Abstract
The acceleration and heating of the solar wind have been studied for decades using satellite observations and models. However, the exact mechanism that leads to solar wind heating and acceleration is poorly understood. In order to improve the understanding of the physical mechanisms that are involved in these processes a combination of modeling and observational analysis is required. Recent models constrained by satellite observations show that wave heating in the low-frequency (MHD), and high-frequency (ion-cyclotron) range may provide the necessary momentum and heat input to coronal plasma and produce the solar wind. This review is focused on the results of several recent solar modeling studies that include waves explicitly in the MHD and the kinetic regime. The current status of the understanding of the solar wind acceleration and heating by waves is reviewed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The solar wind plasma plays a major role in the physical connection between the Sun and the Earth, and affects the plasma conditions in the heliosphere. The solar wind is an important component of space weather, and forms the background upon which solar disturbances, such as CMEs and energetic particles propagate towards the Earth. However, the exact physics of formation of the solar wind is poorly understood. Remote sensing and in-situ observations indicate that there are two types of solar wind: slow and fast. The fast solar wind, reaching the speed of ~ 800 km s−1 at 1 AU, is steady and of low density (few particles per cm3 at 1 AU); the slow solar wind reaches half the above speed with an order of magnitude higher density (see Figure 1). At solar minimum the solar wind speed is a clear function of latitude as measured by Ulysses’ SWOOPS instrument with the fast wind emerging from polar coronal holes, and the slow wind confined to the equatorial regions. Near the solar maximum the corona is dominated by streamers and by slow solar wind. The heavy ion composition of the solar wind is correlated with the fast and slow wind, indicating their coronal origin.
The solar wind speed as a function of latitude (in km s−1) measured by Ulysses’ SWOOPS instrument near solar minimum (left panel) and near solar maximum (right panel). The direction of the magnetic field is marked (red-outward; blue-inward). The typical composite solar images near minimum (8/17/96) and maximum (12/07/00) are shown using data from SOHO/LASCO, EIT, and Mauna Loa K-coronameter images (McComas et al., 2003).
The twin Helios spacecraft investigated the heliosphere in the region 0.3 to 1 AU and found evidence for magnetic fluctuations spectrum, and investigated the radial dependence of plasma parameters and the velocity distributions in the solar wind. These measurements provide the basis of many theoretical studies of solar wind acceleration and heating (see the review by Marsch, 2006). Recent in-situ observations by ACE (Stone et al., 1998), Wind (e.g., Lepping et al., 1995), Ulysses, (e.g., Balogh et al., 1992), and other spacecrafts confirm that the solar wind contains magnetic fluctuations that have power law dependence with frequency (see Figure 2 adapted from Smith et al., 2006). The magnetic fluctuations exhibit high correlation with velocity fluctuations indicating their Alfvénic nature. Remote sensing observations show that the solar wind is heated and accelerated close to the Sun within 10 R⊙ (SOHO/UVCS; Kohl et al., 1997). The observed kinetic and compositional properties provide clues on coronal origin (i.e., coronal holes, active regions) (e.g., Ko et al., 2008), and on the acceleration and heating mechanism. However, the interpretation of observations requires theoretical and computational modeling of the global and kinetic properties of the solar wind to understand the physics and the dynamics of the multi-ion solar wind plasma acceleration and heating, and improve the accuracy of space weather forecasting.
Example of magnetic spectrum from the ACE database. Year/day of sample (decimal day of year in 1998) and Power Spectral Density (PSD) are shown. The top curve represents the summed power in the two components perpendicular to the mean magnetic field, and the lower curve represents the power in the parallel component. The fit functions with power exponent −1.56 ± 0.3 (upper) and −1.8 ± 0.03 (lower) are shown (see Smith et al., 2006, for further details).
In the region between 1 R⊙ and 1 AU the corona and the heliosphere span many orders of magnitudes in relevant temporal-spatial scales, density, magnetic field strength, and in other physical parameters. As a result, the physical processes in the plasma and the modeling approaches are dramatically different in the collisional lower corona with densities on the order of 108–9 cm−3, magnetic field strength of 1 to 100 G, and the heliospheric plasma near 1 AU with densities of few particles per cm−3 and magnetic field strength of few nano-tesla (few tens of micro-Gauss). Correspondingly, the plasma frequency, collision frequency, and the proton gyrofrequency vary over many orders of magnitude between 1 R⊙ and 1 AU. This disparity of scales and physical regimes leads to difficulty in the physical modeling of the heliospheric plasma with a single ‘all-inclusive’ model. For example, solving the Boltzmann equations in three spatial dimensions and six degrees of freedom is not practical with current or foreseeable future computational resources. A practical modeling approach that is applicable on large scales (usually, MHD) can not resolve the physics of the small scale (kinetic) phenomena. The global models provide little or no information on the kinetics of the heating and acceleration processes. The solution of this difficulty is a multi-level modeling approach, where global models are used for large scale structures, with small scales parameterized as external (to MHD) diffusion coefficients and heating/loss functions. Kinetic models are used to study the physics of the local heating and dissipation phenomena on small spatial-temporal scales. The output of the kinetic models can serve as a guide of the diffusion processes that need to be included in global models.
As a result, there are two main types of solar wind models: (1) observationally driven global MHD models that provide the overall global structure of the solar wind as shaped by the interaction with the solar magnetic field, rotation, gravity, and heating; (2) local models that deal with the physical processes of heating and acceleration of the solar wind magnetized plasma with the initial state and boundary conditions not necessarily tied to a particular observation. The output of these models provides the solar wind speed as a function of position, density, temperature, and other parameters. Usually, the acceleration of the solar wind is modeled by introducing simplifying assumption into the energy equation, such as taking the plasma to be isothermal at coronal temperature, or assuming polytropic index below the adiabatic γ = 5/3, that can also vary with heliocentric distance (Cohen et al., 2007). The first isothermal and polytropic solar wind expansion models were developed by Parker (1958, 1963) in one spatial dimension. Present global models provide 3D structure of the solar wind and try to match empirically the observations at 1 AU by adjusting the model parameters (e.g., Mikić et al., 1999; Linker et al., 1999; Usmanov et al., 2000; Roussev et al., 2003; Usmanov and Goldstein, 2003; Cohen et al., 2007). Recently, 2D MHD models that use observations to constrain the solar wind heating function and momentum input were developed (Sittler Jr and Guhathakurta, 1999; Vásquez et al., 2003; Guhathakurta et al., 2006; Sittler Jr and Ofman, 2006). The empirical heating function was recently included in 2.5 solar wind MHD models (Sittler Jr and Ofman, 2006; Airapetian et al., 2011).
On the other end of the scale are the kinetic models which provide the description of the small scale interaction in the solar wind plasma between the waves, the ions, and the background magnetic field. These models usually do not provide the information on the global structure of the solar wind in the heliosphere. However, the kinetic models are well suited for the investigation of the kinetic processes and instabilities involved in heating of solar wind-like plasma. Due to the complexity of the kinetic models, and the necessity to resolve the fine scale on the proton, or even electron Larmor radius scale, it is computationally difficult to include global scale structures.
The range in between the above two modeling approaches is occupied by MHD models that include explicit heating and acceleration of the solar wind by MHD waves. Following Osterbrock (1961) study suggesting MHD waves for the heating of the solar chromosphere and corona, the acceleration of the solar wind by Alfvén waves was studied in the past (Barnes, 1969; Alazraki and Couturier, 1971; Belcher, 1971; Belcher and Davis Jr, 1971; Heinemann and Olbert, 1980). Recently, one-dimensional (Cranmer and van Ballegooijen, 2005; Suzuki and Inutsuka, 2005, 2006; Cranmer et al., 2007) and three-dimensional MHD models (e.g., Usmanov et al., 2000; Evans et al., 2009) were developed (see the review by Ofman, 2005). However, due to the requirements of time step and resolution, the waves are not included explicitly in global models. They are modeled by an additional wave-pressure term, and wave-energy equations. Only few models consider the resolved waves explicitly in 2.5D MHD models (Ofman and Davila, 1997, 1998). The next level of plasma approximation of fully resolved wave driven wind is via multi-fluid models, that describe each particle species as separate fluid (Ofman and Davila, 2001; Ofman, 2004a). The fluids interact through momentum and energy exchanges, and through electromagnetic interactions resulting from quasi-neutrality condition, and through their contribution to the net current. These models can be tested directly by comparing to observations that contain heavy ion emission (e.g., Ofman, 2004b; Abbo et al., 2010).
Observations with SOHO Ultraviolet Coronagraph Spectrometer (UVCS) show that heavy ions such as O5+, and Mg9+ undergo preferential perpendicular heating, causing large temperature anisotropy (T⊥/T∥<10), are hotter and flow faster in coronal holes than protons (Kohl et al., 1997, 1998; Li et al., 1998; Cranmer et al., 1999). Enhanced perpendicular heating of ions compared to protons has also been observed in streamers (Strachan et al., 2002; Uzzo et al., 2007). The magnitude of this effect is significant, but smaller in streamers than in coronal holes. Ulysses and Helios in-situ measurements in the heliosphere have shown that minor ions flow faster than protons by the local Alfvén speed, and are preferentially heated as well, and proton distributions often appear double-peaked with an average relative drift parallel to the background magnetic field (e.g., Marsch et al., 1982b; Feldman et al., 1996; Neugebauer et al., 1996).
The temperature anisotropy of protons deduced from remote sensing and in-situ observations of fast solar wind streams provides indirect evidence for the presence of the ion-cyclotron waves in coronal plasma, since the anisotropy can be produced by the resonant absorption of the ioncyclotron waves. Purely adiabatic expansion of the solar plasma is expected to result in an opposite effect: T⊥<T∥ due to the conservations of magnetic moment of the expanding ions in the decreasing radial magnetic field (e.g., Marsch, 2006). However, T⊥/T∥>1 is observed in the heliosphere (e.g., Marsch et al., 1982b; Gazis and Lazarus, 1982). In the past, several theories of ion-cyclotron resonance have been developed and applied to the heating of the solar corona and the solar wind (e.g., Axford and McKenzie, 1992; Marsch, 1992; Tu and Marsch, 1997; Li et al., 1999; Hollweg, 2000; Hu et al., 2000; Cranmer, 2000; Hollweg and Isenberg, 2002). However, there are theoretical difficulties with the application of the ion-cyclotron mechanism for coronal heating, and its role is not yet fully understood (e.g., Cranmer, 2000; Isenberg, 2004). Most such theories may be classified as either fluid-like or quasi-linear kinetic models. The limitation of the fluid or quasi-linear kinetic models is the assumption of fixed-shape ion velocity distribution and quasi-linear limits (i.e., small magnetic fluctuation amplitude allowing simplified description of wave-particle interactions). In the hybrid models the electrons are treated as a fluid, and the ions are treated fully kinetically as particles. Hybrid simulations (see Section 2.3 below) allow relaxing many approximations used in the fluid, multi-fluid, and in linear or quasi-linear kinetic theory. The model is nonlinear, and can describe both the brief initial linear evolution of the plasma, as well as the nonlinear saturated state. Recently, new kinetic models of heating and acceleration of solar coronal plasma in inhomogeneous magnetic field by Alfvén waves were developed (Galinsky and Shevchenko, 2013a,b). The generation of the solar wind by parallel (Isenberg, 2012; Mecheri, 2013) and oblique (Chandran et al., 2010; Isenberg and Vasquez, 2011) ion-cyclotron waves were also studied. The possible role of kinetic Alfvén waves (KAW) (e.g., Voitenko and Goossens, 2006; Dwivedi et al., 2012) and Alfvén waves turbulence (Chandran, 2010; Chandran et al., 2011; Li et al., 2011; Cranmer and van Ballegooijen, 2012) on the acceleration and heating of the solar wind was recently considered.
Recently, Cranmer and van Ballegooijen (2005) solved the linearized wave equation for Alfvén waves in the heliosphere. The dependence on heliocentric distance of the frequency-integrated Alfvénic velocity amplitude obtained from the solution of the linearized Alfvén wave equation driven by a spectrum of transverse photospheric fluctuations with an amplitude of 3 km s−1 at the photosphere is compared to Alfvén wave amplitude inferred from spectroscopic observations (SOHO/SUMER and UVCS), IPS measurements, and in-situ data in Figure 3. The study shows that there is generally good qualitative agreement between observations and theoretical prediction of the Alfvén wave evolution in the heliosphere, even for a linearized model.
Height dependence of the frequency-integrated velocity amplitude obtained from the solution of the linearized Alfvén wave equation driven by a spectrum of transverse photospheric fluctuations. The solution was obtained in the thin flux tube approximation by Cranmer and van Ballegooijen (2005). Solid lines give the undamped value of 〈δV〉 (the dashed line is for different model parameters). The red line is \(\left\langle {\delta V} \right\rangle _B = \left\langle {\delta B} \right\rangle /\sqrt {4\pi \rho } \) for the 3 km s−1 driving amplitude case. The symbols correspond to observational constraints of the Alfvén waves amplitudes from various observations discussed by Cranmer and van Ballegooijen (2005) (reproduced by permission of the AAS).
The turbulence in the solar wind magnetized plasma has been studied for decades in the past (see the review by Velli, 2003), and recently (Verdini et al., 2009; Chandran and Hollweg, 2009; Chandran et al., 2009; Verdini et al., 2010; Markovskii et al., 2010) as the possible state that leads to cascade of energy from the observed large scale fluctuations and waves to small scale structures, down to dissipation scales that can heat the solar wind plasma. Observations of Alfvénic fluctuations in the solar wind by Helios and Ulysses spacecraft show that the turbulent energy carried by these fluctuations is distributed in frequency according to a power law, at high frequencies going as f−5/3, a Kolmogorov spectrum, while at lower frequencies the spectrum flattens to f−1 (where f is the fluctuation frequency) (Goldstein et al., 1995). Alfvénic turbulence is predominant in fast wind streams while in slow solar wind the turbulence is of more complex nature with low Alfvénicity (see the reviews by Tu and Marsch, 1995; Bruno and Carbone, 2013). Recent observations by ACE spacecraft of the solar wind protons at 1 AU indicate that the turbulent cascade rate agrees better with Kraichnan (f−3/2), rather than with Kolmogorov (f−5/3) rate (Vasquez et al., 2007). Similar results were seen by the Wind spacecraft (Podesta et al., 2006). Part of the fluctuating power at low frequencies can be attributed to propagating structures in the solar wind. However, there is strong evidence that the fluctuations are Alfvénic at frequencies of milli-Hertz and higher.
Recent observations by Hinode satellite show that Alfvénic fluctuations are the likely energy source that drives the solar wind (e.g., De Pontieu et al., 2007; Ofman and Wang, 2008; Hahn et al., 2012; Hahn and Savin, 2013). A review of observational evidence for propagating MHD waves in coronal holes that may accelerate the solar wind is found in Banerjee et al. (2011). Recently launched NASA’s Solar Dynamics Observatory (SDO) provides unparalleled opportunity to look for the solar coronal wave spectrum over the entire disk of the Sun at high temporal and spatial resolution. The analysis of the data from the Atmospheric Imaging Assembly (AIA) onboard SDO will likely provide the constraint on the input wave spectrum that drives the solar wind. Although the observed spectrum is limited to the MHD frequency range, since the temporal resolution does not allow resolving high frequencies down to the gyroresonant scale (∼ kHz), the form of the spectrum is likely to provide clues on the relevant turbulent cascade processes.
The following level of solar wind plasma approximation is via hybrid models (see Section 2.3), that describe protons and other ions kinetically as particles, and electrons as neutralizing background fluid (Winske and Omidi, 1993). Hybrid simulations can represent more completely (than fluid model) and self-consistently the wave-particle interactions in the multi-ion solar wind magnetized plasma. The models can be used to describe the kinetic processes involved in heating by a spectrum of waves, and can be used to study the nonlinear and resonant interactions of the turbulent spectrum with the ions. Such numerical methods have the potential to model the wave-particle interactions, and the corresponding velocity distribution and magnetic fluctuations in the nonlinear saturated state that can be compared to in-situ observations. Recently, one dimensional hybrid simulations of multi-ion solar wind plasma were used to study the heating by wave spectrum, beams, and the stability of solar wind multi-ion plasma (Liewer et al., 2001; Ofman et al., 2001, 2002; Xie et al., 2004; Lu and Wang, 2005; Li and Habbal, 2005; Hellinger et al., 2005; Ofman et al., 2005). Due to the local nature of the hybrid models, they require special treatment taking into account the global properties of the solar wind, such as expansion of the solar wind into the heliosphere (Liewer et al., 2001; Hellinger et al., 2005; Ofman et al., 2011). We will review some of the recent results of hybrid simulation models of solar wind plasma heating.
Two-dimensional hybrid models of homogeneous multi-ion plasma heating were also studied recently (Gary et al., 2001, 2003; Kaghashvili et al., 2003; Hellinger and Trávníček, 2006; Gary et al., 2006). However, only few studies considered the effect of time dependent wave fluctuations on solar wind plasma heating with 2D hybrid models (Ofman and Viñas, 2007; Ofman, 2010; Markovskii et al., 2010). It was found that the input wave spectrum can heat the ions by resonant interaction, as well as through non-resonant parametric decay instability of Alfvén waves (e.g., Araneda et al., 2007). It was also found that the presence of small scale inhomogeneity in the background plasma can enhance the heating by the high frequency Alfvén wave spectrum (Ofman, 2010).
This review is focused on selected wave-acceleration models (both, MHD and kinetic) of the solar wind. Other reviews of solar wind models were recently published (Hansteen and Velli, 2012; Cranmer, 2012).
2 Model Equations
Below we provide the typical basic equations used in the three classes of models reviewed here: MHD, multi-fluid, and hybrid.
2.1 Single fluid MHD
The single-fluid, normalized visco-resistive MHD equations with gravity are (see, e.g., Priest, 1982; Ofman, 2005)
where ρ is the fluid density, v is the fluid velocity, B is the magnetic field, \(J = \nabla \times B\) is the current density, and p is the plasma pressure. The normalization of the magnetic field is by the typical magnetic field B0 at the base of the corona, distances (r) are normalization by the solar radius R⊙, the density normalization is by the typical density ρ0 at the coronal base, the velocity normalization is by Alfvén speed \(V_A = B_0 /(4\pi \rho _0 )^{1/2} \), and the time normalization is by the Alfvén time defined as \(\tau _A = L/V_A \), where L is the typical lengthscale of the problem (for convenience, L = R⊙ is used). The pressure is normalized by p0 = kBn0T0, where kB is the Boltzmann constant, \(n_0 = \rho /(\mu m_p )\) is the typical number density, where mp is the proton mass, and μ is the average mass number density of the coronal plasma, and T0 is the typical temperature at the base of the corona. The Froude number is \(F_r = V_A^2 R_ \odot /(GM_ \odot )\), G is the gravitational constant, R⊙ is the solar radius, M⊙ is the solar mass, \(\beta = 2c_s^2 /(\gamma V_A^2 )\) is the ratio of thermal to magnetic pressure, where \(c_s = (\gamma p/\rho )^{1/2} \) is the sound speed. The Lundquist number \(S = \tau _A /\tau _r \) is the ratio of the typical Alfvén time to the resistive diffusion time (\(\tau _r = 4\pi L^2 /\nu c^2 \), where v is the resistivity, and c is the speed of light), and Fv is the viscous force term (see Braginskii, 1965).
The heating and loss terms are Sh, and Sl, respectively, where Sh is the coronal heating function (assumed, or obtained empirically), and Sl represents the losses due to thermal conduction and radiation (for example, Landi and Landini, 1999; Colgan et al., 2008, for optically thin plasma). The polytropic index γ = 1 in isothermal plasma, γ = 1.05 in a commonly used polytropic model of the solar wind, and γ = 5/3 for solar wind models with explicit heating terms. Variable γ was used by Cohen et al. (2007) to match solar wind properties at 1 AU. The above set of equations is supplemented by the equation of state p = nkBT, and by the solenoidality condition \(\nabla \cdot B = 0\). The visco-resistive single fluid MHD model was used recently to reproduce the global emission properties of the solar corona (Lionello et al., 2009; Downs et al., 2010).
2.2 Multi-fluid models
Here, we describe the multi-fluid equations and model utilized by Ofman (2004a) to model the fast solar wind in coronal holes accelerated by nonlinear MHD waves. Neglecting electron inertia (me≪mp), relativistic effects (V≪c), assuming quasi-neutrality \((n_e = n_p + Zn_i )\), where Z is the charge number, the normalized three-fluid MHD equations can be written as

where the index k = p, i (in Equation (9) k = e, p, i), Hk is the heat conduction term, Sk is the heating term of each fluid, Ckjl is the energy coupling term between the various fluids (Li et al., 1997; Ofman, 2004a), \(F_v = \nabla \cdot \Pi \) is the viscous force term due to ions, where Π the viscous stress tensor and the Coulomb friction terms Fk,coul given by Braginskii (1965), γk = 5/3 is the polytropic index of each species, Ak is the mass number, and \(\Omega _k = \frac{{Z_k eB_0 }} {{A_k m_p c}}\tau _A \) is the normalized gyrofrequency.
The three-fluid equations are normalized by r→r/R⊙, where R⊙ is the solar radius; t→t/τA; V→V/VA; B→B/B0; nk→nk/ne0; Tk→Tk/Tk0. The following parameters enter in the above equations: S the Lundquist number; \(E_{ui} = (k_B T_{i,0} /m_i )/V_A^2 \) the electron and proton Euler number; \(E_{ui} = (k_B T_{i,0} /m_i )/V_A^2 \) the ion Euler number; Fr the Froude number; Ak is the atomic mass of species k; \(b = cB_0 (4\pi en_{e0} R_ \odot V_A )\), Tk,0 is the normalization temperature, mk is the mass of the particles, B0 is the normalization magnetic field. The heat conduction term in Equation (9) is normalized by \(H_k \to H_k (k_B V_A R_ \odot /T_{k0}^{2.5} )\).
In Ofman (2004a) model the fast solar wind is produced by a broad band spectrum of waves. The linearly polarized Alfvén waves are driven at the base of the corona as follows:
where ai = ip/2, p = -1 for the f−1 spectrum, the discrete frequencies are given by \(\omega _i = \omega _1 + (i - 1)\Delta \omega \), and the range is defined by \(\Delta \omega = (\omega _N - \omega _1 )/(N - 1)\), where N is the number of modes, Гi(θ) is the random phase that depends on the solar latitude θ. Typically, the frequencies are in the mHz range, the driving amplitude Vd is few percent of VA, with an order of 100 modes used to model the desired spectrum (see Figure 4). As described by Ofman (2004a) dissipation of the waves occurs through viscous and resistive terms in the momentum and inductance equations, respectively. The dissipation coefficients used in that model are hyper-viscosity and hyper-resistivity, i.e., their values are much larger than the classical resistivity and viscosity, accounting empirically for kinetic and turbulent effects.
In addition to the waves, an empirical heating function is introduced in this model to heat the ions:

where S0,k≡s0,knk is the amplitude of the heat input in normalized units, and λk is the length scale of the heating in R⊙. This is necessary, since the Alfvén wave spectrum constrained by available observations can not account for the observed (e.g., Kohl et al., 1997) preferential acceleration and heating of heavy ions. The asymptotic solar wind parameters (speed of various ion species, mass flux, temperature, etc.), can be matched by fitting the parameters of the heating function, combined with the parameters of the driving Alfvén wave spectrum.
2.3 Hybrid models
In the hybrid model the ions are represented as particles, neglecting collisions, while the electrons are described as a finite temperature massless fluid to maintain quasineutrality of the plasma. This method allows one to resolve the ion dynamics and to integrate the equations over many ion-cyclotron periods, while neglecting the small temporal- and spatial- scales of the electron kinetic motions. In the hybrid model, the three components of order million particle velocities are used to calculate the currents, and the fields in the 1D, 2D, or, in some cases, 3D grid. Note that each numerical particle represents large number of real particles, determined by the density normalization. The required number of particles per cell is determined by the required limitation on the overall statistical noise, and could be increased by an order of magnitude as needed. The following equations of motion are solved for each particle of species (k):
where mk is the particle mass, Z is the charge number, e is the electron charge, and c is the speed of light. The electron momentum equation is solved by neglecting the electron inertia
where pe = kBneTe is used for closure, and quasi-neutrality implies \(n_e = n_p + Zn_i \), where nk is the number density of electron, protons, and ions, respectively. The above equations are supplemented with Maxwell’s equations
where the displacement current is neglected in non-relativistic plasma, and
The field solutions are obtained on the 1D, 2D, or 3D grid, and the proton and ion equations of motions are solved as the particle motions respond to the fields at each time step. The method has been tested and used successfully in many studies.
In Ofman and Viñas (2007) 2D study 128 × 128 grid with 100 particles/cell/species were used. The particle and field equations were integrated in time using a rational Runge-Kutta (RRK) method (Wambecq, 1978) whereas the spatial derivatives were calculated by pseudospectral FFT method. When non-periodic boundary conditions are applied finite difference method is used for the field solver. The hybrid model allows computing the self-consistent evolution of the velocity distribution of the ions that includes the nonlinear effects of wave-particle interactions without additional assumptions. Moreover, the hybrid model is well suited to describe the nonlinear saturated state of the plasma.
Since the hybrid models usually describe a region of several hundred ion inertial length (li = c/ωpi) across, the method is limited to model local small scale structures in the corona. For a typical solar plasma density of 104 cm−3 at 10 R⊙ and a simulation box with a side of 440li we get about 1000 km for the extent of the simulated region in each dimension. At 1 AU the plasma density is much lower and the modeled region covers about 45000 km in each dimension. A way to overcome the computational limitation to small scales is to use an ‘expanding box’ model (e.g., Grappin and Velli, 1996; Liewer et al., 2001; Hellinger et al., 2005). This approach employs transformation of variables to the moving solar wind frame that expands together with the size of the parcel of plasma as it propagates outward from the Sun. In particular, it is assumed that a small packet of plasma of length δr ≪ R0 and width a(t), where a(t)/R0 ≪ 1 expands in the lateral direction only as it moves away from the Sun at constant speed U0. The initial distance R0 is O(R⊙). Thus, the modeled regions position is \(R(t) = R_ \odot + U_0 t\), and the width a(t) = R(t)/R0. Using these transformations the coordinates are transformed as \(x' = x - R(t)\), \(y' = y/a(t)\), and \(z' = z/a(t)\), and the equations of motions together with the field equations are transformed to the moving and expanding frame. Although, the method requires several severe simplifying assumptions (i.e., lateral expansion only, constant solar wind speed) and approximations (the original spherical coordinates and the mean magnetic field transformed to new coordinates using second order expansion (see Liewer et al., 2001) to remain tractable, it provides qualitatively good description of the solar wind expansions, thus connecting the disparate scales of the plasma in the various parts of the heliosphere.
3 Selected Model Results
In this section a brief overview of solar wind model results is given. Here, we concentrate on the results of wave driven 2.5D MHD, 2.5D multi-fluid models, as well as 1D and 2D hybrid models. In the reviewed models the waves are included explicitly, fully resolved, and their damping or resonant absorption was calculated explicitly. This allows more accurate description of the physics and interaction between the waves and the solar wind plasma than in WKB models, or models that parameterize the propagation and dissipation of the waves. The results of a global 3D MHD solar wind model computed with SWMF that incorporates the effects of Alfvén wave heating and acceleration in the WKB approximation is shown in Figure 5. The figure shows a cut of the 3D MHD model results in the meridional plane for an idealized tilted-dipole magnetic field configuration. The formation of the bi-model solar wind with slow wind in the streamer belt and fast at higher latitudes is evident in the radial outflow velocity values.
The radial velocity in the meridional plane for a two-temperature, idealize tilted-dipole simulation with 15° tilt with respect to the rotation axis. The black curves indicate the location of the Alfvénic surface. The red regions show the location of the fast solar wind, and the blue-green show sources of the slow solar wind. Image reproduced by permission from Oran et al. (2013); copyright by AAS.
Wave models in the single fluid MHD are limited to frequencies much smaller than the proton gyrofrequency and correspondingly to wavelengths that are much larger than the proton gyroradius. The acceleration of the solar wind plasma by the waves due to momentum transfer (wave reflection and gradient of the wave pressure is modeled. The dissipation of the waves by Ohmic and viscous dissipation terms is included. The multi-fluid models allow including waves with frequencies in the MHD and in the range of proton and ion gyrosresonant frequency. The multi-ion cyclotron resonant dispersion of waves is reproduced by this model even in the linear regime. It has been shown that multi-fluid dispersion relation is equivalent to Vlasov’s dispersion for cold plasma (for example, see Ofman et al., 2005). In addition, the multi-fluid models can include separate heating and dissipation processes for electrons, protons, and each ion species with different dissipation coefficients. The fluids are coupled through collisional energy exchange terms and Coulomb friction, and through electromagnetic interactions. The multi-fluid models provide the next level of plasma approximation between the MHD and the kinetic descriptions.
The hybrid simulations extend the modeled physics of the solar wind plasma to even smaller scale in time and space to the kinetic regime, and the wave frequencies in the ion- and proton-gyroresonant scale are resolved. In addition, ion velocity space instabilities and ion kinetic processes are modeled fully. The hybrid models are limited to waves with frequencies below the electron gyroresonant frequency, since the electrons are treated as fluid in these models. Other limitations of these models are outlined in Winske and Omidi (1993). The 1D hybrid models are limited to parallel propagating waves in one spatial direction, or oblique waves with fixed angle of propagation. The more general 2D hybrid models include the description of waves with arbitrary propagation direction and can be used to model inhomogeneous plasma in two spatial dimensions.
3.1 Fast solar wind in coronal holes
It is well known that thermally driven Parker’s solar wind model with typical coronal temperature of 1–2 MK can produce the slow solar wind asymptotic speed of about 400 km s−1, but can not explain the fast solar wind that is observed to reach 800 km s−1 within 10 R⊙ and is associated with coronal holes with typical temperatures < 1 MK (Aschwanden, 2004). The common approach is to include an additional source of momentum in the MHD equations, such as Alfvén waves as an empirical WKB momentum addition term (e.g., Usmanov et al., 2000). This approach was recently extended to include the effects of turbulence dissipation in a global wave driven solar wind model, and implemented in the Space Weather Modeling Framework (SWMF) (Tóth et al., 2005) coronal 3D MHD code (Evans et al., 2012; Sokolov et al., 2013; Oran et al., 2013). Two-temperature Alfvén wave driven fast solar wind models were also developed in SWMF (van der Holst et al., 2010).
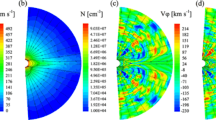
Lau and Siregar (1996) studied the acceleration of the solar wind by resolved nonlinear Alfvén waves in 1.5D MHD model. Ofman and Davila (1997) were the first to use the single fluid 2.5D MHD model to study resolved Alfvén wave driven fast solar wind in a coronal hole. In their model the Alfvén waves were launched at the solar boundary of a coronal hole, and were resolved throughout the coronal hole to 40 R⊙. The acceleration of the solar wind occurs through momentum transfer from the waves to the solar wind plasma. The heating of the solar wind plasma was not included explicitly in this model and an isothermal approximation was used (γ = 1). However, wave dissipation does occur through resistive dissipation with finite value of S. In Figure 6, a snapshot of the spatial dependence of the solutions in terms of Bφ/ρ1/2, vφ, vr, and ρ is shown at t = 255τA = 32.5 h. The velocities and Bφ/ρ1/2 are in units of VA = 1527 km s−1, and the density is in units of 108 cm−3. The monochromatic Alfvén waves launched in this model are evident in Vφ and in Bφ/ρ1/2. The nonlinear longitudinal waves produced by the gradient of the compressions associated with the Alfvén wave, B 2φ , are evident in vr and ρ. The large amplitude, long wavelength compressional velocity and density fluctuation propagate in-phase (Ofman and Davila, 1998). Ofman and Davila (1998) found that low-frequency (0.35 mHz) Alfvén waves with amplitude of 46 km s−1 can produce the fast solar wind in coronal holes.
The result of a 2.5D MHD Alfvén wave driven fast solar wind model in a coronal hole. A snapshot of the spatial dependence of Bφ/ρ1/2, vφ, vr, and ρ is shown at t = 255τA = 32.5 h. The velocities and Bφ/ρ1/2 are in units of VA = 1527 km s−1, and the density is in units of 108 cm−3. The Alfvén waves are evident in Vφ and in Bφ/ρ1/2. The nonlinear longitudinal waves are evident in vr and ρ that propagate in-phase (Ofman and Davila, 1998).
Grappin et al. (2002) were the fist to study resolved Alfvén waves driven wind that include both, closed and open field regions using 2.5D MHD model. They found that onset of Alfvé wave flux in one hemisphere generates a stable global circulation pattern in the closed loops region that can lead to global north-south asymmetry of the solar corona.
In Figure 7 a cut through the center of the coronal hole is shown. The Vr and Vφ solar wind velocity components are shown for two Alfvén wave driving frequencies, and the green curve shows Parker’s isothermal solar wind solution. It is evident that the low frequency waves (f = 0.35 mHz) lead to significant acceleration of the fast solar wind above Parker’s solution, and produce the fast solar wind far from the Sun. The higher frequency waves provide acceleration close to the Sun below 10 R⊙.
Alfvén wave driven fast solar wind obtained with 2.5D MHD model (a cut through the center of the coronal hole is shown). Vr and Vφ solar wind velocities are shown for two Alfvén wave driving frequencies. The green curve shows the Parker’s isothermal solar wind solution (adapted from Ofman and Davila, 1998).
The 2.5D model discussed above includes only the coronal part of the solar wind, with the driving Alfvén waves applied at the lower coronal boundary. Recently, Suzuki and Inutsuka (2005) modeled the acceleration of the fast solar wind by Alfvéen waves from the photosphere to 0.3 AU using a 1.5D model (Figure 8). This approach allowed connecting directly photospheric motions of observationally constrained magnitude to solar wind speed at 0.3 AU. Although the model does not include the effects of cross-field gradients, the model demonstrates that sufficient Alfvén wave energy flux reaches the corona to accelerate the solar wind. The 1.5D model results compare favorably to IPS observation (Grall et al., 1996; Canals et al., 2002) and to SOHO observations (see, Suzuki and Inutsuka, 2005, for the details).
Results from 1.5D solar wind model (red lines) compared to observations (symbols and symbols with error bars). See, Suzuki and Inutsuka (2005) for the details (reproduced by permission of the AAS).
3.2 Fast solar wind: 2.5D multi-fluid models
In Figures 9 and 10 we show the results of the 3-fluid model of the Alfvén wave driven fast solar wind in a coronal hole obtained by Ofman (2004a). In this model a broad band spectrum of Alfvénic fluctuations was applied at the lower coronal hole boundary. The fast solar wind was produced by acceleration and heating with the spectrum of Alfvén waves, that were fully resolved in the model. In Figure 9 the Alfvén waves are evident in Vφ and the accelerating solar wind in Vr velocity components for He++ ions (left panels) and protons (right panels) at t = 114τA are shown. Note that compressive fluctuations are also seen in Vr due to the local variation of wave pressure gradient. The velocity is in units of 1527 km s−1. The distance R is in units of R⊙, and the latitude θ is in radians.
Results of the 3-fluid model of the Alfvén wave driven fast solar wind in a coronal hole. The Vφ and the Vr velocity components for He++ (left panels) and protons (right panels). The velocity is in units of 1527 km s−1. The distance R is in units of R⊙, and the latitude θ is in radians (Ofman, 2004a).
The typical form of the magnetic fluctuations spectrum obtained with the 3-fluid model at 18 R⊙. The solid line shows a fit with ω2, while the dashed curve shows a fit with ω−5/3 (adapted from Ofman, 2004a).
The typical form of the magnetic fluctuations obtained with the 3-fluid model at r = 18 R⊙ is shown in Figure 10. It is interesting to note that the f−1 spectrum launched at the base of the coronal hole results in f−2 spectrum at larger distances. The steepening of the magnetic fluctuations spectrum is expected due to turbulence and dissipation that affects shorter wavelengths and correspondingly higher frequencies more than the long wavelength (low frequencies) fluctuations. The power law dependence is close to Kolmogorov’s turbulent power spectrum of f−5/3. At frequencies higher than 200τ −1A the spectrum steepens due to increased dissipation.
In Figure 11 the θ-averaged outflow speeds of protons, He++, and O5+ ion fluid are shown for four sets of model parameters. The parameters are (a) H0p = 0.5, H0He++ = 12, Vd = 0.034, (b) H0p = 0.5, H0O5+ = 10, Vd = 0.034, and (c) H0p = 0.0, H0He++ = 12, Vd = 0.05, where H0 is the heating rate per particle for an empirical heating term used in Ofman (2004a), and Vd is the amplitude of the Alfvén wave spectrum. The corresponding temperatures and densities are shown in Figure 12. In Figure 11a the solutions of the 3-fluid model with empirical heating term [Equation (12)] in addition to Alfvén wave spectrum are shown. The heating term parameters were chosen to match the observed fast solar wind speed, and the faster outflow of He++ ions compared to protons, observed at 0.3 AU and beyond with Helios and Ulysses spacecraft (Marsch et al., 1982a,b; Feldman et al., 1996; Neugebauer et al., 2001). In Figure 11b the O5+ ions were included as the third fluid, and the heating function parameters for O5+ ions were adjusted to get faster than proton outflow. In Figure 11c the same heating per particle was deposited in protons and He++ ions. Evidently, in this case the He++ ions outflow speed is slower than the proton outflow speed, contrary to observations. In Figure 11d the solar wind protons are accelerated and heated solely by the Alfvén wave spectrum (i.e., H0p = 0). This was achieved by increasing the input wave amplitude, compared to the values used in Figures 11a–c. Note that the temperature structure of protons and O5+ ions as seen in Figure 12b is in qualitative agreement with SOHO/UVCS observations (Kohl et al., 1997; Cranmer et al., 1999; Antonucci et al., 2000) (at present there are no observations of He++ temperature in this region). The model shows that in all cases electron heating can be achieved by thermal coupling between electrons and protons alone (through the Ckjl thermal coupling term in Equation (9)).
Results of the 3-fluid model: the outflow speed of protons (solid) and ions (dashed) in the coronal hole averaged over γ for the fast solar wind in a coronal hole. (a) With preferential heating of He++ ions. (b) Same as (a), but with preferential heating of O5+ as the heavy ions. (c) Solar wind produced with equal heat input per particle for protons and He++ ions. (d) Wave driven wind — no empirical heating of protons, and electrons (adapted from Ofman, 2004a).
In spectroscopic observations of emission lines the observed finite line width is the result of broadening by Doppler shift due to the motion of the emitting ions in the line of sight. The motions are usually attributed to two components: (1) thermal or kinetic motions due to the finite width of the ion velocity distribution; (2) non-thermal motions, arising from any unresolved macroscopic motions of the plasma in the line of sight. The effect of observationally unresolved Alfvén waves on the apparent emission line widths was modeled with the 3-fluid model by Ofman and Davila (2001) and Ofman (2004a). These models allow separating the contribution of waves to the observed line profiles. In Figure 13 the Doppler-broadened emission line, resulting from combined thermal and non-thermal motions calculated with the 3-fluid model is shown. The solid line shows the simulated emission line profile of protons at 4 R⊙ at a temperature of 3.5 MK, and the dashes show the emission line broadened by unresolved Alfvénic fluctuation. In Figure 14 the effective temperature calculated from the kinetic temperature and the Alfvénic wave motion contribution is shown for the wave-driven fast solar wind as a function of the heliocentric distance. The effective proton temperature is affected significantly by the non-thermal component, while the relative effect on He++ is smaller close to the Sun. By comparing the results of the 3-fluid model to observations, it is possible to evaluate better the thermal and non-thermal motions for protons and heavier ions in the observational data.
Doppler broadening of an emission line as a result of unresolved Alfvén wave motions in the line of sight obtained with the 3-fluid model. Thermal (solid line) and simulated (dashed line) line profile at 4 R⊙. The integration time is 1.7 h (adapted from Ofman and Davila, 2001).
The effective temperature and the kinetic temperature for protons (solid) and ions (dashes) for wave driven fast solar wind. The effective temperature that includes the contribution of unresolved Alfvénic fluctuations is shown by thick line style, while the kinetic temperature is shown by thin line style (adapted from Ofman, 2004a).
3.3 1D hybrid models
Recently, Ofman et al. (2002) used 1D hybrid model of initially homogeneous, collisionless plasmas to study the heating of solar wind plasma by a spectrum of ion-cyclotron waves. Motivated by observations the model was driven by circularly polarized Alfvénic fluctuations of the form f−1 and f−5/3 for a limited bandwidth. They found that the ion heating depends on the resonant power in the frequency range of the input spectrum. Preferential heating of minor ions, such as O5+, over protons was demonstrated in this model. In Figure 15 the evolution of the temperature anisotropy for protons and O5+ ions is shown. It is evident that after ∼ 600Ω −1p the perpendicular heating of the ions saturates at anisotropy level of ∼ 7, and the proton are not heated significantly. The level of saturated anisotropy is determined by the temperature dependent nonlinear balance between ion-cyclotron unstable ion velocity distribution that releases electromagnetic ion-cyclotron waves and the resonant absorption of magnetic fluctuations together with parallel heating of the ions. After inspecting the perpendicular and parallel temperatures of O5+ at the end of the run it is evident that the heating was predominantly in the perpendicular direction (Ofman et al., 2002).
The temporal evolution of the O5+ ion (top panel) and proton (lower panel) temperature anisotropy obtained with 1D hybrid model for the driven wave spectrum case (adapted from Ofman et al., 2002).
In Figure 16 the velocity distribution of the protons and O5+ ions is shown at the end of the run. It is evident that the proton velocity distribution is isotropic and the O5+ ions are hotter in the perpendicular direction than in the parallel direction. The O5+ velocity distribution is close to bi-Maxwellian with small non-Maxwellian features in the parallel velocity distribution, likely produced by the small parallel heating due to nonlinear compressive modes driven by the Alfvénic fluctuations spectrum.
The velocity distribution of O5+ ions (left panel) and protons (right panel) obtained with 1D hybrid model of the driven wave spectrum. The Vx is parallel to the background magnetic field shown with the solid curve, the transverse components Vy (dashes), and Vz (dots) are shown (adapted from Ofman et al., 2002).
The relaxation of O5+ ion temperature anisotropy due to ion-cyclotron instability for the parameter range relevant to fast solar wind in coronal holes was recently studied using 1D hybrid model (Ofman et al., 2001) (see Figure 23). The study was motivated by SOHO/UVCS observations indicating large temperature anisotropy of O5+ ions (Kohl et al., 1997; Cranmer et al., 1999). It was found that the scaling of the relaxed \(T_{ \bot i} /T_{\parallel i} - 1\) with the final β∥i (full circles) and the scaling of the relaxation time, trel, with the initial β∥i (circles) agree well with the theoretical scaling law β −0.41∥i (Gary, 1993). The “x”’s mark the values \(T_{ \bot i} /T_{\parallel i} - 1\) at t = 0. The enhanced O5+ abundance relative to protons of 6 × 10−4 in this model was implemented in oder to shorten the computation times. Similar result was found in 2D hybrid model by Gary et al. (2003) (see Section 3.4 and Figure 22 below).
The results of the parametric study with the 1D hybrid simulation of O5+ temperature anisotropy relaxation by Ofman et al. (2001). The scaling of the relaxed \(T_{ \bot i} /T_{\parallel i} - 1\) with the final β∥i (full circles). The scaling of the relaxation time, trel, with the initial β∥i (circles). Both quantities scale as β −0.41∥i . The “x”’s mark the values \(T_{ \bot i} /T_{\parallel i} - 1\) at t = 0. The enhanced O5+ abundance of 6 × 10−4 in this parametric study leads to shorter computation times (Ofman et al., 2001).
Results of the parametric study of He++ anisotropy relaxation obtained with 2D hybrid code by Gary et al. (2003). The parameters were nα/ne = 0.05 with initial \(T_e /T_{\parallel p} = 1.0\), \(T_{ \bot \alpha } /T_{\parallel p} = 4.0\), and isotropic protons. The crosses correspond to t = 0, the squares indicate plasma parameters at saturation of the fluctuating magnetic fields, and the dots represent later times. The dashed line indicates the best fit of the anisotropies at ‖pt = 400 (adapted from Gary et al., 2003).
Recently, Ofman et al. (2005) investigated the effects of high-frequency (of order ion gyrofrequency) Alfvén and ion-cyclotron waves on ion emission lines by studying the dispersion of these waves in a multi-ion coronal plasma. The dispersion relation of parallel propagating Alfvén cyclotron waves in the multi-ions coronal plasma was determined using 1D hybrid model (see Figure 17) and compared with multi-fluid and Vlasov dispersion relation. It was found that the three methods are in good qualitative agreement in the weakly damped regime (kCA/Ωp < 1). The ratio of the ion to proton fluid velocities perpendicular to the direction of the magnetic field was calculated for each wave modes for typical coronal parameters (see Figure 18). It was found that the O6+ perpendicular fluid velocity exhibits strong (factor of 20–100) enhancement and He++ perpendicular velocity is enhanced by a factor of 3.5–5 compared with proton perpendicular fluid velocity, in qualitative agreement with SOHO/UVCS observations of large perpendicular velocity of heavy ions in coronal holes (e.g., Kohl et al., 1997; Cranmer et al., 1999). The study demonstrated how the results of hybrid models can be used to better understand the observations of coronal ion emission.
The dispersion relations obtained from 1D hybrid model in three-ion plasma (p, He++, O6+). The intensity scale shows the power of the Fourier transform of (a) transverse magnetic field fluctuations, and transverse fluid velocities of (b) protons, (c) He++, and (d) O6+ (Ofman et al., 2005).
Velocity amplitude ratios of \(V_{He^{ + + } } /V_p \) (top panel) and \(V_{O^{6 + } } /V_p \) obtained from 1D hybrid simulation dispersion relation. The ratio \(V_{He^{ + + } } /V_p \) is shown in the top panel for \(kC_A /\Omega _p \approx 0\) (solid line), and for \(kC_A /\Omega _p \approx 0.52\) (dashes). Bottom panel: same as top panel, but for the ratio \(V_{O^{6 + } } /V_p \) (Ofman et al., 2005).
Recently, Araneda et al. (2007, 2008) used Vlasov theory and one-dimensional hybrid simulations to study the effects of compressible fluctuations driven by parametric instabilities of Alfvén-cyclotron waves. They found that field-aligned proton beams are generated during the saturation phase of the wave-particle interaction, with a drift speed somewhat above the Alfvén speed. This finding agrees with typically observed velocity distributions of protons in the solar wind that contain a thermal anisotropic core and a beam component (see the review by Marsch, 2006). The expanding box model (Grappin and Velli, 1996; Liewer et al., 2001) was recently applied in 1.5D hybrid models of H+-He++ solar wind plasma heated by a spectrum of turbulent Alfvénic fluctuations and in solar wind plasma with super-Alfvénic ion relative drift (Ofman et al., 2011; Maneva et al., 2013). In particular, Maneva et al. (2013) studied the turbulent heating and acceleration of He++ ions by an initial self-consistent spectra of Alfvén-cyclotron waves in the expanding solar wind plasma using 1.5D hybrid simulations. They found that the He++ ions are preferentially heated by the broad-band initial spectrum, resulting in much more than mass-proportional temperature increase (see Figure 19). Maneva et al. (2013) also found that the differential acceleration of protons and He++ ions depend on the amplitude and spectral index of the magnetic fluctuation, while solar wind expansion suppresses the differential streaming. They also find that the expansion leads in general to perpendicular cooling for protons and alphas. However, the cooling effect of the expansion is small and the waves provide sufficient heating, maintaining significant temperature anisotropy, in agreement with observations. Inspection of the proton and alpha velocity distribution in the V∥-V⊥ plane shows the formation of non-Maxwellian features due to the effects of the broad band spectrum, such as perpendicular broadening (i.e., temperature anisotropy), as well as formation of a population of accelerated particles by the waves (see Figure 20.)
Top: Temporal evolution of the parallel and perpendicular components of the ion temperatures obtained by Maneva et al. (2013) with the 1.5D hybrid model involving broadband spectra. Solid lines denote the evolution without expansion, and the dashed lines illustrate the case when solar wind expansion is considered. Bottom: Temporal evolution of the H+-He++ drift speed for this case. The dashed line shows the result with expansion.
The final stages of the evolution of the proton (top panels) and alpha (bottom panels) velocity distributions in the V∥-V⊥ plane in the 1.5D hybrid model initialized with the broadband spectrum of Alfvén/cyclotron waves. The formation of the accelerated particle population is evident (adapted from Maneva et al., 2013).
3.4 2D hybrid models
The 2D hybrid codes solve similar set of equations as in the 1D hybrid codes but in two spatial dimensions. This allows an additional degree of freedom for particle motions, and the wave propagation is not limited to parallel propagating waves, allowing oblique propagation. In addition, the parallel magnetic field component does not have to be constant in order to conserve ∇·B = 0. As a result, a broader range of possible wave modes, wave-particle, and wave-wave interactions are included in the 2D model compared to 1D model. Obviously, the 2D models are computationally intensive, and may require parallel processing for similar resolution in 2D and similar numbers of particles per cell as in the 1D models that can be run on a desktop workstation.
The 2D hybrid models have been used extensively in the past to model successfully the electromagnetic interactions in magnetized plasmas (McKean et al., 1994; Gary et al., 1997; Daughton et al., 1999; Gary et al., 2000, 2001, 2003; Ofman et al., 2001, 2002; Xie et al., 2004; Ofman and Viñas, 2007). Comparisons between one-and two-dimensional hybrid simulations often show qualitative agreement in the ion response (Winske and Quest, 1986; Ofman and Viñas, 2007). In addition to allowing oblique waves, the 2D code allows including spatial inhomogeneity of plasma density perpendicular to the magnetic field, as well as divergent magnetic field geometry. These features are needed to describe solar wind acceleration and heating more consistently with corona conditions.
Recently, Ofman and Viñas (2007) studied the heating and the acceleration of protons, and heavy ions by a spectrum of waves in the solar wind, as well as the nonlinear influence of heavy ions on the wave structure using the 2D hybrid model. They considered for the first time the heating and acceleration of protons and heavy ions by a driven input spectrum of Alfvén/cyclotron waves, and by heavy ion beam in the multi-species coronal plasma in two spatial dimensions. They found that in the homogeneous plasma the ion beams heat the ions faster than the driven wave spectrum constrained by solar wind parameters, and produce temperature anisotropy with T⊥ > T∥ in qualitative agreement with observation. The beam-heating model requires that the beam speed is larger than the local Alfvén speed. Since any reconnection process produces Alfvénic beams as an exhaust (e.g., Priest, 1982; Aschwanden, 2004), the beams could readily become super-Alfvénic as the plasma moves to regions of lower local Alfvén speed. Since the threshold of beam stability is the Alfvén speed, it is possible that remnants of this process that takes place close to the Sun in the acceleration region of the solar wind are seen in proton data beyond 0.3 AU (Marsch, 2006). Below, the results obtained recently by Ofman and Viñas (2007) are reviewed.
Ofman and Viñas (2007) compared the evolution of O5+ ion anisotropy relaxation by ion cyclotron instability, by modeling the coronal plasma with both 1D and 2D hybrid codes. In Figure 21 the results of a 1D and 2D hybrid models runs are shown. The initial temperature anisotropy was set to 50 in both cases with parallel temperature of 1.4 × 106 K. It is evident that the temperature anisotropy has relaxed to similar values in 1D and 2D runs, close to the marginally stable value of ∼ 10 obtained for the parameters used with the Vlasov stability analysis (Gary, 1993). The agreement that was found between 1D hybrid and 2D hybrid evolution is consistent with the Vlasov dispersion relation that shows maximal growth of the ion cyclotron instability for parallel propagating modes.
Comparison of 1D and 2D model results. The evolution of O5+ temperature anisotropy calculated with the 1D hybrid (dashes) and 2D hybrid (solid) models show good agreement (Ofman and Viñas, 2007).
In Figure 22 the results of the parametric study of He++ anisotropy relaxation obtained with 2D hybrid code by Gary et al. (2003) is shown. In that study the parameters were \(n_\alpha /n_e = 0.05\) with initial \(T_e = T_{\parallel p} ,T_{\parallel \alpha } /T_{\parallel p} = 4.0\), and isotropic protons. The initial anisotropy of He++ was chosen to maximize the linear growth rate of ion-cyclotron instability. The crosses show the anisotropy at t = 0, while the squares show the anisotropy at magnetic energy saturation, and the dots represent later times. The dashed line shows the best fit of the anisotropies at Ωpt = 400, that produces the scaling law \(T_{ \bot \alpha } /T_{\parallel \alpha } - 1 = 0.71/\beta ^{0.45} \). Note the qualitative agreement between the 2D hybrid study for He++ anisotropy relaxation, the 1D hybrid study for the O5+ anisotropy relaxation shown in Figure 23, and the scaling law obtained analytically (Gary, 1993). Gary et al. (2003) have shown that the model results are consistent with Ulysses in-situ observations of solar wind protons and He++ ions.
Ofman and Viñnas (2007) found that the perpendicular heating occurs for the beam-driven instability, which quickly saturates nonlinearly, and due to the driven spectrum of waves. In the driven wave spectrum case the amplitude of the magnetic field fluctuations was δB/B0 = 0.06, and the frequency range of the driver was below the proton gyroresonance. It was found (see Figure 24) that the O5+ anisotropy grows quickly (within 400Ω −1p ) to \(T_ \bot /T_\parallel \approx 4\), and than saturates nonlinearly remaining in the range 4–5 throughout rest of the evolution. The frequency range of the wave spectrum included the O5+ ion resonant frequency at rest. The anisotropy of the protons remains close to unity throughout the run. No significant net drift was found between the protons and O5+ ions in the wave driven case. Similar results were obtained for He++ ions.
The temporal evolution of the temperature anisotropy, and the drift velocity for protons and O5+ ions. (a) Ions heated by the driven wave spectrum. (b) Ions heated by a beam with Vd = 1.5 VA (adapted from Ofman and Viñas, 2007).
The non-Maxwellian features of the ion velocity distribution are evident in the perpendicular to the magnetic field phase space plane. When the initial distribution is drifting Maxwellian with the drift velocity Vd = 1.5 VA, the perpendicular velocity distribution of the O5+ is shell-like, with decreased phase-space density in the central part of the distribution, compared to the perimeter. When the initial drift velocity was increased to 2VA, the shell like structure of the phase-space density of O5+ ions becomes even more apparent (Figure 25). It is interesting to note, that the He++ perpendicular velocity distribution for the drifting case is nearly bi-Maxwellian, and does not exhibit the shell structure.
The perpendicular velocity distribution of the O5+ ions obtained with 2D hybrid model with drift velocity Vd = 2VA (adapted from Ofman and Viñas, 2007).
Recently, Ofman (2010) expanded this study and considered in a parametric study the effect of inhomogeneous background density on the heating by high frequency circularly polarized Alfvén waves with, and without drift between the protons and heavier ions. Ofman (2010) found that the inhomogeneity, and the drift lead to increased heating of the solar wind ions, compared to the homogeneous case, and the spectrum of magnetic fluctuations steepens beyond Kolmogorov’s slope of -5/3. In Figure 26 the magnetic energy fluctuations spectrum obtained in the 2D hybrid simulation with inhomogeneous background density is shown. The dashed-dotted line shows the best fit power law to the spectrum in the regions where the slope did not change considerably. Ofman (2010) found that in the low density region the slope was m = −1.66 for wave driven case, and m = −1.81 for the beam driven case. However, in the high density region the slopes were m = −2.53 for the wave driven case, and m = −2.80 for the beam driven case, indicating enhanced dissipation due to the refraction of Alfvén waves, and the generation of small scale magnetosonic fluctuations that dissipate more effectively than Alfvénic fluctuations. Ofman et al. (2011) explored additional forms of background inhomogeneity on the magnetosonic drift instability and solar wind plasma heating by a spectrum of Alfvénic fluctuations. The expansion of the distant solar wind plasma at 0.3 AU and beyond and the generation of the associated kinetic instabilities and waves was considered in 2D hybrid models by Hellinger and Trvávnvíček (2011, 2013).
The power spectrum of fluctuations in Bz. (a) Middle of low density region, driven waves spectrum. The dashed line is for power law fit with m = −1.66. (b) Same as (a), but in the middle of high density region. The fit is with m = -2.53. (c) Middle of low density region, the case with Vd = 2VA. The dashed line is for power law fit with m = −1.81. (d) Same as (c), but in the middle of the high density region. The dashed line is for power law fit with m = −2.80 (from Ofman, 2010).
4 Open Questions and Challenges
Although significant progress was made in observing and modeling of the solar wind over the past decades, there are still several important questions that are unanswered. This situation stems from the lack of unambiguous observations, which point to a specific physical mechanism for coronal heating, and solar wind accelerations, as well as due to the limitations of present models and theories. In particular, the following questions remain open:
-
1.
What is the exact physical mechanism that produces the fast and slow solar wind? This question relates directly to the question of coronal heating mechanism.
-
2.
What is the role of waves (in a broad frequency range from kinetic to MHD) in the acceleration and heating of the solar wind?
-
3.
What is the role of density inhomogeneity and small scale turbulence (cascade) in the heating and the acceleration of the fast and slow solar wind?
-
4.
How are the non-Maxwellian velocity distributions of protons and ions in the solar wind formed?
-
5.
What determines the heavy ion composition (i.e., elemental abundance and charge states, see Zurbuchen, 2007) of the fast and slow solar wind?
-
6.
What is the role of electrons in solar wind acceleration and heating?
-
7.
How does Earth’s global space environment respond to solar wind variations?
The works reviewed here bear on the first five questions, showing that MHD waves with a given spectrum provide plausible acceleration mechanism of the fast solar wind in coronal holes, and heating of coronal plasma may occur through resonant and non-resonant dissipation of the waves energy. However, the fluid models do not provide the kinetic details of the dissipation processes, and the hybrid models show only limited aspects of the resonant dissipation processes. The formation and the evolution of the ion velocity distribution of the solar wind plasma is not modeled in detail from the Sun to 1 AU. Multi-fluid models address limited aspects (i.e., within the ion-fluids approximation) of the compositional variation of the solar wind in open and closed structures (Ofman, 2000, 2004a). In the reviewed models the electrons are only studied as a fluid and their role in solar wind heating and acceleration only includes basic aspects (i.e., heat conduction, collisions coupling to ions). The last question can be addressed with global models that include the Earth’s magnetosphere and ionosphere. However, the study of the kinetic processes that are at the roots of the solar-wind—magnetosphere—ionosphere interactions is far from complete.
The above questions are on the forefront of current research, and the answer can be obtained by combination of improved observations and modeling. A possible way to answer these questions is by obtaining in-situ measurements of the solar wind plasma in the region close to the Sun, where the acceleration and heating processes are still significant (McComas et al., 2007). This is the goal of the future European Solar Orbiter, and NASA’s Solar Probe Plus missions.
5 Summary and Discussion
Satellite observations provide ample evidence for the presence of low-frequency (MHD) waves in the solar corona and the solar wind. The presence of ion-cyclotron waves and beams is evident as well in in-situ observations at 0.3 AU and beyond, and deduced from remote-sensing spectroscopic observations. Motivated by these observations wave-driven solar wind acceleration and heating models were developed with various degrees of approximation. The formation and the effect of beams on solar wind plasma heating were studied with hybrid models. In the present paper we have reviewed several such models of solar wind acceleration and plasma heating. The emphasis in this review is on wave driven models with fully resolved wave spectrum in 2.5D MHD, 2.5D multi-fluid models, and in hybrid kinetic 1D and 2D models.
Thermal conduction alone can not explain the acceleration of the solar wind to fast wind speed for plasma temperatures of 1–2 MK commonly deduced from observations in open magnetic structures. The 2.5D MHD and multi-fluid models show that Alfvén wave spectrum in the MHD frequency range (millihertz) accelerates the fast solar wind to the observed speed of ∼ 800 km s−1 and provides the necessary energy to heat the solar wind. The advantage of the WKB approximation is that it allows incorporating the effects of Alfvén wave heating and acceleration in global 3D MHD models. However, the models that include fully resolved waves provide more accurate and realistic account of the interaction between the waves and the solar wind plasma than the WKB approximation and the MHD models that use ad-hoc heating function, momentum input, or variation of the polytropic index with distance from the Sun. The main limitations of the wave-driven solar wind MHD models are that the heating is described by Ohmic and viscous dissipation with empirical dissipation coefficients, and the exact kinetic process that underlay the fluid description can only be modeled in detail by kinetic approach.
Multi-fluid models extend beyond MHD by providing insights on the compositional variation of the solar wind plasma, on separate heating processes for electrons, protons, and heavy ions, and on the interactions between the various plasma constituents. The results of multi-fluid models are compared directly with observations of the coronal emission, consisting of ion emission lines, and white light polarized brightness that comes from electron Thompson scattering. These comparisons provide more stringent observational constrains on solar wind models than can be achieved with single fluid MHD, since all modeled particle species must conform to the observed properties (e.g., electron temperature, proton temperature, relative abundance of heavy ions in various magnetic structures, wave signatures in separate fluids, etc.), and the various fluids are coupled through Coulomb and electromagnetic interactions.
The 1D and 2D hybrid models provide the next level of physical modeling, and are reliable tools that have been tested and used for decades to study ion kinetic processes in space plasmas. The reviewed studies concentrate on the resonant dissipation of wave spectrum in the multi-ion solar wind plasma and include the effects of beams. The models show that the high frequency waves in the proton and ion gyrosresonant frequency range can heat the solar wind heavy ions preferentially and anisotropically and produce the anisotropic ion velocity distributions deduced from observations. High-amplitude waves can lead to beam formation, while solar wind expansion can lead to perpendicular cooling of the ions. The hybrid models show that heating can be enhanced further by the instability of super-Alfvénic beams of heavy ions. The reviewed studies show that protons are not heated significantly by these waves due to resonant absorption by heavier ions. Thus, the spectrum of waves that heats and accelerates the solar wind must contain both, lowfrequency (non-resonant) and high-frequency Alfvén waves. The hybrid models do not include the kinetics of electrons, and their possible role in solar wind energy balance and the dissipation of low-frequency waves is not modeled beyond the fluid description.
The planned NASA Solar Probe Plus mission and the European Solar Orbiter missions will provide new measurements in the unexplored region of the inner heliosphere. In particular, in-situ measurement of non-Maxwellian features in proton, ion, and electron velocity distributions such as anisotropy and beams, and measurement of magnetic fluctuations spectrum in the acceleration region of the solar wind close to the Sun will provide the necessary information that will improve our understanding of solar wind acceleration and heating. These measurements will provide improved constraints for future theoretical studies and numerical models of solar wind plasma heating and acceleration for all levels of plasma approximations.
References
Abbo, L., Ofman, L. and Giordano, S., 2010, “Streamers study at solar minimum: combination of UV observations and numerical modeling”, in Twelfth International Solar Wind Conference, Saint-Malo, France, 21–26 June 2009, (Eds.) Maksimovic, M., Issautier, K., Meyer-Vernet, N., Moncuquet, M., Pantelli, F., AIP Conference Proceedings, 1216, pp. 387–390, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on page 7.)
Airapetian, V., Ofman, L., Sittler, E.C. and Kramar, M., 2011, “Probing the Thermodynamics and Kinematics of Solar Coronal Streamers”, Astrophys. J., 728, 67. [DOI], [ADS] (Cited on page 7.)
Alazraki, G. and Couturier, P., 1971, “Solar Wind Accejeration Caused by the Gradient of Alfvén Wave Pressure”, Astron. Astrophys., 13, 380–389. [ADS] (Cited on page 7.)
Antonucci, E., Dodero, M.A. and Giordano, S., 2000, “Fast Solar Wind Velocity in a Polar Coronal Hole during Solar Minimum”, Solar Phys., 197, 115–134. [DOI], [ADS] (Cited on page 21.)
Araneda, J.A., Marsch, E. and Viñnas, A.F., 2007, “Collisionless damping of parametrically unstable Alfvén waves”, J. Geophys. Res., 112(A11), 4104. [DOI], [ADS] (Cited on pages 10 and 27.)
Araneda, J.A., Marsch, E. and Viñas, A.F., 2008, “Proton Core Heating and Beam Formation via Parametrically Unstable Alfvén-Cyclotron Waves”, Phys. Rev. Lett., 100, 125003. [DOI], [ADS] (Cited on page 27.)
Aschwanden, M.J., 2004, Physics of the Solar Corona: An Introduction, Springer-Praxis Books in Geophysical Sciences, Springer; Praxis, Berlin; New York; Chichester. [ADS], [Google Books] (Cited on pages 16 and 31.)
Axford, W.I. and McKenzie, J.F., 1992, “The origin of high speed solar wind streams”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 1–5, Pergamon Press, Oxford; New York. [ADS] (Cited on page 8.)
Balogh, A., Beek, T.J., Forsyth, R.J., Hedgecock, P.C., Marquedant, R.J., Smith, E.J., Southwood, D.J. and Tsurutani, B.T., 1992, “The magnetic field investigation on the Ulysses mission: Instrumentation and preliminary scientific results”, Astron. Astrophys. Suppl., 92, 221–236. [ADS] (Cited on page 6.)
Banerjee, D., Gupta, G.R. and Teriaca, L., 2011, “Propagating MHD Waves in Coronal Holes”, Space Sci. Rev., 158, 267–288. [DOI], [ADS], [arXiv:1009.2980 [astro-ph.SR]] (Cited on page 9.)
Barnes, A., 1969, “Collisionless Heating of the Solar-Wind Plasma. II. Application of the Theory of Plasma Heating by Hydromagnetic Waves”, Astrophys. J., 155, 311. [DOI], [ADS] (Cited on page 7.)
Belcher, J.W., 1971, “Alfvénic Wave Pressures and the Solar Wind”, Astrophys. J., 168, 509–524. [DOI], [ADS] (Cited on page 7.)
Belcher, J.W. and Davis Jr, L., 1971, “Large-Amplitude Alfvén Waves in the Interplanetary Medium, 2”, J. Geophys. Res., 76(16), 3534–3563. [DOI], [ADS] (Cited on page 7.)
Braginskii, S.I., 1965, “Transport processes in plasma”, in Review of Plasma Physics, (Ed.) Leontovich, M.A., Review of Plasma Physics, 1, pp. 201–311, Consultants Bureau, New York (Cited on pages 11 and 12.)
Bruno, R. and Carbone, V., 2013, “The Solar Wind as a Turbulence Laboratory”, Living Rev. Solar Phys., 10, lrsp-2013-2. [DOI], [ADS]. URL (accessed 22 November 2013: http://www.livingreviews.org/lrsp-2013-2 (Cited on page 9.)
Canals, A., Breen, A.R., Ofman, L., Moran, P.J. and Fallows, R.A., 2002, “Estimating random transverse velocities in the fast solar wind from EISCAT Interplanetary Scintillation measurements”, Ann. Geophys., 20, 1265–1277. [DOI], [ADS] (Cited on page 17.)
Chandran, B.D.G., 2010, “Alfvén-wave Turbulence and Perpendicular Ion Temperatures in Coronal Holes”, Astrophys. J., 720, 548–554. [DOI], [ADS], [arXiv:1006.3473 [astro-ph.SR]] (Cited on page 8.)
Chandran, B.D.G. and Hollweg, J.V., 2009, “Alfvén Wave Reflection and Turbulent Heating in the Solar Wind from 1 Solar Radius to 1AU: An Analytical Treatment”, Astrophys. J., 707, 1659–1667. [DOI], [ADS], [arXiv:0911.1068] (Cited on page 8.)
Chandran, B.D.G., Quataert, E., Howes, G.G., Xia, Q. and Pongkitiwanichakul, P., 2009, “Constraining Low-Frequency Alfvénic Turbulence in the Solar Wind Using Density-Fluctuation Measurements”, Astrophys. J., 707, 1668–1675. [DOI], [ADS], [arXiv:0908.0757] (Cited on page 8.)
Chandran, B.D.G., Pongkitiwanichakul, P., Isenberg, P.A., Lee, M.A., Markovskii, S.A., Hollweg, J.V. and Vasquez, B.J., 2010, “Resonant Interactions Between Protons and Oblique Alfvéen/Ion-cyclotron Waves in the Solar Corona and Solar Flares”, Astrophys. J., 722, 710–720. [DOI], [ADS] (Cited on page 8.)
Chandran, B.D.G., Dennis, T.J., Quataert, E. and Bale, S.D., 2011, “Incorporating Kinetic Physics into a Two-fluid Solar-wind Model with Temperature Anisotropy and Low-frequency Alfvén-wave Turbulence”, Astrophys. J., 743, 197. [DOI], [ADS], [arXiv:1110.3029 [astro-ph.SR]] (Cited on page 8.)
Cohen, O., Sokolov, I.V., Roussev, I.I. et al., 2007, “A Semiempirical Magnetohydrodynamical Model of the Solar Wind”, Astrophys. J. Lett., 654, L163–L166. [DOI], [ADS] (Cited on pages 7 and 11.)
Colgan, J., Abdallah Jr, J., Sherrill, M.E., Foster, M., Fontes, C.J. and Feldman, U., 2008, “Radiative Losses of Solar Coronal Plasmas”, Astrophys. J., 689, 585–592. [DOI], [ADS] (Cited on page 11.)
Cranmer, S.R., 2000, “Ion Cyclotron Wave Dissipation in the Solar Corona: The Summed Effect of More than 2000 Ion Species”, Astrophys. J., 532, 1197–1208. [DOI], [ADS] (Cited on page 8.)
Cranmer, S.R., 2012, “Self-Consistent Models of the Solar Wind”, Space Sci. Rev., 172, 145–156. [DOI], [ADS], [arXiv:1007.0954 [astro-ph.SR]] (Cited on page 10.)
Cranmer, S.R. and van Ballegooijen, A.A., 2005, “On the generation, propagation, and reflection of Alfvén waves from the solar photosphere to the distant heliosphere”, Astrophys. J. Suppl. Ser., 156, 265–293. [DOI], [ADS], [astro-ph/0410639] (Cited on pages 7, 8, and 9.)
Cranmer, S.R. and van Ballegooijen, A.A., 2012, “Proton, Electron, and Ion Heating in the Fast Solar Wind from Nonlinear Coupling between Alfvénic and Fast-mode Turbulence”, Astrophys. J., 754, 92. [DOI], [ADS], [arXiv:1205.4613 [astro-ph.SR]] (Cited on page 8.)
Cranmer, S.R., Field, G.B. and Kohl, J.L., 1999, “Spectroscopic Constraints on Models of Ion Cyclotron Resonance Heating in the Polar Solar Corona and High-Speed Solar Wind”, Astrophys. J., 518, 937–947. [DOI], [ADS] (Cited on pages 7, 21, 25, and 27.)
Cranmer, S.R., van Ballegooijen, A.A. and Edgar, R.J., 2007, “Self-consistent Coronal Heating and Solar Wind Acceleration from Anisotropic Magnetohydrodynamic Turbulence”, Astrophys. J. Suppl. Ser., 171, 520–551. [DOI], [ADS], [arXiv:astro-ph/0703333] (Cited on page 7.)
Daughton, W., Gary, S.P. and Winske, D., 1999, “Electromagnetic proton/proton instabilities in the solar wind: Simulations”, J. Geophys. Res., 104(A3), 4657–4668. [DOI], [ADS] (Cited on page 31.)
De Pontieu, B., McIntosh, S.W., Carlsson, M. et al., 2007, “Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind”, Science, 318, 1574–1577. [DOI], [ADS] (Cited on page 9.)
Downs, C., Roussev, I.I., van der Holst, B., Lugaz, N., Sokolov, I.V. and Gombosi, T.I., 2010, “Toward a Realistic Thermodynamic Magnetohydrodynamic Model of the Global Solar Corona”, Astrophys. J., 712, 1219–1231. [DOI], [ADS], [arXiv:0912.2647 [astro-ph.SR]] (Cited on page 11.)
Dwivedi, N.K., Batra, K. and Sharma, R.P., 2012, “Study of kinetic Alfvén wave and whistler wave spectra and their implication in solar wind plasma”, J. Geophys. Res., 117, A07201. [DOI], [ADS] (Cited on page 8.)
Evans, R.M., Opher, M., Jatenco-Pereira, V. and Gombosi, T.I., 2009, “Surface Alfvén Wave Damping in a Three-Dimensional Simulation of the Solar Wind”, Astrophys. J., 703, 179–186. [DOI], [ADS], [arXiv:0908.3146] (Cited on page 7.)
Evans, R.M., Opher, M., Oran, R., van der Holst, B., Sokolov, I.V., Frazin, R., Gombosi, T.I. and Vásquez, A., 2012, “Coronal Heating by Surface Alfvén Wave Damping: Implementation in a global Magnetohydrodynamics Model of the Solar Wind”, Astrophys. J., 756, 155. [DOI], [ADS] (Cited on page 16.)
Feldman, W.C., Barraclough, B.L., Phillips, J.L. and Wang, Y.-M., 1996, “Constraints on high-speed solar wind structure near its coronal base: a ULYSSES perspective”, Astron. Astrophys., 316, 355–367. [ADS] (Cited on pages 8 and 21.)
Galinsky, V.L. and Shevchenko, V.I., 2013a, “Acceleration of the Solar Wind by Alfvén Wave Packets”, Astrophys. J., 763, 31. [DOI], [ADS] (Cited on page 8.)
Galinsky, V.L. and Shevchenko, V.I., 2013b, “Induced Emission of Alfvén Waves in Inhomogeneous Streaming Plasma: Implications for Solar Corona Heating and Solar Wind Acceleration”, Phys. Rev. Lett., 111, 015004. [DOI], [ADS] (Cited on page 8.)
Gary, S.P., 1993, Theory of Space Plasma Microinstabilities, Cambridge Atmospheric and Space Science Series, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on pages 25 and 32.)
Gary, S.P., Wang, J., Winske, D. and Fuselier, S.A., 1997, “Proton temperature anisotropy upper bound”, J. Geophys. Res., 102(A12), 27,159–27,170. [DOI], [ADS] (Cited on page 31.)
Gary, S.P., Yin, L., Winske, D. and Reisenfeld, D.B., 2000, “Electromagnetic alpha/proton instabilities in the solar wind”, Geophys. Res. Lett., 27(9), 1355–1358. [DOI], [ADS] (Cited on page 31.)
Gary, S.P., Yin, L., Winske, D. and Ofman, L., 2001, “Electromagnetic heavy ion cyclotron instability: Anisotropy constraint in the solar corona”, J. Geophys. Res., 106, 10,715–10,722. [DOI], [ADS] (Cited on pages 10 and 31.)
Gary, S.P., Yin, L., Winske, D., Ofman, L., Goldstein, B.E. and Neugebauer, M., 2003, “Consequences of proton and alpha anisotropies in the solar wind: Hybrid simulations”, J. Geophys. Res., 108(A2), 1068. [DOI], [ADS] (Cited on pages 10, 25, 31, and 32.)
Gary, S.P., Yin, L. and Winske, D., 2006, “Alfvén-cyclotron scattering of solar wind ions: Hybrid simulations”, J. Geophys. Res., 111(A10), 6105. [DOI], [ADS] (Cited on page 10.)
Gazis, P.R. and Lazarus, A.J., 1982, “Voyager observations of solar wind proton temperature: 1–10 AU”, Geophys. Res. Lett., 9, 431–434. [DOI], [ADS] (Cited on page 8.)
Goldstein, B.E., Smith, E.J., Balogh, A., Horbury, T.S., Goldstein, M.L. and Roberts, D.A., 1995, “Properties of magnetohydrodynamic turbulence in the solar wind as observed by Ulysses at high heliographic latitudes”, Geophys. Res. Lett., 22, 3393–3396. [DOI], [ADS] (Cited on page 8.)
Grall, R.R., Coles, W.A., Klinglesmith, M.T., Breen, A.R., Williams, P.J.S., Markkanen, J. and Esser, R., 1996, “Rapid acceleration of the polar solar wind”, Nature, 379, 429. [DOI], [ADS] (Cited on page 17.)
Grappin, R. and Velli, M., 1996, “Waves and streams in the expanding solar wind”, J. Geophys. Res., 101, 425–444. [DOI], [ADS] (Cited on pages 14 and 27.)
Grappin, R., Léorat, J. and Habbal, S.R., 2002, “Large-amplitude Alfvén waves in open and closed coronal structures: A numerical study”, J. Geophys. Res., 107, 1380. [DOI], [ADS] (Cited on page 16.)
Guhathakurta, M., Sittler Jr, E.C. and Ofman, L., 2006, “Semiempirically derived heating function of the corona heliosphere during the Whole Sun Month”, J. Geophys. Res., 111, A11215. [DOI], [ADS] (Cited on page 7.)
Hahn, M. and Savin, D.W., 2013, “Observational Quantification of the Energy Dissipated by Alfvén Waves in a Polar Coronal Hole: Evidence that Waves Drive the Fast Solar Wind”, Astrophys. J., 776, 78. [DOI], [ADS], [arXiv:1302.5403 [astro-ph.SR]] (Cited on page 9.)
Hahn, M., Landi, E. and Savin, D.W., 2012, “Evidence ofWave Damping at Low Heights in a Polar Coronal Hole”, Astrophys. J., 753, 36. [DOI], [ADS], [arXiv:1202.1743 [astro-ph.SR]] (Cited on page 9.)
Hansteen, V.H. and Velli, M., 2012, “Solar Wind Models from the Chromosphere to 1 AU”, Space Sci. Rev., 172, 89.121. [DOI], [ADS] (Cited on page 10.)
Heinemann, M. and Olbert, S., 1980, “Non-WKB Alfvén waves in the Solar Wind”, J. Geophys. Res., 85(A3), 1311.1327. [DOI], [ADS] (Cited on page 7.)
Hellinger, P. and Trávnäček, P., 2006, “Parallel and oblique proton fire hose instabilities in the presence of alpha/proton drift: Hybrid simulations”, J. Geophys. Res., 111(A10), 1107. [DOI], [ADS] (Cited on page 10.)
Hellinger, P. and Trávnäček, P.M., 2011, “Proton core-beam system in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 116(A15), A11101. [DOI], [ADS] (Cited on page 34.)
Hellinger, P. and Trávnäček, P.M., 2013, “Protons and alpha particles in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 118, 5421.5430. [DOI], [ADS] (Cited on page 34.)
Hellinger, P., Velli, M., Trávnäček, P., Gary, S.P., Goldstein, B.E. and Liewer, P.C., 2005, “Alfvén wave heating of heavy ions in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 110(9), A12109. [DOI], [ADS] (Cited on pages 10 and 14.)
Hollweg, J.V., 2000, “Cyclotron resonance in coronal holes: 3. A five-beam turbulence-driven model”, J. Geophys. Res., 105(A7), 15,699.15,714. [DOI], [ADS] (Cited on page 8.)
Hollweg, J.V. and Isenberg, P.A., 2002, “Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction”, J. Geophys. Res., 107(A7), 1147. [DOI], [ADS] (Cited on page 8.)
Hu, Y.Q., Esser, R. and Habbal, S.R., 2000, “A four-fluid turbulence-driven solar wind model for preferential acceleration and heating of heavy ions”, J. Geophys. Res., 105, 5093–5112. [DOI], [ADS] (Cited on page 8.)
Isenberg, P.A., 2004, “The kinetic shell model of coronal heating and acceleration by ion cyclotron waves: 3. The proton halo and dispersive waves”, J. Geophys. Res., 109, A03101. [DOI], [ADS] (Cited on page 8.)
Isenberg, P.A., 2012, “A self-consistent marginally stable state for parallel ion cyclotron waves”, Phys. Plasmas, 19(3), 032116. [DOI], [ADS], [arXiv:1203.1938 [physics.plasm-ph]] (Cited on page 8.)
Isenberg, P.A. and Vasquez, B.J., 2011, “A Kinetic Model of Solar Wind Generation by Oblique Ioncyclotron Waves”, Astrophys. J., 731, 88. [DOI], [ADS] (Cited on page 8.)
Kaghashvili, E.K., Vasquez, B.J. and Hollweg, J.V., 2003, “Deceleration of streaming alpha particles interacting with waves and imbedded rotational discontinuities”, J. Geophys. Res., 108(A1), 1036. [DOI], [ADS] (Cited on page 10.)
Ko, Y.-K., Li, J., Riley, P. and Raymond, J.C., 2008, “Large-Scale Coronal Density and Abundance Structures and Their Association with Magnetic Field Structure”, Astrophys. J., 683, 1168–1179. [DOI], [ADS] (Cited on page 6.)
Kohl, J.L., Noci, G., Antonucci, E. et al., 1997, “First Results from the SOHO Ultraviolet Coronagraph Spectrometer”, Solar Phys., 175, 613–644. [DOI], [ADS] (Cited on pages 6, 7, 12, 21, 25, and 27.)
Kohl, J.L., Noci, G., Antonucci, E. et al., 1998, “UVCS/SOHO Empirical Determinations of Anisotropic Velocity Distributions in the Solar Corona”, Astrophys. J. Lett., 501, L127–L131. [DOI], [ADS] (Cited on page 7.)
Landi, E. and Landini, M., 1999, “Radiative losses of optically thin coronal plasmas”, Astron. Astrophys., 347, 401–408. [ADS] (Cited on page 11.)
Lau, Y.-T. and Siregar, E., 1996, “Nonlinear Alfven Wave Propagation in the Solar Wind”, Astrophys. J., 465, 451. [DOI], [ADS] (Cited on page 16.)
Lepping, R.P., Acuña, M.H., Burlaga, L.F. et al., 1995, “The Wind Magnetic Field Investigation”, Space Sci. Rev., 71, 207–229. [DOI], [ADS] (Cited on page 6.)
Li, B., Xia, L.D. and Chen, Y., 2011, “Solar winds along curved magnetic field lines”, Astron. Astrophys., 529, A148. [DOI], [ADS], [arXiv:1103.5211 [astro-ph.SR]] (Cited on page 8.)
Li, X. and Habbal, S.R., 2005, “Hybrid simulation of ion cyclotron resonance in the solar wind: Evolution of velocity distribution functions”, J. Geophys. Res., 110, A10109. [DOI], [ADS] (Cited on page 10.)
Li, X., Esser, R., Habbal, S.R. and Hu, Y., 1997, “Influence of heavy ions on the high-speed solar wind”, J. Geophys. Res., 102(A8), 17,419–17,432. [DOI], [ADS] (Cited on page 12.)
Li, X., Habbal, S.R., Kohl, J. and Noci, G., 1998, “The Effect of Temperature Anisotropy on Observations of Doppler Dimming and Pumping in the Inner Corona”, Astrophys. J. Lett., 501, L133–L137. [DOI], [ADS] (Cited on page 7.)
Li, X., Habbal, S.R., Hollweg, J.V. and Esser, R., 1999, “Heating and cooling of protons by turbulencedrivenion cyclotron waves in the fast solar wind”, J. Geophys. Res., 104(A2), 2521–2535. [DOI], [ADS] (Cited on page 8.)
Liewer, P.C., Velli, M. and Goldstein, B.E., 2001, “Alfvén wave propagation and ion cyclotron interactions in the expanding solar wind: One-dimensional hybrid simulations”, J. Geophys. Res., 106(A12), 29,261–29,282. [DOI], [ADS] (Cited on pages 10, 14, and 27.)
Linker, J.A., Mikić, Z., Biesecker, D.A. et al., 1999, “Magnetohydrodynamic modeling of the solar corona during Whole Sun Month”, J. Geophys. Res., 104, 9809–9830. [DOI], [ADS] (Cited on page 7.)
Lionello, R., Linker, J.A. and Mikić, Z., 2009, “Multispectral Emission of the Sun During the First Whole Sun Month: Magnetohydrodynamic Simulations”, Astrophys. J., 690, 902–912. [DOI], [ADS] (Cited on page 11.)
Lu, Q.-M. and Wang, S., 2005, “Proton and He2+ Temperature Anisotropies in the Solar Wind Driven by Ion Cyclotron Waves”, Chin. J. Astron. Astrophys., 5, 184–192. [DOI], [ADS] (Cited on page 10.)
Maneva, Y.G., Viñas, A.F. and Ofman, L., 2013, “Turbulent heating and acceleration of He++ ions by spectra of Alfvén-cyclotron waves in the expanding solar wind: 1.5-D hybrid simulations”, J. Geophys. Res., 118, 2842–2853. [DOI], [ADS] (Cited on pages 28, 29, and 30.)
Markovskii, S.A., Vasquez, B.J. and Chandran, B.D.G., 2010, “Perpendicular Proton Heating Due to Energy Cascade of Fast Magnetosonic Waves in the Solar Corona”, Astrophys. J., 709, 1003–1008. [DOI], [ADS] (Cited on pages 8 and 10.)
Marsch, E., 1992, “On the possible role of plasma waves in the heating of chromosphere and corona”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 65–68, Pergamon Press, Oxford; New York. [ADS] (Cited on page 8.)
Marsch, E., 2006, “Kinetic Physics of the Solar Corona and Solar Wind”, Living Rev. Solar Phys., 3, lrsp-2006-1. [DOI], [ADS]. URL (accessed 25 January 2010): http://www.livingreviews.org/lrsp-2006-1 (Cited on pages 5, 8, 27, and 31.)
Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R. and Neubauer, F.M., 1982a, “Solar Wind Helium Ions: Observations of the HELIOS Solar Probes Between 0.3 and 1 AU”, J. Geophys. Res., 87(A1), 35–51. [DOI], [ADS] (Cited on page 21.)
Marsch, E., Mühlhäuser, K.-H., Schwenn, R., Rosenbauer, H., Pilipp, W. and Neubauer, F.M., 1982b, “Solar Wind Protons: Three-Dimensional Velocity Distributions and Derived Plasma Parameters Measured Between 0.3 and 1 AU”, J. Geophys. Res., 87, 52–72. [DOI], [ADS] (Cited on pages 8 and 21.)
McComas, D.J., Elliott, H.A., Schwadron, N.A., Gosling, J.T., Skoug, R.M. and Goldstein, B.E., 2003, “The three-dimensional solar wind around solar maximum”, Geophys. Res. Lett., 30, 1517. [DOI], [ADS] (Cited on page 5.)
McComas, D.J., Velli, M., Lewis, W.S. et al., 2007, “Understanding coronal heating and solar wind acceleration: Case for in situ near-Sun measurements”, Rev. Geophys., 45, RG1004. [DOI], [ADS] (Cited on page 37.)
McKean, M.E., Winske, D. and Gary, S.P., 1994, “Two-dimensional simulations of ion anisotropy instabilities in the magnetosheath”, J. Geophys. Res., 99, 11,141–11,154. [DOI], [ADS] (Cited on page 31.)
Mecheri, R., 2013, “Properties of Ion-Cyclotron Waves in the Open Solar Corona”, Solar Phys., 282, 133–146. [DOI], [ADS], [arXiv:1202.5742 [astro-ph.SR]] (Cited on page 8.)
Mikić, Z., Linker, J.A., Schnack, D.D., Lionello, R. and Tarditi, A., 1999, “Magnetohydrodynamic modeling of the global solar corona”, Phys. Plasmas, 6, 2217–2224. [DOI], [ADS] (Cited on page 7.)
Neugebauer, M., Goldstein, B.E., Smith, E.J. and Feldman, W.C., 1996, “Ulysses observations of differential alpha-proton streaming in the solar wind”, J. Geophys. Res., 101(A8), 17,047–17,056. [DOI], [ADS] (Cited on page 8.)
Neugebauer, M., Goldstein, B.E., Winterhalter, D., Smith, E.J., MacDowall, R.J. and Gary, S.P., 2001, “Ion distributions in large magnetic holes in the fast solar wind”, J. Geophys. Res., 106, 5635–5648. [DOI], [ADS] (Cited on page 21.)
Ofman, L., 2000, “Source regions of the slow solar wind in coronal streamers”, Geophys. Res. Lett., 27, 2885–2888. [DOI], [ADS] (Cited on page 37.)
Ofman, L., 2004a, “Three-fluid model of the heating and acceleration of the fast solar wind”, J. Geophys. Res., 109, A07102. [DOI], [ADS] (Cited on pages 7, 11, 12, 20, 21, 22, 23, 24, 25, and 37.)
Ofman, L., 2004b, “The origin of the slow solar wind in coronal streamers”, Adv. Space Res., 33, 681–688. [DOI], [ADS] (Cited on page 7.)
Ofman, L., 2005, “MHD Waves and Heating in Coronal Holes”, Space Sci. Rev., 120, 67–94. [DOI], [ADS] (Cited on pages 7 and 11.)
Ofman, L., 2010, “Hybrid model of inhomogeneous solar wind plasma heating by Alfvén wave spectrum: Parametric studies”, J. Geophys. Res., 115, A04108. [DOI], [ADS] (Cited on pages 10, 33, 34, and 36.)
Ofman, L. and Davila, J.M., 1997, “Do First Results from SOHO UVCS Indicate That the Solar Wind Is Accelerated by Solitary Waves?”, Astrophys. J. Lett., 476, L51–L54. [DOI], [ADS] (Cited on pages 7 and 16.)
Ofman, L. and Davila, J.M., 1998, “Solar wind acceleration by large-amplitude nonlinear waves: Parametric study”, J. Geophys. Res., 103(A10), 23,677–23,690. [DOI], [ADS] (Cited on pages 7, 16, 17, and 18.)
Ofman, L. and Davila, J.M., 2001, “Three-Fluid 2.5-dimensional Magnetohydrodynamic Model of the Effective Temperature in Coronal Holes”, Astrophys. J., 553, 935–940. [DOI], [ADS] (Cited on pages 7 and 24.)
Ofman, L. and Viñas, A.F., 2007, “Two-dimensional hybrid model of wave and beam heating of multi-ion solar wind plasma”, J. Geophys. Res., 112, A06104. [DOI], [ADS] (Cited on pages 10, 14, 31, 32, 34, and 35.)
Ofman, L. and Wang, T.J., 2008, “Hinode observations of transverse waves with flows in coronal loops”, Astron. Astrophys., 482, L9–L12. [DOI], [ADS] (Cited on page 9.)
Ofman, L., Viñs, A. and Gary, S.P., 2001, “Constraints on the O+5 Anisotropy in the Solar Corona”, Astrophys. J. Lett., 547, L175–L178. [DOI], [ADS] (Cited on pages 10, 25, 31, and 33.)
Ofman, L., Gary, S.P. and Viñas, A.F., 2002, “Resonant heating and acceleration of ions in coronal holes driven by cyclotron resonant spectra”, J. Geophys. Res., 107(A12), 1461. [DOI], [ADS] (Cited on pages 10, 24, 25, 26, and 31.)
Ofman, L., Davila, J.M., Nakariakov, V.M. and Viñas, A.-F., 2005, “High-frequency Alfvén waves in multiion coronal plasma: Observational implications”, J. Geophys. Res., 110, A09102. [DOI], [ADS] (Cited on pages 10, 15, 25, 27, and 28.)
Ofman, L., Viñas, A.F. and Moya, P.S., 2011, “Hybrid models of solar wind plasma heating”, Ann. Geophys., 29, 1071–1079. [DOI], [ADS] (Cited on pages 10, 28, and 34.)
Oran, R., van der Holst, B., Landi, E., Jin, M., Sokolov, I.V. and Gombosi, T.I., 2013, “A Global Wavedriven Magnetohydrodynamic Solar Model with a Unified Treatment of Open and Closed Magnetic Field Topologies”, Astrophys. J., 778, 176. [DOI], [ADS], [arXiv:1307.4510 [astro-ph.SR]] (Cited on pages 15 and 16.)
Osterbrock, D.E., 1961, “The Heating of the Solar Chromosphere, Plages, and Corona by Magnetohydrodynamic Waves”, Astrophys. J., 134, 347. [DOI], [ADS] (Cited on page 7.)
Parker, E.N., 1958, “Dynamics of the interplanetary gas and magnetic fields”, Astrophys. J., 128, 664–676. [DOI], [ADS] (Cited on page 7.)
Parker, E.N., 1963, “The Solar-Flare Phenomenon and the Theory of Reconnection and Annihiliation of Magnetic Fields”, Astrophys. J. Suppl. Ser., 8, 177–211. [DOI], [ADS] (Cited on page 7.)
Podesta, J.J., Roberts, D.A. and Goldstein, M.L., 2006, “Power spectrum of small-scale turbulent velocity fluctuations in the solar wind”, J. Geophys. Res., 111, A10109. [DOI], [ADS] (Cited on page 9.)
Priest, E.R., 1982, Solar Magnetohydrodynamics, Geophysics and Astrophysics Monographs, 21, Reidel, Dordrecht; Boston. [ADS], [Google Books] (Cited on pages 11 and 31.)
Roussev, I.I., Gombosi, T.I., Sokolov, I.V. et al., 2003, “A Three-dimensional Model of the Solar Wind Incorporating Solar Magnetogram Observations”, Astrophys. J. Lett., 595, L57–L61. [DOI], [ADS] (Cited on page 7.)
Sittler Jr, E.C. and Guhathakurta, M., 1999, “Semiempirical Two-dimensional MagnetoHydrodynamic Model of the Solar Corona and Interplanetary Medium”, Astrophys. J., 523, 812–826. [DOI], [ADS] (Cited on page 7.)
Sittler Jr, E.C. and Ofman, L., 2006, “2D MHD model of the solar corona and solar wind: Recent results”, in Solar Influence on the Heliosphere and Earth’s Environment: Recent Progress and Prospects, Proceedings of the ILWS Workshop, Goa, India, February 19–24, 2006, (Eds.) Gopalswamy, N., Bhattacharyya, A., pp. 128–131, Quest Publications, Mumbai. [ADS]. Online version (accessed 25 January 2010): http://cdaw.gsfc.nasa.gov/publications/ilws_goa2006/ (Cited on page 7.)
Smith, C.W., Vasquez, B.J. and Hamilton, K., 2006, “Interplanetary magnetic fluctuation anisotropy in the inertial range”, J. Geophys. Res., 111, A09111. [DOI], [ADS] (Cited on page 6.)
Sokolov, I.V., van der Holst, B., Oran, R. et al., 2013, “Magnetohydrodynamic Waves and Coronal Heating: Unifying Empirical and MHD Turbulence Models”, Astrophys. J., 764, 23. [DOI], [ADS], [arXiv:1208.3141 [astro-ph.SR]] (Cited on page 16.)
Stone, E.C., Frandsen, A.M., Mewaldt, R.A., Christian, E.R., Margolies, D., Ormes, J.F. and Snow, F., 1998, “The Advanced Composition Explorer”, Space Sci. Rev., 86, 1–22. [DOI], [ADS] (Cited on page 6.)
Strachan, L., Suleiman, R., Panasyuk, A.V., Biesecker, D.A. and Kohl, J.L., 2002, “Empirical densities, kinetic temperatures, and outflow velocities in the equatorial streamer belt at solar minimum”, Astrophys. J., 571, 1008–1014. [DOI], [ADS] (Cited on page 8.)
Suzuki, T.K. and Inutsuka, S.-i., 2005, “Making the Corona and the Fast Solar Wind: A Self-consistent Simulation for the Low-Frequency Alfvén Waves from the Photosphere to 0.3 AU”, Astrophys. J. Lett., 632, L49–L52. [DOI], [ADS], [arXiv:astro-ph/0506639] (Cited on pages 7, 17, and 19.)
Suzuki, T.K. and Inutsuka, S.-I., 2006, “Solar winds driven by nonlinear low-frequency Alfvén waves from the photosphere: Parametric study for fast/slow winds and disappearance of solar winds”, J. Geophys. Res., 111, A06101. [DOI], [ADS], [arXiv:astro-ph/0511006] (Cited on page 7.)
Tóth, G., Sokolov, I.V., Gombosi, T.I. et al., 2005, “Space Weather Modeling Framework: A new tool for the space science community”, J. Geophys. Res., 110(A9), A12226. [DOI], [ADS] (Cited on page 16.)
Tu, C.-Y. and Marsch, E., 1995, “MHD structures, waves and turbulence in the solar wind: Observations and theories”, Space Sci. Rev., 73(1/2), 1–210. [DOI], [ADS] (Cited on page 9.)
Tu, C.-Y. and Marsch, E., 1997, “Two-Fluid Model for Heating of the Solar Corona and Acceleration of the Solar Wind by High-Frequency Alfvén Waves”, Solar Phys., 171, 363–391. [DOI], [ADS] (Cited on page 8.)
Usmanov, A.V. and Goldstein, M.L., 2003, “A tilted-dipole MHD model of the solar corona and solar wind”, J. Geophys. Res., 108, 1354. [DOI], [ADS] (Cited on page 7.)
Usmanov, A.V., Goldstein, M.L., Besser, B.P. and Fritzer, J.M., 2000, “A global MHD solar wind model with WKB Alfvén waves: Comparison with Ulysses data”, J. Geophys. Res., 105(A6), 12,675–12,696. [DOI], [ADS] (Cited on pages 7 and 16.)
Uzzo, M., Strachan, L. and Vourlidas, A., 2007, “The Physical Properties of Coronal Streamers. II.”, Astrophys. J., 671, 912–925. [DOI], [ADS] (Cited on page 8.)
van der Holst, B., Manchester IV, W.B., Frazin, R.A., Vásquez, A.M., Tóth, G. and Gombosi, T.I., 2010, “A Data-driven, Two-temperature Solar Wind Model with Alfvén Waves”, Astrophys. J., 725, 1373. [DOI], [ADS] (Cited on page 16.)
Vásquez, A.M., van Ballegooijen, A.A. and Raymond, J.C., 2003, “The Effect of Proton Temperature Anisotropy on the Solar Minimum Corona and Wind”, Astrophys. J., 598, 1361–1374. [DOI], [ADS], [arXiv:astro-ph/0310846] (Cited on page 7.)
Vasquez, B.J., Smith, C.W., Hamilton, K., MacBride, B.T. and Leamon, R.J., 2007, “Evaluation of the turbulent energy cascade rates from the upper inertial range in the solar wind at 1 AU”, J. Geophys. Res., 112(A11), 7101. [DOI], [ADS] (Cited on page 9.)
Velli, M., 2003, “MHD turbulence and the heating of astrophysical plasmas”, Plasma Phys. Control. Fusion, 45(26), A205–A216. [DOI], [ADS] (Cited on page 8.)
Verdini, A., Velli, M. and Buchlin, E., 2009, “Turbulence in the Sub-Alfvénic Solar Wind Driven by Reflection of Low-Frequency Alfvén Waves”, Astrophys. J. Lett., 700, L39–L42. [DOI], [ADS], [arXiv:0905.2618] (Cited on page 8.)
Verdini, A., Velli, M., Matthaeus, W.H., Oughton, S. and Dmitruk, P., 2010, “A Turbulence-Driven Model for Heating and Acceleration of the Fast Wind in Coronal Holes”, Astrophys. J. Lett., 708, L116–L120. [DOI], [ADS], [arXiv:0911.5221] (Cited on page 8.)
Voitenko, Y. and Goossens, M., 2006, “Energization of Plasma Species by Intermittent Kinetic Alfvén Waves”, Space Sci. Rev., 122, 255–270. [DOI], [ADS] (Cited on page 8.)
Wambecq, A., 1978, “Rational Runge-Kutta Methods for Solving Systems of Ordinary Differential Equations”, Computing, 20, 333–342. [DOI] (Cited on page 14.)
Winske, D. and Omidi, N., 1993, “Hybrid Codes: Methods and Applications”, in Computer Space Plasma Physics: Simulation Techniques and Software, International School for Space Simulations (ISSS-4), Kyoto, March 25–30, 1990 and Nara, April 2–6, 1990, (Eds.) Matsumoto, H., Omura, Y., pp. 103–160, Terra Scientific Publishing, Tokyo. Online version (accessed 25 January 2010): http://www.terrapub.co.jp/e-library/cspp/ (Cited on pages 9 and 16.)
Winske, D. and Quest, K.B., 1986, “Electromagnetic ion beam instabilities: Comparison of one- and two-dimensional simulations”, J. Geophys. Res., 91, 8789–8797. [DOI], [ADS] (Cited on page 31.)
Xie, H., Ofman, L. and Viñas, A.F., 2004, “Multiple ions resonant heating and acceleration by Alfvén/cyclotron fluctuations in the corona and the solar wind”, J. Geophys. Res., 109, A08103. [DOI], [ADS] (Cited on pages 10 and 31.)
Zurbuchen, T.H., 2007, “A New View of the Coupling of the Sun and the Heliosphere”, Annu. Rev. Astron. Astrophys., 45, 297–338. [DOI], [ADS] (Cited on page 37.)
Acknowledgements
The author would like to acknowledge support by NASA grants NNX08AF85G, NNX08AV88G, and NNX10AC56G.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ofman, L. Wave Modeling of the Solar Wind. Living Rev. Sol. Phys. 7, 4 (2010). https://doi.org/10.12942/lrsp-2010-4
Published:
DOI: https://doi.org/10.12942/lrsp-2010-4