Abstract
Coronal holes are the darkest and least active regions of the Sun, as observed both on the solar disk and above the solar limb. Coronal holes are associated with rapidly expanding open magnetic fields and the acceleration of the high-speed solar wind. This paper reviews measurements of the plasma properties in coronal holes and how these measurements are used to reveal details about the physical processes that heat the solar corona and accelerate the solar wind. It is still unknown to what extent the solar wind is fed by flux tubes that remain open (and are energized by footpoint-driven wave-like fluctuations), and to what extent much of the mass and energy is input intermittently from closed loops into the open-field regions. Evidence for both paradigms is summarized in this paper. Special emphasis is also given to spectroscopic and coronagraphic measurements that allow the highly dynamic non-equilibrium evolution of the plasma to be followed as the asymptotic conditions in interplanetary space are established in the extended corona. For example, the importance of kinetic plasma physics and turbulence in coronal holes has been affirmed by surprising measurements from the UVCS instrument on SOHO that heavy ions are heated to hundreds of times the temperatures of protons and electrons. These observations point to specific kinds of collisionless Alfvén wave damping (i.e., ion cyclotron resonance), but complete theoretical models do not yet exist. Despite our incomplete knowledge of the complex multi-scale plasma physics, however, much progress has been made toward the goal of understanding the mechanisms ultimately responsible for producing the observed properties of coronal holes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coronal holes are regions of low density plasma on the Sun that have magnetic fields opening freely into the heliosphere. Because of their low density, coronal holes tend to be the regions of the outer solar atmosphere that are most prone to behaving as a collisionless plasma. Ionized atoms and electrons flow along the open magnetic fields to form the highest-speed components of the solar wind.
The term “coronal hole” has come to denote several phenomena that may not always refer to the same regions. First, the darkest patches on the solar surface, as measured in ultraviolet (UV) and X-ray radiation, are called coronal holes. Second, the term also applies to the lowest-intensity regions measured above the solar limb, seen either during a total solar eclipse or with an occulting coronagraph. Third, there is a more theoretical usage that equates coronal holes with all open-field footpoints of time-steady solar wind flows. There are good reasons why these three ideas should be related to one another, but the overlap between them is not complete. To avoid possible confusion, this paper will mainly use the first two observational definitions, with the third one being only partly applicable.
During times of low solar activity, when the Sun’s magnetic field is dominated by a rotationally-aligned dipole component, there are large coronal holes that cover the north and south polar caps of the Sun. In more active periods of the solar cycle, coronal holes can exist at all solar latitudes, but they may only persist for several solar rotations before evolving into different magnetic configurations.
Despite not being as visually spectacular as active regions, solar flares, or coronal mass ejections (CMEs), coronal holes are of abiding interest for (at least) three main reasons.
-
1.
The extended corona and solar wind connected with coronal holes tends to exist in an ambient time-steady state, at least in comparison with other regions. This makes coronal holes a natural starting point for theoretical modeling, since it often makes sense to begin with the simplest regions before attempting to understand more complex and variable structures.
-
2.
Coronal hole plasma has the lowest density, which makes it an optimal testbed for studies of collisionless kinetic processes that are the ultimate dissipation mechanisms in many theories of coronal heating. Other regions tend to have higher densities and more rapid Coulomb collisions, and thus the unique signatures of the kinetic processes (in their particle velocity distributions) are not as straightforward to measure as in coronal holes.
-
3.
Coronal holes and their associated high-speed wind streams are also responsible for a fraction of major geomagnetic storms at 1 AU. Corotating interaction regions (CIRs) form when fast and slow wind streams collide with one another, and the subsequent interaction between these structures and the Earth’s magnetosphere can give rise to long-lasting fluxes of energetic electrons.
This paper reviews measurements of the plasma properties of coronal holes and how these measurements have been used to put constraints on theoretical models of coronal heating and solar wind acceleration. There have been several earlier reviews that have focused mainly on the topic of coronal holes, including Zirker (1977), Suess (1979), Harvey and Sheeley Jr (1979), Parker (1991), Kohl and Cranmer (1999), Hudson (2002), Cranmer (2002a), Ofman (2005), de Toma and Arge (2005), Jones (2005), and Wang (2009). Interested readers are urged to survey these other reviews in order to fill in any gaps in topical coverage in the present paper.
The remainder of this paper is organized as follows. Section 2 gives a brief history of the discovery and early years of research on coronal holes. Section 3 summarizes the observations and derived plasma properties of “on-disk” coronal holes (i.e., primarily using the definition of holes as dark patches on the solar surface at UV and X-ray wavelengths). Section 4 reviews the measurements of “off-limb” coronal holes and describes our current knowledge of how these structures are linked to various kinds of solar wind streams measured in situ. Section 5 discusses a broad range of possible theoretical explanations for how the plasma in coronal holes is heated and how the solar wind in these regions is accelerated. Section 6 concludes this paper with a few words about how the study of coronal holes helps to improve our wider understanding of heliophysics, astrophysics, and plasma physics.
2 Historical Overview
Although the term “coronal hole” was not first used until the middle of the 20th century, people have reported the existence of visible features associated with the Sun’s corona — seen during total eclipses — for centuries (see, e.g., Wang and Siscoe, 1980; Vaquero, 2003). A popular astronomy book from the first decade of the 20th century (Serviss, 1909) contained clear descriptions of coronal streamers, eruptive prominences, and polar plumes in coronal holes. The following description of the latter, from an eclipse in 1900, conveys that early speculation may sometimes be prescient:
“The sheaves of light emanating from the poles look precisely like the ‘lines of force’ surrounding the poles of a magnet. It will be noticed in this photograph that the corona appears to consist of two portions: one comprising the polar rays just spoken of, and the other consisting of the broader, longer, and less-defined masses of light extending out from the equatorial and middle-latitude zones. Yet even in this more diffuse part of the phenomenon one can detect the presence of submerged curves bearing more or less resemblance to those about the poles. Just what part electricity or electro-magnetism plays in the mechanism of solar radiation it is impossible to say, but on the assumption that it is a very important part is based the hypothesis that there exists a direct solar influence not only upon the magnetism, but upon the weather of the earth” (Serviss, 1909).
The first quantitative observations of coronal holes were made by Waldmeier (1956, 1957) at the Swiss Federal Observatory in Zürich. These features were identified as long-lived regions of negligible intensity in coronagraphic (off-limb) images of the 5303 Å green emission line (see also Waldmeier, 1975, 1981). Waldmeier called the features that appeared more-or-less circular when projected onto the solar disk Löcher (holes), and the more elongated features were called Kanal (channels) or Rinne (grooves).
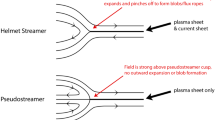
In off-limb eclipse and coronagraph images, the darkest coronal hole regions are surrounded by brighter and more complex streamers. These wispy structures appear to be connected to closed magnetic field lines at the solar surface, but they are often stretched upwards to an elongated cusp-like point, with thin “stalks” of radial rays at the top. For this reason their appearance was likened to a pointed German helmet (or a brush-topped Greek or Roman helmet), and the common phrase helmet streamers is often seen. The earliest studies of coronal morphology tended to concentrate more on streamers than coronal holes because the former are significantly easier to see than the latter (see, e.g., Miller, 1908; Mitchell, 1932; Newkirk Jr, 1967; Pneuman, 1968). Piddington (1972) outlined some early ideas about the global structure of the “quiet” (i.e., solar minimum) corona. Figure 1 compares an adaptation of J. H. Piddington’s sketch of the quiet corona to a more recent photograph from another eclipse around solar minimum.
Left: Adaptation of a sketch of the quiet solar corona made by Piddington (1972), based on prior drawings (Waldmeier, 1955) and photographs (Gold, 1955) of the 30 June 1954 eclipse. Right: Contrast-adjusted eclipse image taken with the POISE instrument on 26 February 1998, in Westpunt, Curaçao. The original image was made available courtesy of the High Altitude Observatory (HAO), University Corporation for Atmospheric Research (UCAR), Boulder, Colorado. UCAR is sponsored by the National Science Foundation.
As the quality of the observations improved, coronal holes became objects of study in their own right. The largest coronal holes were observed to contain fine thread-like polar plumes that appear to follow the superradially expanding open magnetic field lines above the solar limb (Saito, 1958; Stoddard et al., 1966; Newkirk Jr and Harvey, 1968). These elongated structures were found to correlate with bright chromospheric faculae on the surface (e.g., Harvey, 1965) and with longer extensions for the small jet-like spicules that continually rise and fall above the limb (Lippincott, 1957; Beckers, 1968).
Coronal holes were essentially re-discovered in the late 1960s and early 1970s as discrete dark patches on the X-ray and ultraviolet solar disk. Newkirk Jr (1967) reviewed some of the earliest rocket-based measurements in the extreme UV, and Tousey et al. (1968) discussed how the UV emission was “usually weaker over the poles” in images from a series of rocket flights between 1963 and 1967 (around solar minimum). These regions on the solar disk came to be called coronal holes in parallel with the earlier off-limb usage. Munro and Withbroe (1972) analyzed OSO-4 observations to conclude that both the density and electron temperature were lower in these dark regions. In 1973 and 1974, solar instruments on the Apollo telescope mount (ATM) on Skylab confirmed many earlier ideas about coronal holes with data significantly better in quantity and quality (Huber et al., 1974; Kahler, 2000).
In addition to the large north and south polar holes, there were also found to be smaller coronal holes that exist at lower latitudes (often at times other than solar minimum). Sometimes the largest coronal holes can exhibit thin “peninsulas” that jut out from the main regions. Harvey and Recely (2002) called these regions “polar lobes.” Notable examples have been the so-called “Boot of Italy” seen by Skylab in 1974 (e.g., Zirker, 1977) and the “Elephant’s Trunk” seen by SOHO in 1996 (Del Zanna and Bromage, 1999). A third example, from December 2000, is shown in Figure 2.
Additional insights came from the fusion of spectroscopy and coronagraphic occultation. Inspired by rocket-borne UV observations of the extended corona during a solar eclipse in March 1970, Kohl et al. (1978) developed a UV coronagraph spectrometer to measure the profile shape of the bright H I Lyα emission line at 1216 Å. This line is sensitive to several key properties of the velocity distribution of coronal protons, and thus these observations could be used to begin distinguishing proton temperatures from electron temperatures in the collisionless outer regions of coronal holes (see Section 4.3). The rocket-borne UV coronagraph spectrometer was launched three times (in 1979, 1980, and 1982), and the results included the first direct evidence for proton heating and supersonic outflow in coronal holes (Kohl et al., 1980; Strachan et al., 1993; Kohl et al., 2006).
The fact that coronal holes coincide with regions of open magnetic field that expands out into interplanetary space was realized during the first decade of in situ solar wind observations (e.g., Wilcox, 1968; Altschuler et al., 1972; Hundhausen, 1972). Noci (1973) made a theoretical argument, on the basis of measured wave fluxes and heat conduction, that coronal holes should have the largest solar wind kinetic energy fluxes (i.e., the highest speeds). Pneuman (1973) argued that coronal holes need not have lower energy deposition than closed-field regions (as is suggested by the lower intensities of coronal holes) if the solar wind carries away much of that energy. Krieger et al. (1973) utilized X-ray sounding rocket images to identify a large coronal hole as the solar source of a strong high-speed stream as measured by the Pioneer 6 and Vela spacecraft. Around this time it was also realized that coronal holes and high-speed wind streams are also responsible for a fraction of the geomagnetic storms seen at 1 AU (Bell and Noci, 1973; Neupert and Pizzo, 1974; Bell and Noci, 1976; see also Tanskanen et al., 2005 and Zhang et al., 2007). Although there is still no complete understanding of which types of solar wind flow are connected with which types of coronal structures, the causal link between the largest coronal holes and high-speed streams remains firm (see also Section 4.1).
3 Properties of On-Disk Coronal Holes
The traditional observational distinction between coronal holes and their surroundings (i.e., active regions and “quiet Sun”) is that coronal holes have the lowest emission in the UV and X-ray. This definition must be amended, however, to exclude filaments (which are often dark when projected against the solar disk) that are cool magnetic structures and not part of the corona (see, e.g., Scholl and Habbal, 2008; Krista and Gallagher, 2009). Coronal hole magnetic fields are known to be more uniform and unipolar than in other regions (see below). The boundaries between coronal holes and surrounding regions are sometimes sharp, sometimes diffuse, and sometimes filled with many small loops (Hudson, 2002).
Coronal holes are more or less indistinguishable from their surroundings in the photosphere and low chromosphere, and usually one cannot see any significant intensity contrast between hole and non-hole regions until the temperature exceeds about 105 K. Spectra, however, can help make the distinction clearer. Teplitskaya et al. (2007) found that central self-reversals in the chromospheric Ca ii H and K lines are noticeably different in coronal holes as opposed to surrounding quiet-Sun regions. A frequently used observational diagnostic of coronal hole boundaries is the He i 10830 Å near-infrared absorption line triplet (Harvey et al., 1975; Harvey and Recely, 2002). At these wavelengths, the absorption is weakest in coronal holes (i.e., the intensity is highest) and spectroheliogram images show the coronal holes quite clearly. It is somewhat counterintuitive that a spectral line of a neutral species (He0) should be sensitive to the properties of the hot corona. However, the atomic level populations that determine the He i 10830 Å source function are unusually responsive to photoionization from UV wavelengths shortward of 504 Å. The overlying solar corona emits these wavelengths in abundance. In coronal hole regions, though, the corona generally has a lower density and temperature, and thus there is less intense UV and X-ray emission to populate the upper levels of the He0 triplet state (see, e.g., Zirin, 1975; Andretta and Jones, 1997; Centeno et al., 2008). This gives rise to reduced absorption. The He i 10830 Å lines are also good probes of supersonic outflow velocities in distant stellar winds (see, e.g., Dupree et al., 2005; Kwan et al., 2007; Sanz-Forcada and Dupree, 2008).
Another observational diagnostic of coronal holes is their elemental abundance signature (e.g., Feldman, 1998; Feldman and Widing, 2003). In the upper chromosphere, transition region, and low corona, holes exhibit abundances very close to those measured in the photosphere. This stands in contrast to other regions (quiet Sun and active regions), which show significant enhancements in the abundances of elements with low first ionization potential (FIP). This selective fractionation is believed to occur in the upper chromosphere, where low-FIP elements become ionized and high-FIP elements remain more neutral. These patterns extend into the heliosphere, where high-speed flows associated with coronal holes are often identifiable from their near-photospheric FIP abundances (von Steiger et al., 1995; Zurbuchen et al., 2002). However, there is still no widespread agreement about the exact physical processes that give rise to this preferential ionization.
The number, sizes, and heliographic locations of coronal holes vary as a function of the solar activity cycle. Large polar holes exist for about 7 years around solar minimum, and are not present for about 3 or 4 years around solar maximum. However, in the declining phase of activity soon after the maximum, it is possible to see the gradual growth of the new-polarity polar coronal holes. This occurs as a number of smaller high-latitude holes eventually collect together at the poles (Timothy et al., 1975; Harvey and Recely, 2002). Taking this growth phase into account, there are only about 1 or 2 years at solar maximum without any distinct high-latitude coronal hole presence. Figure 3 illustrates the growth phase around the peak of solar cycle 23 in 2001. The growth and full “reappearance” of polar coronal holes at this time was described by Miralles et al. (2001a) and McComas et al. (2002). The post-maximum growth of new polar coronal holes lasts about twice as long as their disappearance in the rising phase of the next maximum (Waldmeier, 1981; Fisher and Sime, 1984).
Polar view of the development of the north polar coronal hole from January to August 2001 (e.g., Carrington rotations 1972 to 1979), using reconstructed coronal hole boundaries from Kitt Peak He i 10830 Å maps. The maximum of solar activity occurred between late 2000 and early 2001. Data from the National Solar Observatory/Kitt Peak were produced cooperatively by NSF/NOAO, NASA/GSFC, and NOAA/SEL.
Many low-latitude coronal holes tend to be situated near the edges of magnetically complex active regions. Sometimes active regions emerge within the coronal holes themselves; these have been called “sea anemone” type regions from their spiky, flower-like appearance (Shibata et al., 1994; Asai et al., 2008). Evolving magnetic interactions between active regions and coronal holes have been studied both as a means of enhancing the mass flux of the associated solar wind on nearby open flux tubes (e.g., Habbal et al., 2008; Wang et al., 2009) and as a possible explanation for the nearly rigid rotation of coronal holes (Wang et al., 1996; Antiochos et al., 2007). A burst of emerging magnetic flux in one of these active regions may give rise to new systems of loop connections in the area bordering the coronal hole, and thus cause the coronal hole to decrease in size. This kind of rapid topological evolution of the magnetic field may be relevant in explaining extreme space weather events such as “the day the solar wind disappeared” (i.e., the dramatic drop in the in situ density seen on 11 May 1999; see Janardhan et al., 2008).
Photospheric magnetograms show that coronal holes are more unipolar than other regions; i.e., they have a larger degree of magnetic flux imbalance between the two polarities (Levine, 1982; Wang, 2009). For the large polar coronal holes, this appears to be the long-term outcome of the decay of active-region magnetic fields and their eventual diffusion up to the poles. The unipolar nature of coronal holes is likely to be related to their connection with open-field solar wind streams. As described in Section 2, one reason why coronal holes are dark is that the solar wind carries away both mass and energy, leaving a lower density and pressure. In addition, Abramenko et al. (2006a) and Hagenaar et al. (2008) found that the local rate of emergence of small-scale magnetic flux (mostly in the form of “ephemeral” small-scale bipoles) is substantially lower in unipolar regions than in more mixed or balanced regions of positive and negative magnetic polarity. In most theories of coronal heating of closed loops, the total flux and the overall complexity of the field both drive the total heating rate. Thus, the lower emergence rate of new flux elements in coronal holes may be another factor determining why they have lower densities and pressures (i.e., less coronal heating; see, e.g., Rosner et al., 1978) and thus why they are dark.
Over the past few decades, the magnetic connection between coronal holes and the fast solar wind has been traced down to ever smaller spatial scales. We now can say with some certainty that much of the plasma that eventually becomes the time-steady solar wind seems to originate in thin magnetic flux tubes (with observed sizes of order 50–200 km) observed mainly in the dark lanes between the ∼ 1000 km size photospheric granulation cells. These strong-field (1–2 kG) flux tubes have been called G-band bright points and network bright points, and groups of them have been sometimes termed “solar filigree” (e.g., Dunn and Zirker, 1973; Spruit, 1984; Berger and Title, 2001; Tsuneta et al., 2008). These flux tubes are concentrated most densely in the supergranular network (i.e., the bright lanes between the larger ∼ 30,000 km size supergranulation cells). Somewhere in the low chromosphere, the thin flux tubes expand laterally to the point where they merge with one another into a more-or-less homogeneous network field distribution of order ∼ 100 G. This merged (mainly vertically oriented) field is associated mainly with the lanes and vertices between supergranular cells. Because this field does not fill the entire coronal volume, it is still susceptible to an additional stage of lateral expansion and weakening. Thus, at a larger height in the chromosphere, these network flux bundles are believed to undergo further broadening into so-called “funnels” (Gabriel, 1976; Dowdy et al., 1986). However, it is still unclear to what extent the closed fields in the supergranular cell centers affect the canopy-like regions between funnels (e.g., Schrijver and Title, 2003). Figure 4 illustrates the successive merging of unipolar field in coronal holes.
Summary of the largely unipolar magnetic field structure of polar coronal holes, with the fields of view successively widening from flux tubes in intergranular lanes (a), to a “funnel” rooted in a supergranular network lane (b), and finally to the extended corona (c). Adapted from Figure 1 of Cranmer and van Ballegooijen (2005).
Observations of blueward Doppler shifts in supergranular network lanes and vertices, especially in large coronal holes, may be evidence for either the “launching” of the solar wind itself or for upward-going waves that are linked to wind acceleration processes (e.g., Hassler et al., 1999; Peter and Judge, 1999; Aiouaz et al., 2005; Tu et al., 2005). These measurements are consistent with several models of the dynamic, multi-species solar wind in superradially expanding funnels (Byhring et al., 2008; Marsch et al., 2008). However, this interpretation of the data is still not definitive, because there are other observational diagnostics that have shown more of a blueshift in the supergranular cell-centers between funnels (e.g., He i 10830 Å; Dupree et al., 1996; Malanushenko and Jones, 2004). There may be subtle radiative transfer effects that preferentially brighten regions of upflow or downflow (see, e.g., Chae et al., 1997; Avrett, 1999), and these may need to be taken into account in order to understand the meaning of the measured Doppler shifts in these regions.
Lastly, it is important to mention the phenomenon of transient coronal holes (sometimes known as “coronal dimmings”). These are rapid reductions in the UV and X-ray intensity in discrete patches that appear to be spatially and temporally correlated with the liftoff of CME plasma (e.g., Rust, 1983; Thompson et al., 2000; Yang et al., 2008). Spectroscopically, these regions are seen to exhibit similar characteristics as normal coronal holes, including Doppler blueshifts (Harra et al., 2007) and large amplitudes of nonthermal wave broadening (McIntosh, 2009). UV coronal dimmings are beginning to be used as diagnostics for the amount of plasma released — i.e., the total mass — in the CME event (e.g., Aschwanden et al., 2009). It should be noted that transient coronal holes represent just one kind of observed dimming that is associated with time-dependent flare/CME activity; there are other types of dimmings that do not resemble coronal holes (Hudson, 2002).
4 Properties of Off-Limb Coronal Holes
Coronal holes observed above the solar limb usually trace out the same regions that are identified as dark coronal-hole “patches” directly on the solar disk. Thus, the lower plasma density that more or less defines the off-limb coronal hole is directly related to the lower density measured on the disk. Section 4.1 briefly discusses how these regions are believed to be connected magnetically with the broader heliosphere. The observations of off-limb coronal holes made with visible-light imaging and polarimetry (Section 4.2) and ultraviolet spectroscopy (Section 4.3) are also summarized below.
4.1 Magnetic connectivity with the solar wind
Although the magnetic field in the solar corona is generally too weak to be measured directly, the overall morphology of the field lines can be extrapolated from magnetograms taken at the level of the photosphere. One popular technique is the “potential field source surface” (PFSS) method, which assumes the corona is current-free out to a spherical surface (set typically at a radius between 2.5 and 3.5 solar radii, or R⊙), above which the field is radial (e.g., Schatten et al., 1969; Altschuler and Newkirk Jr, 1969; Hoeksema and Scherrer, 1986). The PFSS method has been shown to create a relatively good mapping between the Sun and the heliosphere (Arge and Pizzo, 2000; Luhmann et al., 2002; Wang and Sheeley Jr, 2006; Wang, 2009), although the results can be problematic for regions dominated by stream-stream interactions (Poduval and Zhao, 2004).
By far, the strongest causal link between a specific type of coronal structure (measured via remote sensing) and a particular type of quasi-steady solar wind flow (measured in situ) is the connection between large coronal holes and high-speed streams (Wilcox, 1968; Krieger et al., 1973). The general interpretation of this correlation — together with the results of magnetic extrapolation models such as PFSS — is that coronal holes represent a bundle of open flux tubes that flare out horizontally as distance increases. In other words, the coronal hole flux tubes expand superra-dially. Although there are some observations that appear to support other interpretations (Woo et al., 1999; Habbal et al., 2001; Woo, 2005; Woo and Druckmüllerová, 2008), the preponderance of evidence seems clearly to support the idea that fast solar wind streams emerge mainly from superradially expanding coronal holes (e.g., Guhathakurta et al., 1999b; Cranmer et al., 1999b; Jones, 2005; Wang and Sheeley Jr, 2006; Wang et al., 2007).
In contrast to the rather definitive correlation between large coronal holes and the fast solar wind, the coronal sources of the more chaotic slow-speed solar wind are not as well understood (see Schwenn, 2006). Two regions that are frequently cited as sources of slow wind are: (1) boundaries between coronal holes and streamers, and (2) narrow plasma sheets that extend out from the tops of streamer cusps (Wang et al., 2000; Strachan et al., 2002; Susino et al., 2008). These regions tend to dominate around solar minimum. Note that the former type of boundary region tends to contain flux tubes that may be classified as coronal holes when using the theoretical definition (i.e., footpoints of field lines that are open; see Section 1) but would not be defined as such when using the observational definitions (i.e., low emission or low density).
During more active phases of the solar cycle, there is evidence that slow solar wind streams also emanate from small coronal holes (e.g., Nolte et al., 1976; Neugebauer et al., 1998; Zhang et al., 2003) and active regions (Hick et al., 1995; Liewer et al., 2004; Sakao et al., 2007). During the rising phase of solar activity, there seems to be a relatively abrupt (< 6 month) change in the locations of slow wind footpoints: from the high-latitude hole/streamer boundaries to the low-latitude active region and small coronal hole regions (Luhmann et al., 2002). The ability of many of these kinds of regions to produce slow wind was modeled by Cranmer et al. (2007) and Wang et al. (2009); see also Section 5.
4.2 Visible light observations
Measurements of the plasma properties in the extended corona (i.e., r ≈ 1.5 to 10 R⊙, where the main solar wind acceleration occurs) require the bright solar disk to be occulted. The coronal emission is many orders of magnitude less bright than the emission from the solar disk, so even the vast majority of “stray light” that diffracts around the occulting edge must be eliminated. Visible-light coronagraphs that combine stray-light rejection with linear polarimetry have the ability to measure the Thomson-scattered polarization brightness (pB) in the corona. The use of pB rather than the total coronal brightness eliminates the contribution from the dust-scattered F-corona, which is believed to be unpolarized up to distances of about 5 R⊙. Because the coronal plasma is optically thin to the Thomson-scattered photons, pB is proportional to the line-of-sight integral of the electron density ne, multiplied by a known scattering function. Methods for inverting this integral to derive ne as a function of position in various coronal structures have been developed and improved over the years (e.g., van de Hulst, 1950; Altschuler and Perry, 1972; Munro and Jackson, 1977; Guhathakurta and Holzer, 1994; Frazin et al., 2007). For coronal holes, the LASCO (Large Angle and Spectrometric Coronagraph) instrument on SOHO has also been used to probe the superradial expansion of open magnetic flux tubes (DeForest et al., 1997, 2001) and the evolution of transient polar jets (Wang et al., 1998; Wood et al., 1999). The White Light Coronagraphs on Spartan 201 (Fisher and Guhathakurta, 1995) and on the UVCS (Ultraviolet Coronagraph Spectrometer) instrument aboard SOHO (e.g., Kohl et al., 1995; Romoli et al., 2002) have provided electron densities between 1.5 and 5 R⊙ in coronal holes.
Figure 5 illustrates a selection of visible-light measurements of the electron density in coronal holes and compares them to similar measurements of streamers and to a semi-empirical model of the chromosphere, transition region, and low corona (Avrett and Loeser, 2008). The blue coronal hole curves were adapted from the results of Fisher and Guhathakurta (1995) (dotted), Cranmer et al. (1999b) (solid), Doyle et al. (1999) (dashed), and Guhathakurta et al. (1999a) (dot-dashed). The red curves for equatorial helmet streamers were adapted from the results of Sittler Jr and Guhathakurta (1999) (solid) and Gibson et al. (1999) (dashed).
Comparison of empirically determined densities in the upper solar atmosphere. Avrett and Loeser (2008) values of electron number density (solid black curve) and total hydrogen number density (dot-dashed black curve) are compared with various visible-light pB electron number densities for coronal holes (blue curves) and streamers (red curves); see text for details.
Note that streamers are denser than coronal holes by about a factor of 10, but the hole measurements themselves can often exhibit variations in the electron density by factors of the order of 2–3. Much of this spread is likely to be the result of different lines of sight passing through regions that contain varying numbers of polar plumes (see, e.g., Cranmer et al., 1999b, 2008). Some of the cited pB observations were optimized to avoid bright concentrations of plumes, and others have been purposefully averaged over the full range of coronal hole substructure. It is also possible that absolute calibration uncertainties may still exist between the different instruments used to determine pB and ne, and this could compound the reported range of variation in coronal hole electron densities.
For a steady-state solar wind outflow, the conservation of mass demands that the product of density, flow speed, and cross-sectional area of the flux tube remain constant. Thus, if the magnetic geometry and the electron density are known, mass conservation allows the solar wind outflow speed to be computed. Kohl et al. (2006) used the representative values of ne shown in Figure 5 together with a range of estimates for the superradial flux-tube expansion of coronal holes to determine outflow speeds in coronal holes. Figure Fig41a of Kohl et al. (2006) illustrates the result of this process, which shows a large range of values reflecting the uncertainties in both ne and the flux-tube area factor. Despite these uncertainties, though, the electron densities that became available in the 1990s demonstrated that the fast solar wind accelerates rapidly in coronal holes — probably reaching half of its asymptotic terminal speed (u∞ ≈ 700–800 kms−1) by heights no larger than 2–4 R⊙.
The increased sensitivity of the LASCO instrument over earlier coronagraphs revealed a nearly continual release of low-contrast density inhomogeneities, or “blobs,” from the cusps of helmet streamers (Sheeley Jr et al., 1997; Tappin et al., 1999; Wang et al., 2000; Chen et al., 2009). These features were seen to accelerate up to speeds of order 300–400 km s−1 by the time they reached the outer edge of the LASCO field of view (r ≈ 30 R⊙); see also Figure 8 below. The blobs are typically only about 10% to 15% brighter or dimmer than the surrounding streamer material. Because of this low contrast, these features do not appear to comprise a large fraction of the mass flux of the slow solar wind. However, it is still unclear whether blobs are passive “tracers” that flow with the solar wind speed, or whether they are wavelike fluctuations that propagate relative to the background solar wind reference frame. This diagnostic tool has been much more difficult to apply in coronal holes than it has in the bright streamers, so no firm measurements of the fast wind acceleration yet exist from this technique.
Visible light measurements have also revealed evidence for compressive magnetohydrodynamic (MHD) waves that propagate along open field lines in coronal holes. Intensity oscillations measured by the UVCS and EIT instruments on SOHO were found to have periodicities between about 10 and 30 minutes and are consistent with being upwardly propagating slow-mode magnetosonic waves (DeForest and Gurman, 1998; Ofman et al., 1999, 2000). The relative amplitude of the density fluctuations (δn/n0) for these waves was found to range between about 0.03 and 0.15 (see Cranmer, 2004a). This is consistent with measurements of the density fluctuation amplitudes made at larger distances via radio scintillations (Spangler, 2002) and in situ instruments (Tu and Marsch, 1994). There have also been claims that low-frequency oscillations have been measured in H I Lyα emission (Morgan et al., 2004; Bemporad et al., 2008; Telloni et al., 2009). In these cases, however, it is extremely important to take into account all of the relevant instrumental effects. These measurements still appear to be provisional.
As seen in Section 2 above, coronal holes have long been observed as the sites of thin, ray-like polar plumes. The earliest measurements of polar plume properties were made in broad-band visible light, and these dense strands are often seen to stand out distinctly from the ambient interplume corona. It is not clear, though, to what extent off-limb observations (which integrate over long optically thin lines of sight) ever capture only the “pure” plume or interplume plasmas. Space-based observations from, e.g., Spartan 201 and SOHO improved our ability to measure the physical properties in and between plumes (e.g., Fisher and Guhathakurta, 1995; DeForest et al., 1997; Cranmer et al., 1999b; DeForest et al., 2001). Although the brightest plumes are still discernible at the uppermost heights observed by LASCO (i.e., 30–40 R⊙), the plume/interplume density contrast becomes too low to measure clearly in interplanetary space (r > 60 R⊙). However, indirect and possibly plume-related signatures in the in situ data have been reported by Thieme et al. (1990), Reisenfeld et al. (1999), and Yamauchi et al. (2002). The disappearance of plumes probably is the result of some combination of transverse pressure balance (i.e., dense plumes expanding to fill more of the available volume; see Del Zanna et al., 1998) and MHD instabilities that can mix the two components (Parhi et al., 1999; Andries and Goossens, 2001).
4.3 Ultraviolet spectroscopy
Ultraviolet spectroscopy of the corona is a powerful tool for obtaining detailed empirical descriptions of solar plasma conditions (see, e.g., Kohl and Withbroe, 1982; Withbroe et al., 1982). Coronal holes, being the lowest density regions of the outer solar atmosphere, exhibit a complex array of plasma parameters due to their nearly collisionless nature. As a result, every ion species tends to have its own unique temperature, its own type of departure from a Maxwellian velocity distribution, and its own outflow speed. After a brief summary of near-limb measurements made with the SUMER instrument on SOHO, this section mainly describes results at larger heights (in the more clearly collisionless extended corona) from UVCS.
The un-occulted SUMER (Solar Ultraviolet Measurements of Emitted Radiation) spectrometer has observed off-limb regions up to heights of approximately 1.3 R⊙ in coronal holes (Wilhelm et al., 1995, 2000, 2004, 2007). In polar regions at solar minimum, ion temperatures exceed electron temperatures even at r ∼ 1.05 R⊙, where densities were presumed to be so high as to ensure rapid collisional coupling and thus equal temperatures for all species (Seely et al., 1997; Tu et al., 1998; Landi and Cranmer, 2009). Spectroscopic evidence is also mounting for the presence of transverse Alfvén waves propagating into the corona (Banerjee et al., 1998, 2009; Dolla and Solomon, 2008; Landi and Cranmer, 2009).
Electron temperatures derived from line ratios (Habbal et al., 1993; David et al., 1998; Doschek et al., 2001; Wilhelm, 2006; Landi, 2008) exhibit relatively low values in the off-limb coronal holes (Te ∼ 800, 000 K) that are not in agreement with higher temperatures derived from “frozen-in” in situ charge states (Ko et al., 1997). It is difficult to reconcile these observations with one another in the absence of either non-Maxwellian electron velocity distributions or strong differential flows between different ion species near the Sun (Esser and Edgar, 2000). However, some models consistent with both the SUMER temperatures and the in situ charge states are being produced (e.g., Laming and Lepri, 2007).
Figure 6 displays a range of temperatures measured in coronal holes and high-speed wind streams, and it shows how the SUMER electron temperatures (Te) are noticeably lower than the heavy ion temperatures (e.g., shown for the O+5 ions that correspond to the bright O VI 1032, 1037 Å spectral lines) even in the low corona. The degree of agreement between the spectroscopic measurements and one-fluid models of the low corona (i.e., the semi-empirical model of Avrett and Loeser (2008) and the theoretical model of Cranmer et al. (2007)) depends on the height of the sharp transition region between chromospheric (104 K) and coronal (106 K) temperatures.
Radial dependence of empirical and model temperatures in polar coronal holes and fast wind streams. Mean plasma temperatures from a semi-empirical model (dashed black curve; Avrett and Loeser, 2008) and from a turbulence-driven coronal heating model (solid black curve; Cranmer et al., 2007). Te from off-limb SUMER measurements made by Wilhelm (2006) (dark blue bars) and Landi (2008) (light blue bars), Tp from UVCS measurements assembled by Cranmer (2004b) (see text), and perpendicular O+5 ion temperatures from Landi and Cranmer (2009) (open green circles) and Cranmer et al. (2008) (filled green circles). In situ proton and electron temperatures in the fast wind (r > 60 R⊙) are from Cranmer et al. (2009).
The UVCS instrument on SOHO is a combination of an ultraviolet spectrometer and a linearly occulted coronagraph that observes a 2.5 R⊙ long swath of the extended corona, oriented tangentially to the radial direction at heliocentric distances ranging between about 1.5 and 10 R⊙ (Kohl et al., 1995, 1997, 1998, 2006). In coronal holes, UVCS measurements have allowed many key details about the velocity distributions of H0, O+5, and Mg+9 to be derived. For the resonantly scattered emission lines seen at large heights with UVCS, the most straightforward plasma diagnostic is to use the Doppler-broadened line width as a sensitive probe of the overall variance of random particle motions along the line of sight. In other words, measuring the line width provides a constraint on the so-called “kinetic temperature” (i.e., a combination of microscopic stochastic motions and macroscopic [but unresolved] motions due to waves or turbulence) along the direction perpendicular to the (nearly radial) magnetic field lines.
In the ionized solar corona, a given hydrogen nucleus spends most of its time as a free proton, and only a small fraction of time as a bound H0 atom. Thus, the measured plasma properties of neutral hydrogen are considered to be valid proxies of the proton properties below about 3 R⊙ (Allen et al., 2000). Spartan 201 and UVCS observations of the H I Lyα emission line in coronal holes indicated rather large proton kinetic temperatures in the direction perpendicular to the magnetic field (Tp⊥ ∼ 3 MK) and also the possibility of a mild temperature anisotropy (with Tp⊥ > Tp∥) above heights of 2–3R⊙ (Kohl et al., 1997; Cranmer et al., 1999b; Antonucci et al., 2004; Kohl et al., 2006).
UVCS observations indicated that the O+5 ions are much more strongly heated than protons in coronal holes, with perpendicular temperatures in excess of 200 MK (see Figure 7). This exceeds the temperature at the central core of the Sun by an order of magnitude! The UVCS measurements also provided signatures of temperature anisotropies possibly greater than T⊥i/T∥i ≈ 10 (e.g., Cranmer et al., 1999b, 2008). The measured kinetic temperatures of O+5 and Mg+9 are significantly greater than mass-proportional when compared with protons, with Ti/Tp > mi/mp (see also Kohl et al., 1999, 2006). The surprisingly “extreme” properties of heavy ions in coronal holes have led theorists to develop a number of new ideas regarding the heating and acceleration of the solar wind; these are discussed further in Section 5.4.
Combined image of the solar corona from 17 August 1996, showing the solar disk in Fe XII 195 Å intensity from EIT (yellow inner image) and the extended corona in O VI 1032 Å intensity from UVCS (red outer image). Axisymmetric field lines are from the solar-minimum model of Banaszkiewicz et al. (1998), and O VI emission line profiles (bottom) are from SUMER (Warren et al., 1997, left) and UVCS (Kohl et al., 1997, right).
Figure 6 shows UVCS perpendicular temperatures for protons and O+5 ions in coronal holes. The O+5 data points were taken from the recent re-analysis of solar minimum data from 1996–1997 by Cranmer et al. (2008). The proton temperature data were assembled by Cranmer (2004b) from a number of individual measurements of the H I Lyα profile at solar minimum. The sources of these measurements are: Cranmer et al. (1999b) (squares), Esser et al. (1999) (diamonds), Zangrilli et al. (1999) (asterisks), and Antonucci et al. (2000) (triangles). The kinetic proton temperatures are of order 2–3.5 MK, but in Figure 6 we attempted to remove the contribution of nonthermal wave broadening. The semi-empirical model of Cranmer and van Ballegooijen (2005) was used to specify the amplitude of transverse Alfvén waves as a function of height, and their contribution to the line widths was subtracted. The remaining “microscopic” T⊥p does not show as clear a signal of “preferential” proton heating as would be apparent from the larger kinetic temperature. Although one can still marginally see that Tp > Te, the existing measurements of Tp and Te do not fully overlap with one another in radius. Improved measurements are needed in order to better constrain the proton and electron heating rates in the corona.
The UVCS emission line data contain information about the Doppler motions of atoms and ions along the magnetic field (i.e., transverse to the line of sight). The so-called “Doppler dimming” diagnostic technique provides constraints on both the bulk outflow speed along the field and the parallel kinetic temperature (for more details, see Kohl and Withbroe, 1982; Noci et al., 1987; Kohl et al., 2006). In coronal holes, Doppler-dimmed line intensities from UVCS are consistent with the outflow velocity for O+5 being larger than the outflow velocity for protons by as much as a factor of two at large heights (Kohl et al., 1998; Li et al., 1998; Cranmer et al., 1999b). Figure 8 illustrates the outflow speeds measured by UVCS in coronal holes, and compares with the theoretical model of the fast solar wind presented by Cranmer et al. (2007). Also shown for comparison are observational and theoretical data for the slow solar wind associated with equatorial helmet streamers at solar minimum.
Radial dependence of solar wind outflow speeds. UVCS Doppler dimming determinations for protons (red; Kohl et al., 2006) and O+5 ions (green; Cranmer et al., 2008) are shown for polar coronal holes, and are compared with theoretical models of the polar and equatorial solar wind at solar minimum (black curves; Cranmer et al., 2007) and the speeds of “blobs” measured by LASCO above equatorial streamers (open circles; Sheeley Jr et al., 1997).
In contrast to many prior analyses of UVCS data, which concluded that there must be both intense preferential heating of the O+5 ions and a strong field-aligned anisotropy, Raouafi and Solanki (2004), Raouafi and Solanki (2006), and Raouafi et al. (2007) reported that there may not be a compelling need for O+5 anisotropy depending on the assumptions made about the other plasma properties of the coronal hole (e.g., electron density). However, Cranmer et al. (2008) performed a detailed re-analysis of these observations and concluded that there remains strong evidence in favor of both preferential O+5 heating and acceleration and significant O+5 ion anisotropy (in the sense T⊥i > T∥i) above r ≈ 2.1 R⊙ in coronal holes. In determining these properties, it was found to be important to search the full range of possible ion temperatures and flow speeds, and not to make arbitrary assumptions about any given subset of the parameters.
The UVCS results discussed above are similar in character to in situ measurements made in the fast solar wind, but they imply more extreme departures from thermodynamic equilibrium in the extended corona. For example, proton velocity distributions measured in the fast solar wind between 0.3 and 1 AU have anisotropic cores with Tp⊥ > Tp∥, and their magnetic moments increase with increasing distance; this implies net input of perpendicular energy on kinetic scales (e.g., Marsch et al., 1982; Marsch, 2006). Many heavy ions appear to flow faster than the protons by about the local Alfvén speed (Hefti et al., 1998; Reisenfeld et al., 2001), and in the fastest solar wind streams they are also heated preferentially in the same sense as in the corona (Collier et al., 1996).
In the years since the solar minimum of 1996–1997, UVCS observed a large number of other coronal holes that appeared throughout the maximum of solar cycle 23 and the new-millennium solar minimum of 2007–2009. UVCS tends to observe only the largest coronal holes, since when the smallest holes rotate to the solar limb their UV line profiles tend to be contaminated by emission from streamers in the foreground and background. This selection effect naturally screens out small coronal holes that have been correlated with slow solar wind streams at 1 AU (Nolte et al., 1976; Neugebauer et al., 1998). In the cases where UVCS and in situ measurements were made for the same regions associated with large coronal holes, high speeds in excess of 600 km s−1 were inevitably seen in interplanetary space (Miralles et al., 2004, 2006). However, the O+5 outflow speeds measured in the extended corona via Doppler dimming have showed a substantial range of variation. For example, Miralles et al. (2001b) found that the outflow speeds at 2–3 R⊙ in an equatorial coronal hole were approximately three times lower than those measured in the polar coronal holes from 1996–1997 at similar heights (see also Poletto et al., 2002). This implies that the range of coronal heights over which the acceleration of the solar wind occurs can vary greatly, even when the wind at 1 AU ends up similarly fast.
UVCS also has measured the plasma properties in bright polar plumes. The densest concentrations of polar plumes along the line of sight are seen to exhibit narrower line widths — i.e., lower kinetic temperatures — than the lower-density interplume regions (Kohl et al., 1997; Noci et al., 1997; Kohl et al., 2006). Similarly, plumes are seen to have lower outflow speeds than the interplume regions (Giordano et al., 2000; Teriaca et al., 2003; Raouafi et al., 2007), although at low heights the data are not as clear-cut (e.g., Gabriel et al., 2003). UVCS also has put constraints on the plume/interplume density contrast and the filling factor of polar plumes in coronal holes. Cranmer et al. (1999b) used a large number of UVCS synoptic measurements to determine statistically that, at heights around r ≈ 2 R⊙, the plume/interplume density ratio is approximately 2, and polar coronal holes are comprised of about 25% plume and 75% interplume plasma (corresponding to ∼ 40 individual plumes distributed throughout the coronal hole). Earlier measurements made closer to the limb showed a higher density contrast and a smaller filling factor, so the UVCS data are generally consistent with lateral expansion of polar plumes with increasing distance.
It is still relatively unknown how much of the mass, momentum, and energy flux of the fast solar wind comes from polar plumes. Despite that uncertainty, though, there have been several reasonably successful models of polar plume formation. Wang (1994, 1998) presented models of polar plumes as the extensions of flux tubes with concentrated bursts of added coronal heating at the base — presumably via nanoflare-like reconnection events in X-ray bright points (see also DeForest et al., 2001). In these models, the extra basal heat input is balanced by conductive losses to produce the larger plume density. The heating rate in the extended corona is not affected by the basal burst, but the larger density in the flux tube gives rise to less heating per particle at all heights, which leads to lower temperatures in the extended corona and a smaller gas pressure force for solar wind acceleration. This model is consistent with the smaller temperatures and outflow speeds measured in plumes with UV spectroscopy.
UVCS made the first spectroscopic measurements of polar jets in coronal holes (Dobrzycka et al., 2000, 2006). The events observed by EIT, LASCO, and UVCS during the 1996–1997 solar minimum tended to be “cool jets” with higher densities, lower temperatures, and faster outflows than the surrounding coronal holes (see also Wang et al., 1998). More recently, Hinode has observed a new population of “hot” X-ray jets in coronal holes (Culhane et al., 2007; Cirtain et al., 2007; Shimojo et al., 2007; Filippov et al., 2009). UVCS found that some of these events persist up to heights of at least 1.7 R⊙ and that the jet protons remain hotter than the surrounding coronal hole (Miralles et al., 2007). Thus, there appear to exist two distinct kinds of polar jets (cool and hot), with differences possibly related to the relative degrees of heating and adiabatic expansion of the jet parcels. Jets and plumes have roughly similar angular sizes and intensity contrasts near the solar limb, and there is growing evidence that they share a common origin (e.g., Raouafi et al., 2008). It is possible that the only substantial difference between the two phenomena is the duration of the bursts of basal heating; i.e., jets seem to be the result of short-lived bursts of heating, whereas plumes may be the product of base-heating events that last longer than several hours.
5 Coronal Heating and Solar Wind Acceleration
Despite more than a half-century of study, the basic physical processes that are responsible for heating the million-degree corona and accelerating the supersonic solar wind are not known. This section broadens the topic of this paper a bit beyond just coronal holes, since an understanding of solar wind acceleration naturally encompasses not only the question of why fast solar wind streams are fast, but also why (various kinds of) slow solar wind streams are slow. Section 5.1 summarizes some of the major issues regarding coronal energy deposition. The next two subsections describe two alternate views of solar wind acceleration via waves and turbulence in open flux tubes (Section 5.2) and reconnection between open and closed flux tubes (Section 5.3). Lastly, Section 5.4 reviews how collisionless kinetic effects in coronal holes (i.e., preferential ion heating and temperature anisotropies) can be used to more conclusively identify the detailed physical processes that produce the solar wind.
5.1 Sources of energy
Different physical mechanisms for heating the corona probably govern active regions, closed loops in the quiet corona, and the open field lines that give rise to the solar wind (see other reviews by Marsch, 1999; Hollweg and Isenberg, 2002; Longcope, 2004; Gudiksen, 2005; Aschwanden, 2006; Klimchuk, 2006). The ultimate source of the energy is the solar convection zone (e.g., Abramenko et al., 2006b; McIntosh et al., 2007). A key aspect of solving the “coronal heating problem” is thus to determine how a small fraction of that mechanical energy is transformed into magnetic free energy and thermal energy above the photosphere. It seems increasingly clear that loops in the low corona are heated by small-scale, intermittent magnetic reconnection that is driven by the continual stressing of their magnetic footpoints. However, the extent to which this kind of impulsive energy addition influences the acceleration of the solar wind is not yet known.
Intertwined with the coronal heating problem is the heliophysical goal of being able to make accurate predictions of how both fast and slow solar wind streams are accelerated. Empirical correlation techniques have become more sophisticated and predictively powerful (e.g., Wang and Sheeley Jr, 1990, 2006; Arge and Pizzo, 2000; Leamon and McIntosh, 2007; Cohen et al., 2007; Vršnak et al., 2007) but they are limited because they do not identify or utilize the physical processes actually responsible for solar wind acceleration. There seem to be two broad classes of physics-based models that attempt to self-consistently answer the question: “How are fast and slow wind streams heated and accelerated?”
-
1.
In wave/turbulence-driven (WTD) models, it is generally assumed that the convection-driven jostling of magnetic flux tubes in the photosphere drives wave-like fluctuations that propagate up into the extended corona. These waves (usually Alfvén waves) are often proposed to partially reflect back down toward the Sun, develop into strong MHD turbulence, and dissipate over a range of heights. These models also tend to explain the differences between fast and slow solar wind not by any major differences in the lower boundary conditions, but instead as an outcome of different rates of lateral flux-tube expansion over several solar radii as the wind accelerates (see, e.g., Hollweg, 1986; Wang and Sheeley Jr, 1991; Matthaeus et al., 1999; Cranmer, 2005; Suzuki, 2006; Suzuki and Inutsuka, 2006; Cranmer et al., 2007; Verdini and Velli, 2007; Verdini et al., 2009).
-
2.
In reconnection/loop-opening (RLO) models, the flux tubes feeding the solar wind are assumed to be influenced by impulsive bursts of mass, momentum, and energy addition in the lower atmosphere. This energy is usually assumed to come from magnetic reconnection between closed, loop-like magnetic flux systems (that are in the process of emerging, fragmenting, and being otherwise jostled by convection) and the open flux tubes that connect to the solar wind. These models tend to explain the differences between fast and slow solar wind as a result of qualitatively different rates of flux emergence, reconnection, and coronal heating at the basal footpoints of different regions on the Sun (see, e.g., Axford and McKenzie, 1992, 1997; Fisk et al., 1999; Ryutova et al., 2001; Markovskii and Hollweg, 2002, 2004; Fisk, 2003; Schwadron and McComas, 2003; Woo et al., 2004; Fisk and Zurbuchen, 2006).
It is notable that both the WTD and RLO models have recently passed some basic “tests” of comparison with observations. Both kinds of model have been shown to be able to produce fast (υ > 600 km/s), low-density wind from coronal holes and slow (υ < 400 km/s), high-density wind from streamers rooted in quiet regions. Both kinds of model also seem able to reproduce the observed in situ trends of how frozen-in charge states and the FIP effect vary between fast and slow wind streams.
The fact that both sets of ideas described above seem to mutually succeed at explaining the fast/slow solar wind could imply that a combination of both ideas would work best. However, it may also imply that the existing models do not yet contain the full range of physical processes — and that once these are included, one or the other may perform noticeably better than the other. It also may imply that the comparisons with observations have not yet been comprehensive enough to allow the true differences between the WTD and RLO ideas to be revealed.
Several recent observations have pointed to the importance of understanding the relationships and distinctions between the WTD and RLO models. The impulsive polar jets discussed in Section 4 may be evidence that that magnetic reconnection drives some fraction of the fast solar wind (see also Fisk, 2005; Moreno-Insertis et al., 2008; Pariat et al., 2009). Also, direct observations of Alfvén waves above the solar limb indicate the highly intermittent nature of how kinetic energy is distributed in spicules, loops, and the open-field corona (De Pontieu et al., 2007; Tomczyk et al., 2007; Tomczyk and McIntosh, 2009). Spectroscopic observations of blueshifts in the chromospheric network have long been interpreted as the launching points of solar wind streams, but it remains unclear how nanoflare-like events or loop-openings contribute to the interpretation of these diagnostics (He et al., 2007; Aschwanden et al., 2007; McIntosh et al., 2007). Even out in the in situ solar wind — far above the roiling “furnace” of flux emergence at the Sun — there remains evidence for ongoing reconnection (Gosling et al., 2005; Gosling and Szabo, 2008). There is also evidence that the dominant range of turbulence timescales measured in interplanetary space (i.e., tens of minutes to hours) is related to the timescale of flux cancellation in the low corona (Hollweg, 1990, 2006).
Determining whether the WTD or RLO paradigm — or some combination of the two — is the dominant cause of global solar wind variability is a key prerequisite to building physically realistic predictive models of the heliosphere. Many of the widely-applied global modeling codes (e.g., Riley et al., 2001; Roussev et al., 2003; Tóth et al., 2005; Usmanov and Goldstein, 2006; Feng et al., 2007) continue to utilize relatively simple empirical prescriptions for coronal heating in the energy conservation equation. Improving the identification and characterization of the key physical processes will provide a clear pathway for inserting more physically realistic coronal heating “modules” into three-dimensional MHD codes.
5.2 The Wave/Turbulence-Driven (WTD) solar wind idea
There has been substantial work over the past few decades devoted to exploring the idea that the plasma heating and wind acceleration along open flux tubes may be explained as a result of wave damping and turbulent cascade. No matter the relative importance of reconnections and loop-openings in the low corona, we do know that waves and turbulent motions are present everywhere from the photosphere to the heliosphere, and it is important to determine how they affect the mean state of the plasma. A review of the observational evidence for waves and turbulence in the solar wind is beyond the scope of this paper, but several recent reviews of the remote-sensing and in situ data include Tu and Marsch (1995), Mullan and Yakovlev (1995), Goldstein et al. (1997), Roberts (2000), Bastian (2001), and Cranmer (2002a, 2004a, 2007). Although this subsection mainly describes recent work by the author, these results would not have been possible without earlier work on wave/turbulent heating by, e.g., Coleman (1968), Hollweg (1986), Hollweg and Johnson (1988), Isenberg (1990), Li et al. (1999), Matthaeus et al. (1999), Dmitruk et al. (2001, 2002), and many others.
Cranmer et al. (2007) described a set of models in which the time-steady plasma properties along a one-dimensional magnetic flux tube are determined. These model flux tubes are rooted in the solar photosphere and are extended into interplanetary space. The numerical code developed in that work, called ZEPHYR, solves the one-fluid equations of mass, momentum, and energy conservation simultaneously with transport equations for Alfvénic and acoustic wave energy. ZEPHYR is the first code capable of producing self-consistent solutions for the photosphere, chromosphere, corona, and solar wind that combine: (1) shock heating driven by an empirically guided acoustic wave spectrum, (2) extended heating from Alfvén waves that have been partially reflected, then damped by anisotropic turbulent cascade, and (3) wind acceleration from gradients of gas pressure, acoustic wave pressure, and Alfvén wave pressure.
The only input “free parameters” to ZEPHYR are the photospheric lower boundary conditions for the waves and the radial dependence of the background magnetic field along the flux tube. The majority of heating in these models comes from the turbulent dissipation of partially reflected Alfvén waves (see also Matthaeus et al., 1999; Dmitruk et al., 2002; Verdini and Velli, 2007; Chandran et al., 2009a). Photospheric measurements of the horizontal motions of strong-field intergranular flux concentrations (i.e., G-band bright points) were used to constrain the Alfvén wave power spectrum at the lower boundary. This empirically determined power spectrum is dominated by wave periods of order 5–10 minutes. It is important to note, however, that radio and in situ measurements find that most of the fluctuation power in the solar wind is at lower frequencies (i.e., periods of hours). We still do not yet know (1) if the shape of the power spectrum evolves significantly between the lower solar atmosphere and interplanetary space, or (2) if some low-frequency power is missed by the existing measurements of G-band bright point motions. In any case, as seen below, the resulting wave reflection and turbulent dissipation that comes from just the 5–10 minute periods appear to be sufficient to explain the observed levels of coronal heating and solar wind acceleration.
Non-WKB wave transport equations were solved to determine the degree of linear reflection at heights above the photospheric base (see Cranmer and van Ballegooijen, 2005). The resulting values of the Elsasser amplitudes Z±, which denote the energy contained in upward (Z−) and downward (Z+) propagating waves, were then used to constrain the energy flux in the cascade. Cranmer et al. (2007) used a phenomenological form for the damping rate that has evolved from studies of Reduced MHD and comparisons with numerical simulations. The resulting heating rate (in units of erg s−1 cm−3) is given by
where ρ is the mass density and L⊥ is an effective perpendicular correlation length of the turbulence (see, e.g., Hossain et al., 1995; Zhou and Matthaeus, 1990; Breech et al., 2008; Podesta and Bhattacharjee, 2009; Beresnyak and Lazarian, 2009). Cranmer et al. (2007) used a standard assumption that L⊥ scales with the cross-sectional width of the flux tube (Hollweg, 1986). The term in parentheses above is an efficiency factor that accounts for situations in which the cascade does not have time to develop before the waves or the wind carry away the energy (Dmitruk and Matthaeus, 2003). In open field regions, the cascade is “quenched” when the nonlinear eddy time scale teddy becomes much longer than the macroscopic wave reflection time scale tref. In closed field regions, the correction factor may behave in an opposite sense as it does for open field regions (see, e.g., Gómez et al., 2000; Rappazzo et al., 2008). In most of the solar wind models, though, Cranmer et al. (2007) used n = 1 in Equation (1) based on analytic and numerical results (Dobrowolny et al., 1980; Oughton et al., 2006), but they also tried n = 2 to explore a stronger form of the quenching effect.
Figure 9 summarizes the results of varying the magnetic field properties while keeping the lower boundary conditions fixed. For a single choice for the photospheric wave properties, the models produced a realistic range of slow and fast solar wind conditions. A two-dimensional model of coronal holes and streamers at solar minimum reproduces the latitudinal bifurcation of slow and fast streams seen by Ulysses. An active-region-like enhancement of the magnetic field strength in the low corona generates a high mass flux and a slow wind speed, in agreement with observations of open field lines connected with active regions (see also Wang et al., 2009). As predicted by earlier studies, a larger coronal “expansion factor” naturally gives rise to a slower and denser wind, higher temperature at the coronal base, and lower-amplitude Alfvén waves at 1 AU.
Summary of Cranmer et al. (2007) models: (a) The adopted solar-minimum field geometry of Banaszkiewicz et al. (1998), with radii of wave-modified critical points marked by symbols. (b) Latitudinal dependence of wind speed at ∼ 2 AU for models with n = 1 (multi-color curve) and n = 2 (brown curve), compared with data from the first Ulysses polar pass in 1994–1995 (black curve; Goldstein et al., 1996). (c) T(r) for polar coronal hole (red solid curve), streamer edge (blue dashed curve), and strong-field active region (black dotted curve) models.
In these models, the radial gradient of the Alfvén speed affects where the waves are reflected and damped, and thus whether energy is deposited below or above the Parker (1958a) critical point. Early studies of solar wind energetics (e.g., Leer and Holzer, 1980; Pneuman, 1980; Leer et al., 1982) showed that if there is substantial heating below the critical point, its primary impact is to “puff up” the hydrostatic scale height, drawing more particles into the accelerating wind and thus producing a slower and more massive wind. If most of the heating occurs at or above the critical point, the subsonic atmosphere is relatively unaffected, and the local increase in energy flux has nowhere else to go but into the kinetic energy of the wind (leading to a faster and less dense outflow). The ZEPHYR results shown in Figure 9 display this kind of dichotomy because the superradial expansion creates a much higher critical point over the equatorial regions than over the poles. Additional studies of how and where the mass flux and wind speed are determined include Withbroe (1988), Hansteen and Leer (1995), Hansteen et al. (1997), Janse et al. (2007), and Wang et al. (2009).
Perhaps more surprisingly, varying the coronal expansion factor in the models shown in Figure 9 also produces correlative trends that are in good agreement with in situ measurements of commonly measured ion charge state ratios (e.g., O7+/O6+) and FIP-sensitive abundance ratios (e.g., Fe/O). Cranmer et al. (2007) showed that the slowest solar wind streams — associated with active-region fields at the base — can produce a factor of ∼ 30 larger frozen-in ionization-state ratio of O7+/O6+ than high-speed streams from polar coronal holes, despite the fact that the temperature at 1 AU is lower in slow streams than in fast streams. Furthermore, when elemental fractionation is modeled using a theory based on preferential wave-pressure acceleration (Laming, 2004, 2009; Bryans et al., 2009), the slow wind streams exhibit a substantial relative buildup of elements with low FIP with respect to the high-speed streams. Although the WTD models utilize identical photospheric lower boundary conditions for all of the flux tubes, the self-consistent solutions for the upper chromosphere, transition region, and low corona are qualitatively different. Feedback from larger heights (i.e., from variations in the flux tube expansion rate and the resulting heating rate) extends downward to create these differences.
Another empirical “marker” of heliospheric stream structure is the proton specific entropy, or entropy per proton, which is often approximated as being proportional to \({\rm ln}(T_{p}/n_{p}^{\gamma-1})\), where β ≈ 1.5 is an empirical adiabatic index for solar wind protons (e.g., Burlaga et al., 1990; Pagel et al., 2004). When measured in regions of the (non-CME) heliosphere where corotating interaction regions have not yet formed shocks, this quantity is seen to clearly distinguish slow wind streams from fast wind streams. Figure 10 shows how the specific entropy is positively correlated with wind speed, both in measurements made by the Solar Wind Electron Proton Alpha Monitor (SWEPAM) instrument on ACE (McComas et al., 1998) and in the Cranmer et al. (2007) ZEPHYR models discussed above. Each model data point was computed independently of the others. The models had identical lower boundary conditions at the photosphere, and they differed from one another only by having a different radial dependence of the magnetic field. Because entropy should be conserved in the absence of significant small-scale dissipation, the quantity that is measured at 1 AU may be a long-distance proxy for the near-Sun locations of strong coronal heating. In other words, the comparison of measured and modeled solar wind entropy variations may be a key way to discriminate between competing explanations of solar wind acceleration.
Although Equation (1) describes the plasma heating rate in terms of the local properties of MHD turbulence, it is also possible to see that this expression gives a heating rate proportional to the mean magnetic flux density at the coronal base. As illustrated above in Figure 4, the mean field strength in the low corona is determined by both the photospheric field strength in the intergranular bright points and the total number of bright points that eventually merge their fields together in the low corona. The field strength at this merging height can thus be estimated as B ≈ f*B*, where B* ≈ 1500 G is the (nearly universal) photospheric bright-point field strength and f* is the area filling factor of bright points in the photosphere. The latter quantity appears to vary by more than an order of magnitude in different regions on the Sun, from about 0.002 (at low latitudes at solar minimum) to ∼ 0.1 (in active regions). If the regions below the merging height can be treated using approximations from “thin flux tube theory” (e.g., Spruit, 1981; Cranmer and van Ballegooijen, 2005), then it is possible to express each term in Equation (1) as a function of f* and the photospheric properties. For example, B ∝ ρ1/2 applies to thin flux tubes in pressure equilibrium, and thus ρ at the merging height can be estimated as \(f_{\ast}^{2}\rho_{\ast}\) (where ρ* is the photospheric density). For Alfvén waves at low heights, Z± ∝ ρ−1/4, and so Z± at the merging height scales like \(Z_{\pm\ast}/f_{\ast}^{1/2}\). Also, we assumed that L⊥ ∝ B−1/2. If the quenching factor in parentheses in Equation (1) is neglected, then
Equivalently, Equation (2) implies that Q/Q* ≈ B/B*, and thus that the heating in the low corona scales directly with the mean magnetic field strength there. In a more highly structured field, the latter is equivalent to the magnetic “flux density” averaged over a given region. Observational evidence for such a linear scaling has been found for both a variety of solar regions and other stars as well (see, e.g., Pevtsov et al., 2003; Schwadron et al., 2006; Suzuki, 2006; Kojima et al., 2007; Pinto et al., 2009).
5.3 The Reconnection/Loop-Opening (RLO) solar wind idea
It is clear from observations of the Sun’s highly dynamical “magnetic carpet” (Schrijver et al., 1997; Title and Schrijver, 1998; Hagenaar et al., 1999) that much of coronal heating is driven by the continuous interplay between the emergence, separation, merging, and cancellation of small-scale magnetic elements. Reconnection seems to be the most likely channel for the injected magnetic energy to be converted to heat (e.g., Priest and Forbes, 2000). Only a small fraction of the photospheric magnetic flux is in the form of open flux tubes connected to the heliosphere (Close et al., 2003). Thus, the idea has arisen that the dominant source of energy for open flux tubes is a series of stochastic reconnection events between the open and closed fields (e.g., Fisk et al., 1999; Ryutova et al., 2001; Fisk, 2003; Schwadron and McComas, 2003; Feldman et al., 2005; Schwadron et al., 2006; Schwadron and McComas, 2008; Fisk and Zhao, 2009).
The natural appeal of the RLO idea is evident from the fact that open flux tubes are always rooted in the vicinity of closed loops (e.g., Dowdy et al., 1986) and that all layers of the solar atmosphere seem to be in continual motion with a wide range of timescales. In fact, observed correlations between the lengths of closed loops in various regions, the electron temperature in the low corona, and the wind speed at 1 AU (Feldman et al., 1999; Gloeckler et al., 2003) are highly suggestive of a net transfer of Poynting flux from the loops to the open-field regions that may be key to understanding the macroscopic structure of the solar wind. The proposed RLO reconnection events may also be useful in generating energetic particles and cross-field diffusive transport throughout the heliosphere (e.g., Fisk and Schwadron, 2001).
Testing the RLO idea using theoretical models seems to be more difficult than testing the WTD idea because of the complex multi-scale nature of magnetic reconnection. It can be argued that one needs to create fully three-dimensional models of the coronal magnetic field (arising from multiple magnetic elements on the surface) to truly assess the full range of closed/open flux interactions. The idea of modeling the coronal field via a collection of discrete magnetic sources (referred to in various contexts as “magneto-chemistry,” “tectonics,” or “magnetic charge topology”) has been used extensively to study the evolution of the closed-field corona (e.g., Longcope, 1996; Schrijver et al., 1997; Longcope and Kankelborg, 1999; Sturrock et al., 1999; Priest et al., 2002; Beveridge et al., 2003; Barnes et al., 2005; Parnell, 2007; Ng and Bhattacharjee, 2008), but applications to open fields and the solar wind have been rarer (see, however, Fisk, 2005; Tu et al., 2005).
In order to develop the RLO paradigm to the point where it can be tested more quantitatively, several key questions remain to be answered. For example, how much magnetic flux actually opens up in the magnetic carpet? Also, what is the time and space distribution of reconnection-driven energy addition into the (transiently) open flux tubes? Lastly, how is the reconnection energy distributed into various forms (e.g., bulk kinetic energy in “jets,” thermal energy, waves, turbulence, and energetic particles) that each affect the accelerating solar wind in different ways? Combinations of simulations, analytic scaling relations, and observations are needed to make further progress.
5.4 Kinetic microphysics
The theoretical models discussed in the previous two subsections mainly involved a “one-fluid” or MHD approach to the coronal heating and solar wind acceleration. However, at large heights in coronal holes, the collisionless divergence of plasma parameters for protons, electrons, and heavy ions allows the multi-fluid kinetic processes to be distinguished in a more definitive way. The UVCS measurements of strong O+5 preferential heating, preferential acceleration, and temperature anisotropy have spurred a great deal of theoretical work in this direction (see reviews by Hollweg and Isenberg, 2002; Cranmer, 2002a; Marsch, 2005, 2006; Kohl et al., 2006). Specifically, the observed ordering of Ti ≫ Tp > Te and the existence of anisotropies of the form T⊥ > T∥ in coronal holes led to a resurgence of interest in models of ion cyclotron resonance.
The ion cyclotron heating mechanism is a classical resonance between left-hand polarized Alfvén waves and the Larmor gyrations of positive ions around the background magnetic field. If the wave frequency and the natural ion gyrofrequency are equal, then in the rest frame of the ion the oscillating electric and magnetic fields of the wave are no longer felt by the ion to be oscillating. The ion in such a frame senses a constant DC electric field, and it can secularly gain or lose energy depending on the relative phase between the ion’s velocity vector and the electric field direction. In a wave field with random phases, an ion will undergo a random walk in energy. Thus, on average the ions can be considered to “diffuse” into faster (i.e., wider) Larmor orbits with larger perpendicular energy (see Rowlands et al., 1966; Galinsky and Shevchenko, 2000; Isenberg, 2001; Cranmer, 2001; Isenberg and Vasquez, 2009).
In the actual solar corona, however, it is not likely that the situation is as straightforward as summarized above. Instead of a population of pre-existing, linear cyclotron waves that are dissipated, there may be a rich variety of nonlinear plasma mechanisms at play. The observed ion heating is likely to be just the final stage of a multi-step process of energy conversion between waves, turbulent motions, reconnection structures, and various kinds of distortions in the particle velocity distributions. Table 1 surveys the field of suggested possibilities, and the remainder of this section discusses these ideas in more detail.
One potential obstacle to the idea of ion cyclotron heating is that the required gyroresonant wave frequencies in the corona are of order 102 to 104 Hz, whereas the dominant frequencies of Alfvén waves believed to be emitted by the Sun are thought to be much lower (i.e., less than 0.01 Hz, corresponding to periods of minutes to hours). Axford and McKenzie (1992) suggested that the right kinds of high-frequency waves may be generated in small-scale reconnection events in the chaotic “furnace” of the supergranular network. These waves could propagate upwards in height — and downwards in magnetic field strength — until they reached a location where they became cyclotron resonant with the local ions, and thus would damp rapidly to provide the ion heating (see also Schwartz et al., 1981; Tu and Marsch, 1997).
The above scenario of “basal generation” of ion cyclotron waves has been called into question for several reasons. Cranmer (2000, 2001) argued that the passive sweeping of a pre-existing fluctuation spectrum would involve ions with low gyrofrequencies (i.e., small ratios of charge to mass; qi/mi ≈ 0.1 to 0.2 in proton units) encountering waves of a given frequency at lower heights than the ions that have been observed to exhibit preferential heating, like O+5 (qi/mi = 0.31) and Mg+9 (qi/mi = 0.37). Thus, the resonances of many minor ion species may be strong enough to damp out a base-generated spectrum of waves before they can become resonant with the observed species. Furthermore, Hollweg (2000) found that a base-generated spectrum of ion cyclotron waves would exhibit a very different appearance in interplanetary radio scintillations than the observed radio data. There remains some uncertainty about these criticisms of a basal spectrum of ion cyclotron waves, and definitive conclusions cannot yet be made (see discussions in Tu and Marsch, 2001; Hollweg and Isenberg, 2002).
There are several other interesting consequences of the Axford and McKenzie (1992) idea of rapid reconnection events at the coronal base. It is possible, for example, that such microflaring activity would give rise to intermittent bursts of parallel electron beams that propagate up into the extended corona. Sufficiently strong beams may be unstable to the growth of wave power at the ion cyclotron frequencies (Markovskii and Hollweg, 2002, 2004; Voitenko and Goossens, 2002), and these waves would then go on to heat the ions. Also, Lee and Wu (2000) suggested that small-scale reconnection events could produce fast collisionless shocks in the extended corona. For shocks sufficiently thin and strong (i.e., with a bulk velocity jump of at least ∼ 0.3 times the Alfvén speed), ions that cross from one side of the shock to the other remain “nondeflected” by the rapid change in direction of the magnetic field. Thus, they can convert some of their parallel motion into perpendicular gyration. Mancuso et al. (2002) suggested this mechanism may be applied to understanding UVCS measurements of ion heating in shocks associated with CMEs. However, it is unclear to what extent the open magnetic regions in coronal holes are filled with sufficiently strong shocks to enable this process to occur (see also Hollweg and Isenberg, 2002).
In contrast to the ideas of base-generation of ion cyclotron waves, there have been several proposed mechanisms for “gradual generation” of these waves over a range of distances in the corona and solar wind. A natural way to produce such an extended source of fluctuations is MHD turbulent cascade, which continually transports power at large scales to small scales via the stochastic shredding of transient eddies. A strong turbulent cascade is certainly present in interplanetary space (see reviews by Tu and Marsch, 1995; Goldstein et al., 1997). It is well known, though, that in both numerical simulations and analytic descriptions of Alfvén-wave turbulence (with a strong background “guide field” like in the corona) the cascade from large to small length scales (i.e., from small to large wavenumbers) occurs most efficiently for modes that do not increase in frequency. In other words, the cascade acts most rapidly to increase the perpendicular wavenumber k⊥ while leaving the parallel wavenumber k∥ largely unchanged (e.g., Strauss, 1976; Shebalin et al., 1983; Goldreich and Sridhar, 1995; Cho et al., 2002; Oughton et al., 2004). This type of cascade is expected to generate so-called kinetic Alfvén waves (KAWs) with k⊥ ≫ k∥, but not ion cyclotron waves.
Under typical “low plasma beta” conditions in the corona and fast solar wind, the linear dissipation of KAWs would lead to the preferential parallel heating of electrons (Leamon et al., 1999; Cranmer and van Ballegooijen, 2003; Gary and Borovsky, 2008). This is essentially the opposite of what has been observed with UVCS. However, there have been several suggestions for more complex (nonlinear or multi-step) processes that may be responsible for ions to receive perpendicular heating from KAW-type fluctuations.
-
1.
Markovskii et al. (2006) discussed how a perpendicular turbulent cascade produces increasingly strong shear motions transverse to the magnetic field, and that this shear may eventually be unstable to the generation of cyclotron resonant waves that can in turn heat protons and ions (see also Mikhailenko et al., 2008). This effect may also produce a steepening in the power spectrum of the magnetic field fluctuations that agrees with the observed “dissipation range” (Smith et al., 2006).
-
2.
Voitenko and Goossens (2003, 2004) suggested that high-k⊥ KAWs with sufficiently large amplitudes could begin to exhibit nonlinear resonance effects (“demagnetized wave phases”) leading to rapid ion perpendicular heating. There are definite thresholds in the KAW amplitude that must be exceeded for these mechanisms to be initiated, and it is unclear whether the actual coronal turbulent spectrum has enough power in the relevant regions of wavenumber space (see also Wu and Yang, 2006, 2007).
-
3.
The damping of low-frequency KAWs may give rise to substantial parallel electron acceleration. If the resulting electron velocity distributions were sufficiently beamed, they could become unstable to the generation of parallel Langmuir waves. In turn, the evolved Langmuir wave trains may exhibit a periodic electric potential-well structure in which some of the beam electrons can become trapped. Adjacent potential wells can then merge with one another to form isolated “electron phase space holes” of saturated potential. Ergun et al. (1999), Matthaeus et al. (2003), and Cranmer and van Ballegooijen (2003) described how these tiny (Debye-scale) electrostatic structures can heat ions perpendicularly via Coulomblike quasi-collisions.
-
4.
Obliquely propagating MHD waves with large perpendicular and parallel wavenumbers — including KAWs and fast-mode waves — can interact resonantly with positive ions via channels that are not available when either k∥ or k⊥ are small. Li and Habbal (2001) found that oblique fast-mode waves with large wavenumbers may be even more efficient than Alfvén waves at heating ions under coronal conditions. Hollweg and Markovskii (2002) discussed how the higher-order cyclotron resonances become available to obliquely propagating waves with large wavenumbers, and how these can lead to stochastic velocity-space diffusion for ions.
-
5.
On the smallest spatial scales, the plasma in numerical simulations of MHD turbulence is seen to develop into a collection of narrow current sheets undergoing oblique magnetic reconnection (i.e., with the strong “guide field” remaining relatively unchanged). Dmitruk et al. (2004) performed test-particle simulations in a turbulent plasma and found that protons can become perpendicularly accelerated around the guide field because of coherent forcing from the perturbed fields associated with the current sheets (see also Parashar et al., 2009). It remains to be seen whether this process could lead to more than mass-proportional energization for minor ions.
-
6.
If the plasma contains sufficiently small-scale density gradients transverse to the magnetic field (∇⊥ρ), then drift currents can be excited that are unstable to the generation of high-frequency waves (Markovskii, 2001; Zhang, 2003; Vranjes and Poedts, 2008; Mecheri and Marsch, 2008). These instabilities depend on both the amplitudes and scale lengths of ∇⊥ρ. To measure the latter, it is important to take into account both remote-sensing measurements of coronal density inhomogeneities (e.g., Woo, 2006; Pasachoff et al., 2007) and constraints from radio scintillation power spectra at larger distances (Bastian, 2001; Spangler, 2002; Harmon and Coles, 2005).
Despite the fact that theory predicts a predominantly perpendicular cascade, there is some evidence that the turbulent fluctuations in the solar wind have some energy that extends up to large k∥ values in a power-law tail (see, e.g., Bieber et al., 1996; Dasso et al., 2005; MacBride et al., 2008). Whether or not this means that true “parallel cascade” occurs in the corona and solar wind is still not known. However, some progress has been made using a phenomenological approach to modeling the cascade as a combination of advection and diffusion in wavenumber space. In the model of Cranmer and van Ballegooijen (2003), the relative strengths of perpendicular advection and diffusion determine the slope of the power-law spectrum in k∥, and thus they specify the amount of wave energy that is available at the ion cyclotron frequencies (see also Cranmer et al., 1999a; Landi and Cranmer, 2009; Jiang et al., 2009).
There have also been proposals for additional mechanisms that could allow a parallel cascade to occur in the corona and solar wind. Nonlinear couplings between the dominant Alfvén waves and other modes such as fast magnetosonic waves (Chandran, 2005; Luo and Melrose, 2006) and ion-acoustic waves (Yoon and Fang, 2008) have the potential to enhance the wave power at high frequencies. It has also been known for some time that nonlinear coupling between Alfvén and fast-mode waves may help explain why the measured in situ magnetic field magnitude ∣B∣ remains roughly constant while its direction varies strongly (Barnes and Hollweg, 1974; Vasquez and Hollweg, 1996, 1998).
If MHD waves have sufficiently large amplitudes, they may undergo nonlinear wave steepening, which leads to density variations as well as oscillations in the parallel components of the velocity and magnetic field. These may generate progressively smaller scales along the magnetic field (e.g., Medvedev, 2000; Suzuki et al., 2007). There is also a “bootstrap” kind of effect for ion cyclotron wave generation that was discussed by Isenberg et al. (2001). If some outward-propagating cyclotron waves exist, the resonant diffusion may act to produce proton velocity distributions that are unstable to the generation of inward-propagating cyclotron waves. In response, the proton distributions would become further deformed and thus could become unstable to the growth of both inward and outward waves. It is not yet known if this process could reach the point of becoming self-sustaining, but if so, it may also serve as an extended generation mechanism for high-k∥ waves.
In addition to the above ideas that involve large wavenumbers and kinetic effects, there have been other suggested physical processes that do not require high-k resonances to be initially present in order to heat the ions.
-
1.
Particles in large-amplitude Alfvén waves exhibit both E×B drift motions (i.e., their standard velocity amplitude) and a polarization drift velocity Vpol that is smaller than the former by the ratio ω/Ωi, where ω is the wave frequency and Ωi is the ion cyclotron frequency. A sufficiently large Vpol can lead to cross-field currents unstable to the generation of high-frequency waves, and to eventual equipartition between Vpol and the ion thermal speed (Singh and Khazanov, 2004; Singh et al., 2007; Khazanov and Singh, 2007). It is not yet known whether the effective Vpol for the coronal fluctuation spectrum is large enough to provide a significant fraction of the ion thermal speeds.
-
2.
Recently there have been suggested some completely nonresonant mechanisms that depend on the stochasticity of MHD turbulence to produce an effective increase in random ion motions (Lu and Li, 2007; Wu and Yoon, 2007; Bourouaine et al., 2008). Questions still remain, though, concerning the spatial scales over which one should refer to particle motions as “heating” versus “wave sloshing.” This energization mechanism may be just a more chaotic form of the standard velocity amplitude that an ion feels when in the presence of a spectrum of Alfvén waves (see, e.g., Wang and Wu, 2009). In this case, the maximum amount of heating from this process would provide mass-proportional heating for minor ions and protons (i.e., Ti/Tp = mi/mp), and it is clear that the UVCS measurements for O+5 show heating in excess of this amount (see Section 4.3).
-
3.
Both numerical and analytic studies of Alfvén waves show that, at sufficiently large amplitudes, there can be gyroresonance-like ion energization for sets of frequencies at specific fractions of the local ion cyclotron resonance frequency (e.g., Chen et al., 2001; Guo et al., 2008). Like several other processes listed above, this effect becomes active only above certain thresholds of wave amplitude. Also, Markovskii et al. (2009) showed that mildly nonlinear Alfvén waves — with frequencies slightly below the local proton gyrofrequency and power in both the upward and downward directions along the field — can also undergo additional modes of dissipation and proton heating that are not anticipated in linear ion cyclotron resonance theories.
Finally, there has been some development of the so-called velocity filtration theory, which requires neither direct heating nor wave damping in order to energize coronal ions. Spacecraft measurements of plasma velocity distributions, both in the solar wind and in planetary magnetospheres and magnetosheaths, have revealed that “suprathermal” power-law tails are quite common. These observations led to the suggestion by Scudder (1992a, 1994) of an an alternative to theories that demand explicit energy deposition in the low corona (see also Parker, 1958b; Levine, 1974). A velocity distribution having a suprathermal tail will become increasingly dominated by its high-energy particles at larger distances from the solar gravity well. Thus an effective “heating” occurs as a result of particle-by-particle conservation of energy. The major unresolved issue is whether suprathermal tails of the required strength can be produced and maintained in the upper chromosphere and transition region — where Coulomb collisions are traditionally believed to be strong enough to rapidly drive velocity distributions toward Maxwellians. Whether the solar atmosphere actually plays host to strong nonthermal tails is still under debate, with some evidence existing in favor of their presence (e.g., Esser and Edgar, 2000; Ralchenko et al., 2007) and other evidence against them (Anderson et al., 1996; Ko et al., 1996; Feldman et al., 2007).
The original (Scudder, 1992a, b) ideas about suprathermal velocity filtration were applied only to the primary (proton and electron) coronal plasma. More recently, Pierrard and Lamy (2003) and Pierrard et al. (2004) have shown that this mechanism can produce extremely high temperatures for heavy ions in the corona — providing they had suprathermal tails in the chromosphere. The primary quantities presented in these papers, however, were integrated isotropic temperatures T. No information was given about the predicted sense of the temperature anisotropy for the minor ions. For a collisionless exospheric model, there is a suspicion that a combination of several effects (e.g., the initial velocity filtration and subsequent magnetic moment conservation) would result in velocity distributions with T∥ ≫ T⊥, which is not what is observed.
Since it is obvious that not all of the proposed mechanisms described above (and shown in Table 1) can be the dominant cause of the collisionless ion energization in coronal holes, there is a great need to “cut through the jungle” and assess the validity of each of these processes. For many of these suggested ideas, further theoretical development is required so that specific observational predictions can be made. However, there are also several types of measurement that have not been widely recognized or utilized as constraints on theoretical models. A prime example is the use of radio sounding (i.e., interplanetary scintillations and Faraday rotation) to measure the fine structure of the corona and solar wind in density, velocity, and magnetic field strength (see, however, Hollweg and Isenberg, 2002; Spangler, 2002; Harmon and Coles, 2005; Chandran et al., 2009b). Another example is the use of high-resolution UV spectral line profiles to probe departures from Maxwellian or bi-Maxwellian ion velocity distributions (e.g., Cranmer, 2001).
6 Summary and Conclusions
The last decade has seen significant progress toward identifying and characterizing the processes that produce coronal holes. As remote-sensing plasma measurements have become possible in the extended solar corona (i.e., the region of primary acceleration of the solar wind), the traditional gap between solar physics and in situ space physics has become narrower. However, there are still many unanswered questions: How and where in the solar atmosphere are the relevant waves and turbulent motions generated? Which kinds of fluctuation modes (i.e., linear or nonlinear; Alfvén, fast, or slow; high k∥ or high k⊥) are most important? What frequencies dominate the radially evolving power spectrum? What fraction of the interplanetary solar wind comes from filamentary structures such as polar plumes and polar jets? Are there relatively simple “scaling laws” that will allow us to use only the measured properties at the solar surface to predict the resulting amount of coronal heating and solar wind acceleration?
Answering the above questions involves moving forward in both the theoretical and observational directions. Section 5 described the large number of suggested physical processes for energizing the plasma in coronal holes. The validity of many of these processes still needs to be assessed, and their relative contributions to the heating and acceleration of the actual solar corona need to be quantified. If, at the end of this process, there are still a number of mutually inconsistent theories that are still viable, the only way forward is to determine what future measurements would best put the remaining models to the test. These activities are ongoing with the planning of inner heliospheric missions such as Solar Probe (McComas et al., 2007) and Solar Orbiter (Marsden and Fleck, 2007), as well as next-generation ultraviolet coronagraph spectroscopy missions that would follow up on the successes of UVCS/SOHO (see, e.g., Cranmer, 2002b; Gardner et al., 2003; Kohl et al., 2006).
The development of more physically sound models of the solar wind feeds back in many ways to a wider understanding of stellar outflows and star/planet evolution. Figure 11 shows some of the the early stages of evolution for a representative solar-type star. At all ages, cool stars are inferred to exhibit some kind of wind or jet-like outflow (Lamers and Cassinelli, 1999; Wood, 2004; Güdel, 2007; Cranmer, 2008a). Young stars first become visible as dust-obscured cloud cores and protostars (e.g., Lada, 1985; Hartmann, 2000), and these objects are often associated with bipolar, collimated jets. These outflows indicate some kind of transfer of energy from the accretion disk’s orbital motion to torqued magnetic fields (rooted on the stellar surface) that relieve the buildup of angular momentum and eject plasma out the poles (e.g., Blandford and Payne, 1982; van Ballegooijen, 1994). As the accretion rates decrease over time, protostars become visible as classical T Tauri stars (CTTS), and there remains ample evidence for polar outflows in the form of both “disk winds” and true stellar winds (Hartigan et al., 1995; Ferreira et al., 2006; Cranmer, 2008b). The primordial accretion disk is dissipated gradually as the star enters the weak-lined T Tauri star (WTTS) phase, with a likely transition to a protoplanetary dust/debris disk. Strong stellar magnetic activity remains evident during these stages from, e.g., X-rays (Feigelson and Montmerle, 1999). Many “post T Tauri” stars, once they reach the zero-age main sequence (ZAMS), remain rapidly rotating, and for young ZAMS stars such as AB Dor there is evidence for a range of X-ray emitting plasma from dark polar spots (which probably do not correspond to open magnetic field regions like coronal holes) to huge “slingshot prominences” extending over several stellar radii (e.g., Güdel et al., 2001, 2003; Jardine and van Ballegooijen, 2005).
Learning about the fundamental physics responsible for solar coronal holes has relevance that reaches into other areas of study besides astrophysics, including plasma physics, space physics, and astronautical engineering. The practical benefits of improving long-term predictions for the conditions of the Earth’s local space environment are manifold (see, e.g., Feynman and Gabriel, 2000; Eastwood, 2008). In addition, parallel research into the expansion of the polar wind from the Earth’s ionosphere has led to an improved understanding of kinetic processes in plasmas on the boundary between collisional and collisionless conditions (Lemaire and Pierrard, 2001; Barakat and Schunk, 2006). Finally, a growing realization that strict topical compartmentalization is often a hindrance to making progress has given rise to greater interest in interdisciplinary studies of “universal processes in heliophysics” (Crooker, 2004; Davila et al., 2009).
References
Abramenko, V.I., Fisk, L.A. and Yurchyshyn, V.B., 2006a, “The Rate of Emergence of Magnetic Dipoles in Coronal Holes and Adjacent Quiet-Sun Regions”, Astrophys. J. Lett., 641, L65–L68. [ADS] (Cited on page 11.)
Abramenko, V.I., Pevtsov, A.A. and Romano, P., 2006b, “Coronal Heating and Photospheric Turbulence Parameters: Observational Aspects”, Astrophys. J. Lett., 646, L81–L84. [ADS] (Cited on page 23.)
Aiouaz, T., Peter, H. and Lemaire, P., 2005, “The correlation between coronal Doppler shifts and the supergranular network”, Astron. Astrophys., 435(2), 713–721. [DOI], [ADS] (Cited on page 12.)
Allen, L.A., Habbal, S.R. and Li, X., 2000, “Thermal coupling of protons and neutral hydrogen with anisotropic temperatures in the fast solar wind”, J. Geophys. Res., 105, 23123–23134. [ADS] (Cited on page 18.)
Altschuler, M.D. and Newkirk Jr, G., 1969, “Magnetic fields and the structure of the solar corona. I: Methods of calculating coronal fields”, Solar Phys., 9, 131–149. [ADS] (Cited on page 14.)
Altschuler, M.D. and Perry, R.M., 1972, “On Determining the Electron Density Distribution of the Solar Corona from K-Coronameter Data”, Solar Phys., 23, 410–428. [ADS] (Cited on page 15.)
Altschuler, M.D., Trotter, D.E. and Orrall, F.Q., 1972, “Coronal Holes”, Solar Phys., 26, 354–365. [ADS] (Cited on page 8.)
Anderson, S.W., Raymond, J.C. and van Ballegooijen, A., 1996, “Ultraviolet Emission-Line Intensities and Coronal Heating by Velocity Filtration: Collisionless Results”, Astrophys. J., 457, 939–948. [ADS] (Cited on page 34.)
Andretta, V. and Jones, H.P., 1997, “On the Role of the Solar Corona and Transition Region in the Excitation of the Spectrum of Neutral Helium”, Astrophys. J., 489, 375–394. [ADS] (Cited on page 10.)
Andries, J. and Goossens, M., 2001, “Kelvin-Helmholtz instabilities and resonant flow instabilities for a coronal plume model with plasma pressure”, Astron. Astrophys., 368, 1083–1094. [ADS] (Cited on page 17.)
Antiochos, S.K., DeVore, C.R., Karpen, J.T. and Mikic, Z., 2007, “Structure and dynamics of the Sun’s open magnetic field”, Astrophys. J., 671, 936–946. [ADS] (Cited on page 11.)
Antonucci, E., Dodero, M. and Giordano, S., 2000, “Fast Solar Wind Velocity in a Polar Coronal Hole during Solar Minimum”, Solar Phys., 197, 115–134. [ADS] (Cited on page 19.)
Antonucci, E., Dodero, M.A., Giordano, S., Krishnakumar, V. and Noci, G., 2004, “Spectroscopic measurement of the plasma electron density and outflow velocity in a polar coronal hole”, Astron. Astrophys., 416, 749–758. [ADS] (Cited on page 18.)
Arge, C.N. and Pizzo, V.J., 2000, “Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates”, J. Geophys. Res., 105, 10 465–10 480. [ADS] (Cited on pages 14 and 23.)
Asai, A., Shibata, K., Hara, H. and Nitta, N.V., 2008, “Characteristics of Anemone Active Regions Appearing in Coronal Holes Observed with the Yohkoh Soft X-Ray Telescope”, Astrophys. J., 673, 1188–1193. [ADS] (Cited on page 11.)
Aschwanden, M.J., 2006, Physics of the Solar Corona: An Introduction with Problems and Solutions, 2nd ed., Springer-Praxis Books in Geophysical Sciences, Springer; Praxis, Berlin; New York; Chichester (Cited on page 23.)
Aschwanden, M.J., Winebarger, A., Tsiklauri, D. and Peter, H., 2007, “The Coronal Heating Paradox”, Astrophys. J., 659, 1673–1681. [ADS] (Cited on page 24.)
Aschwanden, M.J., Nitta, N.V., Wuelser, J.P., Lemen, J.R., Sandman, A., Vourlidas, A. and Colaninno, R.C., 2009, “First Measurements of the Mass of Coronal Mass Ejections from the EUV Dimming Observed with STEREO EUVI A + B Spacecraft”, Astrophys. J., submitted. Online version (accessed 1 September 2009): http://www.lmsal.com/~aschwand/eprints/2009_dimming.pdf (Cited on page 13.)
Avrett, E.H., 1999, “Combined Effects of Mass Flow and Particle Diffusion on the Ionization Structure of the Solar Transition Region”, in Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, Proceedings of the 8th SOHO Workshop, 22–25 June 1999, Paris, France, (Eds.) Vial, J.-C., Kaldeich-Schümann, B., vol. SP-446 of ESA Conference Proceedings, pp. 141–147, ESA Publications Division, Noordwijk. [ADS] (Cited on page 12.)
Avrett, E.H. and Loeser, R., 2008, “Models of the Solar Chromosphere and Transition Region from SUMER and HRTS Observations: Formation of the Extreme-Ultraviolet Spectrum of Hydrogen, Carbon, and Oxygen”, Astrophys. J. Suppl. Ser., 175, 229–276. [ADS] (Cited on pages 15, 16, 17, and 18.)
Axford, W.I. and McKenzie, J.F., 1992, “The origin of high speed solar wind streams”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., vol. 3 of COSPAR Colloquia Series, pp. 1–5, Pergamon Press, Oxford; New York (Cited on pages 24 and 30.)
Axford, W.I. and McKenzie, J.F., 1997, “The Solar Wind”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 31–66, Arizona University Press, Tucson (Cited on page 24.)
Banaszkiewicz, M., Axford, W.I. and McKenzie, J.F., 1998, “An analytic solar magnetic field model”, Astron. Astrophys., 337, 940–944. [ADS] (Cited on pages 19 and 26.)
Banerjee, D., Teriaca, L., Doyle, J.G. and Wilhelm, K., 1998, “Broadening of Si VIII lines observed in the solar polar coronal holes”, Astron. Astrophys., 339, 208–214. [ADS] (Cited on page 17.)
Banerjee, D., Pérez-Suárez, D. and Doyle, J.G., 2009, “Signatures of Alfvén waves in the polar coronal holes as seen by EIS/Hinode”, Astron. Astrophys., 501, L15–L18. [ADS], [arXiv:0906.4600] (Cited on page 17.)
Barakat, A.R. and Schunk, R.W., 2006, “A three-dimensional model of the generalized polar wind”, J. Geophys. Res., 111, A12314. [ADS] (Cited on page 36.)
Barnes, A. and Hollweg, J.V., 1974, “Large-amplitude hydromagnetic waves”, J. Geophys. Res., 79, 2302–2318. [DOI], [ADS] (Cited on page 32.)
Barnes, G., Longcope, D.W. and Leka, K.D., 2005, “Implementing a Magnetic Charge Topology Model for Solar Active Regions”, Astrophys. J., 629, 561–571. [ADS] (Cited on page 29.)
Bastian, T.S., 2001, “Radio Wave Propagation in the Corona and the Interplanetary Medium”, Astrophys. Space Sci., 277, 107–116. [ADS] (Cited on pages 25 and 32.)
Beckers, J.M., 1968, “Solar Spicules (Invited Review Paper))”, Solar Phys., 3, 367–433. [ADS] (Cited on page 7.)
Bell, B. and Noci, G., 1973, “Are Coronal Holes M Regions?”, Bull. Am. Astron. Soc., 5, 269. [ADS] (Cited on page 8.)
Bell, B. and Noci, G., 1976, “Intensity of the Fe XV emission line corona, the level of geomagnetic activity, and the velocity of the solar wind”, J. Geophys. Res., 81, 4508–4516. [ADS] (Cited on page 8.)
Bemporad, A., Matthaeus, W.H. and Poletto, G., 2008, “Low-frequency Lyα Power Spectra Observed by UVCS in a Polar Coronal Hole”, Astrophys. J. Lett., 677, L137–L140. [ADS] (Cited on page 16.)
Beresnyak, A. and Lazarian, A., 2009, “Structure of Stationary Strong Imbalanced Turbulence”, Astrophys. J., 702, 460–471. [ADS], [arXiv:0904.2574] (Cited on page 25.)
Berger, T.E. and Title, A.M., 2001, “On the Relation of G-Band Bright Points to the Photospheric Magnetic Field”, Astrophys. J., 553, 449–469. [ADS] (Cited on page 12.)
Beveridge, C., Longcope, D.W. and Priest, E.R., 2003, “A model for elemental coronal flux loops”, Solar Phys., 216, 27–40. [ADS] (Cited on page 29.)
Bieber, J.W., Wanner, W. and Matthaeus, W.H., 1996, “Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport”, J. Geophys. Res., 101(A2), 2511–2522. [DOI], [ADS] (Cited on page 32.)
Blandford, R.D. and Payne, D.G., 1982, “Hydromagnetic flows from accretion discs and the production of radio jets”, Mon. Not. R. Astron. Soc., 199, 883–903. [ADS] (Cited on page 35.)
Bourouaine, S., Marsch, E. and Vocks, C., 2008, “‘On the efficiency of nonresonant ion heating by coronal Alfvén waves”, Astrophys. J. Lett., 684, L119–L122. [ADS] (Cited on page 33.)
Breech, B., Matthaeus, W.H., Minnie, J., Bieber, J.W., Oughton, S., Smith, C.W. and Isenberg, P.A., 2008, “Turbulence transport throughout the heliosphere”, J. Geophys. Res., 113, A08105. [ADS] (Cited on page 25.)
Bryans, P., Landi, E. and Savin, D.W., 2009, “A New Approach to Analyzing Solar Coronal Spectra and Updated Collisional Ionization Equilibrium Calculations: II, Updated Ionization Rate Coefficients”, Astrophys. J., 691, 1540–1559. [ADS] (Cited on page 27.)
Burlaga, L.F., Mish, W.H. and Whang, Y.C., 1990, “Coalescence of recurrent streams of different sizes and amplitudes”, J. Geophys. Res., 95, 4247–4255. [ADS] (Cited on page 27.)
Byhring, H.S., Esser, R. and Lie-Svendsen, Ø., 2008, “The Funnel Geometry of Open Flux Tubes in the Low Solar Corona Constrained by O VI and Ne VIII Outflow”, Astrophys. J. Lett., 673, L91–L94. [ADS] (Cited on page 12.)
Centeno, R., Trujillo Bueno, J., Uitenbroek, H. and Collados, M., 2008, “The influence of coronal EUV irradiance on the emission in the He I 10830 Å and D3 multiplets”, Astrophys. J., 677, 742–750. [ADS] (Cited on page 10.)
Chae, J., Yun, H.S. and Poland, A.I., 1997, “Effects of Non-LTE Radiative Loss and Partial Ionization on the Structure of the Transition Region”, Astrophys. J., 480, 817–824. [ADS] (Cited on page 12.)
Chandran, B.D.G., 2005, “Weak Compressible Magnetohydrodynamic Turbulence in the Solar Corona”, Phys. Rev. Lett., 95, 265 004. [ADS] (Cited on pages 30 and 32.)
Chandran, B.D.G., Quataert, E., Howes, G.G., Hollweg, J.V. and Dorland, W., 2009a, “The Turbulent Heating Rate in Strong MHD Turbulence with Nonzero Cross Helicity”, Astrophys. J., 701, 652–657. [ADS], [arXiv:0905.3382] (Cited on page 25.)
Chandran, B.D.G., Quataert, E., Howes, G.G., Xia, Q. and Pongkitiwanichakul, P., 2009b, “Constraining Low-Frequency Alfvénic Turbulence in the Solar Wind Using Density Fluctuation Measurements”, Astrophys. J., submitted. [arXiv:0908.0757] (Cited on page 34.)
Chen, L., Lin, Z. and White, R., 2001, “On resonant heating below the cyclotron frequency”, Phys. Plasmas, 8, 4713–4716. [ADS] (Cited on pages 30 and 33.)
Chen, Y., Li, X., Song, H.Q., Shi, Q.Q., Feng, S.W. and Xia, L.D., 2009, “Intrinsic Instability of Coronal Streamers”, Astrophys. J., 691, 1936–1942. [ADS] (Cited on page 16.)
Cho, J., Lazarian, A. and Vishniac, E.T., 2002, “Simulations of Magnetohydrodynamic Turbulence in a Strongly Magnetized Medium”, Astrophys. J., 564, 291–301. [ADS] (Cited on page 31.)
Cirtain, J.W., Golub, L., Lundquist, L., van Ballegooijen, A., Savcheva, A., Shimojo, M., DeLuca, E., Tsuneta, S., Sakao, T., Reeves, K., Weber, M., Kano, R., Narukage, N. and Shibasaki, K., 2007, “Evidence for Alfvén waves in solar X-ray jets”, Science, 318, 1580–1582. [ADS] (Cited on page 21.)
Close, R.M., Parnell, C.E., Mackay, D.H. and Priest, E.R., 2003, “Statistical Flux Tube Properties of 3D Magnetic Carpet Fields”, Solar Phys., 212, 251–275. [DOI], [ADS] (Cited on page 28.)
Cohen, O., Sokolov, I.V., Roussev, I.I., Arge, C.N., Manchester, W.B., Gombosi, T.I., Frazin, R.A., Park, H., Butala, M.D., Kamalabadi, F. and Velli, M., 2007, “A Semiempirical Magnetohydrodynamical Model of the Solar Wind”, Astrophys. J. Lett., 654, L163–L166. [ADS] (Cited on page 23.)
Coleman, P.J., 1968, “Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma”, Astrophys. J., 153, 371–388. [DOI], [ADS] (Cited on page 25.)
Collier, M.R., Hamilton, D.C., Gloeckler, G., Bochsler, P. and Sheldon, R.B., 1996, “Neon-20, Oxygen-16, and Helium-4 densities, temperatures, and suprathermal tails in the solar wind determined with WIND/MASS”, Geophys. Res. Lett., 23(10), 1191–1194. [DOI], [ADS] (Cited on page 21.)
Cranmer, S.R., 2000, “Ion Cyclotron Wave Dissipation in the Solar Corona: The Summed Effect of more than 2000 Ion Species”, Astrophys. J., 532, 1197–1208. [DOI], [ADS] (Cited on page 30.)
Cranmer, S.R., 2001, “Ion cyclotron diffusion of velocity distributions in the extended solar corona”, J. Geophys. Res., 106(A11), 24,937–24,954. [DOI], [ADS] (Cited on pages 29, 30, and 34.)
Cranmer, S.R., 2002a, “Coronal Holes and the High-Speed Solar Wind”, Space Sci. Rev., 101, 229–294. [DOI], [ADS] (Cited on pages 5, 25, and 29.)
Cranmer, S.R., 2002b, “Solar wind acceleration in coronal holes”, in From Solar Min to Max: Half a Solar Cycle with SOHO, Proceedings of the SOHO-11 Symposium, 11–15 March 2002, Davos, Switzerland, (Ed.) Wilson, A., vol. SP-508 of ESA Conference Proceedings, pp. 361–366, ESA Publications Division, Noordwijk. [ADS] (Cited on page 35.)
Cranmer, S.R., 2004a, “Observational Aspects of Wave Acceleration in Open Magnetic Regions”, in Waves, Oscillations, and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE, Proceedings of the SOHO-13 Workshop, 29 September–3 October 2003, Palma de Mallorca, Spain, (Ed.) Lacoste, H., vol. SP-547 of ESA Conference Proceedings, pp. 353–362, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 16 and 25.)
Cranmer, S.R., 2004b, “Coronal Heating versus Solar Wind Acceleration”, in Coronal Heating, Proceedings of the SOHO-15 Workshop, 6–9 September 2004, St. Andrews, Scotland, UK, (Eds.) Walsh, R.W., Ireland, J., Danesy, D., Fleck, B., vol. SP-575 of ESA Conference Proceedings, pp. 154–163, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 18 and 19.))
Cranmer, S.R., 2005, “Why is the Fast Solar Wind Fast and the Slow Solar Wind Slow? A Survey of Geometrical Models”, in Connecting Sun and Heliosphere, Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, (Eds.) Fleck, B., Zurbuchen, T.H., Lacoste, H., vol. SP-592 of ESA Conference Proceedings, pp. 159–164, ESA Publications Division, Noordwijk. [ADS] (Cited on page 23.)
Cranmer, S.R., 2007, “Turbulence in the solar corona”, in Turbulence and Nonlinear Processes in Astrophysical Plasmas, Proceedings of the 6th Annual International Astrophysics Conference, Oahu, Hawaii, 16–22 March 2007, (Eds.) Shaikh, D., Zank, G.P., vol. 932 of AIP Conference Proceedings, pp. 327–332, American Institute of Physics, Melville, NY. [ADS] (Cited on page 25.)
Cranmer, S.R., 2008a, “Winds of Main-Sequence Stars: Observational Limits and a Path to Theoretical Prediction”, in Cool Stars, Stellar Systems, and the Sun: 14th Cambridge Workshop, 5–10 November 2006, Pasadena, California, (Ed.) van Belle, G., vol. 384 of ASP Conference Series, pp. 317–326, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 35.)
Cranmer, S.R., 2008b, “Turbulence-driven polar winds from T Tauri stars energized by magnetospheric accretion”, Astrophys. J., 689, 316–334. [ADS] (Cited on page 35.)
Cranmer, S.R. and van Ballegooijen, A.A., 2003, “Alfvénic turbulence in the extended solar corona: kinetic effects and proton heating”, Astrophys. J., 594, 573–591. [DOI], [ADS] (Cited on pages 30, 31, and 32.)
Cranmer, S.R. and van Ballegooijen, A.A., 2005, “On the generation, propagation, and reflection of Alfvén waves from the solar photosphere to the distant heliosphere”, Astrophys. J. Suppl. Ser., 156, 265–293. [DOI], [ADS] (Cited on pages 12, 19, 25, and 27.)
Cranmer, S.R., Field, G.B. and Kohl, J.L., 1999a, “Spectroscopic constraints on models of ion cyclotron resonance heating in the polar solar corona and high-speed solar wind”, Astrophys. J., 518, 937–947. [DOI], [ADS] (Cited on page 32.)
Cranmer, S.R., Kohl, J.L., Noci, G., Antonucci, E., Tondello, G., Huber, M.C.E., Strachan, L., Panasyuk, A.V., Gardner, L.D., Romoli, M., Fineschi, S., Dobrzycka, D., Raymond, J.C., Nicolosi, P., Siegmund, O.H.W., Spadaro, D., Benna, C., Ciaravella, A., Giordano, S., Habbal, S.R., Karovska, M., Li, X., Martin, R., Michels, J.G., Modigliani, A., Naletto, G., O’Neal, R.H., Pernechele, C., Poletto, G., Smith, P.L. and Suleiman, R.M., 1999b, “An Empirical Model of a Polar Coronal Hole at Solar Minimum”, Astrophys. J., 511, 481–501. [ADS] (Cited on pages 14, 15, 17, 18, 19, 20, and 21.)
Cranmer, S.R., van Ballegooijen, A.A. and Edgar, R.J., 2007, “Self-consistent coronal heating and solar wind acceleration from anisotropic magnetohydrodynamic turbulence”, Astrophys. J. Suppl. Ser., 171, 520–551. [ADS] (Cited on pages 14, 17, 18, 20, 23, 25, 26, and 27.)
Cranmer, S.R., Panasyuk, A.V. and Kohl, J.L., 2008, “Improved Constraints on the Preferential Heating and Acceleration of Oxygen Ions in the Extended Solar Corona”, Astrophys. J., 678, 1480–1497. [ADS] (Cited on pages 15, 18, 19, and 20.)
Cranmer, S.R., Matthaeus, W.H., Breech, B.A. and Kasper, J.C., 2009, “Empirical Constraints on Proton and Electron Heating in the Fast Solar Wind”, Astrophys. J., 702, 1604–1614. [ADS] (Cited on page 18.)
Crooker, N.U., 2004, “What Is the International Heliophysical Year?”, Eos Trans. AGU, 85(37), 351–353. [ADS] (Cited on page 36.)
Culhane, L., Harra, L.K., Baker, D., van Driel-Gesztelyi, L., Sun, J., Doschek, G.A., Brooks, D.H., Lundquist, L.L., Kamio, S., Young, P.R. and Hansteen, V.H., 2007, “Hinode EUV Study of Jets in the Sun’s South Polar Corona”, Publ. Astron. Soc. Japan, 59, S751–S756. [ADS] (Cited on page 21.)
Dasso, S., Milano, L.J., Matthaeus, W.H. and Smith, C.W., 2005, “Anisotropy in Fast and Slow Solar Wind Fluctuations”, Astrophys. J. Lett., 635, L181–L184. [ADS] (Cited on page 32.)
David, C., Gabriel, A.H., Bely-Dubau, F., Fludra, A., Lemaire, P. and Wilhelm, K., 1998, “Measurement of the electron temperature gradient in a solar coronal hole”, Astron. Astrophys., 336, L90–L94. [ADS] (Cited on page 17.)
Davila, J.M., Gopalswamy, N. and Thompson, B.J., 2009, “Universal processes in heliophysics”, Proc. IAU, 4, 11–16. [DOI], [ADS]. Proceedings of IAU Symposium 257, 15–19 September 2008, Ioannina, Greece (Cited on page 36.))
De Pontieu, B., McIntosh, S.W., Carlsson, M., Hansteen, V.H., Tarbell, T.D., Schrijver, C.J., Title, A.M., Shine, R.A., Tsuneta, S., Katsukawa, Y., Ichimoto, K., Suematsu, Y., Shimizu, T. and Nagata, S., 2007, “Chromospheric Alfvénic waves strong enough to power the solar wind”, Science, 318, 1574–1577. [ADS] (Cited on page 24.)
de Toma, G. and Arge, C.N., 2005, “Multi-wavelength Observations of Coronal Holes”, in Large-scale Structures and their Role in Solar Activity, Proceedings of the 22nd Sacramento Peak Workshop, held at the National Solar Observatory, Sacramento Peak, Sunspot, New Mexico, USA, 18–22 October 2004, (Eds.) Sankarasubramanian, K., Penn, M., Pevtsov, A., vol. 346 of ASP Conference Series, pp. 251–260, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 5.)
DeForest, C.E. and Gurman, J.B., 1998, “Observation of Quasi-periodic Compressive Waves in Solar Polar Plumes”, Astrophys. J. Lett., 501, L217–L220. [DOI], [ADS] (Cited on page 16.)
DeForest, C.E., Hoeksema, J.T., Gurman, J.B., Thompson, B.J., Plunkett, S.P., Howard, R., Harrison, R.C. and Hassler, D.M., 1997, “Polar Plume Anatomy: Results of a Coordinated Observation”, Solar Phys., 175, 393–410. [ADS] (Cited on pages 15 and 17.)
DeForest, C.E., Lamy, P.L. and Llebaria, A., 2001, “Solar Polar Plume Lifetime and Coronal Hole Expansion: Determination from Long-Term Observations”, Astrophys. J., 560, 490–498. [ADS] (Cited on pages 15, 17, and 21.)
Del Zanna, G. and Bromage, B.J.I., 1999, “The Elephant’s Trunk: Spectroscopic diagnostics applied to SOHO/CDS observations of the August 1996 equatorial coronal hole”, J. Geophys. Res., 104, 9753–9766. [ADS] (Cited on page 8.)
Del Zanna, L., von Steiger, R. and Velli, M., 1998, “The Expansion of Coronal Plumes in the Fast Solar Wind”, Space Sci. Rev., 85, 349–356. [ADS] (Cited on page 17.)
Dmitruk, P. and Matthaeus, W.H., 2003, “Low-Frequency Waves and Turbulence in an Open Magnetic Region: Timescales and Heating Efficiency”, Astrophys. J., 597, 1097–1105. [ADS] (Cited on page 25.)
Dmitruk, P., Milano, L.J. and Matthaeus, W.H., 2001, “Wave-driven Turbulent Coronal Heating in Open Field Line Regions: Nonlinear Phenomenological Model”, Astrophys. J., 548, 482–491. [ADS] (Cited on page 25.)
Dmitruk, P., Matthaeus, W.H., Milano, L.J., Oughton, S., Zank, G.P. and Mullan, D.J., 2002, “Coronal Heating Distribution Due to Low-Frequency, Wave-driven Turbulence”, Astrophys. J., 575, 571–577. [ADS] (Cited on page 25.)
Dmitruk, P., Matthaeus, W.H. and Seenu, N., 2004, “Test Particle Energization by Current Sheets and Nonuniform Fields in Magnetohydrodynamic Turbulence”, Astrophys. J., 617, 667–679. [ADS] (Cited on pages 30 and 32.)
Dobrowolny, M., Mangeney, A. and Veltri, P., 1980, “Fully developed anisotropic hydromagnetic turbulence in interplanetary space”, Phys. Rev. Lett., 45, 144–147. [DOI], [ADS] (Cited on page 26.)
Dobrzycka, D., Raymond, J.C. and Cranmer, S.R., 2000, “Ultraviolet Spectroscopy of Polar Coronal Jets”, Astrophys. J., 538, 922–931. [ADS] (Cited on page 21.)
Dobrzycka, D., Raymond, J., DeLuca, E., Gurman, J., Fludra, A. and Biesecker, D., 2006, “SOHO Observations of Polar Coronal Jets over the Last Solar Cycle”, in SOHO-17: 10 Years of SOHO and Beyond, Proceedings of the conference held 7–12 May 2006 at Giardini Naxos, Sicily, Italy, (Eds.) Lacoste, H., Ouwehand, L., vol. SP-617 of ESA Conference Proceedings, pp. 87.1–87.4, ESA Publications Division, Noordwijk. [ADS] (Cited on page 21.)
Dolla, L. and Solomon, J., 2008, “Solar off-limb line widths: Alfvén waves, ion-cyclotron waves, and preferential heating”, Astron. Astrophys., 483, 271–283. [ADS] (Cited on page 17.)
Doschek, G.A., Feldman, U., Laming, J.M., Schühle, U. and Wilhelm, K., 2001, “Properties of Solar Polar Coronal Hole Plasmas Observed above the Limb”, Astrophys. J., 546, 559–568. [ADS] (Cited on page 17.)
Dowdy, J.F., Rabin, D. and Moore, R.L., 1986, “On the magnetic structure of the quiet transition region”, Solar Phys., 105, 35–45. [ADS] (Cited on pages 12 and 28.)
Doyle, J.G., Teriaca, L. and Banerjee, D., 1999, “Coronal hole diagnostics out to 8 R⊙”, Astron. Astrophys., 349, 956–960. [ADS] (Cited on page 15.)
Dunn, R.B. and Zirker, J.B., 1973, “The Solar Filigree”, Solar Phys., 33, 281–304. [ADS] (Cited on page 12.)
Dupree, A.K., Penn, M.J. and Jones, H.P., 1996, “He I 10830 Å Wing Asymmetry in Polar Coronal Holes: Evidence for Radial Outflows”, Astrophys. J. Lett., 467, L121–L124. [ADS] (Cited on page 12.)
Dupree, A.K., Brickhouse, N.S., Smith, G.H. and Strader, J., 2005, “A Hot Wind from the Classical T Tauri Stars: TW Hydrae and T Tauri”, Astrophys. J. Lett., 625, L131–L134. [ADS] (Cited on page 10.)
Eastwood, J.P., 2008, “The science of space weather”, Philos. Trans. R. Soc. London, Ser. A, 366, 4489–4500. [ADS] (Cited on page 35.)
Ergun, R.E., Carlson, C.W., Muschietti, L., Roth, I. and McFadden, J.P., 1999, “Properties of fast solitary structures”, Nonlinear Proc. Geophys., 6, 187–194. [ADS] (Cited on page 32.)
Esser, R. and Edgar, R.J., 2000, “Reconciling Spectroscopic Electron Temperature Measurements in the Solar Corona with In Situ Charge State Observations”, Astrophys. J., 532, L71–L74. [DOI], [ADS] (Cited on pages 17 and 34.)
Esser, R., Fineschi, S., Dobrzycka, D., Habbal, S.R., Edgar, R.J., Raymond, J.C., Kohl, J.L. and Guhathakurta, M., 1999, “Plasma Properties in Coronal Holes Derived from Measurements of Minor Ion Spectral Lines and Polarized White Light Intensity”, Astrophys. J. Lett., 510, L63–L67. [ADS] (Cited on page 19.)
Feigelson, E.D. and Montmerle, T., 1999, “High-energy processes in young stellar objects”, Annu. Rev. Astron. Astrophys., 37, 363–408. [DOI], [ADS] (Cited on page 35.)
Feldman, U., 1998, “FIP Effect in the Solar Upper Atmosphere: Spectroscopic Results”, Space Sci. Rev., 85, 227–240. [ADS] (Cited on page 10.)
Feldman, U. and Widing, K.G., 2003, “Elemental Abundances in the Solar Upper Atmosphere Derived by Spectroscopic Means”, Space Sci. Rev., 107, 665–720. [ADS] (Cited on page 10.)
Feldman, U., Widing, K.G. and Warren, H.P., 1999, “Morphology of the quiet solar upper atmosphere in the 4 × 104 < Te < 1.4 × 106 K temperature regime”, Astrophys. J., 522, 1133–1147. [ADS] (Cited on page 29.)
Feldman, U., Landi, E. and Schwadron, N.A., 2005, “On the sources of fast and slow solar wind”, J. Geophys. Res., 110, A07109. [ADS] (Cited on page 28.)
Feldman, U., Landi, E. and Doschek, G.A., 2007, “Diagnostics of Suprathermal Electrons in Active-Region Plasmas Using He-like UV Lines”, Astrophys. J., 660, 1674–1682. [ADS] (Cited on page 34.)
Feng, X., Zhou, Y. and Wu, S.T., 2007, “A Novel Numerical Implementation for Solar Wind Modeling by the Modified Conservation Element/Solution Element Method”, Astrophys. J., 655, 1110–1126. [ADS] (Cited on page 24.)
Ferreira, J., Dougados, C. and Cabrit, S., 2006, “Which jet launching mechanism(s)) in T Tauri stars?”, Astron. Astrophys., 453, 785–796. [ADS] (Cited on page 35.)
Feynman, J. and Gabriel, S.B., 2000, “On space weather consequences and predictions”, J. Geophys. Res., 105, 10543–10564. [ADS] (Cited on page 35.)
Filippov, B., Golub, L. and Koutchmy, S., 2009, “X-Ray Jet Dynamics in a Polar Coronal Hole Region”, Solar Phys., 254, 259–269. [ADS] (Cited on page 21.)
Fisher, R. and Guhathakurta, M., 1995, “Physical Properties of Polar Coronal Rays and Holes as Observed with the Spartan 201-01 Coronagraph”, Astrophys. J. Lett., 447, L139–L142. [ADS] (Cited on pages 15 and 17.)
Fisher, R. and Sime, D.G., 1984, “Solar activity cycle variation of the K corona”, Astrophys. J., 285, 354–358. [ADS] (Cited on page 10.)
Fisk, L.A., 2003, “Acceleration of the solar wind as a result of the reconnection of open magnetic flux with coronal loops”, J. Geophys. Res., 108, 1157. [ADS] (Cited on pages 24 and 28.)
Fisk, L.A., 2005, “The open magnetic flux of the Sun: I: Transport by reconnections with coronal loops”, Astrophys. J., 626, 563–573. [ADS] (Cited on pages 24 and 29.)
Fisk, L.A. and Schwadron, N.A., 2001, “The Behavior of the Open Magnetic Field of the Sun”, Astrophys. J., 560, 425–438. [ADS] (Cited on page 29.)
Fisk, L.A. and Zhao, L., 2009, “The heliospheric magnetic field and the solar wind during the solar cycle”, Proc. IAU, 4, 109–120. [DOI], [ADS]. Proceedings of IAU Symposium 257, 15–19 September 2008, Ioannina, Greece (Cited on page 28.))
Fisk, L.A. and Zurbuchen, T.H., 2006, “Distribution and properties of open magnetic flux outside of coronal holes”, J. Geophys. Res., 111, A09115. [ADS] (Cited on page 24.)
Fisk, L.A., Schwadron, N.A. and Zurbuchen, T.H., 1999, “Acceleration of the fast solar wind by the emergence of new magnetic flux”, J. Geophys. Res., 104(A9), 19,765–19,772. [DOI], [ADS] (Cited on pages 24 and 28.)
Frazin, R.A., Vasquez, A.M., Kamalabadi, F. and Park, H., 2007, “Three-dimensional Tomographic Analysis of a High-Cadence LASCO-C2 Polarized Brightness Sequence”, Astrophys. J. Lett., 671, L201–L204. [ADS] (Cited on page 15.)
Gabriel, A.H., 1976, “A magnetic model of the solar transition region”, Philos. Trans. R. Soc. London, Ser. A, 281, 339–352. [ADS] (Cited on page 12.)
Gabriel, A.H., Bely-Dubau, F. and Lemaire, P., 2003, “The contribution of polar plumes to the fast solar wind”, Astrophys. J., 589, 623–634. [ADS] (Cited on page 21.)
Galinsky, V.L. and Shevchenko, V.I., 2000, “Nonlinear Cyclotron Resonant Wave-Particle Interaction in a Nonuniform Magnetic Field”, Phys. Rev. Lett., 85, 90–93. [DOI], [ADS] (Cited on page 29.)
Gardner, L.D., Kohl, J.L., Daigneau, P.S., Smith, P.L., Strachan Jr, L., Howard, R.A., Socker, D.G., Davila, J.M., Noci, G., Romoli, M. and Fineschi, S., 2003, “Advanced Spectroscopic and Coronographic Explorer: science payload design concept”, in Polarimetry in Astronomy, Waikoloa, HI, USA 25 August 2002, (Ed.) Fineschi, S., vol. 4843 of Proceedings of SPIE, pp. 1–7, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 35.)
Gary, S.P. and Borovsky, J.E., 2008, “Damping of long-wavelength kinetic Alfvén fluctuations: Linear theory”, J. Geophys. Res., 113, A12104. [ADS] (Cited on page 31.)
Gibson, S.E., Fludra, A., Bagenal, F., Biesecker, D., Del Zanna, G. and Bromage, B., 1999, “Solar minimum streamer densities and temperatures using Whole Sun Month coordinated data sets”, J. Geophys. Res., 104, 9691–9700. [ADS] (Cited on page 15.)
Giordano, S., Antonucci, E., Noci, G., Romoli, M. and Kohl, J.L., 2000, “Identification of the Coronal Sources of the Fast Solar Wind”, Astrophys. J. Lett., 531, L79–L82. [ADS] (Cited on page 21.)
Gloeckler, G., Zurbuchen, T.H. and Geiss, J., 2003, “Implications of the observed anticorrelation between solar wind speed and coronal electron temperature”, J. Geophys. Res., 108, 1158. [ADS] (Cited on page 29.)
Gold, T., 1955, “The symmetry of the corona of 1954 June 30”, Mon. Not. R. Astron. Soc., 115, 340–342. [ADS] (Cited on page 8.)
Goldreich, P. and Sridhar, S., 1995, “Toward a Theory of Interstellar Turbulence: 2, Strong Alfvénic Turbulence”, Astrophys. J., 438, 763–775. [ADS] (Cited on page 31.)
Goldstein, B.E., Neugebauer, M., Phillips, J.L., Bame, S., Gosling, J.T., McComas, D., Wang, Y.-M., Sheeley Jr, N.R. and Suess, S.T., 1996, “Ulysses plasma parameters: Latitudinal, radial, and temporal variations”, Astron. Astrophys., 316, 296–303. [ADS] (Cited on page 26.)
Goldstein, M.L., Roberts, D.A. and Matthaeus, W.H., 1997, “Magnetohydrodynamic Turbulence in Cosmic Winds”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 521–580, University of Arizona Press, Tucson (Cited on pages 25 and 31.)
Gómez, D.O., Dmitruk, P.A. and Milano, L.J., 2000, “Recent theoretical results on coronal heating”, Solar Phys., 195, 299–318. [ADS] (Cited on page 26.)
Gosling, J.T. and Szabo, A., 2008, “Bifurcated current sheets produced by magnetic reconnection in the solar wind”, J. Geophys. Res., 113, A10103. [ADS] (Cited on page 24.)
Gosling, J.T., Skoug, R.M., McComas, D.J. and Smith, C.W., 2005, “Magnetic disconnection from the Sun: Observations of a reconnection exhaust in the solar wind at the heliospheric current sheet”, Geophys. Res. Lett., 32, L05105. [DOI], [ADS] (Cited on page 24.)
Güdel, M., 2007, “The Sun in Time: Activity and Environment”, Living Rev. Solar Phys., 4, lrsp-2007-3. URL (accessed 1 July 2009): http://www.livingreviews.org/lrsp-2007-3 (Cited on page 35.)
Güdel, M., Audard, M., Briggs, K., Haberl, F., Magee, H., Maggio, A., Mewe, R., Pallavicini, R. and Pye, J., 2001, “The XMM-Newton view of stellar coronae: X-ray spectroscopy of the corona of AB Doradus”, Astron. Astrophys., 365, L336–L343. [DOI], [ADS] (Cited on page 35.)
Güdel, M., Arzner, K., Audard, M. and Mewe, R., 2003, “Tomography of a stellar X-ray corona: α Coronae Borealis”, Astron. Astrophys., 403, 155–171. [DOI], [ADS] (Cited on page 35.)
Gudiksen, B.V., 2005, “DC Heating: Is it Enough?”, in Connecting Sun and Heliosphere, Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, (Eds.) Fleck, B., Zurbuchen, T.H., Lacoste, H., vol. SP-592 of ESA Conference Proceedings, pp. 165–169, ESA Publications Division, Noordwijk. [ADS] (Cited on page 23.)
Guhathakurta, M. and Holzer, T.E., 1994, “Density structure inside a polar coronal hole”, Astrophys. J., 426, 782–786. [ADS] (Cited on page 15.)
Guhathakurta, M., Fludra, A., Gibson, S.E., Biesecker, D. and Fisher, R., 1999a, “Physical properties of a coronal hole from a coronal diagnostic spectrometer, Mauna Loa Coronagraph, and LASCO observations during the Whole Sun Month”, J. Geophys. Res., 104, 9801–9808. [ADS] (Cited on page 15.)
Guhathakurta, M., Sittler, E., Fisher, R., McComas, D. and Thompson, B., 1999b, “Coronal magnetic field topology and source of fast solar wind”, Geophys. Res. Lett., 26, 2901–2904. [ADS] (Cited on page 14.)
Guo, Z., Crabtree, C. and Chen, L., 2008, “Theory of charged particle heating by low-frequency Alfvén waves”, Phys. Plasmas, 15, 032311. [ADS] (Cited on pages 30 and 33.)
Habbal, S.R., Esser, R. and Arndt, M.B., 1993, “How reliable are coronal hole temperatures deduced from observations?”, Astrophys. J., 413, 435–444. [ADS] (Cited on page 17.)
Habbal, S.R., Woo, R. and Arnaud, J., 2001, “On the Predominance of the Radial Component of the Magnetic Field in the Solar Corona”, Astrophys. J., 558, 852–858. [ADS] (Cited on page 14.)
Habbal, S.R., Scholl, I.F. and McIntosh, S.W., 2008, “Impact of Active Regions on Coronal Hole Outflows”, Astrophys. J. Lett., 683, L75–L78. [ADS] (Cited on page 11.)
Hagenaar, H.J., Schrijver, C.J., Title, A.M. and Shine, R.A., 1999, “Dispersal of Magnetic Flux in the Quiet Solar Photosphere”, Astrophys. J., 511, 932–944. [ADS] (Cited on page 28.)
Hagenaar, H.J., DeRosa, M.L. and Schrijver, C.J., 2008, “The Dependence of Ephemeral Region Emergence on Local Flux Imbalance”, Astrophys. J., 678, 541–548. [ADS] (Cited on page 11.)
Hansteen, V.H. and Leer, E., 1995, “Coronal heating, densities, and temperatures and solar wind acceleration”, J. Geophys. Res., 100(A11), 21,577–21,594. [ADS] (Cited on page 27.)
Hansteen, V.H., Leer, E. and Holzer, T.E., 1997, “The Role of Helium in the Outer Solar Atmosphere”, Astrophys. J., 482, 498–509. [ADS] (Cited on page 27.)
Harmon, J.K. and Coles, W.A., 2005, “Modeling radio scattering and scintillation observations of the inner solar wind using oblique Alfvén/ion cyclotron waves”, J. Geophys. Res., 110, A03101. [ADS] (Cited on pages 32 and 34.)
Harra, L.K., Hara, H., Imada, S., Young, P.R., Williams, D.R., Sterling, A.C., Korendyke, C. and Attrill, G.D.R., 2007, “Coronal Dimming Observed with Hinode: Outflows Related to a Coronal Mass Ejection”, Publ. Astron. Soc. Japan, 59, S801–S806. [ADS] (Cited on page 13.)
Hartigan, P., Edwards, S. and Ghandour, L., 1995, “Disk Accretion and Mass Loss from Young Stars”, Astrophys. J., 452, 736–768. [ADS] (Cited on page 35.)
Hartmann, L., 2000, Accretion Processes in Star Formation, vol. 32 of Cambridge Astrophysics Series, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on page 35.)
Harvey, J., Krieger, A.S., Timothy, A.F. and Vaiana, G.S., 1975, “Comparison of Skylab X-ray and Ground-based Helium Observations”, in Skylab Solar Workshop, Prelimary Results from the S-054 X-Ray Telescope and the Correlated Ground-Based Observations, Florence, Italy, 21–22 March 1974, (Ed.) Righini, G., vol. 104 of Oss. Mem. Oss. Astrofis. Arcetri, pp. 50–58, Baccini & Chiappi, Florence. [ADS] (Cited on page 10.)
Harvey, J.W., 1965, “Coronal Polar Rays and Polar Magnetic Fields”, Astrophys. J., 141, 832–833. [ADS] (Cited on page 7.)
Harvey, J.W. and Sheeley Jr, N.R., 1979, “Coronal holes and solar magnetic fields”, Space Sci. Rev., 23, 139–158. [ADS] (Cited on page 5.)
Harvey, K.L. and Recely, F., 2002, “Polar Coronal Holes During Cycles 22 and 23”, Solar Phys., 211, 31–52. [ADS] (Cited on pages 8 and 10.)
Hassler, D.M., Dammasch, I.E., Lemaire, P., Brekke, P., Curdt, W., Mason, H.E., Vial, J.-C. and Wilhelm, K., 1999, “Solar Wind Outflow and the Chromospheric Magnetic Network”, Science, 283(5403), 810–813. [DOI], [ADS] (Cited on page 12.)
He, J.-S., Tu, C.-Y. and Marsch, E., 2007, “Can the solar wind originate from a quiet Sun region?”, Astron. Astrophys., 468, 307–312. [ADS] (Cited on page 24.)
Hefti, S., Grünwaldt, H., Ipavich, F.M., Bochsler, P., Hovestadt, D., Aellig, M.R., Hilchenbach, M., Kallenbach, R., Galvin, A.B., Geiss, J., Gliem, F., Gloeckler, G., Klecker, B., Marsch, E., Möbius, E., Neugebauer, M. and Wurz, P., 1998, “Kinetic properties of solar wind minor ions and protons measured with SOHO/CELIAS”, J. Geophys. Res., 103(A12), 29,697–29,704. [DOI], [ADS] (Cited on page 21.)
Hick, P., Jackson, B.V., Rappoport, S., Woan, G., Slater, G., Strong, K. and Uchida, Y., 1995, “Synoptic IPS and Yohkoh soft X-ray observations”, Geophys. Res. Lett., 22, 643–646. [ADS] (Cited on page 14.)
Hoeksema, J.T. and Scherrer, P.H., 1986, “An atlas of photospheric magnetic field observations and computed coronal magnetic fields: 1976–1985”, Solar Phys., 105, 205–211. [ADS] (Cited on page 14.)
Hollweg, J.V., 1986, “Transition region, corona, and solar wind in coronal holes”, J. Geophys. Res., 91, 4111–4125. [ADS] (Cited on pages 23 and 25.)
Hollweg, J.V., 1990, “Heating of the solar corona”, Comput. Phys. Rep., 12, 205–232. [ADS] (Cited on page 24.)
Hollweg, J.V., 2000, “Compressibility of ion cyclotron and whistler waves: Can radio measurements detect high-frequency waves of solar origin in the corona?”, J. Geophys. Res., 105, 7573–7582. [ADS] (Cited on page 30.)
Hollweg, J.V., 2006, “Drivers of the solar wind: Then and now”, Philos. Trans. R. Soc. London, Ser. A, 364, 505–527. [ADS] (Cited on page 24.)
Hollweg, J.V. and Isenberg, P.A., 2002, “Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction”, J. Geophys. Res., 107(A7), 1147. [DOI], [ADS] (Cited on pages 23, 29, 30, 31, and 34.)
Hollweg, J.V. and Johnson, W., 1988, “Transition region, corona, and solar wind in coronal holes: Some two-fluid models”, J. Geophys. Res., 93, 9547–9554. [ADS] (Cited on page 25.)
Hollweg, J.V. and Markovskii, S.A., 2002, “Cyclotron resonances of ions with obliquely propagating waves in coronal holes and the fast solar wind”, J. Geophys. Res., 107(A6), 1080. [DOI], [ADS] (Cited on page 32.)
Hossain, M., Gray, P.C., Pontius, D.H., Matthaeus, W.H. and Oughton, S., 1995, “Phenomenology for the decay of energy-containing eddies in homogeneous MHD turbulence”, Phys. Fluids, 7, 2886–2904. [ADS] (Cited on page 25.)
Huber, M.C.E., Foukal, P.V., Noyes, R.W., Reeves, E.M., Schmahl, E.J., Timothy, J.G., Vernazza, J.E. and Withbroe, G.L., 1974, “Extreme-ultraviolet observations of coronal holes: Initial results from Skylab”, Astrophys. J. Lett., 194, L115–L118. [ADS] (Cited on page 8.)
Hudson, H.S., 2002, “Coronal holes as seen in soft X-rays by Yohkoh”, in From Solar Min to Max: Half a Solar Cycle with SOHO, Proceedings of the SOHO-11 Symposium, 11–15 March 2002, Davos, Switzerland, (Ed.) Wilson, A., vol. SP-508 of ESA Conference Proceedings, pp. 341–349, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 5, 10, and 13.)
Hundhausen, A.J., 1972, Coronal Expansion and the Solar Wind, vol. 5 of Physics and Chemistry in Space, Springer, Berlin; New York (Cited on page 8.)
Isenberg, P.A., 1990, “Investigations of a turbulence-driven solar wind model”, J. Geophys. Res., 95, 6437–6442. [ADS] (Cited on page 25.)
Isenberg, P.A., 2001, “Heating of coronal holes and generation of the solar wind by ion-cyclotron resonance”, Space Sci. Rev., 95(1/2), 119–131. [DOI], [ADS] (Cited on pages 29 and 30.)
Isenberg, P.A. and Vasquez, B.J., 2009, “Preferential acceleration and perpendicular heating of minor ions in a collisionless coronal hole”, Astrophys. J., 696, 591–600. [ADS] (Cited on page 29.)
Isenberg, P.A., Lee, M.A. and Hollweg, J.V., 2001, “The kinetic shell model of coronal heating and acceleration by ion-cyclotron waves: 1. Outward propagating waves”, J. Geophys. Res., 106 (A4), 5649–5660. [ADS] (Cited on page 33.)
Janardhan, P., Tripathi, D. and Mason, H.E., 2008, “The solar wind disappearance event of 11 May 1999: Source region evolution”, Astron. Astrophys., 488, L1–L4. [ADS] (Cited on page 11.)
Janse, Å.M., Lie-Svendsen, Ø. and Leer, E., 2007, “Solar wind originating in funnels: fast or slow?”, Astron. Astrophys., 474, 997–1013. [ADS] (Cited on page 27.)
Jardine, M. and van Ballegooijen, A.A., 2005, “Slingshot prominences above stellar X-ray coronae”, Mon. Not. R. Astron. Soc., 361, 1173–1179. [ADS] (Cited on page 35.)
Jiang, Y.W., Liu, S. and Petrosian, V., 2009, “Cascade and Damping of Alfvén-Cyclotron Fluctuations: Application to Solar Wind Turbulence”, Astrophys. J., 698, 163–183. [ADS] (Cited on page 32.)
Jones, H.P., 2005, “Magnetic Fields and Flows in Open Magnetic Structures”, in Large-scale Structures and their Role in Solar Activity, Proceedings of the 22nd Sacramento Peak Workshop, held at the National Solar Observatory, Sacramento Peak, Sunspot, New Mexico, USA, 18–22 October 2004, (Eds.) Sankarasubramanian, K., Penn, M., Pevtsov, A., vol. 346 of ASP Conference Series, pp. 229–244, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on pages 5 and 14.))
Kahler, S., 2000, “Skylab”, in Encyclopedia of Astronomy and Astrophysics, (Ed.) Murdin, P., p. 2238, Institute of Physics Publishing, Bristol. [DOI], [ADS] (Cited on page 8.)
Khazanov, I. and Singh, N., 2007, “Ion and electron accelerations by large-scale shear Alfvén waves via cross-field instabilities”, Geophys. Res. Lett., 34, L20 111. [ADS] (Cited on pages 30 and 33.)
Klimchuk, J.A., 2006, “On Solving the Coronal Heating Problem”, Solar Phys., 234, 41–77. [ADS] (Cited on page 23.)
Ko, Y.-K., Fisk, L.A., Gloeckler, G. and Geiss, J., 1996, “Limitations on suprathermal tails of electrons in the lower solar corona”, Geophys. Res. Lett., 23, 2785–2788. [ADS] (Cited on page 34.)
Ko, Y.-K., Fisk, L.A., Geiss, J., Gloeckler, G. and Guhathakurta, M., 1997, “An Empirical Study of the Electron Temperature and Heavy Ion Velocities in the South Polar Coronal Hole”, Solar Phys., 171, 345–361. [ADS] (Cited on page 17.)
Kohl, J.L. and Cranmer, S.R. (Eds.), 1999, Coronal Holes and Solar Wind Acceleration, Proceedings of the SOHO-7 Workshop, held at Asticou Inn in Northeast Harbor, Maine, USA from 28 September–1 October 1998, Kluwer Academic Publishers, Dordrecht; Boston. [Google Books]. Reprinted from Space Sci. Rev., 87, (1–2), 1999 (Cited on page 5.)
Kohl, J.L. and Withbroe, G.L., 1982, “EUV spectroscopic plasma diagnostics for the solar wind acceleration region”, Astrophys. J., 256, 263–270. [ADS] (Cited on pages 17 and 20.)
Kohl, J.L., Reeves, E.M. and Kirkham, B., 1978, “The Lyman Alpha Coronagraph”, in New Instrumentation for Space Astronomy, Proceedings of the 20th COSPAR Meeting, Tel Aviv, Israel, 7–18 June 1977, (Eds.) van der Hucht, K.A., Viana, G., pp. 91–94, Pergamon Press, Oxford; New York. [ADS] (Cited on page 8.)
Kohl, J.L., Weiser, H., Withbroe, G.L., Noyes, R.W., Parkinson, W.H., Reeves, E.M., Munro, R.H. and MacQueen, R.M., 1980, “Measurements of coronal kinetic temperatures from 1.5 to 3 solar radii”, Astrophys. J. Lett., 241, L117–L121. [ADS] (Cited on page 8.)
Kohl, J.L., Esser, R., Gardner, L.D., Habbal, S., Daigneau, P.S., Dennis, E.F., Nystrom, G.U., Panasyuk, A., Raymond, J.C., Smith, P.L., Strachan, L., van Ballegooijen, A.A., Noci, G., Fineschi, S., Romoli, M., Ciaravella, A., Modigliani, A., Huber, M.C.E., Antonucci, E., Benna, C., Giordano, S., Tondello, G., Nicolosi, P., Naletto, G., Pernechele, C., Spadaro, D., Poletto, G., Livi, S., von der Lühe, O., Geiss, J., Timothy, J.G., Gloeckler, G., Allegra, A., Basile, G., Brusa, R., Wood, B., Siegmund, O.H.W., Fowler, W., Fisher, R. and Jhabvala, M., 1995, “The Ultraviolet Coronagraph Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 313–356. [ADS] (Cited on pages 15 and 17.)
Kohl, J.L., Noci, G., Antonucci, E., Tondello, G., Huber, M.C.E., Gardner, L.D., Nicolosi, P., Strachan, L., Fineschi, S., Raymond, J.C., Romoli, M., Spadaro, D., Panasyuk, A., Siegmund, O.H.W., Benna, C., Ciaravella, A., Cranmer, S.R., Giordano, S., Karovska, M., Martin, R., Michels, J., Modigliani, A., Naletto, G., Pernechele, C., Poletto, G. and Smith, P.L., 1997, “First Results from the SOHO Ultraviolet Coronagraph Spectrometer”, Solar Phys., 175, 613–644. [ADS] (Cited on pages 17, 18, 19, and 21.)
Kohl, J.L., Noci, G., Antonucci, E., Tondello, G., Huber, M.C.E., Cranmer, S.R., Strachan, L., Panasyuk, A.V., Gardner, L.D., Romoli, M., Fineschi, S., Dobrzycka, D., Raymond, J.C., Nicolosi, P., Siegmund, O.H.W., Spadaro, D., Benna, C., Ciaravella, A., Giordano, S., Habbal, S.R., Karovska, M., Li, X., Martin, R., Michels, J.G., Modigliani, A., Naletto, G., O’Neal, R.H., Pernechele, C., Poletto, G., Smith, P.L. and Suleiman, R.M., 1998, “UVCS/SOHO empirical determinations of anisotropic velocity distributions in the solar corona”, Astrophys. J. Lett., 501, L127–L131. [DOI], [ADS] (Cited on pages 17 and 20.)
Kohl, J.L., Esser, R., Cranmer, S.R., Fineschi, S., Gardner, L.D., Panasyuk, A.V., Strachan, L., Suleiman, R.M., Frazin, R.A. and Noci, G., 1999, “EUV Spectral Line Profiles in Polar Coronal Holes from 1.3 to 3.0 R⊙”, Astrophys. J. Lett., 510, L59–L62. [ADS] (Cited on page 18.)
Kohl, J.L., Noci, G., Cranmer, S.R. and Raymond, J.C., 2006, “Ultraviolet spectroscopy of the extended solar corona”, Astron. Astrophys. Rev., 13, 31–157. [ADS] (Cited on pages 8, 15, 17, 18, 20, 21, 29, and 35.)
Kojima, M., Tokumaru, M., Fujiki, K., Itoh, H., Murakami, T. and Hakamada, K., 2007, “What Coronal Parameters Determine Solar Wind Speed?”, in New Solar Physics with Solar-B Mission, Proceedings of the Sixth Solar-B Science Meeting held 8–11 November 2005 at Kyoto, Japan, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, pp. 549–555, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 28.)
Krieger, A.S., Timothy, A.F. and Roelof, E.C., 1973, “A Coronal Hole and Its Identification as the Source of a High Velocity Solar Wind Stream”, Solar Phys., 29, 505–525. [DOI], [ADS] (Cited on pages 8 and 14.)
Krista, L.D. and Gallagher, P.T., 2009, “Automated Coronal Hole Detection Using Local Intensity Thresholding Techniques”, Solar Phys., 256, 87–100. [ADS] (Cited on page 10.)
Kwan, J., Edwards, S. and Fischer, W., 2007, “Modeling T Tauri Winds from He I 10830 Å Profiles”, Astrophys. J., 657, 897–915. [ADS] (Cited on page 10.)
Lada, C.J., 1985, “Cold outflows, energetic winds, and enigmatic jets around young stellar objects”, Annu. Rev. Astron. Astrophys., 23, 267–317. [ADS] (Cited on page 35.)
Lamers, H.J.G.L.M. and Cassinelli, J.P., 1999, Introduction to Stellar Winds, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on page 35.)
Laming, J.M., 2004, “A Unified Picture of the First Ionization Potential and Inverse First Ionization Potential Effects”, Astrophys. J., 614, 1063–1072. [ADS] (Cited on page 27.)
Laming, J.M., 2009, “Non-WKB Models of the FIP Effect: Implications for Solar Coronal Heating and the Coronal Helium and Neon Abundances”, Astrophys. J., 695, 954–969. [ADS] (Cited on page 27.)
Laming, J.M. and Lepri, S.T., 2007, “Ion Charge States in the Fast Solar Wind: New Data Analysis and Theoretical Refinements”, Astrophys. J., 660, 1642–1652. [ADS] (Cited on page 17.)
Landi, E., 2008, “The off-disk thermal structure of a polar coronal hole”, Astrophys. J., 685, 1270–1276. [ADS] (Cited on pages 17 and 18.)
Landi, E. and Cranmer, S.R., 2009, “Ion temperatures in the low solar corona: Polar coronal holes at solar minimum”, Astrophys. J., 691, 794–805. [ADS] (Cited on pages 17, 18, and 32.)
Leamon, R.J. and McIntosh, S.W., 2007, “Empirical Solar Wind Forecasting from the Chromosphere”, Astrophys. J., 659, 738–742. [ADS] (Cited on page 23.)
Leamon, R.J., Smith, C.W., Ness, N.F. and Wong, H.K., 1999, “Dissipation range dynamics: Kinetic Alfvén waves and the importance of βe”, J. Geophys. Res., 104, 22 331–22 344. [ADS] (Cited on page 31.)
Lee, L.C. and Wu, B.H., 2000, “Heating and Acceleration of Protons and Minor Ions by Fast Shocks in the Solar Corona”, Astrophys. J., 535, 1014–1026. [ADS] (Cited on pages 30 and 31.)
Leer, E. and Holzer, T.E., 1980, “Energy addition in the solar wind”, J. Geophys. Res., 85, 4681–4688. [ADS] (Cited on page 26.)
Leer, E., Holzer, T.E. and Flå, T., 1982, “Acceleration of the solar wind”, Space Sci. Rev., 33, 161–200. [ADS] (Cited on page 26.)
Lemaire, J. and Pierrard, V., 2001, “Kinetic models of solar and polar winds”, Astrophys. Space Sci., 277, 169–180. [ADS] (Cited on page 36.)
Levine, R.H., 1974, “A new theory of coronal heating”, Astrophys. J., 190, 457–466. [ADS] (Cited on page 33.)
Levine, R.H., 1982, “Open Magnetic Fields and the Solar Cycle. I: Photospheric Sources of Open Magnetic Flux”, Solar Phys., 79, 203–230. [DOI], [ADS] (Cited on page 11.)
Li, X. and Habbal, S.R., 2001, “Damping of fast and ion cyclotron oblique waves in the multi-ion fast solar wind”, J. Geophys. Res., 106, 10 669–10 680. [ADS] (Cited on pages 30 and 32.)
Li, X., Habbal, S.R., Kohl, J. and Noci, G., 1998, “The Effect of Temperature Anisotropy on Observations of Doppler Dimming and Pumping in the Inner Corona”, Astrophys. J. Lett., 501, L133–L137. [ADS] (Cited on page 20.)
Li, X., Habbal, S.R., Hollweg, J.V. and Esser, R., 1999, “Heating and cooling of protons by turbulence-driven ion-cyclotron waves in the fast solar wind”, J. Geophys. Res., 104(A2), 2521–2535. [DOI], [ADS] (Cited on page 25.)
Liewer, P.C., Neugebauer, M. and Zurbuchen, T., 2004, “Characteristics of active-region sources of solar wind near solar maximum”, Solar Phys., 223, 209–229. [ADS] (Cited on page 14.)
Lippincott, S.L., 1957, “Chromospheric Spicules”, Smithsonian Contrib. Astrophys., 2, 15–23. [ADS] (Cited on page 7.)
Longcope, D., 2004, “Quantifying Magnetic Reconnection and the Heat it Generates”, in Coronal Heating, Proceedings of the SOHO-15 Workshop, 6–9 September 2004, St. Andrews, Scotland, UK, (Eds.) Walsh, R.W., Ireland, J., Danesy, D., Fleck, B., vol. SP-575 of ESA Conference Proceedings, pp. 198–209, ESA Publications Division, Noordwijk. [ADS] (Cited on page 23.)
Longcope, D.W., 1996, “Topology and Current Ribbons: A Model for Current, Reconnection, and Flaring in a Complex, Evolving Corona”, Solar Phys., 169, 91–121. [DOI], [ADS] (Cited on page 29.)
Longcope, D.W. and Kankelborg, C.C., 1999, “Coronal Heating by Collision and Cancellation of Magnetic Elements”, Astrophys. J., 524, 483–495. [ADS] (Cited on page 29.)
Lu, Q. and Li, X., 2007, “Heating of ions by low-frequency Alfvén waves”, Phys. Plasmas, 14, 042303. [ADS] (Cited on pages 30 and 33.)
Luhmann, J.G., Li, Y., Arge, C.N., Gazis, P.R. and Ulrich, R., 2002, “Solar cycle changes in coronal holes and space weather cycles”, J. Geophys. Res., 107, 1154. [ADS] (Cited on page 14.)
Luo, Q. and Melrose, D., 2006, “Anisotropic weak turbulence of Alfvén waves in collisionless astrophysical plasmas”, Mon. Not. R. Astron. Soc., 368, 1151–1158. [ADS] (Cited on page 32.)
MacBride, B.T., Smith, C.W. and Forman, M.A., 2008, “The Turbulent Cascade at 1 AU: Energy Transfer and the Third-Order Scaling for MHD”, Astrophys. J., 679, 1644–1660. [ADS] (Cited on page 32.)
Malanushenko, O.V. and Jones, H.P., 2004, “Analysis of He I 1083 nm Imaging Spectroscopy Using a Spectral Standard”, Solar Phys., 222, 43–60. [ADS] (Cited on page 12.)
Mancuso, S., Raymond, J.C., Kohl, J., Ko, Y.-K., Uzzo, M. and Wu, R., 2002, “UVCS/SOHO observations of a CME-driven shock: Consequences on ion heating mechanisms behind a coronal shock”, Astron. Astrophys., 383, 267–274. [ADS] (Cited on page 31.)
Markovskii, S.A., 2001, “Generation of ion-cyclotron waves in coronal holes by a global resonant magnetohydrodynamic mode”, Astrophys. J., 557, 337–342. [DOI], [ADS] (Cited on pages 30 and 32.)
Markovskii, S.A. and Hollweg, J.V., 2002, “Electron heat flux instabilities in coronal holes: Implications for ion heating”, Geophys. Res. Lett., 29, 1843. [ADS] (Cited on pages 24, 30, and 31.)
Markovskii, S.A. and Hollweg, J.V., 2004, “Intermittent Heating of the Solar Corona by Heat Flux-generated Ion Cyclotron Waves”, Astrophys. J., 609, 1112–1122. [ADS] (Cited on pages 24, 30, and 31.)
Markovskii, S.A., Vasquez, B.J., Smith, C.W. and Hollweg, J.V., 2006, “Dissipation of the Perpendicular Turbulent Cascade in the Solar Wind”, Astrophys. J., 639, 1177–1185. [ADS] (Cited on pages 30 and 31.)
Markovskii, S.A., Vasquez, B.J. and Hollweg, J.V., 2009, “Proton heating by nonlinear field-aligned Alfvén waves in solar coronal holes”, Astrophys. J., 695, 1413–1420. [ADS] (Cited on page 33.)
Marsch, E., 1999, “Solar wind models from the sun to 1 AU: Constraints by in situ and remote sensing measurements”, Space Sci. Rev., 87(1/2), 1–24. [DOI], [ADS] (Cited on page 23.)
Marsch, E., 2005, “Importance of Kinetic Effects in Heating the Open and Closed Corona”, in Connecting Sun and Heliosphere, Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, (Eds.) Fleck, B., Zurbuchen, T.H., Lacoste, H., vol. SP-592 of ESA Conference Proceedings, pp. 191–198, ESA Publications Division, Noordwijk. [ADS] (Cited on page 29.)
Marsch, E., 2006, “Kinetic Physics of the Solar Corona and Solar Wind”, Living Rev. Solar Phys., 3, lrsp-2006-1. URL (accessed 1 July 2009): http://www.livingreviews.org/lrsp-2006-1 (Cited on pages 21 and 29.)
Marsch, E., Mühlhäuser, K.-H., Schwenn, R., Rosenbauer, H., Pilipp, W.G. and Neubauer, F.M., 1982, “Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 AU”, J. Geophys. Res., 87, 52–72. [DOI], [ADS] (Cited on page 21.)
Marsch, E., Tian, H., Sun, J., Curdt, W. and Wiegelmann, T., 2008, “Plasma flows guided by strong magnetic fields in the solar corona”, Astrophys. J., 685, 1262–1269. [ADS] (Cited on page 12.)
Marsden, R.G. and Fleck, B., 2007, “Solar Orbiter: A Mission Update”, in The Physics of Chromospheric Plasmas, Proceedings of the conference held 9–13 October, 2006 at the University of Coimbra, Portugal, (Eds.) Heinzel, P., Dorotovic, I., Rutten, R.J., vol. 368 of ASP Conference Series, p. 645, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 35.)
Matthaeus, W.H., Zank, G.P., Oughton, S., Mullan, D.J. and Dmitruk, P., 1999, “Coronal Heating by Magnetohydrodynamic Turbulence Driven by Reflected Low-Frequency Waves”, Astrophys. J. Lett., 523, L93–L96. [ADS] (Cited on pages 23 and 25.)
Matthaeus, W.H., Dmitruk, P., Oughton, S. and Mullan, D., 2003, “Turbulent dissipation in the solar wind and corona”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., vol. 679 of AIP Conference Proceedings, pp. 427–432, American Institute of Physics, Melville, NY. [ADS] (Cited on pages 30 and 32.)
McComas, D.J., Bame, S.J., Barker, P., Feldman, W.C., Phillips, J.L., Riley, P. and Griffee, J.W., 1998, “Solar Wind Electron Proton Alpha Monitor (SWEPAM)) for the Advanced Composition Explorer”, Space Sci. Rev., 86, 563–612. [ADS] (Cited on page 27.)
McComas, D.J., Elliott, H.A., Gosling, J.T., Reisenfeld, D.B., Skoug, R.M., Goldstein, B.E., Neugebauer, M. and Balogh, A., 2002, “Ulysses’ second fast-latitude scan: Complexity near solar maximum and the reformation of polar coronal holes”, Geophys. Res. Lett., 29, 1290. [ADS] (Cited on page 10.)
McComas, D.J., Velli, M., Lewis, W.S., Acton, L.W., Balat-Pichelin, M., Bothmer, V., Dirling, R.B., Feldman, W.C., Gloeckler, G., Habbal, S.R., Hassler, D.M., Mann, I., Matthaeus, W.H., McNutt, R.L., Mewaldt, R.A., Murphy, N., Ofman, L., Sittler, E.C., Smith, C.W. and Zurbuchen, T.H., 2007, “Understanding coronal heating and solar wind acceleration: Case for in situ near-Sun measurements”, Rev. Geophys., 45, RG1004. [DOI], [ADS] (Cited on page 35.)
McIntosh, S.W., 2009, “The Inconvenient Truth About Coronal Dimmings”, Astrophys. J., 693, 1306–1309. [ADS] (Cited on page 13.)
McIntosh, S.W., Davey, A.R., Hassler, D.M., Armstrong, J.D., Curdt, W., Wilhelm, K. and Lin, G., 2007, “Observations Supporting the Role of Magnetoconvection in Energy Supply to the Quiescent Solar Atmosphere”, Astrophys. J., 654, 650–664. [ADS] (Cited on pages 23 and 24.)
Mecheri, R. and Marsch, E., 2008, “Drift instabilities in the solar corona within the multi-fluid description”, Astron. Astrophys., 481, 853–860. [ADS] (Cited on page 32.)
Medvedev, M.V., 2000, “Particle Heating by Nonlinear Alfvénic Turbulence in Advection-dominated Accretion Flows”, Astrophys. J., 541, 811–820. [ADS] (Cited on page 33.)
Mikhailenko, V.S., Mikhailenko, V.V. and Stepanov, K.N., 2008, “Ion cyclotron instabilities of parallel shear flow of collisional plasma”, Phys. Plasmas, 15, 092901. [ADS] (Cited on page 31.)
Miller, J.A., 1908, “The Determination of the Heliocentric Position of a Certain Class of Coronal Streamers”, Astrophys. J., 27, 286–295. [ADS] (Cited on page 7.)
Miralles, M.P., Cranmer, S.R. and Kohl, J.L., 2001a, “Ultraviolet Coronagraph Spectrometer Observations of a High-Latitude Coronal Hole with High Oxygen Temperatures and the Next Solar Cycle Polarity”, Astrophys. J. Lett., 560, L193–L196. [ADS] (Cited on page 10.)
Miralles, M.P., Cranmer, S.R., Panasyuk, A.V., Romoli, M. and Kohl, J.L., 2001b, “Comparison of empirical models for polar and equatorial coronal holes”, Astrophys. J. Lett., 549, L257–L260. [ADS] (Cited on page 21.)
Miralles, M.P., Cranmer, S.R. and Kohl, J.L., 2004, “Low-latitude coronal holes during solar maximum”, Adv. Space Res., 33(5), 696–700. [ADS] (Cited on page 21.)
Miralles, M.P., Cranmer, S.R. and Kohl, J.L., 2006, “Coronal Hole Properties During the First Decade of UVCS/SOHO”, in SOHO-17: 10 Years of SOHO and Beyond, Proceedings of the conference held 7–12 May 2006 at Giardini Naxos, Sicily, Italy, (Eds.) Lacoste, H., Ouwehand, L., vol. SP-617 of ESA Conference Proceedings, pp. 15.1–15.4, ESA Publications Division, Noordwijk. [ADS] (Cited on page 21.)
Miralles, M.P., Cranmer, S.R., Raymond, J.C. and Kohl, J.L., 2007, “Multi-Instrument Searches for Polar Jets: Characterizing Jet Heating and Cooling”, 24th IUGG General Assembly, IAGA Symposium ASIV030, conference paper. [ADS] (Cited on page 22.))
Mitchell, S.A., 1932, “The Spectrum of the Corona”, Astrophys. J., 75, 1–33. [ADS] (Cited on page 7.)
Moreno-Insertis, F., Galsgaard, K. and Ugarte-Urra, I., 2008, “Jets in Coronal Holes: Hinode Observations and Three-dimensional Computer Modeling”, Astrophys. J. Lett., 673, L211–L214. [ADS] (Cited on page 24.)
Morgan, H., Habbal, S.R., Rifai, S. and Li, X., 2004, “Hydrogen Lyα Intensity Oscillations Observed by the Solar and Heliospheric Observatory Ultraviolet Coronagraph Spectrometer”, Astrophys. J., 605, 521–527. [ADS] (Cited on page 16.)
Mullan, D.J. and Yakovlev, O.I., 1995, “Remote Sensing of the Solar Wind Using Radio Waves: Part I”, Irish Astron. J., 22, 119–136. [ADS] (Cited on page 25.)
Munro, R.H. and Jackson, B.V., 1977, “Physical properties of a polar coronal hole from 2 to 5 solar radii”, Astrophys. J., 213, 874–886. [ADS] (Cited on page 15.)
Munro, R.H. and Withbroe, G.L., 1972, “Properties of a Coronal ‘hole’ Derived from Extreme-Ultraviolet Observations”, Astrophys. J., 176, 511–520. [ADS] (Cited on page 7.)
Neugebauer, M., Forsyth, R.J., Galvin, A.B., Harvey, K.L., Hoeksema, J.T., Lazarus, A.J., Lepping, R.P., Linker, J.A., Mikic, Z., Steinberg, J.T., von Steiger, R., Wang, Y.-M. and Wimmer-Schweingruber, R.F., 1998, “Spatial structure of the solar wind and comparisons with solar data and models”, J. Geophys. Res., 103, 14 587–14 600. [ADS] (Cited on pages 14 and 21.)
Neupert, W.M. and Pizzo, V., 1974, “Solar coronal holes as sources of recurrent geomagnetic disturbances”, J. Geophys. Res., 79, 3701–3709. [ADS] (Cited on page 8.)
Newkirk Jr, G., 1967, “Structure of the Solar Corona”, Annu. Rev. Astron. Astrophys., 5, 213–266. [ADS] (Cited on page 7.)
Newkirk Jr, G. and Harvey, J., 1968, “Coronal Polar Plumes”, Solar Phys., 3, 321–343. [ADS] (Cited on page 7.)
Ng, C.S. and Bhattacharjee, A., 2008, “A Constrained Tectonics Model for Coronal Heating”, Astrophys. J., 675, 899–905. [ADS] (Cited on page 29.)
Noci, G., 1973, “Energy Budget in Coronal Holes”, Solar Phys., 28, 403–407. [ADS] (Cited on page 8.)
Noci, G., Kohl, J.L. and Withbroe, G.L., 1987, “Solar wind diagnostics from Doppler-enhanced scattering”, Astrophys. J., 315, 706–715. [ADS] (Cited on page 20.)
Noci, G., Kohl, J.L., Antonucci, E., Tondello, G., Huber, M.C.E., Fineschi, S., Gardner, L.D., Naletto, G., Nicolosi, P., Raymond, J.C., Romoli, M., Spadaro, D., Siegmund, O.H.W., Benna, C., Ciaravella, A., Giordano, S., Michels, J., Modigliani, A., Panasyuk, A., Pernechele, C., Poletto, G., Smith, P.L. and Strachan, L., 1997, “First results from UVCS/SOHO”, Adv. Space Res., 20(12), 2219–2230. [ADS] (Cited on page 21.)
Nolte, J.T., Krieger, A.S., Timothy, A.F., Gold, R.E., Roelof, E.C., Vaiana, G., Lazarus, A.J., Sullivan, J.D. and McIntosh, P.S., 1976, “Coronal holes as sources of solar wind”, Solar Phys., 46, 303–322. [ADS] (Cited on pages 14 and 21.)
Ofman, L., 2005, “MHD Waves and Heating in Coronal Holes”, Space Sci. Rev., 120, 67–94. [ADS] (Cited on page 5.)
Ofman, L., Nakariakov, V.M. and DeForest, C.E., 1999, “Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 514, 441–447. [DOI], [ADS] (Cited on page 16.)
Ofman, L., Romoli, M., Poletto, G., Noci, G. and Kohl, J.L., 2000, “UVCS WLC Observations of Compressional Waves in the South Polar Coronal Hole”, Astrophys. J., 529, 592–598. [DOI], [ADS] (Cited on page 16.)
Oughton, S., Dmitruk, P. and Matthaeus, W.H., 2004, “Reduced magnetohydrodynamics and parallel spectral transfer”, Phys. Plasmas, 11, 2214–2225. [ADS] (Cited on page 31.)
Oughton, S., Dmitruk, P. and Matthaeus, W.H., 2006, “A two-component phenomenology for homogeneous magnetohydrodynamic turbulence”, Phys. Rev. Lett., 13, 042306. [ADS] (Cited on page 26.)
Pagel, A.C., Crooker, N.U., Zurbuchen, T.H. and Gosling, J.T., 2004, “Correlation of solar wind entropy and oxygen ion charge state ratio”, J. Geophys. Res., 109, A01113. [DOI], [ADS] (Cited on page 27.)
Parashar, T.N., Shay, M.A., Cassak, P.A. and Matthaeus, W.H., 2009, “Kinetic dissipation and anisotropic heating in a turbulent collisionless plasma”, Phys. Plasmas, 16, 032310. [ADS] (Cited on page 32.)
Parhi, S., Suess, S.T. and Sulkanen, M., 1999, “Can Kelvin-Helmholtz instabilities of jet-like structures and plumes cause solar wind fluctuations at 1 AU?”, J. Geophys. Res., 104, 14 781–14 788. [ADS] (Cited on page 17.)
Pariat, E., Antiochos, S.K. and DeVore, C.R., 2009, “A model for solar polar jets”, Astrophys. J., 691, 61–74. [ADS] (Cited on page 24.)
Parker, E.N., 1958a, “Dynamics of the Interplanetary Gas and Magnetic Fields”, Astrophys. J., 128, 664–676. [DOI], [ADS] (Cited on page 26.)
Parker, E.N., 1958b, “Suprathermal particle generation in the solar corona”, Astrophys. J., 128, 677–685. [ADS] (Cited on page 33.)
Parker, E.N., 1991, “Heating solar coronal holes”, Astrophys. J., 372, 719–727. [ADS] (Cited on page 5.)
Parnell, C.E., 2007, “3D magnetic reconnection, flares and coronal heating”, Mem. Soc. Astron. Ital., 78, 229–235. [ADS] (Cited on page 29.)
Pasachoff, J.M., Rušin, V., Druckmüller, M. and Saniga, M., 2007, “Fine Structures in the White-Light Solar Corona at the 2006 Eclipse”, Astrophys. J., 665, 824–829. [ADS] (Cited on page 32.)
Peter, H. and Judge, P.G., 1999, “On the Doppler Shifts of Solar Ultraviolet Emission Lines”, Astrophys. J., 522, 1148–1166. [ADS] (Cited on page 12.)
Pevtsov, A.A., Fisher, G.H., Acton, L.W., Longcope, D.W., Johns-Krull, C.M., Kankelborg, C.C. and Metcalf, T.R., 2003, “The Relationship Between X-Ray Radiance and Magnetic Flux”, Astrophys. J., 598, 1387–1391. [DOI], [ADS] (Cited on page 28.)
Piddington, J.H., 1972, “A model of the quiet solar atmosphere”, Solar Phys., 27, 402–419. [ADS] (Cited on pages 7 and 8.)
Pierrard, V. and Lamy, H., 2003, “The effects of the velocity filtration mechanism on the minor ions of the corona”, Solar Phys., 216, 47–58. [ADS] (Cited on pages 30 and 34.)
Pierrard, V., Lamy, H. and Lemaire, J., 2004, “Exospheric distributions of minor ions in the solar wind”, J. Geophys. Res., 109(A2), A02118. [DOI], [ADS] (Cited on pages 30 and 34.)
Pinto, R., Grappin, R., Wang, Y.-M. and Léorat, J., 2009, “Time-dependent hydrodynamical simulations of slow solar wind, coronal inflows, and polar plumes”, Astron. Astrophys., 497, 537–543. [ADS] (Cited on page 28.)
Pneuman, G.W., 1968, “Some General Properties of Helmeted Coronal Structures”, Solar Phys., 3, 578–597. [ADS] (Cited on page 7.)
Pneuman, G.W., 1973, “The Solar Wind and the Temperature-Density Structure of the Solar Corona”, Solar Phys., 28, 247–262. [ADS] (Cited on page 8.)
Pneuman, G.W., 1980, “The physical structure of coronal holes: Influence of magnetic fields and coronal heating”, Astron. Astrophys., 81, 161–166. [ADS] (Cited on page 26.)
Podesta, J.J. and Bhattacharjee, A., 2009, “Theory of incompressible MHD turbulence with crosshelicity”, Phys. Rev. Lett., submitted. [arXiv:0903.5041] (Cited on page 25.)
Poduval, B. and Zhao, X.P., 2004, “Discrepancies in the prediction of solar wind using potential field source surface model: An investigation of possible sources”, J. Geophys. Res., 109, A08102. [ADS] (Cited on page 14.)
Poletto, G., Suess, S.T., Biesecker, D.A., Esser, R., Gloeckler, G., Ko, Y.-K. and Zurbuchen, T.H., 2002, “Low-latitude solar wind during the Fall 1998 SOHO-Ulysses quadrature”, J. Geophys. Res., 107(A10), 1300. [DOI], [ADS] (Cited on page 21.)
Priest, E.R. and Forbes, T.G., 2000, Magnetic Reconnection: MHD Theory and Applications, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on page 28.))
Priest, E.R., Heyvaerts, J.F. and Title, A.M., 2002, “A Flux-Tube Tectonics Model for Solar Coronal Heating Driven by the Magnetic Carpet”, Astrophys. J., 576, 533–551. [ADS] (Cited on page 29.)
Ralchenko, Y., Feldman, U. and Doschek, G.A., 2007, “Is There a High-Energy Particle Population in the Quiet Solar Corona?”, Astrophys. J., 659, 1682–1692. [ADS] (Cited on page 34.)
Raouafi, N.-E. and Solanki, S.K., 2004, “Effect of the electron density stratification on off-limb O VI line profiles: How large is the velocity distribution anisotropy in the solar corona?”, Astron. Astrophys., 427, 725–733. [ADS] (Cited on page 20.)
Raouafi, N.-E. and Solanki, S.K., 2006, “Sensitivity of solar off-limb line profiles to electron density stratification and the velocity distribution anisotropy”, Astron. Astrophys., 445, 735–745. [ADS] (Cited on page 20.)
Raouafi, N.-E., Harvey, J.W. and Solanki, S.K., 2007, “Properties of Solar Polar Coronal Plumes Constrained by Ultraviolet Coronagraph Spectrometer Data”, Astrophys. J., 658, 643–656. [ADS] (Cited on pages 20 and 21.)
Raouafi, N.-E., Petrie, G.J.D., Norton, A.A., Henney, C.J. and Solanki, S.K., 2008, “Evidence for Polar Jets as Precursors of Polar Plume Formation”, Astrophys. J. Lett., 682, L137–L140. [ADS] (Cited on page 22.)
Rappazzo, A.F., Velli, M., Einaudi, G. and Dahlburg, R.B., 2008, “Nonlinear Dynamics of the Parker Scenario for Coronal Heating”, Astrophys. J., 677, 1348–1366. [ADS] (Cited on page 26.)
Reisenfeld, D.B., McComas, D.J. and Steinberg, J.T., 1999, “Evidence of a solar origin for pressure balance structures in the high-latitude solar wind”, Geophys. Res. Lett., 26, 1805–1808. [DOI], [ADS] (Cited on page 17.)
Reisenfeld, D.B., Gary, S.P., Gosling, J.T., Steinberg, J.T., McComas, D.J., Goldstein, B.E. and Neugebauer, M., 2001, “Helium energetics in the high-latitude solar wind: Ulysses observations”, J. Geophys. Res., 106(A4), 5693–5708. [DOI], [ADS] (Cited on page 21.)
Riley, P., Linker, J.A. and Mikic, Z., 2001, “An empirically-driven global MHD model of the solar corona and inner heliosphere”, J. Geophys. Res., 106, 15 889–15 902. [ADS] (Cited on page 24.)
Roberts, B., 2000, “Waves and Oscillations in the Corona”, Solar Phys., 193, 139–152. [ADS] (Cited on page 25.)
Romoli, M., Frazin, R.A., Kohl, J.L., Gardner, L.D., Cranmer, S.R., Reardon, K. and Fineschi, S., 2002, “In-flight Calibration of the UVCS White Light Channel”, in The Radiometric Calibration of SOHO, (Eds.) Pauluhn, A., Huber, M.C.E., von Steiger, R., vol. SR-002 of ISSI Scientific Report, pp. 181–201, ESA Publications Division, Noordwijk (Cited on page 15.)
Rosner, R., Tucker, W.H. and Vaiana, G.S., 1978, “Dynamics of the quiescent solar corona”, Astrophys. J., 220, 643–665. [DOI], [ADS] (Cited on page 12.)
Roussev, I.I., Gombosi, T.I., Sokolov, I.V., Velli, M., Manchester, W., DeZeeuw, D.L., Liewer, P., Tóth, G. and Luhmann, J., 2003, “A Three-dimensional Model of the Solar Wind Incorporating Solar Magnetogram Observations”, Astrophys. J. Lett., 595, L57–L61. [ADS] (Cited on page 24.)
Rowlands, J., Shapiro, V.D. and Shevchenko, V.I., 1966, “Quasilinear theory of plasma cyclotron instability”, Sov. Phys. JETP, 23, 651–660 (Cited on page 29.)
Rust, D.M., 1983, “Coronal disturbances and their terrestrial effects”, Space Sci. Rev., 34, 21–36. [ADS] (Cited on page 13.)
Ryutova, M., Habbal, S., Woo, R. and Tarbell, T., 2001, “Photospheric Network as the Energy Source for the quiet-Sun corona”, Solar Phys., 200, 213–234. [ADS] (Cited on pages 24 and 28.)
Saito, K., 1958, “Polar Rays of the Solar Corona”, Publ. Astron. Soc. Japan, 10, 49–78. [ADS] (Cited on page 7.)
Sakao, T., Kano, R., Narukage, N., Kotoku, J., Bando, T., DeLuca, E.E., Lundquist, L.L., Tsuneta, S., Harra, L.K., Katsukawa, Y., Kubo, M., Hara, H., Matsuzaki, K., Shimojo, M., Bookbinder, J.A., Golub, L., Korreck, K.E., Su, Y., Shibasaki, K., Shimizu, T. and Nakatani, I., 2007, “Continuous Plasma Outflows from the Edge of a Solar Active Region as a Possible Source of Solar Wind”, Science, 318, 1585–1588. [ADS] (Cited on page 14.)
Sanz-Forcada, J. and Dupree, A.K., 2008, “Active cool stars and He I 10830 Å: The coronal connection”, Astron. Astrophys., 488, 715–721. [ADS] (Cited on page 10.)
Schatten, K.H., Wilcox, J.M. and Ness, N.F., 1969, “A model of interplanetary and coronal magnetic fields”, Solar Phys., 6, 442–455. [DOI], [ADS] (Cited on page 14.)
Scholl, I.F. and Habbal, S.R., 2008, “Automatic Detection and Classification of Coronal Holes and Filaments Based on EUV and Magnetogram Observations of the Solar Disk”, Solar Phys., 248, 425–439. [ADS] (Cited on page 10.)
Schrijver, C.J. and Title, A.M., 2003, “The Magnetic Connection between the Solar Photosphere and the Corona”, Astrophys. J. Lett., 597, L165–L168. [DOI], [ADS] (Cited on page 12.)
Schrijver, C.J., Title, A.M., van Ballegooijen, A.A., Hagenaar, H.J. and Shine, R.A., 1997, “Sustaining the Quiet Photospheric Network: The Balance of Flux Emergence, Fragmentation, Merging, and Cancellation”, Astrophys. J., 487, 424–436. [DOI], [ADS] (Cited on pages 28 and 29.)
Schwadron, N.A. and McComas, D.J., 2003, “Solar wind scaling law”, Astrophys. J., 599(2), 1395–1403. [DOI], [ADS] (Cited on pages 24 and 28.)
Schwadron, N.A. and McComas, D.J., 2008, “The Solar Wind Power from Magnetic Flux”, Astrophys. J. Lett., 686, L33–L36. [ADS] (Cited on page 28.)
Schwadron, N.A., McComas, D.J. and DeForest, C., 2006, “Relationship between Solar Wind and Coronal Heating: Scaling Laws from Solar X-Rays”, Astrophys. J., 642, 1173–1176. [ADS] (Cited on page 28.)
Schwartz, S.J., Feldman, W.C. and Gary, S.P., 1981, “The source of proton anisotropy in the high-speed solar wind”, J. Geophys. Res., 86, 541–546. [DOI], [ADS] (Cited on page 30.)
Schwenn, R., 2006, “Solar Wind Sources and Their Variations Over the Solar Cycle”, Space Sci. Rev., 124, 51–76. [ADS] (Cited on page 14.)
Scudder, J.D., 1992a, “Why all stars should posses circumstellar temperature inversions”, Astrophys. J., 398(1), 319–349. [DOI], [ADS] (Cited on pages 33 and 34.)
Scudder, J.D., 1992b, “On the causes of temperature change in inhomogenous low-density astrophysical plasmas”, Astrophys. J., 398(1), 299–318. [DOI], [ADS] (Cited on page 34.)
Scudder, J.D., 1994, “Ion and electron suprathermal tail strengths in the transition region: Support for the velocity filtration model of the corona”, Astrophys. J., 427, 446–452. [ADS] (Cited on page 33.)
Seely, J.F., Feldman, U., Schühle, U., Wilhelm, K., Curdt, W. and Lemaire, P., 1997, “Turbulent Velocities and Ion Temperatures in the Solar Corona Obtained from SUMER Line Widths”, Astrophys. J. Lett., 484, L87–L90. [ADS] (Cited on page 17.)
Serviss, G.P., 1909, Curiosities of the Sky: A Popular Presentation of the Great Riddles and Mysteries of Astronomy, Harper & Brothers, New York; London (Cited on page 7.)
Shebalin, J.V., Matthaeus, W.H. and Montgomery, D., 1983, “Anisotropy in MHD turbulence due to a mean magnetic field”, J. Plasma Phys., 29, 525–547. [DOI], [ADS] (Cited on page 31.)
Sheeley Jr, N.R., Wang, Y.-M., Hawley, S.H., Brueckner, G.E., Dere, K.P., Howard, R.A., Koomen, M.J., Korendyke, C.M., Michels, D.J., Paswaters, S.E., Socker, D.G., St Cyr, O.C., Wang, D., Lamy, P.L., Llebaria, A., Schwenn, R., Simnett, G.M., Plunkett, S. and Biesecker, D.A., 1997, “Measurements of Flow Speeds in the Corona between 2 and 30 R⊙”, Astrophys. J., 484, 472–478. [DOI], [ADS] (Cited on pages 16 and 20.)
Shibata, K., Nitta, N., Strong, K.T., Matsumoto, R., Yokoyama, T., Hirayama, T., Hudson, H. and Ogawara, Y., 1994, “A gigantic coronal jet ejected from a compact active region in a coronal hole”, Astrophys. J. Lett., 431, L51–L53. [ADS] (Cited on page 11.)
Shimojo, M., Narukage, N., Kano, R., Sakao, T., Tsuneta, S., Shibasaki, K., Cirtain, J.W., Lundquist, L.L., Reeves, K. and Savcheva, A., 2007, “Fine Structures of Solar X-Ray Jets Observed with the X-Ray Telescope aboard Hinode”, Publ. Astron. Soc. Japan, 59, S745–S750. [ADS] (Cited on page 21.)
Singh, N. and Khazanov, G., 2004, “Numerical simulation of waves driven by plasma currents generated by low-frequency Alfvén waves in a multi-ion plasma”, J. Geophys. Res., 109, A05210. [ADS] (Cited on pages 30 and 33.)
Singh, N., Khazanov, G. and Mukhter, A., 2007, “Electrostatic wave generation and transverse ion acceleration by Alfvénic wave components of broadband extremely low frequency turbulence”, J. Geophys. Res., 112, A06210. [ADS] (Cited on page 33.)
Sittler Jr, E.C. and Guhathakurta, M., 1999, “Semiempirical Two-dimensional Magnetohydrodynamic Model of the Solar Corona and Interplanetary Medium”, Astrophys. J., 523, 812–826. [ADS] (Cited on page 15.)
Smith, C.W., Hamilton, K., Vasquez, B.J. and Leamon, R.J., 2006, “Dependence of the Dissipation Range Spectrum of Interplanetary Magnetic Fluctuationson the Rate of Energy Cascade”, Astrophys. J. Lett., 645, L85–L88. [ADS] (Cited on page 31.)
Spangler, S.R., 2002, “The Amplitude of Magnetohydrodynamic Turbulence in the Inner Solar Wind”, Astrophys. J., 576, 997–1004. [ADS] (Cited on pages 16, 32, and 34.)
Spruit, H.C., 1981, “Motion of magnetic flux tubes in the solar convection zone and chromosphere”, Astron. Astrophys., 98, 155–160. [ADS] (Cited on page 27.)
Spruit, H.C., 1984, “Interaction of Fluxtubes With Convection”, in Small-Scale Dynamical Processes in Quiet Stellar Atmospheres, Proceedings of the Conference held in Sunspot, New Mexico, USA, 25–29 July 1983, (Ed.) Keil, S.L., p. 249, National Solar Observatory, Sunspot, NM. [ADS] (Cited on page 12.)
Stoddard, L.G., Carson, D.G. and Saito, K., 1966, “Polar Rays of the Solar Corona Observed at the 1963 Eclipse”, Astrophys. J., 145, 796–799. [ADS] (Cited on page 7.)
Strachan, L., Kohl, J.L., Weiser, H., Withbroe, G.L. and Munro, R.H., 1993, “A Doppler dimming determination of coronal outflow velocity”, Astrophys. J., 412, 410–420. [ADS] (Cited on page 8.)
Strachan, L., Suleiman, R., Panasyuk, A.V., Biesecker, D.A. and Kohl, J.L., 2002, “Empirical densities, kinetic temperatures, and outflow velocities in the equatorial streamer belt at solar minimum”, Astrophys. J., 571, 1008–1014. [ADS] (Cited on page 14.)
Strauss, H.R., 1976, “Nonlinear, three-dimensional magnetohydrodynamics of noncircular tokamaks”, Phys. Fluids, 19, 134–140. [ADS] (Cited on page 31.)
Sturrock, P.A., Roald, C.B. and Wolfson, R., 1999, “Chromospheric Magnetic Reconnection and its Implication for Coronal Heating”, Astrophys. J. Lett., 524, L75–L78. [ADS] (Cited on page 29.)
Suess, S.T., 1979, “Models of coronal hole flows”, Space Sci. Rev., 23, 159–200. [ADS] (Cited on page 5.)
Susino, R., Ventura, R., Spadaro, D., Vourlidas, A. and Landi, E., 2008, “Physical parameters along the boundaries of a mid-latitude streamer and in its adjacent regions”, Astron. Astrophys., 488, 303–310. [ADS] (Cited on page 14.)
Suzuki, T.K., 2006, “Forecasting Solar Wind Speeds”, Astrophys. J. Lett., 640, L75–L78. [ADS] (Cited on pages 23 and 28.)
Suzuki, T.K. and Inutsuka, S.-I., 2006, “Solar winds driven by nonlinear low-frequency Alfvén waves from the photosphere: Parametric study for fast/slow winds and disappearance of solar winds”, J. Geophys. Res., 111, A06101. [ADS] (Cited on page 23.)
Suzuki, T.K., Lazarian, A. and Beresnyak, A., 2007, “Cascading of Fast-Mode Balanced and Imbalanced Turbulence”, Astrophys. J., 662, 1033–1042. [ADS] (Cited on page 33.)
Tanskanen, E.I., Slavin, J.A., Tanskanen, A.J, Viljanen, A., Pulkkinen, T.I., Koskinen, H.E.J., Pulkkinen, A. and Eastwood, J., 2005, “Magnetospheric substorms are strongly modulated by interplanetary high-speed streams”, Geophys. Res. Lett., 32, L16 104. [ADS] (Cited on page 8.)
Tappin, S.J., Simnett, G.M. and Lyons, M.A., 1999, “A determination of the outflow speeds in the lower solar wind”, Astron. Astrophys., 350, 302–309. [ADS] (Cited on page 16.)
Telloni, D., Antonucci, E., Bruno, R. and D’Amicis, R., 2009, “Persistent and Self-Similar Large-Scale Density Fluctuations in the Solar Corona”, Astrophys. J., 693, 1022–1028. [ADS] (Cited on page 16.)
Teplitskaya, R.B., Turova, I.P. and Ozhogina, O.A., 2007, “The Lower Chromosphere in a Coronal Hole”, Solar Phys., 243, 143–161. [ADS] (Cited on page 10.)
Teriaca, L., Poletto, G., Romoli, M. and Biesecker, D.A., 2003, “The nascent solar wind: Origin and acceleration”, Astrophys. J., 588, 566–577. [ADS] (Cited on page 21.)
Thieme, K.M., Marsch, E. and Schwenn, R., 1990, “Spatial structures in high-speed streams as signatures of fine structures in coronal holes”, Ann. Geophys., 8, 713–723. [ADS] (Cited on page 17.)
Thompson, B.J., Cliver, E.W., Nitta, N., Delannée, C. and Delaboudinière, J.-P., 2000, “Coronal dimmings and energetic CMEs in April–May 1998”, Geophys. Res. Lett., 27, 1431–1434. [ADS] (Cited on page 13.)
Timothy, A.F., Krieger, A.S. and Vaiana, G.S., 1975, “The structure and evolution of coronal holes”, Solar Phys., 42, 135–156. [ADS] (Cited on page 10.)
Title, A.M. and Schrijver, C.J., 1998, “The Sun’s Magnetic Carpet”, in Cool Stars, Stellar Systems, and the Sun: Tenth Cambridge Workshop, Proceedings of a meeting held at Cambridge, Massachusetts, 15–19 July 1997, (Eds.) Donahue, R.A., Bookbinder, J.A., vol. 154 of ASP Conference Series, pp. 345–358, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 28.)
Tomczyk, S. and McIntosh, S.W., 2009, “Time-Distance Seismology of the Solar Corona with CoMP”, Astrophys. J., 697, 1384–1391. [ADS] (Cited on page 24.)
Tomczyk, S., McIntosh, S.W., Keil, S.L., Judge, P.G., Schad, T., Seeley, D.H. and Edmondson, J., 2007, “Alfvén waves in the solar corona”, Science, 317, 1192–1196. [ADS] (Cited on page 24.)
Tóth, G., Sokolov, I.V., Gombosi, T.I., Chesney, D.R., Clauer, C.R., De Zeeuw, D.L., Hansen, K.C., Kane, K.J., Manchester, W.B., Oehmke, R.C., Powell, K.G., Ridley, A.J., Roussev, I.I., Stout, Q.F., Volberg, O., Wolf, R.A., Sazykin, S., Chan, A., Yu, B. and Kóta, J., 2005, “Space Weather Modeling Framework: A new tool for the space science community”, J. Geophys. Res., 110, A12226. [ADS] (Cited on page 24.)
Tousey, R., Sandlin, G.D. and Purcell, J.D., 1968, “On Some Aspects of XUV Spectroheliograms”, in Structure and Development of Solar Active Regions, Proceedings of IAU Symposium 35, 4–8 September 1967, Budapest, Hungary, (Ed.) Kiepenheuer, K.O., pp. 411–419, Reidel, Dordrecht. [ADS] (Cited on page 7.)
Tsuneta, S., Ichimoto, K., Katsukawa, Y., Lites, B.W., Matsuzaki, K., Nagata, S., Orozco Suárez, D., Shimizu, T., Shimojo, M., Shine, R.A., Suematsu, Y., Suzuki, T.K., Tarbell, T.D. and Title, A.M., 2008, “The Magnetic Landscape of the Sun’s Polar Region”, Astrophys. J., 688, 1374–1381. [ADS] (Cited on page 12.)
Tu, C.-Y. and Marsch, E., 1994, “On the nature of compressive fluctuations in the solar wind”, J. Geophys. Res., 99, 21 481–21 509. [ADS] (Cited on page 16.)
Tu, C.-Y. and Marsch, E., 1995, “MHD Structures, Waves and Turbulence in the Solar Wind: Observations and Theories”, Space Sci. Rev., 73(1/2), 1–210. [DOI], [ADS] (Cited on pages 25 and 31.)
Tu, C.-Y. and Marsch, E., 1997, “Two-fluid model for heating of the solar corona and acceleration of the solar wind by high-frequency Alfvén waves”, Solar Phys., 171(2), 363–391. [DOI], [ADS] (Cited on page 30.)
Tu, C.-Y. and Marsch, E., 2001, “On cyclotron wave heating and acceleration of solar wind ions in the outer corona”, J. Geophys. Res., 106, 8233–8252. [ADS] (Cited on page 30.)
Tu, C.-Y., Marsch, E., Wilhelm, K. and Curdt, W., 1998, “Ion Temperatures in a Solar Polar Coronal Hole Observed by SUMER on SOHO”, Astrophys. J., 503, 475–482. [ADS] (Cited on page 17.)
Tu, C.-Y., Zhou, C., Marsch, E., Xia, L.-D., Zhao, L., Wang, J.-X. and Wilhelm, K., 2005, “Solar wind origin in coronal funnels”, Science, 308(5721), 519–523. [DOI], [ADS] (Cited on pages 12 and 29.)
Usmanov, A.V. and Goldstein, M.L., 2006, “A three-dimensional MHD solar wind model with pickup protons”, J. Geophys. Res., 111, A07101. [ADS] (Cited on page 24.)
van Ballegooijen, A.A., 1994, “Energy release in stellar magnetospheres”, Space Sci. Rev., 68, 299–307. [ADS] (Cited on page 35.)
van de Hulst, H.C., 1950, “The electron density of the solar corona”, Bull. Astron. Inst. Neth., 11, 135–150. [ADS] (Cited on page 15.)
Vaquero, J.M., 2003, “The Solar Corona in the Eclipse of 24 June 1778”, Solar Phys., 216, 41–45. [ADS] (Cited on page 7.)
Vasquez, B.J. and Hollweg, J.V., 1996, “Formation of arc-shaped Alfvén waves and rotational discontinuities from oblique linearly polarized wave trains”, J. Geophys. Res., 101, 13,527–13,540. [ADS] (Cited on page 32.)
Vasquez, B.J. and Hollweg, J.V., 1998, “Formation of spherically polarized Alfvén waves and imbedded rotational discontinuities from a small number of entirely oblique waves”, J. Geophys. Res., 103, 335–347. [ADS] (Cited on page 32.)
Verdini, A. and Velli, M., 2007, “Alfvén waves and turbulence in the solar atmosphere and solar wind”, Astrophys. J., 662, 669–676. [ADS] (Cited on pages 23 and 25.)
Verdini, A., Velli, M. and Buchlin, E., 2009, “Reflection Driven MHD Turbulence in the Solar Atmosphere and Wind”, Earth Moon Planets, 104, 121–125. [DOI], [ADS] (Cited on page 23.)
Voitenko, Y.M. and Goossens, M., 2002, “Excitation of high-frequency Alfvén waves by plasma outflows from coronal reconnection events”, Solar Phys., 206, 285–313. [DOI], [ADS] (Cited on page 31.)
Voitenko, Y.M. and Goossens, M., 2003, “Kinetic excitation mechanisms for ion-cyclotron kinetic Alfvén waves in Sun-Earth connection”, Space Sci. Rev., 107, 387–401. [ADS] (Cited on pages 30 and 31.)
Voitenko, Y.M. and Goossens, M., 2004, “Cross-Field Heating of Coronal Ions by Low-Frequency Kinetic Alfvén Waves”, Astrophys. J. Lett., 605, L149–L152. [DOI], [ADS] (Cited on pages 30 and 31.)
von Steiger, R., Wimmer-Schweingruber, R.F., Geiss, J. and Gloeckler, G., 1995, “Abundance variations in the solar wind”, Adv. Space Res., 15(7), 3–12. [ADS] (Cited on page 10.)
Vranjes, J. and Poedts, S., 2008, “Growing drift-cyclotron modes in the hot solar atmosphere”, Astron. Astrophys., 482, 653–656. [ADS] (Cited on page 32.)
Vršnak, B., Temmer, M. and Veronig, A.M., 2007, “Coronal Holes and Solar Wind High-Speed Streams: I. Forecasting the Solar Wind Parameters”, Solar Phys., 240, 315–330. [ADS] (Cited on page 23.)
Waldmeier, M., 1955, “Ergebnisse der Zürcher Sonnenfinsternisexpedition 1954: I. Vorläufige Photometrie der Korona”, Z. Astrophys., 36, 275–292. [ADS] (Cited on page 8.)
Waldmeier, M., 1956, “Synoptische Karten der Sonnenkorona”, Z. Astrophys., 38, 219–236. [ADS] (Cited on page 7.)
Waldmeier, M., 1957, Die Sonnenkorona, vol. 2, Birkhäuser, Basel (Cited on page 7.)
Waldmeier, M., 1975, “The coronal hole at the 7 March 1970 solar eclipse”, Solar Phys., 40, 351–358. [ADS] (Cited on page 7.)
Waldmeier, M., 1981, “Cyclic variations of the polar coronal hole”, Solar Phys., 70, 251–258. [ADS] (Cited on pages 7 and 10.)
Wang, C.B. and Wu, C.S., 2009, “Pseudoheating of protons in the presence of Alfvénic turbulence”, Phys. Plasmas, 16, 020703. [DOI], [ADS] (Cited on page 33.)
Wang, P.K. and Siscoe, G.L., 1980, “Ancient Chinese Observations of Physical Phenomena Attending Solar Eclipses”, Solar Phys., 66, 187–193. [ADS] (Cited on page 7.)
Wang, Y.-M., 1994, “Polar plumes and the solar wind”, Astrophys. J. Lett., 435, L153–L156. [ADS] (Cited on page 21.)
Wang, Y.-M., 1998, “Network Activity and the Evaporative Formation of Polar Plumes”, Astrophys. J. Lett., 501, L145–L148. [ADS] (Cited on page 21.)
Wang, Y.-M., 2009, “Coronal holes and open magnetic flux”, Space Sci. Rev., 144, 383–399. [ADS] (Cited on pages 5, 11, and 14.)
Wang, Y.-M. and Sheeley Jr, N.R., 1990, “Solar wind speed and coronal flux-tube expansion”, Astrophys. J., 355, 726–732. [DOI], [ADS] (Cited on page 23.)
Wang, Y.-M. and Sheeley Jr, N.R., 1991, “Why fast solar wind originates from slowly expanding coronal flux tubes”, Astrophys. J. Lett., 372, L45–L48. [ADS] (Cited on page 23.)
Wang, Y.-M. and Sheeley Jr, N.R., 2006, “Sources of the Solar Wind at Ulysses during 1990–2006”, Astrophys. J., 653, 708–718. [ADS] (Cited on pages 14 and 23.)
Wang, Y.-M., Hawley, S.H. and Sheeley Jr, N.R., 1996, “The magnetic nature of coronal holes”, Science, 271(5248), 464–469. [DOI], [ADS] (Cited on page 11.)
Wang, Y.-M., Sheeley Jr, N.R., Socker, D.G., Howard, R.A., Brueckner, G.E., Michels, D.J., Moses, D., St Cyr, O.C., Llebaria, A. and Delaboudinière, J.-P., 1998, “Observations of Correlated White-Light and Extreme-Ultraviolet Jets from Polar Coronal Holes”, Astrophys. J., 508, 899–907. [ADS] (Cited on pages 15 and 21.)
Wang, Y.-M., Sheeley Jr, N.R., Socker, D.G., Howard, R.A. and Rich, N.B., 2000, “The dynamical nature of coronal streamers”, J. Geophys. Res., 105, 25 133–25 142. [ADS] (Cited on pages 14 and 16.)
Wang, Y.-M., Biersteker, J.B., Sheeley Jr, N.R., Koutchmy, S., Mouette, J. and Druckmüller, M., 2007, “The Solar Eclipse of 2006 and the Origin of Raylike Features in the White-Light Corona”, Astrophys. J., 660, 882–892. [ADS] (Cited on page 14.)
Wang, Y.-M., Ko, Y.-K. and Grappin, R., 2009, “Slow Solar Wind from Open Regions with Strong Low-Coronal Heating”, Astrophys. J., 691, 760–769. [ADS] (Cited on pages 11, 14, 26, and 27.)
Warren, H.P., Mariska, J.T., Wilhelm, K. and Lemaire, P., 1997, “Doppler Shifts and Nonthermal Broadening in the Quiet Solar Transition Region: O VI”, Astrophys. J. Lett., 484, L91–L94. [ADS] (Cited on page 19.)
Wilcox, J.M., 1968, “The Interplanetary Magnetic Field. Solar Origin and Terrestrial Effects”, Space Sci. Rev., 8, 258–328. [ADS] (Cited on pages 8 and 14.)
Wilhelm, K., 2006, “Solar coronal-hole plasma densities and temperatures”, Astron. Astrophys., 455, 697–708. [ADS] (Cited on pages 17 and 18.)
Wilhelm, K., Curdt, W., Marsch, E., Schühle, U., Lemaire, P., Gabriel, A., Vial, J.-C., Grewing, M., Huber, M.C.E., Jordan, S.D., Poland, A.I., Thomas, R.J., Kühne, M., Timothy, J.G., Hassler, D.M. and Siegmund, O.H.W., 1995, “SUMER: Solar Ultraviolet Measurements of Emitted Radiation”, Solar Phys., 162, 189–231. [ADS] (Cited on page 17.)
Wilhelm, K., Dammasch, I.E., Marsch, E. and Hassler, D.M., 2000, “On the source regions of the fast solar wind in polar coronal holes”, Astron. Astrophys., 353, 749–756. [ADS] (Cited on page 17.)
Wilhelm, K., Dwivedi, B.N., Marsch, E. and Feldman, U., 2004, “Observations of the Sun at Vacuum-Ultraviolet Wavelengths from Space, I: Concepts and Instrumentation”, Space Sci. Rev., 111, 415–480. [ADS] (Cited on page 17.)
Wilhelm, K., Marsch, E., Dwivedi, B.N. and Feldman, U., 2007, “Observations of the Sun at Vacuum-Ultraviolet Wavelengths from Space, II: Results and Interpretations”, Space Sci. Rev., 133, 103–179. [ADS] (Cited on page 17.)
Withbroe, G.L., 1988, “The temperature structure, mass, and energy flow in the corona and inner solar wind”, Astrophys. J., 325, 442–467. [ADS] (Cited on page 27.)
Withbroe, G.L., Kohl, J.L., Weiser, H. and Munro, R.H., 1982, “Probing the solar wind acceleration region using spectroscopic techniques”, Space Sci. Rev., 33, 17–52. [ADS] (Cited on page 17.)
Woo, R., 2005, “Relating White-Light Coronal Images to Magnetic Fields and Plasma Flow”, Solar Phys., 231, 71–85. [ADS] (Cited on page 14.)
Woo, R., 2006, “Ultra-fine-Scale Filamentary Structures in the Outer Corona and the Solar Magnetic Field”, Astrophys. J. Lett., 639, L95–L98. [ADS] (Cited on page 32.)
Woo, R. and Druckmüllerová, H., 2008, “Solar Eclipse Images and the Solar Wind”, Astrophys. J. Lett., 678, L149–L152. [ADS] (Cited on page 14.)
Woo, R., Habbal, S.R., Howard, R.A. and Korendyke, C.M., 1999, “Extension of the Polar Coronal Hole Boundary into Interplanetary Space”, Astrophys. J., 513, 961–968. [ADS] (Cited on page 14.)
Woo, R., Habbal, S.R. and Feldman, U., 2004, “Role of Closed Magnetic Fields in Solar Wind Flow”, Astrophys. J., 612, 1171–1174. [ADS] (Cited on page 24.)
Wood, B.E., 2004, “Astrospheres and Solar-like Stellar Winds”, Living Rev. Solar Phys., 1, lrsp-2004-2. URL (accessed 1 July 2009): http://www.livingreviews.org/lrsp-2004-2 (Cited on page 35.)
Wood, B.E., Karovska, M., Cook, J.W., Howard, R.A. and Brueckner, G.E., 1999, “Kinematic Measurements of Polar Jets Observed by the Large-Angle Spectrometric Coronagraph”, Astrophys. J., 523, 444–449. [ADS] (Cited on page 15.)
Wu, C.S. and Yoon, P.H., 2007, “Proton heating via nonresonant scattering off intrinsic Alfvénic turbulence”, Phys. Rev. Lett., 99, 075001. [ADS] (Cited on pages 30 and 33.)
Wu, D.J. and Yang, L., 2006, “Anisotropic and mass-dependent energization of heavy ions by kinetic Alfvén waves”, Astron. Astrophys., 452, L7–L10. [ADS] (Cited on page 31.)
Wu, D.J. and Yang, L., 2007, “Nonlinear interaction of minor heavy ions with kinetic Alfvén waves and their anisotropic energization in coronal holes”, Astrophys. J., 659, 1693–1701. [ADS] (Cited on page 31.)
Yamauchi, Y., Suess, S.T. and Sakurai, T., 2002, “Relation between Pressure Balance Structures and polar plumes from Ulysses high latitude observations”, Geophys. Res. Lett., 29, 1383. [ADS] (Cited on page 17.)
Yang, L.-H., Jiang, Y.-C. and Ren, D.-B., 2008, “Formation of Transient Coronal Holes during Eruption of a Quiescent Filament and its Overlying Sigmoid”, Chinese J. Astron. Astrophys., 8, 329–336. [DOI], [ADS], [arXiv:0901.0784] (Cited on page 13.)
Yoon, P.H. and Fang, T.-M., 2008, “Parallel cascade of Alfvén waves”, Plasma Phys. Control. Fusion, 50, 085007. [ADS] (Cited on pages 30 and 32.)
Zangrilli, L., Nicolosi, P., Poletto, G., Noci, G., Romoli, M. and Kohl, J.L., 1999, “Latitudinal properties of the Lyman alpha and O VI profiles in the extended solar corona”, Astron. Astrophys., 342, 592–600. [ADS] (Cited on page 19.)
Zhang, J., Woch, J., Solanki, S.K., von Steiger, R. and Forsyth, R., 2003, “Interplanetary and solar surface properties of coronal holes observed during solar maximum”, J. Geophys. Res., 108, 1144. [ADS] (Cited on page 14.)
Zhang, J., Richardson, I.G., Webb, D.F., Gopalswamy, N., Huttunen, E., Kasper, J.C., Nitta, N.V., Poomvises, W., Thompson, B.J., Wu, C.-C., Yashiro, S. and Zhukov, A.N., 2007, “Solar and interplanetary sources of major geomagnetic storms (Dst ≤ −100 nT) during 1996–2005”, J. Geophys. Res., 112, A10102. [DOI], [ADS] (Cited on page 8.)
Zhang, T.X., 2003, “Preferential heating of particles by H-cyclotron waves generated by a global magnetohydrodynamic mode in solar coronal holes”, Astrophys. J. Lett., 597, L69–L72. [ADS] (Cited on pages 30 and 32.)
Zhou, Y. and Matthaeus, W.H., 1990, “Transport and turbulence modeling of solar wind fluctuations”, J. Geophys. Res., 95, 10291–10311. [DOI], [ADS] (Cited on page 25.)
Zirin, H., 1975, “The helium chromosphere, coronal holes, and stellar X-rays”, Astrophys. J. Lett., 199, L63–L66. [ADS] (Cited on page 10.)
Zirker, J.B. (Ed.), 1977, Coronal Holes and High-Speed Wind Streams, A Monograph from Skylab Solar Workshop I, Colorado Associated University Press, Boulder (Cited on pages 5 and 8.)
Zurbuchen, T.H., Fisk, L.A., Gloeckler, G. and von Steiger, R., 2002, “The solar wind composition throughout the solar cycle: A continuum of dynamic states”, Geophys. Res. Lett., 29, 1352. [ADS] (Cited on page 10.)
Acknowledgements
I would like to thank the editors of Living Reviews in Solar Physics for the invitation to prepare this review. I gratefully acknowledge John Kohl, Adriaan van Ballegooijen, Leonard Strachan, John Raymond, William Matthaeus, Philip Isenberg, Joseph Hollweg, S. Peter Gary, Eckart Marsch, Marco Velli, Mari Paz Miralles, Larry Gardner, and Enrico Landi for many valuable discussions and collaborations. I would especially like to thank the colleagues with whom I have engaged in more adversarial debates over the years, such as Ian Axford, Chuanyi Tu, Nathan Schwadron, and Nour-Eddine Raouafi. “As brothers fight ye!”
This work was supported by the National Aeronautics and Space Administration (NASA) under grants NNG04GE77G, NNX06AG95G, NNX07AL72G, and NNX09AB27G to the Smithsonian Astrophysical Observatory. SOHO is a project of international cooperation between ESA and NASA. This research made extensive use of NASA’s Astrophysics Data System (ADS) and the John G. Wolbach Library at the Harvard-Smithsonian Center for Astrophysics.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cranmer, S.R. Coronal Holes. Living Rev. Sol. Phys. 6, 3 (2009). https://doi.org/10.12942/lrsp-2009-3
Published:
DOI: https://doi.org/10.12942/lrsp-2009-3