Abstract
We review the properties of solar convection that are directly observable at the solar surface, and discuss the relevant underlying physics, concentrating mostly on a range of depths from the temperature minimum down to about 20 Mm below the visible solar surface.
The properties of convection at the main energy carrying (granular) scales are tightly constrained by observations, in particular by the detailed shapes of photospheric spectral lines and the topology (time- and length-scales, flow velocities, etc.) of the up- and downflows. Current supercomputer models match these constraints very closely, which lends credence to the models, and allows robust conclusions to be drawn from analysis of the model properties.
At larger scales the properties of the convective velocity field at the solar surface are strongly influenced by constraints from mass conservation, with amplitudes of larger scale horizontal motions decreasing roughly in inverse proportion to the scale of the motion. To a large extent, the apparent presence of distinct (meso- and supergranulation) scales is a result of the folding of this spectrum with the effective “filters” corresponding to various observational techniques. Convective motions on successively larger scales advect patterns created by convection on smaller scales; this includes patterns of magnetic field, which thus have an approximately self-similar structure at scales larger than granulation.
Radiative-hydrodynamical simulations of solar surface convection can be used as 2D/3D time-dependent models of the solar atmosphere to predict the emergent spectrum. In general, the resulting detailed spectral line profiles agree spectacularly well with observations without invoking any micro- and macroturbulence parameters due to the presence of convective velocities and atmosphere inhomogeneities. One of the most noteworthy results has been a significant reduction in recent years in the derived solar C, N, and O abundances with far-reaching consequences, not the least for helioseismology.
Convection in the solar surface layers is also of great importance for helioseismology in other ways; excitation of the wave spectrum occurs primarily in these layers, and convection influences the size of global wave cavity and, hence, the mode frequencies. On local scales convection modulates wave propagation, and supercomputer convection simulations may thus be used to test and calibrate local helioseismic methods.
We also discuss the importance of near solar surface convection for the structure and evolution of magnetic patterns: faculae, pores, and sunspots, and briefly address the question of the importance or not of local dynamo action near the solar surface. Finally, we discuss the importance of near solar surface convection as a driver for chromospheric and coronal heating.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Convection is of central importance to the structure and appearance of the Sun, both with respect to its average internal structure and secular evolution, and with respect to the detailed structure and dynamics of the many diverse phenomena that occur at the solar surface. In this review we discuss convection in those layers of the Sun that directly influence what may be observed at the solar surface. In practice, this means that we consider layers ranging from the temperature minimum down to about 20 Mm below the visible surface. Over this range of depths hydrogen ionization goes from essentially zero, with electrons instead supplied mainly by the most abundant metals, to essentially unity. Helium (2nd) ionization is also nearly complete near the bottom of this range of depths.
As illustrated by Figure 1, a depth of 20 Mm corresponds to roughly half the range of pressure or density spanned by the solar convection zone. Thus, even though this layer corresponds to only about 3% of the solar radius, and only about 10% of the geometrical depth of the solar convection zone, mass density and pressure vary by factors of about 105 and 106 across it, respectively.
In these surface and near-surface layers the equation of state of the solar plasma is strongly influenced by the effects of ionization and molecular dissociation. Deeper down the solar plasma is nearly fully ionized, the equation of state is nearly ideal and, hence, the vertical structure of the lower part of the convection zone (90% by depth) is close to that of a perfect polytrope.
The physics of convection near the surface of the Sun is also greatly influenced by the fact that the solar surface is a radiating surface, where the mode of energy transport all of a sudden changes from convective — with energy being carried by moving fluid — to radiative — with energy carried by essentially free-streaming photons.
Each one of these complications — extreme density stratification, ionization and molecule dissociation, and transition to radiative energy transfer — would by itself be sufficient to render analytical treatments impossible and, hence, major progress in modeling these layers could only be achieved via computer simulations and modeling. The subject area was thus truly opened up for study and revolutionized when computer capacity became large enough for realistic simulations to be performed.
Conversely, because of the proximity and large apparent luminosity of the Sun, it is one of the most ideal objects for quantitative and accurate comparisons between numerical simulations and observations — arguably in five dimensions: one has, to a rather unique extent, access to both the time domain and the spatial domain, over a large range of scales, and the available photon flux is large enough to also essentially fully resolve the wavelength domain, from the extreme ultra-violet to the far infrared.
In addition, the Sun is an ideal object for studying magneto-hydrodynamics in an astrophysical context, in that it displays a variety of magnetically related phenomena, ranging in strength from very weak and kinematic, where the evolution of the magnetic field is almost entirely controlled by the fluid motions to the opposite extreme, where the gas pressure is so feeble that fluid motions are totally dominated by the magnetic field.
The comparison of models and observations is thus both particularly challenging and particularly rewarding in this context, and the evolution of the subject area over the last few decades has amply illustrated this state of affairs.
In this review we try to summarize, in a necessarily incomplete and biased way, our current understanding of solar surface convection.
The review is organized as follows: In Section 2 we discuss the principles of hydrodynamics as they apply to solar convection. In Section 3 we discuss the manifestations and properties of the main energy carrying scales, and the granulation pattern that they give rise to. In Section 4 we discuss how larger scale convective patterns arise and are driven, and how they interact with smaller scale patterns. We introduce the concept of a velocity spectrum, and address the question the extent to which the traditional concepts of meso- and supergranulation represent distinct scales of motion. In Section 5 we discuss how spectral line synthesis and comparisons with observed spectral line profiles may be used to asses the accuracy of numerical simulations, and how the resulting spectral line profiles may be used to accurately determine solar chemical abundances. In Section 6 we discuss applications to global and local helioseismology: wave excitation and damping, the influence of convection on the mean structure, and helioseismic diagnostics related to convective flow patterns. In Section 7 we discuss the interaction of convection and solar magnetic fields and, finally, in Section 8 we discuss open questions and directions for future work. Section 9 ends the review with a summary and concluding remarks.
Previous reviews related to this subject include: Bray et al. (1984); Nordlund (1985a); Zahn (1987); Spruit et al. (1990); Nordlund et al. (1996); Spruit (1997); Stix (2004), and Asplund (2005).
2 Hydrodynamics of Solar Convection
Although some of the properties of solar convection may appear strange and unexpected at first, especially in comparison to local laboratory and atmospheric hydrodynamics settings, they of course follow rigorously from the laws of physics, which in the fluid approximations are the laws of compressible hydrodynamics and magnetohydrodynamics. These laws form the basis for numerical modeling, but equally importantly also allow a qualitative and semi-quantitative understanding. We therefore start out by writing down these laws, in forms suitable for the discussion (as well as for computational work in some cases).
2.1 Mass conservation
Mass conservation is expressed in Eulerian form by the continuity equation
or in Lagrangian form
where \({{D\ln \rho} \over {Dt}}\) represents the rate of change of the logarithm of the mass density, ln ρ, following the fluid motion (with velocity u), and \({{D\ln V} \over {Dt}}\) is the logarithmic rate of change of the specific volume V.
These two forms of the continuity equation may already, before one even considers the rest of the equations of hydrodynamics, be used to understand some very fundamental consequences that conservation of mass has for the structure of solar convection.
For example, the Lagrangian form (Equation 2) shows that a fluid parcel that ascends over a number of density scale heights has to expand correspondingly. The Eulerian form (Equation 1) shows, on the other hand, that if the local density does not change much with time, then a rapid decrease of mean density with height in an ascending flow, can be balanced by rapid expansion sideways.
A rapid vertical expansion could in principle also happen, but as we shall see in the next subsection, the equations of motion dictate that the main expansion/contraction of ascending/descending flows happens sideways.
The Eulerian form of the continuity equation is also a central player in the anelastic approximation (Gough, 1969), where one assumes, at least for the purpose of computing the pressure field P(r, t), that one may ignore \({{\partial \rho} \over {\partial t}}\) in comparison to (separately) the contributions from vertical changes of mass flux and horizontal expansion. So, to lowest order one can then assume that
where z is height and t is time, so
showing again that if ln ρ is changing rapidly with height then ascending/descending fluid must expand/contract rapidly.
2.2 Equations of motion
The equations of motion in Eulerian form are
or in Lagrangian form
where P is the gas pressure, Φ is the gravitational potential, and τvisc is the viscous stress tensor.
Near the solar surface, the acceleration of gravity −∇Φ is a nearly constant (per unit mass) downwards vertical force, which needs to be balanced by an equally large pressure gradient \( - {P \over \rho}\nabla \ln P\) ln P acting in the opposite direction. Therefore, if fluid motions are sufficiently slow and large scale (horizontally), so the other terms in the equations of motion may be neglected, then what remains is a condition of hydrostatic equilibrium,
For constant P/ρ (essentially constant temperature), one finds that the logarithmic pressure ln P depends linearly on height, and that the pressure thus decreases exponentially with height,
where the pressure scale height is
These equations, which describe an approximate hydrostatic vertical balance of forces, have some very important consequences in cases where the scale height HP is nearly independent of horizontal position (x, y), while P0 is allowed to vary slowly with horizontal position,
It then follows that the entire pressure field may vary ‘in unison’ vertically, with a common (logarithmic) variation horizontally, leading to horizontal components of the pressure gradient
which are essentially independent of height z. This corresponds to a smoothly undulating surface or atmosphere, where the vertical stratification is similar everywhere, except for a vertical displacement that depends only on (x, y). This is of course somewhat of an idealization, but it is nevertheless an important limiting scenario, where one can have a slowly varying horizontal velocity field that is nearly independent of height.
Returning to the anelastic approximation, ∇ · (ρu) ≈ 0, it may be combined with the equations of motion to obtain
showing that, in this approximation, the pressure is determined (instantaneously) by the per-unit-volume force field — the role of the pressure is essentially that of a constraint, enforcing the condition ∇ · (ρu) = 0.
2.3 Kinetic energy equation, buoyancy work, and gas pressure work
Taking the scalar product of the velocity with the equation of motion yields an equation that describes the time evolution of the kinetic energy,
which shows that local changes of kinetic energy are caused by — in the order of appearance of terms on the right hand side — transport of kinetic energy (divergence of the kinetic energy flux), work by the gas pressure gradient force, work by gravity, and terms related to viscous dissipation. Subtracting off a mean hydrostatic balance \({{\partial P} \over {\partial z}} \approx - \rho \nabla \Phi = \rho {g_z}\) (where for simplicity we ignore the turbulent pressure and assume a constant vertical downward acceleration of gravity gz) we can identify a net force ρ′gz, which is usually referred to as the buoyancy force (cf. the classical principle of Archimedes!).
The work corresponding to the buoyancy force, ρ′u′zgz, where u′z is the horizontal fluctuation of the vertical velocity, is traditionally called the buoyancy work (although buoyancy power would perhaps be more correct). In places where the density of ascending gas is higher than average (e.g., because of the overpressure necessary to accelerate the horizontal flow in large cells) the buoyancy work can be locally negative in upflows — this is referred to as buoyancy braking (Massaguer and Zahn, 1980; Hurlburt et al., 1984; Cattaneo et al., 1991; Rieutord and Zahn, 1995). Averaging the kinetic energy equation over horizontal planes (using 〈…〉 to denote horizontal averages) one finds that there is a contribution from the rate of work done by the buoyancy force,
where u′z is the horizontal fluctuation of the vertical velocity, and the ellipses represent all other terms in the kinetic energy equation. The physical interpretation is apparently clear; fluid that is heavier than average is accelerated downwards while fluid that is lighter than average is accelerated upwards — both give positive contributions to the balance of kinetic energy, so one is led to believe that there is a net positive work done by gravity. However, mass conservation requires that
and hence that
Hence the total work done by gravity vanishes. If we integrate over a volume that entirely encloses the region of convection the integrals of divergence terms vanish, and the only remaining term that can balance the viscous dissipation is
This term is positive on the average because the pressure is higher when the gas expands (on the way up) than when it is compressed (on the way down). So, averaging over the kinetic energy equation tells us that viscous dissipation is balanced by gas pressure work, not by buoyancy work!
But buoyancy forcing of convection is a fundamental and easily understood mechanism; warm gas is lighter and rises, cold gas is denser and sinks. So, how can the total buoyancy work vanish? The solution to this riddle lies in the word “total”. Buoyancy indeed performs positive work on convection cells, maintaining their kinetic energy. It is only when including the ultimate, global scale, the horizontally averaged velocity, that the energy balance score of the buoyancy work is evened out to zero. Because density and velocity are correlated, and because the average mass flux must vanish, the average vertical velocity is upwards, corresponding to negative buoyancy work of a magnitude that exactly cancels the fluctuating buoyancy work!
The root of the somewhat perplexing situation lies in the particular choice of variables that are to be expanded into ‘averages’ and ‘fluctuations’. As a result of choosing density and velocity, rather than for example density and mass flux (which has a vanishing horizontal average) one must include also the (non-vanishing) product of the averages, and not only the average product of the fluctuations.
Perhaps the clearest way of stating the result is to say that there is on the one hand a (generally positive) work done by the buoyancy force (as defined) on the convective motions, and there is on the other hand an equally large but negative work done by the average force of gravity acting on the mean flow. As a result, the total work done by gravity vanishes.
Broadly speaking the positive buoyancy work goes towards maintaining the fluctuating (convective) velocity field against dissipation, but, as illustrated by Equation 17, the most straightforward analysis of work and dissipation is obtained by considering the gas pressure work rather than the buoyancy work.
2.4 Energy transport
The equation describing the evolution of internal energy is, in conservative formFootnote 1,
where E is the internal energy per unit volume, Qrad is the radiative heating or cooling, and Qvisc is the viscous dissipation
or, denoting by sij the symmetric part of the strain tensor \({{\partial {u_i}} \over {\partial {r_j}}}\),
we have
The term P(∇ · u) is the “PdV”-work, which is responsible for adiabatic heating and cooling when gas is compressed or decompressed. This is more clearly brought out by the Lagrangian form of the energy equation,
where e = E/ρ is the energy per unit mass. For an ideal gas
where Γ = (∂ln P/∂ ln ρ)s. In this case e is proportional to temperature T. Since, as per Equation 2, the PdV-term may be written \(-{{P} \over {\rho}} {{D \ {\rm ln} \ \rho} \over {Dt}}\), the adiabatic compression/expansion of an ideal gas is characterized by
Equations 22 and 24 are useful when considering the energy balance of the solar photosphere — cf. further discussion below.
2.4.1 Radiative energy transfer
The radiative heating or cooling Qrad may be written as the negative divergence of the radiative flux,
where
ν is the radiation frequency and Iν is the radiation intensity in direction Ω.
The radiation intensity may be obtained along straight lines of sight by solving the radiative transfer equation
where Sν is the radiative source function (equal to the Planck function Bν if (strong) Local Thermodynamic Equilibrium (LTE) may be assumed), and
is the increment of the optical depth τν over the geometric interval ds, given the monochromatic absorption coefficient κν. Combining Equations 25–28 one also finds that
which lends itself to a direct and intuitive interpretation; it shows that whenever the radiation intensity is lower than the local source function, there is cooling. This happens particularly in surface layers where the outgoing intensity (away from the surface) is similar to the source function, but the incoming intensity is much lower, due to the “dark sky” that is visible from a surface where the optical depth to infinity is less than unity.
Because of the interplay of the ρκν and Iν − Sν factors, the effect is largest in a thin layer near optical depth unity; at larger depths the difference Iν − Sν tends to zero exponentially with optical depth, while at smaller depths the ρκν factor diminishes the effect as well.
The discussion above applies frequency by frequency, and because of variations in the opacity κν with frequency, in particular across spectral lines, the net heating or cooling can only be found by evaluating the integral over frequency that occurs in Equation 29. An approximate way to estimate that integral using a binning method was developed by Nordlund (1982) and applied in subsequent works by Stein, Nordlund and collaborators (e.g., Stein and Nordlund, 1989, 1998; Asplund et al., 2000b; Carlsson et al., 2004). The method has been tested and used by Ludwig and co-workers (Ludwig et al., 1994; Steffen et al., 1995) and by Vögler and co-workers (Vögler et al., 2004; Vögler, 2004; Vögler et al., 2005). Improvements are being developed by Trampedach and Asplund (2003).
2.4.2 Equation of state
Whenever the constituent atoms or molecules of a gas undergo ionization or dissociation, extra energy is required to heat or cool the gas; i.e., the internal energy e varies more with temperature than for an ideal gas. Near the surface of the Sun, both ionization and dissociation are important; ionization of hydrogen and helium influence the equation of state greatly just below the surface, and dissociation of hydrogen molecules is important in the cooler layers of the photosphere.
In general then, one needs to know the relations
and
in order to use Equations 5–18 to evolve the momentum and energy density forward in time (Gustafsson et al., 1975; Mihalas et al., 1988; Däppen et al., 1988; Mihalas et al., 1990; Rogers, 1990; Rogers et al., 1996; Rogers and Iglesias, 1998; Rogers and Nayfonov, 2002; Trampedach, 2004b,a; Trampedach et al., 2006). Since computing these relations from first principles in general is quite expensive the best approach for practical computational work is to tabulate and interpolate in these relations.
2.4.3 Convective and kinetic energy fluxes
By a few algebraic manipulations of the equations of motion and the energy equation one can show that
where Fconv is the convective, enthalpy, flux
Fkin is the kinetic energy flux
and Fvisc is the (generally small) viscous flux
Frad is the radiative energy flux defined by Equation 26. For an ideal gas one may expect the fluctuations in pressure, δP, internal energy per unit volume δE, and the kinetic energy density δ(½ρu2) to be of similar magnitude, and thus the convective and kinetic energy fluxes to also be of similar magnitude (although not necessarily pointing in the same direction). However, as mentioned above, near the solar surface the internal energy becomes dominated by changes in the ionization energy, and the convective flux thus tends to dominate there.
At the solar surface there is a very rapid transition between primarily convective and primarily radiative energy transport. In the atmosphere it is more relevant to consider changes of the radiative flux, through Equation 29.
3 Granulation
With the previous Section providing the physical background, we now have the tools (and the language) to discuss the various manifestations of convection at the surface of the Sun, treating in this Section the energetically most significant pattern; the solar granulation.
The solar granulation pattern was first observed and described by Herschel (1801), who interpreted the pattern as being due to “hot clouds” floating over a cooler solar surface. Nasmyth (1865) later referred to the pattern as one similar to “willow leaves”. Dawes (1864) was the one who coined the term “granules”, contesting the description of Nasmyth with respect to the shapes — this illustrates that already then spatial resolution of observation was a factor of great importance. The first good photographs, published by Janssen (1896) ended the controversy.
The granulation pattern is in fact, as we now know, associated with heat transport by convection, on horizontal scales of the order of a thousand kilometers, or one megameter (Mm). So, Nasmyth was on the right track concerning the temperature, and must have seen essentially the pattern we know today, but the prolific Dawes (who published 5–6 MNRAS papers per year in that period of time) managed to establish the name for it.
3.1 Observational constraints
Paradoxically, the best observational constraints on solar granulation come from completely unresolved observations; observations of the widths, shapes, and strengths of photospheric spectral lines provide constraints that, when combined with numerical models of convection on granular scales, allow quite robust results to be extracted from the numerical models.
Direct observations (e.g., Title et al., 1989; Wilken et al., 1997; Krieg et al., 2000; Müller et al., 2001; Berrilli et al., 2001; Löfdahl et al., 2001; Hirzberger, 2002; Nesis et al., 2002; Hirzberger, 2002; Roudier et al., 2003b; Del Moro, 2004; Puschmann et al., 2005; Nesis et al., 2006; Stodilka and Malynych, 2006, and references therein), have given a wealth of information about the morphology and evolution of the granulation pattern, and about how it is influenced and advected by larger scale flows. However, direct observations of sub-arcsecond size structures are unavoidably affected by image degradation, caused by limited instrumental resolution, scattering in the instrument and, in the case of Earth-based observations, atmospheric blurring and image distortion. Without the access to a sharp reference image or light source, it is not possible to obtain independent measurements of the amount of image degradation, and hence it is also not possible to perform quantitatively well defined image restorations.
In unresolved observations, on the other hand, key properties such as velocity amplitudes and velocity-intensity correlations are encoded in the shapes of the spectral lines. The many photospheric iron lines that can be observed in the solar spectrum are of particular importance, both because they are numerous, which allows a fair number of practically unblended lines to be found, but also because iron is a relatively heavy atom, so the thermal broadening is small (or at least not completely dominating) compared to the Doppler broadening caused by the velocity field.
The widths of spectral lines are thus heavily influenced by the amplitude of the convective velocity field, which overshoots into the stable layers of the solar photosphere where the iron lines are formed. Similarly, correlations of velocity and temperature cause net blueshifts and characteristic asymmetries of spectral lines (cf. Dravins et al., 1981; Dravins, 1982; Asplund, 2005; Gray, 2005). Together, the widths, shifts, and shapes of spectral lines thus constitute a “fingerprint” of the convective motions, which allows detailed and quantitative comparisons between 3D models and observations to be based on spatially unresolved but spectrally very accurate line profile observations. As shown in Asplund et al. (2000a,b), the agreement between observations and high resolution 3D models is excellent. See Section 5 for additional discussion.
Note that the combination of the excellent agreement of spectral line widths (which constrain the velocity amplitudes) and spectral line shifts and asymmetries (which constrain the product of velocity amplitudes and intensity fluctuations) means that the intensity fluctuations obtained from the simulations are very reliable. If they were too large or too small the spectral line shifts and asymmetries would be correspondingly to large or too small as well (cf. Deubner and Mattig, 1975; Nordlund, 1984). Different numerical models give rms intensity fluctuations that agree to within 1–2 percent of the continuum intensity. Observed rms intensity fluctuations are generally much smaller, presumably due to the combined effects of seeing, limited telescope resolution, and scattered light. A detailed comparison of the rms intensity fluctuations observed with Hinode with the results of forward modeling from numerical simulations (Danilovic et al., 2008) concludes that the results are essentially consistent.
3.2 Convective driving
Convection is driven primarily by radiative cooling from a thin thermal boundary layer at the visible surface of the Sun, the layer from which most photons can escape to space. The most prominent intensity variations on the solar surface, aside from sunspots and faculae, are granules — the bright (hot) areas surrounded by dark (cooler) lanes that tile the Sun’s surface (Figure 2). Their diameters are typically of order 1 Mm, and this is the horizontal scale on which radiative cooling drives the convective motions. The bright granules are the locations of upflowing hot plasma, while the dark intergranular lanes are the locations of downflowing cool plasma.
Image of granulation in the G-continuum, showing hot, bright rising fluid surrounded by cooler, darker intergranular lanes. Granules tile the solar surface and are the dominant feature of solar surface convection. Also shown are a few magnetic concentrations, visible as strings of bright beads along the intergranular lanes (image from the Swedish 1m Solar Telescope and Institute of Theoretical Astrophysics, Oslo).
Plasma that reaches the layer where a typical photon’s mean free path equals the distance to space has some of its thermal energy carried away by photons. As a result the plasma cools, so that hydrogen ions capture electrons to become neutral hydrogen atoms and in the process release a large amount of ionization energy that is also carried away to space by photons. The escaping photons, as they remove energy, also remove entropy from the plasma that reaches the surface, producing overdense fluid which is pulled down by gravity (Figure 3). Solar convective motions are driven by buoyancy work, primarily downward on the overdense, low entropy, cool fluid in the intergranular network, and partially upward on the underdense, high entropy, hot fluid in the granule interiors (Figure 4). At increasing depths, more and more of the buoyancy work occurs in the cool downdrafts, rather than the warm upflows. Deeper into the convection zone the magnitude of the entropy fluctuations decreases because the diverging upflowing plasma all has nearly the same entropy, while the turbulent downdrafts entrain and mix with overturning fluid from the upflows which gradually increases their entropy (Figures 3, 5). The result is that, although the convecting plasma is heated at the bottom — as well as cooled at the top — of the convection zone, most of the buoyancy work is due to cooling at the surface which produces large entropy fluctuations, rather than heating at the bottom of the convection zone, which produces only small entropy fluctuations. The role of the lower boundary is to replenish the entropy of fluid parcels that reach the bottom of the convection zone — it is primarily a supplier of heat, and contributes to driving patterns of motion only on the largest, global convection zone scales.
Temporal history of typical fluid parcels that reach the surface: height z (Mm), optical depth τ, log(ρ), radiative heating Qrad (103 erg/gm/s), internal energy E (105 erg/gm), specific entropy S (108 erg/gm/K), fraction ionization to total energy, and vorticity ω (10−2 s−1). Time is counted from when the parcel rises through unit optical depth. When fluid reaches optical depth ρ ∼ 100, it begins to cool rapidly as the gas starts to recombine. Its entropy and energy drop so quickly that its density increases. As it passes above the surface a small amount of radiative reheating occurs and its entropy increases slightly. When it passes back down through optical depth unity it cools some more with a further drop in entropy. As it heads down into the interior it heats up by adiabatic compression and by diffusive energy exchange. The deeper it gets, the more adiabatic its motion becomes (from Stein and Nordlund, 1998).
Buoyancy work at a depth of 0.5 Mm as a function of (a) vertical velocity (downflows are positive) and (b) fluid entropy. Most of the convective driving below the surface occurs in the low entropy downflows produced by radiative cooling at the surface (from Stein and Nordlund, 1998).
Histogram of the entropy (logarithmic color scale with arbitrary units) as a function of depth. Most of the area of a horizontal plane below the surface is occupied by upward moving fluid with close to the maximum entropy. Entropy fluctuations are largest at the surface and decrease with increasing depth due to entrainment of entropy neutral material and, in the case of the simulations, numerical energy diffusion (which however is insignificant in this context — most of the entrainment is due to the overturning forced by mass conservation). Entropy increases above the surface because radiation from the surface heats the gas much above the temperature it would attain if moving adiabatically (from Stein et al., 1997).
3.3 Scale selection
Because of the enormous variation of mass density with depth, conservation of mass plays a central role in determining the convective flow patterns; whenever a fluid parcel moves up or down over a density scale height it must expand or contract with a factor of e. This constraint dictates the scales on which the dominant convective motions occur.
The upper layers of the solar convection zone are indeed highly stratified, with density scale heights that are smaller than the typical horizontal dimensions of granules. The rapid decrease in density with height leads to a marked asymmetry in the convective flows. Fluid moving upward into lower density layers cannot carry all its mass higher. Hence, upward moving fluid must diverge and most of it turns over within a scale height. Downward moving fluid on the other hand is moving into denser regions and gets compressed as it descends. As a result, diverging upflows have their fluctuations smoothed out, while converging downflows have their’s increased and become turbulent. Except within 100 km of the surface, upflows occupy about 2/3 and downflows about 1/3 of the area.
The typical size of granules, and other convective cells deeper inside the convection zone, is set by mass conservation and is a few times the local scale height. To conserve mass, most of the upflow through a convective cell at any given depth must flow out through the sides of the cell over approximately a scale height, H. Hence, approximating the convective cell by a circular cylinder of radius r and height H,
Thus the horizontal cell size must be of order,
A certain minimum vertical velocity is needed to transport sufficient energy to the surface to balance the radiative losses. This can be estimated by balancing the radiative loss from the surface, the solar flux, with the enthalpy flux,
where χ is the hydrogen ionization potential and x is the hydrogen ionization fraction. For an order of magnitude estimate for the required vertical velocity near the surface, assume x ≈ 0.1. This gives a velocity of ∼ 2 km s−1 for the minimum velocity needed to supply the radiative losses from the surface (Nordlund and Stein, 1991). Since the vertical velocity cannot decrease below this value if the granule is to remain bright, the horizontal expansion velocity must increase as the granule size increases to balance the greater volume of fluid being brought to the surface through the larger granule area. However, the horizontal velocities cannot much exceed the sound speed of ≈ 7 km s−1 at the surface. Hence, an upper limit to the size of granules is of order 2r ∼ 4 Mm (H ∼ 300 km near the surface) (Nelson and Musman, 1978; Nordlund, 1978). As a result of the increasing scale height with depth, due to the increasing temperature with depth, the scales of motion increase continually with depth. For simulations extending 20 Mm below the surface, the convective cellular structures reach sizes of about 20–30 Mm (Figure 6). There is no special feature corresponding to mesogranular cells (although that scale is clearly visible in the slice at 4 Mm depth) or the supergranular scale (visible in slices from a depth of about 8 Mm).
The larger scales flow patterns are in a sense also driven by the surface cooling, albeit in a more indirect manner. Rising plasma expands and spreads outwards, and over each density scale height a large fraction turns over and joins the downflowing plasma. Even from a depth of just a few Mm, only a tiny fraction of the ascending flow reaches the surface and is cooled by radiation cooling; the rest turns over and is only cooled by mixing with downflowing material (Stein and Nordlund, 1989). Conversely, descending flows from the surface are being entrained by adiabatic overturning fluid, and turbulent mixing in the downdrafts thus reduces the entropy contrast gradually with depth (cf. Figure 5).
The hierarchy of horizontal scales associated with the gradual increase of scales with depth implies that smaller scales are being advected horizontally by larger scale patterns, and the descending fluid thus forms a hierarchical structure of merging downdrafts (Figure 7). In this hierarchy the granular (surface) scales are driven directly by radiative cooling while the larger scales are driven by the entrained and mixed lower entropy contrast plasma further down in the hierarchy.
mpg-Movie (37870.9150391 KB) Still from a movie showing Vertical velocity (red upward, blue downward) and streaklines (seen more clearly in the movie) in a vertical cut through the 24 Mm wide simulation domain. Diverging upflows sweep downflows toward each other at the boundaries of the larger, deeper lying upflows (movie by Chris Henze, NASA Advanced Supercomputing Division, Ames Research Center). (For video see appendix)
On the average, the plasma at any one level has a slightly superadiabatic stratification, which is a mix of almost perfectly isentropic ascending plasma and cooler descending plasma. Formally, this average structure is convectively unstable according to the Schwarzschild criterion (Schwarzschild, 1958), and one may regard the larger scales as being driven by the corresponding convective instability; a slight perturbation at larger scales is self amplifying, since the diverging upflow sweeps smaller scales downdrafts together, thus amplifying the perturbation (Stein and Nordlund, 1989; Rast, 2003).
3.4 Horizontal patterns and evolution
On the scale of granulation, the shape and evolution of the temperature and velocity patterns also reflects the strong density stratification. The rapid decrease of density with height forces the plasma in each granule to spread outwards (Figure 8). The plasma that reaches the surface looses energy very rapidly by radiative cooling, and as it collides with similar outflows from other granules it forms dark intergranular lanes where the fluid is deflected downwards and along the lanes towards cell vertices. Along the lanes, and particularly at the cell vertices, it forms turbulent downdrafts with low entropy (Figure 9).
Velocity and temperature structure of a granule with a corner cutout. A granule resembles a fountain with warm fluid rising up near the center, diverging horizontally, cooling, being pulled back down by gravity in surrounding intergranular lanes (from Stein and Nordlund, 1998).
Mass conservation takes care of itself by acting through the pressure. Large granules require a large pressure perturbation to drive their horizontal flows. If there is insufficient pressure to push enough mass out horizontally, the density builds up over the granule until the pressure is raised sufficiently to expel it. The excess pressure also decelerates the upflow and thus reduces the energy transport to the surface, in particular near the granule center, which then cools (Massaguer and Zahn, 1980). Hence, as granules grow, the upflow velocity near their center decreases and they develop an edge brightened appearance.
The horizontal flow, driven by the excess pressure in the interiors of the granules, must be halted when it reaches an intergranular lane, by which time it has cooled, become denser and is being pulled down by gravity. This requires an excess pressure also in the intergranular lanes (Hurlburt et al., 1984).
3.5 Exploding granules
Particularly undisturbed granules that grow to sufficient size tend to develop dark centers, where the vertical flow reverses. These so called ‘exploding granules’ have been the topic of a number of observational and theoretical papers (e.g., Musman, 1972; Allen and Musman, 1973; Namba and van Rijsbergen, 1977; Namba, 1986; Simon and Weiss, 1991; Simon et al., 1991a,b; Rast, 1995; Hirzberger et al., 1999; Roudier et al., 2001).
As per the discussion in Section 3.3 above, the reason for the phenomenon is the increase with size of the pressure at the center of granules, which is necessary to drive the increasing horizontal flow that results from the requirement of mass conservation. The increase of the density associated with the increasing pressure leads to a negative buoyancy, which eventually reduces the vertical velocity down below the value needed to maintain the surface luminosity. The resulting cooling then accelerates the process, leading to a rapid cooling and reversal of the vertical flow.
Arguments essentially to this effect were given already by Musman (1972) and Namba and van Rijsbergen (1977).
3.6 Surface entropy jump
Radiation losses and transport near the solar surface not only produces the low entropy, high density fluid that gravity pulls down to drive the convective motions, but also controls what we observe on the Sun. The surface occurs where photons can escape, so neither the diffusion approximation nor the optically thin approximations are valid. The radiation heating/cooling must be obtained by solving the transfer equation for the radiation. Since the temperature varies both in the vertical and horizontal directions, transfer in three-dimensions is needed. Current computers are still not fast enough to solve the full non-LTE (or even LTE) transfer problem at the large number of frequencies needed to cover the continuum and line spectrum for each of the thousands of time steps needed for a reasonable simulation time sequence, so the binning method mentioned in Section 2.4.1 needs to be used.
Photons escape typically from one mean free path into the Sun. The dominant source of opacity at the surface of the Sun is due to the H− ion, whose electron is bound by only 0.75 eV and is easily detached by photons in the near infrared and shorter wavelengths (< 1.64 µm) and by collisions. As a result, the H− opacity is very temperature sensitive, κ ≈ T10. Because of this great sensitivity to the plasma temperature, photons escape from the cool intergranular lanes at larger depths than from the hot granule centers (cf. Pecker, 1996) and the optical depth unity surface is corrugated with an rms height variation of ≈ 35 km in magnetic field free regions and extending as deep as ≈ 350 km in strong magnetic field (≥ 1.5 kG) concentrations (Wilson depression; see Figure 10). This produces a hilly appearance of granules when viewed toward the limb (Figure 11; Carlsson et al., 2004). Another consequence is that we observe a much smaller temperature variation across the surface than is actually present at a given geometrical level (Figure 12; Stein and Nordlund, 1998). We do not observe the hot plasma because at high temperatures we only see photons that escape from higher elevations, which are cooler, since in the photosphere the mean temperature decreases outward.
Correlation of radiation temperature at 1.6 µm with gas temperature at the depth where (τ1.6µm) = 1. We never see the radiation from the high temperature gas because it lies at large local optical depth due to the great temperature sensitivity of the H− opacity (κ × T10) (from Stein and Nordlund, 1998).
Significant absorption and emission occurs in spectral lines above the level from which continuum photons escape. Spectral lines typically cool the plasma where their optical depth is of order unity and heat the plasma where their optical depth is large and they block the escape of radiation; this process is known as “spectral line blanketing” (Mihalas, 1978). Ascending plasma from granule interiors would otherwise adiabatically cool as it expands going from the visible surface to the temperature minimum (∼ 4 scale heights) by a factor of > 3, or from ∼ 6000 K to < 2000 K. This does not happen because the ascending gas is heated by absorbing radiation in optically thick lines and UV continua. Such absorption blocks some of the radiation from escaping producing a greenhouse effect called “back warming”. The photons absorbed above the τ500 = 1 surface reheat the photospheric plasma which then radiates both upward and downward heating the surface above the temperature it would have if all the radiation could escape to space. Realistic horizontal transport in the presence of evacuated magnetic flux concentrations also requires inclusion of optically thick line opacity, because otherwise the flux concentrations become optically thin and do not absorb photons from the hot granule walls and so do not show up as bright points at disk center and faculae toward the limb (Steiner and Stenflo, 1990; Vögler, 2004).
3.7 Temperature fluctuations
As clearly seen from Figure 12, there is a huge temperature difference, a factor of almost two, at mean optical depth unity, between the warm upflows (∼ 10,000 K) and the cool downflows (∼ 6,000 K). Along with the sudden drop in entropy as the fluid begins to be exposed to space (Figure 5), there is a corresponding sudden drop in the temperature of rising fluid parcels (Figure 13). The temperature drop in individual fluid parcels when they can radiate away their energy is far steeper than the average temperature drop. The average includes the cool downflows whose temperature increases gradually as they exchange energy with their surroundings and entrain overturning entropy neutral material from the upflows. It is this drastic difference between the warm upflows and cool downflows at the same geometric height that is the cause of the tremendous temperature fluctuations at the surface.
Temperature as a function of geometric depth at several horizontal locations plus the average temperature profile (dashed). Locally the temperature profile is much steeper than the average profile (from Stein and Nordlund, 1998).
The fluid is always approximately in radiative — convective equilibrium (∇·(Fconv+Frad) ≈ 0) for the atmospheric structure through which it is moving. The upflows transfer their internal energy to radiation between optical depths τ ∼ 30 and τ ∼ 1. Between those depths they have a temperature gradient close to but slightly less than the grey radiative equilibrium value of T ∝ τ1/4 (Figure 14). Their temperature gradient is slightly less than the radiative equilibrium value because the radiative flux is increasing as the optical depth decreases due to the transfer of energy from convection to radiation. This well known gradient on an optical depth scale corresponds to an extremely steep gradient on a geometric depth scale (Figure 13), because of the extreme temperature sensitivity of the dominant H− opacity.
Temperature as a function of optical depth at several horizontal locations plus the average temperature profile (dashed). On an optical depth scale, the temperature profile is similar at all places in the simulation domain, whether in warm upflows or cool downflows. This is because the opacity depends very strongly on temperature, and hence a certain optical depth is reached at nearly the same temperature, whether the temperature rises rapidly (as in upflows) or more slowly (as in downflows) (from Stein and Nordlund, 1998).
3.8 Average structure
The mean atmospheric structure in the 20 Mm deep simulations is shown in Figures 15 and 16. The temperature increases by less than two orders of magnitude from the surface to 20 Mm depth (from ∼ 4300 K to 143,000 K). The density, on the other hand, increases by 5.5 orders of magnitude from the temperature minimum to 20 Mm depth and the pressure varies by 7 orders of magnitude. The 50% ionization depths of H, He i, and He ii occur at ≈ 1, ≈ 6, ≈ 16 Mm, respectively. A 20 Mm deep simulation contains 2/3 of the pressure scale heights within the convection zone.
In general the average structure of 3D models agrees very closely with mixing-length models of the solar envelope, with the main function of the mixing-length parameter being to calibrate the magnitude of the entropy jump at the surface (Rosenthal et al., 1999; Brandenburg et al., 2005).
A 20 Mm deep simulation also contains the entire hydrogen ionization region, helium first ionization and most of the helium second ionization regions (Figure 16). The adiabatic index becomes very small in the hydrogen ionization zone (reaching a minimum of 1.13). The second helium ionization has only a small effect, producing a plateau at Γ = 1.55.
3.9 Vorticity
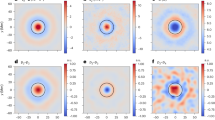
The overturning flow at the edges of granules produces horizontal vortex tubes at the interface between the granule and the intergranular lane. The equation for vorticity ω ≡ ∇ × u is obtained by taking the curl of the equation for the velocity (the equation for the momentum, Equation 6, divided by the density),
The result is (for the case of constant viscosity)
From this equation we see that vorticity is generated where the density and pressure gradients are not parallel, which occurs where radiation transport effects are important, that is near the surface. At the mushroom heads of downdrafts, where there is a change in entropy, so that the density and pressure gradients are not parallel, ring vortices form (Figure 17). These are connected back up to the surface by typically two, but sometimes more, trailing vortices (similar to those from the tips of airplane wings) (Figure 18). The equation for the vorticity also shows that existing vorticity is enhanced by stretching and compression, which occurs primarily in turbulent downflows, and it is diminished by expansion in upflows.
Rendering of vorticity around a single granule showing antiparallel vortex tubes (green, opaque surfaces) at the edges of the intergranular lanes (near the right hand side edge) and a ring vortex at the head of a downdraft with two trailing vortex tubes leading up to the surface (center left). The transparent red and blue shows the velocity divergence ∇ × u red (positive) identifies the diverging flow inside the granule while blue (negative) identifies the converging flow in the intergranular lanes.
3.10 Shocks
Occasional supersonic flows and shocks occur in both the horizontal flows at the intergranular lane boundaries and in the vertical flows below the surface, which results in weak shocks where these downflows collide with the upflows (Stein and Nordlund, 1998). The maximum Mach numbers are about 1.5 for horizontal flows and 1.8 for vertical flows. The maximum Mach numbers occur at the surface for the horizontal flows and half a megameter below the surface for the vertical flows (Figure 19). The largest Mach numbers for both vertical and horizontal flows occur at the boundaries of the granules that overlie the boundaries of the larger scale subsurface flows (Figure 20). It is at these locations that the downdrafts are strongest because they do not have to push against upflowing fluid and it is also here where these strong downflows are the strongest sinks for the diverging horizontal flows in the granules. Observational evidence for shocks waves in the solar photosphere were presented by (Rybák et al., 2004).
Supersonic convective flows were first studied by Cattaneo et al. (1990) and Malagoli et al. (1990) in simple models with polytropic stratification and no radiative energy transfer. They predicted that supersonic flows are most likely to occur close to the photosphere in the case of convection in real stars; the horizontal pressure fluctuations need to be large, and the radiative (or boundary) cooling needs to be efficient, so the sound speed can be efficiently reduced while the flow is being accelerated. This prediction agrees well with what has later been found in models with detailed radiative transfer and non-ideal equations of state (Nordlund and Stein, 1991; Stein and Nordlund, 1998; Wedemeyer et al., 2003, 2004; Schaffenberger et al., 2006; Hansteen, 2008).
3.11 Energy fluxes
About 2/3 of the convective energy flux near the solar surface consists of ionization energy (Figure 21). Thermal energy accounts for a little over 1/6 of the flux and acoustic energy a little under 1/6 of the flux (Stein and Nordlund, 1998). Hence, including ionization of hydrogen, helium, and the other abundant electron donors in the equation of state is necessary to achieve solar values for the velocities and temperature fluctuations. For an ideal gas to be able to carry the solar flux both the vertical velocities and the temperature fluctuations would have to be larger than is observed. Above temperatures of order the He ii ionization energy (∼ 105 K) most of the energy is transported as thermal energy and an ideal gas equation of state for a fully ionized plasma would be a good approximation.
The average thermal, ionization, acoustic, and kinetic fluxes plus their sum, the total energy flux, as a function of depth. The thermal plus ionization energy fluxes together are the internal energy flux (not plotted), and this plus the acoustic flux constitutes the enthalpy or convective flux. The enthalpy flux plus the kinetic energy flux is the total energy flux transported by fluid motions. (The viscous flux is very small.) Energy is transported upward through the convection zone near the surface mostly as ionization energy (∼ 2/3) and thermal energy (∼ 1/3). The kinetic energy flux is downwards and is 10–15% of the total flux near the surface. At larger depths (outside of this plot) both the upward enthalpy flux and the downward kinetic energy flux increase, with the kinetic energy flux reaching about the net solar flux and the enthalpy flux reaching about twice the net solar flux.
3.12 Connections with mixing length recipes
The simplest model of turbulent convection is called “Mixing Length Theory” (MLT; see Böhm-Vitense, 1958). It is extensively used in stellar evolution calculations where the convection zone must be modeled many times during the course of a star’s evolution. MLT is based on an unphysical picture of moving fluid parcels in pressure equilibrium with their surroundings. In a convectively unstable region the entropy increases inward. A fluid parcel moving upward adiabatically will have higher entropy than the surrounding mean atmosphere and so has a higher temperature and lower density than the mean stratification, so it is buoyant and is accelerated upward. Conversely, a fluid parcel moving downward adiabatically will have lower entropy than its surroundings and so has a lower temperature and higher density than the mean stratification and is pulled down by gravity. After moving some characteristic distance ℓ (the mixing length) the fluid parcel dissolves back into its surroundings. The mixing length, ℓ, determines the magnitude of the temperature fluctuations, flow velocities, and consequently the energy flux. Typically this mixing length parameter is taken to be some multiple of the pressure scale height or as the distance to the boundary of the convectively unstable region.
In the first place, this is an unphysical picture. Turbulent convection is best pictured as upflows and downdrafts that can extend over many pressure and density scale heights. MLT is a local theory, where the flow velocities and temperature fluctuations are determined by local conditions. In reality, the entropy and temperature fluctuations are determined primarily by radiative cooling in the thin surface thermal boundary layer.
The free parameter, the mixing length ℓ, is not determined within the theory and varies across the Hertzsprung-Russell diagram according to 3D convection simulations (Abbett et al., 1997; Ludwig et al., 1999; Freytag et al., 1999). Hence, numerical convection simulations are needed to calibrate the mixing length parameter. Furthermore, standard MLT does not allow for overshoot of convective motions into the surrounding stable layers (Deng and Xiong, 2008, but see). It can not, for instance, account for phenomena such as reverse granulation or the observed destruction of lithium in the Sun by mixing below the convection zone. Finally, even with a mixing length that produces the correct interior adiabat, MLT produces a different mean atmosphere structure than given by the numerical simulations. This leads to disagreements between calculated and observed p-mode oscillation frequencies (Rosenthal et al., 1999). However, the mixing length scaling of temperature fluctuations and velocity with the convective flux,
does hold fairly accurately with the proportionality factor depending on viscosity and radiative energy exchange (Brandenburg et al., 2005). Other works that attempt a connection between mixing-length theory and numerical simulations are the ones by Kim et al. (1996) and Robinson et al. (2003).
4 Larger Scale Flows and Multi-Scale Convection
Traditionally, larger scale flows at the solar surface have been classified into mesogranulation, with horizontal scales of the order of 5–10 Mm, supergranulation, with horizontal scales of the order of 20–50 Mm, and giant cells, with horizontal scales of the order of 100 Mm or larger. However, as discussed in more detail below, this distinction is largely of historical origin, and current evidence indicates that there is a continuous spectrum of motions, on all scales from global to sub-granular.
The larger flow scales are related to, and unavoidable consequences of, the larger scale convective flows that exist in the subsurface layers of the solar convection zone. Since the scales of these subsurface flows increase continuously with depth it is also hard to imagine a physical reason that would cause distinct flow scales at the solar surface. Already the fact that there is only a factor ∼ 2 gap between the scales traditionally assigned to granulation, mesogranulation and supergranulation makes it very difficult to imagine a true scale separation.
Below, we first summarize the observational evidence categorized by the traditional flow scale labels, ‘mesogranulation’, ‘supergranulation’, and ‘giant cells’. We then consider multi-scale observations and show that unbiased multi-scale observations, as are available, e.g., from SOHO/MDI, show a smoothly increasing spectrum of velocity amplitudes with increasing wave number (decreasing size), incorporating in a continuous manner the scales with the traditional labels.
4.1 Mesogranulation
Mesogranulation was first detected by Larry November and coworkers (November, 1980; November et al., 1981, 1982), and has since been the subject of a large number of observational papers; (e.g., Oda, 1984; Simon et al., 1988; Brandt et al., 1991; Muller et al., 1992; Roudier et al., 1998; Shine et al., 2000; Roudier and Muller, 2004; Leitzinger et al., 2005). There has also been a heated debate as to the nature of mesogranulation, and about whether mesogranulation is a distinct scale of convection or not; (e.g., Wang, 1989; Deubner, 1989; Stein and Nordlund, 1989; Ginet and Simon, 1992; Straus et al., 1992; Ploner et al., 2000; Cattaneo et al., 2001; Rast, 2003). A recent example of the techniques commonly used to observe mesogranulation is Leitzinger et al. (2005), who used correlation tracking and a running (1 h) mean in time to map the horizontal component of the mesogranulation velocity field, and to study the drifts of mesogranules in the supergranular velocity field. Others (e.g., Brandt et al., 1988; Title et al., 1989; DeRosa and Toomre, 1998; Roudier et al., 1999; Shine et al., 2000; DeRosa and Toomre, 2004) have used similar techniques to study flows on scales ranging from meso- to supergranulation. Inherent in these techniques is that, because of the spatial and temporal averaging, smaller spatial scales and shorter time scales cannot be adequately resolved. In a situation where the velocity amplitudes increase with decreasing motion scale, such a cut-off automatically (but incorrectly) brings out the smallest scale that is adequately resolved as a dominant, distinct scale.
Another inherent limitation of the tracking techniques is the assumption that the granule-scale fragments and features used in the tracking process are actually good tracers of the solar surface velocity field. This is not necessarily the case, since granules are active flow features, whose horizontal motions presumably also sample the conditions over a range of depths. Rieutord et al. (2001) compared the velocity field derived from tracking granule motions in numerical simulations to the actual meso-scale velocity field of the plasma in the simulations. They conclude that neither velocity fields at scales less than 2500 km nor time evolution at scales shorter than 30 min can be faithfully measured by granule tracking, but that at larger scales and over longer time scales granule tracking works well.
4.2 Supergranulation
Supergranulation was first observed by Hart (1956), and was later studied in more detail (and named) by Leighton et al. (1962) and by Simon and Leighton (1964), who emphasized the close correlation between the supergranulation and the chromospheric network.
A large number of works have studied supergranular scale flows observationally and tried to characterize them in terms of, for example, flow velocity as a function of cell size, morphology, clustering, advection of smaller scale flows, divergence and convergence, etc.; some of the most significant ones are, e.g, Deubner (1971); Muller et al. (1992); Hathaway et al. (2000); Zhao and Kosovichev (2003); Del Moro et al. (2004); DeRosa and Toomre (2004) and Meunier et al. (2007).
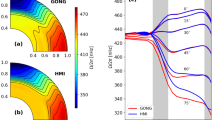
Numerical hydro- and MHD-simulations, with realistic equations of state and radiative energy transfer, are now reaching the scale of supergranulation (Rieutord et al., 2002; Stein et al., 2006a, 2005, 2006b; Ustyugov, 2006; Stein et al., 2007b; Ustyugov, 2007, 2008), and it is thus becoming possible to make quantitative comparisons between observations and simulations. A great benefit of this approach is that if a good match is obtained between the numerical simulations and observations, one may with some confidence use the numerical simulations as proxies or predictions of the subsurface and small scale structure. This allows, e.g., local helioseismology techniques to be further improved and calibrated (Georgobiani et al., 2004; Zhao et al., 2007a; Georgobiani et al., 2007; Birch et al., 2007).
4.3 Giant cells
Reports on velocity field structures significantly larger than supergranulation were sporadic at best (Cram et al., 1983; Hathaway et al., 1996; Ulrich, 1998) until SOHO/MDI made detection of such long-lived and large scale features possible (Beck et al., 1998a,b). Data from SOHO/MDI also made a spherical harmonic analyses possible; Figure 4 of Hathaway et al. (2000) demonstrates conclusively that there is long-lived power at scales corresponding to spherical harmonic wave numbers ℓ ≤ 64; i.e., on scales larger than ∼ 100 Mm (cf. also Figure 22).
Observed and simulated horizontal velocity amplitudes over a wavenumber range extending from global scales to below granulation scales. Observed velocities are from correlation tracking of TRACE and SOHO white light images (Shine, private communication), and from SOHO/MDI Doppler image modeling (Hathaway et al., 2000, and private communication). Simulation results are from Stein and Nordlund (1998) (granulation scales — orange symbols) and Stein et al. (2006a,b) (supergranulation scales — black symbols).
Using local helioseismic techniques, flows on scales larger than supergranulation are now routinely detected and mapped (Hindman et al., 2004b; Featherstone et al., 2004; Hindman et al., 2004a; Featherstone et al., 2006; Hindman et al., 2006).
4.4 Multi-scale convection
With access to extended time series of uniform quality data, especially from SOHO/MDI, but also from TRACE and the best Earth-based observatories, it became possible to simultaneously record motions over a range of scales, and to for example study the advection of mesogranulation scale cells by supergranulation scale motions.
Muller et al. (1992) used a 3 h time series from the Pic du Midi observatory to study the evolution and motion of mesogranules. They were able to show that mesogranules are advected by supergranulation scale motions, and also that the evolution of mesogranules is influenced by their location in larger supergranular scale flows. The evolution of supergranular scale flow fields and their influence on mesogranular scale flows were also studied by DeRosa and Toomre (1998), by Shine et al. (2000), and by DeRosa and Toomre (2004). The latter study provides evidence that flows on different scales are to some extent self-similar, and that they have amplitudes that vary smoothly with spatial and temporal scales. Figure 5 of DeRosa and Toomre (2004) illustrates the smooth behavior of the amplitudes characterizing multi-scale solar convection; over a range of time averaging windows extending from 0.1 to 100 hours the velocity amplitude varies smoothly, deviating from a linear fit in the log-log diagram by less than 10%. Figure 14 of DeRosa and Toomre (2004) illustrates the self-similar behavior, in that folding the data with Gaussians of varying size still leaves the size distributions essentially unchanged, after normalization with the filter size.
Other studies also indicate a close similarity and coupling between patterns at different scales. Schrijver et al. (1997a) compared the cellular patterns of the white light granulation and of the chromospheric Ca ii K supergranular network. They matched the patterns to generalized Voronoi foams and concluded that the two patterns are very similar. Roudier et al. (2003a) and Roudier and Muller (2004) demonstrated that a significant fraction of the granules in the photosphere are organized in the form of ‘trees of fragmenting granules’, which consists of families of repeatedly splitting granules, originating from single granules at their beginnings (see also Müller et al., 2001). Trees of fragmenting granules can live much longer than individual granules, with lifetimes typical of mesogranulation; this illustrates that larger scale flows are able to influence and modulate the evolution of smaller scale flows.
A smooth spectrum of motions was anticipated on theoretical grounds from the very beginning, but at the time it was thought that observations showed otherwise; observations were interpreted as though granulation and supergranulation represented distinct scales of motion, with no significant motions at intermediate scales. This lead to theoretical suggestions specifically aimed at explaining such a state of affairs (e.g., Simon and Weiss, 1968).
The numerical experiments by Stein and Nordlund (1989) showed that the topology of convection beneath the solar surface is dominated by effects of stratification, which lead to gentle, expanding and structure-less warm upflows on the one hand, and strong, converging filamentary cool downdrafts, on the other hand. The horizontal flow topology was shown to be cellular, with a hierarchy of cell sizes; granulation being a shallow surface phenomenon associated with the small scale heights near the surface layers, while deeper layers support successively larger cells. The downflows of small cells close to the surface merge into filamentary downdrafts of larger cells at greater depths. It is the radiative cooling at the surface that provides the entropy-deficient material which drives the circulation. The supply of high entropy fluid from the bottom of the convection zone is maintained by diffusive radiative energy transfer from the central, nuclear burning region, and in this sense the heat supply from below maintains the energy flux through the convection zone, but it is the surface that is responsible for generating the entropy contrast patterns that, via the corresponding buoyancy work, maintains the structure of the convective motions.
DeRosa et al. (2002) constructed the first models of solar convection in a spherical geometry that could explicitly resolve both the largest dynamical scales of the system (of order the solar radius) as well as smaller scale convective overturning motions comparable in size to solar supergranulation (20–40 Mm). They found that convection within these simulations spans a large range of horizontal scales, especially near the top of the domain, where convection on supergranular scales is apparent. The smaller cells are advected laterally by the larger scales of convection, which take the form of a connected network of narrow downflow lanes that horizontally divide the domain into regions measuring approximately 100–200 Mm across. Correspondingly, Stein et al. (2006b,a) found a similarly wide range of scales of motion, with a smooth amplitude spectrum consistent with SOHO/MDI observation (Georgobiani et al., 2007), in simulations covering scales from sub-granular to supergranular.
To properly compare velocity amplitudes over a large range of scales it is useful to display a ‘velocity spectrum’, showing the square root of the velocity power per unit logarithmic interval of wavenumber k
where P(k) is the traditional ‘power spectrum’ (velocity power per unit linear wave number). The quantity kP(k) is the contribution to the total mean square velocity per unit ln k, and is independent of the unit of wavenumber. It has dimension velocity squared, and its square root is a good measure of the velocity amplitude at various scales.
Figure 22 shows a composite of simulated and observed velocities, over a range of scales that extends from global to below granulation scales. Note that the velocities on granular, mesogranular, and supergranular scales are consistent with commonly adopted values (a few km s−1 on granular scales, a few several hundred m s−1 on mesogranular scales, and 100–200 m s−1 on supergranular scales). Note that the velocity spectrum is approximately linear in k, and that it continues to giant cell scales, with no distinct features on scales larger than granulation.
Because of mass conservation large scale convection motions are necessarily dominated by horizontal motions, while on the other hand large scale solar oscillations are dominated by vertical motions near the solar surface. Doppler measurements from, for example, SOHO/MDI are sensitive to a mix of horizontal and vertical motions into the line-of-sight, in that for example the highresolution mode of SOHO/MDI extends over a square of size ∼ 210 Mm, which is often also slightly off-set relative to solar disc center. Figure 23 illustrates these points.
Horizontal and vertical components of the convective and oscillatory components (separated by sub-sonic filtering) of the velocity field in a supergranulation scale convection simulation, compared with the convective and oscillatory components of the line-of-sight velocity field, as observed with SOHO/MDI in high resolution mode. The ‘convective’ and ‘oscillatory’ (‘modes’ in the figure) are separated by a line ω = ck, where c = 7 km s−1 (from the same data set as was used in Stein et al., 2006a).
The velocity spectrum shows that velocities are present over a large range of scales simultaneously, with larger scale motions decreasing in amplitude roughly in inverse proportion to the size. By using a Gaussian filter that leaves approximately the same number of effective resolution elements in picture that vary in size with factors of 2, 4, 8, and 16 one can show that, in addition to being nearly scale-free with respect to the amplitude spectrum, the patterns of motion are also very similar on different scales (cf. Figure 24). The actual sizes of the panels are revealed in Figure 25.
Subsonic filtered line-of-sight velocities from SOHO, Gaussian filtered to the same effective number of pixel elements, for physical sizes of 400, 200, 100, and 50 Mm. The order of the panels has been scrambled, to make the point that the patterns are very similar, and that it is not obvious how to order the panels in a sequence of increasing size, for example (but see Figure 25).
Subsonic filtered line-of-sight velocities from SOHO, with the same order of panels as in Figure 24, but without applying the Gaussian filter that was used there.
5 Spectral Line Formation
Since the convection zone reaches up to the optical surface in the Sun, convection directly influences the spectrum formation both by modifying the mean stratification and by introducing inhomogeneities and velocity fields in the photosphere. Traditionally, convection is incorporated in classical 1D theoretical model atmospheres through the rudimentary mixing length theory (Böhm-Vitense, 1958) or some close relative thereof (e.g., Canuto and Mazzitelli, 1991). These convection descriptions are local, 1D, time-independent and ignore crucial 3D energy exchange effects between the radiation field and the gas (see Section 3.12). Reality is very far from this simple-minded picture. It should not come as a surprise then that the predicted emergent spectrum based on such 1D model atmospheres may be hampered by significant systematic errors.
As an alternative to 1D theoretical model atmospheres solar physicists often prefer the use of semi-empirical model atmospheres such as the Holweger and Müller (1974), Vernazza et al. (1976) (better known as VAL3C) and Fontenla et al. (2007) models, in which the temperature structure is inferred from observations, notably continuum center-to-limb variation and strengths of various spectral lines; the first of these model atmospheres is based on an LTE inversion while the others account for departures from LTE. While the uncertainty in the temperature structure arising from convective motion is thus hopefully largely bypassed, such semi-empirical models are still 1D and, like all 1D models, predict insufficient line broadening that require the introduction of the fudge parameters micro- and macroturbulence (see Gray, 2005, for a general discussion). Such semi-empirical models are not easily constructed for stars other than the Sun due to the inability to observe center-to-limb variations on stars.
Going somewhat beyond the standard 1D modeling, it is possible to combine several 1D atmosphere models corresponding to, for example, typical up- and down-flows to construct multi-component models of solar/stellar granulation (Voigt, 1956; Schröter, 1957; Nordlund, 1976; Kaisig and Schröter, 1983; Dravins, 1990; Borrero and Bellot Rubio, 2002). Bar a few notable exceptions, little effort has been invested in studying the possible impact of multi-component models on solar/stellar abundance determinations (Lambert, 1978; Hermsen, 1982; Frutiger et al., 2000; Bellot Rubio and Borrero, 2002; Ayres et al., 2006).
A more ambitious approach is to make use of the multi-dimensional, time-dependent radiative-hydrodynamical simulations of solar surface convection that are described in this review. These simulations may then be employed as a 2D or 3D solar model atmosphere for spectral line formation purposes (e.g., Dravins et al., 1981; Nordlund, 1985a; Dravins and Nordlund, 1990a,b; Bruls and Rutten, 1992; Atroshchenko and Gadun, 1994; Gadun and Pavlenko, 1997; Gadun et al., 1997; Uitenbroek, 2000a; Asplund et al., 2000a,b,c; Asplund, 2000; Asplund et al., 2004; Asplund, 2004; Asplund et al., 2005a,b; Asplund, 2005; Allende Prieto et al., 2001, 2002; Steffen and Holweger, 2002; Scott et al., 2006; Ljung et al., 2006; Ludwig and Steffen, 2007; Caffau and Ludwig, 2007; Caffau et al., 2007a,b, 2008b,a; Mucciarelli et al., 2008; Centeno and Socas-Navarro, 2008; Ayres, 2008; Basu and Antia, 2008; Meléndez and Asplund, 2008). For computational reasons, most of the calculations have assumed LTE but some studies have braved going beyond this approximation, either in 1.5DFootnote 2 (e.g., Shchukina and Trujillo Bueno, 2001) or in 3D (e.g., Nordlund, 1985b; Kiselman and Nordlund, 1995; Kiselman, 1997, 1998, 2001; Uitenbroek, 1998; Barklem et al., 2003; Asplund et al., 2003, 2004; Allende Prieto et al., 2004). A recent review on 3D spectral line formation is given in Asplund (2005).
5.1 Spatially resolved lines
The spatially resolved spectral line shapes across the solar surface come in an amazing variety of strengths, shifts and asymmetries, as demonstrated in Figure 26. This is a direct reflection of properties of granulation and the correlations between temperature and velocity (e.g., Dravins et al., 1981; Dravins and Nordlund, 1990a; Asplund et al., 2000b). In the warm upflows the continuum intensity is high while the ascending motion shifts the line profiles towards the blue. Furthermore, the steep temperature gradients in the upflows produce strong lines. In contrast, in the downdrafts the continuum intensity is correspondingly lower while the lines are redshifted and weak because of the more shallow temperature structure. The spatially averaged line formation is therefore heavily biased towards the granules, also because of their larger area coverage in the solar atmosphere. This is good news for modeling purposes, since for example the effects of magnetic fields and the use of numerical viscosity on the resulting line formation are then minimized, since both effects tend to be concentrated in the darker intergranular areas. Towards the limb, the relative continuum intensity contrast increases significantly while the correlation between temperature (line strength) and velocities (line shift) becomes much less pronounced.
Upper panel: A selection of spatially resolved line profiles for a typical Fe i line across the solar granulation pattern. The thick curve denotes the spatially averaged profile. Lower panel: The same as above but instead showing the individual line bisectors. Note that the asymmetry of the spatially resolved lines are not at all representative of the spatially averaged profile (thick line) (from Asplund et al., 2000b).
At disk-center, individual line profiles corresponding to different atmospheric columns are largely symmetrical, although the line bisectors in upflows typically have a slight-shape while downflows show slightly more pronounced/-bisectors due to the increasing vertical velocities with depth (Figure 26). Closer to the limb the spatially resolved line profiles become quite distorted. In the line-forming region, the horizontal velocities are typically somewhat larger than the vertical velocities and indeed approach and occasionally exceed the sound speed. The total velocity span of profiles at inclined viewing angles is therefore substantially larger than at disk-center and the lines can develop multiple components as the line-of-sight passes inhomogeneities with distinctly different velocity shifts as well as temperatures. As a consequence the spatially resolved bisectors become very distorted and depend critically on the exact region of the surface that is being observed.
Before a proper comparison can be made between predictions and observations for spatially resolved lines the theoretical line profiles must be convolved appropriately to account for the finite instrumental resolution and atmospheric seeing (e.g., Nordlund, 1984), which unfortunately somewhat limits the information gained from the observations. Nevertheless, such exercises clearly demonstrate the remarkably good agreement between observations and predictions in general (e.g., Dravins et al., 1981; Dravins and Nordlund, 1990a; Kiselman, 1994; Asplund et al., 2000b; Kiselman and Asplund, 2001; Cauzzi et al., 2006; Pereira et al., 2008). Each line has unique fingerprints in correlation maps between for example continuum intensity and line strength, depth, shift, width, and asymmetry across the granulation pattern depending on their height of formation and sensitivity to the atmospheric conditions, as illustrated in Figure 27. Obviously, the agreement between the predicted and observed behavior in this respect is very satisfactory. Indeed, for most lines studied to date this is achieved even within the assumption of LTE in the 3D line formation. Notable exceptions are for weak low-excitation lines of minority species, which strongly suggests that the problem lies with the LTE line formation rather than a shortcoming of the 3D model atmosphere. In fact, when allowing for departures from LTE in the 3D formation of the Li i 670.8 nm line the good agreement is restored (Kiselman, 1998). The unavoidable conclusion is that the statistical properties of photospheric velocity, temperature, and pressure in the 3D simulations closely resemble the real Sun.
The upper left panel shows the predicted continuum intensity across the granulation pattern of one snapshot of a 3D hydrodynamical solar simulation. The other panels illustrate the variation of the predicted (red) and observed (blue) equivalent widths of individual µ = 1 line profiles over the solar surface as a function of the local continuum intensity; each panel is labeled with the species, wavelength, and lower excitation potential of the different transitions. The two crosses denote the values for a typical down- and upflow, with the locations identified in the granulation image. For most lines the 3D LTE and observed behavior agree very well with the exception of low excitation lines of minority ionization stages, such as the 670.8 nm line of Li i, which strongly suggests the presence of non-LTE effects in the line formation (from Asplund, 2005).
5.2 Spatially averaged lines
The widths of spatially averaged photospheric lines are much wider than predicted solely from natural and thermal broadening. As explained in Asplund et al. (2000b), most of the line broadening instead arises from the Doppler shifts associated with granular scale convective motions, with a minor contribution also coming from the photospheric oscillations (the solar p-modes, see Section 6). Since 1D model atmospheres by definition do not predict the photospheric velocity field, the resulting 1D line profiles are too narrow compared with observations; a similar effect is obtained by artificially setting all velocities to zero in the 3D model atmosphere before computing the line formation, as illustrated in Figure 28. To rectify this problem, two fudge parameters, microturbulence and macroturbulence, are introduced in all 1D line formation calculations. The former supposedly represents small-scale velocities while the latter tries to encapsulate the effect of motions occurring on length-scales larger than one optical path-length (e.g., Gray, 2005). The value for the microturbulence parameter is then determined by requiring that the derived elemental abundance is independent of line strength, while the macroturbulence is estimated from the overall widths of spectral lines. However, even with the luxury of having two additional free parameters to tune, 1D calculations cannot explain the detailed shape of the observed lines (nor, as will be demonstrated below, the shifts and asymmetries of lines). Naturally this division into micro- and macroturbulence is too simplistic since the convective motions occur on a range of spatial scales. Furthermore, the names are misleading as the line broadenings have very little to do with turbulence in its classical meaning (Asplund et al., 2000b). Small-scale energy cascades and turbulence associated with a high-Reynolds-number plasma as the solar atmosphere are present but their intensities are very small in the upflows to which the line strengths are strongly biased and thus they do not affect the line formation significantly. As emphasized above, the dominant factor is instead the velocity gradients and the corresponding Doppler shifts stemming from convection and its overshoot in the photosphere.
The predicted spatially and temporally averaged 3D LTE solar line profile of a typical Fe i line (solid line) compared with the corresponding calculation when ignoring all Doppler shifts arising from the photospheric velocity field (dashed line), demonstrating the importance of convective line broadening. The latter profile closely resembles 1D line profiles without application of the fudge parameters micro- and macroturbulence.
In sharp contrast to the 1D case, 3D line formation calculations taking into account the self-consistently predicted velocity field in 3D hydrodynamical solar model atmospheres reproduce the observed line profiles exceedingly well for most lines so far considered, as exemplified in Figure 29. The agreement is equally good for disk-center and flux profiles (Asplund et al., 2000b). Indeed, a comparison between observed and theoretical 3D line shapes is a very powerful tool to identify previously unknown blends or erroneous rest wavelengths for the transition in question.
The predicted temporally and spatially averaged 3D profile (blue solid line) compared with the observed solar disk-center line (red diamonds). Note the excellent agreement as seen in the residuals (the discrepancies in the far red and blue wings are due to unaccounted for blends). Also shown is the best-fitting 1D line profile after having optimized the micro- and macroturbulence (green solid line), which clearly has the wrong shape, asymmetry, and shift.
The correlation of velocity and temperature that is an inherent property of convection causes correlations of radiation intensity and Doppler shifts. This results in both a net blueshift of spectral lines, and a characteristic line asymmetry, which may be quantified by measuring the line shifts (as defined by the wavelength with the minimum intensity/flux in the line profile) or bisectors (the midpoint of the profile at different line depths) (e.g., Dravins et al., 1981; Dravins, 1982; Dravins and Nordlund, 1990a,b; Allende Prieto and García López, 1998; Asplund et al., 2000a,b,c; Asplund, 2005; Gray, 2005). In the Sun, most spatially averaged photospheric lines have a characteristic ⊂-shape, which arises because the upflowing (blueshifted) granular gas is both warmer and have a larger area coverage than the downflowing (redshifted) material in the intergranular lanes. In general, the predicted asymmetries of solar Fe i and Fe ii lines agree very well with the observed bisectors (Asplund et al., 2000b); a few examples are shown in Figure 30. It should be noted that both the theoretical and observed profiles are on an absolute wavelength scale for the Sun and that no arbitrary wavelength shifts have been applied to improve the agreement. Of course, 1D profiles are all completely symmetrical without any line shift. Weak Fe i lines have line shifts of ≈ −500 m s−1 (after correcting for the solar gravitational redshift of 633 m s−1) while Fe ii lines have even larger blueshifts due to their in general greater depths of formation where the granulation contrast and convective velocities are larger. The amount of convective blueshift decreases as the line strength increases when the line-forming region is shifted upwards in the atmosphere until eventually convective (overshoot) motions become unimportant. The theoretical 3D line shifts agree very well with the observed shifts for weak and intermediate strong lines but becomes progressively worse for even stronger lines. This may signal departures from LTE, particularly in the line cores of strong lines, which are formed in high layers with low densities. However, it may also be due to the limited height extension and missing chromospheric physics of the employed 3D simulation (Asplund et al., 2000b; Scott et al., 2006). Towards the limb the convective blueshifts become smaller or vanish due to the smaller granulation intensity contrast compared with at disk-center (Balthasar, 1988).
5.3 Solar abundance analysis
Due to their realistic nature and successful reproduction of key observational constraints, 3D hydrodynamical model atmospheres can be used for elemental abundance determinations. These will then hopefully be more reliable than corresponding 1D analyses since the traditional free parameters used in stellar/solar spectroscopy (mixing length parameters, micro- and macroturbulence) no longer enter into the line formation calculations and because line profile fitting may be routinely employed instead of relying on often uncertain equivalent width measurements. In a series of papers (Allende Prieto et al., 2001, 2002; Asplund, 2000, 2004; Asplund et al., 2000c, 2004, 2005a,b; Scott et al., 2006), a re-analysis of the solar chemical composition was made, using a carefully constructed 3D solar convection simulation with the correct nominal solar effective temperature (Asplund et al., 2000b). The 3D radiative transfer equation was solved at each time-step of the simulation using a realistic equation-of-state (Mihalas et al., 1988) and opacities (Gustafsson et al., 1975; Kurucz, 1993) with the opacity binning technique (Nordlund, 1982). For most elements, LTE was assumed in the line formation calculations but for Li i and O i full 3D non-LTE calculations have been performed (Asplund et al., 2003, 2004). In these studies special effort has been made to adopt the most reliable and up-to-date atomic and molecular input data, such as transition probabilities, partition functions, line broadening parameters and dissociation energies. In the comparison with observations, both disk-center and disk-integrated flux profiles have been used, which give nearly identical results. Similar solar abundance analyses for selected elements assuming LTE have been carried out using an independent 3D hydrodynamical solar model atmosphere computed with the CO5BOLD code (Freytag et al., 2002) with in general good agreement with those presented by Asplund and collaborators when accounting for differences in the adopted atomic line data (Ludwig and Steffen, 2007; Caffau and Ludwig, 2007; Caffau et al., 2007a,b, 2008a,b; Mucciarelli et al., 2008).
5.3.1 Carbon
Of all elements carbon has the most diverse set of indicators that can be employed in deriving a solar elemental abundance. The diagnostics include both high-excitation permitted and low-excitation forbidden C I lines as well as a number of different molecular features, including CH vibration-rotation lines in the infrared, CH electronic lines and C2 electronic transitions in the optical (e.g., Lambert, 1978; Asplund et al., 2005b); CO vibration-rotation lines may also be used but it requires prior knowledge of the solar O abundance (Scott et al., 2006; Ayres et al., 2006). These are all formed in very different atmospheric layers and have distinct dependencies to the atmospheric conditions, in particular the temperature. As some lines are quite weak while others are partly saturated they also have different sensitivity to the predicted convective velocities. For these reasons, achieving consistent results from all different abundance indicators is challenging and provides a very stringent test of the appropriateness of the adopted model atmosphere, line formation calculations and input data for the transitions.
Asplund et al. (2005b) carried out a solar C abundance analysis using a 3D hydrodynamical solar model atmosphere. Table 1 list their derived 3D-based C abundances as well as for two 1D model atmospheres often employed in solar/stellar abundance analyses: the theoretical MARCS (Asplund et al., 1997) and the semi-empirical Holweger and Müller (1974) model atmospheres. Two things are particularly noteworthy. Firstly, only in 3D do the different indicators give consistent results while especially in the Holweger-Müller case there is a range of implied abundances differing by > 0.2 dex. Secondly, the 3D analysis result in significantly lower abundances than the Holweger-Müller, in particular for the molecular transitions. The latter is mainly due to the cooler temperatures in the optically thin layers in the 3D model compared with the 1D semi-empirical model as well as the presence of temperature inhomogeneities. Because of the great temperature sensitivity of molecule formation, both of these factors tend to strengthen the lines in 3D and thus require lower C abundances to explain the observed features. In the 3D case there are no significant abundance trends with wavelength, excitation or line strength, except for C I where there is a slight correlation with the equivalent widths of the lines; we suspect that this is a signature of underestimated non-LTE effects, maybe because here only 1D non-LTE calculations have been used (Fabbian et al., 2006).
The observed strong vibrational-rotational lines of CO in the Sun, in particular towards the limb, have for a long time been a challenge to model and has been argued to be inconsistent with the canonical temperature rise in the lower chromosphere (e.g., Ayres et al., 2006, and references therein). Departures from LTE in the line formation have been demonstrated to be unimportant and thus can not be invoked to explain the strong CO lines (Uitenbroek, 2000b). The presence of temperature atmosphere inhomogeneities in 3D hydrodynamical surface convection simulations on the other hand strengthens the predicted CO lines into better agreement with observations (Uitenbroek, 2000a; Scott et al., 2006); the typically cooler horizontally mean temperature stratification in 3D modeling than in the Holweger and Müller (1974) semi-empirical model is also conducive for molecular formation. Scott et al. (2006) have shown that the 3D-based C abundance from weak CO lines from the fundamental and first overtone bands are in excellent agreement with the other atomic and molecular C abundance indicators (Table 1). Although the situation is markedly better than with the Holweger and Müller (1974) model, the stronger low-excitation CO lines, however, are still predicted to be too weak with the 3D model, suggesting even lower temperatures around the heights of the nominal temperature minimum than the current generation of 3D models implies. In the solar photosphere up to heights of about 700 km above the optical surface, the time-dependent molecule formation of CO has been shown to proceed according to LTE expectations (Asensio Ramos et al., 2003; Wedemeyer-Böhm et al., 2005), which will therefore not affect the derived abundances. The dynamical time-scale in the higher atmospheric layers are much shorter than the time-scale for radiative relaxation, which prevents a CO-driven self-amplified thermal instability to be operative (Wedemeyer-Böhm and Steffen, 2007).
Since previously most trust has been put in the molecular lines, the study by Asplund et al. (2005b) has resulted in a significant lowering of the recommended solar photospheric C abundance to log ∊C = 8.39±0.05. Compared with the compilations of for example Anders and Grevesse (1989) and Grevesse and Sauval (1998) the new value is lower by 0.17 and 0.13 dex, respectively. While for the molecular lines the dominant factor is the use of a realistic 3D model instead of 1D model atmospheres, it should be emphasized that it is not the only factor causing this downward revision. Indeed, for the [C I] 872.7 nm line an improved transition probability is of equal importance while for the C I lines allowing for non-LTE effects is even more important than the 3D effects. The fact that after these significant improvements (3D model atmospheres, non-LTE line formation and better atomic/molecular line data) the derived abundances are in such excellent agreement is very encouraging. Finally, the derived carbon isotopic ratio (12C/13C = 87 ± 4) from CO lines using the same 3D model as above (Scott et al., 2006) is in excellent agreement with the terrestrial value (89 ± 1) while with 1D models the implied ratio is significantly lower (Scott et al., 2006; Ayres et al., 2006).
5.3.2 Nitrogen
Also for N there are both atomic and molecular lines that may be utilized in an abundance analysis, albeit not as many different indicators as for C or O (Asplund et al., 2005a). The forbidden [N I] lines cannot be employed as they are all too weak in the solar spectrum but there are some 20 weak high-excitation N I lines that are suitable for the purpose. In addition there are both vibration-rotation and pure rotation lines of NH in the infrared as well as a multitude of CN transitions from various bands; in the latter case, however, one has to have prior knowledge of the C abundance from other diagnostics. The (still preliminary) results (Asplund, et al., in preparation) in terms of the solar N abundance are given in Table 1. Again, there is very satisfactory agreement between the different indicators in 3D although similar consistency is in fact achieved also with the 1D MARCS model while the Holweger-Müller model returns somewhat larger discrepancies. The mean 3D-based abundance is significantly lower than in previous studies: log ϵN = 7.80 ± 0.05. This is 0.25 dex lower than the value recommended by Anders and Grevesse (1989) and is mainly due to the use of the 3D model with minor changes coming from non-LTE effects for N I, refined atomic/molecular line data and exact choice of lines.
5.3.3 Oxygen
Over the years a large number of studies have been devoted to estimate the solar O abundance, because of its importance in astrophysics stemming from its relatively large abundance, its significant contribution to the opacity in the stellar/solar interior and its diagnostics value for stellar nucleosynthesis and cosmic chemical evolution. In the solar case both atomic and molecular transitions are available for abundance analysis (e.g., Lambert, 1978; Asplund et al., 2004). The high-excitation O I lines (including the well-known 777 nm triplet) are easily measured but are susceptible to significant departures from LTE (e.g., Altrock, 1968; Kiselman, 1993; Kiselman and Nordlund, 1995; Asplund et al., 2004). The forbidden [O I] lines from the ground state at 630 and 636 nm do not suffer from non-LTE effects but are very weak and blended by other lines (Allende Prieto et al., 2001; Asplund et al., 2004; Caffau et al., 2008a; Ayres, 2008). In the infrared there are numerous vibration-rotation as well as pure rotation lines of OH that can be employed (e.g., Sauval et al., 1984; Grevesse et al., 1984; Asplund et al., 2004; Meléndez, 2004); the electronic OH lines in the UV are less suitable for abundance determinations due to the possibility of missing UV opacity (Asplund, 2004). Table 1 summarizes the results of Asplund et al. (2004) based on an analysis using a 3D hydrodynamical solar model atmosphere.
Allende Prieto et al. (2001) utilized the fact that the 3D model can predict the detailed line shapes and asymmetries to a remarkable degree (Section 5.2) to conclude that the [O i] 630 nm line must be blended by a Ni i line (Figure 31), which was suspected already by Lambert (1978). In Allende Prieto et al. (2001) the product of the Ni abundance and the gf-value of the Ni blend was left as a free parameter in the fit of the [O I]+Ni I feature. It is noteworthy from their study that the most important difference compared with previous studies is the allowance of the Ni blend, which by itself lowers the derived O abundance by ≈ 0.13 dex, while the use of the 3D model causes a further 0.08 dex downward revision compared with the case with the Holweger and Müller (1974) model atmosphere. The presence of the Ni blend was subsequently confirmed experimentally by Johansson et al. (2003). Adopting the new laboratory transition probability for the Ni line together with the 3D-based solar Ni abundance (log ϵNi = 6.17 ± 0.04, Scott et al., in preparation) would lead to a 0.12 dex higher log gf · ϵNi than estimated by Allende Prieto et al. (2001) and, hence, a lower left-over contribution of the 630 nm feature to be explained by O I. In terms of abundance this corresponds to a lowering of the O abundance by a further ≈ 0.04 dex compared with what is given in Table 1 at the expense of a degraded agreement with the observed line profile compared with Figure 31.
Upper panel: The observed (dots) feature 630 nm, which corresponds to the main forbidden [O I] line that is blended with a Ni i line. The solid line denote the best fitting 3D-profile consisting of contributions from both [O i] and Ni i (dashed lines). Lower panel: The same as above but ignoring the Ni line. Note that in this case the required O abundance is 0.13 dex higher but that neither the line shape nor the overall line shift of the feature is well explained (from Allende Prieto et al., 2001).
Caffau et al. (2008a) have recently performed an independent analysis of the 630 nm line using an alternative 3D hydrodynamical solar model atmosphere computed with the CO5BOLD code. The two 3D models are based on essentially the same approximations, assumptions and input data but with different and completely independent numerical implementations. The resulting temperature structures are similar, although the CO5BOLD model is slightly warmer in the line-forming region than the 3D model by Asplund et al. (2000b). Caffau et al. (2008a) predict the Ni contribution to the feature by adopting the Johansson et al. (2003) gf-value and the solar Ni abundance of Grevesse and Sauval (1998), which is 0.06 dex higher than the revised value of Scott et al. (in preparation). They find an essentially identical O abundance from this line as Allende Prieto et al. (2001) and Asplund et al. (2004): log ϵO = 8.68±0.15. Ayres (2008) has carried out a similar study but based only on one snapshot of the CO5BOLD 3D solar model. More importantly, he follows the procedure of Allende Prieto et al. (2001) to leave the Ni contribution as a free parameter when obtaining the best fitting line profile, in spite of the new accurate experimental transition probability. He concludes that the Ni line is only 70% as strong as would be expected based on the new gf-value and the Ni abundance of Grevesse and Sauval (1998), a difference which greatly exceeds the quoted uncertainties of these two values. As a result he arrives at a correspondingly higher O abundance: log ϵO = 8.81 ± 0.04.
Centeno and Socas-Navarro (2008) have used a novel alternative method, namely to analyze spectro-polarimetric observations of sunspots and the asymmetry of the Stokes V profile of the [O i] + Ni i blend. They derive an atomic ratio of O/Ni = 210 ± 24, which according to their analysis corresponds to log ϵO = 8.86 ± 0.07 after applying the Ni abundance of Grevesse and Sauval (1998) and correcting for the ∼ 50% of O locked up in CO in the cool environments of sunspots. The asymmetry of the Stokes V profile is relatively model-independent, but the derived oxygen abundance is of course still sensitive to the choice of (gf-values and the C and Ni abundances. Correcting for the use of an outdated gf-value for the [O I] line and employing the new Ni abundance of Scott et al. (in preparation) revises their estimated atomic O abundance from log ϵO = 8.56 to log ϵOI = 8.43. If other molecules can be ignored, as supported by their calculations, the maximum possible total O abundance is obtained by assuming that all of C is tied up in CO. When adopting the solar C abundance of Grevesse and Sauval (1998) this leads to log ϵO = 8.78 while using the value from Asplund et al. (2005b) leads to log ϵO = 8.71, which is quite close to the values found by Allende Prieto et al. (2001) and Asplund et al. (2004). According to the analysis of Asplund et al. (2004), the even weaker [O I] 636 nm line gives results consistent with the 630 nm line, after allowance for two blending CN lines. This is not the case with the analysis of Caffau et al. (2008a), in which the 636 nm line leads to a 0.10 dex higher abundance than the 630 nm line: log ϵO = 8.78 instead of log ϵO = 8.68. The exact reasons for this have not yet been established but it may be partly related to their use of a relatively high solar Ni abundance (Grevesse and Sauval, 1998), which under-estimates the O contribution to the 630 nm feature.
Meléndez and Asplund (2008) has performed a 3D-based analysis of the [O I] line at 557.7 nm not previously considered for abundance purposes. They argue that the significant blending due to two C2 lines can be rather accurately constrained by other nearby C2 lines from the same molecular band with essentially identical excitation potential, line strengths, and thus line formation properties. Using the same 3D solar atmosphere model as employed in the series of papers by Asplund and collaborators, Meléndez and Asplund (2008) find log ϵO = 8.70 ± 0.08. A range of 1D models give however very similar results (e.g., 8.73 with the Holweger and Müller, 1974 model) with the mean value of the tested 3D and 1D models being log ϵO = 8.71 ± 0.02.
After careful inspection of the available permitted neutral oxygen lines, Asplund et al. (2004) selected six O I lines suitable for abundance determination. Full 3D non-LTE line formation calculations were performed, resulting in non-LTE abundance corrections (i.e., 3D non-LTE abundance minus the 3D LTE abundance) ranging from −0.03 to −0.24 dex for the different lines; the 777 nm triplet lines are the most affected in this respect; for the O I lines the main reason for the low estimated O abundance is non-LTE line formation with the effect of the 3D model being quite small. Accounting for departures from LTE greatly improves the agreement with the observed profile as well as the center-to-limb behavior for the 777 nm lines, as shown in Figure 32. In the O atomic model, excitation and ionization from inelastic collisions with H atoms were not considered by Asplund et al. (2004) given the uncertainty surrounding these collisional cross-sections: for the few other elements where laboratory measurements or detailed quantum mechanical calculations exist the classical formula used for the purpose over-estimates the cross-sections by several orders of magnitude (see discussion in Asplund, 2005, and references therein). Allende Prieto et al. (2004) found that the agreement with the observed profiles close to the limb could be improved further by including inelastic H collisions. If correct, this would increase the derived O I abundance given in Table 1 by ≈ 0.06 dex. However, it should be noted that subsequently new quantum mechanical calculations for the electron collisional excitation of O I have been performed (Barklem, 2007a). These imply smaller cross-sections than employed in previous O I non-LTE works and thus one make the non-LTE effects more pronounced by ≈ 0.02 dex (Fabbian et al., 2009).
Center-to-limb variation of the O I 777 nm line strength. The observed behavior is shown as bands with estimated internal errors. The solid lines denote the 3D non-LTE case while the dashed lines correspond to the 3D LTE calculations. Note that in order to have the same disk-integrated equivalent widths, the 3D LTE calculations have been performed with a ≈ 0.2 dex higher O abundance than for the 3D non-LTE profiles (from Asplund et al., 2004).
An independent 3D-based analysis of the permitted O I lines has recently been performed by Caffau et al. (2008a) using a CO5BOLD solar model. In addition to the lines considered by Asplund et al. (2004) they also include the 1130.2 and 1316.4 nm transitions. They include non-LTE abundance corrections but only computed using 1D models, i.e., not full 3D non-LTE computations as in Asplund et al. (2004). Their weighted mean of the eight O I and two [O I] lines is log ϵO = 8.76 ± 0.07, i.e., a value in between the recommended values of Asplund et al. (2005a) and Grevesse and Sauval (1998). Most of the differences with the atomic-based results of Asplund et al. (2004) can be traced to Caffau et al. (2008a) use of rather efficient H collisions for the 1D non-LTE calculations (Δlog ϵO = 0.03 dex) and large adopted equivalent widths.Footnote 3 Their measured equivalent widths are particularly large for the O I 777 nm triplet, indeed deviating by > 3σ compared with the eight most recent influential published solar abundance investigations starting from Lambert (1978). The reasons for these differences have not yet been established. Encouragingly, the particular choice of 3D model does not influence the results significantly. Somewhat earlier, Holweger (2001) obtained a similar O abundance based on an analysis taking multi-dimensional effects into account from a 2D solar granulation simulation and 1D non-LTE line formation: log ϵO = 8.74 ± 0.08.
Asplund et al. (2004) selected the best unblended 70 fundamental vibration-rotation (located around 3 μm) and 127 pure rotation lines (> 9 μm) of OH for abundance analysis. The resulting O abundances are much lower than previously thought from 1D studies: log ϵO = 8.61 and 8.65, respectively. This is a direct reflection of the great temperature sensitivity of the OH lines. There are no apparent abundance trends with wavelength, excitation potential or line strength for the vibration-rotation lines but there is a clear correlation with line strength for the strongest pure rotation lines in the 3D analysis. Since these lines are formed in very high atmospheric layers, this is probably a reflection of shortcomings of the 3D model atmospheres at those heights, such as too high temperatures. The derived low O abundance presented by Asplund et al. (2004) has been supported by a study of the extremely weak first overtone vibration-rotation lines of OH (Meléndez, 2004), which are also included in Table 1.
Asplund et al. (2004) argued that the mean 3D-based oxygen abundance from all the different abundance indicators is log ϵO = 8.66 ± 0.05. The agreement between the different diagnostics is excellent in the 3D case (Δϵ ≤ 0.1 dex) while the corresponding 1D results show quite discrepant results (Δϵ ≥ 0.2 dex) with typically the molecular lines implying a higher abundance than the atomic due to the neglect of atmospheric inhomogeneities and the, in general warmer, mean temperature structure. The estimated abundance is 0.27 dex lower than recommended by Anders and Grevesse (1989), i.e., almost a factor of two downward revision. Given the recent flurry of studies devoted to the topic and the somewhat disparate results obtained, it is clear though that the solar O abundance issue has not yet been resolved once and for all. There are discouraging differences in terms of the observational data used, the collisional data required for the O I non-LTE calculations, the treatment of blending lines and the more reliable 3D atmospheric stratification, which urgently need to be addressed.
The estimated isotopic ratio (16O/18O = 479 ± 29) (Scott et al., 2006) from CO lines using a 3D solar model is in very good agreement with the terrestrial value (499 ± 1). In contrast, with 1D models the implied ratio is significantly lower than the terrestrial value (Ayres et al., 2006), which would be rather surprising.
5.3.4 Fe
Iron is a standard reference element for the overall metallicity of stars and galaxies and thus the solar Fe abundance is of fundamental importance for astronomy. In the 1980s and 1990s a debate raged whether the solar value was low (log ϵFe ≈ 7.50, e.g., Holweger et al., 1995) or high (log ϵFe ≈ 7.65, e.g., Blackwell et al., 1995) which centered around the appropriate choices for the equivalent widths, microturbulence, pressure broadening constants, and transition probabilities. With the application of a 3D hydrodynamical solar model atmosphere the microturbulence parameter becomes obsolete (Asplund et al., 2000b) while the excellent agreement between predicted and observed line shapes allows the use of profile fitting instead of relying on equivalent widths measurements. Asplund et al. (2000c) performed a 3D LTE abundance analysis with the most up-to-date atomic data of both Fe i and Fe ii lines, in both cases finding a low abundance: log ϵFeI = 7.44 and log ϵFeI = 7.45, respectively. There is, however, some evidence that departures from LTE are not insignificant for Fe i, mainly driven by over-ionization due to hot radiation field from below in the upflows (see discussion in Asplund, 2005, and references therein). As for O I lines, the main uncertainty in the available non-LTE calculations appears to be the treatment of inelastic collisions with H. Some calculations (e.g., Shchukina and Trujillo Bueno, 2001) which ignore these collisions altogether imply 1.5D non-LTE abundance corrections of ≈ +0.05 dex for Fe i for the Sun. On the other hand, Korn et al. (2003) find that the H collisions are indeed efficient in thermalizing the Fe i level populations and, hence, that the resulting 1D non-LTE abundance corrections are very small. The jury is still out regarding the H collisions but it is clear that the solar Fe abundance is low, log ϵFe ≤ 7.55, in particular since the solar Fe ii lines now have quite reliable gf-values and are little affected by the uncertainties surrounding the H collisions.
5.3.5 Other elements
To date at least a preliminary 3D-based abundance analysis of all elements up through Ni in the period table plus Zr, Eu, Hf, and Th has been performed; more elements are continually added to this inventory. For the vast majority of elements, solar spectoscopists have to settle for employing only various types of atomic transitions when attempting to estimate the solar abundances. Furthermore, for most elements only atomic lines from one ionization stage are available while often very few lines are suitable for abundance purposes (indeed, in several cases only a handful or fewer lines can be used). Finally, most of the time the appropriate atomic lines for a given element have quite similar sensitivity to the atmospheric conditions. It is therefore difficult to use the results as an indication of the appropriateness of the adopted model atmosphere and line formation calculations, as can be done for C, N, and O as described above, and the resulting 3D-based solar abundances must therefore be taken at face value.
Asplund (2000) found that the solar photospheric Si abundance only needed a 0.04 dex downward revision compared with previous studies. This is quite a significant finding nevertheless as it sets the absolute abundance scale of meteorites since those are depleted in all volatile elements, including hydrogen. In meteorites elemental abundances are therefore measured relative Si. As a consequence knowledge of the photospheric Si abundance is necessary to anchor the photospheric and meteoritic abundances to the same absolute scale. Of the other elements, Asplund et al. (2005a) reported new abundances of the intermediate elements (Na-Ca) while a study of the Fe-peak elements (Sc-Ni) is currently ongoing (Scott et al., in preparation). Asplund (2004) estimated the amount of missing UV opacity from a comparison of the OH lines in the infrared and UV and from this could conclude that the solar photospheric Be abundance is not significantly depleted compared with the meteoritic value. Equipped with new transition probabilities Ljung et al. (2006) re-derived the solar Zr abundance with a 3D-analysis. The here mentioned works have all been based on the 3D solar model of Asplund et al. (2000c), which was also employed in the solar C, N, and O abundance analyses described in previous sections (Asplund et al., 2004, 2005b,a). For most atoms, the impact of 3D models compared with various often-used 1D models is relatively modest in general in contrast to the very model atmosphere-sensitive molecular lines. Typically the derived solar abundances are 0.02–0.1 dex lower than in a corresponding analysis with the Holweger and Müller (1974) model atmosphere when adopting the same input physics otherwise (Asplund et al., 2005a); lines from a minority ionization stage are the most affected in this regard due to their greater temperature dependence (Steffen and Holweger, 2002; Asplund, 2005). This is mainly a reflection of the steeper mean temperature gradient in the line forming region in the 3D model. For the elements for which two ionization stages can be employed, in general more consistent results are obtained with the 3D solar model compared with 1D model atmospheres, theoretical or semi-empirical. Furthermore, the agreement with the revised meteoritic abundance scale (Asplund, 2000) is typically improved, lending further support to the results.
Similar 3D-based determinations of the solar abundances using a CO5BOLD 3D hydrodynamical solar model atmosphere have recently been carried out. Caffau and Ludwig (2007) and Caffau et al. (2007a) have revisited the solar S abundance and find a value in perfect agreement with that of Asplund et al. (2005a). On the other hand, Caffau et al. (2007b) find a solar P abundance 0.1 dex higher than the preliminary analysis of Asplund et al. (2005a); the exact reasons for this difference have not yet been established. In addition, Caffau et al. (2008b) and Mucciarelli et al. (2008) have determined the solar abundances of Eu, Hf, and Th, typically finding ≈ 0.02 dex lower values than the corresponding results with the Holweger and Müller (1974) 1D semi-empirical model; these elements have not yet been studied by Asplund and collaborators.
5.3.6 Implications and reliability of the new solar abundances
The recent revisions of the solar chemical composition based on 3D hydrodynamical model atmosphere, non-LTE line formation when necessary and improved atomic/molecular input data (e.g., Asplund et al., 2004, 2005b,a) has some major implications, if true. First and foremost, due to the large changes of the solar C, N, and O (and by extension also to Ne and ArFootnote 4 abundances in particular, the overall photospheric metallicity is greatly reduced, from Z = 0.0194 (Anders and Grevesse, 1989) or Z = 0.0170 (Grevesse and Sauval, 1998) to Z = 0.0122 (Asplund et al., 2005a). This relatively dramatic downward adjustment brings with it both good and bad news.
The new low solar abundances bring the Sun into agreement with the solar neighborhood as measured by nearby OB-type stars and the local interstellar medium (e.g., Turck-Chièze et al., 2004; Esteban et al., 2005; Przybilla et al., 2008), in particular when considering that the proto-solar abundances must have been 15% higher than the present-day photospheric values due to elemental diffusion (Turcotte et al., 1998). Furthermore, these abundances are consistent with existing models of the Galactic chemical evolution over the past 4.5 Gyr, which predicts that the oxygen abundance in the solar neighborhood has increased with ≈ 0.05 dex since the birth of the Sun. With the old C, N, and O abundances of Anders and Grevesse (1989) and Grevesse and Sauval (1998) there was a sharp conflict between the Sun and its surroundings.
However, the new abundances wreck havoc with the previous impressive agreement between the predicted solar interior sound speed and that measured with helioseismology (e.g., Delahaye and Pinsonneault, 2006; Basu and Antia, 2008). Since in particular C, O, and Ne are significant opacity sources in the solar interior, the reduced abundances change the predicted temperature and density structure of the Sun based on standard solar interior models (e.g., Bahcall et al., 2006). The most noticeable disagreement occurs immediately below the convection zone, which also means that the predicted depth of the convection zone with the new abundances is inconsistent with the value inferred from helioseismology. A great number of possible explanations have been put forward in attempts to resolve the discrepancy, including missing opacity (Badnell et al., 2005), underestimated diffusion (Guzik et al., 2005), accretion of low-metallicity gas (Guzik et al., 2006), internal gravity waves (Young and Arnett, 2005; Charbonnel and Talon, 2005), and underestimated solar Ne abundance (Bahcall et al., 2005; Drake and Testa, 2005) but to date no satisfactory solution has been found to this dilemma.
Another possibility is of course that the new solar abundances are not fully trustworthy and that the real solar C, N, and/or O abundances are significantly higher. Indeed with the values recommended by Grevesse and Sauval (1998) based on an analysis using the modifiedFootnote 5 Holweger and Müller (1974) semi-empirical 1D model atmosphere this solar model problem largely disappears. The reasons for the lowering of the C, N, and O abundances are different for the various abundance indictors. As already mentioned, molecular transitions are particularly sensitive to the model atmosphere temperature structure and presence of inhomogeneities. The atomic lines are also dependent on the adopted model atmosphere but to a lesser extent. Instead the permitted lines such as O I are particularly vulnerable to non-LTE effects and thus the treatment of the poorly known inelastic H collisions but also the measurement of equivalent widths/fitting of line profiles. The forbidden lines are mostly dependent on how blends are accounted for. In all cases, improved atomic/molecular data and selection of lines also have played a role.
One of the key ingredients is the application of 3D, hydrodynamical models of the solar atmosphere instead of 1D hydrostatic models, either theoretical or semi-empirical ones. Such 3D models are still relatively new and thus the possibility of remaining problems with the predicted atmospheric structure in the line-forming region cannot yet be ruled out. As shown in this Section, theoretical 3D line profiles, including their shifts and asymmetries, agree almost perfectly with observations in spite of having no tunable free parameters in the modeling (Asplund et al., 2000b). No 1D model comes close to achieving this. Furthermore, the predicted properties of the 3D simulations resemble very closely the observed solar granulation such as geometry, brightness contrast, velocities, both in terms of statistics and the temporal evolution. However, further confrontations with observational constraints are needed to remove lingering doubts about the 3D models’ appropriateness for abundance analysis purposes. For example, Ayres et al. (2006) argued on the basis of continuum center-to-limb variations and CO line strengths that the 3D model employed by As-plund and co-workers has an erroneous temperature structure. Their conclusion is based on their own calculations using the temporally and spatially averaged mean 3D model; full 3D calculations using the same opacities and equation-of-state used for the hydrodynamical convection simulation instead reveal smaller differences between the predicted and observed limb-darkening behavior by about a factor of two (see also discussion in Koesterke et al. (2008)). It is true though that the 3D model by Asplund et al. (2000b) is not perfect in this respect: in terms of the center-to-limb variation it performs better than theoretical 1D MARCS and Kurucz models but not quite as well as the Holweger and Müller (1974) model, as shown by Koesterke et al. (2008) and Pereira et al. (in preparation). However, in the case of the solar hydrogen lines, which also trace the temperature structure in deep atmospheric layers, the 3D predictions agree better with observations than the Holweger-Müller model, which results in too shallow line wings (Pereira et al., in preparation), in particular when considering the possibility of non-LTE effects in the H line formation (Barklem, 2007b). The CO5BOLD 3D solar model employed by for example Caffau et al. (2008a) performs better in terms of continuum center-to-limb variation than the corresponding 3D model of Asplund et al. and, at least, as well as the Holweger-Müller model, yet it implies essentially the same solar oxygen abundance for atomic lines as advocated by Asplund et al. (2004) when allowing for differences in non-LTE corrections and adopted line strengths. The CO5BOLD model has not yet been applied to molecular transitions but it is expected that it will yield somewhat higher abundances than estimated by Asplund et al. (2004), in which the molecular-based O abundances anyway are slightly lower than the atomic-based values. New 3D solar simulations are currently being carried out with an improved treatment of radiative transfer, including a selective (or sparse) opacity sampling technique rather than opacity binning and proper allowance of scattering (Trampedach et al., in preparation; Hayek et al., in preparation).
Finally, it must be emphasized that the application of a 3D solar model atmosphere is only one of the reasons for the recent downward revision of the solar C, N, and O abundances. Important in this respect are allowances of departures from LTE in the line formation for permitted atomic transitions, recognition of significant blends perturbing some weak lines and improved atomic and molecular input data. Even with the Holweger and Müller (1974) model with its shallow temperature gradient and high temperatures in the line-forming region quite low abundances are derived, as seen in Table 1; note that the molecular abundances are over-estimated in all 1D models on account of the neglect of temperature inhomogeneities.
As described above, there is today no clear consensus what the solar oxygen abundance is (unfortunately carbon and nitrogen have not received nearly as much attention). Asplund and collaborators are currently performing a re-analysis of the solar chemical composition for most accessible elements using a new improved 3D solar atmosphere simulation compared to the old 3D model applied in their previous works on the topic. Preliminary calculations reveal that the value recommended by Asplund et al. (2005a) may need to be revised upwards slightly to log ϵO ≈ 8.70–8.75. This would be in line with the recent estimates of Caffau et al. (2008a), Meléndez and Asplund (2008), and Centeno and Socas-Navarro (2008), when taking into account the recommended adjustments to the input data and analyses discussed in detail above. Such an O abundance would ease but not remove the discrepancy between solar interior models and helioseismology.
6 Applications to Helioseismology
The Sun oscillates. Think of a drum. A drum vibrates when it is hit, which excites its resonant modes. Which modes are excited depends on the skin head and where it is hit. The Sun is similar. It has a resonant cavity in which acoustic waves are trapped, like an organ pipe. Resonance occurs when an integral number of half wavelengths fit into the cavity between the turning points where the waves are reflected or refracted. In the Sun acoustic waves are trapped by reflections near the surface where the temperature drops rapidly and the wavelength of the waves becomes larger than the scale height of the density stratification. The waves are trapped in the solar interior where the increasing temperature and sound speed refracts that waves back up toward the surface.
The Sun’s resonant modes are excited by turbulence in the convection zone. In realistic solar convection zone simulations, acoustic oscillations are also naturally excited. Such simulations have been used to study wave propagation properties, resonant mode excitation, effects on mode frequencies, and as a known data set to test, validate and refine local helioseismic inversion methods. Local helioseismology is a powerful tool for probing the subsurface layers of the Sun. For a review of its methods and results see Gizon and Birch (2005) and Zhao (2008).
6.1 Wave propagation in the convection zone
Understanding how acoustic and surface gravity waves propagate in the solar convection zone is necessary to be able to use observations of these waves to determine the structure of the layers they propagate through (e.g., the sound speed variations, flow velocities, and magnetic fields). The Green’s function for linearized wave propagation determines how the waves respond to small perturbations (Skartlien, 2002; Gizon and Birch, 2005). Green’s functions are the solution of the linearized wave equation with an impulse source in space and time, in an unperturbed mean background state without flows, density or temperature fluctuations (except for the mean vertical stratification) or magnetic fields,
where G is the Green’s function and S is the impulse source. The Green’s functions is then used to compute the response of various observable quantities to perturbations in the background state.
Recently, numerical calculations of linearized wave propagation have been used to study properties for the more complex conditions of the solar atmosphere which is both inhomogeneous and dispersive. There are two important issues: first, because the solar atmosphere is dispersive, waves of different frequencies travel at different speeds (Jefferies et al., 1994), and second, the solar atmosphere’s inhomogeneities in temperature, magnetic field, and density are especially large close to the surface, so they are not small perturbations on a mean background state.
Numerical solutions for linear wave propagation in a mean background solar model with its structure modified so as to be convectively stable (sometimes with a given perturbation) have been used to study various helioseismic issues: How does the dispersive nature of acoustic waves affect their propagation (Tong et al., 2003c; D’Silva, 1998). What is the interaction and coupling between different MHD wave modes (Cally and Goossens, 2007; Rosenthal et al., 2002; Bogdan et al., 2003). How do various types of perturbations and distribution of acoustic sources affect acoustic wave propagation (Tong et al., 2003b,a; Shelyag et al., 2006; Cameron et al., 2007a; Parchevsky and Kosovichev, 2007; Parchevsky et al., 2008). What is the accuracy of time-distance inversion methods — ray tracing and the Born approximation in determining perturbation properties (Hung et al., 2001; Birch et al., 2001; Birch and Felder, 2004; Shelyag et al., 2007). Are there techniques for improving the signal/noise in the observations (Hanasoge et al., 2007). Recently, it has become possible to use realistic models of the near surface layers of the Sun from numerical simulations of solar surface convection to explore the properties of wave propagation and test the accuracy of local helioseismic methods. In such models, p-modes are naturally excited by the convective motions and entropy fluctuations. The mean atmospheric structure is different from the one-dimensional models of the solar atmosphere, which alters the resonant cavity. A complex hierarchy of fluctuations in temperature and sound speed, flow velocities and magnetic flux are present. Such simulations provide the needed test bed of known data against which to test and validate the methods of local helioseismology.
Georgobiani et al. (2003) and Straus et al. (2006) used such three-dimensional simulations to highlight the differences between measuring variables at a constant geometric height in the simulations and at a given local optical depth. The latter corresponds well with observations. Steiner et al. (2007) drove acoustic waves into a magneto-convection simulation from the bottom and then studied the coupling of acoustic and magnetic modes near the β = 1 level, where magnetic pressure becomes equal to the gas pressure. They also calculated the wave travel times between different levels in the atmosphere corresponding to commonly observed lines and showed that such observations may be used to map the topography of the magnetic field. Georgobiani et al. (2007) showed that supergranulation scale (48 Mm wide by 20 Mm deep) simulations of quiet Sun surface convection of Stein et al. (2007a) possessed a k − ω diagram with f- and p1–p4-modes very similar to those observed by MDI and with travel-time maps that were also nearly the same (Figure 33). Zhao et al. (2007b) showed that the horizontal velocities inferred from the ray-tracing inversion of f-mode travel times are in good agreement with the flows actually in the simulation down to depths of about 4 Mm (Figure 34). The vertical velocity inversions, however, were poorly correlated with the actual flows, often having the opposite sign. Within a 48 Mm horizontal extent, the deepest that rays which return to the surface can penetrate is 6.5 Mm. The same set of simulation data has been used to test helioseismic holography by Braun et al. (2007). They found that Born approximation travel times were in good agreement with the model travel times at shallow depths but became less similar at deeper depths, because of near-surface contributions from nearby (and oppositely directed) flows in the near surface side lobes of the kernel functions (Figure 35). As a result, supergranule scale flows are essentially undetectable below depths of about 5 Mm. Longer-lived, larger-scale flows can be detected at greater depths.
Two-dimensional power spectra (ℓ− ν) of the vertical velocity in an 8.5 hour long convection simulation in a domain 48 Mm wide by 20 Mm deep (left) and Doppler velocity from MDI high-resolution observations (right). f- and p1–p4-modes are visible in the simulation data. The dashed curve is the theoretical f-mode ridge. Because of the finite width of the computational box, there are fewer modes which are individually identifiable in the simulation. The low frequency power is convection.
6.2 Excitation of p-modes
Solar oscillations are excited by the convection, both by the entropy fluctuations produced by radiative cooling near the surface and by the Reynolds stresses below the surface where the convective velocities are large (Goldreich et al., 1994). The same processes excite oscillations in convection simulations. In simulations, the spectrum of excited oscillations depends on the size of the computational domain, the wider and deeper it is the richer the spectrum of resonant modes that exist (Figure 33).
Mode excitation may be investigated using the kinetic energy equation for the modes. For radial modes this is the equation for the horizontally averaged variables (indicated by an overbar),
where \(\bar{P}_{g}\) is the gas pressure, \(\bar{P}_{t}\) is the turbulent pressure, and \(\tau_{zz}^{-}\) is the viscous stress tensor, all averaged over horizontal planes. Likewise \(\bar{\rho}=\langle \rho\rangle_{{\rm hor}}\) is the horizontally averaged mass density, and \({\bar u_z} = {\langle {\rho {u_z}} \rangle _{{\rm{hor}}}}/\bar \rho\) is the density weighted average vertical velocity (Nordlund and Stein, 2001). Integrate over the spatial domain and time. If there is no net mass displacement the buoyancy work term vanishes. If there is no displacement on the boundaries (e.g., at the bottom), or if the pressure fluctuations vanish on the boundaries (e.g., at the top), then the integral of the divergence term vanishes. The remaining term is the PdV work integral,
where ξ is the displacement and \(\dot{\xi}\) is the velocity. Here δ denotes the “pseudo-Lagrangian” fluctuation, that is the fluctuation in the frame moving with the average radial velocity ūz in which the net vertical mass flux vanishes (cf. Nordlund and Stein, 2001). The pressure fluctuations and displacement can be split into modal and convective parts. The gas pressure fluctuations can further be split into an adiabatic part (ad) proportional to the density fluctuation,
and the remaining non-adiabatic part (non-ad). The dominant term is the product of the turbulent pressure plus non-adiabatic gas pressure fluctuations with the divergence of the mode displacement, so the change in the mode amplitude in a time interval Δt is,
where Eω, the mode energy per unit surface area (at r = R), is
Here Mω is the mode mass and \(V_{\omega}=\dot{\xi}_{\omega}(R)\) is the mode surface velocity amplitude. The ensemble average >< of the change in mode energy for small changes in amplitude Vω→ Vω + ΔVω over all phases between ΔVω, and Vω is proportional to
The result for the energy increase per unit area in time interval Δt is
whereδP*ω is the imaginary part of the sum of the pseudo-Lagrangian fluctuations of the turbulent pressure (Reynolds stress) and non-adiabatic gas pressure (entropy)
at frequency ω, ξω (z) is the displacement eigenfunction for the mode with frequency ω, and Δν = 1/ΔT, where T is the time interval over which the expression is evaluated. This factor appears when the discrete Fourier transform is normalized such that the sum of the squares of the absolute values of the discrete amplitudes equals the average of the squares of the fluctuations in time (Parseval’s theorem). If the power spectral density were normalized per unit frequency interval, then the factor would disappear and the total power would be the time integral of the squared amplitude rather than its average. The appearance of Eω in the denominator makes the expression independent of the arbitrary normalization of the mode eigenfunctions ξω. The terms in this expression can then be evaluated using the results of realistic convection simulations (Figure 36) which yields good agreement with observations, or using a model of the convective turbulence properties.
Several people have derived equations for p-mode excitation using analytic expressions for the convective kinetic energy and entropy spectra, e.g., (Balmforth, 1992; Goldreich et al., 1994; Samadi and Goupil, 2001). These authors’ formulas and Equation (50) are similar. In all, the excitation rate is proportional to the turbulent pressure and entropy induced pressure fluctuations times the gradient of the displacement eigenfunction divided by the mode mass. The main difference is that Equation (50) contains the absolute value squared of the product of the pressure fluctuations with the mode compression, while the others contain the the absolute value squared of the mode compression times the sum of the absolute values squared of the turbulent pressure and entropy fluctuation contributions. This difference results from the assumption (explicit or implicit) that there are no correlations between the turbulence at different scales and that the mode compression, ∂ξ/∂r, does not change on the length scale of the turbulence and so can be removed from the integral over the local turbulence. Neither of these assumptions is correct and is not necessary. Chaplin et al. (2005) have derived an analytic expression for the mode amplitude where the pressure-mode compression interaction is retained.
Aside from the above simplifying assumptions, there is the question of characterizing the turbulence properties. It is generally assumed that the convective energy spectrum is separable into independent spatial and temporal factors. Convection simulations have revealed that this is not possible. The convection velocity spectrum, Pvel is found to have the form (Georgobiani et al., 2006)
The width and exponent for the vertical velocity are shown in Figure 37.
Samadi et al. (2003a,b) investigated in detail the effects of different assumptions about the turbulence properties on the p-mode excitation rate. They found that the mode driving is particularly sensitive to the turbulence anisotropy factor and to the dynamic properties of the turbulence as represented by the temporal part of the turbulence spectrum. Using the simulation results, fit by analytic expressions for these factors, increases the excitation rate and the contribution of turbulent pressure relative to that of entropy fluctuations.
What physics determines the spectrum of the p-mode driving? Mode driving (Figure 36) decreases at low frequencies for two reasons: first, the mode mass (inertia) increases with decreasing frequency (Figure 38), and second the mode compression decreases with decreasing frequency (Figure 39). The mode driving decreases at high frequencies because convection is a low frequency process (see Figure 33), so the power in the pressure fluctuations decreases at high frequencies (Figure 40).
In the Sun and cool stars the contributions from the Reynolds stresses and entropy fluctuations are comparable at the peak driving frequencies, while the Reynolds stress excitation dominates at lower frequencies where the excitation occurs over a larger range of depths. In hotter stars and giants the Reynolds stress excitation dominates at all frequencies.
P-mode excitation occurs close to the solar surface where the turbulent velocities and entropy fluctuations are largest (Figure 41). As the frequency increases the driving is more and more confined to a shallow layer just below the surface.
P-mode excitation as a function of frequency and depth. The image shows the logarithm (base 10) of the absolute value squared of the work integrand, normalized by the factors in front of the integral in expression for the excitation rate, \({\omega ^2}\vert\delta P_\omega ^{\ast}{\textstyle{{\partial {\xi _\omega}} \over {\partial r}}}{\vert^2}/8\nu {E_\omega}\) (in units of erg/cm4/s).
Jacoutot et al. (2008b) and Jacoutot et al. (2008a) have investigated the influence of the presence of magnetic fields on the excitation of p-modes. They find that regions with magnetic field strengths typical of the peripheries of active regions have enhanced excitation of p-modes, particularly at high frequencies. This is consistent with the observations of so-called “acoustic halos” (Braun et al., 1992; Brown et al., 1992; Hindman and Brown, 1998; Jain and Haber, 2002) around active regions.
6.3 p-mode frequencies
There is a discrepancy between the observed p-mode frequencies and the eigenfrequencies calculated from one-dimensional models. Part of this difference occurs because convection enlarges the p-mode resonant cavity and lowers the frequencies of the higher frequency modes with turning points in the photosphere (Figure 42). This is due to two effects: First, the turbulent pressure is about 15% of the gas pressure near the top of the convection zone and the extra pressure support raises the atmosphere about half a scale height. Second, because of the high temperature sensitivity of the H− opacity, one does not see the hotter gas at the surface. Optical depth unity lies higher in hotter regions where the temperature decreasing outward is lower. Thus the horizontally averaged temperature is actually higher than obtained with a 1D model having the same effective temperature. The higher temperature means the scale height is larger, which raises the atmosphere another half scale height. The total effect is an atmosphere that is extended by a scale height compared to 1D models (Figure 42). The larger cavity reduces the discrepancy between the observed and theoretical mode frequencies as calculated from 1D models (Figure 43) (Rosenthal et al., 1999). The frequency residuals of the f-mode (which is nearly independent of the hydrostatic structure) are unchanged. The residuals of the p-modes from the simulation now are the same order of magnitude as for the f-mode and change sign. This indicates that the remaining discrepancies are due to mode physics effects and depend on depth or frequency or both.
Frequency residuals (observations-calculated) scaled by the ratio Qnℓ of the mode mass to the mode mass of the radial mode with the same frequency. On the left frequencies calculated from the standard 1D solar model S of Christensen-Dalsgaard et al. (1996) and on the right calculated from the horizontal and time averaged 3D simulation extended with a matched mixing length model into the deeper solar layers.
6.4 p-mode line profiles
The interaction between the oscillations, convection and radiation is also responsible for the asymmetry of the mode’s spectra and the reversal of asymmetry between velocity and intensity. There is disagreement as to which is the dominant mechanism producing the asymmetry and its reversal. The Green’s function for the response to excitation has an asymmetry that depends on the depth of the source. The superposition of correlated noise to the oscillation signal will produce a reversal of asymmetry between velocity and intensity (Nigam et al., 1998; Kumar and Basu, 1999). Such a reversal can also be produced by radiative transfer effects (Georgobiani et al., 2003). In addition, the vertical oscillation motions move the height of the steep background temperature gradient in the low photosphere up and down, which tends to cancel the effect caused by oscillation induced opacity fluctuations (Straus et al., 2006). These effects dominate over the intrinsic wave properties in controlling the phase relation between temperature and velocity.
7 Interaction with Magnetic Fields
The strongest magnetic fields near the solar surface are in approximate pressure balance with their surroundings. That is, the magnetic plus gas pressure inside the magnetic concentration is nearly equal to the gas pressure in its neighborhood. This means that the magnetic energy density can be much larger than the kinetic energy of convective motions. However, as one descends into the convection zone the ratio of gas to magnetic pressure quickly becomes very large and the magnetic fields in the quiet Sun get moved around by the convective flows. Diverging upflows sweep magnetic flux to intergranular downflow lanes (Figure 44) (Tao et al., 1998; Thelen and Cattaneo, 2000; Emonet and Cattaneo, 2001; Weiss et al., 2002; Vögler et al., 2005; Stein and Nordlund, 2006). Larger scale, slower flows — mesogranulation and supergranulation — sweep the flux along the intergranular lanes on longer time scales to the boundaries of increasingly larger scale horizontal patterns, while new flux, with mixed polarity, continually emerges throughout the quiet Sun. Eventually a balance is reached where the rate of emergence of new flux balances the rate at which flux is swept to larger horizontal scales, where it encounters existing magnetic flux with which it either cancels or augments (Simon et al., 2001; Krijger and Roudier, 2003; Isobe et al., 2008). This balance empirically occurs at supergranulation scales and produces the magnetic network (Schrijver et al., 1997b, point out that ephemeral active regions are actually a more important source of flux for the quiet-Sun network.). In general, the size and shape of a pattern produced by launching finite life time “corks” in the solar multi-scale velocity field depends both on the amplitude spectrum of the velocities, the morphology of the flows, and on the distribution of life times of the corks.
Granulation image and overlaid magnetogram contours at 30, 50, 70 and 90 G in the Fe i λ6302.5 line (Domínguez Cerdeña et al., 2003). Tickmarks at 1” intervals.
Note that the transportation and concentration of magnetic flux in the solar photosphere — and more generally at a free surface — is a different process than the “flux expulsion” mechanism (Weiss, 1966; Maheswaran, 1969; Peckover and Weiss, 1978; Galloway and Weiss, 1981). Convective motions inside a box with closed boundaries tends to — over a period of time and in the presence of magnetic diffusion — expel magnetic fields from the interior of convection cells. Magnetic field lines penetrating a free surface boundary are efficiently concentrated by purely advective transport, and can subsequently be further concentrated due the suppression of convection associated with a strong magnetic field (Spruit, 1976, 1977a, 1979; Spruit and Zweibel, 1979; Bushby et al., 2008).
7.1 Effects of magnetic fields on convection
As the magnetic flux through a surface patch increases, it has a profound effect on the convective motions and the granulation pattern (Cattaneo et al., 2003; Vögler, 2005). Their simulations, starting with a uniform vertical magnetic field of varying strength, show that as the mean field strength increases first thin sheets of strong (kilogauss) field fill up more and more of the intergranular lanes (Figure 45). Occasionally, micropores form at the downflow vertices. The average size of granules is reduced. When all the intergranular lanes are filled with kilogauss flux, the lanes widen. A few widely separated granule sized upflows persists, with numerous small, weakly magnetized upflow plumes inside the broad lanes of kilogauss field. At average field strengths characteristic of sunspots (2.5 kG) convection occurs as narrow plumes (Weiss et al., 1990, 1996; Schüssler and Vögler, 2006). A feeble initial upflow radiatively cools when it reaches the surface. The reduced pressure induces a strong upflow plume. A narrow return flow surrounding the plume develops. Expansion of the rising plume reduces the magnetic field inside it to a few hundred Gauss. Plumes tend to be elongated in random directions. The upflow is eventually strongly braked by the radiative losses at the surface. The sudden halting of the upflow produces a density buildup at the surface which increases the opacity, so that the τ = 1 surface lies at cooler temperatures and leads to the appearance of a dark lane down the center of the plume.
Emergent intensity (left), and magnetic field (right) at the surface for increasing average vertical field of 0, 200, 800 G (Vögler, 2005). As the magnetic flux increases it fills more of the intergranular lanes, the granules become smaller and eventually have a few large field free granule islands and large field filled lanes with tiny field free granules immersed in them.
Observations of the solar magnetic field show that the magnetic flux is indeed concentrated in the intergranular lanes, as seen in Figure 44 (Domínguez Cerdeña et al., 2003) — see also (Bellot Rubio and Collados, 2003; Martínez González et al., 2006; Khomenko et al., 2008). More magnetic flux emerges as small bipoles in the quiet Sun than in active regions. The number of magnetic concentrations decreases exponentially with increasing magnetic flux (Hagenaar et al., 2003; Domínguez Cerdeña et al., 2006c). The distribution function for the number of magnetic flux concentrations as a function of the flux is a sum of two exponentials: one for small and the other for large fluxes. The distribution of smaller fluxes (<2 × 1019 Mx) does not vary with the solar cycle, while the number of large flux concentrations (and their size) increases from cycle minimum to maximum. This occurs because the larger concentrations are dominated by unipolar regions fed by the dispersal of active regions. The rate of emergence of small bipoles is anti-correlated with the number of sunspots in the magnetic cycle (Hagenaar et al., 2003). The probability density function for magnetic field strength, P(B), cannot be uniquely determined by Zeeman splitting and Hanle depolarization observations. However, Domínguez Cerdeña et al. (2006c) used numerical magneto-convection simulations to constrain P(B) (Figure 46) Magnetic fields with strengths from 0 to 2.5 kG occur at the quiet Sun surface. The distribution function for weak fields (< 500 G) has a log-normal form. The strong fields, observable by Zeeman splitting, occupy only a small fraction (1–10%) of the solar surface, however, they contribute half or more of the magnetic energy and up to half of the magnetic flux. Weak fields cover most of the quiet Sun surface. The magnetic energy density is a significant fraction of the kinetic energy density of granular motions. The most probable magnetic field value is not zero, but of order 100 G. There is a local maximum near the maximum field strength (Figure 46). Simulations with a mean vertical field of 250 G (strong plage) and a horizontal grid size of 25 km have a similar magnetic field distribution but with more area covered by significant field strengths and a larger maximum field strength (Figure 47). Here too only a few percent of the surface has fields below 1 G and the most likely field strength is about 10 G (Figure 48). Steiner (2003) provides a flux based integrated probability density distribution which may be a more robust way to compare observations and models. The main difference between the observations and the simulations is a pronounced maximum in the observed but not the simulated probability density function near the maximum field strength (note that the simulation results may be sensitive to numerical resolution, boundary and initial conditions, and may be influenced by limited statistics). Simulations with no net vertical flux have a stretched exponential distribution of field strengths. A stretched exponential distribution means that the stronger the field the tinier the fraction of the area it occupies. Fields of 3 G, fill all the intergranular lanes and exist even inside some of the granules. Fields stronger than 30 G have been swept out of the granules into the intergranular lanes and even some the intergranular lanes have no field stronger than 30 G. Fields stronger than 300 G are highly intermittent (Figure 49).
Distribution of magnetic field strengths at unit continuum optical depth for case of 250 G mean vertical field. The distribution is similar to that of Vögler and Schüssler (2003) but extends to larger field strengths because τ = 1 lies deeper in regions of strong field, so the field is more concentrated.
Image of magnetic field with superimposed zero velocity contours to outline the granules for the case of a 30 G uniform horizontal seed field. Field magnitudes less than 3, 30, and 300 G respectively are shown in gray. The magnetic field is concentrated into the intergranular lanes. It is highly intermittent, with strong fields occupying a tiny fraction of the total area.
7.2 Center-to-limb behavior
As one observes towards the limb several differences in the surface appearance occur (Figure 51 and Figure 11). First, the granules develop a three-dimensional pillow appearance with the granules higher than the intergranular lanes (see Figure 10), with their near sides brighter than their far sides. This is partly due to the true three-dimensional structure of granulation, the granules are observed higher than the intergranular lanes. Bright granules have their continuum optical depth unity 80 km above the mean surface. Partly it is due to the near side being seen more normal to the line of sight and the far side at a more glancing angle.
At disk center small magnetic concentrations appear as bright points in the intergranular lanes, while larger concentrations are dark. The increased brightness in magnetic concentrations is due to their lower density compared with their surroundings (Figure 50). At a given geometric height granules are hotter than the intergranular lanes, which are in turn hotter than G-band bright points, which are hotter than the large magnetic concentrations. Although at a given geometric height the magnetic elements are cooler than the surrounding medium, one sees into deeper layers, due to the reduced opacity, to where the temperature is higher, in part due to heating from the hot surrounding granules (Spruit, 1976, 1977b; Schüssler et al., 2003; Keller et al., 2004; Carlsson et al., 2004). In the G-band there is an additional, smaller, effect that the CH molecule becomes dissociated in the low density magnetic concentrations. The bottom panel of Figure 50 shows the temperature as function of lg τ500. The contrast in temperature between magnetic concentrations and non-magnetic areas increases with decreasing optical depth giving larger intensity contrast with increasing opacity (e.g., Ca H,K). The G-band has its mean formation height (black line in bottom panel) at lg τ500 = −0.48 corresponding to a mean formation height 54 km above where τ500 = 1, therefore giving a larger contrast than in the continuum. The contrast enhancement by the destruction of CH is seen as a dip in the curve showing the mean formation optical depth in the bottom panel. Note also that the G-band intensity has its peak contribution at similar heights as the continuum (that is why the granulation pattern looks similar). Bright points in the G-band have been used as a proxy for magnetic field concentrations. While G-band bright points are a good proxy for strong magnetic fields, there are many more regions of strong field that appear dark in the G-band, typically because they cover a larger area (Figure 52). Occasionally, especially dark micropores form at the vertices of several intergranular lanes. The contrast in the G-band has also been studied by Rutten et al. (2001), Sánchez Almeida et al. (2001), and Steiner et al. (2001).
Temperature, density, and magnetic field strength along a vertical slice through magnetic and non-magnetic regions, with the average formation height for the G-band intensity for a vertical ray (black line) and at μ = 0.6 (white line). Axes are distances in Mm. The bottom panel shows temperature as function of lg τ500.
mpg-Movie (123750.990234 KB) Still from a movie showing G-band images calculated from the simulation at disk center and towards the limb at μ = 0.8, 0.6, 0.4. At disk center small magnetic concentrations appear bright, while larger ones appear dark. When looking toward the limb the granulation appears hilly and one sees the bright walls of granules where the line of sight passes through a low density magnetic concentration. Movie shows time evolution. Note the formation of a micropore near the upper center (movie by Mats Carlsson). (For video see appendix)
The presence of strong magnetic fields enhances the pillow appearance of granules because their low density and resulting low opacity allow one to see deeper into the hot granules behind them (the “hot wall” effect Spruit, 1976, 1977b; Keller et al., 2004; Shelyag et al., 2004; Carlsson et al., 2004). Where the fields are strong the intergranular lanes are depressed up to 350 km below the mean height. Thus the τ = 1 surface is extremely corrugated. Toward the limb, where the surface is viewed at an angle, the low density and opacity in the strong magnetic elements allows one to see the hot granule walls behind. These are the faculae (Figure 53) (Keller et al., 2004; Carlsson et al., 2004). The excess brightness comes from a thin layer (∼ 30 km) of steep density gradient at the interface between the magnetic and nonmagnetic atmospheres. Typically there is a dark lane just centerward of the bright faculae. As the line of sight moves limbward from granule to faculae, it first intersects a granule top and is bright, then intersects cool material above the granule and inside the magnetic concentration, and finally intersects the hot granule wall on the far side of the magnetic concentration (Figure 54). Variations in the field strength produces variations in the density and opacity which leads to a striated appearance in the bright granule walls. Where the field is weaker, the density is higher, so the opacity larger. This effect is enhanced by a higher CH concentration also due to the higher density. Thus, where the magnetic field is weaker, the radiation emerges from higher, cooler layers, so these locations appear darker.
Schematic sketch of a magnetic flux concentration (region between the thin lines) and adjacent granules (thick lines). The dashed lines enclose the region where 80% of the continuum radiation is formed. Bright facular radiation originates from a thin layer at the hot granule wall behind the limbward side of the optically thin magnetic flux concentration. The line of sight for the dark centerward bands is shown by the dark shaded region (Keller et al., 2004).
High resolution observations of solar faculae show that they have an asymmetric contrast profile, with some brightness extending up to one arcsecond in the limbward direction from their peak in brightness (Hirzberger and Wiehr, 2005). The wide contrast profile cannot be explained solely by the “hot wall” effect, as was noted by Lites et al. (2004). The works by Keller et al. (2004) and Steiner (2005) address this issues, with somewhat conflicting but broadly consistent explanations. One conclusion is that the limbward extension of brightness comes from seeing the granule behind the facular magnetic field through the rarefied facular magnetic flux concentration; a circumstance that observers suspected decades ago. The explanation is corroborated by the direct comparisons of observations and simulations by De Pontieu et al. (2006).
7.3 Magnetic flux emergence
Magnetic flux emergence through the solar surface is driven by two processes: buoyancy and advection. Magnetic concentrations with strong fields rise toward the surface first, because they are buoyant (to maintain approximate pressure equilibrium with their surroundings the density inside the concentration must be smaller than in its surroundings), and second, because they are advected by convective upflows. As it rises, a magnetic concentration will encounter convective downflows piercing the upflows on smaller and smaller scales, with downflow speeds significantly larger than the upflow speeds. The portions of the magnetic concentration in the downflows will be dragged down or at least have their upward motion slowed, while the portions still in the upflows continue to ascend rapidly. This leads to the formation of Ω-loops of successively smaller dimensions as the surface is approached. In general, the asymmetry of upflow and downflows (amplitudes and topology) leads to a tendency for downward transport of magnetic flux; a process known as “magnetic flux pumping” (Petrovay and Szakaly, 1993; Tobias et al., 1998; Dorch and Nordlund, 2000, 2001; Tobias et al., 2001). This process is likely to be of central importance for the overall flux balance of the solar convection zone, and allows storage of considerable magnetic flux inside the convection zone proper.
Yelles Chaouche et al. (2005), Cheung et al. (2007), and Martínez-Sykora et al. (2008) have simulated the rise of a coherent, twisted (necessary to retain its coherence) flux tube through the solar surface. As the tube rises it widens as it enters lower pressure levels. When it reaches the surface (with a width larger than the size if typical granules) it produces a string of larger than normal granules along its length. As it emerges through the surface the granular flows disperse the magnetic field into the intergranular lanes and the granular pattern returns to normal (Figure 55).
Emergent continuum intensity as a twisted flux tube emerges through the solar surface (Yelles Chaouche et al., 2005).
In simulations where a uniform horizontal magnetic field is advected into the computational domain at the bottom by upflows in the interiors of mesogranules, flux emerges through the surface, merges, fragments, cancels, and submerges pulled down by intergranular downflows. An example from the simulation showing both a bipole emerging through the surface and another bipole being pulled back down below the surface is shown in Figure 56. In the emerging bipole, the footpoints spread apart over time and are wider apart at lower elevations. In the submerging bipole, the flux in the upper level weakens over time, while the bipole remains visible at increasingly lower levels as time progresses.
Horizontal slices of magnetic field strength. Rows are time (in seconds) increasing downward. Columns are height (in km) above the mean visible surface decreasing toward the right. Red and yellow have opposite polarity to blue and black. Gray is weak field. At the right of each image is an emerging bipole whose legs separated with decreasing height and increasing time. At the left is a submerging bipole whose legs approach with increasing time and which disappears at higher elevations at later times.
Simulations where uniform horizontal magnetic field is advected in through the bottom of the computational domain can also be used to study “flux tubes”. Figure 57 shows magnetic field lines in the simulation box viewed from the side and slightly above. The red line in the lower left is horizontal field being advected into the domain. In the lower center is a loop like flux concentration rising toward the surface. In the upper right is a vertical flux concentration or “flux tube” through the surface (Stein and Nordlund, 2006). While the field lines form a coherent bundle near the surface, below the surface they become tangled and spread out in many different directions. This “flux tube” and others form by a loop-like flux concentration rising up through the surface and opening up through the upper boundary where the condition is that the field tends toward a potential field. This leaves behind the legs of the loop. Typically one leg is more compact and coherent than the other and persists for a longer time as a coherent entity while the other is quickly dispersed by the convective motions. Cattaneo et al. (2006) have studied the existence of flux tubes using an idealized simulation of a stably stratified atmosphere with shear in both the vertical and one horizontal direction driven by a forcing term in the momentum equation. They find that in the absence of symmetries, even in this laminar flow case, there are no flux surfaces separating the inside of a flux concentration from the outside, so that the magnetic field lines in the concentration connect chaotically to the outside and the “flux tube” is leaky. They conclude that in the highly turbulent solar environment the chance of finding isolated “flux tubes” is slim. Numerical simulations are of course much more magnetically diffusive than the Sun, but here also the field lines in the flux tube connect chaotically to the outside except over a small height range at the surface.
Magnetic field lines in a simulation snapshot viewed from an angle. The red line in the lower left is horizontal field being advected into the domain. In the lower center is a loop like flux concentration rising toward the surface. In the upper right is a vertical flux concentration or “flux tube” through the surface with its field lines connecting chaotically to the outside below the surface.
The fact that magnetic fields that are concentrated close to the surface tend to tangle and spread out in many directions below the surface has been demonstrated earlier by Grossmann-Doerth et al. (1998) — see also Vögler et al. (2005) and Schaffenberger et al. (2005).
Occasionally, in magneto-convection simulations micropores form in the vertices of where several intergranular lanes meet (Bercik, 2002; Bercik et al., 2003; Vögler et al., 2005; Cameron et al., 2007b). In the typical formation scenario a small bright granule is surrounded by strong magnetic fields in the intergranular lanes. The upward velocity in the small granule reverses and it disappears with the area it occupied becoming dark. The surrounding strong fields move into the dark micropore area (Figure 58). On the order of a granular timescale the magnetic field is dispersed and the micropore disappears.
As the upflow velocity in a flux concentration slows and reverses, the upward heat flux decreases and the plasma inside the concentration cools by radiation through the surface (Figure 59). As a result, the density scale height decreases and the plasma settles lower. Initially the material piles up below the surface until a new hydrostatic structure is established (Figure 60).
Magnetic field (filled contours at 250 G intervals from 0 G to 3500 G) and temperature (1000 K intervals from 4000 K to 16,000 K). The τ = 1 depth is shown as the thick line around z = 0 Mm. The flux concentrations are significantly cooler than their surroundings (Bercik, 2002; Bercik et al., 2003).
Magnetic field (filled contours at 250 G intervals) and ln density (in 0.5 intervals from −2 to 4). The τ = 1 depth is shown as the thick line around z = 0 Mm. The established, strong “flux tube” in the center has been evacuated and is in equilibrium. The smaller flux concentrations on either side are in the process of being evacuated, starting above the surface and piling up plasma below the surface (Bercik, 2002; Bercik et al., 2003).
Micropores have an amoeba-like structure with arms extending along the intergranular lanes. Fluid flows are suppressed inside them and they are surrounded by downflowing plasma which is concentrated into a few downdrafts on their periphery (Figure 61). Micropores, like other flux concentrations, are cooled by vertical radiation and heated by radiation from their hotter sidewalls (Figure 62).
Image of vertical velocity (red and yellow down, blue and green up in km s−1) with magnetic field contours at 0.5 kG intervals at the surface (left) and 1.5 Mm below the surface (Bercik, 2002).
Radiative heating and cooling of flux concentrations. The second from top panel shows temperature contours at 1000 K intervals. The third from top panel shows magnetic field contours at 250 G intervals. Units are 1010 erg g−1 s−1. The top three panels show the net radiative heating/cooling and its relation to the temperature and magnetic fields. The bottom three panels show the contribution of vertical, inclined, and nearly horizontal rays (Bercik, 2002).
The ubiquitous occurrence of downflows in the close vicinity but outside magnetic flux concentrations (see for example also Steiner et al., 1998) has been explained in terms of baroclinic flows by Deinzer et al. (1984). The effect has been observationally verified by Langangen et al. (2007).
Emonet and Cattaneo (2001)have shown that dynamo action will occur in a turbulent medium even in the absence of rotation. This led to the suggestion that in addition to the global solar dynamo there is a local, surface dynamo acting in the Sun, a proposition that has recently been confirmed by Vögler and Schüssler (2007). It must be remembered, however, that even though dynamo action occurs in the surface layers of the Sun, these layers are not isolated from the rest of the convection zone. The plasma and magnetic field are mixed throughout the convection zone.
The nature of the large scale solar dynamo has been reviewed by, among many others, Brandenburg and Dobler (2002), Ossendrijver (2003), and Charbonneau (2005).
7.4 Convection as a driver of chromospheric and coronal heating
In a broad sense it is of course generally accepted that the solar convection zone is the ultimate driver of the activity that transpires in the solar chromosphere and corona, since the convection zone is the only available source of mechanical energy. Moreover, since upper atmosphere activity and heating is empirically so intimately connected with the presence of magnetic fields, one must also conclude that it is the Poynting flux (the flux of electromagnetic energy) rather than the acoustic or advective/convective kinetic energy flux that is the main transport agent.
From that point of view the question of chromospheric and coronal driving can in principle be reduced to a question of being able to understand and estimate the Poynting flux passing through the solar surface. In practice, this is not an easy task, and one can furthermore convincingly argue that the magnitude of the Poynting flux indeed depends as much on the sink (the chromosphere and corona) as it depends on the source (the subsurface layers of the convection zone).
If one assumes, for example, that one aspect of the subsurface driving is to twist the magnetic field that passes through the surface, then if there is only a weak resistance to the twist, so the twisting motion can proceed with almost no counteracting force, then very little work is performed, and consequently the Poynting flux through the solar surface must be small. Conversely, if there is a large resistance to the twisting motion, and strong counteracting forces develop, that must correspond to a large Poynting flux through the solar surface.
The key factor that regulates the magnitude of the Poynting flux is the angle that the magnetic field lines make relative to the surface, or relative to the motions that attempt to twist the field lines. If there is a strong resistance to the twisting motion the angle is changed — the field becomes twisted and provides a counteracting force, while if there is almost no resistance the field lines remain straight, and the magnetic field hardly transmits any Poynting flux.
Apart from the twist angle, the Poynting flux is also proportional to the energy density of the magnetic field and to the velocity with which the field is being transported. A knowledge of the these three factors on a boundary is in principle enough to compute the Poynting flux through the boundary. Scaling formulae that express these relations were presented by Parker (1983) and van Ballegooijen (1986). The main uncertainty that one encounters when trying to estimate actual heating rates is the angle factor. Galsgaard and Nordlund (1996) found that simple experiments with boundary driving adhere closely to a scaling law that may be interpreted to mean that the twist angle is always of a size that allows the magnetic field lines to twist around their neighbors about once, from end to end. This rule of thumb is consistent with the stability properties of twisted flux tube, which tend to become unstable (to kinking and similar phenomena) when twisted more than about once.
An important consequence of the scaling is that increased resistivity leads to a decrease of the energy dissipation, in that a larger resistivity allows magnetic field lines to diffuse more quickly, straighten out, and hence become less tilted at the driving boundary (Parker, 1988). Conversely, the work and dissipation obtained for a given resistivity is a lower bound on the work and dissipation obtained at very low resistivities. It is this property that gives hope that numerical experiments can provide accurate predictions of chromospheric and coronal heating.
Indeed, Gudiksen and Nordlund (2005a,b) were able to construct a 3D corona model where sufficient heat was provided exclusively by this mechanism. Synthetic diagnostics from the model (Peter et al., 2005, 2006) fits observed values very well.
The models by Gudiksen and Nordlund (2005a,b) had an artificial velocity field, but with statistical properties consistent with the observed solar surface velocity field, from granular to supergranular scales. Using a fully self-consistent subsurface velocity field, evolved simultaneously with the chromospheric and coronal dynamics requires higher numerical resolution, since one must ideally simultaneously resolve scales from sub-granular sizes up to supergranular or active region sizes. The first steps towards this ultimate goal have been taken (Hansteen and Gudiksen, 2005; Hansteen et al., 2007; Abbett, 2007). Similar studies concentrated on the chromosphere have been initiated by Wedemeyer et al. (2003); see also Schaffenberger et al. (2005) and Schaffenberger et al. (2006).
8 Current Status and Future Directions
As discussed in the previous sections of this review, numerical models of the hydrodynamics and magneto-hydrodynamics of the solar surface layers are becoming increasingly realistic and accurate, both because of the steady growth of computing power, and because of the incorporation of increasingly complex physical mechanisms in the models.
The hydrodynamic aspects of the near-surface regions are now largely understood, both qualitatively and quantitatively, but this cannot at all be said about even the most well-known and and well-studied aspect of solar magneto-hydrodynamics; sunspots and the solar activity cycle.
The study of the magneto-hydrodynamics of the solar surface layers, and even more so the study of the overlying chromosphere and corona, which also provides the opportunity to study phenomena that go beyond classical magneto-hydrodynamics, is now the main focus area in solar physics research.
The results and experiences that will come out of these future efforts will be extremely valuable, also for other branches of astrophysics, where the “five dimensions” that are accessible in solar physics (space, time, and wavelength) are projected down to just a few — essentially one dimension when dealing with stars, and essentially only 2D projections of temporal snapshots when dealing with extended objects such as galaxies or molecular clouds.
To continue the progress the realism of the numerical simulations still needs to be improved: radiation, resolution, diffusion, non-LTE excitation, and ionization are all issues that need more work. Especially the chromospheric and coronal heating problems are also going to benefit from advances in the raw computing power, and from improved and and more efficient approximate methods to model radiation and non-equilibrium processes.
For studies that go beyond classical hydrodynamics and magneto-hydrodynamics a range of new tools need to be developed and deployed: particle-in-cell codes that can describe the near-collisionless conditions in the corona with billions to trillions of particles, codes that use hybrid fluid and particle pictures, diagnostic modules that show what would be observed with the range of new instruments and satellites that will be deployed, etc.
9 Summary and Concluding Remarks
Solar convection is the driver that ultimately controls the Sun’s magnetic field, its explosive events, the interplanetary medium and Earth’s weather and space weather. In this review we have discussed the principles of hydrodynamics as they apply to convection near the solar surface.
In Section 3 we discussed the manifestations and properties of the main energy carrying scales, and the granulation pattern that they give rise to. We emphasized the crucial importance of the density stratification in determining the size and evolution of the granulation pattern, and the importance of the radiative cooling at the solar surface as the provider of the entropy deficient plasma that then drives convective motions over a range of scales.
In Section 4 we discussed how larger scale convective patterns arise and are driven, and how they interact with smaller scale patterns. We introduced the concept of a velocity spectrum, and addressed the question of to what extent or not the traditional concepts of meso- and supergranulation represent distinct scales of motion. We showed that both observations and theoretical models give a smooth velocity spectrum, with velocity amplitudes decreasing approximately linearly with horizontal wave number on scales larger than granulation.
In Section 5 we discussed how spectral line synthesis and comparisons with observed spectral line profiles may be used to assess the accuracy of numerical simulations and how the resulting spectral line profiles may be used to accurately determine solar chemical abundances. We conclude that 3D models with numerical resolutions of the order of 2003 reproduce the widths, shifts, and shapes of photospheric spectral lines with high accuracy, and that the chemical abundances derived from such models have a higher degree of internal consistency with less scatter and fewer systematic trends than the ones obtains from traditional abundance analysis, based on empirical or theoretical one-dimensional model atmospheres.
In Section 6 we discussed applications to global and local helioseismology; wave excitation and damping, the influence of convection on the mean structure, and helioseismic diagnostics related to convective flow patterns. We showed that solar oscillations with realistic overall amplitudes are spontaneously excited in numerical simulations of the solar surface layers, and that solar surface convection directly influences the frequency of the oscillations by changing the size of the resonant cavity.
In Section 7 we discussed the interaction of solar surface convection and solar magnetic fields. In active regions, the presence of magnetic fields causes the brightening of plage regions towards the limb, and increased possibilities for convection to heat the chromosphere and corona.
Finally, in Section 8, we briefly discussed open questions and directions for future work, and emphasized the importance of the Sun as a test bed for astrophysical hydrodynamics, magneto-hydrodynamics, and beyond.
In conclusion, we submit that the Sun is a superb laboratory for investigating dynamical as-trophysical processes and especially plasma physics. Combinations of observations and numerical simulations can provide detailed insights into these physical processes, and can also provide data sets that may be used to validate observational analysis methods and to design future observing programs.
Notes
Erratum 2009-04-15: corrected +P(∇ · u) to −P(∇ · u)
1.5D denotes the case when considering each column in a 2D or 3D model as a separate entity and, thus, ignoring all non-vertical radiative transfer.
We note that the equivalent widths quoted in Asplund et al. (2004) are not measured from the observed spectrum but theoretical values from the best-fitting 3D non-LTE line profiles.
The solar Ne and Ar contents are not inferable from the photospheric spectrum. Instead these abundances are deduced from the coronal Ne/O and Ar/O ratios coupled with the photospheric O abundance, assuming that these ratios are the same in the photosphere and the corona.
In their analysis of the C, N, and O, Grevesse and Sauval (1998) allowed for modifications of the temperature structure of the Holweger and Müller (1974) model in order to remove otherwise unavoidable trends with excitation potential and line strengths for certain species, see also Grevesse and Sauval (1999) for further details.
References
Abbett, W.P., 2007, “The Magnetic Connection between the Convection Zone and Corona in the Quiet Sun”, Astrophys. J., 665, 1469–1488. [DOI], [ADS] (Cited on page 87.)
Abbett, W.P., Beaver, M., Davids, B., Georgobiani, D., Rathbun, P. and Stein, R.F., 1997, “Solar Convection: Comparison of Numerical Simulations and Mixing Length Theory”, Astrophys. J., 480, 395. [DOI], [ADS] (Cited on page 34.)
Allen, M.S. and Musman, S., 1973, “The Location of Exploding Granules”, Solar Phys., 32, 311–314. [DOI], [ADS] (Cited on page 23.)
Allende Prieto, C. and García López, R.J., 1998, “Fe i line shifts in the optical spectrum of the Sun”, Astron. Astrophys. Suppl., 129, 41–44. [ADS], [astro-ph/9710066] (Cited on page 47.)
Allende Prieto, C., Lambert, D.L. and Asplund, M., 2001, “The Forbidden Abundance of Oxygen in the Sun”, Astrophys. J. Lett., 556, L63–L66. [DOI], [ADS], [astro-ph/0106360] (Cited on pages 42, 47, 51, 52, and 53.)
Allende Prieto, C., Lambert, D.L. and Asplund, M., 2002, “A Reappraisal of the Solar Photospheric C/O Ratio”, Astrophys. J. Lett., 573, L137–L140. [DOI], [ADS], [astro-ph/0206089] (Cited on pages 42 and 47.)
Allende Prieto, C., Asplund, M. and Fabiani Bendicho, P., 2004, “Center-to-limb variation of solar line profiles as a test of NLTE line formation calculations”, Astron. Astrophys., 423, 1109–1117. [DOI], [ADS], [astro-ph/0405154] (Cited on pages 42 and 54.)
Altrock, R.C., 1968, “A New Method for the Analysis of Equivalent Widths and its Application to Solar Photospheric Oxygen”, Solar Phys., 5, 260–280. [DOI], [ADS] (Cited on page 51.)
Anders, E. and Grevesse, N., 1989, “Abundances of the elements: Meteoritic and solar”, Geochim. Cosmochim. Acta, 53, 197–214. [DOI], [ADS] (Cited on pages 49, 51, 55, and 57.)
Asensio Ramos, A., Trujillo Bueno, J., Carlsson, M. and Cernicharo, J., 2003, “Nonequilibrium CO Chemistry in the Solar Atmosphere”, Astrophys. J. Lett., 588, L61–L64. [DOI], [ADS], [astroph/0303460] (Cited on page 49.)
Asplund, M., 2000, “Line formation in solar granulation. III. The photospheric Si and meteoritic Fe abundances”, Astron. Astrophys., 359, 755–758. [ADS], [astro-ph/0005322] (Cited on pages 42, 47, and 56.)
Asplund, M., 2004, “Line formation in solar granulation. V. Missing UV-opacity and the photospheric Be abundance”, Astron. Astrophys., 417, 769–774. [DOI], [ADS], [astro-ph/0312291] (Cited on pages 42, 47, 51, and 56.)
Asplund, M., 2005, “New Light on Stellar Abundance Analyses: Departures from LTE and Homogeneity”, Annu. Rev. Astron. Astrophys., 43, 481–530. [ADS] (Cited on pages 8, 15, 42, 45, 47, 54, 55, and 56.)
Asplund, M., Gustafsson, B., Kiselman, D. and Eriksson, K., 1997, “Line-blanketed model atmospheres for R Coronae Borealis stars and hydrogen-deficient carbon stars”, Astron. Astrophys., 318, 521–534. [ADS] (Cited on pages 48 and 50.)
Asplund, M., Ludwig, H.-G., Nordlund, Å. and Stein, R.F., 2000a, “The effects of numerical resolution on hydrodynamical surface convection simulations and spectral line formation”, Astron. Astrophys., 359, 669–681. [ADS], [astro-ph/0005319] (Cited on pages 15, 42, and 47.)
Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C. and Stein, R.F., 2000b, “Line formation in solar granulation. I. Fe line shapes, shifts and asymmetries”, Astron. Astrophys., 359, 729–742. [ADS], [astro-ph/0005320] (Cited on pages 13, 15, 42, 43, 44, 47, 53, 55, and 58.)
Asplund, M., Nordlund, Å., Trampedach, R. and Stein, R.F., 2000c, “Line formation in solar granulation. II. The photospheric Fe abundance”, Astron. Astrophys., 359, 743–754. [ADS], [astro-ph/0005321] (Cited on pages 42, 47, 55, and 56.)
Asplund, M., Carlsson, M. and Botnen, A.V., 2003, “Multi-level 3D non-LTE computations of lithium lines in the metal-poor halo stars HD 140283 and HD 84937”, Astron. Astrophys., 399, L31–L34. [DOI], [ADS], [astro-ph/0302406] (Cited on pages 42 and 47.)
Asplund, M., Grevesse, N., Sauval, A.J., Allende Prieto, C. and Kiselman, D., 2004, “Line formation in solar granulation. IV. [O I], O I and OH lines and the photospheric O abundance”, Astron. Astrophys., 417, 751–768. [DOI], [ADS], [astro-ph/0312290] (Cited on pages 42, 47, 50, 51, 53, 54, 55, 56, 57, and 58.)
Asplund, M., Grevesse, N. and Sauval, A.J., 2005a, “The Solar Chemical Composition”, in Cosmic Abundance as Records of Stellar Evolution and Nucleosynthesis in honor of David L. Lambert, Symposium held 17–19 June, 2004 in Austin, Texas, USA, (Eds.) Barnes III, T.G., Bash, F.N., vol. 336 of ASP Conference Series, pp. 25–38, Astronomical Society of the Pacific, San Francisco. [ADS], [astro-ph/0410214] (Cited on pages 42, 47, 49, 50, 54, 56, 57, and 59.)
Asplund, M., Grevesse, N., Sauval, A.J., Allende Prieto, C. and Blomme, R., 2005b, “Line formation in solar granulation. VI. [C I], C I, CH and C2 lines and the photospheric C abundance”, Astron. Astrophys., 431, 693–705. [DOI], [ADS], [astro-ph/0410681] (Cited on pages 42, 47, 48, 49, 50, 53, 56, and 57.)
Atroshchenko, I.N. and Gadun, A.S., 1994, “Three-dimensional hydrodynamic models of solar granulation and their application to a spectral analysis problem”, Astron. Astrophys., 291, 635–656. [ADS] (Cited on page 42.)
Ayres, T.R., 2008, “Solar forbidden oxygen, revisited”, Astrophys. J., 686, 731–740. [DOI], [ADS] (Cited on pages 42, 51, and 53.)
Ayres, T.R., Plymate, C. and Keller, C.U., 2006, “Solar Carbon Monoxide, Thermal Profiling, and the Abundances of C, O, and Their Isotopes”, Astrophys. J. Suppl. Ser., 165, 618–651. [DOI], [ADS], [astro-ph/0606153] (Cited on pages 42, 48, 49, 55, and 58.)
Badnell, N.R., Bautista, M.A., Butler, K., Delahaye, F., Mendoza, C., Palmeri, P., Zeippen, C.J. and Seaton, M.J., 2005, “Updated opacities from the Opacity Project”, Mon. Not. R. Astron. Soc., 360, 458–464. [DOI], [ADS], [astro-ph/0410744] (Cited on page 57.)
Bahcall, J.N., Basu, S. and Serenelli, A.M., 2005, “What Is the Neon Abundance of the Sun?”, Astrophys. J., 631, 1281–1285. [DOI], [ADS], [astro-ph/0502563] (Cited on page 57.)
Bahcall, J.N., Serenelli, A.M. and Basu, S., 2006, “10,000 Standard Solar Models: A Monte Carlo Simulation”, Astrophys. J. Suppl. Ser., 165, 400–431. [DOI], [ADS], [astro-ph/0511337] (Cited on page 57.)
Balmforth, N.J., 1992, “Solar pulsational stability — III. Acoustical excitation by turbulent convection”, Mon. Not. R. Astron. Soc., 255, 639–649. [ADS] (Cited on page 64.)
Balthasar, H., 1988, “The center-to-limb variation of solar spectral lines”, Astron. Astrophys. Suppl., 72, 473–495. [ADS] (Cited on page 47.)
Barklem, P.S., 2007a, “Electron-impact excitation of neutral oxygen”, Astron. Astrophys., 462, 781–788. [DOI], [ADS], [astro-ph/0609684] (Cited on page 54.)
Barklem, P.S., 2007b, “Non-LTE Balmer line formation in late-type spectra: effects of atomic processes involving hydrogen atoms”, Astron. Astrophys., 466, 327–337. [DOI], [ADS], [astroph/0702222] (Cited on page 58.)
Barklem, P.S., Belyaev, A.K. and Asplund, M., 2003, “Inelastic H+Li and H−+Li+ collisions and non-LTE Li I line formation in stellar atmospheres”, Astron. Astrophys., 409, L1–L4. [DOI], [ADS], [astro-ph/0308170] (Cited on page 42.)
Basu, S. and Antia, H.M., 2008, “Helioseismology and solar abundances”, Phys. Rep., 457, 217–283. [DOI], [ADS], [0711.4590] (Cited on pages 42 and 57.)
Beck, J.G., Duvall Jr, T.L. and Scherrer, P.H., 1998a, “Long-lived giant cells detected at the surface of the Sun”, Nature, 394, 653–655. [ADS] (Cited on page 36.)
Beck, J.G., Duvall Jr, T.L., Scherrer, P.H. and Hocksema, J.T., 1998b, “The Detection of Giant Velocity Cells on the Sun”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, SOHO 6/GONG 98 Workshop, 1–4 June 1998, Boston, Massachusetts, USA, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 725–729, ESA Publications Division, Noordwijk. [ADS] (Cited on page 36.)
Bellot Rubio, L.R. and Borrero, J.M., 2002, “Iron abundance in the solar photosphere. Application of a two-component model atmosphere”, Astron. Astrophys., 391, 331–337. [DOI], [ADS] (Cited on page 42.)
Bellot Rubio, L.R. and Collados, M., 2003, “Understanding internetwork magnetic fields as determined from visible and infrared spectral lines”, Astron. Astrophys., 406, 357–362. [DOI], [ADS] (Cited on page 74.)
Bercik, D.J., 2002, A numerical investigation of the interaction between convection and magnetic field in a solar surface layer, Ph.D. Thesis, Michigan State University, East Lansing. [ADS] (Cited on pages 83, 85, 86, 87, and 88.)
Bercik, D.J., Nordlund, Å. and Stein, R.F., 2003, “Magnetoconvection and micropores”, in Local and Global Helioseismology: The Present and Future, Proceedings of SOHO 12/GONG+ 2002, 27 October–1 November 2002, Big Bear Lake, California, USA, (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 201–206, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 83, 85, and 86.)
Berrilli, F., Consolini, G., Florio, A. and Pietropaolo, E., 2001, “Solar granulation: properties of velocity fields from THEMIS-IPM observations”, Mem. Soc. Astron. Ital., 72, 669–672. [ADS] (Cited on page 15.)
Birch, A.C. and Felder, G., 2004, “Accuracy of the Born and Ray Approximations for Time-Distance Helioseismology of Flows”, Astrophys. J., 616, 1261–1264. [DOI], [ADS] (Cited on page 60.)
Birch, A.C., Kosovichev, A.G., Price, G.H. and Schlottmann, R.B., 2001, “The Accuracy of the Born and Ray Approximations in Time-Distance Helioseismology”, Astrophys. J. Lett., 561, L229–L232. [DOI], [ADS] (Cited on page 60.)
Birch, A.C., Gizon, L., Hindman, B.W. and Haber, D.A., 2007, “The Linear Sensitivity of Helio-seismic Ring Diagrams to Local Flows”, Astrophys. J., 662, 730–737. [DOI], [ADS] (Cited on page 36.)
Blackwell, D.E., Lynas-Gray, A.E. and Smith, G., 1995, “On the determination of the solar iron abundance using Fe i lines”, Astron. Astrophys., 296, 217. [ADS] (Cited on page 55.)
Bogdan, T.J., Carlsson, M., Hansteen, V.H., McMurry, A., Rosenthal, C.S., Johnson, M., Petty-Powell, S., Zita, E.J., Stein, R.F., McIntosh, S.W. and Nordlund, Å., 2003, “Waves in the Magnetized Solar Atmosphere. II. Waves from Localized Sources in Magnetic Flux Concentrations”, Astrophys. J., 599, 626–660. [DOI], [ADS] (Cited on page 60.)
Böhm-Vitense, E., 1958, “Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte”, Z. Astrophys., 46, 108–143. [ADS] (Cited on pages 33 and 39.)
Borrero, J.M. and Bellot Rubio, L.R., 2002, “A two-component model of the solar photosphere from the inversion of spectral lines”, Astron. Astrophys., 385, 1056–1072. [DOI], [ADS] (Cited on page 42.)
Brandenburg, A. and Dobler, W., 2002, “Solar and stellar dynamos — latest developments”, Astron. Nachr., 323, 411–416. [DOI], [ADS], [astro-ph/0207393] (Cited on page 84.)
Brandenburg, A., Chan, K.L., Nordlund, Å. and Stein, R.F., 2005, “Effect of the radiative background flux in convection”, Astron. Nachr., 326, 681–692. [DOI], [ADS], [astro-ph/0508404] (Cited on pages 26 and 34.)
Brandt, P.N., Scharmer, G.B., Ferguson, S., Shine, R.A. and Tarbell, T.D., 1988, “Vortex flow in the solar photosphere”, Nature, 335, 238–240. [DOI], [ADS] (Cited on page 35.)
Brandt, P.N., Ferguson, S., Shine, R.A., Tarbell, T.D. and Scharmer, G.B., 1991, “Variation of granulation properties on a mesogranular scale”, Astron. Astrophys., 241, 219–226. [ADS] (Cited on page 35.)
Braun, D.C., Lindsey, C., Fan, Y. and Jefferies, S.M., 1992, “Local acoustic diagnostics of the solar interior”, Astrophys. J., 392, 739–745. [DOI], [ADS] (Cited on page 66.)
Braun, D.C., Birch, A.C., Benson, D., Stein, R.F. and Nordlund, Å 2007, “Helioseismic Holography of Simulated Solar Convection and Prospects for the Detection of Small-Scale Subsurface Flows”, Astrophys. J., 669, 1395–1405. [DOI], [ADS], [arXiv:0708.0214] (Cited on page 62.)
Bray, R.J., Loughhead, R.E. and Durrant, C.J., 1984, The Solar Granulation, Cambridge University Press, Cambridge; New York, 2nd edn. (Cited on page 8.)
Brown, T.M., Bogdan, T.J., Lites, B.W. and Thomas, J.H., 1992, “Localized sources of propagating acoustic waves in the solar photosphere”, Astrophys. J. Lett., 394, L65–L68. [DOI], [ADS] (Cited on page 66.)
Bruls, J.H.M.J. and Rutten, R.J., 1992, “The formation of helioseismology lines. II. Modeling of alkali resonance lines with granulation”, Astron. Astrophys., 265, 257–267. [ADS] (Cited on page 42.)
Bushby, P.J., Houghton, S.M., Proctor, M.R.E. and Weiss, N.O., 2008, “Convective intensification of magnetic fields in the quiet Sun”, Mon. Not. R. Astron. Soc., 387, 698–706. [DOI], [ADS], [arXiv:0804.1238] (Cited on page 71.)
Caffau, E. and Ludwig, H.-G., 2007, “The forbidden 1082 nm line of sulphur: the photospheric abundance of sulphur in the Sun and 3D effects”, Astron. Astrophys., 467, L11–L14. [DOI], [ADS], [astro-ph/0703423] (Cited on pages 42, 48, and 56.)
Caffau, E., Faraggiana, R., Bonifacio, P., Ludwig, H.-G. and Steffen, M., 2007a, “Sulphur abundances from the S I near-infrared triplet at 1045 nm”, Astron. Astrophys., 470, 699–708. [DOI], [ADS], [arXiv:0704.2335] (Cited on pages 42, 48, and 56.)
Caffau, E., Steffen, M., Sbordone, L., Ludwig, H.-G. and Bonifacio, P., 2007b, “The solar photospheric abundance of phosphorus: results from CO5BOLD 3D model atmospheres”, Astron. Astrophys., 473, L9–L12. [DOI], [ADS], [arXiv:0708.1607] (Cited on pages 42, 48, and 56.)
Caffau, E., Ludwig, H.-G., Steffen, M., Ayres, T.R., Bonifacio, P., Cayrel, R., Freytag, B. and Plez, B., 2008a, “The photospheric solar oxygen project: I. Abundance analysis of atomic lines and influence of atmospheric models”, Astron. Astrophys., 488, 1031–1046. [DOI], [ADS], [arXiv:0805.4398] (Cited on pages 42, 48, 51, 53, 54, 58, and 59.)
Caffau, E., Sbordone, L., Ludwig, H.-G., Bonifacio, P., Steffen, M. and Behara, N.T., 2008b, “The solar photospheric abundance of hafnium and thorium. Results from CO5 BOLD 3D hydrody-namic model atmospheres”, Astron. Astrophys., 483, 591–598. [DOI], [ADS], [arXiv:0803.3585] (Cited on pages 42, 48, and 56.)
Cally, P.S. and Goossens, M., 2007, “Three-Dimensional MHD Wave Propagation and Conversion to Alfvén Waves near the Solar Surface. I. Direct Numerical Solution”, Solar Phys., 251, 251–261. [DOI], [ADS] (Cited on page 60.)
Cameron, R., Gizon, L. and Daiffallah, K., 2007a, “SLiM: a code for the simulation of wave propagation through an inhomogeneous, magnetised solar atmosphere”, Astron. Nachr., 328, 313. [DOI], [ADS] (Cited on page 60.)
Cameron, R., Schüssler, M., Vögler, A. and Zakharov, V., 2007b, “Radiative magnetohydrody-namic simulations of solar pores”, Astron. Astrophys., 474, 261–272. [DOI], [ADS] (Cited on page 83.)
Canuto, V.M. and Mazzitelli, I., 1991, “Stellar turbulent convection: A new model and applications”, Astrophys. J., 370, 295–311. [DOI], [ADS] (Cited on page 39.)
Carlsson, M., Stein, R.F., Nordlund, Å and Scharmer, G.B., 2004, “Observational Manifestations of Solar Magnetoconvection: Center-to-Limb Variation”, Astrophys. J. Lett., 610, L137–L140. [DOI], [ADS], [astro-ph/0406160] (Cited on pages 13, 24, 77, and 80.)
Cattaneo, F., Hurlburt, N.E. and Toomre, J., 1990, “Supersonic convection”, Astrophys. J. Lett., 349, L63–L66. [DOI], [ADS] (Cited on page 30.)
Cattaneo, F., Brummell, N.H., Toomre, J., Malagoli, A. and Hurlburt, N.E., 1991, “Turbulent compressible convection”, Astrophys. J., 370, 282–294. [DOI], [ADS] (Cited on page 11.)
Cattaneo, F., Lenz, D. and Weiss, N., 2001, “On the Origin of the Solar Mesogranulation”, Astrophys. J. Lett., 563, L91–L94. [DOI], [ADS] (Cited on page 35.)
Cattaneo, F., Emonet, T. and Weiss, N.O., 2003, “On the interaction between convection and magnetic fields”, Astrophys. J., 588, 1183–1198. [DOI], [ADS] (Cited on page 71.)
Cattaneo, F., Brummell, N.H. and Cline, K.S., 2006, “What is a flux tube? On the magnetic field topology of buoyant flux structures”, Mon. Not. R. Astron. Soc., 365, 727–734. [DOI], [ADS] (Cited on page 83.)
Cauzzi, G., Ramos, A.A., Reardon, K.P. and Janssen, K., 2006, “Comparison of spatially and spectrally resolved solar data with numerical simulations”, Proc. IAU, 2, 138–143. [DOI], [ADS] (Cited on page 44.)
Centeno, R. and Socas-Navarro, H., 2008, “A new approach to the solar oxygen abundance problem”, Astrophys. J. Lett., 682, L61–L64. [DOI], [ADS], [arXiv:0803.0990] (Cited on pages 42, 53, and 59.)
Chaplin, W.J., Houdek, G., Elsworth, Y., Gough, D.O., Isaak, G.R. and New, R., 2005, “On model predictions of the power spectral density of radial solar p modes”, Mon. Not. R. Astron. Soc., 360, 859–868. [DOI], [ADS] (Cited on page 64.)
Charbonneau, P., 2005, “Dynamo Models of the Solar Cycle”, Living Rev. Solar Phys., 2, lrsp-2005-2. URL (accessed 18 July 2008): http://www.livingreviews.org/lrsp-2005-2 (Cited on page 84.)
Charbonnel, C. and Talon, S., 2005, “Influence of Gravity Waves on the Internal Rotation and Li Abundance of Solar-Type Stars”, Science, 309, 2189–2191. [DOI], [ADS], [astro-ph/0511265] (Cited on page 57.)
Cheung, M.C.M., Schüssler, M. and Moreno-Insertis, F., 2007, “Magnetic flux emergence in granular convection: radiative MHD simulations and observational signatures”, Astron. Astrophys., 467, 703–719. [DOI], [ADS], [astro-ph/0702666] (Cited on page 81.)
Christensen-Dalsgaard, J., Däppen, W., Ajukov, S.V., Anderson, E.R., Antia, H.M., Basu, S., Baturin, V.A., Berthomieu, G., Chaboyer, B., Chitre, S.M., Cox, A.N., Demarque, P., Donatowicz, J., Dziembowski, W.A., Gabriel, M., Gough, D.O., Guenther, D.B., Guzik, J.A., Harvey, J.W., Hill, F., Houdek, G., Iglesias, C.A., Kosovichev, A.G., Leibacher, J.W., Morel, P., Proffitt, C.R., Provost, J., Reiter, J., Rhodes Jr, E.J., Rogers, F.J., Roxburgh, I.W., Thompson, M.J. and Ulrich, R.K., 1996, “The Current State of Solar Modeling”, Science, 272, 1286–1292. [DOI], [ADS] (Cited on page 69.)
Cram, L.E., Durney, B.R. and Guenther, D.B., 1983, “Preliminary observations of velocity fields at the solar poles”, Astrophys. J., 267, 442–454. [DOI], [ADS] (Cited on page 36.)
Danilovic, S., Gandorfer, A., Lagg, A., Schuüssler, M., Solanki, S.K., Vögler, A., Katsukawa, Y. and Tsuneta, S., 2008, “The intensity contrast of solar granulation: comparing Hinode SP results with MHD simulations”, Astron. Astrophys., 484, L17–L20. [DOI], [ADS], [arXiv:0804.4230] (Cited on page 16.)
Däppen, W., Mihalas, D., Hummer, D.G. and Mihalas, B.W., 1988, “The equation of state for stellar envelopes. III. Thermodynamic quantities”, Astrophys. J., 332, 261–270. [DOI], [ADS] (Cited on page 14.)
Dawes, W.R., 1864, “Results of some recent Observations of the Solar Surface, with Remarks”, Mon. Not. R. Astron. Soc., 24, 161. [ADS] (Cited on page 15.)
De Pontieu, B., Carlsson, M., Stein, R., Rouppe van der Voort, L., Löfdahl, M., van Noort, M., Nordlund, Å. and Scharmer, G., 2006, “Rapid Temporal Variability of Faculae: High-Resolution Observations and Modeling”, Astrophys. J., 646, 1405–1420. [DOI], [ADS] (Cited on page 80.)
Deinzer, W., Hensler, G., Schuüssler, M. and Weisshaar, E., 1984, “Model calculations of magnetic flux tubes. II. Stationary results for solar magnetic elements”, Astron. Astrophys., 139, 435. [ADS] (Cited on page 84.)
Del Moro, D., 2004, “Solar granulation properties derived from three different time series”, Astron. Astrophys., 428, 1007–1015. [DOI], [ADS] (Cited on page 15.)
Del Moro, D., Berrilli, F., Duvall Jr, T.L. and Kosovichev, A.G., 2004, “Dynamics and Structure of Supergranulation”, Solar Phys., 221, 23–32. [DOI], [ADS] (Cited on page 36.)
Delahaye, F. and Pinsonneault, M.H., 2006, “The Solar Heavy-Element Abundances. I. Constraints from Stellar Interiors”, Astrophys. J., 649, 529–540. [DOI], [ADS], [astro-ph/0511779] (Cited on page 57.)
Deng, L. and Xiong, D.R., 2008, “How to define the boundaries of a convective zone, and how extended is overshooting?”, Mon. Not. R. Astron. Soc., 386, 1979–1989. [DOI], [ADS], [arXiv:0707.0924] (Cited on page 34.)
DeRosa, M.L. and Toomre, J., 1998, “Correlation Tracking of Mesogranules from SOI-MDI Doppler Images to Reveal Supergranular Flow Fields”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, SOHO 6/GONG 98 Workshop, 1–4 June 1998, Boston, Massachusetts, USA, (Ed.) Korzennik, S., vol. SP-418 of ESA Conference Proceedings, pp. 753–758, ESA Publications Division, Noordwijk, The Netherlands. [ADS] (Cited on pages 35 and 36.)
DeRosa, M.L. and Toomre, J., 2004, “Evolution of Solar Supergranulation”, Astrophys. J., 616, 1242–1260. [DOI], [ADS] (Cited on pages 35 and 36.)
DeRosa, M.L., Gilman, P.A. and Toomre, J., 2002, “Solar Multiscale Convection and Rotation Gradients Studied in Shallow Spherical Shells”, Astrophys. J., 581, 1356–1374. [DOI], [ADS], [astro-ph/0209054] (Cited on page 37.)
Deubner, F.-L., 1971, “Some Properties of Velocity Fields in the Solar Photosphere. III: Oscillatory and Supergranular Motions as a Function of Height”, Solar Phys., 17, 6–20. [DOI], [ADS] (Cited on page 36.)
Deubner, F.-L., 1989, “Mesogranulation: a convective phenomenon”, Astron. Astrophys., 216, 259–264. [ADS] (Cited on page 35.)
Deubner, F.L. and Mattig, W., 1975, “New observations of the granular intensity fluctuations”, Astron. Astrophys., 45, 167–171. [ADS] (Cited on page 16.)
Domínguez Cerdeña, I., Sánchez Almeida, J. and Kneer, F., 2003, “Inter-network magnetic fields observed with sub-arcsec resolution”, Astron. Astrophys., 407, 741–757. [DOI], [ADS], [astroph/0306329] (Cited on pages 72 and 74.)
Domínguez Cerdeña, I., Almeida, J.S. and Kneer, F., 2006a, “Quiet Sun Magnetic Fields from Simultaneous Inversions of Visible and Infrared Spectropolarimetric Observations”, Astrophys. J., 646, 1421–1435. [DOI], [ADS], [astro-ph/0604381] (Cited on page 75.)
Domínguez Cerdeña, I., Sánchez Almeida, J. and Kneer, F., 2006b, “The Distribution of Quiet Sun Magnetic Field Strengths from 0 to 1800 G”, Astrophys. J., 636, 496–509. [DOI], [ADS], [astro-ph/0509243] (Cited on page 75.)
Domínguez Cerdeña, I., Sánchez Almeida, J. and Kneer, F., 2006c, “The Distribution of Quiet Sun Magnetic Field Strengths from 0 to 1800 G”, Astrophys. J., 636, 496–509. [DOI], [ADS] (Cited on page 74.)
Dorch, S.B.F. and Nordlund, Å., 2000, “The Solar Dynamo: Flux Pumping by Stratified Convection”, in The Solar Cycle and Terrestrial Climate, Proceedings of the 1st Solar and Space Weather Euroconference: 25–29 September 2000, Instituto de Astrofisica de Canarias, Santa Cruz de Tenerife, Tenerife, Spain, (Ed.) Wilson, A., vol. SP-463 of ESA Conference Proceedings, pp. 305–308, ESA Publications Division, Nordwijk. [ADS] (Cited on page 81.)
Dorch, S.B.F. and Nordlund, Å., 2001, “On the transport of magnetic fields by solar-like stratified convection”, Astron. Astrophys., 365, 562–570. [DOI], [ADS] (Cited on page 81.)
Drake, J.J. and Testa, P., 2005, “The ‘solar model problem’ solved by the abundance of neon in nearby stars”, Nature, 436, 525–528. [DOI], [ADS], [astro-ph/0506182] (Cited on page 57.)
Dravins, D., 1982, “Photospheric spectrum line asymmetries and wavelength shifts”, Annu. Rev. Astron. Astrophys., 20, 61–89. [DOI], [ADS] (Cited on pages 15 and 47.)
Dravins, D., 1990, “Stellar granulation. VI. Four-component models and non-solar-type stars”, Astron. Astrophys., 228, 218–230. [ADS] (Cited on page 42.)
Dravins, D. and Nordlund, Å, 1990a, “Stellar granulation. IV. Line formation in inhomogeneous stellar photospheres”, Astron. Astrophys., 228, 184. [ADS] (Cited on pages 42, 44, and 47.)
Dravins, D. and Nordlund, Å, 1990b, “Stellar granulation. V. Synthetic spectral lines in disk integrated starlight”, Astron. Astrophys., 228, 203. [ADS] (Cited on pages 42 and 47.)
Dravins, D., Lindegren, L. and Nordlund, Å., 1981, “Solar Granulation: Influence of Convection on Spectral Line Asymmetries and Wavelength Shifts”, Astron. Astrophys., 96, 345–364. [ADS] (Cited on pages 15, 42, 44, and 47.)
D’Silva, S., 1998, “‘Dispersion’ in Time-Distance Heloseismology”, Astrophys. J. Lett., 499, L211–L214. [DOI], [ADS] (Cited on page 60.)
Emonet, T. and Cattaneo, F., 2001, “Small-Scale Photospheric Fields: Observational Evidence and Numerical Simulations”, Astrophys. J. Lett., 560, L197–L200. [DOI], [ADS] (Cited on pages 71 and 84.)
Esteban, C., García-Rojas, J., Peimbert, M., Peimbert, A., Ruiz, M.T., Rodríguez, M. and Carigi, L., 2005, “Carbon and Oxygen Galactic Gradients: Observational Values from H II Region Recombination Lines”, Astrophys. J. Lett., 618, L95–L98. [DOI], [ADS], [astro-ph/0408397] (Cited on page 57.)
Fabbian, D., Asplund, M., Carlsson, M. and Kiselman, D., 2006, “The non-LTE line formation of neutral carbon in late-type stars”, Astron. Astrophys., 458, 899–914. [DOI], [ADS], [astroph/0608284] (Cited on page 49.)
Fabbian, D., Asplund, M., Barklem, P.S., Carlsson, M. and Kiselman, D., 2009, “Neutral oxygen spectral line formation revisited with new collisional data: large departures from LTE at low metallicity”, Astron. Astrophys., accepted. [ADS], [arXiv:0902.4472] (Cited on page 54.)
Featherstone, N., Haber, D.A., Hindman, B.W. and Toomre, J., 2006, “Helioseismic Probing of Giant-Cell Convection”, Bull. Am. Astron. Soc., 38, 257. [ADS] (Cited on page 36.)
Featherstone, N.A., Hindman, B.W., Haber, D.A. and Toomre, J., 2004, “Time-Distance Helioseismology: a Fourier Transform Method and Measurement of Reynolds Stresses”, in Helio- and Asteroseismology: Towards a Golden Future, Proceedings of the SOHO 14/GONG 2004 Workshop, 12–16 July 2004, New Haven, Connecticut, USA, (Ed.) Danesy, D., vol. SP-559 of ESA Conference Proceedings, pp. 428–431, ESA Publications Division, Noordwijk. [ADS] (Cited on page 36.)
Fontenla, J.M., Balasubramaniam, K.S. and Harder, J., 2007, “Semiempirical Models of the Solar Atmosphere. II. The Quiet-Sun Low Chromosphere at Moderate Resolution”, Astrophys. J., 667, 1243–1257. [DOI], [ADS] (Cited on page 39.)
Freytag, B., Ludwig, H.-G. and Steffen, M., 1999, “A Calibration of the Mixing-Length for SolarType Stars Based on Hydrodynamical Models of Stellar Surface Convection”, in Theory and Tests of Convection in Stellar Structure, Proceedings of a meeting held at Granada, Spain, 30 September–2 October 1998, (Eds.) Gimenez, A., Guinan, E.F., Montesinos, B., vol. 173 of ASP Conference Series, pp. 225–228, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 34.)
Freytag, B., Steffen, M. and Dorch, B., 2002, “Spots on the surface of Betelgeuse — Results from new 3D stellar convection models”, Astron. Nachr., 323, 213–219. [DOI], [ADS] (Cited on page 47.)
Frutiger, C., Solanki, S.K., Fligge, M. and Bruls, J.H.M.J., 2000, “Properties of the solar granulation obtained from the inversion of low spatial resolution spectra”, Astron. Astrophys., 358, 1109–1121. [ADS] (Cited on page 42.)
Gadun, A.S. and Pavlenko, Y.V., 1997, “1-D and 2-D model atmospheres: iron and lithium LTE abundances in the Sun”, Astron. Astrophys., 324, 281–288. [ADS] (Cited on page 42.)
Gadun, A.S., Hanslmeier, A. and Pikalov, K.N., 1997, “Bisectors and line-parameter variations over granular and intergranular regions in 2-D artificial granulation”, Astron. Astrophys., 320, 1001–1012. [ADS] (Cited on page 42.)
Galloway, D.J. and Weiss, N.O., 1981, “Convection and magnetic fields in stars”, Astrophys. J., 243, 945–953. [DOI], [ADS] (Cited on page 71.)
Galsgaard, K. and Nordlund, Å, 1996, “Heating and activity of the solar corona 1. Boundary shearing of an initially homogeneous magnetic field”, J. Geophys. Res., 101, 13,445–13,460. [DOI], [ADS] (Cited on page 87.)
Georgobiani, D., Stein, R.F. and Nordlund, Å., 2003, “What Causes p-Mode Asymmetry Reversal?”, Astrophys. J., 596, 698–701. [DOI], [ADS], [astro-ph/0205141] (Cited on pages 61 and 70.)
Georgobiani, D., Stein, R.F., Nordlund, Å., Kosovichev, A.G. and Mansour, N.N., 2004, “High Degree Solar Oscillations in 3D Numerical Simulations”, in Helio- and Asteroseismology: Towards a Golden Future, Proceedings of the SOHO 14/GONG 2004 Workshop, 12–16 July 2004, New Haven, Connecticut, USA, (Ed.) Danesy, D., vol. SP-559 of ESA Conference Proceedings, pp. 267–270, ESA Publications Division, Noordwijk. [ADS] (Cited on page 36.)
Georgobiani, D., Stein, R.F. and Nordlund, Å., 2006, “Spatial and Temporal Spectra of Solar Convection”, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, Proceedings of a meeting held at the NSO/Sac, Sunspot, New Mexico, USA, 18–22 July 2005, (Eds.) Leibacher, J., Stein, R.F., Uitenbroek, H., vol. 354 of ASP Conference Series, p. 109, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 64.)
Georgobiani, D., Zhao, J., Kosovichev, A.G., Benson, D., Stein, R.F. and Nordlund, Å., 2007, “Local helioseismology and correlation tracking analysis of surface structures in realistic simulations of solar convection”, Astrophys. J., 657, 1157–1161. [DOI], [ADS], [astro-ph/0608204] (Cited on pages 36, 37, and 61.)
Ginet, G.P. and Simon, G.W., 1992, “On the evidence for mesogranules in solar power spectra”, Astrophys. J., 386, 359–363. [DOI], [ADS] (Cited on page 35.)
Gizon, L. and Birch, A.C., 2005, “Local Helioseismology”, Living Rev. Solar Phys., 2, lrsp-2005-6. URL (accessed 18 July 2008): http://www.livingreview.org/lrsp-2005-6 (Cited on page 60.)
Goldreich, P., Murray, N. and Kumar, P., 1994, “Excitation of solar p-modes”, Astrophys. J., 424, 466–479. [DOI], [ADS] (Cited on pages 62 and 64.)
Gough, D.O., 1969, “The Anelastic Approximation for Thermal Convection”, J. Atmos. Sci., 26, 448–456. [ADS] (Cited on page 9.)
Gray, D.F., 2005, The Observation and Analysis of Stellar Photospheres, Cambridge University Press, Cambridge; New York, 3rd edn. (Cited on pages 15, 39, 44, and 47.)
Grevesse, N. and Sauval, A.J., 1998, “Standard Solar Composition”, Space Sci. Rev., 85, 161–174. [DOI], [ADS] (Cited on pages 49, 53, 54, and 57.)
Grevesse, N. and Sauval, A.J., 1999, “The solar abundance of iron and the photospheric model”, Astron. Astrophys., 347, 348–354. [ADS] (Cited on page 57.)
Grevesse, N., Sauval, A.J. and van Dishoeck, E.F., 1984, “An analysis of vibration-rotation lines of OH in the solar infrared spectrum”, Astron. Astrophys., 141, 10–16. [ADS] (Cited on page 51.)
Grossmann-Doerth, U., Schüssler, M. and Steiner, O., 1998, “Convective intensification of solar surface magnetic fields: results of numerical experiments”, Astron. Astrophys., 337, 928–939. [ADS] (Cited on page 83.)
Gudiksen, B.V. and Nordlund, A., 2005a, “An Ab Initio Approach to the Solar Coronal Heating Problem”, Astrophys. J., 618, 1020–1030. [DOI], [ADS], [astro-ph/0407266] (Cited on page 87.)
Gudiksen, B.V. and Nordlund, A., 2005b, “An AB Initio Approach to Solar Coronal Loops”, Astrophys. J., 618, 1031–1038. [DOI], [ADS], [astro-ph/0407267] (Cited on page 87.)
Gustafsson, B., Bell, R.A., Eriksson, K. and Nordlund, Å., 1975, “A grid of model atmospheres for metal-deficient giant stars I”, Astron. Astrophys., 42, 407–432. [ADS] (Cited on pages 14 and 47.)
Guzik, J.A., Watson, L.S. and Cox, A.N., 2005, “Can Enhanced Diffusion Improve Helioseismic Agreement for Solar Models with Revised Abundances?”, Astrophys. J., 627, 1049–1056. [DOI], [ADS], [astro-ph/0502364] (Cited on page 57.)
Guzik, J.A., Watson, L.S. and Cox, A.N., 2006, “Implications of revised solar abundances for helioseismology”, Mem. Soc. Astron. Ital., 77, 389. [ADS] (Cited on page 57.)
Hagenaar, H.J., Schrijver, C.J. and Title, A.M., 2003, “The Properties of Small Magnetic Regions on the Solar Surface and the Implications for the Solar Dynamo(s))”, Astrophys. J., 584, 1107–1119. [DOI], [ADS] (Cited on page 74.)
Hanasoge, S.M., Duvall Jr, T.L. and Couvidat, S., 2007, “Validation of Helioseismology through Forward Modeling: Realization Noise Subtraction and Kernels”, Astrophys. J., 664, 1234–1243. [DOI], [ADS] (Cited on page 60.)
Hansteen, V.H., 2008, “Waves and Shocks in the Solar Atmosphere”, in New Solar Physics with Solar-B Mission, Proceedings of the Sixth Solar-B Science Meeting held 8–11 November 2005 at Kyoto, Japan, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, pp. 193–204, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 30.)
Hansteen, V.H. and Gudiksen, B., 2005, “3D Numerical Models of Quiet Sun Coronal Heating”, in Connecting Sun and Heliosphere, Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, (Eds.) Fleck, B., Zurbuchen, T.H., Lacoste, H., vol. SP-592 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on page 87.)
Hansteen, V.H., Carlsson, M. and Gudiksen, B., 2007, “3D Numerical Models of the Chromosphere, Transition Region, and Corona”, in The Physics of Chromospheric Plasmas, Proceedings of the conference held 9–13 October, 2006 at the University of Coimbra, Portugal, (Eds.) Heinzel, P., Dorotovic, I., Rutten, R.J., vol. 368 of ASP Conference Series, pp. 107–114, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:0704.1511] (Cited on page 87.)
Hart, A.B., 1956, “Motions in the Sun at the photospheric level. VI. Large-scale motions in the equatorial region”, Mon. Not. R. Astron. Soc., 116, 38–55. [ADS] (Cited on page 36.)
Hathaway, D., Gilman, P., Harvey, J.W., Hill, F., Howard, R.B., Jones, H.P., Kasher, J., Leibacher, J.B., Pintar, J. and Simon, G.W., 1996, “GONG Observations of Solar Surface Flows”, Science, 272, 1306–1309. [ADS] (Cited on page 36.)
Hathaway, D.H., Beck, J.G., Bogart, R.S., Bachmann, K.T., Khatri, G., Petitto, J.M., Han, S. and Raymond, J., 2000, “The Photospheric Convection Spectrum”, Solar Phys., 193, 299–312. [ADS] (Cited on pages 36 and 38.)
Hermsen, W., 1982, “The influence of temperature inhomogeneities in the solar atmosphere on abundance determinations”, Astron. Astrophys., 111, 233–238. [ADS] (Cited on page 42.)
Herschel, W., 1801, “Observations Tending to Investigate the Nature of the Sun, in Order to Find the Causes or Symptoms of Its Variable Emission of Light and Heat; With Remarks on the Use That May Possibly Be Drawn from Solar Observations”, Philos. Trans. R. Soc. London, 91, 265–318. [ADS] (Cited on page 15.)
Hindman, B.W. and Brown, T.M., 1998, “Acoustic Power Maps of Solar Active Regions”, Astrophys. J., 504, 1029. [DOI], [ADS] (Cited on page 66.)
Hindman, B.W., Featherstone, N.A., Haber, D.A., Musman, S. and Toomre, J., 2004a, “Comparison of Local Helioseismic Techniques Applied to MDI Doppler Data”, in Helio- and Asteroseismology: Towards a Golden Future, Proceedings of the SOHO 14/GONG 2004 Workshop, 12–16 July 2004, New Haven, Connecticut, USA, (Ed.) Danesy, D., vol. SP-559 of ESA Conference Proceedings, pp. 460–463, ESA Publications Division, Noordwijk. [ADS] (Cited on page 36.)
Hindman, B.W., Gizon, L., Duvall Jr, T.L., Haber, D.A. and Toomre, J., 2004b, “Comparison of Solar Subsurface Flows Assessed by Ring and Time-Distance Analyses”, Astrophys. J., 613, 1253–1262. [DOI], [ADS] (Cited on page 36.)
Hindman, B.W., Haber, D.A. and Toomre, J., 2006, “Helioseismically Determined Near-Surface Flows Underlying a Quiescent Filament”, Astrophys. J., 653, 725–732. [DOI], [ADS] (Cited on page 36.)
Hirzberger, J., 2002, “On the brightness and velocity structure of solar granulation”, Astron. Astrophys., 392, 1105–1118. [DOI], [ADS] (Cited on page 15.)
Hirzberger, J. and Wiehr, E., 2005, “Solar limb faculae”, Astron. Astrophys., 438, 1059–1065. [DOI], [ADS] (Cited on page 80.)
Hirzberger, J., Bonet, J.A., Vázquez, M. and Hanslmeier, A., 1999, “Time Series of Solar Granulation Images. III. Dynamics of Exploding Granules and Related Phenomena”, Astrophys. J., 527, 405–414. [DOI], [ADS] (Cited on page 23.)
Holweger, H., 2001, “Photospheric Abundances: Problems, Updates, Implications”, in Solar and Galactic Composition, Proceedings of a Joint Soho / Ace Workshop, Bern, Switzerland, 6–9 March 2001, (Ed.) Wimmer-Schweingruber, R.F., vol. 598 of AIP Conference Proceedings, p. 23, American Institute of Physics, Melville. [ADS], [astro-ph/0107426] (Cited on page 55.)
Holweger, H. and Müller, E.A., 1974, “The photospheric barium spectrum: Solar abundance and collision broadening of Ba ii lines by hydrogen”, Solar Phys., 39, 19–30. [DOI], [ADS] (Cited on pages 39, 48, 49, 50, 51, 53, 56, 57, and 58.)
Holweger, H., Kock, M. and Bard, A., 1995, “On the determination of the solar iron abundance using Fe i lines. Comments on a paper by D.E. Blackwell et al. and presentation of new results for weak lines”, Astron. Astrophys., 296, 233. [ADS] (Cited on page 55.)
Hung, S.-H., Dahlen, F.A. and Nolet, G., 2001, “Wavefront healing: a banana-doughnut perspective”, Geophys. J. Int., 146, 289–312. [DOI], [ADS] (Cited on page 60.)
Hurlburt, N.E., Toomre, J. and Massaguer, J.M., 1984, “Two-dimensional compressible convection extending over multiple scale heights”, Astrophys. J., 282, 557–573. [DOI], [ADS] (Cited on pages 11 and 23.)
Isobe, H., Proctor, M.R.E. and Weiss, N.O., 2008, “Convection-driven Emergence of Small-Scale Magnetic Fields and their Role in Coronal Heating and Solar Wind Acceleration”, Astrophys. J. Lett., 679, L57–L60. [DOI], [ADS] (Cited on page 71.)
Jacoutot, L., Kosovichev, A.G., Wray, A. and Mansour, N.N., 2008a, “Realistic Numerical Simulations of Solar Convection and Oscillations in Magnetic Regions”, Astrophys. J. Lett., 684, L51–L54. [DOI], [ADS] (Cited on page 66.)
Jacoutot, L., Kosovichev, A.G., Wray, A.A. and Mansour, N.N., 2008b, “Numerical Simulation of Excitation of Solar Oscillation Modes for Different Turbulent Models”, Astrophys. J., 682, 1386–1391. [DOI], [ADS], [arXiv:0710.2317] (Cited on page 66.)
Jain, R. and Haber, D., 2002, “Solar p-modes and surface magnetic fields: Is there an acoustic emission? MDI/SOHO observations”, Astron. Astrophys., 387, 1092–1099. [DOI], [ADS] (Cited on page 66.)
Janssen, J., 1896, Ann. Obs. Paris, Meudon, 1, 91 (Cited on page 15.)
Jefferies, S.M., Osaki, Y., Shibahashi, H., Duvall Jr, T.L., Harvey, J.W. and Pomerantz, M.A., 1994, “Use of acoustic wave travel-time measurements to probe the near-surface layers of the Sun”, Astrophys. J., 434, 795–800. [DOI], [ADS] (Cited on page 60.)
Johansson, S., Litzén, U., Lundberg, H. and Zhang, Z., 2003, “Experimental f-Value and Isotopic Structure for the Ni i Line Blended with [O sc i] at 6300 Å”, Astrophys. J. Lett., 584, L107–L110. [DOI], [ADS], [astro-ph/0301382] (Cited on pages 51 and 53.)
Kaisig, M. and Schröter, E.H., 1983, “The asymmetry of photospheric absorption lines. II. The asymmetry of medium-strong Fe i lines in quiet and active regions of the Sun”, Astron. Astrophys., 117, 305–313. [ADS] (Cited on page 39.)
Keller, C.U., Schüssler, M., Vögler, A. and Zakharov, V., 2004, “On the Origin of Solar Faculae”, Astrophys. J. Lett., 607, L59–L62. [DOI], [ADS] (Cited on pages 77 and 80.)
Khomenko, E., Centeno, R., Collados, M. and Trujillo Bueno, J., 2008, “Channeling 5 Minute Photospheric Oscillations into the Solar Outer Atmosphere through Small-Scale Vertical Magnetic Flux Tubes”, Astrophys. J. Lett., 676, L85–L88. [DOI], [ADS], [arXiv:0802.0938] (Cited on page 74.)
Kim, Y.-C., Fox, P.A., Demarque, P. and Sofia, S., 1996, “Modeling Convection in the Outer Layers of the Sun: A Comparison with Predictions of the Mixing-Length Approximation”, Astrophys. J., 461, 499. [DOI], [ADS] (Cited on page 34.)
Kiselman, D., 1993, “The 777 nm oxygen triplet in the Sun and solar-type stars, and its use for abundance analysis”, Astron. Astrophys., 275, 269. [ADS] (Cited on page 51.)
Kiselman, D., 1994, “High-spatial-resolution solar observations of spectral lines used for abundance analysis”, Astron. Astrophys. Suppl., 104, 23–77. [ADS] (Cited on page 44.)
Kiselman, D., 1997, “Formation of Li i Lines in Photospheric Granulation”, Astrophys. J. Lett., 489, L107. [DOI], [ADS], [astro-ph/9708198] (Cited on page 42.)
Kiselman, D., 1998, “The 671 nm Li i line in solar granulation”, Astron. Astrophys., 333, 732–740. [ADS], [astro-ph/9802049] (Cited on pages 42 and 44.)
Kiselman, D., 2001, “NLTE effects on oxygen lines”, New Astron. Rev., 45, 559–563. [ADS], [astro-ph/0010300] (Cited on page 42.)
Kiselman, D. and Asplund, M., 2001, “Spatially Resolved Solar Lines as Diagnostics of NLTE Effects (CD-ROM Directory: contribs/kiselman))”, in Cool Stars, Stellar Systems and the Sun, Proceedings of the 11th Cambridge Workshop held at Puerto de la Cruz, Tenerife, Spain, 4–8 October 1999, (Eds.) García López, R.J., Rebolo, R., Zapaterio Osorio, M.R., vol. 223 of ASP Conference Series, pp. 684–690, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 44.)
Kiselman, D. and Nordlund, Å., 1995, “3D non-LTE line formation in the solar photosphere and the solar oxygen abundance”, Astron. Astrophys., 302, 578. [ADS], [astro-ph/9505037] (Cited on pages 42 and 51.)
Koesterke, L., Allende Prieto, C. and Lambert, D.L., 2008, “Center-to-Limb Variation of Solar Three-dimensional Hydrodynamical Simulations”, Astrophys. J., 680, 764–773. [DOI], [ADS], [arXiv:0802.2177] (Cited on page 58.)
Korn, A.J., Shi, J. and Gehren, T., 2003, “Kinetic equilibrium of iron in the atmospheres of cool stars. III. The ionization equilibrium of selected reference stars”, Astron. Astrophys., 407, 691–703. [DOI], [ADS], [astro-ph/0306337] (Cited on page 56.)
Krieg, J., Kneer, F., Koschinsky, M. and Ritter, C., 2000, “Granular velocities of the Sun from speckle interferometry”, Astron. Astrophys., 360, 1157–1162. [ADS] (Cited on page 15.)
Krijger, J.M. and Roudier, T., 2003, “Photospheric flows measured with TRACE II. Network formation”, Astron. Astrophys., 403, 715–723. [DOI], [ADS] (Cited on page 71.)
Kumar, P. and Basu, S., 1999, “Line Asymmetry of Solar p-Modes: Reversal of Asymmetry in Intensity Power Spectra”, Astrophys. J., 519, 389–395. [DOI], [ADS], [astro-ph/9808144] (Cited on page 69.)
Kurucz, R., 1993, “Atomic data for opacity calculations (Kurucz CD-ROM No. 1)”, data medium, [ADS] (Cited on page 47.))
Lambert, D.L., 1978, “The abundances of the elements in the solar photosphere — VIII. Revised abundances of carbon, nitrogen and oxygen”, Mon. Not. R. Astron. Soc., 182, 249–271. [ADS] (Cited on pages 42, 48, 51, and 54.)
Langangen, Ø., Carlsson, M., Rouppe van der Voort, L. and Stein, R.F., 2007, “Velocities Measured in Small-Scale Solar Magnetic Elements”, Astrophys. J., 655, 615–623. [DOI], [ADS], [astro-ph/0611741] (Cited on page 84.)
Leighton, R.B., Noyes, R.W. and Simon, G.W., 1962, “Velocity Fields in the Solar Atmosphere I. Preliminary Report”, Astrophys. J., 135, 474–499. [ADS] (Cited on page 36.)
Leitzinger, M., Brandt, P.N., Hanslmeier, A., Pützi, W. and Hirzberger, J., 2005, “Dynamics of solar mesogranulation”, Astron. Astrophys., 444, 245–255. [DOI], [ADS] (Cited on page 35.)
Lites, B.W., Scharmer, G.B., Berger, T.E. and Title, A.M., 2004, “Three-Dimensional Structure of the Active Region Photosphere as Revealed by High Angular Resolution”, Solar Phys., 221, 65–84. [DOI], [ADS] (Cited on page 80.)
Ljung, G., Nilsson, H., Asplund, M. and Johansson, S., 2006, “New and improved experimental oscillator strengths in Zr II and the solar abundance of zirconium”, Astron. Astrophys., 456, 1181–1185. [DOI], [ADS] (Cited on pages 42 and 56.)
Löfdahl, M.G., Berger, T.E. and Seldin, J.H., 2001, “Two dual-wavelength sequences of highresolution solar photospheric images captured over several hours and restored by use of phase diversity”, Astron. Astrophys., 377, 1128–1135. [DOI], [ADS] (Cited on page 15.)
Ludwig, H.-G. and Steffen, M., 2007, “Hydrodynamical model atmospheres and 3D spectral synthesis”, in Precision Spectroscopy in Astrophysics, Proceedings of the ESO/Lisbon/Aveiro Conference held in Aveiro, Portugal, 11–15 September 2006, (Eds.) Santos, N.C., Pasquini, L., Correia, A.C.M., pp. 133–138, Springer, Berlin; New York. [DOI], [ADS], [arXiv:0704.1176] (Cited on pages 42 and 48.)
Ludwig, H.-G., Jordan, S. and Steffen, M., 1994, “Numerical simulations of convection at the surface of a ZZ Ceti white dwarf”, Astron. Astrophys., 284, 105–117. [ADS] (Cited on page 13.)
Ludwig, H.-G., Freytag, B. and Steffen, M., 1999, “A calibration of the mixing-length for solartype stars based on hydrodynamical simulations. I. Methodical aspects and results for solar metallicity”, Astron. Astrophys., 346, 111–124. [ADS], [astro-ph/9811179] (Cited on page 34.)
Maheswaran, M., 1969, “Effects of prescribed circulations of magnetic fields”, Mon. Not. R. Astron. Soc., 145, 197. [ADS] (Cited on page 71.)
Malagoli, A., Cattaneo, F. and Brummell, N.H., 1990, “Turbulent supersonic convection in three dimensions”, Astrophys. J. Lett., 361, L33–L36. [DOI], [ADS] (Cited on page 30.)
Martínez González, M.J., Collados, M. and Ruiz Cobo, B., 2006, “On the validity of the 630 nm Fe i lines for magnetometry of the internetwork quiet Sun”, Astron. Astrophys., 456, 1159–1164. [DOI], [ADS], [astro-ph/0605446] (Cited on page 74.)
Martínez-Sykora, J., Hansteen, V. and Carlsson, M., 2008, “Twisted Flux Tube Emergence From the Convection Zone to the Corona”, Astrophys. J., 679, 871–888. [DOI], [ADS], [arXiv:0712.3854] (Cited on page 81.)
Massaguer, J.M. and Zahn, J.-P., 1980, “Cellular convection in a stratified atmosphere”, Astron. Astrophys., 87, 315–327. [ADS] (Cited on pages 11 and 23.)
Meléndez, J., 2004, “A Low Solar Oxygen Abundance from the First-Overtone OH Lines”, Astrophys. J., 615, 1042–1047. [DOI], [ADS], [astro-ph/0407366] (Cited on pages 51 and 55.)
Meléndez, J. and Asplund, M., 2008, “Another forbidden solar oxygen abundance: the [O I] 5577 Å line”, Astron. Astrophys., 490, 817–821. [DOI], [ADS], [arXiv:0808.2796] (Cited on pages 42, 53, and 59.)
Meunier, N., Tkaczuk, R., Roudier, T. and Rieutord, M., 2007, “Velocities and divergences as a function of supergranule size”, Astron. Astrophys., 461, 1141–1147. [DOI], [ADS] (Cited on page 36.)
Mihalas, D., 1978, Stellar atmospheres, W.H. Freeman, San Francisco, 2nd edn. (Cited on page 25.)
Mihalas, D., Däppen, W. and Hummer, D.G., 1988, “The equation of state for stellar envelopes. II. Algorithm and selected results”, Astrophys. J., 331, 815–825. [DOI], [ADS] (Cited on pages 14 and 47.)
Mihalas, D., Hummer, D.G., Mihalas, B.W. and Däppen, W., 1990, “The equation of state for stellar envelopes. IV. Thermodynamic quantities and selected ionization fractions for six elemental mixes”, Astrophys. J., 350, 300–308. [DOI], [ADS] (Cited on page 14.)
Mucciarelli, A., Caffau, E., Freytag, B., Ludwig, H.-G. and Bonifacio, P., 2008, “The solar photospheric abundance of europium. Results from CO5BOLD 3D hydrodynamical model atmospheres”, Astron. Astrophys., 484, 841–845. [DOI], [ADS], [arXiv:0803.0863] (Cited on pages 42, 48, and 56.)
Müller, D.A.N., Steiner, O., Schlichenmaier, R. and Brandt, P.N., 2001, “Time-slice diagrams of solar granulation”, Solar Phys., 203, 211–232. [DOI], [ADS] (Cited on pages 15 and 37.)
Muller, R., Auffret, H., Roudier, T., Vigneau, J., Simon, G.W., Frank, Z., Shine, R.A. and Title, A.M., 1992, “Evolution and advection of solar mesogranulation”, Nature, 356, 322–325. [DOI], [ADS] (Cited on pages 35 and 36.)
Musman, S., 1972, “A Mechanism for the Exploding Granule Phenomenon”, Solar Phys., 26, 290–298. [DOI], [ADS] (Cited on pages 23 and 24.)
Namba, O., 1986, “Evolution of ‘exploding granules’”, Astron. Astrophys., 161, 31–38. [ADS] (Cited on page 23.)
Namba, O. and van Rijsbergen, R., 1977, “Evolution pattern of the exploding granules”, in Problems of Stellar Convection, Proceedings of IAU Colloquium 38, held in Nice, August 16–20, 1976, (Eds.) Spiegel, E.A., Zahn, J.-P., vol. 71 of Lecture Notes in Physics, pp. 119–125, Springer, Berlin; New York. [ADS] (Cited on pages 23 and 24.)
Nasmyth, J., 1865, “The Willow Leaves”, Astron. Reg., 3, 223–224. [ADS] (Cited on page 15.)
Nelson, G.D. and Musman, S., 1978, “The scale of solar granulation”, Astrophys. J. Lett., 222, L69–L72. [DOI], [ADS] (Cited on page 20.)
Nesis, A., Hammer, R., Roth, M. and Schleicher, H., 2002, “Dynamics of the solar granulation. VIII. Time and space development”, Astron. Astrophys., 396, 1003–1010. [DOI], [ADS] (Cited on page 15.)
Nesis, A., Hammer, R., Roth, M. and Schleicher, H., 2006, “Dynamics of the solar granulation. IX. A global approach”, Astron. Astrophys., 451, 1081–1089. [DOI], [ADS] (Cited on page 15.)
Nigam, R., Kosovichev, A.G., Scherrer, P.H. and Schou, J., 1998, “Asymmetry in Velocity and Intensity Helioseismic Spectra: A Solution to a Long-standing Puzzle”, Astrophys. J. Lett., 495, L115. [DOI], [ADS] (Cited on page 69.)
Nordlund, Å., 1976, “A two-component representation of stellar atmospheres with convection”, Astron. Astrophys., 50, 23–39. [ADS] (Cited on page 39.)
Nordlund, Å., 1978, “Solar granulation and the nature of ‘microturbulence’”, in Astronomical Papers Dedicated to Bengt Strömgren, Proceedings of the Symposium, Copenhagen, Denmark, May 30–June 1, 1978, (Eds.) Reiz, A., Andersen, T., pp. 95–115, Copenhagen University Observatory, Copenhagen. [ADS] (Cited on page 20.)
Nordlund, Å., 1982, “Numerical simulations of the solar granulation. I. Basic equations and methods”, Astron. Astrophys., 107, 1–10. [ADS] (Cited on pages 13 and 47.)
Nordlund, Å., 1984, “A Re-evaluation of the Granular Δ Irms”, in Small-Scale Dynamical Processes in Quiet Stellar Atmospheres, Proceedings of the Conference held in Sunspot, New Mexico, USA, 25–29 July 1983, (Ed.) Keil, S.L., p. 174, National Solar Observatory, Sunspot, NM. [ADS] (Cited on pages 16 and 44.)
Nordlund, Å., 1985a, “Solar convection”, Solar Phys., 100, 209–235. [ADS] (Cited on pages 8 and 42.)
Nordlund, Å., 1985b, “NLTE spectral line formation in a three-dimensional atmosphere with velocity fields”, in Progress in Stellar Spectral Line Formation Theory, Proceedings of the NATO Advanced Research Workshop, Trieste, Italy, September 4–7, 1984, (Eds.) Beckman, J.E., Crivellari, L., vol. 152 of NATO ASI Series C, pp. 215–224, Reidel, Dordrecht; Boston. [ADS] (Cited on page 42.)
Nordlund, Å. and Stein, R.F., 1991, “Granulation: Non-adiabatic Patterns and Shocks”, in Challenges to Theories of the Structure of Moderate-Mass Stars, Proceedings of a Conference held at the Institute for Theoretical Physics University of California, Santa Barbara, USA 19–22 June 1990, (Eds.) Gough, D., Toomre, J., vol. 388 of Lecture Notes in Physics, pp. 141–146, Springer, Berlin; New York. [DOI], [ADS] (Cited on pages 20 and 30.)
Nordlund, Å. and Stein, R.F., 2001, “Solar Oscillations and Convection. I. Formalism for Radial Oscillations”, Astrophys. J., 546, 576–584. [DOI], [ADS], [astro-ph/0006336] (Cited on pages 62 and 63.)
Nordlund, Å., Stein, R.F. and Brandenburg, A., 1996, “Supercomputer windows into the solar convection zone”, Bull. Astron. Soc. India, 24, 261. [ADS] (Cited on page 8.)
November, L.J., 1980, Mesogranulation and supergranulation in the Sun, Ph.D. Thesis, University of Colorado at Boulder, Boulder. [ADS] (Cited on page 35.)
November, L.J., Toomre, J., Gebbie, K.B. and Simon, G.W., 1981, “The detection of mesogranulation on the Sun”, Astrophys. J. Lett., 245, L123–L126. [DOI], [ADS] (Cited on page 35.)
November, L.J., Toomre, J., Gebbie, K.B. and Simon, G.W., 1982, “Vertical flows of supergranular and mesogranular scale observed on the Sun with OSO 8”, Astrophys. J., 258, 846–859. [DOI], [ADS] (Cited on page 35.)
Oda, N., 1984, “Morphological study of the solar granulation. III. The mesogranulation”, Solar Phys., 93, 243–255. [ADS] (Cited on page 35.)
Ossendrijver, M., 2003, “The solar dynamo”, Astron. Astrophys. Rev., 11, 287–367. [DOI], [ADS] (Cited on page 84.)
Parchevsky, K.V. and Kosovichev, A.G., 2007, “Three-dimensional Numerical Simulations of the Acoustic Wave Field in the Upper Convection Zone of the Sun”, Astrophys. J., 666, 547–558. [DOI], [ADS], [astro-ph/0612364] (Cited on page 60.)
Parchevsky, K.V., Zhao, J. and Kosovichev, A.G., 2008, “Influence of Nonuniform Distribution of Acoustic Wavefield Strength on Time-Distance Helioseismology Measurements”, Astrophys. J., 678, 1498–1504. [DOI], [ADS], [arXiv:0802.3866] (Cited on page 60.)
Parker, E.N., 1983, “Magnetic neutral sheets in evolving fields. II. Formation of the solar corona”, Astrophys. J., 264, 642. [DOI], [ADS] (Cited on page 84.)
Parker, E.N., 1988, “Nanoflares and the solar X-ray corona”, Astrophys. J., 330, 474–479. [DOI], [ADS] (Cited on page 87.)
Pecker, J.-C., 1996, “The Effects of Non-Sphericity in Diagnosis of Solar and Stellar Atmospheres”, Solar Phys., 169, 277–291. [DOI], [ADS] (Cited on page 24.)
Peckover, R.S. and Weiss, N.O., 1978, “On the dynamic interaction between magnetic fields and convection”, Mon. Not. R. Astron. Soc., 182, 189–208. [ADS] (Cited on page 71.)
Pereira, T., Kiselman, D. and Asplund, M., 2008, “Confronting 3D solar model atmospheres with observations”, in preparation (Cited on page 44.))
Peter, H., Gudiksen, B.V. and Nordlund, Å., 2005, “Coronal Heating Through Braiding of Magnetic Field Lines Synthesized Coronal EUV Emission and Magnetic Structure”, in Chromospheric and Coronal Magnetic Fields, Proceedings of the International Scientific Conference on Chromospheric and Coronal Magnetic Fields, 30 August–2 September 2005, Katlenburg-Lindau, Germany, (Eds.) Innes, D.E., Lagg, A., Solanki, S.A., Danesy, D., vol. SP-596 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on page 87.)
Peter, H., Gudiksen, B.V. and Nordlund, Å., 2006, “Forward Modeling of the Corona of the Sun and Solar-like Stars: From a Three-dimensional Magnetohydrodynamic Model to Synthetic Extreme-Ultraviolet Spectra”, Astrophys. J., 638, 1086–1100. [DOI], [ADS], [astro-ph/0503342] (Cited on page 87.)
Petrovay, K. and Szakaly, G., 1993, “The origin of intranetwork fields: a small-scale solar dynamo”, Astron. Astrophys., 274, 543. [ADS] (Cited on page 81.)
Ploner, S.R.O., Solanki, S.K. and Gadun, A.S., 2000, “Is solar mesogranulation a surface phenomenon?”, Astron. Astrophys., 356, 1050–1054. [ADS] (Cited on page 35.)
Przybilla, N., Nieva, M.-F. and Butler, K., 2008, “A Cosmic Abundance Standard: Chemical Homogeneity of the Solar Neighborhood and the ISM Dust-Phase Composition”, Astrophys. J. Lett., 688, L103–L106. [DOI], [ADS], [arXiv:0809.2403] (Cited on page 57.)
Puschmann, K.G., Ruiz Cobo, B., Vázquez, M., Bonet, J.A. and Hanslmeier, A., 2005, “Time series of high resolution photospheric spectra in a quiet region of the Sun. II. Analysis of the variation of physical quantities of granular structures”, Astron. Astrophys., 441, 1157–1169. [DOI], [ADS] (Cited on page 15.)
Rast, M.P., 1995, “On the nature of ‘exploding’ granules and granule fragmentation”, Astrophys. J., 443, 863–868. [DOI], [ADS] (Cited on page 23.)
Rast, M.P., 2003, “The Scales of Granulation, Mesogranulation, and Supergranulation”, Astrophys. J., 597, 1200–1210. [DOI], [ADS] (Cited on pages 20 and 35.)
Rieutord, M. and Zahn, J.-P., 1995, “Turbulent plumes in stellar convective envelopes”, Astron. Astrophys., 296, 127–138. [ADS] (Cited on page 11.)
Rieutord, M., Roudier, T., Ludwig, H.-G., Nordlund, Å. and Stein, R., 2001, “Are granules good tracers of solar surface velocity fields?”, Astron. Astrophys., 377, L14–L17. [DOI], [ADS], [astro-ph/0108284] (Cited on page 35.)
Rieutord, M., Ludwig, H.-G., Roudier, T., Nordlund, Å. and Stein, R., 2002, “A simulation of solar convection at supergranulation scale”, Nuovo Cimento C, 25, 523–528. [ADS], [astro-ph/0110208] (Cited on page 36.)
Robinson, F.J., Demarque, P., Li, L.H., Sofia, S., Kim, Y.-C., Chan, K.L. and Guenther, D.B., 2003, “Three-dimensional convection simulations of the outer layers of the Sun using realistic physics”, Mon. Not. R. Astron. Soc., 340, 923–936. [DOI], [ADS], [astro-ph/0212296] (Cited on page 34.)
Roca Cortés, T., Jiménez, A., Pallé, P.L. (GOLF and Teams), VIRGO, 1999, “Frequencies of Solar p-Modes from GOLF and VIRGO-SPM (SOHO))”, in Magnetic Fields and, Solar Processes, Proceedings of the 9th European Meeting on Solar Physics, Florence, Italy, 12–18 September, 1999, (Ed.) Wilson, A., vol. SP-448 of ESA Conference Proceedings, pp. 135–140, ESA Publications Division, Noordwijk. [ADS] (Cited on page 65.)
Rogers, F.J., 1990, “A distribution function approach for effective occupation numbers and the equation of state of hydrogen plasmas”, Astrophys. J., 352, 689–697. [DOI], [ADS] (Cited on page 14.)
Rogers, F.J. and Iglesias, C.A., 1998, “Opacity of Stellar Matter”, Space Sci. Rev., 85, 61–70. [DOI], [ADS] (Cited on page 14.)
Rogers, F.J. and Nayfonov, A., 2002, “Updated and Expanded OPAL Equation-of-State Tables: Implications for Helioseismology”, Astrophys. J., 576, 1064–1074. [DOI], [ADS] (Cited on page 14.)
Rogers, F.J., Swenson, F.J. and Iglesias, C.A., 1996, “OPAL Equation-of-State Tables for Astrophysical Applications”, Astrophys. J., 456, 902. [DOI], [ADS] (Cited on page 14.)
Rosenthal, C.S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R.F. and Trampedach, R., 1999, “Convective contributions to the frequencies of solar oscillations”, Astron. Astrophys., 351, 689–700. [ADS], [astro-ph/9803206] (Cited on pages 26, 34, and 69.)
Rosenthal, C.S., Bogdan, T.J., Carlsson, M., Dorch, S.B.F., Hansteen, V., McIntosh, S.W., Mc-Murry, A., Nordlund, Å. and Stein, R.F., 2002, “Waves in the Magnetized Solar Atmosphere. I. Basic Processes and Internetwork Oscillations”, Astrophys. J., 564, 508–524. [DOI], [ADS] (Cited on page 60.)
Roudier, T. and Muller, R., 2004, “Relation between families of granules, mesogranules and photospheric network”, Astron. Astrophys., 419, 757–762. [DOI], [ADS] (Cited on pages 35 and 37.)
Roudier, T., Malherbe, J.M., Vigneau, J. and Pfeiffer, B., 1998, “Solar mesogranule lifetime measurements”, Astron. Astrophys., 330, 1136–1144. [ADS] (Cited on page 35.)
Roudier, T., Rieutord, M., Malherbe, J.M. and Vigneau, J., 1999, “Determination of horizontal velocity fields at the sun’s surface with high spatial and temporal resolution”, Astron. Astrophys., 349, 301–311. [ADS] (Cited on page 35.)
Roudier, T., Eibe, M.T., Malherbe, J.M., Rieutord, M., Mein, P., Mein, N. and Faurobert, M., 2001, “Temporal height properties of the exploding granules”, Astron. Astrophys., 368, 652–661. [DOI], [ADS] (Cited on page 23.)
Roudier, T., Lignières, F., Rieutord, M., Brandt, P.N. and Malherbe, J.M., 2003a, “Families of fragmenting granules and their relation to meso- and supergranular flow fields”, Astron. Astrophys., 409, 299–308. [DOI], [ADS] (Cited on page 37.)
Roudier, T., Malherbe, J.M., Mein, P., Muller, R., Coutard, C., Lafon, M. and Grimaud, F., 2003b, “High spatial resolution capabilities of Doppler measurements with the Pic du Midi MSDP spectrograph”, Astron. Astrophys., 409, 793–797. [DOI], [ADS] (Cited on page 15.)
Rutten, R.J., Kiselman, D., Rouppe van der Voort, L. and Plez, B., 2001, “Proxy Magnetometry of the Photosphere: Why are G-Band Bright Points so Bright?”, in Advanced Solar Polarimetry: Theory, Observation, and Instrumentation, Proceedings of the 20th Sacramento Peak Summer Workshop, held at NSO/Sac, Sunspot, New Mexico, USA, 11–15 September 2000, (Ed.) Sigwarth, M., vol. 236 of ASP Conference Series, pp. 445–452, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 77.)
Rybák, J., Wöhl, H., Kucera, A., Hanslmeier, A. and Steiner, O., 2004, “Indications of shock waves in the solar photosphere”, Astron. Astrophys., 420, 1141–1152. [DOI], [ADS] (Cited on page 30.)
Samadi, R. and Goupil, M.-J., 2001, “Excitation of stellar p-modes by turbulent convection. I. Theoretical formulation”, Astron. Astrophys., 370, 136–146. [DOI], [ADS], [astro-ph/0101109] (Cited on page 64.)
Samadi, R., Nordlund, Å., Stein, R.F., Goupil, M.J. and Roxburgh, I., 2003a, “Numerical constraints on the model of stochastic excitation of solar-type oscillations”, Astron. Astrophys., 403, 303–312. [DOI], [ADS], [astro-ph/0303198] (Cited on page 64.)
Samadi, R., Nordlund, Å., Stein, R.F., Goupil, M.J. and Roxburgh, I., 2003b, “Numerical 3D constraints on convective eddy time-correlations: Consequences for stochastic excitation of solar p modes”, Astron. Astrophys., 404, 1129–1137. [DOI], [ADS], [astro-ph/0304457] (Cited on page 64.)
Sánchez Almeida, J., Asensio Ramos, A., Trujillo Bueno, J. and Cernicharo, J., 2001, “G-Band Spectral Synthesis in Solar Magnetic Concentrations”, Astrophys. J., 555, 978–989. [DOI], [ADS], [astro-ph/0103006] (Cited on page 77.)
Sauval, A.J., Grevesse, N., Zander, R., Brault, J.W. and Stokes, G.M., 1984, “The pure rotation spectrum of OH and the solar oxygen abundance”, Astrophys. J., 282, 330–338. [DOI], [ADS] (Cited on page 51.)
Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O. and Freytag, B., 2005, “Magnetohydro-dynamic Simulation from the Convection Zone to the Chromosphere”, in Chromospheric and Coronal Magnetic Fields, Proceedings of the International Scientific Conference on Chromospheric and Coronal Magnetic Fields, 30 August–2 September 2005, Katlenburg-Lindau, Germany, (Eds.) Innes, D.E., Lagg, A., Solanki, S.A., Danesy, D., vol. SP-596 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 83 and 87.)
Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O. and Freytag, B., 2006, “Holistic MHD-Simulation from the Convection Zone to the Chromosphere”, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, Proceedings of the 23rd Sacramento Peak Summer Workshop, held at NSO/Sac, Sunspot, New Mexico, USA, 18–22 July, 2005, (Eds.) Leibacher, J., Stein, R.F., Uitenbroek, H., vol. 354 of ASP Conference Series, pp. 345–351, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on pages 30 and 87.)
Schrijver, C.J., Hagenaar, H.J. and Title, A.M., 1997a, “On the Patterns of the Solar Granulation and Supergranulation”, Astrophys. J., 475, 328. [DOI], [ADS] (Cited on page 37.)
Schrijver, C.J., Title, A.M., van Ballegooijen, A.A., Hagenaar, H.J. and Shine, R.A., 1997b, “Sustaining the quiet photospheric network: The balance of flux emergence, fragmentation, merging, and cancellation”, Astrophys. J., 487, 424–436. [DOI], [ADS] (Cited on page 71.)
Schröter, E.H., 1957, “Zur Deutung der Rotverschiebung und der Mitte-Rand-Variation der Fraunhoferlinien bei Berücksichtigung der Temperaturschwankungen der Sonnenatmosphäre”, Z. Astrophys., 41, 141–181. [ADS] (Cited on page 39.)
Schüssler, M. and Vögler, A., 2006, “Magnetoconvection in a Sunspot Umbra”, Astrophys. J. Lett., 641, L73–L76. [DOI], [ADS], [astro-ph/0603078] (Cited on page 71.)
Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A. and Solanki, S.K., 2003, “Why solar magnetic flux concentrations are bright in molecular bands”, Astrophys. J. Lett., 597, L173–L176. [DOI], [ADS] (Cited on page 77.)
Schwarzschild, M., 1958, Structure and Evolution of the Stars, Princeton University Press, Princeton (Cited on page 20.)
Scott, P.C., Asplund, M., Grevesse, N. and Sauval, A.J., 2006, “Line formation in solar granulation. VII. CO lines and the solar C and O isotopic abundances”, Astron. Astrophys., 456, 675–688. [DOI], [ADS], [astro-ph/0605116] (Cited on pages 42, 47, 48, 49, 50, and 55.)
Shchukina, N. and Trujillo Bueno, J., 2001, “The Iron Line Formation Problem in Three-dimensional Hydrodynamic Models of Solar-like Photospheres”, Astrophys. J., 550, 970–990. [DOI], [ADS] (Cited on pages 42 and 55.)
Shelyag, S., Schüssler, M., Solanki, S.K., Berdyugina, S.V. and Vögler, A., 2004, “G-band spectral synthesis and diagnostics of simulated solar magneto-convection”, Astron. Astrophys., 427, 335–343. [DOI], [ADS] (Cited on page 80.)
Shelyag, S., Erdélyi, R. and Thompson, M.J., 2006, “Forward Modeling of Acoustic Wave Propagation in the Quiet Solar Subphotosphere”, Astrophys. J., 651, 576–583. [DOI], [ADS] (Cited on page 60.)
Shelyag, S., Erdélyi, R. and Thompson, M.J., 2007, “Forward modelling of sub-photospheric flows for time-distance helioseismology”, Astron. Astrophys., 469, 1101–1107. [DOI], [ADS], [astro-ph/0703067] (Cited on page 60.)
Shine, R.A., Simon, G.W. and Hurlburt, N.E., 2000, “Supergranule and Mesogranule Evolution”, Solar Phys., 193, 313–331. [ADS] (Cited on pages 35 and 36.)
Simon, G.W. and Leighton, R.B., 1964, “Velocity Fields in the Solar Atmosphere. III. Large-Scale Motions, the Chromospheric Network, and Magnetic Fields”, Astrophys. J., 140, 1120–1147. [ADS] (Cited on page 36.)
Simon, G.W. and Weiss, N.O., 1968, “Supergranules and the Hydrogen Convection Zone”, Z. Astrophys., 69, 435. [ADS] (Cited on page 37.)
Simon, G.W. and Weiss, N.O., 1991, “Convective structures in the Sun”, Mon. Not. R. Astron. Soc., 252, 1P–5P. [ADS] (Cited on page 23.)
Simon, G.W., November, L.J., Acton, L.W., Ferguson, S.H. and Shine, R.A., 1988, “Variability of solar mesogranulation”, Adv. Space Res., 8, 169–172. [DOI], [ADS] (Cited on page 35.)
Simon, G.W., Title, A.M. and Weiss, N.O., 1991a, “Simulating exploding granules and mesogranular flows”, Adv. Space Res., 11, 259–262. [DOI], [ADS] (Cited on page 23.)
Simon, G.W., Title, A.M. and Weiss, N.O., 1991b, “Modeling mesogranules and exploders on the solar surface”, Astrophys. J., 375, 775–788. [DOI], [ADS] (Cited on page 23.)
Simon, G.W., Title, A.M. and Weiss, N.O., 2001, “Sustaining the Sun’s Magnetic Network with Emerging Bipoles”, Astrophys. J., 561, 427–434. [DOI], [ADS] (Cited on page 71.)
Skartlien, R., 2002, “Local Helioseismology as an Inverse Source-Inverse Scattering Problem”, Astrophys. J., 565, 1348–1365. [DOI], [ADS] (Cited on page 60.)
Spruit, H., 1997, “Convection in stellar envelopes: a changing paradigm”, Mem. Soc. Astron. Ital., 68, 397–413. [ADS], [astro-ph/9605020] (Cited on page 8.)
Spruit, H.C., 1976, “Pressure equilibrium and energy balance of small photospheric fluxtubes”, Solar Phys., 50, 269–295. [ADS] (Cited on pages 71, 77, and 80.)
Spruit, H.C., 1977a, Magnetic flux tubes and transport of heat in the convection zone of the Sun, Ph.D. Thesis, Utrecht University, Utrecht. [ADS] (Cited on page 71.)
Spruit, H.C., 1977b, “Heat flow near obstacles in the solar convection zone”, Solar Phys., 55, 3–34. [ADS] (Cited on pages 77 and 80.)
Spruit, H.C., 1979, “Convective collapse of flux tubes”, Solar Phys., 61, 363–378. [ADS] (Cited on page 71.)
Spruit, H.C. and Zweibel, E.G., 1979, “Convective instability of thin flux tubes”, Solar Phys., 62, 15–22. [ADS] (Cited on page 71.)
Spruit, H.C., Nordlund, Å. and Title, A.M., 1990, “Solar convection”, Annu. Rev. Astron. Astrophys., 28, 263–301. [DOI], [ADS] (Cited on page 8.)
Steffen, M. and Holweger, H., 2002, “Line formation in convective stellar atmospheres. I. Granulation corrections for solar photospheric abundances”, Astron. Astrophys., 387, 258–270. [DOI], [ADS], [astro-ph/0203127] (Cited on pages 42 and 56.)
Steffen, M., Ludwig, H.-G. and Freytag, B., 1995, “Synthetic spectra computed from hydrodynamical model atmospheres of DA white dwarfs”, Astron. Astrophys., 300, 473. [ADS] (Cited on page 13.)
Stein, R.F. and Nordlund, Å., 1989, “Topology of convection beneath the solar surface”, Astrophys. J. Lett., 342, L95–L98. [DOI], [ADS] (Cited on pages 13, 20, 35, and 37.)
Stein, R.F. and Nordlund, Å., 1998, “Simulations of Solar Granulation. I. General Properties”, Astrophys. J., 499, 914–933. [DOI], [ADS] (Cited on pages 13, 18, 19, 23, 24, 27, 28, 30, 33, and 38.)
Stein, R.F. and Nordlund, Å., 2006, “Solar Small-Scale Magnetoconvection”, Astrophys. J., 642, 1246–1255. [DOI], [ADS] (Cited on pages 71 and 83.)
Stein, R.F., Carlsson, M. and Nordlund, Å., 1997, “Numerical Simulations Can Lead to New Insights”, in Computational Astrophysics; 12th Kingston Meeting on Theoretical Astrophysics, Proceedings of the 12th ‘Kingston Meeting’ on Computational Astrophysics, held in Halifax, Canada October 17–19 1996, (Eds.) Clarke, D.A., West, M.J., vol. 123 of Astronomical Society of the Pacific Conference Series, pp. 72–77, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 19.)
Stein, R.F., Georgobiani, D., Trampedach, R., Ludwig, H.-G. and Nordlund, Å., 2005, “Excitation of P-Modes in the Sun and Stars”, in Highlights of Astronomy, Vol. 13, As Presented at the XXVth General Assembly of the IAU, Sydney, Australia, 13–26 July 2003, (Ed.) Engvold, O., p. 411, IAU, San Francisco. [ADS] (Cited on page 36.)
Stein, R.F., Benson, D., Georgobiani, D. and Nordlund, Å., 2006a, “Supergranule Scale Convection Simulations”, in SOHO 18/Gong 2006/HELAS I: Beyond the Spherical Sun, Proceedings of SOHO 18/GONG 2006/HELAS I, 7–11 August 2006, Sheffield, UK, (Ed.) Thompson, M., vol. SP-624 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 36, 37, 38, and 39.)
Stein, R.F., Benson, D. and Nordlund, Å., 2006b, “Solar Supergranulation Scale Simulations (Abstract No. JD17-15)”, Highlights of Recent Progress in the Seismology of the Sun and Sun-Like Stars, IAU XXVIth General Assembly, Joint Discussion 17, 23 August 2006, Prague, Czech Republic, conference paper. [ADS] (Cited on pages 36, 37, and 38.))
Stein, R.F., Benson, D., Georgobiani, D., Nordlund, Å. and Schaffenberger, W., 2007a, “Surface Convection”, in Unsolved Problems in Stellar Physics, A Conference in Honor of Douglas Gough, Cambridge, UK, 2–6 July 2007, (Eds.) Stancliffe, R.J., Dewi, J., Houdek, G., Martin, R.G., Tout, C.A., vol. 948 of AIP Conference Proceedings, pp. 111–115, American Institute of Physics, Melville. [ADS]. Doi not found anymore 10.1063/1.2818958 (Cited on page 61.)
Stein, R.F., Benson, D. and Nordlund, Å., 2007b, “Solar Magneto-Convection Simulations”, in New Solar Physics with Solar-B Mission, Proceedings of the Sixth Solar-B Science Meeting held 8–11 November 2005 in Kyoto, Japan, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, pp. 87–98, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 36.)
Steiner, O., 2003, “Distribution of magnetic flux density at the solar surface. Formulation and results from simulations”, Astron. Astrophys., 406, 1083–1088. [DOI], [ADS] (Cited on page 74.)
Steiner, O., 2005, “Radiative properties of magnetic elements. II. Center to limb variation of the appearance of photospheric faculae”, Astron. Astrophys., 430, 691–700. [DOI], [ADS] (Cited on page 80.)
Steiner, O. and Stenflo, J.O., 1990, “Model Calculations of the Photospheric Layers of Solar Magnetic Fluxtubes”, in Solar Photosphere: Structure, Convection, and Magnetic Fields, Proceedings of the 138th Symposium of the International Astronomical Union, held in Kiev, U.S.S.R., May 15–20, 1989, (Ed.) Stenflo, J.O., vol. 138 of IAU Symposia, pp. 181–184, Kluwer, Dordrecht; Boston. [ADS] (Cited on page 25.)
Steiner, O., Grossmann-Doerth, U., Knölker, M. and Schüssler, M., 1998, “Dynamical Interaction of Solar Magnetic Elements and Granular Convection: Results of a Numerical Simulation”, Astrophys. J., 495, 468. [DOI], [ADS] (Cited on page 84.)
Steiner, O., Hauschildt, P.H. and Bruls, J., 2001, “Radiative properties of magnetic elements. I. Why are G-band bright points bright?”, Astron. Astrophys., 372, L13–L16. [DOI], [ADS] (Cited on page 77.)
Steiner, O., Vigeesh, G., Krieger, L., Wedemeyer-Böhm, S., Schaffenberger, W. and Freytag, B., 2007, “First local helioseismic experiments with CO5”, Astron. Nachr., 328, 323. [DOI], [ADS], [astro-ph/0701029] (Cited on page 61.)
Stix, M., 2004, The Sun: An Introduction, Astronomy and Astrophysics Library, Springer, Berlin; New York, 2nd corr. edn. (Cited on page 8.)
Stodilka, M.I. and Malynych, S.Z., 2006, “Spatial variations in the velocity field and real solar granulation”, Mon. Not. R. Astron. Soc., 373, 1523–1530. [DOI], [ADS], [astro-ph/0612436] (Cited on page 15.)
Straus, T., Deubner, F.-L. and Fleck, B., 1992, “Is mesogranulation a distinct regime of convection?”, Astron. Astrophys., 256, 652–659. [ADS] (Cited on page 35.)
Straus, T., Severino, G. and Steffen, M., 2006, “Resonant Oscillation Modes and Background in Realistic Hydrodynamical Simulations of Solar Surface Convection”, in SOHO-17: 10 Years of SOHO and Beyond, Proceedings of the conference held 7–12 May 2006 at Giardini Naxos, Sicily, Italy, (Eds.) Lacoste, H., Ouwehand, L., vol. SP-617 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 61 and 70.)
Tao, L., Weiss, N.O., Brownjohn, D.P. and Proctor, M.R.E., 1998, “Flux Separation in Stellar Magnetoconvection”, Astrophys. J. Lett., 496, L39. [DOI], [ADS] (Cited on page 71.)
Thelen, J.-C. and Cattaneo, F., 2000, “Dynamo action driven by convection: the influence of magnetic boundary conditions”, Mon. Not. R. Astron. Soc., 315, L13–L17. [ADS] (Cited on page 71.)
Title, A.M., Tarbell, T.D., Topka, K.P., Ferguson, S.H. and Shine, R.A. (SOUP Team)), 1989, “Statistical properties of solar granulation derived from the SOUP instrument on Spacelab 2”, Astrophys. J., 336, 475–494. [DOI], [ADS] (Cited on pages 15 and 35.)
Tobias, S.M., Brummell, N.H., Clune, T.L. and Toomre, J., 1998, “Pumping of Magnetic Fields by Turbulent Penetrative Convection”, Astrophys. J. Lett., 502, L177–L180. [DOI], [ADS] (Cited on page 81.)
Tobias, S.M., Brummell, N.H., Clune, T.L. and Toomre, J., 2001, “Transport and Storage of Magnetic Field by Overshooting Turbulent Compressible Convection”, Astrophys. J., 549, 1183–1203. [DOI], [ADS] (Cited on page 81.)
Tong, C.H., Thompson, M.J., Warner, M.R. and Pain, C.C., 2003a, “Helioseismic Signals and Wave Field Helioseismology”, Astrophys. J., 593, 1242–1248. [DOI], [ADS] (Cited on page 60.)
Tong, C.H., Thompson, M.J., Warner, M.R. and Pain, C.C., 2003b, “The Significance of Density and Attenuation in the Local Helioseismology”, Astrophys. J. Lett., 596, L263–L266. [DOI], [ADS] (Cited on page 60.)
Tong, C.H., Thompson, M.J., Warner, M.R., Rajaguru, S.P. and Pain, C.C., 2003c, “Acoustic Wave Propagation in the Sun: Implications for Wave Field and Time-Distance Helioseismology”, Astrophys. J. Lett., 582, L121–L124. [DOI], [ADS] (Cited on page 60.)
Trampedach, R., 2004a, “Improved phenomenological equation of state in the chemical picture”, in Equation-of-State and Phase-Transition in Models of Ordinary Astrophysical Matter, Proceedings of the Conference held 2–11 June 2004 in Leiden, The Netherlands, (Eds.) Celebonovic, V., Gough, D., Däppen, W., vol. 731 of AIP Conference Proceedings, pp. 99–105, American Institute of Physics, Melville. [ADS], [astro-ph/0411315] (Cited on page 14.)
Trampedach, R., 2004b, Ingredients for accurate simulations of convection in stellar envelopes, Ph.D. Thesis, Michigan State University, East Lansing, MI. [ADS] (Cited on page 14.)
Trampedach, R. and Asplund, M., 2003, “Radiative Transfer with Very Few Wavelengths”, in 3D Stellar Evolution, Proceedings of the Conference held 22–26 July 2002 at University of California Davis, Livermore, USA, (Eds.) Turcotte, S., Keller, S.C., Cavallo, R.M., vol. 293 of ASP Conference Series, pp. 209–213, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 13.)
Trampedach, R., Däppen, W. and Baturin, V.A., 2006, “A Synoptic Comparison of the Mihalas-Hummer-Däppen and OPAL Equations of State”, Astrophys. J., 646, 560–578. [DOI], [ADS], [astro-ph/0604352] (Cited on page 14.)
Turck-Chièze, S., Couvidat, S., Piau, L., Ferguson, J., Lambert, P., Ballot, J., García, R.A. and Nghiem, P., 2004, “Surprising Sun: A New Step Towards a Complete Picture?”, Phys. Rev. Lett., 93(21), 211102. [DOI], [ADS], [astro-ph/0407176] (Cited on page 57.)
Turcotte, S., Richer, J., Michaud, G., Iglesias, C.A. and Rogers, F.J., 1998, “Consistent Solar Evolution Model Including Diffusion and Radiative Acceleration Effects”, Astrophys. J., 504, 539. [DOI], [ADS] (Cited on page 57.)
Uitenbroek, H., 1998, “The Effect of Photospheric Granulation on the Determination of the Lithium Abundance in Solar-Type Stars”, Astrophys. J., 498, 427. [DOI], [ADS] (Cited on page 42.)
Uitenbroek, H., 2000a, “The CO Fundamental Vibration-Rotation Lines in the Solar Spectrum. I. Imaging Spectroscopy and Multidimensional LTE Modeling”, Astrophys. J., 531, 571–584. [DOI], [ADS] (Cited on pages 42 and 49.)
Uitenbroek, H., 2000b, “The CO Fundamental Vibration-Rotation Lines in the Solar Spectrum. II. Non-LTE Transfer Modeling in Static and Dynamic Atmospheres”, Astrophys. J., 536, 481–493. [DOI], [ADS] (Cited on page 49.)
Ulrich, R.K., 1998, “Large Scale Convection and the Solar Radius”, in New Eyes to See Inside the Sun and Stars: Pushing the Limits of Helio and Asteroseismology with New Observations from the Ground and from Space, Proceedings of the 185th Symposium of the International Astronomical Union, held in Kyoto, Japan, 18–22 August 1997, (Eds.) Deubner, F.-L., Christensen-Dalsgaard, J., Kurtz, D., vol. 185 of IAU Symposia, pp. 59–72, Kluwer, Dordrecht; Boston. [ADS] (Cited on page 36.)
Ustyugov, S.D., 2006, “Magnetohydrodynamic Simulation of Solar Supergranulation”, in Numerical Modeling of Space Plasma Flows, Proceedings of 1ST IGPP-CalSpace International Conference held 26–30 March, 2006, in Palm Springs, California, USA, (Eds.) Zank, G.P., Pogorelov, N.V., vol. 359 of ASP Conference Series, pp. 226–231, Astronomical Society of the Pacific, San Francisco. [ADS], [astro-ph/0605627] (Cited on page 36.)
Ustyugov, S.D., 2007, “Numerical Simulation of Solar Magnetoconvection with Realistic Physics”, in Fifty Years of Romanian Astrophysics, Proceedings of the conference held in Bucharest, Romania, 27–30 September 2006, (Eds.) Dumitrache, C., Popescu, N.A., Suran, M.D., Mioc, V., vol. 895 of AIP Conference Proceedings, pp. 109–114, American Institute of Physics, Melville. [DOI], [ADS] (Cited on page 36.)
Ustyugov, S.D., 2008, “Large Eddy Simulation of Solar Photosphere Convection with Realistic Physics”, in Subsurface and Atmospheric Influences on Solar Activity, Proceedings of a workshop held at the NSO/Sac, Sunspot, New Mexico, USA, 16–20 April 2007, (Eds.) Howe, R., Komm, R.W., Balasubramaniam, K.S., Petrie, G.J.D., vol. 383 of ASP Conference Series, pp. 43–48, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:0710.3023] (Cited on page 36.)
van Ballegooijen, A.A., 1986, “Cascade of magnetic energy as a mechanism of coronal heating”, Astrophys. J., 311, 1001–1014. [DOI], [ADS] (Cited on page 84.)
Vernazza, J.E., Avrett, E.H. and Loeser, R., 1976, “Structure of the solar chromosphere. II. The underlying photosphere and temperature-minimum region”, Astrophys. J. Suppl. Ser., 30, 1–60. [ADS] (Cited on page 39.)
Vögler, A., 2003, Three-dimensional simulations of magneto-convection in the solar photosphere, Ph.D. Thesis, Göttingen University, Göttingen. URL (accessed 27 March 2009): http://webdoc.sub.gwdg.de/diss/2004/voegler/ (Cited on page 75.)
Vögler, A., 2004, “Effects of non-grey radiative transfer on 3D simulations of solar magnetoconvection”, Astron. Astrophys., 421, 755–762. [DOI], [ADS] (Cited on pages 13 and 25.)
Vögler, A., 2005, “On the effect of photospheric magnetic fields on solar surface brightness. Results of radiative MHD simulations”, Mem. Soc. Astron. Ital., 76, 842–849. [ADS] (Cited on pages 71 and 73.)
Vögler, A. and Schüssler, M., 2003, “Studying magneto-convection by numerical simulation”, Astron. Nachr., 324, 399–404. [ADS] (Cited on page 75.)
Vögler, A. and Schüssler, M., 2007, “A solar surface dynamo”, Astron. Astrophys., 465, L43–L46. [DOI], [ADS], [astro-ph/0702681] (Cited on page 84.)
Vögler, A., Bruls, J.H.M.J. and Schüssler, M., 2004, “Approximations for non-grey radiative transfer in numerical simulations of the solar photosphere”, Astron. Astrophys., 421, 741–754. [DOI], [ADS] (Cited on page 13.)
Vögler, A., Shelyag, S., Schüssler, M., Cattaneo, F., Emonet, T. and Linde, T., 2005, “Simulations of magneto-convection in the solar photosphere. Equations, methods, and results of the MURaM code”, Astron. Astrophys., 429, 335–351. [DOI], [ADS] (Cited on pages 13, 71, and 83.)
Voigt, H.-H., 1956, “‘Drei-Strom-Modell’ der Sonnenphotosphäre und Asymmetrie der Linien des infraroten Sauerstoff-Tripletts”, Z. Astrophys., 40, 157. [ADS] (Cited on page 39.)
Wang, H., 1989, “Do mesogranules exist?”, Solar Phys., 123, 21–32. [ADS] (Cited on page 35.)
Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G. and Holweger, H., 2003, “3-D hydrodynamic simulations of the solar chromosphere”, Astron. Nachr., 324, 410–411. [ADS] (Cited on pages 30 and 87.)
Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G. and Holweger, H., 2004, “Numerical simulation of the three-dimensional structure and dynamics of the non-magnetic solar chromosphere”, Astron. Astrophys., 414, 1121–1137. [DOI], [ADS], [astro-ph/0311273] (Cited on page 30.)
Wedemeyer-Böhm, S. and Steffen, M., 2007, “Carbon monoxide in the solar atmosphere. II. Radiative cooling by CO lines”, Astron. Astrophys., 462, L31–L35. [DOI], [ADS], [astro-ph/0612197] (Cited on page 49.)
Wedemeyer-Böhm, S., Kamp, I., Bruls, J. and Freytag, B., 2005, “Carbon monoxide in the solar atmosphere. I. Numerical method and two-dimensional models”, Astron. Astrophys., 438, 1043–1057. [DOI], [ADS], [astro-ph/0503496] (Cited on page 49.)
Weiss, N.O., 1966, “The Expulsion of Magnetic Flux by Eddies”, Proc. R. Soc. London, Ser. A, 293, 310–328. [ADS] (Cited on page 71.)
Weiss, N.O., Brownjohn, D.P., Hurlburt, N.E. and Proctor, M.R.E., 1990, “Oscillatory convection in sunspot umbrae”, Mon. Not. R. Astron. Soc., 245, 434–452. [ADS] (Cited on page 71.)
Weiss, N.O., Brownjohn, D.P., Matthews, P.C. and Proctor, M.R.E., 1996, “Photospheric Convection in Strong Magnetic Fields”, Mon. Not. R. Astron. Soc., 283, 1153–1164. [ADS] (Cited on page 71.)
Weiss, N.O., Proctor, M.R.E. and Brownjohn, D.P., 2002, “Magnetic flux separation in photospheric convection”, Mon. Not. R. Astron. Soc., 337, 293–304. [DOI], [ADS] (Cited on page 71.)
Wilken, V., de Boer, C.R., Denker, C. and Kneer, F., 1997, “Speckle measurements of the centre-to-limb variation of the solar granulation”, Astron. Astrophys., 325, 819–824. [ADS] (Cited on page 15.)
Yelles Chaouche, L., Cheung, M., Lagg, A. and Solanki, S., 2005, “Diagnostics of a Simulated Flux Tube Emergence”, in The Dynamic Sun: Challenges for Theory and Observations, Proceedings of the 11th European Solar Physics Meeting, 11–16 September 2005, Leuven, Belgium, (Eds.) Danesy, D., Poedts, S., De Groof, A., Andries, J., vol. SP-600 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on page 81.)
Young, P.A. and Arnett, D., 2005, “Observational Tests and Predictive Stellar Evolution. II. Nonstandard Models”, Astrophys. J., 618, 908–918. [DOI], [ADS], [astro-ph/0409658] (Cited on page 57.)
Zahn, J.-P., 1987, “Solar and Stellar Convection”, in Solar and Stellar Physics, Proceedings of the 5th European Solar Meeting Held in Titisee/Schwarzwald, Germany, April 27–30, 1987, (Eds.) Schröter, E.-H., Schüssler, M., vol. 292 of Lecture Notes in Physics, pp. 55–71, Springer, Berlin; New York. [ADS] (Cited on page 8.)
Zhao, J., 2008, “Recent progress in time distance helioseismology”, Adv. Space Res., 41, 838–845. [DOI], [ADS] (Cited on page 60.)
Zhao, J. and Kosovichev, A.G., 2003, “On the inference of supergranular flows by time-distance helioseismology”, in Local and Global Helioseismology: The Present and Future, Proceedings of SOHO 12/GONG+ 2002, 27 October–1 November 2002, Big Bear Lake, California, USA, (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 417–420, ESA Publications Division, Noordwijk. [ADS] (Cited on page 36.)
Zhao, J., Georgobiani, D., Kosovichev, A.G., Benson, D., Stein, R.F. and Nordlund, Å., 2007a, “Validation of Time-Distance Helioseismology by Use of Realistic Simulations of Solar Convection”, Astrophys. J., 659, 848–857. [DOI], [ADS], [astro-ph/0612551] (Cited on page 36.)
Zhao, J., Georgobiani, D., Kosovichev, A.G., Benson, D., Stein, R.F. and Nordlund, Å., 2007b, “Validation of Time-Distance Helioseismology by Use of Realistic Simulations of Solar Convection”, Astrophys. J., 659, 848–857. [DOI], [ADS], [astro-ph/0612551] (Cited on page 61.)
Acknowledgments
RFS was supported by NASA grants NNG04GB92G and NAG 5-12450 and by NSF grants AST0205500 and AST0605738. ÅN is grateful to JILA and to the Danish Natural Science Research Council (FNU) for support during a one year sabbatical at the University of Colorado, Boulder. The authors’ simulations were performed on NASA’s project Columbia computer system, at the National Center for Supercomputing Applications, which is supported by the National Science Foundation, at Michigan State University and at the Danish Center for Scientific Computing, Copenhagen.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9167_MOESM1_ESM.mpg
mpg-Movie (37870.9150391 KB) Still from a movie showing Vertical velocity (red upward, blue downward) and streaklines (seen more clearly in the movie) in a vertical cut through the 24 Mm wide simulation domain. Diverging upflows sweep downflows toward each other at the boundaries of the larger, deeper lying upflows (movie by Chris Henze, NASA Advanced Supercomputing Division, Ames Research Center).
41116_2015_9167_MOESM2_ESM.mov
mpg-Movie (8725.79980469 KB) Still from a movie showing Entropy fluctuation from a solar convection simulation. Horizontal scale is 6 Mm and the vertical scale range from the temperature minimum to 2.5 Mm below the surface.
41116_2015_9167_MOESM3_ESM.mov
mpg-Movie (48052.0712891 KB) Still from a movie showing The emergent intensity from a magneto-convection simulation showing changed appearance as one approaches the limb (movie by Mats Carlsson, Oslo).
41116_2015_9167_MOESM4_ESM.mov
mpg-Movie (29986.5087891 KB) Still from a movie showing Magnitude of the vorticity (entrophy) in a single downdraft. Top of the image is the visible solar surface, bottom is 2.5 Mm below the surface. The vertical scale is stretched. Horizontal tickmarks are 237 km apart.
41116_2015_9167_MOESM5_ESM.mov
mpg-Movie (123750.990234 KB) Still from a movie showing G-band images calculated from the simulation at disk center and towards the limb at μ = 0.8, 0.6, 0.4. At disk center small magnetic concentrations appear bright, while larger ones appear dark. When looking toward the limb the granulation appears hilly and one sees the bright walls of granules where the line of sight passes through a low density magnetic concentration. Movie shows time evolution. Note the formation of a micropore near the upper center (movie by Mats Carlsson).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nordlund, Å., Stein, R.F. & Asplund, M. Solar Surface Convection. Living Rev. Sol. Phys. 6, 2 (2009). https://doi.org/10.12942/lrsp-2009-2
Published:
DOI: https://doi.org/10.12942/lrsp-2009-2