Abstract
The Sun’s magnetic activity has steadily declined during its main-sequence life. While the solar photospheric luminosity was about 30% lower 4.6 Gyr ago when the Sun arrived on the main sequence compared to present-day levels, its faster rotation generated enhanced magnetic activity; magnetic heating processes in the chromosphere, the transition region, and the corona induced ultraviolet, extreme-ultraviolet, and X-ray emission about 10, 100, and 1000 times, respectively, the present-day levels, as inferred from young solar-analog stars. Also, the production rate of accelerated, high-energy particles was orders of magnitude higher than in present-day solar flares, and a much stronger wind escaped from the Sun, permeating the entire solar system. The consequences of the enhanced radiation and particle fluxes from the young Sun were potentially severe for the evolution of solar-system planets and moons. Interactions of high-energy radiation and the solar wind with upper planetary atmospheres may have led to the escape of important amounts of atmospheric constituents. The present dry atmosphere of Venus and the thin atmosphere of Mars may be a product of early irradiation and heating by solar high-energy radiation. High levels of magnetic activity are also inferred for the pre-main sequence Sun. At those stages, interactions of high-energy radiation and particles with the circumsolar disk in which planets eventually formed were important. Traces left in meteorites by energetic particles and anomalous isotopic abundance ratios in meteoritic inclusions may provide evidence for a highly active pre-main sequence Sun. The present article reviews these various issues related to the magnetic activity of the young Sun and the consequent interactions with its environment. The emphasis is on the phenomenology related to the production of high-energy photons and particles. Apart from the activity on the young Sun, systematic trends applicable to the entire main-sequence life of a solar analog are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of the past of our Sun and its solar system has become an interdisciplinary effort between stellar astronomy, astrophysics of star and planet formation, astrochemistry, solar physics, geophysics, planetology, meteoritical science and several further disciplines. The interest in understanding the past evolution of our star is obvious; the Sun’s radiative energy, the solar wind, and various forms of transient phenomena (e.g., shock waves, high-energy particle streams during flares) are key factors in the formation and evolution of the planets and eventually the biosphere on Earth.
The Sun is, like almost all cool stars, a “magnetic star” that produces magnetic fields through dynamo operation in the interior. These fields reach the surface where their presence is noticed in the form of sunspots. However, magnetic activity has much more far-reaching consequences: Solar magnetic fields control essentially the entire outer solar atmosphere, they heat coronal gas to millions of degrees, they produce flares whose by-products such as shock waves and high-energy particles travel through interplanetary space to eventually interact with planetary atmospheres; the solar wind is guided by open magnetic fields; this magnetized-wind complex forms a large bubble, an “astrosphere” in interstellar space containing the entire solar system and protecting it from a high dose of cosmic rays.
Was the Sun’s magnetic activity different in its infancy when planets and their atmospheres formed, or when it was still surrounded by an accretion disk? Accumulated direct and indirect evidence indeed points to a much higher level of magnetic activity in the young Sun, in particular in its pre-main sequence (PMS) phase and the subsequent epoch of its settling on the main sequence (MS). Direct evidence includes meteoritic traces and isotopic anomalies that require much higher proton fluxes at early epochs at least partly from within the solar system (Section 6.5 below); indirect evidence comes from systematic comparisons of the contemporary Sun with solar analogs of younger age that unequivocally show a strong trend toward elevated activity at younger ages (Section 5 below). Interestingly, planetary atmospheres offer further clues to strongly elevated activity levels: Evidence for a warmer early climate on Mars or the extremely arid atmosphere of Venus — a sister planet of the water-rich Earth — call for explanations, and such explanations may be found in the elevated activity of the young Sun (see Section 7.2 below). The study of the early solar activity is the theme of the present review article.
The main goal of this article is therefore to demonstrate evidence for a much more active young Sun, and to study the consequences this might have had for the development of the solar environment, including the formation and evolution of planets. Our discussion will therefore take us through the following three major issues:
-
The young Sun’s more rapid rotation induced an internal magnetic dynamo that was much more efficient than the present-day Sun’s. Consequently, stronger surface magnetic fields and/or higher surface magnetic filling factors should have induced enhanced “activity” in all its variations, from larger surface spots to a stronger, extended solar wind. If we can observationally probe the outer magnetic activity of the Sun, we obtain invaluable diagnostics for a deeper theoretical understanding of the internal dynamo.
-
The solar output largely controls planetary atmospheres and their climates. While this is obviously true for the dominant optical and infrared emissions of a star like the Sun, the irradiation of planetary atmospheres by higher-energy ultraviolet and X-ray photons as well as interactions with high-energy particles and the solar wind leads to atmospheric alterations that have been recognized and numerically simulated only recently. The much higher magnetic activity of the young Sun and the resulting higher levels of ultraviolet, X-ray, and particle irradiation were therefore of prime importance for the early evolution of the planets.
The discovery of extrasolar planets in particular around Sun-like stars has also spurred interest in star-planet interactions, e.g., erosion of atmospheres or photochemical reactions, that profit from detailed studies in the solar system.
-
Similarly, at still younger stages of a star’s evolution, its environment is rich in molecular gas and dust, both in the form of a large envelope (in the youngest, protostellar phases of evolution) and a circumstellar gas and dust disk (including the T Tauri phase when planets were forming). Star-disk interactions are manifold, and their role is fundamental in various respects. The optical and ultraviolet radiation heats the disk and therefore primarily determines disk structure and the formation and evolution of planetary systems.
High-energy emission, in particular X-ray radiation, further heats and ionizes parts of the circumstellar disk. Even moderate disk ionization will lead to accretion instabilities if weak magnetic fields are present. Disk heating by X-rays may also produce extreme temperature gradients across the disk that drive complicated chemical networks relevant for the later processing of the disk material into forming planets and planetary atmospheres.
The focus of this review is therefore, on the one hand, on signatures of magnetic activity across the electromagnetic spectrum, representing physical processes in the photosphere, the chromosphere, and the thermal and non-thermal corona of a solar-like star. I will mostly use young solar-like stars to infer conditions that — by analogy — might have prevailed on the young Sun. On the other hand, I will also discuss traces that the elevated activity of the young Sun might have left behind in meteorites and in planetary atmospheres, thus collecting “in-situ” information about the distant past of our own solar system.
While this article focuses on the conditions on the young Sun and in the early solar system, it has proven convenient to study the solar evolution in time systematically from young to old, because a number of trends become evident that can be calibrated with the contemporaneous Sun. We thus not only learn about the young Sun, but we uncover the systematics that made it different from what it is today. This is the approach I adopt in the present work.
This article will not address issues on the formation and evolution of the Sun that are related to its internal constitution, with the exception of cursory reference to the magnetic dynamo that is, of course, at the origin of all solar magnetic activity. I will treat the PMS Sun in separate chapters for three related reasons: First, fundamental properties of the PMS Sun were largely different from those of the contemporaneous Sun (for example, its spectral type, or its photospheric effective temperature). Second, new features not present in the modern Sun become dominant key players related to activity and environment, among them accretion disks, accretion streams, star-disk magnetospheres, outflows, and jets. And third, the PMS behavior of the Sun cannot be assessed in detail judged from the present-day solar parameters; we can only discuss the range of potential evolutionary scenarios now observed in a wide sample of PMS stars (e.g., with respect to mass accretion rate, disk mass, disk dispersal time, rotation period, etc.).
Numerous review articles are available on subjects related to the present one. Without intention to be complete, I refer here in particular to the collection of papers edited by Sonett et al. (1991) and Dupree and Benz (2004), the Cool Stars Workshop series (the latest volume edited by van Belle 2007), and the Protostars and Planets series (in particular the latest volumes by Mannings et al. 2000 and Reipurth et al. 2007). An early overview of solar variability (including that of its activity) can be found in Newkirk Jr (1980). Walter and Barry (1991) specifically reviewed knowledge of the long-term evolution of solar activity as known in the early nineties, in a similar spirit as the present review; numerous older references can be found in that work. For summaries of stellar X-ray and radio emission, I refer to Güdel (2004) and Güdel (2002), respectively. Feigelson and Montmerle (1999) and Feigelson et al. (2007) have summarized PMS aspects of magnetic activity. Glassgold et al. (2005) have reviewed the influence of the magnetic activity of the PMS Sun on its environment, in particular on its circumstellar disk where our planets were forming. Wood (2004) has discussed evidence for winds emanating from solar-like stars, and Goswami and Vanhala (2000) have summarized findings related to radionuclides in meteorites and inferences for the young solar system; the most recent developments in this field have been reviewed by Wadhwa et al. (2007). Kulikov et al. (2007) and Lundin et al. (2007) have provided summaries on interactions between solar high-energy radiation and particles with planetary atmospheres, in particular those of Venus, Earth, and Mars.
2 What is a Solar-Like Star?
The present Sun is a G2 V star with a surface effective temperature of approximately 5780 K. Stellar evolution theory indicates, however, that the Sun has shifted in spectral type by several subclasses, becoming hotter by a few hundred degrees and becoming more luminous (the bolometric luminosity of the Sun in its zero-age main-sequence [ZAMS] phase amounted to only about 70% of the present-day output; Siess et al. 2000). In understanding the solar past, we must therefore also consider stars of mid-to-late spectral class G. On the other hand, alternative evolutionary scenarios have suggested continuous mass loss from the young Sun at a high rate that would require a somewhat earlier spectral classification of the young Sun (Sackmann and Boothroyd, 2003). In any case, magnetic activity in the outer stellar atmospheres is predominantly controlled by the depth of the stellar convection zone and stellar rotation, both of which also evolve during stellar evolution. For our understanding of magnetic activity, the precise spectral subclass is rather likely to play a minor role. When discussing “solar analogs”, I will therefore concentrate on stars mostly of early-to-mid-G spectral types but will occasionally also consider general information from outer atmospheres of somewhat lower-mass stars if available.
The situation is more complex for stars in their PMS stage. The Sun spent much of its PMS life as a mid-K (K5 IV) star when it moved down the Hayashi track. But again, the precise spectral subtype matters even less for magnetic activity in this stage, the more important key parameters being the age of the star (controlling its total luminosity, its radius, and the development and therefore the depth of the convection zone), the presence and dispersal of a circumstellar disk (controlling mass accretion and, via magnetic fields, the spin of the star), and the presence and strength of outflows (controlling, together with accretion, the final evolution of the stellar mass). A somewhat more generous definition of “pre-main sequence solar analogs” is clearly in order, given that the Sun’s history of rotation, accretion, the circumsolar disk, and the solar mass loss cannot be precisely assessed. Quite generally, I will take solar-like stars in the PMS phase to be, from the perspective of “magnetic activity”, stars with masses of roughly 0.5–1.5 solar masses, covering spectral classes from early G to late K/early M.
The expression “solar twin” (Cayrel de Strobel and Bentolila, 1989) is occasionally used. This term should be used solely in the context of a solar analog with an age close to the Sun’s, i.e., of order 4–6 Gyr, an age range in which the internal structure and the rotation period of a 1 M⊙ (and therefore, its activity level) evolve only insignificantly. Efforts toward identifying real solar twins have been important in the context of putting our Sun into a wider stellar context; nearby solar analogs that are essentially indistinguishable from the Sun with regard to spectral type, effective temperature, gravity, luminosity, age, rotation, and magnetic activity (Porto de Mello and da Silva, 1997) prove that the Sun can be robustly used as an anchor to calibrate evolutionary trends — the Sun is not an exception but is representative of its age and mass, a conclusion also reached by Gustafsson (1998) from a rather general comparison of the Sun with sun-like stars.Footnote 1
Table 1 gives a list of terms, symbols, and acronyms used throughout the text.
3 The Sun in Time
3.1 Goals of the “Sun in Time” project
Solar analogs with different ages and therefore activity levels play an important role in our understanding of the past magnetic evolution of the Sun. For stars with masses ≲ 1.5 M⊙ and ages of at least a few 100 Myr, angular momentum loss by a stellar wind brakes rotation in such a way that it is nearly uniquely determined by the stellar age (Soderblom et al., 1993). The only independent variable, the stellar age, then determines the rotation period and, through the internal magnetic dynamo, magnetic activity at all levels of the stellar atmosphere, probably including characteristics of the stellar wind (Wood et al., 2002, 2005; Kulikov et al., 2006). The study of a series of near-solar-mass stars back to ages close to the ZAMS age will therefore be sufficient to reconstruct the history of our Sun and the interaction of its magnetic activity with its environment. This is the goal of the observational “Sun in Time” program (see, e.g., Dorren and Guinan 1994b).
Specifically, the “Sun in Time” program was established to study the long-term magnetic evolution of the Sun during the entire MS lifetime. The primary aims of the program are, (1) to test dynamo models of the Sun in which rotation is the only significant variable parameter, and (2) to determine the spectral irradiance of the Sun over its MS lifetime. Key studies within the “Sun in Time” program comprise the following:
-
the optical (photospheric) and UV “Sun in Time”, the latter studied with IUE (Messina and Guinan, 2002, 2003; Dorren and Guinan, 1994a), to characterize level and extent of surface magnetic activity;
-
the FUV “Sun in Time” as studied with FUSE (Guinan et al., 2003), to infer transition-region magnetic activity;
-
the EUV “Sun in Time” as studied with EUVE (Ayres, 1997; Güdel et al., 1997a; Audard et al., 1999; Ribas et al., 2005), to obtain information on coronal activity;
-
the X-ray “Sun in Time” as studied by ROSAT and ASCA (Güdel et al., 1997b, 1995c; Dorren et al., 1995), to obtain full coverage in coronal temperatures and characterize flares;
-
the X-ray “Sun in Time” as studied spectroscopically with XMM-Newton (Telleschi et al., 2005), to study the thermal stratification and composition of coronae of solar analogs;
-
spectral evolution of the XUV “Sun in Time” (Ribas et al., 2005), to find systematics across the UV-to-X-ray range;
-
the radio “Sun in Time” as studied with the VLA (Güdel et al., 1994, 1995b, c, 1997b; Gaidos et al., 2000; Güdel and Gaidos, 2001), to measure the production of non-thermal particles in magnetic coronae;
-
magnetic cycles of the “Sun in Time” (Messina and Guinan, 2002), measured in the optical or in X-rays;
-
differential rotation of the “Sun in Time” (Messina and Guinan, 2003) as seen in starspot measurements.
A summary of the instruments used for the observations and their wavelength (or energy) ranges covered is given in Table 2. Various project summaries can be found in Dorren and Guinan (1994b), Güdel et al. (1998b), Guinan and Ribas (2002), Guinan et al. (2002), and Güdel (2003).
3.2 Overview of stellar sample
The program uses a homogeneous sample of single nearby G0-5 V MS stars (and one G2 IV subgiant) that all have known rotation periods and well-determined physical properties, including temperatures, luminosities, metal abundances and ages (Table 3). Observations cover spectral ranges from radio to X-rays (excluding the 360–920 Å range, which is a region of very strong absorption by the interstellar medium). The principal stellar sample is given in Table 3; the samples used for particular studies may vary somewhat, depending on the availability of appropriate observational data. The parameters collected in this table are from Dorren and Guinan (1994a), Güdel et al. (1997b), Güdel et al. (1998b), Güdel and Gaidos (2001), Guinan and Ribas (2002), Ribas et al. (2005), and Telleschi et al. (2005). Bolometric luminosities have been derived from absolute visual magnitudes, MV, by applying standard bolometric corrections. I briefly summarize the magnetic-activity properties of a few important “Young Suns” that will be discussed extensively in this paper (further notes can be found in Ribas et al. 2005).
EK Draconis = HD 129333 is an exemplary near-ZAMS solar analog, representing the very active young Sun at the time when planetary atmospheres first formed. EK Dra is a member of the Pleiades Moving Group at a distance of 34 pc. König et al. (2005) estimated an age of only 35 Myr, and a mass of (0.9–1.0)±0.1 M⊙. EK Dra’s optical and UV properties have been studied in detail by Dorren and Guinan (1994a). With a rotation period of 2.7 d, it reveals extreme magnetic activity, showing a photospheric spot coverage of 6% (Dorren and Guinan 1994a, larger fractions were given by König et al. 2005), transition-region line fluxes 20–100 times larger than the Sun’s (Dorren and Guinan, 1994a), a very hot X-ray emitting corona with a luminosity ≈ 1000 times the present-day solar X-ray output (Güdel et al., 1997b; Telleschi et al., 2005), and an extremely luminous non-thermal radio corona exceeding radio luminosities of strong solar flares by orders of magnitude (Güdel et al., 1994, 1995c). EK Dra shows rotational modulation from spots in the optical, and due to inhomogeneous coronal active regions also in the radio and X-ray regimes (Güdel et al., 1995c). It further shows strong evidence for a ≈ 10 yr activity cycle (Dorren and Guinan, 1994a; Dorren et al., 1995; Güdel, 2004; Järvinen et al., 2005). Duquennoy and Mayor (1991) reported a low-mass (M-type) companion star, whose mass was found to be (0.5 ± 0.1) M⊙, and Metchev and Hillenbrand (2004) discussed evidence for another 0.2 M⊙ companion although the latter has been questioned by König et al. (2005). Note that UV, EUV, X-ray, and radio emissions are likely to be dominated by the G star, given the low mass(es) of the companion(s).
47 Cas B = HR 581 = HD 12230 is a somewhat mysterious solar analog in a binary system at a distance of 33.5 pc. It has not been revealed in the optical regime given the primary F0 V star’s overwhelming light. But astrometric, X-ray and radio properties constrain it to be an early-to-mid G-type star, and its likely membership in the Pleiades Moving Group suggests a near-ZAMS age (Güdel et al., 1995a, 1998a). It shows X-rays and radio emission at an even more extreme level than EK Dra, perhaps induced by the even faster rotation; the rotation period has been inferred from periodic X-ray modulation to be about 1 d (Güdel et al., 1995a, 1998a; Telleschi et al., 2005).
π1 UMa = HD 72905 and Χ1 Ori = HD 39587: These are two members of the Ursa Major Stream (King et al., 2003), with an estimated age of 300 Myr (Soderblom and Mayor, 1993). While π1 UMa is considered to be single, Χ1 Ori is orbited by an M-type companion with an orbital period of about 14 yr (Han and Gatewood, 2002) and a mass of 0.15 M⊙ (König et al., 2002), suggesting that most observational signatures of magnetic activity are dominated by the primary.
κ1 Cet = HD 20630 is a Hyades-age solar analog. Its age is not well known but is indirectly inferred from its rotation period and its X-ray luminosity (Ribas et al., 2005).
4 The Solar Magnetic Field in Time
4.1 The young solar photosphere: Large, polar spots
Stellar photospheres provide the crucial interface between the region of magnetic field generation in the stellar interior and the extended outer magnetic fields in the corona and in interplanetary space. Distribution and size of photospheric magnetic features are thought to reflect the location of the magnetic dynamo in the stellar interior; the study of photospheres of young, active solar analogs is therefore important for a closer understanding of the dynamo operating under more extreme conditions, but it of course also gives the boundaries for the extended magnetic-field distribution in the overlying chromosphere, corona, and the stellar wind.
4.1.1 Doppler imaging of young solar analogs
The most advanced (indirect) imaging technique to map magnetic structure in stellar photospheres is Doppler imaging that uses deformations in spectral-line profiles to map starspots (Vogt and Penrod, 1983).
Surface imaging using Doppler reconstruction methods or spot modeling has been performed for several young, active solar analogs. Figure 1 shows views of the three examples discussed below. The colors code for temperature (from http://www.aip.de/groups/activity/DI/maps/).
Three temperature maps of young, active solar analogs, derived from Doppler imaging. From left to right: HD 171488 (P = 1.34 d; Strassmeier et al. 2003), HII 314 (P = 1.47 d; Rice and Strassmeier 2001), and EK Dra (P = 2.7 d; Strassmeier and Rice 1998) (see also http://www.aip.de/groups/activity/DI/maps/), reprinted with permission.
The photosphere of EK Dra has been extensively mapped using spot modeling (Järvinen et al., 2005) and Doppler imaging techniques (Strassmeier and Rice, 1998). Doppler images show spots both close to the visible pole but also near the equator, the dominant feature being located at latitudes of 70–80 deg (Strassmeier and Rice, 1998). This is supported by radial-velocity variations (König et al., 2005). The polar region of EK Dra is, however, less pronounced than in more active (binary) stars, perhaps indicating a trend toward lower-latitude spots for less active stars, as predicted by the Schüssler et al. (1996) theory of Coriolis-force driven magnetic flux tubes that converge to the pole for very rapid rotators (see below).
The Pleiades G dwarf HII 314 (P = 1.47 d) has been Doppler-imaged by Rice and Strassmeier (2001). Again, high-latitude and polar spots are visible. The still younger, “infant Sun” HD 171488 = V889 Her (P = 1.34 d, age = 30 Myr), a star in its last stage of evolution toward the ZAMS, shows very prominent polar spots and various high-latitude dark features (Strassmeier et al., 2003). Further Doppler maps have been presented for the early G-type ultra-fast rotators He 520 (P = 0.49 d) and He 699 (P = 0.61 d). Again, apart from the prominent polar spots, there is a definitive band of low-latitude (l ≲ 30–40 deg) spots on these stars as well (Barnes et al., 1998).
Although these surface spot distributions vary significantly between young solar analogs, there is agreement with regard to high-latitude magnetic activity on all of them (Rice and Strassmeier, 2001; Strassmeier et al., 2003).
The most recent Doppler technique uses spectropolarimetric observations of lines to apply Zeeman-Doppler Imaging (ZDI), which results in maps of radial, azimuthal, and meridional magnetic fields. Successful application to solar analog stars have been presented by Marsden et al. (2006) and Catala et al. (2007); excellent ZDI maps have also been derived for the somewhat cooler, young early-K star AB Dor (Donati et al., 2003b), and put into context with coronal X-rays (Jardine et al., 2002c; McIvor et al., 2003; Hussain et al., 2007). ZDI images (Figure 2) have shown non-solar magnetic features such as high-latitude “rings” of azimuthal (toroidal) field (Donati et al., 2003b; Marsden et al., 2006; Catala et al., 2007), possibly suggesting that the responsible magnetic dynamo is located close to the surface (a “distributed dynamo”) rather than (only) near the tachocline where azimuthal fields are expected for αΩ-type dynamos. The field distribution and orientation also serves as an important diagnostic to study and explain spot lifetimes based on numerical studies (Işik et al., 2007).
Zeeman-Doppler images of the rapidly rotating early G dwarf HD 171488, showing, in polar projection, spot occupancy (upper left), the radial magnetic field (upper right), the azimuthal magnetic field (lower left — note the ring-like high-latitude feature), and the meridional magnetic field (lower right) (from Marsden et al. 2006, reprinted with permission of Blackwell Publishing).
4.1.2 Polar spots
Why are there polar spots in magnetically active stars? Schüssler and Solanki (1992) and Schüssler et al. (1996) suggested that strong Coriolis forces act on magnetic flux bundles that rise from the dynamo region at the boundary between the radiative core and the convective envelope of the star. This force would deflect rising flux to higher altitudes although, given the size of the radiative core, the maximum latitude would probably be no more than about 60 degrees. A parameter study confirms these findings systematically, with flux emergence latitudes increasing with i) rotation rate, ii) decreasing stellar mass (i.e., smaller radiative core radii), and iii) decreasing age; a fraction of the flux tubes will, however, also erupt in near-equatorial regions (Granzer et al., 2000). To produce truly polar spot regions, additional latitudinal transport of flux tubes is still required. A possibility is an additional pole-ward slip of a segment of a flux ring in the stellar interior after the eruption of flux at mid-latitudes in another segment of the same ring (Schüssler et al., 1996).
Alternatively, Schrijver and Title (2001) explored migration of surface magnetic fields toward the poles in a model developed by Schrijver (2001). Here, magnetic bipoles are injected randomly. These flux concentrations migrate pole-ward in a meridional flow and are subject to differential rotation. The bipoles can interact, i.e., fragment, merge, or cancel. The magnetic cycle is simulated by periodically varying the injection latitudes. Schrijver and Title (2001) simulated a star with a bipole injection rate 30 times higher than the present-day Sun, corresponding to a solar analog with a rotation period of 6 d, i.e., an age of a few 100 Myr. The differential rotation profile was assumed to be identical to the present-day Sun’s, and so was the length of the activity cycle (11 yr). In the present-day Sun, the pole-ward migration of the trailing flux in a bipole cancels with existing high-latitude flux of opposite polarity relatively rapidly. In the simulations of the active star, however, the magnetic concentrations contain more flux, resulting in slower diffusion and a longer lifetime before cancellation. The result of these simulations is that, first, there are strong magnetic features accumulating in the polar regions, and second, nested magnetic rings of opposite polarity form around the pole (Figure 3). These are suggestive sites of chromospheric and coronal interactions, perhaps leading to strong coronal heating and flares in these polar regions. As described above, ZDI images indeed provide evidence for high-latitude “rings” of azimuthal (toroidal) field (e.g., Marsden et al. 2006, Figure 2).
Simulations of surface magnetic fields for a star like the Sun (left) and an active star with a bipole emergence rate 30 times higher (right). Various snapshots during the activity cycle are shown (from top to bottom). Note the concentration of magnetic flux in rings of opposite polarity around the pole of the active star (from Schrijver and Title, 2001, reproduced by permission of AAS).
Observationally, the picture is more complicated. In contrast to these simulations and also in contrast to the solar picture, Doppler images of very active, young stars (Figure 1) show intermingling of opposite polarities in longitude also at high latitudes (Mackay et al., 2004). Such features can indeed be reproduced if the latitudes of flux emergence are shifted poleward, to 50–70 degrees, and the meridional flow be made faster (Mackay et al., 2004; Holzwarth et al., 2006). The first modification is of course suggested from the Schüssler et al. (1996) theory.
The structure of polar spots (unipolar, multiple bi-polar regions, or nested rings of different polarity) is indeed also very important for the large-scale coronal field; unipolar magnetic spots suggest the presence of more polar open-field lines, therefore concentrating strong coronal X-ray emission to more equatorial regions, but also reducing the efficiency of angular momentum removal by the magnetized wind due to the smaller lever arm compared to equatorial winds (McIvor et al., 2003).
4.2 Coronal structure of the young Sun
Stellar magnetic fields are anchored in the photospheres, but they can unfold into large, interacting, complicated structures in the solar corona and may reach out into the surrounding “interplanetary” space. Mapping the true 3-D structure of outer stellar atmospheres has therefore been an important goal of stellar coronal physics, but a challenging one. Apart from the complications in inferring the 3-D structure of an optically thin gas that is not spatially resolved by present-day telescopes, the emitting regions (e.g., in X-rays) may not be identical to what we would like to map as “magnetic structure”; further, strong variability in coronal regions on short time scales may make “imaging” challenging. Methods to infer coronal structure include:
-
1.
reconstruction of magnetic features from light curves that are rotationally modulated (at radio or X-ray wavelengths);
-
2.
eclipse image reconstruction for eclipsing binaries (radio and X-rays);
-
3.
theoretical models of magnetic loops, using measurable quantities such as emission measures and temperatures as input (X-rays); specific models have been developed for flaring magnetic loops;
-
4.
implications for coronal structure based on electron density measurements in X-ray spectra;
-
5.
direct imaging using interferometric techniques at radio wavelengths.
Most of these methods are applicable to various types of stars, but results are overall ambiguous. I will not review all aspects of stellar coronal structure (see Güdel, 2004) but concentrate on results that have been obtained — at least in part — specifically for young solar analogs.
4.2.1 Magnetic loop models and active regions
In the simplest approach, let us assume that the observed X-ray luminosity LX is produced by an ensemble of identical magnetic coronal loops with characteristic half-length L, surface filling factor f, and an apex temperature T used for the entire loop; then, on using the Rosner-Tucker-Vaiana (RTV, Rosner et al. 1978) loop scaling law and identifying LX = ∊V where ∊ is the volumetric heating rate (in erg cm−3 s−1), we obtain
This relation can only hold if L is smaller than the pressure scale height. Based on this expression, the luminous, hot plasma component in magnetically active stars seems to invariably require either very large, moderate-pressure loops with a large filling factor, or solar-sized high-pressure compact loops with a very small (< 1%) filling factor (Giampapa et al., 1985; Stern et al., 1986; Schrijver et al., 1989; Giampapa et al., 1996; Güdel et al., 1997b; Preibisch, 1997; Sciortino et al., 1999).
Schrijver et al. (1984) modeled T and the emission measure, EM (= nenHV, where ne and nH are the electron and hydrogen number densities, and V is the volume) of a sample of coronal sources based on RTV loop models and found several trends: i) inactive MS stars such as the Sun are covered to a large fraction by large-scale, cool (2 MK) loops of modest size (0.1 R*); ii) moderately active dwarfs are dominated by very compact, high-density, hot (≈ 20 MK) loops that require high heating rates (up to 20 times more than for solar compact active region loops); iii) the most active stars may additionally form rather extended loops with heights similar to R*.
Similar studies of loop models varied in their results, although for magnetically active stars, most authors reported results that require hot, compact, high-pressure loops (up to several 100 dyn cm−2), somewhat reminiscent of flaring loops (Stern et al., 1986; Giampapa et al., 1996; Maggio and Peres, 1997; Ventura et al., 1998; Sciortino et al., 1999). The hypothesis that the hottest plasma in magnetically active stellar coronae does not form in static loops but in flaring active regions will be encountered again — see Section 5.8.
If the Sun were entirely covered with active regions, the X-ray luminosity would amount to only ≈ (2–3) × 1029 erg s−1 (Vaiana and Rosner, 1978; Wood et al., 1994), short of LX of the most active solar analogs by one order of magnitude. But the X-ray emission measure distributions of such active stars show excessive amounts of plasma around 10–20 MK (Güdel et al., 1997b), which incidentally is the typical range of solar flare temperatures. This again led to the suggestion that the high-T emission measure is in fact due to the superposition of a multitude of temporally unresolved flares (see Section 5.8).
4.2.2 Inferences from coronal density measurements
Comprehensive surveys of stellar coronal electron density (ne) measurements based on X-ray spectroscopic line-flux ratios were presented by Ness et al. (2004) and Testa et al. (2004), including a sample of active solar analogs. These studies concluded that the surface filling factor (derived from the emission measure, the measured ne, and a realistic coronal scale height) of magnetic loops containing cool X-ray emitting material increases from inactive to moderately active stars but then “saturates” at levels of about ten percent. In the most active stars, hot coronal loops are added, with a sharply increasing filling factor, thus probably filling the volume left between the cooler coronal magnetic loops. Observations of rotational modulation in very active solar analogs suggests, however, that the coronal volume filling remains significantly below 100% (see Section 4.2.3 below).
4.2.3 Inferences from rotational modulation
Inhomogeneous coronae may reveal signatures in light curves as the star rotates, although success of this method has been moderate given that coronal features evolve on time scales shorter than one rotation (e.g., owing to flares). Two young, near-ZAMS solar analogs have shown clear signatures of X-ray rotational modulation (EK Dra, Güdel et al. 1995c, and 47 Cas B, Güdel et al. 1995a), pointing to a filling factor below unity. This is unexpected because such stars are in the empirical X-ray saturation regime that has often been suggested to be due to complete filling of the surface with X-ray bright coronal magnetic loops (see Section 5.5 below). EK Dra also showed evidence for radio rotational modulation. The depth and length of the modulation (Figure 4a) constrains the X-ray coronal height, and also the electron densities to ne > 4 × 1010 cm−3, in agreement with spectroscopic measurements (Ness et al., 2004). This leads to the conclusion that much of the emitting material is concentrated in large “active regions”.
Because the X-ray luminosity in very rapidly rotating, “supersaturated” stars (Section 5.5.1) is below the empirical maximum, rotational modulation would give important structural information on the state of such coronae. A deep modulation in the young solar analog VXR45 (Figure 4b) suggests that extreme activity in these stars is again not due to complete coverage of the surface with active regions (Marino et al. 2003a).
4.2.4 Inferences from eclipses
Most binary systems that produce coronal eclipses are close binaries and the components are therefore in no ways similar to the young Sun. A remarkable exception is the relatively wide binary α CrB. Its X-ray active, young (age of few 100 Myr) solar analog of spectral type G5 V is totally eclipsed once every 17 days by the optical primary, an A0 V star that is perfectly X-ray dark. Other parameters are ideal as well, such as the non-central eclipse, the eclipse time-scale of a few hours, and the relatively slow rotation period of the secondary. Eclipse observations obtained by ROSAT (Schmitt and Kürster, 1993) and by XMM-Newton (Güdel et al., 2003a) were used to reconstruct projected 2-D images of the X-ray structure. They consistently reveal patches of active regions across the face of the G star; not much material is found significantly beyond its limb (Figure 5). The structures tend to be of modest size (≈ 5 × 109 cm), with large, X-ray faint areas in between, although the star’s luminosity exceeds that of the active Sun by a factor of ≈ 30. These observations imply moderately high densities in the emitting active regions, and both studies mentioned above yielded average electron densities in the brightest active regions of a few 1010 cm−3. The picture of active coronae consisting of features similar to solar active regions thus seems to hold also for intermediately active, young solar analogs.
Light curve and image reconstruction of the A + G binary a CrB. The left panel shows the light curve from observations with XMM-Newton, the right panel illustrates the reconstructed X-ray brightness distribution on the G star. The axes are such that the larger, eclipsing A-type star moves from left to right parallel to the x-axis, i.e., the polar axis of the orbit is parallel to the y axis. The diameter of the star (outlined by a faint circle) is 0.9 solar diameters or 1.25 × 1011 cm, corresponding to ≈ 365 µ arcsec at a distance of 22.9 pc (after Güdel et al., 2003a, © Springer Verlag, reprinted with permission).
4.2.5 Photospheric-field extrapolation to the corona
Information on coronal structure can also be derived indirectly from surface Zeeman-Doppler images as developed for and applied to the stellar case by Jardine et al. (2002a), Jardine et al. (2002b), Hussain et al. (2002), and Hussain et al. (2007) and further references therein. Jardine et al. (2002a) and Jardine et al. (2002b) explored potential field extrapolation, while Hussain et al. (2002) extended the models to include some form of currents in force-free fields.
Such models also require specification of the base thermal pressure of the plasma with respect to the local magnetic pressure, and some cutoff of the corona at locations where the thermal pressure might open up the coronal field lines. They can successfully recover, at least qualitatively, the total X-ray emission measure, the average electron density, and the low level of rotational modulation observed on very active, young stars such as AB Dor. The X-ray rotational modulation is to a large extent suppressed by the highly complex coronal structure, involving both very large magnetic features and more compact loops anchored predominantly at polar latitudes.
Schrijver and Aschwanden (2002) used the model of surface magnetic-field development devised by Schrijver (2001) and Schrijver and Title (2001) (Section 4.1 above) to extrapolate surface magnetic fields into the corona, assuming a potential-field approach. The resulting magnetic structure is illustrated in Figure 6 for a solar-activity star, and two examples with a 10fold and a 30fold magnetic injection rate (the latter corresponding to a solar analog with an age of a few 100 Myr). Near cycle minimum, the coronae of the active stars are dominated by a large-scale dipolar field although the low-activity example also shows compact active regions, more so than the active stars. At activity maximum, the active stars show magnetic-field arcades between the polar rings of opposite polarity, weakening the contribution from the global dipole components. Not all of these loops will be X-ray bright, however; the loop brightness depends on its heating rate, which in turn depends on the mode of coronal heating of a given magnetic loop (see Schrijver and Aschwanden 2002 for further details).
Magnetic-field geometry of a corona of a solar analog. From left to right: present solar activity, 10fold higher activity, 30fold higher activity. The panels from top to bottom show configurations at different phases of the activity cycle (0.00 = minimum, 0.16, 0.33, 0.49 ≈ maximum, 0.65, and 0.82, respectively). Only field lines with chromospheric footpoint field strengths between 50 G and 600 G are shown. Red and green curves show loops for which the expansion between 10,000 and 30,000 km is less than a factor of 4 and 2, respectively (from Schrijver and Aschwanden, 2002, reproduced by permission of AAS).
4.2.6 Summary on coronal structure
Despite numerous, complementary approaches to the study of coronal structure, the results appear to be inconclusive. Compact active regions are inferred from (and required by) the presence of rotational modulation, and field extrapolation and numerical models suggest compact regions as well. Extended, global fields are more difficult to infer, and this is the consequence of two observational biases rather than implying the absence of such structures. First, most observational methods (e.g., X-ray eclipse and rotational modulation) are insensitive to large structures. Second, the pressure scale height of typical coronal plasma is less than one stellar radius for solar analogs. The ne2 dependence of X-ray emission will therefore bias X-ray loop detection toward low heights. There is, nevertheless, evidence for large-scale magnetic fields on young, active stars, from two directions: surface field extrapolation based on observed spot features or based on numerical models of flux transport (Section 4.2.5) imply the presence of structures resembling global dipole components; and spatially resolved radio observations of active stars indeed do show very extended magnetic structures (predominantly above the polar regions; Benz et al. 1998; Mutel et al. 1998), although such evidence has not yet been demonstrated for young solar analogs. In summary, then, observational evidence and model simulations point to the presence of both compact active regions and extended magnetic structures in the young Sun. The relative proportions are likely to relate to the distribution of magnetic field on the stellar surface, as in the models presented by Schrijver and Aschwanden (2002).
There is clear evidence that the surface magnetic filling factor increases with increasing activity (and decreasing rotation period), both from observations (e.g., Montesinos and Jordan, 1993) and theoretical and modeling studies (Montesinos and Jordan, 1993; Fawzy et al., 2002); in contrast, the photospheric magnetic field strength is thought to be primarily restricted by pressure equilibrium with respect to the ambient gas pressure, i.e., the field strength is primarily dependent on spectral type, although a weak activity dependence is also present (e.g., Montesinos and Jordan, 1993). The higher filling factors lead to less expansion of photospheric/chromospheric flux tubes because the tubes merge with adjacent tubes (Cuntz et al., 1999). Therefore, toward more active stars, coronal magnetic fields interact progressively more frequently due to their denser packing. A higher rate of large flares is a consequence. Since flares enhance the electron density along with the temperature, stars with a higher activity level should reveal a predominance of hotter structures (Güdel et al., 1997b). Such a trend is observationally well supported; as further described in Section 5.5.2 below, coronae at higher activity levels are systematically hotter.
4.3 Activity cycles in the young Sun
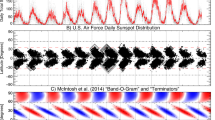
Records of sunspot numbers back over several hundred years show a near-cyclic modulation that has turned out to be a central challenge for dynamo theories. The activity period between two successive spot maxima is approximately 11 years; because the magnetic polarity reverses after one period, the full magnetic cycle amounts to 22 yr. Activity cycles corresponding to the 11 yr solar cycle have been found on many cool stars, mostly as a result of the Mount Wilson HK project (Baliunas et al., 1995) that has collected a continuous data stream of the chromospheric Ca ii H & K line flux diagnostic for many stars over several decades. A subset of stars appear to lack such cycles, however, and very active stars tend to exhibit an irregular rather than a cyclic mode of variability (Hempelmann et al., 1996). An alternative method for finding activity cycles on magnetically active stars is the identification of cycles in the starspot coverage.
4.3.1 Starspot cycles of solar analogs
Messina and Guinan (2002) specifically studied starspot cycles of stars from the “Sun in Time” program. Activity cycles are found in all of them, with periods ranging from 2.1 yr to 13.1 yr. A comparison with the more comprehensive survey and the theoretical interpretations presented by Saar and Brandenburg (1999) confirms the presence of two or three branches: i) inactive solar analogs show cycles about 100 times longer than the rotation period, P; ii) active stars reveal cycles 200–600 times longer than P; iii) and “super-active” stars show cycles about 4 order of magnitude longer than P (Figure 7a). Among G-type stars, only EK Dra appears to be compatible with the third class (Messina and Guinan 2002).
Left (a): Ratio between activity-cycle frequency and rotation frequency plotted vs. the inverse Rossby number, mostly for solar analogs. Three theoretical branches (“inactive”, “active”, and “super-active”) are shown by solid lines. Key to the labels: A = BE Cet, B = κ1 Cet, C = π1 UMa, D = EK Dra, E = HN Peg, F = DX Leo (K0 V), G = AB Dor (KO V), H = LQ Hya (K2 V) (from Messina and Guinan 2002). Right (b): Amplitude of V-band variability as a function of the inverse Rossby number. The labels are as for the left panel (from Messina and Guinan 2002, reprinted with permission).
The brightness amplitude increases with increasing inverse Rossby number (i.e., increasing rotation rate for constant turnover time), indicating that spots produce progressively more modulation toward higher activity levels (Figure 7b). A plateau is suggested for the most active stars, indicating a saturation effect when spots cover a large fraction of the stellar surface (Messina and Guinan, 2002).
The standard near-ZAMS solar analog, EK Dra, has been an important target for cycle studies. Dorren and Guinan (1994a and Dorren and Guinan (1994b) showed that its long-term photometric variations by ≈ 0.07 mag are consistent with a period of about 12 yr. Variations compatible with this time scale are also found in Ca ii HK, Mg ii h and k, and the ultraviolet C iv, C ii, and He ii fluxes (Dorren and Guinan, 1994a), and in X-rays (see Section 4.3.2 below). The spot periodicity has been confirmed by Messina and Guinan (2002) although their best estimate for the period is 9.2 ± 0.4 yr (Figure 8). The star is optically faintest when chromospheric and transition-region activity is highest. On top of this cyclic behavior, there is a long-term trend in the optical light, namely a decline of the blue light by 0.0017 ± 0.0004 mag yr−1 for an investigated time span of 35 yr (Fröhlich et al. 2002; see also Messina and Guinan 2003 and Järvinen et al. 2005). Further, two active longitudes shift in phase in concert with the activity cycles (Järvinen et al., 2005). The dominant spot concentration switches between the two preferred longitudes with a “flip-flop” cycle of about 4–4.5 yr. These features suggest the coexistence of axisymmetric and non-axisymmetric dynamo modes (Berdyugina et al., 2002).
V band photometric time series and sinusoidal (plus long-term trend) fits for EK Dra (left, a) and π1 Cet (right, b) (from Messina and Guinan, 2002, reprinted with permission).
Messina and Guinan (2003) have studied photometric periods from spot modulations, arguing that — as in the solar case — the varying dominant latitudes of the spots should induce a periodic variation of the rotation period in phase with the activity cycle, because of differential rotation. These correlated period variations are indeed present in solar analogs (Messina and Guinan, 2003), although two patterns are seen: either, the period decreases as the cycle proceeds (solar behavior), or it increases (anti-solar behavior). The former effect is due to spot migration toward the equator where the surface rotation is faster. The second effect could be due to pole-ward acceleration of rotation at higher latitudes where active stars predominantly show spots, while the individual spots may still migrate toward the equator. Messina and Guinan (2003), however, suggest that high-latitude spots migrate toward the (slower-rotating) pole, which induces an anti-solar behavior in particular for stars with small inclination angles. This model is preferred because correlations involving the fractional variation in the rotation period show the same behavior for the two subclasses. Support for the model comes from simulations of magnetic-field migration toward the poles in very active stars, as performed by Schrijver and Title (2001) (Section 4.1.2). Specifically, Messina and Guinan (2003) have found a power-law relation between the rotation-period variation, ΔP, and the average rotation period, P, of the form (see Figure 9a)
Left (a): Rotation period variation as a function of the mean rotation period, for a sample of young solar analogs. The solid line is a power-law fit to the entire sample also containing early K stars, while the dotted line is a fit to the G-star sample only. Key to the labels: A = BE Cet, B = κ1 Cet, C = π1 UMa, D = EK Dra, E = HN Peg, F = DX Leo (K0 V), G = AB Dor (K0 V), H = LQ Hya (K2 V), I = 107 Psc (K1 V), L = 61 UMa (G8 V), M = β Com, N = HD 160346 (K3 V), O = 15 Sge, S = Sun (from Messina and Guinan, 2003). Right (b): The activity cycle frequency is shown as a function of the relative surface differential rotation amplitude, ΔΩ/Ω. Vertical dotted lines connect multiple cycles. Three different branches are indicated by the solid curves (from Messina and Guinan, 2003, reprinted with permission).
Further, a tight correlation is found between differential rotation, parameterized by ΔΩ/Ω, and the activity cycle frequency, ωcycl,
suggesting that ΔΩ/Ω is a key parameter controlling the duration of the activity cycle (see Figure 9b).
Differential rotation has also been measured on other very active stars (e.g., Donati et al. 2003a), among them a solar-like post-T Tauri star (Donati et al., 2000), in particular based on Doppler imaging techniques (Section 4.1.1). Differential rotation was found to be solar-like in these examples, although time-variable, which may hint at dynamo processes that periodically convert magnetic into kinetic energy and vice versa (Donati et al., 2003a).
4.3.2 X-ray cycles of solar analogs
Given the much stronger variability in the outer, coronal layers of a stellar atmosphere, an activity cycle may be more easily identified in the X-ray or radio domains. However, such cycles have eluded detection until recently because no appropriate program had been carried out for sufficiently long periods. A few notable examples have now been reported from X-ray monitoring.
First tentative evidence for an X-ray cycle came from the young solar analog EK Dra that was monitored between 1990 and 2000 using ROSAT, ASCA, and XMM-Newton. Initial results were presented in Dorren et al. (1995), a more complete time series has been published by Güdel (2004). There is a suggestive anti-correlation between X-ray flux and photospheric brightness (the star is optically brightest at its activity minimum), although the total X-ray luminosity varies by no more than a factor of ≈ 2–3.
Other reports refer to inactive solar analogs and K-type stars. Hempelmann et al. (2003) and Hempelmann et al. (2006) have reported a correlation between X-ray luminosity and the Ca H & K S index for the two K-type stars 61 Cyg A and B. Both show chromospheric modulations on time scales of about 10 years, one being regular and the other irregular. A gradual X-ray modulation was also seen during a time span 2.5 years in the G2 V star HD 81809, although there seems to be a phase shift by about 1 year with respect to the Ca cycle (Favata et al., 2004).
Additional information on potential coronal activity cycles has been collected from multiple observations of young open clusters and star-forming regions. Generally, such samples indicate that magnetically active, solar-like stars mostly lack well-expressed X-ray cycles unless their cycle-induced variability is no more than a factor of ≈ 2 (Gagné and Caillault, 1994; Gagné et al., 1995a, b; Stern et al., 1994, 1995; Micela et al., 1996; Sciortino et al., 1998; Grosso et al., 2000; Marino et al., 2002, 2003b).
5 Solar Radiation and Wind in Time
The Sun’s magnetic activity has steadily declined throughout its MS lifetime. This is a direct consequence of the declining dynamo as a star spins down by losing angular momentum through its magnetized wind. The distinguishing property of magnetic activity in the context of stellar radiation is excess emission beyond the photospheric thermal spectrum. Because magnetic activity expresses itself by releasing energy, the most relevant radiation signatures of magnetic activity are at wavelengths shorter than the dominant optical light, i.e., at UV wavelengths (emission from active regions in the chromosphere and the transition region), at far-ultraviolet wavelengths (from the transition region), and the extreme-ultraviolet and X-ray ranges (from coronal active regions). Apart from electromagnetic radiation, particles are accelerated as a consequence of magnetic energy release. These particles are either measured in-situ in the solar system, or can be indirectly inferred from non-thermal radio emission. The solar wind of course is another particle stream that requires acceleration related to open magnetic fields.
The present section summarizes our knowledge of these various photon and particle losses from the “Sun in Time”, contrasting the young Sun’s behavior with the contemporaneous Sun by describing the long-term evolution of the radiation and wind signatures. High-energy emission may have been much more important in heating and ionizing planetary atmospheres or, at still earlier stages, circumstellar accretion disks. To understand the young Sun’s influence on its environment, the spectral output in lines and the continuum must be observed for solar analogs with different rotation periods (corresponding to different magnetic activity levels) across the ultraviolet-to-X-ray range. This “Sun in Time” program, introduced in Section 3, has been conducted during the past decade by various groups (e.g., Dorren and Guinan 1994a; Dorren et al. 1995; Güdel et al. 1994, 1995b, 1997b; Ayres 1997; Gaidos et al. 2000; Guinan et al. 2003; Ribas et al. 2005; Telleschi et al. 2005).
I will start with the solar wind that is responsible for the declining solar spin rate, which in turn controls the dynamo; the latter leads to surface activity, and hence to radiation that is again changing on evolutionary time scales. I will discuss consequences of the elevated high-energy output of the young Sun in the subsequent chapters.
5.1 The solar wind in time
Stellar magnetic winds are a crucial consequence of “stellar activity” but their detection in solar analogs is very difficult. Although the wind formation and acceleration mechanisms are still not conclusively understood in the Sun, it is clear that magnetic fields play a major role, be it for acceleration of the wind, for its heating, or for guiding the wind at least out to the Alfvén radius. A close relation between wind and magnetic corona is obvious (Parker, 1958), the former being related to open magnetic field lines and the latter predominantly to closed magnetic structures.
The best — albeit indirect — proof of the presence of magnetized winds is the spin-down of convective stars on the main sequence as such a wind carries away angular momentum from the star. I will discuss this in Section 5.2.
Direct measurement of ionized winds from solar-like stars has not yet succeeded; potential detection methods include the measurement of thermal radio emission from the winds (Lim and White, 1996; Gaidos et al., 2000), and signatures of charge exchange in X-ray spectra (Wargelin and Drake, 2001). Lim and White (1996) and van den Oord and Doyle (1997) gave upper limits to the mass-loss rates of Ṁw ≈ 10−12 M⊙ yr−1 for “solar-like” winds with T ≈ 1 MK emanating from M-type dwarfs. Gaidos et al. (2000) derived upper limits toṀ for three young solar analogs (π1 UMa, κ1 Cet, and β Com), finding Ṁw ≲ (4–5) × 10−11 M⊙ yr−1.
The most promising approach to date is an indirect method making use of Lyα absorption in so-called “astrospheres”; the latter are suggested to be a consequence of interactions between stellar winds and the interstellar medium (ISM). This subject has been extensively reviewed in the Living Reviews in Solar Physics article by Wood (2004); I will therefore only briefly summarize the essential results.
Solar/stellar winds collide with the interstellar medium, forming, with increasing distance from the star, a termination shock (where the wind is shocked to subsonic speeds), a heliospause (separating the plasma flows from the star and the ISM), and the bow shock (where the ISM is shocked to subsonic speeds). The heliosphere is permeated by interstellar H I with T ≈ (2–4) × 104 K (Wood et al., 2002). Much of this gas is piled up between the heliospause and the bow shock, forming the so-called “hydrogen wall” that can be detected as an absorption signature in the Lyα line. The excess absorption from the Sun’s own hydrogen wall is, due to the deceleration of the ISM relative to the star, redshifted, while that of other astrospheres is blueshifted.
The measurable absorption depths are compared with results from hydrodynamic model calculations (Wood et al., 2002, 2005). The important point is that the amount of astrospheric absorption should scale with the wind ram pressure, Pw ∝ ṀwVw, where Vw is the (unknown) wind velocity (Wood and Linsky, 1998). The latter is usually assumed to be the same as the solar wind speed. From this, Ṁw is derived.
The Sun’s hydrogen wall was detected in ultraviolet spectra by Linsky and Wood (1996), and an equivalent astrosphere around α Cen A and B was interpreted by Gayley et al. (1997). Further important wind mass loss measurements based on this method have been presented by Wood et al. (2002) (and references therein) and Wood et al. (2005). A systematic study of all derived mass-loss rates shows that \(\dot{{\cal M}}_{\rm{w}}\) per unit stellar surface correlates with the stellar X-ray surface flux,
(an equivalent relation therefore holds between Ṁw and LX); using the activity-age relation (Section 5.5.1), one finds
(Wood et al., 2005). These two laws indicate that stellar-wind mass loss is — in principle — a genuine activity indicator, the mass-loss being higher in young, magnetically active stars. Extrapolating the above law up to the X-ray saturation limit (FX ≈ 2 × 107 erg cm−2 s−1) would suggest \(\dot{{\cal M}}_{\rm{w}}\) (or Ṁw) of the youngest solar analogs to be about a thousand times higher than the present-day solar mass loss (Ṁ⊙ ≈ 2 × 10−14 M⊙ yr−1; e.g., Feldman et al. 1977). However, this power-law relation breaks down for the most active stars with FX ≳ 8 × 105 erg cm−2 s−1 (Wood et al. 2005, Figure 10). Stars at this limit show Ṁw about 100 times the present solar value, while Ṁw drops toward higher activity levels to about 10 times the solar value. The reason for this breakdown between X-ray activity and wind-mass loss may be related to the appearance of high-latitude active regions (spots) in the most active stars (Section 4.1.2); if the magnetic field becomes more akin to a global dipole, then wind escape may be inhibited in such stars (Wood et al., 2005).
Left (a): Mass-loss rates per unit surface area vs. stellar X-ray surface fluxes. MS stars are shown by filled circles. The trend for inactive stars (shaded area) is not followed by more active stars. — Right (b): Inferred mass-loss history of the Sun. Again, the trend shown for inactive stars (shaded area) breaks down for the most active stars (from Wood et al., 2005, reprinted with permission of AAS).
5.2 The solar spin in time
Stellar magnetic activity is fundamentally determined by the stellar rotation period, as I will further discuss in, e.g., Section 5.5.1. Because the magnetized stellar winds transport angular momentum away from the star, a MS solar analog spins down with age. The rate of change of angular momentum is related to the mass loss rate, the spin rate, and the Alfvén radius, RA. One finds
where m is between 0 and 1 depending on the magnetic field geometry (Weber and Davis, 1967; Mestel, 1984; Stepień, 1988). One further has to couple the average surface magnetic field strength, B0, with Ω. This relation is essentially determined by the magnetic dynamo but can reasonably be parameterized as B0 ∝ Ωp with p probably being 1 or 2 (Mestel, 1984). The approximately observed Ω ∝ t−1/2 law (“Skumanich law”, Skumanich 1972, see below) is recovered for a thermal wind with p = 1 (Mestel, 1984), i.e., a linear dependence between average surface magnetic field strength and rotation rate. For another detailed study of this problem, see Stȩpień (1988).
Empirically, for solar analogs one finds
(Dorren et al., 1994), where t6 is the age in Myr after arrival on the ZAMS. Equivalently, for the rotational (equatorial) velocity and for the rotation rate (for constant R),
(Ayres, 1997) — see Figure 11. These equations imply a decrease in rotation period from ZAMS age to the end of the MS life of a solar analog by a factor of about 20.
Relation between rotational velocity, υ, and age for solar analogs. The diamond-shaped areas show the large scatter of υ in young clusters, before rotational convergence has been attained (from Ayres, 1997, reprinted with permission).
At ages of approximately 100 Myr or younger, the stellar rotation period is not a function of age but of the PMS history such as the history of circumstellar-disk dispersal (e.g., Soderblom et al. 1993, see Figure 11). Once the inner disk disappears, the lack of magnetic locking via stardisk magnetic fields and the contraction of the star toward the MS will spin-up the star and thus determine the initial rotation period on the ZAMS. For example, the rotation periods of G-type stars in the Pleiades and the α Per clusters still scatter considerably, ranging from less than a day (the so-called ultra-fast rotators) to many days (Soderblom et al., 1993; Stauffer et al., 1994; Randich et al., 1996), while they (and therefore the stellar X-ray luminosities, see Section 5.5) have converged to a nearly unique value at the age of the UMa Moving Group (300 Myr) or the Hyades (600–700 Myr; see Soderblom et al. 1993; Stern et al. 1995).
5.3 The ultraviolet Sun in time
Ultraviolet excess emission from late-type stars originates in magnetic chromospheric and transition-zone regions that have been heated to temperatures of order 104–105 K. Magnetic activity thus makes the UV spectra rich in diagnostics (see Figure 12; from Ribas et al. 2005). Dorren and Guinan (1994a) and Ayres (1997) have studied the evolution of ultraviolet (UV) line fluxes in detail, based on spectral measurements obtained by IUE. Ribas et al. (2005) extended these investigations to the “Sun in Time” sample and included spectral information from HST. The bulk of the UV flux in the region shortward of 1700 Å is in emission lines while the continuum is negligible. Emission lines include those of O i λ1304, C ii λ1335, Si iv λ1400, C iv λ1550, He ii λ1640, and C i λ1657.
Extracts of UV spectra of solar analogs with different ages. All spectral fluxes have been transformed to irradiances at 1 AU from the star. The spectra have been shifted along the ordinate, by multiples of 0.2 erg s−1 cm−2 Å−1 (from Ribas et al., 2005, reproduced by permission of AAS).
Dorren et al. (1994) studied the activity-rotation relationship for Mg ii and C iv for solar analogs in the “Sun in Time” sample. They found (I also include their X-ray result for comparison, to be discussed further in Section 5.5.1 below)
Emission from hotter regions is more strongly dependent on rotation. Because P decreases with age, harder emission decays more rapidly than softer emission. I will return to this point in more detail in Section 5.6.
5.4 The far-ultraviolet Sun in time
Guinan et al. (2003) have used the FUSE satellite to probe the transition regions of the “Sun in Time” stars by measuring fluxes of key lines in the 920–1180 Å region. An example is shown in Figure 13. The individual flux measurements have been given by Ribas et al. (2005) and are listed below in Table 4 as irradiances for a distance of 1 AU. Measurements pertaining to the intermediately active Sun are also given (see Ribas et al., 2005, for references).
Extracts of FUV spectra of solar analogs with different ages. The region of the O VI doublet is shown. All spectral fluxes have been transformed to irradiances at 1 AU from the star. The spectra have been shifted along the ordinate, by multiples of 1 erg s−1 cm−2 Å−1 (from Ribas et al., 2005, reproduced by permission of AAS).
These line fluxes have been used to construct surface flux-rotation relations for solar analogs (Guinan et al., 2003). For essentially the entire rotation range of MS solar analogs, the line fluxes follow power-law relations, F ∝ P−α, with α ≈ 1.8. This power-law decay is steeper than for chromospheric lines (Section 5.3), but shallower than for coronal fluxes or luminosities (recalling that the stellar radii are all close to 1 R⊙ and hence the luminosities are proportional to the surface fluxes).
A very important FUV contribution comes from the H I λ1216 Lyα line (Ribas et al., 2005). This holds true throughout the entire MS lifetime of a solar analog although the relative contribution of this line with respect to higher-energy emission increases with age (see Table 4).
5.5 The extreme-ultraviolet and X-ray Sun in time
The present-day Sun’s corona can be characterized by its total radiative output (mostly in the soft-X-ray regime) of a few times 1026 erg s−1 at minimum activity level to a few times 1027 erg s−1 at maximum activity level outside very strong flares; its electron temperature of about 1–5 MK, depending on the magnetic coronal structure under consideration; and its filling factor. The latter is difficult to define as a large variety of (partly expanding) structures confined by closed or open magnetic fields define the magnetic corona. Suffice it to say that the strongest magnetic active regions are confined the volumes closely attached to photospheric sunspot complexes, and the latter cover less than 1% of the solar surface even at activity maximum. Clearly, the solar corona is far from being filled by luminous active regions.
5.5.1 The solar X-ray corona in time
Although coronae radiate across the electromagnetic spectrum, the dominant losses occur in the soft-X-ray range; the radio regime provides complementary diagnostics on non-thermal processes. I concentrate on these two aspects (see Section 5.7 for details on radio emission).
The total X-ray output of a stellar corona depends on the available magnetic energy and is therefore a consequence of the dynamo operation. Younger and more rapidly rotating stars are more X-ray luminous; as is the case for UV and FUV radiation, the X-ray output decreases as the star ages and its rotation period increases. For solar analogs, the decay law is,
(where t9 is the stellar age in Gyr) as derived from small but well-characterized samples (Maggio et al., 1987; Güdel et al., 1997b). This decay law holds for MS stars back in time as long as
-
Equation 12 predicts a luminosity at or below saturation for a solar analog, i.e., LX/Lbol ≲ 10−3, or LX ≲ 4 × 1030 erg s−1;
-
the rotation period is a function of age for a star of given mass.
The second condition is fulfilled only for ages higher than (at least) 100 Myr (Soderblom et al. 1993, see Section 5.2). Consequently, the X-ray luminosity of a solar analog is nearly only a function of rotation period for stars older than ≈ 100–200 Myr, and this dependence is given by
as derived from a sample of nearby solar analogs (Güdel et al. 1997b; see Figure 14; a very similar decay law is found from measurements conducted with broadband spectrometers on board XMM-Newton: LX ∝ 4.04 × 1030 P−2 03±0.35 [erg s−1], see Telleschi et al. 2005). The rotation-activity law (Equation 13) is confirmed by broader studies, also with regard to Rossby number Ro that is defined as the ratio between the two time scales of rotation and convection driving the dynamo (Ro = P/τC, where τC is the convective turnover time; Noyes et al. 1984; Mangeney and Praderie 1984). All studies find roughly LX/Lbol ≈ P−2 for late-type stars (e.g., Randich 2000). Also, other activity indicators such as the surface X-ray flux follow an equivalent law.
Left: X-ray luminosity of solar analogs (from the “Sun in Time” sample), and power-law fit (slope = −2.6). The three objects marked with open squares are close binaries consisting of two early-G solar analogs that rotate synchronously with their orbit motion. These latter stars are in the saturation regime (“RS” and “MEKAL” refer to two different atomic line codes used for the spectral interpretation; from Güdel et al. 1997b, reproduced by permission of AAS). Right: Normalized X-ray and C iv luminosities as a function of rotational velocity for solar analogs. Luminosities of the fastest rotators do not follow the regression laws because of saturation (from Ayres, 1997, reprinted with permission).
Alternatively, the X-ray output roughly scales with the square of the equatorial velocity,
(Pallavicini et al., 1981; Ayres and Linsky, 1980; Maggio et al., 1987; Wood et al., 1994). The X-ray output is an excellent indicator of dynamo activity. The coronal output is strongly determined by parameters that control the magnetic dynamo.
For the most active stars, LX is somewhat suppressed, for reasons that are not well understood. The stars are in a “super-saturated” regime (Randich et al. 1996, see discussion in Güdel 2004).
The overall rotation and activity history of a solar analog star from ZAMS to the terminal stages of its MS life thus proceeds roughly as follows:
-
A star enters on the MS as a fast rotator although the rotation period is not unique, depending on the previous star-disk interaction history. The star thus typically begins its MS life in the saturation regime where LX ≈ (2–4) × 1033 erg s−1. Although it spins down as a consequence of its magnetic-wind mass loss, there is little evolution of the X-ray (and UV, FUV, EUV) output.
-
At an age of around 20–200 Myr, the rotation period has decreased sufficiently so that the star’s corona drops out of the saturation regime (e.g., Patten and Simon 1996; James and Jeffries 1997, and Section 17.5.2 in Güdel 2004). For a G star, saturation holds as long as P < 1.5–2 d.
-
Convergence of rotation periods has been achieved at ages of a few 100 Myr, and by that time a solar analog shows P ≈ 4–5 d and LX ≈ 1029 erg s−1, i.e., less than 10% of the saturation value.
-
From then on, the luminosity decay law holds, because the rotation period is a function of age and increases monotonically. This decay law has been observationally tested until the terminal stages of the MS life of a solar analog.
5.5.2 The coronal temperature in time
The non-flaring corona of the contemporary Sun shows temperatures of a few MK. Active regions tend to be hotter than the quiet corona, and consequently, the average coronal temperature during the Sun’s activity maximum is higher than at minimum. Peres et al. (2000) have studied the full-disk solar coronal emission measure distribution to find peak temperatures of ≈ 1 MK and ≈ 2 MK during minimum and maximum, respectively. The corresponding X-ray luminosities amount to LX ≈ 3 × 1026 erg s−1 and LX ≈ 5 × 1027 erg s−1, respectively. These solar observations suggest that regions of higher magnetic activity, but also episodes of higher overall magnetic activity, not only produce higher-luminosity plasma but also higher temperatures. Does this reflect in coronae of stars with widely varying activity levels?
The spectral evolution of the X-ray and EUV (coronal) Sun in time is illustrated in Figures 15, 16, and 17. These figures of course support the trend of decreasing flux with increasing age as described in Section 5.5.1, but they reveal other important features:
Extracts of the EUV spectra of solar analogs with different ages. All spectral fluxes have been transformed to irradiances at 1 AU from the star. The spectra have been shifted along the ordinate, by multiples of 10 erg cm−2 s−1 Å−1 (from Ribas et al., 2005, reproduced by permission of AAS).
Fluxed high-resolution X-ray spectra of solar analogs with different ages, obtained with the RGS instruments on board XMM-Newton. The topmost two spectra are from K-type T Tauri stars (BP Tau is a classical T Tauri star, V410 Tau a weak-line T Tauri star), while the other spectra are from MS solar analogs. Fluxes are given at a distance of 1 AU from the star, in erg cm−2 s−1 per bin, where the bin width is given in parentheses after the star’s name in each panel (usually 0.05 Å except for β Com where a bin width of 0.0875 Å has been used). Note the anomalously strong O VII (and also Ne ix) lines in the CTTS BP Tau, indicating an excessive amount of cool plasma (the “soft excess”; adapted from Telleschi et al. 2005 and Telleschi et al. 2007b).
Low-resolution CCD X-ray spectra of solar analogs with different ages, obtained with the EPIC MOS instrument on board XMM-Newton. The topmost two spectra are from K-type T Tauri stars (BP Tau is a CTTS, V410 Tau a WTTS), while the other spectra are from MS solar analogs. The sequence of the spectra from top to bottom is reflected in the lower left panel, and also by the colors of the spectra used for the stellar names. Count rate spectra have been normalized to the distance of 47 Cas (33.56 pc); the spectrum of BP Tau has been shifted upward by an additional factor of 30 for clarity (adapted from Telleschi et al. 2005 and Telleschi et al. 2007b).
These spectral features clearly suggest higher temperatures in more active, younger solar analogs.
-
In Figure 15, the EUV spectrum shows prominent lines of highly ionized Fe (Fe XXII, XXIII) in the young EK Dra but these lines rapidly disappear in older stars, where lines of Fe xv and Fe xvi predominate. This is a signature of hotter overall temperatures in the younger, more active solar analogs.
-
In Figure 16, the X-ray spectra of the youngest, most active solar analogs (47 Cas, EK Dra), again reveal strong lines from highly ionized Fe and also a prominent Ne x line (at 12.1 Å); these lines are formed by plasma with temperatures of order 10 MK. In contrast, in the least active star shown (β Com), lines of Fe xvii, Ne ix, and O vii dominate. These lines are formed at temperatures of 2–5 MK.
-
Both Figure 16 and 17 show a more prominent continuum in more active stars. Continuum is predominantly formed by bremsstrahlung and is therefore a sensitive temperature indicator.
From full spectral interpretation, a tight correlation has indeed been found between the characteristic coronal temperature and the normalized coronal luminosity LX/Lbol: Stars at higher activity levels support hotter coronae (Vaiana, 1983; Schrijver et al., 1984; Stern et al., 1986; Schmitt et al., 1990; Dempsey et al., 1993; Maggio et al., 1994; Gagné et al., 1995a; Schmitt et al., 1995; Hünsch et al., 1996; Güdel et al., 1997b; Preibisch, 1997; Schmitt, 1997; Singh et al., 1999).
Figure 18 shows the correlation between average (emission-measure weighted) coronal temperature and the total X-ray luminosity for solar analogs, including solar maximum and minimum values (the latter from Peres et al., 2000). Numerically, the correlation for the stellar sample reads
where Tav is in MK, and LX has been determined in the 0.1–10 keV band (Telleschi et al. 2005, and similar results in Güdel et al. 1997b for the ROSAT energy band). Such relations continue to hold into the PMS domain where exceedingly hot coronae with temperatures up to ≈ 100 MK are found (Imanishi et al., 2001).
Mean coronal temperature of solar analogs as a function of the X-ray luminosity. The dashed and solid lines are the regression fits to results based on different atomic data. The triangles mark the range of the solar corona between activity minimum and maximum (figure from Telleschi et al., 2005, reproduced by permission of AAS).
The trend seen in coronal X-ray emission is similar to the trends described previously for the UV, FUV, and X-ray bands (Sections 5.3, 5.4, and 5.5.1): The emission from stars at higher activity levels is harder, implying that harder emission decays more rapidly in the course of stellar evolution.
Three classes of models have been proposed to explain this correlation:
-
As stellar activity increases, the corona becomes progressively more dominated by hotter and denser features, for example active regions as opposed to quiet areas or coronal holes. Consequently, the average stellar X-ray spectrum indicates more hot plasma (Schrijver et al., 1984; Maggio et al., 1994; Güdel et al., 1997b; Preibisch, 1997; Orlando et al., 2000; Peres et al., 2000).
-
Increased magnetic activity leads to more numerous interactions between adjacent magnetic field structures at the chromospheric level (Cuntz et al., 1999) and therefore at the coronal level, owing to higher magnetic filling factors in the photosphere (Section 4.2.6). The heating efficiency thus increases. Specifically, a higher rate of large flares is expected. Flares produce hot, dense plasma and therefore increase both the X-ray luminosity and the average coronal temperature of a star (Güdel et al., 1997b).
-
Jordan et al. (1987) and Jordan and Montesinos (1991) described an emission measure (EM)-T relation based on arguments of a minimum energy loss configuration of the corona, assuming a fixed ratio between radiative losses and the coronal conductive loss. A relation including the stellar gravity g was suggested, of the form
$$EM \propto {T^3}g,$$(16)which fits to a sample of observations with T taken from single-T fits to stellar coronal spectra. Equation (16) holds because coronal heating directly relates to the production rate of magnetic fields, and the magnetic pressure is assumed to scale with the thermal coronal pressure.
5.6 Putting it all together: The XUV Sun in time
The above subsections provide the input for a comprehensive model of the spectral evolution of the “Sun in Time” in the wavelength band that is relevant for ionization of and chemical reactions in planetary atmospheres and circumstellar disks, namely the 1–1700 Å (≈ 0.007–10 keV) FUV/EUV/X-ray (“XUV”) range. The results are summarized in Tables 4 and 5 compiled using data from Ribas et al. (2005) (for the UV-EUV range) and Telleschi et al. (2005) (for the X-ray range). The table also contains data referring to the classical T Tauri star TW Hya, to be discussed in Section 6, and solar data (see Ribas et al. 2005 for references).Footnote 2 The line fluxes given in Table 4 are normalized to a distance of 1 AU and have also been normalized to the radius our Sun had at the age of the respective star. Note that the Lyα line fluxes were corrected for interstellar H I and D I absorption, i.e., they represent the pure stellar contribution.
Ribas et al. (2005) constructed band-integrated irradiances for the spectral ranges 1–20 Å (X-rays), 20–100 Å (soft X-rays and EUV), 100–360 Å (EUV), and 920–1180 Å (FUV). For the wavelength range of 1180–1700 Å, only line fluxes are provided because of increasing contributions from the photospheric continuum.
All integrated irradiances correlate tightly with the stellar rotation period or age, suggesting a rapid decay of activity at all atmospheric levels in concert. The relations are excellently represented by power laws, as illustrated in Figure 19a. The power-law fits to the fluxes of the form
(α and β being constants) are given in Table 5. Note that the inaccessible spectral range of 360–920 Å (strongly absorbed by interstellar gas) has been interpolated between adjacent spectral ranges, assuming a decay law with β = −1.
Left (a): Power-law decays in time for various spectral ranges, normalized to the present-day solar flux. Note that the hardest emission decays fastest (from Ribas et al., 2005, reproduced by permission of AAS). Right (b): Flux decay slope (given as its absolute value) as a function of formation temperature of the respective line; each cross marks one emission line reported in Table 5 .
The power laws steepen monotonically with decreasing wavelength, i.e., with increasing temperature (or roughly, height) of the atmospheric layer. The steepest decay is seen in the luminosity of the hot corona, with \(F\propto t_{9}^{-1.92}\), while for the ultraviolet transition-region spectrum, \(F\propto t_{9}^{-0.85}\). These power-laws are compared in Figure 19a after normalization to the present-day solar fluxes. For individual lines, the steepness of the decay, β in Equation 17, is compared in Figure 19b for a wide range of line formation temperatures. A fit to β as a function of formation temperature gives
Although the photospheric bolometric luminosity of the Sun has steadily increased during its MS life, starting at a level approximately 30% lower than today, the magnetically induced radiation from the outer atmosphere has steeply decayed during the same time, by factor of ≈ 1500–2000 for coronal X-ray emission and a factor of ≈ 25 for the FUV spectral region. The total XUV emission decayed by a factor of ≈ 100. A summary of the enhancement factors at various stages of the solar past compared to the contemporaneous Sun is given in Table 6. Given the ionizing power of some of this radiation and the importance of UV radiation for line excitation, this emission must have had profound consequences for the environment of the young Sun, most notably circumstellar disks and planetary atmospheres. This will be discussed in Section 6.5 and 7.2. As an example, (see Ribas et al., 2005), for EK Dra, the luminosity of the C III λ977 line alone exceeds the entire integrated luminosity of the present-day Sun below 1200 λ.
This “softening” of the spectral irradiance in time is illustrated in Figure 20 where the entire spectral irradiance from 1–3500 Å (except the strongly absorbed EUV range) is shown for various solar analogs. While the UV flux varies moderately and mostly due to emission lines (Figure 21), the EUV and X-ray level drops dramatically along the MS evolution.
Top: Spectral irradiance of EK Dra for a distance of 1 AU. The various instruments used for the reconstruction are marked. Bottom: Irradiances at 1 AU from solar analogs with different ages (from Guinan and Ribas, 2002, reprinted with permission of ASP).
UV irradiances of EK Dra (upper spectrum) and the very old solar analog, β Hyi (lower spectrum). Note progressively higher flux levels in EK Dra toward shorter wavelengths (from Guinan and Ribas, 2002, reprinted with permission of ASP).
An alternative illustration is provided by the luminosity-luminosity diagram in Figure 22 in which the relation between normalized coronal X-ray and transition-region UV emission is shown for solar-like stars. The two emissions follow a power-law with a slope of 1.9, indicating that toward higher activity levels, X-rays increase more rapidly than UV fluxes (Ayres, 1997).
Correlation between normalized coronal X-ray and transition-region (C iv) UV emission for solar-like field and cluster stars (from the ROSAT/IUE All Sky Survey [RIASS], see Ayres 1997, reprinted with permission).
5.7 The radio Sun in time
Magnetically active stars are sources of vigorous radio emission, which is mostly due to gyroemission from accelerated electrons that are trapped in coronal magnetic fields. Radio emission thus provides diagnostics for coronal magnetic fields and at the same time for high-energy electron populations.
5.7.1 Overview
Solar radio emission is a mixture of various kinds of radiation, some of which are thermal while others are of non-thermal origin. The total solar radio emission is strongly variable and is dominated by different radiation types at different times.
Thermal radiation dominates as long as no strong flares are occurring. Three principal types of thermal radiation are observed (e.g., Gary and Hurford, 1994):
-
1.
Thermal bremsstrahlung from chromospheric layers is seen across the solar disk. The emission is dominated by contributions from the optically thick layer. The brightness temperature is of order 104 K, depending somewhat on wavelength.
-
2.
Above active regions with strong magnetic fields, gyroresonance (cyclotron) emission at low harmonics of the gyrofrequency is often observed. The dominant contributions come from the highest harmonic that is optically thick. This radiation is patchy and covers only a small fraction of the solar disk. Gyroresonance emission may also be accompanied by bremsstrahlung that originates from optically thick layers with coronal temperatures.
-
3.
Some faint, optically thin coronal bremsstrahlung can also be seen from coronal loops that are filled with hot plasma.
The third contribution is usually rather weak; the non-flaring solar radio emission is dominated by the first and second contributions. Although variable, the average radio luminosity at 3.6 cm wavelength from these contributions is log LR ≈ 10.80–11.15 [erg s−1 Hz−1] (Drake et al., 1993). The picture changes entirely during solar flares, when two new contributions dominate the solar radio output:
-
4.
Various forms of non-thermal emission from coherent radiation processes such as electron cyclotron masers or plasma radiation mechanisms are signatures of unstable, non-thermal electron populations. The emission is often (but not exclusively) narrow-band and occurs in short bursts (from milliseconds to a few seconds). More persistent coherent emission is occasionally seen.
-
5.
Gyrosynchrotron radiation originates from non-thermal electron populations that are trapped in magnetic fields. This emission shows a broad spectrum with optically thick and thin components, with a turnover from the former to the latter in the 1–10 GHz range. Gyrosyn-chrotron emission is a direct tracer of accelerated particle populations.
5.7.2 Observational results
The discovery of solar analogs in radio waves (Güdel et al., 1994) was motivated by a correlation between radio and X-ray luminosities that holds for M-type MS stars, but also extends to RS CVn-type binaries and seems to hold similarly for solar flares (Güdel and Benz, 1993; Benz and Güdel, 1994). The following systematics apply:
-
The radio emission of detected solar analogs follows the same radio vs. X-ray luminosity relation as found for active M dwarfs.
-
Only stars with “hard” X-ray spectra, i.e., X-ray emission from very hot coronal plasma (10 MK and more), are non-thermal radio sources.
-
The detected solar analogs that are not components of spun-up binaries are therefore young (≲ a few 100 Myr), magnetically active stars.
Figure 23 shows a summary of normalized radio luminosities of solar analogs with different rotation periods. Like X-ray emission, the radio output decays with increasing rotation period (i.e., decreasing magnetic activity), although the decay is much steeper. The radio decay is reminiscent of the very steep decay of the harder portion of soft X-ray emission which is also an excellent tracer of magnetic activity. The steep decline of non-thermal radio emission therefore extends the trend observed above (Section 5.6): Radio emission originates from the most energetic electrons in the stellar atmosphere.
Relation between LR/Lbol and the stellar rotation period. Note upper limits for slow rotators. The dotted line illustrates the slope of the X-ray decay law as a function of P (Equation 13 ), while the solid line shows the slope of the most rapidly decaying, “hot” X-ray lines (slopes from Table 5 and using Equation 7; adapted from Güdel and Gaidos 2001).
Figure 24 shows the radio luminosity as a function of the average coronal temperature of solar analogs; only radio upper limits are available for the intermediately active coronae with temperatures Tav ≈ 3–5 MK; a regression fit to the points including the upper limits therefore provides a lower limit to the slope:
(based on the APEC emission line code; Telleschi et al. 2005). This empirical relation shows again, and explicitly, that strong non-thermal radio emission develops only in very active stars with hot coronae. Because non-thermal electrons need to be replenished on short time scales, presumably in flare-like processes, a model in which the very hot plasma component is formed by the same flares is suggestive. Alternatively, non-thermal electron distributions may be accelerated continuously out of a Maxwellian distribution into a runaway tail by electric fields (Holman, 1986), a concept also proposed to operate in solar flares (Holman and Benka, 1992). Such mechanisms of course work best if very hot plasmas are present.
Relation between non-thermal radio emission and average coronal temperature (from Telleschi et al., 2005, reproduced by permission of AAS). Open and filled circles refer to different atomic emission line codes used for the temperature determination.
Other types of radio emission are too faint to be detected from solar analogs. Signatures for thermal gyroresonance emission have been found in an M dwarf (Güdel and Benz, 1989), and Drake et al. (1993) reported evidence for non-flaring radio emission probably related to chromospheric bremsstrahlung and some active-region gyroresonance emission in the nearby F-type subgiant Procyon; more systematic observations of solar analogs during all phases of their MS life will require more sensitive radio telescopes than hitherto available.
5.8 Coronal flares in time
5.8.1 Flare energy distributions and coronal heating
Magnetic flares in the solar and stellar atmospheres heat plasma explosively to ≳ 10 MK on time scales of minutes. Large amounts of emission measure are produced, presumably by bringing up heated material from the chromospheric layers, thus increasing the density in coronal regions of magnetic loops. It has been suggested that much, if not all, of the hot coronal plasma has been heated (and evaporated) by flares that may be too small and too frequent to be detected individually. This hypothesis is known as the “microflare” or “nanoflare” hypothesis in solar physics (Parker, 1988). There is observational evidence that numerous small-scale flare events occur in the solar corona at any time (e.g., Lin et al., 1984). Hard-X-ray studies have shown that they are distributed in energy according to a power law,
where dN is the number of flares per unit time with a total energy in the interval [E, E+dE], and k is a constant. If α ≥ 2, then the energy integration (for a given time interval, \(\int_{{E_{\min }}}^{{E_{\max }}} E [dN/dE]dE\)) diverges for Emin → 0, that is, if the power law is extrapolated to small flare energies, a lower cut-off is required for the power-law distribution; arbitrary energy release powers are possible depending on the value of Emin. From solar studies, α ≈ 1.6–1.8 for ordinary solar flares (Crosby et al., 1993), but some recent studies of low-level flaring suggest α = 2.0–2.6 (Krucker and Benz, 1998; Parnell and Jupp, 2000).
5.8.2 Phenomenological evidence
There is abundant evidence that flare-like processes are important in magnetically active stars:
-
A linear correlation between the time-averaged power from optical flares and the low-level, “quiescent” X-ray luminosity suggests that flares are important contributors to the overall stellar coronal heating (Doyle and Butler, 1985; Skumanich, 1985; Whitehouse, 1985).
-
Over the entire solar magnetic cycle, the monthly average soft X-ray luminosity scales in detail and linearly with the rate of detected Hα flares (Pearce et al., 1992).
-
In analogy, the stellar “quiescent” X-ray luminosity correlates approximately linearly with the rate of X-ray flares (above a given lower energy threshold; Audard et al. 2000).
-
The “quiescent” X-ray luminosity of magnetically active stars correlates linearly with the contemporaneous (non-flaring) radio gyrosynchrotron emission. The latter requires accelerated electrons, for which flares are an obvious source (Güdel and Benz, 1993)
-
This latter correlation holds similarly for many solar and stellar flares (Benz and Güdel, 1994).
-
The ratio between energy losses in coronal X-rays and in the chromospheric Mg ii lines is the same in flares and in quiescence (Haisch et al., 1990).
-
The ratio between energy losses in coronal X-rays and in the chromospheric UV emission measured in broad filter bands is the same in flares and in quiescence (Mitra-Kraev et al., 2005).
-
A tight correlation exists between LX and Hγ luminosity that it the same for flares and for quiescence (Mathioudakis and Doyle, 1990).
-
Many observations have shown continuous low-level variability in the stellar X-ray output, with time scales reminiscent of coronal flares (Audard et al. 2003a; see Figure 25 for the X-ray light curve of EK Dra). In particular, a strong temporal correlation between Hγ flare flux and simultaneous low-level X-ray flux in dMe stars suggests that a large number of flare-like events are always present (Butler et al., 1986). Up to 50% of the X-ray output in PMS stars may be due to relatively strong flares (Montmerle et al., 1983), which has become particularly evident in recent observations of the Orion region (Feigelson et al., 2002b; Wolk et al., 2005).
X-ray light curve of the young (ZAMS) solar analog EK Dra, obtained with XMM-Newton. The curves refer to the total 0.2–10 keV photon energy range (black), the soft band (0.2–1 keV; green), the hard band (>1 keV; red), and the ratio of hard/soft (blue; from Telleschi et al. 2005, reproduced by permission of AAS).
5.8.3 Stellar flare energy distributions
Motivated by the above phenomenology, several studies have addressed flare distributions in stellar coronae. Earlier work by Collura et al. (1988) and Pallavicini et al. (1990) indicated power laws with α < 2 although the sensitivities used in those observations were quite limited, and flares from different stars at different distances were lumped together. This also holds for a study by Osten and Brown (1999) for RS CVn-type binaries.
To avoid bias with regard to detection limits at lower energies, new methods have been devised by Audard et al. (1999), Audard et al. (2000), Kashyap et al. (2002), Güdel et al. (2003b), and Arzner and Güdel (2004), the latter three using Monte Carlo forward methods and analytical inversion. Work by Wolk et al. (2005), Arzner et al. (2007), and Stelzer et al. (2007) has extended flare statistics into the PMS domain.
Most of these recent studies converge to α ≈ 2.0–2.5 (Figure 26), indicating a potentially crucial role of flares in coronal heating if the power-law flare energy distribution extends by about 1–2 orders of magnitude below the actual detection limit in the light curves. The X-ray coronae of active stars would be an entirely hydrodynamic phenomenon rather than an ensemble of hydrostatic loops.
Cumulative flare rate distributions in energy for 47 Cas, EK Dra, and both combined. The indices of power-law fits to the cumulative distributions are smaller than those of the differential distributions by one, α − 1. The distributions plotted as solid histograms have been corrected for flare overlap. Also shown are power-law fits to the corrected distributions (solid lines; see Audard et al. 1999 for more details; reproduced by permission of AAS).
5.8.4 Stochastic flares and coronal observations
This mechanism has been studied specifically for young solar analogs by Güdel et al. (1997b), Güdel (1997), Audard et al. (1999), and Telleschi et al. (2005), in particular with regard to synthetic light curves and emission measure distributions.
Güdel et al. (1997b) found that the time-averaged emission measure distribution of solar flares adds a characteristic, separate emission measure component at high temperatures (> 10 MK); numerical simulations support this picture (Güdel, 1997), and corresponding hot emission measure components are indeed also identified in active solar analogs from X-ray spectroscopic observations. If a full distribution of flares contributes, including small flares with lower temperature, then the entire observed X-ray emission measure could be formed by the continually heating and cooling plasma in flares. The predicted steep low-T slope (up to ≈ 4) of an emission measure distribution induced by stochastic flaring compares very favorably with observations of active stars (Güdel et al., 2003b). This holds true specifically for solar analogs for which α = 2.2–2.8 is implied from the emission measure slopes (Telleschi et al., 2005).
Audard et al. (1999) and Audard et al. (2000) derived the flare energy distribution of young solar analogs (Figure 26, where the cumulative distributions are plotted, with a power-law index that is shallower by one unit) and studied consequences for the thermal structure of the active coronae. They speculated that the higher temperatures in active coronae are due to a larger rate of (larger) flares, although they left undecidedwhether there is a larger rate of reheating events of the same coronal structures or whether a higher number of active regions produce the higher flare rate.
5.8.5 Summary: The importance of stochastic flares
The above overview suggests that the young solar corona may have been strongly driven by flares erupting as a consequence of magnetic instabilities. There is no conclusive proof that stochastic flares dominate coronal heating although there is clear evidence that active stellar coronae are continuously variable on time scales similar to flare events, and there is ample circumstantial albeit indirect evidence supporting this model, as described above. There are important implications from flare-heating coronal models:
-
The corona can no longer be treated as an ensemble of static magnetic loops. Scaling laws often used to assess “coronal structure” are meaningless.
-
Solar flares are often accompanied by coronal mass ejections, contributing to the overall mass loss rate. A high rate of coronal flaring may contribute significantly to an enhanced mass loss in the young Sun (see Section 5.1 and Section 7.1.2).
-
Solar flares accelerate electrons and ions to high energies, both within closed magnetic structures (evident by synchrotron emission from mildly relativistic electrons or non-thermal hard X-rays and gamma-rays from collisions in chromospheric gas) and along open field lines toward interplanetary space (measured in situ as “solar energetic particles”). Copious coronal flares in young solar analogs will eject large numbers of energetic particles that are important for non-thermal interactions with planetary atmospheres (Section 7.2.3) and for the irradiation of circumstellar disks and meteoritic material, potentially producing (some of the) well-known isotopic anomalies.
5.9 The solar coronal composition in time
From a naive point of view, the coronal and solar-wind material is expected to show the same overall composition as that of the underlying star and, in particular, its photosphere from where the material has been brought up. However, measurements of the composition of the solar corona and the solar wind have revealed what is commonly known as the “First Ionization Potential (FIP) Effect”; this abundance anomaly results in elements with a FIP below ≈ 10 eV (e.g., Si, Mg, Ca, Fe) being enriched by factor of a few with respect to hydrogen when compared to the photospheric mixture, while elements with a higher FIP (e.g., C, N, O, Ne, Ar) show the photospheric composition. The solar measurements have been summarized comprehensively in the extensive work by Meyer (1985a, b) and Feldman (1992). The same FIP effect is in fact also present in solar energetic particles and — unexpectedly — in cosmic rays.Footnote 3
A discussion of the solar FIP effect is not within the scope of this review, nor are the various physical models that have been proposed for more than two decades. I refer the interested reader to the presentations by Hénoux (1995), Jordan et al. (1998), Drake et al. (1995), and Laming et al. (1995), and also the series of papers in Space Science Reviews, vol. 85 (pp. 283–418, 1998). In short, a fractionation process, probably involving electric and/or magnetic fields or pressure gradients, occurs at chromospheric levels where low-FIP elements are predominantly ionized and high-FIP elements are predominantly neutral. Because ions and neutrals are affected differently by electric and magnetic fields, acceleration or drift of elements with different FIP may occur at different speed or with different efficiency. The FIP effect varies considerably in strength between various types of coronal structure; see, e.g., Jordan et al. (1998). Although it is also expressed in full-disk solar spectral data, it is confined to coronal heights where T ≳ 1 MK, while material at lower temperatures shows the photospheric composition (Laming et al., 1995).
Why are abundance anomalies interesting for the study of the young Sun? The study of solar analogs at different ages has, in fact, shown systematics in the coronal composition that a successful, future model for the generation and heating of stellar coronae must explain. I briefly review the various findings.
5.9.1 Abundances in stellar coronae
Although detailed studies of coronal composition require high-resolution X-ray spectra, anomalies in the coronal composition of magnetically active stars have been recognized already in the early days of X-ray astronomy. Most notably, a significant deficiency of coronal Fe, by factors of a few when compared to the solar composition, has been noted (e.g., Swank et al. 1981; White et al. 1994). There are two caveats with regard to early abundance measurements: i) low-resolution X-ray spectroscopy does not isolate individual spectral lines of any element with the exception of Fe, which produces a line system at 6.7 keV that can be measured by low-resolution (e.g., CCDtype) detectors. This line, however, forms at very high temperatures (formation temperature ≈ 60–70 MK), and knowledge of the thermal structure at those high temperatures is required if the element abundances are to be trusted; ii) more severely, for most stars no reliable photospheric abundances are known (again, the exception is mostly Fe). Because the photospheric composition of stars may significantly differ from the solar photosphere, any coronal abundance anomaly in stars should really be defined with respect to the underlying photosphere. In any case, before the advent of spectroscopy with XMM-Newton and Chandra, a sufficient body of data clearly showed that the most active stars reveal strong depletion of most heavy elements, with little FIP-related systematics (Singh et al., 1999).
Early observations of the extremely active subgiant HR 1099 (Brinkman et al., 2001) and the MS K-type ZAMS star AB Dor (Güdel et al., 2001) with the XMM-Newton Reflection Grating Spectrometer uncovered a new, systematic FIP-related bias in magnetically active stars: In contrast to the solar case, low-FIP abundances are systematically depleted with respect to high-FIP elements, a trend now known as the “inverse FIP effect” (IFIP). The ratio between the abundances of Ne (highest FIP) and Fe (low FIP) is therefore unusually large, of order 10 in the most extreme cases (when compared to the solar photospheric mixture). This pattern has been confirmed for many further active stars (e.g., Drake et al. 2001; Huenemoerder et al. 2001, 2003 etc). Only highly active stars show the IFIP pattern. Toward intermediately active stars, the effect weakens, until eventually flat abundance distributions are recovered (Audard et al., 2003b).
5.9.2 The composition of the young solar corona
Solar analogs provide the best basis for a systematic study of abundance trends because they directly link to the solar case. Fortuitously, many well-studied solar analogs with different ages and activity levels are available for study in the solar vicinity. Again, the “Sun in Time” sample is outstanding in that the photospheric mix has been well documented, often for several elements apart from Fe. The principal result is that all of them show photospheric abundances close to solar (see summary table in Telleschi et al. 2005). The only independent parameter for this sample with regard to coronal abundance anomalies is therefore again the activity level or, equivalently, age.
The sample shows a clear systematic development from an inverse FIP effect in the youngest examples (with underabundances of Fe and Si) to a marked FIP effect in objects at ages of about 300 Myr and older (see Figure 27). As long as the IFIP pattern is present, all abundances appear to be sub-solar, but the Fe/H abundance ratio gradually rises with decreasing coronal activity. The abundance pattern reverts to a normal, solar-type FIP anomaly for stars at activity levels of log LX/Lbol ≲ − 4 (Telleschi et al., 2005). Unexpectedly, this transition also seems to coincide with i) the transition from coronae with a prominent hot (T ≳ 10 MK) component to cooler coronae, and ii) with the transition from prominent non-thermal radio emission to the absence thereof (Telleschi et al., 2005).
Coronal element abundances normalized to the Fe abundance, with respect to the solar photospheric mixture as a function of FIP; the total X-ray luminosities are, from top to bottom: log LX = 30.06 (BP Tau), 30.66 (V410 Tau), 30.39 (47 Cas B), 30.08 (EK Dra), 29.06 (π1 UMa), 28.95 (χ1 Ori), 28.95 (κ1 Cet), 28.26 (β Com) (after Telleschi et al., 2005, 2007b).
5.9.3 The Ne/O abundance ratio: Subject to evolution?
Figure 28 shows an anomaly for the O/Ne ratio which is found at values of 0.3–0.7 times the solar ratio, apparently regardless of the stellar activity level. Because both O and Ne are high-FIP elements, their abundance ratio could reflect the photospheric ratio. But then, the Sun’s composition would be anomalous.
Coronal abundances of Fe (low FIP) and Ne (high FIP — left plot), and ratios of Mg/Fe (low FIP) and O/Ne (high FIP — right plot) for various stars, shown as a function of the average coronal temperature (from Güdel, 2004, © Springer Verlag, reprinted with permission).
The tabulations of several solar element abundances have recently been revised (Asplund et al., 2005b), resulting in significant discrepancies between solar models and helioseismological results (see Antia and Basu, 2005, and references therein) unless further solar abundances were also different. A Ne abundance higher by a factor of at least 2.5 than hitherto assumed would be needed. Therefore, Telleschi et al. (2005) were the first to point out that the systematically nonsolar O/Ne abundance ratio (by a similar factor) calls for a revision of the solar Ne abundance tabulation which at the same time would solve the solar helioseismology problem. This was further elaborated by Drake and Testa (2005) who suggested a factor of 2.7 upward revision of the adopted solar Ne abundance.
Two directions should be taken to verify this suggestion. First, further coronal abundances of low-activity solar-analog stars should be derived. So far, agreement with solar values has in fact been reported for α Cen A (Raassen et al., 2003), Procyon (Raassen et al., 2002), and for β Com, the latter with large error bars, however (Telleschi et al., 2005). There seems to be a trend toward higher O/Ne ratios in Figure 28 indeed. New results for α Cen have been reported by Liefke and Schmitt (2006), placing the Ne/O abundance ratio significantly lower than values for active stars, albeit not as low as the presently accepted solar photospheric value. Second, verification of the solar Ne/O ratio is needed. Although Ne cannot be measured directly in the photosphere, the Ne/O ratio can be derived from coronal measurements the same way as done for stellar observations. Recent analysis of solar active region X-ray spectra and of EUV spectra from transition-region levels (Schmelz et al., 2005; Young, 2005) both report the standard Ne/O abundance ratios, rejecting an upward correction of Ne. The issue should therefore be considered to be open for the time being. A FIP-related, i.e., “evolutionary” enrichment of Ne in active corona remains a viable possibility (Asplund et al., 2005a).
5.10 Summary: The young, active Sun
Although the MS Sun started as a ZAMS star with a bolometric luminosity that was significantly lower than today — by about 30% — a very different picture must be drawn from high-energy observations of solar analogs, including UV, FUV, EUV, X-ray, and non-thermal radio emissions. All signatures of magnetic activity, among them dark starspots, chromospheric and transitionregion line emission, coronal X-rays, and radio gyrosynchrotron emission in young solar analogs point to levels of magnetic activity orders of magnitude above the present solar level. The presentday Sun in fact resides at the lowest levels a solar-like star can attain — near the end of its MS life, as a spun-down star.
Short-wavelength radiation and non-thermal radio emission show power-law decays during the solar evolution that steepen toward higher energies of the underlying electron population. In parallel, the rotation rate of the Sun also decayed, again in a power-law fashion. Rotation is indeed thought to be the ultimate driver of these decay laws, as it is one of the two fundamental ingredients of the magnetic dynamo, the other being convection which does not strongly change during the Sun’s main-sequence life.
The solar wind is another expression of magnetic activity. The mass loss induced by the wind also decays according to a power-law although this does not seem to hold for the youngest and most active examples which show a suppressed wind.
The high level of magnetic activity in the young Sun must have been a pivotal ingredient in shaping the solar environment, in particular planetary atmospheres. The most extreme expressions of magnetic activity, magnetic flares that appear to be dominating contributors to high-energy photon and particle production in young solar analogs, need to be accounted for in planetary atmospheric modeling. I will discuss some of these aspects in Section 7.
6 Further Back in Time: The Pre-Main Sequence Sun
6.1 Where was the cradle of the Sun?
The present-day galactic environment is in no ways related anymore to the place where the Sun was born. The contemporaneous Sun is obviously not a member of a bound cluster. There has consequently been some speculation regarding the environment in which the Sun formed. The large-scale solar environment controls interactions with the outflowing solar wind and is therefore relevant for the influx of cosmic rays into the inner solar system.
During the past 106 years, the Sun has moved from the very hot (≈ 106 K) low-density “local bubble” environment into the cooler and denser (≈ 6900 K, n(H0 + H+) ≈ 0.3 cm−3) “local interstellar cloud” (Frisch, 2000; Frisch and Slavin, 2005, 2006). The pressure characteristics of these two environments are similar, so that the radii of the heliosphere would have been similar (120–130 AU; Frisch 2000). However, the heliospheric structure would shrink to ten percent of its present size if the Sun encountered molecular clouds, and such encounters are likely to have occurred several times in the past (Frisch, 2000).
Moving back in time, the evidence becomes indirect. The best “memory” of the earliest episodes of the Sun’s life is contained in meteorites (Section 6.6). The presence of live 60Fe in the early solar system (see Section 6.6) inferred from meteoritic trace elements (Tachibana and Huss, 2003) cannot be explained by local processes (such as stellar flares, see Section 6.6) but is thought to require supernova explosions (Meyer and Clayton, 2000). The local environment of the forming solar system was therefore likely reminiscent of a high-mass star-forming region like the Orion region; the young Sun and its circumstellar disk may have resided in a H II region for a considerable amount of time (Hester et al., 2004); the intense ultraviolet radiation field from massive stars might have contributed to the evaporation of the molecular environment of the Sun (so-called proplyds in the Orion Nebula, O’Dell 2001, or “evaporating gaseous globules” [EGGs], Hester et al. 1996). These structures contain protostars that can be detected in X-rays (Kastner et al., 2005; Linsky et al., 2007), i.e., deterioration of the environment is due both to the larger-scale “interstellar” environment and the stellar magnetic activity itself.
6.2 New features in the pre-main sequence Sun
6.2.1 Evolutionary stages: Overview
Modern theory of star formation together with results from comprehensive observing programs have converged to a picture in which a forming low-mass star evolves through various stages with progressive clearing of a contracting circumstellar envelope. In its “class 0” stage (according to the mm/infrared classification scheme), the majority of the future mass of the star still resides in the contracting molecular envelope. “Class I” protostars have essentially accreted their final mass while still being deeply embedded in a dust and gas envelope and surrounded by a thick circumstellar disk. Jets and outflows may be driven by these optically invisible “infrared stars”. Once the envelope is dispersed, the stars enter their “Classical T Tauri” stage (CTTS, usually belonging to infrared class II with an IR excess) with excess Hα line emission if they are still surrounded by a massive circumstellar disk; the latter results in an infrared excess. “Weak-line T Tauri” stars (also “naked T Tauri stars”, Walter 1986; usually with class III characteristics, i.e., essentially showing a photospheric spectrum) have lost most of their disk and are dominated by photospheric light (Walter et al., 1988).
6.2.2 New features: Accretion, disks, and jets
Moving back in time from the MS into the PMS era of solar evolution, we encounter changes in the Sun’s internal structure and in fundamental stellar parameters such as radius and Teff. The typical “T Tauri” Sun at an age of 0.5–3 Myr was bolometrically 1–4 times more luminous and 1.7–3.6 times larger in radius, while its surface Teff ≈ 4260 K, corresponding to a K5 star (after Siess et al., 2000). The interior of T Tauri stars evolving on the Hayashi track is entirely convective. The operation of an αΩ dynamo should not be possible, yet very high levels of magnetic activity are clearly observed on T Tauri stars. Alternative dynamos such as convective dynamos may be in operation. “Solar analogy” no longer holds collectively for all stellar parameters, except (roughly) for stellar mass. Also, there is a complex stellar environment, including an accretion disk, outflows and jets, and probably a large-scale stellar magnetosphere that interacts with these structures (Camenzind 1990; Königl 1991; Collier Cameron and Campbell 1993; Shu et al. 1994; Figure 29). Magnetic interactions between the star and its environment are important in the following contexts:
-
Star-disk magnetic fields may form large magnetospheres that lead to star-disk locking and disk-controlled spin rates of the star. Generally, disk-surrounded CTTS rotate relatively slowly, probably due to disk locking, with P = 5–10 d, compared to only a few days for diskless, non-accreting WTTS (Bouvier et al., 1993); if a rotation-induced magnetic dynamo is at work in CTTS, then it may be dampened compared to dynamos in freely (and rapidly) rotating diskless WTTS.
-
Non-synchronized rotation may be possible in particular in very young systems in spite of magnetic fields connecting the star with the inner border of the disk. The different rotation rates produce shear in the star-disk magnetic fields, eventually leading to field lines winding up around the star and reconnecting, releasing energy and plasmoids that stream out along large-scale magnetic fields (Hayashi et al., 1996; Montmerle et al., 2000). This may be a viable model for the production of protostellar jets.
-
Star-disk magnetic fields are thought to define the basic route of material accreting from the disk to the star (Uchida and Shibata, 1984; Camenzind, 1990; Königl, 1991). This star-disk magnetospheric complex (Figure 29) is in the center of present-day studies of PMS magnetic “activity” as it links the accretion process to stellar magnetic fields and probably to outflows and jets. Although the details of the magnetic interface between the star and the circumstellar disk are far from being understood, the physics of mass-loading of the magnetic field lines is being addressed in detail based on theoretical (e.g., Shu et al., 1994; Ferreira and Zanni, 2007) and numerical investigations (e.g., Romanova et al., 2006). Magnetically funneled material forms “hot spots” on the stellar surface that can be observed as an ultraviolet excess (e.g., Calvet and Gullbring, 1998).
Sketch of the environment of a classical T Tauri star or a protostar, showing the star, the circumstellar disk, magnetic field lines, and closed star-disk magnetic field structures that funnel material from the disk to the star (adapted from Camenzind, 1990, © Wiley-VCH Verlag, reproduced with permission).
6.2.3 New emission properties: Solar-like or not?
Given the similarity between WTTS and active, ZAMS stars, “activity” in WTTS as seen in spots, chromospheric and transition-region lines, and X-ray emission has conventionally been attributed to solar-like magnetic activity. Non-thermal gyrosynchrotron radio emission in WTTS suggests processes similar to those observed in active MS stars and subgiant binaries, processes that are thought to be related to electron acceleration in coronal flares (White et al., 1992a, b; Güdel, 2002). As for CTTS, strong optical and ultraviolet emission lines were initially assumed to give evidence for extremely active chromospheres and transition regions (Joy 1945; Herbig and Soderblom 1980, see review by Bertout 1989). Flares and “flashes” (e.g., Ambartsumian and Mirzoyan, 1982) also suggest analogy with magnetic flaring in more evolved stars and the Sun. Arguments in favor of solar-like magnetic coronal activity in all TTS include i) dominant, typical electron temperatures of order 107 K that require magnetic confinement, and ii) the presence of flares (Feigelson and Decampli, 1981; Feigelson and Kriss, 1981, 1989; Walter and Kuhi, 1984; Walter et al., 1988).
However, the solar analogy seems to break down in the optical/UV range where strong flux excesses are recorded; these excesses are uncorrelated with X-rays (Bouvier, 1990) but seem to relate to the accretion process (Section 6.3.2). A similar excess recently discovered in soft X-rays may be related to both coronal magnetic fields and accretion (Güdel and Telleschi 2007, see Section 6.3.4). Also, thermal radio emission observed in CTTS, probably due to optically thick winds but also due to bipolar jets, reaches beyond the solar analogy (Cohen et al., 1982; Bieging et al., 1984). Clearly, emission across the electromagnetic spectrum needs to be understood in the context of the new features around accreting stars, and in particular the related magnetic fields, summarized in Section 6.2.2.
A summary of the present view of activity and other properties of PMS stars from the earliest stages to the arrival on the MS is given in Figure 30 (from Feigelson and Montmerle, 1999).
Summary of properties of PMS objects, in comparison with MS stars (from Feigelson and Montmerle, 1999, © 1999 by Annual Reviews, reprinted with permission).
6.3 The T Tauri Sun
6.3.1 The magnetic field of the T Tauri Sun
Surface magnetic fields have been successfully measured on “solar-analog” T Tauri stars, using Zeeman broadening (Johns-Krull et al., 1999; Valenti and Johns-Krull, 2004; Johns-Krull, 2007a). For example, BP Tau (a 0.65 M⊙ CTTS) maintains a mean magnetic field strength (∑Bf) of 2.6±0.3 kG, i.e., the equivalent of sunspots for f = 1. Such field strengths exceed the equipartition value of T Tauri photospheres (≈ 1 kG, Johns-Krull et al. 1999; Johns-Krull 2007a), which may be a consequence of near-total surface filling (Solanki, 1994; Johns-Krull, 2007a). T Tauri photospheres are therefore dominated by magnetic pressure rather than thermal pressure, in contrast to MS stars and the Sun but similar to stellar coronae in general. The average surface magnetic fields of CTTS also exceed a prediction from X-rays, based on a correlation between X-ray luminosity and photospheric magnetic flux valid for MS stars and the Sun (Pevtsov et al., 2003). Upper limits of the net polarization of photospheric lines suggest that the photospheric magnetic fields form predominantly in small-scale structures, although a dipole may dominate at large distances (Johns-Krull et al., 1999; Valenti and Johns-Krull, 2004; Johns-Krull, 2007a). Large dipole components are also suggested from observations of spots concentrated at the poles of T Tauri stars, similar to active MS solar analogs (e.g., Joncour et al., 1994; Hatzes, 1995; Rice and Strassmeier, 1996). In any case, the observed fields should be strong enough to truncate circumstellar disks indeed (Johns-Krull et al., 1999; Johns-Krull, 2007a), even if rather complex (non-dipolar) surface magnetic field distributions are assumed (Gregory et al., 2006).
Zeeman-Doppler Imaging techniques have successfully been applied to extremely active solar analogs in the PMS phase. A particularly clear case was presented by Donati et al. (2000), finding solar-like differential rotation on a post-T Tauri star (see also Section 4.3.1). More recently, Donati et al. (2007) have reconstructed a rather complex, large-scale magnetic topology on the CTTS V2129 Oph; they found a relatively weak dipole but stronger octupolar fields that are tilted against the rotation axis, with strong near-polar spots. The accretion footpoints are also found to be located at high latitudes. An attempt was made at extrapolating the fields to the inner rim of the disk, showing that some field lines should successfully accrete toward the observed hot spots.
At coronal levels, X-ray rotational modulation provides information on the large-scale distribution of stellar magnetic fields. Rotational modulation is widespread among extremely active T Tauri stars (Flaccomio et al., 2005). Some 10% of the studied stars in the Orion X-ray sample show such evidence, suggesting that: i) the X-ray emitting active regions are not homogeneously distributed on the surface, i.e., despite the X-ray saturation level reached by these stars, the surface cannot be filled with X-ray-bright magnetic loops; ii) the X-ray emitting regions responsible for the rotational modulation are directly associated with the surface and cannot extend much beyond R* (Flaccomio et al., 2005). A comparison of the modulation depth with the Sun’s modulation in fact shows that the longitudinal inhomogeneities are similar (Flaccomio et al., 2005).
6.3.2 The ultraviolet T Tauri Sun
A defining property of (accreting) classical T Tauri stars is their strong line emission of, e.g., Hα or Ca ii H & K. These strong lines were initially thought to be evidence of massive chromospheres similar to those seen on the Sun or in cool stars (see review by Bertout 1989), and the discovery of strong UV lines such as those of Si ii, Si iv, and C iv — equivalent to “transition region” lines in the Sun formed above 104 K — supported this picture.
However, when compared with MS stars, including chromospherically very active examples, UV line and continuum emission is up to 102–104 times stronger in CTTS (see example of TW Hya in Table 4; Canuto et al. 1982, 1983; Bouvier 1990; Valenti et al. 2000), regardless of the photospheric effective temperature or the stellar rotation period but correlated with the mass accretion rates derived from optical continuum data (Bouvier 1990; Johns-Krull et al. 2000; Figure 32a below). Further, UV or Hα line surface fluxes of CTTS show, in contrast to more evolved stars, no correlation with coronal X-rays, the latter being in the range of RS CVn-type active binary systems or very active MS stars but the UV/Hα lines showing a wide range of excess flux (Bouvier, 1990).
Coronal and “chromospheric/transition region” fluxes are thus not correlated in CTTS, contrasting strongly with MS and subgiant stars for which a sharp correlation is taken as evidence for a common physical heating mechanism (operating in related magnetic fields; Section 5.6, Figure 22). An additional mechanism must be responsible for the optical/UV line flux excess. Apart from the line excess fluxes, there is also a strong blue continuum excess that leads to “veiling” in the optical spectrum, i.e., a filling-in of absorption lines by continuum emission; this emission is also not compatible with chromospheric radiation. The most obvious property common only to CTTS among the stars considered above is accretion; downfalling material could provide the energy to generate the optical/UV excess (Bertout et al., 1988; Basri and Bertout, 1989).
Nearly free-falling gas can be heated to maximum temperatures
in shocks forming at the bottom of magnetic accretion funnels (Calvet and Gullbring, 1998). UV and optical line emission could thus provide diagnostics for the accretion velocity, the mass accretion rate, and possibly the surface filling factor of accretion funnels.
The present consensus, based on such concepts as well as line profile properties and correlations with the mass accretion rate, is that the UV excess emission originates from material heated in accretion shocks (e.g., Calvet and Gullbring, 1998; Gullbring et al., 1998). Some of the emission lines (e.g., Hα, Ca ii) may also form in the accretion funnels themselves, or in stellar winds (Ardila et al., 2002).
6.3.3 The X-ray T Tauri Sun in time
Feigelson et al. (2002b), Wolk et al. (2005), and Telleschi et al. (2007b) presented X-ray studies of near-solar-mass stars (stars in the ranges of 0.7 M⊙ ≤ M ≤ 1.4 M⊙ and 0.9 M⊙ ≤ M ≤ 1.2 M⊙, respectively, in the former two studies of the Orion Nebula cluster, and wider in the latter study of the Taurus star-forming region). The sample ages typically comprise the log t = 5.5–7 range and contain both disk-surrounded and disk-less T Tauri stars. The median X-ray luminosity in the Orion sample is found at log LX = 30.25, i.e., three orders of magnitude above the average solar X-ray output, but there is evidence for a slow decay with age, log LX ∝ t−1.1 (Feigelson et al., 2002b; Wolk et al., 2005). A shallower decay was reported by Preibisch and Feigelson (2005) for the same stellar cluster, with an exponent between −0.2 and −0.5, but when considering normalized LX/Lbol or average surface X-ray flux, then both Feigelson et al.’s and Preibisch & Feigelson’s studies indicate that the LX decay law is roughly compatible with full saturation (i.e., LX/Lbol ≈ 10−3) as the star descends the Hayashi track and its bolometric luminosity is decreasing (Feigelson et al., 2002b). Telleschi et al. (2007b) used the Taurus sample over a wider mass range but removed the strong LX versus mass correlation in order to normalize the X-ray evolutionary behavior to a solar-mass star. The slope of the LX vs. age correlation is fully compatible with the Orion results, with a power-law index of −0.36 ± 0.11 although the correlation is dominated by scatter from other sources, and its significance is marginal.
The evolutionary LX decay is thus qualitatively different from that in MS stars: it is due to stellar contraction (and perhaps a change in the internal dynamo while the star transforms from a fully convective to a convective-radiative interior); in contrast, the decay of LX in MS stars is due to stellar spin-down while the stellar structure and size remain nearly constant. Figure 31 shows the long-term evolution of the median X-ray output from PMS stages to the end of the MS evolution, for G-type stars with ages > 10 Myr and K-type stars with ages < 10 Myr (because the predecessors of MS G stars are PMS K stars; data from Güdel 2004). The slight trend toward decreasing LX at ages < 10 Myr follows approximately LX ≈ t−0.3, in agreement with the individual trends for the Orion and the Taurus samples, albeit the scatter is large. No “onset ”of activity can be seen back to ages < 1 Myr.
Evolution of the X-ray luminosity of a near-solar mass star. A sample of field stars from the “Sun in Time” program is shown by filled circles. Open circles show the median LX for G-type stars in open clusters for ages >10 Myr, and for K-type stars in open clusters and star-forming regions for ages <10 Myr. The error bars show the approximate 1σ scatter in the samples (adapted from Güdel, 2004, original data from references given therein; © Springer Verlag, reprinted with permission).
In summary, the age evolution of the X-ray output is modest in PMS stars, the bulk of the X-ray output being determined by other stellar properties. There are at least four such parameters that have been discussed in the recent literature: bolometric luminosity, mass, rotation, and mass accretion rate. I briefly summarize these parameter dependencies in turn:
-
Similar to young MS stars, CTTS and WTTS straddle the empirical X-ray saturation limit, i.e., LX ≈ 10−3.5Lbol (e.g., Preibisch et al., 2005; Telleschi et al., 2007b), pointing to a dynamo process somehow related to the dynamo in MS stars. The long-term evolution of Lbol may then be the principal parameter for the long-term evolution of LX.
-
In contrast to MS stars, PMS stars show a correlation between LX and mass (e.g., Feigelson et al., 1993; Preibisch et al., 2005; Telleschi et al., 2007b). However, if one restricts the MS sample to saturated, young stars, then they follow such a relation as well, owing to the well-known mass-Lbol relation on the MS, Lbol ∝ M3. Conversely, the flatter Lbol − M relation for a given PMS isochrone combined with the saturation law yields an LX vs. mass correlation that is compatible with the observed relation (Telleschi et al., 2007b), i.e., the two relations are interdependent.
-
Rotation is one of the main drivers of the magnetic dynamo and therefore of magnetic activity in MS stars. The near-saturation state of most PMS stars, however, suggests that rotation cannot be a key parameter. This is borne out by explicit correlation studies of the Orion (Preibisch et al., 2005) and the Taurus (Briggs et al., 2007) samples of T Tauri stars that show little in the way of a correlation as seen in MS stars. On the contrary, some apparent trends in this direction are the result of population bias (Briggs et al., 2007). The absence of a decrease in the LX/Lbol ratio up to rotation periods of at least 10 d (in contrast to MS stars) can be explained by the convective turnover time in PMS stars being much larger, yielding smaller Rossby numbers for a given rotation period and therefore saturation up to longer rotation periods (Preibisch et al., 2005; Briggs et al., 2007).
-
Accretion could influence LX either by generating X-rays itself, or by suppressing coronal X-ray production. Empirically, LX is correlated with the mass accretion rate Ṁ but this is not a physical correlation for the following reason. Muzerolle et al. (2003), Muzerolle et al. (2005), and Calvet et al. (2004) described a relation between M and the stellar mass M, approximately reading Ṁ ∝ M2. Because LX correlates with Lbol and therefore, for a typical age isochrone, with mass, LX must correlate with Ṁ. Telleschi et al. (2007b) removed this trend from the Taurus sample. Although the two parameters still do not seem to be fully independent, a clear correlation cannot be established. Accretion does seem to influence magnetic energy output in more subtle ways, however, to be discussed in the Section 6.3.4.
6.3.4 Coronal excesses and deficits induced by activity?
If the photoelectric absorption by the accreting gas is small, then the softest X-ray range may reveal the high-temperature tail of the shock emission measure thought to be responsible for the UV excesses (Section 6.3.2). Telleschi et al. (2007b) and Güdel et al. (2007b) identified an excess in the O VII/O VIII Lyα flux (or luminosity) ratio in CTTS when compared with WTTS or MS stars, the so-called X-ray soft excess of CTTS (Figure 32b). In the most extreme case of the CTTS T Tau, the excess O VII flux is such that this line triplet, formed at only ≈ 2 MK, is the strongest in the soft X-ray spectrum (see Figure 33; Güdel and Telleschi 2007).
Left (a): The ultraviolet excess of CTTS. The figure shows the mean continuum surface flux at ≈ 1958 Å vs. the stellar effective temperature. CTTS are shown by the solid circles, naked (diskless) TTS by asterisks, and MS stars by squares. The solid lines define a fit to the MS stars, the dashed lines giving the lower and upper bounds (from Johns-Krull et al., 2000, reproduced by permission of AAS). Right (b): The X-ray soft excess in CTTS. The figure shows the ratio between O vii r and O viii Lyα luminosities (each in units of erg s−1) vs. LX. Labels give initial letters of stellar names. Crosses mark MS stars (from Ness et al., 2004), triangles solar analogs (from Telleschi et al., 2005), filled (red) circles CTTS, and open (blue) circles WTTS. Two solutions (high- and low-absorption) are given for T Tau, connected by a dotted line. The solid line is a power-law fit to the MS stars with LX > 1027 erg s−1 (from Güdel and Telleschi, 2007, reprinted with permission).
Comparison of fluxed X-ray photon spectra of (from top to bottom, all from XMM-Newton RGS) the active binary HR 1099, the WTTS V410 Tau, the CTTS T Tau, the T Tau spectrum modeled after removal of absorption (two versions, using NH = 3 × 1021 cm−2 and 4.9 × 1021 cm−2, respectively), and the inactive MS star Procyon. The bins are equidistant in wavelength (from top to bottom, the bin widths are, respectively, 0.025 Å, 0.070 Å, 0.058 Å, 0.058 Å, 0.058 Å, and 0.010 Å; from Güdel and Telleschi 2007, reprinted with permission).
Interestingly, however, the X-ray soft excess in CTTS is comparatively moderate, the L(O VII r)/L(O VIII) line flux ratio being enhanced by factors of typically ≈ 3–4 times that of equivalent MS stars or WTTS (Figure 32). Furthermore, the excess X-ray line fluxes do not seem to be correlated with the UV line excesses but are correlated with the overall stellar coronal activity level traced, for example, by the O VIII Lyα line flux (Güdel and Telleschi, 2007). It appears that the X-ray soft excess depends on the level of magnetic (“coronal”) activity although it is, at the same time, related to the presence of accretion. The two dependencies may point to an interaction between accretion and magnetic activity at “coronal” heights.
The shock interpretation of the softest X-rays and the X-ray soft excess is appealing, but remains controversial until a larger sample of CTTS with various accretion properties has been interpreted. In particular, given the appreciable accretion rates, high shock densities of order 1012–1014 cm−3 are expected, as first indeed reported from density-sensitive line diagnostics of O vii and Ne ix in the CTTS TW Hya, forming at only a few MK (Kastner et al., 2002; Stelzer and Schmitt, 2004). However, some accreting PMS stars show much lower densities, such as AB Aur (Telleschi et al., 2007b) and T Tau (Güdel et al., 2007b); the same discrepancy between expected and observed densities has also been reported from ultraviolet density diagnostics (Johns-Krull et al., 2000).
In stark contrast to the X-ray soft excess and the UV excess described above, it is now well established that CTTS show a moderate suppression of 0.1–10 keV soft X-ray emission, typically by a factor of ≈ 2 when compared with WTTS of similar properties (Strom and Strom, 1994; Damiani et al., 1995; Neuhäuser et al., 1995; Stelzer and Neuhäuser, 2001; Flaccomio et al., 2003; Preibisch et al., 2005; Telleschi et al., 2007a). Although selection/detection bias or different photoelectric absorption has been quoted to be responsible for these differences (see Güdel 2004 and references therein), the luminosity deficit in CTTS is now thought to be real; it appears that accretion suppresses coronal heating in a fraction of the coronal volume (Preibisch et al., 2005), or at least leads to larger amounts of cooler plasma, which is perhaps the same plasma inferred from the X-ray soft excess (Telleschi et al., 2007b; Güdel and Telleschi, 2007). Alternatively, the presence of a circumstellar disk could strip the outer parts of the stellar corona, thus reducing LX (Jardine et al., 2006).
6.3.5 X-ray flaring of the T Tauri Sun
A high level of near-continuous flaring is found in PMS solar-mass stars. As much as half of the emitted X-ray energy, if not more, may be due to strong flares (Montmerle et al., 1983), and many TTS are nearly continuously variable probably also owing to flares (Mamajek et al., 2000; Feigelson et al., 2002a; Preibisch and Zinnecker, 2002; Skinner et al., 2003). Examples with extreme luminosities and temperatures up to 100 MK have been reported (e.g., Preibisch et al., 1995; Skinner et al., 1997; Tsuboi et al., 1998, 2000; Imanishi et al., 2002). The most extreme flares are found on CTTS and protostars, a possible hint at star-disk magnetic interactions during flares. Wolk et al. (2005) studied frequency and properties of flares in the Orion Nebula cluster, concluding that the median peak luminosity of their sample was log LX = 30.97, with extremely hard spectra at peak time. The median electron temperature was found at 7 keV. An analogous study has been presented by Stelzer et al. (2007) for T Tauri stars in the Taurus Molecular Cloud. The extreme flaring recorded on these PMS stars may have an important bearing on coronal heating (see Section 5.8) and on the alteration of solids in the young stellar environment (see Section 6.6).
6.3.6 The radio T Tauri Sun in time
Early VLA surveys quickly reported strong radio emission from both CTTS and WTTS. Somewhat unexpectedly, however, radio emission comes in two principal flavors. The early, pioneering studies by Cohen et al. (1982), Bieging et al. (1984), Cohen and Bieging (1986), Schwartz et al. (1984), and Schwartz et al. (1986) recognized thermal wind-type emission with rising spectra and in cases large angular sizes for several CTTS. This radio emission can then be used to estimate mass loss rates; these are found to range up to ≲ 10−7 M⊙ yr−1 (André et al., 1987). The partly enormous kinetic wind energy derived under the assumption of a uniform spherical wind suggests anisotropic outflows while structural changes in the radio sources indicate variable outflows, probably along jet-like features; at shorter radio wavelength, dust emission from the disk becomes apparent as well (Cohen and Bieging, 1986; Rodríguez et al., 1992, 1994; Wilner et al., 1996). The thermal radio emission tells us nothing about the presence or absence of stellar magnetic fields. As described earlier, CTTS do show many signatures of magnetic activity, but whatever the possible accompanying radio emission, it seems to be absorbed by the circumstellar ionized wind.
The situation is different in WTTS in which the presence of huge flares (Feigelson and Montmerle, 1985; Stine et al., 1988; Stine and O’Neal, 1998), longer-term variability, and falling spectra clearly point to non-thermal gyrosynchrotron emission (Bieging et al., 1984; Kutner et al., 1986; Bieging and Cohen, 1989; White et al., 1992a; Felli et al., 1993; Phillips et al., 1996) analogous to radio emission observed in more evolved active stars. Conclusive radio evidence for the presence of solar-like magnetic fields in WTTS came with the detection of weak circular polarization during flares but also in quiescence (White et al., 1992b; André et al., 1992; Skinner, 1993). Extremely energetic particles radiating synchrotron emission may be involved, giving rise to linear polarization in flares on the WTT star HD 283447 (Phillips et al., 1996). VLBI observations showing large (∼ 10 R*) magnetospheric structures with brightness temperatures up to Tb ≈ 109 K fully support the non-thermal picture (Phillips et al., 1991).
As a WTT star ages, its radio emission drops rapidly on time scales of a few million years from luminosities as high as 1018 erg s−1 Hz−1 to values around or below 1015 erg s−1 Hz−1 at ages beyond 10 Myr. Young age of a star is thus favorable to strong radio emission (O’Neal et al., 1990; White et al., 1992a; Chiang et al., 1996), whereas toward the subsequent ZAMS stage it is only the very rapid rotators that keep producing radio emission at the 1015 erg s−1 Hz−1 level (Carkner et al., 1997; Magazzù et al., 1999; Mamajek et al., 1999).
6.3.7 The composition of the T Tauri Sun’s corona
Initial studies of a few accreting T Tau stars, in particular the old (≈ 10 Myr) TW Hya, have shown an abundance pattern in the X-ray source similar to the IFIP effect although the Ne/Fe abundance ratio is unusually high, of order 10 with respect to the solar photospheric ratio, and the N/O and N/Fe ratios are enhanced by a factor of ≈ 3.
These anomalous abundance ratios have been suggested (Stelzer and Schmitt, 2004; Drake and Testa, 2005) to reflect depletion of Fe and O in the accretion disk where almost all elements condense into grains except for N (Savage and Sembach, 1996; Charnley, 1997) and Ne (Frisch and Slavin, 2003) that remain in the gas phase which is accreted onto the star. If accretion occurs predominantly from the gas phase in the higher layers of the disk while the grains grow and/or settle at the disk midplane, then the observed abundance anomaly may be a consequence.
Larger systematics have made this picture less clear, however. Several CTTS and WTTS have revealed large Ne/Fe ratios (≈ 4 or higher), much larger than in MS active solar analogs (Kastner et al., 2004; Argiroffi et al., 2005, 2007; Telleschi et al., 2005, 2007b; Günther et al., 2006) but similar to RS CVn binaries (Audard et al., 2003b). In contrast, the CTTS SU Aur reveals a low Ne/Fe abundance ratio of order unity (Robrade and Schmitt, 2006; Telleschi et al., 2007b), similar to some other massive CTTS (Telleschi et al., 2007b).
Partial clarification of the systematics has been presented by Telleschi et al. (2007b) (see also Güdel et al., 2007b) who found that
-
the abundance trends, and in particular the Ne/Fe abundance ratios, do not depend on the accretion status but seem to depend on spectral type or surface Teff, the later-type stars showing a stronger IFIP effect (larger Ne/Fe abundance ratios); see Figure 34.
-
the same trend is also seen in disk-less ZAMS stars.
The coronal Fe/Ne abundance ratio (with respect to the solar photospheric mixture) in the X-ray sources of various PMS stars and very active MS stars as a function of spectral class. Symbols mark different types of stars: squares: active MS stars; triangles: WTTS; diamonds: CTTS. For details and references, see Telleschi et al. (2007b) and Güdel et al. (2007b).
Anomalously high Ne/O abundance ratios remain, however, for TW Hya (Stelzer and Schmitt, 2004) and V4046 Sgr (Günther et al., 2006) when compared to the typical level seen in magnetically active stars, including PMS objects. The initial idea proposed by Drake et al. (2005) was that the selective removal of some elements from the accretion streams should occur only in old accretion disks such as that of TW Hya where cogulation of dust to larger bodies is ongoing, whereas younger T Tauri stars still accrete the entire gas and dust phase of the inner disk. However, the old CTTS MP Mus does not show any anomaly in the Ne/O abundance ratio (Argiroffi et al., 2007). Larger samples are needed for clarification.
6.4 The protostellar Sun
6.4.1 Magnetic activity in the protostellar Sun
The protostellar Sun was deeply embedded in its molecular cloud envelope. Direct optical observation of protostars is preluded by high extinction; the best access to these objects is through infrared and X-ray observations, the former, however, picking up much of the emission from dust in the disk and the envelope. Recent efforts have succeeded in obtaining photospheric spectra of Class I protostars from light scattered off the bipolar cavities carved by the outflows (White and Hillenbrand, 2004). Somewhat perplexingly, the analysis of the Taurus sample of embedded objects reveals very little statistical diference between Class I and CTTS objects in Taurus, for example with respect to rotation rates, accretion rates, bolometric luminosities, spectral classes, and disk masses, providing evidence that this sample is co-eval with the CTTS sample; the embedded objects seem to be those with the longest envelope dispersal time, while they are all past their main accretion phase (White and Hillenbrand, 2004).
Magnetic field measurements are commensurately challenging. Johns-Krull (2007b) recently succeeded in obtaining near-infrared diagnostics to measure the photospheric magnetic field on a class I protostar. He reports a field strength of 3.6 kG, making this the highest mean surface field so far detected on any young stellar object.
Direct evidence for magnetic activity is seen in X-rays. Strong X-ray activity is found in considerable numbers of “Class I” protostars thanks to Chandra’s and XMM-Newton’s hard-band sensitivity (see, e.g., Imanishi et al., 2001; Preibisch and Zinnecker, 2001, 2002; Preibisch, 2003b; Getman et al., 2002; Güdel et al., 2007a). Their measured characteristic temperatures are very high, of order 20–40 MK (Tsujimoto et al., 2002; Imanishi et al., 2001). Some of these values may, however, be biased by strongly absorbed (“missing”) softer components in particular in spectra with limited signal-to-noise ratios. It is correspondingly difficult to characterize the LX values in traditional soft X-ray bands for comparison with more evolved stars.
6.4.2 Magnetic flaring of the protostellar Sun
Strong X-ray flaring is a characteristic of protostellar solar analogs. Many of these events are extremely large, with total soft X-ray energies of up to ≈ 1037 erg (Koyama et al., 1996; Kamata et al., 1997; Grosso et al., 1997; Ozawa et al., 1999; Imanishi et al., 2001; Preibisch, 2003a; Imanishi et al., 2003). Such flares realistically require large volumes, in fact to an extent that star-disk magnetic fields become a possibility for the flaring region (Grosso et al. 1997 for YLW 15 in p Oph), with important consequences for the irradiation of the stellar environment by high-energy photons and particles (see Section 6.5).
6.4.3 Radio emission from the protostellar Sun
At radio wavelengths, genuine, embedded class I protostars have most often been detected as thermal sources, and this emission is predominantly due to collimated thermal winds or jets. These jets are probably ionized by neutral winds that collide with the ambient medium at distances of around 10 AU and that are aligned with molecular outflows (e.g., Bieging and Cohen 1985; Snell et al. 1985; Brown 1987; Curiel et al. 1989; Rodríguez et al. 1989, 2003; Anglada 1995; Anglada et al. 1998). Ionized circumstellar material and winds easily become optically thick and therefore occult any non-thermal, magnetic emission from close to the star. However, the discovery of polarization in T Tau(S) (Phillips et al., 1993; Smith et al., 2003), in IRS 5 (Feigelson et al., 1998), in protostellar jet sources (Yusef-Zadeh et al., 1990) and the jet outflows themselves (Curiel et al., 1993; Hughes, 1997; Ray et al., 1997), as well as variability and negative spectral indices in T Tau(S) (Skinner and Brown, 1994) provided definitive evidence for magnetic fields and particle acceleration around these class I objects.
6.5 The pre-main sequence Sun’s environment in time
The molecular and dust environment of the very young (PMS) Sun was affected in several ways by ultraviolet radiation, high-energy radiation and high-energy particle streams emitted by the Sun. These often neglected effects have recently attracted considerable attention. Although they apply to the environment of any forming star that is magnetically active, they have been considered in particular for solar-like stars and specifically for the young Sun itself because of various traces that may be observable in the solid bodies of the present solar system. I give a brief overview of the themes in so far as they may relate to the past solar activity.
6.5.1 Circumstellar disk ionization
In terms of physical processes, ionization of the disk is important for the operation of the magneto-centrifugal instability (MRI; Balbus and Hawley 1991) thought to be the main driver of accretion in young stellar objects. Although cosmic rays have long been suspected to be an effective disk ionization source (Gammie, 1996), the high-level, hard coronal emission and frequent stellar flares may be more effective ionizing sources (Glassgold et al., 1997; Feigelson et al., 2002b). This is even more so as young solar analogs in the T Tau stage drive very strong winds that are very likely magnetized; such winds effectively shield the inner disk from cosmic rays, as does the present-day solar wind, at least for cosmic rays with energies < 100 MeV.
The distance to which stellar X-ray ionization dominates over that produced by galactic cosmic rays can be estimated to be (Glassgold et al., 1997; Montmerle, 2001)
where E is the photon energy in the range of 1–20 keV (for other energies, the first term in the parentheses must be generalized to σ(kTX)/σ(1 keV)), ζ is the cosmic ray ionization rate, and J0 is an attenuation factor (J0 ≈ 0. 13 for optical depth of unity for a 1 keV photon). The values given in the parentheses are characteristic for our situation, with the cosmic-ray ionization rate referring to a UV shielded molecular core. Stellar X-ray ionization therefore dominates cosmic ray ionization out to about 1000 AU, i.e., across most of the radius of a typical circumstellar disk. Taking into account frequent, strong flares, significant portions of molecular cores may predominantly be ionized by the central star rather than by cosmic rays.
Glassgold et al. (1997) and Igea and Glassgold (1999) modeled ionization and heating of circum-stellar disks by stellar coronal X-ray sources. The incoming X-ray photons are subject to Compton scattering and photoelectric absorption as they propagate through the disk. X-ray photons may interact with molecules or atoms by ejecting a fast (primary) photoelectron. This photoelectron collisionally produces on average 27 secondary electrons and ions (for a photon energy of 1 keV). Harder photons on average penetrate deeper and thus ionize layers of the disk closer to the equatorial plane, while softer X-rays ionize closer to the disk surface. The disk ionization fraction is then determined when an equilibrium between ionization and recombination has been reached. Electron fractions of 10−15−10−10 are obtained at vertical disk column densities of NH = 1027−1021 cm−2 (as measured from infinity) for distances of 0.1–10 AU from the central star. The precise results depend somewhat on the hardness of the X-ray spectrum (a modest LX = 1029 erg s−1 has been assumed).
The important points here are: 1) that the ionization fraction at the top of the disk is orders of magnitude higher than the ionization fraction that would result from standard cosmic-ray irradiation, and 2) that at vertical column densities of NH = 1024–1025 cm−2 and less, the disk is sufficiently ionized to become unstable against MRI. The disk surface will thus couple to the magnetic field and accrete to the star. In contrast, the deeper layers remain decoupled and therefore “quiescent”, at least within 5 AU (Figure 35, Igea and Glassgold 1999). These are the likely sites of planet formation (Glassgold et al., 1997). Modifications of these calculations by introducing trace heavy metals and diffusion have been discussed by Fromang et al. (2002) and Ilgner and Nelson (2006).
Consequences of X-ray irradiation of a circumstellar disk, shown in the r vs. N⊥ (vertical gas column density) plane. The critical surface (filled circles) separates regions that are coupled to the magnetic field based on a sufficiently high ionization fraction (above) from deeper regions that are uncoupled (below). The various solid lines define the disk midplanes for specific disk models, the bold line characterizing the minimum solar nebula (from Igea and Glassgold, 1999, reproduced by permission of AAS).
Disk irradiation and photoionization by stellar UV photons is further responsible for photoevaporation of gaseous disks (Hollenbach et al., 1994; Clarke et al., 2001; Alexander et al., 2006a, b), and therefore the long-term accretion history of the star-disk system. Additional X-ray irradiation is, however, of secondary importance only (Alexander et al., 2004).
6.5.2 Circumstellar disk heating
Apart from disk ionization, X-ray irradiation also leads to disk heating (Igea and Glassgold, 1999; Glassgold et al., 2004). While dust disks are heated by the central star’s optical and UV light to a few 100 K at distances up to a few AU, the gas component may thermally decouple in particular in the upper layers where the density is small. A model calculation based on accretion viscosity heating combined with X-ray heating due to the central star shows that the upper layers of the gaseous disk (NH ≲ 1021 cm−2) can be heated up to ≈ 5000 K (Figure 36). This holds even for low viscous heating efficiency where the X-ray heating contribution entirely dominates (Glassgold et al., 2004). At the same time, the strong temperature gradients in the temperature inversion region lead to the production of large amounts of “warm” CO. Similar calculations by Gorti and Hollenbach (2004) support the above picture of X-rays dominating gas heating at the disk surface.
Gas and dust temperatures of a circumstellar disk as a function of vertical column density. Different solid lines give the gas temperature for various viscous-heating rates. The leftmost curve is predominantly due to X-ray heating, in the rightmost curve, viscous heating is important. The dashed line gives the dust temperature from a standard dust-disk model (figure from Glassgold et al., 2004, reproduced by permission of AAS).
6.5.3 Observational evidence of disk irradiation
The elevated ultraviolet and X-ray activity level of young low-mass stars leads to significant irradiation of circumstellar accretion disks. Interactions between high-energy photons and disk matter is evident from X-ray photoabsorption in star-disk systems seen edge-on, but also from reprocessed starlight: Spatially unresolved FUV fluorescence lines of H2 have been detected from several CTTS (Brown et al., 1981; Valenti et al., 2000; Ardila et al., 2002; Herczeg et al., 2002, 2006), but usually not from WTTS (Valenti et al., 2000); this emission is reprocessed stellar Lyα emission most intensely radiated from the accretion spots. At least in cases where the line radial velocities are coincident with stellar radial velocities, an origin of the fluorescence in a hydrogenic surface layer of the inner accretion disk at temperatures of 2000–3500 K is likely (Herczeg et al., 2002, 2004) although significantly blueshifted H2 emission points to outflow-related fluorescence in some systems (Brown et al., 1981; Ardila et al., 2002; Walter et al., 2003; Saucedo et al., 2003; Herczeg et al., 2006). Fluorescent emission is also generated by reprocessing of X-ray photons; X-ray fluorescence is seen in particular in the 6.4 keV line of cold iron (Imanishi et al., 2001; Tsujimoto et al., 2005; Favata et al., 2005).
Simple energy considerations are revealing: Herczeg et al. (2004) estimate the rate of energy deposited in the environment of the CTTS TW Hya as a result of Lyα photoexcitation and subsequent far-ultraviolet fluorescence of H2 to be 1.4 × 1029 erg s−1. The total soft X-ray luminosity of ≈ 1.4 × 1030 erg s−1 will at least partially heat the disk surface layer further (Igea and Glassgold, 1999).
Warm H2 has also been detected through infrared 2.12 µm ro-vibrational emission from several T Tauri stars (Weintraub et al., 2000; Bary et al., 2003). This emission is thought to be excited by collisions between H2 molecules and X-ray induced non-thermal electrons, or by an UV radiation field. High temperatures, of order 1000–2000 K, are required, but such temperatures are predicted from disk irradiation by X-rays out to several AU (Glassgold et al., 2004), or by UV radiation from the central star out to ≈ 10 AU if the star shows an UV excess (Nomura and Millar, 2005).
Glassgold et al. (2007) proposed forbidden [Ne II and Ne iii] infrared line emission at 12.81 µm and 15.55 µm, respectively, to be indicative of X-ray irradiation. The high first ionization potential of Ne (21.6 eV) indeed requires Ly continuum or X-ray photons for ionization (or cosmic rays, which are unlikely to be abundant in the inner disk region). The transitions are collisionally excited in warm gas, requiring temperatures of a few 1000 K, attained in disk surface layers out to about 20 AU for X-ray irradiated disks (Glassgold et al., 2004). The [Ne II] 12.81 µm transition has indeed been detected in several CTTS (Pascucci et al., 2007; Lahuis et al., 2007; Ratzka et al., 2007).
As a further consequence, specific chemical reactions may be induced. For example, Lyα itself can dissociate molecules like H2 and H2O and can ionize Si and C (Herczeg et al., 2004). Lyα radiation photodissociates HCN (but not CN), which leads to an enhancement of CN relative to HCN (Bergin et al., 2003).
6.6 The T Tauri Sun’s activity and meteoritics
The presence of chondrules and isotopic anomalies in chondritic meteorites has posed one of the most outstanding problems in our understanding of the young solar system. Chondrules are millimeter-sized spheres of igneous rock embedded in the meteoritical matrix; their content and structure suggests that they were heated to melting temperatures (≈ 2000 K) of solid iron-magnesium silicates for only an hour or less. They must have cooled in an ambient magnetic field of ≈ 10 G (Shu et al., 2001). Calcium-aluminum-rich inclusions (CAIs) are structures in meteorites that vary in shape; they may derive from melt or partial melts. CAIs contain evidence for short-lived radionuclides in the young solar system, in particular of 26Al, 41Ca, 53Mn, and 60Fe with half-lives of 1.1, 0.15, 5.3, and 2.2 Myr, respectively (Lee et al., 1998; Gounelle et al., 2001).
Conventionally, it has been assumed that these short-lived isotopes were injected by external stellar nucleosynthetic events (ejecta from AGB stars, Wolf-Rayet stars, supernova explosions) that at the same time triggered the collapse of the parent molecular cloud, to form the solar system. The fundamental problem with external seeds is the short time required between the formation and injection of live radionuclides and their incorporation into solid CAI structures; this time span should not exceed 105 yr (Lee et al., 1998), i.e., the trigger for the formation of the solar system must have been extremely fast. Observations of galactic star-formation regions show star-forming molecular cloud cores to be rarely within the immediate environment of Wolf-Rayet wind bubbles or supernova shells (Lee et al., 1998); the association of asymptotic giant branch stars with star-forming regions is also very small, making injection of 60Fe into the solar system from such a star improbable (Kastner and Myers, 1994). Also, the assembly of CAIs and chondrules into planetesimals takes much longer, of order 5 Myr (Lee et al., 1998).
These problems can be removed if the short-lived radionuclides were formed locally, namely by bombardment with “cosmic rays” ejected by stellar flares (Lee et al., 1998). While this alternative for the production of the radionuclides is not unanimously accepted or may not be responsible for all isotopic anomalies in meteorites (e.g., Goswami et al., 2001; Wadhwa et al., 2007), I discuss only this hypothesis here as it is directly related to the (undisputed) high activity level of the young Sun in its T Tauri stage.
There is indeed substantial evidence for an active early Sun not only from inferences from active, young solar analogs (Section 5), but also from large enrichments of spallation-produced 21Ne and 38Ar in “irradiated” meteorite grains (i.e., grains that show radiation damage trails from solar-flare Fe-group nuclei), compared to “non-irradiated” grains (Caffee et al. 1987; a summary of further, earlier, albeit ambiguous evidence can be found in Newkirk Jr 1980). Galactic cosmic-ray irradiation would require exposure times in excess of 108 yr for some of these grains, incompatible with other features of the meteorites (Caffee et al., 1987). Alternatively, energetic solar flare protons could be responsible, but the present-day level would again be insufficient to explain the anomaly. Caffee et al. (1987) concluded that an elevated particle flux, related to the enhanced magnetic activity of the young Sun, naturally explains the meteoritic spallation-produced 21Ne enrichment. A flux several orders of magnitude in excess of present-day values and a harder energy spectrum would be required.
Energetic protons required for the generation of radionuclides could be generated in various places in the extended stellar magnetosphere. In the “x-wind” model proposed by Shu et al. (1997, 2001), magnetic reconnection flares occur at the inner border of the accretion disk where closed stellar magnetic fields and open disk fields converge. Flares would flash-melt protochondrules, and the x-wind would eject them to larger solar distances. Radionuclides would be synthesized by flare proton bombardment.
Alternatively, the elevated activity of the central star itself may be sufficient to produce the required proton flux at planetary distances. Feigelson et al. (2002b) estimated the proton flux at 1 AU of a solar analog in its T Tauri phase, from a statistical X-ray study of T Tauri stars in the Orion Nebula Cluster. They found that frequent flares on T Tauri stars are 101.5 times more luminous than the largest solar flares (or 104 times more than solar flares that occur with a daily frequency). These same flares occur at a rate about 102.5 higher than the rate of the largest solar flares. As solar proton fluxes scale non-linearly with the solar X-ray luminosity, Feigelson et al. (2002b) estimated a proton flux about 105 times higher than at present (i.e., 107 protons cm−2 s−1 at 1 AU). Given the high flare rate, this flux was probably present almost continuously.
Regardless of the location of the proton acceleration (flaring) source, I now summarize the relevant results for various radionuclides. For example, 41 Ca is predominantly produced through
where 41Sc electron-captures to 41Ca (Lee et al., 1998). Note that the abundance ratio for 42Ca/40Ca is 6.7 × 10−3 (Lee et al., 1998, and references therein). Summing all three production channels, an isotopic ratio 41Ca/40Ca as inferred from CAIs requires a proton flux of 5 × 103–104 times the present-day value during an irradiation time scale of 5 × 105–106 yr (Goswami et al., 2001). This approximately matches the observational implications from T Tauri flares by Feigelson et al. (2002b).
Similar considerations for 26Al lead to an underproduction by a factor of 20 under the same conditions (Lee et al., 1998). Goswami et al. (2001) require a proton flux 105 times as strong as the present flux at 1 AU to explain the inferred 26Al abundance in the forming CAIs, and irradiation times of about 1 Myr; this is in excellent agreement with the observational inferences made by Feigelson et al. (2002b). However, 3He bombardment of 24Mg may efficiently produce 26Al as well. 3He is preferentially accelerated in solar impulsive (as opposed to gradual) flares (see discussion in Lee et al. 1998 and references therein). The problem then arises that 41Ca is overproduced by two orders of magnitude through reactions involving 3He. Shu et al. (1997, 2001) therefore proposed that CAIs consisting of refractory, Ca-Al-rich material are surrounded by thick mantles of less refractory, Mg-rich material. 3He nuclei would therefore be stopped in the outer mantle where 26Al is produced from 24Mg, while the 40Ca-rich interior remains less affected, i.e., 41Ca production is suppressed. Canonical isotopic ratios can then indeed be derived for most of the species of interest (Gounelle et al., 2001).
The most promising support for local irradiation by solar (or possibly, trapped cosmic ray) protons has been the discovery of 10Be (McKeegan et al. 2000; half-life of 1.5 Myr) and possibly also the extremely short-lived 7Be (Chaussidon et al. 2006; half-life of 53 d). The 10Be isotope could be entirely produced by solar protons and 4He nuclei at asteroidal distances (Gounelle et al., 2001; Marhas and Goswami, 2004) while it is destroyed in the alternative nucleosynthetic production sources such as massive stars or supernova explosions. If the presence of 7Be in young meteorites can be confirmed, then its short half-life precludes an origin outside the solar system altogether and requires a local irradiation source.
Despite the successful modeling of radionuclide anomalies in early CAIs, at least the case of 60Fe remains unsolved in this context. It is difficult to synthesize by cosmic-ray reactions; the production rate falls short of rates inferred from observations by two orders of magnitude (Lee et al., 1998; Goswami et al., 2001) and requires stellar nucleosynthesis or, most likely, a supernova event (Meyer and Clayton, 2000).
Although the formation of radionuclides in early meteorites is under debate (Goswami et al., 2001) and may require several different production mechanisms (Wadhwa et al. 2007; for example, to explain the simultaneous presence of the 60Fe and the 10Be isotopes), the above models are at least promising in explaining some nuclear processing of solar-system material without external irradiation source but with sources whose presence cannot be disputed, namely high-energy particle populations that are a direct consequence of the magnetic activity of the young Sun. Isotopic anomalies in meteorites have opened a window to the violent environment of the young solar system.
6.7 Summary: The violent pre-main sequence Sun
Both the T Tauri and the protostellar Sun were extremely magnetically active, as far as we can tell from observations of contemporaneous objects at these stages. There is no definitive evidence for a turn-on of magnetic activity (for a contrasting view, see Linsky et al., 2007), but the stellar environment (gas and dust disks and envelopes) makes observations challenging. On the other hand, perhaps the most interesting aspect of magnetic activity in this phase is indeed its influence on the environment itself. High X-ray and UV fluxes produced both by magnetic activity and magnetically funneled accretion flows onto the star heat and ionize the circumstellar disk, thus controlling mechanisms as diverse as gas-disk photoevaporation, accretion through the mag-netorotational instability, and chemical networks across the disk. Strong flaring and observations of non-thermal gyrosynchrotron emission in T Tauri and protostars further indicate the presence of strongly elevated particle fluxes in the pre-main sequence Sun’s environment. The impact on solid-state matter forming in the circumstellar disk may be visible to the present day, in the form of daughter products of short-lived radioactive isotopes formed by proton impact. The study of the young Sun’s environment under the aspect of magnetic activity of the central star is still in its early stage and rapidly developing.
7 The Solar System in Time: Solar Activity and Planetary Atmospheres
7.1 The Faint Young Sun Paradox: Greenhouse or deep freeze?
Standard solar models imply that the Sun’s bolometric luminosity has monotonically increased during the past 4.6 Gyr. At its ZAMS stage (t = −4.6 Gyr), the solar luminosity was only 70–75% its present-day level. In the absence of an atmosphere, the Earth’s surface equilibrium temperature would then have amounted to 355 K (Sagan and Chyba, 1997). Assuming an albedo and an atmospheric composition equal to values of the present-day Earth, the mean surface temperature would have been below the freezing point of seawater until ≈ 2 Gyr ago (Sagan and Mullen, 1972). The increase of the surface temperature in the presence of an atmosphere is due to the greenhouse effect, i.e., the property of the atmospheric mixture to be transparent to incoming optical and near-infrared light but to absorb mid-infrared emission that has been re-emitted from the surface. The present-day atmosphere of the Earth rises the surface temperature by only 33 K compared to the atmosphere-free equilibrium value (Sagan and Mullen 1972; Kasting and Catling 2003, see Figure 37).
Illustration of the greenhouse and the Faint Young Sun Paradox for the Earth. The solid line indicates the solar luminosity relative to the present value (right y axis); the lower dashed curve is the effective radiating temperature of the Earth (i.e., its surface being treated as a blackbody radiator); the upper dashed curve shows the calculated, mean global surface temperature affected by the greenhouse (CO2 mixing ratio and relative humidity have been kept fixed; from Kasting and Catling 2003, © 2003 by Annual Reviews, reprinted with permission).
On the other hand, there is clear geologic evidence for a warm climate in the early Earth’s history, with average temperatures perhaps even significantly above present-day values (Kasting and Toon 1989; Kasting 1989; Karhu and Epstein 1986, see also summary of further evidence in Sackmann and Boothroyd 2003). Sedimentary rocks (Bowring et al., 1989) and indirect evidence of microbial life in rock dated to 3.8 Gyr ago (Mojzsis et al. 1996; see also summaries by Nisbet 2000 and Nisbet and Sleep 2001) clearly suggest the presence of liquid water (see also Kasting and Toon, 1989).
There is similar geological evidence for a warmer young Mars, as seen in particular in extensive channels formed by massive streams of liquid water. But again, the mean Martian surface temperature is too low for the presence of liquid water, and the less intense photospheric light from the younger Sun would obviously have aggravated this problem.
The apparent contradiction between implications from the standard solar model and the geologic evidence for a warm early climate on the Earth and Mars is known as the “Faint Young Sun Paradox” (Kasting and Toon, 1989; Kasting and Grinspoon, 1991). This problem has been addressed along two major lines of argumentation of which one (assuming a higher mass loss rate for the young Sun) indirectly relates to the magnetic activity of the young Sun; the other (arguing with greenhouse gases) may be related in as of yet unknown ways to magnetic activity as well (via atmospheric chemistry, see Section 7.2.1), although other processes in no ways related to solar magnetic fields may be relevant. After reviewing these two approaches, I will discuss model calculations that specifically address the influence of magnetic activity on planetary atmospheres (Section 7.2).
7.1.1 The relevance of greenhouse gases
Today’s modest greenhouse effect is due to atmospheric CO2 and H2O (see, e.g., Kasting and Toon, 1989, for a summary). A stronger greenhouse could have been effective in a different atmosphere of the young Earth:
-
1)
A higher content of atmospheric gaseous CO2 might increase the greenhouse effect (Owen et al., 1979; Cess et al., 1980) as in the present-day atmosphere of Venus, but a 100fold increase compared to present-day levels would be required (Kasting and Toon, 1989); such levels of CO2 are plausible because the carbonate-silicate geochemical cycle (which binds CO2 dissolved in rainwater to silicate minerals in the soil) operates in such a way that removal of atmospheric CO2 increases with increasing temperature, thus inducing a negative feedback loop between CO2 greenhouse warming and CO2 removal (Kasting and Toon, 1989). However, the absence of siderite in old soils argues against the required high levels of CO2 (Rye et al., 1995). For Mars, high levels of CO2 in a higher-pressure atmosphere would condense in clouds. The resulting increased global albedo would in fact lead to a net cooling (Kasting, 1991). Although the same clouds may also back-scatter radiation and therefore support the greenhouse (Forget and Pierrehumbert, 1997), experiments suggest that this mechanism is too small to rise the temperatures above the freezing point (Glandorf et al., 2002).
-
2)
Greenhouse gases such as NH3 (Sagan and Mullen, 1972) and CH4 (Sagan and Chyba, 1997) could have been present in appreciable amounts in the young atmospheres, in analogy to the present-day atmosphere of Titan. However, NH3 dissociates rapidly due to solar UV radiation (Kuhn and Atreya 1979; see also Owen et al. 1979). While CH4 is subject to UV dissociation as well, its lifetime is much longer, and biological activity could regenerate it at sufficiently high levels (Pavlov et al., 2000). Moreover, its photolysis may produce a high-altitude haze of organic solids that shields ammonia sufficiently from UV dissociation (Sagan and Chyba, 1997).
How the changes in the atmospheres came about is not entirely clear but may partly be related to the past solar activity (apart from, e.g., weathering, plate tectonics, volcanism, and biological activity). Although enhanced levels of solar EUV and X-ray emission will not directly alter the lower planetary atmospheres but only affect the higher thermosphere (where this radiation is absorbed) and the exosphere (see Section 7.2 below), the complex chemistry induced by photoionization, photodissociation, and heating through enhanced high-energy irradiation may be a key factor in determining what greenhouse gases were available in the young planetary atmospheres, as speculated by Ribas et al. (2005). For example, enhanced photodissociation may have influenced the abundances of ammonia and methane. Also, photochemistry and subsequent production of UV-shielding O3 (Canuto et al., 1982, 1983) was important for the formation and evolution of life, and life itself eventually altered the composition of the young terrestrial atmosphere very significantly.
7.1.2 A bright young Sun?
A more radical remedy of the Faint Young Sun Paradox would be a Sun that was in fact not faint, i.e., did not follow the standard solar model calculations (see Sackmann and Boothroyd, 2003, for a discussion on controversies related to possible greenhouse effects, or their need, in the early atmospheres of Earth and Mars). Such would be possible if the ZAMS Sun had been more massive, having lost its mass in a wind at rates considerably higher than the present-day solar wind. The latter results in a mass loss of (2–3) × 10−14 i⊙ yr−1 (Wood, 2004, and references therein), and the radiative losses of energy transformed in thermonuclear reactions amount to about 3 times this rate. If the Sun had been subject to these present-day losses for its entire lifetime, its ZAMS mass would have been only 0.05% higher than the present-day value (Minton and Malhotra, 2007). This would change the young Sun’s bolometric luminosity negligibly (recall the mass-luminosity relation for MS stars, which requires approximately Lbol ∝ M3; based on Siess et al. 2000 ZAMS calculations for low-mass stars).
Higher wind mass-loss rates would be an interesting alternative (Graedel et al., 1991). Willson et al. (1987) hypothesized that intermediate-mass stars may lose appreciable amounts of mass during their MS life, in particular in the pulsation-instability strip; early G-type stars would then be descendants of A-type stars. Hobbs et al. (1989) concluded that a wind mass loss of 0.041 M⊙ since the Sun’s arrival on the ZAMS would suffice to explain the low Li values observed in the present-day photosphere (because Li would be diluted when the wind-driving surface layer is progressively mixed with Li-free material entering from lower, hotter layers; see also Schramm et al. 1990; note, however, that there are other, and more important, processes that deplete Li, see Sackmann and Boothroyd 2003). A higher mass loss rate for the young Sun is in fact supported by meteoritic and lunar evidence, suggesting that 2.5–3.5 Gyr ago (solar age of 1–2 Gyr), the wind mass loss was on average 10 times higher than at present (Geiss and Bochsler, 1991). This would, however, result in a solar mass still only ≈ 0.1% higher at t = −3 Gyr than now (Sackmann and Boothroyd, 2003). To simultaneously fulfill the requirement of liquid water on young Mars, the initial solar mass would have to be ≳ 1.03 M⊙ (Sackmann and Boothroyd, 2003).
Gaidos et al. (2000) used radio observations of three solar analogs at ages of a few 100 Myr to set upper limits to their present mass-loss rate. Because the spin rates of solar analogs reveal a power-law decay in time, Ω ∝ t−0.6 (Equation 8, also Skumanich 1972 who gave an exponent of −0.5), Gaidos et al. (2000) argued for a power-law decay of the mass-loss rate as well (Equation 6), which, together with the radio upper limits, results in a maximum cumulative mass loss of 6% of the solar mass during the past 4 Gyr. This is close to the suggested mass losses to dilute Li (Hobbs et al. 1989, but note other Li depletion processes), is in agreement with the minimum loss of 3% required to explain liquid water on Mars (Sackmann and Boothroyd, 2003), and is also slightly lower than the upper limit of 7% of M⊙ to avoid runaway greenhouse on Earth (Whitmire et al., 1995; Kasting, 1988) (the runaway greenhouse would evaporate the entire water ocean so that all water would be present in the atmosphere as steam; photodissociation and rapid loss of hydrogen by hydrodynamic escape [see Section 7.2.3 below] would lead to a dry planet — analogous to present-day Venus; see Ingersoll 1969).
Corresponding models have been computed by, among others, Boothroyd et al. (1991), Guzik and Cox (1995), and Sackmann and Boothroyd (2003). The upper limit for the ZAMS Sun allowed by the Li depletion purely due to wind-mass loss was found to be 1.1 M⊙ (Boothroyd et al., 1991; Guzik and Cox, 1995). Helioseismology constraints are compatible with model calculations starting with ZAMS solar masses up to (1.07–1.10) M⊙ (Boothroyd et al., 1991; Guzik and Cox, 1995) but the consequent enhanced mass loss should be confined to the earliest ≈ 200 Myr of the Sun’s life on the MS, implying loss rates as high as 5 × 10−10 M⊙ yr−1 (Guzik and Cox, 1995). Somewhat depending on the precise mass-loss law, the solar flux starts at values up to 7% higher than the present-day value (corresponding to mass-loss rates of ≈ 10−11−10−10 M⊙ yr−1 at ZAMS age) to drop to a minimum no less than 80% after 1–2 Gyr, and to increase again in agreement with the evolution of the standard solar model (Figure 38). The highest acceptable initial solar mass is 1.07 M⊙ to ensure that the young Earth would not lose its water via a greenhouse effect, photodissociation and subsequent loss of hydrogen into space (Sackmann and Boothroyd 2003; see also Section 7.2 below).
Solar flux in time relative to present, for a Sun that was subject to strong mass loss in its past. Different curves show calculations for different initial masses and corresponding mass-loss rates such that the present-day values are obtained. The mass-loss rate declines exponentially in time; the flux increase at later times is due to the luminosity increase of the Sun for nearly constant mass. The double arrow indicates the lower limit for the presence of liquid water on early Mars, the thin arrow an (unrealistic) extreme lower limit (from Sackmann and Boothroyd, 2003, reproduced by permission of AAS).
However, the indirect inferences for the mass-loss rates of the young Sun derived by Wood et al. (2002) and Wood et al. (2005) (see Section 5.1) would again not support a significantly brighter ZAMS Sun. Using the power-law mass-loss decay relation of Wood et al. (2002) back to ZAMS, a total mass-loss of about 0.01 M⊙ would result (Sackmann and Boothroyd, 2003), with an uncertainty of a factor of a few. Most of the mass loss would occur in the first few 100 Myr. The suppressed mass loss at early times, however (Wood et al., 2005), suggests that no more than 0.003 M⊙ could be lost during the Sun’s MS life (Minton and Malhotra, 2007).
In summary, the main problem with the “bright young Sun” model remains the disagreement between climatic requirements for the young-Sun mass (i.e., a ZAMS solar mass of [1.03–1.07] M⊙) and the indirectly measured mass-loss rates (Minton and Malhotra, 2007) that tend to be too small (Wood et al. 2005, i.e., resulting in a ZAMS mass of no more than 1.01 M⊙), although radio upper limits (Gaidos et al., 2000) are still compatible with the required mass-loss rates.
7.1.3 Cosmic rays and a stronger solar wind
Shaviv (2003) suggested a link between the cosmic ray flux and average global temperatures on Earth. Although a physical basis and an accepted proof are still missing, there is suggestive evidence that elevated cosmic-ray fluxes have a cooling effect on the Earth’s atmosphere. In this picture, cosmic rays ionize tropospheric layers, and charged ion clusters lead to condensation nuclei that eventually form clouds. Low-lying clouds have a cooling effect (Shaviv, 2003).
Given that wind of the young Sun was stronger (Section 5.1), the cosmic-ray flux reaching the inner solar system was suppressed compared to present-day fluxes. Cloud formation would thus be suppressed, leading to a warmer climate. Model calculations (also including effects due to variable star-formation rate in the solar vicinity on the cosmic-ray generation, a more rapid rotation of the Earth, and a smaller land mass) suggest that about 2/3 of the temperature reduction associated with the fainter young Sun can be compensated.
7.2 The Sun’s activity in the young solar system
Stellar magnetic activity strongly influences planetary surfaces and atmospheres in at least two ways:
-
The solar wind and high-energy particle streams interact with ions and neutrals in the upper planetary atmospheres, but also with the solid surfaces in the absence of atmospheres. Electron impact ionization, charge exchange, and other processes lead to important alterations of atmospheric or surface materials and to their erosion (e.g., Chassefière and Leblanc, 2004; Kulikov et al., 2007).
-
High-energy (XUV) radiation affects planetary atmospheres through ionization, heating, dissociation and recombination and induced chemistry (e.g., Canuto et al., 1982). Hard radiation also interacts with solid surfaces.
The evolution of planetary surfaces and atmospheres can therefore be understood only in the context of the evolution of the enhanced high-energy solar particle and photon fluxes. For this reason, the past, much higher solar XUV and particle fluxes are crucial elements in our understanding of planet evolution, in particular questions on evaporation of their atmospheres and the loss of water reservoirs. After a short summary of relevant physical effects, I address key issues related to solar-system planets and Saturn’s moon Titan, and conclude with aspects related to “hot Jupiters” around solar analogs.
The evolution of the Earth’s atmosphere is sketched in Figure 39. It indicates a large water reservoir at the earliest times, part of which is thought to have subsequently escaped from Earth (see also Section 7.2.6 below). Note also the rapid increase of biologically produced O2 starting around 2.2 Gyr before present.
Evolution of the constituents of the Earth’s atmosphere in time (adapted from http://science.nasa.gov/headlines/y2002/10jan-exo-atmospheres.htm?list161037, after D. Des Marais and K.J. Zahnle).
7.2.1 Planetary atmospheric chemistry induced by high-energy radiation
The young Sun’s elevated ultraviolet flux had considerable impact on the photochemistry of planetary atmospheres. Ayres (1997) estimated the photoionization rates based on the evolution of ionizing flux of solar analogs. He concluded that photorates scale approximately as t−1, implying rates that were nearly 100 times stronger at a solar age of 100 Myr than at present (Figure 40).
Photoionization rates for H, O, O2, and N2 for different ages of the Sun, derived from the level of ionizing flux of solar analogs. The thick solid lines give the best estimates, the shaded areas give the allowed ranges based on uncertainties in the rotation-activity relationship (from Ayres, 1997, reprinted with permission).
UV radiation initiated the photochemical processes leading to the formation of O2 and O3 in the prebiotic terrestrial atmosphere (Canuto et al., 1982). Ozone absorbs strongly in the 200–300 nm band and therefore protects life from lethal doses of UV radiation.
UV radiation produces oxygen by photolysis of water and CO2:
after which O2 is formed (Canuto et al., 1982). The atomic H can escape into space (see Section 7.2.3 below). Ozone is formed through
(M stands for other molecules; there are also several reactions that destroy O2 and O3; see Canuto et al. 1982). Atmospheric chemical models subject to enhanced UV irradiation show that the surface mixing ratio of O2 increases by a factor of 104–106 above the standard pre-biotic value of 10−15 due to enhanced levels of solar UV radiation (corresponding to 1–300 times the present-day Sun).
The UV irradiation of the young Earth was particularly strong during the Sun’s T Tauri phase, up to factors of 103 above the present solar values. The potential influence on planet formation and the subsequent generation of planetary atmospheres should therefore have been very significant at those epochs — if any of the planetary atmospheres were indeed forming at such early times already. The UV irradiation could increase the total column of O3 by 1–3 orders of magnitude (Canuto et al., 1983), thus shielding incoming solar UV radiation efficiently and protecting early forms of life.
7.2.2 High-energy radiation and the planetary biospheres in habitable zones
Ionizing radiation is of crucial importance also for the evolution of life. While high doses are lethal for life, modest doses are important drivers of genetic mutations and therefore biological evolution. Although at present most high-energy radiation is absorbed in the high atmosphere of the Earth, significant effects may be found in thinner atmospheres (e.g., Mars) or in the environment of the young Sun where the irradiation by XUV photons was hundreds of times stronger. Smith et al. (2004) have computed the propagation of ionizing radiation through model atmospheres of terrestrial-like planets.
The incident spectra are those of supernovae explosions, gamma-ray bursts and, relevant for us, coronal X-ray flares that occurred at a much higher rate and up to much higher total energies in the young Sun compared to the present (Telleschi et al., 2005; Audard et al., 2000). Monte Carlo methods were used to calculate the transfer of incident X-ray and gamma-ray photons via Compton scattering and photoabsorption. The incident high-energy photons ionize molecules, thereby creating primary electrons, which collide further to produce secondary photoelectrons. These excite molecules and create aurora-like emission. A single incident photon can cause ionization of tens of thousands of molecules. For a neutral gas, most of the secondary-electron energy, however, goes into molecule excitation rather than ionization (different from ionized gas; Smith et al. 2004).
Strong re-radiation of the energy will occur in the N2 bands in the UV region (Smith et al., 2004), and at this point, the composition of the atmosphere becomes relevant as a variety of opacity sources and Rayleigh scattering will redistribute the radiation. Smith et al. (2004) studied in particular “habitable” atmospheres, requiring column densities of at least 30–100 g cm−2 for Earth-like planet (the Earth atmosphere’s column density is 1024 g cm−2). Their principal results can be summarized as follows:
-
While the direct transmission of stellar flare X-ray photons to a planetary surface is negligible, in a thin atmosphere with column density of 30–100 g cm−2, pure atmospheric Rayleigh scattering (appropriate for a young terrestrial atmosphere) would transmit ≈ 10% of the incident energy flux as UV radiation; about 1–3% are transmitted as UV photons if only a terrestrial-like O3/O2 molecular absorption screen is present.
-
In denser, Earth-like atmospheres (≳ 100 g cm−2), direct transmission of X-ray photons is essentially zero, but still of order 2 × 10−3 of the incident flux reaches the surface as UV radiation even in the presence of an O3/O2 shield. In a pure Rayleigh-scattering atmosphere (important for the young Earth), the transmission is of order 5%.
Even planets with thick atmospheres that shield evolving life from direct ionizing radiation will shower their surfaces with UV radiation owing to stochastic flares occurring on the host star. The present-day Sun produces about one flare every 100 yr with a transmitted UV surface flux equal to or larger than the continuous solar UV flux in the 200–320 nm band (Smith et al., 2004). Whether the UV irradiation effect is of prime importance for a planet around a young solar-like star is not clear, but it appears to be important for planets orbiting lower-mass M dwarf flare stars (Smith et al., 2004).
7.2.3 Planetary atmospheric loss and high-energy radiation and particles
Various mechanisms induced by solar magnetic activity can lead to escape of planetary atmospheric species, both neutrals and ions. The principal losses strongly depend on the magnetic activity of the host star. Thermal escape processes relate to a Maxwellian particle distribution and are consequently determined by the temperature of the respective atmospheric layer, and therefore by its heating rate. Thermal escape is predominantly controlled by photon irradiation from the host star. Non-thermal escape is due to other processes in which energization and escape are related to microscopic non-thermal processes (e.g., particle acceleration; Lundin and Barabash 2004; Lundin et al. 2007). Key factors are high-energy particle streams from the central star, i.e., the solar/stellar winds, and the magnetic environment of the planet itself.
The heating of planetary upper atmospheres and the generation of ionospheres is primarily due to the solar XUV radiation. The thermosphere is the layer in which most of this radiation is absorbed and is transformed to heat, leading to a positive (upward) temperature gradient. In the exosphere, the mean free path of atmospheric species is large, so that collisions are negligible. The lighter species may escape from this layer into space if their thermal velocity exceeds the gravitational escape velocity. The base of the exosphere, the exobase, is located at the height where the mean free path is equal to the local scale height, H = kTexo/mg, where k is the Boltzmann constant, Texo is the exobase temperature, m is the mass of the main atmospheric species, and g is the gravitational acceleration (Kulikov et al., 2007).
Let us define the thermal escape parameter
as the ratio between the potential energy of a particle and the thermal energy kTexo, where M is the planet’s mass, m is the particle mass (in the following: mostly atomic hydrogen), r is the planetocentric distance, and Texo is the exospheric temperature. Let us now assume a Maxwellian distribution for a given species. If X > 1.5, e.g. for low temperatures, only the particles in the tail of the Maxwellian have kinetic energies sufficient for escape. The particle loss through a spherical surface at radius r is given by the Jeans formula (“Jeans escape”, e.g., Jeans 1925; Öpik 1963; Kulikov et al. 2006),
Here, υ0 = (2kTexo/m)1/2 is the most probable velocity of the particle (see, e.g., Chassefière and Leblanc, 2004; Kulikov et al., 2006).
If the mean thermal energy of the particles (3kTexo/2) exceeds the gravitational energy, i.e., for X < 1.5 or analogously for temperatures Texo > 2GMm/3kr or \(kT\gtrsim mv_{{\rm esc}}^{2}/2\), the exosphere becomes unstable and hydrostatic equilibrium does not apply. The top of the atmosphere “blows off”, i.e., moves radially away from the planet with a velocity near its thermal velocity. To produce sufficiently high temperatures, a high level of EUV irradiation is required. The incoming EUV energy is then no longer converted into thermal energy but directly into kinetic energy. “Hydrodynamic escape” calculations are required (Öpik, 1963; Hunten, 1973; Watson et al., 1981).
The most important heating and cooling processes in the upper atmosphere of the Earth are, following Kulikov et al. (2007) and references therein,
-
heating of the thermosphere due to photoionization of CO2, N2, O2, and O by solar XUV irradiation,
-
heating due to photodissociation of O2 and O3 by solar UV irradiation,
-
chemical heating in exothermic binary and 3-body reactions,
-
molecular heat conduction in neutral gas,
-
cooling by infrared emission in the ro-vibrational bands of CO2, NO, O3, OH, NO+, 14N15N, CO, O2, and others,
-
heating and cooling by contraction and expansion of thermosphere,
-
turbulent energy dissipation and heat conduction.
Models of XUV heating of the present-day Earth’s thermosphere predict an average exospheric temperature of ≈ 1000 K (Kulikov et al., 2007, and references therein), in agreement with measurements. For Venus, Texo = 270 K (Kulikov et al., 2006, 2007) where the low value is due to efficient cooling by CO2. And for Mars, Texo = 220–240 K (Kulikov et al., 2007).
Non-thermal processes are also relevant in outer planetary atmospheres. There are several main types of non-thermal escape processes (Chassefière and Leblanc, 2004; Lundin et al., 2007):
-
Dissociative recombination (photochemical escape): After UV photoionization, ions recombine by forming energetic neutrals that may escape. Dissociative recombination of ionospheric molecular ions and photodissociation of molecular neutrals are sources of suprathermal H, C, N, O, and CO in the exosphere of (present) Venus (Kulikov et al., 2007, and references therein). These atoms are eventually thermalized through collisions, or are lost if they reach the exobase with energies exceeding the escape energy.
-
Ion pick-up escape: Ions are produced by photo-ionization, electron impact, or charge exchange and are dragged along by the magnetic field; a fraction of the particles escape in the solar wind.
-
Ionospheric outflow: Ionospheric matter is accelerated away by the electric field in the solar wind.
-
Ion sputtering: A fraction of the ions produced by photo-ionization, electron impact, or charge exchange re-impact the neutral atmosphere (owing to their large gyroradii) and eject neutral particles. This process is particularly important in the absence of a strong planetary magnetic field.
I now discuss results from applications to solar-system bodies and extrasolar planets.
7.2.4 Mercury: Erosion of atmosphere and mantle?
Mercury stands out among solar-system planets by showing the largest average density, and its core is large compared to other terrestrial planets (60% of its radius). It is possible that strong winds and enhanced XUV irradiation from the young Sun removed much of the early atmosphere and the outer mantle of Mercury (Tehrany et al., 2002; Ribas et al., 2005). It is thus possible that Mercury started as a planet similar in size to Earth but has lost its mantle as a consequence of interactions with the young, active Sun.
7.2.5 Venus: Where has the water gone?
The atmosphere of Venus is extremely dry when compared to the terrestrial atmosphere (a total water content of 2 × 1019 g or 0.0014% of the terrestrial ocean, vs. 1.39 × 1024 g on Earth, Kasting and Pollack 1983). The similar masses of Venus and Earth and their formation at similar locations in the solar nebula would suggest that both started with similar water reservoirs (Kasting and Pollack, 1983). The Venus atmosphere also reveals a surprisingly high deuterium-to-hydrogen (D/H) abundance ratio of (1.6±0.2) × 10−2 or 100 times the terrestrial value of 1.56 × 10−4 (Donahue et al., 1982; Kasting and Pollack, 1983). These observations have motivated a basic model in which water was abundantly available on the primitive Venus. Any water oceans would evaporate, inducing a “runaway greenhouse” in which water vapor would become the major constituent of the atmosphere (Ingersoll, 1969). This vapor was then photodissociated in the upper atmosphere by enhanced solar EUV irradiation (Kasting and Pollack, 1983), followed by the escape of hydrogen (but not deuterium) into space (Watson et al., 1981; Kasting and Pollack, 1983). Oxygen either (partly) followed the same route or (partly) reacted with reduced atmospheric gases or minerals in the crust (Kasting et al., 1984). Judged from the D/H abundance ratio, at least 0.3% of a terrestrial ocean should have been outgassed (Donahue et al., 1982). I summarize some of the results and problems discussed in the literature as far as they refer to solar activity and its much higher level in the early Sun.
Detailed atmospheric models have been calculated by, e.g., Watson et al. (1981), Kasting and Pollack (1983), Kasting et al. (1984), Kasting (1988), Chassefière (1996b), and Kulikov et al. (2006). These models solve the equations of continuity and difusion (e.g., constrained to the vertical direction in 1-D approaches) for a number of species, hydrostatic and heat balance equations, and equations of vibrational kinetics for radiating molecules. They include irradiation by solar XUV and UV and their long-term evolution (see Kulikov et al., 2007, for a review).
Kulikov et al. (2006) and Kulikov et al. (2007) presented results for Venus, assuming no atmospheric (in particular, hydrogenic) loss, i.e., the upper atmospheres are not hydrogen-rich and not humid (Figure 41). For present-day solar XUV irradiation, the calculated exospheric temperature is 270 K, in good agreement with measurements. However, increasing the XUV flux to levels of the young Sun, i.e., a 100fold EUV flux, thermospheric temperatures up to ≈ 8200 K are reached 4.5 Gyr ago, if the CO2 content is the same as today (96%). Higher temperatures are obtained for lower CO2 content.
Modeled temperature profiles for Venus for various solar XUV levels: 1 = present-day, 10 times (3.8 Gyr ago), 50 times (4.33 Gyr ago), and 100 times (4.5 Gyr ago) present levels, based on a 96% CO2 thermosphere (from Kulikov et al., 2007, © Springer Verlag, reprinted with permission.).
The blow-of limit in the exobase is reached at 4000 K, permitting hydrogenic blow-of during the first 250 Myr after the Sun’s arrival on the ZAMS. Detailed hydrodynamic computations by Chassefière (1996b) show high Jeans escape flux even for present-day solar XUV irradiation for a Venus-like planet with a hydrogen atmosphere.
The question on water on the young Venus then concentrates on the availability of water vapor in the young Venus upper atmosphere, that can photodissociate so that H escapes. The critical solar flux leading to complete evaporation of a water ocean (a “runaway greenhouse”, Ingersoll 1969) is ≈ 1.4 Ssun nearly independently of the amount of cooling CO2 in the atmosphere (Kasting, 1988), where Ssun = 1360 Wm−2 is the present-day solar constant. This critical flux is just about the flux expected from the young Sun at the orbit of Venus (and is about 70% of the present-day value at the same solar distance).
These model calculations suggest that the amount of water in the present terrestrial ocean could have escaped from Venus in only 50 Myr if the H2O mass fraction (mass mixing ratio) was at least 0.46, and the XUV flux was 70–100 times the present values (Kulikov et al., 2007).
The remaining problem then is to explain the extremely low oxygen content in the present-day atmosphere of Venus (Chassefière, 1996a). In a strong hydrodynamic escape process on young Venus, heavier gases such as O may be dragged with H (Zahnle and Kasting, 1986; Zahnle et al., 1990) although Chassefière (1996a) concluded that such loss was modest. Ion pick-up by the solar wind and ionospheric erosion by Kelvin-Helmholtz instabilities may be the dominant O+ loss mechanism in the present atmosphere of Venus (Lammer et al., 2006; Chassefière, 1997). The denser, young solar wind (Wood et al., 2002) could in fact easily remove the expected amount of O+ from a massive water ocean (Chassefière, 1997; Kulikov et al., 2006). The equivalent of one terrestrial ocean could be removed in only 10 Myr if the solar wind had been 103–104 times stronger than today, i.e., the escape would be “instantaneous” compared with outgassing time scales (Chassefière, 1997) although it is doubtful whether the young solar wind was indeed as strong as required for such massive losses (Wood et al. 2005, see Section 5.1).
7.2.6 Earth: A CO2 atmosphere and magnetic protection
There is evidence for early hydrodynamic escape from the Earth’s atmosphere. Compared to Venus, the lighter noble gases Ne and Ar are depleted in the Earth’s atmosphere with respect to the heavier Kr and Xe; the isotopic composition of the noble gases points in the same direction (Zahnle and Kasting, 1986; Zahnle et al., 1990; Chassefière and Leblanc, 2004, and references therein).
The Kulikov et al. () model of the terrestrial atmosphere shows that a ten-fold increase of the XUV flux, corresponding to the Sun > 3.8 Gyr ago, leads to exobase temperatures of > 10,000 K, which would imply escape rates not only for H but also for H2, He, N, O, or C. The hydrogenic blow-of temperature is only about 5000 K. As a consequence of dissociation of H2O, large amounts of water would thus have been lost unless there was a significantly higher CO2 content in the early atmosphere, because CO2 is efficiently cooling the upper atmosphere by radiation in the 15 band (Kulikov et al., 2007) Given the high early solar XUV flux, the atmospheric CO2 content in the young Earth’s atmosphere may have been at similar levels as in the atmospheres of the present-day Venus and Mars (≈ 95%; Kulikov et al. 2007). Its reduction and consequently, the rise of Texo, due to weathering onto the surface and the seafloor during the first 500 Myr was accompanied by a rapid decay of the solar EUV irradiation so that Texo was kept below blow-of conditions.
An important factor of the young Earth’s atmosphere is the relatively strong (as compared to Venus or evolved Mars) terrestrial magnetosphere that protects the atmosphere from solar-wind pickup erosion. An early on-set of the dynamo was therefore essential to protect the atmosphere and the large water reservoir of the Earth (Kulikov et al., 2007; Lundin et al., 2007).
7.2.7 Mars: Once warmer and wetter?
There is substantial evidence for a warmer and wetter climate on ancient Mars (Carr, 1986). The presence of valley networks in the highlands as well as some crater morphology require the presence of liquid water (e.g., Craddock and Maxwell 1993). Using Mars Global Surveyor images and altimeter data, Carr and Head (2003) estimated the depth of a primitive Martian ocean at 150 m (over the whole planet). Judged from the near-absence of valleys in the younger northern areas, liquid water disappeared suddenly 3.5–4 Gyr ago (Chassefière and Leblanc, 2004). Temperatures above 0° C and a massive atmosphere were required at earlier epochs, with a substantial content of greenhouse gases (Chassefière and Leblanc, 2004).
Massive atmospheric loss is relatively easy to explain, given Mars’ low surface gravity and the absence of a global magnetic field protecting the atmosphere from the solar wind after about 700 Myr of the planet’s formation (Acuña et al., 1998). Intense erosion by direct interaction between solar wind and the extended atmosphere is thus possible although significant suppression of non-thermal escape by the magnetic field would be possible during the first 200–300 Myr (Hutchins et al., 1997; Kulikov et al., 2007). In present-day Mars, hydrogen is predominantly lost through thermal escape (five times more efficiently than by non-thermal escape), while loss of oxygen to space requires non-thermal processes (Lammer et al., 2003a).
Like for other planets, the thermal escape of the young atmosphere of Mars depended strongly on the solar EUV irradiation, and non-thermal escape processes would also have depended on the ancient solar wind strength. Blow-of conditions are reached for an exospheric temperature Texo ≳ 1000 K (Lammer et al., 2003a). This requires an EUV flux ≈ 100 times the present solar value (Kulikov et al. 2007, see Figure 42), i.e., blow-off may apply to the the earliest times of the solar evolution, namely the first few 100 Myr after the Sun’s arrival on the ZAMS (when a strong solar wind would perhaps provide additional support, Chassefière 1996b, 1997; Chassefière and Leblanc 2004). For solar conditions 2.5 Gyr and 3.5 Gyr ago, Lammer et al. (2003a) concluded that the exospheric temperature was only Texo = 350 K and 600 K, respectively (with a 3 times and 6 times higher solar EUV flux, respectively), insufficient for blow-off unless a significantly lower CO2 mixing ratio applied (Kulikov et al., 2007), although Jeans escape and non-thermal escape of H remained operational.
Modeled temperature profiles for Mars for various solar XUV levels: 1 = present-day, 10 times (3.8 Gyr ago), 50 times (4.33 Gyr ago), and 100 times (4.5 Gyr ago) present levels, based on a 96% CO2 thermosphere (from Kulikov et al., 2007, © Springer Verlag, reprinted with permission).
Calculations show that in contrast to the situation on Venus and Earth, a considerable fraction of O (from the dissociated H2O molecules) may have been dragged of by the escaping H in the very young Mars (4–4.6 Gyr ago; Chassefière 1996a). Non-thermal escape processes (of O) alone may explain the loss of a 12–15 m Martian ocean during the past 3.5 Gyr (Lammer et al. 2003a; Chassefière and Leblanc 2004, and further references therein converging to similar numbers). Lammer et al. (2003a) and Chassefière and Leblanc (2004) summarized escape rates for three different epochs (present, 2.5 Gyr and 3.5 Gyr ago) to find that oxygen loss to space in the early epochs is predominantly due to sputtering (and also ion pick-up; see also Luhmann et al. 1992; Jakosky et al. 1994), in contrast to the present-day situation. During the last 2 Gyr, however, O escape was not sufficient to balance H escape from dissociated water, implying that oxygen must have reacted efficiently with surface material.
7.2.8 Venus, Earth, Mars: Similar start, different results?
Even if Venus, Earth, and Mars might all have started with dense, CO2 rich atmospheres and a large reservoir of water, the outcome of atmospheric evolution shows three very different planets: a very arid Venus with its dense, greenhouse-effective hot CO2 atmosphere; a water-rich Earth with a biologically transformed, intermediate-density atmosphere; and a cold Mars with frozen water reservoirs and a greenhouse-ineffective CO2 atmosphere. Key factors that led to the variations between the present-day planets are, among others: the close distance of Venus to the Sun, potentially allowing for a runaway greenhouse leading to the complete escape of water into space; the Earth’s magnetic field that protected the atmosphere from erosion by the early and stronger solar wind, together with the biological activity unfolding on young Earth; and the low surface gravity of Mars coupled with the absence of a magnetic field that led, except during the initial few 100 Myr, to more efficient erosion of the early atmosphere. Further factors such as continents (allowing for a carbonate-silicate geochemical cycle and thus the removal of CO2, see Section 7.1.1), plate tectonics (allowing for release of CO2, see Kasting and Toon 1989), or volcanic activity may matter as well. Nevertheless, in all cases, the level of XUV emission and the strength of the solar wind in the early solar system were of prime importance. Figure 43 shows a sketch of the different evolutionary paths of the atmospheres of Venus, Earth, and Mars considering the long-term evolution of the Sun’s XUV radiation and the solar-wind strength (from Kulikov et al. 2007; see also Lundin et al. 2007).
Comparison of evolutionary paths of Venus, Earth, and Mars, accounting for the influence of solar XUV and particle radiation (from Kulikov et al., 2007, © Springer Verlag, reprinted with permission).
7.2.9 Titan: Early atmospheric blow-off?
The same atmospheric methodology as described for Venus and Mars can be applied to other solar-system atmospheres. There is a particularly interesting isotopic anomaly in the atmosphere of Titan, namely a 15N enrichment with respect to 14N by a factor of 3.9–4.5 (Penz et al., 2005, and references therein). Non-thermal escape processes alone cannot account for the enrichment unless an unrealistically strong solar wind is assumed for the first 500 Myr after the origin of the solar system (Lammer et al., 2000; Penz et al., 2005).
It is important to note that present-day Titan’s orbit resides entirely within Saturn’s magnetosphere, i.e., its atmosphere is protected from the solar wind. Because the latter has decayed during the Sun’s evolution (Section 5.1), Titan spent most of its time outside Saturn’s magnetosphere at ages of about 100 Myr, and still more than half of the time at an age of 1 Gyr; its atmosphere was therefore subject to direct solar-wind interactions. Nevertheless, sputtering and ion pick-up are not sufficient to explain the anomalous 15N/14N ratio (Penz et al., 2005).
Thermal escape is an alternative. The present exospheric temperature is in the range of Texo ≈ 150–180 K, while for blow-off, Texo > 8040 K is required (see Penz et al., 2005, and references therein). Scaling the present Texo by using the XUV flux decay law derived for solar analogs (Section 5.6), one finds blow-off conditions for Titan during the first 200 Myr. Only 50 Myr would in fact suffice to remove 30 Titan atmospheres, needed to explain the anomalous 15N/14N isotopic ratio (Penz et al. 2005; see also Lunine et al. 1999).
7.2.10 Hot Jupiters: Mass evolution by evaporation?
The discovery of extrasolar, Jupiter-class planets very close to their parent stars (Mayor and Queloz, 1995) immediately brought up the question on the stability of such objects. Gaseous planets close to a solar-like star will efficiently evaporate. However, as discussed above, it is not the radiative effective temperature, Teff, that is relevant for evaporation, but rather the exospheric temperature, Texo, which is determined by the stellar XUV flux, and is therefore a consequence of stellar activity.
A “Hot Jupiter” orbiting a star like the present-day Sun at a distance of 0.04 AU is, with regard to solar XUV irradiation, an analog to a Jupiter-like planet in orbit around the ZAMS Sun at a distance of 1.3 AU. The analogy does not hold for the stellar wind, and there may also be a substantial effect due to synchronous (i.e., slow) rotation of hot Jupiters (Grießmeier et al., 2004).
Lammer et al. (2003b) derived the escape rate of a hydrogen atmosphere of a Jupiter-like exoplanet based on exospheric XUV absorption and heating. They used the time-dependent XUV fluxes from the “Sun in Time” program (Section 5.6). Although for Jupiter in its 5.2 AU orbit around the present-day Sun, XUV heating leads to Texo ≈ 140 K only, a close-in hydrogen-rich Jupiter at distances < 0.3 AU may suffer blow-off temperatures Texo > 2 × 104 K. The XUV-absorbing atmospheric layer (the “exobase”) expands to several planetary radii, which has been directly confirmed by a planetary transit observation (Vidal-Madjar et al., 2003). The initial calculations by Lammer et al. (2003b led to very high mass-loss rates, initially criticized by Yelle (2004) who derived 20 times smaller escape rates by also including atmospheric chemistry in their calculations; in particular, they considered thermospheric cooling by H3+ and the lowering of the solar energy deposition rate by ionization of H to H+, which either escapes, or recombines by emitting a photon, which escapes as well. In this case, the escape rate will not be large enough to substantially affect the planetary evolution. This was substantially confirmed by new calculations performed by the previous group (see Penz et al., 2007) who considered Roche-lobe effects to the hydrodynamic loss, and used realistic heating efficiencies (rather than an energy-limited, 100% efficiency assumption) and IR cooling terms for HD 209458b, a Jupiter-sized planet in orbit around an old, inactive solar analog. The temperatures at 1.5 Rplanet then reach 6000–10,000 K (Figure 44) which, however, leads to blow-of thanks to gravitational effects by the Roche lobe. Loss rates of 7 × 1010 g s−1 are obtained, in agreement with calculations by Yelle (2004) and Yelle (2006). Extrapolated to young MS ages of the host star (applying elevated XUV irradiation, i.e., a factor of 100 at an age of 0.1 Gyr, see Table 6), the loss rate may exceed 1012 g s−1, leading to an integrated mass loss of 1–3.4% of the present mass over the entire MS life time of the host star, a fraction that is not leading to substantial alterations in the planet. However, higher evaporation fractions are possible for planets orbiting closer to the host star.
Temperature profile through the atmosphere of the “hot Jupiter” HD 209458b in a 0.046 AU orbit around its solar-analog host star, for different XUV radiation levels corresponding to ages of 4, 2, 1, 0.5, 0.2, and 0.1 Gyr (from Penz et al., 2007, reprinted with permission).
In summary, hot Jupiters around young solar analogs should be in a state of extensive atmospheric loss for four reasons. The first three, close distance, high XUV flux, and strong wind of the host star have been discussed above. The fourth is the lack of a strong planetary dynamo owing to the slow, synchronous rotation of the planet. This prevents the planet from building up an extensive magnetosphere that protects the upper atmospheric layers from erosion by the solar wind. In fact, during the first 500 Myr, the magnetosphere may not protect the atmospheres of hot Jupiters even if tidal locking were ignored (Grießmeier et al., 2004). The “hot Jupiter” would therefore interact with the solar/stellar wind in a similar way as present-day Venus. Such interactions are even further enhanced by collisions with coronal mass ejections (CMEs). Given that these were probably much more frequent in the young Sun, significant effects are expected for planets at larger distances. Khodachenko et al. (2007) found that in order to prevent atmospheric erosion down to the planetary core, a sufficiently strong planetary magnetic field must be present to deflect CME plasma at stand-off distances of at least 1.3 Rplanet for hot Jupiters like HD 209458b. The very existence of numerous Jupiter-mass planets very close to their host stars may indicate that the planets are able to retain substantial magnetic moments (Khodachenko et al., 2007).
7.3 Summary: The high-energy young solar system
The young, ZAMS Sun was fainter than the present-day Sun in optical light by about 30%, and the consequent lowered irradiance of solar-system planets poses serious problems as the Earth should have been in deep freeze if its atmosphere was not fundamentally different from today’s; however, for both the Earth and Mars, there is evidence for a mild climate in the early days of the Sun’s main-sequence life. But the optical and infrared radiation is not the only, and perhaps not even the key player. Ultraviolet radiation affects the chemistry of the upper atmospheres, and EUV and X-ray radiation is absorbed in the upper layers, ionizing and heating the atmospheric gas. Subsequent thermal or non-thermal processes, notably also interactions with the solar wind, led to escape of atmospheric constituents. Irradiation by UV, EUV, and X-ray photons as well as the solar wind were tens to hundreds of times stronger in the early solar system and should have played a key role in affecting and modifying young planetary atmospheres. Most notably, the loss of water, for example on Venus, is an inevitable product of photodissociation and various loss mechanisms, in particular for the light hydrogen. It may be the Earth’s strong magnetic field that protected it sufficiently from suffering a similar fate as either Venus or Mars.
8 Summary and Conclusions
Only a few decades ago, the past of our Sun since its arrival on the ZAMS was gauged essentially by its modest bolometric luminosity. Stellar evolution calculations have consistently shown that the young (ZAMS) Sun was in fact fainter than the present-day Sun, albeit by only about 30% or so. Small as this difference is, it was at least sufficient to recognize a fundamental problem that might have arisen in the young solar system (Sagan and Mullen, 1972): Both Earth and Mars should have been in deep freeze, perhaps being covered by glaciers all over, not permitting water to flow and shape the Earth’s and Mars’ surface and to eventually serve as the medium in which life formed.
About 3 decades ago, satellites such as IUE and Einstein opened the window to stellar ultraviolet and X-ray sources, entirely changing our view of stellar evolution in particular in the context of magnetic fields and the “activity” they induce. Young stars seen in open clusters and in star-forming regions are not feeble UV and X-ray sources only growing up to the mature solar level. On the contrary, almost every young (ZAMS, PMS) solar analog dwarfs the present-day magnetically induced radiative output of the Sun by orders of magnitude. A common X-ray luminosity level of a ZAMS Sun is 1000 times the present solar level. The same holds true for the production of high-energy particles as seen by their radio emission. The contemporaneous Sun does not get close to a young star’s radio output even during the strongest flares. While observationally more challenging, evidence for winds has been found for solar analogs, and the picture is the same: The present-day Sun occupies a place at the low end of the range of stellar winds, as it does with respect to X-ray, ultraviolet, and radio emission.
The total energy output in the magnetically induced radiation (mostly in coronal soft X-rays and in chromospheric/transition region ultraviolet) from the most active, young solar analogs is still relatively small, amounting to about 1% of the bolometric energy loss of the Sun (Ribas et al., 2005). So, why should we worry?
The real power of magnetically induced radiation is not in its total luminosity but in the ability of individual photons (and high-energy particles) to affect the stellar environment. Ultraviolet and X-ray photons are, in contrast to optical photons, strongly absorbed at large heights in planetary atmospheres. They ionize and heat these layers, leading to complex chains of reactions including chemical networks producing, for example, O2 and O3 that shield the surface from any lethal dose of ultraviolet light; and they heat the thermosphere and exosphere, leading to escape of light elements in possibly significant numbers.
The impact may have been enormous. It is quite possible that Venus, the Earth, and Mars started as similar bodies in the young solar system, but the present-day diferences between them could hardly be larger: the extremely arid, dense, and greenhouse-heated atmosphere of Venus, the biologically active surface of the Earth, and the cold but water-bearing Mars may owe much of their present state to the action of an extremely magnetically active young Sun — through its magnetically induced high-energy emission rather than the optical and infrared emission. Similar things may apply to other solar-system bodies and also to extrasolar planets. Once high levels of short-wavelength radiation from young stars had been reported from observations, its potential role in transforming young planetary atmospheres was rapidly recognized (e.g., Sekiya et al. 1980; Zahnle and Walker 1982; Canuto et al. 1982, 1983; Kasting and Pollack 1983).
The magnetic, solar wind may have been responsible for the fate of solar-system bodies as well. It is an important factor in non-thermal escape processes occurring in upper planetary atmospheres, but it might even have had some indirect influence on the lower atmospheres by removing mass from the young Sun. If the young Sun were indeed slightly more massive and therefore more luminous, the “Faint Young Sun Paradox” may disappear. This solution is currently not preferred given estimates for young solar winds that would fall short of the required mass-loss rates by orders of magnitude. However, the picture of the past solar wind is still not very complete. A direct detection of any wind of a solar analog (e.g., through its radio emission) has yet to be reported.
Magnetic activity was perhaps even more fundamentally important in the PMS Sun when the latter was surrounded by a circumstellar disk in which planets formed. Not only are magnetic fields crucial for guiding accretion flows onto the star and perhaps lock the stellar rotation to the orbit period of the disk; the magnetically induced radiation is also important in ionizing and partly heating the upper layers of the accretion disk, thus driving accretion toward the stars and chemical networks across the disk. Further, high-energy particles produced by gigantic stellar flares may have left their traces in meteoritic material, providing a direct window to past conditions in the young, forming solar system.
The big picture of the young Sun’s activity and its influence on the solar-system environment is, in many ways, rather incomplete and at places controversial. What could be classified as solid knowledge, and where is more research investment needed?
While even the answer to this question may not be unanimous among various researchers, the following is probably safe to say, as far as “established facts” and “issues open to speculation” are concerned:
-
Judged from all observational evidence, the young Sun was much more magnetically active, due to its higher rotation rate. We are not precisely sure what the maximum activity level (and correspondingly, the shortest rotation period) of the young Sun was, but a rotation period about ten times shorter than at present and consequently elevated high-energy (X-ray) losses of order 100 times the present level are likely, at least as long as we consider the Sun to follow typical trends rather than being a maverick. Higher activity levels are possible but difficult to prove from statistical stellar studies.
-
Direct interactions between contemporaneous “solar activity” and upper planetary atmospheres are well established and can be studied in-situ in present-day atmospheres (e.g., Lammer et al., 2003a). The detailed mechanisms having occurred in the young solar system are still subject to some speculation as several ingredients are difficult to know: What was the composition of the initial atmospheres, was there plate tectonics, were there continents, how much water was present on the early planets, how much CO2 was in the atmospheres? In what ways did early life alter the chemical composition of the Earth’s atmosphere? Was there a magnetic field strong enough to shield the atmospheres from the strong solar wind? Regardless of these partly open questions, sophisticated models are available that make predictions that can be tested. In particular, these models include the higher activity level of the young Sun and can successfully explain the loss of water from Venus and the loss of a dense atmosphere from Mars.
-
The magnetic activity of the young, PMS Sun was undoubtedly affecting the complex, molecular environment of the forming solar system through ionization, heating, nuclear reactions, and induced chemistry. Such mechanisms are beginning to be studied and modeled in detail in other stellar systems. A precise assessment is difficult for the young Sun as we have little information on its actual UV, X-ray and particle output at those phases, but again, indirect evidence may shed light on these issues. The presence of chondrules, CAIs with their isotopic anomalies as well as traces of irradiation damage in meteoritical material (by nuclei ejected from the Sun) may at least partly be due to elevated activity of the young Sun, although alternative theories need to be tested.
The young solar system was a place permeated by short-wavelength radiation, high-energy particles, and an intense wind. Interactions with solar-system bodies and the initial circumsolar disk were of fundamental importance much more so than in the relatively quiescent present-day solar system. The basic driver of all these mechanisms was the enhanced solar magnetic field. Solar magnetic activity is by no means a phenomenon localized in the immediate surrounding of the Sun itself; it has been of relevance in shaping the entire solar system and the individual bodies back to the earliest times of its evolution.
Notes
The star claimed to be “the closest ever solar twin” (Porto de Mello and da Silva, 1997), HR 6060, shows parameters nearly indistinguishable from solar values indeed: L/L⊙ = 1.05 ± 0.02; spectral type G2 Va (Sun: G2 V); B − V = 0.65 (Sun: 0.648); U − B = 0.17 (Sun: 0.178); Teff = 5789 K (Sun: 5777 K; ΔTeff = 12 ± 30 K); log g = 4.49 (Sun: 4.44; Δlog g = 0.05 ± 0.12), microturbulence velocity ξ = 1.54 km s−1 (Sun: 1.52 km s−1; Δξ = [0.02 ± 0.04] km s−1); element abundances solar within 1σ, in particular [Fe/H] = 0.05 ± 0.06; Mount Wilson activity index < S > = 0.174 (Sun: 0.177 in 1980); rotational velocity υ sin i < 3.0 km s−1 (Sun: υ = 2 km s−1).
The line fluxes of O viii, O vii, N vii, and C vi were determined from a model spectrum synthesized in the XSPEC software (Arnaud, 1996) using the vapec model (Smith et al., 2001). The model is based on an isothermal plasma with a temperature of 2 MK normalized such that the 0.1–10 keV luminosity is 2 × 1027 erg s−1. The low-FIP element abundances were set to values four times higher than standard photospheric abundances, while the high-FIP element abundances were photospheric; the S abundance was set to an intermediate value of 2× the photospheric value.
Meyer normalized the abundances such that the low-FIP element abundances were photospheric and the high-FIP abundances depleted, whereas the present-day view is that high-FIP elements are at photospheric levels, see Feldman (1992).
References
Acuña, M.H., Connerney, J.E.P., Wasilewski, P., Lin, R.P., Anderson, K.A., Carlson, C.W., McFadden, J., Curtis, D.W., Mitchell, D., Reme, H., Mazelle, C., Sauvaud, J.A., D’Uston, C., Cros, A., Medale, J.L., Bauer, S.J., Cloutier, P., Mayhew, M., Winterhalter, D., Ness, N.F., 1998, “Magnetic Field and Plasma Observations at Mars: Initial Results of the Mars Global Surveyor Mission”, Science, 279, 1676–1680. ADS: http://adsabs.harvard.edu/abs/1998Sci...279.1676A
Alexander, R.D., Clarke, C.J., Pringle, J.E., 2004, “The effects of X-ray photoionization and heating on the structure of circumstellar discs”, Mon. Not. R. Astron. Soc., 354, 71–80. ADS: http://adsabs.harvard.edu/abs/2004MNRAS.354...71A
Alexander, R.D., Clarke, C.J., Pringle, J.E., 2006a, “Photoevaporation of protoplanetary discs — I. Hydrodynamic models”, Mon. Not. R. Astron. Soc., 369, 216–228. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.369..216A
Alexander, R.D., Clarke, C.J., Pringle, J.E., 2006b, “Photoevaporation of protoplanetary discs — II. Evolutionary models and observable properties”, Mon. Not. R. Astron. Soc., 369, 229–239. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.369..229A
Ambartsumian, V.A., Mirzoyan, L.V., 1982, “An observational approach to the early stages of stellar evolution”, Astrophys. Space Sci., 84, 317–330. ADS: http://adsabs.harvard.edu/abs/1982Ap&SS..84..317A
André, P., Montmerle, T., Feigelson, E.D., 1987, “A VLA survey of radio-emitting young stars in the p Ophiuchi dark cloud”, Astron. J., 93, 1182–1198. ADS: http://adsabs.harvard.edu/abs/1987AJ.....93.1182A
André, P., Deeney, B.D., Phillips, R.B., Lestrade, J.-F., 1992, “VLBI survey of ρ Ophiuchi: A population of magnetized, diskless young stellar objects”, Astrophys. J., 401, 667–677. ADS: http://adsabs.harvard.edu/abs/1992ApJ...401..667A
Anglada, G., 1995, “Centimeter Continuum Emission from Outflow Sources”, in Circumstellar Disks, Outflows and Star Formation, (Eds.) Lizano, S., Torrelles, J.M., Circumstellar Disks, Outflows and Star Formation, Cozumel, Mexico, Nov 28–Dec 2, 1994, vol. 1 of Revista Mexicana de Astronomia y Astrofisica Serie de Conferencias, pp. 67–76, UNAM, Mexico D.F., Mexico. ADS: http://adsabs.harvard.edu/abs/1995RMxAC...1...67A
Anglada, G., Villuendas, E., Estalella, R., Beltran, M.T., Rodriguez, L.F., Torrelles, J.M., Curiel, S., 1998, “Spectral Indices of Centimeter Continuum Sources in Star-forming Regions: Implications on the Nature of the Outflow Exciting Sources”, Astron. J., 116, 2953–2964. ADS: http://adsabs.harvard.edu/abs/1998AJ....116.2953A
Antia, H.M., Basu, S., 2005, “The Discrepancy between Solar Abundances and Helioseismology”, Astrophys. Lett., 620, L129–L132. ADS: http://adsabs.harvard.edu/abs/2005ApJ...620L.129A
Ardila, D.R., Basri, G., Walter, F.M., Valenti, J.A., Johns-Krull, C.M., 2002, “Observations of T Tauri Stars using Hubble Space Telescope GHRS. I. Far-Ultraviolet Emission Lines”, Astrophys. J., 566, 1100–1123. ADS: http://adsabs.harvard.edu/abs/2002ApJ...566.1100A
Argiroffi, C., Maggio, A., Peres, G., Stelzer, B., Neuhäuser, R., 2005, “XMM-Newton spectroscopy of the metal depleted T Tauri star TWA 5”, Astron. Astrophys., 439, 1149–1158. ADS: http://adsabs.harvard.edu/abs/2005A&A...439.1149A
Argiroffi, C., Maggio, A., Peres, G., 2007, “X-ray emission from MP Muscae: an old classical T Tauri star”, Astron. Astrophys., 465, L5–L8. ADS: http://adsabs.harvard.edu/abs/2007A&A...465L...5A
Arnaud, K.A., 1996, “XSPEC: The First Ten Years”, in Astronomical Data Analysis Software and Systems V, (Eds.) Jacoby, G.H., Barnes, J., vol. 101 of ASP Conference Series, pp. 17–20, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/1996ASPC..101...17A
Arzner, K., Güdel, M., 2004, “Are Coronae of Magnetically Active Stars Heated by Flares? III. Analytical Distribution of Superposed Flares”, Astrophys. J., 602, 363–376. ADS: http://adsabs.harvard.edu/abs/2004ApJ...602..363A
Arzner, K., Güdel, M., Briggs, K., Telleschi, A., Audard, M., 2007, “Statistics of superimposed flares in the Taurus molecular cloud”, Astron. Astrophys., 468, 477–484. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..477A
Asplund, M., Grevesse, N., Güdel, M., Sauval, A.J., 2005a, “The solar model problem resurrected”, Nature, 436, 525–528. ADS: http://adsabs.harvard.edu/abs/2005astro.ph.10377A
Asplund, M., Grevesse, N., Sauval, A.J., 2005b, “The Solar Chemical Composition”, in Cosmic Abundance as Records of Stellar Evolution and Nucleosynthesis in honor of David L. Lambert, (Eds.) Barnes III, T.G., Bash, F.N., Symposium held 17–19 June, 2004 in Austin, Texas, vol. 336 of ASP Conference Series, pp. 25–38, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2005ASPC..336...25A
Audard, M., Güdel, M., Guinan, E.F., 1999, “Implications from Extreme-Ultraviolet Observations for Coronal Heating of Active Stars”, Astrophys. J. Lett., 513, L53–L56. ADS: http://adsabs.harvard.edu/abs/1999ApJ...513L..53A
Audard, M., Güdel, M., Drake, J.J., Kashyap, V.L., 2000, “Extreme-Ultraviolet Flare Activity in Late-Type Stars”, Astrophys. J., 541, 396–409. ADS: http://adsabs.harvard.edu/abs/2000ApJ...541..396A
Audard, M., Güdel, M., Skinner, S.L., 2003a, “Separating the X-Ray Emissions of UV Ceti A and B with Chandra”, Astrophys. J., 589, 983–987. ADS: http://adsabs.harvard.edu/abs/2003ApJ...589..983A
Audard, M., Güdel, M., Sres, A., Raassen, A.J.J., Mewe, R., 2003b, “A study of coronal abundances in RS CVn binaries”, Astron. Astrophys., 398, 1137–1149. ADS: http://adsabs.harvard.edu/abs/2003A&A...398.1137A
Ayres, T.R., 1997, “Evolution of the solar ionizing flux”, J. Geophys. Res., 102, 1641–1652. ADS: http://adsabs.harvard.edu/abs/1997JGR...102.1641A
Ayres, T.R., Linsky, J.L., 1980, “Outer atmospheres of cool stars. V. IUE observations of Capella: The rotation-activity connection”, Astrophys. J., 241, 279–299. ADS: http://adsabs.harvard.edu/abs/1980ApJ...241..279A
Balbus, S.A., Hawley, J.F., 1991, “A powerful local shear instability in weakly magnetized disks. I — Linear analysis. II — Nonlinear evolution”, Astrophys. J., 376, 214–233. ADS: http://adsabs.harvard.edu/abs/1991ApJ...376..214B
Baliunas, S.L., Donahue, R.A., Soon, W.H., Horne, J.H., Frazer, J., Woodard-Eklund, L., Bradford, M., Rao, L.M., Wilson, O.C., Zhang, Q., Bennett, W., Briggs, J., Carroll, S.M., Duncan, D.K., Figueroa, D., Lanning, H.H., Misch, T., Mueller, J., Noyes, R.W., Poppe, D., Porter, A.C., Robinson, C.R., Russell, J., Shelton, J.C., Soyumer, T., Vaughan, A.H., Whitney, J.H., 1995, “Chromospheric variations in main-sequence stars. II”, Astrophys. J., 438, 269–287. ADS: http://adsabs.harvard.edu/abs/1995ApJ...438..269B
Barnes, J.R., Collier Cameron, A., Unruh, Y.C., Donati, J.F., Hussain, G.A.J., 1998, “Latitude distributions and lifetimes of star-spots on G dwarfs in the α Persei cluster”, Mon. Not. R. Astron. Soc., 299, 904–920. ADS: http://adsabs.harvard.edu/abs/1998MNRAS.299..904B
Bary, J.S., Weintraub, D.A., Kastner, J.H., 2003, “Detections of Rovibrational H2 Emission from the Disks of T Tauri Stars”, Astrophys. J., 586, 1136–1147. ADS: http://adsabs.harvard.edu/abs/2003ApJ...586.1136B
Basri, G., Bertout, C., 1989, “Accretion disks around T Tauri stars. II — Balmer emission”, Astrophys. J., 341, 340–358. ADS: http://adsabs.harvard.edu/abs/1989ApJ...341..340B
Benz, A.O., Güdel, M., 1994, “X-ray/microwave ratio of flares and coronae”, Astron. Astrophys., 285, 621–630. ADS: http://adsabs.harvard.edu/abs/1994A&A...285..621B
Benz, A.O., Conway, J., Güdel, M., 1998, “First VLBI images of a main-sequence star”, Astron. Astrophys., 331, 596–600. ADS: http://adsabs.harvard.edu/abs/1998A&A...331..596B
Berdyugina, S.V., Pelt, J., Tuominen, I., 2002, “Magnetic activity in the young solar analog LQ Hydrae. I. Active longitudes and cycles”, Astron. Astrophys., 394, 505–515. ADS: http://adsabs.harvard.edu/abs/2002A&A...394..505B
Bergin, E., Calvet, N., D’Alessio, P., Herczeg, G.J., 2003, “The Effects of UV Continuum and Lya Radiation on the Chemical Equilibrium of T Tauri Disks”, Astrophys. J. Lett., 591, L159–L162. ADS: http://adsabs.harvard.edu/abs/2003ApJ...591L.159B
Bertout, C., 1989, “T Tauri stars — Wild as dust”, Annu. Rev. Astron. Astrophys., 27, 351–395. ADS: http://adsabs.harvard.edu/abs/1989ARA&A..27..351B
Bertout, C., Basri, G., Bouvier, J., 1988, “Accretion disks around T Tauri stars”, Astrophys. J., 330, 350–373. ADS: http://adsabs.harvard.edu/abs/1988ApJ...330..350B
Bieging, J.H., Cohen, M., 1985, “Multifrequency radio images of L1551 IRS 5”, Astrophys. J. Lett., 289, L5–L8. ADS: http://adsabs.harvard.edu/abs/1985ApJ...289L...5B
Bieging, J.H., Cohen, M., 1989, “On the radio variability of V410 Tauri”, Astron. J., 98, 1686–1692. ADS: http://adsabs.harvard.edu/abs/1989AJ.....98.1686B
Bieging, J.H., Cohen, M., Schwartz, P.R., 1984, “VLA observations of T Tauri stars. II — A luminosity-limited survey of Taurus-Auriga”, Astrophys. J., 282, 699–708. ADS: http://adsabs.harvard.edu/abs/1984ApJ...282..699B
Boothroyd, A.I., Sackmann, I.-J., Fowler, W.A., 1991, “Our Sun. II. Early mass loss of 0.1M⊙ and the case of the missing lithium”, Astrophys. J., 377, 318–329. ADS: http://adsabs.harvard.edu/abs/1991ApJ...377..318B
Bouvier, J., 1990, “Rotation in T Tauri stars. II — Clues for magnetic activity”, Astron. J., 99, 946–964. ADS: http://adsabs.harvard.edu/abs/1990AJ.....99..946B
Bouvier, J., Cabrit, S., Fernandez, M., Martín, E.L., Matthews, J.M., 1993, “COYOTES I: the photometric variability and rotational evolution of T Tauri stars”, Astron. Astrophys., 272, 176–206. ADS: http://adsabs.harvard.edu/abs/1993A&A...272..176B
Bowring, S.A., Williams, I.S., Compston, W., 1989, “3.96 Ga gneisses from the Slave province, Northwest Territories, Canada”, Geology, 17, 971–975
Briggs, K.R., Güdel, M., Telleschi, A., Preibisch, T., Stelzer, B., Bouvier, J., Rebull, L., Audard, M., Scelsi, L., Micela, G., Grosso, N., Palla, F., 2007, “The X-ray activity-rotation relation of T Tauri stars in Taurus-Auriga”, Astron. Astrophys., 468, 413–424. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..413B
Brinkman, A.C., Behar, E., Güdel, M., Audard, M., den Boggende, A.J.F., Branduardi-Raymont, G., Cottam, J., Erd, C., den Herder, J.W., Jansen, F., Kaastra, J.S., Kahn, S.M., Mewe, R., Paerels, F.B.S., Peterson, J.R., Rasmussen, A.P., Sakelliou, I., de Vries, C., 2001, “First light measurements with the XMM-Newton reflection grating spectrometers: Evidence for an inverse first ionisation potential effect and anomalous Ne abundance in the Coronae of HR 1099”, Astron. Astrophys., 365, L324–L328. ADS: http://adsabs.harvard.edu/abs/2001A&A...365L.324B
Brown, A., 1987, “Radio emission from pre-main-sequence stars in Corona Australis”, Astrophys. J. Lett., 322, L31–L34. ADS: http://adsabs.harvard.edu/abs/1987ApJ...322L..31B
Brown, A., Jordan, C., Millar, T.J., Gondhalekar, P., Wilson, R., 1981, “H2 emission in the EUV spectrum of T Tauri and Burnham’s nebula”, Nature, 290, 34–36. ADS: http://adsabs.harvard.edu/abs/1981Natur.290...34B
Butler, C.J., Rodono, M., Foing, B.H., Haisch, B.M., 1986, “Coordinated EXOSAT and spectro-scopic observations of flare stars and coronal heating”, Nature, 321, 679–682. ADS: http://adsabs.harvard.edu/abs/1986Natur.321..679B
Caffee, M.W., Hohenberg, C.M., Swindle, T.D., Goswami, J.N., 1987, “Evidence in meteorites for an active early Sun”, Astrophys. J. Lett., 313, L31–L35. ADS: http://adsabs.harvard.edu/abs/1987ApJ...313L..31C
Calvet, N., Gullbring, E., 1998, “The Structure and Emission of the Accretion Shock in T Tauri Stars”, Astrophys. J., 509, 802–818. ADS: http://adsabs.harvard.edu/abs/1998ApJ...509..802C
Calvet, N., Muzerolle, J., Briceño, C., Hernández, J., Hartmann, L., Saucedo, J.L., Gordon, K.D., 2004, “The Mass Accretion Rates of Intermediate-Mass T Tauri Stars”, Astron. J., 128, 1294–1318. ADS: http://adsabs.harvard.edu/abs/2004AJ.....128.1294C
Camenzind, M., 1990, “Magnetized Disk-Winds and the Origin of Bipolar Outflows”, in Accretion and Winds, (Ed.) Klare, G., vol. 3 of Reviews in Modern Astronomy, pp. 234–265, Springer, Berlin, Germany; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1990RvMA....3..234C
Canuto, V.M., Levine, J.S., Augustsson, T.R., Imhoff, C.L., 1982, “UV radiation from the young sun and oxygen and ozone levels in the prebiological palaeoatmosphere”, Nature, 296, 816–820. ADS: http://adsabs.harvard.edu/abs/1982Natur.296..816C
Canuto, V.M., Levine, J.S., Augustsson, T.R., Imhoff, C.L., Giampapa, M.S., 1983, “The young Sun and the atmosphere and photochemistry of the early Earth”, Nature, 305, 281–286. ADS: http://adsabs.harvard.edu/abs/1983Natur.305..281C
Carkner, L., Mamajek, E., Feigelson, E., Neuhauser, R., Wichmann, R., Krautter, J., 1997, “Radio Emission from ROSAT-discovered Young Stars in and around Taurus-Auriga”, Astrophys. J., 490, 735–743. ADS: http://adsabs.harvard.edu/abs/1997ApJ...490..735C
Carr, M.H., 1986, “Mars: A water-rich planet?”, Icarus, 68, 187–216. ADS: http://adsabs.harvard.edu/abs/1986Icar...68..187C
Carr, M.H., Head, J.W., 2003, “Oceans on Mars: An assessment of the observational evidence and possible fate”, J. Geophys. Res., 108, 8–1. ADS: http://adsabs.harvard.edu/abs/2003JGRE.108e....8C7.2.7
Catala, C., Donati, J.-F., Shkolnik, E., Bohlender, D., Alecian, E., 2007, “The magnetic field of the planet-hosting star τ Bootis”, Mon. Not. R. Astron. Soc., 374, L42–L46. ADS: http://adsabs.harvard.edu/abs/2007MNRAS.374L..42C
Cayrel de Strobel, G., Bentolila, C., 1989, “In search of real solar twins. II”, Astron. Astrophys., 211, 324–340. ADS: http://adsabs.harvard.edu/abs/1989A&A...211..324C
Cess, R.D., Ramanathan, V., Owen, T., 1980, “The Martian paleoclimate and enhanced atmospheric carbon dioxide”, Icarus, 41, 159–165. ADS: http://adsabs.harvard.edu/abs/1980Icar...41..159C
Charnley, S.B., 1997, “Chemical models of interstellar gas-grain processes — III. Molecular depletion in NGC 2024”, Mon. Not. R. Astron. Soc., 291, 455–460. ADS: http://adsabs.harvard.edu/abs/1997MNRAS.291..455C
Chassefière, E., 1996a, “Hydrodynamic Escape of Oxygen from Primitive Atmospheres: Applications to the Cases of Venus and Mars”, Icarus, 124, 537–552. ADS: http://adsabs.harvard.edu/abs/1996Icar..124..537C
Chassefière, E., 1996b, “Hydrodynamic escape of hydrogen from a hot water-rich atmosphere: The case of Venus”, J. Geophys. Res., 101, 26 039–26 056. ADS: http://adsabs.harvard.edu/abs/1996JGR...10126039C
Chassefière, E., 1997, “Loss of Water on the Young Venus: The Effect of a Strong Primitive Solar Wind”, Icarus, 126, 229–232. ADS: http://adsabs.harvard.edu/abs/1997Icar..126..229C
Chassefière, E., Leblanc, F., 2004, “Mars atmospheric escape and evolution; interaction with the solar wind”, Planet. Space Sci., 52, 1039–1058. ADS: http://adsabs.harvard.edu/abs/2004P&SS...52.1039C
Chaussidon, M., Robert, F., McKeegan, K.D., 2006, “Li and B isotopic variations in an Allende CAI: Evidence for the in situ decay of short-lived 10Be and for the possible presence of the short-lived nuclide 7Be in the early solar system”, Geochim. Cosmochim. Acta, 70, 224–245. ADS: http://adsabs.harvard.edu/abs/2006GeCoA..70..224C
Chiang, E., Phillips, R.B., Lonsdale, C.J., 1996, “A λ3.6 cm Radio Survey of Low-Mass, Weak-Line T Tauri Stars in Taurus-Auriga”, Astron. J., 111, 355–364. ADS: http://adsabs.harvard.edu/abs/1996AJ....111..355C
Chmielewski, Y., Friel, E., Cayrel de Strobel, G., Bentolila, C., 1992, “The 1992 detailed analyses of α Centauri A and α Centauri B”, Astron. Astrophys., 263, 219–231. ADS: http://adsabs.harvard.edu/abs/1992A&A...263..219C
Clarke, C.J., Gendrin, A., Sotomayor, M., 2001, “The dispersal of circumstellar discs: the role of the ultraviolet switch”, Mon. Not. R. Astron. Soc., 328, 485–491. ADS: http://adsabs.harvard.edu/abs/2001MNRAS.328..485C
Cohen, M., Bieging, J.H., 1986, “Radio variability and structure of T Tauri stars”, Astron. J., 92, 1396–1402. ADS: http://adsabs.harvard.edu/abs/1986AJ.....92.1396C
Cohen, M., Bieging, J.H., Schwartz, P.R., 1982, “VLA observations of mass loss from T Tauri stars”, Astrophys. J., 253, 707–715. ADS: http://adsabs.harvard.edu/abs/1982ApJ...253..707C
Collier Cameron, A., Campbell, C.G., 1993, “Rotational evolution of magnetic T Tauri stars with accretion discs”, Astron. Astrophys., 274, 309–318. ADS: http://adsabs.harvard.edu/abs/1993A&A...274..309C
Collura, A., Pasquini, L., Schmitt, J.H.M.M., 1988, “Time variability in the X-ray emission of dM stars observed by EXOSAT”, Astron. Astrophys., 205, 197–206. ADS: http://adsabs.harvard.edu/abs/1988A&A...205..197C
Craddock, R.A., Maxwell, T.A., 1993, “Geomorphic evolution of the Martian highlands through ancient fluvial processes”, J. Geophys. Res., 98, 3453–3468. ADS: http://adsabs.harvard.edu/abs/1993JGR.....98.3453C
Crosby, N.B., Aschwanden, M.J., Dennis, B.R., 1993, “Frequency distributions and correlations of solar X-ray flare parameters”, Solar Phys., 143, 275–299. ADS: http://adsabs.harvard.edu/abs/1993SoPh..143..275C
Cuntz, M., Rammacher, W., Ulmschneider, P., Musielak, Z.E., Saar, S.H., 1999, “Two-Component Theoretical Chromosphere Models for K Dwarfs of Different Magnetic Activity: Exploring the Ca ii Emission-Stellar Rotation Relationship”, Astrophys. J., 522, 1053–1068. ADS: http://adsabs.harvard.edu/abs/1999ApJ...522.1053C
Curiel, S., Rodríguez, L.F., Bohigas, J., Roth, M., Cantó, J., Torrelles, J.M., 1989, “Extended radio continuum emission associated with V645 CYG and MWC1080”, Astrophys. Lett. Comm., 27, 299–309. ADS: http://adsabs.harvard.edu/abs/1989ApL&C..27..299C
Curiel, S., Rodríguez, L.F., Moran, J.M., Cantó, J., 1993, “The triple radio continuum source in Serpens: The birth of a Herbig-Haro system?”, Astrophys. J., 415, 191–203. ADS: http://adsabs.harvard.edu/abs/1993ApJ...415..191C
Damiani, F., Micela, G., Sciortino, S., Harnden Jr, F.R., 1995, “Einstein Observations of T Tauri Stars in Taurus-Auriga. I. Properties of X-Ray Emission”, Astrophys. J., 446, 331–340. ADS: http://adsabs.harvard.edu/abs/1995ApJ...446..331D
Dempsey, R.C., Linsky, J.L., Schmitt, J.H.M.M., Fleming, T.A., 1993, “The ROSAT All-Sky Survey of active binary coronae. II. Coronal temperatures of the RS Canum Venaticorum systems”, Astrophys. J., 413, 333–338. ADS: http://adsabs.harvard.edu/abs/1993ApJ...413..333D
Donahue, T.M., Hoffman, J.H., Hodges, R.R., Watson, A.J., 1982, “Venus Was Wet: A Measurement of the Ratio of Deuterium to Hydrogen”, Science, 216, 630–633. ADS: http://adsabs.harvard.edu/abs/1982Sci...216..630D
Donati, J.-F., Mengel, M., Carter, B.D., Marsden, S., Collier Cameron, A., Wichmann, R., 2000, “Surface differential rotation and prominences of the Lupus post T Tauri star RX J1508.6-4423”, Mon. Not. R. Astron. Soc., 316, 699–715. ADS: http://adsabs.harvard.edu/abs/2000MNRAS.316..699D
Donati, J.-F., Collier Cameron, A., Petit, P., 2003a, “Temporal fluctuations in the differential rotation of cool active stars”, Mon. Not. R. Astron. Soc., 345, 1187–1199. ADS: http://adsabs.harvard.edu/abs/2003MNRAS.345.1187D
Donati, J.-F., Collier Cameron, A., Semel, M., Hussain, G.A.J., Petit, P., Carter, B.D., Marsden, S.C., Mengel, M., López Ariste, A., Jeffers, S.V., Rees, D.E., 2003b, “Dynamo processes and activity cycles of the active stars AB Doradus, LQ Hydrae and HR 1099”, Mon. Not. R. Astron. Soc., 345, 1145–1186. ADS: http://adsabs.harvard.edu/abs/2003MNRAS.345.1145D
Donati, J.-F., Jardine, M.M., Gregory, S.G., Petit, P., Bouvier, J., Dougados, C., Moenard, F., Cameron, A.C., Harries, T.J., Jeffers, S.V., Paletou, F., 2007, “Magnetic fields and accretion flows on the classical T Tauri star V2129 Oph”, Mon. Not. R. Astron. Soc., 380, 1297–1312. ADS: http://adsabs.harvard.edu/abs/2007MNRAS.380.1297D
Dorren, J.D., Guinan, E.F., 1994a, “HD 129333: The Sun in its infancy”, Astrophys. J., 428, 805–818. ADS: http://adsabs.harvard.edu/abs/1994ApJ...428..805D
Dorren, J.D., Guinan, E.F., 1994b, “The Sun in Time: Detecting and Modelling Magnetic Inhomogenities on Solar-Type Stars”, in The Sun as a Variable Star: Solar and Stellar Irradiance Variations, (Eds.) Pap, J.M., Fröhlich, C., Hudson, H.S., Solanki, S.K., Proceedings of IAU Colloquium 143, held in Boulder, Colorado, USA, June 20–25, 1993, pp. 206–216, Cambridge University Press, Cambridge, U.K.; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1994svsp.coll..206D
Dorren, J.D., Guinan, E.F., Dewarf, L.E., 1994, “The Decline of Solar Magnetic Activity with Age”, in Cool Stars, Stellar Systems, and the Sun: Eighth Cambridge Workshop, (Ed.) Caillault, J.-P., Athens, Georgia, October 11–14, 1993, vol. 64 of ASP Conference Series, pp. 399–401, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/1994ASPC...64..399D
Dorren, J.D., Guüdel, M., Guinan, E.F., 1995, “X-Ray Emission from the Sun in Its Youth and Old Age”, Astrophys. J., 448, 431–436. ADS: http://adsabs.harvard.edu/abs/1995ApJ...448..431D
Doyle, J.G., Butler, C.J., 1985, “Ultraviolet radiation from stellar flares and the coronal X-ray emission for dwarf-Me stars”, Nature, 313, 378–380. ADS: http://adsabs.harvard.edu/abs/1985Natur.313..378D
Drake, J.J., Testa, P., 2005, “The ‘solar model problem’ solved by the abundance of neon in nearby stars”, Nature, 436, 525–528. ADS: http://adsabs.harvard.edu/abs/2005Natur.436..525D
Drake, J.J., Laming, J.M., Widing, K.G., 1995, “Stellar coronal abundances. II. The first ionization potential effect and its absence in the corona of procyon”, Astrophys. J., 443, 393–415. ADS: http://adsabs.harvard.edu/abs/1995ApJ...443..393D
Drake, J.J., Brickhouse, N.S., Kashyap, V., Laming, J.M., Huenemoerder, D.P., Smith, R., Wargelin, B.J., 2001, “Enhanced Noble Gases in the Coronae of Active Stars”, Astrophys. J. Lett., 548, L81–L85. ADS: http://adsabs.harvard.edu/abs/2001ApJ...548L..81D
Drake, J.J., Testa, P., Hartmann, L., 2005, “X-Ray Diagnostics of Grain Depletion in Matter Accreting onto T Tauri Stars”, Astrophys. J. Lett., 627, L149–L152. ADS: http://adsabs.harvard.edu/abs/2005ApJ...627L.149D
Drake, S.A., Simon, T., Brown, A., 1993, “Detection of radio continuum emission from Procyon”, Astrophys. J., 406, 247–251. ADS: http://adsabs.harvard.edu/abs/1993ApJ...406..247D
Dravins, D., Lindegren, L., Vandenberg, D.A., 1998, “Beta Hydri (G2 IV): a revised age for the closest subgiant”, Astron. Astrophys., 330, 1077–1079. ADS: http://adsabs.harvard.edu/abs/1998A&A...330.1077D
Dupree, A.K., Benz, A.O. (Eds.), 2004, Stars as suns: Activity, evolution and planets, Proceedings of the 219th Symposium of the IAU held during the IAU General Assembly XXV, Sydney, Australia, 21–25 July 2003, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2004IAUS..219....D
Duquennoy, A., Mayor, M., 1991, “Multiplicity among solar-type stars in the solar neighbourhood. II. Distribution of the orbital elements in an unbiased sample”, Astron. Astrophys., 248, 485–524. ADS: http://adsabs.harvard.edu/abs/1991A&A...248..485D
Favata, F., Micela, G., Baliunas, S.L., Schmitt, J.H.M.M., Guüdel, M., Harnden Jr, F.R., Sciortino, S., Stern, R.A., 2004, “High-amplitude, long-term X-ray variability in the solar-type star HD 81809: The beginning of an X-ray activity cycle?”, Astron. Astrophys., 418, L13–L16. ADS: http://adsabs.harvard.edu/abs/2004A&A...418L..13F
Favata, F., Micela, G., Silva, B., Sciortino, S., Tsujimoto, M., 2005, “A survey for Fe 6.4 keV emission in young stellar objects in ρ Oph: The strong fluorescence from Elias 29”, Astron. Astrophys., 433, 1047–1054. ADS: http://adsabs.harvard.edu/abs/2005A&A...433.1047F
Fawzy, D., Stȩpień, K., Ulmschneider, P., Rammacher, W., Musielak, Z.E., 2002, “Acoustic and magnetic wave heating in stars. III. The chromospheric emission-magnetic filling factor relation”, Astron. Astrophys., 386, 994–1000. ADS: http://adsabs.harvard.edu/abs/2002A&A...386..994F
Feigelson, E.D., Decampli, W.M., 1981, “Observations of X-ray emission from T Tauri stars”, Astrophys. J. Lett., 243, L89–L93. ADS: http://adsabs.harvard.edu/abs/1981ApJ...243L..89F
Feigelson, E.D., Kriss, G.A., 1981, “Discovery of three X-ray luminous pre-main-sequence stars”, Astrophys. J. Lett., 248, L35–L38. ADS: http://adsabs.harvard.edu/abs/1981ApJ...248L..35F
Feigelson, E.D., Kriss, G.A., 1989, “Soft X-ray observations of pre-main-sequence stars in the Chamaeleon dark cloud”, Astrophys. J., 338, 262–276. ADS: http://adsabs.harvard.edu/abs/1989ApJ...338..262F
Feigelson, E.D., Montmerle, T., 1985, “An extremely variable radio star in the rho Ophiuchi cloud”, Astrophys. J. Lett., 289, L19–L23. ADS: http://adsabs.harvard.edu/abs/1985ApJ...289L..19F
Feigelson, E.D., Montmerle, T., 1999, “High-Energy Processes in Young Stellar Objects”, Annu. Rev. Astron. Astrophys., 37, 363–408. ADS: http://adsabs.harvard.edu/abs/1999ARA&A..37..363F
Feigelson, E.D., Casanova, S., Montmerle, T., Guibert, J., 1993, “ROSAT X-Ray Study of the Chamaeleon I Dark Cloud. I. The Stellar Population”, Astrophys. J., 416, 623–646. ADS: http://adsabs.harvard.edu/abs/1993ApJ...416..623F
Feigelson, E.D., Carkner, L., Wilking, B.A., 1998, “Circularly Polarized Radio Emission from an X-Ray Protostar”, Astrophys. J. Lett., 494, L215–218. ADS: http://adsabs.harvard.edu/abs/1998ApJ...494L.215F
Feigelson, E.D., Broos, P., Gaffney III, J.A., Garmire, G., Hillenbrand, L.A., Pravdo, S.H., Townsley, L., Tsuboi, Y., 2002a, “X-Ray-emitting Young Stars in the Orion Nebula”, Astrophys. J., 574, 258–292. ADS: http://adsabs.harvard.edu/abs/2002ApJ...574..258F
Feigelson, E.D., Garmire, G.P., Pravdo, S.H., 2002b, “Magnetic Flaring in the Pre-Main-Sequence Sun and Implications for the Early Solar System”, Astrophys. J., 572, 335–349. ADS: http://adsabs.harvard.edu/abs/2002ApJ...572..335F
Feigelson, E.D., Townsley, L., Güdel, M., Stassun, K., 2007, “X-Ray Properties of Young Stars and Stellar Clusters”, in Protostars and Planets V, (Eds.) Reipurth, B., Jewitt, D., Keil, K., pp. 313–328, University of Arizona Press, Tucson, U.S.A. ADS: http://adsabs.harvard.edu/abs/2007prpl.conf..313F
Feldman, U., 1992, “Elemental abundances in the upper solar atmosphere”, Phys. Scripta, 46, 202–220. ADS: http://adsabs.harvard.edu/abs/1992PhST...46..202F
Feldman, W.C., Asbridge, J.R., Bame, S.J., Gosling, J.T., 1977, “Plasma and Magnetic Fields from the Sun”, in The Solar Output and its Variation, (Ed.) White, O.R., p. 351, Colorado Associated University Press, Boulder, U.S.A. ADS: http://adsabs.harvard.edu/abs/1977soiv.conf..351F
Felli, M., Taylor, G.B., Catarzi, M., Churchwell, E., Kurtz, S., 1993, “The Orion Radio Zoo Revisited — Source Variability”, Astron. Astrophys. Suppl., 101, 127–151. ADS: http://adsabs.harvard.edu/abs/1993A&AS..101..127F
Ferreira, J., Zanni, C., 2007, “On some MHD aspects of star-disc-jets systems”, Mem. Soc. Astron. Ital., 78, 348–355. ADS: http://adsabs.harvard.edu/abs/2007MmSAI..78..348F
Flaccomio, E., Micela, G., Sciortino, S., 2003, “Time evolution of X-ray coronal activity in PMS stars; a possible relation with the evolution of accretion disks”, Astron. Astrophys., 402, 277–292. ADS: http://adsabs.harvard.edu/abs/2003A&A...402..277F
Flaccomio, E., Micela, G., Sciortino, S., Feigelson, E.D., Herbst, W., Favata, F., Harnden Jr, F.R., Vrtilek, S.D., 2005, “Rotational Modulation of X-Ray Emission in Orion Nebula Young Stars”, Astrophys. J. Suppl. Ser., 160, 450–468. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..450F
Forget, F., Pierrehumbert, R.T., 1997, “Warming Early Mars with Carbon Dioxide Clouds That Scatter Infrared Radiation”, Science, 278, 1273–1276. ADS: http://adsabs.harvard.edu/abs/1997Sci...278.1273F
Frisch, P.C., 2000, “The galactic environment of the Sun”, J. Geophys. Res., 105, 10279–10290. ADS: http://adsabs.harvard.edu/abs/2000JGR...10510279F
Frisch, P.C., Slavin, J.D., 2003, “The Chemical Composition and Gas-to-Dust Mass Ratio of Nearby Interstellar Matter”, Astrophys. J., 594, 844–858. ADS: http://adsabs.harvard.edu/abs/2003ApJ...594..844F
Frisch, P.C., Slavin, J.D., 2005, “Heliospheric implications of structure in the interstellar medium”, Adv. Space Res., 35, 2048–2054. ADS: http://adsabs.harvard.edu/abs/2005AdSpR..35.2048F
Frisch, P.C., Slavin, J.D., 2006, “The Sun’s journey through the local interstellar medium: the paleoLISM and paleoheliosphere”, Astrophys. Space Sci. Trans., 2, 53–61. URL (cited on 09 April 2007): http://www.astrophys-space-sci-trans.net/2/53/2006/. ADS: http://adsabs.harvard.edu/abs/2006ASTRA...2...53F
Fröhlich, H.-E., Tschaüpe, R., Ruüdiger, G., Strassmeier, K.G., 2002, “EK Draconis: Long-term photometry on Sonneberg Sky-Patrol plates”, Astron. Astrophys., 391, 659–663. ADS: http://adsabs.harvard.edu/abs/2002A&A...391..659F
Fromang, S., Terquem, C., Balbus, S.A., 2002, “The ionization fraction in α models of protoplanetary discs”, Mon. Not. R. Astron. Soc., 329, 18–28. ADS: http://adsabs.harvard.edu/abs/2002MNRAS.329...18F
Gagné, M., Caillault, J.-P., 1994, “The complete Einstein Observatory X-ray survey of the Orion Nebula region”, Astrophys. J., 437, 361–383. ADS: http://adsabs.harvard.edu/abs/1994ApJ...437..361G
Gagné, M., Caillault, J.-P., Stauffer, J.R., 1995a, “Spectral and Temporal Characteristics of X-Ray-bright Stars in the Pleiades”, Astrophys. J., 450, 217–232. ADS: http://adsabs.harvard.edu/abs/1995ApJ...450..217G
Gagné, M., Caillault, J.-P., Stauffer, J.R., 1995b, “Deep ROSAT HRI observations of the Orion nebula region”, Astrophys. J., 445, 280–313. ADS: http://adsabs.harvard.edu/abs/1995ApJ...445..280G
Gaidos, E.J., Güdel, M., Blake, G.A., 2000, “The Faint Young Sun Paradox: An Observational Test of an Alternative Solar Model”, Geophys. Res. Lett., 27, 501–503. ADS: http://adsabs.harvard.edu/abs/2000GeoRL..27..501G
Gammie, C.F., 1996, “Layered Accretion in T Tauri Disks”, Astrophys. J., 457, 355–362. ADS: http://adsabs.harvard.edu/abs/1996ApJ...457..355G
Gary, D.E., Hurford, G.J., 1994, “Coronal temperature, density, and magnetic field maps of a solar acitve region using the Owens Valley Solar Array”, Astrophys. J., 420, 903–912. ADS: http://adsabs.harvard.edu/abs/1994ApJ...420..903G
Gayley, K.G., Zank, G.P., Pauls, H.L., Frisch, P.C., Welty, D.E., 1997, “One- versus Two-Shock Heliosphere: Constraining Models with Goddard High Resolution Spectrograph Lya Spectra toward α Centauri”, Astrophys. J., 487, 259–270. ADS: http://adsabs.harvard.edu/abs/1997ApJ...487..259G
Geiss, J., Bochsler, P., 1991, “Long time variations in solar wind properties — Possible causes versus observations”, in The Sun in Time, (Eds.) Sonett, C.P., Giampapa, M.S., Matthews, M.S., pp. 98–117, University of Arizona Press, Tucson, U.S.A.
Getman, K.V., Feigelson, E.D., Townsley, L., Bally, J., Lada, C.J., Reipurth, B., 2002, “Chandra Study of Young Stellar Objects in the NGC 1333 Star-forming Cloud”, Astrophys. J., 575, 354–377. ADS: http://adsabs.harvard.edu/abs/2002ApJ...575..354G
Giampapa, M.S., Golub, L., Peres, G., Serio, S., Vaiana, G.S., 1985, “Closed coronal structures. VI. Far-ultraviolet and X-ray emission from active late-type stars and the applicability of coronal loop models”, Astrophys. J., 289, 203–212. ADS: http://adsabs.harvard.edu/abs/1985ApJ...289..203G
Giampapa, M.S., Rosner, R., Kashyap, V., Fleming, T.A., Schmitt, J.H.M.M., Bookbinder, J.A., 1996, “The Coronae of Low-Mass Dwarf Stars”, Astrophys. J., 463, 707–725. ADS: http://adsabs.harvard.edu/abs/1996ApJ...463..707G
Glandorf, D.L., Colaprete, A., Tolbert, M.A., Toon, O.B., 2002, “CO2 Snow on Mars and Early Earth: Experimental Constraints”, Icarus, 160, 66–72. ADS: http://adsabs.harvard.edu/abs/2002Icar..160...66G
Glassgold, A.E., Najita, J., Igea, J., 1997, “X-Ray Ionization of Protoplanetary Disks”, Astrophys. J., 480, 344–350. ADS: http://adsabs.harvard.edu/abs/1997ApJ...480..344G
Glassgold, A.E., Najita, J., Igea, J., 2004, “Heating Protoplanetary Disk Atmospheres”, Astrophys. J., 615, 972–990. ADS: http://adsabs.harvard.edu/abs/2004ApJ...615..972G
Glassgold, A.E., Feigelson, E.D., Montmerle, T., Wolk, S., 2005, “X-Ray Flares of Sun-like Young Stellar Objects and Their Effects on Protoplanetary Disks”, in Chondrites and the Protoplanetary Disk, (Eds.) Krot, A.N., Scott, E.R.D., Reipurth, B., vol. 341, pp. 165–180, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2005ASPC..341..165G
Glassgold, A.E., Najita, J.R., Igea, J., 2007, “Neon Fine-Structure Line Emission by X-Ray Irradiated Protoplanetary Disks”, Astrophys. J., 656, 515–523. ADS: http://adsabs.harvard.edu/abs/2007ApJ...656..515G
Gorti, U., Hollenbach, D., 2004, “Models of Chemistry, Thermal Balance, and Infrared Spectra from Intermediate-Aged Disks around G and K Stars”, Astrophys. J., 613, 424–447. ADS: http://adsabs.harvard.edu/abs/2004ApJ...613..424G
Goswami, J.N., Vanhala, H.A.T., 2000, “Extinct Radionuclides and the Origin of the Solar System”, in Protostars and Planets IV, (Eds.) Mannings, V., Boss, A., Russell, S.S., Space Science Series, pp. 963–994, University of Arizona Press, Tucson, U.S.A. ADS: http://adsabs.harvard.edu/abs/2000prpl.conf..963G
Goswami, J.N., Marhas, K.K., Sahijpal, S., 2001, “Did Solar Energetic Particles Produce the Short-lived Nuclides Present in the Early Solar System?”, Astrophys. J., 549, 1151–1159. ADS: http://adsabs.harvard.edu/abs/2001ApJ...549.1151G
Gounelle, M., Shu, F.H., Shang, H., Glassgold, A.E., Rehm, K.E., Lee, T., 2001, “Extinct Radioactivities and Protosolar Cosmic Rays: Self-Shielding and Light Elements”, Astrophys. J., 548, 1051–1070. ADS: http://adsabs.harvard.edu/abs/2001ApJ...548.1051G
Graedel, T.E., Sackmann, I.-J., Boothroyd, A.I., 1991, “Early solar mass loss — A potential solution to the weak sun paradox”, Geophys. Res. Lett., 18, 1881–1884. ADS: http://adsabs.harvard.edu/abs/1991GeoRL..18.1881G
Granzer, T., Schässler, M., Caligari, P., Strassmeier, K.G., 2000, “Distribution of starspots on cool stars. II. Pre-main-sequence and ZAMS stars between 0.4M⊙and 1.7M⊙”,Astron. Astrophys., 355, 1087–1097. ADS: http://adsabs.harvard.edu/abs/2000A&A...355.1087G
Gregory, S.G., Jardine, M., Simpson, I., Donati, J.-F., 2006, “Mass accretion on to T Tauri stars”, Mon. Not. R. Astron. Soc., 371, 999–1013. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.371..999G
Grießmeier, J.-M., Stadelmann, A., Penz, T., Lammer, H., Selsis, F., Ribas, I., Guinan, E.F., Motschmann, U., Biernat, H.K., Weiss, W.W., 2004, “The effect of tidal locking on the magne-tospheric and atmospheric evolution of “Hot Jupiters””, Astron. Astrophys., 425, 753–762. ADS: http://adsabs.harvard.edu/abs/2004A&A...425..753G
Grosso, N., Montmerle, T., Feigelson, E.D., André, P., Casanova, S., Gregorio-Hetem, J., 1997, “An X-ray superflare are from an infrared protostar”, Nature, 387, 56–58. ADS: http://adsabs.harvard.edu/abs/1997Natur.387...56G
Grosso, N., Montmerle, T., Bontemps, S., André, P., Feigelson, E.D., 2000, “X-rays and regions of star formation: a combined ROSAT-HRI/near-to-mid IR study of the ρ Oph dark cloud”, Astron. Astrophys., 359, 113–130. ADS: http://adsabs.harvard.edu/abs/2000A&A...359..113G
Güdel, M., 1997, “Are Coronae of Magnetically Active Stars Heated by Flares?”, Astrophys. J. Lett., 480, L121–L124. ADS: http://adsabs.harvard.edu/abs/1997ApJ...480L.121G
Güdel, M., 2002, “Stellar Radio Astronomy: Probing Stellar Atmospheres from Protostars to Giants”, Annu. Rev. Astron. Astrophys., 40, 217–261. ADS: http://adsabs.harvard.edu/abs/2002ARA&A..40..217G
Güdel, M., 2003, “The Sun in Time: From PMS to Main Sequence”, in Magnetism and Activity of the Sun and Stars, (Eds.) Arnaud, J., Meunier, N., Proceedings of an international conference to honor the work of Jean-Louis Leroy, Toulouse, France, September 17–21, 2002, vol. 9 of EAS Publications Series, pp. 339–348, EDP Sciences, Les Ulis, France. ADS: http://adsabs.harvard.edu/abs/2003EAS.....9..339G
Güdel, M., 2004, “X-ray astronomy of stellar coronae”, Astron. Astrophys. Rev., 12, 71–237. ADS: http://adsabs.harvard.edu/abs/2004A&ARv..12...71G
Güdel, M., Benz, A.O., 1989, “Broad-band spectrum of dMe star radio emission”, Astron. Astrophys., 211, L5–L8. ADS: http://adsabs.harvard.edu/abs/1989A&A...211L...5G
Güdel, M., Benz, A.O., 1993, “X-ray/microwave relation of different types of active stars”, Astrophys. J. Lett., 405, L63–L66. ADS: http://adsabs.harvard.edu/abs/1993ApJ...405L..63G
Güdel, M., Gaidos, E.J., 2001, “Deep Radio Observations of Young Solar Analogs”, in Cool Stars, Stellar Systems and the Sun: 11th Cambridge Workshop, (Eds.) García López, R.J., Rebolo, R., Zapaterio Osorio, M.R., Proceedings of a meeting held at Puerto de la Cruz, Tenerife, Spain, 4–8 October 1999, vol. 223 of ASP Conference Series, pp. 662–667, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2001ASPC..223..662G
Güdel, M., Telleschi, A., 2007, “The X-ray soft excess in classical T Tauri stars”, Astron. Astrophys., 474, L25–L28. ADS: http://adsabs.harvard.edu/abs/2007A&A...474L..25G
Güdel, M., Schmitt, J.H.M.M., Benz, A.O., 1994, “Discovery of Microwave Emission from Four Nearby Solar-Type G Stars”, Science, 265, 933–935. ADS: http://adsabs.harvard.edu/abs/1994Sci...265..933G
Güdel, M., Schmitt, J.H.M.M., Benz, A.O., 1995a, “A bright X-ray and radio corona on the F0V star 47 Cas?”, Astron. Astrophys., 293, L49–L52. ADS: http://adsabs.harvard.edu/abs/1995A&A...293L..49G
Güdel, M., Schmitt, J.H.M.M., Benz, A.O., 1995b, “Microwave emission from X-ray bright solarlike stars: the F-G main sequence and beyond”, Astron. Astrophys., 302, 775–787. ADS: http://adsabs.harvard.edu/abs/1995A&A...302..775G
Güdel, M., Schmitt, J.H.M.M., Benz, A.O., Elias II, N.M., 1995c, “The corona of the young solar analog EK Draconis”, Astron. Astrophys., 301, 201–212. ADS: http://adsabs.harvard.edu/abs/1995A&A...301..201G
Güdel, M., Guinan, E.F., Mewe, R., Kaastra, J.S., Skinner, S.L., 1997a, “A Determination of the Coronal Emission Measure Distribution in the Young Solar Analog EK Draconis from ASCA/EUVE Spectra”, Astrophys. J., 479, 416–426. ADS: http://adsabs.harvard.edu/abs/1997ApJ...479..416G
Güdel, M., Guinan, E.F., Skinner, S.L., 1997b, “The X-Ray Sun in Time: A Study of the Long-Term Evolution of Coronae of Solar-Type Stars”, Astrophys. J., 483, 947–960. ADS: http://adsabs.harvard.edu/abs/1997ApJ...483..947G
Güdel, M., Guinan, E.F., Etzel, P.B., Mewe, R., Kaastra, J.S., Skinner, S.L., 1998a, “Assembling the Pieces of the Puzzle: A Nearby, Rapidly Rotating Young Sun in 47 Cas?”, in Cool Stars, Stellar Systems, and the Sun: Tenth Cambridge Workshop, (Eds.) Donahue, R.A., Bookbinder, J.A., Proceedings of a meeting held at Cambridge, Massachusetts, 15–19 July 1997, vol. 154 of ASP Conference Series, pp. 1247–1256, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/1998ASPC..154.1247G
Güdel, M., Guinan, E.F., Skinner, S.L., 1998b, “The X-Ray and Radio Sun in Time: Coronal Evolution of Solar-Type Stars with Different Ages”, in Cool Stars, Stellar Systems, and the Sun: Tenth Cambridge Workshop, (Eds.) Donahue, R.A., Bookbinder, J.A., Proceedings of a meeting held at Cambridge, Massachusetts, 15–19 July 1997, vol. 154 of ASP Conference Series, pp. 1041–1050, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/1998ASPC.154.1041G
Güdel, M., Audard, M., Briggs, K., Haberl, F., Magee, H., Maggio, A., Mewe, R., Pallavicini, R., Pye, J., 2001, “The XMM-Newton view of stellar coronae: X-ray spectroscopy of the corona of AB Doradus”, Astron. Astrophys., 365, L336–L343. ADS: http://adsabs.harvard.edu/abs/2001A&A...365L.336G
Güdel, M., Arzner, K., Audard, M., Mewe, R., 2003a, “Tomography of a stellar X-ray corona: α Coronae Borealis”, Astron. Astrophys., 403, 155–171. ADS: http://adsabs.harvard.edu/abs/2003A&A...403..155G
Güdel, M., Audard, M., Kashyap, V.L., Drake, J.J., Guinan, E.F., 2003b, “Are Coronae of Magnetically Active Stars Heated by Flares? II. Extreme Ultraviolet and X-Ray Flare Statistics and the Differential Emission Measure Distribution”, Astrophys. J., 582, 423–442. ADS: http://adsabs.harvard.edu/abs/2003ApJ...582..423G
Güdel, M., Briggs, K.R., Arzner, K., Audard, M., Bouvier, J., Feigelson, E.D., Franciosini, E., Glauser, A., Grosso, N., Micela, G., Monin, J.L., Montmerle, T., Padgett, D.L., Palla, F., Pillitteri, I., Rebull, L., Scelsi, L., Silva, B., Skinner, S.L., Stelzer, B., Telleschi, A., 2007a, “The XMM-Newton Extended Survey of the Taurus Molecular Cloud (XEST)”, Astron. Astrophys., 468, 353–377. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..353G
Güdel, M., Skinner, S.L., Mel’nikov, S.Y., Audard, M., Telleschi, A., Briggs, K.R., 2007b, “X-rays from T Tau: A test case for accreting T Tauri stars”, Astron. Astrophys., 468, 529–540. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..529G
Guinan, E.F., Ribas, I., 2002, “Our Changing Sun: The Role of Solar Nuclear Evolution and Magnetic Activity on Earth’s Atmosphere and Climate”, in The Evolving Sun and its Influence on Planetary Environments, (Eds.) Montesinos, B., Gimenez, A., Guinan, E.F., Proceedings of a workshop held at Instituto de Astrofísica de Andalucía, Granada, Spain, 18–20 June 2001, vol. 269 of ASP Conference Series, pp. 85–106, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2002ASPC..269...85G
Guinan, E.F., Ribas, I., Harper, G.M., 2002, “Reconstructing the Sun’s Magnetic History and Spectral Irradiance Evolution from X-ray, EUV, and FUV Observations of Solar Proxies with Different Ages”, in Continuing the Challenge of EUV Astronomy: Current Analysis and Prospects for the Future, (Eds.) Howell, S.B., Dupuis, J., Golombek, D., Walter, F.M., Cullison, J., vol. 264 of ASP Conference Series, pp. 139–153, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2002ASPC..264..139G
Guinan, E.F., Ribas, I., Harper, G.M., 2003, “Far-Ultraviolet Emissions of the Sun in Time: Probing Solar Magnetic Activity and Effects on Evolution of Paleoplanetary Atmospheres”, Astrophys. J., 594, 561–572. ADS: http://adsabs.harvard.edu/abs/2003ApJ...594..561G
Gullbring, E., Hartmann, L., Briceño, C., Calvet, N., 1998, “Disk Accretion Rates for T Tauri Stars”, Astrophys. J., 492, 323–341. ADS: http://adsabs.harvard.edu/abs/1998ApJ...492..323G
Günther, H.M., Liefke, C., Schmitt, J.H.M.M., Robrade, J., Ness, J.-U., 2006, “X-ray accretion signatures in the close CTTS binary V4046 Sagittarii”, Astron. Astrophys., 459, L29–L32. ADS: http://adsabs.harvard.edu/abs/2006A&A...459L..29G
Gustafsson, B., 1998, “Is the Sun a Sun-Like Star?”, Space Sci. Rev., 85, 419–428. ADS: http://adsabs.harvard.edu/abs/1998SSRv...85..419G
Guzik, J.A., Cox, A.N., 1995, “Early Solar Mass Loss, Element Diffusion, and Solar Oscillation Frequencies”, Astrophys. J., 448, 905–914. ADS: http://adsabs.harvard.edu/abs/1995ApJ...448..905G
Haisch, B.M., Butler, C.J., Foing, B., Rodono, M., Giampapa, M.S., 1990, “Rotational modulation and flares on RS Canum Venaticorum and BY Draconis-type stars. XV. Observations of Proxima Centauri and solar calibration data”, Astron. Astrophys., 232, 387–395. ADS: http://adsabs.harvard.edu/abs/1990A&A...232..387H
Han, I., Gatewood, G., 2002, “A Precise Orbit Determination of χ1 Orionis from Astrometric and Radial Velocity Data”, Publ. Astron. Soc. Pac., 114, 224–228. ADS: http://adsabs.harvard.edu/abs/2002PASP..114..224H
Hatzes, A.P., 1995, “Doppler Imaging of the Cool SPOT Distribution on the Weak T Tauri Star V410 Tauri”, Astrophys. J., 451, 784–794. ADS: http://adsabs.harvard.edu/abs/1995ApJ...451..784H
Hayashi, M.R., Shibata, K., Matsumoto, R., 1996, “X-Ray Flares and Mass Outflows Driven by Magnetic Interaction between a Protostar and Its Surrounding Disk”, Astrophys. J. Lett., 468, L37–L40. ADS: http://adsabs.harvard.edu/abs/1996ApJ...468L..37H
Hempelmann, A., Schmitt, J.H.M.M., Stȩpień, K., 1996, “Coronal X-ray emission of cool stars in relation to chromospheric activity and magnetic cycles”, Astron. Astrophys., 305, 284–295. ADS: http://adsabs.harvard.edu/abs/1996A&A...305..284H
Hempelmann, A., Schmitt, J.H.M.M., Baliunas, S.L., Donahue, R.A., 2003, “Evidence for coronal activity cycles on 61 Cygni A and B”, Astron. Astrophys., 406, L39–L42. ADS: http://adsabs.harvard.edu/abs/2003A&A...406L..39H
Hempelmann, A., Robrade, J., Schmitt, J.H.M.M., Favata, F., Baliunas, S.L., Hall, J.C., 2006, “Coronal activity cycles in 61 Cygni”, Astron. Astrophys., 460, 261–267. ADS: http://adsabs.harvard.edu/abs/2006A&A...460..261H
Hénoux, J.-C., 1995, “Models for explaining the observed spatial variation of element abundances — A review”, Adv. Space Res., 15, 23–32. ADS: http://adsabs.harvard.edu/abs/1995AdSpR..15...23H
Herbig, G.H., Soderblom, D.R., 1980, “Observations and interpretation of the near-infrared line spectra of T Tauri stars”, Astrophys. J., 242, 628–637. ADS: http://adsabs.harvard.edu/abs/1980ApJ...242..628H
Herczeg, G.J., Linsky, J.L., Valenti, J.A., Johns-Krull, C.M., Wood, B.E., 2002, “The Far-Ultraviolet Spectrum of TW Hydrae. I. Observations of H2 Fluorescence”, Astrophys. J., 572, 310–325. ADS: http://adsabs.harvard.edu/abs/2002ApJ...572..310H
Herczeg, G.J., Wood, B.E., Linsky, J.L., Valenti, J.A., Johns-Krull, C.M., 2004, “The Far-Ultraviolet Spectra of TW Hydrae. II. Models of H2 Fluorescence in a Disk”, Astrophys. J., 607, 369–383. ADS: http://adsabs.harvard.edu/abs/2004ApJ...607..369H
Herczeg, G.J., Linsky, J.L., Walter, F.M., Gahm, G.F., Johns-Krull, C.M., 2006, “The Origins of Fluorescent H2 Emission From T Tauri Stars”, Astrophys. J. Suppl. Ser., 165, 256–282. ADS: http://adsabs.harvard.edu/abs/2006ApJS..165..256H
Hester, J.J., Scowen, P.A., Sankrit, R., Lauer, T.R., Ajhar, E.A., Baum, W.A., Code, A., Currie, D.G., Danielson, G.E., Ewald, S.P., Faber, S.M., Grillmair, C.J., Groth, E.J., Holtzman, J.A., Hunter, D.A., Kristian, J., Light, R.M., Lynds, C.R., Monet, D.G., O’Neil Jr, E.J., Shaya, E.J., Seidelmann, K.P., Westphal, J.A., 1996, “Hubble Space Telescope WFPC2 Imaging of M16: Photoevaporation and Emerging Young Stellar Objects”, Astron. J., 111, 2349–2360. ADS: http://adsabs.harvard.edu/abs/1996AJ.....111.2349H
Hester, J.J., Desch, S.J., Healy, K.R., Leshin, L.A., 2004, “The Cradle of the Solar System”, Science, 304, 1116–1117. ADS: http://adsabs.harvard.edu/abs/2004Sci...304.1116H
Hobbs, L.M., Iben, I.J., Pilachowski, C., 1989, “On lithium removal from G dwarfs”, Astrophys. J., 347, 817–820. ADS: http://adsabs.harvard.edu/abs/1989ApJ...347..817H
Hollenbach, D., Johnstone, D., Lizano, S., Shu, F., 1994, “Photoevaporation of disks around massive stars and application to ultracompact H II regions”, Astrophys. J., 428, 654–669. ADS: http://adsabs.harvard.edu/abs/1994ApJ...428..654H
Holman, G.D., 1986, “Coronal Heating and the X-Ray and Microwave Emission from M-Dwarf Flare Stars”, in Cool Stars, Stellar Systems and the Sun, (Eds.) Zeilik, M., Gibson, D.M., Proceedings of the Fourth Cambridge Workshop, held in Santa Fe, New Mexico, October 16–18, 1985, vol. 254 of Lecture Notes in Physics, pp. 271–274, Springer, Berlin, Germany; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1986LNP...254..271H
Holman, G.D., Benka, S.G., 1992, “A hybrid thermal/nonthermal model for the energetic emissions from solar flares”, Astrophys. J. Lett., 400, L79–L82. ADS: http://adsabs.harvard.edu/abs/1992ApJ...400L..79H
Holzwarth, V., Mackay, D.H., Jardine, M., 2006, “The impact of meridional circulation on stellar butterfly diagrams and polar caps”, Mon. Not. R. Astron. Soc., 369, 1703–1718. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.369.1703H
Huenemoerder, D.P., Canizares, C.R., Schulz, N.S., 2001, “X-Ray Spectroscopy of II Pegasi: Coronal Temperature Structure, Abundances, and Variability”, Astrophys. J., 559, 1135–1146. ADS: http://adsabs.harvard.edu/abs/2001ApJ...559.1135H
Huenemoerder, D.P., Canizares, C.R., Drake, J.J., Sanz-Forcada, J., 2003, “The Coronae of AR Lacertae”, Astrophys. J., 595, 1131–1147. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595.1131H
Hughes, V.A., 1997, “An Evolving Radio Source in the Young Star-forming Region Cepheus A”, Astrophys. J., 481, 857–865. ADS: http://adsabs.harvard.edu/abs/1997ApJ...481..857H
Hünsch, M., Schmitt, J.H.M.M., Schroeder, K.-P., Reimers, D., 1996, “ROSAT X-ray observations of a complete, volume-limited sample of late-type giants”, Astron. Astrophys., 310, 801–812. ADS: http://adsabs.harvard.edu/abs/1996A&A...310..801H
Hunten, D.M., 1973, “The Escape of Light Gases from Planetary Atmospheres”, J. Atmos. Sci., 30, 1481–1494. ADS: http://adsabs.harvard.edu/abs/1973JAtS...30.1481H
Hussain, G.A.J., van Ballegooijen, A.A., Jardine, M., Collier Cameron, A., 2002, “The Coronal Topology of the Rapidly Rotating K0 Dwarf AB Doradus. I. Using Surface Magnetic Field Maps to Model the Structure of the Stellar Corona”, Astrophys. J., 575, 1078–1086. ADS: http://adsabs.harvard.edu/abs/2002ApJ...575.1078H
Hussain, G.A.J., Jardine, M., Donati, J.-F., Brickhouse, N.S., Dunstone, N.J., Wood, K., Dupree, A.K., Collier Cameron, A., Favata, F., 2007, “The coronal structure of AB Doradus determined from contemporaneous Doppler imaging and X-ray spectroscopy”, Mon. Not. R. Astron. Soc., 377, 1488–1502. ADS: http://adsabs.harvard.edu/abs/2007MNRAS.377.1488H
Hutchins, K.S., Jakosky, B.M., Luhmann, J.G., 1997, “Impact of a paleomagnetic field on sputtering loss of Martian atmospheric argon and neon”, J. Geophys. Res., 102, 9183–9190. ADS: http://adsabs.harvard.edu/abs/1997JGR...102.9183H
Igea, J., Glassgold, A.E., 1999, “X-Ray Ionization of the Disks of Young Stellar Objects”, Astrophys. J., 518, 848–858. ADS: http://adsabs.harvard.edu/abs/1999ApJ...518..848I
Ilgner, M., Nelson, R.P., 2006, “On the ionisation fraction in protoplanetary disks. II. The effect of turbulent mixing on gas-phase chemistry”, Astron. Astrophys., 445, 223–232. ADS: http://adsabs.harvard.edu/abs/2006A&A...445..223I
Imanishi, K., Koyama, K., Tsuboi, Y., 2001, “Chandra Observation of the ρ Ophiuchi Cloud”, Astrophys. J., 557, 747–760. ADS: http://adsabs.harvard.edu/abs/2001ApJ...557..747I
Imanishi, K., Tsujimoto, M., Koyama, K., 2002, “Chandra and ASCA Observations of the X-Ray-brightest T Tauri Stars in the ρ Ophiuchi Cloud”, Astrophys. J., 572, 300–309. ADS: http://adsabs.harvard.edu/abs/2002ApJ...572..300I
Imanishi, K., Nakajima, H., Tsujimoto, M., Koyama, K., Tsuboi, Y., 2003, “A Systematic Study of X-Ray Flares from Low-Mass Young Stellar Objects in the ρ Ophiuchi Star-Forming Region with Chandra”, Publ. Astron. Soc. Japan, 55, 653–681. ADS: http://adsabs.harvard.edu/abs/2003PASJ...55..653I
Ingersoll, A.P., 1969, “The Runaway Greenhouse: A History of Water on Venus”, J. Atmos. Sci., 26, 1191–1198. ADS: http://adsabs.harvard.edu/abs/1969JAtS...26.1191I
Işik, E., Schüssler, M., Solanki, S.K., 2007, “Magnetic flux transport on active cool stars and starspot lifetimes”, Astron. Astrophys., 464, 1049–1057. ADS: http://adsabs.harvard.edu/abs/2007A&A...464.1049I
Jakosky, B.M., Pepin, R.O., Johnson, R.E., Fox, J.L., 1994, “Mars atmospheric loss and isotopic fractionation by solar-wind-induced sputtering and photochemical escape”, Icarus, 111, 271–288. ADS: http://adsabs.harvard.edu/abs/1994Icar..111..271J
James, D.J., Jeffries, R.D., 1997, “Rotation, activity and lithium in NGC 6475”, Mon. Not. R. Astron. Soc., 292, 252–272. ADS: http://adsabs.harvard.edu/abs/1997MNRAS.292..252J
Jardine, M., Collier Cameron, A., Donati, J.-F., 2002a, “The global magnetic topology of AB Doradus”, Mon. Not. R. Astron. Soc., 333, 339–346. ADS: http://adsabs.harvard.edu/abs/2002MNRAS.333..339J
Jardine, M., Wood, K., Collier Cameron, A., Donati, J.-F., Mackay, D.H., 2002b, “Inferring X-ray coronal structures from Zeeman-Doppler images”, Mon. Not. R. Astron. Soc., 336, 1364–1370. ADS: http://adsabs.harvard.edu/abs/2002MNRAS.336.1364J
Jardine, M., Wood, K., Collier Cameron, A., Donati, J.-F., Mackay, D.H., 2002c, “Inferring X-ray coronal structures from Zeeman-Doppler images”, Mon. Not. R. Astron. Soc., 336, 1364–1370. ADS: http://adsabs.harvard.edu/abs/2002MNRAS.336.1364J
Jardine, M., Collier Cameron, A., Donati, J.-F., Gregory, S.G., Wood, K., 2006, “X-ray emission from T Tauri stars”, Mon. Not. R. Astron. Soc., 367, 917–927. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.367..917J
Järvinen, S.P., Berdyugina, S.V., Strassmeier, K.G., 2005, “Spots on EK Draconis. Active longitudes and cycles from long-term photometry”, Astron. Astrophys., 440, 735–741. ADS: http://adsabs.harvard.edu/abs/2005A&A...440..735J
Jeans, J.H., 1925, The Dynamical Theory of Gases, Cambridge University Press, Cambridge, U.K., 4th edn.
Johns-Krull, C.M., 2007a, “The Magnetic Fields of Classical T Tauri Stars”, Astrophys. J., 664, 975–985. ADS: http://adsabs.harvard.edu/abs/2007ApJ...664..975J
Johns-Krull, C.M., 2007b, “The Magnetic Field of the Class I Protostar WL 17”, conference paper. Poster #I.6
Johns-Krull, C.M., Valenti, J.A., Koresko, C., 1999, “Measuring the Magnetic Field on the Classical T Tauri Star BP Tauri”, Astrophys. J., 516, 900–915. ADS: http://adsabs.harvard.edu/abs/1999ApJ...516..900J
Johns-Krull, C.M., Valenti, J.A., Linsky, J.L., 2000, “An IUE Atlas of Pre-Main-Sequence Stars. II. Far-Ultraviolet Accretion Diagnostics in T Tauri Stars”, Astrophys. J., 539, 815–833. ADS: http://adsabs.harvard.edu/abs/2000ApJ...539..815J
Joncour, I., Bertout, C., Menard, F., 1994, “Doppler imaging of the T Tauri star V410 Tau”, Astron. Astrophys., 285, L25–L28. ADS: http://adsabs.harvard.edu/abs/1994A&A...285L..25J
Jordan, C., Montesinos, B., 1991, “The dependence of coronal temperatures on Rossby numbers”, Mon. Not. R. Astron. Soc., 252, 21P–26P. ADS: http://adsabs.harvard.edu/abs/1991MNRAS.252P..21J
Jordan, C., Ayres, T.R., Brown, A., Linsky, J.L., Simon, T., 1987, “The chromospheres and coronae of five G-K main-sequence stars”, Mon. Not. R. Astron. Soc., 225, 903–937. ADS: http://adsabs.harvard.edu/abs/1987MNRAS.225..903J
Jordan, C., Doschek, G.A., Drake, J.J., Galvin, A.B., Raymond, J.C., 1998, “Coronal Abundances: What are They?”, in Cool Stars, Stellar Systems, and the Sun: Tenth Cambridge Workshop, (Eds.) Donahue, R.A., Bookbinder, J.A., Proceedings of a meeting held at Cambridge, Massachusetts, 15–19 July 1997, vol. 154, pp. 91–109, Astronomical Society of the Pacific, San Franciso, U.S.A. ADS: http://adsabs.harvard.edu/abs/1998ASPC..154...91J
Joy, A.H., 1945, “T Tauri Variable Stars.”, Astrophys. J., 102, 168–195. ADS: http://adsabs.harvard.edu/abs/1945ApJ...102..168J
Kamata, Y., Koyama, K., Tsuboi, Y., Yamauchi, S., 1997, “X-Ray Analysis of the ρ Ophiuchi Dark Cloud with ASCA: Source Identification, X-Ray Spectra, and Temporal Variability”, Publ. Astron. Soc. Japan, 49, 461–470. ADS: http://adsabs.harvard.edu/abs/1997PASJ...49..461K
Karhu, J., Epstein, S., 1986, “The implication of the oxygen isotope records in coexisting cherts and phosphates”, Geochim. Cosmochim. Acta, 50, 1745–1756. ADS: http://adsabs.harvard.edu/abs/1986GeCoA..50.1745K
Kashyap, V.L., Drake, J.J., Güdel, M., Audard, M., 2002, “Flare Heating in Stellar Coronae”, Astrophys. J., 580, 1118–1132. ADS: http://adsabs.harvard.edu/abs/2002ApJ...580.1118K
Kasting, J.F., 1988, “Runaway and moist greenhouse atmospheres and the evolution of earth and Venus”, Icarus, 74, 472–494. ADS: http://adsabs.harvard.edu/abs/1988Icar...74..472K
Kasting, J.F., 1989, “Long-term stability of the Earths’s climate”, Palaeogeogr. Palaeoclimatol. Palaeoecol., 75, 83–95
Kasting, J.F., 1991, “CO2 condensation and the climate of early Mars”, Icarus, 94, 1–13. ADS: http://adsabs.harvard.edu/abs/1991Icar...94....1K
Kasting, J.F., Catling, D., 2003, “Evolution of a Habitable Planet”, Annu. Rev. Astron. Astrophys., 41, 429–463. ADS: http://adsabs.harvard.edu/abs/2003ARA&A..41..429K
Kasting, J.F., Grinspoon, D.H., 1991, “The faint young sun problem”, in The Sun in Time, (Eds.) Sonett, C.P., Giampapa, M.S., Matthews, M.S., pp. 447–462, University of Arizona Press, Tucson, U.S.A.
Kasting, J.F., Pollack, J.B., 1983, “Loss of water from Venus. I — Hydrodynamic escape of hydrogen”, Icarus, 53, 479–508. ADS: http://adsabs.harvard.edu/abs/1983Icar...53..479K
Kasting, J.F., Toon, O.B., 1989, “Climate evolution on the terrestrial planets”, in Origin and Evolution of Planetary and Satellite Atmospheres, (Eds.) Atreya, S.K., Pollack, J.B., Matthews, M.S., pp. 423–449, University of Arizona Press, Tucson, U.S.A.
Kasting, J.F., Pollack, J.B., Ackerman, T.P., 1984, “Response of Earth’s atmosphere to increases in solar flux and implications for loss of water from Venus”, Icarus, 57, 335–355. ADS: http://adsabs.harvard.edu/abs/1984Icar...57..335K
Kastner, J.H., Myers, P.C., 1994, “An observational estimate of the probability of encounters between mass-losing evolved stars and molecular clouds”, Astrophys. J., 421, 605–615. ADS: http://adsabs.harvard.edu/abs/1994ApJ...421..605K
Kastner, J.H., Huenemoerder, D.P., Schulz, N.S., Canizares, C.R., Weintraub, D.A., 2002, “Evidence for Accretion: High-Resolution X-Ray Spectroscopy of the Classical T Tauri Star TW Hydrae”, Astrophys. J., 567, 434–440. ADS: http://adsabs.harvard.edu/abs/2002ApJ...567..434K
Kastner, J.H., Huenemoerder, D.P., Schulz, N.S., Canizares, C.R., Li, J., Weintraub, D.A., 2004, “The Coronal X-Ray Spectrum of the Multiple Weak-lined T Tauri Star System HD 98800”, Astrophys. J. Lett., 605, L49–L52. ADS: http://adsabs.harvard.edu/abs/2004ApJ...605L..49K
Kastner, J.H., Franz, G., Grosso, N., Bally, J., McCaughrean, M.J., Getman, K., Feigelson, E.D., Schulz, N.S., 2005, “X-Ray Emission from Orion Nebula Cluster Stars with Circumstellar Disks and Jets”, Astrophys. J. Suppl. Ser., 160, 511–529. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..511K
Kervella, P., Thévenin, F., Ségransan, D., Berthomieu, G., Lopez, B., Morel, P., Provost, J., 2003, “The diameters of alpha Centauri A and B. A comparison of the asteroseismic and VINCI/VLTI views”, Astron. Astrophys., 404, 1087–1097. ADS: http://adsabs.harvard.edu/abs/2003A&A...404.1087K
Khodachenko, M.L., Lammer, H., Lichtenegger, H.I.M., Langmayr, D., Erkaev, N.V., Grießmeier, J.-M., Leitner, M., Penz, T., Biernat, H.K., Motschmann, U., Rucker, H.O., 2007, “Mass loss of Hot Jupiters: Implications for CoRoT discoveries. Part I: The importance of magnetospheric protection of a planet against ion loss caused by coronal mass ejections”, Planet. Space Sci., 55, 631–642. ADS: http://adsabs.harvard.edu/abs/2007P&SS...55..631K
King, J.R., Villarreal, A.R., Soderblom, D.R., Gulliver, A.F., Adelman, S.J., 2003, “Stellar Kinematic Groups. II. A Reexamination of the Membership, Activity, and Age of the Ursa Major Group”, Astron. J., 125, 1980–2017. ADS: http://adsabs.harvard.edu/abs/2003AJ....125.1980K
König, B., Fuhrmann, K., Neuhäuser, R., Charbonneau, D., Jayawardhana, R., 2002, “Direct detection of the companion of χ1 Orionis”, Astron. Astrophys., 394, L43–L46. ADS: http://adsabs.harvard.edu/abs/2002A&A...394L..43K
König, B., Guenther, E.W., Woitas, J., Hatzes, A.P., 2005, “The young active binary star EK Draconis”, Astron. Astrophys., 435, 215–223. ADS: http://adsabs.harvard.edu/abs/2005A&A...435..215K
Königl, A., 1991, “Disk accretion onto magnetic T Tauri stars”, Astrophys. J. Lett., 370, L39–L43. ADS: http://adsabs.harvard.edu/abs/1991ApJ...370L..39K
Koyama, K., Hamaguchi, K., Ueno, S., Kobayashi, N., Feigelson, E.D., 1996, “Discovery of Hard X-Rays from a Cluster of Protostars”, Publ. Astron. Soc. Japan, 48, L87–L92. ADS: http://adsabs.harvard.edu/abs/1996PASJ...48L..87K
Krucker, S., Benz, A.O., 1998, “Energy Distribution of Heating Processes in the Quiet Solar Corona”, Astrophys. J. Lett., 501, L213–L216. ADS: http://adsabs.harvard.edu/abs/1998ApJ...501L.213K
Kuhn, W.R., Atreya, S.K., 1979, “Ammonia photolysis and the greenhouse effect in the primordial atmosphere of the earth”, Icarus, 37, 207–213. ADS: http://adsabs.harvard.edu/abs/1979Icar...37..207K
Kulikov, Y.N., Lammer, H., Lichtenegger, H.I.M., Terada, N., Ribas, I., Kolb, C., Langmayr, D., Lundin, R., Guinan, E.F., Barabash, S., Biernat, H.K., 2006, “Atmospheric and water loss from early Venus”, Planet. Space Sci., 54, 1425–1444. ADS: http://adsabs.harvard.edu/abs/2006P&SS...54.1425K
Kulikov, Y.N., Lammer, H., Lichtenegger, H.I.M., Penz, T., Breuer, D., Spohn, T., Lundin, R., Biernat, H.K., 2007, “A Comparative Study of the Influence of the Active Young Sun on the Early Atmospheres of Earth, Venus, and Mars”, Space Sci. Rev., 129, 207–243. ADS: http://adsabs.harvard.edu/abs/2007SSRv..129..207K
Kutner, M.L., Rydgren, A.E., Vrba, F.J., 1986, “Detection of 6 CM radio emission from late-type PMS stars with weak chromospheric emission”, Astron. J., 92, 895–897. ADS: http://adsabs.harvard.edu/abs/1986AJ.....92..895K
Lahuis, F., van Dishoeck, E.F., Blake, G.A., Evans, II, N.J., Kessler-Silacci, J.E., Pontoppidan, K.M., 2007, “c2d Spitzer IRS Spectra of Disks around T Tauri Stars. III. [Ne II], [Fe I], and H2 Gas-Phase Lines”, Astrophys. J., 665, 492–511. ADS: http://adsabs.harvard.edu/abs/2007ApJ...665..492L
Laming, J.M., Drake, J.J., Widing, K.G., 1995, “Stellar coronal abundances. 3: The solar first ionization potential effect determined from full-disk observation”, Astrophys. J., 443, 416–422. ADS: http://adsabs.harvard.edu/abs/1995ApJ...443..416L
Lammer, H., Stumptner, W., Molina-Cuberos, G.J., Bauer, S.J., Owen, T., 2000, “Nitrogen isotope fractionation and its consequence for Titan’s atmospheric evolution”, Planet. Space Sci., 48, 529–543. ADS: http://adsabs.harvard.edu/abs/2000P&SS...48..529L
Lammer, H., Lichtenegger, H.I.M., Kolb, C., Ribas, I., Guinan, E.F., Abart, R., Bauer, S.J., 2003a, “Loss of water from Mars: Implications for the oxidation of the soil”, Icarus, 165, 9–25. ADS: http://adsabs.harvard.edu/abs/2003Icar..165....9L
Lammer, H., Selsis, F., Ribas, I., Guinan, E.F., Bauer, S.J., Weiss, W.W., 2003b, “Atmospheric Loss of Exoplanets Resulting from Stellar X-Ray and Extreme-Ultraviolet Heating”, Astrophys. J. Lett., 598, L121–L124. ADS: http://adsabs.harvard.edu/abs/2003ApJ...598L.121L
Lammer, H., Lichtenegger, H.I.M., Biernat, H.K., Erkaev, N.V., Arshukova, I.L., Kolb, C., Gunell, H., Lukyanov, A., Holmstrom, M., Barabash, S., Zhang, T.L., Baumjohann, W., 2006, “Loss of hydrogen and oxygen from the upper atmosphere of Venus”, Planet. Space Sci., 54, 1445–1456. ADS: http://adsabs.harvard.edu/abs/2006P&SS...54.1445L
Lee, T., Shu, F.H., Shang, H., Glassgold, A.E., Rehm, K.E., 1998, “Protostellar Cosmic Rays and Extinct Radioactivities in Meteorites”, Astrophys. J., 506, 898–912. ADS: http://adsabs.harvard.edu/abs/1998ApJ...506..898L
Liefke, C., Schmitt, J.H.M.M., 2006, “The coronal Ne/O abundance of α Centauri”, Astron. Astrophys., 458, L1–L4. ADS: http://adsabs.harvard.edu/abs/2006A&A...458L...1L
Lim, J., White, S.M., 1996, “Limits to Mass Outflows from Late-Type Dwarf Stars”, Astrophys. J. Lett., 462, L91–L94. ADS: http://adsabs.harvard.edu/abs/1996ApJ...462L..91L
Lin, R.P., Schwartz, R.A., Kane, S.R., Pelling, R.M., Hurley, K.C., 1984, “Solar hard X-ray microflares”, Astrophys. J., 283, 421–425. ADS: http://adsabs.harvard.edu/abs/1984ApJ...283..421L
Linsky, J.L., Wood, B.E., 1996, “The α Centauri Line of Sight: D/H Ratio, Physical Properties of Local Interstellar Gas, and Measurement of Heated Hydrogen (The ‘Hydrogen Wall’) Near the Heliopause”, Astrophys. J., 463, 254–270. ADS: http://adsabs.harvard.edu/abs/1996ApJ...463..254L
Linsky, J.L., Gagné, M., Mytyk, A., McCaughrean, M., Andersen, M., 2007, “Chandra Observations of the Eagle Nebula. I. Embedded Young Stellar Objects near the Pillars of Creation”, Astrophys. J., 654, 347–360. ADS: http://adsabs.harvard.edu/abs/2007ApJ...654..347L
Luhmann, J.G., Johnson, R.E., Zhang, M.H.G., 1992, “Evolutionary impact of sputtering of the Martian atmosphere by O(+) pickup ions”, Geophys. Res. Lett., 19, 2151–2154. ADS: http://adsabs.harvard.edu/abs/1992GeoRL..19.2151L
Lundin, R., Barabash, S., 2004, “Evolution of the Martian atmosphere and hydrosphere: Solar wind erosion studied by ASPERA-3 on Mars Express”, Planet. Space Sci., 52, 1059–1071. ADS: http://adsabs.harvard.edu/abs/2004P&SS...52.1059L
Lundin, R., Lammer, H., Ribas, I., 2007, “Planetary Magnetic Fields and Solar Forcing: Implications for Atmospheric Evolution”, Space Sci. Rev., 129, 245–278. ADS: http://adsabs.harvard.edu/abs/2007SSRv..129..245L
Lunine, J.I., Yung, Y.L., Lorenz, R.D., 1999, “On the volatile inventory of Titan from isotopic abundances in nitrogen and methane”, Planet. Space Sci., 47, 1291–1303. ADS: http://adsabs.harvard.edu/abs/1999P&SS...47.1291L
Mackay, D.H., Jardine, M., Collier Cameron, A., Donati, J.-F., Hussain, G.A.J., 2004, “Polar caps on active stars: magnetic flux emergence and transport”, Mon. Not. R. Astron. Soc., 354, 737–752. ADS: http://adsabs.harvard.edu/abs/2004MNRAS.354..737M
Magazzù, A., Umana, G., Martín, E.L., 1999, “Radio emission from RASS sources south of Taurus-Auriga”, Astron. Astrophys., 346, 878–882. ADS: http://adsabs.harvard.edu/abs/1999A&A...346..878M
Maggio, A., Peres, G., 1997, “Loop modeling of coronal X-ray spectra. IV. One- and two-loop model fitting of ROSAT PSPC spectra: three test cases”, Astron. Astrophys., 325, 237–248. ADS: http://adsabs.harvard.edu/abs/1997A&A...325..237M
Maggio, A., Sciortino, S., Vaiana, G.S., Majer, P., Bookbinder, J., Golub, L., Harnden Jr, F.R., Rosner, R., 1987, “Einstein Observatory survey of X-ray emission from solar-type stars: The late F and G dwarf stars”, Astrophys. J., 315, 687–699. ADS: http://adsabs.harvard.edu/abs/1987ApJ...315..687M
Maggio, A., Sciortino, S., Harnden Jr, F.R., 1994, “ROSAT X-ray observations of late-type evolved stars: On the relationship between coronal temperatures and luminosities”, Astrophys. J., 432, 701–709. ADS: http://adsabs.harvard.edu/abs/1994ApJ...432..701M
Mamajek, E.E., Lawson, W.A., Feigelson, E.D., 1999, “A radio survey of older T Tauri stars in the eta Chamaeleontis cluster”, Publ. Astron. Soc. Australia, 16, 257–61. ADS: http://adsabs.harvard.edu/abs/1999PASA...16..257M
Mamajek, E.E., Lawson, W.A., Feigelson, E.D., 2000, “The η Chamaeleontis Cluster: Origin in the Sco-Cen OB Association”, Astrophys. J., 544, 356–374. ADS: http://adsabs.harvard.edu/abs/2000ApJ...544..356M
Mangeney, A., Praderie, F., 1984, “The influence of convection and rotation on X-ray emission in main sequence stars”, Astron. Astrophys., 130, 143–150. ADS: http://adsabs.harvard.edu/abs/1984A&A...130..143M
Mannings, V., Boss, A.P., Russell, S.S. (Eds.), 2000, Protostars and Planets IV, Refereed review chapters presented in early form at a conference held at the University of California, Santa Barbara in July 1998, University of Arizona Press, Tucson, U.S.A. ADS: http://adsabs.harvard.edu/abs/2000prpl.conf.....M
Marhas, K.K., Goswami, J.N., 2004, “Low energy particle production of short-lived nuclides in the early solar system”, New Astron. Rev., 48, 139–144. ADS: http://adsabs.harvard.edu/abs/2004NewAR..48..139M
Marino, A., Micela, G., Peres, G., Sciortino, S., 2002, “On X-ray variability in ROSAT-PSPC observations of F7-K2 stars”, Astron. Astrophys., 383, 210–217. ADS: http://adsabs.harvard.edu/abs/2002A&A...383..210M
Marino, A., Micela, G., Peres, G., Sciortino, S., 2003a, “X-ray rotational modulation of a supersaturated star in IC 2391”, Astron. Astrophys., 407, L63–L66. ADS: http://adsabs.harvard.edu/abs/2003A&A...407L..63M
Marino, A., Micela, G., Peres, G., Sciortino, S., 2003b, “X-ray variability of Pleiades late-type stars as observed with the ROSAT-PSPC”, Astron. Astrophys., 406, 629–638. ADS: http://adsabs.harvard.edu/abs/2003A&A...406..629M
Marsden, S.C., Donati, J.-F., Semel, M., Petit, P., Carter, B.D., 2006, “Surface differential rotation and photospheric magnetic field of the young solar-type star HD 171488 (V889 Her)”, Mon. Not. R. Astron. Soc., 370, 468–476. ADS: http://adsabs.harvard.edu/abs/2006MNRAS.370..468M
Mathioudakis, M., Doyle, J.G., 1990, “Chromospheric/coronal emission correlations in ‘quiescent’ and eruptive phenomena in M-dwarf stars”, Astron. Astrophys., 240, 357–359. ADS: http://adsabs.harvard.edu/abs/1990A&A...240..357M
Mayor, M., Queloz, D., 1995, “A Jupiter-Mass Companion to a Solar-Type Star”, Nature, 378, 355–359. ADS: http://adsabs.harvard.edu/abs/1995Natur.378..355M
McIvor, T., Jardine, M., Collier Cameron, A., Wood, K., Donati, J.-F., 2003, “Polar fields for AB Doradus”, Mon. Not. R. Astron. Soc., 345, 601–608. ADS: http://adsabs.harvard.edu/abs/2003MNRAS.345..601M
McKeegan, K.D., Chaussidon, M., Robert, F., 2000, “Incorporation of Short-Lived 10Be in a Calcium-Aluminum-Rich Inclusion from the Allende Meteorite”, Science, 289, 1334–1337. ADS: http://adsabs.harvard.edu/abs/2000Sci...289.1334M
Messina, S., Guinan, E.F., 2002, “Magnetic activity of six young solar analogues I. Starspot cycles from long-term photometry”, Astron. Astrophys., 393, 225–237. ADS: http://adsabs.harvard.edu/abs/2002A&A...393..225M
Messina, S., Guinan, E.F., 2003, “Magnetic activity of six young solar analogues II. Surface Differential Rotation from long-term photometry”, Astron. Astrophys., 409, 1017–1030. ADS: http://adsabs.harvard.edu/abs/2003A&A...409.1017M
Mestel, L., 1984, “Angular momentum loss during pre-main sequence contraction”, in Cool Stars, Stellar Systems, and the Sun: Third Cambridge Workshop, (Eds.) Baliunas, S.L., Hartmann, L., Proceedings of a meeting held in Cambridge, Massachusetts, October 5–7, 1983, pp. 49–59, Springer, Berlin, Germany; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1984LNP...193...49M
Metchev, S.A., Hillenbrand, L.A., 2004, “Initial Results from the Palomar Adaptive Optics Survey of Young Solar-Type Stars: A Brown Dwarf and Three Stellar Companions”, Astrophys. J., 617, 1330–1346. ADS: http://adsabs.harvard.edu/abs/2004ApJ...617.1330M
Meyer, B.S., Clayton, D.D., 2000, “Short-Lived Radioactivities and the Birth of the sun”, Space Sci. Rev., 92, 133–152. ADS: http://adsabs.harvard.edu/abs/2000SSRv...92..133M
Meyer, J.-P., 1985a, “The baseline composition of solar energetic particles”, Astrophys. J. Suppl. Ser., 57, 151–171. ADS: http://adsabs.harvard.edu/abs/1985ApJS...57..151M
Meyer, J.-P., 1985b, “Solar-stellar outer atmospheres and energetic particles, and galactic cosmic rays”, Astrophys. J. Suppl. Ser., 57, 173–204. ADS: http://adsabs.harvard.edu/abs/1985ApJS...57..173M
Micela, G., Sciortino, S., Kashyap, V., Harnden Jr, F.R., Rosner, R., 1996, “ROSAT Observations of the Pleiades. I. X-Ray Characteristics of a Coeval Stellar Population”, Astrophys. J. Suppl. Ser., 102, 75–103. ADS: http://adsabs.harvard.edu/abs/1996ApJS..102...75M
Minton, D.A., Malhotra, R., 2007, “Assessing the massive young Sun hypothesis to solve the warm young Earth puzzle”, Astrophys. J., 660, 1700–1706. ADS: http://adsabs.harvard.edu/abs/2007ApJ...660.1700M
Mitra-Kraev, U., Harra, L.K., Güdel, M., Audard, M., Branduardi-Raymont, G., Kay, H.R.M., Mewe, R., Raassen, A.J.J., van Driel-Gesztelyi, L., 2005, “Relationship between X-ray and ultraviolet emission of flares from dMe stars observed by XMM-Newton”, Astron. Astrophys., 431, 679–686. ADS: http://adsabs.harvard.edu/abs/2005A&A...431..679M
Mojzsis, S.J., Arrhenius, G., McKeegan, K.D., Harrison, T.M., Nutman, A.P., Friend, C.R.L., 1996, “Evidence for life on Earth before 3,800 million years ago”, Nature, 384, 55–59. ADS: http://adsabs.harvard.edu/abs/1996Natur.384...55M
Montesinos, B., Jordan, C., 1993, “On Magnetic Fields Stellar Coronae and Dynamo Action in Late Type Dwarfs”, Mon. Not. R. Astron. Soc., 264, 900–918. ADS: http://adsabs.harvard.edu/abs/1993MNRAS.264..900M
Montmerle, T., 2001, “X-ray Irradiation and Feedback Effects on Circumstellar and Interstellar Matter”, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, (Eds.) Montmerle, T., André, P., vol. 243 of ASP Conference Series, pp. 731–744, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2001ASPC..243..731M
Montmerle, T., Koch-Miramond, L., Falgarone, E., Grindlay, J.E., 1983, “Einstein observations of the Rho Ophiuchi dark cloud: an X-ray Christmas tree”, Astrophys. J., 269, 182–201. ADS: http://adsabs.harvard.edu/abs/1983ApJ...269..182M
Montmerle, T., Grosso, N., Tsuboi, Y., Koyama, K., 2000, “Rotation and X-Ray Emission from Protostars”, Astrophys. J., 532, 1097–1110. ADS: http://adsabs.harvard.edu/abs/2000ApJ...532.1097M
Mutel, R.L., Molnar, L.A., Waltman, E.B., Ghigo, F.D., 1998, “Radio Emission from Algol. I. Coronal Geometry and Emission Mechanisms Determined from VLBA and Green Bank Interferometer Observations”, Astrophys. J., 507, 371–383. ADS: http://adsabs.harvard.edu/abs/1998ApJ...507..371M
Muzerolle, J., Hillenbrand, L., Calvet, N., Briceño, C., Hartmann, L., 2003, “Accretion in Young Stellar/Substellar Objects”, Astrophys. J., 592, 266–281. ADS: http://adsabs.harvard.edu/abs/2003ApJ...592..266M
Muzerolle, J., Luhman, K.L., Briceño, C., Hartmann, L., Calvet, N., 2005, “Measuring Accretion in Young Substellar Objects: Approaching the Planetary Mass Regime”, Astrophys. J., 625, 906–912. ADS: http://adsabs.harvard.edu/abs/2005ApJ...625..906M
Ness, J.-U., Güdel, M., Schmitt, J.H.M.M., Audard, M., Telleschi, A., 2004, “On the sizes of stellar X-ray coronae”, Astron. Astrophys., 427, 667–683. ADS: http://adsabs.harvard.edu/abs/2004A&A...427..667N
Neuhäuser, R., Sterzik, M.F., Schmitt, J.H.M.M., Wichmann, R., Krautter, J., 1995, “ROSAT survey observation of T Tauri stars in Taurus.”, Astron. Astrophys., 297, 391–417. ADS: http://adsabs.harvard.edu/abs/1995A&A...297..391N
Newkirk Jr, G., 1980, “Solar variability on time scales of 10 to the 5th years to 10 to the 9.6th years”, in The Ancient Sun: Fossil Record in the Earth, Moon and Meteorites, (Eds.) Pepin, R.O., Eddy, J.A., Merrill, R.B., Proceedings of the conference held at Boulder, Colorado, October 16–19, 1979, pp. 293–320, Pergamon Press, New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1980asfr.symp..293N
Nisbet, E.G., 2000, “The realms of Archaean life”, Nature, 405, 625–626
Nisbet, E.G., Sleep, N.H., 2001, “The habitat and nature of early life”, Nature, 409, 1083–1091. ADS: http://adsabs.harvard.edu/abs/2001Natur.409.1083N
Nomura, H., Millar, T.J., 2005, “Molecular hydrogen emission from protoplanetary disks”, Astron. Astrophys., 438, 923–938. ADS: http://adsabs.harvard.edu/abs/2005A&A...438..923N
Noyes, R.W., Hartmann, L.W., Baliunas, S.L., Duncan, D.K., Vaughan, A.H., 1984, “Rotation, convection, and magnetic activity in lower main-sequence stars”, Astrophys. J., 279, 763–777. ADS: http://adsabs.harvard.edu/abs/1984ApJ...279..763N
O’Dell, C.R., 2001, “The Orion Nebula and its Associated Population”, Annu. Rev. Astron. Astrophys., 39, 99–136. ADS: http://adsabs.harvard.edu/abs/2001ARA&A..39...990
O’Neal, D., Feigelson, E.D., Mathieu, R.D., Myers, P.C., 1990, “A radio survey of weak T Tauri stars in Taurus-Auriga”, Astron. J., 100, 1610–1617. ADS: http://adsabs.harvard.edu/abs/1990AJ....100.16100
Öpik, E.J., 1963, “Selective escape of gases”, Geophys. J. R. Astron. Soc., 7, 490–509
Orlando, S., Peres, G., Reale, F., 2000, “The Sun as an X-Ray Star. I. Deriving the Emission Measure Distribution versus Temperature of the Whole Solar Corona from theYohkoh/Soft X-Ray Telescope Data”, Astrophys. J., 528, 524–536. ADS: http://adsabs.harvard.edu/abs/2000ApJ...528..5240
Osten, R.A., Brown, A., 1999, “Extreme Ultraviolet Explorer Photometry of RS Canum Venaticorum Systems: Four Flaring Megaseconds”, Astrophys. J., 515, 746–761. ADS: http://adsabs.harvard.edu/abs/1999ApJ...515..7460
Owen, T., Cess, R.D., Ramanathan, V., 1979, “Enhanced CO2 greenhouse to compensate for reduced solar luminosity on early Earth”, Nature, 277, 640–642
Ozawa, H., Nagase, F., Ueda, Y., Dotani, T., Ishida, M., 1999, “Detection of Hard X-Rays from a Class I Protostar in the HH 24–26 Region in the Orion Molecular Cloud”, Astrophys. J. Lett., 523, L81–L84. ADS: http://adsabs.harvard.edu/abs/1999ApJ...523L..810
Pallavicini, R., Golub, L., Rosner, R., Vaiana, G.S., Ayres, T., Linsky, J.L., 1981, “Relations among stellar X-ray emission observed from Einstein, stellar rotation and bolometric luminosity”, Astrophys. J., 248, 279–290. ADS: http://adsabs.harvard.edu/abs/1981ApJ...248..279P
Pallavicini, R., Tagliaferri, G., Stella, L., 1990, “X-ray emission from solar neighbourhood flare stars — A comprehensive survey of EXOSAT results”, Astron. Astrophys., 228, 403–425. ADS: http://adsabs.harvard.edu/abs/1990A&A...228..403P
Parker, E.N., 1958, “Dynamics of the Interplanetary Gas and Magnetic Fields”, Astrophys. J., 128, 664–676. ADS: http://adsabs.harvard.edu/abs/1958ApJ...128..664P
Parker, E.N., 1988, “Nanoflares and the solar X-ray corona”, Astrophys. J., 330, 474–479. ADS: http://adsabs.harvard.edu/abs/1988ApJ...330..474P
Parnell, C.E., Jupp, P.E., 2000, “Statistical Analysis of the Energy Distribution of Nanoflares in the Quiet Sun”, Astrophys. J., 529, 554–569. ADS: http://adsabs.harvard.edu/abs/2000ApJ...529..554P
Pascucci, I., Hollenbach, D., Najita, J., Muzerolle, J., Gorti, U., Herczeg, G.J., Hillenbrand, L.A., Kim, J.S., Carpenter, J.M., Meyer, M.R., Mamajek, E.E., Bouwman, J., 2007, “Detection of [Ne II] Emission from Young Circumstellar Disks”, Astrophys. J., 663, 383–393. ADS: http://adsabs.harvard.edu/abs/2007ApJ...663..383P
Patten, B.M., Simon, T., 1996, “The Evolution of Rotation and Activity in Young Open Clusters: IC 2391”, Astrophys. J. Suppl. Ser., 106, 489–531. ADS: http://adsabs.harvard.edu/abs/1996ApJS..106..489P
Pavlov, A.A., Kasting, J.F., Brown, L.L., Rages, K.A., Freedman, R., 2000, “Greenhouse warming by CH4 in the atmosphere of early Earth”, J. Geophys. Res., 105, 11981–11990. ADS: http://adsabs.harvard.edu/abs/2000JGR...10511981P
Pearce, G., Harrison, R.A., Bromage, B.J.I., Pickering, A.G.M., 1992, “The relationship between global X-ray luminosity and flaring on the sun”, Astron. Astrophys., 253, 601–603. ADS: http://adsabs.harvard.edu/abs/1992A&A...253..601P
Penz, T., Lammer, H., Kulikov, Y.N., Biernat, H.K., 2005, “The influence of the solar particle and radiation environment on Titan’s atmosphere evolution”, Adv. Space Res., 36, 241–250. ADS: http://adsabs.harvard.edu/abs/2005AdSpR..36..241P
Penz, T., Erkaev, N.V., Kulikov, Y.N., Langmayr, D., Lammer, H., Micela, G., Cecchi-Pestelli, C., Biernat, H.K., Selsis, F., Barge, P., Deleuil, M., Leger, A., 2007, “Mass loss of “Hot Jupiters” — Implications for CoRoT discoveries. Part II: Long time thermal atmospheric evaporation modelling”, Planet. Space Sci., submitted
Peres, G., Orlando, S., Reale, F., Rosner, R., Hudson, H., 2000, “The Sun as an X-Ray Star. II. Using theYohkoh/Soft X-Ray Telescope-derived Solar Emission Measure versus Temperature to Interpret Stellar X-Ray Observations”, Astrophys. J., 528, 537–551. ADS: http://adsabs.harvard.edu/abs/2000ApJ...528..537P
Perryman, M.A.C., Lindegren, L., Kovalevsky, J., Hoeg, E., Bastian, U., Bernacca, P.L., Crézé, M., Donati, F., Grenon, M., van Leeuwen, F., van der Marel, H., Mignard, F., Murray, C.A., Le Poole, R.S., Schrijver, H., Turon, C., Arenou, F., Froeschlé, M., Petersen, C.S., 1997, “The HIPPARCOS Catalogue”, Astron. Astrophys., 323, L49–L52. ADS: http://adsabs.harvard.edu/abs/1997A&A...323L..49P
Pevtsov, A.A., Fisher, G.H., Acton, L.W., Longcope, D.W., Johns-Krull, C.M., Kankelborg, C.C., Metcalf, T.R., 2003, “The Relationship Between X-Ray Radiance and Magnetic Flux”, Astrophys. J., 598, 1387–1391. ADS: http://adsabs.harvard.edu/abs/2003ApJ...598.1387P
Phillips, R.B., Lonsdale, C.J., Feigelson, E.D., 1991, “Milliarcsecond radio structure of weak-lined T Tauri stars”, Astrophys. J., 382, 261–269. ADS: http://adsabs.harvard.edu/abs/1991ApJ...382..261P
Phillips, R.B., Lonsdale, C.J., Feigelson, E.D., 1993, “Magnetic nonthermal activity in the T Tauri system”, Astrophys. J. Lett., 403, L43–L46. ADS: http://adsabs.harvard.edu/abs/1993ApJ...403L..43P
Phillips, R.B., Lonsdale, C.J., Feigelson, E.D., Deeney, B.D., 1996, “Polarized Radio Emission From the Multiple T Tauri System HD 283447”, Astron. J., 111, 918–929. ADS: http://adsabs.harvard.edu/abs/1996AJ....111..918P
Porto de Mello, G.F., da Silva, L., 1997, “HR 6060: The Closest Ever Solar Twin?”, Astrophys. J. Lett., 482, L89–92. ADS: http://adsabs.harvard.edu/abs/1997ApJ...482L..89P
Preibisch, T., 1997, “ROSAT coronal temperatures of young late type stars”, Astron. Astrophys., 320, 525–539. ADS: http://adsabs.harvard.edu/abs/1997A&A...320..525P
Preibisch, T., 2003a, “XMM-Newton study of the star forming region NGC 1333”, Astron. Astrophys., 401, 543–555. ADS: http://adsabs.harvard.edu/abs/2003A&A...401..543P
Preibisch, T., 2003b, “XMM-Newton study of the Serpens star-forming region”, Astron. Astrophys., 410, 951–959. ADS: http://adsabs.harvard.edu/abs/2003A&A...410..951P
Preibisch, T., Feigelson, E.D., 2005, “The Evolution of X-Ray Emission in Young Stars”, Astrophys. J. Suppl. Ser., 160, 390–400. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..390P
Preibisch, T., Zinnecker, H., 2001, “Deep Chandra X-Ray Observatory Imaging Study of the Very Young Stellar Cluster IC 348”, Astron. J., 122, 866–875. ADS: http://adsabs.harvard.edu/abs/2001AJ....122..866P
Preibisch, T., Zinnecker, H., 2002, “X-Ray Properties of the Young Stellar and Substellar Objects in the IC 348 Cluster: The Chandra View”, Astron. J., 123, 1613–1628. ADS: http://adsabs.harvard.edu/abs/2002AJ....123.1613P
Preibisch, T., Neuhauser, R., Alcala, J.M., 1995, “A giant X-ray flare on the young star P1724”, Astron. Astrophys., 304, L13+. ADS: http://adsabs.harvard.edu/abs/1995A&A...304L..13P
Preibisch, T., Kim, Y.-C., Favata, F., Feigelson, E.D., Flaccomio, E., Getman, K., Micela, G., Sciortino, S., Stassun, K., Stelzer, B., Zinnecker, H., 2005, “The Origin of T Tauri X-Ray Emission: New Insights from the Chandra Orion Ultradeep Project”, Astrophys. J. Suppl. Ser., 160, 401–422. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..401P
Raassen, A.J.J., Mewe, R., Audard, M., Guüdel, M., Behar, E., Kaastra, J.S., van der Meer, R.L.J., Foley, C.R., Ness, J.-U., 2002, “High-resolution X-ray spectroscopy of Procyon by Chandra and XMM-Newton”, Astron. Astrophys., 389, 228–238. ADS: http://adsabs.harvard.edu/abs/2002A&A...389..228R
Raassen, A.J.J., Ness, J.-U., Mewe, R., van der Meer, R.L.J., Burwitz, V., Kaastra, J.S., 2003, “Chandra-LETGS X-ray observation of α Centauri: A nearby (G2V + K1V) binary system”, Astron. Astrophys., 400, 671–678. ADS: http://adsabs.harvard.edu/abs/2003A&A...400..671R
Randich, S., 2000, “Coronal activity among open cluster stars”, in Stellar Clusters and Associations: Convection, Rotation, and Dynamos, (Eds.) Pallavicini, R., Micela, G., Sciortino, S., Proceedings for a meeting held in Mondello, Palermo, Italy, 25–28 May, 1999, vol. 198 of ASP Conference Series, pp. 401–410, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2000ASPC..198..401R
Randich, S., Schmitt, J.H.M.M., Prosser, C.F., Stauffer, J.R., 1996, “The X-ray properties of the young open cluster around α Persei”, Astron. Astrophys., 305, 785–805. ADS: http://adsabs.harvard.edu/abs/1996A&A...305..785R
Ratzka, T., Leinert, C., Henning, T., Bouwman, J., Dullemond, C.P., Jaffe, W., 2007, “High spatial resolution mid-infrared observations of the low-mass young star TW Hydrae”, Astron. Astrophys., 471, 173–185. ADS: http://adsabs.harvard.edu/abs/2007A&A...471..173R
Ray, T.P., Muxlow, T.W.B., Axon, D.J., Brown, A., Corcoran, D., Dyson, J., Mundt, R., 1997, “Large-scale magnetic fields in the outflow from the young stellar object T Tauri S”, Nature, 385, 415–417. ADS: http://adsabs.harvard.edu/abs/1997Natur.385..415R
Reipurth, B., Jewitt, D., Keil, K. (Eds.), 2007, Protostars and Planets V, Proceedings of a conference held at the Hilton Waikoloa Village on the Big Island of Hawaii on October 24–28, 2005, University of Arizona Press, Tucson, U.S.A. ADS: http://adsabs.harvard.edu/abs/2007prpl.conf.....R
Ribas, I., Guinan, E.F., Güdel, M., Audard, M., 2005, “Evolution of the Solar Activity over Time and Effects on Planetary Atmospheres. I. High-Energy Irradiances (1–1700 Å)”, Astrophys. J., 622, 680–694. ADS: http://adsabs.harvard.edu/abs/2005ApJ...622..680R
Rice, J.B., Strassmeier, K.G., 1996, “Doppler imaging of stellar surface structure. II. The weak-lined T Tauri star V410 Tauri”, Astron. Astrophys., 316, 164–172. ADS: http://adsabs.harvard.edu/abs/1996A&A...316..164R
Rice, J.B., Strassmeier, K.G., 2001, “Doppler imaging of stellar surface structure. XVII. The solar-type Pleiades star HII 314 = V1038 Tauri”, Astron. Astrophys., 377, 264–272. ADS: http://adsabs.harvard.edu/abs/2001A&A...377..264R
Robrade, J., Schmitt, J.H.M.M., 2006, “XMM-Newton X-ray spectroscopy of classical T Tauri stars”, Astron. Astrophys., 449, 737–747. ADS: http://adsabs.harvard.edu/abs/2006A&A...449..737R
Rodríguez, L.F., Myers, P.C., Cruz-Gonzalez, I., Terebey, S., 1989, “Radio continuum observations of IRAS sources associated with dense cores”, Astrophys. J., 347, 461–467. ADS: http://adsabs.harvard.edu/abs/1989ApJ...347..461R
Rodríguez, L.F., Cantó, J., Torrelles, J.M., Gómez, J.F., Ho, P.T.P., 1992, “VLA imaging of a possible circumstellar disk around HL Tauri”, Astrophys. J. Lett., 393, L29–L31. ADS: http://adsabs.harvard.edu/abs/1992ApJ...393L..29R
Rodríguez, L.F., Cantó, J., Torrelles, J.M., Gómez, J.F., Anglada, G., Ho, P.T.P., 1994, “Subarc-second VLA maps of the disk and the jet in HL Tauri”, Astrophys. J. Lett., 427, L103–L106. ADS: http://adsabs.harvard.edu/abs/1994ApJ...427L.103R
Rodríguez, L.F., Porras, A., Claussen, M.J., Curiel, S., Wilner, D.J., Ho, P.T.P., 2003, “The Binary Jet in L1551 IRS 5”, Astrophys. J. Lett., 586, L137–L139. ADS: http://adsabs.harvard.edu/abs/2003ApJ...586L.137R
Romanova, M.M., Kulkarni, A., Long, M., Lovelace, R.V.E., Wick, J.V., Ustyugova, G.V., Koldoba, A.V., 2006, “2D and 3D MHD simulations of disk accretion by rotating magnetized stars: Search for variability”, Adv. Space Res., 38, 2887–2892. ADS: http://adsabs.harvard.edu/abs/2006AdSpR..38.2887R
Rosner, R., Tucker, W.H., Vaiana, G.S., 1978, “Dynamics of the quiescent solar corona”, Astrophys. J., 220, 643–645. ADS: http://adsabs.harvard.edu/abs/1978ApJ...220..643R
Rye, R., Kuo, P.H., Holland, H.D., 1995, “Atmospheric carbon dioxide concentrations before 2.2 billion years ago”, Nature, 378, 603–605. ADS: http://adsabs.harvard.edu/abs/1995Natur.378..603R
Saar, S.H., Brandenburg, A., 1999, “Time Evolution of the Magnetic Activity Cycle Period. II. Results for an Expanded Stellar Sample”, Astrophys. J., 524, 295–310. ADS: http://adsabs.harvard.edu/abs/1999ApJ...524..295S
Sackmann, I.-J., Boothroyd, A.I., 2003, “Our Sun. V. A Bright Young Sun Consistent with Helioseismology and Warm Temperatures on Ancient Earth and Mars”, Astrophys. J., 583, 1024–1039. ADS: http://adsabs.harvard.edu/abs/2003ApJ...583.1024S
Sagan, C., Chyba, C., 1997, “The early faint sun paradox: Organic shielding of ultraviolet-labile greenhouse gases”, Science, 276, 1217–1221. ADS: http://adsabs.harvard.edu/abs/1997Sci...276.1217S
Sagan, C., Mullen, G., 1972, “Earth and Mars: Evolution of Atmospheres and Surface Temperatures”, Science, 177, 52–56. ADS: http://adsabs.harvard.edu/abs/1972Sci...177...52S
Saucedo, J., Calvet, N., Hartmann, L., Raymond, J., 2003, “The Spatial Distribution of Fluorescent H2 Emission near T Tauri”, Astrophys. J., 591, 275–282. ADS: http://adsabs.harvard.edu/abs/2003ApJ...591..275S
Savage, B.D., Sembach, K.R., 1996, “Interstellar Abundances from Absorption-Line Observations with the Hubble Space Telescope”, Annu. Rev. Astron. Astrophys., 34, 279–330. ADS: http://adsabs.harvard.edu/abs/1996ARA&A..34..279S
Schmelz, J.T., Nasraoui, K., Roames, J.K., Lippner, L.A., Garst, J.W., 2005, “Neon Lights up a Controversy: The Solar Ne/O Abundance”, Astrophys. J. Lett., 634, L197–L200. ADS: http://adsabs.harvard.edu/abs/2005ApJ...634L.197S
Schmitt, J.H.M.M., 1997, “Coronae on solar-like stars”, Astron. Astrophys., 318, 215–230. ADS: http://adsabs.harvard.edu/abs/1997A&A...318..215S
Schmitt, J.H.M.M., Kürster, M., 1993, “A Spatially Resolved X-ray Image of a Star Like the Sun”, Science, 262, 215–218. ADS: http://adsabs.harvard.edu/abs/1993Sci...262..215S
Schmitt, J.H.M.M., Collura, A., Sciortino, S., Vaiana, G.S., Harnden Jr, F.R., Rosner, R., 1990, “Einstein Observatory coronal temperatures of late-type stars”, Astrophys. J., 365, 704–728. ADS: http://adsabs.harvard.edu/abs/1990ApJ...365..704S
Schmitt, J.H.M.M., Fleming, T.A., Giampapa, M.S., 1995, “The X-Ray View of the Low-Mass Stars in the Solar Neighborhood”, Astrophys. J., 450, 392–400. ADS: http://adsabs.harvard.edu/abs/1995ApJ...450..392S
Schramm, D.N., Steigman, G., Dearborn, D.S.P., 1990, “Main-sequence mass loss and the lithium dip”, Astrophys. J. Lett., 359, L55–L58. ADS: http://adsabs.harvard.edu/abs/1990ApJ...359L..55S
Schrijver, C.J., 2001, “The Coronae of the Sun and Solar-type Stars”, in Cool Stars, Stellar Systems and the Sun: 11th Cambridge Workshop, (Eds.) García López, R.J., Rebolo, R., Zapaterio Osorio, M.R., Proceedings of a meeting held at Puerto de la Cruz, Tenerife, Spain, 4–8 October 1999, vol. 223 of ASP Conference Series, pp. 131–144, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/2001ASPC..223..131S
Schrijver, C.J., Aschwanden, M.J., 2002, “Constraining the Properties of Nonradiative Heating of the Coronae of Cool Stars and the Sun”, Astrophys. J., 566, 1147–1165. ADS: http://adsabs.harvard.edu/abs/2002ApJ...566.1147S
Schrijver, C.J., Title, A.M., 2001, “On the Formation of Polar Spots in Sun-like Stars”, Astrophys. J., 551, 1099–1106. ADS: http://adsabs.harvard.edu/abs/2001ApJ...551.1099S
Schrijver, C.J., Mewe, R., Walter, F.M., 1984, “Coronal activity in F-, G-, and K-type stars. II. Coronal structure and rotation”, Astron. Astrophys., 138, 258–266. ADS: http://adsabs.harvard.edu/abs/1984A&A...138..258S
Schrijver, C.J., Lemen, J.R., Mewe, R., 1989, “Coronal activity in F-, G-, and K-type stars. IV. Evidence for expanding loop geometries in stellar coronae”, Astrophys. J., 341, 484–492. ADS: http://adsabs.harvard.edu/abs/1989ApJ...341..484S
Schüssler, M., Solanki, S.K., 1992, “Why rapid rotators have polar spots”, Astron. Astrophys., 264, L13–L16. ADS: http://adsabs.harvard.edu/abs/1992A&A...264L..13S
Schüssler, M., Caligari, P., Ferriz-Mas, A., Solanki, S.K., Stix, M., 1996, “Distribution of starspots on cool stars. I. Young and main sequence stars of 1M⊙”, Astron. Astrophys., 314, 503–512. ADS: http://adsabs.harvard.edu/abs/1996A&A...314..503S
Schwartz, P.R., Simon, T., Zuckerman, B., Howell, R.R., 1984, “The T Tauri radio source”, Astrophys. J. Lett., 280, L23–L26. ADS: http://adsabs.harvard.edu/abs/1984ApJ...280L..23S
Schwartz, P.R., Simon, T., Campbell, R., 1986, “The T Tauri radio source. II — The winds of T Tauri”, Astrophys. J., 303, 233–238. ADS: http://adsabs.harvard.edu/abs/1986ApJ...303..233S
Sciortino, S., Damiani, F., Favata, F., Micela, G., 1998, “An X-ray study of the PMS population of the Upper Sco-Cen association”, Astron. Astrophys., 332, 825–841. ADS: http://adsabs.harvard.edu/abs/1998A&A...332..825S
Sciortino, S., Maggio, A., Favata, F., Orlando, S., 1999, “X-ray spectroscopy of the active dM stars: AD Leo and EV Lac”, Astron. Astrophys., 342, 502–514. ADS: http://adsabs.harvard.edu/abs/1999A&A...342..502S
Sekiya, M., Nakazawa, K., Hayashi, C., 1980, “Dissipation of the Primordial Terrestrial Atmosphere Due to Irradiation of the Solar EUV”, Prog. Theor. Phys., 64, 1968–1985. ADS: http://adsabs.harvard.edu/abs/1980PThPh..64.1968S
Shaviv, N.J., 2003, “Toward a solution to the early faint Sun paradox: A lower cosmic ray flux from a stronger solar wind”, J. Geophys. Res., 108, 3–1. ADS: http://adsabs.harvard.edu/abs/2003JGRA.108l.SSH3S
Shu, F., Najita, J., Ostriker, E., Wilkin, F., Ruden, S., Lizano, S., 1994, “Magnetocentrifugally driven flows from young stars and disks. I. A generalized model”, Astrophys. J., 429, 781–796. ADS: http://adsabs.harvard.edu/abs/1994ApJ...429..781S
Shu, F.H., Shang, H., Glassgold, A.E., Lee, T., 1997, “X-rays and fluctuating X-winds from protostars”, Science, 277, 1475–1479. ADS: http://adsabs.harvard.edu/abs/1997Sci...277.1475S
Shu, F.H., Shang, H., Gounelle, M., Glassgold, A.E., Lee, T., 2001, “The Origin of Chondrules and Refractory Inclusions in Chondritic Meteorites”, Astrophys. J., 548, 1029–1050. ADS: http://adsabs.harvard.edu/abs/2001ApJ...548.1029S
Siess, L., Dufour, E., Forestini, M., 2000, “An internet server for pre-main sequence tracks of low-and intermediate-mass stars”, Astron. Astrophys., 358, 593–599. ADS: http://adsabs.harvard.edu/abs/2000A&A...358..593S
Singh, K.P., Drake, S.A., Gotthelf, E.V., White, N.E., 1999, “X-Ray Spectroscopy of Rapidly Rotating, Late-Type Dwarf Stars”, Astrophys. J., 512, 874–891. ADS: http://adsabs.harvard.edu/abs/1999ApJ...512..874S
Skinner, S., Gagnié, M., Belzer, E., 2003, “A Deep Chandra X-Ray Observation of the Embedded Young Cluster in NGC 2024”, Astrophys. J., 598, 375–391. ADS: http://adsabs.harvard.edu/abs/2003ApJ...598..375S
Skinner, S.L., 1993, “Circularly polarized radio emission from the T Tauri star Hubble 4”, Astrophys. J., 408, 660–667. ADS: http://adsabs.harvard.edu/abs/1993ApJ...408..660S
Skinner, S.L., Brown, A., 1994, “The enigmatic T Tauri radio source”, Astron. J., 107, 1461–1468. ADS: http://adsabs.harvard.edu/abs/1994AJ.....107.1461S
Skinner, S.L., Guedel, M., Koyama, K., Yamauchi, S., 1997, “ASCA Observations of the Barnard 209 Dark Cloud and an Intense X-Ray Flare on V773 Tauri”, Astrophys. J., 486, 886–902. ADS: http://adsabs.harvard.edu/abs/1997ApJ...486..886S
Skumanich, A., 1972, “Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion”, Astrophys. J., 171, 565–568. ADS: http://adsabs.harvard.edu/abs/1972ApJ...171..565S
Skumanich, A., 1985, “Evidence for a common magnetic driver for flares and quiescent coronae/chromospheres”, Aust. J. Phys., 38, 971–974. ADS: http://adsabs.harvard.edu/abs/1985AuJPh..38..971S
Smith, D.S., Scalo, J., Wheeler, J.C., 2004, “Transport of ionizing radiation in terrestrial-like exoplanet atmospheres”, Icarus, 171, 229–253. ADS: http://adsabs.harvard.edu/abs/2004Icar..171..229S
Smith, K., Pestalozzi, M., Güdel, M., Conway, J., Benz, A.O., 2003, “VLBI observations of T Tauri South”, Astron. Astrophys., 406, 957–967. ADS: http://adsabs.harvard.edu/abs/2003A&A...406..957S
Smith, R.K., Brickhouse, N.S., Liedahl, D.A., Raymond, J.C., 2001, “Collisional Plasma Models with APEC/APED: Emission-Line Diagnostics of Hydrogen-like and Helium-like Ions”, Astrophys. J. Lett., 556, L91–L95. ADS: http://adsabs.harvard.edu/abs/2001ApJ...556L..91S
Snell, R.L., Bally, J., Strom, S.E., Strom, K.M., 1985, “Radio and optical observations of the jets from L1555 IRS 5”, Astrophys. J., 290, 587–595. ADS: http://adsabs.harvard.edu/abs/1985ApJ...290..587S
Soderblom, D.R., Mayor, M., 1993, “Stellar kinematic groups. I. The Ursa Major group”, Astron. J., 105, 226–249. ADS: http://adsabs.harvard.edu/abs/1993AJ....105..226S
Soderblom, D.R., Stauffer, J.R., MacGregor, K.B., Jones, B.F., 1993, “The evolution of angular momentum among zero-age main-sequence solar-type stars”, Astrophys. J., 409, 624–634. ADS: http://adsabs.harvard.edu/abs/1993ApJ...409..624S
Solanki, S.K., 1994, “Must the Magnetic Field Saturate on Rapidly Rotating Stars?”, in Cool Stars, Stellar Systems, and the Sun: Eighth Cambridge Workshop, (Ed.) Caillault, J.-P., Athens, Georgia, October 11–14, 1993, vol. 64 of ASP Conference Series, pp. 477–479, Astronomical Society of the Pacific, San Francisco, U.S.A. ADS: http://adsabs.harvard.edu/abs/1994ASPC...64..477S
Sonett, C.P., Giampapa, M.S., Matthews, M.S. (Eds.), 1991, The Sun in Time, University of Arizona Press, Tucson, U.S.A.
Stauffer, J.R., Caillault, J.-P., Gagne, M., Prosser, C.F., Hartmann, L.W., 1994, “A deep imaging survey of the Pleiades with ROSAT”, Astrophys. J. Suppl. Ser., 91, 625–657. ADS: http://adsabs.harvard.edu/abs/1994ApJS...91..625S
Stȩpień, K., 1988, “Spin-down of cool stars during their main-sequence life”, Astrophys. J., 335, 907–913. ADS: http://adsabs.harvard.edu/abs/1988ApJ...335..907S
Stelzer, B., Neuhäuser, R., 2001, “X-ray emission from young stars in Taurus-Auriga-Perseus: Luminosity functions and the rotation — activity — age — relation”, Astron. Astrophys., 377, 538–556. ADS: http://adsabs.harvard.edu/abs/2001A&A...377..538S
Stelzer, B., Schmitt, J.H.M.M., 2004, “X-ray emission from a metal depleted accretion shock onto the classical T Tauri star TW Hya”, Astron. Astrophys., 418, 687–697. ADS: http://adsabs.harvard.edu/abs/2004A&A...418..687S
Stelzer, B., Flaccomio, E., Briggs, K., Micela, G., Scelsi, L., Audard, M., Pillitteri, I., Güdel, M., 2007, “A statistical analysis of X-ray variability in pre-main sequence objects of the Taurus Molecular Cloud”, Astron. Astrophys., 468, 463–475. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..463S
Stern, R.A., Antiochos, S.K., Harnden Jr, F.R., 1986, “Modeling of coronal X-ray emission from active cool stars. I Hyades cluster”, Astrophys. J., 305, 417–432. ADS: http://adsabs.harvard.edu/abs/1986ApJ...305..417S
Stern, R.A., Schmitt, J.H.M.M., Pye, J.P., Hodgkin, S.T., Stauffer, J.R., Simon, T., 1994, “Coronal X-ray sources in the Hyades: A 40 kilosecond ROSAT pointing”, Astrophys. J., 427, 808–821. ADS: http://adsabs.harvard.edu/abs/1994ApJ...427..808S
Stern, R.A., Schmitt, J.H.M.M., Kahabka, P.T., 1995, “ROSAT All-Sky Survey Observations of the Hyades Cluster”, Astrophys. J., 448, 683–708. ADS: http://adsabs.harvard.edu/abs/1995ApJ...448..683S
Stine, P.C., O’Neal, D., 1998, “Radio Emission from Young Stellar Objects near LkHa 101”, Astron. J., 116, 890–894. ADS: http://adsabs.harvard.edu/abs/1998AJ....116..890S
Stine, P.C., Feigelson, E.D., Andre, P., Montmerle, T., 1988, “Multi-epoch radio continuum surveys of the ρ Ophiuchi dark cloud”, Astron. J., 96, 1394–1406. ADS: http://adsabs.harvard.edu/abs/1988AJ.....96.1394S
Strassmeier, K.G., Rice, J.B., 1998, “Doppler imaging of stellar surface structure. VI. HD 129333 = EK Draconis: a stellar analog of the active young Sun”, Astron. Astrophys., 330, 685–695. ADS: http://adsabs.harvard.edu/abs/1998A&A...330..685S
Strassmeier, K.G., Pichler, T., Weber, M., Granzer, T., 2003, “Doppler imaging of stellar surface structure. XXI. The rapidly-rotating solar-type star HD 171488 = V889 Hercules”, Astron. Astrophys., 411, 595–604. ADS: http://adsabs.harvard.edu/abs/2003A&A...411..595S
Strom, K.M., Strom, S.E., 1994, “A multiwavelength study of star formation in the L1495E cloud in Taurus”, Astrophys. J., 424, 237–256. ADS: http://adsabs.harvard.edu/abs/1994ApJ...424..237S
Swank, J.H., Holt, S.S., White, N.E., Becker, R.H., 1981, “Two-component X-ray emission from RS Canum Venaticorum binaries”, Astrophys. J., 246, 208–214. ADS: http://adsabs.harvard.edu/abs/1981ApJ...246..208S
Tachibana, S., Huss, G.R., 2003, “The Initial Abundance of 60Fe in the Solar System”, Astrophys. J. Lett., 588, L41–L44. ADS: http://adsabs.harvard.edu/abs/2003ApJ...588L..41T
Tehrany, M.G., Lammer, H., Hanslmeier, A., Ribas, I., Guinan, E.F., Kolb, C., 2002, “Erosion and Sublimation Effects On Mercury’s Surface: Past and Present”, conference paper. ADS: http://adsabs.harvard.edu/abs/2002EGSGA..27.1903T, abstract EGS02-A-01908
Telleschi, A., Güdel, M., Briggs, K., Audard, M., Ness, J.-U., Skinner, S.L., 2005, “Coronal Evolution of the Sun in Time: High-Resolution X-Ray Spectroscopy of Solar Analogs with Different Ages”, Astrophys. J., 622, 653–679. ADS: http://adsabs.harvard.edu/abs/2005ApJ...622..653T
Telleschi, A., Güdel, M., Briggs, K.R., Audard, M., Palla, F., 2007a, “X-ray emission from T Tauri stars and the role of accretion: inferences from the XMM-Newton extended survey of the Taurus molecular cloud”, Astron. Astrophys., 468, 425–442. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..425T
Telleschi, A., Güdel, M., Briggs, K.R., Audard, M., Scelsi, L., 2007b, “High Resolution X-ray Spectroscopy of T Tauri Stars in the Taurus-Auriga Complex”, Astron. Astrophys., 468, 443–462. ADS: http://adsabs.harvard.edu/abs/2007A&A...468..443T
Testa, P., Drake, J.J., Peres, G., 2004, “The Density of Coronal Plasma in Active Stellar Coronae”, Astrophys. J., 617, 508–530. ADS: http://adsabs.harvard.edu/abs/2004ApJ...617..508T
Tsuboi, Y., Koyama, K., Murakami, H., Hayashi, M., Skinner, S., Ueno, S., 1998, “ASCA Detection of a Superhot 100 Million K X-Ray Flare on the Weak-lined T Tauri Star V773 Tauri”, Astrophys. J., 503, 894–901. ADS: http://adsabs.harvard.edu/abs/1998ApJ...503..894T
Tsuboi, Y., Imanishi, K., Koyama, K., Grosso, N., Montmerle, T., 2000, “Quasi-periodic X-Ray Flares from the Protostar YLW 15”, Astrophys. J., 532, 1089–1096. ADS: http://adsabs.harvard.edu/abs/2000ApJ...532.1089T
Tsujimoto, M., Koyama, K., Tsuboi, Y., Goto, M., Kobayashi, N., 2002, “X-Ray Properties of Young Stellar Objects in OMC-2 and OMC-3 from the Chandra X-Ray Observatory”, Astrophys. J., 566, 974–981. ADS: http://adsabs.harvard.edu/abs/2002ApJ...566..974T
Tsujimoto, M., Feigelson, E.D., Grosso, N., Micela, G., Tsuboi, Y., Favata, F., Shang, H., Kastner, J.H., 2005, “Iron Fluorescent Line Emission from Young Stellar Objects in the Orion Nebula”, Astrophys. J. Suppl. Ser., 160, 503–510. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..503T
Uchida, Y., Shibata, K., 1984, “Magnetically buffered accretion to a young star and the formation of bipolar flows”, Puhl. Astron. Soc. Japan, 36, 105–118. ADS: http://adsabs.harvard.edu/abs/1984PASJ...36..105U
Vaiana, G.S., 1983, “Stellar X-ray emission as an indicator of stellar magnetic activity”, in Solar and Stellar Magnetic Fields: Origins and Coronal Effects, (Ed.) Stenflo, J.O., IAU Symposium no. 102, held in Zurich, Switzerland, August 2–6, 1982, pp. 165–185, Reidel, Dordrecht, Netherlands; Boston, U.S.A. ADS: http://adsabs.harvard.edu/abs/1983IAUS..102..165V
Vaiana, G.S., Rosner, R., 1978, “Recent advances in coronal physics”, Annu. Rev. Astron. Astrophys., 16, 393–428. ADS: http://adsabs.harvard.edu/abs/1978ARA&A..16..393V
Valenti, J.A., Johns-Krull, C.M., 2004, “Observations of Magnetic Fields on T Tauri Stars”, Astrophys. Space Sci., 292, 619–629. ADS: http://adsabs.harvard.edu/abs/2004Ap&SS.292..619V
Valenti, J.A., Johns-Krull, C.M., Linsky, J.L., 2000, “An IUE Atlas of Pre-Main-Sequence Stars. I. Co-added Final Archive Spectra from the SWP Camera”, Astrophys. J. Suppl. Ser., 129, 399–420. ADS: http://adsabs.harvard.edu/abs/2000ApJS..129..399V
van Belle, G. (Ed.), 2007, Cool Stars, Stellar Systems and the Sun: Fourteenth Cambridge Workshop, Proceedings of a meeting held 6–10 November 2006 in Pasadena, U.S.A., Astronomical Society of the Pacific, San Francisco, U.S.A. Upcoming
van den Oord, G.H.J., Doyle, J.G., 1997, “Constraints on mass loss from dMe stars: theory and observations”, Astron. Astrophys., 319, 578–588. ADS: http://adsabs.harvard.edu/abs/1997A&A...319..578V
Ventura, R., Maggio, A., Peres, G., 1998, “Loop modeling of coronal X-ray spectra. V. One- and two-loop model fitting of G-type star ROSAT/PSPC spectra”, Astron. Astrophys., 334, 188–200. ADS: http://adsabs.harvard.edu/abs/1998A&A...334..188V
Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., Ballester, G.E., Ferlet, R., Hébrard, G., Mayor, M., 2003, “An extended upper atmosphere around the extrasolar planet HD209458b”, Nature, 422, 143–146. ADS: http://adsabs.harvard.edu/abs/2003Natur.422..143V
Vogt, S.S., Penrod, G.D., 1983, “Doppler Imaging of spotted stars — Application to the RS Canum Venaticorum star HR 1099”, Publ. Astron. Soc. Pac., 95, 565–576. ADS: http://adsabs.harvard.edu/abs/1983PASP...95..565V
Wadhwa, M., Amelin, Y., Davis, A.M., Lugmair, G.W., Meyer, B., Gounelle, M., Desch, S.J., 2007, “From Dust to Planetesimals: Implications for the Solar Protoplanetary Disk from Shortlived Radionuclides”, in Protostars and Planets V, (Eds.) Reipurth, B., Jewitt, D., Keil, K., pp. 835–848, University of Arizona Press, Tucson, U.S.A.
Walter, F.M., 1986, “X-ray sources in regions of star formation. I — The naked T Tauri stars”, Astrophys. J., 306, 573–586. ADS: http://adsabs.harvard.edu/abs/1986ApJ...306..573W
Walter, F.M., Barry, D.C., 1991, “Pre- and main-sequence evolution of solar activity”, in The Sun in Time, (Eds.) Sonett, C.P., Giampapa, M.S., Matthews, M.S., pp. 633–657, University of Arizona Press, Tucson, U.S.A.
Walter, F.M., Kuhi, L.V., 1984, “X-ray photometry and spectroscopy of T Tauri stars”, Astrophys. J., 284, 194–201. ADS: http://adsabs.harvard.edu/abs/1984ApJ...284..194W
Walter, F.M., Brown, A., Mathieu, R.D., Myers, P.C., Vrba, F.J., 1988, “X-ray sources in regions of star formation. III — Naked T Tauri stars associated with the Taurus-Auriga complex”, Astron. J., 96, 297–325. ADS: http://adsabs.harvard.edu/abs/1988AJ.....96..297W
Walter, F.M., Herczeg, G., Brown, A., Ardila, D.R., Gahm, G.F., Johns-Krull, C.M., Lissauer, J.J., Simon, M., Valenti, J.A., 2003, “Mapping the Circumstellar Environment of T Tauri with Fluorescent H2 Emission”, Astron. J., 126, 3076–3089. ADS: http://adsabs.harvard.edu/abs/2003AJ.....126.3076W
Wargelin, B.J., Drake, J.J., 2001, “Observability of Stellar Winds from Late-Type Dwarfs via Charge Exchange X-Ray Emission”, Astrophys. J. Lett., 546, L57–L60. ADS: http://adsabs.harvard.edu/abs/2001ApJ...546L..57W
Watson, A.J., Donahue, T.M., Walker, J.C.G., 1981, “The dynamics of a rapidly escaping atmosphere — Applications to the evolution of earth and Venus”, Icarus, 48, 150–166. ADS: http://adsabs.harvard.edu/abs/1981Icar...48..150W
Weber, E.J., Davis, L.J., 1967, “The Angular Momentum of the Solar Wind”, Astrophys. J., 148, 217–227. ADS: http://adsabs.harvard.edu/abs/1967ApJ...148..217W
Weintraub, D.A., Kastner, J.H., Bary, J.S., 2000, “Detection of Quiescent Molecular Hydrogen Gas in the Circumstellar Disk of a Classical T Tauri Star”, Astrophys. J., 541, 767–771. ADS: http://adsabs.harvard.edu/abs/2000ApJ...541..767W
White, N.E., Arnaud, K., Day, C.S.R., Ebisawa, K., Gotthelf, E.V., Mukai, K., Soong, Y., Yaqoob, T., Antunes, A., 1994, “An ASCA observation of one orbital cycle of AR Lacertae”, Publ. Astron. Soc. Japan, 46, L97–L100. ADS: http://adsabs.harvard.edu/abs/1994PASJ...46L..97W
White, R.J., Hillenbrand, L.A., 2004, “On the Evolutionary Status of Class I Stars and Herbig-Haro Energy Sources in Taurus-Auriga”, Astrophys. J., 616, 998–1032. ADS: http://adsabs.harvard.edu/abs/2004ApJ...616..998W
White, S.M., Pallavicini, R., Kundu, M.R., 1992a, “A 5 GHz radio survey of selected POST T Tauri and naked T Tauri stars”, Astron. Astrophys., 257, 557–566. ADS: http://adsabs.harvard.edu/abs/1992A&A...257..557W
White, S.M., Pallavicini, R., Kundu, M.R., 1992b, “Radio flares and magnetic fields on weak-line T Tauri stars”, Astron. Astrophys., 259, 149–154. ADS: http://adsabs.harvard.edu/abs/1992A&A...259..149W
Whitehouse, D.R., 1985, “Coronal heating and stellar flares”, Astron. Astrophys., 145, 449–450. ADS: http://adsabs.harvard.edu/abs/1985A&A...145..449W
Whitmire, D.P., Doyle, L.R., Reynolds, R.T., Matese, J.J., 1995, “A slightly more massive young Sun as an explanation for warm temperatures on early Mars”, J. Geophys. Res., 100, 5457–5464. ADS: http://adsabs.harvard.edu/abs/1995JGR...100.5457W
Willson, L.A., Bowen, G.H., Struck-Marcell, C., 1987, “Mass loss on the main sequence”, Comments Astrophys., 12, 17–34. ADS: http://adsabs.harvard.edu/abs/1987ComAp..12...17W
Wilner, D.J., Ho, P.T.P., Rodríguez, L.F., 1996, “Subarcsecond VLA Observations of HL Tauri: Imaging the Circumstellar Disk”, Astrophys. J. Lett., 470, L117–121. ADS: http://adsabs.harvard.edu/abs/1996ApJ...470L.117W
Wolk, S.J., Harnden Jr, F.R., Flaccomio, E., Micela, G., Favata, F., Shang, H., Feigelson, E.D., 2005, “Stellar Activity on the Young Suns of Orion: COUP Observations of K5-7 Pre-Main-Sequence Stars”, Astrophys. J. Suppl. Ser., 160, 423–449. ADS: http://adsabs.harvard.edu/abs/2005ApJS..160..423W
Wood, B.E., 2004, “Astrospheres and Solar-like Stellar Winds”, Living Rev. Solar Phys., 1, lrsp-2004-2. URL (cited on 09 April 2007): http://www.livingreviews.org/lrsp-2004-2
Wood, B.E., Linsky, J.L., 1998, “The Local ISM and Its Interaction with the Winds of Nearby Late-Type Stars”, Astrophys. J., 492, 788–803. ADS: http://adsabs.harvard.edu/abs/1998ApJ...492..788W
Wood, B.E., Brown, A., Linsky, J.L., Kellett, B.J., Bromage, G.E., Hodgkin, S.T., Pye, J.P., 1994, “A volume-limited ROSAT survey of extreme ultraviolet emission from all nondegenerate stars within 10 parsecs”, Astrophys. J. Suppl. Ser., 93, 287–307. ADS: http://adsabs.harvard.edu/abs/1994ApJS...93..287W
Wood, B.E., Muüller, H.-R., Zank, G.P., Linsky, J.L., 2002, “Measured Mass-Loss Rates of Solarlike Stars as a Function of Age and Activity”, Astrophys. J., 574, 412–425. ADS: http://adsabs.harvard.edu/abs/2002ApJ...574..412W
Wood, B.E., Müller, H.-R., Zank, G.P., Linsky, J.L., Redfield, S., 2005, “New Mass-Loss Measurements from Astrospheric Lya Absorption”, Astrophys. J. Lett., 628, L143–L146. ADS: http://adsabs.harvard.edu/abs/2005ApJ...628L.143W
Yelle, R.V., 2004, “Aeronomy of extra-solar giant planets at small orbital distances”, Icarus, 170, 167–179. ADS: http://adsabs.harvard.edu/abs/2004Icar..170..167Y
Yelle, R.V., 2006, “Corrigendum to ‘Aeronomy of extra-solar giant planets at small orbital distances’ [Icarus 170 (2004), 167–179]”, Icarus, 183, 508–508. ADS: http://adsabs.harvard.edu/abs/2006Icar..183..508Y
Young, P.R., 2005, “The Ne/O abundance ratio in the quiet Sun”, Astron. Astrophys., 444, L45–L48. ADS: http://adsabs.harvard.edu/abs/2005A&A...444L..45Y
Yusef-Zadeh, F., Cornwell, T.J., Reipurth, B., Roth, M., 1990, “Detection of synchrotron emission from a unique HH-like object in Orion”, Astrophys. J. Lett., 348, L61–L64. ADS: http://adsabs.harvard.edu/abs/1990ApJ...348L..61Y
Zahnle, K., Kasting, J.F., Pollack, J.B., 1990, “Mass fractionation of noble gases in diffusion-limited hydrodynamic hydrogen escape”, Icarus, 84, 502–527. ADS: http://adsabs.harvard.edu/abs/1990Icar...84..502Z
Zahnle, K.J., Kasting, J.F., 1986, “Mass fractionation during transonic escape and implications for loss of water from Mars and Venus”, Icarus, 68, 462–480. ADS: http://adsabs.harvard.edu/abs/1986Icar...68..462Z
Zahnle, K.J., Walker, J.C.G., 1982, “The evolution of solar ultraviolet luminosity”, Rev. Geophys. Space Phys., 20, 280–292. ADS: http://adsabs.harvard.edu/abs/1982RvGSP..20..280Z
Acknowledgements
It is a pleasure to thank Sami Solanki and the editorial board of Living Reviews in Solar Physics for inviting me to write the present review article, and the editorial staff of Living Reviews for their professional help and their patience when unforeseen events took over. I am much indebted to my two referees, Jeffrey L. Linsky and Thierry Montmerle, whose thorough and critical reviews of this paper have improved both content and presentation. Special thanks go to Helmut Lammer, Yuri Kulikov, and Thomas Penz for providing me their new manuscripts before publication. Discussions with Tom Ayres and Helmut Lammer have stimulated inclusion of issues that I would otherwise have failed to mention. I thank the following colleagues for giving me permission to reproduce their original figures: Marc Audard, Tom Ayres, Max Camenzind, Alfred Glassgold, Christopher Johns-Krull, Eric Feigelson, James Kasting, Yuri Kulikov, Helmut Lammer, Antonietta Marino, Stephen Marsden, Sergio Messina, Thomas Penz, Ignasi Ribas, I.-Juliana Sackmann, Carolus Schrijver, Klaus Strassmeier, Alessandra Telleschi, and Brian Wood.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Güdel, M. The Sun in Time: Activity and Environment. Living Rev. Sol. Phys. 4, 3 (2007). https://doi.org/10.12942/lrsp-2007-3
Published:
DOI: https://doi.org/10.12942/lrsp-2007-3