Abstract
Space weather effects arise from the dynamic conditions in the Earth’s space environment driven by processes on the Sun. While some effects are influenced neither by the properties of nor the processes within the Earth’s magnetosphere, others are critically dependent on the interaction of the impinging solar wind with the terrestrial magnetic field and plasma environment. As the utilization of space has become part of our everyday lives, and as our lives have become increasingly dependent on technological systems vulnerable to space weather influences, understanding and predicting hazards posed by the active solar events has grown in importance. This review introduces key dynamic processes within the magnetosphere and discusses their relationship to space weather hazards.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The first steps of Sun-Earth connection science were made by Edmund Halley, who following the spectacular auroral displays in Europe in March 1716, suggested that particles moving along the Earth’s magnetic field lines were the cause of the aurora. Following that, Anders Celcius and Olav Hiorter in 1747 discovered the temporal coincidence between compass needle variations and bright auroral displays. Comparing simultaneous magnetic variations in London and in Uppsala they further realized that the phenomena they were studying were related to processes in the planetary scale. The geomagnetic activity connection to solar processes was established by mid-nineteenth century: Solar flare correlation with active, bright auroras and geomagnetic disturbances was found by Carrington in 1860, and long-term observations showed 11-year variability both in sunspot numbers and occurrence frequency of magnetic disturbances and auroras.
While the modern space era with detailed in-situ and remote sensing measurements in and from space have resolved many issues concerning the behavior of the Sun, the solar wind, and the terrestrial space environment, many of the basic physics questions concerning the Sun-Earth connection remain open. On the other hand, the utilization of space has added a new practical flavor to the academic research, because the rapid time variations in the space plasma systems pose a hazard to technological systems and humans in space as well as on Earth. The term “space weather” now refers to conditions on the Sun and in the solar wind, magnetosphere, ionosphere, and thermosphere (upper parts of the atmosphere) that can influence the performance and reliability of space-borne and ground-based technological systems and can endanger human life or health. The adverse conditions in the space environment can cause disruption of satellite operations, communications, navigation, and electric power distribution grids on ground, leading to a variety of societal and economic losses.
The time scales interesting to studies of space weather processes are determined both by the intrinsic time scales of the processes themselves, but also on the lead time that predictions can be given. The solar and magnetospheric processes pose several timescales ranging from solar cycle and longer (long-term solar activity variations) to 27 days (recurrent solar activity), days (magnetic storms), hours (magnetospheric substorms) and even minutes and seconds (particle acceleration events, plasma instability growth times). On the other hand, before an event can be predicted, some indication of its occurrence must have been observed. Energetic particles reach the Earth within only a few, maybe up to ∼20 min after their release from the solar surface or interplanetary shock front giving only a very short lead time after a warning can be given. The solar wind travel time from the Sun to the Earth is of the order of 80 hours, while solar wind monitors at the first Lagrangian point (L1), 1.4 million km from the Earth, provide measurements of the incoming solar wind that reaches the outer edges of the magnetosphere within about 40 minutes to 1 hour of their detection. Thus, as our capability of predicting solar wind properties from solar observations alone is poor, we are at the moment limited to at best warnings 80 hours in advance and predictions at maximum 1 hour before the event starts.
Today’s challenge for space weather research is to (i) learn to quantitatively predict the state of the magnetosphere and ionosphere from measured solar wind and interplanetary magnetic field conditions, (ii) to extend the physical understanding also to solar processes such that predictions can be made using solar observations to gain more lead time. In addition to that, we need engineering and life sciences to evaluate the hazards and risks on a variety of technological systems and humans in space, onboard high-altitude aircraft, and on ground.
This article reviews the basic properties of the magnetosphere and open questions regarding its dynamics, the most typical solar activity events that cause space weather effects, and the effects caused by solar activity that are seen on space-borne and ground-based technological systems as well as on humans. More details of the solar processes associated with space weather phenomena can be found in a review by Schwenn (2006).
2 Solar Influence on Geospace
The Sun affects the Earth and its environs in a variety of ways and on many different timescales. Events on the Sun leading to large perturbations in the coupled magnetosphere-ionosphere system are called geoeffective. From space weather point of view the key question is how to distinguish those solar events that are geoeffective from those that are not.
On average, the solar wind at Earth orbit has mean density of about 4 cm−3, mean velocity of about 400 kms−1, and mean interplanetary magnetic field (IMF) magnitude of 5 nT. The average direction of the interplanetary magnetic field along the Parker spiral in the ecliptic plane is at an angle of about 45° from the radial direction (Hundhausen, 1972). Geomagnetic activity is primarily driven by magnetic reconnection between the IMF and the terrestrial magnetic field. As the dipole is close to perpendicular to the ecliptic plane, it is primarily dependent on the southward component of the IMF, and the reconnection rate is proportional to the Y component of the motional electric field (E = −VSW × BIMF) of the solar wind (Vasyliunas, 1975). Coherent solar wind structures containing southward magnetic fields and high velocities are thus most efficient drivers of space weather events.
In the longer term, the solar activity varies with the well-known 11-year cycle, which introduces an 11-year activity cycle also to the geomagnetic records. As the orientation of the dipole axis relative to the Sun-Earth line changes over the course of the year, the activity is largest during the equinoxes when the dipole is tilted along the Earth’s orbital track and the projection of the IMF to the geomagnetic field maximizes (Russell and McPherron, 1973). Similarly, the activity level is at minimum during solstices when the projection of the IMF to the Earth’s field is on average at minimum. Figure 1 illustrates the close relationship of the long-term solar activity (characterized by the monthly mean of the sunspot number) and the geomagnetic activity using the planetary magnetic Ap index as a proxy. The left panels show the long-term solar cycle variability with geomagnetic activity after the solar cycle maximum. The top right panel illustrates how the geomagnetic activity maximizes during the declining phase of the solar cycle. The bottom right panel shows the semiannual variations obtained by averaging the monthly values in the left hand plots. While the solar activity shows no annual variation, there is a clear signal in the geomagnetic records arising from the Russell-McPherron effect due to the varying orientation of the Earth’s rotation axis relative to the Sun-Earth line as the Earth rotates around the Sun.
Periodicities in solar and geomagnetic activity. The left panels show time series of the monthly values of the sunspot number and the geomagentic Ap index. The top right panel shows the solar cycle variation present both in the geomagnetic and solar records, showing peak geomagnetic activity during the declining phase of the solar cycle. The bottom right panel shows the semiannual variation in the geomagnetic data not visible in the solar records. The data were obtained from ftp://ftp.ngdc.noaa.gov/STP/.
Coronal mass ejections (CME) expel vast clouds of solar magnetic flux and plasma into interplanetary space. The interplanetary structure formed by the coronal mass ejection (ICME) propagates outward from the Sun, often at high velocity (Schwenn, 2006). The coherent magnetic field structure, the strongly varying field and plasma density in the sheath region preceding the ICME proper, the fast solar wind speed, as well as the interplanetary shock itself are all effective drivers of geomagnetic activity (Farrugia et al., 1997). While the strongly southward field inside the ICME proper tends to drive high ring current activity, the more variable fields and densities in the sheath region drive strongest activity at the high-latitude auroral regions (Huttunen and Koskinen, 2004). As ICMEs are more frequent during solar maximum than during solar minimum (Bothmer and Schwenn, 1998), they contribute to the 11-year cycle in magnetospheric activity. Similarly to ICMEs, any coherent solar wind structures including long-lasting, high-intensity southward interplanetary fields drive magnetic storm activity with its many signatures in the magnetosphere-ionosphere system.
High-speed solar wind streams encountering the Earth most often originate from low-latitude coronal holes. Such high-speed streams are often associated with strong Alfvénic fluctuations leading to strong fluctuations of the IMF Bz and solar wind velocity. These periods are effective drivers of medium-level activity in the high-latitude magnetosphere and in the ring current (Tsurutani and Gonzalez, 1987). The high-speed streams are especially efficient in accelerating relativistic electron populations in the outer van Allen belt. The electron fluxes maximize during the declining phase of the solar activity when the high-speed streams are most frequent, and minimize during solar minimum (Paulikas and Blake, 1979).
During the declining phase of solar cycles, the coronal holes extend to low latitudes sometimes even reaching the ecliptic plane. When the high-speed solar wind emanating from the coronal holes runs into the slower solar wind, the interaction leads to a compression of the plasma and magnetic fields, forming corotating interaction regions (CIR) (Crooker et al., 1999). The CIRs seldom have fast shocks or continuous, strongly southward IMF Bz, and thus drive only moderate magnetospheric activity (Alves et al., 2006; Borovsky and Denton, 2006). CIRs, being associated with the coronal hole structure, also exhibit 27-day periodicity (Schwenn, 1990).
Interplanetary shocks when interacting with the Earth’s bow shock cause direct energy transfer into the magnetosphere. The ram pressure pulse associated with the shock compresses the dayside magnetopause, and the compression effects travel tailward at the solar wind speed causing strong auroral activity observable almost instantaneously all around the auroral oval (Zhou and Tsurutani, 2001).
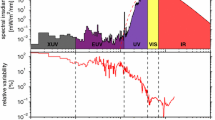
In addition to the interaction with the solar wind, the Sun affects the Earth’s environment also through electromagnetic radiation that reaches the Earth much faster than the solar wind flow. This most familiar form of the Sun’s influence on the Earth is a factor also for space weather: Increases of the solar irradiance cause heating of the upper atmosphere, which affects the drag experienced by low-Earth-orbiting satellites. The irradiance exhibits both long-term (solar cycle) variations as well as shorter term changes related to active solar events, both of which can be monitored using the F10.7 radio flux as a proxy (Lean, 1991).
Solar energetic particles affect the space environment in multiple ways. In the outer magnetosphere (especially near the geostationary region), their presence is a hazard for the satellite systems and instrumentation (Baker, 2000). If they become trapped in the inner magnetosphere dipolar field, they populate the van Allen belts, residing in the magnetosphere for extended periods (Hudson et al., 2004). As the energetic particles can penetrate to 20–40 km altitude (depending on their energy), they also affect the middle and upper atmospheric chemistry while colliding with the atmospheric constituents: The particle precipitation leads to an enhancement of NO2 in the atmosphere, which in turn is a catalyst for ozone distruction. This way the solar activity also affects the long-term balance of the atmospheric chemistry (Seppälä et al., 2006).
Thus, solar irradiation, energetic particle fluxes from the Sun, and the solar wind with its multiple structures all drive geomagnetic activity and are thus potential sources for space weather events. In the following, we review the basic properties of the structure and dynamics of the magnetosphere and associate these drivers with their consequences, both to the plasma environment and to the technological systems, in the terrestrial space environment.
3 The Magnetosphere
A magnetosphere is a cavity in the solar wind flow formed by the interaction of the solar wind and interplanetary magnetic field with the intrinsic magnetic field or ionized upper atmosphere of a planetary body. In the terrestrial case, the interaction is dominated by the strong intrinsic quasidipolar magnetic field; this is also the case of the outer giant planets Jupiter, Saturn, Uranus and Neptune (Southwood and Kivelson, 2001). On the other hand, the inner solar system, Earth-like planets Venus and Mars possess no intrinsic magnetic field, and the magnetosphere is then mostly formed by interaction of the atmosphere and ionosphere with the solar wind flow (Lundin et al., 2001). Mercury has a small intrinsic field but no atmosphere, there the solar wind interacts directly with the surface and exosphere (Killen et al., 2001). The types of space weather phenomena at the different planets depend critically on the magnitude of the intrinsic magnetic field, on the existence and characteristics of the planetary atmosphere and ionosphere, and on the distance from the Sun determining the properties of the driving solar wind and IMF. In the following, we only treat the terrestrial magnetosphere, which is characterized by a dense atmosphere and ionosphere and by a strong intrinsic geomagnetic field, but no internal plasma sources other than the ionosphere.
3.1 Magnetospheric structure
The intrinsic geomagnetic field of the Earth has an intensity of about 50,000 nT in the polar regions and about 30,000 nT at the equator. The size of the magnetospheric cavity is determined by the magnetic pressure of the internal field on one hand, and on the solar wind dynamic pressure on the other: The magnetospheric boundary, the magnetopause, forms at a location where the solar wind and magnetospheric plasmas and magnetic fields are in pressure balance. Typical solar wind conditions give a standoff distance of the magnetopause at about 10 RE (Earth radius = 6370 km) upstream of the Earth, but under strong solar wind driving the magnetopause can be pushed well inside the geostationary orbit (at 6.6 RE where a satellite orbiting around the Earth has a 24-hour rotation period and thus remains at a constant longitude above the Earth). In the antisunward direction, the solar wind flow deforms the dipolar magnetic field to a cometary taillike shape where the magnetopause is on average about 30 RE from the Sun-Earth line, depending on the solar wind pressure. The magnetotail extends far beyond lunar orbit at least a few hundred RE in the antisunward direction. As the solar wind flow past the magnetosphere is both supersonic and super-Alfvénic, a bow shock is formed upstream of the magnetopause, and the flow is decelerated within the magnetosheath between the shock and the magnetopause (see Figure 2).
Basic structure of the magnetosphere. The faint blue arrows show the magnetic field direction toward the Earth in the northern tail lobe, away from the Earth in the southern lobe, and northward at the dayside magnetosphere. The red regions in the inner magnetosphere contain both the ring current and the outer van Allen belt, where the ions and electrons are trapped on closed drift paths. Direction of the Sun is to the left (courtesy ESA).
The low-density tail lobes in the nightside magnetotail connect magnetically to the high-latitude polar caps at one end and to the interplanetary field at the other end. The effects of the strong dipole are not seen tailward of about 20 RE. Beyond that distance, the fields in the northern and southern tail lobes are nearly antiparallel and have an almost constant intensity of about 20 nT over a long range of distances from the Earth. The plasma sheet separating the northern and southern lobes hosts densities of the order of 1 cm−3 and partially very low magnetic field values reaching only a few nT. Thus, while the plasma beta (ratio of plasma and magnetic pressures, β = 2 μ0p/B2) is very low in the tail lobes, it generally exceeds unity at the center of the field reversal region. The inner part of the plasma sheet with its weak field and at times intense cross-tail current sheet is highly variable with bursts of fast flows, magnetic reconnection, and large-scale reconfiguration events. In the inner magnetosphere, particles can become trapped on closed orbits drifting around the Earth guided by the quasi-dipolar intrinsic field. The ring current located roughly at 4–6 RE radial distance encircles the Earth with highly variable intensity also modulated by the level of geomagnetic activity.
The magnetospheric structure is maintained by intense electric current systems at the magnetospheric boundaries, across the tail plasma sheet, and parallel to the magnetic field lines connecting the ionosphere with various parts of the magnetosphere (Figure 3). These field-aligned currents mediate a strong coupling between the ionosphere and the magnetosphere: The plasma sheet is magnetically connected to the auroral ovals, which encircle the magnetic poles and host continuous, diffuse auroral precipitation in addition to the bright auroral displays associated with events of geomagnetic activity. The geocentric solar magnetospheric coordinate system (GSM) is used in the following discussion. In that system, the x-axis points Sunward along the Sun-Earth line, the z-axis is in the plane containing the Sun-Earth line and the dipole axis and points northward, and the y-axis completes the right-handed triad pointing duskward.
Large-scale current systems in the magnetosphere. An enlargement of the Earth showing the auroral oval, auroral electrojet currents, and the large-scale Region 1 (more poleward) and Region 2 (more equatorward) currents bounding the high-latitude polar cap is shown in the background (Figure: Teemu Makinen/Finnish Meteorological Institute).
The solar wind motional electric field in the Earth’s frame of reference (E = −VSW × BIMF) imposes a large-scale convection pattern within the magnetosphere and ionosphere (Dungey, 1961). Dayside reconnection allows solar wind plasma and field entry to the dayside magnetosphere, from where the plasma convects across the polar cap and tail lobes to another reconnection location in the distant tail. At the distant tail reconnection region, plasmas are accelerated toward and away from the reconnection region such that within the tail plasma sheet, the flows are Earthward on the Earthward side of the reconnection region and away from the Earth in the tailward side of the reconnection region (Lyons and Williams, 1984). In the ionosphere, this large-scale convection pattern induces antisunward flow across the polar cap and sunward plasma flow in the auroral region ionosphere (Heelis et al., 1982). This basic flow pattern (in highly variable forms) can always be found underlying the temporal changes associated with the space weather events.
3.2 Magnetospheric plasmas
While the magnetospheric field in general excludes the solar wind plasma from the magnetosphere, at times the solar wind can gain entry into the magnetosphere through the magnetopause. This occurs when the IMF and the magnetospheric fields are antiparallel and magnetic reconnection creates an “open magnetosphere” configuration with a field component normal to the boundary (Dungey, 1961). The plasma entry is strongly modulated by the orientation of the interplanetary magnetic field, and thus enhanced during periods of southward IMF (Russell and McPherron, 1973). While the plasma enters mostly through the dayside magnetopause, a portion of the particles gain entry through the magnetopause boundary layers at low latitudes, well tailward of the terminator (Paschmann, 1997). During northward IMF, high-latitude reconnection over the magnetic poles allows for particle entry to the high-latitude plasma mantle. A minor portion of the energy, estimated to be about 10%, enters via viscous interaction processes (Axford and Hines, 1961). The solar wind plasma, consisting mostly of protons and a small percentage of doubly charged helium and other heavier ions, populates much of the outer magnetosphere through these processes.
In addition to the solar wind flow, the atmosphere contributes both to the neutral and charged particle density in the magnetosphere. The neutral exosphere, or the upward extension of the atmosphere, fills the near-Earth space with an exponentially decreasing density (Chamberlain, 1963; Tinsley et al., 1986). While the neutral atoms and molecules are not influenced by the electromagnetic forces, the geocorona is significant to space physics processes in at least two ways: Coulomb collisions and charge-exchange processes with neutral atoms are significant loss mechanisms for energetic charged particles in the inner magnetosphere (Fok et al., 1995), and thus contribute to the recovery of quiet conditions after a magnetic storm. Furthermore, the slow neutral atoms charge-exchanging with fast charged particles create a population of high-speed neutrals that propagate linearly away from the collision site. During active times, when the flux of energetic charged particles is sufficiently high, this provides (the only) means to image the inner parts of the magnetosphere (Bertaux et al., 1989; Williams et al., 1992).
Above about 80 km altitude, the solar ultraviolet radiation ionizes a small portion of the atmospheric gas creating what is known as the ionosphere. The ionospheric plasma processes couple both to the neutral atmosphere below and to the magnetospheric processes above. From space weather point of view, the ionosphere is significant both because of its effects on radio waves and because it hosts strong electric currents whose effects extend to the ground. The solar wind electric field drives a global convection pattern in the ionosphere, which produces convection electrojets carried by drift currents flowing eastward on the duskside and westward on the dawnside of the ionosphere (Weimer, 1995). Consequently, the plasma flows from the dayside toward the nightside over the polar cap, returning to the dayside along the lower latitudes, consistent with the Dungey cycle (Dungey, 1961). The ionosphere is coupled to the magnetosphere by highly structured and dynamic field-aligned currents, which on an average sense form a pair of large-scale field-aligned current sheets (see Figure 3). The more poleward current Region 1 currents couple to the magnetotail and magnetospheric boundaries, whereas the more equatorward Region 2 currents couple to the ring current in the inner magnetosphere (Iijima and Potemra, 1976). The region encircling the magnetic poles where the current systems flow is also called the auroral oval, as this is the region where particles precipitating from the plasma sheet and colliding with atmospheric atoms and molecules create visible auroral light (Lui and Anger, 1973). During active magnetospheric processes, auroral precipitation is enhanced, localized, and highly structured, especially in the nightside oval.
The upward extension of the ionosphere, the plasmasphere, is a torus filled with low-energy (around 1 eV), dense (10–1000cm−3) plasma originating from the ionosphere. The plasmasphere consists mostly of protons, with singly charged helium accounting for about 20% of the number density. The radius of the torus is variable, but typically the plasmasphere extends close to geostationary orbit, being more compressed during geomagnetically active times and more extended during long periods of magnetic quiescence (Grebovsky, 1970). The Earth’s rotation sets up an electric field, which drags the cold plasma into a corotational motion. The interplay between the solar wind-imposed electric field and the corotation electric field creates a boundary inside of which particles are trapped on closed orbits around the Earth. In the vicinity of this boundary, the plasma density has a sharp gradient; this is known as the plasmapause (Goldstein et al., 2003). Particles inside the trapping boundary remain on closed drift paths around the Earth while those outside the trapping boundary drift under the dawn-to-dusk electric field to the dayside boundary and are lost in the outer magnetosphere and eventually to the solar wind.
The ring current encircling the Earth roughly in the region 2–7 RE from the Earth consists of plasmas originating both from the solar wind and the ionosphere (Daglis et al., 1999). The ring current typically consists of ions in the energy range from a few tens of keV to several hundred keV, and has a highly variable intensity controlled by the level of geomagnetic activity. During magnetically active times, ion outflow from the ionosphere is greatly enhanced, and consequently the ring current composition changes from being dominated by solar wind protons and doubly charged helium to consisting large percentages (up to dominating the mass and energy density) of ionospheric oxygen and to lesser amounts of singly charged helium (Daglis et al., 1999). The ring current decays via charge exchange processes and Coulomb collisions with the exospheric particles.
The outer van Allen radiation belt consists mainly of electrons in the energy range from hundreds of keV to several MeV. The electrons reside colocated with the ring current and the plasmasphere in the inner magnetosphere, roughly from 3 RE to slightly beyond geostationary orbit. These relativistic electron fluxes show sharp dropouts and enhancements in response to the varying geomagnetic activity (Baker et al., 2001), and their dynamics is key to space weather, as these electrons pose a hazard to satellites in Earth orbit. Their rapid drift motion around the Earth is largely controlled by the magnetic field geometry, in contrast to the cold particles that are guided both by the electric and magnetic fields. The electron acceleration and loss processes are strongly dependent on the electric field structure and the wave-particle interactions in the inner magnetosphere (Friedel et al., 2002).
The variety of processes bringing particles into the inner magnetosphere, the fact that the quasi-dipolar field allows trapping of the particles to closed drift orbits, and the relatively low collision frequencies that keep the system from obtaining thermal equilibrium all contribute to the complexity and variability of the inner magnetosphere plasma populations. It is important to note that the dynamic processes all occur on time scales that are short compared to collision times, which means that the plasma populations can retain their characteristics without being thermalized, and that the plasma distribution functions can significantly deviate from simple Maxwellians. Figure 4 shows the key plasma populations in the magnetosphere.
3.3 Magnetospheric dynamics
Energy, momentum, and plasma enter the magnetosphere both via magnetic reconnection at the magnetospheric boundaries in regions where the interplanetary and terrestrial fields are antiparallel and via viscous interactions along the boundary (Dungey, 1961; Axford and Hines, 1961). In a quiescent situation, energy inflow is gradual, the energy is dissipated in the ionosphere, and magnetic flux opened at the dayside reconnection process is closed by a quasistatic reconnection process in the distant magnetotail at about 100–200 RE from the Earth. Energy transfer is most efficient when the reconnection process takes place at the dayside magnetopause, which occurs during periods when the interplanetary field points southward and is thus antiparallel to the intrinsic geomagnetic field (Akasofu, 1981; Laitinen et al., 2006).
Variability in the north-south orientation of the interplanetary magnetic field causes episodic energy loading-dissipation cycles termed magnetospheric substorms (Baker et al., 1996; Sergeev et al., 1996b). Substorms typically occur at a rate of four to five per day, each lasting typically two to three hours. They are initiated by enhanced dayside reconnection and hence increased energy input to the magnetosphere. This causes a configuration change in the magnetosphere including enhancement of the magnetospheric current systems and formation of a thin and intense current sheet from near-geostationary distance outward (McPherron, 1970; Pulkkinen et al., 1992). The current sheet at the tail center has a thickness of only a few hundred kilometers (comparable to the thermal ion gyroradius), and the magnetic field component normal to the current sheet becomes very small, only a few nanotesla (Sergeev et al., 1993). As this thin current sheet grows unstable, a rapid dissipation process quickly expands to a large-scale reconnection event whose effects are observable over a large portion of the coupled magnetosphere-ionosphere system (Hones Jr, 1979). Because the reconnection region is limited in the cross-tail direction, the flow shear between the fast outflow from the reconnection region and the ambient Earthward plasma flow within the plasma sheet creates a pair of field-aligned current sheets, where the current flows to the ionosphere at the eastern edge of the reconnection region and out from the ionosphere at the western edge (McPherron et al., 1973). On ground, magnetospheric substorms are seen as disturbances in the geomagnetic field caused by the field-aligned current systems and auroral electrojet currents in the ionosphere (Baumjohann et al., 1981). Energetic electrons precipitating into the ionosphere and colliding with the atmospheric constituents create bright auroral displays in the night sector auroral region (Elphinstone et al., 1993). Figure 5 shows a schematic of the magnetotail reconfiguration process during a substorm.
A schematic of the magnetospheric substorm. After the onset of dayside reconnection, energy is loaded into the magnetotail, which leads to the formation of a large-scale thin (ion gyroradius scale) current sheet. Magnetic reconnection at a near-Earth neutral line is associated with the bursty energy release, followed by ejection of plasma in the form of a plasmoid back to interplanetary space.
Magnetic reconnection in the tail leads to formation of a plasma structure where the field lines are no longer connected to the Earth. This plasmoid is accelerated tailward and ejects a large portion of the plasma sheet plasma, magnetic flux, and energy back to the solar wind (Hones Jr, 1979). It is estimated that about half of the energy that enters via the dayside reconnection process is processed in the inner magnetosphere and ionosphere, while the other half is carried by the plasmoid(s) back to the solar wind (Ieda et al., 1998).
Magnetospheric substorms require a period of enhanced energy input (southward interplanetary field) from 30 minutes to 1 hour. If the energy input continues significantly longer (≥3 h), a magnetic storm develops (Gonzalez et al., 1994). As it takes several hours of southward interplanetary field and/or high solar wind speed to create a magnetic storm, they often follow from the interaction of a fast solar wind stream, an interplanetary magnetic cloud, an ICME, or other coherent solar wind structure. Magnetic storms typically last from about 12 hours to a few days. Storms are characterized by the formation of an intense ring current encircling the Earth with current peak at about 4 RE, i.e., well inside the geostationary orbit. The ring current is populated both by efficient convection and injection of plasma sheet particles into the inner region and by strongly enhanced ion outflow from the ionosphere. At times, the ionospheric outflow can be strong enough for the ionospheric oxygen to dominate the energy density in the ring current (Daglis, 1997). Storms as largest magnetospheric disturbances are associated with many of the space weather phenomena.
While substorms can occur without magnetic storms, almost all storms include also substorm activity. The interaction of the inner magnetosphere storm-associated processes with the magnetotail substorm-associated processes is highly complex, and presently under active study. Especially, it is debated whether the substorm-associated magnetic field variations and the associated (inductive) electric fields are necessary for the buildup of the ring current energy density (McPherron, 1997; Daglis and Kamide, 2003). While some researchers argue that convection alone can account for the ring current increase (Ebihara and Ejiri, 2003), others have concluded that especially the energization process to energies exceeding 100 keV needs smaller-scale, time-varying electric fields (Ganushkina et al., 2005).
The magnetospheric substorms and storms are the most commonly occurring responses to enhanced solar wind driving, but the magnetosphere can enter into a variety of other dynamic states. Steady convection intervals (SMC) are periods of steadily southward IMF and steady, relatively slow solar wind flow that drive continuous, low-level auroral activity without evident substorm expansion phase activity (Sergeev et al., 1996a). On the other hand, stronger levels of driving may lead to sawtooth oscillations, which are large-scale substorms associated with strong, longitudinally extended, quasi-simultaneous injections at geostationary orbit recurring every 2–3 h (Henderson et al., 2006; Pulkkinen et al., 2006). Magnetic storms include, in addition to strong substorm activity, also other kinds of strong activity, field-aligned currents, and inner magnetosphere disturbances (McPherron, 1997).
4 Monitoring the Magnetosphere
The magnetosphere-ionosphere system has been explored by a multitude of Earth-orbiting spacecrafts, but still the sparsity of the satellite fleet and the vast regions to be covered means that, at any given time, direct measurements of the magnetospheric processes are limited to only a few points in space. The European Space Agency’s Cluster mission with its four satellites flying in constellation has for the first time allowed for separation of space and time and by identification of full three-dimensional vector quantities from four point measurements (see, e.g., Escoubet et al., 2001, and other articles in the same volume). However, the limited number of measurement points still means that many quantities must be evaluated using proxy parameters derived either from point measurements in space or from ground-based observations.
For a long time, the auroral light from the polar region ionospheres was the only source that could provide two-dimensional images of the large-scale space plasma processes. Recently, the NASA IMAGE mission with its onboard neutral atom imagers demonstrated that also the charge-exchange processes with the neutral geocorona and the charged ring current particles can be strong enough to produce enough signal to monitor the plasmaspheric and ring current dynamics in the inner magnetosphere. As these are populations highly sensitive to processes occurring during space weather events, neutral atom imaging is becoming a new tool to monitor the state of the inner regions of the magnetosphere (Burch, 2000; Burch et al., 2001). However, the low signal to noise ratio and the complex inversion process from the line-of-sight measurements to spatially resolved ion distributions still limits the imaging applications. Figure 6 from Fok et al. (2003) shows an example of neutral atom imaging results during a magnetic storm. The red and green colors reflect the enhanced fluxes of energetic neutral atoms that are created by Coulomb collisions between the energetic ring current ions and cold geocoronal material. Such recreation of the ring current particle population requires detailed modeling of the neutral geocorona and the charge-exchange processes.
Ring current evolution during a magnetic storm on August 12, 2000. Top panel: Geomagnetic SYM-H (proxy for ring current intensity) and ASY-H (proxy for ring current asymmetry) indices. Bottom panel: Observations made by the HENA energetic neutral atom imager onboard the IMAGE satellite. The polar plots show the equatorial ion fluxes in units of 1/keV/s/sr/cm2 averaged over pitch-angle in the energy range 27–39 keV. The direction to the Sun is to the left and dawn is up. (From Fok et al., 2003).
However, even with neutral atom imaging, much of the magnetosphere remains invisible to our eyes and instrumentation. To provide conceptual and predictive models of the magnetospheric evolution, large-scale global magnetohydrodynamic (MHD) simulations have been developed (Lyon et al., 2004; Janhunen, 1996). These models describe the solar wind-magnetosphere interaction as well as the coupling to the ionosphere in the single-fluid approximation. With limitations discussed in more detail below, these models have been successfully utilized to provide a large-scale framework for local observations as well as to infer global quantities that cannot be obtained directly from observations.
This section summarizes the most commonly used observational parameters and methods used in space weather research and gives an overview of the global MHD simulations whose results will be presented and discussed in the following Sections 5 and 6.
4.1 Observations
The size and shape of the magnetosphere is controlled by the interaction of the interplanetary magnetic field and solar wind flow with the internal geomagnetic field and the magnetospheric plasma environment. The size is largely controlled by the solar wind dynamic pressure, which is balanced by the magnetic pressure inside the magnetosphere. The tail radius and flaring angle (deviation from a cylindrical shape) are to some extent controlled by the interplanetary magnetic field direction, which controls the intensity of reconnection at the nose of the magnetosphere. An empirical model developed by Shue et al. (1997) and tuned for extreme conditions by Shue et al. (1998) gives the standoff distance of the magnetopause (R(φ)) as a function of the solar zenith angle (φ) as
where the factors α and R0 depend on the IMF Bz and solar wind dynamic pressure (Psw)
The model assumes the magnetopause to be rotationally symmetric with respect to the Sun-Earth line.
Lacking global measurements of the energy transfer from the interplanetary medium into the magnetosphere, the solar wind energy input is either assumed proportional to the solar wind motional electric field EY = − VswBZ,IMF or approximated by an empirical parameter
where Vsw is the solar wind speed, B the interplanetary magnetic field magnitude, and tan(θ) = By/Bz (in the GSM coordinate system) is the IMF clock angle in a plane perpendicular to the Sun-Earth line (Perreault and Akasofu, 1978; Akasofu, 1981). The scale length 7 RE is an empirical scaling parameter originally obtained by comparing the energy input as measured by ϵ and the energy dissipation in the known energy sinks, the ionospheric Joule heating, the auroral precipitation, and the ring current. While later analyses have significantly revised the relative roles of the various energy sinks, the original scaling is still used with the understanding that the ϵ is more accurate in giving temporal variations than absolute magnitudes of the energy input (Koskinen and Tanskanen, 2002).
The level of geomagnetic activity is often characterized in terms of magnetic indices created using a variety of ground magnetic records. The auroral electrojet indices are derived from the north-south components of 12 northern-hemisphere auroral-latitude (around 70° latitude) magnetic stations as the minimum (AL or auroral lower) or maximum (AU or auroral upper) of the 12 measurements at each time instant at one minute temporal cadence. The auroral electrojet index (AE) is then given as the difference of the two (AE = AU − AL). The AL index responds to the enhancement of westward electrojet currents (southward horizontal disturbance field at the Earth’s surface) and is a measure of the intensity of substorm expansion phase activity in the magnetosphere. The AU index responds to the eastward currents, and is a measure of the strength of large-scale convection in the magnetosphere-ionosphere system. While the ionospheric currents are sufficiently close to the ground-based measurement stations so that other magnetospheric current systems do not significantly disturb the measurements, signal arising from ground induction can contribute to the index by as much as 40% during rapidly varying current systems when the induction currents are strongest (Tanskanen et al., 2001). Other geomagnetic indices include the planetary Kp index, which is a quasi-logarithmic scale of geomagnetic activity ranging from 0 to 9, computed from 13 geomagnetic observatories in subauroral latitudes (44–60°). The Ap index ranging from 0 to 32 is derived similarly to the Kp index.
For studies of energy transport through the magnetosphere-ionosphere system, the AE-indices can be used to estimate the amount of energy dissipatedin the ionosphere by frictional Joule heating and by particle precipitation using
(Tanskanen et al., 2002; Ahn et al., 1983; Østgaard et al., 2002), where the factor 2 accounts for precipitation and Joule heating in both northern and southern hemisphere polar regions.
The north-south components of four midlatitude (around 20–40° latitude) stations are used to create the Dst index, which gives a proxy for the intensity of the ring current encircling the Earth. As the amount of ring current intensification is a key parameter in the magnetic storm evolution, this index is used to characterize magnetic storm intensity. The Dst index is computed as an average of the station measurements weighted by the cosines of the station colatitudes (Dst = ΣnΔHn/Σn cos θn) to compensate for the effects of the varying latitudes of the stations. The Dst index is given as hourly values. A high-resolution SYM-H index is computed in an almost similar way but with 1-min temporal cadence.
The ring current consists of two parts, a symmetric ring current encircling the Earth and an asymmetric part carried by particles on open drift paths drifting from the magnetotail to the dayside magnetopause. This partial ring current is closed by field-aligned currents to and from the ionosphere. The ASY-H index is a measure of the asymmetric ring current and is given as the difference between the maximum and minimum disturbances (weighted similarly to Dst) as measured at the six stations distributed around the globe.
As the magnetometers integrate over all current systems, the SYM-H and ASY-H as well as the Dst indices are sensitive not only to the ring current, but as well to the cross-tail current, the field-aligned currents, the magnetopause currents, and currents induced within the conducting Earth. While during quiet times the contributions from the other current systems can be assumed to be small, during magnetic storms (exactly when the indices are most needed) all currents intensify and move closer to the Earth such that the contributions from the other systems can be as large as 50% (Turner et al., 2000; Ohtani et al., 2001; Hakkinen et al., 2002).
The energy input to the ring current trapped particle population has been modeled by Burton et al. (1975), who give the temporal evolution of the Dst index as a function of the driving solar wind electric field and magnetospheric losses. However, as the magnetopause currents can significantly contribute to the Dst index at times when the magnetic pressure is high, the Dst index is first pressure-corrected to the form
where Psw is the solar wind dynamic pressure and the correction factors have been recently redefined by O’Brien and McPherron (2000). For the pressure-corrected Dst* one can then write
where Bs is the southward component of the IMF, critical value for the solar wind electric field is Ec = 0.49 mV/m below which the driver function Q(t) = 0, and τ is the ring current decay time in hours.
Figure 7 shows an example of a large storm that occurred on April 6–7, 2000. The storm was driven by a strongly negative IMF Bz within the sheath region of an interplanetary CME, and caused significant ring current enhancement, strong auroral activity (Huttunen et al., 2002), and space weather effects both in space and on ground (Pulkkinen et al., 2003). A specific feature of this storm was that the solar wind density and dynamic pressure were high, which created much more intense ring current activity than that predicted by the Burton et al. formulation. The left panel shows the driving solar wind and IMF parameters, while the ionospheric dissipation parameters as well as the ring current dissipation (both observed and predicted) are shown in the right panels.
Magnetic storm on April 6–7, 2000. Left, from top to bottom: interplanetary magnetic field Bx and By, Bz, solar wind density and pressure, speed, and motional electric field. Right, from top to bottom: ϵ-parameter giving a measure of the energy input to the system; AU and AL indices giving a proxy of the ionospheric electrojet current activity; AL-index-based proxies for ionospheric Joule heating and particle precipitation power; Dst index and its pressure-corrected variant Dst*, Dst* and its prediction using Equation 7 that provide an estimate of the ring current intensity.
4.2 Global MHD simulations
Global magnetohydrodynamic (MHD) simulations are presently the only means to self-consistently model the plasma processes throughout the solar wind, magnetosphere, and ionosphere: the large range of magnetic field values ranging from 50,000 nT at the Earth’s surface to only a few nT at the magnetotail current sheet, and of plasma densities and temperatures ranging from 1012 cm−3 and a few eV in the ionosphere to less than 1 cm−3 and a few MeV in the magnetosphere set stringent requirements for the numerical solutions. Furthermore, the large system size (several hundred RE or 109 km) compared to the characteristic thermal particle gyroradii (of the order of 102 km) limit the possibilities to describe individual particle dynamics in the entire simulation domain.
Global MHD simulations are used by several research groups to gain a global view of the dynamic processes in the coupled solar wind-magnetosphere-ionosphere system (Lyon et al., 2004; Raeder et al., 1995; Janhunen, 1996; Gombosi et al., 2000). While the codes differ in many details, basically they all solve the (ideal) MHD equations in a large box extending out to at least 30 RE in the Sunward direction, about 60 RE in the perpendiculardirections, and several hundred RE in the downtail direction. This way, the box completely encompasses the magnetosphere in all but the tailward direction, and as the flow is supersonic at the tailward boundary, there is no feedback from that boundary to the other parts of the simulation. With the modern computing capabilities, the variable-size grids can resolve minimum cell sizes of only a fraction of RE, which allows resolving structures to the thermal ion gyroradius scale.
Near the inner boundary, the MHD magnetosphere is coupled to an electrostatic model of the ionosphere. The details of how the ionosphere is treated in the simulations varies quite significantly, and both the coupling to the ionosphere as well as the details of the ionospheric solution are still being refined many of the modeling groups. The inner boundary of the MHD simulation box is located between 2 and 4 RE to avoid very short time steps associated with the large wave speeds in the high-field region near the Earth. The field-aligned currents obtained from the MHD simulation at the inner boundary are mapped to the ionospheric altitude along dipolar magnetic field lines. The ionospheric module solves the potential equation using the field-aligned currents, ionospheric conductances, and Ohm’s law in the ionosphere to get the horizontal ionospheric currents and potential pattern. The electric field computed from the ionospheric potential is then mapped to the inner boundary of the magnetosphere, where it is used as a boundary condition for the MHD simulation part. The ionospheric conductances are determined by the solar illumination and in many models by parametrized electron precipitation from the magnetosphere. The space between the ionosphere and the inner boundary of the MHD simulation part is a passive medium, which only transmits electromagnetic effects along dipolar magnetic field lines. Thus there is no plasma or currents perpendicular to the magnetic field in that region. Figure 8 shows a diagram of the simulation scheme.
Schematic of the structure of a global MHD simulation. Measured solar wind and IMF values are used as input at the Sunward boundary of the MHD simulation box. The MHD part solves the temporal evolution of the plasmas and electromagnetic fields, and feeds the field-aligned currents and electron precipitation to the ionospheric simulation. The ionospheric part solves the potential equation using the magnetospheric input as well as the solar EUV values to compute the ionospheric current and potential pattern and feeds the electric potential pattern back to the MHD simulation.
The simulations are driven by the solar wind and IMF values at the Sunward boundary of the simulation box and the F10.7 flux that determines the level of ionospheric ionization and hence the conductivity. The models can either use idealized solar wind and IMF conditions to gain understanding of the generic dynamic properties of the magnetosphere or use real spacecraft measurements to model the evolution of individual events.
In cases where the global MHD simulations solve the ideal MHD equations with zero resistivity, magnetic reconnection occurs in the simulations only through numerical diffusion. In case the resistivity is explicitly accounted for, it is most often parametrized to scale with the current density; the magnetospheric plasmas are fully collisionless and hence the classical collisional resistivity is zero. This and the lack of microphysical processes below the MHD scale naturally limits the applicability of the models to describe the details of the reconnection process either at the magnetopause or in the magnetotail. However, it has been shown that in the large scale, the simulation results are consistent with the conceptual understanding of when and where reconnection in the magnetosphere should occur (Hones Jr, 1979) and with case studies where in-situ satellite observations of reconnection events are available (Pulkkinen and Wiltberger, 2000).
Figure 9 shows MHD simulation results compared with observations during the storm on April 2000. The top left panel shows the ϵ parameter as a reference for the level of energy input to the magnetosphere. The next two panels show geosynchronous orbit magnetic field measurements from two GOES spacecraft. As the geostationary field is under normal conditions dominated by the strong dipole field pointing northward, the fact that Bz changes sign and becomes strongly negative is a clear indication that the satellites have crossed the magnetopause boundary and entered in the magnetosheath. This time period is highlighted with the green shading. The fourth panel in Figure 9 shows the empirical Shue et al. (1998) model for the subsolar magnetopause position shaded in dark blue (Equation 2). The model correctly predicts that the magnetopause was near or inside the geostationary orbit at 6.6 RE for a large part of the storm main phase. The black curves show two measures of the magnetopause position in the MHD simulation: the upper curve is determined from the maximum current density flowing at the boundary, while the lower curve is defined from the open-closed field-line boundary separating field lines tying to the Earth from the disconnected solar wind field lines. The bottom panel shows Geotail measurements from just upstream of the magnetopause (blue). The measurements trace the IMF Bz variations but are much enhanced, indicating that Geotail was located in the shocked magnetosheath flow between the magnetopause and the shock. The shaded region shows the time period when the simulation (shown black) predicts Geotail position in the solar wind upstream of the shock, and thus overpredicts the amount of inward motion of the shock. However, as the two snapshots of plasma density in the equatorial plane on the right show, Geotail was very close to the shock, and thus even a small error in the shock location may lead to erroneous prediction of the region where the spacecraft resides.
Magnetic storm on April 6–7, 2000. Left, from top to bottom: ϵ parameter characterizing energy input, Bz component of the magnetic field at GOES-10 and GOES-8 (negative Bz is an indication of the satellite being outside the magnetosphere), empirical Shue et al. model for the subsolar magnetopause position (blue) and two measures of the subsolar magnetopause position from the GUMICS-4 MHD simulation (current maximum, upper black curve, and open-closed field line boundary, lower black curve), and Bz from the Geotail spacecraft (blue) and from the GUMICS-4 MHD simulation (black). Right: Two equatorial plane cuts of plasma density from the GUMICS-4 MHD simulation. The direction of the Sun is to the left, and the black sphere at the center marks the inner boundary of the MHD simulation at 3.7 RE. The large black dot shows the Geotail satellite position inside the magnetosheath at 16:00 UT and outside in the solar wind at 21:00 UT as the magnetosphere is compressed during the storm main phase.
In addition to reconnection modeling, the inner magnetosphere also poses significant challenges to the MHD simulations. As the simulations include only one ion population, it describes the entire distribution with a single temperature. This is not realistic in the inner magnetosphere, where the ring current is carried by ions with significantly higher energies than the average plasma sheet population. Furthermore, the ion sources from the ionosphere (plasmasphere, ion outflows associated with geomagnetic activity) are not included in most simulations. As a consequence, the MHD simulations predict a much more dipolar inner magnetosphere than is observed, and do not reproduce the strong inner magnetosphere field depression associated with stormtime ring current. A variety of efforts to couple the inner magnetosphere simulation part with other, more detailed models of the inner magnetosphere are currently underway to address this issue.
Even given their limitations in describing details of reconnection, multicomponent plasma systems, or the physics associated with non-adiabatic ion motion or anisotropic pressures, the global MHD simulations are presently the best tool to obtain a large-scale view of the magnetospheric activity. As such, they are widely developed for use in space weather applications (Raeder et al., 2001; Manchester IV et al., 2004).
5 Solar Wind Energy Entry into the Magnetosphere
As all magnetospheric activity is powered by energy input from the solar wind, detailed understanding of the energy transfer processes and mechanisms is a key challenge for space weather applications. As described in the previous section, observationally we lack global measurements of the energy transfer and thus are limited to the use of proxies. However, global MHD simulations can be used to trace the energy transfer through the simulation magnetopause and through the magnetosphere-ionosphere system. In this section, we analyze the energy transfer using the GUMICS-4 global MHD simulation (Janhunen, 1996) and compare and contrast the results with those obtained using the empirical proxies.
In the MHD formulation applied in the global MHD simulations, the total energy flux is given by
where \(U = P/(\gamma - 1) + \rho {V^2}/2 + {B^2}/2{\mu _0}\) is the total energy density, P the plasma pressure, and γ = 5/3 is the ratio of specific heats. The total energy flux is a conserved quantity in the simulation, and thus it is possible to trace energy flow lines, and the energy transfer through the magnetopause can be evaluated by following the energy flux flow lines and computing its normal component at the boundary.
The challenge in this approach is the determination of the magnetopause surface in the simulation. Observationally, the magnetopause is a current layer (often a tangential discontinuity) that separates the solar wind and interplanetary field from the magnetospheric plasma and field. Thus, from in situ satellite observations, the magnetopause can be distinguished as the location of the current maximum or as the (often very sharp) discontinuity in the magnetic field and plasma density. After trying several methods, the chosen solution for finding the magnetopause in the GUMICS-4 simulation was to define the magnetosphere as a cavity carved by the solar wind plasma flow lines (Palmroth et al., 2003). The magnetopause is then the surface defined by the innermost plasma flow lines encircling the magnetosphere. This method has proven to be quite robust and consistent with other definitions of the magnetopause.
The energy entering from the solar wind into the magnetosphere is dominated by the Poynting flux, and is only modulated by the dominant energy source, solar wind kinetic energy flux. As the ϵ parameter essentially is the Poynting flux toward the magnetopause, it is a good proxy also for the energy transfer rate. The magnetospheric magnetic field topology and the electric field imposed by the solar wind flowing past the magnetosphere create a geometry where a large portion of the entering Poynting flux is focussed to the inner magnetotail (Papadopoulos et al., 1999). Figure 10 illustrates how the Poynting flux entering through the magnetopause is directed toward the central plasma sheet under the Earthward pointing magnetic field in the northern tail lobe and cross-tail (out of the plane of the figure) electric field. In the magnetotail, the energy is converted from magnetic to plasma energy at the cross-tail current sheet.
Poynting flux enters through the magnetopause and focuses toward the inner magnetosphere. The left panel shows the noon-midnight meridian plane with direction of the Sun to the left and the right panel shows the equatorial plane with direction of the Sun to the top. The plots illustrate how the energy enters through the high-latitude boundary and is focussed toward the inner magnetotail and finally toward the ionosphere.
The amount of energy conversion in the magnetotail can be quantified by evaluating the integral of the Poynting flux divergence (∫ dV ∇ · S) in a region that encompasses most of the inner magnetosphere, and hence the region that is mostly affecting space weather phenomena (Laitinen et al., 2005). While this method does not exactly specify the region where the energy conversion takes place, selecting a suitably large region ensures that no major dissipation locations are left out, while the energy conversion outside the active regions is small enough not to produce errors in the evaluation.
Figure 11 shows three frames from a simulation showing the magnetopause size and shape as well as the locations of energy entry from the solar wind into the magnetosphere during the magnetic storm on April 6, 2000 (for observations see Figures 7 and 9). Energy transfer from the solar wind into the magnetosphere is shown in blue and energy escape from the magnetosphere to the magnetosheath is shown in red. Note also the highly variable size of the magnetosphere as the increasing solar wind dynamic pressure compresses the magnetosphere to almost half its original size. As shown previously, in this event the compression was strong enough to push the magnetopause inside the geostationary orbit for an extended period during the storm main phase (Huttunen et al., 2002).
mpg-Movie (12664.8046875 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Magnetopause shape and size and the energy transfer through the magentopause surface during three time instants from the GUMICS-4 global MHD simulation. The magnetospheric boundary is viewed from a direction upstream (Sunward) of the magnetosphere. Note that the energy entry shown in blue is concentrated at the nose of the magnetosphere as well as in two high-latitude regions which are in sectors roughly parallel to the interplanetary magnetic field direction. (For video see appendix)
Integration of the energy flow vector over the magnetopause surface yields a total energy input per unit time, i.e., power transfer through the boundary. The top panel of Figure 12 shows a comparison of the total energy computed from the simulation with the empirical ϵ parameter. Note that the scale for the empirical parameter is different from the simulation one: the two quantities do not agree in magnitude, which indeed is expected. While the energy input through the simulation boundary is a total energy entering the system, the scaling for the ϵ parameter was empirically obtained to match the inner magnetosphere and ionosphere energy dissipation (free scaling parameter 7 RE in Equation 3). Thus, the difference in the magnitudes is a measure of the amount of solar wind energy input that becomes geoeffective in the inner magnetosphere.
Magnetic storm on April 6–7, 2000. Panels from top to bottom: Total power input through the magnetopause from the GUMICS-4 global MHD simulation (black) and ϵ-parameter (blue, scale on the right). Note how the energy entry in the simulation continues after the IMF has turned northward even though the ϵ-proxy would indicate very small energy input. Ionospheric Joule heating integrated over both hemispheres from GUMICS-4 (black) and AE-based proxy from Ahn et al. (1983) (blue, scale on the right). Note the large energy input associated with the solar wind pressure pulse seen in the simulation, but not in the observational proxies. Energy input rate from particle precipitation from GUMICS-4 (black) and from AE-based proxy from Østgaard et al. (2002) (blue, scale on the right).
Detailed analysis of the energy input locations shows that most of the energy enters the magnetosphere through the magnetopause Earthward of about −10 RE, which gives two main regions of energy input, the dayside, and the nightside boundary in the inner magnetotail region. Further down the tail, the energy transfer through the boundary is very small, as the Poynting flux flows very closely parallel to the boundary. If one looks at the azimuthal sectors (in a plane perpendicular to the Sun-Earth line), it can be seen that the energy is mostly entering in sectors that are parallel or antiparallel to the IMF orientation. This means that for southward IMF, the energy is mainly gaining access through the high-latitude regions in both hemispheres. This is consistent with the conceptual picture of the reconnecting magnetopause where the reconnection occurs close to the subsolar point and the open flux is transported across the high-latitude regions (Dungey, 1961).
Mainly two processes consume energy in the ionosphere: Joule heating resulting from the ionospheric closure of field-aligned currents and precipitation of magnetospheric electrons causing the auroral displays. Both quantities can be computed from the ionospheric solution of the global simulation. Total integrated power from Joule heating is obtained from PJH = ∫ ΣPE2dS. The energy of the precipitating electrons is integrated from the innermagnetosphere plasma parameters as \({E_{{\rm{PREC}}}} = {n_e}T_e^{3/2}\sqrt {2/\pi {m_e}}\). The two bottom panels of Figure 12 show line plots of the values integrated over the polar cap and compared with the empirical proxies discussed in Section 4. Figures 13 and 14 show excerpts from two simulations showing the ionospheric Joule heating and the auroral Hall conductivity, which is enhanced in regions of auroral precipitation, and hence proportional to the precipitation energy.
mpg-Movie (3098.69921875 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Northern hemisphere Joule heating during three instants from the GUMICS-4 global MHD simulation. The polar plots are drawn with Sun to the top and dusk to the left. Note how the auroral precipitation energy (shown in Figure 14 ) is concentrated in the auroral oval region and the dayside cusp where solar wind has direct access, while the Joule heating maximizes in the polar cap where the electric field is largest. (For video see appendix)
mpg-Movie (3046.00488281 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Northern hemisphere auroral precipitation during three instants from the GUMICS-4 global MHD simulation. The polar plots are drawn with Sun to the top and dusk to the left. Note how the auroral precipitation energy is concentrated in the auroral oval region and the dayside cusp where solar wind has direct access, while the Joule heating (shown in Figure 13 ) maximizes in the polar cap where the electric field is largest. (For video see appendix)
It is obvious that the strong activity drives highly enhanced auroral precipitation to a wide and expanded auroral oval. Furthermore, the ionospheric Joule heating is large both in the auroral oval region and in the polar cap, due to the very strong electric fields in the polar cap region. The MHD precipitation tends to follow closely the solar wind driver, while the AE-based proxy shows lower level of variability. On the other hand, the MHD simulation produces a large peak at the time of a solar wind pressure pulse, which is not present in the AE-based proxy for the Joule heat. As solar wind pressure pulses are known to be associated with enhanced ionospheric Joule heating (Palmroth et al., 2004), it is not clear to what extent the discrepancies are associated with limitations of the simulation and to what extent they are caused by the use of index-based proxies that may miss large parts of the dissipation if the measuring stations are not suitably located to record the disturbances. This is clearly an area where more work, both simulation and observational, is required for enhanced understanding of the coupling of the solar wind and the ionospheric processes.
6 Reconnection in the Magnetotail
Space weather events are largely driven by dynamic processes that occur within the magnetotail plasma sheet separating the low-density tail lobes. As was shown before, the large-scale structure of the magnetosphere causes the incoming Poynting flux to focus toward the plasma sheet. This leads to structural changes in the current sheet separating the antiparallel magnetic fields in the lobes, and may lead to bursts of reconnection associated with fast flows both Earthward and tailward of the reconnection region.
The magnetotail plasma sheet is a highly dynamic and structured region. Plasma flows in this region are not laminar, and during most times the net Earthward plasma flow imposed by the large-scale convection pattern is composed of short-lived (1–10 min) bursts of fast flow while the ambient plasma velocity distribution is very nearly isotropic. These flows are most likely created by localized reconnection events initiated either by internal tail processes or by external driving conditions (Baumjohann, 1993; Nagai et al., 2005). While such bursts of fast flow can be observed during all magnetospheric activity conditions, they become more numerous, more intense, and have larger scale sizes during magnetically active conditions. As this is the region which feeds the inner magnetosphere with both plasma, energetic particles, and magnetic flux, the plasma sheet dynamics is crucially important for space weather applications.
As the magnetospheric activity conditions are largely controlled by the stability properties of the cross-tail current sheet, and as the magnetotail current sheet shares many of the properties of dynamically important current sheets found e.g. in the solar plasmas, the dynamics of the cross-tail current has been intensively studied in recent years. In the quiet state, the cross-tail current sheet is rather thick, and the plasma and current sheet tailward of the quasi-dipolar region can be described by a simple one-dimensional Harris current sheet, where the magnetic field is given by Bx = B0 tanh(Z/λ), where B0 is the lobe magnetic field, Z is the coordinate across the current sheet, and λ defines the scale thickness of the current sheet. Closer to the Earth, inside of about 15 RE distance, the current sheet starts to deviate from the one-dimensional structure as the dipole introduces a component perpendicular to the current sheet. In the inner magnetosphere, the multiple plasma populations introduce their own complexity to the system.
As the IMF turns southward, dayside reconnection changes the conditions at the magnetospheric boundaries and begins to increase the open flux content in the magnetotail. In order to maintain pressure balance between the plasma sheet plasma pressure and the lobe magnetic pressure, the cross-tail current intensifies and the plasma sheet is compressed. However, in the region tailward of geostationary orbit out to about 20–30 RE the changes in the current density are not uniform: the total current is distributed between the pre-existing thick plasma/current sheet and a newly formed thin current sheet embedded within the plasma sheet. The thin current sheet is often in the ion gyroradius scale, and can host very high current densities at the field reversal region (1); Sitnov et al., 2006). Furthermore, complex, bifurcated current sheets and large-scale wavy structures have been identified from multi-spacecraft analyses.
During magnetospheric substorms, a thin and intense current sheet forms in the inner part of the magnetotail as a consequence of the intensified driving. This current intensification is seen as an increase of the lobe field Bx and a decrease in the normal component Bz at the inner magnetotail current sheet. Figures 15 and 16 show observations during a substorm event on December 10, 1996. The top panel of Figure 15 shows the IMF Bz which turned southward shortly after 06:00 UT. The next panels show the intensification of the lobe field recorded by the Interball satellite and thinning of the current sheet measured by the geostationary orbit satellite GOES-9 and the Geotail spacecraft in the tail plasma sheet. Figure 16 shows frames of the Lyon-Fedder-Mobarry (LFM) global MHD simulation code that was run for the substorm. The gray shading outlines the closed flux within the plasma sheet. The changes from the first to second frame illustrate the strong compression and thinning of the plasma sheet. The third panel shows the pinching off of the plasmoid and reduction of the volume of the closed-flux region. The last panel illustrates return to quiet conditions. These changes are consistent with those suggested by the schematic in Figure 5. Figure 17 shows a frame from the same simulation, now plotted in an equatorial plane projection and showing the electric field with the color coding. The region of the thin current sheet is shown with the red and yellow colors indicating highest electric field intensity. The white circle shows the thin current sheet location as derived from an empirical model (Pulkkinen and Wiltberger, 2000), in remarkable agreement with the simulation result. The white arrows representing the flow velocity show a flow channel that is intruding into the inner magnetosphere and interacting with the thin current sheet region. The simulation shows a series of such localized flow bursts that penetrate to the inner magnetosphere, finally disrupting the thin current sheet when the substorm expansion phase begins.
Substorm on December 10, 1996. Left, from top to bottom: North-south component of the IMF. Magnetotail observations of the thinning and intensification of the tail current sheet. The period of energy storage is bracketed with the vertical lines. Increasing BX in the magnetotail lobe recorded by Interball is a measure of increasing magnetic flux content in the tail. Decreasing Bz in the plasma sheet at geostationary orbit (recorded by GOES-9) and at about 25 RE distance (recorded by Geotail) reflects the increasing tail current intensity.
mpg-Movie (3926.05761719 KB) Still from a movie showing Substorm on December 10, 1996. Four snapshots of the LFM global MHD simulation. The color coding shows the plasma density in the noon-midnight meridian plane. The gray shading outlines the last closed flux surface indicating the large-scale magnetic topology of the system. The topological changes are consistent with those presented in the schematic picture in Section 3 . The direction of the Sun is to the left. (For video see appendix)
mpg-Movie (16560.6015625 KB) Still from a movie showing Substorm on December 10, 1996. LFM global MHD simulation results of the magnetotail flows in an equatorial plane projection. The direction of the Sun is to the left. The color coding shows the cross-tail electric field, with brighter colors showing higher electric field values indicative of a thin and intense current sheet at that location (highlighted by the white circle). The white arrows depict the flow velocity. Note a flow channel initiating from about 40 RE distance and focusing toward the thin current sheet region (outlined with the white dotted line). Such flow channels become larger and more frequent during substorm activity and finally lead to disruption of the intense inner-tail current sheet during the substorm expansion phase. (For video see appendix)
As the flows created by magnetic reconnection in the tail enter the inner magnetosphere, the large-scale magnetic field configuration changes rapidly from highly taillike to a much more quasidipolar state. Furthermore, the reconnection process is associated with rapid and significant energy conversion from magnetic energy in the magnetotail lobes to particle kinetic energy and heat in the plasma sheet. The tail field reconfiguration is also associated with strong field-aligned currents to and from the ionosphere, which in part contribute to the energy dissipation in the ionosphere. Thus, the large-scale current disruption, configuration change, and field reconfiguration all are associated with a major energy dissipation process in the magnetosphere.
The structure and dynamics of the current sheet in the magnetotail control the energy storage and release processes initiated with the enhanced dayside reconnection at the magnetopause. The high-speed plasma flows, strong particle energization processes, and rapid reconfiguration all are major parts in creating the space weather effects in the inner magnetosphere.
7 Space Weather in the Inner Magnetosphere
The quasi-dipolar inner magnetosphere extending roughly out to geostationary distance has a variable field structure caused by the competing effects of the internal dipole field, magnetotail current sheet, dayside magnetopause currents, and the ring current within the region itself. Furthermore, the inner magnetosphere hosts multiple plasma populations: the hot ion ring current in the tens to hundreds of keV energy range, the outer van Allen belt electrons with energies from 100 keV up to several MeV, and the cold plasmaspheric plasma (from a few eV to few hundred eV) originating from the ionosphere. Recent research results have emphasized how effectively all these seemingly distinct populations and their dynamics are coupled together (Meredith et al., 2006).
Relativistic electrons in the inner magnetosphere are a major hazard for Earth-orbiting spacecraft, and therefore prediction of the electron fluxes especially at geostationary orbit is one of the key targets for space weather applications. Figure 18 from Li et al. (2001) shows the long-term variation of the relativistic electrons in the outer van Allen belt color coded as a function of time and distance from the Earth (L giving roughly the distance from the Earth in the equatorial plane) and the Dst index which is assumed to reflect the intensity of the ring current carried by the energetic ions. It is evident that in the large scale, there is an association between the magnetic storm activity (Dst) and the relativistic electron fluxes. Note also that the electron fluxes are significantly lower and further away from the Earth during the solar minimum period in 1996–1997.
The top panel shows the inner belt proton flux in red and the sunspot number in black. The bottom panel shows the relativistic electron distribution in the inner magnetosphere. Color coding shows the inner magnetosphere relativistic electron flux intensity as a function of time and L shell giving the equatorial distance from the Earth. The black curve overlaid shows the daily averages of the Dst index (scale on the right), used here as a measure of the ring current energetic ion flux with more negative values indicating larger ring current (from Li et al., 2001).
7.1 Time-variable electromagnetic fields
Magnetic storms and substorms affect the electromagnetic field configuration in the inner magnetosphere over time scales of minutes to hours and days. During substorms, the intense current sheet can stretch the quasi-dipolar field lines at geostationary orbit to highly taillike ones, which together with the enhancing electric field causes significant changes in particle drift paths and allows for penetration of the plasma sheet plasma deep inside the inner magnetosphere. In the same way, the strong ring current causes stretching of the magnetic field during magnetic storms, but in this case the changes occur over time scales of days rather than hours. Substorm activity during magnetic storms causes quasiperiodic stretching-dipolarization cycles embedded within the longer-term ring current-associated changes.
There are a number of large-scale magnetospheric magnetic field models that give the field configuration as a function of either solar wind conditions or magnetospheric activity parameters (Tsyganenko, 1989, 1995; Tsyganenko et al., 2003). While these models give the large-scale evolution of the field quite well, the smaller-scale and shorter-term variations associated with substorms cannot be accurately represented by these models (Ganushkina et al., 2004). Figure 19 shows results from Ganushkina et al. (2005), who modeled the large-scale magnetic field evolution during a storm on May 2–4, 1998 by fitting an empirical model with free parameters to observed magnetic field values. The figure shows three snapshots of the current configuration at the equatorial plane as well as in the noon-midnight meridian plane prior to the storm, during the storm main phase, and during the recovery phase. Before the storm, the ring current is weak and the tail current intensity varies in response to substorm activity. After the storm onset, the ring current in the inner magnetosphere as well as the magnetotail current are strongly enhanced. During the storm recovery, both current systems weaken, but the ring current decay time is much longer than that of the tail current. On top of these large-scale field variations, there are rapid, large-amplitude, and localized variations of the magnetic field as well in the inner magnetosphere as in the magnetotail.
Magnetic storm on May 2–4, 1998. Magnetotail electric current intensity variations during May 4, 1998. The color coding shows the perpendicular current intensity in the equatorial plane (top panels) and in the noon-midnight meridian plane (bottom panels). Note the strong enhancement of both the ring and tail currents during the storm main phase (from Ganushkina et al., 2005).
The rapidly varying magnetic field induces an electric field (∇ × E = − ∂B/∂t) in the magnetosphere. These induced electric fields are much larger than the large-scale, weak convection electric field imposed by the solar wind flow past the magnetosphere. The small-scale fields can be very intense, include high-frequency fluctuations, and be highly localized in space, which makes their characterization difficult. The large-scale convection field can be given in a simple formulation parametrized by magnetospheric activity or by solar wind parameters (see Section 4). Because of the associated difficulties, there are to date only very few attempts to describe the time-varying, smaller-scale electric fields. However, Li et al. (1998) and Sarris et al. (2002) have described the substorm-associated magnetic field dipolarization and Earthward plasma flows in terms of Earthward-propagating, localized electric field pulses. By computing the magnetic field changes from the electric field and adding those to a simple dipole field and tracing particle drifts under the resulting electromagnetic fields, they were able to reproduce the substorm-associated energetic electron signatures at geostationary orbit. The role of electric fields in the ring current formation and acceleration is treated in more detail below.
7.2 Storm-time ring current
The increased solar wind electric field imposed on the magnetosphere increases the ring current, as described by the dynamic evolution equation of the ground-based Dst index (see Section 4). For many purposes, the particle motion in the magnetosphere can be described in terms of the guiding center motion, which gives an average over the gyromotion around the magnetic field lines and bouncing between the mirror points. In that approximation, the particles drift under the electric and magnetic fields with a total drift velocity (Roederer, 1970)
where the first adiabatic invariant
is conserved. When this approximation is valid, particles convecting toward the increasing magnetic field in the quasi-dipolar inner magnetosphere are adiabatically energized.
The Burton et al. (1975) equation described earlier assumes that when the magnetopause is opened by reconnection, the solar wind electric field penetrates into the magnetosphere and drives convection that transports particles into the inner magnetosphere. Furthermore, it is often assumed that the magnetic field lines are equipotentials. This means that it is sufficient to know the electric field in one plane only, and the electric field measured in the ionosphere can be mapped to the magnetosphere. A simple but robust description of the inner tail electric field in the equatorial plane of the magnetosphere is given by the Volland-Stern electric potential Φconv in the form
where A determines the intensity of the convection electric field, γ is a shielding factor, φ is the magnetic local time, φ0 is the offset angle from the dawn-dusk meridian, and often used values are γ = 2 and φ0 = 0 (Volland, 1973; Stern, 1975). The intensity of the electric field can then be related to magnetic activity indices such as Kp (Maynard and Chen, 1975) by writing
On the other hand, the convection electric field can also be given as a function of the solar wind and IMF values by using the Boyle et al. (1997) function for the polar cap potential Φ in the form
where θIMF = tan−1(Bz/By) is the IMF clock angle, R is the radial distance, and RB = 10.47RE. Both of these electric potential models yield a large-scale potential structure in the magnetosphere, where the electric field in the magnetotail is predominantly in the dawn-dusk direction and thus lead to transport from the tail toward the inner magnetosphere.
The drift approximation has been quite successfully applied to model inner magnetosphere plasma transport and energization during magnetic storms (Liemohn et al., 2001; Jordanova et al., 2001). However, it has become clear that simplified assumptions about the electric field (assuming large-scale convection only) and magnetic field configuration (assuming time-invariant dipole field) are not sufficient to account for many of the phenomena observed during storms. Replacing the magnetic field with a more realistic (time stationary) model allows plasma transport closer to the Earth in the magnetotail region, as the E × B drift dominates in the taillike magnetic field. On the other hand, a realistic representation of the magnetopause leads to significant particle losses from the dayside magnetosphere. Thus, the effect of a realistic magnetic field model is to decrease the total ring current energy content and make it more asymmetric as the dayside losses decrease the morning-sector fluxes (Ganushkina et al., 2005). Adding localized, time-varying electric field pulses to the model causes significant changes in the energy spectrum: while steady convection creates an intense but rather low-energy ring current, the electric field pulses are effective in accelerating particles to energies of 100 keV and above.
Figure 20 based on results in Ganushkina et al. (2005) shows a composite of calculations of the ring current energy content under a variety of magnetic and electric field models. The black curves show the time evolution of the total ring current energy content during a double storm on May 2–4, 1998. The colored curves show contributions from low (blue), medium (green) and high (red) energy particles. The left column shows observations made by the CAMMICE energetic particle instrument onboard the Polar spacecraft. In the right column, the top panel shows a computation using a large-scale convection electric field to drive the particle motion under a dipole magnetic field. The second panel illustrates the energy density development using a more realistic magnetic and electric field models, the T96 (Tsyganenko, 1995) magnetic field and Boyle et al. (1997) electric field. The third panel shows the same calculation, but now in addition to the convection electric field, traveling electric field pulses representing substorms have been added to the model. The bottom panel shows the Dst index during the storm. It is evident that after the second storm peak, only the third panel shows a large increase of the energy in the highest-energy particles (red curves) consistent with the observations shown in the left panels. Ganushkina et al. (2005) conclude that the localized, pulsed electric fields are necessary for the formation of the high-energy ring current and that any enhancement of the large-scale convection electric field cannot produce the observed energy spectrum. This result highlights the fact that in order to understand the ring current intensification and energization processes we need to gain knowledge of the detailed evolution of the electromagnetic fields and their time variations.
Magnetic storm on May 2–4, 1998. Ring current energy content as a function of time. Total energy content is shown in black, red shows the energy contribution from high-energy particles (80–200 keV), green shows the energy content in the medium energy particles (20–80 keV) and blue shows the contribution of the low-energy particles (1–20 keV). The left panels show observations from the Polar spacecraft. The observations indicate strong enhancement of the high-energy component during the later part of the storm (lowest panel shown in red). The three panels on the right show results from drift computations using different magnetic and electric field models, from top to bottom: dipole magnetic field and Volland-Stern convection electric field, T96 magnetic field model and Boyle et al. (1997) convection electric field, T96 magnetic field, Boyle et al. (1997) convection electric field, and substorm-associated electric field pulses. The bottom panel shows the Dst index during the storm. Only the model including the pulsed small-scale electric fields is able to reproduce the strong increase the high-energy component (after Ganushkina et al., 2005).
7.3 Changes in the cold plasmasphere
The plasmasphere encircling the Earth is formed by cold ionospheric plasma flowing outward along magnetic field lines. At low latitudes, close to the Earth, magnetic flux tubes follow drift paths that co-rotate with the Earth and therefore are filled with escaping ionospheric plasma in time scales of several days. The location of the outer boundary of the plasmasphere, the plasmapause, is controlled by the relative intensities of the solar wind-imposed electric field and the co-rotation electric field. Although roughly circular in shape, the plasmapause often shows an elongation in the duskside, following the general electric field pattern (Lyons and Williams, 1984). Statistical studies have shown that the position of the plasmapause is correlated with geomagnetic activity, being at smaller radial distances during higher levels of activity (Moldwin et al., 2003). This can be understood by the enhanced convection electric field moving the boundary between the convection-dominated outer region and the co-rotation-dominated inner region closer to the Earth. During magnetic quiescence, the plasmasphere is expanded and the plasmapause can be located outside geostationary orbit. Particularly during low magnetic activity conditions, there is significant variability in the plasmapause location.
During storms, the plasmapause moves inward due to the enhanced solar wind driving, while a drainage plume develops in the dusk sector (Elphic et al., 1996). Within this plume, the cold plasma flows outward toward the magnetopause thus escaping from the plasmasphere. In the nightside, the inward motion of the plasmapause is of the order of 0.5 RE/h, with the changes following the interplanetary magnetic field variations with 20–30 min delay (Spasojević et al., 2003). After the field lines reconnect at the magnetopause, they convect over the polar cap toward the magnetotail, thus providing an additional source of plasma to the tail plasma sheet during storms (Elphic et al., 1997). As the storm driving subsides, the plasmasphere slowly recovers its quiet-time size. The recovery time scale is associated both with the recovery of the quiet-time electric field structure and with the outflow time scale of the cold plasma from the ionosphere. As discussed below, the location of the plasmapause during storms has been shown to be a significant factor in determining the fate of the relativistic electron population in the outer van Allen belt.
7.4 Relativistic electron acceleration and losses
The most significant hazard to Earth-orbiting satellites is posed by high fluxes of relativistic electrons, which can penetrate the spacecraft systems. These electrons are transported under the same electric and magnetic fields as the ring current ions, but their higher speed makes them less sensitive to the details of the electric field structure.
The relativistic electron intensity variations are driven by the solar wind and interplanetary magnetic field conditions. Early studies found a correlation between the relativistic electron flux enhancements and solar wind high speed streams (Paulikas and Blake, 1979). This result was later augmented by the understanding that those high-speed streams that were coincident with southward interplanetary magnetic field were more efficient in enhancing the electron fluxes (Blake et al., 1997). As southward interplanetary field and high solar wind speed are the main drivers of magnetospheric storm activity, it is not surprising that the average electron flux levels trace geomagnetic activity as shown in Figure 18.
Figure 21 shows the 2–6 MeV relativistic electron fluxes as a function of L (distance from the Earth) and time as measured by the low-Earth orbiting SAMPEX satellite. At storm onset, the electron fluxes often decrease, which has been attributed partially to strong stretching of the field and the spacecraft moving to higher magnetic latitudes, relative to that of the undisturbed field, and hence measuring equatorial fluxes further from the Earth (Reeves, 1998), and partially to real loss of electrons either out from the magnetosphere or into the ionosphere. During this event, the flux dropout at storm onset is clearly seen over a wide range of L-values. Somewhat later, the fluxes were strongly enhanced reaching the usually empty slot region below L = 3. The electron fluxes remained at an elevated level for several weeks after the storm.
Magnetic storm on May 2–4, 1998. Relativistic electron distribution in the inner magnetosphere. Logarithmic color coding shows the daily values inner magnetosphere relativistic electron flux intensity (#/cm2-s-sr) as a function of time and L shell (in 0.1 bins) giving the equatorial distance from the Earth during April 1–June 30, 1998. Note the dropout prior to the storm as well as the strong intensification and Earthward intrusion of the electron population after the storm onset (courtesy X. Li/University of Colorado).
However, more detailed analyses revealed that during any individual storm event, the geostationary orbit fluxes can either increase, decrease, or show no effect at storm onset (Reeves, 1998; Reeves et al., 2003). Furthermore, although there is a general correlation between storm activity and electron enhancement, there is no one-to-one correlation that would indicate that higher peak intensity would necessarily lead to higher electron flux levels (O’Brien et al., 2001). Finding the relevant processes has proven to be difficult, as the net change in the fluxes is a consequence of a delicate balance of dynamic and adiabatic effects as well as acceleration and loss processes.
The candidate processes that can account for acceleration of the magnetospheric electrons to relativistic energies can be divided into three major categories: radial diffusion, rapid transport by intense electric field pulses, and local heating via wave-particle interactions. The recirculation model assumes that radial diffusion combined with pitch-angle scattering close to the ionosphere as well as in the equatorial plane can lead to inward motion and hence adiabatic energization of the electrons (Fujimoto and Nishida, 1990). The same adiabatic effects that lead to local reduction of the electron fluxes at storm onset can account for an increase during the storm recovery phase as the magnetospheric activity subsides and the inner magnetosphere recovers its quiet-time quasi-dipolar configuration. Substorm-associated injections transport both electrons and ions rapidly and non-adiabatically over a range of L-shells, which can lead to significant energization. If a suitable seed population of electrons with energies in the several hundred keV range is already present in the inner magnetosphere or near-magnetotail, this process can account for acceleration of electrons to the required MeV energies. Rostoker et al. (1998) proposed that long-duration elevated Pc 5 ultra-high frequency (ULF) wave activity can lead to inward transport and adiabatic heating of electrons whose drift frequency is in resonance with the pulsations. Finally, electrons can be heated by cyclotron resonance with whistler mode chorus waves outside the dusk-sector plasmapause (Summers et al., 1998). During any given storm, one or more of these processes may be active in producing the observed electron acceleration (Friedel et al., 2002).
Electron losses are similarly a combination of many processes (Koskinen, 2005): convective losses by electrons drifting to the dayside magnetopause are significant especially at storm onset when the magnetosphere is often rapidly compressed to almost half of its original size. Several wave modes interacting with the electrons at resonant energies can scatter them to the atmospheric loss cone hence leading to increased precipitation and loss of electrons from the magnetosphere. Plasmaspheric hiss is a wave mode confined within the plasmasphere, driven unstable by gyroresonant interaction with energetic electrons. Lightning-induced whistler modes or man-made very low frequency (VLF) signals in the inner magnetosphere interact strongly with relativistic electrons. Electromagnetic ion cyclotron (EMIC) waves in turn are excited near the duskside plasmapause as a result of cyclotron resonance with anisotropic ring current ions, and also interact with the van Allen belt electron population. Again, it is likely that more than one process is active in the inner magnetosphere during any given time.
Results presented in this section highlight the strong coupling between the different plasma and energetic particle populations in the inner magnetosphere: The magnetic field configuration is a key element in determining the adiabatic transport properties of both electrons and ions. The field configuration is determined by the large-scale current systems, in the inner magnetosphere mainly the ring current carried by energetic ions. Hence, the ring current ions affect the relativistic electron population through their influence on the field configuration and through their influence on wave development. Changes in the large-scale convection electric field change the plasmaspheric configuration thus changing the locations where the plasmaspheric hiss (in the nightside, inside the plasmapause), EMIC waves (in the dusk sector, inside the plasmapause), and whistler mode chorus waves (in the morning sector, outside the plasmapause) occur. As these wave modes are key elements for both acceleration and loss of the relativistic electrons, the plasmasphere and its dynamics driven by the large-scale convection electric field play a key role in the relativistic electron problem. Substorms are associated with inductive, localized electric fields, and are effective in transporting both electrons and ions to the inner magnetosphere. The rapid field variations provide a means for pitch-angle scattering as well as inward transport and adiabatic energization of the electrons. The substorm-associated energetic electrons can act as a seed population that, if further energized, can become part of the outer van Allen belt relativistic electron population. In summary, while the relativistic electrons themselves interact relatively weakly with the other plasma populations, it seems that resolving their temporal evolution requires detailed knowledge of the dynamics and coupling of as well the cold plasmasphere, hot ring current, tail plasma sheet as the electromagnetic fields guiding the particle motions.
8 Space Weather Effects
The dynamic processes associated with the solar wind-magnetosphere-ionosphere coupling processes can have significant effects in the near-Earth space environment, in the atmosphere, and on the Earth’s surface (Lanzerotti, 2001a). As our lives have become increasingly dependent on technological systems that are vulnerable to electromagnetic disturbances and bombardment by energetic electrons and ions, understanding these processes is important both for the design and maintenance of these systems. Figure 22 graphically illustrates the chain of events leading to space weather effects on ground.
8.1 Effects in the magnetosphere
High-energy ions trapped in the Earth’s magnetic field can cause significant effects in spacecraft systems. While malfunctions such as memory upsets can occur almost anywhere, a vast majority of the events are observed in the southern hemisphere over the South Atlantic Anomaly region where the Earth’s magnetic field is weakest and the energetic particles thus have best access to altitudes where the low-Earth-orbiting spacecraft reside (∼ 300–1000km altitude). Furthermore, the high energies above tens of MeV make galactic cosmic rays highly penetrating into the satellite systems, where they can cause a wide variety of harmful effects (Baker et al., 2001).
Solar energetic particles arising from active events on the Sun cause degradation and failure of space-borne systems. Especially, single event upsets can occur in electronic components when a charged particle (e.g., a heavy ion) ionizes a track along a sensitive part of the circuit and causes the circuit to change state. Single event upsets are commonly detected in transistors and spacecraft memory devices. Error-correcting software solutions have been developed to decrease the damages to the satellite operations.
High-energy electrons in the outer Van Allen radiation belts can penetrate through spacecraft walls and through electronics boxes and become buried in dielectric materials (Baker et al., 1987). The excess negative charge can give rise to potential differences, which in turn can lead to intense voltage discharges and surges of electric energy deep inside the electric circuits of the spacecraft causing severe damage to various subsystems. The discharges can produce short-lived (fractions of a microsecond) but intense (several Amperes) current pulses. As the anomalies tend to occur only during relatively long-duration events, it is not only the peak intensity of the electron flux but also the duration of the exposure that determines the amount of excess charge accumulation.
Moderate-energy electrons associated with substorms cause spacecraft surface charging (Garrett, 1981). During a surface charging event, insulated surfaces may charge to several kilovolts potential (typically negative relative to the ambient plasma). In hot, tenuous plasmas, the incident electrons and ions and the secondary photoelectrons and scattered electrons are not in current balance, which leads to potential buildup at the spacecraft. Differential charging of spacecraft surfaces can lead to harmful discharges, which introduce noise to the system and may interrupt normal spacecraft operations and/or represent false commands for the spacecraft. The discharge breakdown can cause physical damage which can change the satellite conductivity or thermal, chemical or optical properties.
Besides being a threat to technological systems, energetic particles pose a hazard to astronauts on space missions. The atmosphere effectively shields the Earth from high-energy particles such that only the highest-energy particles can gain access to the lower layers of the atmosphere, and only in the polar regions where the geomagnetic field is weakest. However, astronauts in orbit are relatively unprotected especially during the high-latitude parts of the spacecraft orbit. For example, the International Space Station reaches latitudes above 50°, which is sufficiently high to increase the health risks especially during extra-vehicular operations. Furthermore, as the atmospheric shielding is significantly reduced above 10 km altitude, aircraft crews and passengers on transpolar routes are subjected to increased radiation doses from the energetic particles. In practice, this problem is dealt with by limiting the number of transpolar flights the crewmembers can take in a given time period. As the fluxes of energetic particles are strongly modulated by the solar activity, these problems are largest during sunspot maxima.
8.2 Effects in the ionosphere
Satellite navigation systems such as the U.S. Global Positioning System (GPS) or the European Galileo operate by transmitting radio waves from the spacecraft to ground-based receivers. Signals from several satellites are then used to calculate the observing position to high accuracy. As the signals propagate through the ionosphere, they are refracted and slowed especially when they traverse regions of intense auroral currents. In addition, ionospheric scintillations can cause loss of signal lock and thereby lose the positioning capability. While many of the malfunctions associated with energetic particles can be counteracted by engineering the spacecraft with more shielding and redundancy in the systems, this is one where accurate specification of the ionospheric conditions and modeling their effects on the signal propagation is the only way the high accuracy of the positioning information can be maintained with single-frequency receivers.
The ionosphere is heavily utilized as a transmitter of radio-frequency communication signals. As every radio amateur knows, the radio wave communication is significantly influenced by the ionospheric properties and especially the auroral currents. High frequency (HF) radio wave communications are most affected, as they utilize reflection from the ionosphere to carry the signal to distances beyond the local horizon. At times of high auroral activity, the signal can be even completely absorbed making the HF radio propagation impossible. Furthermore, the telecommunication systems increasingly utilize ultra-high-frequency (UHF) bands to transmit signal to satellites to be relayed to other locations. Also this frequency range is vulnerable to the auroral currents in the ionosphere, and can be degraded or even completely lost during times of high activity (Lanzerotti, 2001b).
8.3 Effects in the atmosphere
Low-Earth-orbiting satellites are gradually slowed by the atmospheric drag, which finally leads to the spacecraft re-entry. The atmospheric drag depends on the atmospheric neutral density, which at a given altitude is strongly modulated by the heating and increase of the scale height associated with geomagnetic activity. The increasing atmospheric density during only a single storm can cause a major loss of altitude of the spacecraft. On a longer time scale, changes in the ionization caused by the solar UV radiation cause a significant solar cycle modulation on the neutral density (Hastings and Garret, 1996).
In the middle atmosphere, precipitating energetic particles can significantly affect the chemical processes that are involved in the formation of odd nitrogen compounds. Recent simultaneous observations of a strong increase of solar protons and the global NOx concentration in the atmosphere have clearly established the causal relationship between the solar proton events and the enhancement of odd nitrogen compounds. If sufficient downward transport is available, these nitrogen compounds can reach the stratospheric altitudes and through catalytic reaction chains to strong decrease of the stratospheric ozone Seppälä et al. (2006). The effects caused by these short-lived solar proton events can last for months in the atmosphere. Similarly, relativistic electrons from the magnetosphere affect the nitrogen chemistry at somewhat higher altitudes (50–100 km).
As the amount of energy from the Sun reaching the surface of the Earth is variable, it is only natural to expect that its long-term variations would affect the large-scale climatology of the Earth. The “solar constant” that averages to about 1368 W/m2 has been shown to exhibit a distinct solar cycle variation. The total solar irradiance also varies at 27-day intervals, the variability being larger during high solar activity than during solar minimum conditions. The ultraviolet part of the spectrum is also a strong modulator of the production of ozone, which is clearly demonstrated in the annual variation of the polar ozone holes which intensify during the local spring when the amount of UV radiation increases.
Any change in the balance between incident and outgoing radiation can have an effect on the climate. Changes in the incoming energy may be associated with changes in cloudiness, amount of volcanic dust in the atmosphere, and amounts of either natural or anthropogenic origin aerosols. Changes in the amount of energy radiated away from Earth can be associated with the varying amounts of greenhouse gases in the atmosphere such as carbon dioxide, methane, CFCs, or ozone. The surface properties are also important for the reflected radiation, as the albedos for ice cover, vegetation, and soil are quite different.
There is experimental evidence that the global temperature variations are correlated with a number of space physic parameters: the long term temperature anomaly follows the filtered solar cycle length, which is a measure of the intensity of the solar cycle (Friis-Christensen and Lassen, 1991). The global cloud coverage anomalies are correlated with the mean values of the galactic cosmic ray flux, which is modulated by the solar cycle as the stronger solar wind pressure during solar maximum tends to decrease the amount of anomalous cosmic rays that can reach the inner solar system (Marsh and Svensmark, 2000).
While statistical studies have found strong correlations of solar activity parameters and climatological parameters, the reasons for these changes are not fully understood. Furthermore, it is probable that several different processes influence the observed correlations. The effects of the varying total solar irradiance are too small to be of major importance for the climate change. The correlation of cosmic rays on only low-altitude cloud cover suggests that the cosmic rays may influence the formation of aerosols and through that the abundance of condensation nuclei in the atmosphere which can form liquid water drops. At ground level, the cosmic ray particles cause ionization, and the associated vertical electric currents can influence the production of ice-forming nuclei and clouds in the upper troposphere. These effects might be related to local decreases in the amount of cloud cover associated with short-term changes in the cosmic rays due to increased solar activity.
8.4 Effects on ground
Space weather effects are seen even on ground, as strong currents in the ionosphere can induce currents in long baseline conductor systems on ground. Affected systems include electric power transmission networks, oil and gas pipelines, telecommunication cables and railways systems. In power grids, these geomagnetically induced currents cause saturation of transformers, which tends to distort and increase the excitation current. The excitation current in turn induces harmonics in the electricity, unwanted relay trippings, large reactive power consumption, or voltage fluctuations, which can lead to black-outs or to permanent damage of transformers (Kappenman, 1996).
In buried pipelines, geomagnetically induced currents and the associated pipe-to-soil voltages contribute to corrosion and disturb corrosion control surveys and protection systems (Boteler, 2000). Telecommunication devices may experience overvoltages. As optical fibre cables do not carry induced currents, space weather risks on telecommunication equipment are probably smaller today than they were earlier. However, metal wires are still used in parallel with optical cables for the power to repeat stations.
The first observations of space weather-associated induced currents were made already in early telegraph systems more than 150 years ago (Boteler et al., 1998). In general, being related to auroral phenomena, the geomagnetically induced currents are a high-latitude problem, affecting most regions such as the Scandinavian countries, Russia, and Canada. The amount of induced current in a system is not directly related to the distance to the auroral currents; the ground resistivity and the particular network configuration and its resistances have an important contribution in determining the size of the disturbance. This makes the observed induced current values highly variable from site to site and from system to system. The current magnitudes that are a potential risk for a power transmission system are highly dependent on transformer design and on other engineering details of the network. This means that any space weather hazard assessment must include the details of the engineering solutions in the estimates.
9 Space Weather Predictions
Electron radiation belt climatology has shown that the entire outer radiation zone tends to vary in a relatively coherent way under the influece of major external drivers (high-speed solar wind streams, CMEs, magnetic clouds). Thus, it is possible to use the gross behavior of the outer zone electron population on day timescales using a single or a few satellites only. Specification models that use magnetic activity indices can be used to characterize the state of the outer radiation belt (Moorer and Baker, 2001). Prediction schemes have been developed based on a combination of earlier values of radiation belt fluxes, and past and present solar wind parameters. When these conditions are compared against a database of earlier driver-effect events, the closest comparison event can be used as a forecast of what lies 24–48 hours ahead. Because both past radiation belt and solar wind driver information is used, this analogue forecast method is robustly successful for both quiet and disturbed conditions.
Coronal mass ejection occurrence is routinely recorded and their travel direction determined from solar coronagraph data. Space weather warnings are given for those ICME events that propagate in a direction that probably will lead to encounter with the Earth’s space environment. However, the effects in the near-Earth environment critically depend on the polarity of the magnetic cloud, i.e., whether the magnetic field rotates from north to south or vice versa. From solar observations alone, it is impossible to detect either the solar wind speed in interplanetary space (which is different from the speed near the solar surface) or the structure of the magnetic field and hence the intensity and duration of the geoeffective southward field direction. However, the polarity of the ICME structure shows a statistical dependence on the solar cycle: the preferred leading polarity rotating from south to north is observed during the rising phase of odd-numbered solar cycles, while the opposite polarity is observed during the rising phase of even-numbered cycles (Bothmer and Rust, 1997). Details of the storm intensity can only be predicted when the ICME has propagated to L1 distance (First Lagrangian point at 220 RE upwind from the Earth) where the solar wind monitors (presently SOHO and ACE) record the polarity and intensity of the interplanetary magnetic field and the velocity and density structure of the solar wind plasma. Thus, more detailed predictions of ICMEs as well as any predictions of activity driven by other solar wind and IMF structures not observable by means other than in-situ measurements are available only 30–60 minutes prior to its arrival at Earth.
As the energetic solar particles travel to the Earth within a few tens of minutes, detection of active events in the Sun means an almost instantaneous response at Earth. Solar X-ray monitors routinely monitor the Earth’s environment providing nowcasts of the space environment.
Longer-term space weather predictions can only be given if we obtain observations from a vantage point that allows us to monitor also the face of the Sun not visible from Earth. While future missions such as NASA’s STEREO will obtain a view of the far side of the Sun as well as much improved geometry for ICME detection near the Sun (viewing the propagation sideways rather than face-on), the SWAN instrument onboard ESA’s SOHO spacecraft is already providing first hints of activity on the far side of the Sun. Figure 23 shows two maps of Lyman α intensity over the full sky. The left panels show the hemisphere in the direction of the Sun, thus reflecting activity on the far side of the Sun. The middle panels show the hemisphere in the antisunward direction, which is where activity from the disk visible from the Earth (and SOHO) would propagate. During the first time period (top row), the front side of the Sun shows an active region, which lights up the emissions coming from the antisunward direction (top middle frame). On the other hand, the emissions associated with coronal activity shown in the second time period (bottom row) clearly light up the sky in Lyman a measurements (bottom middle frame). From these correlations it can be deduced that during the first time period there were no active regions in the far side of the Sun (top left frame), while there was an active region during the second time period (bottom left frame). The latter was indeed verified as the active region rotated with the Sun to be visible from the Earth. While this method is not accurate enough to provide sufficiently detailed predictions at Earth orbit, it is a good demonstration of the possibilities that we have for long-term (2-week) predictions in the future.
Measurements of the Lyman-α intensity of the entire sky during two days. The left and middle panels show the Lα intensity over the entire sky in two different look directions, while the right panels show images of the Sun. Left panels: SWAN full-sky Lα image showing the celestial hemisphere in the direction of the Sun. Middle panels: SWAN full-sky Lα image showing the celestial hemisphere in the direction away from the Sun. Right panels: EIT image in the EUV wavelength. The top row shows a time period when there was a bright activation on the solar surface. Consequently, the anti-sunward side hemisphere, which is illuminated by the Sun as viewed from EIT, shows a brightening. The bottom panel shows a day when there were no activations on the visible solar surface, and consequently the anti-sunward hemisphere is in darkness. On the other hand, the sunward hemisphere shows a brightening, which is taken as an indicator of a bright spot on the far side of the Sun. This was verified as the bright spot became visible a few days later (from Bertaux et al., 2000).
10 Concluding Remarks
This review presents the physical basics for understanding why and how solar activity affects technological systems and humans in space and on ground. The final goal of space weather research is to be able to produce reliable forecasts and nowcasts of the space environment as well as assess the risks that are associated with a wide variety of technological applications. While tremendous progress has been made during the recent years, the field still faces several major challenges.
Observations of the near-Earth space environment are sparse and information of the global properties are often not available, as the plasmas for the most part are too tenuous for imaging. Beginning from the solar wind observations, a single point measurement in the solar wind, sometimes far away from the Sun-Earth line, is not always sufficient to determine what impinges on the magnetopause an hour later. In the magnetosphere, the lack of global observations of the mass and energy circulation as well as the dynamics of the electromagnetic fields still limit our capabilities to evaluate the variety of physical processes that can be associated with the observed phenomena. On the ground, the largest and most harmful currents are highly localized, which makes their detection as well as prediction challenging. In many instances, the magnetospheric activity can be quantitatively classified only based on a variety of magnetic indices and proxies derived using the solar wind input and the magnetic indices. It is clear that such proxies include both systematic and statistical errors, which limits our capability to establish causal correlations.
Large-scale or global models of the coupled solar wind-magnetosphere-ionosphere system have advanced greatly in the recent past, both due to better understanding of the critical processes and due to the increased computational capabilities. Global MHD simulations can be run in near-real time, and in many cases reproduce the observed topological changes and even in-situ measurements to quite good accuracy. On the other hand, their use still has serious limitations, both due to missing physics especially in the ionosphere and in the inner magnetosphere, and due to the limitations of the MHD approach in describing the collisionless, multicomponent plasmas in the magnetosphere. While hybrid codes describing the full ion motion while treating the electrons as a fluid already are available for our sister planets, the strong magnetic field and the large system size still limits that approach to localized problems in the terrestrial magnetosphere.
For prediction of the hazards, it is important to note that the effects are dependent both on the space environment and on the engineering and operations of the technological system, be that a telecommunication satellite or a power transmission line on ground. Warnings and predictions can be effectively used to schedule non-standard or maintenance operations during periods of low solar activity, while better shielding and other design improvements are key for successful operations and long lifetime of the systems. To reach these goals requires close contacts between space physics and engineering sciences.
References
Ahn, B.-H., Akasofu, S.-I., Kamide, Y., 1983, “The Joule heat production rate and the particle energy injection rate as a function of the geomagnetic indices AE and AL”, J. Geophys. Res., 88, 6275–6287
Akasofu, S.-I., 1981, “Energy coupling between the solar wind and the magnetosphere”, Space Sci. Rev., 28, 121–190. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1981SSRv...28..121A
Alves, M.V., Echer, E., Gonzalez, W.D., 2006, “Geoeffectiveness of corotating interaction regions as measured by Dst index”, J. Geophys. Res., 111
Axford, W.I., Hines, C.O., 1961, “A unifying theory of high-latitude geophysical phenomena and geomagnetic storms”, Can. J. Phys., 39, 1433
Baker, D.N., 2000, “The occurrence of operational anomalies in spacecraft and their relationship to space weather”, IEEE Trans. Plasma Sci., 28, 2007–2016
Baker, D.N., Belian, R.D., Higbie, P.R., Klebesadel, R.W., Blake, J.B., 1987, “Deep dielectric charging effects due to high energy electrons in Earth’s outer magnetosphere”, J. Electrost., 20, 3
Baker, D.N., Pulkkinen, T.I., Angelopoulos, V., Baumjohann, W., McPherron, R.L., 1996, “The neutral line model of substorms: Past results and present view”, J. Geophys. Res., 101, 12,975
Baker, D.N., Kanekal, S.G., Blake, J.B., Pulkkinen, T.I., 2001, “The global efficiency of relativistic electron production in the Earth’s magnetosphere”, J. Geophys. Res., 106, 19,169
Baumjohann, W., 1993, “The near-Earth plasma sheet: An AMPTE/IRM perspective”, Space Sci. Rev., 64, 141–163. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1993SSRv...64..141B
Baumjohann, W., Pellinen, R.J., Opgenoorth, H.J., Nielsen, E., 1981, “Joint two-dimensional observations of ground magnetic and ionospheric electric fields associated with auroral zone currents: Current systems associated with local auroral break-ups”, Planet. Space Sci., 29, 431. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1981P7.26SS...29..431B
Bertaux, J.-L., Texier, H. Le, Goutail, F., Lallement, R., Kockarts, G., 1989, “Lyman alpha observations of geocoronal and interplanetary hydrogen from Spacelab-1: Exospheric temperature and density and hot emission”, Ann. Geophys., 7, 549–564
Bertaux, J.-L., Quemerais, E. and Lallement, R., Lamassoure, E., Schmidt, W., Kyrölä, E., 2000, “Monitoring solar activity on the far side of the Sun from sky reflected Lyman α radiation”, Geophys. Res. Lett., 27(9), 1331–1334
Blake, J.B., Baker, D.N., Turner, N., Ogilvie, K.W., Lepping, R.P., 1997, “Correlation of changes in the outer-zone relativistic electron population with upstream solar wind and magnetic field measurements”, Geophys. Res. Lett., 24, 927–929
Borovsky, J.E., Denton, M.H., 2006, “Differences between CME-driven storms and CIR-driven storms”, J. Geophys. Res., 111, A07S08
Boteler, D.H., 2000, “Geomagnetic effects on pipe-to-soil potentials of a continental pipeline”, Adv. Space Res., 26, 15–20. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/2000AdSpR..26...15B
Boteler, D.H., Pirjola, R.J., Nevanlinna, H., 1998, “The effects of geomagnetic disturbances on electrical systems at the earth’s surface”, Adv. Space Res., 26, 17–27. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1998AdSpR..22...17B
Bothmer, V., Rust, D.M., 1997, “The field configuration of magnetic clouds and the solar cycle”, in Coronal Mass Ejections, (Eds.) Crooker, N., Joselyn, J.A., Feynman, J., vol. 99 of Geophysical Monograph, pp. 137–146, American Geophysical Union, Washington, U.S.A.
Bothmer, V., Schwenn, R., 1998, “The structure and origin of magnetic clouds in the solar wind”, Ann. Geophys., 16, 1–24
Boyle, C.B., Reiff, P.H., Hairston, M.R., 1997, “Empirical polar cap potentials”, J. Geophys. Res., 102, 111–125
Burch, J.L., 2000, “IMAGE mission overview”, Space Sci. Rev., 91, 1–14
Burch, J.L., Mende, S.B., Mitchell, D.G., Moore, T.E., Pollock, C.J., Reinisch, B.W., Sandel, B.R., Fuselier, S.A., Gallagher, D.L., Green, J.L., Perez, J.D., Reiff, P.H., 2001, “Views of Earth’s Magnetosphere with the IMAGE Satellite”, Science, 291, 619–624
Burton, R.K., McPherron, R.L., Russell, C.T., 1975, “An empirical relationship between interplanetary conditions and Dst”, J. Geophys. Res., 80, 4204–4214
Chamberlain, J.W., 1963, “Planetary coronae and atmospheric evaporation”, Planet. Space Sci., 11, 901–960. Related online version (cited on 9 Janury 2007): http://adsabs.harvard.edu/abs/1963P7.26SS...11..901C
Crooker, N.U., Gosling, J.T., Bothmer, V., Forsyth, R.J., Gazis, P.R., Hewish, A., Horbury, T.S., Intriligator, D.S., Jokipii, J.R., Kota, J., Lazarus, A.J., Lee, M.A.1, Lucek, E., Marsch, E., Posner, A., Richardson, I.G., Roelof, E.C., Schmidt, J.M., Siscoe, G.L., Tsurutani, B.T., Wimmer-Schweingruber, R.F., 1999, “CIR Morphology, Turbulence, Discontinuities, and Energetic Particles”, Space Sci. Rev., 89, 179–220
Daglis, I.A., 1997, “The role of magnetosphere-ionosphere coupling in magnetic storm dynamics”, in Magnetic Storms, (Eds.) Tsurutani, B.T., Gonzalez, W.D., Kamide, Y., Arballo, J.K., vol. 98 of Geophysical Monograph, p. 107, American Geophysical Union, Washington, U.S.A.
Daglis, I.A., Kamide, Y., 2003, “The role of magnetosphere-ionosphere coupling in magnetic storm dynamics”, in Disturbances in Geospace: The Storm-Substorm Relationship, (Eds.) Sharma, A.S., Kamide, Y., Lakhina, G.S., vol. 142 of Geophysical Monograph, pp. 119–129, American Geophysical Union, Washington, U.S.A.
Daglis, I.A., Thorne, R.M., Baumjohann, W., Orsini, S., 1999, “The terrestrial ring current: Origin, formation, and decay”, Rev. Geophys., 37, 407–438. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1999RvGeo..37..407D
Dungey, J.W., 1961, “Interplanetary magnetic field and the auroral zones”, Phys. Rev. Lett., 6, 47–48. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1961PhRvL...6...47D
Ebihara, Y., Ejiri, M., 2003, “Numerical simulation of the ring current: Review”, Space Sci. Rev., 105, 377–452
Elphic, R.C., Weiss, L.A., Thomsen, M.F., McComas, D.J., Moldwin, M.B., 1996, “Evolution of plasmaspheric ions at geosynchronous orbit during times of high geomagnetic activity”, Geophys. Res. Lett., 23, 2189–2192
Elphic, R.C., Thomsen, M.F., Borovsky, J.E., 1997, “The fate of the outer plasmasphere”, Geophys. Res. Lett., 24, 365
Elphinstone, R.D., Hearn, D.J., Murphree, J.S., Cogger, L.L., 1993, “The auroral distribution and its mapping according to substorm phase”, J. Atmos. Terr. Phys., 55, 1741
Escoubet, C.P., Fehringer, M., Goldstein, M., 2001, “The Cluster mission”, Ann. Geophys., 19, 1197–1200
Farrugia, C.J., Burlaga, L.F., Lepping, R.P., 1997, “Magnetic clouds and the quiet-storm effect at Earth”, in Magnetic Storms, (Eds.) Tsurutani, B.T., Gonzalez, W.D., Kamide, Y., Arballo, J.K., vol. 98 of Geophysical Monograph, pp. 91–106, American Geophysical Union, Washington, U.S.A.
Fok, M.-C., Moore, T.E., Kozyra, J.U., Ho, G.C., Hamilton, D.C., 1995, “Three-dimensional ring current decay model”, J. Geophys. Res., 100, 9619–9632
Fok, M.-C., Moore, T.E., Wilson, G.R., Perez, J.D., Zhang, X.X., Brandt, P.C., Mitchell, D.G., Roelof, E.C., Jahn, J.-M., Pollock, C.J., Wolf, R.A., 2003, “Global ENA IMAGE simulations”, Space Sci. Rev., 109, 77–103. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/2003SSRv..109...77F
Friedel, R.H.W., Reeves, G.D., Obara, T., 2002, “Electron dynamics in the inner magnetosphere: A review”, J. Atmos. Sol.-Terr. Phys., 64, 265–282
Friis-Christensen, E., Lassen, K., 1991, “Length of the solar cycle: an indicator of solar activity closely associated with climate”, Science, 254, 698–700
Fujimoto, M., Nishida, A., 1990, “Energization and anisotropization of energetic electrons in the Earth’s radiation belt by the recirculation process”, J. Geophys. Res., 95, 4265–4270
Ganushkina, N.Y., Pulkkinen, T.I., Kubyshkina, M.V., Singer, H.J., Russell, C.T., 2004, “Longterm evolution of magnetospheric current systems during storm periods”, Ann. Geophys., 22, 1317–1334
Ganushkina, N.Y., Pulkkinen, T.I., Fritz, T., 2005, “Role of substorm-associated impulsive electric fields in the ring current development during storms”, Ann. Geophys., 23, 579–591
Garrett, H.B., 1981, “The charging of spacecraft surfaces”, Rev. Geophys., 19, 577
Goldstein, J., Spasojevic, M., Reiff, P.H., Sandel, B.R., Forrester, W.T., Gallgher, D.L., Reinisch, B.W., 2003, “Identifying the plasmapause in IMAGE EUV data using IMAGE RPI in situ steep density gradients”, J. Geophys. Res., 108, 1147
Gombosi, T.I., De Zeeuw, D.L., Groth, C.P.T., Powell, K.G., 2000, “Magnetospheric configuration for Parker-spiral IMF conditions: Results of a 3D AMR MHD simulation”, Adv. Space Res., 26, 139–149. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/2000AdSpR..26..139G
Gonzalez, W.D., Joselyn, J.A., Kamide, Y., Kroehl, H.W., Rostoker, G., Tsurutani, B.T., Vasyliunas, V.M., 1994, “What is a geomagnetic storm?”, J. Geophys. Res., 99, 5771
Grebovsky, J.M., 1970, “Model study of plasmapause motion”, J. Geophys. Res., 75, 4329–4334
Hakkinen, L.V.T., Pulkkinen, T.I., Nevanlinna, H., Pirjola, R.J., Tanskanen, E.I., 2002, “Effects of induced currents on Dst and on magnetic variations at mid-latitude stations”, J. Geophys. Res., 107, 1014
Hastings, D.E., Garret, H., 1996, Spacecraft-Environment Interactions, Cambridge Atmospheric and Space Science Series, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Heelis, R.A., Lowell, J.K., Spiro, R.W., 1982, “A model of the high-latitude ionospheric convection pattern”, J. Geophys. Res., 87, 6339–6345
Henderson, M.G., Reeves, G.D., Skoug, R.M., Thomsen, M.F., Denton, M.H., Mende, S.B., Immel, T.J., Brandt, P.C., Singer, H.J., 2006, “Magnetospheric and auroral activity during the April 18, 2002 Sawtooth Event”, J. Geophys. Res., 111, A01S90
Hones Jr, E.W., 1979, “Plasma flow in the magnetotail and its implications for substorm theories”, in Dynamics of the magnetosphere, (Ed.) Akasofu, S.-I., Proceedings of the A.G.U. Chapman Conference ‘Magnetospheric Substorms and Related Plasma Processes’, held at Los Alamos Scientific Laboratory, Los Alamos, N.M., U.S.A., October 9–13, 1978, vol. 78 of Astrophysics and Space Science Library, pp. 545–562, D. Reidel, Dordrecht, Netherlands; Boston, U.S.A.
Hudson, M.K., Kress, B.T., Mazur, J.E., Perry, K.L., Slocum, P.L., 2004, “3D modeling of shock-induced trapping of solar energetic particles in the Earth’s magnetosphere”, J. Atmos. Terr. Phys., 66, 1389–1397
Hundhausen, A.J., 1972, Coronal Expansion and Solar Wind, vol. 5 of Physics and Chemistry in Space, Springer, Berlin, Germany; New York, U.S.A.
Huttunen, K.E.J., Koskinen, H.E.J., 2004, “Importance of post-shock streams and sheath region as drivers of intense magnetospheric storms and high-latitude activity”, Ann. Geophys., 22, 1729–1738
Huttunen, K.E.J., Koskinen, H.E.J., Pulkkinen, T.I., Pulkkinen, A.A., Palmroth, M., Reeves, G.D., Singer, H.J., 2002, “April 2000 magnetic storm: Solar wind driver and magnetospheric response”, J. Geophys. Res., 107, 1440
Ieda, A., Machida, S., Mukai, T., Saito, Y., Yamamoto, T., Nishida, A., Terasawa, T., Kokubun, S., 1998, “Statistical analysis of the plasmoid evolution with Geotail observations”, J. Geophys. Res., 103, 4453
Iijima, T., Potemra, T.A., 1976, “The amplitude distribution of field aligned currents at northern high latitudes observed by Triad”, J. Geophys. Res., 81, 2165
Janhunen, P., 1996, “GUMICS-3: A global ionosphere-magnetosphere coupling simulation with high ionospheric resolution”, in Environment Modelling for Space-based Applications, (Eds.) Hilgers, A., Guyenne, T.-D., Proceedings of the symposium held at ESTEC, Noordwijk, 18–20 September 1996, vol. SP-392 of ESA Conference Proceedings, p. 233, ESA Publications Division, Nordwijk, Netherlands. Related online version (cited on 8 January 2007): http://www.ava.fmi.fi/~pjanhune/papers/ESTEC96/ESTEC96.html
Jordanova, V.K., Kistler, L.M., Farrugia, C.J., Torbert, R.B., 2001, “Effects of inner magnetospheric convection on ring current dynamics: March 10–12, 1998”, J. Geophys. Res., 106, 29,705
Kappenman, J.G., 1996, “Geomagnetic Storms and Their Impact on Power Systems”, IEEE Power Eng. Rev., 16, 5–8
Killen, R.M., Potter, A.E., Reiff, P., Sarantos, M., Jackson, B.V., Hick, P., Giles, B., 2001, “Evidence for space weather at Mercury”, J. Geophys. Res., 106, 20,509–20,526
Koskinen, H.E.J., 2005, “Energetic particle losses from the inner magnetosphere”, in The Inner Magnetosphere: Physics and Modeling, (Eds.) Pulkkinen, T.I., Tsyganenko, N.A., Friedel, R.H.W., vol. 155 of Geophysical Monograph, pp. 23–31, American Geophysical Union, Washington, U.S.A.
Koskinen, H.E.J., Tanskanen, E.I., 2002, “Magnetospheric energy budget and the epsilon parameter”, J. Geophys. Res., 107, 1415
Laitinen, T.V., Pulkkinen, T.I., Palmroth, M., Janhunen, P., Koskinen, H.E.J., 2005, “The magnetotail reconnection region in a global MHD simulation”, Ann. Geophys., 23, 3753
Laitinen, T.V., Janhunen, P., Pulkkinen, T.I., Palmroth, M., Koskinen, H.E.J., 2006, “On the characterization of magnetic reconnection in MHD simulations”, Ann. Geophys., 24, 3059–3069
Lanzerotti, L.J., 2001a, “Space weather effects on technologies”, in Space Weather, (Eds.) Song, P., Singer, H.J., Siscoe, G.L., p. 11, American Geophysical Union, Washington, U.S.A.
Lanzerotti, L.J., 2001b, “Space Weather Effects on Communications”, in Space Storms and Space Weather Hazards, (Ed.) Daglis, I.A., Proceedings of the NATO Advanced Study Institute, Greece 19–29 June, 2000, vol. 38 of NATO Science Series II, pp. 313–334, Kluwer, Dordrecht, Netherlands; Boston, U.S.A.
Lean, J., 1991, “Variations in the Sun’s radiative output”, Rev. Geophys., 29, 505–535
Li, X., Baker, D.N., Temerin, M., Reeves, G.D., Belian, R.D., 1998, “Simulation of dispersionless injections and drift echoes of energetic electrons associated with substorms”, Geophys. Res. Lett., 25, 3763–3766
Li, X., Baker, D.N., Kanekal, S.G., Looper, M., Temerin, M., 2001, “Long term measurements of radiation belts by SAMPEX and their variations”, Geophys. Res. Lett., 28, 3827–3830
Liemohn, M.W., Kozyra, J.U., Thomsen, M.F., Roeder, J.L., Lu, G., Borovsky, J.E., Cayton, T.E., 2001, “Dominant role of the asymmetric ring current in producing the stormtime Dst”, J. Geophys. Res., 106, 10,883–10,904
Lui, A.T.Y., Anger, C.D., 1973, “A uniform belt of diffuse auroral emission seen by the ISIS-2 scanning photometer”, Planet. Space Sci., 21, 799–802. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1973P726SS...21..799L
Lundin, R., Barabash, S., Andersson, H., Holmstrom, M., Grigoriev, A., Yamauchi, M., Sauvaud, J.-A., Fedorov, A., Budnik, E., Thocaven, J.-J., Winningham, D., Frahm, R., Scherrer, J., Sharber, J., Asamura, K., Hayakawa, H., Coates, A., Linder, D.R., Curtis, C., Hsieh, K.C., Sandel, B.R., Grande, M., Carter, M., Reading, D.H., Koskinen, H.E.J., Kallio, E., Riihela, P., Schmidt, W., Sales, T., Kozyra, J., Krupp, N., Woch, J., Luhmann, J., McKenna-Lawler, S., Cerulli-Irelli, R., Orsini, S., Maggi, M., Mura, A., Milillo, A., Roelof, E.C., Williams, D.J., Livi, S., Brandt, P.C., Wurz, P., Bochsler, P., 2001, “Solar Wind-Induced Atmospheric Erosion at Mars: First Results from ASPERA-3 on Mars Express”, Science, 305, 1933–1936
Lyon, J.G., Fedder, J.A., Mobarry, C.M., 2004, “The Lyon-Fedder-Mobarry (LFM) global MHD magnetospheric simulation code”, J. Atmos. Sol.-Terr. Phys., 66, 1333
Lyons, L.R., Williams, D.J., 1984, Quantitative Aspects of Magnetospheric Physics, Geophysics and Astrophysics Monographs, D. Reidel, Dordrecht, Netherlands; Boston, U.S.A.
Manchester IV, W.B., Gombosi, T.I., Roussev, I., Ridley, A., De Zeeuw, D.L., Sokolov, I.V., Powell, K.G., Toth, G., 2004, “Modeling a space weather event from the Sun to the Earth: CME generation and interplanetary propagation”, J. Geophys. Res., 109
Marsh, N.D., Svensmark, H., 2000, “Low Cloud Properties Influenced by Cosmic Rays”, Phys. Rev. Lett., 85, 5004–5007. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/2000PhRvL..85.5004M
Maynard, N.C., Chen, A.J., 1975, “Isolated cold plasma regions: Observations and their relation to possible production mechanisms”, J. Geophys. Res., 80, 1009–1013
McPherron, R.L., 1970, “Growth phase of magnetospheric substorms”, J. Geophys. Res., 75, 5592
McPherron, R.L., 1997, “The role of substorms in generation of magnetic storms”, in Magnetic Storms, (Eds.) Tsurutani, B.T., Gonzalez, W.D., Kamide, Y., Arballo, J.K., vol. 98 of Geophysical Monograph, p. 131, American Geophysical Union, Washington, U.S.A.
McPherron, R.L., Russell, C.T., Aubry, M.P., 1973, “Satellite studies of magnetospheric substorms on August 15, 1968”, J. Geophys. Res., 78, 3131
Meredith, N.P., Horne, R.B., Glauert, S.A., Thorne, R.M., Summers, D., Albert, J.M., Anderson, R.R., 2006, “Energetic outer zone electron loss timescales during low geomagnetic activity”, J. Geophys. Res., 111
Moldwin, M.B., Mayerberger, S., Rassoul, H.K., Barnicki, T., Anderson, R.R., 2003, “Plasmapause response to geomagnetic storms: CRRES results”, J. Geophys. Res., 108, 1399
Moorer, D.R., Baker, D.N., 2001, “Specification of Energetic Magnetospheric Electrons”, in Space Weather, (Eds.) Song, P., Singer, H.J., Siscoe, G.L., vol. 125 of Geophysical Monograph, pp. 3321–328, American Geophysical Union, Washington, U.S.A.
Nagai, T., Fujimoto, M., Nakamura, R., Baumjohann, W., Ieda, A., Shinohara, I., Machida, S., Saito, Y., Mukai, T., 2005, “Solar wind control of the radial distance of the magnetic reconnection site in the magnetotail”, J. Geophys. Res., 110
O’Brien, T.P., McPherron, R.L., 2000, “An empirical phase space analysis of ring current dynamics: Solar wind control of injection and decay”, J. Geophys. Res., 105, 7707
O’Brien, T.P., McPherron, R.L., Sornette, D., Reeves, G.D., Friedel, R.H.W., Singer, H.J., 2001, “Which magnetic storms produce relativistic electrons at geosynchronous orbit?”, J. Geophys. Res., 106, 15,533–15,544
Ohtani, S., Nose, M., Rostoker, G., Singer, H.J., Lui, A.T.Y., Nakamura, M., 2001, “Storm-substorm relationship: Contribution of the tail current to Dst”, J. Geophys. Res., 106, 21,199–21,209
Østgaard, N.R., Vondrak, R., Gjerloev, J.W., Germany, G.A., 2002, “A relation between the energy deposition by electron precipitation and geomagnetic indices during substorms”, J. Geophys. Res., 107, 1246
Palmroth, M., Pulkkinen, T.I., Janhunen, P., Wu, C.-C., 2003, “Stormtime energy transfer in global MHD simulation”, J. Geophys. Res., 108, 1048
Palmroth, M., Pulkkinen, T.I., Janhunen, P., McComas, D.J., Smith, C.W., Koskinen, H.E.J., 2004, “Role of solar wind dynamic pressure in driving ionospheric Joule heating”, J. Geophys. Res., 109
Papadopoulos, K., Goodrich, C., Wiltberger, M., Lopez, R.E., Lyon, J.G., 1999, “The physics of substorms as revealed by the ISTP”, Phys. Chem. Earth, 24, 189–202
Paschmann, G., 1997, “Observational Evidence for Transfer of Plasma Across the Magnetopause”, Space Sci. Rev., 80, 217–234
Paulikas, G.A., Blake, J.B., 1979, “Effects of the solar wind on magnetospheric dynamics: Energetic electrons at the synchronous orbit”, in Quantitative modeling of magnetospheric processes, (Ed.) Olson, W.P., vol. 21 of Geophysical Monograph, pp. 180–202, American Geophysical Union, Washington, U.S.A.
Perreault, P., Akasofu, S.-I., 1978, “A study of geomagnetic storms”, Geophys. J. R. Astron. Soc., 54, 547–573
Pulkkinen, A.A., Thomson, A., Clarke, E., McKay, A., 2003, “April 2000 geomagnetic storm: ionospheric drivers of large geomagnetically induced currents”, Ann. Geophys., 21, 709–717
Pulkkinen, T.I., Wiltberger, M., 2000, “Thin Current Sheet Evolution as seen in Observations, Empirical Models and MHD Simulations”, Geophys. Res. Lett., 27, 1363
Pulkkinen, T.I., Baker, D.N., Pellinen, R.J., Buächner, J., Koskinen, H.E.J., Lopez, R.E., Dyson, R.L., Frank, L.A., 1992, “Particle scattering and current sheet stability in the geomagnetic tail during the substorm growth phase”, J. Geophys. Res., 97, 19,283
Pulkkinen, T.I., Ganushkina, N.Y., Tanskanen, E.I., Kubyshkina, M.V., Reeves, G.D., Thomsen, M.F., Russell, C.T., Singer, H.J., Slavin, J.A., Gjerloev, J.W., 2006, “Magnetospheric current systems during stormtime sawtooth events”, J. Geophys. Res., 111
Raeder, J., Walker, R.J., Ashour-Abdalla, M., 1995, “The structure of the distant geomagnetic tail during long periods of northward IMF”, Geophys. Res. Lett., 22, 349
Raeder, J., Wang, Y.L., Fuller-Rowell, T.J., Singer, H.J., 2001, “Global Simulation of Magnetospheric Space Weather Effects of the Bastille Day Storm”, Solar Phys., 204, 323–337. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/2001SoPh..204..323R
Reeves, G.D., 1998, “Relativistic electrons and magnetic storms: 1992–1995”, Geophys. Res. Lett., 25, 1817–1820
Reeves, G.D., McAdams, K.L., Friedel, R.H.W., O’Brien, T.P., 2003, “Acceleration and loss of relativistic electrons during geomagnetic storms”, Geophys. Res. Lett., 30, 1529
Roederer, J.G., 1970, Dynamics of Geomagnetically Trapped Radiation, vol. 2 of Physics and Chemistry in Space, Springer, Berlin, Germany; New York, U.S.A.
Rostoker, G., Scone, S., Baker, D.N., 1998, “On the origin of relativistic electrons in the magnetosphere associated with some geomagnetic storms”, Geophys. Res. Lett., 25, 3701
Runov, A., Sergeev, V.A., Nakamura, R., Baumjohann, W., Apatenkov, S., Asano, Y., Takada, T., Volwerk, M., Voros, Z., Zhang, T.L., Sauvaud, J.-A., Reme, H., Balogh, A., 2006, “Local structure of the magnetotail current sheet: 2001 Cluster observations”, Ann. Geophys., 24, 247–262
Russell, C.T., McPherron, R.L., 1973, “Semiannual variation of geomagnetic activity”, J. Geophys. Res., 78, 92
Sarris, T.E., Li, X., Tsaggas, N., Paschalidis, N., 2002, “Modeling energetic particle injections in dynamic pulse fields with varying propagation speeds”, J. Geophys. Res., 107, 1033
Schwenn, R., 1990, “Large-Scale Structure of the Interplanetary Medium”, in Physics of the Inner Heliosphere, Vol. I: Large-Scale Phenomena, (Eds.) Schwenn, R., Marsch, E., vol. 20 of Physics and Chemistry in Space, pp. 99–181, Springer, Berlin, Germany; New York, U.S.A.
Schwenn, R., 2006, “Space Weather: The Solar Perspective”, Living Rev. Solar Phys., 3, lrsp-2006-2. URL (cited on 8 January 2007): http://www.livingreviews.org/lrsp-2006-2
Seppälä, A., Verronen, P.T., Sofieva, V.F., Tamminen, J., Kyrola, E., Rodger, C.J., Clilverd, M.A., 2006, “Destruction of the tertiary ozone maximum during a solar proton event”, Geophys. Res. Lett., 33
Sergeev, V.A., Mitchell, D.G., Russell, C.T., Williams, D.J., 1993, “Structure of the tail plasma/current sheet at ∼ 11RE and its changes in the course of a substorm”, J. Geophys. Res., 98, 17,345–17,366
Sergeev, V.A., Pellinen, R.J., Pulkkinen, T.I., 1996a, “Steady magnetospheric convection: A review of recent results”, Space Sci. Rev., 75, 551–604. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1996SSRv...75..551S
Sergeev, V.A., Pulkkinen, T.I., Pellinen, R.J., 1996b, “Coupled-mode model for the magnetospheric dynamics”, J. Geophys. Res., 101, 13,047
Shue, J.-H., Chao, J.K., Fu, H.C., Russell, C.T., Song, P., Khurana, K.K., Singer, H.J., 1997, “A new functional form to study the solar wind control of the magnetopause size and shape”, J. Geophys. Res., 102, 9497
Shue, J.-H., Song, P., Russell, C.T., Steinberg, J.T., Chao, J.K., Zastenker, G.N., Vaisberg, O.L., Kokubun, S., Singer, H.J., Detman, T.R., Kawano, H., 1998, “Magnetopause location under extreme solar wind conditions”, J. Geophys. Res., 103, 17,691–17,700
Sitnov, M.I., Swisdak, M., Guzdar, P.N., Runov, A., 2006, “Structure and dynamics of a new class of thin current sheets”, J. Geophys. Res., 111, A08204
Southwood, D.J., Kivelson, M.G., 2001, “A new perspective concerning the influence of the solar wind on the Jovian magnetosphere”, J. Geophys. Res., 106, 6123–6130
Spasojević, M., Goldstein, J., Carpenter, D.L., Inan, U.S., Sandel, B.R., Moldwin, M.B., Reinisch, B.W., 2003, “Global response of the plasmasphere to a geomagnetic disturbance”, J. Geophys. Res., 108, 1340
Stern, D.P., 1975, “The motion of a proton in the equatorial magnetosphre”, J. Geophys. Res., 80, 595
Summers, D., Thorne, R.M., Xiao, F., 1998, “Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere.”, J. Geophys. Res., 103, 20,487
Tanskanen, E.I., Viljanen, A.T., Pulkkinen, T.I., Pirjola, R.J., Häakkinen, L.V.T., Pulkkinen, A.A., Amm, O., 2001, “At substorm onset, 40% of AL comes from underground”, J. Geophys. Res., 106, 13,119–13,134
Tanskanen, E.I., Pulkkinen, T.I., Koskinen, H.E.J., 2002, “Substorm energy budget near solar minimum and maximum: 1997 and 1999 compared”, J. Geophys. Res., 107
Tinsley, B.A., Hodges Jr, R.R., Rhorbaugh, R.P., 1986, “Monte carlo models for the terrestrial exosphere over a solar cycle”, J. Geophys. Res., 91, 13,631–13,647
Tsurutani, B.T., Gonzalez, W.D., 1987, “The cause of high-intensity long-duration continuous AE activity (HILDCAAs): Interplanetary Alfvén wave trains”, Planet. Space Sci., 35, 405–412. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1987P7.26SS...35..405T
Tsyganenko, N.A., 1989, “Magnetospheric magnetic field model with a warped tail current sheet”, Planet. Space Sci., 37, 5–20. Related online version (cited on 9 January 2007): http://adsabs.harvard.edu/abs/1989P%26SS...37 5T
Tsyganenko, N.A., 1995, “Modeling the Earth’s magnetospheric magnetic field confined within a realistic magnetopause”, J. Geophys. Res., 100, 5599
Tsyganenko, N.A., Singer, H.J., Kasper, J.C., 2003, “Storm-time distortion of the inner magnetosphere: How severe can it get?”, J. Geophys. Res., 108, 1209
Turner, N.E., Baker, D.N., Pulkkinen, T.I., McPherron, R.L., 2000, “Evaluation of the tail current contribution to Dst”, J. Geophys. Res., 105, 5431–5440
Vasyliunas, V.M., 1975, “Theoretical models of magnetic field line merging. I”, Rev. Geophys. Space Phys., 13, 303–336
Volland, H., 1973, “Semiempirical model of large-scale magnetospheric electric field”, J. Geophys. Res., 78, 171
Weimer, D.R., 1995, “Models of high-latitude electric potentials derived with a least error fit of spherical harmonic coefficients”, J. Geophys. Res., 100, 19,595–19,608
Williams, D.J., Roelof, E.C., Mitchell, D.G., 1992, “Global magnetospheric imaging”, Rev. Geophys., 30, 183–208
Zhou, X., Tsurutani, B.T., 2001, “Interplanetary shock triggering of nightside geomagnetic activity: Substorms, pseudobreakups, and quiescent events”, J. Geophys. Res., 106, 18,957–18,968
Acknowledgements
The author thanks Minna Palmroth and Tiera Laitinen for many useful discussions on global MHD simulations as well as for providing GUMICS-4 simulation results for this paper. Mike Wiltberger is thanked for providing LFM simulation results. Nataly Ganushkina and Marina Kubyshkina are thanked for useful discussions regarding the inner magnetosphere empirical modeling and for providing model results for this paper.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9173_MOESM1_ESM.avi
mpg-Movie (12664.8046875 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Magnetopause shape and size and the energy transfer through the magentopause surface during three time instants from the GUMICS-4 global MHD simulation. The magnetospheric boundary is viewed from a direction upstream (Sunward) of the magnetosphere. Note that the energy entry shown in blue is concentrated at the nose of the magnetosphere as well as in two high-latitude regions which are in sectors roughly parallel to the interplanetary magnetic field direction.
Electronic supplementary material
41116_2015_9173_MOESM2_ESM.mpeg
mpg-Movie (3098.69921875 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Northern hemisphere Joule heating during three instants from the GUMICS-4 global MHD simulation. The polar plots are drawn with Sun to the top and dusk to the left. Note how the auroral precipitation energy (shown in Figure 14 ) is concentrated in the auroral oval region and the dayside cusp where solar wind has direct access, while the Joule heating maximizes in the polar cap where the electric field is largest.
Electronic supplementary material
41116_2015_9173_MOESM3_ESM.mpeg
mpg-Movie (3046.00488281 KB) Still from a movie showing Magnetic storm on April 6–7, 2000. Northern hemisphere auroral precipitation during three instants from the GUMICS-4 global MHD simulation. The polar plots are drawn with Sun to the top and dusk to the left. Note how the auroral precipitation energy is concentrated in the auroral oval region and the dayside cusp where solar wind has direct access, while the Joule heating (shown in Figure 13 ) maximizes in the polar cap where the electric field is largest.
Electronic supplementary material
41116_2015_9173_MOESM4_ESM.mpg
mpg-Movie (3926.05761719 KB) Still from a movie showing Substorm on December 10, 1996. Four snapshots of the LFM global MHD simulation. The color coding shows the plasma density in the noon-midnight meridian plane. The gray shading outlines the last closed flux surface indicating the large-scale magnetic topology of the system. The topological changes are consistent with those presented in the schematic picture in Section 3 . The direction of the Sun is to the left.
Electronic supplementary material
41116_2015_9173_MOESM5_ESM.mpg
mpg-Movie (16560.6015625 KB) Still from a movie showing Substorm on December 10, 1996. LFM global MHD simulation results of the magnetotail flows in an equatorial plane projection. The direction of the Sun is to the left. The color coding shows the cross-tail electric field, with brighter colors showing higher electric field values indicative of a thin and intense current sheet at that location (highlighted by the white circle). The white arrows depict the flow velocity. Note a flow channel initiating from about 40 RE distance and focusing toward the thin current sheet region (outlined with the white dotted line). Such flow channels become larger and more frequent during substorm activity and finally lead to disruption of the intense inner-tail current sheet during the substorm expansion phase.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pulkkinen, T. Space Weather: Terrestrial Perspective. Living Rev. Sol. Phys. 4, 1 (2007). https://doi.org/10.12942/lrsp-2007-1
Published:
DOI: https://doi.org/10.12942/lrsp-2007-1