Local Helioseismology

Abstract

We review the current status of local helioseismology, covering both theoretical and observational results. After a brief introduction to solar oscillations and wave propagation through in-homogeneous media, we describe the main techniques of local helioseismology: Fourier-Hankel decomposition, ring-diagram analysis, time-distance helioseismology, helioseismic holography, and direct modeling. We discuss local helioseismology of large-scale flows, the solar-cycle dependence of these flows, perturbations associated with regions of magnetic activity, and solar supergranulation.

Outline

Helioseismology is a powerful tool to study the interior of the Sun from surface observations of naturally-excited internal acoustic and surface-gravity waves. Helioseismological studies based on the interpretation of the eigenfrequencies of the resonant modes of oscillations have yielded many exciting results about the internal structure and dynamics of the Sun (see, e.g., Christensen-Dalsgaard, 2002). For example, a major achievement has been the inference of the large-scale rotation as a function of depth and unsigned latitude (see, e.g., Thompson et al., 2003). The angular velocity inside the Sun is now known to be larger at the equator than at the poles throughout the convection zone, while the radiative interior rotates nearly uniformly. The layer of radial shear at the bottom of the convection zone, known as the tachocline, is commonly believed to be the seat of the solar dynamo (see, e.g., Gilman, 2000). The current research focuses on small temporal variations connected to the solar cycle that are likely to be related to the magnetic dynamo.

With global-mode helioseismology, however, it is not possible to detect longitudinal variations or flows in meridional planes. To complement global helioseismology, techniques of local helioseismology¹ are being developed to probe local perturbations in the solar interior or on its surface (see review by Duvall Jr, 1998). The goal of local helioseismology is to interpret the full wave field observed at the surface, not just the eigenmode frequencies. Local helioseismology provides a three-dimensional view of the solar interior, which is important to understand large-scale flows, magnetic structures, and their interactions in the solar interior.

Local helioseismology includes a number of different approaches that complement each other. This paper is an attempt to review all these techniques and their achievements. Not all methods of local helioseismology have reached the same degree of maturity. In Section 2 we give basic information about the data that are currently most commonly used for local helioseismology and about the properties of solar oscillations. In Section 3 we discuss equations of motion for solar oscillations, Green’s functions for the response of solar models to forcing, and basic perturbation methods and their range of validity. The main methods of local helioseismology, i.e., Fourier-Hankel decomposition, ring-diagram analysis, time-distance helioseismology, helioseismic holography, and direct modeling, are described in Section 4. In Section 5 we give a summary and discussion of the main results obtained using local helioseismology regarding global-scale features, active regions and sunspots, excitation of waves by flares, and supergranulation. Whenever possible, we discuss the physical implications of the observations.

Observations of Solar Oscillations

Data for local helioseismology

The fundamental data of modern helioseismology are high-resolution Doppler images of the Sun’s surface. Local helioseismology started with observations of acoustic absorption by sunspots using data from the Kitt Peak vacuum telescope (Braun et al., 1987, 1988). Observations obtained by Hill (1988, 1989) at the Sacramento Peak vacuum tower telescope demonstrated that local spectra of solar oscillations provide measurable information about internal horizontal flows. Continuous data from the 1988 south pole expedition lead to direct measurements of local travel times of acoustic waves (Duvall Jr et al., 1993). Today, the development of local helioseismology is fueled by high-quality data from space and ground based networks. The main datasets are provided by the Taiwan Oscillation Network (TON), the Global Oscillation Network Group (GONG), and the Michelson Doppler Imager (MDI) aboard the ESA/NASA SOHO spacecraft in a halo orbit around the Li Sun-Earth Lagrange point.

The TON consists of six identical telescopes at appropriate longitude around the globe. The data are series of 1080 × 1080 full-disk Ca⁺ K-line intensity images recorded at a rate of one image per minute. A description of the TON project is given by Chou et al. (1995). The TON data may be requested by contacting the Principal Investigator, Dr. Dean-Yi Chou (chou@phys.nthu.edu.tw).

The GONG is an international network of six extremely sensitive and stable solar velocity imagers that provide nearly continuous observations of solar oscillations (Leibacher, 1999). The GONG instruments, which are Michelson-interferometer-based Fourier tachometers, observe the Ni I 6768 Å line. In addition to Doppler and intensity images every minute, GONG provides full-disk magnetograms nominally every 20 minutes. The system became operational in October 1995, and will operate for at least an eleven-year solar cycle. The observation duty cycle has averaged about 90%. The original instruments used 256 × 256 pixel CCD cameras, which where replaced in 2001 by 1024 × 1024 square-pixel cameras. The GONG data products can be accessed at the project’s website (GONG, 2002).

The MDI has provided line-of-sight Doppler velocity images since 1996 with an excellent duty cycle (Scherrer et al., 1995). MDI Dopplergrams are obtained by combining 4 filtergrams on the wings and core of the Ni 6788 Å absorption line, formed just above the photosphere. Dopplergrams are available at a one minute cadence. MDI operates under several observing modes. The Dynamics Program runs for 2 to 3 months each year and provides 1024 × 1024 full-disk Doppler images; the plate scale is 2″ per pixel, or 0.12 heliographic degrees (1.45 Mm at disk center). The Structure Program provides continuous coverage: full-disk images are binned onboard into a set of about 20,000 regions of roughly similar projected areas on the Sun to make use of the narrow telemetry channel. The Structure Program data are used to measure mode frequencies up to spherical harmonics degrees of 250. MDI can also operate in High-Resolution mode by zooming on a 11′ square field of the Sun with a plate scale of 0.625″ per pixel and a diffraction-limited resolution of 1.25″. MDI data can be accessed at the project’s website (MDI, 1997).

Properties of solar oscillations

The five-minute solar oscillations were first discovered by Leighton et al. (1962) and interpreted as standing acoustic waves by Ulrich (1970) and Leibacher and Stein (1971). Deubner (1975) then confirmed that the power in the oscillations is concentrated at discrete frequencies for any given horizontal wavenumber, as predicted by Ulrich’s theory. The driving mechanism of solar oscillations is believed to be near-surface turbulent convection (Goldreich and Keeley, 1977). Solar and stellar oscillations are discussed in details by Cox (1980), Gough (1993), Unno et al. (1989), and Christensen-Dalsgaard (2002). Particularly useful are the lecture notes of J. Christensen-Dalsgaard (Christensen-Dalsgaard, 2003).

The small oscillations of a sphere can be represented by a linear superposition of eigenmodes, each characterized by a set of three indices: the radial order n the spherical harmonic degree l and the azimuthal order m. For instance, the radial displacement of a fluid element can be written as

$$\delta r(r,\theta,\phi,t)=\sum\limits_{n,l}{}\sum\limits_{m=-l}^l{{a_{nlm}}}\;{\xi_{nl}}(r)Y_l^m(\theta,\phi){e^{{\bf{i}}{\omega_{nlm}}t}},$$

(1)

where r is the radius, θ and φ are spherical-polar coordinates (colatitude and longitude), and t is time. The $Y_{l}^{m}$ are spherical harmonics, a_nlm is a complex mode amplitude, and ξ_nl(r) is the radial eigenfunction of the mode with frequency ω_nlm. By convention, n corresponds to the number of nodes of the radial eigenfunction, l indicates the total number of nodal lines on spheres, and m tells how many of these nodal lines cross the equator. A spherically symmetric star would give rise to a spectrum of azimuthally degenerate frequencies. However, rotation and other perturbations lift the (2l + 1)-fold m-degeneracy of the frequency of nonradial mode (n, l).

Figure 1 shows m-averaged power spectra of solar oscillations derived from series of tracked Doppler images of size 30° × 30° (near disk center) observed simultaneously by the MDI and TON instruments. Each ridge in the power spectrum corresponds to a different radial order n. The lowest frequency ridge (n = 0) is for the fundamental (f) modes. The f modes are identified as surface gravity waves, with nearly the dispersion relation for deep water waves, ω² = gk, where ω is the angular temporal frequency, g = 274 m s⁻² is the gravitational acceleration at the Sun’s surface, k ≃ l/R_⊙ is the horizontal wavenumber, and R_⊙ = 696 Mm is the solar radius. The f modes propagate horizontally. All other ridges, denoted p_n, correspond to acoustic modes, or p modes. The restoring force for p modes is pressure. The ridge immediately above the f mode ridge is p₁, the next one p₂, and so forth. Low-l and high-n modes penetrate deeper inside the Sun. For frequencies above the acoustic cutoff frequency (5.3 mHz), acoustic waves are not trapped inside the Sun. Acoustic modes with similar values of ω_nlm/l propagate to similar depths inside the Sun. For degrees larger than about 150, wave damping becomes significant and modes are not resolved anymore (continuous ridges). Figure 2 is another beautiful example of a power spectrum of solar oscillations, obtained from data collected during the 1994 south pole campaign.

Figure 1:

m-averaged power spectra of solar oscillations obtained from 512 min series of tracked Doppler images of size 30° × 30° (near disk center) observed by MDI (left) and TON (right), versus spherical harmonic degree l and temporal frequency. The ridges are labelled by the value of the radial order n. From González Hernández et al. (1998).

Figure 2:

Power spectrum of solar oscillations observed in brightness from the geographic south pole in 1994 (Ca II K₁ line, 6 Å bandpass). Notice that ridges of power can be seen well beyond the acoustic cutoff frequency. Courtesy of T.L. Duvall.

Models of Solar Oscillations

In order to understand local helioseismology it is crucial to understand wave propagation through generic solar models, including models with local inhomogeneities. In Section 3.1 we review the equations of motion for linear waves moving through non-magnetic backgrounds. The sources of excitation of solar oscillations are characterized in Section 3.2. In Section 3.3 we discuss methods for computing the Green’s functions for solar models. We describe the zero-order problem in Section 3.4 and the effects of weak steady perturbations in Section 3.5. Numerical tests of the Born approximation are described in Section 3.6. Some effects of magnetic fields are briefly reviewed in Section 3.7.

Throughout this section we will address two general classes of models: general models and plane-parallel models. We will not explicitly consider the case of spherically symmetric models. In general we will use the symbol r to denote position in three dimensions. For plane-parallel models we decompose the position vector as r = (x, z), where x is a two-dimensional horizontal vector and z is the height coordinate. The plane-parallel approximation is valid for very high degree modes, which are routinely used in local helioseismology. Plane-parallel models are often assumed for the interpretation of data collected over a small patch of the Sun: images may be remapped onto a grid which is, locally, approximately Cartesian.

Linear waves

We begin by assuming that we have a steady, wave-free, non-magnetic background state. For discussions of background states see for example Cox (1980) or Unno et al. (1989). In general, the background will satisfy the force balance

$${\rho _0}{v_0} \cdot {\bf{\nabla}} {v_0} = - {\bf{\nabla}} {p_0} + {\rho _0}{g_0},$$

(2)

where ρ₀, ρ₀, v₀, and g₀ are the density, pressure, velocity, and gravitational acceleration in the background state. The energy equation and equation of state must also be satisfied in the background state (see, e.g., Cox, 1980; Unno et al., 1989, for details).

We describe the wave motions that occur on top of the background state by the displacement ξ(r, t), which is the displacement of a fluid parcel that would have been at location r at time t had there been no wave motion. The continuity equation for the wave motion is then

$$\delta \rho + {\rho _0}{\bf{\nabla}} \cdot \xi = 0,$$

(3)

where δρ is the Lagrangian density perturbation. Notice that Equation (3) holds even when the background flow v₀ is non zero. The momentum equation can be written as (Lynden-Bell and Ostriker, 1967)

$${\cal L}\xi = 0,$$

(4)

with

$${\cal L}\xi = - {\rho _0}{{d_0^2\xi} \over {d{t^2}}} + {\bf{\nabla}} [\gamma {p_0}{\bf{\nabla}} \cdot \xi + \xi \cdot {\bf{\nabla}} {p_0}] - ({\bf{\nabla}} \cdot \xi){\bf{\nabla}} {p_0} - \xi \cdot {\bf{\nabla}} ({\bf{\nabla}} {p_0}).$$

(5)

The symbol d₀/dt = ∂_t + v₀ · ∇ is the material derivative in the background flow. To obtain Equation (4) Lynden-Bell and Ostriker (1967) assumed that the Lagrangian pressure and density changes associated with the wave are related by

$${{\delta p} \over {{p_0}}} = \gamma {{\delta \rho} \over {{\rho _0}}}.$$

(6)

For the case of adiabatic motion, γ is the first adiabatic exponent. Equation (4) is the equation of motion for small amplitude waves that we will refer to throughout this review.

Wave excitation

It is generally agreed that solar oscillations are excited by near surface turbulent convection (see, e.g., Goldreich et al., 1994). The two main approaches to modeling wave excitation have been numerical convection simulations and analytical models based on mixing length convection models.

Goldreich et al. (1994) used a mixing length model of solar convection to compute the energy input rates for modes with angular degree less than 60. The model energy input rates were very similar to the observed rates. In the Goldreich et al. (1994) model the main source of wave excitation was entropy fluctuations. Numerical simulations of near-surface turbulent convection have also been able to explain the observed frequency dependence of the energy input and damping rates (see, e.g., Stein and Nordlund, 2001). In the Stein and Nordlund (2001) model, the main source of wave excitation is Reynold’s stresses (turbulent pressure) near the boundaries of granules. Samadi et al. (2003a) compared wave excitation in a 3d numerical simulation and 1d mixing length based models. The numerical simulation gave about five times more energy input into the p-modes than did the mixing length model. In the numerical simulations of Samadi et al. (2003a), excitation by entropy fluctuations dominates over excitation by Reynold’s stresses. Samadi et al. (2003b) used a 3d numerical simulation to study the covariance function of the near-surface turbulent velocity and found that the temporal covariance was not Gaussian. As we will discuss in Section 3.4, this covariance is important for computing the power spectrum of solar oscillations.

As both the numerical convection simulations and the analytical convection models become more developed, it seems likely that they will converge and produce a definitive answer as to the source of solar oscillations.

In order to model the driving of solar oscillations by turbulent convection we add a source term S to the right hand side of Equation (4), to obtain

$${\cal L}\xi = S.$$

(7)

The function S can be thought of as one realization of a stochastic process (granulation). We will later show that the physical quantities that we are interested in, e.g., power spectra, cross-covariances, or ingression-egression correlations, can be written in terms of the covariance of the source function. Following Gizon and Birch (2002), we define the source covariance matrix as

$${M_{ij}}(r,t;{r^{\prime}},{t^{\prime}}) = E[{S_i}(r,t){S_j}({r^{\prime}},{t^{\prime}})].$$

(8)

The indices i and j refer to components of the vector valued source function S. The operator E takes the expectation value of the expression in brackets. When the source model is translation invariant in the horizontal directions and stationary in time, we can write the source covariance as a function of the horizontal separation x − x′, the time difference t − t′, and the two depths z and z′,

$${M_{ij}}(r,t;{r^{\prime}},{t^{\prime}}) = {M_{ij}}[(x - {x^{\prime}},t - {t^{\prime}},z,{z^{\prime}})].$$

(9)

In this case it is convenient to write the source covariance in terms of a Fourier-domain source covariance,

$${M_{ij}}(x,t,z,{t^{\prime}}) = \int {{d^2}} k\;d\omega \;{M_{ij}}(k,\omega, z,{z^{\prime}}){e^{{\rm{i}}(k \cdot x - \omega t)}}.$$

(10)

For any particular type of source model we can obtain the corresponding form for the source covariance M.

Response to an impulsive source

Of central importance to the theory of local helioseismology is the concept of Oreen’s functions. The Oreen’s functions are the impulse responses of the solar model and solve

$${\cal L}{G^i}(r,t;{r^{\prime}},{t^{\prime}}) = {\hat e_i}({r^{\prime}}){\delta _{\rm{D}}}(r - {r^{\prime}}){\delta _{\rm{D}}}(t - {t^{\prime}}),$$

(11)

where δ_D is the Dirac delta function in one or two dimensions. For each i = 1, 2, 3, the ê_i(r′) is the unit vector in the i-th direction at r′, and ℒ is the wave operator for the displacement (see Equation 7). For example, in the non-magnetic case ℒ as given by Equation (5). Because it describes a displacement vector, Gⁱ is a vector. Taken together, the three Green’s vectors Gⁱ form a Green’s tensor, $\{G_{j}^{i}\}$. The function $G_{j}^{i}(r,t;,r^{\prime},t,^{\prime})$ is the displacement in the j-th direction at (r, t) that results from a unit source acting in the i-th direction at (r′, t′)

There are three approaches to solving Equation (11). In the case of very simple problems it is sometimes possible to solve analytically for the Green’s functions in the Fourier domain (see, e.g., Gizon and Birch, 2002). Another, more general approach, is direct numerical solution (Section 3.3.1). An efficient approximate solution is normal mode summation (Section 3.3.2).

Direct solution in plane-parallel models

For plane-parallel steady models with horizontal translation invariance, the Green’s functions will be of the form Gⁱ(x − x′, t − t′, z, z′) where now r = (x, z) and r′ = (x′, z′) are the decompositions of r and r′ into horizontal, x and x′, and vertical, z and z′, components. In this case we can write the Green’s functions as the inverse Fourier transforms of Fourier domain Green’s functions

$${G^i}(x,t,z,{z^{\prime}}) = \int {{d^2}} k\;d\omega \;{G^{\prime}}(k,\omega, z,{z^i}){e^{{\rm{i}}(k \cdot x - \omega t)}},$$

(12)

where k is the horizontal wavevector and ω is the temporal angular frequency. We can then obtain the equation satisfied by Gⁱ(k, ω, z, z′) from Equation (11), for any particular choice of ℒ. The result will be an inhomogeneous set of ordinary differential equations (ODEs) in the variable z for the components of Gⁱ. These ODEs can then be integrated numerically to obtain Gⁱ(k, ω, z, z′) for given k, ω, and z′. Care must be taken with the treatment of the delta function on the right hand side of Equation (11); this can treated by folding the computational domain so that the jump condition across the delta function becomes a non-local boundary condition (Birch et al., 2004).

Normal-mode summation approximation

Dahlen and Tromp (1998) give an excellent discussion of the normal-mode summation approach to the computation of Green’s functions. For a detailed discussion in the context of helioseismology, see Birch et al. (2004). The basic notion of the normal-mode summation approximation is that the Green’s function can be represented as a sum over normal modes. Intuitively, the idea is to compute the amplitude to which a particular source excites each mode in the model, and then to let each mode evolve in time. For example, for the case of undamped modes, Dahlen and Tromp (1998) write

$$G_j^i(r,t;{r^{\prime}},{t^{\prime}}) = \sum\limits_\beta {s_j^\beta} (r)s_i^\beta ({r^{\prime}})\sin [{\omega _\beta}(t - {t^{\prime}})],\quad \quad t > {t^{\prime}}.$$

(13)

Here the index i refers to the direction of the source, and the index j to the component of the response that we are looking at. For t < t′ the Green’s function is zero. The sum over β is taken over all normal modes of the background model. By normal mode we mean a solution of Equation (4) of the form s(r)e^−iwt, with the normalization ∫_⊙ dr ρ₀∥s∥² = 1. In the case of spherical background models the modes are described by the radial order n the angular degree l and the azimuthal order m. In this case we have β = (n, l, m). For the case of plane-parallel models, modes can be labeled by a radial order n and a horizontal wavevector k. In this case we have β = (n, k). The situation is somewhat more complicated for the case of non-adiabatic modes, although it can still be addressed in much the same way (see Chapter six of Dahlen and Tromp, 1998).

Figure 3 compares Green’s functions computed numerically and approximated via normal-mode summation. Notice that the exact numerical result shows a discontinuity at the source depth; this comes from the jump across the delta function on the right hand side of Equation (11). The normal mode approximation, being a finite sum of continuous functions, is everywhere continuous.

Figure 3:

Real (red) and imaginary (blue) parts of the horizontal component of normal-mode and numerical Green’s functions (G_h) for k = 1 Mm⁻¹, ν = 3.92 mHz (just above the n = 2 resonance), z_src = −3.7 Mm, and a vertical momentum source. The Green’s function has been scaled by the square root of the background density. The horizontal axis is acoustic depth in minutes. The vertical scale is arbitrary. The source depth is shown by the solid blue vertical line. The photosphere is shown by the vertical blue dashed line. The solid curves show the numerical results. The real part of the numerical result has a discontinuity at the source depth while the imaginary part is continuous there. The dashed curves show the normal-mode summation approximation. Notice that the normal-mode approximation is continuous at the source depth. This is because we have used only a finite number of modes (radial orders not greater than 15). From Birch et al. (2004).

In the case of plane-parallel translation-invariant isotropic models where the only restoring forces are pressure and gravity, it can be shown that the Green’s functions, in the Fourier domain, can be decomposed as

$${G^i}(k,\omega, z,{z^{\prime}}) = \hat zG_z^i(k,\omega, z,{z^{\prime}}) + {\rm{i}}\hat kG_{\rm{h}}^i(k,\omega, z,{z^{\prime}}).$$

(14)

This decomposition is useful as now for any source we need only to compute two components of the response rather than three. Also notice that $G_{z}^{i}$ and $G_{{\rm h}}^{i}$ depend only on the wavenumber k, defined by $k=k\hat{k}$. A similar decomposition can be done for the dependence on the source direction (Birch et al., 2004).

Green’s functions for the observable

For the remainder of this review, it will be convenient to have a Green’s function for the response of the observable to a wave source. We denote the observable wavefield by the scalar Φ. For most current helioseismology work, the observable is the line-of-sight Doppler velocity. As a result, we define

$$\Phi (x,t) = {\cal F}\left\{{\hat \ell \cdot v(x,{z_{\rm{o}}},t)} \right\},$$

(15)

where v(x, z_o, t) is the Eulerian velocity at horizontal location x, at depth z_o, and time t. The line-of-sight unit vector $\hat{\ell}$ may depend on x. The operator ℱ describes the filter used in the data analysis, which includes the time window, instrumental effects, and other filtering.

As will become obvious in the following sections, it is convenient to introduce a Green’s function for the observable Φ (see Equation 15), given by:

$${{\cal G}^i}(x,t;{r^{\prime}},{t^{\prime}}) = {\cal F}\left\{{\hat \ell \cdot [{\partial _t}{G^i}(x,{z_{\rm{o}}},t;{r^{\prime}},{t^{\prime}}) + {G^i}(x,{z_{\rm{o}}},t;{r^{\prime}},{t^{\prime}}) \cdot {\bf{\nabla}} {v_0}(x,{z_{\rm{o}}})]} \right\}.$$

(16)

The function ${\cal G}^{i}$ is the response of the observable to a unit source acting in the i-th direction. Notice that for the special case when the steady background flow v₀ is constrained to be horizontal at the surface and the line of sight is vertical $(\hat{\ell}=\hat{z})$, we simply have

$${{\cal G}^i}(x,t;{r^{\prime}},{t^{\prime}}) = {\cal F}\{{\partial _t}G_z^i(x,{z_{\rm{o}}},t;{r^{\prime}},{t^{\prime}})\}.$$

(17)

For plane-parallel steady models with horizontal translation invariance, the Green’s functions for the observable are of the form ${\cal G}^{2}(x,t;r^{\prime},t^{\prime})={\cal G}^{i}(x-x^{\prime},t-t^{\prime},z^{\prime})$ where r′ = (x′, z′). In this case we can write the Fourier domain Green’s functions for the observable as ${\cal G}^{i}(k,\omega,z^{\prime})$, according to

$${{\cal G}^i}(x,t,{z^{\prime}}) = \int {{d^2}} k\;d\omega \;{{\cal G}^i}(k,\omega, {z^{\prime}}){e^{{\rm{i}}(k \cdot x - \omega t)}}.$$

(18)

In the short notation ${\cal G}^{i}(k,\omega,z^{\prime})$, the z′ always refers to the vertical position of the source of excitation.

The zero-order problem

The zero-order problem is to solve the driven equations of motion, Equation (7), when there are no perturbations to the background model. By the background model we mean a description of the background state together with specifications for wave damping and the statistics of wave excitation. As discussed in Section 3.1 we assume that the background state is a steady, wave-free, non-magnetic background solar model. The statistics of wave excitation which are needed to compute the wavefield covariance are described by the source covariance matrix M_ij (see Section 3.2). Wave damping can be described either physically (e.g., Balmforth, 1992) or phenomenologically (e.g., Gizon and Birch, 2002).

To obtain the zero-order problem we break the various quantities into unperturbed components (superscript 0) and first-order corrections (prefix δ). In particular we have

$${\cal L} = {{\cal L}^0} + \delta {\cal L},$$

(19)

$$\xi = {\xi ^0} + \delta \xi,$$

(20)

$$S = {S^0} + \delta S.$$

(21)

From Equation (7) we can then obtain the governing equations for the zero-order and perturbed problems.

To lowest order Equation (7) becomes

$${{\cal L}^0}{\xi ^0} = {S^0}.$$

(22)

The solution to this equation can be written in terms of the Green’s tensor G (Section 3.3):

$${\xi ^0}(r,t) = \int {{d^3}} {r_{\rm{s}}}d{t_{\rm{s}}}\;{G^i}(r,t;{r_{\rm{s}}},{t_{\rm{s}}})S_i^0({r_{\rm{s}}},{t_{\rm{s}}}),$$

(23)

where summation over the index i is implied. From Equation (23) together with the definition of the observable in terms of ξ and the definition of the Green’s functions for the observable we obtain the solution for the observable in terms of the wave source

$$\Phi (x,t) = \int {{d^3}} {r_{\rm{s}}}d{t_{\rm{s}}}{G^i}(x,t;{r_{\rm{s}}},{t_{\rm{s}}})S_i^0({r_{\rm{s}}},{t_{\rm{s}}}).$$

(24)

From Equation (24), supplemented with a model for the statistics of S⁰, we can obtain all of the information about the unperturbed problem, in particular the power spectrum, the time-distance cross-correlation, and the ingression-egression correlation.

Let us now consider the power spectrum of the observable Φ. There are two reasons to want to know the power spectrum of any particular model: Comparison between the model power spectrum and observations can be used to verify that the wave excitation model is reasonable, and local power spectra are the zero-order model for ring-diagram analysis (see Section 4.2). We define the power spectrum as

$$P(k,\omega) = {{{{(2\pi)}^3}} \over {AT}}E\left[ {\vert \Phi (k,\omega){\vert ^2}} \right],$$

(25)

where A is the area and T the time duration that the observations are taken over. The factor (2π)³ is included in the definition for the sake of clarity in some of the following results. Here Φ(k, ω) is the spatial and temporal Fourier transform of the observable. When the source model is translation invariant in the horizontal directions and stationary in time we can write the power spectrum as

$$P(k,\omega) = {(2\pi)^6}\int {dz} \int {d{z^{\prime}}} {G^i}(k,\omega,z){G^{\ast j}}(k,\omega,{z^{\prime}}){M_{ij}}(k,\omega,z,{z^{\prime}}).$$

(26)

For the definition of the source covariance M_ij see Equation (10). For the definition of the Green’s function for the observable see Equation (16).

Notice that we have not attempted to include various corrections to the power spectrum (although it could in principle be done). For example, we have neglected the effects of the temporal and spatial window functions. Having observations over a finite spatial area or a finite amount of time will lead to smearing and lack of resolution in the k and ω domains. Also, we have ignored sphericity. Analyzing solar data as if the Sun were flat, which is common in local-helioseismology, leads to distortions in power spectra due to use of FFTs on data that have been projected onto a plane. Line-of-sight projection effects have also been ignored (local helioseismology typically uses the Doppler velocity as input data). For example, waves moving toward disk center are more visible than waves moving in the perpendicular direction; this results in anisotropic power spectra.

The telescope also introduces artifacts into the power spectrum. Because of the finite spatial resolution of the instrument, given by the point-spread function, the power at high wavenumbers is reduced below what it would be for an instrument with perfect spatial resolution. In general the point spread function is not azimuthally symmetric, and so the power is reduced more in some directions than others. The effect of the instrument on the power spectrum is summarized in the modulation transfer function (MTF) which satisfies

$$P(k,\omega) = {\rm{MTF}}(k){P_\odot}(k,\omega),$$

(27)

where P is the power spectrum seen by the instrument and P_⊙ is solar power spectrum.

Figure 4 shows an example comparison of a model power spectrum with real data. The model power is computed from a model with spatially uncorrelated quadrupole sources located 100 km below the photosphere. In order to accurately model the linewidths seen in local power spectra it is crucial to take into account the distortion of the wavefield introduced by the remapping (Birch et al., 2004).

Figure 4:

Comparison of a model filtered power spectrum with the filtered power spectrum of MDI data. The filter is such that most of the power is in the p₁ and p₂ ridges. The model power spectrum is computed for a model with spatially uncorrelated quadrupole sources located at 100 km below the photosphere. The model includes the effects of the spatial and temporal window functions and the broadening of the spectrum by the remapping. Without these corrections the model power spectrum would have linewidths much smaller than those of the data. Upper left panel: Observed filtered power spectrum. Upper right panel: Model filtered power spectrum. The solid lines in the upper panels show the location of the f-mode ridge, for reference. Lower left panel: Average over wavenumbers of the observed (dashed line) and model (solid line) filtered power spectra. Lower right panel: Average over frequencies of the observed (dashed line) and model (solid line) filtered power spectra. From Birch et al. (2004).

Effects of small steady perturbations

In order to do linear inversions of helioseismic data, it is necessary to first solve the linear forward problem. The linear forward problem is to compute the first-order effect of small perturbations to the solar model. By first-order we mean first order in the strength of the perturbations. Essentially all inversions that have been done have assumed that the perturbations to the solar model are time-independent over the time duration during which the observations are made.

In general the linear forward problem can be written as

$$\delta {d_i}\sum\limits_\alpha {\int_\odot {{d^3}}} r\;K_\alpha ^i(r)\delta {q_\alpha}(r).$$

(28)

The δd_i are the first-order changes in the observed helioseismic parameters, for example changes in travel times, ring-fit parameters, or changes in ingression-egression correlations (which will be described in Section 4). The kernel functions $K_{\alpha}^{i}(r)$ depend on the three-dimensional position vector r. The first-order changes to the solar model are given by the functions $\delta q_{\alpha}(r)$, where the index α refers to the type of the perturbation, for example we can look at the effect of flows, changes in sound speed, and changes in wave excitation and damping. For each type of perturbation α, corresponds a particular kernel function K_α. Notice that we have assumed the functions q_α to be constant in time. The goal of the linear forward problem is to compute the functions $K_{\alpha}^{i}$ for any particular type of measurement d_i.

There have been numerous efforts to approximate the kernel functions K for time-distance travel times. These efforts will be described in Section 4.3.5. The kernel functions for ring diagrams have typically been approximated as constant within the area the ring is measured over, with a depth dependence derived from normal mode theory (see Section 4.2.3).

The linear forward problem for normal-mode frequencies is quite well known (see the upcoming Living Reviews paper on global helioseismology, Thompson (2005)). For example, Gough and Thompson (1990), Goldreich et al. (1991), and Dziembowski and Goode (2004) applied first-order perturbation theory to estimate the effect of magnetic fields on normal mode frequencies. This work may be helpful for computing the effects of magnetic fields on local helioseismic measurements.

In local helioseismology, the sensitivity functions K_α may be computed using the Born approximation. The first Born approximation gives the lowest order approximation for estimating scattering amplitudes (Born, 1926); this method appears to have been first used by Strutt (1881). As explained below, the Born approximation is essentially an equivalent-source description of wave interaction. For small perturbations to a solar model, it is used to compute the first-order change in the wavefield. The first-order change in any particular helioseismic parameter can then be obtained from the first-order, as well as the zero-order, wavefields. To compute the first-order change in the wavefield we begin from Equation (7) and Equations (19, 20, 21). To first order we have

$${{\cal L}^0}\delta \xi = - \delta {\cal L}{\xi ^0} + \delta S.$$

(29)

This is the equation for the first Born approximation. The first-order correction to the observed wavefield is therefore given by

$$\matrix{{\delta \Phi (x,t) = - \int {{d^3}} {r^{\prime}}d{t^{\prime}}{d^3}{r_{\rm{s}}}d{t_{\rm{s}}}\;{{\cal G}^i}(x,t;{r^{\prime}},{t^{\prime}}){{\{\delta {\cal L}{{\bf{G}}^j}({r^{\prime}},{t^{\prime}};{r_{\rm{s}}},{t_{\rm{s}}})\}}_i}S_j^0({r_{\rm{s}}},{t_{\rm{s}}})} \hfill \cr {\quad \quad \quad \quad + \int {{d^3}} {r_{\rm{s}}}d{t_{\rm{s}}}\;{{\cal G}^i}(x,t;{r_{\rm{s}}},{t_{\rm{s}}})\delta {S_i}({r_{\rm{s}}},{t_{\rm{s}}}),} \hfill \cr}$$

(30)

where $\{\delta{\cal L}{\bf{G}}^{j}\}_{i}$ is the i-th component of the vector δℒG^j and summation on repeated indices is implied. From Equation (30) we can predict the first-order change in any quantity in local helioseismology that will result from a small change in the model. We can look at, for example, first-order changes in the cross-covariance, travel times, power spectrum, or holographic measurements.

An alternative to the Born approximation is the Rytov approximation. In the Rytov approximation one computes the first order correction to the phase of the wavefield rather than the correction to the wavefield itself. For applications in the context of helioseismology, see Brüggen (2000) and Jensen and Pijpers (2003). The Born and Rytov approximations have been compared by Keller (1969).

Tests of Born approximation for sound speed and flow perturbations

The range of validity of the Born approximation is an important question for local helioseismology, as the linear forward problem proceeds naturally in the Born approximation.

Birch et al. (2001) simulated the scattering of sound waves by a spherical region of perturbed sound speed. The geometry and the essential result are shown in Figure 5. The main result, which was also found by Hung et al. (2001) in the context of geophysics, is that in the limit of weak perturbations the Born approximation is valid, while the ray approximation can fail badly. The Born approximation becomes less accurate as the strength, or spatial extent, of the perturbation is increased. Notice that there have not yet been any studies, in the context of helioseismology, on the accuracy of waveforms, rather than travel times, computed in the Born approximation.

Figure 5:

A numerical experiment of wave scattering by a spherical region of perturbed sound speed. The left panel shows the geometry and a single frame from a numerical simulation. The circular contours are contours of the sound-speed perturbation, which is a raised cosine with radius R and with a maximum fractional sound speed perturbation of A. The curved heavy lines show example ray paths leaving the source, at x = 0, y = −45 Mm, and going through the receiver location, at x = 0, y = 45 Mm. The middle and right-hand panels show the numerical travel times perturbations (solid lines), the Born approximation travel time perturbations (dashed lines), and the first-order ray approximation for the perturbed travel times (dotted lines), for positive and negative five percent changes in the sound speed (A = ±0.01, middle panel) and positive and negative ten percent changes in the sound speed (A = ±0.1, right panel). In both cases, the different travel time perturbations δt are shown as functions of the sphere radius R. Also in both cases, the travel times for negative sound-speed perturbations have δt > 0 and for positive sound-speed perturbations have δt < 0. From Birch et al. (2001).

Birch et al. (2004) studied the validity of the Born approximation for the effect of flows on time-distance travel times. Figure 6 shows the geometry for the numerical experiment, and Figure 7 shows the basic results. For weak flows, the Born approximation is valid as long as the acoustic waves were not traveling nearly upstream or downstream. They also found that strong flows can reflect incoming waves, which leads to a failure of the Born approximation.

Figure 6:

Geometry for a numerical test of the Born approximation. The wave source is located at the origin of the coordinate system. The open circles show the locations where the wavefield is observed. There is a background flow in the $+\hat{x}$ direction confined between the solid horizontal lines. The flow strength varies as a raised cosine, centered between the two horizontal lines, on the y coordinate and has a maximum of value of 1/6 of the background sound speed, which is spatially uniform and equal to 10 km s⁻¹. The lines emanating from the source show example ray traces. The flow reflects waves that hit it at x > 50. The travel times are shown in Figure 7. From Birch and Felder (2004).

Figure 7:

Travel times in the Born approximation (heavy line), ray approximation (thin line), and computed numerically (open circles) for the geometry and jet-flow configuration described in Figure 6. The top panel is for waves that cross the jet-like flow and the bottom panel is for the waves that do not cross the jet. The horizontal axis is the distance in the upstream or downstream direction traveled by the wave before it is observed, i.e., x = 0 is for waves traveling perpendicular to the direction of the flow. For the waves that cross almost perpendicularly to the flow direction the Born and ray approximations are good. For waves that hit the jet at a glancing angle, a strong reflected wave is seen and the Born approximation fails. From Birch and Felder (2004).

Strong perturbations: magnetic tubes and sunspots

The interaction of solar waves with photospheric magnetic fields has been studied extensively in recent years. Yet, applications in the context of local helioseismology have proved difficult. The source of this difficulty is that magnetic perturbations are not small near the solar surface (e.g., Crouch and Cally, 2004): the first Born approximation cannot be applied there. Only deeper inside the Sun, can magnetic effects be treated as small perturbations. In this paragraph, we review theoretical results regarding wave interaction with magnetic flux tubes and sunspots.

Near the photosphere magnetic fields appear to be clumped into intense flux tubes with a typical field strength of order 1 kG and diameters of about 100 km. It is well known (see, e.g., Hollweg, 1990) that flux tubes support various modes of oscillation: the Alfvén modes (twisting motion), the sausage modes (propagating change in the cross-section of the tube), and the kink modes (bending of the tube). The interaction of acoustic waves with thin flux tubes, i.e., tubes with diameters much less than the wavelengths, has been studied extensively (see, e.g., Ryutova and Priest, 1993; Bogdan and Zweibel, 1985; Bogdan et al., 1996; Tirry, 2000). There is general agreement that scattering of acoustic waves by flux tubes contributes to the observed damping rates and frequency shifts (Rajaguru et al., 2001; Komm et al., 2002).

Finsterle et al. (2004b) have detected the interaction of high-frequency acoustic waves with the canopy magnetic field in the solar chromosphere. These exciting results were obtained by making observations of solar oscillations at different heights in the atmosphere (Finsterle et al., 2004a). We note that there have been theoretical studies of the effect of the magnetic canopy on acoustic modes (see, e.g., Campbell and Roberts, 1989; Goldreich et al., 1991).

Thomas et al. (1982) first predicted that solar oscillations could be used to probe the internal structure of sunspots. Sunspots are known to absorb incident p-mode energy (Braun et al., 1987), introduce phase shifts between the incident and scattered waves (Braun et al., 1992; Duvall Jr et al., 1996; Lindsey and Braun, 2004), and cause mode mixing (Braun, 1995). Effects that have been suggested to cause phase shifts are the Wilson depression (Braun and Lindsey, 2000), flows (see, e.g., Duvall Jr et al., 1996; Kosovichev, 1996), inhomogeneous absorption (Woodard, 1997), temperature/density/wave-speed anomalies (see, e.g., Kosovichev, 1996; Brüggen and Spruit, 2000; Tong et al., 2003), and the direct effect of magnetic fields. Bogdan et al. (1998) and Cally et al. (2003) have produced models of the coupling of ambient p and f modes with various magnetic waves in the sunspot that explain some aspects of the data, and demonstrate that magneto-atmospheric waves can not be ignored in local helioseismology. Yet, according to Bogdan (2000), ‘ignorance triumphs over knowledge’. The main difficulties are nonlinear aspects of wave propagation, radiative transfer in magnetised plasmas, and the relationship between velocity measurements in sunspots and real fluid motions. The theoretical study of oscillations in sunspots is an entire field of research and is crucial for the interpretation of local helioseismic measurements in and around sunspots. We refer the reader to the reviews by Bogdan and Braun (1995) and Bogdan (2000) for further details and references.

Methods of Local Helioseismology

Fourier-Hankel spectral method

Wavefield decomposition

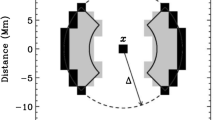
The Hankel spectral analysis was introduced by Braun et al. (1987) in order to study the relationship between inward and outward traveling waves around sunspots. Consider a spherical polar coordinate system (colatitude θ, azimuth ψ) with a sunspot situated on the polar axis θ = 0, and an annular region on the solar surface surrounding the sunspot (θ_min < θ < θ_max). The goal is to decompose the oscillation signal in the annular region, Φ(θ, ψ, t), into components of the form

$${\Phi _{Lm}}(\theta, \psi, t) = \left[ {{A_m}(L,\nu)H_m^{(1)}(L\theta) + {B_m}(L,\nu)H_m^{(2)}(L\theta)} \right]{e^{{\rm{i}}(m\psi + 2\pi \nu t)}},$$

(31)

where m is the azimuthal order, L = [l(l + 1)]^1/2, l is the spherical harmonic degree, ν is the temporal frequency, and $H_{m}^{(1,2)}$ are Hankel functions of the first and second kind. Hankel functions are used as numerical approximations,

$$H_m^{(1,2)}(L\theta) \simeq {(- 1)^m}{{(l - m)!} \over {(l + m)!}}\left[ {P_l^m(\cos \theta) \pm {{2i} \over \pi}Q_l^m(\cos \theta)} \right],$$

(32)

to the more exact combination of the Legendre functions P and Q used in spherical geometry. This approximation, valid in the limit l ≫ m, is always good in practice and is not a limitation of the technique (Braun, 1995). For reference, we recall that in the far-field approximation (θ ≫ 1/L),

$$H_m^{(1,2)}(L\theta) \simeq \sqrt {{2 \over {\pi L\theta}}} {e^{\pm {\rm{i}}(L\theta - m\pi/2 - \pi/4)}},$$

(33)

which makes clear that the functions A_m(L, ν) and B_m(L, ν) represent the complex amplitudes of the incoming and outgoing waves respectively. The wave amplitudes are computed according to (Braun et al., 1992):

$${A_m}({L_i},{\nu _j}) = {{{C_i}} \over {2\pi T}}\int_0^T {dt} \int_0^{2\pi} {d\psi} \int_{{\theta _{\min}}}^{{\theta _{\max}}} \theta \;d\theta \;\Phi (\theta, \psi, t)H_m^{(2)}({L_i}\theta){e^{- {\rm{i}}(m\psi + 2\pi {\nu _j}t)}},$$

(34)

$${B_m}({L_i},{\nu _j}) = {{{C_i}} \over {2\pi T}}\int_0^T {dt} \int_0^{2\pi} {d\psi} \int_{{\theta _{\min}}}^{{\theta _{\max}}} \theta \;d\theta \;\Phi (\theta, \psi, t)H_m^{(1)}({L_i}\theta){e^{- {\rm{i}}(m\psi + 2\pi {\nu _j}t)}},$$

(35)

In these expressions, T is the duration of the observation and C_i ≃ πL_i/(2Θ) is a normalisation constant, where Θ = θ_max − θ_min. The procedure to perform the numerical transforms is discussed by Braun et al. (1988). The time and azimuthal transforms use the standard fast Fourier transform algorithm, with azimuthal orders in the range |m| < 20. In particular, the frequency grid is given by ν_j = jΔν, where Δν = 1/T and j is an integer value. The spatial Hankel transform is computed for a set of discrete values L_i, that provide an orthogonal set of Hankel functions:

$$\int_{{\theta _{\min}}}^{{\theta _{\max}}} {H_m^{(1)}} ({L_i}\theta)H_m^{(2)}({L_k}\theta)\;\theta \;d\theta = 0\quad \quad {\rm{for}}\quad \quad i \ne k.$$

(36)

This condition is approximately satisfied for L_i = iΔL, where ΔL = 2π/Θ and i is an integer (Braun et al., 1988). The maximum degree is given by the Nyquist value L_max = π/Δθ, where Δθ is the spatial sampling, while the minimum degree below which the orthogonality condition ceases to be valid is L_min = m/θ_min. We note that the outer radius of the annulus, θ_max, must not be too large since waves should remain coherent over the travel distance 2R_⊙θ_max. This implies that θ_max < uτ/(2R_⊙), where u(L, ν) and τ (L, ν) are respectively the group velocity and the lifetime of the waves under study. In addition, the travel time across the annulus should be less than the duration of the observation T (waves must be observed first as incoming waves and later as outgoing waves). This implies θ_max < uT/(2R_⊙).

Absorption coefficient

The original motivation for the Hankel analysis was to search for wave absorption by sunspots. Braun et al. (1987) defined the absorption coefficient by

$${\alpha _m}(L,\nu) = {{{P_{{\rm{out}}}} - {P_{{\rm{in}}}}} \over {{P_{{\rm{out}}}}}} = 1 - {{\vert {B_m}(L,\nu){\vert ^2}} \over {\vert {A_m}(L,\nu){\vert ^2}}}.$$

(37)

Braun (1995) remarks that this definition of the absorption coefficient may not necessarily represent wave dissipation as it ignores mode mixing. In practice, some averaging must be done to reduce the noise level. For example, Braun et al. (1987) averaged |A_m|² and |B_m|² over all azimuthal orders and over the frequency range 1.5 mHz < ν < 5 mHz. Braun (1995) obtained a reasonable signal-to-noise level only by averaging in frequency space over the width of a ridge (radial order n) at fixed L:

$${\alpha _m}(L,n) = 1 - {{{{\langle {\vert {B_m}(L,\nu){\vert ^2} - {\lambda _m}(L,\nu)} \rangle}_n}} \over {{{\langle {\vert {A_m}(L,\nu){\vert ^2} - {\lambda _m}(L,\nu)} \rangle}_n}}},$$

(38)

where the angle brackets denote a frequency average over the width of the n-th ridge around the frequency of the mode (L, n). The function λ_m(L, ν) is introduced to remove the background power (see Figure 8). Braun (1995) also made averages over all azimuthal orders, to obtain an absorption coefficient for each ridge and each wavenumber denoted by α(L, n). Hankel analysis revealed that sunspots are strong absorbers of incoming p and f modes. As a check, the same analysis applied to quiet-Sun data does not show significant absorption.

Figure 8:

The m-averaged net power (incoming plus outgoing) as a function of frequency for two representative values of degree l. These power spectra were obtained from the analysis of 1988 quiet-Sun south pole data. The p-mode ridges are labeled by the value of the radial order n. The dashed lines show the background power λ(L, ν). From Braun (1995).

Phase shifts

Braun et al. (1992) and Braun (1995) were successful at measuring the relative phase shift between outgoing and ingoing waves. Phase shifts measurements require a lot of care. Braun et al. (1992) pointed out that the phases of A_m and B_m represent averages over a resolution element with size (ΔL, Δν). For example, Braun (1995) has ΔL = 20 and Δν = 4 µHz.

The finite resolution in wavenumber introduces spurious phases. This can be seen by considering first the A-transform (Equation (34)) of an incoming wave with amplitude |A|, wavenumber L, azimuthal order m, frequency ν, and phase φ_in. Using the far-field approximation of the Hankel functions, we have

$${{A_m}({L_i},{\nu _j}) \simeq {{\vert A\vert {C_i}} \over {T\Theta}}\int_0^T {{e^{{\rm{i}}2\pi (\nu - {\nu _j})t + i{\phi _{{\rm{in}}}}}}dt} \int_{{\theta _{\min}}}^{{\theta _{\min}}} {{e^{{\rm{i}}{{(L - {L_i})}^\theta}}}d\theta}}$$

(39)

$$\matrix{{= \vert A\vert {\rm{sinc}}[\pi (\nu - {\nu _j})T]{\rm{sinc}}[(L - {L_i})\Theta/2]} \hfill \cr {\quad \times \exp [{\rm{i}}{\phi _{{\rm{in}}}} + {\rm{i}}\pi (\nu - {\nu _j}) - {\rm{i}}({L_i} - L)({\theta _{\min}}{+}{\theta _{{\rm{max}}}})/{\rm{2}}],} \hfill \cr}$$

(40)

where sinc x = sin x/x. The B-transform (Equation (35)) applied to an outgoing wave with amplitude |B|, wavenumber L, azimuthal order m, frequency ν, and phase φ_out, gives

$$\matrix{{{B_m}({L_i},{\nu _j}) \simeq \vert B\vert {\rm{sinc[}}\pi (\nu - {\nu _j})T{\rm{]sinc}}[(L - {L_i})\Theta/2]} \hfill \cr {\quad \quad \quad \quad \;\; \times \exp [{\rm{i}}{\phi _{{\rm{out}}}} + {\rm{i}}\pi (\nu - {\nu _j}) + {\rm{i}}({L_i} - L)({\theta _{\min}} + {\theta _{\max}})/2].} \hfill \cr}$$

(41)

Thus the phase difference between the outgoing and incoming waves measured at grid point (L_i, ν_j) is given by

$$\Delta {\phi ^{{\rm{meas}}}}({L_i},{\nu _j}) \simeq \Delta \phi (L,\nu) + ({L_i} - L)({\theta _{\min}} + {\theta _{\max}}),$$

(42)

where Δφ = φ_out − φ_in is the correct phase difference at wavenumber L, and (L_i − L)(θ_max + θ_min) is a spurious phase shift. (The notations here are not the same as those of Braun (1995).)

Let us now consider actual observations. The p modes are distributed along ridges corresponding to different radial orders n, whose frequency positions in the L-ν diagram are specified by known functions ν_n(L). There may be several unresolved modes in the resolution element (ΔL, Δν). The condition θ_max < uT/(2R_⊙) (Section 4.1.1) is equivalent to ΔL > 2Δν/ν_n′(L), where the prime denotes a derivative. This means that the spread in L of the ridge across the frequency step Δν is much smaller than the wavenumber resolution ΔL. In this case Braun et al. (1992) estimate the spurious phase shift from Equation (42) by letting L equal to the mean wavenumber L of the unresolved modes. Since ${\nu _j} - {\nu _n}({L_i}) \simeq \nu _n^{\prime}({L_i})(\bar L - {L_i})$, the frequency dependence of the spurious shifts is given by (Braun et al., 1992)

$$\Delta {\phi ^{{\rm{spur}}}}({L_i},{\nu _j}) \simeq - {{{\theta _{\max}} + {\theta _{\min}}} \over {\nu _n^{\prime}({L_i})}}[{\nu _j} - {\nu _n}({L_i})].$$

(43)

Figure 9 shows phase shifts measurements for quiet-Sun data (Braun, 1995). The predicted values of the spurious shifts, given by the above equation, agree with the observations. The corrected average phase shift is obtained from the phase of B_mA_m* exp(−iΔφ^spur) averaged over m and some frequency range. As expected for the quiet Sun, the average phase shift is zero once the spurious shift has been subtracted. This control experiment shows, in particular, that the values of ν_n (L_i) and (L_i) interpolated from modern p-mode frequency tables are precise enough for the analysis.

Figure 9:

The total m-summed power as a function of frequency across the p-mode ridge corresponding to n = 5 and l = 205 (top panel) and the raw phase measurements across the same range in frequency (bottom panel). The solid lines indicate the predicted value of the spurious phase shifts. 1988 south pole quiet-Sun data. From Braun (1995).

Mode mixing

Using a similar technique, Braun (1995) measured correlations between incoming and outgoing waves with different radial orders n and n′. He found that sunspots introduce non-zero m-averaged phase shifts for n = n′ ± 1. This observation gives hope for a full characterization of the sunspot-wave interaction, encapsulated in the scattering matrix S_ij defined by

$${B_i} = \sum\limits_j {{S_{ij}}} {A_j},$$

(44)

where the indices i and j refer to individual modes (l, n, m), the A_j are the complex amplitudes of the incoming waves, and the B_i are the complex amplitudes of the outgoing waves. Mode mixing introduced by a scatterer shows as off-diagonal elements in the scattering matrix. All techniques of local helioseismology are based on some knowledge of the scattering matrix, implicitly or explicitly.

Ring-diagram analysis

Local power spectra

Ring-diagram analysis is a powerful tool to infer the speed and direction of horizontal flows below the solar surface by observing the Doppler shifts of ambient acoustic waves from power spectra of solar oscillations computed over patches of the solar surface (typically 15° × 15°). Thus ring analysis is a generalization of global helioseismology applied to local areas on the Sun (as opposed to half of the Sun).

The ring diagram method is based on the computation and fitting of local k − ω power spectra and was first introduced by Hill (1988). A small patch is tracked as it moves across the disk. In this process, images are remapped onto a projection grid, such as the cylindrical equal-area projection, Postel’s azimuthal equidistant projection, or the transverse cylindrical equidistant projection (see, e.g., Corbard et al., 2003). A series of tracked images form a data cube, i.e., the surface Doppler velocity as a function of the two spatial coordinates and time Φ(x, t). The data cube is Fourier transformed to obtain Φ(k, ω), where k is the horizontal wavevector and ω is the angular frequency (approximately a plane-wave decomposition). The three-dimensional power spectrum of the resulting data cube, P(k, ω) = |Φ(k, ω)|², yields the basic input data for ring diagrams. As in the global power spectrum, the main features are the ridges corresponding to the normal modes of the Sun. As there are two wavenumber directions, the ridges now appear as rings when seen in a cut through the spectrum at constant frequency (Figure 10). Flows in regions, over which the power spectrum is computed, introduce Doppler shifts in the oscillation spectrum, and changes in sound speed alter the locations of the rings. Thus by fitting the positions and shapes of the rings in the power spectrum the subsurface flows and sound-speed can be estimated.

Figure 10:

Cuts at constant frequency through the three-dimensional power spectrum. Panels A, B, and C correspond to cuts at frequencies 2.8, 3.5, and 3.8 mHz, respectively. The outermost ring corresponds to the f mode, and the inner rings to p₁, p₂, p₃, and so forth. Displacements of the rings are caused by horizontal flows, while alterations of ring diameters are produced by sound speed perturbations. The spectrum was computed from an image sequence 1664 minutes long beginning on 1999 May 25 for a region near disk center. From Hindman et al. (2004).

Measurement procedure

One method of fitting local power spectra was described by Schou and Bogart (1998) (see also Haber et al., 2002; Howe et al., 2004). The first operation is to construct cylindrical cuts at constant k = ∥k∥ in the 3D power spectrum, denoted by P_k(ψ, ω), where ψ gives the direction of k (the angle between $\hat{x}$ and k) and ω is the angular frequency. The power spectrum is then filtered to remove all but the lowest azimuthal orders m in the expansion of the form

$${P_k}(\psi, \omega) = \sum\limits_m {{a_m}} (\omega)\cos m\psi + {b_m}(\omega)\sin m\psi.$$

(45)

For each p-mode ridge (radial order n), the filtered power spectrum is fitted at constant wavenumber using the maximum likelihood method (see, e.g., Anderson et al., 1990) with a model of the form

$${P_{{\rm{fit}}}}(\psi, \omega) = {A \over {1 + {{(\omega - {\omega _0} - k{U_x}\cos \psi - k{U_y}\sin \psi)}^2}/{\gamma ^2}}} + B{k^{- 3}}.$$

(46)

Here A is an amplitude, γ is the half linewidth, and ω₀ is the frequency at resonance. The ring fit parameters U_x and U_y correspond to a depth-averaged horizontal flow U = (U_x, U_y) causing a Doppler shift k · U. The background noise is modeled by Bk⁻³.

Other fitting techniques are described by Patrón et al. (1997) and Basu et al. (1999). Essentially all ring-diagram fitting has been done assuming symmetric profiles for the ridges in the power spectrum. Basu and Antia (1999) concluded that including line asymmetry in the model power spectrum improves the fits, but does not substantially change the inferred flows.

The most important parameters used in ring-diagram analysis are the flow parameters U_x and U_y, and the central frequency ω₀. For each radial order n and wavenumber k (or spherical harmonical degree l) corresponds a new set of values: It is convenient to use the notations $U_{x}^{nl},U_{y}^{nl}$ for the flow parameters, and δw_nl for the difference between the fitted mode frequency and the mode frequency calculated from a standard solar model.

Figure 11:

Logarithm of the power as a function of k_x and k_y at ω/2π = 3150 µ Hz (left panel) and an unwrapped cylinder at wavenumber $k=(k_{x}^{2}+k_{y}^{2})^{1/2}$ corresponding to angular degree l = 586 as a function of ψ and ω (1 mHz < ω/2π < 5 mHz; right panel). From Schou and Bogart (1998).

Depth inversions

The goal of inverting ring fit parameters is to determine the sound speed, density, and mass flows in the region underneath the tile over which the local power spectrum was computed. Generally, the assumption is that the sound speed, density, and flows are only functions of depth within the region covered by a particular tile. The forward problem for ring diagrams has traditionally been done by analogy with global mode helioseismology.

Inversions for sound speed and density are done using the mode frequencies determined from the ring fitting (e.g., Basu et al., 2004). The changes in the mode frequencies can be related to changes in the sound speed and density according to (Dziembowski et al., 1990):

$${{\delta {\omega _{nl}}} \over {{\omega _{nl}}}} = \int {dz} \;K_{c,\rho}^{nl}(z){\delta \over c}(z) + \int {dz} \;K_{\rho, c}^{nl}(z){{\delta \rho} \over \rho}(z) + {{F({\omega _{nl}})} \over {{I_{nl}}}}.$$

(47)

Here the kernel $K_{c,\rho}^{nl}$, is the sensitivity of the frequency of the mode (n, l) to a fractional change in the sound speed at constant density, and $K_{\rho,c}^{nl}$ is the sensitivity to the fractional change in density at constant sound speed. The function F is a smooth function, I is the mode inertia, and F/I gives the effect of near-surface conditions and non-adiabatic effects on the mode frequencies. We recall that mode inertia is the total kinetic energy of the mode divided by the square of the mode velocity at the solar surface; it has the units of mass and is independent of the choice of normalization of the mode eigenfunction. The kernels K can be computed using normal mode theory (for details see the Living Reviews paper on global helioseismology, Thompson (2005)). The function F is determined as part of the inversion procedure. The inversion problem is then to determine δc/c(z) and δρ/ρ(z) given a set of observed δw_nl.

Horizontal flows in the solar interior are related to a set of ring fit parameters $U_{x}^{nl}$ and $U_{y}^{nl}$, according to

$$U_x^{nl} = \int {dz} \;K_v^{nl}(z){v_x}(z),$$

(48)

$$U_y^{nl} = \int {dz} \;K_v^{nl}(z){v_y}(z),$$

(49)

where v_x and v_y are the two horizontal components of the flow velocity, assumed to be functions of depth only. As for the kernels for sound speed and density, the flow kernel $K_{v}^{nl}(z)$ can be obtained from normal mode theory (flow parameters can be converted to frequency splittings and standard global mode methods applied). The inversion problem is then to use the observed $U_{x}^{nl}$ and $U_{y}^{nl}$ to estimate v_x(z) and v_y(z).

As we have seen, the general one-dimensional ring diagram inversion problem is to use a set of equations of the form

$${d_i} = \int {dz} \;{K^i}(z)f(z)$$

(50)

together with the knowledge of the kernels Kⁱ and a set of observed data d_i to determine the model function f(z). The two main approaches that have been used for the inversion of ring diagram parameters are the regularized least squares (RLS) and the optimally localized averages (OLA) methods.

The RLS method (see, e.g., Hansen, 1998; Larsen, 1998) selects the model that minimizes a combination of the misfit between the observed data and the data predicted by the model and some function of the model, for example the integral of the square of the second derivative. In particular RLS minimizes a function of the form

$${\chi ^2} = \sum\limits_i {{1 \over {\sigma _i^2}}} {\left[ {{d_i} - \int {dz} \;{K^i}(z)f(z)} \right]^2} + \lambda {\cal R}f.$$

(51)

Here we have assumed a diagonal error covariance matrix with σ_i being the standard deviation of the error on the measurement d_i. The regularization operator ℛ takes the function f(z) and returns a scalar. The regularization parameter which controls the relative importance of minimizing the misfit to the data and smoothing the solution is λ. Example resolution kernels for RLS inversion are plotted in Figure 12.

Figure 12:

Representative resolution kernels for (A) RLS and (B) OLA inversions of ring-analysis frequency splittings, plotted as a function of depth. Numbers indicate target depths. The negative sidelobes near the surface, so prevalent in RLS inversion kernels, are almost absent in the OLA kernels. From Haber et al. (2004).

The OLA method (Backus and Gilbert, 1968) attempts to produce localized averaging kernels while simultaneously controlling the error magnification. For a discussion of OLA in ring diagram inversions see Basu et al. (1999) and Haber et al. (2004). The essential idea in OLA methods is that the estimate f of the model f at a particular depth, can be written as a linear combination of the data

$$\tilde f({z_0}) = \sum\limits_i {{a_i}} ({z_0}){d_i},$$

(52)

so that we can write

$$\tilde f({z_0}) = \int {dz} \;\kappa (z,{z_0})f(z),$$

(53)

with the averaging kernels κ given by

$$\kappa (z,{z_0}) = \sum\limits_i {{a_i}} ({z_0}){K^i}(z).$$

(54)

The OLA method then attempts to choose the coefficients a_i(z₀) so as to produce averaging kernels κ that are well localized while at the same time controlling the error variance $\sum\nolimits_{i}a_{i}^{2}(z_{0})\sigma_{i}^{2}$, on the estimate $\tilde{f}(z_{0})$.

Time-distance helioseismology

The purpose of time-distance helioseismology (Duvall Jr et al., 1993) is to measure and interpret the travel times of solar waves between any two locations on the solar surface. A travel time anomaly contains the seismic signature of buried inhomogeneities within the proximity of the ray path that connects two surface locations. An inverse problem must then be solved to infer the local structure and dynamics of the solar interior (see, e.g., Jensen, 2003, and references therein).

Fourier filtering

The first operation in time-distance helioseismology is to track Doppler images at a constant angular velocity to remove the main component of solar rotation, as is done in ring-diagram analysis (see Section 4.2.1). Postel’s azimuthal equidistant projection is often used in time-distance helioseismology. The resulting data cube is Fourier transformed to obtain Φ(k, ω).

A filtering procedure is then applied to the data (Duvall Jr et al., 1997). First, frequencies below 1.5 mHz are filtered out in order to remove granulation and supergranulation noise. The data are further filtered to select parts of the wave propagation diagram.

In the case of p modes, a phase speed filter is applied to the data, and the f-mode ridge is filtered out. This choice of filter is based on the fact that acoustic waves with the same horizontal phase speed ω/k travel the same horizontal distance Δ (see Bogdan, 1997). Thus, to measure the travel time for acoustic waves propagating between two surface locations, it is appropriate to consider only those waves with the same phase speed. The choice of the phase speed depends on the travel distance. A list of Gaussian phase-speed filters,

$${F_i}(k,\omega) = \exp [ - {(\omega/k - {v_i})^2}/(2\delta v_i^2)],$$

(55)

is provided in Table 1 for various distances. Here, v_i is the mean phase speed, δv_i is the dispersion, and k = ∥k∥ is the wavenumber. The filtered signal is given by Ψ(k, ω) = F_i(k, ω)Φ(k, ω). The larger the phase speed, the deeper p-mode wavepackets penetrate inside the Sun.

Table 1: Parameters of Fourier filters used in p-mode time-distance helioseismology. The Gaussian phase-speed filters are defined by ${\rm exp}{{[-(\omega/k - v_i)}^{2}}/(2 \delta v_{i}^{2})]$. Courtesy of T.L. Duvall and S. Couvidat.

A separate filtering procedure is applied for surface gravity waves, which are used to probe the near surface layer. In this case the filter function F (k, w) is 1 if $\vert\omega\pm\sqrt{gk}\vert < kU_{\rm cut}$ and 0 otherwise. The parameter U_cut controls the width of the region around the f-mode dispersion relation ω² = gk. A reasonable choice is U_cut = 1 km s⁻¹. This value allows for large Doppler frequency shifts introduced by flows, and does not let the p₁ ridge through.

There is some freedom in the selection of the Fourier filters. For example one may construct filters that depend explicitly on the direction of the wavevector k, and not simply on the wavenumber (see, e.g., Giles, 1999).

Cross-covariance functions

The basic computation in time-distance helioseismology is the temporal cross-covariance between filtered signals at two points x₁ and x₂ on the solar surface,

$$C({x_1},{x_2},t) = {h \over {T - \vert t\vert}}\sum\limits_{{t^{\prime}}} \Psi ({x_1},{t^{\prime}})\Psi ({x_2},{t^{\prime}} + t),$$

(56)

where h_t is the temporal sampling and T is the time duration of the observation. Times are evaluated at discrete values t_i = ih_t. Multiplication by the temporal window function is already included in the definition of Ψ, and the sum over t′ is a short notation to mean the sum over all discrete times in the interval −T/2 ≤ t′ < T/2. The normalization factor 1/(T − |t|) is a correction that becomes significant only when T is small. We note that in practice it is faster to compute the time convolution in the Fourier domain. The positive time lags (t > 0) give information about waves moving from x₁ to x₂, and the negative time lags about waves moving in the opposite direction.

The cross-correlation is useful as it is a phase-coherent average of inherently random oscillations. It can be seen as a solar seismogram, providing information about travel times, amplitudes, and the shape of the wave packets traveling between any two points on the solar surface. Figure 13 shows a theoretical cross-covariance Δ as a function of distance between x₁ and x₂, and time lag t. This time-distance diagram was computed for a spherically symmetric solar model (see Sekii and Shibahashi, 2003). The first ridge corresponds to acoustic waves propagating between the two points without additional reflection from the solar surface. The next ridge corresponds to waves which arrive after one reflection from the surface, and the ridges at greater time delays result from waves arriving after multiple bounces. The backward branch associated with the second ridge corresponds to waves reflected on the far-side of the Sun. In most applications, only the direct (first-bounce) travel times are measured. Figure 14 shows the p-mode cross-covariance function at short distances, computed with the Fourier filters given in Table 1. In this example, cross-covariance functions were averaged over pairs of points at fixed distance to reduce noise. An example cross-covariance function for the f-mode ridge is plotted in Figure 15.

Figure 13:

Theoretical cross-covariance function for p modes, C(x₁, x₂, t), as a function of time lag and arc distance, also called the time-distance diagram. In this calculation the solar model is spherically symmetric. Hence C only depends on the distance between x₁ and x₂ and is symmetric with respect to the time lag t. Courtesy of A.G. Kosovichev.

Figure 14:

Cross-covariance function computed for the Fourier filters given in Table 1. The data are averaged over all pairs of points that correspond to a given distance. Each panel is labelled (on top) by the index i of the phase-speed filter listed in the table. The main branch corresponds to the first bounce of p-mode wavepackets. The correlation at shorter times is an artifact, while the correlation at later times corresponds to the second-bounce branch. Courtesy of S. Couvidat.

Figure 15:

Surface gravity wave cross-covariances. Left panel: Observed cross-covariance C(x₁, x₂, t) averaged over all possible pairs of points (x₁, x₂), as a function of distance Δ = ∥ x₂ − x₁∥ and time lag t. Red refers to positive values and blue to negative values. The observations are 8-hr time series from the MDI high-resolution field of view. The Fourier filter is chosen to isolate surface gravity waves. Right panel: Theoretical cross-covariance from a solar model. From Gizon and Birch (2002).

The travel times of the wave packets are measured from the (first-bounce) cross-covariance function. Local inhomogeneities in the Sun will affect travel times differently depending on the type of perturbation. For example, temperature perturbations and flow perturbations have very different signatures. Given two points x₁ and x₂ on the solar surface the travel time perturbation due to a temperature anomaly is, in general, independent of the direction of propagation between x₁ and x₂. However, a flow with a component directed along the direction x₁ → x₂ will break the symmetry in travel time for waves propagating in opposite directions: Waves move faster along the flow than against it. Magnetic fields introduce a wave speed anisotropy and will have yet another travel time signature (this has not been detected yet).

Travel time measurements

Cross-covariance functions can have a large amount of realization noise due to the schochastic nature of solar oscillations, and it has proved difficult to measure travel times between two individual pixels on the solar surface. Some averaging is often required. The time over which the cross-covariances are computed is usually T ≥ 8 hr (this puts a limit on the temporal scale of the solar phenomena that can be studied). In order to further enhance the signal-to-noise ratio, Duvall Jr et al. (1993) and Duvall Jr et al. (1997) suggested to average C(x₁, x₂, t) over points x₂ that belong to an annulus or quadrants centered at x₁. For instance, to measure flows in the east-west direction in the neighborhood of point x, cross-covariances are averaged over two quadrant arcs ${\cal A}_{\rm w}(x,\Delta)$ and ${\cal A}_{\rm e}(x,\Delta)$ that include points a distance Δ from x:

$${C_{{\rm{ew}}}}(x,t;\Delta) = \sum\limits_{{x^{\prime}} \in {{\cal A}_{\rm{w}}}} {C(x,{x^{\prime}},t)} + \sum\limits_{{x^{\prime}} \in {{\cal A}_{\rm{e}}}} {C({x^{\prime}},x,t)},$$

(57)

Figure 16 shows the geometry of the averaging procedure. An example cross-covariance C_ew is shown in Figure 17 in the f-mode case. Correlations at positive times (t > 0) correspond to waves that propagate westward, and correlations at t < 0 to waves that propagate eastward. As shown in Figure 17, cross-covariances can be further averaged along lines of constant phase within a range of distances. Likewise an average cross-correlation C_sn is constructed from south-north quadrants to measure flows in the meridional direction. Another average C_ann is obtained by averaging over the whole annulus,

$${C_{{\rm{ann}}}}(x,t;\Delta) = \sum\limits_{{x^{\prime}} \in {\cal A}} {C(x,{x^{\prime}},t),} $$

(58)

where ${\cal A}(x,\Delta)$ is an annulus of radius Δ centered at x. This average can be used to measure separately the waves that propagate inward and outward from the central point.

Figure 16:

Quadrant geometry used in the time-distance averaging procedure to measure flows in the east-west direction. Here the spatial sampling is 1.46 Mm (MDI full-disk data). The black regions show the pixels that belong to the east and west quadrants at distance Δ from a central location x, denoted by ${\cal A}_{\rm e}$ and ${\cal A}_{\rm w}$ in the text. The average cross-covariance C_ew is computed according to Equation (57). The gray regions include the pixels used for three separate distances. Combined, these four distances are those displayed in Figure 17. From Hindman et al. (2004).

Figure 17:

Left panel: Measured f-mode cross-covariance functions C_ew(x, Δ, t) at a particular pixel position x and for distances in the range 5.1 Mm < Δ < 11 Mm (full-disk MDI data, T = 8 hr). Middle panel: Cross-covariance functions are shifted along a line of constant phase, such that the reference shift is the same for all x. Right panel: Average of the (shifted) cross-covariances over Δ. This type of averaging is also done for p-mode data. From Hindman et al. (2004).

At fixed x and Δ, the cross-covariance function oscillates around two characteristic (first-bounce) times t = ±t_g. Center-to-annulus or center-to-quadrants travel times are often measured by fitting Gaussian wavelets (Duvall Jr et al., 1997; Kosovichev and Duvall Jr, 1997). This procedure distinguishes between group and phase travel times by allowing both the envelope and the phase of the wavelet to vary independently. The positive-time part of the cross-correlation is fitted with a function of the form

$${w_+}(t) = A\exp [ - {\gamma ^2}{(t - {t_{\rm{g}}})^2}]\cos [{\omega _0}(t - {\tau _+})],$$

(59)

where all parameters are free, and the negative-time part of the cross-correlation is fitted separately with

$${w_-}(t) = A\exp [ - {\gamma ^2}{(t - {t_{\rm{g}}})^2}]\cos [{\omega _0}(t - {\tau_-})].$$

(60)

The times τ₊ and τ₋ are the so-called phase travel times. The basic observations in time-distance helioseismology are the travel time maps τ₊(x, Δ) and τ₋(x, Δ), measured for each of the three averaged cross-correlations C_ew(x, t; Δ), C_sn(x, t; Δ), and C_ann(x, t; Δ). The travel time differences τ_diff = τ₊ − τ₋ are mostly sensitive to flows while the mean travel times τ_mean = (τ₋ + τ₊)/2 are sensitive to wave-speed perturbations. Maps of measured travel times are shown in Figure 18: Most of the signal in these maps is due to supergranular flows (15–30 Mm length scales). We note that an alternative definition of travel time can be obtained by fitting a model cross-covariance function to the data (Gizon and Birch, 2002). This last definition is often used in geoseismology (see, e.g., Zhao and Jordan, 1998).

Figure 18:

Maps of measured travel times (quadrant/annulus geometry). The eight pictures vertically are for eight different annulus sizes. The sizes of the annuli are shown, smallest at the top and largest at the bottom. The horizontal size of each image is 370 Mm. Left column: Travel times for outward-going waves minus inward-going waves with the white displayed as a negative signal. The rms signal in the top image is 0.2 min. Second-to-left column: Westward travel times minus eastward travel times. Third-to-left column: Northward travel times minus southward travel times. Fourth-to-left column: Average of inward and outward travel times with a negative signal displayed as white. The rms signal in the top image is 0.05 min. A correlation with the location of the magnetic features can be seen. Top figure in right column: Magnetic field as seen by MDI. Bottom figure in right column: Average MDI Dopplergram observed for the 8.5 hr interval. From Duvall Jr et al. (1997).

In order to maximize the potential resolution of time-distance helioseismology it is desirable to obtain travel times from cross-covariances measured with shorter T and with as little spatial averaging as possible. However conventional fitting methods will fail when the cross-covariance is too noisy. A new robust definition of travel time was introduced by Gizon and Birch (2004) to measure travel times between individual pixels and T as short as 2 hr. According to this definition, the point-to-point travel time for waves going from x₁ to x₂, denoted by τ₊(x₁, x₂), and the travel time for waves going from x₂ to x₁, denoted by τ₋(x₁, x₂), are given by

$${\tau_\pm}({x_1},{x_2}) = {h_t}\sum\limits_t {{W_\pm}} ({\bf{\Delta}},t)[C({x_1},{x_2},t) - {C^0}({\bf{\Delta}},t)],$$

(61)

with the weight functions W_± given by

$${W_\pm}({\bf{\Delta}},t) = {{\mp f(\pm t)\partial {C^0}({\bf{\Delta}},t)} \over {{h_t}\sum\nolimits_{{t^{\prime}}} f (\pm {t^{\prime}}){{[{\partial _{{t^{\prime}}}}{C^0}({\bf{\Delta}},{t^{\prime}})]}^2}}}.$$

(62)

In this expression C⁰ is a (smooth) reference cross-covariance function computed from a solar model and Δ = x₂ − x₁. The window function f(t′) is a one-sided function (zero for t′ negative) used to separately examine the positive- and negative-time parts of the cross-correlation. The window f(t′) is used to measure τ₊, and f(−t′) is used to measure τ₋. A standard choice is a window that isolates the first-skip branch of the cross-covariance.

This definition has a number of useful properties. First, it is very robust with respect to noise. The fit reduces to a simple sum that can always be evaluated whatever the level of noise. Second, it is linear in the cross-covariance. As a consequence, averaging various travel time measurements is equivalent to measuring a travel time on the average cross-covariance. This is unlike previous definitions of travel time that involve non-linear fitting procedures. Third, the probability density functions of τ₊ and τ₋ are unimodal Gaussian distributions. This means, in particular, that it makes sense to associate an error to a travel time measurement. The Born sensitivity kernels discussed in Section 4.3.5 were derived according to this definition of travel times.

Noise estimation

In global helioseismology, it is well understood that the precision of the measurement of the pulsation frequencies is affected by realization noise resulting from the stochastic nature of the excitation of solar oscillations (see, e.g., Woodard, 1984; Duvall and Harvey, 1986; Libbrecht, 1992; Schou, 1992). It is important to study these properties since the presence of noise affects the interpretation of travel time data. In particular, the correlations in the travel times must be taken into account in the inversion procedure.

An interesting approach, pioneered by Jensen et al. (2003a), consists of estimating the noise directly from the data by measuring the rms travel time within a quiet Sun region. The underlying assumptions are that the fluctuations in the travel times are dominated by noise, not by ‘real’ solar signals, and that the travel times measured at different locations can be seen as different realizations of the same random process. By ‘real’ solar signals we mean travel time perturbations due to inhomogeneities in the solar interior that are slowly varying over the time of the observations. Jensen et al. (2003a) studied the correlation between the center-to-annulus travel times as a function of the distance between the central points, at fixed annulus radius.

Gizon and Birch (2004) derived a simple model for the full covariance matrix of the travel time measurements. This model depends only on the expectation value of the filtered power spectrum and assumes that solar oscillations are stationary and homogeneous on the solar surface. The validity of the model is confirmed through comparison with MDI measurements in a quiet Sun region. Gizon and Birch (2004) showed that the correlation length of the noise in the travel times is about half the dominant wavelength of the filtered power spectrum. The signal-to-noise ratio in quiet-Sun travel time maps increases roughly like the square root of the observation time and is maximum for a distance near half the length scale of supergranulation.

Travel time sensitivity kernels

In this section we show example computations of travel time sensitivity kernels. Kernels are the functions K_α that connect small changes in the solar model with small changes in travel times

$${\delta _\tau}({x_1},{x_2}) = \sum\limits_\alpha {\int_\odot {{d^3}}} r\;{K_\alpha}({x_1},{x_2};r)\delta {q_\alpha}(r).$$

(63)

The sum over α is taken over all possible relevant types of perturbations to the model, for example local changes in sound speed, density, flows, magnetic field, or source properties. For each type of perturbation a there is a corresponding kernel K_α(x₁, x₂; r) that depends on a, the observation points x₁ and x₂ that the travel time is measured between, and a spatial location r that ranges over the entirety of the solar interior. In this section we will describe the various types of approximate calculations of the K_α that have been done.

Notice that kernels can be computed for quantities other than travel times. For example, in geophysics Dahlen and Baig (2002) computed the first-order sensitivity of the amplitude of the observed waveform to a small local change in sound speed. In particular it might be helpful to compute kernels for the mean frequency and amplitude of the cross-correlations, with the aim of using these quantities to help constrain inversions.

Ray approximation

The first efforts at computing the sensitivity of travel times to changes in the solar model (see, e.g., Kosovichev, 1996; D’Silva et al., 1996; D’Silva, 1996; Kosovichev and Duvall Jr, 1997) were based on the ray approximation. In the ray approximation the travel time perturbation is approximated as an integral along the ray path. Fermat’s principle (see, e.g., Gough, 1993) says that in order to compute the first order change in the travel time we do not need to compute the first order change in the ray path, i.e., we can simply take the integral over the unperturbed ray path. In particular, we have (Kosovichev and Duvall Jr, 1997):

$${\delta _\tau}({x_1},{x_2}) = - \int_\Gamma {ds} \left[ {{{\hat n \cdot U} \over {{c^2}}} + {1 \over {{v_{\rm{p}}}}}{{\delta c} \over c} + \left({{{\delta {\omega _{\rm{c}}}} \over {{\omega _{\rm{c}}}}}} \right){{\omega _{\rm{c}}^2{v_{\rm{p}}}} \over {{\omega ^2}{c^2}}} + {1 \over 2}\left({{{c_{\rm{A}}^2} \over {{c^2}}} - {{{{(k \cdot {c_{\rm{A}}})}^2}} \over {{k^2}{c^2}}}} \right)} \right],$$

(64)

where the ray path connecting x₁ and x₂ is denoted by Γ. The increment of path length is ds and $\hat{n}$ is a unit vector directed along the path, in the sense of going from x₁ to x₂. The other quantities in Equation (64) are the change in the sound speed δc, the mass flow U, the Alfvén velocity $c_{\rm A}=B/\sqrt{4\pi\rho}$, the acoustic cut-off frequency ω_c, and the phase speed v_p = ω/k.

Ray theory is based on the assumption that the perturbations to the model are smooth and that the wavepacket frequency bandwith is very large. Bogdan (1997) showed that the energy density of a realistic wavepacket was substantial away from the ray path. This result strongly suggested that perturbations located away from the ray path could have substantial effects on travel times. It is now well known that ray theory fails when applied to perturbations that are smaller that the first Fresnel zone (see, e.g., Hung et al., 2001; Birch et al., 2001).

Finite-wavelength kernels in the single-source approximation

The three approximations that have been used to treat small scale perturbations for time-distance helioseismology are the Born approximation, the Rytov approximation, and the Fresnel zone approximation. Here we describe some results that have been obtained using these methods in the single-source approximation. The single-source approximation, which was motived by the “Claerbout Conjecture” (Rickett and Claerbout, 1999) and by analogy with previous ray-theory based work, says that the one-way travel time perturbation can be found by looking at the time-shift of a wavepacket created at one observation location and then observed at the other. Gizon and Birch (2002) showed that the single-source approximation ignores a potentially important scattering process; this issue is discussed in detail in the paragraph on distributed source models.

Motivated by the use of the Born approximation to compute travel time sensitivities in the context of geophysics (see, e.g., Marquering et al., 1998), Birch and Kosovichev (2000) used the Born approximation to compute travel time kernels for time-distance helioseismology. Figure 19 shows an example result. The shape of the kernel is the characteristic “banana-doughnut” shape first described by Marquering et al. (1998). The kernel is hollow along the ray path, travel times are not sensitive to small-scale sound-speed perturbations located along the ray path. This has been explained in terms of wavefront healing (Nolet and Dahlen, 2000). The ringing in the kernel with distance from the ray path is a result of the finite bandwidth of the wavefield.

Figure 19:

Single-source Born approximation travel time kernel. The left panel is a cut in the plane of the ray path; the right panel is a cut in the plane that is perpendicular to the ray path at the lower turning point. The color scale shows the sensitivity of the travel time to a local change in the sound speed. The solid black line, left panel, shows the ray path. From Birch and Kosovichev (2000).

Another approach to producing finite-wavelength kernels is the Fresnel zone approximation (see, e.g., Sneider and Lomax, 1996; Jensen et al., 2000). The Fresnel zone approach makes a simple parametrized approximation to the kernels. In particular, in the Fresnel zone approximation, the travel time kernels, for fixed x₁ and x₂, are written as (Jensen et al., 2001)

$$K({x_1},{x_2};r) = {A \over {\tau ({x_2}\vert r)\tau (r\vert {x_1})}}\sin ({\omega _0}\;\Delta \tau)\exp \left[ {- {{\left({{{a\;\Delta \tau} \over {{T_0}/2}}} \right)}^2}} \right],$$

(65)

where τ(x|r) is the ray-theoretical travel time from x to r, and Δτ = τ(x₁|r)+ τ(r|x₂) − τ(x₁|x₂). The parameter ω₀ is the central frequency of the wavepacket, T₀ = 2π/ω₀ is the corresponding period, and a is related to the frequency bandwidth of the wavepacket. The amplitude A of the kernel is determined by demanding that the total integral of the kernel be equal to τ(x₁|x₂), which is the ray theory value for the total integral of the kernel. Notice that the value of the kernel goes to infinity as r tends to x₁ or x₂. Jensen et al. (2000) showed, by comparison with direct simulation, that a two dimensional analogue of the Fresnel zone kernel (Equation (65)) was a reasonable approximation to the actual linear sensitivity of travel time to changes in the sound speed.

The Rytov approximation gives a first order correction to the phase of the wavefield, instead of a first order correction to the wavefield itself as one obtains from the Born approximation. Jensen and Pijpers (2003) used the Rytov approximation to write travel time kernels for the effects of sound-speed perturbations. The results were qualitatively similar to the Born approximation results of Birch and Kosovichev (2000). No comparison has been made, in the helioseismology literature, of the ranges of validity of the Rytov and Born approximations.

Distributed source models

Gizon and Birch (2002), motived by Woodard (1997), gave the first comprehensive treatment of the linear forward problem for time-distance helioseismology. Such a treatment must include a physical model of wave excitation which takes into account the fact that waves are stochastically excited by sources (granules) that are distributed over the solar surface (see Section 3.2). An example calculation (Figure 20) demonstrates that the single-source approximation is qualitatively incorrect, as it ignores a scattering process that can be dominant for some perturbations. Figure 20 compares an f-mode travel time kernel for local changes in the wave damping rate, computed in the single-source and distributed-source models. The hyperbolic feature in the distributed-source kernel is not present in the single-source model. As discussed by Gizon and Birch (2002), the single-source approximation ignores the scattered wave that is seen at the observation point that is treated as a source in the single-source approximation.

Figure 20:

Comparison of the distributed stochastic source model (left panel) and the single-source model (right panel) for f-mode travel time kernels for wave damping perturbations. The observation locations are shown as black plus signs. The kernels are for the one-way travel times (from left to right). From Gizon and Birch (2002).

Birch et al. (2004) used the recipe derived by Gizon and Birch (2002) to obtain the linear sensitivity of p-mode travel times to changes in sound speed. The results showed that the sensitivity depends on the filtering that is done to the wavefield before the travel times are measured. Figure 21 shows sound-speed kernels computed for three different cases: a model with no filters, a model with an MTF (see Section 3.4) roughly like the one for MDI full-disk data, and a model with an MTF and also a phase-speed filter of the type employed in routine time-distance analysis. The three kernels are all strikingly different. In the unfiltered case, the kernels looks much like the traditional “banana-doughnut” kernel (see Figure 19). With the introduction of the MTF, the travel time becomes more sensitive to deeper sound-speed perturbations and less sensitive to the near-surface perturbations. This is because the MTF preferentially removes high wavenumbers, and thus modes with low phase speeds and shallow turning points. With the introduction of the phase-speed filter the kernel again changes drastically. The phase-speed filter removes all of the waves with lower turning point much below the turning point of the target ray. As a result, the sensitivity much below the lower turning point of the ray is greatly reduced. This example emphasizes the importance of including the filtering in models of travel time sensitivity kernels. The strong dependence of the shape of the kernels on the filtering suggests that the kernels could to be tailored by adjusting the filters that are used in the data analysis procedure.

Figure 21:

Slices through travel time kernels for the effect of sound-speed perturbations on mean travel times. Top panel: no filters other a filter to remove the f mode; middle panel: also includes an approximate model of the MDI full-disk MTF; bottom panel: also includes a narrow phase speed filter in addition to the MTF. In all of the panels the kernels are shown in the plane of the ray path, which is shown by the black line. From Birch et al. (2004).

Inversions of travel times

The inverse problem is to determine the perturbations δq_α(r) to the solar model that are consistent with a particular set of observed travel times δτ_i. For the inverse problem, the kernel functions and the noise covariance are in general assumed to be known.

Unlike in the ring-analysis case, where a set of one dimensional inversions are performed (see Section 4.2.3), the time-distance inversion procedure is three-dimensional. So far, only RLS inversions have been implemented in time-distance helioseismology. In the RLS approach, the minimization problem reads

$${\chi ^2} = \sum\limits_i {{1 \over {\sigma _i^2}}} {\left[ {\delta {\tau _i} - \sum\limits_\alpha {\int_\odot {{d^3}} r\;K_i^\alpha (r)\delta {q_\alpha}(r)}} \right]^2} + \lambda {\cal R}\{\delta {q_\alpha}\},$$

(66)

where we have assumed, for simplicity of notation, a diagonal covariance matrix. The σ_i are the noise estimates for each of the travel times δ τ_i. The regularization parameter is λ and ℛ is the regularization operator. Notice that we have not assumed any particular parametrization of the perturbations to the solar model δq_α(r). The ideal choice of regularization operator and the optimal method for choosing the regularization parameter are currently open questions.

The minimization of χ², Equation (66), has been done using either the LSQR algorithm (Paige and Saunders, 1982), the multi-channel deconvolution (MCD; Jacobsen et al., 1999), or via singular value decomposition (Hughes and Thompson, 2003). The inputs to either of these methods are the travel time kernels, which result from the linear forward problem (see Section 3.5), the regularization operator, the choice of regularization parameter, and in general also the covariance matrix of the noise.

The central question about inversions is the degree to which any particular inversion method is able to retrieve the true Sun, e.g., the actual sound-speed variations and flows in the interior, from a set of observed travel times. The degree to which any inversion method succeeds will presumably depend on a number of things: (i) the accuracy of the forward model, (ii) the noise level in the travel times, (iii) the depths and spatial scales of the real variations in the Sun, (iv) the number and type of travel times that are available as input to the inversion, and (v) the accuracy of the travel time noise covariance matrix. The two main approaches that have been taken to study inversion methods are either to invert artificial data or to invert real data for perturbations that are relatively well known from global helioseismology or from surface measurements. It is also useful to compare the results of different inversion methods applied to the same set of observed travel times.

The approach of inverting real data is appealing as it is by definition “realistic”. This approach for time-distance was pioneered by Giles (1999) who did ray theory based inversions to measure differential rotation. The results were in approximate agreement with the results of global model inversions, which validated time-distance inversions applied to slowly-varying large scale flows. Gizon et al. (2000) inverted f-mode travel times for horizontal flows in the near-surface. Figure 22 shows a comparison between the projection of the inferred flows onto the line of sight and the directly observed line-of-sight Doppler velocity. The correlation coefficient between the two is 0.7 (Gizon et al., 2000), which shows that their inversion method, an iterative deconvolution, is able to approximately retrieve the horizontal flow velocities from the travel times.

Figure 22:

Results of f-mode time-distance analysis and comparison with the direct Doppler measurements. (a) Direct Doppler measurements averaged over the observation duration (8 hr). (b) Line-of-sight projection of the horizontal vector flow field, inferred using f-mode time-distance. (c) Horizontal divergence of horizontal flows measured by f-mode time-distance analysis 1 Mm beneath the photosphere. (d) Scatter plot of the line-of-sight velocity from time-distance analysis against the observed Doppler velocity. The correlation coefficient is 0.7. From Gizon et al. (2000).

There have been a number of efforts to validate inversions by the generation and inversion of artificial data. These tests are useful as they provide an intuitive understanding of various regularization schemes, the choice of regularization parameter, the effects of limited sets of input travel times, the effects of incorrect assumptions regarding the noise covariance, the potential resolution of any particular inversion, and the cross-talk between different model parameters. A drawback to testing inversions with artificial data is that one always wonders about the realism of the artificial data. Hopefully, in the not distant future quite realistic data will be available for the purpose of testing inversion schemes.

Couvidat et al. (2004) compared inversions done using ray-approximation kernels with inversions done with Fresnel-zone kernels. The results were quite similar for depths between the surface and the lower turning point of the deepest rays used in the inversion. Inversions done with the ray kernels cannot retrieve sound speed perturbations below the lower turning point of the deepest ray, while the Fresnel-zone kernels extend below the depth of the deepest ray. The results of Couvidat et al. (2004), as well as those of Giles (1999), suggest that even though the ray approximation overestimates travel times for small scale perturbations this effect does not seriously corrupt the large scale features found by inversion.

Another test of inversion methods was done by Zhao and Kosovichev (2003a). The two main results of this study, regarding inversions methods, were that there is cross-talk between upflows and convergent flows, and between downflows and divergent flows, and that the MCD and LSQR methods give essentially the same results when applied to quiet sun MDI data. Figure 23 shows an example of a test of the LSQR method. The initial model is shown in the top panel. Travel times were generated using the ray approximation. The travel times were then inverted using five iterations of LSQR to obtain the flow field shown in the second panel of Figure 23. Notice that there are small vertical flows near the surface at the centers and boundaries of the supergranulations cells. After 100 iterations of LSQR, these small vertical velocity features are removed (bottom panel of Figure 23).

Figure 23:

Tests of an RLS inversion for supergranulation-like flows. Top panel: flow field in the model; middle panel: the inversion result after five iterations of LSQR; bottom panel: inversion result after one hundred inversions of LSQR. In practice one hundred iterations would greatly magnify any noise in the data. From Zhao and Kosovichev (2003a).

The first end-to-end test of time distance helioseismology using artificial data was done by Jensen et al. (2003b). In this important study, artificial data were generated by numerical wave propagation through a three-dimensional stratified and horizontally inhomogeneous model. Waves were generated by stochastic sources distributed over a layer 50 km below the upper boundary of the surface of the model. The artificial wave field was “observed” at the spatial resolution and temporal cadence of MDI high-resolution observations. This artificial data set was then subjected to standard time-distance analysis, and the inversion was performed with the Fresnel-zone kernels described by Jensen and Pijpers (2003). Figure 24 shows a comparison of the original sound-speed model and the result of the inversion of the artificial data. Notice that the inversion recovers much of the original structure. The inversion result contains noise, which is to be expected from travel times computed from finite time series. The only noise source in this example is realization noise, noise resulting from the stochastic nature of the wave excitation.

Figure 24:

The sound speed in the model (top panel) and the result of the inversion of the artificial data (lower panel). The gray scale is such that light colors are reduced sound-speed and dark colors are increased sound speed, in both cases relative to the stratified background. From Jensen et al. (2003b).

Helioseismic holography

Helioseismic holography was introduced in detail by Lindsey and Braun (1990), although the basic concept was first suggested by Roddier (1975). For a recent theoretical introduction to helioseismic holography see Lindsey and Braun (2000a). The central idea in helioseismic holography is that the wavefield, e.g., the line-of-sight Doppler velocity observed at the solar surface, can be used to make an estimate of the wavefield at any location in the solar interior at any instant in time. In this sense, holography is much like seismic migration, a technique in geophysics that has been in use since the 1940’s (see, e.g., Hagedoorn, 1954, and references therein). In migration, the wave equation is used to determine the wavefield in the interior of the earth at past times, given the wavefield observed at the surface (see, e.g., Claerbout, 1985).

In Section 4.4.1 we introduce the basic computations of helioseismic holography, the ingression and egression. In Section 4.4.2 we review the various calculations that have been used to obtain the Green’s functions used in holography. In Section 4.4.3 we introduce the notion of the local control correlation. Acoustic power measurements are described in Section 4.4.4. Phase-sensitive holography is introduced in Section 4.4.5. Section 4.4.6 describes the technique of far-side imaging. In Section 4.4.7 we describe acoustic imaging (Chang et al., 1997), a technique closely related to holography.

Ingression and egression

The ingression and egression are attempts to the answer the following question: Given the wavefield observed at the solar surface, what is the best estimate of the wavefield at some point in the solar interior assuming that the observed wavefield resulted entirely from waves diverging from that point (for the egression) or waves converging towards that point (for the ingression)?

The development of holography has, historically, been motived by analogy with optics (e.g., Lindsey and Braun, 2000a) and as a result the holography literature often employs optical terminology. The target point in the solar interior at which we attempt to estimate the wavefield is termed the “focus point”. In practice, only data in a restricted area on the surface above the focus point is used to compute the egression and ingression. This region is called the “pupil”. The choice of pupil geometry depends on the particular application and will be described when we discuss particular applications of holography.

As described by Lindsey and Braun (2000a), a mathematical motivation for the ingression and egression is the Kirchoff integral solution to the wave equation (e.g., Jackson, 1975). Suppose that a scalar field Φ solves the equation

$${k^2}\Phi (r) + {{\bf{\nabla}} ^2}\Phi (r) = 0.$$

(67)

The Green’s function, G, for this problem is defined as the solution to

$${k^2}G(r) + {{\bf{\nabla}} ^2}G(r) = {\delta _{\rm{D}}}(r),$$

(68)

where δ_D is the 3D Dirac delta function. The Kirchoff integral equation for Φ is

$$\Phi (r) = \int_S {ds} \;[\{{\partial _n}G(r - s)\} \Phi (s) - G(r - s){\partial _{\rm{n}}}\Phi (s)].$$

(69)

The integration variable s ranges over any surface S enclosing the locations r. For a derivation see for example the introduction in Jackson (1975), noting that the Kirchoff integral equation is a special case of Green’s second identity. The normal derivative, outwards, is denoted by ∂_n. Equation (69) is interesting as it says that given the value of the field on the surface of a region we can determine the value of the field anywhere inside this region. Holography is an attempt to do just that, determine the wavefield in the solar interior given the wavefield on the solar surface. As discussed in detail by Lindsey and Braun (2004), helioseismic holography is much more complicated than solving the simple scalar wave Equation (67) addressed by the Kirchoff integral.

Motivated by the Kirchoff identity (Equation 69), the egression $H_{+}^{{\cal P}}$ and ingression $H_{-}^{{\cal P}}$ are defined as

$$H_\pm ^{\cal P}(r,\omega) = \int_{\cal P} {{d^2}} {x^{\prime}}G_\pm ^{{\rm{holo}}}(x - {x^{\prime}},z,{\omega ^{\prime}})\Phi ({x^{\prime}},\omega).$$

(70)

The focus point is located at position r = (x, z) in the solar interior. The integration variable x′ denotes horizontal position on the solar surface and ranges over the surface region denoted by the pupil ${\cal P}$, typically an annular region, or a sector of an annular region, centered on the horizontal position of the focus point, x. For examples of pupils see Lindsey and Braun (2000a). The wavefield on the surface is Φ(x′, ω) and ω is temporal angular frequency. Recall that the egression, $H_{+}^{{\cal P}}$, is an attempt to estimate the wavefield at the location r and frequency ω based on the waves that are seen, in the pupil P at the surface, diverging away x. Likewise, the ingression, H₋ is an attempt to estimate the wavefield at the location r and frequency ω based on the waves seen, within the pupil, converging towards the focus point. The holography Green’s functions, which depend on a horizontal displacement x, a focus depth z, and a temporal frequency u are denoted by $G_{\pm}^{{\rm holo}}(r,\omega)$. In the time domain, the causal Green’s function $G_{\pm}^{{\rm holo}}(r,t)$, obtained by temporal inverse Fourier transform from $G_{\pm}^{{\rm holo}}(r,\omega)$, is zero for t < 0. In the time domain, the anti-causal Green’s function is zero for t > 0. The time-domain causal Green’s function and anti-causal Green’s function are related by $G_{-}^{{\rm holo}}(r,t)=G_{+}^{{\rm holo}}(r,-t)$. The holography Green’s function are not defined as the solution to any particular set of equations, but rather we use the symbol $G_{\pm}^{{\rm holo}}$ to denote whatever function is used in practice in the computation of the ingression and egression. There are a number of choices that have been used for these Green’s functions (see Section 4.4.2 for details).

An intuitive way to interpret Equation (70) is to view the Green’s functions as propagators. In this way, the egression can be seen as the result of using the anti-causal Green’s function $G_{+}^{{\rm holo}}$ to propagate the surface wavefield backwards in time. Likewise, the ingression can be seen as the result of using the causal Green’s function $G_{-}^{{\rm holo}}$ to propagate the observed surface wavefield forwards in time.

The egression and ingression are the essential quantities in helioseismic holography. There are many particular ways in which these quantities can be combined to learn about the solar interior. The main techniques are control-correlations (Section 4.4.3), acoustic power holography (Section 4.4.4), phase-sensitive holography (Section 4.4.5), and far-side imaging (Section 4.4.6) which is a special case of phase-sensitive holography. Of central importance to all of these methods is the choice of the holography Green’s function $G_{\pm}^{{\rm holo}}(r,\omega)$, which we now describe.

Holography Green’s functions

The two approaches that have been used to construct the holography Green’s functions, $G_{\pm}^{{\rm holo}}$, involve ray theory and wave theory.

Ray theory

Lindsey and Braun (2000a), motived by ray theory, prescribed the holography Green’s function as

$$G_\pm ^{{\rm{holo}}}(r,t) = \sum\limits_N {{A_N}} (x,z){\delta _{\rm{D}}}(t \pm {\tau _N}(x,z)),$$

(71)

where r = (x, z) and x = ∥x∥ is the horizontal distance. The role of the function $G_{-}^{{\rm holo}}(G_{+}^{{\rm holo}})$ is to propagate the observed surface wavefield forwards (backwards) in time and into the interior of the solar model. Theses functions can also be seen as the “wavefield” response at a horizontal distance x, depth z, and time t to a surface source located at the origin at time t = 0. The observed surface wavefield can be thought of as a source, in the spirit of Huygen’s principle. The index N refers to the number of skips the ray path has taken off the solar surface. Each function A_N(x, z) is the amplitude of a single skip component of the Green’s function and can be estimated from simple ray theory. In particular, in ray theory the amplitude functions A_N are determined by the conservation of energy and the increase, with distance along the ray path, of the cross-sectional area of a ray bundle emerging from the source location. In Equation (71), the functions τ_n are the ray-theoretical travel times along the N-skip ray paths connecting a point on the surface with a point at depth z and a horizontal distance x away from the first point. The sum over skips N in Equation (71) is convenient as it can easily be truncated to estimate, for example, just the “one-skip” Green’s function, i.e., the Green’s function that contains only contributions from waves that have traveled once into the solar interior. The holography Green’s functions in the time domain (Equation 71) must then be Fourier transformed to obtain G_±(r, ω) referred to in Equation (70).

Notice that there are a great many simplifications involved in writing the Green’s function in Equation (71). The substantial frequency dependence of the travel time (e.g., Jefferies et al., 1994) has been ignored. There is no account taken of damping, which is quite significant for high-degree modes (e.g., Duvall Jr et al., 1998). Furthermore, as the ray approximation requires the wavelength to be much smaller than the length scale of the variation of the background medium, the ray approximation is not expected to be valid near the solar surface. Further issues include the neglect of the buoyancy and cut-off frequencies in the calculation of τ_N, and also in the computation of the ray paths themselves (Lindsey and Braun 2000a). Recent work by Lindsey and Braun (2004) suggests that after empirical dispersion corrections have been applied (see Section 4.4.3), the results of ray theory calculations are quite similar to the results of wave theory calculations (see Figure 25).

Figure 25:

Comparison of the amplitudes (left panel) and phases (right panel) of ingression-egression correlations (Section 4.4.5) at a focus depth of 4.2 Mm computed with ray theory (“eikonal”, Equation (71)) and with the wave theory (“hydromechanical”, Equations (72, 73)). In both cases, an empirical dispersion correction has been applied (see Section 4.4.3). The black points correspond to focus points where the photospheric magnetic field is weaker than 10 G and the red points correspond to focus points where the surface magnetic field is larger than 100 G. There is, in general, good correspondence between the results of the two methods, though the scatter in the phases appears to increase with increasing phase shifts. From Lindsey and Braun (2004).

Wave theory

An alternative to the ray calculation is to choose, somewhat arbitrarily, the holography Green’s functions to solve a wave equation for the vertical displacement of a fluid element. This was carried out by Lindsey and Braun (2004). The computation proceeds most simply in the 3D Fourier domain (k-ω domain). For each horizontal wavenumber and frequency component the Green’s function can be found by solving a one-dimensional boundary value problem. This can be seen by considering the equations of motion, written in the Fourier domain (Lindsey and Braun, 2004),

$${\omega ^2}{{dp} \over {dz}} = {k^2}gp + {\rho _0}\left({{\omega ^4} + {\omega ^2}{{dg} \over {dz}} - {k^2}{g^2}} \right){\xi _z},$$

(72)

$${\omega ^2}{{d{\xi _z}} \over {dz}} = \left({{k^2} - {{{\omega ^2}} \over {{c^2}}}} \right){p \over {{\rho _0}}} - {k^2}g{\xi _z}.$$

(73)

Here p and ξ_z are the pressure perturbation and vertical displacement associated with the Green’s function. The acceleration due to gravity is g and the background density and sound speed are ρ₀(z) and c(z), respectively. Equations (72, 73) can be used to find the pressure and vertical displacement given two boundary conditions. The data, however, provide us with only one upper boundary condition. It is for this reason that the assumptions that all of the observed waves are up-going waves at the surface, when computing the egression, and down-going waves at the surface, when computing the ingression, are made (Lindsey and Braun, 2004). In this way the second boundary condition can be generated from the first. Notice that Equations (72, 73) do not include the effect of damping.

Local control correlations

The local control correlation is the correlation between the observed signal at a particular point on the solar surface and the holographic reconstruction of the signal at that same point computed from the data in a surrounding region. In particular the local control correlations are defined as (see, e.g., Lindsey and Braun, 2004)

$${C_-}(x,\omega) = {\langle {\Phi (x,\omega)H_- ^{\ast}(x,{z_{\rm{o}}},\omega)} \rangle _{\Delta \omega}},$$

(74)

$${C_+}(x,\omega) = {\langle {{H_+}(x,{z_{\rm{o}}},\omega){\Phi ^{\ast}}(x,\omega)} \rangle _{\Delta \omega}}.$$

(75)

Here the depth z₀ denotes the z coordinate of the solar surface. The angle brackets denote the average over a frequency band of width Δω centered at frequency ω. Notice that we have not specified the pupil which goes into the ingression/egression calculations. The pupil that is used depends on the particular situation. Figure 26 shows quiet Sun local control correlations, measured using both ray theory and wave theory Green’s functions.

Figure 26:

Spatial averages of quiet Sun local control correlations. (a) Results obtained using the wave theory Green’s functions. (b) Results of using ray theory. The numbers along each curve denote the cyclic frequency ω/2π in units of mHz. In both cases, notice that the phase is not zero. From Lindsey and Braun (2004).

If the egression/ingressions were perfect reconstructions of the observed signal, then the phases of the C_± would both, on average, be zero in the quiet Sun. In practice, this is not the case (Lindsey and Braun, 2004). The phases of the holography Green’s functions are typically corrected so that the phase of the average quiet Sun local control correlation is zero (e.g., Lindsey and Braun, 2000a). We refer to this correction as the empirical dispersion correction.

Acoustic power holography

The goal of acoustic power holography is to estimate the amount of wave power emitted from a particular region, either at particular time or a particular frequency. The estimate of the power emitted at a particular frequency, ω, at horizontal location x and depth z is

$$P(r,\omega) = \vert {H_+}(r,\omega){\vert ^2},$$

(76)

and the estimate of the power emitted at a particular time t is

$$P(r,t) = \vert {H_+}(r,t){\vert ^2}.$$

(77)

Here H₊(r, t) is the temporal Fourier transform of H₊(r, ω). Notice that these estimates depend on the estimate of the Green’s function and the pupil that are used to compute H₊. For further discussions of acoustic power holography see, for example, Lindsey and Braun (1997) and Donea et al. (1999). Acoustic power holography has been used in studies of wave excitation by flares (e.g., Donea et al., 1999) and around active regions (e.g., Donea et al., 2000).

Phase-sensitivity holography

The basic computation in phase-sensitive holography is the ingression-egression correlation (see, e.g., Lindsey and Braun, 2000a, 2004),

$${C_{{\cal P},{{\cal P}^{\prime}}}}(r,\omega) = {\langle {H_- ^{\cal P}(r,\omega)H_+ ^{{\cal P}{^{\prime}_\ast}}(r,\omega)} \rangle _{\Delta \omega}},$$

(78)

where ${\cal P}$ and ${\cal P}^{\prime}$ are two pupils and the angle brackets denote averaging over a frequency range of width Δω centered on frequency ω. Phase-sensitive holography has been used to look for sound-speed perturbations and mass flows. In both cases the geometry is the quadrant geometry that is also used in time-distance measurements. In particular the pupil ${\cal P}$ is chosen to be a quarter of an annulus, let us call it ℒ for “left”, and ${\cal P}^{\prime}$ is chosen to be the quarter annulus located 180° away, call it ℛ for “right”. The symmetric phase is defined as

$${\phi _{\rm{s}}} = {1 \over 2}({\rm{Arg}}\;{C_{{\cal L},{\cal R}}} + {\rm{Arg}}\;{C_{{\cal R},{\cal L}}}).$$

(79)

Here the operator Arg returns the phase. The phase φ_s is mostly sensitive to sound-speed; this can be seen from the symmetry of the definition. In particular, φ_s does not change when the pupils ℒ and ℛ are interchanged. Notice that for a horizontally uniform sound-speed perturbation Arg C_ℒ,ℛ = Arg C_ℒ,ℛ. On the other hand, a uniform horizontal flow gives Arg C_ℒ,ℛ = −Arg C_ℒ,ℛ. Thus φ_s is zero for a horizontally uniform flow and non-zero for a horizontally uniform sound-speed perturbation. The anti-symmetric phase is defined as

$${\phi _{\rm{a}}} = {\rm{Arg}}\;{C_{{\cal L},{\cal R}}} + {\rm{Arg}}\;{C_{{\cal R},{\cal L}}}.$$

(80)

The symmetry of φ_a is such that φ_a changes sign under interchange of the pupils ℒ and ℛ and, thus, the anti-symmetric phase is sensitive to horizontal flows. The phases φ_s and φ_a are analogous to the mean and difference travel times commonly employed in time-distance helioseismology.

Far-side imaging

Far-side imaging is a special case of phase-sensitive holography (e.g., Lindsey and Braun, 2000b; Braun and Lindsey, 2001). The idea is to use the wavefield on the visible disk to learn about active regions on the far-side of the Sun. Figure 27 shows the geometry that was used by Braun and Lindsey (2001). In order to obtain full coverage of the far-side of the Sun, two different geometries were employed. For regions near the antipode of the center of the visible disk a two-skip geometry and two-skip Green’s functions were employed (panel (a) of Figure 27). For focus positions near the limb, the ingression/egression were computed using a single-skip pupil and corresponding Green’s functions, and then correlated with the egression/ingression computed using a three-skip pupil and Green’s functions (the geometry is shown in panel (b) of Figure 27).

Figure 27:

Geometry for far-side imaging. (a) Two-skip correlation scheme. (b) One-skip/three-skip correlation. In far-side imaging the data on the visible disk are used to estimate the wavefield at focal points on the far-side of the Sun. From Braun and Lindsey (2001).

Acoustic imaging

Acoustic imaging was first introduced by Chang et al. (1997); for a recent review see Chou et al. (2003). We have included acoustic imaging in the section on helioseismic holography as the definitions and philosophical motivation for the two techniques are quite similar.

The central computations in acoustic imaging (see, e.g., Chou et al., 1999, 2003) are wavefield reconstructions in the solar interior, Ψ_in and Ψ_out, defined by

$${\Psi _{{\rm{out}},{\rm{in}}}}(r,t) = \sum\limits_{\tau = {\tau _1}}^{{\tau _2}} {W(\tau, z)} \overline \Phi (\Delta (\tau, z),t \pm \tau).$$

(81)

The focus position is r = (x, z). The function $\overline{\Phi}(\Delta,t)$ denotes the azimuthal average, around x, of the surface wavefield Φ measured a horizontal distance Δ away from x. The quantity τ represents the ray-theoretical travel times from the subsurface focus point at r to surface points a horizontal distance Δ away from the focus point. For a given τ, the distance Δ satisfies the time-distance relation established between the focus point and a surface point. This relation, Δ = Δ(τ, z), is computed from a standard solar model, using the ray approximation (see Figure 28). The function W is a smooth weight function of τ (or Δ), explicitly given by Chou et al. (1999). The sum in Equation (81) involves the observed wavefield inside an annulus with inner and outer radii specified by the range τ₁ < τ < τ₂.

Figure 28:

Time-distance relations at various focal depths, computed from a standard solar model, based on ray theory, at 3 mHz. Each curve corresponds to different target depths, as indicated. For each curve, the dots correspond to modes whose l values are multiples of 10, starting with l = 80 at the right end of each curve. The highest-l mode which can reach the target depth is marked by an open circle on each curve. The l value decreases in either direction away from the open circle along the curve. From Chou et al. (1999).

In some sense, acoustic imaging is a special case of holography. Here, the pupil is an annulus with inner radius Δ₁ and outer radius Δ₂ given by the time-distance relation Δ_j = Δ(τ_j, z). The equivalent holography Green’s function is given by Wδ_D(t − τ). The signal Ψ_out corresponds to the egression, i.e., is the signal reconstructed from the observations of waves diverging from the focal point, while corresponds to the ingression, the signal estimated from the waves seen converging towards the focus position.

As with holography, both the amplitudes and phases of Ψ_{out, in} are used to learn about the solar interior. The square of the amplitude of Ψ_out is an estimate of the power contained in the waves seen diverging from the focus position (Chang et al., 1997). In the terminology of holography, the squared of the amplitude of Ψ_out is called the “egression power.” Chen et al. (1998) introduced the correlation

$$C(r,t) = \int {d{t^{\prime}}{\Psi _{{\rm{in}}}}} (r,{t^{\prime}}){\Psi _{{\rm{out}}}}(r,{t^{\prime}} + t)$$

(82)

and then measured phase and group times by fitting a Gaussian wavelet to C(r, t) at fixed target point r. Changes in the phase between Ψ_in and Ψ_out result in changes in C(t) and thus shift the travel times. A phase shift between the two reconstructions, Ψ_out and Ψ_in, is evidence for local changes in sound speed (Chen et al., 1998). Chou and Duvall (2000) discuss the relationship between time-distance travel times and the travel times measured by acoustic imaging.

The forward problem that has received the most attention in acoustic imaging is the dependence of travel times on changes in the sound speed. Chou and Sun (2001) used the ray approximation to estimate the sensitivity of acoustic imaging phase travel times to changes in sound speed. The results showed that in general the horizontal resolution is greater than the vertical resolution and that the resolution decreases with increasing focus depth.

The inverse problem of determining the sound speed from a given set of travel times has been studied in the ray approximation as well. Sun and Chou (2002) tested ray-theory RLS inversions of phase-time measurements on artificial data. These tests showed that the RLS inversions were, for good choices of the regularization parameter, capable of reconstructing the model used to generate the artificial data. Inversions of travel times for sound speed were also discussed in detail by Chou and Sun (2001).

Direct modeling

Woodard (2002) introduced the idea of estimating subsurface flows from direct inversion of the correlations seen in the wavefield in the Fourier domain. The central notion is that for horizontally homogeneous steady models with no flow Fourier components of the physical wavefield are uncorrelated. Departures from horizontal homogeneity or time-dependence in general introduce correlations into the wavefield. Thus observations of the correlations in the Fourier domain can be used to estimate flows in the interior. Woodard (2002) gave a practical demonstration of the ability of the technique to recover near-surface flows from the f-mode part of the spectrum.

Forward problem

The fact that a correlation in the Fourier components of the wavefield is introduced by a perturbation to a translation invariant model can be seen from the Born approximation of the perturbed wavefield, δΦ. Rewriting Equation (30) in terms of Fourier coordinates gives

$$\matrix{{\delta \Phi (k,\omega) = - {{(2\pi)}^3}\int {{d^3}r\;dt\;{d^2}{k^{\prime}}\;d{\omega ^{\prime}}\;d{z_{\rm{s}}}\;{e^{- {\rm{i}}k \cdot x + {\rm{i}}\omega t}}} {G^i}(k, \omega, z)} \hfill \cr {\quad \quad \quad \quad \;\; \times {{\left\{{\delta {L_{(r,t)}}\left[ {{G^j}({k^{\prime}},{\omega ^{\prime}},z,{z_s})\;{e^{{\rm{i}}{k^{\prime}} \cdot x - {\rm{i}}{\omega ^{\prime}}t}}} \right]} \right\}}_i}S_j^0({k^{\prime}},{\omega ^{\prime}},{z_{\rm{s}}}),} \hfill \cr}$$

(83)

where summation is assumed over the repeated indices i and j, r = (x, z) is the scattering location, and the Green’s functions ${\cal G}$ and G are defined in Section 3.3. The perturbations to the source function were ignored for the sake of simplicity. To obtain Equation (83) we used the fact that the operator δℒ, which describes the perturbation to the model at (r, t), is a linear operator. The equation shows that the perturbation to the model in general causes a response at wavevector k and frequency u to a source at k′ and ω′. This response is thus correlated with the unperturbed wave created by the same source. Notice that for a perturbation that depends both on space and time, the operator δℒ explicitly depends on r and t. Using Equation (83) the correlations of the wavefield in the Fourier domain can be approximated, to first order in the strength of the perturbation, as

$$\matrix{{E[\delta \Phi (k,\omega){\Phi ^{\ast}}({k^{\prime}},{\omega ^{\prime}})] = - {{(2\pi)}^6}\int {{d^3}} r\;dt\;d{z_{\rm{s}}}\;dz_{\rm{s}}^{\prime}\;{e^{- {\rm{i}}k\cdot x + {\rm{i}}\omega t}}{{\cal G}^i}(k,\omega,z)} \hfill \cr {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \times {{\left\{{\delta {{\cal L}_{(r,t)}}\left[ {{G^j}({k^{\prime}},{\omega ^{\prime}},z,{z_s}){e^{{\rm{i}}{k^{\prime}}\cdot x + {\rm{i}}{\omega ^{\prime}}t}}} \right]} \right\}}_i}} \hfill \cr {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \times {m_{jk}}({k^{\prime}},{\omega ^{\prime}},{z_{\rm{s}}},z_{\rm{s}}^{\prime}){{\cal G}^{k\ast}}({k^{\prime}},{\omega ^{\prime}},z_{\rm{s}}^{\prime}),} \hfill \cr}$$

(84)

where the source covariances

$$E[S_i^0(k,\omega,{z_{\rm{s}}})S_i^{0\ast}({k^{\prime}},{\omega ^{\prime}},z_{\rm{s}}^{\prime})] = {m_{ij}}(k,\omega,{z_{\rm{s}}},z_{\rm{s}}^{\prime}){\delta _{\rm{D}}}(k - {k^{\prime}}){\delta _{\rm{D}}}(\omega - {\omega ^{\prime}})$$

(85)

express the assumptions of stationarity and horizontal spatial homogeneity (the functions m_ij are equal to the functions M_ij within a multiplicative factor, see Section 3.2). In Equation (84) summation over the repeated indices, i, j, and k, is assumed. This expression is accurate to first order in the strength of the perturbation to the background model, which appears in the operator δℒ.

An example calculation

Let us now connect the result of the previous section with the results of Woodard and Fan (2005). In real space, Woodard and Fan (2005) use

$$\delta {{\cal L}_{(r,t)}} = 2{\rho _0}(z)U(r,t) \cdot {{\bf{\nabla}} _r}{\partial _t}$$

(86)

to model the effect of a flow U. This approximation neglects any possible effect of the flow on the wave sources and wave damping. Woodard and Fan (2005) expand the velocity field in Fourier components, in the horizontal directions and time, and known functions of depth. For the sake of a relatively simple example, let us look at the special case of a vertical flow of the form

$$U(r,t) = \hat z{U_z}(z){e^{{\rm{i}}q \cdot x - {\rm{i}}\sigma t}},$$

(87)

where the vector q is a horizontal wavevector and σ is a temporal frequency. Under these assumptions, we have

$$\delta {{\cal L}_{(r,t)}}\left[ {{G^j}({k^{\prime}},{\omega ^{\prime}},z,{z_{\rm{s}}}){e^{{\rm{i}}{k^{\prime}} \cdot x - {\rm{i}}{\omega ^{\prime}}t}}} \right] = - 2{\rm{i}}{\omega ^{\prime}}{\rho _0}(z){U_z}(z){\partial _z}{G^j}({k^{\prime}},{\omega ^{\prime}},z,{z_{\rm{s}}}){e^{{\rm{i}}({k^{\prime}} + q) \cdot x - {\rm{i}}({w^{\prime}} + \sigma)t}}.$$

(88)

Let us further assume that the sources are all located at a particular depth z_s and that only the j = k = z component of m_jk is non-zero, again only for the sake of simplicity. This is done here only to avoid carrying the integrals over z_s and z_s′. Then Equation (84) becomes

$$\matrix{{E[\delta \Phi (k,\omega){\Phi ^{\ast}}({k^{\prime}},{\omega ^{\prime}})] = 2{\rm{i}}{\omega ^{\prime}}{{(2\pi)}^9}\delta (k - {k^{\prime}} - q)\delta (\omega - {\omega ^{\prime}} - \sigma){m_{zz}}({k^{\prime}},{\omega ^{\prime}}){{\cal G}^{z\ast}}({k^{\prime}},{\omega ^{\prime}},{z_{\rm{s}}})} \hfill \cr {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \times \int {dz} \;{\rho _0}(z){U_z}(z){{\cal G}^i}(k,\omega,z){\partial _z}G_i^z({k^{\prime}},{\omega ^{\prime}},z,z{_s}).} \hfill \cr}$$

(89)

Equation (89) is already quite informative. First of all, note that a velocity field with horizontal wavenumber q only correlates components of the wavefield whose horizontal wavenumbers differ by q. This is sensible. Likewise, velocity fields with harmonic time dependence with frequency a only couple components of the wavefield whose frequencies differ by σ. The above result can be reduced to the equations of Woodard and Fan (2005) by inserting the normal summation approximations for the Greens function’s (see Birch et al., 2004, and Section 3.3.2) into the above result.

Woodard and Fan (2005) make the further approximation that oscillations of different radial orders are excited incoherently. This is certainly not the case in reality, as evidenced by the asymmetry in the power spectrum. It is not clear what effect this approximation will have on the final result, as most of the power is near the resonances, where line-asymmetry is not important.

Notice that we also need to compute the term $E[\Phi(k,\omega)\delta\Phi^{\ast}(k^{\prime},\omega^{\prime})]$ as the final result that we wish to obtain is the first order change in $E[\Phi(k,\omega)\Phi^{\ast}(k^{\prime},\omega^{\prime})]$ introduced by a small change in the model. This second term can be computed in exactly the same manner as the $E[\delta\Phi(k,\omega)\Phi^{\ast}(k^{\prime},\omega^{\prime})]$ term, which we have already done.

Inverse problem

So far we have only addressed the forward problem. The other half of the direct-modeling approach is the inverse problem, that is inferring the flows in the Sun from the Fourier domain correlations seen in the data. The inverse problem in direct modeling has been solved as a linear least-squares problem (Woodard, 2002; Woodard and Fan, 2005). A crucial observation is that a flow with horizontal wavenumber q only couples modes with wavenumbers k and k′ when ∥k − k′∥ = q. This is a result of the assumption that the background model is plane-parallel and translation invariant. As a result the different wavenumber components of the flow can be inferred one at a time, in the spirit of the MCD inversion scheme (Jacobsen et al., 1999). The same argument applies in the time domain, and flows can be inferred one frequency component at a time.

Woodard (2002) tested his direct-modeling approach on a quiet sun region using MDI data. The method was used to invert for near-surface supergranular-scale flow. Although many approximations were made in carrying out the inversion, general agreement (a correlation coefficient of 0.68) was found between the Doppler component of the seismically inferred flow in the photosphere and the directly observed surface Doppler signal (see Figure 29). Thus direct modelling appears to be a very promising technique.

Figure 29:

Line-of-sight velocity maps showing supergranular-scale flow, based on SOHO/MDI high spatial resolution Dopplergrams. Left panel: Line-of-sight projection of near-surface flows inferred from direct modeling of seismic data. Right panel: Velocity map obtained by averaging the 16 hr sequence of Dopplergrams used in the seismic analysis. From Woodard (2002).

Scientific Results from Local Helioseismology

Global scales

Flows in the upper convection zone have been measured by local helioseismology on a wide variety of scales, including differential rotation and meridional circulation, local flows around complexes of magnetic activity and sunspots, and convective flows. Here we mostly discuss the longitudinal averages of flows measured by local helioseismology, and their solar-cycle variations. The focus is on temporal variations that are slow compared to the typical lifetime of active regions. By computing longitudinal averages of rotation and meridional circulation over a few solar rotation periods it is possible to filter out small-scale flows and to reach a sensitivity of the order of 1 m s⁻¹ near the surface. The evolution of flows through cycle 23 reveals connections between mass motions in the solar interior and the large-scale characteristics of the magnetic cycle.

Rotation and torsional oscillations

Measuring the mean rotation using local techniques is a useful exercise, in particular to compare with estimates from inversions of frequency-splitting coefficients. Giles et al. (1998) and Giles (1999) measured rotation with time-distance helioseismology applied to MDI data (structure and dynamics programs; see Scherrer et al., 1995). Figure 30 shows the angular velocity as a function of latitude for radii r > 0.886R_⊙. There is a good qualitative agreement between the time-distance and the global-mode inversions, although the agreement is not as good at high latitudes. Basu et al. (1998, 1999) used the ring-diagram method to obtain the rotational velocity for r > in the latitude range |λ| < 50°. The north-south symmetric component of rotation compares favorably with the rotation determined from the frequency splittings of the global p modes (Figure 31). Since the inversion results of p-mode splittings were not expected to be particularly reliable near the surface, the ring diagram results complement and support the earlier conclusion that rotation increases with depth, near the surface, at low latitudes. Possible explanations for the existence of this near-surface radial shear have been discussed by Gilman (2000) and Robinson and Chan (2001). The local helioseismology results also show measurable differences in the rotation profile between the northern and southern hemispheres (see, e.g., Basu et al., 1999; Giles, 1999; González Hernández and Patrón, 2000). It would be premature, however, to trust the validity of the north-south asymmetry in the rotation rate, since systematic errors are not fully understood and do vary with latitude.

Figure 30:

Comparison of the time-distance and normal mode methods for determining the solar rotation. The angular velocity is plotted versus latitude for six different depths. The solid curve is the symmetric component of the time-distance results, and the dashed lines are formal errors from the inversion. The dotted curve is the result of an OLA inversion of MDI frequency splittings. From Giles (1999).

Figure 31:

North-south average of rotational velocity at different latitude from ring-diagram analysis. The results obtained using RLS inversions are shown by dashed lines (with dotted lines marking the 1σ error limits) and the results obtained by using OLA inversions by crosses with error bars. For comparison, the solid line shows the rotational velocity obtained from inversion of global-mode frequency splittings (after subtracting out the surface rotation velocity used in tracking each region). From Basu et al. (1999).

Howard and Labonte (1980) discovered small (±10 m s⁻¹) latitudinal variations in the surface Doppler rotation profile that propagate toward the equator with the sunspot latitudes. These variations, known as torsional oscillations, have since been confirmed by global helioseismology (Kosovichev and Schou, 1997; Schou, 1999). Inversions of global-mode frequency splittings have shown that torsional oscillations persist at a depth over a large fraction of the convection zone (Howe et al., 2000a), especially at high latitudes where they extend down to the bottom of the convection zone (Vorontsov et al., 2002). At low latitudes, the data support the idea that the torsional oscillation pattern originates inside the convection zone and propagates both upward and equatorward (Vorontsov et al., 2002; Basu and Antia, 2003). Above 45° latitude, bands of faster and slower rotation appear to move toward the poles (Antia and Basu, 2001; Schou, 2003a) suggesting a connection with the poleward migration of high-latitude magnetic activity seen at the surface (see, e.g., Callebaut and Makarov, 1992).

Both time-distance (Giles et al., 1998; Beck et al., 2002; Zhao and Kosovichev, 2004) and ring-diagram (Basu et al., 1999; Basu and Antia, 2000; Haber et al., 2000, 2002) analyses have confirmed the global-mode measurements of torsional oscillations. Figure 32 shows a plot of the zonal flows at depths of 0.9 Mm and 7.1 Mm obtained from ring-diagram analysis. At both these depths, propagating zonal fast bands are seen to migrate toward the equator as the solar cycle progresses. As will be later discussed in Section 5.2, local techniques can also provide information about the longitudinal structure of the zonal flows.

Figure 32:

Zonal flows from ring-diagram analysis at depths of 0.9 Mm (dashed curve) and 7.1 Mm (solid curve). Each panel corresponds to the average over yearly MDI Dynamics Program intervals as indicated. The zonal velocity plots for each year have been offset by subtracting a depth-dependent constant. The error bars shown are 10 times larger than the estimated formal errors in order to be visible. From Haber et al. (2002).

Schüssler (1981) and Yoshimura (1981) suggested that the torsional oscillations may be driven by the Lorentz force due to a migrating dynamo wave. Recent numerical calculations by Covas et al. (2000) seem to be consistent with this hypothesis; their calculations also reproduce the poleward propagating torsional oscillations at high latitudes. Other explanations attribute the torsional oscillations to the feedback of the smaller-scale magnetic fields on the angular momentum transport mechanisms responsible for differential rotation, e.g., changes in the Reynolds/Maxwell stresses (Küker et al., 1996; Kitchatinov et al., 1999) or the local suppression of turbulent viscosity by active regions (Petrovay and Forgács-Dajka, 2002). An alternative explanation by Spruit (2003) suggests that zonal flows may be driven by temperature perturbations near the surface due to the magnetic field: Local flows around regions of enhanced magnetic activity act through the Coriolis force to balance horizontal pressure gradients. The model of Spruit (2003) naturally predicts a solar-cycle variation in the meridional flows. The reader is referred to the review paper of Shibahashi (2004) for other possible explanations.

Meridional flow and its variations

Surface Doppler measurements have shown the existence of a meridional flow from the equator to the poles with an amplitude of about 20 m s⁻¹ (e.g. Hathaway, 1996). Meridional circulation is an important ingredient of solar dynamo models where magnetic flux is transported by a deep equatorward flow (flux-transport dynamo models). In such models, the solar-cycle period is largely determined by the amplitude of the meridional flow near the base of the convection zone (Dikpati and Charbonneau, 1999). Hathaway et al. (2003) claimed that the butterfly diagram is evidence for flux-transport dynamo models, and estimated a 1.2 m s⁻¹ flow at the bottom of the convection zone from the drift of sunspots toward the equator. However, Schüssler and Schmitt (2004) argue that the butterfly diagram is equally well reproduced by a conventional dynamo model with migrating dynamo waves without transport of magnetic flux by a flow. The depth of penetration of the meridional flow is another parameter in some dynamo models (see, e.g., Nandy and Choudhuri, 2002). Knowing meridional circulation is also important to understand its feedback on differential rotation (Rekowski and Rüdiger, 1998; Gilman, 2000).

Meridional circulation was first detected at depth by Giles et al. (1997) with time-distance helioseismology. The inversions, constrained by mass conservation, show that the data are consistent with a meridional circulation which is 20 m s⁻¹ poleward at the solar surface and about 3 m s⁻¹ equatorward at the base of the convection zone, with a turnover point near 0.8R_⊙ (Giles, 1999, see Figure 33). Other estimates of the meridional circulation have been obtained in the near-surface layers with time-distance helioseismology (see, e.g., Duvall Jr and Gizon, 2000; Zhao and Kosovichev, 2004), Hankel analysis (Braun and Fan, 1998), acoustic imaging (e.g. Chou and Dai, 2001), and ring-diagram analysis (see, e.g., Basu et al., 1999; González Hernández et al., 1999, 2000; Haber et al., 2000). Giles (1999) and Haber et al. (2002) found a submerged equatorward flow in the north during the years 1998–2001. This last result, however, may be contaminated in part by errors in the orientation of the MDI Dopplergrams which cause rotation to leak into the meridional flow signal: a P-angle error due to the misalignement of the MDI telescope on the SOHO spacecraft (C. Toner, 2000, private communication) and an error in the Carrington elements that specify the direction of the solar rotation axis (Giles, 1999).

Figure 33:

Meridional circulation in 1996–98 inferred from p-mode travel times at various latitudes as a function of scaled radius r/R_⊙. The blue (red) curves are for the northern (southern) latitudes. The turnover point is roughly at r = 0.8R_⊙. The assymetry between the two hemispheres is probably caused by an error in the orientation of the MDI camera. From Giles (1999).

Meridional circulation (averaged in longitude over several rotation periods) is observed to change from year to year through the solar cycle. To study the time-varying component of meridional circulation, we consider the residuals obtained after subtraction of a temporal average at each latitude. Meridional flow residuals have an amplitude which is less than 10 m s⁻¹. Like torsional oscillations, the north-south flow residuals drift equatorward with active latitudes. Unlike torsional oscillations, the residuals of meridional circulation change sign across the uppermost 70 Mm. Near the surface, the time-varying residuals converge toward active latitudes (Gizon, 2003; Basu and Antia, 2003; Zhao and Kosovichev, 2004, see Figure 34), while at greater depths meridional flow residuals diverge from the dominant latitude of activity (Chou and Dai, 2001; Beck et al., 2002, see Figure 35). The time-varying component of meridional circulation has also been measured near the surface from the advection of supergranulation (Gizon and Duvall Jr, 2004, see Section 5.3.5).

Figure 34:

(a) Meridional flow measured by time-distance helioseismology at depths of 4 Mm (solid lines) and 7 Mm (dash-dotted lines) as a function of latitude for different Carrington rotations. (b) Northward residual flows, computed by removing the CR1911 flow at each Carrington rotation. The grey regions show the latitudes of activity. The residuals are consistent with a converging flow toward the mean latitude of activity. From Zhao and Kosovichev (2004).

Figure 35:

(a) Meridional circulation residuals as a function of time and latitude, measured by time-distance helioseismology at a depth of about 50 Mm. The residuals are obtained by removing a time average. The green (red) shades correspond to excess poleward (equatorward) velocities, with values in the range ±10 m s⁻¹. The thick black line is the mean latitude of activity. The residuals are consistent with a flow diverging from the mean latitude of activity. (b) Zonal flow residuals (torsional oscillations) as a function of time and latitude. The red (blue) shades correspond to flows that are faster (slower) than average. From (Beck et al., 2002).

These observations, summarized in Figure 36, lead Zhao and Kosovichev (2004) to postulate the existence of extra meridional ciculation rolls on each side of the mean latitude of activity, superimposed on the mean global-scale poleward flows. However, it is suggested in Section 5.2 that the changes in the longitudinal averages of meridional flows can be attributed for a large part to flows that are localized both in longitude and latitude around active regions.

Figure 36:

Sketch of the time-varying components of the large-scale flows, averaged in longitude over several rotation periods. Shown is a meridional plane in the northern hemisphere; the prograde direction is coming out of the page. Zonal flows (a) introduce a ±10 m s⁻¹ shear around the mean latitude of activity (AR). Residual meridional flows (< 10 m s⁻¹) converge toward active latitudes near the surface (e) and diverge deeper inside the Sun (d). The whole pattern of flows drifts equatorward through the solar cycle. The dashed streamlines that connect the horizontal flows are a suggestion by Zhao and Kosovichev (2004). From Gizon (2003).

Vertical flows

Because of their small amplitude, vertical flows are much harder to measure than horizontal flows. The ring-diagram analysis is not, in principle, sensitive to vertical flows. However, Komm et al. (2004) showed how to estimate the vertical flows from ring-diagram inversions by adding a mass conservation constraint (using GONG data). This mass conservation constraint is enforced locally for each 15° × 15° region, under the assumption is that horizontal density fluctuations are negligible because of the large size of the region and the large integration time. Figure 37 shows the longitudinal average of the near-surface vertical velocity over one Carrington rotation (Komm et al., 2004). Weak downflows (less than 1 m s⁻¹) are observed near active latitudes. This result is consistent with the observations of a residual horizontal flow converging toward the mean latitude of activity near the surface (see Figure 36). For depths in the range 0–16 Mm, the amplitude of the downflow increases with depth. A small upflow is seen near the equator.

Figure 37:

Vertical velocity from ring-diagram inversions constrained by mass conservation, averaged over Carrington rotation CR 1988 (2002 March 30–April 25), as a function of latitude and depth. Top panel: Surface magnetic flux as a function of latitude (solid line) and averaged over 15° (dotted curve). Bottom panel: Vertical velocity derived from GONG data after removing the large-scale flow components. The dashed line indicates the zero contour; the dotted lines indicate 20%, 40%, 60%, and 80% of the minimum and the maximum of the color scale. The dots indicate the depth-latitude grid. From Komm et al. (2004).

Search for variability at the tachocline

Howe et al. (2000b) discovered temporal changes in the rotational velocity near the bottom of the convection zone with a period of approximately 1.3 yr and a peak amplitude at 0.72R_⊙. The angular velocity variations at 0.72R_⊙ and 0.63R_⊙ are anticorrelated (the signal seemed much weaker near the second half of 2001 but it has come back since). These results are somewhat controversial since they have not been confirmed by others (see, e.g., Basu and Antia, 2001; Vorontsov et al., 2002). However, using wavelet analysis over cycles 21–23, Boberg et al. (2002) found signals with a 1–2 yr period in the solar mean magnetic field and Knaack et al. (2005) detected transient 1.3 yr oscillations in the unsigned photospheric magnetic flux, which may be related to the large-scale magnetic surges towards the poles. The 1.3 yr periodicity is also seen in observations of the interplanetary magnetic field and geomagnetic activity (Lockwood, 2001). Gough (2000) suggested that a 500 G radial magnetic field across the tachocline may lead to exchange of angular momentum with the right time scale, while Covas et al. (2001) suggested a highly non-linear mechanism that does not require different physical time scales for torsional and tachocline oscillations.

A deeply challenging task for local helioseismology is to detect the signature of the magnetic field in the tachocline region. The results of Howe et al. (2000b) have not been confirmed by local helioseismology yet, but there have been a few attempts to search for wave-speed perturbations near the base of the convection zone. Chou and Serebryanskiy (2002) selected wave packets that return to the same spatial point after traveling around the Sun with an integral number of bounces N. The ray paths taking N = 8 bounces to go around the Sun have a lower turning point close to the bottom of the convection zone. Chou and Serebryanskiy (2002) observed that the change in one-bounce travel time at solar maximum relative to minimum is approximately the same for all N values studied, except for N = 8 which shows an additional decrease in travel time. Figure 38 shows the relative decrease in the one-bounce travel time at N = 8 relative to the other N values as a function of time (about 15 ms at solar maximum). The correlation with the sunspot number suggests that the additional decrease in travel time at N = 8 might be caused by wave-speed perturbations at the base of the convection zone. With the simplified assumption that this additional decrease is caused only by a magnetic field perturbation at the base of the convection zone, the field strength was estimated to be 0.4 MG at solar maximum. However, Chou and Serebryanskiy (2002) caution that this interpretation is oversimplified since it would also imply an additional decrease in travel time for the wave packets with N ≥ 7, which is not observed. We note here that Ruzmaikin and Lindsey (2003) argue that only field strengths greater than 1 MG should be detectable near the bottom of the convection zone with currently available data.

Figure 38:

Decrease in the one-bounce travel time at N = 8 relative to the other N’s as a function of time. The filled circles denote the MDI results, and the open circles the GONG results. The horizontal bar associated with each point indicates the duration of each observation (the sequence of observing runs is labelled by a series of increasing numbers). The thick horizontal line indicates the range of solar minimum period used for MDI, and the dashed line for GONG. The solid line is the sunspot number from the Greenwich sunspot data. From Chou and Serebryanskiy (2002).

A different approach by Birch (2002) and Duvall Jr (2003) was to search for longitudinal structures near the bottom of the convection zone. Raw travel times measured between surface points separated by 45° were observed to be correlated from day to day, indicating a real solar signal (Duvall Jr, 2003). However, it is not known whether this signal is due to surface effects or deep perturbations.

It should be mentioned that global seismology may also be used to detect a toroidal magnetic field at the level of a fraction of a megagauss, if such a field were confined to a thin layer near the base of the convective envelope (e.g., Basu, 1997; Dziembowski and Goode, 2004). For example, Basu (1997) gave an upper limit of 0.3 MG near solar minimum.

It is fair to say that local helioseismological techniques have encountered difficulties in probing the tachocline. In order to reach a depth of 200 Mm, it is necessary to consider ray paths that connect surface points separated by almost 45°. All local methods thus suffer from foreshortening near the limb. Also, the plane-wave approximation is obviously not appropriate for probing the deep convection zone. Certain methods, like ring-diagram analysis, need to be adapted to take this into account (see, e.g., Haber et al., 1995).

Active regions and sunspots

Ordered flows near complexes of magnetic activity

Here we consider flows near regions of enhanced magnetic activity. We do not discuss local flows associated with sunspots, but larger-scale flows around complexes of magnetic activity. Using local helioseismology, synoptic maps of local horizontal flows can be constructed by averaging the data in time in a frame of reference that co-rotates with the Sun. Weak 50 m s⁻¹ surface flows that converge toward active regions were detected by Gizon et al. (2001) with time-distance helioseismology (Figure 39). These flows, which exist as far as 30° from the centers of active regions, are also seen in ring diagram analyses with a coarser resolution (Haber et al., 2001). We note that Hindman et al. (2004) have shown that the two methods give remarkably similar results near the surface. Recently, both time-distance (Zhao and Kosovichev, 2004) and ring-diagram (Haber et al., 2004) analyses have provided depth inversions of horizontal flows down to about 15 Mm. Depths inversions indicate that, below 10 Mm, horizontal flows often diverge from active-region centers with velocities on the order of 50 m s⁻¹. Figure 40 shows the flows measured by Haber et al. (2004) around a particular active region. Although vertical flows have not been directly measured yet, motions appear to be organized in the form of a toroidal cell with a surface inflow and a deeper outflow. The picture is not so simple on time scales that are shorter than a week since flows do evolve from day to day.

Figure 39:

Map of near-surface horizontal flows obtained for Carrington rotation 1949 using f-mode time-distance helioseismology. A smooth rotation profile has been subtracted. The dark shades are shorter travel time anomalies that correspond to regions of enhanced magnetic activity. Local flows converge toward complexes of activity with an amplitude of 50 m s⁻¹. Notice also the poleward meridional flow. From Gizon et al. (2001).

Figure 40:

Left column: OLA inversion of horizontal flows around active region NOAA9433 on 23 April 2001 obtained using ring-diagram analysis. The depths shown are 7 Mm (upper panel) and 14 Mm (lower panel). The green and red shades are for the two polarities of the magnetic field. The horizontal and vertical axes give the longitude and the latitude in heliospheric degrees. Right panel: Horizontal flows around NOAA9433 as a function of depth and latitude, averaged over the longitude range (142.5°, 157.5°) and the time period 23–27 April 2001. The transition between inflow and outflow occurs near 10 Mm depth. From Haber et al. (2004).

The observed flows around active regions could be caused by the magnetic field. Indeed, the model of Spruit (2003) mentioned earlier predicts a surface inflow toward regions of enhanced magnetic field. An alternative explanation by Yoshimura (1971) suggests that the longitudinal ordering of solar magnetic fields could be due to the existence of large convective patterns that favor the formation of active regions at particular sites on the solar surface. We note that far away from active regions, complex flows like meanders, jets, and vortices are seen in the synoptic maps (Figure 39); Toomre (2002) suggested that they may be related to the largest scales of deep convection.

Effect on longitudinal averages of large-scale flows

An important question is to know whether the local flows that surround active regions contribute significantly to the solar-cycle variations of the longitudinal averages of rotation and meridional circulation in the upper layers of the convection zone (as discussed in Section 5.1.1 and Section 5.1.2). In other words, are the time-varying components of rotation and meridional circulation global phenomena or are they modulated in longitude by the presence of active regions?

In order to help answer this question, we consider synoptic maps of surface flows obtained in 1999 for Carrington rotations 1948 and 1949. By excluding the local areas of magnetic activity from the computation of the longitudional averages of rotation and meridional circulation, we obtain “quiet-sun” estimates that can be compared to the flows averaged over all longitudes (see Gizon, 2003, for details). From Figure 41 it is obvious that the torsional oscillation (rotational shear at active latitudes) is present in between active longitudes. Thus the time-varying zonal flows appear to be mostly independent of longitude as they slowly drift in latitude through the solar cycle. Yet, active regions do rotate a little faster than their surroundings, thus affecting the mean rotation rate at active latitudes (see, e.g., Zhao et al., 2004). The influence of local active-region flows on longitudinal averages of north-south flows is more serious. Indeed, the 50 m s⁻¹ organized flows that surround active regions introduce a kink at active latitudes in the average meridional circulation profile, on the order of ±5 m s⁻¹. Thus the solar-cycle variations of the meridional circulation (Section 5.1.2) would appear to be caused by active regions: convergence toward active latitudes near the surface and, presumably, divergence below 10 Mm.

Figure 41:

Left column: Longitudinal averages of surface horizontal flows obtained with f-mode time-distance helioseismology (Carrington rotations 1948 and 1949 in 1999). The vertical lines show the mean latitude of activity. The solid curves show zonal flows and meridional circulation averaged over all longitudes and both hemispheres. The zonal flows are obtained after subtraction of a smooth three-term fit to the rotation profile. The dashed curves are averages that exclude local areas in and around active regions (all points within 5° of strongly magnetized regions). Right panel: Sketch of surface flows around active regions: (a) ±10 m s⁻¹ zonal shear flow, (b) 50 m s⁻¹ inflow, (c) active region super-rotation, and (m) 20 m s⁻¹ background meridional circulation. From Gizon (2003).

Sunspot flows

Here we consider flows in the immediate vicinity of sunspots, which should not be confused with the flows discussed in the previous two sections. Duvall Jr et al. (1996) used the technique of time-distance helioseismology to measure the travel time difference between incoming and outgoing p-mode wavepackets around sunspots. They suggested that the observations are consistent with the existence of a downflow below sunspots with a velocity of about 2 km s⁻¹. It was estimated that the downflow persists down to a depth of 2 Mm below the surface. Kosovichev (1996) performed a 3D inversion of travel time measurements. The inversion results are consistent with 1 km s⁻¹ downflows that can reach depths of about 25 Mm.

Lindsey et al. (1996) employed “knife-edge” diagnostics to estimate horizontal flows around sunspots. In knife-edge diagnostics the Fourier transform of the data is multiplied by some filter F(k, ω), and then transformed back to the space-time domain. The square of the absolute value of the signal is then averaged over time. The filter is constructed to let through the part of the signal that has been Doppler shifted by a flow in a particular direction. An estimate of the x component, for example, of the flow is then formed by subtracting the local amplitudes that correspond to waves that have been Doppler shifted in the $+\hat{x}$ and $-\hat{x}$ directions. Using this technique, Lindsey et al. (1996) were able to detect a horizontal outflow from the center of sunspots at depths of about 15 Mm. The amplitude of this flow reaches a maximum of about 180 m s⁻¹ at a distance of 40 Mm from the center of a sunspot.

The Hankel analysis also has the capability of detecting flows below sunspots by interpreting the phase shifts between inward and outward traveling acoustic waves. Braun et al. (1996) applied this technique to south pole data from 1988 and 1991, and reported phase shifts that are consistent with the Doppler effect of a radial outflow from sunspots. The mean horizontal outflow appears to increase with depth and reaches 200 m s⁻¹ at a depth of 20 Mm. A more detailed analysis by Sun et al. (1997) using TON data demonstrates that there is a positive frequency shift between outgoing and ingoing waves which corresponds to a 40–80 m s⁻¹ radial outflow from sunspots. These results exhibit properties similar to those reported by Lindsey et al. (1996).

In order to gain some confidence about flow measurements in sunspots, it is useful to infer surface flows with local helioseismology and check for consistency with direct Doppler measurements. Gizon et al. (2000) used f-mode time-distance helioseismology to study flows very close to the surface (1 Mm deep). Wave-based sensitivity kernels for horizontal flows were used in an iterative deconvolution of the travel times. Figure 42 shows a map of the horizontal flows near the surface for a sunspot observed on 1998 December 6 (the spatial resolution is about 3 Mm). A horizontal outflow around sunspots is observed with an amplitude of about 500 m s⁻¹, which extends to roughly twice the penumbral radius. A high correlation was found between the mean Dopplergram and the projection of the inferred horizontal flows onto the line of sight, confirming the validity of the time-distance inversion. This outflow, often called the moat flow, was seen earlier using surface Dopplergrams (Sheeley, 1972) and magnetic tracers (see, e.g., Brickhouse and Labonte, 1988). The moat flow is believed to be driven by a pressure gradient caused by the blockage of heat by sunspots (see, e.g., Nye et al., 1988).

Figure 42:

Horizontal flows around a sunspot on 1998 December 6, obtained with f-mode time-distance helioseismology. Overplotted is the line-of-sight magnetic field (MDI high resolution) truncated at ±0.5 kG. The moat flow beyond the penumbra (red) is clearly visible. Adapted from Gizon et al. (2000).

Zhao et al. (2001) used a damped least-squares inversion (Tikhonov, 1963) of travel times to infer mass flows around a sunspot below the solar surface. Figure 43 shows the horizontal and vertical components of the flows at three different depths. Converging and downward directed flows were detected at depths of 0–3 Mm, while outflows extending more than 30 Mm from sunspot axis were found below the downward and converging flows. Two vertical cuts through the sunspot, shown in Figure 44, show strong flows across the sunspot at depths of 9–12 Mm, which may provide some evidence in support of the cluster model, as opposed to the monolithic sunspot model. Zhao and Kosovichev (2003b) also applied their time-distance inversion technique to determine the subphotospheric dynamics of an unusually fast-rotating sunspot observed in August 2000, which revealed that the vortical flows can be seen beneath the visible surface of this active region. On the basis of the three-dimensional velocity fields obtained from the time-distance helioseismology inversions, Zhao and Kosovichev (2003b) estimated the subsurface kinetic helicity and concluded that it is comparable to the current helicity estimated from vector magnetograms.

Figure 43:

Flow maps around a sunspot at depths of (a) 0–3 Mm, (b) 6–9 Mm, and (c) 9–12 Mm, infered using p-mode time-distance helioseismology. Arrows show the magnitude and direction of horizontal flows. The color background shows vertical flows (positive values for downward). The contours at the center correspond to the umbral and penumbral boundaries. The longest arrow represents 1 km s⁻¹ for (a) and 1.6 km s⁻¹ for (b) and (c). From Zhao et al. (2001).

Figure 44:

Vertical cuts through the sunspot shown in Figure 43. Upper panel: Cut in the east-west direction. Lower panel: Cut in the north-south direction. The location of the umbra and the penumbra is indicated at the top of each frame. The longest arrow corresponds to a velocity of 1.4 km s⁻¹. From Zhao et al. (2001).

Braun and Lindsey (2003) have recently extended their applications of helioseismic holography to include Doppler diagnostics of quiet Sun regions. Phase-correlation holography measures travel time perturbations from the temporal correlations between the egression and ingression. By dividing the pupil into four quadrants is is possible to infer vector flows. Braun and Lindsey (2003) performed the analysis separately for bands of power around 3, 4, and 5 mHz, and the resulting maps were then averaged together. As shown in Figure 45, it is easy to identify the moat outflow at a focus depths of 3 Mm, as well as supergranules (24 hr time average).

Figure 45:

Horizontal Doppler diagnostics applied to 24 hr data from MDI, which includes sunspot group AR 9363. Left: Observed velocity field, shown as vectors, for a focal depth of 3 Mm and superimposed a magnetogram. Middle: Same vector field as shown in the left panel, but super-imposed over an image of the horizontal divergence of the velocity. Right: Velocity field and its divergence with the focal plane placed 14 Mm below the surface. The companion Movie 46 shows the flow field as a function of focus depth. From Braun and Lindsey (2003).

Figure 46:

avi-Movie (2190.5 KB) Still from a Companion movie to Figure 45, showing the flow field as a function of focus depth. From Braun and Lindsey (2003). (For video see appendix)

Almost all local helioseismology results seem to indicate that there exists a radial outflow around sunspots down to at least 10 Mm, which relates to the moat flow seen at the surface. An exception is the inflow measured with p-mode time-distance helioseismology at a depth of 0–3 Mm. It is especially puzzling that the f-mode and p-mode results are inconsistent. Regarding vertical flows, it is difficult to understand how both downflows and horizontal outflows can coexist just below the sunspot. We caution that many complications introduced by the magnetic field are simply ignored by all local techniques. For example, the effect of the magnetic field on excitation and damping mechanisms is known to introduce a small travel time difference between incoming and outgoing waves (Woodard, 1997; Gizon and Birch, 2002).

Sinks and sources of acoustic waves

The very first success of local helioseismology was the detection of acoustic absorption by sunspots. Braun et al. (1987) decomposed the oscillations in the annular region surrounding a sunspot into incoming waves and outgoing waves (Hankel decomposition, Section 4.1) to measure the incoming and outgoing wave power. It was found that sunspots with a typical radius of 20 Mm absorb as much as 50% of the incoming acoustic power (Braun et al., 1987, 1988). The absorption coefficient reaches 70% for the giant sunspot group studied by Braun and Duvall (1990). Braun et al. (1988) found that the absorption coefficient a increases as a function of horizontal wavenumber k. The decrease of a with m/k is consistent with the absorbing region being mostly confined to the sunspot area. Weaker magnetic regions, such as plage, also display a significant level of p-mode absorption. Using 68 hr of south pole data, Braun (1995) was able to measure the absorption coefficient as a function of degree, azimuthal order, and frequency. It was found that the m dependence is weak for |m| < 20. The m-averaged absorption coefficient is plotted in Figure 47 for two different sunspots as function of frequency and for different harmonic degrees. There is a peak in the absorption around 3 mHz.

Figure 47:

Absorption coefficients plotted as a function of frequency. The left panels show results for sunspot NOAA 5254 and the right panels are for sunspot NOAA 5229. The vertical panels represent different bins of harmonic degree. From Braun (1995).

Spruit and Bogdan (1992) suggested that the partial conversion of the incoming acoustic waves into slow magnetoacoustic waves that propagate downward, channelled by the magnetic field, may explain the observations. Cally and Bogdan (1993), Bogdan (1997), and Cally et al. (2003) showed using numerical models that this mechanism is indeed capable of producing strong absorption coefficients, as defined by Braun. The best agreement is obtained when the magnetic field is inclined to the vertical, to simulate a spreading magnetic field with height (Crouch and Cally, 2003; Cally et al., 2003). In these models the maximum absorption is near 30° inclination.

The acoustic absorption by magnetic regions was confirmed by application of acoustic imaging (Chang et al., 1997) to data from TON. Acoustic holography, applied to MDI data, is ideal for the detection of sources and sinks of acoustic waves on the Sun. Braun and Fan (1998) discovered a region of lower acoustic emission in the 3–4 mHz frequency band which extends far beyond the sunspots (the ‘acoustic moat’). Acoustic moats extend beyond magnetic regions into the quiet Sun. In addition, Braun and Lindsey (1999) discovered high-frequency emission (‘acoustic glories’) surrounding active regions. Figure 48 shows egression power maps of the active region AR 8179 averaged over 24 hr, at different focal depths. The acoustic glory is seen in panel (b) as a bright halo of excess 5 mHz emission surrounding the entire active region complex. Isolated sunspots usually do not have any acoustic glory. The acoustic glory should not be confused with the ‘acoustic halos’ (Doppler acoustic power maps near 6 mHz) that surround all magnetic features (Braun et al., 1992). Neither acoustic halos nor acoustic glories are understood phenomena.

Figure 48:

Egression power maps of active region complex NOAA8179 obtained for the 24 yr period 1998 March 16. (a) MDI magnetogram. Panels (b), (c), and (d) show 5 mHz helioseismic images of the regions with depths at 0, 11.2 and 19.5 Mm below the solar surface, respectively. The dark shades correspond to acoustic absorption. The acoustic glory is seen in panel (b) as a bright halo of excess 5 mHz emission. The linear gray scale at the bottom applies to all of the helioseismic images that are normalized to unity for the mean quiet Sun. From Braun and Lindsey (1999).

We note that acoustic absorption by sunspots may also be studied with local power maps from ring-diagram analysis (e.g., Rajaguru et al., 2001; Howe et al., 2004), and by comparing cross-correlation amplitudes for incoming and outgoing waves in time-distance helioseismology (Duvall, 2002, private communication).

Phase shifts and wave-speed perturbations

The scattering phase shifts induced by sunspots were first measured with Hankel analysis by Braun et al. (1992) and Braun (1995). The m-averaged difference between incoming and outgoing p-mode phases is plotted in Figure 49 for sunspot AR 5254 observed in 1988 at the south pole (Braun, 1995). The f-mode phase shifts could not be determined accurately. The acoustic phase shifts are generaly positive and increase with frequency (or harmonic degree) to reach values in excess of 90°. Notice that the increase with frequency is not linear: The rate of increase is smaller at smaller frequencies. This could indicate that the origin of the scattering phase shifts is due to perturbations that are confined to shallow depths (Braun, 1995). The phase shifts are also observed to decrease with |m|, suggesting that scattering occurs over a small area (Braun, 1995). Fan et al. (1995) estimate that the phase shifts are mostly happening in the region inside the outer edge of the penumbra. Braun (1995) find no significant phase shifts in plage regions. Both the m and frequency dependence of the phase shifts have been modelled successfully by Cally et al. (2003, Figure 49). This provides a strong confirmation of the central physical mechanism that they advocate: partial conversion of incoming waves into downward propagating slow magnetoacoustic waves. We note that organized flows in and around sunspots should also introduce small phase shifts.

Figure 49:

Phase shifts between outgoing and outgoing waves from Hankel analysis, as a function of frequency for several different radial orders n. The data points with error bars are m-averaged values for NOAA5254 (Braun, 1995). The solid lines are from a model by Cally et al. (2003). From Cally et al. (2003).

Chen et al. (1998) used acoustic imaging to map phase shifts as well. They measured phase shifts between ingoing waves and outgoing waves and found a difference between quiet and active regions. Their maps correlate sharply with the surface magnetic field. According to Chou (2000), the phase shifts represent the phase perturbation accumulated along the wave path, which can be due to a change in the phase velocity, wave path, but also magnetic field and changes in the mode cavity. Figure 50 shows phase-shift maps focusing at the solar surface obtained with TON data (Chou et al., 1999). The maps confirm the original findings obtained with Hankel analysis. The acoustic imaging technique is very similar to phase-sensitive holography based on the correlation between the egression and the ingression (Lindsey and Braun, 1997; Braun and Lindsey, 2000, and Section 4.4). The two techniques give consistent results. Braun and Lindsey (2000) report that the phase shifts (or reduced travel time perturbations) increase in amplitude like the logarithm of the surface magnetic flux density.

Figure 50:

Observed acoustic power maps, outgoing intensity maps, phase-shift maps, and envelope-shift maps focusing at the solar surface at 3 mHz (first row), 3.5 mHz (second row), 4 mHz (third row), 4.5 mHz (fourth row), and 5 mHz (fifth row). Gray scales at different frequencies are the same except in the envelope-shift map at 5 mHz, where the gray scale is 1.5 times larger. The envelope peak of the cross-correlation function provides information about wave travel time, associated with the group velocity along the wave path. The phase time of the cross-correlation function between ingoing and outgoing waves provides information about phase changes along the wave path, including the phase change at the boundaries of the mode cavity and flux tubes. From Chou et al. (1999).

The travel time perturbations below active regions was studied by Kosovichev et al. (2000, 2001) using time-distance helioseismology. Mean travel times are usually interpreted in terms of wave speed. Kosovichev et al. (2000) found that the absolute difference in wave-speed between a sunspot (AR 8131) and the quiet Sun is up to 1 km s⁻¹. For reference, the quiet Sun sound speed is about 20 km s⁻¹ at a depth of 4 Mm and 35 km s⁻¹ at 10 Mm. The relative change in the squared sound speed is about (δc²/c² ≃ −0.1 at a depth of 4 Mm, which they say would correspond to a 10% temperature decrease. At greater depths (7–15 Mm), the sound-speed perturbation switches sign and becomes positive. This increase in sound-speed could be due to a temperature change or the direct effect of the magnetic field. The perturbations vanish at depths greater than 15 Mm, which may be an indication of the depth extent of active regions or perhaps of the poor resolution of the inversions there. Kosovichev et al. (2000) also detected the presence of narrow sound-speed anomalies (termed ‘fingers’) that connect internally the sunspot with two nearby pores (confirmed by Couvidat et al., 2004). Kosovichev and colleagues studied several other active regions, including AR 9393 which was seen on the disk for more than 3 months in 2001 (with a different name at each disk passage). The sound-speed perturbations under this giant active region are shown in Figure 51 (movie).

Figure 51:

mpg-Movie (975.834960938 KB) Still from a Wave speed perturbation associated with the active region AR 9393. The positive values are shown in red and the negative ones in blue. The movie shows the evolution of the wave speed perturbation from March 25 until April 1, 2001. Courtesy of A.G. Kosovichev. (For video see appendix)

Surface Doppler velocity measurements are not always reliable in highly magnetized regions. Following a suggestion by Duvall Jr (1995), Duvall Jr and Kosovichev (2001) have implemented a travel time averaging scheme to focus below a sunspot without using surface measurements directly inside the sunspot. This is achieved by considering all the rays that intersect at a target location in the solar interior (deep focusing technique). The standard and deep-focusing time-distance techniques seem to give consistent measurements of wave-speed perturbations (Duvall Jr and Kosovichev, 2001). Another way to avoid contamination is to perform sound-speed inversions of selected travel times that involve only data outside sunspots (Zhao and Kosovichev, 2003b). Figure 52 shows a comparison of sound-speed inversions below a sunspot obtained with and without cropping the data in the sunspot (GONG data; Hughes et al., 2005). The results are qualitatively similar in the two cases, i.e., the sign of the sound-speed perturbation as a function of depth is preserved. General agreement is also found between GONG and MDI for both travel times (Rajaguru et al., 2004) and inversion results (Hughes et al., 2005).

Figure 52:

Horizontal slices through the inferred sound-speed perturbations under a sunspot using GONG data. From top to bottom the rows correspond to the depth ranges 1.7–2.3 Mm, 3.6–4.4 Mm, 6.2–7.3 Mm, and 8.5–9.8 Mm. The inversion results for uncropped (left column) and cropped data (right column) are qualitatively similar. From Hughes et al. (2005).

Kosovichev et al. (2000) studied the emergence in time of an active region. Their results show that the wave-speed perturbations rise very fast across the upper 18 Mm of the convection zone. An analysis for 2 hr time steps suggests that the emerging magnetic flux travels the upper 10 Mm in less than 2 hr, implying a minimum speed of 1.3 km s⁻¹. Jensen et al. (2001) inferred the wave-speed structure beneath the same emerging active region using an inversion technique based on Fresnel-zone sensitivity kernels, as opposed to ray-based kernels. Their results are similar to those of Kosovichev et al. (2000).

Using local mode frequency differences between active and quiet Sun regions measured with the ring-diagram technique (see, e.g., Hindman et al., 2000; Rajaguru et al., 2001), Basu et al. (2004) performed structure inversions to estimate the sound speed and adiabatic index in active regions. The results are for regions with horizontal size 15° and 7-day averages. An attempt was made to remove the uncertainty in the modelisation of the surface layers (Section 4.2.3): inversions do not provide information for depths less than 1 Mm. The uncertainties in modeling the surface layers were ‘removed’ in this process (Section 4.2.3), such that no reliable information at depths of less than 1 Mm could be extracted.

The relative difference of the sound speed between active and quiet regions is plotted in Figure 53 for 12 different active regions. For active regions with strong magnetic fields, a reduction in sound-speed is observed in the upper layers (for depths less than, say, 7 Mm). At greater depths, the sound speed is increased relative to the quiet Sun. This is consistent with the work of Kosovichev et al. (2000) based on time-distance helioseismology. The amplitude of the perturbations are much smaller here than in the time-distance case simply because the magnetic region covers only a few percent of the area of ring-diagram analysis. Because the analysis of Basu et al. (2004) is based on the physics of normal modes, it provides an independent check of the results obtained using time-distance helioseismology.

Figure 53:

Relative differences of the squared sound speed between active and quiet regions obtained by inverting the frequency differences measured using ring-diagram analysis. The blue solid line shows the RLS inversion results, with the blue dotted lines showing the 1σ error limit. The red points are the SOLA (Subtractive OLA) inversion results. The vertical error bars are the 1σ error, and the horizontal error bars mark the distance between the quartile points of the averaging kernels and are a measure of the resolution of the inversions. The magnetic field strengh in each panel is a local magnetic activity index. From Basu et al. (2004).

The wave-speed anomalies below sunspots could be caused by a variety of physical effects, for example thermal and magnetic perturbations. It has not been possible to disentangle these effects yet. The low sound-speed regions just below the surface have been attributed to a smaller temperature (Kosovichev et al., 2000; Basu et al., 2004). On the other hand, the higher wave speeds measured at a depth of 10 Mm below sunspots are unlikely to be due only to the direct effect of the magnetic field (or it would imply very large field strengths of a several tens of kG). The likely cause is a combination of magnetic and structural/thermal effects (Brüggen and Spruit, 2000; Basu et al., 2004). Barnes and Cally (2001) and Cally et al. (2003), however, have questioned the interpretation of travel time anomalies in terms of linear perturbations to the wave speed. Their numerical simulations of wave propagation through a model sunspot have been able to reproduce the phase shifts measured by Hankel analysis without the need for a thermal perturbation. This stresses the need for a proper solution of the forward problem of time-distance helioseismology in sunspots.

Lindsey and Braun (2003) argued that strong magnetic fields near the photosphere introduce large phase shifts in waves passing upwards into the photosphere of active regions and termed this effect the “showerglass” effect. They argue that the showerglass makes measurements of local variations in the subsurface more difficult, and thus attempts should be made to correct for this effect before inverting for subphotospheric structure and flows. Measurements of the showerglass were made by Lindsey and Braun (2003), and in more detail by Lindsey and Braun (2005a). In both cases the local egression and ingression control correlations (Section 4.4.3) were computed in active regions using MDI data. Maps of the phase and amplitude of the control correlations showed a clear relationship with the line-of-sight magnetograms, suggesting that the surface magnetic field was altering the amplitudes and phases of the waves used to compute the control correlation. Lindsey and Braun (2005b) used the measurements of the phase shifts of Lindsey and Braun (2005a) to correct the data before doing phase-sensitive holography (Section 4.4.5). They suggest that with the effect of near-surface magnetic field removed there is no clear evidence for sound-speed perturbations at depths greater than 5 Mm below a sunspot and that the effect of strong photospheric magnetic field on local helioseismic measurements should be studied further.

Far-side imaging

The first observational results from far-side helioseismic holography are due to Lindsey and Braun (2000b). Their results showed that active regions on the far-side of the Sun introduce travel time deficits compared to the quiet Sun of order ten seconds. The demonstration by Lindsey and Braun (2000b) that far-side imaging was practical is important for space weather predictions, as it allows about a week of warning before an active region will be seen at the East limb. Braun and Lindsey (2001) expanded the original idea presented by Lindsey and Braun (2000b) to allow imaging not just of the central region of the far-side of the Sun, but also the regions nearer to the limb. Daily far-side images computed from MDI data are available from the web at http://soi.stanford.edu/data/farside/. Figure 55 shows far-side images computed by Braun and Lindsey (2001) for subsequent days together with magnetograms for the visible part of the disk. Active regions seen on the far-side can be seen in the synoptic magnetogram of the subsequent Carrington rotation. Figure 54 and the companion movie show simultaneously the front-side and farside of the Sun during the period March–June 2001 which saw the evolution of AR 9393.

Figure 54:

mpg-Movie (3136.109375 KB) Still from a Movie showing far-side and front-side images of the Sun from March to June 2001. The large activity complex AR 9393 is seen for several rotation periods. The horizontal axis spans all longitudes measured in the Carrington frame of reference. The fuzzy image shows shorter wave travel times (in red) caused by active regions located on the far-side of the Sun. The Earth-side image of the Sun shows continuum intensity (active regions appear as red/dark shades). (For video see appendix)

Figure 55:

Composite images of SOHO/MDI magnetograms and far-side images made using SOHO/MDI Doppler data. The magnetograms have a higher spatial resolution. The boundary in the far-side images is where the algorithm is switched from two-skip/two-skip imaging, used to image in center of the far-side, to three-skip/one-skip imaging used further from the antipode of the visible disk. See Figure 27 for a diagram of the geometry. The color scale for the far-side images shows the time delay between the egression and the ingression. The sign of the signal in active regions is of the sense of faster propagation time underneath active regions. The top four panels show the far-side images for 1999 April 22–25. The bottom panels shows the magnetogram for Carrington rotation 1999 May 1–28. From Braun and Lindsey (2001).

The sign of the travel time perturbation associated with active regions seen by far-side imaging is consistent with increased wave speeds or shorter paths traveled by the waves. This is consistent with the results of phase-sensitive holography of plage regions on the visible disk (see, e.g., Braun and Lindsey, 2000) and may be related to the observed solar cycle variation of normal mode frequencies (see, e.g., Lindsey and Braun, 2000b, and references therein).

Excitation of waves by flares

Kosovichev and Zharkova (1998) used data from the SOHO/MDI instrument (Scherrer et al., 1995) to make the first clear observations of a helioseismic wave produced by a flare. A roughly circular wave front, though with not insignificant quadrupole component, was seen emerging from the location of the now famous Bastille Day flare, an X-class flare of 1996. The wave packet was seen out to a distance of 120 Mm from the source and took about 55 min to travel that distance (see Figure 56). Earlier attempts using ring diagrams (Haber et al., 1987) and Hankel analysis (Braun and Duvall, 1990) reported small, but not significant, variations of the p-mode signal in flaring regions.

Figure 56:

mpg-Movie (1975.54003906 KB) Still from a Remapped and filtered MDI Dopplergram 25 min after the Bastille Day flare. The flare signal was extracted, enhanced by a factor of 4, and then superimposed on the Dopplergrams. The movie shows the temporal evolution of the signal. From Kosovichev and Zharkova (1998). (For video see appendix)

Later, Donea et al. (1999) used acoustic power holography (see Section 4.4.4) of SOHO/MDI data to investigate the same flare as was studied by Kosovichev and Zharkova (1998). The acoustic power holography showed that the wave source was strongest around 3 mHz, though the signal-to-noise ratio was higher around 6 mHz. The signal in the 6 mHz band appeared about 4 min after the signal in the 3 mHz band. Donea and Lindsey (2004) found significant acoustic power signatures associated with two other flares and showed a possible connection between the fine-scale spatial structure of the acoustic power maps and motions of the footpoints of the flaring loops. We note that detection of flare-induced acoustic waves using ring-diagram analysis has been claimed by Ambastha et al. (2003).

The basic mechanism by which a flare excites helioseismic waves is not entirely clear. Wolff (1972) suggested that the energy released in the flare heats the atmosphere, the expansion of which in turn causes a downward propagating wave. Zharkova and Kosovichev (1998) argue, on the basis of the momentum needed to explain the observed Bastille Day flare wave amplitude, that the shock wave created by chromospheric evaporation may not be the complete explanation and suggested that perhaps momentum transfer by electron or proton beams impacting directly on the photosphere may be important. Zharkova and Kosovichev (2001) argued that electron beams can carry sufficient momentum to explain the observed amplitude of the helioseismic wave caused by the Bastille Day flare.

A separate issue is the mechanism that leads to the initiation of solar flares. The contribution of local helioseismology to this problem has been rather poor so far. We note that Dzifcakova et al. (2003) have searched for a relationship between the evolution of subsurface flows and flaring activity.

Supergranulation

Paradigms

Granulation, with a typical size of 1.5 Mm, is well understood as a convective phenomenon and can be studied with realistic numerical simulations (see, e.g., Stein and Nordlund, 2000). Supergranules, however, have remained puzzling since their detection by Hart (1954, 1956). In a classic paper, Leighton et al. (1962) reported “large cells of horizontally moving material distributed roughly uniformly over the entire solar surface” with a characteristic scale of 30 Mm that are outlined by the chromospheric network; they suggested that the cells are a “surface manifestation of a supergranulation pattern of convective currents”. Unfortunately, there is no accepted theory that explains why solar convection should favor a 30 Mm scale. The solar convection zone is so highly turbulent and stratified that numerical modeling at supergranular scales has remained elusive (see, e.g., Rincon, 2004, and references therein).

Simon and Leighton (1964) presumed that a convective instability due to the recombination of ionized Helium is at the origin of the distinct supergranular scale. Forty years later, this hypothesis has not been proved to be right or wrong. The depth of the supergranulation layer is not known either. We note that Parker (1973) believes that the effect of stratification on convection may imply that supergranules are a deep phenomenon, with depths in excess of their horizontal diameters. Antia and Chitre (1993) investigated the stability of linear convective modes in the solar convection zone and found that a few convective modes dominate the power spectrum, one of which was identified as supergranulation. Using 1D numerical caculations, Ploner et al. (2000) suggested that the scale of supergranulation may be due to the interaction and merging of individual granular plumes (see also Rast, 2003). A somewhat related model was proposed by Rieutord et al. (2000, 2001) whereby supergranulation is the result of a non-linear large-scale instability of the granular flow, triggered by exploding granules. In the two previous models, supergranulation is not a proper scale of thermal convection. Regarding the influence of supergranular flows on magnetic fields, it is well established that a stationary cellular flow tends to expel the magnetic field from the regions of fluid motion and concentrate the magnetic flux into ropes at the cell boundaries (Parker, 1963; Galloway et al., 1977; Galloway and Weiss, 1981).

On the observational side, the original work of Leighton and coworkers has been refined. A variety of methods have been used to characterize the distribution of the cell sizes. A characteristic scale can be obtained from the spatial autocorrelation function (see, e.g., Hart, 1956; Simon and Leighton, 1964; Duvall Jr, 1980), the spatial Fourier spectrum (see, e.g., Hathaway, 1992; Beck, 1997), and segmentation or tessellation algorithms (Hagenaar et al., 1997). Although definitions vary, average cell sizes are in the range 15–30 Mm. It is unclear whether there is a variation of cell sizes with latitude: Rimmele and Schroeter (1989) and Komm et al. (1993a) report a possible decrease with latitude, Berrilli et al. (1999) an increase, and Beck (1997) no significant variation. The typical lifetime of the supergranular/chromospheric network is found to be in the range 1–2 d (e.g Rogers, 1970; Worden and Simon, 1976; Duvall Jr, 1980; Wang and Zirin, 1989). The rms horizontal velocity of supergranular flows is known to be about 300 m s⁻¹ (see, e.g., Hathaway et al., 2000). The vertical component of the flows, however, has been extremely difficult to measure (see, e.g., Giovanelli, 1980) or infer (November, 1989). Indeed, Miller et al. (1984) caution that Doppler velocity measurements at the cell boundaries may be polluted by the network field. Estimates of the rms vertical flow are provided by Chou et al. (1991) and Hathaway et al. (2002) who find speeds of about 30 m s⁻¹ (the topology of the vertical flows is largely unknown). Even more difficult to measure are the related temperature fluctuations. Observers have searched for the thermal signature of a convective process, i.e., rising hot material at the cell centers and sinking cool material at the cell boundaries. Unfortunately, answers vary too widely (see Lin and Kuhn, 1992, and references therein).

Estimates of the pattern rotation rate of supergranulation can be obtained by correlation tracking techniques. Duvall Jr (1980) and Snodgrass and Ulrich (1990) used Doppler scans separated in time by Δt = 24 hr. The results indicate that the equatorial rotation of the supergranulation pattern is faster than the spectroscopic rate (Snodgrass and Ulrich, 1990) by about 4% and faster than the magnetic features (Komm et al., 1993b) by about 2%. Duvall Jr (1980) also considered same-day scans with Δt = 6 hr and found a slightly smaller pattern rotation rate than for Δt = 24 hr.

It was suggested by Foukal (1972) that the difference between the rotation of magnetic features and the spectroscopic rate may be due to magnetic structures being rooted in deeper, more rapidly rotating layers. Supergranules must also sense increase rotation in the shear layer below the surface. However, Beck (2000) remarks that the pattern rotation of supergranulation measured from correlation tracking with Δt = 24 hr is significantly faster than the rotation of the solar plasma measured by helioseismology at any depth in the interior. It is especialy puzzling that the rotation of the magnetic network is significantly less than that of the supergranular pattern, since small magnetic elements are believed to be advected by supergranular flows. Hathaway (1982) suggested that a faster supergranular rate may be a direct consequence of the interaction of convection and rotation.

As explained in the following sections, local heliososeismology has become a powerful tool to study the structure and evolution of supergranular flows. In fact, helioseismological measurements have transformed our knowledge of the dynamics of supergranulation.

Horizontal flows and vertical structure

In order to resolve structures at supergranular scales, Duvall Jr et al. (1996) measured p-mode travel times at distances shorter than 10 Mm over an 8.5 hr time interval. Directional information was obtained by cross-correlating a point on the surface with surrounding quadrants centered on the four cardinal directions. In a first order approximation, the south-north and east-west travel time differences were converted into an apparent horizontal vector flow field without inversion. Duvall Jr et al. (1997) found that the line-of-sight projection of the inferred flow field is highly correlated with the mean MDI Dopplergram (correlation coefficient 0.74). This comparison was initialy used as a validation of the time-distance technique.

Three dimensional inversions of quiet-sun travel times have been presented by Duvall Jr et al. (1997), Kosovichev and Duvall Jr (1997), and Zhao and Kosovichev (2003a). Tests of the ray-based inversion procedure of Zhao and Kosovichev (2003a) show that the horizontal components of the velocity can be infered with some confidence in the upper 5 Mm (and perhaps down to 10 Mm). The small vertical flows, on the other hand, cannot be inferred reliably near the surface due to significant “cross-talk” with the horizontal divergence signal.

Near-surface horizontal flows have been measured at a depth of 1 Mm with f-mode time-distance helioseismology (Duvall Jr and Gizon, 2000). In this case travel time differences are directly sensitive to horizontal flows because f modes propagate horizontaly. The f-mode time-distance technique gives results that are comparable to correlation tracking of granulation (De Rosa et al., 2000). Shown in Figure 22 is an inversion of f-mode travel times that employs 2D Born kernels (Gizon et al., 2000). The correlation coefficient between the estimated line-of-sight velocity and the surface Doppler image is about 0.7.

The holographic technique also measures flows at supergranular scales. As shown earlier in Figure 45, supergranules are easy to identify as regions of outflows for a 3 Mm focus depth (24 hr time average).

A practical way to detect and display supergranulation is to plot the horizontal divergence of the flow field. Time-distance helioseismology applied to f modes is particularly well adapted to measuring the horizontal divergence of the velocity near the surface. Duvall Jr and Gizon (2000) measured the time it takes for solar f modes to propagate from any given point on the solar surface to a concentric annulus around that point. The difference in travel times between inward and outward propagating waves is a proxy for the local horizontal divergence. An example of the divergence signal (inward minus outward travel time) for one 8-hour interval analyzed is shown in Figure 57 with magnetic field information overlaid (MDI full-disk data). A white, or positive signal, corresponds to a horizontal outflow. From the size of the features present, their lifetime, and the presence of the magnetic field in the dark lanes regions, supergranulation is identified as the main contributor to the signal. This can also be seen by making a spatial power spectrum of the divergence signal: Power peaks near degree l = 120. The movie associated with Figure (57) shows that the magnetic features stay in the regions of horizontal convergence over the time interval of the observations (one week).

Figure 57:

mpg-Movie (82945.2949219 KB) Still from a Movie of the divergence signal (inward travel times minus outward times) with magnetic field signal overlaid. The magnetic field is displayed as green and red for the two polarities when the magnitude of the field is larger than 15 G. The gray scale is for the divergence signal with white shades for outflow and dark shades for inflow. The colorbar indicates the travel time difference in seconds. The line Y = 0 corresponds to the equator and X = 0 corresponds to Carrington longitude 180°. The time-distance data is averaged over 8.5 hr starting at the time shown on top. The movie shows the time evolution of the supergranulation pattern over 6 days. From Duvall Jr and Gizon (2000). (For video see appendix)

Local heliososeismology opens prospects for mapping the structure of supergranular flows below the surface. A major goal is to answer the long-standing question of how deep supergranular flows persist below the surface.

Duvall Jr et al. (1997) and Kosovichev and Duvall Jr (1997) presented three-dimensional inversions of quiet-sun travel times using ray-theoretical sensitivity kernels. Figure 58 shows a vertical cut through the velocity field; the horizontal sampling is 4.3 Mm and the vertical sampling is about 1 Mm. In the upper 5 Mm the flows are positively correlated with the direct surface observations. To assess the average structure of superganular flows with depth, Duvall Jr (1998) used the inversion results from Duvall Jr et al. (1997) to measure the correlation of horizontal flows between the surface and any given depth. As seen in Figure 59, the correlation drops to zero at a depth of 5 Mm and is negative in the range 5–8 Mm, suggesting the existence of a “return flow”. Since the correlation seems to disappear below 8 Mm, Duvall Jr (1998) concluded that the depth of supergranulation is 8 Mm. The same type of analysis was repeated by Zhao and Kosovichev (2003a) with more recent (and presumably more reliable) inversions of travel times. They found that the correlation of the horizontal divergence falls off away from the surface, changes sign at a depth of about 6 Mm, and is negative at depths in the range 6–14 Mm (see Figure 59). In particular, Zhao and Kosovichev (2003a) find a correlation coefficient of −0.5 at a depth of 10 Mm. Zhao and Kosovichev (2003a) concluded that supergranulation is about 15 Mm deep.

Figure 58:

Flow field (arrows) and wave-speed perturbations (grey-scale background) inferred by Kosovichev and Duvall Jr (1997) with time-distance helioseismology. Typically there are upflows in the hotter areas where the sound speed is higher, and downflows in the cooler areas. From Kosovichev and Duvall Jr (1997).

Figure 59:

Correlation coefficient between the horizontal divergence at each depth, derived from p-mode time distance helioseismology, and the divergence image of the uppermost layer. The dashed line is from Duvall Jr (1998) and the solid line is from Zhao and Kosovichev (2003a).

We note that inversion results heavily rely on the assumed travel time sensitivity kernels. While most inversions use ray-based kernels, Jensen et al. (2000) and Birch and Kosovichev (2000) showed that finite-wavelength effects must be taken into account. It may be that wave-based kernels could yield depth inversion results that are qualitatively different from the ones presented above.

Braun and Lindsey (2003) used a 24 hr MDI data cube and seismic holography to make maps of convective flows at focus depths from 3 Mm to 37 Mm. The horizontal-divergence maps are shown in the left panels of Figure 60. The behavior of the divergence maps with depth can be studied by making scatter plots of the divergence values observed at a given depth versus the near-surface values. The slope of a line fit to the scatter is observed to change sign at 10 Mm and to remain negative in the range 10–37 Mm. Although it is tempting to interpret the reversal of the horizontal divergence signal at focus depths greater than 10 Mm, Braun and Lindsey (2003) suspect that this reversal could be due to the increasing contribution of oppositely directed surface flows as the pupil increases in size with focus depth. To test this hypothesis, they considered a control experiment in which the observed flows at 3 Mm depth are used to estimate the surface contribution to the seismic measurements at greater focus depths. The divergence maps of the control experiment, which are shown in the right panels of Figure 60, ressemble the observed divergence maps (left panels). The good correspondence between the two suggests that the observations at depths are mostly due to leakage from the surface (the “showerglass effect”). Modelling efforts by Braun et al. (2004) have confirmed that the change of sign of the correlation below 10 Mm is a predominantly surface contamination of the velocity signal from neighboring supergranules. However, the fact that the control data do not reproduce exactly the observations may indicate that there is at least some sensitivity to velocities at depth.

Figure 60:

Comparison of the observed horizontal divergence, derived from seismic holography (left-most panels), with those from a control computation which assumes that the Doppler signatures are concentrated at the solar surface (right-most panels). The middle panels show the weighted pupils used in the analysis. The companion Movie 61 shows the observed and control data as a function of focus depth. From Braun and Lindsey (2003).

Figure 61:

avi-Movie (2464.5 KB) Still from a Companion movie to Figure 60, showing the observed and control data as a function of focus depth. From Braun and Lindsey (2003). (For video see appendix)

It would appear that local helioseismology has not yet provided a definitive answer regarding the depth of supergranulation.

Rotation-induced vorticity

Since the typical lifetime of supergranules is significantly less than the solar rotation period, the influence of rotation on supergranular convection is expected to be small. Solar rotation effects in supergranules were illustrated by Hathaway (1982) in non-linear numerical simulations. The Coriolis force causes divergent and convergent horizontal flows to be associated with vertical components of vorticity of opposite signs (on average). In the northern hemisphere, cells rotate clockwise where the horizontal divergence is positive, while they rotate counterclockwise in the convergent flow towards the sinks. The sense of circulation is reversed in the southern hemisphere.

In general, it is not straightforward to predict the statistical properties of the vorticity in rotating turbulent convection: Vorticity production is due to the effect of the Coriolis force and to vortex stretching and tilting mechanisms. The importance of the Coriolis force is characterized by an inverse Rossby number, or Coriolis number, defined by

$${\rm{Co}} = 2{\tau _{\rm{c}}}\;{\Omega _{{\rm{eq}}}},$$

(90)

where τ_c is a characteristic correlation time and Ω_eq is the equatorial solar angular velocity. The choice τ_c = 48 hr implies Co ≃ 1 for supergranulation. At latitude λ, quasi-linear theory (Rüdiger et al., 1999) predicts that the vertical vorticity of the velocity (denoted below by ‘curl’) and the horizontal divergence of the horizontal velocity (denoted by ‘div’) are correlated according to

$$\langle {{\rm{div}}\;{\rm{curl}}} \rangle \sim - {{{\Omega _{{\rm{eq}}}}} \over {{\tau _{\rm{c}}}}}f(\lambda),$$

(91)

where the brackets denote an expectation value or longitudinal average. The latitudinal variations are given by the function

$$f(\lambda) = \sin (\lambda){{\Omega (\lambda)} \over {{\Omega _{{\rm{eq}}}}}}$$

(92)

and are due to the projection of the local angular velocity vector onto the radial direction.

The effect of rotation on supergranules was first observed by Duvall Jr and Gizon (2000) and Gizon and Duvall Jr (2003)². They computed the vertical vorticity and horizontal divergence from vector flow maps obtained with f-mode time-distance helioseismology (1 Mm deep, 8 hr time invervals). The vertical large-scale vorticity due to differential rotation and meridional circulation was removed to study the vorticity at supergranular scales. Panel (a) of Figure 62 shows the correlation coefficient between div and curl at latitude λ,

$$C(\lambda) = {{\langle {{\rm{div}}\;{\rm{curl}}} \rangle} \over {\sqrt {\langle {{\rm{di}}{{\rm{v}}^2}} \rangle \langle {{\rm{cur}}{{\rm{l}}^2}} \rangle}}},$$

(93)

where the angle brackets denote a spatial average over the area of a 10° longitudinal strip centered around A. In the north, positive (negative) divergence is correlated with clockwise (anticlockwise) vorticity; the correlation changes sign in the south. Thus, away from the equator, the number of right-handed cyclones is not equal to the number of left handed cyclones. The sign and the latitudinal variation of C(λ) are both characteristic of the effect of the Coriolis force on the flows. Panel (b) of Figure 62 shows horizontal averages of the vertical vorticity 〈curl〉_± versus f(λ), where the averages 〈·〉₊ and 〈·〉₋ are restricted to the regions of positive and negative divergence, respectively. Note that there is a small difference between the total area covered by regions of positive and negative divergence (Duvall Jr and Gizon, 2000). A nearly perfect linear relationship between 〈curl〉_± and ∓f(λ) is observed, with 〈curl〉_± = ∓f(λ) Ms⁻¹. This is again consistent with the interpretation as a Coriolis effect.

Figure 62:

Effect of the Coriolis force on supergranular flows. (a) Plot of the correlation coefficient, C(λ), between the vertical vorticity (curl) and the horizontal divergence (div). (b) Horizontal averages of the vorticity, 〈curl〉₊ (solid) and 〈curl〉₋ (dashed), over regions with div > 0 and div < 0, respectively. A vorticity of 1 Ms⁻¹ corresponds to an angular velocity of 2.5° day⁻¹ or a typical circular velocity of 10 m s⁻¹. From Gizon and Duvall Jr (2003).

Observations may be summarized by a measurement of the average correlation between the horizontal divergence and the vertical vorticity (Gizon and Duvall Jr, 2003):

$$\langle {{\rm{div}}\;{\rm{curl}}} \rangle = - 3f(\lambda) \times {10^{- 10}}\;{{\rm{s}}^{- 2}}.$$

(94)

Since Ω_eq/τ_c = 2 × 10⁻¹¹ s⁻² for τ_c = 48 hr, the naive prediction from Equation (91) is one order of magnitude smaller than the measurements (Equation 94). Recent numerical simulations of rotating convection by Egorov et al. (2004) give values of 〈div curl〉 near the top of the convection zone that appear to be close to the observations. They show that a good agreement with the data is obtained for a reasonable Coriolis number (their definition of the Coriolis number is slightly different than ours; Egorov, 2004, private communication). Egorov et al. (2004) predict that the amplitude of the curl-div correlation should decrease fast with depth.

Pattern evolution

As mentioned above, the pattern rotation rate of supergranulation derived from correlation tracking of Doppler scans appears to be significantly faster than the spectroscopic rate (for a 24 hr time lag). Correlation tracking algorithms can also be applied to images of supergranular flows derived from local helioseismology, such as the horizontal divergence signal. Unlike raw Doppler images, the divergence signal has uniform sensitivity across the solar disk and is subject to few systematic errors.

Gizon and Duvall Jr (2003) used a 60-day sequence of 90° × 90° divergence maps obtained with f-mode time-distance helioseismology (0.24° spatial sampling). The original MDI Doppler velocity images were tracked at the Carrington rate to remove the main component of rotation. Small regions, apodized by a Gaussian surface with a full width at half maximum of 3.84° and separated by a time-lag Δt, were spatially cross-correlated. For Δt < 1.5 d the peak of maximum correlation is easy to identify, and the spatial displacement Δx at correlation maximum gives an apparent pattern velocity U_LCT = Δx/Δt, where the subscript LCT stands for ‘local correlation tracking’. Figure 63 shows that the apparent motion of the supergranulation pattern depends on Δt. In particular, the pattern rotation rate increases rapidly with Δt. The apparent meridional motion is poleward for Δt < 18 hr with a very small amplitude (< 5 m s⁻¹), while, suprisingly, it is slightly equatorward for greater time lags. The apparent rotation of supergranulation obtained by tracking the divergence maps confirms the original findings of Duvall Jr (1980) and Snodgrass and Ulrich (1990) obtained by tracking Dopplergrams.

Figure 63:

Anomalous pattern motion of supergranulation measured by tracking the horizontal divergence of the flow field observed with time-distance helioseismology. (a) Pattern rotation for time-lags Δt = 6, 8, 16, and 22 hr. The cross shows the equatorial pattern rotation measured by Snodgrass and Ulrich (1990) for Δt = 24 hr from Mount Wilson Dopplergrams. (b) Meridional motion of the pattern as a function of time-lag Δt. Notice that the meridional motion appears to be equatorward for Δt > 20 hr. A P-angle correction was applied to the data. From Gizon and Duvall Jr (2003).

Beck and Duvall Jr (2001) showed that the observed correlation function of the divergence signal switches sign at Δt ∼ 40 hr. The same analysis is repeated here with the 60-day sequence used by Gizon and Duvall Jr (2003). Figure 64 shows a still at Δt = 24 hr from a movie of the temporal evolution of the spatial correlation, with Δt varying from zero to 5.5 d (equatorial region, 6 hr time steps, Carrington tracking rate). The spatial cross-correlation decays and oscillates as a function of time. For Δt < 36 hr, the peak of maximum correlation is well defined and is surrounded by a ring of negative correlation due to adjacent supergranules. For Δt > 48 hr a peak of negative correlation has appeared (east), which is surrounded by a ring of positive correlation. When the analysis is repeated away from the equator, one finds that the peak of negative correlation forms poleward of the east direction. For Δt ≃ 5.5 d the main correlation peak is again positive and is surrounded by a ring of negative correlation.

Figure 64:

mpg-Movie (373.415039062 KB) Still from a Movie showing the evolution of the spatial cross-correlation of the divergence signal at the equator as a function of Δt from 0 to 5.5 d. (Movie still for time lag Δt = 24 hr.) The original MDI Doppler velocity images were tracked at the Carrington rate. (For video see appendix)

Earlier observations of solar convection assumed that supergranulation can be characterized by an autocorrelation function that exhibits a simple exponential decay in time (Harvey, 1985; Kuhn et al., 2000). It is now obvious that supergranulation does not follow such a simple model. The oscillation period of the correlation function, of the order of 6 d, suggests an underlying long-range order. As shown below, these puzzling observations are easier to describe in Fourier space (Section 5.3.5).

Another interesting method of analysis to study the evolution of the supergranulation pattern is described by Lisle et al. (2004). They used horizontal-divergence maps obtained from local correlation tracking of granules (1 min time lag). Lisle et al. (2004) constructed temporal averages (8 d) of the divergence maps for different tracking velocities v_t. The spatial variations of a 15° × 15° section of the time-averaged divergence map were characterized by the rms values in the east-west (σ_x) and south-north (σ_y) directions. Lisle et al. (2004) found that at the equator the ratio σ_x/σ_y is maximum at a tracking velocity U_LRT which is 110 m s⁻¹ above the Carrington velocity, i.e., faster than any rotation rate measured so far. They suggested that a ratio σ_x/σ_y greater than 1 is an indication that supergranules are preferentially aligned in a north-south direction. Junwei Zhao has recently repeated their analysis using time-distance divergence maps. Figure 66 and the companion Movie ?? shows a 15° × 15° time-averaged divergence map for various tracking velocities. Figure 66 shows the ratio σ_x/σ_y at the equator as a function of tracking velocity, averaged over all available data. The maximum occurs at a tracking rate 123 m s⁻¹ above the Carrington velocity. It is evident that there is another local maximum 8 m s⁻¹ below the Carrington velocity. This local maximum could only be hinted at from the plots of Lisle et al. (2004) due to lack of averaging. We will come back to this observation near the end of the next section.

Figure 65:

mpg-Movie (121.860351562 KB) Still from a Movie showing the evolution of the average map of the divergence signal in a 15° × 15° equatorial region as a function of tracking velocity in the range from −200 m s⁻¹ to 200 ms⁻¹ with respect to the Carrington velocity. The movie still displays the temporal average (5 d) tracked at a velocity 125 m s⁻¹ above the Carrington velocity. This average is constructed from maps derived from time-distance helioseismology every 8 hr. Courtesy of J. Zhao. (For video see appendix)

Figure 66:

Ratio, as defined by Lisle et al. (2004), at the equator as a function of tracking velocity v_t (offset with respect to Carrington velocity). This curve is an average over one month of data. The vertical dashed lines correspond to tracking offsets −8 m s⁻¹ and 123 m s⁻¹. Courtesy of J. Zhao.

Traveling-wave convection

The 3D power spectrum of the divergence signal was studied first by Gizon et al. (2003). The same analysis was extended by Gizon and Duvall Jr (2004) to cover the period from 1996 to 2002. They considered series of MDI full-disk Dopplergrams from the Dynamics campaigns (two to three months each year). Dopplergrams were tracked at the Carrington angular velocity to remove the main component of rotation. Every 12 hr, a 120^° × 120^° map of the horizontal divergence of the near-surface flows was obtained using f-mode time-distance helioseismology. At a given target latitude λ a longitudinal section of the data was extracted, 10° wide in latitude. Gizon and Duvall Jr (2004) rearranged the data in a frame of reference with angular velocity Ω_mag(λ) = 14.43° − 1.77° sin² λ − 2.58° sin⁴ λ d⁻¹ (rotation rate of small magnetic features; Komm et al., 1993b). This choice of reference is convenient, although arbitrary. The position vector is denoted by x = (x, y) in the neighborhood of latitude λ, where coordinate x is prograde and y is northward, with a spatial sampling of 2.92 Mm in both coordinates.

The divergence signal was decomposed into its harmonic components exp(ik · x − iwt) through FFT, where uu is the angular frequency and k = (k_x, k_y) is the horizontal wavevector. The power spectrum of the horizontal divergence signal, denoted by P_div(k, ω), was computed for each target latitude λ with 5° steps. Gizon et al. (2003) discovered that, in the range with 50 < kR_⊙ < 200, the power spectrum of the solar divergence signal can be described accurately by the following parametric model:

$${P_{{\rm{div}}}}(k,\omega) = {1 \over 2}[F(k,\omega) + F(- k, - \omega)],$$

(95)

where

$$F(k,\omega) = {{A(k)} \over {1 + {{[\omega - {\omega _{\rm{r}}}(k)]}^2}/\gamma {{(k)}^2}}} + B(k)$$

(96)

and

$${\omega _{\rm{r}}}(k) = {\omega _0}(k) + k \cdot U(k).$$

(97)

The functions A, ω₀, U, γ, and B, described below, were determined from fits to the data. The fits took into account the ω-convolution of the solar power spectrum with the power in the observation window. The representation of P in terms of F is convenient as it implies P_div(−k, −ω) = P_div(k, ω), i.e., the divergence signal is real.

At fixed k, the power spectrum of the horizontal divergence can be described by the sum of two Lorentz functions with independent amplitudes A(k) and A(−k) and with central frequencies ω_r(k) and −ω_r(−k) respectively. The function A(k) depends on the direction of k and can be parametrized as follows:

$$A(k) = {A_0}(k) + {A_1}(k)\cos (\psi - {\psi _{\max}}) + {A_2}(k)\cos (2\psi - \alpha),$$

(98)

where the azimuth ψ is the direction of the wavector such that k = (k cos ψ, k sin ψ), e.g., ψ = 0 when k points prograde and ψ = π/2 when k points north). The A₂ component includes instrumental astigmatism: a purely spatial distortion which can not easily be separated from a real solar signal. The A₁ component, however, must be of solar origin. The power anisotropy may be defined by the ratio η = 2A₁/A₀, while ψ_max was called the azimuth of maximum power. The background noise B, which is small, was assumed to be independent of frequency but affected by astigmatism. The half width γ at half maximum of the Lorentz profile corresponds to a characteristic e-folding lifetime τ = 1/γ. The frequency shift k · U was interpreted to be a Doppler shift produced by a horizontal flow U = (U_x, U_y) measured in the frame of reference (rotating at Ω_mag), as is done in ring-diagram analysis (Section 4.2.2).

Figure 67 shows a cyclindrical cut in the equatorial power spectrum at a constant k typical of the supergranulation, and a model fit to the data according to Equations (95, 96, 97). For each azimuth ψ, the power has two peaks at frequencies ω₊ = ω_r(k) and ω₋ = −ω_r(−k). Observations show that the difference ω₊ − ω₋ = 2ω₀(k) is independent of azimuth (Gizon et al., 2003). No Galilean transformation can cause these peaks to coalesce, at zero frequency or otherwise. This implies that supergranulation undergoes oscillations. In the plane power is distributed along two parallel sinusoids at frequencies ±ω₀ + kU_x cos ψ + kU_y sin ψ. The presumption by Rast et al. (2004) that power is distributed along two intersecting sinusoids must be rejected: It is inconsistent with the observations. As one does in helioseismological ring analysis (Schou and Bogart, 1998), it is natural to interpret the frequency shift k · U as a Doppler shift produced by an advective flow U (some average flow in the supergranulation layer). The weak k-dependence of the measured U in the range 40 < kR_⊙ < 180 is consistent with this interpretation. Furthermore the functional form of the power is preserved for different tracking rates (i.e., different latitudes). As shown in Figure 68, it is remarkable that the inferred rotation U_x and meridional circulation U_y are both similar to that of the small magnetic features (Komm et al., 1993b, c). This property is consistent with the view that magnetic fields are advected by supergranular flows. In addition, the torsional oscillations are seen with the same phase and amplitude as in global helioseismology. The temporal changes in the meridional circulations are also consistent with an inflows toward the mean latitude of activity (see Section 5.3.4).

Figure 67:

Power spectrum of the horizontal divergence signal for λ = 0 (equator) in 1997. Divergence maps were tracked in a frame of reference with angular velocity Ω_mag (λ = 0) (small magnetic features). Left panel: Cylindrical section at constant wavenumber k = 115/R_⊙, as a function of azimuth ψ and frequency ω/2π. Middle panel: Fit to the data according to the model described in the text. The values of the parameters are measured at fixed k by a two-dimensional fit to the power spectrum in (ψ, ω)-space. For this particular example, η = 1.15 and ψ_max = −2° (excess power in the prograde direction). Right panel: Ratio of the data to the fit; no bias is observed. From Gizon and Duvall Jr (2004).

Figure 68:

(a) Advective flow U_x versus λ at kR_⊙ = 115. Each curve corresponds to a different year (from blue in 1996 to red in 2002). U_x is measured with respect to the reference R_⊙Ω_mag cos λ (small magnetic features). Only the north-south symmetric component is shown. (b) Residuals of U_x after subtraction of a smooth fit (dashed line in panel a). The scale bar has units of ms⁻¹. The black curve is an estimate of the mean latitude of activity. (c) Advective flow U_y versus λ at kR_⊙ = 115. Only the north-south antisymmetric component is shown. (d) Residual meridional circulation with respect to the dashed line in panel (c). The scale bar has units of ms⁻¹.

The dynamics of the supergranulation is best studied once the background flow U has been removed. In a co-moving frame, each spatial component oscillates at a characteristic frequency ω₀. There is a clear relationship between ω₀ and the wavenumber k, well described by a power law (see panel (a) of Figure 69):

$${{{\omega _0}} \over {2\pi}} \simeq 1.8{\left({{{k{R_\odot}} \over {120}}} \right)^{0.45}}\mu \;{\rm{Hz}}.$$

(99)

This is a fundamental relationship as it is measured to be essentialy independent of ψ, λ, and the phase of the solar cycle. The data are consistent with a spectrum of traveling waves with a dispersion relation ω = ω₀(k). The azimuthally averaged power spectrum is shown in panel (b) of Figure 69. In the range 60 < kR_⊙ < 160, the peak of power away from zero temporal frequency is well resolved since the quality factor Q = ω₀/γ is larger than 1. Near kR_⊙ = 120 we have Q ≃ 2. The variations of the oscillation frequency with latitude and time are less than 5% during the period 1996–2002 for kR_⊙ = 115. Since ω₀ and the dominant size of supergranules are observed to be essentially independent of latitude, the general dynamics determining the time scale and the spatial scale of supergranulation is not affected by the Coriolis force associated with the large scale vorticity (rotation). However, there is a pronounced anisotropy in the azimuthal distribution of wave power at fixed k. The power anisotropy is measured to be η ≃ 1 for kR_⊙ = 115. Furthermore, power is maximum in a direction equatorward of the prograde direction in both hemispheres: For |λ| < 25° observations show ψ_max ≃ −λ, and for |λ| > 25° ψ_max ≃ −25°signλ. The pattern therefore senses the effect of rotation. A snapshot of the divergence field would not reveal this as the sum of the powers measured in opposite directions is nearly isotropic. We recall that the effect of rotation on supergranulation was detected in the vorticity field.

Figure 69:

(a) Oscillation frequency ν₀ = ω₀/(2π) versus kR_⊙ at latitudes λ = 0° (solid), λ = ±25° (dotted), and λ = ±50° (dashed). For reference, the orange curve is ν = 1.8(kR_⊙/120)^0.45 µ Hz. Also shown is the half width at half maximum (HWHM, γ/(2π)) of the Lorentzian profiles for the same latitudes. The quality factor is Q = ω₀/γ ≃ 2 at kR_⊙ = 120. (b) Power spectrum corrected for rotation and meridional circulation and averaged over azimuth and latitude. The distribution of power as a function of frequency is affected only by the known temporal window function. From Gizon et al. (2003).

The lifetime of supergranules is about 2.3 d at kR_⊙ = 115, i.e., a somewhat larger value than other estimates derived from the decay of the autocorrelation function. This is because the lifetime is not strictly given the decay of the correlation function at short time lags, but by the decay of the envelope of the correlation function, which oscillates. The lifetime decreases by about 20% at active latitudes (Gizon and Duvall Jr, 2004).

As mentioned earlier, estimates of supergranulation rotation obtained by tracking the Doppler pattern are systematically found to be higher than the rotation of the magnetic network (for large time lags, see panel (a) of Figure 63). This apparent superrotation of the pattern can now be understood as the result of the waves being predominantly prograde. The east-west motion of the pattern is effectively a power-weighted average of the true rotation and the non-advective phase speed u_w = ω₀/k ∼ 65 m s⁻¹ for kR_⊙ = 120. Similarly, the excess of wave power toward the equator is reflected in the equatorward meridional motion of the pattern at large time lags (see panel (b) of Figure 63) even though the advective flow is poleward. Correlation tracking measurements must take into account the fact that the pattern propagates like a modulated traveling wave.

The measurement of the pattern rotation obtained by Lisle et al. (2004) is also a direct consequence of the power spectrum. It is straightforward to show that the ratio σ_x/σ_y (see Section 5.3.4) can be expressed in terms of P_div(k, ω) alone. Plugging in Equations (95, 96, 97), one finds that at the equator the variations of σ_x/σ_y as a function of tracking velocity v_t should display two peaks at v_t ≃ U_x ± u_ω, where u_ω ≃ 65 m s⁻¹ is the dominant wave speed and U_x is the advective velocity. The amplitudes of the peaks are approximately given by

$${{{\sigma _x}} \over {{\sigma _y}}} \simeq \sqrt {{{1 + {Q^2}} \over 2}\left({1 = {\eta \over 2}} \right)} = (1.2,1.8)\quad \quad {\rm{at}}\;{v_t} \simeq {U_x} + {u_{\rm{w}}},$$

(100)

using mean values η ≃ 0.9 and Q ≃ 2. The separation between the two peaks, 2u_w ≃ 130 m s⁻¹, is precisely the observed value (Figure 66). The super-rotation of the pattern obtained by Lisle et al. (2004), U_LRT ≃ U_x + u_w, is understandably faster than measured by other methods, and faster than U_x which is close to the magnetic feature rate. Figure 66 is not only a direct consequence of the observed power spectrum, but it is additional evidence for the existence of prograde and a retrograde components (in a frame rotating at U_x) as well as excess power in the prograde direction. Astigmatism (A₂) would also affect the ratio σ_x/σ_y, but it was neglected in Equation (100) for the sake of simplicity. It is worth noting that σ_x/σ_y > 1 is not a sufficient condition to imply that supergranules are aligned in the north-south direction, since σ_x/σ_y depends on P_div only (phases are needed for pattern characterization).

It was a source of concern that the wavelike properties of supergranulation had not been seen previously in surface Doppler shifts. Schou (2003b) showed that the same phenomenon can be observed directly using MDI Dopplergrams, thereby confirming the observations of Gizon and Duvall Jr (2003). In addition to confirming those results, Schou (2003b) was able to extend the measurements for the rotation and meridional velocities, U_x and U_y, beyond ±70° latitude. We note that, earlier, Beck and Schou (2000) had also used a spectral method to estimate the equatorial rotation of supergranulation from surface Doppler images; this method, however, was incorrect as it did not take account of the full complexity of the power spectrum.

All the evidence shows that supergranulation displays a high level of organization in space and time. Although no serious explanation has been proposed yet, it would seem that supergranulation is an example of traveling-wave convection. The prograde excess of wave power is perhaps due to the influence of rotation (or rotational shear) that breaks the east-west symmetry, allowing for new instabilities to propagate (see, e.g., Busse, 2003, 2004). We note that convection in oblique magnetic fields also exhibits solutions that take the form of traveling waves (Hurlburt et al., 1996). Future work should focus on measuring the evolution of the pattern at different depth in the interior and the phase relationship between the different Fourier components. More than forty years after its discovery, supergranulation remains a complete mystery.