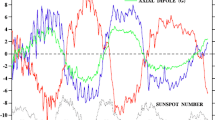1 The Beginning

My introduction to the random walk of magnetic flux on the Sun began on the morning of September 16, 1963 when the phone rang in the 60-foot tower telescope at Mount Wilson. Caltech Professor Robert B. Leighton had just returned from IAU Symposium No. 22 in Rottach-Egern, Germany, and was calling to ask me to meet with him in his office later that day. He had an idea for a possible PhD thesis topic. When I met with him back on the Caltech campus, he said that while he was preparing his IAU talk, he realized that the supergranulation could transport magnetic flux from its origin in sunspot groups and ultimately reverse the polar fields of the Sun (Leighton, 1965a). He said that while he was in his hotel room, he considered what would happen if one inserted a concentration of dye into a non-stationary convective flow like the supergranulation. The dye would be swept to the boundaries of the nearby convective cells, and as the pattern of cells evolved, the dye would be swept to new boundaries again and again until the initial concentration was spread over a wide area. He likened the process to a random walk in which the dye was magnetic flux provided by sunspot groups and the convection was the supergranulation.

The implications were obvious. There were two kinds of flux, positive and negative, which spread out independently from their respective sources in a newly erupted sunspot group and canceled where they overlapped. And, of course, the sunspot groups did not have random properties, but satisfied Hale’s law (positive leading polarity in the north and negative in the south during one sunspot cycle, and opposite during the next cycle) and what Hal Zirin would later call Joy’s law (slightly tilted groups in each hemisphere, with their leading parts closer to the equator and their trailing parts closer to the pole of that hemisphere). In the absence of differential rotation and meridional flow, the amount of flux F from each half of the bipolar region would gradually spread out on the surface and eventually coat it with a uniform average flux density F/(4πR2), where R is the radius of the Sun. At the nearby pole of the Sun, the contribution of each polarity would increase as the flux began to arrive and then decrease again as it spread further out on the Sun. Because the trailing-polarity flux started closer to the pole, it would arrive sooner than the leading-polarity flux and be more concentrated when it arrived. Thus, the net contribution would have the sign of the trailing-polarity flux and a magnitude of order FΔθ/(4πR2), where Δθ is the initial meridional separation of the leading and following parts of the sunspot group. Moreover, it seemed plausible that the accumulated effect of some ∼ 103 sunspot groups that erupt during a given sunspot cycle would be sufficient to reverse the polar fields and replace them with one of opposite polarity.

In the following days, Leighton used idealized ring doublets to represent the longitudinally averaged contribution of sunspot groups, and prepared the punched cards that enabled him to compute the axisymmetric field of the Sun from an equatorial migration of such sources. He acknowledged that I had been working on other topics, but said that measurements to test this new flux-transport hypothesis would make a good thesis project. So while Leighton performed the calculations for his classic paper on flux-transport (Leighton, 1964), I began thinking about measurements that could be used to test the model.

One 11-year sunspot cycle had elapsed since the Babcocks began making daily observations of the Sun’s magnetic field (Babcock and Babcock, 1952), and this interval included the reversal of the polar fields, first at the south pole in 1957 and then at the north pole in 1958 (Babcock and Livingston, 1958; Babcock, 1959). Other reversals were expected, but had not yet been observed. Thus, with the encouragement of Bob Howard, I began looking for indirect evidence of prior polar field reversals on photographic plates that were stored in the basement of the Santa Barbara Street office of the Mount Wilson Observatory. White-light images of the Sun’s disk had been obtained since 1905, and occasionally showed faculae at the poles of the Sun. Hα and Ca-K images were also available, but provided less of a distinction between the polar and low-latitude fields.

A systematic examination of white-light images obtained during 1905–1964 revealed that polar faculae were common in the years around each sunspot minimum, but rare at sunspot maximum (Sheeley Jr, 1964, 1965). Evidently, the polar fields really did reverse around the time of each solar maximum, as predicted by the models of Babcock (1961) and Leighton (1964). However, the yearly averaged numbers of polar faculae occasionally showed short-term fluctuations whose reality was beyond doubt (Sheeley Jr, 1965). Because supergranular diffusion was too slow to cause the polar field to decay appreciably in a year or so, I wondered if intermittent eruptions of flux in the sunspot belts might cause bursts of opposite-polarity flux to arrive at the poles from time to time to suddenly weaken the polar fields. Numerical simulations ultimately showed that the source fluctuations are responsible, but that they must be accompanied by meridional flow in order to reach the poles before they are smoothed out by diffusion (Wang et al., 1989a; Sheeley Jr, 1991).

Aside from Leighton’s (1964) initial flux-transport calculations, there were few numerical studies of flux evolution at that time. Caltech graduate student Phillip Roberts used a true random walk method to extrapolate my measurements of active region fluxes forward in time by a few months and obtained good agreement with the observed fields (Sheeley Jr, 1965, 1966). Leighton experimented with a magneto-kinematic model without meridional flow and was able to reproduce several overall properties of the sunspot cycle (Leighton, 1969). In particular, he obtained the observed equatorward progression of sunspot eruptions (the butterfly diagram) by assuming that the Sun’s internal angular velocity decreases radially outward. However, helioseismology observations have now shown this assumption to be incorrect. As demonstrated by Wang et al. (1991) and Choudhuri et al. (1995), an equatorward progression can be obtained by including meridional circulation with a return flow ∼ 1ms−1 at the base of the convection zone.

The first numerical simulation of the observed large-scale field was performed by Schatten et al. (1972), who combined sources from Mount Wilson Observatory magnetograms with transport by Newton and Nunn (1951) differential rotation and supergranular diffusion at an unspecified rate (presumably in Leighton’s (1964) range of 770–1540 km2 s−1). Their simulations exhibited a quasi-rigid rotation poleward of the sunspot belts. Although this rigid rotation was consistent with the rate obtained from cross-correlations of the observed field (Wilcox et al., 1970), Schatten et al. (1972) thought the field ought to exhibit the same differential rotation used as input to the calculations, and supposed that the result was an artifact of their computational technique. Fifteen years elapsed before we realized that the quasi-rigid rotation was caused by the poleward component of flux transport, diffusion plus meridional flow (Sheeley Jr et al., 1987).

Figure 1:
figure 1

Bob Leighton, examining the spectroheliograph during a visit to Kitt Peak in 1968. His guide, the author, is on the right.

Full size image

2 The 1970s

For his thesis research, Caltech student Jim Mosher compared the evolution of magnetic regions seen on small reproductions of Kitt Peak magnetograms with what he estimated from analytical calculations (Mosher, 1977). He deduced that the effective diffusion rate was only 200–400 km2 s−1 and that it was accompanied by a poleward meridional flow ∼ 3 ms−1. This was an apparent blow to Leighton’s model, which was able to reverse the polar field without the need for meridional flow (provided that the diffusion rate was ∼ 103 km2 s−1), and was especially appealing in the days when there was little observational evidence for the flow. Although Doppler observations of meridional flow were still uncertain (Duvall Jr, 1979; Labonte and Howard, 1982), inferences based on flux evolution continued to accumulate (Howard, 1979; Howard and Labonte, 1981; Topka et al., 1982), and Leighton’s model was increasingly criticized. The status of the model at that time is described in Chapter 2 of the Skylab Active Region Workshop publication (Sheeley Jr, 1981b).

During this era, solar observations were often interpreted in terms of hypothetical properties of the subsurface field. The recurrence patterns of the Sun’s mean line-of-sight field and of the interplanetary field were supposed to originate in rigidly rotating primordial fields below the surface (Svalgaard and Wilcox, 1975). The quasi-rigid rotations of photospheric fields were thought to indicate rotational properties of the subsurface layers in which they were rooted (Stenflo, 1974, 1977; Snodgrass, 1983). Rigid rotations of coronal holes and other coronal structures were interpreted as fundamental manifestations of rigidly rotating subsurface fields (Zirker, 1977; Howard, 1978, 1984). Solar physics had truly entered the ‘dark ages’ of understanding.

3 Early Simulations

The situation turned around in the 1980s, when a confluence of new researchers, improved computing facilities, and high-quality synoptic observations made it possible to begin a more quantitative study of flux transport. During the January 7–10, 1981 meeting of the Solar Physics Division of the American Astronomical Society at Taos, New Mexico, Jay Boris (Director of NRL’s Laboratory for Computational Physics) pointed out that we did not need to listen to speculations about flux transport anymore. We could simulate the evolution of the large-scale field and compare these simulations with synoptic observations from Kitt Peak. So when we returned to NRL, Jay began to write a flux-transport code and I started measuring fluxes in bipolar magnetic regions on Kitt Peak magnetograms. We were soon joined by Rick DeVore, who modified the code for use on the the next generation of computers and used it to simulate the transport of flux in a variety of solar configurations. His analytical and numerical calculations resulted in several papers about magnetic flux transport on the Sun, and a PhD thesis for Princeton University (DeVore, 1986).

It was tedious to measure the coordinates and estimate the fluxes of all of the emerging bipolar magnetic regions on the Kitt Peak magnetograms. Thus, we began with the interval 1976–1981, and recorded the coordinates and pole strengths of idealized newly erupting magnetic ‘doublets’. The list included doublets with pole strengths of 0.1 × 1021 Mx or greater. Our first project was to use these measurements to study the evolution of flux in isolated active regions (Sheeley Jr et al., 1983). We obtained an effective diffusion rate of 730 ± 250 km2 s−1 which overlapped Leighton’s (1964) estimate of 770–1540 km2 s−1, and was much greater than Mosher’s value of 200–400 km2 s−1 (Mosher, 1977). Subsequent studies including meridional flow have reduced the diffusion rate, first to 600 km2 s−1 (Wang et al., 1989b) and then to about 500 km2 s−1 (Wang et al., 2002b).

Next, we simulated the evolution of the Sun’s mean line-of-sight field. The initial result was so encouraging that we extended the source measurements as far as was possible at that time (June 1984), and simulated most of sunspot cycle 21 (DeVore et al., 1985a,b; Sheeley Jr et al., 1985). The sector pattern of the simulated mean field was relatively insensitive to the details of the flux-transport parameters, and left no doubt that the Sun’s mean field was rooted in flux that had originated in active regions. It was no longer necessary to appeal to unknown primordial fields beneath the Sun’s surface; we were coming out of the dark ages.

4 The Era of Enlightenment

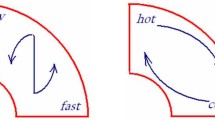
At this point, we realized that the doublet source list and flux-transport code could be used to study a variety of solar magnetic field problems, and we successively considered the decay of the mean field (Sheeley Jr and DeVore, 1986a), the origin of the 28–29 day recurrent patterns (Sheeley Jr and DeVore, 1986b), the total flux on the Sun (Sheeley Jr et al., 1986), and the Sun’s polar magnetic fields (DeVore and Sheeley Jr, 1987). When Yi-Ming Wang and Ana Nash joined the project, we studied the effects of solar rotation on the field, and found that the meridional component of flux transport was responsible for the quasi-rigid rotation of large-scale photospheric magnetic field patterns (Sheeley Jr et al., 1987). This was the result that Schatten et al. (1972) had found, but did not recognize, fifteen years earlier. In his talk at the Tenth Workshop on Cool Stars, Stellar Systems, and the Sun in Cambridge, Massachusetts, Yi-Ming used the ‘swimming duck’ analogy of Figure 2 to illustrate this effect (Wang, 1998).

Figure 2:
figure 2

Ducks enjoying a tour of Boston. Even though the current is faster on one side of the Charles than the other, the ducks form a stationary pattern because they are paddling toward the Boston shore. From Wang (1998).

Full size image

With a few exceptions (Sheeley Jr, 1981a; Wang et al., 1988), we tended to solve the flux-transport equation for the evolving magnetic field, rather than for the amplitudes and phases of its spherical harmonic components. However, in an elegant analytical treatment, Rick DeVore found an approximate solution for the rigidly rotating eigenmodes of the field when both diffusion and meridional flow were included (DeVore, 1987). Fourteen years later, Mike Schulz (2001) would perform a similar study, calculating the eigenmodes numerically for the case of diffusion alone.

When Jay, Rick, and I began the flux-transport simulations, we did not know if meridional flow was present on the Sun, and we couched our language in phrases like, ‘meridional flow (if present) and diffusion will do …’. However, as time passed, it became clear that a better fit between simulations and observations would be obtained if diffusion were assisted by a 10–20 m s−1 poleward meridional flow. For each problem, diffusion alone worked fairly well, but it always worked better if it were accompanied by meridional flow.

The most persuasive arguments concerned the polar fields and the poleward surges of flux from the sunspot belts. First, the topknot structure inferred by Svalgaard et al. (1978) could be explained as a quasi-equlibrium between dispersal via supergranular diffusion and concentration by a poleward flow (DeVore et al., 1984; Sheeley Jr et al., 1989). Second, ‘butterfly diagrams’ of the simulated field, such as those shown in Figure 3, did not reproduce the observed poleward surges of flux unless meridional flow was included in the model (Wang et al., 1989a; Sheeley Jr, 1992). In particular, Wang et al. (1989a) found that enhanced eruption rates and accelerated flows were required to match the episodic poleward surges of flux during sunspot cycle 21. Thus, we became confident that meridional flow was present even though the Doppler measurements were near the limit of credibility, and we dropped the ‘if present’ from our papers.

Figure 3:
figure 3

Time/latitude plots of the axisymmetric component of the simulated photospheric magnetic field during sunspot cycle 21. When the sources are not accompanied by a latitudinal component of transport, wide polarity bands are formed, with the leading polarity dominating near the equator and the trailing polarity dominating at higher latitudes (top panel). When the sources are accompanied by a 600 km2 s−1 diffusion, the equatorial bands of flux are annihilated and the high-latitude bands spread out smoothly to produce the broad latitudinal distribution of a dipole field (middle panel). When the sources are accompanied by diffusion and a steady 10 m s−1 poleward flow, they create several poleward surges of flux and a highly concentrated polar field (bottom panel).

Full size image

Seven years earlier, Topka et al. (1982) had reached the same conclusion from their analysis of the poleward migration of Hα filaments. In fact, their description was similar to that of Babcock (1961) who referred to large regions of trailing polarity drifting to the poles. But, except for Leighton (1964) and later Giovanelli (1984), most researchers did not appreciate that supergranular diffusion was essential for neutralizing the leading polarities and leaving those large regions of trailing polarity in each hemisphere.

Having been convinced that there really is a poleward meridional flow on the Sun’s surface, we wondered if the implied subsurface return flow might be responsible for the equatorward migration of sunspot eruptions (the butterfly diagram) (Wang and Sheeley Jr, 1991). In quantitative simulations of the sunspot cycle without meridional flow, Leighton (1969) obtained stable oscillations with the flux eruptions migrating toward the equator. However, his solution required a negative radial gradient of the Sun’s angular rotation rate, which was contrary to the new helioseismology observations (Duvall Jr et al., 1986). Consequently, we performed quantitative modeling in the spirit of Leighton (1969), and found that a subsurface return flow ∼ 1ms−1 and a subsurface turbulent diffusion rate ∼ 10 km2 s−1 gave cyclic solutions with the flux eruptions migrating toward the equator (Wang et al., 1991). Two-dimensional MHD versions of this flux transport dynamo have since been developed by Choudhuri et al. (1995), Dikpati and Charbonneau (1999), and Charbonneau and Dikpati (2000).

van Ballegooijen et al. (1998) modified the flux-transport model to include the effect of diffusion and flow on the horizontal component of the magnetic field. Their objective was to study the formation of filament channels and to look for systematic chirality relations in the northern and southern hemispheres of the Sun. Using a diffusion rate of 450 km2 s−1, a meridional flow speed of 10 m s−1, and the Snodgrass (1983) differential rotation formula, they obtained good agreement with the longitudinally averaged radial magnetic field observed at the Kitt Peak Observatory, and they reproduced the locations of the observed filament channels. The model seemed to be less successful in predicting the chirality relations, but after modifying the model further and increasing the diffusion rate to 600 km2 s−1, Mackay et al. (2000) were able to recover the observed hemispheric dependence. As described in Section 6, Mackay et al. (2002a,b) would eventually use the model to simulate the evolution of the Sun’s open flux.

Yi-Ming coupled the flux-transport code to the potential-field source-surface extrapolation, and we began to study the rigid rotation of the corona (Wang et al., 1988) and of coronal holes (Nash et al., 1988). The coronal field always rotated rigidly because it originated in a few low-order harmonic components. However, the rigid rate varied during the sunspot cycle as the sources of non-axisymmetric flux changed their latitudes. The same was true of coronal holes. They sheared rapidly when the large-scale non-axisymmetric flux was spread over a wide range of latitudes. But when the flux was concentrated at a specific latitude, a hole would rotate rigidly at the rate of that latitude. Toward sunspot minimum, active regions erupted at low latitudes, causing the meridional extensions of the polar coronal holes to rotate almost rigidly at the equatorial rate, as illustrated in Figure 4.

Figure 4:
figure 4

Longitude/latitude plots of the field consisting of an axisymmetric dipole and an idealized bipolar magnetic region at the equator. The bipolar region distorts the polar-hole boundaries into spurs that are relatively unaffected by differential rotation. Because the bipolar region and the coronal-hole deformations rotate with the 26.9-day equatorial period, they drift very slightly in the 27.27-day Carrington frame used for the maps.

Full size image

Finally, with the link between flux-tube expansion in the corona and solar wind speed far from the Sun (Levine et al., 1977; Wang and Sheeley Jr, 1990a), it became possible to relate solar wind speed variations to the eruption and evolution of photospheric flux (Wang and Sheeley Jr, 1990b; Sheeley Jr and Wang, 1991). For example, it was shown that the small open-field regions that form in active region remnants at sunspot maximum are characterized by rapid flux-tube expansion and therefore produce relatively slow wind. On the other hand, the interaction between two holes of the same polarity results in flux tubes with very low expansion factors. Thus the wind originating from the equatorward extensions of the polar coronal holes is expected to be even faster than that from the poles, a prediction confirmed by Ulysses spacecraft measurements (Phillips et al., 1994).

Although the model had become a powerful tool for analyzing problems involving the large-scale magnetic fields, it was still not universally accepted. Jan Stenflo (1989a,b, 1992) argued that our explanation for the quasi-rigid rotation could not be correct because, for short time lags, the cross-correlations of the simulated field gave the quasi-rigid rotation rate. The model did not reproduce the differential rate that Snodgrass (1983) obtained from cross-correlations of Mount Wilson daily magnetograms. We argued that the Snodgrass differential rate was a consequence of small scale field components, which, of course, are not contained in a diffusing large-scale field. But this argument had little effect until we replaced the diffusion by a discrete random walk and obtained the Snodgrass rate for short time lags (Wang and Sheeley Jr, 1994; Sheeley Jr and Wang, 1994). As we expected, the small-scale features gave the Snodgrass differential rate and the large-scale features gave the quasi-rigid rate. The quasi-rigid rotation could be understood in terms of surface motions alone, and no appeal to the unknown subsurface field was needed.

Although the higher resolution of the random-walk approach provided an appealing match to the resolution of the Mount Wilson magnetograms, we have not used it in our subsequent studies. The diffusion approximation has been adequate for studying the evolution of the large-scale field. However, as mentioned below, Schrijver (2001) has developed a random-walk model whose resolution mimics that of the Kitt Peak and Solar and Heliospheric Observatory (SOHO) magnetographs, and which also includes a procedure for simulating the initial breakup of flux concentrations in active regions.

5 The Australian School

In 1990, Peter Wilson and his colleagues began a long series of papers on the reversal of the Sun’s polar magnetic fields (Wilson et al., 1990; Wilson and McIntosh, 1991; Wilson, 1992; Murray and Wilson, 1992; Wilson and Giovannis, 1994). At first, they argued that the flux-transport model could not work because the surface fields ought to be linked to deep subsurface toroids, which would prevent them from moving freely to the poles. Next, they began their own simulations and concluded that the large-scale fields are not entirely the result of flux from active regions, but require additional contributions from sources in the network. They continued on to papers III (large-scale fields and the first major active regions of cycle 22), IV (polar fields near sunspot maximum), and V (reversal of the polar fields in cycle 22), always concluding that the flux in active regions was not enough to reproduce the large-scale field.

But as they considered the polar field reversals in sunspot cycles 22 (Snodgrass et al., 2000; Kress and Wilson, 2000) and 23 (Durrant and Wilson, 2003), the emphasis of the Australian group seems to have changed. In their most recent paper, Wilson and his colleagues use supergranular diffusion at a rate of 600 km2 s−1 to obtain an improved estimate of the poorly observed polar field reversal time. In addition, McCloughan and Durrant (2002) and Durrant and McCloughan (2004) devised a method for studying the evolution of synoptic maps of the photospheric field and used it to compare their simulations with observations of the polar fields. McCloughan’s 99-page thesis can be found online (McCloughan, 2002).

This change of emphasis seems to be bringing the various schools closer together. Instead of arguing whether the flux-transport model is valid, we were exploiting it to understand properties of the Sun’s magnetic fields. Two new ideas immediately come to mind. First, because the flux does drift to the poles, it must not be permanently attached to subsurface toroids, but must reconnect freely as it seems to do in the corona (Sheeley Jr and Wang, 2002; Sheeley Jr et al., 2004). If the reconnecting fields are so interesting above the surface, what must they be like below the surface? Second, differences in the polar field reversals from one sunspot cycle to the next may reflect differences in the rates of meridional flow. Flow speed variations were suggested by the episodic poleward surges (Labonte and Howard, 1982) which have now been observed in every sunspot cycle since 1964, and by the short-term fluctuations in the numbers of polar faculae since 1905 (Sheeley Jr, 1991). As we shall see in the next section, secular changes in the flow rate of order ± 6 m s−1 are sufficient to preserve the polar field reversal from cycle to cycle (Wang et al., 2002a).

By contrast, the role of small-scale background eruptions is poorly understood. On the one hand, we have been able to reproduce the evolution of the large-scale field without including ephemeral regions in the model. In fact, Sheeley Jr et al. (1985) found that 85% of the sources provided about 50% of the total erupted flux and doublet moment during sunspot cycle 21, but that their exclusion had little effect on either the strength or polarity pattern of the mean field. Similarly, Wang and Sheeley Jr (1991) found that ephemeral regions had no effect on the evolution of the Sun’s axial dipole moment, nor did they give rise to an effective diffusion of flux. Also, at the November 1–5, 1993 Soesterberg Workshop honoring Kees Zwaan, Karen Harvey (1994) presented observations demonstrating that the flux in large-scale unipolar magnetic regions originates in active regions and activity ‘nests’ of the kind that were studied by Gaizauskas et al. (1983). She found that during sunspot cycle 21 the dipole contribution of ephemeral regions was only one-sixth that of active regions and of opposite sign.

On the other hand, Stenflo (1992) and Snodgrass and Wilson (1993) suggested that large-scale regions may sometimes (in Karen’s words) ‘form in situ from a clustering and preferential alignment of the magnetic poles of many small-scale emerging bipolar regions’. More recently, Solanki et al. (2002) argued that ephemeral regions may have contributed to the Sun’s open flux in the past, especially during quiet times like the Maunder Minimum when large active regions were rare. Of course, a sufficiently large number of ephemeral regions will contribute to the large-scale field if the orientations of their doublet moments are not random (as Karen found in cycle 21). However, at present we do not know if these weak background eruptions are the tail of the active-region size distribution with orientations that have been partially randomized during their transit through the convection zone, or an independent component of randomized ‘magnetic foam’. Perhaps future studies of high cadence observations like those of Hagenaar (2001) and high resolution simulations like those of Schrijver (2001) will help to answer this question.

6 Simulations Over Many 11-Year Sunspot Cycles

The next phase was stimulated by interest in the long-term evolution of the Sun’s open magnetic flux. From an analysis of geomagnetic observations, Lockwood et al. (1999) had concluded that the Sun’s open flux doubled during the twentieth century. The variations of open flux and heliospheric magnetic field strength also affect the occurrence of the cosmogenic isotopes of 10Be and 14C, and are thus of interest to researchers working on cosmic rays and solar irradiance variations.

This was the reason that our NRL colleague Judith Lean encouraged us to deduce the long-term variation of the Sun’s open flux from potential-field source-surface extrapolations of the observed photospheric field. We found that the magnitude of the open flux followed the evolution of the Sun’s total dipole during 1971–1999. There was relatively little variation during the sunspot cycle as the dipole evolved from an axisymmetric configuration in the years around sunspot minimum to an equatorial configuration around maximum (Wang et al., 2000a,b) without changing its strength very much. The open flux was approximately constant, except for intermittent fluctuations of a factor of two in the years around or just after sunspot maximum. These fluctuations came from the equatorial dipole, which strengthened when active regions happened to erupt in longitudinal phase with the dipole, and weakened as meridional flow carried the flux to midlatitudes where it was eroded by differential rotation and supergranular diffusion on a 1–2 year time scale (Wang and Sheeley Jr, 2003).

Meanwhile, in Scotland, Duncan Mackay was combining the flux-transport program with the potential-field source-surface model to simulate the evolution of open flux during the sunspot cycle (Mackay et al., 2002a,b). For nominal values of meridional flow speed, the open flux peaked at sunspot minimum, rather than 1–2 years after maximum when the observed open flux (as determined from in situ spacecraft magnetometer measurements) obtained its peak. Mackay et al. concluded that something important must be missing from the model and suggested that the problem might lie with the source-surface component. However, the source-surface model seems to be an unlikely culprit because it correctly reproduces the observed variation of open flux when it is applied to the observed photospheric field (as opposed to the field simulated from the doublet sources) (Wang et al., 2000a; Wang and Sheeley Jr, 2002).

Nevertheless, we also found that the open flux peaked at sunspot minimum when we repeated the Mackay et al. simulation using our estimated doublet sources and nominal flux-transport parameters. Rather than supposing that something was missing from the model, we tried other values of the input parameters to see if we could find a combination that would match the observations. In principle, stronger source fluxes ought to increase the open flux around sunspot maximum. In addition, a faster flow speed with a slightly smaller diffusion rate would weaken the polar field strength (and reduce the open flux) around sunspot minimum. Keep in mind that the ultimate strength of the polar field is determined by the amount of unbalanced flux that is available for meridional flow to transport to the pole, and not on the rate at which the flux is carried there. Thus, a stronger flow speed (relative to diffusion) leaves less unbalanced flux in each hemisphere and produces a weaker, rather than a stronger, polar field. This idea is the key to understanding the polar field reversal when a relatively inactive sunspot cycle follows an active one, as will be discussed below.

To match the simulated and observed open flux, we needed to increase the doublet strengths by a factor of 3, reduce the diffusion rate slightly from 600 km2 s−1 to 500 km2 s−1, and increase the meridional flow rate from ∼ 10 m s−1 to ∼ 25 m s−1 (Wang et al., 2002b). The factor-of-2 increase of flow speed was appreciable, but not unreasonable because the speed still lay in the range of uncertainty obtained from Doppler measurements. By contrast, the factor-of-3 increase of the source strengths was surprising, and made me wonder if active regions really contained 3 times as much flux as I had always supposed. One could rationalize that the process of estimating fluxes from photographic prints of Kitt Peak magnetograms (by measuring areas and using empirical correlations) is not the same as deriving magnetic fluxes from the digital data, and that errors of this magnitude might easily be involved. However, the systematic nature of the correction suggests that it must involve something more fundamental than the use of photographic prints. This means that prior measurements of fluxes in active regions, even though they led to average field strengths of several hundred Gauss in network features, must have been systematically underestimated, perhaps due to weakenings of the Ca Iλ 6103 line used in those measurements (Sheeley Jr, 1966; Chapman and Sheeley Jr, 1968). This possibility is supported by the fact that, during sunspot cycle 21, the total flux on the Sun (as derived from Kitt Peak magnetograms) was 2–3 times larger than that derived from the fields simulated using the doublet sources (cf. Figure 3 of Wang et al. (2002b)). We need to resolve this issue by making improved measurements of the fluxes in newly emerging bipolar magnetic regions, paying careful attention to the fluxes both inside and outside sunspots.

We did not run into this problem until we compared interplanetary field measurements with the open flux simulated using our doublet sources. Evidently, the spacecraft magnetometer measurements provide a constraint on the flux in active regions, and therefore on our doublet-strength calibration. Prior studies, which were not concerned with the absolute amount of flux on the Sun, would not be affected by the doublet-strength calibration (except indirectly through the use of a lower meridional flow speed), nor would studies that used the observed photospheric field as input, instead of the doublet sources. As mentioned above, the open flux, determined from the source-surface extrapolation of the observed photospheric field, agreed well with the open flux derived from interplanetary measurements, assuming that the interplanetary flux is distributed isotropically (Wang and Sheeley Jr, 1995). It is interesting that the Ulrich correction, used to convert the saturated Fe I λ 5250 synoptic measurements of the photospheric field to unsaturated (and therefore more reliable) Fe I λ 5233 measurements, increased the low-latitude flux by a factor ∼ 4 (Ulrich, 1992), and thus had roughly the same effect on the open flux as enhancing the doublet strengths by a factor of 3.

In 2002, flux-transport simulations over many sunspot cycles were providing examples in which the polar fields would not reverse. Schrijver et al. (2002) had recently used source fluxes derived from past sunspot records to simulate the polar field from the mid-17th century to the present, and had found several cases for which the simulated polar fields did not reverse. They noted that this problem would not have occurred if flux emerged on the Sun with a finite life expectancy of about 5 years. At the same time, Judith Lean had used our list of doublets from the years 1976–1986 to create a 110-year series of hypothetical sunspot cycles with intervals in which each cycle was stronger than the next. Judith was motivated by the long-term variation of solar irradiance, and was looking for systematic variations of field strength from one sunspot minimum to the next. As part of that study, she found that the simulated polar fields ultimately became so strong that they would not reverse if the sequence of progressively stronger sunspot cycles were interrupted by a weaker cycle (Lean et al., 2002).

As mentioned above, a variable meridional flow speed (relative to the diffusion rate) provides a possible way of avoiding these puzzling non-reversals of the simulated polar fields. Scaling our doublet sources by past levels of sunspot activity, Yi-Ming simulated the polar field evolution during the past 100 years (Wang et al., 2002a). He varied the meridional flow speed from one cycle to the next so that it was slightly faster in an active cycle and slightly slower during an inactive cycle. For only modest ± 6 m s−1 variations of the flow speed, polar field reversals were obtained in every sunspot cycle, with strengths that were consistent with the polar faculae measurements (Sheeley Jr, 1991). A reassuring aspect of this result is that the positive correlation between flow speed and cycle amplitude is consistent with a negative correlation between flow speed and cycle period. In particular, the flux-transport dynamo calculation of Dikpati and Charbonneau (1999) gives short sunspot cycles when the flow is fast. Because short (or at least rapidly rising) cycles tend to be relatively active according to the sunspot records (Schatten and Hedin, 1984), this implies that fast flow occurs during active cycles.

The flux-transport model has evolved since its birth more than forty years ago. In 1963, it contained differential rotation and supergranular diffusion. Twenty years later, the model included poleward meridional flow and was telling us about coronal holes and sector structure. Now, after twenty more years, the flow speed has temporal variations that are telling us about the long-term behavior of the sunspot cycle, and vice versa. What will be next?

7 Epilogue

This paper concerns the history of magnetic-flux transport and not so much the technical details and consequences of the model, which Marc DeRosa will discuss in a companion paper. I thought it would be interesting to review the history and to write it down before it is forgotten, but I did not want to punish the reader (or myself) by discussing all of the results that we have learned along the way. The interested reader can track them down fairly quickly beginning with the references that are listed here.

In that respect, the referees of this paper provided additional references, some of which I was aware and some of which I was not. The former category includes a review by Rabin et al. (1991), of which Rick DeVore and I are co-authors, but which I had forgotten. The latter category includes papers by Csada (1949, 1955), who presented a mathematical theory of differential rotation and meridional flow in rotating magnetic stars.

A referee also mentioned papers by Plaskett (1959) and Ward (1965). I don’t remember if I was aware of the former paper in the 1963–1965 era when we were beginning our work on flux transport, but I was aware of the latter paper. In 1965, Fred Ward came to Caltech to discuss his idea that the Greenwich sunspot observations show evidence of Rossby waves on the Sun. Leighton was so opposed to Ward’s argument that he wrote a rebuttal (Leighton, 1965b), in which he concluded:

‘To summarize, we have shown that the fluctuations and systematic variations in spot group areas would, a priori, be expected to produce effects of the kinds and approximate magnitudes reported by Ward. While the roughness of our estimates does not yet permit us to be certain that Ward’s results are entirely spurious, the degree of agreement surely suggests that his result be treated with the utmost caution. If the possible sources of difficulty discussed here are in fact less important than estimated, they should be proved so as result of suitable measurements rather than simply by assumption.’

The manuscript is dated May 15, 1965 and contains an inscription indicating that the paper was sent to the Astrophysical Journal. But to my knowledge, it was never published.

One can gain a further sense of the meridional-flow issue by going back a few years earlier to Babcock’s (1961) famous paper, ‘The Topology of the Sun’s Magnetic Field and the 22-Year Cycle’. Here, Babcock cited a previous Babcock and Babcock (1955) paper, in which he and his father had speculated that the poleward migration of the trailing parts of bipolar regions was responsible for the cancellation and reversal of the polar fields, and that the leading parts of the bipolar regions must therefore either be neutralized at the equator or contribute to a quadrupole moment of the Sun. He went on to say that there is no persistent quadrupole, so there must be migration toward the equator at low latitudes and toward the poles at moderate latitudes. However, the cause of this migration was obscure and Babcock could do little more than appeal to supporting observations by Richardson and Schwarzschild (1953), who had reported that individual sunspots drifted slowly away from the 20°latitude circles. For those of us who were skeptical of meridional flow speeds obtained by tracking sunspots, the combination of random-walk diffusion and systematically tilted sunspot groups (Joy’s law) seemed to be a much more convincing way of moving trailing-polarity flux toward the poles and leading-polarity flux toward the equator.

One of the referees wondered if the informal solar lunches and frequent seminars that took place in Pasadena when Zirin, Leighton, and Howard were reinvigorating solar research at Caltech and Mount Wilson played a role in stimulating the development of the flux-transport model. That is an interesting historical question, but the answer is ‘no’. As indicated at the beginning of this paper, Leighton got the idea in September 1963 while he was in Germany preparing his IAU talk on supergranulation. Hal Zirin had not yet arrived at Caltech and the solar lunches were at least a few years in the future. By the time of the solar lunches, I had moved to the Kitt Peak Observatory in Tucson and was less familiar with what was happening at Caltech. However, I think that Leighton had pretty much turned his attention to infrared and millimeter wave astronomy, and that Howard and Zirin were working with a new group of students and post-docs at Mount Wilson and the Big Bear Solar Observatory.

One of them was K. A. Marsh who suggested that the interaction between ephemeral regions and the previously existing network fields might contribute to the large-scale diffusion of flux (Marsh, 1978). The Marsh mechanism was probably an exciting topic of conversation at Caltech lunches when people were trying to reconcile the relatively high diffusion rates ∼ 800 km2 s−1 which Leighton used to reverse the polar fields, and the much slower rates of 100–20 km2 s−1 found by tracking small-scale flux elements. However, the Marsh mechanism did not resolve this discrepancy because the eruption of ephemeral regions with random orientations is not a diffusive process and, in particular, it does not change the large-scale distribution of flux on the Sun (Wang and Sheeley Jr, 1991). More recently, Schrijver et al. (1996) offered a different explanation for the discrepancy, arguing that the traditional methods of tracking flux give smaller diffusion rates because they emphasize the larger, more sluggish, flux elements and underestimate the significant contribution of the many smaller, more mobile, concentrations.

Work on the flux-transport model has waxed and waned over the years. There were relatively few numerical studies from the mid-1960s when Leighton proposed the model until the 1980s when the NRL group started its work. During this interval, observational studies, performed mainly at the Big Bear, San Fernando, Lockheed, and Mount Wilson Observatories, gave results (like small diffusion rates and reports of meridional flow) that were inconsistent with the model as Leighton had originally proposed it. But eventually flow was added to the model and the numerical simulations provided a number of new results and explanations. Additional groups appreciated the usefulness of the model and developed their own flux-transport codes. Now, we are in a new era of extending and improving the flux-transport model (van Ballegooijen et al., 1998; Schrijver, 2001; McCloughan and Durrant, 2002; Mackay et al., 2002a,b; Baumann et al., 2004), and applying it to interesting subjects like the Sun’s long-term behavior and the magnetic fields of other stars (Schrijver and Title, 2001; Mackay et al., 2004).