Coronal Waves and Oscillations

Nakariakov, Valery M.; Verwichte, Erwin

doi:10.12942/lrsp-2005-3

Review Article
Open Access
Published: 07 May 2005

Coronal Waves and Oscillations

Valery M. Nakariakov¹ &
Erwin Verwichte¹

Living Reviews in Solar Physics volume 2, Article number: 3 (2005) Cite this article

5442 Accesses
323 Citations
4 Altmetric
Metrics details

Abstract

Wave and oscillatory activity of the solar corona is confidently observed with modern imaging and spectral instruments in the visible light, EUV, X-ray and radio bands, and interpreted in terms of magnetohydrodynamic (MHD) wave theory. The review reflects the current trends in the observational study of coronal waves and oscillations (standing kink, sausage and longitudinal modes, propagating slow waves and fast wave trains, the search for torsional waves), theoretical modelling of interaction of MHD waves with plasma structures, and implementation of the theoretical results for the mode identification. Also the use of MHD waves for remote diagnostics of coronal plasma — MHD coronal seismology — is discussed and the applicability of this method for the estimation of coronal magnetic field, transport coefficients, fine structuring and heating function is demonstrated.

Introduction

The magnetically dominated plasma of the solar corona is an elastic and compressible medium which can support propagation of various types of waves. For a large class of waves with wavelengths and periods large compared with the ion Larmor radius (< 1 m for almost all combinations of coronal parameters) and the gyroperiod (< 10⁻⁴ s), respectively, the waves can be described using magnetohydrodynamics (MHD). These waves perturb macro-parameters of the coronal plasma, such as density, temperature, bulk velocity and the frozen-in magnetic field. For wavelengths comparable with the characteristic sizes of coronal plasma structures (e.g., loop major and minor radii, widths of plumes and helmet structures, size of active regions, and so on), the typical periods are in the range from a few seconds to several minutes. This range is well covered by temporal resolution of presently available ground-based and spaceborne observational tools, allowing for the observational detection of the waves. However, it is very important to understand that in normal circumstances both spatial and temporal resolution are necessary ingredients of successful detection of the waves: e.g., the pixel size must be much smaller than the wavelength (taking into account the projection effect!) and the cadence time must be shorter than the period. Only in certain exceptional cases, e.g., when the wave passes through a bright object with the geometrical size smaller than the wavelength, the wave can be detected with poorer spatial resolution.

The launch of SOHO and TRACE spacecrafts led a revolutionary breakthrough in the observational study of coronal wave activity, including the discoveries of EIT (or coronal Moreton) waves (Thompson et al., 1998), compressible waves in polar plumes (Ofman et al., 1997; DeForest and Gurman, 1998; Ofman et al., 1999) and in coronal loops (Berghmans and Clette, 1999; De Moortel et al., 2000; Robbrecht et al., 2001), flare-generated global kink oscillations of loops (Aschwanden et al., 1999, 2002; Nakariakov et al., 1999; Schrijver et al., 2002), and longitudinal standing oscillations within loops (Kliem et al., 2002; Wang et al., 2002). Also, ground-based radio observations have long revealed the presence of periodic and quasi-periodic phenomena in the corona (Aschwanden, 1987). Moreover, very recently ground-based optical observations of eclipses have revealed the presence of rapid oscillations in coronal loops (Williams et al., 2001, 2002). Extensive observational reviews of this diversity of coronal oscillations are given in Aschwanden (2003); Nakariakov (2003); Aschwanden (2004). The current state of the theoretical studies of MHD wave propagation in the solar atmosphere is discussed in Roberts (2000, 2002); Goossens et al. (2002b); Roberts and Nakariakov (2003); Roberts (2004).

MHD waves in the corona have been intensively investigated for more than two decades, primarily in the context of the enigmatic problems of coronal heating and acceleration of the fast solar wind. Discussion of those issues is out of scopes of this review and may be found in Walsh and Ireland (2003); Cranmer (2004); Ofman (2004). It is also believed that the coronal MHD waves play an important role in solar-terrestrial connections. The investigation of the coronal waves is now an essential part of solar physics, space physics, geophysics and astrophysics.

The aim of this review is to reflect the current trends in the observational study of coronal wave and oscillatory phenomena, their phenomenology, their interpretation in terms of MHD wave theory, latest achievements in the theoretical modelling of interaction of MHD waves with inhomogeneous plasmas and its relevance to the coronal waves, and recent progress in MHD coronal seismology.

The method of MHD coronal seismology

Despite significant progress in coronal physics over several decades, a number of fundamental questions, for instance, what are the physical mechanisms responsible for the coronal heating, the solar wind acceleration, and solar flares, remain to be answered. All these questions, however, require detailed knowledge of physical conditions and parameters in the corona, which cannot yet be measured accurately enough. In particular, the exact value of the coronal magnetic field remains unknown, because of a number of intrinsic difficulties with applications of direct methods (e.g., based upon the Zeeman splitting and gyroresonant emission), as well as indirect (e.g., based upon extrapolation of chromospheric magnetic sources). Also, the coronal transport coefficients, such as volume and shear viscosity, resistivity, and thermal conduction, which play a crucial role in coronal physics, are not measured even within an order of magnitude and are usually obtained from theoretical estimations. Other obscured parameters are the heating function and filling factors.

The detection of coronal waves provides us with a new tool for the determination of the unknown parameters of the corona — MHD seismology of the corona. Measurement of the properties of MHD waves and oscillations (periods, wavelengths, amplitudes, temporal and spatial signatures, characteristic scenarios of the wave evolution), combined with a theoretical modelling of the wave phenomena (dispersion relations, evolutionary equations, etc.), leads to a determination of the mean parameters of the corona, such as the magnetic field strength and transport coefficients. This approach is illustrated in Figure 1. Philosophically, the method is similar to the acoustic diagnostics of the solar interior, helioseismology. But, MHD coronal seismology is much richer by its very nature as it is based upon three different wave modes, namely, Alfvén, slow, and fast magnetoacoustic modes. These MHD modes have quite different dispersive, polarisation, and propagation properties, which makes this approach even more powerful. A similar method for the determination of physical parameters of laboratory plasmas, MHD spectroscopy, has been successfully used for a decade (see, e.g., the recent review of Fasoli et al., 2002). In particular, the measurements of Alfvén eigenmode frequencies and mode numbers and the comparison between the antenna driven spectrum and that calculated theoretically give information on the bulk plasma, allowing for the improved equilibrium reconstruction in terms of radial profiles of density and safety factor. In contrast with the MHD spectroscopy, MHD coronal seismology utilises propagating waves too.

Originally, the method of MHD coronal seismology was suggested by Uchida (1970) for global and Roberts et al. (1984) for local seismology, and has recently been applied to obtain estimates of the magnetic field (Roberts et al., 1984; Nakariakov and Ofman, 2001), the coronal dissipative coefficients (Nakariakov et al., 1999), and to probe coronal sub-resolution structuring (Robbrecht et al., 2001; King et al., 2003). These implementations are discussed in Sections 3.3, 3.4 and 6.3, respectively.

Properties of MHD Modes of Plasma Structures

In MHD, wave and oscillatory phenomena have spatial and temporal scales much longer than the ion gyroradii and gyroperiods, respectively, the conditions which are satisfied well by the coronal observational constrains. The characteristic speeds of the MHD phenomena are associated with plasma compressibility and elasticity connected with the frozen-in magnetic field of strength B₀ and with gas pressure p₀, and with the ion inertia described by the mass density ρ₀. They are the usual sound speed, C_s = (γp₀/ρ₀)^1/2 with γ the adiabatic index, normally taken to be about 5/3 in the corona, and the Alfvén speed, C_A = B₀/(μ₀ρ₀)^1/2, where μ₀ is the permeability of vacuum. It is convenient to introduce also the cusp or tube speed, $C_{\rm T}=C_{\rm s}C_{\rm A}/(C_{\rm A}^{2}+C_{\rm s}^{2})^{1/2}$ which is a combination of the sound and Alfvén speeds. Typical values of those speeds in coronal active regions vary from a hundred to a few thousand km s⁻¹.

There are three basic MHD waves: an incompressible Alfvén wave and a fast and slow magnetoacoustic waves, which are both essentially compressible. Properties of MHD waves strongly depend upon the angle between the wave vector and the magnetic field, consequently, MHD waves are highly affected by plasma structuring and filamentation. Structuring of the solar coronal plasma modifies those waves and may lead to their coupling, bringing such interesting features of MHD wave dynamics as phase mixing, resonant absorption, and guided wave propagation, dramatically influencing manifestation of the waves in observations. This makes the theory of MHD wave modes of plasma structures to be the key ingredient of the coronal wave study. Also, the theory provides the necessary classification of wave and oscillatory phenomena in coronal plasmas.

MHD modes of a straight cylinder

An important elementary building block of this theory is dispersion relations for modes of a magnetic cylinder (see Figure 2). Magnetic cylinders are believed to model well such common coronal structures as coronal loops, various filaments, polar plumes, etc. Consider a straight cylindrical magnetic flux tube of radius a filled with a uniform plasma of density ρ₀ and pressure p₀ within which is a magnetic field B₀e_z; the tube is confined to r < a by an external magnetic field B_ee_z embedded in a uniform plasma of density ρ_e and pressure p_e (here we neglect the effects of twist and steady flows). The very existence of such a plasma configuration requires the balance of the total pressure P_tot, which is the sum of the plasma and magnetic pressures, between the two media at the boundary. For the equilibrium state, this condition is

$${p_0} + {{B_0^2} \over {2{\mu _0}}} = {p_{\rm{e}}} + {{B_{\rm{e}}^2} \over {2{\mu _0}}}.$$

(1)

Similarly, a magnetic slab may be introduced in much the same way, having a width 2a.

In the internal and external media, the sound speeds are C_s0 and C_se, the Alfvén speeds are C_A0 and C_Ae, and the tube speeds are C_T0 and C_Te, respectively. Relations between those characteristic speeds determine properties of MHD modes guided by the tube.

The presence of the internal spatial scale, the radius of the tube a, brings wave dispersion. The standard derivation of linear dispersion relations is based upon linearisation of MHD equations around the equilibrium. The following system of first order differential equations and algebraic equation governs the behaviour of linear perturbations of the form δP_tot(r) exp[i(k_zz + mϕ − ωt)] (Sakurai et al., 1991a):

$$\matrix{{D{d \over {dr}}(r{\xi _r}) = (C_{\rm{A}}^2 + C_{\rm{s}}^2)({\omega ^2} - C_{\rm{T}}^2k_z^2)\left({{\kappa ^2} + {{{m^2}} \over {{r^2}}}} \right)r\delta {P_{{\rm{tot}}}},} \hfill \cr {{d \over {dr}}(\delta {P_{{\rm{tot}}}}) = {\rho _0}({\omega ^2} - C_{\rm{T}}^2k_z^2){\xi _r},} \hfill \cr}$$

(2)

and

$${\rho _0}({\omega ^2} - C_{\rm{A}}^2k_z^2){\xi _\varphi} = - {{im} \over r}\delta {P_{{\rm{tot}}}},$$

(3)

where ξ_r and ξ_φ are the perturbation displacements in the radial and azimuthal direction, respectively. The quantity D is defined as

$$D = {\rho _0}(C_{\rm{A}}^2 + C_{\rm{s}}^2)({\omega ^2} - C_{\rm{A}}^2k_z^2)({\omega ^2} - C_{\rm{T}}^2C_z^2),$$

(4)

and κ plays the role of the transverse wave number and is defined as

$${\kappa ^2}(\omega) = - {{({\omega ^2} - C_{\rm{s}}^2C_z^2)({\omega ^2} - C_{\rm{A}}^2C_z^2)} \over {(C_{\rm{s}}^2 + C_{\rm{A}}^2)({\omega ^2} - C_{\rm{T}}^2C_z^2)}}.$$

(5)

In each medium separately, the system of Equations (2, 3) can be reduced to the equation

$$({\omega ^2} - C_{{\rm{A}}\alpha}^2k_z^2)\left[ {{{{d^2}} \over {d{r^2}}} + {1 \over r}{d \over {dr}} - \left({\kappa _\alpha ^2 + {{{m^2}} \over {{r^2}}}} \right)} \right]\delta {P_{{\rm{tot}}}} = 0,$$

(6)

where α = 0, e. The first term of Equation (6) represents torsional Alfvén wave solutions with ω = ±C_Aαk_z. The second term is a Bessel-like equation that describes magnetoacoustic wave modes. External and internal solutions of this equation have to be matched by the use of jump conditions: the continuity of total pressure and the normal velocity (see, e.g., Roberts, 1981a,b). Furthermore, a condition of mode localisation is applied, requiring that the wave energy should decline with a lateral distance from the structure (tube or slab). In the presence of a steady flow, the condition of continuity of normal velocity is replaced by continuity of the transverse displacement (see, e.g., Nakariakov and Roberts, 1995a). Applying the boundary conditions to the solutions of the Bessel equation leads to the dispersion relation for magnetoacoustic waves in a magnetic flux tube (Edwin and Roberts, 1983; see also Roberts and Nakariakov, 2003 and references therein)

$${\rho _{\rm{e}}}({\omega ^2} - k_z^2C_{{\rm{Ae}}}^2){\kappa _0}{{I_m^{\prime}({\kappa _0}a)} \over {{I_m}({\kappa _0}a)}} + {\rho _0}(k_z^2C_{{\rm{A}}0}^2 - {\omega ^2}){\kappa _{\rm{e}}}{{K_m^{\prime}({\kappa _{\rm{e}}}a)} \over {{K_m}({\kappa _{\rm{e}}}a)}} = 0.$$

(7)

I_m(x) and K_m(x) are modified Bessel functions of order m, and the prime denotes the derivative of a function I_m(x) or K_m(x) with respect to argument x. The functions κ_e and κ₀ are the transverse wave numbers in the external and internal media, respectively, which are obtained from Equation (5) by the substitution of the appropriate characteristic speeds. For modes that are confined to the tube (evanescent outside, for r > a), the condition $\kappa_{{\rm e},0} > 0$ has to be fulfilled. In the equation, it is assumed that κ_e,0 > 0. The integer m determines the azimuthal modal structure: waves with m = 0 are called sausage modes, waves with m = 1 are kink modes, waves with higher m are sometimes referred to as flute or ballooning modes. The existence and properties of the modes are determined by the equilibrium physical quantities. In particular, a coronal loop or a filament can trap MHD waves if the external Alfvén speed is greater than internal.

Figure 3 shows a typical dispersion diagram of a coronal loop. This figure generalises the dispersion plot given by Edwin and Roberts (1983) to the inclusion of higher-m modes. In the Figure 3, all the possible modes correspond to body modes, which have oscillatory behaviour inside and evanescent behaviour outside. This is in contrast with surface modes, which have evanescent behaviour in both media. Phase speeds of MHD modes guided by the tube can have values in two bands: either between C_A0 and C_Ae (provided C_A0 < C_Ae) and between C_T0 and C_s0. The wave modes in these two bands have been named, respectively, fast and slow, in analogy with the types of magnetoacoustic wave modes present in a homogeneous medium. The fast modes are highly dispersive. In the long wavelength limit, the phase speed of all but sausage fast modes tends to the so-called kink speed

$${C_{\rm{K}}} = {\left({{{B_0^2/{\mu _0} + B_{\rm{e}}^2/{\mu _0}} \over {{\rho _0} + {\rho _{\rm{e}}}}}} \right)^{1/2}} = {\left({{{{\rho _0}C_{{\rm{A}}0}^2 + {\rho _{\rm{e}}}C_{{\rm{Ae}}}^2} \over {{\rho _0} + {\rho _{\rm{e}}}}}} \right)^{1/2}},$$

(8)

which corresponds to the density weighed average Alfvén speed. The sausage mode approaches a cut-off at the external Alfvén speed. Trapped sausage modes do not exist at longer wavelengths. But mode solutions can be found if the condition of mode localisation is relaxed, i.e., if waves are allowed to radiate into the external medium. Such wave modes are called leaky modes and have complex eigenfrequencies. To include leaky modes, dispersion relation (7) is modified such that the modified Bessel functions K_m(x) are replaced by Hankel functions. Details of the leaky solutions may be found in Zaitsev and Stepanov (1975); Cally (1986); Stenuit et al. (1998). In Figure 3, leaky waves would be situated outside the regions of existence of the trapped waves. In particular, the sausage mode continues in the region over the horizontal asymptote C_Ae but its frequency is complex there.

In closed fields of coronal active regions, the longitudinal wave number k_z of standing modes is usually prescribed by the line-tying boundary conditions at the photosphere. Modes with the lowest wave numbers are called global or fundamental.

The magnetoacoustic modes (with an important exception) are collectively supported by the plasma environment, i.e., the wave mode acts across neighbouring magnetic field lines and across transverse plasma inhomogeneities. Alfén waves, though, are locally supported. They have phase and group velocities, with magnitudes equal to the local Alfvén speed, which are directed along the magnetic field. This means that an Alfén wave propagates along its local magnetic field line without interaction with neighbouring field lines. This particular property allows for the existence of continua of eigenfrequencies and which will be discussed in Section 2.2.

In a cylinder model, Alfvén waves are torsional waves that twist tube. In the case of a straight cylinder these modes are incompressible, however in a slightly twisted cylinder they are accompanied by perturbations of plasma density (Zhugzhda and Nakariakov, 1999). In the slab geometry, torsional waves perturb the magnetic field and generate perturbations of plasma velocity in the direction perpendicular to magnetic field and to the direction of the inhomogeneity. Alfvén waves are very weakly dissipative. This means they can propagate very long distances and deposit energy and momentum far from their source. Concerning the generation of Alfvén waves, they can easily be excited by various dynamical perturbations of magnetic field lines. This makes Alfvén waves a promising tool for heating and diagnostics of coronal magnetic structures.

Movies visualising the structure of the MHD modes in a magnetic cylinder are available in Resource 1. Figure 4 shows the transverse and longitudinal density and velocity structure of a magnetic cylinder perturbed by a fundamental fast kink oscillation.

MHD continua

When the group speed of wave modes is directed along the magnetic field, then such modes on neighbouring field lines do not interact with each other. They may oscillate locally with their own eigenfrequency without disturbing the rest of the medium. If the equilibrium parameters of the plasma vary continuously across the magnetic field, then the eigenfrequency of such modes may also vary continuously. This gives rise to continuous intervals of eigenfrequencies, i.e., continua, in frequency space. This situation, though, may change by including resistivity or non-MHD effects (see, e.g., Appert et al., 1986).

In ideal MHD, there exist two continua: the Alfvén continuum and the slow (or cusp) continuum (see Goedbloed, 1983; Goedbloed and Poedts, 2004). Equations (2, 3) are also valid for linear waves in a coronal loop modelled as a plasma cylinder if the equilibrium quantities vary continuously in the radial direction (see, e.g., Sakurai et al., 1991a). The continua are in this case characterised by the frequencies C_A(r)∣k_z∣ and C_T(r)∣k_z∣. There are two effects associated with wave modes from these continua: resonant absorption and phase-mixing.

Resonant absorption

If the loop supports a collective (a mode) wave, either driven externally or set up initially, which has a frequency ω that falls within one of the two continua, a resonance is set up at the location(s) where $\omega^{2}=C_{\rm A}^{2}(r)k_{z}^{2}$ or $\omega^{2}=C_{\rm T}^{2}(r)k_{z}^{2}$ (where Equation (4) becomes zero). The physical location where the resonance occurs is called the resonance layer and in the plasma cylinder model it corresponds to a radial shell (see Figure 5). From now on we shall consider the case of a resonance in the Alfvén continuum only. The locally excited resonant wave mode is a torsional Alfvén wave and its amplitude peaks in the resonance layer where the perturbation develops large gradients. Dissipation has to be taken into account to prevent the perturbation to diverge. The amplitude of the resonant mode scales as Re^1/3 at the resonant layer, where Re is the shear viscous and/or the magnetic Reynolds number (Kappraff and Tataronis, 1977). In the solar corona this number is much larger than unity (Re ∼ 10¹⁴). Since non-resonant modes dissipate with an amplitude proportional to Re, it is clear that the resonantly excited modes experience enhanced dissipation. This also implies that the resonant absorption process is inherently nonlinear, since the amplitude of the resonant mode can not grow to the values implied by the Re^1/3 scaling (Ofman et al., 1994; Ofman and Davila, 1995). Thus, wave energy is extracted secularly through the resonance from the collective wave to the benefit of a local wave mode (mode conversion), which then is dissipated in an enhanced manner. This mechanism of wave heating is called resonant absorption (Goedbloed, 1983, and references therein) and has been put forward in the context of the coronal heating problem (Ionson, 1978) and in sunspot seismology for explaining the loss of acoustic power in sunspots (see, e.g., Sakurai et al., 1991b; Bogdan, 2000, and references therein).

There are inherently two time scales involved. Firstly, there is the damping time scale of the mode conversion from the collective to the local mode, which generally is independent of dissipation. From the point of view of linear theory and classical, theoretical values of dissipation coefficients, it is generally much shorter than the second time scale, which is linked to the dissipative damping of the small-scale perturbations of the local mode in the resonance layer.

Note that for sausage wave modes, where m=0, the equations describing the magnetoacoustic and torsional waves (i.e., Equations (2, 3)) are decoupled so that mode conversion and absorption through the Alfvén resonance cannot take place (the slow resonance can still operate; see, e.g., Erdélyi, 1997). For the slab geometry, this corresponds to propagation parallel to the magnetic field, i.e., k_y = 0.

To study resonant absorption the following procedure is often undertaken. Whilst outside of the resonant layer the ideal MHD equations can be applied, inside the resonant layer dissipative effects have, in principle, to be taken into account to ensure that the solution remains regular. But unless one is interested in the details of the solution in the resonant layer, this can be avoided. The thickness of the resonant layer, δ, is proportional to (ℓL²Re)^−1/3, where ℓ is the length scale over which the Alfvén speed varies around the resonance. In the solar atmospheric context δ can be assumed to be small. The solution in the resonant layer is replaced by a jump relation, which is based upon a Taylor series expansion of the ideal MHD equations around the resonance (Kappraff and Tataronis, 1977; Ionson, 1978; Hollweg, 1987; Hollweg and Yang, 1988; Sakurai et al., 1991a). It is assumed that the quantities that are conserved across the layer in ideal MHD will remain so in weakly dissipative MHD.

Consider a loop model where the internal and external media are homogeneous, except for a loop edge layer of width ℓ where the density varies monotonically from ρ₀ to ρ_e (see Figure 5). A global wave mode is present, which has a frequency ω which matches the Alfvén frequency at C_A(r = r_A)∣k_z∣ within the Alfvén continuum of the edge layer (see Figure 6). In the internal and external media the solutions are calculated using, e.g., Equation (6). Those solutions contain arbitrary integration constants, which are related to each other with use of certain jump relations at the edge layer. The width of the edge layer, ℓ, is considered to be thin, i.e., ℓ ≪ a, but wider than the resonant layer, i.e., δ > ℓ. The jump relations are constructed as follows. Inside the edge layer, the system of Equations (2) is Taylor expanded around the resonance using the small parameter s ≡ r − r_A (∣s∣ ≪ 1). Thus, a second order differential equation for δP_tot/s is derived, which is of the form

$$\left[ {{{{d^2}} \over {d{s^2}}} + {1 \over s}{d \over {ds}} - \left({{1 \over {{s^2}}} + {{{m^2}} \over {r_{\rm{A}}^2}}} \right)} \right]\left({{{\delta {P_{{\rm{tot}}}}} \over s}} \right) = 0.$$

(9)

It has solutions in the form of modified Bessel functions. The total pressure perturbation is described as

$$\delta {P_{{\rm{tot}}}} = a\;s\;{I_1}\left({{{\vert m\vert s} \over {{r_{\rm{A}}}}}} \right) + b\;s\;{K_1}\left({{{\vert m\vert s} \over {{r_{\rm{A}}}}}} \right) \approx b{{{r_{\rm{A}}}} \over {\vert m\vert}},$$

(10)

which is approximately constant across the layer (Hollweg, 1987; Sakurai et al., 1991a). Since for m=0 no resonant coupling can occur, the Equation (10) does not apply for that case. Therefore, the jump relation for the total pressure perturbation is simply [δP_tot] = 0, where the square brackets denote the difference between the solutions in the right and left limits of s tending to zero, respectively. Note that, when the loop is twisted, the total pressure is no longer a conserved quantity (Sakurai et al., 1991a). Similarly, the solution for the radial displacement perturbation can be found to be approximately

$${\xi _r} \approx b{{\vert m\vert} \over {{r_{\rm{A}}}}}{1 \over {{\rho _0}({r_{\rm{A}}})\Delta}}\ln \left({{{\vert m\vert s} \over {2{r_{\rm{A}}}}}} \right) + {\rm{constant,}}$$

(11)

where $\Delta=d(\omega^{2}-C_{\rm A}^{2}k_{z}^{2})/dr_{r=r_{\rm A}}$. ξ_r depends on s through a logarithmic term, which diverges for s tending to zero. The jump relation for ξ_r is

$$[{\xi _r}] = - i\pi {{{m^2}} \over {r_{\rm{A}}^2}}{{{\rm{sign}}\omega} \over {{\rho _0}({r_{\rm{A}}})\vert \Delta \vert}}\delta {P_{{\rm{tot}}}}({r_{\rm{A}}}),$$

(12)

for which the relation [ln(s)] = −iπ sign(ω) sign(Δ) has been used. To match the internal and external solutions, the usual jump conditions of continuity of total pressure and radial displacement are now replaced by the above derived jump relations. Depending on the condition that is imposed at r → ∞, the trapped and/or leaky eigenmodes of the system may be studied (involving a dispersion relation) or the reflection/absorption problem of an externally driven wave that interacts with the loop.

By scanning through the frequency of the collective wave, the wave absorption as a function of ω is studied (see, e.g., the numerical simulations by Poedts et al., 1989). The fractional absorption spectrum often shows well-defined maxima where the absorption reaches 100%. The spatial structure of the excited wave mode at those maxima shows a combination of localised and global behaviour. It is a global wave (e.g., discrete fast eigenmode) with a frequency that lies in the Alfvén continuum and is, therefore, locally coupled to an Alfvén wave. These types of wave modes are known as quasi-modes and they are natural wave modes of the dissipative and inhomogeneous system (Balet et al., 1982; Steinolfson and Davila, 1993; Ofman et al., 1994; Ofman and Davila, 1995; Tirry and Goossens, 1996). Therefore, it is easily understood why maximum absorption occurs when driving at the frequency of a quasi-mode. Also, the presence of steady flows can significantly change the efficiency of resonant absorption (Erdélyi, 1998).

Furthermore, in the absence of flow, these modes are damped (Poedts et al., 1990; Ofman et al., 1994; Wright and Rickard, 1995). From the point of view of the global nature of the mode, the damping is primarily a conversion of energy from the collective to the local. This damping rate has been calculated for various geometries (see, e.g., Lee and Roberts, 1986; Hollweg, 1987; Goossens et al., 1992). Ruderman and Roberts (2002) calculated the damping time, τ, of a global kink wave in a long, thin loop (a ≪ L) in the limits of weak dissipation (Re ≫ 1) and zero plasma-β:

$$\tau = {{2a\vert \Delta \vert {{({\rho _0} + {\rho _{\rm{e}}})}^3}} \over {\pi \rho ({r_{\rm{A}}})\vert {C_{\rm{K}}}{k_z}{\vert ^3}{{({\rho _0} - {\rho _{\rm{e}}})}^2}}}.$$

(13)

This time scale is generally much shorter than the time scale of the dissipative damping of the small-scale perturbations of the local mode in the resonance layer. In Section 3.4 this aspect of rapid mode conversion will be explored further within the context of the observed rapid damping of transverse loop oscillations (Roberts, 2000; Ruderman and Roberts, 2002; Goossens et al., 2002a; Van Doorsselaere et al., 2004).

Ofman et al. (1994) and Ofman and Davila (1995) studied numerically nonlinear resonant absorption and found that the large shear velocities produced at the resonance layer are subject to Kelvin-Helmholtz instabilities. The velocity amplitudes derived from linear theory are much larger than the observed velocities from nonthermal broadening of coronal emission lines. This discrepancy may be explained by a turbulent enhancement of dissipation parameters due to the instabilities. Additional complexity is brought by the effects of boundary conditions in the longitudinal direction, e.g., Beliën et al. (1999) examined numerically the effect of the transition region and chromosphere on the resonant absorption in coronal loops. They found that the nonlinear energy transfer from the Alfvén waves to slow magnetoacoustic waves in the lower atmosphere can much diminish the absorption efficiency compared with models of line-tied loops without a lower atmosphere. The driver they considered was, though, monoperiodic and this study should be extended to include more realistic drivers. Furthermore, the heating of the resonance layer would spread due to thermal conduction and heat the lower atmosphere. The resulting chromospheric evaporation enhances the loop density at the resonance layer and, hence, shifts the Alfvén frequency away from resonance, as well as change the quasi-mode frequencies (see, e.g., the discussion in Ofman and Davila, 1995). Ofman et al. (1998a) considered a broad band Alfvén wave driver (see also DeGroof and Goossens, 2002), and coupling to the chromosphere of the loop density with the use of a quasi-static equilibrium scaling law. They found that the heating is concentrated in multiple resonance layers, rather than in the single layer of previous models, and that these layers drift throughout the loop to heat the entire volume. These properties are in much better agreement with coronal observations that imply multithreaded loop structure.

Alfvén wave phase mixing

Consider again a structure with a continuous inhomogeneity profile across the magnetic field. Instead of an initial collective mode, this time on each field line an Alfvén wave is excited. This wave oscillates independently from its neighbours, with a frequency that lies in the Alfvén continuum. For simplicity a Cartesian geometry is chosen where the magnetic field is in the z-direction and the inhomogeneity is in the x-direction. The Alfvén waves, which are polarised in the y-direction, are described by the wave equation (Heyvaerts and Priest, 1983)

$$\left({{{{\partial ^2}} \over {\partial {t^2}}} - C_{\rm{A}}^2(x){{{\partial ^2}} \over {\partial {z^2}}}} \right){V_y} = 0,$$

(14)

with the solution

$${V_y} = \Psi (x)f(z \mp {C_{\rm{A}}}(x)t),$$

(15)

where f(z) and Ψ(x) are functions prescribed by the initial profile of the wave. The sign in the argument of this function corresponds to a wave propagating in the positive or negative direction of the z-axis, respectively. When Ψ(x) = const, the wave is plane.

Equation (15) shows that the Alfvén waves propagate on different magnetic surfaces, corresponding to different values of x, with different phase speeds equal to the local Alfvén speed C_A(x). If the wave is initially plane in the x direction, it gets gradually inclined. This leads to generation of very small transverse (in the direction of the inhomogeneity) spatial scales. These high transverse gradients, in the presence of finite viscosity or resistivity, which leads to the appearance of a ν∂/∂t ∇²V_y term on the right hand side of Equation (14), are subject to efficient dissipation. Here, ν is the coefficient of viscosity and/or resistivity, small enough so that dissipation may be considered weak. This is the effect of Alfvén wave phase mixing, suggested by Heyvaerts and Priest (1983) as a possible mechanism for heating of open coronal structures.

In the developed stage of phase mixing (when ∂/∂x ≫ ∂/∂z) the Alfvénic perturbations of different magnetic surfaces become uncorrelated with each other, the perturbations decay according to the law (Heyvaerts and Priest, 1983)

$${V_y}(z) \propto {V_y}(0)\exp \left\{{- {{\nu k_z^2} \over {6C_{\rm{A}}^2(x)}}{{\left[ {{{d{C_{\rm{A}}}(x)} \over {dx}}} \right]}^2}{z^3}} \right\},$$

(16)

for propagating harmonic Alfvén waves, and

$${V_y}(t) \propto {V_y}(0)\exp \left\{{- {{\nu k_z^2} \over 6}{{\left[ {{{d{C_{\rm{A}}}(x)} \over {dx}}} \right]}^2}{t^3}} \right\},$$

(17)

for standing harmonic Alfvén waves. The decay time due to phase-mixing is proportional to Re^1/3, similar to the dissipative decay of Alfvén waves due to resonant absorption. Figure 7 shows the dissipative decay of propagating Alfvén waves in a 1D plasma inhomogeneity with Alfvén speed profiles of different steepness, compared with the dissipative decay of Alfvén waves in a homogeneous medium (solid curve).

If instead of a monochromatic wave in the longitudinal direction a localised Alfvén pulse is considered, Heyvaerts and Priest’s expression for the exponential decay (17) should be replaced by the power law

$${V_y} \propto {\left[ {\nu {{\left({{{d\;{C_{\rm{A}}}(x)} \over {dx}}} \right)}^2}{t^3}} \right]^{- 1/2}};$$

(18)

see Hood et al. (2002) and Tsiklauri et al. (2003) for two methods of derivation and comparison with results of numerical modelling.

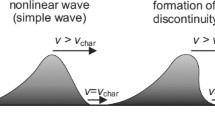
In the nonlinear regime, growing transverse gradients induce oblique fast magnetoacoustic waves (Nakariakov et al., 1997). Consequently, phase mixing regions may be characterised by the presence of compressible perturbations.

Zero plasma-β density profiles

The limiting case of zero plasma-β (where β is the ratio of the gas pressure to the magnetic pressure), when the plasma pressure force is neglected in comparison with the Lorentz force, and there is a one-dimensional profile of the plasma density, embedded in the constant and parallel magnetic field, the eigenvalue problem is similar to the quantum mechanical problem of the interaction of a particle with a nonuniform potential. In this section we restrict our attention to the Cartesian geometry only. The governing equations, in this case, allow for exact analytical solutions. We consider wave propagation along the magnetic field (i.e., k_y = 0) to avoid the Alfvén resonance. Nakariakov and Roberts (1995b) established that the qualitative dispersive properties depend weakly upon the specific profile of the density. Consider a coronal loop as a magnetic slab with a smooth density profile, given by the profile function

$${\rho _0} = {\rho _{\max}}{\rm{sec}}{{\rm{h}}^{\rm{2}}}\left({{x \over a}} \right) + {\rho _\infty},$$

(19)

where ρ_max, ρ_∞ and a are constant. Here, the parameter ρ_max is the density at the centre of the inhomogeneity, ρ_∞ is the density at x = ∞ and a is a parameter governing the inhomogeneity width. This inhomogeneity, plotted in Figure 8, is called the symmetric Epstein profile (see, e.g., Nakariakov and Roberts, 1995b). With an inhomogeneity of this form exact analytical solutions can be obtained. The plasma is inhomogeneous across the straight and uniform magnetic field B₀ = B₀ẑ. In the zero plasma-β limit considered, the equilibrium total pressure balance is identically fulfilled.

According to Nakariakov and Roberts (1995b), linear perturbations of the transverse plasma velocity V_x = U (x) exp (iωt − ik_zz) are described by the equation

$${{{d^2}U} \over {d{x^2}}} + \left[ {{{{\omega ^2}} \over {C_{{\rm{A}}\infty}^2}} - k_z^2 + {{{\omega ^2}} \over {C_{{\rm{Ad}}}^2}}{\rm{sec}}{{\rm{h}}^{\rm{2}}}\left({{x \over a}} \right)} \right]U = 0,$$

(20)

where C_A∞ is the Alfvén speed as x → ∞ and C_Ad is the Alfvén speed based upon the excess density at x = 0, i.e., C_Ad = B₀/(μ₀ρ_max)^1/2. As the corresponding profile of the Alfvén speed has a minimum at the centre of the slab, the slab is a refractive waveguide for fast magnetoacoustic waves (see Edwin and Roberts, 1988, for discussion).

The eigenvalue problem stated by Equation (20) supplemented by the boundary conditions U(x → ±∞) → 0 can be solved analytically (Nakariakov and Roberts, 1995b; Cooper et al., 2003). The eigenfunctions describing kink and sausage modes are respectively given by

$$U = \left\{{\matrix{{A\;{\rm{sec}}{{\rm{h}}^\alpha}({\textstyle{x \over a}})} \hfill & {{\rm{kink}}\;{\rm{mode}}} \hfill \cr {A\;\tanh \;({\textstyle{x \over a}})\;{\rm{sec}}{{\rm{h}}^\alpha}({\textstyle{x \over a}})} \hfill & {{\rm{sausage}}\;{\rm{mode}}} \hfill \cr}}\right.,$$

(21)

where A is the amplitude. Here α is given by

$$\alpha = {{\vert {k_z}\vert a} \over {{C_{{\rm{A}}\infty}}}}\sqrt {C_{{\rm{A}}\infty}^2 - V_{{\rm{ph}}}^2},$$

(22)

with V_ph = ω/k_z being the phase speed, which is determined by the dispersion relations

$$\sqrt {C_{{\rm{A}}\infty}^2 - V_{{\rm{ph}}}^2} = \vert {k_z}\vert a{{{C_{{\rm{A}}\infty}}} \over {{C_{{\rm{A}}0}}}}(V_{{\rm{ph}}}^2 - C_{{\rm{A}}0}^2)$$

(23)

and

$${{\vert {k_z}\vert a} \over {C_{{\rm{A}}0}^2}}(V_{{\rm{ph}}}^2 - C_{{\rm{A}}0}^2) - {2 \over {\vert {k_z}\vert a}} = {3 \over {{C_{{\rm{A}}\infty}}}}\sqrt {C_{{\rm{A}}\infty}^2 - V_{{\rm{ph}}}^2},$$

(24)

where $C_{{\rm A}0}=C_{{\rm A}\infty}C_{\rm Ad}/(C_{{\rm A}\infty}^{2}+C_{{\rm Ad}}^{2})^{1/2}$ is the Alfvén velocity at the centre of the profile, x = 0.

Dispersion relations (23) and (24) and solutions (21) are a convenient tool for the study of the effect of the transverse profile on wave properties. In particular, Figure 9 demonstrates that the sausage mode group speed is affected by the steepness of the profile quite significantly. One of the observational manifestations of this effect is the shape of the fast wave trains formed by the dispersive evolution of initially broad band perturbations. Applications of this theory are discussed in Section 7.

Effects of twisting

It is clear that twisting of the magnetic field in the cylinder will lead to linear coupling of various MHD modes. However, modification of dispersion relation (7) by the twisting is not well understood.

Considering the thin flux tube limit, Zhugzhda and Nakariakov (1999) showed that long-wavelength (k_za ≪ 1) torsional perturbations of a weakly twisted cylinder are described by the dispersion relation

$${\omega ^2} \approx C_{\rm{A}}^2\left({1 + {{K\beta} \over 2}} \right)k_z^2\left({1 + {{{a^2}{K^2}{\beta ^2}(1 - \beta)} \over {16}}k_z^2} \right),$$

(25)

where K = α²a²/8 is the twist parameter (here K ≪ 1), with α = 2J₀/B₀ (J₀ is the current density) being the parameter of force-free magnetic fields and a being the radius of the cylinder. The parameter α = 2J₀/B₀, where J₀ is the current density. The twist results into the appearance of dispersion and modifies the phase speed of the mode. Actually, the considered mode cannot be referred to as a pure torsional mode as it perturbs the plasma density and its phase speed depends upon the plasma-β. The compressibility of the torsional wave in a twisted cylinder may be demonstrated as follows. According to Zhugzhda (1996), the torsional components of the velocity, V_ϕ, and the magnetic field, B_ϕ, are connected with the longitudinal components of the magnetic field B_z and the velocity V_z by the equation

$${\partial \over {\partial t}}\left({{{{B_\phi}} \over {{B_z}}}} \right) + {\partial \over {\partial z}}\left({{V_z}{{{B_\phi}} \over {{B_z}}}} \right) = {{\partial {V_\phi}} \over {\partial z}}.$$

(26)

If the equilibrium value of the twist B_ϕ₀r is non-zero, the torsional motions generate longitudinal flows and, consequently the density perturbations.

Bennett et al. (1999) considered the collective MHD modes of a straight uniformly twisted magnetic cylinder in the incompressible limit, and concluded that the twist leads to the appearance of body modes with phase speeds about the “longitudinal” Alfvén speed (calculated with the use of the longitudinal component of the field only). As well as in the untwisted case, there is a surface mode with the phase speed about the kink speed.

An alternative approach to the modelling of twisted and curved coronal loops was suggested by Cargill et al. (1994), which allowed the authors to take into account the hoop force — the feature missing from the straight cylinder model. The force is connected with both the loop twist and the curvature. The presence of the new restoring force was shown to give rise to a new oscillation mode manifested as the periodic change of the loop major radius and the loop density, whose frequency could be independent of the loop length. Oscillations of the loop minor radius were also found. The oscillation frequencies obtained were significantly different from the frequencies of straight cylinder eigenmodes. This approach certainly requires attention and further development.

Also, oscillations of current carrying loops can be described in terms of the LCR-model, see Section 3.5.

Kink Oscillations of Coronal Loops

TRACE observations

On 14 July 1998, the imaging telescope on board the Transition Region and Coronal Explorer (TRACE) registered, in both 171 Å and 195 Å lines, spatially resolved decaying oscillating displacements of coronal loops in the active region AR 8270 (Aschwanden et al., 1999; Nakariakov et al., 1999; Schrijver et al., 1999). These oscillations happened shortly after a solar flare and, most probably, were generated by the flare. The mechanism of the excitation remains hidden, but it can be connected with a blast wave generated in the flare epicentre. Some of the loops seem to be more responsive to the oscillation than others and it could probably be connected with the magnetic topology of the active regions (Schrijver and Brown, 2000). Oscillations of different loops were not synchronised in phase. The highest amplitude was seen near the loop apices.

Since this discovery, the loop oscillations were subject to an extensive observational study and the results are summarised in Schrijver et al. (2002) and Aschwanden et al. (2002). In particular, it was found that the kink oscillations do not always have a simple form of a global (or principle) mode and there can be higher spatial harmonics observed.

Anyway, the oscillation examined by Nakariakov et al. (1999) may be considered as a typical example of kink oscillations of coronal loops. The analysis of the loop displacement shows that the oscillation is almost harmonic with the period of about P = 256 s (the frequency about 4 mHz). Figure 10 shows the temporal evolution of the displacement at the loop apex. About three periods of oscillation were observed. Displacement amplitudes are several Mm for the distance between the loop footpoints estimated to be about 2L/π = 83 Mm. The displacement amplitude is several times larger than the loop cross-section radius, which was observed to be about 2a = 1 Mm. The oscillation shows evidence of strong damping. Simultaneously, similar quasi-periodic oscillations were observed in several other loops at the distance of several Mm to 60–70 Mm from the flare epicentre (Aschwanden et al., 1999). All these observational findings suggested the oscillations, at least observed in this event, to be interpreted as a kink global standing mode of the loop.

Taking the observed period P and loop length L, and applying that the wavelength of a global standing mode is double the length of the loop, one can estimate the phase speed required as

$${\omega \over k} = {{2L} \over P} \approx 1020 \pm 132\;{\rm{km}}\;{{\rm{s}}^{- 1}}.$$

(27)

According to the theory of MHD modes of a magnetic cylinder, discussed in Section 2, the fast kink magnetoacoustic modes of a magnetic cylinder do not have dispersive cut-offs and exist for all wavenumbers. In all cases, the wavelength of the observed kink oscillations is much longer than the loop cross-section diameter (e.g., the width of the oscillating loop observed on 14 July 1998 is about 1 Mm, while the loop length may be estimated as 261 Mm for the distance between the footpoints of about 83 Mm; Nakariakov and Ofman, 2001). In this limit, the phase speed of fast kink modes waves approaches the kink speed C_K given by Equation (8).

Terradas and Ofman (2004) pointed out intensity variations localised at the tops of some large-amplitude oscillating loops observed with TRACE in the flaring event on 14 July 1998. As no noticeable changes of the plasma temperature were found at those regions, the intensity variations were interpreted as density variations, approximately in the range 14%–52%. The amplitude could possibly be even higher if the filling factor was less than 1. In the analysed loop, the projected maximum amplitude of the oscillations was about 90 km s⁻¹. In the loops oscillating with smaller amplitudes this effect is not detected, indicating its nonlinear nature.

The majority of kink oscillation events corresponds to the horizontal perturbations of coronal loops, which do not change the length of the loop. Recently, Wang and Solanki (2004) found an example of vertically polarised kink oscillations in TRACE 195 Å data. The oscillation period was 3.9 min, the displacement amplitude was about 8 Mm and the decay time was 11.9 min. The main difference of this polarisation from the horizontal one is that in the curved loop the vertically polarised kink mode changes the length of the loop. Consequently, as the mass in the loop should be conserved, this mode can have a significant compressible component. The fractional intensity perturbations associated with this mode were estimated as

$${{\Delta I} \over I} \propto {{2\Delta \rho} \over \rho} \propto {{2\Delta L} \over L},$$

(28)

where Δρ is the density perturbation and ΔL is the perturbation of the loop length. Here it is assumed that the oscillation does not deform the loop cross-section, i.e., Δa/a ≪ ΔL/L. An alternative is associated with bulk field-aligned flows through the loop footpoints, which do not have observational confirmation.

Another possible polarisation of kink oscillations is when the loop moves in the same plane and its apex displaces horizontally. This mode has not been identified yet.

Non-TRACE observations

Kink modes of coronal loops — often erroneously called Alfvén waves (erroneously, because the true Alfvén waves guided by coronal loops are the torsional modes, see Section 8) — can also be observed through modulation of the broadband gyrosynchrotron emission by the periodic variation of the local magnetic field in flaring loops and through periodic variations of the Doppler shift.

The optically thin gyrosynchrotron emission intensity I_f at a frequency f can be estimated with the use of (Dulk and Marsh, 1982)’s approximated formula

$${I_f} \approx 3.3 \times {10^{- 24}}{{BN} \over {2\pi}} \times {10^{- 0.52\delta}}{(\sin \theta)^{- 0.43 + 0.65\delta}}{\left({{f \over {{f_B}}}} \right)^{1.22 - 0.90\delta}},$$

(29)

where N is the concentration of the nonthermal electrons with energies higher than 10 keV, θ is the angle between the magnetic field and the line-of-sight, f_B is the gyrofrequency and δ (usually > 3–5) is the power law spectral index of the electrons. Transverse oscillations are accompanied by the changes of the angle θ and, consequently, modulate the gyrosynchrotron emission coming from the loop. This mechanism can be responsible for quasi-periodic pulsations with periods from several s to several min, abundantly present in the microwave emission coming from flaring loops.

However, confident identification of the kink mode requires observations with high spatial resolution. The pixel size should be smaller than the wave length of the mode. The first spatially resolved detection of microwave quasi-periodic pulsations, which could be associated with the fast kink mode, was performed by Asai et al. (2001) with the Nobeyama Radioheliograph (see Figure 11). The oscillation period was 6. 6 s. They determined the number density in the loop to be 4.5 × 10¹⁶ m⁻³ from filter ratios of soft X-ray images taken by SXT. The loop length was 16 Mm. The microwave pulsations had a less weaker modulated counterpart in hard X-ray emission observed by the HXT on Yohkoh. The modulation of the hard X-ray emission by the kink wave can be connected with modulation of the electron acceleration by the kink oscillation of the flaring loop, or with interaction of the flaring loop with another loop which performs kink oscillations. In both cases the reconnecting magnetic field is periodically fed to the reconnection site by the kink oscillation. As the thickness of the reconnection site is believed to be very small, even weak kink oscillations can produce the required modulation.

When the line of sight has a significant component parallel to the plane of the oscillations, the kink mode can be detected with spectral instruments through the periodically modulated Doppler shift. For example, 300 s, 80 s, and 43 s periodicities were found by Koutchmy et al. (1983) in the Doppler shift of the green coronal line. In this event, no prominent intensity variations were observed. These oscillations were interpreted as standing kink waves by Roberts et al. (1984).

Determination of coronal magnetic fields

In the low plasma-β limit, the expression for the kink speed (8) reduces to

$${C_{\rm{K}}} \approx {\left({{2 \over {1 + {\rho _{\rm{e}}}/{\rho _0}}}} \right)^{1/2}}{C_{{\rm{A}}0}},$$

(30)

and contains two unknown parameters, the Alfvén speed C_A0 and the density ratio ρ_e/ρ₀. By observationally measuring C_K and considering the density ratio as a parameter, the Alfvén speed in the loop can be determined. Assuming a density ratio ρ_e/ρ₀ = 0.1, we obtain C_A = 756 ± 100 km s⁻¹ for the kink speed of 1020 ± 132 km s⁻¹, for the event on the 14 July 1998 (see Nakariakov and Ofman, 2001, for more details).

The Alfvén speed is defined by the magnetic field strength and the density of the medium. Consequently, by using Equation (30), we can estimate the value of the magnetic field in the loop:

$${B_0} = \sqrt {{\mu _0}{\rho _0}} {C_{{\rm{A0}}}} \approx {{\sqrt {2{\mu _0}L}} \over P}\sqrt {{\rho _0}(1 + {\rho _{\rm{e}}}/{\rho _0})},$$

(31)

(there is a typo in Equation (6) of Nakariakov and Ofman (2001), corrected, e.g., in Roberts and Nakariakov (2003)).

A practical formula for the magnetic field determination by the observables is

$${B_0} \approx 1.02 \times {10^{- 12}}{{d\sqrt {\mu {n_0}} \sqrt {1 + {n_{\rm{e}}}/{n_0}}} \over P},$$

(32)

where the magnetic field B₀ is in G, the distance between the footpoints d is in m, the number density in the loop n₀ is in m⁻³, and the oscillation period P is in s; μ is the effective particle mass with respect to the proton mass. In the solar corona, because of the presence of heavier elements, μ = 1.27. Applying this formula, Nakariakov and Ofman (2001) estimated the magnetic field in an oscillating loop observed on the 14 July 1998, as 13 ± 9 G (see Figure 12, where the number density is measured in cm⁻3). This error bar can be significantly reduced by improving the determination of the density in the loop and by better statistics.

A similar estimation for the field strength (about 15 G) was obtained by Roberts et al. (1984) from the observations of Koutchmy et al. (1983) discussed in Section 3.2. However, in contrast with the TRACE observations, the lack of the direct observability of the oscillating loop did not make the interpretation of the oscillations in terms of the kink modes absolutely secure.

Asai et al. (2001) observed microwave quasi-periodic pulsations with a periodicity of 6.6 s, which are associated with a global kink oscillation. Using Equation (32) and assuming n_e/n₀ = 0. 1, we find the loop to have a magnetic field strength of 400 G. This value is consistent with a magnetic field extrapolation (see Asai et al., 2001, which found a magnetic field strength of 300 G). For an alternative interpretation of this observation in terms of the global fast sausage mode, see Section 4.

Decay of the oscillations

The physical mechanism responsible for the quick decay of the oscillations is under intensive discussion. The direct dissipation caused by viscosity or resistivity, considering classical values of the coronal viscosity and resistivity, cannot explain the observed decay times (see the discussion in Roberts, 2000). Ofman et al. (1994) numerically established the scaling law

$${\tau \over P} = 16.3\;{\rm{R}}{{\rm{e}}^{0.22}},$$

(33)

which connects the decay time τ of the oscillation, the Reynolds number Re (= LC_A0/ν) associated with the shear viscosity ν, and the oscillation period P of a fundamental mode with wavelength 2L. In this study, the decay mechanism was resonant absorption (see Section 2.2.1) of a collective kink mode and the authors restricted their attention to linear perturbations only. Applying this law, Nakariakov et al. (1999) suggested that the decay of kink oscillations might be explained by resonant absorption with enhanced shear viscosity. It should be pointed out that this result is not in contradiction to common sense, as enhanced dissipation actually means that the coefficient of shear viscosity in the Braginskii viscosity tensor is comparable to the bulk viscosity coefficient. If so, this must be connected with coronal micro-turbulence. Such a situation is not unusual in astrophysics (e.g., the invoking of turbulent viscosity in the understanding of the physical properties of accretion disks) and is often seen in laboratory plasmas.

The basic idea behind resonant absorption is that the wave energy of the damped global fast kink mode is converted to a localised Alfvén mode through resonant coupling. This coupling occurs in a shell in the loop boundary where the kink mode frequency, which is always between the internal and external Alfvén frequencies, matches the local Alfvén frequency. The combination of these two modes, through resonant coupling, is also called a quasi-mode. In the absence of an equilibrium flow this mode damps independently of dissipation. For a thin, weakly dissipative loop with a thin boundary layer between a − ℓ and a of the form ρ(r) = [(ρ₀ + ρ_e) − (ρ₀ − ρ_e) cos((r − a)π/ℓ)]/2, the global kink wave has a decay time (which may be derived from Equation (13)) (Ruderman and Roberts, 2002)

$${\tau \over P} = {2 \over \pi}{\left({{\ell \over a}} \right)^{- 1}}\left({{{{\rho _0} + {\rho _e}} \over {{\rho _0} - {\rho _e}}}} \right),$$

(34)

where ℓ is the width of the loop boundary, which is assumed to be thin compared with the loop width 2a, and P is the mode period 2L/C_K. This expression does not contain the viscosity coefficient, and the authors concluded that the observed decay time was not connected with dissipation. However, the observed decay times could be explained if ℓ = 0.23a. Sharper profiles give longer damping times; shallower profiles lead to global motions that are rapidly damped. Goossens et al. (2002a) examined the observations further, using the selection of eleven loops presented by Ofman and Aschwanden (2002), and concluded that the resonant absorption decay Equation (34) was able to reproduce the observed decay times provided the inhomogeneity scale ℓ as a fraction of tube radius a ranged in value from ℓ/a = 0. 16 to ℓ/a = 0. 49. This result would violate, though, the assumption ℓ ≪ a. But Van Doorsselaere et al. (2004) showed numerically that, even for this range of values of ℓ/a, the analytical Equation (34) remains valid. Aschwanden et al. (2003) compared the theoretically predicted values of the density ratio ρ_e/ρ₀ with observations and concluded that they are in poor agreement, which was attributed to the narrowness of the TRACE 171 Å temperature bandpass.

In addition, Equation (34) may give unrealistically short decay times comparable with the oscillation period. It is not clear how the phenomenon of resonant absorption can happen in those cases when the decay time is comparable with the oscillation period and, consequently, the oscillation is not harmonic, making the resonance impossible. In any case, resonant absorption remains a plausible interpretation of the decay.

Another alternative interpretation is connected with the effect of phase-mixing (Roberts, 2000; Ofman and Aschwanden, 2002) (see Section 2.2.2). The decay of a standing Alfvén waves by phase-mixing, given by Equation (17), becomes after assuming that dC_A/dx ≈ C_A/ℓ:

$${\tau \over P} = {\left({{3 \over {4{\pi ^2}}}} \right)^{1/3}}{\left({{\ell \over L}} \right)^{2/3}}{\rm{R}}{{\rm{e}}^{{\rm{1/3}}}}.$$

(35)

In principle Re is the shear Reynolds number, Re = LC_A/ν, with ν the kinematic shear viscosity coefficient. If we take the theoretical values for ν, then the decay time due to phase-mixing is orders of magnitude longer than the observed decay. Ofman and Aschwanden (2002) claimed that, due to micro-turbulence or kinetic processes modifying the velocity distribution of ions, ν could be of the same order as the bulk viscosity coefficient, practically returning back to the idea suggested by Nakariakov et al. (1999). Hence, decay due to phase-mixing can be of the same order as the observed decay. We would like to emphasise that in the case discussed here, the phase mixing mechanism does not involve the torsional modes, but is connected with kink perturbations of neighbouring loops.

A different approach to the problem is based on the leakage of wave energy from the loop. Cally (1986, 2003) showed that the fast kink mode is almost identical to a fast leaky kink mode. In the long wavelength limit both modes propagate at the kink speed. In the limit of the plasma-β tending to zero, the amplitude of the leaky kink mode decreases as it radiates into the coronal environment with a decay time (Cally, 2003, note a factor 2 error in his expression)

$${\tau \over P} = {2 \over {{\pi ^4}}}{\left({{a \over L}} \right)^{- 2}}{\left({{{{\rho _0} + {\rho _e}} \over {{\rho _0} - {\rho _e}}}} \right)^2},$$

(36)

which, unless the loop width 2a is considerably larger than the observed loop emission width, is too long to explain the observed decay, especially for large loops (see Figure 13). For example for a loop of length 200 Mm, a needs to be in the range of 10–20 Mm.

The wave energy may also leak through its footpoints. Roberts (2000) concluded from the theoretical study by Berghmans and de Bruyne (1995) that this type of leakage is insufficient to explain the observed decay. De Pontieu et al. (2001), though, argued that this study did not take the chromosphere into account. The amplitude decay of an Alfvén wave leaking into a chromosphere with density scale-height h, typically 150–200 km, is (Hollweg, 1984)

$${\tau \over P} = {1 \over {4{\pi ^2}}}{\left({{h \over L}} \right)^{- 1}},$$

(37)

which is about five times longer than the observed decay (see Figure 13). This was confirmed by the numerical study by Ofman (2002), who also pointed out some inconsistencies in the work by De Pontieu et al. (2001). A similar study of footpoint leakage of fast kink modes themselves has not yet been undertaken but it should take into account the stratification of the external medium and the magnetic field divergence with height. Both effects are expected to increase the efficiency of the reflection of kink modes at the footpoints and, consequently, reduce the leakage.

Ofman and Aschwanden (2002) suggested that observationally determined scaling laws, connecting the decay times with oscillation periods and lengths of oscillating loops, may provide some information allowing us to distinguish between the interpretations discussed above. Indeed different decay mechanisms give different scaling laws: coronal leakage (τ ∝ L²P), footpoint leakage (τ ∝ LP), resonant absorption (τ ∝ P), and phase-mixing (τ ∝ P^2/3). By using the fact that the period is proportional to the loop length, one can be eliminated in favour of the other.

Ofman and Aschwanden (2002) determined scaling laws from observational decay times measured by Nakariakov et al. (1999) and Aschwanden et al. (2002). In particular they found that τ ∝ P^1.17±0.34. They concluded that the mechanism of phase-mixing agrees best with the scaling laws. They, though, assumed that the length ℓ in Equation (35) is proportional to the length of the loop to obtain a modified scaling law for phase-mixing:

$$\tau \propto {(LP)^{2/3}} \propto {P^{4/3}}.$$

(38)

There is indeed a good correspondence between the theoretical and observational power law index. However, it is not clear why ℓ should be proportional to L. If the original scaling law for phase-mixing is considered, then the difference is larger than one standard deviation. Also, the mechanism of resonant absorption, which has a power law index of 1 falls within one standard deviation of the observationally determined power law index and can, therefore, not be excluded. The mechanisms of coronal and footpoint leakage have power law indices of 3 and 2, respectively, which is clearly not consistent with observations.

Figure 13 shows the observationally determined decay times as a function of wavelength and period and uses measurements from Nakariakov et al. (1999), Aschwanden et al. (2002), Wang and Solanki (2004), and Verwichte et al. (2004), which adds two more measurements compared with the study of Ofman and Aschwanden (2002). We have to bear in mind, though, that the measurement from Wang and Solanki (2004) refers to a vertically polarised oscillation and that the measurement from Verwichte et al. (2004) is an averaged value from seven damped kink oscillations in a prominence driven loop arcade. The data points are fitted by power laws which have the dependencies τ ∝ λ^0.70±0.32 and τ ∝ P^1.12±0.36. The dependence on the wavelength seems to favour phase-mixing, without excluding resonant absorption, and the dependence on period seems to favour resonant absorption but is also consistent with the modified scaling law for phase-mixing. In any case, more examples are needed as the data are too scattered.

Verwichte et al. (2004) studied TRACE observations of 15 April 2001 of kink oscillations in a post-flare loop arcade. The loops of this arcade were made to oscillate by the actions of a nearby prominence eruption. The oscillation signatures of nine loops were determined as a function of distance along each loop. They found that the displacement amplitude decreases with distance from the loop top as expected for a fundamental mode. However, two of the loops showed two, simultaneous oscillation modes with the longest period, roughly twice the shortest period. Also, the displacement amplitude of the shortest period oscillation increases with distance from the loop top, which indicates that it is an harmonic mode. The measured decay times of the loop oscillations shows the same dependence on the oscillation period as for previous observations, but with a clear bias towards longer decay times. There are several possible explanations for this bias. Firstly, this study considered an oscillating arcade of post-flare loops, while previous observations are concerned with more isolated active region loops. The decay times may be influenced by the different structuring of post-flare loops or by interactions between neighbouring loops in the arcade. Secondly, the arcade oscillation is driven by a nearby prominence eruption that may have given multiple impulses to the arcade. If a time of 5–10 min is subtracted from all the decay times, then they fall in the range of decay times of the earlier studies. The relationship between the decay time and the period, though, would then be much steeper.

Further development of this discussion on the decay of kink oscillations is connected with the improvement of the observational statistics and high-resolution 3D numerical modelling of oscillating loops. In particular, an important issue is whether the loop cross-section remains unperturbed during kink oscillations. Also, the question of the excitation of these modes, connected with the observational fact that the kink oscillations are a rather rare phenomenon, is still open.

Alternative mechanisms

The idea that a coronal loop is twisted and then carries an electric current gave rise to several alternative mechanisms for the loop oscillations.

An LCR-circuit model developed by Zaitsev et al. (1998) explains the loop oscillations in terms of eigen oscillations of an equivalent electric circuit, where the current is associated with the loop twist. Approximating the magnetic loop by a thin torus and estimating the effective circuit capacitance ${\cal C}$ and inductance ${\cal L}$ as

$${\cal C} = {{{c^4}{\rho _0}{S^2}} \over {2\pi L{I^2}}},$$

(39)

$${\cal L} = 4L\left({\log {{8L} \over {{{(\pi S)}^{1/2}}}} - {7 \over 4}} \right),$$

(40)

where c is the speed of light, ρ₀ is the density inside the loop, L and S are the length and cross-sectional area of the coronal part of the loop, respectively, and I is the electric current along the loop axis. The period of the oscillations is then given by the expression

$$P = {{2\pi} \over c}{({\cal LC})^{1/2}}.$$

(41)

As one of the physical quantities perturbed by this effect is the current (or the twist), its periodic pulsations would be observed through the direct modulation of the gyrosynchrotron emission by the period change of the angle between the LOS and the magnetic field in the emitting region. Also, as the periodic twist is accompanied by perturbations of density — see Equation (26) —, the oscillations would modulate thermal emission as well. Also, twist perturbations could modulate the loop minor radius, resembling the sausage mode. The decay of the oscillations is normally estimated by this model to be very small.

Khodachenko et al. (2003) applied the idea of inductive interaction of electric currents in a group of neighbouring loops to an alternative interpretation of kink oscillations, suggesting that they are caused by the ponderomotoric interaction of currents in groups of inductively coupled current-carrying loops. More specifically, the ponderomotoric interaction of current-carrying magnetic loops can lead to the oscillatory change of the loops inclination. The efficiency of coupling, the period of oscillations and the decay time are connected with mutual inductance of different loops in the active region analysed. Also, it was pointed out that the interaction of the oscillating loop with neighbouring loops can lead to strong damping of the oscillations.

We would like to stress that the periods of loop oscillations described by LCR-contour models should be longer than the Alfvén travel time along the loop, which determines the response time of the current system, so P > L/C_A0.

Dynamic models of magnetic reconnection predict that the processes of tearing instability and coalescence of magnetic islands occur iteratively, leading to an intermittent or impulsive bursty energy release and particle acceleration. Tajima et al. (1987) demonstrated the possibility of oscillatory regimes in coalescence of current carrying loops, combining a simplified 1D analytical approach and numerical modelling. The minimal period of oscillations was found to be

$$P = 2\pi {{C_{{\rm{s}}0}^3\varepsilon} \over {C_{{\rm{A}}0}^4}},$$

(42)

where ε is the characteristic length of the interaction process, connected in this case with the width of a current sheet formed at the boundary between two interacting twisted loops. These oscillations are essentially nonlinear, and it is likely that their period is somehow connected with amplitude.

Sausage Oscillations of Coronal Loops

The fast magnetoacoustic sausage mode (m = 0) is another type of localised, modified fast magnetoacoustic wave. It is associated with perturbations of the loop cross-section and plasma concentration This mode is mainly transverse and the perturbations of plasma velocity in the radial direction are stronger than perturbations along the field. According to Figure 3, the phase speed of this mode is in the range between the Alfvén speed inside and outside the loop. This mode has a long wavelength cutoff (Roberts et al., 1984),

$${k_{zc}}a = {j_0}{\left[ {{{(C_{{\rm{s}}0}^2 + C_{{\rm{A}}0}^2)(C_{{\rm{Ae}}}^2 - C_{{\rm{T}}0}^2)} \over {(C_{{\rm{Ae}}}^2 - C_{{\rm{A}}0}^2)(C_{{\rm{Ae}}}^2 - C_{{\rm{s}}0}^2)}}} \right]^{1/2}},$$

(43)

where j₀ ≈ 2.40 is the first zero of the Bessel function J₀(x). For a magnetic slab with the step function and Epstein density profiles, this value is

$${k_{zc}}a = \sqrt {{{C_{{\rm{A}}0}^2} \over {C_{{\rm{Ae}}}^2 - C_{{\rm{A}}0}^2}}} \;\;\left\{{\matrix{{\pi/2} \hfill & {({\rm{step}}\;{\rm{function}})} \hfill \cr {\sqrt 2} \hfill & {({\rm{Epstein}}\;{\rm{function}})} \hfill \cr}} \right.,$$

(44)

For k − k_zc the mode approaches the cut-off, the phase speed, C_ph, which is equal to ω/k_z, tends to C_Ae from below, and in the short wave length limit, for k − ∞, C_ph tends to C_A0 from above.

The period P_GSM of the global sausage mode of a coronal loop is determined by the loop length L,

$${P_{{\rm{GSM}}}} = {{2L} \over {{C_{{\rm{ph}}}}}},$$

(45)

where C_ph is the specific phase speed of the sausage mode corresponding to the wave number k_z = π/L, C_A0 < C_ph < C_Ae. The length of the loop L should be smaller than π/k_zc to satisfy the condition k > k_c. For a strong density contrast inside and outside the loop, the period of the sausage mode satisfies the condition

$${P_{{\rm{GSM}}}} < {{2\pi a} \over {{j_0}{C_{{\rm{A}}0}}}} \approx {{2.62a} \over {{C_{{\rm{A}}0}}}},$$

(46)

as the longest possible period of the global sausage mode is achieved when k = k_zc. We would like to emphasise that Equation (46) is an inequality, and that the actual resonant frequency is determined by Equation (45), provided Equation (46) is satisfied. Combining Equations (46) and (45), we conclude that the necessary condition for the existence of the global sausage mode is

$${L \over {2a}} < {\pi \over {2{j_0}}}{{{C_{{\rm{Ae}}}}} \over {{C_{{\rm{A}}0}}}} \approx 0.65\sqrt {{{{\rho _0}} \over {{\rho _e}}}},$$

(47)

so the loop should be sufficiently thick and dense (e.g., in the case of a flaring loop).

Nakariakov et al. (2003) demonstrated the applicability of the correct estimation for the global sausage mode period (Equation (45)) by interpreting high spatial and temporal resolution observations of 14–17 s oscillations of coronal loops, performed with the Nobeyama radioheliograph. For the analysed flare, it was found that the time profiles of the microwave emission at 17 and 34 GHz exhibit synchronous quasi-periodical variations of the intensity in different parts of the corresponding flaring loop. The length of the flaring loop is estimated as L = 25 Mm and its width at half intensity at 34 GHz as about 6 Mm. These estimations are confirmed by Yohkoh/SXT images taken on the late phase of the flare. The distribution of the spectral density in the interval 14–17 s along the loop showed the peak of oscillation amplitude near the loop apex and depression at the loop legs, consistent with the structure theoretically predicted for a global (fundamental) mode. Estimation of the period of this mode, according to Equation (47), gives the resonant period in the observed range. Also, for the loop considered, the sausage mode cut-off value k_zca is about 0.25–0.28. Thus, the longest theoretically possible wavelength λ of the trapped sausage mode of the considered loop is λ ≈ (22–25)a. Consequently, as the observed loop radius is about 1/8 of its length, this loop could indeed support the global sausage mode.

Observations in the radioband and in X-rays often show also shorter periodicities, in particular in the range 0.5–10 s (see, e.g., Aschwanden, 1987, 2003). These oscillations are also traditionally associated with sausage (or radial) modes (see, e.g., Zaitsev and Stepanov, 2002, 1989). It was suggested that the energetic particles produced by a flare are somehow modulated by the sausage oscillations of the flaring loop, localised near the top of the loop. The period of this oscillations is supposed to be given by the fast magnetoacoustic wave travel time across the loop, in other words as the ratio of the loop diameter and the fast magnetoacoustic speed $(C_{{\rm A}0}^{2}+C_{{\rm s}0}^{2})^{1/2}$. However, it is not clear what determines the longitudinal length of the oscillation and why it does not propagate along the loop. If the longitudinal wave length is prescribed by the length of the loop, the sausage mode wave number is lower than the cut-off value and the mode is leaking, which is in contradiction with observed high quality of the short period oscillations (see also Aschwanden et al., 2004). The last difficulty can be overcome if there is some mechanism continuously feeding the oscillations or if the leakage is negligible. Also, quasi-periodic pulsations of shorter periods (0.5–10 s) may be associated with sausage modes of higher spatial harmonics (Roberts et al., 1984), if the longitudinal wave length is shorter than the loop length. However, usually the short period oscillations are observed as a single high quality peak in the periodogram, and it is not clear why only this particular harmonics is excited. The role of ballooning modes has not been established yet.

Earlier, we discussed the microwave quasi-periodic pulsations observed by Asai et al. (2001) in the context of a global kink mode. The spatial resolution of the radio data is not sufficient to actually observe the spatial loop displacements. Therefore, can this pulsation also be attributed to a global sausage mode? A sausage mode can more naturally explain the modulation of X-ray emission as it is compressive. Asai et al. (2001) estimated the loop width to be 6 Mm. Condition (47) for the existence of a sausage normal mode restricts the density ratio to be ρ₀/ρ_e > 17, which is reasonable. If we take ρ₀/ρ_e = 20, then the external Alfvén speed is approximately C_Ae ≈ 2L/P = 4850 km s⁻¹. The internal Alfvén speed is then found to be C_A0 ≈ (ρ_e/ρ₀)^1/2C_Ae = 1080 km s⁻¹. Using the value of the loop density determined by Asai et al. (2001), a value for the magnetic field strength of 120 G follows. This value is three times smaller than Asai et al. (2001) obtained from a magnetic field extrapolation. From this point of view the global kink mode seems to be the most likely explanation for the microwave pulsations, but the global sausage mode cannot be dismissed outright.

Acoustic Oscillations of Coronal Loops

Acoustic or, more precisely, slow magnetoacoustic waves are an abundant feature of the coronal wave activity, confidently observed by several instruments, e.g., SOHO (EIT, UVCS, and SUMER), and TRACE. These MHD wave modes are practically longitudinal, perturbing the density of the plasma and the parallel component of the velocity. Consequently, they are observed as disturbances of EUV (and, possibly, X-ray) emission and, if the line of sight has a component parallel to the local magnetic field, as the periodic Doppler shift. Both propagating and standing waves are observed.

Global acoustic mode

The SOHO/SUMER spectral instrument has recently discovered quasi-periodic oscillations of intensity and a Doppler shift in the coronal emission lines Fe xix and Fe xxi (Kliem et al., 2002; Wang et al., 2002, 2003b,a, and references therein). Figure 14 gives an illustration of such oscillations. These spectral lines are associated with a temperature of about 6 MK, corresponding to the sound speed of about 370 km s⁻¹. The observed periods are in the range 7–31 min, with decay times 5.7–36.8 min, and show an initial large Doppler shift pulse with peak velocities up to 200 km s⁻¹. The intensity fluctuation lags the Doppler shifts by 1/4 period. In a statistical study of 54 oscillation cases, Wang et al. (2003a) found that except for a few cases, the presence of definite periodicity in intensity fluctuations is not certain. Moreover, oscillations are not seen in other emission lines observed simultaneously with the oscillating lines. In the initial stage of all 54 cases analysed by Wang et al. (2003a), there is a rapid increase in the line intensity and a large Doppler shift, indicating that the oscillations are excited impulsively.

Ofman and Wang (2002) suggested that these oscillations are produced by the global standing acoustic mode,

$${V_z}(s,t) \propto \cos \left({{{\pi {C_{\rm{s}}}} \over L}t} \right)\cos \left({{\pi \over L}s} \right),$$

(48)

$$\rho (s,t) \propto \sin \left({{{\pi {C_{\rm{s}}}} \over L}t} \right)\sin \left({{\pi \over L}s} \right),$$

(49)

where V_z is the longitudinal velocity, C_s is the speed of sound, L is the loop length, and s is a distance along the loop with the zero at the loop top. More strictly, the phase speed of the longitudinal mode of a coronal loop should, in the long wave length limit, be equal to the tube speed C_T0 inside the tube, however in the low plasma-β plasma of the solar corona this value is very close to the sound speed C_s. From Equation (48), the oscillation period is given by the expression 2L/C_s. According to the thermally conductive, viscous, nonlinear one-dimensional MHD simulations, the short decay time is connected with the dissipation because of high thermal conductivity of the hot plasma filling the loop. Mendoza-Briceño et al. (2004) has recently developed this study, taking into account effects of stratification. It was found that stratification would lead to insignificant changes in the decay times (maximum 15–20%).

There are still several open questions in both the theory and the observations: how are the oscillations triggered and excited; why are intensity oscillations not always seen, whether the occurrence rate of oscillations is temperature dependent (in major cases in Fe xix, i.e., in hot plasma), what is the role of non-adiabatic effects (e.g., thermal instability)?

Also, it is not clear how the SUMER oscillations are related with other coronal oscillations, observed in the radio (e.g., Aschwanden, 2003) and X-ray bands.

Second standing harmonics

Recently, Nakariakov et al. (2004b) modelled the evolution of a coronal loop in response to an impulsive energy release and demonstrated that the second standing acoustic harmonics appears as a natural response of the loop to an impulsive energy deposition. Modelling the loop as a 1D hydrodynamic system with nonlinearity, radiative damping, thermal conduction and accounting for possible chromospheric up and down flows, it was demonstrated that the second harmonics is a common feature of the loop evolution. Figure 15 shows typical time curves of the density and temperature at the loop apex. The quasi-periodic behaviour is clearly seen in the apex density curve, which is consistent with the mode structure

$${V_x}(s,t) = A\cos \left({{{2\pi {C_{\rm{s}}}} \over L}t} \right)\sin \left({{{2\pi} \over L}s} \right),$$

(50)

$$\rho (s,t) = - {{A{\rho _0}} \over {{C_{\rm{s}}}}}\left({{{2\pi {C_{\rm{s}}}} \over L}t} \right)\cos \left({{{2\pi} \over L}s} \right),$$

(51)

where A is the wave amplitude. (The paper of Nakariakov et al., 2004b, contains a misprint, the factor of two is missing from Equations (3) and (4)). The density perturbations have a maximum near the loop apex, while longitudinal velocity perturbations have there a node.

The second standing acoustic mode may be responsible for quasi-periodic pulsation with periods in the range 10–300 s which are often observed in flare light curves in radio and X-ray bands. The SUMER oscillations mentioned above are likely to be associated with some other excitation mechanism, as only a small fraction of SUMER oscillations are observed in association with solar flares (Wang et al., 2003a). Traditionally, the acoustic wave interpretation has been excluded as the waves of these periodicities were supposed to be highly dissipative in the hot plasma of flaring loops. However, the numerical simulations performed by Nakariakov et al. (2004b), as well as the recently gained abundant observational evidence of the presence of acoustic waves in the solar corona, suggest that the observed periodicities can be associated with this mode. The decayless character of these oscillations may be explained in terms of auto-oscillations: By the competition of the oscillation energy losing by dissipation and the energy deposition to the oscillation, e.g., through thermal over-stability.

Propagating Acoustic Waves

Observational results

One of the most wide-spread examples of the coronal wave activity is the slow propagating intensity disturbances observed with imaging telescopes in both open and closed coronal magnetic structures. The standard detection technique is the use of the stroboscopic method: the emission intensities along a chosen path, taken in different instants of time are laid side-by-side to form a time-distance map. Diagonal stripes on these maps exhibit disturbances which change their position in time and, consequently, propagate along the path. This method allows the determination of periods (or wavelengths), relative amplitudes and projected propagation speeds. Usually these waves are observed propagating along the assumed coronal magnetic structures and, thus, along the magnetic field. Their speeds are usually much slower than the expected coronal Alfvén speed which leads to their interpretation as longitudinally propagating slow magnetoacoustic (aka acoustic or longitudinal) waves.

The first observational detection of longitudinal waves came from analysing the polarised brightness (density) fluctuations. The fluctuations with periods of about 9 min, were detected in coronal holes at a height of about 1.9 R_⊙ by Ofman et al. (1997, 1998b) using the white light channel of SOHO/UVCS. Developing this study and analysing several other UVSC data sequences with a 75–125 s cadence time, Ofman et al. (2000b) determined the fluctuation periods in the range of 7–10 min. The propagation speeds of the fluctuations indicated values in the range of 160–260 km s⁻¹ at 2 R_⊙. This value of the speed is slightly below the estimated value of the sound speed. Possibly, a similar phenomenon was observed by Marsh et al. (2002), who detected quasi-periodic variability of coronal EUV emission lines covering a temperature range of log T_e = 5.3–6.1 K with SOHO/CDS. Statistically significant periods were found within the range 100–900 s and 1500 s, also short wavepackets with periods of the order 50–100 s with durations of 2–5 cycles were reported.

DeForest and Gurman (1998), using EIT 171 Å data confirmed this discovery: Outwardly propagating perturbations of the intensity were observed at distances of 1.01–1.2 R_⊙, gathered in quasi-periodic groups of 3–10 periods, with periods of about 10–15 min, The projected speeds are about 75–150 km s⁻¹ and the relative amplitude (in density) was about 2–4 %.

A similar phenomenon was observed near the footpoints of coronal loops, with EIT (Berghmans and Clette, 1999) and TRACE (Nightingale et al., 1999; De Moortel et al., 2000, 2002a,b) imagers as near-isothermal EUV intensity disturbances, which start near the loop footpoints and propagate along the loops at the apparent speed lower than the sound speed. Multi-wavelength observations have been performed by Robbrecht et al. (2001) combining TRACE 171 Å and EIT 195 Å and by King et al. (2003) with TRACE 171 Å and 195 Å. Robbrecht et al. (2001) found the projected propagation speeds to vary roughly between 65 and 150 km s⁻¹ for both instruments, which is close to and below the expected sound speed in the coronal loops, respectively. King et al. (2003) pointed out the high correlation of the disturbances observed in the different bandpasses. Also, recently, a coordinated observation of this phenomenon with SOHO/CDS and TRACE instruments has been carried out Marsh et al. (2003). A propagating oscillation with a period of about 300 s, observed by TRACE in the 171 Å bandpass, was also observed in He i, O v and Mg ix emission lines with CDS, corresponding to the chromospheric, transition region, and coronal temperatures, respectively. This is consistent with about 5 min oscillations observed by O’Shea et al. (2001) with CDS in both velocity and intensity time series associated with the coronal lines Mg ix and Fe xvi, as well as in O v.

A comprehensive overview of observational properties of the longitudinal oscillations, based upon the analysis of 38 examples, is given in De Moortel et al. (2002a), and a more recent one in Nakariakov (2003). The properties of propagating EUV disturbances may be summarised as follows: the projected propagation speed is 35–165 km s⁻¹; the amplitudes are always less than 10 % in intensity (less than 5 % in density); the disturbances are quasi-periodic with the periods about 140–420 s. In most cases, only upwards propagating disturbances have been detected (from the footpoints to the apex of the loop). Sometimes, the waves can be present for several consecutive hours with, more or less, constant period. It is possible that the disturbances with shorter, about 3 min, periods are situated above sunspot regions, whereas disturbances propagating along the loops which are not associated with sunspots have longer periodicity, of about 5 min (De Moortel et al., 2002c). However, King et al. (2003) showed that both 3 min and 5 min perturbations can coexist in the same coronal structure, at least in the analysed example, so the question still remains open.

The propagation direction and speed, together with the fact that the observed waves are compressible suggest their interpretation as slow magnetoacoustic waves. Slow waves of the observed periodicities (shorter than 20 min) can propagate without reflection in the 1.0–2.0 MK corona, as the acoustic cut-off period is about 70 min. According to this interpretation, the waves propagate at about the sound speed in the loop. The observed speed of the waves is reduced by line-of-sight projection.

Waves were also recently detected in the Doppler velocity data in the 1–3 mHz and 5–7 mHz ranges by Sakurai et al. (2002). The line intensity and line width did not show clear oscillations, but their phase relationship with the Doppler velocity indicates propagating waves rather than standing waves. These waves were interpreted as superposition of propagating slow and Alfvén waves.

Theoretical modelling

Theoretical models of the propagation of longitudinal waves in stratified coronal structures, such as polar plumes (Ofman et al., 1999, 2000a) and coronal loops (Nakariakov et al., 2000), describe the evolution of the wave shape and amplitude with the distance along the structure s in terms of the extended Burgers equation

$${{\partial A} \over {\partial s}} - {a_1}A - {a_2}{{{\partial ^2}A} \over {\partial {\xi ^2}}} + {a_3}A{{\partial A} \over {\partial \xi}} = 0,$$

(52)

where the coefficients a₁, a₂, and a₃ are, in general, functions of s and describe: a₁ — the effects of stratification, radiative losses, and heating; a₂ — dissipation by thermal conductivity and viscosity; a₃ — nonlinearity. The ξ = s − C_st is the running coordinate. When a₁ = 0, Equation (52) reduces to the Burgers equation. Specific expressions for the coefficients depend upon the geometry of the problem and are different in the plume and loop cases.

Let us illustrate the derivation of Equation (52) in a specific situation. Following Tsiklauri and Nakariakov (2001), we consider a semi-circular loop of the curvature radius R_L, with the inclination angle α (measured from the normal to the solar surface) and a non-zero offset of circular loop centre from the coronal base line, Z₀ (i.e., distance from the circle’s centre to the solar surface). The loop cross-section is taken to be constant. The loop is filled with a gravitationally stratified magnetised plasma of constant temperature. The sketch of the model is shown in Figure 16.

The gravitational acceleration along the loop is

$$g(s) = {{G{M_ \odot}} \over {R_ \odot ^2}}{{\left[ {{\textstyle{{{X_0}} \over {{R_L}}}}x - {\textstyle{{{Z_0}} \over {{R_L}}}}h} \right]\cos \alpha} \over {{{\left[ {1 + {\textstyle{{{R_L}} \over {{R_ \odot}}}}\left({{\textstyle{{{X_0}} \over {{R_L}}}}h - {\textstyle{{{Z_0}} \over {{R_L}}}}(1 - x)} \right)\cos \alpha} \right]}^2}}},$$

(53)

where h = sin(s/R_L), x = cos(s/R_L), and $X_{0}/R_{L}=(1-Z_{0}^{2}/R_{L}^{2})^{1/2}$. The use of the hydrostatic equilibrium equations and the isothermal equation of state, allows us to write the stationary density profile along the loop as

$${\rho _0}(s) = {\rho _0}(0)\exp \left[{- {{{\textstyle{{\gamma g(0)} \over {C_{\rm{s}}^2}}}[{X_0}h - {Z_0}(1 - x)]\cos \alpha} \over {1 + {\textstyle{{{R_L}} \over {{R_ \odot}}}}\left[ {{\textstyle{{{X_0}} \over {{R_L}}}}h - {\textstyle{{{Z_0}} \over {{R_L}}}}(1 - x)} \right]\cos \alpha}}} \right].$$

(54)

Assuming that the wavelength is much less than the scale height, the dissipation and the nonlinearity lengths, and applying the multi-scale expansion method, we obtain the evolutionary equation for weakly nonlinear, weakly dissipative slow magnetoacoustic waves in stratified coronal loops,

$${{\partial V} \over {\partial s}} - {1 \over {2H(s)}}V + {{\gamma + 1} \over {2{C_{\rm{s}}}}}V{{\partial V} \over {\partial \xi}} - {1 \over {2{\rho _0}(s){C_{\rm{s}}}}}\left[ {{{4{\eta _0}} \over 3} + {{{\kappa _\parallel}{{(\gamma - 1)}^2}} \over {{\cal R}\gamma}}} \right]{{{\partial ^2}V} \over {\partial {\xi ^2}}} = 0,$$

(55)

where an effective scale height is introduced as $H(s)=C_{\rm s}^{2}\gamma g(s),\kappa_{\Vert}$ is the coefficient of thermal conduction, and η₀ denotes the volume viscosity or thermal conductivity.

Similarly, in the radially stratified vertical polar plume, the evolutionary equation is

$${{\partial \rho} \over {\partial R}} + \left({{1 \over R} + {{g(R)} \over {2C_{\rm{s}}^2}}} \right)\rho + {1 \over {{\rho _0}}}\rho {{\partial \rho} \over {\partial \xi}} - {{2\eta} \over {3{C_{\rm{s}}}{\rho _0}(R)}}{{{\partial ^2}\rho} \over {\partial {\xi ^2}}} = 0,$$

(56)

where R is the radial (or vertical) coordinate (see Ofman et al., 2000a, for details; both the viscosity and thermal conduction are included in the dissipative coefficient η).

Solutions of Equation (52) are in a satisfactory agreement with the observed evolution of the wave amplitude: For example, Figure 17 demonstrates the comparison of the observed and theoretically predicted growth of the longitudinal wave amplitude with height. Also, full MHD 2D numerical modelling of these waves gives similar results (see Ofman et al., 1999, 2000a). The comparison of the observed and modelled evolution scenarios give the possibility of estimating, in particular, the efficiency of non-adiabatic processes, such as the competition of heating and radiative losses.

The energy carried and deposited by the observed waves is certainly insufficient for heating of the loop. However, Tsiklauri and Nakariakov (2001) have shown that sufficiently broadband slow magnetoacoustic waves, consistent with currently available observations in the low frequency part of the spectrum, can provide the rate of heat deposition sufficient to heat the loop. In this scenario, the heat would be deposited near the loop footpoints which agrees with observationally determined positioning of the heat source.

Propagating slow waves as a tool for coronal seismology

According to the previous sections, slow magnetoacoustic waves follow magnetic field lines and propagate at the local sound speed. Because of the high coronal thermal conduction along the field, the equilibrium temperature does not experience significant changes in this direction, at least at the distances comparable with the detection distance of the slow waves. As the sound speed is proportional to the temperature squared, the propagation speed should be constant along the structure, and the speed measured observationally would contain information about the temperature and about the value of the adiabatic index γ. However, such a measurement is impossible at the moment, because the observations with the single line of sight provide us with the apparent speed only, which is affected by the projection effect. Possibly, future 3D observations of the propagating slow waves with STEREO will make such an estimation possible.

Another interesting possibility arises when the waves are observed simultaneously in different bandpasses which correspond to different temperatures of the emitting plasma. First such observation was done by Robbrecht et al. (2001) with SOHO/EIT 195 Å filter and TRACE 171 Å filter. It was found that wave propagating along the same coronal structure was detected in both bandpasses. The big difference in spatial resolution of EIT and TRACE imagers (2.5″ vs 0.5″) did not allow to study the correlation in detail. Later on, King et al. (2003) analysed slow waves observed in 171 Å and 195 Å with TRACE, confirming the correlation (see Figure 18). Figure 19 shows the evolution of the correlation coefficient of the perturbations observed in the different bandpasses with distance along the loop. There is a systematic decrease of the correlation coefficient which may be caused by the different propagating speed of the disturbances observed in different bandpasses. This may be interpreted as an indication to the sub-resolution structuring of the analysed active region: The observed loop can be either a bundle of magnetic threads of varying temperature, or have a transverse temperature profile. The further development of this study seems to be promising.

Propagating Fast Waves

Propagating fast waves in coronal loops

Wave lengths of propagating waves should be much shorter than the size of the structure guiding the wave. The shorter wave lengths correspond to shorter periods of the waves, requiring high cadence observational tools. In particular, the typical cadence time of TRACE and EIT EUV imagers is 20–30 s, which gives the minimal period of detected waves to be about 2–3 min. For a typical coronal Alfvén speed of about 1000 km s⁻¹, at least, this corresponds to wavelengths longer than 120–180 Mm, which is comparable with the typical size of a coronal loop. Thus, the EUV imagers cannot normally be used for the detection of propagating fast waves guided by coronal loops. On the other hand, time resolution of a second or better can be achieved with ground based coronographs or radioheliographs.

Recently, Williams et al. (2001, 2002) and Katsiyannis et al. (2003) reported the observational discovery of rapidly propagating compressible wave trains in coronal loops with the SECIS instrument during a full solar eclipse. As the observed speed was estimated at about 2100 km s⁻¹, these waves were interpreted as fast magnetoacoustic modes. The waves were observed to have a quasi-periodic pattern with a mean period of about 6 s. Cooper et al. (2003) found an encouraging agreement between the observed evolution of the wave amplitude along the loop with the theoretical prediction made for kink and sausage modes (see Figure 20). Unfortunately, the high uncertainty in the measurement of the amplitude does not allow the authors to distinguish between the kink and sausage modes in this observation.

The main difference of these works from a number of previous papers analysing eclipse observations is the application of the methods of the time-distance (stroboscopic) plot (Williams et al., 2001, 2002) and of the wavelet transform (Katsiyannis et al., 2003). Those techniques are certainly more preferable in the situation when the waves have modulation or form wave trains. According to dispersion relation (7), fast waves are highly dispersive when their wave length is comparable or longer than the radius of the loop. It is well known that, in a dispersive medium, impulsively generated (or broadband because of another reason) waves evolve into a quasi-periodic wave train with a pronounced period modulation. In the coronal context, it was pointed out by Edwin and Roberts (1983) and Roberts et al. (1983, 1984) that periodicity of fast magnetoacoustic modes in coronal loops is not necessarily connected with the wave source, but can be created by the dispersive evolution of an impulsively generated signal. Studying the dispersive evolution, Roberts et al. (1984) analytically predicted that the development of the propagating sausage pulse forms a characteristic quasi-periodic wave train with three distinct phases. Such evolution scenario is determined by the presence of minimum in the group speed dependence upon the wave number. That analysis was restricted to the case of the slab with sharp boundaries and to sausage modes only. The initial stage of the pulse evolution was numerically modelled by Murawski and Roberts (1993, 1994), Murawski et al. (1998), and was found to be consistent with the analytical prediction.

Nakariakov and Roberts (1995b) studied the case of a smooth density profile of a zero plasma-β plasma,

$${\rho _0} = {\rho _{\max}}{\rm{sec}}{{\rm{h}}^{\rm{2}}}\left[ {{{\left({{x \over a}} \right)}^p}} \right] + {\rho _\infty},$$

(57)

(cf. Equation (19) and Figure 8). The power index p determines the steepness of the profile. The cases when the power index p equals to either unity or infinity correspond to the symmetric Epstein profile or to the step function profile, respectively, both with known analytical solutions in the eigenvalue problem. The group speed has a minimum for all profiles with the power index greater than unity, which are steeper than the symmetric Epstein profile. Thus, the steepness of the profile affects the shape of the wave train and, consequently, the analysis of wave trains can give us information about this profile.

Nakariakov et al. (2004a) numerically simulated the developed stage of the dispersive evolution of a fast wave train in a smooth straight slab of a low plasma-β plasma. It was found that development of an impulsively generated pulse leads to formation of a quasi-periodic wave train with the mean wavelength comparable with the slab width. In agreement with the analytical theory (Roberts et al., 1984), the wave train has a pronounced period modulation which was demonstrated with the wavelet transform technique (see Figure 21). In particular, it is found that the dispersive evolution of fast wave trains leads to the appearance of characteristic “tadpole” wavelet signatures. Similar signatures were found in the wavelet analysis of SECIS data (Katsiyannis et al., 2003), strengthening the interpretation of the SECIS waves as the fast magnetoacoustic wave trains.

This mechanism may also be responsible for the formation of quasi-periodic pulsations with the periods of about a second, observed in association with flares. However, the main property of this effect, which must be taken into account in interpretation, is the period modulation.

Propagating fast kink waves in open structures

Recently, Verwichte et al. (2005) presented for the first time a direct observational study of propagating fast waves in an open magnetic structure, i.e., observations of a long duration flaring event using TRACE 195 Å (a movie of this event can be seen in Resource 2). Because of the presence of an Fe xxiv emission line in the instrumental bandpass, which is sensitive to temperatures of around 20 MK, the hot supra-arcade above the post-flare loop arcade was also visible. The supra-arcade is an open magnetic structure containing plume-like rays. In the particular event analysed, dark, tadpole-like structures appeared in the lanes between the rays. They were density depletions that moved sunwards, decelerating from speeds above 500 km s⁻¹ to less than 100 km s⁻¹. We shall adopt the name tadpole to describe such structures.

Tadpoles were first reported by McKenzie and Hudson (1999) using the Yohkoh Soft X-ray Telescope. Their physical nature is not fully understood and various models have been put forward. Here we shall focus on one particular behavioural feature of tadpoles, namely, after the passage of the tadpole head, the boundaries of the tail regions with the neighbouring rays oscillate transversely. In other words, one can say that the tadpole wiggles its tail. Figure 22 shows slices of the data set analysed by Verwichte et al. (2005). The transverse motions of the tadpole-ray boundaries are clearly visible as wave packets of 3–4 oscillation periods, following the tadpole heads. From this data cube the transverse displacement of four edges, which each may contain multiple tadpole events, have been extracted. Figure 23 illustrates the typical characteristics of these wave packets. A wave packet propagates sunwards, decelerating with phase speeds in the ranges 200–700 km s⁻¹ and 90–200 km s⁻¹ at heights above the post-flare loop footpoints of 90 and 60 Mm, respectively. Simultaneously, the displacement amplitude, which is of the order of several Mm, decreases. The nature of this decrease is not obvious. Besides dissipation, vertical structuring of the supra-arcade may be responsible. The wave periods lie in the range of 90–220 s. The equivalent wavelengths are of the order of 20–40 Mm, which is much shorter than for the standing, fast kink oscillations in coronal loops.

Because of their clear transverse signatures, the tadpole waves are interpreted as fast magnetoacoustic kink waves. They are guided by the vertical, ray-tadpole structure. An MHD model with slab geometry may be used to characterise the structure (Roberts, 1981b). A slab is preferred over a cylindrical model because little is known about the extent of the structure along the line of sight. Because the density is lower in the tadpole than in the ray, the observed waves may be surface modes. Fast surface modes have a phase speed below the minimal Alfvén speed, i.e., the ray Alfvén speed. If we assume that this speed lies plausibly in the range of 500–1000 km s⁻¹, then there is quite a difference with the observed phase speeds, especially at lower heights. This discrepancy may be explained by considering the geometric configuration of the angles between wave propagation, tadpole and ray magnetic field directions and/or by the presence of upflows, possibly connected with the strong Doppler blue shifts reported by SUMER (Innes et al., 2003). In the last case, these waves may be generated by negative energy mechanisms (see, e.g., Ruderman et al., 1996; Joarder et al., 1997), which lead to amplification of waves by nonuniform steady flows.

The period (phase speed) of consecutive tadpole wave packets passing the same neighbouring ray show a linear increase (decrease) with time. This trend can be explained by a density increase in the ray. Using the simple assumptions $I-I_{0}\sim n_{\rm e}^{2}\sim V_{{\rm A},{\rm ray}}^{-4}$ and V_ph ∼ V_A,ray, where V_A,ray is the Alfvén speed in the ray, we find the relations I − I₀ ∼ P⁴ and $I-I_{0}\sim V_{\rm ph}^{-4}$. I₀ is an arbitrarily chosen constant background intensity. A fit to the observed intensity profile yields the dependencies I − I₀ ∼ P^2.8±2.0 and $I-I_{0}\sim V_{\rm ph}^{-3.0\pm 1.5}$. The difference with the theoretical power law indices lies within the error. Theoretical modelling of excitation and propagation of kink waves in supra-arcades has not been fulfilled.

Torsional Modes

Alfvén waves, e.g., as torsional modes of coronal loops (described by the first factor in Equation (6)) are incompressible and, therefore, do not perturb the density and, hence, do not modify the loop emission. In this section we restrict our attention to torsional modes of untwisted magnetic structures. If the loop is twisted, torsional modes are compressible (see Section 2.4 for details). The velocity perturbations of Alfvén waves, though, can be observed through variations of the Doppler shift. Whilst long period waves may show resolved Doppler shifts, short period waves, with periods less than a few minutes, can be observed only indirectly by measuring the additional broadening of coronal emission lines, i.e., non-thermal broadening. An effective temperature T_eff, associated with a coronal optically thin emission line, can be defined that combined the effects of thermal and non-thermal broadening (McClements et al., 1991):

$${T_{{\rm{eff}}}} = {T_{\rm{i}}} + {\cal C}{{{m_{\rm{i}}}} \over {2{k_{\rm{B}}}}}\langle {V_{{\rm{LOS}}}^2} \rangle,$$

(58)

where T_i and m_i are the temperature and mass of the line forming ion, respectively, k_B is the Boltzmann constant, and V_LOS is the velocity in the line of sight. The constant ${\cal C}$ is defined by polarisation and other effects, and its value lies in the interval $2/3 < {\cal C} < 1$.

There have been several attempts to study the evolution of the amplitude of non-thermal broadening along possible wave paths. Banerjee et al. (1998) and Doyle et al. (1999), using SOHO/SUMER, measured the evolution of non-thermal broadening of the emission lines Si viii and O vi in inter-plume regions of polar coronal holes and found that the amplitude of unresolved thermal broadening (possibly, the Alfvén wave amplitude) is growing up to 1.2 R_⊙, then has a plateau to 1.5 R_⊙, and then grows sharply again. The authors suggested that this phenomenon could be associated with nonlinear overturning of the waves, but a rigorous theoretical modelling is still required. Harrison et al. (2002) examined the width of Mg X emission line and found out the emission line narrowing as a function of altitude. This result was interpreted as further evidence for coronal wave activity in closed field regions, and most likely the first evidence of the dissipation of Alfvén waves in the corona. A similar conclusion was reached by O’Shea et al. (2003) by the analysis of the same emission line in polar plumes and inter-plume lanes. However, the analysis of the widths and its height variation of the Mg X doublet lines, in both the quiet equatorial corona and in a polar hole performed by Wilhelm et al. (2004), gave the opposite result: The Doppler width broadened with height in both the equatorial plane and in a polar coronal hole.

An indirect evidence for the presence of unresolved Alfvén waves in the corona was obtained by Erdélyi et al. (1998), who found out that quiet sun line widths increase from the disk centre outwards in SUMER data. This anisotropy of the non-thermal broadening could be caused by transverse waves; however, some other physical processes such as anisotropic turbulence could produce this effect too.

Alfvén waves with sufficiently long wave lengths can be observed directly through the spatial variation of the Doppler shift. Zaqarashvili (2003) suggested that the global torsional oscillations may be observed as a periodical variation of the spectral line width along the loop, as the loop footpoints are likely to provide the waves with rigid wall boundary conditions. The amplitude of the variation must be maximal at the velocity antinodes and minimal at the nodes of the torsional oscillation. The resonant period of a standing torsional mode of n-th order is given by the expression

$$P = 2L/n{C_{{\rm{A}}0}}.$$

(59)

For example, for L = 200 Mm and C_A0 = 1 Mm s⁻¹, there can be several standing torsional modes with periods and wave lengths resolvable with modern coronal spectrometers. Such observational detection can be obtained in the raster mode, as usual 1D slit spectral observations do not give the required spatial information.

Another possibility to observe torsional modes is connected with the gyrosynchrotron emission, which can be detected in the radio band. As the observed emission depends strongly upon the angle ζ between the magnetic field and the LOS, torsional waves changing the local direction of the field can modulate the observed emission. According to the simple estimations made by Tapping (1983) with the use of Equation (29), in the presence of torsional perturbations a substantial fraction of the emission can be observed from the axial direction, e.g., when the perturbed segment of loop is viewed end-on.

Conclusions

Recently achieved spatial and temporal resolution performance of coronal telescopes and spectral instruments, space-borne as well as ground-based, makes possible systematic observational investigations of various waves and oscillations in the corona. The theory of interaction of MHD modes with plasma structures, in particular, of the MHD modes of a magnetic cylinder, developed in early eighties, provides the theoretical basis for interpretation of the phenomena. Observationally determined properties of MHD modes of solar coronal structures, such as active region loops, polar plumes, and other open structures, showed an excellent agreement with the theory. The combination of the observationally gained knowledge with MHD wave theory and direct numerical simulations of the phenomena, gives rise to a new method of investigation of coronal plasmas, the MHD seismology of the corona. This makes the investigation of coronal MHD waves and oscillations to be an interesting, rapidly developing, and promising branch of solar physics.

Some important topics, such as the coronal Moreton or EIT wave, oscillations in coronal bright points, sub-second radio pulsations, nonlinear effects, and other, remained out of the scope of the present version of this review, and will be covered in the next edition.

Resources

Resource 1: Movies visualising the structure of the MHD modes in a magnetic cylinder.

http://solarphysics.livingreviews.org/Articles/lrsp-2005-3/resources/cylindermodes/index.html

Resource 2: Movie of observations of a long duration flaring event using TRACE 195 Å.

http://solarphysics.livingreviews.org/Articles/lrsp-2005-3/resources/tadpolemovie/index.html

References

Appert, K., Collins, G.A., Hellsten, T., Vaclavik, T., Villard, L., 1986, “Theory of MHD waves”, Plasma Phys. Control. Fusion, 28, 133–145. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1986PPCF...28..133A.
ADS Google Scholar
Asai, A., Shimojo, M., Isobe, H., Morimoto, T., Yokoyama, T., Shibasaki, K., Nakajima, H., 2001, “Periodic Acceleration of Electrons in the 1998 November 10 Solar Flare”, Astrophys. J. Lett., 562, L103–L106. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001ApJ...562L.103A.
ADS Google Scholar
Aschwanden, M.J., 1987, “Theory of radio pulsations in coronal loops”, Solar Phys., 111, 113–136. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1987SoPh..111..113A.
ADS Google Scholar
Aschwanden, M.J., 2003, “Review of coronal oscillations — An observer’s view”, in Turbulence, Waves and Instabilities in the Solar Plasma, (Eds.) Erdélyi, R., Petrovay, K., Roberts, B., Aschwanden, M., Proceedings of the NATO Advanced Research Workshop, Lillafüred, Hungary, 16–20 September 2002, vol. 124 of NATO Science Series II, p. 215, Kluwer, Dordrecht, Netherlands; London, U.K.
Google Scholar
Aschwanden, M.J., 2004, Physics of the Solar Corona, Springer, Berlin, Germany; New York, U.S.A.
Google Scholar
Aschwanden, M.J., Fletcher, L., Schrijver, C.J., Alexander, D., 1999, “Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer”, Astrophys. J., 520, 880–894. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999ApJ...520..880A.
ADS Google Scholar
Aschwanden, M.J., Schrijver, C.J., De Pontieu, B., Title, A.M., 2002, “Transverse Oscillations in Coronal Loops Observed with TRACE — II. Measurements of Geometric and Physical Parameters”, Solar Phys., 206, 99–132. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002SoPh..206...99A.
ADS Google Scholar
Aschwanden, M.J., Nightingale, R.W., Andries, J., Goossens, M., Van Doorsselaere, T., 2003, “Observational Tests of Damping by Resonant Absorption in Coronal Loop Oscillations”, Astrophys. J., 598, 1375–1386. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003ApJ...598.1375A.
ADS Google Scholar
Aschwanden, M.J., Nakariakov, V.M., Melnikov, V.F., 2004, “Magnetohydrodynamic sausage-mode oscillations in coronal loops”, Astrophys. J., 600, 458–463. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004ApJ...600..458A.
ADS Google Scholar
Balet, B., Appert, K., Vaclavik, J., 1982, “MHD studies on Alfven wave heating of low-β plasmas”, Plasma Phys., 24, 1005–1023. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1982PlPh...24.1005B.
ADS Google Scholar
Banerjee, D., Teriaca, L., Doyle, J.G., Wilhelm, K., 1998, “Broadening of SI VIII lines observed in the solar polar coronal holes”, Astron. Astrophys., 339, 208–214. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998A&A...339..208B.
ADS Google Scholar
Beliën, A.J.C., Martens, P.C.H., Keppens, R., 1999, “Coronal Heating by Resonant Absorption: The Effects of Chromospheric Coupling”, Astrophys. J., 526, 478–493. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999ApJ...526..478B.
ADS Google Scholar
Bennett, K., Roberts, B., Narain, U., 1999, “Waves in twisted magnetic flux tubes”, Solar Phys., 185, 41–59. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999SoPh..185...41B.
ADS Google Scholar
Berghmans, D., Clette, F., 1999, “Active region EUV transient brightenings — First Results by EIT of SOHO JOP80”, Solar Phys., 186, 207–229. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999SoPh..186..207B.
ADS Google Scholar
Berghmans, D., de Bruyne, P., 1995, “Coronal Loop Oscillations Driven by Footpoint Motions: Analytical Results for a Model Problem”, Astrophys. J., 453, 495–504. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1995ApJ...453..495B.
ADS Google Scholar
Bogdan, T.J., 2000, “Sunspot Oscillations: A Review — (Invited Review)”, Solar Phys., 192, 373–394. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000SoPh..192..373B.
ADS Google Scholar
Cally, P.S., 1986, “Leaky and non-leaky oscillations in magnetic flux tubes”, Solar Phys., 103, 277–298. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1986SoPh..103..277C.
ADS Google Scholar
Cally, P.S., 2003, “Coronal Leaky Tube Waves and Oscillations Observed with Trace”, Solar Phys., 217, 95–108. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003SoPh..217...95C.
ADS Google Scholar
Cargill, P.J., Chen, J., Garren, D.A., 1994, “Oscillations and Evolution of Curved Current-carrying Loops in the Solar Corona”, Astrophys. J., 423, 854–870. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1994ApJ...423..854C.
ADS Google Scholar
Cooper, F.C., Nakariakov, V.M., Williams, D.R., 2003, “Short period fast waves in solar coronal loops”, Astron. Astrophys., 409, 325–330. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...409..325C.
ADS Google Scholar
Cranmer, S.R., 2004, “Observational Aspects of Wave Acceleration in Open Magnetic Regions”, in Proceedings of SOHO 13 ‘Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE’, (Ed.) Lacoste, H., 29 September–3 October 2003, Palma de Mallorca, Balearic Islands, Spain, vol. SP-547 of ESA Conference Proceedings, p. 353, ESA, Noordwijk, Netherlands. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004soho..547..353C.
Google Scholar
De Moortel, I., Ireland, J., Walsh, R.W., 2000, “Observation of oscillations in coronal loops”, Astron. Astrophys., 355, L23–L26. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000A&A...355L..23D.
ADS Google Scholar
De Moortel, I., Hood, A.W., Ireland, J., Walsh, R.W., 2002a, “Longitudinal intensity oscillations in coronal loops observed with TRACE — I. Overview of Measured Parameters”, Solar Phys., 209, 61–88. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002SoPh..209...61D.
ADS Google Scholar
De Moortel, I., Hood, A.W., Ireland, J., Walsh, R.W., 2002b, “Longitudinal intensity oscillations in coronal loops observed with TRACE — II. Discussion of Measured Parameters”, Solar Phys., 209, 89–108. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002SoPh..209...89D.
ADS Google Scholar
De Moortel, I., Ireland, J., Hood, A.W., Walsh, R.W., 2002c, “The detection of 3 & 5 min period oscillations in coronal loops”, Astron. Astrophys., 387, L13–L16. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002A&A...387L..13D.
ADS Google Scholar
De Pontieu, B., Martens, P.C.H., Hudson, H.S., 2001, “Chromospheric Damping of Alfvén Waves”, Astrophys. J., 558, 859–871. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001ApJ...558..859D.
ADS Google Scholar
DeForest, C.E., Gurman, J.B., 1998, “Observation of Quasi-periodic Compressive Waves in Solar Polar Plumes”, Astrophys. J. Lett., 501, L217–L220. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998ApJ...501L.217D.
ADS Google Scholar
DeGroof, A., Goossens, M., 2002, “Fast and Alfvén waves driven by azimuthal footpoint motions. II. Random driver”, Astron. Astrophys., 386, 691–698. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002A&A...386..691D.
ADS Google Scholar
Doyle, J.G., Teriaca, L., Banerjee, D., 1999, “Coronal hole diagnostics out to 8 Rsun”, Astron. Astrophys., 349, 956–960. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999A&A...349..956D.
ADS Google Scholar
Dulk, G.A., Marsh, K.A., 1982, “Simplified expressions for the gyrosynchrotron radiation from mildly relativistic, nonthermal and thermal electrons”, Astrophys. J., 259, 350–358. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1982ApJ...259..350D.
ADS Google Scholar
Edwin, P.M., Roberts, B., 1983, “Wave propagation in a magnetic cylinder”, Solar Phys., 88, 179–191. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1983SoPh...88..179E.
ADS Google Scholar
Edwin, P.M., Roberts, B., 1988, “Employing analogies for ducted MHD waves in dense coronal structures”, Solar Phys., 192, 343–347. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1988A&A...192..343E.
Google Scholar
Erdélyi, R., 1997, “Analytical Solutions for Cusp Resonance in Dissipative MHD”, Solar Phys., 171, 49–59. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1997SoPh..171...49E.
ADS Google Scholar
Erdélyi, R., 1998, “Resonant Absorption of Alfvén Waves in Steady Coronal Loops”, Solar Phys., 180, 213–229.
ADS Google Scholar
Erdélyi, R., Doyle, J.G., Perez, M.E., Wilhelm, K., 1998, “Center-to-limb line width measurements of solar chromospheric, transition region and coronal lines”, Astron. Astrophys., 337, 287–293. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998A&A...337..287E.
ADS Google Scholar
Fasoli, A., Testa, D., Sharapov, S., Berk, H.L., Breizman, B., Gondhalekar, A., Heeter, R.F., Mantsinen, M. (and contributors to the EFDA-JET Workprogramme), 2002, “MHD spectroscopy”, Plasma Phys. Control. Fusion, 44, B159–B172. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002PPCF...44B.159F.
Google Scholar
Goedbloed, J.P., 1983, Lecture Notes on Ideal Magnetohydrodynamics, vol. 83-145 of Rijnhuizen Report, FOM-Instituut voor Plasmafysica ‘Rijnhuizen’, Nieuwegein, Netherlands.
Google Scholar
Goedbloed, J.P., Poedts, S., 2004, Principles of Magnetohydrodynamics: With Applications to Laboratory and Astrophysical Plasmas, Cambridge University Press, New York, U.S.A.
MATH Google Scholar
Goossens, M., Hollweg, J.V., Sakurai, T., 1992, “Resonant behaviour of MHD waves on magnetic flux tubes. III — Effect of equilibrium flow”, Solar Phys., 138, 233–255. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1992SoPh..138..233G.
ADS Google Scholar
Goossens, M., Andries, J., Aschwanden, M.J., 2002a, “Coronal loop oscillations. An interpretation in terms of resonant absorption of quasi-mode kink oscillations”, Astron. Astrophys., 394, L39–L42. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002A&A...394L..39G.
ADS Google Scholar
Goossens, M., De Groof, A., Andries, J., 2002b, “Waves and oscillations in magnetic fields”, in SOLMAG: Magnetic Coupling of the Solar Atmosphere, (Ed.) Sawaya-Lacoste, H., Proceedings of the Euroconference and IAU Colloquium 188, 11–15 June 2002, Santorini, Greece, vol. SP-505 of ESA Conference Proceedings, pp. 137–144, ESA, Noordwijk, Netherlands. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002solm.conf..137G.
Google Scholar
Harrison, R.A., Hood, A.W., Pike, C.D., 2002, “Off-limb EUV line profiles and the search for wave activity in the low corona”, Astron. Astrophys., 392, 319–327. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002A&A...392..319H.
ADS Google Scholar
Heyvaerts, J., Priest, E.R., 1983, “Coronal heating by phase-mixed shear Alfven waves”, Astron. Astrophys., 117, 220–234. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1983A&A...117..220H.
ADS MATH Google Scholar
Hollweg, J.V., 1984, “Resonances of coronal loops”, Astrophys. J., 277, 392–403. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1984ApJ...277..392H.
ADS Google Scholar
Hollweg, J.V., 1987, “Resonance absorption of magnetohydrodynamic surface waves Physical discussion”, Astrophys. J., 312, 880–885. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1987ApJ...312..880H.
ADS Google Scholar
Hollweg, J.V., Yang, G., 1988, “Resonance absorption of compressible magnetohydrodynamic waves at thin ‘surfaces’”, J. Geophys. Res., 93, 5423–5436. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1988JGR....93.5423H.
ADS Google Scholar
Hood, A.W., Brooks, S.J., Wright, A.N., 2002, “Coronal heating by phase mixing of individual pulses propagating in coronal holes”, Proc. R. Soc. London, Ser. A, 458, 2307–2325. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002PRSLAM458.2307H.
ADS MathSciNet MATH Google Scholar
Innes, D.E., McKenzie, D.E., Wang, T., 2003, “Observations of 1000 km s⁻¹ Doppler shifts in 10⁷K solar flare supra-arcade”, Solar Phys., 217, 267–279. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003SoPh..217..267I.
ADS Google Scholar
Ionson, J.A., 1978, “Resonant absorption of Alfvenic surface waves and the heating of solar coronal loops”, Astrophys. J., 226, 650–673. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1978ApJ...226..650I.
ADS Google Scholar
Joarder, P.S., Nakariakov, V.M., Roberts, B., 1997, “A Manifestation of Negative Energy Waves in the Solar Atmosphere”, Solar Phys., 176, 285–297. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1997SoPh..176..285J.
ADS Google Scholar
Kappraff, J.M., Tataronis, J.A., 1977, “Resistive effects on Alfven wave heating”, J. Plasma Phys., 18, 209–226. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1977JPlPh..18..209K.
ADS Google Scholar
Katsiyannis, A.C., Williams, D.R., McAteer, R.T.J., Gallagher, P.T., Keenan, F.P., Murtagh, F., 2003, “Eclipse observations of high-frequency oscillations in active region coronal loops”, Astron. Astrophys., 406, 709–714. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...406..709K.
ADS Google Scholar
Khodachenko, M., Haerendel, G., Rucker, H.O., 2003, “Inductive electromagnetic effects in solar current-carrying magnetic loops”, Astron. Astrophys., 401, 721–732. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...401..721K.
ADS Google Scholar
King, D.B., Nakariakov, V.M., DeLuca, E.E., Golub, L., McClements, K.G., 2003, “Propagating EUV disturbances in the Solar corona: Two-wavelength observations”, Astron. Astrophys., 404, L1–L4. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...404L...1K.
ADS Google Scholar
Kliem, B., Dammasch, I.E., Curdt, W., Wilhelm, K., 2002, “Correlated Dynamics of Hot and Cool Plasmas in the Main Phase of a Solar Flare”, Astrophys. J. Lett., 568, L61–L65. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002ApJ...568L..61K.
ADS Google Scholar
Koutchmy, S., Žugžda, I.D., Locăns, V., 1983, “Short period coronal oscillations — Observation and interpretation”, Astron. Astrophys., 120, 185–191. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1983A&A...120..185K.
ADS Google Scholar
Lee, M.A., Roberts, B., 1986, “On the behavior of hydromagnetic surface waves”, Astrophys. J., 301, 430–439. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1986ApJ...301..430L.
ADS Google Scholar
Marsh, M.S., Walsh, R.W., Bromage, B.J.I., 2002, “A wavelet analysis of quasi-periodic variability across a solar coronal hole region”, Astron. Astrophys., 393, 649–659. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002A&A...393..649M.
ADS Google Scholar
Marsh, M.S., Walsh, R.W., De Moortel, I., Ireland, J., 2003, “Joint observations of propagating oscillations with SOHO/CDS and TRACE”, Astron. Astrophys., 404, L37–L41. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...404L..37M.
ADS Google Scholar
McClements, K.G., Harrison, R.A., Alexander, D., 1991, “The detection of wave activity in the solar corona using UV line spectra”, Solar Phys., 131, 41–48. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1991SoPh..131...41M.
ADS Google Scholar
McKenzie, D.E., Hudson, H.S., 1999, “X-Ray Observations of Motions and Structure above a Solar Flare Arcade”, Astrophys. J. Lett., 519, L93–L96. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999ApJ...519L..93M.
ADS Google Scholar
Mendoza-Briceño, C.A., Erdélyi, R., Sigalotti, L.D.G., 2004, “The Effects of Stratification on Oscillating Coronal Loops”, Astrophys. J., 605, 493–502. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004ApJ...605..493M.
ADS Google Scholar
Murawski, K., Roberts, B., 1993, “Numerical simulations of fast MHD waves in a coronal plasma. II — Impulsively generated linear waves”, Solar Phys., 144, 101–112. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1993SoPh..144..101M.
ADS Google Scholar
Murawski, K., Roberts, B., 1994, “Impulsively Generated MHD Waves in a Coronal Plasma”, Acta Astron., 44, 99–113. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1994AcA....44...99M.
ADS Google Scholar
Murawski, K., Aschwanden, M.J., Smith, J.M., 1998, “Impulsively generated MHD waves and their detectability in solar coronal loops”, Solar Phys., 179, 313–326. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998SoPh..179..313M.
ADS Google Scholar
Nakariakov, V.M., 2003, “Coronal oscillations”, in Dynamic Sun, (Ed.) Dwivedi, B.N., p. 314, Cambridge University Press, New York, U.S.A.
Google Scholar
Nakariakov, V.M., Ofman, L., 2001, “Determination of the coronal magnetic field by coronal loop oscillations”, Astron. Astrophys., 372, L53–L56. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001A&A...372L..53N.
ADS Google Scholar
Nakariakov, V.M., Roberts, B., 1995a, “Magnetosonic Waves in Structured Atmospheres with Steady Flows, I”, Solar Phys., 159, 213–228. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1995SoPh..159..213N.
ADS Google Scholar
Nakariakov, V.M., Roberts, B., 1995b, “On Fast Magnetosonic Coronal Pulsations”, Solar Phys., 159, 399–402. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1995SoPh..159..399N.
ADS Google Scholar
Nakariakov, V.M., Roberts, B., Murawski, K., 1997, “Alfvén wave phase mixing as a source of fast magnetosonic waves”, Solar Phys., 175, 93–105. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1997SoPh..175...93N.
ADS Google Scholar
Nakariakov, V.M., Ofman, L., DeLuca, E.E., Roberts, B., Davila, J.M., 1999, “TRACE observations of damped coronal loop oscillations: implications for coronal heating”, Science, 285, 862–864. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999Sci...285..862N.
ADS Google Scholar
Nakariakov, V.M., Verwichte, E., Berghmans, D., Robbrecht, E., 2000, “Slow magnetoacoustic waves in coronal loops”, Astron. Astrophys., 362, 1151–1157. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000A&A...362.1151N.
ADS Google Scholar
Nakariakov, V.M., Melnikov, V.F., Reznikova, V.E., 2003, “Global sausage modes of coronal loops”, Astron. Astrophys., 412, L7–L10. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...412L...7N.
ADS Google Scholar
Nakariakov, V.M., Arber, T.D., Ault, C.E., Katsiyannis, A.C., Williams, D.R., Keenan, F.P., 2004a, “Time signatures of impulsively generated coronal fast wave trains”, Mon. Not. R. Astron. Soc., 349, 705–709. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004MNRAS.349..705N.
ADS Google Scholar
Nakariakov, V.M., Tsiklauri, D., Kelly, A., Arber, T.D., Aschwanden, M.J., 2004b, “Acoustic oscillations in solar and stellar flaring loops”, Astron. Astrophys., 414, L25–L28. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004A&A...414L..25N.
ADS Google Scholar
Nightingale, R.W., Aschwanden, M.J., Hurlburt, N.E., 1999, “Time Variability of EUV Brightenings in Coronal Loops Observed with TRACE”, Solar Phys., 190, 249–265. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999SoPh..190..249N.
ADS Google Scholar
Ofman, L., 2002, “Chromospheric Leakage of Alfvén Waves in Coronal Loops”, Astrophys. J. Lett., 568, L135–L138. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002ApJ...568L.1350.
ADS Google Scholar
Ofman, L., 2004, “Theoretical Aspects of Wave Acceleration in Open Magnetic Structures”, in Proceedings of SOHO 13 ‘Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE’, (Ed.) Lacoste, H., 29 September — 3 October 2003, Palma de Mallorca, Balearic Islands, Spain, vol. SP-547 of ESA Conference Proceedings, p. 345, ESA, Noordwijk, Netherlands. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004soho..547..3450.
Google Scholar
Ofman, L., Aschwanden, M.J., 2002, “Damping Time Scaling of Coronal Loop Oscillations Deduced from Transition Region and Coronal Explorer Observations”, Astrophys. J. Lett., 576, L153–L156.
ADS Google Scholar
Ofman, L., Davila, J.M., 1995, “Nonlinear resonant absorption of Alfvén waves in three dimensions, scaling laws, and coronal heating”, J. Geophys. Res., 100, 23 427–23 442. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1995JGR...100234270.
ADS Google Scholar
Ofman, L., Wang, T., 2002, “Hot Coronal Loop Oscillations Observed by SUMER: Slow Magnetosonic Wave Damping by Thermal Conduction”, Astrophys. J. Lett., 580, L85–L88. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002ApJ...576L.1530.
ADS Google Scholar
Ofman, L., Davila, J.M., Steinolfson, R.S., 1994, “Coronal heating by the resonant absorption of Alfven waves: The effect of viscous stress tensor”, Astrophys. J., 421, 360–371. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1994ApJ...421..3600.
ADS Google Scholar
Ofman, L., Romoli, M., Poletto, G., Noci, G., Kohl, J.L., 1997, “Ultraviolet Coronagraph Spectrometer Observations of Density Fluctuations in the Solar Wind”, Astrophys. J. Lett., 491, L111–L114. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1997ApJ...491L.1110.
ADS Google Scholar
Ofman, L., Klimchuk, J.A., Davila, J.M., 1998a, “A Self-consistent Model for the Resonant Heating of Coronal Loops: The Effects of Coupling with the Chromosphere”, Astrophys. J., 493, 474–479. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998ApJ...493..4740.
ADS Google Scholar
Ofman, L., Romoli, M., Poletto, G., Noci, G., Kohl, J.L., 1998b, “Ultraviolet Coronagraph Spectrometer Observations of Density Fluctuations in the Solar Wind”, Astrophys. J. Lett., 507, L189–L189. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998ApJ...507L.1890.
ADS Google Scholar
Ofman, L., Nakariakov, V.M., DeForest, C.E., 1999, “Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 514, 441–447.
ADS Google Scholar
Ofman, L., Nakariakov, V.M., Sehgal, N., 2000a, “Dissipation of Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 533, 1071–1083. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000ApJ...533.10710.
ADS Google Scholar
Ofman, L., Romoli, M., Poletto, G., Noci, G., Kohl, J.L., 2000b, “UVCS WLC Observations of Compressional Waves in the South Polar Coronal Hole”, Astrophys. J., 529, 592–598. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999ApJ...514..4410.
ADS Google Scholar
O’Shea, E., Banerjee, D., Doyle, J.G., Fleck, B., Murtagh, F., 2001, “Active region oscillations”, Astron. Astrophys., 368, 1095–1107. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001A&A...368.10950.
ADS Google Scholar
O’Shea, E., Banerjee, D., Poedts, S., 2003, “Variation of coronal line widths on and off the disk”, Astron. Astrophys., 400, 1065–1070. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...400.10650.
ADS Google Scholar
Poedts, S., Goossens, M., Kerner, W., 1989, “Numerical simulation of coronal heating by resonant absorption of Alfven waves”, Solar Phys., 123, 83–815. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1989SoPh..123...83P.
ADS Google Scholar
Poedts, S., Goossens, M., Kerner, W., 1990, “On the efficiency of coronal loop heating by resonant absorption”, Astrophys. J., 360, 279–287. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1990ApJ...360..279P.
ADS MATH Google Scholar
Robbrecht, E., Verwichte, E., Berghmans, D., Hochedez, J.-F., Poedts, S., Nakariakov, V.M., 2001, “Slow magnetoacoustic waves in coronal loops: EIT and TRACE”, Astron. Astrophys., 370, 591–601. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001A&A...370..591R.
ADS Google Scholar
Roberts, B., 1981a, “Wave propagation in a magnetically structured atmosphere. I — Surface waves at a magnetic interface.”, Solar Phys., 69, 27–38. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1981SoPh...69...27R.
ADS Google Scholar
Roberts, B., 1981b, “Wave propagation in a magnetically structured atmosphere. II — Waves in a Magnetic Slab”, Solar Phys., 69, 39–56. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1981SoPh...69...39R.
ADS Google Scholar
Roberts, B., 2000, “Waves and Oscillations in the Corona — (Invited Review)”, Solar Phys., 193, 139–152. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000SoPh..193..139R.
ADS Google Scholar
Roberts, B., 2002, “Waves and Oscillations in the Corona: Theory”, in Solar Variability: From Core to Outer Frontiers, Vol. 2, (Ed.) Wilson, A., Proceedings of the 10th European Solar Physics Meeting, Prague, Czech Republic, 9–14 September 2002, vol. SP-506 of ESA Conference Proceedings, pp. 481–489, ESA, Noordwijk, Netherlands. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002svco.conf..481R.
Google Scholar
Roberts, B., 2004, “MHD Waves in the Solar Atmosphere”, in Proceedings of SOHO 13 ‘Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE’, (Ed.) Lacoste, H., 29 September–3 October 2003, Palma de Mallorca, Balearic Islands, Spain, vol. SP-547 of ESA Conference Proceedings, pp. 1–14, ESA, Noordwijk, Netherlands. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003esasp.547....1R.
Google Scholar
Roberts, B., Nakariakov, V.M., 2003, “Theory of MHD waves in the solar corona”, in Turbulence, Waves and Instabilities in the Solar Plasma, (Eds.) Erdélyi, R., Petrovay, K., Roberts, B., Aschwanden, M., Proceedings of the NATO Advanced Research Workshop, Lillafuüred, Hungary, 16–20 September 2002, vol. 124 of NATO Science Series II, p. 167, Kluwer, Dordrecht, Netherlands; Boston, U.S.A.
Google Scholar
Roberts, B., Edwin, P.M.,, Benz, A.O., 1983, “Fast pulsations in the solar corona”, Nature, 305, 688–690. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1983Natur.305..688R.
ADS Google Scholar
Roberts, B., Edwin, P.M.,, Benz, A.O., 1984, “On coronal oscillations”, Astrophys. J., 279, 857–865. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1984ApJ...279..857R.
ADS Google Scholar
Ruderman, M.S., Roberts, B., 2002, “The Damping of Coronal Loop Oscillations”, Astrophys. J., 577, 475–486. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002ApJ...577..475R.
ADS Google Scholar
Ruderman, M.S., Verwichte, E., Erdélyi, R., Goossens, M., 1996, “Dissipative instability of MHD tangential discontinuity in magnetized plasmas with anisotropic viscosity and thermal conduction”, J. Plasma Phys., 56, 285–206.
ADS Google Scholar
Sakurai, T., Goossens, M., Hollweg, J.V., 1991a, “Resonant behaviour of MHD waves on magnetic flux tubes. I — Connection Formulae at the Resonant Surfaces”, Solar Phys., 133, 227–245. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1991SoPh..133..227S.
ADS Google Scholar
Sakurai, T., Goossens, M., Hollweg, J.V., 1991b, “Resonant behaviour of MHD waves on magnetic flux tubes. II — Absorption of Sound Waves by Sunspots”, Solar Phys., 133, 247–262. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1991SoPh..133..247S.
ADS Google Scholar
Sakurai, T., Ichimoto, K., Raju, K.P., Singh, J., 2002, “Spectroscopic Observation of Coronal Waves”, Solar Phys., 209, 265–286. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002SoPh..209..265S.
ADS Google Scholar
Schrijver, C.J., Brown, D.S., 2000, “Oscillations in the Magnetic Field of the Solar Corona in Response to Flares near the Photosphere”, Astrophys. J. Lett., 537, L69–L72. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2000ApJ...537L..69S.
ADS Google Scholar
Schrijver, C.J., Title, A.M., Berger, T.E., Fletcher, L., Hurlburt, N.E., Nightingale, R.W., Shine, R.A., Tarbell, T.D., Wolfson, J., Golub, L., Bookbinder, J.A., DeLuca, E.E., McMullen, R.A., Warren, H.P., Kankelborg, C.C., Handy, B.N., De Pontieu, B., 1999, “A new view of the solar outer atmosphere by the Transition Region and Coronal Explorer”, Solar Phys., 187, 261–302. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1999SoPh..187..261S.
ADS Google Scholar
Schrijver, C.J., Aschwanden, M.J., Title, A.M., 2002, “Transverse oscillations in coronal loops observed with TRACE — I. An Overview of Events, Movies, and a Discussion of Common Properties and Required Conditions”, Solar Phys., 206, 69–98. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002SoPh..206...69S.
ADS Google Scholar
Steinolfson, R.S., Davila, J.M., 1993, “Coronal heating by the resonant absorption of Alfven waves — Importance of the global mode and scaling laws”, Astrophys. J., 415, 354–363. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1993ApJ...415..354S.
ADS Google Scholar
Stenuit, H., Keppens, R., Goossens, M., 1998, “Eigenfrequencies and optimal driving frequencies of 1D non-uniform magnetic flux tubes”, Astron. Astrophys., 331, 392–404. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998A&A...331..392S.
ADS Google Scholar
Tajima, T., Sakai, J., Nakajima, H., Kosugi, T., Brunel, F., Kundu, M.R., 1987, “Current loop coalescence model of solar flares”, Astrophys. J., 321, 1031–1048. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1987ApJ...321.1031T.
ADS Google Scholar
Tapping, K.F., 1983, “A torsional wave model for solar coronal radio pulsations”, Solar Phys., 87, 177–186. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1983SoPh...87..177T.
ADS Google Scholar
Terradas, J., Ofman, L., 2004, “Loop density enhancement by nonlinear magnetohydrodynamic waves”, Astrophys. J., 610, 523–531. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004ApJ...610..523T.
ADS Google Scholar
Thompson, B.J., Plunkett, S.P., Gurman, J.B., Newmark, J.S., St Cyr, O.C., Michels, D.J., 1998, “SOHO/EIT observations of an Earth-directed coronal mass ejection on May 12, 1997”, Geophys. Res. Lett., 25, 2465–2468. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998GeoRL..25.2465T.
ADS Google Scholar
Tirry, W.J., Goossens, M., 1996, “Quasi-Modes as Dissipative Magnetohydrodynamic Eigenmodes: Results for One-dimensional Equilibrium States”, Astrophys. J., 471, 501–510. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1996ApJ...471..501T.
ADS Google Scholar
Tsiklauri, D., Nakariakov, V.M., 2001, “Wide-spectrum slow magnetoacoustic waves in coronal loops”, Astron. Astrophys., 379, 1106–1112. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001A&A...379.1106T.
ADS Google Scholar
Tsiklauri, D., Nakariakov, V.M., Rowlands, G., 2003, “Phase mixing of a three dimensional magnetohydrodynamic pulse”, Astron. Astrophys., 400, 1051–1055. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...400.1051T.
ADS Google Scholar
Uchida, Y., 1970, “Diagnosis of Coronal Magnetic Structure by Flare-Associated Hydromagnetic Disturbances”, Publ. Astron. Soc. Japan, 22, 341–364. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1970PASJ...22..341U.
ADS Google Scholar
Van Doorsselaere, T., Andries, J., Poedts, S., Goossens, M., 2004, “Damping of Coronal Loop Oscillations: Calculation of Resonantly Damped Kink Oscillations of One-dimensional Nonuniform Loops”, Astrophys. J., 606, 1223–1232. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004ApJ...606.1223V.
ADS Google Scholar
Verwichte, E., Nakariakov, V.M., Ofman, L., DeLuca, E.E., 2004, “Characteristics of transverse oscillations in a coronal loop arcade”, Solar Phys., 223, 77–94. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004SoPh..223...77V.
ADS Google Scholar
Verwichte, E., Nakariakov, V.M., Cooper, F.C., 2005, “Transverse waves in a post-flare supra-arcade”, Astron. Astrophys., 430, L65–L68. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2005A&A...430L..65V.
ADS Google Scholar
Walsh, R.W., Ireland, J., 2003, “The heating of the solar corona”, Astron. Astrophys. Rev., 12, 1–41. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&ARv..12....1W.
ADS Google Scholar
Wang, T.J., Solanki, S.K., 2004, “Vertical oscillations of a coronal loop observed by TRACE, Vertical oscillations of a coronal loop observed by TRACE”, Astron. Astrophys., 421, L33–L36. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004A&A...421L..33W.
ADS Google Scholar
Wang, T.J., Solanki, S.K., Curdt, W., Innes, D.E., Dammasch, I.E., 2002, “Doppler Shift Oscillations of Hot Solar Coronal Plasma Seen by SUMER: A Signature of Loop Oscillations?”, Astrophys. J., 574, L101–L104. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002ApJ...574L.101W.
ADS Google Scholar
Wang, T.J., Solanki, S.K., Curdt, W., Innes, D.E., Dammasch, I.E., Kliem, B., 2003a, “Hot coronal loop oscillations observed with SUMER: Examples and statistics”, Astron. Astrophys., 406, 1105–1121. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...406.1105W.
ADS Google Scholar
Wang, T.J., Solanki, S.K., Innes, D.E., Curdt, W., Marsch, E., 2003b, “Slow-mode standing waves observed by SUMER in hot coronal loops”, Astron. Astrophys., 402, L17–L20. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...402L..17W.
ADS Google Scholar
Wilhelm, K., Dwivedi, B.N., Teriaca, L., 2004, “On the widths of the Mg X lines near 60 nm in the corona”, Astron. Astrophys., 415, 1133–1139. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2004A&A...415.1133W.
ADS Google Scholar
Williams, D.R., Phillips, K.J.H., Rudawy, P., Mathioudakis, M., Gallagher, P.T., O’Shea, E., Keenan, F.P., Read, P., Rompolt, B., 2001, “High-frequency oscillations in a solar active region coronal loop”, Mon. Not. R. Astron. Soc., 326, 428–436. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2001MNRAS.326..428W.
ADS Google Scholar
Williams, D.R., Mathioudakis, M., Gallagher, P.T., Phillips, K.J.H., McAteer, R.T.J., Keenan, F.P., Rudawy, P., Katsiyannis, A.C., 2002, “An observational study of a magneto-acoustic wave in the solar corona”, Mon. Not. R. Astron. Soc., 336, 747–752. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2002MNRAS.336..747W.
ADS Google Scholar
Wright, A.N., Rickard, G.J., 1995, “A numerical study of resonant absorption in a magnetohydrodynamic cavity driven by a broadband spectrum”, Astrophys. J., 444, 458–470. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1995ApJ...444..458W.
ADS Google Scholar
Zaitsev, V.V., Stepanov, A.V., 1975, “On the origin of pulsations of type IV solar radio emission. Plasma cylinder oscillations (I)”, Issled. Geomagn. Aeron. Fiz. Solntsa, 37, 3–10.
ADS Google Scholar
Zaitsev, V.V., Stepanov, A.V., 1989, “Elementary Flare Bursts and the Properties of Eruptive Solar Plasma”, Sov. Astron. Lett., 15, 66–68. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1989SvAL...15...66Z.
ADS Google Scholar
Zaitsev, V.V., Stepanov, A.V., 2002, “On the Origin of the Hard X-ray Pulsations during Solar Flares”, Sov. Astron. Lett., 8, 132–134. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1982SvAL....8..132Z.
ADS Google Scholar
Zaitsev, V.V., Stepanov, A.V., Urpo, S., Pohjolainen, S., 1998, “LRC-circuit analog of current-carrying magnetic loop: diagnostics of electric parameters”, Astron. Astrophys., 337, 887–896. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1998A&A...337..887Z.
ADS Google Scholar
Zaqarashvili, T.V., 2003, “Observation of coronal loop torsional oscillation”, Astron. Astrophys., 399, L15–L18. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?2003A&A...399L..15Z.
ADS Google Scholar
Zhugzhda, Y.D., 1996, “Force-free thin flux tubes: Basic equations and stability”, Phys. Plasmas, 3, 10–21. Related online version (cited on 07 March 2005): http://adsabs.harvard.edu/cgi-bin/bib_query?1996PhPl....3...10Z.
ADS MathSciNet Google Scholar
Zhugzhda, Y.D., Nakariakov, V.M., 1999, “Linear and nonlinear magnetohydrodynamic waves in twisted magnetic flux tubes”, Phys. Lett. A, 252, 222–232.
ADS Google Scholar

Download references

Acknowledgements

VMN acknowledges the support of a Royal Society Leverhulme Trust Senior Research Fellowship. EV is grateful to PPARC for the financial support. The authors are grateful to Leon Ofman, Markus Aschwanden, and Bernie Roberts for a number of valuable comments.

Author information

Affiliations

Physics Department, University of Warwick, Coventry, CV4 7AL, UK
Valery M. Nakariakov & Erwin Verwichte

Authors

Valery M. Nakariakov
View author publications
You can also search for this author in PubMed Google Scholar
Erwin Verwichte
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Valery M. Nakariakov.

Electronic supplementary material

png-Movie (189 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (192 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (192 KB) Still from a movie showing

png-Movie (195 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (197 KB) Still from a movie showing

png-Movie (198 KB) Still from a movie showing

png-Movie (200 KB) Still from a movie showing

png-Movie (207 KB) Still from a movie showing

png-Movie (220 KB) Still from a movie showing

png-Movie (223 KB) Still from a movie showing

png-Movie (231 KB) Still from a movie showing

png-Movie (247 KB) Still from a movie showing

png-Movie (242 KB) Still from a movie showing

png-Movie (213 KB) Still from a movie showing

png-Movie (203 KB) Still from a movie showing

png-Movie (198 KB) Still from a movie showing

png-Movie (197 KB) Still from a movie showing

png-Movie (195 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (192 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (195 KB) Still from a movie showing

png-Movie (192 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (189 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (180 KB) Still from a movie showing

png-Movie (178 KB) Still from a movie showing

png-Movie (179 KB) Still from a movie showing

png-Movie (180 KB) Still from a movie showing

png-Movie (179 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (176 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (176 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (178 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (172 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (179 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (193 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (202 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (171 KB) Still from a movie showing

png-Movie (172 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (170 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (172 KB) Still from a movie showing

png-Movie (171 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (171 KB) Still from a movie showing

png-Movie (172 KB) Still from a movie showing

png-Movie (171 KB) Still from a movie showing

png-Movie (170 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (172 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (173 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (176 KB) Still from a movie showing

png-Movie (174 KB) Still from a movie showing

png-Movie (175 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (178 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (178 KB) Still from a movie showing

png-Movie (177 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (193 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (210 KB) Still from a movie showing

png-Movie (200 KB) Still from a movie showing

png-Movie (213 KB) Still from a movie showing

png-Movie (208 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (179 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (179 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (180 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (180 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (181 KB) Still from a movie showing

png-Movie (182 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (183 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (184 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (191 KB) Still from a movie showing

png-Movie (199 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (199 KB) Still from a movie showing

png-Movie (207 KB) Still from a movie showing

png-Movie (215 KB) Still from a movie showing

png-Movie (203 KB) Still from a movie showing

png-Movie (199 KB) Still from a movie showing

png-Movie (197 KB) Still from a movie showing

png-Movie (195 KB) Still from a movie showing

png-Movie (196 KB) Still from a movie showing

png-Movie (195 KB) Still from a movie showing

png-Movie (194 KB) Still from a movie showing

png-Movie (196 KB) Still from a movie showing

png-Movie (202 KB) Still from a movie showing

png-Movie (200 KB) Still from a movie showing

png-Movie (204 KB) Still from a movie showing

png-Movie (208 KB) Still from a movie showing

png-Movie (200 KB) Still from a movie showing

png-Movie (207 KB) Still from a movie showing

png-Movie (196 KB) Still from a movie showing

png-Movie (208 KB) Still from a movie showing

png-Movie (211 KB) Still from a movie showing

png-Movie (212 KB) Still from a movie showing

png-Movie (214 KB) Still from a movie showing

png-Movie (208 KB) Still from a movie showing

png-Movie (200 KB) Still from a movie showing

png-Movie (198 KB) Still from a movie showing

png-Movie (192 KB) Still from a movie showing

png-Movie (189 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (189 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (190 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (189 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (188 KB) Still from a movie showing

png-Movie (186 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

png-Movie (187 KB) Still from a movie showing

png-Movie (185 KB) Still from a movie showing

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Cite this article

Nakariakov, V.M., Verwichte, E. Coronal Waves and Oscillations. Living Rev. Sol. Phys. 2, 3 (2005). https://doi.org/10.12942/lrsp-2005-3

Download citation

Accepted: 22 March 2005
Published: 07 May 2005
DOI: https://doi.org/10.12942/lrsp-2005-3

Keywords

Coronal Loop
Resonant Absorption
Torsional Wave
Magnetoacoustic Wave
Kink Mode