Large-Scale Dynamics of the Convection Zone and Tachocline

2.1 Global helioseismology

Granulation in the surface layers of the Sun is highly compressible (Mach numbers approaching or exceeding unity) and is therefore a strong source of acoustic waves. These waves propagate throughout the solar interior, reflecting off the surface and interfering with one another to form global standing modes with characteristic periods of about five minutes. In this way the Sun resonates with acoustic oscillations which can be used to probe its internal structure and dynamics².

Helioseismic investigations typically begin with a stellar structure model. Resonant modes of oscillation are then computed by considering linear, adiabatic perturbations about the spherically symmetric background state obtained from these models. Perturbations are typically expressed in terms of spherical harmonic basis functions Y _ℓm in latitude and longitude, and in terms of eigenfunctions in radius characterized by a radial order n. The frequencies of these resonant oscillations depend on the spherical harmonic degree, ℓ, the radial order, n, and the properties of the background state, principally the sound speed and the density (Christensen-Dalsgaard, 2002). The next step is to observe these oscillations on the Sun and compare them to the theoretical predictions. Helioseismic measurements typically consist of a time series of photospheric images in some dynamical variable such as the radial velocity as determined by the Doppler shift of a spectral emission line. These observations are then subjected to spherical harmonic transforms in space and Fourier transforms in time in order to determine oscillation frequencies. The measured frequencies agree remarkably well with the theoretical predictions (Gough, 1996; Christensen-Dalsgaard, 2002) and for low spherical harmonic degree ℓ ≤ 150, they are quantized, indicative of resonant oscillations. At higher spherical harmonic degree, the frequencies are blurred in ℓ due to locally-excited traveling waves which have not yet propagated around the solar sphere to interfere with other waves. These modes form the basis of local-domain helioseismology which will be discussed in Section 2.2 (see also Gizon and Birch, 2005).

Different oscillation modes are sensitive to different regions of the solar interior; for example, high-ℓ modes sample only the near-surface layers whereas low-ℓ modes penetrate much deeper. The oscillation frequencies are weighted integrals over the sampling region (loosely, the ray path) so some inversion procedure is necessary to infer solar interior properties such as the variation of the sound speed with depth (Christensen-Dalsgaard, 2002). The inversions are usually assumed to be linear so weighted summations over different frequencies can be used to derive averaging kernals which are sensitive to localized regions of the solar interior. Parametric representations may also be used, with minimization procedures to determine the best fit to solar data. Global inversions generally become less reliable in the polar regions and in the deep interior which are not well-sampled by observable oscillation modes.

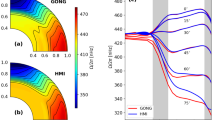
With regard to solar interior dynamics, the most important feature of global acoustic oscillations is their so-called rotational splitting. In a non-rotating star, the frequencies of resonant acoustic oscillations are independent of the spherical harmonic order m (neglecting the asphericity caused by flows or magnetic fields). This is no longer the case when the effects of rotation are included. The resulting frequency shifts are small relative to the reference frequency so they can be reliably treated as perturbations. Helioseismic inversions can then be used to infer the internal rotation profile as a function of latitude and radius as shown in Figure 1.

Open image in new window

A limitation of global helioseismology is that the inversions used to infer rotation profiles or structural quantities such as sound speed are only sensitive to the component which is symmetric about the equator. Furthermore, they are insensitive to meridional circulations and non-axisymmetric convective motions. In order to probe such dynamics other techniques are necessary, the most promising being local helioseismology.

2.2 Local helioseismology

Not all acoustic waves (p-modes) in the Sun are resonant oscillations of the full sphere. Locally-excited waves interact with local variations in sound speed, flow fields, and magnetic activity which alter their propagation characteristics. Thus, a careful analysis of the acoustic wave field in a localized patch of the solar photosphere can potentially reveal a great deal about the subsurface dynamics.

Extracting dynamical information from local wave fields can be more challenging than from global oscillations, primarily because the forward problem is more difficult; for a given structure and flow, what acoustic signal will be manifested on the solar surface? This depends to some degree on the source of the waves, which is complex and intermittent. A thorough understanding of this forward problem is necessary in order to devise reliable inversion techniques for inferring subsurface structure and dynamics from photospheric measurements.

Several related inversion techniques exist for local helioseismology, including ring-diagram analysis (Hill, 1988), time-distance methods (Kosovichev et al., 2000), and acoustic holography (Lindsey and Braun, 2000a). All of these approaches are discussed in detail by Gizon and Birch (2005).

From the perspective of solar interior dynamics, the most important result to come from local helioseismology has been the mapping of horizontal flows in the surface layers of the Sun as shown in Figure 3. Such mappings reveal meandering meridional and zonal circulation patterns as well as intricate smaller-scale flows associated with active regions and supergranulation. The investigation and monitoring of these flows has given rise to the new discipline of solar subsurface weather, SSW (Toomre, 2002). Local helioseismology has also been used to study the acoustic and flow structure underlying sunspots (Kosovichev et al., 2000; Braun and Lindsey, 2000; Zhao et al., 2001; Zhao and Kosovichev, 2003) and to image active regions on the far side of the Sun (Lindsey and Braun, 2000b; Braun and Lindsey, 2001).

The probing of horizontal flows by local helioseismology has provided unpreceded insight into the structure and evolution of differential rotation (Section 3.3), meridional circulation (Section 3.4), and giant cells (Section 3.5). However, like any method, it has its limitations. Most notably, the small-wavelength acoustic waves, which local helioseismology is best suited to investigate, are confined principally to the near-surface layers, r ≥ 0.97R_⊙. Some analyses have attempted to probe deeper (Giles et al., 1997; Braun and Fan, 1998) but the resolution is limited and the results are generally less reliable. There is much promise that with improved instrumentation and analysis techniques local helioseismology can do better and may soon provide information on flow structure, magnetic activity, and thermal asphericity as deep as the tachocline (Gizon and Birch, 2005).

Although local helioseismology can currently only provide detailed dynamical information for the outer few percent of the solar interior, the large-scale flow patterns it reveals may extend deeper into the convective envelope. For the same reason, surface observations are also relevant (Section 2.3).

2.3 Surface and atmospheric observations

Understandably, much of solar physics is concerned with the part of the Sun we can observe directly, namely the photosphere, chromosphere, and corona. Although such observations do not provide direct information on physical conditions in the solar interior, they can provide insight into the nature of solar convection and dynamo processes.

Plasma flows in the photosphere may be measured directly by Doppler imaging or may be inferred by tracking the horizontal movement of magnetic structures, emission features, and convective patterns across the solar disk. Such measurements provide a useful check on near-surface flow fields obtained from helioseismology. Surface measurements also provide an extensive time history of the solar rotation profile, tracing its long-term evolution. The differential rotation of the solar surface has been monitored for almost 150 years (since Carrington, 1863) and careful analysis of prior sunspot records can potentially extend this time coverage even further back (Eddy et al., 1977; Ribes and Nesme-Ribes, 1993). By comparison, helioseismic determinations of the solar rotation only date back to the mid 1980’s.

Doppler maps of photospheric flow fields, known as Dopplergrams, are dominated by granulation: small-scale (∼ 1–2 Mm) turbulent convection cells confined to the near-surface layers and driven by ionization and radiative transfer effects. Characteristic velocity amplitudes depend somewhat on the resolution of the instrument but are, at least, several km s⁻¹. More sophisticated analyses, such as correlation tracking, also reveal another scale of convection known as supergranulation with characteristic length and velocity scales of about 30 Mm and several hundred m s⁻¹ (Leighton et al., 1962; DeRosa and Toomre, 2004). At intermediate scales of ∼ 5 Mm, another pattern known as mesogranulation has also been detected in correlation tracking measurements with characteristic velocity amplitudes of ∼ 60 m s⁻¹ (November et al., 1981; Muller et al., 1992). However, mesogranulation is not apparent in power spectra computed from Doppler measurements of surface velocities whereas granulation and supergranulation are (Hathaway, 1996b; Hathaway et al., 2000). Such patterns must be filtered out or otherwise removed from surface Doppler measurements in order to detect the relatively weak, larger-scale motions more relevant to the dynamics of the deep solar interior, including differential rotation (∼ 200 m s⁻¹), meridional circulation (∼ 20–30 m s⁻¹), and larger-scale convective motions (∼ 10–100 m s⁻¹). The five-minute acoustic oscillations which form the basis of helioseismology must also be filtered out when studying large-scale surface flows by means of Doppler measurements.

Removing contaminating signals arising from rotation, granulation, supergranulation, acoustic oscillations, and small-scale magnetic activity is perhaps the biggest challenge in determining large-scale flow patterns from surface Doppler measurements. Projection effects such as limb darkening also pose problems for both Doppler and tracking techniques, and the non-uniform rotation of the Sun makes it more difficult to identify and monitor long-lived velocity features. Furthermore, techniques which rely on tracking magnetic features or flow patterns via auto-correlations can give misleading results if the features or patterns evolve substantially over the course of the tracking interval or if the features are not just passively advected by the fluid as is implicitly assumed.

Measurements of photospheric intensity or irradiance are also very instructive from the standpoint of solar interior dynamics because they may reflect inhomogeneities in temperature or heat flux induced by large-scale convective motions. However, detecting such large-scale variations is difficult because, like Doppler measurements, solar irradiance measurements are dominated by granulation patterns and small-scale emission features related to magnetic activity such as faculae. After removing these effects, the residual latitudinal variations are only about one part in 10⁴ (Section 3.7).

The Sun exhibits a wide variety of magnetic activity, from the quiet photospheric network to sunspots and coronal loops to MHD waves and explosive events such as flares and coronal mass ejections. Indeed, solar magnetism lies at the heart of nearly all the companion reviews in this journal, including Charbonneau (2005); Fan (2004). Although much of this research focuses on structures in the solar atmosphere, the ultimate origin of this magnetic activity lies below the surface, in the convection zone and tachocline (Section 4.5). Reproducing patterns of magnetic activity such as the solar butterfly diagram (Section 3.8) therefore ranks among the most important and difficult challenges to dynamical models of the solar interior.

3.1 Differential rotation of the solar envelope

The internal rotation of the Sun inferred from global helioseismology is shown in Figure 1. Throughout the convective envelope, the rotation rate decreases monotonically toward the poles by about 30%. Angular velocity contours at mid-latitudes are nearly radial. Near the base of the convection zone, there is a sharp transition between differential rotation in the convective envelope and nearly uniform rotation in the radiative interior. This transition region has become known as the solar tachocline and will be discussed further in the next section (Section 3.2). The rotation rate of the radiative interior is intermediate between the equatorial and polar regions of the convection zone. Thus, the radial angular velocity gradient across the tachocline is positive at low latitudes and negative at high latitudes, crossing zero at a latitude of about 35°.

In addition to the tachocline, there is another layer of comparatively large radial shear in the angular velocity near the top of the convection zone. At low and mid-latitudes there is an increase in the rotation rate immediately below the photosphere which persists down to r ∼ 0.95R_⊙. The angular velocity variation across this layer is roughly 3% of the mean rotation rate and according to the helioseismic analysis of Corbard and Thompson (2002) Ω decreases within this layer approximately as r⁻¹. At higher latitudes the situation is less clear. The radial angular velocity gradient in the subsurface shear layer appears to be smaller and may switch sign (Corbard and Thompson, 2002).

Although helioseismic inversions become less reliable at high latitudes (Section 2.1), available data indicate that the monotonic decrease of angular velocity with latitude continues to the polar regions. Moreover, the inferred rotation rate of the polar regions is even slower than that given by a smooth extrapolation of the rotation rate at low and mid-latitudes (Schou, 1998). This is a striking result, since flows approaching the rotation axis might be expected to spin up the polar regions if they tend to conserve their angular momentum (cf. Sections 6.3 and 6.4).

Finer structure is also present in the rotational inversions, including “wiggles” in the angular velocity contours and propagating, banded zonal flows known as torsional oscillations (Section 3.3). Zonal jets (localized regions of prograde or retrograde flow) may also be present. Schou (1998) reported evidence for a prograde polar jet which can also be seen in the RLS (Regularized Least Squares) inversion results of panel b of Figure 1 (dashed line) at a latitude of 75° and a radius of ∼ 0.95R_⊙. However, some data and analysis techniques spanning the same time interval do not reveal such a jet, so its existence is still questionable (Schou et al., 2002). Spatial and temporal variations in the rotation rate are particularly apparent near the poles where the small moment arm, λ = r sin θ, implies large angular velocity variations even for moderate zonal velocities: Ω = υ _ϕ /λ. Although many of these fluctuations can likely be attributed to observational and analysis errors, some are statistically significant (Toomre et al., 2000).

Global helioseismic inversions such as those shown in Figure 1 can only provide the equatorally-symmetric component of the angular velocity but local helioseismology reveals significant asymmetries, particularly in the torsional oscillations (Haber et al., 2002; Basu and Antia, 2003; Zhao and Kosovichev, 2004).

3.2 The tachocline

The tachocline is a transition layer between two distinct rotational regimes: the differentially-rotating solar envelope and the radiative interior where the rotation is uniform, within the error estimates of the inversions (Figure 1). This transition is sharp and it occurs near the base of the convection zone as determined by helioseismic inversions and solar models (Section 3.6), implying that convection is responsible for the differential rotation of the envelope (Section 4.3). Although some authors incorporate structural information (e.g., subadiabaticity), most define the tachocline solely by means of the rotation profile. We will follow the latter convention.

Recent helioseismic estimates by Charbonneau et al. (1999a) and Basu and Antia (2003) indicate that the tachocline is centered at r_t ∼ 0.693±0.003R_⊙ near the equator. This is below the convection zone base of r_b = 0.713 ± 0.003R_⊙ but it may lie within the overshoot region (Section 3.6). At higher latitudes, the location of the tachocline shifts upward, reaching r_t ∼ 0.717 ± 0.003R_⊙ at a latitude of 60° (Charbonneau et al., 1999a; Basu and Antia, 2003). Thus, the tachocline is significantly prolate. This is in contrast to the base of the convection zone, r_b, in which helioseismic inversions have not yet detected any significant latitudinal variation (Section 3.6).

These helioseismic results suggest that the tachocline lies almost entirely below the convective envelope at low latitudes but it may extend well into the convection zone at high latitudes. Moreover, it appears that the tachocline contains the overshoot region but extends beyond it, perhaps both above and below. However, these results may need to be reexamined in light of new determinations of elemental abundances in the solar envelope, which has important implications for helioseismic inversions (Asplund et al., 2005; Bahcall et al., 2005).

Throughout most of the tachocline, the vertical shear in the mean zonal velocity almost an order of magnitude larger than the latitudinal shear: dυ _ϕ /dr ∼ ±1.5 × 10⁻⁶ s⁻¹ whereas r⁻¹dυ _ϕ /dθ ∼ 2 × 10⁻⁷ s⁻¹. The exception is at latitudes of ∼ 35° where dυ _ϕ /dr changes sign. The total change in the zonal velocity across the tachocline is about 100 m s⁻¹ at the equator and somewhat less at high latitudes, ∼ 90 m s⁻¹.

3.3 Torsional oscillations and other temporal variations in the solar rotation

The rotation rate of the Sun varies on evolutionary timescales; it was once much faster. Here we are concerned with variations on the much shorter dynamical timescales of months, years, and decades. We ask whether the differential rotation profile shown in Figure 1 changes significantly over the course of, for example, the solar activity cycle. The answer is yes. There are two distinct cyclical patterns which have been detected in the solar differential rotation, which we will refer to as torsional oscillations and tachocline oscillations.

The most well-established temporal variations in the solar differential rotation are torsional oscillations, which have been studied using global helioseismology, local helioseismology, and surface Doppler measurements (Howard and LaBonte, 1980; Ulrich et al., 1988; Howe et al., 2000b; Vorontsov et al., 2002; Haber et al., 2002; Basu and Antia, 2003; Zhao and Kosovichev, 2004). These are alternating bands of faster and slower rotation which propagate with a cyclical period of 11 years. At latitudes below about 42°, the bands propagate equatorward but at higher latitudes they propagate poleward. The low-latitude bands are about 15° wide in latitude and extend from the surface down to r ∼ 0.9R_⊙ or deeper, possibly to the base of the convection zone. The high-latitude bands are somewhat wider and deeper, possibly extending to the base of the convection zone (Vorontsov et al., 2002). The amplitude of the angular velocity variation is about 2–5 nHz, which is roughly 1% of the mean rotation rate. This corresponds to a zonal flow of about 5–10 m s⁻¹.

The 11-year period of the torsional oscillations strongly suggests that they are associated in some way with the 22-year solar activity cycle. Indeed, surface magnetic activity correlates well with the oscillation patterns, with activity belts tending to lie on the poleward side of the faster-rotating bands at low latitudes, migrating toward the equator together as the activity cycle progresses (Zhao and Kosovichev, 2004). Recent results by Beck et al. (2002) based on time-distance helioseismology indicate that meridional flows may be diverging out of the activity belts, with equatorward and poleward flows correlating well with the faster and slower bands of the torsional oscillations, respectively. There is some evidence that the zonal bands may get slightly faster at times of peak magnetic activity (Zhao and Kosovichev, 2004). Some evidence has also been found for higher-order harmonics in the torsional oscillation signal (Vorontsov et al., 2002) and for possibly related non-axisymmetric wave patterns having longitudinal wavenumbers up to m = 8 (Ulrich, 2001).

The second type of oscillation which has been detected in the differential rotation profile, first reported by Howe et al. (2000a), is distinct from the torsional oscillation in that it has a shorter period, ∼ 1.3 yr and it is localized around the tachocline and the lower convection zone. Furthermore, there is currently no evidence for latitudinal propagation. Rather, it appears to be a standing wave straddling the base of the convection zone, with angular velocity variations at r = 0.63R_⊙ out of phase with those at r = 0.72R_⊙. The amplitude of the angular velocity variation is about 3 nHz at the equator and perhaps slightly larger, ∼ 4 nHz, at a latitude of 60°. The oscillation may not be strictly periodic; the high-latitude signal in particular appears to be somewhat erratic.

The tachocline oscillation signal is not far from the current sensitivity limits of helioseismic inversions so it is difficult to probe in detail. Basu and Antia (2001) find roughly periodic variations similar to those reported by Howe et al. (2000a) but they argue that the result is not statistically significant. A subsequent analysis by Toomre et al. (2003) further made the case that the oscillations are indeed real but they appear to be varying in amplitude as the solar cycle proceeds, first waning then waxing. Further monitoring of these oscillations is needed in order to verify their presence and better understand their origin.

In addition to the torsional and tachocline oscillation patterns, the solar rotation, particularly at high latitudes, undergoes monthly variations on the order of a few percent or less which appear to be more random (Toomre et al., 2000). Apart from these small variations, the differential rotation profile appears to be remarkably steady. Surface measurements show little variation for well over a century (Gilman, 1974; Schröter, 1985; Rüdiger, 1989). Still, there is some indication that the low-latitude rotation rate as traced by sunspots may increase by as much as a few percent during periods of minimum and to a lesser extent maximum activity (Howard, 1984; Hathaway and Wilson, 1990; Javaraiah, 2003). Longer-term variations may also be present. Javaraiah (2003) has considered rotation data from sunspot groups covering the period from 1879–2002 and has found possible evidence for several patterns, including a speedup of the equatorial rotation rate by ∼ 0.1% in alternate sunspot cycles, accompanyed by an increase in the differential rotation (latitudinal angular velocity gradient) and a greater asymmetry between the northern and southern hemispheres.

Sunspot groups may not be accurate tracers of solar rotation. Small variations in their rotational properties may reflect other physics, such as where they are “anchored” to the plasma. Thus, we are only beginning to explore systematic variations in the solar rotation over time scales of years and decades. High-quality helioseismic inversions have only been available for a single sunspot cycle. Continued monitoring of the internal rotation profile via helioseismology promises to provide new insight into its evolution for many years to come.

3.4 Meridional circulation

The differential rotation is the axisymmetric component of the mean longitudinal flow, < υ _ϕ >. The axisymmetric flow in the meridional plane, < υ _θ > and < υ _r >, is generally known as the meridional circulation.

The meridional circulation in the solar envelope is much weaker than the differential rotation, making it relatively difficult to measure (e.g., Hathaway, 1996a). Furthermore, although it can in principle be probed using global helioseismology (Woodard, 2000), the effect of meridional circulation on global acoustic oscillations is small and may be difficult to distinguish from rotational and magnetic effects (Giles et al., 1997). Thus, we must currently rely on surface measurements and local helioseismology.

Early attempts to measure the mean meridional circulation in the solar photosphere by both Doppler and tracer techniques (reviewed by Hathaway, 1996a; Snodgrass and Dailey, 1996; Latushko, 1996) varied dramatically. Many suggested a poleward flow of ∼ 10–20 m s⁻¹, but others found amplitudes ranging from 1 ∼ 100 m s⁻¹ and complex latitudinal structure with both poleward and equatorward flows, multiple cells, and large asymmetries about the equator.

More recent Doppler measurements of the photospheric meridional circulation by Hathaway (1996b) and Hathaway (1996a) yield a poleward flow of about 20 m s⁻¹ on average, confirming many of the earlier results. This mean poleward flow is nearly symmetric about the equator and peaks at latitudes of about 40°. However, Hathaway (1996a) found substantial monthly and yearly variations in the flow amplitude and profile, reaching speeds of up to 50 m s⁻¹ (panel a in Figure 2). Doppler measurements by Ulrich et al. (1988) showed even larger fluctuations, sometimes reversing sign and becoming equatorward.

Open image in new window

Recent estimates of the meridional circulation obtained from the cross-correlation of magnetic features yield an average latitudinal flow which is poleward at low latitudes and weakly equator-ward at high latitudes, with a peak amplitude of about 15 m s⁻¹ (Komm et al., 1993; Snodgrass and Dailey, 1996; Latushko, 1996). However, these methods too exhibit large temporal variations. In the 26-year interval studied by Snodgrass and Dailey (1996), the meridional flow achieves amplitudes as large as 50 m s⁻¹ and often becomes equatorward at latitudes below 20° and above 40°.

Local helioseismology provides an alternative to surface measurements and gives us the capability of probing the meridional flow below the photosphere. Near the surface the results are generally consistent with Doppler and tracer measurements, showing poleward flow of about 20 m s⁻¹ with substantial time variation and significant asymmetry about the equator (Giles et al., 1997; Chou and Dai, 2001; Haber et al., 2002; Basu and Antia, 2003; Zhao and Kosovichev, 2004).

Below the surface, Haber et al. (2002) have reported a flow reversal in the northern hemisphere where the circulation becomes equatorward at depths greater than about 3 Mm below the photosphere (r ∼ 0.99R_⊙), down to the limit of their sampling domain which lies at a depth of 15 Mm (panel b in Figure 2). Their ring-diagram analysis spans six years, from 1996–2001, with the flow reversal occurring in the latter four, from 1998–2001. Such a flow reversal is not evident in the time-distance results of Zhao and Kosovichev (2004) who present meridional flows averaged over depths of 3–4.5 Mm and 6–9 Mm. Several local helioseismic studies have attempted to probe deeper still. Giles et al. (1997) presented time-distance results for the upper 4% of the solar interior and concluded that the meridional flow throughout this region was poleward. Braun and Fan (1998) similarly find no evidence for a return equatorward flow down to 0.85R_⊙. Inferring the circulation at depth below about 0.98R_⊙ is a difficult task and it is still too early to know what to make of these efforts.

There is evidence from both surface measurements and local helioseismology that the amplitude of the meridional circulation may be anticorrelated with magnetic activity, decreasing during solar maximum and increasing during solar minimum (Komm et al., 1993; Chou and Dai, 2001; Basu and Antia, 2003). Furthermore, a weak meridional circulation component of a few m s⁻¹ has been found which diverges out of magnetic activity belts and propagates with them toward the equator as the activity cycle progresses (Snodgrass and Dailey, 1996; Beck et al., 2002). However, Zhao and Kosovichev (2004) report the opposite: weak meridional flows which converge toward activity belts. They argue that the convergence occurs in the outermost layers, less than ∼ 12 Mm below the photosphere whereas the divergence occurs deeper down.

Although much progress has been made in recent years, improving our understanding of the meridional circulation throughout the convective envelope remains an important challenge for local helioseismology in particular and will be a major research focus in the near future.

3.5 Giant cells, waves, and solar subsurface weather

Differential rotation and meridional circulation are essential components of solar interior dynamics but it is also of fundamental importance to investigate the large-scale convective motions which maintain them and which, therefore, lie at the root of solar variability (Section 1). There is no doubt that large-scale structure (ℓ ≤ 100) is present in surface velocity maps obtained from Doppler measurements, feature tracking, and local helioseismology (e.g., Stix, 2002). However, it has been notoriously difficult to identify characteristic patterns or to obtain quantitative diagnostics of large-scale convective motions.

The convection power spectrum in the photosphere obtained from Doppler measurements peaks at granulation scales (ℓ ≥ 1000), with a secondary peak at ℓ ∼ 120, corresponding to supergranulation (Hathaway, 1996b; Hathaway et al., 2000). At lower wavenumbers, the velocity spectrum appears to drop off nearly linearly: υ(ℓ) ∼ ℓ.

Recently, several groups have reported long-lived features in Dopplergrams which are highly correlated in longitude, corresponding to azimuthal wavenumbers of m = 0–8 (angular extent ≥ 45°) but with a narrow latitudinal extent of not more than about 6° (Ulrich, 1993, 2001; Beck et al., 1998). Although Beck et al. (1998) interpret these features as giant convection cells, Ulrich (2001) argues that they more likely comprise a spectrum of inertial oscillations, possibly related to Rossby wave modes (Appendix A.6) and perhaps also to torsional oscillations (Section 3.3).

Evidence for a dramatically different giant cell structure has been presented by Lisle et al. (2004). They study the supergranulation pattern using correlation tracking and find a tendency for north-south alignment of supergranular cells. Such an alignment would be expected if the supergranulation were advected by larger-scale, latitudinally-elongated lanes of horizontal convergence such as those commonly seen in numerical simulations of solar convection (Section 6.2). Advection by such structures may also help to explain why the supergranulation pattern appears to rotate faster than the surrounding plasma (Lisle et al., 2004).

The most substantial recent advance in the search for large-scale non-axisymmetric motions in the solar envelope has been the mapping of horizontal flows by local helioseismology, as shown in Figure 3. After subtracting out the contributions from differential rotation and meridional circulation, the residual flow maps reveal intricate, evolving flows on a range of spatial scales (Haber et al., 2002; Zhao and Kosovichev, 2004; Komm et al., 2004; Hindman et al., 2004). Such flow patterns have become known as solar subsurface weather, SSW (Toomre, 2002).

Open image in new window

The inferred SSW patterns show a high correlation with magnetic activity, becoming more complex at solar maximum. Near the surface, strong horizontal flows converge into active regions and swirl around them, generally in a cyclonic sense (counter-clockwise in the northern hemisphere and clockwise in the southern hemisphere). Deeper down, roughly 10 Mm below the photosphere, the pattern reverses; here flows tend to diverge away from active regions (Zhao and Kosovichev, 2004).

The distribution and relative amplitude of horizontal divergence and vertical vorticity can provide insight into the nature of the flows and can be used to make contact with theoretical and numerical models. Komm et al. (2004) compute the divergence and vorticity fields from SSW flow maps along with other flow descriptors including the vertical velocity (obtained from the mass continuity equation) and vertical gradients of horizontal flows. The results again show a strong correlation with active regions which are associated with cyclonic vorticity, converging flows, and large velocity gradients.

Other flow diagnostics which can in principle be deduced from SSW flow maps include the horizontal Reynolds stress component < υ′ _θ υ′ _ϕ > (see Section 4.3). Although such quantities have not yet been investigated in detail with helioseismic measurements, they have been measured to some degree using sunspots as tracers. The results yield small but generally positive values, indicating equatorward angular momentum transport (Stix, 2002; Nesme-Ribes et al., 1997).

In addition to giant convective cells, large-scale, non-axisymmetric flow patterns may also arise from wave phenomena. A familiar example is the acoustic wave spectrum which forms the basis of helioseismology. There is also some evidence for the presence of Rossby wave modes or, more generally, inertial oscillations. Ulrich (2001) has interpreted long-lived features in photospheric Dopplergrams as a hierarchy of inertial oscillations with longitudinal wavelengths m ≤ 8. Some hints of these patterns can also be seen in SSW flow maps (Haber et al., 2002). Further evidence for Rossby waves on the Sun has been reported by Kuhn et al. (2000) and Lou (2000). Gizon et al. (2003) have suggested that supergranulation patterns may also exhibit wavelike behavior although this has been disputed by Rast et al. (2004).

3.6 The base of the convection zone

Inversions to determine the radial profile of sound speed and other structure quantities have been used to great effect in improving our understanding of the physics which goes into solar structure models (e.g., Gough, 1996; Christensen-Dalsgaard, 2002). In the context of solar interior dynamics, the most important contribution of structure inversions has been to locate the base of the solar convection zone at r _b = 0.713 ± 0.003R_⊙ (Christensen-Dalsgaard et al., 1991), defined as the radius at which the stratification changes from nearly adiabatic stratification to substantially subadiabatic stratification (see Section 8.1). This result has until recently been viewed as very reliable but new elemental abundance determinations have called it into question (Asplund et al., 2005; Bahcall et al., 2005). Helioseismic estimates further suggest that the extent of the overshoot region below the convection zone is no more than about 5% of a pressure scale height, which is less than 1% of the solar radius (Monteiro et al., 1994; Basu, 1997). Basu and Antia (2001) find no significant variations in either r_b or the thickness of the overshoot region with latitude or time (variations in the structure of the tachocline obtained from rotational inversions are discussed in Sections 3.2 and 3.3).

3.7 Thermal asphericity and subsurface magnetic fields

Latitudinal variations (asphericity) in the sound speed may be caused by temperature perturbations induced by convection or magnetism or they may be caused by the direct influence of the Lorentz force on the propagation speed of acoustic waves. The two effects are difficult to disentangle in helioseismic inversions.

Latitudinal sound speed variations inferred by global helioseismology are found to be very weak (about one part in 10⁴) and appear to be dominated by small-scale magnetic activity near the solar surface (Gough, 1996; Dziembowski et al., 2000; Antia et al., 2001, 2003). In particular, enhancements in the sound speed are found to correlate well with latitudinal bands of magnetic activity in the photosphere which migrate toward the equator during the course of the solar activity cycle. However, weak latitudinal variations have also been detected deeper in the interior. Time-averaged inversions reveal a significant sound speed enhancement throughout the convection zone, peaking at a latitude of ∼ 60° and radius of ∼ 0.92R_⊙ (Dziembowski et al., 2000; Antia et al., 2001, 2003). This feature appears to be present at least over the time interval from 1995 to 2002 and its magnitude is consistent with a fractional sound speed variation of about 10⁻⁴, a magnetic field of strength ∼ 60 kG, or some combination of the two.

Probing magnetic fields near the base of the convection zone is of particular importance to solar dynamo theory since the tachocline and overshoot region are believed to play a key role in generating and storing toroidal magnetic flux which eventually rises to the surface to form active regions (see Section 4.5). Such fields have not yet been unambiguously detected but helioseismic measurements have suggested an upper limit of about 300 kG (Basu, 1997; Antia et al., 2000, 2003).

Thermal asphericity induced by convective motions may also give rise to latitudinal irradiance variations in the photosphere which can in principle be measured. However, in practice, such variations are dominated by magnetic features such as sunspots and faculae, making it difficult to distinguish purely thermal effects (Hudson, 1988). Early estimates of the pole-equator temperature difference (reviewed by Altrock and Canfield, 1972) were only able to set upper limits of a few K. After removing the facular contribution, Kuhn et al. (1988) report residual irradiance variations which they interpret as latitudinal temperature variations. The temperature peaks at low latitudes in warm bands which correlate well with the magnetic activity belts, propagating toward the equator as the cycle progresses. A second component is also present, consisting of warm poles which exhibit little variation over the course of the activity cycle. The amplitudes of the low and high-latitude maxima are about 3 K and 1 K, respectively, relative to the temperature minimum at mid-latitudes. However, further analysis has called this interpretation into question and suggests that the irradiance variations may instead be attributed to emission from diffuse magnetic elements (Woodard and Libbrecht, 2003).

Asphericity in the density field appears to be even weaker than that in the sound speed (fractional variation < 10⁻⁴) and has not yet been reliably detected (Antia et al., 2001).

3.8 Solar magnetism

Observations of magnetic activity on the Sun reveal extremely complex behavior but systematic patterns also exist, at least some of which may be traced back to field generation in the convection zone and tachocline. Thus, a wide variety of magnetic activity is of relevance to solar interior dynamics; here we will only scratch the surface. More comprehensive reviews are given in these volumes by Fan (2004) and Charbonneau (2005), (see also Schrijver and Zwaan, 2000; Ossendrijver, 2003).

The most familiar and compelling magnetic activity pattern in the Sun is the sunspot cycle and the corresponding butterfly diagram (e.g., Stix, 2002). Sunspots and other manifestations of magnetic activity emerge in well-defined latitudinal bands which migrate toward the equator on a timescale of about 11 years. As these activity bands converge on the equator, the polarity of the global field reverses and the emergence pattern repeats, returning to its previous magnetic configuration after two reversals, yielding a net 22-year periodicity.

Sunspot groups are often separated into regions of outward and inward magnetic polarity which are aligned nearly east-west (meaning the neutral line is nearly north-south), but tilted somewhat relative to lines of constant longitude. The polarity of the leading (eastern) side is opposite in each hemisphere and reverses sign every 11 years with the activity cycle (known as Hale’s polarity rules) whereas the tilt angle increases approximately linearly with latitude (known as Joy’s law). These patterns suggest that bipolar active regions are made up of toroidal magnetic flux which has emerged as a loop from below the photosphere and may still be anchored there (Fan, 2004).

The loops which emerge are often twisted and many obey systematic rules for the sense of the twist as defined by the magnetic helicity or current helicity (e.g., Biskamp, 1993). Helicity indicators in the photosphere, chromosphere, and corona are generally positive in the northern hemisphere and negative in the southern hemisphere (Pevtsov et al., 1994, 1995; Zirker et al., 1997; Chae, 2000; Pevtsov, 2002). The pattern is most evident with relatively large-scale structures such as coronal loops.

Another pattern in magnetic activity which has particular relevance to solar interior dynamics is the presence of active nests or active longitudes: localized regions of the solar photosphere where magnetic flux appears to emerge preferentially and repeatedly over the course of multiple rotation periods (Bumba and Howard, 1965; Bogart, 1982; Brouwer and Zwaan, 1990). DeToma et al. (2000) chart a number of such regions during the rising phase of the current solar cycle. They find nests which persist for up to seven rotations, and the number of simultaneous nests increases progressively as the cycle proceeds from zero in late 1995 to three in 1998 (previous studies revealed up to six coexisting longitudinal bands of enhanced activity).

The global structure of the coronal magnetic field as inferred from white light observations can also provide insight into the nature of the solar dynamo operating in the interior, although it is strongly influenced by dynamical processes in the atmosphere as well, such as advection by the solar wind (Aschwanden et al., 2001). Potential-field extrapolations from photospheric measurements and more sophisticated coronal models yield a complex web of magnetic loops and open fields with a range of size scales and connectivity across the solar surface (e.g., Altschuler and Newkirk, 1969; Gibson et al., 1999; Aschwanden et al., 2001; Schrijver and DeRosa, 2003). On the largest scales, the axisymmetric component of the poloidal field is approximately dipolar during solar minimum with an amplitude at the solar photosphere of roughly 10 G. However, as the activity cycle progresses, the field becomes much more complicated and dynamic, with substantial contributions from higher-order multipoles. Figure 4 illustrates the coronal field structure near solar maximum. Note that a potential-field extrapolation as shown does not take into account dynamics occurring above the photosphere and thus may not in general be an accurate indicator of the actual field structure (Gibson et al., 1999; Aschwanden et al., 2001). However, it is a good first approximation and suffices for our purposes here, as a diagnostic of dynamo processes in the solar interior.

Open image in new window

4.1 Governing equations

In order to understand the phenomena described in Section 3, we must consider the equations of magnetohydrodynamics (MHD) which express the conservation of mass, energy, and momentum in a magnetized plasma. Although the dynamics is made more complex by the presence of density stratification, rotation, magnetic fields, and spherical geometry, there is at least one property of the motions which may be safely exploited in order to simplify the equations of motion somewhat: they possess a low Mach number (this can usually be verified a posteriori in any numerical or theoretical model). In other words, the kinetic energy of the convection is small relative to the internal energy of the plasma. Furthermore, the ratio of magnetic to internal energy is also small (implying an Alfvénic Mach number ≪ 1). Under such conditions, it is valid to adopt the anelastic approximation. The anelastic approximation is justified throughout the solar interior with the exception of the near-surface layers (r ≥ 0.98R_⊙) where velocities associated with granulation can exceed the sound speed and where radiative transfer and ionization effects must be taken into account.

In the anelastic approximation the velocity, magnetic fields, and thermodynamic variations induced by convection (or by other means) are treated as perturbations relative to a spherically-symmetric background or reference state. The resulting system of equations is given in Appendix A.2. In numerical applications, the anelastic equations can be much more computationally efficient to implement than the fully compressible MHD equations because they filter out high-frequency acoustic waves which would otherwise severely limit the time step required to maintain numerical stability. Furthermore, from a theoretical standpoint, the anelastic equations are generally more analytically tractable, partly because the velocity field can be expressed in terms of scalar streamfunctions and velocity potentials, thus eliminating one velocity variable (e.g., Glatzmaier, 1984).

In the remainder of this paper, we will use the anelastic equations described in Appendix A.2 to illustrate a few fundamental aspects of solar interior dynamics, the first being energy balance. The reference state density, pressure, specific entropy, and temperature are represented by overbars: \(\bar{\rho},\overline{P},\overline{S}\), and \(\overline{T}\). These same symbols without overbars denote fluctuations about the reference state. For more on notation, see Appendixes A.1 and A.2.

4.2 Energetics

The terms \({\cal F}^{{\rm KE}}\) and \({\cal F}^{{\rm EN}}\) represent kinetic energy and enthalpy flux by convective motions. The latter of these, \({\cal F}^{{\rm EN}}\), dominates the energy flux throughout most of the convective envelope, transporting energy outward from the interior to the surface where it is then radiated into space. By contrast, the kinetic energy flux \({\cal F}^{{\rm KE}}\) is much weaker and is directed inward as a result of the asymmetry between upflows and downflows which is characteristic of compressible convection (see Section 6.2).

In the deep interior, the energy flux is carried by radiative diffusion, \({\cal F}^{{\rm RD}}\), which falls off gradually above the base of the convection zone at r ∼ 0.7R_⊙. The Poynting flux \({\cal F}^{{\rm PF}}\) plays little role in the overall energy balance but can have a significant influence on dynamo processes, particularly if the magnetic boundary conditions permit leakage out of the domain (Brun et al., 2004). The viscous energy flux, \({\cal F}^{{\rm VD}}\), is generally negligible both in the Sun and in numerical models. Many numerical applications also include an additional diffusive heat flux which operates on the entropy gradient and which is intended to represent energy transport by unresolved convective motions (e.g., Miesch et al., 2000). This additional term is designed to carry flux outward near the upper boundary where the convective fluxes vanish and the radiative diffusion is small.

The final term in Equation (2), involving \({\cal F}^{{\rm BS}}\) reflects the internal and gravitational potential energy associated with the background stratification. If the reference state is adiabatic, this term vanishes. Even if the reference entropy gradient is nonzero, the horizontal average of \({\cal F}^{{\rm BS}}\) vanishes so it contributes nothing to the total radial energy flux (see Appendix A.3). However, this term together with the radiative heat flux, \({\cal F}^{{\rm RD}}\), provides the energy input which drives convective motions.

If the anelastic equations are solved within a spherical shell Equation (2) implies that the total energy will be conserved if the net flux through the inner and outer boundaries vanishes. This will be the case if the boundary conditions are impenetrable and stress-free, if no net heat flux is applied, and if the magnetic field is required to be radial at the top and bottom of the shell. Other boundary conditions may lead to energy transport into or out of the domain.

Figure 5 summarizes the exchange of energy between the different reservoirs of the system. Energy is supplied from below via a radiative energy flux which ultimately originates from nuclear burning in the solar core. Convective motions tap this energy source through the buoyancy force which convert thermal energy to kinetic energy. This kinetic energy can then be converted into magnetic energy by the Lorentz force or back into thermal energy by pressure work on expanding or contracting fluid elements through the P∇·v term in the mechanical and internal energy equations (see Appendix A.3). Kinetic and magnetic energy may also be converted into thermal energy by viscous and Ohmic heating. These heating terms are unidirectional, but the buoyancy force, Lorentz force, and compression can operate in both directions, either extracting or injecting kinetic energy. Because we have neglected the centrifugal force, the kinetic energy associated with the uniform component of the solar rotation cannot be tapped directly, although the differential rotation component can be (Section 4.3).

Open image in new window

4.3 Maintenance of differential rotation

The most stringent observational constraints on solar interior dynamics come from helioseismic determinations of the solar differential rotation (reviewed in Section 3). In this subsection we address how this differential rotation is established and maintained.

4.3.1 Angular momentum redistribution

The angular momentum per unit mass is defined as

$${\cal L} = r\sin \theta ({\Omega _0}r\sin \theta + \langle {v_\phi}\rangle) = {\lambda ^2}\Omega,$$

(4)

where Ω₀ is the angular velocity of the rotating coordinate system and λ is the moment arm, λ = r sin θ. An evolution equation for \({\cal L}\) may be derived from the zonal component of the momentum equation, averaged over longitude, and the result may be written as

$$\bar \rho {{\partial {\cal L}} \over {\partial t}} = - \nabla \cdot ({{\bf{F}}^{{\rm{MC}}}} + {{\bf{F}}^{{\rm{RS}}}} + {{\bf{F}}^{{\rm{MS}}}} + {{\bf{F}}^{{\rm{MT}}}} + {{\bf{F}}^{{\rm{VD}}}}).$$

(5)

The right-hand-side includes contributions from the meridional circulation, Reynolds stress, Maxwell stress, mean magnetic fields, and viscous diffusion. Complete expressions for each of these flux terms are given in Appendix A.4.

The first term represents the advection of angular momentum by the mean meridional circulation, having the form \({{\bf{F}}^{{\rm{MC}}}} = \bar \rho \langle {{{\bf{v}}_{\rm{M}}}} \rangle {\cal L}\). The uniform rotation component of this, \(\bar \rho \langle {{{\bf{v}}_{\rm{M}}}} \rangle {\lambda ^2}{\Omega _0}\), represents the Coriolis force which redirects meridional flows into zonal flows. Within the anelastic approximation, the divergence of F^MC may also be expressed as

$$ - {\bf{\nabla}} \cdot {{\bf{F}}^{{\rm{MC}}}} = - \bar \rho \langle {{\bf{v}}_{\rm{M}}}\rangle \cdot {\bf{\nabla}} {\cal L}.$$

(6)

Thus, meridional circulations perpendicular to \({\cal L}\) contours redistribute angular momentum, tending to make \({\cal L}\) constant along streamlines. If there were a global-scale circulation cell in the solar envelope extending from low to high latitudes, it would tend to “spin up” the poles relative to the equator. This is clearly not the case in the Sun (see Figure 1), so there must be more to the story.

The net angular momentum transport through any closed surface of constant L must vanish due to the divergenceless nature of the mass flux. For similar reasons, the component of F^MC due to the uniform rotation, Ω₀, cannot transport angular momentum across cylindrical surfaces aligned with the rotation axis. This result also applies to the more general case of a cylindrical rotation profile Ω(r, θ, t) = Ω(λ, t). Any net transport of angular momentum toward or away from the rotation axis by meridional circulation must come from the advection of the non-cylindrical component of the differential rotation (see also Section 4.3.2).

It may also be noted that angular momentum transport by meridional circulation alone cannot produce localized minima or maxima in \({\cal L}\). This follows from Equation (6), since \({\bf{\Delta }}{\cal L}\) vanishes at local extrema. Isolated features in the differential rotation profile such as jets must be produced by other means.

The main driver in maintaining the solar rotation profile is thought to be the Reynolds stress, F^RS. This term represents the redistribution of angular momentum by non-axisymmetric motions, particularly convection. Rotation, stratification, magnetic fields, and the spherical shell geometry all introduce anisotropies into the flow which give rise to systematic correlations between the fluctuating velocity components. Horizontal velocity correlations 〈 υ′ _θ υ′ _ϕ 〉 produce latitudinal angular momentum transport whereas 〈 υ′ _r υ′ _ϕ 〉 correlations produce radial transport. Elucidating the nature of these correlations ranks among the greatest challenges in solar interior dynamics.

In the solar envelope, the Reynolds stress is dominated by turbulent convection, but other motions may also contribute in the tachocline and radiative interior. Convective overshoot excites a spectrum of internal wave modes, most notably gravity waves, which propagate throughout the radiative interior (see Section 8.4). In the absence of dissipation, linear waves cannot redistribute angular momentum. However, dissipation by thermal diffusion or wave breaking can induce a net angular momentum transport via the Reynolds stress which is generally long-range (non-local) and therefore difficult to model. A reliable model of wave transport requires a realistic depiction of wave generation, propagation, and dissipation, which is a formidable task due to the wide range of spatial scales involved. Other potential sources of Reynolds and Maxwell stresses include shear instabilities (see Section 8.2).

Magnetism can alter the rotation profile either by altering the Reynolds stress or by redistributing angular momentum directly via the Lorentz force. The angular momentum flux by the Lorentz force is here decomposed into contributions from fluctuating (non-axisymmetric) fields, F^MS, and mean (axisymmetric) fields, F^MT. The fluctuating component is known as the Maxwell stress and involves the nonlinear correlations 〈 B′ _θ B′ _ϕ 〉 and 〈 B′ _r B′ _ϕ 〉 Like the Reynolds stress, these may arise from turbulent convection, waves, or instabilities, and understanding their nature is every bit as challenging. The mean-field contribution is more straightforward and can be expressed as

$$ - {\bf{\nabla}} \cdot {{\bf{F}}^{{\rm{MT}}}} = {1 \over {4\pi}}\langle {{\bf{B}}_{\rm{M}}}\rangle \cdot {\bf{\nabla}} (\lambda \langle {B_\phi}\rangle).$$

(7)

In this manner, a mean poloidal field < B_M > will resist deformation in the zonal (ϕ) direction because of the magnetic tension force. This “rubber band effect” will tend to reduce angular velocity gradients. The Maxwell stress may also have a similar “stiffening” effect due to magnetic tension (see Section 6.5).

The viscous contribution, F^VD, is negligible in the Sun but can be significant in numerical and theoretical models (see Section 6.3). This term opposes angular velocity gradients, F^VD ∝ − ∇Ω, driving the system toward uniform rotation.

The primary angular momentum balance in the Sun is thought to be between the Reynolds stress and meridional circulation, with a lesser role played by the Lorentz force. Thus, if the differential rotation is in a statistically steady state, we expect the following to hold, at least in an approximate and time-averaged sense:

$${\bf{\nabla}} \cdot {{\bf{F}}^{{\rm{RS}}}} = - {\bf{\nabla}} \cdot {{\bf{F}}^{{\rm{MC}}}}.$$

(8)

It has been realized for decades that this balance is likely to hold in the solar envelope (e.g., Tassoul, 1978; Zahn, 1992, and references therein) but there had been little further progress until recently, thanks to new insights from helioseismology and high-resolution numerical simulations. Now the specific angular momentum profile, \({\cal L}\), is well-established from global helioseismic inversions (see Figure 1). The meridional circulation is still only known reliably in the solar surface layers (see Section 3.4) but plausible profiles which are consistent with these surface results can be used to compute possible forms for F^MC. Equation (8) may then be used to determine the corresponding Reynolds stress divergence. In other words, if we take the inferred differential rotation profile from helioseismology, we can determine what the Reynolds stress must be doing in order to maintain that profile against redistribution by some assumed meridional circulation. An illustrative example is shown in Figure 6.

Open image in new window

Although the angular velocity in the solar envelope, Ω, varies by ∼ 30% from equator to pole and exhibits nearly radial contours at mid-latitudes (Figure 6, panel a), the corresponding specific angular momentum, \({\cal L} = {\lambda ^2}\Omega\), is approximately cylindrical (Figure 6, panel b). The hypothetical meridional circulation pattern shown in panel c of Figure 6 would redistribute this angular momentum as shown in panel d of Figure 6. Thus, if the balance expressed in Equation (8) holds, the Reynolds stress must act to accelerate the lower convection zone and equatorial regions and to decelerate the upper convection zone in order to offset the advection of angular momentum by the meridional circulation. Any self-consistent mean-field model which exhibits a solar-like differential rotation profile as shown in panel a of Figure 6 and a single-celled meridional circulation pattern as shown in panel c of Figure 6 must include a Reynolds stress parameterization which redistributes angular momentum as shown in panel d of Figure 6 (unless the Lorentz force plays a significant role).

The results shown in Figure 6 are easily generalized to more complicated circulation patterns. If the angular momentum transport by Reynolds stress is to maintain a balance, it must converge wherever the circulation is away from the rotation axis and diverge wherever it is toward the rotation axis. This is best demonstrated by expressing the meridional circulation flux divergence as in Equation (6) and by noting that \({\bf{\Delta }}{\cal L}\) is directed away from the rotation axis. Another perspective can be gained by turning the problem around. For a given model of the Reynolds stress, helioseismic rotation profiles can be used to deduce the meridional circulation needed to maintain an equilibrium. This has been done by Durney (2000a).

If the anelastic equations are solved in a spherical shell with impenetrable, stress-free boundaries, and if the magnetic field is assumed to be radial at the boundaries, then there is no net torque and the total angular momentum of the shell, \(\int\bar{\rho}{\cal L}dV\), is conserved. This is of course just an approximation. In actuality, coupling between the convective envelope and the radiative interior may play a role in the global angular momentum balance (Section 7.3). Angular momentum exchange between the convection zone and the solar atmosphere is likely less important on dynamical timescales, although it is believed that the Sun has lost a large fraction of its initial angular momentum over the course of its lifetime via the solar wind.

4.3.2 The Taylor-Proudman theorem and thermal wind balance

In the previous section we discussed the mechanisms which can redistribute angular momentum in the solar interior, giving rise to differential rotation. There is more we can say about the angular momentum balance which may eventually be achieved if we consider the limit of rapid rotation³ such that Ro ≪ 1, where the Rossby number is defined as

$${\rm{Ro}} \equiv {U \over {2{\Omega _0}r}},$$

(9)

where U is a characteristic velocity scale relative to the rotating reference frame. We neglect viscous diffusion and the Lorentz force, and we assume that the mean flows are in a statistically steady state. With these approximations, the momentum Equation (40) expresses what is called geostrophic (or heliostrophic) and hydrostatic balance:

$$2{{\bf{\Omega}}_0} \times {\langle {\bf{v}} \rangle _{\phi, t}} + {{{\bf{\nabla}} {{\langle P \rangle}_{\phi, t}}} \over {\bar \rho}} + {{{{\langle \rho \rangle}_{\phi, t}}g} \over {\bar \rho}}\hat r = 0.$$

(10)

If we compute the zonal component of the curl of Equation (10), we obtain, with a little manipulation:

$${{\bf{\Omega}}_0} \cdot {\bf{\nabla}} \Omega = {1 \over {2\bar \rho r\lambda}}\left({H_\rho^{- 1}{{\partial {{\langle P \rangle}_{\phi, t}}} \over {\partial \theta}} - g{{\partial {{\langle \rho \rangle}_{\phi, t}}} \over {\partial \theta}}} \right) = {g \over {2{C_P}\lambda r}}{{\partial {{\langle S \rangle}_{\phi, t}}} \over {\partial \theta}}.$$

(11)

The final equality in Equation (11) holds if the reference state is approximately adiabatic and hydrostatic. A more general reference state can be incorporated by interpreting the latitudinal gradient on the right-hand-side as the mean gradient on isobaric (constant pressure) surfaces.

Equation (11) is the well-known Taylor-Proudman theorem (e.g., Pedlosky, 1987), as it applies to the solar differential rotation. If the stratification is perfectly adiabatic (∂S/∂θ = 0), this equation implies that the rotation profile should be cylindrical, i.e., contours of angular velocity Ω should be parallel to the rotation axis, Ω₀. Alternatively, if significant latitudinal entropy gradients are present, then the Taylor-Proudman balance expressed by Equation (11) implies non-cylindrical rotation profiles, such that relatively warm poles (∂S/∂θ < 0 in the northern hemisphere) correspond to a decrease in angular velocity toward higher latitudes (Ω₀·∇Ω < 0). In other words, latitudinal gradients of entropy (or density or temperature) on isobaric surfaces will tend to establish a non-cylindrical differential rotation.

If the rotation profile satisfies Equation (11) it is said to be in thermal wind balance, in analogy with the thermal wind of geophysical fluid dynamics (Pedlosky, 1987). More specifically, the thermal wind component of the differential rotation is the component which is non-cylindrical and which satisfies Equation (11).

In a thermal wind, departures from cylindrical symmetry are maintained by latitudinal entropy gradients. This is consistent with the angular momentum Equation (5) because if the Taylor-Proudman balance is satisfied perfectly, then both the Reynolds stress and the meridional circulation are negligible (as are the Lorentz and viscous forces), so Equation (5) becomes degenerate. However, meridional circulations are the means by which the thermal wind balance is established and maintained in a rapidly-rotating fluid shell. An imbalance in Equation (11) will drive circulations which will redistribute angular momentum until balance is achieved.

In the solar envelope, latitudinal entropy gradients may be established by the influence of rotation on the efficiency of the convection. For example, if convection is more efficient in the polar regions where the rotation vector is nearly vertical, then these regions will be relatively warm. In radiative equilibrium (the net energy flux into the convection zone equals the net flux out through the surface), such efficiency variations must be balanced by latitudinal energy transport as reflected by Equation (2). Thus, the role played by anisotropic energy transport in maintaining the solar differential rotation may potentially be as important as that played by the Reynolds stress, and may be just as enigmatic.

If the solar differential rotation were in thermal wind balance, we would expect thermal variations of a few parts in 10⁶ as shown in Figure 7. If we neglect the pressure contribution to the latitudinal entropy gradient as a first approximation, the resulting temperature variations are about 5 K, increasing from equator to pole (Figure 7, panel b). Thus, if helioseismic inversions were to detect relatively warm poles near the base of the convection zone, this could be interpreted as evidence for thermal wind balance. However, the implied variations are still below the sensitivity limits of current inversions (Section 3.7).

Open image in new window

4.4 Maintenance of meridional circulation

In a compressible fluid, buoyancy cannot generate vorticity directly. However, if the mass flux is divergenceless as in the anelastic approximation, buoyancy can induce overturning circulations as reflected by the term G^BF. In the present context, these may be regarded as axisymmetric convection cells. The Lorentz force may only induce mass flux circulations through magnetic tension, (B·∇)B. This effect is contained in the term G^MT which includes contributions both from fluctuating fields (the Maxwell stress) and from mean fields.

In the Sun the rotational component of G^AD (that involving ω_rot) plays an important role, particularly at low latitudes where the prograde differential rotation is forced outward by the Coriolis force and subsequently turns poleward in the surface layers (see Section 6.4). The buoyancy and Reynolds stress terms (G^BF,G^RS) are also likely to be important (see Section 6.4).

In our anelastic formulation, we have neglected the centrifugal force. It is known that the centrifugal force can produce axisymmetric motions, often called Eddington-Sweet circulations, in the radiative zones of stellar interiors due to the distortion of the gravitational potential surfaces relative to surfaces of constant temperature (e.g., Tassoul, 1978). The mixing of chemicals and angular momentum by such circulations may have important consequences for stellar evolution models or for the relatively “slow” dynamics which may contribute to tachocline confinement (Section 8.5). However, Eddington-Sweet circulations are insignificant in the convection zone and upper tachocline. Measured meridional flows in the solar surface layers imply turnover timescales of years to decades, much longer than the Eddington-Sweet timescale which is more than 10⁶ yr.

In the solar convection zone, the advection of angular momentum by meridional circulation is thought to balance angular momentum transport by the Reynolds stress as expressed by Equation (8). Thus, if the Reynolds stress and rotation profile are given, this equation may similarly be used to determine the equilibrium meridional circulation. However, the thermal wind component of the differential rotation discussed in Section 4.3.2 is independent of the meridional circulation profile. The equation for thermal wind balance (11) may be derived from the meridional circulation maintenance Equation (15) if the uniform rotation component of \({G^{{\rm{AD}}}}(- 2\bar \rho \langle {{v_\phi }} \rangle {{\bf{\Omega }}_0})\) balances the buoyancy term G^BF and if geostrophic balance [Equation (10)] is assumed. Under these conditions, the maintenance Equation (15) becomes independent of ϖ.

4.5 The solar dynamo

As discussed in Sections 1 and 4.2, the magnetic fields which drive solar variability are thought to be generated by fluid motions in the convection zone and tachocline. Kinetic energy is converted to magnetic energy via hydromagnetic dynamo processes and this flux subsequently emerges from the surface, playing a central role in the dynamics of the solar atmosphere and heliosphere.

There are many recent reviews on the solar dynamo so there is no need for a detailed discussion here. For a comprehensive overview of solar dynamo theory as a whole an excellent place to start is the recent article by (Ossendrijver, 2003). Mean-field models of the solar activity cycle are reviewed in these volumes by Charbonneau (2005). Tobias (2004) focuses on the role of the solar tachocline in particular. Further details and perspectives on solar and stellar dynamos are provided by Weiss (1994), Mestel (1999), Schrijver and Zwaan (2000), and Rüdiger and Hollerbach (2004). Dynamo theory from a more general astrophysical perspective has been reviewed comprehensively by Moffatt (1978), Parker (1979), Childress and Gilbert (1995), and most recently by Brandenburg and Subramanian (2004).

The term involving ε represents field generation by turbulent convection or other processes, such as shear instabilities (see Section 8.2). Note that our derivation of Equation (20) involves no additional approximations beyond the standard anelastic (or compressible) MHD equations. However, this equation is the starting point for mean-field dynamo theory in which additional approximations are made in order to make the system more tractable. In many mean-field models the rotation profile Ω and the meridional circulation 〈v_M〉 are specified and the Lorentz force is neglected, making the approach kinematic. Some type of parameterization is then introduced for the turbulent emf ε and Equation (20) is solved for 〈B〉.

In analogy with Equation (22), we will in this paper loosely refer to the α-effect in the general sense of field generation via the turbulent emf term in Equation (20). This does not necessarily imply that the parameterization in Equation (22) is an accurate one. In practice, solar dynamo processes may be much more subtle than this simple expression suggests (see Section 6.5). Still, the classical α-effect is a useful concept and remains an important ingredient of dynamo theory.

Unlike the Ω-effect, the α-effect can work both ways: it may convert toroidal field energy to poloidal field energy or vice versa. The field conversion and amplification process is often associated with vorticity and shear as in the classical scenario, first described by Parker (1955), in which field lines are lifted and twisted by helical eddies. In the special case of homogeneous, pseudo-isotropic turbulence, the a parameter is directly proportional to the mean kinetic helicity of the flow, H_k = 〈ω·v〉 (Moffatt, 1978; Ossendrijver, 2003). Rotation induces vorticity and breaks the reflection symmetry of the fluid equations, so rotating flows are generally helical and tend to be efficient dynamos, although rotation is not required for sustained dynamo action (Cattaneo et al., 2003).

Although Equation (20) only strictly applies to the mean (longitudinally-averaged) field (or some other suitable spatial or ensemble average), similar processes also operate on fluctuating (non-axisymmetric) fields. All toroidal field structures are amplified to some extent by rotational shear and processes akin to the (generalized) α-effect generate magnetic energy on a wide range of spatial scales. Most solar dynamo models focus on the axisymmetric component of the field but observations indicate that the magnetic field structure in the solar photosphere and corona is quite complex, with a large non-axisymmetric component (see Section 3.8 and Figure 4). Solar variability is dominated not by mean fields but by localized structures such as active regions, filaments, and coronal loops.

Our current paradigm for how the solar dynamo operates is illustrated in Figure 8. The density stratification tends to make solar convection highly anisotropic, characterized by relatively weak, broad upflows amid a complex, evolving network of strong downflow lanes and plumes (0). Turbulent downflow plumes possess substantial vorticity and helicity which may amplify fields through the α-effect (1). These fields are then pumped downward by the anisotropic convection and accumulate in the overshoot region and tachocline (2). Intermittent plumes may dredge up some of this flux and return it to the convection zone where it may be further amplified and again pumped down. Differential rotation in the tachocline stretches and amplifies this disorganized field into strong, coherent toroidal flux tubes and sheets (3). As the field becomes stronger, it eventually becomes buoyantly unstable and rises toward the surface (4). The Coriolis force acting on these rising structures twists them in a systematic way which depends on latitude (5). Weaker structures may be shredded by turbulent convection in the envelope and the flux is then recycled (6). Stronger fields and configurations (e.g., twisted tubes) remain coherent throughout the convection zone and emerge from the surface as bipolar active regions (7). Large-scale poloidal fields may be generated by the α-effect (1) or by the turbulent diffusion of surface flux after the tubes have emerged (7). Due to the manner in which field is amplified by the Ω-effect (3) and to the tilts induced in surface active regions due to the Coriolis force (5), surface diffusion would tend to build large-scale poloidal fields opposite in sign to the prevailing field, eventually producing a global polarity reversal.

Open image in new window

This schematic picture of the solar dynamo is compelling but highly simplified. In actuality, each of the processes identified in Figure 8 is complex and researchers are only beginning to understand how they work in detail.

5.1 The challenge

The molecular viscosity in the solar interior may be estimated by ν ∼ 1.2×10⁻¹⁶ ∼ T^5/2ρ⁻¹ cm² s⁻¹, which is valid for a fully ionized hydrogen plasma, neglecting the contribution due to radiation (Parker, 1979). This yields ν ∼ 1 cm² s⁻¹ in the upper convection zone, rising to somewhat higher values near the tachocline. If giant cells have an amplitude of U ∼ 100 m s⁻¹ and scales of L ∼ 200 Mm, this implies Reynolds numbers of R_e = UL/ν ∼ 10¹⁴. In other words, inertia dominate over viscous dissipation, making solar convection strongly nonlinear and thus highly turbulent.

Although solar convection is certainly not homogeneous and isotropic, a rough estimate of the viscous dissipation scale d_v can be obtained by assuming a classical Kolmogorov inertial range (e.g., Lesieur, 1997). The result is \({d_{\rm{v}}}\sim LR_{\rm{e}}^{ - 3/4}\sim 1\;{\rm{cm}}\) — more than ten orders of magnitude smaller than the solar radius! As in most other astrophysical and geophysical systems, direct numerical simulations which capture all the dynamical scales of the system are not feasible because computers simply are not efficient enough to perform all the necessary calculations.

The thermal and magnetic dissipation scales are larger than the viscous dissipation scale but are still beyond the resolution of a global numerical model. We can estimate the magnetic diffusivity by again assuming a fully ionized hydrogen plasma where η = 10¹³ ∼ T^−3/2 cm² s⁻¹ (Parker, 1979). In the solar interior, radiative diffusion dominates over thermal conduction, giving rise to an effective thermal diffusivity of \({\kappa _{\rm{r}}} = 16{\sigma _{{\rm{sb}}}}{T^3}/(3\chi {\rho ^2}{C_P})\), where σ_sb is the Stefan-Boltzman constant and χ is the opacity (Hansen and Kawaler, 1994). Entering values from a solar structure model (model S of Christensen-Dalsgaard, 1996) yields κ_r ≈ η ∼ 10⁵ cm² s⁻¹ near the surface, with κ_r increasing to ∼ 10⁷ cm² s⁻¹ and η decreasing to ∼ 10³ cm² s⁻¹ in the tachocline. These values imply low Prandtl and magnetic Prandtl numbers: P_r = ν/κ ∼ 10⁻³ −10⁻⁶ and P_m = ν/η ∼ 10⁻⁵ −10⁻⁶. The corresponding thermal and magnetic dissipation scales are then several meters to several kilometers.

If motions in the Sun were self-similar then the large dynamical range might not be a problem (see Section 7.2). Although this may be a good approximation for the smallest scales, it does not apply throughout because qualitatively different dynamics occur over a wide range of scales in the solar interior. On the largest scales ∼ 1000 Mm, we have differential rotation and meridional circulation which require the full spherical geometry to be investigated in detail. In the solar surface layers, the strong stratification coupled with ionization and radiation effects drives much smaller-scale motions including granulation (∼ 1 Mm) and supergranulation (∼ 30 Mm). Relatively small-scale motions are also driven by the strong rotational shear and the stiff transition from subadiabatic to superadiabatic stratification at the base of the convection zone, where the region of convective overshoot is thought to be less than 10 Mm thick (Sections 3.6 and 8). In between, in the bulk of the convection zone, we have so-called giant cells (Section 3.5) which likely occupy a wide dynamic range from hundreds of Mm where most of the buoyancy driving occurs down to, at least, supergranulation scales (Section 7.1). The coupling between the bulk of the convection zone and the distinct dynamics occurring in the upper and lower interface regions and beyond is a challenging problem which remains poorly understood (Section 7.3).

The range of temporal scales which characterize solar interior dynamics is every bit as daunting as the range of spatial scales. Granulation evolves over the course of a few minutes, which is comparable to the oscillation frequency of acoustic waves (∼ 5 min). Supergranulation timescales in the surface layers and gravity wave periods in the radiative interior are both somewhat longer — about one day and several hours, respectively. Turnover timescales of giant cells are thought to be comparable to the rotation period of about a month, but substantial evolution likely occurs over the course of days and weeks (Section 6.2). These giant cells likely play a crucial role in the 22-year solar activity cycle (Section 3.8), which must be the ultimate target of any comprehensive dynamical model of the solar interior. Variations of this activity cycle such as the well-known Maunder minimum are known to occur on timescales of centuries or millennia (e.g., Usoskin and Mursula, 2003; Charbonneau, 2005). Meanwhile, thermal relaxation timescales are hundreds of millennia (Section 4.2) and spin-down of the Sun due to magnetic braking and angular momentum loss in the solar wind occurs on still longer timescales — millions to billions of years!

From a modeling perspective, the vast dynamic range of spatial and temporal scales is the most challenging aspect of solar interior dynamics; no single model can hope to capture all the relevant processes. Some approximations must be made.

5.2 numerical simulations

High-resolution numerical simulations provide a powerful means by which to investigate the diverse and complex dynamics occurring in the solar interior. They have as their basis the fundamental equations of mass, energy, and momentum conservation in a magnetized or neutral fluid and explicitly resolve nonlinear interactions over a wide range of spatial scales. As such, they can capture dynamical processes which lie outside the scope of other modeling approaches and they have therefore become an essential tool in solar physics and throughout turbulence research (e.g., Pope, 2000).

Global-scale phenomena such as differential rotation and the solar activity cycle must ultimately be studied using global models. However, in light of the formidable computational challenges highlighted in Section 5.1, much progress can still be made by considering local Cartesian domains intended to represent a small subvolume of the solar envelope. The results, limitations, and promise of global convection simulations will be reviewed at length in Sections 6 and 7.

Although many high-resolution local simulations of solar convection focus on dynamics in the surface layers such as granulation and its interaction with magnetic fields (Weiss et al., 1996, 2002; Stein and Nordlund, 1998, 2000; Hurlburt et al., 2002; Vögler et al., 2005; Rincon et al., 2005), others are concerned with more fundamental fluid dynamical processes which occur throughout the convection zone. These models have been based either on the fully compressible fluid equations (Cattaneo et al., 1991; Brummell et al., 1996, 1998; Brandenburg et al., 1996; Stein and Nordlund, 1998; Porter and Woodward, 2000; Tobias et al., 2001; Brummell et al., 2002b; Ziegler and Rüdiger, 2003) or on the Boussinesq approximation where the compressibility of the fluid is neglected outside of the buoyancy driving (Julien et al., 1996a, b; Weiss et al., 1996, 2002; Cattaneo, 1999; Cattaneo et al., 2003). This is in contrast to recent global models which are based on the anelastic equations described in Appendix A.2. Anelastic models have been developed in local domains but these have thus far focused mainly on the dynamics of magnetic flux structures rather than convection (reviewed by Fan, 2004).

With a few exceptions (e.g., Porter and Woodward, 2000), most local models employ spectral methods for the horizontal dimensions which are treated as periodic. The Cartesian geometry permits the use of fast Fourier transforms (FFTs) which are more computationally efficient than the Legendre transforms necessary for the spherical harmonic algorithm currently used in global simulations. Because of this greater efficiency and the simplified geometry, local models can generally achieve somewhat higher resolution and more turbulent parameter regimes than global simulations and are therefore well equipped to study the fundamental coupling between turbulent convection, rotation, and magnetic fields.

Local simulations were the first to demonstrate the granulation-like character of turbulent compressible convection; broad, relatively weak, relatively laminar upflows surrounded by a network of strong turbulent downflow lanes and plumes where vorticity and magnetic fields are highly concentrated. These strong vortical downflow plumes were identified as the dominant structures of the flow which could remain coherent over multiple density scale heights. Although Boussinesq simulations are symmetric about the mid-plane, they also exhibit an interconnected network of lanes and plumes flowing away from the boundaries which resembles granulation near the top of the layer (e.g., Cattaneo et al., 2003).

Brummell et al. (1996, 1998) found that in the presence of rotation, turbulent plumes tend to align with the rotation axis, altering the Reynolds stress relative to more laminar flows. Quasi-2D vortex interactions among plumes, enhanced by rotation, alter their entrainment and transport properties (Julien et al., 1996a, 1999; Brummell et al., 1996). In particular, vortex interactions can lead to enhanced horizontal mixing and a decorrelation of the temperature and vertical velocity in a plume, reducing the buoyancy driving. The resulting decrease in the convective enthalpy and kinetic energy flux must be compensated by thermal diffusion, leading to a larger superadiabatic entropy gradient in the convection zone relative to comparable non-rotating flows. The Boussinesq simulations by Julien et al. (1996a, 1999) possess both upward and downward plumes which dominate the convective heat flux even though they have a small filling factor. However, downward plumes dominate in compressible flows with a substantial density stratification and the resulting downward kinetic energy flux can nearly balance the upward enthalpy flux such that the plumes contribute little to the net vertical energy transport (Cattaneo et al., 1991). This asymmetry between upflows and downflows also leads to a net downward pumping of magnetic fields from the convection zone to the stably-stratified radiative interior, a process which has also been investigated in detail with local simulations (Brandenburg et al., 1996; Tobias et al., 2001; Dorch and Nordlund, 2001; Ziegler and Rüdiger, 2003).

The highest-resolution simulations of solar convection to date have achieved roughly 1000³ spatial grid points. Thus, even the most ambitious models can only capture a fraction of the vast dynamic range which characterizes solar interior dynamics (Section 5.1). For this reason, all simulations of solar convection should be viewed as large-eddy simulations (LES) in which unresolved subgrid-scale (SGS) processes must be parameterized or otherwise modeled (Section 7.2). Most current models simply treat unresolved motions as an effective turbulent diffusion of momentum, heat, and magnetic fields which is many orders of magnitude larger than the molecular diffusion. Thus, such simulations may also be regarded as direct numerical simulations (DNS) of a hypothetical physical system which is not the Sun.

5.3 Reduced models

High-resolution numerical simulations have become invaluable research tools but they do have their limitations. Because of the computational expense, it is difficult to comprehensively explore the sensitivity of the solutions to parameter values, boundary conditions, and the influence of dynamics which are unresolved or otherwise beyond the scope of the model. Furthermore, it is difficult to investigate relatively slow dynamics such as long-term modulations of the solar activity cycle or the spin-down of a star over the course of its main-sequence lifetime. For these and other purposes, a variety of reduced models have been devised, which are based on some approximated form of the full 3D equations of motion.

The most common approach is to average the equations of motion, generally over longitude, and then to introduce parameterizations for the nonlinear advection terms, including the Reynolds stress, the convective energy fluxes [\({\cal F}^{{\rm EN}}\) and \({\cal F}^{{\rm KE}}\); see Equation (2)], and the turbulent emf (Section 4.5). These parameterizations may themselves be nonlinear and they may introduce additional variables and additional prognostic equations, but they are designed to be more analytically or computationally tractable than the full, 3D equations of motion. The reduced equations are then solved to obtain the structure and evolution of the mean fields which are the quantities of interest. In a solar physics context, this approach is often referred to as mean-field hydrodynamics or mean-field dynamo modeling but it is closely related to what in the turbulence community is called Reynolds-averaged Navier-Stokes (RANS) modeling.

If one specifies the coefficients ν_V, ν_H, Λ_V, and Λ_H and also the meridional circulation, then Equation (5) may be solved numerically to obtain the equilibrium rotation profile (neglecting the Lorentz force). A more self-consistent approach would be to solve the angular momentum equation together with the longitudinally-averaged meridional momentum and thermal energy equations to obtain the full mean flow and thermodynamic fields. In order to do this, similar parameterizations must be introduced to represent the meridional Reynolds stress and the convective heat flux.

Although an anisotropic viscosity alone can induce mean flows, the differential rotation in many mean-field models is driven mainly by either the Λ-effect or by latitudinal variations in the convective heat flux which may drive a thermal wind (Section 4.3.2). The importance of the latter effect in particular has recently been emphasized by Kitchatinov and Rüdiger (1995) and Durney (1999).

As an example of a multi-equation RANS approach, we consider the κ-∊ model which is commonly used in industrial applications (e.g., Pope, 2000; Durbin and Pettersson Reif, 2001). Here the Reynolds stress is expressed in terms of an isotropic turbulent viscosity which is proportional to \(E_{{\rm k}}^{2}/\epsilon\) where E_k is the kinetic energy of the fluctuating velocity field and ∊ is the energy dissipation rate, which is assumed to be scale-invariant within a self-similar inertial range. This expression may be justified using dimensional arguments for homogeneous, isotropic, incompressible flow at high Reynolds numbers. Diagnostic equations for E_k and ∊ may then be derived from the fluctuating flow equations or from phenomenological arguments. These equations are then solved simultaneously along with the mean-field equations.

Similar multi-equation approaches may be followed in the Sun, but they must be somewhat more sophisticated in order to take into account rotation, stratification, shear, and if they’re ambitious enough, magnetic fields. Canuto et al. (1994) have developed a Reynolds stress model based on a hierarchy of equations obtained by taking successive moments of the compressible Navier-Stokes equations and then introducing analytic closures for the highest-order moments. A multi-equation model for the convective energy flux has been developed by Canuto and Dubovikov (1998) and has been used by Marik and Petrovay (2002) to investigate the structure of the overshoot region.

Mean-field hydrodynamics in a solar context has been thoroughly reviewed by Rüdiger (1989), Canuto and Christensen-Dalsgaard (1998), and Rüdiger and Hollerbach (2004). More general reviews of turbulence modeling are given by Cambon and Scott (1999), Pope (2000), Durbin and Pettersson Reif (2001), and Hanjalić (2002).

Mean-field dynamo models are distinct from hydrodynamic models in that many of them are kinematic, based only on the mean induction equation, with a specified mean flow field and parameterizations introduced for the turbulent emf (Section 4.5). Much recent attention has focused on flux-transport dynamo models in which the meridional circulation plays a key role in setting the period of the activity cycle and in establishing emergence patterns of magnetic flux such as the butterfly diagram (Choudhuri et al., 1995; Durney, 1995; Dikpati and Charbonneau, 1999; Dikpati and Gilman, 2001a; Charbonneau, 2005). The literature on mean-field solar dynamo models is vast and we make no attempt to review it here. The reader is referred to Charbonneau (2005) and to the other references given in Section 4.5.

Many dynamo models have been developed which do consider the feedback of magnetic fields on the mean flow, often focusing on temporal variations of the differential rotation (Kitchatinov et al., 1999; Durney, 2000b; Covas et al., 2001, 2004). These models have shown that the torsional oscillations in particular (Section 3.3) are likely due to the action of the Lorentz force from the axisymmetric dynamo-generated field in relation to the activity cycle. This was first suggested by Yoshimura (1981) and Schüssler (1981) soon after the torsional oscillations were discovered.

An alternative to (or in some cases a variation of) mean-field models are phenomenological approaches which are motivated by observations, numerical simulations, or laboratory experiments. Chief among these are the various models which describe solar convection as an ensemble of turbulent plumes (Schmitt et al., 1984; Rieutord and Zahn, 1995; Rast, 2003; Rempel, 2004) or eddies (Kumar et al., 1995). Another type of phenomenological model has been proposed by Longcope et al. (2003) who consider a plasma permeated with thin flux tubes which exert a visco-elastic drag on the mean flow (see also Parker, 1985).

Although they can provide valuable insight, the main disadvantage of reduced models of any kind is that it is difficult to verify whether the parameterizations and approximations introduced are reliable representations of the underlying dynamics. The overwhelming majority of reduced models may be classified as mean-field models and of these, nearly all assume scale separation in space and/or time. There is little empirical or numerical evidence that such scale separation is valid for solar convection. Furthermore, some reduced models are not completely self-consistent. For example, the well-known α-effect parameterization commonly used in mean-field dynamo modeling is based in part on the linearity of the induction equation in B (see Section 4.5). This argument is only strictly valid if the velocity field is independent of B which cannot be the case in any real-world, sustained dynamo where the Lorentz force must react back on the flow to curb unlimited field amplification. Even so, mean-field dynamo models are quite successful at reproducing many features of the solar activity cycle, a result which might provide clues into the nature of the dynamo (see Section 6.5).

Mean-field hydrodynamics is built on a more questionable theoretical foundation than mean-field dynamo modeling. The turbulent viscosity formalism in particular is known to be inaccurate even for the simplest turbulent flows where momentum transport is often not directed down large-scale velocity gradients (e.g., Pope, 2000). Although experimental verification is difficult in a solar context, some testing and calibration of reduced models can be done by comparing them to solar and stellar observations and numerical simulations (e.g., Kupka, 1999).

In principle, there is not a large conceptual gap between mean-field/RANS models and large-eddy simulations (LES); the difference lies mainly in the nature and scale of the averaging. In practice, however, there is usually a substantial gap because mean-field models are generally 2D or much lower resolution. Still, some of the parameterizations and procedures developed for reduced approaches could be incorporated into a large-eddy simulation as a subgrid-scale model (e.g., Canuto, 2000). This will be discussed further in Section 7.2.

5.4 Thin-shell approximations for the tachocline

Another type of reduced model is designed specifically for the lower portion of the solar tachocline where the strong stable stratification inhibits vertical motions, making the dynamics quasi-two-dimensional. Here the equations of motions may be simplified by considering the thin-shell limit δ = Δ_t/r_t ≪ 1 where Δt is the thickness of the tachocline layer and r_t is the radial location. Helioseismic inversions imply that δ is of order 0.05 or less (Section 3.2).

The most extreme form of the thin-shell limit is to neglect vertical motions, magnetic fields, and gradients entirely, leaving the 2D equations of magnetohydrodynamics (MHD) in latitude and longitude. Such models have recently been used to investigate linear MHD shear instabilities in the tachocline and their subsequent nonlinear evolution (see Section 8.2).

Some degree of vertical variation can be taken into account without greatly increasing the mathematical complexity of the problem by treating the upper boundary of the layer as a free surface. In this case one can apply the so-called shallow-water (SW) equations which are commonly used in meteorology and oceanography (e.g., Pedlosky, 1987). Gilman (2000b) has generalized the SW system to include magnetic fields in order to model the stably-stratified portion of the solar tachocline. The upper boundary of this layer is the solar convection zone which is nearly adiabatically-stratified and which therefore should offer little buoyant resistance to surface deformations. This is the rationale behind the SW approach in a tachocline context.

In the SW approximation, motions are assumed to be incompressible and the vertical momentum equation reduces to magneto-hydrostatic balance. Horizontal velocities and magnetic fields are assumed to be independent of height z but unlike the 2D approach, they can possess a horizontal divergence which gives rise to vertical flows and fields. Vertical motions do not overturn; rather, they deform the outer surface. Integrating the magneto-hydrostatic equation over depth gives a direct relationship between the total pressure (gas plus magnetic) and the height of the layer. Thus, the complete SW system consists of the 2D horizontal momentum and induction equations together with another evolution equation for the layer height and divergence-free conditions for the velocity and magnetic fields.

The MHD SW equations conserve energy, mass, momentum, magnetic flux, and other quantities known as Casimir functionals (Dellar, 2002). They also support a variety of wave modes including Alfvén waves and MHD analogues of surface gravity waves (Schecter et al., 2001). Dikpati and Gilman (2001b) have used the shallow water system to investigate dynamical equilibria in the solar tachocline between pressure gradients and the magnetic tension force associated with an axisymmetric ring of toroidal flux. The poleward tension force is balanced by an equatorward pressure gradient supplied by a buildup of mass at the poles, yielding a prolate tachocline structure as suggested by helioseismic inversions (Section 3.2). Rempel and Dikpati (2003) showed that the required prolateness is reduced if the flux ring contains a zonal jet which helps balance the magnetic tension through the Coriolis force. They also showed that the SW treatment of this problem is analogous to one based on the axisymmetric MHD equations in which the latitudinal pressure gradients are supplied by deformations of the isentropic surfaces. The MHD SW equations have also been used to investigate the linear stability of the latitudinal differential rotation in the tachocline (see Section 8.2).

Another approach which has its roots in meteorology and oceanography is to explicitly take the thin-shell limit of the governing equations in a stably-stratified fluid layer, retaining the full height dependence of all flows and fields. This yields what geophysicists call the hydrostatic primitive equations (HPE) which have formed the basis of climate and ocean models for decades (e.g., Pedlosky, 1987; Salby, 1996). An MHD generalization of the HPE system has recently been developed by Miesch and Gilman (2004). This thin-shell system preserves the conservation properties of the full 3D MHD equations (energy, mass, momentum, magnetic helicity) and is dynamically rich enough to incorporate vertical shear, internal gravity waves, and stratified MHD turbulence. Yet, it is more computationally efficient and analytically accessible than the full 3D equations. For example, separation of variables in the thin-shell system has been exploited to obtain analytic results on the penetration of meridional circulation below the solar convection zone (Gilman and Miesch, 2004) and MHD shear instabilities in the tachocline (see Section 8.2).

A limitation of both the SW and the thin-shell systems is that they do not incorporate magnetic buoyancy which requires a complete vertical momentum equation. Other approximations which have been used to simplify the equations of motion in the tachocline and radiative interior include geostrophic balance and axisymmetry. Some of these approaches will be discussed in Section 8.

6.1 Historical perspective

The most conceptually straightforward approach to studying global-scale solar convection is to solve the nonlinear, 3D equations of motion in a rotating spherical shell of fluid heated from below and cooled from above. The first numerical models to do so were developed by Gilman (1977, 1978, 1983), Gilman and Miller (1981, 1986), and Glatzmaier (1984, 1985a, b, 1987). The convection structure was dominated by traveling, columnar convection cells with a north-south alignment and a periodic longitudinal structure (m ∼ 10), similar to the preferred convection modes predicted by linear theory (Busse, 1970; Gilman, 1975). These became known as banana cells because of their elongated appearance, sheared into a crescent shape by the differential rotation they established. These pioneering studies yielded great insight into the nonlinear interaction between convection, rotation, and magnetic fields, but they had limited spatial resolution and were therefore restricted to relatively laminar flows, far from the highly turbulent parameter regimes thought to exist in the solar interior (see Section 5.1).

In the two decades since, many more simulations of convection in rotating spherical shells have appeared, but most have been concerned with physical conditions which are characteristic of the Earth’s outer core and other planetary interiors (e.g., Sun and Schubert, 1995; Tilgner and Busse, 1997; Kageyama and Sato, 1997; Christensen et al., 1999; Roberts and Glatzmaier, 2000; Zhang and Schubert, 2000; Ishihara and Kida, 2002; Busse, 2002; Glatzmaier, 2002). Relative to the Sun, the Earth is rapidly rotating (smaller Rossby number), weakly compressible (smaller density contrast) and highly magnetic (strong Lorentz force). Furthermore, the geometry of the convective shell is somewhat different and physical effects such as compositional gradients and radioactivity play an important role.

In order to revisit solar convection with the latest generation of scalable parallel supercomputers, Clune et al. (1999) developed a numerical model which is now known as the Anelastic Spherical Harmonic (ASH) code. The algorithm is similar to that described by Glatzmaier (1984) and solves the 3D anelastic equations described in Appendix A.2 using a pseudospectral method with spherical harmonic and Chebyshev basis functions. Recent ASH simulations have achieved much higher resolution and subsequently more turbulent parameter regimes than the pioneering studies by Gilman and Glatzmaier referred to above. In the remainder of this section, we will focus on results obtained with the ASH code. For a description of the numerical method see Clune et al. (1999) and Brun et al. (2004). Further details on the scientific results have been reported by Miesch et al. (2000); Elliott et al. (2000); Brun and Toomre (2002); DeRosa et al. (2002) and Brun et al. (2004).

The ASH code is dimensional and uses realistic values for the solar radius, luminosity, and mean rotation rate. The reference state is based on 1D solar structure models. Since global simulations cannot capture the complex dynamics occurring in the near-surface layers (see Section 7.3), the upper boundary of the computational domain is generally placed below the photosphere, at 0.96–0.98R_⊙. For computational efficiency, the lower boundary is often placed at the base of the convection zone (see Section 7.3) but some simulations have included penetration into the radiative interior (Miesch et al., 2000).

6.2 Convection structure

Figure 9 illustrates the variety of convective patterns which have been found in high-resolution simulations of global solar convection. Three simulations are shown, including Case M3 of Brun et al. (2004), Case F of Brun et al. (2005) and Case D2 of DeRosa et al. (2002). The primary difference between Cases M3 and F is that the latter is less dissipative and therefore more turbulent (higher Rayleigh and Reynolds numbers). Case D2 is comparable to Case F but with a thin-shell geometry; the lower boundary was set at r₁ = 0.92R_⊙ as opposed to r₁ = 0.62R_⊙. Cases F and D2 both have an upper boundary at r₂ = 0.98R_⊙, somewhat closer to the solar photosphere than Case M3 (r₂ = 0.96R_⊙). Case M3 is the only one of the three which includes magnetism, although this does not have a substantial influence on the convective patterns shown in Figure 9 (Brun et al., 2004).

Open image in new window

At intermediate Rayleigh (and Reynolds) numbers, there is a marked contrast between the convective structure at low and high latitudes (Figure 9, panel a). Near the equator, the convection is dominated by extended downflow lanes oriented north-south which propagate in longitude faster than the local differential rotation (Miesch et al., 2000). These are reminiscent of the banana cells in earlier more laminar simulations (see Section 6.1) but they are not strictly periodic in longitude, they extend only to mid-latitudes, and they are asymmetric with respect to upflow and downflow due to the density stratification (cf. Section 5.2). Near the poles the convection patterns are more isotropic and homogeneous and the characteristic spatial scales are somewhat smaller.

This variation in convective patterns results arises from the influence of rotation and some insight into its origin can be gained from linear theory (Busse, 1970; Gilman, 1975; Busse and Cuong, 1977). In order to minimize the stabilizing influence of the Coriolis force, convection at low latitudes tends to favor flows which are perpendicular to the rotation axis. If the rotation is rapid, columnar convection cells are preferred which align with the rotation axis and propagate in a prograde direction due to their tendency to conserve angular momentum (or potential vorticity) under the influence of the spherical geometry and density stratification; in this sense they may be regarded as thermal Rossby waves (Glatzmaier and Gilman, 1981; Busse, 2002). At high latitudes, inside the tangent cylinder⁴ overturning motions can no longer remain perpendicular to Ω₀, resulting in more isotropic cells with smaller horizontal scales.

In more turbulent parameter regimes (higher Rayleigh and Reynolds numbers), the convection near the top of the domain exhibits a more granulation-like character across the shell as shown in panel b of Figure 9. As in simulations of turbulent compressible convection in Cartesian domains (see Section 5.2), the convection structure is dominated by an intricate, interconnected network of downflow lanes amidst broader, weaker upflows. Although the patterns appear relatively homogeneous and isotropic with little indication of banana cells, broad upwellings and extended north-south lanes still occur at low latitudes within the more intricate downflow network. These extended downflow lanes generally penetrate deeper into the convection zone than the smaller-scale network patterns (see Figure 12) and play an important role in maintaining the differential rotation (see Section 6.3). Horizontal rolls analogous to north-south downflow lanes are present in even the most turbulent Cartesian simulations of turbulent compressible convection when the rotation vector is made horizontal in order to simulate the equatorial regions (Brummell et al., 2002b).

Although these convective patterns are reminiscent of granulation or supergranulation, their scale is much larger. By eye, the predominant convective cells in panel b of Figure 9 appear to span roughly 10 angular degrees, which corresponds to a horizontal scale of 120 Mm. More localized, swirling structures are also evident near the interstices of the downflow network at midlatitudes. The power spectrum of the radial velocity field peaks at spherical harmonic wavenumbers of ℓ ∼ 50–60, which corresponds to ∼ 80 Mm. Recall that the characteristic scales of granulation and super-granulation are about 1–2 Mm and 30 Mm, respectively (Section 2.3).

Convective motions at supergranular scales have been reported in global simulations by DeRosa et al. (2002) who focused on the upper regions of the solar convection zone. Higher spatial resolution was achieved by limiting the simulation domain to radii between 0.92–0.98R_⊙ and by imposing a four-fold periodicity in longitude. The convection structure in one of these simulations is illustrated in panel c of Figure 9. The pattern exhibits a hierarchy of scales, from supergranular-scale mottling to a network of larger cells and extended north-south downflow lanes more comparable to the deep-shell simulations (cf. Figure 9, panel b). Although provocative, it is premature to identify this small-scale convection pattern too closely with supergranulation on the Sun. Solar supergranulation may involve dynamics which are not captured in these global simulations such as ionization effects or self-organization processes involving smaller-scale granules (Rast, 2003). On the other hand, although simulations of granulation with large aspect ratios exhibit structure on mesogranule scales (∼ 5 Mm), they have not yet achieved larger-scale patterns so the origin of supergranulation remains unclear (Rincon et al., 2005; see also Simon and Weiss, 1991).

In turbulent parameter regimes, the downflow network evolves rapidly, changing substantially over the course of a few days (recall that the rotation period is about a month). This is demonstrated in Figure 10 which follows the radial velocity field near the top of the convection zone in Case F. Advection and distortion of the downflow network by the differential rotation is evident, with low-latitude patterns moving eastward and high-latitude patterns moving westward relative to the rotating coordinate system. Downflow lanes continually merge and re-form as upwellings diverge and fragment. Particularly at high and mid-latitudes, numerous localized vortices appear and disappear near the interstices of the downflow network, often forming new upwellings via the centrifugal siphoning of fluid from below (Brandenburg et al., 1996; Brummell et al., 1996; Miesch, 2000). Such vortices are fed by converging horizontal flows which tend to conserve their angular momentum, spinning up in a cyclonic sense⁵ due to the Coriolis force. This results in intense, intermittent downflow plumes spinning with cyclonic vorticity.

Open image in new window

These vortical downflow plumes appear as cool spots in the temperature field as shown in panel a of Figure 11. Global temperature variations are also apparent, with equatorial and polar regions a few K warmer than mid-latitudes. The local maxima at the poles are often more pronounced in the entropy field than the temperature field, which has implications for the thermal wind component of the differential rotation (Section 6.3). The downflow network is also faintly visible in the temperature field of panel a in Figure 11; in many simulations it leaves a more noticeable imprint (e.g., Thompson et al., 2003, Figure 13).

Open image in new window

The cyclonic nature of the downflow lanes and plumes is evident in the radial vorticity field, shown in panel b of Figure 11. This pattern stands out amid a background of weaker anti-cyclonic vorticity associated with diverging upflows. As expected, the horizontal divergence field, shown in panel c of Figure 11 correlates well with the vertical velocity field shown in panel b of Figure 9. The relative magnitudes of the vortical and divergent components of the horizontal velocity field near the top of the convection zone can potentially be a point of contact between numerical simulations and helioseismic observations Section 3.5. In simulations, the two are generally comparable (the rms values of the vertical vorticity and horizontal divergence fields shown in Figure 11 are 1.6 × 10⁻⁵ s⁻¹ and 1.5 × 10⁻⁵ s⁻¹, respectively).

Deeper in the convection zone, the flow structure changes dramatically as illustrated in Figure 12. Only the strongest downflow plumes and lanes in the near-surface network penetrate to the mid convection zone and the network loses its connectivity. Cool, vortical, intermittent plumes dominate but coherent north-south downflow lanes still persist at low latitudes. In the near-surface layers, the enstrophy (vorticity squared) is dominated by the intense cyclonic vertical vorticity found in the downflow network (Figure 11, panel b). In the mid convection zone, enstrophy is still concentrated in downflows but is now dominated by horizontal entrainment vortices, forming rolls and’ smoke rings’ near the periphery of lanes and plumes (Figure 12, panel c).

Open image in new window

6.3 Differential rotation

The helioseismic and surface observations of the solar differential rotation reviewed in Section 3 present several compelling challenges to theoretical and numerical modelers:

1. 1.

   a monotonic decrease of angular velocity with latitude,

    
2. 2.

   an angular velocity contrast of about 20% (∼ 90 nHz) between the equator and latitudes of ±60°,

    
3. 3.

   nearly radial angular velocity contours at mid-latitudes throughout the bulk of the convection zone,

    
4. 4.

   narrow layers of strong vertical shear in the angular velocity near the top and bottom of the convection zone,

    
5. 5.

   periodic and non-periodic temporal variations.

    

So how are we doing? Results from a recent simulation are shown in Figure 13. On the positive side, the angular velocity exhibits a realistic latitudinal variation and contrast (Challenges 1 and 2), with little radial variation above mid-latitudes (Challenge 3). On the negative side, the low-latitude angular velocity contours are somewhat more cylindrical than suggested by helioseismology, with more radial shear. Furthermore, at present there is little tendency for simulations such as these to form rotational shear layers near the top and bottom of the convection zone (Challenge 4). Although these simulations do exhibit non-periodic angular velocity fluctuations of about the right amplitude relative to helioseismic inversions (a few percent; see Miesch, 2000; Brun and Toomre, 2002), there is currently little evidence for systematic behavior such as torsional oscillations (Challenge 5). We will now proceed to discuss the implications of these results in a little more detail.

Open image in new window

Figure 14 illustrates how the differential rotation in Case M3 is maintained in terms of the angular momentum balance expressed by Equation (5). The Reynolds stress (RS) moves angular momentum outward and equatorward, maintaining the differential rotation against viscous dissipation (VD). The advection of angular momentum by the meridional circulation (MC) also plays an important role, enhancing the outward transport by the Reynolds stress but opposing their latitudinal transport, moving angular momentum toward the poles. As might be expected, magnetic tension tends to suppress the rotational shear in both radius and latitude, but at least in this simulation, the Maxwell stress (MS) is much more effective at this than the mean poloidal field (MT) (see Section 6.5).

Open image in new window

Even in the most turbulent parameter regimes, a persistent feature of global-scale simulations of rotating convection has been the presence of extended downflow lanes at low latitudes aligned in a north-south orientation (see Section 6.2). Such flow structures naturally give rise to prograde equatorial differential rotation as demonstrated in panel a of Figure 15. The Coriolis force tends to divert eastward (prograde) flows toward the equator and westward (retrograde) flows toward the poles, leading to positive < υ′ _θ υ′ _ϕ > correlations which transport angular momentum toward the equator via the Reynolds stress [see Equation (70)]. This is reflected by the Reynolds stress contribution in panel b of Figure 14, which is efficient enough to maintain the differential rotation against meridional circulation, magnetic tension, and viscous diffusion. Similar Coriolis-induced correlations also produce radially outward transport by the Reynolds stress, but these are generally less efficient (Figure 14, panel a).

Open image in new window

Of the challenges listed at the beginning of this section, the first has been particularly difficult. Many simulations of rotating convection in spherical shells exhibit a polar vortex; prograde rotation in the polar regions which arises due to the tendency for flows to conserve angular momentum as they approach the rotation axis. Axisymmetric meridional circulations, in particular, tend to efficiently spin up the poles (see Section 4.3) as reflected by their poleward contribution in panel b of Figure 14. The Reynolds stress must oppose this tendency in order to produce a monotonic decrease in angular velocity with latitude as is apparently the case in the Sun⁶. This is more easily accomplished if the circulation does not extend all the way to the poles. Indeed, a common feature of those simulations which exhibit slow polar rotation, such as Case M3, is the absence of a single-celled meridional circulation which extends from low to high latitudes (Brun and Toomre, 2002). This may have important implications for solar dynamo models (see Section 6.4).

Thus, a polar vortex can be avoided if the meridional circulation is confined mainly to low and mid-latitudes. This will be discussed further in Section 6.4. Alternatively, if the north-south downflow lanes which are primarily responsible for equatorward angular momentum transport were to extend to higher latitudes, they may help spin down the poles. This occurs if the convection zone is made deeper, moving the tangent cylinder closer to the rotation axis (Gilman, 1979; Glatzmaier, 1987). Although this may not be very relevant for the Sun (the convection zone base is reasonably well established from helioseismic inversions, see Section 3.6), it may have implications for less massive stars which have deeper convective envelopes.

An additional complication to the problem of polar spin-up occurs when the convection is allowed to penetrate into an underlying stable region, as demonstrated in panel b of Figure 15. In turbulent parameter regimes, the convection is dominated by downflow plumes and lanes which acquire cyclonic vorticity in the upper convection zone due to the tendency for converging horizontal flows to conserve their angular momentum (see Section 6.2). As these plumes move deeper into the convection zone, they may converge further due to the density stratification and thus spin up even more (although this convergence may be partially suppressed by entrainment, which has a spreading effect). When the plumes reach the overshoot region, they are decelerated by buoyancy and mass is spread out horizontally and redirected into upflows. The Coriolis force acting on these diverging downflows induce anticyclonic vorticity, leading to a sign reversal of the helicity (Miesch et al., 2000).

These downflow plumes are not purely radial. Rather, the influence of the Coriolis force tends to orient them toward the rotation axis in a process known as turbulent alignment (Brummell et al., 1996). Thus, when buoyancy removes the plumes’ vertical momentum in the overshoot region, they have a residual horizontal momentum which diverts them toward the equator. The combination of anticyclonic vorticity and equatorward circulation gives rise to a convergence of angular momentum flux from the Reynolds stress, F^RS, at high latitudes, which tends to spin up the poles. In other words, angular momentum transport in the overshoot region is generally poleward. The meridional circulation component, F^MC, enhances this poleward transport. As a result, sufficiently turbulent global-scale simulations of solar convection which include convective penetration tend to exhibit relatively fast polar rotation (Miesch et al., 2000, 2004). Thus, the slow polar rotation in the Sun remains somewhat enigmatic, although some non-penetrative simulations like Case M3 do a reasonably good job. One possibility is that the transition from sub-adiabatic to super-adiabatic stratification in the penetrative convective simulations is not yet sharp enough (see Section 7.1).

The second challenge listed above has been less problematic; many simulations exhibit an angular velocity contrast between the equator and higher latitudes of about the right amplitude relative to the Sun (∼ 20–30%). However, the third challenge, that of nearly radial angular velocity contours, has proven every bit as difficult as the first. As discussed in Section 4.3, there are two ways to break the tendency for cylindrical angular velocity contours: the Reynolds stress (i.e., the effective Rossby number is not small), and baroclinic driving (latitudinal entropy gradients), which can establish a thermal wind.

Figure 16 illustrates the relative importance of these two contributions in a simulation which exhibits a solar-like rotation profile (Challenges 1–3 are nearly met). This is Case AB of Brun and Toomre (2002), which is a close relative of Case M3 but is non-magnetic. Frames (a) and (b) illustrate the mean zonal velocity and its gradient along the rotation axis. If the differential rotation were in thermal wind balance, then this axial gradient (Figure 16, panel b) would be equal to the baroclinic term on the left-hand-side of Equation (11), which is shown in panel c of Figure 16⁷. The departure from thermal wind balance is demonstrated in panel d of Figure 16.

Open image in new window

The conclusion to be drawn from Figure 16 is that the non-cylindrical component of the angular velocity profile satisfies thermal wind balance in the lower convection zone, but not in the upper convection zone. There the Reynolds stress is responsible for the axial angular velocity gradients. Thus, simulations which come closest to meeting Challenge 3 above do so both by redistributing angular momentum via the Reynolds stress and by establishing latitudinal entropy gradients via anisotropic convective heat transport.

We emphasize that the ASH code was not tuned in any way to achieve the results shown in Figure 13 and elsewhere. The simulations typically begin from uniform rotation or from previous simulations with different parameter values. Boundary conditions are generally stress-free so angular momentum is conserved and uniform-flux or uniform-entropy so a thermal wind is not artificially driven. The subgrid-scale models are purely diffusive. Mean flows and thermal gradients are established solely via momentum and entropy transport by turbulent convection under the influence of rotation. Still, some parameter regimes and boundary conditions do marginally better than others. Low Prandtl numbers (∼ 0.25) tend to produce the most solar-like angular velocity contrasts (Challenge 2) and tend to avoid large-scale meridional circulations which can spin up the poles (Challenge 1). Fixing the heat flux at the boundaries rather than the entropy is more conducive to establishing latitudinal entropy gradients which can help to break the tendency for cylindrical rotational profiles, as discussed above (Challenge 3). Although recent results show a substantial improvement over the early, relatively low-resolution simulations by Gilman and Glatzmier (see Section 6.1), higher Reynolds and Rayleigh numbers do not necessarily yield more solar-like profiles. This may be because the north-south downflow lanes in more turbulent simulations are more confined to lower latitudes than in laminar simulations. Since these structures are primarily responsible for equatorward angular momentum transport as discussed above, the net result is often relatively fast polar rotation and a reduced angular velocity contrast. For further elaboration see Miesch (2000), Elliott et al. (2000) and Brun and Toomre (2002). See also Section 7 where possible resolutions to these issues are discussed.

Global convection simulations are only beginning to address the complicated issues surrounding challenge number 4 above, regarding rotational shear layers. Still, some progress has been made in understanding the speedup of angular velocity below the photosphere, inferred from helioseismic inversions and previously from tracer measurements (see Section 3.1). A plausible origin for this layer is in the tendency for the more vigorous convection in the solar surface layers to conserve angular momentum, spinning up as it approaches the rotation axis. This was first suggested by Foukal and Jokipii (1975) and has generally been borne out in convection simulations by Gilman and Foukal (1979) and more recently by DeRosa et al. (2002). However, these simulations were confined to the upper convection zone; deep shell simulations thus far show little tendency to form near-surface shear layers. Global convection simulations also have yet to form strong shear layers near the base of the convection zone which are comparable in structure to the solar tachocline. This may be because the viscous diffusion is too large and the spatial resolution is insufficient to capture small-scale dynamics occurring in the overshoot region (Section 7). Furthermore, the simulations may have insufficient temporal duration to capture the possibly long-term dynamics which drive the radiative interior toward uniform rotation (see Section 8.5).

Global simulations do not yet exhibit periodic temporal variations such as the solar torsional oscillations discussed in Section 3.3. However, similar torsional oscillations do arise naturally in mean-field dynamo models when the back reaction of the Lorentz force on the differential rotation is taken into account (Yoshimura, 1981; Schüssler, 1981; Kitchatinov et al., 1999; Durney, 2000b; Covas et al., 2001, 2004; Bushby and Mason, 2004). An alternative possibility was recently proposed by Spruit (2003) who argues that torsional oscillations may be a surface phenomenon which arise as a geostrophic flow response to thermally-induced latitudinal pressure gradients associated with belts of magnetic activity. Shorter-period tachocline oscillations may arise from the spatiotemporal fragmentation of torsional oscillations (Covas et al., 2001, 2004) or from the interaction of gravity waves with differential rotation (Section 8.4). Oscillatory shear instabilies may also play a role (Section 8.2).

As a final comment to close this section, we note that the five challenges posed here are in all likelihood intimately connected. Since the radiative interior possesses much more mechanical and thermal inertia than the convective envelope, the differential rotation in the convection zone may be sensitive to the complex dynamics occuring in the tachocline. In other words, we may not fully understand the rotation profile in the convection zone until we get the tachocline right. A realistic tachocline is probably also a prerequisite to achieving the solar-like dynamo cycles and wave-mean flow interactions which appear to be responsible for torsional and tachocline oscillations. These issues will be discussed further in Section 7.3.

6.4 Meridional circulation

In numerical simulations, as in the Sun, the meridional circulation is weak relative to the differential rotation. The kinetic energy is typically smaller by about two orders of magnitude. Sample profiles are illustrated in Figure 17 for case M3 and case P, which is a continuation of Case TUR of Miesch et al. (2000), with increased resolution and lower dissipation⁸.

Open image in new window

The first thing to note about the profiles shown in Figure 17 is that they are much more spatially complex than is assumed in many kinematic dynamo models and other applications. Multiple cells are present in both latitude and radius, and flow patterns are generally not symmetric about the equator. The temporal dependence is equally complex, exhibiting large fluctuations on timescales of weeks and months, as shown in Figure 18. This spatial and temporal complexity can be attributed to the turbulent nature of the convection and to the sensitivity of the meridional circulation to small variations in the differential rotation and Reynolds stress, as will be discussed further later in this section.

Open image in new window

Although the spatial and temporal fluctuations are generally chaotic, systematic patterns emerge when the circulation profiles are averaged over several months. In the equatorial plane, the circulation in the upper convection zone is typically outward, giving rise to poleward flow at low latitudes near the surface. This can be seen for case M3 in panel a of Figure 17 and panel c of Figure 17⁹. This outward flow arises primarily as a result of the centrifugal force acting on the prograde differential rotation at low latitudes.

Another systematic trend which is robust in simulations of penetrative convection is a persistent equatorward circulation in the overshoot region of a few m s⁻¹ (Figure 17, panel d). This can be attributed to the turbulent alignment of downflow plumes as illustrated in panel b of Figure 15 and as discussed in Section 4.3. In turbulent parameter regimes, convective overshoot is dominated by helical downflow plumes which are tilted toward the rotation axis with respect to the vertical. When these plumes reach the overshoot region, negative buoyancy removes their vertical momentum but an equatorward latitudinal momentum remains. This equatorward circulation does not occur in more laminar simulations which do not exhibit turbulent plumes (Miesch et al., 2000).

Near the poles, simulations generally exhibit several circulation cells which span about 10°–15° in latitude and extend from the top of the convection zone to the bottom. The sense of the circulation can vary with time and may or may not be the same in the northern and southern hemispheres. Without exception, simulations which exhibit solar-like differential rotation profiles have such localized circulation cells near the poles. Since axisymmetric circulations tend to conserve angular momentum, a single, global cell extending from low to high latitudes would tend to spin up the poles, driving a polar vortex which is inconsistent with helioseismic inversions (see Section 6.3).

How do these simulation results compare with what we know about the meridional circulation in the Sun? Our knowledge of the solar circulation is currently limited to the uppermost regions of the convection zone (see Section 3.4). There the circulation is generally poleward, although it does fluctuate substantially and is not in general symmetric about the equator. Some of these fluctuations appear to be associated with magnetic activity and exhibit a systematic equatorward propagation over the course of the solar activity cycle in conjunction with torsional oscillations (Snodgrass and Dailey, 1996; Beck et al., 2002; Zhao and Kosovichev, 2004). Fluctuations of comparable amplitude occur in simulations both with and without magnetic fields, but they do not exhibit such systematic latitudinal propagation.

The poleward circulation in the Sun is about the same amplitude as in simulations, ∼ 20 ms⁻¹, but it extends to higher latitudes. Doppler measurements and local helioseismic inversions indicate poleward flow in the solar surface layers up to latitudes of at least 60°. By comparison, the poleward flow near the outer boundary in simulations generally only extends to latitudes of about 30°–50° (Figure 17, panel c). Little is currently known about circulation patterns in the polar regions of the Sun but surface tracer measurements do show some hints of flow reversals at latitudes above 60° (Komm et al., 1993; Snodgrass and Dailey, 1996; Latushko, 1996). Multiple-cell structure in the polar regions such as that seen in simulations has not yet been unambiguously found in surface measurements or helioseismic inversions but it cannot be ruled out.

Further insight into the maintenance of meridional circulation in global convection simulations can be obtained by considering the balance Equation (15). If we apply a Legendre transform to this equation, we obtain an evolution equation for the mass flux vorticity in spectral space: \(\tilde{\varpi}\). We may then multiply by \(\tilde{\varpi}\) and integrate over radius to obtain

$${{\partial {\cal W}(\ell)} \over {\partial t}} = {\rm{RS}}(\ell) + {\rm{AD}}(\ell) + {\rm{BF}}(\ell) + {\rm{VD}}(\ell),$$

(24)

where \({\cal W}(\ell)=\tilde{\varpi}^{2}/2\) is the mass flux enstrophy spectrum associated with the circulation and the terms on the right-hand-side reflect contributions from the Reynolds stress, axisymmetric advection, the buoyancy force, and viscous diffusion (see Appendix A.5). The spectrum \({\cal W}(\ell)\) is shown in Figure 19, frames (a) and (b), along with the corresponding spectrum for the streamfunction, Ψ, defined in Equation (13).

Open image in new window

The density-weighted enstrophy spectrum, \({\cal W}(\ell)\), decays roughly exponentially with the spherical harmonic degree, ℓ, with an e-folding scale of ℓ _ϖ ∼ 31. The streamfunction spectrum is steeper, with an e-folding scale of ℓ_Ψ ∼ 22 over the range shown in panel a of Figure 19. However, it is not as well approximated by an exponential distribution, being somewhat more intermittent. As is most evident in panel b of Figure 19, most of the power in both ϖ and Ψ is concentrated at large scales, ℓ ≤ 20, and in odd values of ℓ. Odd ℓ values correspond to ϖ, Ψ, and < υ _θ > profiles which are antisymmetric about the equator and < υ_r > profiles which are symmetric. For example, a single large-scale circulation cell per hemisphere with upflow at the equator and downflow at the poles is generally dominated by the ℓ = 1 and ℓ = 3 components of ϖ and Ψ (depending on the latitude at which it turns over).

The maintenance terms on the right-hand-side of Equation (24) are shown in panel c of Figure 19. The sum of all contributions is nearly zero, indicating a statistically steady state. Although the G^AD and G^BF terms dominate the total flux represented in Equation (16), they are largely offset by pressure gradients. Large-scale circulations (ℓ = 1–3) are driven by the Reynolds stress (RS) and the residual buoyancy force (BF), which are balanced by axisymmetric advection (AD) and viscous diffusion (VD). On intermediate scales, 4 < ℓ < 10, axisymmetric advection is the primary driving mechanism and the Reynolds stress plays an inhibiting role.

It is instructive to further decompose the Reynolds stress contribution in order to clarify which processes are most relevant. According to Equation (76) in Appendix A.4, the radial component of the Reynolds stress includes contributions from vorticity advection ∝ 〈υ′ _r ω′ϕ〉 and vortex tipping, ∝ 〈υ′ _ϕ ω′ _r 〉 These contributions are plotted separately in panel d of Figure 19 along with that due to the latitudinal component of the Reynolds stress. This figure indicates that the radial tipping term is most important, followed closely by the radial advection term. The latitudinal Reynolds stress is less significant.

Given the important role of the turbulent Reynolds stress, it is perhaps no surprise that the circulation patterns are complex. If the solar meridional circulation is as spatially and temporally variable as the simulations suggest, then this has important implications for kinematic dynamo models. It may pose problems for flux-transport dynamo models in particular which rely on a steady large-scale circulation component to set the period and other aspects of the magnetic activity cycle (Choudhuri et al., 1995; Durney, 1995; Dikpati and Charbonneau, 1999; Dikpati and Gilman, 2001a; Charbonneau, 2005). On the other hand, the success of flux-transport dynamo models in reproducing many features of the solar cycle may point to some shortcomings of global convection simulations. The maintenance of differential rotation in the solar convection zone is subtle, involving small imbalances among relatively large forces. Simulations may be sensitive to dynamics which are not sufficiently resolved or otherwise missing from the model. Still, in light of this delicate balance, it would be surprising if the solar meridional circulation did not fluctuate substantially in space and time.

One feature that global convection simulations and flux-transport dynamo models have in common is an equatorward circulation in the overshoot region. Hathaway et al. (2003) argue that the observed drift speeds of sunspots as a function of latitude support the presence of such a flow. Some flux-transport models require that this equatorial circulation extend even below the overshoot region (Nandy and Choudhuri, 2002). However, any circulation which is driven in the convection zone is unlikely to penetrate deeper than r ∼ 0.7R_⊙ due to the strongly limiting influence of buoyancy and rotation (Gilman and Miesch, 2004). Secondary circulations may be driven by waves and turbulence in the radiative interior but these are likely to be much weaker than those in the convection zone (see Section 8).

6.5 Dynamo processes

The solar dynamo involves an intricate interplay of complex processes occurring over a wide range of spatial and temporal scales (see Section 4.5 and Section 5.1). Consequently, global convection simulations are a long way from making detailed comparisons with photospheric and coronal observations of magnetic activity. Still, they have provided important insight into several key elements of the global dynamo, particularly field generation in the convection zone (processes 0–1 in Figure 8).

Simulations of thermal convection in rotating spherical shells have produced many examples of sustained dynamo action (Gilman and Miller, 1981; Gilman, 1983; Glatzmaier, 1984, 1985a, b; Kageyama and Sato, 1997; Christensen et al., 1999; Roberts and Glatzmaier, 2000; Zhang and Schubert, 2000; Ishihara and Kida, 2002; Busse, 2002; Glatzmaier, 2002; Brun et al., 2004). Most of these are concerned with relatively laminar flows or parameter regimes which are more characteristic of the Earth’s core than the solar interior. Simulations of turbulent convection and dynamo action in more solar-like parameter regimes have recently been investigated by Brun et al. (2004). Results are illustrated in Figures 20 and 21.

Open image in new window

As in Cartesian simulations of MHD convection (e.g., Brandenburg et al., 1996; Cattaneo et al., 2003), radial field near the top of the computational domain is swept into downflow lanes by horizontally converging flows¹⁰. The field distribution is intermittent and confined primarily to the downflow network (Figure 20, panels a and b). Field within the network is of mixed polarity and is wrapped up by cyclonic vorticity, generating large gradients which promote magnetic reconnection. Magnetic helicity is generated locally but it is of mixed sign and no clear global patterns emerge¹¹ (cf. Section 3.8). A potential-field extrapolation of the radial field at the upper boundary exhibits a complex topology, with interconnected loops spanning a wide range of spatial scales (Figure 21, panel a). This may be compared with photospheric extrapolations which are similarly complex (see Figure 4).

Open image in new window

Toroidal fields are somewhat less intermittent and peak in the horizontally-diverging regions between downflow lanes (Figure 20, panel c). These regions tend to be broadest at low latitudes where much of the toroidal field energy is concentrated. Differential rotation stretches fields into toroidal ribbons (Figure 21, panel b) which generally reach higher amplitudes (∼ 3000 G) than poloidal fields (∼ 1000 G). The energy in the mean (axisymmetric) toroidal field exceeds that in the mean poloidal field by about a factor of three, indicating that an Ω-effect is operating (cf. Section 4.5). However, the magnetic energy in the fluctuating (non-axisymmetric) poloidal and toroidal field components is comparable.

In light of the complex topologies evident in Figures 20 and 21 it is no surprise that the axisymmetric field components are relatively small. Fluctuating fields account for 98% of the total magnetic energy in Case M3. Furthermore, there is no clear separation of spatial or temporal scales and nonlinear correlations between fluctuating field components are not small in any sense, calling into question many of the assumptions often used in mean-field dynamo theory (see Section 4.5).

Magnetic fields on the Sun are also complex but they exhibit striking regularities, most notably those associated with the 22-year activity cycle (see Section 3.8). Furthermore, the axisymmetric component of the poloidal field on the Sun is predominantly dipolar, at least during solar minimum. This degree of order amid complexity has not yet been achieved with global simulations. Case M3, for example, does not exhibit cyclic behavior and the mean poloidal field involves dipolar, quadrupolar, and higher-order components (see Brun et al., 2004). Cyclic dipolar dynamos have however been achieved in other parameter regimes. A key element appears to be a strong differential rotation. When the kinetic energy of the differential rotation exceeds that of the convection, cyclic dynamos are more likely. This is a conclusion reached over two decades ago by Gilman (1983) and has generally been borne out in the later work cited at the beginning of this section. Furthermore, many cyclic dynamos operate in the strong field regime in which the magnetic energy exceeds the convection kinetic energy by an order of magnitude or more (e.g., Christensen et al., 1999; Zhang and Schubert, 2000; Ishihara and Kida, 2002). This is appropriate for planetary interiors but not for the Sun, where the rotational influence is much weaker. In Case M3, the kinetic energy in the differential rotation and in the convection are roughly equal while the magnetic energy is about an order of magnitude less.

The importance of a strong differential rotation in achieving cyclic behavior is consistent with mean-field theory where it is known that cycles are more readily achieved with α-Ω dynamos than α² dynamos (Ossendrijver, 2003). If meridional circulation is neglected, the cycle period is determined by the magnitude of a, which in turn is proportional to the kinetic helicity to a first approximation (Section 4.5). To the author’s knowledge, all numerical simulations of thermal convection in rotating spherical shells which have achieved sustained, cyclic, dipolar dynamos (e.g., Gilman, 1983; Glatzmaier, 1985a, b; Kageyama and Sato, 1997; Zhang and Schubert, 2000; Ishihara and Kida, 2002; Busse, 2002) are dominated by so-called banana cells (see Section 6.1). This is either because of low resolution and correspondingly low Reynolds numbers or because of the strong rotational influence characteristic of planetary applications, or both. The Coriolis force acting on these relatively laminar flows induces kinetic helicity which in turn produces efficient poloidal field regeneration via the α-effect¹². An unrealistically large effective value of α was identified as a possible reason why early solar dynamo simulations produced cycle periods of only 1–10 yr, significantly less than the 22-year period of the solar activity cycle (Gilman, 1983; Glatzmaier, 1985a). In more turbulent parameter regimes, nonlinear correlations are likely to be reduced, implying a smaller α. Thus, if cyclic, dipolar dynamos can be achieved in such parameter regimes, there is reason to believe that their periods may be more comparable to the Sun. However, this remains to be seen.

Another difficulty exhibited by the early solar dynamo simulations of Gilman (1983) and Glatzmaier (1985b) is that the toroidal field tended to migrate poleward over the course of a cycle rather than equatorward as in the Sun (Section 3.8). This was attributed to the sign of the kinetic helicity, which determines the propagation direction of dynamo waves in mean-field theory (e.g., Ossendrijver, 2003; Charbonneau, 2005). However, it is well known that the sign of the kinetic helicity in rotating convection simulations reverses near the base of the convection zone (Sections 6.2 and 6.3). For this and other reasons (mainly having to do with the storage and amplification of toroidal flux), it has been argued that the lower convection zone and, in particular, the tachocline likely play a key role in the solar dynamo (e.g., Weiss, 1994; Ossendrijver, 2003).

Global convection simulations have not yet achieved a rotational transition region comparable to the solar tachocline. A realistic modeling effort would require very high spatial resolution (see Section 5.1) and may involve long-term processes which would be difficult to capture in a 3D simulation (see Section 8.5). However, a tachocline can be incorporated in a global model in an approximate way, for example by imposing solid body rotation in the interior via boundary conditions or body forces. This is the frontier for global, 3D, solar dynamo simulations.

The presence of a tachocline in a global simulation may promote more regular, cyclic behavior by providing a reservoir for field storage and a mechanism for field amplification, possibly up to super-equipartition values as is though to occur in the Sun (e.g., Fisher et al., 2000; Fan, 2004). Coupling to the radiative interior may also act to regularize the dynamo by providing thermal, mechanical, and electromagnetic inertia. For example, one of the important contributions of global convection simulations to geodynamo theory over the past decade has been the realization that an electrically conducting core adds stability to the dipolar dynamo, preventing overly sporadic and frequent reversals (e.g., Glatzmaier, 2002). Furthermore, the regularity of the solar cycle suggests that essentially linear processes such as dynamo waves may prevail over more chaotic turbulent processes, meaning the relatively quiescent tachocline may set the rhythm of the solar dynamo.

6.6 Comparisons with mean-field theory

Global convection simulations have provided much insight into solar interior dynamics in general and the maintenance of mean flows and fields in particular. However, in light of their limitations (Section 7), it is prudent to also consider alternative modeling approaches. Mean-field models seek to reproduce the structure and evolution of large-scale flows and fields in the Sun using turbulence models or other physical parameterizations for the Reynold stress, convective heat flux, Maxwell stress, and turbulent emf. The motivation and methodology behind mean-field models was discussed briefly in Section 5.3. Here we review some of the results and insights gained from mean-field modeling and compare them with global convection simulations.

This section is not intended as a comprehensive review. For much more discussion of mean-field hydrodynamics see Rüdiger (1989), Canuto and Christensen-Dalsgaard (1998), and Rüdiger and Hollerbach (2004). For a review of mean-field dynamo models see Ossendrijver (2003), Rüdiger and Hollerbach (2004), and Charbonneau (2005).

7.1 Resolution

In analogy to the shopkeeper’s well-known mantra (location, location, location), one could argue that the three most important factors in improving global-scale solar convection models are resolution, resolution, and resolution.

Global convection simulations are generally well-resolved in the sense that the kinetic, thermal, and magnetic energy spectra peak at relatively large scales (ℓ ∼ 10–50) and their amplitude falls off by at least 2–3 orders of magnitude before reaching the grid scale. Furthermore, the results converge in the sense that a higher-resolution with the same parameters will give statistically the same results. However, simulations are far from the solar parameter regimes (Section 5.1). Thus, as the resolution is increased, parameters are generally not held constant.

In particular, higher resolution allows for higher Reynolds, magnetic Reynolds, and Peclet numbers, R_e, R_m, and P_e, which quantify the relative importance of advection and diffusion. As these ratios are increased, the flow generally becomes more turbulent and the convective patterns and transport properties may change. For example, as the Reynolds number is increased, the downflow lanes and plumes which currently dominate simulations may alter their entrainment properties or even destabilize completely (e.g., Rast, 1998). New convective modes may become unstable, characterized by smaller spatial scales and rapid time variability (Zhang and Schubert, 2000). Nonlinear processes such as tachocline shear instabilities (Section 8.2) may only occur at sufficiently high Reynolds numbers (Section 8.2). Furthermore, the structure of the overshoot region may be sensitive to the Peclet number (Section 8.1).

The hope and expectation is that these changes only occur up to a point. If enough of the global dynamics is explicitly resolved, smaller-scale dynamics may be reliably treated as an effective diffusion or in terms of a more elaborate sub-grid-scale model (Section 7.2). The question is; how much resolution is enough? At the very minimum, simulations must resolve the energy-containing scales. This has already been accomplished; as R_e, R_m, and P_e are further increased, the peaks in the energy spectra will probably not shift significantly. However, spectra only provide part of the story.

Most researchers would agree that the most significant advances in turbulence research over the past few decades have been concerned with coherent structures which arise from self-organization processes such as the selective dissipation of ideal invariants (Cantwell, 1981; Hasegawa, 1985; Lesieur, 1997; Branover et al., 1999). Although such structures may occupy a small volume and possess relatively little energy, they often dominate the transport in inhomogeneous and anisotropic turbulent flows. Symmetry breaking induced by rotation, stratification, and magnetic fields can all give rise to self-organization in the solar convection zone.

A goal for solar convection simulations is therefore to resolve all scales which are significantly influenced by rotation and stratification (i.e., buoyancy) in order to capture such self-organization processes¹⁴. Smaller-scale motions may then behave more like isotropic, homogeneous turbulence which is generally diffusive in nature. This goal may be achievable throughout most of the convection zone. However, magnetic fields will be present everywhere above the magnetic dissipation scale which, at several kilometers, is well beyond the resolution of simulations (Section 5.1). Furthermore buoyancy effects remain important even at the smallest resolvable scales near the photosphere and overshoot region. Thus, subgrid-scale models must be developed which can reliably take into account the effects of magnetism and buoyancy, which may be non-diffusive (Section 7.2).

In any case, it is clear that global simulations are not yet in a regime in which the results are insensitive to viscous, thermal, and magnetic dissipation and consequently, to resolution. Convective patterns and mean flows still depend to some extent to the effective values of R_e, P_e, and R_m (Miesch et al., 2000; Miesch, 2000; Elliott et al., 2000; Brun and Toomre, 2002; Brun et al., 2004).

The transition regions which couple the convection zone to the radiative interior below and the solar atmosphere above are particularly challenging to resolve in global simulations (see Sections 5.1 and 7.3). Granulation in the surface layers will likely remain outside the scope of global models for some time, as will a realistic depiction of penetrative convection and wave dynamics in the overshoot region and tachocline (Section 8). The effect of these transition regions on global-scale dynamics can however be explored in global simulations with the help of appropriate boundary conditions and subgrid-scale models (Sections 7.2 and 7.3).

Improved numerical methods with enhanced resolution near the boundaries and better parallel efficiency may help to mitigate some of the limitations of global simulations in the coming years. Particularly promising in this respect are finite element and finite volume methods which require less inter-processor communication than spectral methods and which, primarily for this reason¹⁵, are becoming more common in atmospheric and oceanic applications (e.g., Lin and Rood, 1997; Marshall et al., 1997; Stuhne and Peltier, 1999; Fournier et al., 2004).

Solar convection simulations must always push the limits of available high-performance computing platforms to achieve ever higher spatial resolution. However, the highest-resolution simulations achievable on a given platform are computationally intensive. Not only do they require more calculations per iteration, but they must take smaller time steps to meet CFL stability conditions, implying more iterations for a particular simulation interval. Thus, it is impractical to run the highest-resolution simulations for the long durations necessary to adequately assess sustained dynamo action or to explore dynamics spanning several solar activity cycles. For such investigations, intermediate-resolution simulations will always remain important. Here again we may be guided by geophysical applications where high-resolution development models may be used to verify and calibrate lower-resolution application models (e.g., Williamson, 2002).

The continued importance of intermediate-resolution simulations further emphasizes the need for reliable subgrid-scale models to account for motions which are not resolved. These will be discussed further in the next section (Section 7.2).

7.2 Subgrid-scale modeling

For as long as we can reasonably speculate, even the most ambitious global simulations will only resolve a small fraction of the dynamical scales which are active in the solar interior. Thus, some type of model is necessary to account for the influence of motions on scales smaller than the grid spacing.

Current subgrid-scale (SGS) models assume that this influence is merely diffusive in nature, acting as an effective scalar viscosity, thermal diffusivity, and magnetic diffusivity which are many orders of magnitude larger than the corresponding molecular values. These scalar coefficients are allowed to vary with depth and are often assumed to be proportional to \(\bar{\rho}^{-1/2}\), as suggested by mixing-length arguments. Such parameterizations are very crude and do not accurately represent the complex dynamics known to occur in rotating, stratified, magnetized flows (e.g., Sections 7.1 and Section 8). More realistic models are necessary in order to make substantial further progress in global simulations.

The extremely high Reynolds numbers characteristic of the solar convection zone suggest that global-scale motions must be essentially inviscid (Section 5.1). Thermal and magnetic diffusion are similarly expected to be insignificant on large scales. This is not the case for current global simulations in which diffusive transport still makes a substantial contribution to the net momentum and energy balance (e.g., Figure 14) and still influences the generation and evolution of the magnetic field. Thus, the first goal of any successful SGS model must be to reduce the influence of this artificial dissipation.

In a spectral model, the most straightforward way to accomplish this is by imposing hyperdiffusion wherein the Laplacian diffusion operator is replaced by or supplemented with a higher-order equivalent (e.g., ∇⁴ or ∇⁸). Thus, the effective diffusion on the largest scales can be greatly reduced while maintaining an efficient dissipation on the smallest scales, preventing a buildup of energy which would otherwise cause numerical instability.

Although hyperdiffusion has benefits, it also has drawbacks. It is a practical construct with little physical justification. Furthermore, higher-order radial derivatives require additional boundary conditions in order to make the problem well-posed, placing artificial constraints on the allowable solutions. Such constraints can be avoided if hyperdiffusion is only implemented on horizontal surfaces while keeping the radial diffusion second-order, an approach which has been used in geodynamo simulations (e.g., Glatzmaier, 2002). However, this introduces an unphysical and largely arbitrary anisotropy into the SGS transport. Hyperviscosity also can introduce spurious overshoot near sharp gradients (related to Gibbs ringing) and may have an adverse effect on dynamo simulations, fundamentally altering the field generation process (Zhang and Schubert, 2000; Busse, 2000). It is therefore important to consider alternatives.

Turbulent flows generally exhibit cascade processes, characterized by a self-similar (scale invariant) exchange of energy or some other ideal invariant between adjacent spectral modes. The most familiar example is the forward cascade of kinetic energy which occurs within the classical inertial range of 3D, homogeneous, isotropic, incompressible turbulence (e.g., Lesieur, 1997; Pope, 2000). Rotation, stratification, and magnetism can also give rise to forward and inverse cascades (e.g., Section 8.3). By narrowing the viscous dissipation range, hyperdiffusion can extend these cascade ranges and thereby better capture the essential dynamics of the largest scales. However, the dynamics within the dissipation range is not accurately represented. A better representation of the resolved flow on all scales might be achieved by assuming from the outset that it will be self-similar on scales comparable to the grid-spacing.

The left-hand-side of Equation (25) can be evaluated directly from the resolved velocity field. However, the right-hand-side involves the unknown correlations \(\overline{v_{i}v_{j}}\) which must be modeled (this is essentially the Reynolds stress). If some parametric form is assumed for τ _ij , Equation (25) may then be used to compute the parameters. For example, if the turbulent transport is assumed to be diffusive, then τ _ij = 2ν_te _ij where ν_t is the turbulentviscosity and e _ij is the strain rate tensor. Equation (25) can then be used to derive v_t as a function of space and time. More commonly, ν_t itself is assumed to be proportional to the trace of e _ij as originally proposed by Smagorinsky (Smagorinsky, 1963; see also Pope, 2000). Equation (25) then yields the proportionality constant (Lesieur and Métais, 1996; Meneveau and Katz, 2000). The only remaining parameter is the ratio of filter scales k₁/k₂, meeting objective 4 above.

Self-similarity models such as these may in principle be applied separately for velocity, thermal, and magnetic fields and they rank among the most promising SGS approaches for solar applications (other promising strategies are reviewed by Lesieur and Métais 1996 and Foias et al. 2001). However, they do not capture nonlocal spectral transfer between large and small scales. Furthermore, they do not account for distinct small-scale dynamics such as granulation which are entirely unresolved, possessing local energy maxima on scales below the grid resolution. For this, separate models must be developed as outlined in objective 3 above. Such models may be based on local-area simulations or on parameterizations and procedures developed in the context of mean-field theory (Section 5.3). In this respect, global solar convection and dynamo simulations may ultimately resemble global circulation models (GCMs) for the Earth’s atmosphere, where unresolved processes are parameterized and where a hierarchy of modeling efforts (macroscale, mesoscale, and microscale) may be used to devise more reliable parameterizations (e.g., Beniston, 1998).

The most straightforward way to evaluate whether an SGS model is reliable and robust is to compare simulations with different resolutions. An intermediate-resolution simulation which incorporates the SGS model should be able to reproduce results from a higher-resolution simulation with only Laplacian diffusion. Furthermore, the LES/SGS model should eventually converge on a statistically equivalent solution as the resolution is increased. Of course, these checks will only work if the assumptions of the model are met. For example, an SGS model which relies on scale invariance will only converge if the cutoff wavenumber corresponding to the grid spacing is well within the inertial range (or some equivalent cascade range). Furthermore, as the resolution is increased, the parameterizations for previously unresolved processes (objective 3) may need to be revised as their characteristic scales begin to overlap with the dynamical range captured by the simulation. This is occurring now in GCMs where increasing the resolution does not necessarily lead to better forecasts (e.g., Williamson, 2002).

Large-eddy simulations with subgrid-scale modeling generally perform well in fundamental turbulence applications (Mason, 1994; Meneveau and Katz, 2000; Pope, 2000). Results have been promising enough that the approach has become standard in engineering and atmospheric applications. It remains to be seen how reliable they will be for solar interior dynamics. Magnetism in particular poses difficult challenges for SGS modeling which have not yet been fully addressed. Rotation and stratification (i.e., buoyancy) must also be incorporated into a realistic model. Furthermore, LES/SGS approaches can run into problems near boundaries where the characteristic scales of the flow can decrease dramatically and where qualitatively different dynamics can occur (Mason, 1994). This is certainly an issue in solar applications where the boundaries of the convection zone are likely to be highly complex (Section 7.3). Still, the prospects are good that improved SGS modeling may lead to substantial advances in global solar convection simulations in the near future.

7.3 Boundary influences

Most global solar convection simulations assume that the upper and lower boundaries of the computational domain are stress-free and impenetrable. Convection is driven by imposing a heat flux on the lower boundary and either a constant heat flux or a constant entropy on the upper boundary. Magnetic boundary conditions are generally either perfectly conducting or matching to an external potential field. All of these conditions are gross simplifications of the complex dynamics which actually couple the solar convection zone to the extended atmosphere above and the radiative interior below.

Although the uppermost layers of the convection zone account for only a small fraction of its total mass, the precipitous drop in entropy near the surface produces strong buoyancy driving. This, when coupled with radiative transfer and ionization effects, maintains granulation and supergranulation. These motions do not penetrate far below the photosphere but stochastic forcing from ensembles of plumes may have a subtle influence on the deeper convective zone. In particular, coupling between supergranulation, mesogranulation, and deeper convective motions may have some bearing on the near-surface shear layer seen in helioseismic rotational inversions (Section 3.1). Furthermore, magnetic flux dispersion by near-surface convective motions might contribute to global polarity reversals as in Babcock-Leighton dynamo models (e.g., Ossendrijver, 2003; Charbonneau, 2005).

Coupling between the convective envelope and the corona can occur through magnetic torques and mass exchange via the solar wind. Such processes generally occur on timescales much longer than the solar activity cycle. However, magnetic helicity flux through the solar surface may play an important role both in the operation of the dynamo (Blackman and Brandenburg, 2003) and in determining the global configuration of the coronal field (Low, 2001; Zhang and Low, 2001, 2003). Understanding the complex process of flux emergence is also essential for interpreting photospheric and coronal observations (e.g., Fan, 2004).

Perhaps an even more important factor in improving global simulations is a more realistic treatment of the complex dynamics occurring at the base of the convection zone, where the solar envelope couples to the radiative interior through the overshoot region and tachocline. This transition region is thought to play a critical role in the solar dynamo (Section 4.5) so it must be represented with some fidelity if global simulations are ever to make meaningful contact with observations of magnetic activity.

The primary difficulty in capturing the dynamics of the overshoot region and tachocline in a global simulation lies in their thin extent (Section 3.2, Section 3.6). Like the near-surface layers, relatively small-scale processes occur which are difficult to resolve (Section 8). This small grid spacing sets corresponding limits on the time steps required for numerical stability, further adding to the computational expense. Such restrictions are overcome in current models by either placing the boundary of the computational domain at the base of the convection zone (no penetration) or by artificially decreasing the subadiabatic stratification in the interior, thereby extending the overshoot region.

Nevertheless, global simulations can potentially capture may aspects of the solar dynamo including turbulent pumping of fields into the overshoot region and amplification by differential rotation in the tachocline (cf. Figure 8). The subsequent formation and rise of flux tubes by buoyancy instabilities may require much higher resolution to reliably model but it should be present to some degree in global simulations which possess a tachocline.

Establishing and maintaining a tachocline in a global convection simulation is a challenge in itself, since it may involve processes which occur on timescales much longer than the solar activity cycle, (Section 8.5). It also requires minimal vertical diffusion to prevent artificial spreading (high R_e, P_e; cf. Section 7.1). Global simulations have only begun to explore penetrative convection in detail and have not yet achieved a rotational shear layer comparable to the tachocline¹⁶.

The tachocline region is not only important from a dynamo perspective; it also mediates angular momentum transport between the convective envelope and the radiative interior. This may occur through magnetic coupling or by through penetrative convection and gravity waves (Section 8.4). Helioseismic inversions suggest that this transport must be relatively efficient, since the mean rotation rate of the convection zone and radiative interior are comparable (Section 3.1).

Angular momentum exchange between the convection envelope and the deep interior plays an important role in the rotational history of the Sun over evolutionary timescales (Charbonneau and MacGregor, 1993). However, it has little bearing on the differential rotation profile of the envelope which is maintained on shorter timescales (Section 4.3). Still, there are several reasons to believe that the differential rotation profile may be sensitive to dynamics near the base of the convection zone.

Turbulent penetrative convection tends to produce poleward angular momentum transport in the overshoot region due to the rotational alignment of downflow plumes (Section 6.3). Since the overshoot region is artificially deep in simulations, we may be overestimating this transport (Miesch, 2005). More generally, poleward angular momentum transport in the tachocline by instabilities and turbulence may balance equatorward transport in the convection zone, giving rise to a global angular momentum cycle which would ultimately determine the equilibrium rotation profile (Gilman et al., 1989).

Thermal effects may also play an important role. The differential rotation in the lower convection zone is probably in thermal wind balance, maintained by latitudinal entropy gradients (Sections 4.3 and 6.3). The radiative interior provides a large thermal reservoir which can influence this balance depending on how it is tapped by penetrative convection. An example of how this may occur has been described by Rempel (2005) in the context of a mean-field model.

In Rempel’s model, differential rotation in the convection zone is maintained by a Λ-effect (Section 5.3) and a meridional circulation which is solved for together with the angular velocity and thermal structure by means of the axisymmetric momentum, energy, and continuity equations. Uniform rotation is imposed on the lower boundary and the system is evolved until a steady state is reached. The competition between the Λ-effect and the lower boundary condition quickly establishes an artificial’ tachocline’; i.e., a large vertical angular velocity gradient near the base of the convection zone. This, in turn, sets up latitudinal entropy gradients in accord with thermal wind balance. These entropy gradients are then transmitted upward into the envelope by convective motions, here treated as an effective thermal diffusion. The net result is a solar-like differential rotation profile in which departures from cylindrical alignment are maintained by latitudinal entropy gradients originating in the tachocline. The model involves many crude simplifications but it illustrates how thermal coupling between the convection zone and radiative interior may influence the differential rotation profile.

More generally, since the convection zone is nearly adiabatic, even small entropy variations originating in the strongly subadiabatic radiative interior may be significant. The depth to which penetrative convection mixes entropy with the interior and the efficiency by which energy is transported through the surface together determine the entropy content, or in other words, the adiabat of the convection zone. This is one more reason why a realistic modeling of these boundary regions may be important for global simulations.

There are many other phenomena which will require detailed modeling of the upper and lower convection zone to fully account for. An example is light element depletion in the Sun and other late-type stars which may arise from chemical transport by gravity waves (Section 8.4). Momentum transport by gravity waves may account for the tachocline oscillations found in helioseismic inversions (Section 3.3). Incorporating all of these influences into global convection simulations is a tall order but it must eventually be done to some degree if we are ever to have a reasonably complete and integrated model of solar interior dynamics. Meeting these challenges will require a combination of increased resolution near the boundaries, sophisticated SGS models, and carefully chosen boundary conditions.

8.1 Convective penetration

Due to its wide applicability in astronomy and geophysics, there is a large body of literature on convective penetration. Much of this work, particularly in a solar context, is concerned with the structure of the overshoot region and how the penetration depth varies with the vigor of the convection and the stiffness of the transition from subadiabatic to superadiabatic stratification.

Figure 22 illustrates the structure of the overshoot region at the base of the solar envelope as suggested by Zahn (1991). In the convection zone, the radial entropy gradient, \(d\overline{S}/dr\), is negative but nearly adiabatic due to the efficient mixing of entropy by turbulent convection. The convective enthalpy flux is positive (outward) and the radiative heat flux normalized by the total flux, L_⊙/4πr² is less than unity. To a good approximation, the normalized convective enthalpy flux and radiative heat flux sum to unity, with smaller contributions from the other terms in Equation (3).

Open image in new window

In many theoretical studies, the base of the convection zone is defined as the point where \(d\overline{S}/dr\) changes sign and becomes positive (subadiabatic). The inertia of convective downflows takes them beyond this point into the stably-stratified interior. Here the enthalpy flux becomes negative (inward) and the outward radiative flux must increase to compensate. Downward motions will be quickly decelerated by buoyancy but the turbulent mixing may still be efficient enough to establish a nearly adiabatic penetration region where \(d\overline{S}/dr\geq 0\). Eventually, downflows will be decelerated enough such that their effective Péclet number, P_e = UL/κ, becomes small and turbulent mixing becomes inefficient relative to thermal diffusion. This occurs in a thin thermal adjustment layer where the enthalpy flux falls to zero and the stratification becomes strongly subadiabatic. Deeper in the interior, the radiative heat flux carries the entire solar luminosity.

Sometimes a distinction is made between convective overshoot and convective penetration. The former is used to describe any convective motions which are carried into a region of stable stratification by their own inertia. By contrast, the latter term often has a more specific meaning, implying that the convection is efficient enough to establish a nearly adiabatic penetration region as indicated in Figure 22. From the perspective of solar structure modeling and helioseismic probing, it is often more convenient to define the base of the convection zone as the bottom of the well-mixed, nearly adiabatic penetration region rather than where the entropy gradient changes sign.

The presence of a nearly adiabatic penetration region in the Sun is currently a matter of some debate. Although many early models and relatively low-resolution 2D and 3D simulations produced a true penetration region where \(d\overline{S}/dr\geq 0\) (reviewed by Brummell et al., 2002b; Rempel, 2004), recent high-resolution simulations of turbulent penetrative convection by Brummell et al. (2002b) exhibited only strongly subadiabatic overshoot. They attributed the absence of a nearly adiabatic penetration region to the small filling factor of downflow plumes, which dominate the flow field in turbulent parameter regimes (see Section 5.2). However, reduced models based on the dynamics of intermittent plumes suggest that such numerical simulations may exhibit more adiabatic penetration if they could achieve more solar-like parameter regimes (Zahn, 1991; Rempel, 2004). In particular, higher Péclet numbers and a lower imposed heat flux may modify the balance between advective and diffusive heat transport enough to produce a nearly adiabatic stratification.

Another challenge to numerical simulations of penetrative convection is achieving a high stiffness parameter S_t, which is a measure of the subadiabatic stratification in the stable zone relative to the superadiabatic stratification in the convection zone. In the Sun this ratio is roughly 10⁵ whereas simulations consider values of at most 10–100. Thus, the depth of penetration, Δ_p, in simulations is artificially high and much work has focused on establishing scaling relations between Δ_p and S in order to extrapolate the results to solar conditions. Analytic estimates by Hurlburt et al. (1994) suggest that the extent of the nearly adiabatic penetration region, if present, scales as \(S_{\rm t}^{-1}\) whereas the depth of the thermal adjustment layer scales as \(S_{\rm t}^{-1/4}\). Numerical simulations are generally consistent with these scaling estimates (Hurlburt et al., 1994; Singh et al., 1995; Brummell et al., 2002b). However, Rogers and Glatzmaier (2005a) have recently achieved stiffness values of over 500 in high-resolution simulations of 2D penetrative convection and they find a much shallower scaling law, \(\Delta_{\rm p}\sim S_{\rm t}^{-0.04}\) for \(S_{\rm t}\geq 10\). When extrapolated to solar conditions, most simulations and models imply penetration depths ranging from about 0.01–1 pressure scale heights H_P, implying a Δ_p of a few percent of the solar radius or less (see, e.g., Rempel, 2004; Stix, 2002). By comparison, upper limits from helioseismology suggest that the overshoot region is no more than about 0.05H_P, which is less than 0.01R_⊙ (Section 3.6). Helioseismic inversions can also set limits on how abruptly the entropy gradient changes at the base of the convection zone, ruling out a very thin thermal adjustment layer (Monteiro et al., 1994; Basu et al., 1994; Roxburgh and Vorontsov, 1994).

Brummell et al. (2002b) also considered the variation of the penetration depth with rotation and latitude, under the f-plane approximation. They found that rotation generally has a stabilizing effect because plumes are tilted away from the vertical by turbulent alignment and weakened by vortex interactions. Similar results were also reported by Julien et al. (1996a, 1999); see Section 5.2. The penetration depth was greatest at the equator and poles, and least at mid-latitudes. The smaller penetration at mid-latitudes relative to high latitudes was attributed to turbulent alignment because tilted plumes have less downward momentum. The enhanced penetration at low latitudes was attributed to the formation of horizontal convective rolls which are analogous to the north-south aligned downflow lanes typically seen in global convection simulations (Section 6.2). Global simulations of penetrative convection by Miesch et al. (2000) do indeed exhibit deeper penetration at the equator, but there is less evidence for enhanced penetration at the poles in turbulent parameter regimes. However, the simulations by Miesch et al. (2000) used a realistic value for the solar luminosity so it was impractical to cover a full thermal equilibration timescale (∼ 10⁵ yr; see Section 5.1). Thus, any conclusions made about the detailed structure of the overshoot region must be regarded as tentative.

Investigating convective penetration with global models remains an important challenge for the near future. Although global models can say little about the thermal structure of the overshoot region at present, they have already produced provocative and robust results regarding its dynamics. In particular, they have indicated that penetrative convection in the Sun is likely to induce equatorward meridional circulation and poleward angular momentum transport in the overshoot region (see Sections 6.3 and 6.4).

Another aspect of penetrative convection which has important implications for solar interior dynamics is the generation of gravity waves. Figure 23 illustrates wave excitation in simulations of penetrative convection by Rogers and Glatzmaier (2005b). The geometry is a 2D circular annulus with the inner boundary placed very near the origin to minimize spurious wave reflection. Gravity waves appear as rings of vorticity in the stable zone propagating outward. This outward phase velocity implies an inward group velocity, and is therefore consistent with wave generation at the base of the convection zone (see Appendix A.7).

Open image in new window

Although gravity waves are present in all simulations of penetrative convection, little is known about the details of wave excitation in the Sun. Unless steps are taken to avoid it, numerical simulations generally suffer from wave reflection at the lower boundary and imposed horizontal periodicities which can substantially alter the spectra, energetics, and transport properties of the waves. Furthermore, obtaining a reliable estimate of gravity wave amplitudes and spectra in a high-resolution simulation of penetrative convection is not a trivial undertaking (e.g., Dintrans and Brandenburg, 2004). The most straightforward method is based on spectral transforms of the velocity or density field in space and time, but this can be unwieldy in a 3D simulation because it requires storing a substantial volume of data at a high temporal cadence and a long enough duration to achieve stable statistics. To date, most investigations of gravity wave excitation in simulations of penetrative convection have been restricted to 2D flows (Hurlburt et al., 1986; Andersen, 1996; Dintrans et al., 2003; Kiraga et al., 2003; Rogers and Glatzmaier, 2005a, b). Theoretical estimates of wave excitation are sensitive to assumptions made about the structure of the convection which are difficult to justify (Goldreich and Kumar, 1990; Fritts et al., 1998; Kumar et al., 1999).

Despite this uncertainty, some general comments can be made. We expect that the gravity wave spectra will peak at spatial and temporal frequencies which correspond to the characteristic scales of the convection which drives them. These are currently uncertain but may be estimated from numerical simulations (Section 6.2). Modes with very small wavelengths (≤ 1 Mm) will be efficiently dissipated by thermal diffusion while modes with horizontal phase velocities comparable to the local differential rotation will be filtered out by critical level absorption and radiative diffusion (Fritts et al., 1998; Kumar et al., 1999; Talon et al., 2002). If the motions are indeed gravity waves, their frequencies will be bounded from above by the Brunt-Väisälä frequency, N, which corresponds to a period of a few hours in the solar interior. However, since the Sun is rotating and magnetized, we might expect a wide variety of waves to be generated by penetrative convection, including inertial gravity waves, Rossby waves, and Alfvén waves. Characteristic velocity amplitudes will vary substantially with radius but may be ∼ 1–10 m s⁻¹ near the overshoot region based on estimates for the vertical velocity in downward plumes, which may reach 100 m s⁻¹, and a moderate conversion efficiency.

No discussion of penetrative convection would be complete without some mention of transport processes. It is well established that turbulent penetrative convection can efficiently pump magnetic fields out of the convection zone into to the overshoot region, and possibly deeper (Brandenburg et al., 1996; Tobias et al., 1998, 2001; Dorch and Nordlund, 2001; Ziegler and Rüdiger, 2003). This is thought to play an integral role in the solar dynamo by continually supplying the tachocline with disordered field which can then be organized and amplified by rotational shear (Section 4.5). Transport of chemical tracers by penetrative convection and the waves it generates can has important implications for solar structure models and spectroscopic measurements of stellar compositional abundances (Montalbán, 1994; Schatzman, 1996; Hurlburt et al., 1994; Pinsonneault, 1997; Fritts et al., 1998; Brummell et al., 2002b; Ziegler and Rüdiger, 2003). Furthermore, angular momentum transport by gravity waves has important implications for understanding the structure and evolution of the solar internal rotation profile as we will discuss further in Sections 8.4 and 8.5.

We emphasize that convective penetration in the Sun is a very intermittent process, dominated by extreme, impulsive events; particularly strong plumes or ensembles of plumes which penetrate deeper than average and then quickly lose coherence. A jackhammer is a better analogy than a drill. Thus, the transport of magnetic fields, chemical tracers, and momentum, is generally deeper than might be expected from average measures such as the mean stratification or the mean kinetic energy density (e.g., Brummell et al., 2002b).

8.2 Instabilities

Penetrative convection occupies only the upper portion of the tachocline, if it overlaps at all (see Section 3.2). The lower portion of the tachocline is convectively stable. However, a variety of other instabilities are likely to occur, driven by shear, buoyancy, and magnetism.

Shear instabilities have been well studied for many years in light of their important geophysical and engineering applications. Undular perturbations in the direction of the mean velocity gradient grow by extracting kinetic energy from the shear flow, eventually overturning and spreading into a turbulent mixing layer. If the shear is vertical, such perturbations are suppressed by sub-adiabatic stratification to a degree which may be quantified by the Richardson number, Ri = (N/|dU/dz|)². If Ri ≥ 0.25, the vertical shear is hydrodynamically stable¹⁷.

For the lower tachocline, N ∼ 10⁻³ s and S ∼ 10⁻⁶ s⁻¹ (see Section 3.2), implying very large Richardson numbers Ri ∼ 10⁶. Vertical shear instabilities should therefore be strongly suppressed. In the overshoot region, N, and therefore Ri, is much smaller, approaching zero at the base of the convection zone. Taking into account the destabilizing influence of thermal diffusion, Schatzman et al. (2000) investigated this problem and concluded that the vertical shear may be hydrodynamically unstable near the base of the convection zone at r = 0.713R_⊙, but that this region of instability is confined to low latitudes and does not extend deeper than r ∼ 0.695. Note that this is a global constraint; stably-stratified flows may still exhibit intermittent turbulence¹⁸ even if Ri ≫ 1 due to wave breaking and horizontal layering which can drive the local Richardson number below 0.25 (Anders Pettersson Reif et al., 2002; Fritts et al., 2003; Petrovay, 2003; Hanazaki and Hunt, 2004). Note also that magnetism and baroclinicity may act to destabilize the vertical shear. We will return to this issue toward the end of this section.

Although the angular velocity gradient in the tachocline is mainly vertical (Section 3.2), stratification does little to suppress horizontal shear instabilities so we might expect that the latitudinal component of the differential rotation is more likely to be unstable. In the absence of magnetic fields, the latitudinal differential rotation will be linearly unstable if the corresponding latitudinal potential vorticity gradient (see Appendix A.6) changes sign somewhere in the domain of interest. This is a variation of Fjortoft’s criterion for a stably-stratified flow, which is in turn related to Rayleigh’s well-known inflexion-point criterion (e.g., Knobloch and Spruit, 1982; Vallis, 2005). Nonlinear stability is another matter; a shear flow which is linearly stable may still be unstable to finite-amplitude perturbations, particularly at high Reynolds numbers (a familiar example is pipe flow; see Drazin and Reid (1981); Tritton (1988); Richard and Zahn (1999)).

In light of the extremely large Reynolds numbers in the solar interior (Section 5.1), Zahn (1992, 1994) has argued that the latitudinal differential rotation should be hydrodynamically unstable to finite-amplitude perturbations. If efficient enough, this nonlinear instability may suppress the latitudinal shear entirely, leading to a state of shellular rotation in which angular velocity is independent of latitude. However, due to the possibly insurmountable difficulties of a complete nonlinear stability analysis, these are mainly empirical arguments based on analogies with laboratory flows. Linear analyses indicate that the latitudinal differential rotation in the tachocline is marginally stable to 2D (latitude/longitude) hydrodynamic perturbations (Charbonneau et al., 1999b) and perhaps only weakly unstable to 3D perturbations near the base of the convection zone (Dikpati and Gilman, 2001c; Cally, 2003). Furthermore, these linear instabilities saturate readily, mixing potential vorticity only enough to smooth local extrema and thus stabilize the flow (Garaud, 2001). It appears then that linear hydrodynamic instabilities, even if they occur, are far too weak to establish uniform rotation on horizontal surfaces. However, the addition of even a weak magnetic field profoundly changes everything.

In a series of papers, Gilman and collaborators have shown that the combination of latitudinal differential rotation and a toroidal field in the tachocline is linearly unstable to 2D perturbations for a wide range of field amplitudes and configurations, from broad distributions which occupy an entire hemisphere to localized bands of flux which span only a few degrees of latitude (Gilman and Fox, 1997, 1999a, b; Dikpati and Gilman, 1999; Gilman and Dikpati, 2000). Possible modes of instability for a toroidal band are illustrated in Figure 24. Similar modes of instability also occur for broad fields.

Open image in new window

A band of toroidal flux will experience a magnetic tension force which will tend to make it contract and move toward the poles (Figure 24, panel a). This is the poleward slip instability first studied using the thin flux tube approximation (Spruit and van Ballegooijen, 1982). In perfectly conducting, 2D, incompressible flow this axisymmetric mode (longitudinal wavenumber m = 0) is excluded because of mass conservation; the ring cannot push fluid uniformly poleward. However, the ring can tip as shown in panel b of Figure 24. This is the m = 1 tipping instability and it generally has the largest growth rate for solar parameter regimes, with timescales of order a few months¹⁹. Higher-wavenumber instabilities may also occur for weak fields (≤ 10⁴ G) which deform the ring as shown in panel b of Figure 24.

Unstable modes grow by extracting energy from the differential rotation or from the magnetic energy of the initial toroidal field, the latter of which becomes significant only for strong fields. The nonlinear saturation and evolution of these 2D instabilities was investigated by Cally (2001) and Cally et al. (2003). It was found that for broad fields, the tipping instability could lead to several different behaviors depending on the relative phases of the northern and southern hemispheres. If they tip out of phase, this leads to a clam-shell instability in which field lines spread out one side of the shell and reconnect on the other, eventually achieving a poloidal configuration. If the tipping occurs in phase, oscillatory solutions are possible in which field lines remain parallel and no reconnection occurs. The clam-shell instability does not occur for banded field profiles, but bands do tip, eventually equilibrating at a tilt angle which increases with the latitude of the initial band (high-latitude bands tip more).

There is little evidence for clam-shell patterns and highly tilted toroidal field bands in the Sun so it is interesting to explore possible mechanisms which may suppress or alter these instabilities. One possibility is that the instabilities may not be as efficient for the more complex toroidal field profiles which are likely to exist in the Sun. Cally et al. (2003) found one mixed profile in particular with low-latitude toroidal bands superposed on a broad field which did not exhibit a clam-shell instability. Another suppression mechanism may arise from the coupling of adjacent horizontal layers by turbulent mixing. This was recently incorporated into the 2D calculations of Dikpati et al. (2004) as an effective kinetic and magnetic drag. Results indicated that the clamshell instability was indeed suppressed for large magnetic drag in particular, but that the tipping instabilities for toroidal bands still equilibrated at tilt angles comparable to the nondiffusive cases.

An efficient mechanism for suppressing the poleward slip instability as well as the tipping instability of a toroidal band arises if the band possesses a coincident prograde zonal jet which provides a gyroscopic inertia (Rempel et al., 2000; Dikpati et al., 2003). Such a jet could be established by conservation of angular momentum in a band which begins to slip poleward and is then stabilized. The resulting centrifugal force can fully or partially balance the latitudinal component of the magnetic tension force in an equilibrium state, with the remaining contribution coming from pressure gradients. Jet formation is indeed observed in nonlinear simulations and contributes to a net flattening of the differential rotation profile (Cally et al., 2003). This flattening is achieved mainly by the Maxwell stress, which transport angular momentum poleward as a result of shear-induced correlations; 〈B′_θB′_ϕ〉.

Subsequent work has shown that similar instabilities also occur in quasi-2D systems under the shallow-water (SW) and thin-shell approximations discussed in Section 5.4 (Dikpati and Gilman, 2001c; Gilman and Dikpati, 2002; Dikpati et al., 2003; Cally, 2003; Gilman et al., 2004). Results again indicate that the tachocline differential rotation is in general unstable and that the m = 1 tipping instability is typically the dominant mode for hydromagnetic perturbations. An additional hydrodynamic mode is also present which may be unstable throughout much of the tachocline even in the absence of magnetic fields (Dikpati and Gilman, 2001c). Although formally allowed, the m = 0 poleward slip instability of a toroidal flux band is suppressed by a restoring pressure force which arise as mass is pushed toward the poles, tending to deform the upper boundary into a prolate shape (Dikpati and Gilman, 2001b).

Growth rates for the m = 1 and m = 2 SW modes of a toroidal band are shown in Figure 25 for parameter values characteristic of the overshoot region and lower tachocline (G is the reduced gravity and s is the fractional angular velocity contrast between the equator and pole). In the overshoot region, weak bands (≤ 10⁴ G) are unstable at all latitudes. For stronger fields, mid-latitude bands are stabilized by a zonal jet but bands at low and high latitudes remain unstable. In the radiative zone, bands at nearly all field strengths considered are stable at low latitudes but unstable at higher latitudes. Strong bands at all latitudes are stabilized by a zonal jet but weak mid-latitude bands remain unstable.

Open image in new window

Using a thin-shell model, Cally (2003) has identified a polar twist instability in which high-latitude toroidal loops lift and twist out of the horizontal plane. This is a different type of m = 1 instability which does not occur in 2D systems and which can exhibit large growth rates (e-folding timescales of months). However, the polar twist instability only operates at high field strengths (≥ 10⁵ G) and large vertical wavenumbers where it may be suppressed by turbulent diffusion. Furthermore, a poloidal field component may stabilize toroidal flux structures near the poles by essentially forming a twisted tube aligned with the rotation axis.

The magneto-shear instabilities studied by Gilman, Fox, Dikpati, and Cally are concerned with the joint instability of latitudinal differential rotation and strong toroidal fields which are thought to exist in the solar tachocline. They are likely related to the toroidal field instabilities described by Tayler (1973), Acheson (1978), and Spruit (1999) but a precise link has not yet been established. Other classes of hydrodynamic and magnetohydrodynamic (MHD) shear instabilities are also likely to operate in the tachocline and radiative interior. Notable among these is the magneto-rotational instability (MRI) described by Velikhov (1959), Chandrasekhar (1961) and Balbus and Hawley (1991) and applied to stellar interiors by Balbus and Hawley (1994). This instability is thought to generate vigorous turbulence in accretion disks which plays an essential role in the global angular momentum balance (Balbus and Hawley, 1998).

Unlike the quasi-2D instabilities studied by Gilman, Fox & Dikpati, the MRI operates mainly on relatively weak poloidal fields which tether axisymmetric rings of fluid to a particular point in the meridional plane. When these rings are perturbed, magnetic tension tends to resist shearing by the differential rotation. If the angular velocity decreases outward from the rotation axis (∂Ω/∂λ > 0), the resulting torques act to amplify the perturbations, leading to instability. When applied to the radiative interior of the Sun, (Balbus and Hawley, 1994) found that the instability was mainly confined to horizontal surfaces by the subadiabatic stratification, producing equatorward angular momentum transport which tends to drive the system toward shellular rotation. Toroidal fields are also subject to MRI as long as the perturbations allow for a poloidal component. However MRI cannot occur in strictly 2D spherical shells so it is distinct from the Gilman-Fox-Dikpati instabilities even in the toroidal field case. Furthermore, the MRI does not operate in regions where ∂Ω/∂λ > 0 or in the equatorial plane where buoyancy resists motions perpendicular to the rotation axis. The MRI criterion ∂Ω/∂λ yt; 0 is more limiting than its hydrodynamic analogue, the Rayleigh instability criterion, which states that a differential rotation profile is unstable if the specific angular momentum decreases outward: \(\partial{\cal L}/\partial\lambda < 0\) (e.g., Knobloch and Spruit, 1982).

As we have discussed, buoyancy in the subadiabatic radiative interior generally has a stabilizing influence on vertical shear but they can also have a destabilizing effect in the presence of rotation and magnetic fields. Rotation can induce baroclinicity, which refers to a state in which isosurfaces of constant density and pressure do not coincide. Fluid particles can tap the gravitational potential energy in such a configuration if they are allowed to move horizontally as well as vertically, in effect circumventing the Schwarzschild criterion for convective stability which applies only to vertical gradients. If a vertical shear is in thermal wind balance as is likely in the lower tachocline (Section 4.3.2), it may be subject to baroclinic instabilities. Such instabilities represent the main driver of weather systems on the Earth despite the large atmospheric Richardson numbers which suggest that the vertical shear would be stable in the absence of baroclinic effects (e.g., Vallis, 2005). Baroclinic instability in a stellar context was studied by Spruit and Knobloch (1984) who concluded that it is probably only significant very near the base of the convection zone where the stratification is relatively weak and where more standard shear instabilities may also occur. However, this work predated the discovery of the tachocline and should perhaps be revisited.

Cally (2000) has argued that a strong uniform toroidal field can further stabilize the vertical shear in a stably-stratified medium. However, if the field strength decreases with height then the fluid is top-heavy and is susceptible to magnetic buoyancy instabilities. Such instabilities likely play an essential role in tachocline dynamics but they have been comprehensively reviewed elsewhere in these volumes by Fan (2004), so we will not address them again here. We merely note that although shear can inhibit magnetic buoyancy instabilities (Tobias and Hughes, 2004), it can also induce them by forming concentrated magnetic structures (Brummell et al., 2002a; Cline et al., 2003a,b).

The presence of a small but finite thermal, magnetic, and viscous diffusion can also induce secular instabilities such as the Goldreich-Schubert-Fricke (GSF) instability (Knobloch and Spruit, 1982; Menou et al., 2004). These generally operate either on small spatial scales or on long temporal scales so they have little bearing on global-scale dynamics which occur over the course of a solar activity cycle. However, they may play a role in tachocline confinement (Section 8.5). Secular instabilities and rotational shear instabilities may also be important for chemical mixing in the radiative interior and light-element depletion in the solar envelope (Zahn, 1994; Pinsonneault, 1997; Barnes et al., 1999; Mathis and Zahn, 2004).

8.3 Rotating, stratified turbulence

Penetrative convection and instabilities will induce motions in the lower, stably-stratified portion of the tachocline which will, in general, undergo further nonlinear interactions. The resulting dynamics are likely to be turbulent in nature as a result of the low molecular dissipation. Shear instabilities and gravity wave breaking, in particular, can generate vigorous turbulence (e.g., Townsend, 1976; Tritton, 1988; Staquet and Sommeria, 2002).

Two-dimensional turbulence has been studied extensively both theoretically and numerically. It is now well known that nonlinear interactions involving triads of wavevectors in 2D turbulence conserve enstrophy (vorticity squared) as well as energy, and that this gives rise to an inverse cascade of energy from small to large scales (e.g., Lesieur, 1997; Pope, 2000)²⁰. This is in stark contrast to 3D turbulence which exhibits a forward cascade of energy from large to small scales where dissipation occurs. The inverse cascade is manifested as small vortices interact and coalesce into larger vortices.

The inverse cascade in 2D turbulence will proceed to the largest scales unless some mechanism suppresses it, such as surface drag in the oceans and atmosphere. Another mechanism for halting the inverse cascade which is more relevant for solar applications occurs in geometries which admit Rossby waves such as rotating spherical shells or β-planes. If the rotation is rapid enough, patches of vorticity can propagate as Rossby wave packets and disperse before they coalesce. Since the phase speed of a Rossby wave increases with the wavelength (see Appendix A.6), this occurs only for wavenumbers below a critical value k _β , often referred to as the Rhines wavenumber after Rhines (1975). At scales above \(k_{\beta}^{-1}\), the flow has a Rossby-wave character and at scales below \(k_{\beta}^{-1}\), it has the character of 2D turbulence.

The most notable thing about the arrest of the inverse cascade by Rossby wave dispersion is that it is anisotropic (Rhines, 1975; Vallis and Maltrud, 1993). Low latitudinal wavenumbers are suppressed, but the cascade can proceed to low longitudinal wavenumbers²¹. This tends to produce banded zonal flows as observed in the jovian planets (Yoden and Yamada, 1993; Nozawa and Yoden, 1997; Huang and Robinson, 1998; Danilov and Gurarie, 2004). Similar processes also occur in shallow-water and two-layer systems, in both freely decaying and forced configurations (Panetta, 1993; Rhines, 1994; Cho and Polvani, 1996a, b; Peltier and Stuhne, 2002; Kitamura and Matsuda, 2004). The number of bands, or jets, is roughly given by Ro^−½. Taking U ∼ 10 m s⁻¹ yields Ro ∼ 0.004 in the solar tachocline, which implies as many as 15 jets.

Does a quasi-2D inverse cascade occur in real 3D flows? It does in the so-called quasi-geostrophic limit first studied by Charney (1971). He showed that in the limit of strong stratification and rapid rotation (Fr² ≪ Ro ≪ 1), nonlinear interactions conserve potential enstrophy (potential vorticity squared; see Appendix A.6) as well as energy, again giving rise to an inverse cascade of energy (see also Salmon, 1978; Vallis, 2005). This has been demonstrated in 3D simulations by Métais et al. (1996). However, the quasi-geostrophic limit does not strictly apply to global-scale motions in spherical shells. It is plausible that similar dynamics occur in spherical systems but this has not yet been rigorously demonstrated.

Thus far in our discussion we have neglected magnetic fields, which can have a profound influence on self-organization processes in turbulent fluids. MHD turbulence does not conserve enstrophy even in the 2D limit, so there is nothing to inhibit a forward cascade of kinetic energy (e.g., Biskamp, 1993; Kim and Dubrulle, 2002). An inverse cascade does occur, but it involves a different ideal invariant, namely magnetic helicity (or in 2D, the magnetic potential). Thus, the physical mechanisms described above which can create banded zonal flows probably do not operate globally in the tachocline, although related dynamics likely occur in relatively field-free regions. Self-organization in MHD turbulence generally proceeds by creating large-scale magnetic structures which can then feed back on mean flows through the Maxwell stress.

Another important factor in a tachocline context is the presence of rotational shear imposed by large-scale stresses from the overlying convective envelope. If the turbulence is itself driven by instabilities of this rotational shear, one may expect it to have a diffusive influence, extracting energy from the shear flow by reducing its amplitude. One may also expect a diffusive behavior if the turbulence is small-scale, isotropic, and homogeneous across horizontal surfaces. In other words, if there is a scale separation with local turbulent mixing. Alternatively, if the flow is dominated by waves, one might expect non-local transport which is in general non-diffusive (e.g., McIntyre, 1998, 2003).

The influence of an imposed differential rotation on 2D turbulence in a β-plane was studied by Shepherd (1987). He found that the shearing of vortices by the differential rotation substantially altered the nonlinear transfer rates among spectral modes. In forced-dissipative simulations, small-scale turbulent motions tended to extract energy from the mean shear but the shear-induced Reynolds stress from the larger-scale wave field (k ≤ k _β ) tended to amplify the mean flow. The net transfer between the mean flow and the fluctuations about it depended sensitively on the parameters of the problem. Shepherd concluded that this complex interaction could not be modeled with a simple linear parameterization, diffusive or otherwise. More recent simulations by Williams (2003) in 2D spherical shells have also shown that the interaction between Rossby wave turbulence and horizontal shear flows can act either to suppress or enhance the shear, depending on the particular details of the problem.

Research into the interaction between a shear flow and 3D, stably-stratified turbulence has focused mainly on the case of non-rotating Cartesian domains with vertical shear. Here an important parameter is the Richardson number Ri = (N/S)² where S is the mean shear (cf. Section 8.2). At small Ri (shear-dominated), the turbulent transport of momentum and buoyancy tends to be down-gradient (diffusive) but at large Ri (buoyancy-dominated), turbulent transport is generally oscillatory and can be persistently counter-gradient (Holt et al., 1992; Galmiche et al., 2002; Jacobitz, 2002). These studies are based on numerical simulations of freely-evolving (decaying) turbulence with homogeneous and isotropic initial conditions and an imposed shear. An effective time-dependent viscosity and diffusivity can be defined based on the instantaneous turbulent fluxes and the mean gradients as shown in Figure 26. Counter-gradient transport is manifested as a negative turbulent viscosity after about 2.5 shear timescales in the strongly-stratified simulation (Figure 26, panel b). Although oscillatory, counter-gradient transport is a robust result of these numerical experiments, it may be a consequence of how they are set up; turbulent fluctuations are sheared by a mean flow which is switched on at some arbitrary time. An analysis in terms of rapid distortion theory by Hanazaki and Hunt (2004) suggests that the counter-gradient fluxes become very weak as Ri → ∞ and may be absent altogether in statistically steady flows.

Open image in new window

Jacobitz (2002) also considered the case of horizontal shear in a vertically stratified domain. In this case the turbulent transport was generally down-gradient (diffusive) even for strong stratification (Figure 26). Similar conclusions were also reached by Miesch (2003) who found down-gradient horizontal angular momentum transport and counter-gradient vertical transport in simulations of rotating, stably-stratified turbulence in thin spherical shells with random external forcing.

Counter-gradient transport in stably-stratified flows is often associated with the presence of waves (although this is not the only mechanism, (e.g., Holt et al., 1992; Galmiche and Hunt, 2002)). Waves carry pseudo-momentum which is conserved until they dissipate, giving rise to long-range transport as described in Section 8.4.

Magnetic fields generally tend to induce down-gradient momentum transport in turbulent shear flows by suppressing upscale kinetic energy transfer (cf. inverse cascades) and by imposing rigidity via magnetic tension. However, the transport efficiency can be reduced due to the partial offset of Reynolds and Maxwell stresses, which often have opposite senses (e.g., Kim et al., 2001). Magnetic fields can also suppress turbulent magnetic diffusion (Cattaneo and Vainshtein, 1991; Yousef et al., 2003). Still, magnetism can also have non-diffusive effects. For example, the balance between the Lorentz and Coriolis forces in toroidal field bands can induce zonal jets (see Section 8.2).

In summary, turbulent transport and self-organization in the tachocline is complex and not well understood. A variety of processes can act to establish or to suppress mean flows. Which of these prevail will depend on the subtleties of how the tachocline couples to the convection zone and radiative interior, a topic which will likely occupy researchers for many years to come.

8.4 Internal waves

Waves are ubiquitous in rotating, stratified flows. In the tachocline, they may be driven by penetrative convection (Section 8.1), shear, or instabilities (Section 8.2). Restoring forces may be provided by buoyancy (gravity waves), the Coriolis force (Rossby and other inertial waves; see Appendix A.6), magnetic tension (Alfvén waves), or some combination of the three²². We will refer to these modes collectively as internal waves.

Linear, non-dissipative waves cannot redistribute momentum in a time-averaged sense. However, waves can redistribute momentum if they dissipate by wave breaking or by thermal or viscous diffusion. Thus, waves induce a momentum transport from regions of excitation to regions of dissipation which is, in general, long-range (non-local) and can be counter-gradient (non-diffusive). There are multiple examples of wave-driven flows in the Earth’s atmosphere where such non-local momentum transport is reasonably well-established (McIntyre, 1998; Shepherd, 2000; Baldwin et al., 2001).

The intrinsic frequency of the wave, σ is set by the wave generation process, for example the timescale which characterizes penetrative convection. As the wave propagates vertically, this frequency is Doppler shifted by the background flow, U₀. For illustration, we will assume U₀ > 0. If the zonal phase speed of the wave is parallel to the mean flow (σk _x > 0), the wave may encounter a critical layer where the Doppler-shifted frequency σ − k _x U₀ approaches zero. The resulting dynamics are illustrated in panel a of Figure 27. In a solar context, the vertical coordinate z may be regarded as increasing downward, with z = 0 at the base of the convection zone.

Open image in new window

As the wave approaches the critical layer z_c, its vertical wavenumber increases and its group velocity slows, making it more susceptible to viscous and thermal diffusion (see Appendix A.7). If it is not dissipated first by diffusion, the wave will increase in amplitude and eventually break before encountering the critical layer. Thus, there is generally a transfer of momentum from waves to the mean flow near a critical layer, a phenomenon which is often referred to as critical layer absorption.

Similar dynamics can also occur in the presence of a horizontal shear, as illustrated in panel b of Figure 27. In this case we have a zonal flow which depends on y, the local latitudinal coordinate, \(U_{0}(y)\hat{x}\). If a wave propagates horizontally against the mean flow, it may encounter a trapping plane at y _t where the Doppler-shifted frequency approaches the Brunt-Väisälä frequency, N. The horizontal group velocity again approaches the mean flow speed, and the latitudinal wavenumber, k _y increases without limit according to WKB theory. The wave will again break or dissipate by thermal or viscous diffusion before y _t is reached, inducing a net momentum flux from the source region of the waves to the vicinity of the trapping plane. The nonlinear breaking of internal gravity waves near a trapping plane and the associated mass and momentum transport has recently been modeled numerically by Staquet and Huerre (2002).

In the Sun, waves are unlikely to dissipate solely by critical layer absorption (or the analogous process near a trapping plane). Rather, they dissipate mainly by radiative diffusion. Still, the processes discussed above give some insight into the resulting momentum transport. In the presence of a prograde zonal flow with vertical shear, a prograde wave will have a lower vertical group velocity and a higher vertical wave number than a retrograde wave. Thus, the prograde wave will be more readily dissipated by thermal diffusion even if it does not encounter a critical layer. The net result is a convergence of prograde momentum which acts to accelerate the mean flow. As the zonal velocity increases, Doppler shifts are amplified and waves travel shorter distances before they are dissipated. The region of convergence moves upward (toward lower z) while lower layers (higher z) decelerate again as a result of the reduced wave flux. In this way, oscillating zonal flows can be established which are analogous to the Quasi-Biennial Oscillation (QBO) in the Earth’s stratosphere (Baldwin et al., 2001).

Wave-driven flows such as these in the solar tachocline have been studied by several authors (Fritts et al., 1998; Kumar et al., 1999; Kim and MacGregor, 2001, 2003; Talon et al., 2002). Kim and MacGregor (2001, 2003), in particular, considered a simple 1D model for a zonal flow with vertical shear U₀ (z), in which momentum transport by radiatively-damped gravity waves is offset by viscous diffusion. Two waves were included in the model, prograde and retrograde, with horizontal velocities parallel and anti-parallel to the mean flow, respectively. As the turbulent viscosity was decreased, the temporal response of the resulting zonal flow underwent a transition from stationary to periodic, to quasi-periodic, and eventually to chaotic. A periodic solution is illustrated in Figure 28. When only a single wave was included in the presence of a background shear, the solutions were stationary and tended to produce counter-gradient angular momentum transport, accelerating the mean flow.

Open image in new window

The selective dissipation of waves with horizontal phase speeds parallel to the mean zonal flow acts as a filtering mechanism, removing these modes from the wave field. This filtering is latitude-dependent, since the radial angular velocity gradient in the tachocline varies from positive values at the equator to negative values at the poles (Section 3.1). Fritts et al. (1998) argue that the momentum redistribution resulting from this inhomogeneous wave filtering will establish a residual meridional circulation which may have implications for chemical transport and the low abundance of Lithium in the solar envelope relative to cosmic abundances. Chemical transport by gravity waves has also been studied by other authors from the perspective of light-element depletion in stars, and is often parameterized in terms of an effective diffusion (Montalbán, 1994; Schatzman, 1996; Pinsonneault, 1997).

Waves which are not filtered out by shear or other processes in the tachocline will propagate deeper into the solar interior. Eventually, these waves too will dissipate, resulting in an exchange of angular momentum between the convective envelope and the radiative interior. In a steady state the net transport must vanish but over evolutionary timescales the Sun is not steady. Rather, the solar envelope is continually losing angular momentum via the solar wind. In this situation, Talon et al. (2002) argue that gravity waves will systematically extract angular momentum from the radiative interior over the lifetime of the Sun. The resulting coupling between the convection zone and radiative interior may help to explain why the mean rotation rate of these two regions is comparable (Section 3.1).

The dynamical influence of a toroidal magnetic field on gravity wave propagation is similar in some ways to that of a zonal flow. Here a magnetic critical layer exists where the horizontal group velocity of the wave approaches the Alfvén speed relative to the mean flow (Barnes et al., 1998; McKenzie and Axford, 2000; MacGregor, 2003). This is analogous to a hydrodynamic critical layer in that the vertical wavenumber increases without bound but the dynamics in the vicinity of the critical layer can be notably different. The presence of a toroidal field significantly limits the range of wavenumbers which can propagate without becoming evanescent. The Doppler-shifted frequency no longer vanishes in the critical layer; rather, it approaches ±k _x υ_A where υ_A is the Alfvén speed. If the field is strong, waves are Alfvénic in nature and propagate along the field lines. Gravity waves may therefore be absorbed by the critical layer (dissipated) or they may be converted to Alfvén modes which propagate horizontally. Such filtering by strong toroidal fields in the tachocline may greatly enhance the shear filtering described above (Kim and MacGregor, 2003).

Shear and magnetic fields not only filter waves by selective dissipation, but they can also reflect waves. In some cases, over-reflection can occur wherein there is a net transfer of energy from the field or shear to the waves. This can increase the amplitude of a wave to the point of nonlinear breaking. Since gravity waves are evanescent in the convection zone, wave reflection by angular velocity shear and toroidal fields in the lower tachocline may essentially create a waveguide, channeling gravity and Alfvén waves into a narrow horizontal layer, where they eventually dissipate by wave breaking or radiative diffusion (MacGregor, 2003).

8.5 Tachocline confinement

One of the most compelling questions about the tachocline is: Why is it so thin? The transition from a ∼ 30% latitudinal variation of angular velocity in the convection zone to nearly uniform rotation in the radiative interior occurs over roughly 5% or less of the solar radius (Section 3.2).

The issue is best illustrated by considering one of the pioneering papers on the subject: The very paper which coined the term tachocline. Soon after the first helioseismic indications that a rotational shear layer exists near the base of the convection zone, Spiegel and Zahn (1992) considered the problem from the perspective of an axisymmetric spin-down scenario. They considered a spherical volume of fluid in hydrostatic and geostrophic balance subject to an imposed latitudinal differential rotation on the upper boundary. This was intended to represent the radiative solar interior under the influence of wind stress from the convective envelope. A meridional circulation was quickly established in which the advective heat flux was balanced by radiative diffusion. If momentum transport by unresolved turbulent motions was neglected, they found that this circulation steadily spread into the radiative interior, redistributing angular momentum away from uniform rotation on a timescale of several billion years. If such a radiative spreading had occurred over the lifetime of the Sun, the differential rotation of the envelope would have spread deep into the solar interior, in marked contrast to the nearly uniform rotation inferred from helioseismic inversions (see Section 3.1). Further numerical calculations were later performed by Elliott (1997), confirming these results.

Thus, the question of why the tachocline is so thin is equivalent to asking what can stop this radiative spreading. Or from a somewhat different perspective, one may instead ask: What process or processes can maintain uniform rotation in the radiative interior, in spite of stresses exerted by the convection zone?

Although Spiegel and Zahn (1992) identified nonlinear hydrodynamic shear instabilities in particular, other mechanisms may produce a similar confinement, provided they induce down-gradient horizontal angular momentum transport. Or, in other words, provided they act as a positive anisotropic turbulent viscosity with ν_H ≫ ν_V. One such alternative mechanism may be provided by the 2D and shallow-water magneto-shear instabilities studied by Gilman, Fox, Dikpati, and Cally which generally transport angular momentum poleward via the Maxwell stress (see Section 8.2). Another possible mechanism might be stratified turbulence induced by penetrative convection (Miesch, 2001, 2003).

These mechanisms may help to explain why the latitudinal differential rotation of the convective envelope does not spread inward, but they do little to explain why the radiative interior as a whole is rotating uniformly. Stratified, rotating turbulence near the base of the convection zone may produce down-gradient angular momentum transport in latitude but this is by no means certain and in any case, the vertical transport is likely to be counter-gradient (see Section 8.3). Deeper in the interior, angular momentum transport by gravity waves would also tend to enhance shear rather than suppress it due to the selective dissipation of prograde and retrograde modes (see Section 8.4). These points have been made repeatedly by McIntyre and others (McIntyre, 1994, 1998, 2003; Gough and McIntyre, 1998; Ringot, 1998). Gravity waves may still play a role in tachocline confinement, but only if there is some additional mechanism such as shear turbulence to provide an effective viscous diffusion (Talon et al., 2002)²³. Hydrodynamic instabilities alone appear to be too inefficient to maintain uniform rotation (Spruit, 1999; Garaud, 2001; Mathis and Zahn, 2004).

The difficulties in producing diffusive angular momentum transport in rotating, stably-stratified flows by purely hydrodynamical means has led some to suggest that magnetic fields are necessary in order to maintain uniform rotation in the radiative interior (Rüdiger and Kitchatinov, 1997; Gough and McIntyre, 1998). Such fields may arise as a remnant, or fossil, left over from the gravitational collapse of the protostellar cloud from which the Sun formed. An axisymmetric poloidal field will resist differential rotation via magnetic tension. The resulting torques will tend to establish uniform rotation along magnetic field lines on an Alfvénic timescale, a result which is known as Ferraro’s theorem (Cowling, 1957; Mestel and Weiss, 1987; MacGregor and Charbonneau, 1999). Turbulence induced by instabilities may then couple adjacent field lines. For example, as the solar wind spins down the convective envelope, angular velocity profiles may be established which decrease outward with cylindrical radius, ∂Ω/∂λ < 0. These would then be subject to magneto-rotational instabilities (Section 8.2) which, together with the torques implied by Ferraro’s theorem, could establish uniform rotation throughout the radiative interior. Diffusive instabilities may also play a role (Menou et al., 2004).

According to Ferraro’s theorem, the fossil field must be confined entirely to the radiative interior in order to maintain uniform rotation. If poloidal field lines were to extend into the convective envelope, then at least some fraction of the differential rotation there would be transmitted into the interior, which would be inconsistent with helioseismic inversions. This expectation is borne out by numerical calculations (MacGregor and Charbonneau, 1999).

In all likelihood, there will be a significant meridional circulation in the tachocline. In the Spiegel and Zahn (1992) scenario discussed above, for example, the differential rotation spreads not by viscous diffusion but by advection due to a radiatively-driven circulation. In this case, MacGregor and Charbonneau (1999) estimate that a field of B₀ ∼ 2 × 10⁻⁴ G would be required for confinement, about two orders of magnitude larger than the viscous estimate implied by Equation (31).

Meridional circulation also plays an essential role in the tachocline model proposed by Gough and McIntyre (1998). Here the circulation is driven by the Reynolds stress in the convection zone through what may be called gyroscopic pumping (McIntyre, 1998). Consider an axisymmetric ring of fluid. If the ring is subject to a prograde longitudinal force it will tend to drift away from the rotation axis due to the Coriolis force. If the force is retrograde, the ring will drift inward. In the solar convection zone, the Reynolds stress act to accelerate the equator relative to the poles, which would tend to establish a global circulation.

In the Gough & McIntyre model, this gyroscopic circulation is prevented from burrowing deep into the radiative interior by a fossil poloidal field as illustrated in Figure 29. The tachocline itself is non-magnetic but there exists a thin boundary layer at its base, called the tachopause, where the circulation is diverted horizontally by the interior field. This gives rise to a horizontal convergence and an associated upwelling at latitudes of about 30°, where the radial shear across the tachocline vanishes. The tachopause occupies only a few percent of the total tachocline width which is given by

$${{{\Delta _{\rm{t}}}} \over {{r_{\rm{t}}}}}\sim 3 \times {10^{- 2}}B_0^{- 1/9}.$$

(33)

This suggests field strengths of ∼ 0.1–1 G but a range of values is consistent with helioseismic inversions because Δ_t is relatively insensitive to B₀.

Open image in new window

The dynamical balance in the tachopause not only keeps the circulation from spreading inward, but it also keeps the fossil field confined to the radiative interior. This can only occur in downwelling regions; upwelling regions are likely to be more complex and may alter this simple picture. In the most recent incarnation of the Gough & McIntyre model (McIntyre, private communication), some of the magnetic field lines in upwelling regions follow the circulation streamlines into the convection zone. Regions in which the angular velocity decreases outward (dΩ/dλ < 0) would then be subject to magneto-rotational instabilities (MRI; see Section 8.2) which would alter the local tachocline structure, still maintaining thermal wind balance.

Although magnetic confinement models are compelling, there are many aspects which need further verification and clarification. Among these is the configuration of the fossil field. Axisymmetric poloidal fields are likely to be unstable over evolutionary timescales so any fossil field which may exist in the solar interior today is probably of mixed poloidal and toroidal topology (Mestel and Weiss, 1987; Spruit, 1999). This has been incorporated into the Gough & McIntyre model, but still only in a schematic way. Another open question is whether a circulation which is driven in the convection zone can overcome the stiff subadiabatic stratification in the lower tachocline and penetrate all the way to the tachopause Gilman and Miesch (2004).

Some aspects of the Gough & McIntyre model have been investigated numerically by Garaud (2002) who solved the axisymmetric MHD equations under the Boussinesq approximation. The circulation in Garaud’s model was driven by Ekman pumping and bore little resemblance to the baroclinic circulations considered by either Gough and McIntyre (1998) or Spiegel and Zahn (1992). Nevertheless, the results did demonstrate that a circulation is capable of confining a poloidal field largely to the radiative interior. Furthermore, the field was able to establish nearly uniform rotation in the interior over an intermediate range of field strengths.

A common feature in nearly all magnetic confinement models is the presence of a polar pit. This is a region near the magnetic poles where the poloidal field is primarily radial and therefore cannot confine the tachocline. Here the meridional circulation and consequently the differential rotation spreads much deeper into the radiative interior. This could in principle be probed with helioseismology, although the low sensitivity of frequency splittings to angular velocity variations near the rotation axis would make it difficult to detect. Currently there is little helioseismic evidence either supporting or refuting the presence of a polar pit.

An alternative to tachocline confinement by a weak fossil field in the radiative interior is tachocline confinement by a strong dynamo field originating in the convection zone. This possibility has been explored by Forgács-Dajka and Petrovay (2002) and Forgács-Dajka (2004) who consider a thin, axisymmetric shell of fluid under the anelastic approximation. A latitudinal differential rotation is imposed on the upper boundary along with an oscillatory poloidal field intended to represent dynamo processes in the convective envelope. The characteristic penetration depth of the field is the electromagnetic skin depth for a conductor, (2η_t/ω_c, where η_t is a turbulent diffusivity and w_c is the frequency of the oscillation. If the turbulent diffusivity is large enough (∼ 10¹⁰ cm s⁻²) and if the imposed field is strong enough (∼ 10³ G), then the field can penetrate deep enough to suppress the spread of differential rotation into the interior.

It is an open question how the relatively weak Lorentz force and circulations associated with magnetic confinement by a fossil field may coexist with and couple to the much stronger forces and motions which exist in the convection zone. In this context, a distinction is often made between fast tachocline dynamics which occur on timescales of weeks to decades and slow tachocline dynamics which occur on much longer timescales (e.g., Gilman, 2000a). Nearly all of the processes discussed in Sections 8.1 and 8.4 fall under the category of fast dynamics. Although they involve relatively weak circulations, the tachocline models of Forgács-Dajka and Petrovay (2002) and Forgás-Dajka (2004) may also be classified as fast because they require efficient turbulent mixing to operate and because they are concerned with dynamo-generated fields with an oscillation period of 22 years. The remaining magnetic confinement models discussed in this section represent slow dynamics. For example, the overturning time scale for the tachocline circulation in the Gough & McIntyre model is of order a million years. Fast dynamics are likely to dominate in the upper tachocline which probably overlaps with the convection zone and overshoot region. However, slow dynamics may be ultimately responsible for the nearly uniform rotation of the radiative interior and may therefore determine the lower boundary of the tachocline.