Abstract
Significant progress has been made in recent years on the development of gravitational-wave detectors. Sources such as coalescing compact binary systems, neutron stars in low-mass X-ray binaries, stellar collapses and pulsars are all possible candidates for detection. The most promising design of gravitational-wave detector uses test masses a long distance apart and freely suspended as pendulums on Earth or in drag-free spacecraft. The main theme of this review is a discussion of the mechanical and optical principles used in the various long baseline systems in operation around the world — LIGO (USA), Virgo (Italy/France), TAMA300 and LCGT (Japan), and GEO600 (Germany/U.K.) — and in LISA, a proposed space-borne interferometer. A review of recent science runs from the current generation of ground-based detectors will be discussed, in addition to highlighting the astrophysical results gained thus far. Looking to the future, the major upgrades to LIGO (Advanced LIGO), Virgo (Advanced Virgo), LCGT and GEO600 (GEO-HF) will be completed over the coming years, which will create a network of detectors with the significantly improved sensitivity required to detect gravitational waves. Beyond this, the concept and design of possible future “third generation” gravitational-wave detectors, such as the Einstein Telescope (ET), will be discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gravitational waves, one of the more exotic predictions of Einstein’s General Theory of Relativity may, after decades of controversy over their existence, be detected within the next five years.
Sources such as interacting black holes, coalescing compact binary systems, stellar collapses and pulsars are all possible candidates for detection; observing signals from them will significantly boost our understanding of the Universe. New unexpected sources will almost certainly be found and time will tell what new information such discoveries will bring. Gravitational waves are ripples in the curvature of space-time and manifest themselves as fluctuating tidal forces on masses in the path of the wave. The first gravitational-wave detectors were based on the effect of these forces on the fundamental resonant mode of aluminium bars at room temperature. Initial instruments were constructed by Joseph Weber [310, 311] and subsequently developed by others. Reviews of this early work are given in [299, 128]. Following the lack of confirmed detection of signals, aluminium bar systems operated at and below the temperature of liquid helium were developed [253, 261, 76, 170], although work in this area is now subsiding, with only two detectors, Auriga [88] and Nautilus [239], continuing to operate. Effort also continues to be pursued into cryogenic spherical bar detectors, which are designed to have a wider bandwidth than the cylindrical bars, with the two prototype detectors the Dutch MiniGRAIL [233, 158] and Brazilian Mário Schenberg [159, 70]. However, the most promising design of gravitational-wave detectors, offering the possibility of very high sensitivities over a wide range of frequency, uses widely-separated test masses freely suspended as pendulums on Earth or in a drag-free craft in space; laser interferometry provides a means of sensing the motion of the masses produced as they interact with a gravitational wave.
Ground-based detectors of this type, based on the pioneering work of Forward and colleagues (Hughes Aircraft) [236], Weiss and colleagues (MIT) [313], Drever and colleagues (Glasgow/Caltech) [130, 129] and Billing and colleagues (MPQ Garching) [95], will be used to observe sources whose radiation is emitted at frequencies above a few Hz, and space-borne detectors, as originally envisaged by Peter Bender and Jim Faller [126, 140] at JILA, will be developed for implementation at lower frequencies.
Gravitational-wave detectors of long baseline have been built in a number of places around the world; in the USA (LIGO project led by a Caltech/MIT consortium) [45, 212], in Italy (Virgo project, a joint Italian/French venture) [61, 304], in Germany (GEO600 project built by a collaboration centred on the University of Glasgow, the University of Hannover, the Max Planck Institute for Quantum Optics, the Max Planck Institute for Gravitational Physics (Albert Einstein Institute), Golm and Cardiff University) [321, 151] and in Japan (TAMA300 project) [78, 294]. A space-borne detector, called LISA [125, 217, 216], was until earlier this year (2011) under study as a joint ESA/NASA mission as one L-class candidate within the ESA Cosmic Visions program (a recent meeting detailing these missions can be found here [118]). Funding constraints within the US now mean that ESA must examine the possibility of flying an L-class mission with European-only funding. The official ESA statement on the next steps for LISA can be found here [240]. When completed, this detector array would have the capability of detecting gravitational wave signals from violent astrophysical events in the Universe, providing unique information on testing aspects of general relativity and opening up a new field of astronomy.
It is also possible to observe the tidal effects of a passing gravitational wave by Doppler tracking of separated objects. For example, Doppler tracking of spacecraft allows the Earth and an interplanetary spacecraft to be used as test masses, where their relative positions can be monitored by comparing the nearly monochromatic microwave signal sent from a ground station with the coherently returned signal sent from the spacecraft [136]. By comparing these signals, a Doppler frequency time series Δν/ν0, where ν0 is the central frequency from the ground station, can be generated. Peculiar characteristics within the Doppler time series, caused by the passing of gravitational waves, can be studied in the approximate frequency band of 10−5 to 0.1 Hz. Several attempts have been made in recent decades to collect such data (Ulysses, Mars Observer, Galileo, Mars Global Surveyor, Cassini) with broadband frequency sensitivities reaching 10−16 (see [85] for a thorough review of gravitational-wave searches using Doppler tracking). There are currently no plans for dedicated experiments using this technique; however, incorporating Doppler tracking into another planetary mission would provide a complimentary precursor mission before dedicated experiments such as LISA are launched.
The technique of Doppler tracking to search for gravitational-wave signals can also be performed using pulsar-timing experiments. Millisecond pulsars [219] are known to be very precise clocks, which allows the effects of a passing gravitational wave to be observed through the modulation in the time of arrival of pulses from the pulsar. Many noise sources exist and, for this reason, it is necessary to monitor a large array of pulsars over a long observation time. Further details on the techniques used and upper limits that have been set with pulsar timing experiments can be found from groups such as the European Pulsar Timing Array [187], the North American Nanohertz Observatory for Gravitational Waves [190, 191], and the Parkes Pulsar Timing Array [179].
All the above detection methods cover over 13 orders of magnitude in frequency (see Figure 1) equivalent to covering from radio waves to X-rays in the electromagnetic spectrum. This broadband coverage allows us to probe a wide range of potential sources.
The sensitivity of various gravitational-wave detection techniques across 13 orders of magnitude in frequency. At the low frequency end the sensitivity curves for pulsar timing arrays (based on current observations and future observations with the Square Kilometre Array [108]) are extrapolated from Figure 4 in [325]. In the mid-range LISA, DECIGO and BBO are described in more detail in Section 7, with the DECIGO and BBO sensitivity curves taken from models given in [323]. At the high frequency the sensitivities are represented by three generations of laser interferometers: LIGO, Advanced LIGO and the Einstein Telescope (see Sections 6, 6.3.1 and 6.3.2). Also included is a representative sensitivity for the AURIGA [88], Allegro [226] and Nautilus [239] bar detectors.
We recommend a number of excellent books for reference. For a popular account of the development of the gravitational-wave field the reader should consult Chapter 10 of Black Holes and Time Warps by Kip S. Thorne [296], or the more recent books, Einstein’s Unfinished Symphony, by Marcia Bartusiak [92] and Gravity from the Ground Up, by Bernard Schutz [283]. A comprehensive review of developments toward laser interferometer detectors is found in Fundamentals of Interferometric Gravitational Wave Detectors by Peter Saulson [277], and discussions relevant to the technology of both bar and interferometric detectors are found in The Detection of Gravitational Waves edited by David Blair [96].
In addition to the wealth of articles that can be found on the home site of this journal, there are also various informative websites that can easily be found, including the homepages of the various international collaborative projects searching for gravitational waves, such as the LIGO Scientific Collaboration [215].
2 Gravitational Waves
Some early relativists were sceptical about the existence of gravitational waves; however, the 1993 Nobel Prize in Physics was awarded to Hulse and Taylor for their experimental observations and subsequent interpretations of the evolution of the orbit of the binary pulsar PSR 1913+16 [185, 295], the decay of the binary orbit being consistent with angular momentum and energy being carried away from this system by gravitational waves [316].
Gravitational waves are produced when matter is accelerated in an asymmetrical way; but due to the nature of the gravitational interaction, detectable levels of radiation are produced only when very large masses are accelerated in very strong gravitational fields. Such a situation cannot be found on Earth but is found in a variety of astrophysical systems. Gravitational wave signals are expected over a wide range of frequencies; from ≃ 10−17 Hz in the case of ripples in the cosmological background to ≃ 103 Hz from the formation of neutron stars in supernova explosions. The most predictable sources are binary star systems. However, there are many sources of much-greater astrophysical interest associated with black-hole interactions and coalescences, neutron-star coalescences, neutron stars in low-mass X-ray binaries such as Sco-X1, stellar collapses to neutron stars and black holes (supernova explosions), pulsars, and the physics of the early Universe. For a full discussion of sources refer to the material contained in [273, 272, 115, 232].
Why is there currently such interest worldwide in the detection of gravitational waves? Partly because observation of the velocity and polarisation states of the signals will allow a direct experimental check of the wave predictions of general relativity; but, more importantly, because the detection of the signals should provide observers with new and unique information about astrophysical processes. It is interesting to note that the gravitational wave signal from a coalescing compact binary star system has a relatively simple form and the distance to the source can be obtained from a combination of its signal strength and its evolution in time. If the redshift at that distance is found, Hubble’s Constant — the value for which has been a source of lively debate for many years — may then be determined with, potentially, a high degree of accuracy [282, 180].
Only now are detectors being built with the technology required to achieve the sensitivity to observe such interesting sources.
3 Detection of Gravitational Waves
Gravitational waves are most simply thought of as ripples in the curvature of space-time, their effect being to change the separation of adjacent masses on Earth or in space; this tidal effect is the basis of all present detectors. Gravitational wave strengths are characterised by the gravitational-wave amplitude h, given by
where ΔL is the change in separation of two masses a distance L apart; for the strongest-allowed component of gravitational radiation, the value of h is proportional to the third time derivative of the quadrupole moment of the source of the radiation and inversely proportional to the distance to the source. The radiation field itself is quadrupole in nature and this shows up in the pattern of the interaction of the waves with matter.
The problem for the experimental physicist is that the predicted magnitudes of the amplitudes or strains in space in the vicinity of the Earth caused by gravitational waves even from the most violent astrophysical events are extremely small, of the order of 10−21 or lower [273, 272]. Indeed, current theoretical models on the event rate and strength of such events suggest that in order to detect a few events per year — from coalescing neutron-star binary systems, for example, an amplitude sensitivity close to 10−22 over timescales as short as a millisecond is required. If the Fourier transform of a likely signal is considered it is found that the energy of the signal is distributed over a frequency range or bandwidth, which is approximately equal to 1/timescale. For timescales of a millisecond the bandwidth is approximately 1000 Hz, and in this case the spectral density of the amplitude sensitivity is obtained by dividing 10−22 by the square root of 1000. Thus, detector noise levels must have an amplitude spectral density lower than ≃ 10−23 Hz−1/2 over the frequency range of the signal. Signal strengths at the Earth, integrated over appropriate time intervals, for a number of sources are shown in Figure 2.
The weakness of the signal means that limiting noise sources like the thermal motion of molecules in the critical components of the detector (thermal noise), seismic or other mechanical disturbances, and noise associated with the detector readout, whether electronic or optical, must be reduced to an extremely low level. For signals above ≃ 10 Hz ground based experiments are possible, but for lower frequencies where local fluctuating gravitational gradients and seismic noise on Earth become a problem, it is best to consider developing detectors for operation in space [125].
3.1 Initial detectors and their development
The earliest experiments in the field were ground based and were carried out by Joseph Weber of the University of Maryland in the 1960s. With colleagues he began by looking for evidence of excitation of the normal modes of the Earth by very low frequency gravitational waves [142]. Efforts to detect gravitational waves via the excitation of Earth’s normal modes was also pursued by Weiss and Block [314]. Weber then moved on to look for tidal strains in aluminium bars, which were at room temperature and were well isolated from ground vibrations and acoustic noise in the laboratory [310, 311]. The bars were resonant at ≃ 1600 Hz, a frequency where the energy spectrum of the signals from collapsing stars was predicted to peak. Despite the fact that Weber observed coincident excitations of his detectors placed up to 1000 km apart, at a rate of approximately one event per day, his results were not substantiated by similar experiments carried out in several other laboratories in the USA, Germany, Britain and Russia. It seems unlikely that Weber was observing gravitational-wave signals because, although his detectors were very sensitive, being able to detect strains of the order of 10−16 over millisecond timescales [310], their sensitivity was far away from what was predicted to be required theoretically. Development of Weber bar type detectors continued with significant emphasis on cooling to reduce the noise levels, although work in this area is now subsiding with efforts continuing on Auriga [88], Nautilus [239], MiniGRAIL [233, 158] and Mario Schenberg [159, 70]. In around 2003, the sensitivity of km-scale interferometric gravitational-wave detectors began to surpass the peak sensitivity of these cryogenic bar detectors (≃ 10−21) and, for example, the LIGO detectors reached their design sensitivities at almost all frequencies by 2005 (peak sensitivity ≃ 2 × 10−23 at ≃ 200 Hz) [315], see Section 6.1 for more information on science runs of the recent generation of detectors. In addition to gaining better strain sensitivities, interferometric detectors have a marked advantage over resonant bars by being sensitive to a broader range of frequencies, whereas resonant bar are inherently sensitive only to signals that have significant spectral energy in a narrow band around their resonant frequency. The concept and design of gravitational-wave detectors based on laser interferometers will be introduced in the following Section 3.2.
3.2 Long baseline detectors on Earth
An interferometric design of gravitational-wave detector offers the possibility of very high sensitivities over a wide range of frequency. It uses test masses, which are widely separated and freely suspended as pendulums to isolate against seismic noise and reduce the effects of thermal noise; laser interferometry provides a means of sensing the motion of these masses produced as they interact with a gravitational wave (Figure 3).
This technique is based on the Michelson interferometer and is particularly suited to the detection of gravitational waves as they have a quadrupole nature. Waves propagating perpendicular to the plane of the interferometer will result in one arm of the interferometer being increased in length while the other arm is decreased and vice versa. The induced change in the length of the interferometer arms results in a small change in the intensity of the light observed at the interferometer output.
As will be explained in detail in the next Section 4, the sensitivity of an interferometric gravitational-wave detector is limited by noise from various sources. Taking this frequency-dependent noise floor into account, a design goal can be estimated for a particular detector design. For example, the design sensitivity for initial LIGO is show in Figure 4 plotted alongside the achieved sensitivities of the three individual interferometers during the fifth science run (see Section 6.1). Such strain sensitivities are expected to allow a reasonable probability for detecting gravitational wave sources. However, in order to guarantee the observation of a full range of sources and to initiate gravitational-wave astronomy, a sensitivity or noise performance approximately ten times better in the mid-frequency range and several orders of magnitude better at 10 Hz, is desired. Therefore, initial detectors will be upgraded to an advanced configuration, such as Advanced LIGO, which will be ready for operation around 2015.
For the initial interferometric detectors, a noise floor in strain close to 2 × 10−23 Hz−1/2 was achieved. Detecting a strain in space at this level implies measuring a residual motion of each of the test masses of about 8 × 10−20 m/Hz−1/2 over part of the operating range of the detector, which may be from ≃ 10 Hz to a few kHz. Advanced detectors will push this target down further by another factor of 10–15. This sets a formidable goal for the optical detection system at the output of the interferometer.
4 Main Noise Sources
In this section we discuss the main noise sources, which limit the sensitivity of interferometric gravitational-wave detectors. Fundamentally it should be possible to build systems using laser interferometry to monitor strains in space, which are limited only by the Heisenberg Uncertainty Principle; however there are other practical issues, which must be taken into account. Fluctuating gravitational gradients pose one limitation to the interferometer sensitivity achievable at low frequencies, and it is the level of noise from this source, which dictates that experiments to look for sub-Hz gravitational-wave signals have to be carried out in space [291, 275, 93, 184]. In general, for ground-based detectors the most important limitations to sensitivity result from the effects of seismic and other ground-borne mechanical noise, thermal noise associated with the test masses and their suspensions, and quantum noise, which appears at high frequency as shot noise in the photocurrent from the photodiode, which detects the interference pattern and can appear at low frequency as radiation pressure noise due to momentum transfer to the test masses from the photons when using high laser powers. The significance of each of these sources will be briefly reviewed.
4.1 Seismic noise
Seismic noise at a reasonably quiet site on the Earth follows a spectrum in all three dimensions close to 10−7f−2 m/Hz1/2 (where here and elsewhere we measure f in Hz) and thus if the disturbance to each test mass must be less than 3 × 10−20 m/Hz1/2 at, for example, 30 Hz, then the reduction of seismic noise required at that frequency in the horizontal direction is greater than 109. Since there is liable to be some coupling of vertical noise through to the horizontal axis, along which the gravitational-wave-induced strains are to be sensed, a significant level of isolation has to be provided in the vertical direction also. Isolation can be provided in a relatively simple way by making use of the fact that, for a simple pendulum system, the transfer function to the pendulum mass of the horizontal motion of the suspension point falls off as 1/(frequency)2 above the pendulum resonance. In a similar way isolation can be achieved in the vertical direction by suspending a mass on a spring. In the case of the Virgo detector system the design allows operation to below 10 Hz and here a seven-stage horizontal pendulum arrangement is adopted with six of the upper stages being suspended with cantilever springs to provide vertical isolation [99], with similar systems developed in Australia [194] and at Caltech [127]. For the GEO600 detector, where operation down to 50 Hz was planned, a triple pendulum system is used with the first two stages being hung from cantilever springs to provide the vertical isolation necessary to achieve the desired performance. This arrangement is then hung from a plate mounted on passive ‘rubber’ isolation mounts and on an active (electro-mechanical) anti-vibration system [257, 298]. The upgraded seismic isolation for Advanced LIGO will also adopt a variety of active and passive isolation stages. The total isolation will be provided by one external stage (hydraulics), two stages of in-vacuum active isolation, and being completed by the test mass suspensions [55, 166]. For clarity, the two stages of in-vacuum isolation are shown in Figure 5, whereas the test-mass suspensions are shown separately in Figure 6.
CAD drawing of quad suspension system for Advanced LIGO, showing the mirror test mass at the bottom and where the uppermost section is attached to the third stage platform of the large chamber seismic isolation system shown in Figure 5.
In order to cut down motion at the pendulum frequencies, active damping of the pendulum modes has to be incorporated, and to reduce excess motion at low frequencies around the micro-seismic peak, low-frequency isolators have to be incorporated. These low-frequency isolators can take different forms — tall inverted pendulums in the horizontal direction and cantilever springs whose stiffness is reduced by means of attractive forces between magnets for the vertical direction in the case of the Virgo system [220], Scott Russell mechanical linkages in the horizontal and torsion bar arrangements in the vertical for an Australian design [322], and a seismometer/actuator (active) system as shown here for Advanced LIGO [55] and also used in GEO600 [256]. Such schemes can provide sufficiently-large reduction in the direct mechanical coupling of seismic noise through to the suspended mirror optic to allow operation down to 3 Hz [98, 134]. However, it is also possible for this vibrational seismic noise to couple to the suspended optic through the gravitational field.
4.2 Gravity gradient (Newtonian) noise
Gravity gradients, caused by direct gravitational coupling of mass density fluctuations to the suspended mirrors, were identified as a potential source of noise in ground-based gravitational-wave detectors in 1972 [313]. The noise associated with gravity gradients was first formulated by Saulson [275] and Spero [291], with later developments by Hughes and Thorne [184] and Cella and Cuoco [93]. These studies suggest that the dominant source of gravity gradients arise from seismic surface waves, where density fluctuations of the Earth’s surface are produced near the location of the individual interferometer test masses, as shown in Figure 7.
The magnitude of the rms motion of the interferometer test masses, \(\tilde x(\omega)\), can be shown to be [184]
where ρ is the Earth’s density near the test mass, G is Newton’s constant, ω is the angular frequency of the seismic spectrum, β (ω); is a dimensionless reduced transfer function that takes into account the correlated motion of the interferometer test masses in addition to the reduction due to the separation between the test mass and the Earth’s surface, and \(\tilde W(\omega)\) is the displacement rms-averaged over 3-dimensional directions. In order to eliminate noise arising from gravity gradients, a detector would have to be operated far from these density fluctuations, that is, in space. Proposed space missions are discussed in Section 7.
However, there are two proposed approaches for reducing the level of gravity-gradient noise in future ground-based detectors. A monitor and subtraction method can be used, where an array of seismometers can be distributed strategically around each test mass to monitor the relevant ground motion (and ground compression) that would be expected to couple through local gravity. A subtraction signal may be developed from knowing how the observed density fluctuations couple to the motion of each test mass, and can potentially allow a significant reduction in gravity-gradient noise.
Another approach is to choose a very quiet location, or better still, to also go underground, as is already going ahead for LCGT [234]. Since the dominant source of gravity-gradient noise is expected to arise from surface waves on the Earth, the observed gravity-gradient noise will decrease with depth into the Earth. Current estimates suggest that gravity-gradient noise can be suppressed down to around 1 Hz by careful site selection and going ∼ 150 m underground [94]. The most promising approach (or likely only approach) to detecting gravitational waves whose frequency is below 1 Hz is to build an interferometer in space.
4.3 Thermal noise
Thermal noise associated with the mirror masses and the last stage of their suspensions is the most significant noise source at the low frequency end of the operating range of initial long baseline gravitational wave detectors [276]. Advanced detector configurations are also expected to be limited by thermal noise at their most sensitive frequency band [211, 238, 168, 121]. Above the operating range there are the internal resonances of the test masses. The thermal noise in the operating range comes from the tails of these resonant modes. For any simple harmonic oscillator such as a mass hung on a spring or hung as a pendulum, the spectral density of thermal motion of the mass can be expressed as [276]
where kB is Boltzmann’s constant, T is the temperature, m is the mass and ϕ (ω) is the loss angle or loss factor of the oscillator of angular resonant frequency ω0. This loss factor is the phase lag angle between the displacement of the mass and any force applied to the mass at a frequency well below ω0. In the case of a mass on a spring, the loss factor is a measure of the mechanical loss associated with the material of the spring. For a pendulum, most of the energy is stored in the lossless gravitational field. Thus, the loss factor is lower than that of the material, which is used for the wires or fibres used to suspend the pendulum. Indeed, following Saulson [276] it can be shown that for a pendulum of mass m, suspended on four wires or fibres of length l, the loss factor of the pendulum is related to the loss factor of the material by
where I is the moment of the cross-section of each wire, and T is the tension in each wire, whose material has a Young’s modulus E. In general, for most materials, it appears that the intrinsic loss factor is essentially independent of frequency over the range of interest for gravitational-wave detectors (although care has to be taken with some materials in that a form of damping known as thermo-elastic damping can become important for wires of small cross-section [246] and for some bulk crystalline materials [102]). In order to estimate the internal thermal noise of a test mass, each resonant mode of the mass can be regarded as a harmonic oscillator. When the detector operating range is well below the resonances of the masses, following Saulson [276], the effective spectral density of thermal displacement of the front face of each mass can be expressed as the summation of the motion of the various mechanical resonances of the mirror as also discussed by Gillespie and Raab [153]. However, this intuitive approach to calculating the thermally-driven motion is only valid when the mechanical loss is distributed homogeneously and, therefore, not valid for real test-mass mirrors. The mechanical loss is known to be inhomogeneous due to, for example, the localisation of structural defects and stress within the bulk material, and the mechanical loss associated with the polished surfaces is higher than the levels typically associated with bulk effects. Therefore, Levin suggested using a direct application of the fluctuation-dissipation theorem to the optically-sensed position of the mirror substrate surface [211]. This technique imposes a notional pressure (of the same spatial profile as the intensity of the sensing laser beam) to the front face of the substrate and calculates the resulting power dissipated in the substrate on its elastic deformation under the applied pressure. Using such an approach we find that Sx(f) can then be described by the relation
where F0 is the peak amplitude of the notional oscillatory force and Wdiss is the power dissipated in the mirror described as,
where ∊(r) and ϕ(r) are the strain and mechanical loss located at specific positions within the volume V. This formalisation highlights the importance of where mechanical dissipation is located with respect to the sensing laser beam. In particular, the thermal noise associated with the multi-layer dielectric mirror coatings, required for high reflectivity, will in fact limit the sensitivity of second-generation gravitational-wave detectors at their most sensitive frequency band, despite these coatings typically being only ∼ 4.5 µm in thickness [168]. Identifying coating materials with lower mechanical loss, and trying to understand the sources of mechanical loss in existing coating materials, is a major R&D effort targeted at enhancements to advanced detectors and for third generation instruments [224].
In order to keep thermal noise as low as possible the mechanical loss factors of the masses and pendulum resonances should be as low as possible. Further, the test masses must have a shape such that the frequencies of the internal resonances are kept as high as possible, must be large enough to accommodate the laser beam spot without excess diffraction losses, and must be massive enough to keep the fluctuations due to radiation pressure at an acceptable level. Test masses currently range in mass from 6 kg for GEO600 to 40 kg for Advanced LIGO. To approach the best levels of sensitivity discussed earlier the loss factors of the test masses must be ≃ 3 × 10−8 or lower, and the loss factor of the pendulum resonances should be smaller than 10−10.
Obtaining these values puts significant constraints on the choice of material for the test masses and their suspending fibres. GEO600 utilises very-low-loss silica suspensions, a technology, which should allow detector sensitivities to approach the level desired for second generation instruments [105, 266, 268], since the intrinsic loss factors in samples of synthetic fused silica have been measured down to around 5 × 10−9 [68]. Still, the use of other materials such as sapphire is being seriously considered for future detectors [104, 195, 266] such as in LCGT [234, 247].
The technique of hydroxy-catalysis bonding provides a method of jointing oxide materials in a suitably low-loss way to allow ‘monolithic’ suspension systems to be constructed [267]. A recent discussion on the level of mechanical loss and the associated thermal noise in advanced detectors resulting from hydroxy-catalysis bonds is given by Cunningham et al. [123]. Images of the GEO600 monolithic mirror suspension and of the prototype Advanced LIGO mirror suspension are shown in Figure 8.
4.4 Quantum noise
4.4.1 Photoelectron shot noise
For gravitational-wave signals to be detected, the output of the interferometer must be held at one of a number of possible points on an interference fringe. An obvious point to choose is halfway up a fringe since the change in photon number produced by a given differential change in arm length is greatest at this point (in practice this is not at all a sensible option and interferometers are operated at, or near, a dark fringe — see Sections 5.1 and 5.4). The interferometer may be stabilised to this point by sensing any changes in intensity at the interferometer output with a photodiode and feeding the resulting signal back, with suitable phase, to a transducer capable of changing the position of one of the interferometer mirrors. Information about changes in the length of the interferometer arms can then be obtained by monitoring the signal fed back to the transducer.
As mentioned earlier, it is very important that the system used for sensing the optical fringe movement on the output of the interferometer can resolve strains in space of 2 × 10−23 Hz−1/2 or lower, or differences in the lengths of the two arms of less than 10−19 m/Hz1/2, a minute displacement compared to the wavelength of light ≃ 10−6 m. A limitation to the sensitivity of the optical readout scheme is set by shot noise in the detected photocurrent. From consideration of the number of photoelectrons (assumed to obey Poisson statistics) measured in a time τ it can be shown [181] that the detectable strain sensitivity depends on the level of laser power P of wavelength λ used to illuminate the interferometer of arm length L, and on the time τ, such that:
or
where c is the velocity of light, h is Planck’s constant and we assume that the photodetectors have a quantum efficiency ≃ 1. Thus, achievement of the required strain sensitivity level requires a laser, operating at a wavelength of 10−6 m, to provide 6 × 106 power at the input to a simple Michelson interferometer. This is a formidable requirement; however, there are a number of techniques which allow a large reduction in this power requirement and these will be discussed in Section 5.
4.4.2 Radiation pressure noise
As the effective laser power in the arms is increased, another phenomenon becomes increasingly important arising from the effect on the test masses of fluctuations in the radiation pressure. One interpretation on the origin of this radiation pressure noise may be attributed to the statistical uncertainty in how the beamsplitter divides up the photons of laser light [133]. Each photon is scattered independently and therefore produces an anti-correlated binomial distribution in the number of photons, N, in each arm, resulting in a \( \propto \sqrt N\) fluctuating force from the radiation pressure. This is more formally described as arising from the vacuum (zero-point) fluctuations in the amplitude component of the electromagnetic field. This additional light entering through the dark-port side of the beamsplitter, when being of suitable phase, will increase the intensity of laser light in one arm, while decreasing the intensity in the other arm, again resulting in anti-correlated variations in light intensity in each arm [109, 110]. The laser light is essentially in a noiseless “coherent state” [154] as it splits at the beamsplitter and fluctuations arise entirely from the addition of these vacuum fluctuations entering the unused port of the beamsplitter. Using this understanding of the coherent state of the laser, shot noise arises from the uncertainty in the phase component (quadrature) of the interferometer’s laser field and is observed in the quantum fluctuations in the number of detected photons at the interferometer output. Radiation pressure noise arises from uncertainty in the amplitude component (quadrature) of the interferometer’s laser field. Both result in an uncertainty in measured mirror positions.
For the case of a simple Michelson, shown in Figure 3, the power spectral density of the fluctuating motion of each test mass m resulting from fluctuation in the radiation pressure at angular frequency ω is given by [133],
where h is Planck’s constant, c is the speed of light and λ is the wavelength of the laser light. In the case of an interferometer with Fabry-Pérot cavities, where the typical number of reflections is 50, displacement noise δx due to radiation pressure fluctuations scales linearly with the number of reflections, such that,
Radiation pressure may be a significant limitation at low frequency and is expected to be the dominant noise source in Advanced LIGO between around 10 and 50 Hz [166]. Of course the effects of the radiation pressure fluctuations can be reduced by increasing the mass of the mirrors, or by decreasing the laser power at the expense of degrading sensitivity at higher frequencies.
4.4.3 The standard quantum limit
Since the effect of photoelectron shot noise decreases when increasing the laser power as the radiation pressure noise increases, a fundamental limit to displacement sensitivity is set. For a particular frequency of operation, there will be an optimum laser power within the interferometer, which minimises the effect of these two sources of optical noise, which are assumed to be uncorrelated. This sensitivity limit is known as the Standard Quantum Limit (SQL) and corresponds to the Heisenberg Uncertainty Principle, in its position and momentum formulation; see [133, 109, 110, 221].
Firstly, it is possible to reach the SQL at a tuned range of frequencies, when dominated by either radiation-pressure noise or shot noise, by altering the noise distribution in the two quadratures of the vacuum field. This effect can be achieved “by squeezing the vacuum field”. There are a number of proposed designs for achieving this in future interferometric detectors, such as a “squeezed-input interferometer” [110, 300], a “variational-output interferometer” [307] or a “squeezed-variational interferometer” using a combination of both techniques. This technique may be of importance in allowing an interferometer to reach the SQL at a particular frequency, for example, when using lower levels of laser power and otherwise being dominated by shot noise. Experiments are under way to incorporate squeezed-state injection as part of the upgrades to current gravitational-wave detectors, and where a squeezing injection bench has already been installed in the GEO600 gravitational-wave detector, which expects to be able to achieve an up-to-6 dB reduction in shot noise using the current interferometer configuration [301]. Similar experiments are also under way to demonstrate variational readout, where ponderomotive squeezing arises from the naturally-occurring correlation of radiation-pressure noise to shot noise upon reflection of light from a mirror [117, 271]
Secondly, if correlations exist between the radiation-pressure noise and the shot-noise displacement limits, then it is possible to bypass the SQL, at least in principle [221]. There are at least two ways by which such correlations may be introduced into an interferometer. One scheme is where an optical cavity is constructed, where there is a strong optical spring effect, coupling the optical field to the mechanical system. This is already the case for the GEO600 detector, where the addition of a signal recycling cavity creates such correlation, where signal recycling is described in Section 5.2. Other schemes of optical springs have been studied, such as optical bars and optical levers [103, 101]. Another method is to use suitable filtering at optical frequencies of the output signal, by means of long Fabry-Pérot cavities, which effectively introduces correlation [201, 116].
5 Laser Interferometric Techniques for Gravitational-Wave Detectors
As explained in Section 4.4.1, high-power laser light is needed to overcome limitations of a detector’s sensitivity due to photoelectron shot noise. The situation can be helped greatly if a multi-pass arrangement is used in the arms of the interferometer as this multiplies up the apparent movement by the number of bounces the light makes in the arms. The multiple beams can either be separate, as in an optical delay line [313, 95], or may lie on top of each other as in a Fabry-Pérot resonant cavity [129], as shown in Figure 9.
Optimally, the light should be stored for a time comparable to the characteristic timescale of the signal. Thus, if signals of characteristic timescale 1 msec are to be searched for, the number of bounces should be approximately 50 for an arm length of 3 km. With 50 bounces the required laser power is reduced to 2.4 × 103 W, still a formidable requirement.
5.1 Power recycling
It can be shown that an optimum signal-to-noise ratio in a Michelson interferometer can be obtained when the arm lengths are such that the output light is very close to a minimum (this is not intuitively obvious and is discussed more fully in [133]). Thus, rather than lock the interferometer to the side of a fringe as discussed above in Section 4.4.1, it is usual to make use of a modulation technique to operate the interferometer close to a null in the interference pattern. An electro-optic phase modulator placed in front of the interferometer can be used to phase modulate the input laser light. If the arms of the interferometer are arranged to have a slight mismatch in length this results in a detected signal, which, when demodulated, is zero with the cavity exactly on a null fringe and changes sign on different sides of the null providing a bipolar error signal; this can be fed back to the transducer controlling the interferometer mirror to hold the interferometer locked near to a null fringe (this is the RF readout scheme discussed in Section 5.4).
In this situation, if the mirrors are of very low optical loss, nearly all of the light supplied to the interferometer is reflected back towards the laser. In other words the laser is not properly impedance matched to the interferometer. The impedance matching can be improved by placing another mirror of correctly chosen transmission — a power recycling mirror — between the laser and the interferometer so that a resonant cavity is formed between this mirror and the rest of the interferometer; in the case of perfect impedance matching, no light is reflected back towards the laser [131, 278]. There is then a power build-up inside the interferometer as shown in Figure 10. This can be high enough to create the required kilowatts of laser light at the beamsplitter, starting from an input laser light of only about 10 W.
To be more precise, if the main optical power losses are those associated with the test mass mirrors — taken to be A per reflection — the intensity inside the whole system considered as one large cavity is increased by a factor given by (πL)/(cAτ), where the number of bounces, or light storage time, is optimised for signals of timescale τ and the other symbols have their usual meaning. Then:
5.2 Signal recycling
To enhance further the sensitivity of an interferometric detector and to allow some narrowing of the detection bandwidth, which may be valuable in searches for continuous wave sources of gravitational radiation, another technique known as signal recycling can be implemented [231, 292, 169]. This relies on the fact that sidebands created on the light by gravitational-wave signals interacting with the arms do not interfere destructively and so do appear at the output of the interferometer. If a mirror of suitably-chosen reflectivity is put at the output of the system as shown in Figure 11, then the sidebands can be recycled back into the interferometer, where they resonate, and hence the signal size over a given bandwidth (set by the mirror reflectivity) is enhanced.
The centre of this frequency band is set by the precise length of the cavity formed by the signal recycling mirror and the cavities in the interferometer arms. Thus, control of the precise position of the signal recycling mirror allows tuning of the frequency at which the performance is peaked.
Often signal recycling will be used to provide a narrow bandwidth to search for continuous wave sources as mentioned above, however it may also be used with a relatively broad bandwidth, centred away from zero frequency, and this application is useful for matching the frequency response of the detector to expected spectral densities of certain broadband or “chirping” signals.
5.3 Application of these techniques
Using appropriate optical configurations that employ power and signal recycling as described in Sections 5.1 and 5.2, the required laser power may thus be reduced to a level (in the range of 10 to 100 W) where laser sources are now available; however stringent requirements on technical noise must be satisfied.
5.3.1 Technical noise requirements
-
Power fluctuations
As described above in Section 5.1 gravitational-wave interferometers are typically designed to operate with the length of the interferometer arms set such that the output of the interferometer is close to a minimum in the output light. If the interferometer were operated exactly at the null point in the fringe pattern, then, in principle, it would be insensitive to power fluctuations in the input laser light. However in practice there will be small offsets from the null position causing some sensitivity to this noise source. In this case, it can be shown [182] that the required power stability of the laser in the frequency range of interest for gravitational-wave detection may be estimated to be
$${{\delta P} \over P} \simeq h{(\delta L/L)^{- 1}},$$(12)where δP/P are the relative power fluctuations of the laser, and δL is the offset from the null fringe position for an interferometer of arm length L. From calculations of the effects of low-frequency seismic noise for the initial designs of long baseline detectors [182] it can be estimated that the rms motion will be on the order of 10−13 m when the system is operating. Taking strains of around 3 × 10−24 Hz−1/2 at 300 Hz, as is the case for Advanced LIGO [166], requires power fluctuations of the laser not to exceed
$${{\delta P} \over P} \leq {10^{- 7}}{\rm{H}}{{\rm{z}}^{- 1/2}}\;\;{\rm{at}} \simeq 300\;{\rm{Hz}}.$$(13)To achieve this level of power fluctuation typically requires the use of active stabilisation techniques of the type developed for argon ion lasers [265]. However, it should be noted that the most stringent constraint on laser-power fluctuations in future ground-based detectors, where circulating laser powers will approach 1 MW or even beyond, will ultimately arise from classical radiation pressure on the mirrors, as described in Section 4.4.2.
-
Frequency fluctuations
For a simple Michelson interferometer it can be shown that a change δx in the differential path length, x, of the interferometer arms causes a phase change δϕ in the light at the interferometer output given by δϕ = (2π/c) (vδx + xδv) where δν is a change in the laser frequency ν and c is the speed of light. It follows that if the lengths of the interferometer arms are exactly equal (i.e., x = 0), the interferometer output is insensitive to fluctuations in the frequency of the input laser light, provided that, in the case of Fabry-Pérot cavities in the arms, the fluctuations are not so great that the cavities cannot remain on resonance. However, in practice, differences in the optical properties of the interferometer mirrors result in slightly different effective arm lengths, a difference of perhaps a few tens of metres. Then the relationship between the limit to detectable gravitational-wave amplitude and the fluctuations dν of the laser frequency ν is given by [182]
$${{\delta \nu} \over \nu} \simeq h{(x/L)^{- 1}}.$$(14)Hence, to achieve the target sensitivity used in the above calculation using a detector with arms of length 4 km, maximal fractional frequency fluctuations of,
$${{\delta \nu} \over \nu} \leq {10^{- 21}}{\rm{H}}{{\rm{z}}^{- 1/2}},$$(15)are required. This level of frequency noise may be achieved by the use of appropriate laser-frequency stabilisation systems involving high finesse reference cavities [182].
Although the calculation here is for a simple Michelson interferometer, similar arguments apply to the more sophisticated systems with arm cavities, power recycling and signal recycling discussed earlier and lead to the same conclusions. Frequency stabilisation is also important in other applications such as in high resolution optical spectroscopy [263], optical frequency standards [223, 312] and fundamental quantum measurements [279]. The best reference cavities, such as those developed by the Ye [245] and Hänsch [75] groups, have reported a frequency stability performance of around 10−16, which is broadly equivalent to that achieved for ground-based gravitational-wave detectors when scaling by cavity length.
-
Beam geometry fluctuations
Fluctuations in the lateral or angular position of the input laser beam, along with changes in its size and variations in its phase-front curvature may all couple into the output signal of an interferometer and reduce its sensitivity. These fluctuations may be due to intrinsic laser mechanical noise (from water cooling for example) or from seismic motion of the laser with respect to the isolated test masses. As an example of their importance, fluctuations in the lateral position of the beam may couple into interferometer measurements through a misalignment of the beamsplitter with respect to the interferometer mirrors. A lateral movement δz of the beam incident on the beamsplitter, coupled with an angular misalignment of the beamsplitter of α/2 results in a phase mismatch δϕ of the interfering beams, such that [270]
$$\delta \phi = (4\pi /\lambda)\alpha \delta z.$$(16)A typical beamsplitter misalignment of ≃ 10−7 radians means that to achieve sensitivities of the level described above using a detector with 3 or 4 km arms, and 50 bounces of the light in each arm, a level of beam geometry fluctuations at the beamsplitter of close to 10−12 m/Hz−1/2 at 300 Hz is required.
Typically, and ignoring possible ameliorating effects of the power recycling cavity on beam geometry fluctuations, this will mean that the beam positional fluctuations of the laser need to be suppressed by several orders of magnitude. The two main methods of reducing beam geometry fluctuations are 1) passing the input beam through a single mode optical fibre [230] and 2) using a resonant cavity as a mode cleaner [270, 288, 317, 83].
Passing the beam through a single mode optical fibre helps to eliminate beam geometry fluctuations, as deviations of the beam from a Gaussian TEM00 mode are equivalent to higher-order spatial modes, which are thus attenuated by the optical fibre. However, there are limitations to the use of optical fibres, mainly due to the limited power-handling capacity of the fibres; care must also be taken to avoid introducing extra beam geometry fluctuations from movements of the fibre itself.
A cavity may be used to reduce beam geometry fluctuations if it is adjusted to be resonant only for the TEM00 mode of the input light. Any higher order modes should thus be suppressed [270]. The use of a resonant cavity should allow the handling of higher laser powers and has the additional benefits of acting as a filter for fast fluctuations in laser frequency and power [288, 317]. This latter property is extremely useful for the conditioning of the light from some laser sources as will be discussed below.
5.3.2 Laser design
From Equation (7) it can be seen that the photon-noise limited sensitivity of an interferometer is proportional to \(\sqrt P\) where P is the laser power incident on the interferometer, and \(\sqrt \lambda\) where λ is the wavelength of the laser light. Thus, single frequency lasers of high output power and short wavelength are desirable. With these constraints in mind, laser development started on argon-ion lasers and Nd:YAG lasers. Argon-ion lasers emitting light at 514 nm were used to illuminate several interferometric gravitational-wave detector prototypes, see, for example, [287, 264]. However, their efficiency, reliability, controllability and noise performance has ruled them out as suitable laser sources for current and future gravitational wave detectors.
Nd:YAG lasers, emitting at 1064 nm or frequency doubled to 532 nm, present an alternative. The longer (infrared) wavelength may initially appear less desirable than the 514 nm of the argon-laser and the frequency doubled 532 nm, as more laser power is needed to obtain the same sensitivity. In addition, the resulting increase in beam diameter leads to a need for larger optical components. For example in an optical cavity the diameter of the beam at any point is proportional to the square root of the wavelength [204] and to keep diffractive losses at each test mass below 1 × 10−6, it can be shown that the diameter of each test mass must be greater than 2.6 times the beam diameter at the test mass. Thus, the test masses for gravitational wave detectors have to be 1.4 times larger in diameter for infrared than for green light. However, Nd:YAG sources at 1064 nm have demonstrated some compelling advantages, in particular the demonstration of scaling the power up to levels suitable for second generation interferometers (∼ 200 W) combined with their superior efficiency [286, 306, 200]. Frequency-doubled Nd:YVO lasers at 532 nm have currently only been demonstrated to powers approaching 20 W and have not been actively stabilised to the levels needed for gravitational-wave detectors [227]. An additional problem associated with shorter wavelength operation is the potential for increased absorption, possibly leading to photochemistry (damage) in the coating materials, in addition to increased scatter. For this reason, all the initial long-baseline interferometer projects, along with their respective upgrades, have chosen some form of Nd:YAG light source at 1064 nm.
As an example, the laser power is being upgraded from 10 W in initial LIGO to 180 W for Advanced LIGO to improve the SNR of the shot-noise-limited regime. This power will be delivered by a three stage injection-locked oscillator scheme [120, 237, 157, 144]. The first stage uses a monolithic non-planar ring oscillator (NPRO) to initially produce 2 W of output power. This output is subsequently amplified by a four-head Nd:YVO laser amplifier to a power of 35 W [143], which is in turn delivered into an injection locked Nd:YAG oscillator to produce 200 W of output power [320].
Other laser developments are being pursued, such as high-power-fibre lasers, which are currently being investigated by the AEI in Germany [280] and prototyped for Advanced VIRGO by Gréverie et al. in France [161]. Fibre amplifiers show great potential for extrapolation to higher laser powers in addition to lower production costs.
Third-generation interferometric gravitational-wave detectors, such as the Einstein Telescope, require input laser powers of around 500 W at 1064 nm in order to achieve their high-frequency shot-noise-limited sensitivities [178]. Low-frequency sensitivity is expected to be achieved through the use of separate low-power interferometers with silicon optics operating at cryogenic temperatures [269, 262]. Longer wavelengths are proposed here due to excessive absorption in silicon at 1064 nm and the expected low absorption (less than 0.1 ppm/cm) at around 1550 nm [160]. Worldwide laser developments may provide new baseline light sources that can provide different wavelength and power options for future detectors. However, the stringent requirements on the temporal and spatial stability for gravitational-wave detectors are beyond that sought in other laser applications. Therefore, a dedicated laser-development program will be required to continue beyond the second-generation interferometers in order to design and build a laser system that meets third-generation requirements, as discussed in more detail in [227].
Another key area of laser development, targeted at improving the sensitivity of future gravitational-wave detectors, is in the use of special optical modes to reduce thermal noise. It can be shown that the amplitude of thermal noise associated with the mirror coatings is inversely proportional to the beam radius [238]. The configuration within current interferometers is designed to inject and circulate TEM00 optical modes, which have a Gaussian beam profile. To keep diffraction losses suitably low for this case (< 1 ppm), a beam radius of a maximum size ∼ 35% of the radius of the test mass mirror can be used. The thermal noise could be further reduced if optical modes are circulated that have a larger effective area, yet not increasing the level of diffraction losses. This would be possible through the use of higher-order Laguerre-Gauss beams, and other “exotic” beams, such as mesa or conical beams. A more in-depth discussion of how these optical schemes can be implemented and the potential increase in detector sensitivity attainable can be found in [303].
5.3.3 Thermal compensation and parametric instabilities
Despite the very-low levels of optical absorption in fused silica at 1064 nm, thermal loading due to high-levels of circulating laser powers within advanced gravitational-wave detectors will cause significant thermal loading. In the case of Advanced LIGO, thermal lensing will be most significant in the input test masses of the Fabry-Pérot cavities, where the beam must transmit through the substrate in addition to the high-power within the cavity being incident on the coating surfaces. Thermal distortion in the optics will be sensed by Hartmann sensors and coupled to two schemes of thermal compensation. Firstly, ring resistance heaters will be installed around the barrel of the input mass in order to compensate for the beam heating the central region of the optics, as demonstrated for radius of curvature tuning in GEO600 [222]. Secondly, a flexible CO2 laser based system will be used to deposit heat onto the reaction mass (otherwise called the compensation plate) for the input test mass, as demonstrated in initial LIGO [209, 308]. The laser beam shape and intensity can be easily modified from outside with the vacuum system and can therefore adapt to non-uniformities in the absorption and other changes in the interferometer’s thermal state.
It should also be noted that energy can couple from the optical modes resonating in the interferometer Fabry-Pérot cavities and the acoustic modes of the test masses. When there is sufficient coupling between these optical and mechanical modes, and the mechanical modes have a suitably high-quality factor, then mechanical resonances can be ‘rung-up’ by the large circulating laser power to the point where the interferometer is no longer stable, a phenomenon called parametric instabilities [106]. Mechanical dampers that are tuned to damp at high-frequency yet not significantly increasing thermal noise at low-frequency are being considered in possible upgrades to advanced detectors, in addition to other schemes, such as active feedback to damp problematic modes provided through the electrostatic actuators.
5.4 Readout schemes
There are various schemes that can be applied to readout the gravitational-wave signal from an interferometer. A good discussion of some of these can be found in [177]. If the interferometer laser has a frequency of f1 then a passing gravitational wave, with frequency fgw, will introduce sidebands onto the laser with a frequency of fs = f1 ± fgw. A readout scheme must be able to decouple the gravitational-wave component, with frequencies of order ∼ 100 Hz, from the far higher laser frequency at hundreds of tera-Hz. To do this it needs to be able to compare the sideband frequency with a known stable optical local oscillator. Ideally this oscillator would be the laser light itself (a homodyne scheme), but the initial generation of gravitational-wave detectors are operated at a dark fringe (i.e., the interferometer is held, so as the light from the arms completely destructively interferes at the beam splitter), so no light at the laser frequency exits (a gravitational wave will alter the arms lengths and constructively interfere, causing light to exit, but only at the sideband frequency).
The standard scheme used by the initial interferometers is a radio frequency (RF) heterodyne readout. In this case the laser light is modulated at an RF (called Schnupp modulation [281]) prior to entering the interferometer arms, giving rise to sidebands offset from the laser frequency at the RF. The interferometer is set up to allow these RF sidebands to exit at the output port. This can be used as a local optical oscillator with which to demodulate the gravitational wave sidebands. However, the demodulation will introduce a beat between the RF and the gravitational wave frequency, which must be removed by a second (hence heterodyne) demodulation at the RF.
The preferred method for future detectors is a DC scheme (see [147, 309, 177] for motivations and advantages of using such a scheme). In this no extra modulation has to be applied to the light. Instead the interferometer is held just off the dark fringe, so some light at the laser frequency reaches the output to serve as the local oscillator.
6 Operation of First-Generation Long-Baseline Detectors
Prior to the start of the 21st century there existed several prototype laser interferometric detectors, constructed by various research groups around the world — at the Max-Planck-Institüt für Quantenoptik in Garching [287], at the University of Glasgow [264], at the California Institute of Technology [56], at the Massachusetts Institute of Technology [148], at the Institute of Space and Astronautical Science in Tokyo [235] and at the astronomical observatory in Tokyo [83]. These detectors had arm lengths varying from 10 m to 100 m and had either multibeam delay lines or resonant Fabry-Pérot cavities in their arms. The 10 m detector that used to exist at Glasgow is shown in Figure 12.
The sensitivities of some of these detectors reached a level — better than 10−18 for millisecond bursts — such that the technology could be considered sufficiently mature to propose the construction of detectors of much longer baseline that would be capable of reaching the performance required to have a real possibility of detecting gravitational waves. An international network of such long baseline gravitational wave detectors has now been constructed and commissioned, and science-quality data from these has been produced and analysed since 2002 (see Section 6.1 and Section 6.2 for a review of recent science data runs and results).
The American LIGO project [212] comprises two detector systems with arms of 4 km length, one in Hanford, Washington, and one in Livingston, Louisiana (also known as the LIGO Hanford Observatory 4k [LHO 4k] and LIGO Livingston Observatory 4k [LLO 4k], or H1 and L1, respectively). One half length, 2 km, interferometer was also contained inside the same evacuated enclosure at Hanford (also known as the LHO 2k, or H2). The design goal of the 4 km interferometers was to have a peak strain sensitivity between 100–200 Hz of ∼ 3 × 10−23 Hz−1/2 [210] (see Figure 15), which was achieved during the fifth science run (Section 6.1). A birds-eye view of the Hanford site showing the central building and the directions of the two arms is shown in Figure 13. In October 2010 the LIGO detectors shut down and decommissioning began in preparation for the installation of a more sensitive instrument known as Advanced LIGO (see Section 6.3.1).
The French/Italian Virgo project [304] comprises a single 3 km arm-length detector at Cascina near Pisa. As mentioned earlier, it is designed to have better performance than the other detectors, down to 10 Hz.
The TAMA300 detector [294], which has arms of length 300 m, at the Tokyo Astronomical Observatory was the first of the “beyond-prototype” detectors to become operational. This detector is built mainly underground and partly has the aim of adding to the gravitational-wave detector network for sensitivity to events within the local group of galaxies, but is primarily a test bed for developing techniques for future larger-scale detectors. Initial operation of the interferometer was achieved in 1999 and power recycling was implemented for data taking in 2003 [81].
All the systems mentioned above are designed to use resonant cavities in the arms of the detectors and use standard wire-sling techniques for suspending the test masses. The German/British detector, GEO600 [151], built near Hannover, Germany, is somewhat different. It makes use of a four-pass delay-line system with advanced optical signal-enhancement techniques, utilises very-low loss-fused silica suspensions for the test masses, and, despite its smaller size, was designed to have a sensitivity at frequencies above a few hundred Hz comparable to the first phases of Virgo and LIGO during their initial operation. It uses both power recycling (Section 5.1) and tunable signal recycling (Section 5.2), often referred to together as dual recycling.
To gain the most out of the detectors as a true network, data sharing and joint analyses are required. In the summer of 2001 the LIGO and GEO600 teams signed a Memorandum of Understanding (MoU), under the auspices of the LIGO Scientific Collaboration (LSC) [215], allowing complete data sharing between the two groups. Part of this agreement has been to ensure that both LIGO and GEO600 have taken data in coincidence (see below). Coincident data taking, and joint analysis, has also occurred between the TAMA300 project and the LSC detectors. The Virgo collaboration also signed an MoU with the LSC, which has allowed data sharing since May 2006.
The operation and commissioning of these detectors is a continually-evolving process, and the current state of this review only covers developments until late-2010. For the most up-to-date information on detectors readers are advised to consult the proceedings of the Amaldi meetings, GWDAW/GWPAW (Gravitational Wave Data Analysis Workshops), and GWADW (Gravitational Wave Advanced Detectors Workshops) — see [165] for a list of past conferences.
For the first and second generations of detector, much effort has gone into estimating the expected number of sources that might be observable given their design sensitivities. In particular, for what are thought to be the strongest sources: the coalescence of neutron-star binaries or black holes (see Section 6.2.2 for current rates as constrained by observations). These estimates, based on observation and simulation, are summarised in Table 5 of [3] and the realistic rates suggest initial detectors would expect to see 0.02, 0.004 and 0.007 events per year for neutron-star-binary, black-hole-neutron-star, and black-hole-binary systems, respectively (it should be noted that there is a range of possible rates consistent with current observations and models)1. Second generation detectors (see Section 6.3.1), which can observe approximately 1000 time more volume than the initial detectors might, expect to see 40, 10, and 20 per year for the same sources. With such rates a great deal of astrophysics could be possible (see [273] for examples).
6.1 Science runs
Over the last decade the commissioning and improvement of the various gravitational-wave detectors has been suspended at various stages to take data for astrophysical analysis. These have been times when it was considered that the detectors were sensitive and stable enough (or had made sufficient improvements over earlier states) to make astrophysical searches worthwhile. Within the LSC these have been called the Science (S) runs, for Virgo they have been the Virgo Science Runs (VSR), and for TAMA300 they have been the Data Taking (DT) periods. A time-line of science runs for the various interferometric detectors, can be seen in Figure 14.
A figure of merit for the sensitivity of a detector is to calculate its horizon distance. This is the maximum range out to which it could see the coalescence of two 1.4 M⊙ neutron stars that are optimally oriented and located (i.e., with the orbital plane perpendicular to the line-of-sight, and with this plane parallel to the detector plane, so that the antenna response is at its maximum) at a signal-to-noise ratio of 8 [18]. The horizon distance can be converted to a range that is an average over all sky locations and source orientations (i.e. not the best case scenario) by dividing it by 2.26 [293])—we shall use this angle averaged range throughout the rest of this review.
6.1.1 TAMA300
The first interferometric detector to start regular data taking with sufficient sensitivity and stability to enable it to potentially detect gravitational waves from the the galactic centre was TAMA300 [79]. Over the period between August 1999 to January 2004 TAMA had nine data-taking periods (denominated DT1-9) over which time its typical strain noise sensitivity, in its most sensitive frequency band improved from ∼ 3 × 10−19 Hz−1/2 to ∼ 1.5 × 10−21 Hz−1/2 [72]. TAMA300 operated in coincidence with the LIGO and GEO600 detectors for two of the science data-taking periods. More recently focus has shifted to the Cryogenic Laser Interferometer Observatory (CLIO) prototype detector [324, 164], designed to test technologies for a future second-generation Japanese detector called the Large-scale Cryogenic Gravitational-Wave Telescope (LCGT) (see Section 6.3.1).
6.1.2 LIGO
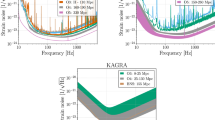
The first LIGO detector to achieve lock (meaning having the interferometer stably held on a dark fringe of the interference pattern, with light resonating throughout the cavity) was H2 in late 2000. By early 2002 all three detectors had achieved lock and have since undergone many periods of commissioning and science data taking. Over the period from mid-2001 to mid-2002 the commissioning process improved the detectors’ peak sensitivities by several orders of magnitude, with L1 going from ∼ 10−17 − 10−20 Hz−1/2 at 150 Hz. In summer 2002 it was decided that the detectors were at a sensitivity, and had a good enough lock stability, to allow a science data-taking run. This was potentially sensitive to local galactic burst events. From 23 August to 9 September 2002 the three LIGO detectors, along with GEO600 (and, for some time, TAMA300), undertook their first coincident science run, denoted S1 (see [12] for the state of the LIGO and GEO600 detectors at the time of S1). At this time the most sensitive detector was L1 with a peak sensitivity at around 300 Hz of 2–3 × 10−21 Hz−1/2. The best strain amplitude sensitivity curve for S1 (and the subsequent LIGO science runs) can be seen in Figure 15. The amount of time over the run that the detectors were said to be in science mode, i.e., stable and with the interferometer locked, called their duty cycle, or duty factor, was 42% for L1, 58% for H1 and 73% for H2. For the most sensitive detector, L1, the inspiral range was typically 0.08 Mpc.
The best strain sensitivities from the LIGO science runs S1 through S6 [213]. The S6 curve is preliminary and based on h(t) data that has not been completely reviewed and may be subject to change. Also shown is the LIGO 4 km design sensitivity.
For the second science run (S2), from 14 February to 14 April 2003, the noise floor was considerably improved over S1 by several upgrades including: improving and stabilising the optical levers used to measure the mirror orientation to reduce the low frequency (≲ 50 Hz) noise; replacing the coil drivers that are used as actuators to control the position and orientation of suspended mirrors, to improve the mid-frequency (∼ 50–200 Hz) noise floor; and increasing the laser power in the interferometer to reduce shot noise and improve the high frequency (≳ 200 Hz) sensitivity (see Section IIA of [22] for a more thorough description of the detector improvements made for S2). These changes improved the sensitivities by about an order of magnitude across the frequency band with a best strain, for L1, of ∼ 3 × 10−22 Hz−1/2 between 200–300 Hz. The duty factor during S2 was 74% for H1, 58% for H2 and 38% for L1, with a triple coincidence time when all three detectors were in lock of 22% of the run. The average inspiral ranges during the run were approximately 0.9, 0.4 and 0.3 Mpc for L1, H1 and H2 respectively. This run was also operated in coincidence with the TAMA300 DT8 run.
For the the third science run (S3), from 31 October 2003 to 9 January 2004, the detectors were again improved, with the majority of sensitivity increase in the mid-frequency range. This run was also operated partially in coincidence with GEO600. The best sensitivity, which was for H1, was ∼ 5 × 10−23 Hz−1/2 between 100–200 Hz. The duty factors were 69% for H1, 63% for H2 and only 22% for L1, with a 16% triple coincidence time. L1’s poor duty factor was due to large levels of anthropogenic seismic noise near the site during the day.
The fourth science run (S4), from 22 February to 23 March 2005, saw less-drastic improvements in detector sensitivity across a wide frequency band, but did make large improvements for frequencies ≲ 70 Hz. Between S3 and S4 a better seismic isolation system, which actively measured and countered for ground motion, was installed in L1, greatly reducing the amount of time it was thrown out of lock. For H1 the laser power was able to be increased to its full design power of 10 W [27]. The duty factors were 80% for H1, 81% for H2 and 74% for L1, with a 56% triple coincidence time. The most sensitive detector, H1, had an inspiral range of 7.1 Mpc.
By mid-to-late 2005 the detectors had equaled their design sensitivities over most of the frequency band and were also maintaining good stability and high duty factors. It was decided to perform a long science run with the aim of collecting one year’s worth of triple coincident data, with an angle-averaged inspiral range of equal to, or greater than, 10 Mpc for L1 and H1, and 5 Mpc or better for H2. This run, S5, spanned from 4 November 2005 (L1 started slightly later on 14 November) until 1 October 2007, and the performance of the detectors during it is summarised in [45]. One year of triple coincidence was achieved on 21 September 2007, with a total triple coincidence duty factor of 52.5% for the whole run. The average insprial range over S5 was ∼ 15 Mpc for H1 and L1, and ∼ 8 Mpc for H2.
After the end of S5 the LIGO H2 detector and GEO600 were kept operational while possible in an evening and weekend mode called Astrowatch. This observing mode continued until early 2009, after which H2 was retired. During this time commissioning of some upgrades to the 4 km LIGO detectors took place for the sixth and final initial LIGO science run (S6) — some of which are summarised in [315]. The aim of these upgrades, called Enhanced LIGO [65], was to try and increase sensitivity by a factor of two. Enhanced LIGO involved the direct implementation of technologies and techniques designed for the later upgrade to Advanced LIGO (see Section 6.3.1) such as, most notably, higher-powered lasers, a DC readout scheme (see Section 5.4), the addition of output mode cleaners and the movement of some hardware into the vacuum system. The lasers, supplied by the Albert Einstein Institute and manufactured by Laser Zentrum Hannover, give a maximum power of ≈ 30 W, which is around 3 times the initial LIGO power. The upgrade to higher power required that several of the optical components needed to be replaced. These upgrades were only carried out on the 4 km H1 and L1 detectors due to the H2 detector being left in Astrowatch mode during the commissioning period. The upgrades were able to produce 1.5–2 times sensitivity increases at frequencies above ≈ 200 Hz, but generally at lower frequencies various sources of noise meant sensitivity increases were not possible. S6 took place from July 2009 until 20 October 2010, at which point decommissioning started for the full upgrade to Advanced LIGO. Typically the detectors ran with laser power at ≈ 10 W during the day (at higher power the detector was less stable and the higher level of anthropogenic noise during the day meant that achieving and maintaining lock required lower power) and ≈ 20 W at night, leading to inspiral ranges from ≈ 10–20 Mpc.
6.1.3 GEO600
GEO600 achieved first lock as a power-recycled Michelson (with no signal recycling) in late 2001. Commissioning over the following year, detailed in [172], included increases in the laser power, installation of monolithic suspensions for the end test masses (although not for the beam splitter and inboard mirrors), rearrangement of the optical bench to reduce scattered light and implementation of an automatic alignment system. For the S1 run, carried out in coincidence with LIGO (and, in part, TAMA300), the detector was kept in this configuration (see [12] for the status of the detector during S1). It had a very high duty factor of ∼ 98%, although its strain sensitivity was ∼ 2 orders of magnitude lower than the LIGO instruments. The auto-alignment system in GEO600 has since meant that it has been able to operate for long periods without manual intervention to regain lock, as has been the case for initial LIGO.
Following S1 the signal recycling mirror was installed and in late 2003 the first lock of the fully dual-recycled system was achieved (see [289, 318, 163] for information on the commissioning of GEO600 as a dual-recycled detector). Other upgrades included the installation of the final mirrors, suspended as triple pendulums, and with monolithic final stages. Once installed it was found that there was a radius of curvature mismatch with one of the mirrors, which had to be compensated for by carefully heating the mirror. Due to this commissioning effort GEO600 did not participate in the S2 run. Very soon after the implementation of dual-recycling GEO600 took part in the S3 run. This occurred over two time intervals from 5–11 November 2003, dubbed S3I, and from 30 December 2003 to 13 January 2004, dubbed S3II. During S3I GEO600 operated with the signal-recycling cavity tuned to ∼ 1.3 kHz, and had a ∼ 95% duty factor, but was then taken off-line for more commissioning work. In the period between S3I and II various sources of noise and lock loss were diagnosed and mitigated, including noise from a servo in the signal recycling cavity and electronic noise on a photo-diode [289]. This lead to improved sensitivity by up to an order of magnitude at some frequencies (see Figure 16). For S3II the signal recycling cavity was tuned to 1 kHz and, due to the upgrades, had an increased duty factor of ∼ 99%. GEO600 operated during the whole of S4 (22 February to 24 March 2004), in coincidence with LIGO, with a ∼ 97% duty factor. It used the same optical configuration as S3, but had sensitivity improvements from a few times to up to an order of magnitude over the S3 values [176].
The typical strain sensitivities from the GEO600 science runs S1 through S5 [150]. Also shown is the theoretical noise budget for the detector when tuned to 550 Hz — the operating position for the S5 run.
The main changes to the detector after S4 were to shift the resonance condition of the signal recycling cavity to a lower frequency, 350 Hz, allowing better sensitivity in the few hundred Hz regime, and increasing the circulating laser power, with an input power of 10 W. The pre-S5 peak sensitivity was ∼ 4 × 10−22 Hz−1/2 at around 400 Hz, with an inspiral range of 0.6 Mpc [173]. GEO600 did not join S5 at the start of the LIGO run, but from 21 January 2006 was in a night-and-weekend data-taking mode whilst noise hunting studies and commissioning were conducted. For S5 the signal recycling cavity was re-tuned up to 550 Hz. It went into full-time data taking from 1 May to 16 October 2006, with an instrumental duty factor of 94%. The average peak sensitivity during S5 was better than 3 × 10−22 Hz−1/2 (see [321] for a summary of GEO600 during S5). After this it was deemed more valuable for GEO600 to continue more noise hunting and commissioning work, to give as good a sensitivity as possible for when the LIGO detectors went offline for upgrading. However, it did continue operating in night-and-weekend mode.
GEO600 continued operating in Astrowatch mode between November 2007 and July 2009 after which upgrades began. The plans for the GEO600 detector are to continue to use it as a test-bed for more novel interferometric techniques whilst focusing on increasing in sensitivity at higher frequencies (greater than a few hundred Hz). This project is called GEO-HF [319]. The upgrading towards GEO-HF has been taking place since Summer 2009 [162]. The main upgrades started during 2009 were to change the read-out scheme from an RF read-out to a DC read-out system [177] (also see Section 5.4), install an output mode cleaner, place the read-out system in vacuum, injecting squeezed light [302, 114] into the output port, and finally increasing the input laser power to 35 W. Running the interferometer with squeezed light will be the first demonstration of a full-scale gravitational-wave detector operating beyond the standard quantum limit. GEO-HF participated in S6 in an overnight and weekend mode, alongside a commissioning schedule, and is continuing in this mode following the end of S6.
6.1.4 Virgo
In summer 2002 Virgo completed the commissioning of the central area interferometer, consisting of a power-recycled Michelson interferometer, but without the 3 km Fabry-Pérot arm cavities. Over the next couple of years various steps were made towards commissioning the full-size interferometer. In early 2004 first lock with the 3 km arms was achieved, but without power-recycling, and by the end of 2004 lock with power recycling was achieved. During summer 2005 the commissioning runs provided order-of-magnitude sensitivity improvements, with a peak sensitivity of 6 × 10−22 Hz−1/2 at 300 Hz, and an inspiral range of over 1 Mpc. In late 2005 several major upgrades brought Virgo to its final configuration. See [58, 59, 60, 61] for more detailed information on the commissioning of the detector.
Virgo joined coincident observations with the LIGO and GEO600 S5 run with 10 weekend science runs (WSRs) starting in late 2006 until March 2007. Over this time improvements were made mainly in the mid-to-low frequency regime (≲ 300 Hz). Full-time data taking, under the title of Virgo Science run 1 (VSR1), began on 18 May 2007 and ended with the end of S5 on 1 October 2007. During VSR1, the science-mode duty factor was 81% and by the end of the run maximum neutron-star-binary inspiral range was frequently up to about 4.5 Mpc. The best sensitivity curves for WSR1, WSR10 and VSR1 can be seen in Figure 17.
At the same time as commissioning for Enhanced LIGO was taking place there was also a similar effort to upgrade the Virgo detector, called Virgo+. The main upgrade was to the lasers to increase their power from 10 to 25 W at the input mode cleaner, with upgrades also to the thermal compensation system on the mirrors, the control electronics, mode cleaners and injection optics [64, 141]. Virgo+ started taking data with Enhanced LIGO for Virgo Science Run 2 (VSR2) and sensitivities of Virgo+ close to the initial Virgo design sensitivity were reached. VSR2 finished on 8 January 2010 to allow for further commissioning and noise hunting. This was followed by VSR3, which began on 11 August 2010 and ran until 20 October 2010. Further Virgo+ runs are expected during 2011. Following these the upgrades to Advanced Virgo will begin.
6.2 Astrophysics results
Prior to the advent of the large scale interferometric detectors there had been some limited effort to produce astrophysical results with the prototype interferometers. The Caltech 40 m detector was used to search for, and set an upper limit on, the gravitational wave emission from pulsar PSR J1939+2134 [171], and on the rate of neutron star binary inspirals in our galaxy, using coincident observations with the University of Glasgow prototype [290] and, more recently, on its own [74]. Coincident observations using the prototype detectors at the University of Glasgow and Max Planck Institute for Quantum Optics, in Garching, Germany, were used to set an upper limit on the strain of gravitational wave bursts [243]. The Garching detector was used to search for periodic signals from pulsars, and in particular set a limit on a potential source in SN 1987A [244]. However since the start of science data taking for the large scale detectors there has been a rapid rise in the number, and scope, of science result papers being published. With the vastly improved sensitivities pushing upper limits on source populations and strengths towards astrophysically interesting areas.
The recent analysis efforts have generally been split into four broad areas depending on the expected signal type: unmodelled transients or bursts, e.g., supernovae; modelled transients, e.g., inspirals and ring-downs (or more specifically compact binary coalescences, CBC); continuous sources; stochastic sources. Within each area a variety of different sources could exist and a variety of analysis techniques have been developed to search for them. Some electromagnetic sources, such as radio pulsars and γ-ray bursts, are also used to enhance searches. A good review of the data analysis methods used in current searches, and the astrophysical consequences of some of the results described below, can be found in [273].
Here we will briefly summarise the main astrophysics results from the science runs. We will mainly focus on those produced by the LIGO Scientific Collaboration [215] detectors LIGO and GEO600 from S1 to the S5 run. At the time of writing not all of the data from the S6 run had been fully analysed, with more results expected over the next year. Reviews of some early S5, and prior science run, results can also be found in [254, 139]. In none of the searches so far has convincing evidence for a gravitational-wave signal been seen.
6.2.1 Unmodelled bursts
Searches for unmodelled bursts, e.g., from supernova core-collapse, are based on looking for short duration periods of excess power in the detectors. Transients are common features in the data, so to veto these events from true gravitational-wave signals they must be coincident in time, and to some extent amplitude and waveform, between multiple detectors. Various methods to assess instrumental excess power, and inter-detector correlations, are used, some examples of which can be found here [202, 77, 284, 228, 107, 112, 113]. These algorithms will produce triggers, which are periods of excess power that cross a predetermined signal-to-noise ratio threshold (determined by tuning the algorithms on a section of playground data, so that the output produces a desired false alarm rate). The number of triggers are then compared to a background rate. Real signals cannot be turned off, and detectors cannot be shielded from them, so the background rate has to be approximated by time shifting one detector’s data stream with respect the the others. Time shifts should only leave triggers due to random coincidences in detector noise and there should be no contribution from real signals. Once a background is calculated, the statistical significance of the foreground rate can be compared to it. To assess the sensitivity of these searches, hardware (the interferometer mirrors are physically moved via the control system) and software signals are injected into the data stream at various strengths and the efficiency of the algorithms at detecting them is measured. A good description of some of these techniques can be found in [13] and [24].
Data from the LIGO S1 run was searched for gravitational-wave bursts of between 4 to 100 ms, and within the frequency band 150 to 3000 Hz [13]. Triple coincident data from all three detectors was used for the analysis. No plausible candidate event was found, but a 90% confidence upper limit on the event rate of 1.6 events per day was set. The search was typically sensitive, at a ≳ 50% detection efficiency, to bursts with amplitudes of hrss ∼ 10−19 −10−17 Hz−1/2 (defined in terms of \({h_{{\rm{rss}}}} \equiv \sqrt {\int {|h{|^2}{\rm{d}}t}}\), which is the root-sum-squared strain amplitude spectral density). Due, in part, to its lower sensitivity GEO600 data was not used in this analysis. The S2 data’s improved sensitivity, and advances in the analysis techniques, allowed a sensitivity to signals (in the frequency range 100–1100 Hz) in the amplitude range hrss ∼ 10−20 −10−19 Hz−1/2 [22]. Interpreting the best sensitivities astrophysically gave order of magnitude estimates on the visible range of ∼ 100 pc for a class of theoretical supernova waveforms, and 1 Mpc for the merger of 50 M⊙ black holes. Again no signal was seen, but a 90% upper limit of 0.26 events per day was set for strong bursts. In the frequency range 700–2000 Hz TAMA300 data was also used in the search giving amplitude sensitivities of hrss ∼ 1–3 × 10−19 Hz−1/2 and decreasing the rate upper limit to 0.12 events per day [20].
The S3 run produced two searches for burst sources. One used the 8 days of triple coincidence data from the three LIGO detectors to search for sub-second bursts in the frequency range 100–1100 Hz [24]. The search was sensitive to signals with amplitudes over hrss ∼ 1 × 10−20 Hz−1/2, but did not include an astrophysical interpretation of the limit or event rate upper limit. This run included coincident operation with the Italian AURIGA bar detector and this data has been analysed [90]. This search looked for short bursts of less than 20 ms within the 850–950 Hz band (around the bar’s sensitive resonant frequency). This had comparable sensitivity to the LIGO-only S2 search and produced a 90% confidence rate upper limit of 0.52 events/day.
For S4 15.5 days of LIGO data were searched for sub-second bursts in the frequency range 64–1600 Hz [27]. This was sensitive to signals with hrss ≲ 10−20 and set a 90% confidence rate upper limit of 0.15 per day. The search results are also cast as astrophysical limits on source ranges and energetics. These show that there would be a 50% detection efficiency to signals of sine-Gaussian nature (at the most sensitive frequency of 153 Hz and quality factor Q = 8.9) at a distance of 10 kpc for an energy of 10−7 M⊙c2, and would be sensitive to signals out to the Virgo cluster (∼ 16 Mpc) for an energy release of 0.25 M⊙c2. See [27] for a comparison of previous burst searches. There was also a burst search combining S4 GEO600 and LIGO data for the first time. This searched data between 768–2048 Hz where the sensitivities were most comparable and used 257 hours of quadruple coincidence between the detectors and saw no gravitational wave events [35].
For the analysis on the first year of S5 data the frequency range for the all-sky burst search was split — a low frequency search covered the most sensitive region between 60–2000 Hz [46], and a high frequency search covering 1–6 kHz (this being the first time an untriggered burst search looked at frequencies above 3 kHz) [50]. The high frequency search set a 90% upper limit on the rate of 5.4 events per year for strong events. The low frequency search analysed more data than the high frequency and set an event rate limit of 3.6 events per year. The second year of S5 LIGO data was analysed with GEO600 and Virgo VSR1 data [1] to search for bursts over the whole 50–6000 Hz band. Combining this with the earlier S5 searches gave hrss upper limits for a variety of simulated waveforms of 6 × 10−22 Hz−1/2 to 2 × 10−20 Hz−1/2, and a 90% confidence event rate for signals between 64–2048 Hz of less than two per year.
6.2.2 Modelled bursts — compact binary coalescence
Modeled bursts generally mean the inspiral and coalescence stage of binaries consisting of compact objects, e.g., neutron stars and black holes. The signals are generally well approximated by post-Newtonian expansions of the Einstein equation, which give the amplitude and phase evolution of the orbit. More recently signal models have started to include numerical relativity simulations of the merger stage [89]. As mentioned in Section 6 the best estimate of the number of signals observable with initial LIGO at design sensitivity (i.e. during S5) would be 0.02 per year (based on an event rate of 1 × 10−6 per year per MWEG).
The majority of inspiral searches make use of matched filtering in which a template bank of signal models is built [250, 252], with a maximum mismatch between templates that is generally of order ∼ 10%. These templates are then cross-correlated with the data and statistically significant triggers (i.e. times when the template and data are highly correlated) from this are looked for. Triggers must be coincident between detectors and the significance of any trigger is judged against a background calculated in the same way as described in Section 6.2.1. See [18] for a good description of the search method.
The first search for an inspiral signal with data from the LIGO S1 run looked for compact object coalescences with component masses between 1–3 M⊙ and was sensitive to such sources within the Milky Way and Magellanic Clouds [11]. It gave a 90% confidence level upper limit on the rate of 170 per year per MWEG.
For the S2 LIGO analysis the search was split into 3 areas covering neutron-star binaries, black-hole binaries and primordial black-hole binaries in the galactic halo. The neutron-starbinary search [18] used 15 days of data with coincidence between either H1 and L1 or H2 and L1. It had a range of ∼ 1.5 Mpc, which spanned the Local Group of galaxies, and gave a 90% event rate upper limit on systems with component masses of 1–3 M⊙ of 47 per year per MWEG. The black-hole-binary search looked for systems with component masses in the 3–20 M⊙ range using the same data set as the neutron-star-binary search [24]. This search had a 90% detection efficiency for sources out to 1 Mpc and set a 90% rate upper limit of 38 per year per MWEG. The third search looked for low mass (0.2–1 M⊙) primordial black-hole binaries in a 50 kpc radius halo surrounding the Milky Way [19]. This placed a 90% confidence-rate upper limit of 63 events per year per Milky Way halo. The S2 search was performed in coincidence with the TAMA300 DT8 period and an inspiral search for neutron-star binaries was performed on data when TAMA300 and at least one of the LIGO sites was operational. This gave a total of 584 hours of data for the analysis, which set a 90% rate upper limit of 49 per year per MWEG, although this search was only sensitive to sources within the majority of the Milky Way [23].
The search for neutron-star-black-hole binaries in S3 LIGO data used techniques designed specifically for systems with spinning components. It searched for systems with component masses in the range 1–20 M⊙ and analysed 167 hours of triple coincident data and 548 hours of H1–H2 data to set the upper limits [40]. For a typical system with neutron-star and black-hole mass distributions centred on 1.35 M⊙ and 5 M⊙ (from the population statistics discussed in [39]) this search produced a 90% confidence-rate upper limit of 15.9 per year per L10.
The search for a wide range of binary systems with components consisting of primordial black holes, neutron stars, and black holes with masses in the ranges given above was conducted on the combined S3 and S4 data [39]. 788 hours of S3 data and 576 hours of S4 data were used and no plausible gravitational-wave candidate was found. The highest mass range for the black-holebinary search was set at 40 M⊙ for S3 and 80 M⊙ for S4. At peak in the mass distribution of these sources 90% confidence-rate upper limits were set at 4.9 per year per L10 for primordial black holes, 1.2 per year per L10 for neutron-star binaries, and 0.5 per year per L10 for black-hole-binaries. S4 data has also been used to search for ring-downs from perturbed black holes, for example following black-hole-binary coalescence [47]. The search was sensitive to ring-downs from 10–500 M⊙ black holes out to a maximum range of 300 Mpc, and produced a best 90% confidence upper limit on the rate of ring-downs to be 1.6 × 10−3 per year per L10 for the mass range 85–390 M⊙.
One other kind of modeled burst search is that looking for gravitational waves produced by cusps in cosmic (super)strings. Just over two weeks of LIGO S4 data were used to search for such signals [44]. This was used to constrain the rate and parameter space (string tension, reconnection probability, and loop sizes), but was not able to beat limits set by Big Bang nucleosynthesis.
Data from the first [48] and second year of S5 (prior to Virgo joining with VSR1) [49] have been searched for low-mass binary coalescences with total masses in the range 2–35 M⊙. The second year search results have produced the more stringent upper limits with 90% confidence rates for neutron-star-binaries, black-hole-binaries and neutron-star-black-hole systems respectively of 1.4 × 10−2, 7.3 × 10−4 and 3.6 × 10−3 per year per L10. Five months of overlapping S5 and VSR1 data were also searched for the same range of signals [5] giving 90% confidence upper rates of 8.7 × 10−3 per year per L10, 2.2 × 10−3 per year per L10, and 4.4 × 10−4 per year per L10. The whole 2 years of LIGO S5 data were also used to search for higher mass binary coalescences with component mass between 1–99 M⊙ and total masses of 25–100 M⊙. No signal was seen, but a 90% confidence upper limit rate on mergers of black-hole-binary systems with component masses between 19 and 28 M⊙, and with negligible spin, was set at 2.0 Mpc−3 Myr−1 [9].
6.2.3 Externally-triggered burst searches
Many gravitational wave burst sources will be associated with electromagnetic (or neutrino) counterparts, for example short γ-ray bursts (GRBs) are potentially caused by black-hole and neutronstar coalescences. Joint observation of a source as both a gravitational wave and electromagnetic event also greatly increases the confidence in a detection. Therefore many searches have been performed to look for bursts coincident (temporally and spatially) with external electromagnetic triggers, such as GRBs observed by Swift for example. These searches have used both excess power and modeled matched-filter methods to look for signals.
During S2 a particularly bright γ-ray burst event (GRB 030329) occurred and was specifically targeted using data from H1 and H2. The search looked for signals with duration less than ∼ 150 ms and in the frequency range 80–2048 Hz [17]. This produced a best strain upper limit for an unpolarised signal around the most sensitive region at ∼ 250 Hz of hrss = 6 × 10−21 Hz−1/2.
For S4 there were two burst searches targeting specific sources. The first target was the hyperflare from the Soft γ-ray Repeater SGR 1806–20 (SGRs are thought to be “magnetars”, neutron stars with extremely large magnetic fields of order 1015 Gauss) on 27 December 2004 [186] (this actually occurred before S4 in a period when only the H1 detector was operating). The search looked for signals at frequencies corresponding to short duration quasi-periodic oscillations (QPOs) observed in the X-ray light curve following the flare [28]. The most sensitive 90% upper limit was for the 92.5 Hz QPO at hrss = 4.5 × 10−22 Hz−1/2, which corresponds to an energy emission limit of 4.3 × 10−8 M⊙c2 (of the same order as the total electromagnetic emission assuming isotropy). The other search used LIGO data from S2, S3 and S4 to look for signals associated with 39 short duration γ-ray bursts (GRBs) that occurred in coincidence with these runs [38]. The GRB triggers were provided by IPN, Konus-Wind, HETE-2, INTEGRAL and Swift as distributed by the GRB Coordinate Network [149]. The search looked in a 180-second window around the burst peak time (120 seconds before and 60 seconds after) and for each burst there were at least two detectors contributing data. No signal coincident with a GRB was observed and the sensitivities were not enough to give any meaningful astrophysical constraints, although simulations suggest that for S4, as in the general burst search, it would have been sensitive to sine-Gaussian signals out to tens of Mpc for an energy release of order a solar mass.
The first search of Virgo data in coincidence with a GRB was performed on data from a commissioning run in September 2005. The long duration GRB 050915a was observed by Swift on 15 September 2005 and Virgo data was used to search for an unmodelled burst in a window of 180 seconds around (120 s before and 60 s after) the GRB peak time [63]. The search produced a strain upper limit of order 10−20 in the frequency range 200–1500 Hz, but was mainly used as a test-bed for setting up the methodology for future searches, including coincidence analysis with LIGO.
Data from the S5 run has been used to search for signals associated with even more γ-ray bursts. One search looked specifically for emissions from GRB 070201 [156, 155], which showed evidence of originating in the nearby Andromeda galaxy (M31). The data around the time of this burst was used to look for an unmodelled burst and an inspiral signal as might be expected from a short GRB. The analysis saw no gravitational-wave event associated with the GRB, but ruled out the event being a neutron-star-binary inspiral located in M31 with a 99% confidence [36]. Again, assuming a neutron-star-binary inspiral, but located outside M31, the analysis set a 90% confidence limit that the source must be at a distance greater than 3.5 Mpc. Assuming a signal again located in M31, the unmodelled burst search set an upper limit on the energy emitted via gravitational waves of 4.4 × 10−4 M⊙c2, which was well within the allowable range for this being an SGR hyper-flare in M31. Searches for 137 GRBs (both short and long GRBs) that were observed, mainly with the Swift satellite, during S5 and VSR1 have been performed again using unmodelled burst methods [53] and for (22 short bursts) inspiral signals [4]. No evidence for a gravitational-wave signal coincident with these events was seen. The unmodeled burst observations were used to set lower limits on the distance to each GRB, with typical limits, assuming isotropic emission, at \(D \sim 15{\mkern 1mu} {\text{Mpc}}{(E_{{\text{GW}}}^{{\text{iso}}}/0.01{\mkern 1mu} {M_ \odot }{c^2})^{1/2}}\). The inspiral search, which was sensitive to CBCs with total system masses between 2 M⊙ and 40 M⊙, was able to exclude with 90% confidence any bursts being neutron-star-black-hole mergers within 6.7 Mpc, although the peak distance distribution of GRBs is well beyond this.
Another search has been to look for gravitational waves associated with flares from known SGRs and anomalous X-ray pulsars (AXPs), both of which are thought to be magnetars. During the first year of S5 there were 191 (including the December 2004 SGR 1806–20 event) observed flares from SGRs 1806−20 and 1900+14 for which at least one LIGO detector was online [37], and 1279 flare events if extending that to six known galactic magnetars and including all S5 and post-S5 Astrowatch data including Virgo and GEO600 [7]. The data around each event was searched for ring-down signals in the frequency range 1–3 kHz and with decay times 100–400 ms as might be expected from f-mode oscillations in a neutron star. It was also searched for unmodeled bursts in the 100–1000 Hz range. No gravitational bursts were seen from any of the events. For the earlier search [37] the lowest 90% upper limit on the gravitational-wave energy from the ring-down search was \(E_{{\rm{GW}}}^{90\%} = 2.4 \times {10^{48}}\) erg for an SGR 1806–20 burst on 24 August 2006. The lowest 90% upper limit on the unmodeled search was \(E_{{\rm{GW}}}^{90\%} = 2.9 \times {10^{45}}\) erg for an SGR 1806–20 burst on 21 July 2006. The smallest limits on the ratio of energy emitted via gravitational waves to that emitted in the electromagnetic spectrum were of order 10–100, which are into a theoretically-allowed range. The latter search [7] gave the lowest gravitational-wave emission-energy upper limits for white noise bursts in the detector-sensitive band, and for f-mode ring-downs (at 1090 Hz), of 3.0 × 1044 erg and 1.4 × 1047 erg respectively, assuming a distance of 1 kpc. The f-mode energy limits approach the range seen emitted electromagnetically during giant flares. One of these flares, on 29 March 2006, was actually a “storm” of many flares from SGR 1900+14. For this event a more sensitive search has been performed by stacking data around the time of each flare [51]. Waveform dependent upper limits of the gravitational-wave energy emitted were set between 2 × 1045 erg and 6 × 1050 erg, which are an order of magnitude lower than the previous upper limit for this storm (included in the search of [37]) and overlap with the range of electromagnetic energies emitted in SGR giant flares.
Another possible source of gravitational waves associated with electromagnetically-observed phenomenon are pulsar glitches. During these it is possible that various gravitational-wave-emitting vibrational modes of the pulsar may be excited. A search has been performed for fundamental modes (f-modes) in S5 data following a glitch observed in the timing of the Vela pulsar in August 2006 [8]. Over the search frequency range of 1–3 kHz this provided upper limits on the peak strain of 0.6–1.4 × 10−20 depending on the spherical harmonic that was excited.
Already efforts are under way to invert this process of searching gravitational-wave data for external triggers, and instead supplying gravitational-wave burst triggers for electromagnetic follow-up. This is being investigated across the range of the electromagnetic spectrum from radio [259], through optical (e.g., [198, 119]) and X-ray/γ-ray, and even looking for coincidence with neutrino detectors [86, 258, 111]. Having multi-messenger observations can have a large impact on the amount of astrophysical information that can be learnt about an event [255].
6.2.4 Continuous sources
Searches for continuous waves focus on rapidly-spinning neutron stars as sources. There are fully targeted searches, which look for gravitational waves from known radio pulsars in which the position and spin evolution of the objects are precisely known. There are semi-targeted searches, which look at potential sources in which some, but not all, the source signal parameters are known, for example neutron stars in X-ray binary systems, or sources in supernova remnants where no pulses are seen, which have known position, but unknown frequency. Finally, there are all-sky broadband searches in which none of the signal parameters are known. The targeted searches tend to be most sensitive as they are able to perform coherent integration over long stretches of data with relatively low computational overheads, and have a much smaller parameter space leading to fewer statistical outliers. Due to various neutron-star population statistics, creation rates and energetics arguments, there is an estimate that the amplitude of the strongest gravitational-wave pulsar observed at Earth will be h0 ≲ 4 × 10−24 [29] (a more thorough discussion of this argument can be found in [203]), although this does not rule out stronger sources.
The various search techniques used to produce these results all look for statistically-significant excess power in narrow frequency bins that have been Doppler demodulated to take into account the signal’s shifting frequency caused by the Earth’s orbital motion with respect to the source (or also including the modulations to the signal caused by the source’s own motion relative to the Earth, such as for a pulsar in a binary system). The statistical significance of a measured level of excess power is compared to what would be expected from data that consisted of Gaussian noise alone. A selection of the searches are summarised in [260], but for more detailed descriptions of the various methods see [100, 206, 188, 33, 29, 132].
In S1 a fully-coherent targeted search for gravitational waves from the then-fastest millisecond pulsar J1939+2134 was performed [14]. This analysis and the subsequent LSC known-pulsar searches assume that the star is triaxial and emitting gravitational waves at exactly twice its rotation frequency. All the data from LIGO and GEO600 was analysed and no evidence of a signal was seen. A 95% degree-of-belief upper limit on the gravitational-wave strain amplitude was set using data from the most sensitive detector, L1, giving a value of 1.4 × 10−22. This result was also interpreted as an ellipticity of the star given a canonical moment of inertia of 1038 kg m2 at ε = 2.9 × 10−4. However, this was still of order 100 000 times higher than the limit that can be set by equating the star’s rate of loss of rotational kinetic energy with that emitted via gravitational radiation—called the “spin-down limit”. In S2 the number of known pulsar sources searched for with LIGO data increased from 1 to 28, although all of these were isolated pulsars (i.e. not in binary systems, although potentially still associated with supernova remnants or globular clusters). This search used pulsar timing data supplied by Lyne and Kramer from Jodrell Bank Observatory to precisely reconstruct the phase of the gravitational-wave signal over the period of the run. The lowest 95% upper limit on gravitational-waves amplitude was 1.7 × 10−24 for PSR J1910−5959D, and the smallest upper limit on ellipticity (again assuming the canonical moment of inertia) was 4.5 − 10−6 for the relatively-close pulsar PSR J2124−3358 [16], at a distance of 0.25 kpc. The pulsar closest to its inferred spin-down limit was the Crab pulsar (PSR J0534+2200) with an upper limit 30 times greater than that from spin-down. S2 also saw the use of two different all-sky-wide frequency band searches that focused on isolated sources, but also including a search for gravitational waves from the low mass X-ray binary Scorpius X1 (Sco-X1). The first search used a semi-coherent technique to search ∼ 60 days of S2 data in the frequency band between 200–400 Hz and with signal spin-downs between −1.1 × 10−9 and 0 Hz s−1 [15]. This gave a lowest gravitational-wave strain 95% upper limit of 4.4 × 10−23 for the L1 detector at around 200 Hz. The other all-sky search was fully coherent and as such was computationally limited to only use a few hours of the most sensitive S2 data. It searched frequencies between 160–728.8 Hz and spin-downs less than −4 × 10−10 Hz s−1 for isolated sources and gave a 95% upper limit across this band from 6.6 × 10−23 to 1 × 10−21 [29]. The search for gravitational waves from Sco-X1 used the same period of data. It did not have to search over sky position as this is well known, but did have to search over two binary orbital parameters — the projected semi-major axis and the orbital phase reference time. The frequency ranges of this search relied on estimates of the spin-frequency from quasi-periodic oscillations in the X-rays from the source and covered two 20 Hz bands from 464–484 Hz and 604–624 Hz (it should be noted that it is now thought that these estimates of the spin-frequency are unreliable). In these two ranges upper limits of 1.7 × 10−22 and 1.3 × 10−21 were found respectively.
One search that was carried out purely on LIGO S3 data was the coherent all-sky wide-band isolated pulsar search using the distributed computing project Einstein@Home [135]. The project is built upon the Berkeley Open Infrastructure for Network Computing [97] and allows the computational workload to be distributed among many computers generally contributed by the general public who sign up to the project. This used the most sensitive 600 hours of data from H1 and cut it into 60 ten hour stretches on each of which a coherent search could be performed. The data was farmed out to computers owned by participants in the project and ran as a background process or screen saver. The search band spanned the range from 50–1500.5 Hz. The search saw no plausible gravitational-wave candidates and the result is described at [25], but it was not used to produce an upper limit.
In the known pulsar search the number of sources searched for using the combined LIGO data from S3 and S4 was increased to 78. This included many pulsars within binary systems. For many of the pulsars that overlapped with the previous S2 analysis results were improved by about an order of magnitude. The lowest 95% upper limit on gravitational-waves amplitude was 2.6 × 10−25 for PSR J1603−7202, and the smallest ellipticity was again for PSR J2124−3358 at just less than 10−6 [32]. The upper limit for the Crab pulsar was found to be only 2.2 times above that from the spin-down limit. Three different, but related, semi-coherent all-sky continuous wave searches were performed on S4 LIGO data, looking for isolated neutron stars in the frequency range from 50–1000 Hz and the spin-down range from −1 × 10−8 to 0 Hz s−1 [33]. The best 95% upper limit based on an isotropically-distributed, randomly-oriented, population of neutron stars was 4.3 × 10−24 near 140 Hz. This is approaching the amplitude of the strongest potential signal discussed above. For one of the searches, which combined data from the different detectors, an isolated pulsar emitting at near 100 Hz, and with an extreme ellipticity of 10−4 could have been seen at a distance of 1 kpc, although for a more realistic ellipticity of 10−8 only a distance of less than 1 pc would be visible over the entire LIGO band. The Einstein@Home project [135] was also used to search the most sensitive data from S4, which consisted of 300 hours of H1 data and 210 hours of L1 data. The search performed a coherent analysis on 30-hour stretches of this data and covered the frequency range of 50–1500 Hz [43]. The range of spin-downs ḟ was chosen by using a minimum spin-down age τ and having −f/τ < ḟ < 0.1 f/τ (small spin-ups are allowed as some pulsars in globular clusters exhibit this due to their Doppler motions within the clusters), with τ = 1000 years for signals below 300 Hz and τ = 10 000 years above 300 Hz. Approximately 6000 years of computational time spread over about 100 000 computers were required to perform the analysis. No plausible gravitational-wave candidates were found, although the results suggest that 90% of sources with strain amplitudes greater than 10−23 would have been detected by the search. A search designed to produce a sky map of the stochastic background was also used to search for gravitational waves from Sco-X1 using a method of cross-correlating H1 and L1 data [31]. This produced a 90% root-mean-squared upper limit on gravitational wave strain of h = 3.4 × 10−24(f/200 Hz) for frequencies greater than 200 Hz.
The first 8 months of S5 have been used to perform an all-sky search for periodic gravitational waves. This search used a semi-coherent method to look in the frequency range 50–1100 Hz and spin-down range −5 × 10−9 −0 Hz s2 and used data from the H1 and L1 detectors [41]. It obtained 95% strain upper limits of less than 10−24 over a frequency band of 200 Hz. The search would have been sensitive to a neutron star with equatorial ellipticity greater than 10−6 within around 500 pc. Einstein@Home [135] has been used to search for periodic waves of 50–1500 Hz in 860 hours of data from a total span of 66 days of S5 data [42]. This search looked for young pulsars, but saw no significant candidates. It would have been sensitive to 90% of sources in the 125–225 Hz band with amplitudes greater than 3 × 10−24. The first approximately 9 months of S5 data was used for a coherent search for gravitational waves from the Crab pulsar [34]. In this search two methods were used: the first followed the method of the targeted search and assumed that the gravitational waves are phase locked to the electromagnetic pulses; the second allowed for some mechanism, which would cause a small mismatch between the two phases. Two 95% upper limits were set, one using astrophysical constraints on the pulsar orientation angle and polarisation angle [241] and the other applying no such constraints. With the first method these 95% upper limits were 3.4 × 10−25 and 2.7 × 10−25 respectively, which correspond to ellipticities of 1.8 × 10−4 and 1.4 × 10−4 (assuming the canonical moment of inertia). These beat the Crab pulsar’s spin-down limit by 4 to 5 times and can be translated into the amount of the available spin-down power that is emitted via gravitational waves, with the lower of these limits showing that less than 4% of power is going into gravitational waves. For the second search the uniform and restricted prior analyses gave upper limits of 1.7 × 10−24 and 1.2 × 10−24 respectively. The whole of S5 was used to search for emissions from 116 known pulsars [54]. During this search the Crab limit was further brought down to be less than a factor of 7 below the spin-down limit, and the spin-down limit is reached for one other pulsar PSR J0537−6910. Of the other pulsars, the best (lowest) upper limit on gravitational-wave amplitude was 2.3 × 10−26 for PSR J1603−7202 and our best (lowest) limit on the inferred pulsar ellipticity is 7.0 × 10−8 for PSR J2124−3358.
A semi-targeted search was performed with 12 days of S5 data, although this time searching for a source with a known position in the Cassiopeia A (Cas A) supernova remnant, but for which there is no known frequency. The search [2] looked in the frequency band between 100–300 Hz and covered a wide range of first and second frequency derivatives and no signal was seen, but it gave 95% amplitude and ellipticity upper limits over the band of (0.7−1.2) × 10−24 and (0.4−4) 10−4 respectively. These results beat indirect limits on the emission based on energy-conservation arguments (similar, but not the same as the spin-down limits) and were also the first results to be cast as limits on the r-mode amplitude [251].
The Vela pulsar has a spin frequency of ∼ 11 Hz and was not accessible with current LIGO data. However, Virgo VSR2 data had sensitivity in the low frequency band that made a search for it worthwhile. Using ∼ 150 days of Virgo data, three semi-independent methods were used to search for the Vela pulsar [6]. No signal was seen, but a 95% upper limit on the amplitude of ∼ 2 × 10−24 was set, which beat the spin-down limit by ∼ 1.6 times. Other than the Crab pulsar, this is currently the only other object for which the spin-down limit has been beaten.
6.2.5 Stochastic sources
Searches are conducted for a cosmological, or astrophysical, background of gravitational waves that would show up as a coherent stochastic noise source between detectors. This is done by performing a cross-correlation of data from two detectors as described in [73].
In S1 the most sensitive detector pair for this correlation was H2-L1 (the H1–H2 pair are significantly hampered by local environmental correlations) and they gave a 90% confidence upper limit of Ωgw < 44 ± 92 within the 40–314 Hz band, where the upper limit is in units of closure density of the universe and for a Hubble constant in units of 72 km s−1 Mpc−1 [10]. This limit was several times better than previous direct-detector limits, but still well above the concordance ACDM cosmology value of the total energy density of the universe of Ω0 ≈ 1 (see, e.g., [189]).
No published stochastic background search was performed on S2 data, but S3 data was searched and gave an upper limit that improved on the S1 result by a factor of ∼ 105. The most sensitive detector pair for this search was H1-L1 for which 218 hours of data were used [21]. Upper limits were set for three different power-law spectra of the gravitational-wave background. For a flat spectra, as predicted by some inflationary and cosmic string models, a 90% confidence upper limit of Ωgw(f) = 8.4 × 10−4 in the 69–156 Hz range was set (again for a Hubble constant of 72 km s−1 Mpc−1). This is still about 60 times greater than a conservative bound on primordial gravitational waves set by big-bang nucleosynthesis (BBN). For a quadratic power law, as predicted for a superposition of rotating neutron-star signals, an upper limit of Ωgw(f) = 9.4 × 10−4(f/100 Hz)2 was set in the range 73–244 Hz, and for a cubic power law, from some pre-Big-Bang cosmology models, an upper limit of Ωgw(f) = 8.1 × 10−4(f/100 Hz)3 in the range 76–329 Hz was produced.
For S4 ∼ 354 hours of H1-L1 data and ∼ 333 hours of H2-L1 data were used to set a 90% upper limit of Ωgw(f) < 6.5 × 10−5 on the stochastic background between 51–150 Hz, for a flat spectrum and Hubble constant of 72 km s−1 Mpc−1 [30]. This result is still several times higher than BBN limits. About 20 days of H1 and L1 S4 data was also used to produce an upper limit map on the gravitational wave background across the sky as would be appropriate if there was an anisotropic background dominated by distinct sources [31]. This search covered a frequency range between 50–1800 Hz and had spectral power limits (which come from the square of the amplitude h) ranging from 1.2 × 10−48 Hz−1 (100 Hz/f)3 and 1.2 × 10−47 Hz−1(100 Hz/f)3 for an f−3 source power spectrum, and limits of 8.5 × 10−49 Hz−1 and 6.1 × 10−48 Hz−1 for a flat spectrum.
Data from S4 was also used to perform the first cross-correlation between an interferometric and bar detector to search for stochastic backgrounds. L1 data and data from the nearby ALLEGRO bar detector were used to search in the frequency range 850–950 Hz, several times higher than the LIGO only searches [26]. A 90% upper limit on the closure density of Ωgw(f) ≤ 1.02 (for the above Hubble constant) was set, which beat previous limits in that frequency range by two orders of magnitude. This limit beats what would be achievable with LLO-LHO cross correlation of S4 data in this frequency range by a factor of several tens, due to the physical proximity of LLO and ALLEGRO.
The entire two years of S5 data from the LIGO detectors has been used to set a limit on the stochastic background around 100 Hz to be Ωgw(f) < 6.9 × 10−6 at 95% confidence (for a flat gravitational-wave spectrum) [52]. This now beats the indirect limits provided by BBN and cosmic microwave background observations.
6.3 Detector upgrades
All the current detectors have upgrades planned over the next several years. These upgrades will give rise to the second generation of gravitational-wave detectors, which should start to open up gravitational-wave astronomy as a real observational tool. There are also currently plans being made for third generation detectors, which could provide the premier gravitational-wave observatories for the first half of the century. A brief summary of the planned upgrades to current and future detectors is given below. An overview can be also be found here [315]. Some of the technologies for these upgrades are discussed earlier in this review (e.g. Section 5).
6.3.1 Advanced LIGO, Advanced Virgo and LCGT
Advanced LIGO (aLIGO) [166, 214, 66] and Advanced Virgo (AdvVirgo) [62, 67] are the second generation detectors. They are planned to have a sensitivity increase over the levels of the initial detectors by a factor of 10–15 times. These increased sensitivity levels would expand the volume of space observed by the detectors by ∼ 1000 times meaning that there is a realistic detection rate of neutron-star-binary coalescences of around 40 yr−1 [3, 205]. The technological issues required to reach these sensitivities, such as choice of test mass and mirror coating materials, suspension design, interferometric layout, control and readout, would need a separate review article to themselves, but we shall very briefly summarise them here.
Advanced LIGO will consist of three 4 km detectors in the current LIGO vacuum system; two at the Hanford site3 and one at Livingston. It will apply some of the technologies from the GEO600 interferometer, such as the use of a signal recycling mirror at the output port and monolithic silica suspensions for the test masses, rather than the current steel wire slings. Larger test masses will be used with an increase from 11 to 40 kg, although the masses will still be made from fused silica. The mirror coating is likely to consist of multiple alternating layers of silica and tantala, with the tantala layers doped with titania to reduce the coating thermal noise [69]. The seismic isolation systems will be replaced with improved versions offering a seismic cut-off frequency of ∼ 10 Hz as opposed to the current cut-off of ∼ 40 Hz. As stated for Enhanced LIGO (in Section 6.1.2), the laser power will be greater than for initial LIGO and a DC readout scheme will be used. Initial/Enhanced LIGO was shut down to begin the installation of these upgrades on 20 October 2010. The design strain amplitude sensitivity curve for aLIGO (and AdvVirgo and LCGT) is shown in Figure 18.
Design sensitivity curves for the Advanced LIGO, Advanced Virgo and LCGT second-generation detectors. The Advanced LIGO curve comes from [166], the Advanced Virgo curve comes from [67], and the LCGT curve comes from [82]. These curves are based on specific configurations of the detectors and are therefore subject to change.
AdvVirgo will apply similar upgrades to those for aLIGO and over a similar timescale (for details see [141] and [62]). Plans are to add a signal recycling mirror, monolithic suspensions, increased laser power to ∼ 200 W, improved coatings, and to potentially use non-Gaussian beams (see, e.g., [146]), although this option is unlikely. The seismic isolation system will not be changed. Virgo will shut down to begin these upgrades in July 2011.
The Large-scale Cryogenic Gravitational-Wave Telescope (LCGT) [234, 247, 207] is a planned Japanese detector to be sited underground in the Kamioka mine. The LGCT will consist of a detector with 3 km arms, using sapphire mirrors and sapphire suspensions. Initially it will operate at room temperature, but will later be cooled to cryogenic temperatures. This detector is planned to have similar sensitivities to aLIGO and AdvVirgo, with a reach for binary coalescences of about 200 Mpc with SNR of 10. There currently exists a technology demonstrator called the Cryogenic Laser Interferometer Observatory (CLIO) [324, 164], which has a 100 m baseline and is also sited in the Kamioka mine. This is to demonstrate the very stable conditions (i.e., low levels of seismic noise) existing in the mine and also the cryogenically-cooled sapphire mirrors suspended from aluminium wires. In experiments with CLIO at room temperature (i.e. 300 K), using a metallic glass called Bolfur for its wire suspensions, it has already been used to produce an astrophysics result by looking for gravitational waves from the Vela pulsar [71], giving a 99.4% confidence upper limit of h = 5.3 × 10−20. Tests with the cryogenic system activated and using aluminium suspensions allowed two mirrors to be cooled to ∼ 14 K.
Having a network of comparably-sensitive detectors spread widely across the globe is vital to gain the fullest astrophysical insight into transient sources. Position reconstruction for sources relies on triangulating the location based on time-of-flight delays observed between detectors. Therefore, having long baselines, and different planes between as many detectors as possible, gives the best positional reconstruction — in [138] it is shown that for the 2 US aLIGO sites sky localisation will be on the order of 1000 square degrees, whereas this can be brought down to a few square degrees with the inclusion of more sites and detectors. Observation with multiple detectors also provides the best way to give confidence that a signal is a real gravitational wave rather than the accidental coincidence of background noise. Finally, multiple, differently-oriented, detectors will increase the ability to reconstruct a transient sources waveform and polarisation.
6.3.2 Third-generation detectors
Currently design studies are under way for a third-generation gravitational-wave observatory called the Einstein Telescope (ET) [134]. This is a European Commission funded study with working groups looking into various aspects of the design including the site location and characteristics (e.g. underground), suspensions technologies; detector topology and geometry (e.g. an equilateral triangle configuration); and astrophysical aims. The preliminary plan is to aim for an observatory, which improves upon the second-generation detectors by an order of magnitude over a broad band. There are many technological challenges to be faced in attempting to make this a reality and research is currently under way into a variety of these issues.
Investigations into the interferometric configuration have already been studied (see [145, 174, 178]), with suggestions including a triple interferometer system made up from an equilateral triangle, an underground location, and potentially a xylophone configuration (two independent detectors covering different frequency ranges, i.e., ultimately giving six detectors in total, although constructed over a period of years). Three potential sensitivity curves are plotted in Figure 19 for different configurations of detectors.
7 Longer Baseline Detectors in Space
Some of the most interesting gravitational-wave signals, resulting from the mergers of supermassive black holes in the range 103 to 106 M⊙ and cosmological stochastic backgrounds, will lie in the frequency region below that of ground-based detectors. The most promising way of looking for such signals is to fly a laser interferometer in space, i.e. to launch a number of drag-free spacecraft into orbit and to compare the distances between test masses in these craft using laser interferometry.
7.1 Laser Interferometer Space Antenna (LISA)
Until early 2011, the Laser Interferometer Space Antenna (LISA) — see, for example, [125, 272, 217, 216] — was under consideration as a joint ESA/NASA mission as one L-class candidate within the ESA Cosmic Visions program [118]. Funding constraints within the US now mean that ESA must examine the possibility of flying an L-class mission with European-only funding [240]. Accordingly all three L-class candidates are undergoing a rapid redesign phase with the goal of meeting the new European-only cost cap. Financial, programmatic and scientific issues will be reassessed following the redesigns and it is currently expected that the selection of the first L-class mission will take place in 2014.
However, for the rest of this article we will discuss the plans for LISA prior to these developments. More concrete information is expected to emerge very soon.
LISA would consist of an array of three drag-free spacecraft at the vertices of an equilateral triangle of length of side 5 × 106 km, with the cluster placed in an Earth-like orbit at a distance of 1 AU from the Sun, 20° behind the Earth and inclined at 60° to the ecliptic. A current review of LISA technologies, with expanded discussion of, and references for, topics touched upon below, can be found in [192]. Here we will focus upon a couple of topics regarding the interferometry needed to give the required sensitivity.
Proof masses inside the spacecraft (two in each spacecraft) form the end points of three separate, but not independent, interferometers. Each single two-arm Michelson-type interferometer is formed from a vertex (actually consisting of the proof masses in a ‘central’ spacecraft), and the masses in two remote spacecraft as indicated in Figure 21. The three-interferometer configuration provides redundancy against component failure, gives better detection probability, and allows the determination of the polarisation of the incoming radiation. The spacecraft, which house the optical benches, are essentially there as a way to shield each pair of proof masses from external disturbances (e.g., solar radiation pressure). Drag-free control servos enable the spacecraft to follow the proof masses to a high level of precision, the drag compensation being effected using proportional electric thrusters. Illumination of the interferometers is by highly-stabilised laser light from Nd:YAG lasers at a wavelength of 1.064 microns, laser powers of ≃ 2 W being available from monolithic, non-planar ring oscillators, which are diode pumped. For LISA to achieve its design performance strain sensitivity of around 10−20 Hz−1/2, adjacent arm lengths have to be sensed to an accuracy of about 10 pm(Hz)−1/2. Because of the long distances involved and the spatial extent of the laser beams (the diffraction-limited laser spot size, after travelling 5 × 106 km, is approximately 50 km in diameter), the low photon fluxes make it impossible to use standard mirrors for reflection; thus, active mirrors with phase locked laser transponders on the spacecraft will be implemented. Telescope mirrors will be used to reduce diffraction losses on transmission of the beam and to increase the collecting area for reception of the beam. With the given laser power, and using arguments similar to those already discussed for ground-based detectors with regard to photoelectron shot noise considerations, means that for the required sensitivity the transmitting and receiving telescope mirrors on the spacecraft will have diameters of 40 cm.
A design sensitivity amplitude spectral density curve for LISA created using the standard parameters in the online generator at [208]. The curve assumes equal length arms, sensitivity averaged over the whole sky and all polarisations, and an SNR of 1. Also included is a curve showing the expected background noise from galactic white-dwarf-binary systems, which will dominate over the instrumental noise in the range from ∼ 0.1–1 mHz.
Further, just as in the case of the ground-based detectors, the presence of laser frequency noise is a limiting factor. It leads to an error in the measurement of each arm length. If the arms are equal, these errors cancel out, but if they are unequal, the comparison of lengths used to search for gravitational waves may be dominated by frequency noise. For the 5 × 109 m long arms of LISA, a difference in arm length of 108 m is likely. Then, for a relative arm length measurement of 2 × 10−12 m Hz−1/2 (the error budget level allowed in the LISA design for this noise source), Equation (14) suggests that a laser stability of ≃ 6 × 10−6 Hz Hz−1/2 is required, a level much better than can be achieved from the laser on its own. Thus, frequency stabilisation has to be provided. The first method of stabilisation is to lock the frequency of one laser in the system on to a local frequency reference, e.g., a Fabry-Pérot cavity mounted on one of the craft (see, for example, [229]), and then to effectively transfer this stability to other lasers in the system by phase locking techniques. With the temperature fluctuations inside each craft limited in the region of 3 mHz to approximately 10−6 K Hz−1/2 by three stages of thermal insulation, a cavity formed of material of low expansion coefficient such as ULE allows a stability level of approximately 30 Hz Hz−1/2 (again at 3 mHz). This level of laser frequency noise is clearly much worse than the required 1.2 × 10−6 Hz Hz−1/2 (at 3 mHz) and a further correction scheme is needed. A second possible stage of frequency stabilisation is arm-locking [285], which relies on the fact that, by design, the fractional stability of the LISA arms is of order δ/L ∼ 10−21 Hz−1/2 to derive an error signal from the phase difference between the local laser and the received light. As the received light is phase locked with the local laser from the craft that sent it, it caries a replica of the frequency noise of the local laser noise delayed by one round trip time τ = 33 s. Using this fact, this noise can be suppressed at frequencies smaller than the round trip frequency f = 1/τ = 30 mHz. This scheme requires no additional hardware and can be completely implemented in software, but it will still leave frequency noise that is several orders of magnitude above required levels. A third stage frequency stabilisation scheme, which is a post-processing step, is time-delay interferometry (TDI). This makes use of the fact that, because the beams coming down each arm are not combined, the phase of each beam can be measured and recorded. Therefore, correlations in the frequency noise can be calculated and subtracted by algebraically combining phase measurements from different craft delayed by the multiples of the time delay between the spacecraft. The accuracy of this is set by the phase measurement accuracy, which allows frequency noise subtraction to below the required level. A simple TDI scheme, for a much simplified constellation, was first based in the frequency domain [152], but due to complexities in taking into account changing arm lengths and a more complex interferometric scheme, subsequent implementations have been in the time domain. A mathematical overview of the TDI scheme, along with moving spacecraft and unequal arm lengths, can be found in [297].
One of the major components of LISA is the disturbance reduction system (DRS), which is responsible for making sure the test masses follow, as far as possible, purely gravitational orbits. This consists of the gravitational reference sensor (GRS) and the control and propulsion systems used to keep the spacecraft centred on the test mass. The test masses for LISA are 1.96 kg cubes, with sides of 46 mm and made of an alloy of 75% gold and 25% platinum, chosen because of its very small magnetic susceptibility. The masses are housed in a cube of electrodes designed to capacitively sense their position and to have measurement noise levels of 1.8 nm Hz−1/2. The masses need to be tightly held in place during launch and then released, so a caging mechanism has been designed consisting of 8 hydraulic fingers (one for each corner of the mass) pushing with 1200 N of force. There will be adhesion between the fingers and the masses, which will require about 10 N of force per finger to break. To provide this force two plungers will push on the the top and bottom surfaces of the masses releasing them from the fingers, followed by pushing smaller release tips in each plunger, and quickly retracting them, to overcome their adhesion to the masses. Charged particles produced by cosmic radiation interacting with the surrounding spacecraft can cause the test masses to become charged at a rate of about 50 electrons per second. Current plans are to use UV light from mercury lamps (or potentially UV LEDs) to discharge the masses. Another key technology for the DRS are the micro-Newton thrusters, which provide the fine control needed for drag-free flight. These will mainly be used to counteract solar radiation pressure on the spacecraft, which requires about 10 µN per relevant thruster. Thrust noise as a function of frequency is required to be smaller than
Two types of system, both of which meet the requirements, will be tested on LISA Pathfinder: the US colloid micro-Newton thruster (CMNT); and the European field emission electric propulsion system (FEEP). The CMNT uses small drops of a colloid, which it ionises through field emission, accelerates and ejects from the thruster. Two designs of FEEP currently exist, one using Indium and the other Caesium and with different geometries, which, instead of ionising a droplet of colloid, just use single ions. This means FEEPs have a better charge to mass ratio. The current baseline is to use caesium FEEPs. Many of the systems above are being tested in the LISA Pathfinder mission (see below) and use the nominal LISA designs.
There are many other issues associated with laser interferometry, and other aspects of the mission mentioned above, for LISA, which are not dealt with here and the interested reader should refer to [183, 192, 193] for a discussion of some of these.
For LISA the baseline mission design was finalised in 2005. An industrial contract was awarded to Astrium GmbH for the LISA Mission Formulation study [193]. Within the current ESA Science Programme LISA is in the Cosmic Vision 2015–2025 Programme [118], and launch after 2020 seems likely. In 2007 the National Research Council report on the NASA Beyond Einstein Program (soon to become the Physics of the Cosmos Program) gave LISA the highest scientific ranking, and it has been rated very highly in the Astro2010 decadal survey [87]. However, as stated above, as of earlier this year (2011) ESA is considering the feasibility of LISA as a single agency mission [240]. Recent technical reports for LISA can be found at [218].
Several of the key technologies for LISA are being testing on the LISA Pathfinder mission (formerly SMART-2). Details of the current status of this mission can be found in [84]. LISA Pathfinder will fly the LISA Technology Package (LTP), which essentially consists of a downscaled version of one LISA arm compressed from 5 million km to 38 cm. The LTP arm contains two test masses (an emitter and a receiver) with a Doppler link between them. The three main things it will measure are: the acceleration phase noise caused by the relative motion of the emitter and receiver from non-gravitational forces; the readout noise; and noise caused by the departure of the Doppler link from the ideal scheme, due to the fact that we are not truly measuring the relative accelerations of two point particles, but instead a more complex system of multiple Doppler links and extended masses. It is designed to test the accuracy of these to within an order of magnitude of that required by the full LISA. Other aspects of the mission that will be tested are the discharging of the test masses, the caging and release of the masses following launch and the micro-Newton thrusters. As much as possible the nominal LISA systems and hardware are being used. LISA Pathfinder is currently scheduled for launch in mid 2013, after which it will orbit the L1 point, with a 180-day mission plan.
7.2 Other missions
LISA is the most advanced space-based project, but there exist concepts for at least two more detectors. DECIGO (DECi-hertz Interferometer Gravitational Wave Observatory) [274, 199] is a Japanese project designed to fill the gap in frequency between ground-based detectors and LISA, i.e. the 0.1–10 Hz band. It would have a similar configuration to LISA with three drag-free spacecraft, but have far shorter arm lengths at 1000 km. Although still early in its design there are plans for two precursor technology demonstration missions (DECIGO Pathfinder [80] and Pre-DECIGO), with a the main mission having a launch date in the mid-2020s.
A similar mission, in terms of the frequency band it seeks to cover, is the US Big Bang Observer (BBO) (see [122, 124, 167] for overviews of the proposal). One of its main aims will be to detect the stochastic background from the early universe, but it can also be used for high precision cosmology [124]. The current configuration would consist of three LISA-like constellations of three spacecraft each, with 50 000 km arm lengths, and separated in their orbit by 120°. The launch of this mission would be after DECIGO, but is designed to be 2–3 times as sensitive.
At lower frequencies than LISA, ∼ 0.1 µHz–1 mHz, there are Chinese proposals for SuperASTROD (Super Astrodynamical Space Test of Relativity using Optical Devices) [242].
8 Conclusion
Significant effort worldwide has been invested, and is continuing to be invested, in the development of both ground and spaced based gravitational-wave detectors. Over the coming years, ground-based detectors will reach sensitivities that will enable the direct observation of gravitational waves as predicted by Einstein’s General Theory of Relativity and open the exciting new field of gravitational-wave astronomy. Studying the gravitational-wave sky could radically change our understanding of the Universe, expanding our knowledge of fundamental physics, cosmology and relativistic astrophysics. Gravitational-wave observations will allow us to gaze into the heart of the most violent events in the Universe, and will help answer some of the biggest questions, particularly in cosmology when combined with other astronomical observations.
References
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “All-sky search for gravitational-wave bursts in the first joint LIGO-GEO-Virgo run”, Phys. Rev. D, 81, 102001, (2010). [DOI], [arXiv:1002.1036 [gr-qc]]. (Cited on page 37.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “First Search for Gravitational Waves from the Youngest Known Neutron Star”, Astrophys. J., 722, 1504–1513, (2010). [DOI], [arXiv:1006.2535 [gr-qc]]. (Cited on page 43.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Predictions for the rates of compact binary coalescences observable by ground-based gravitational-wave detectors”, Class. Quantum Grav., 27, 173001, (2010). [DOI], [arXiv:1003.2480 [astro-ph.HE]]. (Cited on pages 28, 29, and 44.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Search for Gravitational-wave Inspiral Signals Associated with Short Gamma-ray Bursts During LIGO’s Fifth and Virgo’s First Science Run”, Astrophys. J., 715, 1453–1461, (2010). [DOI], [arXiv:1001.0165 [astro-ph.HE]]. (Cited on page 39.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Search for gravitational waves from compact binary coalescence in LIGO and Virgo data from S5 and VSR1”, Phys. Rev. D, 82, 102001, (2010). [DOI]. (Cited on page 38.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Beating the spin-down limit on gravitational wave emission from the Vela pulsar”, arXiv, e-print, (2011). [arXiv:1104.2712 [astro-ph.HE]]. (Cited on page 43.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Search for Gravitational Wave Bursts from Six Magnetars”, Astrophys. J. Lett., 734, L35, (2011). [DOI], [arXiv:1011.4079 [astro-ph.HE]]. (Cited on page 40.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “A search for gravitational waves associated with the August 2006 timing glitch of the Vela pulsar”, Phys. Rev. D, 83, 042001, (2011). [DOI], [arXiv:1011.1357]. (Cited on page 40.)
Abadie, J. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Search for gravitational waves from binary black hole inspiral, merger and ringdown”, Phys. Rev. D, 83, 122005, (2011). [DOI], [arXiv:1102.3781 [gr-qc]]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Analysis of first LIGO science data for stochastic gravitational waves”, Phys. Rev. D, 69, 122004, (2004). [DOI], [gr-qc/0312088]. (Cited on page 43.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Analysis of LIGO data for gravitational waves from binary neutron stars”, Phys. Rev. D, 69, 122001, (2004). [DOI], [gr-qc/0308069]. (Cited on page 37.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Detector description and performance for the first coincidence observations between LIGO and GEO”, Nucl. Instrum. Methods A, 517, 154–179, (2004). [DOI], [gr-qc/0308043]. (Cited on pages 30 and 32.)
Abbott, B. et al. (LIGO Scientific Collaboration), “First upper limits from LIGO on gravitational wave bursts”, Phys. Rev. D, 69, 102001, (2004). [DOI]. (Cited on page 36.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Setting upper limits on the strength of periodic gravitational waves from PSR J1939+2134 using the first science data from the GEO 600 and LIGO detectors”, Phys. Rev. D, 69, 082004, (2004). [DOI], [gr-qc/0308050]. (Cited on page 41.)
Abbott, B. et al. (LIGO Scientific Collaboration), “First all-sky upper limits from LIGO on the strength of periodic gravitational waves using the Hough transform”, Phys. Rev. D, 72, 102004, (2005). [DOI], [gr-qc/0508065]. (Cited on page 41.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Limits on Gravitational-Wave Emission from Selected Pulsars Using LIGO Data”, Phys. Rev. Lett., 94, 181103, (2005). [DOI], [gr-qc/0410007]. (Cited on page 41.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves associated with the gamma ray burst GRB030329 using the LIGO detectors”, Phys. Rev. D, 72, 042002, (2005). [DOI], [gr-qc/0501068]. (Cited on page 39.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from galactic and extra-galactic binary neutron stars”, Phys. Rev. D, 72, 082001, (2005). [DOI], [gr-qc/0505041]. (Cited on pages 29, 37, and 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from primordial black hole binary coalescences in the galactic halo”, Phys. Rev. D, 72, 082002, (2005). [DOI], [gr-qc/0505042]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration and TAMA Collaboration), “Upper limits from the LIGO and TAMA detectors on the rate of gravitational-wave bursts”, Phys. Rev. D, 72, 122004, (2005). [DOI]. (Cited on page 36.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Upper Limits on a Stochastic Background of Gravitational Waves”, Phys. Rev. Lett., 95, 221101, (2005). [DOI], [astro-ph/0507254]. (Cited on page 43.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Upper limits on gravitational wave bursts in LIGO’s second science run”, Phys. Rev. D, 72, 062001, (2005). [DOI]. (Cited on pages 30 and 36.)
Abbott, B. et al. (LIGO Scientific Collaboration and TAMA Collaboration), “Joint LIGO and TAMA300 search for gravitational waves from inspiralling neutron star binaries”, Phys. Rev. D, 73, 102002, (2006). [DOI], [gr-qc/0512078]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from binary black hole inspirals in LIGO data”, Phys. Rev. D, 73, 062001, (2006). [DOI], [gr-qc/0509129]. (Cited on pages 36, 37, and 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Einstein(AT)Home S3 Analysis Summary”, project homepage, UW-Milwaukee, (2007). URL (accessed 3 October 2008): http://einstein.phys.uwm.edu/FinalS3Results/. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration and ALLEGRO Collaboration), “First cross-correlation analysis of interferometric and resonant-bar gravitational-wave data for stochastic backgrounds”, Phys. Rev. D, 76, 022001, (2007). [DOI], [gr-qc/0703068]. (Cited on page 44.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational-wave bursts in LIGO data from the fourth science run”, Class. Quantum Grav., 24, 5343–5369, (2007). [DOI], [arXiv:0704.0943]. (Cited on pages 32 and 37.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational wave radiation associated with the pulsating tail of the SGR 1806–20 hyperflare of 27 December 2004 using LIGO”, Phys. Rev. D, 76, 062003, (2007). [DOI], [astro-ph/0703419]. (Cited on page 39.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Searches for periodic gravitational waves from unknown isolated sources and Scorpius X-1: Results from the second LIGO science run”, Phys. Rev. D, 76, 082001, (2007). [DOI]. (Cited on page 41.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Searching for a Stochastic Background of Gravitational Waves with the Laser Interferometer Gravitational-Wave Observatory”, Astrophys. J., 659, 918–930, (2007). [DOI], [astro-ph/0608606]. (Cited on page 44.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Upper limit map of a background of gravitational waves”, Phys. Rev. D, 76, 082003, (2007). [DOI], [astro-ph/0703234]. (Cited on pages 42 and 44.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Upper limits on gravitational wave emission from 78 radio pulsars”, Phys. Rev. D, 76, 042001, (2007). [DOI], [gr-qc/0702039]. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “All-sky search for periodic gravitational waves in LIGO S4 data”, Phys. Rev. D, 77, 022001, (2008). [DOI], [arXiv:0708.3818]. (Cited on pages 41 and 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Beating the Spin-Down Limit on Gravitational Wave Emission from the Crab Pulsar”, Astrophys. J. Lett., 683, L45–L49, (2008). [DOI], [arXiv:0805.4758]. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “First joint search for gravitational-wave bursts in LIGO and GEO 600 data”, Class. Quantum Grav., 25, 245008, (2008). [DOI], [arXiv:0807.2834]. (Cited on page 37.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Implications for the Origin of GRB 070201 from LIGO Observations”, Astrophys. J., 681, 1419–1430, (2008). [DOI], [arXiv:0711.1163]. (Cited on page 39.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for Gravitational-Wave Bursts from Soft Gamma Repeaters”, Phys. Rev. Lett., 101, 211102, (2008). [DOI], [arXiv:0808.2050]. (Cited on page 40.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves associated with 39 gamma-ray bursts using data from the second, third, and fourth LIGO runs”, Phys. Rev. D, 77, 062004, (2008). [DOI], [arXiv:0709.0766]. (Cited on page 39.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from binary inspirals in S3 and S4 LIGO data”, Phys. Rev. D, 77, 062002, (2008). [DOI]. (Cited on pages 29 and 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search of S3 LIGO data for gravitational wave signals from spinning black hole and neutron star binary inspirals”, Phys. Rev. D, 78, 042002, (2008). [DOI], [arXiv:0712.2050]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “All-Sky LIGO Search for Periodic Gravitational Waves in the Early Fifth-Science-Run Data”, Phys. Rev. Lett., 102, 111102, (2009). [DOI], [arXiv:0810.0283]. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Einstein(AT)Home search for periodic gravitational waves in early S5 LIGO data”, Phys. Rev. D, 80, 042003, (2009). [DOI], [arXiv:0905.1705]. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Einstein(AT)Home search for periodic gravitational waves in LIGO S4 data”, Phys. Rev. D, 79, 022001, (2009). [DOI], [arXiv:0804.1747]. (Cited on page 42.)
Abbott, B. et al. (LIGO Scientific Collaboration), “First LIGO search for gravitational wave bursts from cosmic (super)strings”, Phys. Rev. D, 80, 062002, (2009). [DOI], [arXiv:0904.4718 [astro-ph.CO]]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “LIGO: the Laser Interferometer Gravitational-Wave Observatory”, Rep. Prog. Phys., 72, 076901, (2009). [DOI]. (Cited on pages 5 and 32.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational-wave bursts in the first year of the fifth LIGO science run”, Phys. Rev. D, 80, 102001, (2009). [DOI], [arXiv:0905.0020 [gr-qc]]. (Cited on page 37.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational wave ringdowns from perturbed black holes in LIGO S4 data”, Phys. Rev. D, 80, 062001, (2009). [DOI], [arXiv:0905.1654]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from low mass binary coalescences in the first year of LIGO’s S5 data”, Phys. Rev. D, 79, 122001, (2009). [DOI], [arXiv:0901.0302]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for gravitational waves from low mass compact binary coalescence in 186 days of LIGO’s fifth science run”, Phys. Rev. D, 80, 047101, (2009). [DOI], [arXiv:0905.3710]. (Cited on page 38.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Search for high frequency gravitational-wave bursts in the first calendar year of LIGO’s fifth science run”, Phys. Rev. D, 80, 102002, (2009). [DOI], [arXiv:0904.4910 [gr-qc]]. (Cited on page 37.)
Abbott, B. et al. (LIGO Scientific Collaboration), “Stacked Search for Gravitational Waves from the 2006 SGR 1900+14 Storm”, Astrophys. J. Lett., 701, L68–L74, (2009). [DOI], [arXiv:0905.0005]. (Cited on page 40.)
Abbott, B. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “An upper limit on the stochastic gravitational-wave background of cosmological origin”, Nature, 460, 990–994, (2009). [DOI]. (Cited on page 44.)
Abbott, B. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Search For Gravitational-wave Bursts Associated with Gamma-ray Bursts using Data from LIGO Science Run 5 and Virgo Science Run 1”, Astrophys. J., 715, 1438–1452, (2010). [DOI6], [arXiv:0908.3824 [astro-ph.HE]]. (Cited on page 39.)
Abbott, B. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Searches for Gravitational Waves from Known Pulsars with Science Run 5 LIGO Data”, Astrophys. J., 713, 671–685, (2010). [DOI], [arXiv:0909.3583 [astro-ph.HE]]. (Cited on page 43.)
Abbott, R. et al., “Seismic isolation for Advanced LIGO”, Class. Quantum Grav., 19, 1591–1597, (2002). [DOI]. (Cited on page 13.)
Abramovici, A. et al., “Improved sensitivity in a gravitational wave interferometer and implications for LIGO”, Phys. Lett. A, 218, 157–163, (1996). [DOI]. (Cited on page 27.)
Accadia, T. et al. (Virgo Collaboration), “Calibration and sensitivity of the Virgo detector during its second science run”, Class. Quantum Grav., 28, 025005, (2011). [DOI], [arXiv:1009.5190 [gr-qc]]. (Cited on page 35.)
Acernese, F. et al. (VIRGO Collaboration), “Status of VIRGO”, in Hough, J. and Sanders, G.H. (VIRGO Collaboration), eds., Gravitational Wave and Particle Astrophysics Detectors, Glasgow, Scotland, UK, 23 June 2004, Proc. SPIE, 5500, pp. 58–69, (SPIE, Bellingham, WA, 2004). [DOI]. (Cited on page 34.)
Acernese, F. et al. (VIRGO Collaboration), “Status of Virgo”, Class. Quantum Grav., 22, S869–S880, (2005). [DOI]. (Cited on page 34.)
Acernese, F. et al. (VIRGO Collaboration), “The status of VIRGO”, Class. Quantum Grav., 23, S63–S69, (2006). [DOI]. (Cited on page 34.)
Acernese, F. et al. (Virgo Collaboration), “Status of Virgo detector”, Class. Quantum Grav., 24, S381–S388, (2007). [DOI]. (Cited on pages 5 and 34.)
Acernese, F. et al. (Virgo Collaboration), Advanced Virgo Preliminary Design, VIR-089A-08, (Virgo, Cascina, 2008). URL (accessed 16 February 2011): https://tds.ego-gw.it/ql/?c=2110. (Cited on pages 44 and 45.)
Acernese, F. et al. (Virgo Collaboration), “Search for gravitational waves associated with GRB 050915a using the Virgo detector”, Class. Quantum Grav., 25, 225001, (2008). [DOI], [ADS], [arXiv:0803.0376 [gr-qc]]. (Cited on page 39.)
Acernese, F. et al. (Virgo Collaboration), “Virgo status”, Class. Quantum Grav., 25, 184001, (2008). [DOI]. (Cited on page 34.)
Adhikari, R., Fritschel, P. and Waldman, S., Enhanced LIGO, LIGO-T060156-01, (LIGO, Pasadena, CA, 2006). URL (accessed 10 November 2008): http://www.ligo.caltech.edu/docs/T/T060156-01.pdf. (Cited on page 32.)
“Advanced LIGO”, project homepage, Massachusetts Institute of Technology. URL (accessed 19 November 2008): http://www.advancedligo.mit.edu/. (Cited on page 44.)
“Advanced Virgo”, project homepage, INFN. URL (accessed 16 February 2011): http://www.virgo.infn.it/advirgo/. (Cited on pages 44 and 45.)
Ageev, A., Palmer, B.C., Felice, A.D., Penn, S.D. and Saulson, P.R., “Very high quality factor measured in annealed fused silica”, Class. Quantum Grav., 21, 3887–3892, (2004). [DOI]. (Cited on page 17.)
Agresti, J., Castaldi, G., DeSalvo, R., Galdi, V., Pierro, V. and Pinto, I.M., “Optimized multilayer dielectric mirror coatings for gravitational wave interferometers”, in Ellison, M.J., ed., Advances in Thin-Film Coatings for Optical Applications III, San Diego, CA, USA, 13 August 2006, Proc. SPIE, 6286, (SPIE, Bellingham, WA, 2006). [DOI]. (Cited on page 45.)
Aguiar, O.D. et al., “The Brazilian gravitational wave detector Mario Schenberg: status report”, Class. Quantum Grav., 23, S239–S244, (2006). [DOI]. (Cited on pages 5 and 10.)
Akutsu, T. et al., “Search for continuous gravitational waves from PSR J0835−4510 using CLIO data”, Class. Quantum Grav., 25, 184013, (2008). [DOI]. (Cited on page 46.)
Akutsu, T. et al. (TAMA Collaboration), “Results of the search for inspiraling compact star binaries from TAMA300’s observation in 2000–2004”, Phys. Rev. D, 74, 122002, (2006). [DOI]. (Cited on page 30.)
Allen, B. and Romano, J.D., “Detecting a stochastic background of gravitational radiation: Signal processing strategies and sensitivities”, Phys. Rev. D, 59, 102001, (1999). [DOI], [gr-qc/9710117]. (Cited on page 43.)
Allen, B. et al., “Observational Limit on Gravitational Waves from Binary Neutron Stars in the Galaxy”, Phys. Rev. Lett., 83, 1498–1501, (1999). [DOI], [gr-qc/9903108]. (Cited on page 35.)
Alnis, J., Matveev, A., Kolachevsky, N., Udem, T. and Hänsch, T.W., “Subhertz linewidth diode lasers by stabilization to vibrationally and thermally compensated ultralow-expansion glass Fabry-Pérot cavities”, Phys. Rev. A, 77, 053809, (2008). [DOI]. (Cited on page 23.)
Amaldi, E. et al., “First gravity wave coincident experiment between resonant cryogenic detectors: Louisiana-Rome-Stanford”, Astron. Astrophys., 216, 325–332, (1989). [ADS]. (Cited on page 5.)
Anderson, W.G., Brady, P.R., Creighton, J.D. and Flanagan, É.É., “Excess power statistic for detection of burst sources of gravitational radiation”, Phys. Rev. D, 63, 042003, (2001). [DOI], [gr-qc/0008066]. (Cited on page 36.)
Ando, M. (TAMA Collaboration), “Current status of TAMA”, Class. Quantum Grav., 19, 1409–1419, (2002). [DOI]. (Cited on page 5.)
Ando, M. et al. (TAMA Collaboration), “Stable Operation of a 300-m Laser Interferometer with Sufficient Sensitivity to Detect Gravitational-Wave Events within Our Galaxy”, Phys. Rev. Lett., 86, 3950–3954, (2001). [DOI], [astro-ph/0105473]. (Cited on page 30.)
Ando, M. et al. (DECIGO Collaboration), “DECIGO pathfinder”, Class. Quantum Grav., 26, 094019, (2009). [DOI]. (Cited on page 51.)
Arai, K. et al. (TAMA Collaboration), “Report on the Observation Run of TAMA300 in the Spring of 2003”, in Kajita, T., Asaoka, Y., Kawachi, A., Matsubara, Y. and Sasaki, M. (TAMA Collaboration), eds., 28th International Cosmic Ray Conference (ICRC 2003), July 31—August 7, 2003, Trukuba, Japan, Frontiers science series, 41, pp. 3085–3088, (Universal Academy Press, Tokyo, 2003). [ADS]. (Cited on page 28.)
Arai, K. et al. (TAMA Collaboration and CLIO Collaboration and LCGT Collaboration), “Status of Japanese gravitational wave detectors”, Class. Quantum Grav., 26, 204020, (2009). [DOI]. (Cited on page 45.)
Araya, A., Mio, N., Tsubono, K., Suehiro, K., Telada, S., Ohashi, M. and Fujimoto, M.-K., “Optical mode cleaner with suspended mirrors”, Appl. Opt., 36(7), 1446–1453, (1997). [DOI]. (Cited on pages 24 and 27.)
Armano, M. et al., “LISA Pathfinder: the experiment and the route to LISA”, Class. Quantum Grav., 26, 094001, (2009). [DOI]. (Cited on page 51.)
Armstrong, J.W., “Low-Frequency Gravitational Wave Searches Using Spacecraft Doppler Tracking”, Living Rev. Relativity, 9, lrr-2006-1, (2006). URL (accessed 14 February 2011): http://www.livingreviews.org/lrr-2006-1. (Cited on page 6.)
Aso, Y., Márka, Z., Finley, C., Dwyer, J., Kotake, K. and Márka, S., “Search method for coincident events from LIGO and IceCube detectors”, Class. Quantum Grav., 25, 114039, (2008). [DOI], [arXiv:0711.0107]. (Cited on page 40.)
“Astro2010: The Astronomy and Astrophysics Decadal Survey”, project homepage, The National Acadamies. URL (accessed 14 December 2010): http://sites.nationalacademies.org/bpa/BPA_049810. (Cited on page 51.)
“AURIGA Home Page”, project homepage, INFN. URL (accessed 14 January 2008): http://www.auriga.lnl.infn.it. (Cited on pages 5, 6, and 10.)
Aylott, B. et al., “Testing gravitational-wave searches with numerical relativity waveforms: results from the first Numerical INJection Analysis (NINJA) project”, Class. Quantum Grav., 26, 165008, (2009). [DOI], [arXiv:0901.4399]. (Cited on page 37.)
Baggio, L. et al. (AURIGA Collaboration and LIGO Scientific Collaboration), “A joint search for gravitational wave bursts with AURIGA and LIGO”, Class. Quantum Grav., 25, 095004, (2008). [DOI]. (Cited on page 37.)
Barriga, P. et al., “AIGO: a southern hemisphere detector for the worldwide array of ground-based interferometric gravitational wave detectors”, Class. Quantum Grav., 27, 084005, (2010). [DOI]. (Cited on page 45.)
Bartusiak, M., Einstein’s Unfinished Symphony: Listening to the Sounds of Space-Time, (Joseph Henry Press, Washington, DC, 2000). [Google Books]. (Cited on page 7.)
Beccaria, M. et al., “Relevance of Newtonian seismic noise for the VIRGO interferometer sensitivity”, Class. Quantum Grav., 15, 3339–3362, (1998). [DOI]. (Cited on pages 13 and 15.)
Beker, M.G. et al., “Improving the sensitivity of future GW observatories in the 1–10 Hz band: Newtonian and seismic noise”, Gen. Relativ. Gravit., 43, 623–656, (2011). [DOI]. (Cited on page 15.)
Billing, H., Maischberger, K., Rüdiger, A., Schilling, R., Schnupp, L. and Winkler, W., “An argon laser interferometer for the detection of gravitational radiation”, J. Phys. E: Sci. Instrum., 12, 1043–1050, (1979). [DOI]. (Cited on pages 5 and 20.)
Blair, D.G., ed., The Detection of Gravitational Waves, (Cambridge University Press, Cambridge, New York, 1991). (Cited on page 7.)
“BOINC: Open-source software for volunteer computing and grid computing”, project homepage, University of California. URL (accessed 3 October 2008): http://boinc.berkeley.edu/. (Cited on page 42.)
Braccini, S. et al., “An improvement in the VIRGO Super Attenuator for interferometric detection of gravitational waves: The use of a magnetic antispring”, Rev. Sci. Instrum., 64, 310–313, (1993). [DOI]. (Cited on page 15.)
Braccini, S. et al., “Seismic vibrations mechanical filters for the gravitational waves detector VIRGO”, Rev. Sci. Instrum., 67, 2899–2902, (1996). [DOI]. (Cited on page 13.)
Brady, P.R. and Creighton, T., “Searching for periodic sources with LIGO. II. Hierarchical searches”, Phys. Rev. D, 61, 082001, (2000). [DOI], [gr-qc/9812014]. (Cited on page 41.)
Braginsky, V.B. and Gorodetsky, M.L., “Optical bars in gravitational wave antenna”, Phys. Lett. A, 232, 340–348, (1997). [DOI]. (Cited on page 20.)
Braginsky, V.B., Gorodetsky, M.L. and Vyatchanin, S.P., “Thermodynamical fluctuations and photo-thermal shot noise in gravitational wave antennae”, Phys. Lett. A, 264, 1–10, (1999). [DOI], [cond-mat/9912139]. (Cited on page 16.)
Braginsky, V.B. and Khalili, F.Y., “Nonlinear meter for the gravitational wave antenna”, Phys. Lett. A, 218, 167–174, (1996). [DOI]. (Cited on page 20.)
Braginsky, V.B., Mitrofanov, V.P. and Panov, V.I., Systems with Small Dissipation, (University of Chicago Press, Chicago, 1985). (Cited on page 17.)
Braginsky, V.B., Mitrofanov, V.P. and Tokmakov, K.V., “Energy dissipation in the pendulum mode of the test mass suspension of a gravitational wave antenna”, Phys. Lett. A, 218, 164–166, (1996). [DOI]. (Cited on page 17.)
Braginsky, V.B., Strigin, S.E. and Vyatchanin, S.P., “Parametric oscillatory instability in Fabry-Perot interferometer”, Phys. Lett. A, 287, 331–338, (2001). [DOI]. (Cited on page 26.)
Cadonati, L., “Coherent waveform consistency test for LIGO burst candidates”, Class. Quantum Grav., 21, S1695–S1703, (2004). [DOI]. (Cited on page 36.)
Carilli, C. and Rawlings, S., eds., Science with the Square Kilometre Array, New Astron. Rev., 48, (Elsevier, Amsterdam, 2004). Online version (accessed 15 June 2011): http://www.skads-eu.org/p/SKA_SciBook.php. (Cited on page 6.)
Caves, C.M., “Quantum-mechanical radiation pressure fluctuations in an interferometer”, Phys. Rev. Lett., 45, 75–79, (1980). [DOI]. (Cited on pages 18 and 19.)
Caves, C.M., “Quantum-mechanical noise in an interferometer”, Phys. Rev. D, 23, 1693–1708, (1981). [DOI]. (Cited on pages 18 and 19.)
Chassande-Mottin, E. (Ligo Scientific Collaboration and Virgo Collaboration), “Joint searches for gravitational waves and high-energy neutrinos”, J. Phys.: Conf. Ser., 243, 012002, (2010). [DOI]. (Cited on page 40.)
Chatterji, S., Blackburn, L., Martin, G. and Katsavounidis, E., “Multiresolution techniques for the detection of gravitational-wave bursts”, Class. Quantum Grav., 21, S1809–S1818, (2004). [DOI]. (Cited on page 36.)
Chatterji, S., Lazzarini, A., Stein, L., Sutton, P.J., Searle, A. and Tinto, M., “Coherent network analysis technique for discriminating gravitational-wave bursts from instrumental noise”, Phys. Rev. D, 74, 082005, (2006). [DOI], [gr-qc/0605002]. (Cited on page 36.)
Chelkowski, S., Vahlbruch, H., Danzmann, K. and Schnabel, R., “Coherent control of broadband vacuum squeezing”, Phys. Rev. A, 75, 043814, (2007). [DOI]. (Cited on page 34.)
Ciufolini, I. and Fidecaro, F., eds., Gravitational Waves: Sources and Detectors, Proceedings of the International Conference, Cascina (Pisa), 19–23 March 1996, Edoardo Amaldi Foundation Series, 2, (World Scientific, Singapore; River Edge, NJ, 1997). (Cited on page 8.)
Corbitt, T. and Mavalvala, N., “Review: Quantum noise in gravitational-wave interferometers”, J. Opt. B: Quantum Semiclass. Opt., 65, S675–S683, (2004). [DOI]. (Cited on page 20.)
Corbitt, T. and Mavalvala, N., “Measurement of radiation-pressure-induced optomechanical dynamics in a suspended Fabry-Perot cavity”, Phys. Rev. A, 74, 021802, (2006). [DOI]. (Cited on page 19.)
“Cosmic Vision L-class missions presentation event 2011”, project homepage, European Space Agency, (2011). URL (accessed 31 May 2011): http://sci.esa.int/Lmissions2011. (Cited on pages 5, 48, and 51.)
Coward, D.M. et al., “The Zadko Telescope: A Southern Hemisphere Telescope for Optical Transient Searches, Multi-Messenger Astronomy and Education”, Publ. Astron. Soc. Australia, 27, 331–339, (2010). [DOI], [arXiv:1006.3933 [astro-ph.IM]]. (Cited on page 40.)
Cregut, O. et al., “18 W single-frequency operation of an injection-locked, CW, Nd:YAG laser”, Phys. Lett. A, 140, 294–298, (1989). [DOI]. (Cited on page 25.)
Crooks, D.R.M. et al., “Excess mechanical loss associated with dielectric mirror coatings on test masses in interferometric gravitational wave detectors”, Class. Quantum Grav., 19, 883–896, (2002). [DOI]. (Cited on page 16.)
Crowder, J. and Cornish, N.J., “Beyond LISA: Exploring future gravitational wave missions”, Phys. Rev. D, 72, 083005, (2005). [DOI], [gr-qc/0506015]. (Cited on page 52.)
Cunningham, L. et al., “Re-evaluation of the mechanical loss factor of hydroxide-catalysis bonds and its significance for the next generation of gravitational wave detectors”, Phys. Lett. A, 374, 3993–3998, (2010). [DOI]. (Cited on page 17.)
Cutler, C. and Holz, D.E., “Ultrahigh precision cosmology from gravitational waves”, Phys. Rev. D, 80, 104009, (2009). [DOI], [arXiv:0906.3752]. (Cited on page 52.)
Danzmann, K. et al. (LISA Study Team), “LISA: Laser Interferometer Space Antenna for Gravitational Wave Measurements”, Class. Quantum Grav., 13, A247–A250, (1996). [DOI]. (Cited on pages 5, 10, and 48.)
Decher, R.J., Randall, L., Bender, P.L. and Faller, J.E., “Design Aspects of a Laser Gravitational Wave Detector in Space”, in Cuneo, W.J., ed., Active Optical Devices and Applications, Washington, DC, USA, April 10–11, 1980, Proc. SPIE, 228, pp. 149–153, (SPIE, Bellingham, WA, 1980). (Cited on page 5.)
DeSalvo, R. et al., “Second generation suspensions for LIGO”, in Trân Than Vân, J., Dumarchez, J., Raynoud, S., Salomon, C., Thorsett, S. and Vinet, J.Y., eds., Gravitational Waves and Experimental Gravity, Proceedings of the XXXIVth Rencontres De Moriond, Les Arcs, France, January 23–30, 1999, (World Publishers, Hanoi, 2000). (Cited on page 13.)
Douglass, D.H. and Braginsky, V.B., “Gravitational-radiation experiments”, in Hawking, S.W. and Israel, W., eds., General Relativity: An Einstein Centenary Survey, pp. 90–137, (Cambridge University Press, Cambridge; New York, 1979). (Cited on page 5.)
Drever, R.W.P., “Interferometric detectors of gravitational radiation”, in Deroulle, N. and Piran, T., eds., Gravitational Radiation (Rayonnenment Gravitationnel), NATO Advanced Study Institute, Centre de physique des Houches, 2–21 June 1982, pp. 321–338, (North Holland; Elsevier, Amsterdam; New York, 1983). (Cited on pages 5 and 20.)
Drever, R.W.P., Hough, J., Edelstein, W.A., Pugh, J.R. and Martin, W., “On Gravitational Radiation Detectors Using Optical Sensing Techniques”, in Bertotti, B., ed., Experimental Gravitation (Gravitazione Sperimentale), Proceedings of the International Meeting, Pavia, 17–20 September 1976, pp. 365–369, (Academic Press, New York, 1977), Accademi Nazionale Dei Lincei. (Cited on page 5.)
Drever, R.W.P. et al., “Gravitational wave detectors using laser interferometers and optical cavities: Ideas, principles and prospects”, in Meystre, P. and Scully, M.O., eds., Quantum Optics, Experimental Gravity, and Measurement Theory, Proceedings of the NATO Advanced Study Institute, held August 16–29, 1981 in Bad Windsheim, Germany, NATO ASI Series B, 94, pp. 503–514, (Plenum Press, New York, 1983). (Cited on page 21.)
Dupuis, R.J. and Woan, G., “Bayesian estimation of pulsar parameters from gravitational wave data”, Phys. Rev. D, 72, 102002, (2005). [DOI], [gr-qc/0508096]. (Cited on page 41.)
Edelstein, W.A., Hough, J., Pugh, J.R. and Martin, W., “Limits to the measurement of displacement in an interferometric gravitational radiation detector”, J. Phys. E: Sci. Instrum., 11(7), 710–711, (1978). [DOI]. (Cited on pages 18, 19, and 20.)
“Einstein Telescope”, project homepage, European Gravitational Observatory (EGO), (2008). URL (accessed 5 January 2009): http://www.et-gw.eu/. (Cited on pages 15 and 46.)
“Einstein(AT)Home”, project homepage, UW-Milwaukee. URL (accessed 3 October 2008): http://einstein.phys.uwm.edu. (Cited on page 42.)
Estabrook, F.B. and Wahlquist, H.D., “Response of Doppler spacecraft tracking to gravitational radiation”, Gen. Relativ. Gravit., 6, 439–447, (1975). [DOI], [ADS]. (Cited on page 5.)
“ET sensitivities page”, project homepage, EGO. URL (accessed 23 December 2010): http://www.et-gw.eu/etsensitivities. (Cited on page 47.)
Fairhurst, S., “Source localization with an advanced gravitational wave detector network”, Class. Quantum Grav., 28, 105021, (2011). [DOI], [arXiv:1010.6192 [gr-qc]]. (Cited on page 46.)
Fairhurst, S., Guidi, G.M., Hello, P., Whelan, J.T. and Woan, G., “Current status of gravitational wave observations”, Gen. Relativ. Gravit., 43, 387–407, (2010). [DOI], [arXiv:0908.4006 [gr-qc]]. (Cited on page 36.)
Faller, J.E., Bender, P.L., Hall, J.L., Hils, D. and Vincent, M.A., “Space antenna for gravitational wave astronomy”, in Longdon, N. and Melita, O., eds., Kilometric Optical Arrays in Space, Proceedings of the Colloquium held 23–25 October 1984, Cargèse, Corsica, France, ESA Conference Proceedings, SP-226, pp. 157–163, (ESA Publications Division, Noordwijk, 1985). (Cited on page 5.)
Flaminio, R. et al. (Virgo Collaboration), Advanced Virgo White Paper, VIR-NOT-DIR-1390-304, (Virgo, Cascina, 2005). URL (accessed 16 February 2011): https://tds.ego-gw.it/ql/?c=1544. (Cited on pages 34 and 45.)
Forward, R.L., Zipoy, D., Weber, J., Smith, S. and Benioff, H., “Upper Limit for Interstellar Millicycle Gravitational Radiation”, Nature, 189, 473, (1961). [DOI]. (Cited on page 10.)
Frede, M., Schulz, B., Wilhelm, R., Kwee, P., Seifert, F., Willke, B. and Kracht, D., “Fundamental mode, single-frequency laser amplifier for gravitational wave detectors”, Opt. Express, 15, 459–465, (2007). [DOI]. (Cited on page 25.)
Frede, M., Wilhelm, R., Kracht, D. and Fallnich, C., “Nd:YAG ring laser with 213 W linearly polarized fundamental mode output power”, Opt. Express, 13, 7516–7519, (2005). [DOI]. (Cited on page 25.)
Freise, A., Chelkowski, S., Hild, S., Del Pozzo, W., Perreca, A. and Vecchio, A., “Triple Michelson Interferometer for a Third-Generation Gravitational Wave Detector”, Class. Quantum Grav., 26, 085012, (2009). [DOI], [arXiv:0804.1036]. (Cited on page 46.)
Freise, A. and Strain, K., “Interferometer Techniques for Gravitational-Wave Detection”, Living Rev. Relativity, 13, lrr-2010-1, (2010). URL (accessed 10 December 2010): http://www.livingreviews.org/lrr-2010-1. (Cited on page 45.)
Fritschel, P, “DC Readout for Advanced LIGO”, LSC meeting, Hannover, 21 August 2003, conference paper, (2003). Online version (accessed 16 February 2011): http://www.ligo.caltech.edu/docs/G/G030460-00/G030460-00.pdf. (Cited on page 26.)
Fritschel, P., González, G., Lantz, B., Saha, P. and Zucker, M., “High Power Interferometric Phase Measurement Limited by Quantum Noise and Application to Detection of Gravitational Waves”, Phys. Rev. Lett., 80, 3181–3184, (1998). [DOI]. (Cited on page 27.)
“GCN: The Gamma-ray Coordinates Network (Transient Astronomy Network)”, project homepage, GSFC/NASA. URL (accessed 3 October 2008): http://gcn.gsfc.nasa.gov/. (Cited on page 39.)
“GEO600 Sensitivity Curves”, project homepage, University of Hannover. URL (accessed 22 January 2008): http://www.geo600.uni-hannover.de/geocurves/. (Cited on page 33.)
“GEO600: The German-British Gravitational Wave Detector”, project homepage, MPI for Gravitational Physics (Albert Einstein Institute). URL (accessed 16 February 2011): http://www.geo600.org/. (Cited on pages 5 and 28.)
Giampieri, G., Hellings, R.W., Tinto, M. and Faller, J.E., “Algorithms for unequal-arm Michelson interferometers”, Opt. Commun., 123, 669–678, (1996). [DOI]. (Cited on page 50.)
Gillespie, A.D. and Raab, F.J., “Thermally Excited Vibrations of the Mirrors of Laser Interferometer Gravitational-Wave Detectors”, Phys. Rev. D, 52, 577–585, (1995). [DOI]. (Cited on page 16.)
Glauber, R.J., “Coherent and Incoherent States of the Radiation Field”, Phys. Rev., 131, 2766, (1963). [DOI]. (Cited on page 18.)
Golenetskii, S., Aptekar, R., Mazets, E., Pal’Shin, V., Frederiks, D. and Cline, T., GRB 070201: clarification on localization and konus-wind spectra, GCN Circular, (GSFC/NASA, Greenbelt, MD, 2007). URL (accessed 16 February 2011): http://gcn.gsfc.nasa.gov/gcn3/6094.gcn3. (Cited on page 39.)
Golenetskii, S. et al., IPN localization of very intense short GRB 070201, GCN Circular, (GSFC/NASA, Greenbelt, MD, 2007). URL (accessed 16 February 2011): http://gcn.gsfc.nasa.gov/gcn/gcn3/6088.gcn3. (Cited on page 39.)
Golla, D., Freitag, I., Zellmer, H., Schone, W., Kropke, I. and Welling, H., “15 W single-frequency operation of a CW diode laser-pumped Nd:YAG ring laser”, Opt. Commun., 98, 86–90, (1993). [DOI]. (Cited on page 25.)
Gottardi, L. et al., “Sensitivity of the spherical gravitational wave detector MiniGRAIL operating at 5 K”, Phys. Rev. D, 76, 102005, (2007). [DOI], [arXiv:0705.0122 [gr-qc]]. (Cited on pages 5 and 10.)
“Graviton Group”, project homepage, DAS/INPE. URL (accessed 14 January 2008): http://www.das.inpe.br/graviton/. (Cited on pages 5 and 10.)
Green, M.A. and Keevers, M.J., “Optical properties of intrinsic silicon at 300 K”, Prog. Photovolt: Res. Appl., 3, 189–192, (1995). [DOI]. (Cited on page 25.)
Gréverie, C., Brillet, A., Man, C.N., Chaibi, W., Coulon, J.P. and Feliksik, K., “High power fiber amplifier for Advanced Virgo”, in Lasers and Electro-Optics (CLEO) and Quantum Electronics and Laser Science Conference (QELS), San Jose, CA, May 16–21, 2010, OSA Technical Digest, (IEEE, Washington, DC, 2010). (Cited on page 25.)
Grote, H. (LIGO Scientific Collaboration), “The GEO 600 status”, Class. Quantum Grav., 27, 084003, (2010). [DOI]. (Cited on page 34.)
Grote, H. et al., “The status of GEO 600”, Class. Quantum Grav., 22, S193–S198, (2005). [DOI]. (Cited on page 33.)
“GW group in ICRR UT”, project homepage, University of Tokyo. URL (accessed 16 February 2011): http://www.icrr.u-tokyo.ac.jp/gr/home/gre.html. (Cited on pages 30 and 46.)
“GWIC Sponsored Conferences”, project homepage, Gravitational Wave International Committee. URL (accessed 8 December 2010): http://gwic.ligo.org/conferences/. (Cited on page 28.)
Harry, G.M. (LIGO Scientific Collaboration), “Advanced LIGO: the next generation of gravitational wave detectors”, Class. Quantum Grav., 27, 084006, (2010). [DOI]. (Cited on pages 13, 19, 22, 44, and 45.)
Harry, G.M., Fritschel, P., Shaddock, D.A., Folkner, W. and Phinney, E.S., “Laser interferometry for the Big Bang Observer”, Class. Quantum Grav., 23, 4887–4894, (2006). [DOI]. (Cited on page 52.)
Harry, G.M. et al., “Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings”, Class. Quantum Grav., 65, 897–917, (2002). [DOI], [gr-qc/0109073]. (Cited on pages 16 and 17.)
Heinzel, G., Strain, K.A., Mizuno, J., Skeldon, K.D., Willke, B., Winkler, W., Schilling, R. and Danzmann, K., “An experimental demonstration of dual recycling on a suspended interferometer”, Phys. Rev. Lett., 81, 5493–5496, (1998). [DOI]. (Cited on page 21.)
Heng, I.S., Blair, D.G., Ivanov, E.N. and Tobar, M.E., “Long term operation of a niobium resonant bar gravitational wave antenna”, Phys. Lett. A, 218, 190–196, (1996). [DOI]. (Cited on page 5.)
Hereld, M., A search for gravitational radiation from PSR 1937+214, Ph.D. Thesis, (California Institute of Technology, Pasadena, CA, 1984). (Cited on page 35.)
Hewitson, M. et al., “A report on the status of the GEO 600 gravitational wave detector”, Class. Quantum Grav., 20, S581–S591, (2003). [DOI]. (Cited on page 32.)
Hild, S. (LIGO Scientific Collaboration), “The status of GEO 600”, Class. Quantum Grav., 23, S643–S651, (2006). [DOI]. (Cited on page 34.)
Hild, S., Chelkowski, S. and Freise, A., “Pushing towards the ET sensitivity using ‘conventional’ technology”, arXiv, e-print, (2008). [arXiv:0810.0604 [gr-qc]]. (Cited on pages 46 and 47.)
Hild, S., Chelkowski, S., Freise, A., Franc, J., Morgado, N., Flaminio, R. and DeSalvo, R., “A xylophone configuration for a third-generation gravitational wave detector”, Class. Quantum Grav., 27, 015003, (2010). [DOI], [arXiv:0906.2655 [gr-qc]]. (Cited on page 47.)
Hild, S., Grote, H., Smith, J.R. and Hewitson, M. (GEO600-team), “Towards gravitational wave astronomy: Commissioning and characterization of GEO600”, J. Phys.: Conf. Ser., 32, 66–73, (2006). [DOI]. (Cited on page 34.)
Hild, S. et al., “DC-readout of a signal-recycled gravitational wave detector”, Class. Quantum Grav., 26, 055012, (2009). [DOI], [arXiv:0811.3242 [gr-qc]]. (Cited on pages 26 and 34.)
Hild, S. et al., “Sensitivity Studies for Third-Generation Gravitational Wave Observatories”, arXiv, e-print, (2010). [arXiv:1012.0908 [gr-qc]]. (Cited on pages 25, 46, and 47.)
Hobbs, G.B. et al., “Gravitational-Wave Detection Using Pulsars: Status of the Parkes Pulsar Timing Array Project”, Publ. Astron. Soc. Australia, 26, 103–109, (2008). [DOI], [arXiv:0812.2721 [astro-ph]]. (Cited on page 6.)
Holtz, D.E. and Hughes, S.A., “Using gravitational-wave standard sirens”, Astrophys. J., 629, 15–22, (2005). [DOI], [astro-ph/0504616]. (Cited on page 8.)
Hough, J., “Prospects for Gravitational Wave Detection with Laser Interferometer Detectors”, in Blair, D.G. and Buckingham, M.J., eds., The Fifth Marcel Grossmann Meeting on recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, Part A, Proceedings of the meeting held at The University of Western Australia, 8–13 August 1988, pp. 265–282, (World Scientific, Singapore; River Edge, NJ, 1989). (Cited on page 18.)
Hough, J. et al., “The stabilisation of lasers for interferometric gravitational wave detectors”, in Blair, D.G., ed., The Detection of Gravitational Waves, pp. 329–351, (Cambridge University Press, Cambridge; New York, 1991). [Google Books]. (Cited on pages 22 and 23.)
Hough, J. et al. (LISA Science Team), “LISA—The Interferometer”, in Wilson, A. (LISA Science Team), ed., Fundamental Physics in Space, Proceedings of the Alpbach Summer School 1997, Alpbach, Tyrol, Austria 22–31 July 1997, ESA Conference Proceedings, SP-420, pp. 253–258, (ESA Publications Division, Noordwijk, 1997). (Cited on page 51.)
Hughes, S.A. and Thorne, K.S., “Seismic gravity-gradient noise in interferometric gravitational-wave detectors”, Phys. Rev. D, 58, 122002, (1998). [DOI]. (Cited on pages 13 and 15.)
Hulse, R.A., “The discovery of the binary pulsar”, Rev. Mod. Phys., 66, 699–710, (1994). [DOI]. (Cited on page 8.)
Hurley, K. et al., “An exceptionally bright flare from SGR 1806–20 and the origins of short-duration γ-ray bursts”, Nature, 434, 1098–1103, (2005). [DOI], [astro-ph/0502329]. (Cited on page 39.)
Janssen, G.H., Stappers, B.W., Kramer, M., Purver, M., Jessner, A. and Cognard, I., “European Pulsar Timing Array”, in Bassa, C., Wang, Z., Cumming, A. and Kaspi, V.M., eds., 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, Montreal, Canada, 12–17 August 2007, AIP Conference Proceedings, 983, pp. 633–635, (American Institute of Physics, Melville, NY, 2008). [DOI]. (Cited on page 6.)
Jaranowski, P., Królak, A. and Schutz, B.F., “Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection”, Phys. Rev. D, 58, 063001, (1998). [DOI], [gr-qc/9804014]. (Cited on page 41.)
Jarosik, N. et al., “Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results”, Astrophys. J. Suppl. Ser., 192, 14, (2011). [DOI], [arXiv:1001.4744 [astro-ph.CO]]. (Cited on page 43.)
Jenet, F.A. et al., “Upper bounds on the low-frequency stochastic gravitational wave background from pulsar timing observations: current limits and future prospects”, Astrophys. J., 653, 1571–1576, (2006). [DOI]. (Cited on page 6.)
Jenet, F. et al., “The North American Nanohertz Observatory for Gravitational Waves”, arXiv, e-print, (2009). [arXiv:0909.1058 [astro-ph.IM]]. (Cited on page 6.)
Jennrich, O., “LISA technology and instrumentation”, Class. Quantum Grav., 26, 153001, (2009). [DOI], [arXiv:0906.2901]. (Cited on pages 48 and 51.)
Johann, U.A., Ayre, M., Gath, P.F., Holota, W., Marenaci, P., Schulte, H.R., Weimer, P. and Weise, D., “The European Space Agency’s LISA mission study: status and present results”, J. Phys.: Conf. Ser., 122, 012005, (2008). [DOI]. (Cited on page 51.)
Ju, L. and Blair, D.G., “Low Resonant-Frequency Cantilever Spring Vibration Isolator for Gravitational-Wave Detectors”, Rev. Sci. Instrum., 65, 3482–3488, (1994). [DOI]. (Cited on page 13.)
Ju, L., Notcutt, M., Blair, D.G., Bondu, F. and Zhao, C.N., “Sapphire beamsplitters and test masses for advanced laser interferometric gravitational wave detectors”, Phys. Lett. A, 218, 197–206, (1996). [DOI]. (Cited on page 17.)
Kalogera, V. et al., “The Cosmic Coalescence Rates for Double Neutron Star Binaries”, Astrophys. J. Lett., 601, L179–L182, (2004). [DOI]. (Cited on page 29.)
Kalogera, V. et al., “Erratum: ‘The Cosmic Coalescence Rates for Double Neutron Star Binaries’”, Astrophys. J. Lett., 614, L137–L138, (2004). [DOI], [astro-ph/0312101]. (Cited on page 29.)
Kanner, J., Huard, T.L., Márka, S., Murphy, D.C., Piscionere, J., Reed, M. and Shawhan, P., “LOOC UP: locating and observing optical counterparts to gravitational wave bursts”, Class. Quantum Grav., 25, 184034, (2008). [DOI], [arXiv:0803.0312]. (Cited on page 40.)
Kawamura, S. et al. (DECIGO Collaboration), “The Japanese space gravitational wave antenna: DEECIGO”, Class. Quantum Grav., 28, 094011, (2011). [DOI]. (Cited on page 51.)
Kerr, G.A. and Hough, J., “Coherent addition of laser oscillators for use in gravitational wave antenna”, Appl. Phys. B, 49, 491–495, (1989). [DOI]. (Cited on page 24.)
Kimble, H.J., Levin, Y., Matsko, A.B., Thorne, K.S. and Vyatchanin, S.P., “Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics”, Phys. Rev. D, 65, 022002, (2002). [DOI]. (Cited on page 20.)
Klimenko, S. and Mitselmakher, G., “A wavelet method for detection of gravitational wave bursts”, Class. Quantum Grav., 21, S1819–S1830, (2004). [DOI]. (Cited on page 36.)
Knispel, B. and Allen, B., “Blandford’s argument: The strongest continuous gravitational wave signal”, Phys. Rev. D, 78, 044031, (2008). [DOI], [arXiv:0804.3075]. (Cited on page 41.)
Kogelnik, H. and Li, T., “Laser beams and resonators”, Proc. IEEE, 54, 1312–1329, (1966). [DOI]. (Cited on page 24.)
Kopparapu, R.K., Hanna, C., Kalogera, V., O’Shaughnessy, R., González, G., Brady, P.R. and Fairhurst, S., “Host Galaxies Catalog Used in LIGO Searches for Compact Binary Coalescence Events”, Astrophys. J., 675, 1459–1467, (2008). [DOI], [arXiv:0706.1283]. (Cited on page 44.)
Krishnan, B., Sintes, A.M., Papa, M.A., Schutz, B.F., Frasca, S. and Palomba, C., “Hough transform search for continuous gravitational waves”, Phys. Rev. D, 70, 082001, (2004). [DOI], [gr-qc/0407001]. (Cited on page 41.)
Kuroda, K. (LCGT Collaboration), “Status of LCGT”, Class. Quantum Grav., 27, 084004, (2010). [DOI]. (Cited on page 45.)
Larson, S., “Sensitivity Curves for Spaceborne Gravitational Wave Observatories”, project homepage, California Institute of Technology. URL (accessed 23 December 2010): http://www.srl.caltech.edu/∼shane/sensitivity/. (Cited on page 49.)
Lawrence, R., Zucker, M., Fritschel, P., Marfuta, P. and Shoemaker, D., “Adaptive thermal compensation of test masses in Advanced LIGO”, Class. Quantum Grav., 19, 1803–1812, (2002). [DOI]. (Cited on page 25.)
Lazzarini, A. and Weiss, R., LIGO Science Requirements Document (SRD), LIGO-E950018-02, (California Institute of Technology, Pasadena, CA, 1996). URL (accessed 16 January 2008): http://www.ligo.caltech.edu/docs/E/E950018-02.pdf. (Cited on page 27.)
Levin, Y., “Internal thermal noise in the LIGO test masses: A direct approach”, Phys. Rev. D, 57, 659–663, (1998). [DOI], [gr-qc/9707013]. (Cited on page 16.)
“LIGO Laboratory Home Page”, project homepage, California Institute of Technology. URL (accessed 15 January 2000): http://www.ligo.caltech.edu. (Cited on pages 5 and 27.)
“LIGO Laboratory Home Page for Interferometer Sensitivities”, project homepage, LIGO/California Institute of Technology. URL (accessed 22 January 2008): http://www.ligo.caltech.edu/∼jzweizig/distribution/LSC_Data/. (Cited on pages 12 and 31.)
LIGO Scientific Collaboration, Advanced LIGO Reference Design, LIGO-M060056-08, (LIGO, Pasadena, CA, 2007). URL (accessed 14 November 2008): http://www.ligo.caltech.edu/docs/M/M060056-08/M060056-08.pdf. (Cited on page 44.)
“LIGO Scientific Collaboration Home Page”, project homepage, California Institute of Technology. URL (accessed 21 January 2008): http://www.ligo.org. (Cited on pages 7, 28, and 36.)
“LISA Home Page (ESA)”, project homepage, European Space Agency. URL (accessed 16 February 2011): http://sci.esa.int/lisa. (Cited on pages 5 and 48.)
“LISA Home Page (NASA)”, project homepage, JPL/NASA. URL (accessed 15 January 2000): http://lisa.jpl.nasa.gov. (Cited on pages 5 and 48.)
“LISA: Laser Interferometer Space Antenna Project—Documentation”, project homepage, GSFC/NASA. URL (accessed 3 September 2009): http://lisa.gsfc.nasa.gov/documentation.html. (Cited on page 51.)
Lorimer, D.R., “Binary and Millisecond Pulsars”, Living Rev. Relativity, 11, lrr-2008-8, (2008). URL (accessed 4 January 2011): http://www.livingreviews.org/lrr-2008-8. (Cited on page 6.)
Losurdo, G. et al., “Active Control Hierarchy in VIRGO Superattenuator: The Role of the Inverted Pendulum”, in Coccia, E., Veneziano, G. and Pizzella, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, Proceedings of the conference held at CERN, Switzerland, 1–4 July, 1997, Edoardo Amaldi Foundation Series, 4, pp. 334–338, (World Scientific, Singapore; River Edge, NJ, 1998). (Cited on page 13.)
Loudon, R., “Quantum limit on the Michelson interferometer used for gravitational-wave detection”, Phys. Rev. Lett., 47, 815–818, (1981). [DOI]. (Cited on page 19.)
Lück, H., Freise, A., Goßler, S, Hild, S., Kawabe, K. and Danzmann, K., “Thermal correction of the radii of curvature of mirrors for GEO 600”, Class. Quantum Grav., 21, S985–S989, (2004). [DOI]. (Cited on page 25.)
Ludlow, A.D., Boyd, M.M., Zelevinsky, T., Foreman, S.M., Blatt, S., Notcutt, M., Ido, T. and Ye, J., “Systematic Study of the 87Sr Clock Transition in an Optical Lattice”, Phys. Rev. Lett., 96, 033003, (2006). [DOI]. (Cited on page 23.)
Martin, I.W. et al., “Measurements of a low-temperature mechanical dissipation peak in a single layer of Ta2O5 doped with TiO2”, Class. Quantum Grav., 25, 055005, (2008). [DOI], [0802.2686]. (Cited on page 17.)
Marx, J. et al., Expanding the LIGO Network: The Case for Installing an Advanced LIGO Detector in Australia, LIGO-M1000115-v6, (LIGO, Pasadena, CA, 2010). URL (accessed 24 November 2010): https://dcc.ligo.org/public/0011/M1000115/006/M1000115-v6-LIGO-AUS_WhitePaper.pdf. (Cited on page 45.)
Mauceli, E., Geng, Z.K., Hamilton, W.O., Johnson, W.W., Merkowitz, S.M., Morse, A., Price, B. and Solomonson, N., “The Allegro gravitational wave detector: Data acquisition and analysis”, Phys. Rev. D, 54, 1264–1275, (1996). [DOI]. (Cited on page 6.)
Mavalvala, N., McClelland, D.E., Mueller, G., Reitze, D.H., Schnabel, R. and Willke, B., “Looking towards third generation gravitational wave detectors”, Gen. Relativ. Gravit., 25, 1–24, (2010). [DOI]. (Cited on pages 24 and 25.)
McNabb, J.W.C. et al., “Overview of the BlockNormal event trigger generator”, Class. Quantum Grav., 21, S1705–S1710, (2004). [DOI]. (Cited on page 36.)
McNamara, P.W., Ward, H., Hough, J. and Robertson, D.I., “Laser frequency stabilization for spaceborne gravitational wave detectors”, Class. Quantum Grav., 14, 1543–1547, (1997). [DOI]. (Cited on page 50.)
Meers, B.J., Some aspects of the development of an optically sensed gravitational-wave detector, Ph.D. Thesis, (University of Glasgow, Glasgow, 1983). (Cited on page 24.)
Meers, B.J., “Recycling in laser-interferometric gravitational-wave detectors”, Phys. Rev. D, 38, 2317–2326, (1988). [DOI]. (Cited on page 21.)
Meshkov, S., ed., Gravitational Waves, Sources and Detectors, Third Edoardo Amaldi Conference, Pasadena, California, 12–16 July, 1999, AIP Conference Proceedings, 523, (American Institute of Physics, Melville, NY, 2000). (Cited on page 8.)
“MiniGRAIL, the first spherical gravitational wave detector”, project homepage, Leiden University. URL (accessed 14 January 2008): http://www.minigrail.nl/. (Cited on pages 5 and 10.)
Miyoki, S. (LCGT Collaboration), “Large scale cryogenic gravitational wave telescope”, Nucl. Phys. B (Proc. Suppl.), 138, 439–442, (2005). [DOI]. (Cited on pages 15, 17, and 45.)
Mizuno, E., Kawashima, N., Miyoke, S., Heflin, E.G., Wada, K., Naito, W., Nagano, S. and Arakawa, K., “Effort of Stable Operation by Noise Rreduction of 100m DL Laser Iinterferometer [TENKO-100] for Gravitational Wave Detection”, in Ciufolini, I. and Fidecaro, F., eds., Gravitational Waves: Sources and Detectors, Proceedings of the International Conference, Cascina (Pisa), 19–23 March 1996, Edoardo Amaldi Foundation Series, 2, pp. 108–110, (World Scientific, Singapore; River Edge, NJ, 1997). (Cited on page 27.)
Moss, G.E., Miller, L.R. and Forward, R.L., “Photon-noise-limited laser transducer for gravitational antenna”, Appl. Opt., 10, 2495, (1971). [DOI]. (Cited on page 5.)
Nabors, C.D., Farinas, A.D., Day, T., Yang, S.T., Gustafson, E.K. and Byer, R.L., “Injection locking of a 13-W CW Nd:YAG ring laser”, Opt. Lett., 14, 1189–1191, (1989). [DOI]. (Cited on page 25.)
Nakagawa, N, Gretarsson, A.M., Gustafson, E.K. and Fejer, M.M.F., “Thermal noise in halfinfinite mirrors with nonuniform loss: A slab of excess loss in a half-infinite mirror”, Phys. Rev. D, 65, 102001, (2002). [DOI], [gr-qc/0105046]. (Cited on pages 16 and 25.)
“NAUTILUS Gravitational Wave Antenna”, project homepage, INFN. URL (accessed 14 January 2008): http://www.roma1.infn.it/rog/. (Cited on pages 5, 6, and 10.)
“Next steps for LISA”, project homepage, European Space Agency. URL (accessed 10 June 2011): http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=48728. (Cited on pages 5, 48, and 51.)
Ng, C.-Y. and Romani, R.W., “Fitting Pulsar Wind Tori. II. Error Analysis and Applications”, Astrophys. J., 673, 411–417, (2008). [DOI], [arXiv:0710.4168]. (Cited on page 43.)
Ni, W.-T., “Super-ASTROD: probing primordial gravitational waves and mapping the outer solar system”, Class. Quantum Grav., 26, 075021, (2009). [DOI], [arXiv:0812.0887]. (Cited on page 52.)
Nicholson, D. et al., “Results of the first coincident observations by two laser-interferometric gravitational wave detectors”, Phys. Lett. A, 218, 175–180, (1996). [DOI], [gr-qc/9605048]. (Cited on page 35.)
Niebauer, T.M., Rüdiger, A., Schilling, R., Schnupp, L., Winkler, W. and Danzmann, K., “Pulsar search using data compression with the Garching gravitational wave detector”, Phys. Rev. D, 47, 3106–3123, (1993). [DOI]. (Cited on page 35.)
Notcutt, M., Ma, L.-S., Ludlow, A.D., Foreman, S.M., Ye, J. and Hall, J.L., “Contribution of thermal noise to frequency stability of rigid optical cavity via Hertz-linewidth lasers”, Phys. Rev. A, 73, 031804, (2006). (Cited on page 23.)
Nowick, A.S. and Berry, B.S., Anelastic Relaxation in Crystalline Solids, Materials Science Series, 1, (Academic Press, New York, 1972). (Cited on page 16.)
Ohashi, M. (LCGT Collaboration), “Status of LCGT and CLIO”, J. Phys.: Conf. Ser., 120, 032008, (2008). [DOI]. (Cited on pages 17 and 45.)
O’Shaughnessy, R., Kim, C., Fragos, T., Kalogera, V. and Belczynski, K., “Constraining Population Synthesis Models via the Binary Neutron Star Population”, Astrophys. J., 633, 1076–1084, (2005). [DOI], [ADS], [astro-ph/0504479]. (Cited on page 29.)
O’Shaughnessy, R., Kim, C., Kalogera, V. and Belczynski, K., “Constraining Population Synthesis Models via Empirical Binary Compact Object Merger and Supernova Rates”, Astrophys. J., 672, 479–488, (2008). [DOI]. (Cited on page 29.)
Owen, B.J., “Search templates for gravitational waves from inspiraling binaries: Choice of template spacing”, Phys. Rev. D, 53, 6749–6761, (1996). [DOI], [gr-qc/9511032]. (Cited on page 37.)
Owen, B.J., “How to adapt broad-band gravitational-wave searches for r-modes”, Phys. Rev. D, 82, 104002, (2010). [DOI], [arXiv:1006.1994 [gr-qc]]. (Cited on page 43.)
Owen, B.J. and Sathyaprakash, B.S., “Matched filtering of gravitational waves from inspiraling compact binaries: Computational cost and template placement”, Phys. Rev. D, 60, 022002, (1999). [DOI], [gr-qc/9808076]. (Cited on page 37.)
Pallottino, G.V., “The Resonant Mass Detectors of the Rome Group”, in Coccia, E., Veneziano, G. and Pizzella, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, Proceedings of the conference held at CERN, Switzerland, 1–4 July, 1997, Edoardo Amaldi Foundation Series, 4, pp. 105–114, (World Scientific, Singapore; River Edge, NJ, 1998). (Cited on page 5.)
Papa, M.A., “Progress towards gravitational-wave astronomy”, Class. Quantum Grav., 25, 114009, (2008). [DOI], [arXiv:0802.0936]. (Cited on page 36.)
Phinney, E.S., “Finding and Using Electromagnetic Counterparts of Gravitational Wave Sources”, arXiv, e-print, (2009). [arXiv:0903.0098 [astro-ph.CO]]. (Cited on page 40.)
Plissi, M.V., Torrie, C.I., Husman, M.E., Robertson, N.A., Strain, K.A., Ward, H., Lück, H. and Hough, J., “GEO 600 triple pendulum suspension system: Seismic isolation and control”, Rev. Sci. Instrum., 71, 2539–2545, (2000). [DOI]. (Cited on page 13.)
Plissi, M.V. et al., “Aspects of the suspension system for GEO 600”, Rev. Sci. Instrum., 69, 3055–3061, (1998). [DOI]. (Cited on page 13.)
Pradier, T. (Antares Collaboration), “The Antares neutrino telescope and multi-messenger astronomy”, Class. Quantum Grav., 27, 194004, (2010). [DOI], [arXiv:1004.5579 [astro-ph.HE]]. (Cited on page 40.)
Predoi, V. et al., “Prospects for joint radio telescope and gravitational-wave searches for astrophysical transients”, Class. Quantum Grav., 27, 084018, (2010). [DOI], [arXiv:0912.0476[gr-qc]]. (Cited on page 40.)
Prix, R. et al. (LIGO Scientific Collaboration), “Gravitational Waves from Spinning Neutron Stars”, in Becker, W. and Huang, H.H. (LIGO Scientific Collaboration), eds., Neutron Stars and Pulsars, 363rd WE-Heraeus Seminar, Bad Honnef, Germany, May 14–16, 2006, Astrophysics and Space Science Library, 357, pp. 651–685, (Springer, Berlin, 2009). [DOI]. Online version (accessed 28 June 2011): http://edoc.mpg.de/288718. (Cited on page 41.)
Prodi, G.A. et al., “Initial Operation of the Gravitational Wave Detector AURIGA”, in Coccia, E., Veneziano, G. and Pizzella, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, Proceedings of the conference held at CERN, Switzerland, 1–4 July, 1997, Edoardo Amaldi Foundation Series, 4, pp. 148–158, (World Scientific, Singapore; River Edge, NJ, 1998). Online version (accessed 2 December 2004): http://www.auriga.lnl.infn.it/auriga/papers_src/amaldi97_prodi.ps.gz. (Cited on page 5.)
Punturo, M. et al., “The Einstein Telescope: a third-generation gravitational wave observatory”, Class. Quantum Grav., 27, 194002, (2010). [DOI]. (Cited on page 25.)
Rafac, R.J., Young, B.C., Beall, J.A., Itano, W.M., Wineland, D.J. and Bergquist, J.C., “Sub-dekahertz Ultraviolet Spectroscopy of 199Hg+”, Phys. Rev. Lett., 85, 2462, (2000). [DOI]. (Cited on page 23.)
Robertson, D.I. et al., “The Glasgow 10 m prototype laser interferometric gravitational wave detector”, Rev. Sci. Instrum., 66 (9), 4447–4452, (1995). [DOI]. (Cited on pages 24 and 27.)
Robertson, N.A., Hoggan, S., Mangan, J.B. and Hough, J., “Intensity stabilisation of an argon laser using an electro-optic modulator”, Appl. Phys. B, 39, 149–153, (1986). [DOI]. (Cited on page 23.)
Rowan, S., Twyford, S.M. and Hough, J., “The design of low loss suspensions for advanced gravitational wave detectors”, in Coccia, E., Veneziano, G. and Pizzella, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, Proceedings of the conference held at CERN, Switzerland, 1–4 July, 1997, Edoardo Amaldi Foundation Series, 4, pp. 363–369, (World Scientific, Singapore; River Edge, NJ, 1998). (Cited on page 17.)
Rowan, S., Twyford, S.M., Hough, J., Gwo, D.-H. and Route, R., “Mechanical losses associated with the technique of hydroxide-catalysis bonding of fused silica”, Phys. Lett. A, 246, 471–478, (1998). [DOI]. (Cited on page 17.)
Rowan, S., Twyford, S.M., Hutchins, R., Kovalik, J., Logan, J.E., McLaren, A.C., Robertson, N.A. and Hough, J., “Q factor measurements on prototype fused quartz pendulum suspensions for use in gravitational wave detectors”, Phys. Lett. A, 233, 303–308, (1997). [DOI]. (Cited on page 17.)
Rowan, S. et al., “Test Mass Materials for a New Generation of Gravitational Wave Detectors”, in Cruise, M. and Saulson, P., eds., Gravitational-Wave Detection, Waikoloa, HI, USA, 23 August 2002, Proc. SPIE, 4856, pp. 292–297, (SPIE, Bellingham, WA, 2003). [DOI]. (Cited on page 25.)
Rüdiger, A., Schilling, R., Schnupp, L., Winkler, W., Billing, H. and Maischberger, K., “A mode selector to suppress fluctuations in laser beam geometry”, Opt. Acta, 26 (5), 641–658, (1981). (Cited on pages 23 and 24.)
Sakata, S., Kawamura, S., Sato, S., Somiya, K., Arai, K., Fukushima, M. and Sugamoto, A., “Development of a control scheme of homodyne detection for extracting ponderomotive squeezing from a Michelson interferometer”, J. Phys.: Conf. Ser., 32, 464–469, (2006). [DOI]. (Cited on page 19.)
Sandford, M.C.W., ed., First International LISA Symposium, Proceedings of the symposium, held at the Rutherford Appleton Laboratory in Chilton, 9–12 July 1996, Class. Quantum Grav., 14, (Institute of Physics Publishing, Bristol, 1997). (Cited on pages 8, 9, and 48.)
Sathyaprakash, B.S. and Schutz, B.F., “Physics, Astrophysics and Cosmology with Gravitational Waves”, Living Rev. Relativity, 12, lrr-2009-2, (2009). [arXiv:0903.0338]. URL (accessed 03 March 2009): http://www.livingreviews.org/lrr-2009-2. (Cited on pages 8, 9, 29, and 36.)
Sato, S. et al. (DECIGO Collaboration), “DECIGO: The Japanese space gravitational wave antenna”, J. Phys.: Conf. Ser., 154, 012040, (2009). [DOI]. (Cited on page 51.)
Saulson, P.R., “Terrestrial gravitational noise on a gravitational wave antenna”, Phys. Rev. D, 30, 732–736, (1984). [DOI]. (Cited on pages 13 and 15.)
Saulson, P.R., “Thermal noise in mechanical experiments”, Phys. Rev. D, 42, 2437–2445, (1990). [DOI]. (Cited on page 16.)
Saulson, P.R., Fundamentals of Interferometric Gravitational Wave Detectors, (World Scientific, Singapore; River Edge, NJ, 1994). (Cited on page 7.)
Schilling, R., personal communication, (1981). (Cited on page 21.)
Schmidt-Kaler, F. et al., “The coherence of qubits based on single Ca+ ions”, J. Phys. B: At. Mol. Opt. Phys., 36, 623, (2003). [DOI]. (Cited on page 23.)
Schnabel, R. et al., “Building blocks for future detectors: Silicon test masses and 1550 nm laser light”, J. Phys.: Conf. Ser., 228, 012029, (2010). [0912.3164]. (Cited on page 25.)
Schnupp, L., “Internal modulation schemes”, Presentation at European Collaboration Meeting on Interferometric Detection of Gravitational Waves, (Sorrent, Italy), conference paper, (1988). (Cited on page 26.)
Schutz, B.F., “Determining the nature of the Hubble constant”, Nature, 323, 310–311, (1986). [DOI]. (Cited on page 8.)
Schutz, B.F., Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity, (Cambridge University Press, Cambridge, 2003). (Cited on page 7.)
Searle, A.C., Sutton, P.J. and Tinto, M., “Bayesian detection of unmodeled bursts of gravitational waves”, Class. Quantum Grav., 26, 155017, (2009). [DOI], [arXiv:0809.2809]. (Cited on page 36.)
Sheard, B.S., Gray, M.B., McClelland, D.E. and Shaddock, D.A., “Laser frequency stabilization by locking to a LISA arm”, Phys. Lett. A, 320, 9–21, (2003). [DOI]. (Cited on page 50.)
Shine Jr, R.J., Alfrey, A.J. and Byer, R.L., “40-W cw, TEM00-mode, diode-laser-pumped, Nd:YAG miniature-slab laser”, Opt. Lett., 20 (5), 459–461, (1995). [DOI]. (Cited on page 24.)
Shoemaker, D.H., Schilling, R., Schnupp, L., Winkler, W., Maischberger, K. and Rüdiger, A., “Noise behavior of the Garching 30-meter prototype gravitational-wave detector”, Phys. Rev. D, 38, 423–432, (1988). [DOI]. (Cited on pages 24 and 27.)
Skeldon, K.D., Strain, K.A., Grant, A.I. and Hough, J., “Test of an 18-m-long suspended modecleaner cavity”, Rev. Sci. Instrum., 67 (7), 2443–2448, (1996). [DOI]. (Cited on page 24.)
Smith, J.R. et al., “Commissioning, characterization and operation of the dual-recycled GEO 600”, Class. Quantum Grav., 21, S1737–S1745, (2004). [DOI]. (Cited on page 33.)
Smith, S.L., A search for gravitational waves from coalesing binary stars using the Caltech 40 meter gravity wave detector, Ph.D. Thesis, (California Institute of Technology, Pasadena, CA, 1988). (Cited on page 35.)
Spero, R.E., “Prospects for Ground Based Detectors of Low Frequency Gravitational Radiation”, in Nieto, M.M., Hoffman, C.M., Kolb, E.W., Sandberg, V.D., Toevs, J.W. and Haxton, W.C., eds., Science Underground, Proceedings of the Workshop, Los Alamos, 1982, AIP Conference Proceedings, 96, pp. 347–350, (American Institute of Physics, Melville, NY, 1983). [DOI]. (Cited on pages 13 and 15.)
Strain, K.A. and Meers, B.J., “Experimental demonstration of dual recycling for interferometric gravitational-wave detectors”, Phys. Rev. Lett., 66, 1391–1394, (1991). [DOI]. (Cited on page 21.)
Sutton, P., S3 Performance of the LIGO Interferometers as Measured by SenseMonitor, LIGO-T030276-00-Z, (LIGO/California Institute of Technology, Pasadena, CA, 2003). URL (accessed 16 January 2008): http://www.ligo.caltech.edu/docs/T/T030276-00.pdf. (Cited on page 30.)
“TAMA300 Project”, project homepage, National Astronomical Observatory of Japan. URL (accessed 15 January 2000): http://tamago.mtk.nao.ac.jp. (Cited on pages 5 and 27.)
Taylor, J.H., “Binary Pulsars and Relativistic Gravity”, Rev. Mod. Phys., 66, 711–719, (1994). [DOI]. (Cited on page 8.)
Thorne, K.S., Black Holes and Time Warps: Einstein’s Outrageous Legacy, (W.W. Norton, New York, 1994). (Cited on page 7.)
Tinto, M. and Dhurandhar, S.V., “Time Delay Interferometry”, Living Rev. Relativity, 8, lrr-2005-4, (2005). URL (accessed 03 September 2009): http://www.livingreviews.org/lrr-2005-4. (Cited on page 50.)
Torrie, C.I. et al., “Suspension system design for the main optics for GEO 600”, in Trân Than Vân, J., Dumarchez, J., Raynoud, S., Salomon, C., Thorsett, S. and Vinet, J.Y., eds., Gravitational Waves and Experimental Gravity, Proceedings of the XXXIVth Rencontres De Moriond, Les Arcs, France, January 23–30, 1999, pp. 235–240, (World Publishers, Hanoi, 2000). (Cited on page 13.)
Tyson, J.A. and Giffard, R.P., “Gravitational-Wave Astronomy”, Annu. Rev. Astron. Astrophys., 16, 521–554, (1978). [DOI]. (Cited on page 5.)
Unruh, W.G., “Quantum Noise in the Interferometer Detector”, in Meystre, P. and Scully, M.O., eds., Quantum Optics, Experimental Gravitation, and Measurement Theory, Proceedings of the NATO Advanced Study Institute on Quantum Optics and Experimental General Relativity, August 1981, Bad Windsheim, Germany, NATO ASI Series B, 94, (Plenum Press, New York, 1983). (Cited on page 19.)
Vahlbruch, H., Khalaidovski, A., Lastzka, N., Gräf, C., Danzmann, K. and Schnabel, R., “Coherent Control of Vacuum Squeezing in the Gravitational-Wave Detection Band”, Phys. Rev. Lett., 97, 011101, (2006). [DOI], [arXiv:0707.0164]. (Cited on page 19.)
Vahlbruch, H. et al., “Observation of Squeezed Light with 10-dB Quantum-Noise Reduction”, Phys. Rev. Lett., 100, 033602, (2008). [DOI], [arXiv:0706.1431]. (Cited on page 34.)
Vinet, J.-Y., “On Special Optical Modes and Thermal Issues in Advanced Gravitational Wave Interferometric Detectors”, Living Rev. Relativity, 12, lrr-2009-5, (2009). URL (accessed 25 January 2011): http://www.livingreviews.org/lrr-2009-5. (Cited on page 25.)
“Virgo”, project homepage, INFN. URL (accessed 16 February 2011): http://www.virgo.infn.it. (Cited on pages 5 and 27.)
“Virgo Sensitivity Curves”, project homepage, Virgo/INFN. URL (accessed 16 February 2011): http://www.virgo.infn.it/DataAnalysis/Calibration/Sensitivity/. (Cited on page 35.)
Vogt, R.E., Drever, R.W.P., Thorne, K.S., Raab, F.J. and Weiss, R., “A Laser Interferometer Gravitational Wave Observatory (Proposal to the National Science Foundation)”, unknown format, (1989). (Cited on page 24.)
Vyatchanin, S.P. and Matsko, A.B., “Quantum limit on force measurements”, J. Exp. Theor. Phys., 77, 218–221, (1993). (Cited on page 19.)
Waldman, S.J. et al. (LIGO Science Collaboration), “Status of LIGO at the start of the fifth science run”, Class. Quantum Grav., 23, S653–S660, (2006). [DOI]. (Cited on page 25.)
Ward, R.L. et al., “dc readout experiment at the Caltech 40m prototype interferometer”, Class. Quantum Grav., 25, 114030, (2008). [DOI]. (Cited on page 26.)
Weber, J., “Evidence for Discovery of Gravitational Radiation”, Phys. Rev. Lett., 22, 1320–1324, (1969). [DOI]. (Cited on pages 5 and 10.)
Weber, J., “Anisotropy and Polarization in the Gravitational-Radiation Experiments”, Phys. Rev. Lett., 25, 180–184, (1970). [DOI]. (Cited on pages 5 and 10.)
Webster, S.A., Oxborrow, M. and Gill, P., “Subhertz-linewidth Nd:YAG laser”, Opt. Lett., 29, 1497–1499, (2004). [DOI]. (Cited on page 23.)
Weiss, R., Electromagnetically Coupled Broadband Gravitational Antenna, Quart. Progr. Rep., 105:54–76, (Research Lab. Electron., MIT, Cambridge, MA, 1972). (Cited on pages 5, 15, and 20.)
Weiss, R. and Block, B., “A Gravimeter to Monitor the 0S0 Dilational Mode of the Earth”, J. Geophys. Res., 70 (22), 6515–5627, (1965). (Cited on page 10.)
Whitcomb, S.E., “Ground-based gravitational-wave detection: now and future”, Class. Quantum Grav., 25, 114013, (2008). [DOI]. (Cited on pages 10, 32, and 44.)
Will, C.M., Theory and Experiment in Gravitational Physics, (Cambridge University Press, Cambridge; New York, 1993), 2nd edition. [Google Books]. (Cited on page 8.)
Willke, B., Uehara, N., Gustafson, E.K., Byer, R.L., King, P.J., Steel, S.U. and Savage Jr, R.L., “Spatial and temporal filtering of a 10-W Nd:YAG laser with a Fabry-Perot ring-cavity premode cleaner”, Opt. Lett., 23 (21), 1704–1706, (1998). [DOI]. (Cited on page 24.)
Willke, B. et al., “Status of GEO 600”, Class. Quantum Grav., 21, S417–S423, (2004). [DOI]. (Cited on page 33.)
Willke, B. et al., “The GEO-HF project”, Class. Quantum Grav., 23, S207–S214, (2006). [DOI]. (Cited on page 34.)
Willke, B. et al., “Stabilized lasers for advanced gravitational wave detectors”, Class. Quantum Grav., 25, 114040, (2008). [DOI]. (Cited on page 25.)
Willke, B. et al. (LIGO Scientific Collaboration), “GEO600: status and plans”, Class. Quantum Grav., 24, S389–S397, (2007). [DOI]. (Cited on pages 5 and 34.)
Winterflood, J. and Blair, D.G., “Ultra-Low Frequency Pre-Isolation in Three Dimensons”, in Coccia, E., Veneziano, G. and Pizzella, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, Proceedings of the conference held at CERN, Switzerland, 1–4 July, 1997, Edoardo Amaldi Foundation Series, 4, pp. 485–489, (World Scientific, Singapore; River Edge, NJ, 1998). (Cited on page 13.)
Yagi, K. and Seto, N., “Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries”, Phys. Rev. D, 83, 044011, (2011). [DOI]. (Cited on page 6.)
Yamamoto, K. et al., “Current status of the CLIO project”, J. Phys.: Conf. Ser., 122, 012002, (2008). [DOI], [arXiv:0805.2384]. (Cited on pages 30 and 46.)
Yardley, D.R.B. et al., “The sensitivity of the Parkes Pulsar Timing Array to individual sources of gravitational waves”, Mon. Not. R. Astron. Soc., 407, 669–680, (2010). [DOI]. (Cited on page 6.)
Acknowledgements
We are grateful to the LSC and the Virgo groups for the use of some of their figures. We are indebted to STFC (U.K.), NSF (U.S.A.), the University of Glasgow, the Royal Society of Edinburgh, and the Royal Society for support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pitkin, M., Reid, S., Rowan, S. et al. Gravitational Wave Detection by Interferometry (Ground and Space). Living Rev. Relativ. 14, 5 (2011). https://doi.org/10.12942/lrr-2011-5
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2011-5
Keywords
Article history
- Gravitational Wave Detection by Interferometry (Ground and Space)
- Published:
- 23 August 2016
DOI: https://doi.org/10.12942/lrr-2000-3
Latest
Gravitational Wave Detection by Interferometry (Ground and Space)- Published:
- 11 July 2011
- Accepted:
- 17 June 2011
DOI: https://doi.org/10.12942/lrr-2011-5