Brane-World Gravity

Abstract

The observable universe could be a 1+3-surface (the “brane”) embedded in a 1+3+d-dimensional spacetime (the “bulk”), with Standard Model particles and fields trapped on the brane while gravity is free to access the bulk. At least one of the d extra spatial dimensions could be very large relative to the Planck scale, which lowers the fundamental gravity scale, possibly even down to the electroweak (∼ TeV) level. This revolutionary picture arises in the framework of recent developments in M theory. The 1+10-dimensional M theory encompasses the known 1+9-dimensional superstring theories, and is widely considered to be a promising potential route to quantum gravity. At low energies, gravity is localized at the brane and general relativity is recovered, but at high energies gravity “leaks” into the bulk, behaving in a truly higher-dimensional way. This introduces significant changes to gravitational dynamics and perturbations, with interesting and potentially testable implications for high-energy astrophysics, black holes, and cosmology. Brane-world models offer a phenomenological way to test some of the novel predictions and corrections to general relativity that are implied by M theory. This review analyzes the geometry, dynamics and perturbations of simple brane-world models for cosmology and astrophysics, mainly focusing on warped 5-dimensional brane-worlds based on the Randall-Sundrum models. We also cover the simplest brane-world models in which 4-dimensional gravity on the brane is modified at low energies — the 5-dimensional Dvali-Gabadadze-Porrati models. Then we discuss co-dimension two branes in 6-dimensional models.

1 Introduction

At high enough energies, Einstein’s theory of general relativity breaks down, and will be superceded by a quantum gravity theory. The classical singularities predicted by general relativity in gravitational collapse and in the hot big bang will be removed by quantum gravity. But even below the fundamental energy scale that marks the transition to quantum gravity, significant corrections to general relativity will arise. These corrections could have a major impact on the behaviour of gravitational collapse, black holes, and the early universe, and they could leave a trace — a “smoking gun” — in various observations and experiments. Thus it is important to estimate these corrections and develop tests for detecting them or ruling them out. In this way, quantum gravity can begin to be subject to testing by astrophysical and cosmological observations.

Developing a quantum theory of gravity and a unified theory of all the forces and particles of nature are the two main goals of current work in fundamental physics. There is as yet no generally accepted (pre-)quantum gravity theory. Two of the main contenders are M theory (for reviews see, e.g., [214, 356, 377]) and quantum geometry (loop quantum gravity; for reviews see, e.g., [365, 409]). It is important to explore the astrophysical and cosmological predictions of both these approaches. This review considers only models that arise within the framework of M theory.

In this review, we focus on RS brane-worlds (mainly the RS 1-brane model) and their generalizations, with the emphasis on geometry and gravitational dynamics (see [304, 314, 269, 424, 348, 268, 360, 120, 49, 267, 270] for previous reviews with a broadly similar approach). Other reviews focus on string-theory aspects, e.g., [147, 316, 97, 357], or on particle physics aspects, e.g., [354, 366, 261, 151, 75]. We also discuss the 5D DGP models, which modify general relativity at low energies, unlike the RS models; these models have become important examples in cosmology for achieving late-time acceleration of the universe without dark energy. Finally, we give brief overviews of 6D models, in which the brane has co-dimension two, introducing very different features to the 5D case with co-dimension one branes.

1.1 Heuristics of higher-dimensional gravity

One of the fundamental aspects of string theory is the need for extra spatial dimensions¹. This revives the original higher-dimensional ideas of Kaluza and Klein in the 1920s, but in a new context of quantum gravity. An important consequence of extra dimensions is that the

4-dimensional Planck scale M_p ≡ M₄ is no longer the fundamental scale, which is M_4+d, where d is the number of extra dimensions. This can be seen from the modification of the gravitational potential. For an Einstein-Hilbert gravitational action we have

$${S_{{\rm{gravity}}}} = {1 \over {2\kappa _{4 + d}^2}}\int {{d^4}} x\,{d^d}y\,\sqrt {{- ^{(4 + d)}}g} \left[ {{}^{(4 + d)}R - 2{\Lambda _{4 + d}}} \right],$$

(1)

$$^{(4 + d)}{G_{AB}} \equiv {\,^{(4 + d)}}{R_{AB}} - {1 \over 2}{\,^{(4 + d)}}{R^{(4 + d)}}{g_{AB}} = - {\Lambda _{4 + d}}{\,^{(4 + d)}}{g_{AB}} + \kappa _{4 + d}^2{\,^{(4 + d)}}{T_{AB}},$$

(2)

where X^A =(x^μ, y¹,…,y^d), and $\kappa _{4 + d}^2$ is the gravitational coupling constant,

$$\kappa _{4 + d}^2 = 8\pi {G_{4 + d}} = {{8\pi} \over {M_{4 + d}^{2 + d}}}.$$

(3)

The static weak field limit of the field equations leads to the 4+d-dimensional Poisson equation, whose solution is the gravitational potential,

$$V(r) \propto {{\kappa _{4 + d}^2} \over {{r^{1 + d}}}}.$$

(4)

If the length scale of the extra dimensions is L, then on scales r ≲ L, the potential is 4+d-dimensional, V ∼ r^−(1+d). By contrast, on scales large relative to L, where the extra dimensions do not contribute to variations in the potential, V behaves like a 4-dimensional potential, i.e., r ∼ L in the d extra dimensions, and V ∼ L^−dr⁻¹. This means that the usual Planck scale becomes an effective coupling constant, describing gravity on scales much larger than the extra dimensions, and related to the fundamental scale via the volume of the extra dimensions:

$$M_{\rm{p}}^2\sim \,M_{4 + d}^{2 + d}\,{L^d}.$$

(5)

If the extra-dimensional volume is Planck scale, i.e., $L \sim M_{\rm{p}}^{- 1}$, then M_4+d ∼ M_p. But if the extra-dimensional volume is significantly above Planck scale, then the true fundamental scale M_4+d can be much less than the effective scale M_p ∼ 10¹⁹ GeV. In this case, we understand the weakness of gravity as due to the fact that it “spreads” into extra dimensions and only a part of it is felt in 4 dimensions.

A lower limit on M_4+d is given by null results in table-top experiments to test for deviations from Newton’s law in 4 dimensions, V ∝ r⁻¹. These experiments currently [294] probe sub-millimetre scales, so that

$$L\underset {\sim}{<} {10^{- 1}}{\rm{mm}}\sim{({10^{- 15}}{\rm{TeV}})^{- 1}} \Rightarrow {M_{4 + d}} \underset {\sim}{>} {10^{(32 - 15d)/(d + 2)}}{\rm{TeV}}.$$

(6)

Stronger bounds for brane-worlds with compact flat extra dimensions can be derived from null results in particle accelerators and in high-energy astrophysics [75, 87, 189, 194].

1.2 Brane-worlds and M theory

String theory thus incorporates the possibility that the fundamental scale is much less than the Planck scale felt in 4 dimensions. There are five distinct 1+9-dimensional superstring theories, all giving quantum theories of gravity. Discoveries in the mid-1990s of duality transformations that relate these superstring theories and the 1+10-dimensional supergravity theory, led to the conjecture that all of these theories arise as different limits of a single theory, which has come to be known as M theory. The 11th dimension in M theory is related to the string coupling strength; the size of this dimension grows as the coupling becomes strong. At low energies, M theory can be approximated by 1+10-dimensional supergravity.

It was also discovered that p-branes, which are extended objects of higher dimension than strings (1-branes), play a fundamental role in the theory. In the weak coupling limit, p-branes (p > 1) become infinitely heavy, so that they do not appear in the perturbative theory. Of particular importance among p-branes are the D-branes, on which open strings can end. Roughly speaking, open strings, which describe the non-gravitational sector, are attached at their endpoints to branes, while the closed strings of the gravitational sector can move freely in the bulk. Classically, this is realised via the localization of matter and radiation fields on the brane, with gravity propagating in the bulk (see Figure 1).

Figure 1

Schematic of confinement of matter to the brane, while gravity propagates in the bulk (from [75]).

In the Horava-Witten solution [203], gauge fields of the standard model are confined on two 1+9-branes located at the end points of an S¹/Z₂ orbifold, i.e., a circle folded on itself across a diameter. The 6 extra dimensions on the branes are compactified on a very small scale close to the fundamental scale, and their effect on the dynamics is felt through “moduli” fields, i.e., 5D scalar fields. A 5D realization of the Horava-Witten theory and the corresponding brane-world cosmology is given in [300, 301, 302].

These solutions can be thought of as effectively 5-dimensional, with an extra dimension that can be large relative to the fundamental scale. They provide the basis for the Randall-Sundrum (RS) 2-brane models of 5-dimensional gravity [359] (see Figure 2). The single-brane Randall-Sundrum models [358] with infinite extra dimension arise when the orbifold radius tends to infinity. The RS models are not the only phenomenological realizations of M theory ideas. They were preceded by the Arkani-Hamed-Dimopoulos-Dvali (ADD) brane-world models [15, 14, 13, 6, 367, 421, 168, 173], which put forward the idea that a large volume for the compact extra dimensions would lower the fundamental Planck scale,

$${M_{{\rm{ew}}}}\sim 1 \, {\rm{TeV}} \lesssim {M_{4 + d}} \leq {M_{\rm{p}}}\sim{10^{16}}\,{\rm{TeV}},$$

(7)

where M_ew is the electroweak scale. If M_4+d is close to the lower limit in Equation (7), then this would address the long-standing “hierarchy” problem, i.e., why there is such a large gap between M_ew and M_p.

Figure 2

The RS 2-brane model. (Figure taken from [87].

In the ADD models, more than one extra dimension is required for agreement with experiments, and there is “democracy” amongst the equivalent extra dimensions, which are typically flat. By contrast, the RS models have a “preferred” extra dimension, with other extra dimensions treated as ignorable (i.e., stabilized except at energies near the fundamental scale). Furthermore, this extra dimension is curved or “warped” rather than flat: The bulk is a portion of anti-de Sitter (AdS₅) spacetime. As in the Horava-Witten solutions, the RS branes are Z₂-symmetric (mirror symmetry), and have a tension, which serves to counter the influence of the negative bulk cosmological constant on the brane. This also means that the self-gravity of the branes is incorporated in the RS models. The novel feature of the RS models compared to previous higher-dimensional models is that the observable 3 dimensions are protected from the large extra dimension (at low energies) by curvature rather than straightforward compactification.

The RS brane-worlds and their generalizations (to include matter on the brane, scalar fields in the bulk, etc.) provide phenomenological models that reflect at least some of the features of M theory, and that bring exciting new geometric and particle physics ideas into play. The RS models also provide a framework for exploring holographic ideas that have emerged in M theory. Roughly speaking, holography suggests that higher-dimensional gravitational dynamics may be determined from knowledge of the fields on a lower-dimensional boundary. The AdS/CFT correspondence is an example, in which the classical dynamics of the higher-dimensional gravitational field are equivalent to the quantum dynamics of a conformal field theory (CFT) on the boundary. The RS model with its AdS₅ metric satisfies this correspondence to lowest perturbative order [129] (see also [342, 375, 193, 386, 390, 290, 347, 180] for the AdS/CFT correspondence in a cosmological context).

Before turning to a more detailed analysis of RS brane-worlds, We discuss the notion of Kaluza-Klein (KK) modes of the graviton.

1.3 Heuristics of KK modes

The dilution of gravity via extra dimensions not only weakens gravity on the brane, it also extends the range of graviton modes felt on the brane beyond the massless mode of 4-dimensional gravity. For simplicity, consider a flat brane with one flat extra dimension, compactified through the identification y ⟷ y + 2πnL, where n = 0, 1, 2,…. The perturbative 5D graviton amplitude can be Fourier expanded as

$$f({x^a},y) = \sum\limits_n {{e^{iny/L}}} \,{f_n}({x^a}),$$

(8)

where f_n are the amplitudes of the KK modes, i.e., the effective 4D modes of the 5D graviton. To see that these KK modes are massive from the brane viewpoint, we start from the 5D wave equation that the massless 5D field f satisfies (in a suitable gauge):

$${}^{(5)}\square\,f = 0 \qquad \Rightarrow\qquad \,\square\,f + \partial _y^2\,f = 0.$$

(9)

It follows that the KK modes satisfy a 4D Klein-Gordon equation with an effective 4D mass m_n,

$$\square f_n=m_n^2\,f_n, \qquad m_n={n\over L}.$$

(10)

The massless mode f₀ is the usual 4D graviton mode. But there is a tower of massive modes, L⁻¹, 2L⁻¹, …, which imprint the effect of the 5D gravitational field on the 4D brane. Compactness of the extra dimension leads to discreteness of the spectrum. For an infinite extra dimension, L → ∞, the separation between the modes disappears and the tower forms a continuous spectrum. In this case, the coupling of the KK modes to matter must be very weak in order to avoid exciting the lightest massive modes with m ≳ 0.

From a geometric viewpoint, the KK modes can also be understood via the fact that the projection of the null graviton 5-momentum ⁽⁵⁾p_a onto the brane is timelike. If the unit normal to the brane is n_A, then the induced metric on the brane is

$${g_{AB}}{= ^{(5)}}{g_{AB}} - {n_A}{n_B},{\qquad ^{(5)}}{g_{AB}}{n^A}{n^B} = 1,\qquad {g_{AB}}{n^B} = 0,$$

(11)

and the 5-momentum may be decomposed as

$${}^{(5)}p_A=mn_A+ p_A, \qquad p_An^A=0, \qquad m= {}^{(5)}p_A\, n^A,$$

(12)

where p_a = g_ab ⁽⁵⁾p^B is the projection along the brane, depending on the orientation of the 5-momentum relative to the brane. The effective 4-momentum of the 5D graviton is thus p_a. Expanding ⁽⁵⁾g_AB ⁽⁵⁾p^{A (5)}p^B = 0, we find that

$$g_{AB}p^Ap^B=-m^2.$$

(13)

It follows that the 5D graviton has an effective mass m on the brane. The usual 4D graviton corresponds to the zero mode, m = 0, when ⁽⁵⁾p_a is tangent to the brane.

The extra dimensions lead to new scalar and vector degrees of freedom on the brane. In 5D, the spin-2 graviton is represented by a metric perturbation ⁽⁵⁾h_AB that is transverse traceless:

$$^{(5)}{h^A}_A = 0 = {\partial _B}{\,^{(5)}}{h_A}^B.$$

(14)

In a suitable gauge, ⁽⁵⁾h_AB contains a 3D transverse traceless perturbation h_ij, a 3D transverse vector perturbation ∑_i, and a scalar perturbation β, which each satisfy the 5D wave equation [130]:

$$^{(5)}{h_{AB}}\quad \rightarrow \quad {h_{ij}},{\Sigma _i},\beta ,$$

(15)

$$h^i{}_i = 0 = \partial_j h^{ij},$$

(16)

$${\partial _i}{\Sigma ^i} = 0,$$

(17)

$$(\square + \partial_y^2) \left({\begin{array}{*{20}c} \beta \\ {{{\Sigma_i}}} \\ {{h_{ij}}} \\ \end{array}} \right) = 0.$$

(18)

The other components of ⁽⁵⁾h_AB are determined via constraints once these wave equations are solved. The 5 degrees of freedom (polarizations) in the 5D graviton are thus split into 2(h_ij) + 2(∑_i) + 1(β) degrees of freedom in 4D. On the brane, the 5D graviton field is felt as

• a 4D spin-2 graviton h_ij (2 polarizations),

• a 4D spin-1 gravi-vector (gravi-photon) ∑_i (2 polarizations), and

• a 4D spin-0 gravi-scalar β.

The massive modes of the 5D graviton are represented via massive modes in all three of these fields on the brane. The standard 4D graviton corresponds to the massless zero-mode of h_ij.

In the general case of d extra dimensions, the number of degrees of freedom in the graviton follows from the irreducible tensor representations of the isometry group as ${1 \over 2}(d + 1)(d + 4)$.

2 Randall-Sundrum Brane-Worlds

RS brane-worlds do not rely on compactification to localize gravity at the brane, but on the curvature of the bulk (sometimes called “warped compactification”). What prevents gravity from ‘leaking’ into the extra dimension at low energies is a negative bulk cosmological constant,

$${\Lambda _5} = - {6 \over {{\ell ^2}}} = - 6{\mu ^2},$$

(19)

where ℓ is the curvature radius of AdS₅ and μ is the corresponding energy scale. The curvature radius determines the magnitude of the Riemann tensor:

$$^{(5)}{R_{ABCD}} = - {1 \over {{\ell ^2}}}\left[ {{\,^{(5)}}{g_{AC}}{\,^{(5)}}{g_{BD}} - {\,^{(5)}}{g_{AD}}{\,^{(5)}}{g_{BC}}} \right].$$

(20)

The bulk cosmological constant acts to “squeeze” the gravitational field closer to the brane. We can see this clearly in Gaussian normal coordinates X^a = (x^μ,y)based on the brane at y = 0, for which the AdS₅ metric takes the form

$$^{(5)}d{s^2} = {e^{- 2\vert y\vert /\ell}}{\eta _{\mu \nu}}d{x^\mu}d{x^\nu} + d{y^2},$$

(21)

with η_μν being the Minkowski metric. The exponential warp factor reflects the confining role of the bulk cosmological constant. The Z₂-symmetry about the brane at y = 0 is incorporated via the ∣y ∣ term. In the bulk, this metric is a solution of the 5D Einstein equations,

$$^{(5)}{G_{AB}} = - {\Lambda _5}{\,^{(5)}}{g_{AB}},$$

(22)

i.e., ⁽⁵⁾T_AB = 0 in Equation (2). The brane is a flat Minkowski spacetime, ${g_{AB}}({x^\alpha},0) = {\eta _{\mu \nu}}{\delta ^\mu}_A{\delta ^\nu}_B$, with self-gravity in the form of brane tension. One can also use Poincare coordinates, which bring the metric into manifestly conformally flat form,

$$^{(5)}d{s^2} = {{{\ell ^2}} \over {{z^2}}}\left[ {{\eta _{\mu \nu}}d{x^\mu}d{x^\nu} + d{z^2}} \right],$$

(23)

where z = ℓe^y/ℓ. The two RS models are distinguished as follows:

RS 2-brane: There are two branes in this model [359], at y = 0 and y = L, with Z₂-symmetry identifications

$$y \leftrightarrow - y,\qquad y + L \leftrightarrow L - y.$$

(24)

The branes have equal and opposite tensions ±λ, where

$$\lambda = {{3M_{\rm{p}}^2} \over {4\pi {\ell ^2}}}.$$

(25)

The positive-tension brane has fundamental scale M₅ and is “hidden”. Standard model fields are confined on the negative tension (or “visible”) brane. Because of the exponential warping factor, the effective Planck scale on the visible brane at y = L is given by

$$M_{\rm{p}}^2 = M_5^3\,\ell \left[ {{e^{2L/\ell}} - 1} \right].$$

(26)

So the RS 2-brane model gives a new approach to the hierarchy problem: even if M₅ ∼ ℓ⁻¹ ∼ TeV, we can recover M_p ∼ 10¹⁶ TeV by choosing L/ℓ large enough. Because of the finite separation between the branes, the KK spectrum is discrete. Furthermore, at low energies gravity on the branes becomes Brans-Dicke-like, with the sign of the Brans-Dicke parameter equal to the sign of the brane tension [155]. In order to recover 4D general relativity at low energies, a mechanism is required to stabilize the inter-brane distance, which corresponds to a scalar field degree of freedom known as the radion [174, 408, 335, 283].

RS 1-brane: In this model [358], there is only one, positive tension, brane. It may be thought of as arising from sending the negative tension brane off to infinity, L → ∞. Then the energy scales are related via

$$M_5^3 = {{M_{\rm{p}}^2} \over \ell}.$$

(27)

The infinite extra dimension makes a finite contribution to the 5D volume because of the warp factor:

$$\int {{d^5}} X\sqrt {{- ^{(5)}}g} = 2\int {{d^4}} x\int\nolimits_0^\infty d y{e^{- 4y/\ell}} = {\ell \over 2}\int {{d^4}} x.$$

(28)

Thus the effective size of the extra dimension probed by the 5D graviton is ℓ.

We will concentrate mainly on RS 1-brane from now on, referring to RS 2-brane occasionally. The RS 1-brane models are in some sense the most simple and geometrically appealing form of a brane-world model, while at the same time providing a framework for the AdS/CFT correspondence [129, 342, 375, 193, 386, 390, 290, 347, 180]. The RS 2-brane introduce the added complication of radion stabilization, as well as possible complications arising from negative tension. However, they remain important and will occasionally be discussed.

2.1 KK modes in RS 1-brane

In RS 1-brane, the negative Λ₅ is offset by the positive brane tension λ. The fine-tuning in Equation (25) ensures that there is a zero effective cosmological constant on the brane, so that the brane has the induced geometry of Minkowski spacetime. To see how gravity is localized at low energies, we consider the 5D graviton perturbations of the metric [358, 155, 171, 122],

$$^{(5)}{g_{AB}}{\rightarrow ^{(5)}}{g_{AB}} + {e^{- 2\vert y\vert /\ell}}{\,^{(5)}}{h_{AB}},{\qquad ^{(5)}}{h_{Ay}} = 0{= ^{(5)}}{h^\mu}_\mu {= ^{(5)}}{h^{\mu \nu}}_{,\nu}$$

(29)

(see Figure 3). This is the RS gauge, which is different from the gauge used in Equation (15), but which also has no remaining gauge freedom. The 5 polarizations of the 5D graviton are contained in the 5 independent components of ⁽⁵⁾h_μν in the RS gauge.

Figure 3

Gravitational field of a small point particle on the brane in RS gauge. (Figure taken from [155].)

We split the amplitude f of ⁽⁵⁾h_AB into 3D Fourier modes, and the linearized 5D Einstein equations lead to the wave equation (y > 0)

$$\ddot f + {k^2}f = {e^{- 2y/\ell}}\left[ {f\prime\prime - {4 \over \ell}\,f\prime} \right].$$

(30)

Separability means that we can write

$$f(t,y) = \sum\limits_m {{\varphi _m}} (t)\,{f_m}(y),$$

(31)

and the wave equation reduces to

$${\ddot \varphi _m} + ({m^2} + {k^2}){\varphi _m} = 0,$$

(32)

$$f_m{\prime\prime} - {4 \over \ell}\,f_m\prime + {e^{2y/\ell}}\,{m^2}{f_m} = 0.$$

(33)

The zero mode solution is

$${\varphi _0}(t) = {A_{0 +}}{e^{+ ikt}} + {A_{0 -}}{e^{- ikt}},$$

(34)

$${f_0}(y) = {B_0} + {C_0}{e^{4y/\ell}},$$

(35)

and the m > 0 solutions are

$${\varphi _m}(t) = {A_{m +}}\exp \left({+ i\sqrt {{m^2} + {k^2}} \,t} \right) + {A_{m -}}\exp \left({- i\sqrt {{m^2} + {k^2}} \,t} \right),$$

(36)

$${f_m}(y) = {e^{2y/\ell}}\left[ {{B_m}{J_2}\left({m\ell {e^{y/\ell}}} \right) + {C_m}{Y_2}\left({m\ell {e^{y/\ell}}} \right)} \right].$$

(37)

The boundary condition for the perturbations arises from the junction conditions, Equation (68), discussed below, and leads to f ′(t, 0) = 0, since the transverse traceless part of the perturbed energy-momentum tensor on the brane vanishes. This implies

$${C_0} = 0,\qquad {C_m} = - {{{J_1}(m\ell)} \over {{Y_1}(m\ell)}}\,{B_m}.$$

(38)

The zero mode is normalizable, since

$$\left\vert {\int\nolimits_0^\infty {{B_0}} {e^{- 2y/\ell}}dy} \right\vert < \infty .$$

(39)

Its contribution to the gravitational potential $V = {1 \over 2}$ ⁽⁵⁾h₀₀ gives the 4D result, V ∝ r⁻¹. The contribution of the massive KK modes sums to a correction of the 4D potential. For r ≪ ℓ, one obtains

$$V(r) \approx {{GM\ell} \over {{r^2}}},$$

(40)

which simply reflects the fact that the potential becomes truly 5D on small scales. For r ≫ ℓ,

$$V(r) \approx {{GM} \over r}\left({1 + {{2{\ell ^2}} \over {3{r^2}}}} \right),$$

(41)

which gives the small correction to 4D gravity at low energies from extra-dimensional effects. These effects serve to slightly strengthen the gravitational field, as expected.

Table-top tests of Newton’s laws currently find no deviations down to ${\mathcal O}({10^{- 1}}\, {\rm{mm}})$, so that ℓ ≲ 0.1 mm in Equation (41). Then by Equations (25) and (27), this leads to lower limits on the brane tension and the fundamental scale of the RS 1-brane model:

$$\lambda > {(1\,\,{\rm{TeV}})^4},\qquad {M_5} > {10^5}\,{\rm{TeV}}.$$

(42)

These limits do not apply to the 2-brane case.

For the 1-brane model, the boundary condition, Equation (38), admits a continuous spectrum m > 0 of KK modes. In the 2-brane model, f ′(t, L) = 0 must hold in addition to Equation (38). This leads to conditions on m, so that the KK spectrum is discrete:

$${m_n} = {{{x_n}} \over \ell}\,{e^{- L/\ell}}\qquad {\rm{where}}\,\,{J_1}({x_n}) = {{{J_1}(m\ell)} \over {{Y_1}(m\ell)}}\,{Y_1}({x_n}).$$

(43)

The limit Equation (42) indicates that there are no observable collider, i.e., ${\mathcal O}({\rm{TeV}})$, signatures for the RS 1-brane model. The 2-brane model by contrast, for suitable choice of L and ℓ so that ${m_1} = {\mathcal O}({\rm{TeV}})$, does predict collider signatures that are distinct from those of the ADD models [189, 194].

2.2 RS model in string theory

There have been interesting developments in realizing the Randall-Sundrum brane-world model in string theory. A concrete example was found in type IIB supergravity [170]. The bosonic part of the 10-dimensional action is given by (see for example [355])

$$\begin{array}{*{20}c} {{S_{{\rm{IIB}}}} = {1 \over {2\kappa _{10}^2}}\int {{d^{10}}} x\sqrt {- {g_{\rm{s}}}} \{{e^{- 2\phi}}\left[ {{R_{\rm{s}}} + 4{{(\nabla \phi)}^2}} \right] - {{F_{(1)}^2} \over 2} - {1 \over {2\cdot 3!}}{G_{(3)}}\cdot{{\bar G}_{(3)}} - {{\tilde F_{(5)}^2} \over {4\cdot 5!}}\}} \\ {+ {1 \over {8i\kappa _{10}^2}}\int {{e^\phi}} {C_{(4)}} \wedge {G_{(3)}} \wedge {{\bar G}_{(3)}} + {S_{{\rm{loc}}}}.\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad} \\ \end{array}$$

(44)

Here g_s denotes the string metric. We have also defined the combined three-flux, G₍₃₎ = F₍₃₎ − _τH₍₃₎, where τ = C₍₀₎ + ie^−ϕ, and

$${\tilde F_{(5)}} = {F_{(5)}} - {1 \over 2}{C_{(2)}} \wedge {H_{(3)}} + {1 \over 2}{B_{(2)}} \wedge {F_{(3)}}.$$

(45)

The term S_loc is the action of localized objects, such as branes.

There is a 10-dimensional solution similar to the one in the RS model

$$ds_{10}^2 = h{(y)^{- {1 \over 2}}}{\eta _{\mu \nu}}d{x^\mu}d{x^\nu} + h{(y)^{{1 \over 2}}}{\tilde g_{mn}}d{y^m}d{y^n},$$

(46)

where x^μ are four-dimensional coordinates and y^m are coordinates on the 6-dimensional compact manifold ${{\mathcal M}_6}$. If there are N coincident D3-branes on the manifold, the 10-dimensional spacetime is described by AdS₅ × X₅ where X₅ is a five-dimensional Einstein manifold. The warp factor is given by [418]

$$h(r)\sim{\left({{L \over r}} \right)^4},$$

(47)

where r is the distance from the D3 branes in the $\tilde{g}_{mn}$ metric and L is given by

$$L = 4\pi a{g_s}N\alpha {\prime ^2}.$$

(48)

Here g_s is the string coupling constant, α′ is related to the string mass scale m_s as $\alpha{\prime} = 1/m_s^2$ and depends on X₅.

Near the D3 branes, the geometry is AdS₅ × S⁵. At large r, the product structure of the 10-dimensional metric breaks down and ceases to be a good coordinate, and the 6D extra-dimensional space ${{\mathcal M}_6}$ is not a product of a five sphere and one-dimensional spacetime. This gives a minimum distance r₀. This cut-off acts as a TeV brane in the RS model. On the other hand, for r > r_max, the AdS geometry smoothly glues into a Calabi-Yau compactification. Thus, the compact manifold plays the role of the Planck brane in the RS model, acting as a cut-off of the spacetime. The minimum warp factor h (r₀)^−1/2 is determined by the flux associated with F₃ and H₃ and thanks to the warping, it is possible to realize a large hierarchy [170]

$${{h({r_0})} \over {h({r_{{\rm{max}}}})}} \gg 1\,.$$

(49)

3 Covariant Approach to Brane-World Geometry and Dynamics

The RS models and the subsequent generalization from a Minkowski brane to a FriedmannRobertson-Walker (FRW) brane [38, 260, 216, 226, 183, 330, 209, 145, 154] were derived as solutions in particular coordinates of the 5D Einstein equations, together with the junction conditions at the Z₂-symmetric brane². A broader perspective, with useful insights into the inter-play between 4D and 5D effects, can be obtained via the covariant Shiromizu-Maeda-Sasaki approach [388], in which the brane and bulk metrics remain general. The basic idea is to use the Gauss-Codazzi equations to project the 5D curvature along the brane. (The general formalism for relating the geometries of a spacetime and of hypersurfaces within that spacetime is given in [423].)

The 5D field equations determine the 5D curvature tensor; in the bulk, they are

$$^{(5)}{G_{AB}} = - {\Lambda _5}{\,^{(5)}}{g_{AB}} + \kappa _5^2{\,^{(5)}}{T_{AB}},$$

(50)

where ⁽⁵⁾T_ab represents any 5D energy-momentum of the gravitational sector (e.g., dilaton and moduli scalar fields, form fields).

Let y be a Gaussian normal coordinate orthogonal to the brane (which is at y = 0 without loss of generality), so that n_adX^A = dy, with n^A being the unit normal. The 5D metric in terms of the induced metric on {y = const.} surfaces is locally given by

$$^{(5)}{g_{AB}} = {g_{AB}} + {n_A}{n_B},{\qquad ^{(5)}}d{s^2} = {g_{\mu \nu}}({x^\alpha},y)d{x^\mu}d{x^\nu} + d{y^2}.$$

(51)

The extrinsic curvature of {y = const.} surfaces describes the embedding of these surfaces. It can be defined via the Lie derivative or via the covariant derivative:

$${K_{AB}} = {1 \over 2}{\pounds_{\bf{n}}}\,{g_{AB}} = {g_A}^C{\,^{(5)}}{\nabla _C}{n_B},$$

(52)

so that

$${K_{[AB]}} = 0 = {K_{AB}}{n^B},$$

(53)

where square brackets denote anti-symmetrization. The Gauss equation gives the 4D curvature tensor in terms of the projection of the 5D curvature, with extrinsic curvature corrections:

$${R_{ABCD}}{= ^{(5)}}{R_{EFGH}}{g_A}^E{g_B}^F{g_C}^G{g_D}^H + 2{K_{A\left[ C \right.}}{K_{\left. D \right]B}},$$

(54)

and the Codazzi equation determines the change of K_ab along {y = const.} via

$${\nabla _B}{K^B}_A - {\nabla _A}K{= ^{(5)}}{R_{BC}}\,{g_A}^B{n^C},$$

(55)

where $K = {K^A}_A$

Some other useful projections of the 5D curvature are:

$$^{(5)}{R_{EFGH}}\,{g_A}^E{g_B}^F{g_C}^G{n^H} = 2{\nabla _{\left[ A \right.}}{K_{\left. B \right]C}},$$

(56)

$$^{(5)}{R_{EFGH}}\,{g_A}^E{n^F}{g_B}^G{n^H} = - {\pounds_{\bf{n}}}{K_{AB}} + {K_{AC}}{K^C}_B,$$

(57)

$$^{(5)}{R_{CD}}\,{g_A}^C{g_B}^D = {R_{AB}} - {\pounds_{\bf{n}}}{K_{AB}} - K{K_{AB}} + 2{K_{AC}}{K^C}_B.$$

(58)

The 5D curvature tensor has Weyl (tracefree) and Ricci parts:

$$^{(5)}{R_{ABCD}} = {\,^{(5)}}{C_{ACBD}} + {2 \over 3}\left({{\,^{(5)}}{g_{A\left[ C \right.}}{\,^{(5)}}{R_{\left. D \right]B}}{- ^{(5)}}{g_{B\left[ C \right.}}{\,^{(5)}}{R_{\left. D \right]A}}} \right) - {1 \over 6}{\,^{(5)}}{g_{A\left[ C \right.}}{\,^{(5)}}{g_{\left. D \right]B}}{\,^{(5)}}R.$$

(59)

3.1 Field equations on the brane

Using Equations (50) and (54), it follows that

$$\begin{array}{*{20}c} {{G_{\mu \nu}} = - {1 \over 2}{\Lambda _5}{g_{\mu \nu}} + {2 \over 3}\kappa _5^2\left[ {{\,^{(5)}}{T_{AB}}{g_\mu}^A{g_\nu}^B + \left({{\,^{(5)}}{T_{AB}}{n^A}{n^B} - {1 \over 4}\,{\,^{(5)}}T} \right){g_{\mu \nu}}} \right]} \\ {+ K{K_{\mu \nu}} - {K_\mu}^\alpha {K_{\alpha \nu}} + {1 \over 2}\left[ {{K^{\alpha \beta}}{K_{\alpha \beta}} - {K^2}} \right]{g_{\mu \nu}} - {E_{\mu \nu}},\quad \quad} \\ \end{array}$$

(60)

where $^{(5)}T = ^{(5)}{T^A}_A$, and where

$${{\mathcal E}_{\mu \nu}}{= ^{(5)}}{C_{ACBD}}\,{n^C}{n^D}{g_\mu}^A{g_\nu}^B,$$

(61)

is the projection of the bulk Weyl tensor orthogonal to n^A. This tensor satisfies

$${{\mathcal E}_{AB}}{n^B} = 0 = {{\mathcal E}_{[AB]}} = {{\mathcal E}_A}^A,$$

(62)

by virtue of the Weyl tensor symmetries. Evaluating Equation (60) on the brane (strictly, as y → ±0, since ${{\mathcal E} _{AB}}$ is not defined on the brane [388]) will give the field equations on the brane.

First, we need to determine K_μν at the brane from the junction conditions. The total energy-momentum tensor on the brane is

$$T_{\mu \nu}^{{\rm{brane}}} = {T_{\mu \nu}} - \lambda {g_{\mu \nu}},$$

(63)

where T_μν is the energy-momentum tensor of particles and fields confined to the brane (so that T_ABn^B = 0). The 5D field equations, including explicitly the contribution of the brane, are then

$$^{(5)}{G_{AB}} = - {\Lambda _5}{\,^{(5)}}{g_{AB}} + \kappa _5^2\left[ {{\,^{(5)}}{T_{AB}} + T_{AB}^{{\rm{brane}}}\delta (y)} \right].$$

(64)

Here the delta function enforces in the classical theory the string theory idea that Standard Model fields are confined to the brane. This is not a gravitational confinement, since there is in general a nonzero acceleration of particles normal to the brane [303].

Integrating Equation (64) along the extra dimension from y = −ϵ to y = +ϵ, and taking the limit ϵ → 0, leads to the Israel-Darmois junction conditions at the brane,

$$g_{\mu \nu}^ + - g_{\mu \nu}^ - = 0,$$

(65)

$$K_{\mu \nu}^ + - K_{\mu \nu}^ - = - \kappa _5^2\left[ {T_{\mu \nu}^{{\rm{brane}}} - {1 \over 3}{T^{{\rm{brane}}}}{g_{\mu \nu}}} \right],$$

(66)

where ${T^{{\rm{brane}}}} = {g^{\mu \nu}}T_{\mu \nu}^{{\rm{brane}}}$. The Z₂ symmetry means that when you approach the brane from one side and go through it, you emerge into a bulk that looks the same, but with the normal reversed, n^A → −n^A. Then Equation (52) implies that

$$K_{\mu \nu}^ - = - K_{\mu \nu}^ + ,$$

(67)

so that we can use the junction condition Equation (66) to determine the extrinsic curvature on the brane:

$${K_{\mu \nu}} = - {1 \over 2}\kappa _5^2\left[ {{T_{\mu \nu}} + {1 \over 3}\left({\lambda - T} \right){g_{\mu \nu}}} \right],$$

(68)

where $T = {T^\mu}_\mu$, where we have dropped the (+), and where we evaluate quantities on the brane by taking the limit y → +0.

Finally we arrive at the induced field equations on the brane, by substituting Equation (68) into Equation (60):

$${G_{\mu \nu}} = - \Lambda {g_{\mu \nu}} + {\kappa ^2}{T_{\mu \nu}} + 6{{{\kappa ^2}} \over \lambda}{{\mathcal S}_{\mu \nu}} - {{\mathcal E}_{\mu \nu}} + 4{{{\kappa ^2}} \over \lambda}{{\mathcal F}_{\mu \nu}}.$$

(69)

The 4D gravitational constant is an effective coupling constant inherited from the fundamental coupling constant, and the 4D cosmological constant is nonzero when the RS balance between the bulk cosmological constant and the brane tension is broken:

$${\kappa ^2} \equiv \kappa _4^2 = {1 \over 6}\lambda \kappa _5^4,$$

(70)

$$\Lambda = {1 \over 2}\left[ {{\Lambda _5} + {\kappa ^2}\lambda} \right].$$

(71)

The first correction term relative to Einstein’s theory is quadratic in the energy-momentum tensor, arising from the extrinsic curvature terms in the projected Einstein tensor:

$${{\mathcal S}_{\mu \nu}} = {1 \over {12}}T{T_{\mu \nu}} - {1 \over 4}{T_{\mu \alpha}}{T^\alpha}_\nu + {1 \over {24}}{g_{\mu \nu}}\left[ {3{T_{\alpha \beta}}{T^{\alpha \beta}} - {T^2}} \right].$$

(72)

The second correction term is the projected Weyl term. The last correction term on the right of Equation (69), which generalizes the field equations in [388], is

$${{\mathcal F}_{\mu \nu}}{= ^{(5)}}{T_{AB}}{g_\mu}^A{g_\nu}^B + \left[ {{\,^{(5)}}{T_{AB}}{n^A}{n^B} - {1 \over 4}{\,^{(5)}}T} \right]{g_{\mu \nu}},$$

(73)

where ⁽⁵⁾T_ab describes any stresses in the bulk apart from the cosmological constant (see [311] for the case of a scalar field).

What about the conservation equations? Using Equations (50), (55) and (68), one obtains

$${\nabla ^\nu}{T_{\mu \nu}} = - 2{\,^{(5)}}{T_{AB}}{n^A}{g^B}_\mu .$$

(74)

Thus in general there is exchange of energy-momentum between the bulk and the brane. From now on, we will assume that

$$^{(5)}{T_{AB}} = 0\quad \Rightarrow \quad {{\mathcal F}_{\mu \nu}} = 0,$$

(75)

so that

$$^{(5)}{G_{AB}} = - {\Lambda _5}{\,^{(5)}}{g_{AB}}\qquad \qquad \qquad \qquad \qquad \quad \,{\rm{in\, the\, bulk}},$$

(76)

$${G_{\mu \nu}} = - \Lambda {g_{\mu \nu}} + {\kappa ^2}{T_{\mu \nu}} + 6{{{\kappa ^2}} \over \lambda}{{\mathcal S}_{\mu \nu}} - {{\mathcal E}_{\mu \nu}}\qquad {\rm{on}}\,{\rm{the}}\,{\rm{brane}}.$$

(77)

One then recovers from Equation (74) the standard 4D conservation equations,

$${\nabla ^\nu}{T_{\mu \nu}} = 0.$$

(78)

This means that there is no exchange of energy-momentum between the bulk and the brane; their interaction is purely gravitational. Then the 4D contracted Bianchi identities (∇^νG_μν = 0), applied to Equation (69), lead to

$${\nabla ^\mu}{{\mathcal E}_{\mu \nu}} = {{6{\kappa ^2}} \over \lambda}\,{\nabla ^\mu}{{\mathcal S}_{\mu \nu}},$$

(79)

which shows qualitatively how 1+3 spacetime variations in the matter-radiation on the brane can source KK modes.

The induced field equations (77) show two key modifications to the standard 4D Einstein field equations arising from extra-dimensional effects:

• ${{\mathcal S}_{\mu \nu}} \sim {({T_{\mu \nu}})^2}$ is the high-energy correction term, which is negligible for ρ ≪ λ, but dominant for ρ ≫ λ:

  $${{\vert {\kappa ^2}{{\mathcal S}_{\mu \nu}}/\lambda \vert} \over {\vert {\kappa ^2}{T_{\mu \nu}}\vert}}\sim{{\vert {T_{\mu \nu}}\vert} \over \lambda}\sim{\rho \over \lambda}.$$

  (80)

• ${{\mathcal E}_{\mu \nu}}$ is the projection of the bulk Weyl tensor on the brane, and encodes corrections from 5D graviton effects (the KK modes in the linearized case). From the brane-observer viewpoint, the energy-momentum corrections in ${{\mathcal S}_{\mu \nu}}$ are local, whereas the KK corrections in ${{\mathcal E}_{\mu \nu}}$ are nonlocal, since they incorporate 5D gravity wave modes. These nonlocal corrections cannot be determined purely from data on the brane. In the perturbative analysis of RS 1-brane which leads to the corrections in the gravitational potential, Equation (41), the KK modes that generate this correction are responsible for a nonzero ${{\mathcal E}_{\mu \nu}}$; this term is what carries the modification to the weak-field field equations. The 9 independent components in the tracefree ${{\mathcal E}_{\mu \nu}}$ are reduced to 5 degrees of freedom by Equation (79); these arise from the 5 polarizations of the 5D graviton. Note that the covariant formalism applies also to the two-brane case. In that case, the gravitational influence of the second brane is felt via its contribution to ${{\mathcal E}_{\mu \nu}}$.

3.2 5-dimensional equations and the initial-value problem

The effective field equations are not a closed system. One needs to supplement them by 5D equations governing ${{\mathcal E}_{\mu \nu}}$, which are obtained from the 5D Einstein and Bianchi equations. This leads to the coupled system [374]

$${\pounds_{\bf{n}}}{K_{\mu \nu}} = {K_{\mu \alpha}}{K^\alpha}_\nu - {{\mathcal E}_{\mu \nu}} - {1 \over 6}{\Lambda _5}{g_{\mu \nu}},$$

(81)

$$\begin{array}{*{20}c} {{\pounds_{\bf{n}}}{{\mathcal E}_{\mu \nu}} = {\nabla ^\alpha}{{\mathcal B}_{\alpha (\mu \nu)}} + {1 \over 6}{\Lambda _5}\left({{K_{\mu \nu}} - {g_{\mu \nu}}K} \right) + {K^{\alpha \beta}}{R_{\mu \alpha \nu \beta}} + 3{K^\alpha}_{(\mu}{{\mathcal E}_{\nu)\alpha}} - K{{\mathcal E}_{\mu \nu}}} \\ {+ \left({{K_{\mu \alpha}}{K_{\nu \beta}} - {K_{\alpha \beta}}{K_{\mu \nu}}} \right){K^{\alpha \beta}},\quad \quad \qquad \qquad \qquad \qquad} \\ \end{array}$$

(82)

$${\pounds_{\bf{n}}}{{\mathcal B}_{\mu \nu \alpha}} = - 2{\nabla _{\left[ \mu \right.}}{{\mathcal E}_{\left. \nu \right]\alpha}} + {K_\alpha}^\beta {{\mathcal B}_{\mu \nu \beta}} - 2{{\mathcal B}_{\alpha \beta \left[ \mu \right.}}{K_{\left. \nu \right]}}^\beta ,$$

(83)

$${\pounds_{\bf{n}}}{R_{\mu \nu \alpha \beta}} = - 2{R_{\mu \nu \gamma \left[ \alpha \right.}}{K_{\left. \beta \right]}}^\gamma - {\nabla _\mu}{{\mathcal B}_{\alpha \beta \nu}} + {\nabla _\mu}{{\mathcal B}_{\beta \alpha \nu}},$$

(84)

where the “magnetic” part of the bulk Weyl tensor, counterpart to the “electric” part ${{\mathcal E}_{\mu \nu}}$, is

$${{\mathcal B}_{\mu \nu \alpha}} = {g_\mu}^A{g_\nu}^B{g_\alpha}^C{\,^{(5)}}{C_{ABCD}}{n^D}.$$

(85)

These equations are to be solved subject to the boundary conditions at the brane,

$${\nabla ^\mu}{{\mathcal E}_{\mu \nu}} \overset{.}{=}\kappa _5^4{\nabla ^\mu}{{\mathcal S}_{\mu \nu}},$$

(86)

$${{\mathcal B}_{\mu \nu \alpha}}\overset{.}{=}2{\nabla _{\left[ \mu \right.}}{K_{\left. \nu \right]\alpha}} \overset{.}{=} - \kappa _5^2{\nabla _{\left[ \mu \right.}}\left({{T_{\left. \nu \right]\alpha}} - {1 \over 3}{g_{\left. \nu \right]\alpha}}T} \right),$$

(87)

where A ≐ B denotes A ∣_brane = B ∣_brane.

The above equations have been used to develop a covariant analysis of the weak field [374]. They can also be used to develop a Taylor expansion of the metric about the brane. In Gaussian normal coordinates, Equation (51), we have £_n = ∂/∂y. Then we find

$$\begin{array}{*{20}c} {{g_{\mu \nu}}(x,y) = {g_{\mu \nu}}(x,0) - \kappa _5^2{{\left[ {{T_{\mu \nu}} + {1 \over 3}(\lambda - T){g_{\mu \nu}}} \right]}_{y = 0 +}}\vert y\vert \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad} \\ {\quad \quad + {{\left[ {- {{\mathcal E}_{\mu \nu}} + {1 \over 4}\kappa _5^4\left({{T_{\mu \alpha}}{T^\alpha}_\nu + {2 \over 3}(\lambda - T){T_{\mu \nu}}} \right) + {1 \over 6}\left({{1 \over 6}\kappa _5^4{{(\lambda - T)}^2} - {\Lambda _5}} \right){g_{\mu \nu}}} \right]}_{y = 0 +}}{y^2} + \ldots} \\ \end{array}$$

(88)

In a non-covariant approach based on a specific form of the bulk metric in particular coordinates, the 5D Bianchi identities would be avoided and the equivalent problem would be one of solving the 5D field equations, subject to suitable 5D initial conditions and to the boundary conditions Equation (68) on the metric. The advantage of the covariant splitting of the field equations and Bianchi identities along and normal to the brane is the clear insight that it gives into the interplay between the 4D and 5D gravitational fields. The disadvantage is that the splitting is not well suited to dynamical evolution of the equations. Evolution off the timelike brane in the spacelike normal direction does not in general constitute a well-defined initial value problem [12]. One needs to specify initial data on a 4D spacelike (or null) surface, with boundary conditions at the brane(s) ensuring a consistent evolution [207]. Clearly the evolution of the observed universe is dependent upon initial conditions which are inaccessible to brane-bound observers; this is simply another aspect of the fact that the brane dynamics is not determined by 4D but by 5D equations. The initial conditions on a 4D surface could arise from models for creation of the 5D universe [154, 257, 10, 44, 379], from dynamical attractor behaviour [334] or from suitable conditions (such as no incoming gravitational radiation) at the past Cauchy horizon if the bulk is asymptotically AdS.

3.3 The brane viewpoint: A 1 + 3-covariant analysis

Following [303], a systematic analysis can be developed from the viewpoint of a brane-bound observer. (See also [228].) The effects of bulk gravity are conveyed, from a brane observer viewpoint, via the local ${{\mathcal S}_{\mu \nu}}$ and nonlocal ${{\mathcal E}_{\mu \nu}}$ corrections to Einstein’s equations. (In the more general case, bulk effects on the brane are also carried by ${{\mathcal F}_{\mu \nu}}$, which describes any 5D fields.) The ${{\mathcal E}_{\mu \nu}}$ term cannot in general be determined from data on the brane, and the 5D equations above (or their equivalent) need to be solved in order to find ${{\mathcal E}_{\mu \nu}}$.

The general form of the brane energy-momentum tensor for any matter fields (scalar fields, perfect fluids, kinetic gases, dissipative fluids, etc.), including a combination of different fields, can be covariantly given in terms of a chosen 4-velocity u^μ as

$${T_{\mu \nu}} = \rho {u_\mu}{u_\nu} + p{h_{\mu \nu}} + {\pi _{\mu \nu}} + {q_\mu}{u_\nu} + {q_\nu}{u_\mu}.$$

(89)

Here ρ and p are the energy density and isotropic pressure, respectively, and

$${h_{\mu \nu}} = {g_{\mu \nu}} + {u_\mu}{u_\nu} = {\,^{(5)}}{g_{\mu \nu}} - {n_\mu}{n_\nu} + {u_\mu}{u_\nu}$$

(90)

projects into the comoving rest space orthogonal to u^μ on the brane. The momentum density and anisotropic stress obey

$${q_\mu} = {q_{\langle \mu \rangle}},\qquad {\pi _{\mu \nu}} = {\pi _{\langle \mu \nu \rangle}},$$

(91)

where angled brackets denote the spatially projected, symmetric, and tracefree part:

$${V_{\langle \mu \rangle}} = {h_\mu}{\,^\nu}{V_\nu},\qquad {W_{\langle \mu \nu \rangle}} = \left[ {{h_{(\mu}}^\alpha {h_{\nu)}}^\beta - {1 \over 3}{h^{\alpha \beta}}{h_{\mu \nu}}} \right]{W_{\alpha \beta}}.$$

(92)

In an inertial frame at any point on the brane, we have

$${u^\mu} = (1,\vec 0),\qquad {h_{\mu \nu}} = {\rm{\backslash diag}}(0,1,1,1),\qquad {V_\mu} = (0,{V_i}),\qquad {W_{\mu 0}} = 0 = \sum {{W_{ii}}} = {W_{ij}} - {W_{ji}},$$

(93)

where i,j = 1, 2, 3.

The tensor ${{\mathcal S}_{\mu \nu}}$ which carries local bulk effects onto the brane, may then be irreducibly decomposed as

$$\begin{array}{*{20}c} {{{\mathcal S}_{\mu \nu}} = {1 \over {24}}\left[ {2{\rho ^2} - 3{\pi _{\alpha \beta}}{\pi ^{\alpha \beta}}} \right]{u_\mu}{u_\nu} + {1 \over {24}}\left[ {2{\rho ^2} + 4\rho p + {\pi _{\alpha \beta}}{\pi ^{\alpha \beta}} - 4{q_\alpha}{q^\alpha}} \right]{h_{\mu \nu}}} \\ {\quad \quad \, - {1 \over {12}}(\rho + 3p){\pi _{\mu \nu}} - {1 \over 4}{\pi _{\alpha \langle \mu}}{\pi _{\nu \rangle}}^\alpha + {1 \over 4}{q_{\langle \mu}}{q_{\nu \rangle}} + {1 \over 3}\rho {q_{(\mu}}{u_{\nu)}} - {1 \over 2}{q^\alpha}{\pi _{\alpha (\mu}}{u_{\nu)}}.} \\ \end{array}$$

(94)

This simplifies for a perfect fluid or minimally-coupled scalar field to

$${{\mathcal S}_{\mu \nu}} = {1 \over {12}}\rho \left[ {\rho {u_\mu}{u_\nu} + \left({\rho + 2p} \right){h_{\mu \nu}}} \right].$$

(95)

The tracefree ${{\mathcal E}_{\mu \nu}}$ carries nonlocal bulk effects onto the brane, and contributes an effective “dark” radiative energy-momentum on the brane, with energy density ${\rho _{\mathcal E}}$, pressure ${\rho _{\mathcal E}}/3$, momentum density $q_\mu ^{\mathcal E}$, and anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$:

$$- {1 \over {{\kappa ^2}}}{{\mathcal E}_{\mu \nu}} = {\rho _{\mathcal E}}\left({{u_\mu}{u_\nu} + {1 \over 3}{h_{\mu \nu}}} \right) + q_\mu ^{\mathcal E}{u_\nu} + q_\nu ^{\mathcal E}{u_\mu} + \pi _{\mu \nu}^{\mathcal E}.$$

(96)

We can think of this as a KK or Weyl “fluid”. The brane “feels” the bulk gravitational field through this effective fluid. More specifically:

• The KK (or Weyl) anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$ incorporates the scalar or spin-0 (“Coulomb”), the vector (transverse) or spin-1 (gravimagnetic), and the tensor (transverse traceless) or spin-2 (gravitational wave) 4D modes of the spin-2 5D graviton.

• The KK momentum density $q_\mu ^{\mathcal E}$ incorporates spin-0 and spin-1 modes, and defines a velocity $\upsilon _\mu ^{\mathcal E}$ of the Weyl fluid relative to u^μ via $q_\mu ^{\mathcal E} = \rho {\mathcal E}\upsilon _\mu ^{\mathcal E}$.

• The KK energy density ${\rho _{\mathcal E}}$, often called the “dark radiation”, incorporates the spin-0 mode.

In special cases, symmetry will impose simplifications on this tensor. For example, it must vanish for a conformally flat bulk, including AdS₅,

$$^{(5)}{g_{AB}}\,{\rm{conformally}}\,{\rm{flat}}\quad \Rightarrow \quad {{\mathcal E}_{\mu \nu}} = 0.$$

(97)

The RS models have a Minkowski brane in an AdS₅ bulk. This bulk is also compatible with an FRW brane. However, the most general vacuum bulk with a Friedmann brane is Schwarzschild-anti-de Sitter spacetime [336, 45]. Then it follows from the FRW symmetries that

$${\rm{Schwarzschild}}\,{\rm{Ad}}{{\rm{S}}_5}{\rm{bulk,}}\,{\rm{FRW}}\,{\rm{brane:}}\qquad q_\mu ^{\mathcal E} = 0 = \pi _{\mu \nu}^{\mathcal E},$$

(98)

where ${\rho _{\mathcal E}} = 0$ only if the mass of the black hole in the bulk is zero. The presence of the bulk black hole generates via Coulomb effects the dark radiation on the brane.

For a static spherically symmetric brane (e.g., the exterior of a static star or black hole) [105],

$${\rm{static}}\,{\rm{spherical}}\,{\rm{brane:}}\qquad q_\mu ^{\mathcal E} = 0.$$

(99)

This condition also holds for a Bianchi I brane [307]. In these cases, $\pi _{\mu \nu}^{\mathcal E}$ is not determined by the symmetries, but by the 5D field equations. By contrast, the symmetries of a Gödel brane fix $\pi _{\mu \nu}^{\mathcal E}$ [25].

The brane-world corrections can conveniently be consolidated into an effective total energy density, pressure, momentum density, and anisotropic stress:

$${\rho _{{\rm{tot}}}} = \rho + {1 \over {4\lambda}}\left({2{\rho ^2} - 3{\pi _{\mu \nu}}{\pi ^{\mu \nu}}} \right) + {\rho _{\mathcal E}},$$

(100)

$${p_{{\rm{tot}}}} = p + {1 \over {4\lambda}}\left({2{\rho ^2} + 4\rho p + {\pi _{\mu \nu}}{\pi ^{\mu \nu}} - 4{q_\mu}{q^\mu}} \right) + {{{\rho _{\mathcal E}}} \over 3},$$

(101)

$$q_\mu ^{{\rm{tot}}} = {q_\mu} + {1 \over {2\lambda}}\left({2\rho {q_\mu} - 3{\pi _{\mu \nu}}{q^\nu}} \right) + q_\mu ^{\mathcal E},$$

(102)

$$\pi _{\mu \nu}^{{\rm{tot}}} = {\pi _{\mu \nu}} + {1 \over {2\lambda}}\left[ {- (\rho + 3p){\pi _{\mu \nu}} - 3{\pi _{\alpha \langle \mu}}{\pi _{\nu \rangle}}^\alpha + 3{q_{\langle \mu}}{q_{\nu \rangle}}} \right] + \pi _{\mu \nu}^{\mathcal E}.$$

(103)

These general expressions simplify in the case of a perfect fluid (or minimally coupled scalar field, or isotropic one-particle distribution function), i.e., for q_μ = 0 = π_μν, to

$${\rho _{{\rm{tot}}}} = \rho \left({1 + {\rho \over {2\lambda}} + {{{\rho _{\mathcal E}}} \over \rho}} \right),$$

(104)

$${p_{{\rm{tot}}}} = p + {\rho \over {2\lambda}}(2p + \rho) + {{{\rho _{\mathcal E}}} \over 3},$$

(105)

$$q_\mu ^{{\rm{tot}}} = q_\mu ^{\mathcal E},$$

(106)

$$\pi _{\mu \nu}^{{\rm{tot}}} = \pi _{\mu \nu}^{\mathcal E}.$$

(107)

Note that nonlocal bulk effects can contribute to effective imperfect fluid terms even when the matter on the brane has perfect fluid form: There is in general an effective momentum density and anisotropic stress induced on the brane by massive KK modes of the 5D graviton.

The effective total equation of state and sound speed follow from Equations (104) and (105) as

$${w_{{\rm{tot}}}} \equiv {{{p_{{\rm{tot}}}}} \over {{\rho _{{\rm{tot}}}}}} = {{w + (1 + 2w)\rho /2\lambda + {\rho _{\mathcal E}}/3\rho} \over {1 + \rho /2\lambda + {\rho _{\mathcal E}}/\rho}},$$

(108)

$$c_{{\rm{tot}}}^2 \equiv {{{{\dot p}_{{\rm{tot}}}}} \over {{{\dot \rho}_{{\rm{tot}}}}}} = \left[ {c_{\rm{s}}^2 + {{\rho + p} \over {\rho + \lambda}} + {{4{\rho _{\mathcal E}}} \over {9(\rho + p)(1 + \rho /\lambda)}}} \right]{\left[ {1 + {{4{\rho _{\mathcal E}}} \over {3(\rho + p)(1 + \rho /\lambda)}}} \right]^{- 1}},$$

(109)

where w = p/ρ and $c_{\rm{s}}^2 = \dot {p}/\dot {\rho}$. At very high energies, i.e., ρ ≫ λ, we can generally neglect ${\rho _{\mathcal E}}$ (e.g., in an inflating cosmology), and the effective equation of state and sound speed are stiffened:

$${w_{{\rm{tot}}}} \approx 2w + 1,\qquad c_{{\rm{tot}}}^2 \approx c_{\rm{s}}^2 + w + 1.$$

(110)

This can have important consequences in the early universe and during gravitational collapse. For example, in a very high-energy radiation era, w = 1/3, the effective cosmological equation of state is ultra-stiff: w_tot ≈ 5/3. In late-stage gravitational collapse of pressureless matter, w = 0, the effective equation of state is stiff, w_tot ≈ 1, and the effective pressure is nonzero and dynamically important.

3.4 Conservation equations

Conservation of T_μν gives the standard general relativity energy and momentum conservation equations, in the general, nonlinear case:

$$\dot \rho + \Theta (\rho + p) + {\vec \nabla ^\mu}{q_\mu} + 2{A^\mu}{q_\mu} + {\sigma ^{\mu \nu}}{\pi _{\mu \nu}} = 0,$$

(111)

$${\dot q_{\langle \mu \rangle}} + {4 \over 3}\Theta {q_\mu} + {\vec \nabla _\mu}p + (\rho + p){A_\mu} + {\vec \nabla ^\nu}{\pi _{\mu \nu}} + {A^\nu}{\pi _{\mu \nu}} + {\sigma _{\mu \nu}}{q^\nu} - {\varepsilon _{\mu \nu \alpha}}{\omega ^\nu}{q^\alpha} = 0.$$

(112)

In these equations, an overdot denotes u^ν ∇_ν, Θ = ∇^μu_μ is the volume expansion rate of the u^μ worldlines, ${A_\mu} = {\dot u_\mu} = {A_{\left\langle \mu \right\rangle}}$ is their 4-acceleration, ${\sigma _{\mu \nu }} = {\vec \nabla _{\left\langle \mu \right.}}{u_{\left. \nu \right\rangle }}$ is their shear rate, and ${\omega _\mu} = - {1 \over 2}{\rm{curl}}\,{u_\mu} = {\omega _{\left\langle \mu \right\rangle}}$ is their vorticity rate.

On a Friedmann brane, we get

$${A_\mu} = {\omega _\mu} = {\sigma _{\mu \nu}} = 0,\qquad \Theta = 3H,$$

(113)

where H = ȧ/a is the Hubble rate. The covariant spatial curl is given by

$${\rm{curl}}\,{V_\mu} = {\varepsilon _{\mu \alpha \beta}}{\vec \nabla ^\alpha}{V^\beta},\qquad {\rm{curl}}\,{W_{\mu \nu}} = {\varepsilon _{\alpha \beta (\mu}}{\vec \nabla ^\alpha}{W^\beta}_{\nu)},$$

(114)

where ε_μαβ is the projection orthogonal to u^μ of the 4D brane alternating tensor, and ${\vec \nabla _\mu}$ is the projected part of the brane covariant derivative, defined by

$${\vec \nabla _\mu}{F^{\alpha \ldots}}_{\ldots \beta} = {\left({{\nabla _\mu}{F^{\alpha \ldots}}_{\ldots \beta}} \right)_{\bot u}} = {h_\mu}^\nu {h^\alpha}_\gamma \ldots {h_\beta}^\delta {\nabla _\nu}{F^{\gamma \ldots}}_{\ldots \delta}.$$

(115)

In a local inertial frame at a point on the brane, with $u^\mu = {\delta^ \mu}_0$, we have: $0=A_0=\omega_0=\sigma_{0\mu}=\varepsilon_{0\alpha\beta}= {\rm curl}\, V_0 = {\rm curl}\, W_{0\mu}$, and

$${\vec \nabla _\mu}{F^{\alpha \ldots}}_{\ldots \beta} = {\delta _\mu}^i{\delta ^\alpha}_j \ldots {\delta _\beta}^k{\nabla _i}{F^{j \ldots}}_{\ldots k}\qquad {\rm{(local}}\,{\rm{inertial}}\,{\rm{frame)}},$$

(116)

where, i, j, k, = 1, 2, 3.

The absence of bulk source terms in the conservation equations is a consequence of having Λ₅ as the only 5D source in the bulk. For example, if there is a bulk scalar field, then there is energy-momentum exchange between the brane and bulk (in addition to the gravitational interaction) [311, 21, 322, 143, 274, 144, 48].

Equation (79) may be called the “nonlocal conservation equation”. Projecting along u^μ gives the nonlocal energy conservation equation, which is a propagation equation for ${\rho _{\mathcal E}}$ In the general, nonlinear case, this gives

$$\begin{array}{*{20}c} {\dot \rho {\mathcal E} + {4 \over 3}\Theta \rho {\mathcal E} + {{\vec \nabla}^\mu}q_\mu ^{\mathcal E} + 2{A^\mu}q_\mu ^{\mathcal E} + {\sigma ^{\mu \nu}}\pi _{\mu \nu}^{\mathcal E} = \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad} \\ {{1 \over {2\lambda}}\left[ {3{\pi ^{\mu \nu}}{{\dot \pi}_{\mu \nu}} + 3(\rho + p){\sigma ^{\mu \nu}}{\pi _{\mu \nu}} + \Theta \left({2{q^\mu}{q_\mu} + {\pi ^{\mu \nu}}{\pi _{\mu \nu}}} \right) + 6{A^\mu}{q^\nu}{\pi _{\mu \nu}}} \right.} \\ {\left. {\quad \quad \quad - 2{q^\mu}{{\vec \nabla}_\mu}\rho + 3{q^\mu}{{\vec \nabla}^\nu}{\pi _{\mu \nu}} + 3{\pi ^{\mu \nu}}{{\vec \nabla}_\mu}{q_\nu} + 3{\sigma ^{\mu \nu}}{\pi _{\alpha \mu}}{\pi _\nu}^\alpha - 3{\sigma ^{\mu \nu}}{q_\mu}{q_\nu}} \right].} \\ \end{array}$$

(117)

Projecting into the comoving rest space gives the nonlocal momentum conservation equation, which is a propagation equation for $q_\mu ^{\mathcal E}$:

$$\begin{array}{*{20}c} {\dot q_{\langle \mu \rangle}^{\mathcal E} + {4 \over 3}\Theta q{{\mathcal E}_\mu} + {1 \over 3}{{\vec \nabla}_\mu}{\rho _{\mathcal E}} + {4 \over 3}{\rho _{\mathcal E}}{A_\mu} + {{\vec \nabla}^\nu}\pi {{\mathcal E}_{\mu \nu}} + {A^\nu}\pi {{\mathcal E}_{\mu \nu}} + {\sigma _\mu}^\nu q{{\mathcal E}_\nu} - {\varepsilon _\mu}^{\nu \alpha}{\omega _\nu}q{{\mathcal E}_\alpha} =} \\ {\qquad \qquad {1 \over {4\lambda}}[ - 4(\rho + p){{\vec \nabla}_\mu}\rho + 6(\rho + p){{\vec \nabla}^\nu}{\pi _{\mu \nu}} + 6{q^\nu}{{\dot \pi}_{\langle \mu \nu \rangle}} + 2{\pi _\mu}^\nu {{\vec \nabla}_\nu}\rho} \\ {\qquad \qquad \qquad - 6{\pi ^{\alpha \beta}}\left({{{\vec \nabla}_\mu}{\pi _{\alpha \beta}} - {{\vec \nabla}_\alpha}{\pi _{\beta \mu}}} \right) - 3{\pi _{\mu \alpha}}{{\vec \nabla}_\beta}{\pi ^{\alpha \beta}} + 12{q^\nu}{{\vec \nabla}_\mu}{q_\nu} - 6{q^\nu}{{\vec \nabla}_\nu}{q_\mu} - 2q\mu {{\vec \nabla}^\nu}{q_\nu}} \\ {\qquad \qquad \qquad - 6{\pi _{\mu \alpha}}{\sigma ^{\alpha \beta}}{q_\beta} + 6{\sigma _{\mu \alpha}}{\pi ^{\alpha \beta}}{q_\beta} + 6{\pi _{\mu \nu}}{\varepsilon ^{\nu \alpha \beta}}{\omega _\alpha}{q_\beta} - 6{\varepsilon _{\mu \alpha \beta}}{\omega ^\alpha}{\pi ^{\beta \nu}}{q_\nu}} \\ {\qquad \qquad \qquad + 4(\rho + p)\Theta {q_\mu} + 2{q_\mu}{A^\nu}{q_\nu} + 6{A_\mu}{q^\nu}{q_\nu} + 4{q_\mu}{\sigma ^{\alpha \beta}}{\pi _{\alpha \beta}}].} \\ \end{array}$$

(118)

The 1+3-covariant decomposition shows two key features:

• Inhomogeneous and anisotropic effects from the 4D matter-radiation distribution on the brane are a source for the 5D Weyl tensor, which nonlocally “backreacts” on the brane via its projection ${{\mathcal E}_{\mu \nu}}$.

• There are evolution equations for the dark radiative (nonlocal, Weyl) energy (${\rho _{\mathcal E}}$) and momentum $q_\mu ^{\mathcal E}$ densities (carrying scalar and vector modes from bulk gravitons), but there is no evolution equation for the dark radiative anisotropic stress ($\pi _{\mu \nu}^{\mathcal E}$) (carrying tensor, as well as scalar and vector, modes), which arises in both evolution equations.

In particular cases, the Weyl anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$ may drop out of the nonlocal conservation equations, i.e., when we can neglect ${\sigma ^{\mu \nu}}\pi _{\mu \nu}^{\mathcal E},\;{\vec \nabla ^\nu}\pi _{\mu \nu}^{\mathcal E}$ and ${A^\nu}\pi _{\mu \nu}^{\mathcal E}$ This is the case when we consider linearized perturbations about an FRW background (which remove the first and last of these terms) and further when we can neglect gradient terms on large scales (which removes the second term). This case is discussed in Section 6. But in general, and especially in astrophysical contexts, the $\pi _{\mu \nu}^{\mathcal E}$ terms cannot be neglected. Even when we can neglect these terms, $\pi _{\mu \nu}^{\mathcal E}$ arises in the field equations on the brane.

All of the matter source terms on the right of these two equations, except for the first term on the right of Equation (118), are imperfect fluid terms, and most of these terms are quadratic in the imperfect quantities q_μ and π_μν. For a single perfect fluid or scalar field, only the ${\vec \nabla _\mu}\rho$ term on the right of Equation (118) survives, but in realistic cosmological and astrophysical models, further terms will survive. For example, terms linear in π_μν will carry the photon quadrupole in cosmology or the shear viscous stress in stellar models. If there are two fluids (even if both fluids are perfect), then there will be a relative velocity υ_μ generating a momentum densityq_μ = ρυ_μ, which will serve to source nonlocal effects.

In general, the 4 independent equations in Equations (117) and (118) constrain 4 of the 9 independent components of ${{\mathcal E}_{\mu \nu}}$ on the brane. What is missing is an evolution equation for $\pi _{\mu \nu}^{\mathcal E}$, which has up to 5 independent components. These 5 degrees of freedom correspond to the 5 polarizations of the 5D graviton. Thus in general, the projection of the 5-dimensional field equations onto the brane does not lead to a closed system, as expected, since there are bulk degrees of freedom whose impact on the brane cannot be predicted by brane observers. The KK anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$ encodes the nonlocality.

In special cases the missing equation does not matter. For example, if $\pi _{\mu \nu}^{\mathcal E} = 0$ by symmetry, as in the case of an FRW brane, then the evolution of ${{\mathcal E}_{\mu \nu}}$ is determined by Equations (117) and (118). If the brane is stationary (with Killing vector parallel to u^μ), then evolution equations are not needed for ${{\mathcal E}_{\mu \nu}}$, although in general $\pi _{\mu \nu}^{\mathcal E}$ will still be undetermined. However, small perturbations of these special cases will immediately restore the problem of missing information.

If the matter on the brane has a perfect-fluid or scalar-field energy-momentum tensor, the local conservation equations (111) and (112) reduce to

$$\dot \rho + \Theta (\rho + p) = 0,$$

(119)

$${\vec \nabla _\mu}p + (\rho + p){A_\mu} = 0,$$

(120)

while the nonlocal conservation equations (117) and (118) reduce to

$$\dot \rho {\mathcal E} + {4 \over 3}\Theta \rho {\mathcal E} + {\vec \nabla ^\mu}q_\mu ^{\mathcal E} + 2{A^\mu}q_\mu ^{\mathcal E} + {\sigma ^{\mu \nu}}\pi _{\mu \nu}^{\mathcal E} = 0,$$

(121)

$$\dot q_{\langle \mu \rangle}^{\mathcal E} + {4 \over 3}\Theta q_\mu ^{\mathcal E} + {1 \over 3}{\vec \nabla _\mu}\rho {\mathcal E} + {4 \over 3}\rho {\mathcal E}{A_\mu} + {\vec \nabla ^\nu}\pi _{\mu \nu}^{\mathcal E} + {A^\nu}\pi _{\mu \nu}^{\mathcal E} + {\sigma _\mu}^\nu q_\nu ^{\mathcal E} - {\varepsilon _\mu}^{\nu \alpha}{\omega _\nu}q_\alpha ^{\mathcal E} = - {{(\rho + p)} \over \lambda}{\vec \nabla _\mu}\rho .$$

(122)

Equation (122) shows that [388]

• if ${{\mathcal E}_{\mu \nu}} = 0$ and the brane energy-momentum tensor has perfect fluid form, then the density ρ must be homogeneous, ${\vec \nabla _\mu}\rho = 0$;

• the converse does not hold, i.e., homogeneous density does not in general imply vanishing ${{\mathcal E}_{\mu \nu}}$.

A simple example of the latter point is the FRW case: Equation (122) is trivially satisfied, while Equation (121) becomes

$${\dot \rho _{\mathcal E}} + 4H{\rho _{\mathcal E}} = 0.$$

(123)

This equation has the dark radiation solution

$${\rho _{\mathcal E}} = {\rho _{{\mathcal E}\,0}}{\left({{{{a_0}} \over a}} \right)^4}.$$

(124)

If ${{\mathcal E}_{\mu \nu}} = 0$, then the field equations on the brane form a closed system. Thus for perfect fluid branes with homogeneous density and ${{\mathcal E}_{\mu \nu}} = 0$, the brane field equations form a consistent closed system. However, this is unstable to perturbations, and there is also no guarantee that the resulting brane metric can be embedded in a regular bulk.

It also follows as a corollary that inhomogeneous density requires nonzero ${{\mathcal E}_{\mu \nu}}$:

$${\vec \nabla _\mu}\rho \neq 0\quad \Rightarrow \quad {{\mathcal E}_{\mu \nu}} \neq 0.$$

(125)

For example, stellar solutions on the brane necessarily have ${{\mathcal E}_{\mu \nu}} \neq 0$ in the stellar interior if it is non-uniform. Perturbed FRW models on the brane also must have ${{\mathcal E}_{\mu \nu}} \neq 0$. Thus a nonzero ${{\mathcal E}_{\mu \nu}}$, and in particular a nonzero $\pi _{\mu \nu}^{\mathcal E}$, is inevitable in realistic astrophysical and cosmological models.

3.5 Propagation and constraint equations on the brane

The propagation equations for the local and nonlocal energy density and momentum density are supplemented by further 1+3-covariant propagation and constraint equations for the kinematic quantities Θ, A_μ, ω_μ, σ_μν, and for the free gravitational field on the brane. The kinematic quantities govern the relative motion of neighbouring fundamental world-lines. The free gravitational field on the brane is given by the brane Weyl tensor C_μναβ. This splits into the gravito-electric and gravito-magnetic fields on the brane:

$${E_{\mu \nu}} = {C_{\mu \alpha \nu \beta}}{u^\alpha}{u^\beta} = {E_{\langle \mu \nu \rangle}},\qquad {H_{\mu \nu}} = {1 \over 2}{\varepsilon _{\mu \alpha \beta}}{C^{\alpha \beta}}_{\nu \gamma}{u^\gamma} = {H_{\langle \mu \nu \rangle}},$$

(126)

where E_μν is not to be confused with ${{\mathcal E}_{\mu \nu}}$. The Ricci identity for u^μ

$${\nabla _{\left[ \mu \right.}}{\nabla _{\left. \nu \right]}}{u_\alpha} = {1 \over 2}{R_{\alpha \nu \mu \beta}}{u^\beta},$$

(127)

and the Bianchi identities

$${\nabla ^\beta}{C_{\mu \nu \alpha \beta}} = {\nabla _{\left[ \mu \right.}}\left({- {R_{\left. \nu \right]\alpha}} + {1 \over 6}R{g_{\left. \nu \right]\alpha}}} \right),$$

(128)

produce the fundamental evolution and constraint equations governing the above covariant quantities. The field equations are incorporated via the algebraic replacement of the Ricci tensor R_μν by the effective total energy-momentum tensor, according to Equation (69). The brane equations are derived directly from the standard general relativity versions by simply replacing the energy-momentum tensor terms ρ…. by ρ_tot,…. For a general fluid source, the equations are given in [303, 228]. In the case of a single perfect fluid or minimally-coupled scalar field, the equations reduce to the following nonlinear equations:

• Generalized Raychaudhuri equation (expansion propagation):

  $$\dot \Theta + {1 \over 3}{\Theta ^2} + {\sigma _{\mu \nu}}{\sigma ^{\mu \nu}} - 2{\omega _\mu}{\omega ^\mu} - {\vec \nabla ^\mu}{A_\mu} - {A_\mu}{A^\mu} + {{{\kappa ^2}} \over 2}(\rho + 3p) - \Lambda = - {{{\kappa ^2}} \over 2}(2\rho + 3p){\rho \over \lambda} - {\kappa ^2}{\rho _{\mathcal E}}.$$

  (129)

• Vorticity propagation:

  $${\dot \omega _{\langle \mu \rangle}} + {2 \over 3}\Theta {\omega _\mu} + {1 \over 2}{\rm{curl}}\,{A_\mu} - {\sigma _{\mu \nu}}{\omega ^\nu} = 0.$$

  (130)

• Shear propagation:

  $${\dot \sigma _{\langle \mu \nu \rangle}} + {2 \over 3}\Theta {\sigma _{\mu \nu}} + {E_{\mu \nu}} - {\vec \nabla _{\langle \mu}}{A_{\nu \rangle}} + {\sigma _{\alpha \langle \mu}}{\sigma _{\nu \rangle}}^\alpha + {\omega _{\langle \mu}}{\omega _{\nu \rangle}} - {A_{\langle \mu}}{A_{\nu \rangle}} = {{{\kappa ^2}} \over 2}\pi _{\mu \nu}^{\mathcal E}.$$

  (131)

• Gravito-electric propagation (Maxwell-Weyl E-dot equation):

  $$\begin{array}{*{20}c} {{{\dot E}_{\langle \mu \nu \rangle}} + \Theta {E_{\mu \nu}} - {\rm{curl}}\,{H_{\mu \nu}} + {{{\kappa ^2}} \over 2}(\rho + p){\sigma _{\mu \nu}} - 2{A^\alpha}{\varepsilon _{\alpha \beta (\mu}}{H_{\nu)}}^\beta - 3{\sigma _{\alpha \langle \mu}}{E_{\nu \rangle}}^\alpha + {\omega ^\alpha}{\varepsilon _{\alpha \beta (\mu}}{E_{\nu)}}^\beta =} \\ {- {{{\kappa ^2}} \over 2}(\rho + p){\rho \over \lambda}{\sigma _{\mu \nu}}\quad \quad \quad \quad \quad \quad \quad \,\,\,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad} \\ {- {{{\kappa ^2}} \over 6}\left[ {4\rho {\mathcal E}{\sigma _{\mu \nu}} + 3\dot \pi _{\langle \mu \nu \rangle}^{\mathcal E} + \Theta \pi _{\mu \nu}^{\mathcal E} + 3{{\vec \nabla}_{\langle \mu}}q_{\nu \rangle}^{\mathcal E} + 6{A_{\langle \mu}}q_{\nu \rangle}^{\mathcal E} + 3{\sigma ^\alpha}_{\langle \mu}\pi _{\nu \rangle \alpha}^{\mathcal E} + 3{\omega ^\alpha}{\varepsilon _{\alpha \beta (\mu}}\pi _{\nu)}^{\mathcal E}{}^\beta} \right].\quad} \\ \end{array}$$

  (132)

• Gravito-magnetic propagation (Maxwell-Weyl H-dot equation):

  $$\begin{array}{*{20}c} {{{\dot H}_{\langle \mu \nu \rangle}} + \Theta {H_{\mu \nu}} + {\rm{curl}}\,{E_{\mu \nu}} - 3{\sigma _{\alpha \langle \mu}}{H_{\nu \rangle}}^\alpha + {\omega ^\alpha}{\varepsilon _{\alpha \beta (\mu}}{H_{\nu)}}^\beta + 2{A^\alpha}{\varepsilon _{\alpha \beta (\mu}}{E_{\nu)}}^\beta =} \\ {\qquad \qquad {{{\kappa ^2}} \over 2}\left[ {{\rm{curl}}\,\pi _{\mu \nu}^{\mathcal E} - 3{\omega _{\langle \mu}}q_{\nu \rangle}^{\mathcal E} + {\sigma _{\alpha (\mu}}{\varepsilon _{\nu)}}^{\alpha \beta}q_\beta ^{\mathcal E}} \right].\quad \quad \quad \quad} \\ \end{array}$$

  (133)

• Vorticity constraint:

  $${\vec \nabla ^\mu}{\omega _\mu} - {A^\mu}{\omega _\mu} = 0.$$

  (134)

• Shear constraint:

  $${\vec \nabla ^\nu}{\sigma _{\mu \nu}} - {\rm{curl}}\,{\omega _\mu} - {2 \over 3}{\vec \nabla _\mu}\Theta + 2{\varepsilon _{\mu \nu \alpha}}{\omega ^\nu}{A^\alpha} = - {\kappa ^2}q_\mu ^{\mathcal E}.$$

  (135)

• Gravito-magnetic constraint:

  $${\rm{curl}}\,{\sigma _{\mu \nu}} + {\vec \nabla _{\langle \mu}}{\omega _{\nu \rangle}} - {H_{\mu \nu}} + 2{A_{\langle \mu}}{\omega _{\nu \rangle}} = 0.$$

  (136)

• Gravito-electric divergence (Maxwell-Weyl div-E equation):

  $$\begin{array}{*{20}c} {{{\vec \nabla}^\nu}{E_{\mu \nu}} - {{{\kappa ^2}} \over 3}{{\vec \nabla}_\mu}\rho - {\varepsilon _{\mu \nu \alpha}}{\sigma ^\nu}_\beta {H^{\alpha \beta}} + 3{H_{\mu \nu}}{\omega ^\nu} = \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,} \\ {\,{{{\kappa ^2}} \over 3}{\rho \over \lambda}{{\vec \nabla}_\mu}\rho + {{{\kappa ^2}} \over 6}\left({2{{\vec \nabla}_\mu}{\rho _{\mathcal E}} - 2\Theta q_\mu ^{\mathcal E} - 3{{\vec \nabla}^\nu}\pi _{\mu \nu}^{\mathcal E} + 3{\sigma _\mu}^\nu q_\nu ^{\mathcal E} - 9{\varepsilon _\mu}^{\nu \alpha}{\omega _\nu}q_\alpha ^{\mathcal E}} \right).} \\ \end{array}$$

  (137)

• Gravito-magnetic divergence (Maxwell-Weyl div-H equation):

  $$\begin{array}{*{20}c} {{{\vec \nabla}^\nu}{H_{\mu \nu}} - {\kappa ^2}(\rho + p){\omega _\mu} + {\varepsilon _{\mu \nu \alpha}}{\sigma ^\nu}_\beta {E^{\alpha \beta}} - 3{E_{\mu \nu}}{\omega ^\nu} = \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad} \\ {{\kappa ^2}(\rho + p){\rho \over \lambda}{\omega _\mu} + {{{\kappa ^2}} \over 6}\left({8{\rho _{\mathcal E}}{\omega _\mu} - 3{\rm{curl}}\,q_\mu ^{\mathcal E} - 3{\varepsilon _\mu}^{\nu \alpha}{\sigma _\nu}^\beta \pi _{\alpha \beta}^{\mathcal E} - 3\pi _{\mu \nu}^{\mathcal E}{\omega ^\nu}} \right).} \\ \end{array}$$

  (138)

• Gauss-Codazzi equations on the brane (with ω_μ = 0):

  $$R_{\langle \mu \nu \rangle}^ \bot + {\dot \sigma _{\langle \mu \nu \rangle}} + \Theta {\sigma _{\mu \nu}} - {\vec \nabla _{\langle \mu}}{A_{\nu \rangle}} - {A_{\langle \mu}}{A_{\nu \rangle}} = {\kappa ^2}\pi _{\mu \nu}^{\mathcal E},$$

  (139)
  $${R^ \bot} + {2 \over 3}{\Theta ^2} - {\sigma _{\mu \nu}}{\sigma ^{\mu \nu}} - 2{\kappa ^2}\rho - 2\Lambda = {\kappa ^2}{{{\rho ^2}} \over \lambda} + 2{\kappa ^2}{\rho _{\mathcal E}},$$

  (140)

  where $R_{\mu \nu}^ \bot$ is the Ricci tensor for 3-surfaces orthogonal to u^μ on the brane, and ${R^ \bot} = {h^{\mu \nu}}R_{\mu \nu}^ \bot$.

The standard 4D general relativity results are regained when λ⁻¹ → 0 and ${{\mathcal E}_{\mu \nu}} = 0$, which sets all right hand sides to zero in Equations (129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140). Together with Equations (119, 120, 121, 122), these equations govern the dynamics of the matter and gravitational fields on the brane, incorporating both the local, high-energy (quadratic energy-momentum) and nonlocal, KK (projected 5D Weyl) effects from the bulk. High-energy terms are proportional to ρ/λ, and are significant only when ρ > λ. The KK terms contain ${\rho _{\mathcal E}},\, q_\mu ^{\mathcal E}$, and $\pi _{\mu \nu}^{\mathcal E}$, with the latter two quantities introducing imperfect fluid effects, even when the matter has perfect fluid form.

Bulk effects give rise to important new driving and source terms in the propagation and constraint equations. The vorticity propagation and constraint, and the gravito-magnetic constraint have no direct bulk effects, but all other equations do. High-energy and KK energy density terms are driving terms in the propagation of the expansion Θ. The spatial gradients of these terms provide sources for the gravito-electric field E_μν. The KK anisotropic stress is a driving term in the propagation of shear σ_μν and the gravito-electric/gravito-magnetic fields, E and H_μν respectively, and the KK momentum density is a source for shear and the gravito-magnetic field. The 4D Maxwell-Weyl equations show in detail the contribution to the 4D gravito-electromagnetic field on the brane, i.e., (E_μν, E_μν), from the 5D Weyl field in the bulk.

An interesting example of how high-energy effects can modify general relativistic dynamics arises in the analysis of isotropization of Bianchi spacetimes. For a Binachi type I brane, Equation (140) becomes [307]

$${H^2} = {{{\kappa ^2}} \over 3}\rho \left({1 + {\rho \over {2\lambda}}} \right) + {{{\Sigma ^2}} \over {{a^6}}},$$

(141)

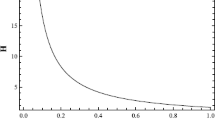
if we neglect the dark radiation, where a and H are the average scale factor and expansion rate, and ∑ is the shear constant. In general relativity, the shear term dominates as a → 0, but in the brane-world, the high-energy ρ² term will dominate if ω > 0, so that the matter-dominated early universe is isotropic [307, 68, 67, 413, 373, 23, 93]. This is illustrated in Figure 4.

Figure 4

The evolution of the dimensionless shear parameter Ω_shear = σ²/ 6H² on a Bianchi I brane, for a $V = {1 \over 2}{m^2}{\phi ^2}$ model. The early and late-time expansion of the universe is isotropic, but the shear dominates during an intermediate anisotropic stage. (Figure taken from [307].)

Note that this conclusion is sensitive to the assumption that ${\rho _{\mathcal E}} \approx 0$, which by Equation (121) implies the restriction

$${\sigma ^{\mu \nu}}\pi _{\mu \nu}^{\mathcal E} \approx 0.$$

(142)

Relaxing this assumption can lead to non-isotropizing solutions [5, 94, 66].

The system of propagation and constraint equations, i.e., Equations (119, 120, 121, 122) and (129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140), is exact and nonlinear, applicable to both cosmological and astrophysical modelling, including strong-gravity effects. In general the system of equations is not closed: There is no evolution equation for the KK anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$.

4 Gravitational Collapse and Black Holes on the Brane

The physics of brane-world compact objects and gravitational collapse is complicated by a number of factors, especially the confinement of matter to the brane, while the gravitational field can access the extra dimension, and the nonlocal (from the brane viewpoint) gravitational interaction between the brane and the bulk. Extra-dimensional effects mean that the 4D matching conditions on the brane, i.e., continuity of the induced metric and extrinsic curvature across the 2-surface boundary, are much more complicated to implement [160, 119, 422, 159]. High-energy corrections increase the effective density and pressure of stellar and collapsing matter. In particular this means that the effective pressure does not in general vanish at the boundary 2-surface, changing the nature of the 4D matching conditions on the brane. The nonlocal KK effects further complicate the matching problem on the brane, since they in general contribute to the effective radial pressure at the boundary 2-surface. Gravitational collapse inevitably produces energies high enough, i.e., ρ ≫ λ, to make these corrections significant.

We expect that extra-dimensional effects will be negligible outside the high-energy, short-range regime. The corrections to the weak-field potential, Equation (41), are at the second post-Newtonian (2PN) level [164, 210]. However, modifications to Hawking radiation may bring significant corrections even for solar-sized black holes, as discussed below.

A vacuum on the brane, outside a star or black hole, satisfies the brane field equations

$${R_{\mu \nu}} = - {{\mathcal E}_{\mu \nu}},\qquad {R^\mu}_\mu = 0 = {{\mathcal E}^\mu}_\mu ,\qquad {\nabla ^\nu}{{\mathcal E}_{\mu \nu}} = 0.$$

(143)

The Weyl term ${{\mathcal E}_{\mu \nu}}$ will carry an imprint of high-energy effects that source KK modes (as discussed above). This means that high-energy stars and the process of gravitational collapse will in general lead to deviations from the 4D general relativity problem. The weak-field limit for a static spherical source, Equation (41), shows that ${{\mathcal E}_{\mu \nu}}$ must be nonzero, since this is the term responsible for the corrections to the Newtonian potential.

4.1 The black string

The projected Weyl term vanishes in the simplest candidate for a black hole solution. This is obtained by assuming the exact Schwarzschild form for the induced brane metric and “stacking” it into the extra dimension [76],

$$^{(5)}d{s^2} = {e^{- 2\vert y\vert /\ell}}{\tilde g_{\mu \nu}}d{x^\mu}d{x^\nu} + d{y^2},$$

(144)

$${\tilde g_{\mu \nu}} = {e^{2\vert y\vert /\ell}}{g_{\mu \nu}} = - (1 - 2GM/r)d{t^2} + {{d{r^2}} \over {1 - 2GM/r}} + {r^2}d{\Omega ^2}.$$

(145)

(Note that Equation (144) is in fact a solution of the 5D field equations (22) if ${\tilde g_{\mu \nu}}$ is any 4D Einstein vacuum solution, i.e., if ${\tilde R_{\mu \nu}} = 0$, and this can be generalized to the case ${\tilde R_{\mu \nu}} = - \tilde \Lambda {\tilde g_{\mu \nu}}$ [11, 20].)

Each {y = const.} surface is a 4D Schwarzschild spacetime, and there is a line singularity along r = 0 for all y. This solution is known as the Schwarzschild black string, which is clearly not localized on the brane y = 0. Although ⁽⁵⁾C_abcd ≠ 0, the projection of the bulk Weyl tensor along the brane is zero, since there is no correction to the 4D gravitational potential:

$$V(r) = {{GM} \over r}\quad \Rightarrow \quad {{\mathcal E}_{\mu \nu}} = 0.$$

(146)

The violation of the perturbative corrections to the potential signals some kind of non-AdS₅ pathology in the bulk. Indeed, the 5D curvature is unbounded at the Cauchy horizon, as y → ∞ [76]:

$$^{(5)}{R_{ABCD}}{\,^{(5)}}{R^{ABCD}} = {{40} \over {{\ell ^4}}} + {{48{G^2}{M^2}} \over {{r^6}}}\,{e^{4\vert y\vert /\ell}}.$$

(147)

Furthermore, the black string is unstable to large-scale perturbations [182].

Thus the “obvious” approach to finding a brane black hole fails. An alternative approach is to seek solutions of the brane field equations with nonzero ${{\mathcal E}_{\mu \nu}}$ [105]. Brane solutions of static black hole exteriors with 5D corrections to the Schwarzschild metric have been found [105, 160, 119, 422, 224, 73, 223], but the bulk metric for these solutions has not been found. Numerical integration into the bulk, starting from static black hole solutions on the brane, is plagued with difficulties [389, 78].

4.2 Taylor expansion into the bulk

One can use a Taylor expansion, as in Equation (88), in order to probe properties of a static black hole on the brane. (An alternative expansion scheme is discussed in [74].) For a vacuum brane metric,

$$\begin{array}{*{20}c} {{{\tilde g}_{\mu \nu}}(x,y) = {{\tilde g}_{\mu \nu}}(x,0) - {{\mathcal E}_{\mu \nu}}(x,0 +){y^2} - {2 \over \ell}{{\mathcal E}_{\mu \nu}}(x,0 +)\vert y{\vert ^3}\quad \quad \quad \quad \quad \quad \quad \quad \quad} \\ {+ {1 \over {12}}{{\left[\square {{{\mathcal E}_{\mu \nu}} - {{32} \over {{\ell ^2}}}{{\mathcal E}_{\mu \nu}} + 2{R_{\mu \alpha \nu \beta}}{{\mathcal E}^{\alpha \beta}} + 6{{\mathcal E}_\mu}^\alpha {{\mathcal E}_{\alpha \nu}}} \right]}_{y = 0 +}}{y^4} + \ldots} \\ \end{array}$$

(148)

This shows in particular that the propagating effect of 5D gravity arises only at the fourth order of the expansion. For a static spherical metric on the brane,

$${\tilde g_{\mu \nu}}d{x^\mu}d{x^\nu} = - F(r)d{t^2} + {{d{r^2}} \over {H(r)}} + {r^2}d{\Omega ^2},$$

(149)

the projected Weyl term on the brane is given by

$${{\mathcal E}_{00}} = {F \over r}\left[ {H\prime - {{1 - H} \over r}} \right],$$

(150)

$${{\mathcal E}_{rr}} = - {1 \over {rH}}\left[ {{{F\prime} \over F} - {{1 - H} \over r}} \right],$$

(151)

$${{\mathcal E}_{\theta \theta}} = - 1 + H + {r \over 2}H\left({{{F\prime} \over F} + {{H\prime} \over H}} \right).$$

(152)

These components allow one to evaluate the metric coefficients in Equation (148). For example, the area of the 5D horizon is determined by ${\tilde g_{\theta \theta}}$; defining ψ (r) as the deviation from a Schwarzschild form for, i.e.,

$$H(r) = 1 - {{2m} \over r} + \psi (r),$$

(153)

where m is constant, we find

$${\tilde g_{\theta \theta}}(r,y) = {r^2} - \psi \prime\left({1 + {2 \over \ell}\vert y\vert} \right){y^2} + {1 \over {6{r^2}}}\left[ {\psi \prime + {1 \over 2}(1 + \psi \prime)(r\psi \prime - \psi)\prime} \right]{y^4} + \ldots$$

(154)

This shows how ψ and its r-derivatives determine the change in area of the horizon along the extra dimension. For the black string ψ = 0, and we have ${\tilde g_{\theta \theta}}(r,y) = {r^2}$. For a large black hole, with horizon scale ≫ ℓ, we have from Equation (41) that

$$\psi \approx - {{4m{\ell ^2}} \over {3{r^3}}}.$$

(155)

This implies that ${\tilde g_{\theta \theta}}$ is decreasing as we move off the brane, consistent with a pancake-like shape of the horizon. However, note that the horizon shape is tubular in Gaussian normal coordinates [163].

4.3 The “tidal charge” black hole

The equations (143) form a system of constraints on the brane in the stationary case, including the static spherical case, for which

$$\Theta = 0 = {\omega _\mu} = {\sigma _{\mu \nu}},\qquad {\dot \rho _{\mathcal E}} = 0 = q_\mu ^{\mathcal E} = \dot \pi _{\mu \nu}^{\mathcal E}.$$

(156)

The nonlocal conservation equations ${\nabla ^\nu}{{\mathcal E}_{\mu \nu}} = 0$ reduce to

$${1 \over 3}{\vec \nabla _\mu}{\rho _{\mathcal E}} + {4 \over 3}{\rho _{\mathcal E}}{A_\mu} + {\vec \nabla ^\nu}\pi _{\mu \nu}^{\mathcal E} + {A^\nu}\pi _{\mu \nu}^{\mathcal E} = 0,$$

(157)

where, by symmetry,

$$\pi _{\mu \nu}^{\mathcal E} = {\Pi _{\mathcal E}}\left({{1 \over 3}{h_{\mu \nu}} - {r_\mu}{r_\nu}} \right),$$

(158)

for some ${\Pi _{\mathcal E}}(r)$, with r_μ being the unit radial vector. The solution of the brane field equations requires the input of ${{\mathcal E}_{\mu \nu}}$ from the 5D solution. In the absence of a 5D solution, one can make an assumption about ${{\mathcal E}_{\mu \nu}}$ or g_μν to close the 4D equations.

If we assume a metric on the brane of Schwarzschild-like form, i.e. H = F in Equation (149), then the general solution of the brane field equations is [105]

$$F = 1 - {{2GM} \over r} + {{2G\ell Q} \over {{r^2}}},$$

(159)

$${{\mathcal E}_{\mu \nu}} = - {{2G\ell Q} \over {{r^4}}}\left[ {{u_\mu}{u_\nu} - 2{r_\mu}{r_\nu} + {h_{\mu \nu}}} \right],$$

(160)

where Q is a constant. It follows that the KK energy density and anisotropic stress scalar (defined via Equation (158)) are given by

$${\rho _{\mathcal E}} = {{\ell Q} \over {4\pi \,{r^4}}} = {1 \over 2}{\Pi _{\mathcal E}}.$$

(161)

The solution (159) has the form of the general relativity Reissner-Nordström solution, but there is no electric field on the brane. Instead, the nonlocal Coulomb effects imprinted by the bulk Weyl tensor have induced a “tidal” charge parameter Q, where Q = Q (M), since M is the source of the bulk Weyl field. We can think of the gravitational field of M being “reflected back” on the brane by the negative bulk cosmological constant [104]. If we impose the small-scale perturbative limit (r ≪ ℓ) in Equation (40), we find that

$$Q = - 2M.$$

(162)

Negative Q is in accord with the intuitive idea that the tidal charge strengthens the gravitational field, since it arises from the source mass M on the brane. By contrast, in the Reissner-Nordström solution of general relativity, Q ∝ + q², where q is the electric charge, and this weakens the gravitational field. Negative tidal charge also preserves the spacelike nature of the singularity, and it means that there is only one horizon on the brane, outside the Schwarzschild horizon:

$${r_{\rm{h}}} = GM\left[ {1 + \sqrt {1 - {{2\ell Q} \over {G{M^2}}}}} \right] = GM\left[ {1 + \sqrt {1 + {{4\ell} \over {GM}}}} \right].$$

(163)

The tidal-charge black hole metric does not satisfy the far-field r⁻³ correction to the gravitational potential, as in Equation (41), and therefore cannot describe the end-state of collapse. However, Equation (159) shows the correct 5D behaviour of the potential (∝ r⁻²) at short distances, so that the tidal-charge metric could be a good approximation in the strong-field regime for small black holes.

4.4 Realistic black holes

Thus a simple brane-based approach, while giving useful insights, does not lead to a realistic black hole solution. There is no known solution representing a realistic black hole localized on the brane, which is stable and without naked singularity. This remains a key open question of nonlinear brane-world gravity. (Note that an exact solution is known for a black hole on a 1+2-brane in a 4D bulk [141], but this is a very special case.) Given the nonlocal nature of ${{\mathcal E}_{\mu \nu}}$ it is possible that the process of gravitational collapse itself leaves a signature in the black hole end-state, in contrast with general relativity and its no-hair theorems. There are contradictory indications about the nature of the realistic black hole solution on the brane:

• Numerical simulations of highly relativistic static stars on the brane [427] indicate that general relativity remains a good approximation.

• Exact analysis of Oppenheimer-Snyder collapse on the brane shows that the exterior is non-static [159], and this is extended to general collapse by arguments based on a generalized AdS/CFT correspondence [406, 139].

The first result suggests that static black holes could exist as limits of increasingly compact static stars, but the second result and conjecture suggest otherwise. This remains an open question. More recent numerical evidence is also not conclusive, and it introduces further possible subtleties to do with the size of the black hole [262, 430].

On very small scales relative to the AdS₅ curvature scale, r ≪ ℓ, the gravitational potential becomes 5D, as shown in Equation (40),

$$V(r) \approx {{G\ell M} \over {{r^2}}} = {{{G_5}M} \over {{r^2}}}.$$

(164)

In this regime, the black hole is so small that it does not “see” the brane, so that it is approximately a 5D Schwarzschild (static) solution. However, this is always an approximation because of the self-gravity of the brane (the situation is different in ADD-type brane-worlds where there is no brane tension). As the black hole size increases, the approximation breaks down. Nevertheless, one might expect that static solutions exist on sufficiently small scales. Numerical investigations appear to confirm this [262, 430]: Static metrics satisfying the asymptotic AdS₅ boundary conditions are found if the horizon is small compared to ℓ, but no numerical convergence can be achieved close to ℓ. The numerical instability that sets in may mask the fact that even the very small black holes are not strictly static. Or it may be that there is a transition from static to non-static behaviour. Or it may be that static black holes do exist on all scales.

The 4D Schwarzschild metric cannot describe the final state of collapse, since it cannot incorporate the 5D behaviour of the gravitational potential in the strong-field regime (the metric is incompatible with massive KK modes). A non-perturbative exterior solution should have nonzero ${{\mathcal E}_{\mu \nu}}$ in order to be compatible with massive KK modes in the strong-field regime. In the end-state of collapse, we expect an ${{\mathcal E}_{\mu \nu}}$ which goes to zero at large distances, recovering the Schwarzschild weak-field limit, but which grows at short range. Furthermore, ${{\mathcal E}_{\mu \nu}}$ may carry a Weyl “fossil record” of the collapse process.

4.5 Oppenheimer-Snyder collapse gives a non-static black hole

The simplest scenario in which to analyze gravitational collapse is the Oppenheimer-Snyder model, i.e., collapsing homogeneous and isotropic dust [159]. The collapse region on the brane has an FRW metric, while the exterior vacuum has an unknown metric. In 4D general relativity, the exterior is a Schwarzschild spacetime; the dynamics of collapse leaves no imprint on the exterior.

The collapse region has the metric

$$d{s^2} = - d{\tau ^2} + {{a{{(\tau)}^2}\left[ {d{r^2} + {r^2}d{\Omega ^2}} \right]} \over {{{(1 + k{r^2}/4)}^2}}},$$

(165)

where the scale factor satisfies the modified Friedmann equation (see below),

$${{{{\dot a}^2}} \over {{a^2}}} = {{8\pi G} \over 3}\rho \left({1 + {\rho \over {2\lambda}} + {{{\rho _{\mathcal E}}} \over \rho}} \right).$$

(166)

The dust matter and the dark radiation evolve as

$$\rho = {\rho _0}{\left({{{{a_0}} \over \mu}} \right)^3},\qquad {\rho _{\mathcal E}} = {\rho _{{\mathcal E}\,0}}{\left({{{{a_0}} \over \mu}} \right)^4},$$

(167)

where a₀ is the epoch when the cloud started to collapse. The proper radius from the centre of the cloud is R (τ) = ra (τ)/($R(\tau) = ra(\tau)/(1 + {1 \over 4}k{r^2})$). The collapsing boundary surface ∑ is given in the interior comoving coordinates as a free-fall surface, i.e., r = r₀ = const., so that ${R_\Sigma}(\tau) = {r_0}a(\tau)/(1 + {1 \over 4}kr_0^2)$

We can rewrite the modified Friedmann equation on the interior side of ∑ as

$${\dot R^2} = {{2GM} \over R} + {{3G{M^2}} \over {4\pi \lambda {R^4}}} + {Q \over {{R^2}}} + E,$$

(168)

where the “physical mass” M (total energy per proper star volume), the total “tidal charge” Q, and the “energy” per unit mass E are given by

$$M = {{4\pi a_0^3r_0^3{\rho _0}} \over {3{{(1 + {1 \over 4}kr_0^2)}^3}}},$$

(169)

$$Q = {{{\rho _{{\mathcal E}\,0}}a_0^4r_0^4} \over {{{(1 + {1 \over 4}kr_0^2)}^4}}},$$

(170)

$$E = - {{kr_0^2} \over {{{(1 + {1 \over 4}kr_0^2)}^2}}} > - 1.$$

(171)

Now we assume that the exterior is static, and satisfies the standard 4D junction conditions. Then we check whether this exterior is physical by imposing the modified Einstein equations (143). We will find a contradiction.

The standard 4D Darmois-Israel matching conditions, which we assume hold on the brane, require that the metric and the extrinsic curvature of ∑ be continuous (there are no intrinsic stresses on ∑). The extrinsic curvature is continuous if the metric is continuous and if Ṙ is continuous. We therefore need to match the metrics and Ṙ across ∑.

The most general static spherical metric that could match the interior metric on ∑ is

$$d{s^2} = - F{(R)^2}\left[ {1 - {{2Gm(R)} \over R}} \right]d{t^2} + {{d{R^2}} \over {1 - 2Gm(R)/R}} + {R^2}d{\Omega ^2}.$$

(172)

We need two conditions to determine the functions F (R) and m (R). Now ∑ is a freely falling surface in both metrics, and the radial geodesic equation for the exterior metric gives Ṙ^{2 =} −1+2Gm (R)/R+Ẽ/F (R)², where Ẽ is a constant and the dot denotes a proper time derivative, as above. Comparing this with Equation (168) gives one condition. The second condition is easier to derive if we change to null coordinates. The exterior static metric, with

$$dv = dt + {{dR} \over {(1 - 2Gm/R)F}},$$

(173)

The interior Robertson—Walker metric takes the form [159]

$$d{s^2} = - {F^2}\left({1 - {{2Gm} \over R}} \right)d{v^2} + 2F\,dv\,dR + {R^2}\,d{\Omega ^2}.$$

(174)

where

$$d\tau = {\tau _{,v}}dv + \left({1 + {1 \over 4}k{r^2}} \right){{dR} \over {r\dot a - 1 + {1 \over 4}k{r^2}}}.$$

Comparing Equations (173) and (174) on ∑ gives the second condition. The two conditions together imply that F is a constant, which we can take as F (R) = 1 without loss of generality (choosing Ẽ = E + 1), and that

$$m(R) = M + {{3{M^2}} \over {8\pi \lambda {R^3}}} + {Q \over {2GR}}.$$

(175)

In the limit λ⁻¹ = 0 = Q, we recover the 4D Schwarzschild solution. In the general brane-world case, Equations (172) and (175) imply that the brane Ricci scalar is

$${R^\mu}_\mu = {{9G{M^2}} \over {2\pi \lambda {R^6}}}.$$

(176)

However, this contradicts the field equations (143), which require

$${R^\mu}_\mu = 0.$$

(177)

It follows that a static exterior is only possible if M/λ = 0, which is the 4D general relativity limit. In the brane-world, collapsing homogeneous and isotropic dust leads to a non-static exterior. Note that this no-go result does not require any assumptions on the nature of the bulk spacetime, which remains to be determined.

Although the exterior metric is not determined (see [178] for a toy model), we know that its non-static nature arises from

• 5D bulk graviton stresses, which transmit effects nonlocally from the interior to the exterior, and

• the non-vanishing of the effective pressure at the boundary, which means that dynamical information from the interior can be conveyed outside via the 4D matching conditions.

The result suggests that gravitational collapse on the brane may leave a signature in the exterior, dependent upon the dynamics of collapse, so that astrophysical black holes on the brane may in principle have KK “hair”. It is possible that the non-static exterior will be transient, and will tend to a static geometry at late times, close to Schwarzschild at large distances.

4.6 AdS/CFT and black holes on 1-brane RS-type models

Oppenheimer-Snyder collapse is very special; in particular, it is homogeneous. One could argue that the non-static exterior arises because of the special nature of this model. However, the underlying reasons for non-static behaviour are not special to this model; on the contrary, the role of high-energy corrections and KK stresses will if anything be enhanced in a general, inhomoge-neous collapse. There is in fact independent heuristic support for this possibility, arising from the AdS/CFT correspondence.

The basic idea of the correspondence is that the classical dynamics of the AdS5 gravitational field correspond to the quantum dynamics of a 4D conformal field theory on the brane. This correspondence holds at linear perturbative order [129], so that the RS 1-brane infinite AdS₅ brane-world (without matter fields on the brane) is equivalently described by 4D general relativity coupled to conformal fields,

$${G_{\mu \nu}} = 8\pi GT_{\mu \nu}^{({\rm{cft}})}.$$

(178)

According to a conjecture [406], the correspondence holds also in the case where there is strong gravity on the brane, so that the classical dynamics of the bulk gravitational field of the brane black hole are equivalent to the dynamics of a quantum-corrected 4D black hole (in the dual CFT-plus-gravity description). In other words [406, 139]:

• Quantum backreaction due to Hawking radiation in the 4D picture is described as classical dynamics in the 5D picture.

• The black hole evaporates as a classical process in the 5D picture, and there is thus no stationary black hole solution in RS 1-brane.

A further remarkable consequence of this conjecture is that Hawking evaporation is dramatically enhanced, due to the very large number of CFT modes of order (ℓ/ℓ_P)². The energy loss rate due to evaporation is

$${{\dot M} \over M}\sim N\left({{1 \over {{G^2}{M^3}}}} \right),$$

(179)

where N is the number of light degrees of freedom. Using N ∼ ℓ²/G, this gives an evaporation timescale [406]

$${t_{{\rm{evap}}}}\sim {\left({{M \over {{M_ \odot}}}} \right)^3}{\left({{{1\;{\rm{mm}}} \over \ell}} \right)^2}\;{\rm{yr}}.$$

(180)

A more detailed analysis [140] shows that this expression should be multiplied by a factor ≈ 100. Then the existence of stellar-mass black holes on long time scales places limits on the AdS5 curvature scale that are more stringent than the table-top limit, Equation (6). The existence of black hole X-ray binaries implies

$$\ell \lesssim {10^{- 2}}\;{\rm{mm}},$$

(181)

already an order of magnitude improvement on the table-top limit.

One can also relate the Oppenheimer-Snyder result to these considerations. In the AdS/CFT picture, the non-vanishing of the Ricci scalar, Equation (176), arises from the trace of the Hawking CFT energy-momentum tensor, as in Equation (178). If we evaluate the Ricci scalar at the black hole horizon, R ∼ 2 GM, using $\lambda = 6M_5^6/M_{\rm{p}}^2$, we find

$${R^\mu}_\mu \sim {{{M_5}^{12}\,{\ell ^6}} \over {{M^4}}}.$$

(182)

The CFT trace on the other hand is given by ${T^{({\rm{cft}})}}\sim NT_{\rm{h}}^4/M_{\rm{p}}^2$, so that

$$8\pi G{T^{({\rm{cft}})}}\sim {{{M_5}^{12}\,{\ell ^6}} \over {{M^4}}}.$$

(183)

Thus the Oppenheimer-Snyder result is qualitatively consistent with the AdS/CFT picture.

Clearly the black hole solution, and the collapse process that leads to it, have a far richer structure in the brane-world than in general relativity, and deserve further attention. In particular, two further topics are of interest:

• Primordial black holes in 1-brane RS-type cosmology have been investigated in [210, 185, 184, 313, 91, 384]. High-energy effects in the early universe (see the next Section 5) can significantly modify the evaporation and accretion processes, leading to a prolonged survival of these black holes. Such black holes evade the enhanced Hawking evaporation described above when they are formed, because they are much smaller than ℓ.

• Black holes will also be produced in particle collisions at energies ≳ M₅, possibly well below the Planck scale. In ADD brane-worlds, where $M_{4+d} = {\mathcal O}(\rm{TeV})$ is not ruled out by current observations if d > 1, this raises the exciting prospect of observing black hole production signatures in the next-generation colliders and cosmic ray detectors (see [75, 169, 138]).

5 Brane-World Cosmology: Dynamics

A 1+4-dimensional spacetime with spatial 4-isotropy (4D spherical/plane/hyperbolic symmetry) has a natural foliation into the symmetry group orbits, which are 1+3-dimensional surfaces with 3-isotropy and 3-homogeneity, i.e., FRW surfaces. In particular, the AdS5 bulk of the RS brane-world, which admits a foliation into Minkowski surfaces, also admits an FRW foliation since it is 4-isotropic. Indeed this feature of 1-brane RS-type cosmological brane-worlds underlies the importance of the AdS/CFT correspondence in brane-world cosmology [342, 375, 193, 386, 390, 290, 347, 180].

The generalization of AdS₅ that preserves 4-isotropy and solves the vacuum 5D Einstein equation (22) is Schwarzschild-AdS₅, and this bulk therefore admits an FRW foliation. It follows that an FRW brane-world, the cosmological generalization of the RS brane-world, is a part of Schwarzschild-AdS₅, with the Z₂-symmetric FRW brane at the boundary. (Note that FRW branes can also be embedded in non-vacuum generalizations, e.g., in Reissner-Nordström-AdS₅ and Vaidya-AdS₅.)

In natural static coordinates, the bulk metric is

$$^{(5)}d{s^2} = - F(R)d{T^2} + {{d{R^2}} \over {F(R)}} + {R^2}\left({{{d{r^2}} \over {1 - K{r^2}}} + {r^2}d{\Omega ^2}} \right),$$

(184)

$$F(R) = K + {{{R^2}} \over {{\ell ^2}}} - {m \over {{R^2}}},$$

(185)

where K = 0, ±1 is the FRW curvature index, and m is the mass parameter of the black hole at R = 0 (recall that the 5D gravitational potential has R⁻² behaviour). The bulk black hole gives rise to dark radiation on the brane via its Coulomb effect. The FRW brane moves radially along the 5th dimension, with R = a (T), where a is the FRW scale factor, and the junction conditions determine the velocity via the Friedmann equation for a [336, 45]. Thus one can interpret the expansion of the universe as motion of the brane through the static bulk. In the special case m = 0 and da/dT = 0, the brane is fixed and has Minkowski geometry, i.e., the original RS 1-brane brane-world is recovered in different coordinates.

The velocity of the brane is coordinate-dependent, and can be set to zero. We can use Gaussian normal coordinates, in which the brane is fixed but the bulk metric is not manifestly static [38]:

$$^{(5)}d{s^2} = - {N^2}(t,y)d{t^2} + {A^2}(t,y)\left[ {{{d{r^2}} \over {1 - K{r^2}}} + {r^2}d{\Omega ^2}} \right] + d{y^2}.$$

(186)

Here a (t) = A (t, 0) is the scale factor on the FRW brane at y = 0, and t may be chosen as proper time on the brane, so that N (t, 0) = 1. In the case where there is no bulk black hole (m = 0), the metric functions are

$$N = {{\dot A(t,y)} \over {\dot a(t)}},$$

(187)

$$A = a(t)\left[ {\cosh \left({{y \over \ell}} \right) - \left\{{1 + {{\rho (t)} \over \lambda}} \right\}\sinh \left({{{\vert y\vert} \over \ell}} \right)} \right].$$

(188)

Again, the junction conditions determine the Friedmann equation. The extrinsic curvature at the brane is

$${K^\mu}_\nu = {\rm{diag}}{\left({{{N{\prime}} \over N},{{A{\prime}} \over A},{{A{\prime}} \over A},{{A{\prime}} \over A}} \right)_{{\rm{brane}}}}.$$

(189)

Then, by Equation (68),

$${\left. {{{N{\prime}} \over N}} \right\vert _{{\rm{brane}}}} = {{\kappa _5^2} \over 6}(2\rho + 3p - \lambda),$$

(190)

$${\left. {{{A{\prime}} \over A}} \right\vert _{{\rm{brane}}}} = - {{\kappa _5^2} \over 6}(\rho + \lambda).$$

(191)

The field equations yield the first integral [38]

$${(AA{\prime})^2} - {{{A^2}} \over {{N^2}}}{\dot A^2} + {{{\Lambda _5}} \over 6}{A^4} + m = 0,$$

(192)

where m is constant. Evaluating this at the brane, using Equation (191), gives the modified Friedmann equation (194).

The dark radiation carries the imprint on the brane of the bulk gravitational field. Thus we expect that ${{\mathcal E}_{\mu \nu}}$ for the Friedmann brane contains bulk metric terms evaluated at the brane. In Gaussian normal coordinates (using the field equations to simplify),

$${{\mathcal E}^0}_0 = 3{\left. {{{A{\prime\prime}} \over A}} \right\vert_{{\rm{brane}}}} + {{{\Lambda _5}} \over 2},\qquad {{\mathcal E}^i}_j = - \left({{1 \over 3}{{\mathcal E}^0}_0} \right){\delta ^i}_j.$$

(193)

Either form of the cosmological metric, Equation (184) or (186), may be used to show that 5D gravitational wave signals can take “short-cuts” through the bulk in travelling between points A and B on the brane [89, 211, 65]. The travel time for such a graviton signal is less than the time taken for a photon signal (which is stuck to the brane) from A to B.

Instead of using the junction conditions, we can use the covariant 3D Gauss-Codazzi equation (140) to find the modified Friedmann equation:

$${H^2} = {{{\kappa ^2}} \over 3}\rho \left({1 + {\rho \over {2\lambda}}} \right) + {m \over {{a^4}}} + {1 \over 3}\Lambda - {K \over {{a^2}}},$$

(194)

on using Equation (124), where

$$m = {{{\kappa ^2}} \over 3}\rho \varepsilon \,{}_0a_0^4.$$

(195)

The covariant Raychauhuri equation (129) yields

$$\dot H = - {{{\kappa ^2}} \over 2}(\rho + p)\left({1 + {\rho \over \lambda}} \right) - 2{m \over {{a^4}}} + {K \over {{a^2}}},$$

(196)

which also follows from differentiating Equation (194) and using the energy conservation equation.

When the bulk black hole mass vanishes, the bulk geometry reduces to AdS₅, and ${\rho _{\mathcal E}} = 0$. In order to avoid a naked singularity, we assume that the black hole mass is non-negative, so that ${\rho _{{\mathcal E}\,0}} \geq 0$.(By Equation (185), it is possible to avoid a naked singularity with negative m when K = −1, provided ∣ m ∣ ≤ ℓ²/ 4.) This additional effective relativistic degree of freedom is constrained by nucleosynthesis and CMB observations to be no more than ∼ 5% of the radiation energy density [271, 24, 208, 47]:

$${\left. {{{\rho \varepsilon} \over {{\rho _{{\rm{rad}}}}}}} \right\vert_{{\rm{nuc}}}} {\lesssim}\, 0.05.$$

(197)

The other modification to the Hubble rate is via the high-energy correction ρ/λ. In order to recover the observational successes of general relativity, the high-energy regime where significant deviations occur must take place before nucleosynthesis, i.e., cosmological observations impose the lower limit

$$\lambda > {(1\;{\rm{MeV}})^4}\quad \Rightarrow \quad {M_5} > {10^4}\;{\rm{GeV}}.$$

(198)

This is much weaker than the limit imposed by table-top experiments, Equation (42). Since ρ²/λ decays as a⁻⁸ during the radiation era, it will rapidly become negligible after the end of the high-energy regime,ρ = λ.

If ${\rho _{\mathcal E}} = 0$ and K = 0 = Λ, then the exact solution of the Friedmann equations for w = p/ρ = const. is [38]

$$a = {\rm{const}}. \times {[t(t + {t_\lambda})]^{1/3(w + 1)}},\qquad {t_\lambda} = {{{M_{\rm{p}}}} \over {\sqrt {3\pi \lambda} (1 + w)}} \lesssim {(1 + w)^{- 1}}{10^{- 9}}\;{\rm{s}},$$

(199)

where w > −1. If ${\rho _{\mathcal E}} \neq 0$ (but K = 0 = Λ), then the solution for the radiation era ($w = {1 \over 3}$) is [24]

$$a = {\rm{const}}. \times {[t(t + {t_\lambda})]^{1/4}},\qquad {t_\lambda} = {{\sqrt 3 \,{M_{\rm{p}}}} \over {4\sqrt {\pi \lambda} \,(1 + \rho \varepsilon /\rho)}}.$$

(200)

For t ≫ t_λ we recover from Equations (199) and (200) the standard behaviour, a ∝ t^{2/3(w + 1)}, whereas for t ≫ t_λ, we have the very different behaviour of the high-energy regime,

$$\rho \gg \lambda \quad \Rightarrow \quad a \propto {t^{1/3(w + 1)}}.$$

(201)

When w = −1 we have ρ = ρ₀ from the conservation equation. If K = 0 = Λ, we recover the de Sitter solution for ${\rho _{\mathcal E}} = 0$ and an asymptotically de Sitter solution for ${\rho _{\mathcal E}} > 0$:

$$a = {a_0}\exp [{H_0}(t - {t_0})],\qquad {H_0} = \kappa \sqrt {{{{\rho _0}} \over 3}\left({1 + {{{\rho _0}} \over {2\lambda}}} \right)} ,\qquad {\rm{for}}\,\rho \epsilon = 0,$$

(202)

$${a^2} = \sqrt {{m \over {{H_0}}}} \sinh [2{H_0}(t - {t_0})]\qquad \qquad \qquad \qquad \qquad \qquad {\rm{for}}\rho \epsilon > 0.$$

(203)

A qualitative analysis of the Friedmann equations is given in [68, 67].

5.1 Brane-world inflation

In 1-brane RS-type brane-worlds, where the bulk has only a vacuum energy, inflation on the brane must be driven by a 4D scalar field trapped on the brane. In more general brane-worlds, where the bulk contains a 5D scalar field, it is possible that the 5D field induces inflation on the brane via its effective projection [231, 195, 146, 368, 198, 197, 407, 426, 259, 275, 196, 46, 325, 221, 315, 149, 18].

More exotic possibilities arise from the interaction between two branes, including possible collision, which is mediated by a 5D scalar field and which can induce either inflation [134, 220] or a hot big-bang radiation era, as in the “ekpyrotic” or cyclic scenario [229, 215, 339, 403, 273, 317, 412], or in colliding bubble scenarios [40, 156, 157]. (See also [26, 98, 299] for colliding branes in an M theory approach.) Here we discuss the simplest case of a 4D scalar field ϕ with potential V (ϕ) (see [287] for a review).

High-energy brane-world modifications to the dynamics of inflation on the brane have been investigated [308, 216, 92, 405, 320, 319, 106, 285, 34, 35, 36, 328, 192, 264, 363, 307]. Essentially, the high-energy corrections provide increased Hubble damping, since ρ ≫ λ implies that H is larger for a given energy than in 4D general relativity. This makes slow-roll inflation possible even for potentials that would be too steep in standard cosmology [308, 99, 312, 369, 346, 286, 205].

The field satisfies the Klein-Gordon equation

$$\ddot \phi + 3H\dot \phi + V{\prime}(\phi) = 0.$$

(204)

In 4D general relativity, the condition for inflation, ä > 0, ${\dot \phi ^2} < V(\phi)$, i.e., $p < - {1 \over 3}\rho$, where $\rho = {1 \over 2}{\dot \phi ^2} + V$ and $p = {1 \over 2}{\dot \phi ^2} - V$ The modified Friedmann equation leads to a stronger condition for inflation: Using Equation (194), with m = 0 = Λ = K, and Equation (204), we find that

$$\ddot a > 0\quad \Rightarrow \quad w < - {1 \over 3}\left[ {{{1 + 2\rho /\lambda} \over {1 + \rho /\lambda}}} \right],$$

(205)

where the square brackets enclose the brane correction to the general relativity result. As ρ/λ → 0, the 4D result $w < - {1 \over 3}$ is recovered, but for ρ > λ, w must be more negative for inflation. In the very high-energy limit ρ/λ → ∞, we have $w < - {2 \over 3}$. When the only matter in the universe is a self-interacting scalar field, the condition for inflation becomes

$${\dot \phi ^2} - V + \left[ {{{{1 \over 2}{{\dot \phi}^2} + V} \over \lambda}\left({{5 \over 4}{{\dot \phi}^2} - {1 \over 2}V} \right)} \right] < 0,$$

(206)

which reduces to ${\dot \phi ^2} < V$ when ${\rho _\phi} = {1 \over 2}{\dot \phi ^2} + V \ll \lambda$

In the slow-roll approximation, we get

$${H^2} \approx {{{\kappa ^2}} \over 3}V\left[ {1 + {V \over {2\lambda}}} \right],$$

(207)

$$\dot \phi \approx - {{V{\prime}} \over {3H}}.$$

(208)

The brane-world correction term V/λ in Equation (207) serves to enhance the Hubble rate for a given potential energy, relative to general relativity. Thus there is enhanced Hubble’ friction’ in Equation (208), and brane-world effects will reinforce slow-roll at the same potential energy. We can see this by defining slow-roll parameters that reduce to the standard parameters in the low-energy limit:

$$\epsilon \equiv - {{\dot H} \over {{H^2}}} = {{M_{\rm{p}}^2} \over {16\pi}}{\left({{{V{\prime}} \over V}} \right)^2}\left[ {{{1 + V/\lambda} \over {{{(1 + V/2\lambda)}^2}}}} \right],$$

(209)

$$\eta \equiv - {{\ddot \phi} \over {H\dot \phi}} = {{M_{\rm{p}}^2} \over {8\pi}}\left({{{V{\prime\prime}} \over V}} \right)\left[ {{1 \over {1 + V/2\lambda}}} \right].$$

(210)

Self-consistency of the slow-roll approximation then requires ϵ, ∣η ∣ ≪ 1. At low energies, V ≪ λ, the slow-roll parameters reduce to the standard form. However at high energies, V ≫ λ, the extra contribution to the Hubble expansion helps damp the rolling of the scalar field, and the new factors in square brackets become ≈ λ/V:

$$\epsilon \approx {\epsilon _{{\rm{gr}}}}\left[ {{{4\lambda} \over V}} \right],\qquad \eta \approx {\eta _{{\rm{gr}}}}\left[ {{{2\lambda} \over V}} \right],$$

(211)

where ϵ_gr, η_gr are the standard general relativity slow-roll parameters. In particular, this means that steep potentials which do not give inflation in general relativity, can inflate the brane-world at high energy and then naturally stop inflating when V drops below λ. These models can be constrained because they typically end inflation in a kinetic-dominated regime and thus generate a blue spectrum of gravitational waves, which can disturb nucleosynthesis [99, 312, 369, 346, 286]. They also allow for the novel possibility that the inflaton could act as dark matter or quintessence at low energies [99, 312, 369, 346, 286, 8, 327, 288, 56, 380].

The number of e-folds during inflation, N = ∫ Hdt, is, in the slow-roll approximation,

$$N \approx - {{8\pi} \over {M_{\rm{p}}^2}}\int\nolimits_{{\phi _{\rm{i}}}}^{{\phi _{\rm{f}}}} {{V \over {V{\prime}}}} \left[ {1 + {V \over {2\lambda}}} \right]d\phi .$$

(212)

Brane-world effects at high energies increase the Hubble rate by a factor V/ 2λ, yielding more inflation between any two values of ϕ for a given potential. Thus we can obtain a given number of e-folds for a smaller initial inflaton value ϕ_i. For V ≫ λ, Equation (212) becomes

$$N \approx - {{128{\pi ^3}} \over {3M_5^6}}\int\nolimits_{{\phi _{\rm{i}}}}^{{\phi _{\rm{f}}}} {{{{V^2}} \over {V{\prime}}}} d\phi .$$

(213)

The key test of any modified gravity theory during inflation will be the spectrum of perturbations produced due to quantum fluctuations of the fields about their homogeneous background values. We will discuss brane-world cosmological perturbations in the next Section 6. In general, perturbations on the brane are coupled to bulk metric perturbations, and the problem is very complicated. However, on large scales on the brane, the density perturbations decouple from the bulk metric perturbations [303, 271, 177, 148]. For 1-brane RS-type models, there is no scalar zero-mode of the bulk graviton, and in the extreme slow-roll (de Sitter) limit, the massive scalar modes are heavy and stay in their vacuum state during inflation [148]. Thus it seems a reasonable approximation in slow-roll to neglect the KK effects carried by ${{\mathcal E}_{\mu \nu}}$ when computing the density perturbations.

To quantify the amplitude of scalar (density) perturbations we evaluate the usual gauge-invariant quantity

$$\zeta \equiv {\mathcal R} - {H \over {\dot \rho}}\delta \rho ,$$

(214)

which reduces to the curvature perturbation ${\mathcal R}$ on uniform density hypersurfaces (δρ = 0). This is conserved on large scales for purely adiabatic perturbations as a consequence of energy conservation (independently of the field equations) [425]. The curvature perturbation on uniform density hypersurfaces is given in terms of the scalar field fluctuations on spatially flat hypersurfaces δϕ by

$$\zeta = H{{\delta \phi} \over {\dot \phi}}.$$

(215)

If one makes the assumption that backreaction due to metric perturbations in the bulk can be neglected, the field fluctuations at Hubble crossing (k = aH) in the slow-roll limit are given by 〈δϕ²〉 ≈ (H/ 2π)², a result for a massless field in de Sitter space that is also independent of the gravity theory [425]. For a single scalar field the perturbations are adiabatic and hence the curvature perturbation ζ can be related to the density perturbations when modes re-enter the Hubble scale during the matter dominated era which is given by $A_{\rm{s}}^2 = 4\langle {\zeta ^2}\rangle/25$. Using the slow-roll equations and Equation (215), this gives

$${\left. {A_{\rm{s}}^2 \approx \left({{{512\pi} \over {75M_{\rm{p}}^6}}\,{{{V^3}} \over {{V{\prime 2}}}}} \right){{\left[ {{{2\lambda + V} \over {2\lambda}}} \right]}^3}} \right\vert_{k = aH}}.$$

(216)

Thus the amplitude of scalar perturbations is increased relative to the standard result at a fixed value of ϕ for a given potential.

A crucial assumption is that backreaction due to metric perturbations in the bulk can be neglected. In the extreme slow-roll limit this is necessarily correct because the coupling between inflaton fluctuations and metric perturbations vanishes; however, this is not necessarily the case when slow-roll corrections are included in the calculation. Previous work [250, 253, 255] has shown that such bulk effects can be subtle and interesting (see also [109, 114] for other approaches). In particular, subhorizon inflaton fluctuations on a brane excite an infinite ladder of Kaluza-Klein modes of the bulk metric perturbations at first order in slow-roll parameters, and a naive slow-roll expansion breaks down in the high-energy regime once one takes into account the backreaction of the bulk metric perturbations, as confirmed by direct numerical simulations [200]. However, an order-one correction to the behaviour of inflaton fluctuations on subhorizon scales does not necessarily imply that the amplitude of the inflaton perturbations receives corrections of order one on large scales; one must consistently quantise the coupled brane inflaton fluctuations and bulk metric perturbations. This requires a detailed analysis of the coupled brane-bulk system [70, 252].

It was shown that the coupling to bulk metric perturbations cannot be ignored in the equations of motion. Indeed, there are order-unity differences between the classical solutions without coupling and with slow-roll induced coupling. However, the change in the amplitude of quantum-generated perturbations is at next-to-leading order [252] because there is still no mixing at leading order between positive and negative frequencies when scales observable today crossed the horizon, so the Bogoliubov coefficients receive no corrections at leading order. The amplitude of perturbations generated is also subject to the usual slow-roll corrections on super-horizon scales. The next-order slow-roll corrections from bulk gravitational perturbations are calculated in [254] and they are the same order as the usual Stewart-Lyth correction [404]. These results also show that the ratio of tensor-to-scalar perturbation amplitudes are not influenced by brane-bulk interactions at leading order in slow-roll. It is remarkable that the predictions from inflation theories should be so robust that this result holds in spite of the leading-order change to the solutions of the classical equations of motion.

The scale-dependence of the perturbations is described by the spectral tilt

$${n_{\rm{s}}} - 1 \equiv {{d\ln A_{\rm{s}}^2} \over {d\ln k}} \approx - 4\epsilon + 2\eta ,$$

(217)

where the slow-roll parameters are given in Equations (209) and (210). Because these slow-roll parameters are both suppressed by an extra factor λ/V at high energies, we see that the spectral index is driven towards the Harrison-Zel’dovich spectrum, n_s → 1, as V/λ → ∞; however, as explained below, this does not necessarily mean that the brane-world case is closer to scale-invariance than the general relativity case.

As an example, consider the simplest chaotic inflation model $V = {1 \over 2}{m^2}{\phi ^2}$. Equation (212) gives the integrated expansion from ϕ_i to ϕ_f as

$$N \approx {{2\pi} \over {M_{\rm{p}}^2}}\left({\phi _{\rm{i}}^2 - \phi _{\rm{f}}^2} \right) + {{{\pi ^2}{m^2}} \over {3M_5^6}}\left({\phi _{\rm{i}}^4 - \phi _{\rm{f}}^4} \right).$$

(218)

The new high-energy term on the right leads to more inflation for a given initial inflaton value ϕ_i.

The standard chaotic inflation scenario requires an inflaton mass m ∼ 10¹³ GeV to match the observed level of anisotropies in the cosmic microwave background (see below). This corresponds to an energy scale ∼ 10¹⁶ GeV when the relevant scales left the Hubble scale during inflation, and also to an inflaton field value of order 3M_p. Chaotic inflation has been criticised for requiring super-Planckian field values, since these can lead to nonlinear quantum corrections in the potential.

If the brane tension λ is much below 10¹⁶ GeV, corresponding to M₅ < 10¹⁷ GeV, then the terms quadratic in the energy density dominate the modified Friedmann equation. In particular the condition for the end of inflation given in Equation (206) becomes ${\dot \phi ^2} < {2 \over 5}V$. In the slow-roll approximation (using Equations (207) and (208)) $\dot \phi \approx - M_5^3/2\pi \phi$, and this yields

$$\phi _{{\rm{end}}}^4 \approx {5 \over {4{\pi ^2}}}{\left({{{{M_5}} \over m}} \right)^2}M_5^4.$$

(219)

In order to estimate the value of ϕ when scales corresponding to large-angle anisotropies on the microwave background sky left the Hubble scale during inflation, we take N_cobe ≈ 55 in Equation (218) and ϕ_f = ϕ_end. The second term on the right of Equation (218) dominates, and we obtain

$$\phi _{{\rm{cobe}}}^4 \approx {{165} \over {{\pi ^2}}}{\left({{{{M_5}} \over m}} \right)^2}M_5^4.$$

(220)

Imposing the COBE normalization on the curvature perturbations given by Equation (216) requires

$${A_{\rm{s}}} \approx \left({{{8{\pi ^2}} \over {45}}} \right){{{m^4}\phi _{{\rm{cobe}}}^5} \over {M_5^6}} \approx 2 \times {10^{- 5}}.$$

(221)

Substituting in the value of ϕ_cobe given by Equation (220) shows that in the limit of strong brane corrections, observations require

$$m \approx 5 \times {10^{- 5}}\,{M_5},\qquad {\phi _{{\rm{cobe}}}} \approx 3 \times {10^2}\,{M_5}.$$

(222)

Thus for M₅ < 10¹⁷ GeV, chaotic inflation can occur for field values below the 4D Planck scale, ϕ_cobe < M_p, although still above the 5D scale M₅. The relation determined by COBE constraints for arbitrary brane tension is shown in Figure 5, together with the high-energy approximation used above, which provides an excellent fit at low brane tension relative to M₄.

Figure 5

The relation between the inflaton mass m/M₄ (M₄ ≡ M_p) and the brane tension ${(\lambda/M_4^4)^{1/4}}$ necessary to satisfy the COBE constraints. The straight line is the approximation used in Equation (220), which at high energies is in excellent agreement with the exact solution, evaluated numerically in slow-roll. (Figure taken from [308].)

It must be emphasized that in comparing the high-energy brane-world case to the standard 4D case, we implicitly require the same potential energy. However, precisely because of the high-energy effects, large-scale perturbations will be generated at different values of V than in the standard case, specifically at lower values of V, closer to the reheating minimum. Thus there are two competing effects, and it turns out that the shape of the potential determines which is the dominant effect [284]. For the quadratic potential, the lower location on V dominates, and the spectral tilt is slightly further from scale invariance than in the standard case. The same holds for the quartic potential. Data from WMAP and 2dF can be used to constrain inflationary models via their deviation from scale invariance, and the high-energy brane-world versions of the quadratic and quartic potentials are thus under more pressure from data than their standard counterparts [284], as shown in Figure 6.

Figure 6

Constraints from WMAP data on inflation models with quadratic and quartic potentials, where R is the ratio of tensor to scalar amplitudes and n is the scalar spectral index. The high energy (H.E.) and low energy (L.E.) limits are shown, with intermediate energies in between, and the 1-σ and 2-σ contours are also shown. (Figure taken from [284].)

Other perturbation modes have also been investigated:

• High-energy inflation on the brane also generates a zero-mode (4D graviton mode) of tensor perturbations, and stretches it to super-Hubble scales, as will be discussed below. This zero-mode has the same qualitative features as in general relativity, remaining frozen at constant amplitude while beyond the Hubble horizon. Its amplitude is enhanced at high energies, although the enhancement is much less than for scalar perturbations [272]:

  $$A_{\rm{t}}^2 \approx \left({{{32V} \over {75M_{\rm{p}}^2}}} \right)\;\left[ {{{3{V^2}} \over {4{\lambda ^2}}}} \right],$$

  (223)
  $${{A_{\rm{t}}^2} \over {A_{\rm{s}}^2}} \approx \left({{{M_{\rm{p}}^2} \over {16\pi}}{{{{V}\prime 2}} \over {{V^2}}}} \right)\;\left[ {{{6\lambda} \over V}} \right].$$

  (224)

  Equation (224) means that brane-world effects suppress the large-scale tensor contribution to CMB anisotropies. The tensor spectral index at high energy has a smaller magnitude than in general relativity,

  $${n_{\rm{t}}} = - 3\epsilon,$$

  (225)

  but remarkably the same consistency relation as in general relativity holds [205]:

  $${n_{\rm{t}}} = - 2{{A_{\rm{t}}^2} \over {A_{\rm{s}}^2}}.$$

  (226)

  This consistency relation persists when Z₂ symmetry is dropped [206] (and in a two-brane model with stabilized radion [172]). It holds only to lowest order in slow-roll, as in general relativity, but the reason for this [381] and the nature of the corrections [64] are not settled. The massive KK modes of tensor perturbations remain in the vacuum state during slow-roll inflation [272, 176]. The evolution of the super-Hubble zero mode is the same as in general relativity, so that high-energy brane-world effects in the early universe serve only to rescale the amplitude. However, when the zero mode re-enters the Hubble horizon, massive KK modes can be excited.

• Vector perturbations in the bulk metric can support vector metric perturbations on the brane, even in the absence of matter perturbations (see the next Section 6). However, there is no normalizable zero mode, and the massive KK modes stay in the vacuum state during brane-world inflation [52]. Therefore, as in general relativity, we can neglect vector perturbations in inflationary cosmology.

Brane-world effects on large-scale isocurvature perturbations in 2-field inflation have also been considered [17]. Brane-world (p)reheating after inflation is discussed in [414, 429, 9, 415, 96].

5.2 Brane-world instanton

The creation of an inflating brane-world can be modelled as a de Sitter instanton in a way that closely follows the 4D instanton, as shown in [154]. The instanton consists of two identical patches of AdS₅ joined together along a de Sitter brane (dS₄) with compact spatial sections. The instanton describes the “birth” of both the inflating brane and the bulk spacetime, which are together “created from nothing”, i.e., the point at the south pole of the de Sitter 4-sphere. The Euclidean AdS₅ metric is

$$^{(5)}ds_{{\rm{euclid}}}^2 = d{r^2} + {\ell ^2}{\sinh ^2}(r/\ell)\left[ {d{\chi ^2} + {{\sin}^2}\chi \,d\Omega _{(3)}^2} \right],$$

(227)

where $d\Omega _{(3)}^2$ is a 3-sphere, and r ≤ r₀. The Euclidean instanton interpolates between r = 0 (“nothing”) and r = r₀ (the created universe), which is a spherical brane of radius

$$H_0^{- 1} \equiv \ell \sinh ({r_0}/\ell){.}$$

(228)

After creation, the brane-world evolves according to the Lorentzian continuation, χ → iH₀t + π/2,

$$^{(5)}d{s^2} = d{r^2} + {(\ell {H_0})^2}{\sinh ^2}(r/\ell)\left[ {- d{t^2} + H_0^{- 2}{{\cosh}^2}({H_0}t)\,d\Omega _{(3)}^2} \right]$$

(229)

(see Figure 7).

Figure 7

Brane-world instanton. (Figure taken from [154].)

5.3 Models with non-empty bulk

The single-brane cosmological model can be generalized to include stresses other than A₅ in the bulk:

• The simplest example arises from considering a charged bulk black hole, leading to the Reissner-Nordström AdS₅ bulk metric [22]. This has the form of Equation (184), with

  $$F(R) = K + {{{R^2}} \over {{\ell ^2}}} - {m \over {{R^2}}} + {{{q^2}} \over {{R^4}}},$$

  (230)

  where q the “electric” charge parameter of the bulk black hole. The metric is a solution of the 5D Einstein-Maxwell equations, so that ⁽⁵⁾T_ab in Equation (50) is the energy-momentum tensor of a radial static 5D “electric” field. In order for the field lines to terminate on the boundary brane, the brane should carry a charge −q. Since the RNAdS₅ metric is 4-isotropic, it is still possible to embed a FRW brane in it, which is moving in the coordinates of Equation (184). The effect of the black hole charge on the brane arises via the junction conditions and leads to the modified Friedmann equation [22],

  $${H^2} = {{{\kappa ^2}} \over 3}\rho \left({1 + {\rho \over {2\lambda}}} \right) + {m \over {{a^4}}} - {{{q^2}} \over {{a^6}}} + {1 \over 3}\Lambda - {K \over {{a^2}}}.$$

  (231)

  The field lines that terminate on the brane imprint on the brane an effective negative energy density −3q²/(κ²a⁶), which redshifts like stiff matter (w = 1). The negativity of this term introduces the possibility that at high energies it can bring the expansion rate to zero and cause a turn-around or bounce (but see [204] for problems with such bounces).

  Apart from negativity, the key difference between this “dark stiff matter” and the dark radiation term m/a⁴ is that the latter arises from the bulk Weyl curvature via the ${{\mathcal E}_{\mu \nu}}$ tensor, while the former arises from non-vacuum stresses in the bulk via the ${{\mathcal F}_{\mu \nu}}$ tensor in Equation (69). The dark stiff matter does not arise from massive KK modes of the graviton.

• Another example is provided by the Vaidya-AdS₅ metric, which can be written after transforming to a new coordinate υ = T + ∫ dR/F in Equation (184), so that υ = const. are null surfaces, and

  $$^{(5)}d{s^2} = - F(R,v)d{v^2} + 2dv\,dR + {R^2}\left({{{d{r^2}} \over {1 - K{r^2}}} + {r^2}d{\Omega ^2}} \right),$$

  (232)
  $$F(R,v) = K + {{{R^2}} \over {{\ell ^2}}} - {{m(v)} \over {{R^2}}}.$$

  (233)

  This model has a moving FRW brane in a 4-isotropic bulk (which is not static), with either a radiating bulk black hole (dm/dυ < 0), or a radiating brane (dm/d υ > 0) [77, 278, 277, 280]. The metric satisfies the 5D field equations (50) with a null-radiation energy-momentum tensor,

  $$^{(5)}{T_{AB}} = \psi {k_A}{k_B},\qquad {k_A}{k^A} = 0,\qquad {k_A}{u^A} = 1,$$

  (234)

  where ψ ∝ dm/dυ. It follows that

  $${{\mathcal F}_{\mu \nu}} = \kappa _5^{- 2}\psi {h_{\mu \nu}}.$$

  (235)

  In this case, the same effect, i.e., a varying mass parameter m, contributes to both ${{\mathcal E}_{\mu \nu}}$ and ${{\mathcal F}_{\mu \nu}}$ in the brane field equations. The modified Friedmann equation has the standard 1-brane RS-type form, but with a dark radiation term that no longer behaves strictly like radiation:

  $${H^2} = {{{\kappa ^2}} \over 3}\rho \left({1 + {\rho \over {2\lambda}}} \right) + {{m(t)} \over {{a^4}}} + {1 \over 3}\Lambda - {K \over {{a^2}}}.$$

  (236)

  By Equations (74) and (234), we arrive at the matter conservation equations,

  $${\nabla ^\nu}{T_{\mu \nu}} = - 2\psi {u_\mu}.$$

  (237)

  This shows how the brane loses (ψ > 0) or gains (ψ < 0) energy in exchange with the bulk black hole. For an FRW brane, this equation reduces to

  $$\dot \rho + 3H(\rho + p) = - 2\psi .$$

  (238)

  The evolution of m is governed by the 4D contracted Bianchi identity, using Equation (235):

  $${\nabla ^\mu}{{\mathcal E}_{\mu \nu}} = {{6{\kappa ^2}} \over \lambda}{\nabla ^\mu}{{\mathcal S}_{\mu \nu}} + {2 \over 3}\left[ {\kappa _5^2\left({\dot \psi + \Theta \psi} \right) - 3{\kappa ^2}\psi} \right]{u_\mu} + {2 \over 3}\kappa _5^2{\vec \nabla _\mu}\psi .$$

  (239)

  For an FRW brane, this yields

  $${\dot \rho _{\mathcal E}} + 4H{\rho _{\mathcal E}} = 2\psi - {2 \over 3}{{\kappa _5^2} \over {{\kappa ^2}}}\left({\dot \psi + 3H\psi} \right),$$

  (240)

  where ${\rho _{\mathcal E}} = 3m(t)/({\kappa ^2}{a^4})$.

• A more complicated bulk metric arises when there is a self-interacting scalar field Φ in the bulk [311, 21, 322, 143, 274, 144, 48]. In the simplest case, when there is no coupling between the bulk field and brane matter, this gives

  $$^{(5)}{T_{AB}} = {\Phi _{,A}}{\Phi _{,B}} - {\;^{(5)}}{g_{AB}}\left[ {V(\Phi) + {1 \over 2}{\;^{(5)}}{g^{CD}}{\Phi _{,C}}{\Phi _{,D}}} \right],$$

  (241)

  where Φ(x,y) satisfies the 5D Klein-Gordon equation,

  $$^{(5)}\square\Phi - V{\prime}(\Phi) = 0{.}$$

  (242)

  The junction conditions on the field imply that

  $${\partial _y}\Phi (x,0) = 0{.}$$

  (243)

  Then Equations (74) and (241) show that matter conservation continues to hold on the brane in this simple case:

  $${\nabla ^\nu}{T_{\mu \nu}} = 0.$$

  (244)

  From Equation (241) one finds that

  $${{\mathcal F}_{\mu \nu}} = {1 \over {4\kappa _5^2}}\left[ {4{\phi _{,\mu}}{\phi _{,\nu}} - {g_{\mu \nu}}\left({3V(\phi) + {5 \over 2}{g^{\alpha \beta}}{\phi _{,\alpha}}{\phi _{,\beta}}} \right)} \right],$$

  (245)

  where

  $$\phi (x) = \Phi (x,0),$$

  (246)

  so that the modified Friedmann equation becomes

  $${H^2} = {{{\kappa ^2}} \over 3}\rho \left({1 + {\rho \over {2\lambda}}} \right) + {m \over {{a^4}}} + {{\kappa _5^2} \over 6}\left[ {{1 \over 2}{{\dot \phi}^2} + V(\phi)} \right] + {1 \over 3}\Lambda - {K \over {{a^2}}}.$$

  (247)

  When there is coupling between brane matter and the bulk scalar field, then the Friedmann and conservation equations are more complicated [311, 21, 322, 143, 274, 144, 48].

6 Brane-World Cosmology: Perturbations

The background dynamics of brane-world cosmology are simple because the FRW symmetries simplify the bulk and rule out nonlocal effects. But perturbations on the brane immediately release the nonlocal KK modes. Then the 5D bulk perturbation equations must be solved in order to solve for perturbations on the brane. These 5D equations are partial differential equations for the 3D Fourier modes, with both initial and boundary conditions needed.

The theory of gauge-invariant perturbations in brane-world cosmology has been extensively investigated and developed [303, 271, 24, 308, 99, 312, 369, 346, 286, 177, 272, 176, 331, 333, 190, 235, 265, 416, 258, 332, 417, 231, 266, 191, 123, 158, 234, 50, 127, 340, 385, 368, 285, 85, 90, 116, 41, 54, 364, 53, 362, 282, 281] and is qualitatively well understood. The key task is integration of the coupled brane-bulk perturbation equations. Special cases have been solved, where these equations effectively decouple [271, 24, 282, 281], and approximation schemes have been developed [398, 428, 387, 399, 400, 245, 361, 51, 201, 136, 321, 323, 27] for the more general cases where the coupled system must be solved. Below we will also present the results of full numerical integration of the 5D perturbation equations in the RS case.

From the brane viewpoint, the bulk effects, i.e., the high-energy corrections and the KK modes, act as source terms for the brane perturbation equations. At the same time, perturbations of matter on the brane can generate KK modes (i.e., emit 5D gravitons into the bulk) which propagate in the bulk and can subsequently interact with the brane. This nonlocal interaction amongst the perturbations is at the core of the complexity of the problem. It can be elegantly expressed via integro-differential equations [331, 333], which take the form (assuming no incoming 5D gravitational waves)

$${A_k}(t) = \int d t{\prime}\,{\mathcal G}(t,t{\prime}){B_k}(t{\prime}),$$

(248)

where ${\mathcal G}$ is the bulk retarded Green’s function evaluated on the brane, and A_k, B_k are made up of brane metric and matter perturbations and their (brane) derivatives, and include high-energy corrections to the background dynamics. Solving for the bulk Green’s function, which then determines ${\mathcal G}$, is the core of the 5D problem.

We can isolate the KK anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$ as the term that must be determined from 5D equations. Once $\pi _{\mu \nu}^{\mathcal E}$ is determined in this way, the perturbation equations on the brane form a closed system. The solution will be of the form (expressed in Fourier modes):

$$\pi _k^{\mathcal E}(t) \propto \int d t{\prime}\,{\mathcal G}(t,t{\prime}){F_k}(t{\prime}),$$

(249)

where the functional F_k will be determined by the covariant brane perturbation quantities and their derivatives. It is known in the case of a Minkowski background [374], but not in the cosmological case.

The KK terms act as source terms modifying the standard general relativity perturbation equations, together with the high-energy corrections. For example, the linearization of the shear propagation equation (131) yields

$${\dot \sigma _{\mu \nu}} + 2H{\sigma _{\mu \nu}} + {E_{\mu \nu}} - {{{\kappa ^2}} \over 2}{\pi _{\mu \nu}} - {\vec \nabla _{\langle \mu}}{A_{\nu \rangle}} = {{{\kappa ^2}} \over 2}\pi _{\mu \nu}^{\mathcal E} - {{{\kappa ^2}} \over 4}(1 + 3w){\rho \over \lambda}{\pi _{\mu \nu}}.$$

(250)

In 4D general relativity, the right hand side is zero. In the brane-world, the first source term on the right is the KK term, and the second term is the high-energy modification. The other modification is a straightforward high-energy correction of the background quantities H and ρ via the modified Friedmann equations.

As in 4D general relativity, there are various different, but essentially equivalent, ways to formulate linear cosmological perturbation theory. First we describe the covariant brane-based approach.

6.1 1 + 3-covariant perturbation equations on the brane

In the 1+3-covariant approach [303, 282, 305], perturbative quantities are projected vectors, V_μ = V 〈_µ 〉, and projected symmetric tracefree tensors, W_μν = W 〈_μv 〉, which are gauge-invariant since they vanish in the background. These are decomposed into (3D) scalar, vector, and tensor modes as

$${V_\mu} = {\vec \nabla _\mu}V + {\bar V_\mu},$$

(251)

$${W_{\mu \nu}} = {\vec \nabla _{\langle \mu}}{\vec \nabla _{\nu \rangle}}W + {\vec \nabla _{\langle \mu}}{\bar W_{\nu \rangle}} + {\bar W_{\mu \nu}},$$

(252)

where ${\bar W_{\mu \nu}} = {\bar W_{\left\langle {\mu \nu} \right\rangle}}$ and an overbar denotes a (3D) transverse quantity,

$${\vec \nabla ^\mu}{\bar V_\mu} = 0 = {\vec \nabla ^\nu}{\bar W_{\mu \nu}}.$$

(253)

In a local inertial frame comoving with u^μ, i.e., ${u^\mu} = (1,\,\vec 0)$, all time components may be set to zero: V_μ = (0, Vi), W_0μ = 0, ${\vec \nabla _\mu} = (0,\,{\vec \nabla _i})$.

Purely scalar perturbations are characterized by the fact that vectors and tensors are derived from scalar potentials, i.e.,

$${\bar V_\mu} = {\bar W_\mu} = {\bar W_{\mu \nu}} = 0.$$

(254)

Scalar perturbative quantities are formed from the potentials via the (3D) Laplacian, e.g., ${\mathcal V} = {\vec \nabla ^\mu}{\vec \nabla _\mu}V \equiv {\vec \nabla ^2}V$. Purely vector perturbations are characterized by

$${V_\mu} = {\bar V_\mu},\qquad {W_{\mu \nu}} = {\vec \nabla _{\langle \mu}}{\bar W_{\nu \rangle}},\qquad {\rm{curl}}{\vec \nabla _\mu}f = - 2\dot f{\omega _\mu},$$

(255)

where ω_μ is the vorticity, and purely tensor by

$${\vec \nabla _\mu}f = 0 = {V_\mu},\qquad {W_{\mu \nu}} = {\bar W_{\mu \nu}}.$$

(256)

The KK energy density produces a scalar mode ${\vec \nabla _\mu}\rho {\mathcal E}$ (which is present even if ${\rho _{\mathcal E}} = 0$ in the background). The KK momentum density carries scalar and vector modes, and the KK anisotropic stress carries scalar, vector, and tensor modes:

$$q_\mu ^{\mathcal E} = {\vec \nabla _\mu}{q^{\mathcal E}} + \bar q_\mu ^{\mathcal E},$$

(257)

$$\pi _{\mu \nu}^{\mathcal E} = {\vec \nabla _{\langle \mu}}{\vec \nabla _{\nu \rangle}}{\pi ^{\mathcal E}} + {\vec \nabla _{\langle \mu}}\bar \pi _{\nu \rangle}^{\mathcal E} + \bar \pi _{\mu \nu}^{\mathcal E}.$$

(258)

Linearizing the conservation equations for a single adiabatic fluid, and the nonlocal conservation equations, we obtain

$$\dot \rho + \Theta (\rho + p) = 0,$$

(259)

$$c_{\rm{s}}^2{\vec \nabla _\mu} + (\rho + p){A_\mu} = 0,$$

(260)

$${\dot \rho _{\mathcal E}} + {4 \over 3}\Theta {\rho _{\mathcal E}} + {\vec \nabla ^\mu}q_\mu ^{\mathcal E} = 0,$$

(261)

$$\dot q_\mu ^{\mathcal E} + 4Hq_\mu ^{\mathcal E} + {1 \over 3}{\vec \nabla _\mu}{\rho _{\mathcal E}} + {4 \over 3}{\rho _{\mathcal E}}{A_\mu} + {\vec \nabla ^\nu}\pi _{\mu \nu}^{\mathcal E} = - {{(\rho + p)} \over \lambda}{\vec \nabla _\mu}\rho .$$

(262)

Linearizing the remaining propagation and constraint equations leads to

$$\dot \Theta + {1 \over 3}{\Theta ^2} - {\vec \nabla ^\mu}{A_\mu} + {1 \over 2}{\kappa ^2}(\rho + 3p) - \Lambda = - {{{\kappa ^2}} \over 2}(2\rho + 3p){\rho \over \lambda} - {\kappa ^2}{\rho _{\mathcal E}},$$

(263)

$${\dot \omega _\mu} + 2H{\omega _\mu} + {1 \over 2}{\rm{curl}}\;{A_\mu} = 0,$$

(264)

$${\dot \sigma _{\mu \nu}} + 2H{\sigma _{\mu \nu}} + {E_{\mu \nu}} - {\vec \nabla _{\langle \mu}}{A_{\nu \rangle}} = {{{\kappa ^2}} \over 2}\pi _{\mu \nu}^{\mathcal E},$$

(265)

$$\begin{array}{*{20}c} {{{\dot E}_{\mu \nu}} + 3H{E_{\mu \nu}} - {\rm{curl}}\;{H_{\mu \nu}} + {{{\kappa ^2}} \over 2}(\rho + p){\sigma _{\mu \nu}} = - {{{\kappa ^2}} \over 2}(\rho + p){\rho \over \lambda}{\sigma _{\mu \nu}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ {- {{{\kappa ^2}} \over 6}\left[ {4{\rho _{\mathcal E}}{\sigma _{\mu \nu}} + 3\dot \pi _{\mu \nu}^{\mathcal E} + 3H\pi _{\mu \nu}^{\mathcal E} + 3{{\vec \nabla}_{\langle \mu}}q_{\nu \rangle}^{\mathcal E}} \right],}\\ \end{array}$$

(266)

$${\dot H_{\mu \nu}} + 3H{H_{\mu \nu}} + {\rm{curl}}\;{E_{\mu \nu}} = {{{\kappa ^2}} \over 2}{\rm{curl}}\;\pi _{\mu \nu}^{\mathcal E},$$

(267)

$${\vec \nabla ^\mu}{\omega _\mu} = 0,$$

(268)

$${\vec \nabla ^\nu}{\sigma _{\mu \nu}} - {\rm{curl}}{\omega _\mu} - {2 \over 3}{\vec \nabla _\mu}\Theta = - q_\mu ^{\mathcal E},$$

(269)

$${\rm{curl}}{\sigma _{\mu \nu}} + {\vec \nabla _{\langle \mu}}{\omega _{\nu \rangle}} - {H_{\mu \nu}} = 0,$$

(270)

$${\vec \nabla ^\nu}{E_{\mu \nu}} - {{{\kappa ^2}} \over 3}{\vec \nabla _\mu}\rho = {{{\kappa ^2}} \over 3}{\rho \over \lambda}{\vec \nabla _\mu}\rho + {{{\kappa ^2}} \over 6}\left[ {2{{\vec \nabla}_\mu}{\rho _{\mathcal E}} - 4Hq_\mu ^{\mathcal E} - 3{{\vec \nabla}^\nu}\pi _{\mu \nu}^{\mathcal E}} \right],$$

(271)

$${\vec \nabla ^\nu}{H_{\mu \nu}} - {\kappa ^2}(\rho + p){\omega _\mu} = {\kappa ^2}(\rho + p){\rho \over \lambda}{\omega _\mu} + {{{\kappa ^2}} \over 6}[8{\rho _{\mathcal E}}{\omega _\mu} - 3\;{\rm{curl}}\;q_\mu ^{\mathcal E}].$$

(272)

Equations (259), (261), and (263) do not provide gauge-invariant equations for perturbed quantities, but their spatial gradients do.

These equations are the basis for a 1+3-covariant analysis of cosmological perturbations from the brane observer’s viewpoint, following the approach developed in 4D general relativity (for a review, see [137]). The equations contain scalar, vector, and tensor modes, which can be separated out if desired. They are not a closed system of equations until $\pi _{\mu \nu}^{\mathcal E}$ is determined by a 5D analysis of the bulk perturbations. An extension of the 1+3-covariant perturbation formalism to 1+4 dimensions would require a decomposition of the 5D geometric quantities along a timelike extension u^A into the bulk of the brane 4-velocity field u^μ, and this remains to be done. The 1+3-covariant perturbation formalism is incomplete until such a 5D extension is performed. The metric-based approach does not have this drawback.

6.2 Metric-based perturbations

An alternative approach to brane-world cosmological perturbations is an extension of the 4D metric-based gauge-invariant theory [236, 329]. A review of this approach is given in [53, 362]. In an arbitrary gauge, and for a flat FRW background, the perturbed metric has the form

(273)

where the background metric functions A, N are given by Equations (187, 188). The scalars ψ,${\mathcal R},\,{\mathcal C}$, α, β, ν represent scalar perturbations. The vectors S_i, F_i, and χ_i are transverse, so that they represent 3D vector perturbations, and the tensor f_ij is transverse traceless, representing 3D tensor perturbations.

In the Gaussian normal gauge, the brane coordinate-position remains fixed under perturbation,

$$^{(5)}d{s^2} = \left[ {g_{\mu \nu}^{(0)}(x,y) + \delta {g_{\mu \nu}}(x,y)} \right]d{x^\mu}d{x^\nu} + d{y^2},$$

(274)

where $g_{\mu \nu}^{(0)}$ is the background metric, Equation (186). In this gauge, we have

$$\alpha = \beta = \nu = {\chi _i} = 0.$$

(275)

In the 5D longitudinal gauge, one gets

$$- {\mathcal B} + \dot{\mathcal C}= 0 = - \beta + {\mathcal C}{\prime}.$$

(276)

In this gauge, and for an AdS₅ background, the metric perturbation quantities can all be expressed in terms of a “master variable” Ω which obeys a wave equation [331, 333]. In the case of scalar perturbations, we have for example

$${\mathcal R} = {1 \over {6A}}\left({\Omega{\prime\prime} - {1 \over {{N^2}}}\,\ddot \Omega - {{{\Lambda _5}} \over 3}\,\Omega} \right),$$

(277)

with similar expressions for the other quantities. All of the metric perturbation quantities are determined once a solution is found for the wave equation

$${\left({{1 \over {N\;{A^3}}}\,\dot \Omega} \right)^\cdot} + \left({{{{\Lambda _5}} \over 6} + {{{k^2}} \over {{A^2}}}} \right){N \over {{A^3}}}\,\Omega = {\left({{N \over {{A^3}}}{\Omega \prime}} \right)\prime}.$$

(278)

The junction conditions (68) relate the off-brane derivatives of metric perturbations to the matter perturbations:

$${\partial _y}\,\delta {g_{\mu \nu}} = - \kappa _5^2\left[ {\delta {T_{\mu \nu}} + {1 \over 3}\left({\lambda - {T^{(0)}}} \right)\delta {g_{\mu \nu}} - {1 \over 3}g_{\mu \nu}^{(0)}\delta T} \right],$$

(279)

where

$$\delta {T^0}_0 = - \delta \rho ,$$

(280)

$$\delta {T^0}_i = {a^2}{q_i},$$

(281)

$$\delta {T^i}_j = \delta p\,{\delta ^i}_j + \delta {\pi ^i}_j.$$

(282)

For scalar perturbations in the Gaussian normal gauge, this gives

$${\partial _y}\psi (x,0) = {{\kappa _5^2} \over 6}(2\delta \rho + 3\delta p),$$

(283)

$${\partial _y}{\mathcal B}(x,0) = \kappa _5^2\delta p,$$

(284)

$${\partial _y}{\mathcal C}(x,0) = - {{\kappa _5^2} \over 2}\delta \pi ,$$

(285)

$${\partial _y}{\mathcal R}(x,0) = - {{\kappa _5^2} \over 6}\delta \rho - {\partial _i}{\partial ^i}\,{\mathcal C}(x,0),$$

(286)

where δπ is the scalar potential for the matter anisotropic stress,

$$\delta {\pi _{ij}} = {\partial _i}{\partial _j}\delta \pi - {1 \over 3}{\delta _{ij}}\,{\partial _k}{\partial ^k}\delta \pi .$$

(287)

The perturbed KK energy-momentum tensor on the brane is given by

$$\delta {{\mathcal E}^0}_0 = {\kappa ^2}\delta {\rho _{\mathcal E}},$$

(288)

$$\delta {{\mathcal E}^0}_i = - {\kappa ^2}{a^2}q_i^{\mathcal E},$$

(289)

$$\delta {{\mathcal E}^i}_j = - {{{\kappa ^2}} \over 3}\delta {\rho _{\mathcal E}}\,{\delta ^i}_j - \delta {\pi ^{{\mathcal E}i}}_j.$$

(290)

The evolution of the bulk metric perturbations is determined by the perturbed 5D field equations in the vacuum bulk,

$$\delta \;{}^{(5)}{G^A}_B = 0.$$

(291)

Then the matter perturbations on the brane enter via the perturbed junction conditions (279).

For example, for scalar perturbations in Gaussian normal gauge, we have

$$\delta {\;^{(5)}}{G^y}_i = {\partial _i}\left\{{- \psi\prime + \left({{{A\prime} \over A} - {{N\prime} \over N}} \right)\psi - 2{{\mathcal R}\prime} - {{{A^2}} \over {2{N^2}}}\left[ {{{\dot{\mathcal B}}\prime} + \left({5{{\dot A} \over A} - {{\dot N} \over N}} \right){{\mathcal B}\prime}} \right]} \right\}.$$

(292)

For tensor perturbations (in any gauge), the only nonzero components of the perturbed Einstein tensor are

$$\delta {\,^{(5)}}{G^i}_j = - {1 \over 2}\left\{{- {1 \over {{N^2}}}{{\ddot f}^i}_j + f\prime {\prime ^i}_j - {{{k^2}} \over {{A^2}}}{f^i}_j + {1 \over {{N^2}}}\left({{{\dot N} \over N} - 3{{\dot A} \over A}} \right){{\dot f}^i}_j + \left({{{N\prime} \over N} + 3{{A\prime} \over A}} \right)f{\prime ^i}_j} \right\}.$$

(293)

In the following, we will discuss various perturbation problems, using either a 1+3-covariant or a metric-based approach.

6.3 Density perturbations on large scales

In the covariant approach, we define matter density and expansion (velocity) perturbation scalars, as in 4D general relativity,

$$\Delta = {{{a^2}} \over \rho}{\vec \nabla ^2}\rho ,\qquad Z = {a^2}{\vec \nabla ^2}\Theta .$$

(294)

Then we can define dimensionless KK perturbation scalars [303],

$$U = {{{a^2}} \over \rho}{\vec \nabla ^2}{\rho _{\mathcal E}},\qquad Q = {a \over \rho}{\vec \nabla ^2}{q^{\mathcal E}},\qquad \Pi = {1 \over \rho}{\vec \nabla ^2}{\pi ^{\mathcal E}},$$

(295)

where the scalar potentials ${q^{\mathcal E}}$ and ${\pi ^{\mathcal E}}$ are defined by Equations (257, 258). The KK energy density (dark radiation) produces a scalar fluctuation U which is present even if ${\rho _{\mathcal E}} = 0$ in the background, and which leads to a non-adiabatic (or isocurvature) mode, even when the matter perturbations are assumed adiabatic [177]. We define the total effective dimensionless entropy S_tot via

$${p_{{\rm{tot}}}}\,{S_{{\rm{tot}}}} = {a^2}{\vec \nabla ^2}{p_{{\rm{tot}}}} - c_{{\rm{tot}}}^2{a^2}{\vec \nabla ^2}{\rho _{{\rm{tot}}}},$$

(296)

where $c_{{\rm{tot}}}^2 = {\dot p_{{\rm{tot}}}}/{\dot \rho _{{\rm{tot}}}}$ tot is given in Equation (109). Then

$${S_{{\rm{tot}}}} = {{9\left[ {c_{\rm{s}}^2 - {1 \over 3} + \left({{2 \over 3} + w + c_{\rm{s}}^2} \right)\rho /\lambda} \right]} \over {[3(1 + w)(1 + \rho /\lambda) + 4{\rho _{\mathcal E}}/\rho ][3w + 3(1 + 2w)\rho /2\lambda + {\rho _{\mathcal E}}/\rho ]}}\,\left[ {{4 \over 3}{{{\rho _{\mathcal E}}} \over \rho}\,\Delta - (1 + w)U} \right].$$

(297)

If ${\rho _{\mathcal E}} = 0$ in the background, then U is an isocurvature mode: S_tot ∝ (1+w)U. This isocurvature mode is suppressed during slow-roll inflation, when 1 + w ≈ 0.

If ${\rho _{\mathcal E}} = 0$ in the background, then the weighted difference between U and Δ determines the isocurvature mode: ${S_{{\rm{tot}}}} \propto (4{\rho _{\mathcal E}}/3\rho)\Delta - (1 + w)U$. At very high energies, ρ ≫ λ, the entropy is suppressed by the factor λ/ρ.

The density perturbation equations on the brane are derived by taking the spatial gradients of Equations (259), (261), and (263), and using Equations (260) and (262). This leads to [177]

$$\dot \Delta = 3wH\Delta - (1 + w)Z,$$

(298)

$$\dot Z = - 2HZ - \left({{{c_{\rm{s}}^2} \over {1 + w}}} \right){\vec \nabla ^2}\Delta - {\kappa ^2}\rho U - {1 \over 2}{\kappa ^2}\rho \left[ {1 + (4 + 3w){\rho \over \lambda} - \left({{{4c_{\rm{s}}^2} \over {1 + w}}} \right){{{\rho _{\mathcal E}}} \over \rho}} \right]\Delta ,$$

(299)

$$\dot U = (3w - 1)HU + \left({{{4c_{\rm{s}}^2} \over {1 + w}}} \right)\;\left({{{{\rho _{\mathcal E}}} \over \rho}} \right)H\Delta - \left({{{4{\rho _{\mathcal E}}} \over {3\rho}}} \right)\;Z - a{\vec \nabla ^2}Q,$$

(300)

$$\dot Q = (3w - 1)HQ - {1 \over {3a}}U - {2 \over 3}a{\vec \nabla ^2}\Pi + {1 \over {3\mu}}\left[ {\left({{{4c_{\rm{s}}^2} \over {1 + w}}} \right){{{\rho _{\mathcal E}}} \over \rho} - 3(1 + w){\rho \over \lambda}} \right]\Delta .$$

(301)

The KK anisotropic stress term Π occurs only via its Laplacian, ${\vec \nabla ^2}\Pi$. If we can neglect this term on large scales, then the system of density perturbation equations closes on super-Hubble scales [303]. An equivalent statement applies to the large-scale curvature perturbations [271]. KK effects then introduce two new isocurvature modes on large scales (associated with U and Q), and they modify the evolution of the adiabatic modes as well [177, 282].

Thus on large scales the system of brane equations is closed, and we can determine the density perturbations without solving for the bulk metric perturbations.

We can simplify the system as follows. The 3-Ricci tensor defined in Equation (140) leads to a scalar covariant curvature perturbation variable,

$$C \equiv {a^4}{\vec \nabla ^2}{R^ \bot} = - 4{a^2}HZ + 2{\kappa ^2}{a^2}\rho \left({1 + {\rho \over {2\lambda}}} \right)\Delta + 2{\kappa ^2}{a^2}\rho U.$$

(302)

It follows that C is locally conserved (along u^μ flow lines):

$$C = {C_0},\qquad {\dot C_0} = 0.$$

(303)

We can further simplify the system of equations via the variable

$$\Phi = {\kappa ^2}{a^2}\rho \Delta .$$

(304)

This should not be confused with the Bardeen metric perturbation variable Φ_H, although it is the covariant analogue of Φ_H in the general relativity limit. In the brane-world, high-energy and KK effects mean that Φ_H is a complicated generalization of this expression [282] involving Π, but the simple Φ above is still useful to simplify the system of equations. Using these new variables, we find the closed system for large-scale perturbations:

$$\dot \Phi = - H\left[ {1 + (1 + w){{{\kappa ^2}\rho} \over {2{H^2}}}\left({1 + {\rho \over \lambda}} \right)} \right]\Phi - \left[ {(1 + w){{{a^2}{\kappa ^4}{\rho ^2}} \over {2H}}} \right]\;U + \left[ {(1 + w){{{\kappa ^2}\rho} \over {4H}}} \right]{C_0},$$

(305)

$$\dot U = - H\left[ {1 - 3w + {{2{\kappa ^2}{\rho _{\mathcal E}}} \over {3{H^2}}}} \right]\;U - {{2{\rho _{\mathcal E}}} \over {3{a^2}H\rho}}\left[ {1 + {\rho \over \lambda} - {{6c_{\rm{s}}^2{H^2}} \over {(1 + w){\kappa ^2}\rho}}} \right]\;\Phi + \left[ {{{{\rho _{\mathcal E}}} \over {3{a^2}H\rho}}} \right]{C_0}.$$

(306)

If there is no dark radiation in the background, ${\rho _{\mathcal E}} = 0$, then

$$U = {U_0}\exp \left({- \int {(1 - 3w)} dN} \right),$$

(307)

and the above system reduces to a single equation for Φ. At low energies, and for constant w, the non-decaying attractor is the general relativity solution,

$${\Phi _{{\rm{low}}}} \approx {{3(1 + w)} \over {2(5 + 3w)}}{C_0}.$$

(308)

At very high energies, for $w \geq - {1 \over 3}$, we get

$${\Phi _{{\rm{high}}}} \rightarrow {3 \over 2}{\lambda \over {{\rho _0}}}(1 + w)\left[ {{{{C_0}} \over {7 + 6w}} - {{2{{\tilde U}_0}} \over {5 + 6w}}} \right],$$

(309)

where ${\tilde U_0} = {\kappa ^2}a_0^2{\rho _0}{U_0}$, so that the isocurvature mode has an influence on Φ. Initially, Φ is suppressed by the factor λ/ρ₀, but then it grows, eventually reaching the attractor value in Equation (308). For slow-roll inflation, when 1 + w ∼ ϵ, with 0 < ϵ ≪ 1 and ${H^{- 1}}\vert \dot \epsilon \vert \, = \, \vert \epsilon{\prime}\vert \, \ll \, 1$, we get

$${\Phi _{{\rm{high}}}}\sim{3 \over 2}\epsilon {\lambda \over {{\rho _0}}}{C_0}{e^{3\epsilon N}},$$

(310)

where N = ln(a/a₀), so that Φ has a growing-mode in the early universe. This is different from general relativity, where Φ is constant during slow-roll inflation. Thus more amplification of Φ can be achieved than in general relativity, as discussed above. This is illustrated for a toy model of inflation-to-radiation in Figure 8. The early (growing) and late time (constant) attractor solutions are seen explicitly in the plots.

Figure 8

The evolution of the covariant variable Φ, defined in Equation (304) (and not to be confused with the Bardeen potential), along a fundamental world-line. This is a mode that is well beyond the Hubble horizon at N = 0, about 50 e-folds before inflation ends, and remains super-Hubble through the radiation era. A smooth transition from inflation to radiation is modelled by $w = {1 \over 3}[(2 - {3 \over 2}\epsilon){\rm{tanh}}(N - 50) - (1 - {3 \over 2}\epsilon)]$, where ϵ is a small positive parameter (chosen as ϵ = 0.1 in the plot). Labels on the curves indicate the value of ρ₀/λ, so that the general relativistic solution is the dashed curve (ρ₀/λ = 0). (Figure taken from [177].)

The presence of dark radiation in the background introduces new features. In the radiation era $w = {1 \over 3}$, the non-decaying low-energy attractor becomes [187]

$${\Phi _{{\rm{low}}}} \approx {{{C_0}} \over 3}(1 - \alpha),$$

(311)

$$\alpha = {{{\rho _{\mathcal E}}} \over \rho} \underset{\sim}{<} 0{.}05{.}$$

(312)

The dark radiation serves to reduce the final value of Φ, leaving an imprint on Φ, unlike the ${\rho _{\mathcal E}} = 0$ case, Equation (308). In the very high energy limit,

$${\Phi _{{\rm{high}}}} \rightarrow {\lambda \over {{\rho _0}}}\left[ {{2 \over 9}{C_0} - {4 \over 7}{{\tilde U}_0}} \right] + 16\alpha {\left({{\lambda \over {{\rho _0}}}} \right)^2}\left[ {{{{C_0}} \over {273}} - {{4{{\tilde U}_0}} \over {539}}} \right].$$

(313)

Thus Φ is initially suppressed, then begins to grow, as in the no-dark-radiation case, eventually reaching an attractor which is less than the no-dark-radiation attractor. This is confirmed by the numerical integration shown in Figure 9.

Figure 9

The evolution of Φ in the radiation era, with dark radiation present in the background. (Figure taken from [187].)

6.4 Curvature perturbations and the Sachs-Wolfe effect

The curvature perturbation ${\mathcal R}$ on uniform density surfaces is defined in Equation (273). The associated gauge-invariant quantity

$$\zeta = {\mathcal R} + {{\delta \rho} \over {3(\rho + p)}}$$

(314)

may be defined for matter on the brane. Similarly, for the Weyl “fluid” if ${\rho _{{\mathcal E}\,}} \neq 0$ in the background, the curvature perturbation on hypersurfaces of uniform dark energy density is

$${\zeta _{\mathcal E}} = {\mathcal R} + {{\delta {\rho _{\mathcal E}}} \over {4{\rho _{\mathcal E}}}}.$$

(315)

On large scales, the perturbed dark energy conservation equation is [271]

$${(\delta {\rho _{\mathcal E}})^\cdot} + 4H\delta {\rho _{\mathcal E}} + 4{\rho _{\mathcal E}}\dot{\mathcal R} = 0,$$

(316)

which leads to

$${\dot \zeta _{\mathcal E}} = 0.$$

(317)

For adiabatic matter perturbations, by the perturbed matter energy conservation equation,

$${(\delta \rho)^\cdot} + 3H(\delta \rho + \delta p) + 3(\rho + p)\dot{\mathcal R} = 0,$$

(318)

we find

$$\dot \zeta = 0.$$

(319)

This is independent of brane-world modifications to the field equations, since it depends on energy conservation only. For the total, effective fluid, the curvature perturbation is defined as follows [271]: If ${\rho _{\mathcal E}} \neq 0$ in the background, we have

$${\zeta _{{\rm{tot}}}} = \zeta + \left[ {{{4{\rho _{\mathcal E}}} \over {3(\rho + p)(1 + \rho /\lambda) + 4{\rho _{\mathcal E}}}}} \right]\left({{\zeta _{\mathcal E}} - \zeta} \right),$$

(320)

and if ${\rho _{\mathcal E}} = 0$ in the background, we get

$${\zeta _{{\rm{tot}}}} = \zeta + {{\delta {\rho _{\mathcal E}}} \over {3(\rho + p)(1 + \rho /\lambda)}}$$

(321)

$$\delta {\rho _{\mathcal E}} = {{\delta {C_{\mathcal E}}} \over {{a^4}}},$$

(322)

where $\delta {C_{\mathcal E}}$ is a constant. It follows that the curvature perturbations on large scales, like the density perturbations, can be found on the brane without solving for the bulk metric perturbations.

Note that ${\dot \zeta _{{\rm{tot}}}} \neq 0$ even for adiabatic matter perturbations; for example, if ${\rho _{\mathcal E}} = 0$ in the background, then

$${\dot \zeta _{\,{\rm{tot}}}} = H\left({c_{{\rm{tot}}}^2 - {1 \over 3}} \right){{\delta {\rho _{\mathcal E}}} \over {(\rho + p)(1 + \rho /\lambda)}}.$$

(323)

The KK effects on the brane contribute a non-adiabatic mode, although ${\dot \zeta _{{\rm{tot}}}} \rightarrow 0$ at low energies.

Although the density and curvature perturbations can be found on super-Hubble scales, the Sachs-Wolfe effect requires $\pi _{\mu \nu}^{\mathcal E}$ in order to translate from density/curvature to metric perturbations. In the 4D longitudinal gauge of the metric perturbation formalism, the gauge-invariant curvature and metric perturbations on large scales are related by

$${\zeta _{{\rm{tot}}}} = {\mathcal R} - {H \over {\dot H}}\left({{{\dot{\mathcal R}} \over H} - \psi} \right),$$

(324)

$${\mathcal R} + \psi = - {\kappa ^2}{a^2}\delta {\pi _{\mathcal E}},$$

(325)

where the radiation anisotropic stress on large scales is neglected, as in general relativity, and $\delta {\pi _{\mathcal E}}$ is the scalar potential for $\pi _{\mu \nu}^{\mathcal E}$, equivalent to the covariant quantity Π defined in Equation (295). In 4D general relativity, the right hand side of Equation (325) is zero. The (non-integrated) Sachs-Wolfe formula has the same form as in general relativity:

$${\left. {{{\delta T} \over T}} \right\vert _{{\rm{now}}}} = ({\zeta _{{\rm{rad}}}} + \psi - {\mathcal R}){\vert _{{\rm{dec}}}}{.}$$

(326)

The brane-world corrections to the general relativistic Sachs-Wolfe effect are then given by [271]

$${{\delta T} \over T} = {\left({{{\delta T} \over T}} \right)_{{\rm{gr}}}} - {8 \over 3}\left({{{{\rho _{{\rm{rad}}}}} \over {{\rho _{{\rm{cdm}}}}}}} \right){S_{\mathcal E}} - {\kappa ^2}{a^2}\delta {\pi _{\mathcal E}} + {{2{\kappa ^2}} \over {{a^{5/2}}}}\int d a\,{a^{7/2}}\,\delta {\pi _{\mathcal E}},$$

(327)

where ${S_{\mathcal E}}$ is the KK entropy perturbation (determined by $\delta {\rho _{\mathcal E}}$). The KK term $\delta {\pi _{\mathcal E}}$ cannot be determined by the 4D brane equations, so that δT/T cannot be evaluated on large scales without solving the 5D equations. (Equation (327) has been generalized to a 2-brane model, in which the radion makes a contribution to the Sachs-Wolfe effect [244].)

The presence of the KK (Weyl, dark) component has essentially two possible effects:

• A contribution from the KK entropy perturbation ${S_{\mathcal E}}$ that is similar to an extra isocurvature contribution.

• The KK anisotropic stress $\delta {\pi _{\mathcal E}}$ also contributes to the CMB anisotropies. In the absence of anisotropic stresses, the curvature perturbation ζ_tot would be sufficient to determine the metric perturbation ${\mathcal R}$ and hence the large-angle CMB anisotropies via Equations (324, 325, 326). However, bulk gravitons generate anisotropic stresses which, although they do not affect the large-scale curvature perturbation ζ_tot, can affect the relation between ζ_tot, ${\mathcal R}$, and ψ, and hence can affect the CMB anisotropies at large angles.

A simple phenomenologic al approximation to $\delta {\pi _{\mathcal E}}$ on large scales is discussed in [24], and the Sachs-Wolfe effect is estimated as

$${{\delta T} \over T}\sim{\left({{{\delta {\pi _{\mathcal E}}} \over \rho}} \right)_{{\rm{in}}}}{\left({{{{t_{{\rm{eq}}}}} \over {{t_{{\rm{dec}}}}}}} \right)^{2/3}}\left[ {{{\ln ({t_{{\rm{in}}}}/{t_4})} \over {\ln ({t_{{\rm{eq}}}}/{t_4})}}} \right],$$

(328)

where t₄ is the 4D Planck time, and t_in is the time when the KK anisotropic stress is induced on the brane, which is expected to be of the order of the 5D Planck time.

A self-consistent approximation is developed in [245], using the low-energy 2-brane approximation [398, 428, 387, 399, 400] to find an effective 4D form for ${{\mathcal E}_{\mu \nu}}$ and hence for $\delta {\pi _{\mathcal E}}$. This is discussed below. In a single brane model in the AdS bulk, full numerical simulations were done to find the behaviour of $\delta {\pi _{\mathcal E}}$ [69], as will be discussed in the next subsection.

6.5 Full numerical solutions

In order to study scalar perturbations fully, we need to numerically solve the coupled bulk and brane equations for the master variable Ω. A thorough analysis was done in [69]. For this purpose, it is convenient to use the static coordinate where the bulk equation is simple and consider a moving FRW brane;

$$^{(5)}d{s^2} = {{{\ell ^2}} \over {{z^2}}}[{\eta _{\mu \nu}}d{x^\mu}d{x^\nu} + d{z^2}].$$

(329)

The bulk master variable satisfies the following wave equation (see Equation (278))

$$0 = - {{{\partial ^2}\Omega} \over {\partial {\tau ^2}}} + {{{\partial ^2}\Omega} \over {\partial {z^2}}} + {3 \over z}{{\partial \Omega} \over {\partial z}} + \left({{1 \over {{z^2}}} - {k^2}} \right)\Omega .$$

(330)

From the junction condition, Ω satisfies a boundary condition on the brane

$${\left[ {{\partial _n}\Omega + {1 \over \ell}\left({1 + {\rho \over \lambda}} \right)\Omega + {{6\rho {a^3}} \over {\lambda {k^2}}}\Delta} \right]_{\rm{b}}} = 0.$$

(331)

where ∂_n is the derivative orthogonal to the brane

$${\partial _n} = {1 \over a}\left({- H\ell {\partial \over {\partial \tau}} + \sqrt {1 + {H^2}{\ell ^2}} {\partial \over {\partial z}}} \right),$$

(332)

and Δ is the density perturbation in the comoving gauge. The subscript b implies that the quantities are evaluated on the brane. On a brane, Δ satisfies a wave equation

$${{{d^2}\Delta} \over {d{\eta ^2}}} + (1 + 3c_s^2 - 6w)Ha{{d\Delta} \over {d\eta}} + \left[ {c_s^2{k^2} + {{3\rho {a^2}} \over {\lambda {\ell ^2}}}A + {{3{\rho ^2}{a^2}} \over {{\lambda ^2}{\ell ^2}}}B} \right]\Delta = {{{k^4}(1 + w){\Omega _{\rm{b}}}} \over {3\ell {a^3}}},$$

(333a)

$$A = 6c_s^2 - 1 - 8w + 3{w^2},\qquad B = 3c_s^2 - 9w - 4,$$

(333b)

where we consider a perfect fluid on a brane with an equation state w and c_s is a sound speed for perturbations. The above ordinal differential equation, the bulk wave equation (330) and the boundary condition (331) comprise a closed set of equations for Δ and Ω_c.

On a brane, we take the longitudinal gauge

$$ds_b^2 = - (1 + 2\psi)d{t^2} + (1 + 2{\mathcal R}){\delta _{ij}}d{x^i}d{x^j}.$$

(334)

Using the expressions for metric perturbations in terms of the master variable Ω (see Equation (277)) and the junction condition Equation (331), ψ and ${\mathcal R}$ are written in terms of Δ and Ω as

$${\mathcal R} = {{3{a^2}\rho (\rho + \lambda)} \over {{k^2}{\ell ^2}{\lambda ^2}}}\Delta + \left({{{3{H^2}{a^2} + {k^2}} \over {6\ell {a^3}}}} \right){\Omega _{\rm{b}}} - {H \over {2\ell {a^2}}}{{d{\Omega _{\rm{b}}}} \over {d\eta}},$$

(335a)

$$\begin{array}{*{20}c} {\psi = - {{3\rho {a^2}(3w\rho + 4\rho + \lambda)} \over {{k^2}{\ell ^2}{\lambda ^2}}}\Delta - \left[ {{{(3w + 4){\rho ^2}} \over {2{\ell ^3}a{\lambda ^2}}} + {{(5 + 3w)\rho} \over {2{\ell ^3}a\lambda}} + {{{k^2}} \over {3\ell {a^3}}}} \right]{\Omega _{\rm{b}}}}\\ {+ {{3H} \over {2\ell {a^2}}}{{d{\Omega _{\rm{b}}}} \over {d\eta}} - {1 \over {2\ell {a^3}}}{{{d^2}{\Omega _{\rm{b}}}} \over {d{\eta ^2}}}.\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;}\\ \end{array}$$

(335b)

Other quantities of interest are the curvature perturbation on uniform density slices,

$$\zeta = {\mathcal R} - {{HaV} \over k} + {\Delta \over {3(1 + w)}} = \left[ {{1 \over 3} - {{3\rho {a^2}(w\lambda - \lambda - \rho)} \over {{k^2}{\ell ^2}{\lambda ^2}}}} \right]{\Delta \over {1 + w}} + {{Ha} \over {{k^2}(1 + w)}}{{d\Delta} \over {d\eta}} + {{{k^2}} \over {6\ell {a^3}}}{\Omega _{\rm{b}}},$$

(336)

where the velocity perturbation V is also written by Δ and Ω_b. There are two independent numerical codes that can be used to solve for Δ and Ωb. The first is the pseudo-spectral (PS) method used in [200] and the second is the characteristic integration (CI) algorithm developed in [70].

Figure 10 shows the output of the PS and CI codes for a typical simulation of a mode with ρ/λ = 50 at the horizon re-enter. As expected we have excellent agreement between the two codes, despite the fact that they use different initial conditions. Note that for all simulations, we recover that Δ and ζ are phase-locked plane waves,

$$\Delta (\eta) \propto \cos {{k\eta} \over {\sqrt 3}},\quad \Delta (\eta) \approx 4\zeta (\eta),$$

(337)

at sufficiently late times kη ≫ 1, which is actually the same behaviour as seen in GR. Figure 11 illustrates how the ordinary superhorizon behaviour of perturbations in GR is recovered for modes entering the Hubble horizon in the low energy era. We see how Δ, ψ and ${\mathcal R}$ smoothly interpolate between the non-standard high-energy behaviour to the usual expectations in GR. Also shown in this plot is the behaviour of the KK anisotropic stress, which steadily decays throughout the simulation. These results confirm that at low energies, we recover GR solutions smoothly.

Figure 10

Comparison between typical results of the PS and CI codes for various brane quantities (left); and the typical behaviour of the bulk master variable (right) as calculated by the CI method. Very good agreement between the two different numerical schemes is seen in the left panel, despite the fact that they use different initial conditions. Also note that on subhorizon scales, Δ and ζ undergo simple harmonic oscillations, which is consistent with the behaviour in GR. The bulk profile demonstrates our choice of initial conditions: We see that the bulk master variable Ω is essentially zero during the early stages of the simulation, and only becomes “large” when the mode crosses the horizon. Figure taken from [69].

Figure 11

The simulated behaviour of a mode on superhorizon scales. On the left we show how the Δ gauge invariant switches from the high-energy behaviour predicted to the familiar GR result as the universe expands through the critical epoch. We also show how the KK anisotropic stress $\kappa _4^2\delta {\pi _{\mathcal E}}$ steadily decays throughout the simulation, which is typical of all the cases we have investigated. On the right, we show the metric perturbations ψ (= Ψ) and ${\mathcal R}(= \Phi)$ as well as the curvature perturbation ζ. Again, note how the GR result Φ ≈ − Ψ ≈ −2ζ/3 is recovered at low energy. Figure taken from [69].

At high energies ρ > λ, there are two separate effects to consider: First, there is the modification of the universe’s expansion at high energies and the ${\mathcal O}(\rho/\lambda)$ corrections to the perturbative equations of motion. Second, there is the effect of the bulk degrees of freedom encapsulated by the bulk master variable Ω (or, equivalently, the KK fluid ${{\mathcal E}_{\mu \nu}}$). To separate out the two effects, it is useful to introduce the 4-dimensional effective theory where all ${\mathcal O}(\rho/\lambda)$ corrections to GR are retained, but the bulk effects are removed by artificially setting Ω = 0. In the case of radiation domination, we obtain equations for the effective theory density contrast Δ_ref and curvature perturbation ζ_ref from Equations (336) and (333) with Ωb = 0:

$$0 = {{{d^2}{\Delta _{{\rm{ref}}}}} \over {d{\eta ^2}}} + \left({{{{k^2}} \over 3} - {{4\rho {a^2}} \over {\lambda {\ell ^2}}} - {{18{\rho ^2}{a^2}} \over {{\lambda ^2}{\ell ^2}}}} \right){\Delta _{{\rm{ref}}}},$$

(338a)

$${\zeta _{{\rm{ref}}}} = \left({{1 \over 4} + {{3\rho {a^2}} \over {2\lambda {k^2}{\ell ^2}}} + {{9{\rho ^2}{a^2}} \over {4{\lambda ^2}{k^2}{\ell ^2}}}} \right){\Delta _{{\rm{ref}}}} + {{3Ha} \over {4k}}{{d{\Delta _{{\rm{ref}}}}} \over {d\eta}}.$$

(338b)

These give a closed set of ODEs on the brane that describe all of the ${\mathcal O}(\rho/\lambda)$ corrections to GR.

Since in any given model we expect the primordial value of the curvature perturbation to be fixed by inflation, it makes physical sense to normalize the waveforms from each theory such that ζ_5D ≈ ζ_ref ≈ ζ_gr ≈ 1 for a ≪ a_*. We can define a set of “enhancement factors”, which are functions of k that describe the relative amplitudes of Δ after horizon crossing in the various theories. Let the final amplitudes of the density perturbation with wavenumber k be ${{\mathcal C}_{5{\rm{D}}}}(k),\,{{\mathcal C}_{{\rm{ref}}}}(k)$ and ${{\mathcal C}_{{\rm{GR}}}}(k)$ for the 5-dimensional, effective and GR theories, respectively, given that the normalization ζ_5D ≈ ζ_ref ≈ ζ_gr ≈ 1 holds. Then, we define enhancement factors as

$${{\mathcal Q}_{{\rm{ref}}}}(k) = {{{{\mathcal C}_{{\rm{ref}}}}(k)} \over {{{\mathcal C}_{{\rm{GR}}}}(k)}},\quad {{\mathcal Q}_{\mathcal E}}(k) = {{{{\mathcal C}_{{\rm{5D}}}}(k)} \over {{{\mathcal C}_{{\rm{ref}}}}(k)}},\quad {{\mathcal Q}_{{\rm{5D}}}}(k) = {{{{\mathcal C}_{{\rm{5D}}}}(k)} \over {{{\mathcal C}_{{\rm{GR}}}}(k)}}.$$

(339)

It follows that ${{\mathcal Q}_{{\rm{ref}}}}(k)$ represents the ${\mathcal O}(\rho/\lambda)$ enhancement to the density perturbation, ${{\mathcal Q}_{\mathcal E}}(k)$ gives the magnification due to KK modes, while ${{\mathcal Q}_{5{\rm{D}}}}(k)$ gives the total 5-dimensional amplification over the GR case. They all increase as the scale is decreased, and that they all approach unity for k → 0. Since ${\mathcal Q}=1$ implies no enhancement of the density perturbations over the standard result, this means we recover general relativity on large scales. For all wavenumbers we see ${{\mathcal Q}_{{\rm{ref}}}} > {{\mathcal Q}_{\mathcal E}} > 1$, which implies that the amplitude magnification due to the ${\mathcal O}(\rho/\lambda)$ corrections is always larger than that due to the KK modes. Interestingly, the ${\mathcal Q}$-factors appear to approach asymptotically constant values for large k:

$${{\mathcal Q}_{{\rm{ref}}}}(k) \approx 3.0,\quad {{\mathcal Q}_{\mathcal E}}(k) \approx 2.4,\quad {{\mathcal Q}_{{\rm{5D}}}}(k) \approx 7.1,\quad k \gg {k_{\rm{c}}},$$

(340)

where k_c is the comoving wavenumber of the mode that enters the horizon when H = ℓ⁻¹.

In cosmological perturbation theory, transfer functions are very important quantities. They allow one to transform the primordial spectrum of some quantity set during inflation into the spectrum of another quantity at a later time. In this sense, they are essentially the Fourier transform of the retarded Green’s function for cosmological perturbations. There are many different transfer functions one can define, but for our case it is useful to consider a function T (k) that will tell us how the initial spectrum of curvature perturbations ${\mathcal P}_\zeta ^{\inf}$ maps onto the spectrum of density perturbations ${{\mathcal P}_\Delta}$ at some low energy epoch within the radiation era. It is customary to normalize transfer functions such that T (k; η) → 1(k → 0), which leads us to the following definition

$$T(k;\eta) = {9 \over 4}{\left[ {{k \over {H(\eta)a(\eta)}}} \right]^{- 2}}{{{\Delta _k}(\eta)} \over {\zeta _k^{{\rm{inf}}}}}.$$

(341)

Here, $\zeta _k^{\inf}$ is the primordial value of the curvature perturbation and Δ_k (η) is the maximum amplitude of the density perturbation in the epoch of interest. As demonstrated in Figure 11, we know that we recover the GR result in the extreme small scale limit (k → 0), which gives the transfer function the correct normalization. In the righthand panel of Figure 12, we show the transfer functions derived from GR, the effective theory and the 5-dimensional simulations. As expected, the T (k; η) for each formulation match one another on subcritical scales k < k_c. However, on supercritical scales we have T_5D > T_ref > T_GR.

Figure 12

Density perturbation enhancement factors (left) and transfer functions (right) from simulations, effective theory, and general relativity. All of the ${\mathcal Q}$ factors monotonically increase with k/k_c, and we see that the Δ amplitude enhancement due to ${\mathcal O}(\rho/\lambda)$ effects ${{\mathcal Q}_{{\rm{ref}}}}$ is generally larger than the enhancement due to KK effects ${{\mathcal Q}_{\mathcal E}}$. For asymptotically small scales k ≫ k_c, the enhancement seems to level off. The transfer functions in the right panel are evaluated at a given subcritical epoch in the radiation dominated era. The T functions show how, for a fixed primordial spectrum of curvature perturbations ${\mathcal P}_\zeta ^{\inf}$, the effective theory predicts excess power in the Δ spectrum ${{\mathcal P}_\Delta} \propto {T^2}{\mathcal P}_\zeta ^{\inf}$ on supercritical/subhorizon scales compared to the GR result. The excess small-scale power is even greater when KK modes are taken into account, as shown by T_5D(k; η). Figure taken from [69].

Note that if we are interested in the transfer function at some arbitrary epoch in the low-energy radiation regime Ha ≫ k_c, it is approximately given in terms of the enhancement factor as follows:

$${T_{{\rm{5D}}}}(k;\eta) \approx \left\{{\begin{array}{*{20}c} {1,\quad \quad \quad \quad \quad \quad} & {k < 3{H_a},} \\ {{{(3Ha/k)}^2}{{\mathcal Q}_{{\rm{5D}}}}(k),} & {k > 3{H_a},} \\ \end{array}} \right.$$

(342)

Now, the spectrum of density fluctuations at any point in the radiation era is given by

$${{\mathcal P}_\Delta}(k;\eta) = {{16} \over {81}}{T^2}(k;\eta){\left({{k \over {Ha}}} \right)^4}{\mathcal P}_\zeta ^{{\rm{inf}}}(k).$$

(343)

Using Equation (342), we see that the RS matter power spectrum (evaluated in the low-energy regime) is ∼ 50 times bigger than the GR prediction on scales given by k ∼ 10³k_c.

The amplitude enhancement of perturbations is important on comoving scales ≲ 10 AU, which are far too small to be relevant to present-day/cosmic microwave background measurements of the matter power spectrum. However, it may have an important bearing on the formation of compact objects such as primordial black holes and boson stars at very high energies, i.e., the greater gravitational force of attraction in the early universe will create more of these objects than in GR (different aspects of primordial black holes in RS cosmology in the context of various effective theories have been considered in [185, 184, 91, 384, 383, 382]).

6.6 Vector perturbations

The vorticity propagation equation on the brane is the same as in general relativity,

$${\dot \omega _\mu} + 2H{\omega _\mu} = - {1 \over 2}{\rm{curl}}\;{A_\mu}.$$

(344)

Taking the curl of the conservation equation (112) (for the case of a perfect fluid, q_μ = 0 = π_μν), and using the identity in Equation (255), one obtains

$${\rm{curl}}\;{A_\mu} = - 6Hc_{\rm{s}}^2{\omega _\mu}$$

(345)

as in general relativity, so that Equation (344) becomes

$${\dot \omega _\mu} + (2 - 3c_{\rm{s}}^2)\;H{\omega _\mu} = 0,$$

(346)

which expresses the conservation of angular momentum. In general relativity, vector perturbations vanish when the vorticity is zero. By contrast, in brane-world cosmology, bulk KK effects can source vector perturbations even in the absence of vorticity [304]. This can be seen via the divergence equation for the magnetic part H_μν of the 4D Weyl tensor on the brane,

$${\vec \nabla ^2}{\bar H_\mu} = 2{\kappa ^2}(\rho + p)\left[ {1 + {\rho \over \lambda}} \right]{\omega _\mu} + {4 \over 3}{\kappa ^2}{p_{\mathcal E}}{\omega _\mu} - {1 \over 2}{\kappa ^2}{\rm{curl}}\,\bar q_\mu ^{\mathcal E},$$

(347)

where ${H_{\mu \nu}} = {\vec \nabla _{\langle \mu}}{\bar H_{\nu \rangle}}$. Even when ω_μ = 0, there is a source for gravimagnetic terms on the brane from the KK quantity curl $\bar q_\mu ^{\mathcal E}$.

We define covariant dimensionless vector perturbation quantities for the vorticity and the KK gravi-vector term:

$${\bar \alpha _\mu} = a\,{\omega _\mu},\qquad {\bar \beta _\mu} = {a \over \rho}{\rm{curl}}\,\bar q_\mu ^{\mathcal E},$$

(348)

On large scales, we can find a closed system for these vector perturbations on the brane [304]:

$${\dot \bar \alpha _\mu} + (1 - 3c_{\rm{s}}^2)\;H{\bar \alpha _\mu} = 0,$$

(349)

$${\dot \bar \beta _\mu} + (1 - 3w)H{\bar \beta _\mu} = {2 \over 3}H\left[ {4(3c_{\rm{s}}^2 - 1){{{\rho _{\mathcal E}}} \over \rho} - 9{{(1 + w)}^2}{\rho \over \lambda}} \right]{\bar \alpha _\mu}.$$

(350)

Thus we can solve for ᾱ_μ and ${\bar \beta _\mu}$ on super-Hubble scales, as for density perturbations. Vorticity in the brane matter is a source for the KK vector perturbation ${\bar \beta _\mu}$ on large scales. Vorticity decays unless the matter is ultra-relativistic or stiffer ($w \geq {1 \over 3}$), and this source term typically provides a decaying mode. There is another pure KK mode, independent of vorticity, but this mode decays like vorticity. For w ≡ p/ρ = const., the solutions are

$${\bar \alpha _\mu} = {b_\mu}{\left({{a \over {{a_0}}}} \right)^{3w - 1}},$$

(351)

$${\bar \beta _\mu} = {c_\mu}{\left({{a \over {{a_0}}}} \right)^{3w - 1}} + {b_\mu}\left[ {{{8{\rho _{{\mathcal E}\,0}}} \over {3{\rho _0}}}{{\left({{a \over {{a_0}}}} \right)}^{2(3w - 1)}} + 2(1 + w){{{\rho _0}} \over \lambda}{{\left({{a \over {{a_0}}}} \right)}^{- 4}}} \right],$$

(352)

where ḃ_μ = 0 = ċ_μ.

Inflation will redshift away the vorticity and the KK mode. Indeed, the massive KK vector modes are not excited during slow-roll inflation [53, 362].

6.7 Tensor perturbations

The covariant description of tensor modes on the brane is via the shear, which satisfies the wave equation [304]

$${\vec \nabla ^2}{\bar \sigma _{\mu \nu}} - {\ddot \bar \sigma _{\mu \nu}} - 5H{\dot \bar \sigma _{\mu \nu}} - \left[ {2\Lambda + {1 \over 2}{\kappa ^2}\left({\rho - 3p - (\rho + 3p){\rho \over \lambda}} \right)} \right]{\bar \sigma _{\mu \nu}} - {\kappa ^2}\left({\dot \bar \pi _{\mu \nu}^{\mathcal E} + 2H\bar \pi _{\mu \nu}^{\mathcal E}} \right).$$

(353)

Unlike the density and vector perturbations, there is no closed system on the brane for large scales. The KK anisotropic stress $\bar \pi _{\mu \nu}^{\mathcal E}$ is an unavoidable source for tensor modes on the brane. Thus it is necessary to use the 5D metric-based formalism. This is the subject of the next Section 7.

7 Gravitational Wave Perturbations in Brane-World Cosmology

7.1 Analytical approaches

The tensor perturbations are given by Equation (273), i.e., (for a flat background brane),

$$^{(5)}d{s^2} = - {N^2}(t,y)d{t^2} + {A^2}(t,y)[{\delta _{ij}} + {f_{ij}}]\;d{x^i}d{x^j} + d{y^2}.$$

(354)

The transverse traceless f_ij satisfies Equation (293), which implies, on splitting fij into Fourier modes with amplitude f (t, y),

$${1 \over {{N^2}}}\left[ {\ddot f + \left({3{{\dot A} \over A} - {{\dot N} \over N}} \right)\dot f} \right] + {{{k^2}} \over {{A^2}}}f = f{\prime\prime} + \left({3{{A{\prime}} \over A} + {{N{\prime}} \over N}} \right)f{\prime}.$$

(355)

By the transverse traceless part of Equation (279), the boundary condition is

$${\left. {{{f{\prime}}_{ij}}} \right\vert _{{\rm{brane}}}} = {\bar \pi _{ij}},$$

(356)

where ${\bar \pi _{ij}}$ is the tensor part of the anisotropic stress of matter-radiation on the brane.

The wave equation (355) cannot be solved analytically except if the background metric functions are separable, and this only happens for maximally symmetric branes, i.e., branes with constant Hubble rate H₀. This includes the RS case H₀ = 0 already treated in Section 2. The cosmologically relevant case is the de Sitter brane, H₀ > 0. We can calculate the spectrum of gravitational waves generated during brane inflation [272, 176, 148, 232], if we approximate slow-roll inflation by a succession of de Sitter phases. The metric for a de Sitter brane dS₄ in AdS₅ is given by Equations (186, 187, 188) with

$$N(t,y) = n(y),$$

(357)

$$A(t,y) = a(t) n(y),$$

(358)

$$n(y) = \cosh \mu y - \left({1 + {{{\rho _0}} \over \lambda}} \right)\sinh \mu \vert y\vert ,$$

(359)

$$a(t) = {a_0}\exp {H_0}(t - {t_0}),$$

(360)

$$H_0^2 = {{{\kappa ^2}} \over 3}{\rho _0}\left({1 + {{{\rho _0}} \over {2\lambda}}} \right),$$

(361)

where μ = ℓ⁻¹.

The linearized wave equation (355) is separable. As before, we separate the amplitude as f = ḟφ_m (t)f_m (y) where m is the 4D mass, and this leads to:

$${\ddot \varphi _m} + 3{H_0}{\dot \varphi _m} + \left[ {{m^2} + {{{k^2}} \over {{a^2}}}} \right]{\varphi _m} = 0,$$

(362)

$$f_m{\prime\prime} + 4{{n\prime} \over n}f_m\prime + {{{m^2}} \over {{n^2}}}{f_m} = 0.$$

(363)

The general solutions for m > 0 are

$${\varphi _m}(t) = \exp \left({- {3 \over 2}{H_0}t} \right){B_\nu}\left({{k \over {{H_0}}}{e^{- {H_0}t}}} \right),$$

(364)

$${f_m}(y) = n{(y)^{- 3/2}}L_{3/2}^\nu \left({\sqrt {1 + {{{\mu ^2}} \over {H_0^2}}n{{(y)}^2}}} \right),$$

(365)

where B_ν is a linear combination of Bessel functions, $L_{3/2}^\nu$ is a linear combination of associated Legendre functions, and

$$\nu = i\sqrt {{{{m^2}} \over {H_0^2}} - {9 \over 4}} .$$

(366)

It is more useful to reformulate Equation (363) as a Schrödinger-type equation,

$${{{d^2}{\Psi _m}} \over {d{z^2}}} - V(z){\Psi _m} = - {m^2}{\Psi _m},$$

(367)

using the conformal coordinate

$$z = {z_{\rm{b}}} + \int\nolimits_0^y {{{d\tilde y} \over {n(\tilde y)}}} ,\qquad {z_{\rm{b}}} = {1 \over {{H_0}}}{\sinh ^{- 1}}\left({{{{H_0}} \over \mu}} \right),$$

(368)

and defining Ψ_m ≡ n^3/2f_m. The potential is given by (see Figure 13)

$$V(z) = {{15H_0^2} \over {4{{\sinh}^2}({H_0}z)}} + {9 \over 4}H_0^2 - 3\mu \left({1 + {{{\rho _0}} \over \lambda}} \right)\delta (z - {z_{\rm{b}}}),$$

(369)

where the last term incorporates the boundary condition at the brane. The “volcano” shape of the potential shows how the 5D graviton is localized at the brane at low energies. (Note that localization fails for an dS₄ brane [225, 396].)

Figure 13

Graviton “volcano” potential around the dS₄ brane, showing the mass gap. (Figure taken from [270].)

The non-zero value of the Hubble parameter implies the existence of a mass gap [154],

$$\Delta m = {3 \over 2}{H_0},$$

(370)

between the zero mode and the continuum of massive KK modes. This result has been generalized: For dS₄ brane(s) with bulk scalar field, a universal lower bound on the mass gap of the KK tower is [148]

$$\Delta m \geq \sqrt {{3 \over 2}} {H_0}.$$

(371)

The massive modes decay during inflation, according to Equation (364), leaving only the zero mode, which is effectively a 4D gravitational wave. The zero mode, satisfying the boundary condition

$${f}_0\prime(x,0) = 0,$$

(372)

is given by

$${f_0} = \sqrt \mu \,F\left({{H_0}/\mu} \right),$$

(373)

where the normalization condition

$$2\int\nolimits_{{z_{\rm{b}}}}^\infty \vert \Psi _0^2\vert dz = 1$$

(374)

implies that the function F is given by [272]

$$F\left(x \right) = {\left\{{\sqrt {1 + {x^2}} - {x^2}\ln \left[ {{1 \over x} + \sqrt {1 + {1 \over {{x^2}}}}} \right]} \right\}^{- 1/2}}.$$

(375)

At low energies (H₀ ≪ μ) we recover the general relativity amplitude: F → 1. At high energies, the amplitude is considerably enhanced:

$${H_0} \gg \mu \quad \Rightarrow \quad F \approx \sqrt {{{3{H_0}} \over {2\mu}}} .$$

(376)

The factor F determines the modification of the gravitational wave amplitude relative to the standard 4D result:

$$A_{\rm{t}}^2 = \left[ {{8 \over {M_{\rm{p}}^2}}{{\left({{{{H_0}} \over {2\pi}}} \right)}^2}} \right]{F^2}({H_0}/\mu){.}$$

(377)

The modifying factor F can also be interpreted as a change in the effective Planck mass [148].

This enhanced zero mode produced by brane inflation remains frozen outside the Hubble radius, as in general relativity, but when it re-enters the Hubble radius during radiation or matter domination, it will no longer be separated from the massive modes, since H will not be constant. Instead, massive modes will be excited during re-entry. In other words, energy will be lost from the zero mode as 5D gravitons are emitted into the bulk, i.e., as massive modes are produced on the brane. A phenomenological model of the damping of the zero mode due to 5D graviton emission is given in [281]. Self-consistent low-energy approximations to compute this effect are developed in [201, 136].

At zero order, the low-energy approximation is based on the following [321, 323, 27]. In the radiation era, at low energy, the background metric functions obey

$$A(t,y) \rightarrow a(t){e^{- \mu y}},\qquad N(t,y) \rightarrow {e^{- \mu y}}.$$

(378)

To lowest order, the wave equation therefore separates, and the mode functions can be found analytically [321, 323, 27]. The massive modes in the bulk, f_m (y), are the same as for a Minkowski brane. On large scales, or at late times, the mode functions on the brane are given in conformal time by

$$\varphi _m^{(0)}(\eta) = {\eta ^{- 1/2}}{B_{1/4}}\left({{{ma_{\rm{h}}^2\,\mu} \over {\sqrt 2}}{\eta ^2}} \right),$$

(379)

where a_h marks the start of the low-energy regime (ρ_h = λ), and B_ν denotes a linear combination of Bessel functions. The massive modes decay on super-Hubble scales, unlike the zero-mode. Expanding the wave equation in ρ₀/λ, one arrives at the first order, where mode-mixing arises. The massive modes $\varphi _m^{(1)}(\eta)$ on sub-Hubble scales are sourced by the initial zero mode that is re-entering the Hubble radius [136]:

$$\left({{{{\partial ^2}} \over {\partial {\eta ^2}}} - {{\partial _\eta ^2a} \over a}} \right)a\varphi _m^{(1)} + {k^2}a\varphi _m^{(1)} + {m^2}{a^3}\varphi _m^{(1)} = - 4{{{\rho _0}} \over \lambda}{I_{m0}}{k^2}a\varphi _0^{(0)},$$

(380)

where I_{m 0} is a transfer matrix coefficient. The numerical integration of the equations [201] confirms the effect of massive mode generation and consequent damping of the zero-mode.

7.2 Full numerical solutions

Full numerical solutions for the tensor perturbations have been obtained by the two methods — the pseudo-spectral (PS) method used in [200, 199] and the characteristic integration (CI) algorithm developed in [70]. It was shown that both methods give identical results and the behaviour of gravitational waves on a brane is quite insensitive to the initial conditions in the bulk as for the scalar perturbations [378]. Here we summarize the results obtained in [199]. It is convenient to use the static bulk metric and consider a moving brane. The simplest initial condition is f (z, τ) = const when the mode is outside the hubble horizon on the brane. If the brane is static, this would give a zero-mode solution f = cos(k (τ − τ₀)) where τ₀ is an initial time. However, due to the motion of the brane, which causes the expansion of the brane universe, KK modes are excited and this solution is modified. Figure 14 demonstrate this effect. Once the perturbation enters the horizon, non-trivial waves are excited in the bulk and the amplitude of the tensor perturbation is damped. Figure 15 shows the behaviour of gravitational waves for two different wave numbers. Here ϵ_* = ρ/λ at the time when the mode re-enters the horizon. As for scalar perturbations, we can define the effective 4D solutions by ignoring the bulk as a reference

$${\ddot h_{{\rm{ref}}}} + 3H{\dot h_{{\rm{ref}}}} + {{{k^2}} \over {a{{(t)}^2}}}{h_{{\rm{ref}}}} = 0.$$

(381)

h_ref only takes into account the effect of the high-energy modification of the Friedmann equation. Figure 15 shows that the full solution has an additional suppression of the amplitude compared with h_ref. This suppression is caused by the excitations of KK modes at the horizon crossing as is seen in Figure 14. The suppression is stronger for modes that enter the horizon earlier ϵ_* > 1 and it becomes negligible at low energies ϵ_* < 1.

Figure 14

The evolution of gravitational waves. We set the comoving wave number to $k = \sqrt 3/\ell$. The right panel depicts the projection of the three-dimensional waves of the left panel. Figure taken from [199].

Figure 15

Squared amplitude of gravitational waves on the brane in the low-energy (left) and the high-energy (right) regimes. In both panels, solid lines represent the numerical solutions. The dashed lines are the amplitudes of reference gravitational waves h_ref obtained from Equation (381). Figure taken from [199].

The ratio |h_5D|h_ref| evaluated at the low-energy regime long after the horizon re-entry time monotonically decreases with the frequency and the suppression of amplitude h_5D becomes significant above the critical frequency f_crit given by

$${f_{{\rm{crit}}}} = {1 \over {2\pi \ell}}{{{a_{{\rm{crit}}}}} \over {{a_{{\rm{eq}}}}}}{{{a_{{\rm{eq}}}}} \over {{a_0}}}$$

(382)

$$= 5.6 \times {10^{- 5}}\;{\rm{Hz}}{\left({{\ell \over {0.1\;{\rm{mm}}}}} \right)^{- 1/2}}{\left({{{{H_0}} \over {72\;{\rm{km/s}}\cdot{\rm{Mpc}}}}} \right)^{1/2}}{\left({{{1 + {z_{{\rm{eq}}}}} \over {3200}}} \right)^{- 1/4}}.$$

(383)

This corresponds to a frequency of the mode that enters the horizon when H_* = ℓ⁻¹ (cf. [202]). The ratio |h_5D/h_ref | obtained from numerical solutions is fitted as

$$\left\vert {{{{h_{{\rm{5D}}}}} \over {{h_{{\rm{ref}}}}}}} \right\vert = \alpha {\left({{f \over {{f_{{\rm{crit}}}}}}} \right)^{- \beta}}$$

(384)

with α = 0.76 ± 0.01 and β = 0.67 ± 0.01.

There are two important effects on the spectrum in the high-energy regime. Let us first consider the non-standard cosmological expansion due to the ρ²-term. The spectrum of the stochastic gravitational waves is modified to

$${\Omega _{{\rm{ref}}}} = \left\{{\begin{array}{*{20}c} {{f^{{{6w - 2} \over {3w + 1}}}}} & {{\rm{for}}\;\;f < {f_{{\rm{crit}}}},}\\ {{f^{{{6w + 2} \over {3w + 2}}}}} & {{\rm{for}}\;\;f > {f_{{\rm{crit}}}},}\\ \end{array}} \right.$$

(385)

where w is an equation of state. This is because gravitational waves re-enter the horizon when the ρ²-term dominates at high frequencies f > f_crit. In the high-energy radiation dominated phase, the spectrum of the stochastic gravitational waves is modified to

$${\Omega _{{\rm{ref}}}} \propto {f^{4/3}}\quad ({f_{{\rm{crit}}}} < f){.}$$

(386)

The other effect is the KK-mode excitations. Taking account of the KK-mode excitations, the spectrum is calculated as

$${\Omega _{{\rm{GW}}}} = {\left\vert {{{{h_{{\rm{5D}}}}} \over {{h_{{\rm{ref}}}}}}} \right\vert ^2}{\Omega _{{\rm{ref}}}},$$

(387)

where we used the fact Ω_GW ∝ h²f². Combining it with the result (384), the spectrum becomes nearly flat above the critical frequency:

$${\Omega _{{\rm{GW}}}} \propto {f^0},$$

(388)

which is shown in filled squares in Figure 16. In this figure, the spectrum calculated from the reference gravitational waves Ω_ref is also shown in filled circles. Note that the normalization factor of the spectrum is determined as Ω_GW = 10⁻¹⁴ from the CMB constraint. The short-dashed line and the solid line represent asymptotic behaviors in the high-frequency region. The spectrum taking account of the two high-energy effects seems almost indistinguishable from the standard four-dimensional prediction shown in long-dashed line in the figure. In other words, while the effect due to the non-standard cosmological expansion enhances the spectrum, the KK-mode effect reduces the GW amplitude, which results in the same spectrum as the one predicted in the four-dimensional theory. Note that the amplitude taking account of the two effects near f ≈ f_crit is slightly suppressed, which agrees with the results in the previous study for ϵ_* ≤ 0.3 using the Gaussian-normal coordinates [201] discussed in the previous subsection.

Figure 16

The energy spectrum of the stochastic background of gravitational wave around the critical frequency f_c in radiation dominated epoch. The filled circles represent the spectrum caused by the non-standard cosmological expansion of the universe. Taking account of the KK-mode excitations, the spectrum becomes the one plotted by filled squares. In the asymptotic region depicted in the solid line, the frequency dependence becomes almost the same as the one predicted in the four-dimensional theory (long-dashed line). Figure taken from [199].

This cancelation of two high energy effects is valid only for w = 1/3. For other equations of state, the final spectrum at high frequencies are different from 4D predictions. For example for w = 1, Ω_GW ∝f^2/5 for f > f_c while the 4D theory predicts Ω_GW ∝ f¹.

8 CMB Anisotropies in Brane-World Cosmology

For the CMB anisotropies, one needs to consider a multi-component source. Linearizing the general nonlinear expressions for the total effective energy-momentum tensor, we obtain

$${\rho _{{\rm{tot}}}} = \rho \left({1 + {\rho \over {2\lambda}} + {{{\rho _{\mathcal E}}} \over \rho}} \right),$$

(389)

$${p_{{\rm{tot}}}} = p + {\rho \over {2\lambda}}(2p + \rho) + {{{\rho _{\mathcal E}}} \over 3},$$

(390)

$$q_\mu ^{{\rm{tot}}} = {q_\mu}\left({1 + {\rho \over \lambda}} \right) + q_\mu ^{\mathcal E},$$

(391)

$$\pi _{\mu \nu}^{{\rm{tot}}} = {\pi _{\mu \nu}}\left({1 - {{\rho + 3p} \over {2\lambda}}} \right) + \pi _{\mu \nu}^{\mathcal E},$$

(392)

where

$$\rho = \sum\limits_i {{\rho _{(i)}}} ,\qquad p = \sum\limits_i {{p_{(i)}}} ,\qquad {q_\mu} = \sum\limits_i {q_\mu ^{(i)}}$$

(393)

are the total matter-radiation density, pressure, and momentum density, respectively, and π_μν is the photon anisotropic stress (neglecting that of neutrinos, baryons, and CDM).

The perturbation equations in the previous Section 7 form the basis for an analysis of scalar and tensor CMB anisotropies in the brane-world. The full system of equations on the brane, including the Boltzmann equation for photons, has been given for scalar [282] and tensor [281] perturbations. But the systems are not closed, as discussed above, because of the presence of the KK anisotropic stress $\pi _{\mu \nu}^{\mathcal E}$, which acts a source term.

In the tight-coupling radiation era, the scalar perturbation equations may be decoupled to give an equation for the gravitational potential Φ, defined by the electric part of the brane Weyl tensor (not to be confused with ${{\mathcal E}_{\mu \nu}}$):

$${E_{\mu \nu}} = {\vec \nabla _{\langle \mu}}{\vec \nabla _{\nu \rangle}}\Phi .$$

(394)

In general relativity, the equation in Φ has no source term, but in the brane-world there is a source term made up of $\pi _{\mu \nu}^{\mathcal E}$ and its time-derivatives. At low energies (ρ ≪ λ), and for a flat background (K = 0), the equation is [282]

$$3x\Phi _k{\prime\prime} + 12\Phi _k\prime + x{\Phi _k} = {{{\rm{const}}.} \over \lambda}\left[ {\pi _k^{{\mathcal E}\prime \prime} - {1 \over x}\pi _k^{{\mathcal E}\prime} + \left({{2 \over {{x^3}}} - {3 \over {{x^2}}} + {1 \over x}} \right)\pi _k^{\mathcal E}} \right],$$

(395)

where x = k/(aH), a prime denotes d/dx, and Φ_k and $\pi _{k}^{\mathcal E}$ are the Fourier modes of Φ and $\pi _{\mu \nu}^{\mathcal E}$, respectively. In general relativity the right hand side is zero, so that the equation may be solved for Φ_k, and then for the remaining perturbative variables, which gives the basis for initializing CMB numerical integrations. At high energies, earlier in the radiation era, the decoupled equation is fourth order [282]:

$$\begin{array}{*{20}c} {729{x^2}\Phi _k{\prime\prime\prime\prime} + 3888x\Phi _k{\prime\prime\prime} + (1782 + 54{x^2})\Phi _k{\prime\prime} + 144x\Phi _k\prime + (90 + {x^2}){\Phi _k}\quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ {= {\rm{const}}. \times \left[ {243{{\left({{{\pi _k^{\mathcal E}} \over \rho}} \right)}{\prime \prime \prime \prime}} - {{810} \over x}{{\left({{{\pi _k^{\mathcal E}} \over \rho}} \right)}{\prime \prime \prime}} + {{18(135 + 2{x^2})} \over {{x^2}}}{{\left({{{\pi _k^{\mathcal E}} \over \rho}} \right)}{\prime \prime}}\quad \quad \quad \quad \quad} \right.}\\ {\left. {- {{30(162 + {x^2})} \over {{x^3}}}{{\left({{{\pi _k^{\mathcal E}} \over \rho}} \right)}\prime} + {{{x^4} + 30(162 + {x^2})} \over {{x^4}}}\left({{{\pi _k^{\mathcal E}} \over \rho}} \right)} \right].}\\ \end{array}$$

(396)

The formalism and machinery are ready to compute the temperature and polarization anisotropies in brane-world cosmology, once a solution, or at least an approximation, is given for $\pi _{\mu \nu}^{\mathcal E}$. The resulting power spectra will reveal the nature of the brane-world imprint on CMB anisotropies, and would in principle provide a means of constraining or possibly falsifying the brane-world models. Once this is achieved, the implications for the fundamental underlying theory, i.e., M theory, would need to be explored.

However, the first step required is the solution for $\pi _{\mu \nu}^{\mathcal E}$ This solution will be of the form given in Equation (249). Once ${\mathcal G}$ and F_k are determined or estimated, the numerical integration in Equation (249) can in principle be incorporated into a modified version of a CMB numerical code. The full solution in this form represents a formidable problem, and one is led to look for approximations.

8.1 The low-energy approximation

The basic idea of the low-energy approximation [398, 428, 387, 399, 400] is to use a gradient expansion to exploit the fact that, during most of the history of the universe, the curvature scale on the observable brane is much greater than the curvature scale of the bulk (ℓ < 1 mm):

$$L\sim\;\vert {R_{\mu \nu \alpha \beta}}\vert ^{{- 1/2}} \gg \ell \sim\;\vert {\;^{(5)}}{R_{ABCD}}\vert ^{{- 1/2}}\quad \Rightarrow \quad \vert {\nabla _\mu}\vert \;\sim{L^{- 1}} \ll \;\vert \;{\partial _y}\vert \;\sim{\ell ^{- 1}}.$$

(397)

These conditions are equivalent to the low energy regime, since ℓ² ∝ λ⁻¹ and |R_μναβ | ∼ |T_μν |:

$${{{\ell ^2}} \over {{L^2}}}\sim{\rho \over \lambda} \ll 1.$$

(398)

Using Equation (397) to neglect appropriate gradient terms in an expansion in ℓ²/L², the low-energy equations can be solved. However, two boundary conditions are needed to determine all functions of integration. This is achieved by introducing a second brane, as in the RS 2-brane scenario. This brane is to be thought of either as a regulator brane, whose backreaction on the observable brane is neglected (which will only be true for a limited time), or as a shadow brane with physical fields, which have a gravitational effect on the observable brane.

The background is given by low-energy FRW branes with tensions ±λ, proper times t_±, scale factors a_±, energy densities ρ_± and pressures p_±, and dark radiation densities${\rho _{{\mathcal E}\, \pm}}$. The physical distance between the branes is $\ell \bar d(t)$, and

$${d \over {d{t_ -}}} = {e^{\bar d}}\,{d \over {d{t_ +}}},\qquad {a_ -} = {a_ +}{e^{- \bar d}},\qquad {H_ -} = {e^{\bar d}}\left({{H_ +} - \dot \bar d} \right),\qquad {\rho _{{\mathcal E}\, -}} = {e^{4\bar d}}{\rho _{{\mathcal E}\, +}}.$$

(399)

Then the background dynamics is given by

$$H_ \pm ^2 = \pm {{{\kappa ^2}} \over 3}({\rho _ \pm} \pm {\rho _{{\mathcal E}\, \pm}}),$$

(400)

$$\ddot \bar d + 3{H_ +}\dot \bar d - {\dot \bar d^2} = {{{\kappa ^2}} \over 6}\left[ {{\rho _ +} - 3{p_ +} + {e^{2\bar d}}({\rho _ -} - 3{p_ -})} \right].$$

(401)

(see [39, 276] for the general background, including the high-energy regime). The dark energy obeys ${\rho _{{\mathcal E} +}} = C/a_ + ^4$, where C is a constant. From now on, we drop the +-subscripts which refer to the physical, observed quantities.

The perturbed metric on the observable (positive tension) brane is described, in longitudinal gauge, by the metric perturbations ψ and ${\mathcal R}$, and the perturbed radion is $d = \bar d + N$. The approximation for the KK (Weyl) energy-momentum tensor on the observable brane is

$${{\mathcal E}^\mu}_\nu = {2 \over {{e^{2d}} - 1}}\left[ {- {{{\kappa ^2}} \over 2}({T_\nu ^\mu + {e^{- 2d}}T_{- \nu}^\mu}) - {\nabla ^\mu}{\nabla _\nu}d + \delta _\nu ^\mu {\nabla ^2}d - \left({{\nabla ^\mu}d{\nabla _\nu}d + {1 \over 2}\delta _\nu ^\mu {{(\nabla d)}^2}} \right)} \right],$$

(402)

and the field equations on the observable brane can be written in scalar-tensor form as

$${G^\mu}_\nu = {{{\kappa ^2}} \over \chi}T_\nu ^\mu + {{{\kappa ^2}{{(1 - \chi)}^2}} \over \chi}T_{- \nu}^\mu + {1 \over \chi}({\nabla ^\mu}{\nabla _\nu}\chi - \delta _\nu ^\mu {\nabla ^2}\chi) + {{\omega (\chi)} \over {{\chi ^2}}}\left({{\nabla ^\mu}\chi {\nabla _\nu}\chi - {1 \over 2}\delta _\nu ^\mu {{(\nabla \chi)}^2}} \right),$$

(403)

where

$$\chi = 1 - {e^{- 2d}},\qquad \omega (\chi) = {3 \over 2}{\chi \over {1 - \chi}}.$$

(404)

The perturbation equations can then be derived as generalizations of the standard equations. For example, the $\delta {G^0}_0$ equation is

$$\begin{array}{*{20}c} {{H^2}\psi - H\dot{\mathcal R} - {1 \over 3}{{{k^2}} \over {{a^2}}}{\mathcal R} = - {1 \over 6}{\kappa ^2}{{{e^{2\bar d}}} \over {{e^{2\bar d}} - 1}}\left({\delta \rho + {e^{- 4\bar d}}\delta {\rho _ -}} \right) + {2 \over 3}{\kappa ^2}{{{e^{2\bar d}}} \over {{e^{2\bar d}} - 1}}{\rho _{\mathcal E}}N\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ {- {1 \over {{e^{2\bar d}} - 1}}\left[ {\left({\dot \bar d - H} \right)\dot N + {{\left({\dot \bar d - H} \right)}^2}N - {{\dot \bar d}^2}\psi + 2H\dot \bar d\psi - \dot \bar d\dot{\mathcal R}- {1 \over 3}{{{k^2}} \over {{a^2}}}N} \right].}\\ \end{array}$$

(405)

The trace part of the perturbed field equation shows that the radion perturbation determines the crucial quantity, $\delta {\pi _{\mathcal E}}$:

$${\mathcal R} + \psi = - {2 \over {{e^{2\bar d}} - 1}}N = - {\kappa ^2}{a^2}\delta {\pi _{\mathcal E}},$$

(406)

where the last equality follows from Equation (325). The radion perturbation itself satisfies the wave equation

$$\begin{array}{*{20}c} {\ddot N + \left({3H - 2\dot \bar d} \right)\dot N - \left({2\dot H + 4{H^2} + 2{{\dot \bar d}^2} - 6H\dot \bar d - 2\ddot \bar d} \right)N + {{{k^2}} \over {{a^2}}}N}\\ {- \dot \bar d\dot \psi + 3\dot \bar d\dot{\mathcal R} + \left({- 2\ddot \bar d - 6H\dot \bar d + 2{{\dot \bar d}^2}} \right)\psi \quad \quad \quad \quad \quad}\\ {= {{{\kappa ^2}} \over 6}\left[ {\delta \rho - 3\delta p + {e^{- 2\bar d}}(\delta {\rho _ -} - 3\delta {p_ -})} \right].}\quad \quad\quad \quad \quad\\ \end{array}$$

(407)

A new set of variables φ±, E turns out be very useful [244, 245]:

$$\begin{array}{*{20}c} {{\mathcal R} = - {\varphi _ +} - {{{a^2}} \over {{k^2}}}H\dot E + {1 \over 3}E,}\\ {\psi = - {\varphi _ +} - {{{a^2}} \over {{k^2}}}(\ddot E + 2H\dot E),}\\ {N = {\varphi _ -} - {\varphi _ +} - {{{a^2}} \over {{k^2}}}\dot \bar d\dot E.\;\;\;\;\;\;\;} \\ \end{array}$$

(408)

Equation (406) gives

$$\ddot E + \left({3H + {{2\dot \bar d} \over {{e^{2\bar d}} - 1}}} \right)\dot E - {1 \over 3}{{{k^2}} \over {{a^2}}}E = - {{2{e^{2\bar d}}} \over {{e^{2\bar d}} - 1}}{{{k^2}} \over {{a^2}}}\left({{\varphi _ +} - {e^{- 2\bar d}}{\varphi _ -}} \right).$$

(409)

The variable E determines the metric shear in the bulk, whereas φ± give the brane displacements in transverse traceless gauge. The latter variables have a simple relation to the curvature perturbations on large scales [244, 245] (restoring the +-subscripts):

$${\zeta _{{\rm{tot}}\, \pm}} = - {\varphi _ \pm} + {{H_ \pm ^2} \over {{{\dot H}_ \pm}}}\left({{{{{\dot \varphi}_ \pm}} \over {{H_ \pm}}} + {\varphi _ \pm}} \right),$$

(410)

where ḟ± ≡ df±/dt±.

8.2 The simplest model

The simplest model is the one in which

$${\rho _{\mathcal E}} = 0 = \dot \bar d$$

(411)

in the background, with p₋/ρ₋ = p/ρ. The regulator brane is assumed to be far enough away that its effects on the physical brane can be neglected over the timescales of interest. By Equation (401) it follows that

$${\rho _ -} = - \rho {e^{2\bar d}},$$

(412)

i.e., the matter on the regulator brane must have fine-tuned and negative energy density to prevent the regulator brane from moving in the background. With these assumptions, and further assuming adiabatic perturbations for the matter, there is only one independent brane-world parameter, i.e., the parameter measuring dark radiation fluctuations:

$$\delta {C_\ast} = {{\delta {\rho _{\mathcal E}}} \over {{\rho _{{\rm{rad}}}}}}.$$

(413)

This assumption has a remarkable consequence on large scales: The Weyl anisotropic stress $\delta {\pi _{\mathcal E}}$ terms in the Sachs-Wolfe formula (327) cancel the entropy perturbation from dark radiation fluctuations, so that there is no difference on the largest scales from the standard general relativity power spectrum. On small scales, beyond the first acoustic peak, the brane-world corrections are negligible. On scales up to the first acoustic peak, brane-world effects can be significant, changing the height and the location of the first peak. These features are apparent in Figure 17. However, it is not clear to what extent these features are general brane-world features (within the low-energy approximation), and to what extent they are consequences of the simple assumptions imposed on the background. Further work remains to be done.

Figure 17

The CMB power spectrum with brane-world effects, encoded in the dark radiation fluctuation parameter δC_* as a proportion of the large-scale curvature perturbation for matter (denoted ζ_* in the plot). (Figure taken from [245].)

A related low-energy approximation, using the moduli space approximation, has been developed for certain 2-brane models with bulk scalar field [361, 51]. The effective gravitational action on the physical brane, in the Einstein frame, is

$${S_{{\rm{eff}}}} = {1 \over {2{\kappa ^2}}}\int {{d^4}} x\sqrt {- g} \left[ {R - {{12{\alpha ^2}} \over {1 + 2{\alpha ^2}}}{{(\partial \phi)}^2} - {6 \over {1 + 2{\alpha ^2}}}{{(\partial \chi)}^2} - V(\phi ,\chi)} \right],$$

(414)

where α is a coupling constant, and ϕ and χ are moduli fields (determined by the zero-mode of the bulk scalar field and the radion). Figure 18 shows how the CMB anisotropies are affected by the χ-field.

Figure 18

The CMB power spectrum with brane-world moduli effects from the field χ in Equation (414). The curves are labelled with the initial value of χ. (Figure taken from [361, 51].)

9 DGP Models: Modifying Gravity at Low Energies

9.1 ‘Self-accelerating’ DGP

Most brane-world models modify general relativity at high energies. The Randall-Sundrum models discussed up to now are a typical example. At low energies, Hℓ ≪ 1, the zero-mode of the graviton dominates on the brane, and general relativity is recovered to a good approximation. At high energies, Hℓ ≫ 1, the massive modes of the graviton dominate over the zero-mode, and gravity on the brane behaves increasingly 5-dimensional. On the unperturbed FRW brane, the standard energy-conservation equation holds, but the Friedmann equation is modified by an ultraviolet correction, (Gℓρ)². At high energies, gravity “leaks” off the brane and H² ∝ ρ².

By contrast, the brane-world model of Dvali-Gabadadze-Porrati [135] (DGP), which was generalized to cosmology by Deffayet [115], modifies general relativity at low energies. This model produces ‘self-acceleration’ of the late-time universe due to a weakening of gravity at low energies. Like the RS model, the DGP model is a 5D model with infinite extra dimensions.³

The action is given by

$${{- 1} \over {16\pi G}}\left[ {{1 \over {{r_c}}}\int\nolimits_{{\rm{bulk}}} {{d^5}} x\,\sqrt {- {g^{(5)}}} \,{R^{(5)}} + \int\nolimits_{{\rm{brane}}} {{d^4}} x\,\sqrt {- g} \,R} \right]\,.$$

(415)

The bulk is assumed to be 5D Minkowski spacetime. Unlike the AdS bulk of the RS model, the Minkowski bulk has infinite volume. Consequently, there is no normalizable zero-mode of the 4D graviton in the DGP brane-world. Gravity leaks off the 4D brane into the bulk at large scales, r ≫ r_c, where the first term in the sum (415) dominates. On small scales, gravity is effectively bound to the brane and 4D dynamics is recovered to a good approximation, as the second term dominates. The transition from 4D to 5D behaviour is governed by the crossover scale r_c. For a Minkowski brane, the weak-field gravitational potential behaves as

$$\psi \propto \left\{{\begin{array}{*{20}c} {{r^{- 1}}\;{\rm{for}}\;\;r \ll {r_c}}\\ {{r^{- 2}}\;{\rm{for}}\;\;r \ll {r_c}} \\ \end{array} .} \right.$$

(416)

On a Friedmann brane, gravity leakage at late times in the cosmological evolution can initiate acceleration — not due to any negative pressure field, but due to the weakening of gravity on the brane. 4D gravity is recovered at high energy via the lightest massive modes of the 5D graviton, effectively via an ultra-light meta-stable graviton.

The energy conservation equation remains the same as in general relativity, but the Friedmann equation is modified [115]:

$$\dot \rho + 3H(\rho + p) = 0\,,$$

(417)

$${H^2} + {K \over {{a^2}}} - {1 \over {{r_c}}}\sqrt {{H^2} + {K \over {{a^2}}}} = {{8\pi G} \over 3}\rho \,.$$

(418)

The Friedmann equation can be derived from the junction condition or the Gauss-Codazzi equation as in the RS model. To arrive at Equation (418) we have to take a square root which implies a choice of sign. As we shall see, the above choice has the advantage of leading to acceleration — but at the expense of a ‘ghost’ (negative kinetic energy) mode in the scalar graviton sector. The ‘normal’ (non-self-accelerating) DGP model, where the opposite sign of the square root is chosen, has no ghost, and is discussed below.

From Equation (418) we infer that at early times, i.e., Hr_c ≫ 1, the general relativistic Friedman equation is recovered. By contrast, at late times in an expanding CDM universe, with ρ ∝ a⁻³ → 0, we have

$$H \rightarrow {H_\infty} = {1 \over {{r_c}}}\,,$$

(419)

so that expansion accelerates and is asymptotically de Sitter. The above equations imply

$$\dot H - {K \over {{a^2}}} = - 4\pi G\rho \left[ {1 + {1 \over {\sqrt {1 + 32\pi Gr_c^2\rho /3}}}} \right].$$

(420)

In order to achieve self-acceleration at late times, we require

$${r_c}\underset{\sim}{>} H_0^{- 1}\,,$$

(421)

since H₀ ≲ H_∞. This is confirmed by fitting supernova observations, as shown in Figures 19 and 20. The dimensionless cross-over parameter is defined as

$${\Omega _{{r_c}}} = {1 \over {4{{({H_0}{r_c})}^2}}}\,,$$

(422)

and the LCDM relation,

$${\Omega _m} + {\Omega _\Lambda} + {\Omega _K} = 1\,,$$

(423)

is modified to

$${\Omega _m} + 2\sqrt {{\Omega _{{r_c}}}} \sqrt {1 - {\Omega _K}} + {\Omega _K} = 1\,.$$

(424)

Figure 19

Joint constraints [solid thick (blue)] from the SNLS data [solid thin (yellow)], the BAO peak at z = 0.35 [dotted (green)] and the CMB shift parameter from WMAP3 [dot-dashed (red)]. The left plot shows LCDM models, the right plot shows DGP. The thick dashed (black) line represents the flat models, Ω_K = 0. (From [306].)

Figure 20

The constraints from SNe and CMB/BAO on the parameters in the DGP model. The flat DGP model is indicated by the vertical dashed-dotted line; for the MLCS light curve fit, the flat model matches to the date very well. The SALT-II light curve fit to the SNe is again shown by the dotted contours. The combined constraints using the SALT-II SNe outlined by the dashed contours represent a poorer match to the CMB/BAO for the flat model. (From [401].)

LCDM and DGP can both account for the supernova observations, with the fine-tuned values $\Lambda \sim H_0^2$ and ${r_c} \sim H_0^{- 1}$, respectively. When we add further constraints to the expansion history from the baryon acoustic oscillation peak at z = 0.35 and the CMB shift parameter, the DGP flat models are in strong tension with the data, whereas LCDM models provide a consistent fit. This is evident in Figures 19 and 20 though this conclusion depends on a choice of light curve fitters in the SNe observations. The open DGP models provide a somewhat better fit to the geometric data — essentially because the lower value of Ω_m favoured by supernovae reduces the distance to last scattering and an open geometry is able to extend that distance. For a combination of SNe, CMB shift and Hubble Key Project data, the best-fit open DGP also performs better than the flat DGP [402], as shown in Figure 21.

Figure 21

The difference in χ² between best-fit DGP (flat and open) and best-fit (flat) LCDM, using SNe, CMB shift and H₀ Key Project data. (From [402].)

Observations based on structure formation provide further evidence of the difference between DGP and LCDM, since the two models suppress the growth of density perturbations in different ways [296, 295]. The distance-based observations draw only upon the background 4D Friedman equation (418) in DGP models — and therefore there are quintessence models in general relativity that can produce precisely the same supernova distances as DGP. By contrast, structure formation observations require the 5D perturbations in DGP, and one cannot find equivalent quintessence models [251]. One can find 4D general relativity models, with dark energy that has anisotropic stress and variable sound speed, which can in principle mimic DGP [263]. However, these models are highly unphysical and can probably be discounted on grounds of theoretical consistency.

For LCDM, the analysis of density perturbations is well understood. For DGP the perturbations are much more subtle and complicated [251]. Although matter is confined to the 4D brane, gravity is fundamentally 5D, and the 5D bulk gravitational field responds to and back-reacts on 4D density perturbations. The evolution of density perturbations requires an analysis based on the 5D nature of gravity. In particular, the 5D gravitational field produces an effective “dark” anisotropic stress on the 4D universe, as discussed in Section 3.4. If one neglects this stress and other 5D effects, and simply treats the perturbations as 4D perturbations with a modified background Hubble rate — then as a consequence, the 4D Bianchi identity on the brane is violated, i.e., ∇^vG_μν ≠ 0, and the results are inconsistent. When the 5D effects are incorporated [251, 71], the 4D Bianchi identity is automatically satisfied. (See Figure 22.)

Figure 22

The growth factor g (a) = Δ(a)/a for LCDM (long dashed) and DGP (solid, thick), as well as for a dark energy model with the same expansion history as DGP (short dashed). DGP-4D (solid, thin) shows the incorrect result in which the 5D effects are set to zero. (From [251].)

There are three regimes governing structure formation in DGP models:

• On small scales, below the Vainshtein radius (which for cosmological purposes is roughly the scale of clusters), the spin-0 scalar degree of freedom becomes strongly coupled, so that the general relativistic limit is recovered [256].

• On scales relevant for structure formation, i.e., between cluster scales and the Hubble radius, the spin-0 scalar degree of freedom produces a scalar-tensor behaviour. A quasi-static approximation (as in the Newtonian approximation in standard 4D cosmology) to the 5D perturbations shows that DGP gravity is like a Brans-Dicke theory with parameter [251]

  $${\omega _{BD}} = {3 \over 2}(\beta - 1),$$

  (425)
  $$\beta = 1 + 2{H^2}{r_c}{\left({{H^2} + {K \over {{a^2}}}} \right)^{- 1/2}}\left[ {1 + {{\dot H} \over {3{H^2}}} + {{2K} \over {3{a^2}{H^2}}}} \right].$$

  (426)

  At late times in an expanding universe, when Hr_c ≳ 1, it follows that β < 1, so that ω_BD < 0. (This is a signal of the ghost pathology in DGP, which is discussed below.)

• Although the quasi-static approximation allows us to analytically solve the 5D wave equation for the bulk degree of freedom, this approximation breaks down near and beyond the Hubble radius. On super-horizon scales, 5D gravity effects are dominant, and we need to solve numerically the partial differential equation governing the 5D bulk variable [71].

On subhorizon scales relevant for linear structure formation, 5D effects produce a difference between ϕ and − ψ [251]:

$${k^2}\phi = 4\pi G{a^2}\left({1 - {1 \over {3\beta}}} \right)\rho \Delta \,,$$

(427)

$${k^2}\psi = - 4\pi G{a^2}\left({1 + {1 \over {3\beta}}} \right)\rho \Delta \,,$$

(428)

so that there is an effective dark anisotropic stress on the brane:

$${k^2}(\phi + \psi) = - {{8\pi G{a^2}} \over {3{\beta ^2}}}\rho \Delta \,.$$

(429)

The density perturbations evolve as

$$\ddot \Delta + 2H\dot \Delta - 4\pi G\left({1 - {1 \over {3\beta}}} \right)\rho \Delta = 0\,.$$

(430)

The linear growth factor, g (a) = Δ(a)/a (i.e., normalized to the flat CDM case, Δ ∝ a), is shown in Figure 22. This illustrates the dramatic suppression of growth in DGP relative to LCDM — from both the background expansion and the metric perturbations. If we parametrize the growth factor in the usual way, we can quantify the deviation from general relativity with smooth dark energy [293]:

$$f: = {{d\ln \Delta} \over {d\ln a}} = {\Omega _m}{(a)^\gamma}\,,\quad \gamma \approx \left\{{\begin{array}{*{20}c} {0{.}55 + 0{.}05[1 + w(z = 1)]} & {{\rm{GR}},\;{\rm{smooth}}\;{\rm{DE}}}\\ {0.68\quad \quad \quad \quad \quad \quad \quad \;\;} & {{\rm{DGP}}\quad \quad \quad \quad}\\ \end{array}} \right.$$

(431)

Observational data on the growth factor [188] are not yet precise enough to provide meaningful constraints on the DGP model. Instead, we can look at the large-angle anisotropies of the CMB, i.e., the ISW effect. This requires a treatment of perturbations near and beyond the horizon scale. The full numerical solution has been given by [71], and is illustrated in Figure 23. The CMB anisotropies are also shown in Figure 23, as computed in [142] using a scaling approximation to the super-Hubble modes [376] (the accuracy of the scaling ansatz is verified by the numerical results [71]).

Figure 23

Left: Numerical solutions for DGP density and metric perturbations, showing also the quasi-static solution, which is an increasingly poor approximation as the scale is increased. (From [71].) Right: Constraints on DGP (the open model in Figure 21 that provides a best fit to geometric data) from CMB anisotropies (WMAP5). The DGP model is the solid curve, QCDM (short-dashed curve) is the GR quintessence model with the same background expansion history as the DGP model, and LCDM is the dashed curve (a slightly closed model that gives the best fit to WMAP5, HST and SNLS data). (From [142].)

It is evident from Figure 23 that the DGP model, which provides a best fit to the geometric data (see Figure 21), is in serious tension with the WMAP5 data on large scales. The problem arises because there is a large deviation of ϕ₋ = (ϕ − ψ)/2 in the DGP model from the LCDM model. This deviation, i.e., a stronger decay of ϕ₋, leads to an over-strong ISW effect (which is determined by ${\dot \phi _ -}$), in tension with WMAP5 observations.

As a result of the combined observations of background expansion history and large-angle CMB anisotropies, the DGP model provides a worse fit to the data than LCDM at about the 5σ level [142]. Effectively, the DGP model is ruled out by observations in comparison with the LCDM model.

In addition to the severe problems posed by cosmological observations, a problem of theoretical consistency arises from the fact that the late-time asymptotic de Sitter solution in DGP cosmological models has a ghost. The ghost is signaled by the negative Brans-Dicke parameter in the effective theory that approximates the DGP on cosmological subhorizon scales: The existence of the ghost is confirmed by detailed analysis of the 5D perturbations in the de Sitter limit [246, 175, 81, 246]. The DGP ghost is a ghost mode in the scalar sector of the gravitational field — which is more serious than the ghost in a phantom scalar field. It effectively rules out the DGP, since it is hard to see how an ultraviolet completion of the DGP can cure the infrared ghost problem. However, the DGP remains a valuable toy model for illustrating the kinds of behaviour that can occur from a modification to Einstein’s equations — and for developing cosmological tools to test modified gravity and Einstein’s theory itself.

9.2 ‘Normal’ DGP

The self-accelerating DGP is effectively ruled out as a viable cosmological model by observations and by the problem of the ghost in the gravitational sector. Indeed, it may be the case that self-acceleration generically comes with the price of ghost states. The ‘normal’ (i.e., non-self-accelerating and ghost-free) branch of the DGP [371], arises from a different embedding of the DGP brane in the Minkowski bulk (see Figure 24). In the background dynamics, this amounts to a replacement r_c → − r_c in Equation (418) — and there is no longer late-time self-acceleration. Therefore, it is necessary to include a Λ term in order to accelerate the late universe:

$${H^2} + {K \over {{a^2}}} + {1 \over {{r_c}}}\sqrt {{H^2} + {K \over {{a^2}}}} = {{8\pi G} \over 3}\rho + {\Lambda \over 3}\,.$$

(432)

(Normal DGP models with a quintessence field have also been investigated [88].) Using the dimensionless crossover parameter defined in Equation (422), the densities are related at the present time by

$$\sqrt {1 - {\Omega _K}} = - \sqrt {{\Omega _{{r_c}}}} + \sqrt {{\Omega _{{r_c}}} + {\Omega _m} + {\Omega _\Lambda}} \,,$$

(433)

which can be compared with the self-accelerating DGP relation (424).

Figure 24

Left: The embedding of the self-accelerating and normal branches of the DGP brane in a Minkowski bulk. (From [81].) Right: Joint constraints on normal DGP (flat, K = 0) from SNLS, CMB shift (WMAP3) and BAO (z = 0.35) data. The best-fit is the solid point, and is indistinguishable from the LCDM limit. The shaded region is unphysical and its upper boundary represents flat LCDM models. (From [279].)

An interesting feature of the normal branch is the ‘degravitation’ property, i.e., that Λ is effectively screened by 5D gravity effects. This follows from rewriting the modified Friedmann equation (432) in standard general relativistic form, with

$${\Lambda _{{\rm{eff}}}} = \Lambda - {3 \over {{r_c}}}\sqrt {{H^2} + {K \over {{a^2}}}} < \Lambda \,.$$

(434)

Thus, 5D gravity in normal DGP can in principle reduce the bare vacuum energy significantly [371, 298]. However, Figure 24 shows that best-fit flat models, using geometric data, only admit insignificant screening [279]. The closed models provide a better fit to the data [167], and can allow a bare vacuum energy term with Ω_Λ > 1, as shown in Figure 25. This does not address the fundamental problem of the smallness of Ω_Λ, but is nevertheless an interesting feature. We can define an effective equation-of-state parameter via

$${\dot \Lambda _{{\rm{eff}}}} + 3H(1 + {w_{{\rm{eff}}}}){\Lambda _{{\rm{eff}}}} = 0\,.$$

(435)

At the present time (setting K = 0 for simplicity),

$${w_{{\rm{eff}},0}} = - 1 - {{({\Omega _m} + {\Omega _\Lambda} - 1){\Omega _m}} \over {(1 - {\Omega _m})({\Omega _m} + {\Omega _\Lambda} + 1)}} < - 1\,,$$

(436)

where the inequality holds because Ω_m < 1. This reveals another important property of the normal DGP model: effective phantom behaviour of the recent expansion history. This is achieved without any pathological phantom field (similar to what can be done in scalar-tensor theories [42]). Furthermore, there is no “big rip” singularity in the future associated with this phantom acceleration, unlike the situation that typically arises with phantom fields. The phantom behaviour in the normal DGP model is also not associated with any ghost problem — indeed, the normal DGP branch is free of the ghost that plagues the self-accelerating DGP [81].

Figure 25

Left: Joint constraints on normal DGP from SNe Gold, CMB shift (WMAP3) and H₀ data in the projected curvature-Λ plane, after marginalizing over other parameters. The best-fits are the solid points, corresponding to different values of Ω_m. (From [167].) Right: Numerical solutions for the normal DGP density and metric perturbations, showing also the quasistatic solution, which is an increasingly poor approximation as the scale is increased. Compare with the self-accelerating DGP case in Figure 23. (From [71].)

Perturbations in the normal branch have the same structure as those in the self-accelerating branch, with the same regimes — i.e., below the Vainshtein radius (recovering a GR limit), up to the Hubble radius (Brans-Dicke behaviour), and beyond the Hubble radius (strongly 5D behaviour). The quasistatic approximation and the numerical integrations can be simply repeated with the replacement r_c → − r_c (and the addition of Λ to the background). In the sub-Hubble regime, the effective Brans-Dicke parameter is still given by Equations (425) and (426), but now we have ω_BD > 0 — and this is consistent with the absence of a ghost. Furthermore, a positive Brans-Dicke parameter signals an extra positive contribution to structure formation from the scalar degree of freedom, so that there is less suppression of structure formation than in LCDM — the reverse of what happens in the self-accelerating DGP. This is confirmed by computations, as illustrated in Figure 25.

The closed normal DGP models fit the background expansion data reasonably well, as shown in Figure 25. The key remaining question is how well do these models fit the large-angle CMB anisotropies, which is yet to be computed at the time of writing. The derivative of the ISW potential ${\dot \phi _ -}$ can be seen in Figure 25, and it is evident that the ISW contribution is negative relative to LCDM at high redshifts, and goes through zero at some redshift before becoming positive. This distinctive behaviour may be contrasted with the behaviour in f (R) models (see Figure 26): both types of model lead to less suppression of structure than LCDM, but they produce different ISW effects. However, in the limit r_r → ∞, normal DGP tends to ordinary LCDM, hence observations which fit LCDM will always just provide a lower limit for r_c.

Figure 26

Top: Measurement of the cross-correlation functions between six different galaxy data sets and the CMB, reproduced from [166]. The curves show the theoretical predictions for the ISW-galaxy correlations at each redshift for the LCDM model (black, dashed) and the three nDGP models, which describe the 1 − σ region of the geometry test from Figure 25. (From [167].) Bottom: Theoretical predictions for a family of f(R) theories compared with the ISW data [166] measuring the angular CCF between the CMB and six galaxy catalogues. The model with B₀ = 0 is equivalent to LCDM, while increasing departures from GR produce negative cross-correlations. (From [165].)

10 6-Dimensional Models

For brane-world models in 6-dimensional spacetime, the codimension of a brane is two and the behaviour of gravity is qualitatively very different from the codimension one brane-world models. Here we briefly discuss some important examples and features of 6-dimensional models.

10.1 Supersymmetric Large Extra Dimensions (SLED) Model

This is a supersymmetric version of the Einstein-Maxwell model [72] (see [57, 58, 59, 247] for reviews). The bosonic part of the action is given by [3, 4, 2]

$$S = \int {{d^6}} x\sqrt {- g} \left[ {{1 \over {2\kappa _6^2}}\left({R - {\partial _M}\phi {\partial ^M}\phi} \right) - {1 \over 4}{e^{- \phi}}{F_{MN}}{F^{MN}} - {e^\phi}{\Lambda _6}} \right].$$

(437)

There exists a solution where the dilaton ϕ is constant, ϕ = ϕ₀. The solution for the 6D spacetime is given by

$$d{s^2} = {\eta _{\mu \nu}}d{x^\mu}d{x^\nu} + {\gamma _{ij}}d{x^i}d{x^j}.$$

(438)

The gauge field is taken to consist of magnetic flux threading the extra dimensional space so that the field strength takes the form

$${F_{ij}} = \sqrt \gamma {B_0}{\epsilon _{ij}},$$

(439)

where B₀ is a constant, γ is the determinant of γ_ij and ϵ_ij is the antisymmetric tensor normalized as ϵ₁₂ = 1. All other components of F_ab vanish. A static and stable solution is obtained by choosing the extra-dimensional space to be a two-sphere

$${\gamma _{ij}}d{x^i}d{x^j} = a_0^2(d{\theta ^2} + {\sin ^2}\theta d{\varphi ^2}){.}$$

(440)

The magnetic field strength B₀ and the radius a₀ are fixed by the cosmological constant

$$B_0^2 = 2{\Lambda _6}{e^{2{\phi _0}}},\quad a_0^2 = {{M_6^4} \over {2{\Lambda _6}{e^{{\phi _0}}}.}}.$$

(441)

The constant value ϕ₀ is determined by the condition that the potential for ϕ has minimum [153]

$$V{\prime}({\phi _0}) = - {1 \over 2}B_0^2{e^{- {\phi _0}}} + {\Lambda _6}{e^{{\phi _0}}} = 0.$$

(442)

This is exactly the condition to have a flat geometry on the brane (see Equation (441))

$$B_0^2{e^{- {\phi _0}}} = 2{\Lambda _6}{e^{{\phi _0}}}.$$

(443)

Thus without tuning the 6D cosmological constant, it is possible to obtain a flat 4D spacetime.

Now we add branes to this solution [72]. The brane action is given by

$${S_4} = - \sigma \int {{d^4}} x\sqrt {- \gamma} .$$

(444)

The solution for the extra dimensions is now given by

$${\gamma _{ij}}d{x^i}d{x^j} = a_0^2(d{\theta ^2} + {\alpha ^2}{\sin ^2}\theta d{\varphi ^2}),$$

(445)

where

$$\alpha = 1 - {\sigma \over {2\pi M_6^2}},\quad a_0^2 = {{M_6^4} \over {2{\Lambda _6}{e^{{\phi _0}}}}}.$$

(446)

The coordinate φ ranges from 0 to 2π. Thus the effect of the brane makes a deficit angle δ = 2π(1 − α) in the bulk (see Figure 27). This is a 6D realization of the ADD model including the self-gravity of branes. An interesting property of this model is that regardless of the tension of the brane, the 4D specetime on the brane is flat. Thus this could solve the cosmological constant problem — any vacuum energy on the brane only changes a geometry of the extra-dimensions and does not curve the 4D spacetime. This idea of solving the cosmological constant problem is known as self-tuning.

Figure 27

Removing a wedge from a sphere and identifying opposite sides to obtain a rugby ball geometry. Two equal-tension branes with conical deficit angles are located at either pole; outside the branes there is constant spherical curvature. From [72].

We should note that there have been several objections to the idea of self-tuning [153, 419, 420]. Consider that a phase transition occurs and the tension of the brane changes from σ₁ to σ₂. Accordingly, α changes from ${\alpha _1} = 1 - {\sigma _1}/(2\pi M_6^4)$ to ${\alpha _2} = 1 - {\sigma _2}/(2\pi M_6^4)$. The magnetic flux is conserved as the gauge field strength is a closed form, dF = 0. Then the magnetic flux which is obtained by integrating the field strength over the extra dimensions should be conserved

$${\Phi _B} = 4\pi {\alpha _1}{B_{0,1}} = 4\pi {\alpha _2}{B_{0,2}}.$$

(447)

The relation between Λ₆ and B₀, Equation (441), that ensures the existence of Minkowski branes cannot be imposed both for B₀ = B_0,1 ^and B₀ = B_0,2 when α₁ ≠ α₂ unless ϕ₀ changes. Moreover, the quantization condition must be imposed on the flux Φ_B. What happens is that a modulus, which is a combination of ϕ and the radion describing the size of extra-dimension, acquires a runaway potential and the 4D spacetime becomes non-static.

An unambiguous way to investigate this problem is to study the dynamical solutions directly in the 6D spacetime. However, once we consider the case where the tension becomes time dependent, we encounter a difficulty to deal with the branes [419]. This is because for co-dimension 2 branes, we encounter a divergence of metric near the brane if we put matter other than tension on a brane. Hence, without specifying how we regularize the branes, we cannot address the question what will happen if we change the tension. Is the self-tuning mechanism at work and does it lead to another static solution? Or do we get a dynamical solution driven by the runaway behaviour of the modulus field?

There was a negative conclusion on the self-tuning in this supersymmetric model for a particular kind of regularization [419, 420]. However, the answer could depend on the regularization of branes and the jury remains out. It is important to study the time-dependent dynamics in the 6D spacetime and the regularization of the branes in detail [410, 60, 62, 411, 61, 33, 110, 338, 350, 100].

10.2 Cosmology in 6D brane-world models

It is much harder to obtain cosmological solutions in 6D models than in 5-dimensional models. In 5D brane-world models, cosmological solutions can be obtained by considering a moving brane in a static bulk spacetime. This is because the motion of the homogeneous and isotropic brane does not change the bulk spacetime thanks to Birkoff’s theorem. However, this is no longer the case in 6D spacetime. Thus we need to find time dependent bulk solutions that are coupled to a motion of a brane, which requires us to solve non-linear partial differential equations numerically. Moreover, as is mentioned above, there appears a curvature singularity if one considers an infinitely thin brane and puts matter other than tension on the brane [419, 420]. Thus we need some regularization scheme to find cosmological solutions.

One of the popular ways to regularize a brane is to promote a brane that is a point-like object in two extra-dimensions to a 5D ring [353]. The ring is a codimension one object and it is possible to consider a motion of this ring. However, a problem is that this ring brane is not homogeneous as one of dimensions on the brane is compact and this breaks Birkhoff’s theorem. It has been shown that cosmology obtained by the motion of a brane in a static bulk shows pathological behaviour [351, 326]. This indicates that we need to find fully time-dependent bulk solutions.

At the moment, the only accessible way is to solve the 6D bulk spacetime using the gradient expansion methods assuming physical scales on a brane are much lower than mass scales in the bulk [150, 16, 233]. It is still an open question what are high energy effects in 6D models.

As in 5D models, there are many generalizations such as the inclusion of the induced gravity term on a brane and the Gauss-Bonnet term in the bulk [43, 222, 101, 84, 349, 239, 83, 82].

10.3 Cascading brane-world model

This is a 6D extension of the DGP model [111, 112]. The action is given by

$$\begin{array}{*{20}c} {S = {1 \over {2\kappa _6^2}}\int {{d^6}} x\sqrt {{-{} ^{(6)}}g} {\;{}^{(6)}}R + {1 \over {2\kappa _5^2}}\int\nolimits_{4 -{\rm{brane}}} {{d^5}} x\sqrt {{-{} ^{(5)}}g} {\;\;{}^{(5)}}R}\\ {+ {1 \over {2\kappa _5^2}}\int\nolimits_{3 - {\rm{brane}}} {{d^4}} x\sqrt {{-\;{} ^{(4)}}g} \left[ {\;{}^{(4)}R + {L_{{\rm{matter}}}}} \right].\;\;\;\;\;\;\;\;\;\;\;}\\ \end{array}$$

(448)

As in the 5D DGP model, we can define the cross over scale. In this model, there are two cross over scales:

$$^{(5)}{r_c} = {{M_5^3} \over {M_4^2}},{\quad ^{(6)}}{r_c} = {{M_6^3} \over {M_5^2}}.$$

(449)

Assuming that ⁽⁶⁾r_c ≫ ⁽⁵⁾r_c, the gravitational potential on the 3-brane cascades from a 1/r (4D gravity) regime at short scales, to a 1/r² (5D gravity) regime at intermediate distance and finally a 1/r³ (6D gravity) regime at large distances.

This model addresses several fundamental issues in induced gravity models in 6D spacetime. Without the induced gravity term on the 4-brane, the 6D graviton propagator diverges logarithmically near the position of the 3-brane [162]. On the other hand, the graviton propagator on the 3-brane in this model behaves like G (p) → log(p⁽⁵⁾r_c) in the M₅ → 0 limit where p is 4D momentum. Thus the cross-over scale ⁽⁵⁾r_c acts as a cut-off for the propagator and it remains finite even at the position of the 3-brane.

A more serious issue in the induced gravity model is that most constructions seem to be plagued by ghost instabilities [128, 152]. Usually, the regularization of the brane is necessary and it depends on the regularization scheme whether there appears a ghost or not [243]. In the cascading model, there is still a ghost if the 3-brane has no tension. However, it was shown that by adding a tension to the 3-brane, this ghost disappears [111, 112, 113]. More precisely, there is a critical tension

$${\lambda _{{\rm{crit}}}} = {2 \over 3}{\;^{(6)}}r_c^{- 2}M_4^2$$

(450)

and above the critical tension λ > λ_crit, the model is free of ghosts. It is still unclear what is the meaning of having the critical tension for the existence of the ghost. For example, what happens if there is a phase transition on the 3-brane and the tension changes from λ > λ_crit to λ < λ_crit? This remains a very interesting open question. This model also provides an interesting insight into the “degravitation” mechanism by which the cosmological constant does not gravitate on the 3-brane [132, 112].

Cosmological solutions in the cascading brane model are again notoriously difficult to find because it is necessary to find 6-dimensional solutions that depend on time and two extra-coordinates [1]. The simplest de Sitter solutions have been obtained [324]. Interestingly, there exists a self-accelerating solution for the 3-brane even when the solution for the 4-brane is in the normal branch. It is still not clear whether this self-accelerating solution is stable or not and it is crucial to check the stability of this new self-accelerating solution.

A similar class of models includes intersecting branes [217, 102, 103]. In this model, we have two 4-branes that intersect and a 3-brane sits at the intersection. Again there are self-accelerating de Sitter solutions and cosmology has been studied by considering a motion of one of the 4-branes. A model without a 4-brane has been studied by regularizing a 3-brane by promoting it to a 5D ring brane [219, 218].

11 Conclusion

Simple brane-world models provide a rich phenomenology for exploring some of the ideas that are emerging from M theory. The higher-dimensional degrees of freedom for the gravitational field, and the confinement of standard model fields to the visible brane, lead to a complex but fascinating interplay between gravity, particle physics, and geometry, that enlarges and enriches general relativity in the direction of a quantum gravity theory.

This review has attempted to show some of the key features of brane-world gravity from the perspective of astrophysics and cosmology, emphasizing a geometric approach to dynamics and perturbations. It has focused mainly on 1-brane RS-type brane-worlds, but also considered the DGP brane-world models. The RS-type models have some attractive features:

• They provide a simple 5D phenomenological realization of the Horava-Witten supergravity solutions in the limit where the hidden brane is removed to infinity, and the moduli effects from the 6 further compact extra dimensions may be neglected.

• They develop a new geometrical form of dimensional reduction based on a strongly curved (rather than flat) extra dimension.

• They provide a realization to lowest order of the AdS/CFT correspondence.

• They incorporate the self-gravity of the brane (via the brane tension).

• They lead to cosmological models whose background dynamics are completely understood and reproduce general relativity results with suitable restrictions on parameters.

The review has highlighted both the successes and some remaining open problems of the RS models and their generalizations. The open problems stem from a common basic difficulty, i.e., understanding and solving for the gravitational interaction between the bulk and the brane (which is nonlocal from the brane viewpoint). The key open problems of relevance to astrophysics and cosmology are

• to find the simplest realistic solution (or approximation to it) for an astrophysical black hole on the brane, and settle the questions about its staticity, Hawking radiation, and horizon; and

• to develop realistic approximation schemes (building on recent work [398, 428, 387, 399, 400, 245, 361, 51, 201, 136]) and manageable numerical codes (building on [245, 361, 51, 201, 136]) to solve for the cosmological perturbations on all scales, to compute the CMB anisotropies and large-scale structure, and to impose observational constraints from high-precision data.

The RS-type models are the simplest brane-worlds with curved extra dimension that allow for a meaningful approach to astrophysics and cosmology. One also needs to consider generalizations that attempt to make these models more realistic, or that explore other aspects of higher-dimensional gravity which are not probed by these simple models. Two important types of generalization are the following:

• The inclusion of dynamical interaction between the brane(s) and a bulk scalar field, so that the action is

  $$\begin{array}{*{20}c} {S = {1 \over {2\kappa _5^2}}\int {{d^5}} x\sqrt {- {}^{(5)}g} \left[ {{}^{(5)}R - \kappa _5^2{\partial _A}\Phi {\partial ^A}\Phi - 2{\Lambda _5}(\Phi)} \right]}\\ {+ \int\nolimits_{{\rm{brane}}({\rm{s}})} {d^4}x\sqrt {- g} \left[ {- \lambda (\Phi) + {K \over {\kappa _5^2}} + {L_{{\rm{matter}}}}} \right]\quad \quad}\\ \end{array}$$

  (451)

  (see [311, 21, 322, 143, 274, 144, 48, 231, 195, 146, 368, 198, 197, 407, 426, 259, 275, 196, 46, 325, 221, 315, 149, 18]). The scalar field could represent a bulk dilaton of the gravitational sector, or a modulus field encoding the dynamical influence on the effective 5D theory of an extra dimension other than the large fifth dimension [26, 98, 299, 361, 51, 55, 242, 212, 352, 179].

  For two-brane models, the brane separation introduces a new scalar degree of freedom, the radion. For general potentials of the scalar field which provide radion stabilization, 4D Einstein gravity is recovered at low energies on either brane [408, 335, 283]. (By contrast, in the absence of a bulk scalar, low energy gravity is of Brans-Dicke type [155].) In particular, such models will allow some fundamental problems to be addressed:

  • The hierarchy problem of particle physics.

  • An extra-dimensional mechanism for initiating inflation (or the hot radiation era with super-Hubble correlations) via brane interaction (building on the initial work in [134, 220, 229, 215, 339, 403, 273, 317, 412, 26, 98, 299, 40, 156, 157]).

  • An extra-dimensional explanation for the dark energy (and possibly also dark matter) puzzles: Could dark energy or late-time acceleration of the universe be a result of gravitational effects on the visible brane of the shadow brane, mediated by the bulk scalar field?

• The addition of stringy and quantum corrections to the Einstein-Hilbert action, including the following:

  • Higher-order curvature invariants, which arise in the AdS/CFT correspondence as next-to-leading order corrections in the CFT. The Gauss-Bonnet combination in particular has unique properties in 5D, giving field equations which are second-order in the bulk metric (and linear in the second derivatives), and being ghost-free. The action is

    $$\begin{array}{*{20}c} {S = {1 \over {2\kappa _5^2}}\int {d^5}x\sqrt {- {}^{(5)}g} \left[ {{}^{(5)}R - 2{\Lambda _5} + \alpha \left({{}^{(5)}{R^2} - 4{}^{(5)}{R_{AB}}{}^{(5)}{R^{AB}} + {}^{(5)}{R_{ABCD}}{}^{(5)}{R^{ABCD}}} \right)} \right]} \\ {+ \int\nolimits_{{\rm{brane}}} {d^4}x\sqrt {- g} \left[ {- \lambda + {K \over {\kappa _5^2}} + {L_{{\rm{matter}}}}} \right],\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;} \\ \end{array}$$

    (452)

    where α is the Gauss-Bonnet coupling constant, related to the string scale. The cosmological dynamics of these brane-worlds is investigated in [121, 343, 345, 341, 161, 80, 289, 37, 318, 291, 181, 125, 19, 124, 79, 310]. In [20] it is shown that the black string solution of the form of Equation (144) is ruled out by the Gauss-Bonnet term. In this sense, the Gauss-Bonnet correction removes an unstable and singular solution.

    In the early universe, the Gauss-Bonnet corrections to the Friedmann equation have the dominant form

    $${H^2} \propto {\rho ^{2/3}}$$

    (453)

    at the highest energies. If the Gauss-Bonnet term is a small correction to the Einstein-Hilbert term, as may be expected if it is the first of a series of higher-order corrections, then there will be a regime of RS-dominance as the energy drops, when H² ∝ ρ². Finally at energies well below the brane tension, the general relativity behaviour is recovered.

  • Quantum field theory corrections arising from the coupling between brane matter and bulk gravitons, leading to an induced 4D Ricci term in the brane action. The original induced gravity brane-world is the DGP model [131, 95, 344, 391], which we investigated in this review as an alternative to the RS-type models. Another viewpoint is to see the induced-gravity term in the action as a correction to the RS action:

    $$S = {1 \over {2\kappa _5^2}}\int {{d^5}} x\sqrt {- {}^{(5)}g} \left[ {{}^{(5)}R - 2{\Lambda _5}} \right] + \int\nolimits_{{\rm{brane}}} {{d^4}} x\sqrt {- g} \left[ {\beta R - \lambda + {K \over {\kappa _5^2}} + {L_{{\rm{matter}}}}} \right],$$

    (454)

    where β is a positive coupling constant.

    The cosmological models have been analyzed in [117, 238, 126, 230, 118, 372, 392, 370, 397, 7, 309, 297, 337, 186, 240]. (Brane-world black holes with induced gravity are investigated in [241].) Unlike RS-type models, DGP models lead to 5D behaviour on large scales rather than small scales. Then on an FRW brane, the late-universe 5D behaviour of gravity can naturally produce a late-time acceleration, even without dark energy, although the self-accelerating models suffer from a ghost. Nevertheless, the DGP model is a critical example of modified gravity models in cosmology that act as alternatives to dark energy.

The RS and DGP models are 5-dimensional phenomenological models, and so a key issue is how to realize such models in 10-dimensional string theory. Some progress has been made. 6-dimensional cascading brane-worlds are extensions of the DGP model. 10-dimensional type IIB supergravity solutions have been found with the warped geometry that generalizes the RS geometry. These models have also been important for building inflationary models in string theory, based on the motion of D3 branes in the warped throat [63, 133] (see the reviews [292, 32] and references therein). The action for D3 branes is described by the Dirac-Born-Infeld action and this gives the possibility of generating a large non-Gaussianity in the Cosmic Microwave Background temperature anisotropies, which can be tested in future experiments [395, 213] (see the reviews [86, 248]).

These models reply on the effective 4-dimensional approach to deal with extra dimensions. For example, the stabilization mechanism, which is necessary to fix moduli fields in string theory, exploits non-perturbative effects and they are often added in the 4-dimensional effective theory. Then it is not clear whether the resultant 4-dimensional effective theory is consistent with the 10-dimensional equations of motion [107, 108, 237, 249]. Recently there has been a new development and it has become possible to calculate all significant contributions to the D3 brane potential in the single coherent framework of 10-dimensional supergravity [31, 30, 28, 29]. This will provide us with a very interesting bridge between phenomenological brane-world models, where dynamics of higher-dimensional gravity is studied in detail, and string theory approaches, where 4D effective theory is intensively used. It is crucial to identify the higher-dimensional signature of the models in order to test a fundamental theory like string theory.

In summary, brane-world gravity opens up exciting prospects for subjecting M theory ideas to the increasingly stringent tests provided by high-precision astronomical observations. At the same time, brane-world models provide a rich arena for probing the geometry and dynamics of the gravitational field and its interaction with matter.