Abstract
The status of experimental tests of general relativity and of theoretical frameworks for analysing them are reviewed. Einstein’s equivalence principle (EEP) is well supported by experiments such as the Eötvös experiment, tests of special relativity, and the gravitational redshift experiment. Future tests of EEP and of the inverse square law will search for new interactions arising from unification or quantum gravity. Tests of general relativity at the post-Newtonian level have reached high precision, including the light defl ection the Shapiro time delay, the perihelion advance of Mercury, and the Nordtvedt effect in lunar motion. Gravitational wave damping has been detected in an amount that agrees with general relativity to half a percent using the Hulse-Taylor binary pulsar, and new binary pulsar systems may yield further improvements. When direct observation of gravitational radiation from astrophysical sources begins, new tests of general relativity will be possible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
At the time of the birth of general relativity (GR), experimental confirmation was almost a side issue. Einstein did calculate observable effects of general relativity, such as the perihelion advance of Mercury, which he knew to be an unsolved problem, and the deflection of light, which was subsequently verified, but compared to the inner consistency and elegance of the theory, he regarded such empirical questions as almost peripheral. But today, experimental gravitation is a major component of the field, characterized by continuing efforts to test the theory’s predictions, to search for gravitational imprints of high-energy particle interactions, and to detect gravitational waves from astronomical sources.
The modern history of experimental relativity can be divided roughly into four periods: Genesis, Hibernation, a Golden Era, and the Quest for Strong Gravity. The Genesis (1887–1919) comprises the period of the two great experiments which were the foundation of relativistic physics — the Michelson-Morley experiment and the Eötvös experiment — and the two immediate confirmations of GR — the deflection of light and the perihelion advance of Mercury. Following this was a period of Hibernation (1920–1960) during which theoretical work temporarily outstripped technology and experimental possibilities, and, as a consequence, the field stagnated and was relegated to the backwaters of physics and astronomy.
But beginning around 1960, astronomical discoveries (quasars, pulsars, cosmic background radiation) and new experiments pushed GR to the forefront. Experimental gravitation experienced a Golden Era (1960–1980) during which a systematic, world-wide effort took place to understand the observable predictions of GR, to compare and contrast them with the predictions of alternative theories of gravity, and to perform new experiments to test them. The period began with an experiment to confirm the gravitational frequency shift of light (1960) and ended with the reported decrease in the orbital period of the Hulse-Taylor binary pulsar at a rate consistent with the general relativity prediction of gravity wave energy loss (1979). The results all supported GR, and most alternative theories of gravity fell by the wayside (for a popular review, see [148]).
Since 1980, the field has entered what might be termed a Quest for Strong Gravity. Many of the remaining interesting weak-field predictions of the theory are extremely small and diffcult to check, in some cases requiring further technological development to bring them into detectable range. The sense of a systematic assault on the weak-field predictions of GR has been supplanted to some extent by an opportunistic approach in which novel and unexpected (and sometimes inexpensive) tests of gravity have arisen from new theoretical ideas or experimental techniques, often from unlikely sources. Examples include the use of laser-cooled atom and ion traps to perform ultra-precise tests of special relativity; the proposal of a “fifth” force, which led to a host of new tests of the weak equivalence principle; and recent ideas of large extra dimensions, which have motived new tests of the inverse square law of gravity at sub-millimeter scales. Several major ongoing efforts also continue, principally the Stanford Gyroscope experiment, known as Gravity Probe-B.
Instead, much of the focus has shifted to experiments which can probe the effects of strong gravitational fields. The principal figure of merit that distinguishes strong from weak gravity is the quantity ∊∼GM/Rc2, where G is the Newtonian gravitational constant, M is the characteristic mass scale of the phenomenon, R is the characteristic distance scale, and c is the speed of light. Near the event horizon of a non-rotating black hole, or for the expanding observable universe, ∊∼0.5; for neutron stars, ∊∼0.2. These are the regimes of strong gravity. For the solar system ∊<10-5; this is the regime of weak gravity. At one extreme are the strong gravitational fields associated with Planck-scale physics. Will unification of the forces, or quantization of gravity at this scale leave observable effects accessible by experiment? Dramatically improved tests of the equivalence principle or of the inverse square law are being designed, to search for or bound the imprinted effects of Planck-scale phenomena. At the other extreme are the strong fields associated with compact objects such as black holes or neutron stars. Astrophysical observations and gravitational wave detectors are being planned to explore and test GR in the strong-field, highly-dynamical regime associated with the formation and dynamics of these objects.
In this Living Review, we shall survey the theoretical frameworks for studying experimental gravitation, summarize the current status of experiments, and attempt to chart the future of the subject. We shall not provide complete references to early work done in this field but instead will refer the reader to the appropriate review articles and monographs, specifically to Theory and Experiment in Gravitational Physics [147], hereafter referred to as TEGP. Additional recent reviews in this subject are [142, 145, 150, 139, 37, 117]. References to TEGP will be by chapter or section, e.g. “TEGP 8.9 [147]”.
2 Tests of the Foundations of Gravitation Theory
2.1 The Einstein equivalence principle
The principle of equivalence has historically played an important role in the development of gravitation theory. Newton regarded this principle as such a cornerstone of mechanics that he devoted the opening paragraph of the Principia to it. In 1907, Einstein used the principle as a basic element of general relativity. We now regard the principle of equivalence as the foundation, not of Newtonian gravity or of GR, but of the broader idea that spacetime is curved.
One elementary equivalence principle is the kind Newton had in mind when he stated that the property of a body called “mass” is proportional to the “weight”, and is known as the weak equivalence principle (WEP). An alternative statement of WEP is that the trajectory of a freely falling body (one not acted upon by such forces as electromagnetism and too small to be affected by tidal gravitational forces) is independent of its internal structure and composition. In the simplest case of dropping two different bodies in a gravitational field, WEP states that the bodies fall with the same acceleration (this is often termed the Universality of Free Fall, or UFF).
A more powerful and far-reaching equivalence principle is known as the Einstein equivalence principle (EEP). It states that:
-
1.
WEP is valid.
-
2.
The outcome of any local non-gravitational experiment is independent of the velocity of the freely-falling reference frame in which it is performed.
-
3.
The outcome of any local non-gravitational experiment is independent of where and when in the universe it is performed.
The second piece of EEP is called local Lorentz invariance (LLI), and the third piece is called local position invariance (LPI).
For example, a measurement of the electric force between two charged bodies is a local non-gravitational experiment; a measurement of the gravitational force between two bodies (Cavendish experiment) is not.
The Einstein equivalence principle is the heart and soul of gravitational theory, for it is possible to argue convincingly that if EEP is valid, then gravitation must be a “curved spacetime” phenomenon, in other words, the effects of gravity must be equivalent to the effects of living in a curved spacetime. As a consequence of this argument, the only theories of gravity that can embody EEP are those that satisfy the postulates of “metric theories of gravity”, which are:
-
1.
Spacetime is endowed with a symmetric metric.
-
2.
The trajectories of freely falling bodies are geodesics of that metric.
-
3.
In local freely falling reference frames, the non-gravitational laws of physics are those written in the language of special relativity.
The argument that leads to this conclusion simply notes that, if EEP is valid, then in local freely falling frames, the laws governing experiments must be independent of the velocity of the frame (local Lorentz invariance), with constant values for the various atomic constants (in order to be independent of location). The only laws we know of that fulfill this are those that are compatible with special relativity, such as Maxwell’s equations of electromagnetism. Furthermore, in local freely falling frames, test bodies appear to be unaccelerated, in other words they move on straight lines; but such “locally straight” lines simply correspond to “geodesics” in a curved spacetime (TEGP 2.3 [147]).
General relativity is a metric theory of gravity, but then so are many others, including the Brans-Dicke theory. The nonsymmetric gravitation theory (NGT) of Moffat is not a metric theory. Neither, in this narrow sense, is superstring theory (see Sec. 2.3), which, while based fundamentally on a spacetime metric, introduces additional fields (dilatons, moduli) that can couple to material stress-energy in a way that can lead to violations, say, of WEP. So the notion of curved spacetime is a very general and fundamental one, and therefore it is important to test the various aspects of the Einstein Equivalence Principle thoroughly.
A direct test of WEP is the comparison of the acceleration of two laboratory-sized bodies of different composition in an external gravitational field. If the principle were violated, then the accelerations of different bodies would differ. The simplest way to quantify such possible violations of WEP in a form suitable for comparison with experiment is to suppose that for a body with inertial mass mI, the passive gravitational mass mP is no longer equal to mI, so that in a gravitational field g, the acceleration is given by mIa=mPg. Now the inertial mass of a typical laboratory body is made up of several types of mass-energy: rest energy, electromagnetic energy, weak-interaction energy, and so on. If one of these forms of energy contributes to mP differently than it does to mI, a violation of WEP would result. One could then write
where EA is the internal energy of the body generated by interaction A, and ηA is a dimensionless parameter that measures the strength of the violation of WEP induced by that interaction, and c is the speed of light. A measurement or limit on the fractional difference in acceleration between two bodies then yields a quantity called the “Eötvös ratio” given by
where we drop the subscript “I” from the inertial masses. Thus, experimental limits on η place limits on the WEP-violation parameters ηA.
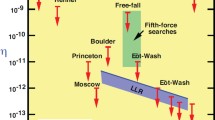
Many high-precision Eötvös-type experiments have been performed, from the pendulum experiments of Newton, Bessel and Potter, to the classic torsionbalance measurements of Eötvös [58], Dicke [55], Braginsky [31] and their collaborators. In the modern torsion-balance experiments, two objects of different composition are connected by a rod or placed on a tray and suspended in a horizontal orientation by a fine wire. If the gravitational acceleration of the bodies differs, there will be a torque induced on the suspension wire, related to the angle between the wire and the direction of the gravitational acceleration g. If the entire apparatus is rotated about some direction with angular velocity ω, the torque will be modulated with period 2π/ω. In the experiments of Eötvös and his collaborators, the wire and g were not quite parallel because of the centripetal acceleration on the apparatus due to the Earth’s rotation; the apparatus was rotated about the direction of the wire. In the Dicke and Braginsky experiments, g was that of the Sun, and the rotation of the Earth provided the modulation of the torque at a period of 24 hr (TEGP 2.4 (a) [147]). Beginning in the late 1980s, numerous experiments were carried out primarily to search for a “fifth force” (see Sec. 2.3), but their null results also constituted tests of WEP. In the “free-fall Galileo experiment” performed at the University of Colorado, the relative free-fall acceleration of two bodies made of uranium and copper was measured using a laser interferometric technique. The “Eöt-Wash” experiments carried out at the University of Washington used a sophisticated torsion balance tray to compare the accelerations of various materials toward local topography on Earth, movable laboratory masses, the Sun and the galaxy [121, 10], and have recently reached levels of 4×10-13. The resulting upper limits on η are summarized in Figure 1 (TEGP 14.1 [147]; for a bibliography of experiments, see [61]).
Selected tests of the weak equivalence principle, showing bounds on η, which measures fractional difference in acceleration of different materials or bodies. The free-fall and Eöt-Wash experiments were originally performed to search for a fifth force. The blue band shows current bounds on η for gravitating bodies from lunar laser ranging (LURE).
The second ingredient of EEP, local Lorentz invariance, has been tested to high-precision in the “mass anisotropy” experiments: The classic versions are the Hughes-Drever experiments, performed in the period 1959–60 independently by Hughes and collaborators at Yale University, and by Drever at Glasgow University (TEGP 2.4 (b) [147]). Dramatically improved versions were carried out during the late 1980s using laser-cooled trapped atom techniques (TEGP 14.1 [147]). A simple and useful way of interpreting these experiments is to suppose that the electromagnetic interactions suffer a slight violation of Lorentz invariance, through a change in the speed of electromagnetic radiation c relative to the limiting speed of material test particles (c0, chosen to be unity via a choice of units), in other words, c≠1 (see Sec. 2.2.3). Such a violation necessarily selects a preferred universal rest frame, presumably that of the cosmic background radiation, through which we are moving at about 300 km/s. Such a Lorentz-non-invariant electromagnetic interaction would cause shifts in the energy levels of atoms and nuclei that depend on the orientation of the quantization axis of the state relative to our universal velocity vector, and on the quantum numbers of the state. The presence or absence of such energy shifts can be examined by measuring the energy of one such state relative to another state that is either unaffected or is affected differently by the supposed violation. One way is to look for a shifting of the energy levels of states that are ordinarily equally spaced, such as the four J=3/2 ground states of the 7Li nucleus in a magnetic field (Drever experiment); another is to compare the levels of a complex nucleus with the atomic hyperfine levels of a hydrogen maser clock. These experiments have all yielded extremely accurate results, quoted as limits on the parameter δ≡c-2−1 in Figure 2. Also included for comparison is the corresponding limit obtained from Michelson-Morley type experiments (for a review, see [75]).
Selected tests of local Lorentz invariance showing the bounds on the parameter δ, which measures the degree of violation of Lorentz invariance in electromagnetism. The Michelson-Morley, Joos, and Brillet-Hall experiments test the isotropy of round-trip speed of light, the latter experiment using laser technology. The centrifuge, two-photon absorption (TPA) and JPL experiments test the isotropy of light speed using one-way propagation. The remaining four experiments test isotropy of nuclear energy levels. The limits assume a speed of Earth of 300 km/s relative to the mean rest frame of the universe.
Recent advances in atomic spectroscopy and atomic timekeeping have made it possible to test LLI by checking the isotropy of the speed of light using oneway propagation (as opposed to round-trip propagation, as in the Michelson-Morley experiment). In one experiment, for example, the relative phases of two hydrogen maser clocks at two stations of NASA’s Deep Space Tracking Network were compared over five rotations of the Earth by propagating a light signal one-way along an ultrastable fiberoptic link connecting them (see Sec. 2.2.3). Although the bounds from these experiments are not as tight as those from mass-anisotropy experiments, they probe directly the fundamental postulates of special relativity, and thereby of LLI (TEGP 14.1 [147], [144]).
The principle of local position invariance, the third part of EEP, can be tested by the gravitational redshift experiment, the first experimental test of gravitation proposed by Einstein. Despite the fact that Einstein regarded this as a crucial test of GR, we now realize that it does not distinguish between GR and any other metric theory of gravity, but is only a test of EEP. A typical gravitational redshift experiment measures the frequency or wavelength shift Z≡Δν/ν=-Δλ/λ between two identical frequency standards (clocks) placed at rest at different heights in a static gravitational field. If the frequency of a given type of atomic clock is the same when measured in a local, momentarily comoving freely falling frame (Lorentz frame), independent of the location or velocity of that frame, then the comparison of frequencies of two clocks at rest at different locations boils down to a comparison of the velocities of two local Lorentz frames, one at rest with respect to one clock at the moment of emission of its signal, the other at rest with respect to the other clock at the moment of reception of the signal. The frequency shift is then a consequence of the first-order Doppler shift between the frames. The structure of the clock plays no role whatsoever. The result is a shift
where ΔU is the difference in the Newtonian gravitational potential between the receiver and the emitter. If LPI is not valid, then it turns out that the shift can be written
where the parameter α may depend upon the nature of the clock whose shift is being measured (see TEGP 2.4 (c) [147] for details).
The first successful, high-precision redshift measurement was the series of Pound-Rebka-Snider experiments of 1960–1965 that measured the frequency shift of gamma-ray photons from 57Fe as they ascended or descended the Jefferson Physical Laboratory tower at Harvard University. The high accuracy achieved — one percent — was obtained by making use of the Mössbauer effect to produce a narrow resonance line whose shift could be accurately determined. Other experiments since 1960 measured the shift of spectral lines in the Sun’s gravitational field and the change in rate of atomic clocks transported aloft on aircraft, rockets and satellites. Figure 3 summarizes the important redshift experiments that have been performed since 1960 (TEGP 2.4 (c) [147]).
The most precise standard redshift test to date was the Vessot-Levine rocket experiment that took place in June 1976 [131]. A hydrogen-maser clock was own on a rocket to an altitude of about 10,000 km and its frequency compared to a similar clock on the ground. The experiment took advantage of the masers’ frequency stability by monitoring the frequency shift as a function of altitude. A sophisticated data acquisition scheme accurately eliminated all effects of the first-order Doppler shift due to the rocket’s motion, while tracking data were used to determine the payload’s location and the velocity (to evaluate the potential difference ΔU, and the special relativistic time dilation). Analysis of the data yielded a limit ∣α∣<2×10-4.
A “null” redshift experiment performed in 1978 tested whether the relative rates of two different clocks depended upon position. Two hydrogen maser clocks and an ensemble of three superconducting-cavity stabilized oscillator (SCSO) clocks were compared over a 10-day period. During the period of the experiment, the solar potential U/c2 changed sinusoidally with a 24-hour period by 3×10-13 because of the Earth’s rotation, and changed linearly at 3×10-12 per day because the Earth is 90 degrees from perihelion in April. However, analysis of the data revealed no variations of either type within experimental errors, leading to a limit on the LPI violation parameter ∣αH−αSCSO∣<2×10-2 [130]. This bound has been improved using more stable frequency standards [68, 109]. The varying gravitational redshift of Earth-bound clocks relative to the highly stable Millisecond Pulsar PSR 1937+21, caused by the Earth’s motion in the solar gravitational field around the Earth-Moon center of mass (amplitude 4000 km), has been measured to about 10 percent, and the redshift of stable oscillator clocks on the Voyager spacecraft caused by Saturn’s gravitational field yielded a one percent test. The solar gravitational redshift has been tested to about two percent using infrared oxygen triplet lines at the limb of the Sun, and to one percent using oscillator clocks on the Galileo spacecraft (TEGP 2.4 (c) [147] and 14.1 (a) [147]).
Modern advances in navigation using Earth-orbiting atomic clocks and accurate time-transfer must routinely take gravitational redshift and time-dilation effects into account. For example, the Global Positioning System (GPS) provides absolute accuracies of around 15 m (even better in its military mode) anywhere on Earth, which corresponds to 50 nanoseconds in time accuracy at all times. Yet the difference in rate between satellite and ground clocks as a result of special and general relativistic effects is a whopping 39 microseconds per day (46 μs from the gravitational redshift, and -7 μs from time dilation). If these effects were not accurately accounted for, GPS would fail to function at its stated accuracy. This represents a welcome practical application of GR! (For the role of GR in GPS, see [8]; for a popular essay, see [140].)
Local position invariance also refers to position in time. If LPI is satisfied, the fundamental constants of non-gravitational physics should be constants in time. Table 1 shows current bounds on cosmological variations in selected dimensionless constants. For discussion and references to early work, see TEGP 2.4 (c) [147].
2.2 Theoretical Frameworks for Analyzing EEP
2.2.1 Schiff’s conjecture
Because the three parts of the Einstein equivalence principle discussed above are so very different in their empirical consequences, it is tempting to regard them as independent theoretical principles. On the other hand, any complete and self-consistent gravitation theory must possess suffcient mathematical machinery to make predictions for the outcomes of experiments that test each principle, and because there are limits to the number of ways that gravitation can be meshed with the special relativistic laws of physics, one might not be surprised if there were theoretical connections between the three sub-principles. For instance, the same mathematical formalism that produces equations describing the free fall of a hydrogen atom must also produce equations that determine the energy levels of hydrogen in a gravitational field, and thereby the ticking rate of a hydrogen maser clock. Hence a violation of EEP in the fundamental machinery of a theory that manifests itself as a violation of WEP might also be expected to show up as a violation of local position invariance. Around 1960, Schiff conjectured that this kind of connection was a necessary feature of any self-consistent theory of gravity. More precisely, Schiff’s conjecture states that any complete, self-consistent theory of gravity that embodies WEP necessarily embodies EEP. In other words, the validity of WEP alone guarantees the validity of local Lorentz and position invariance, and thereby of EEP.
If Schiff’s conjecture is correct, then Eötvös experiments may be seen as the direct empirical foundation for EEP, hence for the interpretation of gravity as a curved-spacetime phenomenon. Of course, a rigorous proof of such a conjecture is impossible (indeed, some special counter-examples are known), yet a number of powerful “plausibility” arguments can be formulated.
The most general and elegant of these arguments is based upon the assumption of energy conservation. This assumption allows one to perform very simple cyclic gedanken experiments in which the energy at the end of the cycle must equal that at the beginning of the cycle. This approach was pioneered by Dicke, Nordtvedt and Haugan (see, e.g. [74]). A system in a quantum state A decays to state B, emitting a quantum of frequency ν. The quantum falls a height H in an external gravitational field and is shifted to frequency ν′, while the system in state B falls with acceleration gB. At the bottom, state A is rebuilt out of state B, the quantum of frequency ν′, and the kinetic energy mBgBH that state B has gained during its fall. The energy left over must be exactly enough, mAgAH, to raise state A to its original location. (Here an assumption of local Lorentz invariance permits the inertial masses mA and mB to be identified with the total energies of the bodies.) If gA and gB depend on that portion of the internal energy of the states that was involved in the quantum transition from A to B according to
(violation of WEP), then by conservation of energy, there must be a corresponding violation of LPI in the frequency shift of the form (to lowest order in hν/mc2)
Haugan generalized this approach to include violations of LLI [74], (TEGP 2.5 [147]).
2.2.2 The TH∊μ formalism
The first successful attempt to prove Schiff’s conjecture more formally was made by Lightman and Lee [86]. They developed a framework called the TH∊¼ formalism that encompasses all metric theories of gravity and many non-metric theories (Box 1). It restricts attention to the behavior of charged particles (electromagnetic interactions only) in an external static spherically symmetric (SSS) gravitational field, described by a potential U. It characterizes the motion of the charged particles in the external potential by two arbitrary functions T(U) and H(U), and characterizes the response of electromagnetic fields to the external potential (gravitationally modified Maxwell equations) by two functions ∊(U) and μ(U). The forms of T, H, ∊ and μ vary from theory to theory, but every metric theory satisfies
for all U. This consequence follows from the action of electrodynamics with a “minimal” or metric coupling:
where the variables are defined in Box 1, and where Fμν≡Aν,μ−Aμ,ν. By identifying g00=T and gij=Hδij in a SSS field, Fi0=Ei and Fij=∊ijkBk, one obtains Eq. (7). Conversely, every theory within this class that satisfies Eq. (7) can have its electrodynamic equations cast into “metric” form. In a given non-metric theory, the functions T, H, ∊ and μ will depend in general on the full gravitational environment, including the potential of the Earth, Sun and Galaxy, as well as on cosmological boundary conditions. Which of these factors has the most influence on a given experiment will depend on the nature of the experiment.
Lightman and Lee then calculated explicitly the rate of fall of a “test” body made up of interacting charged particles, and found that the rate was independent of the internal electromagnetic structure of the body (WEP) if and only if Eq. (7) was satisfied. In other words, WEP→EEP and Schiff’s conjecture was verified, at least within the restrictions built into the formalism.
Certain combinations of the functions T, H, ∊ and μ reflect different aspects of EEP. For instance, position or U-dependence of either of the combinations ∊(T/H)1/2 and μ(T/H)1/2 signals violations of LPI, the first combination playing the role of the locally measured electric charge or fine structure constant. The “non-metric parameters” Γ0 and Λ0 (Box 1) are measures of such violations of EEP. Similarly, if the parameter ϒ0≡1−(TH-1∊μ)0 is non-zero anywhere, then violations of LLI will occur. This parameter is related to the difference between the speed of light c, and the limiting speed of material test particles c0, given by
In many applications, by suitable definition of units, c0 can be set equal to unity. If EEP is valid, Γ0≡Λ0≡ϒ0=0 everywhere.
The rate of fall of a composite spherical test body of electromagnetically interacting particles then has the form
where E ESB and E MSB are the electrostatic and magnetostatic binding energies of the body, given by
where rab=|xa−xb|, nab=(xa−xb)/rab, and the angle brackets denote an expectation value of the enclosed operator for the system’s internal state. Eötvös experiments place limits on the WEP-violating terms in Eq. (11), and ultimately place limits on the non-metric parameters |Γ0|<2×10-10 and |Λ0|<3×10-6. (We set ϒ0=0 because of very tight constraints on it from tests of LLI.) These limits are sufficiently tight to rule out a number of non-metric theories of gravity thought previously to be viable (TEGP 2.6 (f) [147]).
The TH∊μ formalism also yields a gravitationally modified Dirac equation that can be used to determine the gravitational redshift experienced by a variety of atomic clocks. For the redshift parameter α (Eq. (4)), the results are (TEGP 2.6 (c) [147]):
The redshift is the standard one (α=0), independently of the nature of the clock if and only if Γ0≡Λ0≡0. Thus the Vessot-Levine rocket redshift experiment sets a limit on the parameter combination |3Γ0−Λ0| (Figure 3); the null-redshift experiment comparing hydrogen-maser and SCSO clocks sets a limit on \( \left| {{\alpha _{\rm{H}}} - {\alpha _{{\rm{SCSO}}}}} \right| = \frac{3}{2}\left| {{\Gamma _0} - {\Lambda _0}} \right| \) . Alvarez and Mann [4, 3, 5, 6, 7] extended the TH∊μ formalism to permit analysis of such effects as the Lamb shift, anomalous magnetic moments and non-baryonic effects, and placed interesting bounds on EEP violations.
2.2.3 The c2 formalism
The TH∊μ formalism can also be applied to tests of local Lorentz invariance, but in this context it can be simplified. Since most such tests do not concern themselves with the spatial variation of the functions T, H, ∊, and α, but rather with observations made in moving frames, we can treat them as spatial constants. Then by rescaling the time and space coordinates, the charges and the electromagnetic fields, we can put the action in Box 1 into the form (TEGP 2.6 (a) [147])
where c2≡H0/T0∊0μ0=(1−ϒ0)-1. This amounts to using units in which the limiting speed c0 of massive test particles is unity, and the speed of light is c. If c≠1, LLI is violated; furthermore, the form of the action above must be assumed to be valid only in some preferred universal rest frame. The natural candidate for such a frame is the rest frame of the microwave background.
The electrodynamical equations which follow from Eq. (15) yield the behavior of rods and clocks, just as in the full TH∊μ formalism. For example, the length of a rod moving through the rest frame in a direction parallel to its length will be observed by a rest observer to be contracted relative to an identical rod perpendicular to the motion by a factor 1−V2/2+O(V4). Notice that c does not appear in this expression. The energy and momentum of an electromagnetically bound body which moves with velocity V relative to the rest frame are given by
where MR=M0−E ESB , M0 is the sum of the particle rest masses, E ESB is the electrostatic binding energy of the system (Eq. (12) with T 1/20 H0∊ -10 =1), and
where
Note that (c-2−1) corresponds to the parameter δ plotted in Figure 2.
The electrodynamics given by Eq. (15) can also be quantized, so that we may treat the interaction of photons with atoms via perturbation theory. The energy of a photon is ћ times its frequency ω, while its momentum is ћω/c. Using this approach, one finds that the difference in round trip travel times of light along the two arms of the interferometer in the Michelson-Morley experiment is given by L0(v2/c)(c-2−1). The experimental null result then leads to the bound on (c-2−1) shown on Figure 2. Similarly the anisotropy in energy levels is clearly illustrated by the tensorial terms in Eqs. (16) and (18); by evaluating E͂ ES ijB for each nucleus in the various Hughes-Drever-type experiments and comparing with the experimental limits on energy differences, one obtains the extremely tight bounds also shown on Figure 2.
The behavior of moving atomic clocks can also be analysed in detail, and bounds on (c-2−1) can be placed using results from tests of time dilation and of the propagation of light. In some cases, it is advantageous to combine the c2 framework with a “kinematical” viewpoint that treats a general class of boost transformations between moving frames. Such kinematical approaches have been discussed by Robertson, Mansouri and Sexl, and Will (see [144]).
For example, in the “JPL” experiment, in which the phases of two hydrogen masers connected by a fiberoptic link were compared as a function of the Earth’s orientation, the predicted phase difference as a function of direction is, to first order in V, the velocity of the Earth through the cosmic background,
where φ͂=2πνL, ν is the maser frequency, L=21 km is the baseline, and where n and n0 are unit vectors along the direction of propagation of the light at a given time and at the initial time of the experiment, respectively. The observed limit on a diurnal variation in the relative phase resulted in the bound |c-2−1|<3×10-4. Tighter bounds were obtained from a “two-photon absorption” (TPA) experiment, and a 1960s series of “Mössbauer-rotor” experiments, which tested the isotropy of time dilation between a gamma ray emitter on the rim of a rotating disk and an absorber placed at the center [144].
2.3 EEP, particle physics, and the search for new interactions
In 1986, as a result of a detailed reanalysis of Eötvös’ original data, Fischbach et al. [62] suggested the existence of a fifth force of nature, with a strength of about a percent that of gravity, but with a range (as defined by the range λ of a Yukawa potential, e-r/λ/r) of a few hundred meters. This proposal dovetailed with earlier hints of a deviation from the inverse-square law of Newtonian gravitation derived from measurements of the gravity profile down deep mines in Australia, and with ideas from particle physics suggesting the possible presence of very low-mass particles with gravitational-strength couplings. During the next four years numerous experiments looked for evidence of the fifth force by searching for composition-dependent differences in acceleration, with variants of the Eötvös experiment or with free-fall Galileo-type experiments. Although two early experiments reported positive evidence, the others all yielded null results. Over the range between one and 104 meters, the null experiments produced upper limits on the strength of a postulated fifth force between 10-3 and 10-6 of the strength of gravity. Interpreted as tests of WEP (corresponding to the limit of infinite-range forces), the results of two representative experiments from this period, the free-fall Galileo experiment and the early Eöt-Wash experiment, are shown in Figure 1. At the same time, tests of the inverse-square law of gravity were carried out by comparing variations in gravity measurements up tall towers or down mines or boreholes with gravity variations predicted using the inverse square law together with Earth models and surface gravity data mathematically “continued” up the tower or down the hole. Despite early reports of anomalies, independent tower, borehole and seawater measurements now show no evidence of a deviation. Analyses of orbital data from planetary range measurements, lunar laser ranging, and laser tracking of the LAGEOS satellite verified the inverse-square law to parts in 108 over scales of 103 to 105 km, and to parts in 109 over planetary scales of several astronomical units [122]. The consensus at present is that there is no credible experimental evidence for a fifth force of nature. For reviews and bibliographies, see [61, 63, 64, 2, 143].
Nevertheless, theoretical evidence continues to mount that EEP is likely to be violated at some level, whether by quantum gravity effects, by effects arising from string theory, or by hitherto undetected interactions, albeit at levels well below those that motivated the fifth-force searches. Roughly speaking, in addition to the pure Einsteinian gravitational interaction, which respects EEP, theories such as string theory predict other interactions which do not. In string theory, for example, the existence of such EEP-violating fields is assured, but the theory is not yet mature enough to enable calculation of their strength (relative to gravity), or their range (whether they are long range, like gravity, or short range, like the nuclear and weak interactions, and thus too short-range to be detectable).
In one simple example, one can write the Lagrangian for the low-energy limit of string theory in the so-called “Einstein frame”, in which the gravitational Lagrangian is purely general relativistic:
where g͂μν is the non-physical metric, R͂μν is the Ricci tensor derived from it, ϕ is a dilaton field, and G͂, U and M͂ are functions of ϕ. The Lagrangian includes that for the electromagnetic field Fμν, and that for particles, written in terms of Dirac spinors ψ͂. This is not a metric representation because of the coupling of ϕ to matter via M͂(ϕ) and U(ϕ). A conformal transformation g͂μν=F(ϕ)gμν, ψ͂=F(ϕ)-3/4ψ, puts the Lagrangian in the form (“Jordan” frame)
One may choose F(ϕ)=const./M͂(ϕ)2 so that the particle Lagrangian takes the metric form (no explicit coupling to ϕ), but the electromagnetic Lagrangian will still couple non-metrically to U(ϕ). The gravitational Lagrangian here takes the form of a scalar-tensor theory (Sec. 3.3.2). But the non-metric electromagnetic term will, in general, produce violations of EEP. For examples of specific models, see [125, 50].
Thus, EEP and related tests are now viewed as ways to discover or place constraints on new physical interactions, or as a branch of “non-accelerator particle physics”, searching for the possible imprints of high-energy particle effects in the low-energy realm of gravity. Whether current or proposed experiments can actually probe these phenomena meaningfully is an open question at the moment, largely because of a dearth of firm theoretical predictions. Despite this uncertainty, a number of experimental possibilities are being explored.
Concepts for an equivalence principle experiment in space have been developed. The project MICROSCOPE, designed to test WEP to 10-15 has been approved by the French space agency CNES for a possible 2004 launch. Another, known as Satellite Test of the Equivalence Principle (STEP), is under consideration as a possible joint effort of NASA and the European Space Agency (ESA), with the goal of a 10-18 test. The gravitational redshift could be improved to the 10-10 level using atomic clocks on board a spacecraft which would travel to within four solar radii of the Sun. Laboratory tests of the gravitational inverse square law at sub-millimeter scales are being developed as ways to search for new short-range interactions or for the existence of large extra dimensions; the challenge of these experiments is to distinguish gravitation-like interactions from electromagnetic and quantum mechanical (Casimir) effects [88].
3 Tests of Post-Newtonian Gravity
3.1 Metric theories of gravity and the strong equivalence principle
3.1.1 Universal coupling and the metric postulates
The overwhelming empirical evidence supporting the Einstein equivalence principle, discussed in the previous section, supports the conclusion that the only theories of gravity that have a hope of being viable are metric theories, or possibly theories that are metric apart from possible weak or short-range non-metric couplings (as in string theory). Therefore for the remainder of this article, we shall turn our attention exclusively to metric theories of gravity, which assume that (i) there exists a symmetric metric, (ii) test bodies follow geodesics of the metric, and (iii) in local Lorentz frames, the non-gravitational laws of physics are those of special relativity.
The property that all non-gravitational fields should couple in the same manner to a single gravitational field is sometimes called “universal coupling”. Because of it, one can discuss the metric as a property of spacetime itself rather than as a field over spacetime. This is because its properties may be measured and studied using a variety of different experimental devices, composed of different non-gravitational fields and particles, and, because of universal coupling, the results will be independent of the device. Thus, for instance, the proper time between two events is a characteristic of spacetime and of the location of the events, not of the clocks used to measure it.
Consequently, if EEP is valid, the non-gravitational laws of physics may be formulated by taking their special relativistic forms in terms of the Minkowski metric η and simply “going over” to new forms in terms of the curved spacetime metric g, using the mathematics of differential geometry. The details of this “going over” can be found in standard textbooks ([94, 136], TEGP 3.2. [147]).
3.1.2 The strong equivalence principle
In any metric theory of gravity, matter and non-gravitational fields respond only to the spacetime metric g. In principle, however, there could exist other gravitational fields besides the metric, such as scalar fields, vector fields, and so on. If, by our strict definition of metric theory, matter does not couple to these fields, what can their role in gravitation theory be? Their role must be that of mediating the manner in which matter and non-gravitational fields generate gravitational fields and produce the metric; once determined, however, the metric alone acts back on the matter in the manner prescribed by EEP.
What distinguishes one metric theory from another, therefore, is the number and kind of gravitational fields it contains in addition to the metric, and the equations that determine the structure and evolution of these fields. From this viewpoint, one can divide all metric theories of gravity into two fundamental classes: “purely dynamical” and “prior-geometric”.
By “purely dynamical metric theory” we mean any metric theory whose gravitational fields have their structure and evolution determined by coupled partial differential field equations. In other words, the behavior of each field is influenced to some extent by a coupling to at least one of the other fields in the theory. By “prior geometric” theory, we mean any metric theory that contains “absolute elements”, fields or equations whose structure and evolution are given a priori, and are independent of the structure and evolution of the other fields of the theory. These “absolute elements” typically include flat background metrics η, cosmic time coordinates t, and algebraic relationships among otherwise dynamical fields, such as gμν=hμν+kμkν, where hμν and kμ may be dynamical fields.
General relativity is a purely dynamical theory since it contains only one gravitational field, the metric itself, and its structure and evolution are governed by partial differential equations (Einstein’s equations). Brans-Dicke theory and its generalizations are purely dynamical theories; the field equation for the metric involves the scalar field (as well as the matter as source), and that for the scalar field involves the metric. Rosen’s bimetric theory is a prior-geometric theory: It has a non-dynamical, Riemann-flat background metric η, and the field equations for the physical metric g involve η.
By discussing metric theories of gravity from this broad point of view, it is possible to draw some general conclusions about the nature of gravity in different metric theories, conclusions that are reminiscent of the Einstein equivalence principle, but that are subsumed under the name “strong equivalence principle”.
Consider a local, freely falling frame in any metric theory of gravity. Let this frame be small enough that inhomogeneities in the external gravitational fields can be neglected throughout its volume. On the other hand, let the frame be large enough to encompass a system of gravitating matter and its associated gravitational fields. The system could be a star, a black hole, the solar system or a Cavendish experiment. Call this frame a “quasi-local Lorentz frame”. To determine the behavior of the system we must calculate the metric. The computation proceeds in two stages. First we determine the external behavior of the metric and gravitational fields, thereby establishing boundary values for the fields generated by the local system, at a boundary of the quasi-local frame “far” from the local system. Second, we solve for the fields generated by the local system. But because the metric is coupled directly or indirectly to the other fields of the theory, its structure and evolution will be influenced by those fields, and in particular by the boundary values taken on by those fields far from the local system. This will be true even if we work in a coordinate system in which the asymptotic form of gμν in the boundary region between the local system and the external world is that of the Minkowski metric. Thus the gravitational environment in which the local gravitating system resides can influence the metric generated by the local system via the boundary values of the auxiliary fields. Consequently, the results of local gravitational experiments may depend on the location and velocity of the frame relative to the external environment. Of course, local non-gravitational experiments are unaffected since the gravitational fields they generate are assumed to be negligible, and since those experiments couple only to the metric, whose form can always be made locally Minkowskian at a given spacetime event. Local gravitational experiments might include Cavendish experiments, measurement of the acceleration of massive self-gravitating bodies, studies of the structure of stars and planets, or analyses of the periods of “gravitational clocks”. We can now make several statements about different kinds of metric theories.
-
(i)
A theory which contains only the metric g yields local gravitational physics which is independent of the location and velocity of the local system. This follows from the fact that the only field coupling the local system to the environment is g, and it is always possible to find a coordinate system in which g takes the Minkowski form at the boundary between the local system and the external environment. Thus the asymptotic values of gμν are constants independent of location, and are asymptotically Lorentz invariant, thus independent of velocity. General relativity is an example of such a theory.
-
(ii)
A theory which contains the metric g and dynamical scalar fields ϕA yields local gravitational physics which may depend on the location of the frame but which is independent of the velocity of the frame. This follows from the asymptotic Lorentz invariance of the Minkowski metric and of the scalar fields, but now the asymptotic values of the scalar fields may depend on the location of the frame. An example is Brans-Dicke theory, where the asymptotic scalar field determines the effective value of the gravitational constant, which can thus vary as ϕ varies. On the other hand, a form of velocity dependence in local physics can enter indirectly if the asymptotic values of the scalar field vary with time cosmologically. Then the rate of variation of the gravitational constant could depend on the velocity of the frame.
-
(iii)
A theory which contains the metric g and additional dynamical vector or tensor fields or prior-geometric fields yields local gravitational physics which may have both location and velocity-dependent effects.
These ideas can be summarized in the strong equivalence principle (SEP), which states that:
-
1.
WEP is valid for self-gravitating bodies as well as for test bodies.
-
2.
The outcome of any local test experiment is independent of the velocity of the (freely falling) apparatus.
-
3.
The outcome of any local test experiment is independent of where and when in the universe it is performed.
The distinction between SEP and EEP is the inclusion of bodies with self-gravitational interactions (planets, stars) and of experiments involving gravitational forces (Cavendish experiments, gravimeter measurements). Note that SEP contains EEP as the special case in which local gravitational forces are ignored.
The above discussion of the coupling of auxiliary fields to local gravitating systems indicates that if SEP is strictly valid, there must be one and only one gravitational field in the universe, the metric g. These arguments are only suggestive however, and no rigorous proof of this statement is available at present. Empirically it has been found that every metric theory other than GR introduces auxiliary gravitational fields, either dynamical or prior geometric, and thus predicts violations of SEP at some level (here we ignore quantum-theory inspired modifications to GR involving “R2” terms). General relativity seems to be the only metric theory that embodies SEP completely. This lends some credence to the conjecture SEP→General Relativity. In Sec. 3.6, we shall discuss experimental evidence for the validity of SEP.
3.2 The parametrized post-Newtonian formalism
Despite the possible existence of long-range gravitational fields in addition to the metric in various metric theories of gravity, the postulates of those theories demand that matter and non-gravitational fields be completely oblivious to them. The only gravitational field that enters the equations of motion is the metric g. The role of the other fields that a theory may contain can only be that of helping to generate the spacetime curvature associated with the metric. Matter may create these fields, and they plus the matter may generate the metric, but they cannot act back directly on the matter. Matter responds only to the metric.
Thus the metric and the equations of motion for matter become the primary entities for calculating observable effects, and all that distinguishes one metric theory from another is the particular way in which matter and possibly other gravitational fields generate the metric.
The comparison of metric theories of gravity with each other and with experiment becomes particularly simple when one takes the slow-motion, weak-field limit. This approximation, known as the post-Newtonian limit, is sufficiently accurate to encompass most solar-system tests that can be performed in the foreseeable future. It turns out that, in this limit, the spacetime metric g predicted by nearly every metric theory of gravity has the same structure. It can be written as an expansion about the Minkowski metric (ημν=diag(-1, 1, 1, 1)) in terms of dimensionless gravitational potentials of varying degrees of smallness. These potentials are constructed from the matter variables (Box 2) in imitation of the Newtonian gravitational potential
The “order of smallness” is determined according to the rules \( U \sim {v^2} \sim \Pi \sim p/\rho \sim \in ,{v^i} \sim \left| {d/dt} \right|/\left| {d/dx} \right| \sim { \in ^{1/2}} \), and so on (we use units in which G=c= 1; see Box 2).
A consistent post-Newtonian limit requires determination of g00 correct through O(∊2), g0i through O(∊3/2) and gij through O(∊) (for details see TEGP 4.1 [147]). The only way that one metric theory differs from another is in the numerical values of the coefficients that appear in front of the metric potentials. The parametrized post-Newtonian (PPN) formalism inserts parameters in place of these coefficients, parameters whose values depend on the theory under study. In the current version of the PPN formalism, summarized in Box 2, ten parameters are used, chosen in such a manner that they measure or indicate general properties of metric theories of gravity (Table 2). Under reasonable assumptions about the kinds of potentials that can be present at post-Newtonian order (basically only Poisson-like potentials), one finds that ten PPN parameters exhaust the possibilities.
The parameters γ and β are the usual Eddington-Robertson-Schiff parameters used to describe the “classical” tests of GR, and are in some sense the most important; they are the only non-zero parameters in GR and scalar-tensor gravity. The parameter ξ is non-zero in any theory of gravity that predicts preferred-location effects such as a galaxy-induced anisotropy in the local gravitational constant GL (also called “Whitehead” effects); α1, α2, α3 measure whether or not the theory predicts post-Newtonian preferred-frame effects; α3, ζ1, ζ2, ζ3, ζ4 measure whether or not the theory predicts violations of global conservation laws for total momentum. Next to γ and β, the parameters α1 and α2 occur most frequently with non-trivial null values. In Table 2 we show the values these parameters take (i) in GR, (ii) in any theory of gravity that possesses conservation laws for total momentum, called “semi-conservative” (any theory that is based on an invariant action principle is semi-conservative), and (iii) in any theory that in addition possesses six global conservation laws for angular momentum, called “fully conservative” (such theories automatically predict no post-Newtonian preferred-frame effects). Semi-conservative theories have five free PPN parameters (γ, β, ξ, α1, α2) while fully conservative theories have three (γ, β, ξ).
The PPN formalism was pioneered by Kenneth Nordtvedt [98], who studied the post-Newtonian metric of a system of gravitating point masses, extending earlier work by Eddington, Robertson and Schiff (TEGP 4.2 [147]). A general and unified version of the PPN formalism was developed by Will and Nordtvedt. The canonical version, with conventions altered to be more in accord with standard textbooks such as [94], is discussed in detail in TEGP 4 [147]. Other versions of the PPN formalism have been developed to deal with point masses with charge, fluid with anisotropic stresses, bodies with strong internal gravity, and post-post-Newtonian effects (TEGP 4.2, 14.2 [147]).
3.3 Competing theories of gravity
One of the important applications of the PPN formalism is the comparison and classification of alternative metric theories of gravity. The population of viable theories has fluctuated over the years as new effects and tests have been discovered, largely through the use of the PPN framework, which eliminated many theories thought previously to be viable. The theory population has also fluctuated as new, potentially viable theories have been invented.
In this article, we shall focus on general relativity and the general class of scalar-tensor modifications of it, of which the Jordan-Fierz-Brans-Dicke theory (Brans-Dicke, for short) is the classic example. The reasons are several-fold:
-
A full compendium of alternative theories is given in TEGP 5 [147].
-
Many alternative metric theories developed during the 1970s and 1980s could be viewed as “straw-man” theories, invented to prove that such theories exist or to illustrate particular properties. Few of these could be regarded as well-motivated theories from the point of view, say, of field theory or particle physics. Examples are the vector-tensor theories studied by Will, Nordtvedt and Hellings.
-
A number of theories fall into the class of “prior-geometric” theories, with absolute elements such as a flat background metric in addition to the physical metric. Most of these theories predict “preferred-frame” effects, that have been tightly constrained by observations (see Sec. 3.6.2). An example is Rosen’s bimetric theory.
-
A large number of alternative theories of gravity predict gravitational wave emission substantially different from that of general relativity, in strong disagreement with observations of the binary pulsar (see Sec. 7).
-
Scalar-tensor modifications of GR have recently become very popular in unification schemes such as string theory, and in cosmological model building. Because the scalar fields are generally massive, the potentials in the post-Newtonian limit will be modified by Yukawa-like terms.
3.3.1 General relativity
The metric g is the sole dynamical field, and the theory contains no arbitrary functions or parameters, apart from the value of the Newtonian coupling constant G, which is measurable in laboratory experiments. Throughout this article, we ignore the cosmological constant λ. Although λ has significance for quantum field theory, quantum gravity, and cosmology, on the scale of the solar-system or of stellar systems its effects are negligible, for values of λ corresponding to a cosmological closure density.
The field equations of GR are derivable from an invariant action principle δI=0, where
where R is the Ricci scalar, and Im is the matter action, which depends on matter fields ψm universally coupled to the metric g. By varying the action with respect to gμν, we obtain the field equations
where Tμν is the matter energy-momentum tensor. General covariance of the matter action implies the equations of motion Tμν;ν=0; varying Im with respect to ψm yields the matter field equations. By virtue of the absence of prior-geometric elements, the equations of motion are also a consequence of the field equations via the Bianchi identities Gμν;ν=0.
The general procedure for deriving the post-Newtonian limit is spelled out in TEGP 5.1 [147], and is described in detail for GR in TEGP 5.2 [147]. The PPN parameter values are listed in Table 3.
3.3.2 Scalar-tensor theories
These theories contain the metric g, a scalar field ϕ, a potential function V(ϕ), and a coupling function A(ϕ) (generalizations to more than one scalar field have also been carried out [42]). For some purposes, the action is conveniently written in a non-metric representation, sometimes denoted the “Einstein frame”, in which the gravitational action looks exactly like that of GR:
where R͂≡g͂μνR͂μν is the Ricci scalar of the “Einstein” metric g͂μν. (Apart from the scalar potential term V(ϕ), this corresponds to Eq. (20) with G͂(ϕ)≡(4πG)-1, U(ϕ)≡1, and M͂(ϕ)∝A(ϕ).) This representation is a “non-metric” one because the matter fields ψm couple to a combination of ϕ and g͂μν. Despite appearances, however, it is a metric theory, because it can be put into a metric representation by identifying the “physical metric”
The action can then be rewritten in the metric form
where
The Einstein frame is useful for discussing general characteristics of such theories, and for some cosmological applications, while the metric representation is most useful for calculating observable effects. The field equations, post-Newtonian limit and PPN parameters are discussed in TEGP 5.3 [147], and the values of the PPN parameters are listed in Table 3.
The parameters that enter the post-Newtonian limit are
where φ0 is the value of φ today far from the system being studied, as determined by appropriate cosmological boundary conditions. The following formula is also useful: 1/(2+ω)=2α 20 /(1+α 20 ). In Brans-Dicke theory (ω(φ)=constant), the larger the value of ω, the smaller the effects of the scalar field, and in the limit ω→∞(α0→0), the theory becomes indistinguishable from GR in all its predictions. In more general theories, the function ω(φ) could have the property that, at the present epoch, and in weak-field situations, the value of the scalar field φ0 is such that ω is very large and Λ is very small (theory almost identical to GR today), but that for past or future values of φ, or in strong-field regions such as the interiors of neutron stars, ω and Λ could take on values that would lead to significant differences from GR. Indeed, Damour and Nordtvedt have shown that in such general scalar-tensor theories, GR is a natural “attractor”: Regardless of how different the theory may be from GR in the early universe (apart from special cases), cosmological evolution naturally drives the fields toward small values of the function α, thence to large ω. Estimates of the expected relic deviations from GR today in such theories depend on the cosmological model, but range from 10-5 to a few times 10-7 for 1−γ [47, 48].
Scalar fields coupled to gravity or matter are also ubiquitous in particle-physics-inspired models of unification, such as string theory. In some models, the coupling to matter may lead to violations of WEP, which are tested by Eötvös-type experiments. In many models the scalar field is massive; if the Compton wavelength is of macroscopic scale, its effects are those of a “fifth force”. Only if the theory can be cast as a metric theory with a scalar field of infinite range or of range long compared to the scale of the system in question (solar system) can the PPN framework be strictly applied. If the mass of the scalar field is sufficiently large that its range is microscopic, then, on solar-system scales, the scalar field is suppressed, and the theory is essentially equivalent to general relativity. This is the case, for example, in the “oscillating-G” models of Accetta, Steinhardt and Will (see [120]), in which the potential function V(ϕ) contains both quadratic (mass) and quartic (self-interaction) terms, causing the scalar field to oscillate (the initial amplitude of oscillation is provided by an inflationary epoch); high-frequency oscillations in the “effective” Newtonian constant Geff≡G/φ=GA(ϕ)2 then result. The energy density in the oscillating scalar field can be enough to provide a cosmological closure density without resorting to dark matter, yet the value of ω today is so large that the theory’s local predictions are experimentally indistinguishable from GR. In other models, explored by Damour and Esposito-Farèse [43], non-linear scalar-field couplings can lead to “spontaneous scalarization” inside strong-field objects such as neutron stars, leading to large deviations from GR, even in the limit of very large ω.
3.4 Tests of the parameter γ
With the PPN formalism in hand, we are now ready to confront gravitation theories with the results of solar-system experiments. In this section we focus on tests of the parameter γ, consisting of the deflection of light and the time delay of light.
3.4.1 The deflection of light
A light ray (or photon) which passes the Sun at a distance d is deflected by an angle
(TEGP 7.1 [147]), where m⊙ is the mass of the Sun and Ф is the angle between the Earth-Sun line and the incoming direction of the photon (Figure 4). For a grazing ray, d≈d⊙, Ф≈0, and
independent of the frequency of light. Another, more useful expression gives the change in the relative angular separation between an observed source of light and a nearby reference source as both rays pass near the Sun:
where d and dr are the distances of closest approach of the source and reference rays respectively, Фr is the angular separation between the Sun and the reference source, and χ is the angle between the Sun-source and the Sun-reference directions, projected on the plane of the sky (Figure 4). Thus, for example, the relative angular separation between the two sources may vary if the line of sight of one of them passes near the Sun (d∼R⊙, dr≫d, χ varying with time).
It is interesting to note that the classic derivations of the deflection of light that use only the principle of equivalence or the corpuscular theory of light yield only the “1/2” part of the coefficient in front of the expression in Eq. (30). But the result of these calculations is the deflection of light relative to local straight lines, as established for example by rigid rods; however, because of space curvature around the Sun, determined by the PPN parameter γ, local straight lines are bent relative to asymptotic straight lines far from the Sun by just enough to yield the remaining factor “γ/2”. The first factor “1/2” holds in any metric theory, the second “γ/2” varies from theory to theory. Thus, calculations that purport to derive the full deflection using the equivalence principle alone are incorrect.
The prediction of the full bending of light by the Sun was one of the great successes of Einstein’s GR. Eddington’s confirmation of the bending of optical starlight observed during a solar eclipse in the first days following World War I helped make Einstein famous. However, the experiments of Eddington and his co-workers had only 30 percent accuracy, and succeeding experiments were not much better: The results were scattered between one half and twice the Einstein value (Figure 5), and the accuracies were low.
Measurements of the coefficient (1+γ)/2 from light deflection and time delay measurements. Its general relativity value is unity. The arrows denote anomalously large values from early eclipse expeditions. The Shapiro time-delay measurements using Viking spacecraft yielded an agreement with GR to 0.1 percent, and VLBI light deflection measurements have reached 0.02 percent. Hipparcos denotes the optical astrometry satellite, which has reached 0.1 percent.
However, the development of VLBI, very-long-baseline radio interferometry, produced greatly improved determinations of the deflection of light. These techniques now have the capability of measuring angular separations and changes in angles as small as 100 microarcseconds. Early measurements took advantage of a series of heavenly coincidences: Each year, groups of strong quasistellar radio sources pass very close to the Sun (as seen from the Earth), including the group 3C273, 3C279, and 3C48, and the group 0111+02, 0119+11 and 0116+08. As the Earth moves in its orbit, changing the lines of sight of the quasars relative to the Sun, the angular separation δθ between pairs of quasars varies (Eq. (32)). The time variation in the quantities d, dr, χ and Фr in Eq. (32) is determined using an accurate ephemeris for the Earth and initial directions for the quasars, and the resulting prediction for δθ as a function of time is used as a basis for a least-squares fit of the measured δθ, with one of the fitted parameters being the coefficient 1/2(1+γ). A number of measurements of this kind over the period 1969–1975 yielded an accurate determination of the coefficient 1/2(1+γ) which has the value unity in GR. A 1995 VLBI measurement using 3C273 and 3C279 yielded (1+γ)/2=0.9996±0.0017 [85].
A recent series of transcontinental and intercontinental VLBI quasar and radio galaxy observations made primarily to monitor the Earth’s rotation (“VLBI” in Figure 5) was sensitive to the deflection of light over almost the entire celestial sphere (at 90° from the Sun, the deflection is still 4 milliarcseconds). A recent analysis of over 2 million VLBI observations yielded (1+γ)/2=0.99992±0.00014 [59]. Analysis of observations made by the Hipparcos optical astrometry satellite yielded a test at the level of 0.3 percent [66]. A VLBI measurement of the deflection of light by Jupiter was reported; the predicted deflection of about 300 microarcseconds was seen with about 50 percent accuracy [129]. The results of light-deflection measurements are summarized in Figure 5.
3.4.2 The time delay of light
A radar signal sent across the solar system past the Sun to a planet or satellite and returned to the Earth suffers an additional non-Newtonian delay in its round-trip travel time, given by (see Figure 4)
where xe (x⊕) are the vectors, and re (rx⊕) are the distances from the Sun to the source (Earth), respectively (TEGP 7.2 [147]). For a ray which passes close to the Sun,
where d is the distance of closest approach of the ray in solar radii, and r is the distance of the planet or satellite from the Sun, in astronomical units.
In the two decades following Irwin Shapiro’s 1964 discovery of this effect as a theoretical consequence of general relativity, several high-precision measurements were made using radar ranging to targets passing through superior conjunction. Since one does not have access to a “Newtonian” signal against which to compare the round-trip travel time of the observed signal, it is necessary to do a differential measurement of the variations in round-trip travel times as the target passes through superior conjunction, and to look for the logarithmic behavior of Eq. (34). In order to do this accurately however, one must take into account the variations in round-trip travel time due to the orbital motion of the target relative to the Earth. This is done by using radar-ranging (and possibly other) data on the target taken when it is far from superior conjunction (i.e. when the time-delay term is negligible) to determine an accurate ephemeris for the target, using the ephemeris to predict the PPN coordinate trajectory xe(t) near superior conjunction, then combining that trajectory with the trajectory of the Earth x⊕(t) to determine the Newtonian round-trip time and the logarithmic term in Eq. (34). The resulting predicted round-trip travel times in terms of the unknown coefficient 1/2(1+γ) are then fit to the measured travel times using the method of least-squares, and an estimate obtained for 1/2(1+γ).
The targets employed included planets, such as Mercury or Venus, used as passive reflectors of the radar signals (“passive radar”), and artificial satellites, such as Mariners 6 and 7, Voyager 2, and the Viking Mars landers and orbiters, used as active retransmitters of the radar signals (“active radar”).
The results for the coefficient 1/2(1+γ) of all radar time-delay measurements performed to date (including a measurement of the one-way time delay of signals from the millisecond pulsar PSR 1937+21) are shown in Figure 5 (see TEGP 7.2 [147] for discussion and references). The Viking experiment resulted in a 0.1 percent measurement [111].
From the results of VLBI light-deflection experiments, we can conclude that the coeficient 1/2(1+γ) must be within at most 0.014 percent of unity. Scalar-tensor theories must have ω>3500 to be compatible with this constraint.
3.5 The perihelion shift of Mercury
The explanation of the anomalous perihelion shift of Mercury’s orbit was another of the triumphs of GR. This had been an unsolved problem in celestial mechanics for over half a century, since the announcement by Le Verrier in 1859 that, after the perturbing effects of the planets on Mercury’s orbit had been accounted for, and after the effect of the precession of the equinoxes on the astronomical coordinate system had been subtracted, there remained in the data an unexplained advance in the perihelion of Mercury. The modern value for this discrepancy is 43 arcseconds per century. A number of ad hoc proposals were made in an attempt to account for this excess, including, among others, the existence of a new planet Vulcan near the Sun, a ring of planetoids, a solar quadrupole moment and a deviation from the inverse-square law of gravitation, but none was successful. General relativity accounted for the anomalous shift in a natural way without disturbing the agreement with other planetary observations.
The predicted advance per orbit Δῶ, including both relativistic PPN contributions and the Newtonian contribution resulting from a possible solar quadrupole moment, is given by
where m≡m1+m2 and μ≡m1m2/m are the total mass and reduced mass of the two-body system respectively; p≡a(1−e2) is the semi-latus rectum of the orbit, with the semi-major axis a and the eccentricity e; R is the mean radius of the oblate body; and J2 is a dimensionless measure of its quadrupole moment, given by J2=(C−A)/m1R2, where C and A are the moments of inertia about the body’s rotation and equatorial axes, respectively (for details of the derivation see TEGP 7.3 [147]). We have ignored preferred-frame and galaxy-induced contributions to Δῶ; these are discussed in TEGP 8.3 [147].
The first term in Eq. (35) is the classical relativistic perihelion shift, which depends upon the PPN parameters γ and β. The second term depends upon the ratio of the masses of the two bodies; it is zero in any fully conservative theory of gravity (α1≡α2≡α3≡ζ2≡0); it is also negligible for Mercury, since μ/m≈mMerc/m⊙≈2×10-7. We shall drop this term henceforth. The third term depends upon the solar quadrupole moment J2. For a Sun that rotates uniformly with its observed surface angular velocity, so that the quadrupole moment is produced by centrifugal flattening, one may estimate J2 to be ∼1×10-7. This actually agrees reasonably well with values inferred from rotating solar models that are in accord with observations of the normal modes of solar oscillations (helioseismology). Substituting standard orbital elements and physical constants for Mercury and the Sun we obtain the rate of perihelion shift \(\dot \tilde \omega\), in seconds of arc per century,
Now, the measured perihelion shift of Mercury is known accurately: After the perturbing effects of the other planets have been accounted for, the excess shift is known to about 0.1 percent from radar observations of Mercury between 1966 and 1990 [116]. Analysis of data taken since 1990 could improve the accuracy. The solar oblateness effect is smaller than the observational error, so we obtain the PPN bound |2γ−β−1|<3×10-3.
3.6 Tests of the strong equivalence principle
The next class of solar-system experiments that test relativistic gravitational effects may be called tests of the strong equivalence principle (SEP). In Sec. 3.1.2 we pointed out that many metric theories of gravity (perhaps all except GR) can be expected to violate one or more aspects of SEP. Among the testable violations of SEP are a violation of the weak equivalence principle for gravitating bodies that leads to perturbations in the Earth-Moon orbit; preferred-location and preferred-frame effects in the locally measured gravitational constant that could produce observable geophysical effects; and possible variations in the gravitational constant over cosmological timescales.
3.6.1 The Nordtvedt effect and the lunar Eötvös experiment
In a pioneering calculation using his early form of the PPN formalism, Nordtvedt [97] showed that many metric theories of gravity predict that massive bodies violate the weak equivalence principle — that is, fall with different accelerations depending on their gravitational self-energy. Dicke [113] linked such an effect to the possibility of a spatially varying gravitational constant, in theories such as scalar-tensor gravity. For a spherically symmetric body, the acceleration from rest in an external gravitational potential U has the form
where Eg is the negative of the gravitational self-energy of the body (Eg>0). This violation of the massive-body equivalence principle is known as the “Nordtvedt effect”. The effect is absent in GR (η=0) but present in scalartensor theory (η=1/(2+ω)+4Λ). The existence of the Nordtvedt effect does not violate the results of laboratory Eötvös experiments, since for laboratory-sized objects, Eg/m≤10-27, far below the sensitivity of current or future experiments. However, for astronomical bodies, Eg/m may be significant (10-5 for the Sun, 10-8 for Jupiter, 4.6×10-10 for the Earth, 0.2×10-10 for the Moon). If the Nordtvedt effect is present (η≠0) then the Earth should fall toward the Sun with a slightly different acceleration than the Moon. This perturbation in the Earth-Moon orbit leads to a polarization of the orbit that is directed toward the Sun as it moves around the Earth-Moon system, as seen from Earth. This polarization represents a perturbation in the Earth-Moon distance of the form
where ω0 and ωs are the angular frequencies of the orbits of the Moon and Sun around the Earth (see TEGP 8.1 [147] for detailed derivations and references; for improved calculations of the numerical coefficient, see [102, 53]).
Since August 1969, when the first successful acquisition was made of a laser signal reflected from the Apollo 11 retroreflector on the Moon, the lunar laser-ranging experiment (LURE) has made regular measurements of the round-trip travel times of laser pulses between a network of observatories and the lunar retroreflectors, with accuracies that are approaching 50 ps (1 cm). These measurements are fit using the method of least-squares to a theoretical model for the lunar motion that takes into account perturbations due to the Sun and the other planets, tidal interactions, and post-Newtonian gravitational effects. The predicted round-trip travel times between retroreflector and telescope also take into account the librations of the Moon, the orientation of the Earth, the location of the observatory, and atmospheric effects on the signal propagation. The “Nordtvedt” parameter η along with several other important parameters of the model are then estimated in the least-squares method.
Several independent analyses of the data found no evidence, within experimental uncertainty, for the Nordtvedt effect (for recent results see [56, 154, 96]). Their results can be summarized by the bound |η|<0.001. These results represent a limit on a possible violation of WEP for massive bodies of 5 parts in 1013 (compare Figure 1). For Brans-Dicke theory, these results force a lower limit on the coupling constant ω of 1000. Note that, at this level of precision, one cannot regard the results of lunar laser ranging as a “clean” test of SEP until one eliminates the possibility of a compensating violation of WEP for the two bodies, because the chemical compositions of the Earth and Moon differ in the relative fractions of iron and silicates. To this end, the Eöt-Wash group carried out an improved test of WEP for laboratory bodies whose chemical compositions mimic that of the Earth and Moon. The resulting bound of four parts in 1013 [10] reduces the ambiguity in the Lunar laser ranging bound, and establishes the firm limit on the universality of acceleration of gravitational binding energy at the level of η<1.3×10-3.
In GR, the Nordtvedt effect vanishes; at the level of several centimeters and below, a number of non-null general relativistic effects should be present [102].
3.6.2 Preferred-frame and preferred-location effects
Some theories of gravity violate SEP by predicting that the outcomes of local gravitational experiments may depend on the velocity of the laboratory relative to the mean rest frame of the universe (preferred-frame effects) or on the location of the laboratory relative to a nearby gravitating body (preferred-location effects). In the post-Newtonian limit, preferred-frame effects are governed by the values of the PPN parameters α1, α2, and α3, and some preferred-location effects are governed by ξ (see Table 2).
The most important such effects are variations and anisotropies in the locally-measured value of the gravitational constant, which lead to anomalous Earth tides and variations in the Earth’s rotation rate; anomalous contributions to the orbital dynamics of planets and the Moon; self-accelerations of pulsars, and anomalous torques on the Sun that would cause its spin axis to be randomly oriented relative to the ecliptic (see TEGP 8.2, 8.3, 9.3 and 14.3 (c) [147]). An improved bound on α3 of 2×10-20 from the period derivatives of 20 millisecond pulsars was reported in [13]; improved bounds on α1 were achieved using lunar laser ranging data [95], and using observations of the circular binary orbit of the pulsar J2317+1439 [12]. Negative searches for these effects have produced strong constraints on the PPN parameters (Table 4).
3.6.3 Constancy of the Newtonian gravitational constant
Most theories of gravity that violate SEP predict that the locally measured Newtonian gravitational constant may vary with time as the universe evolves. For the scalar-tensor theories listed in Table 3, the predictions for Ġ/G can be written in terms of time derivatives of the asymptotic scalar field. Where G does change with cosmic evolution, its rate of variation should be of the order of the expansion rate of the universe, i.e. Ġ/G∼H0, where H0 is the Hubble expansion parameter and is given by H0=100 h km s-1 Mpc-1=h×10-10 yr-1, where current observations of the expansion of the universe give h≈0.7.
Several observational constraints can be placed on Ġ/G using methods that include studies of the evolution of the Sun, observations of lunar occultations (including analyses of ancient eclipse data), lunar laser-ranging measurements, planetary radar-ranging measurements, and pulsar timing data. Laboratory experiments may one day lead to interesting limits (for review and references to past work see TEGP 8.4 and 14.3 (c) [147]). Recent results are shown in Table 5.
The best limits on Ġ/G still come from ranging measurements to the Viking landers and Lunar laser ranging measurements [56, 154, 96]. It has been suggested that radar observations of a Mercury orbiter over a two-year mission (30 cm accuracy in range) could yield Δ(Ġ/G)∼10-14 yr-1.
Although bounds on Ġ/G from solar-system measurements can be correctly obtained in a phenomenological manner through the simple expedient of replacing G by G0+Ġ0(t−t0) in Newton’s equations of motion, the same does not hold true for pulsar and binary pulsar timing measurements. The reason is that, in theories of gravity that violate SEP, such as scalar-tensor theories, the “mass” and moment of inertia of a gravitationally bound body may vary with variation in G. Because neutron stars are highly relativistic, the fractional variation in these quantities can be comparable to ΔG/G, the precise variation depending both on the equation of state of neutron star matter and on the theory of gravity in the strong-field regime. The variation in the moment of inertia affects the spin rate of the pulsar, while the variation in the mass can affect the orbital period in a manner that can subtract from the direct effect of a variation in G, given by Ṗb/Pb=-2Ġ/G [101]. Thus, the bounds quoted in Table 5 for the binary pulsar PSR 1913+16 [51] and the pulsar PSR 0655+64 [69] are theory-dependent and must be treated as merely suggestive.
3.7 Other tests of post-Newtonian gravity
3.7.1 Tests of post-Newtonian conservation laws
Of the five “conservation law” PPN parameters ζ1, ζ2, ζ3, ζ4, and α3, only three, ζ2, ζ3 and α3, have been constrained directly with any precision; ζ1 is constrained indirectly through its appearance in the Nordtvedt effect parameter η, Eq. (37). There is strong theoretical evidence that ζ4, which is related to the gravity generated by fluid pressure, is not really an independent parameter — in any reasonable theory of gravity there should be a connection between the gravity produced by kinetic energy (ρv2), internal energy (ρП), and pressure (p). From such considerations, there follows [141] the additional theoretical constraint
A non-zero value for any of these parameters would result in a violation of conservation of momentum, or of Newton’s third law in gravitating systems. An alternative statement of Newton’s third law for gravitating systems is that the “active gravitational mass”, that is the mass that determines the gravitational potential exhibited by a body, should equal the “passive gravitational mass”, the mass that determines the force on a body in a gravitational field. Such an equality guarantees the equality of action and reaction and of conservation of momentum, at least in the Newtonian limit.
A classic test of Newton’s third law for gravitating systems was carried out in 1968 by Kreuzer, in which the gravitational attraction of fluorine and bromine were compared to a precision of 5 parts in 105.
A remarkable planetary test was reported by Bartlett and van Buren [11]. They noted that current understanding of the structure of the Moon involves an iron-rich, aluminum-poor mantle whose center of mass is offset about 10 km from the center of mass of an aluminum-rich, iron-poor crust. The direction of offset is toward the Earth, about 14° to the east of the Earth-Moon line. Such a model accounts for the basaltic maria which face the Earth, and the aluminum-rich highlands on the Moon’s far side, and for a 2 km offset between the observed center of mass and center of figure for the Moon. Because of this asymmetry, a violation of Newton’s third law for aluminum and iron would result in a momentum non-conserving self-force on the Moon, whose component along the orbital direction would contribute to the secular acceleration of the lunar orbit. Improved knowledge of the lunar orbit through lunar laser ranging, and a better understanding of tidal effects in the Earth-Moon system (which also contribute to the secular acceleration) through satellite data, severely limit any anomalous secular acceleration, with the resulting limit
According to the PPN formalism, in a theory of gravity that violates conservation of momentum, but that obeys the constraint of Eq. (39), the electrostatic binding energy Ee of an atomic nucleus could make a contribution to the ratio of active to passive mass of the form
The resulting limit on ζ3 from the lunar experiment is ζ3<1×10-8 (TEGP 9.2, 14.3 (d) [147]).
Another consequence of a violation of conservation of momentum is a self-acceleration of the center of mass of a binary stellar system, given by
where δm=m1−m2, a is the semi-major axis, and nP is a unit vector directed from the center of mass to the point of periastron of m1 (TEGP 9.3 [147]). A consequence of this acceleration would be non-vanishing values for d2P=dt2, where P denotes the period of any intrinsic process in the system (orbit, spectra, pulsar periods). The observed upper limit on d2Pp/dt2 of the binary pulsar PSR 1913+16 places a strong constraint on such an effect, resulting in the bound |α3+ζ2|<4×10-5. Since α3 has already been constrained to be much less than this (Table 4), we obtain a strong bound on ζ2 alone [146].
3.7.2 Geodetic precession
A gyroscope moving through curved spacetime suffers a precession of its axis given by
where v is the velocity of the gyroscope, and U is the Newtonian gravitational potential of the source (TEGP 9.1 [147]). The Earth-Moon system can be considered as a “gyroscope”, with its axis perpendicular to the orbital plane. The predicted precession is about 2 arcseconds per century, an effect first calculated by de Sitter. This effect has been measured to about 0.7 percent using Lunar laser ranging data [56, 154].
For a gyroscope orbiting the Earth, the precession is about 8 arcseconds per year. The Stanford Gyroscope Experiment has as one of its goals the measurement of this effect to 5×10-5 (see below); if achieved, this would substantially improve the accuracy of the parameter γ.
3.7.3 Search for gravitomagnetism
According to GR, moving or rotating matter should produce a contribution to the gravitational field that is the analogue of the magnetic field of a moving charge or a magnetic dipole. Although gravitomagnetism plays a role in a variety of measured relativistic effects, it has not been seen to date, isolated from other post-Newtonian effects (for a discussion of the evidence for gravitomagnetism in solar system measurements and the binary pulsar, see [100, 99]). The Relativity Gyroscope Experiment (Gravity Probe B or GP-B) at Stanford University, in collaboration with NASA and Lockheed-Martin Corporation, is in the advanced stage of developing a space mission to detect this phenomenon directly [71]. A set of four superconducting-niobium-coated, spherical quartz gyroscopes will be flown in a low polar Earth orbit, and the precession of the gyroscopes relative to the distant stars will be measured. In the PPN formalism, the predicted effect of gravitomagnetism is a precession (also known as the Lense-Thirring effect, or the dragging of inertial frames), given by
where J is the angular momentum of the Earth, n is a unit radial vector, and r is the distance from the center of the Earth (TEGP 9.1 [147]). For a polar orbit at about 650 km altitude, this leads to a secular angular precession at a rate 1/2(1+γ+1/4α1)42×10-3 arcsec/yr. The accuracy goal of the experiment is about 0.5 milliarcseconds per year. The science instrument package and the spacecraft are in the final phases of assembly, with launch scheduled for 2002.
Another proposal to look for an effect of gravitomagnetism is to measure the relative precession of the line of nodes of a pair of laser-ranged geodynamics satellites (LAGEOS), ideally with supplementary inclination angles; the inclinations must be supplementary in order to cancel the dominant nodal precession caused by the Earth’s Newtonian gravitational multipole moments. Unfortunately, the two existing LAGEOS satellites are not in appropriately inclined orbits, and no plans exist at present to launch a third satellite in a supplementary orbit. Nevertheless, by combing nodal precession data from LAGEOS I and II with perigee advance data from the slightly eccentric orbit of LAGEOS II, Ciufolini et al. reported a partial cancellation of multipole effects, and a resulting 20 percent confirmation of GR [34].
3.7.4 Improved PPN parameter values
A number of advanced space missions have been proposed in which spacecraft orbiters or landers and improved tracking capabilities could lead to significant improvements in values of the PPN parameters, of J2 of the Sun, and of Ġ/G. Doppler tracking of the Cassini spacecraft (launched to orbit and study Saturn in 1997) during its 2003 superior conjunction could measure γ to a few parts in 105, by measuring the time variation of the Shapiro delay [77]. A Mercury orbiter, in a two-year experiment, with 3 cm range capability, could yield improvements in the perihelion shift to a part in 104, in γ to 4×10-5, in Ġ/G to 10-14 yr-1, and in J2 to a few parts in 108. Proposals are being developed, primarily in Europe, for advanced space missions which will have tests of PPN parameters as key components, including GAIA, a high-precision astrometric telescope (successor to Hipparcos), which could measure light-deflection and γ to the 10-6 level [9]. Nordtvedt [103] has argued that “grand fits” of large solar system range data sets, including ranging to Mercury, Mars and the Moon, could yield substantially improved measurements of PPN parameters.
4 Strong Gravity and Gravitational Waves: A New Testing Ground
4.1 Strong-field systems in general relativity
4.1.1 Defining weak and strong gravity
In the solar system, gravity is weak, in the sense that the Newtonian gravitational potential and related variables (U(x, t)∼v2∼p/ρ∼∊) are much smaller than unity everywhere. This is the basis for the post-Newtonian expansion and for the “parametrized post-Newtonian” framework described in Sec. 3.2. “Strong-field” systems are those for which the simple 1PN approximation of the PPN framework is no longer appropriate. This can occur in a number of situations:
-
The system may contain strongly relativistic objects, such as neutron stars or black holes, near and inside which ∊∼1, and the post-Newtonian approximation breaks down. Nevertheless, under some circumstances, the orbital motion may be such that the interbody potential and orbital velocities still satisfy ∊≪1 so that a kind of post-Newtonian approximation for the orbital motion might work; however, the strong-field internal gravity of the bodies could (especially in alternative theories of gravity) leave imprints on the orbital motion.
-
The evolution of the system may be affected by the emission of gravitational radiation. The 1PN approximation does not contain the effects of gravitational radiation back-reaction. In the expression for the metric given in Box 2, radiation back-reaction effects do not occur until O(∊7/2) in g00, O(∊3) in g0i, and O(∊5/2) in gij. Consequently, in order to describe such systems, one must carry out a solution of the equations substantially beyond 1PN order, sufficient to incorporate the leading radiation damping terms at 2.5PN order.
-
The system may be highly relativistic in its orbital motion, so that U∼v2∼1 even for the interbody field and orbital velocity. Systems like this include the late stage of the inspiral of binary systems of neutron stars or black holes, driven by gravitational radiation damping, prior to a merger and collapse to a final stationary state. Binary inspiral is one of the leading candidate sources for detection by a world-wide network of laser interferometric gravitational wave observatories nearing completion. A proper description of such systems requires not only equations for the motion of the binary carried to extraordinarily high PN orders (at least 3.5PN), but also requires equations for the far-zone gravitational waveform measured at the detector, that are equally accurate to high PN orders beyond the leading “quadrupole” approximation.
Of course, some systems cannot be properly described by any post-Newtonian approximation because their behavior is fundamentally controlled by strong gravity. These include the imploding cores of supernovae, the final merger of two compact objects, the quasinormal-mode vibrations of neutron stars and black holes, the structure of rapidly rotating neutron stars, and so on. Phenomena such as these must be analysed using different techniques. Chief among these is the full solution of Einstein’s equations via numerical methods. This field of “numerical relativity” is a rapidly growing and maturing branch of gravitational physics, whose description is beyond the scope of this article. Another is black hole perturbation theory (see [93] for a review).
4.1.2 Compact bodies and the strong equivalence principle
When dealing with the motion and gravitational wave generation by orbiting bodies, one finds a remarkable simplification within general relativity. As long as the bodies are sufficiently well-separated that one can ignore tidal interactions and other effects that depend upon the finite extent of the bodies (such as their quadrupole and higher multipole moments), then all aspects of their orbital behavior and gravitational wave generation can be characterized by just two parameters: mass and angular momentum. Whether their internal structure is highly relativistic, as in black holes or neutron stars, or non-relativistic as in the Earth and Sun, only the mass and angular momentum are needed. Furthermore, both quantities are measurable in principle by examining the external gravitational field of the bodies, and make no reference whatsoever to their interiors.
Damour [39] calls this the “effacement” of the bodies’ internal structure. It is a consequence of the strong equivalence principle (SEP), described in Section 3.1.2.
General relativity satisfies SEP because it contains one and only one gravitational field, the spacetime metric gμν. Consider the motion of a body in a binary system, whose size is small compared to the binary separation. Surround the body by a region that is large compared to the size of the body, yet small compared to the separation. Because of the general covariance of the theory, one can choose a freely-falling coordinate system which comoves with the body, whose spacetime metric takes the Minkowski form at its outer boundary (ignoring tidal effects generated by the companion). There is thus no evidence of the presence of the companion body, and the structure of the chosen body can be obtained using the field equations of GR in this coordinate system. Far from the chosen body, the metric is characterized by the mass and angular momentum (assuming that one ignores quadrupole and higher multipole moments of the body) as measured far from the body using orbiting test particles and gyroscopes. These asymptotically measured quantities are oblivious to the body7#x2019;s internal structure. A black hole of mass m and a planet of mass m would produce identical spacetimes in this outer region.
The geometry of this region surrounding the one body must be matched to the geometry provided by the companion body. Einstein’s equations provide consistency conditions for this matching that yield constraints on the motion of the bodies. These are the equations of motion. As a result the motion of two planets of mass and angular momentum m1, m2, J1 and J2 is identical to that of two black holes of the same mass and angular momentum (again, ignoring tidal effects).
This effacement does not occur in an alternative gravitional theory like scalar-tensor gravity. There, in addition to the spacetime metric, a scalar field φ is generated by the masses of the bodies, and controls the local value of the gravitational coupling constant (i.e. G is a function of φ). Now, in the local frame surrounding one of the bodies in our binary system, while the metric can still be made Minkowskian far away, the scalar field will take on a value φ0 determined by the companion body. This can affect the value of G inside the chosen body, alter its internal structure (specifically its gravitational binding energy) and hence alter its mass. Effectively, each mass becomes several functions mA(φ) of the value of the scalar field at its location, and several distinct masses come into play, inertial mass, gravitational mass, “radiation” mass, etc. The precise nature of the functions will depend on the body, specifically on its gravitational binding energy, and as a result, the motion and gravitational radiation may depend on the internal structure of each body. For compact bodies such as neutron stars, and black holes these internal structure effects could be large; for example, the gravitational binding energy of a neutron star can be 40 percent of its total mass. At 1PN order, the leading manifestation of this effect is the Nordtvedt effect.
This is how the study of orbiting systems containing compact objects provides strong-field tests of general relativity. Even though the strong-field nature of the bodies is effaced in GR, it is not in other theories, thus any result in agreement with the predictions of GR constitutes a kind of “null” test of strong-field gravity.
4.2 Motion and gravitational radiation in general relativity
The motion of bodies and the generation of gravitational radiation are long-standing problems that date back to the first years following the publication of GR, when Einstein calculated the gravitational radiation emitted by a laboratory-scale object using the linearized version of GR, and de Sitter calculated N-body equations of motion for bodies in the 1PN approximation to GR. It has at times been controversial, with disputes over such issues as whether Einstein’s equations alone imply equations of motion for bodies (Einstein, Infeld and Hoffman demonstrated explicitly that they do, using a matching procedure similar to the one described above), whether gravitational waves are real or are artifacts of general covariance (Einstein waffled; Bondi and colleagues proved their reality rigorously in the 1950s), and even over algebraic errors (Einstein erred by a factor of 2 in his first radiation calculation; Eddington found the mistake). Shortly after the discovery of the binary pulsar PSR 1913+16 in 1974, questions were raised about the foundations of the “quadrupole formula” for gravitational radiation damping (and in some quarters, even about its quantitative validity). These questions were answered in part by theoretical work designed to shore up the foundations of the quadrupole approximation, and in part (perhaps mostly) by the agreement between the predictions of the quadrupole formula and the observed rate of damping of the pulsar’s orbit (see Section 5.1). Damour [39] gives a thorough review of this subject.
The problem of motion and radiation has received renewed interest since 1990, with proposals for construction of large-scale laser interferometric gravitational-wave observatories, such as the LIGO project in the US, VIRGO and GEO600 in Europe, and TAMA300 in Japan, and the realization that a leading candidate source of detectable waves would be the inspiral, driven by gravitational radiation damping, of a binary system of compact objects (neutron stars or black holes) [1, 127]. The analysis of signals from such systems will require theoretical predictions from GR that are extremely accurate, well beyond the leading-order prediction of Newtonian or even post-Newtonian gravity for the orbits, and well beyond the leading-order formulae for gravitational waves.
This presented a major theoretical challenge: to calculate the motion and radiation of systems of compact objects to very high PN order, a formidable algebraic task, while addressing a number of issues of principle that have historically plagued this subject, sufficiently well to ensure that the results were physically meaningful. This challenge is in the process of being met, so that we may soon see a remarkable convergence between observational data and accurate predictions of gravitational theory that could provide new, strong-field tests of GR.
Here we give a brief overview of the problem of motion and gravitational radiation.
4.3 Einstein’s equations in “relaxed” form
The Einstein equations Gμν=8πTμν are elegant and deceptively simple, showing geometry (in the form of the Einstein tensor Gμν, which is a function of spacetime curvature) being generated by matter (in the form of the material stress-energy tensor Tμν). However, this is not the most useful form for actual calculations. For post-Newtonian calculations, a far more useful form is the so-called “relaxed” Einstein equations:
where □≡-∂2/∂t2+∇2 is the flat-spacetime wave operator, hαβ is a “gravitational tensor potential” related to the deviation of the spacetime metric from its Minkowski form by the formula hαβ≡ηαβ−(-g)1/2gαβ, g is the determinant of gαβ, and a particular coordinate system has been specified by the de Donder or harmonic gauge condition ∂hαβ/∂xβ=0 (summation on repeated indices is assumed). This form of Einstein’s equations bears a striking similarity to Maxwell’s equations for the vector potential Aα in Lorentz gauge: □Aα=-4πJα, ∂Aα/∂xα=0. There is a key difference, however: The source on the right hand side of Eq. (45) is given by the “effective” stress-energy pseudotensor
where Λαβ is the non-linear “field” contribution given by terms quadratic (and higher) in hαβ and its derivatives (see [94], Eqs. (20.20, 20.21) for formulae). In general relativity, the gravitational field itself generates gravity, a reflection of the nonlinearity of Einstein’s equations, and in contrast to the linearity of Maxwell’s equations.
Equation (45) is exact, and depends only on the assumption that spacetime can be covered by harmonic coordinates. It is called “relaxed” because it can be solved formally as a functional of source variables without specifying the motion of the source, in the form
where the integration is over the past flat-spacetime null cone C of the field point (t, x). The motion of the source is then determined either by the equation ∂ταβ/∂xβ=0 (which follows from the harmonic gauge condition), or from the usual covariant equation of motion Tαβ;β=0, where the subscript ;β denotes a covariant divergence. This formal solution can then be iterated in a slow motion (v<1) weak-field (‖hαβ‖<1) approximation. One begins by substituting h αβ0 =0 into the source ταβ in Eq. (47), and solving for the first iterate h αβ1 , and then repeating the procedure sufficiently many times to achieve a solution of the desired accuracy. For example, to obtain the 1PN equations of motion, two iterations are needed (i.e. h αβ2 must be calculated); likewise, to obtain the leading gravitational waveform for a binary system, two iterations are needed.
At the same time, just as in electromagnetism, the formal integral (47) must be handled differently, depending on whether the field point is in the far zone or the near zone. For field points in the far zone or radiation zone, |x|>λ̴>|x′| (λ̴ is the gravitational wavelength/2π), the field can be expanded in inverse powers of R=|x| in a multipole expansion, evaluated at the “retarded time” t−R. The leading term in 1/R is the gravitational waveform. For field points in the near zone or induction zone, |x|∼|x′|<λ̴, the field is expanded in powers of |x−x′| about the local time t, yielding instantaneous potentials that go into the equations of motion.
However, because the source ταβ contains hαβ itself, it is not confined to a compact region, but extends over all spacetime. As a result, there is a danger that the integrals involved in the various expansions will diverge or be ill-defined. This consequence of the non-linearity of Einstein’s equations has bedeviled the subject of gravitational radiation for decades. Numerous approaches have been developed to try to handle this difficulty. The “post-Minkowskian” method of Blanchet, Damour and Iyer [19, 20, 21, 45, 22, 15] solves Einstein’s equations by two different techniques, one in the near zone and one in the far zone, and uses the method of singular asymptotic matching to join the solutions in an overlap region. The method provides a natural “regularization” technique to control potentially divergent integrals. The “Direct Integration of the Relaxed Einstein Equations” (DIRE) approach of Will, Wiseman and Pati [152, 105] retains Eq. (47) as the global solution, but splits the integration into one over the near zone and another over the far zone, and uses different integration variables to carry out the explicit integrals over the two zones. In the DIRE method, all integrals are finite and convergent.
These methods assume from the outset that gravity is sufficiently weak that ‖hαβ‖<1 and harmonic coordinates exists everywhere, including inside the bodies. Thus, in order to apply the results to cases where the bodies may be neutron stars or black holes, one relies upon the strong equivalence principle to argue that, if tidal forces are ignored, and equations are expressed in terms of masses and spins, one can simply extrapolate the results unchanged to the situation where the bodies are ultrarelativistic. While no general proof of this exists, it has been shown to be valid in specific circumstances, such as at 2PN order in the equations of motion, and for black holes moving in a Newtonian background field [39].
Methods such as these have resolved most of the issues that led to criticism of the foundations of gravitational radiation theory during the 1970s.
4.4 Equations of motion and gravitational waveform
Among the results of these approaches are formulae for the equations of motion and gravitational waveform of binary systems of compact objects, carried out to high orders in a PN expansion. Here we shall only state the key formulae that will be needed for this article. For example, the relative two-body equation of motion has the form
where m=m1+m2 is the total mass, r=|x1−x2|, v=v1−v2, and n̑=(x1−x2)/r. The notation AnPN indicates that the term is O(∊n) relative to the Newtonian term -n̑n. Explicit formulae for terms through various orders have been calculated by various authors: non-radiative terms through 2PN order [40, 38, 72, 39, 27], radiation reaction terms at 2.5PN and 3.5PN order [78, 79, 17], and non-radiative 3PN terms [80, 81, 46, 26, 25]. Here we quote only the first PN corrections and the leading radiation-reaction terms at 2.5PN order:
where η=m1m2/(m1+m2)2. These terms are sufficient to analyse the orbit and evolution of the binary pulsar (Sec. 5.1). For example, the 1PN terms are responsible for the periastron advance of an eccentric orbit, given by ω̇=6πfbm/a(1−e2), where a and e are the semi-major axis and eccentricity, respectively, of the orbit, and fb is the orbital frequency, given to the needed order by Kepler’s third law 2πfb=(m/a3)1/2.
Another product is a formula for the gravitational field far from the system, written schematically in the form
where R is the distance from the source, and the variables are to be evaluated at retarded time t−R. The leading term is the so-called quadrupole formula
where Iij is the quadrupole moment of the source, and overdots denote time derivatives. For a binary system this leads to
For binary systems, explicit formulae for all the terms through 2.5PN order have been derived by various authors [135, 155, 106, 23, 24, 152, 16, 18]. Given the gravitational waveform, one can compute the rate at which energy is carried off by the radiation (schematically ∫ḣḣdΩ, the gravitational analog of the Poynting flux). The lowest-order quadrupole formula leads to the gravitational wave energy flux
Formulae for fluxes of angular and linear momentum can also be derived. The 2.5PN radiation-reaction terms in the equation of motion (48) result in a damping of the orbital energy that precisely balances the energy flux (54) determined from the waveform. Averaged over one orbit, this results in a rate of increase of the binary’s orbital frequency given by
where \({\mathcal M}\) is the so-called “chirp” mass, given by \({\mathcal M} = {\eta ^{3/5}}m\), and F(e)=(1+73e2/24+37e4/96)/(1−e2)7/2. Notice that by making precise measurements of the phase Ф(t)=2π ∫t f(t′)dt′ of either the orbit or the gravitational waves (for which f=2fb for the dominant component) as a function of the frequency, one in effect measures the “chirp” mass of the system.
These formalisms have also been generalized to include the leading effects of spin-orbit and spin-spin coupling between the bodies [83, 82].
Another approach to gravitational radiation is applicable to the special limit in which one mass is much smaller than the other. This is the method of blackhole perturbation theory. One begins with an exact background spacetime of a black hole, either the non-rotating Schwarzschild or the rotating Kerr solution, and perturbs it according to gμν=g (0) μν +hμν. The particle moves on a geodesic of the background spacetime, and a suitably defined source stress-energy tensor for the particle acts as a source for the gravitational perturbation and wave field hμν. This method provides numerical results that are exact in v, as well as analytical results expressed as series in powers of v, both for non-rotating and for rotating black holes. For non-rotating holes, the analytical expansions have been carried to 5.5PN order, or ∊5.5 beyond the quadrupole approximation. All results of black hole perturbation agree precisely with the m1→0 limit of the PN results, up to the highest PN order where they can be compared (for a detailed review see [93]).
4.5 Gravitational wave detection
A gravitational wave detector can be modelled as a body of mass M at a distance L from a fiducial laboratory point, connected to the point by a spring of resonant frequency ω0 and quality factor Q. From the equation of geodesic deviation, the infinitesimal displacement ξ of the mass along the line of separation from its equilibrium position satisfies the equation of motion
where F+(θ,φ,ψ) and F×(θ,φ,ψ) are “beam-pattern” factors, that depend on the direction of the source (θ,φ) and on a polarization angle ψ, and h+(t) and h×(t) are gravitational waveforms corresponding to the two polarizations of the gravitational wave (for a review, see [126]). In a source coordinate system in which the x−y plane is the plane of the sky and the z-direction points toward the detector, these two modes are given by
where hij represent transverse-traceless (TT) projections of the calculated waveform of Eq. (51), given by
where N̑j is a unit vector pointing toward the detector. The beam pattern factors depend on the orientation and nature of the detector. For a wave approaching along the laboratory z-direction, and for a mass whose location on the x−y plane makes an angle φ with the x axis, the beam pattern factors are given by F+=cos2φ and F×=sin2φ. For a resonant cylinder oriented along the laboratory z axis, and for source direction (θ, φ), they are given by F+=sin2ψcos2ψ, F×=sin2θsin2ψ (the angle ψ measures the relative orientation of the laboratory and source x-axes). For a laser interferometer with one arm along the laboratory x-axis, the other along the y-axis, and with ξ dedined as the differential displacement along the two arms, the beam pattern functions are F+=1/2(1+cos2θ)cos2φcos2ψ−cosθsin2φsin2ψ and F×=1/2(1+cos2θ)cos2φsin2ψ+cosθsin2φcos2ψ.
The waveforms h+(t) and h×(t) depend on the nature and evolution of the source. For example, for a binary system in a circular orbit, with an inclination i relative to the plane of the sky, and the x-axis oriented along the major axis of the projected orbit, the quadrupole approximation of Eq. (53) gives
where Фb(t)=2π∬tfb(t′)dt′ is the orbital phase.
5 Stellar System Tests of Gravitational Theory
5.1 The binary pulsar and general relativity
The 1974 discovery of the binary pulsar PSR 1913+16 by Joseph Taylor and Russell Hulse during a routine search for new pulsars provided the first possibility of probing new aspects of gravitational theory: the effects of strong relativistic internal gravitational fields on orbital dynamics, and the effects of gravitational radiation reaction. For reviews of the discovery and current status, see the published Nobel Prize lectures by Hulse and Taylor [76, 123]. For a thorough review of pulsars, including binary and millisecond pulsars, see the Living Review by Dunc Lorimer [89].
The system consists of a pulsar of nominal period 59 ms in a close binary orbit with an as yet unseen companion. The orbital period is about 7.75 hours, and the eccentricity is 0.617. From detailed analyses of the arrival times of pulses (which amounts to an integrated version of the Doppler-shift methods used in spectroscopic binary systems), extremely accurate orbital and physical parameters for the system have been obtained (Table 6). Because the orbit is so close (≈1R⊙) and because there is no evidence of an eclipse of the pulsar signal or of mass transfer from the companion, it is generally believed that the companion is compact: Evolutionary arguments suggest that it is most likely a dead pulsar. Thus the orbital motion is very clean, free from tidal or other complicating effects. Furthermore, the data acquisition is “clean” in the sense that by exploiting the intrinsic stability of the pulsar clock combined with the ability to maintain and transfer atomic time accurately using such devices as the Global Positioning System, the observers can keep track of the pulsar phase with an accuracy of 15 μs, despite extended gaps between observing sessions (including a several-year gap during the middle 1990s upgrade of the Arecibo radio telescope). The pulsar has shown no evidence of “glitches” in its pulse period.
Three factors make this system an arena where relativistic celestial mechanics must be used: the relatively large size of relativistic effects [vorbit≈(m/r)1/2≈10-3], a factor of 10 larger than the corresponding values for solar-system orbits; the short orbital period, allowing secular effects to build up rapidly; and the cleanliness of the system, allowing accurate determinations of small effects. Because the orbital separation is large compared to the neutron stars’ compact size, tidal effects can be ignored. Just as Newtonian gravity is used as a tool for measuring astrophysical parameters of ordinary binary systems, so GR is used as a tool for measuring astrophysical parameters in the binary pulsar.
The observational parameters that are obtained from a least-squares solution of the arrival-time data fall into three groups: (i) non-orbital parameters, such as the pulsar period and its rate of change (defined at a given epoch), and the position of the pulsar on the sky; (ii) five “Keplerian” parameters, most closely related to those appropriate for standard Newtonian binary systems, such as the eccentricity e and the orbital period Pb; and (iii) five “post-Keplerian” parameters. The five post-Keplerian parameters are: 〈ω̇〉, the average rate of periastron advance; γ′, the amplitude of delays in arrival of pulses caused by the varying effects of the gravitational redshift and time dilation as the pulsar moves in its elliptical orbit at varying distances from the companion and with varying speeds; Ṗb, the rate of change of orbital period, caused predominantly by gravitational radiation damping; and r and s=sin i, respectively the “range” and “shape” of the Shapiro time delay of the pulsar signal as it propagates through the curved spacetime region near the companion, where i is the angle of inclination of the orbit relative to the plane of the sky.
In GR, these post-Keplerian parameters can be related to the masses of the two bodies and to measured Keplerian parameters by the equations (TEGP 12.1, 14.6 (a) [147])
where m1 and m2 denote the pulsar and companion masses, respectively. The formula for 〈ω̇〉 ignores possible non-relativistic contributions to the periastron shift, such as tidally or rotationally induced effects caused by the companion (for discussion of these effects, see TEGP 12.1 (c) [147]). The formula for Ṗb includes only quadrupole gravitational radiation; it ignores other sources of energy loss, such as tidal dissipation (TEGP 12.1 (f) [147]). Notice that, by virtue of Kepler’s third law, (2πfb)2=m/a3, (2πmfb)2/3∼m/a∼∊, thus the first two post-Keplerian parameters can be seen as O(∊), or 1PN corrections to the underlying variable, while the third is an O(∊5/2), or 2.5PN correction. The current observed values for the Keplerian and post-Keplerian parameters are shown in Table 6. The parameters r and s are not separately measurable with interesting accuracy for PSR 1913+16 because the orbit’s 47° inclination does not lead to a substantial Shapiro delay.
Because fb and e are separately measured parameters, the measurement of the three post-Keplerian parameters provide three constraints on the two unknown masses. The periastron shift measures the total mass of the system, Ṗb measures the chirp mass, and γ′ measures a complicated function of the masses. GR passes the test if it provides a consistent solution to these constraints, within the measurement errors.
From the intersection of the 〈ω̇〉 and γ′ constraints we obtain the values m1=1.4411±0.0007M⊙ and m2=1.3873±0.0007M⊙. The third of Eqs. (60) then predicts the value Ṗb=-2.40243°0.00005×10-12. In order to compare the predicted value for Ṗb with the observed value of Table 6, it is necessary to take into account the small effect of a relative acceleration between the binary pulsar system and the solar system caused by the differential rotation of the galaxy. This effect was previously considered unimportant when Ṗb was known only to 10 percent accuracy. Damour and Taylor [52] carried out a careful estimate of this effect using data on the location and proper motion of the pulsar, combined with the best information available on galactic rotation, and found
Subtracting this from the observed Ṗb (Table 6) gives the residual
which agrees with the prediction within the errors. In other words,
The consistency among the measurements is displayed in Figure 6, in which the regions allowed by the three most precise constraints have a single common overlap.
Constraints on masses of the pulsar and its companion from data on PSR 1913+16, assuming GR to be valid. The width of each strip in the plane reflects observational accuracy, shown as a percentage. An inset shows the three constraints on the full mass plane; the intersection region (a) has been magnified 400 times for the full figure.
A third way to display the agreement with general relativity is by comparing the observed phase of the orbit with a theoretical template phase as a function of time. If fb varies slowly in time, then to first order in a Taylor expansion, the orbital phase is given by Фb(t)=2πfb0t+πḟb0t2. The time of periastron passage tP is given by Ф(tP)=2πN, where N is an integer, and consequently, the periastron time will not grow linearly with N. Thus the cumulative difference between periastron time tP and N/fb0, the quantities actually measured in practice, should vary according to tP−N/fb0=ḟb0N2/2f 3b0 ≈-ḟb0≈-2fb0)t2. Figure 7 shows the results: the dots are the data points, while the curve is the predicted difference using the measured masses and the quadrupole formula for ḟb0 [137].
The consistency among the constraints provides a test of the assumption that the two bodies behave as “point” masses, without complicated tidal effects, obeying the general relativistic equations of motion including gravitational radiation. It is also a test of strong gravity, in that the highly relativistic internal structure of the neutron stars does not influence their orbital motion, as predicted by the strong equivalence principle of GR.
Recent observations [84, 138] indicate variations in the pulse profile, which suggests that the pulsar is undergoing precession as it moves through the curved spacetime generated by its companion, an effect known as geodetic precession. The amount is consistent with GR, assuming that the pulsar’s spin is suitably misaligned with the orbital angular momentum. Unfortunately, the evidence suggests that the pulsar beam may precess out of our line of sight by 2020.
5.2 A population of binary pulsars?
Since 1990, several new massive binary pulsars similar to PSR 1913+16 were discovered, leading to the possibility of new or improved tests of GR.
-
PSR 1534+12. This is a binary pulsar system in our galaxy. Its pulses are significantly stronger and narrower than those of PSR 1913+16, so timing measurements are more precise, reaching 3 μs accuracy. Its parameters are listed in Table 7 [118, 119]. The orbital plane appears to be almost edge-on relative to the line of sight (i≃80°); as a result the Shapiro delay is substantial, and separate values of the parameters r and s have been obtained with interesting accuracy. Assuming general relativity, one infers that the two masses are m1=1.335±0.002M⊙ and m2=1.344±0.002M⊙. The rate of orbit decay Ṗb agrees with GR to about 15 percent, the precision limited by the poorly known distance to the pulsar, which introduces a significant uncertainty into the subtraction of galactic acceleration. Independently of Ṗb, measurement of the four other post-Keplerian parameters gives two tests of strong-field gravity in the non-radiative regime [124].
-
PSR 2127+11C. This system appears to be a clone of the Hulse-Taylor binary pulsar, with very similar values for orbital period and eccentricity (see Table 7). The inferred total mass of the system is 2.706±0.011M⊙. Because the system is in the globular cluster M15 (NGC 7078), it suffers Doppler shifts resulting from local accelerations, either by the mean cluster gravitational field or by nearby stars, that are more difficult to estimate than was the case with the galactic system PSR 1913+16. This may make a separate, precision measurement of the relativistic contribution to Ṗb impossible.
-
PSR 1855+09. This binary pulsar system is not particularly relativistic, with a long period (12 days) and highly circular orbit. However, because we observe the orbit nearly edge on, the Shapiro delay is large and measurable, as reflected in the post-Keplerian parameters r and s.
-
PSR 0655+64. This system consists of a pulsar and a white dwarf companion in a nearly circular orbit. Only an upper limit on Ṗb has been placed.
5.3 Binary pulsars and alternative theories
Soon after the discovery of the binary pulsar it was widely hailed as a new testing ground for relativistic gravitational effects. As we have seen in the case of GR, in most respects, the system has lived up to, indeed exceeded, the early expectations.
In another respect, however, the system has only partially lived up to its promise, namely as a direct testing ground for alternative theories of gravity. The origin of this promise was the discovery that alternative theories of gravity generically predict the emission of dipole gravitational radiation from binary star systems. In general relativity, there is no dipole radiation because the “dipole moment” (center of mass) of isolated systems is uniform in time (conservation of momentum), and because the “inertial mass” that determines the dipole moment is the same as the mass that generates gravitational waves (SEP). In other theories, while the inertial dipole moment may remain uniform, the “gravity wave” dipole moment need not, because the mass that generates gravitational waves depends differently on the internal gravitational binding energy of each body than does the inertial mass (violation of SEP). Schematically, in a coordinate system in which the center of inertial mass is at the origin, so that mI,1x1+mI,2x2=0, the dipole part of the retarded gravitational field would be given by
where v=v1−v2 and η and m are defined using inertial masses. In theories that violate SEP, the difference between gravitational wave mass and inertial mass is a function of the internal gravitational binding energy of the bodies. This additional form of gravitational radiation damping could, at least in principle, be significantly stronger than the usual quadrupole damping, because it depends on fewer powers of the orbital velocity v, and it depends on the gravitational binding energy per unit mass of the bodies, which, for neutron stars, could be as large as 40 percent (see TEGP 10 [147] for further details). As one fulfillment of this promise, Will and Eardley worked out in detail the effects of dipole gravitational radiation in the bimetric theory of Rosen, and, when the first observation of the decrease of the orbital period was announced in 1979, the Rosen theory suffered a terminal blow. A wide class of alternative theories also fails the binary pulsar test because of dipole gravitational radiation (TEGP 12.3 [147]).
On the other hand, the early observations of PSR 1913+16 already indicated that, in GR, the masses of the two bodies were nearly equal, so that, in theories of gravity that are in some sense “close” to GR, dipole gravitational radiation would not be a strong effect, because of the apparent symmetry of the system. The Rosen theory, and others like it, are not “close” to general relativity, except in their predictions for the weak-field, slow-motion regime of the solar system. When relativistic neutron stars are present, theories like these can predict strong effects on the motion of the bodies resulting from their internal highly relativistic gravitational structure (violations of SEP). As a consequence, the masses inferred from observations of the periastron shift and γ′ may be significantly different from those inferred using general relativity, and may be different from each other, leading to strong dipole gravitational radiation damping. By contrast, the Brans-Dicke theory is “close” to GR, roughly speaking within 1/ωBD of the predictions of the latter, for large values of the coupling constant ωBD (here we use the subscript BD to distinguish the coupling constant from the periastron advance ω̇). Thus, despite the presence of dipole gravitational radiation, the binary pulsar provides at present only a weak test of Brans-Dicke theory, not yet competitive with solar-system tests.
5.4 Binary pulsars and scalar-tensor gravity
Making the usual assumption that both members of the system are neutron stars, and using the methods summarized in TEGP 10–12 [147], one can obtain formulas for the periastron shift, the gravitational redshift/second-order Doppler shift parameter, and the rate of change of orbital period, analogous to Eqs. (60). These formulas depend on the masses of the two neutron stars, on their self-gravitational binding energy, represented by “sensitivities” s and ι*, and on the Brans-Dicke coupling constant ωBD. First, there is a modification of Kepler’s third law, given by
Then, the predictions for 〈ω̇〉, γ′ and Ṗb are
where \({\mathcal M} \equiv {\chi ^{3/5}}{{\mathcal G}^{ - 4/5}}{\eta ^{3/5}}m\), and, to first order in ξ≡(2+ωBD)-1, we have
The quantities sa and κ *a a are defined by
and measure the “sensitivity” of the mass ma and moment of inertia Ia of each body to changes in the scalar field (reflected in changes in G) for a fixed baryon number N (see TEGP 11, 12 and 14.6 (c) [147] for further details). The quantity sa is related to the gravitational binding energy. Notice how the violation of SEP in Brans-Dicke theory introduces complex structure-dependent effects in everything from the Newtonian limit (modification of the effective coupling constant in Kepler’s third law) to gravitational radiation. In the limit ¾→0, we recover GR, and all structure dependence disappears. The first term in Ṗb (Eq. (68)) is the effect of quadrupole and monopole gravitational radiation, while the second term is the effect of dipole radiation.
In order to estimate the sensitivities sa and κ *a , one must adopt an equation of state for the neutron stars. It is sufficient to restrict attention to relatively stiff neutron star equations of state in order to guarantee neutron stars of sufficient mass, approximately 1.4M⊙. The lower limit on ωBD required to give consistency among the constraints on 〈ω̇〉, γ and Ṗb as in Figure 6 is several hundred [153]. The combination of 〈ω̇〉 and γ give a constraint on the masses that is relatively weakly dependent on ξ, thus the constraint on ξ is dominated by Ṗb and is directly proportional to the measurement error in Ṗb; in order to achieve a constraint comparable to the solar system value of 3×10-4, the error in Ṗ OBSb would have to be reduced by more than a factor of ten.
Alternatively, a binary pulsar system with dissimilar objects, such as a white dwarf or black hole companion, would provide potentially more promising tests of dipole radiation. Unfortunately, none has been discovered to date; the dissimilar system B0655+64, with a white dwarf companion is in a highly circular orbit, making measurement of the periastron shift meaningless, and is not as relativistic as 1913+16. From the upper limit on Ṗb (Table 7), one can infer at best the weak bound ωBD>100.
Damour and Esposito-Farèse [42] have generalized these results to a broad class of scalar-tensor theories. These theories are characterized by a single function α(ϕ) of the scalar field ϕ, which mediates the coupling strength of the scalar field. For application to the solar system or to binary systems, one expands this function about a cosmological background field value ϕ0:
A purely linear coupling function produces Brans-Dicke theory, with α 20 =1/(2ωBD+3). The function α(ϕ) acts as a potential function for the scalar field ω, and, if β0>0, during cosmological evolution, the scalar field naturally evolves toward the minimum of the potential, i.e. toward α0≈0, ωBD→∞, or toward a theory close to, though not precisely GR [47, 48]. Bounds on the parameters α0 and β0 from solar-system, binary-pulsar and gravitational wave observations (see Sec. 6.3) are shown in Figure 8 [44]. Negative values of β0 correspond to an unstable scalar potential; in this case, objects such as neutron stars can experience a “spontaneous scalarization”, whereby the interior values of ϕ can take on values very different from the exterior values, through non-linear interactions between strong gravity and the scalar field, dramatically affecting the stars’ internal structure and the consequent violations of SEP. On the other hand, β0<0 is of little practical interest, because, with an unstable ϕ potential, cosmological evolution would presumably drive the system away from the peak where α0≈0, toward parameter values that could easily be excluded by solar system experiments. On the α0−β0 plane shown in Figure 8, the α0 axis corresponds to pure Brans-Dicke theory, while the origin corresponds to pure GR. As discussed above, solar system bounds (labelled “1PN” in Figure 8) still beat the binary pulsars. The bounds labelled “LIGO-VIRGO” are discussed in Sec. 6.3.
The region of the scalar-tensor theory α0−β0 plane allowed by solarsystem, binary-pulsar, and future gravitational wave observations. A polytropic equation of state for the neutron stars was assumed. The shaded region is that allowed by all tests. For positive values of β0, solar-system bounds (labelled 1PN) still are the best. (From [44], ©1998 by the American Physical Society, reproduced by permission.)
6 Gravitational Wave Tests of Gravitational Theory
6.1 Gravitational wave observatories
Some time in the next decade, a new opportunity for testing relativistic gravity will be realized, with the commissioning and operation of kilometer-scale, laser interferometric gravitational wave observatories in the U.S. (LIGO project), Europe (VIRGO and GEO600 projects) and Japan (TAMA300 project). Gravitational-wave searches at these observatories are scheduled to commence around 2002. The LIGO broad-band antennas will have the capability of detecting and measuring the gravitational waveforms from astronomical sources in a frequency band between about 10 Hz (the seismic noise cutoff) and 500 Hz (the photon counting noise cutoff), with a maximum sensitivity to strain at around 100 Hz of h∼Δl/l∼10-22 (rms). The most promising source for detection and study of the gravitational wave signal is the “inspiralling compact binary” — a binary system of neutron stars or black holes (or one of each) in the final minutes of a death dance leading to a violent merger. Such is the fate, for example, of the Hulse-Taylor binary pulsar PSR 1913+16 in about 300 million years. Given the expected sensitivity of the “advanced LIGO” (around 2007), which could see such sources out to hundreds of megaparsecs, it has been estimated that from 3 to 100 annual inspiral events could be detectable. Other sources, such as supernova core collapse events, instabilities in rapidly rotating nascent neutron stars, signals from non-axisymmetric pulsars, and a stochastic background of waves, may be detectable (for reviews, see [1, 127]; for updates on the status of various projects, see [65, 32]).
A similar network of cryogenic resonant-mass gravitational antennas have been in operation for many years, albeit at lower levels of sensitivity (h∼10-19). While modest improvements in sensitivity may be expected in the future, these resonant detectors are not expected to be competitive with the large interferometers, unless new designs involving bars of spherical, or nearly spherical shape come to fruition. These systems are primarily sensitive to waves in relatively narrow bands about frequencies in the hundreds to thousands of Hz range [104, 73, 14, 110].
In addition, plans are being developed for an orbiting laser interferometer space antenna (LISA for short). Such a system, consisting of three spacecraft separated by millions of kilometers, would be sensitive primarily in the very low frequency band between 10-4 and 10-1 Hz, with peak strain sensitivity of order h∼10-23 [54].
In addition to opening a new astronomical window, the detailed observation of gravitational waves by such observatories may provide the means to test general relativistic predictions for the polarization and speed of the waves, and for gravitational radiation damping.
6.2 Polarization of gravitational waves
A laser interferometric or resonant bar gravitational wave detector measures the local components of a symmetric 3×3 tensor which is composed of the “electric” components of the Riemann curvature tensor, R0i0j, via the equation of geodesic deviation, given for a pair of freely falling particles by ẍi=-R0i0jxj, where xi denotes the spatial separation. In general there are six independent components, which can be expressed in terms of polarizations (modes with specific transformation properties under rotations and boosts). Three are transverse to the direction of propagation, with two representing quadrupolar deformations and one representing a monopole “breathing” deformation. Three modes are longitudinal, with one an axially symmetric stretching mode in the propagation direction, and one quadrupolar mode in each of the two orthogonal planes containing the propagation direction. Figure 9 shows the displacements induced on a ring of freely falling test particles by each of these modes. General relativity predicts only the first two transverse quadrupolar modes (a) and (b) independently of the source; these correspond to the waveforms h+ and h× discussed earlier (note the cos 2φ and sin 2φ dependences of the displacements). Scalar-tensor gravitational waves can in addition contain the transverse breathing mode (c). More general metric theories predict additional longitudinal modes, up to the full complement of six (TEGP 10.2 [147]).
The six polarization modes for gravitational waves permitted in any metric theory of gravity. Shown is the displacement that each mode induces on a ring of test particles. The wave propagates in the +z direction. There is no displacement out of the plane of the picture. In (a), (b) and (c), the wave propagates out of the plane; in (d), (e), and (f ), the wave propagates in the plane. In general relativity, only (a) and (b) are present; in scalar-tensor gravity, (c) may also be present.
A suitable array of gravitational antennas could delineate or limit the number of modes present in a given wave. The strategy depends on whether or not the source direction is known. In general there are eight unknowns (six polarizations and two direction cosines), but only six measurables (R0i0j). If the direction can be established by either association of the waves with optical or other observations, or by time-of-flight measurements between separated detectors, then six suitably oriented detectors suffice to determine all six components. If the direction cannot be established, then the system is underdetermined, and no unique solution can be found. However, if one assumes that only transverse waves are present, then there are only three unknowns if the source direction is known, or five unknowns otherwise. Then the corresponding number (three or five) of detectors can determine the polarization. If distinct evidence were found of any mode other than the two transverse quadrupolar modes of GR, the result would be disastrous for GR. On the other hand, the absence of a breathing mode would not necessarily rule out scalar-tensor gravity, because the strength of that mode depends on the nature of the source.
Some of the details of implementing such polarization observations have been worked out for arrays of resonant cylindrical, disk-shaped, spherical and truncated icosahedral detectors (TEGP 10.2 [147], for recent reviews see [87, 133]); initial work has been done to assess whether the ground-based or space-based laser interferometers (or combinations of the two types) could perform interesting polarization measurements [134, 33, 90, 67]. Unfortunately for this purpose, the two LIGO observatories (in Washington and Louisiana states, respectively) have been constructed to have their respective arms as parallel as possible, apart from the curvature of the Earth; while this maximizes the joint sensitivity of the two detectors to gravitational waves, it minimizes their ability to detect two modes of polarization.
6.3 Gravitational radiation back-reaction
In the binary pulsar, a test of GR was made possible by measuring at least three relativistic effects that depended upon only two unknown masses. The evolution of the orbital phase under the damping effect of gravitational radiation played a crucial role. Another situation in which measurement of orbital phase can lead to tests of GR is that of the inspiralling compact binary system. The key differences are that here gravitational radiation itself is the detected signal, rather than radio pulses, and the phase evolution alone carries all the information. In the binary pulsar, the first derivative of the binary frequency ḟb, was measured; here the full nonlinear variation of fb as a function of time is measured.
Broad-band laser interferometers are especially sensitive to the phase evolution of the gravitational waves, which carry the information about the orbital phase evolution. The analysis of gravitational wave data from such sources will involve some form of matched filtering of the noisy detector output against an ensemble of theoretical “template” waveforms which depend on the intrinsic parameters of the inspiralling binary, such as the component masses, spins, and so on, and on its inspiral evolution. How accurate must a template be in order to “match” the waveform from a given source (where by a match we mean maximizing the cross-correlation or the signal-to-noise ratio)? In the total accumulated phase of the wave detected in the sensitive bandwidth, the template must match the signal to a fraction of a cycle. For two inspiralling neutron stars, around 16,000 cycles should be detected during the final few minutes of inspiral; this implies a phasing accuracy of 10-5 or better. Since v∼1/10 during the late inspiral, this means that correction terms in the phasing at the level of v5 or higher are needed. More formal analyses confirm this intuition [35, 60, 36, 108].
Because it is a slow-motion system (v∼10-3), the binary pulsar is sensitive only to the lowest-order effects of gravitational radiation as predicted by the quadrupole formula. Nevertheless, the first correction terms of order v and v2 to the quadrupole formula were calculated as early as 1976 [135] see TEGP 10.3 [147]).
But for laser interferometric observations of gravitational waves, the bottom line is that, in order to measure the astrophysical parameters of the source and to test the properties of the gravitational waves, it is necessary to derive the gravitational waveform and the resulting radiation back-reaction on the orbit phasing at least to 2PN order beyond the quadrupole approximation, and probably to 3PN order.
For the special case of non-spinning bodies moving on quasi-circular orbits (i.e. circular apart from a slow inspiral), the evolution of the gravitational wave frequency f=2fb through 2PN order has the form
where η=m1m2/m2. The first term is the quadrupole contribution (compare Eq. (55)), the second term is the 1PN contribution, the third term, with the coefficient 4π, is the “tail” contribution, and the fourth term is the 2PN contribution, first reported jointly by Blanchet et al. [24, 23, 152]. Calculation of the higher-order contributions is nearing completion.
Similar expressions can be derived for the loss of angular momentum and linear momentum. (For explicit formulas for non-circular orbits, see [70].) These losses react back on the orbit to circularize it and cause it to inspiral. The result is that the orbital phase (and consequently the gravitational wave phase) evolves non-linearly with time. It is the sensitivity of the broad-band LIGO and VIRGO-type detectors to phase that makes the higher-order contributions to df/dt so observationally relevant. A ready-to-use set of formulae for the 2PN gravitational waveform template, including the non-linear evolution of the gravitational wave frequency (not including spin effects) have been published [28] and incorporated into the Gravitational Radiation Analysis and Simulation Package (GRASP), a software toolkit used in LIGO.
If the coefficients of each of the powers of f in Eq. (72) can be measured, then one again obtains more than two constraints on the two unknowns m1 and m2, leading to the possibility to test GR. For example, Blanchet and Sathyaprakash [30, 29] have shown that, by observing a source with a sufficiently strong signal, an interesting test of the 4π coefficient of the “tail” term could be performed.
Another possibility involves gravitational waves from a small mass orbiting and inspiralling into a (possibly supermassive) spinning black hole. A general non-circular, non-equatorial orbit will precess around the hole, both in periastron and in orbital plane, leading to a complex gravitational waveform that carries information about the non-spherical, strong-field spacetime around the hole. According to GR, this spacetime must be the Kerr spacetime of a rotating black hole, uniquely specified by its mass and angular momentum, and consequently, observation of the waves could test this fundamental hypothesis of GR [114, 107].
Thirdly, the dipole gravitational radiation predicted by scalar-tensor theories will result in a modification of the gravitational radiation back-reaction, and thereby of the phase evolution. Including only the leading quadrupole and dipole contributions, one obtains, in Brans-Dicke theory,
where \({\mathcal M} = \left( {{\chi ^{3/5}}{{\mathcal G}^{ - 4/5}}} \right){\eta ^{3/5}}m\), and b is the coefficient of the dipole term, given by \(b = \left( {5/48} \right)\left( {{\chi ^{ - 1}}{{\cal G}^{4/3}}} \right)\xi {{\cal S}^2}\), where χ, G, S are given by Eqs. (69), and ξ=1/(2+ωBD). The effects are strongest for systems involving a neutron star and a black hole. Double neutron star systems are less promising because the small range of masses available near 1.4M⊙ results in suppression of dipole radiation by symmetry (the sensitivity s turns out to be a relatively weak function of mass near 1.4M⊙, for typical equations of state). For black holes, s=0.5 identically, consequently double black-hole systems turn out to be observationally identical in the two theories.
But for a 1.4M⊙ neutron star and a 10 M⊙ (3 M⊙) black hole at 200 Mpc, the bound on ωBD could be 600 (1800) (using advanced LIGO noise curves). The bound increases linearly with signal-to-noise ratio [149]. If one demands that this test be performed annually, thus requiring observation of frequent, and therefore more distant, weaker sources, the bounds on ωBD will be too weak to compete with existing solar-system bounds (this corresponds to the “LIGO-VIRGO” bound on the α0 axis in Figure 8, which assumes a signal-to-noise ratio of 10). However, if one is prepared to wait 10 years for the lucky observation of a nearby, strong source, the resulting bound could exceed the current solar-system bound. The bounds are illustrated in Figure 10 by the curves marked N=1 and N=1/10. Figure 10 assumes a double-neutron-star inspiral rate of 10-6 per year per galaxy, and a black-hole-neutron-star rate β times that, where β is highly uncertain. Values of β=1/10, 1, and 10 are shown. For the general class of scalar-tensor theories, the corresponding bounds are plotted on the α0−β0 plane in Figure 8, under the restrictive assumption of a signal-to-noise ratio (S/N) of 10 [44]. All other factors being equal, the bound achievable on the α0−β0 parameters of scalar-tensor gravity is inversely proportional to S/N.
6.4 Speed of gravitational waves
According to GR, in the limit in which the wavelength of gravitational waves is small compared to the radius of curvature of the background spacetime, the waves propagate along null geodesics of the background spacetime,i.e. they have the same speed c as light (in this section, we do not set c=1). In other theories, the speed could differ from c because of coupling of gravitation to “background” gravitational fields. For example, in the Rosen bimetric theory with a flat background metric η, gravitational waves follow null geodesics of η, while light follows null geodesics of g (TEGP 10.1 [147]).
Another way in which the speed of gravitational waves could differ from c is if gravitation were propagated by a massive field (a massive graviton), in which case vg would be given by, in a local inertial frame,
where mg and E are the graviton rest mass and energy, respectively. For a recent review of the idea of a massive graviton along with a model theory, see [132].
The most obvious way to test this is to compare the arrival times of a gravitational wave and an electromagnetic wave from the same event, e.g. a supernova. For a source at a distance D, the resulting value of the difference 1−vg/c is
where Δt≡Δta(1+Z)Δte is the “time difference”, where Δta and Δte are the differences in arrival time and emission time, respectively, of the two signals, and Z is the redshift of the source. In many cases, Δte is unknown, so that the best one can do is employ an upper bound on Δte based on observation or modelling. The result will then be a bound on 1−vg/c.
For a massive graviton, if the frequency of the gravitational waves is such that hf≫mgc2, where h is Planck’s constant, then vg/c≈1−1/2(c/λgf)2, where λg=h/mgc is the graviton Compton wavelength, and the bound on 1−vg/c can be converted to a bound on λg, given by
The foregoing discussion assumes that the source emits both gravitational and electromagnetic radiation in detectable amounts, and that the relative time of emission can be established to sufficient accuracy, or can be shown to be sufficiently small.
However, there is a situation in which a bound on the graviton mass can be set using gravitational radiation alone [151]. That is the case of the inspiralling compact binary. Because the frequency of the gravitational radiation sweeps from low frequency at the initial moment of observation to higher frequency at the final moment, the speed of the gravitons emitted will vary, from lower speeds initially to higher speeds (closer to c) at the end. This will cause a distortion of the observed phasing of the waves and result in a shorter than expected overall time Δta of passage of a given number of cycles. Furthermore, through the technique of matched filtering, the parameters of the compact binary can be measured accurately, (assuming that GR is a good approximation to the orbital evolution, even in the presence of a massive graviton), and thereby the emission time Δte can be determined accurately. Roughly speaking, the “phase interval” fΔt in Eq. (76) can be measured to an accuracy 1/ρ, where ρ is the signal-to-noise ratio.
Thus one can estimate the bounds on λg achievable for various compact inspiral systems, and for various detectors. For stellar-mass inspiral (neutron stars or black holes) observed by the LIGO/VIRGO class of ground-based interferometers, D≈200 Mpc, f≈100 Hz, and fΔtρ-1≈1/10. The result is λg>1013 km. For supermassive binary black holes (104 to 107M⊙) observed by the proposed laser interferometer space antenna (LISA), D≈3 Gpc, f≈10-3 Hz, and fΔt∼ρ-11/1000. The result is λg>1017 km.
A full noise analysis using proposed noise curves for the advanced LIGO and for LISA weakens these crude bounds by factors between two and 10. These potential bounds can be compared with the solid bound λg>2.8×1012 km, [122] derived from solar system dynamics, which limit the presence of a Yukawa modification of Newtonian gravity of the form
and with the model-dependent bound λg>6×1019 km from consideration of galactic and cluster dynamics [132].
6.5 Other strong-gravity tests
One of the central difficulties of testing general relativity in the strong-field regime is the possibility of contamination by uncertain or complex physics. In the solar system, weak-field gravitational effects could in most cases be measured cleanly and separately from non-gravitational effects. The remarkable cleanliness of the binary pulsar permitted precise measurements of gravitational phenomena in a strong-field context.
Unfortunately, nature is rarely so kind. Still, under suitable conditions, qualitative and even quantitative strong-field tests of general relativity can be carried out.
One example is in cosmology. From a few seconds after the big bang until the present, the underlying physics of the universe is well understood, although significant uncertainties remain (amount of dark matter, value of the cosmological constant, the number of light neutrino families, etc.). Some alternative theories of gravity that are qualitatively different from GR fail to produce cosmologies that meet even the minimum requirements of agreeing qualitatively with big-bang nucleosynthesis (BBN) or the properties of the cosmic microwave background (TEGP 13.2 [147]). Others, such as Brans-Dicke theory, are sufficiently close to GR (for large enough ωBD) that they conform to all cosmological observations, given the underlying uncertainties. The generalized scalar-tensor theories, however, could have small ωBD at early times, while evolving through the attractor mechanism to large ωBD today. One way to test such theories is through big-bang nucleosynthesis, since the abundances of the light elements produced when the temperature of the universe was about 1 MeV are sensitive to the rate of expansion at that epoch, which in turn depends on the strength of interaction between geometry and the scalar field. Because the universe is radiation-dominated at that epoch, uncertainties in the amount of cold dark matter or of the cosmological constant are unimportant. The nuclear reaction rates are reasonably well understood from laboratory experiments and theory, and the number of light neutrino families (3) conforms to evidence from particle accelerators. Thus, within modest uncertainties, one can assess the quantitative difference between the BBN predictions of GR and scalar-tensor gravity under strong-field conditions and compare with observations. The most sophisticated recent analysis [49] places bounds on the parameters α0 and β0 of the generalized framework of Damour and Esposito-Farèse (see Sec. 5.4 and Fig. 8) that are weaker than solar-system bounds for β0<0.3, but substantially stronger for β>0.3.
Another example is the exploration of the spacetime near black holes via accreting matter. Observations of low-luminosity binary X-ray sources suggest that a form of accretion known as advection-dominated accretion flow (ADAF) may be important. In this kind of flow, the accreting gas is too thin to radiate its energy efficiently, but instead transports (advects) it inward toward the central object. If the central object is a neutron star, the matter hits the surface and radiates the energy away; if it is a black hole, the matter and its advected energy disappear. Systems in which the accreting object is believed to be a black hole from estimates of its mass are indeed observed to be underluminous, compared to systems where the object is believe to be a neutron star. This has been regarded as the first astrophysical evidence for the existence of black hole event horizons (for a review, see [92]). While supporting one of the critical strong-field predictions of GR, the observations and models are not likely any time soon to be able to distinguish one gravitational theory from another (except for theories that do not predict black holes at all).
Another example involving accretion purports to explore the strong-field region just outside massive black holes in active galactic nuclei. Here, iron in the inner region of a thin accretion disk is irradiated by X-ray-emitting material above or below the disk, and fluoresces in the Kα line. The spectral shape of the line depends on relativistic Doppler and curved-spacetime effects as the iron orbits the black hole near the innermost stable circular orbit, and could be used to determine whether the hole is a non-rotating Schwarzschild black hole, or a rotating Kerr black hole. Because of uncertainties in the detailed models, the results are inconclusive to date, but the combination of higher-resolution observations and better modelling could lead to striking tests of strong-field predictions of GR.
7 Conclusions
We find that general relativity has held up under extensive experimental scrutiny. The question then arises, why bother to continue to test it? One reason is that gravity is a fundamental interaction of nature, and as such requires the most solid empirical underpinning we can provide. Another is that all attempts to quantize gravity and to unify it with the other forces suggest that the standard general relativity of Einstein is not likely to be the last word. Furthermore, the predictions of general relativity are fixed; the theory contains no adjustable constants so nothing can be changed. Thus every test of the theory is either a potentially deadly test or a possible probe for new physics. Although it is remarkable that this theory, born 80 years ago out of almost pure thought, has managed to survive every test, the possibility of finding a discrepancy will continue to drive experiments for years to come.
References
Abramovici, A., Althouse, W. E., Drever, R. W. P., Gürsel, Y., Kawamura, S., Raab, F. J., Shoemaker, D., Siewers, L., Spero, R. E., Thorne, K. S., Vogt, R. E., Weiss, R., Whitcomb, S. E., and Zucker, M. E., “LIGO: The laser interferometer gravitational-wave observatory”, Science, 256, 325–333, (1992). 4.2, 6.1
Adelberger, E. G., Heckel, B. R., Stubbs, C. W., and Rogers, W. F., “Searches for new macroscopic forces”, Annu. Rev. Nucl. Sci., 41, 269–320, (1991). 2.3
Alvarez, C., and Mann, R. B., “The equivalence principle and anomalous magnetic moment experiments”, Phys. Rev. D, 54, 7097–7107, (1996). For a related online version see: C. Alvarez, et al., “The equivalence principle and anomalous magnetic moment experiments”, (November, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9511028. 2.2.2
Alvarez, C., and Mann, R. B., “Testing the equivalence principle by Lamb shift energies”, Phys. Rev. D, 54, 5954–5974, (1996). For a related online version see: C. Alvarez, et al., “Testing the equivalence principle by Lamb shift energies”, (July, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9507040. 2.2.2
Alvarez, C., and Mann, R. B., “The equivalence principle and g-2 experiments”, Phys. Lett. B, 409, 83–87, (1997). For a related online version see: C. Alvarez, et al., “The Equivalence Principle and g-2 Experiments”, (October, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9510070. 2.2.2
Alvarez, C., and Mann, R. B., “The Equivalence Principle in the Non-baryonic Regime”, Phys. Rev. D, 55, 1732–1740, (1997). For a related online version see: C. Alvarez, et al., “The equivalence principle in the non-baryonic regime”, (September, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9609039. 2.2.2
Alvarez, C., and Mann, R. B., “Testing the equivalence principle using atomic vacuum energy shifts”, Mod. Phys. Lett. A, 11, 1757–1763, (1997). For a related online version see: C. Alvarez, et al., “Testing the Equivalence Principle using Atomic Vacuum Energy Shifts”, (December, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9612031. 2.2.2
Ashby, N., “Relativistic effects in the Global Positioning System”, in Dadhich, N., and Narlikar, J. V., eds., Gravitation and Relativity: At the Turn of the Millenium. 15th International Conference on General Relativity and Gravitation, 231–258, (Inter-University Center for Astronomy and Astrophysics, Pune, India, 1998). 2.1
Astrophysics Division of the Space Science Department at ESA, “GAIA — The Galactic Census Project”, (October, 2000), [Online HTML Document]: cited on 15 January 2001, http://astro.estec.esa.nl/GAIA/.3.7.4
Baessler, S., Heckel, B. R., Adelberger, E. G., Gundlach, J. H., Schmidt, U., and Swanson, H. E., “Improved test of the equivalence principle for gravitational self-energy”, Phys. Rev. Lett., 83, 3585–3588, (1999). 2.1, 3.6.1
Bartlett, D. F., and van Buren, D., “Equivalence of active and passive gravitational mass using the moon”, Phys. Rev. Lett., 57, 21–24, (1986). 3.7.1
Bell, J. F., Camilo, F., and Damour, T., “A tighter test of local Lorentz invariance using PSR J2317+1439”, Astrophys. J., 464, 857, (1996). For a related online version see: J. F. Bell, et al., “A Tighter Test of Local Lorentz Invariance using PSR J2317+1439”, (December, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9512100. 3.6.2
Bell, J. F., and Damour, T., “A new test of conservation laws and Lorentz invariance in relativistic gravity”, Class. Quantum Grav., 13, 3121–3128, (1996). For a related online version see: J. F. Bell, et al., “A new test of conservation laws and Lorentz invariance in relativistic gravity”, (June, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9606062. 3.6.2
Blair, D. G., Heng, I. S., Ivanov, E. N., and Tobar, M. E., “Present status of the resonant-mass gravitational-wave antenna NIOBE”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 127–147, (World Scientific, Singapore, 1998). 6.1
Blanchet, L., “Second-post-Newtonian generation of gravitational radiation”, Phys. Rev. D, 51, 2559–2583, (1995). For a related online version see: L. Blanchet, “Second-post-Newtonian generation of gravitational radiation”, (January, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9501030. 4.3
Blanchet, L., “Energy losses by gravitational radiation in inspiralling compact binaries to 5/2 post-Newtonian order”, Phys. Rev. D, 54, 1417–1438, (1996). For a related online version see: L. Blanchet, “Energy losses by gravitational radiation in inspiralling compact binaries to five halves post-Newtonian order”, (March, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9603048. 4.4
Blanchet, L., “Gravitational radiation reaction and balance equations to post-Newtonian order”, Phys. Rev. D, 55, 714–732, (1997). For a related online version see: L. Blanchet, “Gravitational radiation reaction and balance equations to post-Newtonian order”, (September, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9609049. 4.4
Blanchet, L., “Quadrupole-quadrupole gravitational waves”, Class. Quantum Grav., 15, 113–141, (1998). For a related online version see: L. Blanchet, “Gravitational-wave tails of tails”, (October, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9710038. 4.4
Blanchet, L., and Damour, T., “Radiative gravitational fields in general relativity. I. General structure of the field outside the source”, Philos. Trans. R. Soc. London, Ser. A, 320, 379–430, (1986). 4.3
Blanchet, L., and Damour, T., “Tail-transported temporal correlations in the dynamics of a gravitating system”, Phys. Rev. D, 37, 1410–1435, (1988). 4.3
Blanchet, L., and Damour, T., “Post-Newtonian generation of gravitational waves”, Ann. Inst. Henri Poincaré, A, 50, 377–408, (1989). 4.3
Blanchet, L., and Damour, T., “Hereditary effects in gravitational radiation”, Phys. Rev. D, 46, 4304–4319, (1992). 4.3
Blanchet, L., Damour, T., and Iyer, B. R., “Gravitational waves from inspiralling compact binaries: Energy loss and waveform to second-post-Newtonian order”, Phys. Rev. D, 51, 5360–5386, (1995). For a related online version see: L. Blanchet, et al., “Gravitational waves from inspiralling compact binaries: Energy loss and waveform to second-post-Newtonian order”, (January, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9501029. 4.4, 6.3
Blanchet, L., Damour, T., Iyer, B. R., Will, C. M., and Wiseman, A. G., “Gravitational-radiation damping of compact binary systems to second post-Newtonian order”, Phys. Rev. Lett., 74, 3515–3518, (1995). For a related online version see: L. Blanchet, et al., “Gravitational-Radiation Damping of Compact Binary Systems to Second Post-Newtonian order”, (January, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9501027. 4.4, 6.3
Blanchet, L., and Faye, G., “General relativistic dynamics of compact binaries at the third post-Newtonian order”, Phys. Rev. D. For a related online version see: L. Blanchet, et al., “General relativistic dynamics of compact binaries at the third post-Newtonian order”, (July, 2000), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/0007051. In press. 4.4
Blanchet, L., and Faye, G., “On the equations of motion of point-particle binaries at the third post-Newtonian order”, Phys. Lett. A. For a related online version see: L. Blanchet, et al., “On the equations of motion of point-particle binaries at the third post-Newtonian order”, (April, 2000), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/0004009. In press. 4.4
Blanchet, L., Faye, G., and Ponsot, B., “Gravitational field and equations of motion of compact binaries to 5/2 post-Newtonian order”, Phys. Rev. D, 58, 124002, (1998). For a related online version see: L. Blanchet, et al., “Gravitational field and equations of motion of compact binaries to 5/2 post-Newtonian order”, (April, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9804079. 4.4
Blanchet, L., Iyer, B. R., Will, C. M., and Wiseman, A. G., “Gravitational waveforms from inspiralling compact binaries to second post-Newtonian order”, Class. Quantum Grav., 13, 575–584, (1996). For a related online version see: L. Blanchet, et al., “Gravitational waveforms from inspiralling compact binaries to second post-Newtonian order”, (February, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9602024. 6.3
Blanchet, L., and Sathyaprakash, B. S., “Signal analysis of gravitational wave tails”, Class. Quantum Grav., 11, 2807, (1994). 6.3
Blanchet, L., and Sathyaprakash, B. S., “Detecting a tail effect in gravitational-wave experiments”, Phys. Rev. Lett., 74, 1067–1070, (1995). 6.3
Braginsky, V. B., and Panov, V. I., “Verification of the equivalence of inertial and gravitational mass”, Sov. Phys. JETP, 34, 463–466, (1972). 2.1
Brillet, A., “VIRGO — Status report, November 1997”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 86–96, (World Scientific, Singapore, 1997). 6.1
Brunetti, M., Coccia, E., Fafone, V., and Fucito, F., “Gravitational-wave radiation from compact binary systems in the Jordan-Brans-Dicke theory”, Phys. Rev. D, 59, 044027, (1999). For a related online version see: M. Brunetti, et al., “Brunetti, M. and Coccia, E. and Fafone, V. and Fucito, F.”, (May, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9805056. 6.2
Ciufolini, I., Pavlis, E., Chieppa, F., Fernandes-Vieira, E., and Pérez-Mercader, J., “Test of general relativity and measurement of the Lense-Thirring effect with two Earth satellites”, Science, 279, 2100–2103, (1998). 3.7.3
Cutler, C., Apostolatos, T. A., Bildsten, L., Finn, L. S., Flanagan, É. É., Kennefick, D., Marković, D. M., Ori, A., Poisson, E., Sussman, G. J., and Thorne, K. S., “The last three minutes: Issues in gravitational wave measurements of coalescing compact binaries”, Phys. Rev. Lett., 70, 2984–2987, (1993). For a related online version see: C. Cutler, et al., “The Last Three Minutes: Issues in Gravitational Wave Measurements of Coalescing Compact Binaries”, (August, 1992), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9208005. 6.3
Cutler, C., and Flanagan, É. É., “Gravitational waves from merging compact binaries: How accurately can one extract the binary’s parameters from the inspiral waveform?”, Phys. Rev. D, 49, 2658–2697, (1994). For a related online version see: C. Cutler, et al., “Gravitational Waves from Mergin Compact Binaries: How Accurately Can One Extract the Binary’s Parameters from the Inspiral Waveform?”, (February, 1994), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9402014. 6.3
Damour, T., “Gravitation, experiment and cosmology”, in Proceedings of the 5th Hellenic School on Elementary Particle Physics. For a related online version see: T. Damour, “Gravitation, experiment and cosmology”, (June, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9606079. In press. 1
Damour, T., “Problème des deux corps et freinage de rayonnement en relativité général”, Comptes Rendus Acad. Sci. Ser. II, 294, 1355–1357, (1982). 4.4
Damour, T., “The problem of motion in Newtonian and Einsteinian gravity”, in Hawking, S. W., and Israel, W., eds., 300 Years of Gravitation, 128–198, (Cambridge University Press, Cambridge, 1987). 4.1.2, 4.2, 4.3, 4.4
Damour, T., and Deruelle, N., “Radiation reaction and angular momentum loss in small angle gravitational scattering”, Phys. Lett., 87A, 81–84, (1981). 4.4
Damour, T., and Dyson, F., “The Oklo bound on the time variation of the fine-structure constant revisited”, Nucl. Phys. B, 480, 37–54, (1996). For a related online version see: T. Damour, et al., “The Oklo bound on the time variation of the fine-structure constant revisited”, (June, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/hep-ph/9606486. 2.1
Damour, T., and Esposito-Farèse, G., “Tensor-multi-scalar theories of gravitation”, Class. Quantum Grav., 9, 2093–2176, (1992). 3.3.2, 5.4
Damour, T., and Esposito-Farèse, G., “Tensor-scalar gravity and binary-pulsar experiments”, Phys. Rev. D, 54, 1474–1491, (1996). For a related online version see: T. Damour, et al., “Tensor-scalar gravity and binary-pulsar experiments”, (February, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9602056. 3.3.2
Damour, T., and Esposito-Farèse, G., “Gravitational-wave versus binary-pulsar tests of strong-field gravity”, Phys. Rev. D, 58, 042001, (1998). For a related online version see: T. Damour, et al., “Gravitational-wave versus binary-pulsar tests of strong-field gravity”, (March, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9803031. 5.4, 8, 6.3
Damour, T., and Iyer, B. R., “Post-Newtonian generation of gravitational waves. II. The spin moments”, Ann. Inst. Henri Poincaré, A, 54, 115–164, (1991). 4.3
Damour, T., Jaranowski, P., and Schäfer, G., “Poincaré invariance in the ADM Hamiltonian approach to the general relativistic two-body problem”, Phys. Rev. D, 62, 021501, (2000). For a related online version see: T. Damour, et al., “PoincarÉ invariance in the ADM Hamiltonian approach to the general relativistic two-body problem”, (March, 2000), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/0003051. 4.4
Damour, T., and Nordtvedt, K., “General relativity as a cosmological attractor of tensor-scalar theories”, Phys. Rev. Lett., 70, 2217–2219, (1993). 3.3.2, 5.4
Damour, T., and Nordtvedt, K., “Tensor-scalar cosmological models and their relaxation toward general relativity”, Phys. Rev. D, 48, 3436–3450, (1993). 3.3.2, 5.4
Damour, T., and Pichon, B., “Big bang nucleosynthesis and tensor-scalar gravity”, Phys. Rev. D, 59, 123502, (1999). For a related online version see: T. Damour, et al., “Big bang nucleosynthesis and tensor-scalar gravity”, (July, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9807176. 6.5
Damour, T., and Polyakov, A. M., “The string dilaton and a least coupling principle”, Nucl. Phys. B, 423, 532–558, (1994). 2.3
Damour, T., and Taylor, J. H., “On the orbital period change of the binary pulsar PSR 1913+16”, Astrophys. J., 366, 501–511, (1991). 3.6.3
Damour, T., and Taylor, J. H., “Strong-field tests of relativistic gravity and binary pulsars”, Phys. Rev. D, 45, 1840–1868, (1992). 5.1
Damour, T., and Vokrouhlický, D., “Equivalence principle and the Moon”, Phys. Rev. D, 53, 4177–4201, (1996). For a related online version see: T. Damour, et al., “Equivalence principle and the Moon”, (July, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9507016. 3.6.1
Danzmann, K., “LISA — An ESA cornerstone mission for a gravitational-wave observatory”, Class. Quantum Grav., 14, 1399–1404, (1997). 6.1
Dicke, R. H., Gravitation and the Universe, volume 78 of Memoirs of the American Philosophical Society, Jayne Lecture for 1969, (American Philosophical Society, Philadelphia, USA, 1970). 82 pages. 2.1
Dickey, J. O., Bender, P. L., Faller, J. E., Newhall, X. X., Ricklefs, R. L., Ries, J. G., Shelus, P. J., Veillet, C., Whipple, A. L., Wiant, J. R., Williams, J., and Yoder, C. F., “Lunar laser ranging: A continuing legacy of the Apollo Program”, Science, 265, 482–490, (1994). 3.6.1, 3.6.3, 3.7.2
Drinkwater, M. J., Webb, J. K., Barrow, J. D., and Flambaum, V. V., “New limits on the possible variation of physical constants”, Mon. Not. R. Astron. Soc., 295, 457–462, (1998). For a related online version see: M. J. Drinkwater, et al., “New limits on the possible variation of physical constants”, (November, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9711290. 2.1
Eötvös, R. V., Pekàr, V., and Fekete, E., “Beitrage zum Gesetze der Proportionalität von Trägheit und Gravität”, Ann. Phys. (Leipzig), 68, 11–66, (1922). 2.1
Eubanks, T. M., Martin, J. O., Archinal, B. A., Josties, F. J., Klioner, S. A., Shapiro, S., and Shapiro, I. I., “Advances in solar system tests of gravity”, (August, 1999), [Online Preprint]: cited on 15 January 2001, ftp://casa.usno.navy.mil/navnet/postscript/prd_15.ps. 3.4.1
Finn, L. S., and Chernoff, D. F., “Observing binary inspiral in gravitational radiation: One interferometer”, Phys. Rev. D, 47, 2198–2219, (1993). For a related online version see: L. S. Finn, et al., “Observing binary inspiral in gravitational radiation: One interferometer”, (January, 1993), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9301003. 6.3
Fischbach, E., Gillies, G. T., Krause, D. E., Schwan, J. G., and Talmadge, C., “Non-Newtonian graviaty and new weak forces: An index of Measurements and Theory”, Metrologia, 29, 213–260, (1992). 2.1, 2.3
Fischbach, E., Sudarsky, D., Szafer, A., Talmadge, C., and Aronson, S. H., “Reanalysis of the Eötvös experiment”, Phys. Rev. Lett., 56, 3–6, (1986). Erratum: Phys. Rev. Lett., 56, 1427 (1986). 2.3
Fischbach, E., and Talmadge, C., “Six years of the fifth force”, Nature, 356, 207–215, (1992). 2.3
Fischbach, E., and Talmadge, C., The search for non-Newtonian gravity, (Springer-Verlag, New York, 1999). 2.3
Fritschel, P., “The LIGO project: Progress and plans”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 74–85, (World Scientific, Singapore, 1998). 6.1
Froeschlé, M., Mignard, F., and Arenou, F., “Determination of the PPN Parameter γ with the Hipparcos Data”, (1997), [Online Preprint]: cited on 15 January 2001, http://astro.estec.esa.nl/Hipparcos/venice-proc/poster01_03.ps.gz. In Proceedings of the Hipparcos Venice 1997 Symposium, available at http://astro.estec.esa.nl/Hipparcos/venice.html. 3.4.1
Gasperini, M., “On the response of gravitational antennas to dilatonic waves”, Phys. Lett. B, 470, 67–72, (1999). For a related online version see: M. Gasperini, “On the response of gravitational antennas to dilatonic waves”, (October, 1999), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9910019. 6.2
Godone, A., Novero, C., and Tavella, P., “Null gravitational redshift experiment with nonidentical atomic clocks”, Phys. Rev. D, 51, 319–323, (1995). 2.1
Goldman, I., “Upper limit on G variability derived from the spin-down of PSR 0655+64”, Mon. Not. R. Astron. Soc., 244, 184–187, (1990). 3.6.3
Gopakumar, A., and Iyer, B. R., “Gravitational waves from inspiraling compact binaries: Angular momentum flux, evolution of the orbital elements and the waveform to the second post-Newtonian order”, Phys. Rev. D, 56, 7708–7731, (1997). For a related online version see: A. Gopakumar, et al., “Gravitational waves from inspiraling compact binaries: Angular momentum flux, evolution of the orbital elements and the waveform to the second post-Newtonian order”, (October, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9710075. 6.3
Gravity Probe B Project at Stanford University, “Home Page”, [Online HTML Document]: cited on 15 January 2001, http://einstein.stanford.edu/. 3.7.3
Grishchuk, L. P., and Kopejkin, S. M., “Equations of motion for isolated bodies with relativistic corrections including the radiation-reaction force”, in Kovalevsky, J., and Brumberg, V. A., eds., Relativity in Celestial Mechanics and Astrometry, 19–34, (Reidel, Dordrecht, 1986). 4.4
Hamilton, W. O., “The ALLEGRO detector and the future of resonant detectors in the USA”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 115–126, (World Scientific, Singapore, 1998). 6.1
Haugan, M. P., “Energy conservation and the principle of equivalence”, Ann. Phys. (N. Y.), 118, 156–186, (1979). 2.2.1, 2.2.1
Haugan, M. P., and Will, C. M., “Modern tests of special relativity”, Phys. Today, 40, 69–76, (1987). 2.1
Hulse, R. A., “Nobel Lecture: The discovery of the binary pulsar”, Rev. Mod. Phys., 66, 699–710, (1994). 5.1
Iess, L., Giampieri, G., Anderson, J. D., and Bertotti, B., “Doppler measurement of the solar gravitational de ection”, Class. Quantum Grav., 16, 1487–1502, (1999). 3.7.
Iyer, B. R., and Will, C. M., “Post-Newtonian gravitational radiation reaction for two-body systems”, Phys. Rev. Lett., 70, 113–116, (1993). 4.4
Iyer, B. R., and Will, C. M., “Post-Newtonian gravitational radiation reaction for two-body systems: Non-spinning bodies”, Phys. Rev. D, 52, 6882–6893, (1995). 4.4
Jaranowski, P., and Schäfer, G., “3rd post-Newtonian higher order Hamilton dynamics for two-body point-mass systems”, Phys. Rev. D, 57, 7274–7291, (1998). For a related online version see: P. Jaranowski, et al., “3rd post-Newtonian higher order Hamilton dynamics for two-body point-mass systems”, (December, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9712075. 4.4
Jaranowski, P., and Schäfer, G., “The binary black-hole problem at the third post-Newtonian approximation in the orbital motion: Static part”, Phys. Rev. D, 60, 124003, (1999). For a related online version see: P. Jaranowski, et al., “The binary black-hole problem at the third post-Newtonian approximation in the orbital motion: Static part”, (June, 1999), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9906092. 4.4
Kidder, L. E., “Coalescing binary systems of compact objects to (post)5/2-Newtonian order. V. Spin effects”, Phys. Rev. D, 52, 821–847, (1995). For a related online version see: L. E. Kidder, “Coalescing binary systems of compact objects to (post)5/2-Newtonian order. V. Spin effects”, (June, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9506022. 4.4
Kidder, L. E., Will, C. M., and Wiseman, A. G., “Spin effects in the inspiral of coalescing compact binaries”, Phys. Rev. D, 47, R4183–4187, (1993). For a related online version see: L. E. Kidder, et al., “Spin effects in the inspiral of coalescing compact binaries”, (November, 1992), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9211025. 4.4
Kramer, M., “Determination of the geometry of the PSR B1913+16 system by geodetic precession”, Astrophys. J., 509, 856–860, (1998). For a related online version see: M. Kramer, “Determination of the geometry of the PSR B1913+16 system by geodetic precession”, (August, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9808127. 5.1
Lebach, D. E., Corey, B. E., Shapiro, I. I., Ratner, M. I., Webber, J. C., Rogers, A. E. E., Davis, J. L., and Herring, T. A., “Measurement of the solar gravitational deflection of radio waves using very-long-baseline interferometry”, Phys. Rev. Lett., 75, 1439–1442, (1995). 3.4.1
Lightman, A. P., and Lee, D. L., “Restricted proof that the Weak Equivalence Principle implies the Einstein Equivalence Principle”, Phys. Rev. D, 8, 364–376, (1973). 2.2.2
Lobo, J. A., “Spherical GW detectors and geometry”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 168–179, (World Scientific, Singapore, 1998). 6.2
Long, J. C., Chan, H. W., and Price, J. C., “Experimental status of gravitational-strength forces in the sub-centimeter regime”, Nucl. Phys. B, 539, 23–34, (1999). For a related online version see: J. C. Long, et al., “Experimental status of gravitational-strength forces in the sub-centimeter regime”, (May, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/hep-ph/9805217. 2.3
Lorimer, D., “Binary and millisecond pulsars”, (September, 1998), [Article in Online Journal Living Reviews in Relativity]: cited on 15 January 2001, http://www.livingreviews.org/Articles/Volume1/1998-10lorimer. 5.1
Maggiore, M., and Nicolis, A., “Detection strategies for scalar gravitational waves with interferometers and resonant spheres”, Phys. Rev. D, 62, 024004, (1999). For a related online version see: M. Maggiore, et al., “Detection strategies for scalar gravitational waves with interferometers and resonant spheres”, (July, 1999), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9907055. 6.2
Malaney, R. A., and Mathews, G. J., “Probing the early universe: A review of primordial nucleosynthesis beyond the standard big bang”, Phys. Rep., 229, 147–219, (1993). 2.1
Menou, K., Quataert, E., and Narayan, R., “Astrophysical evidence for black-hole event horizons”, in Piran, T., and Ruffini, R., eds., Proceedings of the Eighth Marcel Grossmann Meeting on General Relativity, 204–224, (World Scientific, Singapore, 1999). For a related online version see: K. Menou, et al., “Astrophysical evidence for black hole event horizons”, (December, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9712015. 6.5
Mino, Y., Sasaki, M., Shibata, M., Tagoshi, H., and Tanaka, T., “Black hole perturbation”, Prog. Theor. Phys. Suppl., 128, 1–121, (1997). For a related online version see: Y. Mino, et al., “Black hole perturbation”, (December, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9712057. 4.1.1, 4.4
Misner, C. W., Thorne, K. S., and Wheeler, J. A., Gravitation, (Freeman, San Francisco, 1973). 3.1.1, 3.2, 4.3
Müller, J., Nordtvedt, K., and Vokrouhlický, D., “Improved constraint on the α1 PPN parameter from lunar motion”, Phys. Rev. D, 54, R5927–R5930, (1996). 3.6.2
Müller, J., Schneider, M., Nordtvedt, K., and Vokrouhlický, D., “What can LLR provide to relativity?”, in Piran, T., and Ruffini, R., eds., Proceedings of the 8th Marcel Grossman Meeting on General Relativity, 1151–1153, (World Scientific, Singapore, 1999). 3.6.1, 3.6.3
Nordtvedt, K., “Equivalence principle for massive bodies. I. Phenomenology”, Phys. Rev., 169, 1014–1016, (1968). 3.6.1
Nordtvedt, K., “Equivalence principle for massive bodies. II. Theory”, Phys. Rev., 169, 1017–1025, (1968). 3.2
Nordtvedt, K., “Existence of the gravitomagnetic interaction”, Int. J. Theor. Phys., 27, 1395–1404, (1988). 3.7.3
Nordtvedt, K., “Gravitomagnetic interaction and laser ranging to Earth satellites”, Phys. Rev. Lett., 61, 2647–2649, (1988). 3.7.3
Nordtvedt, K., “Ġ/G and a cosmological acceleration of gravitationally compact bodies”, Phys. Rev. Lett., 65, 953–956, (1990). 3.6.3
Nordtvedt, K., “The relativistic orbit observables in lunar laser ranging”, Icarus, 114, 51–62, (1995). 3.6.1
Nordtvedt, K., “Improving gravity theory tests with solar system ‘grand fits”’, Phys. Rev. D, 61, 122001, (2000). 3.7.4
Pallottino, G. V., “The resonant-mass detectors of the Rome group”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 105–114, (World Scientific, Singapore, 1998). 6.1
Pati, M. E., and Will, C. M., “Post-Newtonian gravitational radiation and equations of motion via direct integration of the relaxed Einstein equations. Foundations”, Phys. Rev. D. For a related online version see: M. E. Pati, et al., “Post-Newtonian gravitational radiation and equations of motion via direct integration of the relaxed Einstein equations. I. Foundations”, (July, 2000), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/0007087. In press. 4.3
Poisson, E., “Gravitational radiation from a particle in circular orbit around a black hole. I. Analytic results for the nonrotating case”, Phys. Rev. D, 47, 1497–1510, (1993). 4.4
Poisson, E., “Measuring black-hole parameters and testing general relativity using gravitational-wave data from space-based interferometers”, Phys. Rev. D, 54, 5939–5953, (1996). For a related online version see: E. Poisson, “Measuring black-hole parameters and testing general relativity using gravitational-wave data from space-based interferometers”, (June, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9606024. 6.3
Poisson, E., and Will, C. M., “Gravitational waves from inspiralling compact binaries: Parameter estimation using second-post-Newtonian waveforms”, Phys. Rev. D, 52, 848–855, (1995). For a related online version see: E. Poisson, et al., “Gravitational waves from inspiralling compact binaries: Parameter estimation using second-post-Newtonian waveforms”, (February, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9502040. 6.3
Prestage, J. D., Tjoelker, R. L., and Maleki, L., “Atomic clocks and variations of the fine structure constant”, Phys. Rev. Lett., 74, 3511–3514, (1995). 2.1
Prodi, G. A., Conti, L., Mezzena, R., Vitale, S., Taffarello, L., Zendri, J. P., Baggio, L., Cerdonio, M., Colombo, A., Crivelli Visconti, V., Macchietto, R., Falferi, P., Bonaldi, M., Ortolan, A., Vedovato, G., Cavallini, E., and Fortini, P., “Initial operation of the gravitational-wave detector AURIGA”, in Coccia, E., Pizzella, G., and Veneziano, G., eds., Second Edoardo Amaldi Conference on Gravitational Waves, 148–158, (World Scientific, Singapore, 1998). 6.1
Reasenberg, R. D., Shapiro, I. I., MacNeil, P. E., Goldstein, R. B., Breidenthal, J. C., Brenkle, J. P., Cain, D. L., Kaufman, T. M., Komarek, T. A., and Zygielbaum, A. I., “Viking relativity experiment: Verification of signal retardation by solar gravity”, Astrophys. J. Lett., 234, L219–L221, (1979). 3.4.2
Reeves, H., “On the origin of the light elements (Z<6)”, Rev. Mod. Phys., 66, 193–216, (1994). 2.1
Roll, P. G., Krotkov, R., and Dicke, R. H., “The equivalence of inertial and passive gravitational mass”, Ann. Phys. (N. Y.), 26, 442–517, (1964). 3.6.1
Ryan, F. D., “Gravitational waves from the inspiral of a compact object into a massive, axisymmetric body with arbitrary multipole moments”, Phys. Rev. D, 52, 5707–5718, (1995). 6.3
Salomon, C., Sortais, Y., Bize, S., Abgrall, M., Zhang, S., Nicolas, C., Mandache, C., Lemonde, P., Laurent, P., Santarelli, G., Clairon, A., Dimarcq, N., Petit, P., Mann, A., Luiten, A., and Chang, S., “Cold Atom Clocks”, in Inguscio, M., and Arimondo, E., eds., Proceedings of the International Conference on Atomic Physics 2000, (Singapore, World Scientific, 2000). In press. 2.1
Shapiro, I. I., “Solar system tests of general relativity”, in Ashby, N., Bartlett, D. F., and Wyss, W., eds., General Relativity and Gravitation: 12th International Conference on General Relativity and Gravitation, 313–330, (Cambridge University Press, Cambridge, 1990). 3.5
Shapiro, I. I., “A century of relativity”, Rev. Mod. Phys., 71, S41–S53, (1999). 1
Stairs, I. H., Arzoumanian, Z., Camilio, F., Lyne, A. G., Nice, D. J., Taylor, J. H., Thorsett, S. E., and Wolszczan, A., “Relativistic orbital decay in PSR B1534+12”, Astrophys. J., 505, 352–357, (1998). For a related online version see: I. H. Stairs, et al., “Relativistic orbital decay in the PSR B1534+12 binary system”, (December, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9712296. 7, 5.2
Stairs, I. H., Nice, D. J., Thorsett, S. E., and Taylor, J. H., “Recent Arecibo timing of the relativistic binary PSR B1534+12”, in Gravitational Waves and Experimental Gravity: XXXIV Rencontres de Moriond. For a related online version see: I. H. Stairs, et al., “Recent Arecibo timing of the relativistic binary PSR B1534+12”, (March, 1999), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9903289. In press. 7, 5.2
Steinhardt, P. J., and Will, C. M., “High-frequency oscillations of Newton’s constant induced by inflation”, Phys. Rev. D, 52, 628–639, (1995). For a related online version see: P. J. Steinhardt, et al., “High-frequency oscillations of Newton’s constant induced by in ation”, (September, 1994), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/astro-ph/9409041. 3.3.2
Su, Y., Heckel, B. R., Adelberger, E. G., Gundlach, J. H., Harris, M., Smith, G. L., and Swanson, H. E., “New tests of the universality of free fall”, Phys. Rev. D, 50, 3614–3636, (1994). 2.1
Talmadge, C., Berthias, J.-P., Hellings, R. W., and Standish, E. M., “Model-independent constraints on possible modifications of Newtonian gravity”, Phys. Rev. Lett., 61, 1159–1162, (1988). 2.3, 6.4
Taylor, J. H., “Nobel Lecture: Binary pulsars and relativistic gravity”, Rev. Mod. Phys., 66, 711–719, (1994). 5.1
Taylor, J. H., Wolszczan, A., Damour, T., and Weisberg, J. M., “Experimental constraints on strong-field relativistic gravity”, Nature, 355, 132–136, (1992). 5.2
Taylor, T. R., and Veneziano, G., “Dilaton coupling at large distance”, Phys. Lett. B, 213, 450, (1988). 2.3
Thorne, K. S., “Gravitational radiation”, in Hawking, S. W., and Israel, W., eds., 300 Years of Gravitation, 330–458, (Cambridge University Press, Cambridge, 1987). 4.5
Thorne, K. S., “Gravitational waves”, in Kolb, E. W., and Peccei, R., eds., Proceedings of the Snowmass 94 Summer Study on Particle and Nuclear Astrophysics and Cosmology, 160–184, (World Scientific, Singapore, 1995). For a related online version see: K. S. Thorne, “Gravitational waves”, (June, 1995), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9506086. 4.2, 6.1
Thorsett, S., “The Pulsar Catalog”, (1999), [Web Interface to Database]: cited on 15 January 2001, http://pulsar.ucolick.org/cog/pulsars/catalog. Web acess to information from the pulsar catalog of J. H. Taylor, R. N. Manchester, and A. G. Lyne. 6, 7
Treuhaft, R. N., and Lowe, S. T., “A measurement of planetary relativistic de ection”, Astron. J., 102, 1879–1888, (1991). 3.4.1
Turneaure, J. P., Will, C. M., Farrell, B. F., Mattison, E. M., and Vessot, R. F. C., “Test of the principle of equivalence by a null gravitational redshift experiment”, Phys. Rev. D, 27, 1705–1714, (1983). 2.1
Vessot, R. F. C., Levine, M. W., Mattison, E. M., Blomberg, E. L., Hoffman, T. E., Nystrom, G. U., Farrell, B. F., Decher, R., Eby, P. B., Baugher, C. R., Watts, J. W., Teuber, D. L., and Wills, F. O., “Test of relativistic gravitation with a space-borne hydrogen maser”, Phys. Rev. Lett., 45, 2081–2084, (1980). 2.1
Visser, M., “Mass for the graviton”, Gen. Relativ. Gravit., 30, 1717–1728, (1998). For a related online version see: M. Visser, “Mass for the graviton”, (May, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9705051. 6.4, 6.4
Wagoner, R. V., “Resonant-mass detection of tensor and scalar waves”, in Marck, J.-A., and Lasota, J.-P., eds., Relativistic Gravitation and Gravitational Radiation, 419–432, (Cambridge University Press, Cambridge, 1997). 6.2
Wagoner, R. V., and Kalligas, D., “Scalar-tensor theories and gravitational radiation”, in Marck, J.-A., and Lasota, J.-P., eds., Relativistic Gravitation and Gravitational Radiation, 433–446, (Cambridge University Press, Cambridge, 1997). 6.2
Wagoner, R. V., and Will, C. M., “Post-Newtonian gravitational radiation from orbiting point masses”, Astrophys. J., 210, 764–775, (1976). 4.4, 6.3
Weinberg, S.W., Gravitation and Cosmology, (Wiley, New York, 1992). 3.1.1
Weisberg, J. M., and Taylor, J. H., private communication. 5.1
Weisberg, J. M., and Taylor, J. H., “General relativistic precession of the spin axis of binary pulsar B1913+16: First two-dimensional maps of the emission beam”, in Kramer, M., Wex, N., and Wielebinski, R., eds., Pulsar Astronomy — 2000 and Beyond, (2000). In press. 5.1
Will, C. M., “The confrontation between general relativity and experiment: A 1998 update”, (November, 1998), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9811036. In Dixon, L., ed., Gravity: From the Hubble Length to the Planck Length. XXVI SLAC Summer Institute on Particle Physics, available at http://www.slac.stanford.edu/gen/meeting/ssi/1998/manu_list.html. 1
Will, C. M., “Einstein’s relativity and everyday life”, (October, 2000), [Article in Online Resource Physics Central]: cited on 15 January 2001, http://www.physicscentral.com/writers. 2.1
Will, C. M., “Active mass in relativistic gravity: Theoretical interpretation of the Kreuzer experiment”, Astrophys. J., 204, 224–234, (1976). 3.7.1
Will, C. M., “Experimental gravitation from Newton’s Principia to Einstein’s general relativity”, in Hawking, S. W., and Israel, W., eds., 300 Years of Gravitation, 80–127, (Cambridge University Press, Cambridge, 1987). 1
Will, C. M., “Twilight time for the fifth force?”, Sky and Telescope, 80, 472–479, (1990). 2.3
Will, C. M., “Clock synchronization and isotropy of the one-way speed of light”, Phys. Rev. D, 45, 403–411, (1992). 2.1, 2.2.3, 2.2.3
Will, C. M., “The confrontation between general relativity and experiment: A 1992 update”, Int. J. Mod. Phys. D, 1, 13–68, (1992). 1
Will, C. M., “Is momentum conserved? A test in the binary system PSR 1913+16”, Astrophys. J. Lett., 393, L59–L61, (1992). 3.7.1
Will, C. M., Theory and experiment in gravitational physics, (Cambridge University Press, Cambridge, 1993), 2nd edition. 1, 2.1, 2.1, 2.1, 2.1, 2.1, 2.1, 1, 2.2.1, 2.2.2, 2.2.3, 3.1.1, 3.2, 1, 3.3, 3.3.1, 3.3.2, 3.4.1, 3.4.2, 3.4.2, 3.5, 3.6.1, 3.6.2, 3.6.3, 3.7.1, 3.7.1, 3.7.2, 3.7.3, 5.1, 5.1, 5.3, 5.4, 5.4, 6.2, 6.2, 6.3, 6.4, 6.5
Will, C. M., Was Einstein right?, (Basic Books / Perseus Group, New York, 1993), 2nd edition. 1
Will, C. M., “Testing scalar-tensor gravity with gravitational-wave observations of inspiralling compact binaries”, Phys. Rev. D, 50, 6058–6067, (1994). For a related online version see: C. M. Will, “Testing scalar-tensor gravity with gravitational-wave observations of inspiralling compact binaries”, (June, 1994), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9406022. 6.3
Will, C. M., “The confrontation between general relativity and experiment: A 1995 update”, in Hall, G. S., and Pulham, J. R., eds., General Relativity: Proceedings of the 46th Scottish Universities Summer School in Physics, 239–282, (Institute of Physics Publishing, Bristol, 1996). 1
Will, C. M., “Bounding the mass of the graviton using gravitional-wave observations of inspiralling compact binaries”, Phys. Rev. D, 57, 2061–2068, (1998). For a related online version see: C. M. Will, “Bounding the mass of the graviton using gravitional-wave observations of inspiralling compact binaries”, (September, 1997), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9709011. 6.4
Will, C. M., and Wiseman, A. G., “Gravitational radiation from compact binary systems: Gravitational waveforms and energy loss to second post-Newtonian order”, Phys. Rev. D, 54, 4813–4848, (1996). For a related online version see: C. M. Will, et al., “Gravitational radiation from compact binary systems: Gravitational waveforms and energy loss to second post-Newtonian order”, (August, 1996), [Online Los Alamos Archive Preprint]: cited on 15 January 2001, http://xxx.lanl.gov/abs/gr-qc/9608012. 4.3, 4.4, 6.3
Will, C. M., and Zaglauer, H. W., “Gravitational radiation, close binary systems and the Brans-Dicke theory of gravity”, Astrophys. J., 346, 366–377, (1989). 5.4
Williams, J. G., Newhall, X. X., and Dickey, J. O., “Relativity parameters determined from lunar laser ranging”, Phys. Rev. D, 53, 6730–6739, (1996). 3.6.1, 3.6.3, 3.7.2
Wiseman, A. G., “Coalescing binary systems of compact objects to (post)5/2-Newtonian order. II. Higher-order waveforms and radiation recoil”, Phys. Rev. D, 46, 1517–1539, (1992). 4.4
Wolszczan, A., “Binary pulsars and relativistic gravitation”, Class. Quantum Grav., 11, A227–A242, (1994). 7
Acknowledgements
This work was supported in part by the National Science Foundation, Grant Number PHY 96-00049.
Author information
Authors and Affiliations
Rights and permissions
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 4, 4 (2001). https://doi.org/10.12942/lrr-2001-4
Published:
DOI: https://doi.org/10.12942/lrr-2001-4
Keywords
- Binary Pulsar
- Nordtvedt Effect
- Gravitational Waves
- Einstein Equivalence Principle (EEP)
- Dipole Gravitational Radiation
Article history
Latest
The Confrontation between General Relativity and Experiment- Published:
- 01 December 2014
- Accepted:
- 06 June 2014
DOI: https://doi.org/10.12942/lrr-2014-4
- The Confrontation between General Relativity and Experiment
- Published:
- 27 March 2006
- Accepted:
- 27 February 2006
DOI: https://doi.org/10.12942/lrr-2006-3
Original
The Confrontation between General Relativity and Experiment- Published:
- 11 May 2001
DOI: https://doi.org/10.12942/lrr-2001-4