Abstract
Perturbations of stars and black holes have been one of the main topics of relativistic astrophysics for the last few decades. They are of particular importance today, because of their relevance to gravitational wave astronomy. In this review we present the theory of quasi-normal modes of compact objects from both the mathematical and astrophysical points of view. The discussion includes perturbations of black holes (Schwarzschild, Reissner-Nordström, Kerr and Kerr-Newman) and relativistic stars (non-rotating and slowly-rotating). The properties of the various families of quasi-normal modes are described, and numerical techniques for calculating quasi-normal modes reviewed. The successes, as well as the limits, of perturbation theory are presented, and its role in the emerging era of numerical relativity and supercomputers is discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Helioseismology and asteroseismology are well known terms in classical astrophysics. From the beginning of the century the variability of Cepheids has been used for the accurate measurement of cosmic distances, while the variability of a number of stellar objects (RR Lyrae, Mira) has been associated with stellar oscillations. Observations of solar oscillations (with thousands of nonradial modes) have also revealed a wealth of information about the internal structure of the Sun [204]. Practically every stellar object oscillates radially or nonradially, and although there is great difficulty in observing such oscillations there are already results for various types of stars (O, B, …). All these types of pulsations of normal main sequence stars can be studied via Newtonian theory and they are of no importance for the forthcoming era of gravitational wave astronomy. The gravitational waves emitted by these stars are extremely weak and have very low frequencies (cf. for a discussion of the sun [70], and an important new measurement of the sun’s quadrupole moment and its application in the measurement of the anomalous precession of Mercury’s perihelion [163]). This is not the case when we consider very compact stellar objects i.e. neutron stars and black holes. Their oscillations, produced mainly during the formation phase, can be strong enough to be detected by the gravitational wave detectors (LIGO, VIRGO, GEO600, SPHERE) which are under construction.
In the framework of general relativity (GR) quasi-normal modes (QNM) arise, as perturbations (electromagnetic or gravitational) of stellar or black hole spacetimes. Due to the emission of gravitational waves there are no normal mode oscillations but instead the frequencies become “quasi-normal” (complex), with the real part representing the actual frequency of the oscillation and the imaginary part representing the damping.
In this review we shall discuss the oscillations of neutron stars and black holes. The natural way to study these oscillations is by considering the linearized Einstein equations. Nevertheless, there has been recent work on nonlinear black hole perturbations [101, 102, 103, 104, 100] while, as yet nothing is known for nonlinear stellar oscillations in general relativity.
The study of black hole perturbations was initiated by the pioneering work of Regge and Wheeler [173] in the late 50s and was continued by Zerilli [212]. The perturbations of relativistic stars in GR were first studied in the late 60s by Kip Thorne and his collaborators [202, 198, 199, 200]. The initial aim of Regge and Wheeler was to study the stability of a black hole to small perturbations and they did not try to connect these perturbations to astrophysics. In contrast, for the case of relativistic stars, Thorne’s aim was to extend the known properties of Newtonian oscillation theory to general relativity, and to estimate the frequencies and the energy radiated as gravitational waves.
QNMs were first pointed out by Vishveshwara [207] in calculations of the scattering of gravitational waves by a Schwarzschild black hole, while Press [164] coined the term quasi-normal frequencies. QNM oscillations have been found in perturbation calculations of particles falling into Schwarzschild [73] and Kerr black holes [76, 80] and in the collapse of a star to form a black hole [66, 67, 68]. Numerical investigations of the fully nonlinear equations of general relativity have provided results which agree with the results of perturbation calculations; in particular numerical studies of the head-on collision of two black holes [30, 29] (cf. Figure 1) and gravitational collapse to a Kerr hole [191]. Recently, Price, Pullin and collaborators [170, 31, 101, 28] have pushed forward the agreement between full nonlinear numerical results and results from perturbation theory for the collision of two black holes. This proves the power of the perturbation approach even in highly nonlinear problems while at the same time indicating its limits.
QNM ringing after the head-on collision of two unequal mass black holes [29]. The continuous line corresponds to the full nonlinear numerical calculation while the dotted line is a fit to the fundamental and first overtone QNM.
In the concluding remarks of their pioneering paper on nonradial oscillations of neutron stars Thorne and Campollataro [202] described it as “just a modest introduction to a story which promises to be long, complicated and fascinating”. The story has undoubtedly proved to be intriguing, and many authors have contributed to our present understanding of the pulsations of both black holes and neutron stars. Thirty years after these prophetic words by Thorne and Campollataro hundreds of papers have been written in an attempt to understand the stability, the characteristic frequencies and the mechanisms of excitation of these oscillations. Their relevance to the emission of gravitational waves was always the basic underlying reason of each study. An account of all this work will be attempted in the next sections hoping that the interested reader will find this review useful both as a guide to the literature and as an inspiration for future work on the open problems of the field.
In the next section we attempt to give a mathematical definition of QNMs. The third and fourth section will be devoted to the study of the black hole and stellar QNMs. In the fifth section we discuss the excitation and observation of QNMs and finally in the sixth section we will mention the more significant numerical techniques used in the study of QNMs.
2 Normal Modes — Quasi-Normal Modes — Resonances
Before discussing quasi-normal modes it is useful to remember what normal modes are!
Compact classical linear oscillating systems such as finite strings, membranes, or cavities filled with electromagnetic radiation have preferred time harmonic states of motion (ω is real):
if dissipation is neglected. (We assume χ to be some complex valued field.) There is generally an infinite collection of such periodic solutions, and the “general solution” can be expressed as a superposition,
of such normal modes. The simplest example is a string of length L which is fixed at its ends. All such systems can be described by systems of partial differential equations of the type (χ may be a vector)
where A is a linear operator acting only on the spatial variables. Because of the finiteness of the system the time evolution is only determined if some boundary conditions are prescribed. The search for solutions periodic in time leads to a boundary value problem in the spatial variables. In simple cases it is of the Sturm-Liouville type. The treatment of such boundary value problems for differential equations played an important role in the development of Hilbert space techniques.
A Hilbert space is chosen such that the differential operator becomes symmetric. Due to the boundary conditions dictated by the physical problem, A becomes a self-adjoint operator on the appropriate Hilbert space and has a pure point spectrum. The eigenfunctions and eigenvalues determine the periodic solutions (1).
The definition of self-adjointness is rather subtle from a physicist’s point of view since fairly complicated “domain issues” play an essential role. (See [43] where a mathematical exposition for physicists is given.) The wave equation modeling the finite string has solutions of various degrees of differentiability. To describe all “realistic situations”, clearly C∞ functions should be sufficient. Sometimes it may, however, also be convenient to consider more general solutions.
From the mathematical point of view the collection of all smooth functions is not a natural setting to study the wave equation because sequences of solutions exist which converge to non-smooth solutions. To establish such powerful statements like (2) one has to study the equation on certain subsets of the Hilbert space of square integrable functions. For “nice” equations it usually happens that the eigenfunctions are in fact analytic. They can then be used to generate, for example, all smooth solutions by a pointwise converging series (2). The key point is that we need some mathematical sophistication to obtain the “completeness property” of the eigenfunctions.
This picture of “normal modes” changes when we consider “open systems” which can lose energy to infinity. The simplest case are waves on an infinite string. The general solution of this problem is
with “arbitrary” functions A and B. Which solutions should we study? Since we have all solutions, this is not a serious question. In more general cases, however, in which the general solution is not known, we have to select a certain class of solutions which we consider as relevant for the physical problem.
Let us consider for the following discussion, as an example, a wave equation with a potential on the real line,
Cauchy data χ(0, x), ∂tχ(0, x) which have two derivatives determine a unique twice differentiable solution. No boundary condition is needed at infinity to determine the time evolution of the data! This can be established by fairly simple PDE theory [116].
There exist solutions for which the support of the fields are spatially compact, or — the other extreme — solutions with infinite total energy for which the fields grow at spatial infinity in a quite arbitrary way!
From the point of view of physics smooth solutions with spatially compact support should be the relevant class — who cares what happens near infinity! Again it turns out that mathematically it is more convenient to study all solutions of finite total energy. Then the relevant operator is again self-adjoint, but now its spectrum is purely “continuous”. There are no eigenfunctions which are square integrable. Only “improper eigenfunctions” like plane waves exist. This expresses the fact that we find a solution of the form (1) for any real ω and by forming appropriate superpositions one can construct solutions which are “almost eigenfunctions”. (In the case V(x) = 0 these are wave packets formed from plane waves.) These solutions are the analogs of normal modes for infinite systems.
Let us now turn to the discussion of “quasi-normal modes” which are conceptually different to normal modes. To define quasi-normal modes let us consider the wave equation (5) for potentials with V ≥ 0 which vanish for |x| > x0. Then in this case all solutions determined by data of compact support are bounded: |χ(t, x)| < C. We can use Laplace transformation techniques to represent such solutions. The Laplace transform ̂χ(s, x) (s > 0 real) of a solution χ(t, x) is
and satisfies the ordinary differential equation
where
is the homogeneous equation. The boundedness of χ implies that ̂χ is analytic for positive, real s, and has an analytic continuation onto the complex half plane Re(s) > 0.
Which solution ̂χ of this inhomogeneous equation gives the unique solution in spacetime determined by the data? There is no arbitrariness; only one of the Green functions for the inhomogeneous equation is correct!
All Green functions can be constructed by the following well known method. Choose any two linearly independent solutions of the homogeneous equation f-(s, x) and f+(s, x), and define
where W(s) is the Wronskian of f- and f+. If we denote the inhomogeneity of (7) by j, a solution of (7) is
We still have to select a unique pair of solutions f-, f+. Here the information that the solution in spacetime is bounded can be used. The definition of the Laplace transform implies that ̂χ is bounded as a function of x. Because the potential V vanishes for |x| > x0, the solutions of the homogeneous equation (8) for |x| > x0 are
The following pair of solutions
which is linearly independent for Re(s) > 0, gives the unique Green function which defines a bounded solution for j of compact support. Note that for Re(s) > 0 the solution f+ is exponentially decaying for large x and f- is exponentially decaying for small x. For small x however, f+ will be a linear combination a(s)e-sx + b(s)esx which will in general grow exponentially. Similar behavior is found for f-.
Quasi-Normal mode frequencies sn can be defined as those complex numbers for which
that is the two functions become linearly dependent, the Wronskian vanishes and the Green function is singular! The corresponding solutions f+(sn, x) are called quasi eigenfunctions.
Are there such numbers sn? From the boundedness of the solution in space-time we know that the unique Green function must exist for Re(s) > 0. Hence f+, f- are linearly independent for those values of s. However, as solutions f+, f- of the homogeneous equation (8) they have a unique continuation to the complex s plane. In [35] it is shown that for positive potentials with compact support there is always a countable number of zeros of the Wronskian with Re(s) < 0.
What is the mathematical and physical significance of the quasi-normal frequencies sn and the corresponding quasi-normal functions f+? First of all we should note that because of Re(s) < 0 the function f+ grows exponentially for small and large x! The corresponding spacetime solution \({e^{{s_n}}}^t{f_ + }({s_n}, \:x)\) is therefore not a physically relevant solution, unlike the normal modes.
If one studies the inverse Laplace transformation and expresses ω as a complex line integral (a > 0),
one can deform the path of the complex integration and show that the late time behavior of solutions can be approximated in finite parts of the space by a finite sum of the form
Here we assume that Re(sn+1) < Re(sn) < 0, sn = αn + iβn. The approximation ∼ means that if we choose x0, x1, ∊ and t0 then there exists a constant C(t0, x0, x1, ∊) such that
holds for t > t0, x0 < x < x1, ∊ > 0 with C(t0, x0, x1, ∊) independent of t. The constants an depend only on the data [35]! This implies in particular that all solutions defined by data of compact support decay exponentially in time on spatially bounded regions. The generic leading order decay is determined by the quasi-normal mode frequency with the largest real part s1, i.e. slowest damping. On finite intervals and for late times the solution is approximated by a finite sum of quasi eigenfunctions (15).
It is presently unclear whether one can strengthen (16) to a statement like (2), a pointwise expansion of the late time solution in terms of quasi-normal modes. For one particular potential (Pöschl-Teller) this has been shown by Beyer [42].
Let us now consider the case where the potential is positive for all x, but decays near infinity as happens for example for the wave equation on the static Schwarzschild spacetime. Data of compact support determine again solutions which are bounded [117]. Hence we can proceed as before. The first new point concerns the definitions of f±. It can be shown that the homogeneous equation (8) has for each real positive s a unique solution f+(s, x) such that limx→∞(esxf+(s, x)) = 1 holds and correspondingly for f-. These functions are uniquely determined, define the correct Green function and have analytic continuations onto the complex half plane Re(s) > 0.
It is however quite complicated to get a good representation of these functions. If the point at infinity is not a regular singular point, we do not even get converging series expansions for f±. (This is particularly serious for values of s with negative real part because we expect exponential growth in x).
The next new feature is that the analyticity properties of f± in the complex s plane depend on the decay of the potential. To obtain information about analytic continuation, even use of analyticity properties of the potential in x is made! Branch cuts may occur. Nevertheless in a lot of cases an infinite number of quasi-normal mode frequencies exists.
The fact that the potential never vanishes may, however, destroy the exponential decay in time of the solutions and therefore the essential properties of the quasi-normal modes. This probably happens if the potential decays slower than exponentially. There is, however, the following way out: Suppose you want to study a solution determined by data of compact support from t = 0 to some large finite time t = T. Up to this time the solution is — because of domain of dependence properties — completely independent of the potential for sufficiently large x. Hence we may see an exponential decay of the form (15) in a time range t1 < t < T. This is the behavior seen in numerical calculations. The situation is similar in the case of α-decay in quantum mechanics. A comparison of quasi-normal modes of wave equations and resonances in quantum theory can be found in the appendix, see section 9.
3 Quasi-Normal Modes of Black Holes
One of the most interesting aspects of gravitational wave detection will be the connection with the existence of black holes [201]. Although there are presently several indirect ways of identifying black holes in the universe, gravitational waves emitted by an oscillating black hole will carry a unique fingerprint which would lead to the direct identification of their existence.
As we mentioned earlier, gravitational radiation from black hole oscillations exhibits certain characteristic frequencies which are independent of the processes giving rise to these oscillations. These “quasi-normal” frequencies are directly connected to the parameters of the black hole (mass, charge and angular momentum) and for stellar mass black holes are expected to be inside the bandwidth of the constructed gravitational wave detectors.
The perturbations of a Schwarzschild black hole reduce to a simple wave equation which has been studied extensively. The wave equation for the case of a Reissner-Nordström black hole is more or less similar to the Schwarzschild case, but for Kerr one has to solve a system of coupled wave equations (one for the radial part and one for the angular part). For this reason the Kerr case has been studied less thoroughly. Finally, in the case of Kerr-Newman black holes we face the problem that the perturbations cannot be separated in their angular and radial parts and thus apart from special cases [124] the problem has not been studied at all.
3.1 Schwarzschild Black Holes
The study of perturbations of Schwarzschild black holes assumes a small perturbation hμν on a static spherically symmetric background metric
with the perturbed metric having the form
which leads to a variation of the Einstein equations i.e.
By assuming a decomposition into tensor spherical harmonics for each hμν of the form
the perturbation problem is reduced to a single wave equation, for the function χℓm(r, t) (which is a combination of the various components of hμν). It should be pointed out that equation (20) is an expansion for scalar quantities only. From the 10 independent components of the hμν only htt, htr, and hrr transform as scalars under rotations. The htθ, htϕ, hrϕ, and hrϕ transform as components of two-vectors under rotations and can be expanded in a series of vector spherical harmonics while the components hθθ, hθϕ, and hϕϕ transform as components of a 2 × 2 tensor and can be expanded in a series of tensor spherical harmonics (see [202, 212, 152] for details). There are two classes of vector spherical harmonics (polar and axial) which are build out of combinations of the Levi-Civita volume form and the gradient operator acting on the scalar spherical harmonics. The difference between the two families is their parity. Under the parity operator π a spherical harmonic with index ℓ transforms as (-1)ℓ the polar class of perturbations transform under parity in the same way, as (-1)ℓ, and the axial perturbations as (-1)ℓ+1Footnote 1. Finally, since we are dealing with spherically symmetric spacetimes the solution will be independent of m, thus this subscript can be omitted.
The radial component of a perturbation outside the event horizon satisfies the following wave equation,
where r* is the “tortoise” radial coordinate defined by
and M is the mass of the black hole.
For “axial” perturbations
is the effective potential or (as it is known in the literature) Regge-Wheeler potential [173], which is a single potential barrier with a peak around r = 3M, which is the location of the unstable photon orbit. The form (23) is true even if we consider scalar or electromagnetic test fields as perturbations. The parameter σ takes the values 1 for scalar perturbations, 0 for electromagnetic perturbations, and -3 for gravitational perturbations and can be expressed as σ = 1-s2, where s = 0, 1, 2 is the spin of the perturbing field.
For “polar” perturbations the effective potential was derived by Zerilli [212] and has the form
where
Chandrasekhar [54] has shown that one can transform the equation (21) for “axial” modes to the corresponding one for “polar” modes via a transformation involving differential operations. It can also be shown that both forms are connected to the Bardeen-Press [38] perturbation equation derived via the Newman-Penrose formalism. The potential Vℓ(r*) decays exponentially near the horizon, r* → -∞, and as r -2* for r* → +∞.
From the form of equation (21) it is evident that the study of black hole perturbations will follow the footsteps of the theory outlined in section 2.
Kay and Wald [117] have shown that solutions with data of compact support are bounded. Hence we know that the time independent Green function G(s, r*, r ′* ) is analytic for Re(s) > 0. The essential difficulty is now to obtain the solutions f± (cf. equation (10)) of the equation
(prime denotes differentiation with respect to r*) which satisfy for real, positive s:
To determine the quasi-normal modes we need the analytic continuations of these functions.
As the horizon (r* → ∞) is a regular singular point of (26), a representation of f-(r*, s) as a converging series exists. For \(M = \frac{1}{2}\) it reads:
The series converges for all complex s and |r - 1| < 1 [162]. (The analytic extension of f- is investigated in [115].) The result is that f- has an extension to the complex s plane with poles only at negative real integers. The representation of f+ is more complicated: Because infinity is a singular point no power series expansion like (28) exists. A representation coming from the iteration of the defining integral equation is given by Jensen and Candelas [115], see also [159]. It turns out that the continuation of f+ has a branch cut Re(s) ≤ 0 due to the decay r-2 for large r [115].
The most extensive mathematical investigation of quasi-normal modes of the Schwarzschild solution is contained in the paper by Bachelot and Motet-Bachelot [35]. Here the existence of an infinite number of quasi-normal modes is demonstrated. Truncating the potential (23) to make it of compact support leads to the estimate (16).
The decay of solutions in time is not exponential because of the weak decay of the potential for large r. At late times, the quasi-normal oscillations are swamped by the radiative tail [166, 167]. This tail radiation is of interest in its own right since it originates on the background spacetime. The first authoritative study of nearly spherical collapse, exhibiting radiative tails, was performed by Price [166, 167].
Studying the behavior of a massless scalar field propagating on a fixed Schwarzschild background, he showed that the field dies off with the power-law tail,
at late times, where P = 1 if the field is initially static, and P = 2 otherwise. This behavior has been seen in various calculations, for example the gravitational collapse simulations by Cunningham, Price and Moncrief [66, 67, 68]. Today it is apparent in any simulation involving evolutions of various fields on a black hole background including Schwarzschild, Reissner-Nordström [106], and Kerr [132, 133]. It has also been observed in simulations of axial oscillations of neutron stars [18], and should also be present for polar oscillations. Leaver [136] has studied in detail these tails and associated this power low tail with the branch-cut integral along the negative imaginary ω axis in the complex ω plane. His suggestion that there will be radiative tails observable at \({{\mathcal J}^ + }\) and \({{\mathcal H}^ + }\) has been verified by Gundlach, Price, and Pullin [106]. Similar results were arrived at recently by Ching et al. [62] in a more extensive study of the late time behavior. In a nonlinear study Gundlach, Price, and Pullin [107] have shown that tails develop even when the collapsing field fails to produce a black hole. Finally, for a study of tails in the presence of a cosmological constant refer to [49], while for a recent study, using analytic methods, of the late-time tails of linear scalar fields outside Schwarzschild and Kerr black holes refer to [36, 37].
Using the properties of the waves at the horizon and infinity given in equation (27) one can search for the quasi-normal mode frequencies since practically the whole problem has been reduced to a boundary value problem with s = iω being the complex eigenvalue. The procedure and techniques used to solve the problem will be discussed later in section 6, but it is worth mentioning here a simple approach to calculate the QNM frequencies proposed by Schutz and Will [180]. The approach is based on the standard WKB treatment of wave scattering on the peak of the potential barrier, and it can be easily shown that the complex frequency can be estimated from the relation
where r0 is the peak of the potential barrier. For ℓ =2 and n = 0 (the fundamental mode) the complex frequency is Mω ≈ (0.37, -0.09), which for a 10M⊙ black hole corresponds to a frequency of 1 .2 kHz and damping time of 0.55 ms. A few more QNM frequencies for ℓ = 2, 3 and 4 are listed in table 1.
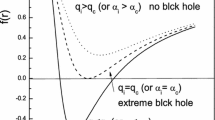
Figure 2 shows some of the modes of the Schwarzschild black hole. The number of modes for each harmonic index ℓ is infinite, as was mathematically proven by Bachelot and Motet-Bachelot [35]. This was also implied in an earlier work by Ferrari and Mashhoon [85], and it has been seen in the numerical calculations in [25, 157]. It can be also seen that the imaginary part of the frequency grows very quickly. This means that the higher modes do not contribute significantly in the emitted gravitational wave signal, and this is also true for the higher ℓ modes (octapole etc.). As is apparent in figure 2 that there is a special purely imaginary QNM frequency. The existence of “algebraically special” solutions for perturbations of Schwarzschild, Reissner-Nordström and Kerr black holes were first pointed out by Chandrasekhar [57]. It is still questionable whether these frequencies should be considered as QNMs [137] and there is a suggestion that the potential might become transparent for these frequencies [11]. For a more detailed discussion refer to [144].
The spectrum of QNM for a Schwarzschild black-hole, for ℓ = 2 (diamonds) and ℓ = 3 (crosses) [25]. The 9th mode for ℓ = 2 and the 41st for ℓ = 3 are “special”, i.e. the real part of the frequency is zero (s = iω).
As a final comment we should mention that as the order of the modes increases the real part of the frequency remains constant, while the imaginary part increases proportionally to the order of the mode. Nollert [157] derived the following approximate formula for the asymptotic behavior of QNMs of a Schwarzschild black hole,
where γ1 = 0.343, 0.7545 and 2.81 for ℓ = 2, 3 and 6, correspondingly, and n → ∞. The above relation was later verified in [10] and [143].
For large values of ℓ the distribution of QNMs is given by [164, 86, 85, 113]
For a mathematical proof refer to [39].
The perturbations of Reissner-Nordström black holes, due to the spherical symmetry of the solution, follow the footsteps of the analysis that we have presented in this section. Most of the work was done during the seventies by Zerilli [213], Moncrief [153, 154] and later by Chandrasekhar and Xanthopoulos [55, 209]. For an extensive discussion refer to [56]. We have again wave equations of the form (21), one for each parity with potentials which are like (23) and (24) plus extra terms which relate to the charge of the black hole. An interesting feature of the charged black holes is that any perturbation of the gravitational (electromagnetic) field will also induce electromagnetic (gravitational) perturbations. In other words, any perturbation of the Reissner-Nordström spacetime will produce both electromagnetic and gravitational radiation. Again it has been shown that the solutions for the odd parity oscillations can be deduced from the solutions for even parity oscillations and vice versa [55]. The QNM frequencies of the Reissner-Nordström black hole have been calculated by Gunter [108], Kokkotas, and Schutz [129], Leaver [137], Andersson [9], and lately for the nearly extreme case by Andersson and Onozawa [26].
3.2 Kerr Black Holes
The Kerr metric represents an axisymmetric, black hole solution to the source free Einstein equations. The metric in (t, r, θ, φ) coordinates is
with
M is the mass and 0 ≤ a ≤ M the rotational parameter of the Kerr metric. The zeros of Δ are
and determine the horizons. For r+ ≤ r < ∞ the spacetime admits locally a timelike Killing vector. In the ergosphere region
the Killing vector ∂/∂t which is timelike at infinity, becomes spacelike. The scalar wave equation for the Kerr metric is
where σ = 0, ±1, ±2 for scalar, electromagnetic or gravitational perturbations, respectively. As the Kerr metric outside the horizon (r > r+) is globally hyperbolic, the Cauchy problem for the scalar wave equation (37) is well posed for data on any Cauchy surface. However, the coefficient of ∂2χ/∂φ2 becomes negative in the ergosphere. This implies that the time independent equation we obtain after the Fourier or Laplace transformation is not elliptic!
For linear hyperbolic equations with time independent coefficients, we know that solutions determined by data with compact support are bounded by ceγt, where γ is independent of the data. It is not known whether all such solutions are bounded in time, i.e. whether they are stable.
Assuming harmonic time behavior χ = eiωt̂χ(r, θ, φ), a separation in angular and radial variables was found by Teukolsky [196]:
Note that in contrast to the case of spherical harmonics, the separation is ω-independent. To be a solution of the wave equation (37), the functions R and S must satisfy
where K = (r2 + a2)ω + am, λ = E + a2ω2 + 2amω - σ (σ + 1), and E is the separation constant.
For each complex a2ω2 and positive integer m, equation (39) together with the boundary conditions of regularity at the axis, determines a singular Sturm-Liouville eigenvalue problem. It has solutions for eigenvalues E(ℓ, m2, a2ω2), |m| ≤ ℓ. The eigenfunctions are the spheroidal (oblate) harmonics Sℓ|m|(θ). They exist for all complex ω2. For real ω2 the spheroidal harmonics are complete in the sense that any function of z = cos θ, absolutely integrable over the interval [-1, 1], can be expanded into spheroidal harmonics of fixed m [181]. Furthermore, functions A(θ, φ) absolutely integrable over the sphere can be expanded into
For general complex ω2 such an expansion is not possible. There is a countable number of “exceptional values” ω2 where no such expansion exists [148].
Let us pick one such solution Sℓ|m|(θ, ω) and consider some solutions R(r, ω) of (40) with the corresponding E(ℓ, |m|, ω). Then Rℓ|m|(r, ω)Sℓ|m|eimφe-iωt is a solution of (37). Is it possible to obtain “all” solutions by summing over ℓ, m and integrating over ω? For a solution in spacetime for which a Fourier transform in time exists at any space point (square integrable in time), we can expand the Fourier transform in spheroidal harmonics because ω is real. The coefficient R(r, ω, m) will solve equation (40). Unfortunately, we only know that a solution determined by data of compact support is exponentially bounded. Hence we can only perform a Laplace transformation.
We proceed therefore as in section 2. Let ̂χ(s, r, θ, φ) be the Laplace transform of a solution determined by data χ(t, r, θ, φ) = 0 and ∂tχ(t, r, θ, φ) = ρ, while χ is analytic in s for real s > γ ≥ 0, and has an analytic continuation onto the half-plane Re(s) ≥ γ. For real s we can expand ̂χ into a converging sum of spheroidal harmonics [148]
R(ℓ, m, s) satisfies the radial equation (9) with iω = s. This representation of ̂χ does, however, not hold for all complex values in the half-plane on which it is defined. Nevertheless is it true that for all values of s which are not exceptional an expansion of the form (42) existsFootnote 2.
To define quasi-normal modes we first have to define the correct Green function of (40) which determines R(ℓ, m, s) from the data ρ. As usual, this is done by prescribing decay for real s for two linearly independent solutions ±R(ℓ, m, s) and analytic continuation. Out of the Green function for R(ℓ, m, s) and Sℓ|m|(-s2, θ) for real s we can build the Green function G(s, r, r′, θ, θ′, ϕ, ϕ′) by a series representation like (42). Analytic continuation defines G on the half plane Re(s) > γ. For non exceptional s we have a series representation. (We must define G by this complicated procedure because the partial differential operator corresponding to (39), (40) is not elliptic in the ergosphere.)
Normal and quasi-normal modes appear as poles of the analytic continuation of G. Normal modes are determined by poles with Re(s) > 0 and quasi-normal modes by Re(s) < 0. Suppose all such values are different from the exceptional values. Then we have always the series expansion of the Green function near the poles and we see that they appear as poles of the radial Green function of R(ℓ, m, s).
To relate the modes to the asymptotic behavior in time we study the inverse Laplace transform and deform the integration path to include the contributions of the poles. The decay in time is dominated either by the normal mode with the largest (real) eigenfrequency or the quasi-normal mode with the largest negative real part.
It is apparent that the calculation of the QNM frequencies of the Kerr black hole is more involved than the Schwarzschild and Reissner-Nordström cases. This is the reason that there have only been a few attempts [135, 185, 123, 160] in this direction.
The quasi-normal mode frequencies of the Kerr-Newman black hole have not yet been calculated, although they are more general than all other types of perturbation. The reason is the complexity of the perturbation equations and, in particular, their non-separability. This can be understood through the following analysis of the perturbation procedure. The equations governing a perturbing massless field of spin σ can be written as a set of 2σ + 1 wavelike equations in which the various different helicity components of the perturbing field are coupled not only with each other but also with the curvature of the background space, all with four independent variables as coordinates over the manifold. The standard problem is to decouple the 2σ + 1 equations or at least some physically important subset of them and then to separate the decoupled equations so as to obtain ordinary differential equations which can be handled by one of the previously stated methods. For a discussion and estimation of the QNM frequencies in a restrictive case refer to [124].
3.3 Stability and Completeness of Quasi-Normal Modes
From the normal modes one can learn a lot about stability. Take as an example linear stellar oscillation within the framework of Newton’s theory of gravity. As outlined at the beginning of section 2, we have a sequence of normal modes ωn with ω2 real. The general solution is a convergent linear combination of the corresponding eigenfunctions. Hence all eigenfunctions are bounded if ω is purely imaginary, i.e. ω2 < 0.
Therefore the spectrum contains all the information about stability. To discuss stability for systems with quasi-normal modes, let us consider a case like equation (5) with the assumption that V is of compact support but not necessarily positive.
Data of compact support define solutions which grow at most exponentially in time
where a is independent of the data. As outlined in appendix 9, eigenvalues necessarily have sn > 0 and the eigenfunctions determine solutions growing exponentially in time. If no eigenvalues exist, the solution can not grow exponentially. Polynomial growth is still possible and related to the properties of the Laplace transform of the Green function at s = 0. As the potential has compact support, the functions f±(s, x) are analytic for all s. Hence, the Green function can at most have a pole at s = 0. A pole of order two and higher implies polynomial growth in time. If the potential is positive, energy conservation shows that the field can grow at most linearly in time and therefore we can have at most a pole of order 2 at s = 0.
If we define stability as boundedness in time for all solutions with data of compact support, properties of quasi-normal modes can not decide the stability issue. However, the appearance of a normal mode proves instability. If the support of the potential is not compact everything becomes more complicated. In particular, it is a non trivial problem to obtain the behavior of the Green function at s = 0.
In the case of the Schwarzschild black hole, stability is demonstrated by Kay and Wald [117] who showed the boundedness of all solutions with data of compact support.
The issue is more subtle for Kerr. There is a conserved energy, but because of the ergoregion its integrand is not positive definite, hence the conserved energy could be finite while the field still might grow exponentially in parts of the spacetime. Papers by Press and Teukolsky [165], Hartle and Wilkins [109], and Stewart [193] try to exclude the existence of an exponentially growing normal mode. Their work makes the stability very plausible but is not as conclusive as the Wald-Kay result. However this is a delicate issue as we see if, for example, we multiply the Regge-Wheeler potential by a factor ∊: For any ∊ > 0 we obtain an infinite number of QNMs, for ∊ = 0, however there is no QNM! Whiting [208] has proven that there are no exponentially growing modes, and in his proof he showed that the growth of the modes is at most linear. Recent numerical evolution calculations [132, 133] for slowly and fast rotating Kerr black holes pick up all the expected features (QNM ringing, tails) and show no sign of exponential growth. It should be noted that the massive scalar perturbations of Kerr are known to be unstable [72, 214, 77]. These unstable modes are known to be very slowly growing (with growth times similar to the age of universe).
Let us finally turn to the “completeness of QNMs”. A general mathematical theorem (spectral theorem) implies that for systems like strings or membranes the general solution can be expanded into a converging sum of normal modes. A similar result can not be expected for QNMs, the reasons are given in section 2. There is, however, the possibility that an infinite sum of the form (15) will be a representation of a solution for late times. This property has been shown by Beyer [42] for the Pöschl-Teller potential which has a similar form as the potential on Schwarzschild (23). The main difference is its exponential decay at both ends. In [158] Nollert and Price propose a definition of completeness and show its adequateness for a particular model problem. There are also systematic studies [63] about the relation between the structure of the QNM’s of the Klein-Gordon equation and the form of the potential. In these studies there is a discussion on both the requirements for QNMs to form a complete set and the definition of completeness.
4 Quasi-Normal Modes of Relativistic Stars
Pulsating stars are important sources of information for astrophysics. Nearly every star undergoes some kind of pulsation during its evolution from the early stages of formation until the very late stages, usually the catastrophic creation of a compact object (white dwarf, neutron star or black hole). Pulsations of supercompact objects are of great importance for relativistic astrophysics since these pulsations are accompanied by the emission of gravitational radiation. Neutron star oscillations were also proposed to explain the quasi-periodic variability found in radio-pulsar and X-ray burster signals [206, 146]. In this chapter we shall discuss various features of neutron star non-radial pulsations i.e. the various modes of pulsation, mode excitation, detection probability and the possibility to extract information (to estimate, for example, the radius, mass and stellar equation of state) from the detection of the associated gravitational waves. It is not in our plans to discuss rotating relativistic stars; the interested reader should refer to another review in this journal [192]. Radial oscillations are also not discussed since they are not interesting for gravitational wave research.
4.1 Stellar Pulsations: The Theoretical Minimum
For the study of stellar oscillations we shall consider a spherically symmetric and static spacetime which can be described by the Schwarzschild solution outside the star, see equation (17). Inside the star, assuming that the stellar material is behaving like an ideal fluid, we define the energy momentum tensor
where p(r) is the pressure, ρ(r) is the total energy density. Then from the conservation of the energy-momentum and the condition for hydrostatic equilibrium we can derive the Tolman-Oppenheimer-Volkov (TOV) equations for the interior of a spherically symmetric star in equilibrium. Specifically,
and the “mass inside radius r” is represented by
This means that the total mass of the star is M = m(R), with R being the star’s radius. To determine a stellar model we must solve
where
These equations should of course, be supplemented with an equation of state p = p(ρ, …) as input. Usually is sufficient to use a one-parameter equation of state to model neutron stars, since the typical thermal energies are much smaller than the Fermi energy. The polytropic equation of state p = Kρ1+1/N where K is the polytropic constant and N the polytropic exponent, is used in most of the studies. The existence of a unique global solution of the Einstein equations for a given equation of state and a given value of the central density has been proven by Rendall and Schmidt [174].
If we assume a small variation in the fluid or/and in the spacetime we must deal with the perturbed Einstein equations
and the variation of the fluid equations of motion
while the perturbed metric will be given by equation (18).
Following the procedure of the previous section one can decompose the perturbation equations into spherical harmonics. This decomposition leads to two classes of oscillations according to the parity of the harmonics (exactly as for the black hole case). The first ones called even (or spheroidal, or polar) produce spheroidal deformations on the fluid, while the second are the odd (or toroidal, or axial) which produce toroidal deformations.
For the polar case one can use certain combinations of the metric perturbations as unknowns, and the linearized field equations inside the star will be equivalent to the following system of three wave equations for unknowns S, F, H:
and the constraint
The linear functions Li, (i = 1, 2, 3, 4) depend on the background model and their explicit form can be found in [118, 5]. The functions S and F correspond to the perturbations of the spacetime while the function H is proportional to the density perturbation and is only defined on the background star. With cs we define the speed of sound and with a prime we denote differentiation with respect to r*:
Outside the star there are only perturbations of the spacetime. These are described by a single wave equation, the Zerilli equation mentioned in the previous section, see equations (21) and (24). In [118] it was shown that (for background stars whose boundary density is positive) the above system — together with the geometrical transition conditions at the boundary of the star and regularity conditions at the center — admits a well posed Cauchy problem. The constraint is preserved under the evolution. We see that two variables propagate along light characteristics and the density H propagates with the sound velocity of the background star.
It is possible to eliminate the constraint — first done by Moncrief [152] — if one solves the constraint (54) for H and puts the corresponding expression into L2. (The characteristics for F change then to sound characteristics inside the star and light characteristics outside.) This way one has just to solve two coupled wave equations for S and F with unconstrained data, and to calculate H using the constraint from the solution of the two wave equations. Again the explicit form of the equation can be found in [5].
Turning next to quasi-normal modes in the spirit of section 2, we can Laplace transform the two wave equations and obtain a system of ordinary differential equations which is of fourth order. The Green function can be constructed from solutions of the homogeneous equations (having the appropriate behavior at the center and infinity) and its analytic continuation may have poles defining the quasi-normal mode frequencies.
From the form of the above equations one can easily see two limiting cases. Let us first assume that the gravitational field is very weak. Then equation (51) and (52) can be omitted (actually S → 0 in the weak field limit [200, 5]) and we find that one equation is enough to describe (with acceptable accuracy) the oscillations of the fluid. This approach is known as the Cowling approximation [64]. Inversely, we can assume that the coupling between the two equations (51) and (52) describing the spacetime perturbations with the equation (53) is weak and consequently derive all the features of the spacetime perturbations from only the two of them. This is what is called the “inverse Cowling approximation” (ICA) [22].
For the axial case the perturbations reduce to a single wave equation for the spacetime perturbations which describes toroidal deformations
where X ∼ hrϕ. Outside the star, pressure and density are zero and this equation is reduced to the Regge-Wheeler equation, see equations (21) and (24). In Newtonian theory, if the star is non-rotating and the static model is a perfect fluid (i.e. shear stresses are absent), the axial oscillations are a trivial solution of zero frequency to the perturbation equations and the variations of pressure and density are zero. Nevertheless, the variation of the velocity field is not zero and produces non-oscillatory eddy motions. This means that there are no oscillatory velocity fields. In the relativistic case the picture is identical [202] nevertheless; in this case there are still QNMs, the ones that we will describe later as “spacetime or w-modes” [125].
When the star is set in slow rotation then the axial modes are no longer degenerate, but instead a new family of modes emerges, the so-called r-modes. An interesting property of these modes that has been pointed out by Anders-son [14, 94] is that these modes are generically unstable due the Chandrasekhar-Friedman-Schutz instability [53, 95] and furthermore it has been shown [23, 142] that these modes can potentially restrict the rotation period of newly formed neutron stars and also that they can radiate away detectable amounts of gravitational radiation [161]. The equations describing the perturbations of slowly rotating relativistic stars have been derived by Kojima [120, 121], and Chandrasekhar and Ferrari [61].
4.2 Mode Analysis
The study of stellar oscillations in a general relativistic context already has a history of 30 years. Nevertheless, recent results have shown remarkable features which had previously been overlooked.
Until recently most studies treated the stellar oscillations in a nearly Newtonian manner, thus practically ignoring the dynamical properties of the space-time [202, 198, 171, 199, 200, 141, 147, 79, 146]. The spacetime was used as the medium upon which the gravitational waves, produced by the oscillating star, propagate. In this way all the families of modes known from Newtonian theory were found for relativistic stars while in addition the damping times due to gravitational radiation were calculated.
Inspired by a simple but instructive model [128], Kokkotas and Schutz showed the existence of a new family of modes: the w-modes [130]. These are spacetime modes and their properties, although different, are closer to the black hole QNMs than to the standard fluid stellar modes. The main characteristics of the w-modes are high frequencies accompanied with very rapid damping. Furthermore, these modes hardly excite any fluid motion. The existence of these modes has been verified by subsequent work [138, 21]; a part of the spectrum was found earlier by Kojima [119] and it has been shown that they exist also for odd parity (axial) oscillations [125]. Moreover, sub-families of w-modes have been found for both the polar and axial oscillations i.e. the interface modes found by Leins et al. [138] (see also [17]), and the trapped modes found by Chandrasekhar and Ferrari [60] (see also [125, 122, 17]). Recently, it has been proven that one can reveal all the properties of the w-modes even if one “freezes” the fluid oscillations (Inverse Cowling Approximation) [22]. In the rest of this section we shall describe the features of both families of oscillation modes, fluid and spacetime, for the case ℓ = 2.
4.2.1 Families of Fluid Modes
For non-rotating stars the fluid modes exist only for polar oscillations. Here we will describe the properties of the most important modes for gravitational mode frequency damping time wave emission. These are the fundamental, the pressure and the gravity modes; this division has been done in a phenomenological way by Cowling [64]. For an extensive discussion of other families of fluid modes we refer the reader to [98, 99] and [147, 146]. Tables of frequencies and damping times of neutron star oscillations for twelve equations of state can be found in a recent work [19] which verifies and extends earlier work [141]. In Table 2 we show characteristic frequencies and damping times of various QNM modes for a typical neutron star.
-
The f-mode (fundamental) is a stable mode which exists only for non-radial oscillations. The frequency is proportional to the mean density of the star and it is nearly independent of the details of the stellar structure. An exact formula for the frequency can be derived for Newtonian uniform density stars
$${\omega ^2} = \frac{{2\ell (\ell - 1)}}{{2\ell + 1}}\frac{M}{{{R^3}}}.$$((57))This relation is approximately correct also for the relativistic case [17] (see also the discussion in section 5.4). The f-mode eigenfunctions have no nodes inside the star, and they grow towards the surface. A typical neutron star has an f-mode with a frequency of 1.5 – 3 kHz and the damping time of this oscillation is less than a second (0.1 – 0.5 sec). Detailed data for the frequencies and damping times (due to gravitational radiation) of the f-mode for various equations of state can be found in [141, 19]. Estimates for the damping times due to viscosity can be found in [69, 71].
-
The p-modes (pressure or acoustic) exist for both radial and non-radial oscillations. There are infinitely many of them. The pressure is the restoring force and it experiences substantial fluctuations when these modes are excited. Usually, the radial component of the fluid displacement vector is significantly larger than the tangential component. The oscillations are thus nearly radial. The frequencies depend on the travel time of an acoustic wave across the star. For a neutron star the frequencies are typically higher than 4 – 7 kHz (p1-mode) and the damping times for the first few p-modes are of the order of a few seconds. Their frequencies and damping times increase with the order of the mode. Detailed data for the frequencies and damping times (due to gravitational radiation) of the p1-mode for various equations of state can be found in [19].
-
The g-modes (gravity) arise because gravity tends to smooth out material inhomogeneities along equipotential level-surfaces and buoyancy is the restoring force. The changes in the pressure are very small along the star. Usually, the tangential components of the fluid displacement vector are dominant in the fluid motion. The g-modes require a non-zero Schwarzschild discriminant in order to have non-zero frequency, and if they exist there are infinitely many of them. If the perturbation is stable to convection, the g-modes will be stable (ω2 > 0); if unstable to convection the g-modes are unstable (ω2 < 0); and if marginally stable to convection, the g-mode frequency vanishes. For typical neutron stars they have frequencies smaller than a hundred Hz (the frequency decreases with the order of the mode), and they usually damp out in time much longer than a few days or even years. For an extensive discussion about g-modes in relativistic stars refer to [87, 88]; and for a study of the instability of the g-modes of rotating stars to gravitational radiation reaction refer to [134].
-
The r-modes (rotational) in a non-rotating star are purely toroidal (axial) modes with vanishing frequency. In a rotating star, the displacement vector acquires spheroidal components and the frequency in the rotating frame, to first order in the rotational frequency Ω of the star, becomes
$${\omega _r} = \frac{{2m\Omega }}{{\ell (\ell + 1)}}.$$((58))
An inertial observer measures a frequency of
From (58) and (59) it can be deduced that a counter-rotating (with respect to the star, as defined in the co-rotating frame) r-mode appears as co-rotating with the star to a distant inertial observer. Thus, all r-modes with ℓ-mode ≥ 2 are generically unstable to the emission of gravitational radiation, due to the Chandrasekhar-Friedman-Schutz (CFS) mechanism [53, 95]. The instability is active as long as its growth-time is shorter than the damping-time due to the viscosity of neutron star matter. Its effect is to slow down, within a year, a rapidly rotating neutron star to slow rotation rates and this explains why only slowly rotating pulsars are associated with supernova remnants [23, 142, 131]. This suggests that the r-mode instability might not allow millisecond pulsars to be formed after an accretion induced collapse of a white dwarf [23]. It seems that millisecond pulsars can only be formed by the accretion induced spin-up of old, cold neutron stars. It is also possible that the gravitational radiation emitted due to this instability by a newly formed neutron star could be detectable by the advanced versions of the gravitational wave detectors presently under construction [161]. Recently, Andersson, Kokkotas and Stergioulas [24] have suggested that the r-instability might be responsible for stalling the neutron star spin-up in strongly accreting Low Mass X-ray Binaries (LMXBs). Additionally, they suggested that the gravitational waves from the neutron stars, in such LMXBs, rotating at the instability limit may well be detectable. This idea was also suggested by Bildsten [44] and studied in detail by Levin [139].
A graph which shows all the w-modes: curvature, trapped and interface both for axial and polar perturbations for a very compact uniform density star with M/R = 0.44. The black hole spectrum is also drawn for comparison. As the star becomes less compact the number of trapped modes decreases and for a typical neutron star (M/R = 0.2) they disappear. The Im(ω) = 1/damping of the curvature modes increases with decreasing compactness, and for a typical neutron star the first curvature mode nearly coincides with the fundamental black hole mode. The behavior of the interface modes changes slightly with the compactness. The similarity of the axial and polar spectra is apparent.
4.2.2 Families of Spacetime or w-Modes
The spectra of the three known families of w-modes are different but the spectrum of each family is similar both for polar and axial stellar oscillations. As we have mentioned earlier they are clearly modes of the spacetime and from numerical calculations appear to be stable.
-
The curvature modes are the standard w-modes [130]. They are the most important for astrophysical applications. They are clearly related to the spacetime curvature and exist for all relativistic stars. Their main characteristic is the rapid damping of the oscillations. The damping rate increases as the compactness of the star decreases: For nearly Newtonian stars (e.g. white dwarfs) these modes have not been calculated due to numerical instabilities in the various codes, but this case is of marginal importance due to the very fast damping that these modes will undergo. One of their main characteristics is the absence of significant fluid motion (this is a common feature for all families of w-modes). Numerical studies have indicated the existence of an infinite number of modes; model problems suggest this too [128, 40, 13]. For a typical neutron star the frequency of the first w-mode is around 5 – 12 kHz and increases with the order of the mode. Meanwhile, the typical damping time is of the order of a few tenths of a millisecond and decreases slowly with the order of the mode.
-
The trapped modes exist only for supercompact stars (R ≤ 3M) i.e. when the surface of the star is inside the peak of the gravitational field’s potential barrier [60, 125]. Practically, the first few curvature modes become trapped as the star becomes more and more compact, and even the f-mode shows similar behavior [122, 17]. The trapped modes, as with all the spacetime modes, do not induce any significant fluid motions and there are only a finite number of them (usually less than seven or so). The number of trapped modes increases as the potential well becomes deeper, i.e. with increasing compactness of the star. Their damping is quite slow since the gravitational waves have to penetrate the potential barrier. Their frequencies can be of the order of a few hundred Hz to a few kHz, while their damping times can be of the order of a few tenths of a second. In general no realistic equations of state are known that would allow the formation of a sufficiently compact star for the trapped modes to be relevant.
-
The interface modes [138] are extremely rapidly damped modes. It seems that there is only a finite number of such modes (2 – 3 modes only) [17], and they are in some ways similar to the modes for acoustic waves scattered off a hard sphere. They do not induce any significant fluid motion and their frequencies can be from 2 to 15 kHz for typical neutron stars while their damping times are of the order of less than a tenth of a millisecond.
4.3 Stability
The stability of radial oscillations for non-rotating stars in general relativity is well understood. Especially, the stability of static spherically symmetric stars can be determined by examining the mass-radius relation for a sequence of equilibrium stellar models, see for example Chapter 24 in [150]. The radial perturbations are described by a Sturm-Liouville second order equation with the frequency of the mode being the eigenvalue ω2, then for real ω the modes will be stable while for imaginary ω they will be unstable [52], see also Chapter 17.2 in [188].
The stability of the non-radially pulsating stars (Newtonian or relativistic) is determined by the Schwarzschild discriminant
where Γ1 is the star’s adiabatic index. This can be understood if we define the local buoyancy force f per unit volume acting on a fluid element displaced a small radial distance δr to be
where g is the local acceleration of gravity. When S is negative in some region the buoyancy force is positive and the star is unstable against convection, while when S is positive the buoyancy force is restoring and the star is stable against convection. Another way of discussing the stability is through the so-called Brunt-Väisälä frequency N2 = gS(r) which is the characteristic frequency of the local fluid oscillations. Following earlier discussions when N2 is positive, the fluid element undergoes oscillations, while when N2 is negative the fluid is locally unstable. In other words, in Newtonian theory stability to non-radial oscillations can be guaranteed only if S > 0 everywhere within the star [65]. In general relativity [78], this is a sufficient condition, and so if S > 0 the quasi-normal modes are stable. For an extensive discussion of stellar instabilities for both non-rotating and rotating stars (which are actually more interesting for the gravitational wave astronomy) refer to [177, 140, 192].
For completeness the same applies as outlined at the end of section 3.3. A model calculation of Price and Husain [168], however indicated that the nearly Newtonian quasi-normal modes might be a basis for the fluid perturbations. Further mathematical investigation is needed to clarify this issue.
5 Excitation and Detection of QNMs
A critical issue related to the discussions of the previous sections is the excitation of the QNMs. The truth is that, although the QNMs are predicted by our perturbation equations, it is not always clear which ones will be excited and under what initial conditions. As we have already mentioned in the introduction there is an excellent agreement between results obtained from perturbation theory and full nonlinear evolutions of Einstein equations for head-on collisions of two black holes. Still there is a degree of arbitrariness in the definition of initial data for other types of stellar or black hole perturbations. This due to the arbitrariness in specifying the gravitational wave content in the initial data.
The construction of acceptable initial data for the evolution of perturbation equations is not a trivial task. In order to specify astrophysically relevant initial data one should first solve the fully nonlinear 3-dimensional initial value problem for (say) a newly formed neutron star that settles down after core collapse or two colliding black holes or neutron stars. Afterwards, starting from the Cauchy data on the initial hypersurface, one can evolve forward in time with the linear equations of perturbation theory instead of the full nonlinear equations. Then most of the long-time evolution problems of numerical relativity (throat stretching when black holes form, numerical instabilities or effects due to the approximate outer boundary conditions) are avoided. Additionally, the interpretations of the computed fields in terms of radiation is immediate [2]. This scheme has been used by Price and Pullin [170] and Abrahams and Cook [1] with great success for head-on colliding black holes. The success was based on the fact that the bulk of the radiation is generated only in the very strong-field interactions around the time of horizon formation and the radiation generation in the early dynamics can be practically ignored (see also the discussion in [3]). The extension of this scheme to other cases, like neutron star collisions or supernovae collapse, is not trivial. But if one can define even numerical data on the initial hypersurface then the perturbation method will be probably enough or at least a very good test for the reliability of fully numerical evolutions. For a recent attempt towards applying the above techniques in colliding neutron stars see [6, 20].
Before going into details we would like to point out an important issue, namely the effect of the potential barrier on the QNMs of black holes. That is, for any set of initial data that one can impose, the QNMs will critically depend on the shape of the potential barrier, and this is the reason that the close limit approximation of the two black-hole collision used by Price and Pullin [170] was so successful, because whatever initial data you provide inside the r < 3M region (the peak of the potential barrier is around 3M) the barrier will “filter” them and an outside observer will observe only the QNM ringing (see for example recent studies by Allen, Camarda and Seidel [7]). This point of view is complementary to the discussion earlier in this section, since roughly speaking even before the creation of the final black hole the common potential barrier has been created and anything that was to be radiated had to be “filtered” by this common barrier.
5.1 Studies of Black Hole QNM Excitation
In the study of QNMs of black holes the attention, in most cases, was focused on estimating the spectrum and its properties. But there is limited work in the direction of understanding what details of the perturbation determine the strength of the QNM ringing.
In 1977 Detweiler [76] discussed the resonant oscillations of a rotating black hole, and after identifying the QNMs as “resonance peaks” in the emitted spectrum he showed that the modes formally correspond to poles of a Green function to the inhomogeneous Teukolsky equation [197]. This idea has been extended in a more mathematically rigorous way by Leaver [136]. Leaver extracts the QNM contribution to the emitted radiation as a sum over residues. This sum arises when the inversion contour of the Laplace transform, which was used to separate the dependence on the spatial variables from the time dependence, is deformed analytically in the complex frequency plane. In this way the contribution from the QNM can be accounted for. Sun and Price [194, 195] discussed in detail the way that QNM are excited by given Cauchy data based to some extent on numerical results obtained by Leaver [136]. Lately, Andersson [12] used the phase-integral method to determine some characteristics of the QNM excitation.
5.2 Studies of Stellar QNM Excitation
The discussion in the previous sections has shown that we have an acceptable knowledge of stellar pulsations and that we can extract information from the detection of such oscillations. But as was clear from the discussion earlier in this section, the energy released as gravitational radiation during the stellar collapse is basically unknown. Additionally, it is not known how the energy is distributed in the various fluid and spacetime modes. Both uncertainties depend strongly on the details of gravitational collapse, or in general the mechanism that excites the modes. Unless full 3D general relativistic codes are generated for the gravitational collapse or the final stages of binary coalescence we will never be able to give definite answers to the above questions. In the meantime, perturbation theory is a reliable way to get some first hints and indications. A survey of the literature reveals several indications that the pulsation modes are present in the gravitational wave signals from coalescing stars. Waveforms obtained by Nakamura and Oohara [155] show clear mode presence. Ruffert et al. [175] have also obtained gravitational wave signals from coalescing stars that show late-time oscillations. Their waveforms and spectra show oscillations at frequencies between 1.5 and 2 kHz.
The situation is similar for rotating core collapse. Most available studies use Newtonian hydrodynamics and account for gravitational wave emission through the quadrupole formula. The collapse of a non-rotating star is expected to bounce at nuclear densities, but if the star is rotating the collapse can also bounce at subnuclear densities because of the centrifugal force. In each case, the emerging gravitational waves are dominated by a burst associated with the bounce. But the waves that follow a centrifugal bounce can also show large amplitude oscillations that may be associated with pulsations in the collapsed core. Such results have been obtained by Mönchmeyer et al. [151]. Some of their models show the presence of modes with different angular dependence superimposed. Typically, these oscillations have a period of a few ms and damp out in 20 ms. The calculations also show that the energy in the higher multipoles is roughly three orders of magnitude smaller than that of the quadrupole. More recent simulations by Yamada and Sato [210] and Zwerger and Müller [215] also show post-bounce oscillations. The cited examples are encouraging, and it seems reasonable that besides the fluid modes the spacetime modes should also be excited in a generic case. To show that this is the case one must incorporate general relativity in the simulations of collapse and coalescence. As yet there have been few attempts to do this, but an interesting example is provided by the core collapse studies of Seidel et al. [187, 186, 182, 183]. They considered axial (odd parity) or polar (even parity) perturbations of a time-dependent background (that evolves according to a specified collapse scenario). The extracted gravitational waves are dominated by a sharp burst associated with the bounce at nuclear densities. But there are also features that may be related to the fluid and the w-modes. Especially for the axial case, since there are no axial fluid modes for a non-rotating star, it is plausible that this mode corresponds to one of the axial w-modes of the core. Furthermore, the power spectrum for one of the simulations discussed in [187] (cf. their Fig. 2) shows some enhancement around 7 kHz.
Recently, Andersson and Kokkotas [18] have studied the excitation of axial modes by sending gravitational wave pulses to hit the star (see figure 5). The results of this study are encouraging because they provide the first indication that the w-modes can be excited in a dynamical scenario. Similar results have recently been obtained by Borelli [48] for particles falling onto a neutron star. The excitation of the axial QNMs by test particles scattered by a neutron star have been recently studied in detail [203, 84, 27] and some interesting conclusions can be drawn. For example, that the degree of excitation depends on the details of the particle’s orbit, or that in the cases that we have strong excitation of the quadrapole oscillations there is a comparable excitation of higher multipole modes.
Time evolution of axial perturbations of a neutron star, here only axial w-modes are excited. It is apparent in panel D that the late time behavior is dominated by a time tail. In the left panels (A and C) the star is ultra compact (M/R = 0.44) and one can see not only the curvature modes but also the trapped modes which damp out much slower. The stellar model for the panels (B and D) is a typical neutron star (M/R = 0.2) and we can see only the first curvature mode being excited.
These results have prompted the study of an astrophysically more relevant problem, the excitation of even parity (or polar) stellar oscillations. In recent work Allen et al. [5] have studied the excitation of the polar modes using two sets of initial data. First, as previously for the axial case, they excited the modes by an incoming gravitational wave pulse. In the second case, the initial data described an initial deformation of both the fluid and the spacetime. In the first case the picture was similar to that of the axial modes i.e. the star was excited and emitted gravitational waves in both spacetime and the fluid modes. Nearly all of the energy was radiated away in the w-modes.
This should be expected since the incoming pulse does not have enough time to couple to the fluid (which has a much lower speed of propagation of information). The infalling gravitational waves are simply affected by the spacetime curvature associated with the star, and the outgoing radiation contains an unmistakable w-mode signature. In the second case one has considerable freedom in choosing the degree of initial excitation of the fluid and the spacetime. In the study the choice was some “plausible” initial data inspired by the treatment of the problem in the Newtonian limit. Then the energy emitted as gravitational waves was more evenly shared between the fluid and the spacetime modes, and one could see the f, p, and w modes in the signal. The characteristic signal was (as expected) a short burst (w-modes) followed by a slowly damped sinusoidal wave (fluid modes).
The previous picture emerged as well in a recent study in the close limit of head-on collision of two neutron stars [6]. There the excitation of both fluid and spacetime modes is apparent but most of the energy is radiated via the fluid modes. These new results show the importance of general relativity for the calculation of the energy emission in violent processes. Up to now the general way of calculating the energy emission has been the quadrupole formula. But this formula only accounts for the fluid deformations and motions, and as we have seen this accounts only for a part of the total energy.
5.3 Detection of the QNM Ringing
It is well known in astrophysics that many stars will end their lives with a violent supernova explosion. This will leave behind a compact object which will oscillate violently in the first few seconds. Huge amounts of gravitational radiation will be emitted and the initial oscillations will consequently damp out. The gravitational waves will carry away information about the compact object. If the supernova remnant is a black hole we will observe a short monochromatic burst lasting a few tenths of a millisecond (see figures 1 and 4). If it is a neutron star we will observe a more complicated signal which will be the overlapping of several frequencies (see figure 6). The stellar signal will consist of a short burst (similar to that from a black hole) followed by a long lasting sinusoidal wave. Supernovae are quite frequent, the expected event rate is 5.8 ± 2.4 events per century per galaxy [205]. The amount of energy emitted in such an event depends on the details of the collapse. A spherical collapse will not produce any gravitational waves at all, while as much as 10-3M⊙c2 [179] can be radiated away in a highly nonspherical one. The collapse releases an enormous amount of energy, at least equal to the binding energy of a neutron star, about 0.15M⊙c2. Most of this energy should be carried away by neutrinos, and this is supported by the neutrino observations at the time of supernova SN1987A. But even if only 1% of the energy released in neutrinos is radiated in gravitational waves then the above number makes sense. The present numerical codes used to simulate collapse predict that the energy emitted as gravitational waves will be of the order of 10-4 – 10-7M⊙c2 [47]. However, most of these codes are based on Newtonian dynamics and the few fully general relativistic ones are not 3-dimensional. Modern computers are still not able to perform realistic simulations of gravitational collapse in 3D, including all the important nuclear reactions and neutrino and photon transport. For example, most of the codes fail to explain the high average pulsar velocity which is believed to be a result of a boost that the neutron star gets during the collapse due to anisotropy in the neutrino distribution [51].
Excitation of polar modes due to an initial deformation of the star. The initial burst which is dominated mainly by the first w-mode is followed by a sinusoidal waveform dominated by the f and the first p-mode. In the upper panel the actual waveform is shown, while in the lower panel is its power spectrum. The wide peak in the power spectrum corresponds to the w-mode, while the sharp peaks correspond to the various fluid modes.
Although collapse may be the most frequent source for excitation of black hole and stellar oscillations there are other situations in which significant pulsations take place. For example, after the merger of two coalescing black holes or neutron stars it is natural to expect that the final object will oscillate. Thus the well known waveform for inspiralling binaries [45] will be followed by a short, but not yet properly known, period (the merger phase) and will end with the characteristic quasi-normal signal (ringing) of the newly created neutron star or black hole. During the inspiralling phase the stellar oscillations can be excited by the tidal fields of the two stars [127]. A detailed description of the gravitational wave emission and detection from binary black hole coalescences can be found in two recent articles by Flanagan and Hughes [90, 91]. In the same way smaller bodies falling on a neutron star or black hole will excite oscillations. Stellar or black hole oscillations can also be excited by a close encounter with another compact object [203, 84, 27].
Another potential excitation mechanism for stellar pulsation is a starquake, e.g., associated with a pulsar glitch. The typical energy released in this process may be of the order of 10-10M⊙c2. This is an interesting possibility considering the recent discovery of so-called magnetars: Neutron stars with extreme magnetic fields [81]. These objects are sometimes seen as soft gamma-ray repeaters, and it has been suggested that the observed gamma rays are associated with starquakes. If this is the case, a fraction of the total energy could be released through nonradial oscillations in the star. As a consequence, a burst from a soft gamma-ray repeater may be associated with a gravitational wave signal.
Finally, a phase-transition could lead to a sudden contraction during which a considerable part of the stars gravitational binding energy would be released, and it seems inevitable that part of this energy would be channeled into pulsations of the remnant. Transformation of a neutron star into a strange star is likely to induce pulsations in a similar fashion.
One way of calibrating the sensitivity of detectors is to calculate the amplitude of the gravitational wave that would be produced if a certain fraction of the released energy were converted into gravitational waves. To obtain rough estimates for the typical gravitational wave amplitudes from a pulsating star we use the standard relation for the gravitational wave flux which is valid far away from the star [178]
where h is the gravitational wave amplitude and r the distance of the detector from the source. Combining this with
-
i)
dE/dt = E/2τ where τ is the damping time of the pulsation and E is the available energy,
-
ii)
the assumption that the signal is monochromatic (with frequency f), and
-
iii)
the knowledge that the effective amplitude achievable after matched filtering scales as the square root of the number of observed cycles, \({t_{{\rm{eff}}}} = h\sqrt n = h\sqrt {f\tau } \), we get the estimates [18, 19]
$${h_{{\rm{eff}}}} \sim 2.2 \times {10^{ - 21}}{\left( {\frac{E}{{{{10}^{ - 6}}{M_ \odot }{c^2}}}} \right)^{1/2}}{\left( {\frac{{2\;{\rm{kHz}}}}{{{f_{gw}}}}} \right)^{1/2}}\left( {\frac{{50\;{\rm{kpc}}}}{r}} \right)$$((63))for the f-mode, and
$${h_{{\rm{eff}}}} \sim 9.7 \times {10^{ - 22}}{\left( {\frac{E}{{{{10}^{ - 6}}{M_ \odot }{c^2}}}} \right)^{1/2}}{\left( {\frac{{10\;{\rm{kHz}}}}{{{f_{gw}}}}} \right)^{1/2}}\left( {\frac{{50\;{\rm{kpc}}}}{r}} \right)$$((64))for the fundamental w-mode.
Here we have used typical parameters for the pulsation modes, and the distance scale used is that to SN1987A. In this volume of space one would not expect to see more than one event per ten years or so. However, the assumption that the energy release in gravitational waves in a supernova is of the order of 10-6M⊙c2 is very conservative [179].
Similar relations can be found for black holes [178]:
for stellar black holes, and
for galactic black holes.
An important factor for the detection of gravitational waves are the pulsation mode frequencies. Existing resonant gravitational wave detectors, as well as laser interferometric ones which are under construction, are only sensitive in a certain bandwidth. The spherical and bar detectors are typically tuned to 0.6 – 3 kHz, while the interferometers are sensitive within 10 – 2000 Hz. The initial part of the QNM waveform, which carries away whatever deformation a collapse left in the spacetime, is expected to be for a neutron star in the frequency range of 5 – 12 kHz (w-mode). The subsequent part of the waveform is constructed from combination of the f- and p-modes. Still the present gravitational wave detectors are sensitive only in the frequencies of the f-mode. For a black hole the frequency will depend on the mass and rotation rateFootnote 3, thus for a 10 solar mass black hole the frequency of the signal will be around 1 kHz, around 100 Hz for a 100 M⊙ black hole and around 1 mHz for galactic black holes.
5.4 Parameter Estimation
For astronomy it is important not only to observe various astronomical phenomena but also to try to mine information from these observations. From the observations of solar and stellar oscillations (of normal stars) astronomers have managed to get details of the internal structure of stars. In our days the GONG program [110] for detailed observation of the solar seismology is well underway. This has suggested that, in a similar way, information about neutron star parameters (mass, radius), and internal structure or the mass and the rotation rate of black holes can be found, using the theory of QNMs. It will be instructive to briefly examine the case of oscillating black holes since they are much “cleaner” objects than stars. From the normal mode analysis of black hole oscillations we can get a spectrum which is related to the parameters of the black hole (mass M and angular momentum a). In particular, for the frequency of the first quasi-normal mode (which as we have stated previously is the most important one for the gravitational wave detection) the following approximate relations have been suggested [83, 89]:
These two relations can be inverted and thus from the “observed” frequency and the damping time we can derive the parameters of the oscillating black hole. In practice, the noise of the detector will contaminate the signal but still (depending on the signal to noise ratio) we will get a very accurate estimate of the black hole parameters. A similar set of empirical relations cannot be derived in the case of neutron star oscillations since the stars are not as “clean” as black holes, since more than one frequency contributes. Although we expect that most of the dynamical energy stored in the fluid oscillations will be radiated away in the f-mode, some of the p-modes may be excited as well and a significant amount of energy could be radiated away through these modes [5]. As far as the spacetime modes are concerned we expect that only the curvature modes (the standard w-modes) will be excited, but it is possible that the radiated energy can be shared between the first two w-modes [5]. Nevertheless, Andersson and Kokkotas [19], using the properties of the various families of modes (f, p, and w), managed to create a series of empirical relations which can provide quite accurate estimates of the mass, radius and equation of state of the oscillating star, if the f and the first w-mode can be observed. In figure 7 one can see an example of the relation between the stellar parameters and the frequencies of the f and the first w-mode for various equations of state and various stellar models. There it is apparent that the relation between the f-mode frequencies and the mean density is almost linear, and a linear fitting leads to the following simple relation:
We can also find the following relation for the frequency of the first w-mode:
The upper graph shows the numerically obtained f-mode frequencies plotted as functions of the mean stellar density. In the second graph the functional Rωω is plotted as a function of the compactness of the star (M and R are in km, ωf-mode and ωw-mode in kHz). The letters A, B, C, … correspond to different equations of state for which one can refer to [19].
From tests performed using polytropic stars to provide data for the above relations it was seen that these equations predict the masses and the radii of the polytropes usually with an error less than 10%. There is work underway towards extracting the parameters of the star from a noisy signal [126].
6 Numerical Techniques
For each candidate source of gravitational waves, gravitational wave astronomy needs answers to two questions. Firstly, how much energy will be carried away by the emitted gravitational waves? Secondly, which are the “preferred” frequencies at which a 10 M⊙ black hole or a neutron star will oscillate? The answer to the first question is that the energy will depend on the degree of asymmetry that the process generates, and it will depend critically on the initial data. In the previous section we have tried to provide some guesstimates for the energy emitted during the oscillation phase of black holes and neutron stars. The answer to the second question is related to the numerical solution of the perturbation equations. The numerical schemes developed for this purpose will be described in this section.
Let us describe why the numerical calculation of quasi-normal mode frequencies is delicate. Consider again the case treated in section 2 of the wave equation with a potential with compact support. We try to find a complex number s with negative real part such that the solution which is e-sx for large positive x, is esx for large negative x. Note that these solutions grow exponentially with |x| and therefore one has to be very careful to make sure that there is no exponentially decaying part in the solution. The situation becomes even more complicated if we do not know f± explicitly because one can not characterize the correct solution by some growth property. This is for example the case for the Schwarzschild solution.
6.1 Black Holes
We would like to point out here that the attempts to calculate the QNM frequencies date back to the beginning of 70s. More specifically in their study of the black hole oscillations excited by an infalling particle Davis et al. [73] found that the peak of the spectrum is (for a Schwarzschild black hole) at around Mω = 0.32 (geometrical units). This number is very close to the one calculated by much more accurate methods later. In what will follow we will describe the various methods used to calculate the QNM frequencies.
6.1.1 Evolving the Time Dependent Wave Equation
This approach was actually the first one used to study the QNM excitation by Vishveshwara [207] but it has only been recently revived thanks to increased power of computers. In general, one does not need to Fourier decompose the perturbed Einstein equations but instead evolve them for given sets of initial data and at the end to Fourier analyze the resulting waveform. This procedure has certain advantages since one does not need to be so careful in considering the appropriate boundary conditions on the horizon, at infinity, on the surface or at the center of the star. This does not mean that these boundaries are not important for the evolution schemes. The difference is that in the time independent case one formulates a boundary value problem, and the eigenvalues (quasi-normal frequencies) depend critically on the correct conditions on the various boundaries. A major disadvantage of the evolution schemes is that one cannot get the complete spectrum of the QNMs neither for a star nor for a black hole. The reason is that although any perturbation is the sum of the harmonics involved, in practice only a few of them will be observed and in the best case one can succeed in getting a few extra modes by “playing” around with the initial data.
To be more specific, by evolving a perturbation on a black hole background one can get a QNM signal as the one shown in figure 4, but in this signal the Fourier transform will show that there are present at most two frequencies (the slowest damped ones); then by doing “matched filtering” of this signal we will get the right frequencies and damping times, but then all the extra modes of the spectrum are missing! See for example the work by Bachelot and Motet-Bachelot [35, 34], and Krivan et al [132, 133]. This is true also for stars; in recent evolutions of axial perturbations of stellar backgrounds Andersson and Kokkotas [18] saw only a few of the w-modes (the ones that damped slowest), while in similar calculations for even parity stellar perturbations Allen et al. [5] have seen only the f-mode, 2 – p-modes and two of the w-modes.
Of course with more detailed studies for various sets of initial data one might be successful to get a few more modes, but more important than deriving extra modes is understanding the physical situation which generates the appropriate initial data.
Finally, the evolutions of the time dependent perturbation equations can be extremely useful (and probably will be the only way) for the calculation of the QNM frequencies and waveforms for the perturbations of the Kerr-Newman black hole and for slowly and fast rotating relativistic stars.
6.1.2 Integration of the Time Independent Wave Equation
This technique was used by Chandrasekhar and Detweiler [58] and is based on the definition of QNMs given in section 2. They assumed that a QNM is a solution corresponding to incoming waves on the horizon and outgoing at infinity. Then by taking a series expansion of the Zerilli wave equation (21, 23, 24) at both limits (horizon and infinity) of the form given by (27) they found initial values for the numerical integration of the equation. Their integration goes from both limits towards a common point which was set close to the peak of the potential i.e. around r = 3M. The values of ω for which the Wronskian of the two numerically taken solutions vanishes are the quasieigensolutions of the problem. In this way they managed to calculate the first 2 – 3 QNM frequencies of the Schwarzschild black hole for various harmonic indices. The accuracy of the method improves for increasing ℓ. Later, Gunter [118] and Kokkotas with Schutz [129] used the same approach to calculate the QNMs of the Reissner-Nordström black hole.
The approach used by Nollert and Schmidt [156, 159] is more elaborate and based on a better estimate of the values of the quasi-eigenfunctions on both boundaries (±∞); this leads to a more accurate estimate of frequencies and one also finds frequencies which damp extremely fast. Andersson [8] suggested an alternative integration scheme. The key idea is to separate ingoing and outgoing wave solutions by numerically calculating their analytic continuations to a place in the complex r-coordinate plane where they have comparable amplitudes. This method is extremely accurate.
6.1.3 WKB Methods
This technique, originally in the form suggested by Schutz and Will [180], based on elementary quantum mechanical arguments, was later developed into a powerful technique with which accurate results have been derived. The idea is that one can reduce the QNM problem into the standard WKB treatment of scattering of waves on the peak of the potential barrier. The simplest way to find the QNM frequencies is to use the well known Bohr-Sommerfeld (BS) rule. Using this rule it is possible to reproduce not only the Schutz-Will formula (30) but also to give a way to extend the accuracy of that formula by taking higher order terms [114, 105]. The classical form of the BS rule for equations like (21) is
where rA, rB are the two roots (turning points) of ω2 - V(r) = 0. A more general form can be found [82, 41] which is valid for complex potentials. This form can be extended to the complex r plane where the contour encircles the two turning points which are connected by a branch cut. In this way one can calculate the eigenfrequencies even in the case of complex potentials, as it is the case for Kerr black holes.
This method has been used for the calculation of the eigenfrequencies of the Schwarzschild [113], Reissner-Nordström [129], Kerr [185, 123] and Kerr-Newman [124] black holes (restricted case). In general with this approach one can calculate quite accurately the low-lying (relatively small imaginary part) QNM modes, but it fails to give accurate results for higher-order modes.
This WKB approach was improved considerably when the phase integral formalism of Fröman and Fröman [97] was introduced. In a series of papers [96, 25, 15, 32] the method was developed and a great number of even extremely fast damped QNMs of the Schwarzschild black hole have been calculated with a remarkable accuracy. The application of the method for the calculation of QNM frequencies of the Reissner-Nordström black hole [16] has considerably improved earlier results [129] for the QNMs which damp very fast. Close to the logic of this WKB approach were the attempts of Blome, Mashhoon and Ferrari [46, 86, 85] to calculate the QNM modes using an inversion of the black hole potential. Their method was not very accurate but stimulated future work using semianalytic methods for estimating QNMs.
6.1.4 The Method of Continued Fractions
In 1985, Leaver [135] presented a very accurate method for calculating the QNM frequencies. His method can be applied to the calculation of the QNMs of Schwarzschild, Kerr and, with some modifications, Reissner-Nordström black holes [137]. This method is very accurate also for the high-order modes.
His approach was analogous to the determination of the eigenvalues of the H+ ion developed in [33]. A series representation of the solution f- is assumed to represent also f+ for the value of the quasi-normal mode frequency. For normal modes the method may work because f+ is certainly bounded at infinity. In the case of quasi-normal modes this is not so clear because f+ grows exponentially. Nevertheless, the method works very well numerically and was improved by Nollert [157] such that he was able to calculate very high mode numbers (up to 100, 000!). In this way he obtained the asymptotic distributions of modes described in (31). An alternative way of using the recurrence relations was suggested in [145].
Nollert [156] explains in his PhD thesis why the method works. As initiated by Heisenberg et al. [111] he considers potentials depending analytically on a parameter λ such that for λ = 1 the potential has bound states — normal modes — and for for λ = 1 just quasi-normal modes. This is, for example, the case if we multiply the Regge-Wheeler potential (23) by -λ. Assuming that the modes depend continuously on λ, one can try to relate normal modes to quasi-normal modes and their methods of calculation.
In the case of QNMs of the Kerr black hole, one has to deal in practice with two coupled equations, one which governs the radial part (40) and another which governs the angular dependence of the perturbation (39). For both of them one can construct recurrence relations for the coefficients of the series expansion of their solutions, and through them calculate the QNM frequencies.
For the case of the QNMs of the Reissner-Nordström black hole, the asymptotic form of the solutions is similar to that shown in equation (28) but the coefficients an are determined via a four term recurrence relation. This means that the nice properties of convergence of the three term recurrence relations have been lost and one should treat the problem with great caution. Nevertheless, Leaver [137] has overcome this problem and showed how to calculate the QNMs for this case.
As a final comment on this excellent method we should point out that it has a disadvantage compared to the WKB based methods in that it is a purely numerical method and it cannot provide much intuition about the properties of the QNM spectrum.
6.2 Relativistic Stars
Although the perturbation equations in the exterior of a star are similar to those of the black-hole and the techniques described earlier can be applied here as well, special attention must be given to the interior of the star where the perturbation equations are more complicated.
For the time independent case the system of equations (51, 52, 53) inside the star reduces to a 4th order system of ODEs [79]. One can then even treat it as two coupled time independent wave equationsFootnote 4. The first equation will correspond to the fluid and the second equation will correspond to spacetime perturbations. In this way one can easily work in the Cowling approximation (ignore the spacetime perturbations) if the aim is the calculation of the QNM frequencies of the fluid modes (f, p, g, …) or the Inverse Cowling Approximation [22] (ignore the fluid perturbations) if the interest is in w-modes. The integration procedure inside the star is similar to those used for Newtonian stars and involves numerical integration of the equations from the center towards the surface in such a way that the perturbation functions are regular at the center of the star and the Lagrangian variation of the pressure is zero on the surface (for more details refer to [141, 130]). The integrations inside the star should provide the values of the perturbation functions on the surface of the star where one has to match them with the perturbations of the spacetime described by Zerilli’s equation (21, 23, 24).
In principle the integrations of the wave equation outside the star can be treated as in the case of the black holes. Leaver’s method of continued fraction has been used in [119, 138], Andersson’s technique of integration on the complex r plane was used in [21] while a simple but effective WKB approach was used by Kokkotas and Schutz [130, 211].
Finally, there are a number of additional approaches used in the past which improved our understanding of stellar oscillations in GR. In the following paragraphs they will be discussed briefly.
-
Resonance Approach. This method was developed by Thorne [199], the basic assumption being that there are no incoming or outgoing waves at infinity, but instead standing waves. Then by searching for resonances one can identify the QNM frequencies. The damping times can be estimated from the half-width of each resonance. This is a simple method and can be used for the calculations of the fluid QNMs. In a similar fashion Chandrasekhar and Ferrari [59] have calculated the QNM frequencies from the poles of the ratio of the amplitudes of the ingoing and outgoing waves.
-
Direct Numerical Integration. This method was used by Lindblom and Detweiler [141] for the calculation of the frequencies and damping times of the f-modes for various stellar models for thirteen different equations of state. In this case, after integration of the perturbation equations inside the star, one gets initial data for the integration of the Zerilli equation outside. The numerical integration is extended up to “infinity” (i.e. at a distance where the solutions of Zerilli equations become approximately simple sinusoidal ingoing and outgoing waves), where this solution is matched with the asymptotic solutions of the Zerilli equations which describe ingoing and outgoing waves. The QNM frequencies are the ones for which the amplitude of the incoming waves is zero. This method is more accurate than the previous one at least in the calculation of the damping times as has been verified in [19], but still is not appropriate for the calculation of the w-modes.
-
Variational Principle Approach. Detweiler and Ipser [78] derived a variational principle for non-radial pulsational modes. Associated with that variational principle is a conservation law for the pulsational energy in the star. The time rate of change of that pulsational energy, as given by the variational principle, is equal to minus the power carried off by gravitational waves. This method was used widely for calculating the f [74] and g-modes [87] and in studies of stability [78, 75].
-
WKB. This is a very simple method but quite accurate, and contrary to the previous three methods it can be used for the calculation of the QNM frequencies of the w-modes (this was the first method used for the derivation of these modes). In practice one substitutes the numerical solutions of the Zerilli equation with their approximate WKB solutions and identifies the QNM frequencies as the values of the frequency for which the amplitude of the incoming waves is zero [130, 211].
-
WKB-Numerical. This is a combination of direct integration of the Zerilli equation and the WKB method. The trick is that instead of integrating outwards, one integrates inwards (using initial data at infinity for the incoming wave solution); this procedure is numerically more stable than the outward integration. On the stellar surface one needs of course not the solution for incoming waves but the one for outgoing ones. But through WKB one can derive approximately the value of the outgoing wave solution from the value of the incoming wave solution. In this way errors are introduced, nevertheless the results are quite accurate [130].
7 Where Are We Going?
From the previous discussions we can draw some general conclusions and suggestions for future work. We believe that independent of the advancement of numerical relativity and computer power there remains much future work in perturbation theory, in particular parallel to the numerical relativity efforts.
7.1 Synergism Between Perturbation Theory and Numerical Relativity
Fifteen years ago with the advancements in computer power, we could not think that perturbation theory would continue to play such an important role in many problems. Today it is widely accepted that there is a need for the development of new approximation schemes to accompany large scale simulations. Fully relativistic computer simulations give only numerical answers to problems; often these answers do not provide physical understanding of which principles are important, or even what principles govern a given process. Even more, in some cases, simulation results can be simply incorrect or misleading. By closely coupling various perturbation schemes it is possible to interpret and confirm simulation results.
For example, during the late stages of black hole or stellar coalescence or supernovae collapse, the system settles down to a slightly perturbed black hole or neutron star. Numerical codes, evolving the full nonlinear Einstein equations, should be able to accurately compute the waveforms required for gravitational wave detection. Parallel to this, it should be possible to evolve the perturbations of both black holes and stars (governed by their own linear evolution equations) for the same set of initial data. This is an important check of the fully nonlinear codes. An excellent example is the head-on collision of two black holes. This sounds like an impossible task for perturbation theory but it can be achieved if the two black holes are close together and they can be considered as having already merged into a single perturbed black hole (close limit); see more details in a recent review by Pullin [172]. Much work has already been performed for head-on collisions of two non-rotating black holes but the more realistic problem for the inspiral collision of rotating black holes is still open.
Following in the same spirit are more recent calculations [6] of the close limit for two identical neutron stars. The results show the excitation of stellar QNMs and it remains for numerical relativity to verify the results.
Finally, perturbation theory can be also used as a tool to construct a gauge invariant measure of the gravitational radiation in a numerically generated perturbed black hole spacetime [7, 184].
7.2 Second Order Perturbations
A basic feature of linearized perturbation theory is that there is no “built-in” indication of how good the approximation is. But if one has results for a physical quantity to second order in a perturbation parameter, then the difference between the results of the first and second order theory is a quantitative indication of the error in the perturbation calculation. From this point of view second order perturbation theory is a practical tool for calculations. Nevertheless, there remain many technical problems in this approach, for example the gauge that should be used [100, 50] and the amount of calculations. Thus second order perturbation theory has turned out to be much more difficult than linearized theory, but if one overcomes these difficulties second order calculations will be a great deal easier than numerical relativity. From this point of view we encourage work in this direction. In particular, the perturbations of stellar oscillations should be extended to second order, and the study of the second order perturbations of black holes extended to the Kerr case.
7.3 Mode Calculations
Although the modes have been well studied there remain a few open issues. In the black hole case, the Kerr-Newman spectrum is known only in a restricted case [124], so the general case should be studied, probably by evolving the perturbation equations. For non-rotating stars, there remain certain technical questions, i.e. to find if there exist a class of w-modes with even larger imaginary part or the existence of extra interface modes. But for rotating stars, even slowly rotating ones, there remains much work [192]. There should be estimates of the fluid and spacetime modes for slowly rotating stars for various realistic equations of state, and the results should be incorporated into the method suggested in [19] for the estimates of the stellar parameters. There should be work towards understanding the possible interaction of r-modes with g-modes [176, 93]. And finally the time dependent perturbation equations for rotating stars should be evolved, because in this way we expect to see most of the new features that rotation induces in the spectra (splitting, instabilities etc).
7.4 The Detectors
As we have mentioned earlier in section 5, there are techniques available for the extraction of the QNM signal from the noise of the detectors [83, 90, 91]. But there are still issues related to the sensitivity of the planned detectors in parts of the spectrum. For example, the QNM frequencies of stellar black holes (10 – 100M⊙) will be of around 100 – 1000 Hz, i.e. in the frequencies where the laser interferometers are sensitive. The QNM frequencies of galactic size black holes will be detectable only from space (LISA) since their frequencies will be in the mHz regime. For the QNM frequencies of stars, there is a lack of appropriate detectors. Laser interferometers will be sensitive enough in the frequency regime of the f-mode but it will be very hard to detect signals in the frequencies of the p- and w-modes. Nevertheless, from the discussion in section 5 it is apparent that there is a wealth of information in the signal of oscillating neutron stars, and in order to extract this information we need the p- or/and w-modes. This suggests that the ideas considering detectors, or arrays of detectors, in this high frequency regime [92] should be considered more seriously.
Notes
In the literature the polar perturbations are also called even-parity because they are characterized by their behavior under parity operations as discussed earlier, and in the same way the axial perturbations are called odd-parity. We will stick to the polar/axial terminology since there is a confusion with the definition of the parity operation, the reason is that to most people, the words “even” and “odd” imply that a mode transforms under π as (-1)2n or (-1)2n+1 respectively (for n some integer). However only the polar modes with even ℓ have even parity and only axial modes with even ℓ have odd parity. If ℓ is odd, then polar modes have odd parity and axial modes have even parity. Another terminology is to call the polar perturbations spheroidal and the axial ones toroidal. This definition is coming from the study of stellar pulsations in Newtonian theory and represents the type of fluid motions that each type of perturbation induces. Since we are dealing both with stars and black holes we will stick to the polar/axial terminology.
The definition of Sℓ|m|(-s2, θ) on the complex plane is made unique by fixing certain conventions about the branch cuts. The exceptional points are the beginnings of branch cuts. R(l, m, s) as a solution of (40) is defined also at the exceptional points; just the series does not exist there.
For neutron stars the frequencies depend not only on the mass and rotation rate, but also on the radius and the equation of state.
Chandrasekhar and Ferrari [59] have also reduced the time independent perturbation equations (using a different gauge) into a 5th order system which involves only the spacetime perturbations with the fluid perturbations being calculated via algebraic relations from the spacetime perturbations. It was later proven by Ipser and Price [112, 169] that this system of ODEs can be reduced to the standard equations in the Regge-Wheeler gauge. That this is possible is apparent from equations (51, 52, 53, 54) and it is discussed in [5]
References
Abrahams, A.M., and Cook, G.B., “Collisions of boosted black holes: Perturbation theory prediction of gravitational radiation”, Phys. Rev. D, 50, R2364–R2367, (1994). For a related online version see: A.M. Abrahams, et al., “Collisions of boosted black holes: perturbation theory prediction of gravitational radiation”, (1994), [Online Los Alamos Archive Preprint]: cited on 23 May 1994, http://xxx.lanl.gov/abs/gr-qc/9405051. 5
Abrahams, A.M., and Price, R.H., “Applying black hole perturbation theory to numerically generated space-times.”, Phys. Rev. D, 53, 1963–1971, (1996). For a related online version see: A.M. Abrahams, et al., “Applying black hole perturbation theory to numerically generated spacetimes”, (1995), [Online Los Alamos Archive Preprint]: cited on 28 August 1995, http://xxx.lanl.gov/abs/gr-qc/9508059. 5
Abrahams, A.M., Shapiro, S.L., and Teukolsky, S.A., “Calculation ofgrav-itational waveforms from black hole collisions and disk collapse: Applying perturbation theory to numerical scpacetimes”, Phys. Rev. D, 51, 42954301, (1995). For a related online version see: A.M. Abrahams, et al., “Calculation of gravitational wave forms from black hole collisions and disk collapse: Applying perturbation theory to numerical spacetimes”, (1994), [Online Los Alamos Archive Preprint]: cited on 29 August 1994, http://xxx.lanl.gov/abs/gr-qc/9408036. 5
Albererio, S., Ferreira, L.S., and Streit, L., eds., Lecture Notes in Physics 211 Proceedings Bielefeld, (Springer-Verlag, Berlin, 1984). 9
Allen, G., Andersson, N., Kokkotas, K.D., and Schutz, B.F., “Gravitational waves from pulsating stars: Evolving the perturbation equations for a relativistic star”, Phys. Rev. D, 58, 124012, (1998). For a related online version see: G. Allen, et al., “Gravitational waves from pulsating stars: Evolving the perturbation equations for a relativistic star”, (1997), [Online Los Alamos Archive Preprint]: cited on 8 April 1997, http://xxx.lanl.gov/abs/gr-qc/9704023. 4.1, 4.1, 5.2, 5.4, 6.1.1, 4
Allen, G.D., Andersson, N., Kokkotas, K.D., Laguna, P., Pullin, J., and Ruoff, J., “The close-limit approximation to neutron star collisions”, Phys. Rev. For a related online version see: G.D. Allen, et al., “The close-limit approximation to neutron star collisions”, (1999), [Online Los Alamos Archive Preprint]: cited on 29 March 1999, http://xxx.lanl.gov/abs/gr-qc/9903100. accepted for publication. 5, 5.2, 7.1
Allen, G.D., Camarda, K., and Seidel, E., “Evolution of Distorted Black Holes: A Perturbative Approach”, (June, 1998), [Online Los Alamos Archive Preprint]: cited on 3 June 1998, http://xxx.lanl.gov/abs/gr-qc/9806014. 5, 7.1
Andersson, N., “A numerically accurate investigation of black-hole normal modes”, Proc. R. Soc. London, 439, 47–58, (1992). 6.1.2
Andersson, N., “Normal-mode frequencies of Reissner-Nordström black holes”, Proc. R. Soc. London, 442, 427–4 6, (1993). 1
Andersson, N., “On the asymptotic distribution of quasinormal-mode frequencies for Schwarzschild black holes”, Class. Quantum Grav., 10, L61–L67, (1993). 1
Andersson, N., “Total transmission through the Schwarzschild black hole potential barrier”, Class. Quantum Grav., 11, L39–L44, (1994). 1
Andersson, N., “Excitation of Schwarzschild black hole quasinormal modes”, Phys. Rev. D, 51, 353–363, (1995). 5.1
Andersson, N., “Two simple models for gravitational-wave modes of compact stars”, Gen. Relativ. Gravit., 28, 1433–1445, (1996). 4.2.2
Andersson, N., “A New class of unstable modes of rotating relativistic stars”, Astrophys. J., 502, 708–713, (1998). For a related online version see: N. Andersson, “A new class of unstable modes of rotating relativistic stars”, (1997), [Online Los Alamos Archive Preprint]: cited on 24 June 1997, http://xxx.lanl.gov/abs/gr-qc/9706075. 4.1
Andersson, N., Araujo, M.E., and Schutz, B.F., “The phase-integral method and the black hole normal modes”, Class. Quantum Grav., 10, 735–755, (1993). 6.1.3
Andersson, N., Araujo, M.E., and Schutz, B.F., “Quasinormal modes of Reissner-Nordström black holes: Phase-integral approach”, Phys. Rev. D, 49, 2703–2709, (1994). 6.1.3
Andersson, N., Kojima, Y., and Kokkotas, K.D., “On the oscillation spectra of ultracompact stars: An Extensive survey of gravitational wave modes”, Astrophys. J., 462, 855–864, (1996). For a related online version see: N. Andersson, et al., “On the oscillation spectra of ultracom-pact stars: An extensive survey of gravitational-wave modes”, (1995), [Online Los Alamos Archive Preprint]: cited on 29 December 1995, http://xxx.lanl.gov/abs/gr-qc/9512048. 4.2, 4.2.1, 4.2.2
Andersson, N., and Kokkotas, K.D., “Gravitational waves and pulsating stars: What can we learn from future observations?”, Phys. Rev. Lett., 77, 4134–4137, (1996). For a related online version see: N. Andersson, et al., “Gravitational waves and pulsating stars: What can we learn from future observations?”, (1996), [Online Los Alamos Archive Preprint]: cited on 16 October 1996, http://xxx.lanl.gov/abs/gr-qc/9610035. 1, 5.2, 5.3, 6.1.1
Andersson, N., and Kokkotas, K.D., “Towards gravitational wave astero-seismology”, Mon. Not. R. Astron. Soc., 299, 1059–1068, (1998). For a related online version see: N. Andersson, et al., “Towards gravitational-wave asteroseismology”, (1997), [Online Los Alamos Archive Preprint]: cited on 28 November 1997, http://xxx.lanl.gov/abs/gr-qc/9711088. 4.2.1, 4.2.1, 5.3, 5.4, 7, 4, 7.3
Andersson, N., Kokkotas, K.D., Laguna, P., Papadopoulos, P., and Sipior, M.S., “Construction of Astrophysical Initial Data for Perturbations of Relativistic Stars”, Phys. Rev. For a related online version see: N. Andersson, et al., “Construction of Astrophysical Initial Data for Perturbations of Relativistic Stars”, (1999), [Online Los Alamos Archive Preprint]: cited on 23 April 1999, http://xxx.lanl.gov/abs/gr-qc/9904059. accepted for publication. 5
Andersson, N., Kokkotas, K.D., and Schutz, B.F., “A New numerical approach to the oscillation modes of relativistic stars”, Mon. Not. R. Astron. Soc., 274, 1039–1048, (1995). For a related online version see: N. Andersson, et al., “A New numerical approach to the oscillation modes of relativistic stars”, (1995), [Online Los Alamos Archive Preprint]: cited on 8 March 1995, http://xxx.lanl.gov/abs/gr-qc/9503014. 4.2, 4
Andersson, N., Kokkotas, K.D., and Schutz, B.F., “Space-time modes of relativistic stars”, Mon. Not. R. Astron. Soc., 280, 1230–1234, (1996). For a related online version see: N. Andersson, et al., “Space-time modes of relativistic stars”, (1996), [Online Los Alamos Archive Preprint]: cited on 10 January 1996, http://xxx.lanl.gov/abs/gr-qc/9601015. 4.1, 4.2, 4
Andersson, N., Kokkotas, K.D., and Schutz, B.F., “Gravitational radiation limit on the spin of young neutron stars”, Astrophys. J., 510, 846–853, (1999). For a related online version see: N. Andersson, et al., “Gravitational radiation limit on the spin of young neutron stars”, (1998), [Online Los Alamos Archive Preprint]: cited on 17 May 1998, http://xxx.lanl.gov/abs/astro-ph/9805225. 4.1, 4.2.1
Andersson, N., Kokkotas, K.D., and Stergioulas, N., “On the relevance of the r-mode instability for accreting neutron stars and white dwarfs”, As-trophys. J., 516, 307–314, (1999). For a related online version see: N. An-dersson, et al., “On the relevance of the r-mode instability for accreting neutron stars and white dwarfs”, (1998), [Online Los Alamos Archive Preprint]: cited on 5 June 1998, http://xxx.lanl.gov/abs/astro-ph/9806089. 4.2.1
Andersson, N., and Linnaeus, S., “Quasinormal modes of a Schwarzschild black hole: Improved phase-integral treatment”, Phys. Rev. D, 46, 4179–4187, (1992). 1, 2, 6.1.3
Andersson, N., and Onozawa, H., “Quasinormal modes of nearly extreme Reissner-Nordström black holes”, Phys. Rev. D, 54, 7470–7475, (1996). For a related online version see: N. Andersson, et al., “Quasinormal modes of nearly extreme Reissner-Nordström black holes”, (1996), [Online Los Alamos Archive Preprint]: cited on 23 July 1996, http://xxx.lanl.gov/abs/gr-qc/9607054. 1
Andrade, Z., and Price, R.H., “Excitation of the odd-parity quasi-normal modes of compact objects”, (February, 1999), [Online Los Alamos Archive Preprint]: cited on 20 February 1999, http://xxx.lanl.gov/abs/gr-qc/9902062. 5.2, 5.3
Andrade, Z., and Price, R.H., “Headon collisions of unequal mass black holes: close limit predictions.”, Phys. Rev. D, 56, 6336–6350, (1997). For a related online version see: Z. Andrade, et al., “Headon collisions of unequal mass black holes: close limit predictions.”, (1996), [Online Los Alamos Archive Preprint]: cited on 8 November 1996, http://xxx.lanl.gov/abs/gr-qc/9611022. 1
Anninos, P., and Brandt, S., “Head-on collision of two unequal mass black holes”, (June, 1998), [Online Los Alamos Archive Preprint]: cited on 6 June 1998, http://xxx.lanl.gov/abs/gr-qc/9806031. 1, 1
Anninos, P., Hobill, D., Seidel, E., Smarr, L., and Suen, W.-M., “The Collision of two black holes”, Phys. Rev. Lett., 71, 2851–2854, (1993). For a related online version see: P. Anninos, et al., “The Collision of two black holes”, (1993), [Online Los Alamos Archive Preprint]: cited on 14 September 1993, http://xxx.lanl.gov/abs/gr-qc/9309016. 1
Anninos, P., Price, R.H., Pullin, J., Seidel, E., and Suen, W.-M., “Headon collision of two black holes: Comparison of different approaches.”, Phys. Rev. D, 52, 4462–4480, (1995). For a related online version see: P. Anninos, et al., “Headon collision of two black holes: Comparison of different approaches.”, (1995), [Online Los Alamos Archive Preprint]: cited on 23 May 1995, http://xxx.lanl.gov/abs/gr-qc/9505042. 1
Araujo, M.E., Nicholson, D., and Schutz, B.F., “On the Bohr-Sommerfeld formula for black hole normal modes”, Class. Quantum Grav., 10, 11271138, (1993). 6.1.3
Baber, W.G., and Hassé, H.R., “The two centre problem in wave mechanics”, Proc. Cambridge Philos. Soc. London, 25, 564–581, (1935). 6.1.4
Bachelot, A., and Motet-Bachelot, A., “Resonances of Schwarzschild black holes”, in Proceedings of the IV International Conference on Hyperbolic Problems, Taosmina, (1992). 6.1.1
Bachelot, A., and Motet-Bachelot, A., “Les resonances d’un trou noir de Schwarzschild”, Ann. Inst. Henri Poincare, 59, 3, (1993). 2, 2, 1, 1, 6.1.1
Barack, L., “Late time dynamics of scalar perturbations outside black holes. II. Schwarzschild geometry”, Phys. Rev. D, 59, 044017, (1999). For a related online version see: L. Barack, “Late time dynamics of scalar perturbations outside black holes. II. Schwarzschild geometry”, (1998), [Online Los Alamos Archive Preprint]: cited on 10 November 1998, http://xxx.lanl.gov/abs/astro-ph/9811028. 1
Barack, L., and Ori, A., “Late-time decay of scalar perturbations outside rotating black holes”, (February, 1999), [Online Los Alamos Archive Preprint]: cited on 25 February 1999, http://xxx.lanl.gov/abs/gr-qc/9902082. 1
Bardeen, J.M., and Press, W.H., “Radiation fields in the Schwarzschild background”, J. Math. Phys., 14, 7–19, (1973). 1
Barreto, A.S., and Zworski, M., “Distribution of resonances for spherical black holes”, Math. Res. Lett., 4, 103–121, (1997). 1
Baumgarte, T., and Schmidt, B.G., “Quasi-normal modes in coupled systems”, Class. Quantum Grav., 10, 2067–2076, (1993). 4.2.2
Bender, C.M., and Orszag, S.A., Advanced Mathematical Methods for Scientists and Engineers, (McGraw-Hill, New York, 1978). 6.1.3
Beyer, H.R., “On the Completeness of the Quasinormal Modes of the Pöschl-Teller Potential”, Commun. Math. Phys., 204, 397–423, (1999). For a related online version see: H.R. Beyer, “On the Completeness of the Quasinormal Modes of the Pöschl-Teller Potential”, (1998), [Online Los Alamos Archive Preprint]: cited on 10 March 1999, http://xxx.lanl.gov/abs/gr-qc/9803034. 2, 3.3
Beyer, H.R., and Schmidt, B.G., “Newtonian stellar oscillations”, Astron. Astrophys., 296, 722–726, (1995). 2
Bildsten, L., “Gravitational Radiation and Rotation of Accreting Neutron Stars”, Astrophys. J., L89–L93, (1998). For a related online version see: L. Bildsten, “Gravitational Radiation and Rotation of Accreting Neutron Stars”, (1998), [Online Los Alamos Archive Preprint]: cited on 29 April 1998, http://xxx.lanl.gov/abs/astro-ph/9804325. 4.2.1
Blanchet, L., Iyer, B.R., Will, C.M., and Wiseman, A.G., “Gravitational waveforms from inspiralling compact binaries to second-post-Newtonian order”, Class. Quantum Grav., 13, 575–584, (1996). For a related online version see: L. Blanchet, et al., “Gravitational waveforms from inspiralling compact binaries to second-post-Newtonian order”, (1996), [Online Los Alamos Archive Preprint]: cited on 13 February 1996, http://xxx.lanl.gov/abs/gr-qc/9602024. 5.3
Blome, H.J., and Mashhoon, B., “Quasi-normal oscillations of Schwarzschild black hole”, Phys. Lett. A, 100, 231–234, (1984). 6.1.3
Bonazzola, S., and Marck, J.-A., in Relativity in General, (Editions Fron-tieres, Gif-sur-Yvette, Cedex, 1994). 5.3
Borelli, A., “Gravitational radiation emitted when a mass falls onto a compact star”, Nuovo Cimento, 112 B, 225–241, (1997). 5.2
Brady, P.R., Chambers, C.M., Krivan, W., and Laguna, P., “Telling tails in the presence of a cosmological constant”, Phys. Rev. D, 55, 7538–7545, (1997). For a related online version see: P.R. Brady, et al., “Telling tails in the presence of a cosmological constant”, (1996), [Online Los Alamos Archive Preprint]: cited on 23 November 1996, http://xxx.lanl.gov/abs/astro-ph/9611056. 1
Bruni, M., Matarrese, S., Mollerach, S., and Sonego, S., “Perturbations of spacetime: gauge transformations and gauge invariance at second order and beyond”, Class. Quantum Grav., 14, 2585–2606, (1997). For a related online version see: M. Bruni, et al., “Perturbations of spacetime: gauge transformations and gauge invariance at second order and beyond”, (1996), [Online Los Alamos Archive Preprint]: cited on 13 September 1996, http://xxx.lanl.gov/abs/gr-qc/9609040. 7.2
Burrows, A., and Hayes, J., “Pulsar recoil and gravitational radiation due to asymmetrical stellar collapse and explosion”, Phys. Rev. Lett., 76, 352355, (1996). For a related online version see: A. Burrows, et al., “Pulsar Recoil and Gravitational Radiation due to Asymmetrical Stellar Collapse and Explosion”, (1995), [Online Los Alamos Archive Preprint]: cited on 22 November 1995, http://xxx.lanl.gov/abs/astro-ph/9511106. 5.3
Chandrasekhar, S., “The dynamical instability of gaseous masses approaching the Scwharzschild limit in general relativity”, Astrophys. J., 140, 417–433, (1964). 4.3
Chandrasekhar, S., “Solutions of two problems in the theory of gravitational radiation”, Phys. Rev. Lett., 24, 611–614, (1970). 4.1, 4.2.1
Chandrasekhar, S., “On the equations governing the perturbations of the Schwarzschild black hole”, Proc. R. Soc. London, Ser. A, 343, 289–298, (1975). 1
Chandrasekhar, S., “On one-dimensional potential barriers having equal reflexion and transmission coefficients”, Proc. R. Soc. London, Ser. A, 369, 425–433, (1980). 1
Chandrasekhar, S., The Mathematical Theory of Black Holes, (Clarendon Press, Oxford, 1983). 1
Chandrasekhar, S., “On algebraically special perturbations of black holes”, Proc. R. Soc. London, Ser. A, 392, 1–13, (1984). 1
Chandrasekhar, S., and Detweiler, S., “The quasi-normal modes of the Schwarzschild black hole”, Proc. R. Soc. London, Ser. A, 344, 441–452, (1975). 6.1.2
Chandrasekhar, S., and Ferrari, V., “On the non-radial oscillations of a star”, Proc. R. Soc. London, Ser. A, 432, 247–279, (1991). 4
Chandrasekhar, S., and Ferrari, V., “On the non-radial oscillations of a star. III — A reconsideration of the axial modes”, Proc. R. Soc. London, Ser. A, 434, 449–457, (1991). 4.2, 4.2.2
Chandrasekhar, S., and Ferrari, V., “On the non-radial oscillations of slowly rotating stars induced by the Lense-Thirring effect”, Proc. R. Soc. London, Ser. A, 433, 423–440, (1991). 4.1
Ching, E.S.C., Leung, P.T., Suen, W.-M., and Young, K., “Wave propagation in gravitating systems: Late time behavior”, Phys. Rev. D, 52, 2118–2132, (1995). For a related online version see: E.S.C. Ching, et al., “Wave Propagation in Gravitational Systems: Late Time Behavior”, (1995), [Online Los Alamos Archive Preprint]: cited on 14 July 1995, http://xxx.lanl.gov/abs/gr-qc/9507035. 1
Ching, E.S.C., Leung, P.T., Suen, W.-M., and Young, K., “Wave propagation in gravitational systems: Completeness of quasinormal modes”, Phys. Rev. D, 54, 3778–3791, (1996). For a related online version see: E.S.C. Ching, et al., “Wave Propagation in Gravitational Systems: Completeness of Quasinormal Modes”, (1995), [Online Los Alamos Archive Preprint]: cited on 14 July 1995, http://xxx.lanl.gov/abs/gr-qc/9507034. 3.3
Cowling, T.G., Mon. Not. R. Astron. Soc., 101, 367, (1941). 4.1, 4.2.1
Cox, J.P., Theory of Stellar Pulsation, (Princeton University Press, 1980). 4.3
Cunningham, C.T., Price, R.H., and Moncrief, V., “Radiation from collapsing relativistic stars. I. Linearized odd-parity radiation”, Astrophys. J., 224, 643–667, (1978). 1, 1
Cunningham, C.T., Price, R.H., and Moncrief, V., “Radiation from collapsing relativistic stars. I. Linearized even-parity radiation”, Astrophys. J., 230, 870–892, (1979). 1, 1
Cunningham, C.T., Price, R.H., and Moncrief, V., “Radiation from collapsing relativistic stars III. Second order perurbations of collapse with rotation”, Astrophys. J., 236, 674–692, (1980). 1, 1
Cutler, C., and Lindblom, L., “The effect of viscosity on neutron star oscillations”, Astrophys. J., 314, 234–241, (1987). 4.2.1
Cutler, C., and Lindblom, L., “Gravitational helioseismology?”, Phys. Rev. D, 54, 1287–1290, (1996). 1
Cutler, C., Lindblom, L., and Splinder, R.J., “Damping times for neutron star oscillations”, Astrophys. J., 363, 603–611, (1990). 4.2.1
Damour, T., Deruelle, N., and Ruffini, R., “On quantum resonances in stationary geometries”, Lett. Nuovo Cimento, 15, 257, (1976). 3.3
Davis, M., Rufinni, R., Press, W.H., and Price, R.H., “Gravitational radiation from a particle falling radially into a Schwarzschild black hole”, Phys. Rev. Lett., 27, 1466–1469, (1971). 1, 6.1
Detweiler, S.L., “A variational calculation of the fundamental frequencies of quadrupole pulsation of fluid spheres in general relativity”, Astrophys. J., 197, 203–217, (1975). 4
Detweiler, S.L., “A variational principle and a stability criterion for the dipole modes of pulsation of stellar models in general relativity”, Astrophys. J., 201, 440–446, (1975). 4
Detweiler, S.L., “On resonant oscillations of a rapidly rotating black hole”, Proc. R. Soc. London, Ser. A, 352, 381–395, (1977). 1, 5.1
Detweiler, S.L., “Klein-Gordon equation and rotating black holes”, Phys. Rev. D, 22, 2323–2326, (1980). 3.3
Detweiler, S.L., and Ipser, J., “A variational principle and a stability criterion for the nonradial modes of pulsation of stellar models in general relativity”, Astrophys. J., 185, 685–707, (1973). 4.3, 4
Detweiler, S.L., and Lindblom, L., “On the nonradial pulsations of general relativistic stellar models”, Astrophys. J., 292, 12–15, (1985). 4.2, 6.2
Detweiler, S.L., and Szedenits, E., “Black holes and gravitational waves. II — Trajectories plunging into a nonrotating hole”, Astrophys. J., 231, 211–218, (1979). 1
Duncan, R.C., and Thompson, C., “Formation of very strongly magnetized neutron stars: Implications for gamma-ray bursts”, Astrophys. J., 392, L9–L13, (1992). 5.3
Dunham, J.L., “The Wentzel-Brillouin-Kramers method of solving the wave equation”, Phys. Rev., 41, 713–720, (1932). 6.1.3
Echeverria, F., “Gravitational wave measurements of the mass and angular momentum of a black hole”, Phys. Rev. D, 40, 3194–3203, (1989). 5.4, 7.4
Ferrari, V., Gualtieri, L., and Borrelli, A., “Stellar pulsations excited by a scattered mass”, Phys. Rev. D, 59, 124020, (1999). For a related online version see: V. Ferrari, et al., “Stellar Pulsations excited by a scattered mass”, (1999), [Online Los Alamos Archive Preprint]: cited on 22 January1999, http://xxx.lanl.gov/abs/gr-qc/9901060. 5.2, 5.3
Ferrari, V., and Mashhoon, B., “New approach to the quasinormal modes of a black hole”, Phys. Rev. D, 30, 295–304, (1984). 1, 1, 6.1.3
Ferrari, V., and Mashhoon, B., “Oscillations of a black hole”, Phys. Rev. Lett., 52, 1361–1346, (1984). 1, 6.1.3
Finn, L.S., “g-modes of non-radially pulsating relativistic stars: The slow-motion formalism”, Mon. Not. R. Astron. Soc., 222, 393–416, (1986). 2, 4.2.1, 4
Finn, L.S., “g-modes in zero-temperature neutron stars”, Mon. Not. R. Astron. Soc., 227, 265–293, (1987). 4.2.1
Finn, L.S., “Detection, measurement and gravitational radiation”, Phys. Rev. D, 46, 5236–5249, (1992). 5.4
Flanagan, E.E., and Hughes, S.A., “Measuring gravitational waves from binary black hole coalescences. I. Signal to noise for inspiral, merger, and ringdown”, Phys. Rev. D, 57(8), 4535–4565, (1998). For a related onlineversion see: E.E. Flanagan, et al., “Measuring gravitational waves from binary black hole coalescences: I. Signal to noise for inspiral, merger, and ringdown”, (1997), [Online Los Alamos Archive Preprint]: cited on 16 January 1997, http://xxx.lanl.gov/abs/gr-qc/9701039. 5.3, 7.4
Flanagan, E.E., and Hughes, S.A., “Measuring gravitational waves from binary black hole coalescences. II. The wave’s information and its extraction, with and without templates”, Phys. Rev. D, 57(8), 4566–4587, (1998). For a related online version see: E.E. Flanagan, et al., “Measuring gravitational waves from binary black hole coalescences: II. the waves’ information and its extraction, with and without templates”, (1997), [Online Los Alamos Archive Preprint]: cited on 30 October 1997, http://xxx.lanl.gov/abs/gr-qc/9710129. 5.3, 7.4
Frasca, S., and Papa, M.A., “Networks of resonant gravitational-wave antennas”, Int. J. Mod. Phys. D, 4, 1–50, (1995). 7.4
Friedman, J.L., private communication. 7.3
Friedman, J.L., and Morsink, S., “Axial instability of rotating relativistic stars”, Astrophys. J., 502, 714–720, (1998). For a related online version see: J.L. Friedman, et al., “Axial instability of rotating relativistic stars”, (1997), [Online Los Alamos Archive Preprint]: cited on 23 June 1997, http://xxx.lanl.gov/abs/gr-qc/9706073. 4.1
Friedman, J.L., and Schutz, B.F., “Secular instability of rotating newtonian stars”, Astrophys. J., 222, 281–296, (1998). 4.1, 4.2.1
Fröman, N., Fröman, P.O., Andersson, N., and Hökback, A., “Black hole normal modes: Phase integral treatment”, Phys. Rev. D, 45, 2609–2616, (1992). 6.1.3
Fröman, P.O., and Fröman, N., JWKB Approximation, Contributions to the Theory, (North-Holland, Amsterdam, 1965). 6.1.3
Gautschy, A., and Saio, H., “Stellar pulsations across the HR diagram: Part I”, Annu. Rev. Astron. Astrophys., 33, 75–113, (1995). 4.2.1
Gautschy, A., and Saio, H., “Stellar pulsations across the HR diagram: Part II”, Annu. Rev. Astron. Astrophys., 34, 551, (1996). 4.2.1
Gleiser, R.J., Nicasio, C.O., Price, R.H., and Pullin, J., “Gravitational radiation from Schwarzschild black holes: the second order formalism”, Phys. Rep. For a related online version see: R.J. Gleiser, et al., “Gravitational radiation from Schwarzschild black holes: the second order formalism”, (1998), [Online Los Alamos Archive Preprint]: cited on 29 July 1998, http://xxx.lanl.gov/abs/gr-qc/9807077. submitted. 1, 7.2
Gleiser, R.J., Nicasio, C.O., Price, R.H., and Pullin, J., “Colliding black holes: How far can the close approximation go?”, Phys. Rev. Lett., 77, 4483–4486, (1996). For a related online version see: R.J. Gleiser, et al., “Colliding black holes: how far can the close approximation go?”, (1996), [Online Los Alamos Archive Preprint]: cited on 9 September 1996, http://xxx.lanl.gov/abs/gr-qc/9609022. 1
Gleiser, R.J., Nicasio, C.O., Price, R.H., and Pullin, J., “Second order perturbations of a Schwarzschild black hole”, Class. Quantum Grav., 13, L117–L124, (1996). For a related online version see: R.J. Gleiser, et al., “Second order perturbations of a Schwarzschild black hole”, (1995), [Online Los Alamos Archive Preprint]: cited on 24 October 1995, http://xxx.lanl.gov/abs/gr-qc/9510049. 1
Gleiser, R.J., Nicasio, C.O., Price, R.H., and Pullin, J., “Evolving the Bowen-York initial data for spinning black holes”, Phys. Rev. D, 57, 3401–3407, (1998). For a related online version see: R.J. Gleiser, et al., “Evolving the Bowen-York initial data for spinning black holes”, (1997), [Online Los Alamos Archive Preprint]: cited on 21 October 1997, http://xxx.lanl.gov/abs/gr-qc/9710096. 1
Gleiser, R.J., Nicasio, C.O., Price, R.H., and Pullin, J., “The Collision of boosted black holes: Second order close limit calculation”, Phys. Rev. D, 59, 044024, (1999). For a related online version see: R.J. Gleiser, et al., “The Collision of boosted black holes: Second order close limit calculation”, (1998), [¿Online Los Alamos Archive Preprint]: cited on 3 March 1998, http://xxx.lanl.gov/abs/gr-qc/9802063. 1
Guinn, J.W., Will, C.M., Kojima, Y., and Schutz, B.F., “High-overtone normal modes of Schwarzschild black holes”, Class. Quantum Grav., 7, L47–L53, (1990). 6.1.3
Gundlach, C., Price, R.H., and Pullin, J., “Late time behavior of stellar collapse and explosions: 1. Linearized perturbations”, Phys. Rev. D, 49, 883–889, (1994). 1
Gundlach, C., Price, R.H., and Pullin, J., “Late time behavior of stellar collapse and explosions: 2. Nonlinear evolution”, Phys. Rev. D, 49, 890–899, (1994). For a related online version see: C. Gundlach, et al., “Late time behavior of stellar collapse and explosions: 2. Nonlinear evolution”, (1993), [Online Los Alamos Archive Preprint]: cited on 12 July 1993, http://xxx.lanl.gov/abs/gr-qc/9307010. 1
Gunter, D.L., “A study of the coupled gravitational and electromagnetic perturbations to the Reissner-Nordström black hole: The scattering matrix, energy conversion, and quasi-normal modes”, Philos. Trans. R. Soc. London, A 296, 497–526, (1980). 1, 6.1.2
Hartle, J.B., and Wilkins, D.C., “Analytic properties of the Teukolsky equation”, Commun. Math. Phys., 38, 47–63, (1974). 3.3
Harvey, J.W. et al., “The Global Oscillation Network Group (GONG) Project”, Science, 272, 1284–1286, (1996). 5.4
Heisenberg, W. et al., “Der mathematiche Rahmen der Quantentheorie der Wellenfelder”, Z. Naturforsch., 1, 608, (1946). 6.1.4
Ipser, J., and Price, R.H., “Nonradial pulsations of stellar models in general relativity”, Phys. Rev. D, 43, 1768–1773, (1991). 4
Iyer, S., “Black-hole normal modes: A WKB approach. II. Schwarzschild black holes”, Phys. Rev. D, 35, 3632–3636, (1987). 1, 6.1.3
Iyer, S., and Will, C.M., “Black-hole normal modes: A WKB approach. I Foundations and application of a higher WKB analysis of potential-barrier scattering”, Phys. Rev. D, 35, 3621–3631, (1987). 6.1.3
Jensen, B.P., and Candelas, P., “Schwarzschild radial functions”, Phys. Rev. D, 33, 1590–1595, (1986). 1
John, F., Partial Differential Equations, (Springer-Verlag, New York, 1991). 2
Kay, B.S., and Wald, R.M., “Linear stability of Schwarzschild under perturbations which are non-vanishing on the bifurcation 2-sphere”, Class. Quantum Grav., 4, 893–898, (1987). 2, 1, 3.3
Kind, S., Ehlers, J., and Schmidt, B.G., “Relativistic stellar oscillations treated as an initial value problem”, Class. Quantum Grav., 10, 21372152, (1993). 4.1, 4.1
Kojima, Y., “Two families of normal modes in relativistic stars”, Prog. Theor. Phys., 79, 665–675, (1988). 4.2, 4
Kojima, Y., “Equations governing the nonradial oscillations of a slowly rotating relativistic star”, Phys. Rev. D, 46, 4289–4303, (1992). 4.1
Kojima, Y., “Normal modes of relativistic stars in slow rotation limit”, Astrophys. J., 414, 247–253, (1993). 4.1
Kojima, Y., Andersson, N., and Kokkotas, K.D., “On the oscillation spectra of ultracompact stars”, Proc. R. Soc. London, Ser. A, 451, 341–348, (1995). For a related online version see: Y. Kojima, et al., “On the oscillation spectra of ultracompact stars”, (1995), [Online Los Alamos Archive Preprint]: cited on 7 March 1995, http://xxx.lanl.gov/abs/gr-qc/9503012. 4.2, 4.2.2
Kokkotas, K.D., “Normal modes of the Kerr black hole”, Class. Quantum Grav., 8, 2217–2224, (1991). 2, 6.1.3
Kokkotas, K.D., “Normal modes of the Kerr-Newmann black hole”, Nuovo Cimento B, 108, 991–998, (1993). 3, 2, 6.1.3, 7.3
Kokkotas, K.D., “Axial modes for relativistic stars”, Mon. Not. R. Astron. Soc., 268, 1015–1018, (1994). 4.1, 4.2, 4.2.2
Kokkotas, K.D., Apostolatos, T., and Andersson, N., “The inverse problem for pulsating neutron stars: A’ fingerprint analysis’ for the supranu-clear equation of state”, Mon. Not. R. Astron. Soc., (1999). 1999For a related online version see: K.D. Kokkotas, et al., “The inverse problem for pulsating neutron stars: A”, (1999), [Online Los Alamos Archive Preprint]: cited on 25 January 1999, http://xxx.lanl.gov/abs/gr-qc/9901072. submitted. 5.4
Kokkotas, K.D., and Schafer, G., “Tidal and Tidal-resonant Effects in Close Binary Systems”, Mon. Not. R. Astron. Soc., 275, 301–308, (1995). For a related online version see: K.D. Kokkotas, et al., “Tidal and Tidal-resonant Effects in Close Binary Systems”, (1995), [Online Los Alamos Archive Preprint]: cited on 17 February 1995, http://xxx.lanl.gov/abs/gr-qc/9502034. 5.3
Kokkotas, K.D., and Schutz, B.F., “Normal modes of a model radiating system”, Gen. Relativ. Gravit., 18, 913–921, (1986). 4.2, 4.2.2
Kokkotas, K.D., and Schutz, B.F., “Black hole normal modes: A WKB approach. III The Reissner-Nordström black hole”, Phys. Rev. D, 37, 3378–3387, (1988). 1, 6.1.2, 6.1.3
Kokkotas, K.D., and Schutz, B.F., “W-modes: A new family of normal modes for pulsating relativistic stars”, Mon. Not. R. Astron. Soc., 255, 119–128, (1992). 4.2, 4.2.2, 4
Kokkotas, K.D., and Stergioulas, N., “Analytic description of the r-mode instability in uniform density neutron stars”, Astron. Astrophys., 341, 110–116, (1999). For a related online version see: K.D. Kokkotas, et al., “Analytic description of the r-mode instability in uniform density stars”, (1997), [Online Los Alamos Archive Preprint]: cited on 22 May 1998, http://xxx.lanl.gov/abs/astro-ph/9805297. 4.2.1
Krivan, W., Laguna, P., and Papadopoulos, P., “Dynamics of scalar fields in the background of rotating black holes”, Phys. Rev. D, 54, 4728–4734, (1996). For a related online version see: W. Krivan, et al., “Dynamics of Scalar Fields in the Background of Rotating Black Holes”, (1996), [Online Los Alamos Archive Preprint]: cited on 4 June 1996, http://xxx.lanl.gov/abs/gr-qc/9606003. 1, 3.3, 6.1.1
Krivan, W., Laguna, P., Papadopoulos, P., and Andersson, N., “Dynamics of perturbations of rotating black holes”, Phys. Rev. D, 56, 3395–3404, (1997). For a related online version see: W. Krivan, et al., “Dynamics of perturbations of rotating black holes”, (1997), [Online Los Alamos Archive Preprint]: cited on 24 February 1997, http://xxx.lanl.gov/abs/gr-qc/. 1, 3.3, 6.1.1
Lai, D., “Secular Instability of g-Modes in Rotating Neutron Stars”, Mon. Not. R. Astron. Soc., 307, 1001–1007, (1999). For a related online version see: D. Lai, “Secular Instability of g-Modes in Rotating Neutron Stars”, (1998), [Online Los Alamos Archive Preprint]: cited on 29 June 1998, http://xxx.lanl.gov/abs/astro-ph/9806378. 4.2.1
Leaver, E.W., “An analytic representation for the quasi-normal modes of Kerr black holes”, Proc. R. Soc. London, Ser. A, 402, 285–298, (1985). 1, 2, 6.1.4
Leaver, E.W., “Spectral decomposition of the perturbation response of the Schwarzschild geometry”, Phys. Rev. D, 34, 384–408, (1986). 1, 5.1
Leaver, E.W., “Quasinormal modes of Reissner-Nordström black holes”, Phys. Rev. D, 41, 2986–2997, (1990). 1, 1, 6.1.4
Leins, M., Nollert, H.-P., and Soffel, M.H., “Nonradial oscillations of neutron stars: A new branch of strongly damped normal modes”, Phys. Rev. D, 48, 3467–3472, (1993). 4.2, 4.2.2, 4
Levin, Y., “Runaway heating by r-modes of neutron stars in low-mass X-Ray binaries”, Astrophys. J., 517, 328–333, (1999). For a related online version see: Y. Levin, “Runaway Heating By R-modes of Neutron Stars in Low Mass X-ray Binaries”, (1998), [Online Los AlamosArchive Preprint]: cited on 29 October 1998, http://xxx.lanl.gov/abs/astro-ph/9810471. 4.2.1
Lindblom, L., “Stellar Stability according to Newtonian Theory and General Relativity”, in Francaviglia, M., Longhi, G., Lusanna, L., and Sorace, E., eds., General Relativity and Gravitation — Proceedings of the GR 14 conference, (1997). 4.3
Lindblom, L., and Detweiler, S.L., “The quadrupole oscillations of neutron stars”, Astrophys. J. Suppl. Ser., 53, 73–92, (1983). 4.2, 4.2.1, 4.2.1, 4
Lindblom, L., Owen, B.J., and Morsink, S.M., “Gravitational Radiation Instability in Hot Young Neutron Stars”, Phys. Rev. Lett., 80, 4843–4846, (1998). For a related online version see: L. Lindblom, et al., “Gravitational Radiation Instability in Hot Young Neutron Stars”, (1998), [Online Los Alamos Archive Preprint]: cited on 13 March 1998, http://xxx.lanl.gov/abs/gr-qc/9803053. 4.1, 4.2.1
Liu, H., “Asymptotic behaviour of quasi-normal mode od Schwarzschild black holes”, Class. Quantum Grav., 12, 543–552, (1995). 1
Liu, H., and Mashhoon, B., “On the spectrum of oscillations of a Schwarzschild black hole”, Class. Quantum Grav., 13, 233–251, (1996). 1
Majumdar, B., and Panchapakesan, N., “Schwarzschild black-hole normal modes using the Hill determinant”, Phys. Rev. D, 40, 2568–2571, (1989). 6.1.4
McDermott, P.N., Van Horn, H.M., and Hansen, C.J., “Nonradial oscillations of neutron stars”, Astrophys. J., 325, 725–748, (1988). 4, 4.2, 4.2.1
McDermott, P.N., Van Horn, H.M., and Scholl, J.F., “Nonradial g-mode oscillations of warm neutron stars”, Astrophys. J., 268, 837–848, (1983).4.2, 4.2.1
Meixner, J., and Schäfke, F.W., Mathieusche Functionen und Sphäroidfunctionen, (Springer Verlag, Berlin, 1954). 3.2
Melrose, R., Geometrical Scattering Theory, (Cambridge University Press, 1995). 9
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W. H. Freeman, New York, 1973). 4.3
Mönchmeyer, R., Schoäfer, G., Müller, E., and Kates, R.E., “Gravitational waves from the collapse of rotating stellar cores”, Astron. Astrophys., 246, 417–440, (1991). 5.2
Moncrief, V., “Gravitational perturbations of spherically symmetric systems. I. The exterior problem”, Ann. Phys. (N. Y.), 88, 323–342, (1974). 3.1, 4.1
Moncrief, V., “Odd-parity stability of a Reissner-Nordström black holes”, Phys. Rev. D, 9, 2707–2709, (1974). 1
Moncrief, V., “Stability of a Reissner-Nordström black hole”, Phys. Rev. D, 10, 1057–1059, (1974). 1
Nakamura, T., and Oohara, K., “Gravitational radiation from coalescing binary neutron stars. IV. Tidal disruption”, Prog. Theor. Phys., 86, 7388, (1991). 5.2
Nollert, H.-P., Astrophysik in der Schwarzschildmetrik am Beispiel von Quasi-Normalmoden schwarzer Löcher und Lichtablenkung bei Röntgenpulsaren, PhD thesis, (University of Tubingen, 1990). 6.1.2, 6.1.4
Nollert, H.-P., “Quasinormal modes of Schwarzschild black holes: The determination of quasinormal frequencies with very large imaginary parts”, Phys. Rev. D, 47, 5253–5258, (1993). 1, 1, 6.1.4
Nollert, H.-P., and Price, R.H., “Quantifying excitations of quasinormal mode systems”, J. Math. Phys., 40, 980–1010, (1999). For a related online version see: H.-P. Nollert, et al., “Quantifying excitations of quasinormal mode systems”, (1998), [Online Los Alamos Archive Preprint]: cited on22 October 1998, http://xxx.lanl.gov/abs/gr-qc/9810074. 3.3
Nollert, H.-P., and Schmidt, B.G., “Quasinormal modes of Schwarzschild black holes: Defined and calculated via Laplace transformation”, Phys. Rev. D, 45, 2617–2627, (1992). 1, 6.1.2
Onozawa, H., “Detailed study of quasinormal frequencies of the Kerr black hole”, Phys. Rev. D, 55, 3593–3602, (1997). For a related online version see: H. Onozawa, “A detailed study of quasinormal frequencies of the Kerr black hole”, (1996), [Online Los Alamos Archive Preprint]: cited on 22 October 1996, http://xxx.lanl.gov/abs/gr-qc/9610048. 2
Owen, B.J., Lindblom, L., Cutler, C., Schutz, B.F., Vecchio, A., and An-dersson, N., “Gravitational waves from hot young rapidly rotating neutron stars”, Phys. Rev. D, 58, 084020, (1998). For a related online version see: B.J. Owen, et al., “Gravitational waves from hot young rapidly rotating neutron stars”, (1998), [Online Los Alamos Archive Preprint]: cited on 20 April 1998, http://xxx.lanl.gov/abs/gr-qc/9804044. 4.1, 4.2.1
Persides, S., “On the radial wave equation in Schwarzschild space-time”, J. Math. Phys., 14, 1017–1021, (1973). 1
Pijpers, F.P., “Helioseismic determination of the solar gravitational quadrupole moment”, Mon. Not. R. Astron. Soc., 297, L76–L80, (1998). 1
Press, W.H., “Long wave trains of gravitational waves from a vibrating black hole”, Astrophys. J., 170, L105–L108, (1971). 1, 1
Press, W.H., and Teukolsky, S., “Perturbations of a rotating black hole. II Dynamical stability of the Kerr metric”, Astrophys. J., 185, 649–673, (1973). 3.3
Price, R.H., “Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations”, Phys. Rev. D, 5, 24192438, (1972). 1
Price, R.H., “Nonspherical perturbations of relativistic gravitational collapse. II. Integer-spin, zero-rest-mass fields”, Phys. Rev. D, 5, 2439–2454, (1972). 1
Price, R.H., and Husain, V., “Model for the completeness of quasinormal modes of relativistic stellar oscillations”, Phys. Rev. Lett., 68, 1973–1976, (1992). 4.3
Price, R.H., and Ipser, J., “Relation of gauge formalisms for pulsations of general-relativistic stellar models”, Phys. Rev. D, 44, 307–313, (1991). 4
Price, R.H., and Pullin, J., “Colliding black holes: The Close limit”, Phys. Rev. Lett., 72, 3297–3300, (1994). For a related online version see: R.H.Price, et al., “Colliding black holes: The Close limit”, (1994), [OnlineLos Alamos Archive Preprint]: cited on 22 February 1994, http://xxx.lanl.gov/abs/gr-qc/9402039. 1, 5
Price, R.H., and Thorne, K.S., “Non-radial pulsation of general-relativistic stellar models. II Properties of the gravitational waves”, Astrophys. J., 155, 163–182, (1969). 4.2
Pullin, J., “Colliding black holes: Analytic insights”, in Dadhich, N., and Narlikar, J., eds., Gravitation and Relativity: At the turn of the Millennium, Proceedings of the GR-15 Conference, 87–106, (IUCCA, Pune, 1998). For a related online version see: J. Pullin, “Colliding black holes: analytic insights”, (1998), [Online Los Alamos Archive Preprint]: cited on2 March 1998, http://xxx.lanl.gov/abs/gr-qc/9803005. 7.1
Regge, T., and Wheeler, J.A., “Stability of a Schwarzschild singularity”, Phys. Rev., 108, 1063–1069, (1957). 1, 1
Rendall, A.D., and Schmidt, B.G., “Existence and properties of spherically symmetric static fluid bodies with a given equation of state”, Class. Quantum Grav., 8, 985–1000, (1991). 4.1
Ruffert, M., Janka, H.Th., and Schäfer, G., “Coalescing neutron stars-a step towards physical models I. Hydrodynamical evolution and gravitational-wave emission”, Astron. Astrophys., 311, 532–566, (1995). 5.2
Schutz, B.F., private communication. 7.3
Schutz, B.F., “Relativistic gravitational instabilities”, in Hartle, B., and Carter, J. B., eds., Gravitation in Astrophysics, 123–154, (Plenum Press, New York, 1987). 4.3
Schutz, B.F., “Gravitational wave sources”, Class. Quantum Grav., 13, A219–A238, (1996). 5.3, 5.3
Schutz, B.F., “The detection of gravitational waves”, in J.A. Lasota, J.P. Marck, ed., Relativistic Gravitation and Gravitational Radiation, (1997). 5.3, 5.3
Schutz, B.F., and Will, C.M., “Black hole normal modes: a semianalytic approach”, Astrophys. J., 291, L33–L36, (1985). 1, 6.1.3
Seidel, E., “A comment on the eigenvalues of spin-weighted spheroidal functions”, Class. Quantum Grav., 6, 1057–1062, (1989). 3.2
Seidel, E., “Gravitational radiation from even-parity perturbations of stellar collapse: Mathematical formalism and numerical methods”, Phys. Rev. D, 42, 1884–1907, (1990). 5.2
Seidel, E., “Normal-mode excitation from stellar collapse to a black hole: Odd-parity perturbations”, Phys. Rev. D, 44, 950–965, (1991). 5.2
Seidel, E., “The synergy between numerical and perturbative approaches to black holes”, in Iyer, B., and Bhawal, B., eds., On the Black Hole Trail. Kluwer, (1999). For a related online version see: E. Seidel, “The synergy between numerical and perturbative approaches to black holes”, (1998), [Online Los Alamos Archive Preprint]: cited on 23 June 1998, http://xxx.lanl.gov/abs/gr-qc/9806087. 7.1
Seidel, E., and Iyer, S., “Black hole normal modes: A WKB approach. IV Kerr black holes”, Phys. Rev. D, 41, 374–382, (1990). 2, 6.1.3
Seidel, E., and Moore, T., “Gravitational radiation from realistic relativistic stars: odd parity fluid perturbations”, Phys. Rev. D, 35, 2287–2296, (1987). 5.2
Seidel, E., Myra, E.S., and Moore, T., “Gravitational radiation from type II supernova: The effect of the high density equation of state”, Phys. Rev. D, 38, 2349–2356, (1988). 5.2
Shapiro, S., and Teukolsky, S., Neutron Stars, White Dwarfs and Black Holes, (Willey Interscience, New York, 1983). 4.3
Simon, B., “Resonances and complex scaling — rigorous overview”, Int. J. Quantum Chem., XIV, 529, (1978). 9
Skibsted, K., “Truncated Gamow functions, alpha-decay and the exponential law”, Commun. Math. Phys., 104(4), 591–604, (1986). 9
Stark, R.F., and Piran, T., “Gravitational-wave emission from rotating gravitational collapse”, Phys. Rev. Lett., 55, 891–894, (1985). 1
Stergioulas, N., “Rotating Stars in Relativity”, (June, 1998), [Article in Online Journal Living Reviews in Relativity]: cited on 20 August 1999, http://www.livingreviews.org/Articles/Volume1/1998-8stergio. 4, 4.3, 7.3
Stewart, J.M., “On the stability of Kerr’s space-time”, Proc. R. Soc. London, Ser. A, 344, 65–79, (1975). 3.3
Sun, Y., and Price, R.H., “Excitation of quasinormal ringing of a Schwarzschild black hole”, Phys. Rev. D, 38, 1040–1052, (1988). 5.1
Sun, Y., and Price, R.H., “Excitation of Schwarzschild quasinormal modes by collapse”, Phys. Rev. D, 41, 2492, (1990). 5.1
Teukolsky, S., “Rotating black holes: Separable wave equations for gravitational and electromagnetic perturbations”, Phys. Rev. Lett., 29, 1114–1118, (1972). 3.2
Teukolsky, S., “Perturbations of a rotating black hole. I. Fundamental equations for gravitational, electromagnetic, and neutrino-field perturbations”, Astrophys. J., 185, 635–648, (1973). 5.1
Thorne, K.S., “Gravitational radiation damping”, Phys. Rev. Lett., 21, 320–323, (1968). 1, 4.2
Thorne, K.S., “Nonradial pulsation of general-relativistic stellar models. III. Analytic and numerical results for neutron star”, Astrophys. J., 158, 1–16, (1969). 1, 4.2, 4
Thorne, K.S., “Nonradial pulsation of general-relativistic stellar models. IV. The weak-field limit”, Astrophys. J., 158, 997–1019, (1969). 1, 4.1, 4.2
Thorne, K.S., “Probing Black Holes and Relativistic Stars with Gravitational Waves”, in Black Holes and Relativistic Stars, (University of Chicago Press, 1998). 3
Thorne, K.S., and Campolattaro, A., “Non-radial pulsation of general-relativistic stellar models. I. Analytic analysis for ℓ ≥ 2”, Astrophys. J., 149, 591–611, (1967). 1, 3.1, 4.1, 4.2
Tominaga, K., Saijo, M., and Maeda, K., “Gravitational waves from a test particle scattered by a neutron star: axial mode case”, Phys. Rev. D, 60, 024004, (1999). For a related online version see: K. Tominaga, et al., “Gravitational waves from a test particle scattered by a neutron star: axial mode case”, (1999), [Online Los Alamos Archive Preprint]: cited on 14 January 1999, http://xxx.lanl.gov/abs/gr-qc/9901040. 5.2, 5.3
Unno, W., Osaki, Y., Ando, H., Saio, H., and Shibahashi, H., Non-radial Oscillations of Stars, (University Tokyo Press, Tokyo, 1989). 1
Van den Bergh, S., and Tammann, G.A., “Galactic and extragalactic supernova rates”, Annu. Rev. Astron. Astrophys., 29, 363–407, (1991). 5.3
Van Horn, H.M., “Micropulses, drifting subpulses, and nonradial oscillations of neutron stars”, Astrophys. J., 236, 899–903, (1980). 4
Vishveshwara, C.V., “Scattering of gravitationa radiation by a Schwarzschild black-hole”, Nature, 227, 936–938, (1970). 1, 6.1.1
Whiting, B.F., “Mode stability of the Kerr black hole”, J. Math. Phys., 30, 1301–1305, (1989). 3.3
Xanthopoulos, B., “Metric and electromagnetic perturbations of the Reissner-Nordstroum black hole”, Proc. R. Soc. London, Ser. A, 378, 7388, (1981). 1
Yamada, S., and Sato, K., “Gravitational Radiation from Rotational Collapse of a Supernova Core”, Astrophys. J., 450, 245–252, (1995). 5.2
Yoshida, S., Eriguchi, Y., and Futamase, T., “Quasinormal modes of boson stars”, Phys. Rev. D, 50, 6235–6246, (1994). 4
Zerilli, F.J., “Gravitational field of a particle falling in a Schwarzschild geometry analysed in tensor harmonics”, Phys. Rev. D, 2, 2141–2160, (1970). 1, 3.1, 1
Zerilli, F.J., “Perturbation analysis for gravitational and electromagnetic radiation in a Reissner-Nordstroum geometry”, Phys. Rev. D, 9, 860, (1974). 1
Zouros, T.J.M., and Eardley, D.M., “Instabilities of massive scalar perturbations of a rotating black hole”, Ann. Phys. (N. Y.), 118, 139–155, (1979). 3.3
Zwerger, T., and Müller, E., “Dynamics and gravitational wave signature of axisymmetric rotational core collapse”, Astron. Astrophys., 320, 209–227, (1997). 5.2
Acknowledgments
We are grateful to G. Allen for the suggestions and the careful reading of the manuscript. Suggestions by N. Andersson, H. Beyer, A. Rendall and N. Stergioulas are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix: Schrödinger Equation Versus Wave Equation
Appendix: Schrödinger Equation Versus Wave Equation
The purpose of this appendix is a brief comparison of properties of the Schrödinger equation
and the wave equation
for the same potential V(x).
The ansatz of “stationary states”
leads to the time independent Schrödinger equation
The ansatz (corresponding to Laplace transformation)
gives for the wave equation
The equations (75) and (77) are the same if we set E = -s2. Hence time independent scattering theory — the theory of the operator -d2/dx2 + V(x) — does not know whether we deal with the wave equation or the Schrödinger equation.
Consider first a positive potential of compact support. From quantum mechanics we know that there are no bound states. This is easy to understand: outside the support of the potential the solutions are \({\rm{exp}}\left( { \pm x\sqrt { - E} } \right)\), hence only negative values of E are possible eigenvalues. However, if we multiply (75) by ψ and integrate over all x we obtain a contradiction because of the positivity of V. Hence the operator -d2/dx2 + V(x) has no eigenfunctions and there are only scattering states, the continuous spectrum. The operator is selfadjoint on the Hilbert space of square integrable functions on the real line. Its resolvent, RE is defined for all complex E outside the continuous spectrum, which consists of the non negative real numbers. RE is an integral operator whose kernel is the Green function constructed in section 1. There G(s, x, x′) was considered as a function of s. As a function of E, G is analytic on the whole complex plane with the exception of real E ≤ 0, the continuous spectrum. In terms of s, the Green function — and the resolvent — is defined on the “physical half space” Re(s) > 0.
Resonances of Schrödinger operators can be defined as the poles of the analytic extension of the Green function or the resolvent. There is a huge amount of literature on the subject, in particular mathematical papers. A convenient starting point may be the proceedings of a conference on resonances in 1984 [4]. Existence of resonances, asymptotic distribution and also their interpretation is treated. There is in particular the recent development of “Geometric scattering Theory”, where the use of “pseudo differential operators” gives strong and interesting results [149]. We describe one such result on the asymptotic distribution of quasi-normal mode frequencies of the Schwarzschild spacetime in section 2. It is amusing to note that in the field of quantum mechanics the same difficulties in defining the notion of a resonance occurred as in relativity in the context of “normal modes of black holes”! [189] is a good reference explaining this point.
Historically, quasi-normal modes appeared the first time in Gamow’s treatment of the α-decay. The model he studies is a potential with two positive square potentials. Radioactive decay is exponential in experiments. However, even the decay in time of solutions of the free Schrödinger equation is a power law decay (1/t for 1-dimensional systems), similarly for potentials with compact support. So we face the difficulty to characterize that part of the time evolution, in which exponential decay is a good approximation, knowing that the final decay is polynomial! In [190] such estimates are derived.
Let us finally consider general potentials of compact support. If the potential well is deep enough a finite number of negative eigenvalues En may exist describing bound states of the quantum system. What are the properties of the corresponding solutions of the wave equation? Let ψn(x) be an eigenfunction of -d2/dx2 + V(x) with eigenvalue En < 0. Then (E = -s2)
is a solution of the wave equation. For large positive x we have
as the only square integrable solution of the Schrödinger equation with vanishing potential. Thus the solution of the wave equation for large x is
This solution grows exponentially in time and falls off exponentially in space for x → ∞. This apparently strange behaviour is possible because the energy density of the conserved energy of the wave equation
is not positive definite, if the potential is somewhere negative. In this situation the solution can grow in time and nevertheless have conserved finite energy.
In the complex s plane the eigenvalues appear as poles of the Green function with values \({s_n} = \sqrt { - {E_n}} \). To the right of the largest eigenvalue we have analyticity of the Green function.
Let us close this section by remarking that functional analysis techniques can also be used to develop existence theory: In the case discussed above, -d2/dx2 + V(x) is selfadjoint on the space of square-integrable function. “Functional calculus” can be used to show the existence and uniqueness of solutions of the time dependent Schrödinger and wave equation, given appropriate initial data. From this point of view the time independent Green function is the primary object, which is unique because there is a unique selfadjoint operator -d2/dx2 + V(x) on the real line.
Rights and permissions
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kokkotas, K.D., Schmidt, B.G. Quasi-Normal Modes of Stars and Black Holes. Living Rev. Relativ. 2, 2 (1999). https://doi.org/10.12942/lrr-1999-2
Published:
DOI: https://doi.org/10.12942/lrr-1999-2