Introduction

Massive multiple-input multiple-output (maMIMO) systems have recently gained a lot of attention due to their huge energy and spectrum efficiency improvements [1]. In a maMIMO system, the base station (BS) has several antennas that are substantially larger than the mobile terminals. The PSs are sent to the BS by each mobile terminal in the maMIMO system, and the uplink (UL) channel is estimated by the BS [2]. The time-division duplex (TDD) protocol is preferred over the frequency-division duplex (FDD) protocol for maMIMO systems because of the channel reciprocity in a TDD system, and UL training can be employed to obtain the DL CSI. Because of the scarcity of channel coherence time and the huge number of mobile terminals in the multi-cell network, mobile terminals will inevitably use the same set of training sequences again. As a result, there will be a PC, which implies that mobile terminals utilizing the same set of pilot sequences or non-orthogonal PS will corrupt the estimated channels at the BS. Several techniques have been recommended in literature to alleviate PC problems and have been extensively discussed in the related works section.

The remaining sections of the paper are structured as follows: the very first section is the paper’s “Introduction,” the second section discusses the “System model,” and then the “Methods” under which we discussed Formulation of problem, Pilot assignment with LAP, Greedy algorithm, and Tools and parameters used in the simulation forms the third section. In the fourth section, “Results and discussion” is presented. We finally conclude the paper in the “Conclusions” section.

Notation

The bold letter case represents vectors, and the bold uppercase symbolizes matrices. \({\mathbf{I}}_{M}\) denotes identity matrices of dimension \(M\times M\). \((.{)}^{T}, ({.)}^{-1}, \mathrm{and} (.{)}^{H}\) are operators which define transpose, inverse, and conjugate transpose operations, respectively. \(E[.]\) denotes the operator for expectation.

Related works

For PC mitigation, several conventional algorithms based on pilot assignment have been proposed [3,4,5]. In [3], a vertex graph-coloring-based pilot assignment was proposed, in which pilot sequences were assigned to mobile terminals based on the ICI graph. The evaluation of an ICI graph is dependent on both the angle of arrival (AoA) correlation and the distance between the mobile terminals, but the problem with the scheme is that it needs a second-order channel information to function effectively. A deep learning-based pilot allocation scheme (DL-PAS) was done by [5] to solve problems caused by PC in maMIMO systems. The learning process for this algorithm is based on the correlation between mobile terminal location and pilot assignment. To process the data, however, the DL algorithm demands a lot of data, and it requires much longer time.

The location-based pilot assignment methods for pilot decontamination were developed by the authors in [6] and [7]. LoS interference was given a new expression in [6], and it is regarded as the selection criteria for pilots. Although the sum spectral efficiency (SE) is increased, it still takes longer to implement the pilot assignment process, especially in enormous networks. The pilot assignment process was used to eliminate interference in the angular region of the targeted user as described in [7]. The BS antenna array numbers and the position of the mobile terminals both contribute to the description of this angular region. Nevertheless, the joint optimization problems used to formulate the pilot assignment problem result in extreme computational complexity. In [8, 9], the pilot allocation depending on pilot reuse (that is a reuse factor more than one) is also selected for the PC’s eradication method. A thoroughly composed pilot reuse approach was proposed by [8]. In accordance with the tree division, this method allows neighboring cells to use various sets of pilot sequences. The depth of the tree increases linearly with the severity of the PC. To improve performance, ensure greater distances between cells that share the same pilot sets. This method works well when the ratio of the channel coherence time to the number of mobile terminals in each cell is relatively massive. A soft pilot reuse (SPR) scheme was developed by [9] to enhance the quality of service (QoS) of the edge users. The channel quality for each user is initially compared with a threshold before the pilot allocation procedure, but an increase in complexity occurs due to the additional computation expenses incurred by determining the ideal threshold value. Pilot allocation schemes were proposed to mitigate PC by weighing fairness among mobile terminals [10, 11]. The pilot assignment based on the harmonic SINR utility function was introduced to control the fairness among users for the purpose of PC mitigation in [11]. However, as the number of mobile terminals and network size increases to more than two cells, the complexity of the system also increases as well.

The pilot allocation methods in [4, 12] aim to improve the performance of the mobile terminals with SINR. The pilot allocation described in [12] was centered on maximizing the system’s overall capacity for pilot decontamination. In their work, users with poor channel conditions were initially given the pilot sequences. However, as the network size grows, the pilot assignment process becomes more complex. In [4], an SPA scheme was proposed to help users with low SINR perform better. Low interference was achieved by assigning users with poor channel quality to PS. However, this scheme’s success is limited because it did not put into consideration the ICI that resulted in PC.

As indicated in [13, 14], some authors have attempted to combine two schemes for improve performance. In an effort to minimize the impact of PC, [13] proposed a joint pilot assignment scheme that combined the time-shifted [2] and SPA [4] schemes. Inter-group interference was minimized in [2] strategy, whereas SPA was applied to lower intragroup interference. Even though the performance in total had improved, the mutual interference between the uplink pilot signals and downlink data could not be eradicated completely even with the use of the SPA scheme. For maMIMO downlink, another pilot assignment method such as greedy based and swapping based was developed along with a PC precoding scheme (PCP) [14]. The PCP matrix was altered in accordance with the updated information on the pilot assignment, but this combination significantly outperformed the random pilot assignment.

We considered the source of ICI throughout the pilot assignment, which is the fundamental cause of the PC in maMIMO systems, in contrast to the works mentioned in [4, 15]. The availability of some factors, such as mobile terminal location, AoA, or LoS interference, is difficult to estimate, and it is a requirement for pilot assignment in some other works [3, 5,6,7], while in our proposed scheme, we only need large-scale fading coefficients that are easy to track because they do not change quickly during the coherence interval. Our proposed scheme is not computationally intensive and can be easily implemented in large-scale systems. In addition to comparisons to prior works in [4, 16], our work aims at improving the performance of mobile terminals with serious PC issues. A typical problem in assigning PSs to terminals at a targeted cell surrounded by neighboring cells is studied. Unlike random assignment technique, which randomly allocate PS to mobile terminals, our proposed scheme optimizes all users in the targeted cell’s minimal uplink’s SINR. The BS first evaluates the ICI of each PS caused by terminals with the same PS in other neighboring cells, taking advantage of the large-scale (LS) characteristics of fading channels. The channel characteristics of distinct mobile terminals in the targeted cell to the BS may then be identified, which typically vary from one terminal to the next. The proposed scheme allocates pilot sequences to the right mobile terminals to achieve the least ICI. Some theories will be derived, and simulations were conducted to validate the effectiveness of the proposed GreedyLAP scheme in maMIMO systems.

System model

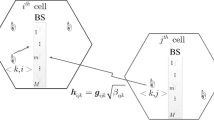
A multi-cell multiuser maMIMO system comprises of L hexagonally shaped cells is considered as seen in Fig. 1, each of which contains M BS antenna arrays and \(K(K\ll M)\) single-antenna mobile terminals [1, 16]. The vector of the channel \({h}_{ijk}\in {\mathcal{C}}^{M\times 1}\) from the \(k-th\) mobile terminal in the \(j-th\) cell to the BS in the \(i-th\) cell can be modelled and given below.

$${\mathbf{h}}_{ijk}={\mathbf{g}}_{ijk}\sqrt{{\beta }_{ijk}}$$
(1)

Where \({\beta }_{ijk}\) is the coefficient for the large-scale (LS) fading, it changes gradually and can be tracked easily [17,18,19], and \({g}_{ijk}\sim \mathcal{C}\mathcal{N}(0,{{\varvec{I}}}_{\mathrm{M}})\) represents the small-scale fading vectors. We utilize the widely established time block fading model to investigate a typical TDD protocol in maMIMO system, in which the channel vector \({h}_{ijk}\) stays constant during the coherence interval \({\tau }_{c}={B}_{c}{T}_{c}\)[1] \({B}_{c}\) represents bandwidth, and \({T}_{c}\) represents coherent time respectively.

Fig. 1
figure 1

Illustration of PC in massive MIMO system

Full size image

In the \(j-th\) cell, the channel matrix of all the K mobile terminals and the BS in the \(i-th\) cell can be expressed as

$${\mathbf{H}}_{ij}=\left[{\mathbf{h}}_{i,j,1}, {\mathbf{h}}_{i,j,2}, \dots , {\mathbf{h}}_{i,j,K}\right]=[{g}_{i,j,1}\,{g}_{i,j,2},\dots ,{g}_{i,j,K}{]\mathbf{D}}_{i,j}^\frac{1}{2}$$
(2)

where \({\mathbf{D}}_{i,j}=diag({\beta }_{i,j,1},{\beta }_{i,j,2},\dots ,{\beta }_{i,j,K})\) and represents the LS fading matrix which relates to all the K mobile terminals in the \(j-th\) cell to the BS of the \(i-th\) cell.

The BS acquires the downlink (DL) estimated channel by using the TDD protocol and using the reciprocity of the UL and DL channels. To be more specific, for both the DL and UL directions, both the small-scale fading vectors and the LS fading coefficients may be regarded as identical, provided the bandwidth is adequately low to avoid independent fading of the DL and UL. During the coherence interval, we utilize the commonly applied time block fading model, in which the vector of the channel \({h}_{ijk}\) stays unchanged. Assuming the PS \(\Phi =[{\phi }_{1},{\phi }_{2},\dots ,{\phi }_{K}{]}^{T}\in {\mathcal{C}}^{K\times 1}\) with length of \(\tau\) employed in one cell orthogonal \(({\varvec{\Phi}}{{\varvec{\Phi}}}^{H}={\mathbf{I}}_{K})\), and the same pilot group is used again in neighboring cells because pilot resource is scarce [16]. The PS \({\phi }_{k}\) is normally assigned to the \(k-th\) mobile terminal utilizing conventional or randomized pilot assignment method. It ignores the fact that various users have variable channel quality [11, 16]. Thus, the received PS \({\mathbf{Y}}_{i}^{P}\in {\mathcal{C}}^{M\times \tau }\) at the BS in the \(i-th\) cell can be expressed as follows:

$${\mathbf{Y}}_{i}^{P}=\sqrt{{\rho }_{P}}\sum_{j=1}\nolimits^{L}\sum_{k=1}\nolimits^{K}{\mathbf{h}}_{ijk}{\phi }_{k}^{T}+{\mathbf{N}}_{i}^{P}$$
(3)

where \({\rho }_{P}\) represents the pilot transmission power and \({\mathbf{N}}_{i}^{P}\in {\mathcal{C}}^{M\times 1}\) represents the additive white Gaussian noise (AWGN) matrix with independently and identically distributed (i.i.d.) Gaussian random variable entries with zero mean and variance of \({\sigma }_{N}^{2}\). In the \(i-th\) cell, the user data \({y}_{i}^{u}\in {\mathcal{C}}^{M\times 1}\) received at the BS is expressed in Eq. (4) below.

$${y}_{i}^{u}=\sqrt{{\rho }_{u}}\sum_{j=1}\nolimits^{L}\sum_{k=1}\nolimits^{K}{\mathbf{h}}_{ijk}{x}_{jk}^{u}+{\mathbf{n}}_{i}^{u}$$
(4)

where \({x}_{jk}^{u}\) depicts the symbol from the \(k-th\) mobile terminal in the \(j-th\) cell with \(E\left\{|{x}_{jk}^{u}{|}^{2}\right\}=1\), \({\rho }_{u}\) represents the UL data transmission power, and \({\mathbf{n}}_{i}^{u}\in {\mathcal{C}}^{M\times 1}\) represents the AWGN vector with \(E\{{\mathbf{n}}_{i}^{u}\left({\mathbf{n}}_{i}{)}^{H}\right\}={\sigma }_{n}^{2}{\mathbf{I}}_{M}\). By correlating the PS \({\mathbf{Y}}_{i}^{P}\) received with pilot sequence \({\phi }_{k}\), the estimated channel of the \(k-th\) user in the \(i-th\) cell is expressed as shown in Eq. (5).

$${\widehat{h}}_{iik}=\frac{1}{\sqrt{{\rho }_{P}}}{\mathbf{Y}}_{i}^{P}{\phi }_{k}^{H}=\sum\nolimits_{j=1}^{L}{\mathbf{h}}_{ijk}+{\mathbf{v}}_{ik}$$
(5)

where \({\mathbf{v}}_{ik}=\frac{1}{\sqrt{{\rho }_{P}}}{\mathbf{N}}_{i}^{P}{\phi }_{k}^{H}\) denotes the equivalent noise. The estimated channel of the \(k-th\) mobile terminal in the \(i-th\) cell, \({\widehat{h}}_{iik}\), linearly combines with the channels \({h}_{ijk}, j=\mathrm{1,2},\dots ,L,\) of the users with identical PS in all cells, which is commonly known as PC. By applying the matched-filter (MF) detector depending on the estimated channel \({\widehat{h}}_{iik},\) the symbol detected for the \(k-th\) mobile terminals is located in the \(i-th\) cell, and it is expressed as follows:

$$\begin{aligned} &{\widehat{x}}_{ik}^{u}={\widehat{\mathbf{h}}}_{iik}^{H}{{\varvec{y}}}_{i}^{u}=(\sum_{j=1}^{L}{h}_{ijk}+{v}_{ik}{)}^{H} \left(\sqrt{{\rho}_{u}}\sum_{j=1}^{L}\sum_{{k}^{^{\prime}}=1}^{K}{h}_{ij{k}^{^{\prime}}}{x}_{j{k}^{^{\prime}}}^{u}+{n}_{i}^{u}\right)\\ &M\to \infty =M\sqrt{{\rho }_{u}}\left({\beta }_{iik}{x}_{ik}^{u}+{\sum }_{j\ne i}{\beta }_{ijk}{x}_{ik}^{u}\right)\\ &M\to \infty =M\sqrt{{\rho }_{u}}\left({\beta }_{iik}{x}_{ik}^{u}+{\sum }_{j\ne i}{\beta }_{ijk}{x}_{ik}^{u}\right) \end{aligned}$$
(6)

Where \({\varepsilon }_{ik}^{u}\) represents intra-cell interference and uncorrelated noise, both types of noise can be considerably decreased by making the BS antenna numbers large [1]. Then, the UL SINR of the \(k-th\) mobile terminal in the \(i-th\) cell is written as in Eq. (7) shown below.

$${SINR}_{ik}^{u}=\frac{|{\mathbf{h}}_{iik}^{H}{{\mathbf{h}}_{iik}|}^{2}}{\sum_{j\ne i}|{{\varvec{h}}}_{ijk}^{H}{\mathbf{h}}_{ijk}{|}^{2}+\frac{|{\varepsilon }_{ik}^{u}{|}^{2}}{{\rho }_{u}}}{\begin{array}{c}M\to \infty \\ \to \end{array}\frac{{\beta }_{iik}^{2}}{{\sum }_{j\ne i}{\beta }_{ijk}^{2}}}_{.}$$
(7)

The average capacity for UL of this mobile terminal can be expressed as \({C}_{ik}^{u}=(1-\) \(\mu )E\left\{{log}_{2}\left(1+{SINR}_{ik}^{u}\right)\right\}\), where \(0<\mu <1\). As M approaches infinity, it is evident that thermal noise and small-scale fading impacts can obviously be averaged out. The average UL capacity, on the other hand, is constrained by PC and cannot be simply increased by increasing the transmission or pilot power.

The PC equally affects transmission in the DL. For the transmission in the DL, the MF precoding matrix is normalized [20]. This is normally applied to the DL transmission, and it is represented by \({\mathbf{W}}_{i}=\frac{1}{\sqrt{{\gamma }_{i}}}{\widehat{\mathbf{H}}}_{i,i}^{*}\) and \({\gamma }_{i}=Tr({\widehat{\mathbf{H}}}_{i,i}^{T}{\widehat{\mathbf{H}}}_{i,i}^{*})/K\) which represent normalization factor. The BS located in the \(i-th\) cell will transmit an M dimensional signal vector \({s}_{i}^{d}={\mathbf{W}}_{i}{x}_{i}^{d}\) where \({\mathrm{X}}_{i}^{d}=[{x}_{i,1}^{d } {x}_{i,2}^{d} {x}_{i,3}^{d}\dots {x}_{i,K}^{d}{]}^{T}\) where \(E\left\{.|{{x}_{i,k}^{d}|}^{2}\right\}=1\) represents source symbol vector for the K mobile terminal located in the \(i-th\) cell. The signals received from the K mobile terminal in the \(i-th\) cell can be bundled together to form \({y}_{i}^{d}=\sqrt{{\rho }_{d}}\sum_{j=1}^{L}{\mathbf{H}}_{j,i}^{T}\frac{1}{\sqrt{{\gamma }_{j}}}{\widehat{\mathbf{H}}}_{i,i}^{*}{x}_{j}^{d}+{\mathbf{n}}_{i}^{d}\), where \({\mathbf{n}}_{i}^{d}\) represents the channel AWGN vector of the DL associated with \(E\{{{\varvec{n}}}_{i}^{d}\left({{\varvec{n}}}_{i}^{d}{)}^{H}\right\}=({{\varvec{\sigma}}}_{i}^{d}{)}^{2}{\mathbf{I}}_{M}\). This derivative equivalent is shown in Eq. (7); the SINR for the DL for the \(k-th\) mobile terminal located in the \(i-th\) cell can be given as follows:

$${SINR}_{ik}^{d}=\frac{|{\mathbf{h}}_{iik}^{T}{{\mathbf{h}}_{iik}^{*}|}^{2}}{\sum_{j\ne i}|{{\varvec{h}}}_{ijk}^{T}{\mathbf{h}}_{ijk}^{*}{|}^{2}+\frac{|{\varepsilon }_{ik}^{d}{|}^{2}}{{\rho }_{d}}}{\begin{array}{c}M\to \infty \\ \to \end{array}\frac{{\beta }_{iik}^{2}}{{\sum }_{j\ne i}{\beta }_{ijk}^{2}}}_{.}$$
(8)

where \({\varepsilon }_{ik}^{d}\) represents the equivalent interference similar to \({\varepsilon }_{ik}^{u}\) in Eq. (6). The DL rate can also be denoted as \({C}_{ik}^{d}=(1-\) \(\mu )E\left\{{log}_{2}\left(1+{SINR}_{ik}^{d}\right)\right\}.\)

Methods

The optimization problem for assigning pilot for a cell that is targeted is first articulated in this section. The GreedyLAP strategy is then provided as a greedy way of approaching the optimization solution.

Formulation of the problem

The pilot allocation for a particular cell, that is, the \(i-th\) cell, is referred to as the target cell, whereas the respective BS independently regulate the pilot allocation for other cells. The number of distinct kinds of pilot allocation between K users \([{U}_{1}, {U}_{2},\dots ,{U}_{K}]\) and K PS \(\left[{\phi }_{1}, {\phi }_{2},\dots , {\phi }_{K}\right]\) is enormous for this cell, that is, \(P\left(K,K\right)=K!\). In the random pilot assignment scheme, [1, 16], the \(k-th\) user (\({U}_{k})\) is randomly assigned to the pilot sequence \({\phi }_{K}\).

The main aim is to maximize the least UL SINR of all K mobile terminals in the target cell, and this can be expressed as the optimization problem below.

$$\mathcal{P} :\begin{array}{c}max\\ {\{\mathcal{R}}_{s}\}\end{array} \begin{array}{c}min\\ {\forall }_{k}\end{array} \frac{|{{\varvec{h}}}_{i,i,{r}_{s}^{k}}^{H}{{\varvec{h}}}_{i,i{r}_{s}^{k}}{|}^{2 }}{{\sum }_{j\ne i}|{{\varvec{h}}}_{ijk}^{H}{{\varvec{h}}}_{ijk}{|}^{2}+\frac{|{\varepsilon }_{{ir}_{s}^{k}{|}^{2}}^{u}}{{\rho }_{u}}}$$
(9)

where \(\{{\mathcal{R}}_{s}:s=\mathrm{1,2},3,\dots ,K!\}\) represents all the potential K! kind of pilot assignments.

\({\mathcal{R}}_{s}=[{r}_{s}^{1}, {r}_{s}^{2},\dots ,{r}_{s}^{k}]\) represents the \(s-th\) assignment, and an assumption is that the PS \({\phi }_{k}\) is assigned to the \(k-th\) mobile terminal \({U}_{k}\) in all other cells. However, it appears that we will be unable to solve this optimization problem \(\mathcal{P}\) due to inaccurate estimated channel under PC, as seen in (9). Fortunately, the constraint of the UL SINR can be denoted by the LS fading coefficients \({\beta }_{ijk}\) as seen in (9) [17,18,19].

We cannot get an accurate estimated channel under PC; thus, solving this optimization problem \(\mathcal{P}\) appears to be impossible.

As M the BS antennas approaches infinity, the optimization problem can then be simplified as shown in Eq. (10) below.

$$\mathcal{P}\to {\mathcal{P}}^{^{\prime}} as\,M\to \infty :\begin{array}{c}max\\ {\mathcal{R}}_{s}\end{array} \begin{array}{c}min\\ {\forall }_{k}\end{array} \frac{{\beta }_{ii{r}_{s}^{k}}^{2}}{{\sum }_{j\ne i}{\beta }_{ijk}^{2}}$$
(10)

Optimization problem \({\mathcal{P}}^{^{\prime}}\) can be solved in a greedy way.

Pilot assignment with LAP

One of the most effective techniques for optimization problem \({\mathcal{P}}^{^{\prime}}\) to be solved is to search through all possible assignments and select the best one. This is computationally complex because to search through all possible assignments is enormous as K!. The optimization problem \({\mathcal{P}}^{^{\prime}}\) is to be solved in low complexity in a greedy way [4].

For the cell targeted, we defined certain parameters \(\{{\alpha }_{k}{\}}_{k=1}^{K}\) the channel for K mobile terminals can be quantified as follows:

$${\alpha }_{k}={\beta }_{iik}^{2}, k=\mathrm{1,2},\mathrm{3,4},\dots ,K.$$

For the K PS \(\left[{\phi }_{1}, {\phi }_{2},{\phi }_{3},\dots ,{\phi }_{K}\right],\) we express the parameters \(\{{b}_{k}{\}}_{k=1}^{K}\) the ICI of each PS caused by the mobile terminals repeating the same sets of PS in other neighboring cells or using non-orthogonal PS can also be quantified and written as follows:

$${b}_{k}={\sum }_{j\ne i}{\beta }_{ijk}^{2}, k=\mathrm{1,2},3.4,\dots ,K$$

This varies between the K pilot sequence. For a particular assignment \({\mathcal{R}}_{s}=\left[{r}_{s}^{1}, {r}_{s}^{2},\dots ,{r}_{s}^{K}\right]\), the PS \({\phi }_{k}\) is assigned to the terminal \({U}_{{r}_{s}^{k}}\), whereby the constraints of UL SINR of the terminal \({U}_{{r}_{s}^{k}}\), i.e., \({SINR}_{ik}^{u}\to {a}_{{r}_{s}^{k}/{b}_{k}}\), are decided by two as follows:

  1. 1

    The quality of the channel \({\alpha }_{{r}_{s}^{k}}\) of the terminal \({U}_{{r}_{s}^{k}}\)

  2. 2

    The ICI \({(b}_{k})\) is created because the mobile terminals share the same set of pilot sequence \({\phi }_{k}\) with the neighboring cells. To increase the least UL SINR of all users in the cell that is targeted, we must avert assigning a high ICI to a terminal with poor channel quality which will result in a relatively low UL SINR [4].

The proposed GreedyLAP scheme assigns pilot sequences to mobile terminals to achieve the lowest intercell interference.

Assignment problems are a type of linear programming problems (LAP) that deal with the one-to-one allocation of diverse resources to activities.

The LAP consciously matches equal number of workers to a task in a unique way. In our work, we match pilot sequences to terminals. The proposed scheme performs the pairing to achieve minimum ICI or maximum SINR.

K pilot sequence is sorted out according to their ICI in any order, i.e.,

$${\mathcal{R}}_{p}:\left[{\phi }_{{r}_{p}^{1}, }{\phi }_{{r}_{p}^{2}}, \dots ,{\phi }_{{r}_{p}^{K}}\right]$$
(11)

Similarly, K mobile terminals are also sorted out according to their channel qualities in any order, i.e.,

$${\mathcal{R}}_{q} :\left[{U}_{{r}_{q}^{1}}, {U}_{{r}_{q}^{2}},\dots ,{U}_{{r}_{q}^{K}}\right]$$
(12)

Pairing between K pilot sequence (\({\phi }_{{r}_{p}^{K}})\) and K mobile terminals \({(U}_{{r}_{q}^{K}})\) will produce the smallest ICI \(({b}_{k})\) using the proposed scheme, comparable to weighed bipartite graph in finding a perfect match.

There may be several viable assignments for minimal interference, but we are only interested in identifying one. Assuming m is the number of users, n is the number of pilot sequences subject to the assignment constraints.

The problem can be formulated as an integer linear programming problem and then expressed below as in Eq. (13).

Linear assignment problem (LAP)

Objective function of LAP

$$min\sum_{n=1}\nolimits^{K}\sum_{m=1}\nolimits^{\phi }{b}_{k,nm}j{x}_{nm}$$
(13)

Subject to the following:

\({\sum }_{n=1}^{K}{x}_{n,m}=1, m=\mathrm{1,2},\mathrm{3,4},\dots ,K\) (every row of permutation matrix sums to 1).

\({\sum }_{m=1}^{\phi }{x}_{n,m}=1, i=\mathrm{1,2},\dots ,\upphi\) (every column of permutation matrix sums to 1).

\({x}_{n,m}=0\) or \({x}_{n,m}=1\) (permutation matrix has only entries 0 or 1).

\({x}_{n,m}=1 ,\) if Kth user is assigned to the best \(\phi\) th pilot sequence.

\({x}_{i,j}=0\), if Kth user is not assigned to the best \(\phi\) th pilot sequence [21].

Greedy algorithm for linear assignment problem

A greedy algorithm is one that chooses the locally optimal option at each step while disregarding the global optimality. A greedy algorithm for the linear assignment problem would try to assign PS to the right user with the lowest interference, regardless of the impact on the other assignments.

Pilot sequence \(\phi\) is assigned to mobile terminals in all j cells for all 1,2, 3…,L.

figure a

Algorithm 1. Greedy algorithm for the LAP

Making allocation and linkage for the assignment, it is \(\mathcal{O}\left(K\right)\) and mesh \(\mathcal{O}\left({K}^{2}\right);\) for queuing, it is\(\mathcal{O}(2{K}^{2}\mathrm{log}K+ {K}^{2})\). Therefore, initialization requires \(\mathcal{O}({K}^{2}\mathrm{log}K )\) time. The loop’s body necessitates a consistent temporal allocation of pilot to terminals and \(\mathcal{O}\left(2k-1\right)\) time to eliminate the row and column from \(k\times k\) matrix using an enhanced depth first search. Thus, the loop accounts for \(\mathcal{O}({K}^{2})\) time. The resulting time complexity is therefore \(\mathcal{O}({K}^{2}\mathrm{log}K)\).

Tools and parameters used in the simulation

We perform Monte Carlo simulation experiments using MATLAB and offer numerical results for the problem of pilot assignment and to validate the performance of GreeLAP technique. We examine a three-celled maMIMO system with the radius R of the cell and K mobile terminals distributed evenly within each cell. The cell that is targeted is surrounded by neighboring cells. Table 1 summarizes some key parameters that were utilized in this simulation, and the base code used can also be found in [1, 22].

Table 1 Parameters used in the simulation
Full size table

Results and discussion

The linear assignment problem with greedy algorithms is evaluated and measured against conventional or random assignment scheme [16]; this assigns pilot sequences to active mobile terminals randomly and smart pilot assignments [4] and also assigns pilot sequences with the least ICI to the terminals with the worst quality of channel.

Figure 2 illustrates the cumulative distribution function (CDF) of SINRs for the terminals with the various schemes when the BS antennas M = 100. It can obviously be seen that GreedyLAP scheme outperformed SPA and random scheme. The reason being that they could have been affected by ICI due to the presence of PC. The proposed scheme performed best because they assigned pilots to the more deserving mobile terminals that resulted in the least ICI and therefore improved their SINR significantly.

Fig. 2
figure 2

Cumulative distribution function (CDF) for the various schemes

Full size image

Figure 3 illustrates the sum rate (bps/Hz) plotted against the number of base station antennas. As the BS antenna numbers increase, the sum rates also increase. The sum rate of GreedyLAP is observed to be better than those of SPA and randomly assigned schemes. This performance is because the proposed scheme combats interference from the adjacent cells by reducing the consequence of PC.

Fig. 3
figure 3

The sum rate vs the number of BS antennas for the various schemes

Full size image

Figure 4 demonstrates a graph of the sum rate plotted against the number of BS antennas in the target cell for the three schemes. It can be observed that the sum rate is reduced as the number of mobile terminals increases and the proposed scheme performed better than the random and SPA schemes. This indicates that the proposed scheme can serve more mobile terminals with slightly better performance.

Fig. 4
figure 4

Sum rate vs the number of BS antennas per cell

Full size image

Figure 5 shows the sum rate plotted against SNR for the proposed random and SPA schemes. It can be observed that the sum rate for the GreedyLAP or proposed scheme performed better than the other two schemes when compared. The reason being that the proposed scheme (GreedyLAP) assigns pilot sequences according to the LS fading mobile terminals for all the cells, while SPA assigns pilots separately and random scheme assigns pilots without using any information.

Fig. 5
figure 5

The sum rate vs SNR for different pilot assignments schemes

Full size image

Conclusions

In this paper, a GreeyLAP pilot assignment scheme was proposed to alleviate the consequences of PC in a maMIMO system. Optimization problem was formulated and solved to enhance the systems throughput in the UL direction. This was attained by assigning pilots sequence to mobile terminals that achieved the least ICI. This was accomplished by utilizing linear assignment problem with greedy algorithm. Simulations were conducted, and the results obtained proved that the proposed scheme performed better than both random assignment and smart pilot assignment schemes when compared.