1 Introduction

Three-dimensional (3D) imaging at the nanometer scale enables important insights in biology and material behaviors, including virus function [1], structural damage [2], nanoelectronics [3], etc. One way is to do this destructively, i.e. immobilize the specimen, etch the top layer finely with a particle beam, image the revealed features with a scanning electron microscope or similar high-resolution methods, and repeat this process until the entire specimen volume has been consumed [4, 5]. However, in many instances, it is preferable to operate non-destructively, and then a form of tomography is necessary. This is more challenging than, say, the medical case, for two main reasons: (i) as feature sizes approach the radiation wavelength, e.g. X-rays, diffraction and scattering effects influence image fidelity more strongly; and (ii) the number of voxels (resolvable 3D elements) within a macroscopic volume can become very large. For example, at \(\left( 10\,\text {nm}\right) ^3\) 3D sampling rate, the number of voxels in a \(1\,\text {cm}\times 1\,\text {cm}\times 100\,\upmu \text {m}\) volume is \(\sim 10^{16}\). In this paper, we use integrated circuits (IC) as an exemplar, because they present some practical conveniences—ICs are rigid and, thus, require no fixing—and it is also very useful, for example in manufacturing process verification, failure analysis and counterfeits detection [3, 6]. On the other hand, the challenge of 3D IC imaging grows with time due to Moore’s law [7].

For nondestructive 3D IC imaging at the nanoscale, hard X-rays are ideal probes because of their long penetration depth and short wavelength. Unlike medical X-ray tomography, however, which operates almost always on the intensity of the projections, in the nanoscale case it is common to seek the complex field via ptychography [8] first, and then do tomography. This combined scheme is also known as X-ray ptychographic tomography (ptycho-tomography) [9]. There are several reasons to do this: for example, if the projection approximation is still applicable, then we can perform two tomographic reconstructions in parallel, one on the field amplitude yielding the imaginary part of the refractive index (attenuation) at each voxel and one on the field phase yielding the real part; most materials exhibit phase variations by 10 times larger than their respective absorption changes [10].

X-ray ptycho-tomography reconstructions are performed in the same sequence as experimental acquisition, i.e. in a two-step approach [9, 11]. First, 2D projections are retrieved from far-field diffraction patterns using phase-retrieval algorithms [12,13,14], and then, tomographic reconstructions are implemented to recover the real and/or imaginary parts of a 3D object from 2D projections [15,16,17,18]. Many applications have been successfully demonstrated with this two-step approach: IC imaging [3, 19], microscopic organism imaging [9, 20] and studies of material properties such as fracture [21], percolation [22] and hydration [23]. However, both ptychography and tomography demand large redundancy in the data [24, 25], leading to long acquisition and processing times generally.

One way to reduce the acquisition time is through high-precision scanners that can reliably work with efficient scanning schemes [26,27,28] and at high scanning velocities [29, 30]. Reducing the data redundancy requirements in ptycho-tomography is an alternate way to speed up data acquisition but introduces ill-posedness. However, with reduced data, the conventional reconstruction algorithms are likely to produce artifacts and a general loss of fidelity.

Studies have coupled computationally the ptychography and tomography reconstruction processes to improve reconstruction qualities under limited data acquisition. One way is to split the whole problem into two sub-problems, as conventional two-step approaches, and perform them iteratively, to mildly relax the data redundancy requirements without sacrificing fidelity. For example, tomography naturally provides angular intersections of beams as they pass through the object, which is employed to coarsen the ptychographic sampling in each projection with iterative two-step algorithms [31,32,33,34]. The angular requirements in tomography could be eased as well [35,36,37,38,39] through physically modeling the interactions between X-ray and object with a multi-slice propagation model instead of projection approximation [40]. Depth information is resolved partially in individual projection planes to help relax the usual Crowther criterion for tomography. On the other hand, the coupling between ptychography and tomography could be expressed as a single optimization problem to reconstruct 3D objects from diffraction patterns directly instead of two separate cost functions [41,42,43] to further reduce the required number of measurements. Still, however, severe image artifacts are to be expected if data reduction is aggressive beyond a certain limit. Moreover, all the above mentioned variants of X-ray ptycho-tomographic reconstruction are computationally intensive and, hence, scale prohibitively with sample volume.

In general, regularization resolves ill-posedness by rejecting invalid objects and, hence, eliminating reconstruction artifacts that would be incompatible with our prior knowledge about the object. For example, handcrafted priors, such as sparsity, piecewise constancy, etc. are routinely incorporated in X-ray ptycho-tomography problems to improve reconstruction qualities to some extent [31,32,33, 43, 44]. Recently, deep neural networks (DNNs) have yielded even better regularization performance under severe ill-posedness, e.g. 2D phase retrieval through scattering media [45, 46] and under extremely low light conditions [47, 48], digital staining [49, 50], limited-angle 3D volumetric reconstruction [51, 52], etc. These works are based on supervised learning, where the regularizing priors are learned from large datasets of available typical objects. Non-supervised approaches are also possible [53, 54] but not of interest for our present work. The purpose of this paper is to use DNN-based regularizers to radically increase the allowable angular reduction and associated gains in both acquisition and computation time in X-ray ptycho-tomography, which hasn’t been explored in experimental X-ray ptycho-tomography yet [55].

Poor image fidelities resulting from severe ill-posedness in X-ray ptycho-tomography is difficult to improve if we naïvely apply a vanilla 3D DNN structure with the kernels size of \(3\times 3\times 3\) [56], i.e., each layer’s receptive field extends to the next layer by a single pixel away only. To perform image correction in hard cases (i.e., large angular reduction) one needs DNNs with many layers or large size kernels, and that is disadvantageous both because it introduces too many parameters, especially in 3D, and because training may saturate early, even with residuals [57]. On the other hand, the physics of tomographic image reconstruction suggests that larger receptive fields in the convolutional layers should be effective in a shallower network while still requiring a large number of parameters. The atrous convolution methods [58, 59] combat this problem by forcing all connections within the receptive field to be zero, except the ones at the outermost corners. Moreover, the implementation of atrous convolution in a Spatial Pyramid Pooling (ASPP) module is known to perform well in extracting long-range and multi-scale information [60, 61].

2 Results

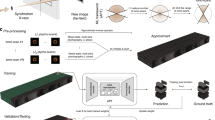
In this study, we propose the novel deep learning-based pipeline for reduced-angle ptycho-tomography, RAPID. Our method works as follows: first, the far-field diffraction patterns obtained from reduced 21-angle acquisitions are pre-processed together to produce an Approximant [51]. This is a preliminary 3D reconstruction of the object’s interior and generally exhibits low quality. The Approximant is obtained by gradient descent inversion on a multi-slice propagation model [40, 62]. Subsequently, the Approximant is fed into the RAPID network. During the training phase, matching the network’s output to the corresponding golden standard is used to adjust the network weights in a standard stochastic gradient descent fashion. During testing, the network’s output is the final reconstruction of the given volume. The procedure is schematically depicted in Fig. 1 and described in detail in the Methods section.

A new DNN structure is proposed by incorporating the atrous module in the 3D U-net structure [63, 64] to improve the image qualities. Here we modify the atrous module anisotropically to account for the 3D point spread function (PSF). We use the term “anisotropy” here in the sense that the atrous convolutional kernels are different along the x, y, and z axes.

In the experimental demonstration, the IC sample consists of 13 circuit layers. The layers have a different thickness each. The total thickness is unknown, but we estimated it based on the golden standard to be \(3.92\, \upmu \text {m}\). The area of each circuit layer is \(25.10 \times 93.18\, \upmu \text {m}^2\). The upper part of the IC, relative to the optical axis, is used to pre-train the network. This training segment has a total volume of \(20.60\times 93.18 \times 3.92\,\upmu \text {m}^3\). The remaining part, with volume \(4.48 \times 93.18 \times 3.92\,\upmu \text {m}^3\), serves for testing.

Better reconstruction performance can be expected as the number of rotation angles increases, at the expense of longer experimental and computational time. We explore the best scanning condition that results in the minimum feasible acquisition time. Starting from the extreme condition of a single angle, we gradually increase N to 349 by adding angular measurements uniformly within maximum angular range \(\theta _{max} = 140.8^\circ \). The improvement is noticeable quantitatively and visually when the total number of rotation angles is small, e.g. from 1 to 5, as shown in Fig. 2a, b; Additional file 1: Fig. S2. However, above 21 angles the improvement is marginal. Therefore, this represents a good compromise between accuracy and acquisition cost.

Fig. 1
figure 1

Schematic of the proposed RAPID framework. a Reduced-angle ptycho-tomography experiment to collect diffraction pattern measurements via translational and rotational scanning. Raw diffraction patterns are pre-processed to generate the approximant as the input to the pre-trained network, and volumetric distribution are obtained as the final output. b Network training process. Diffraction patterns acquired from reduced-angle ptycho-tomography are pre-processed to get the approximant as the network input, and a two-step conventional approach is employed to generate the high-resolution golden standard (GS) as the ground truth to train the DNN

Full size image
Fig. 2
figure 2

Quantitative comparison among different scanning strategies for testing volumes. a, b Show the performance change with the increase of the number of rotation angles. c, d Show the performance change with the increase of angular range

Full size image

We further explore the influence of maximum angular range \(\theta _{\text {max}}\) with fixed number of rotation angles as \(N = 21\). Figure 2c, d and Additional file 1: Fig. S3 show quantitative and qualitative performance when increasing \(\theta _{\text {max}}\) from \(8^\circ \) to \(140.8^\circ \). Small angles such as \(8^\circ \) and \(16^\circ \) perform badly. Increasing \(\theta _{\text {max}}\) improves up to \(32^\circ \) and beyond the returns become diminishing again but without any added cost in computational time. Therefore, we can afford to use the full range of \(140.8^\circ \).

Fig. 3
figure 3

Performance of RAPID under \(N_\theta =21\) acquisition within the range \(\theta = 140.8^\circ \). a, b Quantitative (PCC, MS-SSIM, BER, and DICE) comparison among approximant, RAPID, FBP, and SART. c–g Layer-wise visualization of the reconstruction results from different methods, including the golden standard reconstructed from \(N_\theta =349\) angles, Approximant, RAPID, FBP, and SART recovered from \(N_\theta =21\) angles. h PSD distribution in \(k_z\)-\(k_x\) plane of different methods. For \(k_z\)-\(k_y\) and \(k_x\)-\(k_y\) planes, refer to the Additional file 1: Fig. S4

Full size image

Figure 3 describes typical testing results the \(N=349\) angles and \(\theta _{\text {max}} = 140.8^\circ \) for the golden standard compared with our optimal compromise, i.e. \(N=21\) angles and \(\theta _{\text {max}} = 140.8^\circ \). Parts (a) and (b) show quantitative metrics of image quality. We have chosen four: Pearson Correlation Coefficient (PCC), Multi-scale Structural Similarity Metric (MS-SSIM) [65], Bit Error Rate (BER) [66], and the Dice coefficient [67] (Detailed in Methods section). The first two are used often in statistics and image processing, while the third and fourth are information- and set-theoretic, respectively. The results indicate that the RAPID method indeed can learn to regularize better than the conventional filtered backprojection (FBP) and simultaneous algebraic reconstruction technique (SART) methods.

Figure 3c–g show the golden standard and how well various reconstruction approaches come to approximate it, for several circuit layers and orientations. As expected, the Approximant (Fig. 3d) is of rather poor quality because of the severe missing wedge problem in our reduced-angle configuration. The RAPID method does not fully eliminate the axial artifacts, but significantly reduces them—almost to the same extent as the golden standard (Fig. 3c). Part (h) shows the power spectral densities (PSD) of the whole testing volume in \(k_x-k_z\) plane (the performances of \(k_x-k_y\) and \(k_y-k_z\) planes are shown in Additional file 1: Fig. S4), corresponding to methods of (c–g). Notable are the differences in coverage of the space between the measured slices (emerging as radial spokes in the PSD) and of the missing wedges.

Fig. 4
figure 4

Quantitative and qualitative comparison among the reconstruction results from different network architectures. a Layer-wise visualization of the reconstructions from different network architectures, A: 3D U-net structure as the baseline method; and modified 3D U-net by replacing the first convolutional kernels at each hierarchical level in the encoder as B: the combination of \(x-y\), \(y-z\), and \(x-z\) convolution kernels without atrous; C: 3D isotropic atrous module, D: 3D anisotropic atrous module with the same max atrous rate \(a_1 = a_2 = 18\), E–G: 3D anisotropic atrous module with different max atrous rates ((\(a_1 = 24\) and \(a_2 = 30\)), (\(a_1 = 30\) and \(a_2 = 36\)), and (\(a_1 = 36\) and \(a_2 = 42\)), respectively). The results of method E are shown in Fig. 3e. b, c Quantitative comparison of the testing volumes

Full size image

For the same configuration \(N=21\) angles and \(\theta _{\text {max}} = 140.8^\circ \), Fig. 4 studies the influence of atrous anisotropy in our method and compares with different combinations of isotropic or partially anisotropic scheme. To make the comparison fair, all methods are designed with a similar number of total parameters and trained with the same strategy. Extending the anisotropic kernel range along the axis of the missing wedge tends to effectively compensate for the axial artifacts. Results E, F, and G in the figure indicate that the choice of atrous parameters does not impact performance significantly.

Table 1 Experimental and computational time (hours) and reduction ratio of the whole testing volume \(4.50 \times 93.18 \times 3.92\, \upmu \text {m}^3\) from conventional two-step approaches with N=349 angles as the golden standard, RAPID, FBP, and SART methods with \(N=21\) angles
Full size table

Table 1 shows the data acquisition time, computational reconstruction time, and total pipeline duration for the techniques under comparison. RAPID is \(\times 16\) faster in terms of data acquisition and \(\times 175\) faster for image reconstruction compared to the golden standard. The aggregate acceleration for the entire pipeline is \(\times 140\). The absolute durations for the golden standard and RAPID were \(\sim 66\) h \(30'\) and \(\sim 30'\), respectively.

3 Discussion

To address severely ill-posed problems in X-ray imaging, we introduced anisotropic atrous spatial pyramid pooling modules which increase the size of the receptive field to enable long-range and multi-scale extraction of underlying features. This augmentation largely improves performance compared to non-atrous implementations. The max atrous rates in this novel module can be more rigorously determined by feature size, scattering potential, dataset sampling size, etc. For example, it would be worthwhile to investigate the relationship between max atrous rate and the anisotropy in the PSF of the imaging system. Alternatively, by means of global-range self-attention, transformer architectures [68, 69] have also been demonstrated for reduced-angle ptycho-tomography [70]. Detailed comparison between these two methods is beyond the scope of the present paper.

Different from cylinder-shaped samples [9], the penetration path length of a plate-shaped sample increases significantly with the rotation angle. When the penetration path length is larger than the depth of field, multi-slice techniques are necessary to account for propagation effects within the sample when generating the approximant. In our implementation, we run a five-slice ptychographic algorithm under a reduced-angle framework for two iterations to speed up the computation, resulting in vague layer separation from each angle. The improvement in the reconstruction quality flattens after 21 projections as shown in Fig. 2a, b is related to this approximant generation algorithm. As reconstructions from adjacent angles are similar, adding more angles will not improve the approximant quality significantly and thus the final reconstruction. Besides, a multi-slice ptychographic algorithm can relax the Crowther criterion due to more frequency coverage in the Fourier domain for each projection angle [39], which also indicates the information from neighboring angles are similar. On the other hand, the plateau after 32° in Fig. 2c, d shows that measurements sampled from the angular range over 32° contribute similarly to the approximant compared to the 32° case when fixing the total number of rotation angles as 21. More slices may be required to count for the diffraction effects at larger angles, but in turn, increase the computation burden. The theoretical proof for the turning point in terms of the number of projections and maximum angular range is out of the scope of this manuscript but is interesting for future study. On the other hand, the laminography technique [71, 72] compensates for uneven propagation lengths by scanning the illumination wavevectors along a conical surface. In either case, it may be possible to modify RAPID to further reduce the total scanning time by skipping steps in the ptychographic scan as well [73].

Supervised learning approaches often is a cause for concern regarding the generalization ability to new and unseen data. We propose a strategy to train on a subset of the sample, where a trustable but otherwise very slow alternative method can be used to obtain ground truths; and then use the train network on the rest of the sample, significantly speeding up the entire operation. This approach is appealing for integrated circuits or other large 3D specimens [74]. Besides, it is possible that transfer learning [75] might alleviate the efforts for training RAPID anew for new experiments. For even more general specimens, like viruses, nanoparticles, etc. comparable performance may be expected, but most likely at the cost of some redesign in the learning architecture.

4 Method

4.1 X-ray ptychographic tomography experiment of integrated circuits

X-ray ptychographic tomography experiment was carried out using the Velociprobe with a Dectris Eiger 500K detector (\(75\,\upmu \text {m}\) pixel size) positioned at a distance of \(1.92\, \text {m}\) from the sample at the Advanced Photon Source of the Argonne National Laboratory, USA. A schematic of the Velociprobe was shown in the previous paper [30]. The photon energy of 8.8 keV with a spectral bandwidth of \(10^{-4}\) was selected using a double-crystal silicon monochromator. A Fresnel zone plate with \(50\, \text {nm}\) outmost zone width and \(180\,\upmu \text {m}\) diameter was installed on the zone plate scanner. The first order diffracted beam from the zone plate was selected by the combined use of a \(60\, \upmu \text {m}\) diameter tungsten central stop and a \(30\, \upmu \text {m}\) diameter order-sorting aperture placed \(\sim 62 \, \text {mm}\) downstream of the zone plate. The illumination spot size on the sample is about \(1.4\, \upmu \text {m}\). The sample was fly-scanned in a snake pattern [30] with a 100-nm and 500-nm step size in the horizontal and vertical directions, respectively.

A total number of 349 rotation angles with the angle spacing \(0.4^\circ \) within the angular range of \(\theta _{\text {max}} = 140.8^\circ \) from the reference axis was acquired for an IC produced with \(16\,\textrm{nm}\) technology with the size of \(25.09\times 93.18\,\times 3.92\,\upmu \text {m}^3\). \(\sim 60k\) diffraction patterns were captured at each angle. The field of view of the projection at each angle was \(30 \times 100\,\upmu \text {m}^2\) with the detector frame rate of \(500\,\text {Hz}\), giving \(2\,\text {ms}\) exposure time per scan. It took about \(129\,\text {s}\) for each rotation angle and the total data acquisition time for 349 angles was \(\sim 13\) h. For reduced-angle ptycho-tomography, we increased the angular spacing proportionally. The experiment time for the whole testing volume was estimated linearly according to the ratio of testing volume to the whole volume and the number of reduced angles to the whole angle, which is reasonable as the translational and angular scanning scheme of ptycho-tomography.

4.2 Multi-slice forward and inverse models for reduced-angle acquisition

We applied the multi-slice propagation method to model the measurements exiting the object. In the multi-slice propagation model, the object f is divided into L slices along the beam propagation direction, as \([f_1,\,f_2,\,,...,\,f_L]\). Each slice is with the thickness of \(\Delta z\). The wave field \(u_{l,j}(x,y,z_l)\) from probe position j entering \(l\hbox {th}\) slice is modulated by the slice \(f_{l}\) to yield a wave field \(u'_{l+1,j}(x,y,z_{l+1})\) as \( u'_{l,j}(x,y,z_{l}) = u_{l,j}(x,y,z_l)f_{l}(x,y,z_{l})\). The wavefront is then propagated to the next slice according to the Fresnel diffraction integral given by

$$\begin{aligned} \begin{aligned} u_{l+1,j}(x,y,z_{l+1})&= {\mathcal {P}}_{\Delta z} u'_{l+1,j}(x,y,z_{l+1}) \\&= {\mathcal {F}}^{-1}\{{\mathcal {F}}\{u'_{l+1,j}(x,y,z_{l+1})\}h_{\Delta z})\}. \end{aligned} \end{aligned}$$
(1)

Here \(h_{\Delta z} = \exp (-i(q-\sqrt{q^2-q_x^2-q_y^2}))\) and q is the reciprocal domain coordinate. This process is repeated for all L layers until one obtains the exit wave leaving the object \(\psi _{L,j}\), represented as \(\psi _{L,j} = f_{L}{\mathcal {P}}_{\Delta z}f_{L-1}...{\mathcal {P}}_{\Delta z}f_{2}{\mathcal {P}}_{\Delta z}f_{1}u_{1,j}\). Here \(u_{1,j}\) is the incident probe at scan position j. Then we apply the far-field propagation operator \({\mathcal {P}}_d\) to take the exit wave \(\psi _{L,j}\) from the object to the plane of the detector, which is performed with a simple Fourier transform as \(u_{j}(q) = {\mathcal {P}}_d \psi _{L,j} = {\mathcal {F}}\{\psi _{L,j}\}\).

In this experiment, the quasi-coherent X-ray illumination was modeled as the combination of multiple coherent modes with the index of \(m = [1,2,...,M]\) to improve the accuracy. Thus, the far-field diffraction measurements were represented as the sum of each coherent mode. In addition, reduced-angle ptycho-tomography requires the illumination of the object from several rotation angles \(\theta \). Here we rotated the object according to a constant wave propagation direction, which was performed with a rotation operation \(f_{\theta } = {\mathcal {R}}_\theta f\), and the rotated object \(f_{\theta }\) is further sliced into L different layers \([f_{\theta ,1},\,f_{\theta ,2},\,,...,\,f_{\theta ,L}]\). This leads to a combined forward operation of

$$\begin{aligned} \begin{aligned} H_{\theta , j}&= \underset{m}{\sum }\ |u^{(m)}_{\theta ,j}(q)|^2\\&= \underset{m}{\sum }\ |{\mathcal {P}}_d f_{\theta ,L}{\mathcal {P}}_{\Delta z}f_{\theta ,L-1}...{\mathcal {P}}_{\Delta z}f_{\theta ,1}{\mathcal {P}}_{\Delta z}f_{\theta ,1}u^{(m)}_{1,j} |^2. \end{aligned} \end{aligned}$$
(2)

In order to apply the gradient descent updates to find optimal f, we start with the data fidelity term of the loss function

$$\begin{aligned} {\mathcal {L}} = \frac{1}{2}\frac{1}{N_\theta N_j}\underset{\theta , j}{\sum }\Vert \underset{m}{\sum } |u^{(m)}_{\theta ,j}(q)|^2-g_{\theta ,j}\Vert ^2_2 =\frac{1}{N_\theta }\underset{\theta }{\sum }{\mathcal {L}}_\theta . \end{aligned}$$
(3)

The gradient of \({\mathcal {L}}\) with respect to f is derived as

$$\begin{aligned} \begin{aligned} \nabla _f {\mathcal {L}}&= \frac{1}{N_\theta }\underset{\theta }{\sum }\frac{\partial {\mathcal {L}}_\theta }{\partial f}\\&=\frac{1}{N_\theta }\underset{\theta }{\sum }\left[ \frac{\partial {\mathcal {L}}_\theta }{\partial f_{\theta ,1}},\, \frac{\partial {\mathcal {L}}_\theta }{\partial f_{\theta ,2}},\, ...\frac{\partial {\mathcal {L}}_\theta }{\partial f_{\theta ,L}} \right] \frac{\partial f_\theta }{\partial f}. \end{aligned} \end{aligned}$$
(4)

The term \(\frac{\partial f_\theta }{\partial f}\) could be obtained with the rotation matrix. We derive the formula of \(\frac{\partial {\mathcal {L}}_\theta }{\partial f_{\theta }}\) to get the \(\nabla _f {\mathcal {L}}\) with the chain rule as

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathcal {L}}_\theta }{\partial f_\theta }&= \underset{m,j}{\sum }\frac{\partial {\mathcal {L}}}{\partial {|u^{(m)}_{\theta ,j}|}} \frac{\partial {|u^{(m)}_{\theta ,j}|}}{\partial f_\theta }\\&= \frac{1}{N_j}\underset{m,j}{\sum }\left(\underset{m}{\sum } |u^{(m)}_{\theta ,j}(q)|^2-g_{\theta ,j}\right)2|u^{(m)}_{\theta ,j}|\frac{\partial {|u^{(m)}_{\theta ,j}|}}{\partial f_\theta } \end{aligned} \end{aligned}$$
(5)

Following the similar notation as ref. [76], we employ the auxiliary variable \(\chi ^{(m)}_{\theta ,j}\) as

$$\begin{aligned} \chi ^{(m)}_{\theta ,j} = {\mathcal {F}}^{-1}\left\{2\left(\underset{m}{\sum } |u^{(m)}_{\theta ,j}(q)|^2-g_{\theta ,j}\right)u^{(m)}_{\theta ,j}\right\}. \end{aligned}$$
(6)

In this way, the gradient of the loss function \({\mathcal {L}}_\theta \) with respect to the object \(f_\theta \) is defined as

$$\begin{aligned} \frac{\partial {\mathcal {L}}_\theta }{\partial f_{\theta ,l}} = \left\{ \begin{array}{lcl} \frac{1}{N_j}\underset{m,j}{\sum }\chi ^{(m)*}_{\theta ,j}u^{(m)}_{\theta ,j,L}; &{} &{} {l=L}\\ u^{(m)}_{\theta ,j,l}{\mathcal {P}}_{-\Delta z}\left\{ \frac{\partial {\mathcal {L}}_\theta }{\partial u^{(m)}_{\theta ,j,l+1}}\right \}^*; &{} &{}{1\le l<L}\\ \end{array} \right.. \end{aligned}$$
(7)

where the asterisk represents the complex conjugate. Here \(\frac{\partial {\mathcal {L}}_\theta }{\partial u^{(m)}_{\theta ,j,l}}\) was derived as follows

$$\begin{aligned} \frac{\partial {\mathcal {L}}_\theta }{\partial u^{(m)}_{\theta ,j,l}} = \left\{ \begin{array}{lcl} \frac{1}{N_j}\chi ^{(m)*}_{\theta ,j}f_{\theta ,L}; &{} &{} {l=L}\\ f_{\theta ,l}{\mathcal {P}}_{-\Delta z}\{ \frac{\partial {\mathcal {L}}_\theta }{\partial u^{(m)}_{\theta ,j,l+1}} \}^*; &{} &{}{1\le l<L}\\ \end{array} \right. \end{aligned}$$
(8)

4.3 Computation of the approximant

The performance of the DNN is significantly improved if the raw measurements are preprocessed by considering the imaging formation as an approximation of the solution, which is also known as Approximant [47]. Here we treated the reconstruction of 3D refractive index of an object \(f(r) = \exp [\alpha (r)+i\phi (r)]\) from multi-angle ptychographic diffraction measurements g as a nonlinear optimization problem by minimizing the loss function

$$\begin{aligned} {\hat{f}} = \underset{f}{\textrm{argmin}}\{\Vert H(f)-g\Vert ^2+\gamma \Phi (f)\}, \end{aligned}$$
(9)

where the first component is known as the data fidelity term, which models the physical relationship between the object f and the measurements g in a reduced-angle setting; \(\Phi \) is the regularizer expressing the prior knowledge of the object, which is learned from the volumetric pairs of golden standard IC patterns reconstructed from 349 rotation angles with a two-step reconstruction method, and the approximant retrieved from the one-step multi-slice preprocessor with 21 rotation angles; and \(\gamma \) is the regularization parameter controlling the competition between the data fidelity term and regularization term. We assume that the sample is a pure phase object, i.e., \(\alpha (r)=0\), which is reasonable as the phase contrast is about 10 times larger than the absorption contrast in X-ray experiments for IC samples.

The approximant was generated by iteratively updating the data fidelity term (Eq. 3) via gradient descent \(f^{(k+1)} = f^{(k)} - s(\nabla _f {\mathcal {L}})_{f^{(k)}}\). Here k denotes the iteration step, s is the step size, and \((\nabla _f {\mathcal {L}})_{f^{(k)}}\) is the gradient of \({\mathcal {L}}\) with respect to f evaluated at \(f^{(k)}\), as shown in Eq. 4. Raw diffraction patterns g of \(256\times 256\,\text {px}^2\) were downsampled by \(\times 2\) to accelerate the computation, which results in the Approximant \(\times 2\) smaller in x and y directions compared to the golden standard. In this work, we chose \(k=2\) to further speed up the computation, \(L=5\) by considering the depth of focus of our system, and \(M=12\) coherent modes of the synchrotron X-ray for the reconstruction. The number of desired reconstruction slices is much larger, i.e. 280, so we simply dilated the generated slices to match it. As a result, the quality of network input is poor.

4.4 Network architecture and implementation details

RAPID is an encoder-decoder network architecture based on 3D U-net via including a special convolution module, the anisotropic atrous module, at each hierarchical level in the encoding branch, as shown in Additional file 1: Fig. S1a. The original 2D ASPP module contains one \(1\times 1\) convolution and three \(3\times 3\) convolutions with isotropic atrous rates = (6, 12, 18). Here we extend it to a 3D version by incorporating the 3D atrous convolution, which is defined as

$$\begin{aligned} g(i,j,k) = \sum _{l=1}^L\sum _{m=1}^M\sum _{n=1}^Nf(i-r_1l,j-r_2m,k-r_3n)h(l,m,n). \end{aligned}$$
(10)

Here, (i, j, k) is the voxel in the original volume f and filtered volume g, (l, m, n) is the voxel in the convolutional kernel h, \(r_1, r_2,\) and \(r_3\) are atrous rates in x, y and z axes. \(r_1, r_2\) and \(r_3\) are generally the same, which is also known as isotropic atrous convolution.

Additional file 1: Figure S1b shows the design of the anisotropic atrous module including three anisotropic ASPP modules in \(x-y\), \(y-z\), and \(x-z\) planes and an additional 3D convolution module to capture features in 3D. The features extracted from these four branches are fused via concatenation and passed through another standard \(3\times 3\times 3\) convolution kernels. Inter-slice cross-talking in the Approximant, originating from the nature of multi-slice reconstruction model, makes feature separation in the z direction difficult. To emphasize this artifact and achieve isotropic volumetric resolution, we include two more anisotropic atrous convolutions \(a = a_1,\, a_2\) to address the severe feature residuals along the z direction for atrous convolution operated in \(y-z\) and \(x-z\) planes.

The whole volumes were split into 2781 examples with the size of \(128\times 128\times 280\) for the golden standard, and \(64\times 64\times 280\) for the Approximant. The split volumes overlapped 50% between each other. As mentioned before, the upper part with respect to the beam propagation direction was used for training, which contained 2060 volumes; and the lower part was used for testing, which included 618 volumes. There was no overlap between the training and testing volumes. We employed a negative Pearson correlation coefficient (NPCC = −PCC) as the loss function and the training runs for 200 epochs with a batch size of 2. The PCC is defined as

$$\begin{aligned} PCC(A,B) = \frac{\sum _i(A_i-{\bar{A}})(B_i-{\bar{B}})}{\sqrt{\sum _i(A_i-{\bar{A}})^2\sum _i(B_i-{\bar{B}})^2}}, \end{aligned}$$
(11)

for two volumes A and B. Adam optimizer for stochastic optimization [77] with a polynomial learning rate schedule was used to update a learning rate as

$$ lr({\text{step}}) = (lr(0)-lr({\text{end}}))\times \left( 1 - \frac{{\text{step}}}{{\text{T}}}\right) ^p,$$
(12)

where the initial learning rate \(lr(0) = 2e-4\), the end learning rate \(lr(\text {end}) = 5e-5\), the total decay steps \(T = 3e4\), and \(p = 0.5\). The rest parameters of Adam optimizer were set as default values.

For training processes, we used the MIT Supercloud with an Intel Xeon Gold 6248 CPU with 384 GB RAM and dual NVIDIA Volta V100 GPUs with 32 GB VRAM. Once the network was trained, it took less than one minute for giving predictions over each test volume with a single NVIDIA Volta V100 GPU. And the whole testing area took around 125 seconds to get the final result. Our scripts for training and testing are publicly available in https://github.com/Ziling-Wu.

4.5 Two-step reconstruction as the ground truth and comparison algorithms

The ptychography reconstruction was conducted with the multi-slice least square maximum likelihood algorithm [78] for 600 iterations to generate the phase projections at each tomographic angle in PtychoShelves [79]. In total, it took \(\sim \) 360 h for ptychographic reconstruction for all 349 angles with 8 Tesla V100 GPUs in parallel. We further aligned all 349 projections in the form of a phase ramp removal process and post-process with a pre-trained super-resolution network to refine the projections, which took about \(\sim 5\) h with a single Tesla V100 GPU. The final tomographic reconstruction was performed with 10 iterations of SART [17] to generate a 3D reconstruction of the IC sample with the isotropic \(14\, \text {nm}\) voxel size, which took about 1 h using 8 Tesla V100 GPUs.

We compared our algorithm with two conventional approaches for 21-angle X-ray ptycho-tomography . The experiment time was reduced by \(\times \)16 as a result of the angular reduction. In terms of computation, ptychography reconstruction and projection refinement were performed as the golden standard for diffraction measurements from \(N=21\) angles. The final tomographic reconstruction was conducted with FBP and SART (10 iterations) algorithms implemented in TomoPy with the ASTRA toolbox [80, 81]. The computation time for ptychographic reconstruction and refinement was also reduced linearly according to angular reduction compared to the golden standard. The tomographic reconstructions were performed with the same configuration as our method, which took \(116\,{\rm s}\) and \(1678\,{\rm s}\) for the whole volume with FBP and SART (10 iterations), respectively. The computation time for the whole testing volume was estimated proportionally.

4.6 Quantitative comparison metrics

We used PCC, MS-SSIM, BER, and DICE metrics to quantify our proposed method. PCC and MS-SSIM are used to quantify the correlation between two volumes. PCC is defined in the Eq. (12), and MS-SSIM [65] is a weighted similarity metric with fixed weights on SSIM values from different scales.

The remaining two metrics DICE and BER are used to quantify the segmentation volumes. DICE, also known as F1 score, is broadly used to compare the similarity among two segmented volumes via calculating overlapping size over their total size. Similarly, BER quantifies the ratio of erroneously classified voxels. Both of them involve the derivation of probability distribution functions, thus probabilistic, and are based on binary classification as follows

$$\begin{aligned} \text {DICE} = \frac{2\cdot \text {TP}}{2\cdot \text {TP} + \text {FN} + \text {FP}}, \end{aligned}$$
(13)

and

$$\begin{aligned} \text {BER} = \frac{\text {FP} + \text {FN}}{\text {TP}+\text {TN}+\text {FP}+\text {FN}}, \end{aligned}$$
(14)

where \(\text {TP}\), \(\text {TN}\), \(\text {FP}\), and \(\text {FN}\) indicate the number of true positives, true negatives, false positives, and false negatives, respectively. For the gold standard, the binary thresholds and prior probabilities p(0), p(1) required for these quantities were estimated by an Expectation Maximization (EM) algorithm. For testing, we used Bayes’ rule \(p(x|0)p(0) = p(x|1)p(1)\) with p(0), p(1) same as for the gold standard.