1 Introduction

Cherenkov radiation arises when a charged particle moves with a velocity exceeding the phase velocity of light in a transparent medium [1, 2]. In transparent dielectric materials, Cherenkov radiation is an extended mode (i.e., a packet of Cherenkov photons) propagating into the infinity at a constant emission angle \(\theta_{c}\). This so-called Cherenkov angle depends on the particle velocity \(v\) as \(\cos \theta_{c} = \frac{c}{nv}\) [3], where \(c\) is the light speed in the vacuum and \(n\) is the refractive index of the background medium. As a key application in particle physics, Cherenkov radiation has been widely deployed for particle discrimination, i.e. the particle velocity can be determined with high accuracy by measuring the Cherenkov angle of emitted photons [4,5,6,7,8,9]. Emerging communication applications call for a route map towards the miniaturization of Cherenkov devices [10,11,12,13,14,15]. However, the major challenge to scale down Cherenkov detectors arises from the large footprint of photon detection apparatus.

In recent decades, surface waves have drawn extensive attention in nanotechnology owing to their ability to confine electromagnetic waves in subwavelength domains [16,17,18,19]. Surface plasmon-polariton (SPP) existing at metal/dielectric interfaces is perhaps the most well-known example [20,21,22,23]. Its enhanced photonic density of states leads to a wealth of nanotechnological breakthroughs in super-resolution imaging, ultrasensitive biosensing, efficient light emission, etc [24,25,26]. On the other hand, light–matter interactions with surface phonon-polariton (SPhP) at the interface of van der Waals materials attracts increased research interest mainly due to the high confinement and moderate losses of SPhP in the mid-infrared frequency [27, 28]. Especially, recent advances in particle physics have shown that SPPs/SPhPs may also provide a route to control Cherenkov radiation at the subwavelength scale [29, 30]. This so-called surface-polariton Cherenkov radiation exhibits several unique features including enhanced photon emission, reversed Cherenkov cone and vanishing Cherenkov threshold [31,32,33,34,35,36,37,38]. However, realization of miniaturized Cherenkov detectors with SPPs/SPhPs is still challenging, probably because of the non-negligible dissipation losses and strong chromatic dispersion of used materials [39]. For instance, the large metallic dissipation inevitably prohibits the detection of surface-polariton Cherenkov radiation beyond the plasmon propagation length (which is usually several micrometers at optical frequencies). On the other hand, the strong chromatic dispersion makes the emission angle of surface-polariton Cherenkov radiation highly wavelength-dependent and therefore unavoidably limits the working bandwidth of designed Cherenkov detectors. These problems become more severe when the particle velocity approaches the Cherenkov threshold, where the photon emission is inherently weak. Hence, an alternative approach with suppressed dissipation and dispersion effects is still highly demanded for the design of compact Cherenkov detectors.

Here, we show that Dyakonov surface waves (DSWs) supported by transparent birefringent materials provide a feasible solution to these problems [40]. We investigate systematically surface Dyakonov–Cherenkov radiation at the surface of a birefringent crystal in contact with an isotropic background medium and find that the emission behaviors are strongly susceptible to the particle velocity and trajectory. Remarkably, the excitation of DSWs significantly enhances the photon emission by several orders of magnitude when the particle velocity approaches to the threshold velocity of the swift charge in surrounding medium. This unique feature greatly facilitates the particle identification around the velocity cutoff. In addition, DSWs have another two distinct advantages over conventional surface plasmons: first, their negligible dissipation losses not only enhance the photon extraction efficiency, but also significantly increase the propagation length of surface waves, facilitating the far-field detection of Cherenkov signals; second, their small chromatic dispersion dramatically broadens the working bandwidth of particle detectors. Our studies add a new perspective on enhanced particle–photon–matter interactions and open up an opportunity for achieving high-performance Cherenkov detectors on chip.

2 Results and discussions

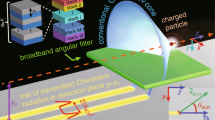
Without loss of generality, we consider a swift charged particle of velocity \(\overline{v}\) travelling parallel to the interface of an isotropic background medium (with a refractive index \(n_{a}\)) and a uniaxial birefringent crystal (with ordinary and extraordinary refractive indices denoted as \(n_{o}\) and \(n_{e}\), respectively). The distance between the particle trajectory and the interface is \(y_{0} = 200\) nm. The optical axis of birefringent crystal is orientated parallel to the interface, as shown in Fig. 1a. In this configuration, DSWs exist if \(n_{e} > n_{a} > n_{o}\) [41,42,43,44,45]. To satisfy this condition, we choose Si3N4 as the isotropic background medium and YVO4 as the birefringent crystal. The refractive indices of studied materials are \(n_{a} = 2.04\), \(n_{o} = 1.99\) and \(n_{e} = 2.22\). In general, DSWs are highly directional and exist only within small angular regions in four quadrants (i.e., \(\theta_{d}\), \(\pi - \theta_{d}\), \(\pi + \theta_{d}\), \(2\pi - \theta_{d}\)), where \(\theta_{d} \in \left[ {29.43^\circ , \;30.15^\circ } \right]\) is the angle between the phase velocity of DSWs and the optical axis of the YVO4 crystal. In this study, we focus our discussions on the behaviors of DSWs in the first quadrant. Owing to the mirror symmetry, our results also apply to DSWs in other three quadrants.

Fig. 1
figure 1

Emission behaviors of a swift charged particle in an all-dielectric structure made of a semi-infinite istrotropic medium Si3N4 and a semi-infinite uniaxial crystal YVO4. a The schematic of the setup. A swift charged particle moves parrallel to the interface between the isotropic medium Si3N4 and the uniaxial crystal YVO4. The angle between the particle velocity and the optical axis of the uniaxial crystal is denoted as \(\theta_{q}\). b–d Time-domain radiation-field distributions of the charged particle in the cross section formed by the surface normal and the particle trajectory. When \(v = 0.50c\) and \(\theta_{q} = 40.9^\circ\), the swift charged particle excites both free-space Cherenkov photons and DSWs in b; when \(v\) is changed to \(0.51c\) (c) or \(\theta_{q}\) is changed to be \(41.4^\circ\) (d), only free-space Cherenkov photons are produced. In all the plots, the distance between the particle trajectory and the interface is fixed as \(y_{0} = 200\) nm, and the integration range of the wavelength is \(\lambda \in \left[ {0.2,2} \right]\) μm in free space

Full size image

We begin our analysis by studying the excitation condition of DSWs by the swift charged particle. Denote \(\theta_{q}\) as the angle between the optical axis and the particle trajectory (Fig. 1a). We find that the excitation of Dyakonov surface modes requires \(\theta_{q}\) fulfilling the following condition (Additional file 1: Section S4):

$$\theta_{q} = \theta_{d} \pm \cos^{ - 1} \left( {\frac{\omega }{{k_{d} v}}} \right),$$
(1)

where \(\omega\) is the angular frequency; \(k_{d}\) is the magnitude of in-plane wavevector of the Dyakonov surface mode. Unlike conventional Cherenkov photons which can be produced by charged particles travelling along any direction (i.e. regardless of \(\theta_{q}\)), Dyakonov surface modes can be excited only for some specific \(\theta_{q}\).

The radiation field pattern from the swift charged particle is very susceptible to the magnitude and direction of the particle velocity in our platform. To illustrate this point and reveal the impact of DSWs, we plot in Fig. 1b–d radiation field patterns for three circumstances. When Eq. (1) is rigorously satisfied, the radiation mode is a superposition of the conventional Cherenkov photons and DSWs, as shown in Fig. 1b. In this case, the radiation field can penetrate deeply into the YVO4 crystal. Such a large penetration length results from the weak longitudinal confinement of DSWs on the interface [17]. In addition, surface Dyakonov–Cherenkov radiation also features an extremely asymmetric field pattern in the transverse plane (Additional file 1: Fig. S5). On the other hand, when the magnitude or direction of the particle velocity changes slightly such that Eq. (1) is no longer satisfied, the swift charged particle emits only conventional Cherenkov photons. As a result, the radiation field decays rapidly in the YVO4 crystal (Fig. 1c, d) and the field pattern becomes symmetric in the transverse plane (Additional file 1: Fig. S5). These results clearly demonstrate that the excitation of DSWs relies heavily on the particle trajectory. This property provides an effective way to determine simultaneously the particle velocity and trajectory for high-energy particles whose directions are oriented parallel to the surface of the birefringent crystal, through the direct measurement of the radiation field pattern.

Excitation of DSWs modifies not only the near-field pattern, but also the energy loss of the swift particle. As shown in Fig. 2, the power spectral density is quite susceptible to the particle velocity and trajectory, and increases dramatically when Eq. (1) is satisfied. To explore the underlying physical mechanism, we divide the total radiation power into two parts, i.e., the radiation loss \(G_{{{\text{ph}}}}\) through the emission of free-space Cherenkov photons and the radiation loss \(G_{{{\text{DSW}}}}\) through the excitation of DSWs.

Fig. 2
figure 2

Energy loss of a swift charged particle emitting Dyakonov surface wave. A power spectral density \(G_{{{\text{DSW}}}}\) (owing to the excitation of DSWs) as a function of the normalized particle velocity \(v/c\) and the angle \(\theta_{q}\) (corresponding to the orientation of the particle trajectory). \(G_{{{\text{DSW}}}}\) acquires a nonzero value only when \(v\) and \(\theta_{q}\) satisfy the phase matching condition given by Eq. (1). b The total power spectral density \(G_{{{\text{DSW}}}} + G_{{{\text{ph}}}}\) (where \(G_{{{\text{ph}}}}\) refers to the radiation loss of free-space Cherenkov photons) versus the normalized particle velocity \(v/c\) for angle \(\theta_{q} = 40.9^\circ\), \(64.8^\circ\), \(75.1^\circ\) and \(81.8^\circ\), respectively. c The total power spectral density \(G_{{{\text{DSW}}}} + G_{{{\text{ph}}}}\) versus the angle \(\theta_{q}\) for particle velocity \(v = 0.5c\), \(0.6c\), \(0.7c\) and \(0.8c\), respectively. θq,max (θq at the maximum energy loss) is marked for each velocity in c. In particular, we denote \(G_{{{\text{ph}}}}\) as the straight dashed line b, c. d The maximum achievable photon number \(N_{{{\text{DSW}}}} \left( {\theta_{{q,{\text{max}}}} } \right)\) of DSW generated per unit length of the particle path at each particle velocity. For comparison, we also plot the photon number \(N_{{{\text{ph}}}}\) of free-space Cherenkov radiation as a function of particle velocity. The studied wavelength is 0.635 µm

Full size image

Figure 2b, c clarify quantitatively the respective contributions of \(G_{{{\text{ph}}}}\) and \(G_{{{\text{DSW}}}}\) to the total power spectral density at λ = 0.635 µm. Our results show that \(G_{{{\text{ph}}}}\) and \(G_{{{\text{DSW}}}}\) display distinctly different responses to the particle velocity and trajectory. On the one hand, \(G_{{{\text{ph}}}}\) (as denoted as the straight dashed line) increases smoothly as the particle velocity increases (Fig. 2b) while at the same time remains almost a constant over a broad angular band (Fig. 2c). Such a behavior makes particle detection with traditional Cherenkov photons difficult. On the other hand, \(G_{{{\text{DSW}}}}\) is much more sensitive to small variations in particle velocity/trajectory and acquires a nonzero value only when v and θq strictly satisfy the condition given by Eq. (1) (see Fig. 2a and the bulges in Fig. 2b, c). The velocity range for nonzero \(G_{{{\text{DSW}}}}\) is generally smaller than 0.02c, e.g., from 0.502c to 0.498c, 0.596c to 0.604c, 0.694c to 0.706c, and 0.792c to 0.808c for \(\theta_{q} = 40.9^\circ\), \(64.8^\circ\), \(75.1^\circ\), and \(81.8^\circ\), respectively; the angular band for nonzero \(G_{{{\text{DSW}}}}\) is generally smaller than 1°, e.g., from 40.4° to 41.4°, 64.3° to 65.3°, 74.6° to 75.6°, and 81.3° to 82.3° for \(v = 0.5c\), \(0.6c\), \(0.7c\), and \(0.8c\), respectively. θq,max (i.e., θq at the maximum energy loss) shows excellent agreement with θq fulfilling Eq. (1). The enhanced sensitivity in energy loss offers an alternative approach to measure simultaneously the particle velocity and trajectory. We also reveal that the maximum achievable photon number \(N_{{{\text{DSW}}}} \left( {\theta_{{q,{\text{max}}}} } \right)\) of DSW generated per unit length of the particle path is greater than that \(N_{{{\text{ph}}}}\) of free-space Cherenkov radiation in the low-speed regime (i.e., 0.49c < v < 0.7c), while \(N_{{{\text{ph}}}}\) dominates the total photon number in the high-speed regime (i.e., 0.7c < v < c) (Fig. 2d). The consideration of realistic chromatic dispersion of materials will not affect our findings (Additional file 1: Figs. S9, S10).

The negligible chromatic dispersion and small dissipation loss of our structure can greatly enhance the photon extraction by means of DSWs, facilitating particle detection in the far field. To highlight this point, we compare the power flow density of surface Dyakonov–Cherenkov radiation with that of surface-polariton Cherenkov radiation [46]. In our comparison, the surface-polariton Cherenkov radiation is investiageted in the plasmonic system made of Aluminum Oxide (Al2O3) and Gold (Au), such that the corresponding SPPs have a propagation constant identical to that of DSWs at a wavelength of \(\lambda = 0.641{ }\) µm (Additional file 1: Fig. S8). Meanwhile, the distance from the particle trajectory and the interface is set as y0 = 0.09δ (with δ as the penetration depth of the surface mode in the superstrate) such that the interaction strengths between the swift charge and surface waves are the same for both configurations. Here, the dielectric constants of Al2O3 and Au are taken from the experimental data [47, 48]. Figure 3 demonstrates that DSWs are more strongly excited than conventional SPPs despite of their weak confinement along the longitudinal direction. First, the photon extraction efficiency of DSWs is much higher (i.e. the power flow density is an orders of magnitude larger) than that of conventional SPPs at \(l = 0\) μm, as shown in Fig. 3c. Second, DSWs have a much longer propagation distance and remain detectable in the far field, e.g. the Poynting power of DSWs attenuates less than 5% over a distance of 10 μm, while conventional SPPs have already faded away over such a distance. On the other hand, owing to the long penetration depth δDSW (22 times larger than that of SPPs at 0.641 μm), the excitation efficiency of DSWs is robust against the variation of y0, e.g. from 0 to 200 nm (Fig. 3b). In sharp contrast, the swift particle cannot efficiently excite SPPs when y0 > δSPP = 100 nm.

Fig. 3
figure 3

Comparison between surface Dyakonov–Cherenkov radiation and surface-polariton Cherenkov radiation. a The contour plot of the power flow density in the cross section formed by the surface normal \(\hat{y}\) and the power flow direction \(\overline{P}_{{{\text{sw}}}}\) of DSWs. b The contour plot of the power flow density in the cross section formed by the surface normal \(\hat{y}\) and the power flow direction \(\overline{P}_{{{\text{sw}}}}\) of conventional SPPs. In a, b, \(y_{0} = 0.09\delta\), which is the penetration depth in the superstrate \(\delta = 2.2\) µm (\(\delta = 0.1\) µm) for DSWs (SPPs) at \(\lambda = 0.641\) µm. The insets of a, b highlight the orientations of studied cross sections (as marked in cyan) to the particle velocity. c The Poynting power \(\overline{P}_{sw}\) integrated along the y-direction versus the propagation distance l, when y0 = 0.9δ, 0.09δ and 0.009δ, respectively. In our comparison, we choose Si3N4–YVO4 and Al2O3–Au as the platforms to excite DSWs and SPPs, respectively, such that the corresponding DSWs and SPPs have an identical effective mode index \(n_{{{\text{eff}}}} = 2.0309\) at \(\lambda = 0.641\) µm. The particle velocity is \(v = 0.5c\) for both configurations. As a result, DSWs/SPPs propagate in a direction with \(14.02^\circ\)/\(11.21^\circ\) to the particle trajectory (see insets of a, b)

Full size image

Finally, to demonstrate that surface Dyakonov–Cherenkov radiation can be used for the particle detection, we plot θq,max (i.e. θq at the maximum energy loss) as a function of the velocity/momentum of particles. As shown in Fig. 4, measuring θq,max not only determines the particle velocity, but also offers a possible route for the particle discrimination, e.g. θq,max for electron, pion, kaon and proton are 90.45°, 89.55°, 80.41° and 54.35°, respectively, at the momentum of 0.6 GeV/c. Such a strong variation in θq,max indicates that our configuration provides a high detection sensitivity when applied to particle detection.

Fig. 4
figure 4

Particle detection with surface Dyakonov–Cherenkov radiation. a The angle θq,max versus the normalized particle velocity v/c. b The angle θq,max versus the particle momenta for four elementary particles

Full size image

3 Conclusions

We demonstrate that DSWs offer a powerful platform to manipulate Cherenkov radiation at the nanoscale. Different from conventional Cherenkov or surface-polariton Cherenkov radiation, surface Dyakonov–Cherenkov radiation is highly susceptible to the particle trajectory. Small chromatic dispersion and negligible propagation loss make our all-dielectric structure highly suitable for particle detection on chip. We highlight that the birefringence of the host material can strongly impact the behavior of surface Dyakonov–Cherenkov radiation (Additional file 1: Fig. S2). Particularly, larger birefringence gives rise to a larger angular existing domain for DSWs. As a result, surface Dyakonov–Cherenkov radiation becomes less sensitive to the particle trajectory. Thus, the usage of strongly anisotropic materials such as van der Waals materials and hyperbolic metamaterials [47,48,49] will not lead to our key findings. For the practical implementation, the optical axis orientation (and hence \(\theta_{q}\)) can be effectively controlled by constructing a cascade structure and/or applying a Galvo motor [50], providing a route to control surface Dyakonov–Cherenkov radiation (see more discussions in Additional file 1: Section S8).

4 Methods

4.1 Photon emission from a swift charged particle atop the interface between a birefringent crystal and an isotropic background medium

The corresponding setup is depicted in Fig. 1a. In the isotropic dielectric background, the swift charged particle with an effective current density \(\overline{J}\left( {\overline{r},t} \right) = \hat{z}vq_{0} \delta \left( x \right)\delta \left( {y - y_{0} } \right)\delta \left( {z - vt} \right)\) induces a scalar potential, which can be expressed in the frequency domain as

$$\phi_{0} \left( {\overline{r},\omega } \right) = \smallint \limits_{ - \infty }^{ + \infty } {\text{d}}k_{x} \frac{{{\text{i}}q_{0} }}{{8\pi^{2} k_{ya} }}{\text{e}}^{{\text{i}k_{x} x + \text{i}k_{ya} \left| {y - y_{0} } \right| + \text{i}k_{z} z}} .$$

As a result, the frequency-domain source fields are calculated as,

$$\overline{E}\left( {\overline{r},\omega } \right) = \frac{\text{i}}{{\omega \varepsilon_{0} \varepsilon_{a} }}\nabla \times \nabla \times \left( {\hat{z}\phi_{0} } \right),$$
$$\overline{H}\left( {\overline{r},\omega } \right) = \nabla \times \left( {\hat{z}\phi_{0} } \right),$$

where \(\varepsilon_{a} = n_{a}^{2}\) is the permittivity of the isotropic dielectric. In particular, the source field with the wavevector of \(\overline{k}_{a}^{s} = \left[ {\begin{array}{*{20}c} 0 & { - k_{ya} } & {k_{{{\text{in}}}} } \\ \end{array} } \right]\) in the (u, y, w) coordinate system can be decoupled into p- and s-polarized field, respectively, where \(k_{{{\text{in}}}} = \sqrt {k_{x}^{2} + k_{z}^{2} }\) is the in-plane wavevector. Light incident upon the boundary between the isotropic dielectric and birefringent crystal is reflected as p- and s-polarized light, while transmitted as ordinary (o) and extraordinary (e) light. Wavevectors of reflected as p- and s-polarized light are identical and given by \(\overline{k}_{a} = \left[ {\begin{array}{*{20}c} 0 & {k_{ya} } & {k_{{{\text{in}}}} } \\ \end{array} } \right]\), while wavevectors of transmitted o and e light are different and given by \(\overline{k}_{o} = \left[ {\begin{array}{*{20}c} 0 & { - k_{yo} } & {k_{{{\text{in}}}} } \\ \end{array} } \right]\) and \(\overline{k}_{e} = \left[ {\begin{array}{*{20}c} 0 & { - k_{ye} } & {k_{{{\text{in}}}} } \\ \end{array} } \right]\), respectively. By applying the boundary conditions, reflection coefficients \(R_{p}\), \(R_{s}\) and transmission coefficients \(T_{o}\), \(T_{e}\) can be determined. Our analytical expressions provided in Additional file 1: Section S2 show that these coefficients depend on both the magnitude and direction of the particle velocity.

4.2 Energy loss spectrum of the swift charged particle

The total power dissipation (i.e. the energy loss per particle per second) is evaluated as

$$P = - 4\pi \smallint {\text{d}}\omega \cdot\smallint\smallint\smallint {\text{d}}V{\text{Re}} \left[ {E\left( {\overline{r},\omega } \right) \cdot \overline{J}\left( {\overline{r},\omega } \right)} \right].$$

Detailed derivations provided in Additional file 1: Section S3 show that the total energy loss \(P\) takes the following analytical form,

$$P = \frac{{q_{0}^{2} v\mu_{0} }}{4\pi } \smallint \limits_{0}^{\infty } {\text{d}}\omega \left[ {\omega \left( {1 - \frac{{c^{2} }}{{\varepsilon_{a} v^{2} }}} \right)u\left( {1 - \frac{{c^{2} }}{{\varepsilon_{a} v^{2} }}} \right)} \right] + 2q_{0} v \smallint \limits_{0}^{\infty } {\text{d}}\omega \smallint \limits_{ - \infty }^{ + \infty } \text{d}k_{x} {\text{Re}} \left[ {\frac{{k_{x} R_{s} + k_{ya} k_{z} R_{p} }}{{\sqrt {k_{x}^{2} + k_{z}^{2} } }}} e^{{{\text{i}}k_{ya} y_{0} }} \right],$$

where \(u\left( t \right)\) is the Heaviside step function. Notably, our method does not consider the secondary particle production, resulting from the interaction between the moving charged particle and high-density dielectrics. However, the consideration of secondary particle production is no longer necessary if we adopt, for example, the multilayered structure as shown in Additional file 1: Fig. S11a in practical applications (see more discussions in Additional file 1: Section S8).