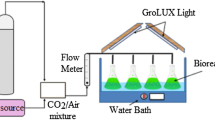
Abstract
Background
Removal of Cr(VI) from wastewater is essential as it is potentially toxic and carcinogenic in nature. Bioremediation of heavy metals using microalgae is a novel technique and has several advantages such as microalgae remove metals in an environmentally friendly and economic manner. The present study deals with modeling and optimization of the phycoremediation of Cr(VI) from synthetic wastewater. The initial concentration of Cr(VI), initial pH, and inoculum size were considered as input factors, and the percentage removal of Cr(VI) was chosen as a response.
Results
An accurate data-driven genetic programming model was developed with the experimental data of other scientists to find a relation between the percentage removal of Cr(VI) and all input parameters. To maximize the removal of Cr(VI), the grey wolf optimization technique was applied to determine the optimal values of input parameters.
Conclusion
These optimum input parameters are difficult to get through experimentation using the trial-and-error method. The established modelling and optimization technique is generic and can be applied to any other experimental study.
Graphical Abstract

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.1 Background
Modeling of chemical processes requires a deep understanding of phenomenology. The bulk of chemical processes is enormously complicated, with limited knowledge of their mechanisms. Due to a lack of understanding, developing the first principle-based phenomenological model is challenging and time-consuming. Different researchers have tried different numerical and mathematical algorithm to model the system from input–output data where process phenomenology is not known. Alternative route of numerical analysis currently emerging is artificial intelligence (AI)-based modeling technique [7, 23, 28, 33, 42]. In this scenario, an artificial intelligence-based data-driven modeling technique can be a feasible alternative where process phenomenology is not required. In this decade, artificial neural network (ANN) and support vector machine (SVM) algorithms have established themselves as powerful data-driven black-box modeling technique. In the last 20 years, ANN and SVM have been applied to a large number of research and industrial applications in diverse fields. ANN, on the other hand, generates a complex sigmoidal function at the end with several tuning constants known as weights and biases. These complex sigmoidal equations are black box in nature and do not give any insights into the process phenomenology. In addition, it is very difficult to get a possible explanation of the processes from these equations. Both ANN and SVM models suffer from these limitations of explainability despite their superior prediction capability. Due to these reasons, ANN and SVM models are not favoured by the engineers working in the industry and by the researchers working in R&D laboratories. Plant engineers and R&D researchers typically want manageable equations in differential/algebraic form that relate output variables to input features so that they can have a better understanding of the desired benefits. In this work, an attempt has been made to explore alternative computational methods for modelling the less understood chemical processes.
It is found in the literature that genetic programming (GP), which is a branch of evolutionary modeling techniques, has the capability to remove the above drawbacks of ANN and SVM models. Genetic programming automatically generates nonlinear structured models as closed-form equations relating the input and output of the system from available data. Not only does GP identify the structure of the equation, but also it estimates the different parameters of the equations so that it accurately predicts the output. At the time of building up MISO (multiple input, single output) models by using GP, the probability of survival of a particular model to its next generations depends on its prediction accuracy and followed ‘survival of the fittest’ principles. Recombination of components of survived models continuously takes place to form a new model aiming at increasing predictability in each generation. In the literature, the breakthrough in GP can be seen in the late 1980s with the experiments of Koza on symbolic regression [17]. The versatility of the GP algorithm is proved by Koza and Rice by applying it in diverse fields of robotics, games, control, etc. [15].
Multi-gene genetic programming (MGGP) is one of the robust variants of GP and claims to be more effective than GP in nonlinear modeling [35, 36]. MGGP is designed to generate mathematical models of predictor response data that are ‘multi-gene’ in nature, i.e. linear combinations of low-order nonlinear transformations of the input variables. The conventional GP is mainly based on the evaluation of a single tree (model) expression. In the multi-gene approach, several individual genes are combined to construct a single one [36]. It has been proved that MGGP regression is capable of providing a more accurate and computationally efficient model in comparison to conventional GP [35, 36]. It can be seen in many cases that MGGP performed better than other machine learning methods, viz. ANN, SVM, etc., in terms of predictability and model simplicity [6, 10, 12, 24].
Since the beginning of industrialization, industrial wastewater carrying various contaminants has been dumped directly or indirectly into water bodies, disrupting the aquatic biota. This has made water pollution a serious environmental problem. Due to their poisonous and carcinogenic nature, heavy metals in wastewater play a key role among other contaminants including organic or inorganic compounds, dyes, and pesticides [37]. Additionally, they cannot biodegrade but rather bioaccumulate in living tissue, posing major health risks and even fatalities [40]. The specific gravities of heavy metals are five times larger than those of water, and their atomic weights range from 63.5 to 200.6 [39]. In 2015, the Agency for Toxic Substances and Disease Registry (ATSDR) ranked Cr(VI) as the sixteenth most dangerous substance [11]. According to a recent study by Yen et al. [43], Cr(VI) is the second most prevalent heavy metal (pollutant) in the environment, with concentration in groundwater ranging from 0.008 to 173 mM [43]. Natural sources and anthropogenic sources are the two main sources of chromium pollution. Leaching from rocks and topsoil are two natural sources of chromium pollution of surface water. The effluents from industrial sectors such as electroplating, leather tanning, anodizing, ink manufacturing, pigments, dyeing, glass, ceramics, glues, wood processing, paint industry, metal cleaning, mining, and textile industries are some of the main anthropogenic sources of chromium in surface water bodies [30]. The most stable forms of chromium are Cr(III) and Cr(VI). Cr(III) is used as an essential nutrient for animals; however, due to its strong teratogenic, mutagenic, and carcinogenic effects, Cr(VI) is over 300 times more hazardous than Cr(III) [27]. Due to its high solubility, Cr(VI) can easily pass through cell membranes. The inappropriate disposal of solid waste from chromate-processing facilities is mostly to blame for groundwater pollution with chromium. The dose of chromium, the length of exposure, and the type of compound all affect one’s health. Acute exposure to chromate leads to several health problems in human beings, like gastrointestinal disorders, haemorrhagic diathesis, and convulsions. In extreme circumstances, it could also result in cardiovascular shocks and death [32]. Additionally, it is known that hexavalent chromium causes cancer in human beings and genetic changes that result in birth abnormalities in unborn infants [25]. The World Health Organization (WHO) states that the acceptable limits for total chromium in drinking water, which includes Cr(III) and Cr(VI), are 0.05 mg/L and 2 mg/L, respectively [14]. For public water systems, the Environmental Protection Agency (EPA), USA, limits the maximum total chromium contaminant level in drinking water to 100 µg/L or 100 ppb [41]. Therefore, before discharging wastewater into the environment, chromium must be removed from it. Chromium removal from wastewater has been accomplished using several conventional treatment methods, including solvent extraction, membrane separation, ion exchange, and chemical precipitation [26]. Conventional methods, however, have drawbacks such as high chemical or energy requirements, secondary pollution development, high cost, production of toxic sludge, etc. Additionally, they are ineffective for metal concentrations below 100 mg/L [4, 14]. As a result, research is currently leaning towards alternative environmentally benign, economically feasible processes. There are about 7000 different types of algae worldwide. Microalgae can bio-reduce CO2 from waste gases and the atmosphere; they can use low-quality water, including municipal runoff and industrial wastewater containing toxic metals and organic matter. Moreover, algal bodies can survive in natural weather conditions. Algae can produce significantly more biomass when grown in wastewater; thus, high-quality agricultural land is not necessary to grow the algal cells [29]. Even though there have been many studies on the reduction of Cr(VI) utilizing microalgal/cyanobacterial biomass, very few of them address the intricate mathematical analysis supported by experimental results. Sen et al. [38] used Chlorococcum sp. to remove Cr(VI) from simulated wastewater [38].
In the present article, the phycoremediation method for the removal of Cr(VI), a very complex process, was chosen as a case study. The experimental data as reported by Sen et al. [38] were used for modeling and optimization using MGGP and grey wolf optimization (GWO) techniques, respectively. In the present study, an attempt was made to explore the relationship between the removal of Cr(VI) with input parameters like pH, inoculum size, initial concentration of Cr(VI), and time. Once a model was built through the application of MGGP, that model was utilized to get the phenomenological insights of the phycoremediation process. One major objective of the application of MGGP was to develop an accurate phycoremediation model which is a closed-form equation, portable, and can be used by the plant engineers to gain insight into the process. The second objective of the study was to use the developed model to maximize the removal of Cr(VI). This was accomplished by using a nature-inspired metaheuristic optimization method for the optimization of the input process parameters [1,2,3, 5]. To produce Pareto optimal solutions that meet the goals in the most efficient way possible, the grey wolf optimization (GWO) was utilized to improve the input space of the MGGP model for phycoremediation. GWO has the following advantages: (i) it is a nature-inspired modern optimization technique and has world-spread applicability; (ii) GWO has not been used so far to optimize complex phycoremediation models.
Therefore, overall novelties of the present study are: (i) MGGP has been used to solve an industrial problem; (ii) as far as known, MGGP has not been used to build a phycoremediation model; (iii) out of several good performing models, those models are sorted out which actually obey the internal phenomenology; and (iv) grey wolf optimization (GWO), a nature-inspired metaheuristic optimization algorithm, has been used to optimize the process parameters.
2 Methods
2.1 Generation of data for model building
Sen et al. [38] performed experiments on the removal of Cr(VI) using the Chlorococcum sp., a cyanobacterial species. They had 82 experimental data points. In the present study, using 82 data points and ‘Plot Digitizer’ software 897 data points were generated for better MGGP model building. After building a reliable MGGP model for the phycoremediation process, the model equation is optimized through the grey wolf optimization (GWO) technique. The ranges of four variables, including pH, inoculum size (IS), initial concentrations (IC) of Cr(VI), and time, are shown in Table 1. Table 2 shows some of the experimental data which are generated by ‘Plot Digitizer’ software.
2.2 Multi-gene genetic programming: at a glance
GP is a type of metaheuristic symbolic modeling technique that creates equations for solving problems based on Darwinian natural selection’s ‘survival of the fittest’ concept [13]. The following is the general form of the process model to be obtained (Eq. 1)
where \(y\) indicates the process output variable (removal of Cr(VI)); \(X\) is the N-dimensional vector of input variables like pH, inoculum size, initial concentration of Cr(VI), etc.
and \(f\) denotes a nonlinear function whose parameters are defined in terms of a P-dimensional vector, \(\left( {\beta \left[ {\beta_{1} ,\beta_{{2, \ldots ,\beta_{K} }} } \right]^{P} } \right)\). If phycoremediation data of input and output variables are given, the GP algorithm tries to best fit the data by changing its functional form and parameter vector \(\beta\). Genetic programing iterative modelling process is shown in Fig. 1.
2.2.1 Executional steps of genetic programming
The algorithm of GP is illustrated in Fig. 2. The execution steps of GP are mentioned below [31]:
Step 1 (Initialization) In the first step, the GP algorithm creates random equations to fit the data defined in Eq. (1). These equations are commonly called the population of strings (chromosomes) representing candidate solutions. Basically, a population member consists of functions and terminals combined in a hierarchical manner, which is termed the tree. The function set may contain algebraic operators and Boolean logical operators. The terminal set may consist of variables and numerical and logical constants. A typical tree is shown in Fig. 1.
Step 2 (Generation) This step is an iterative procedure to generate the population with a high fitness value and consists of the following sub-steps (Fig. 2):
-
(a)
The fitness of each population is evaluated using a prespecified fitness function. A coefficient of determination (R2) dependent or error-dependent fitness function can be used for this purpose. Higher the value of R2 or lower the value of error, the more the fitness of a particular population. In this study, root-mean-squared error (RMSE) was considered an error parameter.
-
(b)
Select individual equations from the population with the help of probabilistic determination of fitness.
-
(c)
Create new individual equations with the help of genetic operators such as (Fig. 2):
-
(i)
Reproduction During reproduction, the algorithm copies the existing population into a new generation without any change.
-
(ii)
Crossover In the crossover, offspring is produced by the interchanging of chromosomes of the parent generation.
-
(iii)
Mutation In mutation, the replacement of existing elements in offspring with other elements takes place.
-
(i)
The reproduction, crossover, and mutation steps are illustrated in Fig. 1.
Step 3 (Termination) When the termination criteria are met, the best program will be the approximate solution to the problem (Fig. 2).
2.2.2 Structure of MGGP
Usually, symbolic regression uses GP to create a population of trees. Each of these trees is basically a mathematical expression. In MGGP, a multiple tree structure is used to predict the output as shown below.
Each of these trees can be considered a gene. A typical multi-gene model is shown in Fig. 3. This model predicts an output variable using three input variables (\(x_{1} , x_{2} , x_{3}\)). The characteristics of this model structure are though it contains nonlinear terms (like a square), it is linear in the parameter concerning the coefficients \(C_{0} , C_{1} , {\text{and}} C_{2}\). The maximum allowable number of genes (\(G_{\max }\)) for a model and the maximum tree depth (\(D_{\max }\)) have a profound effect on the final model structure and are usually specified by the users. From the literature, it is found that a maximum tree depth of 4 or 5 nodes usually gives a compact efficient model. The linear coefficients \(C_{0} , C_{1} , {\text{and}} C_{2}\) are usually evaluated by applying the ordinary least square method to the training data. In the literature, multi-gene symbolic regression is reported as more accurate and efficient than the standard GP.
2.2.3 Application of MGGP in phycoremediation process modeling
This paper tries to explore the MGGP modeling technique for the phycoremediation process to obtain a meaningful nonlinear relationship between the removal of heavy metals with various input parameters like pH, time, inoculum size, and initial concentrations of heavy metals.
2.2.4 Selection of input and output variables for modeling
Since the removal percentage of Cr(VI) has a large impact on wastewater, this parameter is kept as the output variable. All the input variables which can impact the Cr(VI) removal are studied in the literature [8, 34, 37]. Four input variables are finally shortlisted and shown in Table 1.
2.2.5 Modeling through multi-gene genetic programming (MGGP)
The experimental data were taken for GP-based modeling. Random partitioning of the dataset comprising four input variables and one output variable (Table 1) into a training set (80% of whole data) and test set (20% of whole data) was performed. The training set was used to compute the model by maximizing the fitness value, whereas the test data set was used for cross-validation of the expression developed. The main objective of cross-validation is to make the model more generalizable.
Open-source GPTIPS toolkit coupled with subroutines written in MATLAB 2019a was utilized to construct the GP-based model [36]. In this study, the root-mean-squared error (RMSE) between actual and predicted outputs was employed as a fitness function, and the program was run in such a way that the RMSE value was kept as low as possible. Due to the stochastic character of the GP, the software was run 100 times to build the model.
2.3 Optimization through grey wolf optimization (GWO)
Mirjalili et al. [20] developed GWO which is a stochastic and metaheuristic optimization methodology. This bionic optimization algorithm stimulates the rank-based mechanisms and attacking behaviour of the grey wolf pack. The lead wolf helps the other wolves to capture the prey through the surrounding, haunting, and attacking process. This large-scale search methodology centred on the three best grey wolves, but there is no elimination mechanism. The optimization technique is different from others in terms of modeling. It constitutes a strict hierarchical pyramid. The group size is 5–12 on average. Layer α, consisting of a male and a female leader, is the strongest and most capable individual for deciding the team’s predation actions and other activities. Layer β and layer δ are the second and third layers, respectively, in the hierarchy, responsible for assisting α in the behaviour of group organizations. The bottom ranking of the pyramid is occupied by the majority of the total, named ω. They are mainly responsible for satisfying the entire pack by balancing the internal relationship of the populations, looking after the young, and maintaining the dominant structure [20]. The social hierarchy, encircling, hunting, attacking prey (exploitation), and searching for prey are the main key elements of the GWO model (exploration). The detailed mathematical modeling of GWO has been described by Mirjalili et al. [20].
This metaheuristic approach is applied in various real-world problems because of its efficient and simple performance ability by tuning the fewest operators [9, 16, 18, 21, 22]. Recent research in this regard looks forward to the further development of the optimization algorithm. The detail of the GWO algorithm is depicted in Fig. 4.
3 Results
3.1 Performance of the MGGP model
The main objective of the present study is to generate a closed-form model equation of the phycoremediation process which is accurate, simple, and portable. Eight hundred and ninety-seven data sets were qualified for model building. The values of MGGP parameters required for modelling were decided based on a trial-and-error approach and literature survey and are shown in Table 3 [36]. A sensitivity analysis was performed where the population size, maximum generation, and maximum number of genes were varied. A balance has been made between model complexity and prediction accuracy as shown in Pareto diagram (Fig. 5). The maximum allowable number of genes (\(G_{\max }\)) for a model and the maximum tree depth (\(D_{\max }\)) have a profound effect on the final model structure and are usually specified by the users. From the literature, it is found that a maximum tree depth of 4 or 5 nodes usually gives a compact efficient model. Population size, maximum generations, \(G_{\max } {\text{and}} D_{\max }\) were kept at 500, 150, 6, and 4, respectively. The linear coefficients \(C_{0} , C_{1} , {\text{and}} C_{2}\) are usually evaluated by applying the ordinary least square method to the training data [36]. Each run consists of more than 10,000 iterations as long as MGGP is able to improve the R2 value and minimize the RMSE value. The stopping criteria for MGGP are when RMSE drops below the threshold value of 0.001 or maximum execution time is achieved. Since MGGP is stochastic in nature, 20 such runs were done to conclude the final model. Further increase in run up to 100 has no substantial benefit on prediction accuracy.
3.2 Developing closed-form model equations
GP generates a lot of promising model equations during its run. Table 4 summarizes the most prominent closed-form equations generated by GP for the removal percentage of Cr(VI). For each run of GP, one Pareto diagram was developed (Fig. 5). Pareto diagrams represent the plot of expressional complexity (represented by the number of nodes in the equation) vs. prediction accuracy represented by (1 − R2).
3.3 Controlling model complexity
The use of regression models frequently suffers from the phenomenon called ‘bloat’, vertical and horizontal bloat. The tendency to evolve trees with terms that provide little or no performance benefit is known as vertical bloat. This is connected to the phenomena of overfitting in terms of model development. Researchers have used a different approach to handle overfitting. Miriyala et al. in their paper conducted six tests for the overfitting, viz. information theory test, cross-validation test, held-out sample test, testing with noisy data, and goodness-of-fit test [19]. In the present study, by the restriction on tree depth and use of the Pareto tournament between expressional complexity and accuracy the vertical bloats were ameliorated. Tree depth was kept 4 by trial-and-error method, and the Pareto diagram is generated as shown in Fig. 5.
Sometimes during execution multi-gene models add additional genes which do not give significant performance enhancement but add to the model complexity. This phenomenon is known as horizontal bloat. The simplest technique to avoid horizontal bloat in multi-gene regression is to limit the number of genes allowed in the model. In this study, the maximum number of genes is kept at 6 after the trial-and-error method.
3.4 Shortlisting the models
Out of potential candidates or representative model equations (Table 4) with varying degrees of complexity and accuracy, for the selection of a suitable model, the following criteria were kept in mind:
-
(i)
Simplicity: The model complexity should be as low as possible.
-
(ii)
Prediction accuracy: The developed model should have low RMSE and high R2.
-
(iii)
The model equation should capture the underlying physics of the process. In other words, model equations are not merely a predictive correlation but also should have a physical sense of the system under study. This is a prime consideration to develop real-life models. To judge this capability, domain experts’ qualitative knowledge about phycoremediation behaviour is collected from the literature and experiment. The operating skill, circumstance, and surveillance of phycoremediation behaviour are summarized in Table 5.
3.5 Shortlisting the model based on phenomenology
All thirteen equations in Table 4 are subjected to the above scrutiny to judge whether the developed equation is in agreement with real observations. All the developed models are passed through rigorous testing. For example, ten test data set was generated where all the variables are kept at their 50-percentile value except pH which was varied from its minimum value to maximum value by 10 equal intervals. These test data were put in equations of Table 4, and respective 10-set removal percentage data were generated. After that, the first pH vs removal percentage was plotted. From these plots, observation number 1 of Table 5 was verified. In the same way, all other plots were generated which are shown in Fig. 6. Final model equation is as follows:
Table 6 shows the coefficient of determination (R2), root-mean-squared error (RMSE), and mean absolute error (MAE) values for training and test data.
3.6 Generation of explainable model equations
One of the major advantages of the GP modeling technique over ANN and SVR techniques is that it generates a closed form equation (like Eq. 10), which is portable, and easy to understand. GP develops a closed-form equation with a high prediction capability, but the created equation is vast and complex, and it can be difficult to interpret directly. In the present study, a methodology is developed to enhance the interpretability of the developed equations. Figures 6 and 7 summarize the developed methodology. Figure 6 is created by varying one variable at a time from its minimum to the maximum value (10 steps) while maintaining the average value of the other three input variables. Cr(VI) removal equations developed by GP are used to predict the output value in each case of these simulated test data. After plotting was done, a trendline was drawn through each data. Based on eye inspection and R2 value, a trend line curve was chosen (such as a straight line, or a polynomial of degree 2 or 3 or more) that almost matches the data.
On the other hand, Fig. 7 depicts the actual phenomenology of the phycoremediation process for the removal of Cr(VI). From the figure, it is seen that the removal of Cr(VI) increases with the initial concentration of Cr(VI) up to 20 mg/L. Further increase in initial concentration decreases the removal percentage. pH was varied from 7 to 11, and it is seen that removal of Cr(VI) increases with time and reaches its maximum value at pH 9. Further increases in pH decrease the removal of Cr(VI). Inoculum size was varied from 2 to 10%, and it is observed that the removal of Cr(VI) monotonically increases with inoculum size. Kinetic study was performed with respect to the initial concentration (10–25 mg/L), pH (7–11), and inoculum size (2–10%). In all the cases of kinetic study, it is seen that removal of Cr(VI) increases with time.
3.7 Optimization through GWO
Once the reliable models were successfully developed, the models were subjected to optimization. The purpose of optimization is to find out the finest combination of input parameters that correspond to the highest Cr(VI) removal. One of the most significant jobs for any process optimization is to define the search space in which the optimal process conditions should be found.
GWO code in MATLAB is used to optimize the input parameters (pH, inoculum size, and the number of days) which gives maximum removal of Cr(VI). Optimization conditions and the optimal solutions are shown in Tables 7 and 8, respectively.
4 Discussion
4.1 MGGP modeling
In the current research work, basic arithmetic operators and functions, the population size of 500, maximum generation of 150, maximum tree depth of 4, and a maximum number of genes of 6 were proved to be the best for modeling (shown in Table 3). If these parameters are taken with high values, the model accuracy may increase but the complexity of the solutions also increases, and also the program becomes computationally expensive.
As shown in Table 4, there is always a conflicting objective between model complexity (denoted by a number of tree nodes) and model prediction accuracy (denoted by coefficient of determinations (R2)). More accurate models are more complex and vice versa. Complex models are difficult to interpret and unnecessarily overfit the data.
Pareto diagrams represent the plot of expressional complexity (represented by the number of nodes in the equation) vs. prediction accuracy represented by (1 − R2). An optimum point was found as the final model with a low value of (1 − R2) and an acceptable value of model complexity. The red triangular point in the Pareto diagram was chosen as a model.
All thirteen equations in Table 4 are subjected to scrutiny to judge whether the developed equation is in agreement with real observations. All the developed models are passed through rigorous testing. The scrutiny is necessary because in any modeling, besides the accuracy of the model, the developed relationship between output and input variables should be in agreement with the underlying physics of the process. In most cases, data-driven models with high accuracy end up being only black-box models without any insight into the system. In this procedure, the two parameters have been kept in mind, firstly accuracy and secondly obeying underlying physics.
From the shortlisted model equations, only one model equation for the removal percentage of Cr(VI) was finally selected (Eq. 10): This equation is considered the representative model equation for the removal of metals as it is highly accurate, obeys Table 5 observations, and captures the internal physics of the process. Figure 7 shows the actual phenomenology of the phycoremediation process.
The high R2 and low RMSE values for the Cr(VI) removal model (Table 6) show that the predicted and actual output values are comparable, and the models created are trustworthy, fairly accurate, and represent the phycoremediation process’ underlying physics. The high R2 value on unseen test data and low RMSE further suggest the model’s generalizability and accurate learning on nonlinear input and output relationships.
Figure 8 depicts the models’ prediction performance on training and testing data. The almost overlapping nature of the actual vs predicted curve indicates the model’s good prediction accuracy.
The generated model is highly accurate and dependable, as evidenced in Table 6, Figs. 6, 7, and 8. It also works well with unknown test data.
As seen from Fig. 6, the developed trend lines are very decisive and monotonically increasing/decreasing. As mentioned earlier, they all match the actual observations (Fig. 7) and obey Table 5. In short, developed models capture the nonlinear relationship between the removal percentage of Cr(VI) and the operating parameters of the phycoremediation process. These trend lines can be used by plant operating engineers to get insights into how a particular input parameter affects the removal percentage of Cr(VI).
4.2 GWO optimization
In the present study, since the initial concentrations of Cr(VI) are not under our control and they are fixed as per wastewater data, it is not considered an optimization parameter (Case 1–Case 6). Here, there are only three optimization variables (pH, inoculum size, and the number of days). The input parameters pH (x1), inoculum size (x2), and time (x4) are varied in the range of 7–11, 2–10%, and 2–14 days, respectively. In case 7, initial concentration of Cr(VI) also has been considered as optimization parameter. The lower bounds (LB) and upper bounds (UB) explored in these scenarios are shown in Table 7.
It is observed from Table 8 that removal of Cr(VI) increases with the initial concentration of Cr(VI) up to 20 mg/L (Case 1–Case 4). Further increase in Cr(VI) concentration decreases the removal percentage (Case 5–Case 6). In Case 7, pH, IS, IC, and time are the optimization parameters. It is observed from Table 8 that if wastewater contains Cr(VI) at a concentration level of 14 mg/L, then if pH is kept at 9.48 (x1), IS (x2) at 10%, then within 13.4 days, 99% Cr(VI) removal is possible.
5 Conclusions
This study uses multi-gene genetic programming techniques to develop an accurate model of a phycoremediation process from the experimental data. The study’s key contribution is the development of an extremely precise and explainable model equation that comes with an understanding of the process. The produced model equations are based on the process’s underlying physics and correspond to the expert’s observations and experiences. Developed model equations are then used to generate optimal solutions to maximize the removal percentage of Cr(VI). Also, it has been shown that if the operating parameters are adjusted as prescribed by optimization results, it can be possible to increase the removal percentage up to 99%.
Availability of data and materials
All the data presented in the article are produced or evaluated during the research.
Abbreviations
- GP:
-
Genetic programming
- MGGP:
-
Multi-gene genetic programming
- GWO:
-
Grey wolf optimization
- ANN:
-
Artificial neural network
- SVM:
-
Support vector machine
- R&D:
-
Research and development
- MISO:
-
Multiple input single output
- WHO:
-
World Health Organization
- IS:
-
Inoculum size
- IC:
-
Initial concentration
- RMSE:
-
Root-mean-squared error
- \(R^{2}\) :
-
Coefficient of determination
- \(G_{\max }\) :
-
Maximum number of allowable genes
- \(D_{\max }\) :
-
Maximum tree depth
- MAE:
-
Mean absolute error
- LB:
-
Lower bounds
- UB:
-
Upper bounds
- AI:
-
Artificial intelligence
- ATSDR:
-
Agency for Toxic Substances and Disease Registry
- mM:
-
Millimole
- EPA:
-
Environmental Protection Agency
- USEPA:
-
United States Environmental Protection Agency
- C0, C1, C2 :
-
Linear coefficients
- ppb:
-
Parts per billion
References
Abo-Hammour Z, Alsmadi O, Momani S, Arqub OA (2013) A genetic algorithm approach for prediction of linear dynamical systems. Math Probl Eng. https://doi.org/10.1155/2013/831657
Abo-Hammour Z, Arqub OA, Momani S, Shawagfeh N (2014) Optimization solution of Troesch’s and Bratu’s problems of ordinary type using novel continuous genetic algorithm. Discrete Dyn Nat Soc. https://doi.org/10.1155/2014/401696
Abu O, Abo-hammour Z (2014) Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf Sci. https://doi.org/10.1016/j.ins.2014.03.128
Anjana K, Kaushik A, Kiran B, Nisha R (2007) Biosorption of Cr(VI) by immobilized biomass of two indigenous strains of cyanobacteria isolated from metal contaminated soil. J Hazard Mater 148:383–386. https://doi.org/10.1016/j.jhazmat.2007.02.051
Arqub OA, Abo-hammour Z, Momani S, Shawagfeh N (2012) Solving singular two-point boundary value problems using continuous genetic algorithm. Abstr Appl Anal. https://doi.org/10.1155/2012/205391
Barati R, Neyshabouri SAAS, Ahmadi G (2014) Development of empirical models with high accuracy for estimation of drag coefficient of flow around a smooth sphere: an evolutionary approach. Powder Technol 257:11–19. https://doi.org/10.1016/j.powtec.2014.02.045
Bilal S, Ali I, Akgu A, Botmart T, Sayed E, Yahia IS (2022) A comprehensive mathematical structuring of magnetically effected Sutterby fluid flow immersed in dually stratified medium under boundary layer approximations over a linearly stretched surface. Alex Eng J 61:11889–11898. https://doi.org/10.1016/j.aej.2022.05.044
Dorman L, Rodgers JH, Castle JW (2010) Characterization of ash-basin waters from a risk-based perspective. Water Air Soil Pollut 206:175–185. https://doi.org/10.1007/s11270-009-0094-9
Emary E, Zawbaa HM, Hassanien AE (2016) Binary grey wolf optimization approaches for feature selection. Neurocomputing 172:371–381. https://doi.org/10.1016/j.neucom.2015.06.083
Floares A, Luludachi I (2014) Inferring transcription networks from data XX. 1 Introduction and background. In: Springer Handbook of Bio-/Neuroinformatics, pp 311–326
ATSDR (Agency for Toxic Substances and Disease Registry). 2017. ATSDR’s substance priority list. Accessed April 28, 2017. https://www.atsdr.cdc.gov/spl/
Gandomi AH, Alavi AH (2012) A new multi-gene genetic programming approach to nonlinear system modeling. Part I: materials and structural engineering problems. Neural Comput Appl 21:171–187. https://doi.org/10.1007/s00521-011-0734-z
Grosman B, Lewin DR (2002) Automated nonlinear model predictive control using genetic programming. Comput Chem Eng 26:631–640. https://doi.org/10.1016/S0098-1354(01)00780-3
Gupta VK, Rastogi A (2009) Biosorption of hexavalent chromium by raw and acid-treated green alga Oedogonium hatei from aqueous solutions. J Hazard Mater 163:396–402. https://doi.org/10.1016/j.jhazmat.2008.06.104
Koza JR, Rice JP (1992) Genetic programming: the movie. The MIT Press, Cambridge
Kohli M, Arora S (2018) Chaotic grey wolf optimization algorithm for constrained optimization problems. J Comput Des Eng 5:458–472. https://doi.org/10.1016/j.jcde.2017.02.005
Koza JR (1994) Genetic programming: on the programming of computers by means of natural selection. In: Koza JR (ed) A bradford book. MIT Press, Cambridge
Lu Q, He ZL, Graetz DA, Stoffella PJ, Yang X (2010) Phytoremediation to remove nutrients and improve eutrophic stormwaters using water lettuce (Pistia stratiotes L.). Environ Sci Pollut Res 17:84–96. https://doi.org/10.1007/s11356-008-0094-0.
Miriyala SS, Mittal P, Majumdar S, Mitra K (2016) Comparative study of surrogate approaches while optimizing computationally expensive reaction networks. Chem Eng Sci 140:44–61. https://doi.org/10.1016/j.ces.2015.09.030
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007
Mirjalili S, Saremi S, Mirjalili SM, Coelho LDS (2016) Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization. Expert Syst Appl 47:106–119. https://doi.org/10.1016/j.eswa.2015.10.039
Mittal N, Singh U, Sohi BS (2016) Modified grey wolf optimizer for global engineering optimization. Appl Comput Intell Soft Comput. https://doi.org/10.1155/2016/7950348
Modanli M, Go E, Khalil EM, Akgu A (2022) Two approximation methods for fractional order Pseudo-Parabolic differential equations. Alex Eng J 61:10333–10339. https://doi.org/10.1016/j.aej.2022.03.061
Pan I, Pandey DS, Das S (2013) Global solar irradiation prediction using a multi-gene genetic programming approach. J Renew Sustain Energy. https://doi.org/10.1063/1.4850495
Pradhan D, Behari L, Sawyer M, Rahman PKSM (2017) Recent bioreduction of hexavalent chromium in wastewater treatment: a review. J Ind Eng Chem 55:1–20. https://doi.org/10.1016/j.jiec.2017.06.040
Qasem NAA, Mohammed RH, Lawal DU (2021) Removal of heavy metal ions from wastewater: a comprehensive and critical review. npj Clean Water. https://doi.org/10.1038/s41545-021-00127-0
Qu Y, Zhang X, Xu J, Zhang W, Guo Y (2014) Removal of hexavalent chromium from wastewater using magnetotactic bacteria. Sep Purif Technol 136:10–17. https://doi.org/10.1016/j.seppur.2014.07.054
Qureshi ZA, Sultana M, Botmart T, Zahran HY, Yahia IS (2022) Mathematical analysis about influence of Lorentz force and interfacial nano layers on nanofluids flow through orthogonal porous surfaces with injection of SWCNTs. Alex Eng J 61:12925–12941. https://doi.org/10.1016/j.aej.2022.07.010
Ramanan R, Kannan K, Deshkar A, Yadav R, Chakrabarti T (2010) Enhanced algal CO2 sequestration through calcite deposition by Chlorella sp. and Spirulina platensis in a mini-raceway pond. Bioresour Technol 101:2616–2622. https://doi.org/10.1016/j.biortech.2009.10.061
Rangabhashiyam S, Selvaraju N (2015) Adsorptive remediation of hexavalent chromium from synthetic wastewater by a natural and ZnCl2 activated Sterculia guttata shell. J Mol Liq 207:39–49. https://doi.org/10.1016/j.molliq.2015.03.018
Sadhu T, Banerjee I, Lahiri SK, Chakrabarty J (2020) Modeling and optimization of cooking process parameters to improve the nutritional profile of fried fish by robust hybrid artificial intelligence approach. J Food Process Eng 43:1–13. https://doi.org/10.1111/jfpe.13478
Saha R, Nandi R, Saha B (2011) Sources and toxicity of hexavalent chromium. J Coord Chem. https://doi.org/10.1080/00958972.2011.583646
Sajid M, Waqas M, Ahmed N, Akgül A, Rafiq M, Raza A (2023) Numerical simulations of nonlinear stochastic Newell-Whitehead-Segel equation and its measurable properties. J Comput Appl Math 418:114618. https://doi.org/10.1016/j.cam.2022.114618
Salama ES, Roh HS, Dev S, Khan MA, Abou-Shanab RAI, Chang SW, Jeon BH (2019) Algae as a green technology for heavy metals removal from various wastewater. World J Microbiol Biotechnol. https://doi.org/10.1007/s11274-019-2648-3
Searson D, Willis M, Montague G (2007) Co-evolution of non-linear PLS model components. J Chemom 21:592–603. https://doi.org/10.1002/cem.1084
Searson DP, Leahy DE, Willis MJ (2010) GPTIPS: an open source genetic programming toolbox for multigene symbolic regression. In: Proceedings of the International multiconference of engineers and computer scientists 2010, IMECS 2010 I, pp 77–80
Sen S, Dutta S, Guhathakurata S, Chakrabarty J, Nandi S, Dutta A (2017) Removal of Cr(VI) using a cyanobacterial consortium and assessment of biofuel production. Int Biodeterior Biodegrad 119:211–224. https://doi.org/10.1016/j.ibiod.2016.10.050
Sen S, Rai A, Chakrabarty J, Lahiri SK, Dutta S (2021) Parametric modeling and optimization of phycoremediation of Cr(VI) using artificial neural network and simulated annealing, Algae. Multifarious Appl Sustain World. https://doi.org/10.1007/978-981-15-7518-1_6
Shanab S, Essa A, Shalaby E (2012) Bioremoval capacity of three heavy metals by some microalgae species (Egyptian isolates). Plant Signal Behav 7:392–399. https://doi.org/10.4161/psb.19173
Tangahu BV, Sheikh Abdullah SR, Basri H, Idris M, Anuar N, Mukhlisin M (2011) A review on heavy metals (As, Pb, and Hg) uptake by plants through phytoremediation. Int J Chem Eng. https://doi.org/10.1155/2011/939161
USEPA. 2017. Chromium in drinking water. Accessed April 28, 2017. http://www.epa.gov/dwstandardsregulations/chromium-drinking-water
Xu C, Farman M, Hasan A, Akgu A, Zakarya M, Albalawi W, Park C (2022) Lyapunov stability and wave analysis of Covid-19 omicron variant of real data with fractional operator. Alex Eng J 61:11787–11802. https://doi.org/10.1016/j.aej.2022.05.025
Yen H, Chen P, Hsu C, Lee L (2017) The use of autotrophic Chlorella vulgaris in chromium (VI) reduction under different reduction conditions. J Taiwan Inst Chem Eng 74:1–6. https://doi.org/10.1016/j.jtice.2016.08.017
Acknowledgements
The authors sincerely acknowledge the computational and analytical instrumentation support received from DST-FIST, GOI by the Department of Chemical Engineering, National Institute of Technology, Durgapur, India.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
BS is the investigator and performed the process optimization, modelling, and paper writing. SS is the investigator and was involve in paper writing. SD contributed to conceptualization, supervision, and reviewing and final editing the paper thoroughly. SKL was involved in conceptualization, supervision, modelling, optimization, and reviewing and final editing the paper thoroughly. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
There are no competing interests between the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sarkar, B., Sen, S., Dutta, S. et al. Application of multi-gene genetic programming technique for modeling and optimization of phycoremediation of Cr(VI) from wastewater. Beni-Suef Univ J Basic Appl Sci 12, 27 (2023). https://doi.org/10.1186/s43088-023-00365-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43088-023-00365-w