1 Background

Mathematical models are important techniques that have been greatly explored to describe the transmission dynamics of evolving and re-evolving diseases in epidemiology. The essence of epidemic models is to understand, prepare for future occurrence of epidemic breakout, and to implement necessary intervention strategies to curtail the spread of diseases in human and environment host population. One of the earliest publications on mathematical models of infectious disease are the works of [1,2,3]. The authors discussed on the division of the human host population into compartments and epidemic interactions between them. Also, several mathematical techniques have been employed by authors to quantitatively and qualitatively describe the dynamics of models of many diseases like onchocerciasis [4, 5], conjunctivitis [6], co-infection of malaria with filariasis and toxoplasmosis [7, 8], as well as using stability theorems and optimal control analysis to qualitatively and quantitatively analyse epidemic models [9,10,11]. Medical awareness programs through media outlets like radio, electronic prints, television, and social media are means of communicating to the human host community to be aware of how to mitigate disease spread and forestall healthy living [12, 13]. The basic reproduction number Rr is an epidemic threshold used to determine the number of secondary cases of infections arising as a result of an introduction of an infected individual into a susceptible host population during his or her period of infection. Rr have been used immensely to describe the reproductive rate of many diseases [14]. Also, [15] worked on the analysis of an SEIR epidemic model with saturated incidence and saturated treatment functions, while [16] investigated the impact of vaccination strategies for a SISV epidemic model guaranteeing the nonexistence of endemic solutions. In addition, [17] worked on the SEIR model formulation and compartmental epidemic interactions in the human population, while [18] worked on assessing the inference of the basic reproduction number Rr in SIR model incorporating growth scaling parameter, see also [19, 20]. Other works on SEIR modeling includes [21,22,23,24], while the publications of [25, 26] proved useful to this study by employing the use of Lyapunov functions to analyze model stability domain. Numerical methods of Runge-Kutta and DTM have proved useful in obtaining the convergent approximate solutions of epidemic models, see [27, 28]. In view of the cited publications, we consider the SEIR epidemic model with two groups of infected individuals who attend or are compliant to medical awareness program and those who did not attend or are non-compliant to medical awareness program, with saturated incidence function. Section 2 discusses the positivity and invariant region analysis of the model, while the equilibria of the model and basic reproduction number Rr is obtained. Section 3 involves the local and global stability of model system at the disease-free and endemic equilibrium solutions. Furthermore, we employ the DTM and Runge-Kutta fourth-order method to obtain the approximate solutions of the model. The results obtained agreeably compare with each other. Also, we performed simulations involving some parameters of the model when Rr < 1 and Rr > 1.

2 Model establishment and analytical results

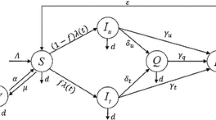
The total human host population denoted N(t), at time t > 0 is classified into five compartments of susceptible denoted S(t), which are the individuals who are at risk of acquiring the disease. Also, people who have been latently infected but are not yet infectious are denoted by E(t), symptomatic individuals who did not attend medical awareness program are denoted by Iu(t), symptomatic individuals who did attend medical awareness program are denoted by Iv(t), and the recovered individuals are denoted by R(t), so that

$$ N(t)=S(t)+E(t)+{I}_u(t)+{I}_v(t)+R(t). $$
(1)

The susceptible population is increased by the recruitment of individuals at the rate A, following an effective contact with infected individuals in the Iu and Iv compartment, the force of infection is denoted λ(t), and described by the quantity

$$ \lambda (t)=\upbeta \left(\frac{{\mathrm{I}}_{\mathrm{u}}}{1+{\upphi}_1{\mathrm{I}}_{\mathrm{u}}} + \frac{\uptheta {\mathrm{I}}_{\mathrm{v}}}{1+{\phi}_2{\mathrm{I}}_{\mathrm{v}}\ }\right). $$
(2)

In (2), λ(t) is the force of infection that takes into account the high saturation of infected individuals in the human host community, where β is the transmission rate of infection and θ is the modification parameter that takes into account the relative infectiousness of medical awareness non-compliant individuals to transmit infection at a higher rate than medical awareness compliant individuals. We adopt a nonlinear saturated incidence rate in the two groups of individuals to describe the behavioral change and crowding effect of infected humans where ϕ1 and ϕ2 measures the inhibitory effect. But if ϕ1 and ϕ2 are zeros, then the incidence function follows a bilinear incidence which is commonly adopted in many models. The population of the susceptible individuals is further decreased by natural death rate μ. Thus, the rate of change of the susceptible population is given by

$$ \frac{dS}{\kern0.5em dt}=A-\left(\mu +\lambda (t)\right)S. $$
(3)

The population of exposed individuals is increased by the force of infection λ(t). The compartment is further on decreased by the development of clinical symptoms, natural death and the disease-induced mortality at the rate ϵ, μ and d respectively, so that

$$ \frac{dE}{dt}=\lambda (t)S-\left(\in +\upmu +d\right)E. $$
(4)

The population of the symptomatic individuals who did not attend medical awareness program is increased at the rate ϵ. It is decreased by natural recovery rate γo, the rate of emergence of new symptoms σ, natural death μ1, and disease-induced mortality rate α1. This is given by

$$ \frac{dI_u}{dt}=\in E-\left({\upgamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right){I}_u. $$
(5)

The population of infected individuals who attended medical awareness program is increased progressively at the rate σ. The compartment is decreased by recovery rate γ1, natural death rate μ2, and disease-induced mortality α2. It is assumed that the disease-induced mortality rate of individuals who attended medical awareness program is low in comparison with infected individuals who did not attend medical awareness program, such that α2 < α1. Hence, the rate of change of this population is given by

$$ \frac{d{I}_v}{dt}=\sigma {I}_u-\left({\upmu}_2+{\upgamma}_1+{\alpha}_2\right){I}_v. $$
(6)

Finally, the population of recovered individuals is generated by the recovery of individuals who attend and who did not attend medical awareness program at the rate γo and γ1, while it is decreased by natural death rate μ, so that

$$ \frac{dR}{dt}={\upgamma}_o{I}_u+{\upgamma}_1{I}_v-\upmu \mathrm{R}. $$
(7)

Thus, the model for the transmission dynamics of a generalized infectious disease with non-linear incidence of two groups of infected individuals who attend and did not attend medical awareness follows a first order system of ordinary differential equations given by

$$ {\displaystyle \begin{array}{l}\frac{dS}{dt}=A-\left(\mu +\lambda \left(\mathrm{t}\right)\right)S,\\ {}\frac{dE}{dt}=\lambda (t)S-\left(\upepsilon +\mu +d\right)E,\\ {}\begin{array}{l}\ \frac{d{I}_u}{dt}=\epsilon E-\left({\gamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right){I}_u,\kern0.5em \\ {}\frac{d{I}_v}{dt}=\sigma {I}_u-\left({\upmu}_2+{\upgamma}_1+{\alpha}_2\right){I}_v,\\ {}\frac{dR}{dt}={\gamma}_o{I}_u+{\gamma}_1{I}_v-\mu R.\end{array}\end{array}} $$
(8)

Subject to the initial conditions S(0) = So, E(0) = Eo, Iu(0) = Iuo, Iv(0) = Ivo, R(0) = Ro.

2.1 Positivity of the model

It is assumed that the initial conditions of the model are non-negative and it is necessary to show that the solution of the model is positive.

Theorem 1: Let Ω = {(S, E, Iu, Iv, R) ∈ R+5 : So > 0, Eo > 0, Iuo > 0, Ivo > 0, Ro > 0}. Then the solutions of S, E, Iu, Iv, R are positive for t ≥ 0.

Proof: From the model system of differential Eq. (8), considering the first state equation given by

$$ {\displaystyle \begin{array}{l}\frac{\mathrm{dS}}{\mathrm{dt}}=\mathrm{A}-\left(\upmu +\uplambda \right)\mathrm{S},\\ {}\mathrm{so}\ \mathrm{that}\\ {}\begin{array}{l}\frac{\mathrm{dS}\left(\mathrm{t}\right)}{\mathrm{dt}}\ge \left(\upmu +\uplambda \right)\mathrm{S},\\ {}\frac{\mathrm{dS}\left(\mathrm{t}\right)}{\mathrm{S}}\ge \left(\lambda +\mu \right) dt,\\ {}\begin{array}{l}\mathrm{and}\\ {}\int \frac{\mathrm{dS}\left(\mathrm{t}\right)}{\mathrm{S}}\ge \kern0.5em \int \left(\uplambda +\upmu \right)\mathrm{dt}.\end{array}\end{array}\end{array}} $$
(9)

Solving (9) using separation of variable and applying the initial condition S(0) = So, yields

$$ S(t)\ge {S}_o{e}^{-\left(\uplambda +\upmu \right)t}\ge 0. $$
(10)

Also, from the second state equation of (8),

$$ \frac{dE}{dt}=\lambda S-\left(\epsilon +\mu +d\right)E. $$
(11)

Simplifying (11) further yields

$$ {\displaystyle \begin{array}{l}\frac{dE}{dt}\ge \kern0.5em \left(\epsilon +\mu +d\right)E\\ {}\mathrm{and}\\ {}\int \frac{dE}{E}\ge \kern0.5em \int \left(\ \epsilon +\mu +d\right) dt.\end{array}} $$
(12)

On solving (12) using separation of variable and applying initial condition E(0) = Eo, yields

$$ E(t)\ge {E}_o{e}^{-\left(\epsilon +\mu +d\right)t}\ge 0. $$
(13)

From the third state equation in (8),

$$ \frac{d{I}_u}{dt}=\epsilon E(t)-\left({\gamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right){I}_u, $$
(14)

Simplifying (14) further become,

$$ {\displaystyle \begin{array}{l}\frac{dI_u}{dt}\ge \left({\upgamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right){I}_u\\ {}\mathrm{and}\\ {}\int \frac{dI_u}{I_u}\ge \int \left({\upgamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right)d(t).\end{array}} $$
(15)

Solving (15) using separation of variable and applying initial condition Iu(0) = Iuo, yields

$$ {I}_u(t)\ge {I}_{uo}{e}^{-\left({\gamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right)t}\ge 0. $$
(16)

In addition, taking the fourth state equation of (8),

$$ \frac{d{I}_v}{dt}=\sigma {I}_u(t)-\left({\upmu}_2+{\upgamma}_1+{\alpha}_2\right){I}_v $$
(17)

where

$$ \int \frac{dI_v}{I_v}\ge -\int \left({\upmu}_2+{\upgamma}_1+{\upalpha}_2\right) dt. $$
(18)

Solving (18) using separation of variable and applying initial condition Iv(0) = Ivo, yields

$$ {I}_v(t)\ge {I}_{vo}{e}^{-\left({\upmu}_2+{\upgamma}_1+{\upalpha}_2\right)t}\ge 0. $$
(19)

Finally, taking the fifth state equation of (8),

$$ \frac{dR}{dt}={\gamma}_o{I}_u(t)+{\upgamma}_1{I}_v(t)-\upmu \mathrm{R}. $$
(20)

The simplification of (20) yields

$$ {\displaystyle \begin{array}{l}\frac{dR}{dt}\ge -\upmu \mathrm{R},\\ {}\mathrm{and}\\ {}\begin{array}{l}\frac{dR}{R}\ge -\upmu \mathrm{dt},\\ {}\int \frac{dR}{R}\ge -\int \upmu \mathrm{dt}.\end{array}\end{array}} $$
(21)

Solving (21) using separation of variable and applying initial condition R(0) = Ro, yields

$$ R(t)\ge {R}_o{e}^{-\upmu t}\ge 0. $$
(22)

From (10), (13), (16), (19), and (22), it is clear that at time t > 0, the model solutions are positive.

This completes the proof of the theorem.

2.2 Invariant region

In this section, the model system is analyzed in an invariant region and shown to be bounded. The addition of the whole model system Eq. (8) yields

$$ \mathrm{N}=\mathrm{S}+\mathrm{E}+{I}_u+{I}_v+R, $$
(23)

such that

$$ \frac{dN}{dt}=\frac{dS}{dt}+\frac{dE}{dt}+\frac{d{I}_u}{dt}+\frac{d{I}_v}{dt}+\frac{dR}{dt} $$
(24)

and

$$ \frac{dN}{dt}=A-\mu N- dE-{\upalpha}_1{I}_u-{\upalpha}_2{I}_v. $$
(25)

In the absence of natural and mortality due to disease, i.e., (d = 0, α1 = 0, α2 = 0), (25) becomes

$$ \frac{dN}{dt}=A-\mu N. $$
(26)

Integrating both side of (26) yields

$$ \int \frac{dN}{A-\mu N}\le \int \mathrm{dt} $$
(27)

and

$$ \frac{1}{\upmu}\ \ln\ \left(A-\mu N\right)\le t. $$
(28)

Simplification of (28) become

$$ \mathrm{A}-\mu N\ge {e}^{-\mu t}. $$
(29)

Applying the initial condition, N(0) = No, (29) yields A = A − μNo. Substituting A = A − μNo into (29) yields

$$ A-\mu {N}_o\ge \left(A-\mu {N}_o\right){e}^{-\mu t}. $$
(30)

Further simplification and re-arrangement of (30) yields

$$ N\le \left(\frac{A}{\upmu}-\frac{A-\upmu {\mathrm{N}}_{\mathrm{o}}}{\upmu}\right)\ {e}^{-\mu t}. $$
(31)

As t → ∞ in (31), the population size \( N\to \frac{A}{\mu } \) implies that \( 0\le N\le \frac{A}{\mu } \). Thus, the feasible solution set of the system equations of the model start and end in the region

$$ \Omega =\left(\left\{S,E,{I}_u,{I}_v,R\right\}\in {R^{+}}^5:N\le \frac{A}{\mu}\right). $$
(32)

Therefore, the basic model (8) is well posed mathematically and epidemiologically reasonable. Hence, it is sufficient to study the dynamics of the model system (8) in Ω.

2.3 Equilibria

To find the disease-free equilibrium solutions, the right-hand side of the model system (8) is equated to zero, evaluating it at when there is no disease in the system, i.e., E = Iu = Iv = 0. Therefore, the disease-free equilibrium solutions are given by

$$ {E}_o=\left(S,\kern0.5em E,{I}_u,{I}_v,R\right)=\left(\frac{A}{\mu },0,0,0,0\right). $$
(33)

The endemic equilibrium is denoted E∗∗ = (S∗∗, E∗∗, Iu∗∗,  Iv∗∗, R∗∗) and it occurs when a disease persist in the human host population. Therefore

$$ {E}^{\ast \ast }=\left({S}^{\ast \ast },{E}^{\ast \ast },{I_u}^{\ast \ast },{I_v}^{\ast \ast },{R}^{\ast \ast}\right)=\left({S}^{\ast }=\frac{A}{{\mathrm{m}}_1}, \kern0.5em {E}^{\ast }=\frac{\lambda A}{{\mathrm{m}}_2{\mathrm{m}}_3},\kern0.75em {I}_u^{\ast }=\frac{\lambda \epsilon A}{{\mathrm{m}}_1{\mathrm{m}}_2{\mathrm{m}}_3},{I}_v^{\ast }=\frac{\lambda \sigma \epsilon A}{{\mathrm{m}}_1{\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4},{R}^{\ast }=\frac{1}{\mu\ }\left[\frac{\lambda \epsilon {\gamma}_oA}{{\mathrm{m}}_1{\mathrm{m}}_2{\mathrm{m}}_3}\kern0.5em +\frac{\lambda \sigma \epsilon {\upgamma}_1A}{{\mathrm{m}}_1{\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4\ }\right]\right). $$
(34)

Where m1 = (λ + μ), m2 = (ϵ + μ + d), m3 = (γo + μ1 + α1 + σ), m4 = (μ2 + γ1 + α2).

2.4 Basic reproduction number (R r)

We want to show how the threshold that governs the spread of a disease, called the basic reproduction number is obtained.

Theorem 2.

Define Xs = {X = 0| Xi, i = 1, 2, 3, …}, in order to obtain Rr, new infections are distinguished from other changes in the populations. Such that, Fi(x) is the rate of new manifestations of clinical symptoms in compartment i. Also, let \( {V}_i^{+} \) be the rate at which individuals move out of compartment i. Then xi = Fi(x) − Vi(x), i = 1, 2, 3, …. , and \( {V}_i(x)={V}_i^{-}-{V}_i^{+} \). F is a non negative matrix and V is a non-singular matrix.

Proof: We applied the next generation matrix method to the model equations starting with newly infective classes given by

$$ \left.\begin{array}{l}\frac{dE}{dt}=\lambda (t)S-{\mathrm{m}}_2E,\\ {}\frac{dI_u}{dt}=\varepsilon E-{\mathrm{m}}_3{I}_u,\\ {}\frac{dI_v}{dt}=\sigma {I}_{\mathrm{u}}-{\mathrm{m}}_4{I}_v.\end{array}\right\} $$
(35)

The rate of new clinical symptoms is given by

$$ \mathrm{F}=\left(\genfrac{}{}{0pt}{}{\upbeta \mathrm{S}\left(\frac{{\mathrm{I}}_{\mathrm{u}}}{1+{\upphi}_1{\mathrm{I}}_{\mathrm{u}}} + \frac{\uptheta {\mathrm{I}}_{\mathrm{v}}}{1+{\phi}_2{\mathrm{I}}_{\mathrm{v}}\ }\right)}{\begin{array}{c}0\\ {}0\end{array}}\right) $$
(36)

And the rate of transfer terms of individuals is given by

$$ \mathrm{V}=\left(\genfrac{}{}{0pt}{}{\begin{array}{c}{\mathrm{m}}_2E\\ {}\epsilon E-{\mathrm{m}}_3{I}_u\end{array}}{\sigma {I}_{\mathrm{u}}-{\mathrm{m}}_4{I}_v}\right). $$
(37)

The Jacobian matrices of F and V evaluated at disease-free equilibrium solution (33) are given by

$$ \mathrm{F}=\left(\begin{array}{c}0\kern3em 0\kern4em \frac{\upbeta \mathrm{A}}{\mu\ }\\ {}0\kern3.5em 0\kern4.5em 0\\ {}0\kern3.25em 0\kern4.5em 0\ \end{array}\right) $$
(38)

and

$$ V=\left(\begin{array}{c}{\mathrm{m}}_2\kern4.25em 0\kern5.25em 0\\ {}\upepsilon \kern4.75em {\mathrm{m}}_3\kern5em 0\\ {}0\kern5em \sigma \kern5em {\mathrm{m}}_4\end{array}\right). $$
(39)

The inverse of V is given by

$$ {V}^{-1}=\left(\begin{array}{ccc}\frac{1}{{\mathrm{m}}_2}& 0& 0\\ {}\frac{\upepsilon}{{\mathrm{m}}_2{\mathrm{m}}_3}&\ \frac{1}{{\mathrm{m}}_3}& 0\\ {}\frac{\upepsilon \sigma }{{\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4}& \frac{\sigma }{{\mathrm{m}}_4}&\ \frac{1}{{\mathrm{m}}_4}\end{array}\right) $$
(40)

and

$$ F{V}^{-1}=\left(\begin{array}{ccc}\frac{\lambda A\upepsilon \sigma }{\mu {\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4}& \frac{\lambda A\sigma}{\mu {\mathrm{m}}_3{\mathrm{m}}_4}& \frac{\lambda A}{\mu {\mathrm{m}}_4}\\ {}0& 0& 0\\ {}0& 0& 0\end{array}\right). $$
(41)

The eigenvalues of FV−1 in (41) are given by

$$ {\displaystyle \begin{array}{l}{\uplambda}_1={\uplambda}_2=0\\ {}\mathrm{and}\\ {}{\uplambda}_3=\frac{\lambda A\in \sigma }{\mu {\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4}.\end{array}} $$
(42)

The dominant eigenvalue in (42) is λ3. Therefore, the basic reproduction number Rr is given by

$$ {R}_r=\frac{\lambda A\upepsilon \sigma }{\mu {\mathrm{m}}_2{\mathrm{m}}_3{\mathrm{m}}_4}. $$
(43)

The threshold in (43) measures the rate at which new cases of infection arises, when a typical infected individual is introduced into a susceptible population of humans during their course of infection.

3 Stability analysis of the model system equilibria

3.1 Local stability of the disease-free equilibrium

Theorem 2: The disease-free equilibrium solution Eo (33) is locally asymptotically stable if Rr < 1.

Proof: The Jacobian matrix of system (8) at the disease-free equilibrium solution Eo of (33) is given by

$$ J\left({E}_o\right)=\left(\begin{array}{c}\begin{array}{c}-{\mathrm{m}}_1\kern2em 0\kern2.75em 0\kern2.75em 0\kern3em 0\\ {}\kern0.5em \uplambda \kern2em -{\mathrm{m}}_2\kern1.75em 0\kern2.5em 0\kern3.5em 0\\ {}\kern0.5em 0\kern2.75em {\upvarepsilon}_{\mathrm{o}}\kern1.5em -{\mathrm{m}}_3\kern2em 0\kern2.75em 0\end{array}\\ {}\kern0.5em 0\kern2.75em 0\kern2.75em \upsigma \kern1.75em -{\mathrm{m}}_4\kern2.25em 0\\ {}\kern1em 0\kern3em 0\kern2.75em {\gamma}_o\kern3em {\upgamma}_1\kern1.75em -\upmu \end{array}\right). $$
(44)

The eigenvalues obtained in (44) yield

$$ \left.\begin{array}{l}-\mu, \\ {}{m}_1=-\left(\lambda +\mu \right),\\ {}{m}_2=-\left(\in +\upmu +d\right).\end{array}\right\} $$
(45)

The remaining characteristics polynomial is given by

$$ {\lambda}^2+\lambda\ \left({\mathrm{m}}_3+{\mathrm{m}}_4\right)+{\mathrm{m}}_3{\mathrm{m}}_4=0. $$
(46)

It is observed that (46) has strictly negative real root if and only if m3 > 0 and m4 > 0, and m3 > m4. Also, m3 is positive and for m4 to be positive, 1−Rr must be positive which leads to Rr < 1. Therefore, the disease-free equilibrium Eo (33) of model (8) is locally asymptotically stable if Rr < 1.

3.2 Global stability of disease-free equilibrium

Theorem: The disease free equilibrium solution Eo (33) of model system (8) is globally asymptotically stable whenever Rr < 1.

Proof: A Lyapunov function is derived for the model system such that

$$ \mathrm{F}=\left(\frac{\epsilon {m}_4+\sigma }{m_2{m}_3}\right)\mathrm{E}+\left(\frac{m_4+\sigma }{m_3}\right)\ {I}_u+{\mathrm{I}}_{\mathrm{v}}. $$
(47)

Where

$$ \dot{F}=\left(\frac{\epsilon {m}_4+\sigma }{m_2{m}_3}\right)\frac{dE}{dt}+\left(\frac{{\mathrm{m}}_4+\sigma }{{\mathrm{m}}_3}\right)\ \frac{d{I}_u}{dt}+\frac{d{I}_v}{dt} $$
(48)

and

$$ \dot{F}=\left(\frac{\epsilon {m}_4+\sigma }{m_2{m}_3}\right)\left(\upbeta S-{m}_3\mathrm{E}\right)+\left(\frac{{\mathrm{m}}_4+\sigma }{{\mathrm{m}}_3}\right)\left(\upepsilon \mathrm{E}+{m}_3{I}_u\right)+\left(\sigma {I}_u-{m}_4{I}_v\right). $$
(49)

Since \( \frac{A}{\mu } \) in (33), further simplification becomes

$$ \dot{F}\le \left(\frac{\epsilon {m}_4+\sigma }{m_2{m}_3}\right)\left(\frac{\upbeta A}{\mu }-{m}_3\mathrm{E}\right)+\left(\frac{m_4+\sigma }{m_3}\right)\left(\upepsilon \mathrm{E}+{m}_3{I}_u\right)+\left(\sigma {I}_u-{m}_4{I}_v\right) $$
(50)

and

$$ \dot{F}=\frac{\lambda A\epsilon \left({\mathrm{m}}_4+\sigma \right)}{\mu {\mathrm{m}}_2{\mathrm{m}}_3}+\left(\sigma -\left({\mathrm{m}}_4+\sigma \right)\right){I}_u-{\mathrm{m}}_4{I}_{\mathrm{v}}. $$
(51)

Therefore

$$ \dot{F}={\mathrm{m}}_4\left({R}_{tr}-\frac{\lambda A\epsilon}{\mu {\mathrm{m}}_2{\mathrm{m}}_3}\ {I}_u+{I}_v\right). $$
(52)

Since all the parameters and variables of the model system (8) are nonnegative, it follows that \( \dot{F} \) ≤ 0 for Rr < 1 with \( \dot{F} \) = 0 if and only if E = Iu = Iv = 0. Hence, \( \dot{F} \) is a Lyapunov function in Ω. Therefore, the largest compact invariant subset of the set where \( \dot{F} \) = 0 is the singleton {(E, Iu, Iv) = (0, 0, 0)}. Thus, it follows, from the La-Salle’s invariant principle [19], that as t →  ∞ ,

$$ \left(E,{I}_u,{I}_v\right)\to \left(0,0,0\right). $$
(53)

Therefore the disease-free equilibrium (33), of model (8) is globally asymptotically stable if Rtr < 1.

3.3 Global stability of endemic equilibrium

Theorem: If Rr > 1, the endemic equilibrium solution (34) of the model system (8) is globally asymptotically stable.

Proof: A Lyapunov function candidate of the form

$$ \mathrm{L}\left(\mathrm{t}\right)=\left(\mathrm{S}-{\mathrm{S}}^{\ast }-{\mathrm{S}}^{\ast}\mathrm{Loge}\frac{S}{{\mathrm{S}}^{\ast }}\right)+\left(\mathrm{E}-{\mathrm{E}}^{\ast }-{\mathrm{E}}^{\ast}\mathrm{Loge}\frac{E}{{\mathrm{E}}^{\ast }}\right)+\left({I}_u-{I}_u^{\ast }- Loge\frac{I_u}{I_u^{\ast }}\right)+\left({I}_{\mathrm{v}}-{I}_v^{\ast }-{I}_v^{\ast } Loge\frac{I_v}{I_v^{\ast }}\right)+\left(\mathrm{R}-{\mathrm{R}}^{\ast }-{\mathrm{R}}^{\ast}\mathrm{Loge}\frac{R}{{\mathrm{R}}^{\ast }}\right) $$
(54)

is derived, such that the time derivative of (54) becomes

$$ \frac{dL}{dt}=\left(\frac{S-{S}^{\ast }}{S}\right)\frac{dS}{dt}+\left(\frac{E-{E}^{\ast }}{E}\right)\frac{dE}{dt}+\left(\frac{I_u-{I_u}^{\ast }}{I_u}\right)\frac{d{I}_u}{dt}+\left(\frac{I_v-{I_v}^{\ast }}{I_v}\right)\frac{d{I}_v}{dt}+\left(\frac{R-{R}^{\ast }}{R}\right)\frac{dR}{dt}, $$
(55)

so that

$$ \frac{dL}{dt}=\left(\frac{S-{S}^{\ast }}{S}\right)\left(A-{m}_1S\right)+\left(\frac{E-{E}^{\ast }}{E}\right)\left(\lambda S-{m}_2E\right)+\left(\frac{I_u-{I_u}^{\ast }}{I_u}\right)\left(\epsilon E-{m}_3{I}_u\right)+\left(\frac{I_v-{I_v}^{\ast }}{I_v}\right)\left(\sigma {I}_u-{m}_4{I}_v\right)+\left(\frac{R-{R}^{\ast }}{R}\right)\left({\gamma}_o{I}_u+{\upgamma}_1{I}_v-\upmu \mathrm{R}\right). $$
(56)

and

$$ \frac{dL}{dt}=\left(\frac{S-{S}^{\ast }}{S}\right)\left(A-{m}_1\left(S-{S}^{\ast}\right)\right)+\left(\frac{E-{E}^{\ast }}{E}\right)\left(\lambda \left(S-{S}^{\ast}\right)-{m}_2\left(E-{E}^{\ast}\right)\right)+\left(\frac{I_u-{I_u}^{\ast }}{I_u}\right)\left(\epsilon \left(E-{E}^{\ast}\right)-{m}_3\left({I}_u-{I_u}^{\ast}\right)\right)\left(\frac{I_v-{I_v}^{\ast }}{I_v}\right)-{m}_4+\left(\frac{R-{R}^{\ast }}{R}\right)\left({\gamma}_o\left({I}_u-{I_u}^{\ast}\right)+{\upgamma}_1\left({I}_v-{I_v}^{\ast}\right)-\upmu \left(\mathrm{R}-{\mathrm{R}}^{\ast}\right)\right). $$
(57)

Further simplification of (57) yields

$$ \frac{dL}{dt}=\left(\frac{{\left(S-{S}^{\ast}\right)}^2}{S}\right)\left(\frac{A}{\left(S-{S}^{\ast}\right)}-{m}_1\right)+\left(\frac{{\left(E-{E}^{\ast}\right)}^2}{E}\right)\left(\ \frac{\lambda \left(S-{S}^{\ast}\right)}{\left(E-{E}^{\ast}\right)}-{m}_2\right)+\left(\frac{{\left({I}_u-{I_u}^{\ast}\right)}^2}{I_u}\right)\left(\frac{\epsilon \left(E-{E}^{\ast}\right)}{\left({I}_u-{I_u}^{\ast}\right)}-{\mathrm{m}}_3\right)+\left(\frac{{\left({I}_v-{I_v}^{\ast}\right)}^2}{I_v}\right)\left(\frac{\sigma \left({I}_u-{I_u}^{\ast}\right)}{\left({I}_v-{I_v}^{\ast}\right)}-{\mathrm{m}}_4\right)+\left(\frac{{\left(R-{R}^{\ast}\right)}^2}{R}\right)\left(\frac{\gamma_o\left({I}_u-{I_u}^{\ast}\right)}{\left(R-{R}^{\ast}\right)}+\frac{\gamma_1\left({I}_v-{I_v}^{\ast}\right)}{\left(R-{R}^{\ast}\right)}-\upmu \right) $$
(58)

and

$$ \frac{dL}{dt}=\frac{A\left(S-{S}^{\ast}\right)}{S}+\frac{\lambda \left(S-{S}^{\ast}\right)\left(E-{E}^{\ast}\right)}{E}+\frac{\epsilon \left(E-{E}^{\ast}\right)\left({I}_u-{I_u}^{\ast}\right)}{I_u}+\frac{\sigma \left({I}_u-{I_u}^{\ast}\right)\left({I}_v-{I_v}^{\ast}\right)}{I_v}+\frac{\gamma_o\left({I}_u-{I_u}^{\ast}\right)\left(R-{R}^{\ast}\right)}{R}+\frac{\upgamma_1\left({I}_v-{I_v}^{\ast}\right)\left(R-{R}^{\ast}\right)}{R}-\frac{m_1{\left(S-{S}^{\ast}\right)}^2}{S}-\frac{m_2{\left(E-{E}^{\ast}\right)}^2}{E}-\frac{{\mathrm{m}}_3{\left({I}_u-{I_u}^{\ast}\right)}^2}{I_u}-\frac{{\mathrm{m}}_4{\left({I}_v-{I_v}^{\ast}\right)}^2}{I_v}-\frac{\upmu {\left(R-{R}^{\ast}\right)}^2}{R}. $$
(59)

Hence, by collecting positive terms together and negative terms together in (59) becomes

$$ \frac{dL}{dt}={B}_1-{B}_2. $$
(60)

Where

$$ {B}_1=\frac{A\left(S-{S}^{\ast}\right)}{S}+\frac{\lambda \left(S-{S}^{\ast}\right)\left(E-{E}^{\ast}\right)}{E}+\frac{\epsilon \left(E-{E}^{\ast}\right)\left({I}_u-{I}_u\ast \right)}{I_u}+\frac{\sigma \left({I}_u-{I_u}^{\ast}\right)\left({I}_v-{I_v}^{\ast}\right)}{I_v}+\frac{\gamma_o\left({I}_u-{I_u}^{\ast}\right)\left(R-{R}^{\ast}\right)}{R}+\frac{\upgamma_1\left({I}_v-{I_v}^{\ast}\right)\left(R-{R}^{\ast}\right)}{R} $$
(61)

And

$$ {B}_2=\kern0.5em \frac{m_1{\left(S-{S}^{\ast}\right)}^2}{S}+\frac{m_2{\left(E-{E}^{\ast}\right)}^2}{E}+\frac{m_3{\left({I}_u-{I_u}^{\ast}\right)}^2}{I_u}+\frac{m_4{\left({I}_v-{I_v}^{\ast}\right)}^2}{I_v}+\frac{\upmu {\left(R-{R}^{\ast}\right)}^2}{R}. $$
(62)

Thus if B1 < B2, then \( \frac{dL}{dt} \) ≤ 0. Note that, \( \frac{dL}{dt} \)= 0 if and only if \( \left(S={S}^{\ast }\ E={E}^{\ast },\kern0.5em {I}_u={I}_u^{\ast },\kern0.5em {I}_v={I}_v^{\ast },\kern0.5em R={R}^{\ast}\right) \). Therefore, the largest compact, invariant set in \( \left[\right({S}^{\ast },{E}^{\ast },{I}_u^{\ast },{I}_V^{\ast },{R}^{\ast } \)) ∈Ω: \( \frac{dL}{dt} \) = 0] is the singleton set E∗∗, where E∗∗ is the endemic equilibrium solution (34) of the model system (8). By La-Salle’s invariant principle [20], E∗∗ is globally asymptotically stable in Ω if B1 < B2.

3.4 Approximate solution of the SEIR epidemic model

In this section, the approximate solution of the model system (8) is obtained, using the Runge-Kutta fourth order and DTM. The concept of DTM was first proposed by Zhou [28] for solving linear and nonlinear initial value problems in electrical circuit analysis. The method in many instances have been adopted to solve series of models based on differential equations. The concept of DTM is derived from the Taylor series expansion. This method requires that a system of differential equations together with its initial and boundary conditions are transformed into recurrent power series solutions.

Taylor series expansion of a function f(x) about the point x = 0 is given by

$$ f(x)={\sum}_{n=1}^{\infty}\frac{1}{k!}\left({\mathrm{f}}^{\mathrm{k}}\left(\mathrm{c}\right){\left(\mathrm{x}-\mathrm{c}\right)}^{\mathrm{k}}\right)=0. $$
(63)

For all x ∈ (c − r, c + r) such that x = c converges to f(x).

Definition 1: The differential transformation F(k) of a function f(x) is defined as

$$ F(k)=\frac{1}{k!}{\left(\frac{d^{\mathrm{k}}f(x)}{dt^k}\right)}_{k=0}. $$
(64)

Definition 2: It follows from Eqs. (63) and (64) that the differential inverse transformation f (x) of F (k) is given by

$$ f(x)={\sum}_{k=0}^{\infty}\frac{t^k}{k!}{\frac{{\mathrm{d}}^{\mathrm{k}}\mathrm{f}\left(\mathrm{t}\right)}{{\mathrm{d}\mathrm{t}}^{\mathrm{k}}}}_{\mathrm{x}={\mathrm{x}}_{\mathrm{o}}}. $$
(65)

Using (63)–(64), the following basic operations of DTM [26, 28] is tabulated below;

If S(k), E(k), Iu(k), Iv(k), and R(k) denote the differential transformation of S(t), E(t), Iu(t), Iv(t), and R(t) respectively, then the following recurrence relation of model system (8) are given by

$$ {\displaystyle \begin{array}{l}S\left(k+1\right)=\frac{1}{k+1}\left( A\delta (k)-\upmu \mathrm{S}\left(\mathrm{k}\right)-\upbeta {\sum}_{m=1}^{\infty}\left(\frac{S(m){I}_u\left(k-m\right)}{\delta (k)+{\upphi}_1{I}_u\left(\mathrm{k}\right)}+\frac{S(m){I}_v\left(k-m\right)}{\delta (k)+{\upphi}_2{I}_v\left(\mathrm{k}\right)}\right)\right),\\ {}E\left(k+1\right)=\frac{1}{k+1}\left(-\left(\upepsilon +\mu +d\right)E\left(\mathrm{k}\right)+\upbeta {\sum}_{m=1}^{\infty}\left(\frac{S(m){I}_u\left(k-m\right)}{\delta (k)+{\upphi}_1{I}_u\left(\mathrm{k}\right)}+\frac{S(m){I}_v\left(k-m\right)}{\delta (k)+{\upphi}_2{I}_v\left(\mathrm{k}\right)}\right)\right),\\ {}\begin{array}{l}{I}_{\mathrm{u}}\left(k+1\right)=\frac{1}{k+1}\left(\upepsilon E(k)-\left({\gamma}_o+{\upmu}_1+{\upalpha}_1+\sigma \right){I}_{\mathrm{u}}(k)\right),\\ {}{I}_v\left(k+1\right)=\frac{1}{k+1}\left(\sigma {I}_u(k)-\left({\upmu}_2+{\upgamma}_1+{\alpha}_2\right){I}_v(k)\right),\\ {}R\left(k+1\right)=\frac{1}{k+1}\left(\ {\gamma}_o{I}_u(k)+{\upgamma}_1{I}_v(k)-\mu R(k)\right).\end{array}\end{array}} $$
(66)

Applying the values of variables and parameters in Table 1 together with the initial conditions of the model, yields the following results given by

$$ S(1)=-17.768,E(1)=16.089,{I}_u\ (1)=-5.322,{I}_v(1)=27.500,R(1)=-2.162,S(2)=-10.330,E(2)=9.559,{I}_u(2)=1.496,{I}_v(2)=5.710,R(2)=1.513,S(3)=0.878,E(3)=0.778,{I}_u(3)=-0.252,{I}_v(3)=-1.591,R(3)=0.946. $$
(67)
Table 1 The meanings of variables and parameters of the SEIR model (8)
Full size table

Substituting the values in (67) into (66) yields, the recurrence relation given by the following;

$$ {\displaystyle \begin{array}{l}S(t)=\sum \limits_{k=1}^{\infty }{t}^k\ S(k)=S(0)+ tS(1)+{t}^2S(2)+{t}^3S(3)+\dots, \\ {}E(t)=\sum \limits_{k=1}^{\infty }{t}^k\ E(k)=E(0)+ tE(1)+{t}^2E(2)+{t}^3E(3)+\dots, \\ {}{I}_u(t)=\sum \limits_{k=1}^{\infty }{t}^k\ {I}_u(k)={I}_u(0)+{tI}_u(1)+{t}^2{I}_u(2)+{t}^3{I}_u(3)+\dots, \\ {}{I}_v(t)=\sum \limits_{k=1}^{\infty }{t}^k\ {I}_v(k)={I}_v(0)+{tI}_v(1)+{t}^2{I}_v(2)+{t}^{{}^3}{I}_v(3)+\dots, \\ {}R(t)=\sum \limits_{k=1}^{\infty }{t}^k\ R(k)=R(0)+ tR(1)+{t}^2R(2)+{t}^{{}^3}R(3)+\dots, \end{array}}. $$
(68)

The closed form solutions when k = 3, in (68) is given by

$$ {\displaystyle \begin{array}{l}S(t)=50-17.768t-10.330{t}^2+0.878{t}^3+\dots, \\ {}E(t)=20+16.089t+9.5585{t}^2+0.778{t}^3+\dots, \\ {}\begin{array}{l}{I}_u(t)=10-5.322t+1.496{t}^2-0.252{t}^3+\dots, \\ {}{I}_v(t)=7+27.500t+5.710{t}^2-1.591{t}^3+\dots, \\ {}R(t)=3+2.162t+1.513{t}^2-0.946{t}^3+\dots .\end{array}\end{array}} $$
(69)

Also, the idea of Runge-Kutta method was conceived by Carl Runge and Wilhem Kutta. This work employs the Runge-Kutta fourth-order method because of its accuracy and faster convergence, which have been employed to solve several problems in differential equations applied to science, engineering, economics etc. The numerical scheme for this method is given by

$$ {y}_{n+1}={y}_n+\frac{1}{6}\left({z}_1+2{z}_2+2{z}_3+{z}_4\right). $$
(70)

Where

$$ \left.\begin{array}{l}{z}_1= hf\left({x}_n,{y}_n\right),\\ {}{z}_2= hf\left({x}_n+\frac{1}{2}h,{y}_n+\frac{1}{2}{z}_1\right),\\ {}{z}_3= hf\left({x}_n+\frac{1}{2}h,{y}_n+\frac{1}{2}{z}_2\right),\\ {}{z}_4= hf\left({x}_n+h,{y}_n+{z}_3\right).\end{array}\right\} $$
(71)

Applying the Runge-Kutta scheme to the model system (8) yields

$$ \left.\begin{array}{l}{S}_{n+1}={S}_n+\frac{1}{6}\left({q}_1+2{q}_2+2{q}_3+{q}_4\right)h\\ {}{E}_{n+1}={E}_n+\frac{1}{6}\left({y}_1+2{y}_2+2{y}_3+{y}_4\right)h\\ {}{I}_{vn+1}={I}_{vn}+\frac{1}{6}\left({x}_1+2{x}_2+2{x}_3+{x}_4\right)h\\ {}{I}_{un+1}={I}_{vn}+\frac{1}{6}\left({u}_1+2{u}_2+2{u}_3+{u}_4\right)h\\ {}{R}_{n+1}={R}_n+\frac{1}{6}\left({v}_1+2{v}_2+2{v}_3+{v}_4\right)h\end{array}\right\} $$
(72)

Where

$$ {\displaystyle \begin{array}{l}{q}_1=A-\mu {S}_n-\beta \left(\frac{I_{un}}{1+{\phi}_1{I}_{un}}+\frac{\theta {I}_{vn}}{1+{\phi}_2{I}_{vn}}\right){S}_n,\\ {}{y}_1=\beta \left(\frac{I_{un}}{1+{\phi}_1{I}_{un}}+\frac{\theta {I}_{vn}}{1+{\phi}_2{I}_{vn}}\right){S}_n-\left(\epsilon +\mu +d\right){E}_n,\\ {}\begin{array}{l}{x}_1=\epsilon {E}_n-\left({\gamma}_o+{\mu}_1+{\alpha}_1+{\sigma}_1\right){I}_{un},\\ {}{u}_1=\sigma {I}_{un}-\left({\mu}_1+{\gamma}_1+{\alpha}_2\right){I}_{vn},\\ {}{v}_1={\gamma}_o{I}_{un}+{\gamma}_1{I}_{vn}-\mu {R}_n.\end{array}\end{array}} $$
(73)

Also,

$$ {\displaystyle \begin{array}{l}{q}_2=A-\mu \left({S}_n+{q}_1\frac{h}{2}\right)-\beta \left(\frac{\left({I}_{un}+{q}_1\frac{h}{2}\right)}{1+{\phi}_1\left({I}_{un}+{q}_1\frac{h}{2}\right)}+\frac{\left({I}_{vn}+{q}_1\theta \frac{h}{2}\right)}{1+{\phi}_1\left({I}_{vn}+{q}_1\frac{h}{2}\right)}\right)\left({S}_n+{q}_1\frac{h}{2}\right),\\ {}{y}_2=\beta \left(\frac{\left({I}_{un}+{y}_1\frac{h}{2}\right)}{1+{\phi}_1\left({I}_{un}+{y}_1\frac{h}{2}\right)}+\frac{\left({I}_{vn}+{y}_1\theta \frac{h}{2}\right)}{1+{\phi}_1\left({I}_{vn}+{y}_1\frac{h}{2}\right)}\right)\left({S}_n+{y}_1\frac{h}{2}\right)+\left(\epsilon +\mu +d\right)\left({E}_n+{y}_1\frac{h}{2}\right),\\ {}\begin{array}{l}{x}_2=\epsilon \left({E}_n+{y}_1\frac{h}{2}\right)+\left({\gamma}_o+{\mu}_1+{\alpha}_1+\sigma \right)\left({\mathrm{I}}_{\mathrm{un}}+{x}_1\frac{h}{2}\right),\\ {}{u}_2=\sigma \left({I}_{un}+{x}_1\frac{h}{2}\right)+\left({\gamma}_1+{\mu}_1+{\alpha}_2\right)\left({\mathrm{I}}_{\mathrm{vn}}+{u}_1\frac{h}{2}\right),\\ {}{v}_2={\gamma}_o\left({I}_{un}+{x}_1\frac{h}{2}\right)+{\gamma}_1\left({I}_{vn}+{u}_1\frac{h}{2}\right)-\mu \left({R}_n+{v}_1\frac{h}{2}\right).\end{array}\end{array}} $$
(74)

and

$$ {\displaystyle \begin{array}{l}{q}_3=A-\mu \left({S}_n+{q}_2\frac{h}{2}\right)-\beta \left(\frac{\left({I}_{un}+{q}_2\frac{h}{2}\right)}{1+{\phi}_1\left({I}_{un}+{q}_2\frac{h}{2}\right)}+\frac{\left({I}_{vn}+{q}_2\theta \frac{h}{2}\right)}{1+{\phi}_1\left({I}_{vn}+{q}_2\frac{h}{2}\right)}\right)\left({S}_n+{q}_2\frac{h}{2}\right),\\ {}{y}_3=\beta \left(\frac{\left({I}_{un}+{y}_2\frac{h}{2}\right)}{1+{\phi}_1\left({I}_{un}+{y}_2\frac{h}{2}\right)}+\frac{\left({I}_{vn}+{y}_2\theta \frac{h}{2}\right)}{1+{\phi}_1\left({I}_{vn}+{y}_2\frac{h}{2}\right)}\right)\left({S}_n+{y}_2\frac{h}{2}\right)+\left(\epsilon +\mu +d\right)\left({E}_n+{y}_2\frac{h}{2}\right),\\ {}\begin{array}{l}{x}_3=\epsilon \left({E}_n+{y}_2\frac{h}{2}\right)+\left({\gamma}_o+{\mu}_1+{\alpha}_1+\sigma \right)\left({\mathrm{I}}_{\mathrm{un}}+{x}_2\frac{h}{2}\right),\\ {}{u}_3=\sigma \left({I}_{un}+{x}_2\frac{h}{2}\right)+\left({\gamma}_1+{\mu}_1+{\alpha}_2\right)\left({\mathrm{I}}_{\mathrm{vn}}+{u}_2\frac{h}{2}\right),\\ {}{v}_3={\gamma}_o\left({I}_{un}+{x}_2\frac{h}{2}\right)+{\gamma}_1\left({I}_{vn}+{u}_2\frac{h}{2}\right)-\mu \left({R}_n+{v}_2\frac{h}{2}\right),\end{array}\end{array}} $$
(75)

And

$$ {\displaystyle \begin{array}{l}{q}_4=A-\mu \left({S}_n+{z}_3h\right)-\beta \left(\frac{\left({I}_{un}+{z}_3h\right)}{1+{\phi}_1\left({I}_{un}+{z}_3h\right)}+\frac{\left({I}_{un}+{z}_3\theta h\right)}{1+{\phi}_1\left({I}_{un}+{z}_3h\right)}\right)\left({S}_n+{z}_3h\right),\\ {}{y}_4=\beta \left(\frac{\left({I}_{un}+{z}_3h\right)}{1+{\phi}_1\left({I}_{un}+{z}_3h\right)}+\frac{\left({I}_{un}+{z}_3\theta h\right)}{1+{\phi}_1\left({I}_{un}+{z}_3h\right)}\right)\left({S}_n+{z}_3h\right)-\left(\epsilon +\mu +d\right)\left({E}_n+{y}_3h\right),\\ {}\begin{array}{l}{x}_4=\epsilon \left({E}_n+{y}_3h\right)-\left({\gamma}_o+{\mu}_1+{\alpha}_1+{\sigma}_1\right)\left({I}_{un}+{x}_3h\right),\\ {}{u}_4=\sigma \left({I}_{un}+{x}_3h\right)-\left({\mu}_1+{\gamma}_1+{\alpha}_2\right)\left({I}_{vn}+{u}_3h\right),\\ {}{v}_4={\gamma}_o\left({I}_{un}+{x}_3h\right)+{\gamma}_1\left({I}_{vn}+{u}_3h\right)-\mu \left({R}_n+{v}_3h\right).\end{array}\end{array}} $$
(76)

Substituting (73) to (76), together with the parameter values and initial conditions of the model system (8) into (72) yield the numerical results in Table 2.

Table 2 Numerical results of the model system equations using Runge-Kutta method
Full size table

3.5 Results

Simulations are carried out by varying some parameters of the models when the basic reproduction number Rtr < 1 as shown in Figs. 1, 2, 3, 4, 5, and 6, that is, the parameter solutions converges to the disease-free equilibrium. Tables 1 and 3 display the parameter and variable values used in the simulations of the model and the basic operations of DTM. Also, the numerical results of the model system is presented using Runge-Kutta fourth order and differential transform method (DTM) in Tables 2 and 4 which compare agreeably with each other, and the DTM performs better. Figure 1 is the description of the impact of disease transmission rate β. As time increases, transmission of disease increases, but the steady decline, indicate that more humans are being aware of their disease status leading to quick movement to recovery state or probably death in the case of fatality. It is observed in Fig. 2 that there is a decrease of infection from the 1st–6th month as time increases, but a gradual rise of infection from the 7th–12th month depict that emergence of infection will be on the rise in the absence of health intervention policies. Figures 3 and 4 is the depiction of the high saturation of diseases in human host population as time increases. Strict compliance, increase of medical awareness programs, and treatment are needed to mitigate the high saturation of the disease in human host community, while Figs. 5 and 6 is the depiction of the impact of the variation of treatment rates γo and γ1 in infected humans. As time increases, a steady rise in the curve indicate that treatment is essential in minimizing infection in human host community.

Fig. 1
figure 1

Varying β(0.001 − 0.027) when Rr < 1

Full size image
Fig. 2
figure 2

Varying ϵ(0.001 − 0.0041) when Rr < 1

Full size image
Fig. 3
figure 3

Varying ϕ1(0.212 − 0.612) when Rr < 1

Full size image
Fig. 4
figure 4

Varying ϕ2(0.40 − 0.220) when Rr < 1

Full size image
Fig. 5
figure 5

Varying γo(0.123 − 0.203) when Rr < 1

Full size image
Fig. 6
figure 6

Varying γ1(0.100 − 0.164) when Rr < 1

Full size image
Table 3 Basic Operations of DTM
Full size table
Table 4 Numerical results of the model system equations using DTM
Full size table

In addition, simulations of variations of some increased parameter values displayed in Figs. 7, 8, 9, 10, 11, and 12 reveal that the parameter solutions converges to the endemic state, that is, Rr > 1. This implies that, for the system not to remain in the endemic state, transmission and new clinical manifestations of disease must be minimized by scaling up treatment and medical awareness program rate.

Fig. 7
figure 7

Varying β(0.710 − 0.960) when Rr > 1

Full size image
Fig. 8
figure 8

Varying ϵ(0.260 − 0.661) when Rr > 1

Full size image
Fig. 9
figure 9

Varying ϕ1(0.412 − 0.812) when Rr > 1

Full size image
Fig. 10
figure 10

Varying ϕ2(0.500 − 0.680) when Rr > 1

Full size image
Fig. 11
figure 11

Varying γ1(0.300 − 0.436) when Rr > 1

Full size image
Fig. 12
figure 12

Varying γo(0.420 − 0.490) when Rr > 1

Full size image

Figure 13 is the description of the sub-population of susceptible individuals who are at the risk of acquiring the disease. As time increases in the absence of control, more susceptible individuals become exposed to the disease. Figure 14 is the description of the sub-population of exposed individuals who are latently infected. As time increases, there is a quick inflow of exposed individuals moving into the infectious class. Figure 15 is the depiction of the behavior of sub-population of infected individuals who attend or are compliant to medical awareness program. As time increases, their compliance to medical awareness program leads to decrease of infected individuals as they are available to treatment, care, etc. Figure 16 is description of the behavior of the sub-population of infected individuals who did not attend or are non-compliant to medical awareness program. As time increases, non compliance to medical awareness program results to fatal cases and probably death. Figure 17 is the description of the behavior of the recovered sub-population. Recovered humans increases as healthy measures are adopted by infected individuals leading to the reduction and elimination of the disease prevalence in human host community as time increases.

Fig. 13
figure 13

Description of the sub-population of susceptible individuals who are at the risk of acquiring the disease

Full size image
Fig. 14
figure 14

Description of the sub-population of exposed individuals who are latently infected

Full size image
Fig. 15
figure 15

Depiction of the behavior of sub-population of infected individuals who attend or are compliant to medical awareness program

Full size image
Fig. 16
figure 16

Description of the behavior of the sub-population of infected individuals who did not attend or are non-compliant to medical awareness program

Full size image
Fig. 17
figure 17

Description of the behavior of the recovered sub-population

Full size image

4 Conclusion

A generalized SEIR model describing the transmission of disease in human host community of infected individuals who attend or compliant and who did not attend (non-compliant) medical awareness program is established. Qualitative and quantitative mathematical techniques were used to analyze the invariant region and boundedness of the model. Also, the basic reproduction number (Rr) and the equilibria is obtained to show that if Rr < 1, the SEIR model disease-free equilibrium is locally and globally asymptotically stable and if Rr > 1, the endemic equilibrium solution is globally asymptotically stable. Numerical methods of DTM and Runge-Kutta fourth-order method are employed to obtain the approximate solutions of the model as shown in Tables 2 and 4, which reveal that the two methods agree favorably with each other. Simulations of the model parameters when Rr < 1 and Rr > 1 is performed in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 and the graphical behavior of the model in Figs. 13, 14, 15, 16 and 17 reveal that educational awareness about an epidemic breakout is essential in curbing the menace and endemicity of a disease. However, the limitation of this study is that the model cannot incorporate all the complexities involving human behavioral change toward compliance to medical awareness program and lack of real life data involving registration of human individuals that are medical awareness compliant or not in any endemic disease setting. To this end, this work is still recommended further for proper data fit to the model.