Introduction

With the rapid development of new technologies and materials, a substantial number of long-span bridges have sprung up, e.g. Russky Bridge, Sutong Bridge, Hongkong-Zhuhai-Macau Bridge etc. These bridges are generally flexible and sensitive to ambient excitations such as wind, traffic, tidal currents, and their combination. Therefore, monitoring the dynamic deformation in these structures under ambient excitations via using field measurement techniques is an extremely important task. Excessive deformation can cause structural damage and or even destruction [1,2,3].

At present, accelerometer is widely employed as an effective monitoring technique to derive the dynamic responses of bridges [4,5,6]. It has the advantages of high measurement accuracy, high sampling frequency and good sensitivity. However, the displacement information obtained by carrying out the operation of double integral to the acceleration signal will deviate from the true value, which is difficult to meet the requirements of displacement measurement accuracy [7, 8]. Subsequently, the emergence of GPS (Global Positioning System) overcomes this problem better. GPS can monitor the three-dimensional coordinate information of bridges for all-weather in real time. Real Time Kinematic (RTK) is a positioning method based on the carrier phase double difference model, which is an important development to aid GPS real-time dynamic measurement [9]. Especially, the advent of multi-constellation Global Navigation Satellite System (multi-GNSS) makes this technique get a better development. Nevertheless, it is noteworthy that GNSS sensors are insensitive to the high frequency vibration of structures, and it is difficult to track the target even with high sampling rate. Meanwhile, the existence of various error sources, including troposphere delay, ionosphere delay, troposphere error, satellite clock difference, multipath effect, etc., results in the limited positioning accuracy of GNSS. Although several errors can be eliminated in RTK mode, the multipath effect is still a main problem to be addressed for GNSS-RTK measurement.

Considering GNSS and accelerometer sensors have their own advantages and disadvantages, an integrated approach can be employed to increase the accuracy of the monitoring system. In this context, Smyth and Wu [10] put forward a multi-rate Kalman filtering approach to fuse acceleration and displacement data sampled at different frequencies. They demonstrated that the proposed algorithm can accurately estimate the displacement and velocity from noise contaminated measurements of displacement and acceleration via various numerical examples. Enlightened by this study, Kim et al. [11] presented a new algorithm of the multi-rate Kalman filtering via introducing acceleration measurement bias. Experimental verification was that the proposed algorithm can improve the accuracy of displacement estimation compared with reference in the previous literature [10]. Subsequently, Xu et al. [12] proposed a novel step of employing maximum likelihood estimation (MLE) to determine the necessary noise parameters required by the Kalman filter algorithm. Their study validated that MLE is an effective method for accurately estimating the noise parameters of measurement signals via a numerical example and a field measurement test. In the aforementioned studies, the correlated process and measurement noises were deemed to white Gaussian noises. However, this assumption does not in accordance with the general case. Hence it can only derive the suboptimal fusion estimation. Previous studies have indicated that the multipath error is the main factor affecting the positioning accuracy of GNSS-RTK sensors, which is mainly distributed in the low frequency range of GNSS signal [13]. Furthermore, Górski [14] has verified that the low frequency background noise of GNSS sensors does not follow Gaussian distribution via a stability test. Due to the vibration forms of a large number of long-span bridges belong to low frequency vibration, the low frequency noise of GNSS has a more significant influence on monitoring results than that of high frequency noise. Based on the above-mentioned analysis, considering the influence of colored measurement noise, incorporating dynamic displacement from acceleration into GNSS-derived displacement can be seen promising in achieving accurate displacement measurement.

An principal goal of accurate displacement measurement is to extract structural modal parameters (i.e. natural frequencies, mode shapes and damping ratios). These parameters are important indicators for evaluating the safety and stability performances of bridges [15,16,17]. They are bound up with material characteristics, structural stiffness, mass distribution, foundation types, etc., hence their predictions are sophisticated. Nowadays, the frequently used methods for modal parameter identification can be divided into two types, i.e. traditional modal analysis (TMA) [18, 19] and operational modal analysis (OMA) [20,21,22] methods. TMA requires to measure excitation forces and responses of structures simultaneously. This method needs expensive excitation equipment and requires interrupting the normal operation of structures. Moreover, artificial excitation is often applied to the local position of the structure, which can easily cause damage to the structure. Whereas OMA can identify the modal parameters of the structure without artificial excitation and only rely on the response information of the structure, hence, this method is used more often [23,24,25]. Based on accurate displacement measurement, the OMA method is used to accurately extract structural modal parameters, which is an important task in structural health monitoring (SHM) for long-span bridges.

Inspired by the above research, this study presents a multi-rate weighted data fusion approach with colored measurement noise for estimating displacement responses of long-span bridges under operational conditions. The developed approach can derive a high-sampling rate displacement with improved accuracy via fusing the GNSS signal and the acceleration signal. Compared with the structural modes extracted by GNSS-derived displacement, higher-order modes can be determined from the estimated displacement. A numerical model and a practical bridge test are conducted to verify the performance of the developed approach.

Methodology

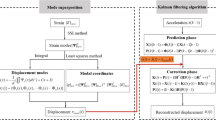
This study develops a multi-rate data fusion approach, as illustrated in Fig. 1. This approach involves two parts: (1) Local estimation: the Kalman filter algorithm with colored measurement noise is used to derive the results of local estimation of each sensor. (2) Fusion estimation: a weighted fusion criterion of scalar linear minimum variance is employed to fuse the local estimations for obtaining accurate displacement measurement. Then, structural modal parameters are determined by using data-driven stochastic subspace identification (SSI) algorithm based on accurate displacement measurement.

Fig. 1
figure 1

Flow chart of displacement estimation and operational modal analysis based on data fusion and SSI algorithms

Full size image

Displacement estimated based on data fusion

This section presents the proposed data fusion approach based on the Kalman filter with colored measurement noise. The presence of colored noise is likely to lead to incorrect analysis of bridge deformation signals and affect the estimation of modal parameter [26, 27]. Ignoring the impact of colored noise may degrade the performance of identification algorithms [28].

Assuming that the sampling interval of acceleration is Ta, and the sampling interval of displacement is Td. They have the following relationship, i.e., \({{T_{d} } \mathord{\left/ {\vphantom {{T_{d} } {T_{a} }}} \right. \kern-0pt} {T_{a} }} = M\). \(\beta_{d}\) and \(\beta_{a}\) the associated measurement noise of displacement and acceleration with covariance r and q; \(\beta_{d} \sim N\left( {0\quad {\mathbf{R}}} \right)\); \(\beta_{a} \sim N\left( {0\quad {\mathbf{Q}}} \right)\); \({\mathbf{Q}} = \left[ \begin{gathered} {0}\quad {0} \hfill \\ {0}\quad q \hfill \\ \end{gathered} \right]\); \({\mathbf{R}} = r\). The measurement process can be modeled by using the following equation:

$$\left\{ \begin{array}{ll} {\varvec{x}}_{k} = {\mathbf{A}}{\varvec{x}}_{k - 1} + {\mathbf{B}}{\varvec{a}}_{k - 1} + {\varvec{\omega}}_{k - 1} \hfill \\ {\varvec{z}}_{k} = {\mathbf{H}}{\varvec{x}}_{k} + {\varvec{\eta}}_{k} \hfill \\ \end{array} \right.$$
(1)

where \({\mathbf{A}} = \left[ \begin{gathered} 1\quad T_{a} \hfill \\ 0\quad 1 \hfill \\ \end{gathered} \right]\); \({\mathbf{B}} = \left[ \begin{gathered} {{T_{a}^{2} } \mathord{\left/ {\vphantom {{T_{a}^{2} } 2}} \right. \kern-0pt} 2} \hfill \\ \;\;T_{a} \hfill \\ \end{gathered} \right]\); \({\mathbf{H}} = \left[ {1\quad 0} \right]\); \({\varvec{\omega}}_{k}\) and \({\varvec{\eta}}_{k}\) are uncorrelated white noise sequences with zero mean value, which satisfy the following conditions:

$$\left\{ \begin{array}{ll} {\varvec{Q}}_{k} = E\left( {{\varvec{\omega}}_{k} {\varvec{\omega}}_{j}^{T} } \right) = q\left[ \begin{gathered} {{T_{a}^{2} } \mathord{\left/ {\vphantom {{T_{a}^{2} } 2}} \right. \kern-0pt} 2}\quad {{T_{a}^{3} } \mathord{\left/ {\vphantom {{T_{a}^{3} } 2}} \right. \kern-0pt} 2} \hfill \\ {{T_{a}^{2} } \mathord{\left/ {\vphantom {{T_{a}^{2} } 2}} \right. \kern-0pt} 2}\quad \;\;T_{a} \hfill \\ \end{gathered} \right] \hfill \\ {\varvec{R}}_{k} = E\left( {{\varvec{\eta}}_{k} {\varvec{\eta}}_{j}^{T} } \right) = \frac{{\mathbf{R}}}{{T_{a} }} \hfill \\ \end{array} \right.$$
(2)

where \({\varvec{Q}}_{k}\) and \({\varvec{R}}_{k}\) are the variance matrix of system noise and measurement noise respectively. The whole process of the traditional Kalman filtering can be described as the following five equations [26, 27]:

$$\left\{ \begin{array}{ll} \hat{\user2{x}}_{k|k - 1} = {\mathbf{A}}\hat{\user2{x}}_{k - 1|k - 1} \hfill \\ {\boldsymbol{P}}_{k|k - 1} = {\mathbf{A}}{\boldsymbol{P}}_{k - 1|k - 1} {\mathbf{A}}^{\mathrm{T}} + {\boldsymbol{Q}}_{k - 1} \hfill \\ {\boldsymbol{K}}_{k} = {\boldsymbol{P}}_{k|k - 1} {\mathbf{H}}^{\mathrm{T}} \left[ {{\mathbf{H}}{\boldsymbol{P}}_{k|k - 1} {\mathbf{H}}^{\mathrm{T}} + {\boldsymbol{R}}_{k} } \right]^{ - 1} \hfill \\ \hat{\user2{x}}_{k|k} = \hat{\user2{x}}_{k|k - 1} + {\boldsymbol{K}}_{k} \left[ {{\boldsymbol{z}}_{k} - {\mathbf{H}}\hat{\user2{x}}_{k|k - 1} } \right] \hfill \\ {\boldsymbol{P}}_{k|k} = \left[ {{\boldsymbol{I}} - {\boldsymbol{K}}_{k} {\mathbf{H}}} \right]{\boldsymbol{P}}_{k|k - 1} \hfill \\ \end{array} \right.$$
(3)

where \(\hat{\user2{x}}_{k|k - 1}\) is the prior estimation; \(\hat{\user2{x}}_{k - 1|k - 1}\) is the posteriori estimation; \({\varvec{P}}_{k - 1}\) is the state error covariance matrix; \({\varvec{K}}_{k}\) is the Kalman filter gain matrix; If the initial values of \(\hat{\user2{x}}_{0}\) and \({\varvec{P}}_{0}\) are known, the system state \(\hat{\user2{x}}_{k}\) can be estimated via employing the measured value \({\varvec{z}}_{k}\). If the measurement noise \({\varvec{\eta}}_{k}\) is of a colored noise, \({\text{cov}} \left( {{\varvec{\eta}}_{k} ,\;{\varvec{\eta}}_{j} } \right) \ne 0\left( {k \ne j} \right)\). In this case, \({\varvec{\eta}}_{k}\) in Eq. (1) can be expressed as [29, 30]:

$${\varvec{\eta}}_{k} = {\varvec{\psi}}_{k - 1} {\varvec{\eta}}_{k - 1} + {\varvec{\zeta}}_{k - 1} ,\quad {\varvec{\zeta}}_{k} \sim N\left( {0,\;{\varvec{R}}_{k} } \right)$$
(4)

where \({\varvec{\psi}}_{k}\) is the measurement noise transfer matrix. The pseudo-measurement is introduced to whiten the colored measurement noise, as follows:

$${\varvec{y}}_{k} = {\varvec{z}}_{k + 1} - {\varvec{\psi}}_{k} {\varvec{z}}_{k} = {\mathbf{C}}_{k} {\varvec{x}}_{k} + {\varvec{\nu}}_{k}$$
(5)
$$\left\{ \begin{array}{ll} E\left( {{\boldsymbol{\nu}}_{k} {\boldsymbol{\nu}}_{j}^{\mathrm{T}} } \right) = \overline{\user2{R}} \hfill \\ E\left( {{\boldsymbol{\omega}}_{k} {\boldsymbol{\nu}}_{j}^{\mathrm{T}} } \right) = {\boldsymbol{Q}}_{k} {\mathbf{H}}^{\mathrm{T}} \hfill \\ \end{array} \right.$$
(6)

where \({\mathbf{C}}_{k} = {\mathbf{HA}} - {\varvec{\psi}}_{k} {\mathbf{H}}\); \({\varvec{\nu}}_{k} = {\mathbf{H}}{\varvec{\omega}}_{k} + {{\zeta}}_{k}\); \(\overline{\user2{R}}_{k} = {\mathbf{H}}{\mathbf{Q}}_{k} {\mathbf{H}}^{\mathrm{T}} + {\mathbf{R}}_{k}\). The decorrelation analysis method can be used to filter out the correlation between stochastic noise and measurement noise [30], as follows:

$$\begin{array}{ll} {\varvec{x}}_{k} = {\mathbf{A}}{\varvec{x}}_{k - 1} + {\varvec{\omega}}_{k - 1} + {\varvec{J}}_{k - 1} \left( {{\varvec{y}}_{k - 1} - {\mathbf{C}}_{k - 1} {\varvec{x}}_{k - 1} - {\varvec{\nu}}_{k - 1} } \right) \hfill \\ \quad \, = {\mathbf{D}}_{k - 1} {\varvec{x}}_{k - 1} + {\varvec{J}}_{k - 1} {\varvec{y}}_{k - 1} + {\varvec{\mu}}_{k - 1} \hfill \\ \end{array}$$
(7)
$$\left\{ \begin{array}{ll} E\left( {{\boldsymbol{\mu}}_{k} {\boldsymbol{\mu}}_{j}^{\mathrm{T}} } \right) = \overline{\user2{Q}}_{k} \hfill \\ E\left( {{\boldsymbol{\mu}}_{k} {\boldsymbol{\nu}}_{j}^{\mathrm{T}} } \right) = {\mathbf{Q}}_{k} {\mathbf{H}}^{\mathrm{T}} - {\boldsymbol{J}}_{k} \overline{\user2{R}}_{k} \hfill \\ \end{array} \right.$$
(8)

where \(\overline{\user2{Q}}_{k} = {\boldsymbol{Q}}_{k} + {\boldsymbol{J}}_{k} \overline{\user2{R}}_{k} {\boldsymbol{J}}_{k}^{\mathrm{T}} - {\boldsymbol{Q}}_{k} {\mathbf{H}}^{\mathrm{T}} {\boldsymbol{J}}_{k}^{\mathrm{T}} - {\boldsymbol{J}}_{k} {\mathbf{H}}{\boldsymbol{Q}}_{k}\); \({\mathbf{D}}_{k} = {\mathbf{A}} - {\varvec{J}}_{k} {\mathbf{C}}_{k}\); \({\varvec{\mu}}_{k - 1} = {\varvec{\omega}}_{k} \user2{ - J}_{k} {\varvec{\nu}}_{k}\).

To make \(E\left( {{\boldsymbol{\mu}}_{k} {\boldsymbol{\nu}}_{j}^{\mathrm{T}} } \right)\) is equal to zero, it requires:

$${\varvec{J}}_{k} = {\boldsymbol{Q}}_{k} {\mathbf{H}}^{\mathrm{T}} \left( {\overline{\user2{R}}_{k} } \right)^{ - 1}$$
(9)

After the above treatment, we can get the new state space model:

$$\left\{ \begin{array}{llll} {\varvec{x}}_{k} = {\mathbf{D}}_{k - 1} {\varvec{x}}_{k - 1} + {\varvec{J}}_{k - 1} {\varvec{y}}_{k - 1} + {\varvec{\mu}}_{k - 1} \quad {\varvec{\mu}}_{k - 1} \sim N\left( {0,\,\overline{\user2{Q}}_{k} } \right) \hfill \\ {\varvec{y}}_{k} = {\mathbf{C}}_{k} {\varvec{x}}_{k} + \nu_{k} \quad \quad \quad \quad \quad \quad \;\;\nu_{k - 1} \sim N\left( {0,\,\overline{\user2{R}}_{k} } \right) \hfill \\ \end{array} \right.$$
(10)

Then, the Kalman filter algorithm with colored measurement noise can be described as:

Time update:

$$\left\{ \begin{array}{ll} \hat{\user2{x}}_{k|k - 1} = {\mathbf{D}}_{k - 1} \hat{\user2{x}}_{k - 1|k - 1} + {\boldsymbol{J}}_{k - 1} {\boldsymbol{y}}_{k - 1} \hfill \\ {\boldsymbol{P}}_{k|k - 1} = {\mathbf{D}}_{k - 1} {\boldsymbol{P}}_{k - 1|k - 1} {\mathbf{D}}_{k - 1}^{\mathrm{T}} + \overline{\user2{Q}}_{k - 1} \hfill \\ \end{array} \right.$$
(11)

Measurement update:

$$\left\{ \begin{array}{ll} \hat{\user2{x}}_{k|k} = \hat{\user2{x}}_{k|k - 1} + {\varvec{C}}_{k} \left[ {{\varvec{y}}_{k} - {\mathbf{C}}_{k} \hat{\user2{x}}_{k|k - 1} } \right] \hfill \\ {\varvec{P}}_{k|k} = \left[ {{\varvec{I}} - {\varvec{K}}_{k} {\mathbf{C}}_{k} } \right]{\varvec{P}}_{k|k - 1} \hfill \\ \end{array} \right.$$
(12)

Kalman gain matrix:

$${\varvec{K}}_{k} = {\boldsymbol{P}}_{k|k - 1} {\mathbf{C}}_{k}^{\mathrm{T}} \left[ {{\mathbf{C}}_{k} {\boldsymbol{P}}_{k|k - 1} {\mathbf{C}}_{k}^{\mathrm{T}} + \overline{\user2{R}}_{k} } \right]^{ - 1}$$
(13)

Note that the measured displacements are unavailable between the times kTd, only the time update based on Eq. (11) is performed. When the measured displacements are available at times kTd, both the time update and measurement update should be performed.

Thus, a series of local estimations are derived (i.e., displacement: \(\hat{\user2{X}}_{1,k|k} ,\;\hat{\user2{X}}_{2,k|k} ,\; \cdots ,\;\hat{\user2{X}}_{M,k|k}\); and covariance: \({\varvec{P}}_{1,k|k} ,\;{\varvec{P}}_{2,k|k} ,\; \cdots ,\;{\varvec{P}}_{M,k|k}\)). If the local estimation errors are uncorrelated, the optimal fusion estimation results \(\hat{\user2{X}}_{k|k}\) can be derived via using a weighted fusion criterion of scalar linear minimum variance. It can be written as:

$$\hat{\user2{X}}_{k|k} = \alpha_{1} \hat{\user2{X}}_{1,k|k} + \alpha_{2} \hat{\user2{X}}_{2,k|k} + \cdots + \alpha_{j} \hat{\user2{X}}_{j,k|k} + \cdots + \alpha_{M} \hat{\user2{X}}_{M,k|k}$$
(14)

where \(\hat{\user2{X}}_{j,k|k}\) is the local estimation value obtained after Kalman filter by the j-th sensor; \(\alpha_{j}\) is the weight coefficient, which can be expressed in the following form:

$$\alpha_{j} = \rho /{\mathbf{tr}}{\boldsymbol{P}}_{j,k|k}$$
(15)

where \(\rho = \left( {\frac{1}{{\mathrm{tr}{\boldsymbol{P}}_{1,k|k} }} + \frac{1}{{\mathrm{tr}{\boldsymbol{P}}_{2,k|k} }} + \cdots + \frac{1}{{\mathrm{tr}{\boldsymbol{P}}_{j,k|k} }} + \cdots + \frac{1}{{\mathrm{tr}{\boldsymbol{P}}_{M,k|k} }}} \right)^{ - 1}\). The corresponding covariance matrix \({\varvec{P}}_{0,k|k}\) of the estimation error has the following form:

$${\varvec{P}}_{0,k|k} = \alpha_{1} {\varvec{P}}_{1,k|k} + \alpha_{2} {\varvec{P}}_{2,k|k} + \cdots + \alpha_{j} {\varvec{P}}_{j,k|k} + \cdots + \alpha_{M} {\varvec{P}}_{M,k|k}$$
(16)

Operational modal analysis algorithm

The SSI is a widely used OMA approach for estimating structural modal parameters because it combines a good robustness and a high estimation accuracy [31, 32]. It is divided into two sub methods, i.e. data-driven SSI and covariance-driven SSI. In particular, data-driven SSI can identify modal parameters directly from the measured data, unlike covariance-driven SSI where one needs to derive the covariance matrix relating all of the measured outputs. Hence, data-driven SSI approach is employed in this study. Its basic principle (shown in Fig. 2) can consult the literature [33, 34]. Once the system matrix A* and output matrix H* of state-space model of a structure are determined, the modal frequency and damping ratio can be identified by conducting eigenvalue decomposition of matrix A* while the mode shape coefficients can be derived by the eigenvectors multiplied based on matrix H*.

Fig. 2
figure 2

The working principle of data-driven SSI

Full size image

The eigenvalue decomposition of matrix A* can be expressed as:

$${\text{A*}} = {\mathbf{\Phi \Lambda \Phi }}^{ - 1}$$
(17)

where \({{\varvec{\Phi}}}\) is eigenvector matrix in discrete time. \({\mathbf{\Lambda = }}\,\mathrm{diag}\left( \lambda \right)\), \(\lambda\) is the eigenvalue in discrete time. It is related to the eigenvalue \(\lambda_{c}\) in continuous time, as follows:

$$\lambda_{c} = \frac{{\mathrm{ln}\left( \lambda \right)}}{\Delta t}$$
(18)

The modal frequency \(f\) and damping ratio \(\xi\) can be computed as:

$$f = \frac{{\sqrt {{\text{Re}}^{2} \left( {\lambda_{c} } \right) + {\text{Im}}^{2} \left( {\lambda_{c} } \right)} }}{2\pi }$$
(19)
$$\xi = - \frac{{{\text{Re}} \left( {\lambda_{c} } \right)}}{2\pi f}$$
(20)

The corresponding mode shape \(\user2{\varphi }\) is computed as:

$$\user2{\varphi = }{\text{H*}} \cdot {{\varvec{\Phi}}}$$
(21)

Preliminary validation of proposed approach on numerical model

The purpose of this section is to evaluate the performance of the proposed data fusion algorithm with a simplified numerical model. Considering a four-DOF linear time-invariant spring-mass-damper model (shown in Fig. 3):

Fig. 3
figure 3

Four degree-of-freedom linear spring-mass-damper model

Full size image

Assume that the basic parameters of this model are

$${\mathbf{M}} = \left[ \begin{array}{ll} 1\\ \quad \;2 \hfill \\ \quad \quad \;\,3 \hfill \\ \quad \quad \quad \;\,{\kern 1pt} 4\\ \end{array} \right],\quad {\mathbf{K}} = \left[ \begin{gathered} \;\;{\kern 1pt} 800\quad - 800\quad \quad \;\,0\quad \quad \quad \;0\quad \hfill \\ - 800\quad \;2400\quad - 1600\quad \quad \;\;0\quad \hfill \\ \quad 0\quad \, - 1600\quad \;\;\,4000\quad - 2400 \hfill \\ \quad 0\quad \quad \;\;\,0\quad \;\;{\kern 1pt} - 2400\quad \;\;\,5600 \hfill \\ \end{gathered} \right],\quad {\mathbf{C}} = \alpha {\mathbf{M}} + \beta {\mathbf{K}}$$

The damping factors for mass proportional damping were set to \(\alpha = 0.1\), \(\beta = 0\). Colored noise was employed to excite the model with four-DOF. The responses of displacement and acceleration of the model were derived via using Newmark method, as shown in Fig. 4(a) and (b). The sample rate is taken as 50 Hz for measured displacement and 100 Hz for measured acceleration. This displacement obtained directly from the model is the real displacement of the system. It can be used as the reference to evaluate the working performance of the proposed approach. To simulate the field measurement data, a colored noise is added into the true displacement and acceleration responses. First, a Gaussian white noise with signal-to-noise ratio (SNR) of 5 dB is generated. Then, a shaping filter is designed to filter the generated white noise to derive a colored noise of non-uniform power spectral density (PSD). This is a relatively weak level of noise. Figure 4(c) and (d) show the displacement and acceleration responses after adding colored noise. In particular, a comparative study was carried out to investigate the performance of the following six cases. Cases 1–3 process the simulated signal with colored noise based on the assumption of white noise, while cases 4–6 consider the impact of colored noise. The purpose of implementing these cases is, on the one hand, to reveal the influence of white noise and colored noise on the estimation results, and on the other hand, to compare the estimation accuracy of single sensor with that of multi-sensor fusion.

  • Case 1: Displacement estimation was derived based on only displacement measurement by using Kalman filter method with white measurement noise;

  • Case 2: Displacement estimation was derived based on only acceleration measurement by using Kalman filter method with white measurement noise.

  • Case 3: Displacement estimation was derived based on combined measurements by using Kalman filter method with white measurement noise;

  • Case 4: Displacement estimation was derived based on only displacement measurement by using Kalman filter method with colored measurement noise;

  • Case 5: Displacement estimation was derived based on only acceleration measurement by using Kalman filter method with colored measurement noise;

  • Case 6: Displacement estimation was derived based on combined measurements by using the proposed approach.

Fig. 4
figure 4

Displacement and acceleration of a four-DOF model under colored noise excitation: (a) original displacement response; (b) original acceleration response; (c) displacement response with added noise; (d) acceleration response with added noise

Full size image

Figures 5(a)-(f) indicate the results of displacement estimation under different cases. To quantify the accuracy of the estimated results, the normalised root mean square error (NRMSE) was introduced. It can be expressed as the following form:

$$\mathrm{NRMSE} = \frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\hat{x}_{i} - x_{i} } \right)^{2} } } }}{{\max \left( {x_{i} } \right) - \min \left( {x_{i} } \right)}}$$
(22)

where \(x_{i}\) and \(\hat{x}_{i}\) represent the real and estimated value at time step \(i\), \(n\) is the number of sampled data points.

Fig. 5
figure 5

Displacement estimation of a SDOF system under different cases

Full size image

Table 1 lists the NRMSE values under six different cases based on Eq. (22). It can be seen that the estimated results of cases 4, 5 and 6 are better than cases 1, 2 and 3 respectively. This is mainly because the simulated signal contains colored noise. If it is processed as white noise, the estimation accuracy is relatively low. Additionally, it can be found that when the (100 Hz) acceleration data is combined with the (50 Hz) sampled displacement, the estimation results have a drastic improvement. In other words, the estimated result of multi-sensor fusion is better than that of single sensor when the measurement noise is given. Specially, the estimated result of case 6 is superior to other cases. This implies that the proposed approach is an effective method for estimating the real displacement of the system with a higher accuracy.

Table 1 NRMSE values of estimated displacements under six different cases
Full size table

Next, the SSI algorithm was used to calculate the modal parameters of the model. Figure 6 shows the identified mode shapes. The modal frequencies and damping ratios were presented in Table 2. The modal assurance criterion (MAC) is used to evaluate the accuracy of mode shapes, as follows:

$${\text{MAC}} = \frac{{\left( {\Phi_{a}^{\mathrm{T}} \cdot \Phi_{b} } \right)^{2} }}{{\left( {\Phi_{a}^{\mathrm{T}} \cdot \Phi_{a} } \right)\left( {\Phi_{b}^{\mathrm{T}} \cdot \Phi_{b} } \right)}}$$
(23)

where \(\Phi_{a}\) and \(\Phi_{b}\) represent the theoretical and estimated mode shapes, respectively. It can be found that the results have a good agreement with the theoretical values.

Fig. 6
figure 6

Identified and theoretical mode shapes: (a) The 1st mode; (b) The 2nd mode; (c) The 3rd mode; (d) The 4th mode

Full size image
Table 2 Estimated modal parameters of the numerical example
Full size table

Application to a long-span cable-stayed bridge

In this section, the proposed approach was applied to displacement estimation and modal identification of a long-span cable-stayed bridge named Tianjin Yonghe (shown in Fig. 7), located in Tianjin, China, from the GNSS and accelerometer monitoring data. The bridge was built in 1983 and opened to traffic at the end of 1987, and it is a pre-stressed concrete cable-stayed bridge with three-span, couple tower and couple cable. The total length of the bridge is 510 m, and the main span and each side span are 260 m and 125 m respectively. It is noted that several damage patterns, i.e. cracks at the bottom of the mid-span girder and corroded cables, were detected in 2005. Therefore, the bridge was closed and repaired between 2005 and 2007. Subsequently, the bridge was reopened to traffic at the end of 2007 with a sophisticated health monitoring system. The bridge has been in operation for approximately 15 years, and the structural modal parameters may have changed. Notably, the position accuracy of GNSS under RTK mode was limited. Therefore, before the field measurement, a stability experiment of GNSS was performed.

Fig. 7
figure 7

Panoramic schematic of Tianjin Yonghe Bridge

Full size image

FE analyses of the target bridge

Before the field measurement, a Finite Element (FE) model of the bridge was established via using ANSYS 14.5 software. The purpose of establishing the FE model is to optimize the layout of the measured points and compare it with the experimental results. In this model, there are 475 nodes and 566 elements. The bridge towers and the main girder were modelled via employing BEAM44 element. The concrete transverse beams were individually simplified as the mass element MASS21 every 2.9 m along the bridge. The stay cables were modelled via employing LINK10 element. The bridge deck was simulated via employing SHELL63 element. The main girder was modelled as floating on the main tower, and all of the towers were fixed to the ground. The longitudinal restriction effect of the rubber supports was modelled via employing COMBIN14 elements. The Young’s moduli of the towers and girder are \(3.55 \times 10^{10} \;{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{{2}} }}} \right. \kern-0pt} {{\text{m}}^{{2}} }}\), and their material densities are \(2,550\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{{3}} }}} \right. \kern-0pt} {{\text{m}}^{{3}} }}\). The Young’s modulus of the cables is \(2.0 \times 10^{11} \;{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{{2}} }}} \right. \kern-0pt} {{\text{m}}^{{2}} }}\), and its material density is \(7,850\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{{3}} }}} \right. \kern-0pt} {{\text{m}}^{{3}} }}\). The mass of a single concrete transverse beam is \(6,932.8\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{{3}} }}} \right. \kern-0pt} {{\text{m}}^{{3}} }}\). The Young’s modulus of the bridge deck is \(2.85 \times 10^{10} \;{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{{2}} }}} \right. \kern-0pt} {{\text{m}}^{{2}} }}\), and its material density is \(2,500\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{{3}} }}} \right. \kern-0pt} {{\text{m}}^{{3}} }}\). It is noteworthy that the status of the bridge has changed after a long time of operation. Several damage patterns, i.e. cracks at the bottom of the mid-span girder and corroded cables, were detected in 2005. Therefore, the bridge was closed and repaired between 2005 and 2007. Subsequently, the bridge was reopened to traffic at the end of 2007 with a sophisticated health monitoring system. This study established a benchmark finite element model based on the design value, and then further modified this model by using preliminary measurements. Based on the FE modal analysis results, the first to eighth vertical vibration frequencies (i.e., 0.3996 Hz、0.5522 Hz、0.9332 Hz、1.0559 Hz、1.4217 Hz、1.5961 Hz、1.6662 Hz and 1.7231 Hz) and the corresponding mode shapes were derived, as shown in Fig. 8(a)-(h).

Fig. 8
figure 8

Finite element modal analysis results of the Bridge: (a) The 1st mode; (b) The 2nd mode; (c) The 3rd mode; (d) The 4th mode; (e) The 5th mode; (f) The 6th mode; (g) The 7th mode; (h) The 8th mode

Full size image

Experimental scheme and measurement

Based on the FE analysis results from Fig. 8, it can be seen that the largest deformation of the bridge are presented at 1/4, 1/2 and 3/4 of the main span, and 1/2 of the side spans. The sensors arranged at these positions can effectively reveal the vibration characteristics of the structure. Therefore, this experiment used six GNSS receivers (Sampling rate: 50 Hz) and five accelerometer sensors (Sampling rate: 100 Hz) to monitor the vibration response of the bridge. One GNSS receiver was placed on a stable ground as the reference station and approximately 50 m away from the bridge, as shown in Fig. 9(a). From Fig. 9(b), five GNSS receivers in association with five accelerometers were fixed at 1/4, 1/2 and 3/4 of the main span, and 1/2 of the side spans as the rover stations. Figure 9(c) depicts the specific locations of the measuring points (i.e., C1-C5). This experiment lasted for 9 h from 9:00 a.m. to 6:00 p.m. on 12 July 2019 local time.

Fig. 9
figure 9

Schematic figure for the field measurement: (a) GNSS reference station; (b) GNSS rover station and accelerometer sensor; (c) The position of measuring points

Full size image

Data processing and analysis

In section "Preliminary validation of proposed approach on numerical model", the superiority of the proposed approach has been verified by a numerical example. This section reports the results of employing the proposed data fusion approach to the field data recorded on Tianjin Yonghe Bridge.

Figure 10 depicts the original GNSS data of Point C3, and the corresponding PSD function. It can be seen that there are two notable peaks (i.e., 0.4150 Hz and 0.5981 Hz) corresponding to the first two vertical modes of the bridge from PSD distribution. Moreover, It can also be found that the modal frequencies identified via PSD function are agree with the results of FE analysis with a little difference. Figure 11 presents the original acceleration data of Point C3, and the corresponding PSD function. It can be observed that there are five obvious peaks (i.e., 0.4150 Hz, 0.5859 Hz, 0.9644 Hz, 1.0860 Hz and 1.4530 Hz) corresponding to the first five modal information of the bridge. In particular, it is noteworthy that Figs. 10 and 11 only show the 200 s vibration response, and the corresponding PSD and the follow-up modal calculation are calculated with 1000 s sample data. From Fig. 10, there were no apparent peaks about the third to fifth modes based on GNSS data. This implies that compared with acceleration sensors, GNSS can only detect a few number of low order modes even with a high sampling rate. Theoretically, the GNSS measurement has the chance to detect the higher vertical modes but in fact it has failed to do so. This is mainly because the positioning accuracy of GNSS is limited while the dynamic component of displacement is relatively small and easily contaminated by the measurement noise.

Fig. 10
figure 10

GNSS signal and its PSD function

Full size image
Fig. 11
figure 11

Acceleration signal and its PSD function

Full size image

Next, the proposed multi-rate weighted data fusion approach was used to fuse the GNSS and acceleration data. However, it is worth noting that the measured GNSS data includes not only the dynamic part of displacement but also the quasi-static part. This study mainly focused on investigating the dynamic displacements of bridges under ambient excitation. Hence, a second-order type 1 Chebyshev high-pass digital filter with the cut-off frequency of 0.05 Hz was first adopted to remove the quasi-static part of displacement. Then, the remained dynamic part of GNSS and acceleration were fused via the developed approach. In addition, previous studies have proved that smoothing can produces a much better estimation after fusion [10, 35]. Therefore, a smoothing technique named Savitzky-Golay (SG) approach was used in this section [36]. The SG approach was a data smoothing approach depended on local least-squares polynomial approximation. It has been demonstrated that least-squares smoothing reduces noise while ensuring the height and shape of waveform peaks [37]. The final estimated displacements from GNSS, acceleration and data fusion and their PSD functions were illustrated in Fig. 12. It can be found that the estimated result based on GNSS data can identify first three modes of the bridge, but before that, only the first two modes can be detected. This implies that the filtering and smoothing approaches reduce the noise and make the dynamic components of GNSS clear. However, it was still failed to extract the fourth and fifth modes of the bridge. From Fig. 12(b), it was also seen that five distinct modes were identified via using the developed data fusion approach. Furthermore, the identified results of modal frequencies were consistent with the acceleration-derived displacement. To some extent, the problem that GNSS is insensitive to high frequency vibration of structures is alleviated. Note that the sampling rate of the estimated displacement via using the proposed approach is 100 Hz. The standard deviations of three different estimation results were calculated (i.e., GNSS-derived displacement: 0.0104 m; Acceleration-derived displacement: 0.0101 m; Data fusion-derived displacement: 0.0089 m).

Fig. 12
figure 12

Estimated displacements and the corresponding PSD functions

Full size image

The data-driven SSI algorithm is performed on the estimated displacements. The modal frequencies and the corresponding damping ratios were listed in Table 3. It can be seen that the modal frequencies identified via GNSS-derived displacement, acceleration-derived displacement and data fusion-derived displacement are consistent. However, there is a large deviation in the damping identification results. The accurate estimation of damping is difficult because the bridge contains several sources of energy dissipation, and their lesser known combinations. Figure 13 illustrates the extracted results of the mode shapes. It can be observed that the identified results are in good agreement with the theoretical values based on the FE analysis. The MAC values (shown in Table 4) confirmed that the mode shapes identified based on data fusion-derived displacement were better than those GNSS-derived and acceleration-derived displacements. This further proves that the developed approach has an accuracy advantage to those of the local estimations from single type sensors. Thus far, all the modal parameters of the structure were successfully obtained.

Table 3 Estimated modal parameters for Tianjin Yonghe Bridge based on field measurement
Full size table
Fig. 13
figure 13

Identified first five vertical mode shapes

Full size image
Table 4 The MAC values of GNSS-derived, acceleration-derived and data fusion-derived displacements
Full size table

Conclusions

In this study, a multi-rate weighted data fusion approach based Kalman filter with colored measurement noise was developed to estimate dynamic displacement of a long-span bridge based on GNSS and acceleration measurements. Then, the data-driven SSI method was employed to identify modal parameters of the bridge from the estimated displacement. The method is tested using a four-DOF system and an actual long-span bridge. The following conclusions are summarized:

  • The proposed data fusion approach is capable of accurately estimating structural dynamic displacements. The feasibility and effectiveness of the approach were validated by a comparative study of a spring-mass-damper model. On the premise of a given measurement noise, the estimated result of multi-sensor fusion performs better than that of single sensor. Moreover, the proposed approach with considering colored measurement noise is superior to the general approach with considering white measurement noise. The corresponding NRMSE index decreased from 0.0475 to 0.0320.

  • The proposed approach can improve the accuracy of GNSS-derived displacement and expand recognizable frequency range by fusing acceleration information. Based on raw GNSS data, only the first two modes of the bridge were detected even with high sampling rate. However, the third mode of the bridge became distinct based on GNSS local estimation obtained by Kalman filtering. This is mainly because the noise reduction makes the dynamic components of displacement clear. Importantly, the fourth and fifth modes of the bridge can be extracted if the measured displacement from GNSS was fused with accelaration information using the developed approach. In other words, the developed fusion strategy alleviates the problem of low dynamic tracking accuracy of GNSS.

  • The identified modal frequencies based on GNSS-derived, acceleration-derived and data fusion-derived displacements are consistant. Meanwhile, they are in agreement with the theoretical values based on the FE analysis. Moreover, the MAC values demonstrated that the modes identified via fusion-derived displacement are better than GNSS-derived and acceleration-derived displacements. This further reveals that multi-sensor fusion has an accuracy improvement over single type of sensors.