Abstract
To achieve higher automation level of vehicles defined by the Society of Automotive Engineers, safety is a key requirement affecting navigation accuracy. We apply Light Detection and Ranging (LiDAR) as a main auxiliary sensor and propose LiDAR-based Simultaneously Localization and Mapping (SLAM) approach for Positioning, Navigation, and Timing. Furthermore, point cloud registration is handled with 3D Normal Distribution Transform (NDT) method. The initial guess of the LiDAR pose for LiDAR-based SLAM comes from two sources: one is the differential Global Navigation Satellite System (GNSS) solution; the other is Inertial Navigation System (INS) and GNSS integrated solution, generated with Extended Kalman Filter and motion constraints added, including Zero Velocity Update and Non-Holonomic Constraint. The experiment compares two initial guesses for scan matching in terms navigation accuracy. To emphasize the importance of a multi-sensor scheme in contrast to the conventional navigation method using the stand-alone system, the tests are conducted in both open sky area and GNSS signal block area, the latter might cause Multipath and Non-Line-Of-Sight effects. To enhance the navigation accuracy, the Fault Detection and Exclusion (FDE) mechanism is applied to correct the navigation outcome. The results show that the application of NDT and FDE for INS/GNSS integrated system can not only reach where-in-lane level navigation accuracy (0.5 m), but also enable constructing the dynamic map.
Similar content being viewed by others
Introduction
To navigate a vehicle safely and autonomously from one place to another, its position shall be accurately localized, even at lane level (Stephenson, 2016). The conventional navigation method relies on Global Navigation Satellite System (GNSS) (Noureldin et al., 2013) and Inertial Navigation System (INS) (Nassar, 2003). But the error of INS will accumulate over time; meanwhile, GNSS can’t provide accurate position in challenging environments, and its positioning errors affected by several factors, including the multipath effect and ionosphere errors (Groves & Jiang, 2013; Rahmani et al., 2020). To deal with these problems, several auxiliary sensors were tested, including camera (Mur et al., 2015), Radio Detection and Ranging (Radar) (Wang, 2016), Light Detection and Ranging (LiDAR) (Cheng & Wang, 2018; Gao et al., 2015), etc. However, the camera might be affected by light conditions and weather events and the modeling definition of the radar is too low, while LiDAR can overcome the disadvantages that camera and radar might have. Therefore, we utilize the INS and Differential GNSS (DGNSS) to output an integrated navigation solution to initialize the LiDAR pose, yet apply Extended Kalman Filter (EKF) as framework. Note that there are other methods for updating other than the Kalman Filter used in this research. Yet, the EKF can deal with continuous-time system model since the measurements are nonlinear. To define the initial pose of LiDAR, one shall transform the initial guess to the center of LiDAR in the LiDAR frame by the transformation relationship of lever arm and boresight, which is the so-called Direct Georeferencing (DG) (Reshetyuk, 2009). After DG, the dynamic map can be built by matching consecutive frames of point cloud data. There are several registration methods, which can generally be divided into three categories, which are point-based, feature-based, and distribution-based. However, compared to the point-based and feature-based methods (Zhang et al., 2014), the distribution-based Normal Distribution Transform (NDT) (Magnusson, 2009; Magnusson et al., 2009) not only copes with a larger range of initial pose offset, but also needs less computational time than Iterative Closest Point (ICP) method (Aghili & Su., 2016).
Numerous studies were conducted on the development of NDT and its variants to deal with LiDAR data. Recently, some research tried to emphasize the initial pose correction ability of NDT and process experiments took place in GNSS challenging areas, including indoor and urban environments (Chen et al., 2021; Wen et al., 2018; Zhou et al., 2017). While others conducted real-time Simultaneously Localization and Mapping (SLAM) (Chen et al., 2021; Deng et al., 2021). Furthermore, the concept of High Definition Map (HD Map) with dense and robust point cloud (Zhou et al., 2017; Liu et al., 2020) was applied in LiDAR scan for HD map registration to output better initial pose correction.
Nevertheless, compared to camera and radar, LiDAR has a disadvantage that it is relatively expensive, making its application to autonomous vehicles infeasible. Meanwhile, the construction of HD Map is costly, which is not applicable immediately over the world. In this research, we simulate the situation without HD Map, which means the navigation only can be conducted by an initial guess from INS/GNSS, and the point cloud map is constructed frame by frame through NDT. For this purpose, it only relies on the initial guess of position, velocity, and attitude from INS/GNSS integrated navigation solution or navigation solution from GNSS stand-alone system.
This paper has three contributions as follows: first, to meet the feasible cost in the application of LiDAR for future development in autonomous vehicle applications, the low-cost LiDAR “single VLP16” is selected. Second, to provide not only reliable initial guess for LiDAR SLAM but also applicable for real-world coordinate system, the INS/GNSS based integrated navigation solution is generated with EKF and in the Earth frame. Third, the Fault Detection and Exclusion (FDE) schemes are applied to reject false measurements to maintain the navigation accuracy. To sum up, a low-cost INS/GNSS/LiDAR integrated system is proposed in this paper to conduct Positioning, Navigation, and Timing (PNT).
The structure of this paper is arranged in the following sequence. “Methods” section presents the PNT structure and the methodologies applied to fulfill multi-sensors integration scheme with different initial guesses. "Experiments" section introduces the experiment setup, test field selection, and point cloud data preprocessing. The results and discussions of the experiments will be shown in “Results and discussion” section. Finally, the conclusion is made in “Conclusions” section.
Methods
Architecture design
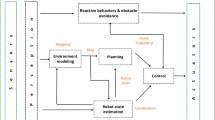
The proposed LiDAR-SLAM-based structure for PNT is illustrated in Fig. 1. GNSS in Fig. 1 refers to the DGNSS with the measurements received from multi-constellation system, which takes GPS, GLONASS, and BeiDou systems into consideration. The more measurements from multi-constellation system will result in more precise positioning solution in diverse scenarios. This is applicable for the following content as well. The initial guess for LiDAR-SLAM comes from two sources. One is the INS/GNSS integrated navigation solution with EKF after Rauch–Tung–Striebel (RTS) smoother (Chiang et al., 2009; Särkkä, 2008), which predicts and updates the velocity, position, and attitude information and feedbacks the bias and scale factor from EKF to INS mechanism. The other is directly from DGNSS stand-alone system with the position and velocity information only. The whole LiDAR-SLAM process includes point cloud preprocessing, DG, 3D NDT scan matching, and FDE. Especially, the FDE mechanism involves the two-step-functions, which are LiDAR Odometry (LO) and LiDAR Mapping (LM).
Initial guesses
INS/GNSS integrated navigation solution
In this research, the INS and DGNSS sensors integration system is developed utilizing the Loosely Coupled (LC) scheme, which needs an optimal estimator to compare the difference between each measurement with predicted variables and establish the error model, in order to estimate the possible error. The Least-Square (LS) method is the most used optimal estimator (Parvazi et al., 2020). To deal with continuous measurements, the Recursive Least-Square (RLS) method, the derivative of LS can update the previous optimal estimates with the current observations. However, RLS is only suitable for time-invariant system, while the Kalman filter can cope with time-varying system (Zangeneh-Nejad et al., 2018). The fundamental equations of EKF based on RLS are as follows.
The state vector \({x}_{k}\) for EKF input is showed in Eq. 1 (Shin and El, 2002; Shin, 2005), where each element involves the values in x, y, and z three axes.
where \(r\) is the position vector in the Earth frame (latitude, longitude, height); \(v\) is velocity vector recorded in North, East, and Downward sequence; \(\varphi\) is the attitude rotating from the body frame to mapping frame, while body frame is known as the vehicle frame, and mapping frame refers to the local level frame; \({b}_{a}\) is the bias of accelerometer in IMU; \({b}_{g}\) is the bias of gyroscope in IMU; \({s}_{a}\) and \({s}_{g}\) are the scale factors of accelerometer and gyroscope, respectively.
With the state vector, we can construct two functions. One is function f, which utilizes the state vector at epoch k to predict the state vector at the next epoch k + 1. The other is function h, which can compute the measurements updated at epoch k + 1 by multiplying the predicted state from function f with observation matrix H and adding the observation error \({v}_{k}\).
Because the state transition and measurement update model are nonlinear, the previous functions shall pass through partial derivatives before putting them into Kalman Filter, which can be divided into two parts: prediction and measurement update. The prediction process estimates the state and noise at epoch k + 1 from the observation at epoch k, and the estimated value from prediction is denoted with superscript (–).
The measurement update process is conducted by updating the state with the observation at epoch k + 1. It put the \({K}_{k+1}\) as Kalman gain into consideration. When the prediction model is more reliable, the weight for residual will be smaller, and vice versa. The combination and evaluation about the weights of observations from two sources (INS and GNSS) are critical (Teunissen & Amiri-Simkooei, 2008), while the suitable weight settings can improve the quality of unknown parameters. Meanwhile, the weighting should also take the grade of the sensor into consideration.
DGNSS stand-alone navigation solution
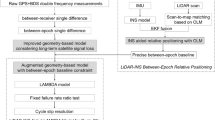
The concept of DGNSS is that the base station and the rover station simultaneously receive GNSS signals, while the latter is mounted on the vehicle. By subtracting the positioning data of the base (also named as the reference station) and rover stations, it can turn out the differential GNSS data. Compared to real-time DGNSS, the post-processing DGNSS applied in this research can achieve higher accuracy (Yoshimura & Hasegawa, 2004). The schematic diagram of DGNSS is shown in Fig. 2a. In this paper, the satellites’ data are continuously received by several Virtual Reference Stations (VRS), which therefore forms a GPS network to estimate the GPS error model in a specific area, the corrections will be send back to the rover station via the network to update the position of the vehicle. It is noteworthy that the established GPS network of multi reference stations can not only reduce the ionosphere and tropospheric delay errors, but also enhance the rover station’s ability to resolve phase ambiguity, increasing the positioning solution reliability.
Because the GNSS only provides position and velocity data, the initial heading at the first epoch comes from the reference, and the heading values at the following epochs are calculated by the positions at current epoch and previous epoch. The method is described in Fig. 2b.
Direct georeferencing
While each sensor is in different frame, the initial guess received by GNSS antenna is in Earth frame, and the point cloud is in LiDAR frame. To fulfill multi-sensors integration, it must transform them into a uniform frame by performing the translation and rotation with the three axes (Chiang et al., 2019), the so-called DG process. In this research, we transform each frame into the mapping frame with the coordinate at the first epoch as the origin. The transformation relationship between each pair of sensor frames is shown in Fig. 3, while \({r}_{b}^{m}\) and \({R}_{b}^{m}\) represent the translation and rotation of body frame with respect to the mapping frame and so on.
After DG, it can define the initial pose and construct the environment where the vehicle is by the initial guess generated in previous sub-section after the compensation of lever arm and boresight. However, the distribution of the point cloud is based on the rough initial guess. To correct the initial pose of the vehicle, it shall go through scan to dynamic map registration to adjust it, which will be mentioned in the next sub-section.
3D normal distribution transform
Although the initial guess can estimate the pose of the point cloud, in GNSS challenging environment, the initial guess might lead to a large pose offset of the vehicle. To prevent the failure of scan matching caused by the initial pose offset, if the points of each frame are well-matched, it can correct the error in the initial guess. This paper applies NDT for scan matching, which is a distribution-based registration method and more robust to deal with initial pose offset.
As we receive the consecutive frames of point cloud from LiDAR, the previous frame of point cloud is cut in a constant voxel size. Each voxel shall contain at least three points. Later, it processes the NDT by matching points after voxelization from moving frame (current frame) to the distribution of the fixed frame (previous frame) and turns out the normal distribution modeling \(N(q, \sum )\) for each voxel (Akai et al., 2017; Biber & Straßer, 2003).
where \({x}_{i}\) is the point in the voxel; n is the number of points in a specific voxel; q is the mean value and Σ is the covariance value of the voxel.
After registration, it can calculate the score value. To minimize the score value, it iteratively updates the rotation and translation in three axes of consecutive frames and applies the Newton’s algorithm to optimize. It’s worth noticing that during the coordinate transformation process, the estimation of the weights for unknowns can enhance the registration results (Amiri-Simkooei., 2018), such as the calculation of six Degrees of Freedom (6DOF) may refer to the slant distance from the center to each point to set the corresponding weight.
For the research settings, the iteration won’t stop until it meets some criteria, such as the iteration number of scan matching, or the rotation and translation differences between consecutive frames fall within a predefined tolerance. To prevent the rotation and translation differences from falling into a local minimum, Iterative Discretization Method-NDT (IDM-NDT) registers the point cloud in three rounds by iteratively decreasing the voxel size. The schematic diagram of the NDT process mentioned above is shown in Fig. 4.
Fault detection and exclusion scheme
While processing the NDT algorithm, the error in height and rotation angle will drift with time. It leads to error propagation and NDT failure, resulting from the miss-registration caused by the large offset in translation and rotation output from previous NDT (Al et al., 2017). To this end, FDE mechanism (Akai et al., 2017) is added after the NDT process to detect the faults and exclude them from LiDAR-SLAM-based navigation solution. The concept of FDE applied in this research is described in Fig. 5. The FDE mechanism operates in two steps: the LiDAR Mapping and LiDAR Odometry. Due to NDT being sensitive to the height offset, FDE for LiDAR Mapping can constraint the translation offset in height and the rotation in pitch and roll, then update the transformation matrix to register the point cloud again and build robust dynamic map for autonomous vehicle without HD map. For the FDE in LiDAR Odometry, it compares the initial guess and the initial guess added with NDT, then outputs a relatively accurate one which is treated as the navigation solution outcome of LiDAR-SLAM.
Experiments
Equipment setup
The sensors for experiment setup were mounted on the top of a vehicle as shown in Fig. 6, including LiDAR, the VLP16, and the antennas. The initial guesses of INS and GNSS were received by tactical grade IMU, the Novatel PwrPak7; while the reference was collected by the navigation grade IMU GNSS, the iMAR-RQH. The reference was computed by commercial INS/GNSS processing software with EKF using the Tightly Coupled scheme in two-step smoothing, the forward and backward sequentially. For more information about the performance of the two IMUs is shown in Table 1.
Test field selection
The experiment took place around the Taiwan Cheng Kung University campus. To examine how the initial pose offset will affect LiDAR-SLAM-based PNT estimation, two test fields were selected. One was in open sky area, which can receive steady GNSS signal as Fig. 7 shows, and the other was in the GNSS challenging environment, which might lead to worse initial pose offset. The route is plotted in Fig. 8. The red line represents the reference, the blue line represents the INS/GNSS integrated navigation solution, and the green line represents the GNSS stand-alone navigation solution. To better show the GNSS positioning accuracy over time, the Position Dilution of Precision (PDOP) values were recorded in Fig. 9. It can tell that the PDOP values are relatively small in the open sky area, but large in the GNSS-challenging environment due to signals blocked by the surrounding buildings or the unevenly geometric distribution of the satellites.
Point cloud data preprocessing
To utilize the reliable point cloud to process NDT, for the points whose Euclidean distances to the transmitter are larger than a certain distance, the pulses are more possible be refracted by obstacles in line-of-sight during emission and transmission. Meanwhile, the points that are too close to LiDAR also might be refracted by adjacent sensors. Therefore, only the points within a predefined distance are extracted to process NDT.
The fixed frame in this experiment was formed by merging the previous five frames as the sliding window to reduce computational time and constraint error propagation. In the NDT process every frame of the point cloud was adopted to construct a more robust dynamic map, because the point cloud received by VLP-16 is too sparse. In this paper, the voxel size is decreased from 2.5 to 1.5 m, and then to 1 m for each round of the NDT process, sequentially.
Results and discussion
Results in open sky area
For mapping evaluation, Fig. 10 shows the dynamic maps built with two different initial guesses in the open sky area. Figure 10a and c is the dynamic map built with INS/GNSS-based initial guess, while Fig. 10b and d is constructed with GNSS-based initial guess. As Fig. 10 shows, in the open sky area GNSS can provide a reliable initial guess for INS/GNSS integrated navigation solution and GNSS stand-alone navigation solution, although GNSS stand-alone system cannot provide rotation information. At the same time, FDE constraints the drift in height and the offsets in rotation, which turns out two initial guesses methods can help construct steady dynamic map. For statistical analysis, the mean errors of INS/GNSS-based and GNSS-based solutions generated from LiDAR SLAM in open sky area under three different mechanisms are given in Tables 2 and 3, where the percentage of improvement for the mechanisms is also calculated by subtracting and dividing the mean error of initial guess.
In Tables 2 and 3 the along-track means the longitudinal or the movement direction of the vehicle, while the cross-track means the lateral direction with respect to the right-handed system. It can be found out that with the conventional navigation method both the initial guesses for INS/GNSS and GNSS stand-alone navigation solutions can provide accurate localization. While applying initial guesses with NDT, the errors in along-track affect the 3D localization accuracy with worse by 377.27% and 348.38% for INS/GNSS-based and GNSS-based navigation solutions, respectively. Due to fewer features in the along-track direction for scan matching the errors are large, while cross-track errors can be constrained by man-made structures, e.g., walls, buildings, and curbs, which can provide robust features for NDT scan matching. It’s worth noting that due to the initial guesses with FDE mechanism in LM, the drift in height can be maintained to a certain extent. Finally, the previous outcome is added with the FDE mechanism in LO. However, the accuracy is not much improved much in both INS/GNSS-based and GNSS-based navigation solutions. Theoretically speaking, the accuracy shall be further improved, yet they are similar to initial guesses, it is because the conventional methods are reliable enough.
The trajectories of navigation solutions mentioned in Tables 2 and 3 are plotted in Fig. 11. The red line represents the reference, the purple line represents the initial guess, the green line represents the initial guess added with NDT and FDE (LM), and the blue dashed line represents the initial guess added with NDT and FDE (LM and LO).
Results in GNSS challenging environment
Mapping evaluation in GNSS challenging environment is depicted in Fig. 12, and the dynamic maps are built with INS/GNSS integrated navigation solution and GNSS stand-alone navigation solution. In Fig. 12b and d, due to GNSS signal disturbance and lacking rotation information from INS, the dynamic map built with GNSS-based initial guess after NDT scan matching is unstable. The reason is probably caused by inaccurate heading angle based on GNSS position, while GNSS positioning is unreliable in this environment, which leads to large translation and rotation offsets at the same time. Therefore, it causes NDT failure. Compared to Fig. 12b and d, the assistance of INS and EKF constrains the offsets to a certain extent in translation and rotation, then constructs robust dynamic maps in Fig. 12a and c, respectively.
The statistical analysis is given in Tables 4 and 5. One can find out the mean errors in the two tables remain a big gap compared with the results in the open sky area. Compared with the conventional methods, INS/GNSS integrated navigation solution performs steady, while the positioning errors of GNSS stand-alone system reach several meters, especially in height. Under the circumstance with the limitation set by the FDE mechanism in LM, it can significantly reduce the mean error in height of GNSS from 7 to 0.47 m with an improvement by 69.62%. However, the application of NDT in the GNSS challenging environment shares the same characteristics as the results in the open sky area. Lacking robust features in the along-track direction leads to a relatively a large error in this direction in a comparison with the cross-track error. Finally, applying an aid with the FDE mechanism in LO, a significant improvement in accuracy can be achieved in the GNSS-challenging environment, 8.33% for INS/GNSS-based navigation solution, while 73.81% for GNSS-based navigation solution. The trajectories of navigation solutions mentioned in Tables 4 and 5 are plotted in Fig. 13.
To sum up, in the open sky area both the INS/GNSS integrated solution and the DGNSS solution can achieve the lane-level navigation grade accuracy (0.5 m) without LiDAR assistance. However, in the GNSS challenging environment with unreliable initial guess, the FDE refuses to apply a false initial guess, and the LiDAR shows error constraint ability by scan to dynamic map. Meanwhile, the other application of the FDE effectively assist the system to output more accurate navigation solution, especially in GNSS challenging scenario.
Conclusions
This paper analyzes the performance with the different initial guesses for the LiDAR-SLAM-based PNT estimation system through the NDT scan matching. The initial guesses for LiDAR SLAM are received by conventional sensors, one is the GNSS stand-alone navigation system and the other is the integration of INS/GNSS after the EKF Loosely Coupled scheme. The low-cost LiDAR sensor, the VLP16, can only receive the sparse point cloud, so it has more limitations while doing scan matching. Therefore, the NDT method is selected to realize distribution-based scan matching between consecutive point clouds. However, the height will drift with time in the raw NDT process, while NDT is sensitive to initial pose offset. To this end, the FDE mechanism is applied sequentially, which is for LiDAR Mapping and LiDAR Odometry.
To test the effect of the initial pose offset on the LiDAR-SLAM-based PNT system, the experiment was conducted with two scenes: an open sky area and GNSS challenging environment. The results turn out that conventional navigation sensors can provide more accurate navigation solution than the one adding NDT in open sky area. As the conventional method can reach where-in-lane level grade accuracy (0.5 m), and there are fewer robust man-made structures in along-track direction for NDT scan matching.
However, in GNSS-challenging environment, it’s obvious that in the environment with less reliable GNSS signal, the INS/GNSS integrated shows a better navigation result than DGNSS stand-alone solution, but it still falls within lane level navigation grade accuracy (1.5 m). Although with unreliable initial guess, the application with NDT and FDE works well with the accuracy of where-in-lane level grade (0.5 m) with the INS/GNSS integrated system and 74% improvement in the navigation accuracy with the DGNSS stand-alone system.
For future work, the FDE mechanism will be added before the initial guess is treated as the input of LiDAR-SLAM-based PNT system, to remove unreliable positioning results in the GNSS-challenging area. It can also make the initial guesses more robust and, output a more accurate navigation solution after the LiDAR-SLAM-based PNT system.
Availability of data and materials
The INS/GNSS/LiDAR data applied in this research were collected by real tests. In addition, if required, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- AKF:
-
Adaptive Kalman filter
- DG:
-
Direct georeferencing
- DGNSS:
-
Differential global navigation satellite system
- EKF:
-
Extended Kalman filter
- FDE:
-
Fault detection and exclusion
- GNSS:
-
Global navigation satellite system
- GPS:
-
Global positioning system
- HD Map:
-
High definition map
- ICP:
-
Iterative closest point
- IE:
-
Inertial explorer
- IMU:
-
Inertial measurement unit
- INS:
-
Inertial navigation system
- LC:
-
Loosely coupled
- LiDAR:
-
Light detection and ranging
- LO:
-
LiDAR odometry
- LOAM:
-
Lidar odometry and mapping
- LM:
-
LiDAR mapping
- NDT:
-
Normal distribution transform
- NHC:
-
Non-holonomic constraints
- NLOS:
-
Non-Line-Of-Sight
- PDOP:
-
Position dilution of precision
- PNT:
-
Positioning, navigation and timing
- Radar:
-
Radio detection and ranging
- RTS:
-
Rauch–Tung–Striebel
- SAE:
-
Society of automotive engineers
- SLAM:
-
Simultaneously localization and mapping
- UAV:
-
Unmanned aerial vehicle
- ZUPT:
-
Zero velocity update
References
Aghili, F., & Su, C. Y. (2016). Robust relative navigation by integration of ICP and adaptive Kalman filter using laser scanner and IMU. IEEE/ASME Transactions on Mechatronics, 21(4), 2015–2026.
Akai, N., Morales, L. Y., Takeuchi, E., Yoshihara, Y., & Ninomiya, Y. (2017). Robust localization using 3D NDT scan matching with experimentally determined uncertainty and road marker matching. In 2017 IEEE intelligent vehicles symposium (IV) (pp. 1356–1363). IEEE.
Al Hage, J., El Najjar, M. E., & Pomorski, D. (2017). Multi-sensor fusion approach with fault detection and exclusion based on the Kullback-Leibler divergence: Application on collaborative multi-robot system. Information Fusion, 37, 61–76.
Amiri-Simkooei, A. R. (2018). Parameter estimation in 3D affine and similarity transformation: Implementation of variance component estimation. Journal of Geodesy, 92(11), 1285–1297.
Biber, P., & Straßer, W. (2003). The normal distributions transform: A new approach to laser scan matching. In Proceedings 2003 IEEE/RSJ international conference on intelligent robots and systems (IROS 2003) (Cat. No. 03CH37453) (Vol. 3, pp. 2743–2748). IEEE.
Chen, S., Zhou, B., Jiang, C., Xue, W., & Li, Q. (2021). A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization. Remote Sensing, 13(14), 2720. https://doi.org/10.3390/rs13142720
Cheng, Y., & Wang, G. Y. (2018). Mobile robot navigation based on lidar. In 2018 Chinese control and decision conference (CCDC) (pp. 1243–1246). IEEE.
Chiang, K. W., Lin, Y. C., Huang, Y. W., & Chang, H. W. (2009). An ANN–RTS smoother scheme for accurate INS/GPS integrated attitude determination. GPS Solutions, 13(3), 199–208.
Chiang, K. W., Tsai, G. J., Chang, H. W., Joly, C., & El-Sheimy, N. (2019). Seamless navigation and mapping using an INS/GNSS/grid-based SLAM semi-tightly coupled integration scheme. Information Fusion, 50, 181–196.
Deng, Q., Sun, H., Chen, F., Shu, Y., Wang, H., & Ha, Y. (2021). An optimized FPGA-based real-time NDT for 3D-LiDAR localization in smart vehicles. IEEE Transactions on Circuits and Systems II: Express Briefs, 68(9), 3167–3171.
Gao, Y., Liu, S., Atia, M. M., & Noureldin, A. (2015). INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm. Sensors, 15(9), 23286–23302.
Groves, P. D., & Jiang, Z. (2013). Height aiding, C/N0 weighting and consistency checking for GNSS NLOS and multipath mitigation in urban areas. The Journal of Navigation, 66(5), 653–669.
Liu, R., Wang, J., & Zhang, B. (2020). High definition map for automated driving: Overview and analysis. The Journal of Navigation, 73(2), 324–341. https://doi.org/10.1017/S0373463319000638
Magnusson, M. (2009). The three-dimensional normal-distributions transform: an efficient representation for registration, surface analysis, and loop detection. Ph.D. Dissertation, orebro university, orebro, sweden.
Magnusson, M., Nuchter, A., Lorken, C., Lilienthal, A. J., & Hertzberg, J. (2009). Evaluation of 3D registration reliability and speed-A comparison of ICP and NDT. In 2009 IEEE international conference on robotics and automation (pp. 3907–3912). IEEE.
Mur-Artal, R., Montiel, J. M. M., & Tardos, J. D. (2015). ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Transactions on Robotics, 31(5), 1147–1163.
Nassar, S. (2003). Improving the inertial navigation system (INS) error model for INS and INS/DGPS applications (pp. 10–32). Ph.D. Dissertation, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada.
Noureldin, A., Karamat, T. B., & Georgy, J. (2013). Fundamentals of inertial navigation, satellite-based positioning and their integration. Springer.
Parvazi, K., Farzaneh, S., & Safari, A. (2020). Role of the RLS-VCE-estimated stochastic model for improvement of accuracy and convergence time in multi-GNSS precise point positioning. Measurement, 165, 108073.
Rahmani, Y., Alizadeh, M. M., Schuh, H., Wickert, J., & Tsai, L. C. (2020). Probing vertical coupling effects of thunderstorms on lower ionosphere using GNSS data. Advances in Space Research, 66(8), 1967–1976.
Reshetyuk, Y. (2009). Self-calibration and direct georeferencing in terrestrial laser scanning Ph.D. Dissertation, University of Gävle, Gävleborg, Sweden.
Särkkä, S. (2008). Unscented Rauch--Tung--Striebel smoother. IEEE Transactions on Automatic Control, 53(3), 845–849.
Shin, E. H. (2005). Estimation techniques for low-cost inertial navigation. UCGE report, 20219.
Shin, E. H., & El-Sheimy, N. (2002). Accuracy improvement of low cost INS/GPS for land applications. In Proceedings of the 2002 national technical meeting of the institute of navigation (pp. 146–157).
Stephenson, S. (2016). Automotive applications of high precision GNSS. Ph.D. Dissertation, University of Nottingham, Nottingham, UK.
Teunissen, P. J., & Amiri-Simkooei, A. R. (2008). Least-squares variance component estimation. Journal of Geodesy, 82(2), 65–82.
Wang, W. Q. (2016). Overview of frequency diverse array in radar and navigation applications. IET Radar, Sonar & Navigation, 10(6), 1001–1012.
Wen, W., Hsu, L. T., & Zhang, G. (2018). Performance analysis of NDT-based graph SLAM for autonomous vehicle in diverse typical driving scenarios of Hong Kong. Sensors, 18(11), 3928. https://doi.org/10.3390/s18113928
Yoshimura, T., & Hasegawa, H. (2004). Effects of post-processed and real-time DGPS on the precision and accuracy of GPS positioning in forested areas. Journal of the Japan Forest Engineering Society, 19(2), 135–140.
Zangeneh-Nejad, F., Amiri-Simkooei, A. R., Sharifi, M. A., & Asgari, J. (2018). Recursive least squares with additive parameters: Application to precise point positioning. Journal of Surveying Engineering, 144(4), 04018006.
Zhang, J., & Singh, S. (2014). LOAM: Lidar odometry and mapping in real-time. Robotics: Science and Systems., 2, 9.
Zhou, B., Tang, Z., Qian, K., Fang, F., & Ma, X. (2017). A lidar odometry for outdoor mobile robots using ndt based scan matching in gps-denied environments. In 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER) (pp. 1230–1235). IEEE.
Acknowledgements
Not applicable.
Funding
Authors would like to acknowledge the financial support provided by the MOST Taiwan with the project no. 109-2121-M-006-011-MY3.
Author information
Authors and Affiliations
Contributions
KC is the supervisor who proposed the idea and modified this paper; YC executed the experiment and analysis to draft the manuscript; SS made suggestions for the framework and participated in architecture construction; MT assisted in article revision. All the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chiang, K., Chiu, Y., Srinara, S. et al. Performance of LiDAR-SLAM-based PNT with initial poses based on NDT scan matching algorithm. Satell Navig 4, 3 (2023). https://doi.org/10.1186/s43020-022-00092-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43020-022-00092-0