Abstract
This research work compares the performance of a conventional solar still (CSS) with a modified CSS (MSS) that uses Plexiglas and jute fabric to increase heat localization and thin-film evaporation. Two solar stills with identical 1 m2 basin areas were designed and constructed using Fiberglass reinforced plastic for experimentation. A heat transfer model based on linear regression was utilized in the theoretical analysis. Performance analysis was determined based on exergy analysis, and a cost per litre was also included in the research work. It was found that the MSS achieved a distillate output 35% higher than the CSS. Also, MSS led to a 45% reduction in the costs of distillate output of water than CSS.
Similar content being viewed by others
1 Introduction
The availability of secure and uncontaminated potable water, a vital necessity for human existence, is progressively declining annually. The depletion is mainly related to the rapid rise of the world population and the rising industrial sector. The global water scarcity issue is a significant challenge almost every country encounters. Many conventional methods to convert brackish water into potable water rely on fossil fuels. With the depletion of fossil fuels anticipated in the future, there is now a change in attention towards economically feasible, renewable, and sustainable methods to address the increasing needs of the population. Solar energy is an excellent option because of its abundance, renewability, sustainability, and environmental friendliness [1]. The Conventional Solar Still (CSS) is a passive device that works on the greenhouse effect and harnesses solar energy to desalinate brackish or saline water. It is an effective solution in areas lacking robust power infrastructure, especially in arid and coastal regions. Despite its merits, CSS needs help with low distillate output and efficiency. Therefore, the scientific community is actively working to enhance CSS performance, making it more widely available to diverse populations [2].
Numerous researchers have provided a comprehensive chronological overview of CSS development [2,3,4]. Factors such as the inclination of the glass cover, geographical location, seasonal variations, and salt concentration in the feedwater have been investigated [4,5,6,7]. Additionally, enhancements have been explored using porous fins, wax-filled finned cups, dried pond fibres, and small solar fountains [8,9,10,11,12,13,14,15]. Many CSS devices augmented with nanofluids and sensible heat storage materials have been studied to increase distillate output [16,17,18,19,20,21,22]. A detailed technical overview and recent developments have been reported by Singh et al. [23]. Peng and Sharshir have presented a detailed review of the performance of multi-stage solar stills [24].
Another area of focus has been using phase change materials (PCMs) to store sensible and latent heat, resulting in improved CSS performance. Various PCMs have been explored, such as copper oxide micro-flakes, graphite, cuprous oxide-coated absorber plates, and nanofluids [25,26,27]. Furthermore, porous media, shape-stabilizing PCMs, and different wick materials have enhanced CSS performance [28,29,30,31,32,33,34]. In an experimental study, Nagaraju et al. [35] have reported the integration of sand troughs with the single slope solar still.
To address the issue of water scarcity, this study explores a novel approach that centres on thin-film evaporation and heat localization. A Plexiglas (with holes) floating on the water basin is covered in jute and placed in the solar still. The Plexiglas acts as an insulator, concentrating heat on the jute cover, resulting in a thin film of water with low heat capacity, which evaporates rapidly. The research objectives encompass understanding the thermodynamic behaviour of these modifications, assessing their economic viability, and conducting a comparative exergy and economic analysis of the CSS and Modified Solar Stills (MSS).
2 Experimental setup
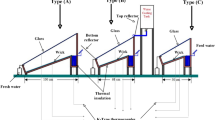
Two identical solar stills were manufactured using Fiberglass Reinforced Plastic (FRP) having a thickness of 5 mm. The chosen thickness ensures the stills are durable during transportation while concurrently minimizing the rate of heat loss (as has also been mentioned by several past studies [36,37,38]). Both solar stills have different vertical wall heights, with a lower wall of 0.2 m and a higher wall of 0.48 m. A Galvanized Iron tray measuring 1 m \(\times\) 1 m \(\times\) 0.1 m contained the water within the basin. The inside and the basin water tray were coated with black paint to enhance the absorption of incident solar radiation. An iron transparent glass cover with a thickness of 4 mm was placed on top of the solar stills at an inclination angle of 15.6°. One of the solar stills was modified by adding Plexiglas and jute during the experiments, referred to as the MSS, while the other was referred to as CSS for comparison. The purpose of using Plexiglas is to hinder the thermal energy transfer directly to the basin water due to its low thermal conductivity, resulting in heat localization on top of the Plexiglas sheet. This will enhance the water evaporative heat transfer rate ( \({\dot{q}}_{ew}\)) from the jute cloth above it.
Both solar stills were positioned to face southward. Schematic diagrams of the CSS and MSS configurations can be observed in Fig. 1.
Most of the incident solar radiation that strikes the glass cover is transmitted through the water in the basin, with the remaining portion being absorbed by the tray holding the water. The absorbed solar radiation raises the temperature of the water, leading to increased \({\dot{q}}_{ew}\) driven by the greenhouse effect. This results in the upward movement of water vapour from the water surface to the inner condensing cover (Tci), where it condenses, releasing its latent heat of vaporization. The condensed water forms a thin film on the underside of the glass. As it accumulates a sufficient mass, it drips into the distillate collection tray for potable water collection.
A Plexiglas float is positioned on the basin water surface in the MSS. The Plexiglas is enveloped with a layer of jute cloth from above, with several holes drilled into it to allow water to contact the jute from beneath. Capillary action causes the water to rise within the jute cloth, forming an extremely thin film of water on its surface. Positioned holes ensure uniform water distribution, preventing uneven wetting and promoting consistent capillary rise. Moreover, the chosen hole distances form an optimal thin water film on the jute cloth, maximizing its efficiency in promoting evaporation. Also, it has been observed that the chosen hole spacing has regulated the water flow, preventing excessive saturation and ensuring uniform wetting of the jute cloth. Even hole distribution aids in maintaining a consistent and efficient heat transfer to the jute cloth, promoting optimal conditions for the distillation process.
Solar radiation that falls on the jute surface rapidly heats the water due to its minimal heat capacity, as there is a relatively small quantity of water on the surface. This leads to the quick vaporization of the water from the jute surface, primarily due to heat localization. Therefore, the Plexiglas serves a dual purpose: it supports the jute cloth and acts as a heat insulator. This insulating property prevents the solar radiation that falls on the jute from being trapped, thanks to Plexiglas’s low thermal conductivity, which typically ranges from 0.17 to 0.2 W m−1 K−1. As a result, heat is localized, enhancing the system’s efficiency.
The jute material used in this setup has specific characteristics, including a weight of 0.4 kg, fibre fineness of 2.08 Tex, and a density of 1.45 g cm−3. Over time, salt may accumulate and form a layer on the surface of the jute cover. To maintain efficiency, this layer needs to be cleaned every month and can be reused. Figure 2 shows the schematic diagram of plexiglass with holes.
The MSS and CSS temperatures were monitored using K-type thermocouples (specifically K 7/32-2 C-TEF). Temperature data was recorded using a DTC324A-2 temperature indicator. Incident solar radiation was measured using an LX-107 solar power meter. Hourly distillate production was collected and measured using a Borosil graduated cylinder. The instruments used for these measurements had specified operating ranges, accuracies, and standard uncertainties, detailed in Table 1.
The standard uncertainty was calculated using the following expression [39]:
Here, α represents the accuracy of the instruments.
The experiments were conducted in April–May 2020 at Jaypee University of Engineering and Technology in Guna, India. The basin water mass was carefully chosen to be 40 kg, a result of multiple trials, to ensure an optimal water depth and the proper buoyancy of the Plexiglas on the water surface. The experiments had a total duration of 10 h. At hourly intervals throughout the experiments, the following observations were recorded:
-
Temperatures of the glass, basin water, atmospheric conditions, and jute cloth.
-
Solar radiation intensity.
-
Hourly distillate production.
3 Theoretical background
3.1 Thermodynamic analysis
The primary factor propelling vapour movement within solar still is natural convection. The transfer of heat through convection from the water to the inner condensing surface can be modelled using Newton’s law of cooling, as elaborated in a previous investigation by Dumka and Mishra [40].
In Eq. (1), where Tw and Tci represent the water and glass temperatures, the parameter hcw is initially unknown and needs to be calculated. In the case of natural convection, the Nusselt number (Nu) is influenced by the Prandtl (Pr) and Grashof (Gr) numbers, as described by Bergman et al. [41]:
Equation (2) can also be expressed in an alternative mathematical form known as a power law, as detailed in the work by Dumka et al. [42] and Dumka and Mishra [43]:
The thermal properties of moist air, which are essential for calculating Gr and Pr numbers, have been sourced from Tsilingiris [44,45,46] and employed in this study. The evaluation of convective heat transfer coefficient (hcw) in Eq. (3) requires the determination of the constants C and n. Numerous numerical models, as documented in the literature [47,48,49,50], offer methods to estimate the values of C and n. However, the model that Kumar and Tiwari [51] developed was chosen. This model relies on a simple linear regression technique that is not dependent on the Gr number range. The specific numerical values for C and n obtained from this model are provided below [51].
where, \(y=\text{ln}\left(\frac{{\dot{m}}_{ew}}{R}\right)\), \(x=\text{l}\text{n}(Pr\times Gr)\), and \(R=0.0163\left({P}_{w}-{P}_{ci}\right)\frac{k}{d}\frac{3600}{L}\). Pw, Pci, k, d, and L are the partial pressure of vapour on the water surface, partial pressure of vapour on the Tci, thermal conductivity of vapour, character dimension of still, and latent heat of water, respectively.
With the values of C and n determined, the hcw can be calculated using Eq. (3). Subsequently, the evaporative heat transfer coefficient (hew) and the corresponding \({\dot{q}}_{ew}\)can be derived as follows [50]:
The theoretical distillate output (\({\dot{m}}_{ew}\)) can now be calculated using the following equations, as described in Dumka and Mishra [52]:
Radiative heat transfer is a heat exchange mode that occurs independently within the solar still. This type of heat transfer can be quantified using the formula described in the studies conducted by others [52,53,54,55,56].
Where, \({\dot{q}}_{rw}\) is the radiative heat transfer rate hrw is the radiative heat transfer coefficient which is defined in terms of effective emissivity (\({\epsilon }_{eff}\)) as: \({h}_{rw}={\epsilon }_{eff} \sigma ({T}_{w}+{T}_{ci}+546.2)({\left({T}_{w}+273.15\right)}^{2}+{\left({T}_{ci}+273.15\right)}^{2})\) and \({\epsilon }_{eff}=\frac{1}{\frac{1}{{\epsilon }_{w}}+\frac{1}{{\epsilon }_{ci}}-1}\) .
The overall heat transfer thus can be evaluated as shown in Eq. (10).
where h1w (overall heat transfer coefficient) is the sum of radiative, evaporative, and convective heat transfer coefficients. The concept of energy fractions is a valuable tool for determining the dominant mode of heat transfer within the solar still. These energy fractions can be calculated using the following methods:
The first law efficiency, also known as instantaneous efficiency (ηi), for solar stills can be calculated as follows [50, 57, 58]:
In Eq. (12), I(t) represents the instantaneous solar radiation intensity, while As refers to the water surface area, which is notably larger in the MSS when compared to the CSS.
The first law of efficiency primarily involves comparing different modes of energy transfer within a system. In contrast, second law efficiency provides a more comprehensive understanding of a system’s performance by comparing the quality of energy. Exergy, in this context, refers to the maximum useful work a system can accomplish before reaching a state of thermodynamic equilibrium, often called the “dead state.” A higher exergy or exergy efficiency signifies that a system performs its designated tasks more effectively. This concept is encapsulated in the following expressions (as documented in the references provided: Dumka and Mishra [40], Petela [59, 60], Shoeibi [21], Rashidi et al. [61], and Shoeibi et al. [22]):
Let us expand upon the expressions for \({\dot{Ex}}_{in}\) and \({\dot{Ex}}_{evap}\), representing the input and output exergy to and from solar stills, respectively. These are detailed as follows:
where, \({T}_{a}\) and \({T}_{s}\) are the local atmospheric temperature and the temperature of sun respectively. The exergy destruction, which indicates the loss of exergy or useful work potential within various sections of the solar stills, is calculated as follows:
Where, \({\dot{Ex}}_{dest, basin}\), \({\dot{Ex}}_{dest, glass}\), and \({\dot{Ex}}_{dest,water}\) are the exergy destruction ins basin, glass, and water, respectively. \({\dot{Ex}}_{water}\), \({\dot{Ex}}_{insu}\), \({\dot{Ex}}_{trans(water\to glass)}\), \(\dot{E}{x}_{trans(glass\to air)}\) are the exergy utilized to raise the temperature of saline water, exergy loss trough FRP insulation, exergy transfer from water to glass, and exergy transfer from glass to water respectively. And τ & α are the transmissivity and absorptivity.
3.2 Cost analysis
The capital recovery factor (CRF) and sinking fund factor (SFF), which are used to evaluate economic parameters, can be obtained as follows, as per literature [37, 62, 63]: The formulas for CRF and SFF depend on the life expectancy (\(n{\prime }\)) and the annual interest rate (i), and they are calculated as follows:
CRF and SFF factors are used in economic analysis to determine costs and savings over the life span of a system or investment. The CRF represents the annual payment required to recover the capital investment, while the SFF is used for savings and investments. In the manuscript, the values of \(n{\prime }\) and i were considered as 15 years (which is the typical life span of an FRP still) and 12%, respectively. After determining CRF and SFF, you can calculate the first annual cost (FAC) and annual salvage value (ASV) as described by several researchers [57, 64,65,66,67,68]:
These economic parameters help assess the annual financial aspects of the solar still system, considering factors like depreciation and potential savings over time. Therefore, the annual cost (AC) can be calculated using the following formula, taking into account the initial investment (P), salvage value of salvageable items (S), FAC, and annual maintenance cost (AMC):
The Eq. (23) helps estimate the yearly operating and maintenance costs, including the depreciation and any potential savings due to salvageable items. The annual maintenance cost (AMC) is considered as 15% of the FAC, as described in the work of Dumka and Mishra [10, 58]. Ultimately, the CPL can be calculated following the methodology:
Here, AC represents the annual cost calculated earlier, and AY represents the yearly distillate production in liters. This equation allows you to determine the cost of producing one liter of distillate from the solar still. The calculations, data analysis, and graph generation were carried out using the MATLAB 2015 software platform. The reason for choosing MATLAB is its user-friendly interface and easy-to-implement programming syntax.
4 Result and discussion
Figure 3a illustrates the variation of the measured solar radiation intensity over time. At 9:00 a.m., the recorded value stood at 580 W m−2 during the experimental day. Subsequently, it steadily rose to 990 W m−2 by 1:00 p.m. and gradually decreased, reaching 0 W m−2 by 6:30 p.m.
Figure 3b demonstrates the temperature variations for water, the inner glass, and atmosphere throughout the experimental day. During the experiment, it was observed that the water temperature (Tw) on the jute fabric in the MSS was higher than that in the CSS until about 2:30 p.m. After that time, it started to cool down. The initial elevated temperature within MSS can be attributed to heat confinement effects and a thin water layer on the jute cover. Conversely, with its larger water volume, CSS initially absorbed and retained energy for an extended period. At 9:00 a.m., Tw in MSS surpassed that in CSS by 32%, reaching its difference at 10:30 a.m., with MSS outpacing CSS by 56%. The rapid increase in Tw for MSS is a result of the heating of the thin water layer. By 1:00 p.m., CSS had accumulated substantial energy, reducing the difference in Tw between MSS and CSS to 15%. After 2:30 p.m., as solar radiation began to decrease, the temperature of the water film on the jute fabric in MSS decreased while it increased within CSS. At 3:00 p.m., MSS exhibited a 5% difference compared to CSS, which reduced to 13% by 6:30 p.m. In MSS, the high condensation rate on the (Tci) sustained its temperature higher than that of CSS until 2:00 p.m., after which CSS assumed the lead and retained it until the experiment’s conclusion.
Throughout the experiment, It was found that the heat transfer coefficient related to evaporation, represented as hew, exhibited higher values in the MSS when compared to the CSS (as indicated in Fig. 3c). The difference in performance can be attributed to the impact of heat confinement and water evaporation from the jute cover caused by surface tension in MSS compared to CSS. At the experiment’s outset, hew in MSS exceeded that in CSS by 55% due to the higher water temperature on the jute cover within MSS in contrast to the water within CSS. As the day progressed, there was an enhancement in the value of hew for MSS compared to CSS. The highest recorded value of hew occurred at 1:30 p.m., with MSS exceeding CSS by 216%. Subsequently, there was a marked decline in hew for MSS as solar radiation intensity diminished, resulting in a 66% reduction from the peak value at 1:30 p.m. by the experiment’s conclusion at 6:30 p.m. At 6:30 p.m., MSS held a 65% advantage over CSS.
Conversely, CSS maintained a relatively consistent hew value after 1:00 p.m., around an average of 12.2 W m-2 K-1. This stability is attributable to the substantial heat capacity of water within CSS. To sum it up, there was an overall enhancement of 140% in the value of hew for MSS in comparison to CSS, primarily attributed to the effects of heat confinement and thin film evaporation.
Figure 3d illustrates the time-dependent changes in the hcw from the water surface to the Tci in MSS and CSS. Throughout the experimentation, the hcw for the MSS was observed to be higher than that of the CSS. This difference can be attributed to the greater temperature differential between the evaporating and condensing surfaces in MSS due to heat localization. From the experimental results, MSS held the lead over CSS by 17.49%. The highest value of hcw in MSS was obtained at 12:30 p.m., standing at 142% above its CSS. In contrast, CSS achieved its peak value at 4:30 p.m., trailing MSS by 114%. The heat localization significantly increased the value of hcw for MSS by 110% compared to CSS. At 6:30 p.m., MSS maintained a lead of 95% over CSS at the experiment’s end.
Figure 4a illustrates the temporal evolution of the hrw from the water surface to the Tci in MSS and CSS both. It was found that the hrw value gradually increased from 9:00 a.m. to 1:30 p.m. and subsequently declined. Initially, the values were 5.0 W m-2 K-1 for CSS and 5.3 W m-2 K-1 for MSS. At 9:00 a.m., MSS held a 6% advantage over CSS. The water surface temperatures (Tw) and Tci influence the radiative heat transfer coefficient. As the temperature difference between these two variables diminished after 1:30 p.m., there was a reduction in the hrw value for MSS compared to CSS. Overall hrw value for MSS was 3% higher than that of CSS.
Figure 4b depicts the time-dependent changes in the, h1w, which essentially represents the cumulative effect of all internal heat transfer coefficients within the solar stills. This coefficient signifies the collective efficiency of heat transfer from the evaporating surface to the condensing surface in the solar still. In addition, Fig. 4c provides a representation of the energy fractions that reveal the predominant mode of heat transfer within the still. Furthermore, owing to the influences of heat localization and the presence of a thin water film in MSS, the effectiveness of Few was notably superior compared to CSS from 9:00 a.m. to 6:00 p.m. As the day progressed and solar radiation diminished, the fraction of Few, decreased in MSS. Consequently, the overall improvement in heat transfer from the water to the glass in MSS was estimated to be 87% higher than in CSS.
Figure 4c depicts the variations in energy fractions for MSS and CSS over time during the experimental day. Around 11:00 a.m., there was a sudden increase in solar radiation intensity, resulting in a rise in the water temperature. Consequently, the hew began to take the lead. It continued to rise until it reached its peak value, surpassing both the radiative (hrw) and convective (hcw) heat transfer coefficients. After 1:00 p.m., hew began to decline, corresponding to the gradual reduction in solar radiation intensity. This observation highlights that the most significant portion of energy transfer from the evaporating surface to the condensing cover is attributed to evaporative heat transfer, while the smallest contribution comes from convective heat transfer. Hence, the highest energy fraction is for evaporative and least for convective.
Figure 4d illustrates the distillate output for both MSS and CSS over time, as seen in experimental and theoretical results. The experimental distillate output for MSS was 35% higher than that for CSS during the 11:00 am during the experimental day. This enhancement can be attributed to rapid evaporation from the jute cloth and heat localization. MSS consistently demonstrated a notably higher distillate output in the initial seven hours than CSS, primarily due to the heat localization in the evaporation process. However, as the day progressed, the distillate output of MSS gradually decreased, influenced by the reduction in radiation intensity and the greater heat capacity of water in CSS. The Kumar and Tiwari [51] theoretical models displayed 11% and 25% deviations from the experimental results.
Figure 5a illustrates the variations in theoretical and experimental instantaneous efficiencies for the CSS and the MSS over time. At 9:00 a.m., the experimental efficiency of MSS surpassed that of CSS by 59%, while its theoretical efficiency lagged behind CSS by 90.5%. By 11:00 a.m., when the distillate output was minimal, theoretical and experimental efficiencies reached their lowest values, with values of 0.9 and 1.4% for MSS and 14.2 and 14.3% for CSS, respectively. An interesting observation can be made from 2:30 p.m. to 4:30 p.m., during which the instantaneous efficiency of MSS decreased to 11% relative to the experimental distillate output concerning incident solar radiations. This decline in instantaneous efficiency in MSS resulted in a significant drop in its theoretical efficiency compared to the experimental efficiency. By 3:30 p.m., MSS’s experimental and theoretical efficiencies were 15 and 54% higher than those of CSS, respectively. It has been found that heat localization had a notable positive impact on the average instantaneous efficiency of MSS, enhancing it by 18%. However, it is important to note that the data is presented only up to 3:30 p.m., as beyond 4:00 p.m., there was a sharp decrease in solar radiation intensity compared to distillate output.
Figure 5b illustrates the variations in exergy efficiency for both the MSS and CSS over time. Exergy, which represents the maximum possible work obtainable from a system in equilibrium with its surroundings, is a measure of the portion of energy available for practical use. The introduction of heat localization had a substantial positive impact on the exergy efficiency of MSS compared to CSS. Between 9:00 a.m. and 10:00 a.m., the exergy efficiency of MSS was only slightly higher than CSS, at 84%. However, after 11:00 a.m., MSS experienced a significant increase in exergy efficiency compared to CSS. By 11:30 a.m., MSS led CSS by an impressive 429%. The highest increase in exergy efficiency for MSS was observed at 1:30 p.m., reaching 608% higher than CSS. Overall, due to heat localization, the exergy efficiency of MSS surpassed that of CSS by 114%. This signifies the remarkable improvement in the practical usability of energy achieved with heat localization in the MSS compared with CSS.
Figure 5c presents the exergy destruction in the basin, Tci, and water for both the MSS and CSS over time. Evaluating exergy destruction helps assess the performance of solar stills by examining the wastage of available energy. The highest exergy destruction was observed in the basin area, while the minimum was found in the glass and water sections. The peak exergy destruction in the basin area for MSS occurred at 11:30 a.m., measuring 642 W, which was 25% lower than CSS. This indicates that the heat localization in MSS has substantially reduced exergy destruction in the basin area. For CSS, the maximum values of exergy destruction in the glass and water sections were similar or 41 W. In contrast, for MSS, these values were 52 and 30 W, respectively. This data reflects the differences in exergy destruction between both solar stills, highlighting the advantages of heat localization in reducing the wastage of available energy.
Table 2 provides a detailed breakdown of the component costs and salvage values for the MSS and CSS. The salvage value reflects the estimated worth of the equipment after a 15-yr operational lifespan, which is the standard life expectancy for FRP solar stills. This information is essential for evaluating the long-term cost-effectiveness and return on investment for these solar stills.
Table 3 presents an overview of various factors and their associated costs for calculating CPL for the MSS and CSS. Using jute-covered Plexiglas in MSS resulted in a noteworthy reduction of 45% in the distillate output compared to CSS. This indicates that the MSS represents a promising option to enhance its performance in distillate output and economic efficiency.
Table 4 presents the average values for overall heat transfer coefficient, exergy, and instantaneous efficiency of CSS and MSS. The distillate output represents the cumulative distillate output obtained over a full day of observation (11 h).
5 Conclusions
The following points are concluded from the present research work:
-
i.
MSS found significant advantages from heat localization during the peak radiation periods, resulting in a heightened temperature differential between the inner condensing cover and the evaporating surface compared to CSS.
-
ii.
MSS significantly enhances evaporative, convective, radiative, and overall heat transfer coefficients. MSS experiences improvements of 140, 110, 3 and 87%, to CSS.
-
iii.
MSS leverages capillary action in the jute fabric, leading to escalated evaporation rates and a 35% augmentation in the cumulative distillate output relative to CSS.
-
iv.
The theoretical outcomes from the Kumar and Tiwari model exhibit a minimal deviation of 11% for MSS.
-
v.
The MSS demonstrates improved exergy and instantaneous efficiency, with respective increases of 114 and 19% compared to the CSS.
-
vi.
During the first six hours of the experimental day, MSS exhibits a significant decrease in exergy degradation compared to CSS, mostly due to increased rates of evaporation and condensation.
-
vii.
The CPL of distillate derived from MSS is subject to a 45% reduction compared to CSS, rendering it a more cost-effective selection.
In conclusion, augmenting solar still with jute cloth and Plexiglas enhances its distillate output, efficiency, and economic viability.
Availability of data and materials
Data will be available as per the reasonable request.
Change history
27 March 2024
A Correction to this paper has been published: https://doi.org/10.1186/s42834-024-00210-4
References
WWC. 8th World Water Forum Highlights. Marseille: World Water Council; 2018.
Kabeel AE, El-Agouz SA. Review of researches and developments on solar stills. Desalination. 2011;276:1–12.
Ayoub GM, Malaeb L. Developments in solar still desalination systems: A critical review. Crit Rev Env Sci Tec. 2012;42:2078–112.
Abujazar MSS, Fatihah S, Rakmi AR, Shahrom MZ. The effects of design parameters on productivity performance of a solar still for seawater desalination: A review. Desalination. 2016;385:178–93.
Kabeel AE, Muthu Manokar A, Sathyamurthy R, Prince Winston D, El-Agouz SA, Chamkha AJ. A review on different design modifications employed in inclined solar still for enhancing the productivity. J Sol Energy Eng. 2019;141:031007.
Khalifa AJN. On the effect of cover tilt angle of the simple solar still on its productivity in different seasons and latitudes. Energ Convers Manage. 2011;52:431–6.
Dumka P, Mishra DR. Influence of salt concentration on the performance characteristics of passive solar still. Int J Ambient Energy. 2021;42:1463–73.
Afrand M, Karimipour A. Theoretical analysis of various climatic parameter effects on performance of a basin solar still. J Power Technol. 2017;97:44–51.
Panchal H, Sathyamurthy R. Experimental analysis of single-basin solar still with porous fins. Int J Ambient Energy. 2020;41:563–9.
Dumka P, Mishra DR. Comparative experimental evaluation of conventional solar still (CSS) and CSS augmented with wax-filled metallic finned-cups. FME Trans. 2020;48:482–95.
Suraparaju SK, Natarajan SK. Performance analysis of single slope solar desalination setup with natural fibre. Desalin Water Treat. 2020;193:64–71.
Suraparaju SK, Dhanusuraman R, Natarajan SK. Performance evaluation of single slope solar still with novel pond fibres. Process Saf Environ. 2021;154:142–54.
Suraparaju SK, Natarajan SK. Augmentation of freshwater productivity in single slope solar still using Luffa acutangula fibres. Water Sci Technol. 2021;84:2943–57.
Dumka P, Sharma S, Gautam H, Gunawat C. Impact of solar powered fountain on the performance of conventional solar still. Int J Eng Res Technol. 2021;10:109–12.
Karthick M, Joe Patrick Gnanaraj S, Appadurai M, Jeshurun SB. Productivity enhancement of a single slope solar still with energy storage medium. Mater Today Proc. 2022;60:889–93.
Sangeetha A, Shanmugan S, Alrubaie AJ, Jaber MM, Panchal H, Attia MEH, et al. A review on PCM and nanofluid for various productivity enhancement methods for double slope solar still: Future challenge and current water issues. Desalination. 2023;551:116367.
Kabeel AE, Omara ZM, Essa FA, Abdullah AS, Arunkumar T, Sathyamurthy R. Augmentation of a solar still distillate yield via absorber plate coated with black nanoparticles. Alex Eng J. 2017;56:433–8.
Elango T, Kannan A, Murugavel KK. Performance study on single basin single slope solar still with different water nanofluids. Desalination. 2015;360:45–51.
Sharshir SW, Peng G, Wu L, Essa FA, Kabeel AE, Yang N. The effects of flake graphite nanoparticles, phase change material, and film cooling on the solar still performance. Appl Energ. 2017;191:358–66.
Mohamed AF, Hegazi AA, Sultan GI, El-Said EMS. Augmented heat and mass transfer effect on performance of a solar still using porous absorber: Experimental investigation and exergetic analysis. Appl Therm Eng. 2019;150:1206–15.
Shoeibi S. Numerical analysis of optimizing a heat sink and nanofluid concentration used in a thermoelectric solar still: an economic and environmental study. Environ Res Eng Manag. 2021;77:110–22.
Shoeibi S, Rahbar N, Abedini Esfahlani A, Kargarsharifabad H. Application of simultaneous thermoelectric cooling and heating to improve the performance of a solar still: An experimental study and exergy analysis. Appl Energ. 2020;263:114581.
Singh SK, Kaushik SC, Tyagi VV, Tyagi SK. Comparative performance and parametric study of solar still: A review. Sustain Energy Techn. 2021;47:101541.
Peng G, Sharshir SW. Progress and performance of multi-stage solar still – A review. Desalination. 2023;565:116829.
Shukla A, Kant K, Sharma A. Solar still with latent heat energy storage: A review. Innov Food Sci Emerg. 2017;41:34–46.
Cheng WL, Huo YK, Nian YL. Performance of solar still using shape-stabilized PCM: Experimental and theoretical investigation. Desalination. 2019;455:89–99.
Kabeel AE, El-Agouz SA, Sathyamurthy R, Arunkumar T. Augmenting the productivity of solar still using jute cloth knitted with sand heat energy storage. Desalination. 2018;443:122–9.
Srivastava PK, Agrawal SK. Winter and summer performance of single sloped basin type solar still integrated with extended porous fins. Desalination. 2013;319:73–8.
Srivastava PK, Agrawal SK. Experimental and theoretical analysis of single sloped basin type solar still consisting of multiple low thermal inertia floating porous absorbers. Desalination. 2013;311:198–205.
Rabhi K, Nciri R, Nasri F, Ali C, Ben Bacha H. Experimental performance analysis of a modified single-basin single-slope solar still with pin fins absorber and condenser. Desalination. 2017;416:86–93.
Alaian WM, Elnegiry EA, Hamed AM. Experimental investigation on the performance of solar still augmented with pin-finned wick. Desalination. 2016;379:10–5.
Abdullah AS, Essa FA, Omara ZM. Effect of different wick materials on solar still performance – a review. Int J Ambient Energy. 2021;42:1055–82.
Rashidi S, Akar S, Bovand M, Ellahi R. Volume of fluid model to simulate the nanofluid flow and entropy generation in a single slope solar still. Renew Energ. 2018;115:400–10.
Natarajan SK, Suraparaju SK, Elavarasan RM, Pugazhendhi R, Hossain E. An experimental study on eco-friendly and cost-effective natural materials for productivity enhancement of single slope solar still. Environ Sci Pollut R. 2022;29:1917–36.
Nagaraju V, Murali G, Bewoor AK, Kumar R, Sharifpur M, Assad MEH, et al. Experimental study on performance of single slope solar still integrated with sand troughs. Sustain Energy Techn. 2022;50:101884.
Tiwari GN, Tiwari AK. Solar Distillation Practice For Water Desalination Systems. New Delhi: Anamaya Publishers; 2008.
Mukherjee K, Tiwari GN. Economic analyses of various designs of conventional solar stills. Energ Convers Manage. 1986;26:155–7.
Sharma M, Tiwari AK, Mishra DR. A review on desalination of water using single slope passive solar still. Int J Dev Res. 2016;6:10002–12.
Holman JP. Experimental Methods for Engineers. 8th ed. New York: McGraw-Hill; 2011.
Dumka P, Mishra DR. Performance evaluation of single slope solar still augmented with the ultrasonic fogger. Energy. 2020;190:116398.
Bergman TL, Lavine AS, Incropera FP, DeWitt DP. Fundamentals of Heat and Mass Transfer. 8th ed. Hoboken: John Wiley & Sons; 2018.
Dumka P, Jain A, Mishra DR. Energy, exergy, and economic analysis of single slope conventional solar still augmented with an ultrasonic fogger and a cotton cloth. J Energy Storage. 2020;30:101541.
Dumka P, Mishra DR. Energy and exergy analysis of conventional and modified solar still integrated with sand bed earth: Study of heat and mass transfer. Desalination. 2018;437:15–25.
Tsilingiris PT. Combined heat and mass transfer analyses in solar distillation systems – The restrictive conditions and a validity range investigation. Sol Energy. 2012;86:3288–300.
Tsilingiris PT. Modeling heat and mass transport phenomena at higher temperatures in solar distillation systems – The Chilton–Colburn analogy. Sol Energy. 2010;84:308–17.
Tsilingiris PT. The application and experimental validation of a heat and mass transfer analogy model for the prediction of mass transfer in solar distillation systems. Appl Therm Eng. 2013;50:422–8.
Tsilingiris PT. Parameters affecting the accuracy of Dunkle’s model of mass transfer phenomenon at elevated temperatures. Appl Therm Eng. 2015;75:203–12.
Clark JA. The steady-state performance of a solar still. Sol Energy. 1990;44:43–9.
Dunkle RV. Solar water distillation, the roof type still, and a multiple effect diffusion still. In: International Heat Transfer Conference. Boulder: Commonwealth Scientific and Industrial Research Organization, Victoria, Australia; 1961. 28–Sep 1.
Kiatsiriroat T, Bhattacharya SC, Wibulswas P. Prediction of mass transfer rates in solar stills. Energy. 1986;11:881–6.
Kumar S, Tiwari GN. Estimation of convective mass transfer in solar distillation systems. Sol Energy. 1996;57:459–64.
Dumka P, Mishra DR. Experimental investigation of modified single slope solar still integrated with earth (I) & (II): Energy and exergy analysis. Energy. 2018;160:1144–57.
Panchal H. Progress in passive solar still for enhancement in distillate output. In: Kumar A, Prakash O, editors. Solar Desalination Technology. Singapore: Springer; 2019.
Panchal HN. Use of thermal energy storage materials for enhancement in distillate output of solar still: A review. Renew Sust Energ Rev. 2016;61:86–96.
Panchal H, Mohan I. Various methods applied to solar still for enhancement of distillate output. Desalination. 2017;415:76–89.
Panchal H, Patel DK, Patel P. Theoretical and experimental performance analysis of sandstones and marble pieces as thermal energy storage materials inside solar stills. Int J Ambient Energy. 2018;39:221–9.
Awasthi A, Kumari K, Panchal H, Sathyamurthy R. Passive solar still: recent advancements in design and related performance. Environ Technol Rev. 2018;7:235–61.
Dumka P, Mishra DR. Energy, exergy and techno-economic analysis of novel solar stills for sea coastal area. Int J Ambient Energy. 2022;43:5207–17.
Petela R. Exergy of Heat Radiation. ASME J Heat Mass Transf. 1964;86:187–92.
Petela R. Exergy of undiluted thermal radiation. Sol Energy. 2003;74:469–88.
Rashidi S, Rahbar N, Valipour MS, Esfahani JA. Enhancement of solar still by reticular porous media: Experimental investigation with exergy and economic analysis. Appl Therm Eng. 2018;130:1341–8.
Shoeibi S, Rahbar N, Esfahlani AA, Kargarsharifabad H. Energy matrices, exergoeconomic and enviroeconomic analysis of air-cooled and water-cooled solar still: Experimental investigation and numerical simulation. Renew Energ. 2021;171:227–44.
Shoeibi S, Kargarsharifabad H, Mirjalily SAA, Zargarazad M. Performance analysis of finned photovoltaic/thermal solar air dryer with using a compound parabolic concentrator. Appl Energ. 2021;304:117778.
Tiwari GN. Economic analysis of some solar energy systems. Energ Convers Manage. 1984;24:131–5.
Shoeibi S, Rahbar N, Abedini Esfahlani A, Kargarsharifabad H. A comprehensive review of Enviro-Exergo-economic analysis of solar stills. Renew Sust Energ Rev. 2021;149:111404.
Sharon H, Reddy KS. Performance investigation and enviro-economic analysis of active vertical solar distillation units. Energy. 2015;84:794–807.
Kumar Singh A, Material conscious energy matrix and enviro-economic analysis of passive ETC solar still. Mater Today Proc. 2021;38:1–5.
Joshi P, Tiwari GN. Energy matrices, exergo-economic and enviro-economic analysis of an active single slope solar still integrated with a heat exchanger: A comparative study. Desalination. 2018;443:85–98.
Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project number (RSPD2024R999), King Saud University, Riyadh, Saudi Arabia.
Funding
No funding is received.
Author information
Authors and Affiliations
Contributions
All authors have equal contribution in the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article was revised: “Author name correction”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dumka, P., Mishra, D.R., Singh, B. et al. Enhancing solar still performance with Plexiglas and jute cloth additions: experimental study. Sustain Environ Res 34, 3 (2024). https://doi.org/10.1186/s42834-024-00208-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42834-024-00208-y