Abstract
A novel blending approach has been introduced for fluoride removal by means of electrocoagulation. A blend was prepared by mixing synthetic phosphoric acid plant wastewater and gypsum plaster (GP) rich wastewater. This study explores defluoridation of wastewater using the simultaneous effect of chemical precipitation and electrocoagulation. Fourier transform infrared spectroscopy analysis of sludge confirms the presence Ca-F bond, which proves that enhancement in fluoride removal with blending of GP rich wastewater is due to simultaneous action of chemical precipitation and electrocoagulation. Optimization and statistical modeling were done with the help of MINITAB 17 software. Response surface methodology was performed using Box-Behnken Design to predict the fluoride removal efficiency and energy consumption. R2 values of 0.9485 and 0.9998 shows a good agreement between experimental and predicted values of responses. Kinetic study was done to determine the rate constant and it is found out that fluoride removal follows second order kinetic model. Blending approach confirmed the assistive role of GP rich wastewater in the enhancement of fluoride removal efficiency.
Similar content being viewed by others
Introduction
Water contamination of fluoride is an issue related to drinking water, as excess fluoride exhibits hazardous health effects like dental fluorosis, skeletal fluorosis etc. [1]. Excess fluoride in water could be due to natural causes like volcanic ash, fluoride rich minerals etc. or anthropogenic causes like fly ash, fertilizer plant wastewater [2]. According to literature, the majority of researcher’s work on defluoridation is about the treatment of target drinking water source. All these work have tried to remove fluoride from drinking water as per WHO norms, i.e., max 1.5 mg L− 1 of F− ion [3]. If we consider the wastewaters from semiconductor or phosphate fertilizer industries, excess fluoride from these waters acts as a source for drinking water contamination. According to Central Pollution Control Board of India, maximum fluoride limit for industrial wastewater is 15 mg L− 1 for discharge to public sewers or marine coastal areas [4].
Fluoride removal from contaminated water can be done using various processes like adsorption, chemical precipitation, reverse osmosis, electrocoagulation, and ion exchange [5]. Each method has its own operational favorability and constraints. Electrocoagulation as a method of defluoridation has received considerable attention in recent years. It is an electrochemical approach to water treatment with its operational favorability of less sludge generation, higher percentage removal, faster coagulation and simple operation [6]. A typical electrocoagulation unit consists of an electrochemical cell which can be a batch or continuous reactor with metal electrodes connected to a DC power supply. Mechanism of electrocoagulation is similar to chemical coagulation with the only difference in that in electrocoagulation the coagulant is generated by electrochemical dissolution of sacrificial anode [7]. When the sacrificial anode is made up of aluminum metal, the supply of electric current produces trivalent aluminum hydroxide flocs. These coagulant species form agglomerates with negatively charged fluoride ions and precipitates out as sludge [8].
Reactions occurring in electrocoagulation process when aluminum is used as a sacrificial anode can be represented as follows [9].
Anode:
Cathode:
Precipitation of F − ions with coagulant species:
Recently the major portion of studies has done optimization and statistical modeling of electrocoagulation process using response surface methodology (RSM). It is a statistical modeling technique used to create empirical models, study interactions among factors and to find out optimized parametric conditions for a target response [10]. The main advantage of using RSM for designing experiments is that it allows us to study interactions among different variables and optimize the specified response with a limited number of planned experiments [11]. It has been used to optimize electrocoagulation process with drinking water using a new flow column electrocoagulation reactor [12], chicken processing industry wastewater [13], palm oil mill effluent [14], raw landfill leachate [15], and molasses wastewater [16].
This study covers fluoride removal from wastewater of phosphoric acid plant using the simultaneous effect of chemical precipitation and electrocoagulation. A blending approach has been selected and the blend represents the combination of wastewaters viz. fluoride contaminated wastewater and gypsum plaster (GP) rich wastewater. GP is a calcium sulfate hemihydrate (CaSO4⦁0.5H2O) so GP rich wastewater acts as a source of calcium ions which induces precipitation of fluoride ions [17]. In India, many religious activities like idol (GP based) immersion leads to increase in calcium ions concentration in lake/rivers [18]. This wastewater could be used as a source of calcium ions. In this research paper, the combined effect of chemical precipitation and electrocoagulation for defluoridation of wastewater was studied. The reaction mechanism of precipitation of fluoride ions with gypsum dissolved in water can be represented as follows [19]:
A critical literature survey has been carried out and it is observed that we are offering a new approach of blending for defluoridation. Furthermore, statistical modeling using RSM has been carried out. Also, in this research paper, wastewater containing high initial fluoride concentration (200 mg L− 1) was selected, over the work done by most of the researchers taking a low concentration of fluoride, i.e., 25 mg L− 1 [20].
Material and methods
Preparation of synthetic wastewater samples
Stock solution simulating wastewater from the phosphoric acid plant was prepared by adding sodium fluoride (Fisher Scientific, 97%) and potassium dihydrogen orthophosphate (Fisher Scientific, 99%) in distilled water [21]. F− ion and \( P{O}_4^{-} \) ion concentration in stock solution was 200 and 1800 mg L− 1 respectively.
GP rich wastewater was prepared by dissolving commercial grade plaster of Paris powder (4 g L− 1) in distilled water. The duo was stirred for 20 min and then allowed to be settled for around 20 min. Finally, top clear GP rich wastewater was used for blending purpose.
Experimental setup
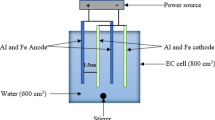
An acrylic cylindrical shaped flat bottom vessel (90 mm internal diameter, 220 mm height) was used as a reactor in electrocoagulation process as shown in Fig. 1a. The reactor consists of two aluminum plate electrodes viz. cathode and anode, with an arrangement of variable inter-electrode distance on supporting rod. The thickness of each aluminum electrode and the effective surface area is 3 mm and 125 cm2, respectively. A constant current was supplied using DC power supply (Scientific, PSD3210, 0–10 A, 0–30 V). Stirring was carried out using a magnetic stirrer. Schematic representation of experimental setup is shown in Fig. 1b.
Experimental procedure
A blend was prepared by mixing of 500 mL of synthetic phosphoric acid plant wastewater, GP rich wastewater as per its level in designed experiments and distilled water to make up the final volume up to 1 L. pH was measured with pH electrode (HACH, Intellical™ PHC101). In all combinations, pH of the blend was in the range of 6–6.5. This pH value is favorable for dominance of solid Al(OH3) coagulant species which precipitates out F− ions [9]. Initial conductivity was maintained at 5 mS cm− 1 using NaCl. NaCl in water provides Cl− ion which helps to eliminate passive layer formation on aluminum electrodes [10]. Conductivity measurement was done using standard conductivity electrode (HACH, CDC 40101). Stirring was carried out at 650 rpm. Fluoride concentration was analyzed using fluoride ion selective electrode (HACH, ISEF12101). Percentage fluoride removal and energy consumption were calculated using following equations.
Where Ci and Cf represent initial and final F− ion concentration.
Fourier transform infrared spectroscopy (FTIR) analysis
The FTIR analysis of dried sludge was carried out in IRAffinity-1 Shimadzu FTIR spectrometer. The discs of sludge samples were prepared using potassium bromide (sludge sample: potassium bromide, 1:14). FTIR spectrum was recorded in the range of 4000–400 cm− 1.
Statistical experimental design
A statistical experimental design was carried out using MINITAB 17. Variables such as time (A), current density (B), interelectrode distance (C) and GP rich wastewater volume (D) were selected and responses viz. are percentage fluoride removal (Y1) and energy consumption (Y2) has been analyzed. Variable levels for a design of experiments are shown in Table 1.
RSM has been performed using Box-Behnken Design (BBD) to predict the responses viz. Y1 and Y2. The generalized form of BBD model can be represented as Eq. (9) [22].
Where Y is predicted response, xi and xj are variables, β0, βj, βjj and βijare the regression coefficients for intercept, linear, square and interaction terms, respectively, and ei is the error.
Results and discussion
Development of regression model and statistical analysis
Response surface analysis has been carried out with the regression models developed as in Eqs. (10) and (11).
Table 2 represents experimental and predicted values of Y1 and Y2 for 27 runs. The data from Table 2 show a good fit between predicted and experimental values with R2 values of 0.9485 and 0.9998 for Y1 and Y2, respectively.
Analysis of variance (ANOVA) was done by opting 95% confidence level. ANOVA output for Y1 and Y2 is provided in Tables 3 and 4, respectively. ANOVA gives us the information about the level of significance in terms of p-value which should be less than 0.05 for a term to be significant [23]. It is observed that all the linear terms viz. time, current density, inter-electrode distance and GP rich wastewater volume are significant terms for the fluoride removal (%). However, all the linear terms are significant except GP rich wastewater volume in case of energy consumption. This may be because of constant conductivity in all experiments nullified the effect of GP rich wastewater volume on energy consumption.
Effects of time, current density, and inter-electrode distance
Run time is one of the important variables where with the increase in time, there is an increase in coagulant species formation and ultimately more fluoride removal has been observed. This could be possible because of the removal efficiency of any charged pollutants directly depends on the rate of anodic dissolution [24]. Figure 2a represents this direct relationship between time and fluoride removal. Similarly increase in time leads to increase in consumption of electrical energy, and same has been reported in Fig. 3a.
Current density is electric current supplied per unit surface area of an electrode. From Fig. 2a, it is observed that with the increase in current density there is an increase in fluoride removal. This trend can be explained by the fact that more current supplied to electrodes will result in more coagulant dosage into the water [25]. It is also observed that there is an increase in energy consumption with an increase in current density, as shown in Fig. 3a.
Figure 2b shows that there is an inverse relation between inter-electrode distance and fluoride removal. This may be because of two reasons, firstly, the short inter-electrode distance will cause rise in mass transfer rate of coagulant due to increase in turbulence [26] and next could be the increase in electrode distance offering more resistance to current flow between electrodes, which leads to decrease in anodic dissolution resulting in lower fluoride removal. Large inter-electrode distance demands more voltage to maintain constant current flow which causes more energy consumption, as shown in Fig. 3b.
Main effects plot of all linear variables on fluoride removal (%) is shown in Fig. 4. From this plot it can be easily inferred that time (A), current density (B) and volume of GP rich wastewater (D) have a positive effect and inter-electrode distance (C) has a negative effect over the removal of fluoride.
Effect of GP rich wastewater blending
Mixing of GP rich wastewater introduces calcium ions in the blend of wastewaters. It is seen that an increase in the volume of GP rich wastewater in a blend causes an increase in fluoride removal efficiency as shown in Fig. 2b, it is on account of more calcium ions available for precipitating out fluoride ions. This enhancement in removal efficiency by electrocoagulation can be attributed to simultaneous chemical coagulation of F− ions by calcium ions as illustrated in Eqs. (5) and (6). In general, the addition of the GP rich wastewater improves the conductivity of blend, so that the required voltage will diminish and it will result in low energy consumption at constant supplied current. But in this study conductivity of blend was kept constant by adding NaCl to avoid the variations in current flow. That is why the volume of GP rich wastewater has no significant effect on energy consumption and same has been reported in terms of the p-value in Table 4.
Optimization of process variables
In this study, process variables were optimized for two objectives: first is to achieve maximum fluoride removal with minimum energy consumption and second is to achieve 95% of fluoride removal without any constraints on energy consumption. A target value of 95% fluoride removal has been selected, as it would give a final fluoride concentration of 10 mg L− 1 which is well below the limits set by Central Pollution Control Board India for effluent discharge.
After statistical analysis response optimizer tool of MINITAB 17 has been used to optimize the process variables without any constraints on input variables. Two response goals (viz. to maximize fluoride removal and to minimize energy consumption) have been assigned for first objective. Similarly, for the second objective a target of 95% removal efficiency has been assigned with no constraints on energy consumption. Optimized process variables for the first objective are run time of 20 min, current density of 0.0064 A cm− 2, an inter-electrode distance of 1.2 cm and 500 mL of GP rich wastewater. While for the second objective, optimized process variables are run time of 23.17 min, current density of 0.0052 A cm− 2, an inter-electrode distance of 1.2 cm and 500 mL of GP rich wastewater. Triplicates experiments have been performed to confirm the experimental values with predicted results. It is observed that experimental values are in a good agreement with predicted values; hence it validated the optimization results.
Energy consumption in first objective (3.42 Wh) is greater than that of second objective (2.82 Wh) and current density is 0.006 and 0.005 A cm− 2 respectively. Similarly, removal of fluoride in the first objective (96%) is greater than that of second objective (95%). While the time required is less in first objective (20 min) than that of second objective (23.2 min). We can conclude that on increasing current density, fluoride removal will enhance while run time will be reduced. We can also conclude that volume of GP rich wastewater is one of the more significant factors in defluoridation by electrocoagulation viz. more the volume of GP rich wastewater, less will be the run time.
FTIR characterization
FTIR analysis ranged from wave numbers between 4000 and 400 cm− 1 was performed to analyze the chemical bonds of the elements present in the dried sludge sample. A generated FTIR spectrum is shown in Fig. 5. The peak at 628 cm− 1 can be ascribed to the stretching of F-Al-F bond [27]. The peak at 453 cm− 1 is likely attributed to presence of calcium fluoride in sludge, as Ca-F bond is represented at 450 cm−1on IR absorbance band [28]. Hence FTIR analysis confirms the presence of Ca-F bond in the sludge. Thus, we can conclude that chemical precipitation plays a vital role in fluoride removal according to Eq. (6). Hence presence of Ca-F and F-Al-F bonds in the sludge samples validates that enhancement in fluoride removal with blending of GP rich waste water is due to simultaneous action of electrocoagulation and chemical precipitation according to Eqs. (4) and (6) respectively.
Fluoride removal kinetic
Experiments were carried out at optimum conditions to study the fluoride removal kinetic at different initial fluoride concentrations. Change in initial fluoride concentration with respect to time was measured in interval of 5 min. Results in terms of removal of fluoride vs. time are plotted in Fig. 6a. It is observed that we could express rate of change of fluoride concentration as a second order kinetic model according to Eq. (12), which is clearly seen in Fig. 6b.
On integration Eq. (12), yields
Where Ct, C0 and k are fluoride concentration at any time t, initial fluoride concentration and, rate constant respectively.
In Fig. 6b, (1/Ct) is plotted against time t at different initial fluoride concentrations with operating variables as current density of 0.0064 A cm− 2, an inter-electrode distance of 1.2 cm and volume of GP rich wastewater as 500 mL. At all different initial fluoride concentrations, the plot gave the intercept approximately equal to (1/C0), which confirmed that fluoride removal follows the second order kinetic model. And it can be seen that value of kinetic constant k increases as the initial fluoride concentration decreased from 140 to 60 mg L− 1.
Conclusions
In this study, a novel blending approach for defluoridation of wastewater in electrocoagulation process using GP rich wastewater has been studied successfully. Optimization of fluoride removal by electrocoagulation using RSM has been carried out. Regression analysis was done to generate mathematical model equations for predicting fluoride removal efficiency and energy consumption. R2 values of 0.9485 and 0.9998 shows a good agreement between experimental and predicted values of responses. Optimized process variables for maximum fluoride removal efficiency with minimum energy consumption obtained are run time of 20 min, current density of 0.0064 A cm− 2, an inter-electrode distance of 1.2 cm and volume of GP rich wastewater as 500 mL. While for a target value of 95% fluoride removal efficiency obtained optimized process variables are run time of 23.2 min, current density of 0.0052 A cm− 2, an inter-electrode distance of 1.2 cm and volume of GP rich wastewater as 500 mL. Trends of 3D surface plots confirm the enhancive role of GP rich wastewater blending in the defluoridation process using electrocoagulation. FTIR analysis validates that enhancement in fluoride removal with blending of GP rich waste water is due to simultaneous action of chemical precipitation and electrocoagulation. This study also confirms that by blending two different wastewaters, we could treat industrial wastewaters with high fluoride concentration and bring down the fluoride in effluent discharge well below the CPCB limits.
References
Kut KMK, Sarswat A, Srivastava A, Pittman CU, Mohan D. A review of fluoride in African groundwater and local remediation methods. Groundwater Sustain Dev. 2016;2–3:190–212.
Brindha K, Elango L. Fluoride in groundwater: causes, implications and mitigation measures. In: Monroy SD, editor. Fluoride properties, applications and environmental management. Hauppauge: Nova Science Publishers; 2011. p. 111–36.
Cai JG, Zhang YY, Pan BC, Zhang WM, Lv L, Zhang QX. Efficient defluoridation of water using reusable nanocrystalline layered double hydroxides impregnated polystyrene anion exchanger. Water Res. 2016;102:109–16.
MoEF. The Environment (Protection) Rules. New Delhi: Ministry of Environmenrt and Forest; 1986.
Loganathan P, Vigneswaran S, Kandasamy J, Naidu R. Defluoridation of drinking water using adsorption processes. J Hazard Mater. 2013;248-249:1–19.
Moussa DT, El-Naas MH, Nasser M, Al-Marri MJ. A comprehensive review of electrocoagulation for water treatment: potentials and challenges. J Environ Manag. 2017;186:24–41.
Mouedhen G, Feki M, Wery MDP, Ayedi HF. Behavior of aluminum electrodes in electrocoagulation process. J Hazard Mater. 2008;150:124–35.
Zhu J, Zhao HZ, Ni JR. Fluoride distribution in electrocoagulation defluoridation process. Sep Purif Technol. 2007;56:184–91.
Emamjomeh MM, Sivakumar M, Varyani AS. Analysis and the understanding of fluoride removal mechanisms by an electrocoagulation/flotation (ECF) process. Desalination. 2011;275:102–6.
Behbahani M, Moghaddam MRA, Arami M. Techno-economical evaluation of fluoride removal by electrocoagulation process: optimization through response surface methodology. Desalination. 2011;271:209–18.
Thirugnanasambandham K, Sivakumar V, Maran JP. Optimization of process parameters in electrocoagulation treating chicken industry wastewater to recover hydrogen gas with pollutant reduction. Renew Energy. 2015;80:101–8.
Hashim KS, Shaw A, Al Khaddar R, Pedrola MO, Phipps D. Defluoridation of drinking water using a new flow column-electrocoagulation reactor (FCER) - experimental, statistical, and economic approach. J Environ Manage. 2017;197:80–8.
Thirugnanasambandham K, Sivakumar V, Maran JP. Efficiency of electrocoagulation method to treat chicken processing industry wastewater-modeling and optimization. J Taiwan Inst Chem Eng. 2014;45:2427–35.
Nasution A, Ng BL, Ali E, Yaakob Z, Kamarudin SK. Electrocoagulation of palm oil mill effluent for treatment and hydrogen production using response surface methodology. Pol J Environ Stud. 2014;23:1669–77.
Huda N, Raman AAA, Bello MM, Ramesh S. Electrocoagulation treatment of raw landfill leachate using iron-based electrodes: effects of process parameters and optimization. J Environ Manag. 2017;204:75–81.
Tsioptsias C, Petridis D, Athanasakis N, Lemonidis I, Deligiannis A, Samaras P. Post-treatment of molasses wastewater by electrocoagulation and process optimization through response surface analysis. J Environ Manag. 2015;164:104–13.
Al-Rawajfeh AE, Al-Hawamdeh S, Al-Hawamdeh S, Al-Dharaba’a S. Defluoridation of water by natural materials: is it adsorption? In: 13th International Conference of Environmental Science and Technology. Athens; 2013 Sep 5–7.
Ujjania NC, Multani AA. Impact of Ganesh idol immersion activities on the water quality of Tapi River, Surat (Gujarat) India. Res J Biol. 2011;1:11–5.
Masamba WRL, Sajidu SM, Thole B, Mwatseteza JF. Water defluoridation using Malawi’s locally sourced gypsum. Phys Chem Earth. 2005;30:846–9.
Pulkka S, Martikainen M, Bhatnagar A, Sillanpaa M. Electrochemical methods for the removal of anionic contaminants from water - a review. Sep Purif Technol. 2014;132:252–71.
Patwardhan AD. Industrial wastewater treatment. 2nd ed. Delhi: PHI Learning Private Limited; 2017.
Maran JP, Sivakumar V, Thirugnanasambandham K, Sridhar R. Response surface modeling and analysis of barrier and optical properties of maize starch edible films. Int J Biol Macromol. 2013;60:412–21.
Jang S, Lee AY, Lee AR, Choi G, Kim HK. Optimization of ultrasound-assisted extraction of glycyrrhizic acid from licorice using response surface methodology. Integr Med Res. 2017;6:388–94.
Drouiche N, Aoudj S, Hecini M, Ghaffour N, Lounici H, Mameri N. Study on the treatment of photovoltaic wastewater using electrocoagulation: fluoride removal with aluminium electrodes - characteristics of products. J Hazard Mater. 2009;169:65–9.
Un UT, Koparal AS, Ogutveren UB. Electrocoagulation of vegetable oil refinery wastewater using aluminum electrodes. J Environ Manag. 2009;90:428–33.
Martinez-Villafane JF, Montero-Ocampo C, Garcia-Lara AM. Energy and electrode consumption analysis of electrocoagulation for the removal of arsenic from underground water. J Hazard Mater. 2009;172:1617–22.
Gross U, Rudiger S, Kemnitz E, Brzezinka KW, Mukhopadhyay S, Bailey C, et al. Vibrational analysis study of aluminum trifluoride phases. J Phys Chem A. 2007;111:5813–9.
Al-Ajely MS, Ziadan KM, Al-Bader RM. Preparation and characterization of calcium fluoride nano particles for dental applications. Int J Res Granthaalayah. 2018;6:338–46.
Acknowledgements
The authors wish to express their gratitude to the Visvesvaraya National Institute of Technology, Nagpur for providing infrastructural and other necessary facilities to carry out this research.
Author information
Authors and Affiliations
Contributions
VJ carried out electrocoagulation fluoride removal studies including optimization using RSM, kinetics. KJ participated in the design of the elctrocoagulation acrylic apparatus. SK concieved the study and participated in its design and co-ordination. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Jadhao, V.K., Kodape, S. & Junghare, K. Optimization of electrocoagulation process for fluoride removal: a blending approach using gypsum plaster rich wastewater. Sustain Environ Res 29, 6 (2019). https://doi.org/10.1186/s42834-019-0002-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42834-019-0002-y