Two-phase mixed convection nanofluid flow of a dusty tangent hyperbolic past a nonlinearly stretching sheet

Abstract

A theoretical analysis for magnetohydrodynamic (MHD) mixed convection of non-Newtonian tangent hyperbolic nanofluid flow with suspension dust particles along a vertical stretching sheet is carried out. The current model comprises of non-linear partial differential equations expressing conservation of total mass, momentum, and thermal energy for two-phase tangent hyperbolic nanofluid phase and dust particle phase. Primitive similarity formulation is given to mutate the dimensional boundary layer flow field equations into a proper nonlinear ordinary differential system then Runge-Kutta-Fehlberg method (RKF45 method) is applied. Distinct pertinent parameter impact on the fluid or particle velocity, temperature, concentration, and skin friction coefficient is illustrated. Analysis of the obtained computations shows that the flow field is affected appreciably by the existence of suspension dust particles. It is concluded that an increment in the mass concentration of dust particles leads to depreciate the velocity distributions of the nanofluid and dust phases. The numerical computations has been validated with earlier published contributions for a special cases.

Introduction

The flow and heat transfer investigations about non-Newtonian fluids has been of widely importance due to the characteristics of fluid with suspended particles cannot be completely depicted by classical Newtonian fluids theory. Non-Newtonian liquids are widespread fluids in industrial and engineering operations in which linear relationship between stress and deformation rate cannot be obtained. No single non-Newtonian model exists that depicts all the properties of fluids. Tangent hyperbolic fluid model signifies one of interesting non-Newtonian models that developed for chemical engineering systems. This rheological formulation is derived from kinetic theory of liquids rather than the empirical relations. One of the non-Newtonian models introduced by Pop and Ingham [1] was hyperbolic tangent model. Nadeem and Akram[2] has inspected MHD peristaltic flow of a hyperbolic tangent fluid due to a vertical asymmetric channel with heat transfer. Akbar et al. [3] has reported MHD boundary layer flow of non-Newtonian tangent hyperbolic fluid by a stretched sheet numerically. Entropy analysis in MHD steady non-Newtonian tangent hyperbolic nanofluid regime through an accelerated stretching cylinder with variable wall temperature has been investigated by Mahdy [4]. Kumar et al. [5] inspected the aspect of partial slip on peristaltic motion of non-Newtonian tangent hyperbolic fluid flow along an inclined cylindrical channel. Naseer et al. [6] have reported the tangent hyperbolic boundary layer fluid flow due to a vertical stretching cylinder. Malik et al. [7] have inspected the MHD flow of non-Newtonian tangent hyperbolic fluid through a stretching cylinder. Hayat et al. [8] have examined the impact of thermal radiation in the two-dimensional free and forced convection flow of a tangent hyperbolic fluid nearby a stagnation point. Some extensive contributions of non-Newtonian fluids have been considered under unlike physical circumstances (Abdul Gaffar et al. [9]; Salahuddin et al. [10]; Nadeem et al. [11]; Mahdy and Chamkha [12], Nadeem and Maraj [13]; Hady et al. [14], Hayat et al. [15]; Mahanthesh et al. [16]).

In higher-power output devices, the forced convection alone is not sufficient in order to dissipate all the heat. As such, combining natural and forced convection (mixed) will usually give desired results. Mainly, the mixed convection phenomenon is found in several industrial and technical applications, for instance, a heat exchanger, nuclear reactors cooling during an emergency shutdown, electronic devices cooled by fans, and solar collectors. Additionally, dusty convective fluid flow has some various applications such as power plant piping, petroleum transport, and wastewater handling and combustion. Gireesha et al. [17, 18] have analyzed steady and unsteady MHD boundary layer flow and heat transfer of dusty fluid due to a stretching sheet. Sadia et al. [19] exhibited two-phase free convection flow of nanofluid past a vertical wavy plate. Singleton [20] depicted the boundary layer analysis for dusty fluid. Vajravelu and Nayfeh [21] have explored MHD dusty fluid flow past a stretching sheet. The dynamics of two-phase flow was scrutinized by a number of authors with some various physical conditions (Sivaraj and Kumar [22]; Singh and Singh [23]; Dalal [24]). Flows of mixed convection are of massive interest due to their variety scientific, engineering, and industrial applications in heat and mass transfer. Free and forced convection of mass and heat transfer exist simultaneously in the design fields of chemical operations equipment, distributions of temperature, and formation and dispersion of fog. Also, analysis of flows due to stretched surface through heat transfer has acknowledged ample consideration owing to their possible demands in several industrial procedures, for instance, in metal extrusion, continuous casting, hot rolling, and drawing of plastic films. Particularly in polymer industry, aerodynamic extrusion of plastic sheets has a major significant. This procedure includes the heat transfer between the surrounding and surface fluid. Moreover, the rate of stretching in hot/cold fluids greatly depends upon the quality of the material with desired properties. In such process, heat transfer has an essential role in controlling the cooling rate. Some published investigations can be consulted (Hady et al. [25]; Zeeshan [26]; Khan et al. [27]; Gorla et al. [28]; Mahdy [29–31]; Srinivasacharya and Reddy [32]).

Furthermore, the theory of nanofluids represents an old notion, and it was first presented by Choi and Eastman [33] as they were looking for novel cooling technologies and coolants; thereafter, it became common on account of its extensive applications in heat exchangers, nuclear reactor systems, boilers energy storage, and electronic cooling devices (Ostrach [34]). The ultra-small particle size and thermal conductivity represent the worthy thermophysical properties of nanofluids, and as a result, nanofluids give significantly better performance with comparison to the normal single/multi-phase fluids. Makinde [35] analyzed computational modeling of time-dependent nanofluid flow past convectively heated stretched surface. The stagnation point flow of a nanofluid due to unsteady stretching sheet in the presence of slip impacts has been illustrated by Malvandi et al. [36], Mahdy [37], and Mahdy and Sameh [38]. Zheng at al. [39] addressed the behavior of velocity slip in nanofluid flow through a stretching sheet. Also see [40–44].

To the best of the author’s knowledge, investigations on mixed convection flow and heat transfer on hydromagnetic dusty non-Newtonian nanofluid flow over a nonlinearly stretching sheet have not been considered so far. In the present analysis, we look at the non-linearly stretching flow of a dusty non-Newtonian tangent hyperbolic nanofluid flow. Numerical computations has been given to illustrate the behavior of nanofluid and dust particles. In our current analysis, we will examine whether the suspension dust particles in nanofluids affects the physical characteristics or not.

Flow field analysis

A subclass of non-Newtonian fluids is so-called tangent hyperbolic fluid. Actually, in this sort of non-Newtonian fluids [1], the Cauchy stress tensor is given by:

$$ \tau=\left(\mu_{\infty}+(\mu_{0}+\mu_{\infty})\tanh(\Gamma\dot{\gamma})^{n} \right) $$

(1)

in which τ points out extra stress tensor, μ_∞ signifies the infinite shear rate viscosity, μ₀ means the zero shear rate viscosity, Γ gives the constant of time-dependent material, n refers to the power-law index, i.e., flow behavior index, and $\dot {\gamma }$ is given by the formula

$$ \dot{\gamma}=\sqrt{\frac{1}{2}\sum_{i}\sum_{j}\dot{\gamma}_{ij}\dot{\gamma}_{ji}}=\sqrt{\frac{1}{2}\Pi} $$

(2)

Here, $\Pi =\frac {1}{2}trac(\nabla V+(\nabla V)^{T})^{2}$, and V denotes the velocity vector. We use Eq. (1) for the case as μ_∞=0 since it is not possible to examine the problem for the infinite shear rate viscosity and since we are applying tangent hyperbolic fluid that depicts shear thinning impacts; hence, $\Gamma \dot {\gamma }\ll 1$. Therefor, Eq. (1) mutates to the formula

$$\begin{array}{@{}rcl@{}} \tau&&=\mu_{0}[(\Gamma \dot{\gamma})^{n}]\dot{\gamma} \\ &&=\mu_{0}[(1+\Gamma \dot{\gamma}-1)^{n}]\dot{\gamma}\\ &&=\mu_{0}[1+n(\Gamma \dot{\gamma}-1)]\dot{\gamma} \end{array} $$

(3)

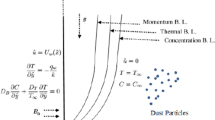
Now, let us scrutinize a steady, 2-D, incompressible, laminar, boundary layer MHD mixed convection flow of non-Newtonian tangent hyperbolic nanofluid embedded with dust particles towards a vertical nonlinearly stretching sheet. The scenario of a typical flow has been depicted in Fig. 1. As clarified, the orthogonal system (x,y) is chosen, in which the x-axis varies along the same stretched sheet direction with stretching rate U_w(x)=ax^m, with a>0, and the other axis, i.e., y-axis, is being perpendicular to the sheet surface and keeping the origin point to be fixed. An external magnetic field of strength B₀ is acting in the direction of y-axis. As a result to this, the induced current is produced in the fluid and magnetic Reynolds number is treated to be as a small enough such that the induced magnetic field can be ignored.

Fig. 1

Orthogonal system and flow model

T_∞ gives the fluid temperature far away from the stretching sheet with observation that T_w<T_∞ and T_w>T_∞ refers to the opposing and assisting flows, respectively. By following the habitual boundary layer and Boussinesq approximations, the flow-governing equations of the steady-state dynamics of a non-Newtonian tangent hyperbolic fluid are given as [3, 17–19, 21]

Fluid phase equations

$$ \frac{\partial{u}}{\partial x}+\frac{\partial v}{\partial y}=0 $$

(4)

$$\begin{array}{@{}rcl@{}} \rho_{f}\left(u\frac{\partial u}{\partial x}+ v\frac{\partial u}{\partial y}\right)= &&\mu_{f} \left((1-n)+\sqrt{2} n\Gamma\frac{\partial u}{\partial y}\right)\frac{\partial^{2} u}{\partial y^{2}}+\frac{\rho_{p}}{\jmath}(u_{p}-u) -\sigma B_{0}^{2} u\\ &&+ g\left((1-C_{\infty})\rho_{f}\beta(T-T_{\infty})-(\rho_{np}-\rho_{f})(C-C_{\infty})\right) \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} (\rho c)_{f} \left(u\frac{\partial T}{\partial x}+ v\frac{\partial T}{\partial y}\right)= k_{f}\frac{\partial^{2} T}{\partial y^{2}}&+ (\rho c)_{np}\left(D_{B}\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\left(\frac{D_{T}}{T_{\infty}}\right)\left(\frac{\partial T}{\partial y}\right)^{2} \right) \\ &+\frac{\rho_{p} c_{s}}{\jmath^{\star}}(T_{p}-T)+\frac{\rho_{p}}{\jmath}(u_{p}-u)^{2} \end{array} $$

(6)

$$ u\frac{\partial C}{\partial x}+ v\frac{\partial C}{\partial y}= D_{B}\frac{\partial^{2} C}{\partial y^{2}}+\left(\frac{D_{T}}{T_{\infty}}\right)\frac{\partial^{2} T}{\partial y^{2}} $$

(7)

Particle phase equations

$$ \frac{\partial{u_{p}}}{\partial x}+\frac{\partial v_{p}}{\partial y}=0 $$

(8)

$$ \rho_{p}\left(u_{p}\frac{\partial u_{p}}{\partial x}+ v_{p}\frac{\partial u_{p}}{\partial y}\right)= -\frac{\rho_{p}}{\jmath}(u_{p}-u) $$

(9)

$$ \rho_{p} c_{s}\left(u_{p}\frac{\partial T_{p}}{\partial x}+ v_{p}\frac{\partial T_{p}}{\partial y}\right)= -\frac{\rho_{p} c_{s}}{\jmath^{\star}}(T_{p}-T) $$

(10)

with (u,v) and (u_p,v_p) signifying the tangent hyperbolic nanofluid and particle phase velocity components through x and y axes, respectively; ρ_f,ρ_p give the fluid and dust particle phases density, ρ_np is the density of nanoparticles; ȷ,ȷ^⋆ refer to the dust particles momentum and thermal relaxation time; and c_f,c_s denote specific heat for the fluid and particle phases. T,T_p indicate the fluid and dust particle phase temperatures inside the boundary layer; g signifies acceleration due to the gravity; Γ indicates the Williamson parameter; n symbolizes the power law index; D_B,D_T give the Brownian and thermophoresis diffusion coefficients; C points out the resealed nanoparticle volume fraction; β means the coefficient of thermal expansion; and B₀,σ point out the magnetic field strength and electrical conductivity.

The above-stated essential equations must be solved with the appropriate boundary conditions, in order to evaluate the fluid flow fields and the dust particles. Hence, the convenient boundary conditions for our problem are as follows.

Fluid and particle phases boundary conditions are:

$$\begin{array}{@{}rcl@{}} &&\quad \eta=0,\quad u=U_{w},\quad v=0,\quad T=T_{w},\quad D_{B}\frac{\partial C}{\partial y} + D_{T}\frac{\partial T}{\partial y}=0\\ && \quad \eta\rightarrow\infty,\quad u,u_{p}\rightarrow0,\quad v_{p}=v\quad T,T_{p}\rightarrow T_{\infty},\quad C\rightarrow C_{\infty} \end{array} $$

(11)

Now, to mutate the fundamental governing flow field equations and boundary conditions, namely Eqs. (4)–11), the following dimensionless transformation have been given [12, 45]:

$$\begin{array}{@{}rcl@{}} &&\eta =\left(\frac{a(m+1)}{2\nu_{f}}\right)^{1/2} x^{\frac{m-1}{2}}y,\qquad \psi=\left(\frac{2a\nu_{f}}{m+1}\right)^{1/2}x^{\frac{m+1}{2}}F(\eta),\\ &&\psi_{p}=\left(\frac{2a\nu_{f}}{m+1}\right)^{1/2}x^{\frac{m+1}{2}}S(\eta),\quad\theta(\theta_{p})=\frac{T(T_{p})-T_{\infty}}{T_{w}-T_{\infty}},\quad \phi=\frac{C-C_{\infty}}{C_{\infty}} \end{array} $$

(12)

It is evident that Eqs. (4) and (8) are satisfied automatically where the stream functions ψ and ψ_p are given as $u=\frac {\partial \psi }{\partial y}$, $v=-\frac {\partial \psi }{\partial x}$ and $u_{p}=\frac {\partial \psi _{p}}{\partial y}$, $v_{p}=-\frac {\partial \psi _{p}}{\partial x}$.

Via the similar transformation that clarified in Eq. (12), the boundary layer Eqs. (5)–(11) are re-presented as:

$$\begin{array}{@{}rcl@{}} \frac{m+1}{2}\left((1-n+{nW}_{e}F^{\prime\prime})F^{\prime\prime\prime}+FF^{\prime\prime}\right)&&-mF'^{2}+\lambda(\theta-N_{r}\phi)\\ &&+D_{p}\alpha_{d}(S'-F')-M_{g} F'=0 \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} \frac{1}{Pr}\theta^{\prime\prime}+F\theta'+N_{b}\theta'\phi'+N_{t}\theta'^{2}&&+\frac{4D_{p}\alpha_{d} }{3(m+1) Pr}(\theta_{p}-\theta)\\ &&+\frac{2}{m+1}D_{p}E_{c}\alpha_{d}(S'-F')^{2}=0 \end{array} $$

(14)

$$ \phi^{\prime\prime}+Le F\phi'+\frac{N_{t}}{N_{b}}\theta^{\prime\prime}=0 $$

(15)

$$ SS^{\prime\prime}-\frac{2m}{m+1}S'^{2}-\frac{2\alpha_{d}}{m+1}(S'-F')=0 $$

(16)

$$ S\theta'_{p}-\frac{4 \alpha_{d}}{3(m+1)\gamma Pr}(\theta_{p}-\theta)=0 $$

(17)

subjected to the following converted fluid and dust particle phase boundary conditions:

$$\begin{array}{@{}rcl@{}} &&F(0)=0,\qquad F'(0)=1,\qquad \theta(0)=1, \qquad N_{b}\phi'(0)+N_{t}\theta'(0)=0, \\ && F'(\infty)\rightarrow0,\qquad \theta(\infty)\rightarrow0,\qquad\phi(\infty)\rightarrow0\\ && S(\infty)=F(\infty),\qquad S'(\infty)\rightarrow0,\qquad\theta_{p}(\infty)\rightarrow0 \end{array} $$

(18)

The resultant parameters are as follows: $W_{e}=\frac {\sqrt {m+1}\Gamma a^{3/2}x^{\frac {3m-1}{2}}}{\nu _{f}^{1/2}}$ signifies Weissenberg number; $M_{g}=\frac {\sigma B_{0}^{2}}{\rho _{f} a x^{m-1}}$ points out magnetic field parameter; $\lambda =\frac {Gr}{Re^{2}}$ denotes the mixed convection parameter; $Gr=\frac {g\beta (1-C_{\infty })(T_{w}-T_{\infty })x^{3}}{\nu _{f}^{2}}$ refers to Grashof number; $Re=\frac {a x^{m+1}}{\nu _{f}}$ points out Reynolds number, $N_{r}=\frac {(\rho _{np}-\rho _{f}) C_{\infty }}{\rho _{f} \beta (T_{w}-T_{\infty })(1-C_{\infty })}$ gives the buoyancy ratio parameter; $D_{p}=\frac {\rho _{p}}{\rho _{f}}$ refers to relative density; $\alpha _{d}=\frac {1}{\jmath a x^{m-1}}$ means fluid particle interaction parameter; $Pr=\frac {\mu _{f} k_{f}}{c_{f}}$ and $Le=\frac {\nu _{f}}{D_{B}}$ mean Prandtl and Lewis numbers; $N_{b}=\frac {(\rho c)_{np}D_{B}C_{\infty }}{(\rho c)_{f}\nu _{f}}$, $N_{t}=\frac {(\rho c)_{np}D_{T}(T_{w}-T_{\infty })}{(\rho c)_{f}T_{\infty }\nu _{f}}$ indicate the Brownian motion and thermophoresis parameters; and $E_{c}=\frac {a^{2}x^{2m}}{c_{f}(T_{w}-T_{\infty })}$ denotes Eckert number. Note $\jmath ^{\star }=\frac {3}{2} \gamma \jmath Pr$; $\gamma =\frac {c_{s}}{c_{f}}$ means the specific heat ratio of the mixture. It is significant to state here that for various mixtures, the term of interaction γ has values lies between 0.1 and 10.0 Rudinger (1980). It is noticable that for α_d=0, the flow is purely governed by the mixed convection in the absent of dusty particles (i.e., carrier phase only).

The skin friction factor C_f, Nusselt number Nu_x, and Sherwood number Sh_x represent the two major salient quantities of practical interest in the present investigation which are given as follows:

$$ C_{f}=\frac{\tau_{w}}{\frac{1}{2}\rho U_{w}^{2}},\quad Nu=\frac{xq_{w}}{k_{f} (T_{w}-T_{\infty})},\quad {Sh}_{x}=\frac{xq_{m}}{D_{B} C_{\infty}} $$

(19)

The wall shear stress τ_w and surface heat and mass transfer rate per unit area q_w,q_m:

$$\begin{array}{@{}rcl@{}} \tau_{w}=\mu_{f}\left((1-n)\frac{\partial u}{\partial y}+\frac{n\Gamma}{\sqrt{2}}\left(\frac{\partial u}{\partial y}\right)^{2} \right)_{y=0},&\; q_{w}=-k_{f}\left.\frac{\partial T}{\partial y}\right|_{y=0},&\; q_{m}=-D_{B}\left.\frac{\partial C}{\partial y}\right|_{y=0} \end{array} $$

(20)

Therefore, from the similarity transformation which is clarified in Eq. (12), the local skin friction factor and Nusselt and Sherwood numbers in non-dimensional formula are:

$$\begin{array}{@{}rcl@{}} &&\frac{1}{2}Re^{1/2}\;C_{f}=\sqrt{\frac{m+1}{2}}\left((1-n)F^{\prime\prime}(0)+\frac{1}{2}{nW}_{e}{F}^{\prime\prime{2}}(0) \right)\\ &&Re^{-1/2}\;{Nu}_{x}=-\sqrt{\frac{m+1}{2}}\theta'(0)\\ &&Re^{-1/2}\;{Sh}_{x}=-\sqrt{\frac{m+1}{2}}\phi'(0) \end{array} $$

(21)

Results and discussion

The present part provides the graphical and tabular results of the influences of different physical governing parameters on representative velocity, temperature of fluid and dusty particle phases, and concentration distribution which are delineated through Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 and Tables 1, 2, and 3. The highly non-linear ordinary differential Eqs. (13)–(17) with respect to the boundary condition (18) have been solved numerically via Runge-Kutta-Fehlberg technique with the help of Matlab software. In this method, the boundary value problem have to be mutated into the initial value problem. Additionally, it is pivotal to choose a finite values of η_∞. In order to appraise the accuracy of the present numerical results, a comparison of heat transfer results is done with the formerly published data (Rana and Bhargava [46] and Mabood et al. [47]) for the case of clean fluid (non suspended dust particles). The comparison is given in Table 1, and an excellent agreement was noticed. Furthermore, Tables 2 and 3 illustrate the impact of governing parameters on skin friction factor and Nusselt and Sherwood numbers. From these two tables, one observation is that the Nusselt number improves with γ,m,N_b, and Pr while it reduces with the other parameters. In addition, the skin friction factor reduces with λ,E_c,m,N_t, and N_b, whereas it enhances with the other parameters. Here, to illustrate the impact of any physical parameter, the other parameters are considered to be Pr=5,λ=0.2,W_e=0.7,M_g=0.5,N_r=1,n=0.3,N_b=N_t=0.4,α_d=0.1,D_ρ=1,E_c=0.3,Le=5,γ=0.3,and m=0.5

Fig. 2

Velocity and temperature of fluid and dust phase for Dp parameter

Fig. 3

Velocity and temperature of fluid and dust phase for α_d parameter

Fig. 4

Velocity and temperature of fluid and dust phase for Mg parameter

Fig. 5

Velocity and temperature of fluid and dust phase for m parameter

Fig. 6

Velocity and temperature of fluid and dust phase for Nr parameter

Fig. 7

Fluid and dust temperature phase for Nt, Nb parameters

Fig. 8

Concentrations profiles for Nb parameter and Le number

Fig. 9

Fluid and dust temperature phase for Ec, Pr numbers

Fig. 10

Velocity and temperature of fluid and dust phase for γ parameter

Fig. 11

Velocity and temperature of fluid and dust phase for λ parameter

Table 1 Comparison of −θ^′(0) with Pr=Le=2 without dust nanoparticles

Table 2 F^″(0) and −θ^′(0) for various governing parameters

Table 3 F^′′(0),−θ^′(0), and −ϕ^′(0) for different N_t,N_b and Pr

Figure 2 is prepared to portray the impact of mass concentration of the dust particle parameter D_ρ on tangent hyperbolic nanofluid and dust particle phase velocities F^′,S^′ and temperatures θ,θ_p. An increment in dust particle volume fraction leads to improve the drag force within the fluid, and therefore, velocities are reduced. Again, the aspect of D_ρ on nanofluid temperature θ and dust temprature θ_p is depicted in Fig. 2. With increasing, D_ρ maximizes the thermal field of both phases. Theoretically, for larger D_ρ, more dust particles gain the heat energy from the tangent hyperbolic nanofluid. As a result, cleans fluid’s temperature diminished, and relatively the particulate fluid temperature is also diminished.

Figure 3 illustrates the plots for dust particle-fluid interaction parameter α_d on the velocity and temperature for nanofluid and dust phases. The tangent hyperbolic nanofluid velocity field F^′ is reduced whereas dust particles velocity profile S^′ improved for higher values of α_d. Physically, a large α_d turns to reduce the relaxation time of particle phase and therefore improve the drag force on the fluid in contact with it. It is seen from the figure that, for larger α_d, the dust particle phase will become in equilibrium with the nanofluid phase. At this point, the temperature and velocity distributions for dust phase become parallel. Truly, due to the interaction with dust particles, the carrier fluid losses the kinetic and thermal energy. Therefore, the carrier nanofluid velocity/temperature field minifies for larger values of α_d parameter. This phenomenon indeed occurs for dust particle phase velocity/temperature. The velocity field of accelerated tangent hyperbolic nanofluid, dusty particles, and related momentum boundary layer thicknesses dwindle with increasing of magnetic field parameter M_g. This can be clarified as the fact that magnetic force acts like resistive force to fluid flow. This means that the applied magnetic field creates a resistive force known as “Lorentz force” which dwindles the fluid motion and results in a thinner momentum boundary layer thickness. The created intensive Lorentz force is accountable for the improvement both of dust temperature θ_p and nanofluid temperature θ profiles (Fig. 4). For strong magnetic force, this Lorenz force becomes predominant and temperature of fluid rose.

Figure 5 widths the aspect of nonlinear stretching parameter m on the dimensionless velocity and temperature of nanofluid and dust particle phases. It is observed that the velocity profile of dust particle are insignificantly reduced with increasing values of m=0.1,0.5,1,2, and 5, but the velocity profile of nanofluid is increased. From the same Fig. 5, it is clear that the variation in the dimensionless dust particle temperature phase due to nonlinear stretching parameter m reduces. Besides, it is seen that an increase in m parameter tends to enhance the temperature gradient at the wall (Table 2). Figure 6 displays the impact of buoyancy ratio N_r parameter on the dimensionless velocity and temperature profiles for fluid and dust particle phases. An increment in buoyancy ratio leads to thicken the thermal boundary layer, hence detracting the temperature gradient at the wall, as given in Table 2. Velocity components of nanofluid and dust particle phases reduce with higher values of buoyancy ratio parameter. The temperature profiles of tangent hyperbolic nanofluid and dust particle phases θ and θ_p for different values of N_t and N_b are shown in Fig. 7. This figure illustrates that as N_t becomes higher, the magnitude of the dimensionless temperatures θ and θ_p reduces. The diffusion of nanoparticles into the fluid maximizes with the rising in N_b, and hence, rescaled temperature profiles are improvements (Fig. 7). Impacts of Brownian motion parameter N_b and Lewis number Le on concentration distributions are plotted in Fig. 8. The Brownian motion parameter can be illustrated as the ratio of the nanoparticle diffusion, which is due to the Brownian motion impact, to the thermal diffusion in the nanofluid. For the value N_b=0, thermal transport is absent due to buoyancy impacts produced as a result of nanoparticle concentration gradients. Lewis number Le means the ratio of thermal diffusivity to mass diffusivity. Figure 8 imply that concentration profile is a decreasing function of Lewis number Le. Indeed, gradual enlarging values of Lewis number and Brownian motion parameter correspond to minimal mass diffusivity which is accountable in lessening of concentration distribution. Figures 7 and 8 show that the aspects of variations in N_b on the variations in concentration profiles are higher than those impacts on the non-dimensional temperature profiles.

The aspect of Eckert number E_c for nanofluid and dust temperature distribution were displayed in Fig. 9. From this figure, it is clarified that the nanofluid and dust temperature phases profiles enhance by increasing values of E_c. It is due to the heat energy is stored in the liquid according to frictional heating and this is true in both cases. Prandtl number Pr impact on the heat transfer is plotted in Fig. 9. The relative thickening of momentum and thermal boundary layers is governed by Prandtl number. Small values of Pr will possess higher thermal conductivities, hence heat can diffuse from the sheet very quickly compared to the velocity. Furthermore, it depicts that the temperature reduces with upgrade in the value of Pr. Prandtl number can be used to enhance the rate of cooling. By analyzing the figure, it illustrates that the influence of enlarging Pr turns to decrease the nanofluid and dust temperature curves in the flow region, and it is evident that high values of Prandtl number results in thinning of thermal boundary layer. A slight influence has obtained a mixture of specific heat ratio parameter γ for velocity and temperature profiles for fluid and dust particle phases in Fig. 10, but γ has a strong effect on dust particle temperature distribution. θ_p reduces by increasing γ.

The impact of mixed convection parameter λ on the velocity and temperature curves of nanofluid and dust particle phases is depicted in Fig. 11. The figure reveals that the velocity profiles F^′ and S^′ improve via larger values of mixed convection parameter. The mixed convection parameter presents the ratio of the buoyancy to inertial forces. That is, for higher mixed convection parameter, the buoyancy force overbears the inertial force which enhances the fluid velocity. In addition, the momentum boundary layer thickness improves. Figures 12 and 13 indicate the aspect of the Weissenberg number W_e and power law index parameter n on the velocity and temperature profiles for fluid F^′ and dust particles S^′ phases. Both F^′ and S^′ and the associated boundary layer thickness give decreasing behavior for higher values of Weissenberg number W_e and power law index parameter n (Fig. 12). In addition, an opposite behavior is shown for temperature of fluid and dust particle phases (Fig. 13).

Fig. 12

Velocity and temperature of fluid and dust phase for W_e number

Fig. 13

Velocity and temperature of fluid and dust phase for n parameter

Conclusions

This analysis addressed the MHD mixed convection flow of non-Newtonian tangent hyperbolic nanofluid with suspension dust nanoparticles along a nonlinear stretching sheet. Numerical computations are given in tabular and graphical forms in order to clarify the features of nanofluid flow, heat transfer, and dust particle phases. The obtained conclusions are summarized as:

• 1. Tangent hyperbolic nanofluid phase temperature is greater than the dust particles phase temperature.

• 2. Both W_e and n tend to enhance skin friction factor and reduce rate of heat transfer.

• 3. Increasing the fluid particle interaction parameter α_d leads to reduce the fluid velocity but enhances the velocity and temperature of particle phase.

• 4. Higher mass concentration of the dust particle parameter gives lower velocities of fluid and dust phases.

• 5. Nonlinear stretching parameter m has pronounced impact on dust particle phase.