Abstract
Partly because of advances in power electronic converters, the share of renewable energy in power generation is steadily increasing. The main medium of interface for integrating renewable energy sources to the utility grid is the power electronic inverter. Virtual oscillator control (VOC) is a time-domain approach for controlling parallel inverters in a standalone microgrid (MG). The concept is to simulate nonlinear deadzone oscillator dynamics in a system of inverters to ensure a stable AC MG in the absence of communication. VOC is a time-domain and self-synchronizing controller that simply requires the measurement of filter current, whereas traditional droop control and the virtual synchronous machine (VSM) require low pass filters for active and reactive power calculations. In this work, a particle swarm optimization (PSO)-based VOC method (VOC-PSO) is proposed, in which the parameters of the VOC are designed using the PSO algorithm. The system performance using droop, VSM, VOC, and VOC-PSO controllers are investigated using MATLAB and Opal-RT real-time digital simulator platforms. The results show that the proposed VOC-PSO gives improved performance over other control strategies. The efficacy of the proposed VOC-PSO control method is also demonstrated by the experimental results.
Similar content being viewed by others
1 Introduction
1.1 Motivation
Excessive usage of fossil fuels has resulted in significant emissions of greenhouse gases into the atmosphere, which has considerably harmed the ecosystem. As a result, renewable energy sources (RESs) received a lot of attentions and development as they produce efficient electric power with no pollution. Solar photovoltaics, wind energy, and geothermal energy are a few examples of RESs. Various control algorithms, power converter topologies, and power tracking systems have been developed for the efficient harvesting of electricity from RESs. Research is constantly being carried out on effective integration of RESs into the power grid for increased efficiency. Because of their critical significance in power conversion and output power regulation from these resources, increasing attention is being paid to power converters and their control.
1.2 Literature review
Control strategies for parallel inverters in the microgrid (MG) can be classified as master/slave (MS), current sharing, droop control, virtual synchronous machine (VSM)-based and virtual oscillator control (VOC) methods. The MS and current sharing methods both have the disadvantage of requiring communication networks (CN). This adds a single point of failure into the system. In MS methods, one master inverter is selected to control the voltage in the system, and other slave inverters are used to feed current to the system [1, 2]. If the master inverter fails, one of the slave inverters should immediately take over as the master inverter, otherwise the whole system would fail. Thus, a CN that can dynamically reassign inverter functions is required for this capability. Alternatively, the current sharing approach necessitates the detection of the overall load current and inverters are regulated to deliver a proportion of the total current after the load current is shared by the inverters in the system [3,4,5]. Because MS and current sharing techniques need system level control, they are unable to provide a true distributed plug and play MG design solution.
Droop control is the most common MG inverter control approach that does not need explicit communication among the parallel inverters [6]. This approach is established based on simulating the physical properties of synchronous machines (SMs), and inverters are designed to replicate the dynamics of traditional SMs by following the normal Q–V and P–f droop laws. Therefore, the behavior of droop regulated inverters is similar to that of SMs [7, 8]. In [9], this control is used to both 3-phase and 1-phase systems, while it focuses on enhancing inverter sharing accuracy in [10]. In [11], droop-controlled inverters are modelled as coupled Kuramoto oscillators, with adequate convergence and system stability requirements. The work in [12,13,14] provide advanced droop control algorithms for parallel inverters to enhance reactive power sharing with different line impedance values.
In comparison to a classical droop controller, the VSM control method has several benefits. However, the majority of VSM-based investigations in the literature concentrate on active power and frequency characteristics of the system [15,16,17]. In the standalone AC MG, because of the nature of the inductive load, fluctuations occur in reactive power [18]. This is the key research gap discovered from prior VSM-based research. In the case of a traditional droop controller or a VSM-based controller, the reactive power oscillation problem weakens as the droop gain or virtual inertia increases [19]. Thus, a fast change of AC load with inductive properties could disrupt the stability of an AC MG [20]. Research has demonstrated that a VSM controller may be used in a variety of applications.
VOC is a solution for parallel-connected 1-phase and 3-phase inverters in an MG [21,22,23,24]. In the context of VOC, inverters are designed to imitate the dynamics of non-linear weakly coupled oscillators (deadzone or Van der Pol), and the steady-state oscillations are approximately sinusoidal. VOC is a time domain and self-synchronizing controller that simply requires the measurement of filter current. The ability of nonlinearly coupled oscillators to self-synchronize to a steady-state limit cycle from random initial conditions (excluding the origin) is known as self-synchronization. References [23, 24] describe the synchronization criteria for parallel-connected VOC inverters. Since VOC does not need AC-cycle averaging and phase locked loop (PLL), while also avoids the use of low pass filters and active and reactive power measurements (which are required in other control methods), it can be configured to have a greater dynamic response than traditional droop control [21]. However, in contrast to droop control, the output voltage of a VOC-controlled inverter will always have harmonics. Thus, it is a design choice between quick inverter dynamic response and harmonics. In recent studies, VOC has been applied to grid-connected VSIs [25,26,27,28], but the parameter selection in conventional deadzone-based VOC is lengthy and time consuming. In this work, an optimization scheme is used to design the parameters of the VOC. It is simple to apply while improving system performance.
1.3 Contribution and paper organization
The contributions of this paper can be summarized as follows:
-
(a)
A particle swarm optimization (PSO)-based VOC method is proposed for parallel inverters in a standalone MG;
-
(b)
Implementation of different control algorithms, such as droop, VSM, and VOC in an islanded MG;
-
(c)
Eigenvalue or stability analysis of the system with the proposed and aforementioned control methods;
-
(d)
MATLAB and Opal-RT real-time digital simulator studies and comparison of the results with different control methods;
-
(e)
Hardware experimentation on a 3-phase inverter employing VOC-PSO in an islanded MG.
The rest of the paper is organized thus: Sect. 2 illustrates the system description while Sect. 3 discusses the controllers and their implementation. Section 4 explains the proposed PSO-based VOC control concept and its function. Eigenvalue studies of the droop, VSM, VOC, and VOC-PSO methods are carried out in Sect. 5, while Sects. 6 and 7 give the results of the MATLAB and Opal-RT simulations, respectively. The experimental findings of VOC-PSO controlled inverter system are presented in Sect. 8, while Sect. 9 gives an overall conclusion.
2 System description
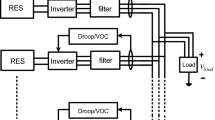
As seen in Fig. 1, the system contains two 3-phase VSIs that are interconnected and operated in an islanded MG. The input DC supply is Vdc, which is time varying and results from renewable energy resources such as solar panels or fuel cells. The DC link capacitor C is responsible for smoothing the DC bus voltage. The filter inductance, capacitance, and resistance are represented by Lf, Cf, and Rf, respectively. The on-state resistance of the IGBTs is denoted by ron. Specifically, Vta, Vtb, and Vtc are the inverter’s terminal voltages, while Vsa, Vsb, and Vsc are the voltages after the filter. Ifa, Ifb, Ifc, are capacitor currents, and ILa, ILb, ILc are load currents. In this paper, the inverters are regulated using a variety of sophisticated control methods to guarantee that the desired frequency and voltage of the MG are achieved.
3 Control structures
3.1 Droop control
In this subsection, the fundamentals and implementation of the droop controller are presented. Figure 2 shows the implementation of the droop controlled inverter in an islanded MG. As shown, the power detector measures the active power (AP) and reactive power (RP) from the sensed current and voltage values. Based on the AP and RP, the droop control generates the command signals to the inner voltage controller, which then outputs command signals to the inner current controller. The inner control loops produce the control signals to generate the switching pulses for the inverter. The equivalent model of a standalone inverter connected to PCC is shown in Fig. 3.
The output AP and RP can be calculated from Fig. 3 as:
where P and Q are the AP and RP of the VSI. RL and XL are the equivalent line resistance and reactance, respectively, while V1 and V2 are the respective voltages at the sending and receiving ends.\(\delta_{p}\) is the power angle which is very small in practice. Thus \(\sin \delta_{p} \approx 0\) and \(\cos \delta_{p} \approx 1\). Therefore, Eqs. (1) and (2) can be simplified to:
From [7], applying phasor calculus to (3) and (4) yields:
In this work, the P–f and Q–V droop control laws are considered, as:
where kp and kq are the AP and RP droop coefficients, respectively. f0 and V0 are the rated frequency and voltage, while f and V = V1 are the output frequency and voltage of the inverter, respectively. The frequency and voltage set points are decided from (7 to 8). The characteristic equation of the droop controlled inverter and eigenvalue analysis are presented in Sect. 5.
3.2 Virtual synchronous machine
The droop features and swing equation of a traditional SM are the inspiration for the VSM design. In comparison to the well-known droop control, VSM has good dynamic performance, and its typical implementation is shown in Fig. 4. From [16, 17], the mathematical modeling of the inverter can be understood. The swing equation, which includes the droop and damping effects, is directly treated in this section, as:
The virtual mechanical input power, virtual mechanical speed, and electrical output power of VSM are represented by the variables P*, \(\omega_{vsm}\), and Pout, respectively. The time constant is denoted by the \(\tau_{a}\), while the damping and droop constants of VSM are denoted by the kd and kw, respectively. The characteristic equation of the VSM controlled inverter is taken from [18] and the eigenvalue plots are shown in the stability analysis in Sect. 5.
3.3 Virtual oscillator control
VOC is stimulated by the occurrence of synchronization of non-linear coupled oscillators [24], and its representation is shown in Fig. 5a. VOC is composed of two subsystems, i.e., an RLC circuit and a voltage-dependent-current-source (VDCS). These are, derived from the nonlinear deadzone oscillator (DZo), as:
In Fig. 5b, the characteristics of deadzone and VDCS are depicted. The VDCS is \(g(v_{C} ) = f(v) - \sigma v,\) where f(v) is the DZ function given as
The schematic of the VO-controlled VSI is shown in Fig. 6, while Fig. 7 illustrates the VO-controlled VSI in the MG. The design process for the VOC parameters is clarified in detail in [24], while an optimization technique to design the VOC parameters is proposed in the next section.
4 PSO-based VOC
Parameter selection is lengthy and time consuming in conventional VOC. In this work, a PSO scheme is used to design the parameters of the VOC. This is simple to apply and improves system performance. PSO is a population-based approach and an evolutionary method that iteratively tries to develop solutions for diverse parameter values [29]. PSO was inspired by the behaviors of a flock of birds, or a school of fish etc., fishes, birds and other organisms always travel in groups, altering their positions and velocities based on group knowledge to avoid colliding with other members. This strategy eliminates the need for individuals to search for food, housing, or other necessities.
4.1 Design problem statement
The process for designing VOC parameters is described in [21, 22], and the main steps are as follows.
-
a.
Set the voltage gain (kv) to generate the required output voltage of the VSI, i.e., \(k_{v} = \sqrt 2 V_{rated} .\)
-
b.
Tune the offset voltage parameter (\(\varphi\)) to ensure that the system can function within the specified voltage range under diverse load scenarios.
-
c.
Adjust the current gain (ki) such that during rated operation, the system works at the lowest possible voltage.
-
d.
The L and C parameters of the harmonic oscillator can be selected using (13).
-
e.
The harmonic oscillator resistance (R), as well as the slope of the DZ function (\(\sigma\)), are chosen in order to meet (14).
-
f.
The other parameters of the VOC are chosen so that the synchronization criterion is fulfilled, as stated in (15).
-
g.
Finally, all the parameters of the VOC should minimize (12) to get a pure sinusoidal modulating signal from the proposed controller.
From the above design procedure, the minimum value of the fitness function matches the optimal set of parameter values. In this analysis, the fitness function is expressed in (12), and the constraints are expressed in (13–15). \(Z_{net} (j\omega )\) is the filter impedance.
The flowchart of the PSO algorithm with VO-controlled inverter is shown in Fig. 8, while Fig. 9 shows the plot between fitness function values and the number of iterations for the VO-controlled inverter. The values of the PSO algorithm are listed in Table 1.
5 Eigenvalue analysis
For eigenvalue analysis, the linearized expressions of the aforementioned control strategies from reference work are used. The droop controlled inverter transfer function model is taken from [30], the VSM eigenvalue concept from [31], and the VO-controlled inverter from [32]. The characteristic equation of the droop, and VO controlled VSI are shown in (16), and (17) respectively.
where
The system is linearized to produce the subsequent small signal model to examine the transient response of the VO-driven inverter system. The state space equations for the overall VOC are given as:
where \(\lambda = \frac{{\sigma (1 - \frac{{3\beta V^{2} }}{2})}}{2C}\). From (18), the characteristic equation of the VO-controlled inverter is given as:
Figure 10i–iv display the eigenvalue plots of the system with different controllers, while changing the filter resistance. Similarly, Figs. 11i–iv shows the eigenvalue plots of the system while varying the filter inductance. Selected eigenvalues for different filter resistance and inductance values are also listed in Tables 2 and 3, respectively. In comparison to the other approaches, the negative real parts of the VOC and VOC-PSO eigenvalues move far away from the imaginary axis, as shown in Figs. 10 and 11. As a result, VOC's response is more damped and faster than the others.
6 Simulation results and discussion
Two 3-phase VSIs connected to separate DC sources are operated in parallel in the simulation model and simulations are conducted for the standalone MG system as shown in Fig. 1. A 3-phase balanced load is shared by both inverters. In the droop and VSM controllers, current sharing is determined by the droop coefficients, whereas in VOC, it is determined by the inverter power rating. During the simulation, the initial load is 2 kW, but is increased to 3 kW at 0.4 s and then goes back to 2 kW at 0.6 s, as shown in Fig. 12. The current sharing is evident in VOC and VOC-PSO, shown in Figs. 13(iii) and (iv), and the zero crossing points of the currents in inverters are also the same. As illustrated in Fig. 13(i) and (ii), the zero-crossing points in droop and VSM do not exactly match. In comparison to the droop and VSM control methods, the VOC and VOC-PSO methods perform better.
Figure 14(i–iv) illustrate the synchronization of the inverter output voltages in droop, VSM, VOC, and VOC-PSO. In droop and VSM, load voltage changes are bigger than those in VOC and VOC-PSO when the load is changed at 0.4 s and 0.6 s. The VOC concept is based on the deadzone oscillator, in which it maintains a constant output voltage and frequency. Therefore, when the load rises quickly, the load side voltage varies less in VO controlled inverters than in droop and VSM control methods, while the proposed VO-controlled VSIs also allow faster output voltage synchronization over the classical VOC method.
Figure 15(i–iv) demonstrate the load current with the four aforementioned control schemes. The steady state responses in all controllers are nearly identical for the same load change as indicated earlier. However, compared to droop control and VSM, the dynamic behaviors of the system employing VOC and VOC-PSO are superior. The VSM-based system has a better dynamic response than the droop-based system. All inverters in VOC have the same zero-crossing point for currents, while the zero-crossing positions in droop and VSM differ.
Figure 16a depicts the system frequency when employing the three distinct control mechanisms outlined above, during the load disturbance shown in Fig. 16d. As seen in Fig. 16a, in the droop control approach, the system frequency abruptly drops when load variation occurs, resulting in a high rate of change of frequency. This indicates poor stability (potentially causing unnecessary df/dt relay tripping). As demonstrated in Figs. 16b, c, the frequency change rates in VSM are lower than in droop and VOC. Because VOC uses immediate current feedback signals, the rates of change of frequency are much higher than VSM. In comparison to droop and VSM, the steady-state frequency errors in VOC and VOC-PSO are lower.
Figure 17 demonstrates the AP tracking results for droop, VSM, VOC, and VOC-PSO. VOC is a time-domain control method that reacts instantly and does not need further computation, whereas droop and VSM use phasor values that are not well characterized in real-time. In comparison to droop and VSM control approaches, the VOC and VOC-PSO dynamic responses are extremely quick, while VSM-based system has better dynamic response than the droop-based system. The rise and settling times with the four aforementioned controllers are shown in Table 4, where, tr, ts, and ess are the rise time, settling time, and steady-state error, respectively. The overshoot is less with faster response in the proposed VOC-PSO than with the conventional VOC method.
The robustness of the VOC and VOC-PSO controllers for load variations of 25–200% are shown in Figs. 18, 19, 20 and 21, which demonstrate the terminal voltage and current sharing of inverters employing VOC and VOC-PSO controllers. The voltage dips during substantial fluctuations in load are reduced in both situations as seen in Figs. 18 and 19, and the controllers maintain the output voltage within the required limits. The current sharing between the two VSIs is prominent, as seen in Figs. 20 and 21. VOC-PSO reaches its steady state quicker at starting than VOC control.
7 Real-time digital simulator results
In this section, the real-time digital simulator (Model: OP-5142) is used (shown in Fig. 22) to test the system performance with different controllers. Figures 23, 24 and 25 depict the current distribution, voltage synchronization of inverters, and system load current with a sudden change in load, for droop, VSM, VOC, and VOC-PSO control methods. As seen the VOC-PSO outperforms all other control systems and has the best response.
8 Hardware results and discussion
The proposed VOC control technique has an improved enactment over traditional droop and VSM, as demonstrated by simulation and Opal-RT studies. The VOC-PSO control technique is thus used to implement hardware testing in the lab. Figure 26 depicts the experimental setup.
The main components in the hardware experimentation can be seen in Fig. 26, while the complete hardware circuit diagram is shown in Fig. 27. A Semikron inverter is used to provide the desired DC to VSI conversion through an auto-transformer. Low voltage DC power supplies are used to supply the current sensor, logic circuits, level shifters, and opto-isolators. The current sensor gives the feedback current to the Opal-RT controller (only one current signal is required which is the main advantage of this controller). The top views of the current sensor and LC filter are also clearly shown in Fig. 26. Figure 28 shows the gate pulses of one leg of the VSI, while Fig. 29 shows the transient response of the inverter with the proposed control during load transients. As seen, the performance during load transients is largely inline with the simulation, and is satisfactory.
9 Conclusions
In an islanded MG, droop, VSM, VOC, and VOC-PSO control techniques are implemented to control parallel inverters, and to ensure synchronization and power sharing. VOC-PSO provides improved synchronization and current sharing among all the different control methods, while the synchronization condition in VOC is unaffected by the load characteristics or the number of inverters. All control schemes require no communicating between different inverters. Eigenvalue analysis of the system with the aforementioned controllers is discussed. When compared to other control methods, the VOC method has the lowest real-parts of the eigenvalues and these are far away from the imaginary axis, resulting in a rapid and damped response. The change in frequency rate is less in VSM, while PSO provide superior VOC design parameters such that the proposed PSO based VOC has faster synchronization than the conventional VOC. The active power tracking is also excellent in the proposed control method. VOC-PSO outperforms droop and VSM control in MATLAB and Opal-RT digital simulations, while the efficacy of the proposed VOC control strategy is also demonstrated by the experimental results.
Availability of data and materials
Not applicable.
Abbreviations
- VOC:
-
Virtual oscillator control
- MG:
-
Microgrid
- VSM:
-
Virtual synchronous machine
- PSO:
-
Particle swarm optimization
- MS:
-
Master/slave
- CN:
-
Communication network
- SMs:
-
Synchronous machines
- PCC:
-
Point pf common coupling
- RESs:
-
Renewable energy sources
- VSI:
-
Voltage source inverter
- PLL:
-
Phase locked loop
- VDCS:
-
Voltage dependent current source
- DZo:
-
Deadzone oscillator
References
Chen, J. F., & Chu, C. L. (1995). Combination voltage-controlled and current-controlled PWM inverters for UPS parallel operation. IEEE Transactions on Power Electronics, 10(5), 547–558.
Zhao, B., Zhang, X., & Chen, J. (2012). Integrated microgrid laboratory system. IEEE Transactions on Power Systems, 27(4), 2175–2185.
Kawabata, T., & Higashino, S. (1988). Parallel operation of voltage source inverters. IEEE Transactions on Industry Applications, 24(2), 281–287.
Sun, X., Lee, Y.-S., & Dehong, X. (2003). Modeling, analysis, and implementation of parallel multi-inverter systems with instantaneous average-current-sharing scheme. IEEE Transactions on Power Electronics, 18(3), 844–856. https://doi.org/10.1109/TPEL.2003.810867
Chen, Y. K., Wu, Y. E., Wu, T. F., & Ku, C. P. (2003). ACSS for paralleled multi-inverter systems with DSP-based robust controls. IEEE Transactions on Aerospace and Electronic Systems, 39(3), 1002–1015.
Piagi, P., & Lasseter, R. (2006). Autonomous control of microgrids. IEEE Transactions on Industry Applications, 6, 1–8.
Chandorkar, M., Divan, D., & Adapa, R. (1993). Control of parallel connected inverters in standalone ac supply systems. IEEE Transactions on Industry Applications, 29(1), 136–143.
Guerrero, J., de Vicuna, L., Matas, J., Castilla, M., & Miret, J. (2004). A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems. IEEE Transactions on Power Electronics, 19(5), 1205–1213.
Matas, J., Castilla, M., de Vicuña, L., Miret, J., & Vasquez, J. (2010). Virtual impedance loop for droop-controlled single-phase parallel inverters using a second-order general-integrator scheme. IEEE Transactions on Power Electronics, 25(12), 2993–3002.
De, D., & Ramanarayanan, V. (2010). Decentralized parallel operation of inverters sharing unbalanced and nonlinear loads. IEEE Transactions on Power Electronics, 25(12), 3015–3025.
Simpson-Porco, J. W., Dörer, F., & Bullo, F. (2013). Synchronization and power sharing for droop-controlled inverters in islanded microgrids. Automatica, 49(9), 2603–2611.
Yao, W., Chen, M., Matas, J., Guerrero, J. M., & Qian, Z.-M. (2011). Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing. IEEE Transactions on Industrial Electronics, 58(2), 576–588.
Lee, C. T., Chu, C. C., & Cheng, P. T. (2013). A new droop control method for the autonomous operation of distributed energy resource interface converters. IEEE Transactions on Power Electronics, 28(4), 1980–1993.
Han, H., Liu, Y., Sun, Y., Su, M., & Guerrero, J. M. (2015). An improved droop control strategy for reactive power sharing in islanded microgrid. IEEE Transactions on Power Electronics, 30(6), 3133–3141.
Roldán-pérez, J., Prodanovic, M., Rodríguez-cabero, A., Guerrero, J. M., & García-Cerrada, A. (2019). Finite-gain repetitive controller for harmonic sharing improvement in a VSM microgrid. IEEE Transactions on Smart Grid, 10(6), 6898–6911.
Wang, Z., Zhuo, F., Yi, H., Wu, J., Wang, F., & Zeng, Z. (2019). Analysis of dynamic frequency performance among voltage-controlled inverters considering virtual inertia interaction in microgrid. IEEE Transactions on Industry Applications, 55(4), 4135–4144.
Hou, X., Sun, Y., Zhang, X., Lu, J., Wang, P., & Guerrero, J. M. (2019). Improvement of frequency regulation in VSG-based AC microgrid via adaptive virtual inertia. IEEE Transactions on Power Electronics, 35(2), 1589–1602.
Vijay, A. S., Chandorkar, M. C., & Doolla, S. (2019). A system emulator for AC microgrid testing. IEEE Transactions on Industry Applications, 55(6), 6538–6547.
Ebrahimi, M., Khajehoddin, S. A., & Karimi-ghartemani, M. (2019). An improved damping method for virtual synchronous machines. IEEE Transactions on Sustainable Energy, 10(3), 1491–1500.
Hossain, M. J., Rafi, F. H., Town, G., & Lu, J. (2018). Multifunctional three-phase four-leg PV-SVSI with dynamic capacity distribution method. IEEE Transactions on Industrial Informatics, 14(6), 2507–2520.
Mauroy, A., Sacré, P., & Sepulchre, R. (2012). Kick synchronization versus diffusive synchronization. In 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), pp. 7171–7183.
Johnson, B. B., Dhople, S. V., Hamadeh, A. O., & Krein, P. T. (2014). Synchronization of nonlinear oscillators in an LTI electrical power network. IEEE Transactions on Circuits and Systems I: Regular Papers, 61(3), 834–844.
Sinha, M., Dörfler, F., Johnson, B. B., & Dhople, S. V. (2017). Uncovering droop control laws embedded within the nonlinear dynamics of van der pol oscillators. IEEE Transactions on Control of Network Systems, 4(2), 347–358.
Johnson, B. B., Dhople, S. V., Hamadeh, A. O., & Krein, P. T. (2014). Synchronization of parallel single-phase inverters with virtual oscillator control. IEEE Transactions on Power Electronics, 29(11), 6124–6138.
Gurugubelli, V., Ghosh, A., Panda, A. K., & Rudra, S. (2021). Implementation and comparison of droop control, virtual synchronous machine, and virtual oscillator control for parallel inverters in standalone microgrid. International Transactions on Electrical Energy Systems., 31(5), e12859.
Luo, S., Wu, W., Koutroulis, E., Chung, H. S. H., & Blaabjerg, F. (2021). A new virtual oscillator control without third-harmonics injection For DC/AC Inverter. IEEE Transactions on Power Electronics, 36(9), 10879–10888.
Yu, H., Awal, M. A., Tu, H., Husain, I., & Lukic, S. (2021). Comparative transient stability assessment of droop and dispatchable virtual oscillator controlled grid-connected inverters. IEEE Transactions on Power Electronics, 36(2), 2119–2130.
Lin, J. (2021). Virtual oscillator control of distributed power filters for selective ripple attenuation in DC systems. IEEE Transactions on Power Electronics, 36(7), 8552–8560.
Ghosh, A., Banerjee, S., Sarkar, M. K., & Dutta, P. (2016). Design and implementation of Type-II and Type-III controller for DC–DC switched modeboost converter by using K-factor approach and optimization techniques. IET Power Electronics, 9(5), 938–950.
Rui, W., Qiuye, S., Pinjia, Z., Yonghao, G., Dehao, Q., & Peng, W. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Transactions on Energy Conversion, 35(3), 1585–1595.
D’Arco, S., Suul, J. A., & Fosso, O. B. (2015). A virtual synchronous machine implementation for distributed control of power converters in SmartGrids. Electric Power Systems Research, 122, 180–197. https://doi.org/10.1016/j.epsr.2015.01.001
Johnson, B., Rodriguez, M., Sinha, M. & Dhople, S. (2017). Comparison of virtual oscillator and droop control. In IEEE Workshop on Control and Modeling for Power Electronics pp. 1–6.
Acknowledgements
The idea of work is supported by DST project Scheme for Young Scientists and Technologists (SP/YO/2019/1349).
Funding
No funding.
Author information
Authors and Affiliations
Contributions
Each author contributed significantly to the design and implementation of the proposed work. All authors read and approved the final manuscript.
Author's information
Vikash Gurugubelli received B.Tech and M.Tech degrees in Electrical and Electronics Engineering from JNTU Kakinada, Andhra Pradesh, India, in 2014 and 2017, respectively. He is currently working towards Ph.D. degree in Electrical Engineering at National Institute of Technology, Rourkela, Odisha, India. His research interests include modeling, analysis, and control of power electronics and power systems with a focus on renewable integration.
Arnab Ghosh received the B.Tech. and M.Tech. degrees from West Bengal University of Technology, Kolkata, India, in 2010 and 2012, respectively, and the Ph.D. degree from the National Institute of Technology Durgapur, Durgapur, India, in 2017, all in electrical engineering. He is currently an Assistant Professor in the Department of Electrical Engineering, National Institute of Technology Rourkela, India. He has published several research papers in national/international journals and conference proceedings. His research interests include design of power electronics converters, renewable energy sources, microgrid and smart grid, electric vehicles and vehicle to grid applications.
Anup Kumar Panda received the B.Tech degree in Electrical Engineering from Sambalpur University, India, M. Tech in Power Electronics and Drives from Indian Institute of Technology, Kharagpur, India and Ph.D. from Utkal University in 1987, 1993 and 2001 respectively. In 1990 he joined as a lecturer in IGIT, Sarang, served there for 11 years and then in January 2001 joined National Institute of Technology, Rourkela as an Assistant Professor and currently continuing as a Professor HAG in the Department of Electrical Engineering, National Institute of Technology Rourkela. He has published more than two hundred articles in journals and conferences. He has completed two MHRD projects, one CSIR and one NaMPET project. Guided twenty Ph.D. scholars and presently guiding ten scholars in the area of Power Electronics & Drives. He is a Fellow of Institute of Engineering and Technology UK, Institute of Engineers India and Institute of Electronics and Telecommunication Engineering. He is also a senior member of IEEE USA. He was awarded the Institute Endowed Chair Professor Award in 2018. His research interest includes design of high frequency power conversion circuits and applications of soft computing techniques, improvement in multilevel converter topology, power factor improvement, power quality improvement in power system and electric drives.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix
Appendix
1.1 Simulation parameters
-
System parameters: PCC voltage = 415 V (line–line rms); frequency = 50 Hz; Lf = 3.5 mH, Cf = 50 µF; DC supply = 800 V; switching frequency = 12 kHz.
-
Droop control parameters: droop constants: kp1 = 0.6/2000, kq1 = 10/1000, kp2 = 0.3/2000, kq2 = 5/1000.
-
VSM parameters: ωvsm = 314.15 rad/s, kw = 20, kd = 150,\(\tau_{a}\) = 1, 2 for VSI (i) and (ii) individually.
-
VOC parameters: oscillator RLC parameters: R = 10 Ω, L = 250 µH, C = 28.14 mF. Oscillator non-linear parameters: σ = 1S, φ = 0.47 V. Voltage and current gains: kv = 338.85, ki = 2.984 × 10–3.
-
VOC-PSO parameters: oscillator RLC parameters: R = 11.87Ω, L = 271.59 µH, C = 37.31 mF. Oscillator non-linear parameters: σ = 1.78S, φ = 0.47 V. Voltage and current gains: kv = 338.85, ki = 2.984 × 10–3.
1.2 Hardware details
DC supply = 260 V, DC link capacitor (SKC 4M7), IGBT modules in inverter is (SKM75GB12T4)), Lf = 12 mH and Cf = 36 µF, a load (balanced and resistive load) is varies from 350 to 700 W. The controller is OPAL-RT (OP5142). Optoisolator (MCT2E), NOT gate (IN74LS04N), level shifter (CD4502BE), current sensor (LA 55-P), and DC power supplies.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gurugubelli, V., Ghosh, A. & Panda, A.K. Parallel inverter control using different conventional control methods and an improved virtual oscillator control method in a standalone microgrid. Prot Control Mod Power Syst 7, 27 (2022). https://doi.org/10.1186/s41601-022-00248-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41601-022-00248-9