1 Introduction

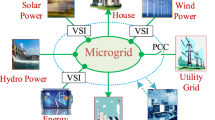
Consumption of electrical energy is increasing rapidly, following the rapid growth of the world’s population. To meet the demand, largely fossil fuels have been used. However, fossil fuels pollute the environment. At the same time, they are also depleting dramatically [1, 2]. To overcome this problem, renewable energy is one of the prime solutions, and different renewable energy generating units such as wind turbine, photovoltaic (PV), hydro, bio-mass, hydrogen fuel cells have been considered as distributed generator (DG) units located at customer sites [3, 4]. These DGs are connected to the utility grid through microgrid (MG) systems. Furthermore, the MG contains various loads including linear and nonlinear, balanced and unbalanced, static and dynamic types, as well as lines and distribution transformers, and energy storage systems (ESS) [5,6,7]. It is also worth noting that DG units cannot provide accurate 50/60 Hz power supply to the MG owing to their characteristics. To interface an MG with DG units, voltage source inverters (VSI) are used, and thus, to obtain the quality voltage and power outputs, VSI control is extremely important [8]. A simple MG structure with some conventional DG units, VSI and loads is depicted in Fig. 1.

Fig. 1
figure 1

Microgrid configuration

Full size image

An MG must have the ability to accommodate any uncertainty and abnormality, and bring the system back into an equilibrium position within the shortest possible time after a disturbance. The functions of an MG can be segmented into non-isolated (grid connected) mode and isolated (autonomous) mode [9]. In non-isolated mode, the utility grid controls the voltage and frequency of the MG, and the MG is treated as a controllable generator or load. In the case of autonomous mode, the MG itself has to control the different parameters including voltage, frequency, active and reactive power, power-factor etc. Thus, a robust control system is necessary for satisfactory operation of an autonomous MG.

Research has made significant progress on MG controlling technology for maintaining good performance. The linear quadratic regulator (LQR) [10, 11], integral-LQR (I-LQR) [12], linear quadratic Gaussian (LQG) [13], and integral-LQG (I-LQG) [14] are well-known controllers based on linearization techniques. These have been proposed for the voltage control of an MG. Accurate voltage tracking is the main advantage of these controllers, but the dynamics of these controllers depend on the dynamics of the plant and their performance degrades if the plant changes. Furthermore, according to the order of the plant dynamics, the order of the controller also increases. Proportional integral derivative (PID) [15] and proportional integral (PI) [16] controllers are very common and widely used for voltage and power control of an MG because of their simplicity and easy implementation. However, during disturbances, their performance degrades and steady-state errors occur because of the unbalanced system. In addition, if the operating point changes, the performance of the controllers is also hampered.

Decentralized and distributed control strategies [17,18,19] are two more control systems frequently used in an MG to compensate for deviations in frequency and voltage. These controllers require parameters which are measured by remote sensing blocks and sent back to the controller through low bandwidth communication systems. Thus, the low bandwidth and slow control loop are the principal drawbacks of these controllers.

An H-infinity controller [20, 21] has been proposed to acquire good stabilization with guaranteed performance of an MG. However, the order of the system is a big issue for such a controller and advanced digital signal processing (DSP) is required for satisfactory performance. In addition, high mathematical understanding is needed for modeling this controller, while its slow dynamic response restricts its use. The hierarchical control technique [22, 23] which is another well-known controller, is commonly used in a power system to control voltage and frequency. Three different levels are required, where each level is assigned to perform a distinctive control action. If one of the control levels collapses, the whole control system fails.

Model predictive control (MPC) [24, 25] is an advanced control technique extensively used to control an MG system while satisfying some constraints. Lower switching frequency and accurate voltage control with lower total harmonic distortion (THD) are the main advantages of this controller. However, sensitivity to parameter variations, as well as the need for an advanced DSP system to implement the higher order system are its major limitations. The hysteresis controller, which is another control technique based on the current controlled pulse width modulation (PWM) technique proposed in [26, 27], has fast transient response and low complexity in design. However, the considerable amount of ripple in current and variation of switching frequency limit its use at large scale. The repetitive controller [28, 29] is also a good competitor for voltage control of an MG. It is designed to eliminate periodic disturbance and minimize harmonics in the system. However, it is difficult to stabilize the controller against all unknown load disturbances, and it responds sluggishly while loads fluctuate.

In order to damp out the resonant mode in a power system, different damping controllers have been proposed, such as the proportional resonant (P-RC) [30, 31] and proportional integral resonant controllers (PI-RC) [32]. These improve the performance of the MG. These controllers are simple in structure, and can efficiently control selective harmonics and show negligible steady-state error. However, they are extremely sensitive to frequency variation and require accurate tuning. Negative imaginary (NI) based-resonant (NI-R) [33], proportional resonant [34] and proportional plus lead compensator controllers [35] also promote voltage tracking performance along with damping resonant peak in islanded MG system, and exhibit robust performance against different load dynamics. However, they show poor performance in minimizing transient oscillation in some cases, and also the magnitude and phase errors in voltage tracking degrade their performance.

The above descriptions demonstrate the need for further improvements in voltage control of an MG system for precise reference tracking. Therefore, in this paper, a robust high-performance controller is designed to amend voltage tracking performance against various uncertainties and different loads in autonomous MG technology for both single-phase and three-phase systems. The designed controller is modeled with a resonant (R) controller, series connected with a lead-lag compensator (LLC), which obeys the NI theorem for guaranteeing system stability, abbreviated to ‘NI-RLLC’ controller. The NI-RLLC controller rigorously eliminates the drawbacks mentioned above, and has the advantages of both the resonant controller and lead-lag compensator. The lead compensator shifts the root locus to the left for achieving good transient stability, while steady state errors in phase and magnitude are minimized through the lag compensator. The pole and zero of the lag compensator are placed near the origin and close to each other to avoid the instability problem. The main focus of the proposed work is to control the output voltage to track the reference to ensure the lowest magnitude and phase errors as well as THD, considering different uncertainties, nonlinearities and unknown dynamics of loads. To prove the superiority of the designed NI-RLLC controller, its performance is compared with the well-known LQR, MPC and NI-R controllers. The controller and the system are simulated through MATLAB software.

The rest of the paper is structured as follows. Section 2 describes MG modeling while Sect. 3 presents the design procedure of the NI-RLLC controller. Comparison of controllers is discussed in Sect. 4 and the performance of the controller is evaluated in Sect. 5. Section 6 concludes the paper.

2 Modeling of autonomous MG technology

The configuration and modelling of single-phase and three-phase autonomous MGs are provided in this section.

2.1 Autonomous MG configuration

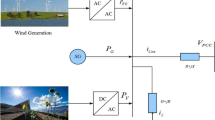
An MG mainly consists of three essential elements: an input energy source, an energy conversion unit and a filter. A single-phase MG system with these elements is shown in Fig. 2a. For modeling purposes, a DC voltage source is used as the source for generating power, and an IGBT-based full bridge VSI is used to convert the DC voltage into AC. In order to eliminate high frequency harmonic components from the VSI output, a filter consisting of inductor and capacitor is used after the VSI. As the MG system operates at low voltage with short lines, only the series resistance is considered here as line impedance [36]. Figure 2b depicts the three-phase MG system, where a three-phase VSI and a filter are used to regulate voltage and current. Additionally, the three-phase MG has step-up transformer, point of common coupling (PCC) and loads, where loads are connected to the high voltage side of the transformer at PCC [37].

Fig. 2
figure 2

Closed-loop configuration of MG technology for a single-phase system and b three-phase system

Full size image

Figure 2a, b also show the closed-loop control structures of single-phase and three-phase MG systems, respectively. Measured output voltages and reference voltages are injected to the controllers as shown in Fig. 2a, b. Necessary actions are imposed to generate proper control signals which are sent to the PWM blocks to control the IGBT switches.

2.2 Mathematical modeling of single-phase MG system

In this subsection, a state space mathematical model is provided for the autonomous MG technology as shown in Fig. 2a. Considering \({\hat{V}}_{L}\) as the voltage across inductor \(L_{s}\), and \({\hat{I}}_{L}\) as inductor current, there is [38, 39]:

$${\hat{V}}_{L} = L_{s} \frac{{d{\hat{I}}_{L} }}{dt}.$$
(1)

Applying KVL yields:

$${\hat{V}}_{sw} = {\hat{V}}_{L} + {\hat{V}}_{G}$$
(2)

Substituting (1) into (2) yields:

$$\frac{{d{\hat{I}}_{L} }}{dt} = \frac{{{\hat{V}}_{L} }}{{L_{s} }} = \frac{{{\hat{V}}_{sw} - {\hat{V}}_{G} }}{{L_{s} }}$$
(3)

where \({\hat{V}}_{sw}\) and \({\hat{V}}_{G}\) represent input voltage and output voltage, respectively. \({\hat{V}}_{sw} = \tau {\hat{V}}_{DC}\) is the average switching voltage and duty ratio \(\tau \in \{ - 1,1\}\).

Considering \({\hat{I}}_{C}\) as the current through the capacitor and \({\hat{V}}_{G}\) the capacitor voltage, there is:

$${\hat{I}}_{C} = C_{s} \frac{{d{\hat{V}}_{G} }}{dt}.$$
(4)

Using KCL obtains:

$${\hat{I}}_{L} = {\hat{I}}_{C} + {\hat{I}}_{G}$$
(5)

Substituting (4) into (5) yields:

$$\frac{{d{\hat{V}}_{G} }}{dt} = \frac{{{\hat{I}}_{C} }}{{C_{s} }} = \frac{{{\hat{I}}_{L} - {\hat{I}}_{G} }}{{C_{s} }}.$$
(6)

Equations (3) and (6) can be represented in the time-domain as:

$$\frac{d}{dt}\left[ {\begin{array}{*{20}l} {{\hat{I}}_{L} } \hfill \\ {{\hat{V}}_{G} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{L_{s} }}} \\ {\frac{1}{{C_{s} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\hat{I}}_{L} } \hfill \\ {{\hat{V}}_{G} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\frac{1}{{L_{s} }}} \hfill \\ 0 \hfill \\ \end{array} } \right]{\hat{V}}_{sw} + \left[ {\begin{array}{*{20}c} 0 \\ { - \frac{1}{{C_{s} }}} \\ \end{array} } \right]{\hat{I}}_{G} .$$
(7)

Loads in MG are considered as black box as they change randomly and abruptly, and thus, \({\hat{I}}_{G}\) in (7) is treated as disturbance. As the purpose is to follow the reference voltage properly, \({\hat{V}}_{G}\) is considered as output, i.e.:

$$y = [{\hat{V}}_{G} ] = [\begin{array}{*{20}c} 0 & 1 \\ \end{array} ]\left[ {\begin{array}{*{20}c} {{\hat{I}}_{L} } \\ {{\hat{V}}_{G} } \\ \end{array} } \right].$$
(8)

Considering (7) and (8), the general form of the system in the Laplace domain can be written as [40]:

$$W(s) = W_{0} (s) + \Delta_{t} (s)$$
(9)

where \(W_{0} (s) = C_{t} (sI - A_{t} )^{ - 1} B_{t} + D_{t}\) is the plant transfer function, and \(\Delta_{t} (s) = \left[ {\begin{array}{*{20}c} 0 \\ { - \frac{1}{{C_{s} }}} \\ \end{array} } \right]{\hat{I}}_{G} (s)\) is the output to input uncertainty. Also, the system matrix is \(A_{t} = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{L_{s} }}} \\ {\frac{1}{{C_{s} }}} & 0 \\ \end{array} } \right]\), the input matrix \(B_{t} = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{s} }}} \\ 0 \\ \end{array} } \right]\); the output matrix \(C_{t} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]\), and the feed-through matrix \(D_{t} = 0\). The required parameters of the single-phase MG system are listed in Table 1.

Table 1 Parameters of single-phase MG
Full size table

2.3 Mathematical modeling of three-phase MG system

Mathematical analysis of the three-phase MG system is constructed with the aid of Fig. 2b. The dynamical equation of the topology in the abc-frame can be expressed as [41, 42]:

$$\overline{I}_{t,abc} = C_{f} \frac{{d{\overline{V}}_{abc} }}{dt}$$
(10)
$${\overline{V}}_{t,abc} = L_{f} \frac{{d\overline{I}_{t,abc} }}{dt} + R_{f} \overline{I}_{t,abc} + {\overline{V}}_{abc} .$$
(11)

In (10) and (11), \({\overline{V}}_{t,abc}\), \(\overline{I}_{t,abc}\) and \({\overline{V}}_{abc}\) are \(3 \times 1\) matrices consisting of independent phase quantity in the time-domain. Rearranging (10) and (11) leads to:

$$\frac{{d{\overline{V}}_{abc} }}{dt} = \frac{1}{{C_{f} }}\overline{I}_{t,abc}$$
(12)
$$\frac{{d\overline{I}_{t,abc} }}{dt} = \frac{1}{{L_{f} }}{\overline{V}}_{t,abc} - \frac{{R_{f} }}{{L_{f} }}\overline{I}_{t,abc} - \frac{1}{{L_{f} }}{\overline{V}}_{abc} .$$
(13)

Assuming balanced DG units and loads, Eqs. (12) and (13) can be transformed into a rotating dq-frame using the Park transformation as:

$$\frac{{d{\overline{V}}_{dq} }}{dt} = \frac{1}{{C_{f} }}\overline{I}_{t,dq} - j\omega_{f} {\overline{V}}_{dq}$$
(14)
$$\frac{{d\overline{I}_{t,dq} }}{dt} = \frac{1}{{L_{f} }}{\overline{V}}_{t,dq} - \frac{{R_{f} }}{{L_{f} }}\overline{I}_{t,dq} - \frac{1}{{L_{f} }}{\overline{V}}_{dq} - j\omega_{f} \overline{I}_{t,dq} .$$
(15)

Equations (14) and (15) consist of components in the d- and q-axes, where the d- and q-axes represent real and imaginary parts, respectively. Dissociating these two components, Eqs. (14) and (15) are formed as:

$$\frac{{d{\overline{V}}_{d} }}{dt} = \frac{1}{{C_{f} }}\overline{I}_{t,d} + \omega_{f} {\overline{V}}_{q}$$
(16)
$$\frac{{d{\overline{V}}_{q} }}{dt} = \frac{1}{{C_{f} }}\overline{I}_{t,q} - \omega_{f} {\overline{V}}_{d}$$
(17)
$$\frac{{d\overline{I}_{t,d} }}{dt} = \frac{1}{{L_{f} }}{\overline{V}}_{t,d} - \frac{{R_{f} }}{{L_{f} }}\overline{I}_{t,d} - \frac{1}{{L_{f} }}{\overline{V}}_{d} + \omega_{f} \overline{I}_{t,q}$$
(18)
$$\frac{{d\overline{I}_{t,q} }}{dt} = \frac{1}{{L_{f} }}{\overline{V}}_{t,q} - \frac{{R_{f} }}{{L_{f} }}\overline{I}_{t,q} - \frac{1}{{L_{f} }}{\overline{V}}_{q} + \omega_{f} \overline{I}_{t,d} .$$
(19)

The standard state space equations of the MG system can be expressed as:

$$\dot{x}(t) = A_{m} x(t) + B_{m} u(t)\quad y(t) = C_{m} x(t) + D_{m} u(t)$$
(20)

where, \(A_{m} = \left[ {\begin{array}{*{20}c} 0 & {\omega_{f} } & {\frac{1}{{C_{f} }}} & 0 \\ { - \omega_{f} } & 0 & 0 & {\frac{1}{{C_{f} }}} \\ { - \frac{1}{{L_{f} }}} & 0 & { - \frac{{R_{f} }}{{L_{f} }}} & {\omega_{f} } \\ 0 & { - \frac{1}{{L_{f} }}} & {\omega_{f} } & { - \frac{{R_{f} }}{{L_{f} }}} \\ \end{array} } \right]\), \(B_{m} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ {\frac{1}{{L_{f} }}} & 0 \\ 0 & {\frac{1}{{L_{f} }}} \\ \end{array} } \right]\), \(C_{m} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right]\) and \(D_{m} = 0\). Also, the state vectors are \(x(t) = \left[ {\begin{array}{*{20}c} {{\overline{V}}_{d} } & {{\overline{V}}_{q} } & {\overline{I}_{t,d} } & {\overline{I}_{t,q} } \\ \end{array} } \right]^{T}\), the input or control vectors are \(u(t) = \left[ {\begin{array}{*{20}c} {{\overline{V}}_{t,d} } & {{\overline{V}}_{t,q} } \\ \end{array} } \right]^{T}\), and the output vectors are \(y(t) = \left[ {\begin{array}{*{20}c} {{\overline{V}}_{d} } & {{\overline{V}}_{q} } \\ \end{array} } \right]\).

To design an MIMO control system for a three-phase MG in the s-domain, illustrated in Fig. 3a, the nominal plant transfer function is obtained from (20), thus:

$$W_{m} (s) = C_{m} (sI - A_{m} )^{ - 1} B_{m} + D_{m}$$

Table 2 lists the necessary parameters required for the three-phase MG system.

Fig. 3
figure 3

a Closed-loop control structure of MG system both for single-phase and three-phase b bode plot of different transfer functions for single-phase

Full size image
Table 2 Parameters of three-phase MG
Full size table

3 Controller design for single-phase and three-phase autonomous MG systems

3.1 Controller design for single-phase MG system

Figure 3a shows the block diagram of the closed-loop control structure for an autonomous MG system. Here, the reference signal is defined as \(R(s)\) and the output signal is \(Y(s)\). For a single-phase system, \(W(s)\) represents the nominal plant transfer function between input voltage \({\hat{V}}_{sw}\) and output voltage \({\hat{V}}_{G}\), \(H(s)\) is the resonant controller and \(C(s)\) is the lead-lag compensator. For robust performance, the feedback compensator \(C(s)\) is connected in series with the resonant controller \(H(s)\). The transfer function of the resonant controller \(H(s)\) for a simple single input single output (SISO) system can be expressed as [33, 43, 44]:

$$H(s) = - k_{s} \frac{{s(s + 2\xi_{s} \omega_{s} )}}{{s^{2} + 2\xi_{s} \omega_{s} s + \omega_{s}^{2} }}$$
(21)

where \(k_{s}\) is the resonant gain of the controller, \(\xi_{s}\) is the damping co-efficient, and \(\omega_{s}\) is the resonant frequency. For proper stabilization of this controller, all its parameters are higher than zero. The optimized value of \(\xi_{s}\) is taken, as a large value leads to low damping while a small value provides unwanted phase shift. The closed-loop transfer function of the system \(W(s)\) associating with the resonant controller \(H(s)\) can be expressed as:

$${\hat{W}}_{Cl} (s) = \frac{W(s)}{{1 - W(s)*H(s)}}$$
(22)

This resonant controller H(s) is designed by the NI theorem (NI-R) [33], which is a simple second order controller. However, this controller has steady-state phase and amplitude errors, and also shows poor performance in transient condition with considerable oscillations.

To alleviate these drawbacks, a lead-lag compensator \(C(s)\) is cascaded in series with the resonant controller \(H(s)\), i.e., RLLC controller, for better and robust performance. The RLLC controller is designed to satisfy the NI theorem, and is thus called NI-RLLC. According to the NI theorem [43, 45], the positive feedback interconnection of two NI systems will be stable if one of the systems is strictly negative imaginary (SNI) and the DC loop gain remains less than unity. From Fig. 3b, it is clear that the phase of the plant transfer function \(W(s)\) lies within − 180° and 0°, which implies that the system is an NI system. The transfer function of the lead-lag compensator \(C(s)\) with a gain \(k_{c}\) can be written as [46, 47]:

$$C(s) = k_{c} \frac{{(s + z_{s1} )(s + z_{s2} )}}{{(s + p_{s1} )(s + p_{s2} )}}$$
(23)

The zero and pole of the lead compensator are denoted by \(z_{s1}\) and \(p_{s1}\), respectively, and \(\left| {p_{s1} } \right| > \left| {z_{s1} } \right|\). For the lag compensator, \(z_{s2}\) and \(p_{s2}\) are the zero and pole, respectively, and \(\left| {z_{s2} } \right| > \left| {p_{s2} } \right|\). The values of the parameters are chosen as \(k_{c} = 3.5\), \(z_{s1} = 4100\), \(p_{s1} = 9600\), \(z_{s2} = 4\) and \(p_{s2} = 3\). The overall closed-loop transfer function with the designed NI-RLLC controller can be written as:

$$W_{Cl} (s) = \frac{W(s)}{{1 - W(s)*F(s)}}$$
(24)

where \(F(s) = H(s)*C(s)\).

Figure 3b shows that the loop gain \(W(s)*F(s)\) is still less than unity at low frequency which stabilizes the designed controller. Nyquist and root-locus plots are depicted in Fig. 4a, b, respectively. It can be seen that the stability criterion of the designed NI-RLLC controller is guaranteed, as no root is located in the right-half plane. The performance of the designed NI-RLLC controller is examined through imposing different uncertainties and various load dynamics. Different parameters of the SISO NI-RLLC controller are listed in Table 3.

Fig. 4
figure 4

a Nyquist and b root-locus plot for single-phase MG system

Full size image
Table 3 Parameters of SISO NI-RLLC controller
Full size table

3.2 Controller design for three-phase MG system

Designing a multiple input multiple output (MIMO) controller is much more challenging as multiple subsystems may consist of a number of power sources in each subsystem, while the numbers of control inputs and outputs increase. The closed-loop control technique for three-phase MG technology is shown in Figs. 2b and 3a, where \({\overline{V}}_{t,d}\) and \({\overline{V}}_{t,q}\) are the two control inputs, and \({\overline{V}}_{d}\), \({\overline{V}}_{q}\) are the two output signals to be controlled. The transfer function matrix of the MIMO closed-loop system for plant \(W_{m} (s)\) and controller \(F_{m} (s)\) can be formed as:

$$W_{mCl} (s) = \frac{{W_{m} (s)}}{{1 - W_{m} (s)*F_{m} (s)}}$$
(25)

where \(F_{m} (s) = H_{m} (s)*C_{m} (s)\).

For the MIMO system, \(H_{m} (s)\) and \(C_{m} (s)\) can be provided in the following way:

$$H_{m} (s) = - k_{m} \frac{{s(s + 2\xi_{m} \omega_{m} )}}{{s^{2} + 2\xi_{m} \omega_{m} s + \omega_{m}^{2} }}\beta_{m \times m}$$
(26)
$$C_{m} (s) = k_{p} \frac{{(s + z_{m1} )(s + z_{m2} )}}{{(s + p_{m1} )(s + p_{m2} )}}\eta_{m \times m}$$
(27)

\(\beta_{m \times m}\) and \(\eta_{m \times m}\) are square matrices of order 2 × 2 for a two-state MG system. The compensator gains are chosen as: \(k_{p} = 2\), \(z_{m1} = 3800\), \(p_{m1} = 8600\), \(z_{m2} = 4\) and \(p_{m2} = 3\). The values of various parameters are listed in Table 4. For better perception of the control mechanism, a flowchart is given in Fig. 5 for the MIMO NI-RLLC controller. In the case of the SISO system, \(\beta_{m \times m}\) and \(\eta_{m \times m}\) are 1 × 1 matrices, and there is no need to dissociate the input voltage. However, the rest of the procedure is identical for the two systems. Since the objective is to control the voltage of the autonomous MG system, the corresponding load voltages of the SISO and MIMO systems are considered as inputs, and the outputs of the control systems are the regulated PWM signals for the inverter IGBTs.

Table 4 Parameters of MIMO NI-RLLC controller
Full size table
Fig. 5
figure 5

Flowchart of designed NI-RLLC controller incorporating nominal plant

Full size image

4 Comparative study of controllers

To evaluate the superior performance of the designed NI-RLLC controller, time-domain and frequency-domain comparisons are displayed in Figs. 6 and 7, respectively, for single-phase and three-phase systems. Commonly used controllers, including LQR and MPC together with NI-R controller are considered for comparison. The design procedure of LQR, MPC, and NI-R is adopted from [33, 48, 49], respectively. For fair comparison, the resonant controller parameters of the NI-R controller and the designed NI-RLLC controller are kept the same as shown in Tables 3 and 4, respectively. The required parameters of the LQR controller are chosen as follows:

$$\begin{gathered} {\text{SISO LQR:}}\;Q_{s} = \left[ {\begin{array}{*{20}c} {10} & 0 \\ 0 & {10^{ - 2} } \\ \end{array} } \right]\;{\text{and}}\;R_{s} = 14.\\ {\text{MIMO LQR:}}\;Q_{m} = \left[ {\begin{array}{*{20}c} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 5 & 0 \\ 0 & 0 & 0 & 3 \\ \end{array} } \right]\;{\text{and}}\;R_{m} = \left[ {\begin{array}{*{20}c} {300} & 0 \\ 0 & {350} \\ \end{array} } \right].\hfill \\ \end{gathered}$$
Fig. 6
figure 6

Single-phase a step response comparison of different controllers and b bode plot comparison of different controllers

Full size image
Fig. 7
figure 7

Three-phase step response comparison for different controllers for a d-axis and b q-axis; bode plot comparison for different controllers for c d-axis and d q-axis

Full size image

For the SISO MPC controller, the prediction horizon and control horizon are selected as 10 and 1, respectively, and the weights are chosen as 0.1 and 11. Prediction and control horizons are kept unchanged whereas weights are selected as {0.1, 0.1} and {13, 200} for MIMO MPC.

Numerical values of different terms for different controllers which represent the step responses for single-phase and three-phase systems are listed in Tables 5 and 6, respectively. It is clear from the tables that the designed NI-RLLC controller for both SISO and MIMO systems achieves outstanding performance. The step response of the closed-loop system using the designed SISO NI-RLLC controller approaches steady-state with null offset, nearly 76.39%, 86.92% and 77.63% faster than the NI-R controller, LQR and MPC, respectively. Incorporating rapid rise time and peak time, the designed NI-RLLC controller reduces the overshoot by around 54.35%, 67.31% and 59.41% with respect to the NI-R controller, LQR and MPC, respectively. It is also notable that better performance is obtained for the three-phase system, with lower percentage of overshoot, faster rise time and peak time, as well as lower settling time with zero steady-state error. Obviously, these relative analyses prove that the designed NI-RLLC controller is more reliable than the other controllers in all aspects for voltage tracking of an autonomous MG system.

Table 5 Step response comparison of different controllers for single-phase
Full size table
Table 6 Step response comparison of different controllers for three-phase
Full size table

5 Performance evaluation for single-phase autonomous MG system

5.1 Performance over different uncertainties

Uncertainties in a system arise on account of unknown load parameters, unmodeled load dynamics, load variation etc. In order to achieve robust performance, a controller must perform sensitively under various uncertainties. For robust analysis of the designed NI-RLLC controller, multiplicative input uncertainty, inverse additive uncertainty and inverse multiplicative input uncertainty are imposed on the plant, whose block diagrams are depicted in Fig. 8a–c, respectively, where \(W_{0} (s)\), \(E_{0}\) and \(\Delta_{t} (s)\) represent plant transfer function, scalar weights and plant variation, respectively. The values of \(E_{0}\) and \(\Delta_{t} (s)\) are selected by considering 25% of reference amplitudes as plant variation. Effectiveness of the controller against all the uncertainties is shown in Fig. 8d–f. It is clear that the open-loop responses become severely distorted because of plant variation, whereas the NI-R controller and the designed NI-RLLC controller show good performance, while the designed controller attains relatively higher damping than the NI-R controller. It is worth mentioning that the literature and previous discussions indicate that the NI-R has better responses than both MPC and LQR. Thus, it validates the claim of superior performance of the designed NI-RLLC controller over other controller designs.

Fig. 8
figure 8

Block diagram of a multiplicative input uncertainty b inverse additive uncertainty and c inverse multiplicative input uncertainty for single-phase MG system. Bode plot of d multiplicative input uncertainty e inverse additive uncertainty and f inverse multiplicative input uncertainty for single-phase MG system

Full size image

5.2 Performance over changing reference value

As the prime objective of this paper is to design a controller for tracking reference voltage rigorously, the performance of this controller is verified with varying reference value. The following conditions are considered for changing reference grid voltage, \(V_{G}^{ * }\):

  • \(V_{G}^{ * }\) = 200 V; 0 s < t < 0.035 s;

  • \(V_{G}^{ * }\) = 250 V; 0.035 s < t < 0.065 s;

  • \(V_{G}^{ * }\) = 150 V; 0.065 s < t < 0.1 s;

Figure 9 verifies the robust reference tracking performance of the designed NI-RLLC controller, despite changing the reference value randomly. The NI-R controller exhibits a greater magnitude error than the designed NI-RLLC controller, and the NI-R controller shows higher oscillations during an abrupt change of reference.

Fig. 9
figure 9

Performance check for changing reference value a normal view b zoomed view

Full size image

5.3 Performance over some conventional loads

Commonly, an MG system deals with ranges of known and unknown loads, and their characteristics may disturb normal operation. With the aid of the designed controller, these problems can be easily addressed. To verify the effectiveness of the designed NI-RLLC controller, some common loads are modeled in Fig. 10, and a brief description of these loads is given in Table 11 in the “Appendix”.

Fig. 10
figure 10

Block diagram of single-phase a consumer load, b harmonic load, c unknown load, d nonlinear load, e dynamic load

Full size image

5.3.1 Consumer load

This type of load is modeled in Fig. 10a, and improved voltage tracking of the designed NI-RLLC controller for such load is demonstrated in Fig. 11a, f. Apart from having the lowest amplitude error, a higher amount of active power is evolved using NI-RLLC controller as shown in Fig. l1k.

Fig. 11
figure 11

Single-phase load voltage comparison of load a consumer, b harmonic, c unknown, d nonlinear, e dynamic. Zoomed view of load voltage of load f consumer, g harmonic, h unknown, i nonlinear, and j dynamic. Active power measurement of load k consumer, l harmonic, m unknown, n nonlinear and o dynamic

Full size image

5.3.2 Harmonic load

Harmonics originate because of different nonlinear loads such as semiconductor devices, switching elements etc. These loads are the prime reason of over-heating of motors, cables, and capacitors etc. In order to simulate the effects of harmonic loads, they are modeled as shown in Fig. 10b. The open-loop and NI-R controller in Fig. 11b, g show more transient oscillations, but the designed NI-RLLC controller mitigates the oscillations and tracks the voltage waveform more accurately with fewer harmonics. It is apparent from Fig. 11l that the open-loop can extract a very low amount of power, while NI-R improves this problem significantly, but the designed NI-RLLC has the highest power extraction capability.

5.3.3 Unknown load

Modeling of an unknown load is shown in Fig. 10c, while open-loop, NI-R and NI-RLLC controller responses for this type of load are reported in Fig. 11c, h. It is seen that the designed NI-RLLC controller tracks the voltage most effectively with least tracking error despite changing load dynamics. In correspondence to least magnitude error, a comparatively higher amount of power is derived for the NI-RLLC controller as shown in Fig. 11m.

5.3.4 Nonlinear load

Often an MG system faces nonlinear loads, e.g., rectifiers, semiconductor devices, computers, printers, electronic lighting ballasts etc. For simulation purposes and simple representation, this type of load is configured as shown in Fig. 10d. Figure 11d, i show that the NI-R controller performs better than the open-loop system but exhibits some phase shift in voltage tracking. However, the designed NI-RLLC controller diminishes the harmonics to a greater extent and has better voltage tracking capability than the others. In terms of power extraction, the designed NI-RLLC controller also indicates the best performance as can be seen from Fig. 11n.

5.3.5 Dynamic load

Dynamic loads as configured in Fig. 10e have considerable effects on an MG system. Large transient oscillations in voltage waveform are noted for the open-loop and NI-R controller, while the designed NI-RLLC controller effectively mitigates these oscillations and tracks the reference voltage with near zero tracking error, as shown in Fig. 11e, j. Moreover, relatively higher active power is also obtained for the designed NI-RLLC controller as shown in Fig. 11o.

5.4 Quantitative analysis of simulation performances

Quantitative analysis for the open-loop system, NI-R and NI-RLLC controllers is carried out with different loads. The THD analysis, and errors of RMS voltage and active power are investigated based on Fig. 11, and are presented in Tables 7, 8 and 9, respectively. Table 7 indicates that the lowest THD are obtained for all kinds of loads with the designed NI-RLLC controller. This is followed by the NI-R controller. In the case of RMS voltage error, the designed NI-RLLC controller minimizes the error noticeably for all loads. Taking the average RMS voltage error, a maximum error of 17.5 V is found for the open loop system, followed by 0.52 V for NI-R controller and 0.30 V for the NI-RLLC controller. It is clear from Table 9 that the highest active power is extracted by the NI-RLLC controller under all types of loads. On average, 1242.84 W active power is extracted with the designed NI-RLLC controller. This is 5.06 W and 230.82 W higher than the NI-R controller and the open-loop system, respectively. These results demonstrate that the NI-RLLC controller has better performance under various load conditions than the others.

Table 7 Total harmonic distortion (THD) for different loads of SISO system
Full size table
Table 8 RMS voltage error for different loads of SISO system
Full size table
Table 9 Active power (watt) measurement for different loads of SISO system
Full size table

5.5 Performance evaluation for three-phase MG system

Simulation performance of the designed MIMO NI-RLLC controller is examined by imposing various types of three-phase loads, whose details are noted in Table 12 in the “Appendix”. Among different types of loads, consumer load is the most common form of load as depicted in Fig. 12a. The closed-loop with the NI-RLLC controller and open-loop system responses are presented in Fig. 12e, i, respectively. These indicate that the closed-loop system performs much better than the open-loop system by keeping the load voltage within the desired 1 pu value, while the open-loop system has a voltage profile of around 2 pu.

Fig. 12
figure 12

Block diagram of three-phase load a consumer, b nonlinear, c unknown, d unbalanced. Three-phase load voltage for closed-loop with MIMO NI-RLLC controller for load e consumer, f nonlinear, g unknown, h unbalanced. Open-loop load voltage response of load i consumer, j nonlinear, k unknown and l unbalanced

Full size image

After connecting the nonlinear load as shown in Fig. 12b to the MG system, the NI-RLLC controller keeps the load voltage stable and helps it return to its normal state (1 pu) within a minimum time period as shown in Fig. 12f. On the other hand, the output voltage moves from the desirable load level because of the insertion of nonlinear load as shown in Fig. 12j.

The unknown load for a three-phase system is modeled in Fig. 12c, and the consequence of such load is shown in Fig. 12g, k for closed-loop and open-loop systems, respectively. The NI-RLLC controller shows a desirable response against this changing load dynamics by maintaining the load voltage to the level of 1 pu, but the open-loop system cannot meet the requirement at all.

In order to investigate the performance of the NI-RLLC controller during unbalanced condition, an unbalanced load is modeled as shown in Fig. 12d. Because of the control action of the NI-RLLC controller, imbalance among phases is controlled rigidly, while the open loop system fails to minimize the effects of unbalanced load as is clearly visible in Fig. 12h, l. Therefore, the desired level of load voltage is obtained for closed-loop, but the open-loop system completely loses its control after connecting the unbalanced load.

5.6 Power quality constraint measurement

Some power quality constraints, such as THD, voltage deviation and voltage imbalance ratio are considered in order to justify the use of the MIMO NI-RLLC controller. For the steady-state condition, numerical values are measured for various loads and listed in Table 10. It is clear that all the measured values satisfy the standard IEEE Std-1547 [50]. This affirms the robust performance of this NI-RLLC controller for three-phase MG technology.

Table 10 Power quality constraints measurement with the designed MIMO NI-RLLC controller
Full size table

6 Conclusion

This paper presents a lead-lag compensator conjugated resonant controller, designed by following the negative imaginary theorem, abbreviated as NI-RLLC controller for both single-phase and three-phase autonomous MG systems. The efficacy of the proposed controller is proven by comparing its performance with LQR, MPC and NI-R controllers and open-loop response. From the simulation results and numerical analysis, the following can be stated:

  • Step response and bode plots confirm that the designed NI-RLLC controller has better responses than the LQR, MPC and NI-R controller for both single-phase and three-phase MG systems. Furthermore, the Nyquist plot and root-locus indicate that system stability is guaranteed.

  • The NI-RLLC controller attains 139.64 dB damping which is 11.74 dB higher than its closest competitor, i.e., NI-R controller. In addition, 722 rad/s higher bandwidth is obtained for the NI-RLLC controller than the NI-R controller.

  • The NI-RLLC controller maintains its superiority for different uncertainties and for continuously changing reference value.

  • For a SISO system, the NI-RLLC controller has the best performance in terms of THD and RMS voltage error, while it also has the capability to extract the highest amount of active power for several types of loads. Similarly, for the MIMO system, the NI-RLLC controller maintains all power quality constraints within the IEEE Std-1547 standard.

  • For both SISO and MIMO, the proposed NI-RLLC controllers have the best voltage tracking capability for different load dynamics.