Abstract
Large integration of doubly-fed induction generator (DFIG) based wind turbines (WTs) into power networks can have significant consequences for power system operation and the quality of the energy supplied due to their excessive sensitivity towards grid disturbances. Under voltage dips, the resulting overcurrent and overvoltage in the rotor circuit and the DC link of a DFIG, could lead to the activation of the protection system and WT disconnection. This potentially results in sudden loss of several tens/hundreds of MWs of energy, and consequently intensifying the severity of the fault. This paper aims to combine the use of a crowbar protection circuit and a robust backstepping control strategy that takes into consideration of the dynamics of the magnetic flux, to improve DFIG’s Low-Voltage Ride Through capability and fulfill the latest grid code requirements. While the power electronic interfaces are protected, the WTs also provide large reactive power during the fault to assist system voltage recovery. Simulation results using Matlab/Simulink demonstrate the effectiveness of the proposed strategy in terms of dynamic response and robustness against parametric variations.
Similar content being viewed by others
1 Introduction
In the last few decades, there have been significant development and utilization of wind energy conversion systems (WECs). In the early stage of wind energy development, generated wind power was allowed to be injected to the networks with minimum technical requirements, respecting only some grid connection criteria, for instance, the voltage plans between different areas and harmonics. However, the ever-growing and massive integration of wind energy has led the power system operators to modify the connection requirements and thoroughly revise the grid codes specifications.
Voltage dips are common grid disturbances, and can have considerable effects on the stability and operation of wind generation, for instance, resulting in frequent disconnection by the WT protection system. In large wind power penetrations, the disconnection of WTs deprives the electrical system from several tens/hundreds of MWs of energy, which can intensify the severity of the fault, threatening thereby the stability of the power system in its entirety [1].
Consequently, one of the most restrictive requirements for wind power generation in recent times is the capability of grid-connected WTs to ensure Low Voltage Ride Through (LVRT). This connection rule specifies that wind generators must remain connected in the presence of severe voltage dips. For instance, Fig. 1 shows the evolution of the characteristics for this requirement between 2004 and 2016 for the German electrical network [1]. WECSs are now required to remain connected and disconnection is only allowed when the voltage drops below the critical limit specified by the voltage curves. Besides, the latest grid codes specify that wind turbines must also participate in restoring voltage by supplying large amounts of reactive energy to the networks during the faults. For instance, in Germany, the transmission system operator “TSO-EO-Netz” specifies that for a 5% voltage drop [2], additional reactive power must be injected into the grid by its offshore WTs. Figure 2 illustrates the quantity of the required reactive current as a function of the voltage magnitude. It indicates that when the voltage drops below 50% of its rated value, only reactive power should be injected into the power system [1, 2].
Nowadays, owing to its high-energy conversion efficiency, robustness, and inexpensive power electronic converters that carry only one-third of the generator’s rated power [3], the DFIG has emerged as one of the most prominent wind energy conversion technologies.
However, the main disadvantage of DFIG is its sheer sensitivity towards grid disturbances [4, 5]. An abrupt change of the voltage at its terminals, particularly a voltage dip, could cause overcurrent and overvoltage in the rotor terminals and the DC link, which may lead to the activation of the protection system to disconnect the WT d [5, 6].
Significant efforts have been made by both academia and industry to design suitable protection systems and control solutions to fulfill the latest grid code connection requirements. Early proposed solutions to protect the power electronic interfaces, as addressed in [7], used an electronic device called crowbar, to provide an alternative path for the fault current while the converter is deactivated. Despite its reliability and widespread usage, the crowbar solution can no longer be used alone because the machine loses its control when the rotor side converter is deactivated, meaning that the generation system cannot produce the required reactive power injection during the fault. In contrast, as it has been detailed in [8], the machine draws very high short circuit current and large reactive power when the crowbar is activated. Therefore, this solution was only acceptable when the wind power constituted only an insignificant share of the system generation.
Some researches [9, 10], have suggested the use of static synchronous compensators (STATCOM) at the terminals of the DFIG to assist in recovering the voltage during the fault. However, the high costs of such a solution are not very encouraging.
Other works [11,12,13], have proposed modified control schemes to improve LVRT. These control strategies can mainly be distinguished into two categories: (1) the decomposition of the current/voltage into symmetrical components, and (2) the regulation of the rotor current using traditional PI controllers [14,15,16]. These control schemes suffer however from stability problems due to the considerable time delay introduced during the decomposition process and the sluggish transient response of PI current controllers [14, 17, 18]. In addition, these control strategies can only be effective when the voltage dip is short and not severe enough (very high overcurrent induced in the rotor windings) to urge for crowbar assistance.
Based on the theoretical analysis of the DFIG’s dynamic behavior during a severe voltage dip, this work proposes a combination of active crowbar hardware solution and robust control strategy that takes into consideration the dynamics of the generator magnetic flux, to fulfill the latest grid code requirements.
In the event of a severe voltage dip, the crowbar will be activated first to protect the converters for a limited period of time, during which the overcurrent in the rotor windings is too high for the power electronic interfaces to handle. The power converters are the reactivated and a backstepping control strategy takes over of the rotor side converter (RtSC), to stabilize the magnetic state of the DFIG by dumping down of the flux oscillations and to generate large reactive power to assist the power system in the voltage recovery process.
To ensure high performance and faster dynamic respond, the current controllers are implemented using the backstepping control approach. A robustness test is carried out in the paper to compare the performances of the proposed control strategy and the classical PI controller during parametric variations.
2 System discerptions
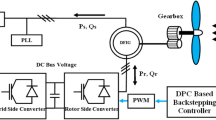
The basic configuration of DFIG based wind turbine is shown in Fig. 3 [19]. The electrical generator mounted to the shaft of the gearbox is a wound rotor induction machine, with its stator windings directly connected to the network and rotor windings linked to the grid through a set of back-to-back converters that consist of a rotor side converter (RtSC) and a grid side converter (GdSC).
The DFIG can be modeled in a rotating Park reference frame using the following set of Equations [3]:
Moreover, the electromagnetic torque is given by:
Finally, the active and reactive power can be determined by:
The crowbar is activated only after the appearance of the voltage dip to protect the back-to-back converters by providing an alternative path for the fault current induced in the rotor circuit.
The crowbar circuit employs a diode bridge assembled with a dissipation resistance via a Gate Turn-off Thyristor (GTO) or an insulated gate bipolar transistor (IGBT) as shown in Fig. 3. However, the use of GTO or “Insulated Gate Commutated Thyristor” (IGCT) is more advantageous than IGBT for this application because GTO and IGCT are normally designed to withstand higher overcurrents than IGBTs.
2.1 System operation under voltage disturbance
This section briefly carries out the theoretical analysis of the DFIG’s dynamic behavior during grid fault. Although the analysis can be used with any type of voltage disturbances, it is focused on symmetrical dips here given that they exhibit the severest reaction especially in terms of the fault current induced in the rotor terminals. For the following analysis, the superscripts (s, r) denote that the variables are expressed in the stationary reference frame linked to the stator (α, β) or to the rotating reference frame linked to the rotor (D, Q), respectively.
Under normal operation, neglecting the stator resistance Rs, which is a realistic approximation for multimegawatts DFIG, the stator flux phasor can be expressed by [5]:
This indicates that, in steady state, the stator flux is a space vector, rotating at the synchronism speed ωs with a magnitude \( {\hat{\psi}}_s \) proportional to its stator voltage \( {\hat{V}}_{pre} \). On some occasions, this is called the forced flux \( {\overrightarrow{\psi}}_{sf}^s \).
The rotor flux can be obtained from (2) as:
According to Faraday’s law, the rotor voltage can be expressed by:
Replacing (6) into (7) yields:
The first term of (8) corresponds to the EMF induced by the magnetic flux in the rotor circuit, while, the second term \( {\overrightarrow{v}}_{r0}^r \) corresponds to the voltage drop in the rotor resistance Rr and inductance Lr.
Considering a sudden voltage dip at the DFIG stator terminals at t = t0, the voltage magnitude changing from \( {\hat{V}}_{pre} \) (pre-fault) to \( {\hat{V}}_{fault} \) (at fault), can be mathematically expressed by:
The sudden drop of the voltage magnitude across the stator terminals mainly affects the magnetic state of the generator. However, as the flux is a state variable whose change cannot be discontinuous or instantaneous like that of the voltage, it can be expressed into two terms as [5]:
where, τ = Ls/Rs is the time constant of the stator.
The first term in (10) is called the natural flux \( {\overrightarrow{\psi}}_{sn}^s \), which represents the transient component induced by the sudden change in the stator voltage and decreases exponentially allowing a continuous and progressive passage of the total flux from its pre-fault value to the steady-state value. The second term is the forced magnetic rotating flux \( {\overrightarrow{\psi}}_{sf}^s \), which corresponds to the steady-state value, and as previously mentioned, depends only on the new magnitude of the stator voltage. Figure 4 shows the evolution of the stator flux during the dip, and Fig. 5 displays the trajectory of the flux phasor before, during, and after the dip in a stationary (α, β) reference frame linked to the stator.
Each of the flux components induces different EMF in the rotor circuit. Neglecting the voltage drop in the rotor voltage Eq. (8) and substituting the stator flux expression of (10) into (8), the rotor voltage can be expressed as the superposition of two terms:
To express the stator flux given in (9) in a reference frame linked to rotor, it must be multiplied by \( {\mathrm{e}}^{-\mathrm{j}{\upomega}_{\mathrm{m}}} \) such that [6]:
Equation (11) shows that the EMF induced by the forced flux component \( {\overrightarrow{\mathrm{e}}}_{\mathrm{r}\mathrm{f}}^{\mathrm{r}} \) is very low as it depends on the slip (s) and the new voltage magnitude, which are both very small. On the other hand, the EMF induced by the natural flux is high as it is proportional to the depth of the voltage drop and (1-s).
Figure 6 shows the evolution of the rotor voltage at the appearance of a voltage dip (D = 0.7), while the machine is operating at slip s = 0.2. It can be observed that the natural component of the flux increases the voltage, and the waveform is also modified due to the superposition of the two sinusoidal components with different frequencies as indicated in (11). Subsequently, the component induced by the natural flux disappears after an initial transient and the voltage obtained at the steady-state corresponds to that induced by the forced flux only.
The overvoltage induced in the rotor terminals will significantly affect the DFIG’s control loops, but more importantly, the converters must be designed to withstand the maximum voltage that can reach during the fault. In the worst case, during a total voltage dip, they must be able to support the full stator voltage that has disappeared. This means that an oversizing of the converters must be considered, thus losing one of the DFIG main advantages [6].
3 The proposed control strategy
3.1 Control objectives
The section proposes a robust control strategy based on the backstepping approach, to allow DFIG based WT to respond to the latest grid connection requirements under grid voltage disturbances. The proposed control algorithm protects the power electronic interfaces and to ensures (LVRT) preventing the disconnection of the WTs, while generating large reactive power during the fault, to assist power system voltage recovery.
As being analyzed, the main difficulty comes with the natural flux component at the beginning of the voltage dip, which is responsible for the excessive increases of the current and voltage. Therefore, the control strategy aims to damp down the natural flux component as fast as possible, i.e., to reduce the time that it takes for the DFIG to demagnetize, by imposing a rapid passage of the total flux to its steady state forced flux value.
As will be shown in the next section, the traditional DFIG vector control strategies are not capable of dealing with voltage dips, because they are designed under the assumption of a stable electrical network with ψsd = Vs/ωs, ψsq = 0. However, under faulty conditions, the dynamic of the flux can no longer be neglected. From (2) the stator current expressions are given as:
Substituting (13) into (2) results in the expression of the rotor fluxes:
Substituting the rotor flux (14) in the respective rotor and stator voltages in (1) yields:
In order to enhance system robustness, the proposed control strategy revolves around the backstepping control approach, which is a recursive and systematic control methodology used for nonlinear systems control, such that, the feedback control loop that guarantees the overall system stability and behavior can be efficiently elaborated. Figure 7 shows the block diagram of the proposed RtSC control [20].
The backstepping control design methodology uses the so-called virtual control variables (VCVs) to decompose a complex nonlinear control scheme into smaller control design problems called steps [21].
In each step, it virtually handles a simple one-input-one-output subsystem. Thus, each step provides a reference for the following one, while the final step, provides the so-called actual control variable (ACV). Therefore, the final control law that guarantees the overall system stability and performance is built up in a constructive manner using Lyapunov’s functions.
As shown in Fig. 7 the control diagram includes two external control blocks (Normal and LVRT control) to compute the VCV, the rotor current in this case, and to deliver to the following control blocks through a switch that selects the appropriate references depending on the operation mode.
Then, the internal control block computes the ACV, in this case, the rotor voltage, which is transmitted to the PWM block to determine switching of the RtSC (note that only the faulty operation condition will be considered in the paper). In order to regulate the stator flux around its forced component, the following references are chosen:
Based on (15) and (16), the state model of the DFIG can be obtained as:
where:
μ = ωrσLr; δ = ωr(Lm/Ls); α = (1/σLr).
This indicates 2 second order systems and according to the backstepping theory the control design will be carried out in the following two steps.
3.2 Step 1 – virtual control variables computation (VCVs)
First, the error variables are defined as:
Then, the quadratic Lyapunov’s functions that are simple and effective, and have proven to be a very powerful tool for assessment of various performances such as robustness, disturbance rejection and forced oscillation as:
According to the backstepping theory, to ensure a stable tracking behavior, the derivatives of the chosen Lyapunov’s functions must be strictly negative, i.e.:
where bs1 and bs2 are positive constants called the backstepping setting coefficients. From (18)–(22), the VCV can be determined by:
with, \( A=\left(\frac{L_s}{L_m{R}_s}\right) \).
3.3 Step 2 – actual control variables computation (ACVs)
Note that, the VCVs from the previous step will serve as references for this step. Again, the error variables are defined as:
And the Lyapunov’s function are selected as:
Similarly, in order to ensure stable tracking, the derivatives of the chosen Lyapunov’s functions must be strictly negative, i.e.:
From (24)–(26), (21) and (23) the ACV can easily be determined as:
where, (bs1, bs2, bs3, bs4) are positive constants called the backstepping setting coefficients, used to guarantee the stability of the system and to ensure a fast controller dynamic response.
4 Simulation results and discussions
This section examines the performance of the proposed control strategy on a multimegawatts DFIG bases WT, under a severe 3-phase voltage dip (with a depth of D = 70% and a duration of 700 ms) as shown in Fig. 8.
As the fault duration is short compared to wind fluctuation all simulations are performed in the Matlab/Simulink with a constant wind speed v of 9 m/s. The system parameters are given in the Appendix.
4.1 Simulations – without the proposed control strategy
To highlight the benefit of the proposed control algorithm, system behavior using only the “normal control” strategy is studied first.
As indicated in Fig. 9, a sudden drop in the stator voltage leads to a reduction of the internal flux of the DFIG. As mentioned previously, this demagnetization does not happen instantly, and therefore, the natural flux component allows a gradual variation of the magnetic state of the machine. Moreover, the latter generates reactive power during its demagnetization, and consequently, the resulting peaks of the stator current are very high in Fig. 10.
At the same time, the DFIG experiences overcurrent at the rotor windings, as shown in Fig. 11, induced mainly due to the magnetic bond between the stator and rotor. It can be observed that the current waveforms have also been modified due to the addition of the two sinusoidal components with different frequencies.
Unlike the stator overcurrent, which can be tolerated by the machine thermal capacity, the overcurrent in the rotor terminals could damage the power electronic interfaces, normally designed to carry only around one-third of the generator rated power [20]. Figure 12 shows the overvoltage induced at the DC bus capacitor during the fault.
The demagnetization of the generator during the dip reduces its electromechanical conversion capacity. Consequently, the electromagnetic torque and the stator active power are reduced as shown in Figs. 13 and 14, respectively. Moreover, the behavior of the DFIG becomes heavily unbalanced due to the slow reduction of the flux transient component (the natural flux).
In addition, as the mechanical power, largely depending on the wind profile, remains unchanged, the reduction of the WT electric power leads to excess of power expressed by:
Consequently, the WT accelerates as shown in Fig. 15.
4.2 Simulations – with the proposed control strategy
The performance of the proposed control strategy is examined here. Before the fault (t < 3 s), the WT operates with the “Normal control” control, ensuring a maximum wind power conversion. During the voltage dip (t > =3 s), the sequence of events that occur can be summarized as follows:
-
i.
The protection system monitors the following anomalies: overcurrent in the rotor circuit or an overvoltage in the DC bus [4] to determine the switching order from the normal to LVRT operation.
-
ii.
Once the fault is detected (usually within a few milliseconds), the crowbar is activated to short-circuit the rotor terminals. Simultaneously, for safety measures, the RtSC is blocked so the fault current is evacuated through the crowbar. Figure 16 shows the current in the crowbar circuit.
-
iii.
To comply with the grid code requirements, it is important to make sure that the controllability of the system is maintained for most of the fault duration. Therefore, the crowbar is activated and the power electronic interfaces are blocked, only for a very limited period of time (10 ms), during which the rotor current is too high for the RtSC to handle.
-
iv.
The crowbar is deactivated and the RtSC is re-enabled allowing the proposed backstepping control strategy to take over.
Figures 17 and 18 highlight the evolution of the direct and quadrature components of the flux, respectively. It can be observed that during the normal operation mode the two components follow their references perfectly. During the fault and after the deactivation of the crowbar, the two components recover to their exact references after transient regimes characterized by very small oscillations that appear at the beginning and end of the fault.
Figure 19 shows the evolution of the stator flux module. Comparing the results in Figs. 9 and 19, it can be observed that the activation of the crowbar not only absorbs the fault current during the beginning of the dip but also accelerates the demagnetization of the DFIG. After the crowbar deactivation, the proposed control strategy succeeds in regulating the internal flux around its forced components \( {\overrightarrow{\psi}}_{sf}^s \).
In order to meet the specific requirements related to the contribution of WTs to voltage restoration by providing large reactive power during the fault [2, 22], e.g., Germany’s EO-Netz reactive power requirements in Fig. 2, the control strategy is modified. After a few milliseconds of the crowbar deactivation, and RtSC reactivation, the DFIG injects no active power but only the maximum reactive power by specifying the new references for \( {\mathrm{I}}_{\mathrm{rq}}^{\ast } \) and \( {\mathrm{I}}_{\mathrm{rd}}^{\ast } \) as:
Figures 20 and 21 highlight the evolution of the active and reactive current, respectively. During the normal operation, the two components follow their references, while during the dip, the high peaks observed in the first few moments (3 ~ 3.1 s) of the fault are inevitable, as they are induced due to the natural flux component. During the short time period, the converters are blocked for safety reason and the control is lost, so the current peaks completely absorbed by the crowbar resistance. A after a few milliseconds after the reactivation of the RtSC, the reactive current takes 100% of the rated rotor current of the DFIG, while the active current is down to zero. The reactive current oscillation just before the fault clearance (t = 3.6) is due to the DFIG re-magnetization. After the fault clearance (t > 3.7), the rotor current returns to its pre-fault reference.
To highlight the merits of the backstepping control strategy, system performances under some disturbances are analyzed. As the generator’s parameters are usually exposed to many forms of inaccuracies and variations due to the identification methodology, measuring devices or natural phenomena, e.g. operating temperature variation, a robustness test is carried out to compare the performances of the proposed control strategy with the classical PI controller when parametric variations are registered. The test consists of intentionally modifying the stator resistance Rs and rotor resistance Rr of the DFIG by 50%, and the stator inductance Ls and rotor inductance Lr by 20% from their nominal values.
The simulation results shown in Figs. 17, 18, 19, 20 and 21, highlight the superiority of the proposed control strategy compared to the traditional PI controller. It can be seen that the traditional PI controller is highly sensitive towards parametric variation, whereas the proposed backstepping control algorithm shows an exquisite disturbance rejection so all the outputs (ψsd and ψsq components of the magnetic flux, and the active Irq and reactive Ird current) converge correctly to their designated references.
Figures 22 and 23 show the variation of the stator active and reactive powers, respectively. Before the dip, both powers follow their references specified by the “Normal control” block, which equal to the maximum extractable active power (MPPT operation) and zero reactive power, respectively. At the appearance of the fault, the control switches to “LVRT control” and both powers go through a transient regime, characterized by oscillations, due to the sudden demagnetization of the DFIG before finally finding their exact setpoints after a few milliseconds of the crowbar deactivation. Moreover, it can also be observed that the DFIG generates a large amount of reactive power for most of the fault duration as the grid codes demanded. After the fault clearance, the active and reactive power return to their pre-fault references.
The comparison of Figs. 12 and 24 highlights additional benefit of activating the crowbar and blocking the RtSC during the first instants of the dip. As shown in Fig. 24 the GdSC succeeds in regulating the DC bus voltage around its reference value during the fault.
5 Conclusion
This paper has examined the dynamic behavior of a multimegawatts DFIG based wind turbine in the event of a severe voltage dip, and subsequently proposed control solutions to fulfill the latest grid code requirements. It reveals that the natural flux component at the beginning of the dip is responsible for all the sudden changes of all electrical variables’ magnitudes, potentially leading to the activation of the protection system, and consequently the disconnection of the wind turbine.
The proposed scheme uses the active crowbar hardware solution, in the first instants of the fault, during which the rotor current is too high for the rotor side converter to operate. The robust backstepping control strategy then takes over to reduce the time required for the generator to demagnetize during the dip, and to eliminate the natural flux component and control the stator flux to around its forced steady state value. Simulation results show that the proposed control algorithm successfully meets the control objectives in the presence of a severe symmetrical voltage dip. The converters and the DC link capacitor are protected, and the LVRT of the WT is achieved while providing large reactive power to the network during the fault to assist system voltage recovery.
6 Nomenclatures
6.1 Variables
v Voltages (V)
i Current (A)
φ Flux linkage (Wb)
R Resistance (Ω)
L Inductance (H)
ω Angular speed
p Pair of poles
T Torque
P Active power
Q Reactive power
Udc DC bus voltage
D Depth of the voltage dip
τ Stator time constant
e Error variable
V Lyapunov’s function
bs Setting coefficients
6.2 Subscripts
s Stator
r Rotor
m Mechanical
f Forced flux
n Natural flux
6.3 Superscript
s Stationary reference frame (α, β)
r Rotating reference frame (D, Q)
\( \hat{\mathrm{x}} \) Magnitude
\( \overrightarrow{\mathrm{x}} \) Phasor
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Jotwani, A., & Rather, Z. (2017). An advanced investigation on lvrt requirement in wind integrated power systems. In 1st International Conference on large-scale grid integration of renewable energy in India.
Teninge, A., Roye, D., & Bacha, S. (2010). Reactive power control for variable speed wind turbines to low voltage ride through grid code compliance. In The XIX International Conference on Electrical Machines-ICEM 2010, (pp. 1–6).
Poitiers, F., Bouaouiche, T., & Machmoum, M. (2009). Advanced control of a doubly-fed induction generator for wind energy conversion. Electric Power Systems Research, 79(7), 1085–1096.
Jiang, H., Zhang, C., Zhou, T., Zhang, Y., & Zhang, F. (2019). An adaptive control strategy of crowbar for the low voltage ride-through capability enhancement of DFIG. Energy Procedia, 158, 601–606.
Abad, G., López, J., Rodríguez, M., Marroyo, L., & Iwanski, G. (2011). Analysis of the DFIM under voltage dips.
Abad, G., & Iwanski, G. (2014). Properties and control of a doubly fed induction machine. Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications, 18, 270–318.
Peng, L., Francois, B., & Li, Y. (2009). Improved crowbar control strategy of DFIG based wind turbines for grid fault ride-through. In 2009 twenty-fourth annual IEEE applied power electronics conference and exposition, (pp. 1932–1938).
Morren, J., & De Haan, S. W. H. (2007). Short-circuit current of wind turbines with doubly fed induction generator. IEEE Transactions on Energy Conversion, 22(1), 174–180.
Zhou, L., Liu, J., & Liu, F. (2010). Design and implementation of STATCOM combined with series dynamic breaking resistor for low voltage ride-through of wind farms. In 2010 IEEE energy conversion congress and exposition, (pp. 2501–2506).
El-Moursi, M. S., Bak-Jensen, B., & Abdel-Rahman, M. H. (2009). Novel STATCOM controller for mitigating SSR and damping power system oscillations in a series compensated wind park. IEEE Transactions on Power Electronics, 25(2), 429–441.
Xiang, D., Ran, L., Tavner, P. J., & Yang, S. (2006). Control of a doubly fed induction generator in a wind turbine during grid fault ride-through. IEEE Transactions on Energy Conversion, 21(3), 652–662.
López, J., Gubía, E., Olea, E., Ruiz, J., & Marroyo, L. (2009). Ride through of wind turbines with doubly fed induction generator under symmetrical voltage dips. IEEE Transactions on Industrial Electronics, 56(10), 4246–4254.
Yao, J., Li, H., Liao, Y., & Chen, Z. (2008). An improved control strategy of limiting the DC-link voltage fluctuation for a doubly fed induction wind generator. IEEE Transactions on Power Electronics, 23(3), 1205–1213.
Hu, J., He, Y., & Xu, L. (2010). Improved rotor current control of wind turbine driven doubly-fed induction generators during network voltage unbalance. Electric Power Systems Research, 80(7), 847–856.
Gomis-Bellmunt, O., Junyent-Ferre, A., Sumper, A., & Bergas-Jane, J. (2008). Ride-through control of a doubly fed induction generator under unbalanced voltage sags. IEEE Transactions on Energy Conversion, 23(4), 1036–1045.
Zhou, T. (2009). Control and energy management of a hybrid active wind generator including energy storage system with super-capacitors and hydrogen technologies for micro-grid application.
Feltes, C., Engelhardt, S., Kretschmann, J., Fortmann, J., Koch, F., & Erlich, I. (2008). High voltage ride-through of DFIG-based wind turbines. In 2008 IEEE power and energy society general meeting-conversion and delivery of electrical energy in the 21st century, (pp. 1–8).
Rahimi, M., & Parniani, M. (2010). Grid-fault ride-through analysis and control of wind turbines with doubly fed induction generators. Electric Power Systems Research, 80(2), 184–195.
Nadour, M., Essadki, A., & Nasser, T. (2017). Comparative analysis between PI & backstepping control strategies of DFIG driven by wind turbine. International Journal of Renewable Energy Research, 7(3), 1307–1316.
Nadour, M., Essadki, A., & Nasser, T. (2019). Robust coordinated control using backstepping of flywheel energy storage system and DFIG for Power smoothing in wind power plants. International Journal of Power Electronics and Drive Systems, 10(2), 1110–1122.
Nadour, M., Essadki, A., Fdaili, M., & Nasser, T. (2019). Inertial response using backstepping control from DFIG based wind power plant for short-term frequency regulation. In 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), (pp. 268–273).
Beltran-Pulido, A., Cortes-Romero, J., & Coral-Enriquez, H. (2018). Robust active disturbance rejection control for LVRT capability enhancement of DFIG-based wind turbines. Control Engineering Practice, 77, 174–189.
Acknowledgements
Not applicable.
About the authors
Mohamed Nadour, He received the M. S degree in electrical engineering in 2016 from Mohammed V University, ENSET Rabat-Morocco. Currently he is working toward the Ph.D. in the Research Centre of Engineering and Health Sciences and Technologies (STIS), since 2017. His research interests are related to renewable energy. His current activities include robust control strategies of a wind-energy conversion system for ancillary services.
Ahmed Essadki, is currently a Research Professor in the Research Centre of Engineering and Health Sciences and Technologies (STIS). And a professor in the electrical engineering at ENSET, Mohammed V University, Morocco. In 2000, He received his PhD degree from Mohammadia Engineering School (EMI), (Morocco). From 1990 to 1993, he pursued his Master program at UQTR University, Quebec Canada, respectively, all in electrical engineering. His current research interests include renewable energy, motors drive and power system.
Tamou Nasser, is currently an Associate Professor at the communication networks department of National High School for Computer Science and Systems (ENSIAS), Mohammed V University, Morocco, since 2009. She received her PhD degree in 2005 and her research MS degree, in 2000, respectively, all in electrical engineering from Mohammadia Engineering School (EMI), Morocco. Her research interests include renewable energy, motor drives, power system, and smart grid.
Funding
The research work is not supported by any funding agency.
Author information
Authors and Affiliations
Contributions
MN as the corresponding author, modeled the system, designed and tested the proposed control strategy and wrote the papers. AE and TN as supervisor and co-supervisor respectively, contribute to revise the manuscript and perform some additional changes. All authors have read and approve the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Appendix
Appendix
Wind turbine parameters | ||
Quantity | Symbol | Value |
Blades radius | R | 45 m |
Gearbox | G | 90 |
Maximum power coefficient | Cpmax | 0.44 |
Total inertia (WT + DFIG) | J | 1000 kg/m2 |
Damping coefficient | f | 0.017 N.m. s/rd |
Density of air | ρ | 1.2 kg/m3 |
DFIG’s parameters | ||
Rated power | P | 2 MW |
Number of pole pairs | p | 2 |
Stator rated voltage | Vs | 690 V |
Stators rated frequency | fs | 50 Hz |
Stator resistance | Rs | 2.6mΩ |
Rotor resistance | Rr | 2.9mΩ |
Stator inductance | Ls | 2.6 mH |
Rotor inductance | Lr | 2.6 mH |
Mutual inductance | Lm | 2.6 mH |
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nadour, M., Essadki, A. & Nasser, T. Improving low-voltage ride-through capability of a multimegawatt DFIG based wind turbine under grid faults. Prot Control Mod Power Syst 5, 33 (2020). https://doi.org/10.1186/s41601-020-00172-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41601-020-00172-w