1 Introduction

In recent years, there has been an increasing demand for the use of multi-level converters in power electronics applications. The increase in the number of voltage levels in the converter output voltage leads to a satisfactory level of total harmonic distortion (THD) while reducing the stress in each switching component by reducing their supported voltages especially in high power applications. The lower cost of low voltage switches further makes multi-level converters even more attractive [1]. The common neutral point clamped (NPC) inverter is one of the most used multi-level topologies in industrial applications [2] because of the several advantages offered in terms of its reduced stress across the semiconductors, less harmonic content, and lower voltage distortion [3, 4]. A sinusoidal pulse width modulation (SPWM) strategy is commonly used for converter operation [5]. Variable speed drive of electric motors continues to be the objective of scientific research because of the technological evolution of converters and the development of increasingly efficient control laws. Direct torque control (DTC) is one of the strategies for a high performance motor drive. Its principle is to obtain decoupled control of the stator flux and electromagnetic torque based on hysteresis controllers and a switching table [6]. DTC has a relatively simple control structure, is less sensitive to variations in motor parameters (as only the stator resistance is used to estimate the stator flux), and offers a higher dynamic performance than conventional vector control [7]. However, the variable switching frequency caused by hysteresis regulators results in unwanted ripples in flux and torque responses, increased acoustic noise and increased control difficulty in low speed regions [8]. Several improvements have been proposed to overcome these problems. Model predictive control (MPC) is one of the methods used to determine an appropriate voltage vector which can reduce the ripples, though the great complexity of the control law and the unsatisfactory performance in the steady state limit its uses [1, 9]. The DTC method with constant switching frequency based on SPWM has been presented to circumvent the aforementioned drawbacks, as this strategy is based on PI regulators. This improves the system dynamics while eliminating the static errors between the estimated quantities and the references [10]. However, the linear mathematical model of the SPWM-DTC generally contains approximate assumptions and unspecified dynamics. These can affect the stability and robustness of the entire system. Another method proposed in the literature is the DTC based on an artificial neural network. Despite having good performance this strategy needs a very long process that doesn’t allow real-time command especially when the motor is fed by a multilevel inverter [11]. This paper presents a DTC method based on sliding mode control (SMC) which is one of the robust and non-linear strategies widely used in the field of electric motor drives. This technique is characterized by good dynamic performance since it forces the system trajectory to move along the sliding surface according to a control law whose stability is verified analytically by Lyapunov theory [12]. The most powerful advantages of this technique include high robustness against various system uncertainties, fast dynamic response and simplicity in implementation [13]. In a high-performance control system, the accuracy of the state feedback parameters is an important factor which influences the reliability of the whole system, in particular the flux and torque which must be estimated with precision. In this regard, optimal observers can be designed to improve the performance of asynchronous motor drives [14]. In the literature, various observers have been proposed such as Luenberger observers [15], sliding mode observers (SMO) [16], extended Kalman filters (EKF) [17] etc. The observer based on SMO used in this work; presents the advantage of an exact convergence of the real system states even in the presence of disturbances due to a nonlinear switching term called sliding surface [18]. This type of observer also has other advantages such as rapid response, insensitivity to changes in parameters and good robustness.

Therefore, the main purpose of this work is to propose an enhanced sensorless sliding mode technique based on direct torque control (SM-DTC) via a three-level NPC inverter in which principles of DTC, SMC, SPWM, multi-level inverter and SMO are combined for improved robustness, minimized ripples and higher operating performance. Moreover, this paper proposes an advanced SMO of stator flux which directly allows the determination of the estimated speed, torque and rotor flux to reduce structural complexity and increase estimation accuracy. To highlight the aforementioned advantages of the whole proposed structure, simulation results are compared between the proposed strategy (SM-DTC) using a three-level inverter, the same SM-DTC using a two-level inverter, and the PI-DTC-SPWM using the three-level inverter.

The paper is structured as follows. The modeling of the asynchronous motor is briefly summarized in Section 2 and the proposed SM-DTC strategy is described in detail in Section 3. Section 4 introduces the NPC topology and the use of the SMO for stator flux estimation is outlined in Section 5. The simulation results are presented and discussed in Section 6 and a general conclusion is presented in Section 7.

2 Mathematical model

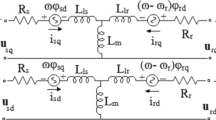
The mathematical model of an asynchronous motor in the stationary reference frame is given as follows:

$$ \left\{\begin{array}{l}{V}_{ds}={R}_s{I}_{ds}+\frac{d{\varphi}_{ds}}{dt}-{\omega}_s{\varphi}_{qs}\\ {}{\mathrm{V}}_{qs}={R}_s{I}_{qs}+\frac{d{\varphi}_{qs}}{dt}+{\omega}_s{\varphi}_{ds}\end{array}\right.\kern0.75em \left\{\begin{array}{l}0={R}_r{I}_{dr}+\frac{d{\varphi}_{dr}}{dt}-{\omega}_g{\varphi}_{qr}\\ {}0={R}_r{I}_{qr}+\frac{d{\varphi}_{qr}}{dt}+{\omega}_g{\varphi}_{dr}\end{array}\right. $$
(1)

where Vds and Vqs are the direct and quadrature stator voltage components, respectively. Ids, Iqs and Idr, Iqr are the direct and quadrature stator and rotor current components, respectively. φds, φqs and φdr, φqr are the respective direct and quadrature stator and rotor flux components. Rs and Rr are the stator and rotor resistances, respectively.

The fundamental mechanical equation and the electromagnetic torque can be expressed as:

$$ {\mathrm{T}}_e=\frac{3}{4}P\left({\varphi}_{ds}{I}_{qs}-{\varphi}_{qs}{I}_{ds}\right) $$
(2)
$$ \mathrm{J}\frac{d\varOmega}{d t}={T}_e-{T}_L- f\varOmega $$
(3)

where P is the number of pole pairs, Ω is the motor mechanical speed, and TL is the load torque. f and J are the friction and the moment of inertia coefficients, respectively.

3 Application of the sliding mode technique (SM) in direct torque control (DTC)

The block diagram of the variable-structure sliding mode control of an asynchronous motor (SM-DTC) is illustrated in Fig. 1. The quantities that are required are the stator flux, the torque and the motor speed. It is possible, in certain cases, to suppress the speed control loop and to control the motor using only its torque and flux [19]. The combination of the SMC with the DTC-SPWM provides a robust control which keeps the parameters to be adjusted within a well-defined range (Fig. 1) [20].

Fig. 1
figure 1

General diagram of the SM-DTC method applied to an asynchronous motor supplied by a three-level inverter with a sliding mode observer

Full size image

The complete flowchart of the proposed algorithm is illustrated in Fig. 2.

Fig. 2
figure 2

Flowchart of the SM-DTC algorithm

Full size image

3.1 Stator flux and torque control

The main task of the variable structure controller, illustrated in Fig. 3, is to obtain a fast and reliable control of the torque and the stator flux. For this reason, two sliding mode controllers with PI regulators are designed, and the direct and quadrature reference voltages are obtained at the output of the controller to generate the SPWM. In the following illustration, the reference and the estimated values are designated respectively by (*) and (^).

Fig. 3
figure 3

Stator flux and torque regulation loops with the SM-DTC

Full size image

Based on (1)–(2) and under the assumed orientation where the d component is aligned to the stator flux vector direction, i.e., the quadrature stator flux is zero ‘φqs = 0’, the developed equations can be written as:

$$ \left\{\begin{array}{l}{V}_{ds}={R}_s{I}_{ds}+\frac{d{\varphi}_{ds}}{dt}\\ {}{\mathrm{V}}_{qs}={R}_s{I}_{qs}+{\omega}_s{\varphi}_{ds}\\ {}{T}_e=\frac{3P}{4}\frac{\varphi_{ds}}{R_s}\left({\mathrm{V}}_{qs}-{\omega}_s{\varphi}_{ds}\right)\end{array}\right. $$
(4)

The above equations indicate that the direct and quadrature stator voltage components Vds and Vqs can be employed for flux and torque control, respectively.

From the same perspective as the PI-DTC-SPWM control strategy, two sliding surfaces (S1,S2) are selected according to (4), in which S1 is defined from the error of the stator flux to control the direct voltage component, while the surface S2 represents the error of the electromagnetic torque to allow the determination of the quadrature voltage component. Since defining a sliding surface based only on the error will not allow the imposition of the dynamics for the error correction [17], these two surfaces S1 and S2 are designed so as to enforce sliding-mode operation with first-order dynamics of \( {\mathrm{S}}_1={\dot{\mathrm{S}}}_1=0 \) and \( {\mathrm{S}}_2={\dot{\mathrm{S}}}_2=0 \) as:

$$ \left[\begin{array}{c}{S}_1\\ {}{S}_2\end{array}\right]=\left[\begin{array}{c}{e}_{\varphi s}+{c}_{\varphi s}\frac{de_{\varphi s}}{dt}\\ {}{e}_{Te}+{c}_{Te}\frac{de_{Te}}{dt}\end{array}\right] $$
(5)

where cφs and cTe are constant gains to be defined according to the desired dynamics. eφs and eTe are theerror functions that must be minimized:

$$ \left\{\begin{array}{l}{e}_{\varphi s}=\left|{\varphi}_s^{\ast}\right|-\left|{\hat{\varphi}}_s\right|\\ {}\ {e}_{Te}={T}_e^{\ast }-{\hat{T}}_e\end{array}\right. $$
(6)

In sliding mode, the control laws limit the state of the system to the surfaces (S1 and S2) and their behavior is exclusively governed by (S1 = S2 = 0). First-order linear torque and flux error dynamics resulting from (5) are:

$$ \left\{\begin{array}{c}{e}_{\varphi s}=-{c}_{\varphi s}\frac{de_{\varphi s}}{dt}\\ {}{e}_{Te}=-{c}_{Te}\frac{de_{Te}}{dt}\end{array}\right. $$
(7)

Then, the control law can be proposed in a similar way as:

$$ \left\{\begin{array}{l}{V}_{ds}=\left({K}_{p\varphi s}+\frac{K_{I\varphi s}}{S}\right) sat\left({S}_1\right)\\ {}{V}_{qs}=\left({K}_{p Te}+\frac{K_{I Te}}{S}\right) sat\left({S}_2\right)+{\omega}_s{\hat{\varphi}}_s\end{array}\right. $$
(8)

where Kpφs, KpTe are the proportional gains of the PI regulators which allow the convergence of the errors, and must be chosen to satisfy the condition of stability \( {S}_1\frac{dS_1}{dt}<0\ \mathrm{et}\ {S}_2\frac{dS_2}{dt}<0 \) using the Lyapunov criterion [21]. KIφs, KITe are the integral gains which also ensure convergence of the errors and decoupling between the torque and the flux. In order to reduce chattering phenomena, the traditional sign function of the switching control is replaced by a more flexible saturation function “sat(S1) and sat(S2)”.

3.2 Speed control

Figure 4 shows the speed loop using sliding mode control. The controller is designed so that the regulation loop generates the reference of the electromagnetic torque with a rapid dynamic response. The speed sliding surface is defined by:

$$ \left\{\begin{array}{c}{S}_{\varOmega }={\Omega}^{\ast }-\hat{\Omega}\\ {}{\dot{S}}_{\Omega}={\dot{\Omega}}^{\ast }-\hat{\dot{\Omega}}\end{array}\right. $$
(9)
Fig. 4
figure 4

Speed loop in sliding mode control

Full size image

The mechanical equation of the asynchronous motor is given by:

$$ J\dot{\varOmega}={T}_e-{T}_L-f\hat{\varOmega} $$
(10)

By substituting (9) into (10), the surface derivative is:

$$ {\dot{S}}_{\varOmega }=\dot{\Omega}\ast -\frac{1}{J}\left({T}_e-{T}_L-f\hat{\Omega}\right) $$
(11)

Based on the sliding mode theory, there is:

$$ {T}_e={T}_{eeq}+{T}_{en} $$
(12)

The equivalent command part (Teeq) is defined during the sliding mode state with ṠΩ = 0, Ten = 0 and \( {\dot{\varOmega}}^{\ast } \) =0, and is:

$$ {T}_{eeq}={T}_L+f\Omega $$
(13)

The non-linear part (Ten) is defined as:

$$ {T}_{en}={c}_{\varOmega } sat\left({S}_{\varOmega}\right) $$
(14)

From (13) and (14) the torque control equation in sliding mode is given by:

$$ {T}_e={T}_L+f\hat{\varOmega}+{c}_{\varOmega } sat\left({S}_{\varOmega}\right) $$
(15)

where cΩ is a positive gain.

4 Three-level NPC inverter

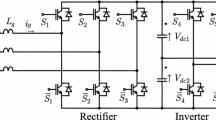
Multi-level inverters are increasingly used for drive and control of AC motors because of their multiple advantages over the two-level inverters especially in medium and high power applications [22, 23]. A simplified circuit diagram of a three-level NPC inverter is shown in Fig. 5. Each phase is made by four switches Si1-Si4 with four freewheeling diodes Di1-Di4, where “i” corresponds to one of the phase segments a, b, or c. The DC bus voltage Vdc is divided into two equal parts by the line capacitors C1 and C2, which provide a neutral point N. The clamping diodes Dsi1 and Dsi2 are used to clamp the output potential to the neutral point N. This generates an additional zero voltage level, i.e., +Vdc/2, 0 and -Vdc/2 taking the neutral point as a reference [24].

Fig. 5
figure 5

Three-phase three-level inverter supplying an asynchronous motor

Full size image

The phase to neutral (Van, Vbn, Vcn) and the phase to phase (Vab, Vbc, Vca) output voltages are expressed as:

$$ \left.\begin{array}{l}\left[\begin{array}{c}{\mathrm{V}}_{\mathrm{a}\mathrm{n}}\\ {}{\mathrm{V}}_{\mathrm{b}\mathrm{n}}\\ {}{\mathrm{V}}_{\mathrm{c}\mathrm{n}}\end{array}\right]=\frac{{\mathrm{V}}_{\mathrm{dc}}}{6}\left[\begin{array}{ccc}2& \hbox{-} 1& \hbox{-} 1\\ {}\hbox{-} 1& 2& \hbox{-} 1\\ {}\hbox{-} 1& \hbox{-} 1& 2\end{array}\right]\left[\begin{array}{c}{\mathrm{s}}_{\mathrm{a}}\\ {}{\mathrm{s}}_{\mathrm{b}}\\ {}{\mathrm{s}}_{\mathrm{c}}\end{array}\right]\\ {}\left[\begin{array}{c}{\mathrm{V}}_{\mathrm{a}\mathrm{b}}\\ {}{\mathrm{V}}_{\mathrm{b}\mathrm{c}}\\ {}{\mathrm{V}}_{\mathrm{c}\mathrm{a}}\end{array}\right]=\frac{{\mathrm{V}}_{\mathrm{dc}}}{2}\left[\begin{array}{ccc}1& \hbox{-} 1& 0\\ {}0& 1& \hbox{-} 1\\ {}\hbox{-} 1& 0& 1\end{array}\right]\left[\begin{array}{c}{\mathrm{s}}_{\mathrm{a}}\\ {}{\mathrm{s}}_{\mathrm{b}}\\ {}{\mathrm{s}}_{\mathrm{c}}\end{array}\right]\end{array}\right\} $$
(16)
$$ \mathrm{With}:{\mathrm{s}}_a=\left\{\begin{array}{c}2\mathrm{if}{\mathrm{S}}_{a1}= on\mathrm{and}{S}_{a2}= on\\ {}\begin{array}{l}1\mathrm{if}{\mathrm{S}}_{a2}= on\mathrm{and}{S}_{a3}= on\\ {}0\mathrm{if}{\mathrm{S}}_{a3}= on\mathrm{and}{S}_{a4}= on\end{array}\end{array}\right.\operatorname{} $$
(17)

A number of modulation techniques can be used to control three-phase multi-level converters. These modulation techniques are used to generate the PWM pulses in order to meet the objectives of converter control, such as low THD, etc. [25]. In SPWM, the switching states of the switches are obtained by comparing a balanced three-phase reference voltage with two triangular high frequency carriers. Variations in the amplitude and frequency of the reference voltage modify the generated pulse patterns which determine the inverter output.

5 Sliding mode observer

The sliding mode observers (SMO) offer high efficiency, ease of implementation with no in-depth calculation, and good robustness against the variation of machine parameters [26]. The objective of the flux observer in sliding mode is to reconstruct the stator flux components and to use them for torque and speed estimation (as shown in Fig. 6). According to the characteristic equations of the asynchronous motor (1), the variations of the stator flux and current are obtained as:

$$ \left\{\begin{array}{l}\frac{d{\varphi}_s}{dt}={V}_s-{R}_s{I}_s+j{\omega}_s{\varphi}_s\\ {}\frac{dI_s}{dt}=-\frac{1}{\sigma}\left(\frac{1}{T_r}+\frac{1}{T_s}\right){I}_s+\frac{1}{\sigma {L}_s}\left(\frac{1}{T_r}-j{\omega}_s\right){\varphi}_s+\frac{1}{\sigma {L}_s}{V}_s\end{array}\right. $$
(18)

where: \( {T}_s=\frac{L_s}{R_s}\ and\ {T}_r=\frac{L_r}{R_r} \) are the stator and rotor time constants and \( \sigma =1-\frac{L_m}{L_s{L}_r} \) is the leakage coefficient. The term (ωsφs) contains the pulsation and stator flux considered as a perturbation for the design of the observer. Thus, the estimated stator flux and current are:

$$ \left\{\begin{array}{l}\frac{d{\hat{\varphi}}_s}{dt}={V}_s-{R}_s{I}_s- Ksat\left({S}_I\right)\\ {}\frac{d{\hat{I}}_s}{dt}=-\frac{1}{\sigma}\left(\frac{1}{T_r}+\frac{1}{T_s}\right){I}_s+\frac{1}{\sigma {L}_s{T}_r}{\varphi}_s+\frac{1}{\sigma {L}_s}{V}_s- Ksat\left({S}_I\right)\end{array}\right. $$
(19)

where K is the observer gain which must be positive, and SI is the sliding surface of the current error. A PI controller is proposed to impose the error convergence as:

$$ {S}_I=\left({K}_p+\frac{K_I}{S}\right)\left({\hat{I}}_s-{I}_s\right) $$
(20)
Fig. 6
figure 6

Stator flux observer in sliding mode

Full size image

The advantage of the stator flux observer lies in the fact that it is not related to the rotor speed, while the latter can be estimated as:

$$ \hat{\Omega}=\frac{1}{\varphi_r^2}\left(\frac{d{\hat{\varphi}}_{\beta r}}{dt}{\hat{\varphi}}_{\alpha r}-\frac{d{\hat{\varphi}}_{\alpha r}}{dt}{\hat{\varphi}}_{\beta r}\right)-\frac{4}{3}\frac{R_s{\hat{T}}_e}{P{\varphi}_r^2} $$
(21)

Rotor flux and torque can be estimated as:

$$ {\hat{\varphi}}_r=\frac{L_r{\hat{\varphi}}_s-{L}_r{L}_s\sigma {I}_s}{L_m} $$
(22)
$$ {\hat{T}}_e=\frac{3}{4}P\left({\hat{\varphi}}_{\alpha s}{I}_{\beta s}-{\hat{\varphi}}_{\beta s}{I}_{\alpha s}\right) $$
(23)

6 Simulation results and discussion

The global control and observation algorithms presented previously are simulated using MATLAB/SIMULINK in this section. The simulation results are obtained for a 300 W three-phase squirrel cage asynchronous motor, with its characteristics given in Table 1. The results are compared between SM-DTC via a three-level NPC inverter, the same control with a two-level inverter and PI-DTC using the three-level NPC inverter. The motor flux magnitudes are taken from a sliding mode observer applied to all schemes. The figures are specified by (a) for SM-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter, and (c) for PI-DTC with the three-level NPC inverter.

Table 1 Motor Parameters
Full size table

Figure 7 illustrates the speed tracking performance to the reference of 1146 rpm while the load torque is applied at t = 0.3 s. It can be noticed that Fig. 7(a) and (b), presenting the SM-DTC, have the fastest responses at startup by reaching the steady state in only 0.17 s, and very minimal overshoots of less than 6.385% compared to that in Fig. 7(c) with PI-DTC. They are also least affected by the application of load. The SM-DTC strategy with the three-level inverter offers the best reference tracking according to the zoomed part of Fig. 7(a) (with negligible error) compared to the other two strategies (with errors around 0.5%).

Fig. 7
figure 7

Motor speed response (rpm) (a) for SM-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter and (c) for PI-DTC with a three-level NPC inverter

Full size image

Figure 8 shows the torque responses for the three systems when the load is introduced at t = 0.3 s. In steady state, it is clearly seen that the proposed strategy shown in Fig. 8(a) has smaller ripples compared to the others presented in Fig. 8(b) and (c). In addition, the transient response time and overshoot are minimized with the SM-DTC with both the two-level and three-level inverter cases. It can also be observed that the SM-DTC strategy has a smaller initial settings torque than that of the PI-DTC-SPWM because of the control strategy which minimizes the startup current.

Fig. 8
figure 8

Electromagnetic torque response (rpm) (a) for SM-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter and (c) for PI-DTC with a three-level NPC inverter

Full size image

Figure 9 illustrates the stator current with their zoomed waveforms.

Fig. 9
figure 9

Stator currents (A) (a) for SM-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter and (c) for PI-DTC with a three-level NPC inverter

Full size image

As can be seen, Fig. 9(a) and (b) show good sine waveforms that quickly reach the steady state after the application of the load. In addition, the SM-DTC strategy, with either the two-level or three-level inverter, limits the current drawn at startup (around half of that with PI-DTC-SPWM) indicating a significant advantage.

Figure 10 compares the current harmonic spectra of the three cases. It can be seen that the cases with the three-level inverter shown in Fig. 10(a) and (c) have lower harmonic distortion than the two-level shown in Fig. 10(b). In addition, SM-DTC produces lower ripples in the stator current, torque and flux than those of PI-DTC, and thus further improves the THD, as can be seen from Fig. 10(a) and (c).

Fig. 10
figure 10

Harmonic spectra of the stator current (A) (a) for M-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter and (c) for PI-DTC with a three-level NPC inverter

Full size image

From the stator flux amplitude waveforms shown in Fig. 11, it can be observed that the stator flux in the three cases follows the reference 0.9960 Wb with great precision. The SM-DTC algorithm associated with the three-level inverter has reduced flux ripples (0.4%) compared to those of the PI-DTC-SPWM strategy with the same inverter (0.55%) and the SM-DTC strategy with the two-level inverter (5%). In addition, the SM-DTC strategy associated with the three-level inverter shows excellent controllability during load disturbance.

Fig. 11
figure 11

Stator flux magnitude (Wb) (a) for SM-DTC with a three-level NPC inverter, (b) for SM-DTC with a two-level inverter and (c) for PI-DTC with a three-level NPC inverter

Full size image

From the above analysis, the proposed method that combines the SM-DTC with the three-level inverter and the SMO shows the following characteristics:

  • Good reference tracking with almost zero static error.

  • Reduced ripples in flux and torque.

  • Limited current drawn at start-up.

  • Low THD.

  • Excellent controllability during load disturbance.

  • Simplified structure with a single observer.

7 Conclusion

This paper presents a comparative analysis of a cage asynchronous motor supplied by a three-level NPC inverter with SM-DTC, a conventional two-level inverter with the same SM-DTC, and the three-level NPC inverter with PI-DTC-SPWM. The study shows that the use of the three-level inverter considerably reduces the ripples and the THD of the motor current, while the adoption of the robust SM-DTC control law offers good tracking of the references, a significant reduction of the starting current and faster dynamic response. In conclusion, the use of the three-level NPC inverter with the variable structure strategy SM-DTC and the SMO results in excellent control of the drive system.

8 Nomenclature

DTC Direct Torque Control

NPC Neutral Point Clamped

MPC Model Predictive Control

PI-DTC-SPWM Direct Torque Control based on PI regulators using Sinusoidal Pulse Width Modulation

SMC Sliding Mode Control

SMO Sliding Mode Observer

SM-DTC Sliding Mode based on Direct Torque Control

SPWM Sine Pulse Width Modulation

THD Total Harmonic Distortion

Vds, Vqs Direct and quadrature stator voltages

Ids, Iqs Direct and quadrature stator currents

Idr, Iqr Direct and quadrature rotor currents

Rs, Rr Stator and Rotor resistances

Ls, Lr Stator, Rotor and mutual inductances

ωs Synchronous speed

Te, TL Electromagnetic and load torques

Ω Mechanical Speed

P Number of Pole Pairs

J, f Moment of inertia and friction coefficients

φds, φqs Direct and quadrature stator flux

φdr, φqr Direct and quadrature rotor flux

Ts, Tr Stator and rotor time constants

σ Leakage coefficient

KPTe, KPφs proportional gains of the PI regulators

KITe, KIφs Integral gains of the PI regulators

K Observer’s gain

cΩ, cφs, cTe Speed, stator flux and torque sliding mode gains

SI, S1, S2, SΩ Sliding surfaces of the current, stator flux, torque and speed errors

eφs, eTe Stator flux and torque error functions