Abstract
Under frequency load shedding is an effective approach to maintain or restore the steady-state operation of the power system when frequency accidents occur. An improved under frequency load shedding strategy based on dynamic power flow tracking is proposed. The expression of the kinetic energy theorem in power system is derived and combined with the power flow tracing method to analyze the relation between system energy distribution and its frequency. The power system frequency influencing factors are then constructed and applied to find the reasons of frequency decline and to quantify the contributions of the mechanical power of the generators, the load power and the transmission losses for the frequency deviation. Finally, considering a variety of unbalanced power scenarios in the system, the modified load shedding strategy is designed. Based on the results of dynamic power flow tracing, the strategy can choose the suitable load node to control, and the defined load frequency contribution indicator is utilized to determine the load shedding amount which each control object undertakes. The proposed methodology is verified by the fault scenarios when the generator sets mistakenly cut off and the trip of important tie-lines in the IEEE 39-bus system. Compared with the conventional strategies, the proposed strategy is more selective, can reduce the blackout range, and improve the effect of stable frequency recovery.
Similar content being viewed by others
Introduction
Under frequency load shedding (UFLS) is an effective approach to maintain frequency stability in power system. It prevents the system from frequency collapse in the presence of a serious active power deficit and is one of the most important components of the “Three Defensive Lines” strategy in China [1].
Recently, academic papers about the UFLS can be largely divided into three categories: 1) optimization algorithms on location of load shedding and allocation of its amount by using some constructed indicators [2, 3]. In [3], a centralized adaptive load shedding scheme is proposed, and the optimal amount and location of load shedding and the proposed strategies are specified in the second stage; 2) study on how to set specified load shedding steps and the corresponding frequency thresholds [4]; 3) research on modified UFLS schemes when there are new equipment or components installed in the power system [5,6,7].
However, the above-mentioned methodologies do not analyze the detailed frequency dynamic process in power system. Most of them just apply the simplified system frequency response model (SFR) [8] to study the frequency stability. This SFR model is a simplified equivalent model, and its modeling procedure is based on the generator parameters. So the disadvantage of such model is the weak adaptiveness for the multi-machine power system. Besides, the SFR model cannot reveal the influencing degree and mechanism of different loads on frequency in detail.
As a consequence, most proposed methodologies utilize all resettable loads to operate the load shedding process. Reference [9] distributes the load shedding amount to all loads, which lacks pertinence and increases the blackout area. In addition, its frequency recovery effect is far from satisfaction. Reference [10] applies the load power data of the fault nodes to construct the corresponding load shedding proportion. However, it only considers the power flow tracing in steady state, and does not take into account of the dynamic changes of load power during the fault. An improved power flow tracing method is given in [11] to operate the risk assessment in power systems, but it cannot be adaptive to variety of contingencies.
As different loads have different impacts on the frequency recovery in the process of frequency decline, it is appropriate to allocate the load shedding amount to the load buses which have great influence on restoring frequency [2], rather than to all resettable load buses. Thus, the operated load bus and its load shedding proportion can be obtained through the detailed analysis of the load response when the frequency decreases.
With the widely application of the wide area measurement system (WAMS) [12], it is feasible to acquire the operating parameters of the entire power system in real-time. The WAMS can provide the synchronously measured data, such as the magnitude and angle of the voltage and current, the frequency and its rate of change, etc. Based on the measured data, the power flow and load power data of the entire system can be obtained in real-time.
This paper proposes a methodology to analyze the frequency transient process of every generator. The method combines the power flow tracing algorithm with the kinetic energy theorem of power systems, to obtain the frequency influencing factors of every generator. On the basis of that, it can quantify the contribution of the mechanical power of the generators, the load power and the transmission losses for the frequency deviation. The improved under frequency load shedding strategy is then designed according to the proposed methodology. The simulation results show that the proposed strategy is adaptive to different faults. The proposed strategy can determine the load bus to be curtailed and is more beneficial for the frequency recovery when compared with the conventional schemes.
Methods
The kinetic energy theorem of power system
For a power system with n generators, the motion equation [13] for the rotor of generator i is given as
In (1), δ i is the power-angle of generator i in unit of rad; Δω i is the deviation of the angular speed of generator i in unit of rad/s; M i is the inertia constant of generator i in unit of s; ω N =2πf N represents the angular speed of the generator in steady state; ω i * represents the angular speed of generator i in per unit, which cannot be neglected in analyzing frequency stability; time variable t is measured in unit of s; P mi and P ei represent the per unit mechanical and electromagnetic power of generator i respectively. Unless otherwise mentioned, all power in this paper is in per unit, while the unit value of power is 100 MW.
Multiplying the second equation in (1) by the actual value of the angular frequency ω i , and applying proper mathematical conversions, yield
Implementing integral computation to (2) in the region of [t 0, t 1] as
Applying expansion to the left side of (3) and dividing throughout by \( {\omega}_{\mathrm{N}}^2 \) yield
1/2M i ω i *2 is defined as the kinetic energy of generator i and (4) is the expression of the kinetic energy theorem in power systems. It indicates that the kinetic energy difference of one generator equals the difference of the work of its mechanical power and electromagnetic power during this period.
The Power flow tracing method
The electromagnetic power of the generators flows through the transmission network to loads, with some being consumed by the loads and some being consumed by the lines it flowing through. Generally, there are many generators and loads in power systems, and each generator undertakes different load. Power flow tracing method, widely applied in the analysis of electric power market and based on the fundamental assumption of power distribution following proportional sharing principle [14], can determine the way how the power of one generator is allocated to the load.
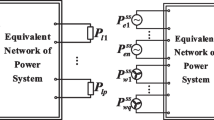
Based on the power flow in Fig. 1 and the power flow tracing method [15], it can calculate the contribution quota of the output power P Gj (P Gj = 0 if there is no generator at this node) of the generator at node j to load P Lk at node k, namely P Gj,Lk , and the power loss P Gj,Loss in the power transmission, shown in (5) and (6) respectively as
Besides, it can also calculate the contribution quota of the input power on line i-j to its downstream load k and power transmission loss, shown in (7) and (8) respectively as
The majority of the proposed power flow tracing method simply takes the steady state power flow into account. However, the one-to-one correspondence can be obtained between the load power and generator power through the dynamic power flow tracing method in each moment. This is because that the input and output power of the load node is always equal at any time.
The analysis of the frequency influencing factor
If the distributed power and new energy source are not considered, the output electromagnetic power of any generator can be represented by its load and power transmission loss as
In (9), number j is the node number that refers to generator i. Substituting (9) into (4) gives
The mechanical power variation ΔP mi , which is compared to its value at steady state, is given as
In (11), \( {P}_{\mathrm{m} i}^{\mathrm{S}} \) is the per unit mechanical power at steady state. Since the mechanical power of one generator equals its electromagnetic power in steady state, that is
Given that,
In (13), ΔP Gj, Lk represents the transmission power variation compared to its stable value in the situation that generator at node j transmits power to load at node k; ΔP Gj,Loss represents the transmission power loss compared to its stable value, which is supplied by the generator at node j.
Substituting (11–13) into (10) yields
From (14) it can be seen that, at time of t 1, the angular speed (namely frequency) of generator i is determined by the following four parts:
-
1)
The kinetic energy of the generator at time of t 0: \( \frac{1}{2}{M}_i{\omega_i^{*}}^2\left({t}_0\right) \);
-
2)
The work done by the mechanical power variation during the period of [t 0, t 1]: \( {\displaystyle {\int}_{t_0}^{t_1}\varDelta {P}_{\mathrm{m} i}\mathrm{d} t} \);
-
3)
The work of load power variation which is supplied by the generator during the period of [t 0, t 1]: \( {\displaystyle \sum_{k=1}^m{\displaystyle {\int}_{t_0}^{t_1}-\varDelta {P}_{\mathrm{G} j,\mathrm{L} k}\mathrm{d} t}} \);
-
4)
The work of the transmission power loss variation undertaken by the generator during the period of [t 0, t 1]: \( {\displaystyle {\int}_{t_0}^{t_1}-\varDelta {P}_{\mathrm{G} j,\mathrm{Loss}}\mathrm{d} t} \).
Therefore, by analyzing each generator using (14), the frequency change and its influencing factors for each generator can be acquired. Since the first part of (14) is a constant, the second to the fourth parts can be considered as the main influencing factors which result in the frequency change of the generator.
The design of load shedding strategy
In generally, the following scenarios can lead to unbalanced power in the system [16]: Generator sets are mistakenly removed, resulting in significant reduction of the power supply; Transmission equipment such as tie-line is removed by relay protection because of transmission power overload or other reasons, causing power islands; The electricity load is suddenly increased leading to power shortage. The proposed load shedding strategy in the paper mainly deals with the first two scenarios.
The situation where generator set is mistakenly removed
It is assumed that multiple generators are mistakenly removed, and these faulty generator nodes compose set D. When generator node j∈D, load power variation on node k which is supplied by the generator is ΔP Gj, Lk . Load nodes, which meet (15) when frequency declines, should be removed and all of them compose set C j .
Formula (15) shows that the faulty generator on node j reduces the supply of load power which belongs to set C j and this part of load should be shed.
Then, the load frequency contribution indicator ρ j,k is defined to indicate the allocation of load shedding amount, which is shown as
In (16), the integral lower limit t 0 and upper limit t 1 should be defined. Any moment in steady state can be chosen as t 0, so the initial kinetic energy \( 1/2{M}_i{\omega_i^{*}}^2\left({t}_0\right) \) is the rated kinetic energy, because the deviation of the rated frequency is the main concern when considering frequency stability. Load shedding devices are only triggered when the frequency reduces to a pre-specified threshold value and the time of the trigging is chosen as t 1.
According to (16), the more work of the load power variation has done which is supplied by the generator during the period of [t 0, t 1], the bigger its load frequency contribution indicator will be. This is due to the fact that larger work done by the load power variation leads to bigger reduction of the load power by the faulty generator and this part of the load power shortage will have to be supplied by other healthy generators. That is to say, the healthy generators will support not only the load which has more work of its load power variation, but also the one being discarded by the faulty generator. Thus, it is beneficial to shed this type of load for better frequency recovery.
The active power deficit of the fault generator can be calculated as
where ΔP j represents the active power deficit of the generator on node j; \( {P}_{\mathrm{m} j}^{\mathrm{S}} \) is the steady-state mechanical power of the generator on node j; \( {P}_{\mathrm{m} j}^{\mathrm{fault}} \) stands for the mechanical power of the generator on node j at the failure moment.
So the load at bus k needed to shed can be calculated as
The Removal of tie-lines resulting in power islands
When some important tie-lines are mistakenly or abnormally removed, the power system will be divided into multiple power islands. Frequency instability could occur in some power islands with heavy load, so it is necessary to shed load for maintaining system stability.
For the following analysis, grids A and B are considered to be connected by the tie-line L 12 and L 34, and the directions of power flow for both lines are from grid A to grid B. The transmitted power is P 12 and P 34, respectively. When L 12 and L 34 are disconnected, there will be power deficit of P 12 + P 34 in grid B. Under such conditions, the load needed to shed in grid B can also be calculated by applying power flow tracing method and kinetic energy theorem. Suppose all tie-lines which are disconnected compose set A and all loads in grid B compose set B. The set of loads needed to shed is C j , which should meet the following requirement
where \( {P}_{ij,\mathrm{L} k}^{\mathrm{S}} \) is the load power at bus k supplied by line i-j calculated using (7) in steady state. The load nodes which meet (19) are the loads in grid B supplied by grid A.
Line i-j can be equivalent to a power supply which transmits power to grid B. Similarly, the load frequency contribution indicator ρ ij,k is defined as
where ΔP ij, Lk is the variation between the actual and steady state load power at bus k supplied by line i-j and is given as
If the moment in steady state is chosen as t 0, ΔP ij, Lk =0 is true before the fault and P ij, Lk =0 is true after the fault. Thus (20) can be modified as
Therefore, the load at bus k required to shed in grid B can be calculated as
Results and Discussions
Digital simulation
The IEEE 39-bus system is used to simulate the proposed strategy and the system parameters can be found in [17]. There are governors and exciters in the generators at bus 30–38. The generator model is biaxial transient model considering damping windings. The generator 39 uses classic second-order model without governor and exciter. The load model represents 30% constant impedance component, 50% constant current component and 20% constant power component, and the load frequency regulation effect is also considered. The rated frequency is 50 Hz, the rated active power is 6192 MW and the maximal active power is 6372 MW.
Failure 1: Removal of generator set by mistake
Assuming false protection operation at 0.2 s and the generator 35 is removed leading to a reduction of 500 MW power generation. At this time, the frequency will decline due to unbalanced power. Generator 35 (G-35) has the highest frequency fluctuation and thus, G-35 will discard a part of load which has to be supported by other healthy generators. After a while, the frequency fluctuation of all generators slows down and the system frequency tends to be gradually converged. The whole fluctuation process can be used to understand the redistribution of load power and the result of the process tends to make the frequency of each generator to be uniform.
In Fig. 2, the integral starting point is selected as the time of failure (0.2 s), and the abscissa represents the terminal time of the integral. The Y-axis represents per unit value of the energy work and the labels in the Fig. 2 such as ‘-ΔP G35,L3’, refer to the energy work value from 0.2 s to t 1, e.g. -ΔP G35,L3= \( {\displaystyle {\int}_{0.2}^{t_1}-\varDelta {P}_{\mathrm{G}35,\mathrm{L}3}\mathrm{d} t} \).
From Fig. 2 it can be seen that, the energy work of the load supplied by G-35 decreases after the accident, and the energy work of each load power variation is different. The load discarded by G-35 will be supported by other healthy generators. Taking the load at bus-16 for example, the load power of bus-16 supplied by the system generators after the accident is shown in Fig. 3.
Fig. 3 shows that the decreased load power of bus-16 which is supplied by G-35 is mainly supported by G-33 with other healthy generators making small contributions. Similarly, other load discarded by G-35 will also be supported by other healthy generators, and this causes their frequencies to decline due to the required additional power support.
The required load shedding amount at the moment can be calculated according to (17) and (18). From Fig. 2 it can be concluded that all the loads meet (15) which indicates that G-35 reduces the power of all of its supplied loads. Therefore, the set of shedding load in this case is C 35 = {3, 4, 15,16,18,21, 23, 24,27}.
For comparison, different load shedding strategies have also been simulated. Strategy 1 applies the steady state load power and Δf to guide the load shedding [9], while strategy 2 [10] conducts load shedding according to steady power flow tracking results and Δf. The traditional load shedding method [18] which acts step by step is referred as strategy 3. The system inertia center frequency recovery of the four different load shedding strategies is shown in Fig. 4.
Figure 4 shows that the system frequency of the proposed strategy recovers fast than the other ones. This is because the proposed strategy is better targeted and uses the characteristics of the faulty generator which will decrease the power supply when frequency declines to make load shedding strategy. Strategy 1 and 3 choose all system buses to shed their load. This enlarges the power cut range and its frequency recovery is not satisfactory. The reason for this is that loads at some buses are not associated with the faulty generator. Strategy 2 applies steady power flow tracking results to make load shedding scheme, but the dynamic load variation is not considered adequately. Therefore, the accuracy cannot be improved.
The load power which is supplied by G-35 after the proposed load shedding strategy is shown in Fig. 5. From Fig. 5, G-35 again decreases the load power of bus-21. However, this is due to the load-shedding of bus-21 load and is not related to the discard of the power supply. However, there is a small increase in other bus load. The proposed strategy redistributes the load power after load shedding and the healthy generators will not support the load which is discarded by the faulty one. Taking the bus-16 load as an example, the load power of bus-16 supplied by each generator after the proposed strategy is shown in Fig. 6.
In Fig. 6, it can be seen that the bus-16 load power which is supplied by the generators returns to the steady state level after using the proposed strategy except the faulty generator G-35. This indicates that other healthy generators will not support the load which was initially supplied by G-35, and the active power deficit of G-35 is solved by load shedding. The power supply of other bus load is similar to this. Thus, it can be concluded that the proposed strategy selectively sheds the bus load which contributes to frequency decline, viz. the load discarded by the faulty generator and those supported by other healthy generators.
Figure 7 compares the load power of bus-16 supplied by G-33 after using the proposed strategy, strategy 1 and strategy 2, respectively.
The bus-16 load power supplied by G-33 is about 1.8 p.u. under steady state. Figure 7 shows that the bus-16 load power supported by G-33 is still maintained at a high level after using strategy 1 indicating that the bus-16 load is still supported by G-33 after load shedding. In strategy 1, all system bus loads will be chosen to trip which sacrifices the load power not related to the faulty generator to support the load of bus-16. Comparing the proposed strategy with strategy 2 it can be seen that the bus-16 load power supplied by G-33 of the former is closer to the steady state value than the latter. As the dynamic power flow tracing combined with the kinetic energy theorem is applied in the proposed strategy, the analysis can reflect the dynamic energy variation in power systems leading to a more reliable load shedding scheme.
Failure 2: Removal of important tie-lines
In the IEEE 39-bus system, the tie-line 19–16 is an important line and the power system will be divided into 2 power grids if it is disconnected. One of the grid is called power grid A composed of bus-19, bus-20, bus-33 and bus-34 with the remaining system node constituting power grid B.
A part of the load in grid B is supplied by grid A through the tie-line 19–16. When the system is in steady state, the active power from the generators of bus-33 and bus-34 to bus-16 is about 451 MW which flows through the tie-line 19–16.
Therefore, there is 451 MW active power deficit in the power grid B after tie-line 19–16 is disconnected and the system frequency declines. Using (23), the load shedding amount for each load bus can be calculated. The system inertia center frequency of power grid B after load shedding is given in Fig. 8. For comparison, strategy 1 and 3 are also simulated, and their corresponding system frequency variations are also shown in Fig. 8 (strategy 2 is not simulated as it can only be applied in Failure 1). From Fig. 8 it can be seen that the proposed strategy can also improve the effect of frequency recovery in this failure mode.
In fact, if the disconnected tie-line is considered to be equivalent to a power source which supplies power to grid B, the analysis on failure 2 becomes similar to the scheme for failure 1. From (23), there is:
Thus the following equation can be derived
Equation (25) indicates that the load shedding amount of node k is approximately equal to the node k load power supplied by tie-line i-j. Therefore, it is appropriate to cut off the load power which is supplied by the faulty tie-line so as to avoid the shedding of the unrelated bus load.
Conclusion
The paper derives the expression of the kinetic energy theorem in power systems, which is combined with the power flow tracing method to analyze the relationship between dynamic distribution of energy and frequency variation in a power system. It can be concluded that the main factors causing the generator frequency variation are the work done by the mechanical power variation, the work of load power variation supplied by the generators, and the work of transmission power loss variation undertaken by the generators.
The system frequency influencing factors are then applied to analyze the transient process of frequency, and the reason for generator frequency decline is divided into two types. The reason of the faulty generator frequency decline is due to the decrease of its mechanical power, and to repress further frequency decline it directly reduces its supplied load power. For other healthy generators, the reason for their frequency decrease is due to the additional supply to the load discarded by the faulty generators.
Based on the analysis, a distributed load shedding strategy is proposed which is based on the load frequency contribution indicator to allocate the load shedding amount of each load node. The simulation results show that the system load power can be redistributed after the implementation of the load shedding control. The healthy generators no longer supply the load power which is discarded by the fault generator, and their load power supply almost recovers to the steady state value. In addition, this strategy can improve the effect of frequency recovery and reduce the blackout range.
Change history
28 August 2017
An erratum to this article has been published.
References
Lu, M., ZainalAbidin, W. A. W., Masri, T., et al. (2016). Under-Frequency Load Shedding (UFLS) Schemes - A Survey. International Journal of Applied Engineering Research, 11(2), 456–472.
Tang, J., Liu, J., Ponci, F., et al. (2013). Adaptive load shedding based on combined frequency and voltage stability assessment using synchrophasor measurements. IEEE Transactions on Power Systems, 28(2), 2035–2047.
Shekari, T., Gholami, A., Aminifar, F., Sanaye-Pasand, M. An Adaptive Wide-Area Load Shedding Scheme Incorporating Power System Real-Time Limitations. IEEE Systems Journal, 2016. doi:10.1109/JSYST.2016.2535170.
Guowei, C., Zhenglong, S., Yuwei, W., et al. (2013). Optimization of under frequency load shedding scheme based on improved system frequency response model. Power System Technology, 37(11), 3131–3136.
Das, K., Nitsas, A., Altin, M., Hansen, A., & Sorensen, P. (2017). Improved Load Shedding Scheme considering Distributed Generation. IEEE Transactions on Power Delivery, 32(1):515–524.
Pulendran, S., Tate, J. E. Energy Storage System Control for Prevention of Transient Under-Frequency Load Shedding. IEEE Transactions on Smart Grid, 2015. doi:10.1109/TSG.2015.2476963.
Sigrist, L., Egido, I., Lobato Miguélez, E., & Rouco, L. (2015). Sizing and controller setting of ultracapacitors for frequency stability enhancement of small isolated power systems. IEEE Transactions on Power Systems, 30(4), 2130–2138.
Shekari, T., Aminifar, F., & Sanaye-Pasand, M. (2016). An analytical adaptive load shedding scheme against severe combinational disturbances. IEEE Transactions on Power Systems, 31(5), 4135–4143.
Mingliang, Q., & Xiuchao, Y. (2002). Measures to reduce over-shedding caused by under-frequency load shedding project[J]. Power System Technology, 26(3), 83–86.
Yaodong, W., Haifeng, L., & Yajing, G. (2015). Research on adaptive UFLS strategy based on power flow tracing algorithm[J]. Electric Power, 48(3), 61–66.
Niu, R., Zeng, Y., Cheng, M., et al. Study on Load-shedding Model Based on Improved Power Flow Tracing Method in Power System Risk Assessment, DRPT, 2011
Rudez, U. & Mihalic, R. WAMS Based Under frequency Load Shedding With Short-Term Frequency Prediction. (2016) IEEE Transactions on Power Delivery. 31(4):1912–1920.
Rudez, U., & Mihalic, R. (2011). Monitoring the first frequency derivative to improve adaptive under frequency load-shedding schemes[J]. IEEE Transactions on Power Systems, 26(2), 839–846.
Jianwen, R., Sha, L., Minmin, Y., et al. (2013). Emergency control strategy for line overload based on power flow tracing algorithm[J]. Power System Technology, 31(2), 392–397.
Boming, Z., Shousun, C., & Zheng, Y. (2007). Higher power network analysis[M]. Beijing: Tsinghua University Press.
Anderson, P. M., & Fouad, A. A. (2003). Power system control and stability [M]. Piscataway: IEEE Press Wiley-Interscience.
Vital, V. (1992). Transient stability test systems for direct stability methods [J]. IEEE Trans on Power Systems, 7(1), 37–43.
Guancheng, Y., & Da, X. (2012). The principle of power system automation equipment [M]. Beijing: China Electric Power Press.
Acknowledgment
This work was supported by the project “Research on coordination, online diagnostics and auxiliary decision-making technology of multi-zone stability control system”, approved by science and technology project of State Grid Corporation in China.
Funding
Chinese National Natural Science Foundation (51507116).
Authors’ contributions
SL proposed the dynamic power flow tracing based frequency stability emergency control strategy and drafted the manuscript. BC verified the proposed methodology through simulations. All authors read and approved the final manuscript.
Authors’ information
Shun Li, was born in Hunan, China, in 1993. He received the B.S. degree from Wuhan University, China, in 2015. He is currently pursuing the M.S. degree in School of Electrical Engineering, Wuhan University. His research interests include power system stability analysis, evaluation and control.
Qingfen Liao, was born in Zhejiang, China, in 1975. She received the Ph. D. degree from Wuhan University, China. She is currently an Associate Professor in School of Electrical Engineering, Wuhan University. Her research interests include power system stability analysis and control.
Dichen Liu, was born in Hubei, China, in 1953. He received the Ph. D. degree from Wuhan University, China. He is currently a Full Professor and a doctoral supervisor in School of Electrical Engineering, Wuhan University. His research interests include power system operation and control, distributed generation and micro power grid.
Bingcheng Cen, was born in Guangdong, China, in 1991. He received the B.S. degree from Wuhan University, China, in 2013. He is currently pursuing the M.S. degree in School of Electrical Engineering, Wuhan University. His research interests include power system stability analysis and control.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are retracting this article. After publication we became aware of the following errors in the methodology:
(1) Our article states: “ If the distributed power and new energy source are not considered, the output electromagnetic power of any generator can be represented by its load and power transmission loss”. However, formula (9) is wrong when considering the spinning reserve capacity and the adjustment of the balancing machine in the power system.
(2) In our article formula (16) and formula (20) use the time integral of load change to determine the load frequency contribution factor, and these two formulae only consider the voltage characteristics of the load. In the simulations, the constant impedance model or the constant impedance+constant power combination model are applied, so the load change is caused by the change of the node voltage when the system frequency drops. Therefore, in our article, formula (16) and formula (20) used to determine the effect of load power on system frequency are wrong. In addition, if the load is all constant power model, then the load power will not change when the frequency drops, and the load frequency contribution factor cannot be obtained correspondingly.
In summary, the actual power system will quickly operate the spinning reserve capacity in the event of failure and its load composition varied, so the simulation results obtained in our article can only be established under special conditions. In most actual power systems, our proposed methodology is invalid and the simulation results are wrong.
An erratum to this article is available at https://doi.org/10.1186/s41601-017-0064-y.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, S., Liao, Q., Liu, D. et al. RETRACTED ARTICLE: An improved under frequency load shedding strategy based on dynamic power flow tracing. Prot Control Mod Power Syst 2, 4 (2017). https://doi.org/10.1186/s41601-016-0031-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41601-016-0031-z