Abstract
Background
Understanding the pattern of COVID-19 infection progression is critical for health policymakers. Reaching the exponential peak of cases, flattening the curve, and treating all of the active cases are the keys to success in reducing outbreak transmission. The objective of this study was to determine the most effective model for predicting the peak of COVID-19 in Indonesia, using a deterministic model.
Methods
The SEI2RS model considers five strategies for control, namely: large-scale social restriction (u1), contact tracing (u2), mass testing (u3), case detection and treatment (u4), and the wearing of face masks (u5). Three scenarios were developed, each differentiated by the controls. The model used April 10, 2020, and December 31, 2020, as the initial and final times.
Results
The simulation results indicated that the peak of COVID-19 cases for scenarios 1, 2, and 3 occur on the 59th day with 33,151 cases, on the 38th day with 37,908 cases, and on the 40th day with 39,305 cases. For all of the scenarios, the decline phase shows a slow downward slope and about 8000 cases of COVID-19 still active by the end of 2020.
Conclusion
The study concludes that scenario 2, which consists of large-scale social restriction (u1), contact tracing (u2), case detection and treatment (u4), and the wearing of face masks (u5), is the most rational scenario to control COVID-19 spreading in Indonesia.
Similar content being viewed by others
Background
The outbreak of coronavirus disease (COVID-19) has spread to nearly every country around the world. With a high density population, Indonesia is predicted to have a high number of infectious persons and, consequentially, suffer over a longer time period [1]. The first positive cases of COVID-19 in Indonesia were confirmed with two cases in Java Island on March 2, 2020, then spreading to other islands [2, 3]. As of the first week of April, there are about 3000 cases reported (Fig. 1). However, there is skepticism about whether the true number of COVID-19 cases in the community is higher than reported, due to inadequate testing and under detecting [4].
Without well prepared interventions, the number of COVID-19 cases will grow exponentially. Though delayed, the Indonesian government has taken numerous measures to control the community spread of COVID-19. Control measures, such as large-scale social restriction policies in specific provinces, a campaign for frequent hand washing and face mask use, and rapid testing suspected cases, have been implemented across Indonesia [5]. Indonesia benefits from being a country of a thousand islands, as this geography may delay disease transmission from the main epicenter on Java Island to surrounding islands.
Considering limited knowledge of COVID-19 in Indonesia, where the number of cases has been fast-growing since the onset of the epidemic, this study proposes a deterministic mathematical model based on the susceptible (S), exposed (E), infectious (I), recovered (R)-(SEIR) model [6,7,8]. Selected control variables were simulated, representing measures that have been and will be implemented by the Indonesian government to detect and reduce COVID-19 transmission. These measures include large-scale social restriction (u1), contact tracing (u2), mass rapid antibody testing (u3), case detection and treatment (u4), and the wearing of face masks (u5). Using a mathematical model as an approach to solving problems can help in explaining current phenomena [9, 10]. A mathematical model may help us to understand patterns in disease outbreak, especially that of COVID-19, and lead to a more public health informed policy making process [11, 12].
Applying optimal control to a mathematical model can predict, forecast, estimate, or choose the best scenario to eliminate a disease in a dynamical system, based on epidemiological characteristics [13]. In the phenomenon of the COVID-19 outbreak, there are lags among the real on-going spread of infection, the case detection and report and the response action. If the case load could be properly predicted, the government would have the ability to fine tune their reaction, such as adjustment of the intensity of social distancing, preparation of medical resources to cope with the case load, and planning for socio-economic recovery at proper time points.
Methods
SEI2RS model formulation
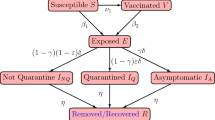
A deterministic mathematical model is applied by dividing populations into several compartments. The basis of the mathematical model in this study, SEIR, is modified to be the susceptible (S), exposed (E), carrier (I1), infectious (I2), recovery (R), susceptible (S)-(SEI2RS) Model. The cumulative number of cases (in the infectious compartment (I2)) will increase depending on the movement of the suspect population (in the exposed compartment (E)) and the number of undetected cases (in the carrier compartment (I1)). The number of I2 cases will decrease as there is increased movement of infectious cases to the recovery compartment. This compartmental model was modified not only to obtain a realistic mathematical model for the Indonesian setting, but to also follow the pathogenesis of COVID-19.
Susceptible (S) refers to the individuals deemed susceptible to COVID-19 infection during the period of outbreak. A susceptible person may be a healthy individual, but based on currently available information and clinical expertise, are at higher risk for severe illness, such as older adults and people of any age who have serious underlying medical conditions. Since local transmission has been reported in Indonesia, all patients presenting with symptoms of acute respiratory infection in primary care or the accident and emergency department of a hospital (first contact with the healthcare system) will be considered as suspected cases, regardless of their presumed susceptibility.
Indonesian guidelines divide the patient’s health status by confirmed cases and suspect cases. Exposed (E) individuals refer to suspect cases. Suspected cases include Person Under Monitoring (PUM) and Patient Under Supervision (PUS). PUM is an individual who traveled to the coronavirus epicenter or has made contact with a person suspected to be positive for COVID-19 but does not show any symptoms themselves. PUS is an individual who has shown symptoms of coronavirus infection, ranging from mild to severe pneumonia. A PUS is then categorized as a positive COVID-19 case if a swab test produces positive results.
Also included in the model, the carrier (I1) refers to individuals in the community that go undetected and may spread the disease while unaware of their infectious status. This category contains people who remain asymptomatic or develop major noticeable symptoms but are not detected as a suspected case in health facilities. This study considers carrier (I1) as a compartment because the previous study found around 86% of those infected had remained asymptomatic (or had flu-like mild symptoms). This group of individuals makes transmission control particularly difficult, as they may unknowingly transmit the disease to vulnerable individuals (such as elderly people and people with underlying diseases) [14].
Infectious (I2) individuals refer to confirmed COVID-19 cases that are detected by a health facility and then receive treatment. Recovery (R) individuals refer to the people who recover from COVID-19 infection due to their improving immunity and successful hospital treatment. The total population considered at the time (t) in this study can be denoted by N (t), as calculated in the following equation:
Parameters were also developed while implementing this mathematical model. Λ symbolizes the natural birth rate, (μ) symbolizes the natural death rate, including the susceptible, exposed, carrier and recovery compartments, and (μ1) is the death rate in the infectious compartment. There are three infected rates used in the model; the infected rate of S to I1 (α1), the infected rate of S to I2 (α2), and the infected rate of S to E (α3). β1 is the diagnostic error rate of E to S and β2 is the development rate of E to I2. γ1 and γ2 are the recovery rates from I2 to R explained by immunity, and the development rate of I1 to I2 because of the positive rapid test result, respectively.
Furthermore, θ1 and θ2 are the treatment success rates from I2 to R, and the diagnostic error rate of I2 to S. θ2 is very likely to occur in developing countries because of limited access to resources and advanced clinical capabilities. This model considers varying possible results for the specified rates. The last parameter in this model is the loss of immunity rate of R to S. Assumptions for this model include waning immunity, in that someone who has recovered from COVID-19 will later lose their immunity and return to susceptible individual category.
All parameters included in the mathematical model are assumed to be positive and constant. Based on these assumptions, a flowchart for COVID-19 transmission could be constructed, as shown in Fig. 2. According to the flowchart, the differential equations used for the model are:
The parameters used in Eq. (2) are constant and non-negative, detailed in Table 2. Then, Eq. (2) has a biological region as a solution 5-dimensional positive real numbers denoted as: [23]
Endemic equilibrium and its stability
The equilibrium point is obtained by accounting for the first derivative of the equation [24]. This derivative describes the gradient of a particular value environment, which in this case, is the peak point or valley. A problem in initial values and parameters applied to the system model Eq. (2) results in instability at the equilibrium point (S∗ = 895,722,037, E∗ = 0, \( {I}_1^{\ast } \) = 0, \( {I}_2^{\ast } \) = 459,601 and R∗ = 2071). The eigenvalue analysis of the J matrix is in the form of five negative values, which guarantees that the resulting system is asymptotic and stable. The eigenvalues obtained are − 0.0255, − 0.0346, − 1.9516 × 10− 5, − 0.0033 and − 0.0029.
Optimal control
The control variables are strategies to detect and reduce COVID-19 transmission in Indonesia, including large-scale social restriction (u1), contact tracing (u2), mass testing (u3), case detection and treatment (u4) and the wearing of face masks (u5), as proposed in currently evolving scenarios. The large-scale social restriction is an effort to slow the spread of coronavirus by encouraging people to do their routine activity at home, keep a minimum of 1.5 m distance from other individuals while talking, and avoid public gatherings. Contact tracing is a systematic effort to track and trace people who may have been exposed to an infectious disease, COVID-19 in this instance, to categorize them as a Person Under Monitoring (PUM) or a Patient Under Supervision (PUS). If available, the rapid test would be conducted on the individual to confirm their infection status.
Mass testing is an effort to aggressively test healthy individuals who remain asymptomatic. Mass testing will detect new infections earlier and provide a more complete picture of spread within a community, by capturing positive cases that would have never shown symptoms. This testing approach could be implemented by using the rapid test. Case detection and treatment is an effort to detect the virus in exposed individuals, so they can be moved to the infectious individual category using polymerase chain reaction (PCR) testing methods and be guaranteed high-quality treatment. The last control is the widespread wearing of face masks. This control is used to protect an individual not currently infected by COVID-19 and to control the transmission from an asymptomatic virus carrier.
Based on the function of these controls, three scenarios were made to estimate the incidence and the peak of cumulative COVID-19 cases in Indonesia. The first scenario includes three control variables, large-scale social restriction (u1), case detection and treatment (u4), and wearing of face masks (u5). The second scenario includes large-scale social restriction (u1), contact tracing (u2), case detection and treatment (u4), and the wearing of face masks (u5). The third scenario applies all of the previously listed control functions.
In the model, large-scale social restriction (u1) and mass testing (u3) are included in compartment S and I1. Employing large-scale social restriction (u1) on compartment S will reduce the number of people infected with COVID-19 in the subsequent time period. The mass testing (u3) aims to move a number of susceptible individuals to the more accurate infectious individuals category. At the same time, contact tracing (u2) is applied to compartment E. This contact tracing approach aims to move exposed individuals to infectious individuals in the compartment I1.
Furthermore, the case detection and treatment (u4) control function is employed on compartment I1. This process aims to reduce the number of infectious individuals by moving them to the recovered individuals category. The last control strategy is to wear face masks (u5). Face masks as a mitigation strategy is put on compartment S, E, and I1. The aim of (u5) is to keep the individuals in their specified compartment, as well as prevent others from transferring between compartments, during the outbreak of COVID-19.
Based on the optimal control problem, the formulated mathematical model is:
The goal of the control variables is to find the optimal scenario to minimize the exposed, carrier, and infectious individuals. To reduce COVID-19 transmission, infectious individuals need to be treated while simultaneous efforts are made to screen and treat exposed and carrier individuals to prevent the occurrence of new COVID-19 cases. The efforts made in the objective function are assumed to be a non-linear and quadratic function. The quadratic function is the common form of an objective function in an OCT problem [25]. The objective function minimized in this model is as follows:
The model parameters t0 and tf are the initial and final time. They are taken as t0= April 10, 2020, and tf= December 31, 2020, for a duration of 266 days. The weight coefficients, A1, A2, A3, A4, and A5 are chosen to balance the population value during the minimization process [25]. The study aims to obtain the optimal control while satisfying \( {u}_1^{\ast },{u}_2^{\ast },{u}_3^{\ast },{u}_4^{\ast } \) and \( {u}_5^{\ast } \).
where Ω = {(u1, u2, u3, u4, u5 )ϵ L1 (t0; tf)| 0 ≤ ui ≤ 1 for i = 1, 2, 3, 4, 5}. In the ui control range, no investment in control is made if the value of ui = 0. In When the control value is 1, the maximum effort is made on the control in question. The vector Ω is considered to be in the Lebesgue space with p-norm, which is p = 1. The vector was stated as Lebesgue measurable and was successful in several cases of optimal control such as malaria, tuberculosis, and tumor treatment [23, 26,27,28]. Euclid space, L2(t0, tf), was considered and the functional analysis results were shown in Appendix 2.
The control strategy was assumed to affect the model in all scenarios, so several cases that accommodate these assumptions were considered. The weight parameters in the model were then set as A1 =25, A2 =15, A3 =10, A4 =90, and A5 =20. Values of Ai were weighted so that the control variable ui could be considered as the minimum objective. Further, the Fourth order Runge-Kutta method was also considered to solve the optimal control problem (power of error about \( \mathcal{O}\left({h}^5\right),h<1 \)). Analyses were performed using MATLAB software and visualization of the results was done on R software.
State variables and parameters
For computation, the newest COVID-19 data from Indonesia is used as baseline data. Baseline refers to data per April 10, 2020, or 40 days after the first reported cases. Appropriate estimations are provided by looking at the stability of the data pattern while considering the results of current national policies being implemented, such as large-scale social restriction, mass rapid antibody testing, and obligatory face mask policy.
The study was conducted by gathering the initial values of state variables and parameters from various valid sources (Table 1). The number of exposed individuals (E), reported infectious cases (I1), and recovery (R) cases was obtained from provincial and national data sources. The number of viral carriers (I2) was best estimated based on other studies [14]. The number of susceptible individuals (S) was estimated by calculating the total population minus the number of exposed individuals, carrier individuals, infectious individuals, and recovery individuals, as follows: S = N- E- I1- I2- R.
The parameter values used in the study were chosen and calculated to be as close to Indonesia’s true condition as possible, see Table 2. Some parameters in the model were calculated through estimation because precise data were not available. According to the pathogenesis of COVID-19, infectious individuals can infect up to 2–2.5 other people in the course of 4 days, based on the reproduction number of COVID-19 cases [30, 31]. Based on this statement, the infection rate between susceptible individuals and exposed individuals was calculated by the number of infectious individuals multiplied by 2.5 and then divided by the number of susceptible individuals, as shown by: α3 = (I2 × 2.5)/ S. Following the same method, the infection rate between susceptible individuals and infectious individuals is also calculated: α1 = (I1 × 2.5)/ S. Additionally, the loss immunity rate (φ2) is estimated based on the calculation of 1 minus the death rate in the R compartment and relapse rate, as follows: φ2 = 1 − μR − φ2. Based on these formulae, the resulting values are α3 = 3.586 × 10− 5, α1 = 2.203 × 10− 4 and φ2 = 0.96228. The diagnostic error rate of E to S is assumed to be 95% until December 2020. θ2 is the diagnostic error rate of I2 to S. The diagnostic error rate is the rate of false positive results of a rapid test, which although rare, still occur.
Results
Three scenarios were simulated by plotting all control strategies as a function of time in the model. Scenario 1 includes large-scale social restriction (u1), case detection and treatment (u4), and the wearing of face masks (u5). Scenario 2 includes large-scale social restriction (u1), contact tracing (u2), case detection and treatment (u4), and the wearing of face masks (u5). Lastly, scenario 3 added control mass testing (u3) to all controls included in scenario 2.
In all of the modeled scenarios, the optimal control u1 remained near the upper bound, around 1.00, until 264 days after the initial application. After that critical point, u1 dropped dramatically to the lower bound at the final captured time frame. The optimal control u4 and u5 for scenario 1, 2, and 3 were continuously at the upper bound from the initial time until the final time recorded. u2 and u3 react differently in the control profile, as u2 was fully applied for only a few months and remained around 0.99 for scenario 2 and 3, before decreasing linearly towards the lower bound. The last, u3 was around the upper bound at 0.99 until 246 days after initiation, and then it decreased linearly towards the lower bound by the final time recorded (Fig. 3).
The changing of each control profile is implied in different scenarios and resulted in a varying amount of change between the population of each compartment. As shown in Fig. 4, each scenario will have a different impact on the spread of COVID-19 and the culmination of cases. The objective function of the proposed mathematical model, applying optimal control as in Eq. (5) by Eq. (6), is to minimize the number of suspect (or exposed) individuals, the number of carrier individuals (or undetected cases), and the number of infectious individuals, in Indonesia.
The simulation showed that the number of suspect individuals, the number of carrier individuals, and the number of infectious individuals at final time for all scenarios is 148,401 cases, 23,601 cases, and 3842 cases, respectively. Figure 4 shows the peak in the number of infectious individuals for each of the simulated scenarios. The peak for scenario 1, 2, and 3 are 33,151 cases on the 59th day, 37,908 cases on the 38th day, and 39,305 cases on the 40th day. Predictions extend until the end of 2020, showing that cases of COVID-19 will still be active.
To examine the impact of the control profile on overall transmission, the number of suspect individuals, the number of carrier individuals, and the number of infectious individuals was counted at the end of projected time for each scenario. The analysis shows the projected counts of 15 cases, 8473 cases, and 11,935 cases, respectively, in Scenario 1. At the final time reported in scenario 2 there are 0 cases, 8473 cases, and 10,919 cases for the number of suspect individuals (or exposed), carrier individuals (or undetected cases), and infectious individuals, respectively. In scenario 3, the number for suspect individuals, carrier individuals, and infectious individuals are 0 cases, 6802 cases, 14,016 cases, respectively. Based on the results, scenario 2 shows the shortest amount of time between control measure initiation and the peak of COVID-19 cases in Indonesia. The peak of COVID-19 cases for scenario 2 and 3 does not differ significantly. However, the duration of time to the peak of infectious cases will take the most time in Scenario 1, an estimated 59 days.
Discussion
This paper highlights the changes to COVID-19 control measure variables to estimate the time to the peak of cases, while attempting to limit the spread of the outbreak in several scenarios. Analysis is based on the Susceptible-Exposed-Infectious-Recovered’ (SEIR) model, which has been globally accepted. A main limitation of this model when considering application to other countries is the variance in control strategies implemented by the region’s government, which may reflect a level of decentralization of power in COVID-19 control. Scenario 2 is the fastest projected scenario to reach the peak of COVID-19 cases in Indonesia. This scenario includes the implementation of large-scale social restriction (u1), contact tracing (u2), case detection and treatment (u4), and the wearing of face masks (u5).
The number of detected cases was accounted for, as this count is highly correlated with the number of tests available and conducted. Compared to other countries, Indonesia has a relatively small number of tests being conducted in health facilities and throughout the community. Indonesia has conducted just 0.13 COVID-19 tests per thousand people, or 34,975 in total (as of April 16, 2020) [32]. There are still many people who have not been confirmed as COVID-19 patients and may be unknowingly spreading the virus through the community, due to the limited resources and government capability to conduct tests at an adequate rate. As of the first week of April, the capacity for daily PCR testing is still limited to just 12 laboratories throughout Indonesia. When this study began, the Indonesian government had attained a testing machine that can process up to 1000 tests a day, and planned to place it in more than 49 laboratories through-out the country. In this rapidly evolving global crisis, our prediction of the peak of the epidemic should be interpreted based on parameters per April 10, 2020.
Theoretically, when the government and healthcare facilities have the ability to test for all cases in the community and treat the detected infectious cases, the number of new COVID-19 cases will slow until completely stopped. Results show that mass testing (u3) does not have a significant effect on the scenario’s timeline or peak. This conclusion may be attributed to the antibody rapid test assumption in this model, which failed to increase the number of cases detected. An increase in availability and implementation of PCR tests is suggested. Scenario 2 suggests that it is important to detect at least 40,000 cases in the first week of May 2020 and to identify efforts to reach the carrier cases in the simulation. Resulting scenarios highlight the key to successful outbreak control is to find the infectious case as fast as possible, so the patient can be treated as well as socially restricted, separating the carrier cases from other individuals that may be susceptible to the disease.
Learning from other country’s actions, it is also possible that Indonesia will experience a second wave of COVID-19, resulting in a second peak. The influx of possibly infectious people traveling from other countries or from delayed disease onset are risks that need to be considered. Though not considered in the model, the possibility of recovering cases being re-infected, or experiencing a relapse needs to be examined. Large-scale social restriction (u1) should be maintained, as well as wearing face masks (u5) and case detection and treatment programs (u4). The decline in number of infectious cases looks slow sloping and shows that even at the end of 2020, there will still be about 20,000 cases. This result can be explained by a relatively slow recovery rate and a simultaneous movement of individuals from the susceptible to the infectious compartment. The discovery of effective drugs as treatment may reduce the number of infectious cases at a rapid rate, unseen up to the current time. A vaccine is the most effective solution for preventing movement from the susceptible group to active infectious cases, thus reducing the spread of the disease. These assumptions point to COVID-19 becoming endemic in parts of the world, much like a number of other infectious diseases.
Assumptions for this model were developed from reported cases that had been tested prior to 10 April 2020. During this time, there may have been significant change in policy or unsuccessful policy implementation, deeming the prediction inaccurate. Indonesia can consider implementing the scenario 2 control profile, with limited resources, throughout the year 2020, based on this study. This scenario requires increased public awareness to adhere to physical distancing and face mask guidelines. The government can continue their efforts to accurately track and trace cases, as well as improving the health care facilities. Due to non-significant results, mass antibody testing is not recommended. Further evaluation research would be useful to measure the results of this policy.
This model is relatively simple and estimates are concurrent with previous studies. The model holds merit in its consideration of essential elements, including the control variable from government efforts, although geographical compartment groups that may impact the number of cases in each scenario are not considered. Caution should be taken in interpreting the model.
Conclusion
Optimal control application was derived and analyzed to pattern the progression of COVID-19 cases in Indonesia. The SEI2RS model is a stable model, based on equilibrium results. Estimating the number of cases and the time period between control measure initiation and the peak number of cases is important for policymakers and public health officials to assess effectiveness of control measures in this exponential phase of the COVID-19 outbreak. According to this study, the Indonesian government should be prepared for an increasing number of cases in the middle of May 2020. Even after reaching the peak, the declining slope of infectious cases will be slow and even at the end of 2020, there will still be about 20,000 active cases.
It seems that COVID-19 will remain endemic in parts of the world, like other infectious diseases. The model provides evidence that while the control profile of Scenario 2 is implemented through the year, a number of COVID-19 cases will still exist in the end of 2020. Thus, if all of the control profiles were to be lost, the number of cases would presumably be higher than previously predicted.
Availability of data and materials
All the primary data and materials involved in this paper are from the published articles and web links, and they are all available online. If readers need more information about data and materials, please contact the corresponding author for data requests.
Abbreviations
- COVID-19:
-
Coronavirus disease 2019
- SEIR:
-
Susceptible, exposed, infectious, recovered
- SEI2RS:
-
Susceptible, exposed, carrier, infectious, recovery, susceptible
- PUM:
-
Person under monitoring
- PUS:
-
Patient under supervision
- PCR:
-
Polymerase chain reaction
- OCT:
-
Optimal control theory
References
Syakriah A. Bappenas, UI modeling shows grim projection of COVID-19 spread in Indonesia - National - The Jakarta Post: Jakarta Post; 2020. p. 1. https://www.thejakartapost.com/news/2020/03/31/bappenas-ui-modeling-shows-grim-projection-of-covid-19-spread-in-indonesia.html. Accessed 20 Apr 2020.
World Health Organization. Coronavirus disease 2019 (COVID-19): situation report 42: World Health Organization; 2020. p. 1. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200302-sitrep-42-covid-19.pdf?sfvrsn=224c1add_2. Accessed 6 Apr 2020.
Ministry of Health of the Republic of Indonesia. Novel coronavirus (covid-19) situation on 2 Maret 2020: Ministry of Health of the Republic of Indonesia; 2020. p. 1–3. https://covid19.kemkes.go.id/situasi-infeksi-emerging/info-corona-virus/situasi-terkini-perkembangan-covid-19-17-maret-2020/#.XnC5aXIzbIU. Accessed 6 Apr 2020.
Pablo DSM, Niehus R, Taylor A, Buckee C, Lipsitch M. Using predicted imports of 2019-nCoV cases to determine locations that may not be identifying all imported cases. Med. 2020:1–13. https://doi.org/10.1101/2020.02.04.20020495.
Djalante R, Lassa J, Setiamarga D, Sudjatma A, Indrawan M, Haryanto B, et al. Review and analysis of current responses to COVID-19 in Indonesia: period of January to March 2020. Prog Disaster Sci. 2020;6:100091. https://doi.org/10.1016/j.pdisas.2020.100091.
Chen X, Yu B. First two months of the 2019 coronavirus disease (COVID-19) epidemic in China: real-time surveillance and evaluation with a second derivative model. Glob Health Res Policy. 2020;5:7. https://doi.org/10.1186/s41256-020-00137-4.
Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health. 2020;5:e261–70. https://doi.org/10.1016/S2468-2667(20)30073-6.
Pan J, Yao Y, Liu Z, Li M, Wang Y, Dong W, et al. Effectiveness of control strategies for coronavirus disease 2019: a SEIR dynamic modeling study. MedRxiv. 2020. https://doi.org/10.1101/2020.02.19.20025387.
Idroes R, Maulana A, Noviandy TR, Suhendra R, Sasmita NR, Lala A, et al. A genetic algorithm to determine research consultation schedules in campus environment. IOP Conf Ser Mater Sci Eng. 2020. https://doi.org/10.1088/1757-899X/796/1/012033.
Idroes R, Noviandy TR, Maulana A, Suhendra R, Sasmita NR, Muslem M, et al. Retention index prediction of flavor and fragrance by multiple linear regression and the genetic algorithm. Int Rev Model Simulations. 2019;12:373. https://doi.org/10.15866/iremos.v12i6.18353.
Sasmita NR, Geater AF, Kammanee A, Chongsuvivatwong V. Is the recovery rate in latent tuberculosis infection significant in reducing tuberculosis transmission in Indonesia?: a mathematical model study in epidemiology. In: RSU Res. Conf. 2019. Pathum Thani: Rangsit University; 2019. p. 101–11.
Yang C, Wang J. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math Biosci Eng. 2020;17:2708–24. https://doi.org/10.3934/mbe.2020148.
Moore SE, Okyere E. Controlling the transmission dynamics of COVID-19. ArXiv. 2020;2004.00443.
Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science (80- ). 2020;3221:eabb3221. https://doi.org/10.1126/science.abb3221.
World Bank. Birth rate, crude (per 1,000 people): World Bank; 2018. https://data.worldbank.org/indicator/SP.DYN.CBRT.IN. Accessed 25 Mar 2020.
World Bank. Death rate, crude (per 1,000 people): World Bank; 2018. https://data.worldbank.org/indicator/SP.DYN.CDRT.IN?locations=ID. Accessed 24 Mar 2020.
Gugus Tugas Percepatan Penanganan COVID-19. Situasi virus corona – Covid19.go.id. Gov Repub Indones 2020:1. https://www.covid19.go.id/situasi-virus-corona/. Accessed 11 Apr 2020.
Government of West Java Indonesia. Pemdaprov Jabar Tindaklanjuti Hasil Rapid Test Kabupaten/Kota. Gov West Java; 2020:1. https://jabarprov.go.id/index.php/news/37231/2020/04/01/Pemdaprov-Jabar-Tindaklanjuti-Hasil-Rapid-Test-KabupatenKota. Accessed 11 Apr 2020.
Qifang B, Yongsheng W, Shujiang M, Chenfei Y, Xuan Z, Zhen Z, et al. Epidemiology and transmission of COVID-19 in Shenzhen China: analysis of 391 cases and 1,286 of their close contacts. MedRxiv. 2020:1–22. https://doi.org/10.1101/2020.03.03.20028423.
Prem K, Liu Y, Russell T, Kucharski AJ, Eggo RM, Davies N, et al. The effect of control strategies that reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China. MedRxiv. 2020;2667:2020.03.09.20033050. https://doi.org/10.1101/2020.03.09.20033050.
Ivorra B, Ferrandez MR, Perez MV, Ramos A. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. ResearchGate. 2019;2020:1–28. https://doi.org/10.13140/RG.2.2.21543.29604.
Fidinillah M, Eko S. Kasus di Wuhan: 3-10% Pasien Sembuh COVID-19 Bisa Terjangkit Lagi: DetikCom; 2020. p. 1. Available from https://20.detik.com/e-flash/20200326-200326083/kasus-di-wuhan-3-10-pasien-sembuh-covid-19-bisa-terjangkit-lagi. Accessed 2 Apr 2020.
Okosun KO, Rachid O, Marcus N. Optimal control strategies and cost-effectiveness analysis of a malaria model. Biosystems. 2013;111:83–101. https://doi.org/10.1016/j.biosystems.2012.09.008.
Sitti Rosnafian S, Mardlijah, Hariyanto. Stability analysis on the spread of the ebola virus considering changes in human behavior and climate (case study: Democratic Republic of the Congo). J Phys Conf Ser. 2019:1373. https://doi.org/10.1088/1742-6596/1373/1/012043.
Kim S, de los Reyes AA, Jung E. Mathematical model and intervention strategies for mitigating tuberculosis in the Philippines. J Theor Biol. 2018;443:100–12. https://doi.org/10.1016/j.jtbi.2018.01.026.
Choi S, Jung E. Optimal tuberculosis prevention and control strategy from a mathematical model based on real data. Bull Math Biol. 2014;76:1566–89. https://doi.org/10.1007/s11538-014-9962-6.
Whang S, Choi S, Jung E. A dynamic model for tuberculosis transmission and optimal treatment strategies in South Korea. J Theor Biol. 2011;279:120–31. https://doi.org/10.1016/j.jtbi.2011.03.009.
Pang L, Zhao Z, Song X. Cost-effectiveness analysis of optimal strategy for tumor treatment. Chaos Soliton Fract. 2016;87:293–301. https://doi.org/10.1016/j.chaos.2016.03.032.
World Health Organization. Global tuberculosis report 2019. France: WHO; 2019.
Ferguson NM, et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID- 19 mortality and healthcare demand. Imp Coll. 2020:1–20. https://doi.org/10.25561/77482.
World Health Organization. Coronavirus disease 2019 (COVID-19): situation report-46. Geneva: WHO; 2020.
Hasell J, Ospina E-O, Mathieu E, Ritchie H, Beltekian D, Roser M. To understand the global pandemic, we need global testing – the Our World in Data COVID-19 Testing dataset. Our World in Data 2020:1–1. Available from https://ourworldindata.org/covid-testing#thailand. Accessed 17 Apr 2020.
Safitri E, Tarmizi T, Ramli M, Wahyuni S, Ikhwan M. Model of virus therapy and chemotherapy for cancer. IOP Conf Ser Earth Environ Sci. 2019;364:012029. https://doi.org/10.1088/1755-1315/364/1/012029.
Acknowledgments
We thank Dr. Satiti Palupi from East Java CDC and the other two reviewers for their excellent comments about health policy implication of this mathematical model. The authors would like to express sincere appreciation to Madeline Bernard from the University of Michigan, School of Public Health, USA, for proofreading this manuscript while the study was conducted.
Funding
None
Author information
Authors and Affiliations
Contributions
NRS, MI, SS and VC contributed equally to this manuscript. NRS and SS designed the study and prepared the first draft. MI conducted the analyses. NRS, SS and VC reviewed the literature, contributed to the interpretation of the results, and review the manuscript. All authors commented on this draft and contributed to the final version. All authors had full access to all of the data (including statistical reports and tables) in the study and can take responsibility for the integrity of the data and the accuracy of the data analysis. The author(s) read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
The Author did not obtain ethical approval for this study. All of the data used in this paper was available online from the COVID-19 surveillance report at Indonesia Ministry of Health website and did not contain personal information.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Appendices
Appendix 1
Characteristics of equilibrium
The equilibrium point is formed by \( \frac{dS}{dt}=\frac{dE}{dt}=\frac{d{I}_1}{dt}=\frac{d{I}_2}{dt}=\frac{dR}{dt}=0 \).
The equilibrium point is obtained as follows.
The stability at the equilibrium point (8) is obtained by assuming f1, f2, f3, f4, and f5 in which \( \dot{S},\dot{E},{\dot{I}}_1,{\dot{I}}_2 \) and \( \dot{R} \), consecutive. Then the linearization of system (7) can be written with the following Jacobian matrix [33]:
Appendix 2
Characteristics of optimal control
The necessary conditions for optimal control are satisfied with Pontryagin’s Minimum Principle.
where Ω = {(u1, u2, u3, u4, u5)ϵ L1(April 10, 2020; December 31, 2020)| 0 ≤ ui ≤ 1 for i = 1, 2, 3, 4, 5}.
Consider Lebesgue space Lp(ℝn). For p = 1 and p = 2, the space is composed of all functions f : ℝn → ℝ with
Normed space that formed is
for p = 1 and
for p = 2, and both of them fulfill three norm properties.
In case Ω = {(u1, u2, u3, u4, u5)ϵ L1(t0, tf)| 0 ≤ ui ≤ 1 for i = 1, 2, 3, 4, 5}.
Property 1 clearly fulfill based on 0 ≤ ui ≤ 1.
‖u‖ ≥ 0 for any u ∈ U = {u1, u2, u3, u4, u5}, and ‖u‖ = 0 if and only if u = 0.
Property 2 is shown as follows
‖αu‖ = |α| ‖u‖ for any u ∈ U and α ∈ ℝ.
Evidence conducted as discrete αu1 + αu2 + … + αun = α (u1 + u2 + … + un).
Property 3 is shown as follows
‖u + v‖ ≤ ‖u‖ + ‖v‖, for any u, v ∈ U.
Evidence conducted as discrete (u1 + v1) + (u2 + v2) + … + (un + vn) = (u1 + u2 + … + un) + (v1 + v2 + … + vn).
In case Ω = {(u1, u2, u3, u4, u5)ϵ L2(t0, tf)| 0 ≤ ui ≤ 1 for i = 1, 2, 3, 4, 5}
Property 1
‖u‖ ≥ 0 for any u ∈ U = {u1, u2, u3, u4, u5}, and ‖u‖ = 0 if and only if u = 0. Based on 0 ≤ ui ≤ 1, it represented as discrete \( {\left({u}_1^2+{u}_2^2+\dots +{u}_n^2\right)}^{0.5} \) would be positive number and become 0 if and only if u = 0
Property 2 (cancelation proof)
‖αu‖ = |α| ‖u‖ for any u ∈ U and α ∈ ℝ. Cancelation conducted as discrete
By the normed space, L1 is used in this paper.
The necessary conditions can be generated from the Hamiltonian equation. Based on that principle, the system of Eqs. (4) and (5) is converted to the Hamiltonian (H) given by
Where gi symbolizes the right-hand side of the differential equation of the i th state variable. More notably, the state variable is analyzed. Where \( {\dot{x}}_i \) is state equations containing \( \dot{S},\dot{E},{\dot{I}}_1,{\dot{I}}_2, \) and \( \dot{R} \). the state equation is obtained by \( {\dot{x}}_i=\partial H/\partial {\lambda}_i. \)
Furthermore, adjoint equations are \( {\dot{\lambda}}_i=-\partial H/\partial {x}_i \) and follow transversality conditions \( {\lambda}_i^{\ast}\left({t}_f\right)=0 \). Where i = 1, …, 5. So,
The optimality conditions are obtained by ∂H/∂ui = 0, where i = 1, 2, 3, 4. So,
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sasmita, N.R., Ikhwan, M., Suyanto, S. et al. Optimal control on a mathematical model to pattern the progression of coronavirus disease 2019 (COVID-19) in Indonesia. glob health res policy 5, 38 (2020). https://doi.org/10.1186/s41256-020-00163-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41256-020-00163-2