Abstract
This paper proposes a fast recognition method based on generalized similarity measure (GSM). The GSM achieves good recognition accuracy for face recognition, but has a scalability problem. Because the GSM method requires the similarity measures between a query and all samples to be calculated, the computational cost for recognition is in proportion to the number of samples. A reasonable approach to avoiding calculating all the similarity measures is to limit the number of samples used for calculation. Although approximate nearest neighbor search (ANNS) methods take this approach, they cannot be applied to the GSM-based method directly because they assume that similarity measure is the Euclidean distance. The proposed method embeds the GSM into the Euclidean distance so that it may be applied in existing ANNS methods. We conducted experiments on face, object, and character datasets, and the results show that the proposed method achieved fast recognition without dropping the accuracy.
Similar content being viewed by others
1 Introduction
The generalized similarity measure (GSM), a similarity measure expressed by a linear combination of the Mahalanobis distance and bilinear similarity, obtains good recognition accuracy for face recognition [1]. The GSM is also practical because learning the GSM is expressed as a convex optimization problem and the global solution can be found by existing algorithms. While the GSM shows good accuracy and practicability, it still has a scalability issue. To deal with massive data from the web, scalability becomes as important as accuracy and practicability. When recognizing a query, the similarity measures must be calculated for all samples to find the closest sample. Hence, computing the similarity measures is expensive if the number of samples is large.
A feasible way to reduce the computational cost is to limit the samples used for calculating the similarity measures. This can be realized using approximate nearest neighbor search (ANNS) methods such as locality sensitive hashing (LSH) [2], fast library for approximate nearest neighbors (FLANN) [3], and bucket distance hashing (BDH) [4]. However, they are not directly applicable to the GSM because the GSM is different from any similarity measures on which existing ANNS methods work; few acceleration methods based on other similarity measures include the binary similarity measure based recognition, which was accelerated by introducing LSH [5], and the cosine similarity measure based recognition with LSH [6]. To the best of our knowledge, no method accelerates recognition based on the GSM.
In this paper, we propose an acceleration method based on the GSM using an ANNS method. We embed the GSM in d-dimensional space into (d+1)-dimensional Euclidean space, where d is the dimensionality of feature space. This enables us to use the GSM with a Euclidean distance-based ANNS method, so that the computational cost of the GSM-based search can be reduced. Experimental results show that the proposed method realizes fast recognition without degrading accuracy on face, object, and character datasets.
2 GSM
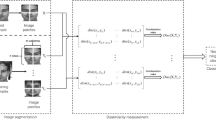
In this section, we explain the GSM [1], which is the similarity measure of the proposed method. The GSM is defined as a linear combination of the Mahalanobis distance and bilinear similarity. The bilinear similarity measure is adopted as one of the GSM components because it shows favorable recognition results [7]. The GSM is more useful than the cosine similarity measure [8] because the cost function for learning the GSM is convex with respect to M and G. Let x and y be feature vectors. The GSM f (M,G)(x,y) is expressed with the Mahalanobis distance d M (x,y)=(x−y)⊤ M(x−y) and the bilinear similarity measure s G (x,y)=x ⊤ G y as follows:
To reduce the effect of the intra-class variations, Eq. (1) uses mapped feature vectors x and y according to [1]. Let \(\boldsymbol {z}_{i}^{{\phantom {.}}j}\) be the feature extracted from jth image of the subject i∈{1…,S}. The intra-class covariance matrix is then defined by
Let (λ 1,…,λ l ), V=(v 1,…,v l ) and X be the top l eigenvalues, eigenvectors of C S , and the original feature vector of x, respectively. A mapped feature vector x is expressed as
The parameters of the GSM, M and G, are learned by similarity metric learning on the intra-class subspace (sub-SML) [1].
3 Acceleration of the GSM-based nearest neighbor search
The computational cost of nearest neighbor search based on the GSM is expensive because the value of f (M,G)(·,·) in Eq. (1) is recalculated for each sample in a database. Our idea is to accelerate the search by introducing an ANNS method. Thanks to approximation and efficient calculation, ANNS can be realized by calculating only a limited number of distances. The biggest problem to introducing an ANNS method to a search is that function f (M,G)(·,·) in Eq. (1) cannot be directly treated as an L n norm such as the Euclidean and Manhattan distances because it consists of two terms with different characteristics. Thus, we transform Eq. (1) so it can be calculated as an L 2 norm (i.e., the Euclidean distance).
Suppose that x is a mapped sample feature in a database and y is a mapped query feature. The GSM of x and y is expressed by the following equation:
Let x p=(G+2M)x, and Eq. (4) can be rewritten as
The first term in Eq. (5) is the dot product of y and x p. Hence, it is represented using the Euclidean distance ∥y−x p∥ as
We substitute Eq. (6) into Eq. (5) and obtain
where
Note that because the second and third terms \(\frac {1}{2} \|\boldsymbol {y}\|^{2}-\boldsymbol {y}^{\top }M\boldsymbol {y}\) in the right-hand side (RHS) of Eq. (7) can be ignored (because it is the common term for all samples in the database), only the first term \( -\frac {1}{2} \|\boldsymbol {y}-\boldsymbol {x}^{{\phantom {.}}p}\|^{2} \) is a function of y. This term cannot be calculated until a query y is given. In contrast, the third term \(-\frac {1}{2} L(\boldsymbol {x})\) can be calculated before the query is given. As a consequence, Eq. (7) can be obtained by adding the third term to the Euclidean distance calculated by the first term. Though this is not the Euclidean distance, it can be transformed into the Euclidean distance by introducing augmented vectors that have one more dimension than the original vectors. Augmented vectors \(\phantom {\dot {i}\!}\boldsymbol {x}^{p'},\boldsymbol {y}'\) are given as
In order to make \(\sqrt {L(\boldsymbol {x})}\) in Eq. (9) real, L(x)≥0 should be satisfied. Here, ∥M∥≤0.5 is required because {2M−(G+2M)⊤(G+2M)} in Eq. (8) must be a positive-semidefinite matrix to satisfy L(x)≥0. Using Eqs. (9) and (10), we can rewrite Eq. (7) with \(\phantom {\dot {i}\!}\boldsymbol {x}^{p'}\) and y ′ as
As the second and third terms in the RHS of Eq. (11) can be ignored, Eq. (11) is expressed as the Euclidean distance between \(\phantom {\dot {i}\!}\boldsymbol {x}^{p'}\) and y ′. Thus, we can apply ANNS.
4 Experiments
We used three datasets for the evaluation: the Labeled Face in the Wild dataset (LFW) [9], Amsterdam Library of Object Images (ALOI) [10], and ETL9B1. We describe the experimental setting and results in each dataset.
4.1 LFW
LFW is a celebrity face database from Yahoo! News2. It has 13,233 images of 5790 subjects. The image set we used was called “LFW-a” [11], whose images were cropped and normalized to 250 × 250 pixels by a commercial face detector. We used 482 subjects for learning M and G, and 1198 subjects for the gallery and probe. The subjects used for learning did not overlap with the subjects for the gallery and probe. We used both 50 and 482 subjects for learning M and G. When we used 50 subjects, the number of images in each subject was fixed to 22. When we used 482 subjects, the number of images was different in each subject and the average number of images was 22 per subject. We chose one image per subject for the gallery and one image per subject for the probe. We evaluated the computational time and recognition rate by increasing the number of subjects for the gallery and probe from 100 to 1000 in increments of 100. We extracted features following Cao’s method [1]. That is, nine feature points were fixed as shown in Fig. 1, and the SIFT descriptor [12] was extracted on the points at three scales: 2, 6, and 10. Extracted features were concatenated and the dimensionality was reduced to 100 using principal component analysis. In the recognition process, we used the 1-nearest neighbor. We used the BDH [4] as the ANNS method. Figure 2 shows the recognition rates and average search times of the proposed method 1000 subjects for the gallery when the BDH parameters changed. This indicates that the recognition rate and speed depend on the BDH parameters. Therefore, we experimented many times with different parameters and present the best recognition rate in the paper.
We compared the proposed method with the face recognition method proposed in [13], called local generic representation (LGR). The LGR focuses on improving recognition accuracy when a single image per person is available for the gallery and probe. In the literature, the best recognition rate on the LFW database is 30.4% with 50 subjects [13]. We used only 50 subjects for learning in the LGR because the number of images in each subject must be uniform for learning in the LGR. We could evaluate the LGR up to 400 subjects in the gallery because of the memory limitation. We also compared the proposed method with the fast face recognition method proposed in [14], which uses the PCA-SIFT for image representation and BDH for search. In the literature, a 100% cumulative recognition rate with 139-ms search time on an original 5 million-item database has been presented [14].
All experiments were conducted on a PC with an Intel Xeon E5-4627 v2 (3.30 GHz) processor and 8 GB of RAM running the Debian 4.9.2-10 operating system using a single processor core. We measured the search time for all queries and calculated the average search time of each query. The search time excluded feature extraction time and learning time.
The recognition rate and average search time are shown in Fig. 3. In Fig. 3 a, “without ANNS” is the method which ANNS is excluded in the proposed method, “BDH+PCA-SIFT” is the method proposed in [14], and the following numbers represent the number of subjects used for learning. The proposed method showed the same recognition rate as “without ANNS” in Fig. 3 a. This indicates that the proposed method can recognize subjects without reducing the accuracy. The proposed method showed better recognition rate than the LGR and “BDH+PCA-SIFT.” This indicates that the proposed method can achieve satisfactory accuracy for the face recognition task.
In Fig. 3 b, the proposed method and “without ANNS” used the parameters learned with the 482 subjects. Figure 3 b shows that the proposed method is about 24,000 times faster than the LGR, 88 times faster than “without ANNS,” and about 1600 times faster than “BDH+PCA-SIFT”.
4.2 ALOI
ALOI is an object image database that consists of 110,250 color images of 1000 small objects. We used a part of the ALOI called “ALOI-VIEW,” whose images were taken from 72 different directions by rotating objects on the plane at intervals of 5 degrees. The number of objects is 1000 and the total number of images is 7200. The image size is 384 × 288 pixels. We sampled images according to the rotation of the objects to use for learning parameters: every 180 degrees (0+k180), 90 degrees (0+k90), 45 degrees (0+k45), 20 degrees (0+k20), and 10 degrees (0+k10). We also used the sampled data for the gallery, and the rest were used for the probe in the recognition process. We fixed the number of objects used for the gallery and probe to 100, 200, 500, 700, and 1000, and evaluated the computational time and recognition rate. We used the bag-of-feature model with the SIFT features for image representation. To acquire the whole image feature, we sampled feature points at every 5 pixels horizontally and vertically, and extracted the SIFT descriptors from these points. The scales of the SIFT were fixed to 20 and 30. We fixed the number of visual words to 300 based on preliminary experimental results. We used a soft-voting k-Nearest Neighbor (k-NN) classifier in which the voting weight was given by the similarity score. We fixed parameter k to 100.
We compared the proposed method with a multiclass SVM [15]. The training and probe data were identical to the proposed method, and we used a linear function as a kernel function. We also compared the k-NN classifier with the Euclidean distance. We conducted experiments on the same PC used for the LFW experiments.
Figure 4 shows the recognition rates and search time. Figure 4 a shows that the proposed method obtained a better recognition rate than other methods when the learning data were identical. In Fig. 4 b, the proposed method was faster than the other methods under almost all experimental settings. When the learning data were 0+k180 and 0+k90, and the number of subjects was 100, the multiclass SVM was faster than the proposed method. However, when the number of subjects increased to more than 200, the proposed method was faster than the multiclass SVM. This indicates that the proposed method has better scalability than the multiclass SVM.
4.3 ETL9B
ETL9B is a handwriting Japanese character database that is a binarized version of ETL9 [16] and consists of 3036 Japanese characters and 200 images per character. The size of character images is 64 × 63 pixels. We used the first 100 images in each character for learning and the gallery, and the rest for the probe. We fixed the number of characters for the gallery and probe to 100, 500, 1000, 2000, and 3036, to evaluate the proposed method. We resized the images to 16 × 16 pixels, and converted the resized images to vector features by concatenating the pixel values. We also used the directional element features [17], which have a dimensionality of 196, to represent the images. The recognition method was same as ALOI, and the PC used for evaluation was the same as LFW. We compared the proposed method with a Euclidean distance-based k-NN classifier. Figure 5 shows the recognition rate and average search time. In Fig. 5 a, the proposed method shows the same recognition rate as the method without the ANNS method, just as for LFW and ALOI. Figure 5 b shows that the computational time increased in a sublinear manner. Consequently, we confirmed that the proposed method was much faster than existing methods and, with respect to recognition accuracy, no worse than existing methods.
5 Conclusions
In this paper, we proposed a fast recognition method based on the GSM. The proposed method embeds the GSM into the Euclidean distance and applies an existing ANNS method to reduce the number of calculated similarity measures. The experimental results show that the proposed method was 88 times faster than before acceleration. In addition, an evaluation on three databases demonstrates that increase in the computational time of the proposed method was sublinear when the number of subjects in the gallery increased.
References
Cao Q, Ying Y (2013) Similarity metric learning for face recognition In: Proc. of ICCV, 2408–2415.
Datar M, Immorlica N, Indyk P, Mirrokni VS (2004) Locality-sensitive hashing scheme based on p-stable distributions In: Proc. of SCG, 253–262.
Muja M, Lowe DG (2014) Scalable nearest neighbour algorithms for high dimensional data. IEEE Trans PAMI 36(11): 2227–2240.
Iwamura M, Sato T, Kise K (2013) What is the most efficient way to select nearest neighbor candidates for fast approximate nearest neighbor search? In: Proc. of ICCV, 3535–3542.
Deng J, Berg AC, Fei-Fei L (2011) Hierarchical semantic indexing for large scale image retrieval In: Proc. of CVPR, 785–792.
Ravichandran D, Pantel P, Hovy E (2005) Randomized algorithms and NLP: using locality sensitive hash function for high speed noun clustering In: Proc. of ACL, 622–629.
Chechik G, Sharma V, Shalit U, Bengio S (2010) Large scale online learning of image similarity through ranking. JMLR 11: 1109–1135.
Nguyen HV, Bai L (2011) Cosine similarity metric learning for face verification In: Proc. of ACCV, 709–720.
Huang GB, Ramesh M, Berg T, Learned-Miller E (2009) Labeled faces in the wild: a database for studying face recognition in unconstrained environments. Technical report, University of Massachusetts, Amherst.
Geusebroek J, Burghouts GJ, Smeulders AWM (2005) The Amsterdam library of object images. IJCV 61(1): 103–112.
Wolf L, Hassner T, Taigman Y (2011) Effective unconstrained face recognition by combining multiple descriptors and learned background statistics. IEEE Trans PAMI 33(10): 1978–1990.
Lowe DG (2004) Distinctive image features from scale-invariant keypoints. IJCV 60(2): 91–110.
Zhu P, Yang M, Zhang L, Lee I (2014) Local generic representation for face recognition with single sample per person In: Proc. of ACCV, 34–50.
Utsumi Y, Sakano Y, Maekawa K, Iwamura M, Kise K (2014) Scalable face retrieval by simple classifiers and voting scheme In: Proc. of Intel. Workshop on FFER-ICPR, 99–108.
Chang C, Lin C (2011) LIBSVM : A library for support vector machines. ACM TIST 2(3): 1–27.
Saito T, Yamada H, Yamamoto K (1985) On the data base ETL9 of handprinted characters in JIS chinese characters and its analysis. Trans IEICEJ68-D(4): 757–764.
Kato N, Suzuki M, Omachi S, Aso H, Nemoto Y (1999) A handwritten character recognition system using directional element feature and asymmetric Mahalanobis distance. IEEE Trans PAMI 21(3): 258–262.
Funding
This work was supported by KDDI, SCAT Research Grant Programs, and JSPS KAKENHI Grant Number JP25240028.
Availability of data and materials
The code of the proposed method will be made public later.
Authors’ contributions
YU designed the proposed method and drafted the manuscript. TM participated in the design of the proposed method and implemented the proposed method. MI participated in designing the proposed method and helped in drafting the manuscript. KK supervised the work. All authors reviewed and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Utsumi, Y., Mizuno, T., Iwamura, M. et al. Fast search based on generalized similarity measure. IPSJ T Comput Vis Appl 9, 11 (2017). https://doi.org/10.1186/s41074-017-0024-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41074-017-0024-5