Abstract
Credit risk assessment involves conducting a fair review and evaluation of an assessed subject’s solvency and creditworthiness. In the context of real estate enterprises, credit risk assessment provides a basis for banks and other financial institutions to choose suitable investment objects. Additionally, it encourages real estate enterprises to abide by market norms and provide reliable information for the standardized management of the real estate industry. However, Chinese real estate companies are hesitant to disclose their actual operating data due to privacy concerns, making subjective evaluation approaches inevitable, occupying important roles in accomplishing Chinese real estate enterprise credit risk assessment tasks. To improve the normative and reliability of credit risk assessment for Chinese real estate enterprises, this study proposes an integrated multi-criteria group decision-making approach. First, a credit risk assessment index for Chinese real estate enterprises is established. Then, the proposed framework combines proportional hesitant fuzzy linguistic term sets and preference ranking organization method for enrichment evaluation II methods. This approach is suitable for processing large amounts of data with high uncertainty, which is often the case in credit risk assessment tasks of Chinese real estate enterprises involving massive subjective evaluation information. Finally, the proposed model is validated through a case study accompanied by sensitivity and comparative analyses to verify its rationality and feasibility. This study contributes to the research on credit assessment for Chinese real estate enterprises and provides a revised paradigm for real estate enterprise credit risk assessment.
Similar content being viewed by others
Introduction
The real estate industry is a capital-intensive industry with the following characteristics: (1) Land development cost is high; (2) Buildings are of great value; (3) The transaction taxes are premium; and (4) Developers and investors put high expectations on real estate development Yumei and Dandan (2011). Commercial banks are financial institutions that accept deposits, offer checking account services, grant various loans, and provide basic financial products like certificates of deposit and savings accounts to individuals and small businesses, commercial banks play an important role in providing credit to real estate enterprises. In 2022, six state-owned banks in China intentionally financed 12 domestic real estate enterprises with a total of 93.6 billion dollars.Footnote 1 However, commercial banks face non-negligible investment risks due to the uncertainty of the real estate enterprise’s solvency.
The credit of a real estate enterprise refers to its ability and willingness to fulfill its obligations under a loan contract. According to the Basel Committee, credit risk is the most basic and significant risk faced by banks among the eight financial risks. This is because the failure of the credit risk trustee to fulfill its obligations in the contract can directly and completely cause economic losses to banks Yumei and Dandan (2011). Therefore, it is critical to comprehensively evaluate the credit risk of real estate enterprises based on their operating conditions and financial status Salas and Saurina (2002); Breuer et al. (2008). Additionally, real estate enterprise credit risk assessment contributes to national economic risk control.
Credit risk assessment for real estate enterprises is a financial risk control activity that aims to predict their ability to repay loans on time. Data related to the business activities and finances of the evaluation object are critical to the accuracy of credit risk assessment (Chen et al. 2016). However, managers are sensitive to disclosing information about their company operations (Ferreira and Rezende 2007) because competitors may adopt corresponding strategies based on the disclosed information, causing companies to lose in market competition. Therefore, it is challenging to obtain operational and financial information on real estate enterprises for credit risk assessment. Subjective evaluation information from industry experts plays an essential role in evaluating credit risk for real estate enterprises. Multiple methods, such as Credit Metrics by JP Morgan, the Kealhofer, McQuown and Vasicek (KMV) model of the KMV Company, and the Credit Suisse Financial Products (CSFP) CreditRisk+, are used to predict and evaluate the default risk of real estate enterprises. Previous studies have provided innovative views on credit risk evaluation for real estate enterprises. For example, Kerr (2002) combined an accounting model and structural model to predict the default risk of real estate enterprises, while Liow (2008) used a logistic regression model to evaluate the credit risk of listed real estate companies. Mah-Hui (2008) proposed a commercial real estate credit risk assessment method based on professional judgment, considering the particularity of commercial real estate credit risk, and considered both quantitative and qualitative credit factors. Derbali (2012) constructed a model linking macroeconomic variables directly to aggregate measures of credit risk in selected industries. These methods perform well in processing subjective credit risk evaluation information.
Affected by the national economic and land systems, and financing methods, China’s real estate industry has distinct characteristics. The existing international mainstream real estate enterprise credit risk assessment methods are not always suitable for China’s real estate industry. China’s land is owned by collectives and the state, and land resources are highly monopolized by the government. The industry is subject to macro-control by the state, and the operating decisions of real estate companies cannot be fully adjusted in accordance with the relationship between market supply and demand. Therefore, Chinese real estate companies are unique due to the influence of the government’s active involvement, and the credit risk assessment information of Chinese real estate companies is highly uncertain. The current credit risk assessments of real estate companies that are popular in the world are mainly aimed at the real estate industry that is regulated by the market, and its credit risk is more predictable. Therefore, establishing a credit risk evaluation index system and method for Chinese real estate companies is of great significance for the risk control of commercial banks and the stability of China’s real estate industry.
This paper aims to evaluate Chinese real estate enterprise credit risk to provide scientific references for bank investment decisions. The main work is summarized as follows:
-
Constructing credit risk assessment indexes for real estate enterprises in China based on their characteristics and business models.
-
Constructing a composite weight model consisting of objective weights. Objective weights are determined based on the similarity between experts’ evaluation information, while subjective weights are determined based on the experience and reputation of decision experts.
-
Proposing the PHFLTS-PROMETHEE method by combining proportional hesitant fuzzy linguistic term set (PHFLTS) and preference ranking organization method for enrichment evaluation (PROMETHEE) II. This method improves the practicality and accuracy of the traditional PROMETHEE method and provides a solution for prioritizing real estate enterprises in China based on credit risk assessment.
The remainder of this paper is structured as follows. “Literature review” section provides a review of the related literature on real estate enterprise credit risk assessment and the application of multi-criteria group decision-making (MCGDM) methods in complex and multi-dimensional uncertain evaluation problems. “Preliminaries” section clarifies the basic concepts and operations that are relevant to this research. “Credit ranking of real estate enterprises by a bank based on the PHFLTS-PROMETHEE II model” section establishes the index system for real estate credit risk assessment and proposes a novel real estate enterprise credit risk evaluating method. “Case study” section presents a case study of the proposed method. “Comparison and sensitivity analysis” section demonstrates the superiority of the proposed credit risk evaluating method through the comparative and sensitivity analyses. Finally, “Conclusion and future direction” section summarizes the main contributions of this study and presents future perspectives.
Literature review
This study contributes to the field of real estate enterprise credit risk assessment by proposing an integrated framework that combines the PHFLTS and PROMETHEE II methods. As such, we have divided our literature review into two subsections to provide an in-depth understanding of these two methods.
Real estate enterprise credit risk assessment
Loans to real estate development enterprises account for a significant proportion of the overall loans issued by commercial banks. Consequently, credit risk assessment for real estate enterprises has been the subject of widespread discussions.
The existing literature on credit risk assessment can be broadly categorized into two groups. One group of studies investigates credit risk assessments based on the impact of real estate enterprises’ credit on their own development. For instance, Kanno (2020) conducted a credit risk assessment of Japan’s real estate investment trust from a macro perspective using a binary logistic regression model. The study mainly considered the financial factors, including the financial health of the real estate industry, the downside risk in the asset value or cash flow of the property holdings, sponsor support circumstances, and some network centralities as proxies for the interactions in the block holding and lending networks. Kanno (2020) also applied the random forest method to predict the credit default of real estate enterprises, which provided novel insights for credit risk management. However, acquiring the dataset is a challenging task. Zhu et al. (2010) built an artificial BP neural network evaluation model to evaluate the credit risk of the real estate industry. COVID-19 has had a significant impact on small and medium-sized enterprises (SMEs), making credit risk management particularly important for supply chain finance. To address this issue, Yang et al. (2021) constructed a risk evaluation index system based on non-financial data, determined the key factors affecting credit, identified corporate risk factors using the lasso logistic model, and predicted the credit risk of the enterprise. Wu (2017) constructed a multi-criteria cluster decision model based on gray correlation analysis for credit risk analysis and corporate strategy adjustment guidance. Another category focuses on the impact of credit risk of real estate enterprises on investing banks and the industry as a whole. Li and Guo (2022)constructed the structural characteristics of the real estate company’s related network and discussed the contagion law of the associated credit risk in the network. They emphasized that the credit status of real estate companies not only affects enterprise’s own development but also may trigger large-scale risk contagion within the real estate industry. Other studies contribute to credit risk management. Jin et al. (2011) established an incidence identification method based on grey incidence analysis to identify the industry and macroeconomic factors that could affect the impaired loan ratio of banks. Their research provides implications for credit risk control of banks. Gao and Xiao (2021)constructed a machine learning-based method to discriminate normal loans and default loans, which is significant for banks to control potential financial risks. Some studies combined different techniques for better credit risk assessment. Yang et al. (2019) used gray correlation analysis and the technique for order preference by similarity to an ideal solution (TOPSIS) to establish a green credit rating mechanism that includes environmental and social benefits, which can be used by banks to encourage enterprises to focus on green development through green credit. Locurcio et al. (2021) analyzed real estate credit risk by establishing credit real estate risk indicators, allowing for more approvals of debt restructuring procedures and facilitating restructuring debt operations, benefiting smaller banks and SMEs. Kanno (2022) analyzed the network structure of syndicated loans to Japan’s real estate investment trusts (J-REITs) and the credit and systemic risk in the J-REITs bank loan market from the perspective of financial networks and risk resilience using key centrality indicators, and thus provided an effective methodology to assess the interconnectedness of loans in a bimodal network of syndicated loans and the risk contagion from borrowers to lenders. Due to the relatively short development time of China’s real estate industry, various problems are faced such as unsustainable development of excessive profitability. Cheng et al. (2020) combined the KMV model with the genetic algorithm (GA) to construct a GA-KMV model for analyzing the relationship between debt financing of real estate companies and their credit risk, providing a reference for banks to invest in the real estate industry.
There are many studies on credit risk management through multi-criteria indicators in various areas, not just limited to the real estate industry. For example, to reduce the number of non-performing loans in personal loans, Zhang et al. (2018) combined personal socio-demographic information, loan application information, and applicant dynamic transaction behavior data to construct a personal credit evaluation model based on radial basis function multiple instances learning to extract features. With online transactions becoming the main pattern of consumer shopping, merchant credit is one of the main factors affecting consumer decisions. Nana et al. (2022) introduced a profit function and constructed a game model to analyze and explore the causes of credit risk formation in e-commerce and made suggestions for reducing losses caused by credit risk in e-commerce. In agriculture, farmers’ demands for operational loan components have increased. To solve the problem of credit difficulties in agricultural development, Xia et al. (2022) constructed a sustainable agricultural supply chain finance risk indicator system from five aspects, including farmers’ credit status and core enterprise qualifications, and used the neutrosophic enhanced best-worst method and combined compromise solution model to assess the credit risk.
Previous literature has contributed to the standardized development of real estate enterprise credit by discussing the contagion of associated credit risk in real estate networks and evaluating and predicting the credit risk of the real estate industry. Existing credit risk assessment methods include logistic regression models, machine learning, big data, and grey incidence analysis. These evaluation methods typically assess the overall credit level of the industry using macro and financial data of the real estate industry, providing guidance for banks’ investment decisions. However, in practice, the credit risk assessment of specific real estate enterprises has greater reference value for banks’ investment decisions and risk control. Moreover, the existing research on the credit risk of real estate enterprises is general, and China’s real estate industry is subject to national macro-control, with unique financing methods. Consequently, there are few available risk assessment methods for Chinese real estate enterprises.
This study aims to establish a novel credit assessment index for evaluating the credit risk of Chinese real estate enterprises. To achieve this goal, an MCGDM method is utilized for credit risk evaluation, which will be reviewed in the next section.
The application of MCGDM method in complex and multi-dimensional uncertain evaluation problems
The MCGDM problems inherently present high-dimensional uncertainty provoked by the changing decision-making contexts and their associated complexity (Chen et al. 2023; Zha et al. 2020; Zhang et al. 2020; Chen et al. 2022). One particular tool for dealing with such complexity is the concept of hesitant fuzzy set (HFS) proposed by Torra (2010), which can better adapt to the decision-making environment with hesitant information. However, the limitation of individual subjective judgment and incomplete knowledge of problem aspects makes it difficult for experts to evaluate decision objects with accurate numerical values. Therefore, Rodriguez et al. (2012) proposed the HFLTSs using linguistic terms to effectively reflect expert preferences. The emergence of HFLTS has led scholars from different professions to address various MCGDM issues. For example, Sansabas-Villalpando et al. (2019) analyzed the influencing factors with HFLTS to develop methodological strategies and sustainability priorities for organizational development, while Liao et al. (2019) proposed the extended multi-objective optimization on the basis of ratio analysis plus full multiplicative form method based on HFLTS to solve the investment problem of bike sharing. Additionally, Isik and Kaya (2022) proposed a new HFLTS method to solve the product acceptance problem by overcoming the traditional HFLTS accuracy problem.
As the research progresses, some scholars have found that relying solely on HFLTSs to reflect expert assessment information is not appropriate. This is because the proportional information in the assessment data provided by decision experts is ignored, which affects the accuracy of decision-making (Xiong et al. 2018). To address this issue, Chen et al. (2016) proposed the notion of PHFLTS. PHFLTS is an important extension of HFLTS, which greatly reduces the loss of evaluation information by considering both the linguistic terms of expert evaluation and the corresponding proportional information in the MCGDM environment. To improve the applicability and integrity of PHFLTS, Liu and Rodríguez (2014) defined some novel manipulations such as comparison, arithmetic operations, aggregation operators, cosine similarity, and distance measures. They also developed two MCGDM methods to deal with the MCGDM problem with PHFLTS information. Moreover, Xiong et al. (2023) expanded the practical application scope of the power geometric operator and utilized it to develop a proportional hesitant fuzzy linguistic large-scale group decision-making model. Additionally, Yang et al. (2022) combined PHFLTS and extended cumulative prospect theory to facilitate the translation of customer requirements into engineering characteristics. Several studies have been conducted on the application of PROMETHEE to the fuzzy environment. For instance, Hesamian and Shams (2015) proposed a fuzzy multi-criteria decision-making (MCDM) method that combines the analytic hierarchy process (AHP) and PROMETHEE. Furthermore, Meng and Chen (2015) applied PROMETHEE to a 2-tuple linguistic environment. Liao et al. (2015) conducted a well-integrated study of PHFLSs with PROMETHEE II for MCGDM problems to identify the most suitable decision alternatives. Lastly, Farhadinia (2016) presented a new hybrid decision-making support method that jointly uses AHP, quality function deployment, PROMETHEE II, and HFLTS to capture hesitation and aggregate divergent opinions from different experts.
Most of the existing research on Chinese enterprise credit risk adopts traditional and modern credit risk measurement models that mainly rely on quantitative indicators. However, indicators that impact the credit risk of real estate development enterprises also include qualitative indicators, such as the external environment, industry status, market position, competitive advantage, and government policies. Enterprises consider their actual operating conditions and financial risks as private information, and their willingness to disclose such information is weak. Therefore, it is difficult for banks to obtain comprehensive quantitative data related to corporate credit risks. To cope with the lack of quantitative information, banks usually obtain subjective evaluations of credit risks of real estate enterprises by inviting industry experts. Thus, a reasonable combination of quantitative and qualitative evaluations is crucial to the reliability of assessment results. However, there is no good combination of qualitative and quantitative indicators in the current research on enterprise credit risk. Moreover, China’s real estate enterprises lack objective operational data, and the evaluation of credit risk of China’s real estate enterprises relies mainly on the subjective evaluation information of a large number of experts. PHFLTS considers not only the linguistic information but also the proportional information of different linguistics when processing the subjective evaluation information of experts. This approach can more accurately represent the hesitancy and preference of experts. PROMETHEE II has incomplete compensation to overcome the mutual substitutability of indicators and does not require dimensionless or standardized treatment of indicators (Wang and Yang 2007). Therefore, this study proposes the PHFLTS-PROMETHEE method by combining PHFLTS with PROMETHEE II. This method has the ability to handle a large amount of high uncertainty data and applies to the credit risk assessment of Chinese real estate enterprises with massive subjective evaluation information. Furthermore, the PHFLTS-PROMETHEE method improves the practicality and accuracy of the traditional PROMETHEE method, solving the dilemma of the lack of operational data of real estate enterprises in China.
Preliminaries
In this section, we present a review of the tools and the methods used for credit evaluation and ranking of real estate enterprises before bank loans. We will specifically focus on HFLTS and PHFLTS.
Hesitant fuzzy linguistic term sets (HFLTS)
In the actual decision-making process, numerical scales may not accurately and effectively reflect the preferences of experts (Torra 2010; Zadeh 1975) when evaluating certain qualitative indicators. To address this issue and better represent the subjective judgment of experts, linguistic terms are often used to evaluate decision objects.
Definition 1
Zadeh (1975) Let \({\varvec{S}} = \left\{ {{s_0},{s_1}, \ldots ,{s_g}} \right\}\) be a linguistic term set (LTS), where \({s_i}\left( {i = 0,1,\cdots ,g} \right)\) is a linguistic term, and g + 1 is an odd number known as the granularity of \({\varvec{S}}\). Generally, the linguistic term set \({\varvec{S}}\) must satisfy the following conditions:
-
(1)
Orderliness once \(i > j\), then \({s_i} > {s_j}\);
-
(2)
Maximization operator once \({s_i} > {s_j}\), then \(\mathsf{{Max}}\left( {{s_i},{s_j}} \right) = {s_i}\);
-
(3)
Minimization operator once \({s_i} \ge {s_j}\), then \(\mathsf{{Min}}\left( {{s_i},{s_j}} \right) = {s_j}\);
-
(4)
Negation operator \(\mathsf{{Neg}}\left( {{s_i}} \right) = {s_j}\), where \(j\mathrm{{ = }}g - i\).
Traditional linguistic decision models are limited in their ability to express experts’ evaluation information with only one linguistic term. They do not apply when experts hesitate among several possible linguistic terms Rodriguez et al. (2012). To address this limitation, Rodriguez et al. (2012) proposed the concept of HFLTS based on the idea of HFSs and LTS.
Definition 2
Rodriguez et al. (2012) Let \({\varvec{S}} = \left\{ {{s_0},{s_1}, \ldots ,{s_g}} \right\}\) be an LTS. An HFLTS, which can be abbreviated as \(\varvec{{H_S}}\), is an ordered and finite subset of the consecutive linguistic term of \({\varvec{S}}\). For easy understanding, \(\varvec{{H_S}}\) can be represented as
where \({s_t} \in {\varvec{S}}\), \(t \in \left\{ {i,i + 1,\cdots ,j} \right\}\), \(i,j \in \left\{ {0,1,\cdots ,g} \right\}\), and \(i \le j\).
Definition 3
Rodriguez et al. (2012) Let \({\varvec{S}}\) be a LTS and \(\varvec{{H_S}}\) be an HFLTS. \(\varvec{{H_S}^ +}\), \(\varvec{{H_S}^ -}\), which represent the upper and lower bounds of the HFLTS \(\varvec{{H_S}}\), are defined as
-
(1)
\(\varvec{{H_S}^ + } = \mathsf{{Max}}\left\{ {{s_i}} \right\} = {s_j},{s_i} \in \varvec{H_S}\), and \({s_i} \le {s_j},\forall i\);
-
(2)
\(\varvec{{H_S}^ -} = \mathsf{{Min}}\left\{ {{s_i}} \right\} = {s_j},{s_i} \in \varvec{H_S}\), and \({s_i} \ge {s_j},\forall i\).
Definition 4
Rodriguez et al. (2012) Let \({\varvec{S}}\) be as before. \(\varvec{{H_S}}\), \(\varvec{{H_S}^1}\), and \(\varvec{{H_S}^2}\) are three arbitrary HFLTS on \({\varvec{S}}\). The complement, union, and intersection of the HFLTSs are computed as follows:
-
(1)
\(\varvec{{H_S}^c} = {\varvec{S}} - \varvec{{H_s}} = \left\{ {{s_i}|{s_i} \in {\varvec{S}},\mathrm{{and}}\;{s_i}\, \notin \varvec{{H_S}}} \right\}\);
-
(2)
\(\varvec{{H_S}^1 }\cup \varvec{{H_S}^2} = \left\{ {\,{s_i}|{s_i} \in \varvec{{H_S}^1}\,or\,{s_i} \in \varvec{{H_S}^2}} \right\}\);
-
(3)
\(\varvec{{H_S}^1} \cap \varvec{{H_S}^2} = \left\{ {{s_i}|{s_i} \in \varvec{{H_S}^1}\,and\,{s_i} \in \varvec{{H_S}^2}} \right\}\).
Although HFLTSs use consecutive linguistic terms to elicit opinions, human beings do not naturally express their opinions in this manner; they use linguistic expressions. To address this issue, Rodriguez et al. (2012) proposed the use of context-free grammar to construct comparative linguistic expressions that are closer to the reasoning process of human beings.
Definition 5
Rodriguez et al. (2012) Let \({\varvec{S}}\) be as before. A context-free grammar can be denoted as \(\varvec{{G_H}}\left( {\varvec{V_N},\varvec{V_T},{\varvec{I}},{\varvec{P}}} \right)\), where \(\varvec{V_N}\) is the nonterminal symbols set, \(\varvec{V_T}\) is the terminal symbols set, \({\varvec{I}}\) is the starting symbol, and \({\varvec{P}}\) is the production rules set. The elements of \(\varvec{{G_H}}\left( {\varvec{V_N},\varvec{V_T},{\varvec{I}},{\varvec{P}}} \right)\) are defined below: \(\begin{array}{l} \varvec{V_N} = \left\{ {\left\langle {primary\, \, term} \right\rangle ,\left\langle {composite\, \, term} \right\rangle ,\left\langle {unary\, {} term} \right\rangle ,\left\langle {binary\, {} term} \right\rangle ,\left\langle {conjunction} \right\rangle } \right\} ;\\ \varvec{V_T} = \left\{ {lower\, {} than,greater\, {} than,at\, {} least,at\, {} most,between,and,{s_0},{s_1}, \cdots ,{s_g}} \right\} ;\\ {\varvec{I}} \in \varvec{V_N}. \end{array}\) The production rules are defined in an extended Backus-Naur form, where brackets enclose optional elements and the symbol | indicates alternative elements Bordogna and Pasi (1993). The production rules of \(\varvec{{G_H}}\) are shown below: \(\begin{array}{l} {\varvec{P}} = \{ I::\, = \left\langle {\mathrm{{primary~ term}}} \right\rangle |\left\langle {\mathrm{{composite~ term}}} \right\rangle \\ \left\langle {\mathrm{{composite~ term}}} \right\rangle ::\, = \left\langle {\mathrm{{unary~ relation}}} \right\rangle \left\langle {\mathrm{{primary~ term}}} \right\rangle |\left\langle {\mathrm{{binary~ relation}}} \right\rangle \\ \left\langle {\mathrm{{primary~ term}}} \right\rangle \left\langle {\mathrm{{conjunction}}} \right\rangle \left\langle {\mathrm{{primary~ term}}} \right\rangle \\ \left\langle {\mathrm{{primary~ term}}} \right\rangle ::\, = \,{s_0}|{s_1}| \cdots |{s_g}\\ \left\langle {\mathrm{{unary~ relation}}} \right\rangle ::\, = \,\mathrm{{lower~ than}}|\mathrm{{greater~ than}}|\mathrm{{at~ least}}|\mathrm{{at~ most}}\\ \left\langle {\mathrm{{binary~ relation}}} \right\rangle ::\, =\,\mathrm{{between }}\\ \left\langle {\mathrm{{conjunction}}} \right\rangle ::\, = \,\mathrm{{and\} }} \end{array}\).
To perform computation processes with these linguistic expressions, Rodríguez et al. (2013) defined a conversion function that transforms comparative linguistic expressions into HFLTS:
Definition 6
Rodríguez et al. (2013) Let \({\varvec{S}}\) be the LTS used by \(\varvec{{G_H}}\) and \(\varvec{S_{ll}}\) be the expression domain based on \(\varvec{{G_H}}\). The linguistic expressions \(ll \in \varvec{S_{ll}}\) are generated by the context-free grammar \(\varvec{{G_H}}\). \(\varvec{E_{{G_H}}}\) is a conversion function that transforms \(ll \in \varvec{S_{ll}}\) into HFLTS, that is \(\varvec{E_{{G_H}}}\): \(\varvec{S_{ll}} \rightarrow \varvec{{H_S}}\). \(\varvec{S_{ll}}\) is transformed into HFLTS using the following transformations:
-
(1)
\(\varvec{ E_{{G_H}}}\left( {{s_i}} \right) = \left\{ {{s_i}} \right\} \;\mathrm{{for~ arbitrary }}\;{s_i} \in {\varvec{S}}\);
-
(2)
\(\varvec{E_{{G_H}}}\left( {\mathrm{{at~ least~ }}{s_i}} \right) = \left\{ {{s_j}|{s_j} \ge {s_i}\;and\;{s_j} \in {\varvec{S}}} \right\} \;\);
-
(3)
\(\varvec{E_{{G_H}}}\left( {\mathrm{{at~ most~ }}{s_i}} \right) = \left\{ {{s_j}|{s_j} \le {s_i}\;and\;{s_j} \in {\varvec{S}}} \right\} \;\);
-
(4)
\(\varvec{E_{{G_H}}}\left( {\mathrm{{lower~ than }}\,{s_i}} \right) = \left\{ {{s_j}|{s_j} < {s_i}\;and\;{s_j} \in {\varvec{S}}} \right\} \;\);
-
(5)
\(\varvec{E_{{G_H}}}\left( {\mathrm{{greater~ than }}\,{s_i}} \right) = \left\{ {{s_j}|{s_j} > {s_i}\;and\;{s_j} \in {\varvec{S}}} \right\} \;\);
-
(6)
\(\varvec{E_{{G_H}}}\left( {\mathrm{{between }}{s_i}\;\mathrm{{and}}\;{s_j}} \right) = \left\{ {{s_k}|{s_j} \ge {s_k} \ge {s_i}\;and\;{s_k} \in {\varvec{S}}} \right\} \;\).
In the actual decision-making process, it is often necessary to integrate multiple HFLTSs. Therefore, it is also important to understand the relevant operations of HFLTS, which provide a foundation for its logical and algorithmic developments.
Following the correlation operations of HFSs by Torra (2010), Wei et al. (2013) defined the negation, max-union, and min-intersection operations on HFLTSs.
Definition 7
Wei et al. (2013) Let \({\varvec{S}}\) be as before. \(\varvec{{H_S}}\), \(\varvec{{H_S}^1}\), and \(\varvec{{H_S}^2}\) are three arbitrary HFLTSs defined on \({\varvec{S}}\).
-
(1)
The negation of \(\varvec{H_S}\): \(\varvec{{H_S}^{neg} }= \left\{ {{s_{g - i}}|i \in Ind\left( \varvec{{{H_S}}} \right) } \right\}\), where Ind() represents the index set of the linguistic terms in an HFLTS;
-
(2)
The max-union of \(\varvec{{H_S}^1}\) and \(\varvec{{H_S}^2}\): \(\varvec{{H_S}^1} \vee \varvec{{H_S}^2} = \left\{ {\mathsf{{Max}} \left\{ {{s_i},{s_j}} \right\} \mathrm{{|}}{s_i} \in \varvec{{H_S}^1},{s_j} \in \varvec{{H_S}^2}} \right\}\);
-
(3)
The min-intersection of \(\varvec{{H_S}^1}\) and \(\varvec{{H_S}^2}\): \(\varvec{{H_S}^1} \wedge \varvec{{H_S}^2} = \left\{ {\mathsf{{Min}}\left\{ {{s_i},{s_j}} \right\} \mathrm{{|}}{s_i} \in \varvec{{H_S}^1},{s_j} \in \varvec{{H_S}^2}} \right\}\).
Gou and Xu (2016) defined the following basic operational laws of HFLTS:
Definition 8
Gou and Xu (2016) Let \(\varvec{{H_S}}\), \(\varvec{{H_S}^1}\), and \(\varvec{{H_S}^2}\) be the three arbitrary HFLTSs defined on \({\varvec{S}}\).
-
(1)
\(\varvec{{H_S}^1} \oplus \varvec{{H_S}^2} = {f^{ - 1}}\left( {{ \cup _{{\gamma _1} \in f\left( \varvec{{{H_S}^1}} \right) ,{\gamma _2} \in f\left( \varvec{{{H_S}^2}} \right) }}\left\{ {{\gamma _1} + {\gamma _2} - {\gamma _1}{\gamma _2}} \right\} } \right)\);
-
(2)
\(\varvec{{H_S}^1} \otimes \varvec{{H_S}^2} = {f^{ - 1}}\left( {{ \cup _{{\gamma _1} \in f\left( \varvec{{{H_S}^1}} \right) ,{\gamma _2} \in f\left( \varvec{{{H_S}^2}} \right) }}\left\{ {{\gamma _1}{\gamma _2}} \right\} } \right)\);
-
(3)
\(\lambda \varvec{{H_S}} = {f^{ - 1}}\left( {{ \cup _{\gamma \in f\left( \varvec{{{H_S}}} \right) }}\left\{ {1 - {{\left( {1 - \gamma } \right) }^\lambda }} \right\} } \right)\);
-
(4)
\({\left( \varvec{{{H_S}}} \right) ^\lambda } = {f^{ - 1}}\left( {{ \cup _{\gamma \in f\left( \varvec{{{H_S}}} \right) }}\left\{ {{\gamma ^\lambda }} \right\} } \right)\);
-
(5)
\({\lambda _1}\varvec{{H_S}} \oplus {\lambda _2}\varvec{{H_S}} = \left( {{\lambda _1} + {\lambda _2}} \right) \varvec{{H_S}}\);
-
(6)
\({\left( \varvec{{{H_S}}} \right) ^{{\lambda _1}}} \otimes {\left( \varvec{{{H_S}}} \right) ^{{\lambda _2}}} = {\left( \varvec{{{H_S}}} \right) ^{\left( {{\lambda _1} + {\lambda _2}} \right) }}\);
where \(\lambda,\lambda_1,\lambda_2\) are any real numbers, f and \({f^{ - 1}}\) are the two linguistic scale functions between HFSs and HFLTSs, defined as follows:
where \(Ind\left( {{s_i}} \right)\) represents a function to derive the subscript of linguist term \({s_i}\), \(Ind\left( {{s_i}} \right) = i\).
Wei et al. (2013) generated a convex combination of two HFLTSs based on the convex combination of LTSs. The definition is as follows:
Definition 9
Wei et al. (2013) Let \(\varvec{{H_S}^1}\) and \(\varvec{{H_S}^2}\) be two HFLTSs defined on \({\varvec{S}}\), where \({\varvec{S}}\) is an LTS. The convex combination of \({H_S}^1\) and \({H_S}^2\) can be defined as follows:
where \({\omega _i} \ge 0\left( {i = 1,2} \right)\) and \({\omega _1}\mathrm{{ + }}{\omega _2}\mathrm{{ = }}1\).
Liao et al. (2014) defined the Euclidean distance of \(\varvec{H_S^1}\left( {{x_i}} \right)\) and \(\varvec{H_S^2}\left( {{x_i}} \right)\) as shown below.
Definition 10
Liao et al. (2014) Let \({\varvec{S}}\) be as before, \({\varvec{X}}= \left\{ {{x_0},{x_1}, \ldots ,{x_n}} \right\}\) be a reference set, \(\varvec{H_S^1}\left( {{x_i}} \right) = { \cup _{\left( {{S_{\delta _q^1}} \in \varvec{H_S^1}} \right) }}\left\{ {{s_{\delta _q^1}}\mathrm{{|}}q = 1,\cdots ,\# \varvec{H_S^1}} \right\}\) and \(\varvec{H_S^2}\left( {{x_i}} \right) = { \cup _{\left( {{S_{\delta _q^2}} \in \varvec{H_S^2}} \right) }}\left\{ {{s_{\delta _q^2}}\mathrm{{|}}q = 1,\cdots ,\# \varvec{H_S^2}} \right\}\) be two HFLTSs on \({\varvec{X}}\), where \(\# {H_S^1}\) and \(\# {H_S^2}\) represent the number of linguistic terms in \(\varvec{{H_S}^1}\) and \(\varvec{{H_S}^2}\), respectively. The Euclidean distance of \(\varvec{H_S^1}\left( {{x_i}} \right)\) and \(\varvec{H_S^2}\left( {{x_i}} \right)\) are defined as follows:
where \(Q = \#{H_S^1 }= \#{H_S^2}\) (if \(\# {H_S^1} \ne \# {H_S^2}\), we can use extension rules to make the number of linguistic terms the same in both linguistic terms), \(\delta _q^1\) represents the subscript of the qth linguistic term in \(\varvec{{H_S}^1}\), where \(0 \le \delta _q^1 \le g\) and \(0 \le \delta _q^2 \le g\).
When calculating the distance between two HFLTSs, it is necessary for the number of linguistic terms to be the same. However, in general, the number of linguistic terms in different HFLTSs is not necessarily equal. Therefore, it is necessary to use the expansion rule of HFLTSs to make the number of linguistic terms included in HFLTSs the same. Garmendia et al. (2017) proposed the HFS extension rule based on the minimum common multiple, which is defined as follows:
Definition 11
Garmendia et al. (2017) Let \({\varvec{A}}= \left\{ {{a_1},{a_2},\cdots ,{a_n}} \right\}\) and \({\varvec{B}} = \left\{ {{b_1},{b_2},\cdots ,{b_m}} \right\}\) be two finite subsets of the unit interval and \(lcm\left( {n,m} \right)\) be the least common multiple of n and m. The extended sets \({\varvec{A}}\) and \({\varvec{B}}\) are as follows:
where \(lcm\left( {n,m} \right) = r \cdot n = y \cdot m\).
Proportional hesitant fuzzy linguistic term set (PHFLTS)
Although HFLTSs serve as successful information representation models for individuals, they are not effective in modeling group assessments where the assessments are collected from a subset of individual HFLTS inputs. Information loss or distortion is inevitable because the objective proportions of expert subgroups with the same individual assessment cannot be reflected well. To address this issue, the concept of a PHFLTS was introduced by integrating the proportional information of each generalized linguistic term, providing a new dimension to construct a group information representation using HFLTSs. PHFLTSs offer a new perspective on understanding the collective decision matrix construction paradigm, as they not only improve the quality of evaluations by including objective statistical information but also provide a simple solution to gather individual opinions. To consider hesitant linguistic assessments of experts and the proportional information of each generalized linguistic term in group decision-making settings simultaneously, Chen et al. (2016) proposed the concept of PHFLTS, as described below.
Definition 12
Chen et al. (2016) Let \({\varvec{S}}\) be as before and \(\varvec{{H_S}^l}\left( {l = 1,2,\cdots ,t} \right)\) be t HFLTSs provided by a panel of decision experts \(d{e_l}\left( {l = 1,2,\cdots ,t} \right)\). The PHFLTS, denoted as \( \varvec{P_{{H_S}}}\), is an ordered finite proportional linguistic pairs set for the linguistic variable \(\vartheta\) generated by the union of \(\varvec{{H_S}^l}\left( {l = 1,2,\cdots ,t} \right)\).
where \({\varvec{P}}= {\left( {{p_0},{p_1},\cdots ,{p_g}} \right) ^{\,T}}\) is a proportional vector, \({p_i}\) indicates the possibility degree that the alternative possesses the evaluation value \({s_i}\) provided by the decision experts group, \(0 \le {p_i} \le 1\left( {i = 0,1,\cdots ,g} \right)\) and \(\sum \limits _{i = 0}^g {{p_i}} = 1\), the binary group \(\left( {{s_i},{p_i}} \right) \;\left( {i = 0,1,\cdots ,g} \right)\) can be defined as proportional linguistic pairs.
The probability-theory-based comparison method for PHFLTSs was proposed by Chen et al. (2016), and some related concepts are introduced as follows:
Definition 13
Chen et al. (2016) Let \({\varvec{S}}\) be as before, \({s_i}\) and \({s_j}\) be any two linguistic terms of \({\varvec{S}}\), \({p_i}\) and \({p_j}\) be the proportions of \({s_i}\) and \({s_j}\), respectively. The binary relation is defined as follows:
Definition 14
Chen et al. (2016) Let \({\varvec{S}}\) be as before, \(\varvec{P_{_{{H_S}}}}^1 = \left\{ {\,\left( {{s_i},{p_i}^1} \right) |{s_i} \in {\varvec{S}},\;i \in Ind\left( {\varvec{P_{_{{H_S}}}}^1} \right) \,} \right\}\) and \(\varvec{P_{_{{H_S}}}}^2 = \left\{ {\,\left( {{s_i},{p_i}^2} \right) |{s_i} \in {\varvec{S}},\;i \in Ind\left( {\varvec{P_{_{{H_S}}}}^2} \right) \,} \right\}\) be the two PHFLTSs. The degree of possibility \(L\left( {\varvec{P_{_{{H_S}}}}^1 \ge \varvec{P_{_{{H_S}}}}^2} \right)\) and \(L\left( {\varvec{P_{_{{H_S}}}}^1 \le \varvec{P_{_{{H_S}}}}^2} \right)\) can be defined as follows:
In general, the number of proportional linguistic pairs in different PHFLTSs varies. To simplify operations, Yang et al. (2019) proposed the following extension rules that ensure an equal number of elements in different PHFLTSs.
Definition 15
Yang et al. (2019) Let \(\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{1\,l},{p_i}^{1\,l}} \right) \;} \right| \;{s_i}^{1\,l} \in {\varvec{S}},\;0 \le {p_i}^{1\,l} \le 1,\;\sum \limits _{i = 1}^g {{p_i}^{1\,l} = 1,\;i = 0,1,\cdots ,g} \,,l = 1,2,\cdots ,{L_1}} \right\}\) and \(\varvec{P_{_{{H_S}}}}^2\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{2\,l},{p_i}^{2\,l}} \right) \;} \right| \;{s_i}^{2\,l} \in {\varvec{S}},\;0 \le {p_i}^{2\,l} \le 1,\;\sum \limits _{i = 1}^g {{p_i}^{2\,l} = 1,\;i = 0,1,\cdots ,g} \,,l = 1,2,\cdots ,{L_2}} \right\}\) be the two PHFLTSs with different numbers of elements. Let \({\varvec{P}} = {\left( {{p_1}\mathrm{{*}},{p_2}\mathrm{{*}}\cdots ,{p_K}\mathrm{{*}}} \right) ^{\,\textrm{T}}}\) be the adjusted proportion vector of \(\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right)\) and \(\varvec{P_{_{{H_S}}}}^2\left( \vartheta \right)\), where \({L_1}\), \({L_2}\), and K represent the number of PHFLTS in the set of PHFLTSs. The adjusted PHFLTSs can be represented as
\(\varvec{{\tilde{P}}_{{H_S}}}^1\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{1k},{p_k}^*} \right) \;} \right| \;{s_i}^{1k} \in {\varvec{S}},\;0 \le {p_k}^* \le 1,\;\sum \limits _{k = 1}^K {{p_k}^* = 1,\;i = 0,1,\cdots ,g} \,} \right\}\) and
\(\varvec{{\tilde{P}}_{_{{H_S}}}}^2\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{2k},{p_k}^*} \right) \;} \right| \;{s_i}^{2k} \in {\varvec{S}},\;0 \le {p_k}^* \le 1,\;\sum \limits _{k = 1}^K {{p_k}^* = 1,\;i = 0,1,\cdots ,g} \,} \right\}\), where
-
(1)
\({p_1}^* = \mathsf{{Min}} \left\{ {{p^{11}},{p^{21}}} \right\}\);
-
(2)
if \(p_1^{\mathrm{{*}}} = {p^{11}}\), then \(p_2^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{12}},{p^{21}} - p_1^*} \right\}\);
-
(3)
or if \(p_1^{\mathrm{{*}}} = {p^{21}}\), then \(p_2^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{22}},{p^{11}} - p_1^*} \right\}\);
-
(4)
if \(p_1^{\mathrm{{*}}} = {p^{11}}\) and \(p_2^{\mathrm{{*}}} = {p^{12}}\), then \(p_3^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{13}},{p^{21}} - \left( {p_1^* + p_2^*} \right) } \right\}\);
-
(5)
or if \(p_1^{\mathrm{{*}}} = {p^{11}}\) and \(p_2^{\mathrm{{*}}} = {p^{21}} - p_1^{\mathrm{{*}}}\), then \(p_3^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{12}} - p_2^*,{p^{22}}} \right\}\);
-
(6)
or if \(p_1^{\mathrm{{*}}} = {p^{21}}\) and \(p_2^{\mathrm{{*}}} = {p^{22}}\), then \(p_3^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{23}},{p^{11}} - \left( {p_1^* + p_2^*} \right) } \right\}\);
-
(7)
or if \(p_1^{\mathrm{{*}}} = {p^{21}}\) and \(p_2^{\mathrm{{*}}} = {p^{11}} - p_1^{\mathrm{{*}}}\), then \(p_3^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{22}} - p_2^*,{p^{12}}} \right\}\);
\(\cdots\)
\(p_k^{\mathrm{{*}}} = \mathsf{{Min}} \left\{ {{p^{1{L_1}}},{p^{2{L_2}}}} \right\}\).
To perform the operations on PHFLTS, Yang et al. (2019) established fundamental operational laws for PHFLTS.
Definition 16
Yang et al. (2019) Let \({\varvec{S}}\) be as before, \(\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{1k},{p_k}^*} \right) \;} \right| \;{s_i}^{1k} \in {\varvec{S}},\;0 \le {p_k}^* \le 1,\;\sum \limits _{k = 1}^K {{p_k}^* = 1,\;i = 0,1, \cdots ,g} \,} \right\}\) and \(\varvec{P_{_{{H_S}}}}^2\left( \vartheta \right) = \left\{ {\,\left. {\left( {{s_i}^{2k},{p_k}^*} \right) \;} \right| \;{s_i}^{2k} \in {\varvec{S}},\;0 \le {p_k}^* \le 1,\;\sum \limits _{k = 1}^K {{p_k}^* = 1,\;i = 0,1, \cdots ,g} \,} \right\}\) be two PHFLTSs with the same proportional vector \({\varvec{P}} = {\left( {{p_1}\mathrm{{*}},{p_2}\mathrm{{*}}, \cdots ,{p_K}\mathrm{{*}}} \right) ^{\,T}}\), and \(\lambda\) be a positive real number. The basic operational laws can be obtained as follows:
-
(1)
\(\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) \oplus \varvec{P_{_{{H_S}}}}^2\left( \vartheta \right) = \left\{ {\;\left[ {{f^{ - 1}}\left( {f\left( {{s_i}^{1k}} \right) + f\left( {{s_i}^{2k}} \right) - f\left( {{s_i}^{1k}} \right) f\left( {{s_i}^{2k}} \right) } \right) ,{p_k}^*} \right] \;\left| {\;{s_i}^{1k} \in \varvec{P_{_{{H_S}}}}^1,{s_i}^{2k} \in \varvec{P_{_{{H_S}}}}^2} \right. } \right\}\);
-
(2)
\(\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) \otimes \varvec{P_{_{{H_S}}}}^2\left( \vartheta \right) = \left\{ {\;\left[ {{f^{ - 1}}\left( {f\left( {{s_i}^{1k}} \right) \cdot f\left( {{s_i}^{2k}} \right) } \right) ,{p_k}^*} \right] \;\left| {\;{s_i}^{1k} \in \varvec{P_{_{{H_S}}}}^1,{s_i}^{2k} \in \varvec{P_{_{{H_S}}}}^2} \right. } \right\}\);
-
(3)
\(\lambda \varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) = \left\{ {\;\left[ {{f^{ - 1}}{{\left( {1 - f\left( {{s_i}^{1k}} \right) } \right) }^\lambda },{p_k}^*} \right] \;\left| {\;{s_i}^{1k} \in \varvec{P_{_{{H_S}}}}^1} \right. } \right\}\);
-
(4)
\({\left( {\varvec{P_{_{{H_S}}}}^1\left( \vartheta \right) } \right) ^\lambda } = \left\{ {\;\left[ {{f^{ - 1}}{{\left( {f\left( {{s_i}^{1k}} \right) } \right) }^\lambda },{p_k}^*} \right] \;\left| {\;{s_i}^{1k} \in \varvec{P_{_{{H_S}}}}^1} \right. } \right\}\);
where \(i = 0,1,\cdots ,g\) and \(k = 1,2,\cdots ,K\). f and \({f^{ - 1}}\) are defined in Definition 8.
Based on the operational laws of PHFLTS, the proportional hesitant fuzzy linguistic weighted averaging (PHFLWA) operator and the proportional hesitant fuzzy linguistic ordered weighted averaging operator were developed for PHFLTSs. For more information on PHFLTS and its associated concepts, theorems, and recent advancements, please refer to Chen et al. (2016), Yang et al. (2019), Xiong et al. (2023).
Credit ranking of real estate enterprises by a bank based on the PHFLTS-PROMETHEE II model
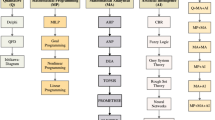
The PROMETHEE method is an interactive MCDM approach designed to handle both quantitative and qualitative criteria with discrete alternatives. In this method, pairwise comparison of the alternatives is performed to compute a preference function for each criterion. Based on this preference function, a preference index for each alternative is determined. This preference index is the measure that supports the hypothesis that an alternative is preferred. The PROMETHEE method has significant advantages over other MCDM approaches, such as multi-attribute utility theory and AHP, as it can classify alternatives that are difficult to compare due to trade-off relations of evaluation standards as non-comparable alternatives. It is quite different from AHP in that there is no need to perform pairwise comparisons again when comparative alternatives are added or deleted, making its calculation intuitive and uncomplicated. As the main financing source of real estate enterprises, the risks of real estate enterprises have a direct impact on banks. Therefore, banks must conduct credit risk assessments on real estate enterprises before granting loans to achieve the best allocation of credit resources, thereby reducing the bank’s risk of loans to real estate enterprises. PHFLTS is a way of eliciting expert evaluation information, which can effectively reduce the loss of information. PROMETHEE II is an MCDM method with a higher level than the relationship and has been widely used in transportation management, manufacturing (Venkata Rao and Patel 2010), and many other fields. The current section proposes the PHFLTS-PROMETHEE II model to evaluate the credit risk of real estate enterprises. The flowchart of the model is shown in Fig. 1, where each specific step is described in further detail in the following subsections.
Establishment of an experienced decision-making team
Given that many aspects of this method are determined by the evaluation information of experts, it is critical to prepare by constructing an experienced decision-making team whose members have rich experience, knowledge, and reputation in the field of real estate credit evaluation. We denote the set of experts as \(\varvec{DE} = \left\{ {d{e_1},\,de{}_2, \ldots ,\,d{e_t}} \right\}\), where t is the number of experts in the decision-making process.
Determination of credit evaluation criteria and establishment of the credit evaluation index system for real estate
To evaluate and rank the credit of real estate enterprises before banks grant loans, it is necessary to first determine the evaluation criteria used in the decision-making process. Let \({\varvec{E}} = \left\{ {{e_1},\,e{}_2, \ldots ,\,{e_m}} \right\}\) be the set of real estate enterprises applying for loans, where m is the number of enterprises.
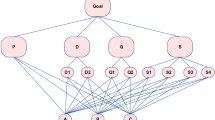
With the promulgation of a series of real estate regulation policies by the Chinese government, real estate enterprises are facing greater competitive pressure and capital demand (Li et al. 2020). Bank loans are the primary source of capital for China’s real estate industry (Fung et al. 2006). Thus, the establishment of a credit risk index system for real estate companies by banks is of great significance to increase the security of bank operations and enhance their ability to prevent and resist unexpected risks. To reduce the risk of bank loans, this thesis constructs a credit risk evaluation index system for real estate companies, which consists of a quantitative indicator system and a qualitative indicator system. The quantitative indicators mainly include financial indicators, while the qualitative indicators mainly include non-financial indicators. The qualitative index system includes four criteria: (i) external environment and industry status, (ii) market position and competitive advantage, (iii) management level and operation status, and (iv) bank-enterprise relationship. The quantitative index system includes four criteria: solvency, profitability, development ability, and operating ability. Let \({\varvec{C}} = \left\{ {{c_1},\,c{}_2, \ldots ,\,{c_n}} \right\}\) denote the set of criteria in the index system, where n is the number of criteria. Moreover, each criterion contains multiple sub-criteria. The selection process for sub-criteria is as follows:
-
We collect and sort the indicators used by banks to evaluate the credit of loan enterprises and the credit evaluation indicators in the literature related to real estate evaluation, based on the characteristics and business model of the real estate enterprise. We use the frequency statistics method to carry out the preliminary selection of the sub-criteria for real estate credit evaluation.
-
We invite relevant experts and experienced personnel to provide recommendations on the initial sub-indicators. We then review the indicators based on the experts’ recommendations and adjust by adding or subtracting indicators as necessary to determine the final index system used in this study.
We have presented a review of the criteria selected from the relevant literature in Table 1.
Through the literature review, we sorted out the overall index table, as shown in Fig. 2.
We excluded some molecular indicators through a questionnaire survey of experts, which is provided in Appendix B.
Thus, the credit evaluation index system for real estate companies includes two parts: a quantitative index system and a qualitative index system. The quantitative index system contains eight first-level indicators and twenty-two second-level indicators, as shown in Fig. 3.
Professionals and seasoned individuals with expertise in evaluating credit risk for real estate development firms were invited to assign scores to the sub-criteria that were initially chosen (see Appendix B for details). The sub-criteria were then reviewed based on their recommendations, and adjustments were made by either increasing or decreasing the indicators. Ultimately, the indicator system employed in this investigation can be established.
Quantitative indicator system
The financial index of a real estate enterprise is a crucial quantitative indicator of credit evaluation (Tian et al. 2014). By analyzing the financial index data of the enterprise, we can determine the internal factors that affect the credit evaluation of the company, such as its solvency, profitability, development ability, and operating ability.
(1) Solvency
Solvency refers to the ability of a real estate development enterprise to repay debt with its assets, which can measure the enterprise’s current financial ability, especially the liquidity of its current assets. The solvency of a real estate enterprise can be evaluated through the following four indicators:
-
Adjusted quick ratioThis index is a financial evaluation index that measures the short-term debt repayment and ability to pay. It reflects the circulating cash scale and cash payment ability of the company’s normal operating turnover activities. However, relying solely on the adjusted quick ratio may not provide a reliable picture of a firm’s financial condition if the company has accounts receivable that take longer than usual to collect or current liabilities that are due but have no immediate payment needed.
-
Cash current liabilities ratio This is a liquidity measure that shows the company’s ability to cover its short-term obligations using only cash and cash equivalents. It fully reflects the extent to which the net cash flow generated by the business activities can guarantee the repayment of current liabilities in the current period, given that the cash earned may not necessarily be enough to pay off the debt. A calculation greater than 1 means that a company has more cash on hand than current debts, while a calculation less than 1 means that a company has more short-term debt than cash.
-
Asset-liability ratio This index shows the ratio of assets provided by creditors and non-creditors to all assets. It considers all of the company’s debt, not just loans and bonds payable, and all assets, including intangibles. The total-debt-to-total-assets ratio is calculated by dividing the company’s total amount of debt by its total amount of assets. This ratio reflects the risk of creditor and non-creditor assets and the enterprise’s leverage ability.
-
Interest protection multiple This index reflects the number of times the operating income of the enterprise covers the debt interest to be paid. As long as the interest protection multiple is large enough, the enterprise has sufficient capacity to pay interest and vice versa.
(2) Operation capability
This factor reflects the operating ability of the enterprise in relation to its total assets and constituent elements. The strength of this ability is determined by the management level, operating conditions, and turnover speed of the assets. The operating ability of a real estate development enterprise refers to the efficiency and turnover rate of the funds required for operation in the process of production and operation.
-
Accounts receivable turnover This index reflects the efficiency of managing enterprise accounts receivable and the speed of their realization.
-
Inventory turnover This index reflects the management efficiency of real estate development enterprises, including production and sales, and has an absolute impact on the profitability and solvency of the enterprises.
-
Total asset turnover This index reflects the speed at which total assets turn over and the enterprise’s sales capacity. A higher turnover rate indicates a faster asset turnover and stronger sales capacity.
(3) Profitability
This factor reflects the ability of the enterprise to increase the value of its capital, which is reflected in its income level. The risk of real estate investment is large, and its profitability is directly related to whether the enterprise can continue to operate, and it is an important source of funds for debt repayment and a guarantee for investors and creditors to receive compensation.
-
Operating profit margin This index measures the income level of an enterprise and reflects the ability of enterprise managers to obtain profits. It represents the competitiveness of the company’s industry to a certain extent.
-
Rate of return on total assets This index measures the profit of the enterprise using the total amount of creditors’ and owners’ equity. It reflects the profitability of the enterprise’s total assets and the effectiveness of the comprehensive utilization of its assets. It is a concrete embodiment of the company’s management performance.
-
Return on equity This index measures the efficiency of the enterprise’s asset utilization and reflects the ability of investors to obtain net profits from their investments. It helps analyze the efficiency of the enterprise’s capital utilization.
(4) Development ability
This factor refers to the potential ability of the enterprise to expand its strength and scale based on survival. Analyzing the future development potential of the enterprise can help evaluate its future operation and profitability, and assist creditors in making correct decisions. For real estate enterprises, strong development potential is beneficial to their continuous and healthy operation and also provides a guarantee for the repayment of their subsequent debts.
-
Operating income growth rate This index reflects the change in operating income for real estate development enterprises. It helps evaluate a company’s development abilities and growth prospects.
-
Capital accumulation rate This index is important for measuring the ability of an enterprise to grow its capital. It reflects changes in the enterprise owner’s equity and the accumulation of enterprise capital. It also reflects the growth and preservation of the capital invested by investors in a real estate development enterprise.
-
Total asset growth rate This index reflects the development ability of the real estate enterprise by tracking the expansion of its asset scale, indicating the impact of the growth of the real estate enterprise on its future development.
Qualitative indicator system
As financial statements of real estate enterprises mainly reflect their past operating situation, the data can be easily manipulated and there may be a time lag (Atiya 2001). Therefore, solely relying on financial data to evaluate the credit risk of real estate enterprises is defective and inadequate. This study selects eight non-financial indicators from the following four aspects, which can reflect the company’s soft power, and make the index system construction more comprehensive and scientific. This approach also improves the limitations of the evaluation of financial indicators. This study selects the four primary indicators of external environment and industry status, market position and competitive advantage, management level, and the operation condition and bank-enterprise relationship as qualitative evaluation indicators of real estate credit rating. These indicators aid in a full understanding of the risk factors related to corporate credit.
-
(1)
External environment and industry status
-
Regional real estate industry development The real estate industry’s situation directly affects real estate enterprises’ operations and, to some extent, can reflect their credit risk.
-
Local government support China’s real estate investment is more regulated and influenced by the government than any other investment behavior. In recent years, the rapid increase in commercial housing prices in China has had some negative effects. The government has introduced many policies to regulate the real estate market, such as land supply and financial policies.
-
-
(2)
Market position and competitive advantage
-
Land reserve area This indicator is unique to real estate companies and is an important indicator for examining their long-term capabilities. Given the scarcity and non-replacement of land resources, an appropriate amount of land reserve must be held to ensure the long-term sustainable development of enterprises.
-
Enterprise reputation Enterprise reputation is an external expression of corporate spirit and culture, which is the overall impression felt by the public during their contact with the enterprise. The brand effect is the key factor in enhancing the company’s popularity and comprehensive strength. A famous real estate brand attracts customers, increases the company’s output value, promotes the continued growth of the company, and increases the guarantee for the company’s credit rating.
-
-
(3)
Management level and operation status
-
Management experience Whenever an unexpected event occurs, the ability of management to make an appropriate response is key to maintaining the development of the enterprise. In this context, this indicator has become important. Generally, the longer the main leaders of real estate companies have been engaged in real estate development, the more familiar they are with the characteristics of the industry, and the stronger their ability to deal with practical problems that arise in the operation of the enterprise. Therefore, this article uses the length of time that major leaders of real estate development companies have been engaged in this industry to evaluate their experience.
-
Building capacity development This indicator is based on the qualification assessment of the Ministry of Construction of China, and it incorporates qualification indicators such as development capability into the indicator system of the thesis research. The goal is to combine with the qualification assessment of real estate development enterprises to improve the social acceptance of credit evaluation.
-
Sales area/completed area This indicator reflects the market acceptance of the real estate company’s products and can indicate the turnover and recovery ability of the company’s main business funds. The larger the index, the stronger the turnover and recovery capacity of the company’s main business funds.
-
-
(4)
Years of cooperation with banks
If a company has a long-standing relationship with a bank, the bank will have a better understanding of the company and its creditworthiness. If the company’s credit standing is not good, the bank may not cooperate with the company over a long period of time.
Determination of the linguistic term set and the semantics of its elements
Real estate credit evaluation includes qualitative and quantitative indicators, which can be regarded as an MCGDM problem that combines qualitative and quantitative evaluation. Thus, defining a reasonable LTS and the semantics that can be used for both qualitative and quantitative index evaluation is integral. As g is an even number, in order to better identify the differences between adjacent linguistic terms and improve the accuracy of the results (Chen et al. 2021), the LTS will be constructed in the subsequent "Case study" section.
Expert evaluation of all enterprises to obtain the initial linguistic decision matrix
Experts evaluate all enterprises using linguistic expressions ll generated according to \(\varvec{G_H}\) given in Definition 5. This produces the initial linguistic decision matrix of each expert. Since quantitative and qualitative indicators are not easy to handle simultaneously, we require experts to convert the evaluation of quantitative indicators into linguistic evaluation values when dealing with quantitative indicators. Experts offer their linguistic expressions based on the financial statements of each enterprise and international standards. Therefore, theoretically, the quantitative indicators’ evaluation results of each expert should be consistent. The initial linguistic decision matrix of \(d{e_l}\) can be represented as \({\varvec{Lde}}{^l} = {(ld{e_{ji}}^l)_{m \times n}}\), where \(ld{e_{ji}}^l\) represents the linguistic evaluation of enterprise \({e_j}\) for criterion \({c_i}\) provided by expert \(d{e_l}\), i belongs to \({{\varvec{N}}} = \left\{ {1, 2, \cdots ,n} \right\}\), j belongs to \({{\varvec{M}}} = \left\{ {1, 2, \cdots ,m} \right\}\), and l belongs to \({\varvec{T}} = \left\{ {1,2, \cdots ,t} \right\}\).
Normalization of initial linguistic decision matrix
-
(1)
We convert the linguistic expression ll in each \(\varvec{ Ld{e^l}}\) to HFLTS on the basis of the transformation function \(\varvec{E_{{G_H}}}\), which is set in Definition 6. We then construct the hesitant fuzzy linguistic evaluation matrix \(\varvec{H_S^l }= {({H_{{S_{ji}}}}^l)_{m \times n}}\), where \({H_{{S_{ji}}}}^l\) is an HFLTS, which has the same meaning as \(ld{e_{ji}}^l\).
-
(2)
We normalize the hesitant fuzzy linguistic evaluation matrix \(\varvec{H_S^l} = {({H_{{S_{ji}}}}^l)_{m \times n}}\) of each expert to \(\varvec{{B^l}} = {({b_{ji}}^l)_{m \times n}}\) by using the following rules:
$$\begin{aligned} {b_{ji}}^l = \left\{ {\begin{array}{*{20}{c}} {{H_{{S_{ji}}}}^l,\quad \mathrm{{benefit~ criterion}}\;{\mathrm{{c}}_i}}\\ {{{({H_{{S_{ji}}}}^l)}^{neg}},\quad \mathrm{{cost~}}\;\mathrm{{criterion}}\;{\mathrm{{c}}_i}} \end{array}\quad (i \in {{\varvec{N}}},\;j \in {{\varvec{M}}})} \right. \end{aligned}$$where \({b_{ji}}^l\) is an HFLTS and \({\left( {{H_{{S_{ji}}}}^l} \right) ^{neg}}\) can be obtained by Definition 10.
-
(3)
We standardize HFLTSs. Given that the number of elements in different HFLTSs of the hesitant fuzzy linguistic evaluation matrix by each expert is usually different, comparing the size or calculating the distance between different HFLTSs can be difficult. Therefore, it is necessary to standardize the matrix \(\varvec{{B^l} }= {({b_{ji}}^l)_{m \times n}}\) by using the expansion rules given in Definition 11 to ensure that the number of linguistic terms in each HFLTS in the matrix \(\varvec{{B^l}} = {({b_{ji}}^l)_{m \times n}}\) is the same.
Determination of the comprehensive weights of experts
In the process of solving the MCGDM problem, experts coming from different research fields have varying levels of knowledge and practical experience, leading to different evaluations of the same decision-making problem. Therefore, it is necessary for each expert to assign a weight that corresponds to their importance in the problem. The weights of experts reflect their discourse power and directly impact the decision results. The expert weights consist of two parts: subjective weights and objective weights.
-
(1)
The subjective weights of experts The bank manager determines the subjective weights of experts based on their experience and reputation. If an expert has dealt with many related projects and has a good reputation in the relevant field, they should be assigned a higher weight. Conversely, if the expert has less experience and reputation, they should be assigned a lower weight. The subjective weights of experts can be represented as \(\varvec{{u^S}} = \left( {{u_1}{^S},\;{u_2}{^S},\;\cdots \;,\;{u_t}^S} \right)\).
-
(2)
The objective weights of experts The objective weights of experts are determined based on the consensus among the experts. If the consensus among the experts is higher, it indicates that the expert evaluations are more reasonable, and the evaluation questions are more professional. Therefore, giving a higher weight to the expert who has a higher consensus is reasonable. The objective weights of experts can be represented as \(\varvec{{u^O}} = \left( {{u_1}{^O},\;{u_2}{^O},\;\cdots \;,\;{u_t}^O} \right)\). Let \(d{e_l}\) and \(d{e_k}\) represent two experts, and \({H_{{S_{ji}}}}^l\) and \({H_{{S_{ji}}}}^k\) indicate the evaluations of experts \(d{e_l}\) and \(d{e_k}\) on enterprise \({e_j}\) under criterion \({c_i}\), respectively, where l and k belong to \({\varvec{T}}\). The process of determining the objective weights involves seven sub-steps.
Step 1 When evaluating \({e_j}\) under the criterion \({c_i}\), the degree of consistency between the opinions of \(d{e_l}\) and \(d{e_k}\) is defined as follows:
where \(0 \le AC_l^k({e_j},{c_i}) \le 1\), and the larger the value, the higher the consistency between \(d{e_l}\) and \(d{e_k}\). The distance between \({H_{{S_{ji}}}}^l\) and \({H_S}{_{_{ji}}^k}\) is calculated using the equation given in Definition 10.
Step 2 The consistency of \(d{e_l}\) and \(d{e_k}\) is calculated when evaluating all enterprises under all criteria.
Therefore, the consistency degree between any two experts can be represented by a consistency matrix.
Step 3 The average consistency degree of \(d{e_l}\) is expressed as follows:
Step 4 The degree of consistency normalized between \(d{e_l}\) and all other experts is given by:
Step 5 The objective weight of each expert is obtained as follows:
-
(3)
The comprehensive weight of each expert is calculated as follows:
$$\begin{aligned} {u_l} = \frac{{{u_l}^O + {u_l}^S}}{{\sum \nolimits _{l = 1}^t {({u_l}^O + {u_l}^S} )}},\;l \in {\varvec{T}}. \end{aligned}$$(9)
Generation of the group decision matrix of PHFLTS
-
(1)
Generation of standard PHFLTS Given that HFLTS is a special form of PHFLTS where the proportion of each evaluation value in PHFLTS is equal, the first step is to convert HFLTS to PHFLTS. Then the PHFLTS is converted to the standard PHFLTS format according to Definition 15. Finally, we can obtain the individual decision matrix \(\varvec{{P^l}} = {({p_{ji}}^l)_{m \times n}}\), where \({p_{ji}}^l\) is a PHFLTS, and \({l \in \varvec{T}}\).
-
(2)
Generation of the group decision matrix of PHFLTS The individual decision matrix \(\varvec{{P^l}} = {({p_{ji}}^l)_{m \times n}}\) is aggregated using the PHFLWA operator, which was introduced in Yang et al. (2019). This way, we obtain the PHFLTS group decision matrix \(\varvec{\tilde{P} }= {\left( {{{{\tilde{p}}}_{ji}}} \right) _{m \times n}}\), where \({{{{\tilde{p}}}_{ji}}}\) is a PHFLTS that represents the group evaluation of \({e_j}\) under criterion \({c_i}\).
Determination of the weights of criteria
Criteria weights play a crucial role in MCGDM. Different criteria weighting can lead to different decision results. Therefore, the allocation of criteria weight should be thoroughly considered in the decision-making process.
Experts determine the criteria weights \({\varvec{w}}= \left( {{w_1}\,,\;{w_2}\,,\;\cdots \;,\;{w_n}} \right)\). Compared to commonly used methods for determining weights such as AHP and Delphi, the calculation of BWM is simpler, and the evaluation consistency is stronger. The fuzzy best-worst method (FBWM) is a new method based on BWM, which considers the ambiguity and uncertainty of experts in the decision-making process, and integrates fuzzy theory (Guo and Zhao 2017). Therefore, in this study, we use FBWM to determine the weights of criteria. The specific process of FBWM is as follows.
Step 1 Establishment of a set of decision criteria.
Step 2 Determination of the best criterion and the worst criterion.
Step 3 Determination of the fuzzy preference degree of the best criterion over all other criteria and the fuzzy preference degree of the worst criterion over all other criteria.
The experts compare the importance of the indicators based on their knowledge and professional experience level. The comparison results are expressed in linguistic terms, which include five levels in this study. These linguistic terms need to be converted into fuzzy evaluations, which are represented by triangular fuzzy numbers. The conversion rules are shown in Guo and Zhao (2017).
-
(1)
Determination of the fuzzy preference degree of the best criterion over all other criteria Experts compare the importance of the best criterion with the other criteria and express the comparison results in linguistic terms. These terms are then transformed into triangular fuzzy numbers using the conversion rules listed in Guo and Zhao (2017). The resulting fuzzy best-to-others vector, denoted by \(\varvec{{{\tilde{A}}_B}}\), can be constructed as follows:
$$\begin{aligned} \varvec{{{\tilde{A}}_B}} = \left( {{{{\tilde{a}}}_{B1}},\;{{\tilde{a}}_{B2}},\;\cdots ,\;{{{\tilde{a}}}_{Bn}}} \right) , \end{aligned}$$(10)where \({{\tilde{a}}_{Bi}}\) denotes the fuzzy preference degree of the best criterion \({c_B}\) over criterion \({c_i}\), where \(i \in {{\varvec{N}}}\). Note that \(\varvec{{{\tilde{a}}_{BB}}} = \left( {1,1,1} \right)\).
-
(2)
Determining the fuzzy preference degree of the worst criterion over all other criteria
Experts compare the importance of all criteria relative to the worst criterion using the linguistic terms. These terms are then converted to triangular fuzzy numbers based on the conversion rules given in Guo and Zhao (2017). The resulting fuzzy others-to-worst vector, denoted by \(\varvec{{{\tilde{A}}_W}}\), can be determined as follows:
where \({{\tilde{a}}_{iW}}\) denotes the fuzzy preference degree of criterion \({c_i}\) over the worst criterion \({c_B}\) and \(i \in {{\varvec{N}}}\). Note that \(\varvec{{{\tilde{a}}_{WW}}} = \left( {1,1,1} \right)\).
Step 4 Calculation of the optimal fuzzy weights \(\varvec{\omega } = \left( {{\omega _1}\,,\;{\omega _2}\,,\;\cdots \;,\;{\omega _n}} \right)\) of the criteria.
The optimal fuzzy weights of the criteria for this study are calculated using a nonlinear constrained optimization model proposed in Guo and Zhao (2017). The model can be expressed as follows:
where \(\varvec{{{\tilde{a}}_{iW}}}\mathrm{{ = }}\left( {{l_{iW}},{m_{iW}},{u_{iW}}} \right)\); \(\varvec{{\tilde{a}_{Bi}}}\mathrm{{ = }}\left( {{l_{Bi}},{m_{Bi}},{u_{Bi}}} \right)\); \(\varvec{{{\tilde{w}}_i}}\mathrm{{ = }}\left( {l_i^w,m_i^w,u_i^w} \right)\) is the optimal fuzzy weight of criterion \({c_i}\); \(\varvec{{{\tilde{w}}_B}}\mathrm{{ = }}\left( {l_B^w,m_B^w,u_B^w} \right)\) is the optimal fuzzy weight of the best criterion; \(\varvec{{{\tilde{w}}_W}}\mathrm{{ = }}\left( {l_W^w,m_W^w,u_W^w} \right)\) is the optimal fuzzy weight of the worst criterion; and l, m, u represent the lower, median, and upper values, respectively. \(R\left( {{{{\tilde{w}}}_i}} \right) = \frac{{l_i^w + 4m_i^w + u_i^w}}{6}\) is a function that transforms the fuzzy weight of criterion \({c_i}\) into an accurate value. \(\varvec{{\xi ^{\mathrm{{*}}}}}\mathrm{{ = }}\left( {{k^*},{k^*},{k^*}} \right)\) is the optimal target value.
Solving the above model allows us to obtain the optimal fuzzy weights denoted by \(\left( {{\tilde{w}}_1^*,{\tilde{w}}_2^*,\cdots ,\tilde{w}_n^*} \right)\). The final criteria weights \(\left( {{w_1},{w_2},\cdots ,{w_n}} \right)\) can be obtained using the function \({R\left( {{{{\tilde{w}}}_i}} \right) } = \frac{{l_i^w + 4m_i^w + u_i^w}}{6}\).
Use of the probability-based PHFLTS-PROMETHEE II method to sort all enterprises
The specific steps of the probability-based PHFLTS-PROMETHEE II method are detailed below.
Step 1 Calculation of the probability degree between two enterprises.
To obtain the probability \({L_i}\left( {{e_r},{e_k}} \right)\) that \({e_r}\) is better than \({e_k}\) under criterion \({c_i}\), we use the equation given in Definition 14
Step 2 Construction of a probability matrix of pairwise comparisons of enterprise evaluation values for each criterion \({c_i}\left( {i \in {{\varvec{N}}}} \right)\).
where \(L\left( {{p_{ri}} \ge {p_{ki}}} \right) \in \left[ {0,1} \right]\). A higher value of \(L\left( {{p_{ri}} \ge {p_{ki}}} \right)\) indicates that \({e_r}\) is better than \({e_k}\), while a smaller value of \(L\left( {{p_{ri}} \ge {p_{ki}}} \right)\) suggests a smaller difference between \({e_r}\) and \({e_k}\). \(L\left( {{p_{ri}} \ge {p_{ki}}} \right) \mathrm{{ = }}0\) indicates that \({e_r}\) and \({e_k}\) are indistinguishable.
Step 3 Determination of the preference index \(\prod {\,\left( {{e_r},\,{e_k}} \right) }\).
This index represents the outranking degree of every \({e_r}\) over \({e_k}\).
Step 4 The positive flow \({\varphi ^ + }\left( e \right)\) and negative flow \({\varphi ^ - }\left( e \right)\) of each enterprise based on the preference index.
Step 5 The net ranking \(\varphi \left( e \right)\) of each enterprise.
Step 6 All enterprises according to the net ranking \(\varphi \left( e \right)\) of each enterprise.
The enterprise with a higher net ranking is considered to have better credit.
Case study
Bank A (anonymized) is one of the five largest state-owned commercial banks in China. As real estate development loans are susceptible to macroeconomic conditions and national regulations, Bank A has gradually begun to control the issuance of credit to the real estate industry. Five real estate enterprises, namely \(\left\{ {{e_1},{e_2},{e_3},{e_4},{e_5}} \right\}\), have applied for real estate development loans from the Hunan Branch of Bank A. In order to achieve the best allocation of credit resources and reduce the risk of loans to real estate companies, this study proposes a credit risk assessment model based on the PHFLTS-PROMETHEE II method for real estate enterprises. This model ranks the real estate companies according to their level of credit risk. The specific steps of the model are outlined below.
Establishment of an experienced decision-making team
We formed a team of five decision experts, denoted as \(\varvec{DE}\mathrm{{ = }}\left\{ {d{e_1},\;d{e_2},\;d{e_3},\;d{e_4},\;d{e_5}} \right\}\), consisting of five experts with rich experience and knowledge in bank credit evaluation and the real estate industry. The team was tasked with ranking several real estate enterprises and selecting the enterprise with the best credit. The profiles of the experts are shown in Table 2.
Eight criteria for credit risk assessment
There are eight criteria for credit risk assessment, which are as follows: solvency (\({c_1}\)), operation capability (\({c_2}\)), profitability (\({c_3}\)), development ability (\({c_4}\)), external environment and industry status (\({c_5}\) ), market position and competitive advantage (\({c_6}\)), management level and operational status (\({c_7}\)), and years of cooperation with banks (\({c_8}\)). The set of criteria is denoted by \({\varvec{C}}=\left\{ {{c_1},\;{c_2},\;{c_3},\;{c_4},\;{c_5},{c_6},\;{c_7},\;{c_8}} \right\}\).
Definition of LTS with seven terms
The representation of LTS is as follows.
Evaluation of five enterprises under eight criteria
Five experts were invited to evaluate the five enterprises under the eight criteria using comparative linguistic expressions. The initial decision matrix is presented in Table 3.
Normalization of initial linguistic decision matrix
-
(1)
Transformation of the linguistic expression ll in Table 3 into HFLTS using \(\varvec{E_{{G_H}}}\). The resulting HFLTS evaluation matrix is shown in Table 4.
-
(2)
Conversion of cost criterion into benefit criterion.
Given that all eight criteria are already benefit criteria, converting any cost criterion is unnecessary.
-
(3)
Generate the standardized HFLTS matrix.
To facilitate the calculation of the size and distance between two HFLTSs, we use the extended rule presented in Definition 11 to ensure that the number of linguistic terms used by different experts to evaluate the HFLTSs under criterion \({c_i}\) for each enterprise was the same. The resulting standardized HFLTS matrix is shown in Table 5.
Determination of the comprehensive weights of experts
-
(1)
Determining the subjective weights of experts.
The subjective weights of experts are determined by a bank manager based on three aspects: reputation in the industry, number of processed projects, and years of experience in the industry. The higher the reputation, the more projects processed, and the longer the experience, the higher the score. The score range for each expert is 0–100, and the score of each expert is normalized to 0–1 as the weight. The subjective weight of each expert can be obtained as \(\varvec{{u^S}} = \left( {0.18,\;0.16,\;0.2,\;0.22,\;0.24} \right)\).
-
(2)
Determining the objective weights of experts.
Given that \({c_1} - {c_4}\) are quantitative indicators, the five expert evaluations of \({c_1} - {c_4}\) are nearly the same. Thus, we only consider the expert evaluation of \({c_5} - {c_8}\).
Step 1 We calculate the distance and consistency between the evaluations of expert \(d{e_l}\) and \(d{e_k}\) for enterprise \({e_j}\) under criterion \({c_i}\). The consistency matrices are as follows:
\(\varvec{A{C_1}^2 }= \left[ {\begin{array}{*{20}{c}} {0.774}&{}{0.857}&{}{0.816}&{}{0.495}\\ {0.899}&{}{0.899}&{}1&{}{0.636}\\ {0.816}&{}{0.899}&{}{0.816}&{}{0.816}\\ {0.899}&{}{0.899}&{}{0.816}&{}{0.816}\\ {0.276}&{}1&{}{0.899}&{}{0.816} \end{array}} \right]\), \(\varvec{A{C_1}^3} = \left[ {\begin{array}{*{20}{c}} {0.774}&{}{0.774}&{}{0.816}&{}{0.774}\\ {0.774}&{}1&{}{0.857}&{}{0.636}\\ {0.714}&{}{0.899}&{}{0.883}&{}{0.816}\\ {0.899}&{}{0.883}&{}{0.691}&{}{0.857}\\ {0.495}&{}{0.714}&{}{0.899}&{}{0.816} \end{array}} \right]\),
\(\varvec{A{C_1}^4 }= \left[ {\begin{array}{*{20}{c}} {0.899}&{}{0.899}&{}{0.899}&{}{0.495}\\ {0.857}&{}{0.899}&{}{0.816}&{}{0.857}\\ {0.899}&{}{0.899}&{}1&{}{0.899}\\ 1&{}{0.691}&{}{0.691}&{}{0.857}\\ {0.353}&{}{0.816}&{}{0.883}&{}1 \end{array}} \right]\), \(\varvec{A{C_1}^5} = \left[ {\begin{array}{*{20}{c}} {0.899}&{}{0.636}&{}1&{}{0.774}\\ {0.774}&{}{0.857}&{}{0.816}&{}{0.899}\\ {0.774}&{}{0.899}&{}{0.816}&{}{0.816}\\ 1&{}{0.691}&{}{0.714}&{}{0.857}\\ {0.899}&{}{0.816}&{}{0.883}&{}{0.816} \end{array}} \right]\),
\(\varvec{A{C_2}^3 }= \left[ {\begin{array}{*{20}{c}} 1&{}1&{}1&{}{0.714}\\ {0.816}&{}{0.899}&{}{0.857}&{}1\\ {0.816}&{}{0.816}&{}{0.857}&{}1\\ {0.883}&{}{0.899}&{}{0.857}&{}{0.883}\\ {0.774}&{}{0.714}&{}1&{}1 \end{array}} \right]\), \(\varvec{A{C_2}^4} = \left[ {\begin{array}{*{20}{c}} {0.816}&{}{0.816}&{}{0.899}&{}1\\ {0.899}&{}1&{}{0.816}&{}{0.774}\\ {0.774}&{}{0.816}&{}{0.816}&{}{0.774}\\ {0.899}&{}{0.774}&{}{0.857}&{}{0.883}\\ {0.899}&{}{0.816}&{}{0.899}&{}{0.816} \end{array}} \right]\),
\(\varvec{A{C_2}^5} = \left[ {\begin{array}{*{20}{c}} {0.816}&{}{0.857}&{}{0.816}&{}{0.714}\\ {0.691}&{}{0.899}&{}{0.816}&{}{0.714}\\ {0.899}&{}{0.816}&{}{0.714}&{}1\\ {0.899}&{}{0.774}&{}{0.816}&{}{0.883}\\ {0.353}&{}{0.816}&{}{0.899}&{}{0.714} \end{array}} \right]\), \(\varvec{A{C_3}^4} = \left[ {\begin{array}{*{20}{c}} {0.816}&{}{0.816}&{}{0.899}&{}{0.714}\\ {0.899}&{}{0.899}&{}{0.691}&{}{0.774}\\ {0.636}&{}1&{}{0.883}&{}{0.774}\\ {0.899}&{}{0.714}&{}1&{}1\\ {0.857}&{}{0.816}&{}{0.899}&{}{0.816} \end{array}} \right]\),
\(\varvec{A{C_3}^5} = \left[ {\begin{array}{*{20}{c}} {0.816}&{}{0.857}&{}{0.816}&{}1\\ {0.571}&{}{0.857}&{}{0.691}&{}{0.714}\\ {0.899}&{}1&{}{0.857}&{}1\\ {0.899}&{}{0.714}&{}{0.883}&{}1\\ {0.571}&{}{0.816}&{}{0.899}&{}{0.714} \end{array}} \right]\), \(\varvec{A{C_4}^5 }= \left[ {\begin{array}{*{20}{c}} 1&{}{0.691}&{}{0.899}&{}{0.714}\\ {0.636}&{}{0.899}&{}1&{}{0.899}\\ {0.714}&{}1&{}{0.816}&{}{0.774}\\ 1&{}1&{}{0.883}&{}1\\ {0.429}&{}1&{}1&{}{0.816} \end{array}} \right]\).
Step 2 We calculate the consistency of \(d{e_l}\) and \(d{e_k}\) when evaluating all enterprises under all criteria and obtain the consistency matrix.
Step 3 We calculate the average consistency of each expert.
Step 4 We normalize the degree of consistency between expert \(d{e_l}\) and all other experts.
Step 5 We obtain the objective weight of each expert.
-
(3)
Comprehensive weights of each expert.
$$\begin{aligned} {u_1} = 0.188, \,{u_2} = 0.180, \,{u_3} = 0.201, \,{u_4} = 0.212, \,and \,{u_5} = 0.219. \end{aligned}$$
Generation of the group decision matrix of PHFLTS
Given that HFLTS is a special case of PHFLTS where the proportion of each evaluation value is equal, Table 5 can be represented as Table 6. The evaluation matrices of the experts shown in Table 5 are aggregated to obtain the PHFLTS group decision matrix shown in Table 7.
The rest of Table 6 is presented in Appendix A to save space here.
Calculation of the weights of criteria by using FBWM
Step 1 Establishment of a set of decision criteria.
For this study, eight credit risk assessment criteria have been identified for the enterprise credit risk assessment; these include solvency [\({c_1}\)], operation capability [\({c_2}\)], profitability [\({c_3}\)], development ability [\({c_4}\)], external environment and industry status [\({c_5}\)], market position and competitive advantage [\({c_6}\)], management level and operational status [\({c_7}\)], and years of cooperation with banks [\({c_8}\)].
Step 2 Determination of the best and the worst criteria.
Based on expert consensus, \({c_3}\) is identified as the best criterion, and \({c_8}\) is identified as the worst criterion.
Step 3 Determination of the fuzzy preference degree of the best and worst criteria over all other criteria.
The comparison results of the importance of the best criterion, worst criterion, and other criteria provided by experts are shown in Tables 8 and 9.
Thus, the fuzzy best-to-others vector can be obtained by Table 3 and Eq. (10) as follows:
The fuzzy others-to-worst vector can be obtained by Table 3 and Eq. (11) as follows:
Step 4 Calculation of the optimal fuzzy weights \(\varvec{\omega } = \left( {{\omega _1}\,,\;{\omega _2}\,,\;\cdots \;,\;{\omega _n}} \right)\) of the criteria.
In this study, according to the fuzzy best-to-others vector \(\varvec{{{\tilde{A}}_B}}\) and the fuzzy others-to-worst vector \(\varvec{{{\tilde{A}}_W}}\), the following model for calculating the optimal weight of the criterion can be established.
The nonlinear constrained optimization equation represented by specific numbers can be obtained, as shown below.
By solving Eq. (17), the optimal fuzzy weights of eight criteria can be calculated as follows:
Then, the final criteria weights \(\left( {{w_1},{w_2},\cdots ,{w_n}} \right)\) can be obtained by the function \(R\left( {{{{\tilde{w}}}_i}} \right) = \frac{{l_i^w + 4m_i^w + u_i^w}}{6}\). The weights are as follows:
Use of the probability-based PHFLTS-PROMETHEE II method to sort all enterprises
Step 1 Calculation of the probability degree between two enterprises under each criterion.
The probability matrix of pairwise comparisons of enterprise evaluation values under each criterion is shown below:
Step 2 Determination of the preference index \(\prod {\,\left( {{e_r}\,,\,{e_k}} \right) }\).
Step 3 Calculation of the positive flow \({\varphi ^ + }\left( e \right)\) and negative flow \({\varphi ^ - }\left( e \right)\) of each enterprise based on the preference index.
Step 4 Calculation of the net ranking \(\varphi \left( e \right)\) of each enterprise.
Based on the value of the net ranking \(\varphi \left( e \right)\), we can rank all enterprises as follows: \({e_3}> {e_4}> {e_1}> {e_2} > {e_5}\). The credit of enterprise \({e_3}\) is the best among them. Therefore, the bank should choose enterprise \({e_3}\) for the loan to minimize credit risk.
Comparison and sensitivity analysis
To validate the effectiveness and practicality of the proposed PHFLTS-PROMETHEE II method, we compare it with the following methods: Pang et al.’s method (2016), Xiong et al.’s method (2022), and Liu et al.’s method (2017).
Comparison analysis
In Pang et al. (2016), evaluation information is expressed using probabilistic linguistic term sets (PLTSs), and two models are proposed to calculate the completely unknown or partially unknown condition of criterion weight information. Specifically, two methods are proposed in Pang et al. (2016): the extended TOPSIS method and the aggregation-based method. In this section, we compare our method with TOPSIS. The seven steps described in Pang et al. (2016) are as follows.
Step 1 The linguistic evaluation values of experts are aggregated to obtain a probabilistic linguistic decision matrix \({\varvec{R}} = {\left[ {{L_{ji}}\left( p \right) } \right] _{m \times n}}\), where \({L_{ji}}\left( p \right) = \left\{ {\left. {{L_{ji}}^{\left( k \right) }\left( {p_{_{ji}}^{\left( k \right) }} \right) } \right| k = 1,2,\cdots ,\# {L_{ji}}\left( p \right) } \right\}\) and \(\# {L_{ji}}\left( p \right)\) is the number of different terms in \({L_{ji}}\left( p \right)\).
Step 2 The criteria weight vector \({\varvec{w}}= {\left( {{w_1},{w_2},\cdots ,{w_n}} \right) ^T}\) is calculated by using the maximizing deviation method.
where \(d\left( w \right)\) is the deviation degree and \({L_{ji}}\left( p \right)\) is a PLTS, which represents the criteria values over the enterprises \({e_j}\left( {j = 1,2, \cdots ,m} \right)\) with respect to the criteria \({c_i}\left( {i = 1,2, \cdots ,n} \right)\). The deviation degree between \({L_{ji}}\left( p \right)\) and \({L_{qi}}\left( p \right)\) is \(d\left( {{L_{ji}}\left( p \right) ,{L_{qi}}\left( p \right) } \right) = \sqrt{\sum \nolimits _{k = 1}^{\# {L_{ji}}\left( p \right) } {{{\left( {{p_{ji}}^{\left( k \right) }{r_{ji}}^{\left( k \right) } - {p_{qi}}^{\left( k \right) }{r_{qi}}^{\left( k \right) }} \right) }^2}/\# {L_{ji}}\left( p \right) } }\). In addition, \({p^{\left( k \right) }}\) is the probability of the linguistic term, and \({r^{\left( k \right) }}\) is the subscript of the linguistic term.
Step 3 The positive ideal solution (PIS) \(L{\left( p \right) ^ + }\) and negative ideal solution (NIS) \(L{\left( p \right) ^ - }\) of enterprises are obtained.
Step 4 The deviation degree \(d\left( {{e_j},L{{\left( p \right) }^ + }} \right)\) between each enterprise and PIS and the deviation degree \(d\left( {{e_j},L{{\left( p \right) }^ - }} \right)\) between each enterprise and NIS are obtained.
The better enterprise \({e_j}\) has a smaller distance \(d\left( {{e_j},L{{\left( p \right) }^ + }} \right)\) and a larger distance \(d\left( {{e_j},L{{\left( p \right) }^ - }} \right)\).
Step 5 \({d_{\mathsf{{Min}} }}\left( {{e_j},L{{\left( p \right) }^ + }} \right)\) and \({d_{\mathsf{{Max}}}}\left( {{e_j},L{{\left( p \right) }^ - }} \right)\) are determined by the formulas, as shown below.
Step 6 The closeness coefficient CI of each enterprise is calculated.
where \(CI\left( {{e_j}} \right) \le 0\left( {j = 1,2,\cdots ,m} \right)\). The better enterprise \({e_j}\) has a larger closeness coefficient.
Step 7 Enterprises are sorted according to the closeness coefficient CI.
Applying the above steps to the case in “Credit ranking of real estate enterprises by a bank based on the PHFLTS-PROMETHEE II model” section, the following results can be obtained.
We can obtain the ranking of enterprises using Pang et al.’s method (2016) as \({e_4}> {e_3}> {e_1}> {e_2} > {e_5}\). In addition, the ranking of enterprises from Xiong et al.’s method (2022) is \({e_3}> {e_4}> {e_1}> {e_2} > {e_5}\), and the ranking from Liu et al.’s method (2017) is \({e_4}> {e_3}> {e_1}> {e_2} > {e_5}\). The relevant calculation process is provided in Appendix C.
The ranking results with different methods are depicted in Fig. 4.
The enterprise ranking results of the proposed method, Pang et al.’s method, Xiong et al.’s method, and Liu et al.’s method are generally similar. However, there is a small deviation for enterprises \({e_3}\) and \({e_4}\). The reason for this is two-fold. First, Pang et al.’s method adds the expected smaller linguistic terms directly after standardizing the proportional linguistic term set, whereas other methods add them proportionally, which effectively reduces information change. Second, although Pang et al.’s, Xiong et al.’s, and Liu et al.’s methods consider the evaluation information of several experts, they do not have a model for determining the expert weights, while the expertise and experience of different experts can affect the evaluation results. Therefore, the present study comprehensively considers the subjective and objective weights of experts, making the evaluation results more accurate and reliable.
Sensitivity analysis
To investigate the influence of expert weights and assessment criteria on the ranking results of the proposed method and the extended TOPSIS method, we conduct a sensitivity analysis of the decision results with respect to \(\varphi\).
In this subsection, we conduct sensitivity analysis by varying the weight of each criterion to avoid the impact of data randomness. Firstly, we increase the weight of each criterion by 30\(\%\) and 60\(\%\). At the same time, the weights of the remaining criteria are adjusted proportionally to ensure that the sum of expert weights is equal to 1. The decision information, parameters, thresholds, and other aspects of the proposed model remain unchanged. For each change in the criterion weight, we obtain five experimental ranking results. Finally, we conduct 16 experiments, as shown in Figs. 5, 6, 7, and 8. From the figures, we can conclude that the ranking results of the proposed method are slightly sensitive to changes in the weight of the criteria, but the range of change is small in this process. As shown in Fig. 5, the ranking results of the proposed method change when we adjust the weights of the second, fourth, and seventh criteria. The main reason for this is the significant preference differences among them, which affect similar enterprises 3 and 4. We also conducted comparative experiments on other methods by changing the weight of the criteria. It can be seen from the figures that the ranking of enterprises obtained by other methods is more susceptible to changes in the control group of weights. This is because the proposed method takes into account the weight of experts, which results in a more significant difference in preferences.
In conclusion, the introduction of the proposed method allows us to fully consider individual experts who have significant differences in assessment information from others, leading to a more comprehensive assessment. The sensitivity of the ranking results also reminds us to determine the weights of criteria accurately to obtain more accurate and reliable decision results.
Conclusion and future direction
Conclusion
Credit risk assessment of Chinese real estate enterprises is crucial to commercial banks for control financial risk. However, accurately evaluating credit risk in this industry is challenging due to its distinctive characteristics. Firstly, the Chinese real estate industry is heavily influenced by the government, requiring a novel credit risk evaluation index for real estate enterprises that is tailored to the Chinese market. Secondly, information related to the operations of Chinese real estate enterprises is rarely disclosed, leading to high uncertainty in credit risk evaluation. To address this challenge, this study proposes a PHFLTS-PROMETHEE method for evaluating the credit risk of Chinese real estate companies. The main contributions and innovations of this study are summarized below:
-
This study develops a credit risk assessment index for Chinese real estate enterprises, utilizing both quantitative and qualitative indicators that reflect the unique characteristics of the industry. The index provides commercial banks with assessment criteria and contributes to the research on credit risk assessment for Chinese real estate enterprises.
-
This study proposes the PHFLTS-PROMETHEE method for evaluating credit risk in Chinese real estate enterprises. This method utilizes the defined PHFLTS distance measurement and replaces the traditional PROMETHEE method. The extended PHFLTS-PROMETHEE method can be applied for expressing the evaluation information in PHFLTS, and the preference function in the PROMETHEE method is replaced by a possibility degree, improving its applicability and accuracy. The PHFLTS-PROMETHEE method can overcome the challenge of a lack of operational data in the Chinese real estate industry and has the advantage of integrating subjective judgment under both quantitative and qualitative indicators.
-
The study presents a comprehensive weight distribution model that enhances the rationality of decision-making. The model determines objective weights of experts by calculating the similarity measure between evaluation information provided by experts, while subjective weights are determined based on their experience and reputation. The study integrates the obtained objective and subjective weights to obtain comprehensive weights for experts, which improves the accuracy and reliability of the decision-making process.
-
This study demonstrates the effectiveness of the PHFLTS-PROMETHEE method through empirical analysis of bank loans towards real estate enterprises and comparative analysis with similar methods. The comparative analysis reveals that the PHFLTS-PROMETHEE method is flexible in various decision-making contexts and can produce reliable results, thus confirming the validity and practicality of the approach.
Future direction
This study presents an effective method through empirical analysis of bank loans towards real estate enterprises, demonstrating its flexibility in various decision-making contexts and ability to obtain reliable results. However, the proposed PHFLTS-PROMETHEE II method may require further improvement, particularly regarding the simultaneous involvement of subjective and objective weights in determining the weights of criteria. Future research will focus on developing accurate, efficient, and general methods to analyze the credit risk of real estate companies in practical applications. For example, the evaluation of quantitative indicators can be improved using scientific and reasonable methods such as the KMV model. Additionally, future research will focus on allocating credit funds based on the credit risk of real estate development enterprises and the loan amount they apply for. This approach will ensure reasonable allocation of resources and mitigate financial risks for commercial banks.
Despite its effectiveness, this study has certain limitations. Firstly, the amount of data is limited, as only five enterprises were considered for credit risk rating. Future research should focus on big data analysis to provide a more comprehensive understanding of credit risk in the Chinese real estate industry. Additionally, the reliability and quality of data should be improved for more accurate analysis. Advanced subjective evaluation processing techniques can also be explored in future research to process expert evaluations. To promote and deepen continuing research, further studies should investigate new issues and potential areas of improvement.
Availability of data and materials
Not applicable.
References
Adair A, Hutchison N (2005) The reporting of risk in real estate appraisal property risk scoring. J Proper Invest Financ 23(3): 254–268
Atiya AF (2001) Bankruptcy prediction for credit risk using neural networks: a survey and new results. IEEE Trans Neural Netw 12:929–935
Bernhardsen E, Larsen K (2007) Modelling credit risk in the enterprise sector-further development of the SEBRA model. Norges Bank. Econ Bullet 78:102
Bordogna G, Pasi G (1993) A fuzzy linguistic approach generalizing boolean information retrieval: a model and its evaluation. J Am Soc Inf Sci 44:70–82
Breuer T, Jandacka M, Rheinberger K, Summer M (2008) Regulatory capital for market and credit risk interaction: is current regulation always conservative? Bundesbank Series 2 Discussion Paper No. 2008,14. Available at SSRN: https://ssrn.com/abstract=2794017
Chai N, Wu B, Yang W, Shi B (2019) A multicriteria approach for modeling small enterprise credit rating: evidence from china. Emerg Mark Financ Trade 55:2523–2543
Chang Y-C, Chang K-H, Wu G-J (2018) Application of extreme gradient boosting trees in the construction of credit risk assessment models for financial institutions. Appl Soft Comput 73:914–920
Chen Z-S, Chin K-S, Li Y-L, Yang Y (2016) Proportional hesitant fuzzy linguistic term set for multiple criteria group decision making. Inf Sci 357:61–87
Chen N, Ribeiro B, Chen A (2016) Financial credit risk assessment: a recent review. Artif Intell Rev 45:1–23
Chen Z-S, Zhang X, Pedrycz W, Wang X-J, Chin K-S, Martínez L (2021) K-means clustering for the aggregation of HFLTS possibility distributions: N-two-stage algorithmic paradigm. Knowledge-Based Syst 227:107230
Chen Z-S, Zhang X, Rodríguez RM, Pedrycz W, Martínez L, Skibniewski MJ (2022) Expertise-structure and risk-appetite-integrated two-tiered collective opinion generation framework for large scale group decision making. IEEE Trans Fuzzy Syst 30:5496–5510
Chen Z-S, Zhou M-D, Chin K-S, Darko A, Wang X-J, Pedrycz W (2023) Optimized decision support for BIM maturity assessment. Autom Constr 149:104808
Cheng Y-Q, Xu Z-D (2019) Credit risk evaluation of small enterprises based on revised ELECTRE III by theil index. Chin J Manag Sci 27:22–33
Cheng X, Sun Z, Bao W (2020) Study on credit risk of real estate industry based on genetic algorithm KMV model. J Phys Conf 1629:012072
Choi Y, Ye X, Zhao L, Luo AC (2016) Optimizing enterprise risk management: a literature review and critical analysis of the work of wu and olson. Ann Oper Res 237:281–300
D. Kerr, The ‘place’ of land in japan’s postwar development, and the dynamic of the (1980) real-estate ‘bubble’ and 1990s banking crisis. Environ Plann D Soc Space 20(2002):345–374
Derbali AMS (2012) The current models of credit portfolio management: a comparative theoretical analysis. Int J Manag Bus Res 2:271–292
Farhadinia B (2016) Multiple criteria decision-making methods with completely unknown weights in hesitant fuzzy linguistic term setting. Knowledge-Based Syst 93:135–144
Ferreira D, Rezende M (2007) Corporate strategy and information disclosure. RAND J Econ 38:164–184
Fung HG, Huang AG, Liu QW, Shen MX (2006) The development of the real estate industry in China. Chin Econ 39(1):84–102
Gao L, Xiao J (2021) Big data credit report in credit risk management of consumer finance. Wirel Commun Mob Comput 2021:1–7
Garmendia L, del Campo RG, Recasens J (2017) Partial orderings for hesitant fuzzy sets. Int J Approx Reason 84:159–167
Gaudêncio J, Mazany A, Schwarz C (2019) The impact of lending standards on default rates of residential real-estate loans, ECB Occasional Paper No. 220. ISBN 978-92-899-3685-9. Available at SSRN: https://ssrn.com/abstract=3356407
Gou X, Xu Z (2016) Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Inf Sci 372:407–427
Guo S, Zhao H (2017) Fuzzy best-worst multi-criteria decision-making method and its applications. Knowledge-Based Syst 121:23–31
Hesamian G, Shams M (2015) Measuring similarity and ordering based on hesitant fuzzy linguistic term sets. J Intel Fuzzy Syst 28:983–990
Huang X, Liu X, Ren Y (2018) Enterprise credit risk evaluation based on neural network algorithm. Cogn Syst Res 52:317–324
Isik G, Kaya I (2022) A novel hesitant fuzzy linguistic term sets approach and its application on acceptance sampling plans. Iran J Fuzzy Syst 19:175–192
Jin J, Yu Z, Mi C (2011) Commercial bank credit risk management based on grey incidence analysis. In: Proceedings of 2011 IEEE international conference on grey systems and intelligent services. IEEE, pp 534–538
Kanno M (2020) Credit risk assessment in real estate investment trusts: a perspective on blockholding and lending networks. Int Rev Financ Anal 71:101556
Kanno M (2022) Exploring risks in syndicated loan networks: evidence from real estate investment trusts. Econ Model 115:105953
Lee M-C (2012) Enterprise credit risk evaluation models: a review of current research trends. Int J Comput Appl 44:37–44
Li Y, Guo C (2022) The contagion of associated credit risk based on the real estate companies network. Proc Comput Sci 199:479–486
Li Y, Zhu D, Zhao J, Zheng X, Zhang L (2020) Effect of the housing purchase restriction policy on the Real Estate Market: Evidence from a typical suburb of Beijing, China. Land Use Policy 94:104528
Liao H, Xu Z, Zeng X-J (2014) Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Inf Sci 271:125–142
Liao H, Xu Z, Zeng X-J, Merigó JM (2015) Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets. Knowledge-Based Syst 76:127–138
Liao H, Qin R, Gao C, Wu X, Hafezalkotob A, Herrera F (2019) Score-hedlisf: a score function of hesitant fuzzy linguistic term set based on hesitant degrees and linguistic scale functions: An application to unbalanced hesitant fuzzy linguistic MULTIMOORA. Inf Fusi 48:39–54
Liow KH (2008) Financial crisis and Asian real estate securities market interdependence: some additional evidence. J Prop Res 25:127–155
Liu W (2021) Enterprise credit risk management using multicriteria decision-making. Math Probl Eng 2021:6191167
Liu H, Rodríguez RM (2014) A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making. Inf Sci 258:220–238
Liu P, You X (2017) Probabilistic linguistic TODIM approach for multiple attribute decision-making. Granul Comput 2:333–342
Locurcio M, Tajani F, Morano P, Anelli D, Manganelli B (2021) Credit risk management of property investments through multi-criteria indicators. Risks 9:106
Mah-Hui ML (2008) Old wine in new bottles: subprime mortgage crisis-causes and consequences. J Appl Res Account Financ 3:3–13
Medeiros Assef F, Arns Steiner MT (2020) Ten-year evolution on credit risk research: a systematic literature review approach and discussion. Ingenieria e Investigacion 40:50–71
Meng F, Chen X (2015) A hesitant fuzzy linguistic multi-granularity decision making model based on distance measures. J Intel Fuzzy Syst 28:1519–1531
Mou W, Wong W-K, McAleer M (2018) Financial credit risk evaluation based on core enterprise supply chains. Sustainability 10:3699
Nana Z, Xiujian W, Zhongqiu Z (2022) Game theory analysis on credit risk assessment in E-commerce. Inf Process Manag 59:102763
Pang Q, Wang H, Xu Z (2016) Probabilistic linguistic term sets in multi-attribute group decision making. Inf Sci 369:128–143
Rodríguez RM, Martínez L, Herrera F (2012) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20:109–119
Rodríguez RM, Martínez L, Herrera F (2013) A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf Sci 241:28–42
Salas V, Saurina J (2002) Credit risk in two institutional regimes: Spanish commercial and savings banks. J Financ Serv Res 22:203–224
Sansabas-Villalpando V, Pérez-Olguín IJC, Pérez-Domínguez LA, Rodríguez-Picón LA, Mendez-González LC (2019) CODAS HFLTS method to appraise organizational culture of innovation and complex technological changes environments. Sustainability 11:7045
Sun H, Guo M (2015) Credit risk assessment model of small and medium-sized enterprise based on logistic regression. In: 2015 IEEE international conference on industrial engineering and engineering management (IEEM), IEEE, pp 1714–1717
Tian XR, Jiang HD, Liu JL (2014) The research of financial risk warning model about real estate enterprises in China. Adv Mater Res 989:2625–2628
Torra V (2010) Hesitant fuzzy sets. Int J Intel Syst 25:529–539
Venkata Rao R, Patel BK (2010) Decision making in the manufacturing environment using an improved PROMETHEE method. Int J Prod Res 48:4665–4682
Wang G, Ma J (2012) A hybrid ensemble approach for enterprise credit risk assessment based on support vector machine. Expert Syst Appl 39:5325–5331
Wang J-J, Yang D-L (2007) Using a hybrid multi-criteria decision aid method for information systems outsourcing. Comput Operat Res 34:3691–3700
Wang F, Ding L, Yu H, Zhao Y (2020) Big data analytics on enterprise credit risk evaluation of e-business platform. Inf Syst e-Business Manag 18:311–350
Wei C, Zhao N, Tang X (2013) Operators and comparisons of hesitant fuzzy linguistic term sets. IEEE Trans Fuzzy Syst 22:575–585
Wu W (2017) Grey relational analysis method for group decision making in credit risk analysis. EURASIA J Math Sci Technol Educ 13:7913–7920
Xia Y, Long H, Li Z, Wang J (2022) Farmers’ credit risk assessment based on sustainable supply chain finance for green agriculture. Sustainability 14:12836
Xiong S-H, Chen Z-S, Chin K-S (2018) A novel MAGDM approach with proportional hesitant fuzzy sets. Int J Comput Intel Syst 11:256–271
Xiong S-H, Chen Z-S, Chiclana F, Chin K-S, Skibniewski MJ (2022) Proportional hesitant 2-tuple linguistic distance measurements and extended vikor method: Case study of evaluation and selection of green airport plans. Int J Intel Syst 37:4113–4162
Xiong S-H, Zhu C-Y, Chen Z-S, Deveci M, Chiclana F, Skibniewski MJ (2023) On extended power geometric operator for proportional hesitant fuzzy linguistic large-scale group decision-making. Inf Sci 632:637–663
Yang C-C, Ou S-L, Hsu L-C (2019) A hybrid multi-criteria decision-making model for evaluating companies’ green credit rating. Sustainability 11:1506
Yang Q, Li Y-L, Chin K-S (2019) Constructing novel operational laws and information measures for proportional hesitant fuzzy linguistic term sets with extension to PHFL-VIKOR for group decision making. Int J Comput Intel Syst 12:998–1018
Yang Y, Chu X, Pang R, Liu F, Yang P (2021) Identifying and predicting the credit risk of small and medium-sized enterprises in sustainable supply chain finance: evidence from China. Sustainability 13:5714
Yang Q, Chen Z-S, Chan CY, Pedrycz W, Martínez L, Skibniewski MJ (2022) Large-scale group decision-making for prioritizing engineering characteristics in quality function deployment under comparative linguistic environment. Appl Soft Comput 127:109359
Yao G, Hu X, Wang G (2022) A novel ensemble feature selection method by integrating multiple ranking information combined with an svm ensemble model for enterprise credit risk prediction in the supply chain. Expert Syst Appl 200:117002
Yumei W, Dandan L (2011) The financial risk and precaution of real estate enterprises. In: 2011 International conference of information technology, computer engineering and management sciences, vol 4. IEEE, pp 96–99
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning–i. Inf Sci 8:199–249
Zha Q, Kou G, Zhang H, Liang H, Chen X, Li C-C, Dong Y (2020) Opinion dynamics in finance and business: a literature review and research opportunities, Financial. Innovation 6:1–22
Zhang M, He Y, Zhou Z-F (2013) Study on the influence factors of high-tech enterprise credit risk: empirical evidence from china’s listed companies. Proc Comput Sci 17:901–910
Zhang T, Zhang W, Wei X, Haijing H (2018) Multiple instance learning for credit risk assessment with transaction data. Knowl-Bas Syst 161:65–77
Zhang H, Zhao S, Kou G, Li C-C, Dong Y, Herrera F (2020) An overview on feedback mechanisms with minimum adjustment or cost in consensus reaching in group decision making: Research paradigms and challenges. Inf Fus 60:65–79
Zhao Y, Zheng X (2018) Credit risk evaluation and management of commercial banks for small and medium sized enterprises. In: 2018 2nd international conference on education science and economic management (ICESEM 2018). Atlantis Press, pp 1028–1033
Zhu C, Zhan Y, Jia S (2010) Research on BP neural network evaluation model of credit risk of bank clients. In: 2010 International conference on management and service science. IEEE pp 1–5
Acknowledgements
The authors would like to express their gratitude to the EIC, AE, and three anonymous reviewers for their prompt, thorough, and insightful comments on this paper. The quality of the paper was significantly enhanced by the valuable comments and suggestions provided by the editors and reviewers.
Funding
This work was supported by the National Natural Science Foundation of China (Grant Nos. 72171182 and 72031009), the Spanish Ministry of Economy and Competitiveness through the Spanish National Research Project (Grant No. PGC2018-099402-B-I00), the Spanish postdoctoral fellowship program Ramon y Cajal (Grant No. RyC-2017-21978).
Author information
Authors and Affiliations
Contributions
ZSC: Conceptualization; Data collection, Funding acquisition, Project administration, Supervision, Writing—original draft, Writing—review and editing. JZ: Formal analysis, Data collection, Investigation, Methodology, and Writing—original draft. CYZ: Resources, Validation, Writing—review and editing. ZJW: Software, Writing—review and editing. SHX: Writing—review and editing. RMR: Writing—review and editing. LM: Writing—review and editing. MS: Writing—review and editing. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare having no known competing financial interests or personal relationships that could have appeared to influence the work reported in this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Continued from Table 6: Standard PHFLTS evaluation matrix
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) | \(c_{7}\) | \(c_{8}\) | ||
|---|---|---|---|---|---|---|---|---|---|
\(de_{2}\) | |||||||||
\(e_{1}\) | {(\(s_{4}\),1)} | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6)} | |
\(e_{2}\) | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1)} | {(\(s_{2}\),1)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6)} | |
\(e_{3}\) | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(e_{4}\) | {(\(s_{5}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{6}\),1)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6)} | |
\(e_{5}\) | {(\(s_{2}\),1)} | {(\(s_{3}\),1)} | {(\(s_{3}\),1)} | {(\(s_{2}\),1)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) | \(c_{7}\) | \(c_{8}\) | ||
|---|---|---|---|---|---|---|---|---|---|
\(de_{3}\) | |||||||||
\(e_{1}\) | {(\(s_{4}\),1)} | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | |
\(e_{2}\) | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1)} | {(\(s_{2}\),1)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6)} | |
\(e_{3}\) | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{3}\),1)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(e_{4}\) | {(\(s_{5}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{6}\),1)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | |
\(e_{5}\) | {(\(s_{2}\),1)} | {(\(s_{3}\),1)} | {(\(s_{3}\),1)} | {(\(s_{2}\),1)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) | \(c_{7}\) | \(c_{8}\) | ||
|---|---|---|---|---|---|---|---|---|---|
\(de_{4}\) | |||||||||
\(e_{1}\) | {(\(s_{4}\),1)} | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6)} | |
\(e_{2}\) | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1)} | {(\(s_{2}\),1)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6)} | |
\(e_{3}\) | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | |
\(e_{4}\) | {(\(s_{5}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{6}\),1)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | |
\(e_{5}\) | {(\(s_{2}\),1)} | {(\(s_{3}\),1)} | {(\(s_{3}\),1)} | {(\(s_{2}\),1)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) | \(c_{7}\) | \(c_{8}\) | ||
|---|---|---|---|---|---|---|---|---|---|
\(de_{5}\) | |||||||||
\(e_{1}\) | {(\(s_{4}\),1)} | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | |
\(e_{2}\) | {(\(s_{3}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1)} | {(\(s_{2}\),1)} | {(\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6), (\(s_{0}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6)} | |
\(e_{3}\) | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{3}\),1/6), (\(s_{3}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | |
\(e_{4}\) | {(\(s_{5}\),1)} | {(\(s_{4}\),1)} | {(\(s_{4}\),1)} | {(\(s_{6}\),1)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | |
\(e_{5}\) | {(\(s_{2}\),1)} | {(\(s_{3}\),1)} | {(\(s_{3}\),1)} | {(\(s_{2}\),1)} | {(\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{5}\),1/6), (\(s_{5}\),1/6), (\(s_{6}\),1/6), (\(s_{6}\),1/6)} | {(\(s_{1}\),1/6), (\(s_{1}\),1/6), (\(s_{2}\),1/6), (\(s_{2}\),1/6), (\(s_{3}\),1/6), (\(s_{3}\),1/6)} | {(\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6), (\(s_{4}\),1/6)} | |
Appendix B
Investigation on the Importance of Evaluation Indicators of “Credit Risk Assessment of Real Estate Development Enterprises—From the Perspective of Commercial Banks”
Solvency | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Adjust rate | |||||||
Cash flow liability ratio | |||||||
Asset liability ratio | |||||||
Interest coverage ratio | |||||||
Profitability | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Operating profit margin | |||||||
Return on total assets | |||||||
Return on net assets | |||||||
Net profit margin on sales | |||||||
Developing capacity | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Operating profit margin | |||||||
Capital accumulation rate | |||||||
Total asset growth rate | |||||||
Operating profit growth rate | |||||||
Operational capability | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Accounts Receivable Turnover | |||||||
Rate of stock turnover | |||||||
Turnover of total capital | |||||||
Velocity of liquid assets | |||||||
External environment and industry conditions | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Prosperity of the local real estate industry | |||||||
Local government support | |||||||
Monetary and credit policy | |||||||
Land tax policy | |||||||
Market position and competitive advantage | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Land bank | |||||||
Corporate reputation | |||||||
New project development strategy | |||||||
Regional market position | |||||||
Management level and operating conditions | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Management experience | |||||||
Develop building capabilities | |||||||
Sales area/Completed area | |||||||
Shareholder control | |||||||
Bank-enterprise relationship | |||||||
|---|---|---|---|---|---|---|---|
Very important | Important | A little important | Normal | Not very important | Not important | Very not important | |
Years of cooperation with the bank | |||||||
Enterprise historical credit rating | |||||||
Financing default rate | |||||||
Transaction Default Rate | |||||||
Appendix C
Xiong’s method
Step 1 Calculate the PHFLTS group decision matrix. The decision matrix is shown in Table 10.
Step 2 The weighting vector of the decision?making attribute is
Step 3 The distance between the comprehensive assessment value and the best value for the corresponding attribute is:
Step 4 Calculate the comprehensive evaluation value of each green airport plan as:
\({H_1} = 0.523;\,{H_2} = 0.798;\,{H_3} = 0.000;\,{H_4} = 0.332;\,{H_5} = 1.000.\)
Step 5 The ranking of the alternative green airport plans according to group utility is
\({e_3}> {e_4}> {e_1}> {e_2} > {e_5}.\)
Liu’s method
Step 1 Standardize the decision matrix. The decision matrix is shown in Table 11.
Step 2 Obtain attribute weight vector for \({c_1},{c_2},\cdots ,{c_8}\).
\(w_1^ * = 0.0923;\,w_2^ * = 0.0612;\,w_3^ * = 0.2381;\,w_4^ * = 0.1848; w_5^ * = 0.1083;\,w_6^ * = 0.1846;\,w_7^ * = 0.0750;\,w_8^ * = 0.0557.\)
Step 3 Obtain the relative weight \({w_{{{jr}}}}\) of the attribute \({C_r}\) to the reference \({C_j}\) by
\(w_{14}^ * = 0.387;\,w_{24}^ * = 0.257;\,w_{34}^ * = 1;\,w_{44}^ * = 0.776; w_{54}^ * = 0.455;\,w_{64}^ * = 0.775;\,w_{74}^ * = 0.315;\,w_{84}^ * = 0.234.\)
Step 4 Obtain the overall prospect value of the alternative.
\(\delta \left( {{x_1}} \right) = 0.627;\,\delta \left( {{x_2}} \right) = 0.498;\,\delta \left( {x3} \right) = 0.814;\,\delta \left( {{x_4}} \right) = 1.000;\,\delta \left( {{x_5}} \right) = 0.000.\)
Step 5 Sort the alternatives by their \(\delta \left( {{x_i}} \right)\). The biggerd \(\delta \left( {{x_i}} \right)\) is, the better alternative is, we get:
\({e_4}> {e_3}> {e_1}> {e_2} > {e_5}.\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, ZS., Zhou, J., Zhu, CY. et al. Prioritizing real estate enterprises based on credit risk assessment: an integrated multi-criteria group decision support framework. Financ Innov 9, 120 (2023). https://doi.org/10.1186/s40854-023-00517-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40854-023-00517-y