Abstract
Background
Advanced lightweight laminated composite shells are increasingly being used in modern aerospace structures to enhance their structural efficiency and performance. Such thin-walled structures are susceptible to buckling when subjected to static and dynamic compressive stresses. This paper reports on the numerical (finite element method (FEM)) study on buckling of carbon fibre-reinforced plastic (CFRP) layered composite cylinders under displacement and load-controlled static axial compression.
Methods
The effects of geometric properties, lamina lay-up, amplitudes of imperfection and parametric research of the shape (square, circular) and the dimensions (axial and circumferential sizes, diameter) of the opening on the strength of the cylinders under compression were studied. The measurement of imperfections on the cylindrical surface is achieved using the interpolation method and Fourier series.
Results
The analysis indicates that the critical load is sensitive to the circumferential size of the opening. The function (critical load-circumferential size of the opening) is linear for large openings and independent of the geometrical imperfections of the shell. However, for small openings, it is necessary to take into account the coupling between the initial geometrical imperfections and the openings.
Conclusions
The linear approach does not fit due to the importance of the evolution of the displacements near the openings. Also, it was shown that the buckling behaviour of thin composite cylindrical shells can be evaluated accurately via modelling to determine the imperfections and the material properties in FEM.
Similar content being viewed by others
Background
Composite cylindrical shells, used in weight sensitive structures such as aircraft fuselages, submarine hulls and space launch vehicles, are constantly subjected to membrane stresses. They are made efficient due to their high strength-to-weight and stiffness-to-weight ratios (Jones 1975). However, they are vulnerable to instabilities (buckling) when subjected to static or dynamic compressive stresses (Weaver 2000). Due to the fact that there are no substances that can satisfy all of these requirements, a substitute material should be determined, which in this case, was determined to be composites. In many industrial applications, shells are equipped with openings of various shapes, sizes and locations within the lateral surface. Cutouts in aerial structures such as aircraft and missiles are created to provide fuel or windows, and these structures are subjected to a combination of loads in plane, out of plane and shear during application. Due to the geometry and general loads of these structures, buckling is one of the most important failure criteria. A cylindrical shell under compression in the meridional direction can fail by overall buckling (global/Euler), local buckling or the material strength being exceeded. Various failure mechanisms of composite cylindrical shells, as affected by initial geometric imperfections, boundary conditions, lamina stacking sequence, anisotropic coupling effects, different cutouts and load eccentricity, were identified by Weaver (2000), in terms of laminate configurations and shell proportions. The buckling response of the shells is very sensitive to changes in boundary conditions. A significant discrepancy between theory and experiment is possible in the case of cylindrical shells, unless the boundary and loading conditions are accurately modelled, and the initial geometric imperfections are precisely taken into consideration in any theoretical model. Unlike shells made of isotropic materials, composite cylindrical shells could experience failure due to a stronger coupling between membranes and bending strains. The degradation of the buckling strength of composite laminates may also occur due to delamination, resulting from poor fabrication (Singer et al. 2002). While numerous experimental and theoretical studies are available on the buckling and post-buckling characteristics of isotropic shells, including the effects of geometric imperfections, relatively few have been reported on the buckling behaviour of laminated composite shells. Many experimental studies only involved curved composite laminate panels, mostly to avoid the high cost and complexities involved in the fabrication and testing of the full composite cylindrical shells (Singer et al. 2002). Analysis of post-buckling of shear-deformable anisotropic laminated cylindrical shells subjected to axial compression was studied by Li and Shen (2008). They found that there exists a compressive stress along with an associate shear stress and twisting when the shear-deformable anisotropic laminated cylindrical shell is subjected to axial compression. Tennyson (1975; 1968) reviewed, in detail, the theoretical and experimental investigations on buckling of laminated cylinders and experimented on the effect of small circular openings on shell buckling in the elastic range. This included the effects of material, geometric nonlinearities and boundary conditions on buckling strength of the shell, as well as correlation studies between theory and experiments. This work was followed by Starnes (1974) and Toda (1983), who tested shells with a larger range of opening diameters. Knodel and Schulz (1988) were the first to perform tests on steel cylinders with a large spectrum of imperfection (geometry, loading, material). This created the possibility for a statistical evaluation of the buckling strength of shells. Simultaneously, no physical understanding of the phenomenon was gained. The first numerical calculations on cylindrical shells with cutouts were reported by Almroth and Holmes (1972). Based on the available results, Samuelson and Eggwertz (1992) proposed a simple analytical description of the effect of the diameter of the hole on the buckling strength of shells. Similar investigations on filament wound glass-epoxy thick and thin cylinders (having various radius-to-thickness ratios) with circumferential and helical windings were described in the works of Card (1969), Tsai et al. (1965) and Hahn et al. (1994). Analysis of buckling and post-buckling of an anisotropic laminated thin cylindrical shell of finite length subjected to combined loading of external pressure and axial compression using the boundary layer theory presented by Li and Qiao (2015). They obtained the governing equations utilizing classic shell theory and von Karman-Donnell strain displacement relations. Axial compression tests on these shells revealed that for some winding angles, compressive load induces shear, resulting in new buckling failure modes. Shells having smaller radius-to-thickness ratios experienced catastrophic material failure under shear stress, while the large ones exhibited failure by the classical diamond-shaped shell buckling mode. The experimental buckling loads were about 65–85 % of the theoretical linear elastic buckling loads. Papers dealing with the effect of imperfection and cutouts in laminated composite structures (Leissa 1985) are available in the literature, based on Koiter’s (1970) imperfection shell theory. These indicate reasonably good estimates of the buckling loads for axial compression and bending loading. The effects of local geometric imperfections on the buckling and post-buckling of composite laminated cylindrical shells subjected to combined axial compression and uniform temperature rise using Reddy’s higher-order shear deformation shell theory and employing a von Karman type of kinematic nonlinearity investigated by Shen and Li (2002). The main difficulty in developing post-buckling theories, required to assess the imperfection sensitivity of composite cylindrical shells, is the lack of reliable imperfection data (Singer et al. 2002). In the 1970s and 1980s, several analytical and experimental studies were conducted on the buckling behaviour of composite cylinders fabricated from prepregs, considering the effect of assumed axisymmetric initial geometric imperfections having similar RMS value amplitudes, as measured in the works of Tennyson et al. (1971) and Tennyson and Hansen (1983). The discrepancy between the theory and experiments were about 20 %. Geier et al. (2002; 1991) also revealed that sensitivity to geometric and loading imperfections was influenced by the laminates’ lay-up and the fact that a strong interaction exists between shape and loading imperfections. In the absence of such data, approximate knockdown factors were used to determine the critical buckling load. In order to include a nonlinear, pre-buckling behaviour and imperfection sensitivity of general shells, an asymptotic analysis was performed using a Lyapunov-Schmidt-Koiter decomposition and an asymptotic expansion technique in the framework of the finite element method proposed by Kheyrkhahan and Peek (1999). Weaver et al. (2002) described experimental investigations on the advantage of using an anti-symmetric lay-up for a laminate over a symmetric laminate in spiral buckling modes. They also showed, based on Onoda’s solution (Onoda 1985), that in order to eliminate the anisotropic coupling effects, which lower the buckling loads, a laminate with a minimum of 48 plies is required. However, their study ignored the effect of initial imperfections. Developing design strategies based on the use of ring stiffeners as a way of preventing global buckling (i.e., buckling modes that have large displacements around the top edge) was introduced by Schmidt et al. (1998). Their design recommendations are supported by computational results for perfect cylindrical shells. Wullschleger and Meyer-Piening (2002) recommended, based on extensive buckling tests and analyses, that for the most reliable evaluation of the instability of imperfect carbon fibre-reinforced plastic (CFRP) cylinders, proper imperfection measurements, with a nodal resolution in the order of the mesh size used for the nonlinear pre-buckling analyses, are needed. Bisagni (2000) reported the correlation to be within 15–20 % between the numerical and experiments in composite shell buckling, using the measured imperfections in the finite element model. None of the above-mentioned researches provided sufficient information to develop a reliable physical model of the considered problem or to deduce a general understanding. Furthermore, the analysis of coupling geometrical imperfections with openings has not been carried out. In order to achieve this goal, a new study has been performed on composite cylindrical shells subjected to axial compressive load.
This paper presents details of a numerical (finite element method (FEM)) study on CFRP composite cylinders under load-controlled static axial loading conditions. It was shown that the buckling behaviour of thin composite cylindrical shells can be predicted by accurately measuring initial geometric imperfections and modelling it appropriately in FEM using the measured material properties. The numerical study involves carbon fibre composite cylinders made from eight layers of unidirectional carbon-epoxy prepregs, with a symmetric balanced lay-up of [0°/45°/−45°/0°], made using hand lay-up of prepregs. Details of a FEM based on parametric study on the effects of specimen geometry and different shapes (square, circular) and sizes of openings and lay-up sequences are included. One of the current objectives is to improve the understanding of the effect of cutouts with and without initial imperfection on the critical buckling load of thin cylindrical shells. Methods of manufacture, imperfection measurement using interpolation method and Fourier series, and the results of the investigation on a few CFRP cylinders under static axial compression are presented. It is shown that the buckling characteristics of thin composite cylindrical shells can be predicted to less than 5 % error.
Parametric study using FEM
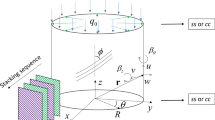
Some parametric studies are required to determine the effect of length (L)-to-mean radius (r) (L/r) ratio, mean radius-to-thickness (t) (r/t) ratio, and the lay-up sequence on the buckling strength of cylindrical shell. A carbon-epoxy composite cylindrical shell with a 300-mm inner diameter, 400-mm length, 1-mm thickness and a lay-up sequence of [0°/45°/45°/0°] was selected for the numerical study. The buckling behaviour of the CFRP cylindrical shells was studied numerically using ABAQUS (Version 6.10), a general-purpose finite element program with linear static capabilities (Onoda 1985). The complete shell geometry was modelled as required in composite laminates exhibiting coupling (Tennyson and Hansen 1983) using 4-noded S4R shell elements, with reduced integration. These shell elements have six degrees of freedom at each node and are free from shear locking and hour glass mode (Onoda 1985). In the model, all six degrees of freedom (three rotations and three translations) were arrested at one (supported) end of the shell, and at the other end (loaded), all the degrees of freedom, with the exception of the axial deformation degree of freedom, were arrested. The results of the parametric studies are given below. The properties of the prepreg, as supplied by the manufacturer, were used in the model (Table 1).
The effect of L/r and r/t ratios on the linear elastic buckling load
The different values of L/r (ranging from 0.5 to 3.0) and r/t ratios (ranging from 60 to 300) were chosen, keeping the inner diameter of the shell constant at 300 mm, and varying the length and the thickness of the shell. Four-layer balanced lay-up sequence (0°/45°/45°/0°) and a symmetric balanced lay-up (45°/−45°/−45°/45°) were chosen for the study. The variation of the linear elastic buckling stress (P cr/A) with respect to L/r and r/t ratios is shown in Fig. 1 for both lay-up sequences. It is seen that the influence of L/r for shells having L/r ≥1 on the buckling stress is hardly noticeable in each of the lay-up sequence, while in both lay-ups, the effect of radius-to-thickness (r/t) ratio is quite evident. This implies that the buckling strength of the shell depends mainly on the radius-to-thickness ratio and the lay-up sequence of lamina in the composite laminated shell in the range of parameters being studied. Hence, the choice of the length in the study can be freely made for L/r ≥1, while the thickness may be chosen based on the behaviour and strength requirements.
Linear elastic instability (eigenvalue) analysis
Linear elastic buckling loads of composite cylindrical shells can be evaluated by eigenvalue analysis. Generally, this analysis is carried out on a perfect model without taking into account the imperfections. However, in this study, the linear elastic instability analysis was carried out on models with and without imperfections to study its effect on the linear elastic buckling load. The buckling load predicted by this method on the model without imperfections normally gives an idea of the upper limit of the ultimate strength of the cylindrical shell and is usually much higher than that from tests and nonlinear FEA due to the imperfections. In a shell with imperfections, the actual ultimate load and the buckling mode may be considerably different from that obtained by the linear buckling analysis of model without imperfections. However, the linear instability load serves as a guideline nonlinear analysis and is computationally much simpler and faster than the nonlinear analysis. The eigenvalue analysis was conducted using the finite element code ABAQUS/Standard. Prior to the analysis, a mesh refinement study was performed to ensure that satisfactory convergence has been achieved in the model. From the study, a mesh with 13,320 elements, 180 along the circumferential direction, and 74 along the meridional direction, was chosen, as it was a good compromise between accuracy and CPU time. This model, and the previous model, with 170 elements along the circumferential direction and 69 elements along the meridional direction, had a convergence error of 0.4 %. The buckling load of shell obtained from the linear elastic analysis was 166.401 kN. The buckling loads and the mode shapes obtained from the linear elastic static buckling analysis without any initial geometric imperfections are shown in Fig. 2.
Measurement of imperfections
Before the strain gauges were mounted, the outer surface’s initial imperfections were measured (Fig. 3). For this purpose, the specimen was mounted on a turn table, which can be rotated about the axis of the shell. Externally, a 20-mm range linear variable differential transducer (LVDT), having a least count of 1/1000 mm, was mounted on a support for contact with the outer surface of the shell in the radial direction and is able to move up and down parallel to the meridional axis. The LVDT was connected to a data acquisition system, and the data was recorded at points on the outer surface of the shell at 5° apart in the circumferential direction, and 10 mm in the meridional direction. Using the data on radial variation of the surface, the mean cylinder diameter was determined to obtain the least square of the error. The measured coordinates of the specimen surface’s points were further modelled in MATLAB to reconstruct the real shape of the imperfections in the specimen. This is plotted for specimen 2 in Fig. 4. The shell’s surface opens out to a horizontal plane. The imperfection in the cylinder was taken as the radial distance between the best-fit cylinder and the actual shell surface, as measured in the work of Priyadarsini et al. (2012).
Variation of initial imperfection (−2 mm, 2 mm) of the outer surface of the cylindrical shell (Priyadarsini et al. 2012)
Apply imperfection
For the purpose of comparing the FEM results with the experimental values, they were superimposed onto the cylinder to create the actual geometry with imperfections for the analysis. A cylindrical coordinate system was employed, and the radial distance of the nodal coordinate was taken as R = r 0 + δ 0, where r is the mean radius of the best-fit cylinder, and δ 0 is the imperfection amplitude.
The imperfection shown in Fig. 4 must be applied to all nodes of cylindrical shell. First, the curves and the equations of curves 1 and 2 in Fig. 4 are obtained (Figs. 5 and 6). To obtain these curves and equations, the Fourier series is used; Fourier series equations are a form of Fortran code. Since nodes are in the Cartesian coordinates, it must be converted to cylindrical coordinates, with each node having one θ (0 ≤ θ ≤ 360). Substituting θ into the equations resulted in two series of imperfections. By interpolating these two imperfections, the imperfections of the other nodes were obtained. The expressions for applying the imperfections are:
Imperfection, as shown in Fig. 4, is between −2 and 2 mm. Applying imperfection has a great influence on the shape of buckling of cylindrical shell. Figure 7 clearly shows the differences between these two states.
As expected, the buckling loads of the composite cylindrical shells decreases as the amplitude of the imperfection increases, and this rate of decrease is more for changes in imperfection amplitudes at lower values (Fig. 8).
The following observations are made from the comparison of the analyses and experiments of the specimen in the work of Priyadarsini et al. (2012). The interpolation method and approximation of curves of Figs. 5 and 6 results in some errors but is nevertheless in good agreement with the results of the reference.
Validation
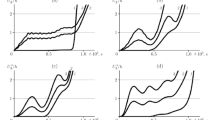
The results from the present ABAQUS models were compared with those from the experimental and numerical investigations reported by Priyadarsini, R. S et al. (2012). It can be seen that the results of the present study, as shown in Figs. 9 and 10, are comparable with those of Priyadarsini, R. S et al. Hence, the present finite element method was regarded as being suitable.
Comparison of the buckling of composite cylindrical shell (with imperfection) with the reference (Priyadarsini et al. 2012)
Comparison of the buckling of composite cylindrical shell (with imperfection) with the reference (Priyadarsini et al. 2012)
Influence of lay-up sequence on the elastic buckling load and buckling mode
A parametric study was carried out to determine the buckling mode shapes corresponding to different lay-up sequences with and without imperfections, and also the lay-up corresponding to the maximum linear elastic buckling load of a cylindrical shell, of 300-mm inner diameter, 400-mm length and 1-mm thickness (made of 8 unidirectional prepregs). The lay-up sequences chosen for the study and the corresponding linear elastic buckling loads obtained are shown in Table 2. The fibre orientations are measured from the meridional direction of the shell, while the stacking sequence was ordered from the innermost to the outermost layers.
It is seen that even for the overall dimensions, the length and thickness remained similar, and the variation in the lay-up sequence of the prepregs could have lead to considerable variation in the elastic buckling load and buckling modes (Figs. 11 and 12). Most of the specimens experienced spiral mode of buckling, except the specimen with the anti-symmetric lay-up, which experienced the axisymmetric buckling mode and the specimen having orthogonal lay-up, which experienced the diamond-shaped buckling mode. The shell have a lay-up of (0°/0°/30°/−30°/−30°/30°/0°/0°), with fibres oriented closer to the meridional direction, which lacks the largest elastic buckling strength. It was also seen that the anisotropy factor increases the pitch of the spiral buckling mode.
Effect of circular and square cutout on axial buckling
In many industrial applications such as aircraft, missiles, reservoirs, pipelines, automobiles and some submarine structures, shells are equipped with openings of various shapes, sizes and locations within the lateral surface. These components, during their lifetime, may buckle under compressive axial loads. In addition, they might have some discontinuities, such as cutouts. These discontinuities can influence the stability of the structures. The objective of this section is to improve the understanding of the effect of circular and square cutouts on the critical buckling load of thin cylindrical shells.
Square openings
For a given dimension of the square and centred opening under consideration, the force-displacement characteristic of the shell remains linear up to the first local buckling (LB), which occurs in the vicinity of a contour of the opening. After this point, the behaviour is linear and stable, with a reduced slope until a global buckling (collapse buckling, CB) takes place, which involves the entire shell. A square cutout in a cylindrical shell subjected to axial compression reduces the first local buckling load and the global collapse buckling load (Fig. 11). In the pre-buckling range prior to the first local buckling, large radial displacements develop near the edges of the openings, particularly around the rims of the hole.
Circular openings
A cylindrical shell with a circular opening of a diameter equal to the width of the square opening develops similar collapse buckling load (Fig. 12). Simultaneously, the first load buckling was not observed in this case. The results indicate that the occurrence of the first local buckling is preceded by a redistribution of stresses, due to stress concentration at the corners of the square cutouts. For this type of opening, the effect of a small hole dimension was also analysed. It was confirmed that very small holes do not cause any appreciable change in the critical load.
The effect of imperfections must be coupled with a cutout. Simultaneously, for very small openings, their size is unimportant compared with a significant imperfection sensitivity of cylinders subjected to compressive loads. In the case of small openings, it is necessary to include a coupling between the geometrical imperfection and presence of an opening in the analysis. In the range of moderately large openings, the existence of geometrical imperfections of any size is negligible (Figs. 13 and 14).
Conclusions
This work deals with the numerical (FEM) study on the buckling behaviour of thin CFRP cylindrical shells under static axial compression. It was shown that the ultimate strength is affected by the lay-up sequence, radius-to-thickness ratio, geometric imperfections and any kinds of opening. The effect of the ratio of the length-to-radius is negligible. Also, the effect of a hole on the critical load of a cylindrical shell with an opening under axial compression is studied; the behaviour shows two large zones: for small openings, where there is a coupling between the geometrical imperfection and the presence of an opening, and for a moderately larger opening, the existence of geometrical imperfections of any size can be neglected. The results of this work should be useful for future designs of aerospace shell structures possessing cutouts. These will assist the designers in comparing the effects of changes in geometrical dimensions and material properties on the buckling response of shells without the expense of experimental testing.
The results from this study indicated that numerical modelling can be used to evaluate the buckling strength accurately, provided the material properties and initial imperfections are properly modelled.
Abbreviations
- P :
-
Linear elastic buckling load
- P cr :
-
Ultimate strength at failure
- A :
-
Area of cross section of the cylinder
- U :
-
Amplitude of initial imperfections (corresponding to first buckling mode)
- L :
-
Total free length of cylinder between supports
References
Almroth, BO, & Holmes, AM. (1972). Buckling of shells with cutouts. Experimental and analysis. Journal of Solids Structures, 8, 1057–1566.
Bisagni, C. (2000). Numerical analysis and experimental correlation of composite shell buckling and post-buckling. Composite: Part B, 31, 655–667.
Card, MF. (1969). The sensitivity of buckling of axially compressed fibre-reinforced cylindrical shells to small geometric imperfections, NASA TMX-61914.
B. Geier, H. Klein and R. Zimmermann, Buckling tests with axially compressed unstiffened cylindrical shells made from CFRP, in: Buckling of shell structures, on land, in the sea and in the air, Proceedings of the International Conference, J.F. Jullien, ed., INSA Lyon, Elsevier Applied Science, London, New York (September 1991), pp. 498-507
Geier, B, Meyer-Piening, HR, & Zimmermann, R. (2002). On the influence of laminate stacking on buckling of composite cylindrical shells subjected to axial compression. Composite Structures, 55, 467–474.
Hahn, HT, Jensen, DW, Claus, SJ, & Hipp, PA. (1994). Structural design criteria for filament wound composite shells, NASA CR-195125.
Jones, RM. (1975). Mechanics of composite materials (McGraw hill).
Kheyrkhahan, M, & Peek, R. (1999). Postbuckling analysis and imperfection sensitivity of general shells by the finite element method. International journal of solids and structures, 36(18), 2641–2681.
Knodel, P, & Schulz, U. (1988). Stabilite´de chemine´es d’acier a` ouvertures dans les tuyaux. Stahlbau (Der), 57(1), 13–21.
Koiter, WT. (1970). On the stability of elastic equilibrium. Delft: Doctoral Thesis, 1945. English Translation: AFFDL-TR-70 25.
Leissa, AW. (1985). Buckling of laminated composite plates and shell panels, Report AFWAL-TR-85-3069 (AF Wright Aeronautical Laboratories).
Li, Z-M, & Qiao, P. (2015). Buckling and postbuckling of anisotropic laminated cylindrical shells under combined external pressure and axial compression in thermal environments. Composite Structures, 119, 709–726.
Li, Z-M, & Shen, H-S. (2008). Postbuckling of shear-deformable anisotropic laminated cylindrical shells under axial compression. International Journal of Structural Stability and Dynamics, 8(03), 389–414.
Onoda, J. (1985). Optimal laminate configuration of cylindrical shells for axial buckling. AIAA Journal, 23(7), 1093.
Priyadarsini, R. S., V. Kalyanaraman, and S. M. Srinivasan (2012). Numerical and experimental study of buckling of advanced fiber composite cylinders under axial compression. International Journal of Structural Stability and Dynamics 12, no. 04:401–423.
Samuelson, AL, & Eggwertz, S. (1992). Shell stability handbook (p. 278). London: Elsevier Applied Science.
Schmidt, H, Binder, B, & Lange, H. (1998). Postbuckling strength design of open thin-walled cylindrical tanks under wind load. Thin-Walled Structures, 31(1), 203–220.
Shen, H-S, & Li, QS. (2002). Thermomechanical postbuckling of shear deformable laminated cylindrical shells with local geometric imperfections. International Journal of Solids and Structures, 39(17), 4525–4542.
Singer, J, Arbocz, J, & Weller, T. (2002). Buckling experiments, experimental methods in buckling of thin-walled structures, volume 2, shells, built-up structures, composites and additional topics. Hoboken, NJ, USA: John-Wiley.
Starnes, JH. (1974). The effects of cutouts on the buckling of thin shells. In YC Fung & EE Sechler (Eds.), Thin shell structures (pp. 289–304). Englewood Cliffs, New York: Prentice Hall, Inc.
Tennyson RC (1968). The effect of unreinforced circular cutouts on the buckling of circular cylindrical shells under axial compression. Journal of Manufacturing Science and Engineering 90, no. 4:541–546.
R.C. Tennyson (1975). Buckling of laminated composite cylinders: a review. Composites, 17-24.
Tennyson, RC, & Hansen, JS. (1983). Optimum design for buckling of laminated cylinders. In JMT Thompson & GW Hunt (Eds.), Collapse: the buckling of structures in theory and practice (pp. 409–429). Cambridge: Cambridge University Press.
R.C. Tennyson, K.H. Chan, and D.B. Muggeridge (1971). The effect of axisymmetric shape imperfections on the buckling of laminated anisotropic circular cylinders. Transactions of the Canadian Aeronautics and Space Institute, 4(2):131–139.
Toda, S. (1983). Buckling of cylinders with cutouts under axial compression. Journal of Experimental Mechanics, 3, 414–417.
Tsai, J, Feldman, A, & Stang, DA. (1965). The buckling strength of filament wound cylinders under axial compression, NASA, CR-266.
Weaver, PM. (2000). Design of laminated composite shells under axial compression. Composites Part B, 31(8), 669–679.
Weaver, PM, Driesen, JR, & Roberts, P. (2002). Anisotropic effects in the compression buckling of laminated composite cylindrical shells. Composites Science and Technology, 62, 91–105.
Wullschleger, L, & Meyer-Piening, HR. (2002). Buckling of geometrically imperfect cylindrical shells—definition of a buckling load. International Journal of Nonlinear Mechanics, 37, 645–657.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AS and BB modeled and analyzed the studies, participated in the sequence alignment and drafted the manuscript. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shahrjerdi, A., Bahramibabamiri, B. The effect of different geometrical imperfection of buckling of composite cylindrical shells subjected to axial loading. Int J Mech Mater Eng 10, 6 (2015). https://doi.org/10.1186/s40712-015-0033-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40712-015-0033-z