Introduction

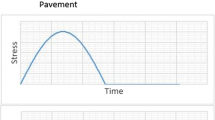
Excess pore water pressure generation in a subgrade soil layer is identified as one of the key parameters affecting the behavior and long-term performance of any sub-structure (railway or pavement) subjected to cyclic traffic loading. By understanding the mechanisms behind excess pore water pressure generation, engineers and designers can develop improved design practices that take these effects into account and help to prevent or mitigate its potential impacts. It should be noted that when a saturated subgrade is subjected to cyclic loading, excess pore water pressure accumulation can be generated with time, and eventually, it could lead to migration of particles into the overlying granular layers [1, 2, 17, 45]. The migration of subgrade soil to the upper layers would lead to clogging of pores in the contaminated coarse aggregate layers and a reduction in the drainage capacity of the upper layers [29, 30]. This condition would lead build-up of excess pore water pressure when a saturated subgrade is subjected to cyclic loading. The build-up of excess pore water pressure under cyclic traffic loadings seem to be similar to the rapidly increasing excess pore water pressure initiated during an earthquake [24, 26]. As the drainage capability is decreased under continuous cyclic loading, excess pore water pressure does not have enough time to dissipate and eventually leading the build-up of excess pore water pressure [3, 15, 16, 43, 46, 59, 60]. However, the build-up of excess pore water pressure under cyclic traffic loadings could result in loss of strength and stiffness of the subgrade soil and eventually reduce the stability of pavements [24, 26, 54]. Cedergren [10] indicated that poor and inadequate drainage condition induced by subgrade particles clogging the sub-base layer is a primary reason for the early deterioration of pavement. Indraratna et al. [25] mentioned that the migration of fine particles to the upper ballast layer could cause differential settlement and, eventually, frequently required track maintenance or upgrading. For example, the maintenance could cost hundreds of millions of dollars every year in the United States [24, 26]. Christopher et al. [11] and Holtz et al. [21] reported that the development of pore water pressure at the subgrade-subbase interface of pavement would lead to erosion and subsequent movement of soil particles into the subbase. Trani and Indraratna [56] reported that excess pore water pressure applies a vertical seepage force on fine soil particles of a subgrade and hence reduces the effective stress and consequently shear strength of the overlying layers (sub-ballast or ballast). Therefore, it is crucial to understand the mechanisms of excess pore water pressure generated in subgrades for both designing and further maintenance purposes. To date, there have been a number of studies addressing the pore water pressure generation in subgrade soils under cyclic traffic loading [15, 19, 23, 24, 26, 37, 39, 40, 48, 51, 59, 60, 62, 64]. In the study by Sangrey et al. [51], a series of designed tests were performed to examine the behavior of saturated clay soil under repeated loading. The cyclic strain and excess pore water pressure were measured at every stage of the tests. The test results provided in-depth knowledge into cyclic responses (strain and excess pore water pressure) of saturated clayey soil under repeated loading. However, the very slow rate of cyclic loading, i.e., ten hours per cycle, in their study would not be appropriate to the contemporary traffic speed. Yasuhara et al. [62] performed a series of stress-controlled cyclic triaxial tests on a remolded soft marine clay to investigate the effect of frequency on the generation of excess pore water pressure. Their results indicated that the generation of excess pore water pressure in the used soft marine clay was more predominant at a higher frequency of the cyclic loading. Loh [39] studied the cyclic responses (strain and excess pore water pressure) of a typical fine-grained reconstituted kaolinite clay soil, simulating the characteristic subgrade responses under the passing axles/wheel load. An insight into the effects of consolidated states, stress history, and cyclic stress ratios on the cyclic response of the kaolinite clay soil was provided. However, the reconstituted kaolin clay used in his study is known as non-structured clay. The cyclic responses obtained from the experimental program would not be the same as those from other clay soils. In the study by Wang et al. [59, 60], a series of high cycle (50,000 cycles) triaxial tests were performed on a soft marine clay under various cyclic stress ratios and three different confining pressures. The purpose of their study was to investigate the development of strain and excess pore water pressure with a large number of cycles. Their results indicated that the development of excess pore water pressures depended on the cyclic stress ratio (CSR) values. In addition, a relationship between strain and excess pore water pressure was proposed. Lei et al. [37] attempted to study the cyclic behavior of ultrasoft soil under cyclic loading. They found that the frequency had no significant effect on the excess pore pressure of ultrasoft soil. The obtained curves of excess pore pressure at different frequencies were similar. The excess pore pressure increased rapidly at an early stage and then tended to be stabilized as the number of cycles increased. More recently, research on the generation of pore water pressure under cyclic loading have been reported by Ichii and Mikami [23], Gluchowski et al. [19], and Indraratna et al. [24, 26]. While Ichii and Mikami [23] used torsional hollow cylinder cyclic shearing tests for clay and sand samples, Gluchowski et al. [19] and Indraratna et al. [24, 26] both employed cyclic undrained triaxial tests for cohesive soil and low-plastic soil, respectively. Interestingly, the same finding observed from the three studies was that the generation of excess pore pressure related to the development of axial strain due to cyclic loading. This relationship is influenced by factors such as effective consolidation stress [19, 23], soil properties [23, 24, 26], and loading characteristics [24, 26]. Special interest in the factors affecting the cyclic pore water pressure generation in a subgrade soil have also been addressed in the literature. For example, frequency [24, 26, 40, 44, 48, 62, 64], density, CSR [12, 14, 49] and drainage condition [4, 64]. Most abovementioned studies mainly focused on the excess pore water pressure generation in soft fine-grained subgrade soils which contain a high proportion of fine particles, such as silty clay or clay. These soils are often referred to as “cohesive” soils (e.g., cohesive and plastic soils). In addition, the natural water content of these soils is relatively high; close to the liquid limit. In practice, however, some other fine granular materials, such as non-cohesive and non-plastic soils (e.g., silty sand, silt, tailings) would also be involved in the generation of excess pore water pressure and migration of fine particles under cyclic loading. Therefore, this study focuses on the excess pore water pressure generated in fine granular materials under cyclic loading. Figure 1 shows two examples of mud pumping phenomenon involved the excess pore water pressure generation in fine granular materials, i.e., non-plastic silty sand [55] (Fig. 1a) and tailings [31] (Fig. 1b).

Fig. 1
figure 1

Mud pumping phenomenon under cyclic traffic loading: (railway track (Trafikverket) and b porous piers in a tailings dam (Boliden)

Full size image

In this research, a series of undrained cyclic triaxial tests were performed to broaden the understanding of the excess pore water pressure in fine granular materials (railway sand and tailings). The cyclic response of excess pore water pressure in this study was evaluated and compared to that from the literature. A relationship between excess pore water pressure and cyclic axial strain of the fine granular materials was then discovered.

Experimental program

Materials

Two types of fine granular materials were selected for this study. The first one was a sandy soil, as a granular material that originated from a railway embankment (Inlandsbanans sträckning), in Sweden. The second one was tailings, as an artificial fine granular material taken from a tailings dam in Kiruna, Sweden. The tests were carried out on reconstituted samples. Both materials, after taken from the field, were first dried in an oven at 105 ℃ until a constant weight was attained. The railway sand was then passed through a 1.0-mm size sieve to eliminate unnecessary large particles and approach the particle size of fine granular materials. The physical properties of railway sand and tailings are tabulated in Table 1. The particle size distribution curves of the railway sand and tailings are shown in Fig. 2.

Table 1 Physical properties of the granular materials used in this study
Full size table
Fig. 2
figure 2

Particle size distribution curves of the fine granular materials used in this study

Full size image

Sample preparation

Sample preparation is extremely important for cyclic triaxial tests since the method of specimen preparation has a significant effect upon the cyclic resistance measured [34, 42, 58]. All samples in this study were introduced into specimens by the tamping method following the procedure of ASTM D 5311. The materials with optimum water contents were compacted into five layers inside a manufactured mold (tailings samples) or standard triaxial mold (railway sand samples). For tailings specimens, the manufactured mold (50 × 100 mm) was used for the reconstitution. In this study, the non-linear undercompaction method proposed by Jiang et al. [28], was applied to tailings samples to ensure the homogeneity of specimens. The tailings sample preparation using the non-linear undercompaction method can be found in detail in the study by the author [13]. Based on the undercompaction method, a designated portion for each layer is determined before specimen preparation. This method has been successfully employed in many previous research studies as it could consider the factor that the bottom layers also absorb the compaction energy from the layers above [8, 24, 26, 33,34,35, 53]. For railway sand samples, sand was mounted on the base of the cyclic triaxial apparatus and supported by the standard triaxial mold (the split mold) since it was unable to stand on during specimen extrusion. Pre-determined quantities of sand were spread carefully and sequentially in five layers into the mold. Each layer was densified by tamping with a steel rod that was marked for five designated portions. In order to obtain uniform density within the entire height of the sample, the number of regular hand tamping for each layer was kept consistently during the preparation. The top of the sample was then covered with filter paper, and a porous stone was placed on top of the filter paper. By using the above technique, both railway sand and tailings samples with different target dry densities were prepared.

Testing procedure

After the successful sample preparation, all specimens were tested using a servo-hydraulic dynamic triaxial system consisting of a hydraulic pump, a hydraulically controlled piston and sensors to measure load, LVDT for displacement measurement, pressure controllers, data acquisition system, and a full cell. Once the cell with a mounted sample was assembled and placed in the loading frame, water was used to fill the cell. This was then followed by the cell de-air with three de-air valves on the top of the cell. Afterward, the hydraulic piston was manually lowered to approximately 2 mm above the internal loading piston. In order to keep the vertical alignment between the two rods, an exterior coupler was then used to connect the hydraulic piston to the internal loading rod. With the system assembled, an initial condition was applied to the entire system with a cell pressure of 30 kPa, a back pressure of 20 kPa to stabilize the specimen inside the cell. For all samples in this study, the minimum back pressure of 600 kPa was used and applied to assist the specimen in reaching full saturation, i.e., targeted to a minimum B-value of 0.93. The effective stress of 10 kPa was applied during the saturation. The samples were then consolidated to the low effective confining pressure of 30 kPa, representing the condition of the shallow tailings layers under the pier or subgrade layers under the railway embankment. This stress level, i.e., low effective confining pressure of 30 kPa, used in this study was in line with previous research works on railway sub-structures [18, 27, 57]. It should be noted that the actual magnitude of effective confining pressure is dependent on the wheel load, and the thickness of the overlying layers. However, the effects of effective confining pressure on the cyclic response of excess pore water pressure were not considered in this study. Eventually, all samples were sheared cyclically by using the one-way stress-controlled loading scheme under various cyclic stress ratios (CSR)

$$ CSR = \frac{{q_{cyc} }}{{2 \times \sigma_{c}^{,} }} $$
(1)

where qcyc is the amplitude of cyclic stress (see Fig. 3) and σc’ is the effective confining pressure. It should be noted that this stress-controlled loading was widely used in many previous studies on cyclic characteristics of soils under traffic loading [6, 9, 20, 24, 26, 39, 41]. During the cyclic loading phase, samples were subjected to axial loading and unloading under the constant cell pressure condition. Drainage was closed and variation of pore water pressure was measured by a pore pressure transducer installed at the bottom of the cell. The data was then logged by the data acquisition system at a regular interval within each cycle. The state of stress during cyclic loading used for all samples in this study can be seen in Fig. 3, where qcyc and f are applied cyclic deviatoric stress and frequency, respectively.

Fig. 3
figure 3

State of stress during cyclic loading (compression)

Full size image

The procedures in the ASTM Standards (D 5311) were used for the performance of the cyclic triaxial tests in this study. The experimental program is presented in detail in Table 2. The frequency f = 1 Hz (one cycle per second) was chosen in this study. This frequency simulates the cyclic nature of stress near subgrade surface due to traffic loading traveling at a low speed of 45 km/h [24, 26, 39]. Wheeler et al. [61] observed the pumping of subgrade fines with train speeds as low as 40 km/h. Knutsson and Laue [31] reported the pumping of tailings at the surface of a porous pier where the speed of dump haulers is typically limited to 40 km/h. The cyclic triaxial tests were terminated after reaching either 5% cyclic axial strain or 1000 cycles for tailings series and 3000 cycles for railway sand series. It should be noted that the number and speed of dump haulers driving on the porous pier are limited during construction. In addition, the 750 m long heavy-haul trains with 68 wagons [38], assuming a four-axle wagon, can generate 272 loading cycles with every passage. The selected 3000 cycles for railway sand series simulated approximately ten continuous passes of the train in one day, but without any rest period. As reported by LKAB [38], there are ten passes of the train traveling on the ore Railway (Kiruna to Narvik or Kiruna to Luleå) every day. It should be noted that the excess pore water pressure would be dissipated during the rest periods in between each pass of the train [50].

Table 2 An experimental program for all undrained cyclic triaxial tests
Full size table

Testing program

Table 2 presents the experimental program in detail consisting of two series of tests, so-called tailings series and railway sand series. With these series, the roles of material types (tailings and railway sand), density conditions (or relative compactions), and loading characteristics (applied cyclic stress) are addressed and investigated. Each test in Table 2 is given a name which is a set of characters containing alphanumeric characters. The labels ‘‘Ta” and ‘‘RaSa” indicate tailings and railway sand, respectively. CYC refers to the type of test performed (undrained cyclic triaxial test). The second set of characters signifies the level of applied cyclic stress ratio and relative density, e.g., 0.12(84) indicates the applied cyclic stress ratio of 0.12 and the relative compaction of 84%.

Results and discussion

Excess pore water pressure generation in tailings

The excess pore water pressure (PWP) response of tailings samples under undrained cyclic loading is presented as residual PWP ratios against number of cycles. The idea of the residual PWP, i.e., the troughs of each cycle, is presented in Fig. 4. The excess PWP response is represented by the excess pore water pressure ratios (ru), which is commonly known as the ratio between pore pressure development and the initial effective stress. Figure 5 shows excess PWP response of tailings samples under undrained cyclic triaxial loading. As can be observed, excess PWP increased with respect to the number of cycles. However, the excess PWP response was significantly dependent on the CSR. When CSR was small, i.e., CSR = 0.12 for Ta_CYC0.12(84) and CSR = 0.25 for Ta_CYC0.25(90), excess pore water pressure ratios (ru) increased and reached 0.39 and 0.15, respectively, after 1000 cycles. However, when CSR was higher, i.e., CSR > 0.15 for tailings samples with RC = 84% and CSR > 0.40 for tailings samples with RC = 90%, excess pore water pressure ratios (ru) grew rapidly up to 1.0 at an early stage (samples reached a failure state after a certain number of cycles). In this sense, the critical CSR values (CSRru=1.0) for tailings samples with RC = 84% and RC = 90% were found to be 0.15 and 0.40. It should be noted that ru = 1.0 is traditionally used for the evaluation of the pore pressure response (when liquefaction) during cyclic loading [5, 52, 63]. Apart from CSR, the excess PWP response of tailings was also affected by relative compaction. The samples with higher relative compaction tended to resist cyclic loads better than those with lower relative compaction under the same loading conditions. Take CSR = 0.25 as an example, while the excess pore water pressure ratio of Ta_CYC0.25(84) increased rapidly and reached 1.0 after only 95 cycles (failure), that of Ta_CYC0.25(90) increased slightly and reached only 0.15 after 1000 cycles (not failure). Take CSR = 0.40 as another example; the excess pore water pressure ratios of both Ta_CYC0.40(84) and Ta_CYC0.40(90) reached 1.0. However, in order to reach ru = 1.0, the sample with higher relative compaction, i.e., Ta_CYC0.40(90) took more cycles (77 cycles) than sample with lower relative compaction, i.e., Ta_CYC0.40(84) (18 cycles).

Fig. 4
figure 4

Development of residual excess pore water pressure ratio of Ta_CYC0.15(84), Ta_CYC0.30(84)

Full size image
Fig. 5
figure 5

Excess PWP response under undrained cyclic triaxial loading: a tailings samples with relative compaction 84%; b tailings samples with relative compaction 90%

Full size image

Figure 6 illustrates the relationship between the excess pore water pressure ratio, ru, and the normalized number of cycles, N, by the number of cycles at ru = 1 (Nru=1). For reference, data in this study were compared to those from the literature. Note that Zhang et al. [63] proposed a model to predict cyclic pore pressure response, based on various undrained cyclic triaxial tests of tailings materials, which is expressed as

$$ r_{u} = \frac{4}{\pi }\arctan \left( {\frac{N}{{N_{{r_{u} = 1}} }}} \right)^{1/2\theta } $$
(2)

where θ is an empirical constant determined from laboratory testing. As shown, most data in this study fell into the pore water pressure envelope by Zhang et al. [63] with the optimal values of θ = 0.2 (lower bound) and θ = 0.6 (upper bound). The relationship between excess PWP ratio (ru) and the normalised number of cycles (N) by the number of cycles at ru = 1 is also in line with previous studies on excess PWP of tailings materials under cyclic loading reported by Hu et al. [22].

Fig. 6
figure 6

Relationship between excess PWP ratio (ru) and the normalised number of cycles (N) by the number of cycles at ru = 1

Full size image

Excess pore water pressure generation in railway sand

Figure 7 shows the excess PWP response under undrained cyclic triaxial loading of all railway sand samples. Note that data in Fig. 7 were only plotted until ru = 1.0 as the soil sample failure or liquefaction. As a result, a similar trend is observed in the cyclic strain response of the railway sand samples to that of tailings samples, i.e., the excess PWP accumulation with respect to the number of cycles and the dependency of cyclic PWP response on the CSR. Despite the variation in types of materials and density conditions, the similarity of the curves appears to indicate the fundamental cyclic PWP response of granular materials. At low CSR values, i.e., CSR = 0.20 for RaSa_CYC0.20(84) and CSR = 0.40 for RaSa_CYC0.40(90), excess pore water pressure ratios (ru) increased and reached 0.25 and 0.74 after 3000 cycles and 1148 cycles, respectively. When CSR was higher, i.e., CSR > 0.40 for railway sand samples with RC = 84% and CSR > 0.85 for railway sand samples with RC = 90%, excess pore water pressure ratios turned into a highly unstable state (i.e., sharp increase) at earlier cycles. The critical CSR values (CSRru=1.0) of railway sand samples were higher than those of tailings samples. In this sense, railway sand samples tended to resist cyclic loads better than tailings samples. This is mainly due to the much finer grain size of tailings than that of railway sand. It should be noted that, in addition to particle size, the shape of particles also plays a crucial role in influencing the cyclic response but it has not investigated in this study. In general, soil composed of angular-shaped particles tends to possess higher shear strength due to their strong interlocking with rounded particles. Furthermore, angular particles generally exhibit lower susceptibility to deformation under cyclic loading as they are less compressible than rounded particles. In contrast, rounded particles typically have smoother surfaces that facilitate easier sliding past each other, resulting in lower shear strength of the soil. Additionally, they are generally more prone to deformation under cyclic loading due to their higher compressibility compared to angular particles.

Fig. 7
figure 7

Excess PWP response under undrained cyclic triaxial loading: a railway sand samples with relative compaction 84%; b railway sand samples with relative compaction 90%

Full size image

Afterward, all data sets in this study were also compared to those from the cyclic pore pressure predictive model proposed by Seed et al. [52] (Fig. 8), which is expressed as

$$ r_{u} = \frac{2}{\pi }\arcsin \left( {\frac{N}{{N_{{r_{u} = 1}} }}} \right)^{1/2\theta } $$
(3)

where θ is an empirical constant determined from laboratory testing, and θ = 0.70 is the average value for sand. As shown, most data in this study met the pore water pressure envelope by Seed et al. [52] with the empirical coefficient of θ = 0.3 (lower bound) and θ = 1.1 (upper bound). A similar trend can also be found in the previous studies on the cyclic PWP response on sandy soils [7, 32, 36, 47].

Fig. 8
figure 8

Relationship between excess PWP ratio (ru) and the normalised number of cycles (N) by the number of cycles at ru = 1

Full size image

Relationship between excess pore water pressure and cyclic axial strain from undrained cyclic triaxial tests

The relationship between excess pore water pressure and cyclic axial strain can be established based on excess pore water pressure and cyclic axial strain responses of both tailings and railway sand. For this purpose, the excess pore water pressure generation of both these granular materials should be looked at more closely at different stages. As discussed earlier, the excess pore water pressure response was evaluated based on plotting data in terms of the excess pore water pressure ratio against the number of cycles or the normalized number of cycles (N) by the number of cycles at ru = 1. Additional insight into the development of excess PWP can be obtained by looking into the incremental increase of excess PWP per cycle. Two typical patterns characterized for the incremental increase of all samples were discovered. The incremental increase of excess PWP of the selected samples is shown in Fig. 9a (Ta_CYC0.30(84) and Fig. 9b (RaSa_CYC0.85(90). Two separated components can be clearly observed from Fig. 9a: (a) plateau zone with an almost constant incremental increase of excess PWP; and (b) rapid increasing incremental increase until the sample failure. For the incremental increase of excess PWP curve in Fig. 9b, three distinct regions can be identified: (a) plateau zone with an almost constant incremental increase of excess PWP; (b) rapid increasing incremental increase until reaching a peak; and (c) decreasing incremental increase. A critical point, NAcc, which is the number of cycles at which the incremental increase starts accelerating, is then identified in both Fig. 9a, b.

Fig. 9
figure 9

Incremental increase of excess PWP of the selected samples: a Ta_CYC0.30(84) sample and b RaSa_CYC0.85(90)

Full size image

With the excess pore water pressure and cyclic axial strain data at NAcc and Nru=1, combined with those at N = 1 cycle, N = 2 cycles, N = 5 cycles, and N = 10 cycles, the relationship between excess pore water pressure and cyclic axial strain of all prepared samples (both tailings and railway sand samples) was plotted (log scale). A general trend can be observed in Fig. 10. The excess pore water pressure was proportional to the cyclic axial strain, regardless of the number of cycles, CSR, density conditions, and material types. In addition, the interpretation shown can be separated into four stages of behaviors, corresponding to four zones in Fig. 10. Up to the cyclic axial strain of 0.2% (Zone 1), the excess pore water pressure ratio (ru) increases slightly and reaches approximately 0.20. In this stage, the samples are considered as “stable”. At the cyclic axial strain between 0.2 and 1.0% (Zone 2), the pore pressure ratios range from moderate to relatively high. In this stage, the samples are considered as “metastable”. Zone 3 (at the cyclic axial strain between 1.0 and 2.67%) includes all excess pore water pressure data at NAcc, involving the acceleration of the excess pore water pressure incremental increase as mentioned earlier. In this stage, the samples are considered as “unstable”. Finally, Zone 4 (at the cyclic axial strain larger than 2.34%) includes all excess pore water pressure data at Nru=1, relating to the liquefaction. In this stage, the samples are considered as “failure”.

Fig. 10
figure 10

Excess pore water pressure build-up versus cyclic axial strain of all prepared samples (both tailings and railway sand samples)

Full size image

Conclusions

This study presents an experimental investigation on excess pore water pressure generation in fine granular materials under cyclic loading. A series of undrained cyclic triaxial tests were performed to study the excess pore water pressure generation in two selected fine granular materials, railway sand and tailings. Based on the results of this investigation, the following conclusions can be drawn:

  • The test results showed excess pore water pressure accumulated over time due to cyclic loading. However, its accumulation was significantly dependent on CSR values, density conditions, and material types. At low CSR values, the excess pore water pressure showed a slight increase, but a sharp increase was observed at higher CSR values, ultimately leading to a failure state after a certain number of cycles. Moreover, the samples with higher relative compaction demonstrated greater resistance to cyclic loads compared to those with lower relative compaction under identical loading conditions.

  • The relationship between excess pore water pressure and cyclic axial strain of the selected fine granular materials was discovered based on all outputs from the undrained cyclic triaxial tests. The excess pore water pressure increased with an increase in cyclic axial strain, regardless of the number of cycles, CSR, density conditions, and material types.

  • The excess pore water pressure in fine granular materials under cyclic loading displays different behavior at various levels of cyclic axial strain. At cyclic axial strains up to 0.2% (“stable” condition), the excess pore water pressure ratio exhibits a slight increase. At cyclic axial strains between 0.2 and 1.0% (“metastable” condition), the pore pressure ratios range from moderate to relatively high. At cyclic axial strains between 1.0 and 2.67% (“unstable” condition), the excess pore water pressure data at NAcc represent the acceleration of the excess pore water pressure incremental increase. At cyclic axial strains larger than 2.34% (“failure” condition), the excess pore water pressure ratios reach 1.0, which is related to liquefaction.