Abstract
Slope instability occurrences as damaging shallow-landslides in the residual soil around mountains has been widely studied with geophysical, geotechnical and hydrogeological techniques but relating soil electrical resistivity to hydraulic conductivity for characterisation of lithology inducing of these landslides is not common. In this study, we used Electrical Resistivity Tomography (ERT) data and Hydraulic Conductivity (HC) data obtained from soil samples collected within 1–4.5 m depth in the borehole to assess the characteristics of soil that can induce landslide in the study location. The HC data were derived empirically from Beyer, Kozeny-Carman and Slitcher formula which were validated with HC obtained from laboratory experiment. The Empirical Derived Hydraulic Conductivities (EDHC) were correlated with the soil resistivity. The result shows a strong correlation between soil resistivity and HC with regression values of R2 = 0.9702, R2 = 0.9153 and R2 = 0.9232 for Beyer, Kozeny-Carman and Slitcher formula, respectively. The ERT model revealed a possible sliding surface between two contrasting resistive top material and underneath conductive materials at about 4 m depth. The HC assessment result corroborated the ERT model result because high and low-HC values were obtained in the borehole soil samples within 0–4 m and > 4 m depths from EDHC, respectively. The low-HC zone below 4 m depth was responsible for the occurrences of the shallow-landslides in the study.
Key points
-
Relationship between soil electrical resistivity and hydraulic conductivity were examined for assessment of lithology inducing shallow-landslide.
-
Soil electrical resistivity delineated a boundary between two contrasting resistive and conductive lithologies at 4 m depth.
-
Strong correlation ranged between R2 = 0.9153 to 0.9702 were observed between soil resistivity and hydraulic conductivity for the soil samples examined.
-
The conductive lithology with low hydraulic conductivity below 4 m depth was responsible for the occurrences of the shallow-landslides.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Slope instabilities are common occurrences in the residual soil that have developed on mountains in the humid climate regions as damaging landslides. These landslides have the potential of creating havoc to the lives and properties located around such mountains. In order to effectively predict and manage the occurrences of these slope instabilities, one needs to relate hydrogeological properties of the soil to its electrical properties, which requires a good knowledge of the soil hydraulic conductivity and electrical resistivity of the residual soil. This study examines the relationship between soil electrical resistivity and hydraulic conductivity influence on characterisation of lithology inducing slope instability in residual soil developed around mountains in humid regions.
Several researchers have reported widely on slope instabilities using Electrical Resistivity Tomography (ERT) survey [5, 8, 15, 32, 35, 42]. ERT has been commonly used for slope instability assessment because it is responsive to changes in pore water or fluid of soil or rock. Electrical resistivity method is an indirect, non-invasive measurement of changes in soil water content from the ground surface. It is a function of porosity which helps to distinguish between lithology of contrasting resistivity or the presence of clay particles [3, 39]. Coarse grained soils derived from silica quartz minerals have lesser voids and pore spaces through which electric current flows. These voids and pore spaces were connected and may affect the amount of pore fluid present in it which will significantly influences the results obtained from the resistivity investigation. However, fine grained soil (clay minerals) has lower soil resistivity than that of granular (sands or gravels) due to the flow of electric current through surface conduction. This flow and distribution of ions through the surfaces of clay particles is called double layer [12]. Therefore, the presence of large amount of clay in the soil is usually related to a low resistivity value [19, 47, 49].
Also, subsurface water movement depends on soil hydraulic conductivity, which is the ease of water or fluid flow through the pore spaces of the soil. This movement or flow of soil water or fluid through the pore spaces depend on the porosity of soils. It is higher in coarse grained soil (sand) than in fine grained soil (silt and clay) [37]. Seasonal changes in soil water content affects the hydraulic conductivity of the soil [14]. Therefore, a good knowledge of soil hydraulic conductivity is vital for slope instability assessment in the residual soil. Several studies of the impact of hydraulic conductivity on slope instabilities have been published, which were based on its hydromechanical contributions to hillslope hydrological process [4, 27, 44, 50]. However, in the past decade researchers have made efforts to develop a relation between hydraulic conductivity and electrical resistivity from the understanding that the flow of water can be compared to the flow of electric current through a saturated aquifer medium for groundwater management [25, 33, 38, 45]. Sattar et al. [38] developed a direct relationship equation between hydraulic conductivity and electrical resistivity in a complex floodplain geologic environment to solve the problem of random drilling, resulting in low yield or dry boreholes. The results showed that hydraulic conductivity values can be obtained from electrical resistivity data where there is no pumping test information from borehole. Niwas and Celik [25] have used two theoretical methods based on Kozeny and Archie equations to estimate porosity and hydraulic conductivity of an aquifer from Vertical Electrical Soundings (VES) data. The results showed good correlation between estimated hydraulic conductivity values from electrical resistivity (VES) data and measured hydraulic conductivity values from pumping test. Vogelgesang et al. [45] have also used high resolution electrical resistivity to estimate hydraulic conductivity in shallow alluvial aquifers for large scale groundwater modelling and characterisation of aquifer heterogeneity. The result showed that electrical resistivity data can improve the quantity and spatial distribution of hydraulic conductivity, especially in the sites where there is no available boreholes for pumping test. These previous studies have revealed that soil resistivity and hydraulic conductivity are strongly related but they have not been able to show how it affects porosity for characterizing lithology. However, the analysis of the relationship between soil electrical resistivity and hydraulic conductivity for characterization of lithology inducing slope instability is rare.
This article is organised in five sections. Following introduction section is regional setting, which presents the site selection, area of study, geology and soil characterisation. The review of theoretical background and basis for the work contained in the subsequent material and methods section detailed the procedures of data acquisition, analysis and interpretation. Section 4 presents the experimental and investigation results and discussion of results of the outcomes of the methods described in Sect. 3. Section 5 summarizes the significant findings and conclusion of the research.
Regional setting
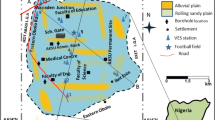
Study area and site selection
The study site is located in the Penang Island (Fig. 1). It has a daily maximum high temperature of 35 °C, annual average rainfall as high as 647 cm and daily relative humidity as high as 96.8% in some cases [1, 2]. These climatic factors are responsible for rapid weathering of the granitic rocks into residual soil which makes the slope potentially unstable resulting in shallow landslide in Balik Pulau and Paya Terubong axis. Penang Island is occupied majorly by central highlands of granitic origin with little lowland areas around the coast flanks. The lowland areas have been fully developed due to urban populace because of rapid industrialization [9]. Land reclamation has been ongoing for years between 1960 to present in the coastal areas [10]. However, urbanization and population growth have resulted in expansion into the slope areas [36, 48]. These slope areas are prone to slope instability. Shallow landslides are most prevalent slope instability affecting the residual soil in the slope areas in the past few years due to prolong heavy rainfall. This geomorphic event has been gradually reducing the highland areas to lowland thereby influences the landform and landscape in the area which creates land for building and farming. Recent shallow landslide occurrence in the early 2018 in the Relau Metropolitan Gardens, Sungai Ara along Paya Terubong road gives a preference choice to conduct this study in the landslide vicinity.
Geology and soil characterisation
The geology of Pulau Pinang is predominantly granitic rocks of igneous origin which can be divided into two types namely: Type I (Sungai Ara Type) and Type II (Bukit Bendera Type) (Fig. 2). Type I is of late carboniferous to early Permian in age, medium grained and contains primary muscovite while Type II is of Triassic age, is coarse grained and does not contain primary muscovite [43]. Type I (Sg. Ara, Batu Maung and Paya Terubong) is also refers to as the South Penang Pluton (SPP) while Type II (Bukit Bendera and Tanjung Bungah) is also refers to as the North Penang Pluton (NPP) [1]. The study site is located within the Type I South Penang Pluton between Paya Terubong and Sungai Ara.
Geological Map of Penang Island showing the study site location in the medium to coarse grained Biotite Granite [31]
Chemical weathering of these granitic rocks produce residual soil commonly found in the slope area of the island. Ali et al. [2] have shown that these residual soils consists of gravel, sand, silt and clay with their percentages varying with depth from the study carried out on several boreholes in the Paya Terubong area. Gravel, sand and silt have high percentages of greater than 25% while clay with percentage of less than 18% at about 0–5 m depth but thicker clay was found below 5 m depth. The depth to bedrock in the area ranges from 0.9 to 23.55 m with mean value of 10.9 m [1].
Materials and methods
Review of the relationship between hydraulic conductivity and electrical resistivity
The review of the relationship between hydraulic conductivity and electrical resistivity was developed based on two fundamental flow laws: laminar water flow and electric current flow.
According to Darcy law, the flow of water through the pores or voids in a soil can be laminar. Darcy’s empirical law, water flows through a fully saturated soil in one dimension.
The laminar velocity, \(v\), is proportional to the hydraulic gradient, \(i\) in Eq. (1)
But,
where, q is the total rate of flow through the cross-sectional area, A and the constant of proportionality, k is called the coefficient of permeability, ∆h is the head loss and L is the length in Eq. (2) [13]. Equation (2), \(q= kiA\) is referred to as Darcy’s law. Where, \(i= \frac{\Delta h}{l}\) is hydraulic gradient, q is rate of discharge (m3/s), v is velocity, A is cross section area, k is hydraulic conductivity (m/day).
Then,
Also, according to ohm’s law for the flow of electric current in pores and voids
V = potential difference, I = current flow, R = resistant of the material. Equation (4) can be written in the differential form as
J = current density (A/m2), σ = electrical conductivity (inverse of resistivity is an isotropic medium) and E = electric field applied. Based on Nath et al., [24] the resistivity of the soil is given by Eq. (6) as,
ρ is the constant of proportionality for the expression of total resistivity (A) of a cylinder of length, L, and cross-sectional area, D, of uniform composition. If we consider a geological section of a block of weathered material resting on a slope showing a series of lithological defined layer of interfaces having a unit cross-section with layer thicknesses, hi, and layer resistivities, ρi. The transverse resistance, R, normal to the face of the block and longitudinal conductance, S, parallel to the face of the block can be given as [34].
And
R and S are Dar Zarrouk parameters. These two Eqs. (7) and (8) are applied to a block of geological section of aquifer materials [40]. Transmissivity, T, is the product of aquifer layer thickness and hydraulic connectivity, which the layer thickness can be derived from R and S from Eqs. (7) and (8) above [34].
And
Therefore,
And
From Eqs. (11) and (12) either of the two conductivity factors kσ = constant or \(\frac{k}{\sigma }\) = constant could be true for a layered aquifer similar for this study as observed by Niwas and Singhal [26]. The total resistivity of the aquifer material, A, is correlated or directly proportional to hydraulic conductivity, k, in the relation in Eq. (13) which has been used by Dassargues [11]
where
\(\sum { \rho }_{i}\) is the summation of resistivity of different layers of aquifer. Sattar et al., [38] have correlated hydraulic conductivity with electrical resistivity using the Eq. (13) and established the fact that variations in resistivity are due to variations in geological formation. Since, electrical resistivity and hydraulic conductivity are function of porosity, electric current and water would have a better flow in larger pores of soil which are connected. It therefore means that this relationship in Eq. (13) between electrical resistivity and hydraulic conductivity is feasible. Archie [3] observed a direct relationship between the bulk resistivity of rock, Ro, and fully saturated aqueous fluid resistivity, Rw given as.
The constant of proportionality, F = formation factor which describes the effect of presence of the rock matrix, F ≥ 1. Archie established that F is influenced by porosity, pore shape and cementation.
Equation (16) is the Archie first law, a = constant, ɸ = porosity, m = cementation factor, which are influenced by geometry of pores, compaction, mineral composition and cementation. Equation (16) is valid for fully saturated clean formation only where grains are insulators. Archie also observed that when the medium is partially saturated such that changes in degree of water saturation affect porosity, the bulk resistivity of the rock, Rt is given as.
I is the resistivity index which describes the effect of partial desaturation of the rock, if I = 1 the or soil is fully saturated but if the soil or rock is filled dry air i.e., no fluid \(I\to \bowtie \).
Then,
where Sw = water saturation, n = saturation index. Equation (18) is called Archie second law. In Archie’s law, the rock formation factor varies with rock structure only but for the sediment with clay, formation factor varies with sediment composition or structure and pore water resistivity. This formation factor value is referred to as Apparent Formation Factor (AFF) see Eq. (18). Therefore, AFF removes the effect of pore water resistivity, Rw, which makes it a standard practice to use resistivity data to solve F in Eq. (18).
ERT data acquisition
The electric resistivity tomography data were acquired along two profiles A and B using Wenner-Schlumberger array configuration because it is able to map both vertical and horizontal structures thereby able to delineate faults and bedding discontinuities. Wenner-Schlumberger array also has a good resolution and penetration depth. Profiles A and B have total survey length of 60 m, 1.5 m electrode spacing and depth of investigation of 11 m to target the weathered basement in the locality. Record of past research conducted in the study location has shown that average depth of weathered basement was 11 m and shallow landslides occurred at 2–5 m [17]. Profile A was conducted in the east–west direction on the 23rd January 2020 while profile B was conducted in the north–south direction on 25th January 2020. Profile B crosses profile A at 41 m while profile A crosses profile B at 25 m. The data were acquired using four electrodes which is based on fixed spacing between potential dipole whereas the spacing between current electrode is increased and after a series of measurements the spacing of the potential electrodes is increased to obtain a deeper depth of investigation [20, 30]. The obtained resistivity data was inverted into ERT model using RES2DINV software. However, bad data points were edited out of the field data because they introduce noise which are misfits in the inversion process. A smoothness-constrained least squares method was adopted for the inversion [18]. The measured resistance values were converted to Apparent Resistivity (AR) in the inversion process from the result of the ratio between measured potential difference and electric current injected to the ground multiplied by the Wenner-Schlumberger geometric factor. The ERT model have better resolution after three (3) to four (4) iterations of the inversion with Root Mean Square (RMS) errors 19.8% and 18.6% for profile A and profile B, respectively.
Hydrogeological data collection for estimation of hydraulic conductivity
The ERT model resistivity values distribution guided the location of three boreholes (BH1, BH2, BH3) for the collection of soil samples in the study site for particle size distribution analysis and estimation of hydraulic conductivity. Borehole samples were taken between 1.0 and 4.5 m depth. Geotechnical analysis was used for classification and distribution tests such as moisture contents and particle size distribution, which were determined on the soil samples in accordance with the British Standard [6]. The mechanical wet sieving were used for the analysis of soil particles greater than 0.0625 mm in diameter while a calibrated hydrometer was used to analyse finer grains size with diameter less than 0.0625 mm. The hydraulic conductivity data were derived empirically from Beyer, Kozeny-Carman and Slitcher formula using the collected soil samples from these boreholes. The review of the three formulae of estimation Beyer, Kozeny-Carman and Slitcher can be found in the Olabode and San [28]. Parameters such as D10, D30 and D60 are sieve diameters corresponding to 10%, 30% and 60% finer, respectively and porosity (n) were extracted from the curve. Porosity (n) was derived from the empirical relationship with the coefficient of grain uniformity (\({C}_{u}\)) as follows: \(n=0.255(1+{0.83}^{{C}_{u}})\) [46]. These parameters were used to estimate hydraulic conductivity empirically using Beyer, Kozeny-Carman and Slitcher formulae [28]. The EDHC from soil samples collected within 1 to 4.5 m depth in the boreholes were correlated with the soil resistivity to define spatial distribution of hydraulic conductivity for lithology characterisation and validation of ERT results. All calculations were based on SI units and temperature of 25 °C was included in the kinematic viscosity.
Two soil samples were sampled with cylindrical core cutters at 1.0–2.0 m and 4.0–4.5 m depths in one representative borehole (BH1) in an undisturbed state for laboratory permeability experiments. The Laboratory Derived Hydraulic Conductivity (LDHC) values of the samples were determined from both falling head and constant head permeability tests in accordance with International Standard [7].
Results and discussion
ERT model interpretation
ERT model results were classified as saturated zones, weathered granite zones and boulders with resistivity values of less than 400 Ωm, 500–5000 Ωm and greater than 4000 Ωm respectively [23, 30] (Figs. 3, 4). An interpreted boulder located besides the saturated zone in profile A, covering a distance ranging from 35 to 41 m at the point where profile B crosses profile A, is prone to instability and movement during heavy and continuous rainfall [30]. In profile B, another boulder was interpreted within the distance of 25 to 33 m on the top of the saturated zone close to the point where profile A crosses profile B and it is also prone to sliding downslope during heavy rainfall. It can be deduced that this boulder on both profiles A and B is the same.
Also, higher resistivity values were observed at shallow depth of about 0–4 m whereas lower resistivity values were observed at depth below 4 m indicating changes in lithology in both profiles A and B. The boundary between the saturated zones and weathered layer in profile B is interpreted as a possible sliding surface at about 4 m depth because it is contrasting between resistive top material and underneath conductive materials (Fig. 4). Previous studies around the world have shown that this boundary was a result of changes in soil water saturation and lithology from dry and coarse-grained material to wet and fine-grained material, respectively [16, 29, 32]. Table 1 shows the average resistivity values obtained at depth in each borehole location from model blocks of RES2DINV. It can be observed that the resistivity values decrease with depth and the lowest value of 398 Ωm recorded at 4.0–4.5 m depth. It therefore suggests that more porous or saturated materials may be present at this depth.
Hydraulic conductivity versus soil resistivity
The particle size distribution analysis revealed that the study site is composed of gravelly sand soil in the upper part from 0 to 4 m depth, which is composed largely of coarse-grained soil. Whereas fine grained silt and clay soil dominates below 4 m depth. It can be observed that soil sample below 4 m depth has higher soil moisture content of 38.00% than soil samples located above 4 m depth with soil moisture contents that ranged from 11.05% to 30.02% as shown in Table 2. The highest moisture content of 38.00% is found in soil sample located at 4.0–4.5 m depth indicative of higher saturation than those above it as observed in the low resistivity value recorded at the same depth in Table 1 above. Figure 5 shows a typical grain size distribution analysis curve obtained in the study site. The gravelly sand is indicated with the blue colour while the silt and clay is indicated with the brown colour. The results of the particle size distribution and soil indices parameters is shown in Fig. 5 and Table 3.
The particle size distribution curve analysis revealed that the boreholes soil samples compose of gravelly sand to clayey sand soil. The soil samples obtained at 4.0 to 4.5 m depth have the highest silt and clay fraction of 23.74%, however, the silt and clay fractions ranged between 5.78 and 23.74% in all samples. Table 3 shows that the soil sampled at 4.0–4.5 m depth has the highest estimated porosity of 32.70% indicative of higher porous soil. Table 4 shows the EDHC values obtained from Beyer, Kozeny-Carman and Slitcher formula with the soil resistivity and boreholes depth at distances 25 m, 36 m and 51 m on profile A and B in the study location.
Hydraulic conductivity values estimated from Beyer formula ranged from 10 m/day to 4.5 m/day for 1.0 -2.0 to 4.0–4.5 m depths respectively (Table 4).Whereas hydraulic conductivity values estimated from Kozeny-Carman and Slitcher formulae for 1.0–2.0 to 4.0–4.5 m depths ranged from 3.5 m/day to 2 m/day and 1.56 m/day to 0.5 m/day, respectively (Table 4).
However, the LDHC values obtained for the depths of 1.0–2.0 m and 4.0–4.5 m depths were 1.21 m/day and 0.33 m/day respectively.
The main observation of the borehole data is the spatial variation of the soil resistivity decreasing with depth [22]. Figures 6, 7 and 8 show the correlation of the measured field soil resistivity data (ERT) plotted against the hydraulic conductivity (EDHC values) where pumping test data were not available. They are scatter plots of empirical relationship in Eq. (13) as shown in Figs. 6, 7 and 8. There is a strong correlation between soil resistivity and hydraulic conductivity with regression value R2 = 0.9702 for Beyer formula as shown in Fig. 6. Kozeny-Carman and Slitcher also have strong correlation of R2 = 0.9153 and R2 = 0.9232, respectively (Fig. 7, 8). It was observed that Beyer formula has higher values of hydraulic conductivity than Kozeny-Carman and Slitcher. The lower hydraulic conductivity values observed in both Kozeny-Carman and Slitcher may be due to the inclusion of porosity in the estimation formulae. Beyer formular does not take porosity into consideration in the estimation but it rather consider the coefficient of uniformity of the soils.
The hydraulic conductivity values of 1.82 m/day to 3.53 m/day obtained for Kozeny-Carman were in close agreement with values of 0.06 m/day to 4.68 m/day obtained in a similar geology of granitic rock in Selangor as reported by [21]. Hydraulic conductivity values of 0.50 m/day to 1.56 m/day obtained for Slitcher were also in accordance with values of 0.02 m/day to 1.31 m/day obtained in a fractured geology in Kerry Hill, Malaysia as reported by Zaini and Roslan [51]. The results of the LDHC values of 1.21 m/day and 0.33 m/day for the 1.0–2.0 and 4.0–4.5 m depths have validated the results of EDHC for Slitcher formula of 1.56 m/day to 0.50 m/day for the same depths. Beyer and Kozeny-Carman formulae may have overestimated the hydraulic conductivity values. Therefore, the Slitcher formula proved to be the best estimator of the hydraulic conductivity. Since Eq. (13) shows that the hydraulic conductivity directly proportional to soil resistivity, it can therefore be used for lithological characterisation of ERT data. This variation is true and in agreement with the electric current flow in a coarse-grained soil. In coarse grained soil, soil resistivity is influenced by the grain size distribution, which as well influences the porosity. The study site is composed of gravelly sand, which is a coarse-grained medium. The particle grains present a very high resistance to the flow of electric current. It is evident in the result of the ERT models of profiles A and B in Figs. (3, 4) in the present study location. Therefore, the gravelly sand within 0–4 m depth is characterized as permeable soil as observed in the ERT with high resistivity values, consequently, the soil hydraulic conductivity is increased as shown in Figs. 6, 7 and 8, which agrees with the results obtain in alluvium aquifers from the published research work by Sinha et al. [41]. However, low soil resistivity observed below 4 m depth is due to the presence of considerable amount of clay in the soil as shown in Fig. 5 and it is classified as clayey sand, which have ion exchange property. The clayey sand soil has low permeability and it presents low resistance to the flow of electric current due to surface conduction of the clay particles particularly at 4.0–4.5 m depth. This surface boundary between the permeable gravelly sand and low permeability clayey sand soil is inimical to failure due to landslide as reported in the clay embarkment work of Gunn et al. [12].
Conclusion
The ERT model revealed a possible sliding surface between two contrasting resistive top material and underneath conductive materials at about 4 m depth. The hydrogeological assessment result corroborated the ERT model result because high and low hydraulic conductivity values were obtained in the borehole soil samples within 0–4 m and > 4 m depths from EDHC and LDHC, respectively. It agrees with the electric current flow in a soil because soil resistivity is influenced by the grain size distribution, which as well influences the porosity. The particle grains present a very high resistance to the flow of electric current within 0–4 m depth as observed in the ERT model results, which characterized the medium as permeable with the high hydraulic conductivity obtained from the hydrogeological assessment result. However, the particle grains below 4 m depth show low resistivity because of the presence of considerable amount of clay in the clayey sand soil, which have ion exchange property and low hydraulic conductivity. Clayey sand soil has low permeability and it presents low resistance to the flow of electric current due to surface conduction of the clay particles presence in the soil matrix. This surface conduction would cause the high resistive permeable materials on top to slide relative to the clay particles below which are conductive with low hydraulic conductivity due to its negative charge alignment. Therefore, the low hydraulic conductivity zone was responsible for the occurrences of the shallow landslides in the study location.
Availability of data and materials
The data archiving for this work are underway at the Universiti Sains Malaysia (USM) repository link http://eprints.usm.my/.
References
Ahmad F, Yahaya AS, Farooqi MA (2006) Characterization and geotechnical properties of Penang residual soils with emphasis on landslides. Am J Environ Sci 2(4):121–128. https://doi.org/10.3844/ajessp.2006.121.128
Ali MM, Ahmad F, Yahaya AS, Farooqi MA (2011) Characterization and hazard study of two areas of penang Island, Malaysia. Human Ecol Risk Assessment 17(4):915–922. https://doi.org/10.1080/10807039.2011.588156
Archie GE (2003) The electrical resistivity log as an aid in determining some reservoir characteristics. SPE Reprint Series 55:9–16. https://doi.org/10.2118/942054-g
Bernatek-Jakiel A, Poesen J (2018) Subsurface erosion by soil piping: significance and research needs. Earth Sci Rev 185(August):1107–1128. https://doi.org/10.1016/j.earscirev.2018.08.006
Boyle A, Wilkinson PB, Chambers JE, Meldrum PI, Uhlemann S, Adler A (2018) Jointly reconstructing ground motion and resistivity for ERT-based slope stability monitoring. Geophys J Int 212(2):1167–1182. https://doi.org/10.1093/gji/ggx453
BS 1377 Part 2 (1990) Methods of test for soils for civil engineering purposes. Vol. 3, Issue 1.
BS EN ISO 17892-11 (2014) Geotechnical Investigation and testing—laboratory testing of soil—permeability tests. International Standard, 2014, 25
Cebulski J, Pasierb B, Wieczorek D, Zieliński A (2020) Reconstruction of landslide movements using digital elevation model and electrical resistivity tomography analysis in the polish outer carpathians. CATENA 195:104758. https://doi.org/10.1016/j.catena.2020.104758
Chan NW (1996) Environmental hazards associated with hill land development in Penang Island, Malaysia: some recommendations on effective management. Disaster Prevent Manage Int J 7(4):305–318. https://doi.org/10.1108/09653569810230148
Chee SY, Othman AG, Sim YK, Mat Adam AN, Firth LB (2017) Land reclamation and artificial islands: walking the tightrope between development and conservation. Global Ecol Conserv 12:80–95. https://doi.org/10.1016/j.gecco.2017.08.005
Dassargues A (1997) Modeling baseflow from an alluvial aquifer using hydraulic-conductivity data obtained from a derived relation with apparent electrical resistivity. Hydrogeol J 5(3):97–108. https://doi.org/10.1007/s100400050125
Gunn DA, Chambers JE, Uhlemann S, Wilkinson PB, Meldrum PI, Dijkstra TA, Haslam E, Kirkham M, Wragg J, Holyoake S, Hughes PN, Hen-Jones R, Glendinning S (2015) Moisture monitoring in clay embankments using electrical resistivity tomography. Constr Build Mater 92:82–94. https://doi.org/10.1016/j.conbuildmat.2014.06.007
Holtz RD, Kovacs WD (1981) An introduction to geotechnical engineering, vol 123. Prentice-Hall Inc, USA
Hu W, Shao MA, Si BC (2012) Seasonal changes in surface bulk density and saturated hydraulic conductivity of natural landscapes. Eur J Soil Sci 63(6):820–830. https://doi.org/10.1111/j.1365-2389.2012.01479.x
Hussain Y, Cardenas-Soto M, Martino S, Moreira C, Borges W, Hamza O, Prado R, Uagoda R, Rodríguez-Rebolledo J, Silva RC, Martinez-Carvajal H (2019) Multiple geophysical techniques for investigation and monitoring of Sobradinho Landslide, Brazil. Sustainability (Switzerland) 11(23):6672. https://doi.org/10.3390/su11236672
Hussain Y, Hamza O, Cárdenas-Soto M, Borges WR, Dou J, Rebolledo JFR, Prado RL (2020) Characterization of sobradinho landslide in fluvial valley using MASW and ERT methods. REM Int Eng J 73(4):487–497. https://doi.org/10.1590/0370-44672019730109
Lateh H, Muqtada MAK, Jefriza M (2011) Monitoring of shallow landslide in Tun Sardon KM 3.9. Int J Phys Sci 6(12):2989–2999. https://doi.org/10.5897/IJPS11.118
Loke MH, Barker RD (1996) Rapid least-squares inversion of apparent resistivity pseudosections by a quasi-Newton method1. Geophys Prospect 44(1):131–152. https://doi.org/10.1111/j.1365-2478.1996.tb00142.x
Martin L (2019) Effects of electro-osmotic consolidation of clays and its improvement using ion exchange membranes [Dissertations, 1424.]. https://digitalcommons.njit.edu/dissertations/1424
Metwaly M, Alfouzan F (2013) Application of 2-D geoelectrical resistivity tomography for subsurface cavity detection in the eastern part of Saudi Arabia. Geosci Front 4(4):469–476. https://doi.org/10.1016/j.gsf.2012.12.005
Mohamad H, Roslan N (2017) Groundwater in fractured granite in Selangor. Warta Geolog 43(3):250
Mollehuara Canales R, Kozlovskaya E, Lunkka JP, Guan H, Banks E, Moisio K (2020) Geoelectric interpretation of petrophysical and hydrogeological parameters in reclaimed mine tailings areas. J Appl Geophys 181:104139. https://doi.org/10.1016/j.jappgeo.2020.104139
Muztaza NM, Ghafar SHMA, Sukri S, Jinmin M (2018) Identification of slope failure using 2-D resistivity method. Int J Adv Sci Eng Technol 6(2):13–17
Nath SK, Patra HP, Shahid S (2000) Geophysical prospecting for ground water. Oxford and IBH Publishing, Oxford
Niwas S, Celik M (2012) Equation estimation of porosity and hydraulic conductivity of Ruhrtal aquifer in Germany using near surface geophysics. J Appl Geophys 84:77–85. https://doi.org/10.1016/j.jappgeo.2012.06.001
Niwas S, Singhal DC (1981) Estimation of aquifer transmissivity from Dar-Zarrouk parameters in porous media. J Hydrol 50:393–399. https://doi.org/10.1016/0022-1694(81)90082-2
Okeke ACU, Wang F (2016) Hydromechanical constraints on piping failure of landslide dams: an experimental investigation. Geoenviron Disasters 3(1):1–17. https://doi.org/10.1186/s40677-016-0038-9
Olabode OP, San HL (2022) Hydrogeological assessment of hydraulic conductivity on gully formation in erosion degraded residual soil of an unstable slope. Indian Geotech J 52:519. https://doi.org/10.1007/s40098-021-00585-w
Olabode OP, San HL, Ramli MH (2022) Geophysical and geotechnical evaluation of landslide slip surface in a residual soil for monitoring of slope instability. Earth Space Sci 9:1–17. https://doi.org/10.1029/2022EA002248
Olabode OP, San LH, Ramli MH (2020) Analysis of geotechnical-assisted 2-d electrical resistivity tomography (ERT) monitoring of slope instability in residual soil of weathered granitic basement. Front Earth Sci 7(11):1–15. https://doi.org/10.3389/feart.2020.580230
Ong WS (1993) The geology and engineering geology of Penang Island. Geological Survey of Malaysia.
Pasierb B, Grodecki M, Gwóźdź R (2019) Geophysical and geotechnical approach to a landslide stability assessment: a case study. Acta Geophys 67(6):1823–1834. https://doi.org/10.1007/s11600-019-00338-7
Purvance DT, Andricevic R (2000) On the electrical-hydraulic conductivity correlation in aquifers. Water Resour Res 36(10):2905–2913. https://doi.org/10.1029/2000WR900165
Reynolds JM (1997) An introduction to applied and environmental geophysics. Wiley, USA. https://doi.org/10.1071/pvv2011n155other
Rezaei S, Shooshpasha I, Rezaei H (2019) Reconstruction of landslide model from ERT, geotechnical, and field data, Nargeschal landslide, Iran. Bull Eng Geol Environ 78(5):3223–3237. https://doi.org/10.1007/s10064-018-1352-0
Samat N, Mahamud MA, Tan ML, Tilaki MJM, Tew YL (2020) Modelling land cover changes in peri-urban areas: a case study of George town conurbation, Malaysia. Land 9(10):1–16. https://doi.org/10.3390/land9100373
Saravanan S, Parthasarathy KSS, Sivaranjani S (2019) Chapter 10—Assessing coastal aquifer to seawater intrusion: application of the GALDIT Method to the Cuddalore Aquifer, India. In: Ramkumar M, James RA, Menier D, Kumaraswamy KBT-CZM (eds) Coastal zone management global perspectives, regional processes, local issues. Elsevier, Amsterdam, pp 233–250. https://doi.org/10.1016/B978-0-12-814350-6.00010-0
Sattar GS, Keramat M, Shahid S (2016) Deciphering transmissivity and hydraulic conductivity of the aquifer by vertical electrical sounding (VES) experiments in Northwest Bangladesh. Appl Water Sci 6(1):35–45. https://doi.org/10.1007/s13201-014-0203-9
Shevnin V, Mousatov A, Ryjov A, Delgado-rodriquez O (2007) Estimation of clay content in soil based on resistivity modelling and laboratory measurements. Geophys Prospect 55(2):265–275. https://doi.org/10.1111/j.1365-2478.2007.00599.x
Singh UK, Das RK, Hodlur GK (2004) Significance of Dar-Zarrouk parameters in the exploration of quality affected coastal aquifer systems. Environ Geol 45(5):696–702. https://doi.org/10.1007/s00254-003-0925-8
Sinha R, Israil M, Singhal DC (2009) A hydrogeophysical model of the relationship between geoelectric and hydraulic parameters of anisotropic aquifers. Hydrogeol J 17(3):495–503. https://doi.org/10.1007/s10040-008-0424-9
Soto J, Galve JP, Palenzuela JA, Azañón JM, Tamay J, Irigaray C (2017) A multi-method approach for the characterization of landslides in an intramontane basin in the Andes (Loja, Ecuador). Landslides 14(6):1929–1947. https://doi.org/10.1007/s10346-017-0830-y
Tan BK (1994) Engineering properties of granitic soils and rocks of Penang Island, Malaysia. Bull Geolog Soc Malaysia 35:69–77. https://doi.org/10.7186/bgsm35199408
Vardon PJ, Liu K, Hicks MA (2016) Reduction of slope stability uncertainty based on hydraulic measurement via inverse analysis. Georisk 10(3):223–240. https://doi.org/10.1080/17499518.2016.1180400
Vogelgesang JA, Holt N, Schilling KE, Gannon M, Tassier-Surine S (2020) Using high-resolution electrical resistivity to estimate hydraulic conductivity and improve characterization of alluvial aquifers. J Hydrol 580:123992. https://doi.org/10.1016/j.jhydrol.2019.123992
Vukovic M, Soro A (1992) Determination of hydraulic conductivity of porous media from grain-size composition. Water Resources Publications (Illustrate). Water Resources Publications. http//:trove.nla.gov.au/version/28823874
Waxman MH, Smits LJM (1968) Electrical conductivities in oil-bearing shaly sands. Soc Petrol Eng J 8(02):107–122. https://doi.org/10.2118/1863-A
Yahaya NS, Ramli Z, Thompson A, Pereira JJ (2019) Landslides in Penang Island, Malaysia: insights on emerging issues and the role of geoscience. Warta Geologi 45:37–43
Yamakawa Y, Kosugi K, Masaoka N, Sumida J, Tani M, Mizuyama T (2012) Combined geophysical methods for detecting soil thickness distribution on a weathered granitic hillslope. Geomorphology 145–146:56–69. https://doi.org/10.1016/j.geomorph.2011.12.035
Yeh HF, Wang J, Shen KL, Lee CH (2015) Rainfall characteristics for anisotropic conductivity of unsaturated soil slopes. Environ Earth Sci 73(12):8669–8681. https://doi.org/10.1007/s12665-015-4032-4
Zaini N, Roslan N (2017) Groundwater in fractured metasedimentary rocks of Kenny hill formation. Warta Geologi 43(3):250
Acknowledgements
We would like to thank my colleagues that assisted in the fieldwork exercises. All supports from USM and various parties are gratefully acknowledged. We also acknowledged the support of Universiti Sains Malaysia (USM) and Federal University Oye-Ekiti, Nigeria.
Funding
This work is financially supported by the grant “Burning in the Southeast Asian Maritime Continent: Solving Smoke Direct and Semi-Direct Radiative Forcing Through AERONET and MPLNET Constraint” (1001.PFIZIK.8011079), which is under the Research University Grants (RUI) grant from Universiti Sains Malaysia (USM) and Federal University Oye-Ekiti who is responsible for the payment of O. P. Olabode’s salary.
Author information
Authors and Affiliations
Contributions
Conceptualization, OPO; Methodology, OPO; Software, OPO; Formal Analysis, OPO; Investigation, OPO; Resources, LHS; Data Curation, OPO; Writing—Original Draft Preparation, OPO; Writing—Review and Editing, OPO; Supervision, LHS; Project Administration, OPO; Funding Acquisition, LHS. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest. The funding sponsors had no role in the conceptualization, design, methodology of the study; in the data collection, analysis, data interpretation; in the writing of the manuscript and in the decision to publish the obtained results.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Olabode, O.P., San, L.H. Analysis of soil electrical resistivity and hydraulic conductivity relationship for characterisation of lithology inducing slope instability in residual soil. Geo-Engineering 14, 7 (2023). https://doi.org/10.1186/s40703-023-00184-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40703-023-00184-z