Introduction

Particle breakage plays an important role in determining the constitutive relation for granular materials at high or medium high stress. For one-dimensional compression, the slope of normal compression line and the plastic deformation were found to significantly affected by the particle breakage [1, 21, 23, 24, 29]. Constitutive relation incorporated with particle breakage was developed theoretically for one-dimensional compression [5], tri-axial conditions [14, 16, 17, 28, 34]. McDowell [20] suggested that macroscopic yielding stress dominated by the average tensile strength. Single particle crushing tests were carried out to determine average tensile strength on a wide range of size of grains and verity of minerals [7, 20, 30, 41]. This finding provides valuable information for calibration of crushable particle during discrete-element method modelling [10, 25, 26]. Physical test and numerical simulations have been used to understand the load-deformation behavior of individual particle or the stress–strain response under macro stress. However, limited studies were carried out to study the role of fundamental parameters on single-particle fracture or stress–strain response.

Particle size distribution, particle shape and mineralogy are basic fundamental parameters used to describe of sands. Image based methods were used to quantify particle shape in geomechanics and geology, for example, roundness [33, 36], sphericity [11, 27]. Particle shape has a great effect on the mechanical properties of sand, for example, the relative density [11, 27], stiffness [11], breakage [4, 35] and mechanical behavior [3]. Although particle shape for 36 kinds of sands was investigated by Altuhafi et al. [2], they have not studied the effects of shapes on mechanical behavior. Besides, due to the practical problems, behavior of different mineralogy sand, such as crushable carbonate sand [7, 12, 13, 40], volcanic ash [19] and tailing sand [6, 8, 9] have been studied in recent decades. Since the complex of nature sand, the contribution of the particle shape or mineralogy on mechanical behavior is not easy to distinguish. Thus, this paper focus on investigating the influence of particle shape and mineralogy on average tensile strength, particle breakage and compressibility. Four widely used sands, such as weathered completely decomposed granite (CDG), carbonate sand (CS), Leighton Buzzard sand (LBS) and nature volcanic eruption deposit pumice sand (PM) were used in this paper for comparison.

Test materials and methods

Four kinds of material were used in this study, including completely decomposed granite (CDG), carbonate sand (CS), standard Leighton Buzzard sand (LBS) and pumice deposits (PM). Figure 1 shows an example of Leica microscope image and Fig. 2 shows scanning electron microscope (SEM) image (Hitachi S3400N VP scanning electron microscope) for CDG, CS, LBS and PM with grain size of 0.6–1.18 mm and 1.18–2.0 mm (mechanical sieved following British standard BS1377-2:1990). An advanced particle size analysis and shape evaluation apparatus (QicPic made by a Germany company SYMPATEC) was applied to measure shape of each material. Two main shape factor, aspect ratio (AR) and sphericity was applied in this paper to describe shape of particles. Aspect ratio is a ratio of Feretmin over Feretmax. Feretmin or Feretmax is the minimum or maximum distances between two parallel tangents lines around the particle. Sphericity is a parameter described degree of similarity between a particle to a sphere [2], which is the ratio of equivalent perimeter of a circle with equivalent area with projected area to real perimeter of a projected particle. Thus, AR could be a parameter to represent the irregular shape of particle while sphericity could be a parameter to represent how smooth or roughness of particle.

Fig. 1
figure 1

Microscope images for test materials with size of 0.6–1.18 mm: a completely decomposed granite; b carbonate sand; c Leighton Buzzard sand; d pumice sand

Full size image
Fig. 2
figure 2

Scanning electron microscope images for test materials with size of 0.6–1.18 mm: a completely decomposed granite; b carbonate sand; c Leighton Buzzard sand; d pumice sand

Full size image

CDG is the product of old Hong Kong granite rock that has weathered into soil particles ranging in size from coarse sand to silt. The mineralogy of the soil grains consists of mica and feldspar, and it is not difficult to distinguish these two different components from Fig. 1. The Mica looks transparent, is monoclinic and has perfect cleavage as a result of its atoms being arranged of hexagonal sheet like. Mica and Feldspar were picked out to determine the mineral elements by spectrum processing separately. Figure 3 shows scanning electron microscope images for Completely decomposed granite with mineral compositions of feldspar and mica at magnitude of 200×. The mineral elements of Mica are predominantly Si and O, and include a small amount of K, Na, Al and Fe to formal group of silicate minerals. Feldspar is a group of rock-forming tectosilicate minerals and it was found to be majorly KAlSi3O8 and NaAlSi3O8.

Fig. 3
figure 3

Scanning electron microscope images for completely decomposed granite with size of 0.6–1.18 mm at magnification of ×200: a feldspar; b mica

Full size image

CS examined in this study comes from South China sea is the product of corals, mollusc shells and algae, and the mineral components are Ca, C and O predominantly (98.13%) [13], with negligible quantities of, Na, Mg, Al and S. LBS is rounded and mainly quartztic. It is found that LBS does not only include Si, O, but also a small amount of C, Fe and K which could be due to impurities attached on the surface. Pumice (PM) deposits are a light, porous volcanic rock that generated from the explose of the eruptions when the lava is permeated with gas bubbles during the solidification process, resulting in pumice deposits being characterized by the vesicular material. The mineralogy components are majorly 71.0% silica, 13.0% aluminum oxide and 2.0% ferric oxide [32].

The single particle crushing tests were carried out on the apparatus used for unconfined compression test suggested by Mcdowell and Amon [22]. The top platen is fixed and the bottom platen moves up. The force F applied to the grains is measured by the proving ring dial gauge and the stress applied to the particles is computed as Eq. (1):

$$\sigma = \frac{F}{d}$$
(1)

where d is the diameter of particle and the unit is mm. The load measuring capacity of the device is 10 kN with a resolution of 0.001 N, and the resolution of displacement measuring is 0.1 mm. The loading rate is 0.1 mm/s suggested by Nakata et al. [30]. Weibull [37] suggested that the probability \(P\) of choosing at random an individual have a \(X\) equal to or less than x, and could have

$$P(X \le x) = F(x)$$
(2)

He also considered that any distribution may be written in the form:

$$F(x) = 1 - e^{ - \varphi (x)}$$
(3)

Thus, for a great number of individual \(n\), the probability of failure is \(P_{n}\) while the probability of nonfailure \((1 - P_{n} )\) is equal to the probability of the simultaneous non failure of all \((1 - P_{n} ) = (1 - P)^{n}\). Thus, the survival probability \(P_{s}\) of a volume \(V_{0}\) under a uniform tensile stress \(\sigma\) is given by:

$$P_{s} (V_{0} ) = 1 - P_{n} = \exp \left[ { - \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{m} } \right]$$
(4)

where if the stress \(\sigma = \sigma_{0}\), \(P_{s} (V_{0} )\) is equal to 37%, and thus σ0 is the stress for 37% of tested specimens survive, and m is Weibull modulus.

The procedure of one-dimensional consolidation tests followed the British standard (BS 1377-5:1990). The specimens were prepared by dry deposition, then tamping into an initial pre-set height, and all the tests are carried out under dry condition. The initial void ratio was calculated using three different methods relying on independent measurements [1], for which the difference in void ratios was found to be within ± 0.01. The final grading was estimated after each test by mechanical dry sieving.

Results

Figure 4 shows the particle shape distribution, which present the cumulative percentage passing by volume across the entirety of shape factors. CS as a product of corals, mollusc shells and algae was considered as a very irregular and fragile material like Dog’s Bay sand [12, 15, 31], or contains several intra-voids [38], but it is surprising to note that AR50 of CDG is smallest among four kinds of materials, which indicate that CDG could be the most irregular material instead of CS from statistic quantification. LBS as a British standard quartz sand is rounded, where the line for AR in Fig. 3a located in the right-most. From Fig. 3b, sphericity distribution of CDG, CS and PM are very close, while that of LBS is far right from those three materials, because the surface of LBS is very smooth as shown in Fig. 1. Thus, LBS is a regular shape grains, while CDG is the most irregular shape grains instead of the CS among four sands.

Fig. 4
figure 4

Shape distribution: a aspect ratio; b sphericity

Full size image

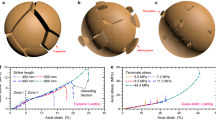
Figure 5 shows the Weibull modulus and the 37% survival possibility strength of CDG. Mica and feldspar within CDG were measured separately by single particle crushing tests, and it was found that the 37% survival possibility strength of mica with size of 0.6–1.18 mm is 94.8 MPa, while that of feldspar is 38.1 MPa. For CDG with size of 1.18–2.0 mm, the 37% survival possibility strength of mica is 79.5 MPa, while that of feldspar is 16.8 MPa as shown in Table 1. This is in a good agreement with Mcdowell and Amon [22] that the 37% survival possibility strength is decreasing with the increase of size of particle because the large particle could include more defects. It seems that the tensile strength of feldspar is much lower than that of mica. Zhao et al. [41] found that feldspar includes fractures caused the failure of feldspar along with the crystallographic planes, where has a very low bonding stress. Although PM include 71% of silica, average tensile strength of PM is 31.92 MPa shown in Fig. 6b, which is even less than that of feldspar, this could because PM includes a great number of intra-voids caused the structure of PM like a honeycomb. It is well known that CS includes several intra-voids as well [12], but the 37% survival possibility strength of CS is 41.5 MPa, which is much higher than that of PM. It seems that intra-voids within PM is far more than that of CS, because the specific gravity of PM is 2.28 while the specific gravity of CS is 2.75.

Fig. 5
figure 5

The 37% survival possibility strength of CDG

Full size image
Table 1 Shape factors for test materials and the 37% average tensile strength (σ0) measured by single particle crushing tests
Full size table
Fig. 6
figure 6

The 37% survival possibility strength of CS and PM

Full size image

Figure 6 shows the relationship between the void ratio and logarithm effective vertical stress among four sands under one-dimensional compression tests. It should be noted that it is impossible to prepare the same initial void ratio specimen due to the minimum void ratio among four sands are quite different. Here the yielding stress has been taken to be the point of maximum curvature on the \(e\) − log \(\sigma_{0}\), which are approximately 5 MPa, 9 MPa, 11 MPa and 15 MPa for PM, CS, CDG and LBS, respectively, and the yielding stress could be four times less than the 37% survival possibility strength suggested by McDowell [20]. This seems to indicate that the strength of four sands are in order of PM, CS, CDG and LBS. Although average tensile strength of mica in CDG is highest, a great number of feldspar in CDG caused the yielding stress of CDG is smaller than that of LBS. The yielding stress of CDG depends on the tensile strength of feldspar instead of mica because the yielding strength dominated by the weakest grains in a specimen.

Figure 7b shows particle size distribution after one-dimensional compression at a stress of 18 MPa. The relative breakage (Br) was calculated by using Hardin’s method [18]. Br of CDG, CS, LBS and PM are 0.335, 0.217, 0.067 and 0.487 respectively. PM suffered the largest particle breakage, while breakage of CS and CDG are quite close. Breakage of LBS is far less than that of other three sands, even the 37% survival possibility strength of LBS is 66.7 MPa suggested by McDowell [20], which is far less than 94.8 MPa of mica within CDG. Particle breakage also depends on the strength of weakest sands. Zhang and Baudet [39] found the breakage in gap-graded soils depends on the size of large particle, nor the ratio of large to small size of particle. This could be the same reason that particle breakage is dominated by the weakest particle, where tensile strength of larger size particle in the same ratio gap-graded soil is less than that of smaller size of large particle.

Fig. 7
figure 7

Experimental results for one-dimensional compression tests of four sands: a the void ratio against logarithm effective vertical stress; b particle size distribution curves

Full size image

Discussions

Particle shape, mineralogy and texture seem to have a mutual effect on the strength, particle breakage and compressibility among four sands. The mineral compositions of PM, CDG and LBS are majorly silica and the contents of silica in CDG, PM and LBS are approximately 40%, 70% and 90%. However, the 37% survival possibility strength and yielding stress of CDG lies between PM and LBS. It seems that the mineral composition plays a minor role in the 37% survival possibility strength, yielding stress and particle breakage.

It is worth noticing that regular LBS has the highest AR50 and S50, and the 37% survival possibility strength, yielding stress and particle breakage also reach the maximum value among four sands. In compare to AR50 and S50 of CDG and CS, CDG seems to be more angular than CS through quantitatively analysis, result in the 37% survival possibility strength and yielding stress of CDG is slightly lower than those of CS, result in Br of CS is lower than that of CDG under the same compression stress, even CS includes a greater number of intro-voids. It seems that particle shape influences on the 37% survival possibility strength and yielding stress. Apart from mineralogy and particle shape, it was found that the 37% survival possibility strength and yielding stress of CS is greater than that of PM due to the significantly greater number of intro-voids of PM irrespective to the mineralogy and shape, although AR50 and S50 of CS is similar with that of PM and both particles have honeycomb structure.

Conclusions

Sands from a variety of origins, CDG, CS, LBS and PM, were examined through shape analysis, single particle crushing tests and one-dimensional compression tests. It was found mineralogy plays a minor role, but the particle shape seems to have an influence on 37% survival possibility, yielding stress and particle breakage. Besides, the texture of particle seems also important, and the weakest mineral of particle could become dominant the strength when particle with mixed mineralogy.