Introduction

The disposal of fly ash industrial wastes coming out of the thermal power plants is a major concern and requires a large land area. The structural fills or embankments are one of the promising areas of utilization of fly ash. Nowadays, even the use of other industrial waste materials such as ground granulated blast furnace slag,\copper slag, etc. containing Pozzolanic properties, has also gained a wide popularity in the embankment construction since their safe disposal also assumes the serious problem. This utilization of such waste materials in the geotechnical and highway construction can reduce the construction cost significantly apart from encouraging the sustainable development and reducing the environmental problems. There are many situations where the foundations need to be located either on the top of a embankment slope or on the slope itself and the slopes may be made up of fly ash and other Pozzolanic materials apart from the natural soil. Under such circumstances, there may be significant reduction in the strength of the embankment slope or bearing capacity of the footing (foundation) depending upon the location of the footing with respect to the slope. The improvement of the load carrying capacity of such loaded slopes is, therefore, one of the important aspects of geotechnical engineering practice as the structures resting on the slopes are liable to be unsafe due to slope failure. One of the possible solutions to improve the bearing capacity would be to reinforce the sloped fill. To design a footing on a sloped fill requires a thorough understanding of both—the bearing capacity behaviour of the footing and the mechanical behaviour of slope.

Although decreasing availability of good construction sites and increasing construction activities for infrastructural developments have impelled civil engineers in the developing countries like India to use unsuitable sites, particularly low lying areas after filling them with fly ash and other Pozzolanic materials, there may be difficulty in constructing a stable structural fill due to poor load carrying capacity of fly ash and such other materials, especially when loaded on the top of the fill slope. During last three decades, several researchers presented extensively the use of geosynthetic reinforcement for improving the load bearing capacity of foundation soils. The possibility of using polymeric reinforcements within the fill made up of Pozzolanic waste materials may provide the most viable option for enhancing the load carrying capacity of the embankment slopes made up of such waste materials and if found effective, it may lead to the bulk utilization of these materials in geotechnical applications, particularly for road and rail embankments. However, before application in the prototype, establishment of the role of reinforcement in conjunction with such waste materials in improving the strength of the embankment slopes is essential to be carried out by studying the behaviour of footings located near the crest of the slope of such embankments through experimental and numerical studies.

Review of literature

There have been several studies reported in the literature [21, 46, 48] concerning with the bearing capacity behaviour of strip footings on the sloeps made up of granular soil where the investigations were carried out with the single slope ranging between 20° and 35°. Some of the researchers [12, 13] worked on fly ash structural fills. Few researchers [27, 52] presented investigations on the utilization of Pozzolanic materials such as mine waste in conjunction with coal ash and furnace slag by studying the bearing capacity behaviour of footing on such embankments. Lim and Chu [35] assessed the use of spent copper slag for land reclamation. Havanagi [25, 26] reported the utilization of copper slag wastes in embankment and pavement construction. They, further, presented the design and stability analysis of such embankments. Several researchers [3, 5, 34, 36, 47, 55], have reported on the behaviour of footings constructed on the stabilized and reinforced slopes of sandy soil. Bhardwaj and Mandal [5] presented the study on the behaviour of polypropylene fiber reinforced fly ash slopes. Pointing out the availability of the limited investigations in the literature on load carrying capacity of reinforced fly ash slopes, Choudhary and co-authors [9, 19, 30] reported experimental, theoretical and numerical studies on the bearing capacity behaviour of strip footing on reinforced fly ash slope. Nadaf and Mandal [40] presented model studies on fly ash slopes reinforced with planer steel grids. Dhatrak and Gandhi [11] evaluated bearing capacity of square and circular footings on reinforced fly ash slope.

Some of the researchers presented the use of discarded tyres wastes as a sustainable material which can be used in the civil engineering construction, especially in fills and embankments. Edil and Bosscher [14] investigated the feasibility of using shredded waste tyres to reinforce the sand. Foose et al. [17] opined shredded waste tyres could be used as a lightweight fill in the highway applications. Tatlisoz and Benson [51] investigated the feasibility of reclaimed high density polythene (HDPE) as the reinforcement for reinforcing the soils. Wasti and Bunton [54] conducted series of laboratory model tests on a strip footing supported by sand, reinforced with randomly distributed polypropylene fiber and mesh elements. Nilay et al. [41] assessed the potential advantage of using soil- tyre chip mixtures as backfill materials for the geosynthetic reinforced retaining walls and embankments. O’Shaughnessy and Garga [42] studied the feasibility of using non-shredded scrap tyres as soil reinforcement in tyre reinforced slopes. Yoon et al. [56] presented the benefits of using discarded car tyres in construction of test embankment using a sand-tyre shred mixture as fill material. Hataf and Rahimi [22] conducted series of laboratory test on the model of shallow footing on sand reinforced with tyre shreds. Yoon et al. [57] investigated the reinforcing effect of the tyre cell material, made from treads of waste tyres, in sand. Tanchaisawat et al. [50] investigated the behaviour of lightweight geomaterials made up of tyre chip-sand mixtures reinforced with geogrid for use as embankment construction on soft ground. Dewaikar et al. [10] reported the use of rubbergrid, geotextiles and geogrid in conjunction with mine waste for evaluating the bearing capacity of footings in the context of the centric loading. Moghaddas and Norouzi [37] investigated the feasibility of using randomly distributed rubber shreds as a soil reinforcement beneath footing. Srivastava et al. [49] reviewed studies on utilization of shredded rubber as the reinforcement material for soil improvement which focussed on the utilization of tyre chips to increase the strength behaviour of soil. Still, the literature concerning the utilization of tyre waste in conjunction with the Pozzolanic materials is scanty.

In recent years, numerical analyses (e.g. finite difference, finite element, discrete element) have gained popularity in the design practices as they can model several parameters precisely which can not be accounted for in the experimental or theoretical works. There have been few significant studies [1, 2, 4, 5, 8, 19, 20, 23, 24, 28, 29, 31,32,33, 39] which reported the numerical analysis of the reinforced embankment slope of sand or other types of slopes, [19] and 2013 presented the numerical analysis of the geogrid reinforced fly ash slope in conjunction with the experimental studies. Yet much needs to be investigated with respect to numerical analysis, particularly in the context of the safe and economical design of footings resting on reinforced embankment slopes made up different Pozzolanic waste materials.

The review of literature indicates that although significant work has been carried out on the load carrying capacity of the embankment slopes made up of soils, considerably less work has been reported with respect to the embankment slopes made up of fly ash and other Pozzolanic materials such as ground granulated blast furnace slag (GGBFS), copper slag. Further, the studies carried out on blast furnace slag and copper slags are relatively less as compared with the fly ash slope. Pursuant to this, Patil [43] carried out the comprehensive investigations on the strength and stability of the reinforced embankment slopes made up of fly ash and blast furnace slag. Various parameters such as effect of edge distance from slope crest, slope angle, the embedment depths of the reinforcement and number of layers, etc. were considered. Further, two types of reinforcements (geogrid and the rubbergrid) derived out of the discarded waste tyres) were also used. Patil and Chore [44] reported the experimental investigations on the strength evaluation of unreinforced embankment slopes made up of two different Pozzolanic materials (fly ash and GGBFS) by studying the bearing capacity behaviour of a strip footing on model slopes). They also presented the limited investigation on the load carrying capacity of geogrid reinforced fly ash slope with respect to critical slope angle observed by Patil and Chore [45] and in respect of only one embedment depth. Experiments with the Pozzolanic materials have their merits, there are various conditions and parameters that can not be examined in the laboratory. Therefore, development of the numerical procedure for predicting the performance consistent with the values observed experimentally may be fruitful.

Based on the afore-mentioned review of literature, the objective of the present work reported in this paper to examine the efficacy of the geogrid and rubbergrid reinforced fly ash and GGBFS embankment through the numerical analysis using finite element based software PLAXIS. The scope of the present paper is to report the load—deformation behaviour obtained numerically in view of the model study through the bearing capacity behaviour of the footing resting on the embankment slope and to compare the results obtained with those obtained experimentally and reported in the published literature [44, 45].

Laboratory model tests

In the numerical analysis, unreinforced embankment slopes made up of fly ash and GGBFS and geogrid reinforced fly ash embankment slope corresponding to the experimental work reported in the literature [44] were considered. In both the experimental investigations, model tests were conducted in plain strain conditions to study the behaviour of shallow footings placed on the top of the embankment slope under applied loads. The effect of various parameters on the load carrying capacity of the embankment slopes were studied in the investigations. Patil and Chore [44] dealt with the unreinforced fly ash and GGBFS embankments. In this study, series of plain strain model tests were conducted. Three slope angles (β = 31°, 39° and 45°) were considered and further, three edge distances (De = 1B, 2B and 3B) were considered in respect of fly ash embankment. Further, as the slope angle of 45 was found to be critical giving least load carrying capacity, the investigations on GGBFS slope was carried out for critical slope only, i.e., β = 45° and for all the edge distances. Subsequently, in an another study, Patil and Chore [45] reported limited experimental investigation on the geogrid reinforced fly ash slope for the critical slope (β = 45°) in the context of the geogrid reinforcement located at the embedment depth ratio of 0.3 with respect to all the three edge distances considered by them in their earlier study. The particulars of the experimental set up including loading frame, preparation of the fly ash and GGBFS slopes, strip model footing and test procedure have already been dealt with in detail in the works reported by the authors [44, 45] and hence are not described here. The Pozzolanic materials and the reinforcements considered in the investigation along with their properties used in the numerical analysis and the particulars of the model footing used as the load transferring medium are briefly described here.

Materials

Fly ash

The fly ash procured from Eklahare Thermal Power Plant, Nashik, Maharashtra, India was used throughout the investigation. The geotechnical properties of fly ash are shown in Table 1 [44]. The fly ash used in the experiment had a wide range of size of particles that were well rounded and spherical in shape, with surfaces that appeared to be very smooth and non plastic (NP).

Table 1 Geotechnical properties of fly ash and GGBFS (after [44])
Full size table

Ground granulated blast furnace slag (GGBFS)

The GGBFS procured from JSW Cement Industry, Raigad, Maharashtra (India) was used in the present investigation. It consists of essential silica and alumina of calcium. The material has a glossy structure and is ground to less than 45 microns. The ground slag in the presence of water hydrates and sets with time. The geotechnical properties of GGBFS are shown in Table 1 along with that of fly ash [44].

Model geogrid

Commercially available 1 mm thick bi-axial polymeric coated polyester model geogrid (PET) was used in the present investigation (Fig. 1a). This is made from high tenacity polypropylene rods which are polymeric coated. Different rib layout patterns give rise to different styles of uni-directional and bi-directional products. The average tensile strength of the model geogrid having dimensions 35 mm × 63 mm was observed to be 33.7 kN/m at 12.5% [45].

Fig.1
figure 1

Different reinforcement considered in the investigation

Full size image

Rubbergrid

It is recognized that, the rubber has many excellent mechanical properties in comparison to other materials. These include impact resistance, flexibility, abrasion resistance, and resistance to bio-degradation. These properties point to the potential of its being a great engineering material, like earth reinforcement. In the present investigations, scrap tyres have been used for deriving the rubber grid, which could act as the reinforcement and substitute to the geo grid. The rubbergrids were derived manually from the side wall and tread of the tyres of heavy vehicle tyres in 5 mm thick string (Fig. 1 b). The rubbergrids were formed in the size as that of geo grid (65 mm × 35 mm) with the help of aluminium wires reinforcing strips were derived from the sidewall and tread of the tyre. The strips of size, 5 mm × 5 mm were cut from these parts. The size was restricted to 5 mm, due to model testing and difficulties in manual cutting. Different rib layout engineering properties of truck tyres, as reported by Dewaikar et al. [10], are presented in Table 2.

Table 2 Engineering properties of truck tyres (after [10])
Full size table

Footing

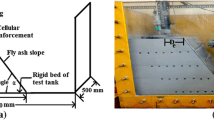
The rigid foundation was modeled by footing made up of good quality well seasoned Sal wood. The model footing of size 300 mm × 100 mm was used for conducting the model tests. The length of the footing was kept equal to the width of the test tank so as to simulate a strip or continuous footing conditions [34]. The thickness of the model footing was kept 100 mm.

Test parameters

The geometry of the footing test configuration considered in this investigation is shown in Fig. 2 with respect to model slopes made up of fly ash and GGBFS. The variables considered in a parametric study through the numerical analysis presented here are indicated in Table 3.

Fig. 2
figure 2

Schematic view of the geometry of test configuration

Full size image
Table 3 Variables considered in the parametric study of the embankment slope
Full size table

Numerical modeling

A series of two dimensional finite element simulations on footing- embankment slope system were performed to understand the deformation trends within the fly ash and GGBFS embankment mass. The analyses was performed using the finite element programme PLAXIS 2D (Version 8.6) which is capable of handling a wide range of geotechnical problems such as deep excavations, tunnels and earth structures such as retaining walls, slopes, embankments, etc. The analysis problem is considered as the plane—strain condition of the embankment. The embankment material (Fly ash and GGBFS) is modeled using non-linear Mohr- Coulomb criteria owing to its simplicity, practical importance and the availability of the parameters and further, 15 noded triangular coarse elements are considered. Similar approach has been used in literature [18, 20, 39]. The nodes at right and left vertical boundaries are not allowed to displace horizontally (horizontal fixity), but allowed to undergo vertical displacement whereas for the nodes at the bottom surface, both- horizontal and vertical displacements, are arrested (total fixity). The geometry of embankment and material properties used for numerical model (footing-slope system) is the same as that of the laboratory model tests. The dimensions adopted for the numerical model is kept same as that of laboratory model tests. Similar approach is also reported by Muthukkumaran and Almas Begum [39].

After setting geometry of problem, the material set is defined as per respective properties as shown in Figs. 3(a) and 4 (a) and Table 4. The nonlinear behavior of fill material is modeled using the non-linear Mohr– Coulomb criterion. The elasto-plastic Mohr–Coulomb model involves five input parameters, namely- Young’s modulus (E), Poisson’s ratio (µ) for soil elasticity, friction angle (ϕ), cohesion (c), for soil plasticity and angle of dilatancy (ψ). This Mohr–Coulomb model presents a first order approximation of soil behavior. The parameters used for numerical analysis are obtained from the basic tests on fly ash and GGBFS samples; and properties of geogrid are taken as provided by the supplier (Table 4). The properties of the footing considered in the analysis are also given in Table 4.

Fig. 3
figure 3

Numerical response for unreinforced fly ash embankment slope (β = 45°; De/B = 1)

Full size image
Table 4 Properties used in the finite element analyses (FEA)
Full size table

The geogrids are used to model the reinforcement in the numerical analysis presented here. Geogrids are assumed to be composed of geogrid elements (line elements) with two translation degrees of freedom at each node. The only material property required for geogrid is its elastic normal (axial) stiffness EA, which can be specified in the material data base. Geogrids are assumed as the slender structure with some non-zero value of normal stiffness and zero bending stiffness since it can sustain only tensile force and no compression [7]. The other properties used for the numerical analysis are well defined in PLAXIS 2D manual. Similar is the analogy followed for modeling another reinforcement, i.e., rubbergrid, considered in the investigation.

The footing is treated as an elasto-plastic plate with significant flexural rigidity (EI) and normal stiffness (EA). This software enables the automatic generation of 15 node triangle plane strain elements for the soil which provides a fourth order interpolation for displacements and the numerical integration involves twelve Gauss points (stress points).

Numerical analysis

In order to simulate the construction stage sequence of the Pozzolanic material (fly ash and GGBFS) slope with and without geogrid reinforcement, slope model of size (height 0.75 m, length 2.4 m and width 0.31 m) is formed with respective materials in PLAXIS 2D numerical analysis. The coarse mesh is generated by considering the entire element in place through automatic mesh generation system of PLAXIS 2D software. In this analysis, the specification of initial stresses is generated using K0 procedures or gravity loading. K0 is a coefficient representing the ratio of horizontal and vertical effective stress. A similar approach is also reported in the literature [6, 20, 38, 39].

The interaction between the geogrid and surrounding material is simulated by interface elements located between the reinforcement and fill material surfaces. The interface properties are calculated from the material properties available in the associated data set and the strength reduction factor is determined by applying the rules as given in the PLAXIS reference manual. PLAXIS allows for a fully automatic mesh generation of finite element meshes. A prescribed footing load is then applied in increments (load control method) accompanied by iterative analysis up to failure. The load advancement procedures (ultimate level and number of steps) make use of an automatic step size algorithm [53]. The size of the first load step was chosen automatically depending on the applied algorithm.

When a new load step is applied, a series of iteration are carried out to reach equilibrium. There are three possible outcomes in this process. In case-1, the solution reaches equilibrium within a number of iteration that is less than the desired minimum (04) whereas in case 2, the solution fails to converge within a desired maximum (10) number of iteration and for case-3 the number of required iterations lies between the desired minimum and maximum. And the load increment size for case-3 is assumed to be satisfactory.

After the iterations are complete, next calculation step begins. When soil plasticity is involved in a finite element calculation then each calculation phase needs to be solved in a series of calculation steps (load steps). The size of the first load step is obtained automatically which performs a trial calculation step and determines a suitable step size. This automatic step size procedure is primarily used for calculation where a certain state or load level (the ultimate state or ultimate level) has to be reached. This procedure terminates the calculation when the specified state or load level is reached or when material failure is detected. By default the number of additional step set is 250 and in most cases the calculation stops before the number of additional steps is reached (www.plaxis.nl). There are various procedures available (load advancement ultimate level, load advancement number of steps and automatic time stepping) for solution of non-linear plastic problems.

All the procedures are based on automatic step size selection and it automatically selects the most appropriate procedure by itself to guarantee optimum performance. There is a convenient default setting for most control parameters which strikes a balance between robustness, accuracy and efficiency. Domain size adopted for numerical analysis is same, as considered in the laboratory model tests, with one-to-one correspondence. Fixities are selected from the load submenu. In the geometry model, distinction can be made between horizontal fixities (ux = 0) and vertical fixities (uy = 0). In addition, one can select total fixities (ux = uy = 0). Standard fixities are selected from the load submenu, which automatically imposed a set of general boundary conditions to the geometry model. The boundary conditions of the model are assumed such that the vertical boundaries are free vertically and constrained horizontally while the bottom horizontal boundary is fully fixed.

The typical response of the unreinforced fly ash embankment slope analyzed numerically in respect of critical unreinforced fly ash slope (β = 45°) and critical edge distance (De = 1B) is shown graphically in Fig. 3(a–f).

The corresponding response for the geogrid reinforced fly ash embankment is indicated graphically in Fig. 4(a–f).

Fig. 4
figure 4

Numerical response for geogrid reinforced fly ash embankment slope (β = 45°; De/B = 1)

Full size image

A typically deformed FE mesh for footing on unreinforced fly ash slope and single geogrid reinforced fly ash slope are shown in Figs. 3(b) and 4(b) respectively. These deformed meshes are in the context of critical slope angle (β = 45˚) and edge distance (De/B = 1) in respect of unreinforced and geogrid reinforced fly ash slope and Z/B = 0.3 as in case of reinforced slope. It can be seen that the deformation is less when the loaded footing rests on the reinforced slope as compared to unreinforced slope. The reinforcing layer decreases subgrade deformation and prevents particles from moving to the region surrounded by the reinforcing layer. This can be observed and compared through the deformed FE mesh images [Figs. 3 (b) and 4(b)]. The reinforcement also provides lateral restraint, which confines the horizontal movement of fly ash particles under the base of footing and mitigates slope deformation when compared with unreinforced slope [Figs. 3 (b) and 4(b)]. The reinforcing layer also decreases the horizontal movement of subgrade particles. The extreme total displacement developed with two slopes  Figs. 3(d) and 4(d) gives confirmed advantage of reinforcing layer inclusion with the locking displacement beyond the region away from the slope. Effective principal stress vector variation is seen to have been differently spread over in case of unreinforced slope (Fig. 3c) and that in case of geogrid reinforcement slope (Fig. 4 c). In case of geogrid reinforced fly ash slope, the result of FE analysis shows that around 25% more effective principal stress are induced before ultimate failure as compared to that in case of unreinforced fly ash slope with similar slope angle and edge distances. The inclusion of geogrid reinforcement at significant embedment depth from top of slope is found to decrease the deformation of slope and footing resting on it as compared to that in unreinforced slope.

The slope failure mechanism on the reinforced slope can be discussed on the basis of the FE output, total and vertical displacement within the slopes [Figs. 3(d–e) and 4(d–e)]. The total and vertical displacements in the right part, which confirms the occurrence of failure as mentioned by principal strain locations, can be compared with the help of these figures to assess the improvement in the bearing capacity improvement, especially, through the strains concentrated below the confined region and extended toward the bottom of slope in form of stress isobars. The total displacements (Figs. 3d and 4d) indicate the end points on the outside of slope toe in form of these isobars. The vertical displacements (Figs. 3e and 4e) follow the similar pattern but with less stress contours as compared to the total displacement curves seen in Figs. 3(d) and 4(d). The shear strain with vertical displacement stress isobars (Fig. 4e) in respect of reinforced slope indicates more close isobars as compared to that in respect of unreinforced slope (Fig. 3e). This can be confirmed with total as well as vertical displacement which shows around 51% more settlement capacity before the failure of the slope (Figs. 3d–e and 4 d–e).

From Figs. 3(a–e) and 4(a–e), it can be pointed out that the inclusion of the geogrid reinforcement in fly ash slope modifies and balances the effective stresses below the base of footing. The legendary color shading with Figs. 3 and 4 compares the load bearing capacity, settlement and the slope stability improvement in respect of unreinforced and reinforced slope.

For unreinforced slope it is found that the bearing pressure action reaches the ultimate failure of slope and shows the pressure—settlement curve and pressure decreases suddenly resulting continuous increase in the settlement. From the FE analysis, the plastic and tension cutoff points are obtained for all slope angles, edge distances in case of unreinforced as well as reinforced slopes. Stress points below the footing in the plastic states are indicated in Figs. 3(f) and 4(f). The FE analysis is seen to induce different arrangements of plastic points near the footing base depending on the footing location and further, condition of the reinforcement along with the variation in slope angle. The Fig. 4(f) illustrating the point points in case of geogrid reinforced fly ash slope shows the more intense plastic points generated at the verge of collapse for the footing near the sloped ground. It can be observed from Fig. 3(f) that the plastic points below footing are in the widening condition in case of unreinforced slope. This clearly shows as to how the shear failure pattern below footing is stressed towards the toe of unreinforced fly ash slope and also shows as to how the geogrid reinforcement layer limits the dissipation of relative shear stress towards the toe of slope (Figs. 3 f and 4f).

Results and discussion

Following the analysis with respect to all the constant and variable parameters indicated in Table 3 for different types of embankment slopes, the results in the form of pressure- settlement characteristics, ultimate bearing capacity, settlement ratio and the bearing capacity ratio are obtained. The results for different types of embankment configurations (Table 3) are discussed in the sequential manner.

Unreinforced fly ash and GBBFS embankment

The typical curves indicating the variation of bearing pressure (q) and the settlement ratio (∆) in respect of the unreinforced fly ash and GGBFS embankment slopes w.r.t. to the values obtained numerically are shown in Figs. 5 and 6, respectively. Further, the variation as reported in the literature [44] w.r.t. the values observed experimentally in respect of the unreinforced fly ash slope is indicated in Fig. 5 and that in respect of unreinforced GGBFS slope with critical slope angle of 45° is indicated in Fig. 6(c). The footing settlement (s is expressed as the settlement ratio (∆ in terms of the footing width (B [∆ = (S/B × 100%].

Fig. 5
figure 5

Pressure-settlement curve for unreinforced fly ash slope

Full size image
Fig. 6
figure 6

Pressure-settlement curves for unreinforced GGBFS embankment

Full size image

It is seen that with increase in slope angle, the ultimate bearing capacity is found to decrease for all the edge distances considered in the investigations. Notwithstanding from the results, it can be concluded that the effect of slope angle on the bearing capacity (BC) is more significant when the footing is located neared to the crest, i.e., De = 1B or even less; but it starts diminishing as the edge distance increases to 2B or 3B. It is also seen that the ultimate bearing pressure of the footing increases with increase in edge distance in both the cases. It may be noted that the bearing capacity in respect of the critical slope angle (β = 45°) corresponding to edge distance 2B and 3B is on higher side by 4.17% and 7.13%, respectively when compared with that obtained for the edge distance of 1B. The bearing capacity in respect of GGBFS embankment also shows the similar trend as seen in case of fly ash embankment. The capacity at the edge distance of 2B and 3B in case of GGBFS embankment is found to be on higher side by 8.3% and 18.3%, respectively corresponding to the edge distance of 2B and 3B as compared with 1B. The edge distance of 1B can be referred to as the critical edge distance. The total displacement for unreinforced fly ash embankment slope is found to be 14.24 × 10–3 m, 13.42 × 10–3 m and 10.42 × 10–3 m for the critical depth of 1B of embankment slopes of 31°, 39° and 45°, respectively. Further, when the bearing capacity of the fly ash and GGBFS embankment is compared for the slope angle of 45°, it is seen that the strength of GGBGS embankment is on higher side.

Similar trend of variation in bearing capacity with slope angle for all the edge distances in case of unreinforced fly ash embankment slope and with edge distance in GGBFS embankment has been reported in the experimental investigation [44]. Further, when the results obtained through the numerical analysis are compared with those obtained in the experimental studies, it is seen that the values obtained numerically are on lower side for all the slope angles in respect of fly ash slope and the critical slope angle (45°) in respect of GGBFS embankment. It indicates that the numerical analysis underestimates the value of the ultimate bearing capacity in the range of 33.3–40.2%, 35–39% and 12.7–33.11% in respect of fly ash embankment for the slope angles of 31°, 39° and 45°, respectively. In respect of GGBFS embankment, the corresponding variation is found to be 4.05–13.04% for the critical slope (45°). The percentage variation in the ultimate values of the bearing capacity corresponding to critical slope and critical edge distance (De = 1B) is observed to be near about same. The settlement ratio, expressed as percentage, is found to be 10.42 obtained by the numerical analysis as against 5.1 obtained experimentally in case of reinforced fly ash embankment slope corresponding to critical slope. Similarly, the corresponding values are 16.14 and 6.2 in case of unreinforced GGBFS embankment. The values of the settlement ratio as obtained in the experimental studies are on lesser side as compared to that obtained numerically.

Reinforced fly ash slope

Geogrid

The pressure-settlement characteristics for different embedment depth rations (Z/B = 0.3, 0.6, 0.9, 1.2, 1.8, 2.4 and 3) and further for all the slope angles (β = 31°, 39° and 45°) and edge distances (De/B = 1, 2 and 3) with respect to the values obtained numerically are shown in Fig. 7(a–i).

Fig. 7
figure 7figure 7

Pressure-settlement curve for geogrid reinforced fly ash slopes

Full size image

It is seen that with increase in embedment depth ratio (Z/B) from 0.3 to 1.2, the bearing capacity improvement ratio (BCI) is found to increase by 6% approximately and with further increase in Z/B from 1.2–3, the BCI is found to reduce from its peak value. Therefore, it can be said that the bearing capacity increases with increase in embedment depth ratio (Z/B) up to a certain critical value and thereafter, it decreases with further increase in Z/B ratio in all the cases of slope angles and edge distances. The maximum value of the bearing capacity in case of reinforced fly ash slope is obtained corresponding to the embedment depth ratio of 1.2. The load transfer mechanism seems to reach its optimum value when the embedment depth ratio (Z/B) is around 1. As regards the trend of variation in bearing capacity in case of reinforced slopes with a peak value in between, similar trend has been reported by the few researchers [34, 47, 55] for reinforced sand slopes although the fill used in the present investigation is fly ash and GGBFS, relatively much weaker material than sand and the slope angle used in the present investigation is much higher. Moreover, the results are quite consistent with those reported by some of the researchers [6, 15, 16, 20, 38, 39] in the recent past wherein the bearing capacity improvement in the fly ash with inclusion of geogrid was studied.

Figure 7 indicates that wherever excessive settlement is the controlling factor in determining the allowable bearing capacity, incorporation of the layer of geogrid reinforcement in the fly ash fill slope may significantly decrease the settlement ratio for the same level of bearing pressure. It is observed that, the provision of layer of geogrid reinforcement increases the ultimate bearing capacity of the fly ash embankment. When the values of the ultimate bearing capacity corresponding to Z/B = 1.2 are considered, the increase in the bearing capacity is found to be in the range of 9.62–14%, 10–16.98% and 10.4–16.5% for the slope angles of 31, 39 and 45, respectively.

The tendency of the footing to rotate or move towards the face of the embankment is clearly noticed. It is also observed that, with the increase in the embedment depth of the reinforcement layer, the load carrying capacity improves. However, this improvement in the bearing capacity is accompanied by increase in settlements. The total displacement in respect of the unreinforced fly ash slope which is 10.42 × 10–3 m is found to increase to 15.79 × 10–3 m with the insertion of the layer of geogrid. The reinforcement layer limits the spreading and lateral deformation of soil particles. The mobilized tension in the reinforcement enables it to resist the imposed horizontal shear stresses built up in the soil mass under the loaded area. This results in the improvement in the bearing capacity of the reinforced fill. When reinforcement is placed at a depth (Z/B = 1.2), the plastic failure zones do not extend much below the reinforcement layer in case of both fly ash as well as GGBFS embankment. However, when the reinforcements lies around 1 (Z/B = 1.2), the reinforcements enable much better load distribution over larger area below the reinforced zone.

When the effective stress distribution with respect to an unreinforced and reinforced fill is compared, it can be observed that the failure zones are widely distributed underneath the footing for greater width and depth in respect of reinforced case than that in respect of unreinforced case. It is obvious that the geogrid layer prevents the lateral movement of a fill material towards the face of the slope and pushes it downward to a greater depth, thus, spreading the footing load wider and deeper into the fly ash.

When the values of the bearing capacity in case of geogrid reinforced fly ash embankment slope (β = 45°) for Z/B = 0.3 reported by Patil and Chore [45] in respect of experimental investigations are compared with those obtained numerically for the corresponding slope angle and embedment depth ratio, the numerical values are on lower side as compared with those obtained experimentally. The bearing capacity obtained numerically is found to be underestimated by 17–27%. When the values of the ultimate bearing capacity for different slope angles and edge distances obtained experimentally [43] is compared with those obtained numerically for the embedment depth ratio (Z/B) = 1.2, the numerical analysis is found to underestimate the experimental values by 43.7–48.65%. The value of the ultimate bearing capacity obtained numerically is found to underestimate the experimental value by 46.5% corresponding to the critical edge distance of 1B in respect of critical slope for Z/B = 1.2. Similarly, the settlement ratio is found to be 15.8% from the numerical analysis whereas the same is calculated to be 3.1% with respect to the observations recorded in the experimental studies.

Rubbergrid

The effect of rubbergrid reinforcement on the behaviour of footing resting on the top of the fly ash slope is also studied for all the three slope angles and edge distances. The variation of BCI with embedment depth obtained through numerical analysis is indicated in Fig. 8.

Fig. 8
figure 8

BCI with rubber grid reinforced fly ash slope

Full size image

When the variation of bearing capacity is studied with respect to different embedment depth ratios, it is seen that the capacity attains the maximum value corresponding to the embedment depth ratio of 1.2, exactly similar to that seen in case of the geogrid reinforced fly ash slope. Further, when the bearing capacity for different slope angles and edge distances are considered corresponding to Z/B = 1.2, it is observed that the bearing capacity decreases with increase in slope angle for any edge distance and it increases with the edge distance from the slope crest. Similar observation is seen in case of geogrid reinforced fly ash embankment. The corresponding increase in bearing capacity with respect to the edge distance of 2B and 3B is found to be 5.17% and 8.62%, 8% and 9.7%, 3.44% and 10.3% for 31°, 39° and 45° slope angles, respectively. This clearly indicates that the slope angle of 45° and the edge distance of 1B are the critical values similar to that is seen in case of unreinforced and geogrid reinforced fly ash slope. Further, when the values of the ultimate bearing capacity for geogrid reinforced and rubbergrid reinforced fly ash slopes obtained numerically are compared, it is found that the values are on higher side in case of the rubbergrid reinforcement; the increase being in the range of 0.5–1.75%, 1.5–5% and 3.3–9.5% for the slope angles of 31°, 39° and 45°, respectively. This demonstrates the better performance of rubbergrid derived out of the discarded waste tyres vis-à-vis geogrid. The better performance of the rubber grid could be due to the better frictional adherence between the longitudinal members of the grid and soil which is influenced by the surface properties and coefficient of friction between them. The nylon belt provided within the tread and sidewalls of the tyre remains protruded even after stripping. This helps in creating the desired roughness in the rubber grid and in turn develops greater frictional resistance, although its tensile strength is less than that of geo grid. The semi-elastic properties of rubber grid develop better pseudo- cohesion owing to the temporary deformation of rubber grid. However, this mechanism is not present in case of other conventional geogrids. Further, the apertures present in the grid structure, there are chances for better interlocking of the sub-grade and the reinforcement along with the backfill material. Hence, the performance of rubbergrid is better than that of geogrid.

The trend of better performance of rubbergrid as compared to geogrid is consistent with that reported in the literature [10]. Further, when the values of the bearing capacity obtained numerically in respect of critical slope of 45° are compared to that observed in an experimental study [43], the numerical values are found to underestimate the experimental values by 44.2–46.2%. Similarly, the better performance of rubbergrid as compared to geogrid is also evident from the experimental results.

It can be concluded that the effect of slope angle on the bearing capacity is more significant when the footing is located in the nearby vicinity of the crest, i.e., De = 1B or even less. But this, effect starts diminishing with the increase in the edge distance beyond 1B. In general, the ultimate bearing capacity of the footing with its location increases with an increase in edge distance from the slope crest. This is attributed to the passive resistance of the fly ash offered by the respective reinforcements (geogrid and rubbergrid) from the slope side. When the footing is placed at sufficient distance from the slope crest, the passive resistance from the slope side to the failure wedge under the footing increases, whereas the reinforcement reduces the lateral displacement. This results in a wider and deeper failure zone, thereby increasing the bearing capacity. Further, the trend of increase in strength with edge distance in all the cases of the slope angles and the decrease in strength with slope angle for any value of the edge distance as seen in case of unreinforced fly ash embankment holds good here as well. It is also consistent with the afore-mentioned published literature and also observed experimentally.

Geogrid reinforced GGBFS embankment

The numerical analysis is extended to evaluate the bearing capacity of the geogrid reinforced GGBFS embankment in respect of critical slope (45°) and edge distance corresponding to the embedment depth ratio (Z/B) of 1.2. The strength of the geogrid GGBFS embankment is found to be 3.33% more as compared to unreinforced GGBFS embankment. However, this improvement in bearing capacity is accompanied by increase in settlements as it retains its capacity. The total displacement in respect of unreinforced GGBFS embankment is found to be 16.14 × 10–3 m and the same increases to 24.19 × 10–3 m with the inclusion of a layer of geogrid reinforcement within a fill. The ultimate bearing capacity of the geogrid reinforced GGBFS slope obtained through numerical analysis is found to underestimate the experimental value by 19.5%. When the effective stress distribution with respect to an unreinforced and reinforced GGBFS fill is compared, unlike that in case of geogrid reinforced fly ash sloped fill, inclusion of geogrid reinforcement within the GGBFS sloped fill is seen to have failed in improving the bearing capacity that significantly as the effective stresses are comparatively more, which results in larger failure surface with more settlement and bearing capacity. Further, when the gain in the strength of the FA and GGBFS embankment slope in the context of geogrid reinforcement, the increase in the ultimate bearing capacity in case of reinforced fly ash and GGBFS embankments are found to be 10.4% and 3.33%, respectively when compared with the bearing capacity obtained for unreinforced embankments. The gain due single layer of geogrid reinforcement in the bearing capacity seems to be significant in case of fly ash embankment as compared to that in GGBFS embankment. Further, it is found that the embankment slope reinforced with a layer of geogrid reinforcement and made up of GGBFS corresponding to optimum embedment depth ratio is found to exhibit more strength, i.e., 17% higher, as compared to similar embankment slope made up of fly ash.

Limitations

The numerical modeling in the present investigation is carried out on the premise of non-linear behavior of the fill material. For simulating non-linear behavior of the fill material, non-linear Mohr–Coulomb elasto-plastic model is used. The Mohr–Coulomb model is a first order model and it includes only limited number of features exhibiting the behavior of soil or soil materials such as fly ash and ground granulated blast furnace slag. This model neither includes stress dependency nor anisotropic stiffness. The Pozzolanic materials considered in the present study have a tendency to wick water into itself and it may be possible that the lower extremities of the embankments made up of such waste materials will get saturated and further, would result into a loss of shear strength. Therefore, the base of such embankments should not be made exposed to the free moisture or presence of high water table conditions. In order to avoid the seepage in such embankments, a drainage layer should be provided at their base. Moreover, the compacted fly ash and GGBFS slopes must be protected from erosion by placing the soil cover of suitable thickness. The unavailability of the standard data in respect of the rubbergrid derived out of discarded waste tyre has also been the limitation in the present investigation. All the same, the results obtained are consistent with those reported by several researchers who worked on the similar theme irrespective of the materials.

Summary and conclusions

The bearing capacity behaviour of a strip footing resting on the top of embankment slopes made up of two Pozzolanic materials such as fly ash and GGBFS reinforced with a layer of the geogrid and the rubbergrid, derived from the discarded waste tyres, is studied numerically through a finite element based software, PLAXIS. Some of the important conclusions inferred from the numerical analysis are deduced as under.

  • Numerical analysis can be used for predicting the performance of the footing resting on the top of the embankments for various conditions and parameters which are otherwise difficult to be considered in the experimental studies.

  • Several parameters such as slope angle, location of the footing from the crest of the slope, depth of embedment of the reinforcement from top affects the load carrying capacity of the embankment slopes.

  • The reinforcement has a considerable effect on improving the bearing capacity which indicates a significant perfection in the stiffness of the fill and shear strength; and further provides ideal densifications o the fill. A layer of the reinforcement within the sloped fill improves the bearing capacity to the maximum extent when the same is located at a depth of 1.2 times the width of footing, i.e., Z/B = 1.2. Beyond this value, there is no significant improvement in the bearing capacity.

  • With increase in the edge distance from the crest of the slope, the bearing capacity decreases for any slope angle irrespective of the material and reinforcement. The edge distance of 1B considered in the present investigation is found to give least bearing capacity irrespective of the slope angle, fill material and the reinforcement.

  • With increase in slope angle, the ultimate bearing capacity decreases for any edge distance in case of unreinforced fly ash and GGBFS embankment slope; and geogrid and rubbergrid reinforced fly ash slopes. The slope angle of 45° seems to be critical. The percentage decrease in the bearing capacity for this angle is found to be in the range of 3.84–7.7 and 3.5–7 in case of unreinforced and geogrid reinforced fly ash slope, respectively. In case of rubbergrid reinforced fly ash slope, the corresponding decrease is in the range of 1–2.6%.

  • The strength of geogrid reinforced fly ash embankment slope vis-à-vis unreinforced fly ash slope is found to be in the range of 9.6- 17% considering all slope angles and edge distances.

  • The strength of the unreinforced GGBFS embankment is found to be on higher side by 25–38% as compared to that of unreinforced fly ash embankment for the critical slope considered in the study considering all the edge distances and the strength of geogrid reinforced GGBFS embankment for critical slope and the edge distance is 4.2% more than that of unreinforced GGBFS embankment.

  • The strength of the rubbergrid reinforced fly ash embankment is found to be slightly more as compared to that of the geogrid reinforced fly ash embankment by 0.5–9.5% considering all the slope angles and edge distances.

  • Numerical analysis helps in better understanding the deformation behaviour of the embankment slope with respect to embedment depth of the reinforcement, slope angle and edge distance. It presents the picture of different stresses with load transfer mechanism and provides a realistic failure mechanism. In addition, it demonstrates as to how the reinforcement layer can protect the slope from collapse by decreasing the slope deformation.

The trend of the results with respect to various parameters obtained in the present study is similar to that reported by the authors with respect to experimental study and further, consistent with that reported by several researchers. The results obtained numerically when compared with the experimental results reported in respect of the similar studies and published elsewhere, are found to be underestimated. However, similar trend of results has been reported by few other researchers who worked on the similar lines and reported the experimental as well as numerical studies. The study presented here indicates that the industrial waste materials such as fly ash and GGBFS can be advantageously used in the embankment construction. Further, the discarded waste tyres can also be used effectively as the reinforcement. The utilization of such waste material can solve the problem of waste disposal and it may result in the sustainable construction material.