Abstract
Footings placed on or near a slope, the slope face act as a finite boundary that leads to an inappropriate and inadequate development of the plastic region of failure as the foundation approaches the limit state under the applied loading. Depending upon the position of the footing and steepness of the slope, the above-mentioned phenomena might lead to considerable decrease in the bearing capacity of the foundation. A sequence of finite element analysis has been carried out using Plaxis 2D v2015.02 to inspect the ultimate bearing capacity of strip footings placed at the crest of the c–φ soil slope. The effect of various geo-parameters namely internal angle of friction (φ), cohesion (c), setback distance (b), width of footing (B), slope angle (β) and embedment depth of footing (Df) on the ultimate bearing capacity of the footing have been investigated and the outputs obtained are appropriately elucidated. In addition, large database of numerically simulated ultimate bearing capacity has been considered to develop and verify the ANN model to establish the relative importance of the input parameters.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
The ultimate bearing capacity (UBC) of foundation is defined as the maximum stress that it can carry without undergoing a shear failure. Based on the shear strength parameters of the soil, Terzaghi [39] was the first to estimate the UBC of a strip footing placed on a uniform horizontal ground. The basic proposal for the bearing capacity of strip footings has undergone several modifications, primarily related to the bearing capacity factors, as well as inclusion of several new contributory factors [20, 29, 40]. Moreover, in order to accommodate different shapes of the footings (square, rectangular, circular or combined), shape factors were introduced in the bearing capacity expressions [20, 40].
Rapid growth of urbanization in hilly regions of India has resulted in myriads of residential and commercial constructions. The foundations of such constructions are mostly shallow, and are located either on the crest or on the benched face of the slopes. Apart from the urban constructions, transmission towers, mobile tower, retaining walls, water tanks, bridge abutments and even foundations for transportation links are mostly placed on the slopes. Foundation on slopes is a challenging and complex problem for the geotechnical engineers.
There exists limited researches on experimental and numerical investigations connected to the estimation of the bearing capacity of a footing located on a slope [1, 4,5,6, 9, 22, 23, 37, 38]. Most of the investigations have been done to estimate the bearing capacity of shallow footings, resting on dry cohesionless sandy soil slope to examine the effects of geo-parameters. Very few literatures exist related to the numerical investigations for strip footings resting on a c–φ soil slope [26].
Neural networks have been initiating from the research of McCulloch and Pitts [28], who recognized the capability of interconnected neurons to estimate some logical functions. Hebb [21] investigated the importance of the synaptic connections in the learning process. Later, Rosenblatt [35] had provided the first operational model of a neural network: the ‘Perceptron’. The perceptron, built as an analogy to the visual system, was able to learn some logical functions by modifying the synaptic connections. Artificial neural networks (ANNs) usually considered when the relationship between the input and output is complex in nature or application of another available method takes a large computational time and effort is very expensive.
Many researchers in different field of the civil engineering have considered ANNs. Lee and Lee [25], Das and Basudhar [11] and Momeni et al. [31] used ANN for forecasting the pile bearing capacity. Ghaboussi et al. [18] had showed that ANNs were powerful tools for the mathematical constitutive modelling of geomechanics. Shahin et al. [36] had applied successfully back propagation and Multi-Layer Perceptron’s (MLPs) to predict the settlement of shallow foundations on granular soils. Goh [19] had demonstrated that ANNs have capability to model the complex relationship between seismic soil parameters and liquefaction potential using actual field records. The prediction of swelling pressure and hydraulic conductivity characteristics of clayey soil have been investigated by several researchers [12, 13, 16, 30]. Noorzaei et al. [34], Kuo et al. [24], Behera et al. [7, 8] had used ANNs to predict the UBC of strip footing resting on horizontal ground surface loaded with centrically and eccentrically loading.
Habitats in the hilly regions mostly comprise of the houses resting either on the slope face or on the slope crest. A ‘Compilation of the catalogue of the building typologies in India’ revealed that most of the buildings located in the hilly terrains in the North-Eastern regions of India are supported by shallow footings [33]. It has been perceived from the field study [33] that in the hilly region the foundations are constructed on the slope by cutting and filling the slope face. Strip footings are commonly considered for building foundations over the slope. Hence, it is important to research and comprehend the failure mechanism of strip footings resting on the c–φ soil-slope. Hence, based on 2-D finite element (FE) analysis considering Plaxis 2D, this article reports the effect of various geo-parameters on the normalised UBC [qu/γHs where, qu = ultimate bearing capacity, γ = unit weight of soil and Hs = height of slope] of a strip footing resting on crest of c–φ soil-slopes. The 2D numerical model also provides a description of the failure mechanism involved in the process of loading and failure of the footing. An artificial neural network (ANN) model has been made for the prediction of normalised ultimate bearing capacity (qu/γHs) of strip footing resting on crest of c–φ soil-slope from the outcomes of the parametric investigation. From the ANN results, a sensitivity analysis has been performed to comprehend the importance of various geo-parameters considered for assessing UBC.
Numerical analysis
Plaxis 2D v2015.02 is a finite element (FE) tool intended for two-dimensional analysis of deformation, stability and ground water flow in geotechnical engineering. Plaxis 2D is equipped with several features to deal with various aspects of complex geotechnical problems incorporating advanced constitutive models for analysis of time-dependent, non-linear and anisotropic behaviour of soil or rock. It has been observed from the past researches [1, 22] that dry cohesionless sandy soil-slope has been considered for experimental and numerical investigation for estimating UBC of footings resting on or near the slope. In case of practical scenario, hill-slopes are made of different types of soils, ranging from fine silts, marginal soil mixtures, gravels, as well as highly weathered rock masses. As a result, finite element 2-D analysis has been carried out to study the behaviour of a strip footing resting on a c–φ soil slope with an aim to represent the commonly occurring building foundations on the hill slopes of India.
Description of the modelling
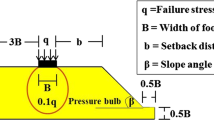
The model geometry has been developed for strip footing located on the crest of the slope as shown typically in Fig. 1. In accordance to the Boussinesq’s elastic stress theory, the “0.1q” (q is the stress applied on the footing up to its failure) stress contour represents the outermost significant isobar, beyond which the effect of the applied stress is considered negligible. The model dimensions have been so chosen that the significant isobar is not intersected by the model boundaries (Fig. 1). From the past researches [2, 3, 10], it has been perceived that the bearing capacity of strip footing remains unaffected beyond an optimal depth of 3B (B is footing width) from base of footing. In case of embedded footing, the depth of the domain has been changed. For the embedment depth of footing 1B, the domain depth has been changed to 4B plus the footing thickness of 0.2 m. The model dimension and boundary condition have been chosen in such a way that the slip mechanism generated beneath the strip footing resting on crest of slope should not be affected by the model boundaries. Moreover, the slip lines have not been reached to toe of the slope model.
In the numerical model, “standard fixity” condition has been employed. Horizontal fixity was applied to the vertical edges, while the bottom edge of the model is assumed to be non-yielding and restrained from both vertical and horizontal movements (Fig. 2). The inclined slope face is devoid of any fixity, allowing for free deformation occurring due to the location and loading of the footing. In order to estimate the bearing capacity of footing in the numerical framework, various locations of a strip footing have been chosen for the numerical analyses. Figure 3 shows the different locations of the surface and embedded footings on the crest or the face of the sloping ground.
To perform finite element calculation, the model geometry is discretized into smaller finite number of elements. In Plaxis 2D, the basic soil elements are the 6-noded and 15-noded triangular elements. In the present research, 15-noded triangular elements were used (Fig. 2) as it provides more nodes and Gauss points aiding in comparatively precise determination of displacements and stresses as compared to the 6-noded triangular elements. Plaxis 2D program allows for a fully automatic generation of finite element meshes using the ‘robust triangulation scheme’. In Plaxis 2D, five basic types meshing is available namely ‘very coarse’, ‘coarse’, ‘medium’, ‘fine’, and ‘very fine’, each having progressively refined mesh coarseness factor. The mesh should be sufficiently and optimally fine to obtain correct numerical results. A very coarse mesh may fail to capture the important responses of the domain while beyond optimally fine meshed, there are chances of the accumulation of numerical errors. Moreover, very fine meshing should be avoided since it will take excessive time for calculations. Any basic meshing scheme can be adopted, with further provisions of local refinements, as demanded by the merit of the problem and the location of the response points in the numerical simulation. The present numerical investigation has been done with fine meshing as shown in Fig. 2.
For the present study, the soil is modelled by linear elastic-perfectly plastic Mohr–Coulomb (M–C) model which involves five input parameters, i.e. elastic parameters (stiffness E and Poisson’s ratio ν) and strength parameter (soil plasticity parameters: c, cohesion; φ, angle of internal friction and dilatancy parameters: ψ, angle of dilatancy). Plasticity theory specifies that, if the dilatancy angle is not identical to the friction angle, the material follows a non-associated flow rule. The dilatancy angle varies from zero to the soil friction angle. Correspondingly, dilative coefficient, η, which relates the dilatancy angle to the soil friction angle, is defined as \(\eta = \psi /\varphi\), where, φ is the friction angle and ψ is the dilatancy angle. Theoretically, the magnitude of dilative coefficient is \(0 \le \eta \le 1\). The case η = 1 directs that the material follows an associated flow rule [15, 41]. In the present investigation associated flow rule has been taken into account, for each value of friction angle φ, dilation angle ψ has been considered equal to φ (associative flow rule). The various combinations of geotechnical and geometrical parameters used in the present study are given in Fig. 4. It has been perceived from past research [1] that the unit weight of soil has negligible effect on the UBC (qu). In the present numerical investigation, the unit weight of soil has been taken 16 kN/m3 as constant.
The rigid rough strip footing, formed with M20 concrete material, was represented by using linearly elastic model and the parameters are tabulated in Table 1. An interface element is provided at the boundary of the concrete and soil elements, the stiffness matrix of which was obtained using Newton–Cotes integration points [32]. The interface parameters were simulated by assigning a suitable value to the interface strength reduction factor (Rinter) which controls the soil strength mobilized at the interface during the deformation. For the present study, the strength reduction factor for the soil-concrete interface was assigned to be 1, thus allowing no relative movement between the footing and the soil; hence, the footing is modelled as rough strip footing.
The failure mechanism generated beneath the footing resting on horizontal ground has been postulated by Terzaghi [39] on the basis of the assumption that the base of the footing is rough. In the same fashion, the base of the footing has been considered as rough base by taken into account Rinter = 1 to comprehend the failure mechanism of footing resting on or near the slope. The rough base indicates high friction between footing base and soil. Hence, relative horizontal movement between soil and foundation base is zero.
In Plaxis simulations, initial stresses need to be specified. Two possibilities remain for the specification of these stresses, namely ‘K0-procedure’ and ‘Gravity loading’. As a rule, K0-procedure should be used in case of horizontal surface and with any soil layer and phreatic lines parallel to the surface. For all other circumstances, Gravity loading should be considered.
In the current research, Gravity loading has been taken into account for strip footing resting on crest of slope. The initial stresses, in this case, are set up by considering the soil self-weight in the first calculation phase. In Mohr–Coulomb model, the final value of K0 depends strongly on the assumed values of Poisson’s ratio (\(v\)). It is important to choose magnitude of Poisson’s ratio that provides realistic values of K0. The magnitude of K0 has been given by Eq. 1. In the present study, the magnitude of Poisson’s ratio (\(v\)) has been taken as 0.3.
In the current investigation, load controlled analysis has been considered. The vertical load has been provided over the strip footing till failure. In the present analysis, the embedded footing has been modelled by considering the practical construction sequences. Firstly, the soil has been deactivated from the foundation pit. The boundary conditions have been applied to the excavated pit by providing horizontal and vertical fixities to the vertical walls and bottom of the pit. Afterwards, the footing and the soil cluster over the footing have been activated. Then the given fixities have been removed. Finally, load has been activated over the footing till failure.
Artificial neural networks modelling
Neural networks are data processing systems consisting of a large number of simple, highly interconnected processing elements (artificial neurons) in an architecture inspired by the structure of the central cortex of the brain. They operate as black box and powerful tools to capture and learn significant structures in data. Neural networks can provide meaningful answer even when the data to be processed include errors or are incomplete and can process information extremely rapidly when applied to solve real world problems.
A commercial Microsoft Windows-based ANN software, Matlab v2015A [27] was used throughout the study. This software allows the user to select the number of hidden layers and hidden layer nodes (neurons), iterations used during the model training, learning algorithm and transfer functions. A multilayer feed-forward back-propagation network, which was created by generalizing the Levenberg–Marquardt’s [30] learning rule to multiple layer networks and nonlinear differential transfer functions, was used in the modelling. In the present study, the network architecture consisted of an input layer with six neurons, an output layer with one neuron, and a hidden layer with nine neurons as shown in Fig. 5. The number of hidden nodes in a network is critical to network performance. Too few nodes can lead to under fitting. Too many nodes can lead the system toward memorizing the patterns in the data or learn noise [11]. The transfer function used in the model is hyperbolic tangent sigmoidal signal function for both inputs to hidden and hidden to output layers. The idea behind choosing sigmoidal functions as transfer functions is that it bears a greater resemblance to the biological neurons. In case of sigmoidal functions, the output of the neurons varies continuously but not linearly with the input. The maximum epochs have been set to 10,000. The Root Mean Square Error (RMSE) specifies the error generated while learning and can be calculated using Eq. (2).
where, N is the total number of data, OSimulation is the numerical simulated values of property and OANN is the predicted values of this last one. The error (E) values between the simulated results and the predicted results with the present ANNs models are expressed by Eq. (3).
Stages of analysis
Based on the developed 2D simulation models, several numerical analyses have been conducted in order to investigate the following:
-
Validation of the numerical model.
-
Convergence study to determine the optimum mesh configuration.
-
Effect of the variation of geotechnical and geometrical parameters, specifically angle of internal friction of soil (φ), cohesion (c), slope angle (β), footing width (B), setback distance (b) and embedment depth of footing (Df).
-
Development of ANN model for prediction of normalised ultimate bearing capacity (qu/γHs) and recognition of the relative importance of the various geotechnical and geometrical parameters used for evaluating the UBC (qu).
Results and discussion
Validation study
The experimental work done by Keskin and Laman [22] for strip footing resting on crest of the slope has been validated by Plaxis 2D v2015.02 to understand the intricacies of 2D simulations and to get confidence on the efficacy of the simulation models. For the validation, a soil sample of φ = 41.8°, Dr = 65%, and γ = 17 kN/m3, has been taken. A strip footing of 70 mm width resting on the crest of the slope (β = 30°) with setback distance of b/B = 0, has been simulated. In the numerical investigation same model dimension has been taken as considered by the researchers. In Plaxis 2D various meshing schemes are available like very coarse, coarse, medium, fine and very fine. In order to choose a suitable mesh for the numerical simulation, a convergence test has been conducted and it has been found that for the present study, the choice of the fine mesh (non-dimensional average length of 0.04) is sufficient to provide the optimal results, as shown in Fig. 6. Non-dimensional average length is the ratio of average element length and the length of the domain. It has been perceived from the Fig. 7 that there is significant match between the numerical result and experimental result obtained from Keskin and Laman [22]. In Fig. 7, q is bearing capacity and S is the settlement of footing.
Validation of the numerical model with experimental investigation done by Keskin and Laman [22] for setback ratios: (a) b/B = 0 and (b) b/B = 2
In validation study, the load–displacement pattern obtained from numerical analysis is abrupt in nature for footing resting on crest of slope with zero setback distance (b/B = 0) as shown in Fig. 7a. Footing resting on crest of slope with zero setback distance (b/B = 0) is the most critical situation where the passive resistance is minimum. Hence, in case of zero setback distance, the UBC is least and load–displacement pattern is brittle in nature. The stability of foundation has been improved with increasing the setback distance as shown in Fig. 7b. Hence the UBC and passive resistance have been increased with increasing setback distance. Moreover, the load–displacement pattern (Fig. 7b) is not abrupt and the UBC can easily be obtained from it.
As earlier, the numerical simulation of strip footings resting on sloping ground, with various setback ratios (b/B), slope angles (β), footing widths (B) and embedment ratios (Df/B) had been checked for mesh convergence, the typical results of which are illustrated in Fig. 8. It can be observed that beyond a fine mesh (average non-dimensional mesh size of nearly 0.047), the obtained results are nearly identical, and hence, all the further studies for the sloping ground have been carried out with the same. To determine the non-dimensional mesh size, the length of the model for this study has been considered to be 28 m, which remains invariant for all the simulation scenarios.
Parametric study
For footing resting on a sloping ground, the setback distance is perceived as one of the most important governing parameter in the assessment of bearing and deformation characteristics of the footing. The lesser the setback distance, higher is the possibility of failure of the footing exhibiting conditions of distress due to the deformation of the slope face. Hence, in order to highlight the effect of various parameters, a detailed parametric study has been conducted keeping the setback distance as one of the contributing parameters of the simulation. For a footing resting on a sloping ground, ten different setback ratios were considered in the analysis, namely b/B = 0–10, and the same is represented in Fig. 3.
Variation of cohesion (c)
The variation of cohesion (c) on the normalised ultimate bearing capacity (qu/γHs) has been exhibited in Fig. 9. It has been perceived that the combined variation of setback ratio (b/B) and cohesion have significant effect on the UBC. It can be seen that up to setback ratio 6, the increase in c resulted in the increase in the magnitude of qu/γHs, the effect being more prominent at higher values of c. Increase of UBC approves the fact that increase in cohesion comprises increase in shear strength of foundation soil.
Slope angle (β)
Change in the slope angle (β) can significantly alter the stability conditions and bearing capacity characteristics of the footing resting on the sloping ground. A footing exhibits a higher bearing capacity while resting on or near a slope with lesser inclination. Moreover, the natural stability of the slope is governed by the slope angle in relation to the angle of internal friction and cohesion of the constituent material. For the present study, three different slope angles have been considered namely β = 20°, 30° and 40°. It can be observed from Fig. 10 that qu/γHs decreases with the increase in the angle of inclination of the slope. This is attributed to the fact that more steeper is the slope, the zone of passive resistance will be smaller and hence, less resistance towards failure will be offered by the soil located towards the slope face.
Width of footing (B)
Three different footing widths have been elected namely B = 0.5 m, 1 m and 2 m. Figure 11 shows the variation of normalised ultimate bearing capacity (qu/γHs) for various footing widths. Increase of UBC reconfirms the fact that a greater footing width involves a larger soil domain to support the incumbent load.
Angle of internal friction (φ)
Figure 12 demonstrates the effect of variation of angle of internal friction (φ) on the normalised ultimate bearing capacity (qu/γHs). It can be observed that the combined variation of setback ratio and angle of internal friction have substantial effect on the above estimates. Increase of UBC agrees the facts that increase in angle of internal friction involves increase in confinement between soil particles hence increase in shear strength of foundation soil.
Embedment depth ratio of footing (D f/B)
Three different embedment ratios were chosen for footing resting on the crest of a sloping ground having Df/B were considered to be 0, 0.5 and 1, so that the footings can be considered to behave as shallow footings. Figure 13 shows that for up to setback distance 6, the normalised ultimate bearing capacity (qu/γHs) increases with the increase in the embedment ratio of footing (Df/B), the effect being more prominent when the footing is located away from the face of the slope i.e. the footing exhibits a higher setback distance.
Study of failure mechanism
For strip footings located at various setback distances from the slope face, Fig. 14 portrays the role of the sloping face in intersecting the repelling passive zone beneath the footing, and thus reducing the bearing capacity. It has been witnessed that for a footing placed at the crest of the slope (b/B = 0), the formation of passive zone is largely one-directional and curtailed by the slope face, due to the dominant free deformation of the soil upon loading of the footing to failure.
This phenomenon results in a considerable decrease of the confinement pressure, and hence, attenuation of the bearing capacity. As the setback ratio increases, the influencing effect of the slope face on the development of the passive mechanism gradually diminishes, as can be observed from the Fig. 14. It is noted that beyond a critical setback ratio (b/B) critical of 6, the footing behaves as if resting on horizontal ground, wherein the developed displacement contours for the passive zone remains unaffected from the influence of the slope face.
ANN results
Number of hidden neurons in hidden layer
In the present investigation, a convergence study has been conducted for achieving optimum number of neurons in the hidden layer. The number of neurons in the hidden layer is varied and the minimum root mean square error (RMSE) value of 1.67 has been obtained with nine hidden neurons as shown in Fig. 15. So with six inputs (c, φ, B, b/B, β and Df/B) and nine hidden neurons and single (1) output (qu/γHs), the ANN is described as a 6–9–1 network architecture (Fig. 5).
Neural network training, testing and validation
A neural computing system can adjust its behaviour in response to its environment. When sets of inputs are shown to the network, it will self-adjust to produce reliable responses through a process called training. Training is the process of altering the weights methodically in order to attain some desired results for a given set of inputs. The aim of training is to find a set of connection weights that will reduce the MSE predicting error in the shortest possible training time [14]. In total, 80% of the data are used for training and 20% are used for validation. The training data are further divided into 70% for the training set and 30% for the testing set [18].
Comparison of UBC of strip footing predicted by ANN and simulation for 70% training data set is shown in Fig. 16. The coefficients of efficiency (R2) between the simulated and predicted values are found to be 0.998 for training data. In the training process, weights and biases are constantly adjusted to minimize the error between the actual and the desired outputs of the units in the output layer. It should be reported that at the beginning of the training, a set of inappropriate random initial values of weights and biases always resulted in the training divergence. This shows that the combination of weights and biases strongly influences the training process. When the training was over, the weights and biases were fixed. After successful training has been reached, the network weights and biases are fixed and used for predicting the output corresponding to any set of values of the input parameters.
After the network was trained, to highlight the capability of the developed ANN model for UBC of foundation soil, an effort has been made to predict the UBC of foundation soil for new sets of data. As already mentioned, for the testing purpose, 30% of data have been used. A comparison between the UBC of foundation soil predicted through the ANN and the numerical simulation evidence for testing set is shown in Fig. 17. An important observation in this figure is that the results of ANN are very close to the simulated data. The coefficients of efficiency (R2) between the simulated and predicted values are found to be 0.996 for testing data. This indicates that ANN model is capable of predicting UBC of foundation soil with acceptable accuracy.
Once the training phase of the model has been successfully accomplished, the performance of the trained model is validated using the validation data, which have not been used as part of the model building process. The purpose of the model validation phase is to ensure that the model has the ability to generalize within the limits set by the training data, rather than simply having memorized the input–output relationships that are contained in the training data. Comparison of value of UBC in validation sets (20% of total) between simulated value (target value) and predicted value (network value) is shown in Fig. 18. The coefficients of efficiency (R2) between the simulated and predicted values are found to be 0.998 for validation data.
Sensitivity analysis
Sensitivity analysis is of extreme apprehension for selection of important input variables. Different tactics have been suggested to select the important input variables. Goh [19] and Shahin et al. [36] have used Garson’s algorithm (1991) in which the input-hidden and hidden-output weights of trained ANN model are partitioned and the absolute values of the weights are taken to select the important input variables (Eqs. 4 and 5). The methodology for this algorithm is as follows [30]:
-
a.
For each hidden neuron h, divide the absolute value of the input-hidden layer connection weight by the sum of the absolute value of the input-hidden layer connection weight of all input neurons, i.e. for h = 1 to nh, and i = 1 to ni:
$$A_{ih} = \frac{{\left| {W_{ih} } \right|}}{{\sum\nolimits_{i = 1}^{ni} {\left| {W_{ih} } \right|} }}$$(4) -
b.
For each input neuron i, divide the sum of the Aih for each hidden neuron by the sum for each hidden neuron of the sum for each input neuron of Aih, multiply by 100. The relative importance of all output weights attributable to the given input variable is then obtained. For i = 1 to ni:
$$RI(\% ) = \frac{{\sum\nolimits_{n = 1}^{nh} {A_{ih} } }}{{\sum\nolimits_{n = 1}^{nh} {\sum\nolimits_{i = 1}^{ni} {A_{ih} } } }} \times 100$$(5)
The sensitivity analysis has been done as per Garson’s method [11, 17, 36] to find out important input parameters are presented in Table 2. The angle of internal friction, φ has been found to be the most important input parameter followed by c, B, Df/B, b/B, and β as shown in Fig. 19.
Conclusions
Based on the present study, the following significant conclusions are drawn:
-
Mesh convergence study aided to define a non-dimensional optimal mesh size for the Plaxis 2D models so as to obtain accurate solutions from the numerical simulation.
-
Ultimate bearing capacity increases with the increase in the angle of internal friction and cohesion for footing resting on sloping ground owing to the fact that increase in the shear strength of foundation soil.
-
Ultimate bearing capacity increases with an increase of embedment depth of the footing owing to increase in the degree of confinement restricting the movement of the soil towards the sloping face.
-
Ultimate bearing capacity gets significantly increased with the increase in the footing width.
-
Ultimate bearing capacity with the increase of slope angle, which is associated with the increased soil movement towards the slope.
-
Ultimate bearing capacity increases with the increasing setback distance. Beyond a setback ratio (b/B) critical = 6, the footing behaves similar to that on horizontal ground.
-
The ANN model with c, φ, B, b/B, β and Df/B as input parameters is the ‘best’ model, based on coefficient of efficiency, for training, testing and validation data set.
-
Based on sensitivity analyses; it has been perceived from Garson’s algorithm that angle of internal friction, φ and, c are the most important input parameters for estimating the ultimate bearing capacity of strip footing resting on crest of sloping ground.
References
Acharyya R, Dey A (2017) Finite element investigation of the bearing capacity of square footings resting on sloping ground. INAE Lett 2–3:97–105
Acharyya R, Dey A (2018) Assessment of bearing capacity of interfering strip footings located near sloping surface considering Ann-technique. J Mt Sci 15–12:2766–2780
Acharyya R, Dey A (2018) Importance of dilatancy on the evolution of failure mechanism of a strip footing resting on horizontal ground. INAE Lett 3–3:131–142
Azzam WR, El-Wakil AZ (2015) Experimental and numerical studies of circular footing resting on confined granular subgrade adjacent to slope. Int J Geomech 16–1:1–15
Azzam WR, Farouk A (2010) Experimental and numerical studies of sand slopes loaded with skirted strip footing. Electron J Geotech Eng 15:795–812
Bauer GE, Shields DH, Scott JD, Gruspier JE (1981) Bearing capacity of footing in granular slope. In: Proceedings of 11th international conference on soil mechanics and foundation engineering, Balkema, Rotterdam, The Netherlands, Vol 2, pp 33–36
Behera RN, Patra CR, Sivakugan N, Das BM (2013) Prediction of ultimate bearing capacity of eccentrically inclined loaded strip footing by ANN: part I. Int J Geotech Eng 7–1:36–44
Behera RN, Patra CR, Sivakugan N, Das BM (2013) Prediction of ultimate bearing capacity of eccentrically inclined loaded strip footing by ANN: part II. Int J Geotech Eng 7–2:165–172
Castelli F, Lentini V (2012) Evaluation of the bearing capacity of footings on slopes. Int J Phys Model Geotech 12–3:112–118
Das BM (2009) Shallow foundations. CRC Press, Taylor and Francis Group, New York
Das SK, Basudhar PK (2006) Undrained lateral load capacity of piles in clay using artificial neural network. Comput Geotech 33:454–459
Das SK, Samui P (2010) Prediction of swelling pressure of soil using artificial intelligence technique. Environ Earth Sci 61:393–403
Das SK, Samui P, Sabat AK (2012) Prediction of field hydraulic conductivity of clay liners using an artificial neural network and support vector machine. Int J Geomech 12:606–611
Demuth HB, Hagan MT (1996) Neural network design. PWS Publishing Company, Boston
Drescher A, Detournay E (1993) Limit load in translational failure mechanisms for associative and non-associative materials. Geotechnique 43–3:443–456
Erzin Y, Gumaste SD, Gupta AK, Singh DN (2009) Artificial neural network (ANN) models for determining hydraulic conductivity of compacted fine-grained soils. Can Geotech J 46:955–968
Garson GD (1991) Interpreting neural-network connection weights. Artif Intell Expert 6–7:47–51
Ghaboussi J, Sidarta DE, Lade PV (1994) Neural network based modelling in geomechanics. Computer methods and advances in geomechanics. Rotterdam Publishing, Balkema, pp 153–164
Goh ATC (1994) Seismic liquefaction potential assessed by neural networks. J Geotech Geoenviron Eng 120(9):1467–1480
Hansen JB (1970) A revised and extended formula for bearing capacity. Danish Geotechnical Institute, Bulletin 28, pp 5–11
Hebb DO (1949) The organization of behaviour. Wiley, New York
Keskin MS, Laman M (2013) Model studies of bearing capacity of strip footing on sand slope. KSCE J Civil Eng 17–4:699–711
Kumar SVA, Ilamparuthi K (2009) Response of footing on sand slopes. In: Indian geotechnical conference, Guntur, India, pp 622–626
Kuo YL, Jaksa MB, Lyamin AV, Kaggwa WS (2009) ANN-based model for predicting the bearing capacity of strip footing on multi-layered cohesive soil. Comput Geotech 36:503–516
Lee MI, Lee HJ (1996) Prediction of pile bearing capacity using neural networks. Comput Geotech 18–3:189–200
Leshchinsky B (2015) Bearing capacity of footings placed adjacent to c′–φ′ slopes. J Geotechn Geoenviron Eng 141–6:1–13
MathWorks (2001) Matlab user’s manual, Version 2015A. The MathWorks Inc, Natick
McCulloch WS, Pitts W (1943) A logical calculus in the ideas immanent in nervous activity. Bull Math Biophys 5:115–133
Meyerhof GG (1951) The ultimate bearing capacity of foundations. Geotechnique 2:301–332
Mishra AK, Kumar B, Dutta J (2016) Prediction of hydraulic conductivity of soil bentonite mixture using hybrid-ANN approach. J Environ Inform 27–2:98–105
Momeni E, Nazir R, Armaghani DJ, Maizir H (2014) Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement 57:122–131
Nasr AM (2014) Behaviour of strip footing on fiber-reinforced cemented sand adjacent to sheet pile wall. Geotext Geomembr 42:599–610
NDMA (2013) Catalogue of building typologies in India: Seismic vulnerability assessment of building types in India, A report submitted by the Seismic Vulnerability Project Group of IIT Bombay, IIT Guwahati, IIT Kharagpur, IIT Madras and IIT Roorkee to the National Disaster Management Authority, India
Noorzaei J, Hakim SJS, Jaafar MS (2008) An approach to predict ultimate bearing capacity of surface footings using artificial neural network. Indian Geotechn J 38–4:513–526
Rosenblatt F (1958) The perception: a probabilistic model for information storage and organization in brain. Psychol Rev 68:368–408
Shahin MA, Maier HR, Jaksa MB (2002) Predicting settlement of shallow foundations using neural networks. J Geotechn Geoenviron Eng 128–9:785–793
Shields DH, Scott JD, Bauer GE, Deschenes JH, Barsvary AK (1977) Bearing capacity of foundation near slopes. In: Proceedings of the 10th international conference on soil mechanics and foundation engineering Japanese society of soil mechanics and foundation engineering, Tokyo, Japan, Vol 2, pp 715–720
Shukla RP, Jakka RS (2016) Discussion on Experimental and numerical studies of circular footing resting on confined granular subgrade adjacent to slope by WR Azzam and AZ El-Wakil. Int J Geomech 17–2:1–3
Terzaghi K (1943) Theoretical soil mechanics. Wiley, New York
Vesic AS (1973) Analysis of ultimate loads of shallow foundation. J Soil Mech Found Div ASCE 99(SM1):45–73
Xiao-Li Y, Nai-Zheng G, Lian-Heng Z, Jin-Feng Z (2007) Influences of non-associated flow rules on seismic bearing capacity factors of strip footing on soil slope by energy dissipation method. J Central South Univ Technol 6:842–846
Authors’ contributions
The author read and approved the final manuscript.
Acknowledgements
The author expresses his gratitude to Dr. Arindam Dey, Associate Professor, Civil Engineering, IIT Guwahati for his valuable support and guidance in comprehending the topics of strip footings on or near the slope which immensely assisted in evaluating the ultimate bearing capacity and failure mechanism of strip footing resting on crest of slope.
Competing interests
The author declares that he has no competing interest.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Acharyya, R. Finite element investigation and ANN-based prediction of the bearing capacity of strip footings resting on sloping ground. Geo-Engineering 10, 5 (2019). https://doi.org/10.1186/s40703-019-0100-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40703-019-0100-z