Abstract
This study examines the effects of slope geometry and Geo-mechanical parameters of tailing dumps at Enyigba mine, Nigeria. Fifty-two slopes were studied, with seven sampled for laboratory analysis. Correlation matrix and principal component analysis were employed in the data interpretations. The mechanical properties of the slope materials were investigated using geotechnical tests such as sieve analysis, Atterberg limits, compaction and undrained triaxial tests. Shear strength parameters generated from the triaxial tests were utilized in slope stability analysis executed with the Slope/W Geostudio software. Both statistical and slope stability methods suggested a combination of height and width (dimensions) has more significance on the stability of the dump slopes at Enyigba mine than slope angles (inclination). Height and width constituted 83.61% of the total variance data and represented 16.39%. Particle size distribution of the slope materials showed high percentage of fines. The computed factor of safety of the slopes ranged from 1.00 to 1.30, implying critical stability which indicates liability of the slopes to failure when predisposed to landslide triggering agents. Therefore, slope dimension optimization and stabilization are required on the tailing dumps at Enyigba to prevent severe landslide occurrence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Background
The slope angle and height of dumps are very critical to mine economics because of shortage of horizontal space available for dumping and stability concerns. Increasing rate of mine activities in Enyigba has led to large dump accumulations formed in and around the mining areas. Mandal and Sengupta [40] noted that the internal mine dumps are often located close to active haul roads of the mine (Fig. 1a) and failure of these dumps may result in heavy loss of life and property. The failure of slopes can happen in either sudden or slow modes. The sudden failures which could be dangerous to humans and the environment usually follow extreme events such as large precipitations, earthquakes or volcanic activity. Research on management of mine waste dumps have increased since it has been established that the waste do play significant role in mine functioning and mining economics [63].
The slope geometry and the geo-mechanical strength of dump materials mostly control the stability of the dump [7, 19, 42]. Das [18] and McCurthy and David [41] asserted various factors responsible for failure of dump slopes such as geology and hydrogeology of the dumping area, gravitational force, seepage of water from dump to slope, lowering of water adjacent to a slope, changes of stress and erosion of dump (removal of lateral support) caused by flowing water. Other factors such as dump slope angle (slope inclination), natures of the dump materials (material properties), degree of compaction, dump height and changes in cohesion of interface materials have also been pointed by other workers [34, 48, 57].
A good understanding these factors that influence slope instability or reduction in shear strength of slope materials provides vital information for mine design and safe mining operations. Abramson et al. [1] noted that the role of the mentioned factors of slope failure can be summarized into two processes: increased shear stresses (triggered by removal of support, overloading, earthquakes, decrease in lateral pressure) or decreased shear strength of the soil (as a result of stratification, hydration of minerals and pore pressure due to rainfall event or melting snow).
The mechanical properties of the slope mixture have great significance for determining the operating cost and reducing the footprint of surface mines [10]. The most important mechanical property of a material is shear strength which sequentially depend on parameters such as cohesion (c) and internal friction angle (ø). Knowledge about these two shear strength parameters is necessary for optimizing the benches on dumps [68]. The shear strength of a material at a point on a particular plane was expressed by Coulomb as a linear function of the normal stress on that plane expressed by the equation:
where τ is the shear strength, σ is normal stress, φ is angle of internal friction and c is the cohesive strength of the material [67].
The cohesion and friction angle of slope materials are influenced by the particle size distribution characteristics and other conditions, especially the water content [67]. The mine dumps of Enyigba are made up primarily of soil–rock aggregate. The formation history of rock–soil aggregate is very complicated, and the material composition of rock–soil aggregate is also complex. The extremely irregular structure distribution of rock–soil and other characteristics add to the complexity [50, 55, 66]. Ultimately, experience with the behavior of slopes, and often with their failure, has led to development of improved understanding of the changes in soil properties that can occur over time, recognition of the requirements and limitations of laboratory and in situ testing, and lots more.
In the assessment of slopes, the factor of safety values still remain the key index for determining how close or how far slopes are from failure [13, 37, 44]. Factor of safety (FS) is expressed as the ratio of soil shear stress to soil shear strength imposed along a slip surface. A factor of safety of unity theoretically means that the failure mass is on the verge of sliding [22]. Previous researchers focused on the properties of the dump materials to ascertain the stability of the tailings. However, this paper focuses mainly on the effect of slope geometry and mechanical properties of slope materials on the stability of Enyigba tailings. The authors hope to apply stability analysis in evaluating the waste dump stability so as to suggest economical, sustainable and safe disposal of the mine tailings.
Study area
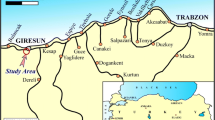
The study area is situates south of Abakaliki town, Ebonyi state of Nigeria. It lies within longitudes 006°05′N and 006°15′N and 008°05′E and 008°10′E (Fig. 2). It is accessed through major federal highway: Abakaliki-Afikpo road and minor roads (local road networks within the area). The mine is about 14.2 km from Abakaliki, the capital city of Ebonyi State, which lies within the Guinea Savannah region of South-eastern Nigeria [8]. The area has a humid tropical climate, with the vegetation characterized by grasses and parkland trees of various sizes. The area experiences a rainfall of more than 1200 mm yearly (Fig. 3). The mean annual temperature stands at 28 °C [51]. The area experiences 8 months of rainy season and 4 months of dryness within the year. The area is drained by a major river known as Ebonyi River and its tributaries (Iyiudene and Iyiokwu). Both tributaries are perennial and usually overflow their banks at the peak of the rainy season. The drainage system of the area is dendritic pattern (Fig. 2), which is mostly controlled by the geology of the area (Fig. 4).
The study area is underlain predominantly by shale of low erodibility potentials but the topography is generally undulating, with no area exceeding 400 ft above-sea-level (Fig. 5). The area is part of the “Abakaliki anticlinorium” (Fig. 6), and it is underlain by the Abakalikishales of the Asu River Group (Albian-Cretaceous sediments), which falls under the lower Benue Trough. Simpson [59] described the Asu River Group as consisting largely of olive brown sandy shales, fine-grained micaceous sandstone and mudstone. The formation is overlain unconformably by the Eze-Aku Shale of Turonian Age. The Lithostratigraphic succession of the area include: Albian–Cenomanian–Turonian–Conaician–Santonian–Campanian–Maastrichtian (Table 1). Rocks within the study area are extensively fractured, folded, jointed and faulted (Fig. 4), particularly following the series of tectonic episodes which have acted on them from the Santonian times [6]. Obiora and Charan [52] reported that the highly indurated shales of the Asu River Group have undergone low grade metamorphism, which is the reason for its usage as construction material. However, the mine area consists of expansive clay and shale that are fine-grained and dark-grey in colour. And like the rocks of the region, the shale is fissile, highly folded, fractured and faulted, and primarily makes up the mine tailings.
Methodology
Field mapping and laboratory analyses of samples were the stages adopted in the course of this research. Field mapping involved reconnaissance survey and detailed field investigations. The field mapping was undertaken to carefully observe the visible features on the tailings, generate coordinates of the area for map productions, measure geometry of the dump slopes and to collect samples for laboratory analyses. Fifty-two slopes were studied, and seven samples were collected randomly. The samples were labeled AM 1, AM2, EN3, EN10, EN14, EN15 and EN16 (Figs. 4, 5).
Samples were analyzed in the laboratory to determine the geo-mechanical properties of the slope materials. Properties such as natural moisture content, permeability, Atterberg limits, specific gravity, compaction and shear strength of the materials were evaluated. The laboratory tests were carried out according to relevant American Society for Testing and Materials (ASTM) standard of soil testing. Coordinates of the study area were used to develop digital elevation model of the area (Fig. 5). Slope/WGeostudio 2012 software was used to produce a modeled diagram of slope morphology for failure prediction (in terms of factor of safety) on the slopes. The analysis type used was the Morgenstern-Price limit equilibrium method. Parameters from the geotechnical test used for the analyses were slope geometry, unit weight, cohesion and internal friction angle. SPSS software was used to run the statistical analysis.
Results and discussion
Tailing geotechnical properties
The samples presented a wide range of heterogeneity in their geo-mechanical properties. The particle size distribution result revealed that the content of gravel, sand and fines in the tailing dump units are 0–40.2, 10.7–47.8 and 34.9–80.7% respectively (Table 2). This result indicated a high percentage of fines, which could suggest clay dominated material, and thereby signifying cohesive slope materials. Although Mugagga et al. [47] reported that material with clay content greater than 20% exhibited expansion abilities, Baynes [4] suggested that 10% clay content should been used as an indicator for soil expansion potential. Therefore with average clay content of 55.95%, the studied samples could imply medium to high expansive potential. High clay content have been noted to have impact on slope failure by many researchers such as Knapen et al. [36], Yang et al. [65], Kitutu et al. [35] and Wati et al. [64].
The result of Atterberg limits and moisture content tests are shown in Table 2. The materials’ natural moisture content ranged from 3 to 13%, signifying low to medium water content in the soil. The liquid limit (LL) ranged from 24 to 59% and the plastic limit (PL) ranged from 24 to 35%, while PI ranges between 9 and 26%. These consistency limit values suggested that the soils possess low to medium plasticity, which agrees with the soil low to moderate moisture content. Thus the soils can be classified as ML or CH according to the Unified Soil Classification System (USCS) as seen in Fig. 7.
Much emphasis have been made by many authors on the role of LL in characterizing the problematic soils [4, 21, 45]. The LL of the materials at the mine is absolutely higher than the threshold of 25% recommended for stable soil in tropical Africa. Consequently, the high LL coupled with high clay content might certify the soils as problematic soils that could be susceptible to landslides [47].
The tailing dump materials have average value of PI to be 17%. The average values of PI and LL of the studied materials might be suggestive of low to moderate expansion potential of the clay, thereby agreeing to the tailing dumps vulnerability to landslides [47]. This swelling ability could signify the presence of swelling clay minerals.
The determined permeability coefficient (k) of the slope materials ranged from 1.49 × 10−4 to 9.04 × 10−8cm/s (Table 2). These values of k are considered to be low and in the range of fine grained materials, which agrees with the particle size distribution result. This low value of k suggests on the water holding ability of the soil. Excess pore pressure can build up on such materials on moisture influx due to the low permeability, thus reducing the strength of materials, and consequently leads to slope failure. Due to the reduction of shear resistance, sliding have been found to be prevalent in plastic inorganic soils during rainfall events [17, 47]. Therefore, these plastic inorganic clays could be susceptible to sliding even under moderate rainfall events due to reduction of shear resistance.
The bulk density (γb) of the slope samples ranged between 1.79 and 2.21 Mg/m3 (Table 2). These values of (γb) fall within range of swelling clays as suggested by Seedman [54] and Hong et al. [25], who observed that osmotic swelling occurs in clays with bulk density less than 2.45 Mg/m3. This could be the effect of high activity within the clay due to high water absorption into the clay by smectite minerals, thereby increasing the natural moisture content of the soil.
Figure 8 shows compaction curves of the samples. The compaction result showed that the soil optimum moisture content (OMC) ranged between 13.45 and 17.05%, while the maximum dry density (MDD) ranged from 1.86 to 2.22 g/cm3 (Table 2). These values are suggestive of slope material with average OMC and moderate MDD. The curves represent that of low to medium plastic clays described by Maduka et al. [39], thus assenting with the consistency limits. Arora [3] noted that heavy clays of very high plasticity have very low–moderate dry density and high optimum water content, which is consistent with the view that high OMC and low–moderate MDD is suggestive of moderate materials.
The soil specific gravity (Gs) is presented in Table 2. The values ranged from 2.58 to 2.70. These Gs values are in agreement with the report of Tuncer and Lohnes [62], who noted that the specific gravity of clayey and silty soils varies from 2.60 to 2.90. Therefore, with average value of 2.63, the Gs are indicative of high clay content materials. However, Reidenouer [53] reported that materials of Gs below 2.65 usually deteriorate at engineering sites, mainly on moisture influx due to weakness and non-durability.
The shear test is one of the key proofs in verifying the strength of a material since it generates the shear strength parameters (cohesion and angle of internal friction). It has been noted by Gupta and Paul [23] that slope geometry and the strength of materials on it ultimately determines the stability of a slope. Table 2 shows that the range of the angle of internal resistance and cohesion of the slope materials are 8°–37° and 13–34kN/m2 respectively. Some of the Mohr envelopes of the samples are shown in Fig. 9. These values implied low to moderate values of cohesion and low values of internal friction angle. The low shear strength parameter values could be the consequence of presence of expansive minerals [38, 39].
The strength of a soil has been observed to drop whenever permeability inhibits drainage from the material voids owing to upsurge in hydrostatic pore pressure within the soil [9]. Therefore, water infiltration could induce failure by weakening slopes via reduction in suction and strength [16, 26, 29]. This strength reduction only become noticeable when the mobilized forces become lesser than the shear forces, and steep slopes are mainly affected on account of increasing shear stress against reducing shear strength, thereby causing a significant fall in the slope factor of safety [28, 47, 64, 65]. This reduction in shear strength is capable of triggering a landslide in a tailing dump slope along the weak planes [5].
Relationship between dump slope geotechnical parameters
A statistical method known as Pearson’s correlation matrix was used to determine the relationship between the slope material’s geotechnical properties (Table 3). From the correlation table, it can be observed that there is a strong positive correlation between LL and PI (0.963), and this could be as a result of their strong relationship with fines (clay and silt size materials) and soil plasticity [49, 56, 61]. A confirmed relationship has been noted to exist between high plasticity and fine-grained inorganic clay and silts [33]. Plasticity index and liquid limit have been reported to be influenced by clay content [38]. These soil properties have also been observed to have strong impact on slope stability and landslide incidences [20, 35, 36, 47, 64, 65].
Liquid limit (LL) and plasticity index (PI) are noted in Table 3 to correlate positively (0.863 and 0.963 respectively) with cohesion (c) but recorded negative correlations (− 0.973 and − 0.968 respectively) with angle of internal friction (ø), though c and ɸ are both shear strength parameters. This disparity in relationship of LL and PI with c and ɸ could be associated to the connection of c and ø with fines and sand size particles respectively. The connection of c and ø to different sources such as fines and sand particles can be observed in their strong negative (− 0.792) correlation (Table 3).
However, increase in both strength parameters have been reported to increase the stability of slopes [15, 48]. Cohesion is seen to have moderate positive correlations (0.538 and 0.575) with maximum dry density and Optimum moisture content (OMC) respectively and a strong correlation (0.718) with bulk density (Table 3). These moderate positive relationships between c and MDD, OMC and ϒb could be suggestive of the amount of clay content in material. Loose broken materials usually have low shear strength but its strength increases with time as it becomes more and more compact [34].
The very strong positive (0.844) relationship between natural moisture content (NMC) and OMC could be partly due to their connection with clay content and partly due to closeness in amount (3–13% and 13–17%) in the slope material. In general, water content has been reported to influence the stability of slopes [20].
The strong relationship (0.721) between specific gravity (Gs) which is the weighted average of soil minerals (excluding air and water) and bulk density could be pointing to the type of material that made up the slopes, whether they are competent materials or incompetent materials that deteriorate on moisture influx [2]. Generally, the soil properties linked with slope failure were observed to range between low to moderate in slope material (see Table 2), which could be the reason for the moderate stability recorded by the analyzed slopes (see FS results in Table 4 and Fig. 10).
Dump slope physical attribute
Slope geometry and other measurements were taken on fifty slopes in the study area. Most slopes were observed to be concave in curvature (Fig. 1), and from the field measurements, slope angles of the individual slopes ranged from 30° to 60° (Table 5). Most landslide events have normally been reported to occur on concave slopes with slope angle ranging between 36° and 58° [27, 28, 46, 47].
A spatial correlation between landslide occurrence and topographical concavity has been noted by Mugagga [46]. Igwe [27] also reported that positive correlation exist between frequency of landslide and slope angle, but however noted that landslides occur more on slopes with angles greater than 30° but less than 40°. Thus slope geometry could be one of the causes of the shallow sliding on the slope surfaces shown in Fig. 1b, since it presents moderate to high slope angles (35°–45°). The dump slope geometry (height, width and angle) recorded in Table 5 were analyzed using a statistical method known as principal component analysis (PCA) to decipher which geometric components would have more influence on the stability of the dump slopes [11, 12, 24]. The method is commonly used in the field of geosciences [14, 24].
Tables 6, 7, 8 shows the results of the principal component analysis (PCA) and Pearson correlation matrix. Table 6 shows the loading of variables on each component and percentage of data variance in the data set. The three components shown in the table account for 100% of the total variance in the data set with each of component 1, 2 and 3 having percentage variance of 48.7, 34.9 and 16.3% respectively. However, only two components were extracted as principal component (PC) for considerations (Using their high eigenvalues of 1.047 and 1.461), which accounted for 83.6% of the total data variance (Table 6).
PCs with score loadings at 0.5 and above were considered significant controlling processes. The 1st components that could have significant influence on the stability of the studied slopes are height and width of the slope with component matrix of 0.875 and 0.712, while the slope angles could have a secondary influence on the slopes with a matrix of 0.850 (Table 7).
The PCA results agree with the Pearson’s correlation result where there is a moderate relationship (0.401) between slope height and width (Table 8). Result from principal component analysis suggested that combination of height and width (dimensions) as factors of slope failure are more significant on the stability of slopes in Enyigba mine dumps than slope angles (inclinations), and therefore implies that slope height and width could be key determinants of slope failure in the area. Also, results of the PCA and Pearson’s correlation signifies that there could be many factors that causes slope instability or decrease in shear strength of slope materials [43], but some factors could be more prominent depending on the area [27].
Stability analysis of the dumps
Limit equilibrium method (LEM) of numerical analysis was used to carry out a slope stability analysis on one of the tailing dump slopes. Currently, LEM is the conventional stability approach in numerical stability analysis according to Cheng and Lau [13]. The Morgenstern-Price limit equilibrium method was adopted in the present study due to its vital advantage over other methods such as the Bishops, Spencer and Ordinary methods. The very important conditions that must be satisfied in this method are that equilibrium must be attained in terms of total stresses, and all forces acting on the dump must be included in the analysis. Finally, a factor of safety (FS) for the slope will be computed. The FS is the ratio of the shear strength of the soil against the shear stress required for equilibrium.
The FS generated for slope EN14 was 1.12, implying marginally stable slope (Fig. 10). The FS of some of the other slopes in Enyigba mine dumps are shown in Table 4. The FS recorded at the site ranges from 1.00 to 1.30, implying critical stability to marginally stable slopes (Table 4). To enable the plot of a safety map for the studied slope, several trial slip surfaces were analyzed at the time. Two hundred trial slip surfaces were evaluated (Fig. 10c), and FS generated was between 1.12 and 1.79. The safety map generated is shown in Fig. 10d, and has the color band covering FS between 1.12 and 1.37. The map showed the zones of which FS are similar. The most critical slip surfaces (lowest factors of safety) lie within the red band, which is the area of interest, and on which safety of a slope is considered. The areas under the red band cover the range of FS between 1.12 and 1.17 (Fig. 10d). These are the range of FS at which a possible slope failure could occur. Outside these zones (red bands), slope failure may likely not occur.
However, the computed FS of 1.12 in Fig. 10a was computed at the middle of the dry season, with little or no water in the tailing slope. From field observations, however, it was evident that the area was waterlogged (flooded) during the rainy season (Fig. 11). The FS dropped from 1.12 to 1.08 as soon as the likely effect of groundwater within the dump slope was incorporated into the analysis (Fig. 10e). Then, the FS decreased further down to 1.00 with the consideration of impact of flooding (Fig. 10f). Consequently, the FS diminished from slightly stable to critical stability.
With water in and around the tailing slope, activating forces could be greater than the resisting forces through increase in pore pressure. Figure 12 revealed that pore pressure acting on the base of the analyzed could be as low as between 0 and 20 kPa during the dry period (Fig. 12a) but could rise to 60–80 kPa during the rainy season as seen in Fig. 12b. This rise in pore pressure may cause a decrease in shear strength, and possibly triggering a slope failure if it persists.
The drop in FS may continue as water surges within and around the slopes until failure is initiated at FS < 1.0. At FS < 1, a mass wasting process such as landslide or mudflow might be imminent since the activating forces would be greater than resisting forces. It is noteworthy to say that the volume of the sliding materials in landslide episodes could be increased with water in and around the slopes. This assertion was evident from the numerical analysis were the sliding mass increased from 67.97 to 71.51 m3 as water increased within the tailing slope as seen in Fig. 10b, f. This observation is inconsistent with the findings of Maduka et al. [38].
Slope height and angle optimization
It is not in the best interest of slope management to go for flatter waste dump deposits all the time because of shortage of horizontal space available for dumping (which is usually the constraint in dump slope design) and cost of evacuating to other storage sites. Therefore, there is a need to always go for steeper slopes, but with a limit through the option of slope optimization.
The best and appropriate optimization of tailing dump slope requires a slope to be at optimal height and angle at the same time, with a view to creating space for more waste dumps accommodation, without compromising the stability and safety of such slopes. This apparently is one of the main challenges of tailing dumps management and slope stability. However, the risk of slope instability can be considerably reduced if a good correlation can be made between shear strength parameters, slope height and angle and groundwater [60]. For such correlation to be made with a view of optimizing the slope profiles, it is advisable to use the proposed dump slope material parameters in carrying out several models with modifications on the slope geometry while keeping groundwater conditions unaltered. Thus, the slope materials and slope groundwater conditions as well as either of slope height or slope angle remains unaltered while the other is varied. The factors of safety for all prevailing scenarios of the dump slope should be determined as shown in Tables 9, 10, 11, 12, 13.
Tables 9 and 10 are results of the effect of height and angle variations on FS of an average strength dump slope. The results of the effects of slope height and angle were plotted in the same plot area as shown in Fig. 13. From Fig. 13; FS is 3.4 at 5 m slope height which signifies a very stable slope. But same slope at 25 m high and above presented FS (ranging from 0.94 to 0.82) lower than 1, implying very unstable or failed slope. The critical stability was observed at 20 m with FS (1.12) marginally greater than 1 (Fig. 13). Other authors have observed that FS reduced logarithmically with respect to increase in dump height [34, 48]. The case of slope angle presented a similar FS trend as that of height (Fig. 13). Slope angle of 30° and below generated a FS greater than 1 (i.e. 1.42–3.08) while slope angle greater than 40° produced a FS below 1 (i.e. 0.80–0.93). These FS results suggest that the analyzed slope would be theoretically stable at slope angle less than 30° and unstable at slope angle greater than 35°. It is observable from the graph (Fig. 13) that the analyzed slope could be stable at slope angle as high as 38° with FS of 1.1, though slightly critical. However, the overall results mean that as we go on reducing the overall height and slope angle, FS will continue to increase. Although most mining companies have operated on dump angle ranging between 37° and 39° [34], the need for a balance between slope height and angle (optimization) cannot be over emphasized due to incessant dump slope failure recorded over the last few years [34, 48, 57, 58].
For a slope optimization, it would be better to consider both slope geometric properties simultaneously by correlating their graphs. Looking at the graphs (Fig. 13), it is interesting to observe that both graphs intercepted at various points, and these could be points of balance of both of their effects on the FS. These points could be harnessed in striking a balance between what heights or slope angles are suitable for a dump waste design. From Fig. 13, the slope can be noticed to be stable at both points (A and B) of interceptions with FS at approximately 1.2 and 2.8 respectively. At point A, slope height and angle are 20 m and 35° while at point B, both are 7 m and 11° respectively. Therefore, to solve the stability challenge, it would be good to design the dump waste storage fitting to point B. But to overcome the space limitations and cost of managing several slope, it would be proper to optimize the waste dump design to Point A for maximum storage. This could be the reason why earlier analyzed slope (see Fig. 10) and other slope on the studied site are still stable at their various height and angle range (between 18–20 and 30–40° respectively). In a situation where the predesign model intercepted once, it would be proper to design according to the single point of interception.
For slope optimization to be effective, the predesign models must be done using the actual strength parameters (cohesion and angle of internal friction) of the proposed waste dump material, and not with estimated strength properties. It is possible that any dump storage higher than the optimized height and slope angle might be liable to failure. Therefore such slope must be supported by special ground preparation before dumping and/or any type of stabilization method [48]. However, in as must as optimization of slope could guarantee slope stability on a site, the probability of local failure may not be totally overcome due to inhomogeneity of materials and extreme mining site activities.
Effects of material strength and groundwater table on slope stability
The strength of a slope materials and groundwater depth (GWD) could have severe implications on the stability of the slope (Tables 11, 12, 13). Figure 14 shows the variations of FS with respect to groundwater level (depth). As earlier suggested, the material properties were kept constant together with the slope geometry (height = 35 m and angle = 40°).
The factor of safety was computed to be 1.1 for groundwater depth of 35 m below the slope surface and decreased to 0.64 with increase in groundwater to 5 m from the slope surface (Fig. 14). This is 41.8% decrease in FS in 85.7% increase in groundwater depth, which is to say that the effect of the increase (decrease in FS) is almost half of the increase itself (increase in GWD). Therefore, water is playing a significant role in the stability of waste dump. This result agrees with the findings of other workers on effect of groundwater depth on waste dump stability, who noted that a rise in groundwater level of dump slope reduces drastically the slope factor of safety [48]. Figure 14 indicated that groundwater should be reduced beyond 25 m (35–10 m) below the slope surface in order to reduce the risk of instability.
Combining simultaneously the effects of slope height, slope angle, and groundwater level presented just one optimization point (Fig. 15) which is different from the two presented by the combined effects of slope angle and height only in Fig. 14. The factor of safety dropped from 1.2 to 1.0 but the height and slope angle increased from 22 to 26 m and 38° to 40° respectively. This implies that the studied slope could be unstable at height more than 26 m and angle higher than 40° if the combined effects of the slope geometry and groundwater level are considered (Fig. 15).
Cohesion and angle of internal friction are essential material properties in describing the strength of any soil material, and any variation in their value in same material is mostly due to amount of water in material [60]. Several simulations of 40 m high dump slopes with different ranges of cohesion and angle of internal friction were numerically solved and analyzed to ascertain the role of material strength on factor of safety of slope and its stability. On each modeled scenario, different combination of cohesion ranging from 5 to 40 kPa and frictional angle ranging from 5° to 40° were alternated. To determine the effects of change in one of the strength parameters, the other as well as the slope profile is kept constant. The factors of safety generated for change in cohesion and internal friction angle are shown in Tables 12 and 13 respectively.
Figure 16 illustrates the influence of effective cohesion and internal angle of friction (which are the shear strength parameters shown in Eq. 1 on FS. The graphs showed that when there is a decrease in either of cohesion and internal friction, there will be a considerable decrease in FS (Fig. 16) and invariably a fall in stability of slope. Therefore, the higher the cohesion and internal friction of waste dump materials, the higher factor of safety and slope stability [48]. This implies that lower values of both strength properties (mostly caused by a reduction) would cause a failure of the slope, and the condition is often as a result of external weakening influences such as severe precipitation and moisture influx, ground vibrations caused by induced blasting and seismicity. Therefore, any activities that can cause a reduction in either of effective cohesion or internal friction angle to zero must be avoided within the perimeter of a waste dump site.
It can also be observed from the two graphs that FS increases in a linear progression with increase in either of the shear strength parameters. These linear relationships reinforces that dump waste materials obey Mohr–Coulomb principles [60]. However, the inclination of the FS is more noticeable with friction angle than cohesion for similar ranges of variation of cohesion and internal friction (Fig. 16). All the values of FS that fall below 1 (which is the minimum threshold value required to keep a slope theoretically stable) suggests that the slope is unstable at that values of cohesion and friction angles or have probably failed [27, 28, 30,31,32, 38, 60], and probably by circular mode. This suggests that the analyzed slope would be critically stable with cohesion at 40 kPa and/or internal friction angle greater 35° with FS marginally above 1.0. But, it should be noted that with FS equal to 1 or slightly greater than 1, the slope would require stabilization to increase the FS to 1.5 which is often recommended and normally used to augment for the inconsistencies in modeling. The method of benching (which help moderate slope height and angle) proposed by Maduka et al. [38] can be employed to improve the slope stability.
Conclusions
The tailing dumps slopes at Enyigba mine southeastern Nigeria were carefully studied, and were observed to be liable to slope failure by sliding. The slope materials at the site have been characterized largely to be dark grey shale, and from the geotechnical and numerical analyses, few conclusions were made.
The tailing clay content, moisture content, permeability, compaction and shear strength indicated low to medium plastic soil, with low to medium water holding ability that could reduce the strength of the dump materials. These geotechnical attributes of the slope could be as a result of soil mineralogy. Materials with the above traits have been observed to exhibit low strength either as foundation or slope materials, and are capable of initiating engineering failures at sites on moisture influx.
The steepness of the slopes and slope curvature could be pointed out as some of the factors that would negate the stability of the slopes. However, while the slope dimension (height and width) was observed as a primary factor affecting the dump slope stability at the mine, slope angles could be the secondary.
The studied tailing slopes were inferred to be either critically or marginally stable, with a range of generated factor of safety between 1.00 and 1.30, hinting on the possibility of landslide occurrences on the tailing dumps within the mine site.
It was also concluded that increase in strength parameters (cohesion and angle of internal friction) have positive influence on the stability of the dump slopes while increase in slope height, slope angle and groundwater level have damaging and destructive influences on such slopes.
Therefore, after a thorough assessment of the slopes and materials of the tailing dumps, the authors recommended a number of precautions that could be beneficial in the design of tailing dumps for safe and durable storage. Effort should be made to avoid flooding within the mine perimeter, thereby reducing water level to as low as possible around and within the dump slope. Slope height and angle optimization must be a common cautious exercise in the design of tailing dump storage. Slopes with higher height and angle than the optimal and/or high groundwater level must undergo stabilization, using any affordable method such as the benching method. The method helps reduce high slope height and angle and also reduces sliding mass in the event of possible slope failure.
References
Abramson LW, Lee TS, Sharma S, Boyce GM (2002) Slope stability and stabilization methods, 2nd edn. Wiley, New York
Aghamelu OP, Okogbue CO (2011) Geotechnical assessment of road failures in the Abakiliki Area, southeastern Nigeria. Int J Civil Environ Eng 11(2):12–21
Arora KR (2008) Soil mechanics and foundation engineering (geotechnical engineering), 8th edn. Lomus Offset Press, Delhi, p 953
Baynes FJ (2008) Anticipating problem soils on linear projects. In: Conference proceedings on problem soils in South Africa, vol 34. pp 9–21
Behera PK, Sarkar K, Singh AK, Verma AK, Singh TN (2016) Dump slope stability analysis—a case study. J Geol Soc India 88:725–735
Benkhelil J (1986) Structure et evolution geodynamique due basin intercontinental de la Benoue (Nigeria) Bull CentresRech Explor—Prod Elf-Aquitaine 12(1): 29–128
Bishop AW (1955) The use of the slip circle in the stability analysis of earth slopes‖. Geotechnique 5(1):7–17
Blench PO (2004) Regional stratigraphy of Abakaliki, Southeastern Nigeria. Corral Publishers Ltd., North Vancouver, pp 14–50
Blyth FGH, De Feritas MH (1984) A geology for engineers. Arnold Intern Students, 7th edn. Arnold Publishing, London
Cai QX, Zhou W, Shu JS, Liu Y, Peng HG (2008) Analysis and application on end-slope timeliness of internal dumping under flat dipping ore body in large surface coal min. J China Univ Min Technol 37(6):740–744
Chalouan A, Michard A (2004) The Alpine Rif Belt (Morocco): a case of mountain building in a subduction–subduction-transform fault triple junction. Pure Appl Geophys 161:489–519
Chalouan A, Michard A, Feinberg H, Montigny R, Saddiqi O (2001) The Rif mountain building (Morocco): a new tectonic scenario. Bull Soc Géol Fr 172(5):603–616
Cheng YM, Lau CK (2014) Slope stability analysis and stabilization, 2nd edn. Taylor & Francis Group, New York, pp 17–97
Cirac P (1985) Le bassinsud-rifain occidental au Néogènesupérieur. Évolution de la dynamiquesédimentaireet de la paléogéographie au coursd’une phase de comblement. Thèsees Sciences, Université de Bordeaux I, France, p 283
Coulibaly C, Tikou B, LiZhen C (2017) Numerical analysis and geophysical monitoring for stability assessment of the Northwest tailings dam at Westwood Mine. Int J Min Sci Technol. https://doi.org/10.1016/j.ijmst.2017.05.012
Crosta G, Frattini P (2008) Rainfall-induced landslides and debris flows. Hyd Proc 22(4):473–477
Dai FC, Lee CF, Ngai YY (2002) Landslide risk assessment and management: an overview. Eng Geol 64(1):65–87
Das G (2011) Analysis of slope stability for waste dumps in a Mine. BSc thesis, Department of Mining Engineering, National Institute of Technology Rourkela
Dawson E, Roth W, Drescher A (1999) Slope stability analysis by strength reduction. Geotechnique 49(6):835–840
Emeh C, Igwe O (2016) Variations in soils derived from an erodible sandstone formation and factors controlling their susceptibility to erosion and landslide. J Geol Soc India 90(3):259–384
Fauziah A, Yahaya AS, Farooqi MA (2006) Characterization and geotechnical properties of Penang residual soils with emphasis on landslides. Am J Environ Sci 2(4):121–128. https://doi.org/10.3844/ajessp.2006.121.128
Gofar N, Kassim KA (2007) Introduction to geotechnical engineering. Prentice Hall/Pearson Education South Asia, London
Gupta AK, Paul B (2016) Augmenting the stability of OB dump by using fly ash: a geotechnical approach to sustainably manage OB dump at Jharia Coal Field, India. Current World Environ 11(1):204–211
Haddou MB, Essahlaoui A, Boujlal M, Elouali A, El- Hmaidi A (2013) Study of the geotechnical parameters of the different soils by correlation analysis and statistical, in the Kenitra Region (Morocco). J Earth Sci Geotech Engs 3(2):51–60
Hong JC, Jong KM, Il SJ (2012) A study of decreasing behavior of strength and elastic parameters due to water infiltration in rock cores. J Korean Geotech Soc 28(1):69–83
Igwe O (2014) The compressibility and shear characteristics of soils associated with landslides in geologically different localities—case examples from Nigeria. Arab J Geosci. https://doi.org/10.1007/s12517-014-1616-3
Igwe O (2015) The geotechnical characteristics of landslides on the sedimentary and metamorphic terrains of south-east Nigeria. Geoenviron Dis, West Africa. https://doi.org/10.1186/s40677-014-0008-z
Igwe O (2015) Stability analysis and simulated hydrologic response of some vulnerable slopes in Nigeria: implications for rainfall-induced landslides. IOSR J Appl Geol Geophy (IOSR-JAGG) 3(3):48–56. https://doi.org/10.9790/0990-03314856
Igwe O, Fukuoka H (2014) The effect of water-saturation on the stability of problematic slopes at the Iva Valley area. Arab J Geosci, Southeast Nigeria. https://doi.org/10.1007/s12517-014-1398-7
Igwe O, Brooks AE, Maduka RI, Oha IA (2015) Landslide investigation of Ikwette, Obudu local government area of Cross River State, Nigeria. IOSR J Appl Geol Geophy (IOSR-JAGG) 3(3):1–12
Igwe O, Fukuoka H, Sassa K (2012) The effect of relative density and confining stress on shear properties of sands with varying grading. Geotech Geol Eng 30:1207–1229
Igwe O, Mode W, Nnebedum O, Okonkwo I, Oha I (2013) The analysis of rainfallinduced slope failures at Iva Valley area of Enugu State. Environ Earth Sci DOI, Nigeria. https://doi.org/10.1007/s12665-013-2647-x
Isik Y, Keskin Y (2008) GIS based statistical and physical approaches to landslide susceptibility mapping (Sebinkarahisar, Turkey). Bull EngGeol Environ 68:459–471
Kainthola A, Verma D, Gupte SS, Singh TN (2011) A coal mine dump stability analysis—a case study. Int J Geomater 1:1–13
Kitutu MG, Muwanga A, Poesen J, Deckers JA (2009) Influence of soil properties on landslide occurrence in Bududa district, Eastern Uganda. Afr J Agric Res 4(7):611–620
Knapen A, Kitutu MG, Poesen J, Breugelmans W, Deckers J, Muwanga A (2006) Landslides in a densely populated county at the footsteps of Mount Elgon (Uganda): characteristics and causal factors. Geomorphology 73:149–165
Lin H, Zhong W, Xiong W, Tang W (2014) Slope stability analysis using limit equilibrium method in nonlinear criterion. Sci World J 2014:7
Maduka RI, Igwe O, Ayogu NO, Ayogu CN, Nwachukwu M (2017) Geotechnical assessment of road failure and slope monitoring along Nsukka-Adoru-Idah highway. Southeastern Nigeria Environ Monit Assess 189:1–18
Maduka RI, Ayogu NO, Ayogu NC, Gbakurun GA (2016) Role of smectite-rich shales in frequent foundation failures in southeast Nigeria. J Earth Syst Sci. https://doi.org/10.1007/s12040-016-0727-5
Mandal A, Sengupta D (2000) The Analysis of fatal accidents in Indian Coal Mines. ISO India, Kolkata
McCarthy David F (2007) Essentials of soil mechanics and foundations. Pearson Prentice Hall publication, London, pp 657–718
Morgenstern N, Price VE (1965) The analysis of the stability of general slip surfaces. Geotechnique 15(1):79–93
Moser M, Hohensinn F (1983) Geotechnical aspects of soil slips in Alpine regions. Eng Geo 19(3):185–211
Moudabel OA (2013) Slope stability case study by limit equilibrium and numerical methods. MSc thesis. Tripoli University Tripoli, Libya, p 78
Msilimba GG, Holmes PJ (2005) A landslide hazard assessment and vulnerability appraisal procedure:vunguvungu/Banga catchment, Northern Malawi. Nat Hazards 34(2):199–216. https://doi.org/10.1007/s11069-004-1513-2
Mugagga F (2011) Land use change, landslide occurrence and livelihood strategies on Mount Elgon slopes, eastern Uganda. Unpublished PhD thesis. Nelson Mandela Metropolitan University, Port Elizabeth
Mugagga F, Kakembo V, Buyinza M (2011) A characterisation of the physical properties of soil and the implications for landslide occurrence on the slopes of Mount Elgon. Nat Hazards, Eastern Uganda. https://doi.org/10.1007/s11069-011-9896-3
Muthreja IL, Yerpude RR, Jethwa JL (2012) Role of site selection on the stability of surface coal mine waste dumps. Indian Min Eng J 51:9
Nath A, Dalal SS (2004) The role of plasticity index in predicting compression behavior of clays. Elect J Geotech Eng 9:1–7
Noda A, TuZino T (2007) “Characteristics of sediments and their dispersal systems along the shelf and slope of an active forearc margin” eastern Hokkaido, northern Japan. Sedimentary Geol 201(3–4):341–364
Nweke OM (2015) Evaluating the suitability of clays from Abakaliki Area, Southeastern Nigeria for oil industrial application using geotechnical and rheological properties. Sci Innov 3(2):22–31. https://doi.org/10.11648/j.si.20150302.11
Obiora SC, Charan SN (2011) Geochemistry of regionally metamorphosed sedimentary rocks from the lower Benue rift: implications for provenance and tectonic setting of the Benue rift sedimentary suite. S Afr J Geol 114:25–40
Reidenouer DR (1970) Shale suitability, phase ii: pennsylvania department of transportation, Bureau of materials, testing and research. Interim Rep 1:198
Seedman R (1986) The behavior of clay shales in water. Canadian Geotech J 23(1):18–22
Selley RC (2000) Applied rock–soil aggregateology, 2nd edn. Academic Press, Berkeley
Sen B, Pal SK (2014) Index properties of soils collected from different locations and correlations of parameters. Elect J Geotech Eng 19:3443–3452
Sengupta S, Sharma S, Roy I (2016) Stability analysis of overburden internal dump materialofamlohri opencast coal mine, india. ARPN J Earth Sci 5(1):50–57
Sharma S, Roy I (2015) Slope failure of waste rock dump at Jayant opencast mine, india: a case study. Int J Appl Eng Res 10(13):33006–33012
Simpson A (1954) The Nigerian coal field—the geology of parts of Onitsha, Owerri and Benue provinces. Geol Surv Nig Bull, No, p 24
Singh TN, Pradhan SP, Vishal V (2013) Stability of slopes in a fire-prone mine in Jharia Coalfield, India. Arab J Geosci 6(2):419–427
Sudha Rani Ch, Phani Kumar V (2011) Prediction of compression index of soils using artificial neural networks (Anns). Int J Eng Res Appl (IJERA) 1(4):1554–1558
Tuncer OD, Lohnes CG (1977) Specific gravity of soils. J Geol 75:432–534
Vishal V, Pradhan SP, Singh NT (2010) Instability assessment of mine slope—a finite element approach. Int J Earth Sci Eng 3:11–23
Wati SE, Hastuti T, Wijojo S, Pinem F (2010) Landslide susceptibility mapping with heuristic approach in mountainous areaA case study in Tawangmangu sub District, Central Java, Indonesia. Int Arch Photo RS Spat InfSci 38(8):248–253
Yang H, Adler R, Huffman G (2007) Use of satellite remote sensing in the mapping of global landslide susceptibility. Nat Hazards 43(2):245–256. https://doi.org/10.1007/s11069-006-9104-z
Zhou JW, Xu YW, Yang XG, Shi C, Yang ZH (2010) The 28 October 1996 landslide and analysis of the stability of the current Huashiban slope at the Liangjiaren Hydropower Station, Southwest China. Eng Geol 114(1–2):45–56
Zhou J, Shi C, Xu F (2013) Geotechnical characteristics and stability analysis of rock–soil aggregate slope at the Gushui Hydropower Station, Southwest China. Sci World J 2013:16
Zhou Z, Wang H-G, Fu H-L, Liu B-C (2009) Influences of rainfall infiltration on stability of accumulation slope by in situ monitoring test. J Central South Univ Technol 16:297–302
Authors’ contributions
The first author developed the concepts and theories that guided the research. The author also verified and validated the research outcome. The second author applied the concepts in the field and laboratory assessments. The resaerch is part of the second author's postgraduate thesis. Both authors read and approved the final manuscript.
Acknowledgements
The authors heartily acknowledge the lecturers of Geology department, University of Nigeria, Nsukka, who have contributed immensely to the success of this research work. Special thanks go to Raphael, Chiedu, and Rev. Chukwu for their financial support. God bless you.
Competing interests
The authors declare that they have no competing interests.
Ethics approval and consent to participate
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Igwe, O., Chukwu, C. Evaluation of the mechanical properties and critical slope parameters of mine tailings at Enyigba, South eastern, Nigeria. Geo-Engineering 9, 7 (2018). https://doi.org/10.1186/s40703-018-0075-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40703-018-0075-1