Background

A rock bolt is a support (preliminary one) to create a stable underground space, used with shotcrete and steel rib. The rock bolt is widely used due to a variety of its functions: formation of a confined pressure range in a strip shape inside the jointed mass around the tunnel face, arching effects, hanging effects, shape retention effects, suture action, etc.

The research on the rock bolt at home and abroad has been conducted mainly focused on the development of new rock bolt methods (shape, material, fixing method, etc.); however, the experimental study on the reinforcing effects of the rock bolt is insufficient. The analysis of the existing studies found that these studies were conducted through a numerical analysis in the concept of the support and others (shotcrete, steel rib, etc.) in terms of the rock bolt. Thus, there have been few experimental studies on the reinforcing effects of the rock bolt only [1].

This study thus attempted to confirm the reinforcing effects of the jointed rock mass in terms of the rock bolt by creating a concrete block ground that has simulated the uniform jointed rock mass and conducting a large scale model test based on the pretension of the rock bolt and the length of the reinforced ground as parameters. To obtain the reinforcing effects that only the rock bolt exerts, the elastic modulus of the model ground reinforced by the rock bolt reinforcing the rock bolt was derived by creating the model ground into a cantilever shape, excavating the bottom ground of the concrete block, and measuring the maximum deflection of the model ground.

Deflection of cantilever

The free statically determinate structure on which one side has been fixed and the other side has no support is referred to as a cantilever beam. In general, the fixed part is called a cantilever or a cantilever beam. In general, the fixed side is called a fixed end and the side without a support a free end. The deflection of the cantilever subject to uniformly distributed loading under the experimental conditions can be calculated based on the following empirical formula with the distance (x) from the free end [2].

$$\delta = \frac{\text{q}}{{24\,{\text{EI}}}} \cdot \left( {{\text{x}}^{4} - 4{\text{x}}^{3} {\text{l}} + 3{\text{l}}^{4} } \right)^{2}$$

where, δ: deflection (m), q: uniformly distributed load (kN/m), x: distance from free end (m), l: cantilever length (m), E: modulus of elasticity (kPa), I: geometrical moment of inertia (m4).

The relationship between the modulus of elasticity and the deflection in accordance with the formula is inverses as shown in the following Fig. 1a. The relationship between the length and deflection of the cantilever according to the experimental formula for the cantilever length applied to the model test is shown as in Fig. 1b.

Fig. 1
figure 1

Deflection curve of cantilever. a Modulus of elasticity-deflection curve. b Cantlever length-deflection curve

Full size image

This study attempted to quantitatively analyze the reinforcing effects of the rock bolt by substituting the cantilever deflection measured through a model test into the formula and inversely deriving the elastic modulus of the model ground.

Large scale model test

Test overviews

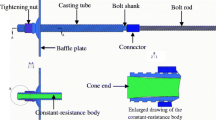
In a large model test, the model ground in a cantilever shape was created so that the rock bolt and the model ground (concrete block) move for the clear reinforcing effects. Additionally, to maintain the confined zone; the same reinforcing zone 0.18 m2 (0.4 m × 0.45. length × width) per rock bolt was applied to maintain the thickness of the confine zone by reinforcing rock bolts. The model ground was installed to ensure the pattern bolting or system bolting to install rock bolts by increasing the cantilever length (ground length) by 0.4 m. Figure 2 is a conceptual diagram of the large scale model test created with a cantilever.

Fig. 2
figure 2

Experimental concept. a 2L. b 3L. c 4L

Full size image

Large scale model test equipment and model ground

The type of the large model test and the creature of the model ground are shown in Fig. 3 below. The model ground is divided into the two layers: the upper layer and the lower layer. The upper layer was created in a scale of full size 4.0 × 0.45 × 0.75 m (length × width × height). For the lower ground, sandy soil (sand) was used. It was created by reinforcing it in a sand curtain way to create an uniform ground to simulate the excavation. The center of the model ground is a fixed end, manufactured to ensure the upper ground (concrete block ground) allows for the complete cantilever behavior according to the excavation of the lower ground (sand) and to conduct an efficient test by differently loading the pretension of the rock bolt on the left and right sides.

Fig. 3
figure 3

Large scale model tester. a Front view. b Side view

Full size image

The model ground of the large scale test and the properties of the rock bolt are as follow Table 1.

Table 1 Properties of model ground and rock bolt
Full size table

Methods

In this study, a test was conducted by adopting the cantilever length (model ground length and the pretension of the rock bolt as parameters. For reinforcing length, 0.4 m per rock bolt was expressed into L. Then, a large scale model test was carried out for 3 cases—0.8 m (2L), 1.2 m (3L), and 1.6 m (4L)—in the model ground length and for the total of 6 cases L according to of 15kN and 25kN in the rock bolt pretension. The concept and parameters of the large scale model experiment are shown in Fig. 4 [3].

Fig. 4
figure 4

Conceptual view and test parameters of the large scale model test. a 2L, b 3L, c 4L, d test parameters

Full size image

The test was conducted in the following order.

  1. 1.

    The excavated ground was created by grouting the sand (SP) in the same particle size.

  2. 2.

    A jointed rock mass was created on the upper of the lower of the excavated ground with a concrete block (for the zone where the rock bolt was installed, a drilled concrete block was used).

  3. 3.

    The confining load was applied to create cantilever conditions.

  4. 4.

    The installed rock bolt was combined with the concrete block.

  5. 5.

    A load cell was installed in the upper of the rock bolt and the pretension was loaded.

  6. 6.

    A linear variable differential transformer (LVDT) was installed on the top, middle, and bottom of the position where the rock bolt has been installed.

  7. 7.

    The lower ground was excavated and the deflection of the upper ground and the side force of the rock bolt were measured.

Results

Deflection after excavation

The tendency of deflection occurred significantly as the cantilever length (ground length, arm length) increased and the distance from the fixed end was farther away. As the pretension increased, the deflection decreased. For the shortest cantilever length 2L (RB2), the deflection difference according to the pretension slightly increased. The deflection according to the cantilever length is shown in Fig. 5 below and the front view of the large scale model tester is shown in Fig. 6.

Fig. 5
figure 5

Deflection according to rock bolt location per cantilever length. a 2L, b 3L, c 4L, d comparison with the max. deflection by a formula

Full size image
Fig. 6
figure 6

View after Test (RB4PT15, RB4PT25)

Full size image

The deflection based on the formula Fig. 5d is a value calculated to obtain the max. deflection by cantilever length using the cantilever deflection formula. Compared to the formula, the deflection that has occurred during the test decreased by 60–67 % for pretension 15 kN and by 66–80 % for pretension 25 kN (Table 2). The results can be explained by the reinforcing effects of the rock bolt where pretension has been loaded.

Table 2 Max. deflection according to cantilever length
Full size table

Reinforcing effects according to pretension of rock bolts

It was found that as pretension increases, deflection decreases and the modulus of elasticity increases. The modulus of elasticity according to the pretension by cantilever length is shown in Fig. 7. (However, the modulus of elasticity when the pretension reaches 0 kN was assumed to be 0).

Fig. 7
figure 7

Modulus of elasticity according to pretension. a 2L, b 3L, c 4L

Full size image

The modulus of elasticity has a correlation between pretension and the linear (linear equation). As a result of the regression analysis, the relationship between the pretension of the rock bolt and the modulus of elasticity of the reinforced ground can be expressed into the following equation.

$${\text{E}}_{\text{P}} = \alpha \cdot {\text{P}}$$

where, EP: modulus of elasticity of reinforced ground of rock bolt (MPa), α: constant according to pretension (Table 3), P: rock bolt pretension (kN).

Table 3 Constant according to pretension of rock bolt
Full size table

Reinforcing effects according to cantilever length

Figure 8 shows the graphs of the modulus of elasticity according to the cantilever length by pretension. The modulus of elasticity tends to increase with the cantilever increasing.

Fig. 8
figure 8

Modulus of elasticity according to cantilever length. a 15 kN, b 25 kN

Full size image

The modulus of elasticity has a polynomial (quadratic) correction with the cantilever length. As a result of the regression analysis, the relationship can be expressed into the following equation.

$${\text{E}}_{\text{L}} = {\text{aL}}^{2} + {\text{bL}} + {\text{c}}$$

where, EL: Modulus of elasticity (MPa) of rock bolt-reinforce ground; a, b, c: constants according to cantilever length (Table 4); L: cantilever length (m).

Table 4 Constants according to cantilever length
Full size table

Supporing increasing effects by pattern bolting

Figure 9 is a graph drawn to show the modulus of elasticity according to the position of the rock bolt from the fixed end. In general, the modulus of elasticity tended to decrease as it moved away from the fixed end (as it got close to the free end. However, for 4L, the longest modulus of elasticity, the modulus of elasticity decreased and increased as it moved away from the fixed end, showing the max. value. The results of the analysis of the growth of the modulus of elasticity by cantilever length revealed an decrease in 2L (65–70 %) and 3L (23–60 %), while an increase in 4L (42–52 %).

Fig. 9
figure 9

Modulus of elasticity according to distance from fixed end. a 2L, b 3L, c 4L

Full size image

Compared to the modulus of elasticity (min. value), close to the free end, the modulus of elasticity was found to increase as the cantilever length increased (2L < 3L < 4L). This increase may be explained by an increase of the reinforcing effects due to pattern bolting. The effects on pattern bolting were proposed with the following equation

$$\lambda = \frac{{4 \cdot {\text{n}} \cdot {\text{d}} \cdot {\text{l}}}}{{{\text{s}}_{ 1} \cdot {\text{s}}_{\text{c}} }}$$

where, λ: coefficient according to reinforcing effects of pattern bolting; n: number of rock bolts (per); d: diameter of rock bolt (m); l: length of rock bolt (m); sl, sc: perpendicular and horizontal installation interval (m).

Conclusion

This study attempted to derive the modulus of elasticity of the ground by creating the model ground that has simulated the jointed rock mass with a concrete block to confirm the reinforcing effects of a rock bolt and conducting a model test based on the pretension of the rock bolt and the cantilever length as parameters after excavating the lower ground. As a result, the following conclusions were derived for the reinforcing effects of the jointed rock mass by the rock bolt.

  1. 1.

    In the model ground, a rhombic-shaped reinforcing zone is formed due to the pretension of the rock bolt. As the pretension increases, the deflection decreases and the modulus of elasticity increases. This reinforces the reinforcing effects.

  2. 2.

    In general, the deflection tends to increase according to the cantilever length, while decreases as the modulus of elasticity increases due to the effects of pattern bolting according to an increase in the number of reinforcing rock bolts.

  3. 3.

    The correlation between the modulus of elasticity and the pretension of the rock bolt shows a linear equation (linear) form, while the correlation between the modulus of elasticity and the cantilever length a polynomial (quadratic) form.

  4. 4.

    The modulus of elasticity after the rock bolt reinforcement is expressed into the following correlation in consideration of the pretension of the rock bolt, the cantilever length, and the pattern bolting efficiency.

    $${\text{Er}} = \frac{{\alpha \cdot {\text{P}}}}{{\left( {\beta {\text{L}} - \gamma } \right)^{2} }} \cdot \lambda$$

    where Er: modulus of elasticity in rock bolts-reinforced ground (MPa); P: pretension of rock bolt (kN); L: cantilever length (m); α: constant after pretension of rock bolt; β, γ: β2 = a, 2βγ = b, γ2 = c; λ: coefficient according to reinforcing effects of pattern bolting.