Abstract
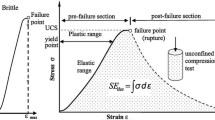
The drop modulus is an important parameter to estimate the post peak behavior of rock mass. It is the slope for the softening stage of rock mass that related to quality of rock mass and confinement stress as increasing in the quality of rock mass and decreasing in the confinement stress can increase the drop modulus and it is true inversely. One of the most important applications of this parameter is to predict the rock burst, squeezing and etc because the mentioned phenomena are directly related to post peak behavior of rock mass. In this study, a new empirical method is proposed to estimate the drop modulus using the double shield TBM specifications of Karaj–Tehran water conveyance tunnel in Iran. It is estimated based on the penetration rate of TBM, the equivalent thrust per cutter and the torque of TBM. The result shows that there are inverse relations between the drop modulus of rock mass with the penetration rate and the torque of TBM and a direct relation between the drop modulus and the equivalent thrust per cutter. In this study, new power equations are proposed to estimate the drop modulus using the penetration rate and the equivalent thrust per cutter respectively. Also a new linear equation is suggested to estimate the drop modulus using the torque of TBM. Finally, the most useful equation to estimate the drop modulus is achieved using the ratio of the equivalent thrust per cutter to product of TBM penetration rate on torque of TBM because it is a function of three parameters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
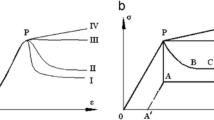
Hoek and Brown [7] suggested guidelines to estimate the post failure behavior types of rock mass according to rock mass quality. These guidelines are based on rock types: for very good quality hard rock masses, with a high GSI value (70 < GSI < 90), the rock mass behavior is elastic brittle; for averagely jointed rock (50 < GSI < 65), moderate stress levels result in a failure of joint systems and the rock becoming gravely; for heavily jointed rock (40 < GSI < 50), strain softening is assumed; and for very weak rock (GSI < 30), the rock mass behaves in an elastic perfectly plastic manner and no dilation are assumed. These concepts are illustrated in Fig. 1. The strain softening behavior can accommodate purely brittle behavior and elastic perfectly plastic behavior, so brittle and elastic perfectly plastic behaviors are special cases of the strain softening behavior [2, 3]. Concept of the strain softening behavior of rock mass is explained in the next section.
Concept of the strain softening behavior
Strain-softening behavior is characterized by a gradual transition from a peak to a residual failure criterion that is governed by the softening parameter η. In this model when the softening parameter is null, an elastic regime exists, whenever 0 <η < η*, the softening regime occurs and the residual state takes place when η > η*, with η*, defined as the value of the softening parameter controlling the transition between the softening and residual stages. This model is illustrated in Fig. 2. It is obvious that perfectly brittle or elastic–brittle–plastic and perfectly plastic models are special cases of the strain-softening model. The following information is needed to characterize a strain-softening rock mass: (1) peak and residual failure criteria, (2) elastic parameters (Young’s modulus and Poisson’s ratio), and (3) post-failure deformability parameters. Joints, micro-cracks, and groundwater reduce strength of rock mass. The GSI, as a scaling parameter is used to provide an estimate of the decreased rock mass strength based on the Hoek–Brown criterion. The GSI is an empirically dimensionless number that varies over a range between 10 and 100. By definition, GSI values close to 10 correspond to very-poor-quality rock mass while GSI values close to 100 correspond to excellent-quality rock masses [4, 7, 8, 11]. When the GSI scale factor is introduced, the Hoek–Brown failure criterion for the rock mass is given as follows:
The parameter mb, in Eq. 1 depends on the following: the intact rock parameter, mi, the value of GSI, and disturbance factor D, as defined by the Eq. 2:
D is a factor which depends upon the degree of disturbance to which the rock mass has been subjected by blast damage and stress relaxation. According to Table 1, it varies from 0 for undisturbed in situ rock masses to 1 for very disturbed rock masses in tunnels [7, 8, 9]. The parameter, s, depends empirically on the value of GSI and D as follows,
The parameter, a, also depends empirically on the value of GSI, as Eq. 4:
Determining the appropriate value of σ3 for use in Eq. 1 is very important. It is estimated based on Eq. 5:
where σcm, is the rock mass strength, defined by Eq. 6, γ, is the unit weight of the rock mass and H, is the depth of the tunnel below surface. In case the horizontal stress is higher than the vertical stress, the horizontal stress value should be used in place of γ·H [9].
where c is the cohesion of rock mass and Ф is the friction angle of rock mass.
Cai [5] proposed estimating the residual strength of rock masses by adjusting peak GSI to the residual GSIres value by using of two major controlling factors in the GSI system including residual block volume Vrb and residual joint condition factor Jrc. The proposed method for estimating residual strength of rock mass was validated with actual examples based on using in situ block shear test data from three large-scale cavern construction sites and data from a back analysis of the rock slope. In order to obtain this, peak failure criterion can be used of GSIpeak in the mentioned equations. The residual failure criterion is similarly obtained by changing the value of the peak geotechnical quality GSIpeak to that of the residual geotechnical quality GSIres. The guidelines given by [5] used to estimate GSIres. It is mentioned in Table 2.
The slope for the softening stage or drop modulus is denoted by M. if the drop modulus approach to infinity, perfectly brittle behavior appears, whereas perfectly plastic behavior is obtained if this modulus approaches to zero [2].
One of the most important parameters affect on drop modulus is confinement stress as with increasing this parameter, the rock mass behaviors become more and more ductile and finally behave ideally plastic [13] and drop modulus tend to zero and with decreasing the confinement stress, the rock mass behavior tend to brittle and the drop modulus increases to infinite. The conclusion of Seeber [14] showed that ideally plastic behavior, without strain softening post failure, may be expected when the confinement pressure σ3, is equal to or greater than one-fifth of the axial stress at failure (Fig. 3).
Dependence of the post-failure behavior of granite samples on the confinement pressure. a Results of a numerical simulation of the 3-axial tests. b, Schematic behavior [6]
Assuming the failure criterion of Hoek and Brown, based on Seeber’s condition, the relation between the confinement pressure and the uniaxial compressive strength σc, of the intact rock can be obtained [6, 16, 17]. This relation can be approximated by:
where, mb is the product of a parameter m depending on the lithology, with a reduction factor depending on the degree of fracturing of the rock.
As mentioned above it has been observed in the field that the deformability post-failure behavior of rock masses is highly dependent on rock mass quality and confinement stress. Based on these observations, the following values proposed by [2] to estimate the drop modulus of the rock mass according to the peak rock mass quality given by GSI peak and to the level of confinement stress expressed in terms of the rock mass compressive strength given by \(\sqrt {{\text{S}}^{\text{peak}} } \cdot \sigma_{\text{ci}}\). The values obtained thus take into account the assumption of a continuous trend, from brittle behavior in high-quality rock masses subjected to unconfined conditions, to pure ductile behavior in poor-quality rock masses for extremely high confinement stresses. The value of the drop modulus depends on the deformation’s modulus Erm, according to the next equation:
The value of the ratio ω, depends on the GSI peak and confinement-stress level and can be estimated according to Eqs. 9 and 10:
If confinement stresses is not considered in calculation, the drop modulus can be estimated according to the next equation:
A more complex approach to estimate of drop modulus, including the effect of σci, is:
The following equation is used as a first approach to estimate the drop modulus, if one uses more complex strain softening models with confinement stress dependent drop modulus [2, 3]:
The most complex equation to estimate the drop modulus is defined as Eq. 14:
Equation 14 is used for GSI ranges from 20 to 75 and more effective factors such as GSI, confinement stress, σ3, unixial strength of intact rock σci, are applied in this equation [2, 3].
The deformation modulus of rock mass is the most important parameter affecting the mechanical behavior of rock mass. There are several methods to estimate this parameter such as in situ tests, back analysis using numerical methods and empirical equations, which are based on the application of rock mass classifications. Although the best method to estimate this parameter is in situ tests, it is costly and often very difficult. Because of such difficulties, determining the modulus of deformation of the rock masses with other methods continues to attract the attention of rock engineers and engineering geologists. Thus, Erm can be generally estimated and easily be acquired by means of empirical methods.
The pre failure deformability was obtained using empirical approaches. The deformation modulus, Erm, can be obtained from Hoek and Diederichs approach according to Eq. 15 because more effective factors on deformability such as the elastic modulus of intact rock, Ei, disturbance factor, D, and GSI are used in this equation [8, 16, 17].
The main purpose of this study is to estimate the drop modulus based on TBM specifications (TBM Penetration rate, torque and the equivalent thrust per cutter) of Karaj–Tehran water conveyance tunnel of Iran.
Projects description and geology
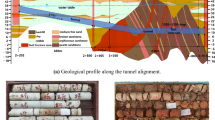
Karaj–Tehran water conveyance tunnel (lot 2) is one of the components of a water management system in Iran which has been excavated using double shield TBM Herrenknecht model S323. This tunnel was located in the Chaloos road, about 35 km west of Tehran. The circular-shaped tunnel is 4.66 m in diameter and has a cross-sectional area of 17.05 m2 and a length of 13.45 km. The portal of this tunnel was shown in Fig. 4. Five rock mass types were observed in this tunnel such as Siltstone, Sandstone, Tuff, Gabbro and Diorite. Geological and geomechanical properties of rock mass types were mentioned in Table 3. All rock mass types of tunnel were classified as fair rock mass condition (25 < GSI < 75). Geology longitudinal profile of Karaj–Tehran water conveyance tunnel was shown in Fig. 5.
The geology longitudinal profile of Karaj–Tehran water conveyance tunnel [15]
Estimation of the drop modulus using TBM operational parameters
In this section the drop modulus of rock mass was estimated in four stages as mentioned follow. Therefore, in the first stage, estimation of the drop modulus was estimated using the penetration rate of TBM and in the second stage, the relation between the drop modulus and the equivalent thrust per cutter was estimated. Then, a new relation to determine the drop modulus based on the torque of TBM was proposed and finally, the drop modulus was estimated using all mentioned parameters (TBM penetration rate, torque and equivalent thrust per cutter).
Estimation of the drop modulus based on the penetration rate of TBM
The penetration rate of TBM is one of the most important parameters which is defined in terms of the excavated distance divided by the operating time during a continuous excavation phase [1]. TBM penetration rate depends on the machine characteristics and the rock mass properties. When TBM is operating, a chronometer on the TBM records all operating times. This operating times are used to calculate the penetration rate (ROP) as a measure of the cutter head advance per unit excavating time. ROP is often calculated as an average hourly value over a specified basis of time (i.e., instantaneous, hour, shift, day, month, year, or the entire project), and the basis for calculation should be clearly defined. Penetration rate can also be calculated on the basis of the distance excavated per cutter head rotation and expressed as an instantaneous penetration or as the average over each thrust cylinder cycle or other time periods listed above. Therefore,
where pr (m/h) is the rate of penetration (m/h) and ROP (mm/rev) is the amount of cutter penetration.
The aim of this section is to predict the drop modulus of rock mass in Karaj–Tehran water conveyance tunnel of Iran by considering the effect of the penetration rate of TBM. Technical specifications of double shield TBM Herrenknecht model S323 was shown in Table 4. For this reason, 15 sections in different zones of Karaj–Tehran water conveyance tunnel were considered. The minimum and maximum of absolute value of drop modulus (|M| using of Eqs. 9–11 to calculate the drop modulus) vary between 0.127–186.11 GPa, depending on the quality of rock mass and confinement stress. So an increase in the confinement stress and a decrease in the quality of rock mass can decrease |M| It can be true inversely, too. As the first step, regression analysis was used to investigate the kind of relation between both parameters. It was shown in Fig. 6. The results show that there is an inverse relation between both parameters and a new exponential equation was proposed to predict the drop modulus. The best correspondence between both parameters was achieved when Alejano’s drop modulus equations (estimated based on calculating the reduction coefficient of deformation modulus, ω) were used to estimate the drop modulus. Based on the statistical analysis, the following equation between both parameters with R2 = 0.6403 was obtained:
where ROP and M are the penetration rate of TBM (mm/rev) and the drop modulus (GPa), respectively.
The effect of other operational parameters of TBM hasn’t been considered in this section but it is very important parameter because the drop modulus highly depends on mentioned parameter. One of the most important operational parameters is the equivalent thrust per cutter. The effect of this parameter is investigated in the following “Estimation of the drop modulus using the equivalent thrust per cutter”section.
Estimation of the drop modulus using the equivalent thrust per cutter
The equivalent thrust per cutter is an important parameter affecting operation machine. This factor is for cutter diameter 483 mm (19 in.) and average cutter spacing 70 mm [15, 18]. For diverging cutter dimensions, the equivalent thrust is given by the formula:
where, MB, kd and ka are the applied thrust per cutter (KN), the correction factor for cutter diameter as given in Fig. 7, and the correction factor for cutter spacing as given in Fig. 8, respectively. These correction factors can also be found from the expressions 19 and 20 [15, 18].
where Dc and Sc are the cutter diameter and the spacing between the cutters, respectively.
In this study, the equivalent thrust per cutter was calculated using mentioned equations.
The relation between the drop modulus and the equivalent thrust per cutter in Karaj–Tehran water conveyance tunnel of Iran was investigated using the statistical analysis. The equivalent thrust per cutter was calculated from Eq. 18 using the mentioned specifications in Table 4.
Based on the statistical analysis, the following equation between both parameters with R2 = 0.5648 was obtained:
where Meq and M are the equivalent thrust per cutter (KN) and the drop modulus (GPa), respectively. The results show that there is a direct relation between both parameters. Also the correlation between both parameters was shown in Fig. 9. As mentioned in the previous section, the best correspondence between both parameters was achieved when Alejano’s drop modulus equations (Eqs. 8–10), were used to estimate the drop modulus. In the next section, based on the torque of TBM, the drop modulus of rock mass is proposed using the mentioned parameter.
Estimation of the drop modulus using the torque of TBM
One of the most important operational parameters of TBM that related with rock mass quality is the torque of TBM as with increasing this parameter, the rock mass quality and the drop modulus is decreased and it is true inversely [15]. According to the regression analysis (using 15 data of Karaj–Tehran water conveyance tunnel of Iran), the relation between the absolute value of drop modulus and the torque of TBM is suggested to the next equation. It is shown in Fig. 10.
where M and T are the drop modulus (GPa) and the torque of TBM (KN.m), respectively.
A more comprehensive model to estimate the drop modulus
Three factors were used to produce the proposed model such as TBM penetration rate, the equivalent thrust per cutter and the torque of TBM. The input parameters to estimate the drop modulus of rock mass are intact rock properties, pre and post failure properties of rock mass and behavior of rock mass. Also the input parameters to estimate the equivalent thrust per cutter are applied thrust per cutter, cutter spacing and cutter diameter.
As mentioned above, the drop modulus has an inverse relation with TBM penetration rate and torque of TBM and a direct relation with the equivalent thrust per cutter.
In this section, to obtain a more comprehensive model to estimate the drop modulus, the ratio of the equivalent thrust per cutter to product of TBM penetration rate on torque of TBM was calculated and finally, the relation between the mentioned ratio and the absolute value of drop modulus was investigated. The correlation between mentioned ratio with the drop modulus was shown in Fig. 11.
Based on the statistical analysis, the following power equation with R2 = 0.7482 was obtained:
where M, ROP, Meq and T are drop modulus (GPa), penetration rate of TBM (mm/rev), equivalent thrust per cutter (KN) and the torque of TBM (KN.m), respectively.
The best correspondence was achieved using all mentioned parameters to estimate the drop modulus.
Conclusions
As mentioned above, the drop modulus is the slope of the softening stage of rock mass that directly related to the quality of rock mass and inversely related to the confinement stress. it is applicable to estimate the post peak behavior of rock mass and directly used to predict the rock burst and squeezing phenomena. In this paper, the drop modulus was estimated using the operational parameters of TBM because the mentioned parameters are automatically recorded due to excavation by TBM. So, using the operational parameters of TBM to estimate the drop modulus is more comfortable than using the classifications of rock mass such as GSI, RMR and etc because of difficulties to estimate the rock mass classifications in mechanized excavations. In this paper, the following results were obtained:
-
1.
The best correspondence between parameters is achieved when Alejano’s drop modulus equations (Eqs. 8–10), were used to estimate the strain energy ratio.
-
2.
Based on the statistical analysis, it became apparent that the drop modulus has a direct relation with the equivalent thrust per cutter and an inverse relation with TBM penetration rate and torque.
-
3.
In this study, new exponential equations is proposed to predict the drop modulus, using TBM penetration rate and the equivalent thrust per cutter respectively. Also a new polynomial equation is proposed to predict the drop modulus based on the torque of TBM.
-
4.
The most useful equation to estimate the drop modulus is achieved using TBM penetration rate, the equivalent thrust per cutter and the torque of TBM because it is a function of three parameters and finally a new power equation was proposed to estimate the drop modulus using the ratio of the equivalent thrust per cutter to product of TBM penetration rate on torque of TBM.
References
Alber M (1996) Prediction of penetration and utilization for hard rock TBMs. In: Baria M (ed) Prediction and performance in Rock Mech. and Rock Eng. Torino, vol 2. Balkema, Rotterdam, pp 721–725
Alejano LR, Rodriguez-Dono A, Alonso E, Fdez-Manin G (2009) Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behavior. Tunn Undergr Sp Tech 24(6):689–705
Alejano LR, Alonso E, Rodriguez-Dono A, Fernandez-Manin G (2009) Application of the convergence-confinement-method to tunnels in rock masses exhibiting Hoek-Brown strain-softening behaviour. Int J Rock Mech Min Sci 47(1):150–160
Cai M, Kaiser PK, Uno H, Tasaka Y, Minami M (2004) Estimation of rock mass deformation modulus and strength of jointed rock masses using the GSI system. Int J Rock Mech Min Sci 41(1):3–19
Cai M, Kaiser PK, Tasakab Y, Minami M (2007) Determination of residual strength parameters of jointed rock masses using the GSI system. Int J Rock Mech Min Sci 44(2):247–265
Egger P (2000) Design and construction aspects of deep tunnels (with particular emphasis on strain softening rocks). Tunnelling Underground Space Technol 15(4):403–408
Hoek E, Brown ET (1997) Practical estimates of rock mass strength. Int J Rock Mech Sci Geom Abstr 34(8):1165–1186
Hoek E, Diederichs MS (2006) Empirical estimation of rock mass modulus. Int J Rock Mech Min Sci 43(2):203–215
Hoek E, Carranza-Torres C, Diederichs MS, Corkum B (2008) Kersten lecture: integration of geotechnical and structural design in tunnelling. In: Proceedings University of Minnesota 56th Annual geotechnical engineering conference. Minneapolis, pp 1–53
Khademi Hamidi J, Shahriar K, Rezai B, Rostami J (2010) Performance prediction of hard rock TBM using Rock Mass Rating (RMR) system. Tunn Undergr Sp Tech 25(4):333–345
Nelson P, O’Rourke TD (1983) Tunnel boring machine performance in sedimentary rocks. Report to Goldberg-Zoino Associates of New York, P.C., by School of Civil and Environmental of Civil Engineering. Cornell University. Geotechnical Engineering Report 83-3. Ithaca, New York, p 438
Rocscience, Roclab (2002) Rocscience Inc., Toronto, Canada
Rummel F, Fairhurst C (1970) Determination of the post failure behavior of brittle rock using a servo-controlled testing machine. Rock Mech 2(4):189–204
Seeber G (1999) Druckstollen und Druckschächte: Bemessung-Konstruktion-Ausführung. Enke im Georg Thieme Verlag
Soleiman Dehkordi M, Lazemi, HA, Shahriar K (2015) Application of the strain energy and the equivalent thrust per cutter to predict the penetration rate of TBM case study: karaj–tehran water conveyance tunnel of iran. Arab J Geosci 8(7):4833–4842
Soleiman Dehkordi M, Shahriar K, Maarefvand P, Gharouninik M (2011) Application of the strain energy to estimate the rock load in non-squeezing ground condition. Arch Min Sci 56(3):551–566
Soleiman Dehkordi M, Shahriar K, Maarefvand P, Gharouninik M (2013) Application of the strain energy to estimate the rock load in squeezing ground condition of Emamzade Hashem tunnel in Iran. Arab J Geosci 6(4):1241–1248
Tarkoy PJ (1987) Practical geotechnical and engineering properties for tunnel-boring machine performance analysis and prediction transportation research record 1087. Transportation Research Board. National Research Council, pp 62–78
Authors’ contributions
All steps of this article such as collecting data, performing data processing and analysis were performed by both authors. MSD designed and wrote the manuscript and HAL revised the manuscript. All authors read and approved the final manuscript.
Acknowledgements
The authors are indebted to staff of all consulting engineers, contractors and employers to offer data to us and to any people who help to us to preparation this paper. The authors are also indebted to reviewers, whose comments lead to a hopefully more accurate estimation of drop modulus.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lazemi, H.A., Dehkordi, M.S. Application of TBM operational parameters to estimate the drop modulus, case study: Karaj–Tehran water conveyance tunnel of Iran. Geo-Engineering 7, 6 (2016). https://doi.org/10.1186/s40703-016-0020-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40703-016-0020-0