Effects of the lateral stress on the inner frictional resistance of pipe piles driven into sand

Abstract

The inner frictional resistance of pipe piles depends on the degree of soil plugging. Many factors including pile diameter, lateral stress at the pile tip and geometrical conditions of piles could influence the soil plugging. In this paper, the effects of inner sleeves attached at the pile base on the inner frictional resistance are discussed, particularly highlighting the lateral stresses at the sleeve using small-scale steel pipe piles penetrated into a medium dense sandy ground. A closed-ended pile of the same diameter was also tested to compare it with similar open-ended piles. The results of incremental filling ratio (IFR) and plug length ratio (PLR) were also discussed. A simple method was also proposed to evaluate IFR and PLR for the sleeved piles since they have originally been defined for non-sleeved piles. The results of the IFR indicate that all the piles penetrated under partially-plugged or unplugged state producing smaller penetration resistance than a similar closed-ended pile. The results of the corrected IFR give a better indication of the soil plugging of the sleeved piles, particularly at shallow penetration depths. The results also suggest that the inner frictional resistance increase with the sleeve height. The results of the coefficient of lateral earth pressure, K _h also indicate that K _h increases with the sleeve height. The effects however become less significant at higher sleeve heights. Therefore, we can recommend the use of the inner sleeve as an improvement method to increase the bearing capacity of open-ended piles installed in sandy grounds.

Background

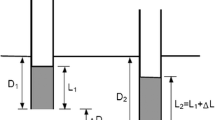
In recent times, open-ended driven piles have gained popularity as deep foundations, particularly in offshore deep foundations due to smaller driving resistance compared to closed-ended piles. The constructions of large structures such as seaports and airports have resulted in high demands for long and large diameter steel pipe piles. Previous studies have shown that the behaviour of open-ended piles is different from closed-ended piles [1–3]. It is accepted that a short open-ended pile produces a smaller bearing capacity than a similar closed-ended pile [4]. However, a long open-ended pile can produce a similar bearing capacity as a closed-ended pile due to large inner frictional resistance mobilised between the inner pile shaft and inner soil [5]. The ultimate bearing capacity of an open-ended pile consists of three components as given in Eq. 1 (see Fig. 1 also). The bearing capacity of an open-ended pile could be influenced significantly by the plug capacity (see Eq. 2), which is influenced by the degree of soil plugging.

Fig. 1

The components of the bearing capacity of an open-ended pile

$$Q_{\text{u}} = Q_{\text{an}} + Q_{\text{out}} + Q_{\text{plug}}$$

(1)

where Q _u is ultimate bearing capacity, Q _an is annulus resistance, Q _out is outer frictional resistance and Q _plug is plug resistance (see Eq. 2).

$$Q_{\text{plug}} = \hbox{min} \,(Q_{\text{in}} ,\,Q_{\text{b}} )$$

(2)

where Q _plug is plug resistance, Q _in is inner frictional resistance and Q _b is base resistance.

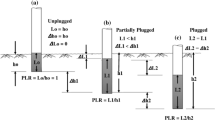
When an open-ended pile is driven into a soil, underneath soil penetrates into the pile and generates a soil plug. As penetration continues, inner frictional resistance mobilised between the pile inner shaft and inner soil may develop and prevent further soil intrusion. Depending on the degree of soil plugging, an open-ended pile can produce a similar bearing capacity as a closed-ended pile. Figure 2a–d show the modes of penetration of open- and closed-ended piles. A fully-plugged open-ended pile (see Fig. 2c) behaves similar to a closed-ended pile (see Fig. 2d). However, most piles in practice are driven under partially-plugged mode [6, 7]. Due to lack of inner frictional resistance, an unplugged (or fully coring) open-ended pile produces a smaller bearing capacity than its fully-plugged or partially-plugged counterparts. Although a large soil plug is developed in an unplugged open-ended pile (see Fig. 2a), it does not produce inner frictional resistance due to the upward movement of the soil plug relatively to the pile. The soil plug settles with the pile as an intact body in a fully-plugged pile during pile installation (or loading).

Fig. 2

The modes of penetrations: a fully coring, b partially-plugged and c fully-plugged mode for an open-ended pile and d a closed-ended pile

Many factors of pile installation and ground conditions can affect the mechanism of the soil plugging [8]. Henke and Grabe [9, 10] compared the effects of installation methods on the degree of soil plugging using static and dynamic pile installation methods. They concluded that dynamic installation methods such as impact and vibratory pile driving do not encourage soil plugging compared to the static methods. Previous studies have also reported that loose ground conditions lead to higher degree of soil plugging conditions [11, 12]. The effects of lateral stress on shaft friction have been included in the design methods by Jardine et al. [13] and Lehane et al. [14]. However, their proposed formulae were based on closed-ended piles where the shaft friction is limited to the outer pile shaft and outer soil. Recently, Henke and Bienen [15] discussed the effects of lateral stress on inner frictional resistance. However, the discussions were limited to the pile diameters.

The lack of knowledge on the mechanism of soil plugging has resulted various design methods adopting different design parameters for open-ended piles. In Japan, most of the pile foundations are designed based on the JRA specifications for highway bridges [16], which specifies the ratio of embedment length to pile outer diameter as the main factor governing inner frictional resistance regardless of the ground conditions or the geometrical properties of the piles except pile outer diameter. In contrast, the ICP [13] method considers inner diameter and relative density as the main factors governing soil plugging and base capacity [17]. The main problem of the ICP method as well as the API method [18] is that they classify any pile into either fully-plugged or unplugged mode whereas most piles in practice are driven under partially-plugged mode. As partially-plugged piles can be classified into the unplugged mode, the ICP and API methods may underestimate the inner frictional resistance of partially-plugged open-ended piles. Among the many design methods, only the UWA-05 design method incorporates the degree of soil plugging in the evaluation of bearing capacity directly [14]. As reported in many design methods, it can be seen that that the evaluation of inner frictional resistance has not been universally established due to uncertainty of the mechanism of the soil plugging.

The effects of ground conditions on the soil plug formation have been sufficiently investigated [11, 12, 19]. While the effects of pile diameter on the inner frictional resistance have been studied adequately [15, 20], the effects of outer or inner sleeves (i.e., attachments at the pile base) on the mechanism of soil plugging have hardly been studied. Therefore, the mechanism of soil plugging on the sleeved-piles are still unknown. In this research, the behaviour of open-ended piles attached with inner sleeves was studied.

Methods

The model ground was prepared in a soil tank with the dimension of 300 mm inner diameter and 250 mm height as shown in Fig. 3a. The bearing house fitted on the top cover was designed to maintain the verticality of the piles during the pile installation and loading. The loading apparatus is shown in Fig. 3b. Silica sand was used to prepare the model ground. The physical properties and particle size distribution of silica sand are given in Table 1 and Fig. 4 respectively. The model ground was prepared with 60 % of relative density. The sand was poured from a tube of 30 mm diameter from a constant height to produce the required relative density (i.e., air pluviation method). Static penetration with a penetration rate of 3 mm/min was applied during pile penetration.

Fig. 3

a Schematic diagram of soil tank and b a photograph of the loading apparatus

Table 1 Physical properties of silica sand

Fig. 4

Particle size distribution of silica sand

The penetration resistance and penetration depth were measured during the loading. Soil plug height was measured using a scaled-mark string connected to a small weight at the bottom by stopping loading at 10 mm intervals as shown in Fig. 5. The loading was manually stopped at each 10 mm of penetration. After unloading disconnects the pile head and loading rod, the soil tank is shifted slightly using the bottom sliding plate, on which the soil tank is placed. Then, the string is inserted into the pile and measure the height using the scale-marked on it.

Fig. 5

The measurement method of soil plug length

Stainless steel piles were used in the experimental work. Five open-ended piles and one closed-ended pile of different geometrical properties were used for the tests as given in Table 2 and Fig. 6. In pile notations of P₅₀-4.0-10 (see Table 2), 50 is pile outer diameter (in mm), 4.0 is wall thickness at the pile tip (in mm) and 10 is sleeve height (in mm). The open-ended piles have 50 mm of outer diameter (D), 380 mm of pile length and 2 mm of top thickness (t _top). When the top wall thickness is considered as the wall thickness, the piles give a ratio of 25 for D/t _top which is within the range (i.e., 15–45) reported by Jardine and Chow [21] for typical offshore piles. However, when the inner sleeves are introduced to the piles (which gives 4 mm wall thickness at the pile base), the ratio reduced to 12.5, which is slightly below the range for typical offshore piles. However, given our discussion is not on the absolute value of the bearing capacity, the piles should give acceptable results. The closed-ended pile (i.e., P₅₀-0.0-380) too has 50 mm diameter and 380 mm of pile length. Kikuchi [6] reported that the inner frictional resistance is mobilised within 2D distance (D is pile outer diameter) from the pile tip. Therefore, we selected the sleeve height, l such that l = 10 mm and 0.5, 1.0 and 2.0D (see Table 2). However, for the non-sleeved pile of 2 mm wall thickness (i.e., P₅₀-2.0-380), the entire pile length (i.e., 380 mm) is considered as the sleeve height simply for comparison purposes.

Table 2 The details of the model piles

Fig. 6

Schematic diagram of an open-ended pile

Results

Two indexes widely used to describe the degree of soil plugging of open-ended piles, called plug length ratio (PLR) and incremental filling ratio (IFR) are defined in Eqs. 3 and 4 respectively [22, 23]. The PLR indicates an average behaviour of plugging state for a long penetration depth. In contrast, the IFR indicates the instantaneous plugging state at small penetration depth. As plug condition may change discontinuously with pile penetration, the IFR is a better indication of plugging condition than the PLR [22, 23].

$$PLR = \frac{h}{H}$$

(3)

where PLR is plug length ratio, h is soil plug height and H is penetration depth (see Fig. 5).

$$IFR = \frac{\varDelta h}{\varDelta H} \times 100\,(\% )$$

(4)

where IFR is incremental filling ratio, Δh is the change of soil plug height for penetration depth of ΔH (see Fig. 5).

Effects of tip thickness

Figure 7 shows the results of penetration resistance versus penetration depth for the piles. As shown in Fig. 7, the closed-ended pile (i.e., P₅₀-0.0-380) produces a larger penetration resistance than similar open-ended piles. Theoretically, only a fully-plugged open-ended pile (i.e., IFR = 0 %) can produce a penetration resistance similar to a closed-ended pile. Figure 7 indicates that the thick-walled piles produce larger penetration resistance than thin-walled piles (by comparing the piles of 2.0 and 4.0 mm of wall thickness, t), which can be attributed to larger annular area (see Table 2). The effects of the wall thickness on the bearing capacity of the piles used in practice (particularly when large diameter piles are used, e.g., in Japan, more than 1.5 m diameter piles are sometimes used) might not be significant compared to the model piles tested in this study simply due to a slightly smaller ratio of A _an/A _t (A _an in annular area and A _t is total area covered by the pile outer diameter). However, when small-scale piles are used, the effects of wall thickness on the bearing capacity may not be insignificant.

Fig. 7

Penetration resistance versus penetration depth

Effects of sleeve height

As shown in Fig. 7, in the piles of 4.0 mm of wall thickness (i.e., P₅₀-4.0-10, P₅₀-4.0-25, P₅₀-4.0-50 and P₅₀-4.0-100) with different sleeve heights (i.e., l = 10, 25, 50 and 100 mm), the penetration resistance is a function of the sleeve height. Figure 7 clearly shows that the piles with higher sleeve height produce larger penetration resistance. Therefore, we can conclude that the sleeve height influences the bearing capacity. As annular area is equal for these piles (i.e., P₅₀-4.0-10, P₅₀-4.0-25, P₅₀-4.0-50 and P₅₀-4.0-100), the annulus resistance can be assumed to be equal. Then, the difference in penetration resistance can be attributed to the difference in inner frictional resistance since the outer frictional resistance should be same.

Inner frictional resistance

As outer frictional resistance (see Eqs. 5 and 6) was found to be 19 N at 150 mm depth (assuming 35° of soil frictional angle, φ; 0.6 φ of frictional angle between the pile shaft and soil, δ; 0.45 of coefficient of lateral earth pressure, K _h according to Tomlinson [7]), it was ignored in the analysis. Annulus resistance, Q _an was calculated using the area ratio given in Table 2 and Q _t (Q _t is total resistance and is equal to the penetration resistance) of the respective closed-ended pile as given in Eq. 7. Then, inner frictional resistance, Q _in was calculated subtracting Q _an from Q _t.

$$Q_{\text{out}} = Aq$$

(5)

where Q _out is outer frictional resistance, A is circumferential area of pile shaft and q is unit outer frictional resistance as given in Eq. 6.

$$q = K_{\text{h}} \sigma \tan \delta$$

(6)

where q is unit outer frictional resistance, K _h is coefficient of lateral earth pressure, σ is effective overburden pressure and δ is frictional angle between the pile shaft and soils.

$$Q_{{{\text{an}},t = 4.0}} = \frac{{A_{\text{an}} }}{{A_{\text{t}} }}Q_{{{\text{t}},D = 50}}$$

(7)

where Q _an,t=4.0 is annulus resistance of t = 4.0 mm piles (t is wall thickness at the pile tip), A _an is annular area (see Eq. 8), A _t is total area covered by pile outer diameter, D and Q _t,D=50 is total resistance of 50 mm diameter closed-ended pile.

$$A_{\text{an}} = \frac{\pi }{4}\left( {D^{2} - d^{2} } \right)$$

(8)

where A _an is annular area, D and d are pile outer and inner diameter respectively.

Figure 8a shows the inner frictional resistance, Q _in versus penetration depth, H. If the value of Q _out is included in the analysis, then all the Q _in-H curves would have the same trend shown now with a slightly smaller value of Q _in since Q _out is equal in all the piles. Figure 8b shows the Q _in versus sleeve height, l. The inner frictional resistance shown in Fig. 8b (i.e., Q _in,150) was calculated at 150 mm penetration depth, which is equal to 5D of penetration depth (D is pile outer diameter). As field piles could be penetrated into even greater depths, we selected the maximum depth possible in the model piles to calculate the inner frictional resistance. As shown in Fig. 8b, inner frictional resistance, Q _in is influenced by the sleeve height, l and is a linear function of l. The results indicate that a higher sleeve height is necessary to produce a large inner frictional resistance. However, it should be noted that the inner frictional resistance may not increase with the sleeve height up to the total pile length as reported by Kikuchi [6].

Fig. 8

Inner frictional resistance versus (a) penetration depth and (b) versus sleeve height

Plug length ratio and incremental filling ratio

Plug length ratio, PLR and incremental ratio, IFR (see Eqs. 3 and 4 respectively) have originally been defined for the non-sleeved piles. Therefore, soil plug height, h should be corrected to evaluate them for the sleeved-piles. The corrected soil plug height, h _cor was evaluated assuming the soil volume of a sleeved pile is equal to its virtual non-sleeved pile as given in Eq. 9 (see also Fig. 9).

Fig. 9

The definition of the inner diameter of a virtual non-sleeved pile

$$h_{\text{cor}} = \left( {\frac{d}{{d_{\text{cor}} }}} \right)^{2} h$$

(9)

where h _cor is the corrected soil plug height, d is pile inner diameter, d _cor is inner diameter of its non-sleeved pile and h is the measured soil plug height (see Fig. 9).

The PLR and IFR were then evaluated using the corrected soil plug height, h _cor as given in Eqs. 10 and 11 respectively. Figure 10a, b show the measured soil plug height, h and corrected soil plug height, h _cor versus penetration depth, H respectively. Figure 10a, b indicate that the non-sleeved piles penetrate closer to unplugged state than the sleeved piles. Although the variations in Fig. 10a is relatively smaller, Fig. 10b shows that the sleeve height influences the soil plug height with clear variations. Figure 10b further indicates that the piles with a higher sleeve height produce a smaller soil plug height.

Fig. 10

a Measured and b corrected soil plug height versus penetration depth

$$PLR_{\text{cor}} = \frac{{h_{\text{cor}} }}{H}$$

(10)

$$IFR_{\text{cor}} = \frac{{\varDelta h_{\text{cor}} }}{\varDelta H} \times 100\,(\% )$$

(11)

where PLR _cor is the corrected plug length ratio, IFR _cor is the corrected incremental filling ratio and h _cor is the corrected soil plug height.

Figure 11a, b show the results of the original and corrected incremental filling ratios, IFR and IFR _cor respectively versus penetration depth, H. The IFRs were calculated at 20 mm intervals although the measurements were taken at 10 mm intervals to reduce scattering of the data. As shown in Fig. 11a, b, a comparison of the results of 46 and 42 mm inner diameter piles (see Table 2) indicates that the smaller diameter piles (using the pile inner diameter, d here since the outer diameter is equal for all the piles) produce higher degree of soil plugging (i.e., smaller values of IFR). A comparison of 4 mm thickness piles in Fig. 11a, b indicate that sleeve height, l affects degree of soil plugging, where it clearly shows that a higher sleeve height, l produces higher degree of soil plugging (i.e., smaller values of IFR). The results of Fig. 11a, b also show that the corrected IFR gives better indication of soil plugging at shallow depth (or where the depth is equal to the sleeve height).

Fig. 11

a Original and b corrected incremental filling ratio versus penetration depth

Figure 12a, b show the results of the original and corrected plug length ratios, PLR and PLR _cor respectively versus penetration depth, H. It should be noted that the value of the PLR can be greater than the unity for a fully coring pile since the top of the soil column inside the pile is above the ground level [24, 25]. A few published papers provide the evidence of the PLR being greater than the unity [11, 26]. As shown for the soil plug height, h in Figs. 10, 12b also shows clear differences of the PLRs among the sleeved-piles than Fig. 12a after PLR is corrected for its virtual non-sleeved pile. As mentioned earlier, the PLR indicates the average behaviour of soil plugging over a large penetration depth. Therefore, we can say that the piles with a higher sleeve produce, on average higher degree of soil plugging.

Fig. 12

a Original and b corrected plug length ratio versus penetration depth

Lateral earth pressure

The soil plug can be treated simplistically as a series of horizontal slices, with each slice acted on by vertical stresses above and below it [27–29]. The vertical stress acting z distance from the pile tip, σ _v,z can be calculated using Eq. 12 [28, 29].

$$\sigma_{\text{v,z}} = \left( {\sigma_{\text v,0} + \frac{{\gamma_{\text t} D}}{{4\mu K_{\text h} }}} \right)\exp \left( {\frac{{4\mu K_{\text h} }}{D}\left( { - z} \right)} \right) - \frac{{\gamma_{\text t} D}}{{4\mu K_{\text h} }}$$

(12)

where σ _v,z is vertical stress at z distance from the pile tip, σ _v,0 is vertical stress at the pile tip, γ _t is soil unit weight, D is pile outer diameter, μ is coefficient of friction between the pile shaft and soil, K _h is coefficient of lateral earth pressure and z is distance from the pile tip.

We calculated the coefficient of lateral earth pressure, K _h under two conditions that the vertical stress acting at z distance from the pile tip, σ _v,z (see Eq. 12) becomes zero at the top of soil plug, h _max and 2D (D is pile outer diameter) distance from the pile tip (i.e., σ _v,z = 0 at z = h _max and 2D respectively). In Eq. 12, it was assumed 0.53 for μ, which comes from a 28° interface frictional angle between the pile and soil. The vertical stress at the pile tip, σ _v,0 was calculated as given in Eq. 13. The inner frictional resistance in Eq. 13 was considered at 150 mm penetration depth.

$$\sigma_{{{\text{v,}}0}} = \frac{{Q_{\text{in}} }}{{\left( {\frac{\pi }{4}d^{2} } \right)}}$$

(13)

where σ _v,0 is vertical stress at the pile base, d is pile inner diameter and Q _in inner frictional resistance.

Figure 13a, b show the results of K _h for the two conditions considered (i.e., σ _v,z being zero at h _max and 2D from the pile tip respectively). Figure 13a, b indicate that the sleeve height, l influences K _h where the pile with a higher value of l results in higher value of K _h. The values of K _h increase from 0.78 to 1.41 when the sleeve height is increased from 10 to 100 mm in the case of zero σ _v,z at the top of soil plug, h _max. The value of K _h increases from 1.08 to 1.75 in the case of zero σ _v,z at 2D distance from the pile tip as reported in Kikuchi [6]. The results indicate that K _h increases with the sleeve height. The results also indicate that larger inner diameter piles produce smaller value of K _h (i.e., 0.29 and 0.59 for the pile of 46 mm of inner diameter, d for h _max and 2D conditions respectively whereas they are 0.78–1.41 and 1.08–1.75 for the piles of 42 mm of d for h _max and 2D conditions respectively).

Fig. 13

The coefficient of lateral earth pressure versus distance from the pile tip, z for zero vertical stress at a h _max and b 2D of z (σ_v,z is vertical stress at z distance from the pile tip, h _max is maximum soil plug height and D is pile outer diameter)

Figure 14a, b show the variation of the coefficient of lateral earth pressure along the penetration depth for the two conditions considered in the analysis. In Fig. 14b, which assumed the vertical stress at 2D distance from the pile tip to be zero, the maximum soil plug height, h _max was considered instead of 2D when it is less than 2D distance (i.e., z = h _max if h _max <2D, see Fig. 14b for more details). Both cases indicate that the value of K _h decreases along the penetration depth. The results also indicate that the variation of the sleeved piles within shallow depth (e.g., less than 50 mm or the depth of 1D distance) is negligible. Also, we can see from Fig. 14a, b that the variations of K _h reduces when a higher sleeve height is used.

Fig. 14

The coefficient of lateral earth pressure versus penetration depth for zero vertical stress at a h _max and b 2D of z (σ_v,z is vertical stress at z distance from the pile tip, z is distance from the pile tip, h _max is maximum soil plug height and D is pile outer diameter)

Conclusions

In this paper, the effects of inner sleeves attached at the pile base on the bearing capacity, particularly inner frictional resistance are discussed using small-scale model piles driven into a sandy ground. The discussion is mainly focused on the mechanism of soil plugging of open-ended piles, in particular the effects of lateral stress at the pile base. The results of IFR and PLR are also discussed. A simple method is also proposed to evaluate the IFR and PLR for sleeved piles in this study since the original equations have been defined for non-sleeved piles.

The results of the IFR indicate that all the piles penetrated under partially-plugged or unplugged state producing smaller penetration resistance than a similar closed-ended pile. The results of the corrected soil plug height clearly indicate the variations of it and the PLR among the sleeved piles. The corrected IFR also gives a better indication of the soil plugging for the sleeved piles, particularly at shallow penetration depth. The results further indicate that soil plug height is dependent of sleeve height, where a higher sleeve height produces a smaller soil plug height. The results indicate that bearing capacity increases with tip thickness, which can be attributed to the increase in annular area. The results also suggest a higher sleeve height produces a larger inner frictional resistance, with the results showing a linear relationship until a 2D height of a sleeve (D is pile outer diameter). The results of the coefficient of lateral earth pressure, K _h also indicate that K _h increases with the sleeve height. The effects of sleeve height on K _h becomes less significant at higher sleeve heights though. As an overall conclusion, we can recommend the use of an inner sleeve at the pile base to increase inner frictional resistance.