Stochastic regularity of a quadratic observable of high-frequency waves

Abstract

We consider high-frequency waves satisfying the scalar wave equation with highly oscillatory initial data. The wave speed, and the phase and amplitude of the initial data are assumed to be uncertain, described by a finite number of random variables with known probability distributions. We define quantities of interest (QoIs), or observables, as local averages of the squared modulus of the wave solution. We aim to quantify the regularity of these QoIs in terms of the input random parameters, and the wave length, i.e., to estimate the size of their derivatives. The regularity is important for uncertainty quantification methods based on interpolation in the stochastic space. In particular, the size of the derivatives should be bounded independently of the wave length. In this paper, we are able to show that when these QoIs are approximated by Gaussian beam superpositions, they indeed have this property, despite the highly oscillatory character of the waves.

1 Background

Many physical phenomena can be described by propagation of high-frequency waves. Such problems arise, for example, in optics, acoustics, geophysics or oceanography. By high frequency, it is understood that the wavelength is very short compared to the distance travelled by the wave. Uncertainty may often be introduced through one or multiple sources: Either the model parameters are incomplete or it is due to the intrinsic variability of the problem. An example of such uncertain high-frequency wave propagation is an earthquake where seismic waves with uncertain epicenter travel through the layers of the Earth with uncertain soil characteristics.

As a simplified model of the wave propagation, we consider the scalar wave equation

$$\begin{aligned}&u^\varepsilon _{tt}(t,\mathbf x ,\mathbf{y })- c(\mathbf x ,\mathbf{y })^2 \, \varDelta u^\varepsilon (t,\mathbf x ,\mathbf{y }) = 0, \quad \text {in } [0,T] \times {{\mathbb {R}}}^n \times \varGamma ,\end{aligned}$$

(1a)

$$\begin{aligned}&u^\varepsilon (0,\mathbf x ,\mathbf{y })=B_0(\mathbf x ,\mathbf{y }) \, \hbox {e}^{i \, \varphi _0(\mathbf x ,\mathbf{y })/\varepsilon }, \quad \text {in } {{\mathbb {R}}}^n \times \varGamma ,\end{aligned}$$

(1b)

$$\begin{aligned}&u^\varepsilon _t(0,\mathbf x ,\mathbf{y })=\frac{1}{\varepsilon }B_1(\mathbf x ,\mathbf{y }) \, \hbox {e}^{i \, \varphi _0(\mathbf x ,\mathbf{y })/\varepsilon }, \quad \text {in } {{\mathbb {R}}}^n \times \varGamma , \end{aligned}$$

(1c)

with highly oscillatory initial data represented by the wavelength $\varepsilon$, which is assumed to be much smaller than both the typical scale of variations in the wave speed and the wave propagation distance. Such initial data generate high-frequency waves propagating in low-frequency media. By $t\in [0,T]$ we denote the time and by $\mathbf x = (x_1,\ldots ,x_n)\in \mathbb {R}^n$ the spatial variable. The uncertainty in the model is described by the random variables $\mathbf{y }= (y_1,\cdots ,y_N) \in \varGamma \subset \mathbb {R}^N$ where N is a positive integer. Their joint probability density is assumed to be bounded. Two sources of uncertainty are considered: the local speed, $c = c(\mathbf x ,\mathbf y )$, and the initial data, $B_0=B_0(\mathbf x ,\mathbf y ), B_1=B_1(\mathbf x ,\mathbf y ), \varphi _0=\varphi _0(\mathbf x ,\mathbf y )$. The solution is therefore also a function of the random parameter, $u^{\varepsilon }=u^{\varepsilon }(t,\mathbf x ,\mathbf y )$. The initial data and the local speed are all assumed to be smooth functions.

In this work, we are interested in observables, or quantities of interest (QoI) defined as functionals of the solution $u^\varepsilon$ to (1) for each ${\mathbf{y }}\in \varGamma$. These observables often carry important physical information. They are functions of the random variable $\mathbf{y }$, and we want to determine their statistical moments, for example the expected value and the variance. This means that we first need to solve (1), then evaluate the functional and finally integrate in $\mathbf y$ over $\varGamma$, which typically is in a high-dimensional space.

Hence, when computing the statistical moments, we are facing two problems: high frequencies and high-dimensional integrals. Firstly, modeling of a high-frequency problem by direct methods is not feasible. The accuracy of direct methods is determined by the number of points per wavelength. For a given accuracy, the wave resolution cost grows rapidly when shrinking the wavelength. As a consequence, direct numerical methods become very expensive at high frequencies. Secondly, the dimension of the random space is typically large which results in a fast growth of the number of mesh points in standard numerical integration schemes. This phenomenon is referred to as the curse of dimensionality.

In [18], we proposed a method for computing the statistics of quantities of interest that deals efficiently with both difficulties. It consists of two techniques: the Gaussian beam superposition method for treating the high frequencies and the sparse stochastic collocation for treating the uncertainty. The Gaussian beam method is an asymptotic technique largely based on the geometrical optics approach. It has been extensively studied in [4, 16, 23, 29]. The sparse grid collocation method has been used in forward propagation of uncertainty in many PDE models, see [16, 25]. The two methods separately are in use, but their combination offers a new powerful tool.

In order for the sparse stochastic collocation to converge fast, high stochastic regularity of the QoI is crucial. That is, the derivatives of the QoI with respect to $\mathbf y$ should exist and be small. In the high-frequency setting, the QoI will depend on the wavelength $\varepsilon$ and it is important that the derivatives are bounded independently of $\varepsilon$. In particular, the QoI should not oscillate with period $\varepsilon$. The objective of this paper is to show such bounds for a certain observable.

Natural choices of QoI include the solution itself in a fixed point $(T,\mathbf x _0)$,

$$\begin{aligned} u^{\varepsilon }(T,\mathbf x _0,\mathbf y ), \end{aligned}$$

or more generally the weighted mean value of the solution,

$$\begin{aligned} \int _{\mathbb {R}^n}u^{\varepsilon }(T,\mathbf x ,\mathbf y )\psi (\mathbf x )\hbox {d}\mathbf x , \quad \psi \in C^\infty _c(\mathbb {R}^n). \end{aligned}$$

In our case, however, neither of these QoIs is interesting due to the high-frequency nature of $u^{\varepsilon }$. In the first case, the pointwise QoI is itself highly oscillatory in $\mathbf y$ and its derivatives cannot be bounded by constants that are independent of $\varepsilon$. In the second case, the mean value tends to zero as $\varepsilon \rightarrow 0$ due to the stationary phase lemma [9], and little new information is given by the QoI.

Quadratic quantities present another choice of observables. In this paper, we will consider:

$$\begin{aligned} {{\mathcal {Q}}}^\varepsilon (\mathbf{y }) = \int _{{{\mathbb {R}}}^n} |u^\varepsilon (T, \mathbf{x }, \mathbf{y })|^2 \, \psi (\mathbf{x }) \, \hbox {d}\mathbf{x }, \end{aligned}$$

(2)

where $\psi$ is again a given real-valued compactly supported smooth function referred to as the QoI test function. QoI (2) has an important physical motivation. Since the square of the wave amplitude $|u^\varepsilon |^2$ represents energy density, the weighted integration of the wave amplitude represents the weighted average strength of the wave inside the support of $\psi$. For example, if the solution $u^{\varepsilon }$ describes the acoustic pressure, $\mathcal {Q}^\varepsilon$ represents the local acoustic potential energy.

It was conjectured in [18] that the QoI (2) computed by the Gaussian beam method, ${\mathcal {Q}}_{\mathrm{GB}}^\varepsilon$, has high stochastic regularity, more precisely, that

$$\begin{aligned} \sup _\mathbf{y \in \varGamma }\left| \partial _\mathbf{y }^{\varvec{\varvec{\sigma }}} {\mathcal {Q}}_{\mathrm{GB}}^\varepsilon (\mathbf{y })\right| \le C_{\varvec{\sigma }}, \quad \forall \, {\varvec{\sigma }} \in {\mathbb {N}}_0^N. \end{aligned}$$

(3)

The result (3) may seem counterintuitive as the solution itself oscillates with $\varepsilon$. However, formal theoretical arguments and numerical examples presented in [18] showed that $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$ is indeed non-oscillatory. As a consequence, the convergence of the sparse stochastic collocation method was exponential, contrasting the rather slow convergence for Monte Carlo simulations.

The main result of this work is Theorem 1 in Sect. 5, where (3) is proved. This shows the suitability of the sparse grid collocation method for computation of the statistics of the QoI. The proof is based on techniques presented in [16]. We stress that (3) is shown for the approximate solution. Whether it holds also for the exact solution with matching initial data is an open question. A simple argument based on the accuracy of the Gaussian beam solution gives that at least $|\mathcal {Q}^\varepsilon _{\mathrm{GB}}-\mathcal {Q}^\varepsilon |=O(\varepsilon ^{k/2-1})$, for kth-order beams, see Remark 1. Hence, for sufficiently high-order beams $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$ is close to $\mathcal {Q}^\varepsilon$. Based on numerical experiments, we conjecture that it is in fact close for all beam orders.

The paper is organized as follows: In Sect. 2, we introduce precise assumptions. In Sect. 3, we present the sparse collocation technique and a numerical example. Section 4 contains the Gaussian beam approximation description and properties. In Sect. 5, we prove the main result on stochastic regularity of the QoI.

2 Preliminaries and assumptions

In this section, we introduce notation used in the paper and formulate precise assumptions for the high-frequency wave propagation problem (1) with stochastic parameters. We write $|\mathbf x |$ for the Euclidean norm of a vector $\mathbf x \in \mathbb {R}^n$. For a multi-index $\varvec{\alpha }=(\alpha _1,\ldots ,\alpha _n)\in \mathbb {N}^n_0$, we, however, use the standard convention that $|\varvec{\alpha }|= \alpha _1+\cdots +\alpha _n$. We frequently use the simple estimate,

$$\begin{aligned} |\mathbf x ^{\varvec{\alpha }}|\le |\mathbf x |^{|\varvec{\alpha }|},\quad \mathbf x \in \mathbb {R}^n,\quad \varvec{\alpha }\in \mathbb {N}^n_0. \end{aligned}$$

For a function $f:\mathbb {R}^n\mapsto \mathbb {R}$, we let $\nabla f(\mathbf x )$ denote its gradient, $\varDelta f(\mathbf x )$ represents the Laplacian of f with respect to the spatial variable $\mathbf x$, and $D^2f(\mathbf x )$ its Hessian. Partial derivatives of order $\varvec{\alpha }$ are written as $\partial _\mathbf{x }^{\varvec{\alpha }} f(\mathbf x )$, where

$$\begin{aligned} \partial _\mathbf{x }^{\varvec{\alpha }}f := \frac{\partial ^{|{\varvec{\alpha }}|}f}{\partial x_1^{\alpha _1} \, \cdots \, \partial x_n^{\alpha _n}},\quad \mathbf x = (x_1,\ldots , x_n)^{\top }. \end{aligned}$$

For a vector-valued function $\mathbf f :\mathbb {R}^n\mapsto \mathbb {R}^n$, we denote the Jacobian matrix by $D\mathbf f (\mathbf x )$. Finally, we let $a^*$ denote the complex conjugate of a complex number a.

We make the following precise assumptions:

• (A1) Strictly positive, smooth and bounded speed of propagation,

  $$\begin{aligned} c\in C^\infty (\mathbb {R}^n\times \varGamma ),\quad 0<c_{\mathrm{min}} \le c(\mathbf x ,\mathbf{y }) \le c_{\mathrm{max}} < \infty , \quad \forall \, \mathbf{x } \in {{\mathbb {R}}}^n, \quad \forall \, \mathbf{y } \in \varGamma . \end{aligned}$$

• (A2) Smooth and (uniformly) compactly supported initial amplitudes,

  $$\begin{aligned} B_{{\ell }}\in C^\infty (\mathbb {R}^n\times \varGamma ),\quad \mathrm{supp}\,B_{{\ell }}(\,\cdot \,,\mathbf{y })\subset K_0, \quad \ell =0,1,\quad \forall \mathbf y \in \varGamma , \end{aligned}$$

  where $K_0\subset \mathbb {R}^n$ is a compact set.

• (A3) Smooth initial phase with nonzero gradient,

  $$\begin{aligned} \varphi _0\in C^\infty (\mathbb {R}^n\times \varGamma ),\quad |\nabla \varphi _0(\mathbf{x },\mathbf{y })|>0,\quad \forall \, \mathbf{x } \in {{\mathbb {R}}}^n, \quad \forall \, \mathbf{y } \in \varGamma . \end{aligned}$$

• (A4) Compact support in random space: The set $\varGamma$ is the closure of a bounded open set.

• (A5) High frequency,

  $$\begin{aligned} 0<\varepsilon \le 1. \end{aligned}$$

• (A6) Smooth and compactly supported QoI test function,

  $$\begin{aligned} \psi \in C_c^\infty ({\mathbb {R}}^n). \end{aligned}$$

3 Forward propagation of uncertainty

There are in general two types of numerical methods for propagating uncertainty in PDE models subject to stochastic uncertainty: (1) intrusive methods and (2) non-intrusive methods. Intrusive methods, such as stochastic Galerkin [2, 33], are based on a weak formulation of the problem and are combined with direct simulations such as the finite element method. Consequently, their application to high-frequency waves is not feasible, since direct solvers require a large number of elements to resolve the wave’s high oscillations. On the contrary, non-intrusive methods, such as Monte Carlo [6] and stochastic collocation [1, 20, 32], are sample-based approaches and rely on a set of deterministic models corresponding to a set of realizations. Consequently, asymptotic techniques for approximating deterministic high-frequency waves [5, 22, 27], such as Gaussian beam superposition (presented in Sect. 4), can be employed within the framework of a non-intrusive method.

In this section, we discuss and motivate the applicability and efficiency of two popular non-intrusive methods, Monte Carlo and stochastic collocation, for approximating the statistics of the QoI in (2).

3.1 Non-intrusive numerical methods

Two popular non-intrusive methods, combined with Gaussian beam superposition, have been proposed in the high-frequency wave community: a Monte Carlo method [31] and a sparse stochastic collocation method [18]. In both methods, the solution to problem (1) is approximated in space and time by the Gaussian beam superposition (see Sect. 4). This gives the Gaussian beam QoI ${{\mathcal {Q}}}^\varepsilon _{\text {GB}}(\mathbf{y })$ in (13), which is evaluated at some set of points $\{ \mathbf{y }^{(m)}\}_{m=1}^{\eta }$. The two methods differ in treating the Gaussian beam QoI in the stochastic space, including the selection of the set of points $\{ \mathbf{y }^{(m)}\}_{m=1}^{\eta }$. Here, we briefly review and compare the convergence rates of the two methods.

Monte Carlo. The Monte Carlo method approximates the statistical moments of a stochastic quantity by sample averages. For instance, let $\{ \mathbf{y }^{(m)} \}_{m=1}^\eta \in \varGamma$ be a set of $\eta$ independent and identically distributed samples of the random vector $\mathbf{y }$. Then, the Monte Carlo estimator [31] computes the first moment of the quantity ${{\mathcal {Q}}}^\varepsilon$ by sample averages of the Gaussian beam QoI:

$$\begin{aligned} {{\mathbb {E}}}[{{\mathcal {Q}}}^\varepsilon ] \approx {{\mathbb {E}}}[{{\mathcal {Q}}}_{\text {GB}}^\varepsilon ] \approx \frac{1}{\eta } \sum _{m=1}^\eta {{\mathcal {Q}}}_{\text {GB}}^\varepsilon (\mathbf{y }^{(m)}), \end{aligned}$$

where ${{\mathcal {Q}}}_{\text {GB}}^\varepsilon (\mathbf{y }^{(m)})$ is the Gaussian beam QoI (13) evaluated at $\mathbf{y }^{(m)}$.

Sparse stochastic collocation. Stochastic collocation is another non-intrusive technique, which exploits the stochastic regularity of the QoI, if available, to obtain a much faster, possibly spectral convergence. In stochastic collocation, ${{\mathcal {Q}}}^\varepsilon _{\text {GB}}(\mathbf{y })$ in (13) is collocated in the points $\{ \mathbf{y }^{(m)} \}_{m=1}^{\eta } \in \varGamma$, giving the $\eta$ Gaussian beam quantities $\{{{\mathcal {Q}}}^\varepsilon _{\text {GB}}(\mathbf{y }^{(m)})\}_{m=1}^{\eta }$. Then, a global polynomial approximation, ${{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta }$, is built upon those evaluations,

$$\begin{aligned} {{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta } (\mathbf{y })= \sum _{m=1}^{\eta } {{\mathcal {Q}}}^\varepsilon _{\text {GB}}(\mathbf{y }^{(m)}) \, L_m(\mathbf{y }), \end{aligned}$$

(4)

for suitable multivariate polynomials, $\{ L_m (\mathbf{y })\}_{m=1}^{\eta }$, such as Lagrange interpolating polynomials. It is important to note that the statistical moments of the quantity ${{\mathcal {Q}}}^\varepsilon$ can directly be computed without forming the polynomial approximation ${{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta } (\mathbf{y })$ in (4). For instance, the first moment of the quantity ${{\mathcal {Q}}}^\varepsilon$ is computed by

$$\begin{aligned} {{\mathbb {E}}}[{{\mathcal {Q}}}^\varepsilon ] \approx {{\mathbb {E}}}[{{\mathcal {Q}}}_{\text {GB}}^\varepsilon ] \approx \sum _{m=1}^\eta {\theta }_m \, {{\mathcal {Q}}}_{\text {GB}}^\varepsilon (\mathbf{y }^{(m)}), \quad \theta _m = \int _{\varGamma } L_m(\mathbf{y }) \, \rho (\mathbf{y }) \, \hbox {d}\mathbf{y }. \end{aligned}$$

(5)

The choice of the set of collocation points, $\{ \mathbf{y }^{(m)} \}_{m=1}^{\eta }$, i.e., the type of computational grid in the N-dimensional stochastic space, is crucial in the computational complexity of stochastic collocation. A full tensor grid, based on the Cartesian product of mono-dimensional grids, can only be used when the dimension of the stochastic space, N, is small, since the computational cost grows exponentially fast with N (the curse of dimensionality). In this case, the grid consists of $\eta = (p + 1)^N$ collocation points, where p is the polynomial degree in each direction. Alternatively, sparse grids, such as total degree and hyperbolic cross grids, can reduce the curse of dimensionality. In both full tensor and sparse grids, typical choices of grid points to be used include Gauss abscissas [30], Clenshaw–Curtis abscissas [30] and Leja abscissas [24]. The statistical moments of the QoI can then be computed using Gauss or Clenshaw–Curtis quadrature formulas applied to (4). See [18] for more details.

3.2 Convergence of numerical methods

By the central limit theorem [6], if the variance of $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$ is bounded, then the convergence rate of Monte Carlo estimator is ${{\mathcal {O}}}(\eta ^{-1/2})$. Therefore, while being very flexible and easy to implement, Monte Carlo sampling features a very slow convergence rate. Multi-level Monte Carlo [7, 19], multi-index Monte Carlo [8], and quasi-Monte Carlo methods [11] have been proposed to accelerate the convergence of Monte Carlo sampling. It is to be noted that these recent techniques have not been applied to high-frequency wave propagation problems.

The rate of convergence of stochastic collocation for approximating a stochastic function $v(\mathbf{y })$ depends on the regularity of the function in stochastic space, i.e., the regularity of the mapping $v: \varGamma \rightarrow {{\mathbb {R}}}$. Fast convergence with respect to the number of collocation points is attained in the presence of high stochastic regularity. For instance, for a stochastic function $v(\mathbf{y })$ with $s \ge 1$ bounded mixed derivatives, $\partial _{y_1}^{s} \, \partial _{y_2}^{s} \cdots \partial _{y_N}^{s} v \in L^\infty (\varGamma )$, the error in stochastic collocation on sparse Smolyak grids based on Gauss–Legendre abscissas satisfies (see Theorem 5 in [20])

$$\begin{aligned}&||v - v_{\eta }||_{L^2_{\rho }(\varGamma )} \le C \, \left( 1+ \log _2 \frac{\eta }{N} \right) ^{2 \, N} \, \eta ^{- s \, \frac{\log _e 2}{\xi + \log _e N}},\nonumber \\&\quad \xi = 1 + (\log _e 2) (1 + \log _2 1.5) \approx 2.1, \end{aligned}$$

where $\Vert \;\cdot \;\Vert _{L^2_{\rho }(\varGamma )}$ is the weighted $L^2$-norm with bounded weight function $\rho$ and

$$\begin{aligned} C = C_{s,N} \, || \rho ||_{\infty }^{1/2} \, \max _{n=1,\cdots ,N} \, \, \max _{0\le k_1, \cdots , k_n \le s} || \partial _{y_1}^{k_1} \cdots \partial _{y_n}^{k_n} v ||_{L^2(\varGamma )}. \end{aligned}$$

Here, the constant C depends on $s, N, \rho$ and the function v, but not on $\eta$. Therefore, the larger s, or equivalently the higher the regularity of v, the faster the convergence rate in $\eta$. In particular, when the stochastic function has infinitely many bounded mixed derivatives, the convergence rate is close to spectral. See also [3, 20, 21].

In the case of high-frequency waves with a highly oscillatory wave solution, the constant C depends in general also on the wavelength $\varepsilon$. To maintain fast convergence, it is therefore crucial that C remains bounded as $\varepsilon \rightarrow 0$. Since C depends on the size of the $\mathbf y$-derivatives of v on $\varGamma$, we need uniform bounds for the $\mathbf{y }$-derivatives of $\mathcal {Q}^\varepsilon _{\text {GB}}(\mathbf y )$ independent of $\varepsilon$ to obtain fast convergence for all $\varepsilon$. We emphasize that since the Gaussian beam quantity $\mathcal {Q}^\varepsilon _{\text {GB}}(\mathbf y )$ is used in the stochastic collocation approximation (4)–(5), it is the stochastic regularity of the Gaussian beam quantity $\mathcal {Q}^\varepsilon _{\text {GB}}(\mathbf y )$ that determines the convergence rate, not the regularity of the analytical quantity $\mathcal {Q}^\varepsilon (\mathbf y )$.

3.3 Example

Let us present a numerical example to illustrate the discussion in Sect. 3.2. We introduce two 2D pulses, nearly disjoint in the beginning and moving toward each other. At a finite time, they start to overlap which leads to oscillations of order $\varepsilon$ in the magnitude of the solution. We consider three uniformly distributed independent random variables $\mathbf{y }=(y_1, y_2, y_3)$ characterizing a random speed, $c=c(\mathbf y )=y_1$, and a random initial position of the second pulse, $\mathbf s _2 = \mathbf s _2(\mathbf y ) = (y_2,y_3)$. We use the smooth test function

$$\begin{aligned} \psi (\mathbf{x }) = \left\{ \begin{array}{ll} \hbox {e}^{-\frac{|\mathbf{x }|^2}{1/4-|\mathbf{x }|^2}}, &{}\quad |\mathbf{x }| < 1/2.\\ 0, &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

The initial data in (1) read

$$\begin{aligned} \varphi _0(\mathbf{x }) = |x_1|, \quad B_0(\mathbf{x },\mathbf{y }) = \hbox {e}^{-5|\mathbf{x }-\mathbf{s }_1|^2} + \hbox {e}^{-5|\mathbf{x }-\mathbf{s }_2(\mathbf{y })|^2}, \end{aligned}$$

where $\mathbf{s }_1 = (-1,0)$. We consider the random variables to span

$$\begin{aligned} y_1\sim {{\mathcal {U}}}(0.8,1), \quad y_2 \sim {{\mathcal {U}}}(1,1.5), \quad y_3 \sim {{\mathcal {U}}}(0,0.5). \end{aligned}$$

The amplitude $B_1$ is chosen such that the pulses move toward each other, without producing any backward propagating waves. The first-order Gaussian beam method from Sect. 4 has been utilized to compute the solution $u^{\varepsilon }$. Figure 1 shows the absolute value of $u^{\varepsilon }$ with $\mathbf y =(0.8,1,0.5)$ and wavelength $\varepsilon = 1/40$ at various times. At time $T = 1$, the pulses reach the central circle indicating the support of the QoI test function with oscillations emerging in the overlap area.

Fig. 1

Time evolution of $|u^{\varepsilon }(T,\mathbf{x },\mathbf{y })|$ with wavelength $\varepsilon = 1/40$ and $\mathbf y =(0.8,1,0.5)$ in the example in Sect. 3.3. Panels show snapshots of $|u^\varepsilon |$ at the given time values T. The central circle indicates the support of the QoI test function

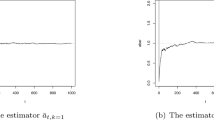
In Fig. 2, we plot the quantity of interest (13) and its first and second derivatives along the line $\mathbf{y }(r) = (0.8+0.2r,1+0.5r,0.5r), r\in [0,1]$ at time $T=1$. We note that the solution $u^{\varepsilon }$ oscillates with $\varepsilon$; however, this is not the case for the QoI and its derivatives. This suggests bounds of the type (3).

Fig. 2

QoI $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$ and its first and second derivatives along the line $\mathbf{y }(r) = (0.8+0.2r,1+0.5r,0.5r)$ where $r \in [0,1]$, for wavelengths $\varepsilon =[1/40,1/80,1/160]$. a ${{\mathcal {Q}}}^\varepsilon (\mathbf{y }(r))$. b $\frac{\hbox {d}}{\hbox {d}r}{{\mathcal {Q}}}^\varepsilon (\mathbf{y }(r))$. c $\frac{\hbox {d}^2}{\hbox {d}r^2}{{\mathcal {Q}}}^\varepsilon (\mathbf{y }(r))$

Fig. 3

Relative error $e(\eta )$ at time $T=1$ versus the number of collocation points $\eta$ (or the number of samples in the case of Monte Carlo sampling), for various wavelengths

Figure 3 shows the relative error of the approximate expected value of the Gaussian beam QoI

$$\begin{aligned} e(\eta ) := \frac{ \Bigl | {{\mathbb {E}}}[ {{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta _{\text {ref}}}] - {{\mathbb {E}}}[ {{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta }] \Bigr |}{\Bigl |{{\mathbb {E}}}[{{\mathcal {Q}}}^\varepsilon _{\text {GB}, \eta _{\text {ref}}}] \Bigr |}, \end{aligned}$$

versus the number of collocation points $\eta$ for various wavelengths. The Gaussian beam quantity is computed by (4) on the sparse Smolyak grid at time $T=1$. To obtain a reference solution, we use $\eta _{\text {ref}}$ = 30,465 collocation points. The figure also compares convergence of the Monte Carlo and the stochastic collocation methods. A simple linear regression through the Monte Carlo data points shows that the rate of convergence of Monte Carlo is approximately 0.46. We observe a fast spectral convergence of the stochastic collocation error due to the high stochastic regularity of the Gaussian beam QoI. Moreover, the decay rate does not deteriorate as $\varepsilon$ decreases.

4 Gaussian beams

In this section, we briefly describe the Gaussian beam approximation. We restrict the description to the points that are relevant for the analysis in Sect. 5. For a more detailed account with a general derivation for hyperbolic equations, dispersive wave equations and Helmholtz equation, we refer to [12,13,14, 16, 26, 28].

Individual Gaussian beams are asymptotic solutions to the wave equation that concentrate around a central ray in space-time. We denote the k-th-order Gaussian beam and the central ray starting at $\mathbf z \in K_0$ by $v_k(t,\mathbf y ;\mathbf z )$ and $\mathbf q (t,\mathbf y ;\mathbf z )$, respectively. The beam has the following form,

$$\begin{aligned} v_{k}(t,\mathbf x ,\mathbf y ;\mathbf z ) = A_{k}(t,\mathbf x -\mathbf q (t,\mathbf y ;\mathbf z ),\mathbf y ;\mathbf z )\hbox {e}^{i\varPhi _{k}(t,\mathbf x -\mathbf q (t,\mathbf y ;\mathbf z ),\mathbf y ;\mathbf z )/\varepsilon }, \end{aligned}$$

(6)

where

$$\begin{aligned} \varPhi _{k}(t,\mathbf x ,\mathbf y ;\mathbf z ) = \phi _{0}(t,\mathbf y ;\mathbf z ) + \mathbf x \cdot \mathbf p (t,\mathbf y ;\mathbf z ) + \frac{1}{2}\,\mathbf x \cdot M(t,\mathbf y ;\mathbf z ) \mathbf x + \sum _{|\varvec{\beta }|=3}^{k+1} \frac{1}{\varvec{\beta }!}\phi _{\varvec{\beta }}(t,\mathbf y ;\mathbf z ) \mathbf x ^{\varvec{\beta }}, \end{aligned}$$

is the k-th-order phase function and

$$\begin{aligned} A_{k}(t,\mathbf x ,\mathbf y ;\mathbf z )= \sum _{j=0}^{\lceil \frac{k}{2} \rceil -1} \varepsilon ^j \bar{a}_{j,k}(t,\mathbf x ,\mathbf y ;\mathbf z ), \end{aligned}$$

(7)

is the k-th-order amplitude function, with

$$\begin{aligned} \bar{a}_{j,k}(t,\mathbf x ,\mathbf y ;\mathbf z ) = \sum _{|\varvec{\beta }|=0}^{k-2j-1} \frac{1}{\varvec{\beta }!}a_{j,\varvec{\beta }}(t,\mathbf y ;\mathbf z ) \mathbf x ^{\varvec{\beta }} \ . \end{aligned}$$

(8)

Single beams are summed together to form the k-th-order Gaussian beam superposition solution $u_k(t,\mathbf x ,\mathbf y )$,

$$\begin{aligned} u_{k}(t,\mathbf x ,\mathbf y ) = \left( \frac{1}{2\pi \varepsilon }\right) ^\frac{n}{2} \int _{K_0} v_{k}(t,\mathbf x ,\mathbf y ;\mathbf z ) \varrho _\eta (\mathbf x -\mathbf q (t,\mathbf y ;\mathbf z )) \hbox {d}\mathbf z , \end{aligned}$$

(9)

where the integration in $\mathbf z$ is over the support of the initial data $K_0\subset \mathbb {R}^n$. Since the wave equation is linear, the superposition of beams is still an asymptotic solution. The function $\varrho _\eta \in C^\infty (\mathbb {R}^n)$ is a real-valued cutoff function with radius $0<\eta \le \infty$ satisfying,

$$\begin{aligned} \varrho _\eta (\mathbf x ) \ge 0 \quad \text{ and } \quad \varrho _\eta (\mathbf x )= \left\{ \begin{array}{ll}\begin{array}{l} 1 \quad \text{ for } |\mathbf x |\le \eta , \\ 0 \quad \text{ for } |\mathbf x |\ge 2\eta , \end{array} &{} \text{ for } 0<\eta <\infty , \\ \begin{array}{l} 1, \end{array}&\text{ for } \eta =\infty . \end{array}\right. \end{aligned}$$

(10)

As shown in (P4), if $\eta >0$ is sufficiently small, it is ensured that $\text {Im}\ \varPhi _k>0$ on the support of $\varrho _\eta$ and the Gaussian beam superposition is well behaved. For first-order beams, $k=1$, the cutoff function is not needed and we can take $\eta =\infty$.

Since the wave equation (1) is a second-order equation, two modes and two Gaussian beam superpositions are needed, one for forward and one for backward propagating waves. We denote the corresponding coefficients by ${}^+$ and ${}^-$, respectively, and write the solution

$$\begin{aligned} {\tilde{u}}_{k}(t,\mathbf x ,\mathbf y )&= \left( \frac{1}{2\pi \varepsilon }\right) ^\frac{n}{2} \int _{K_0} \left[ v^+_{k}(t,\mathbf x ,\mathbf y ;\mathbf z )\varrho _\eta (\mathbf x -\mathbf q ^+(t,\mathbf y ;\mathbf z ))\right. \\&\ \ \ \ \ \left. + v^-_{k}(t,\mathbf x ,\mathbf y ;\mathbf z )\varrho _\eta (\mathbf x -\mathbf q ^-(t,\mathbf y ;\mathbf z ))\right] \hbox {d}\mathbf z , \end{aligned}$$

where $v_k^{\pm }$ are built from the central rays $\mathbf q ^\pm (t,\mathbf y ;\mathbf z )$ and coefficients $\phi _{0}^\pm , \mathbf p ^\pm , M^\pm , \phi ^\pm _{\varvec{\beta }}, a^\pm _{j,\varvec{\beta }}$.

The central rays $\mathbf q ^\pm (t,\mathbf y ;\mathbf z )$ and all the coefficients of the two modes $\phi _{0}^\pm , \mathbf p ^\pm , M^\pm , \phi ^\pm _{\varvec{\beta }}$ and $a^\pm _{j,\varvec{\beta }}$ satisfy ODEs in t. The dependence on $\mathbf z$ is only via the initial data. The leading-order ODEs are

$$\begin{aligned} \partial _t \mathbf{q }^\pm&= \pm c(\mathbf{q }^\pm )\frac{\mathbf{p }^\pm }{|\mathbf{p }^\pm |},\end{aligned}$$

(11a)

$$\begin{aligned} \partial _t \mathbf{p }^\pm&= \mp \nabla c(\mathbf q ^\pm ) |\mathbf{p }^\pm |,\end{aligned}$$

(11b)

$$\begin{aligned} \partial _t \phi ^\pm _0&= 0,\end{aligned}$$

(11c)

$$\begin{aligned} \partial _t M^\pm&= \mp (E + B^T M^\pm + M^\pm B + M^\pm C M^\pm ), \end{aligned}$$

(11d)

$$\begin{aligned} \partial _t a^\pm _0&= \pm \frac{1}{2 |\mathbf{p }^\pm |} \left( \mathbf{p }^\pm \cdot \nabla c(\mathbf{q }^\pm ) +\frac{c(\mathbf{q }^\pm )\, \mathbf{p }^\pm \cdot M \mathbf{p }^\pm }{|\mathbf{p }^\pm |^2} -c(\mathbf{q }^\pm ) \, \text {Tr}(M^\pm ) \right) a^\pm _0, \end{aligned}$$

(11e)

with

$$\begin{aligned} E= |\mathbf{p }^\pm | D^2 c(\mathbf{q }^\pm ), \quad B = \frac{\mathbf{p }^\pm \otimes \nabla c({\mathbf{q }}^\pm )}{|\mathbf{p }^\pm |}, \quad C = \frac{c(\mathbf{q }^\pm )}{|\mathbf{p }^\pm |}\mathrm{Id}_{n\times n} - \frac{c(\mathbf{q }^\pm )}{|\mathbf{p }^\pm |^3} \mathbf{p }^\pm \otimes \mathbf{p }^\pm . \end{aligned}$$

There are similar linear ODEs for higher-order coefficients $\phi ^\pm _{\varvec{\beta }}$ and $a^\pm _{j,\varvec{\beta }}$, see, e.g., [26, 28].

Each Gaussian beam $v^\pm _{k}(t,\mathbf x ,\mathbf y ;\mathbf z )$ requires initial values for the central ray and all of the amplitude and phase Taylor coefficients. The appropriate choice of these initial values will make ${\tilde{u}}_k(0,\mathbf x ,\mathbf y )$ asymptotically converge to the initial conditions in (1). As shown in [16], initial data for the central ray and phase coefficients should be chosen as follows:

$$\begin{aligned} \mathbf q ^\pm (0,\mathbf y ;\mathbf z )&= \mathbf z , \end{aligned}$$

(12a)

$$\begin{aligned} \mathbf p ^\pm (0,\mathbf y ;\mathbf z )&= \nabla \varphi _0(\mathbf z ,\mathbf y ), \end{aligned}$$

(12b)

$$\begin{aligned} \phi ^\pm _0(0,\mathbf y ;\mathbf z )&= \varphi _0(\mathbf z ,\mathbf y ), \end{aligned}$$

(12c)

$$\begin{aligned} M^\pm (0,\mathbf y ;\mathbf z )&= D^2\varphi _0(\mathbf z ,\mathbf y ) + i\ \mathrm{Id}_{n\times n},\end{aligned}$$

(12d)

$$\begin{aligned} \phi ^\pm _{\varvec{\beta }}(0,\mathbf y ;\mathbf z )&= \partial _\mathbf{x }^{\varvec{\beta }}\varphi _0(\mathbf z ,\mathbf y ), \quad |\varvec{\beta }|= 3,\ldots ,k+1 \ . \end{aligned}$$

(12e)

The initial data for the amplitude coefficients are more complicated, and we refer the reader to [16] for more detailed description.

In the remainder of the paper, we will restrict ourselves to only one of the two modes and drop the ± subscript. This means that we only consider high-frequency wave solutions that propagate in one direction from the initial source. Note that the interaction between the two modes could potentially introduce more oscillations in $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$. An analysis of this will be reported elsewhere.

4.1 Gaussian beam quantity of interest

Instead of the full quantity of interest defined in (2), we here consider the corresponding quantity of interest computed based on the Gaussian beam approximation with one mode,

$$\begin{aligned} {{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon (\mathbf{y }) = \int _{{{\mathbb {R}}}^n} |u_{k}(T, \mathbf{x }, \mathbf{y })|^2 \, \psi (\mathbf{x }) \, \hbox {d}\mathbf{x }, \end{aligned}$$

(13)

where $u_{\mathrm{k}}$ is given by (9) and $v_k$ is either $v_k^+$ or $v_k^-$, with corresponding $\mathbf q ^+$ or $\mathbf q ^-$ respectively. Since $u_k$ is a good approximation of $u^\varepsilon$, the QoI $\mathcal Q^\varepsilon _{GB}$ in (13) is a good approximation to $\mathcal Q^\varepsilon$, see Remark 1.

We get

$$\begin{aligned} {{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon (\mathbf{y })&= \left( \frac{1}{2\pi \varepsilon }\right) ^n \int _{\mathbb {R}^n}\int _{K_0\times K_0} v_{k}(T,\mathbf x ,\mathbf y ; \mathbf z )\varrho _\eta (\mathbf x -\mathbf q (T,\mathbf y ;\mathbf z ))\nonumber \\&\quad \times v^*_{k}(T,\mathbf x ,\mathbf y ; \mathbf z ')\varrho _\eta (\mathbf x -\mathbf q (T,\mathbf y ;\mathbf z ')) \, \psi (\mathbf{x })\hbox {d}\mathbf{z } \, \hbox {d}\mathbf{z }' \hbox {d}\mathbf{x }\nonumber \\&=: \left( \frac{1}{2\pi \varepsilon }\right) ^n \int _{K_0\times K_0} I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }') \, \hbox {d}\mathbf{z } \, \hbox {d}\mathbf{z }'. \end{aligned}$$

(14)

Since $(a \hbox {e}^{i \phi })^* = a^* \hbox {e}^{- i \phi ^*}$, we can write using (6),

$$\begin{aligned}&I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }')\\&\quad = \int _{\mathbb {R}^n} \sum _{j,m = 0}^{\lceil k/2\rceil -1} \sum _{|\varvec{\alpha }|=0}^{k-2j-1} \sum _{|\varvec{\beta }|=0}^{k-2m-1} \varepsilon ^{j+m} g_{j,m,\varvec{\alpha },\varvec{\beta }}(T,\mathbf{x },\mathbf{y };\mathbf{z },\mathbf{z }')\, (\mathbf{x } - \mathbf{q }(T,\mathbf{y };\mathbf{z }))^{\varvec{\alpha }}\nonumber \\&\quad \quad \times \, (\mathbf{x } - \mathbf{q }(T,\mathbf{y };\mathbf{z }'))^{\varvec{\beta }} \, \hbox {e}^{i [ \varPhi _k(T, \mathbf{x } - \mathbf{q }(T,\mathbf y ;\mathbf{z }), \mathbf y ;\mathbf{z }) - \varPhi _k^*(T, \mathbf{x } - \mathbf{q }(T,\mathbf y ;\mathbf{z }'), \mathbf y ;\mathbf{z }') ] / \varepsilon } \, \hbox {d}\mathbf x , \end{aligned}$$

where $g_{j,m,\varvec{\alpha },\varvec{\beta }}$ is given by

$$\begin{aligned} g_{j,m,\varvec{\alpha },\varvec{\beta }} = \frac{1}{\varvec{\alpha }!\,\varvec{\beta }!} \, a_{j,\varvec{\alpha }}(T,\mathbf y ;\mathbf z ) \, a^*_{m,\varvec{\beta }}(T,\mathbf y ;\mathbf z ') \, \varrho _\eta (\mathbf x -\mathbf q (T,\mathbf y ;\mathbf z )) \, \varrho _\eta (\mathbf x - \mathbf q (T,\mathbf y ;\mathbf z '))\,\psi (\mathbf x ). \end{aligned}$$

To simplify the expressions, we introduce the symmetrizing variables

$$\begin{aligned} {\bar{\mathbf{q }}}= & {} {\bar{\mathbf{q }}}(T,\mathbf{y };\mathbf{z }, \mathbf{z }') = \frac{\mathbf{q }(T,\mathbf{y };\mathbf{z }) + \mathbf{q }(T,\mathbf{y };\mathbf{z }')}{2},\nonumber \\ \varDelta \mathbf{q }= & {} \varDelta \mathbf{q }(T,\mathbf{y };\mathbf{z }, \mathbf{z }') = \frac{\mathbf{q }(T,\mathbf{y };\mathbf{z }) - \mathbf{q }(T,\mathbf{y };\mathbf{z }')}{2}, \end{aligned}$$

(15)

and write

$$\begin{aligned}&I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }') \nonumber \\&\quad =\int _{\mathbb {R}^n} \sum _{j,m = 0}^{\lceil k/2\rceil -1}\sum _{|\varvec{\alpha }|=0}^{k-2j-1} \sum _{|\varvec{\beta }|=0}^{k-2m-1} \varepsilon ^{j+m} {\bar{g}}_{j,m,\varvec{\alpha },\varvec{\beta }} \, (\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} (\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }} \hbox {e}^{i \varPsi / \varepsilon } \, \hbox {d}\mathbf x , \end{aligned}$$

(16)

where

$$\begin{aligned} \varPsi (T, \mathbf{x }, \mathbf y ;\mathbf{z },\mathbf{z }') = \varPhi _k(T, \mathbf{x } - \varDelta \mathbf{q }, \mathbf y ;\mathbf{z }) - \varPhi _k^*(T, \mathbf{x } + \varDelta \mathbf{q }, \mathbf y ;\mathbf{z }') \end{aligned}$$

(17)

is the symmetrized phase and

$$\begin{aligned}&{\bar{g}}_{j,m,\varvec{\alpha },\varvec{\beta }}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \nonumber \\&\quad = \frac{1}{\varvec{\alpha }!\varvec{\beta }!} \, a_{j,\varvec{\alpha }}(T,\mathbf y ;\mathbf z ) \, a^*_{m,\varvec{\beta }}(T,\mathbf y ;\mathbf z ') \, \, \varrho _\eta (\mathbf x -\varDelta \mathbf q ) \, \varrho _\eta (\mathbf x + \varDelta \mathbf q )\,\psi (\mathbf x + \bar{\mathbf{q }}). \end{aligned}$$

(18)

Remark 1

In [16], it was proved that under the given smoothness conditions and for a small enough cutoff radius $\eta$,

$$\begin{aligned} \sup _{0\le t\le T} ||u^{\varepsilon }(t,\cdot ) - u_{k}(t,\cdot )||_{H^1} \le C(T) \varepsilon ^{k/2-1}, \end{aligned}$$

if initial data are sufficiently well approximated by the beams. This immediately gives the same estimate for ${{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon$ when $\psi \ge 0$. Indeed, for a fixed ${\mathbf{y }}$,

$$\begin{aligned}&|{{\mathcal {Q}}}^\varepsilon ({\mathbf{y }})-{{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon ({\mathbf{y }})| = \left| \int |u^{\varepsilon }(T,{\mathbf{x }},{\mathbf{y }})|^2-|u_{k}(T,{\mathbf{x }},{\mathbf{y }})|^2\psi ({\mathbf{x }})\hbox {d}{\mathbf{x }}\right| \\&\quad \le \int |u^{\varepsilon }(T,{\mathbf{x }},{\mathbf{y }})-u_k(T,{\mathbf{x }},{\mathbf{y }})|\cdot \left( |u^{\varepsilon }(T,{\mathbf{x }},{\mathbf{y }})|+|u_k(T,{\mathbf{x }},{\mathbf{y }})|\right) \psi ({\mathbf{x }})\hbox {d}{\mathbf{x }}\\&\quad \le ||u^{\varepsilon }(T,\,\cdot \,,{\mathbf{y }}) - u_{k}(T,\,\cdot \,,{\mathbf{y }})||_{L^2}\left( \sqrt{{{\mathcal {Q}}}^\varepsilon ({\mathbf{y }})} + \sqrt{{{\mathcal {Q}}}^\varepsilon _{\mathrm{GB}}({\mathbf{y }})}\right) \\&\quad \le C(T,{\mathbf{y }})\,\varepsilon ^{k/2-1} \left( 2\sqrt{1+{{\mathcal {Q}}}^\varepsilon _{\mathrm{GB}}({\mathbf{y }})} + |{{\mathcal {Q}}}^\varepsilon ({\mathbf{y }})-{{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon ({\mathbf{y }})| \right) . \end{aligned}$$

For small enough $\varepsilon$ and $k\ge 3$, we can move the second term over to the left-hand side and get the estimate,

$$\begin{aligned} |{{\mathcal {Q}}}^\varepsilon ({\mathbf{y }})-{{\mathcal {Q}}}_{\mathrm{GB}}^\varepsilon ({\mathbf{y }})| \le \tilde{C}(T,{\mathbf{y }}) \varepsilon ^{k/2-1} \sqrt{1+{{\mathcal {Q}}}^\varepsilon _{\mathrm{GB}}({\mathbf{y }})}. \end{aligned}$$

Below we show that ${{\mathcal {Q}}}^\varepsilon _{\mathrm{GB}}$ is bounded independently of $\varepsilon$, and the estimate therefore implies that ${{\mathcal {Q}}}^\varepsilon _{\mathrm{GB}}({\mathbf{y }})$ is close to ${{\mathcal {Q}}}^\varepsilon ({\mathbf{y }})$ for small $\varepsilon$, at least if we use beams of third order or higher. We do not believe this estimate is sharp, however. In particular, in computations we see a small difference already with first-order beams.

4.2 Gaussian beam phase properties

In this section, we present some consequences of assumptions (A1)–(A4) for the Gaussian beam coefficient functions, the whole phase $\varPhi _k$ and the symmetrized phase $\varPsi$. The properties are of great importance in the subsequent estimates in Sect. 5. They also show the significance of the cutoff function introduced in Sect. 4 and indicate how the width $\eta$ should be chosen. Following (P4), we make the definition:

Definition 1

The cutoff width $\eta$ used for the Gaussian beam approximation is called admissible for $\varPhi _k$ if it is small enough in the sense of property (P4) in Proposition 1.

Throughout this paper, we will consider the cutoff function $\varrho _\eta$ in the Gaussian beam approximation (9) to be chosen such that $\eta$ is admissible in the sense of Definition 1.

Because of the cutoff function, the terms $g_{j,m,{\varvec{\alpha }},{\varvec{\beta }}}$ in (18) are zero unless $|\mathbf x -\varDelta \mathbf q |$ and $|\mathbf x +\varDelta \mathbf q |$ are both small enough. We introduce the subsets $\varOmega _\mu \subset \mathbb {R}^n$, parameterized by $\mu$, to describe this

$$\begin{aligned} \varOmega _\mu =\varOmega _\mu (t,\mathbf y ;\mathbf z , \mathbf z ') =\left\{ \mathbf x \in \mathbb {R}^n\ :\ |\mathbf x + \varDelta \mathbf q |\le 2\mu \text { and } |\mathbf x - \varDelta \mathbf q |\le 2\mu \right\} . \end{aligned}$$

We note that since $|\mathbf x |^2\le |\mathbf x |^2+|\varDelta \mathbf q |^2=|\mathbf x + \varDelta \mathbf q |^2/2+|\mathbf x - \varDelta \mathbf q |^2/2$, we have the inclusion

$$\begin{aligned} \varOmega _{\mu }\subset B_{2\mu },\quad B_{\mu } := \left\{ \mathbf x \in \mathbb {R}^n\ :\ |\mathbf x |\le \mu \right\} . \end{aligned}$$

(19)

The components of the Gaussian beam approximation then have the following properties.

Proposition 1

Under assumptions (A1)–(A4),

• (P1) $\phi _0, \mathbf p , \mathbf q , M, \phi _{\varvec{\beta }}, a_{j,\varvec{\beta }}\in C^\infty (\mathbb {R}\times \varGamma \times \mathbb {R}^n)$ and

  $$\begin{aligned} \mathrm{supp}\,a_{j,\varvec{\beta }}(t,\mathbf y ;\,\cdot \,)\subset K_0,\quad \forall t\in \mathbb {R},\ \mathbf y \in \varGamma . \end{aligned}$$

  (20)

• (P2) $\varPhi _k\in C^\infty (\mathbb {R}\times \mathbb {R}^n\times \varGamma \times \mathbb {R}^n)$,

• (P3) For each $T>0$, there is a constant $C>0$ such that

  $$\begin{aligned} |\mathbf p (t,\mathbf y ;\mathbf z )-\mathbf p (t,\mathbf y ;\mathbf z ')|+ |\mathbf q (t,\mathbf y ;\mathbf z )-\mathbf q (t,\mathbf y ;\mathbf z ')| \ge C|\mathbf{z }-\mathbf{z }'|\ , \end{aligned}$$

  for all $t\in [0,T], \mathbf{z },\mathbf{z }'\in K_0$ and $\mathbf{y }\in \varGamma$.

• (P4) For each $T>0$ and beam order k, there is a Gaussian beam cutoff width $\eta >0$ and constant $\delta >0$, such that for all $\mathbf x \in B_{2\eta }$,

  $$\begin{aligned} \text {Im}\, \varPhi _k(t,\mathbf x ,\mathbf y ;\mathbf z )\ge \frac{1}{2}\delta |\mathbf x |^2\ ,\quad \forall t\in [0,T],\ \mathbf y \in \varGamma , \ \mathbf z \in K_0, \end{aligned}$$

  (21)

  Moreover, for the symmetrized phase, when $\mathbf x \in \varOmega _{\eta }$,

  $$\begin{aligned} \text {Im}\,\varPsi (t,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \ge \frac{1}{2}\delta \left[ |\mathbf x + \varDelta \mathbf q |^2 + |\mathbf x -\varDelta \mathbf q |^2\right] = \delta |\mathbf x |^2 + \delta |\varDelta \mathbf q |^2, \end{aligned}$$

  (22)

  for all $t\in [0,T], \mathbf y \in \varGamma$ and $\mathbf z ,\mathbf z '\in K_0$. When $k=1$ the width $\eta$ can be any positive value and (21, 22) hold for all $\mathbf x \in \mathbb {R}^n$.

• (P5) The following statement holds for all $t \in \mathbb {R}, \mathbf y \in \varGamma$ and $\mathbf z \in \mathbb {R}^n$,

  $$\begin{aligned} \nabla _\mathbf{z } \phi _0(\mathbf y ;\mathbf z ) = D_\mathbf{z }\mathbf q (t,\mathbf y ;\mathbf z )^T\mathbf p (t,\mathbf y ;\mathbf z ). \end{aligned}$$

• (P6) Let $\mathbf z ,\mathbf z '\in K_0$ be such that $|\mathbf q (t,\mathbf y ;\mathbf z ) - \mathbf q (t,\mathbf y ;\mathbf z ')| \le \theta |\mathbf z -\mathbf z '|$ for fixed $t\in [0,T]$ and $\mathbf y \in \varGamma$. Then, for small enough $\theta$ and $\mu$, there exists a constant $C(\theta ,\mu )>0$ such that

  $$\begin{aligned} \inf _\mathbf{x \in \varOmega _{\mu }} |\nabla _\mathbf{x } \varPsi (t,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ')|\ge C(\theta ,\mu ) |\mathbf z -\mathbf z '|. \end{aligned}$$

  The constant is independent of $\mathbf z , \mathbf z ', t$ and $\mathbf y$.

The proof of these properties essentially follows the same steps as in the corresponding lemmas in [15, 16]. The details are provided in [17].

5 Stochastic regularity

In this section, we prove the main result of the paper, namely that the derivative $\partial _{\mathbf{y }}^{\varvec{\varvec{\sigma }}} {\mathcal {Q}}_{\mathrm{GB}}^\varepsilon$ is uniformly bounded in $\mathbf{y }$ and $\varepsilon$. More precisely, we show the following theorem.

Theorem 1

Under assumptions (A1)–(A6), for the Gaussian beam quantity of interest (13) where the cutoff parameter $\eta$ is admissible in the sense of Definition 1, there are constants $C_\sigma$, independent of $\varepsilon$, such that

$$\begin{aligned} \sup _{\mathbf{y }\in \varGamma } \left| \frac{\partial ^{\varvec{\varvec{\sigma }}} {\mathcal {Q}}_{\mathrm{GB}}^\varepsilon (\mathbf{y })}{\partial \mathbf{y }^{\varvec{\varvec{\sigma }}}}\right| \le C_{\varvec{\varvec{\sigma }}}, \quad \forall \, {{\varvec{\varvec{\sigma }}}} \in {\mathbb {N}}_0^N. \end{aligned}$$

In Sect. 5.1, we prove various prerequisite lemmas needed for the proof of Theorem 1 and introduce notation used in the rest of the paper. Section 5.2 is devoted to rewriting the QoI and its derivatives. In Sect. 5.3, several important estimates are presented. In Sect. 5.4, the actual proof of Theorem 1 is carried out.

5.1 Preliminaries

Let $\mathcal U_\eta$ denote the space

$$\begin{aligned} \mathcal U_\eta = \{f\in C^{\infty }(\mathbb {R}\times \mathbb {R}^n \times \varGamma \times \mathbb {R}^n \times \mathbb {R}^n) :\, \text {supp}\, f(t,\,\cdot \,,\,\mathbf y ;\mathbf z ,\mathbf z ') \subset \varOmega _{\eta }(t,\mathbf y ;\mathbf z ,\mathbf z ')\}. \end{aligned}$$

We also use the shorthand

$$\begin{aligned} \mathcal V = C^{\infty }(\mathbb {R}\times \varGamma \times \mathbb {R}^n\times \mathbb {R}^n), \end{aligned}$$

and note that if $u,v\in \mathcal U_\eta$ and $w \in \mathcal V$, then both $uv \in \mathcal U_\eta$ and $uw \in \mathcal U_\eta$. Consequently, for ${\bar{g}}_{j,m,\varvec{\alpha },\varvec{\beta }}$ in (18), it holds that ${\bar{g}}_{j,m,\varvec{\alpha },\varvec{\beta }}\in \mathcal U_\eta$ due to (A6), (10) and (P1).

We first note that the Taylor expansion remainder of a smooth function belongs to $\mathcal V$.

Lemma 1

Let f be a scalar function such that $f\in C^\infty (\mathbb {R}\times \varGamma \times \mathbb {R}^n)$, then its Taylor expansion to k-th order reads

$$\begin{aligned} f(t,\mathbf y ; \mathbf z ') = \sum _{|\varvec{\alpha }| \le k}\frac{\partial ^{\varvec{\alpha }}_\mathbf{z } f(t,\mathbf y ;\mathbf z )}{\varvec{\alpha }!}(\mathbf z -\mathbf z ')^{\varvec{\alpha }} + \sum _{|\varvec{\beta }|=k+1}R_{\varvec{\beta }}(t,\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf z -\mathbf z ')^{\varvec{\beta }}, \end{aligned}$$

(23)

where $R_{\varvec{\beta }} \in \mathcal V$. Similarly, for a vector-valued function $\mathbf g \in C^\infty (\mathbb {R}\times \varGamma \times \mathbb {R}^n)$, there exists a matrix valued function $G\in \mathcal V$ so that

$$\begin{aligned} \mathbf g (t,\mathbf y ;\mathbf z ')=\mathbf g (t,\mathbf y ;\mathbf z ) + G(t,\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf z -\mathbf z '). \end{aligned}$$

(24)

Proof

This follows from Taylor’s theorem by considering the integral form of the remainder terms. $\square$

We will often use the following lemma.

Lemma 2

For a matrix $A \in \mathcal V$ and $\mathbf u \in \mathbb {R}^n$, there exists function $c_{\varvec{\beta }} \in \mathcal V$ such that

$$\begin{aligned} \left( A(t,\mathbf y ;\mathbf z ,\mathbf z ')\,\mathbf u \right) ^{\varvec{\alpha }} = \sum _{|\varvec{\beta }|=|\varvec{\alpha }|}c_{\varvec{\beta },\varvec{\alpha }}(t,\mathbf y ;\mathbf z ,\mathbf z ')\mathbf u ^{\varvec{\beta }}. \end{aligned}$$

(25)

Proof

We recall that for any vectors $\mathbf a , \mathbf a _j, j = 1,\ldots n$, scalar u and multi-indices $\varvec{\alpha }, \varvec{\gamma }_j$,

$$\begin{aligned} (\mathbf a _1 + \cdots +\mathbf a _n)^{\varvec{\alpha }} = \sum _{\varvec{\gamma }_1+\cdots +\varvec{\gamma }_n=\varvec{\alpha }}\frac{\varvec{\alpha }!}{\varvec{\gamma }_1! \ldots \varvec{\gamma }_n!}\mathbf a _1^{\varvec{\gamma }_1}\ldots \mathbf a _n^{\varvec{\gamma }_n}, \quad (u \mathbf a )^{\varvec{\alpha }} = u^{|\varvec{\alpha }|}\mathbf a ^{\varvec{\alpha }}. \end{aligned}$$

Letting $\mathbf a _j$ be the column vectors of A and $u_j$ the elements of $\mathbf u$, we then have

$$\begin{aligned} (A\mathbf u )^{\varvec{\alpha }}&= (u_1 \mathbf a _1 + u_2 \mathbf a _2 +\cdots +u_n \mathbf a _n)^{\varvec{\alpha }}\\&= \sum _{\varvec{\gamma }_1+\cdots +\varvec{\gamma }_n=\varvec{\alpha }} \frac{\varvec{\alpha }!}{\varvec{\gamma }_1!\ldots \varvec{\gamma }_n!}(u_1 \mathbf a _1)^{\varvec{\gamma }_1}\ldots (u_n \mathbf a _n)^{\varvec{\gamma }_n} \\&=\sum _{\varvec{\gamma }_1+\cdots +\varvec{\gamma }_n=\varvec{\alpha }}\frac{\varvec{\alpha }!}{\varvec{\gamma }_1!\ldots \varvec{\gamma }_n!}\mathbf a _1^{\varvec{\gamma }_1}\ldots \mathbf a _n^{\varvec{\gamma }_n} \,u_1^{|\varvec{\gamma }_1|}\ldots u_n^{|\varvec{\gamma }_n|}. \end{aligned}$$

Hence, $(A\mathbf u )^{\varvec{\alpha }}$ will be of the form

$$\begin{aligned} \left( A\mathbf u \right) ^{\varvec{\alpha }} = \sum _{|\varvec{\beta }|=|\varvec{\alpha }|}\,c_{\varvec{\beta },\varvec{\alpha }} \mathbf u ^{\varvec{\beta }}, \end{aligned}$$

where $c_{\varvec{\beta },\varvec{\alpha }}\in \mathcal V$. $\square$

5.2 Derivatives of the quantity of interest

By (14), differentiating $\mathcal {Q}^\varepsilon _{\mathrm{GB}}$ with respect to $\mathbf{y }$ gives

$$\begin{aligned} \partial ^{\varvec{\sigma }}_{\mathbf{y }} { \mathcal {Q}^\varepsilon _{\mathrm{GB}}}(\mathbf{y })=\left( \frac{1}{2\pi \varepsilon }\right) ^n \int _{K_0\times K_0} \partial ^{\varvec{\sigma }}_{\mathbf{y }} I^\varepsilon (T,\mathbf{y };\mathbf{z },\mathbf{z }') \,\hbox {d}\mathbf{z } \hbox {d}\mathbf{z }'. \end{aligned}$$

(26)

In this section, we first rewrite the integral $I^\varepsilon$ (Proposition 2) employing Lemma 3, and phase $\varPsi$ (Lemma 4). The form of $\partial ^{\varvec{\sigma }}_\mathbf{y }I^\varepsilon$ then follows from Proposition 3.

Lemma 3

There exists $f_{\varvec{\mu },\varvec{\nu },\varvec{\alpha },\varvec{\beta }}\in \mathcal V$ such that

$$\begin{aligned} (\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} \, (\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }} = \sum _{|\varvec{\mu }+ \varvec{\nu }| = |\varvec{\alpha }+ \varvec{\beta }|} f_{\varvec{\mu },\varvec{\nu },\varvec{\alpha },\varvec{\beta }}(t,\mathbf y ; \mathbf z , \mathbf z ') (\mathbf z -\mathbf z ')^{\varvec{\mu }} \mathbf x ^{\varvec{\nu }}. \end{aligned}$$

(27)

Proof

Let us recall the definition of $\varDelta \mathbf q$ in (15). From (P1), $\mathbf q \in C^\infty (\mathbb {R}^n \times \varGamma \times \mathbb {R}^n)$ and hence according to (24), we conclude that

$$\begin{aligned} \varDelta \mathbf q (t,\mathbf y ;\mathbf z ,\mathbf z ') = Q(t,\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf z -\mathbf z '), \end{aligned}$$

with $Q\in \mathcal V$. From (25), we then have

$$\begin{aligned} \varDelta \mathbf q ^{\varvec{\alpha }} = \left( Q(t,\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf z -\mathbf z ')\right) ^{\varvec{\alpha }} = \sum _{|\varvec{\varvec{\sigma }}|=|\varvec{\alpha }|}f_{{\varvec{\sigma },\varvec{\alpha }}} (t,\mathbf y ; \mathbf z , \mathbf z ') (\mathbf z -\mathbf z ')^{\varvec{\varvec{\sigma }}}, \end{aligned}$$

(28)

for some $f_{\varvec{\varvec{\sigma }},\varvec{\alpha }} \in \mathcal V$. By the generalized binomial theorem and (28), $(\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }}$ reads

$$\begin{aligned} (\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} = \sum _{\varvec{\beta }+\varvec{\gamma }= \varvec{\alpha }} {\varvec{\alpha }\atopwithdelims ()\varvec{\gamma }} \, (-1)^{\varvec{\beta }}\,\varDelta \mathbf q ^{\varvec{\beta }} \mathbf x ^{\varvec{\gamma }} = \sum _{|\varvec{\varvec{\sigma }} + \varvec{\gamma }| = |\varvec{\alpha }|} h_{{\varvec{\sigma }},\varvec{\gamma },\varvec{\alpha }}(t,\mathbf y ;\mathbf z ,\mathbf z ')\,(\mathbf z -\mathbf z ')^{\varvec{\varvec{\sigma }}} \mathbf x ^{\varvec{\gamma }}, \end{aligned}$$

where $h_{\varvec{\varvec{\sigma }},\varvec{\gamma },\varvec{\alpha }}\in \mathcal V$.

The terms $(\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }}$ can be expanded in a similar manner:

$$\begin{aligned} (\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }} = \sum _{|\varvec{\delta }+ \varvec{\omega }| = |\varvec{\beta }|} {\widetilde{h}}_{\varvec{\delta },\varvec{\omega },\varvec{\beta }}(t,\mathbf y ;\mathbf z ,\mathbf z ')\,(\mathbf z -\mathbf z ')^{\varvec{\delta }} \mathbf x ^{\varvec{\omega }}, \end{aligned}$$

for some ${\widetilde{h}}_{\varvec{\delta },\varvec{\omega },\varvec{\alpha }}\in \mathcal V$. Then

$$\begin{aligned} (\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} \, (\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }}&= \sum _{|\varvec{\varvec{\sigma }} + \varvec{\gamma }| = |\varvec{\alpha }|} \sum _{|\varvec{\delta }+ \varvec{\omega }| = |\varvec{\beta }|} h_{{\varvec{\sigma }},\varvec{\gamma },\varvec{\alpha }} {\widetilde{h}}_{\varvec{\delta },\varvec{\omega },\varvec{\beta }}\,(\mathbf z -\mathbf z ')^{\varvec{\sigma }+\varvec{\delta }} \mathbf x ^{\varvec{\gamma }+\varvec{\omega }}\\&= \sum _{|\varvec{\mu }+ \varvec{\nu }| = |\varvec{\alpha }+ \varvec{\beta }|} f_{\varvec{\mu },\varvec{\nu },\varvec{\alpha },\varvec{\beta }}(\mathbf z -\mathbf z ')^{\varvec{\mu }} \mathbf x ^{\varvec{\nu }}, \end{aligned}$$

where $f_{\varvec{\mu },\varvec{\nu },\varvec{\alpha },\varvec{\beta }}\in \mathcal V$. This concludes the proof. $\square$

Utilizing the results of Lemma 3, we are ready to reformulate $I^\varepsilon$ in (16) in terms of $\mathbf x$ and $\mathbf z -\mathbf z '$.

Proposition 2

The quantity $I^\varepsilon$ in (16) can be rewritten as

$$\begin{aligned}&I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }') \nonumber \\&\quad = \sum _{j = 0}^{2\lceil k/2\rceil -2}\sum _{|\varvec{\mu }+\varvec{\nu }|=0}^{2(k-j-1)} \, \varepsilon ^{j} (\mathbf z -\mathbf z ')^{\varvec{\mu }} \int _{\mathbb {R}^n} \mathbf x ^{\varvec{\nu }}\, g_{j,\varvec{\mu },\varvec{\nu }}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \, \hbox {e}^{i \varPsi (T, \mathbf x , \mathbf y ;\mathbf z ,\mathbf z ') / \varepsilon } \, \hbox {d}\mathbf x , \end{aligned}$$

(29)

with $g_{j,\varvec{\mu },\varvec{\nu }}\in \mathcal U_\eta$.

Proof

We start by noting that the expression for $I^\varepsilon$ in (16) can be simplified to

$$\begin{aligned} I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }') = \sum _{j = 0}^{2\lceil k/2\rceil -2}\sum _{|\varvec{\alpha }+\varvec{\beta }|=0}^{2(k-j-1)} \varepsilon ^{j} \int _{\mathbb {R}^n} {\bar{g}}_{j,\varvec{\alpha },\varvec{\beta }} \, (\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} (\mathbf x + \varDelta \mathbf q )^{\varvec{\beta }} \hbox {e}^{i \varPsi / \varepsilon } \, \hbox {d}\mathbf x , \end{aligned}$$

where $\bar{g}_{j,\varvec{\alpha },\varvec{\beta }}\in \mathcal U_\eta$ are either sums of $\bar{g}_{j,m,\varvec{\alpha },\varvec{\beta }}\in \mathcal U_\eta$ in (18) or identically zero. Recalling Lemma 3, this can be reformulated as

$$\begin{aligned} I^\varepsilon (T,\mathbf{y };\mathbf{z }, \mathbf{z }')&= \sum _{j = 0}^{2\lceil k/2\rceil -2}\sum _{|\varvec{\alpha }+\varvec{\beta }|=0}^{2(k-j-1)} \varepsilon ^{j} \int _{\mathbb {R}^n} \sum _{|\varvec{\mu }+ \varvec{\nu }| = |\varvec{\alpha }+ \varvec{\beta }|} {\bar{g}}_{j,\varvec{\alpha },\varvec{\beta }} f_{\varvec{\mu },\varvec{\nu },\varvec{\alpha },\varvec{\beta }} (\mathbf z -\mathbf z ')^{\varvec{\mu }} \mathbf x ^{\varvec{\nu }}\, \hbox {e}^{i \varPsi / \varepsilon } \, \hbox {d}\mathbf x \\&=: \sum _{j = 0}^{2\lceil k/2\rceil -2}\sum _{|\varvec{\mu }+\varvec{\nu }|=0}^{2(k-j-1)} \varepsilon ^{j} (\mathbf z -\mathbf z ')^{\varvec{\mu }} \int _{\mathbb {R}^n} g_{j,\varvec{\mu },\varvec{\nu }} \mathbf x ^{\varvec{\nu }}\, \hbox {e}^{i \varPsi / \varepsilon } \, \hbox {d}\mathbf x , \end{aligned}$$

where $g_{j,\varvec{\mu },\varvec{\nu }}\in \mathcal U_\eta$.

This concludes the proof. $\square$

Similarly as for $I^\varepsilon$, let us first express the Gaussian beam phase $\varPsi$ in terms of $\mathbf x$ and $\mathbf z -\mathbf z '$.

Lemma 4

For the k-th-order Gaussian beam phase $\varPsi$, there exist $g_{\varvec{\alpha },\varvec{\beta }} \in \mathcal V$ such that

$$\begin{aligned} \varPsi (T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') = \sum _{|\varvec{\alpha }+\varvec{\beta }|=2}^{k+1} g_{\varvec{\alpha },\varvec{\beta }}(T,\mathbf y ;\mathbf z ,\mathbf z ') \, (\mathbf z -\mathbf z ')^{\varvec{\alpha }} \, \mathbf x ^{\varvec{\beta }}. \end{aligned}$$

(30)

Proof

Recall the definition of $\varPsi$ in (17). For k-th-order beams, we write (dropping T)

$$\begin{aligned} \varPsi (\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ')&= F(\mathbf y ;\mathbf z ,\mathbf z ')+\mathbf x ^T[\mathbf p (\mathbf y ;\mathbf z )-\mathbf p (\mathbf y ;\mathbf z ')] \nonumber \\&\quad + \frac{1}{2}(\mathbf x -\varDelta \mathbf q )^TM(\mathbf y ;\mathbf z )(\mathbf x -\varDelta \mathbf q )-\frac{1}{2}(\mathbf x +\varDelta \mathbf q )^T\,{M^*(\mathbf y ;\mathbf z ')}(\mathbf x +\varDelta \mathbf q ) \nonumber \\&\quad + \sum _{|\varvec{\gamma }|=3}^{k+1}\frac{1}{\varvec{\gamma }!}\phi _{\varvec{\gamma }}(\mathbf z )(\mathbf x -\varDelta \mathbf q )^{\varvec{\gamma }} - \sum _{|\varvec{\gamma }|=3}^{k+1}\frac{1}{\varvec{\gamma }!}{\phi ^*_{\varvec{\gamma }}(\mathbf z ')}(\mathbf x +\varDelta \mathbf q )^{\varvec{\gamma }}, \end{aligned}$$

(31)

where

$$\begin{aligned} F(\mathbf y ;\mathbf z ,\mathbf z ') =\phi _0(\mathbf y ;\mathbf z )- \phi _0(\mathbf y ;\mathbf z ') -\frac{1}{2}(\mathbf q (\mathbf y ;\mathbf z )-\mathbf q (\mathbf y ;\mathbf z '))(\mathbf p (\mathbf y ;\mathbf z )+\mathbf p (\mathbf y ;\mathbf z ')). \end{aligned}$$

We show that all the terms of $\varPsi$ in (31) are of the form (30). First, we note that for all $\mathbf y$

$$\begin{aligned} F(\mathbf y ;\mathbf z ,\mathbf z )=0,\quad \nabla _\mathbf{z '} F(\mathbf y ;\mathbf z ,\mathbf z )= -\nabla _\mathbf{z } \phi _0(\mathbf y ;\mathbf z ) + D_\mathbf{z }\mathbf q (T,\mathbf y ;\mathbf z )^T\mathbf p (\mathbf y ;\mathbf z )=0, \end{aligned}$$

where the second equality follows from (P5). By (P1), $F\in \mathcal V$, hence due to (23) there exists a function $g_{\varvec{\alpha }} \in \mathcal V$ such that,

$$\begin{aligned} F(\mathbf y ;\mathbf z ,\mathbf z ') = \sum _{|\varvec{\alpha }|=2} g_{\varvec{\alpha }}(\mathbf y ;\mathbf z ,\mathbf z ')\,\left( \mathbf z -\mathbf z '\right) ^{\varvec{\alpha }}. \end{aligned}$$

The second term in (31) includes $\mathbf x ,\mathbf p$ that are both in $C^\infty (\mathbb {R}\times \varGamma \times \mathbb {R}^n)$ by (P1) and hence (24) can be applied:

$$\begin{aligned} \mathbf x ^T(\mathbf p (\mathbf y ;\mathbf z )-\mathbf p (\mathbf y ;\mathbf z ')) = \mathbf x ^TG(\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf z -\mathbf z ') = \sum _{|\varvec{\alpha }| = |\varvec{\beta }| = 1} h_{\varvec{\alpha },\varvec{\beta }}(\mathbf y ;\mathbf z ,\mathbf z ') \,(\mathbf z -\mathbf z ')^{\varvec{\alpha }} \, \mathbf x ^{\varvec{\beta }}, \end{aligned}$$

with $h_{\varvec{\alpha },\varvec{\beta }} \in \mathcal V$. Similarly,

$$\begin{aligned} (\mathbf x - \varDelta \mathbf q )^TM(\mathbf y ;\mathbf z )(\mathbf x - \varDelta \mathbf q )&= \sum _{|\varvec{\alpha }|=2} m_{\varvec{\alpha }}(\mathbf y ;\mathbf z ,\mathbf z ')(\mathbf x - \varDelta \mathbf q )^{\varvec{\alpha }} \\&= \sum _{|\varvec{\alpha }+\varvec{\beta }|= 2} \ell _{\varvec{\alpha },\varvec{\beta }}(\mathbf y ;\mathbf z ,\mathbf z ')\,(\mathbf z -\mathbf z ')^{\varvec{\alpha }}\, \mathbf x ^{\varvec{\beta }}, \end{aligned}$$

where $m_{\varvec{\alpha }}, \ell _{\varvec{\alpha },\varvec{\beta }} \in \mathcal V$. Again, we used (P1) and (24). The term $(\mathbf x + \varDelta \mathbf q )^T{M^*(\mathbf y ;\mathbf z )}(\mathbf x +\varDelta \mathbf q )$ can be formulated in a similar fashion. The last two terms in (31) include the quantity $(\mathbf x \pm \varDelta \mathbf q )^{\varvec{\gamma }}$, which can be expanded by (27), namely

$$\begin{aligned} \sum _{|\varvec{\gamma }|=3}^{k+1}\frac{1}{\varvec{\gamma }!}\phi _{\varvec{\gamma }}(\mathbf z )(\mathbf x -\varDelta \mathbf q )^{\varvec{\gamma }} = \sum _{|\varvec{\alpha }+\varvec{\beta }|=3}^{k+1} p_{\varvec{\alpha },\varvec{\beta }}(\mathbf y ; \mathbf z , \mathbf z ') \, (\mathbf z - \mathbf z ')^{\varvec{\alpha }}\,\mathbf x ^{\varvec{\beta }}, \end{aligned}$$

with $p_{\varvec{\alpha },\varvec{\beta }}\in \mathcal V$. Analogously, $\sum _{|\varvec{\gamma }|=3}^{k+1}\frac{1}{\varvec{\gamma }!}{\phi ^*_{\varvec{\gamma }}{(\mathbf z ')}}(\mathbf x +\varDelta \mathbf q )^{\varvec{\gamma }}$ is of the same form.

To summarize, all the terms of (31) are indeed of the form (30). Their sums are finite and hence the union is also finite, which concludes the claim of the lemma. $\square$

The first step in proving Theorem 1 is to express $\partial ^{\varvec{\varvec{\sigma }}}_{\mathbf{y }} I^\varepsilon (T,\mathbf{y };\mathbf{z },\mathbf{z }')$ using the lemmas above.

Proposition 3

There exist functions $b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}} \in \mathcal U_\eta$ such that the derivatives of $I^\varepsilon$ in (16) with respect to $\mathbf y$ read:

$$\begin{aligned}&\partial ^{\varvec{\varvec{\sigma }}}_\mathbf{y } I^\varepsilon (T,\mathbf y ;\mathbf z ,\mathbf z ') \nonumber \\&\quad = \sum _{j=-|\varvec{\varvec{\sigma }}|}^{2\lceil k/2\rceil -2} \sum _{|\varvec{\alpha }+\varvec{\beta }|= \max (-2j,0)}^{(|\varvec{\varvec{\sigma }}|+2)(k-1)-2j} \varepsilon ^{j} (\mathbf z -\mathbf z ')^{\varvec{\alpha }} \int _{{\mathbb {R}}^n} \mathbf x ^{\varvec{\beta }} b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \hbox {e}^{i\varPsi /\varepsilon } \mathrm{d}\mathbf{x }. \end{aligned}$$

(32)

Proof

The proof will be carried out by mathematical induction. Let us define an index set ${\mathcal {J}}^{\varvec{\varvec{\sigma }}}$ which corresponds to the double sum in (32), namely

$$\begin{aligned} {\mathcal {J}}^{\varvec{\varvec{\sigma }}} = \{(j,\varvec{\alpha },\varvec{\beta }) : -|\varvec{\varvec{\sigma }}| \le j\le 2(\lceil k/2\rceil -1), \quad 0 \le |\varvec{\alpha }+\varvec{\beta }|+2j\le (|\varvec{\varvec{\sigma }}|+2)(k-1)\}, \end{aligned}$$

for all $\varvec{\varvec{\sigma }} \in {\mathbb {N}}^n_0$. First, we show that the statement (32) is valid for $\varvec{\varvec{\sigma }} \equiv 0$. Next, while assuming that the claim holds for $\varvec{\varvec{\sigma }} \in {\mathbb {N}}^n_0$ we prove that it is valid for any $\bar{\varvec{\varvec{\sigma }}} = \varvec{\varvec{\sigma }} + \mathbf{e }_\ell$.

• 1. $\varvec{\varvec{\sigma }}= 0$: The sums in (29) are (32) in this case, with $b_{j,\varvec{\alpha },\varvec{\beta },0}=g_{j,\varvec{\alpha },\varvec{\beta }}$.

• 2. $\bar{\varvec{\varvec{\sigma }}} = \varvec{\varvec{\sigma }} + \mathbf{e }_\ell$: We assume (32) to hold for $\varvec{\varvec{\sigma }} \in {\mathbb {N}}^n_0$. Then

  $$\begin{aligned}&\partial ^{\bar{\varvec{\varvec{\sigma }}}}_\mathbf{y } I^\varepsilon (T,\mathbf y ;\mathbf z ,\mathbf z ') = \partial _{y_\ell } \left( \partial ^{\varvec{\varvec{\sigma }}}_\mathbf{y } I^\varepsilon (T,\mathbf y ;\mathbf z ,\mathbf z ')\right) \nonumber \\&\quad = \sum _{(j,\varvec{\alpha },\varvec{\beta }) \in {\mathcal {J}}^{\varvec{\varvec{\sigma }}}} \varepsilon ^{j} (\mathbf z -\mathbf z ')^{\varvec{\alpha }} \int _{{\mathbb {R}}^n} \mathbf x ^{\varvec{\beta }} \, \partial _{y_\ell } b_{j,\varvec{\alpha },\varvec{\beta },{\varvec{\sigma }}}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf x \, \end{aligned}$$

  (33)
  $$\begin{aligned}&\ \ \quad + \sum _{(j,\varvec{\alpha },\varvec{\beta }) \in {\mathcal {J}}^{\varvec{\varvec{\sigma }}}} \varepsilon ^{j} (\mathbf z -\mathbf z ')^{\varvec{\alpha }} \int _{{\mathbb {R}}^n} \mathbf x ^{\varvec{\beta }} \, b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ')\, \partial _{y_\ell } \hbox {e}^{i\varPsi /\varepsilon } \, \hbox {d}\mathbf x \,. \end{aligned}$$

  (34)

  In (33), $\partial _{y_\ell } b_{j,\varvec{\alpha },\varvec{\beta },{\varvec{\sigma }}} \in \mathcal U_\eta$ and ${\mathcal {J}}^{\varvec{\varvec{\sigma }}} \subset {\mathcal {J}}^{\bar{\varvec{\varvec{\sigma }}}}$. The derivative $\partial _{y_\ell } \hbox {e}^{i\varPsi /\varepsilon }$ in (34) can be expressed from Lemma 4 as

  $$\begin{aligned} \partial _{y_\ell } \hbox {e}^{i\varPsi /\varepsilon } = \frac{i}{\varepsilon } \,\hbox {e}^{i \varPsi /\varepsilon }\partial _{y_\ell }\varPsi = \sum _{|\varvec{\gamma }+\varvec{\delta }|=2}^{k+1} \varepsilon ^{-1}\, (\mathbf z -\mathbf z ')^{\varvec{\gamma }}\, \mathbf x ^{\varvec{\delta }} \, h_{\varvec{\gamma },\varvec{\delta },\mathbf{e }_\ell }(T,\mathbf y ;\mathbf z ,\mathbf z ') \, \hbox {e}^{i\varPsi /\varepsilon }, \end{aligned}$$

  with $h_{\varvec{\gamma },\varvec{\delta },\mathbf{e }_\ell }=i \,\partial _{y_\ell }g_{\varvec{\gamma },\varvec{\delta }} \in \mathcal V$, with $g_{\varvec{\gamma },\varvec{\delta }}$ from (30). The terms in (34) are hence of the form

  $$\begin{aligned} \varepsilon ^{{\bar{j}}}(\mathbf z -\mathbf z ')^{\bar{\varvec{\alpha }}} \int _{{\mathbb {R}}^n} \mathbf x ^{\bar{\varvec{\beta }}} \, g_{}(T,\mathbf x ,\mathbf y ;\mathbf z ,\mathbf z ') \, \hbox {e}^{i\varPsi /\varepsilon } \hbox {d}\mathbf x \end{aligned}$$

  with $g := b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}} \,h_{\varvec{\gamma },\varvec{\delta },\mathbf{e }_\ell } \in \mathcal U_\eta$ and ${\bar{j}}=j-1, \bar{\varvec{\alpha }} = \varvec{\alpha }+\varvec{\gamma }, \bar{\varvec{\beta }} = \varvec{\beta }+\varvec{\delta }$. Note that $2\le |\varvec{\gamma }+\varvec{\delta }|\le k+1$ and since $(j,\varvec{\alpha },\varvec{\beta }) \in {\mathcal {J}}^{\varvec{\varvec{\sigma }}}$,

  $$\begin{aligned} 0 \le |{\varvec{\alpha }} + {\varvec{\beta }}|+2j + |\varvec{\gamma }+\varvec{\delta }|-2 = |\bar{\varvec{\alpha }} + \bar{\varvec{\beta }}|+2{\bar{j}}\le (|\varvec{\varvec{\sigma }}|+3)(k-1), \end{aligned}$$

  where $-|\varvec{\varvec{\sigma }}|-1 \le {\bar{j}} \le 2\lceil k/2\rceil -2$. Therefore, $({\bar{j}},\bar{\varvec{\alpha }},\bar{\varvec{\beta }}) \in {\mathcal {J}}^{\bar{\varvec{\varvec{\sigma }}}}$ which concludes the induction and proves Proposition 3. $\square$

5.3 Estimates for derivatives of the quantity of interest

We build the proof of Theorem 1 on estimates presented in this section for the derivatives of the quantity of interest (13). We first note that the n-dimensional Gaussian integral can be computed as

$$\begin{aligned} \int _{\mathbb {R}^n} |\mathbf x |^{|\varvec{\alpha }|} \hbox {e}^{-a\mathbf | \mathbf x |^2/\varepsilon } \, \hbox {d}\mathbf x = C \varepsilon ^{n/2+|\varvec{\alpha }|/2}, \end{aligned}$$

(35)

where C does not depend on $\varepsilon$. We will use this result in several places below.

Lemma 5

Let $g \in \mathcal U_\eta$, and $\eta$ be admissible in the sense of Definition 1. Then, for any $t\in [0,T], \varvec{\beta }\in \mathbb {N}^n_0$, there is a constant C and $\delta >0$, independent of $t, \mathbf z , \mathbf z ', \mathbf{y }$ and $\varepsilon$ such that

$$\begin{aligned} \left| \int _{{\mathbb {R}}^n}\mathbf{x }^{\varvec{\beta }} \, g(t,\mathbf{x },\mathbf{y }, \mathbf{z }, \mathbf{z }') \, \mathrm{e}^{i\varPsi (t,\mathbf{x },\mathbf{y }, \mathbf{z }, \mathbf{z }')/\varepsilon }\, \hbox {d}\mathbf{x } \right| \le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \mathrm{e}^{-\delta |\varDelta \mathbf{q }(t,\mathbf y ;\mathbf{z }, \mathbf{z }')|^2 /\varepsilon }. \end{aligned}$$

(36)

Proof

Integral (36) reads

$$\begin{aligned} I:= \left| \int _{{\mathbb {R}}^n}\mathbf{x }^{\varvec{\beta }} \, g \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \right| = \left| \int _{\varOmega _{2\eta }}\mathbf{x }^{\varvec{\beta }} \, g \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \right| . \end{aligned}$$

By (P4) and since g is uniformly bounded in $\mathbf{y }$ by (A4), we have

$$\begin{aligned} I&\le \int _{\varOmega _{2\eta }}\mathbf{x }^{\varvec{\beta }} \, |g| \, \hbox {e}^{-\mathrm{Im}\ \varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \le C \, \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \varDelta \mathbf{q } |^2} \, \int _{\varOmega _{2\eta }} | \mathbf{x } |^{|\varvec{\beta }|} \, \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \mathbf{x } |^2} \, \hbox {d}\mathbf{x }\\&\le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \, \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \varDelta \mathbf{q } |^2}, \end{aligned}$$

where we recalled (35) in the last inequality. We note that the constant C may depend on n and $\varvec{\beta }$, but is independent of $\mathbf z , \mathbf z ', \mathbf{y }$ and $\varepsilon$. $\square$

Lemma 6

Let $g \in \mathcal U_\eta$ and $\eta$ be admissible in the sense of Definition 1. Suppose further that for fixed $t\in [0,T]$ and $\mathbf{y }\in \varGamma$ it holds that $|\mathbf q (t,\mathbf y ;\mathbf z )-\mathbf q (t,\mathbf y ; \mathbf z ')|\le \theta |\mathbf z -\mathbf z '|$ for some $\theta >0$ and $\mathbf z , \mathbf z '\in K_0$. Then, for any $\varvec{\beta }\in \mathbb {N}^n_0, K \in {\mathbb {N}}_0$, and if $\theta$ is small enough, there is a constant C, independent of $t, \mathbf z , \mathbf z ', \mathbf y$ and $\varepsilon$ such that

$$\begin{aligned} \left| \int _{{\mathbb {R}}^n}\mathbf{x }^{\varvec{\beta }} \, g(t,\mathbf{x },\mathbf{y }, \mathbf{z }, \mathbf{z }') \, \mathrm{e}^{i\varPsi (t,\mathbf{x },\mathbf{y }, \mathbf{z }, \mathbf{z }')/\varepsilon }\, \hbox {d}\mathbf{x } \right| \le C \, \varepsilon ^{\frac{n+ |{\varvec{\beta }}|}{2}} \frac{1}{1 + \bigl | \frac{\mathbf{z }-\mathbf{z }'}{\sqrt{\varepsilon }} \bigr |^K}. \end{aligned}$$

(37)

Proof

Take $\mu$ and $\theta$ such that they are small enough in the sense of (P6), and also $\mu <\eta$. We simplify our notation by omitting the functions’ arguments and introduce two smooth test functions $\varphi _1, \varphi _2 \in C_{\text {c}}^{\infty }({{\mathbb {R}}}^n)$ with the following properties:

$$\begin{aligned} \varphi _1(\mathbf{x }) = \left\{ \begin{array}{l l} 1 \, &{} \, \, \mathbf{x } \in \varOmega _{\mu /2},\\ 0 \, &{} \, \, \mathbf{x } \in \varOmega _{\eta } {\setminus } \varOmega _{\mu }, \end{array} \right. \quad \varphi _2(\mathbf{x }) = 1 - \varphi _1(\mathbf{x }), \end{aligned}$$

and let $\varphi _1$ be monotonic on $\varOmega _{\mu } {\setminus } \varOmega _{\mu /2}$. By forming a smooth partition of unity, we split the function g into two parts:

$$\begin{aligned} g = (\varphi _1 + \varphi _2) \, g = \varphi _1 \, g + \varphi _2 \, g =: g_1 + g_2, \end{aligned}$$

where ${\text {supp}}(g_1) = \varOmega _{\mu } \subset \varOmega _{\eta }$, which implies that $g_1 \in \mathcal U_\eta$, and ${\text {supp}}(g_2) = \varOmega _{\eta } {\setminus } \varOmega _{\mu /2}$, see Fig. 4.

Fig. 4

A one-dimensional schematic representation of partitioning the function g

Accordingly, we can split the integral on the left-hand side of the inequality in (37) into two parts and using the triangular inequality write:

$$\begin{aligned} I:= \left| \int _{{\mathbb {R}}^n}\mathbf{x }^{\varvec{\beta }} \, g \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \right| \le \left| \int _{\varOmega _{\mu }}\mathbf{x }^{\varvec{\beta }} \, g_1 \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \right| + \left| \int _{\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}}\mathbf{x }^{\varvec{\beta }} \, g_2 \, \hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \right| =: {I}_1 + {I}_2. \end{aligned}$$

We first estimate ${I}_1$. We recall Lemma 5 and write

$$\begin{aligned} {I}_1 \le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \hbox {e}^{-\frac{\delta }{\varepsilon }|\varDelta \mathbf q |^2} \le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}}. \end{aligned}$$

We note that the constant C may depend on $(n, \varvec{\beta })$, but is independent of $\mathbf{y }$ and $\varepsilon$. This proves the needed estimate for ${I}_1$ for the case $K=0$ as well as the case $K>0$ when $\mathbf z =\mathbf z '$. Therefore, in the remainder of the proof we will consider the case $K \ne 0$ and $\mathbf z \ne \mathbf z '$.

From (P6), since $\mu$ and $\theta$ are small enough, there exists a constant $C>0$ such that $\inf _\mathbf{x \in \varOmega _{\mu }} |\nabla \varPsi |\ge C|\mathbf z -\mathbf z '|>0$. Since the gradient of $\varPsi$ does not vanish, we employ the non-stationary phase lemma (see [10]). Since $g_1\in \mathcal U_\mu$, we get

$$\begin{aligned} I_1&\le C_{K} \, {\varepsilon }^K \, \sum _{|\mathbf{m }| \le K} \int _{\varOmega _{\mu }} \frac{|\partial _\mathbf{x }^\mathbf{m } (\mathbf{x }^{\varvec{\beta }} \, g_1)|}{|\nabla \varPsi |^{2K - |\mathbf{m }|} } \, \hbox {e}^{- \text {Im } \varPsi / \varepsilon } \, \hbox {d}\mathbf{x }\\&\le C_{K} \, {\varepsilon }^K \, \sum _{|\mathbf{m }| \le K}{|\mathbf z -\mathbf z '|^{|\mathbf{m }|-2K} } \underbrace{\int _{\varOmega _{\mu }} |\partial _\mathbf{x }^\mathbf{m } (\mathbf{x }^{\varvec{\beta }} \, g_1)| \, \hbox {e}^{- \text {Im } \varPsi / \varepsilon } \, \hbox {d}\mathbf{x }}_{(*)}, \end{aligned}$$

where we used (P6). Employing the general Leibniz rule, $(*)$ can be estimated as

$$\begin{aligned} (*)&\le C \sum _{\begin{array}{c} \mathbf{m }_1 + \mathbf{m }_2 = \mathbf{m }\\ \mathbf{m }_1 \le \varvec{\beta } \end{array}} \int _{\varOmega _{\mu }} |\partial _\mathbf{x }^{\mathbf{m }_1} \mathbf{x }^{\varvec{\beta }}| \, | \partial _\mathbf{x }^{\mathbf{m }_2} g_1| \, \hbox {e}^{- \text {Im } \varPsi / \varepsilon } \, \hbox {d}\mathbf{x }\\&\le C \sum _{\begin{array}{c} \mathbf{m }_1 + \mathbf{m }_2 = \mathbf{m }\\ \mathbf{m }_1 \le \varvec{\beta } \end{array}} \int _{\varOmega _{\mu }} |\mathbf{x }|^{|\varvec{\beta }| - |{\mathbf{m }_1}|} \, \hbox {e}^{- \text {Im } \varPsi / \varepsilon } \, \hbox {d}\mathbf{x }, \end{aligned}$$

where the last inequality follows because $g_1$ has bounded derivatives with respect to $\mathbf{x }$, independent of $\mathbf{y }$ and $\varepsilon$, which is a consequence of (A4) and the smoothness of $\varphi _1$ and g on the compact sets $\varOmega _{\mu }$ and $\varOmega _{\eta }$, respectively. Using (P4) and (35), we have

$$\begin{aligned} \int _{\varOmega _{\mu }}|\mathbf{x }|^{|\varvec{\beta }| - |{\mathbf{m }_1}|}\, \hbox {e}^{- \text {Im } \varPsi / \varepsilon } \, \hbox {d}\mathbf{x }&\le \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \varDelta \mathbf{q } |^2} \int _{\varOmega _{\mu }}|\mathbf{x }|^{|\varvec{\beta }| - |{\mathbf{m }_1}|}\, \hbox {e}^{- \frac{\delta }{\varepsilon } \,|\mathbf x |^2} \, \hbox {d}\mathbf{x } \\&\le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }| - |{\mathbf{m }_1}|}{2}} \le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }| - |{\mathbf{m }}|}{2}}, \end{aligned}$$

where we used that $\mathbf m _1\le \mathbf m$ and (A5) in the last step. Consequently, we obtain

$$\begin{aligned} I_1 \le C_{K} \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \, \sum _{|\mathbf{m }| \le K}\left( \frac{|\mathbf z -\mathbf z '|}{\sqrt{\varepsilon }}\right) ^{|\mathbf{m }|-2K}. \end{aligned}$$

Now since when $K=0: I_1 \le C \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}}, \,$ in the general case of $K \ge 0$, we can write

$$\begin{aligned} I_1\le C_K \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \, \min \biggl (1, \, \sum _{|\mathbf{m }| \le K} \left( \frac{|\mathbf z -\mathbf z '|}{\sqrt{\varepsilon }}\right) ^{|\mathbf{m }|-2K} \biggr ). \end{aligned}$$

Since for positive numbers $a,b,c> 0$, the following inequalities hold:

$$\begin{aligned} \min (a,b+c) \le \min (a,b) + \min (a,c) \quad {\text {and}} \quad \min (1, 1/a) \le 2/(1+a), \end{aligned}$$

then

$$\begin{aligned} I_1 \le C_K \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \, \sum _{|\mathbf{m }| \le K} \frac{2}{1 + \left( \frac{|\mathbf z -\mathbf z '|}{\sqrt{\varepsilon }}\right) ^{2 K - |\mathbf{m }|}} \le C_K \, \varepsilon ^{\frac{n+ |\varvec{\beta }|}{2}} \, \frac{1}{1 + \left( \frac{|\mathbf z -\mathbf z '|}{\sqrt{\varepsilon }}\right) ^K}. \end{aligned}$$

It remains to show that $I_2$ can be estimated in a similar way. By (P4) and since $g_2$ is uniformly bounded in $\mathbf{y }$ and by (A4), we have

$$\begin{aligned} I_2&\le C \, \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \varDelta \mathbf{q } |^2} \, \int _{\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}} | \mathbf{x } |^{|\varvec{\beta }|} \, \hbox {e}^{- \frac{\delta }{\varepsilon } \, | \mathbf{x } |^2} \, \hbox {d}\mathbf{x } \\&= C \, \hbox {e}^{- \frac{\delta }{2\varepsilon } \, | \varDelta \mathbf{q } |^2} \, \int _{\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}} | \mathbf{x } |^{|\varvec{\beta }|} \, \hbox {e}^{- \frac{\delta }{2\varepsilon } \, (| \mathbf{x } |^2+|\varDelta \mathbf q |^2)} \hbox {e}^{- \frac{\delta }{2\varepsilon } \, | \mathbf{x } |^2}\, \hbox {d}\mathbf{x }\\&\le C \, \int _{\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}} \,| \mathbf{x } |^{|\varvec{\beta }|} \hbox {e}^{- \frac{\delta }{4\varepsilon } \, (|\mathbf{x } + \varDelta \mathbf{q }|^2 + |\mathbf{x } - \varDelta \mathbf{q }|^2 )} \hbox {e}^{- \frac{\delta }{2\varepsilon } \, | \mathbf{x } |^2}\, \hbox {d}\mathbf{x }, \end{aligned}$$

where the last inequality follows from $|\mathbf{x }|^2 + | \varDelta \mathbf{q }|^2 = |\mathbf{x } + \varDelta \mathbf{q }|^2/2 + |\mathbf{x } - \varDelta \mathbf{q }|^2/2$ and ${\hbox {e}^{- \frac{\delta }{2\varepsilon } \, | \varDelta \mathbf{q } |^2}\le 1}$. Since on $\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}$, at least one of the following inequalities holds:

$$\begin{aligned} | \mathbf{x } + \varDelta \mathbf{q } |> \mu \quad {\text {or}} \quad | \mathbf{x } - \varDelta \mathbf{q } |> \mu \quad {\text {or}} \quad | \mathbf{x } \pm \varDelta \mathbf{q } | > \mu , \end{aligned}$$

we have

$$\begin{aligned} I_2 \le C \hbox {e}^{- \frac{\delta }{4\varepsilon }\,\mu ^2}\, \int _{\varOmega _{\eta } {\setminus } \varOmega _{\mu /2}} \,| \mathbf{x } |^{|\varvec{\beta }|} \hbox {e}^{- \frac{\delta }{2\varepsilon } \, | \mathbf{x } |^2}\, \hbox {d}\mathbf{x }. \end{aligned}$$

From (35), this yields

$$\begin{aligned} I_2 \le C \hbox {e}^{- \frac{\delta }{4\varepsilon }\,\mu ^2} \, \varepsilon ^{\frac{|\varvec{\beta }|+n}{2}} \le C_s \, \varepsilon ^s, \quad \forall s >0. \end{aligned}$$

This means that $I_2$ is of order $\mathcal O(\varepsilon ^{\infty })$. Let us find s such that $I_2$ satisfies the estimate (37). We have

$$\begin{aligned} I_2\le C_s\,\varepsilon ^s \le C_s \, \varepsilon ^s \frac{1 + \text {diam}(K_0)^K}{\varepsilon ^{K/2} + \text {diam}(K_0)^K} = C_s \, \varepsilon ^{s-K/2} \frac{1 + \text {diam}(K_0)^K}{1+ \left( \frac{\text {diam}(K_0)}{\sqrt{\varepsilon }}\right) ^K}, \end{aligned}$$

where $\text {diam}(K_0)<\infty$ denotes the diameter of $K_0$, which is finite since $K_0$ is compact (see (A2)). As $|\mathbf z -\mathbf z '|\le \text {diam}(K_0)$, we get

$$\begin{aligned} I_2\le {\tilde{C}}_s \,\frac{\varepsilon ^{s-K/2}}{1+ \left( \frac{|\mathbf z -\mathbf z '|}{\sqrt{\varepsilon }}\right) ^K}, \end{aligned}$$

so we have the same estimate as (37) if we take $s=(K+n+|\varvec{\beta }|)/2$. The proof of Lemma 6 is complete. $\square$

5.4 Proof of Theorem 1

Let us recall the form of $\partial ^{\varvec{\varvec{\sigma }}}_\mathbf{y } { \mathcal {Q}^\varepsilon _{\mathrm{GB}}}(\mathbf y )$ in (26). We express $\partial _\mathbf{y }^{\varvec{\varvec{\sigma }}} I^\varepsilon (\mathbf y ;\mathbf z ,\mathbf z ')$ from Proposition 3 and estimate $|\partial ^{\varvec{\varvec{\sigma }}}_\mathbf{y } { \mathcal {Q}^\varepsilon _{\mathrm{GB}}}(\mathbf y )|$, dropping the T-argument, as

$$\begin{aligned} \left| \partial ^{\varvec{\varvec{\sigma }}}_\mathbf{y } { \mathcal {Q}^\varepsilon _{\mathrm{GB}}}(\mathbf{y })\right|&\le \left( \frac{1}{2\pi \varepsilon }\right) ^n \sup _{\mathbf{ z }'\in K_0}\int _{K_0} \left| \partial ^{\varvec{\varvec{\sigma }}}_{\mathbf{y }} I^\varepsilon (\mathbf{y };\mathbf{z }, \mathbf{z }') \right| \hbox {d}\mathbf{z } \nonumber \\&\le \left( \frac{1}{2\pi \varepsilon }\right) ^n \sup _{\mathbf{z }'\in K_0} \sum _{j=-|\varvec{\varvec{\sigma }}|}^{2(\lceil k/2\rceil -1)} \sum _{|\varvec{\alpha }+\varvec{\beta }|=\max (-2j,0)}^{(|\varvec{\varvec{\sigma }}|+2)(k-1)-2j} \nonumber \\&\quad \varepsilon ^{j} \underbrace{\int _{K_0} |\mathbf{z }-\mathbf{z }'|^{|\varvec{\alpha }|} \left| \int _{{\mathbb {R}}^n} {\mathbf{x }}^{\varvec{\beta }}\, b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}}(\mathbf{x },\mathbf{y };\mathbf{z },\mathbf{z }')\,\hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \, \right| \hbox {d}\mathbf{z }.}_{(*)} \end{aligned}$$

(38)

To begin with $(*)$, let us first divide the set $K_0 \times K_0$ into two sets: the non-caustic region where $|\varDelta \mathbf q | \ge \theta |\mathbf z -\mathbf z '|$ and the caustic region where $|\varDelta \mathbf q | < \theta |\mathbf z -\mathbf z '|$, for small enough $\theta$ in the sense of (P6).

• 1. Non-caustic region $|\varDelta \mathbf q | \ge \theta |\mathbf z -\mathbf z '|$.

  The function $b_{j,\varvec{\alpha }, \varvec{\beta },\varvec{\varvec{\sigma }}}$ in (38) belongs to $\mathcal U_\eta$ and we can apply the results of Lemma 5. Then $(*)$ reads:

  $$\begin{aligned}&\int _{K_0} |\mathbf{z }-\mathbf{z }'|^{|{\varvec{\alpha }}|} \left| \int _{{\mathbb {R}}^n} \mathbf{x }^{\varvec{\beta }}\, b_{j,\varvec{\alpha },\varvec{\beta },\varvec{\varvec{\sigma }}}(\mathbf{x }, \mathbf{y };\mathbf{z },\mathbf{z }')\,\hbox {e}^{i\varPsi /\varepsilon }\, \hbox {d}\mathbf{x } \, \right| \hbox {d}\mathbf{z }\nonumber \\&\quad \le C \varepsilon ^{\frac{n+|\varvec{\beta }|}{2}} \int _{K_0} |\mathbf{z }-\mathbf{z }'|^{|\varvec{\alpha }|} \hbox {e}^{-\delta |\varDelta \mathbf{q }|^2 /\varepsilon } \hbox {d}\mathbf{z } \nonumber \\&\quad \le C \varepsilon ^{\frac{n+|\varvec{\beta }|}{2}} \int _{K_0} |\mathbf{z }-\mathbf{z }'|^{|{\varvec{\alpha }}|} \hbox {e}^{-\delta \theta ^2 |\mathbf{z }-\mathbf{z }'|^2 /\varepsilon } \hbox {d}\mathbf{z } \le C\varepsilon ^{\frac{n+|{\varvec{\beta }}|}{2}} \varepsilon ^{\frac{n+|{\varvec{\alpha }}|}{2}}, \end{aligned}$$

  where we used the fact that $|\varDelta \mathbf q | \ge \theta |\mathbf z -\mathbf z '|$ and recalled the Gaussian integral formula (35) in the last step. Consequently, (38) reduces to

  $$\begin{aligned} \left| \partial _\mathbf{y }^{{\varvec{\sigma }}} {\mathcal {Q}^\varepsilon _\mathrm{GB}}(\mathbf y )\right| \le C_{\varvec{\varvec{\sigma }}} \sum _{j=-|{\varvec{\sigma }}|}^{2(\lceil k/2\rceil -1)} \sum _{|{\varvec{\alpha }}+{\varvec{\beta }}|=\max (-2j,0)}^{(|{\varvec{\sigma }}|+2)(k-1)-2j} \varepsilon ^{j + \frac{|{\varvec{\beta }}|+|{\varvec{\alpha }}|}{2}}. \end{aligned}$$

  (39)

• 2. Caustic region $|\varDelta \mathbf{q }| < \theta |\mathbf{z }-\mathbf{z }'|$.

  Relation (38) fulfills the prerequisites of Lemma 6 and hence $(*)$ reads, for all $K\ge 0,$

  $$\begin{aligned}&\int _{K_0} |\mathbf{z }-\mathbf{z }'|^{|{\varvec{\alpha }}|} \left| \int _{{\mathbb {R}}^n}\mathbf{x }^{{\varvec{\beta }}}\, b_{j,{\varvec{\alpha }},{\varvec{\beta }},{\varvec{\sigma }}}(\mathbf{x },\mathbf{y };\mathbf{z },\mathbf{z }')\,\hbox {e}^{i\Psi /\varepsilon }\, \hbox {d}\mathbf{x } \, \right| \hbox {d}\mathbf{z }\\&\quad \le C \varepsilon ^{\frac{n+|{\varvec{\beta }}|}{2}} \int _{K_0} \frac{|\mathbf{z }-\mathbf{z }'|^{|{\varvec{\alpha }}|}}{1 + (|\mathbf{z }-\mathbf{z }'|/\sqrt{\varepsilon })^K} \, \hbox {d}\mathbf{z } \le C \varepsilon ^{\frac{n+|{\varvec{\beta }}|}{2}} \varepsilon ^{\frac{n+|{\varvec{\alpha }}|}{2}}\int _{{\mathbb {R}}^n} \frac{|t|^{|{\varvec{\alpha }}|}}{1 + |t|^K} \, \hbox {d}t. \end{aligned}$$

  The integral is bounded when $K > n + |\varvec{\alpha }|$; hence, we arrive at the same conclusion as in (39).

In both the caustic and non-caustic regions, the same inequality has been obtained. The exponent of $\varepsilon$ is always positive as $0\le |\varvec{\alpha }+\varvec{\beta }|+2j$ and hence

$$\begin{aligned} \left| \partial _\mathbf{y }^{\varvec{\varvec{\sigma }}} { \mathcal {Q}^\varepsilon _{\mathrm{GB}}}(\mathbf y )\right| \le C_{\varvec{\varvec{\sigma }}}, \end{aligned}$$

which concludes the proof of Theorem 1.