1 Introduction

For a smooth projective variety X of dimension n and a birational self-map \(f{:}\,X \dasharrow X\), one can define a tuple of real numbers

$$\begin{aligned} \lambda _0 (f) = 1,\; \lambda _2 (f), \ldots , \lambda _{n-1}(f), \; \lambda _n (f) =1, \end{aligned}$$

where \(\lambda _i(f)\ge 1\) for \(2\le i\le n-1\), called the dynamical degrees of f. See Sect. 2 for two equivalent definitions of these numbers. The dynamical degrees turn out to be invariant under birational conjugacy, so that the dynamical spectrum

$$\begin{aligned} \varLambda (X) = \left\{ \lambda (f) :=\left( \lambda _1 (f), \ldots , \lambda _{n-1}(f)\right) \mid f \in \mathrm {Bir}(X) \right\} \subset {\mathbb {R}}^{n-1} \end{aligned}$$

is a birational invariant of the variety X. One thus might, for example, try to use it to distinguish very general (conjecturally irrational) cubic fourfolds X from \({\mathbb {P}}^4\). Here are some ideas how the spectra might differ:

  1. (1)

    As point sets, that is, there might be a tuple \(\lambda (f)\) in the spectrum of \({\mathbb {P}}^4\) which is not in the spectrum of X. This could, for example, be proven if one could show that on X the dynamical degrees have to satisfy other additional inequalities, coming from the geometry of X, which can be violated on \({\mathbb {P}}^4\). For this, one has, in particular, to develop certain semi-continuity properties and computational tools for dynamical degrees, which we start doing in the subsequent sections.

  2. (2)

    As metric (or only topological) spaces: for example, one can consider, for every k, the smallest gap in the spectrum after 1, if there is any, that is,

    $$\begin{aligned} g_k:=\inf _{f \in \mathrm {Bir}(X), \; \lambda _k (f) \ne 1} (\lambda _k(f) -1). \end{aligned}$$

    It is possible that these numbers differ for X and \({\mathbb {P}}^4\), but the drawback is that it is not easy to see how to relate them to accessible geometric features of X. In other words, it seems very hard to compute or estimate them. On the topological side, it may happen that the Cantor–Bendixson ranks of the dynamical spectra or some linear slices in them differ, but again these are very hard to access.

  3. (3)

    Arithmetically: it could happen that for both X and \({\mathbb {P}}^4\), the dynamical degrees are algebraic integers, but for X they may satisfy some additional arithmetic constraints. For example, the number fields generated by each tuple of dynamical degrees on X might differ from the ones for \({\mathbb {P}}^4\). But also this seems very hard to detect.

We thus concentrate on (1) for the moment.

The paper is organized as follows. In Sect. 2, we recall some basic facts about cycles and dynamical degrees. In Sect. 3, we prove Theorem 3.1 which says that the dynamical degrees are lower semi-continuous functions for families over smooth bases, if one understands lower semi-continuity in a slightly generalized sense, namely that (downward) jumps may occur on countable unions of closed subsets. Moreover, in Proposition 3.4 we collect some results that point out the importance of the questions of existence of (finite-dimensional, connected, non-trivial) algebraic subgroups in \(\mathrm {Bir}(X)\) and of the classification of birational automorphisms with all dynamical degrees equal to 1 for the irrationality problem for cubic fourfolds X. In Sect. 4, we study the relationship between dynamical degrees and Cremona degrees under some assumptions and prove a submultiplicativity result, Theorem 4.3. Section 5 is devoted to reflections on cubic fourfolds, and in Theorem 5.5, we show, under some assumptions, the equality of the first and second dynamical degrees of a composition of reflections on a smooth cubic fourfolds. This is a sample of a type of result which says that special dynamical degrees can only arise in the presence of special dynamics. Such implications are very important for making progress on the irrationality problem for cubics, too. Finally, in “Appendix” we describe generalized Picard–Manin spaces which might prove useful in the study of dynamical degrees on fourfolds in the future.

Conventions We work over the field of complex numbers \({\mathbb {C}}\) throughout the paper. A variety is a reduced and irreducible scheme of finite type over \({\mathbb {C}}\). A prime k-cycle on a variety is an (irreducible) subvariety of dimension k. A k-cycle is a formal linear combination of prime k-cycles. If \(f{:}\,X\dasharrow Y\) is a rational map between varieties, we denote by \(\mathrm {dom}(f)\) the largest open subset of X on which f is a morphism. The graph \(\varGamma _f \subset X \times Y\) of f is the closure of the locus of points (x, f(x)) with \(x \in \mathrm {dom}(f)\).

2 Preliminaries

2.1 Cycles

Let X be a smooth projective variety of dimension n. Following [6], we will denote by \(A_k(X),\,B_k(X)\) and \(H_k(X)\) the groups of algebraic cycles of dimension k modulo rational, algebraic and homological equivalence, respectively. Roughly speaking, a cycle is rationally equivalent to zero if it can be written as the difference of two fibers of a family over \({\mathbb {P}}^1\); algebraically equivalent to zero if it can be written as the difference of two fibers of a family over a smooth curve; and homologically equivalent to zero if it maps to zero under the cycle map .

Any zero cycle \(\alpha \in A_0(X)\) has a well-defined degree, see [6, Def. 1.4].

As usual, \(A^k(X),\,B^k(X),\,H^k(X)\) will denote the groups of cycles of codimension k. There are surjections

for all possible k.

Given a proper map of some relative dimension l, one can define pushforward maps and, if f is also flat, pullback maps , see [6, Sect. 1]. For instance, for the pullback under a flat map one simply takes the class of the preimage of a prime cycle and extends this definition linearly. One can also define pullback maps for morphisms between smooth varieties which are not necessarily flat, but this is slightly more complicated and involves some intersection theory, see [6, Ch. 8].

Also recall that the collection of all groups \(A_*(X)=\oplus _{k=0}^n A_k(X)\) is a commutative ring with respect to the intersection pairing (here we need X smooth). More precisely, there are pairings for all possible k, l. In other words, \(A^*(X)\) is a graded ring.

An important result about cycles which we will use below is the “Principle of Conservation of Number”, see [6, Subsect. 10.2].

Theorem 2.1

Let be a proper morphism of varieties, \(\dim T=m\), and \(\alpha \) be an m-cycle on \(\mathcal {Y}\). Then the cycle classes \(\alpha _t \in A_0 (\mathcal {Y}_t)\) for \(t \in T\) a regular closed point, all have the same degree.

Remark 2.2

Here, if \(\beta \) is an \((m+k)\)-cycle \(\beta \) on \(\mathcal {Y}\) (where k is not necessarily zero), then fiber cycle classes \(\beta _t\) are in general defined via \(\beta _t = t^{!} (\beta )\), where \(t^{!}\) is a refined Gysin homomorphism associated with the regular embedding , see [6, Subsect. 10.1]; however, in all our applications below, there is a much simpler way to think of \(\beta _t\): indeed, we will always have that the embedding \(i_t\) of the fiber \(Y_t=p^{-1}(t)\) into \(\mathcal {Y}\) will be regular of codimension m, and \(Y_t\) and \(\mathcal {Y}\) will be smooth. Then \(\beta _t = i^{*}_t (\beta )\) (the cycle pullback) by [6, Ex. 10.1.2]. Even more concretely, suppose that \(\beta \) is represented by some subvariety of \(\mathcal {Y}\) that is generically transverse to \(i_t\) in the sense of [5, Def. 1.22], i.e., \(i_t^{-1}(\beta )\) (scheme-theoretic preimage) is generically reduced and \(\mathrm {codim}_{Y_t}(i_t^{-1}(\beta )) = \mathrm {codim}_{\mathcal {Y}} (\beta )\), i.e., the intersections take place in the expected codimensions. Then the cycle pullback \(i_t^{*}(\beta )\) is represented by the class of \(i_t^{-1}(\beta )\) by [5, Thm. 1.23(a)]. We use this fact in the sequel to understand the geometric meaning of fiber cycle classes \(\beta _t\) (e.g., if this is a zero cycle, we will identify its degree with Cremona degrees in certain setups).

2.2 Dynamical degrees

Let X be a smooth projective variety of dimension n, fix an ample divisor H on X and let \(f{:}\,X \dasharrow X\) be a birational map. Setting \(H^k_{\mathbb {R}}(X):=H^k(X)\otimes {\mathbb {R}}\), we define a linear map

where are the projections and \(\varGamma _f\subset X\times X\) is the graph of f.

Definition 2.3

Let X and f be as above. The kth dynamical degree of f is

where \(\rho ((f^m)^*)\) is the spectral radius of the linear map \((f^m)^*\). Recall that the spectral radius of a linear map is the maximum among the absolute values of its eigenvalues.

Equivalently, one can choose any resolution Z of singularities of \(\varGamma _f\), consider the induced diagram

and define \(f^* = \pi _{1*}\circ \pi _2^*\). For the equivalence of these two approaches, see [10, Subsect. 3.1].

There is yet another way of defining the dynamical degrees. First, one can define the Cremona degree \(\deg _k (f)\) of f with respect to H as the degree (i.e., the intersection number with \(H^{n-k}\)) of the birational transform under \(f^{-1}\) of a general element in the system of cycles homologically equivalent to \(H^k\). In symbols,

$$\begin{aligned} \deg _k(f)=H^{n-k} \cdot f^* H^k. \end{aligned}$$

One then puts

the growth rate of the Cremona degrees of the iterates of f. This definition does not depend on the choice of H and is equivalent to the previous one, see [10, Thm. 1.1] for a statement valid over any algebraically closed field of characteristic zero or [7, Thm. 2.4] for a more analytic statement.

Remark 2.4

Before the existence of the limit was proven, a definition involving a limes inferior of Cremona degrees or spectral radii was sometimes used in the literature.

The dynamical degrees satisfy several numerical properties, such as log-concavity, and are related to the topological entropy of f, see [7].

Finally, for the convenience of the reader we recall the statement of [3, Lem. 2.3] since it is used below.

Lemma 2.5

Let be a morphism of varieties over an algebraically closed field k and let \(W \subset Z\) be a constructible subset. Then there is a finite collection of locally closed subsets \(\varOmega _i \subset \varOmega ,\,1\le i\le N\), and closed subsets \(Y_i \subset p^{-1}(\varOmega _i)\) such that \(\varOmega = \bigcup _{i=1}^N \varOmega _i\) and for any \(i,\,1\le i\le N\), and any point \(\omega \in \varOmega _i\), the fiber \((Y_i)_{\omega }\) is equal to the closure of \(W_{\omega }\) in \(Z_{\omega }\).

3 Semi-continuity of dynamical degrees

In this section, we will prove Theorem 3.1, providing estimates on dynamical degrees in families.

Theorem 3.1

Let

be a smooth projective family of smooth varieties \(X_s \subset {\mathbb {P}}^N\) over a variety S. Let

be a birational map such that no entire fiber of \(\pi \) is in the indeterminacy or exceptional locus of f, i.e., fiberwise, \(f_s {:}\,X_s \dasharrow X_s\) is a well-defined birational map (if this is not satisfied at the beginning, we can always achieve it by replacing S by a non-empty open subset). Consider the function

associating with \(s\in S\) the jth dynamical degree \(\lambda _j (f_s)\) of \(f_s\). Then \(\lambda _j\) is lower semi-continuous in the following generalized sense :  the sets

$$\begin{aligned} V_a:=\left\{ s \in S \mid \lambda _j (s) \le a \right\} , \quad a \in {\mathbb {R}}, \end{aligned}$$

are countable unions of Zariski closed subsets in S.

Remark 3.2

We would like to draw attention to a subtlety in the structure of the proof of Theorem 3.1 at this point already. First of all, notice that to prove Theorem 3.1 for given and f, it is sufficient to prove it for the base change family and \(f_{\tilde{S}}{:}\,X_{\tilde{S}} \dashrightarrow X_{\tilde{S}}\) for a desingularization . This is so because all the hypotheses hold for the family after the base change, and the sets \(V_a=V_a(S)\) on S are the images under the proper morphism b of the corresponding sets \(V_a(\tilde{S})\) on \(\tilde{S}\).

This being so, we will prove Theorem 3.1 by a descending induction on \(\dim S\), and for this we will need the statement of the Theorem for arbitrary bases S (non-singular or not) as hypothesis in the induction step. In the course of the proof, we will have to apply the principle of conservation of number Theorem 2.1, however, which will require the bases of the families under consideration to be smooth. The remark above shows that this is no serious restriction in our setup: we can always pass to an appropriate non-singular base \(\tilde{S}\) if necessary.

We begin with the following result, which generalizes [12, Lem. 4.1].

Lemma 3.3

In the setup of Theorem 3.1, let \(H \subset {\mathbb {P}}^N\) be the linear system of hyperplanes in \({\mathbb {P}}^N\). Let \(\deg _j (f_s)\) be the jth Cremona degree of \(f_s\). Then

is a lower semi-continuous function on S.

Proof

Passing to a desingularization of S and the pullback family as in Remark 3.2 if necessary, we may as well assume that S is smooth. Consider the graph \(\varGamma _f \subset X \times _S X \subset {\mathbb {P}}^N \times {\mathbb {P}}^N \times S\) and the two (flat) projections \(p_1, p_2\)

Let \(H^j_S \subset {\mathbb {P}}^n\times S\) be the pullback to \({\mathbb {P}}^N \times S\) of the algebraic equivalence class \(H^j\), that is, an intersection of j relative hyperplanes in \({\mathbb {P}}^N\times S\). Then, by Theorem 2.1 applied to \(\mathcal {Y}={\mathbb {P}}^N \times {\mathbb {P}}^N \times S,\,T = S\) and \(\alpha = \varGamma _f \cdot p_1^* (H_S^{\dim X_s -j}) \cdot p_2^* (H_S^{j})\) (an easy computation shows that this is indeed a \(\dim (S)\)-cycle), the degree of \(\alpha _t \in A_0 (\mathcal {Y}_t)\) is constant. Note that the cycle pullbacks via the flat morphisms (or, in any case, via morphisms between smooth varieties) and the intersection product in the ambient smooth variety \({\mathbb {P}}^N \times {\mathbb {P}}^N \times S\) are well-defined. Note also that \(\deg \alpha _s\) is equal to the Cremona degree \(\deg _j (s)\) for s in a non-empty Zariski open subset \(\varOmega \subset S\), because, firstly, for s in a dense Zariski open subset of S we have

$$\begin{aligned} (\varGamma _f)_s = \varGamma _{f_s} \end{aligned}$$

by an application of Lemma 2.5: just apply it to \(Z = X\times _S X,\,\varOmega =S\) and the constructible set W consisting of the points (x, f(x)) for \(x \in \mathrm {dom}(f)\) to conclude that there is an open dense subset of points in S with the desired property. Note that for special \(s \in Z:=S{{\backslash }} \varOmega ,\,\varGamma _{f_s}\) may be a proper component of \((\varGamma _f)_s\). Now, secondly, provided that \((\varGamma _f)_s = \varGamma _{f_s}\), we can calculate the restriction \(\alpha _s\) of \(\alpha \) to \(\mathcal {Y}_s=Y_s={\mathbb {P}}^N \times {\mathbb {P}}^N \times \{s\}\) via the geometric method explained at the end of Remark 2.2 to find that then

$$\begin{aligned} \alpha _s = \varGamma _{f_s}\cdot \mathrm {pr}_1^* H^{\dim X_s -j} \cdot \mathrm {pr}_2^* H^j, \end{aligned}$$

which has degree equal to the Cremona degree \(\deg _j(s)\) by the definition of Cremona degree.

Thus we see that on \(\varOmega \), the function \(\deg _j\) is constant by Theorem 2.1. Let us check that \(\deg _j\) can only get smaller at a point \(z_0 \in Z\). This will imply the assertion by descending induction on \(\dim S\). Indeed, if \(\deg _j = a\) generically on S, there is a proper closed subset \(S' \subset S\) such that \(\{ s \in S \mid \deg _j (s) \le a-1 \} \subset S'\). Now considering the irreducible components of \(S'\), and the restriction of the family X to each of these implies the assertion.

To see that \(\deg _j\) can only drop at \(z_0 \in Z\), we can assume that \(\dim S >0\) and then take a smooth curve \(C \subset S\) with \(z_0 \in C\) and \(C \cap \varOmega \ne \emptyset \), and restrict the family to C, i.e., consider and the restriction \(f_C{:}\,X_C \dasharrow X_C\) of f to \(X_C\). Then we can do the above construction with S replaced by C, that is, we can consider \(\varGamma _{f_C}\) and a relative cycle \(\alpha _C\). Note that since \(\varOmega \cap C \ne \emptyset \), for a general point \(c\in C\) the degree of \((\alpha _C)_c\) will be equal to \(\deg _j (f_c)\) again by Lemma 2.5 and Remark 2.2.

Now there is a finite set of points \(\mathcal {P} \subset C\), where we can assume that \(z_0 \in \mathcal {P}\), such that for \(c\in C {{\backslash }} \mathcal {P}\), the fiber \((\varGamma _{f_C})_c\) of \(\varGamma _{f_C}\) over c is nothing but the graph of \((f_C)_c\).

The graph \(\varGamma _{f_C}\) is, by definition, the closure of in \({\mathbb {P}}^N \times {\mathbb {P}}^N \times C\). Now the advantage of working over a curve C is that, by the valuative criterion of properness and the properness of Chow schemes of cycles in \({\mathbb {P}}^N \times {\mathbb {P}}^N\), the limits \((\varGamma _{f_C})_z\), for \(z \in \mathcal {P}\), of the family will be cycles of dimension \(\dim X_s\), that is, all components of \((\varGamma _{f_C})_{z_0}\) have dimension \(\dim X_s\). This allows us to interpret the degree of the zero cycle \((\alpha _C)_{z_0}\) geometrically. First of all, \(\deg (\alpha _C)_{z_0}= \deg (\alpha _C)_c = \deg _j (f_c)\) for \(c\in C\) general, by Theorem 2.1. Note that it is here that we need the assumption C smooth (hence also had to be able to assume S smooth before to ensure the existence of such a C) because otherwise conservation of number does not hold: think of the normalization of a curve with a double point as a relative zero cycle over the singular curve downstairs.

On the other hand, \(\deg (\alpha _C)_{z_0}\) is nothing but the sum of the numbers \(\mathcal {G} \cdot \mathrm {pr}_1^* (H^{\dim X_s -j}). \mathrm {pr}_2^* (H^{j})\) running over the irreducible components \(\mathcal {G}\) of \((\varGamma _{f_C})_{z_0}\), possibly counted with suitable multiplicities, cf. [6, 10.1, p. 176 bottom]. Here \(\mathrm {pr}_i\) are the projections of \({\mathbb {P}}^N\times {\mathbb {P}}^N\) onto its factors. Since \(\varGamma _{f_{z_0}}\) is one of the components, we see that the Cremona degree can only drop at a special point \(z_0\). \(\square \)

Proof of Theorem 3.1

By definition, we have

Applying Lemma 3.3 to each iterate of f, we see that for each \(n \in {\mathbb {N}}\), there is a proper closed subset \(Z_n \subset S\) such that on \(S{\backslash } Z_n,\,\deg _j (f_s^n)\) is constant. Thus outside the countable union of proper closed subsets

$$\begin{aligned} \bigcup _{k_0 \ge 1} \left( \bigcap _{k \ge k_0} Z_{k} \right) \end{aligned}$$

the function is constant (here we use Remark 2.4). Now arguing again by induction on the dimensions of the irreducible components of the closed subsets in the previous countable union (these are countably many proper closed subsets) gives the assertion. \(\square \)

One instance where one can use the above considerations is the following result, which might be useful when trying to prove irrationality of very general cubic fourfolds. It is based on a suggestion by Miles Reid.

Let G be an algebraic group. Recall that given an injective map of (abstract) groups , we get an action of G on X by birational isomorphisms, and we say that G is an algebraic subgroup of \(\mathrm {Bir}(X)\) if the domain of definition of the partially defined map \(G\times X \dasharrow X,\,\), contains a dense open set of \(G \times X\) and coincides on it with a rational map (in the sense of algebraic geometry). By a theorem of Rosenlicht [8, Thm. 2], one can characterize algebraic subgroups G equivalently by saying that they are those subgroups for which there is a birational model \(Y \dasharrow X\) such that G acts on Y via biregular maps/automorphisms.

Proposition 3.4

Let X be a smooth cubic fourfolds. For a line \(l \subset X\) denote by the associated conic fibration, and by

$$\begin{aligned} \mathrm {Bir}_{\varphi _l}(X) \subset \mathrm {Bir}(X) \end{aligned}$$

the subgroup consisting of birational self-maps which preserve the fibration \(\varphi _l\), i.e., map a general fiber into itself. The following hold.

  1. (1)

    X is rational if and only if there is an algebraic subgroup \(({\mathbb {C}}^*)^2\) in \(\mathrm {Bir}(X)\).

  2. (2)

    If X is rational, then there is a family of birational maps

    such that for any \(s \in S:= ({\mathbb {C}}^*)^2\) all dynamical degrees of \(f_s:=f\mid _{X_s}\) are equal to 1 and such that the set \(\{ f_s \}_{s\in ({\mathbb {C}}^*)^2}\) is contained in no subgroup \(\mathrm {Bir}_{\varphi _l}(X)\) as above.

  3. (3)

    If X is rational, then there is some birational self-map \(f \in \mathrm {Bir}(X)\) with all dynamical degrees equal to 1 and such that f is contained in no subgroup \(\mathrm {Bir}_{\varphi _l}(X)\). There is even such a map f with the property that the growth of the Cremona degrees of the iterates of f is bounded.

Proof

For (1) note that if X is rational, \(\mathrm {Bir}(X)\) certainly contains a subgroup \(({\mathbb {C}}^*)^2\), e.g., coordinate rescalings. Conversely, if there is an algebraic subgroup \(({\mathbb {C}}^*)^2\) in \(\mathrm {Bir}(X)\), then X is birationally a \(({\mathbb {C}}^*)^2\)-principal bundle over a unirational, hence rational, surface (note that \(({\mathbb {C}}^*)^2\), being abelian, will act generically freely once it acts faithfully). Since any such \(({\mathbb {C}}^*)^2\)-principal bundle is Zariski locally trivial (\(({\mathbb {C}}^*)^2\) is a special group in the sense of Serre), X is rational in this case.

To prove (2), note that the existence of the family is clear by (1) (the family is simply induced by the rational action of \(({\mathbb {C}}^*)^2\) on X), so we only have to see that for any \(s \in S:= ({\mathbb {C}}^*)^2\) all dynamical degrees of \(f_s=f\mid _{X_s}\) are equal to 1. Now by Lemma 3.3, clearly all Cremona degrees are bounded in the family. On the other hand, since it arises from a subgroup \(({\mathbb {C}}^*)^2\) of \(\mathrm {Bir}(X)\), for any \(f_s,\,f_s^n\) is again in the family, i.e., equal to some \(f_t\). Hence all dynamical degrees are equal to 1. Moreover, the set \(\{ f_s \}_{s\in ({\mathbb {C}}^*)^2}\) is contained in no subgroup \(\mathrm {Bir}_{\varphi _l}(X)\), since the images of

(i.e., the \(({\mathbb {C}}^*)^2\)-orbits) are rational surfaces for a general point \(p\in X\) if we construct the family \(\{ f_s \}\) from a subgroup \(({\mathbb {C}}^*)^2\) in \(\mathrm {Bir}(X)\) as in (1). But if \(\{ f_s \}_{s\in ({\mathbb {C}}^*)^2}\) were contained in a subgroup \(\mathrm {Bir}_{\varphi _l}(X)\), these images would be conics.

To prove (3), suppose that

$$\begin{aligned} \varPhi {:}\,{\mathbb {P}}^4 \dasharrow X \end{aligned}$$

is a birational map, and suppose that \(x\in {\mathbb {P}}^4\) is a point in which \(\varPhi \) is defined and is a local isomorphism. Our goal is now to find a one-parameter group

$$\begin{aligned} \{ f_t \}, \quad t \in {\mathbb {C}}^*, \quad f_{t}\circ f_s = f_{ts} \end{aligned}$$

of birational self-maps of X such that \(\varGamma \), the (closure of the) image of

is a curve on X through p which is not a conic. Here we want all \(f_t\) to be birational self-maps with all dynamical degrees equal to 1. So \(\varGamma \) is an orbit under the action of \({\mathbb {C}}^*\) on X. If we can find such a one-parameter group, we are done: namely, if we choose t to be of infinite order, then \(f:=f_t\) has the required properties; indeed, if f preserved a conic fibration, then the iterates \(f^n (p),\,n\in {\mathbb {N}}\), would all have to lie in a conic Q. These iterates also lie on the curve \(\varGamma \) and are distinct by our choice of t; thus, \(\varGamma \) and Q would coincide (they have infinitely many points in common), a contradiction.

One way to construct such a one-parameter subgroup is as follows: consider the family of all conics \(\mathcal {C}_p\) through \(p=\varPhi (x)\). For every conic \(C \in \mathcal {C}_p\), consider its birational transform \(\varPhi ^{-1}_{\mathrm {bir}}(C)\) in \({\mathbb {P}}^4\) through x. Now the degrees of the curves \(\varPhi ^{-1}_{\mathrm {bir}}(C)\) for C ranging over \(\mathcal {C}_p\) are bounded above since degrees are lower semi-continuous in families (compare also Lemma 4.4 below, and its proof). Assume without loss of generality that x is the point \((1,1,1,1) \in {\mathbb {C}}^4 \subset {\mathbb {P}}^4\). Now consider the one-parameter subgroups

$$\begin{aligned} \mathrm {diag}(t^a, t^b, t^c, t^d) \subset \mathrm {GL}_4 ({\mathbb {C}}), \quad t \in {\mathbb {C}}^*, \quad a,b,c,d \in {\mathbb {N}}. \end{aligned}$$

These give families of birational maps of \({\mathbb {P}}^4\) via rescaling the coordinates. The orbit closures of these subgroups (which are all isomorphic to \({\mathbb {C}}^*\)) are rational curves in \({\mathbb {P}}^4\) whose degree is unbounded. Hence, one of them is certainly not in the set of curves \(\varPhi ^{-1}_{\mathrm {bir}}(C)\). This achieves our goal. The dynamical degrees of the resulting f are equal to 1 since it is contained in an algebraic subgroup \({\mathbb {C}}^*\) by construction. \(\square \)

Remark 3.5

Note the similarity of the argument used in the proof of (1) of Proposition 3.4 with [2, Prop. 3.1]. Also note that Proposition 3.4 continues to hold for any fourfolds with birationally a conic bundle structure over \({\mathbb {P}}^3\).

One might hope that birational self-maps f with all dynamical degrees equal to 1 are in some sense “classifiable” on a very general cubic fourfolds. Restricting this class even further, the maps whose iterates have bounded growth of the Cremona degrees can be studied. For surfaces, such maps f are often called elliptic and it is known, see [1], that they are precisely those that are virtually isotopic to the identity, that is, on some model, an iterate \(f^{n_0}\) belongs to the connected component of the identity of the (biregular) automorphism group. On varieties of higher dimension, the term elliptic does not seem so appropriate, so we call them bounded maps here for now. Note that not only the dynamical degrees, but also the growth rate of the sequence of Cremona degrees is invariant under birational conjugacy. So bounded maps are a birationally invariant class. These maps have topological entropy equal to zero and hence are what is sometimes called topologically deterministic. If on a very general cubic fourfolds it were true that any such map is a birational automorphism of finite order (we believe this could be true, at least none of the examples we know contradicts it), then Proposition 3.4. (3) would imply that a very general cubic fourfolds is irrational.

Remark 3.6

In part (3) of Proposition 3.4, one can even assume that the sequence of Cremona degrees is constant. This follows from Lemma 3.3: if \(f_t\) is a family of birational self-maps of X parametrized by an algebraic subgroup \({\mathbb {C}}^* \subset \mathrm {Bir}(X)\), then the Cremona degrees are constant outside of a finite set of points in \({\mathbb {C}}^*\). Now \(f_s^n = f_{s^n}\), and for general s, the set of its powers \(s^n\) avoids the previous finite set of points.

4 Upper bounds for dynamical degrees in terms of degrees

For birational maps \(f, g{:}\,{\mathbb {P}}^n \dasharrow {\mathbb {P}}^n\), the kth Cremona degree \(\deg _k\) is submultiplicative in the sense that

$$\begin{aligned} \deg _k (fg) \le \deg _k (f)\deg _k(g) \end{aligned}$$

whence also \(\deg _k(f^n) \le \deg _k(f)^n\) and \(\lambda _k(f) \le \deg _k (f)\); see [9, Lem. 4.6]. As we will see, another application of Theorem 2.1 easily yields a result for certain varieties more general than \({\mathbb {P}}^n\).

We will use the following result.

Lemma 4.1

  1. (1)

    Let be a surjective morphism of smooth projective varieties. For any \(l \in {\mathbb {N}}\), let

    $$\begin{aligned} Y_l := \left\{ y \in Y \mid \dim f^{-1}(y) \ge l \right\} , \end{aligned}$$

    and suppose that V is a subvariety of Y which intersects all irreducible components of the subvarieties \(Y_l\), as l ranges over \({\mathbb {N}}\), as well as their mutual intersections properly. Then the pullback class \(f^*[V]\) in \(A^* (X)\) is represented by \(f^{-1}(V)\) which is equal to the birational transform of V under \(f^{-1}\).

  2. (2)

    Now let \(g{:}\,X_1 \dasharrow X_2\) be a birational map. Pick a resolution of \(g^{-1}\)

    where q is a succession of blowups in subvarieties lying over components of the base locus \(\mathrm {Bs}(g^{-1})\subset X_2\). Suppose that Z is a subvariety of \(X_2\) which satisfies the conditions for V in part (1) with respect to the morphism q and which is also not contained in \(\mathrm {Exc}(g^{-1})\), the union of the subvarieties in \(X_2\) contracted by \(g^{-1}\). Then \(g^*[Z]\) is represented by the birational transform of Z under \(g^{-1}\).

Proof

Part (1) is [5, Thm. A.6 and Thm. 1.23] or [10, Lem. 3.1] and proof of Lem. 3.2(a) ibid. For part (2), we can apply part (1) to conclude that \(q^*[Z]\) is represented by the birational transform of Z under \(q^{-1}\) on \({\widetilde{X}}_2\). But \(g^*[Z]\) is equal to \(p_*q^*[Z]\), and \(p_*\) is an isomorphism onto its image on \(q^*[Z]\) outside of the strict transforms on \({\widetilde{X}}_2\) of the subvarieties contracted by g, hence the claim. \(\square \)

Definition 4.2

We will call a Z as in part (2) of Lemma 4.1 g-adapted.

Theorem 4.3

Let X be a smooth projective variety such that \(H^k_{{\mathbb {R}}}(X)\) is one-dimensional generated by \(H^k\) where \(H\subset X\) is a very ample divisor. For any birational map \(f{:}\,X \dasharrow X\), consider the map defined in Sect. 2. Suppose this map is multiplication by \(\delta _k (f) \in {\mathbb {N}}\). Also suppose that for any birational map \(g {:}\,X \dasharrow X\), there is an \(m\in {\mathbb {N}}\) and a flat family of effective irreducible codimension k cycles homologically equivalent to \(\delta _k(f)mH^k\) over a smooth irreducible base S such that \(\mathcal {C}_{s_0}\) is the birational transform under \(f^{-1}\) of a general element in \(mH^k\), and for general \(s\in S,\,\mathcal {C}_s\) is g-adapted in the sense of Definition 4.2. Then

$$\begin{aligned} \delta _k (f \circ g) \le \delta _k (f) \cdot \delta _k (g). \end{aligned}$$

In particular, \(\lambda _k(f) \le \delta _k (f)\) for such a birational map \(f{:}\,X \dasharrow X\).

To prove Theorem 4.3, we use the following Lemma.

Lemma 4.4

Let X be a smooth and projective variety of dimension n with a very ample class \(H,\,S\) be a smooth variety and let be a flat family of irreducible k-cycles of some fixed degree on \(X \times S,\,\) be the inclusion, and \(g{:}\,X \dasharrow X\) a birational map such that \(g^{-1} \circ \iota _s\) is a well-defined birational map on every fiber \(\mathcal {C}_s\). Then the function

which associates with a point \(s\in S\) the degree of the birational transform of the cycle \(\mathcal {C}_s\) under \(g^{-1} \circ \iota _s\) (with respect to H) is a lower semi-continuous function on S.

Proof

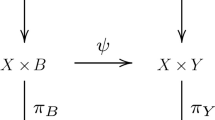
Again we employ Theorem 2.1. Let \(\mathcal {Y} = X \times X \times S\) with projections and . Moreover, for the fiberwise birational map \(g^{-1} \times \mathrm {id}_S{:}\,X \times S \dashrightarrow X \times S\), consider the composite

and (the closure in \(\mathcal {Y}\) of) its graph \(\varGamma _{(g^{-1}\times \mathrm {id}_S)\circ \iota }\).

Consider the cycle \(\alpha =\varGamma _{(g^{-1}\times \mathrm {id}_S)\circ \iota } \cdot p_2^* (H^{i}_S)\) on \(\mathcal {Y}\), where i is chosen appropriately such that \(\alpha _s\) is a zero cycle for all s. Then arguing as in the proof of Lemma 3.3, we find that for general s in S, the degree of \(\alpha _s\) is equal to \( \deg ((g^{-1}\circ i_s)_*(\mathcal {C}_s))\), whereas at special points it only gives an upper bound. Since the degree of \(\alpha _s\) is constant by Theorem 2.1, we get the assertion. \(\square \)

Proof of Theorem 4.3

Replacing \(H^k\) by \(mH^k\), we can assume \(m=1\). Then \(\delta _k (f)\) is the degree of the birational transform under \(f^{-1}\) of a general element \(H^k\), divided by \(H^n\), and the same holds for g. In symbols: \(\frac{f^{*}H^k\cdot H^{n-k}}{H^n}=\delta _k(f)\).

On the other hand, for \(\delta _k (f \circ g)\) we first consider the birational transform \(\mathcal {C}_{s_0}\) under \(f^{-1}\) of a general element \(H^k\), and \(\mathcal {C}_{s_0}\) is now a special element in \(B^k (X)\). We then have to compute the degree of the birational transform under \(g^{-1}\) of \(\mathcal {C}_{s_0}\) and divide it by \(H^n\), and this is \(\delta _k (f \circ g)\).

By hypothesis, we can deform \(\mathcal {C}_{s_0}\) in the homological equivalence class of \(\delta _k (f) H^k\) to a general element \(\mathcal {C}_{s}\) in that class via the family whose existence is assumed in Theorem 4.3. Then the birational transform, for general \(s\in S\), under \(g^{-1}\) of \(\mathcal {C}_s\) is in \(\delta _k(g) \delta _k(f)H^k\) since \(\mathcal {C}_s\) is g-adapted and Lemma 4.1 (2) holds. But the birational transform under \(g^{-1}\) of \(\mathcal {C}_{s_0}\) may lie in \(d H^k\) with \(d \le \delta _k (g) \delta _k (f)\) by Lemma 4.4. Thus Theorem 4.3 follows. \(\square \)

Remark 4.5

For example, Theorem 4.3 is applicable for a birational map \(g{:}\,X \dasharrow X\) of a very general cubic fourfolds, and a reflection \(f = \sigma _p{:}\,X \dasharrow X\) in a point \(p\in X\); in this case, \(\mathcal {C}_{s_0}\) is the birational transform under f of an element which is general in \(H^2\), for some very ample divisor H. Then we can find an irreducible family \(\mathcal {C}\) with the required properties, taking as elements of \(\mathcal {C}\) the birational transforms of 2-cycles A under \(\sigma _q\), for q varying in X and A varying in the system of complete intersections of two hyperplanes \(H^2\).

5 Degrees of iterated birational transforms of surfaces in fourfolds

5.1 An iterative set-up

When computing dynamical degrees, especially \(\lambda _2\) on fourfolds, one frequently has to understand how the degrees of successive birational transforms of some general surface in the initial variety change.

We therefore study the following set-up: let X be a smooth projective fourfolds with a very ample divisor H. Let \(f{:}\,X \dasharrow X\) be a birational map. We want to compute the first and second Cremona degrees of the iterates of f successively. Let \(i\in {\mathbb {Z}}\) be the iteration index.

To begin with, we let \(S_0\subset X\) be a surface which is the intersection of two very general elements in H. In particular, we assume \(S_0\) is smooth. Let

be the inclusion. Moreover, we write \(h_0\subset S_0\) for the intersection with \(S_0\) of a very general element of H. Then \(h_0\) defines a very ample class on \(S_0\). Moreover, we also put \(D_0:= h_0\).

Now suppose inductively that \(S_i\) and a morphism , together with divisors \(h_i, D_i \subset S_i\), have already been defined. We then define \(S_{i+1}\) and \(s_{i+1}\), with \(h_{i+1}\) and \(D_{i+1}\), in the following way. Consider the diagram

Here \(\sigma _i\) is a sequence of blowups of S in reduced points such that the rational map \(f\circ s_i\) becomes a morphism \(s_{i+1}\) on the blown-up surface \(S_{i+1}\). We will describe more precisely how to construct \(\sigma _i\) in a moment. Once this is done, we define

$$\begin{aligned} h_{i+1}= \sigma _i^* (h_i), \quad D_{i+1} = s_{i+1}^* (H) \end{aligned}$$

and we would like to compute the quantities

$$\begin{aligned} d_2^{(i+1)}:= D_{i+1}^2, \quad d_1^{(i+1)} := D_{i+1}\cdot h_{i+1} \end{aligned}$$

in terms of data associated with the resolution map \(\sigma _i\) and of \(d_2^{(i)}, \, d_1^{(i)}\). Note that \(d_2^{(i+1)}\) is the second Cremona degree (with respect to the chosen H) of \(f^{i+1}\), and \(d_1^{(i+1)}\) is its first Cremona degree.

Let us now say how \(\sigma _i\) is defined. The map f can be given by a certain linear system; i.e., there is a line bundle \(\mathcal {L}\) on X, a subspace of sections \(V \subset H^0 (X, \mathcal {L})\) and the associated linear system \(|V| = {\mathbb {P}}(V) \subset {\mathbb {P}}(H^0 (X, \mathcal {L}))\) of divisors defining f. Recall that there is an evaluation morphism for sections which determines a morphism whose image is called the base ideal

$$\begin{aligned} \mathfrak {b}(|V|) \subset \mathcal {O}_X \end{aligned}$$

of the linear system |V|. The closed subscheme \(\mathrm {Bs}(|V|)\subset X\) it defines is called the base scheme of the linear system |V|.

Since \(S_0\) is chosen very general, the image of is not contained in \(\mathrm {Bs}(|V|)\) for any i, and the composite rational map \(f\circ s_i\) is defined by the linear system attached to the pullback space of sections \(s_i^*(V) \subset H^0 (S_i, s_i^*\mathcal {L})\). Its base scheme is defined by the inverse image ideal sheaf \(s_i^{-1}(\mathfrak {b}(|V|))\) which we call \(\mathcal {I}_i\) for the sake of explaining how to construct \(\sigma _i\) with simpler notation. Let \(Z_i\subset S_i\) be the closed subscheme which \(\mathcal {I}_i\) defines.

Now we construct \(\sigma _i\) inductively as a composite of point blowups as follows. Put \(\mathcal {I}^{(0)}_i := \mathcal {I}_i,\,Z_i^{(0)}:= Z_i\) and \(S_i^{(0)}:= S_i\). We wish to construct a sequence of morphisms

where each is a blowup in a finite set of reduced points in \(S_i^{(j)}\).

Step 1 Suppose we have already constructed \(S_i^{(j)}\) together with \(\mathcal {I}^{(j)}_i,\,Z_i^{(j)}\). Then if \(Z^{(j)}_i\) is zero-dimensional, we put \(Z^{(j)}_i (\mathrm {point}) := Z^{(j)}_i\). If \(Z^{(j)}_i\) is one-dimensional, then we can write

$$\begin{aligned} Z^{(j)}_i = \mathfrak {D}^{(j)}_i \cup \mathfrak {E}^{(j)}_i, \end{aligned}$$

where \(\mathfrak {D}^{(j)}_i\) is the union of the one-dimensional isolated components in a primary decomposition of \(\mathcal {I}^{(j)}_i\). These define a unique divisor \( \mathfrak {D}^{(j)}_i\), whereas \(\mathfrak {E}^{(j)}_i\), which may contain embedded point components, is not unique: recall for example that locally around the origin in \({\mathbb {A}}^2\), the ideal \((xy,y^2)\) can be written in many ways as an intersection of primary ideals:

$$\begin{aligned} (xy,y^2) = (y) \cap (x^2, xy, y^2, x+ \alpha y), \quad \alpha \in {\mathbb {C}}, \end{aligned}$$

and the embedded point component defined by any \((x^2, xy, y^2, x+ \alpha y)\) is not unique at all. Let \(\mathcal {O} (- \mathfrak {D}^{(j)}_i)\) be the ideal sheaf of \(\mathfrak {D}^{(j)}_i\), and put

$$\begin{aligned} Z^{(j)}_i (\mathrm {point}) := V \left( \left( \mathcal {I}^{(j)}_i : \mathcal {O} (- \mathfrak {D}^{(j)}_i) \right) \right) , \end{aligned}$$

which is a well-defined ideal sheaf with support in a finite set of points. Note that whereas the embedded point components are not well-defined, the quotient ideal sheaf \( \left( \mathcal {I}^{(j)}_i : \mathcal {O} (- \mathfrak {D}^{(j)}_i) \right) \) is and defines a certain zero-dimensional subscheme \(Z^{(j)}_i (\mathrm {point})\). In the example above, it is just the reduced origin corresponding to (x, y).

Step 2 Define as the blowup of \(S_i^{(j)}\) in the reduced subscheme (a finite set of points) whose support agrees with \(Z^{(j)}_i (\mathrm {point})\). Let

$$\begin{aligned} Z^{(j+1)}_i:=\pi _j^{-1} (Z^{(j)}_i (\mathrm {point}) ) \end{aligned}$$

be the scheme-theoretic preimage with ideal sheaf \(\mathcal {I}_i^{(j+1)}\). In other words, if \(\mathcal {I}^{(j)}_i (\mathrm {point})\) is the ideal sheaf of \(Z^{(j)}_i (\mathrm {point})\), the subscheme \(Z^{(j+1)}_i\subset S_i^{(j+1)}\) is defined by the ideal sheaf which is the image of \(\pi _j^*(\mathcal {I}^{(j)}_i (\mathrm {point}))\) in \(\mathcal {O}_{S^{(j+1)}_i}\). This is, by definition, the inverse image ideal sheaf \(\pi _j^{-1}(\mathcal {I}^{(j)}_i (\mathrm {point}))\). It is not necessarily principal of course, since we have blown up in the reduced subscheme underlying \(Z^{(j)}_i (\mathrm {point})\), and not in \(Z^{(j)}_i (\mathrm {point})\) itself.

At any rate, it is easy to compute \(Z^{(j+1)}_i\) in local coordinates on the blown-up surface simply by substituting these in the original ideal downstairs. With \(Z^{(j+1)}_i\) now go back to Step 1. The process terminates since the length of the scheme \(Z^{(j)}_i (\mathrm {point})\) drops strictly in each step until it becomes the empty set.

It is now easy to describe what \(D_{i+1}\) is on \(S_{i+1}= S^{(N)}_{i+1}\). In particular, this then allows us to compute \(d_2^{(i+1)}= D_{i+1}^2, \, d_1^{(i+1)} = D_{i+1}\cdot h_{i+1}\). If D is a divisor which lives on some surface in the tower

then we denote the pullback of D to the top floor \(S_{i+1}\) of the tower simply by putting a hat on it: \(\hat{D}\). Then

$$\begin{aligned} D_{i+1} = \hat{D}_i - \sum _j \hat{\mathfrak {D}}^{(j)}_i. \end{aligned}$$

5.2 Geometry of a reflection on a cubic fourfolds

As an illustration, let us prove a result about equality of dynamical degrees when X is a very general cubic fourfolds and f is a certain suitably general composition of reflections in points on X. We will say what suitably general means below.

First we recall some facts about the geometry of a reflection \(\sigma _p{:}\,X \dasharrow X\) on a smooth cubic fourfolds in a very general point p. Compare [4, Sect. 3] for these. A general line in \({\mathbb {P}}^5\) through p intersects X in two points away from p, and \(\sigma _p\) is the birational involution interchanging these points. One main fact we will use is that the birational self-map \(\sigma _p\) lifts to an automorphism \({\widetilde{\sigma }}_p\) on a suitable model \({\widetilde{X}}\):

and we can construct \({\widetilde{X}}\) in two steps , where each map is a blowup in a certain smooth center. See Fig. 1 for a schematic picture, which we will explain now in some more detail.

Fig. 1
figure 1

Geometry of the resolution of a reflection

Full size image

The embedded tangent hyperplane \({\mathbb {T}}_pX\) intersects X in a cubic threefold Y(p) with a node at p; the lines on X through p sweep out a surface S(p) which coincides with the surface of lines on Y(p). The tangent cone to Y(p) in p is a cone over a smooth quadric \(Q \simeq {\mathbb {P}}^1\times {\mathbb {P}}^1\) in the hyperplane \({\mathbb {P}}^3_{\infty } \subset {\mathbb {T}}_pX\), and S(p) is a cone over a curve C of bidegree (3, 3) in Q. The indeterminacy locus of \(\sigma _p\) is S(p), and \(\sigma _p\) contracts Y(p) to the point p.

Definition 5.1

We call a point \(p\in X\) good if C is a smooth curve.

A general point p will be good. To simplify, we will only consider reflections in good points in the sequel. Now is the blowup of X in p with exceptional divisor \(E'(p) \simeq {\mathbb {P}}(T_pX) \simeq {\mathbb {P}}^3\). Inside \(E'(p)\) we retrieve \(Q \simeq {\mathbb {P}}^1\times {\mathbb {P}}^1\) as the set of all tangent directions of smooth curve germs in Y(p) through p, and inside this, there is a copy of C, the set of directions of lines on X through p. The strict transform \(Y'(p)\) of Y(p) on \(X'\) is the blowup of Y(p) in the node, which gets replaced by \({\mathbb {P}}^1\times {\mathbb {P}}^1\simeq Q\). The strict transform \(S'(p)\) of S(p) on \(X'\) is smooth because p is a good point.

Now is the blowup of \(X'\) in \(S'(p)\). We call the resulting exceptional divisor \({\widetilde{F}}(p)\). It is a \({\mathbb {P}}^1\)-bundle over \(S'(p)\). The strict transform of \(Y'(p)\) on \({\widetilde{X}}\) is called \(\widetilde{Y}(p)\). The strict transform of \(E'(p)\) on \({\widetilde{X}}\), denoted by \({\widetilde{E}}(p)\), is the blowup of \(E'(p)\) in C. We also denote by \({\widetilde{H}}\) the pullback of a hyperplane section H to \({\widetilde{X}}\) via the modification .

Proposition 5.2

  1. (1)

    The classes \({\widetilde{H}}, {\widetilde{E}}(p), {\widetilde{F}}(p)\) are a basis of \(\mathrm {Pic}({\widetilde{X}})\). Moreover,

    $$\begin{aligned} \widetilde{Y}(p) \equiv {\widetilde{H}} - 2{\widetilde{E}}(p) - {\widetilde{F}}(p) \end{aligned}$$
    (5.1)

    and

    $$\begin{aligned}&({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) \equiv 2 {\widetilde{H}} - 3 {\widetilde{E}}(p) - {\widetilde{F}}(p), \end{aligned}$$
    (5.2)
    $$\begin{aligned}&({\widetilde{\sigma }}_p)^* ({\widetilde{E}}(p)) \equiv \widetilde{Y}(p)\equiv {\widetilde{H}} - 2{\widetilde{E}}(p) - {\widetilde{F}}(p), \end{aligned}$$
    (5.3)
    $$\begin{aligned}&({\widetilde{\sigma }}_p)^* ({\widetilde{F}}(p)) \equiv {\widetilde{F}}(p). \end{aligned}$$
    (5.4)
  2. (2)

    We have

    $$\begin{aligned}&({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) \cdot \widetilde{Y}(p) \equiv 0, \end{aligned}$$
    (5.5)
    $$\begin{aligned}&{\widetilde{H}} \cdot {\widetilde{E}}(p) \equiv 0. \end{aligned}$$
    (5.6)
  3. (3)

    We have

    $$\begin{aligned}&({\widetilde{\sigma }}_p)^* ({\widetilde{H}})^2 \equiv 2{\widetilde{H}}^2+3{\widetilde{E}}(p)\cdot {\widetilde{E}}(p) - {\widetilde{F}}(p)\cdot {\widetilde{H}} + {\widetilde{E}}(p)\cdot {\widetilde{F}}(p), \end{aligned}$$
    (5.7)
    $$\begin{aligned}&-\widetilde{Y}(p)^2 \equiv {\widetilde{H}}^2 - 2\left( - {\widetilde{E}}(p)^2\right) - {\widetilde{H}}\cdot {\widetilde{F}}(p) + {\widetilde{E}}(p)\cdot {\widetilde{F}}(p). \end{aligned}$$
    (5.8)

Proof

Part (1) is straightforward and can be found in [4, Sect. 3, Prop. 3.2 ff]. As for (2), note that by the projection formula

$$\begin{aligned} ({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) \cdot \widetilde{Y}(p) \equiv {\widetilde{H}} \cdot ({\widetilde{\sigma }}_p)_* (\widetilde{Y}(p)) \equiv {\widetilde{H}}\cdot {\widetilde{E}}(p) \equiv 0 \end{aligned}$$

since a general hyperplane section H of X does not meet p.

For (3) we compute

$$\begin{aligned} ({\widetilde{\sigma }}_p)^* ({\widetilde{H}})^2&\equiv ({\widetilde{\sigma }}_p)^* ({\widetilde{H}})\cdot ({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) - ({\widetilde{\sigma }}_p)^* ({\widetilde{H}})\cdot \widetilde{Y}(p)\\&\equiv ({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) \cdot ( ({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) - \widetilde{Y}(p))\\&\equiv (2 {\widetilde{H}} - 3 {\widetilde{E}}(p) - {\widetilde{F}}(p) ) \cdot ({\widetilde{H}} - {\widetilde{E}}(p))\\&\equiv 2 {\widetilde{H}}\cdot {\widetilde{H}} - 3 {\widetilde{H}}\cdot {\widetilde{E}}(p) - {\widetilde{H}}\cdot {\widetilde{F}}(p) - 2{\widetilde{H}}\cdot {\widetilde{E}}(p) + 3 {\widetilde{E}}(p)\cdot {\widetilde{E}}(p) + {\widetilde{F}}(p)\cdot {\widetilde{E}}(p)\\&\equiv 2{\widetilde{H}}\cdot {\widetilde{H}}+3{\widetilde{E}}(p)\cdot {\widetilde{E}}(p) - {\widetilde{F}}(p)\cdot {\widetilde{H}} + {\widetilde{E}}(p)\cdot {\widetilde{F}}(p), \end{aligned}$$

where one uses the second formula of (2) (\({\widetilde{H}} \cdot {\widetilde{E}}(p) \equiv 0\)) in the last step and the first formula of (2) in the first step. Now

$$\begin{aligned} -\widetilde{Y}(p)^2&\equiv ({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) \cdot \widetilde{Y}(p) - \widetilde{Y}(p)^2\\&\equiv (({\widetilde{\sigma }}_p)^* ({\widetilde{H}}) - \widetilde{Y}(p) ) \cdot \widetilde{Y}(p)\\&\equiv ({\widetilde{H}} - {\widetilde{E}}(p))\cdot ({\widetilde{H}} - 2{\widetilde{E}}(p) - {\widetilde{F}}(p))\\&\equiv {\widetilde{H}}^2 - 2{\widetilde{H}}\cdot {\widetilde{E}}(p) - {\widetilde{H}}\cdot {\widetilde{F}}(p) - {\widetilde{E}}(p)\cdot {\widetilde{H}}(p) + 2{\widetilde{E}}(p)^2 + {\widetilde{E}}(p)\cdot {\widetilde{F}}(p)\\&\equiv {\widetilde{H}}^2 + 2{\widetilde{E}}(p)^2 - {\widetilde{H}}\cdot {\widetilde{F}}(p) + {\widetilde{E}}(p)\cdot {\widetilde{F}}(p). \end{aligned}$$

\(\square \)

Now we pass to an iterative setup again. Namely, consider a sequence of points \(\{ p_i \}_{i =1, 2, \ldots }\) on X and the corresponding sequence of reflections \(\{ \sigma _{p_i} \}_{i=1, \ldots }\) Take a surface \(S_0 \subset X\) which is the intersection of two very general elements in H, and let \(h_0\subset S_0\) be the intersection of \(S_0\) with a very general element in H. Thus \(S_0\) and \(h_0\) are, respectively, a smooth cubic surface and a smooth cubic curve on X. We want to study the successive birational transforms of \(S_0\) and \(h_0\) when we apply \(\sigma _{p_1}\), then \(\sigma _{p_2},\,\sigma _{p_3}\) and so forth. In particular, we want to study the degrees of those birational transforms. Let

$$\begin{aligned} d_1^{(i)},\,\,d_2^{(i)} \end{aligned}$$

be the degrees, respectively, of the birational transforms of \(h_0\) resp. \(S_0\) under \(\sigma _{p_i}\circ \cdots \circ \sigma _{p_1}\). To study iterates of a single map, let us assume that the sequence of points is periodic with period N, i.e.,

$$\begin{aligned} p_{i+N} = p_i\quad \forall i. \end{aligned}$$

Let us also assume that all the points \(p_i\) are good. The growth rates of the degrees \(d_1^{(i)}\) resp. \(d_2^{(i)}\) for are then the first resp. second dynamical degrees of the composite

$$\begin{aligned} \sigma _{p_N} \circ \cdots \circ \sigma _{p_1}. \end{aligned}$$

To compute the degrees, we first define a sequence of auxiliary surfaces \(S_i\) with morphisms inductively as follows: for \(i=0,\,S_0\) has already been defined, and \(s_0\) is the inclusion into X. Suppose now has been defined. Look at the commutative diagram

(5.9)

Here is the modification described above: blow up the point \(p_{i+1}\) on X and then the strict transform of the surface of lines through \(p_{i+1}\). The morphism is a composite of blowups in reduced points, constructed in the way described at the beginning of this section, such that the diagonal dotted arrow becomes a morphism \({\widetilde{s}}_i\). Then \(s_{i+1}\) is simply the composite

$$\begin{aligned} s_{i+1} = \mu _{i+1}\circ {\widetilde{\sigma }}_{p_{i+1}} \circ {\widetilde{s}}_i. \end{aligned}$$

Now, in the notation of Proposition 5.2, we have divisor classes \({\widetilde{H}}_{i+1}, {\widetilde{E}}(p_{i+1}),\) \( {\widetilde{F}}(p_{i+1}), \widetilde{Y}(p_{i+1})\) and \(({\widetilde{\sigma }}_{p_{i+1}})^*({\widetilde{H}}_{i+1})\) on \({\widetilde{X}}_{i+1}\) and we give names to their pullbacks via \({\widetilde{s}}_i\) to \(S_{i+1}\):

$$\begin{aligned} D_{i+1}:= & {} ({\widetilde{s}}_i)^* (({\widetilde{\sigma }}_{p_{i+1}})^*({\widetilde{H}}_{i+1})), \\ E_{i+1}:= & {} ({\widetilde{s}}_i)^* ({\widetilde{E}}(p_{i+1})), \\ F_{i+1}:= & {} ({\widetilde{s}}_i)^* ( {\widetilde{F}}(p_{i+1})), \\ Y_{i+1}:= & {} ({\widetilde{s}}_i)^* ( \widetilde{Y}(p_{i+1})). \end{aligned}$$

Note that by the commutativity of the diagram (5.11), the equality

$$\begin{aligned} ({\widetilde{s}}_i)^* ({\widetilde{H}}_{i+1})&=({\widetilde{s}}_i)^* (\mu _{i+1}H)=\pi _{i+1}^*s_i^*H\\&=\pi _{i+1}^*({\widetilde{s}}_{i-1}^*{\widetilde{\sigma }}_{p_i}^*\mu _i^*H)=\pi _{i+1}^* (D_i) \end{aligned}$$

holds, so we do not need a new name for \(({\widetilde{s}}_i)^* ({\widetilde{H}}_{i+1})\). Then the morphism is defined by the linear system \(|D_i|\), i.e., \(s_i^*(H) = D_i\). Moreover, we make the following simplifying notational convention: if some divisor class D lives on \(S_j\), then for any \(i > j\) we denote the pullback of D to \(S_i\) via the composite

simply by the same letter D. Thus, for example, \(h_0\subset S_0\) defines a class on each surface \(S_i\) by pullback, and we denote all of them by the same letter, where, in a given equation, the context makes it clear on which \(S_i\) this holds.

Now all Eqs. (5.1)–(5.8) give equations on any surface \(S_{i+1}\) by pulling the divisors back via \({\widetilde{s}}_i\). However, we want to impose a certain genericity condition on the points \(p_1, \ldots , p_N\) such that these equations take a simpler form.

Assumption 5.3

The N-periodic sequence of good points \(p_i\) can be chosen such that for a very general \(S_0\) and \(h_0\), the following equations hold on any blown-up surface \(S_{i+1}\):

$$\begin{aligned} F_{i+1}\cdot \,D_i = 0, \quad E_{i+1}\cdot F_{i+1} = 0. \end{aligned}$$

In fact, we will assume something a little bit stronger, which implies the previous assumption, but can be expressed more geometrically in terms of the successive birational transforms of \(S_0\):

Assumption 5.4

The N-periodic sequence of good points \(p_i\) can be chosen such that for a very general \(S_0\) and \(h_0\), the surface \(s_i(S_i) \subset X\) is \(\sigma _{p_{i+1}}\)-adapted in the sense of Definition 4.2 except for the following phenomenon which we allow to cause failure of \(\sigma _{p_{i+1}}\)-adaptedness: for a point \(p_{k}\) there can be a point \(p_{\tau (k)}\) such that all points

$$\begin{aligned} \sigma _{p_l}\circ \cdots \circ \sigma _{p_{k+1}}(p_k), \quad k\le l \le \tau (k)-2 \end{aligned}$$

land in the open set where \(\sigma _{p_{l+1}}\) is a local isomorphism onto the image, and

$$\begin{aligned} p_{\tau (k)}= \sigma _{p_{\tau (k) -1}}\circ \cdots \circ \sigma _{p_{k+1}}(p_k). \end{aligned}$$

Moreover, the birational transform \(s_{\tau (k)-1}(S_{\tau (k)-1}) \subset X\) is such that its strict transform in \(X'_{\tau (k)}\) (obtained from X by blowing up the point \(p_{\tau (k)}\)) meets the exceptional divisor in a curve, \(\varGamma _{\tau (k)}\) say, which does not coincide with the curve \(C_{\tau (k)}\) of directions of lines through \(p_{\tau (k)}\). In fact, this condition ensures that \(E_{\tau (k)}\cdot F_{\tau (k)} =0\) on \(S_{\tau (k)}\): this is clear if \(\varGamma _{\tau (k)}\) and \(C_{\tau (k)}\) are even disjoint; but if they meet in only finitely many points, then, looking back at Fig. 1, we find that \(S_{\tau (k)}\) can be viewed as a blowup of a surface \(S'_{\tau (k)}\) such that \(E_{\tau (k)}\) is a pullback of a divisor on \(S'_{\tau (k)}\) and \(F_{\tau (k)}\) is exceptional for \(\pi \).

Intuitively, we can express Assumption 5.4 by saying that we allow a curve in a certain birational transform of \(S_0\) to be contracted to a reflection point \(p_k\) at some stage of the iteration, and this point then wanders around, always staying in the domain of definition and away from the exceptional locus of the respective next reflection, until at some later time it gets mapped to \(p_{\tau (k)}\) after applying \(\sigma _{p_{\tau (k)-1}}\). We then also assume that the directions of smooth curve germs which lie on the birational transform \(s_{\tau (k)-1}(S_{\tau (k)-1}) \subset X\) and which pass through \(p_{\tau (k)}\) are not identical with the directions of lines through \(p_{\tau (k)}\).

In this way, we will always have \(E_{i+1}\cdot F_{i+1}=0\) under Assumption 5.4 as well as \(F_{i+1}\cdot D_i = 0\) since the birational transforms of \(S_0\) intersect the surfaces of lines attached as indeterminacy loci to subsequent reflections only in points. Thus Assumption 5.4 is stronger than Assumption 5.3. Moreover, we then have the successor function , which associates with k the value \(\tau (k)\) if \(p_k\) gets mapped to \(p_{\tau (k)}\) after a while as in Assumption 5.4, or is equal to \(\infty \) if there is no successor (if the point never gets mapped unto another reflection point).

For the time being, we will not discuss whether the genericity Assumption 5.4 can be satisfied by a certain configuration of points \(p_1, \ldots , p_N\) on X. Also, this is not so important from our point of view. Rather, we would like to demonstrate that one can prove that some property (P) of dynamical degrees forces special geometric configurations on X, or conversely, that for suitably general configurations, the dynamical degrees fail to have property (P), if the configuration is realizable. The following result is a sample for this.

Theorem 5.5

Suppose that \(\{ p_i \}\) is an N-periodic sequence of good points on X which satisfy Assumption 5.4. Then the first and second dynamical degrees of the map

$$\begin{aligned} \sigma _{p_N} \circ \cdots \circ \sigma _{p_1} \end{aligned}$$

are equal.

Proof

Under the hypotheses, we have the equations on \(S_{i+1}\)

$$\begin{aligned} D_{i+1}^2 = 2 D_{i}^2 + 3 E_{i+1}^2,\\ -Y_{i+1}^2 = D_i^2 - 2\left( -E_{i+1}^2\right) \end{aligned}$$

from (5.1), (5.2), and from (5.7) and (5.8)

$$\begin{aligned} D_{i+1}\cdot h_0 = 2D_{i}\cdot h_0 - 3 E_{i+1}\cdot h_0,\\ Y_{i+1}\cdot h_0 = D_i\cdot h_0 - 2E_{i+1}\cdot h_0 \end{aligned}$$

since \(F_{i+1}.h_0 =0\) because \(F_{i+1}\) lies over points in \(S_0\). Note that these equations are valid universally, but \(E_{i+1}\) may very well be zero, and indeed will be unless \(i+1\) is of the form \(\tau (k)\). Now note that

$$\begin{aligned} d_2^{(i+1)}= D_{i+1}^2, \quad d_1^{(i+1)} = D_{i+1}\cdot h_0 \end{aligned}$$

and abbreviate

$$\begin{aligned} t_2^{(i+1)}:= -Y_{i+1}^2, \quad t_1^{(i+1)}:= Y_{i+1}\cdot h_0. \end{aligned}$$

Moreover, note that under our geometric Assumption 5.4, we have

$$\begin{aligned} E_{\tau (k)} = Y_k. \end{aligned}$$

Thus we get the recursions

$$\begin{aligned} d_2^{(i+1)}= & {} 2 d^{(i)}_2 - 3 t_2^{(\tau ^{-1}(i+1))}, \end{aligned}$$
(5.10)
$$\begin{aligned} t_2^{(i+1)}= & {} d_2^{(i)} - 2 t_2^{(\tau ^{-1}(i+1))}, \end{aligned}$$
(5.11)

where we agree to put

$$\begin{aligned} t_2^{(\tau ^{-1}(i+1))} := 0 \; \mathrm {if} \; \tau ^{-1}(i+1)= \emptyset \end{aligned}$$

by definition. Also,

$$\begin{aligned} d_1^{(i+1)}= & {} 2 d^{(i)}_1 - 3 t_1^{(\tau ^{-1}(i+1))}, \end{aligned}$$
(5.12)
$$\begin{aligned} t_1^{(i+1)}= & {} d_1^{(i)} - 2 t_1^{(\tau ^{-1}(i+1))}. \end{aligned}$$
(5.13)

Note that \(\tau ^{-1}(1) = \emptyset \). Hence, the two sequences \(d^{(i)}_1\) and \(d^{(i)}_2\) are determined by the same set of recursions, starting from \(d^{(0)}_1=d^{(0)}_2=3,\,t_1^{(0)}=t_2^{(0)}=0\), and thus coincide. In particular, the first and second dynamical degrees of \(\sigma _{p_N} \circ \cdots \circ \sigma _{p_1}\) are equal. \(\square \)

Remark 5.6

In the setup of Theorem 5.5, put

$$\begin{aligned} C:= \mathrm {l.c.m.}_{i=1, \ldots , N} \left\{ N, \tau (1) -1, \tau (2) -2, \ldots , \tau (N) -N \right\} . \end{aligned}$$

Then the recursions (5.11), (5.12) resp. (5.13), (5.14) show that there is a \(2C\times 2C\) matrix M (with constants as entries) such that for the vectors

$$\begin{aligned} v_1^{(i)}= & {} \left( d^{(C+iC)}_1, \ldots , d_1^{(1+iC)}, t_1^{(C+iC)}, \ldots , t_1^{(1+iC)}\right) ,\\ v_2^{(i)}= & {} \left( d^{(C+iC)}_2, \ldots , d_2^{(1+iC)}, t_2^{(C+iC)}, \ldots , t_2^{(1+iC)}\right) , \end{aligned}$$

we have

$$\begin{aligned} v_1^{(i+1)} = Mv_1^{(i)}, \quad v_2^{(i+1)} = M v_2^{(i)}. \end{aligned}$$

This can be used to compute the dynamical degrees for concretely given successor functions \(\tau \). Under certain generality assumptions, they will be equal to the spectral radius of M.