Abstract
This paper proposes a mathematical model and formalism to study coded exposure (flutter shutter) cameras. The model includes the Poisson photon (shot) noise as well as any additive (readout) noise of finite variance. This is an improvement compared to our previous work that only considered the Poisson noise. Closed formulae for the mean square error and signal to noise ratio of the coded exposure method are given. These formulae take into account for the whole imaging chain, i.e., the Poisson photon (shot) noise, any additive (readout) noise of finite variance as well as the deconvolution and are valid for any exposure code. Our formalism allows us to provide a curve that gives an absolute upper bound for the gain of any coded exposure camera in function of the temporal sampling of the code. The gain is to be understood in terms of mean square error (or equivalently in terms of signal to noise ratio), with respect to a snapshot (a standard camera).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background
Since the seminal papers [1–6] of Agrawal and Raskar coded exposure (flutter shutter) method has received a lot of follow-ups [7–39]. In a nutshell, the authors proposed to open and close the camera shutter, according to a sequence called “code,” during the exposure time. By this clever exposure technique, the coded exposure method permits one to arbitrarily increase the exposure time when photographing (flat) scenes moving at a constant velocity. Note that with a coded exposure method only one picture is stored/transmitted. A rich body of empirical results suggest that the coded exposure method allows for a gain in terms of Mean Square Error (MSE) or Signal to Noise Ratio (SNR) compared to a classic camera, i.e., a snapshot. Therefore, the coded exposure method seems to be a magic tool that should equip all cameras.
We now briefly expose the different applications, variants, and studies that surround the coded exposure method. An application of the coded exposure method to bar codes is given in [16, 35], to fluorescent cell image in [27], to periodic events in [25, 34, 36], to multi-spectral imaging in [10], and to iris in [21]. Application to motion estimation/deblurring are presented in [9, 19, 20, 26, 31, 33, 37, 38]. An extension for space-dependent blur is investigated in [28]. Methods to find better or optimal sequences as investigated in [12–14, 22, 23, 39] or in [15] that aims at adapting the sequence to the velocity. Diverse implementations of the method are presented in [17, 18, 24, 32]. The method is used for spatial/temporal trade-off in [7, 8, 11]. A numerical and mathematical investigation of the gain of the method is in [29, 30] but their camera model contains only photon (shot) noise and neglects all other noise sources, contrarily to the model we shall develop in this paper.
Therefore, as far as we know, little is known on the coded exposure method from a rigorous mathematical point of view and it seems useful for the applications to build a theory to shed some light on this promising coded exposure method. For instance, to the best of our knowledge, little is know on the gain, in terms of MSE and SNR, of this coded exposure method compared to a standard (snapshot) camera. This paper proposes a mathematical model of photon acquisition by a light sensor. The model can cope with any additive readout noise of finite variance in addition to the Poisson photon (shot) noise. The model is compatible with the Shannon–Whittaker framework, assumes that the relative camera scene velocity is constant and known, that the sensor does not saturate, that the readout noise has finite variance and that the coded exposure method allows for an invertible transformation among the class of band-limited functions (this means that the observed image can be deblurred using a filter). Note that with this model the image has a structure: the image is assumed to be band limited. This set of assumptions represents an ideal mathematical framework that allows us to give a rigorous analysis of the limits, in terms of MSE and SNR, of the coded exposure method. For instance, it is clear that the MSE (resp. SNR) will increase (resp. decrease) if one needs to estimate the velocity from the observed data, compared to the formulae we shall prove in this theoretical paper.
To be thorough, a mathematical analysis of a camera requires to go rigorously from the continuous observed scene to the discrete samples of the final restored image. This is needed to mathematically analyze the whole image chain: from the photon emission to the final restored image via the observed discrete samples measured by the camera. As far as we know, the coded exposure method is very useful for moving scenes. Consequently, we need a formalism capable of dealing with moving scenes. Since the observed scene moves continuously with respect to the time we adopt a continuous point of view. This means that we shall model the observed scene as a function s. Loosely speaking, s(x) give the light intensity at a spatial position x (by opposition, a discrete formalism would model the observed scene as a vector of \(\mathbb {R}^n\) but requires a more restrictive assumption, see below). We shall rely on the Shannon–Whittaker framework (see, e.g., [40]) to perform the mathematical analysis of sampling-related questions. This framework requires the structure of band-limited (with a cutoff frequency) signals or images and will allow us to perform a rigorous mathematical analysis of the coded exposure method. Recall that a discrete formalism would model the observed scene as a vector of \(\mathbb {R}^n\) and the convolution would use Toepliz matrices. Therefore, the scene would be assumed to be periodic and also band limited for sampling purposes. Note that the continuous formalism that we shall develop in this paper does not require to assume that the observed scene s is periodic (most natural scenes are not periodic). However, the adaptation of the formalism that we shall develop in this paper to periodic band-limited scene is straightforward if needed for some application.
Our first goal is to provide closed mathematical formulae that give the MSE and SNR of images obtained by a coded exposure camera. Therefore, we shall start by carefully modeling the photon acquisition by a light sensor then deduce a mathematical model of the coded exposure method.
The mathematical model of camera that we shall develop in this paper has not, to the best of our knowledge, been developed in the existing literature on the coded exposure method. Indeed, the model we shall develop in this paper is able to cope with the Poisson photon (shot) noise in addition to any additive (sensor readout) noise of finite variance and does not require to assume that the observed scene is periodic. For example, the model developed in [30] does not consider any additive (sensor readout) noise. The formulae that give the MSE and SNR of the final crisp image
-
Assume the Shannon–Whittaker framework that (1) requires band-limited (with a frequency cutoff) images, and that (2) the pixel size is designed according to the Shannon–Whittaker theory. In this paper, we prove the validity of the Shannon–Whittaker for non-stationary noises (see also Sect. 2.2).
-
Assume that the relative camera scene velocity is constant and known.
-
Assume that the sensor does not saturate.
-
Assume that the additive (sensor readout) noise has zero mean and finite variance (this term contains, without loss of generality, the quantization noise).
-
Assume that the coded exposure allows for an invertible transformation among the class of band-limited functions (this means that the observed image can be deblurred using a filter).
-
Neglects the boundaries effects for the deconvolution (the inverse filter of a coded exposure camera has larger support than the inverse filter of a snapshot. Thus, this slightly overestimates the gain of the coded exposure method with respect to the snapshot).
We assume that the sensor readout (additive) noise has zero mean. However, with our formalism, the adaptation to non-zero mean additive (sensor readout) noise is straightforward if needed for some application. This zero mean assumption for the additive noise can be found in e.g., [41, 1st paragraph and Eqs. (22)–(25)]. It can also be found in [42, p. 2, 3rd paragraph] and [43, p. 554, column 2, “noise model” paragraph] (for HDR sensors). It is also common for CMOS (3T) APS sensors, see, e.g., [44, p. 179, paragraph 2] and certain infrared sensors (microbolometers), see, e.g., [45, p. 98] that states that these devices have the readout noise of a CMOS device.
The paper is organized as follows. Section 2 gives a mathematical model of classic cameras. This mathematical model is extended in Sect. 3 to model coded exposure cameras. Section 4 gives an upper bound for the gain of the coded exposure method, in terms of MSE and SNR with respect to a snapshot, in function of the temporal sampling of the code. The upper bound of Corollary 4.2 is illustrated on Fig. 2. In addition, Table 1 provides numerical experiments illustrating these results. The Appendix A–L contain several proofs of propositions that are used throughout this paper. A glossary of notations is in Appendix M (in the sequel latin numerals refer to the glossary of notations).
2 A mathematical model of classic cameras
The goal of this section is to provide a mathematical model of the photon acquisition by a light sensor and the formalism that we shall use to model the coded exposure method in the sequel.
As usual in the coded exposure literature [2, 3, 9, 21, 22, 30, 35, 46] and for the sake of the clarity we shall formalize the coded exposure method using a one-dimensional framework. In other words, the sensor array and the observed image are assumed be one-dimensional. One could think that this one-dimensional framework is a limitation of the theory. However, this one-dimensional framework is no limitation. Indeed, as we have seen, we assume that the image acquisition obeys the Shannon–Whittaker sampling theory. This means that the frequency cutoff is compatible with the image grid sampling. The extension to any two-dimensional grid (and two-dimensional images) is straightforward (the sketch of the proof is in Appendix A). Therefore, the one-dimensional framework that we shall consider is no limitation for the scope of this paper that proposes a mathematical analysis of coded exposure cameras. A fortiori, the calculations of MSE and SNR that we shall propose in this paper remain valid for two-dimensional images. The noise is, in general, non-stationary. This due both to the sensor (see, e.g., [47]) and to the observed scene. In this paper, we also prove the validity of the Shannon–Whittaker interpolation is valid for non-stationary noises (see also Sect. 2.2). In addition, we shall assume that the motion blur kernel is known, i.e., the relative camera scene velocity vector and the exposure code (or function) are known (this kernel is called “PSF motion” in, e.g., [1] and is also assumed to be known [1, p. 2]).
We now turn to the mathematical model of photons acquisition by a light sensor.
2.1 A mathematical model of photons acquisition by a light sensor
The goal of this subsection is to give a rigorous mathematical definition (see Definition 2) of the samples produced by a pixel sensor that observes a moving scene. This definition of the observed sample can cope with any additive zero mean (sensor readout) noise of finite variance in addition to the standard Poisson photon (shot) noise. Note that the model developed in [30] do not consider any additive (sensor readout) noise. Therefore, the results of [30] do not include this more elaborated mathematical model. In particular, the advantages of the coded exposure method in terms of MSE, with this more elaborated set up, are, to the best of our knowledge, open questions.
We consider a continuous formalism in order to ease the transition from steady scenes to scenes moving at an arbitrary real velocity. Another advantage of this continuous formalism is that it allows us to avoid the implicit periodic assumption of the observed scene needed if one uses Toeplitz matrices to represent the convolutions see, e.g., [1, Eq. 2, p. 3] (this is needed because, in general, natural scenes are not periodic).
We now sketch the construction of our camera model. We first consider the photon emission, and finally include the optical and sensor kernels, then include the effect of the exposure time and of the motion to our model. The lasts two steps consists in adding the Poisson photon (shot) noise and the additive (sensor readout) noise to our camera model. The camera model that we shall consider in this paper is depicted in Fig. 1.
Schematic diagram of our camera model. The observed scene emits light and moves at velocity \(v \in \mathbb {R}\). The light undergoes the blur of the optical system and is measured by a pixel sensor. The pixel sensor produces a Poisson random variable (shot noise) that is further corrupted by an additive (sensor readout) noise of finite variance to produce the observed sample
We assume that the observed scene emits photons at a deterministic rate s defined by
Here and in the sequel, the variable \(x\in \mathbb {R}\) represents the spatial position (we will precise the unit of x, i.e., the unit we shall use to measure distances when we introduce the pixel sensor). Intuitively, \(s\) represents the ideal crisp image, i.e., the image that one would observed if there were no noise whatsoever, no motion, with a perfect optical system (formally the point spread function is a Dirac-mass) and the pixel sensor has an infinitesimal area. In a nutshell, \(s(x)\) would be the gray-level of the image at position \(x \in \mathbb {R}\) in the idealistic case mentioned above. The quantity \(s(x)\) can also be seen as the intensity of light emission at position x.
We now introduce the optical system in our model. The effect of the optical system is described by its point spread function (PSF) denoted \(g\), and we assume that \(g\ge 0\). Formally, the effect of the point spread function is modeled by a convolution in space (see, e.g., [48, Eq. 7.1, p. 171] see also, e.g., [1, Eq. 1, Sect. 2]). Therefore, in the noiseless case, if there is no motion, the gray level of the acquired image at position \(x \in \mathbb {R}\) is, formally, described by
where \(*\) denotes the convolution (see (ix) for the definition) (recall that here and in the rest of the text, Latin numerals refer to the formulae in the final glossary). We shall give the assumptions on \(g\) and \(s\) so that the quantity in (1) is well defined later on.
A pixel sensor can be small but has nevertheless a positive area. Indeed, a pixel sensor integrates the incoming light \(g*s\) (the scene is observed through the optical system) on some surface element of the form \([x_1,x_2]\subset \mathbb {R}\) with \(x_1<x_2\). Therefore, formally, the output of a pixel sensor supported by \([x_1,x_2]\), in the noiseless case and without motion, is
In the sequel, we shall assume that all the pixel sensors of the sensor array have the same length. Mathematically, we can normalize this length so that every pixel sensors of the array have unit length. This corresponds to using the pixel sensor length as unit to measure distances. Thus, this represents no limitation. Hence, from now on the unit of x is the pixel sensor length. By definition, with this unit, all the pixel sensor have lengths 1. Therefore, from now on when we speak of a pixel sensor centered at x we mean that the pixel sensor is supported on the interval \([x-\frac{1}{2},x +\frac{1}{2}]\). Hence, from (2) we deduce that the output of a pixel sensor supported on the interval \([x-\frac{1}{2}, x+ \frac{1}{2}]\), that stares at the scene s through the optical system modeled by \(g\), is, in the noiseless case and without motion,
Remark
We implicitly assume a 100 % fill factor for the sensor as the pixel sensor is supported on \([-\frac{1}{2},\frac{1}{2}]\) and we have a pixel sensor at every unit. This is no loss of generality for studying the gain of the flutter with respect to a snapshot. Indeed, the fill factor impacts equally the snapshot and the flutter. In addition, the RMSE calculations are carried out using the function u in (3) as reference and using an unbiased estimator for u. Thus, all results we give in this paper hold if one replace u by \(u=\mathbb {1}_{[-\varepsilon ,\varepsilon ]}*g*s\) in (3) for any \(\varepsilon \in (0,\frac{1}{2}]\).
Consider the deterministic function formally defined by \(u:=\mathbb {1}_{[-\frac{1}{2},\frac{1}{2}]}*g*s\). The deterministic quantity u(x) represents the gray level of the image at position x if there were no noise and no motion. Indeed, u contains the kernels of the optical system \(g\) and of the sensor. Note that the quantity u(x) can also be seen as an intensity of light emission received by a unit pixel sensor centered at x. With the formalism of, e.g., [1, Eq. 1, Sect. 2] \(\mathbb {1}_{[-\frac{1}{2},\frac{1}{2}]}\) represents “\(h_{\text {sensor}}\)” and \(g\) represents “\(h_{\text {lens}}\).”
We now introduce the exposure time in our model. Indeed, the sensor accumulates the light during a time span of the form \([t_1,t_2]\subset \mathbb {R}\), with \(t_1<t_2\). We denote by \(\Delta t\) the positive quantity \(\Delta t:=t_2-t_1\) that we shall call exposure time. Thus, from (3), the output of a pixel sensor centered at x that integrates on the time interval \([t_1,t_2]\) is, in the noiseless case
Note that the quantity in (4) is the amount of light measured by the pixel sensor, and it evolves linearly with the exposure time \(\Delta t~(=t_2-t_1)\).
We now extend the above formalism to cope with moving scenes. Without loss of generality (w.l.o.g.) we assume that the camera is steady while the scene \(s\) moves. The coded exposure method permits to deal with uniform motions. Therefore, we assume that the scene \(s\) moves at a constant velocity \(v \in \mathbb {R}\) (measured in pixel per second) during the exposure time interval \([t_1,t_2]\). This means that the scene evolves with respect to the time as \(s(x-vt)\). Here and in the sequel the temporal variable is denoted by t. Therefore, from (4) we deduce that the output of a pixel sensor centered at x and integrating on the time interval \([t_1,t_2]\) is, in the noiseless case,
For example, suppose that we take a constant velocity \(v=1\) in (5). In this case, the output of a pixel sensor centered at x is, in the noiseless case,
where \(\mathbb {1}_{[a,b]}\) represents the characteristic function of the interval [a, b] (see (3) for the last equality). From this simple example we can qualitatively describe where the exposure code will act. Indeed, by a clever exposure technique, the coded exposure method will allow to replace the function \(\mathbb {1}_{[t_1,t_2]}\) in the above formula by a more general class of functions that does not need to be window functions. With the formalism of, e.g., [1, Eq. 1, Sect. 2], \(\mathbb {1}_{[t_1,t_2]}\) represents “\(h_{\text {motion}}\)” for a classic camera.
We now extend our model to cope with the Poisson photon (shot) noise and then will add the readout noise. The photon emission follows a Poisson distribution see, e.g., [49] (tf X is a random variable that follows a Poisson distribution then all the possible realization of X are in \(\mathbb {N}\). In addition, the probability of the event \(X=k\) is \(\mathbb {P}\ (X=k)=\frac{\lambda ^k e^{-\lambda }}{k!}\), where \(\lambda >0\) is the intensity of the Poisson random variable). We assume that a pixel sensor behaves as a photon counter.Footnote 1 That is to say, we assume that a pixel sensor integrates the photons that are emitted by the moving observed scene \(s\) on some surface element of the form \([x_1,x_2]\) on the time span \([t_1,t_2]\) and produces a sample. This sample follows a Poisson random variable. From (5), this means that the sample produced by a pixel sensor supported by \([x_1,x_2]\) and that integrates on the time span \([t_1,t_2]\) has law
where the notation \(\mathcal {P}(\lambda )\) denotes a Poisson random variable of intensity \(\lambda \). With (3) the above equation can be rewritten as
Thus, the value of this sample can be any realization a Poisson random variable with intensity \(\int _{t_1}^{t_2} u(x-vt)\mathrm{d}t\). Consequently, the probability that the sample has value \(k\in \mathbb {N}\) when observing the scene \(s\) on the time span \([t_1,t_2]\) with the pixel sensor centered at x is
This quantity is nothing but the probability that the pixel sensor counts \(k \in \mathbb {N}\) photons during the time interval \([t_1,t_2]\).
With the formalism we introduced we can compute the SNR of the produced image, just to verify that we retrieved the fundamental theorem of photography that underlies statements like “the capture SNR increases proportional to the square root of the exposure time” that can be found in, e.g., [2, p. 1, column 2, 1st paragraph]. To this aim, consider the case where \(v=0\), \(t_1=0\), \(t_2=\Delta t\) in (7). If the observed value \(\mathrm{obs}(x)\) at position \(x \in \mathbb {R}\) follows \(\mathcal {P}\left( \int _0^{\Delta t} u(x)\mathrm{d}t \right) \) we have \(\mathbb {E}(\mathrm{obs}(x))=\Delta t u(x)\). This means that, in expectation, the number of photon caught by the pixel sensor centered at x increases linearly with the exposure time. If we time-normalize the obtained quantity and consider, formally, a random variable \(\mathbb {u}_\mathrm{est}(x)\) that follows \(\frac{\mathcal {P}\left( \int _0^{\Delta t} u(x)\mathrm{d}t \right) }{\Delta t}\) we obtain \(\mathbb {E}\left( \mathbb {u}_\mathrm{est}(x) \right) =u(x)\). This means that \(\mathbb {u}_\mathrm{est}(x)\) estimates u(x) without bias. In addition, we have \(\mathrm {var}\left( \mathbb {u}_\mathrm{est}(x) \right) =\frac{\Delta t u(x)}{ \Delta t^2}=\frac{u(x)}{\Delta t}.\)
Consider the SNR on the spatial interval \([-R,R]\) given by \(\frac{\frac{1}{2R}\int _{-R}^R \mathbb {E}\left( \mathbb {u}_\mathrm{est}(x)\right) \mathrm{d}x}{\sqrt{\frac{1}{2R}\int _{-R}^R \mathrm {var}\left( \mathbb {u}_\mathrm{est}(x)\right) \mathrm{d}x}}\). This definition of the SNR can be found in, e.g., [48, Eq. 1.39, p. 42], [46, Eq. 15, p. 4], [2, Eq. 1, p. 2562]. We have
Therefore, assuming that \(\mu \) the “mean signal level” [48, p. 42] (\(\mu \) relates to \(\bar{i}_0\) in, e.g., [2, Sect. 2])
is finite we can define the SNR by
Thus, we have \(\text {SNR}(\mathbb {u}_\mathrm{est})=\sqrt{\mu \Delta t}\). For example, if the mean photon emission \(\mu \) doubles then the SNR is multiplied by a factor \(\sqrt{2}\) (and we retrieve the fundamental theorem of photography namely the \(\mathrm {SNR} \rightarrow + \infty \) when \(\Delta t\rightarrow +\infty \)). Note that if we have no control over the photon emission then the only sure way to increase the SNR with a given camera is to increase the exposure time \(\Delta t\). Similarly, we can define the MSE by
whenever the limit exists, and we have \(\text {MSE}\left( \mathbb {u}_\mathrm{est}\right) =\mu \Delta t\).
We are now in position to extend our model to include the additive (readout) noise. Here and in the sequel the additive (readout) noise of a pixel sensor centered at x is modeled by a zero-mean real random variable of finite variance denoted by \(\eta (x)\). Therefore, from (6), the output of the pixel sensor centered at x that integrates photons on the time span \([t_1,t_2]\) can be, formally, any realization of the sum of the random variables
or equivalently (see (3)),
Recall that the deterministic quantity u(x) represents the gray level of the image at position x if there were no noise and no motion as it is seen by a pixel sensor centered at x. The quantity \(\int _{t_1}^{t_2} u(x-vt)\mathrm{d}t\) represents the amount of light received on the time interval \([t_1,t_2]\) by a steady pixel sensor centered at x that gathers the light emitted by the observed scene that moves at velocity \(v\in \mathbb {R}\).
We now give a mathematical framework to make precise the above formulae. We shall assume that the scene \(s\in L^1_{loc}(\mathbb {R})\) so that the convolution in (3) is well defined. We shall assume that the PSF \(g\) belongs to the Schwartz class that, hereinafter, we shall denote \(S(\mathbb {R})\). In addition, we shall assume that the PSF \(g\in S(\mathbb {R})\) furnishes a cutoff frequency. This assumption is needed by the Shannon–Whittaker sampling theory. We shall assume that the frequency cutoff of \(g\) is \(\pi \), i.e., \(g\) is \([-\pi ,\pi ]\) band limited. In other words, \(\hat{g}(\xi )=0\) for any \(\xi \in \mathbb {R}\) such that \(|\xi |>\pi \), where, here and in the sequel, we denote by \(\hat{g}\) or \(\mathcal {F}(g)\) the Fourier transform of \(g\) [see (14) for the definition of the Fourier transform] and (here and elsewhere) \(\xi \in \mathbb {R}\) represents the (Fourier) frequency coordinate. One could think that this \([-\pi ,\pi ]\) is a limitation for the theory. However, it is not. The choice of \([{-\pi ,\pi }]\) in the following definition is thoroughly justified in Appendix B.
Definition 1
(The observable scene u) We call observable scene any non-negative deterministic function u of the form \( u=\mathbb {1}_{[-\frac{1}{2},\frac{1}{2}]} *g*s.\) Recall that the \(\mathbb {1}_{[-\frac{1}{2},\frac{1}{2}]}\) denotes the characteristic function of the interval \([-\frac{1}{2},\frac{1}{2}]\) and is related to the normalized pixel sensor. The PSF satisfies \(g\in S(\mathbb {R})\), \(g\ge 0\), and is \([-\pi ,\pi ]\) band limited. The (non-negative) photon emission intensity is denoted \(s\in L^1_{loc}(\mathbb {R})\). We have that \(u\in L_{loc}^1(\mathbb {R})\) and we assume that u satisfies \(\mu :=\lim _{TR\rightarrow +\infty }\frac{1}{2R}\int _{-R}^{R^{}} u(x)\mathrm{d}x \in \mathbb {R}^+\). In addition, we assume that \(\tilde{u}:=u-\mu \in L^1(\mathbb {R}) \cap L^2(\mathbb {R})\).
Note that u is the sum of the constant \(\mu \) and of \(\tilde{u} \in L^1(\mathbb {R})\). Thus, we have \(u\in S'(\mathbb {R})\) (the space of tempered distributions). This means that u enjoys a Fourier transform in \(S'(\mathbb {R})\), see, e.g., [50, p. 173], see also [51, p. 23]. In addition, u and \(\tilde{u}\) inherit the frequency cutoff of the PSF \(g\). Therefore, u and \(\tilde{u}\) are \([-\pi ,\pi ]\) band limited. In addition note that the assumption \(\tilde{u} \in L^2(\mathbb {R}) \) is w.l.o.g. Indeed, since \(\tilde{u} \in L^1(\mathbb {R})\), from Riemann–Lebesgue theorem (see e.g., [52, Proposition 2.1]), we have that \(\hat{\tilde{u}}\) is continuous. In addition, since \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited we have that \(\hat{\tilde{u}}\) is continuous and has compact support. We deduce that \(\hat{\tilde{u}}\in L^2(\mathbb {R})\). Therefore, we obtain that \(\tilde{u} \in L^2(\mathbb {R})\) w.l.o.g.
We can now give a definition of the observed sample at a pixel centered at \(x \in \mathbb {R}\) that we shall denote \(\mathrm{obs}(x)\).
Definition 2
(Observed sample of a of pixel that includes any additive (sensor readout) noise of finite variance in addition to the Poisson photon (shot) noise) We assume that the observed sample produced by a unit pixel sensor centered at \(x \in \mathbb {R}\) is corrupted by an additive noise \(\eta (x)\) that we shall call readout noise. We assume that \(\mathbb {E}(\eta (x))=0\) and that \(\mathrm {var}(\eta (x))=\sigma _r<+\infty \). Hereinafter, we shall denote this observed sample by \(\mathrm{obs}(x)\). From (9), we have that \(\mathrm{obs}(x)\) satisfies, for any \(x \in \mathbb {R}\),
where \([t_1,t_2]\) is the time exposure interval, the observable scene u is defined by Definition 1 and moves at velocity \(v\in \mathbb {R}\). The notation \(X\sim Y\) means that the random variables X and Y have the same law.
In the sequel we will need to compute MSEs as well as SNRs. Therefore, we will need to compute expected values and variances of the observed samples. Thus, we need to justify the validity of these operations. This is done in Appendix C.
The Definition 2 entails that \(\mathrm{obs}(x)\), the observed sample of a pixel sensor centered at position x, is a measurable function (a random variable see, e.g., [p. 168] shiriaev1984probability) for which it is mathematically possible to compute, e.g., the expectation and the variance.
The images produced by a digital camera are discrete. In addition, the image obtained by a coded exposure camera requires to undergo a deconvolution to get the final crisp image. The calculation of the adequate deconvolution filter requires a continuous model. Thus, we now turn to the sampling and interpolation in order to go comfortably from the discrete observations to the latent continuous image.
2.2 Sampling and interpolation
This section recalls the principles of the Shannon–Whittaker interpolation that applies to, e.g., images that have the band limitedness structure. Consider a \([-\pi ,\pi ]\) band-limited deterministic function \(f\in L^1(\mathbb {R})\cap L^2(\mathbb {R})\). From the values f(n) for \(n \in \mathbb {Z}\) the Shannon–Whittaker interpolation of f is

and the above series converges uniformly to f(x) for any \(x \in \mathbb {R}\) (see, e.g., [40, p. 354]).
We recall that Appendix B proves that it is no loss to assume that u is \([-\pi ,\pi ]\) band limited. However, the sample \(\mathrm{obs}(x)\) defined in Definition 2 produced by the sensor is noisy. Indeed, the sample \(\mathrm{obs}(x)\) contains the Poisson photon (shot) noise and the additive sensor readout noise. This means that \( \mathbb {R}\ni x \mapsto \mathrm{obs}(x)\) is not a deterministic function and that \(\mathrm{obs}\) does not belong to any Lebesgue space. The Shannon–Whittaker theorem is usually applied to deterministic functions. Some generalization exists in the case where the observed samples are corrupted by an additive noise, see, e.g., [54, p. 111], or to sample wide-sense stationary stochastic signals, see, e.g., [54, p. 148]. However, the Poisson photon shot noise is not additive. Therefore, the first generalization is not applicable. In addition, from Definition 1 we deduce that the autocorrelation function \(\mathbb {E}\left( \mathrm{obs}(x) \mathrm{obs}(y) \right) \) is not a function of the variable \(x-y\). This means that the samples of a coded exposure camera cannot be seen as the samples of a wide-sense stationary stochastic process (see, e.g., [55, p. 17] for the definition). In addition, the sensor itself can introduce non-stationary noise, see, e.g., [47]. Thus, to the best of our knowledge, the existing generalizations of the Shannon–Whittaker theorem are not sufficient to treat the observed samples of a coded exposure camera (defined in Definition 2). Consequently, in the sequel, we shall carefully prove that

is mathematically feasible for the \(\mathrm{obs}\) defined in Definition 2.
Therefore, in the sequel, we assume that the observed samples are obtained from a sensor array and that the sensor array is designed according to the Shannon–Whittaker sampling theory. Thus, we assume that the samples \(\mathrm{obs}(x)\) are obtained at a unit rate, i.e., for \(x \in \mathbb {Z}\). Consequently, we shall denote the observed samples by \(\mathrm{obs}(n)\). This means that, in the sequel, we shall neglect the boundaries effect due to the deconvolution. This is another way to get rid of the boundaries effects without assuming that the observed scene is periodic as required by linear algebra (with Toepliz matrices) model based (see, e.g., [1–3, 5, 12, 25, 29, 30]) (this is needed because most natural scenes are not periodic). Note that this slightly overestimates the gain of the coded exposure method with respect to the snapshot. Indeed, the support of the coded exposure function is larger than the support of the exposure function of a snapshot. This means that in practice the boundaries artifacts due to the deconvolution are stronger with the coded exposure method.
Hereinafter, we assume that the sequence of random variables \((\eta (n))_{n \in \mathbb {Z}}\) are mutually independent, identically distributed, and independent from the shot noise, i.e., independent from \(\mathcal {P}\left( \int _{t_1}^{t_2} u(n-vt) \mathrm{d}t\right) \) where \(n \in \mathbb {Z}\). This independence assumption represents no limitation for the model. Indeed, a photon can only be sensed once. In addition, the additive (sensor readout) noise comes from an inaccurate reading of the sample value that does not depend on the light intensity emission or on the Poisson photon (shot) noise.
We have defined the observed samples produced by a light sensor in Definition 2. This definition includes both the Poisson photon (shot) noise and an additive (readout) noise of finite variance. We now turn to the mathematical formalization of the coded exposure method.
3 A mathematical model of coded exposure camera that includes any additive (sensor readout) noise of finite variance in addition to the Poisson photon (shot) noise
The goal of this section is to formalize the coded exposure method. In this section, we consider invertible “exposure codes” and provides the MSE and SNR of these exposure strategies. The study yields to Theorem 3.4.
The coded exposure (flutter shutter) method permits to modulate, with respect to the time, the photons flux caught by the sensor array. Indeed, the Agrawal and Raskar coded exposure method [1–6] consists in opening/closing the camera shutter on sub-intervals of the exposure time. In such a situation the exposure function that controls when the shutter is open or closed is binary and piecewise constant. Since it is piecewise constant it is possible to encode this function using an “exposure code.” (We give a mathematical definition of these objects).
Note that neither the model nor the results of [30] can be used in this paper. Indeed, in [30] the additive (sensor readout) noise is neglected. Therefore, the formalism of [30] does not hold with the more elaborated set up that we shall consider here. Indeed, this paper considers any additive sensor readout noise of finite variance in addition to the Poisson photon (shot) noise.
As we have seen, in their seminal work [1–6], Agrawal and Raskar propose to use binary exposure codes. Yet, mathematically, one could envisage smoother exposure codes that are not binary. Indeed, with a bigger searching space for the exposure code the MSE and SNR can be expected to be better than with the smaller set of binary codes. Therefore, in the sequel, we shall assume that the exposure codes have values in [0, 1]. The value 0 means that the shutter is closed while the value 1 means the shutter is open and, e.g., \(\frac{1}{2}\) means that half of the photons are allowed to reach the sensor. We do not consider the practical feasibility of these non-binary exposure codes as this is out of the scope of this paper which proposes a mathematical framework and formulae.
We first formalize the fact that the exposure code method modulates temporally the flux of photons that are allowed to reach the sensor by giving an adequate definition of an “exposure function” that, hereinafter, we shall denote \(\alpha \). To be precise, the gain \(\alpha (t)\) at time t is defined as the proportion of photons that are allowed to travel to the sensor. We then give the formula of the observed samples taking the exposure function into account (see Definition 4).
Definition 3
(Exposure function, exposure code) We call exposure function any function \(\alpha \) of the form
We assume that \(a_k \in [0,1]\), for any k, that \((a_k)_k \in \ell ^1(\mathbb {Z})\) and that \(\Delta t>0\). The sequence \((a_k)_k\) is called exposure code.
Remark
It is easy to see that \(\alpha \in L^1(\mathbb {R}) \cap L^2(\mathbb {R}) \cap L^\infty (\mathbb {R})\) and that the above definition can cope with finitely supported codes, e.g., the Agrawal and Raskar code [5, p. 5] and patent application [6, p. 5].
We have defined the exposure function that controls with respect to the time the camera shutter. We now give the formula of the observed samples of a coded exposure camera.
Let \(\alpha \) be an exposure function and \(u(x-vt)\) a scene moving at velocity \(v \in \mathbb {R}\). Recall that \(\alpha (t)\) is nothing but the percentage of photons allowed to reach the sensor at time t. Therefore, from Definition 2, we deduce that \(\mathrm{obs}(n)\), the observed sample at a position \(n \in \mathbb {Z}\), is a random variable that satisfies, for any \(n \in \mathbb {Z}\),
This yields
Definition 4
(Observed samples of a coded exposure camera) Let \(\alpha \) be an exposure function. We call observed samples at position n of the scene u (defined in Definition 1) moving at velocity \(v \in \mathbb {R}\) the random variable
Recall that the random variables \(\mathrm{obs}(n)\) observed for \(n \in \mathbb {Z}\) are mutually independent. From Definition 1 we have that u is of the form \(L^1(\mathbb {R})\) plus constant and is band limited. From Definition 3 we have that \(\alpha \in L^1(\mathbb {R})\). We obtain that the convolution in (13) is well defined everywhere. In addition, note that the pixels are read only once as in, e.g., [1–6]. (Only one image is observed, stored and transmitted).
Proposition 3.1
Let \(\mathrm{obs}\) be as in Definition 4. For any \(n \in \mathbb {Z}\), we have
Proof
The proof is a direct consequence of Definition 4. \(\square \)
Remark
(The motion blur of a standard camera is not invertible as soon as its support exceeds two pixels) A standard camera can be seen as a coded exposure camera if the exposure function \(\alpha \) is of the form \(\alpha =\mathbb {1}_{[0,\Delta t]}\), where \(\Delta t>0\) is the exposure time measured in second(s). Consider the idealistic noiseless case where, from (13), one would observe
From Definition 1 u is \([-\pi ,\pi ]\) band limited. Therefore, we deduce that the convolution in (15) is non-invertible as soon as the Fourier transform of \(\frac{1}{|v|}\mathbb {1}_{[0,\Delta t]} \left( \frac{\cdot }{v}\right) \) is zero on \([-\pi ,\pi ]\). For any \(\xi \in \mathbb {R}\), we have \(\mathcal {F}\left( \frac{1}{|v|}\mathbb {1}_{[0,\Delta t]} \left( \frac{\cdot }{v}\right) \right) (\xi )=\mathcal {F}\left( \mathbb {1}_{[0,\Delta t]}\right) (\xi v)\). In addition, from the definition of the Fourier transform (14), for any \(\xi \in \mathbb {R}\) we have
Therefore, for any \(\xi \in \mathbb {R}\), we have \(\mathcal {F}\left( \frac{1}{|v|}\mathbb {1}_{[0,\Delta t]} \left( \frac{\cdot }{v}\right) \right) (\xi )= \Delta t \ \mathrm {sinc}\ \left( \frac{\xi v \Delta t}{2\pi }\right) e^{\frac{-i\xi v\Delta t}{2}}.\) From the Definition (16) of the sinc function, we deduce that the convolution in (15) is not invertible as soon as the blur support \(|v| \Delta t\) satisfies \(|v| \Delta t \ge 2\). Since, the velocity v is measured in pixel(s) per second, and the exposure time \(\Delta t\) is measured in second(s) we deduce that as soon as the blur support \(|v|\Delta t\) exceeds two pixels the motion blur of a standard camera is not invertible.
The observed samples of any coded exposure camera are formalized in Definition 4. We wish to compute the MSE and SNR of a deconvolved crisp image with respect to the continuous observable scene u. To this aim a continuous deconvolved crisp signal \(\mathbb {u}_\mathrm{est}\) must be defined from the observed samples \(\mathrm{obs}(n)\) observed for \(n \in \mathbb {Z}\). Thus, we (1) prove the mathematical feasibility of the Shannon–Whittaker interpolation “\(\mathrm{obs}(x)=\sum _{n \in \mathbb {Z}} \mathrm{obs}(n) \ \mathrm {sinc}\ (x-n)\)”, (2) deduce the conditions on the exposure function \(\alpha \) for the existence of an inverse filter \(\gamma \) that deconvolves the observed samples, (3) define the final crisp image \(\mathbb {u}_\mathrm{est}\) and (4) give the formulae for the MSE and SNR of \(\mathbb {u}_\mathrm{est}\). The study yields to Theorem 3.4.
The mathematical feasibility of the Shannon–Whittaker interpolation is formalized by
Proposition 3.2
(Mathematical feasibility of the Shannon–Whittaker interpolation of the observed samples \(\mathrm{obs}(n)\) \(n\in \mathbb {Z}\)) Let \(\mathrm{obs}\) be as in Definition 4. For any \(x \in \mathbb {R}\), the series
converges in quadratic mean. In addition, for any \(x \in \mathbb {R}\), we have
Proof
See Appendix D. \(\square \)
We now treat the step 2. We cannot recur to a Wiener filter to define \(\gamma \). Indeed, due to the Poisson photon (shot) noise, the noise in of our observations \(\mathrm{obs}(n)\) defined in Definition 4 is not additive. Therefore, the Wiener filter is not defined (see, e.g., [56, p. 205], [55, p. 95], [57, p. 159] see also [58, p. 252] for a definition). Instead of using a Wiener filter we shall propose a filter designed so that the restored crisp image \(\mathbb {u}_\mathrm{est}\) is unbiased. This is also the set up considered in, e.g., [1, Sect. 3.1, p. 6]. We now provide the condition under which an inverse filter \(\gamma \) will yield to an unbiased restored crisp image \(\mathbb {u}_\mathrm{est}\).
If the exposure function \(\alpha \) defined in Definition 3 satisfies \(\hat{\alpha }(\xi v)= 0\) for some \(\xi \in [-\pi ,\pi ]\) the convolution in (18) is not invertible and some information is destroyed. Therefore, it is no more possible to retrieve any observed scene u (in a discrete setting, that would mean that the Toepliz matrix associated with the convolution kernel is not invertible). Thus, if \(\hat{\alpha }(\xi v)\ne 0\) for some \(\xi \in [-\pi ,\pi ]\) there exists no inverse filter \(\gamma \) capable of giving back an arbitrary observed scene u. Hence, we assume that the exposure function \(\alpha \) satisfies \(\hat{\alpha }(\xi v)\ne 0\) for any \(\xi \in [-\pi ,\pi ]\). Under that condition the convolution \(\left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) \right) *u\) in (18) is invertible because u is \([-\pi ,\pi ]\) band limited. Therefore, we have
Definition 5
(Admissible \(\alpha \) and definition of the inverse filter \(\gamma \) ) Let \(\alpha \) as in Definition 3. If \(\alpha \) satisfies \(\hat{\alpha }(\xi v)\ne 0\) for any \(\xi \in [-\pi ,\pi ]\) then the inverse filter \(\gamma \), that deconvolves the observed samples (and will be proved to give back a crisp image), exists and is defined by [its inverse Fourier transform (14)]
Remark
From Definition 5, we deduce that \(\mathbb {R}\ni \xi \mapsto \hat{\gamma }(\xi )\) is bounded and has compact support. Hence, we have \(\hat{\gamma }\in L^1(\mathbb {R}) \cap L^2(\mathbb {R})\) and therefore \(\gamma \in L^2(\mathbb {R})\). In addition, from Riemann–Lebesgue theorem we have that \(\gamma \) is continuous and bounded. Consequently, \(\gamma \) is \([-\pi ,\pi ]\) band limited and \(C^{\infty }(\mathbb {R})\), bounded, and belongs to \( L^2(\mathbb {R})\).
We now treat the step 3. The mathematical feasibility of deconvolved crisp signal \(\mathbb {u}_\mathrm{est}\) is formalized by
Proposition 3.3
(Validity/existence of the crisp deconvolved image \(\mathbb {u}_\mathrm{est}\)) Let \(\mathrm{obs}\) be as in Definition 4 and \(\alpha \), \(\gamma \) be as in Definition 5. For any \(x \in \mathbb {R}\), the series
converges in quadratic mean. In addition, for any \(x \in \mathbb {R}\), we have
This proposition means that \(\mathbb {u}_\mathrm{est}\) is an unbiased estimator of the observable scene u.
Proof
See Appendix F. \(\square \)
We now treat the step 4. We have
Theorem 3.4
(MSE and SNR of the coded exposure method) Let \(\mathbb {u}_\mathrm{est}\) be as in Proposition 3.3. Consider a scene \(u(x-vt)\) (see Definition 1) that moves at velocity \(v\in \mathbb {R}\) and let \(\sigma _r^2\) be the (finite) variance of the additive (readout) noise.
The MSE and SNR of the final crisp image \(\mathbb {u}_\mathrm{est}\) satisfy
Proof
See Appendix I. \(\square \)
We now connect the formulae in Theorem 3.4 with the existing literature on the coded exposure method. We have that the mean photon emission \(\mu \) relates to \(\bar{i}_0\) in, e.g., [2, Sect. 2]. In addition, from (25), we have that for fixed exposure function \(\alpha \) and additive (readout) noise variance \(\sigma _r^2\) the SNR evolves proportionally to \(\sqrt{\frac{\mu }{1 +\frac{\sigma _r^2}{\mu }}}\) with the mean photon emission \(\mu \). In particular, from (25), if \(\sigma _r^2=0\) and for a fixed \(\alpha \) we deduce that the SNR evolves proportionally to \(\sqrt{\mu }\) and we retrieve the fundamental theorem of photography. Note that it is equivalent to minimize (24) or to maximize (25) with respect to the exposure function \(\alpha \). Therefore, in the sequel we choose w.l.o.g. to use formula (24) and to evaluate the performance of the coded exposure method in terms of MSE. The calculation for the SNR can be immediately deduced. As an easy application of Theorem 3.4, we have the following corollary that provides the MSE of any invertible snapshot, i.e., that satisfies \(|v|\Delta t<2\) (see the Sect. 5) where \(\Delta t\) is the exposure time. This corollary will also be needed to compare the coded exposure method and the snapshot, in terms of MSE, in Sect. 4.
Corollary 3.5
(MSE of a snapshot with an exposure time of \(\Delta t\)) Let \(\mathbb {u}_\mathrm{est}\), v, \(u(x-vt)\), and \(\sigma _r^2\) be as in Theorem 3.4 and \(\Delta t\) be such that \(|v|\Delta t <2\). The MSE of a snapshot with exposure time \(\Delta t\) is
Proof
The proof is immediate combining (16) and (24). \(\square \)
We now turn to Sect. 4 that proposes a theoretical evaluation of the gain of the coded exposure method, with respect a snapshot.
4 An upper bound of performance for coded exposure cameras
This section study the gain, in terms of MSE, of the coded exposure method, with respect to a snapshot, as a function of the exposure code sampling rate. The study yields to a theoretical bound that is formalized in Theorem 4.1 and Corollary 4.2. The bound is valid for any exposure code provided \(|v|\Delta t \le 1\) (we recall that the exposure code sampling rate \(\Delta t\) is defined in Definition 3). This means that the proposed bound is an upper bound for the gain of any coded exposure camera, provided \(|v|\Delta t \le 1\). We have
Theorem 4.1
(A lower bound for the MSE of coded exposure cameras) Let \(\mathbb {u}_\mathrm{est}\), v, \(u(x-vt)\), and \(\sigma _r^2\) be as in Theorem 3.4. The MSE of any coded exposure camera satisfies, as soon as \(|v|\Delta t \le 1\),
Proof
See Appendix J. \(\square \)
We also have
This figure depicts the upper bound proved in Corollary 4.2. The x axis represents the quantity \(|v|\Delta t\) that is inversely proportional to the frequency sampling of the exposure function. The x axis varies in the interval [0, 1] because Corollary 4.2 is valid in this range. The y axis represents the upper bound of the gain, in terms of root mean square error, of the flutter with respect to a snapshot with an exposure time \(\Delta t=\frac{1}{|v|}\). Note that the curve is an upper bound. Thus, the actual gain of the coded exposure method is below this curve
In this experiment, we assume that the scene s moves at velocity \(v=1\) pixel per second. The additive (readout) noise is Gaussian with a standard deviation equal to 10. We also assume that the scene emits 625 photons per seconds (for other values see Table 1) On the top left panel: the observed image using the Agrawal and Raskar code [5, 6]. On the top right panel: the observed image for snapshot an exposure time of 1 second, i.e., the blur support is 1 pixel. On the bottom left panel: the reconstructed image for the Agrawal and Raskar code [5, 6]. On the bottom right panel: the reconstructed image for the snapshot (blur support of 1 pixel). This means that for the Agrawal and Raskar code the blur has a support of 52 pixels. In other words, this code permits to increase the exposure time by a factor 52 compared to the snapshot. The RMSE using the Agrawal and Raskar code is equal to 9.84. The RMSE of the snapshot is equal to 5.96. We refer to Table 1 for different values of mean photon count and additive (readout) noise variance. This simulation is based on a variant of [29]
Corollary 4.2
(Upper bound of any coded exposure camera in terms of MSE with respect to a snapshot) Let \(\mathbb {u}_\mathrm{est}\), v, \(\Delta t\), \(u(x-vt)\) and \(\sigma _r^2\) be as in Theorem 4.1. We have
Proof
See Appendix K. \(\square \)
Corollary 4.2 directly provides an upper bound for the gain, of the coded exposure method, in terms of MSE with respect to a snapshot. Given our hypothesis this bound is valid for any code as soon as \(|v|\Delta t \le 1\). We now depict, in Fig. 2, the upper bound of Corollary 4.2 varying the quantity \(|v|\Delta t\). Note that the quantity \(|v|\Delta t\) is inversely proportional to the temporal frequency sampling of the exposure code. Note that the curve is an upper bound. Thus, the actual gain of the coded exposure method is below this curve.
We now illustrate numerically Corollary 4.2 in Fig. 3 and Table 1.
5 Limitations and discussion
We have proposed a mathematical model of coded exposure cameras. The model includes the Poisson photon (shot) noise and any additive readout noise of finite variance. The model is based on the Shannon–Whittaker framework that assumes band-limited images. This formalism has allowed us to give closed formulae for the Mean Square Error and Signal to Noise Ratio of coded exposure cameras. In addition, we have given an explicit formula that gives an absolute upper bound for the gain of any coded exposure cameras, in terms of Mean Square Error, with respect to a snapshot. The calculations take into account the whole imaging chain that includes Poisson photon (shot) noise, any additive (readout) noise of finite variance in addition to the deconvolution. Our mathematical model does not allow us to prove that the coded exposure method allows for very large gains compared to an optimal snapshot. This may be the result of an imperfect model of our mathematical coded exposure camera. Indeed, our model assumes that the sensor does not saturate, that the relative camera scene velocity is known, that the scene has finite energy and is observed through an optical system that provides a cutoff frequency, that the additive (readout) noise has a finite variance and neglects the boundaries effects due to the deconvolution. How the results change if one has to, e.g., estimate the velocity is, to the best of our knowledge, an open question.
Notes
Single-photon avalanche detectors (SPADS) is a possible implementation of a photon counter. Any light sensing device that produces, when the quantization is neglected, a signal in biunivocal relationship with the photon count can be w.l.o.g. assumed to be photon counter. The quantization noise will w.l.o.g. be included in the additive (readout) noise later on.
References
Agrawal, A., Raskar, R.: Resolving objects at higher resolution from a single motion-blurred image. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1–8 (2007)
Agrawal, A., Raskar, R.: Optimal single image capture for motion deblurring. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2560–2567 (2009)
Agrawal, A., Xu, Y.: Coded exposure deblurring: Optimized codes for PSF estimation and invertibility. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2066–2073 (2009)
Raskar, R.: Method and apparatus for deblurring images. Google Patents. US Patent 7,756,407 (2010)
Raskar, R., Agrawal, A., Tumblin, J.: Coded exposure photography: motion deblurring using fluttered shutter. ACM Trans. Graph. 25(3), 795–804 (2006)
Raskar, R., Tumblin, J., Agrawal, A.: Method for deblurring images using optimized temporal coding patterns. Google Patents. US Patent 7,580,620 (2009)
Agrawal, A., Gupta, M., Veeraraghavan, A., Narasimhan, S.G.: Optimal coded sampling for temporal super-resolution. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 599–606 (2010)
Dengyu, L., Jinwei, G., Hitomi, Y., Gupta, M., Mitsunaga, T., Nayar, S.K.: Efficient space-time sampling with Pixel-Wise coded exposure for high-speed imaging. IEEE Trans. Pattern Anal. Mach. Intell. 36(2), 248–260 (2014)
Ding, Y., McCloskey, S., Yu, J.: Analysis of motion blur with a flutter shutter camera for non-linear motion. In: Proceedings of the Springer-Verlag European Conference on Computer Vision (ECCV), pp. 15–30 (2010)
Gao, D., Liu, D., Xie, X., Wu, X., Shi, G.: High-resolution multispectral imaging with random coded exposure. J. Appl. Remote Sens. 7(1), 73695–73695 (2013)
Holloway, J., Sankaranarayanan, A.C., Veeraraghavan, A., Tambe, S.: Flutter shutter video camera for compressive sensing of videos. In: Proceedings of the IEEE International Conference on Computational Photography (ICCP), pp. 1–9 (2012)
Huang, K., Zhang, J., Li, G.: Noise-optimal capture for coded exposure photography. Opt. Eng. 51(9), 093202–10932026 (2012)
Jelinek, J.: Designing the optimal shutter sequences for the flutter shutter imaging method. In: SPIE defense, security, and sensing, pp. 77010–77010. International Society for Optics and Photonics (2010)
Jelinek, J., McCloskey, S.: Method and system for designing optimal flutter shutter sequence. Google Patents. US Patent 8,537,272 (2013)
McCloskey, S.: Velocity-dependent shutter sequences for motion deblurring. In: Proceedings of the Springer-Verlag European Conference on Computer Vision (ECCV), pp. 309–322 (2010)
Mccloskey, S.: Acquisition system for obtaining sharp barcode images despite motion. EP Patent 2,284,764 (2011)
McCloskey, S.: Temporally coded flash illumination for motion deblurring. In: Proceedings of the IEEE International Conference on Computer Vision (ICCV), pp. 683–690 (2011)
McCloskey, S.: Fluttering illumination system and method for encoding the appearance of a moving object. Google Patents. US Patent 8,294,775 (2012)
McCloskey, S.: Heterogeneous video capturing system. Google Patents. US Patent 8,436,907 (2013)
McCloskey, S.: Motion Deblurring: Algorithms and Systems. Chap. 11: Coded exposure motion deblurring for recognition. Cambridge University Press, Cambridge (2014)
McCloskey, S., Au, W., Jelinek, J.: Iris capture from moving subjects using a fluttering shutter. In: Proceedings of the IEEE International Conference on Biometrics: theory applications and systems (BTAS), pp. 1–6 (2010)
McCloskey, S., Ding, Y., Yu, J.: Design and estimation of coded exposure point spread functions. IEEE Trans. Pattern Anal. Mach. Intell. 34(10), 2071–2077 (2012)
McCloskey, S., Jelinek, J., Au, K.W.: Method and system for determining shutter fluttering sequence. Google Patents. US Patent 12/421,296 (2009)
McCloskey, S., Muldoon, K., Venkatesha, S.: Motion invariance and custom blur from lens motion. In: Proceedings of the IEEE International Conference on Computational Photography (ICCP), pp. 1–8 (2011)
Reddy, D., Veeraraghavan, A., Raskar, R.: Coded strobing photography for high-speed periodic events. In: Imaging systems. Optical Society of America (2010)
Sarker, A., Hamey, L.G.C.: Improved reconstruction of flutter shutter images for motion blur reduction. In: Proceedings of the IEEE International Conference on Digital Image Computing: Techniques and Applications (DICTA), pp. 417–422 (2010)
Schonbrun, E.F., Gorthi, S.S., Schaak, D.: Fluorescence flutter shutter for imaging cells in flow. In: Computational optical sensing and imaging, pp. 4–4. Optical Society of America (2013)
Tai, Y.W., Kong, N., Lin, S., Shin, S.Y.: Coded exposure imaging for projective motion deblurring. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2408–2415 (2010)
Tendero, Y.: The flutter shutter camera simulator. Image Process. Line 2, 225–242 (2012)
Tendero, Y., Morel, J.-M., Rougé, B.: The flutter shutter paradox. SIAM J. Imaging Sci. 6(2), 813–847 (2013)
Torii, S., Shindo, Y.: Information processing apparatus and method for synthesizing corrected image data. Google Patents. US Patent 8,379,096 (2013)
Tsai, R.: Pulsed control of camera flash. Google Patents. US Patent 7,962,031 (2011)
Tsutsumi, S.: Image processing apparatus and method. Google Patents. US Patent App. 13/104,476 (2011)
Veeraraghavan, A., Reddy, D., Raskar, R.: Coded strobing photography: compressive sensing of high speed periodic events. IEEE Trans. Pattern Anal. Mach. Intell. 33(4), 671–686 (2011)
Xu, W., McCloskey, S.: 2D Barcode localization and motion deblurring using a flutter shutter camera. In: Proceedings of the IEEE Workshop on Applications of Computer Vision (WACV), pp. 159–165 (2011)
Asif, M.S., Reddy, D., Boufounos, P.T., Veeraraghavan, A.: Streaming compressive sensing for high-speed periodic videos. In: Proceedings of the IEEE International Conference on Image Processing (ICIP), pp. 3373–3376 (2010)
Tendero, Y., Morel, J.-M.: An optimal blind temporal motion blur deconvolution filter. IEEE Trans. Signal Process. Lett. 20(5), 523–526 (2013)
Tendero, Y., Morel, J.-M., Rougé, B.: A formalization of the flutter shutter. J. Phys. 386(1), 012001 (2012)
Tendero, Y.: The flutter shutter code calculator. Image Process. Line 5, 234–256 (2015)
Gasquet, C., Witomski, P.: Fourier analysis and applications: filtering, numerical computation, Wavelets. Texts in applied mathematics. Springer, New York (1999)
Healey, G.E., Kondepudy, R.: Radiometric CCD camera calibration and noise estimation. IEEE Trans. Pattern Anal. Mach. Intell. 16(3), 267–276 (1994)
Kavusi, S., El Gamal, A.: Quantitative study of high-dynamic-range image sensor architectures. In: Electronic Imaging 2004, pp. 264–275. International Society for Optics and Photonics (2004)
Hasinoff, S.W., Durand, F., Freeman, W.T.: Noise-optimal capture for high dynamic range photography. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 553–560 (2010)
Fowler, B.A., El Gamal, A., Yang, D.X., Tian, H.: Method for estimating quantum efficiency for CMOS image sensors. In: Photonics West’98 Electronic Imaging, pp. 178–185. International Society for Optics and Photonics (1998)
Daniels, A.: Field guide to infrared systems, detectors, and FPAs. Field guide series. Society of Photo Optical, Bellingham, Washington (2010)
Agrawal, A., Xu, Y., Raskar, R.: Invertible motion blur in video. ACM Trans. Graph. 28(3), 95–1958 (2009)
Degerli, Y., Lavernhe, F., Magnan, P., Farre, J.: Non-stationary noise responses of some fully differential on-chip readout circuits suitable for CMOS image sensors. IEEE Trans. Circuits Syst. II 46(12), 1461–1474 (1999)
Lukac, R.: Computational photography: methods and applications, 1st edn. CRC Press Inc, Boca Raton (2010)
Boracchi, G., Foi, A.: Uniform motion blur in poissonian noise: blur/noise tradeoff. IEEE Trans. Image Process. 20(2), 592–598 (2011)
Bony, J.-M.: Cours -d’analyse: Théorie des distributions et analyse de fourier. Éditions de l’École Polytechnique, Palaiseau (2001)
Stein, E.M., Weiss, G.L.: Introduction to Fourier analysis on Euclidean spaces. Mathematical series. Princeton University Press, Princenton (1971)
Krantz, S.G.: A panorama of harmonic analysis. Carus Mathematical Monographs 27. Mathematical Association of America, United States (1999)
Shiryaev, A.N.: Probability. Graduate texts in mathematics. Springer, New York (1984)
Marks, R.J.: Introduction to Shannon sampling and interpolation theory. Springer texts in electrical engineering. Springer, New York (1991)
Chonavel, T., Ormrod, J.: Statistical signal processing: modelling and estimation. Advanced textbooks in control and signal processing. Springer, London (2002)
Kovacevic, B., Durovic, Z., Durović, Z.: Fundamentals of Stochastic signals, systems and estimation theory: with worked examples. Springer, Berlin, Heidelberg (2008)
Zaknich, A.: Principles of adaptive filters and self-learning systems. Advanced textbooks in control and signal processing. Springer, London (2006)
Dahlhaus, R.: Mathematical methods in signal processing and digital image analysis. Springer complexity. Springer, Berlin, Heidelberg (2008)
Karr, A.F.: Probability. Springer texts in statistics. Springer, New York (1993)
Resnick, S.: A probability path. Birkhäuser, Boston (1999)
Makarov, B., Podkorytov, A.: Real analysis: measures. Integrals and applications. Universitext. Springer, London (2013)
Wiener, N.: The Fourier integral and certain of its applications. Cambridge mathematical library. Cambridge University Press, Cambridge (1988)
Durán, A.L., Estrada, R., Kanwal, R.P.: Extensions of the Poisson summation formula. J. Math. Anal. Appl. 218(2), 581–606 (1998)
Katznelson, Y.: An introduction to Harmonic analysis. Cambridge Mathematical Library. Cambridge University Press, Cambridge (2004)
Butzer, P.L., Stens, R.L.: The Euler-MacLaurin summation formula, the sampling theorem, and approximate integration over the real axis. Linear Algebra Appl. 52, 141–155 (1983)
Timan, A.F.: Theory of approximation of functions of a real variable. Dover books on advanced mathematics. Pergamon Press, New York (1963)
Authors' contributions
YT and SO equally contributed to this work. Both authors read and approved the final manuscript.
Acknowledgements
Yohann Tendero is happy to deeply thank “les milieux autorisés”: Igor Ciril (IPSA, MITE), Jérôme Darbon (CNRS, UCLA and the “others offices”), Marc Sigelle (Télécom ParisTech), the one who knocks and the Betches family for their careful readings of the drafts. Indeed, their feedbacks have been duly noted. Research partially supported on the ONR Grants N000141410683, N000141210838, and DOE Grant DE-SC00183838. Part of this work was done at the UCLA Math. Dept.
Research partially supported on the ONR Grants N000141410683, N000141210838 and DOE Grant DE-SC00183838.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Validity of the one-dimensional framework
Without loss of generality, we express the coordinates of the two-dimensional camera scene velocity vector using the sampling axis grid as Galilean reference frame. Therefore, in this reference frame, the angle \(\theta \) between the two-dimensional velocity vector and, e.g., the x-axis of the sampling grid is known. Consider the rotation re-sampling operator of angle \(-\theta \) on \(L^2(\mathbb {R}^2)\). This rotation operator re-sample the image so that the motion is parallel to one of the grid axis, e.g., the x-axis. The motion blur is a one-dimensional phenomenon. Therefore, we can apply the motion blur model to each line of the image parallel to the x-axis. Thus, from the mathematical viewpoint, the motion blur is mathematically equivalent to a one-dimensional convolution of a exposure function by the one-dimensional observed stochastic scene. Indeed, the whole convolution/deconvolution model is applied to each line of the image parallel to the x-axis. In addition, the image rotation operator is isometric in \(L^2(\mathbb {R}^2)\). Therefore, the calculations of MSE and SNR as if the images were one-dimensional signals hold for two-dimensional images by easy expectation and variance calculations. This means that the theorems that we shall prove in the sequel are valid for two-dimensional images.
Appendix B: It is enough to study only \([-\pi ,\pi ]\) band-limited functions
This section justifies that it is enough to consider only \([-\pi ,\pi ]\) band-limited functions. As we have seen, it is enough to model the coded exposure method as if the images were one-dimensional signals. For the sake of the clarity, consider momentarily that the deterministic function f represents a sound (this example is illustrative of our situation because u defined in Definition 1 is one-dimensional). Since we consider a sound f, we also momentarily consider that the unit of the variable x in (14) is the second (denoted s). From the definition of \(\hat{f}\) [see (14)] we deduce that \(\xi \) is in \(\frac{\text {Hz}}{2\pi }\) (Hz denotes Hertz). If \(\hat{f}\) satisfies \(\hat{f}(\xi )=0\) for any \(\xi \in \mathbb {R}\) such that \(|\xi |>\pi \), i.e., is \([-\pi ,\pi ]\) band limited then the maximal frequency of f is \(\frac{\pi }{2\pi } \) in Hz. Therefore, from the Shannon–Whittaker sampling theorem, f is well sampled with one sample every second.
Consider now an arbitrary function f and a positive real number c. If f is sampled with one sample every \(\frac{1}{c}\) s then, from the Shannon–Whittaker sampling theorem, one can recover any \([-c\pi ,c\pi ]\) band-limited functions. This means that f must not contain any frequency above \(\frac{\pi c}{2\pi }\) in Hz. In other words, by diminishing adequately the sampling step one can recover any band-limited function. Consider another time unit \(\frac{\text {s}}{c}\), and a zoomed version of f defined by \(\tilde{f}(\cdot ):=f\left( \frac{\cdot }{c} \right) \). As we have seen, if we have access to the samples \(\ldots ,f\left( \frac{-1}{c}\right) ,f\left( \frac{0}{c}\right) ,f\left( \frac{1}{c}\right) ,f\left( \frac{2}{c}\right) ,\ldots \) or equivalently that we have access to \(\ldots , \tilde{f}(-1),\tilde{f}(0),\tilde{f}(1),\tilde{f}(2),\ldots \) then f and therefore \(\tilde{f}\) are well sampled from the Shannon–Whittaker theory point of view. One the one hand, f is \([-c\pi ,c\pi ]\) band limited with an arbitrary positive constant c. This means that \(\hat{\tilde{f}}(\xi )=0\) as soon as \(|c\xi |>|c\pi |\). Therefore, from its definition, \(\hat{\tilde{f}}\) is \([-\pi ,\pi ]\) band limited. In other words, f can be seen as a \([-\pi ,\pi ]\) band-limited function provided we use an adequate time scale, i.e., use an adequate unit to measure the time. This time scale is given by the Shannon–Whittaker sampling theorem and, implicitly, implies that \(\xi \) is measured in \(\frac{\pi }{2\pi c}\) Hz. Therefore, if we assume that the sampling system respects the Shannon–Whittaker theorem we can without loss of generality assume that f is \([-\pi ,\pi ]\), where the frequencies of f does not exceed \(\frac{\pi }{2\pi \times \text {``sampling step in s''}}\) Hz.
In conclusion, we assume that the couple optical system/sensor array are designed according to the Shannon–Whittaker sampling theory. Therefore, the adequate unit for the distances \(x \in \mathbb {R}\) is the distance between pixel centers. With this unit of distance the signal is \([-\pi ,\pi ]\) band limited, where the frequencies are measured in \(\frac{\pi }{2\pi \text {``pixel length''}}\) Hz. Therefore, the physical frequency cutoff is arbitrary. This means that the theory we shall develop covers any band-limited function, and any positive fill factors. Our hypothesis is that, the couple optical system/sensor permits to obtain well-sampled signal in the sense of the Shannon–Whittaker sampling theorem. Mathematically, we can, w.l.o.g. assume that the cutoff frequency comes from the PSF \(g\) as in Definition 1 that is \(g\) is \([-\pi ,\pi ]\) band limited.
Appendix C: Measurability
We need to prove that the samples are random variables, i.e., measurable functions (see, e.g., [53, p. 168], see also [59, p. 44]). For any \(x \in \mathbb {R}\) let the random variables \(\eta (x)\) be defined by \(\eta (x):(\Omega ,\mathcal {T}_\eta ,\mathbb {P}_\eta ) \rightarrow (\mathbb {R},\mathcal {B} or(\mathbb {R}))\) where, \(\Omega :=\mathbb {R}\) is the sample space, \(\mathcal {B}or(\mathbb {R})\) is the Borel sigma-algebra on \(\mathbb {R}\), \(\mathcal {T}_\eta \) is chosen as the smallest sigma-algebra on \(\Omega \) that makes \(\eta (x)\) measurable, i.e., \(\mathcal {T}_\eta =\{\eta (k)^{-1} B : B \in \mathcal {B} or(\mathbb {R}) \}\). The Poisson random variables are defined on \(\mathcal {P}(\lambda ):(\mathbb {N},\mathcal {T}_\mathbb {N},\mathbb {P}_{\mathrm{Poisson}(\lambda )}) \rightarrow (\mathbb {R},\mathcal {B} or(\mathbb {R}))\), where \(\mathcal {T}_\mathbb {N}\) is the smallest sigma-algebra (in the sense of the inclusion) that contains \(\mathbb {N}\). Assume that at a pixel sensor centered at \(x\in \mathbb {R}\) we have \(\int _{t_1}^{t_2} u(x-vt) \mathrm{d}t=\lambda \). From Eq. (10) and for any \(x \in \mathbb {R}\), \(\mathrm{obs}(x)\) is the sum of a Poisson and of an additive random variables \(\mathcal {P}(\lambda )+\eta (x):(\Omega ,\mathcal {T}, \mathbb {P}) \rightarrow (\mathbb {R},\mathcal {B} or(\mathbb {R}))\). Therefore, \(\mathrm{obs}\) is measurable with the sigma-algebra \(\mathcal {T}=\{(\mathcal {P}(\lambda )+\eta (k))^{-1} B : B \in \mathcal {B} or(\mathbb {R}) \}\).
Appendix D: Proof of Proposition 3.2 p. 3.2
We first give a lemma and its corollary that will be useful for the proof and then give the construction details.
Lemma D.1
The deterministic function \(\mathbb {R}\ni x \mapsto \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (x)\) is \([-\pi ,\pi ]\) band limited, uniformly bounded and for any \(x \in \mathbb {R}\) we have
Proof
See Appendix E. \(\square \)
Corollary D.2
The deterministic function \(\mathbb {Z}\ni n\mapsto \mathrm {var}\left( \mathrm{obs}(n)\right) \) is uniformly bounded.
Proof
The proof is immediate from Proposition 3.1 and Lemma D.1. \(\square \)
For any \(n \in \mathbb {Z}\), consider the centered random variables
The proof is in three steps. The step (a) proves that, for any \(x \in \mathbb {R}\), the series
converges in quadratic mean. The step (b) proves that, for any \(x \in \mathbb {R}\), the series
converges to a deterministic constant. These two steps entail that the series in (17) converges, for any \(x \in \mathbb {R}\), in quadratic mean. The step (c) provides explicit formulae for the expectation and variance of (17) (these calculations will be needed for the computation of MSE and SNR of the deconvolved crisp image. We now turn to the proof of step (a).
Step (a) From (30), for any \(n \in \mathbb {Z}\), we have
Consider the finite sums of independent random variables
Note that hereinafter, \(\tilde{o}^N\) denotes the N-th term of the sequence defined in (32).
For any \(N\ge M\) and any \(x \in \mathbb {R}\), we have that
Therefore, combining (31) and (33) we deduce that
for any \(x \in \mathbb {R}\). From Corollary D.2 we have that \(\sup _n\mathrm {var}(\mathrm{obs}(n))<+\infty \). Hence, from (34) we have
for any \(x \in \mathbb {R}\). The series \(\sum _{n=-\infty }^{+\infty } \ \mathrm {sinc}\ ^2(x-n)\) converges for any \(x \in \mathbb {R}\). Consequently, from (35), for any \(x \in \mathbb {R}\) and \(\epsilon >0\) we deduce that there exists \(M_0\in \mathbb {N}\) such that if \(M_0 \le M\le N\) we have
Therefore, from the Cauchy criterion (see, e.g., [60, Theorem 6.6.2]) we deduce that, for any \(x \in \mathbb {R}\), the series \(\tilde{\mathrm{obs}}(x)=\sum _{n=-\infty }^{+\infty } \tilde{\mathrm{obs}}(n)\ \mathrm {sinc}\ (x-n)\) converges in quadratic mean to a limit that we can therefore call \(\tilde{\mathrm{obs}}(x)\). This concludes step (a). We now turn to step (b) that proves that, for any \(x \in \mathbb {R}\), the series \(\sum _{n=-\infty }^{+\infty } \mathbb {E} \left( \mathrm{obs}(n)\right) \ \mathrm {sinc}\ (x-n)\) converges to a deterministic constant.
Step (b) From Proposition 3.1, for any \(x \in \mathbb {R}\), we have
Combining (29) and (37), we have that, for any \(x\in \mathbb {R}\),
We first deal with of the first term on the right-hand side (RHS) of (38). From Definition 1 we have \(\tilde{u} \in L^1(\mathbb {R})\) and \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. From Definition 3 \(\alpha \in L^1(\mathbb {R})\). Therefore, from Young inequality (see, e.g., [61, p. 525]) we have that \( \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *\tilde{u} \right) \in L^1(\mathbb {R})\) and is \([-\pi ,\pi ]\) band limited since \(\tilde{u}\) is band limited in this range. Hence, we deduce (see, e.g., [40, p. 354]) that, for any \(x \in \mathbb {R}\), there holds
We now deal with of the second term on the RHS of (38). For any \(x\in \mathbb {R}\), we have \(\sum _{n=-\infty }^{+\infty } \ \mathrm {sinc}\ (x-n)=1\). Thus, combining (38) and (39) we have that, for any \(x\in \mathbb {R}\), there holds
From Definition 1, for any \(x \in \mathbb {R}\), we have that \(u(x)=\tilde{u}(x) + \mu \). In addition, \(\int _{-\infty }^\infty \frac{1}{|v|} \alpha (\frac{t}{v}) \mu \mathrm{d}t=\mu \int _{-\infty }^\infty \alpha (t)\mathrm{d}t\). Hence, from (40) we obtain that, for any \(x \in \mathbb {R}\), there holds
This concludes step (b).
We now combine the steps (a) and (b). Combining (17) and (30), the series
converges, for any \(x \in \mathbb {R}\), in quadratic mean to a limit that we can therefore call \(\mathrm{obs}(x)\). Indeed, from step (a), it is the sum of the quadratic mean convergent series \(\sum _{n\,=\,-N}^N \tilde{\mathrm{obs}}(n)\ \mathrm {sinc}\ (x-n)\) and, from (41), of the deterministic constant \( \left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) (x)\).
Consequently, we deduce that, for any \(x \in \mathbb {R}\), the series defined in (17) converges in quadratic mean. Thus, for any \(x \in \mathbb {R}\), we call \(\mathrm{obs}(x)\) this limit. We now turn to step (c) that gives explicit formulae for the expectation and variance of the quadratic mean convergent series \(\mathrm{obs}(x)\) defined in (17).
Step (c) The convergence in quadratic mean implies the convergence of the two firsts moments (see [59, Example 5.6(a), (b), p. 158]). Therefore, for any \(x \in \mathbb {R}\) we have


In addition, the linearity of the expectation and the independence of the observed samples \(\mathrm{obs}(n)\) imply that, for any \(x \in \mathbb {R}\),
Therefore, combining (42) with (44) and the Definition (17) of \(\mathrm{obs}(x)\) we have

for any \(x \in \mathbb {R}\). Similarly, combining (43) with (45) and the Definition (17) of \(\mathrm{obs}(x)\) we have that

for any \(x \in \mathbb {R}\). Combining (41) and (46) we have that, for any \(x \in \mathbb {R}\),
Hence, we proved (18). From Proposition 3.1 and (47) we deduce that, for any \(x\in \mathbb {R}\),

Since, for any \(x\in \mathbb {R}\), we have \(\sum _{n=-\infty }^{+\infty } \ \mathrm {sinc}\ ^2(x-n)=1\), from (48) we deduce that, for any \(x \in \mathbb {R}\),
Hence, we proved (19). In addition, from Corollary D.2, we deduce that, for any \(x \in \mathbb {R}\), \(\mathrm {var}(\mathrm{obs}(x))\) is finite. This concludes our proof.
Appendix E: Proof of Lemma D.1 p. 20
From its Definition 1 the deterministic function \(\tilde{u}=u-\mu \) is \([-\pi ,\pi ]\) band limited. Therefore, we deduce that the function \(\mathbb {R}\ni x \mapsto \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\right) (x)\) is \([-\pi ,\pi ]\) band limited. In addition, since \(u(\cdot )=\tilde{u}(\cdot ) +\mu \) (see Definition 1) we deduce that, for any \(x \in \mathbb {R}\), (29) holds. We now prove that u is uniformly bounded. From the remark we have \(\alpha \in L^1(\mathbb {R})\). Recall that from Definition 1 we have \(\tilde{u} \in L^1(\mathbb {R})\). Hence, from Young inequality (see, e.g., [61, p. 525]) we deduce that \(\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\right) \in L^1(\mathbb {R})\). Therefore, by Riemann–Lebesgue theorem (see e.g., [52, Proposition 2.1]) we have that \(\mathbb {R}\ni \xi \mapsto \mathcal {F}\left( \alpha \left( \frac{\cdot }{v}\right) *\tilde{u} \right) (\xi )\) is continuous. In addition, from Definition 1 we have that \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. Therefore, \(\mathbb {R}\ni \xi \mapsto \mathcal {F}\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\right) (\xi )\) is compactly supported. Hence, we deduce that \(\mathcal {F}\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\right) \in L^1(\mathbb {R})\). Thus, by Riemann–Lebesgue theorem we have that \(\frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\) is uniformly bounded. It follows from (29) that \(\frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\) is uniformly bounded. This concludes our proof.
Appendix F: Proof of Proposition 3.3 p. 15
We first prove (21) then (22) and (23).
We need to recur, again, to a convergence argument prove the validity of (21).
Therefore, for any \(x\in \mathbb {R}\), we set
Note that hereinafter, \(\mathbb {u}_\mathrm{est}^N(x)\) denotes the N-th term of the sequence defined in (50). From Definition 5, we deduce that \(\gamma \) satisfies
Hence, from (51) \(\gamma \) obeys the same decay as the \({\mathrm {sinc}}\). Thus, we deduce that the rest of the proof follows exactly the same arguments as for the construction of \(\mathrm{obs}(x)\) leading to Proposition 3.2. Therefore, we obtain that, for any \(x \in \mathbb {R}\), \(\mathbb {u}_\mathrm{est}^N(x)=\sum _{n\,=\,-N}^N \mathrm{obs}(n)\ \mathrm {sinc}\ (x-n)\) converges, in quadratic mean, to a limit that we can therefore call \(\mathbb {u}_\mathrm{est}(x)\). This proves (21). Quadratic mean convergence implies the convergence of the two firsts moments (see [59, Example 5.6(a)–(b), p. 158]). Therefore, we again obtain that, for any \(x \in \mathbb {R}\),


It remains to prove (22) and (23). To this aim the next lemma will be useful.
Lemma F.1
(The inverse filter \(\gamma \) gives back an unbiased estimator of u) Let \(\alpha \) and \(\gamma \) be as in Definition 5. For any \(x \in \mathbb {R}\), we have
Proof
The proof is in Appendix G. \(\square \)
Combining Proposition 3.1 and (50), for any \(x \in \mathbb {R}\), we have
From Lemma F.1 we deduce that, for any \(x \in \mathbb {R}\),

Combining (52) and (56) we retrieve (22). The independence of \(\mathrm{obs}(n)\) implies that, for any \(x\in \mathbb {R}\), \(\mathrm {var}\left( \mathbb {u}_\mathrm{est}^N(x)\right) =\sum _{-N}^{N}\mathrm {var}\left( \mathrm{obs}(n)\right) \gamma ^2(x-n)\). Hence, from (53), for any \(x \in \mathbb {R}\), we have that \(\mathrm {var}\left( \mathbb {u}_\mathrm{est}(x) \right) =\sum _{-\infty }^{+\infty }\mathrm {var}\left( \mathrm{obs}(n)\right) \gamma ^2(x-n)\). We now justify that \(\mathrm {var}\left( \mathbb {u}_\mathrm{est}(x)\right) \) is finite for any \(x \in \mathbb {R}\). From Corollary D.2, we have \(\sup _n \mathrm {var}\left( obs(n)\right) <+\infty \). Thus, it remains to show that \(\sum _{n=-\infty }^{+\infty }\gamma ^2(x-n)\) is finite for any \(x \in \mathbb {R}\). From Definition 5 we have that \(\gamma \) is \([-\pi ,\pi ]\) band limited. In addition, from (51) we have that \(\gamma ^2 \in L^1(\mathbb {R})\). Hence, we deduce that \(\gamma ^2\) is such that \(\widehat{\gamma ^2}(\xi )\) is supported on \([-2\pi ,2\pi ]\). Moreover, from the definition of \(\gamma \) 5 we have
The integrand in (57) is non-zero only on the zero Lebesgue measure set \(\{\pi \}\). Therefore, we have \(\widehat{\gamma ^2}(2\pi )=0\). Similarly, we have \(\widehat{\gamma ^2}(-2\pi )=0\). Thus, from the Poisson formula (see Appendix L) we deduce that
since, from remark we have that \(\gamma \in L^2(\mathbb {R})\). This concludes our proof.
Appendix G: Proof of Lemma F.1 p. 23
The proof is based on the Poisson summation formula (see Appendix L) and on the following lemma.
Lemma G.1
(Poisson like formula for the inverse filter \(\gamma \)) Let \(\alpha \) and \(\gamma \) be as in Definition 5 (page 15). For any \(x \in \mathbb {R}\), we have \(\sum _{n=-\infty }^{+\infty }\gamma (x-n)=\frac{1}{\int _{\mathbb {R}}\alpha (x)\mathrm{d}x}. \)
Proof
The proof is in Appendix H. \(\square \)
We now give the calculations details.
The proof is in three steps. The step (a) proves that, for any \(x \in \mathbb {R}\),
The step (b) proves that, for any \(x\in \mathbb {R}\),
The step (c) combines the steps a) and b) with Lemma G.1 and (29) to deduce (54). We now turn to step (a).
Step (a) For any \(x \in \mathbb {R}\), we have
To justify (61), consider the intermediate function \(f_x\) defined by
With the help of the function \(f_x\) defined in (62), the left hand side of (61) rewrites as
Using the Poisson summation formula (see Appendix L) we will prove that
Provided (64) holds, the equality in (61) follows from the definition of the Fourier transform \(\hat{f}_x(0)=\int _\mathbb {R}f_x(y)\mathrm{d}y\). Indeed, from the Definition (62) of \(f_x\) we have \(\int _\mathbb {R}f_x(y)\mathrm{d}y=\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *\tilde{u}\right) (y)\gamma (x-y)\mathrm{d}y\) which coincides with the RHS of (61). Therefore, provided we prove that (64) holds the equality in (61) holds. We now turn to the validity of (64).
Using the Poisson summation formula (see Appendix L), we now justify (64). In order to apply the Poisson formula we first need to prove that \(f_x \in L^1(\mathbb {R})\) and band limited. From Cauchy–Schwartz inequality (see, e.g., [61, p. 140]) we have
In addition, from Young inequality (see, e.g., [61, p. 525]), we have
Therefore, combining (65) and (66) we have
Furthermore, from Definition 1 we have \( \tilde{u} \in L^1(\mathbb {R})\), from remark we have \( \alpha \in L^2(\mathbb {R})\) and from the remark we have \(\gamma \in L^2(\mathbb {R})\). Therefore, from (67) we deduce that \(f_x \in L^1(\mathbb {R})\). From its Definition 1 \(\tilde{u}\) is band limited. Therefore, from its Definition (62), we deduce that \(f_x\) is band limited. This means that we can apply the Poisson formula to \(f_x\). The Poisson summation formula (see Appendix L) applied to \(f_x\) entails
Recall that we need to prove that (64) holds. Therefore, we need to prove that the term \(m=0\) is the only non-zero term in the RHS of (68).
From the Definition (62) of \(f_x\) we have
for any \(\xi \in \mathbb {R}\). From Definition 1 we have that u is \([-\pi ,\pi ]\) band limited. This implies that the function \(\mathbb {R}\ni \xi \mapsto \hat{\alpha }(\xi v) \hat{\tilde{u}} (\xi )\) is \([-\pi ,\pi ]\) band limited. From its Definition 5 \(\gamma \) is also \([-\pi ,\pi ]\) band limited. Therefore, from (69), we deduce that \(\hat{f}_x(\xi )=0\) for all \(\xi \in \mathbb {R}\) such that \(|\xi |>2\pi \). Thus, from (68) we deduce that
Yet, to prove that (64) holds we need to show that \(\hat{f}_x(-2\pi )=\hat{f}_x(2\pi )=0\). We now show in details that \(\hat{f}_x(2\pi )=0\). From (69), \(\hat{f}_x(\xi )\) is given by a convolution [see (9) for the definition]. Thus, the evaluation of (69) at \(\xi =2\pi \) yields
Recall that, from Definition 1, \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. Thus, from (71) we deduce that
The integrand in (72) is non-zero only on the zero Lebesque measure set \(\{\pi \}\). Hence, we deduce that \(\hat{f}_x(2\pi )=0\). Similarly we obtain \(\hat{f}_x( -2\pi )=0\). Thus, we proved that (64) holds, i.e., we can remove the question mark in (64). Consequently, we have that (61) holds. Furthermore, from the Definition (9) of the convolution we have
for any \(x \in \mathbb {R}\). Hence, combining (61) and (73), for any \(x \in \mathbb {R}\), we obtain (59). This concludes the step (a). We now turn to step (b).
Step (b) From the Definition (14) of the Fourier and the inverse Fourier transforms, for any \(x\in \mathbb {R}\), we have
Since \(\mathcal {F}\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) \right) = \hat{\alpha }(\xi v)\), from (74) we have
for any \(x \in \mathbb {R}\). From the definition of the inverse Fourier transform (xiv) and (75) we deduce that, for any \(x \in \mathbb {R}\),
From Definition 1 we have that \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. Consequently, from (76) we deduce that, for any \(x \in \mathbb {R}\),
From the definition of \(\gamma \) (20) we have that \(\hat{\gamma }(\xi ) = \frac{1}{\hat{\alpha }(\xi v)}\) for any \(\xi \in [-\pi ,\pi ]\). Hence, we deduce that, for any \(x \in \mathbb {R}\),
From Definition 1 we have that \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. This implies that, for any \(x \in \mathbb {R}\),
where the last equality is justified by the definition of the inverse Fourier transform (14). Thus, combining (78) and (79) we obtain (60). This completes the step (b). We now turn to the step (c) that completes our proof.
Step (c) Combining (59) and (60), for any \(x \in \mathbb {R}\), we have
From Lemma G.1 we deduce that, for any \(x \in \mathbb {R}\),
Therefore, combining (29), (80) and (81) we deduce that, for any \(x \in \mathbb {R}\),
From the definition of u 1 we have \(u(\cdot )=\tilde{u}(\cdot ) +\mu \). Thus, from (82) we obtain that, for any \(x \in \mathbb {R}\), (54) holds. This concludes our proof.
Appendix H: Proof of Lemma G.1 p. 24
Consider the \(2\pi \) periodic function \(g:\mathbb {R}\rightarrow \mathbb {C}\) defined as
and the Dirichlet kernel \(D_n(\xi )=\frac{1}{2\pi }\sum _{k=-n}^{n} e^{ik\xi }\). From its Definition 3 we have \(\alpha \in L^1(\mathbb {R})\). Therefore, by Riemann–Lebesque (see e.g., [52, Proposition 2.1]) we have that \(\hat{\alpha }\) is continuous. From Definition 5 and (83), we have \(g(\xi )=\gamma (\xi )=\frac{1}{\hat{\alpha }(\xi v)}\) for any \(\xi \in [-\pi ,\pi ]\). Since \(\hat{\alpha }(\xi v) \ne 0\) for any \(\xi \in [-\pi ,\pi ]\), we obtain that g is continuous on \([-\pi ,\pi ]\) and that \(g \in L^1(-\pi ,\pi )\). Since \(g\in L^1(-\pi ,\pi )\) it has a Fourier series decomposition [see (18)]. From the Fourier series decomposition we have
where, for any \(k \in \mathbb {Z}\),
We shall now pass to the limit \(n \rightarrow +\infty \) in (84). The Fourier series theory entails that  for any \(\xi \in \mathbb {R}\) where g is continuous at \(\xi \). Therefore, we obtain that
for any \(\xi \in \mathbb {R}\) where g is continuous at \(\xi \). Therefore, we obtain that
for any \(\xi \in \mathbb {R}\) where g is continuous at \(\xi \). We have that g is continuous at \(\xi =0\). Therefore, from (86) we obtain that
Hence, combining (83), (85), and (87) we deduce that
Since, from its Definition 5, \(\gamma \) is \([-\pi ,\pi ]\) band limited we obtain that
In addition, from (51) we have \(\gamma \in L^2(\mathbb {R})\). From (14), for any \(k \in \mathbb {Z}\), we have
Hence, combining (88) and (89) we deduce that
This applies for any shift \(x \in \mathbb {R}\) of \(\gamma \). Hence, from (90) we deduce that
for any \(x \in \mathbb {R}\). In addition, from Definition 5, we have
Thus, combining (92) and (91) we deduce that \(\sum _{k=-\infty }^{+\infty }\gamma (x-k)=\frac{1}{\int _{\mathbb {R}}\alpha (t)\mathrm{d}t}, \) for any \(x \in \mathbb {R}\). This concludes our proof.
Appendix I: Proof of Theorem 3.4 p. 15
In order to provide closed formulae for the MSE and SNR we first evaluate \(\mathrm {var}(\mathbb {u}_\mathrm{est}(x))\) and then the limit of \(\frac{1}{2R} \int _{-R}^R \mathrm {var}(\mathbb {u}_\mathrm{est}(x))\mathrm{d}x\) when \(R \rightarrow + \infty \).
Combining (14) and (23), for any \(x \in \mathbb {R}\), we have
Therefore, from (93) we deduce that, for any \(x \in \mathbb {R}\),
From Definition 3, we have that \(\alpha \) is non-negative. Therefore, \( \Vert \alpha \Vert _{L^1(\mathbb {R})} = \int _{\mathbb {R}} \alpha (t)\mathrm{d}t\). Hence, combining (29) and (94), for any \(x \in \mathbb {R}\), we have
Hence, combining (58) and (95), for any \(x \in \mathbb {R}\), we have
Moreover, from the Definition 5 and Plancherel identity (140) we have
Thus, combining (96) and (97) we deduce that, for any \(x\in \mathbb {R}\),
From Proposition 3.3, for any \(x \in \mathbb {R}\), we have
Therefore, for any \(x \in \mathbb {R}\), we have
Hence, combining (98) and (100), for any \(x \in \mathbb {R}\), we have
With the help of (101), we now calculate the limit of \(\frac{1}{2R} \int _{-R}^R \mathrm {var}(\mathbb {u}_\mathrm{est}(x))\mathrm{d}x\) when \(R \rightarrow + \infty \). The function \(\mathbb {R}\ni x \mapsto \sum _{n=-\infty }^\infty \left[ \left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *\tilde{u}\right) (n)(\gamma (x-n))^2\right] \) belongs to \(L^1(\mathbb {R})\). Indeed, we have

Hence, it follows from (102) and Fubini theorem (see, e.g., [53, p. 196]) that
For any \(n \in \mathbb {Z}\), we have
Therefore, from (103) we deduce that
From Definition 1 we have \(\tilde{u} \in L^1(\mathbb {R})\) and \(\tilde{u}\) is \([-\pi ,\pi ]\) band limited. From Definition 3 \(\alpha \in L^1(\mathbb {R})\). Therefore, from the Poisson summation formula (see Appendix L) we obtain that
Indeed, from Young inequality (see, e.g., [61, p. 525]) we have that \(\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v} \right) *\tilde{u} \right) \in L^1(\mathbb {R})\). In addition, from (51) \(\gamma \in L^2(\mathbb {R})\). Thus, combining (104) and (105) we deduce that
and therefore obtain

For any \(R>0\), from (98) we have that
Combining (106) and (107)–(108), we obtain

Hence, combining (100) and (109), we deduce that, for any \(x \in \mathbb {R}\),

Therefore, (24) is proved. The proof of (25) follows from the definition of u (Definition 1), (22) and the above equation. This concludes our proof.
Appendix J: Proof of Theorem 4.1
From Theorem 3.4 we have
where \(\mathrm{d}\lambda \) denotes the Lebesgue measure on \(\left( \mathbb {R}, \mathcal {B}(\mathbb {R})\right) \). Let \(S:=\big \{ \alpha \mathrm{of \ the\ form~(12)}, \alpha \in L^1(\mathbb {R}),~ 0\le \alpha \le 1\big \}\). From Definition 3, we deduce that optimizing the coded exposure method boils down to finding \(\alpha \in S\) that minimizes (110). We wish to prove that (27) holds true. Our proof is in 4 steps. Step (a) proves that, for any \(\alpha \in S\), (110) is bounded from below, namely that there holds
Step (b) proves that as soon as \(|v|\Delta t\le 1\) the RHS of (111) can be rewritten in terms of Fourier series and that there holds
Step (c) proves that the RHS of (112) is attained by constructing an adequate f that allows to show that
Step (d) proves that (27) holds by giving a closed form of the RHS of (113), and giving a formula for the constant C. We now turn to step (a).
Step (a) From its Definition 3 we have that \(\alpha (t) \in [0,1]\) for any \(t\in \mathbb {R}\) and that \(\alpha \in L^1(\mathbb {R})\). Hence, we deduce that \(\alpha ^2 \le \alpha \) and that \(\int _{\mathbb {R}} |\alpha (x)|\mathrm{d}x\ge \int _{\mathbb {R}} |\alpha (x)|^2\mathrm{d}x\). Hence, from (110) and the definition of S, we obtain that
In addition, the form of \(\alpha \) given in Definition 3 and the fact that \(\ell ^1(\mathbb {Z}) \subset \ell ^2(\mathbb {Z})\), imply that \(S \subset \left\{ \alpha \ \mathrm{of \ the \ form~(12)},~\alpha \in L^2(\mathbb {R}), 0\le \alpha \le 1 \right\} \). Thus, from (114) we deduce that
Consider the set \(T:=\left\{ \alpha \mathrm{of \ the\ form~(12)},~\alpha \in L^2(\mathbb {R}), -1\le \alpha \le 1 \right\} .\) We have that \(S\subset \left\{ \alpha \mathrm{\;of \; the\ form~(12)},~\alpha \in L^2(\mathbb {R}), 0\le \alpha \le 1 \right\} \subset T\). Therefore, combining (114) and (115) we deduce that
Our goal is to evaluate the RSH of the above equation. From Definition 3, by an easy calculation of a Fourier transform (14), we deduce that, for any \(\xi \in \mathbb {R}\), there holds
Hence, combining (116) and (117) we deduce that
Thus, by a change of variable, from (118) we deduce that
This concludes step 1. We now turn to step (b).
Step (b) Since, by assumption, we have \(|v|\Delta t\le 1\) we deduce that \([-\pi |v|\Delta t,\pi |v|\Delta t] \subset [-\pi ,\pi ]\) (note that \(\mathrm {sinc}^2\left( \frac{\xi }{2\pi }\right) \ne 0\) for any \(\xi \in [-\pi ,\pi ]\)). As soon as \(|v|\Delta t\le 1\), the term \(\sum _{k \in \mathbb {Z}} \alpha _k e^{-ik \xi }\) that appears in the RHS of (119) is the Fourier series (18) synthesis formula of some \(f \in L^2(-\pi ,\pi )\) function evaluated at \(-\xi \). In other words, as soon as \(|v|\Delta t\le 1\), \(\alpha _k=c_k(f)\) for any \(k\in \mathbb {Z}\), for some \(f \in L^2(-\pi ,\pi )\). From Parseval identity (18) we have \(\sum _k |\alpha _k|^2=\Vert f\Vert _{L^2(-\pi ,\pi )}^2\). Thus, form (119) and Riesz–Fischer theorem (see, e.g., [62, p. 27]), as soon as \(|v|\Delta t\le 1\), we obtain
where \(U:=\{f\in L^2(-\pi ,\pi ), -1\le f \le 1\}\). This concludes step (b). We now turn to step (c).
Step (c) On the one hand, \(\alpha _k=c_k(f) \in \mathbb {R}\) for any \(k\in \mathbb {Z}\) and the Hermitian symmetry implies that \(|f(-\xi )|=|f(\xi )|\). On the other hand, the function \((0,+\infty ) \ni x \mapsto \frac{1}{x}\) is strictly convex. In addition, we have \(\frac{\mathrm{d} \lambda ([-\pi ,\pi ])}{2\pi }=1\). Thus, by Jensen inequality (see, e.g., [59, p. 232]), from (120) we obtain that
The strict convexity of \((0,+\infty ) \ni x \mapsto \frac{1}{x}\) implies that the equality case in (121) is realized when \( \xi \mapsto \mathrm {sinc}^2\left( \frac{\xi }{2\pi }\right) \left| f(\xi )\right| ^2 \) is constant say \(C>0\) on the interval \([-\pi |v|\Delta t,\pi |v|\Delta t]\). We choose to set \(f(\xi ):=\frac{C}{\mathrm {sinc}\left( \frac{\xi }{2\pi }\right) }\) for any \(\xi \in [-\pi |v|\Delta t,\pi |v|\Delta t]\). It remains to extend this f on \([-\pi ,\pi ] \backslash [-\pi |v|\Delta t,\pi |v|\Delta t]\), and discuss the value of C, to give a complete definition of an \(f \in L^2(\mathbb {R})\) that provides, through its Fourier series, a lower bound for the MSE of any coded exposure method. From the term \( \Vert f\Vert _{L^2(-\pi ,\pi )}^2\) in (121) it is easy to see that we need to extend f by zero on \([-\pi ,\pi ] \backslash [-\pi |v|\Delta t,\pi |v|\Delta t]\). This yield to the definition of \(f \in L^2(-\pi ,\pi )\) of the form
where C is a positive constant. Being real and even, this f therefore entails that the \(a_k=c_k(f)\) are real. The f given in (122) provide the equality case in (121). Thus, combining (120) and the equality case in (121) given by the definition of f (122) we deduce that, as soon as \(|v|\Delta t \le 1\), there holds
where C is a positive constant. It remains to set the value of C in (122) so that \(f \in U\), i.e., to ensure that \(|\alpha _k|\le 1\) (recall Definition 3). From (123) it is easy to see that we would like C as large as possible, while \(|c_k(f)|\le 1\) so that \(f \in U\). From their Definition (18) we have that \(|c_k(f)|\le \frac{1}{2\pi } \int _{-\pi |v|\Delta t}^{\pi |v| \Delta t} \frac{C}{ \ \mathrm {sinc}\ \left( \frac{\xi }{2\pi }\right) })\mathrm{d}\xi \). Therefore, we deduce that we need \(C \le \frac{1}{\frac{1}{2\pi }\int _{-\pi |v|\Delta t }^{\pi |v| \Delta t} \frac{C}{\ \mathrm {sinc}\ \left( \frac{\xi }{2\pi }\right) }\mathrm{d}\xi }\) in order to ensure that \(|c_k(f)|\le 1\) for any \(k \in \mathbb {Z}\). Therefore, we deduce that the choice
in the definition of f is enough to provide a lower bound to the MSE of coded exposure cameras. That is this choice for f realizes in infinimum of the RHS of (120). In other words, from (123) we deduce that, as soon as \(|v|\Delta t \le 1\),
with C given by (124). From (125), as soon as \(|v|\Delta t \le 1\), we obtain
This concludes step (c). We now turn to step (d).
Step (d) It remains to give a closed form for (126). On the one hand, we have
On the other hand, from (124), we have
Thus, combining (127)–(128) and (129) we deduce that
and therefore
Combining (126) and (130)–(131) we obtain (27) and conclude our proof.
Appendix K: Proof of Corollary 4.2 p. 17
In order to evaluate the maximal theoretical “gain” of coded exposure camera we need to compare the bound in terms of MSE given in Theorem 4.1 namely (27) with the MSE of a snapshot. Therefore, the proof is in two steps. The first step prove an upper bound for the MSE of the optimal snapshot. Step (b) calculates the ratio of these MSE and prove (28). We now turn to step (a).
Step (a) From Corollary 3.5 and the definition of the sinc function (16) we have
Hence, we deduce
and therefore obtain
Thus, combining (26) and (132), we deduce that the MSE of a snapshot with exposure time equal to \(\Delta t:=\frac{1}{|v|}\) (this implies that support of the blur kernel is 1 pixel) satisfies
Indeed, the optimal snapshot, if it exists has, by definition, a MSE lower or equal to the one in Eq. (133). In other words, (133) provides an upper bound for the MSE of the optimal snapshot. We now compare the MSE of the coded exposure method given by Theorem 4.1 namely Eq. (27) and the MSE of this snapshot in step (b).
Step (b) From Theorem 4.1 (p. 17), as soon as \(|v|\Delta t<1\) we have
In addition, by Jensen inequality (see, e.g., [59, p. 232]), we have
Hence, we deduce that
Thus, combining (134)–(135) and (136) we deduce that
and therefore obtain
Thus, combining (133) and (137) we obtain
and therefore
Equation (138) is valid for any \(\alpha \) that satisfies Definition 3 and \(|v|\Delta t\le 1\). In other words, (138) is valid for any coded exposure method that satisfies \(|v|\Delta t\le 1\). Hence (28) is proven. This concludes our proof.
Appendix L: Poisson summation formula for \(L^1(\mathbb {R})\) band-limited functions
This section proves that the Poisson summation formula that we use in this paper is valid.
The Poisson summation formula is, formally,
However, (139) is not always valid when \(f \in L^1(\mathbb {R})\). Indeed, even when both sides of (139) converge absolutely the equality may fail (see, e.g., [63] and [64, Example 1.17, p. 163] for an example of \(f\in L^1(\mathbb {R})\) such that \(\hat{f} \in L^1(\mathbb {R})\) for which (139) fails). A classic condition that ensures that (139) holds involves decay estimates of both f and \(\hat{f}\) at the infinity (see, e.g., [61, Theorem 1, p. 628]) and does not apply if f is just in \(L^1(\mathbb {R})\) and band limited. Other results involve bounded variation assumption (see, e.g., [63]) on f that are not applicable here. Therefore, we shall now provide a proof that (139) holds in our case that is for an \(f \in L^1(\mathbb {R})\) and band limited. Our proof is based on [65]. Let \(f \in L^1(\mathbb {R})\) be such that \(\hat{f}(\xi ) =0\) for any \(\xi \) such that \(|\xi |>C\) for some constant C. From Riemann–Lebesgue theorem (see e.g., [52, Proposition 2.1]) we have \(\hat{f}\) is continuous. From the band-limited assumption we deduce that \(\hat{f} \in L^1(\mathbb {R})\). Since f is band limited the series \(\sum _{m=-\infty }^{+\infty } \hat{f}\left( 2\pi m -x\right) \) is finite and therefore converges uniformly in \(x\in \mathbb {R}\). By Plancherel–Pólya inequality (see [66, Eqs. (25) and (26), p. 233], since \(f \in L^1(\mathbb {R})\) and band limited it satisfies the growth condition) we obtain that \( \sum _{k=-\infty }^{+\infty }|f(k)| \le A \Vert f\Vert _{L^1(\mathbb {R})}\) for some positive constant A. Therefore, the series \(\sum _{k=-\infty }^{+\infty }f(k)\) converges. Thus, we can apply [65, Theorem 2, p. 147] (with \(g:=\hat{f}\) and \(W=\frac{1}{2\pi }\)) to deduce that (139) is valid for any \(f \in L^1(\mathbb {R})\) band limited.
Appendix M: Main notations and formulae
-
1.
\(t\ge 0\) time variable.
-
2.
\(\Delta t\) length of a time interval (exposure time).
-
3.
\(x \in \mathbb {R}\) spatial variable.
-
4.
\(X \sim Y\) means that the random variables X and Y have the same law.
-
5.
\(\mathbb {P}(A)\) probability of an event A.
-
6.
\(\mathbb {E}(X)\) expected value of a random variable X.
-
7.
\(\mathrm {var}(X)\) variance of a random variable X.
-
8.
\(\mathcal P(\lambda )\) Poisson random variable with intensity \(\lambda >0\). Thus, if \(X \sim \mathcal P (\lambda )\) we have \(\mathbb {P}(X=k)=\frac{\exp (-\lambda )\lambda ^k}{k!}\).
-
9.
\(f *g\) convolution of two functions \((f *g)(x) = \int _{\mathbb {R}} f(y) g(x-y) \mathrm{d}y\).
-
10.
\(\mathrm{obs}(n)\), \(n \in \mathbb {Z}\) observation of the scene at a pixel at position n.
-
11.
v relative velocity between the scene and the camera (unit: pixel(s) per second).
-
12.
\(\alpha (\cdot )=\sum _{k=-\infty }^{+\infty } \alpha _k \mathbb {1}_{\left[ k\Delta t,(k+1)\Delta t\right) }(\cdot )\) exposure function (\((\alpha _k)_k \in \ell ^1(\mathbb {Z})\)).
-
13.
\( \Vert f \Vert _{L^1(\mathbb {R})}= \int _\mathbb {R}|f(x)| \mathrm{d}x\), \( \Vert f \Vert _{L^2(\mathbb {R})}= \sqrt{\int _\mathbb {R}|f(x)|^2 \mathrm{d}x}\).
-
14.
Let \(f,g \in L^1(\mathbb {R})\) or \(L^2(\mathbb {R})\), then \(\mathcal {F}(f)(\xi ):=\hat{f} (\xi ):=\int _{\mathbb {R}} f(x) e^{-ix \xi } \mathrm{d}x\) and
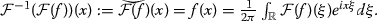 Moreover \(\mathcal {F}(f*g)(\xi )=\mathcal {F}(f)(\xi )\mathcal {F}(g)(\xi )\) and (Plancherel) $$\begin{aligned} \int _{\mathbb {R}} |f(x)|^2\mathrm{d}x= \Vert f \Vert _{L^2(\mathbb {R})}^2=\frac{1}{2 \pi } \int _{\mathbb {R}} \left| \mathcal {F}(f)\right| ^2(\xi ) \mathrm{d}\xi = \frac{1}{2\pi } \Vert \mathcal {F}(f) \Vert _{L^2(\mathbb {R})}^2\qquad \quad \end{aligned}$$(140)
Moreover \(\mathcal {F}(f*g)(\xi )=\mathcal {F}(f)(\xi )\mathcal {F}(g)(\xi )\) and (Plancherel) $$\begin{aligned} \int _{\mathbb {R}} |f(x)|^2\mathrm{d}x= \Vert f \Vert _{L^2(\mathbb {R})}^2=\frac{1}{2 \pi } \int _{\mathbb {R}} \left| \mathcal {F}(f)\right| ^2(\xi ) \mathrm{d}\xi = \frac{1}{2\pi } \Vert \mathcal {F}(f) \Vert _{L^2(\mathbb {R})}^2\qquad \quad \end{aligned}$$(140) -
15.
u ideal (noiseless) observable scene.
-
16.
\(\ \mathrm {sinc}\ (x)=\frac{\sin (\pi x)}{\pi x}=\frac{1}{2 \pi } \mathcal {F}(\mathbb {1}_{[-\pi ,\pi ]})(x)=\mathcal {F}^{-1}(\mathbb {1}_{[-\pi ,\pi ]})(x)\).
-
17.
\(\mathbb {1}_{[a,b]}\) indicator function of an interval [a, b].
-
18.
Let \(f\in L^1(-\pi ,\pi )\) or \(f\in L^2(-\pi ,\pi )\). The n-th Fourier series coefficient of f is \(c_n(f):=\frac{1}{2\pi }\int _{-\pi }^\pi f(t)e^{-in t}\mathrm{d}t\) and we have \(f(t)=\sum _{n=-\infty }^{+\infty } c_n(f)e^{+int}\). Moreover we have (Parseval)
$$\begin{aligned} \sum _{n=-\infty }^{+\infty }\left| c_n(f)\right| ^2=\Vert f\Vert _{L^2(-\pi ,\pi )}^2:=\frac{1}{2\pi }\int _{-\pi }^\pi \left| f(t)\right| ^2\mathrm{d}t. \end{aligned}$$(141)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tendero, Y., Osher, S. On a mathematical theory of coded exposure. Res Math Sci 3, 4 (2016). https://doi.org/10.1186/s40687-015-0051-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40687-015-0051-8
Keywords
- Coded exposure
- Computational photography
- Flutter shutter
- Motion blur
- Mean square error (MSE)
- Signal to noise ratio (SNR)








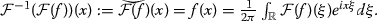 Moreover
Moreover