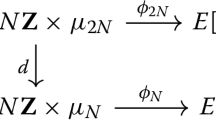Abstract
Let q be a prime and \(K={\mathbb Q}(\sqrt{-D})\) be an imaginary quadratic field such that q is inert in K. If \(\mathfrak {q}\) is a prime above q in the Hilbert class field of K, there is a reduction map
from the set of elliptic curves over \(\overline{{\mathbb Q}}\) with complex multiplication by the ring of integers \({\mathcal {O}}_K\) to the set of supersingular elliptic curves over \({\mathbb {F}}_{q^2}.\) We prove a uniform asymptotic formula for the number of CM elliptic curves which reduce to a given supersingular elliptic curve and use this result to deduce that the reduction map is surjective for \(D \gg _{\varepsilon } q^{18+\varepsilon }.\) This can be viewed as an analog of Linnik’s theorem on the least prime in an arithmetic progression. We also use related ideas to prove a uniform asymptotic formula for the average
of central values of the Rankin–Selberg L-functions \({L(f \times {\Theta _{\chi}},s)}\) where f is a fixed weight 2, level q arithmetically normalized Hecke cusp form and \(\Theta _\chi \) varies over the weight 1, level D theta series associated to an ideal class group character \(\chi \) of K. We apply this result to study the arithmetic of Abelian varieties, subconvexity, and \(L^4\) norms of autormorphic forms.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Bertolini, M., Darmon, H.: A rigid analytic Gross–Zagier formula and arithmetic applications. Ann. Math. 146, 111–147 (1997)
Blomer, V., Harcos, G.: Hybrid bounds for twisted L-functions. J. Reine Angew. Math. 621, 53–79 (2008)
Blomer, V., Khan, R., Young, M.: Distribution of mass of Hecke eigenforms. Duke Math. J. 162, 2609–2644 (2013)
Blomer, V., Michel, P.: Sup-norms of eigenfunctions on arithmetic ellipsoids. Int. Math. Res. Not. IMRN 21, 4934–4966 (2011)
Buttcane, J., Khan, R.: L norms of Hecke newforms of large level. http://arxiv.org/abs/1305.1850 (2013, preprint)
Cornut, C.: Mazur’s conjecture on higher Heegner points. Invent. Math. 148, 495–523 (2002)
Duke, W.: Hyperbolic distribution problems and half-integral weight Maass forms. Invent. Math. 92, 73–90 (1988)
Duke, W.: The critical order of vanishing of automorphic L-functions with large level. Invent. Math. 119, 165–174 (1995)
Elkies, N., Ono, K., Yang, T.H.: Reduction of CM elliptic curves and modular function congruences. Int. Math. Res. Not. 44, 2695–2707 (2005)
Feigon, B., Whitehouse, D.: Averages of central L-values of Hilbert modular forms with an application to subconvexity. Duke Math. J. 149, 347–410 (2009)
Feigon, B., Whitehouse, D.: Exact averages of central values of triple product L-functions. Int. J. Number Theory 6, 1609–1624 (2010)
Gelbart, S., Jacquet, H.: A relation between automorphic representations of GL(2) and GL(3). Ann. Sci. École Norm. Sup. 11, 471–542 (1978)
Gross, B.: Heights and the special values of L-series. Number theory (Montreal, Que., 1985). In: CMS Conference Proceedings, vol. 7, pp. 115–187. Amer. Math. Soc., Providence (1987)
Gross, B., Kudla, S.: Heights and the central critical values of triple product L-functions. Compositio Math. 81, 143–209 (1992)
Hoffstein, J., Kontorovich, A.: The first non-vanishing quadratic twist of an automorphic L-series. http://arxiv.org/abs/1008.0839 (2010, preprint)
Holowinsky, R., Munshi, R.: Level aspect subconvexity for Rankin–Selberg L-functions, to appear in automorphic representations and L-functions. Tata Institute of Fundamental Research, Mumbai. http://arxiv.org/abs/1203.1300 (2012)
Holowinsky, R., Templier, N.: First moment of Rankin–Selberg central L-values and subconvexity in the level aspect. Ramanujan J. 33, 131–155 (2014)
Iwaniec, H.: Fourier coefficients of modular forms of half-integral weight. Invent. Math. 87, 385–401 (1987)
Iwaniec, H., Kowalski, E.: Analytic number theory. American Mathematical Society Colloquium Publications, vol. 53, pp. xii+615. American Mathematical Society, Providence (2004)
Iwaniec, H., Luo, W., Sarnak, P.: Low lying zeros of families of L-functions. Inst. Hautes Études Sci. Publ. Math. 91(2000), 55–131 (2001)
Jackson, J., Knightly, A.: Averages of twisted L-functions, p. 24 (2015, preprint)
Jetchev, D., Kane, B.: Equidistribution of Heegner points and ternary quadratic forms. Math. Ann. 350, 501–532 (2011)
Kane, B.: Representations of integers by ternary quadratic forms. Int. J. Number Theory 6, 127–159 (2010)
Kane, B.: CM liftings of supersingular elliptic curves. J. Théor. Nombres Bordeaux 21, 635–663 (2009)
Kohel, D.: Endomorphism rings of elliptic curves over finite fields. University of California, Berkeley, Thesis (1996)
Kohnen, W., Sengupta, J.: On quadratic character twists of Hecke L-functions attached to cusp forms of varying weights at the central point. Acta Arith. 99, 61–66 (2001)
Kohnen, W., Zagier, D.: Values of L-series of modular forms at the center of critical strip. Invent. Math. 64, 175–198 (1981)
Li, X.: Upper bounds on L-functions at the edge of the critical strip. IMRN 4, 727–755 (2010)
Liu, S.-C., Masri, R., Young, M.P.: Subconvexity and equidistribution of Heegner points in the level aspect. Compositio Math. 149, 1150–1174 (2013)
Michel, P.: The subconvexity problem for Rankin–Selberg L-functions and equidistribution of Heegner points. Ann. Math. 160, 185–236 (2004)
Michel, P., Ramakrishnan, D.: Consequences of the Gross–Zagier formulae: stability of average L. Number theory, analysis and geometry, pp. 437–459. Springer, New York (2012)
Michel, P., Venkatesh, A.: Heegner points and non-vanishing of Rankin/Selberg L-functions. Analytic number theory, Clay Math. Proc., vol. 7, pp. 169–183. Amer. Math. Soc., Providence (2007)
Nelson, P.: Stable averages of central values of Rankin–Selberg L-functions: some new variants. http://arxiv.org/abs/1202.6313 (2012, preprint)
Vatsal, V.: Uniform distribution of Heegner points. Invent. Math. 148, 1–46 (2002)
Yang, T.H.: Minimal CM liftings of supersingular elliptic curves. Pure Appl. Math. Q. 4, 1317–1326 (2008)
Acknowledgements
R. M. and M. Y. were supported by the National Science Foundation under agreement Nos. DMS-1162535 (R. M.) and DMS-1101261 (M. Y.). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, SC., Masri, R. & Young, M.P. Rankin–Selberg L-functions and the reduction of CM elliptic curves. Mathematical Sciences 2, 22 (2015). https://doi.org/10.1186/s40687-015-0040-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40687-015-0040-y
Keywords
- Supersingular elliptic curves
- Equidistribution
- Gross points
- Heegner points
- Mean values of L-functions
- \(L^4\) norm