Abstract
Background
This paper presents a detailed analysis of a composite Climate Vulnerability Index (CVI) to examine and compare climate change vulnerability and its dimensions adaptive capacity, sensitivity and exposure. Thereby, we are mainly interested on climate change vulnerability at community-level watershed development programmes and how the different implementing agencies could help to address the problems associated with climate change in future planning and implementation.
Method
The primary data used for this study was obtained from household surveys (n=215) in three watershed communities of Kerala, India. We use bootstrap sampling and a leave-one-out sensitivity analysis to compare the climate vulnerability of the three examined watersheds in detail. By introducing the bootstrapping method and sensitivity analysis into the research field of climate vulnerability, the paper describes significant differences in CVI values and the influencing indicators to the overall vulnerability at the watershed community level.
Results
The results show that there are significant differences in the exposure and sensitivity dimensions of vulnerability even if the overall CVI shows less variability and no significant differences among the three watersheds. The sensitivity analysis emphasizes that ‘Livelihood Strategies’ and ‘Social Network’ are the most influencing major components of vulnerability. This suggests that implementing agencies should focus on these two major components in order to improve the watershed development programmes.
Conclusion
The bootstrapping approach is transferable to evaluate the degree of influence of indicators on a composite index like the CVI. Moreover, it allows us to evaluate the potential effectiveness of various other climate change programmes where the evaluation is commonly done by field surveys. This thereby helps to increase the credibility in the examination of the impacts of climate change at different scales in order to find key areas for better policy planning.
Similar content being viewed by others
Background
Climate change adaptation strategies are given high priority in developing countries due to their social, technological and financial resource scarcity for adapting to anticipated climate change and variability [1]. One billion people in Asia could face water shortage which leads to drought and land degradation by the 2050s [2]. By 2030, these countries will require about USD 28-67 billion to enable proper and timely adaptation to climate change depending on the geographical, social, cultural, economic and political situation [1]. Therefore, quantification of vulnerability is very important to help the vulnerable regions in the prioritisation and planning of activities to tackle the impacts of climate change [3].
Although vulnerability is not a directly observable phenomenon, because of the policy-driven needs and assessments [3, 4], researchers have proposed and applied a set or composite of proxy indicators to quantify the vulnerability [5, 6]. Composite indices are analytical, communicative and collaborative tools which help to raise awareness, support decision making, facilitate planning and policy development through improved understanding of a complex multidimensional problem [7, 8]. This gets even more complicated when assessments of continual stress like climate change are taken into account. Moreover, it can be more challenging when local geographical, ecological and socio-economical contexts vary substantially within a given area of interest [7]. Thus, it would be unwise to adopt a national level index approach to local scale study and vice versa [9] without adequate modifications and adjustments [10]. In addition, available indices are limited in their applicability by considerable subjectivity and uncertainties in the selection of indicators [7, 8, 11, 12], their weights [4, 6], as well as by the availability of data at various scales and in space [8, 13].
There are a number of previous studies on quantifying and comparing vulnerability in terms of an index [6, 13–18]. Analysing climate vulnerability and research into the development of appropriate indicators has gained awareness since the groundbreaking paper of Smit and Wandel [19] and the IPCC assessment report published in 2007 [2]. To date, the majority of these studies have focused merely on developing a Climate Vulnerability Index (CVI) for specific climatic disasters such as droughts or floods and for specific communities. In addition, these studies were proposing policy suggestions for improved adaptation strategies and mitigation solutions. However, the CVIs used in the past studies do not explore the robustness of comparisons, significant differences of vulnerability indicators [20] or the significance of the associated policy messages at local to community level [7]. While a number of general, regional and subject-specific indicators have been developed [21], we found less work that investigated or at least discussed the issue of uncertainty. Already in 2011, Preston et al. [22] stated that “Unfortunately, the tendency within vulnerability assessments is to neglect the issue of uncertainty almost entirely-an occurrence that is likely to undermine the uptake of vulnerability assessments in decision support.” [22].
There are a few uncertainty and sensitivity analyses done for other composite indices like the Technology Achievement Index [12], Composite Learning Index [23], Social Vulnerability Index [24, 25], Human Development Index [26] and Environmental Performance Index [27] at national to global level. These studies confirm that uncertainty is an unavoidable factor for composite indices [21, 22]. The reason is that the value of a composite indicator is not a simple number, but a distribution of values. According to Saisana et al. [12], the composite indicator’s ‘simple big picture’ may direct to misleading non-robust policy messages if they are not interpreted in combination with the sub-indicators. Thus, it emphasizes the need and urgency to conduct sensitivity analysis of CVI rather than merely developing a composite index for policy implications.
Sensitivity analysis examines the robustness, i.e. the degree of influence of each indicator on the index output, thereby revealing which input choices are most or least influential [25]. Shukla et al. [28] have evaluated solely the robustness of inherent vulnerability ranks to compare mountainous agricultural communities in Uttarakhand state of India. Uncertainty in the estimation of climate vulnerability can have several sources. The selection of the composite indicator is one of these sources. Vulnerability is largely depending on the composition and construction of the method applied, as was shown in a multi-index method intercomparison [29]. In case spatial assessment is conducted, the variability of input data introduce a further component, i.e. the spatial uncertainty [22]. Additional uncertainty can arise through weighing the various indicators or components that are used in the estimation of the vulnerability indices [29, 30]. The question remains, how much uncertainty is introduced by a single indicator into the assessment of vulnerability and how much a single (or several) indicator affects the overall outcome. Just recently in parallel to our work, Fernandez et al. [31] investigated the effect of particular indicators on the overall outcome of their index. They studied the substitutional power of indicators by various aggregation schemes. Our study takes a different approach. By adopting the bootstrap methodology we aim at identifying the robustness of our calculated index in view of the selection of input data, in our case the survey data. Through this systematic analysis of the CVI, we are able to provide the specific driving factors which contribute to the adverse effects of climate change.
For this study, we considered the CVI developed at Indian watershed community level. We are specifically interested in the climate vulnerability at watershed household level to identify the main drivers of climate change vulnerability and thus how the different implementing agencies could help to address the problems associated with climate change in future planning and implementation. In addition, we believe that climate change is particularly noticeable at this aggregation level and illustrate the differences between the Watershed Development Programmes (WDP). Fifty-five percent of Indian farmers rely on rainfed systems in which ‘delayed, deficient or erratic rains’ lead to a severe decline in productivity [32, 33]. Another stressor, climate change, affects weather patterns, availability of water, temperature and soil moisture, thereby resulting in low crop yields and degraded land with increased sensitivity of food-insecure households [3]. To change the situation of these rainfed areas, the Government of India initiated WDPs in 1973-74. WDP refer to the conservation, regeneration and the judicious use of all the resources - natural (like land, water, plants, animals) and human - within the watershed area. Samuel et al. [34] indicate that community-led watershed development has the potential to make a significant contribution to reduce the vulnerability, enhance resilience and build adaptive capacities of communities to climate-induced shocks. Moreover, integration of climate change aspects into ongoing development efforts with special attention to location specific knowledge is required for better adaptation strategies [35]. For this, policies and programmes need to be fine tuned with respect to technology, processes and institutions to make the watersheds more resilient to variability and extreme climate risks [34]. The assessment of vulnerability at the watershed community level has just recently begun.
A preliminary study has been conducted by us among three watershed communities in Kerala, the southernmost state of India [36]. The implementation of the programme was done by three different agencies: the State Government (SG) through the department of Soil Survey & Conservation, a Non-Governmental Organization (NGO) and the Local Self-Government (LG). Our approach used primary data collected from household surveys (n=215) to construct the index. Qualitative data obtained through Focus Group Discussions (FGDs) and Key Informant Interviews was used to support the results. Through a theory driven and deductive approach [37], the best possible location specific indicators were identified and aggregated at watershed community level under the three dimensions of vulnerability: adaptive capacity, sensitivity and exposure to form the index [6, 9]. Under these three dimensions, 10 major components and 59 sub-indicators for the major components were identified. The major components were calculated as an average score of the sub-indicators [6]. The CVI is then estimated as the weighted average of the major components [8]. The number of sub-indicators in each major component has been taken as the weight for calculating the CVI. More detailed information on the computation methods of the individual sub-indicators can be found in Raghavan Sathyan et al. [36] and in Additional file 1: Table A2. However, the CVIs for the three watershed communities were rather similar, while there were differences in the dimensions and major components. The results show that the watershed implemented by the NGO exhibits relatively the highest vulnerability, followed by the LG and SG. The largest difference between the watersheds was found for the exposure. Exposure was more pronounced and on a similar level in LG and NGO, while the SG depicts a substantially lower index value. As the derived CVI values for the three watersheds are almost similar, an in-depth data analysis is necessary to identify the degree of influence of each indicator on the CVI output.
Given this background, the main objective of this paper is to develop and to apply a method to investigate the further applicability of the CVI. Despite the obvious similarities of the CVI values, we hypothesize that there exist significant differences between the dimensions and its major components for the three WDPs. The focus thereof is to explore and compare the CVIs of the three examined WDPs in more detail by obtaining the distribution and computing significant differences through bootstrapping.
Thus, we contribute to the literature in two ways. First, by introducing the use of the bootstrapping method in this field of climate vulnerability research, and second, by analysing and comparing the CVIs based on the major components in detail. Thereby, we derive a reliable statement about the significance of our results and the most influencing indicators of the CVI. The approach can be replicated to evaluate the potential effectiveness of watershed programmes, climate change adaptation programmes and to analyse the plausible impacts of climate change at local community level.
Methods
Theoretical framework
Vulnerability has been conceptualised and understood under various contexts. In the words of McCarty et al. [38] vulnerability to climate change is the degree to which a system is susceptible to or unable to cope with adverse effects of climate change including climate variability and extremes. It is a function of adaptive capacity, sensitivity and exposure dimensions [39]. The term ‘exposure’ indicates the nature and degree to which the system is exposed to climatic variations and extreme events [40]. The system’s susceptibility to such kind of exposures makes it sensitive and thus vulnerable to climate change [40, 41]. But the ability of systems, institutions, humans and other organisms to adjust to potential damage via taking advantage of opportunities and thus responding to consequences make them adaptive. Thus, by increasing the adaptive capacity, the opportunity of systems to manage varying ranges and magnitudes of climate improves [19]. In a nutshell, a system is vulnerable if it is exposed and sensitive to the effects of climate change with limited adaptive capacity and vice versa [37, 42]. Hence, development programmes play a decisive role when it comes to facilitate the enhancement of adaptive capacity of the system and thus reduce the sensitivity to climate change by programmes specific interventions.
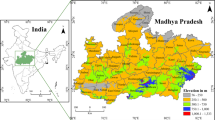
Study area
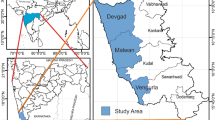
Kerala state lies between the Arabian Sea in the west and the Western Ghats Mountains in the east. The state is divided into three physiographically distinct regions: the eastern highlands, the central midlands and the western lowlands. It is unique in its socio-economic conditions such as high population density (859 persons/km2), high literacy (93%) with heavy unemployment, highly developed health care system and rapid urbanization [43]. Kerala experiences tropical monsoon climate with heavy annual rainfall of 3000 mm. In recent years, there is both spatial and temporal variation in monsoon rainfall [44] along with more intense short term droughts [45] compared to the previous years. The temperature reaches up to more than 32°C during March to April with a relative humidity of 73–89%. Any sort of climate change will be detrimental to thermo-sensitive crops like cardamom, coffee, tea, cocoa and black pepper cultivation in Kerala and other cropping patterns in the state [46]. In recent years, the state faces deterioration of natural resources, increased number of landslides, severe forest and biodiversity degradation, soil erosion, lower river water quality, conversion of paddy lands, water scarcity and decrease in productivity which is accelerated by the climate change dimension. Forty percent of the total cropped area is prone to soil erosion. This underlines the importance of integrated soil and water conservation programmes in Kerala on watershed basis [43]. Among the 14 districts of Kerala, Palakkad is listed as one of the highly vulnerable districts to climate change due to its specific geographic location, humid climate, high percentage of population relying on agriculture, low ranking in the human development index, high social deprivation and high degree of vulnerability to natural hazards like flood and drought with impacts on human life [43]. Thus, the district was purposively selected for the study. Based on the WDP completion year and the implementing agencies, Adakkaputhur (A. Puthur), Akkiyampadam (A. Padam) and Eswaramangalam (E. Mangalam) watersheds, implemented by SG, NGO, LG respectively, have been selected for the study. Table 1 summarizes some basic facts about these WDPs.
Each WDP is implemented according to certain guidelines issued by the central/state government. Here, the SG implemented WDP was under the National Watershed Development Project for Rainfed Areas, while the NGO and LG implemented WDPs were under the Western Ghat Development Programme. There were differences in the mode of project administration, implementation and major activities as given in Table 2. The main WDP activities carried out in the watersheds were under Natural Resource Management (NRM) which aims at conservation of soil, water and biomass, Production System Management (PSM) to increase the area and productivity and Livelihood Support System (LSS) activities to support landless and marginal sections of the community with an alternative source of income.
Household survey
The watersheds selected for the study have completed all the programmes activities before 2014. The household interviews were conducted during the period from August to November 2015. Out of the total 215 households covered in the field survey, 70 households were in A. Puthur (SG), 70 households in A. Padam (NGO) and 75 households in E. Mangalam (LG). Hereafter, the three watersheds are denoted as SG, NGO and LG corresponding to the names of the respective implementing agencies of WDP for better readability. The sampling method used for selection of households was cluster sampling. Based on the secondary data collected from the agricultural office of the locality, we categorized the farmers into small, marginal, medium and large farmers. Within these categories purposive selection was done to include at least one respondent from labourers, self-help group members, watershed committee members and women. To get an overview of the implementation of the programmes, two FGDs were conducted with men and women groups in each watershed. The discussions were centered on climate related extremes and contribution of the WDP activities on climate variability risk mitigation and adaptation strategies. The outcome of the FGDs were used to support the forthcoming results part.
Bootstrapping method
The focus of our research is to analyse and compare the climate vulnerability of the three examined WDPs in more detail. For this, we use bootstrap sampling and a leave-one-out sensitivity analysis. After introducing and computing the CVI, we are particularly interested to know if the three observed programmes are significantly different from each other or not. In general, one could use a two sample difference in the mean test for comparing mean values. Nevertheless, the usually computed Z-score or t-test is not applicable to our circumstances as we merely have one observed value without knowing the underlying data generating process of our computed parameters. In addition, there is a reason to believe that asymptotic theory provides a poor guide to the precision of our computed values as the assumption of independence might be violated.
We decided to use the bootstrapping method as an alternative way of obtaining the distribution and comparing the test statistics of interest. Introduced by Efron [47] and Efron and Tibshirani [48], bootstrap sampling has become increasingly popular in all sorts of econometric applications. Bootstrapping provides a way of finding the sampling distribution for the observed sample. The main advantage of bootstrapping is that we do not need to make an assumption about the underlying data generating process. This follows the basic idea that all information of the true and unknown data generating process is included in the observed sample. If this is the case, then resampling from the observed sample is the same as randomly drawing from the data generating process of the population itself. Thus, bootstrapping allows for statistical inference based on the sampling distributions of the sample statistic of interest.
Suppose we observe the realisation x=(x1,x2,…,x n ) as the outcome of an independent and identically distributed (iid) random variable X=(X1,X2,…,X n ) of the unknown Cumulative Distribution Function (CDF) F. In general, we are interested in some population parameter θ=t(F) that is some function of the true and unknown distribution. Thus, \(\widehat {\theta _{n}} = t(\widehat {F_{n}})\) is the calculated estimate of θ from which we would like to draw inference statements. Thereby, \(\widehat {F_{n}} \) denotes the Empirical Distribution Function (EDF) of our observed random sample with size n. The EDF is an estimate for F and is defined as the discrete distribution that puts a probability 1/n on each observed value x. We can use the EDF for bootstrapping since all information about F is contained in x as e.g. shown by Efron and Tibshirani [48]. Thus, we define the bootstrap sample \(\boldsymbol {x}^{\ast }=\left (x_{1}^{\ast }, x_{2}^{\ast }, \ldots, x_{n}^{\ast }\right)\) to be an iid sample of size n that is drawn with replacement from \(\widehat {F_{n}}\) of our observed sample x. The algorithm for the non-parametric bootstrap applied can in general be described in four steps:
-
1.
Sample a new data set x∗ of size n with replacement from x.
-
2.
Compute the statistic of interest, \(\widehat {\theta ^{\ast }} = t\left (\widehat {F^{\ast }}\right)\), for this resample.
-
3.
Repeat the steps 1 and 2 N times, where N denotes the number of bootstrap replications.
-
4.
Use the EDF of \(\left (\widehat {\theta _{1}^{\ast }}, \ldots, \widehat {\theta _{N}^{\ast }}\right)\) as an approximation for the true distribution of \(\widehat {\theta }\).
Additional and more detailed information on the use and limitations of bootstrapping in econometrics can for example be found in Horowitz [49], Davidson and MacKinnon [50] and MacKinnon [51].
Based on the household surveys performed for SG, NGO and LG watershed we proceed as follows. First, we create N=10,000 bootstrap samples by sampling with replacement from the original household surveys. To be more precise, we resample the interviewed families while holding constant the answers given by each family. Thus, each new sample has the same size as the original sample we obtained for the three regions and the same structure of the answers given by the individual family. Secondly, we calculated the 59 sub-indicators for each resample as proposed by Raghavan Sathyan et al. [36]. The resulting EDF allows us in a third step to draw conclusions about the shape, mean and variance of the individual sub-indicators.
In addition, we now are able to examine the differences between the three programmes and make a statement about the statistical significance of difference in this context. The latter will be done by constructing a Confidence Interval (CI) for the parameter of interest. One could use the bootstrap percentile interval method for this purpose. This is done by ordering the bootstrap replications \(\widehat {\theta }\) such that \(\widehat {\theta _{1}}< \ldots < \widehat {\theta _{N}}\). Afterwards, the upper and lower confidence bounds for the significance level α are computed as the N·α/2-th and N·(1−α/2)-th ordered element. This yields the CI \(\left [\widehat {\theta }_{N\cdot \alpha /2}, \widehat {\theta }_{N\cdot (1-\alpha /2)}\right ]\). Generally, this will be an appropriate solution if the observed distribution is symmetric.
Nevertheless, if the distribution is skewed or heavily tailed, the percentile interval will be too narrow. Thus, we use the bias corrected and accelerated percentile method (BC a ), which has a smaller coverage error in this situation [52]. Now, we can use the BC a CI to test whether the difference between the CVI of any two regions A and B is significantly different from zero. Therefore, we compute the bootstrap distribution of the difference between A and B by subtracting \(\widehat {\theta }_{A}\) from \(\widehat {\theta }_{B}\). Thus, we can use an approximate two-sided test of a null hypothesis of the form \(H_{0} = \widehat {\theta }_{A} - \widehat {\theta }_{B} = 0\) vs. the alternative hypothesis \(H_{1} = \widehat {\theta }_{A} - \widehat {\theta }_{B} \neq 0\). Then, we construct the BC a CI for the difference distribution under the null hypothesis. We reject H0 on the significance level α if 0 lies outside the computed CI.
Results
In order to evaluate the climate change adaptation strategies of the three investigated watershed programmes, the bootstrap results will be discussed first. Subsequently, the distribution of the CVIs, the three dimensions adaptive capacity, sensitivity and exposure as well as the ten major components will be examined using descriptive statistics. Thereby, we can address a systematic distortion of the evaluated components and get a first insight into the driving factors of the vulnerability. Moreover, we discuss if there exists a significant difference between the WDPs using the two-sided bootstrap test described above. Furthermore, we conducted a sensitivity analysis to identify the importance of the ten major components on the overall CVIs using a leave-one-out sensitivity analysis.
Descriptive analysis
Figure 1 shows the box plots for the ten major components sorted by the three dimensions. When comparing the individual components of the adaptive capacity in Fig. 1a-e, one can observe that the median values are to some extent different between the regions while the variation seems to be comparable over all major components.
Of particular importance is that the strong overlap of the range between the whiskers for ‘Socio-Economic Assets’, ‘Livelihood Strategies’ and ‘Agricultural’ provides an initial indication that these components might not be significantly different. This does not hold for the ‘Socio-Demographic Profile’ and ‘Social Network’. Here, there appears to be a noticeable difference between the medians. In addition, there seems to be a general tendency of the median of SG and LG watersheds to being closer together than NGO. A different picture emerges for the sensitivity and exposure dimension shown in Fig. 1f-h and i, j. While the component ‘Water’ displays an overlap between the regions, ‘Food’ and ‘Climate Variability’ seem to differ substantially. The components ‘Health’ and ‘Natural Disaster and Impact’ are problematic in a different sense. Due to the highly homogeneous answers given by the families in the original sample, the bootstrap distribution reveals gaps and therefore deviates from the other distributions. For instance, all of the interviewed families in the NGO implemented watershed responded that there were no health issues in their region. Thus, if there is no or little variability in the data, the bootstrap method reveals limitations since almost all of the variation of the bootstrap distributions comes from the original sample. Thus, even increasing the number of bootstrap samples would not enlarge the variation substantially in this situation.
Next, we consider the three different dimensions of vulnerability and the CVIs in more detail. Table 3 summarizes the location and control parameters of the respective distributions. Although the mean of the CVI values and adaptive capacity are close together for the three regions, sensitivity and exposure demonstrate a distinct difference in relation to the mean vulnerability. Furthermore, six out of the twelve bootstrap distributions are not normally distributed on a significance level based on a Jarque-Bera Test. Figure 2 visualizes the difference between the distributions with a histogram and kernel density plot. The kernel density plots display a kernel density which has been estimated using a triangular kernel with a bandwidth of j=0.9T0.2·min(σ,IQR/1.34) suggested by [53], where IQR denotes the Inter Quartile Range. Thereby, we emphasize that there might be a significant difference for the mean values at least for exposure (c) and in parts for sensitivity (d). At the same time CVI (a) and adaptive capacity (b) plots indicate no significant differences between the WDPs.
Significant differences
The significant differences will be examined based on the two-sided test described in the method section. Table 4 summarizes the mean values and the significance of the three null hypotheses: \(H_{0} = \widehat {\theta }_{SG} -\widehat {\theta }_{NGO} \), \(H_{0} = \widehat {\theta }_{SG} -\widehat {\theta }_{LG}\) and \(H_{0} = \widehat {\theta }_{NGO} -\widehat {\theta }_{LG}\). The results confirm our initial impression that the three regions are not significantly different in terms of their overall CVIs. Nevertheless, we find significant regional variations for most of the major components as well as for the dimensions, exposure and sensitivity; except for adaptive capacity. At the same time there are significant differences in a few major components of adaptive capacity between the programmes. The major components of the dimension adaptive capacity, ‘Socio-Demographic Profile’ and in parts ‘Livelihood Strategies’ and ‘Social Network’ display significant differences between the three watershed programmes. Aside from ‘Socio-Demographic Profile’, there is no significant difference for any of the major components between SG implemented and LG implemented watersheds for the adaptive capacity dimension, which again confirms our initial statement that these two regions and WDPs respectively seem to be similar. The major component ‘Food’ under the sensitivity dimension exhibits significant differences between the three programmes while the other components ‘Water’ and ‘Health’ show significant differences only in part. To be precise, there is no significant difference between WDPs implemented by NGO and LG in the ‘Water’ and ‘Health’ components. Under the exposure dimension, the ‘Climate Variability’ component is significantly different in all of the three watersheds.
Additional file 1: Table A1 depicts the results of all components based on the mean of the bootstrap distributions. Thereby, the indicator values for the sub-indicators ‘Family dependency index’, ‘Poverty index’, ‘Indebtedness index’, ‘Percent of high income household’ and ‘Religious diversity index’ show high variation among the watersheds.
For instance, the ‘Family dependency ratio’ was the highest for the WDP implemented by NGO (0.506) while the LG WDP had the least (0.285). In NGO, 40% of the households had to take care of members aged above 60 years in addition to the school attending children. The increased number of young children and ailing elderly people demand lots of time, resources and energy from the earning members in the family and particularly the women [54]. This reduces the adaptive capacity and thus adds to the climate vulnerability. In addition, 80% of the interviewed households were in debt in the SG implemented watershed while only 59% in the LG implemented faced this problem.
In the SG WDP, most of the crop loans availed were utilized for non-productive purposes. Hence, the families could often not pay back their loans on time. This again emphasizes, that there exists a great variation in the major component ‘Socio-Demographic Profile’ between the three watershed programmes. While considering the major component ‘Social Networks’, we found distinct variations in the sub-indicators among the three watersheds. The ‘Percent of beneficiaries’, ‘Percentage of households with membership in cooperative institutions’ and ‘No beneficiary contribution’ were with wider variations compared to other sub-indicators. Twenty-eight percent of the households received some kind of benefit from the programme in the LG watershed while there was a greater share (66%) for the SG watershed. Among the beneficiaries in SG, 68% were neither aware about the beneficiary contribution nor contributed their share for the activities undertaken in their fields. Only 3% of the beneficiaries in the NGO watershed have not contributed to their part for benefits. This variability contributes to the significant differences in the ‘Social Network’ component among the three watersheds.
Moreover, the LG watershed reacts significantly less in terms of ‘sensitivity’ as compared to SG and NGO. Due to the aggregation/construction scheme of all the indicators, we find no difference between the latter two. Although there exist significant differences for all three major components, ‘Water’ and ‘Health’ offset the oppositely directed value of ‘Food’ almost completely. The sub-indicators ‘Poor support from the government’ contributed to this variability in the ‘Food’ component. Ninety-four percent of the households in the NGO watershed opined that there were no improvements in government support for food sufficiency enhancement in general and through the Public Distribution System (fair price shops for food grains) in specific. But only 6% of the households in the SG watershed were in disagreement with government support. This wider variation in opinion could explain the significant difference in the ‘Food’ component. Furthermore, the LG watershed reacts most vulnerable to the exposure dimension, followed by the NGO and SG watershed communities. This is not surprising as the LG watershed was heavily affected by wind in 2015 which led to crop loss and property damage while the other two were not affected by such catastrophes. In the SG watershed, only 60% of the households opined Medium-High and High temperature increase during the last ten years while it was 94% and even 99% for the NGO and LG watersheds, respectively. Extreme climate event incidences were the highest in the LG watershed with an index value of 0.573 while the least was 0.043 in NGO. In addition, ‘Climate Variability’ is also significantly different between the three regions. The SG implemented watershed is least affected followed by the LG and NGO watersheds.
Sensitivity analysis
We complete our study by conducting a leave-one-out sensitivity analysis which means that we compute the CVI again by leaving out one major component at a time. This allows for a more detailed look at the importance of the individual indicators. We use the already familiar boxplots in Fig. 3 to summarize the main findings.
a-c Sensitivity analysis. Sensitivity analysis of the CVI and the major components for the three WDPs. For reasons of comparison, the original CVI is plotted and its median value is represented by the dashed line. The major component on the horizontal axis denotes the one that is left out of the computation of the CVI
For reasons of comparison, the original CVI is plotted and its median value is represented by the dashed line. Except for the ‘Socio-Demographic Profile’, ‘Climate Variability’ and ‘Water’, we find consistent results for the direction of change of all other major components on the CVIs of the three watershed programmes. Thus, ‘Socio-Economic Assets’, ‘Health’, ‘Food’ and ‘Natural Disaster and Impact’ when left out of the computation, lead to a higher CVI. Thus at present watershed community level, these components are contributing well to the non-vulnerable situation. On the other hand, if we neglect these major components and sub-indicators, it seemingly leads to a more vulnerable community. In addition, ‘Livelihood Strategies’, ‘Agricultural’ and ‘Social Network’ have a diminishing effect on the overall CVI for all three regions. It indicates that at present it holds a high vulnerable index value. Consequently, these are the major areas where policy interventions should be performed. Of particular relevance seems to be ‘Livelihood Strategies’ and ‘Social Network’ for the vulnerability analysis. These components have a negative effect and increase the vulnerability of the observed region.
In addition, we find differences between the regions for the remaining major components. While the ‘Socio-Demographic Profile’ has a negative effect in SG and LG, it is positive for NGO on the vulnerability. ‘Water’ has a positive impact in SG, almost none in NGO and a negative one for LG watershed. Furthermore, a higher ‘Climate Variability’ leads to an increase in vulnerability in NGO and LG, while the effect is opposite for NGO. Especially, the effects of ‘Livelihood Strategies’ and ‘Social Network’ on the overall CVI leave room for improvement of the adaptation strategies and allows us to draw policy implications for the three watershed programmes in the discussion part.
Discussion
Composite indices are an analytical, communicative, and collaborative tool, which help to raise awareness and improve understanding of a complex, multidimensional issue. An index can be better communicated to policy makers, stakeholders and decision makers when the sensitivity of the input factors are taken into consideration. When it comes to the reduction of climate vulnerability, community-level watershed programmes play an important role to build up adaptive capacities to climate induced shocks [34]. Thus, the main focus of our research was to do an in-depth analysis of the already developed CVI, a composite indicator, of three WDPs implemented by different agencies. Here, we assessed the vulnerability based on its three dimensions adaptive capacity, sensitivity and exposure. We have investigated the significant differences between the CVIs, its dimensions and done sensitivity analysis of the CVI for the three watershed communities. To our knowledge, this is the first time of such a thorough statistical analyses of CVI other than local sensitivity analysis performed to address the change in the ranks of inherent vulnerability of mountain agricultural communities at village level done by Shukla et al. [28]. Their main consideration was based solely on adaptive capacity and sensitivity of the communities. In contrast to Shukla et al. [28], we focused on the sensitivity analysis of the CVI and addressed the systematic distortions of the evaluated components, which allowed us to identify the driving factors of vulnerability.
Our study put forward two major features of vulnerability in the WDP areas. First and foremost, there are no significant differences in the adaptive capacity between the three communities while there are significant differences in sensitivity and exposure dimensions. The WDPs have equal opportunity to improve and enhance the adaptive capacity of the community through region-specific policies. Pandey and Jha [15] assessed and compared the vulnerability of lower Himalayan households, but stated only minor differences in the CVI and component values. One of the main limitations of the study was statistical variability. In addition, Chaliha et al. [14] investigated the vulnerability in villages of flood prone district of Assam, India. The authors faced the problem of missing some of the indicator values in the field survey as well as carrying out the normalisation of the indicators throughout. Even though it was a bottom up level study useful for microlevel planning, the limitations have greater influence in formulating efficient adaptation measures to flood in the district.
Secondly, the sensitivity analysis of the CVI shows that ‘Livelihood Strategies’ and ‘Social Network’ are the most influencing major components of vulnerability in all the watersheds. This suggests that one should focus on these two major components in order to improve the WDPs. Policy makers may enact measures to promote diversification of livelihoods, ensure peoples participation in developmental programmes, promote capacity building programmes to augment social capital and improve access to information technology for better communication. This stands in line with the results of Shukla et al. [28] that ‘Livelihood Dependency’ and ‘Institutional Capacity’ were the sub-dimensions which influenced the vulnerability ranking of villages in Uttarakhand state of India. The statistical property consideration of vulnerability dimensions and underlying indicators provide clear motivation to focus on the key areas of interventions [25]. A single aggregate index representation of climate vulnerability dimensions like adaptive capacity may be appealing for policy makers but would be inaccurate and highly misleading [9]. Moreover, vulnerability assessments based on indicators are not robust to changes in the assumptions with respect to the substitution or compensation between the indicators [31]. Thus a continual process of refinement is essential so that the indicators and the index have the greatest possible validity and thus utility [13].
There are other components of uncertainty which need to be explored in future research such as data uncertainty, uncertainty in building a composite index such as alternative normalisation methods for sub-indicator values and different weighting approaches of the sub-indicators. This study used household surveys for primary data collection. Even though survey research has expanded to address complex substantive issues, there has been a growing reluctance among many households to participate in surveys. The demographics, economic conditions, environmental influences, culture and societal differences such as average household size, or percentage of young children may have influenced our survey leading to wrong judgement by interviewers and interviewees. This in turn leads to increased uncertainty about the performance of survey design, challenges the cost of data collection in meeting the goals for numbers of interviews [55] and eventually the quality of resulting statistics [55, 56]. We also faced such kind of issues in this survey research. Because of some vague answers, non-responsiveness, general uncertainty and the limited data of questionnaires, it is important to assess how uncertain and reliable the CVIs are.
Conclusion
This paper introduces the bootstrapping technique into CVI sensitivity analysis and considered a part of the underlying uncertainty which is replicable for any bottom up level vulnerability assessments. Index development involves different steps such as indicator selection, variable transformation, weighting, aggregation and plausible subjectivity on selection [25]. So, as to address these issues the composite index should be tested using uncertainty analysis to add transparency to the index construction process and explore the robustness of composite index design [8, 9]. The future research may concentrate on such refinement of index composition and construction method to improve the reliability and accuracy of the index results.
References
UNFCCC. Climate change: Impacts, vulnerabilities and adaptation in developing countries. 2007. http://unfccc.int/resource/docs/publications/impacts.pdf.
Cruz RV, Harasawa H, Lal M, Wu SYA, Punsalmaa B, Honda Y, Jafari M, Li C, Huu Ninh N. Asia. climate change 2007: Impacts, adaptation and vulnerability In: van der Linden P, Parry M, Canziani O, Palutikof J, Hanson C, editors. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: Cambridge University Press: 2007. p. 469–506.
Krishnamurthy PK, Lewis K, Choularton RJ. A methodological framework for rapidly assessing the impacts of climate risk on national-level food security through a vulnerability index. Glob Environ Chang. 2014; 25:121–32. https://doi.org/10.1016/j.gloenvcha.2013.11.004.
Luers AL, Lobell DB, Sklar LS, Addams CL, Matson PA. A method for quantifying vulnerability, applied to the agricultural system of the yaqui valley, mexico. Glob Environ Chang. 2003; 13(4):255–67. https://doi.org/10.1016/S0959-3780(03)00054-2.
Moss RH, Brenkert RL, Malone RL. Vulnerability to Climate Change: A Quantitative Approach. Richland: Pacific Northwest National Laboratory; 2001.
Hahn MB, Riederer AM, Foster SO. The livelihood vulnerability index: a pragmatic approach to assessing risks from climate variability and change—a case study in mozambique. Glob Environ Chang. 2009; 19(1):74–88. https://doi.org/10.1016/j.gloenvcha.2008.11.002.
Sandra R. Bapista. Design and use of composite indices in assessments of climate change vulnerability and resilience. Washington: USAID; 2014. http://www.ciesin.org/documents/Design_Use_of_Composite_Indices.pdf.
Sullivan C, Meigh J. Targeting attention on local vulnerabilities using an integrated index approach: The example of the climate vulnerability index. Water Sci Technol J Int Assoc Water Pollution Res. 2005; 51(5):69–78.
Vincent K. Uncertainty in adaptive capacity and the importance of scale. Glob Environ Chang. 2007; 17(1):12–24. https://doi.org/10.1016/j.gloenvcha.2006.11.009.
Mclaughlin S, Cooper JAG. A multi-scale coastal vulnerability index: A tool for coastal managers?Environ Hazards. 2010; 9(3):233–48. https://doi.org/10.3763/ehaz.2010.0052.
OECD. Handbook on Constructing Composite Indicators: Methodology and User Guide. Paris: OECD Publishing; 2008. https://doi.org/10.1787/9789264043466-en.
Saisana M, Saltelli A, Tarantola S. Uncertainty and sensitivity analysis techniques as tools for the quality assessment of composite indicators. J R Stat Soc Series A (Stat Soc). 2005; 168(2):307–23. https://doi.org/10.1111/j.1467-985X.2005.00350.x.
Vincent K. Creating an index of social vulnerability to climate change for Africa. Tyndall Center for Climate Change Research. Working Paper. 2004; 56:41.
Chaliha S, Sengupta A, Sharma N, Ravindranath NH. Climate variability and farmer’s vulnerability in a flood–prone district of assam. Int J Climate Change Strat Manag. 2012; 4(2):179–200. https://doi.org/10.1108/17568691211223150.
Pandey R, Jha S. Climate vulnerability index - measure of climate change vulnerability to communities: A case of rural lower himalaya, india. Mitig Adapt Strateg Glob Chang. 2012; 17(5):487–506. https://doi.org/10.1007/s11027-011-9338-2.
Pandey R, Bardsley DK. Social-ecological vulnerability to climate change in the nepali himalaya. Appl Geogr. 2015; 64:74–86. https://doi.org/10.1016/j.apgeog.2015.09.008.
Pandey R, Kala S, Pandey VP. Assessing climate change vulnerability of water at household level. Mitig Adapt Strateg Glob Chang. 2015; 20(8):1471–1485. https://doi.org/10.1007/s11027-014-9556-5.
Piya L, Joshi NP, Maharjan KL. Vulnerability of chepang households to climate change and extremes in the mid-hills of nepal. Climatic Change. 2016; 135(3-4):521–37. https://doi.org/10.1007/s10584-015-1572-2.
Smit B, Wandel J. Adaptation, adaptive capacity and vulnerability. Glob Environ Chang. 2006; 16(3):282–92. https://doi.org/10.1016/j.gloenvcha.2006.03.008.
Eakin H, Luers AL. Assessing the vulnerability of social-environmental systems. Annu Rev Environ Resour. 2006; 31(1):365–94. https://doi.org/10.1146/annurev.energy.30.050504.144352.
Tonmoy FN, El-Zein A, Hinkel J. Assessment of vulnerability to climate change using indicators: A meta-analysis of the literature. Wiley Interdisci Rev Clim Chang. 2014; 5(6):775–92. https://doi.org/10.1002/wcc.314.
Preston BL, Yuen EJ, Westaway RM. Putting vulnerability to climate change on the map: A review of approaches, benefits, and risks. Sustain Sci. 2011; 6(2):177–202. https://doi.org/10.1007/s11625-011-0129-1.
Saisana M. The 2007 composite learning index: Robustness issues and critical assessment. Italy: EUR 23274, European Commission, JRC-IPSC; 2008.
Schmidtlein MC, Deutsch RC, Piegorsch WW, Cutter SL. A sensitivity analysis of the social vulnerability index. Risk Anal Off Publication Soci Risk Anal. 2008; 28(4):1099–114. https://doi.org/10.1111/j.1539-6924.2008.01072.x.
Tate E. Social vulnerability indices: A comparative assessment using uncertainty and sensitivity analysis. Nat Hazards. 2012; 63(2):325–47. https://doi.org/10.1007/s11069-012-0152-2.
Aguña CG, Kovacevic M. Uncertainty and sensitivity analysis of the human development index. Human Dev ResPaper. 2010; 2010(47):1–61.
Saisana M, Saltelli A. European Commission, Joint Research Centre & Institute for the Protection and the Security of the Citizen. Uncertainty and sensitivity analysis of the 2010 Environmental Performance Index. Luxembourg: 2010. https://doi.org/10.2788/67623.
Shukla R, Sachdeva K, Joshi PK. Inherent vulnerability of agricultural communities in himalaya: A village-level hotspot analysis in the uttarakhand state of india. Appl Geography. 2016; 74:182–98. https://doi.org/10.1016/j.apgeog.2016.07.013.
Wiréhn L, Danielsson Å, Neset TSS. Assessment of composite index methods for agricultural vulnerability to climate change. J Environ Manag. 2015; 156:70–80. https://doi.org/10.1016/j.jenvman.2015.03.020.
Song JY, Chung ES. Robustness, uncertainty and sensitivity analyses of the topsis method for quantitative climate change vulnerability: A case study of flood damage. Water Resources Manag. 2016; 30(13):4751–71. https://doi.org/10.1007/s11269-016-1451-2.
Fernandez MA, Bucaram S, Renteria W. (non-) robustness of vulnerability assessments to climate change: An application to new zealand. J Environ Manag. 2017; 203(Pt 1):400–12. https://doi.org/10.1016/j.jenvman.2017.07.054.
Planning Commission. Final report of minor irrigation and watershed management for the twelfth five year plan (2012-2017). New Delhi; 2012. http://planningcommission.gov.in/aboutus/committee/wrkgrp12/wr/wg_migra.pdf.
Wani SP, Rockström J, Oweis T. Rainfed Agriculture: Unlocking the Potential. Comprehensive assessment of water management in agriculture series, vol. 7. Wallingford: CABI; 2009. https://doi.org/10.1079/9781845933890.0000.
Samuel AL, Lobo C, Zade D, Srivatsa S, Phadtare A, Gupta N, Raskar V. Watershed Development, Resilience and Livelihood Security: An Empirical Analysis. India: Pune; 2015. http://wotr.org/system/files/research_outputs/WSD,%20Resilience%20and%20Livelihood%20Security.pdf.
Wisner B. Climate change and cultural diversity. Int Soc Sci J. 2010; 61(199):131–40. https://doi.org/10.1111/j.1468-2451.2010.01752.x.
Raghavan Sathyan A, Aenis T, Breuer L. Participatory vulnerability analysis of watershed development programmes as a basis for climate change adaptation strategies in kerala, india. J Environ Res Dev. 2016; 11(1):196–209.
Niemeijer D. Developing indicators for environmental policy: Data-driven and theory-driven approaches examined by example. Environ Sci Policy. 2002; 5(2):91–103. https://doi.org/10.1016/S1462-9011(02)00026-6.
McCarty JJ, Canziani OF, Leary NA, Dokken DJ, White KS, (eds).Climate Change 2001: Impacts, Adaptation, and Vulnerability, Climate change 2001. vol. Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: Cambridge Univ. Press; 2001. http://www.grida.no/publications/other/ipcc_tar/.
In: Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC, Girma B, Kissel ES, Levy AN, MacCracken S, Mastrandrea PR, White LL, (eds).Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. United Kingdom and New York: Cambridge University Press; 2014.
Aleksandrova M, Lamers JPA, Martius C, Tischbein B. Rural vulnerability to environmental change in the irrigated lowlands of central asia and options for policy-makers: A review. Environ Sci Policy. 2014; 41:77–88. https://doi.org/10.1016/j.envsci.2014.03.001.
Engle NL. Adaptive capacity and its assessment. Glob Environ Chang. 2011; 21(2):647–56. https://doi.org/10.1016/j.gloenvcha.2011.01.019.
Mearns R, Norton A. Social Dimensions of Climate Change: Equity and Vulnerability in a Warming World. New Frontiers of Social Policy. Washington: World Bank; 2012. http://hdl.handle.net/10986/2689.
Government of Kerala. Kerala sta te action plan on climate change - 2014, Thiruvanathapuram, Kerala. 2014. http://www.indiaenvironmentportal.org.in/files/file/keralaon.
Nikhil Raj PP, Azeez PA. Trend analysis of rainfall in bharathapuzha river basin, kerala, india. Int J Climatol. 2012; 32(4):533–9. https://doi.org/10.1002/joc.2283.
Thomas J, Prasannakumar V. Temporal analysis of rainfall (1871–2012) and drought characteristics over a tropical monsoon-dominated state (kerala) of india. J Hydrol. 2016; 534:266–80. https://doi.org/10.1016/j.jhydrol.2016.01.013.
Gopakumar CS. Impacts of Climate variability on Agriculture in Kerala. Cochin: Cochin University of Science and Technology; 2011. https://dyuthi.cusat.ac.in/jspui/bitstream/purl/2940/1/Dyuthi-T0931.pdf.
Efron B. Bootstrap methods: Another look at the jackknife. Ann Stat. 1979; 7(1):1–26. https://doi.org/10.1214/aos/1176344552.
Efron B, Tibshirani RJ. An Introduction to the Bootstrap, [reprint] edn. Monographs on statistics and applied probability, vol. 57. Boca Raton: Chapman & Hall; 1998.
Horowitz JL. The bootstrap In: Heckman JJ, editor. Handbook of Econometrics. Handbooks in economics, vol. 5. Amsterdam: Elsevier: 2008. p. 3159–228. https://doi.org/10.1016/S1573-4412(01)05005-X.
Davidson R, MacKinnon JG. Bootstrap methods in econometrics In: Hassani H, Mills TC, Patterson K, editors. Palgrave Handbook of Econometrics. Basingstoke: Palgrave Macmillan: 2009. p. 812–38.
MacKinnon JG. Bootstrap methods in econometrics. Econ Rec. 2006; 82(s1):2–18. https://doi.org/10.1111/j.1475-4932.2006.00328.x.
Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy: Rejoinder. Stat Sci. 1986; 1(1):77. https://doi.org/10.1214/ss/1177013817.
Silverman BW. Density Estimation for Statistics and Data Analysis. Boston: Springer US; 1986. https://doi.org/10.1007/978-1-4899-3324-9.
Shah KU, Dulal HB. Household capacity to adapt to climate change and implications for food security in trinidad and tobago. Regional Environ Change. 2015; 15(7):1379–91. https://doi.org/10.1007/s10113-015-0830-1.
Groves RM, Heeringa SG. Responsive design for household surveys: Tools for actively controlling survey errors and costs. J R Stat Soc Series A (Stat Soc). 2006; 169(3):439–57. https://doi.org/10.1111/j.1467-985X.2006.00423.x.
Groves RM, Couper MP. Nonresponse in Household Interview Surveys. Wiley Series in Survey Methodology. New York: Wiley; 2012. https://doi.org/10.1002/9781118490082.
People Service Society. Detailed Project Report of Akkiyampadam watershed. Palakkad: PSS; 2009.
Integrated Rural Technology Center. Detailed Project Report of Eswaramangalam watershed. 2009.
Government of India. WARASA-Guidelines for National Watershed Development Project for Rainfed Areas (NWDPRA). Ministry of Agriculture. Department of Agriculture & Cooperation. Rainfed farming system division. New Delhi: 2008.
Acknowledgements
We would like to gratefully acknowledge funding from Deutscher Akademischer Austauschdienst (DAAD), Bonn, Germany (ST42 for Development-Related Post Graduate Courses, 50077057 & PKZ: 91538032) for conducting the field study and research. We honour the valuable time and contribution of inhabitants in the watershed areas for their kind support and participation during the data collection. We are also grateful to the field assistants who provided help and support for the data collection.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional file
Additional file 1
Table A1. Bootstrapped mean index values for the sub-indicators under the major components. Table A2. Dimensions, major components and sub-indicators of the CVI. Adapted from [36]. (PDF 196 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Raghavan Sathyan, A., Funk, C., Aenis, T. et al. Sensitivity analysis of a climate vulnerability index - a case study from Indian watershed development programmes. Clim Chang Responses 5, 1 (2018). https://doi.org/10.1186/s40665-018-0037-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40665-018-0037-z