Abstract
Background
Camera calibration, which translates reconstructed count map into absolute activity map, is a prerequisite procedure for quantitative SPECT imaging. Both planar and tomographic scans using different phantom geometries have been proposed for the determination of the camera calibration factor (CF). However, there is no consensus on which approach is the best. The aim of this study is to evaluate all these calibration methods, compare their performance, and propose a practical and accurate calibration method for SPECT quantitation of therapeutic radioisotopes. Twenty-one phantom experiments (Siemens Symbia SPECT/CT) and 12 Monte Carlo simulations (GATE v6.1) using three therapy isotopes (131I, 177Lu, and 188Re) have been performed. The following phantom geometries were used: (1) planar scans of point source in air (PS), (2) tomographic scans of insert(s) filled with activity placed in non-radioactive water (HS + CB), (3) tomographic scans of hot insert(s) in radioactive water (HS + WB), and (4) tomographic scans of cylinders uniformly filled with activity (HC). Tomographic data were reconstructed using OSEM with CT-based attenuation correction and triple energy window (TEW) scatter correction, and CF was determined using total counts in the reconstructed image, while for planar scans, the photopeak counts, corrected for scatter and background with TEW, were used. Additionally, for simulated data, CF obtained from primary photons only was analyzed.
Results
For phantom experiments, CF obtained from PS and HS + WB agreed to within 6% (below 3% if experiments performed on the same day are considered). However, CF from HS + CB exceeded those from PS by 4–12%. Similar trend was found in simulation studies. Analysis of CFs from primary photons helped us to understand this discrepancy. It was due to underestimation of scatter by the TEW method, further enhanced by attenuation correction. This effect becomes less important when the source is distributed over the entire phantom volume (HS + WB and HC).
Conclusions
Camera CF could be determined using planar scans of a point source, provided that the scatter and background contributions are removed, for example using the clinically available TEW method. This approach is simple and yet provides CF with sufficient accuracy (~ 5%) to be used in clinics for radiotracer quantification.
Similar content being viewed by others
Background
In single-photon emission computed tomography (SPECT), quantification of radiotracer distribution has recently become an increasingly important component of many clinical studies [1, 2]. In particular, quantitative SPECT can be very helpful in the diagnosis of multi-vessel heart disease and assessment of myocardial blood flow reserve [3], as well as in quantitative evaluation of the lungs, kidneys, brain [4] and other organs.
However, the most important role activity quantitation has to play is in the targeted radionuclide therapies (TRT) [5]. The assessment of tumor burden, prediction of potentially critical organs and normal tissue toxicities, and calculation of the radiation dose are all necessary elements of the personalized, image-based therapy planning as well as evaluation of patient’s response to this therapy. They all require accurate absolute quantification of the amount of the radioactive material that is localized in tumor(s) and critical organs and characterization of its changes over time (biokinetics) [6, 7].
There are three essential steps, which have to be performed for quantification of SPECT images. The first step involves quantitative SPECT reconstructions. Since the data acquired in projections are affected by physical phenomena such as photon attenuation and scatter, collimator blurring, camera dead-time and partial volume effects; in order to get quantitatively accurate images, all these factors must be properly compensated for during the reconstruction process. Fortunately, in the past few decades, considerable technical advancement has been achieved in both SPECT hardware and data processing software. Particularly, with the introduction of hybrid SPECT/CT imaging systems and the development of statistical iterative reconstruction algorithms, quantitative reconstructions have become available for the majority of the commercial SPECT/CT cameras [8,9,10].
The second step is to apply camera calibration factor (CF) to the reconstructed images, which will translate the three-dimensional (3D) count maps into 3D activity maps. It is important to stress at this point that CF provides only a numerical coefficient necessary for this “translation”. The value of CF depends on the energy of the measured photons; therefore, it is radioisotope specific and represents the joint sensitivity of the camera and the collimator for detection of a particular isotope’s emissions in the energy window(s) that is used for data acquisition. Please note that the value of CF might be influenced by the potential errors in dose calibrator readings when measuring the activity.
Finally, in order to obtain a quantitative value of the activity contained in any particular volume of tissue (for example in an organ or a tumor), the third step involving segmentation of this activity map must be performed. As segmented volumes will be affected by partial volume effects (PVE), for accurate activity quantification, appropriate PVE correction methods must be applied [11]. For example, one such method would be to use experimentally determined recovery coefficients (RC) [12, 13].
The most reliable method to determine CF of the camera is to perform an experimental measurement using an accurately calibrated radioactive source. Considering that quantitative reconstruction methods generate images from primary photons (PP) (as quantitative reconstruction has already removed the scattered photons and corrected for losses due to attenuation), CF must relate these PP images to the activity which produced them.
Different camera calibration methods have been proposed, but there is still no consensus which method is the best. Some researchers use planar scans of a small (point-like) source (PS) placed in air at a certain distance (usually 20–30 cm) from the collimator surface [14,15,16,17,18,19]. This is a simple method where the CF is directly calculated from the acquired planar images. Care must be taken, however, that photon scatter is accounted for and that attenuation in the source and source support are minimized. Different small-volume geometries ranging from a vial to a syringe [15, 18]and a small container [14] to a petri dish (following NEMA protocol for camera sensitivity test [19]) have been employed. Some researchers even performed tomographic scans of such a point source [16]; however, it is not clear what would be the advantage of such acquisition.
Alternatively, tomographic scans of large cylindrical phantoms containing accurately measured amounts of radioactive materials have been proposed [12, 13, 20,21,22,23,24,25,26]. This approach is more cumbersome, especially when radioisotopes with long half-lives are used. However, its rationale is that the geometry of the extended calibration phantom better models the body of a patient and the physical effects (photon attenuation and scatter) which occur in patients’ acquisitions. Therefore, all approximations (and potential inaccuracies) due to the clinical reconstruction method which may affect the accuracy of patient images will be replicated in the reconstructed images of the calibration phantom. The geometries which have been used in the extended phantom experiments can be divided into three categories: (a) small container(s) filled with activity (hot sources (HS)) placed in the large cylinder filled with non-radioactive water (cold background (CB)) [13, 22, 23, 26], (b) small container(s) with activity placed in the large cylinder filled with radioactive water (warm background (WB)) [21], and (c) large cylinders with no inserts, filled uniformly with activity (hot-cylinder (HC)) [12].
The purpose of the present study is to evaluate all these methods, compare their performance and check if, and under what conditions, the planar calibration and tomographic calibration produce equivalent results. A large series of phantom experiments, as well as extensive simulation studies, have been performed. The objective of the simulations (done with GATE Monte Carlo program [27]) was to generate the true CF values, and to investigate and understand the physical effects, which may be responsible for the discrepancies observed between CFs obtained using different experimental methods. Three popular therapeutic radioisotopes (emitting beta particles and also gamma radiation) were investigated, namely, 131I, 177Lu and 188Re.
Methods
Our study was composed of two parts: (1) phantom experiments and (2) Monte Carlo simulations. In both parts, 131I, 177Lu and 188Re radioisotopes were used, and in total, 21 experimental scans and 12 simulation runs were performed. The information about the isotopes’ half-lives, their most intensive gamma emissions and maximum and mean energy of their beta emission, is provided in Table 1.
Phantom experiments
For each isotope, the data were acquired using the following three experimental configurations (see Fig. 1 and Table 2):
-
A.
Planar acquisition of a small source suspended in air (PS; Table 2: experiments #1, #6–7, and #15–17)
-
B.
Tomographic (SPECT/CT) acquisition of hot inserts (spheres and/or cylinders) placed in non-radioactive water (HS + CB; Table 2: experiments #2–3, #8–9, and #18–19)
-
C.
Tomographic (SPECT/CT) acquisition of the same set of hot inserts placed in radioactive water (HS + WB; Table 2: experiments #4–5, #10–13, and #20–21)
Additionally, for 177Lu, the following fourth configuration was used:
-
D.
Tomographic (SPECT/CT) acquisition of a cylindrical phantom filled with uniform activity (HC; Table 2: experiment #14)
All data acquisitions were performed using Symbia SPECT/CT cameras (Siemens Healthineers, Germany). The acquisitions #6–13 for 177Lu and #15–21 for 188Re were performed at the Vancouver General Hospital, Nuclear Medicine Department, Vancouver (Canada). Experiments with 131I (acquisitions #1–5) were done at the Department of Radiology, University of Michigan Medical School, Ann Arbor (USA). And finally, the 177Lu acquisition #14 was performed at the Department of Radiology and Nuclear Medicine, Université Laval, Quebec (Canada). The acquisition conditions, the camera model, the collimators, and the total activities used in the experiments are specified in Table 2.
For experiments performed using configuration A, the volume of the point source was always equal to or less than 1 mL. In each case, a syringe containing the point source was suspended in air between the detectors and it was equally spaced from each collimator surface (Fig. 1a and Table 2). The scan duration ranged from 5 to 20 min.
For tomographic acquisitions, cylindrical phantoms with hot spherical and/or cylindrical inserts were used (Fig. 1b and Table 2). The total volume of the hot inserts varied between experiments and ranged from 58 to 560 mL, while the volume of the cylinder was about 6 L (Jaszczak phantom) and 10 L (Elliptical Thorax phantom). In the experiments where inserts were placed in the hot background, the ratio of sphere to background activity concentration was always close to 6:1 (which corresponds to that often observed in clinical studies).
For each phantom configuration and each experiment, the total activity in the phantom was sufficiently low that the camera did not display any dead time effects. For all scans, the projection data were acquired in three abutting energy windows, namely the 20% photopeak window (PW), the lower scatter window (LSW) and the upper scatter window (USW). The data in these three windows were subsequently used to perform triple energy window (TEW) scatter correction. The acquisition times ranged from 8 to 40s per projection with a total of 60–96 projection (30–48 camera stops). Table 3 provides energy window settings used in our experiments and simulations (for 177Lu, only the 208 keV photopeak was used).
Monte Carlo simulation experiments
The Geant4 Applications for Tomographic Emission (GATE version 6.1 [27]) Monte Carlo code was used for the simulated experiments. The Siemens SymbiaT dual head SPECT imaging system was modeled. The system geometry (detector, collimator and shielding) used in our simulations was identical to that described and validated in our previous study [28].
The emission energy spectra of the three isotopes, which have complex decay schemes, are built-in into GATE and included accurate modeling of β− and gamma emissions. The simulated radionuclides were distributed uniformly within their respective source volume, as described in the next paragraph.
For each radionuclide, four phantom configurations (analogous to those used in the experiments) were simulated:
-
I.
Point source (1-mL sphere) in air
-
II.
100-mL spherical source placed in the center of a cylinder filled with non-radioactive water
-
III.
100-mL spherical source placed in the center of a cylinder filled with radioactive water
-
IV.
Cylinder filled with uniform activity
In all simulation experiments, the phantoms were placed at the center of the field of view (FOV) of the camera. The distance from the source to each of the collimator surfaces was equal to 25 cm. The cylindrical phantom used in these simulations had the same dimensions as that used in the experiments. Although multiple inserts with different sizes were used in the phantom experiments, while only a single sphere was used in the simulations, the characteristics of photons recorded by the camera when using this simple phantom model were very similar to those from the experiments, providing us with information sufficient to explain discrepancies in CF values obtained by different methods.
The total number of decays (Ntot) simulated for each phantom configuration and corresponding activities (assuming in each case 5 min acquisition time) are listed in Table 4 (Ntot was selected so that the total number of photons detected in PW was more than 15,000 in order to ensure errors are < 1%). For each simulation experiment, the projection images corresponding to the true primary photons and the total photons recorded in the photopeak window (PW), as well as those recorded in the two scatter windows (LSW and USW), were generated.
For all phantom configurations, only one planar projection was simulated for each of the photopeak windows (PW) and for each of the two scatter energy windows (LSW and USW). Benefiting from the cylindrical symmetry of the simulated phantoms, the tomographic images were created by replicating these single projections 90 times with Poisson noise added to the data.
Image reconstruction
The images from the experimentally acquired tomographic projection datasets, as well as these from simulations, were reconstructed using in-house developed software packages (MIRG software [29] for 177Lu and 188Re, UM software [30] for 131I). In all cases, the OSEM algorithm (see Table 5 for details), with CT-based attenuation correction and TEW scatter correction [31, 32], was employed.
Additionally, 177Lu datasets were reconstructed using the Siemens software available on the camera (Flash3D) [20]. By definition, these reconstructions included resolution recovery (RR) correction. This correction, however, should have no effect on the total number of counts recorded in the reconstructed image. Therefore, CFs obtained from images reconstructed with and without RR should be considered to be equivalent. In all cases, the matrix size was 128 × 128 × 128 with the pixel size equal to 4.79 mm.
Moreover, for each isotope and each phantom configuration, the images were reconstructed from the simulated data corresponding to the primary photons only. In this case, no scatter correction was required so only attenuation correction was included in the reconstruction. The attenuation maps used in all reconstructions of the simulated data were generated using cylindrical phantom shapes filled with narrow-beam attenuation coefficients.
Determination of camera calibration factor
The camera calibration factor (CF) can be determined using the following general formula:
where C is the number of photons emitted by the source having the activity A and recorded by the camera in time t. This general formula formed the bases of all our data processing; the details of calculations are summarized in Table 6. For simulated data, the product of activity and time was replaced by the total number of decays.
Planar acquisitions (experimental and simulated configurations—PS)
For planar acquisitions, the CF was directly calculated from the acquired planar images; no reconstruction was required. The counts collected in the entire field of view of the camera were employed and CPWSC corresponding to the PW counts corrected for scatter using the TEW method was used.
Additionally, our simulated data provided us with the estimate of the number of primary photons. This allowed us to calculate CPPsim (the “true” CF), which was not affected by approximations related to the TEW scatter correction.
Tomographic acquisitions (experimental and simulated configurations—HS + CB, HS + HB and HC)
For tomographic phantom experiments, the total numbers of counts, summed over the entire 3D image, were used to determine the CFs corresponding to each isotope and each phantom configuration.
Additionally, for simulated data, the CF factors were calculated using the images reconstructed from primary photons only (see Table 6).
In Table 6, the CF symbols corresponding to the values obtained from planar data are marked with subscript PW for “photopeak window” and PWSC for “photopeak window scatter corrected”; CF obtained from tomographic data are marked with subscript R for “reconstructed” and superscript B, C or D indicating configuration of the phantom. Furthermore, the CF obtained from simulated data was labeled with subscript sim, while CF calculated from primary photons only are additionally marked with subscript PP.
Results
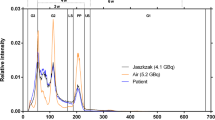
Figure 2 presents the energy spectra for the three investigated radioisotopes, generated by our GATE simulations. The phantoms used in these simulations corresponded to a point source scanned in air (blue line), a 100-mL sphere filled with activity placed at the center of a cylinder filled with cold (black line) and warm (red line) water.
Simulated energy spectra as would be acquired by the SPECT camera from emissions of 131I, 177Lu, and 188Re. For each isotope, a point source scanned in air (blue line) and a 100-mL hot sphere placed at the center of a 20-cm diameter cylindrical phantom filled with non-radioactive water (black line) and warm (red line) water were simulated
Tables 7 and 8 summarize the CF values obtained using all planar and tomographic configurations (as outlined in Table 6) from simulations and phantom experiments, respectively. Additionally, these results are presented in a graphical form in Figs. 3 and 4. Since the CF values for 177Lu data obtained from MIRG and Siemens reconstructions agreed to within 3%, only CF from MIRG reconstructions were used in the subsequent analysis.
Summary of CF obtained from simulated phantom experiments performed using different phantom configurations. a shows CFs obtained from primary photons only normalized using CFPPsim, while CFs shown in b were calculated using total counts recorded in the photopeak window corrected for scatter with TEW and normalized using CFPWSCsim
In order to facilitate comparison of CFs obtained from different experiments with different phantom configurations, the CF values in Figs. 3 and 4 are presented in relative units. For simulated data, shown in Fig. 4a, CF obtained from primary photons recorded in the photopeak window of the planar acquisition of a point source were considered to be the “true” CF values and were set to 1. For the experimental data presented in Fig. 3 and for simulations shown in Fig. 4b, the data were normalized using counts in the planar acquisition of a point source corrected for scatter, i.e. CFPWSC and CFPWSCsim, respectively.
Discussion
The spectra presented in Fig. 2 allow us to evaluate the contribution of scattered photons to the photopeak energy window for different phantom configurations. While scatter component in point source (PS) scans of 177Lu is relatively low, for 131I and 188Re, the photons from high-energy gamma transitions, which were scattered mostly in the camera and its components, substantially increase the background. This observation supports our claim that scatter correction should be performed when CF is derived from the data obtained using planar scans of point sources. The scatter correction method, which is the most popular in clinics, is TEW. Besides being simple and easy to implement, TEW allows us to correct not only for self-scattered photons, but also for high-energy scatter and other background.
Further analysis of the data presented in Fig. 2 confirms that scatter correction should be included in all tomographic image reconstructions. All energy spectra for HS + CB and HS + WB phantom configurations that were used in our tomographic acquisitions, and which model patient scans better than point sources, display large scatter background under the photopeaks.
For all isotopes (131I, 177Lu and 188Re), the experimental CFs (summarized in Fig. 3 and Table 7) show relatively good agreement between CFPWSC obtained from planar scans corrected for scatter and \( {\mathrm{CF}}_R^C \) obtained from tomographic scans performed using hot sources placed in warm background (HS + WB). These CF values agree to within 6%. The agreement usually improves (to below 3%) when CF obtained from the experiments performed on the same day are considered. This improvement may be attributed to the fact that for the same-day experiments, all errors in activity determination are minimized, as the activity measurements are performed using the same vial and same dose calibrator settings. However, the differences between CFPWSC and \( {\mathrm{CF}}_R^B \) (HS + CB) values are much larger, for 177Lu and 188Re even reaching 12%.
The explanation of all these effects can be provided by the analysis of our MC simulation results. Firstly, as expected, when considering only primary photons, for all radioisotopes, CFs obtained from planar scans (CFPPsim) and those reconstructed from tomographic data (with attenuation correction) agree to within 1–3% (see Table 8 and Fig. 4a). Such small differences may be caused by statistical fluctuations and small approximations in attenuation correction used in reconstructions of simulated tomographic data (voxelized attenuation maps were used in reconstructions, while in GATE analytical shapes are used).
However, larger discrepancies, similar to those observed in experimental data, are found when comparing CFs obtained from simulated PS scans corrected for scatter CFPWSCsim and simulated tomographic scans (Table 8 and Fig. 4b). The differences between CFPWSCsim and both \( {\mathrm{CF}}_{R\mathrm{sim}}^C \) and \( {\mathrm{CF}}_{R\mathrm{sim}}^D \) remain below 5%, while \( {\mathrm{CF}}_{R\mathrm{sim}}^C \) and \( {\mathrm{CF}}_{R\mathrm{sim}}^D \) agree with each other to within 1%. However, the differences between CFPWSCsim and \( {\mathrm{CF}}_{R\mathrm{sim}}^B \) increase to 12–16%. These effects are caused by the approximations of the TEW scatter correction method, which can be visualized when considering the shapes of the profiles presented in Fig. 5.
The energy spectra obtained from the simulations of the phantom scanned in configuration B (HS + CB). The counts recorded in the photopeak window and correspond to the ROI drawn on the projection images: around the hot object (column b), in the background surrounding this ROI (column c), and in the entire image (column d). Column a shows the simulated PW projections. The hot object ROI was placed inside the red circle while the background ROI comprised all counts found on the outside of the red circle
Simulated spectra presented in Fig. 5 correspond to the phantom configuration B (HS + CB). The graphs compare the shapes of the photopeak, the true scatter component observed in PW and the scatter estimated by the TEW method using counts recorded in LSW + USW. Counts in the three regions were analyzed. Spectra presented in Fig. 5b correspond to counts recorded in the source ROI, and Fig. 5a shows the location of the source ROI drawn in the projection images of each isotope. Spectra in Fig. 5c correspond to counts recorded in the background region around the source, and Fig. 5d shows spectra of counts recorded in the entire image (these counts were used for the CF determination). Please note that Fig. 5c for 131I contains a small peak corresponding to septal penetration of the collimator by 364 keV photons.
The analysis of these graphs clearly demonstrates that for all isotopes, the TEW method (area under the red line) underestimates the true scatter (marked by the blue line) in the source ROI region while overestimates it in the background region. As a result, the source region seems to have more counts, while counts in the background around the source seem to be lower than they should be. This “surplus” is further enhanced by the attenuation correction, which boosts the excess of counts in the source region, because it is located in the center of the phantom where attenuation correction is the highest.
On the other hand, when scatter correction is done by subtracting projections, before image reconstruction, the overestimation of scatter counts in the background may potentially create negative counts. However, in our reconstructions, these negative counts could not occur because the TEW scatter estimate was included in the denominator of the OSEM formula. As a result, the total number of reconstructed counts used for CF calculation is higher than the truth and also higher than that determined from planar scans. This effect is relatively smaller for phantom configurations in which activity is distributed over the entire phantom (HS + WB and HC).
Additionally, please note that although CFs determined experimentally and obtained from simulations are quite similar, CF from simulations exceed experimental values by 3–10%. In our opinion, these differences should be attributed to approximations made in the simulated camera model [28] and inaccuracies in dose calibrator measurements of source activities.
At this point, it is important to emphasize that the CF value, as defined in our study, corresponds purely to the camera efficiency for given radioisotope, collimator and energy window settings. It does not depend on the camera and image resolution, the size and shape of the imaged object, the signal-to-background ratio and other factors. Although some authors propose to combine CF and RC into a single calibration coefficient [33], such approach would be very challenging, as it is impossible to design a calibration experiment which would model every patient geometry and every activity distribution. More importantly, in order to account for these different conditions, such a “combined” approach would require not a single value of CF, but a large table of values, which additionally would depend on the segmentation method that was used to generate RC.
This is not to say that the proposed CF allows us to avoid the challenges related to image segmentation. Still, the activity maps, which are obtained by multiplying patient images (i.e. count-maps) by CF, must be segmented if one wants to get activity in any particular volume. The advantage of the proposed method is that CF determined using a single planar scan can be repeatedly applied to many patient studies, as long as they were acquired using the same camera, collimator, radioisotope and energy window settings. It has been shown that, under normal exploitation conditions, the camera sensitivity (thus this CF) will remain unchanged over a long period of time [18].
Actually, another observation from this study (and also from our previous experience) is that often calibration experiments performed using the same type of camera (from the same manufacturer) and same acquisition protocols (collimator and energy window settings) but located in different Nuclear Medicine departments (often even in different countries) result in very similar values of CFs. This fact may be illustrated by the experimental CFs for 177Lu phantom configuration C and D, which agree well (within 6%) in spite of the fact that one of these studies was done using Siemens camera located in Vancouver and the other camera in Quebec City.
Conclusions
Accurate determination of the gamma camera CF is critical for quantitative imaging to translate counts in the reconstructed images into activity values. However, currently, there is no consensus about the calibration method, both planar and tomographic scans have been performed and the resulting CF applied in research and clinical studies.
We have shown that planar acquisition of a point-like source provides CF very close to those obtained from tomographic images (reconstructed with attenuation and scatter corrections) of a phantom where the activity is distributed over the entire volume (with or without the hot object(s) in its center). The value of CF determined using these two approaches agree to within 3% when experiments are performed on the same day and to 6% for experiments done over the period of several months. Usually, such phantom configuration is considered to be a good approximation of activity distribution encountered in clinical patient studies. However, our analysis suggests that, for all investigated radiotherapy isotopes, the camera calibration based on a planar scan of a point source must include scatter correction. This is because photopeak windows for 131I and 188Re, and to a lesser degree for 177Lu, contain important component from scattered high-energy gamma emissions (and septal penetration for 131I).
Additionally, our experiments indicate that camera calibration performed using tomographic scan of a source(s) placed in non-radioactive (cold) background may overestimate CF by more than 10%. Thus, the use of this method is not recommended for determination of the camera CF. Analysis of simulations helped us to understand that this rather large discrepancy is due to approximations made by the TEW scatter correction, even further enhanced by attenuation correction performed during image reconstruction.
Based on these considerations, we conclude that camera CF may be confidently determined using planar scans of the point source, provided that the background contribution to the photopeak is removed, for example using the TEW method. The approach is simple and easy to perform and provides CF with sufficient accuracy (~ 5%) to be used in clinical quantitative imaging studies. The proposed method is general and is expected to provide good results for other isotopes than those reported here.
Abbreviations
- 3D:
-
Three-dimensional
- CB:
-
Cold background
- CF:
-
Calibration factor
- FOV:
-
Field of view
- GATE:
-
Geant4 Applications for Tomographic Emission
- HC:
-
Hot cylinder
- HS:
-
Hot sources
- LSW:
-
Lower scatter window
- PP:
-
Primary photons
- PS:
-
Point source
- PVE:
-
Partial volume effects
- PW:
-
Photopeak window
- RC:
-
Recovery coefficients
- ROI:
-
Region of interest
- RR:
-
Resolution recovery
- SPECT:
-
Single photon emission computed tomography
- TEW:
-
Triple energy window
- TRT:
-
Targeted radionuclide therapies
- USW:
-
Upper scatter window
- WB:
-
Warm background
References
Frey EC, Humm JL, Ljungberg M. Accuracy and precision of radioactivity quantification in nuclear medicine images. Semin Nucl Med. 2012;42(3):208–18.
Bailey DL, Willowson KP. An evidence-based review of quantitative SPECT imaging and potential clinical applications. J Nucl Med. 2013;54(1):83–9.
Da Silva a J, Tang HR, Wong KH, Wu MC, Dae MW, Hasegawa BH. Absolute quantification of regional myocardial uptake of 99mTc-sestamibi with SPECT: experimental validation in a porcine model. J Nucl Med. 2001;42(5):772–9.
Ohno Y, Koyama H, Nogami M, Takenaka D, Matsumoto S, Yoshimura M, et al. Postoperative lung function in lung cancer patients: comparative analysis of predictive capability of MRI, CT, and SPECT. AJR Am J Roentgenol. 2007;189(2):400–8.
Dewaraja YK, Frey EC, Sgouros G, Brill B, Roberson P, Zanzonico PB, et al. MIRD pamphlet no. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy. J Nucl Med. 2012;53(8):1310–25.
Strigari L, Konijnenberg M, Chiesa C, Bardies M, Du Y, Gleisner KS, et al. The evidence base for the use of internal dosimetry in the clinical practice of molecular radiotherapy. Eur J Nucl Med Mol Imaging. 2014;41(10):1976–88.
Williams LE, DeNardo GL, Meredith RF. Targeted radionuclide therapy. Med Phys. 2008;35(7Part1):3062–8.
Bailey DL, Willowson KP. Quantitative SPECT/CT: SPECT joins PET as a quantitative imaging modality. Eur J Nucl Med Mol Imaging. 2014;41(SUPPL. 1):17–25.
Ritt P, Vija H, Hornegger J, Kuwert T. Absolute quantification in SPECT. Eur J Nucl Med Mol Imaging. 2011;38(SUPPL. 1):69–77.
Seret A, Nguyen D, Bernard C. Quantitative capabilities of four state-of-the-art SPECT-CT cameras. EJNMMI Res. 2012;2(1):45.
Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys Med Biol. 2012;57(21):R119–59.
Sanders JC, Kuwert T, Hornegger J, Ritt P. Quantitative SPECT/CT imaging of 177Lu with in vivo validation in patients undergoing peptide receptor radionuclide therapy. Mol Imaging Biol. 2015;17(4):585–93.
Hippeläinen E, Tenhunen M, Mäenpää H, Sohlberg A. Quantitative accuracy of (177)Lu SPECT reconstruction using different compensation methods: phantom and patient studies. EJNMMI Res. 2016;6(1):16.
Willowson K, Bailey DL, Baldock C. Quantitative SPECT reconstruction using CT-derived corrections. Phys Med Biol. 2008;53(12):3099–112.
He B, Du Y, Song X, Segars WP, Frey EC. A Monte Carlo and physical phantom evaluation of quantitative In-111 SPECT. Phys Med Biol. 2005;50(17):4169–85.
de Wit TC, Xiao J, JFW N, van het Schip FD, Staelens SG, van Rijk PP, et al. Hybrid scatter correction applied to quantitative holmium-166 SPECT. Phys Med Biol. 2006;51(19):4773–87.
Shcherbinin S, Grimes J, Bator A, Cwikla JB, Celler A. Three-dimensional personalized dosimetry for (188)Re liver selective internal radiation therapy based on quantitative post-treatment SPECT studies. Phys Med Biol. 2013;59(1):119–34.
Anizan N, Wang H, Zhou XC, Hobbs RF, Wahl RL, Frey EC. Factors affecting the stability and repeatability of gamma camera calibration for quantitative imaging applications based on a retrospective review of clinical data. EJNMMI Res. 2014;4(1):1–11.
Pacilio M, Cassano B, Pellegrini R, Di Castro E, Zorz A, De Vincentis G, et al. Gamma camera calibrations for the Italian multicentre study for lesion dosimetry in 223Ra therapy of bone metastases. Phys Medica. 2017;41:117–23.
Zeintl J, Vija AH, Yahil A, Hornegger J, Kuwert T. Quantitative accuracy of clinical 99mTc SPECT/CT using ordered-subset expectation maximization with 3-dimensional resolution recovery, attenuation, and scatter correction. J Nucl Med. 2010;51(6):921–8.
Koral KF, Yendiki A, Lin Q, Dewaraja YK. Comparison of 3D OSEM vs 1D SAGE for focal total-activity quantification in I-131 SPECT with HE and UHE collimation. IEEE Trans Nuc Sci. 2005;52(1):154–8.
McDougald WA, Miyaoka RS, Alessio AM, Harrison RL, Lewellen TK. A study of SPECT/CT camera stability for quantitative imaging. EJNMMI Phys. 2016;3(1):14.
Beauregard JM, Hofman MS, Pereira JM, Eu P, Hicks RJ. Quantitative 177Lu SPECT (QSPECT) imaging using a commercially available SPECT/CT system. Cancer Imaging. 2011;11(1):56–66.
Sandström M, Garske U, Granberg D, Sundin A, Lundqvist H. Individualized dosimetry in patients undergoing therapy with 177Lu-DOTA-D-Phe1-Tyr3-octreotate. Eur J Nucl Med Mol Imaging. 2010;37(2):212–25.
Sandström M, Ilan E, Karlberg A, Johansson S, Freedman N, Garske-Román U. Method dependence, observer variability and kidney volumes in radiation dosimetry of (177)Lu-DOTATATE therapy in patients with neuroendocrine tumours. EJNMMI Phys. 2015;2(1):24.
D’Arienzo M, Cozzella ML, Fazio A, De Felice P, Iaccarino G, D’Andrea M, et al. Quantitative 177Lu SPECT imaging using advanced correction algorithms in non-reference geometry. Phys Medica. 2016;32(12):1745–52.
Jan S, Benoit D, Becheva E, Carlier T, Cassol F, Descourt P, et al. GATE V6: a major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol. 2011;56:881–901.
Uribe CF, Esquinas PL, Gonzalez M, Celler A. Characteristics of bremsstrahlung emissions of 177Lu, 188Re, and 90Y for SPECT/CT quantification in radionuclide therapy. Phys Medica. 2016;32(5):691–700.
Uribe CF, Esquinas PL, Tanguay J, Gonzalez M, Gaudin E, Beauregard J-M, et al. Accuracy of 177Lu activity quantification in SPECT imaging: a phantom study. EJNMMI Phys. 2017;4(1):2.
Dewaraja YK, Wilderman SJ, Ljungberg M, Koral KF, Zasadny K, Kaminiski MS. Accurate dosimetry in 131I radionuclide therapy using patient-specific, 3-dimensional methods for SPECT reconstruction and absorbed dose calculation. J Nucl Med. 2005;46(5):840–9.
Ogawa K, Harata Y, Ichihara T, Kubo A, Hashimoto S. A practical method for position-dependent Compton-scatter correction in single photon emission CT. IEEE Trans Med Imaging. 1991;10(3):408–12.
de Nijs R, Lagerburg V, Klausen TL, Holm S. Improving quantitative dosimetry in 177Lu-DOTATATE SPECT by energy window-based scatter corrections. Nucl Med Commun. 2014;35(5):522–33.
Wevrett J, Fenwick A, Scuffham J, Nisbet A. Development of a calibration protocol for quantitative imaging for molecular radiotherapy dosimetry. Radiat Phys Chem. 2017;140(November 2016):355–60.
Khazov Y, Mitropolsky I, Rodionov A. Nuclear data sheets for A = 131. Nucl Data Sheets. 2006;107(11):2715–930.
Kondev FG. Nuclear data sheets for A = 177. Nucl Data Sheets. 2003;98(3):801–1095.
Singh B. Nuclear data sheets for A = 188 *. Nucl Data Sheets. 2002;387(2):387–541.
Dewaraja YK, Ljungberg M, Green AJ, Zanzonico PB, Frey EC, Bolch WE, et al. MIRD pamphlet no. 24: guidelines for quantitative 131I SPECT in dosimetry applications. J Nucl Med. 2013;54(12):2182–8.
Ljungberg M, Celler A, Konijnenberg MW, Eckerman KF, Dewaraja YK, Sjogreen GK. MIRD pamphlet no. 26: joint EANM/MIRD guidelines for quantitative 177Lu SPECT applied for dosimetry of radiopharmaceutical therapy. J Nucl Med. 2015;9881(26):151–62.
Esquinas PL, Rodríguez-Rodríguez C, Carlos De La Vega J, Bokharaei M, Saatchi K, Shirmohammad M, et al. 188Re image performance assessment using small animal multi-pinhole SPECT/PET/CT system. Phys Medica. 2016;33:26–37.
Acknowledgments
The publication of this article was supported by funds of the European Association of Nuclear Medicine (EANM).
Funding
The funding for the project has been provided by the Canadian Institutes of Health Research (CIHR) grant MOP-142233 and the Natural Sciences and Engineering Research Council (NSERC) Discovery grant RGPIN-2017-04914. Additionally, one of the authors (YKD) would like to acknowledge grant support from R01 EB022075 awarded by the National Institute of Health, USA.
Availability of data and materials
The phantom images and the simulated phantom data are stored in the Medical Imaging Research Group Server, Vancouver, Canada.
Author information
Authors and Affiliations
Contributions
WZ was responsible for the acquisitions, reconstructions, and data analysis and participated in the study design with AC, and AC, PE, and XH assisted with the acquisitions and analysis of data. MG and CU assisted with the acquisitions in Vancouver, Canada. JMB assisted with the acquisitions in Quebec, Canada. YKD assisted with the acquisitions in Michigan, USA. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Authors’ information
Yuni K Dewaraja/consultant/MIM Software Inc., Cleveland, USA.
Carlos F Uribe/postdoctoral fellow/GE Healthcare/Data Driven Gating/Monetary.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, W., Esquinas, P.L., Hou, X. et al. Determination of gamma camera calibration factors for quantitation of therapeutic radioisotopes. EJNMMI Phys 5, 8 (2018). https://doi.org/10.1186/s40658-018-0208-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40658-018-0208-9