Zeros of harmonic polynomials, critical lemniscates, and caustics

Abstract

In this paper, we sharpen significantly several known estimates on the maximal number of zeros of complex harmonic polynomials. We also study the relation between the curvature of critical lemniscates and its impact on geometry of caustics and the number of zeros of harmonic polynomials.

1 Introduction

We concern ourselves in this paper with complex harmonic polynomials, i.e., polynomials which admit a decomposition

$$\begin{aligned} h(z) = p(z) + \overline{q(z)}, \end{aligned}$$

where $p=p_n$ and $q=q_m$ are analytic polynomials of degrees n and m, respectively. An interesting open question is, for given n and m, to find the maximal number of solutions to the equation $h(z)=0$, i.e., extending the Fundamental Theorem of Algebra to harmonic polynomials, see [9] and references therein. Throughout the paper, we assume $n>m$, for the case $n=m$ could give an infinite solution set.

Wilmshurst [20, 21], in his doctoral thesis, proved the following:

Theorem

(Wilmshurst) The equation $h(z) = 0$ has at most $n^2$ solutions.

The proof of this result readily follows from Bezout’s theorem [4].

Seeking to improve on this bound, Wilmshurst conjectured that the equation $h(z) = 0$ has at most $3n-2 + m(m-1)$ solutions. Khavinson and Swia̧tek [8] confirmed Wilmshurst’s conjecture when $m=1$ using complex dynamics, and the bound was shown to be sharp by Geyer [6]. However, as was shown by Lee et al. [10], the conjecture is not true in general, for example, when $m=n-3$. Also see [7] for many more counterexamples.

Our first theorem bounds the number of roots off the coordinate axes for the harmonic polynomials $h=p_n+\overline{q_m}$, where $n>m$, with real coefficients.

Theorem 1

For a harmonic polynomial $h(z) = p_n(z) + \overline{q_m(z)}$ with real coefficients, the equation $h(z) = 0$ has at most $n^2 - n$ solutions that satisfy $(\mathrm{Re}\,z) (\mathrm{Im} z)\ne 0.$

Our next two theorems provide lower bounds on the maximal number of roots.

Theorem 2

For all $n>m$ , there exists a harmonic polynomial $h(z) = p_n(z) + \overline{q_m(z)}$ with at least $3n-2$ roots.

Theorem 3

For all $n>m$ , there exists a harmonic polynomial $h(z) = p_n(z) + \overline{q_m(z)}$ with at least $m^2+m+n$ roots.

The above three theorems will be proved in Sect. 2.

Remark

• (i) The reason why in Theorem 1 we only consider roots off the coordinate axes is the following. Consider $p(z)=z^n + (z-1)^n$ and $q(z)=z^n - (z-1)^n$. Then $h(z)=p(z)+\overline{q(z)}$ has $n^2$ number of roots including the root at 0 with the multiplicity n. In fact, this is the polynomial that Wilmshurst used (with a slight perturbation to split the multiple root at the origin) to show that the maximal bound $n^2$ is sharp. This example shows that Theorem 1 is sharp. Theorem 1 also yields that the harmonic polynomial with real coefficients and with the maximal ($n^2$) number of roots should have at least n roots on the coordinate axes as in the above example.

• (ii) Theorems 2 and 3 complement each other. Theorem 2 is stronger than Theorem 3 when $m^2+m+2<2n$ and Theorem 3 is stronger than Theorem 2 when $m^2+m+2>2n$. In addition, Theorem 2 is not at all trivial, since the argument principle for harmonic functions [5, 17, 19] only yields that h has at least n zeroes (see Fact 1 in Sect. 2.2).

• (iii) Note that, compared to Wilmshurst’s conjecture, Theorem 3 undercounts the number of roots by $2(n-m-1)$. See Sect. 2.4 for the in-depth discussion.

Theorem 3 allows the following important corollary.

Corollary 1

Let $Z_{n,m}$ denote the maximal possible number of zeros of $h=p_n+\overline{q_m}.$ Then, for any fixed integer $a\ge 1$ , we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{Z_{n,n-a}}{n^2}=1. \end{aligned}$$

More generally, if $m= \alpha n + o(n)$ with $0\le \alpha \le 1$ , we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{Z_{n,m}}{n^2}\ge \alpha ^2. \end{aligned}$$

Proof

From Theorem 3, we have $Z_{n,m}\ge n^2+2(1-a) n + a(a-1)$ for the first case, and $Z_{n,m}\ge \alpha ^2 n^2+o(n^2)$ for the second case. $\square$

We note that the first asymptotic statement about the case when $m = n-a$ follows from Theorem 2 in [7]. This corollary yields that the maximal number of roots is asymptotically given by Wilmshurst’s theorem. This answers a question posed by the first author more than a decade ago. In addition, this corollary complements the estimates on the expected number of zeros of Gaussian random harmonic polynomials obtained by Li and Wei in [13] and, more recently, by Lerario and Lundberg in [11]. For example, for $m=\alpha n$, $\alpha <1$, the expected number of zeros is $\sim n$ [13] for the Gaussian harmonic polynomials and $\sim c_\alpha n^{3/2}$ [11] for the truncated Gaussian harmonic polynomials. Yet, Corollary 1 yields that among all harmonic polynomials, the maximal number $\sim \alpha n^2$ of zeros occurs with positive probability, thus expanding further the results in [3] for $m=1$.

To state our last theorem, we have to introduce the set

$$\begin{aligned} \Omega = \{z : |f(z)|<1 \}, \end{aligned}$$

(1)

where

$$\begin{aligned} f(z)=\frac{p'_n(z)}{q_m'(z)}. \end{aligned}$$

For a harmonic function $h(z) = p(z) + \overline{q(z)}$, we note that h is sense-preserving at a point z if the Jacobian of h:

$$\begin{aligned} \det \left[ \begin{array}{cc} \partial _{x} \mathrm{Re} \,h(x+iy ) &{} \partial _{y} \mathrm{Re} \,h(x+iy ) \\ \partial _{x} \mathrm{Im} \,h(x+iy ) &{} \partial _{y} \mathrm{Im} \,h(x+iy ) \end{array} \right] _{x+iy=z} = |p'(z) |^2 - |q'(z) |^2, \end{aligned}$$

is positive, and sense-reversing at z if the Jacobian is negative at z. Otherwise, we say that h is singular at z. Note that the mapping $z\mapsto h(z)$ is sense-reversing precisely on $\Omega$. The boundary $\partial \Omega$ is the lemniscate $\{z:|f(z)|=1\}$.

Each connected component of $\Omega$ must contain at least one critical point of $p_n$. Indeed, if there is a connected component without a critical point, by applying the maximum modulus principle to f(z) and 1/f(z) with $|f(z)|=1$ on the boundary of that component, we have that f is a unimodular constant, a contradiction.

This implies that there are at most $\deg p_n'=n-1$ connected components of $\Omega$.

For $m=1$ (when Wilmshurst’s conjecture was proven to hold [8]), Wilmshurst guessed ([20], p. 73) that the following might be true: “In each component of $\Omega$ where $h(z)=p_n(z)+\overline{z}$ is sense-reversing, the behavior of h will be essentially determined by the $\overline{z}$ term so there will only be one zero of h”. From that the maximal number of roots (i.e., $3n-2$ for $m=1$) may be obtained by the argument principle when each connected component of $\Omega$ contains a zero.

The statement above is true when the component of $\Omega$ is convex according to the following result (see [20], p. 75).

Theorem

(Sheil-Small) If g(z) is an analytic function in a convex domain D and $|g'(z)|<1$ in D, then $\overline{z}+g(z)$ is injective on D.

Note that the theorem relates the geometry of critical lemniscates with the number of zeros, because D can have at most one zero of the function $\overline{z}+g(z)$ if the latter is injective. In a non-convex component of $\Omega$, it is possible to have more than one zero of h(z). In [20], an example is given where a non-convex component of $\Omega$ contains two critical points of $p_n$ and two zeros of $h(z)=p_n(z)+\overline{z}$. This is not surprising, because each component of $\Omega$ can have a zero of h and, therefore, one can have two zeros in a component by merging two components into one. The resulting component then has two critical points of $p_n$. It was, however, not clear whether a connected component containing a single critical point of $p_n$ could possibly have more than one zero of h.

Here, we show that it is, indeed, possible and, also, present a necessary and sufficient condition for having more than one zero of h in a connected component of $\Omega$ that contains a single critical point of $p_n$. The theorem holds for general m and n.

Theorem 4

Let $n>m$. Let D be a connected component of $\Omega$ [defined by (1)] containing exactly one zero of $p'_n$, counting multiplicity. On a smooth part of the curve $q_m(\partial D)$ (the image of $\partial D$ under $q_m$) let $\kappa$ be the curvature of $q_m(\partial D)$ with respect to the counterclockwise arclength parametrization of $\partial D$. Then, the following are equivalent:

• (i) Let $f(z)=p_n'(z)/q_m'(z)$ . There exists $z\in \partial D,$ such that

  $$\begin{aligned} \frac{\kappa (z)}{|f'(z)|}<-\frac{1}{2}. \end{aligned}$$

• (ii) There exists $\theta \in {\mathbb R}$ and $A\in {\mathbb C},$ such that

  $$\begin{aligned} \widetilde{p}_n(z)-\overline{q_m(z)} \end{aligned}$$

  has at least two zeros in D, where $\widetilde{p}_n(z)= e^{i\theta } p_n(z)+A.$

Remark

• (a) Note that $\kappa$ is the curvature of $\partial D$ when $q_m(z)=z$. In this case, the theorem tells us exactly how “non-convex” the domain D needs to be to have multiple zeros of h, improving upon Sheil-Small’s theorem.

• (b) In statement (ii) of Theorem 4, we note that $|\widetilde{p}'_n(z)|=| p'_n(z)|$. The corresponding lemniscate, $\{z:|\widetilde{p}_n'(z)/q'_m(z)|=1\}$, is, therefore, the same for all $\theta$ and A.

For $(n,m)=(4,1)$, we provide an example where a component of $\Omega$ with one critical point of $p_n$ contains two zeros of h, see Fig. 1. Note that the roots appear where $\Omega$ is (slightly) concave. The example is produced based on the discussion following our final Proposition 1 in Appendix A regarding the shapes of critical lemniscates.

Fig. 1

Roots (dots) for $h(z)=-\,(0.934124 +0.356949 i) z^*+(0.0581623 +0.156514 i) z^4+(0.354765-0.131835 i) z^3-(0.116325 +0.313028 i) z^2-(1.06429 -0.395504 i) z+(0.247627\, +0.020994 i)$. The stars are for the zeros of f and the shaded region is $\Omega$. The right picture is a zooming image of the top component of $\Omega$

2 Proofs of Theorems 1, 2 and 3

2.1 Proof of Theorem 1

Given a bivariate real polynomial P defined by the following:

$$\begin{aligned} P(x,y)=\sum \limits _{i=0}^n \sum \limits _{j=0}^m a_{ij}x^iy^j,\quad a_{ij}\in \mathbb {R}, \end{aligned}$$

the Newton polygon ${\mathcal N}_P$ of P is the convex hull of $N_P\subset {\mathbb R}^2$ where $N_P= \left\{ (i,j) : a_{ij}\ne 0\right\}$.

Given two polynomials P and Q with Newton polygons $\mathcal {N}_P$ and $\mathcal {N}_Q$, let $\mathcal {M}_{P,Q}$ be the Minkowski sum of $\mathcal {N}_P$ and $\mathcal {N}_Q$, defined by the following:

$$\begin{aligned} \mathcal {M}_{P,Q} = \{(i_1+i_2,j_1+j_2) \vert (i_1,j_1) \in \mathcal {N}_P, (i_2,j_2) \in \mathcal {N}_Q\}. \end{aligned}$$

Let [X] denote the area of a set $X \subset \mathbb {R}^2$. We then define the mixed area of P and Q as $[\mathcal {M}_{P,Q}] - [\mathcal {N}_P] - [\mathcal {N}_Q]$.

Theorem

(D. Bernstein; cf. [18], or the original articles [2, 16]) The number of solutions to the system of polynomial equations $p(x,y)=q(x,y)=0$ satisfying $x y \ne 0$ does not exceed the mixed area of p and q.

For analytic polynomials with real coefficients, $p_n(z)$ and $q_m(z)$ of degrees n, m, respectively, we have

$$\begin{aligned} h(x+iy)=p_n(x+iy)+\overline{q_m(x+iy)} = A(x,y)+iB(x,y), \end{aligned}$$

where A and B are polynomials with real coefficients. Let $\mathcal {N}_A$ be the Newton polygon of A(x, y) and $\mathcal {N}_B$ be the Newton polygon of B(x, y). As we will see below, the polynomials $p_n$ and $q_n$ having real coefficients lead to a certain structure of ${\mathcal N}_A$ and ${\mathcal N}_B$.

Lemma 1

Given a generic h(z) with only real coefficients let ${\mathcal N}_A$ and ${\mathcal N}_B$ be defined as above. If n is even, ${\mathcal N}_A$ is the isosceles triangle with vertex set $\{(0,0),(0,n),(n,0)\}$ and ${\mathcal N}_B$ is the trapezoid with vertex set $\{(0,1),(0,n-1),(1,n-1),(n-1,1)\}$. If n is odd, ${\mathcal N}_A$ is the trapezoid with vertex set $\{(0,0),(0,n-1),(1,n-1),(n,0)\}$ and ${\mathcal N}_B$ is the isosceles triangle with vertex set $\{(0,1),(0,n),(n-1,1)\}$ (see Fig. 2).

Fig. 2

Newton polygons $\mathcal {A}$ (left) and $\mathcal {B}$ (right) for $n=6$ (top) and $n=5$ (bottom), respectively

Proof

The lemma follows directly from the fact that:

$$\begin{aligned} A(x,y) = \sum _{ \begin{array}{c} j+k \le n,\\ k\text { is even} \end{array} } a_{jk}x^jy^k, \qquad B(x,y) = \sum _{\begin{array}{c} j+k \le n,\\ k\text { is odd} \end{array}} b_{jk}x^jy^k , \qquad a_{jk}, b_{jk} \in \mathbb {R}. \end{aligned}$$

The condition, $j+k\le n$, on the summation indices follows from $\deg h=\deg p_n =n$. The condition on k to be even or odd comes from $p_n$ and $q_m$ having real coefficients. Note that in the expansion of $p_n(x+iy)$ or, of $q_m(x+iy)$, the “i” comes only together with y—for a term of the form $x^j y^k$, the power of “i” is given by k, the power of y.

We need to show that all the coefficients that correspond to the extreme points of the convex hulls are nonvanishing. First of all, those that satisfy $j+k=n$:

$$\begin{aligned}&a_{0,n}, a_{n,0}, b_{1,n-1}\quad \mathrm{and}\quad b_{n-1,1}\quad \text { for even } n,\\&a_{1,n-1}, a_{n,0}, b_{0,n}\quad \mathrm{and}\quad b_{n-1,1}\quad \text { for odd } n, \end{aligned}$$

are all nonvanishing, because $\deg p_n=n$.

Using $h(z)=p_n(z)+\overline{q_m(z)}$, we note that

$$\begin{aligned} h(x), \quad \frac{\partial }{\partial y}h(x+i y)\bigg |_{y=0}, \quad \frac{\partial ^{n-1}}{\partial y^{n-1}}h(x+i y)\bigg |_{y=0} \end{aligned}$$

are all nontrivial polynomials in x, due to the presence of the terms, $x^n$, $x^{n-1}y,$ and $x y^{n-1}$ in $h(x+iy),$ respectively. Therefore, there exists $x_0\in \mathbb {R},$ such that, when $x=x_0$, none of the above three polynomials vanishes. Defining

$$\begin{aligned} \widetilde{h}(z)= h(z+ x_0),\quad x_0\in \mathbb {R}, \end{aligned}$$

$\widetilde{h}$ is a real polynomial (of the same holomorphic and antiholomorphic degrees) and has the same number of zeros as h. Moreover, the coefficients at the extreme points are all nonvanishing, because

$$\begin{aligned} a_{0,0}&= \widetilde{h}(0) = h(x_0),\\ b_{0,1}&=\frac{\partial }{\partial y}\widetilde{h}(i y)\bigg |_{y=0}=\frac{\partial }{\partial y}h(x_0+i y)\bigg |_{y=0},\\ \heartsuit _{0,n-1}&=\frac{1}{(n-1)!}\frac{\partial ^{n-1}}{\partial y^{n-1}}\widetilde{h}(i y)\bigg |_{y=0}=\frac{1}{(n-1)!}\frac{\partial ^{n-1}}{\partial y^{n-1}}h(x_0+i y)\bigg |_{y=0}, \end{aligned}$$

where, in the last line, the symbol $\heartsuit$ stands for a, when n is odd, and for b, when n is even. $\square$

Now, we prove Theorem 1. We divide the proof into two cases.

Case 1 Let n be even. From Lemma 1, $\mathcal {A}$ is an isosceles triangle with vertex set $\{(0,0), (0,n),(n,0)\}$ and $\mathcal {B}$ is the trapezoid with vertex set $\{(0,1),(0,n-1),(1,n-1),(n-1,1)\}$. Now, the Minkowski sum $\mathcal {M}$ of $\mathcal {A}$ and $\mathcal {B}$ is a trapezoid with vertex set $\{(0,1), (0,2n-1), (1,2n-1),(2n-1,1)\}$. The mixed area is then

$$\begin{aligned}{}[\mathcal {M}] - [\mathcal {A}] - [\mathcal {B}] = (2n^2 - 2n)-\frac{n^2}{2} - \frac{n^2-2n}{2}= n^2 - n. \end{aligned}$$

Case 2 Let n be odd. From the lemma, $\mathcal {A}$ is the trapezoid with vertex set $\{(0,0),(0,n-1),(1,n-1),(n,0)\}$ and $\mathcal {B}$ is the isosceles triangle with vertex set $\{(0,1),(0,n),(n-1,1)\}$. The Minkowski sum $\mathcal {M}$ of $\mathcal {A}$ and $\mathcal {B}$ is then the trapezoid with vertex set $\{(0,1),(0,2n-1),(1,2n-1),(2n-1,1)\}$. The mixed area is

$$\begin{aligned}{}[\mathcal {M}] - [\mathcal {A}] - [\mathcal {B}] = (2n^2 - 2n) - \frac{n^2-1}{2} - \frac{(n-1)^2}{2}=n^2-n. \end{aligned}$$

2.2 Proof of Theorem 2

For an oriented, closed curve $\Gamma ,$ such that a continuous function F does not vanish on $\Gamma$, we denote by $\Delta _{\Gamma }\arg F(z)$ the increment in the argument of F along $\Gamma$. The following is well known.

Theorem

(The argument principle for harmonic functions [5, 17]) Let H be a harmonic function in a Jordan domain D with boundary $\Gamma$. Suppose that H is continuous in $\overline{D}$ and $H\ne 0$ on $\Gamma$. Suppose that H has no singular zeros in D, and let $N=N_+ - N_-$, where $N_+$ and $N_-$ are the number of sense-preserving zeros and sense-reversing zeros of H in D, respectively. Then, $\Delta _{\Gamma }\arg H(z)=2\pi N.$

We also say that h is regular if all the zeros of h are either sense-reversing, or sense-preserving. The next fact [8] follows then by applying the argument principle to a circle of a sufficiently large radius, where $|p_n|\gg |q_m|.$

Fact 1

Let $h=p_n+\overline{q_m}$ be regular. Let $N_+$ be the number of sense-preserving zeros of h and $N_-$ be the number of sense-reversing zeros. Then,

$$\begin{aligned} n=N_+ - N_-. \end{aligned}$$

An elegant proof (due to Donald Sarason) of the following lemma can be found in [8].

Lemma 2

If p(z) is a polynomial of degree greater than 1, then the set of complex numbers c for which $p(z) +\overline{q(z)} - c$ is regular is open and dense in $\mathbb {C}.$

For $m=1$, more is known about the space of regular polynomials. Bleher et al. [3] proved that in the space $\mathbb {C}^{n+1}$ of harmonic polynomials $p_n(z)+\overline{z}$ of degree $n\ge 2,$ the set of “simple polynomials”, i.e., regular polynomials with k zeros, is a non-empty open subset of $\mathbb {C}^{n+1}$ if and only if $k = n,n+2,\ldots , 3n-4,3n-2$, and that the non-simple polynomials are contained in a real algebraic subset of $\mathbb {C}^{n+1}.$

The following fact is noted in [14], Theorem 3.1. Here, we provide a slightly different proof.

Lemma 3

If the function $h(z) = p_n(z) + \overline{z}$ has $3n-2$ zeros, then h(z) is regular.

Proof

Assume h is not regular and has exactly $3n-2$ roots. The number of roots that are not sense-preserving is at most $n-1,$ because each of those roots attracts a critical point of $p_n$ under the iteration of $z\mapsto p_n(z)$, cf. Proposition 1 in [8]. Therefore, the number of sense-preserving roots must be at least $2n-1$. For all non-singular roots $z_j$’s, there exists $\epsilon >0,$ such that the disks, $B_{\epsilon }(z_j) = \{ z : |z - z_j |< \epsilon \}$, do not intersect each other, do not intersect the singular set $\{z : |p'(z)|=1\}$, and $\Delta _{\partial B_\epsilon (z_j)}\arg h =\pm \, 2\pi$. Defining

$$\begin{aligned} \delta = \min _{z\in \partial B_\epsilon (z_j)} |h(z)|, \end{aligned}$$

for any $c\in {\mathbb C}$ with $|c |< \delta,$ we have $\Delta _{\partial B_\epsilon (z_j)}\arg h =\Delta _{\partial B_\epsilon (z_j)}\arg (h - c)$ and, using the argument principle for harmonic functions, the equation $h(z) - c$ has exactly one zero in each $B_{\epsilon }(z_j).$

Suppose that $z_0$ is a singular zero of h. Since $h(z_0) = 0$ and h is continuous near $z_0$, there is an $\eta >0,$ such that $B_{\eta }(z_0)$ does not intersect any $B_\epsilon (z_j)$ and

$$\begin{aligned} |h(z) |< \delta\quad \text { for all }z \in B_{\eta }(z_0). \end{aligned}$$

Furthermore, the set $B_{\eta }(z_0)$ intersects sense-preserving region, since, otherwise, $\log |p'(z)|$ would be constant over $B_\eta (z_0)$ by the maximum modulus principle. Let $\zeta$ be a sense-preserving point in $B_{\eta }(z_0)$. We can set $c=h(\zeta ),$ since $|h(\zeta ) |< \delta$, and $h(z)-c=h(z)-h(\zeta )$ must have zeros in each $B_{\epsilon }(z_j)$ and at $\zeta \in B_\eta (z_0).$ Consequently, $h(z)-h(\zeta )$ has at least 2n sense-preserving zeros. By Lemma 2, we can choose $\zeta ,$ such that $h(z)-h(\zeta )$ is a regular polynomial, which contradicts the result of Khavinson and Swia̧tek [8] that the regular polynomial can have at most $2n-1$ sense-preserving roots. $\square$

We now complete the proof of Theorem 2.

Proof

Let $p_n(z)$ be an analytic polynomial, such that the equation $p_n(z) + \overline{z}=0$ has $3n-2$ solutions. By Lemma 3, the polynomial $h(z)=p_n(z)+\overline{z}$ is regular. Let $z_0$ be a zero of h. One can find a circle, $\Gamma$, centered at $z_0$ with radius $\epsilon ,$ such that h does not vanish on $\Gamma$ and $\Delta _{\Gamma }\arg h=\pm\,2\pi.$ As in a standard proof of Rouché’s theorem, taking $\delta ,$ such that

$$\begin{aligned} 0<\delta < \frac{\min _{z\in \Gamma }|h(z)|}{\max _{z\in \Gamma }(|z|^m+1)}, \end{aligned}$$

we have the perturbed mapping, $z \mapsto h(z) + \delta \overline{z}^m$, that preserves the winding number of $h(\Gamma )$, that is, the perturbed mapping also vanishes in the interior of $\Gamma.$ Applying the same argument to all $3n-2$ zeros of h, we can choose $\delta ,$ such that $h(z)+\delta \overline{z}^m$ has (at least) $3n-2$ zeros. Setting now $q_m(z)=\delta z^m+z$ completes the proof. $\square$

Remark

This proof suggests that if the equation $p_n(z) + \overline{q_{m-1}(z)}=0$ has at least k solutions, then there exists a harmonic polynomial $p_n(z) + \overline{q_m(z)}$ with k zeros. However, a proof of this, following the above argument, would require that $p_n(z) + \overline{q_{m-1}(z)}$ be regular.

2.3 Proof of Theorem 3

Let us sketch the procedure (similar to [7, 10]) that allows creating examples of harmonic polynomials with a large number of roots (cf. Fig. 3).

Fix n and $m<n.$ Let

$$\begin{aligned} \begin{array}{ll} S(z)=z^n,\\ T(z)=(z-b)^{m+1}(z^{n-m-1}+t_{n-m-2}z^{n-m-2}+\cdots +t_0). \end{array} \end{aligned}$$

The $n-m-1$ complex parameters $t_j$’s in T(z) are uniquely determined by the condition that $S(z) -T(z)$ is a polynomial of degree m. Then, we choose $a\in {\mathbb C}$ and $b\in {\mathbb C}$ by hand to maximize the number of intersections between the two sets:

$$\begin{aligned} \Gamma _T=\{z\,|\, \mathrm{Im}\,T(z)=0\},\quad \Gamma _S=\{z\,|\, \mathrm{Re}\,S(z)=0\}. \end{aligned}$$

These intersections are the roots of the equation $p_n(z)+\overline{q_m(z)}=0,$ where

$$\begin{aligned} p_n(z)=S(z) + T(z),\quad q_m(z)=S(z)-T(z), \end{aligned}$$

since

$$\begin{aligned} p_n(z)+\overline{q_m(z)}=2\,\mathrm{Re}\,S(z)+2\,i\, \mathrm{Im}\,T(z) . \end{aligned}$$

Fig. 3

Curves $\Gamma _T$ (black) and $\Gamma _S$ (red) for $n=4, 5$ and $m=2$. The shaded region is $\Omega$. For $n=4$ (left), we choose $a=0$ and $b=1.1-0.1i$ to produce 12 roots. For $n=5$ (right), we choose $S(z)=(z-a)^{n-1}(z+(n-1)a)$ where $a=1.5-0.5i$ and $b=-\,0.05+0.92i$ to produce 15 roots

Theorem 3 can be stated equivalently as follows:

Theorem

For a generic choice of $b\in {\mathbb C}$ , the equation $p_n+\overline{q_m}=0$ defined in terms of S and T (as above) has at least $m^2+m+n$ roots.

Proof

Let $\Gamma _S$ be the set of rays emanating from the origin and extending to the infinity, i.e., $\Gamma _S=\{ z{:} \mathrm{arg\,} z = (\frac{1}{2}+k)\pi /n,k=0,1,\ldots ,2n-1\}$. Note that $\Gamma _T$ has $2m+2$ curved rays emanating from b where every ray asymptotically approaches the infinity towards $\{z{:}\arg z=l\pi /n\}_{l\in N_{2m+2}},$ such that: (i) different rays correspond to different values of l, and (ii) l is chosen in a subset, that we will denote by $N_{2m+2}$, containing $2m+2$ numbers from $\{0,1,\ldots ,2n-1\}$. We assume that $b\notin \Gamma _S$. We first assume that none of the rays in $\Gamma _{T}$ hit any critical point of T(z) except at $z=b,$ so that those rays do not intersect each other away from b.

Let $W_l$ ($l=0,1,\ldots ,2n-1$) denotes the connected component (that we will call “sector”) in $\mathbb {C}\setminus \Gamma _S$ that intersects $\{z {:} \arg z=l\pi /n\}$ as |z| goes to $\infty$. A simple geometric consideration tells us that the number of intersections between $\Gamma _S$ and a curved ray starts from $b\in W_{l_1}$ and continues into $W_{l_2}$ without passing through the origin, is at least

$$\begin{aligned} \min (|l_2-l_1|,2n-|l_2-l_1|). \end{aligned}$$

This means that the minimal possible number of intersections between $\Gamma _S$ and “the $2m+2$ curved rays in $\Gamma _T$” is as follows:

$$\begin{aligned} \sum _{l_2\in N_{2m+2} }\min (|l_2-l_1|,2n-|l_2-l_1|)\ge 0+2(1+2+\cdots + m ) + (m+1) = (m+1)^2. \end{aligned}$$

The inequality is obtained by letting the summands in the left-hand side assume the minimal possible values. The remaining part of $\Gamma _T$ (i.e., that is not connected to b) approaches the infinity in $2n-2m-2$ different sectors $W_l$, that are not already taken by the rays from b. Assuming that there are no critical points of T in $\Gamma _T$ except the one at b, each curve in the “remaining part of $\Gamma _T$” must connect two sectors from the $2n-2m-2$ sectors, such that, around $\infty$, each sector is “hit” by one curve only. Since there is at least one intersection between each curve and $\Gamma _S$, the minimal number of intersections between the “remaining part of $\Gamma _T$” and $\Gamma _S$ is $n-m-1$ and the minimal number of intersections between $\Gamma _T$ and $\Gamma _S$ is given by $(m+1)^2+n-m-1=m^2+m+n$.

When $\Gamma _{T}$ hit a critical point of T(z) outside $z=b$, and if $\Gamma _S$ does not intersect the same critical point, all the arguments in the proof can be carried through by considering a proper deformation of $\Gamma _T$ near the critical point.

This leaves us with the case when both $\Gamma _T$ and $\Gamma _S$ hits a critical point of T(z) outside $z=b$. Then, one may add a small (imaginary) constant to T(z), so that $\Gamma _T$ avoids that critical point, and hence, this case is not generic. This ends the proof.

The referee has kindly suggested a different, shorter, route to the proof of the theorem, that is worth sketching here. Let $p_{m+1}$ and $q_m$ be the polynomials of degree $m+1$ and m, respectively, so that Eq. $p_{m+1}(z) + \overline{q_{m}(z)} = 0$ has $(m + 1)^2$ many solutions. Such examples exist from Wilmshursts original construction [20, 21], and the solutions are regular. By the argument principle, one checks that the number of sense-reversing zeros is $m(m + 1)/2$. One can consider a perturbation to the original equation, $\epsilon z^n +p_{m+1}(z) + \overline{q_{m}(z)}=0,$ such that it keeps the same number of sense-reversing zeros for a small $\epsilon$. However, now, the winding number on large circles is n. This forces $n-m-1$ new (sense-preserving) zeros to appear, so that the total number of zeros is $m^2 + m + n$. We also note that this simpler construction has exactly this many zeros, whereas the former construction potentially has additional zeros. $\square$

2.4 A remark on Wilmshurst’s conjecture

Fig. 4

Roots and $\Omega$ (shaded region) for $(n,m)=(9,7)$, $a=0$ and $b=1.1-0.1 i$

Comparing with Wilmshurst’s conjecture, Theorem 3 undercounts the number of roots by

$$\begin{aligned} 3n-2+m(m-1) - (m^2+m+n) = 2(n-m-1). \end{aligned}$$

(2)

One can show that the corresponding lemniscate has $2m+2$ curves that connects b and a (cf. Fig. 4). The numerics suggests that the $2m+1$ regions in between these curves have, respectively:

$$\begin{aligned} m-1,m-2,\ldots ,2,1,1,2,\ldots ,m-1,m, \end{aligned}$$

(counting from top to bottom in Fig. 4) roots. Among these exactly $1+2+\cdots +m=m(m+1)/2$ of them are found in the sense-reversing region (with m components; the shaded part in Fig. 4) and, therefore, the total number of roots must be at least

$$\begin{aligned} 2\times \frac{m^2+m}{2}+ n = m^2+ m + n \end{aligned}$$

(3)

by Fact 1, giving the same number as in Theorem 3.

Since there can be at most $n-1$ components in $\Omega$, there can be $n-m-1$ extra components in the sense-reversing region, and these components are not connected to the point b. Wilmshurst’s count is obtained when each of these components has exactly one root. This increases the total number of sense-reversing roots by $n-m-1$ and, hence, increases the total number of roots by $2(n-m-1)$, cf. (3), which is precisely Wilmshurst’s count, cf. (2).

The various counterexamples studied in [7, 10] indicate that the $n-m-1$ “extra components” of $\Omega$ (that are not connected to b) can have more than one root in each component. For example, Fig. 4 shows that there are two roots inside the component of $\Omega$ that is not connected to b.

For $m=n-2$, our numerical experiment supports the structure shown in Fig. 4: there are $m^2+m+n$ roots that are counted in terms of the $2m+2$ curves connecting a and b, and the excessive zeros are twice the number of zeros found in the component of $\Omega$ that is not connected to b. Choosing $b=e^{i\pi /(2n)}+\epsilon$ ($\epsilon \ne 0$ is needed, so that the origin is not a root), we found that the number of “excessive zeros”, i.e., (the total number of zeros) $-\,(m^2+m+n)$, increases by 4 whenever n hits the numbers:

$$\begin{aligned} 7, 15, 22, 30, 37, 45, 52, 60, 68, 75, 83, 90, 98, 105, 113, 120, 128, 136,\ldots . \end{aligned}$$

For example, for $n=100$, there are total 13 numbers before 100 from the list, and the total number of zeros is $4\times 13 +(m^2+m+n) = 52+9998$, exceeding Wilmshurst’s count by $4\times 13 -2(n-m-1) = 52 - 2 = 50$. These experiments prompt us to suggest the following conjecture.

Conjecture

When $m=n-2$, the maximal number of roots of $h=p_n+\overline{q_m}$ is given by

$$\begin{aligned} n^2 - \frac{3}{2} n + o(n) \end{aligned}$$

as n grows to $\infty$ (which is larger than Wilmshurst’s count of $n^2-2n+4$).

Remark

While this paper was under review, two of the authors proved in the recent publication [12] that the maximal number of roots in the above conjecture is bounded below by $n^2 - C n + {\mathcal O}(1)$ with a constant $C\approx 1.47052$.

3 Geometry of caustics: Proof of Theorem 4

As before, let $\Omega$ be defined by (1). Setting

$$\begin{aligned} f(z)=p'_n(z)/q'_m(z), \end{aligned}$$

let D be a connected component of $\Omega$ with exactly k (counting the multiplicities) zeros of f in D. It is well known (cf. [1]) that $f{:} D\rightarrow {\mathbb D}$, where ${\mathbb D}$ is the unit disk, is a branched covering of degree k of D onto ${\mathbb D}$.

When D contains exactly one critical point of $p_n$, $f:D\rightarrow {\mathbb D}$ is a univalent map. In this case, let $\eta{:}[0,2\pi )\rightarrow \partial D$ be the parametrization of $\partial D$ given by

$$\begin{aligned} \eta (\theta ) = f^{-1}(e^{i\theta }), \end{aligned}$$

where $f^{-1}$ on $\partial {\mathbb D}$ is obtained by the continuous extension of $f^{-1:}{\mathbb D}\rightarrow D$. This parametrization of $\partial D$ is given by the harmonic measure of D (normalized by the factor $2\pi$) with respect to the pole at the zero of f, that is

$$\begin{aligned} \mathrm{d}\theta = \mathrm{d}\,\arg f(z),\quad z\in \partial D. \end{aligned}$$

(4)

This viewpoint can be generalized when there are k zeros of f in D. In this case, the same Eq. (4) defines the parametrization, $\eta :[0,2\pi k)\rightarrow \partial D$, by the harmonic measure of k-sheeted disk.

On a smooth part of the curve $\partial D$ (i.e., where $f'\ne 0$), let v(z) be the tangent vector of the curve $\partial D$ at $z\in \partial D$ given by

$$\begin{aligned} v(z)= \frac{\mathrm{d} \eta (\theta )}{\mathrm{d}\theta }=i\frac{f(z)}{f'(z)}. \end{aligned}$$

(5)

Let us consider the image of $\partial D$ under h. For each $z\in \partial D$ with $f'(z)\ne 0$ we obtain a tangent vector of the curve $h(\partial D)$ at h(z) as follows (v is the tangent vector to $\partial D$, cf. (5), $|f|=1$ on $\partial D$):

$$\begin{aligned} V(z) = \Big (v(z)\partial +\overline{v(z)}\, \overline{\partial }\Big ) h(z) = v(z) p'_n(z) +\overline{v(z)} \,\overline{q'_m(z)}, \end{aligned}$$

(6)

assuming that this expression does not vanish. The next two lemmas deal with the geometry of the caustic that we identify now.

Definition

The image of the critical lemniscate $h(\partial \Omega )$ is called the caustic.

The following lemma is essentially Lemma 2.3 in [15].

Lemma 4

Let D be a component of $\Omega$ with exactly k zeros (counting multiplicity) of f and $\partial D$ is parametrized by $\eta :[0,2\pi k)\rightarrow \partial D,$ such that ${\rm d} \arg f(\eta (\theta )) ={\rm d}\theta.$ At $z=\eta (\theta )\in \partial D$ where $f'(z)\ne 0$ and $\mathrm{Re}\big (v(z) q'_m(z) \sqrt{f(z)}\big )\ne 0$, we have

$$\begin{aligned} \frac{\mathrm{d} \arg V(\eta (\theta ))}{\mathrm{d}\theta }=\frac{1}{2}. \end{aligned}$$

In other words, the caustic, away from the possible singularities, has constant curvature with respect to the special parametrization defined above.

Lemma 5

The only singularities of the curve $h(\partial D)$ are cusps. When $z_0\in \partial D$ is not in the branch cut of $\sqrt{f},$ there is a cusp at $h(z_0)$ if and only if the mapping from $\partial D$ to ${\mathbb R}$ given by

$$\begin{aligned} z\mapsto \mathrm{Re}\Big (v(z) q'_m(z) \sqrt{f(z)}\Big ) \text {~~ on }\partial D, \end{aligned}$$

changes sign across $z_0$ . When $z_0$ is on the branch cut of $\sqrt{f}$ , the cusp occurs at $h(z_0)$ if and only if the mapping,

$$\begin{aligned} z\mapsto \mathrm{Re}\left( \frac{\sqrt{f(z)}}{\sqrt{f(z_0)}}\right) \,\mathrm{Re}\Big (v(z) q'_m(z) \sqrt{f(z)}\Big ) \text {~~ on }\partial D, \end{aligned}$$

changes sign across $z_0.$

The proof of the Lemma can be found in [15]. This lemma characterizes the “possible singularities” of the caustic. According to [15], they correspond to the “critical points of the 1st kind” generically. In fact, that paper contains the comprehensive description of the singularities that can happen in the so-called “light harmonic mappings” in the author’s terminology. The latter include all the harmonic polynomial mappings considered in our paper.

If $f'(z_0)=0$ for $z_0\in \partial D$, multiple components of $\Omega$ merge together at $z_0$. They are called “The critical points of the third kind” in [15]. It turns out that the image of $\partial \Omega$ under h has an interesting structure, as we will see below.

Remark

(a critical point on the critical lemniscate) Let $z_0\in \partial \Omega$ satisfy $f'(z_0)=\cdots =f^{(k-1)}(z_0)=0$ and $f^{(k)}(z_0)\ne 0$, that is

$$\begin{aligned} f(z)=f(z_0) + \frac{f^{(k)}(z_0)}{k!}(z-z_0)^{k}+{\mathcal O}\big ((z-z_0)^{k+1}\big ). \end{aligned}$$

Taking the absolute value and rotating if necessary, we obtain

$$\begin{aligned} |f(z)|=|f(z_0)| + \frac{|f(z_0)|}{k!}\mathrm{Re}\left[ \frac{f^{(k)}(z_0)}{f(z_0)}(z-z_0)^{k}\right] +{\mathcal O}\big ((z-z_0)^{k+1}\big ). \end{aligned}$$

(7)

Locally, the lemniscate consists of 2k curved rays meeting at $z_0$ and it divides the plane into 2k wedge-shaped sections with the angle $\pi /k$ at $z_0$. Among them, total k sections, equally spaced, are included in $\Omega$. To be more precise, taking a sufficiently small disk B centered at $z_0$, $B\cap \Omega$ has exactly k components, such that $B\cap \partial \Omega$ consists of 2k curves emanating from $z_0$ with the angular directions given by

$$\begin{aligned} \theta _j= \frac{1}{k}\arg \frac{f(z_0)}{f^{(k)}(z_0)}+\frac{\pi }{k}\bigg (j+\frac{1}{2}\bigg ),\quad j=0,1,\ldots ,2k-1. \end{aligned}$$

Note that the sections between $\theta _{2\ell }$ and $\theta _{2\ell +1}$ for every $\ell =0,1,\ldots , k-1$ are in $\Omega$. Therefore, taking the single component (let us denote it by $D_\ell$) of $B\cap \Omega$ between $\theta _{2\ell }$ and $\theta _{2\ell +1}$, the tangent vector of its boundary changes angular direction from $\theta _{2\ell +1}-\pi$ to $\theta _{2\ell }$ at $z_0$. Using Lemma 5, assuming that $z_0$ is not in the branch cut of $\sqrt{f}$, the corresponding tangent vector of $h(\partial D_\ell )$ changes the direction by $\pi$ at $h(z_0)$ (i.e., has a cusp singularity) if and only if

$$\begin{aligned} \mathrm{Re}\left( e^{i(\theta _{2\ell +1}-\pi )}q'_m(z_0)\sqrt{f(z_0)}\right) \mathrm{Re}\left( e^{i\theta _{2\ell }}q'_m(z_0)\sqrt{f(z_0)}\right) <0 \end{aligned}$$

or, equivalently,

$$\begin{aligned} \theta _{2\ell }+\arg \left( q'_m(z_0)\sqrt{f(z_0)}\right) \in \left( 0,\frac{k-1}{k}\pi \right) \cup \left( \pi , \frac{2k-1}{k}\pi \right) . \end{aligned}$$

When k is even (respectively, odd), there can be at most two (respectively, one) values of $\ell$’s that do not satisfy the above condition. It means that for those values of $\ell$’s, $h(\partial D_\ell )$ has a smooth boundary at $h(z_0)$, and for the other values of $\ell$’s, $h(\partial D_\ell )$ has a cusp at $h(z_0)$. In Fig. 5, the middle picture shows a caustic where the critical point $z_0=0$ corresponds to the three cusps at the origin, and the last picture shows a caustic, where one component (red) of the lemniscate maps $z_0$ to a regular point of the caustic.

Fig. 5

Lemniscate (left) and caustics, $h(z)=\frac{z^4}{4}-z-e^{i\theta }\overline{z}$ for $\theta =0$ and $\theta =\frac{\pi }{6}$

Lemma 6

Let D be a simply connected component of $\Omega$ with exactly k zeros of $q'_m\cdot p'_n$ counting multiplicity. The number of cusps in $h(\partial D)$ is odd (resp. even) when k is odd (resp. even) and, moreover, is $\ge 2+k.$

Proof

According to Lemma 5, a cusp in $h(\partial D)$ occurs whenever $\mathrm{Re}\big ( v \,q'_m \sqrt{f} \big )$ changes sign. To locate such events, it is convenient to define the function, $\Psi :[0,2\pi k)\rightarrow \mathbb {R}$ by

$$\begin{aligned} \Psi :\theta \rightarrow \arg \Big ( v(z) \,q'_m(z) \sqrt{f(z)} \Big )_{z=\eta (\theta )} = \arg v(\eta (\theta )) + \arg q'_m(\eta (\theta )) + \arg \sqrt{f(\eta (\theta ))}. \end{aligned}$$

(8)

For the term $\arg q'_m(\eta (\theta ))$, we choose the branch of the function “$\arg ,$” such that the term is continuous with respect to $\theta$. For the term $\sqrt{f(\eta (\theta ))},$ we choose the branch of $\sqrt{f}$ and “$\arg$” function (separately from the previous one), so that term is continuous. Finally, for the first term, $\arg v$, we choose the branch of “$\arg ,$” such that the term is a piecewise continuous function where the only discontinuities are at the critical points of the lemniscate (i.e., where $f'(\eta (\theta ))=0$). At the discontinuity $\arg v$ jumps by a positive angle, $\frac{k-1}{k\pi }\in [\pi /2,\pi )$ from $\theta _{2\ell +1}-\pi$ to $\theta _{2\ell }$ using the notations in the above Remark “a critical point on the critical lemniscate”; the angle can vary according to the order $k\ge 2$ of the critical point. As a consequence, $\Psi$ is a continuous function with only discontinuities being the jump(s) by angles in $[\pi /2,\pi ]$ at the critical points of the lemniscate.

For a cusp to occur at $\theta$, the condition in Lemma 5 gives that

$$\begin{aligned} \bigcap _{\epsilon >0}(\Psi (\theta -\epsilon ),\Psi (\theta +\epsilon )) \text {~contains } l\pi \text { for some integer}\,l. \end{aligned}$$

(9)

Let us look at the three terms in $\Psi$ individually. The last term is linear in $\theta$ with the slope 1/2 by the definition of $\eta$ and, therefore, $\Delta \arg \sqrt{f} = k\pi$. Here and below $\Delta$ stands for the increment over $\partial D$. Note that k equals $\#(p'_n)-\#(q'_m)$ where $\#(A)$ is the number of zeros of the polynomial A in D. The second term, $\arg q'_m$, is a continuous function and $\Delta \arg q'_m=2\pi \#(q'_m)$. Finally, the first term, $\arg v$, is a piecewise continuous function with $\Delta \arg v = 2\pi$ where the only discontinuities are at the critical points of the lemniscate (i.e., where $f'(\eta (\theta ))=0$). Summing up, the total increment of $\Psi$ over $[0,2k\pi )$ is $(2+k+2\#(q'_m))\pi =(2+\#(p'_n)+\#(q'_m))\pi$ and, therefore, there are at least $\#(p'_n)+\#(q'_m)+2$ points (and exactly $\#(p'_n)+\#(q'_m)+2$ if $\Psi$ is monotone) where the condition (9) holds.

Suppose now that $\Psi$ is not monotone. For any point $\theta$ that satisfies the condition (9), there are two possibilities: as $\epsilon \rightarrow +0:$

$$\begin{aligned} \text {(A):}~~ \Psi (\theta -\epsilon )<l\pi \text { and } \Psi (\theta +\epsilon )>l\pi \quad \text { or }\quad \text {(B):}~~\Psi (\theta -\epsilon )>l\pi \text { and } \Psi (\theta +\epsilon )<l\pi . \end{aligned}$$

Since the total increment of $\Psi$ is $(\#(p'_n)+\#(q'_m)+2)\pi$, the number of points satisfying the condition (A) must be larger than those satisfying (B) by exactly $\#(p'_n)+\#(q'_m)+2.$ Therefore, the number of points satisfying either (A) or (B) can be bigger than $\#(p'_n)+\#(q'_m)+2$ by an even number. As a consequence, the number of cusps is always odd (respectively, even) when k is odd (respectively, even). $\square$

Lemma 7

Let D be a component of $\Omega$ with a single zero of f. If $h(\partial D)$ has only three cusps, then it is a Jordan curve. There are more than three cusps in $h(\partial D)$ (hence, five or more according to Lemma 6 (if and only if there exists a point relative to which the winding number of $h(\partial D)$ is larger than one, i.e., there exists $p\in \mathbb {C},$ such that $\Delta _{\partial D}\arg (h(\cdot )-p)> 2\pi.$

Proof

To prove the first statement of the lemma, it suffices to show that the three smooth (open) arcs between the three cusps do not intersect each other. Choosing any two arcs, there exists a cusp where the two arcs meet. Since the tangent vector rotates at most by $\pi$ over a smooth part of the curve (cf. Lemma 4), the two arcs can only get farther from each other as one moves along the arcs starting from the common cusp. Note, however, that, if the constant curvature is bigger than 1/2, $h(\partial D)$ can self-intersect.

To prove the second statement, assume that $h(\partial D)$ has five or more cusps. Let $\Gamma$ be a smooth curve that is obtained by slightly “smoothing” all the cusps of $h(\partial D)$, see the left picture in Fig. 6. Considering infinitesimally small smoothing, such deformation indicates that the tangent vector of $\Gamma$ rotates by

$$\begin{aligned} \frac{1}{2}\cdot 2\pi -\#\{\text {cusps}\}\pi \le \pi -5\pi = - 4\pi \end{aligned}$$

over the whole curve.

Fig. 6

Cusp in caustic (left). Dotted line shows a “cusp after smoothing”. Relative winding numbers in a region around an intersection point (right)

Therefore, $\Gamma$ cannot be a (smooth) Jordan curve and $h(\partial D)$ must have a self-intersection (that cannot be removed by a small perturbation, such as the one in the right picture of Fig. 6).

Let us define the orientation on $h(\partial D)$ by the orientation inherited from $\partial D$. For each point $p\notin h(\partial D)$, one can consider the winding number of $h(\partial D)$ around p. The winding number of $h(\partial D)$ on the left side (with respect to the orientation) is bigger than the one on the right side by $+1$. Then, in a neighborhood of a self-intersection, there must be a pair of regions where the winding numbers differ by 2, see the right picture in Fig. 6. $\square$

Proof of Theorem 4

To have more than three cusps, the function $\Psi$ that is defined in the proof of Lemma 6 must be non-monotonic, i.e., there must be a point where the slope of the graph of $\Psi$ is negative, that is

$$\begin{aligned} \frac{\mathrm{d}\Psi (\theta )}{\mathrm{d}\theta }= \frac{\mathrm{d}\,\arg v(\eta (\theta ))}{\mathrm{d}\theta } + \frac{\mathrm{d}\,\arg q'_m(\eta (\theta ))}{\mathrm{d}\theta } + \frac{1}{2}<0. \end{aligned}$$

(10)

Note that the first two terms in the left-hand side give the curvature of $q_m(\partial D)$ with respect to the parametrization by $\theta$ or, equivalently, $\kappa /|f'|$ where $\kappa$ is the curvature with respect to the arclength on $\partial D$ (cf. (5)):

$$\begin{aligned} \left| \frac{\mathrm{d}\eta (\theta )}{\mathrm{d}\theta }\right| \kappa = \frac{\mathrm{d}}{\mathrm{d}\theta }\,\arg \frac{\mathrm{d} q_m(\eta (\theta ))}{\mathrm{d}\theta } =\frac{\mathrm{d}\,\arg v(\eta (\theta ))}{\mathrm{d}\theta } + \frac{\mathrm{d}\arg q'_m(\eta (\theta ))}{\mathrm{d}\theta }. \end{aligned}$$

Therefore, the inequality (10) is exactly the one that appears in (i) of Theorem 4.

Once the graph of $\Psi$ is non-monotonic, one can create more roots of $\Psi \equiv 0 \mod \pi$ by vertically shifting this graph. This is done by the following transformation, which preserves the lemniscate $\{z:|p'_n(z)/q'_m(z)|=1\}{:}$

$$\begin{aligned} p_n \rightarrow e^{i\varphi } p_n, \quad \varphi \in {\mathbb R}. \end{aligned}$$

Under this transformation,

$$\begin{aligned} \arg (v\,q'_m\sqrt{f}) \rightarrow \arg (v\,q'_m\sqrt{f})+\varphi /2 \end{aligned}$$

because of the term $\sqrt{f}.$ This means that, for some $\varphi$, $h(\partial D)$ can have more than five cusps. By Lemma 7, there exists a point, say $p\in {\mathbb C}$, where $\Delta _{\partial D}(h(\cdot )-p)>2\pi.$ This means that

$$\begin{aligned} \widetilde{p}_n(z) = e^{i\varphi } p_n(z) - p \end{aligned}$$

satisfies $\Delta _{\partial D}\widetilde{h}>2\pi$ where $\widetilde{h} = \widetilde{p}_n +\overline{q_m}$ and, therefore, $\widetilde{h}$ has at least two roots inside D. This ends the proof of Theorem 4. $\square$

Appendix A. Construction of non-convex lemniscate

Let us recall that the original motivation of the paper was to sort out whether a connected component of $\Omega$ with a single critical point of $p_n$ could possibly have more than one zero of h. Theorem 4 suggests that the answer is “yes” if the boundary of the component is sufficiently concave. The following proposition gives one way of finding such concave component. Our example in Fig. 1 has been found using the subsequent proposition and its corollary.

Proposition 1

Let f be a rational function and $\Omega =\{z:|f(z)|<1\}$ . Let $z_0 \in \partial \Omega,$ $f'(z_0) = 0$ and $(\log f)''(z_0) \ne 0$ . In a neighborhood of $z_0,$ $\partial \Omega$ is a union of two smooth arcs that intersect perpendicularly at $z_0$ . Moreover, the point $z_0$ is not an inflection point (i.e., the curvature is strictly positive or negative at $z_0$ ) for either of the arcs if and only if

$$\begin{aligned} \mathrm{Re}\bigg ( e^{\pm i\pi /4} \frac{(\log f)'''(z_0)}{(\log f)''(z_0)^{3/2}}\bigg )\ne 0. \end{aligned}$$

Corollary 2

If $z_0\in \partial \Omega$ satisfies the assumptions in Proposition 1 and furthermore, is not an inflection point of $\partial \Omega$ , then there is a connected component of $\Omega$ whose curvature of the boundary (with respect to the counterclockwise orientation) converges to a negative value at $z_0.$

Proof

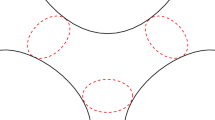
According to Proposition 1, there exists an open neighborhood U of $z_0,$ such that $\Omega \cap U$ is the disjoint union of two domains, see Fig. 7 for an illustration ($\Omega \cap U$ is the shaded region). When the “no inflection” condition in Proposition 1 is satisfied, the local configuration of $\Omega$ has two possibilities: $\Omega \cap U$ is the disjoint union of a convex and a non-convex domain (left in Fig. 7) or, $\Omega \cap U$ is the disjoint union of two non-convex domains (right in Fig. 7). In either case, there exists a connected component of $\Omega \cap U$ whose boundary has a negative curvature in a neighborhood of $z_0$. $\square$

Fig. 7

Lemniscate near $z_0$, see text below Proposition 1.

Remark

To relate Proposition 1 to our harmonic polynomials, we take $f(z) = p_n'(z)/q_m'(z)$. For $m=1$, as z approaches $z_0$ along the “concave” arc, $\kappa (z)<0$ by Corollary 2 and $|f'(z)|\rightarrow 0$. Therefore, one obtains that $\kappa (z)/|f'(z)|\rightarrow -\infty$ as z approaches $z_0$ along the “concave” arc. Hence, we obtain the “non-convex” domain D as is needed to satisfy the condition $\kappa /|f'|<-1/2$ in Theorem 4.

In the rest of this section, we prove Proposition 1.

Let f be a meromorphic function. Let $\gamma :\mathbb {R}\rightarrow \mathbb {C}$ be the parametrization of a curve in $\mathbb {C},$ such that $\gamma (0) = z_0$ and $f'(z_0) = 0$. Taking the derivatives of $\log |f(\gamma (t)) |$ at $t=0,$ we obtain:

$$\begin{aligned} \frac{\text {d}}{\text {d}t} \log |f(\gamma (t)) |\bigg |_{t=0}=0, \end{aligned}$$

$$\begin{aligned} \frac{\text {d}^2}{\text {d}t^2} \log |f(\gamma (t)) |\bigg |_{t=0} = \text {Re}\Big (\dot{\gamma }(0)^2 (\log f)''(z_0)\Big ), \end{aligned}$$

$$\begin{aligned} \frac{\text {d}^3}{\text {d}t^3}\log |f(\gamma (t)) |\bigg |_{t=0}= \text {Re}\Big (3\dot{\gamma }(0)\ddot{\gamma }(0) (\log f)''(z_0)+\dot{\gamma }(0)^3(\log f)'''(z_0)\Big ). \end{aligned}$$

Above, $\dot{\gamma }$ and $\ddot{\gamma }$ denote, respectively, the derivative and the second derivative of $\gamma$ with respect to t. Consider the Taylor expansion of $\log |f(\gamma (t))|$ around $t=0$. We have

$$\begin{aligned} \begin{array}{ll} \log |f(\gamma (t))|&{}= \text {Re}\Big (\dot{\gamma }(0)^2 (\log f)''(z_0)\Big )\frac{t^2}{2} \\ &{} \quad +\,\text {Re}\Big (3\dot{\gamma }(0)\ddot{\gamma }(0) (\log f)''(z_0)+\dot{\gamma }(0)^3(\log f)'''(z_0)\Big )\frac{t^3}{6} + {\mathcal O}(t^4). \end{array} \end{aligned}$$

If $\gamma$ parametrizes the lemniscate $\partial \Omega$ passing through $z_0$, where $\Omega$ is as in (1), then we have $\log |f(\gamma (t))|=0$ identically for all t, and all the coefficients in the above Taylor series must vanish. The first coefficient vanishes when

$$\begin{aligned} \dot{\gamma }(0)^2 = i c_1 \overline{(\log f)''(z_0)},\quad c_1\in \mathbb {R}. \end{aligned}$$

(11)

We may assume that $\gamma$ is the arclength parametrization, i.e., $|\dot{\gamma }|\equiv 1$. Then, $\ddot{\gamma }\overline{\dot{\gamma }}$ is purely imaginary and

$$\begin{aligned} \ddot{\gamma }(0)=i c_2\, \dot{\gamma }(0) \end{aligned}$$

(12)

for some real constant $c_2$. The second coefficient in the Taylor series gets simplified as

$$\begin{aligned} \begin{array}{ll} &{} \text {Re}\Big (3\dot{\gamma }(0)\ddot{\gamma }(0) (\log f)''(z_0)+\dot{\gamma }(0)^3(\log f)'''(z_0)\Big ) \\ &{} =- 3c_1c_2 |(\log f)''(z_0)|^2 -c_1 \mathrm{Im}\Big ( \dot{\gamma }(0)\overline{(\log f)''(z_0)} (\log f)'''(z_0)\Big ), \end{array} \end{aligned}$$

using (11) and (12). The above expression vanishing implies that

$$\begin{aligned} c_2 = - \frac{1}{3}\mathrm{Im}\bigg ( \dot{\gamma }(0)\frac{(\log f)'''(z_0)}{(\log f)''(z_0)}\bigg ). \end{aligned}$$

Summarizing, we obtain

$$\begin{aligned} \gamma (t) = z_0 + \dot{\gamma }(0) t - \frac{i\,\dot{\gamma }(0)}{6}\mathrm{Im}\bigg ( \dot{\gamma }(0)\frac{(\log f)'''(z_0)}{(\log f)''(z_0)}\bigg ) t^2 + {\mathcal O}(t^3), \end{aligned}$$

where, using (11)

$$\begin{aligned} \dot{\gamma }(0)=\pm \,e^{\pm i\pi /4}i \frac{\overline{\sqrt{(\log f)''(z_0)}}}{|\sqrt{(\log f)''(z_0)}|}=\pm \,e^{\pm i\pi /4}i \frac{|\sqrt{(\log f)''(z_0)}|}{\sqrt{(\log f)''(z_0)}}. \end{aligned}$$

The two signs can be chosen arbitrarily and independently. This proves that there are two different arcs orthogonal at $z_0$. The curve $\partial \Omega$ does not have an inflection point at $z_0$ when the quadratic term in the Taylor expansion of $\gamma (t)$ is non-zero, that is

$$\begin{aligned} \mathrm{Re}\bigg ( e^{\pm i\pi /4} \frac{(\log f)'''(z_0)}{(\log f)''(z_0)^{3/2}}\bigg )\ne 0. \end{aligned}$$

The proof is now complete.