Constellation design and performance of future quantum satellite gravity missions

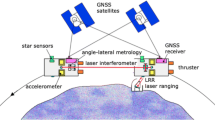
Abstract

Temporal aliasing is currently the largest error contributor to time-variable satellite gravity field models. Therefore, the evolution of sensor technologies has to be complemented by strategies to reduce temporal aliasing errors. The most straightforward way to improve temporal aliasing is through extended satellite constellations because they improve the observation geometry and increase the achievable temporal resolution. Therefore, strategies to optimize the design of larger satellite constellations are investigated in this contribution. A complete constellation modeling procedure is presented, starting from primary design variables (such as the required targeted resolutions) and concluding with concrete orbital elements for the individual satellites. In parallel, it is evaluated if improved instrument sensitivities based on quantum technologies (cold atom interferometry) can be fully exploited in the case of larger constellations. For this, future quantum satellite gravity missions adopting the gradiometry concept (similar to the GOCE mission) and the low-low satellite-to-satellite tracking concept (similar to GRACE/-FO) are simulated on optimized constellations with up to 6 satellites/pairs. The retrieval performance of a 6-pair mission in terms of the global equivalent water height RMS can be improved by a factor of roughly 3 compared to an inclined double-pair mission. 3D-gradiometry intrinsically has a better de-aliasing behavior but has extremely high accuracy requirements for the gradiometer (about 10 µEotvos) and the attitude reconstruction to be of any benefit. All simulations show that when incorporating improved sensor technologies, such as future quantum sensing instruments in extended constellations, temporal aliasing will remain the dominant error source by far, up to five orders of magnitude larger than the instrument errors. Therefore, improving sensor technologies has to go hand in hand with larger satellite constellations and improved space–time parameterization strategies to further reduce temporal aliasing effects.

Graphical Abstract

1 Introduction

Current satellite missions for observing the Earth’s time-variable gravity, such as the Gravity Recovery and Climate Experiment mission (GRACE, Tapley et al. 2004) and the GRACE Follow-On mission (GRACE-FO, Kornfeld et al. 2019), are confined in their accuracy mainly due to instrument errors and temporal aliasing introduced by the limited spatio-temporal coverage achievable by a single satellite/-pair (cf. Flechtner et al. 2016). Through technological advancements, it can be expected that the noise level of the instruments for future satellite gravity missions can still be significantly reduced. Especially, upcoming quantum technologies are promising for increasing the sensitivity of future instruments even further (Encarnação et al. 2024). Future quantum accelerometers based on cold atom interferometry (CAI) might become particularly useful for observing gravity from space since they are currently rapidly evolving (Lévèque et al. 2022). In view of this progress in technology, the reduction of temporal aliasing errors will become even more relevant in the future. To achieve this, the European Space Agency (ESA) plans to launch the Next Generation Gravity Mission (NGGM, Daras et al. 2024) which consists of a low-low satellite-to-satellite tracking (SST) pair at an inclined controlled orbit around 397 km orbital altitude, which will complement the GRACE-Continuity polar pair mission (GRACE-C, German Aerospace Center 2024). It is foreseen that, together, both missions will form the Mass Change and Geoscience International Constellation (MAGIC, Heller-Kaikov et al. 2023; Daras et al. 2024). In the case of SST, a second inclined pair helps to significantly improve the observation geometry by introducing a second observation direction and, in addition, ground track crossover points, which might help to equilibrate instrument errors (discussed in Sect. 2.1). Eventually, this increases the overall space–time sampling and homogeneity of the observation considerably, which allows a substantial reduction of temporal aliasing and, thus, results in more accurate time-variable gravity field solutions.

However, even if a MAGIC double-pair mission considerably reduces this effect, temporal aliasing still remains the dominant error in such a constellation (cf. Heller-Kaikov et al. 2023), which means that a possible future quantum mission will be even more affected because the relative error contribution of temporal aliasing errors compared to further reduced instrument errors will be even more significant. Hence, the question arises: what would be needed for a quantum satellite gravity mission beyond MAGIC to reduce temporal aliasing even further? Since it is known that (temporal) aliasing is caused by an insufficient (temporal) sampling rate (see Shannon 1949), it is evident that an increase of the (temporal) sampling rate is necessary to mitigate it. For satellite gravity missions, the temporal sampling rate can be defined as the period needed to achieve global observation coverage with a desired spatial resolution. Through a suitable constellation design (see Sect. 2), the achievable temporal sampling rate (i.e., the retrieval period) can be reduced linearly with the number of satellites resp. satellite-pairs (in the case of SST). This implies that, theoretically, temporal aliasing can fundamentally be avoided through an arbitrarily large constellation.

Hence, more sophisticated constellations will be essential for future satellite gravity mission designs. To tackle this subject, this contribution aims to highlight how larger satellite constellations for future gravity field missions can be defined (Sect. 2) by introducing a general design strategy and by providing the necessary theory and methodology. Based on the presented approach, several examples for constellations of up to 6 satellites/pairs are subsequently derived and evaluated regarding their stability for retrieving gravity fields. Subsequently (in Sect. 3), the impact of such larger constellations on the performance of future quantum satellite gravity missions will be assessed in depth by conducting realistic full-scale simulations. For all simulations, optimistic future quantum instrument noise models, according to Encarnação et al. (2024), are applied. These models were developed in the frame of the same ESA study (QSG4EMT, see acknowledgments) with the purpose of enabling profound simulations of future quantum satellite gravity missions. Hence, particular attention is paid to evaluating the impact of these quantum instruments on the overall gravity field retrieval performance considering different constellations.

Up to now, recovering time-variable gravity through the satellite gravity gradiometry concept (SGG, like the GOCE mission, see Drinkwater et al. 2003), is deemed impossible since it requires a very accurate gradiometer, which, at the time of writing, is not realizable by means of conventional sensors (Heller et al. 2020). However, future quantum gradiometers promise a performance that is several orders of magnitudes better than what is currently possible (Encarnação et al. 2024). Hence, with the availability of superior future quantum sensors, SGG might become a serious competitor of SST because, compared to SST, SGG also has some advantages, such as the availability of collocated multi-directional observations (see discussion in Sect. 3). Therefore, scenarios for quantum SGG missions will also be simulated in addition to SST scenarios, and both concepts will be compared.

Next to the conventional SST and SGG concepts, possible alternative concepts will also be addressed (in Sect. 4) to emphasize that the presented constellation design may not only be limited to the classical concepts. To highlight this, the impact and benefits of the so-called across-track SST concept are investigated, where satellites of one pair are orbiting roughly side by side (i.e., orthogonal to their flight direction) instead of behind one another (as in the case of in-line SST). For this alternative across-track SST concept, future quantum sensors can also be applied (Encarnação et al. 2024).

Finally, in Sect. 5, a summary of all findings and achievements is provided, highlighting the impact of larger constellations and future quantum instruments. Special attention will also be given to the conclusions regarding temporal aliasing by discussing remaining limitations that will path the way for future investigations.

2 Constellation design

In this section, strategies for designing low Earth orbiting satellite constellations are discussed that are suitable for future satellite gravimetry missions (such as SST and SGG) and all other Earth observation satellite missions that require observations with a specific spatial and temporal resolution (e.g., altimetry missions). For this, a three-step approach is presented (see Fig. 1): firstly, a set of primary design variables is determined (Sect. 2.1). Based on these, concrete (Keplerian) orbits can be derived (Sect. 2.2). In a last step, these simplified orbits can be refined to be stable (by exhibiting a repeating ground track) in the Earth’s actual (static) gravity field so that they may serve as actual nominal orbits for a satellite mission (Sect. 2.3). Finally (in Sect. 2.4), a set of concrete constellations is exemplarily introduced (up to six satellites/pairs) to practically apply the previously presented theory. Additionally, a direct stability measure is presented to assess the constellation’s behavior regarding global gravity field retrieval. These constellations will be further used (in Sects.  3 and 4) to highlight their impact on actual satellite gravity mission performances.

Fig. 1

Flowchart of the constellation design procedure. Rectangular boxes describe design steps, rounded boxes data items. Data items might either be inputs resp. prerequisites (shown in black color) or (intermediate) results (shown in green color and dotted if optional). Data flow is depicted by solid lines. Possibly needed iterations are visualized as dotted lines. For the definition of the individual items, please refer to the appropriate section

2.1 Primary design variables

Mainly independent from the concrete concept, for satellite gravity missions, four general shape patterns/variables can be identified for satellite constellations that directly impact the retrievability of global gravity field models. Likewise, these variables represent the initial degrees of freedom in the constellation design.

Time to global coverage (TTGC). Gaps in the global observation coverage lead to numerical instabilities in the global gravity field retrieval and, eventually, hinder the calculation of independent solutions. Hence, one must ensure that a constellation achieves a global observation coverage that is as homogeneous as possible. In addition, for time-variable gravity field retrieval, one has to ensure that this is achieved in specific periods. These requirements lead to the definition of the so-called time to global coverage (TTGC), which shall be an essential attribute of the (gravity mission) constellation. To safely enable a repeating TTGC, only constellations consisting of satellites on repeating orbits will be investigated that exhibit a common repeat cycle (hence, leading to a repeating constellation). When introducing sub-cycles (see Sect. 2.2), a constellation can have even more than one TTGC. Hence, usually, several TTGCs can be defined for one constellation. However, it needs to be ensured that these also exist for an actual setup (since fitting sub-cycles may not always exist, cf. Section 2.2). Eventually, the chosen TTGCs will correspond to the primary gravity field retrieval periods targeted by the mission. Since mitigating temporal aliasing is the main objective of this study, selecting the TTGCs first seems to be the most intuitive approach. If one has other priorities, the determination order of the primary design variables (see below) might need to be adjusted.

Orbital altitude range. Gravity field retrieval from space is, concerning its spatial resolution, primarily limited through the signal attenuation of the shorter wavelengths of the body’s gravity field which effect increases with observation distance. Thus, choosing an orbital altitude as low as possible is usually desirable. However, there might be several mission parameters that limit the achievable minimum altitude (mainly due to aerodynamic drag). The altitude poses, thus, for most missions, a critical input parameter that is pre-defined by the fundamental satellite/mission design. To implement the desired TTGCs for the constellation, it is necessary to initially allow a specific altitude range since the required repeat and sub-cycles directly depend on the altitude (see Sect. 2.2). For larger constellations with satellites at different inclinations, different altitudes (for the individual inclinations) might be necessary (since repeat and sub-cycles also depend on the inclination). The larger the allowed altitude range, the more likely a good TTGC configuration can be found. Since observation homogeneity is generally beneficial, choosing eccentric orbits usually does not benefit satellite gravity missions. This further limits the search space for the satellite orbits to (near) circular orbits.

Spatial resolution/number of satellites. Once the TTGCs and the altitude is determined, the required spatial resolution still needs to be defined regarding a specific TTGC. If the resolution has been determined, the minimum number of needed satellites (resp. satellite pairs) for the chosen altitude can be estimated. Assuming an optimal distribution of the satellites (e.g., simplified on polar orbits), the maximum spacing in longitudinal direction ${d}_{lon}(t)$ is inversely proportional to the number of ascending nodes (i.e., the number satellite revolutions) ${n}_{rev}(t)$ within the appropriate TTGC $=t$ and the number of satellites ${n}_{sat}$:

$${d}_{lon}\left(t\right)\le \frac{2\pi }{{n}_{rev}\left(t\right)\cdot {n}_{sat}},$$

(1)

$${l}_{max}\left(t\right)\approx \frac{\pi }{{d}_{lon}\left(t\right)}\ge \frac{1}{2}\cdot {n}_{rev}\left(t\right)\cdot {n}_{sat},$$

where ${l}_{max}$ approximates the maximum degree and order (d/o) of a spherical-harmonic (SH) gravity field model, which can still be stably solved through the given spacing (when assuming a regular grid with the specific spacing). This formula can be interpreted as an extension of the well-known Colombo–Nyquist sampling rule (see Colombo 1984) for more than one satellite/pair. Note that the inequality sign is intentionally swapped compared to Colombo (1984; see discussion below). Using Kepler’s third law, the number of satellite revolutions ${n}_{rev}$ can be approximated sufficiently well through:

$${n}_{rev}\left(t,a\right)=\frac{t\cdot {\omega }_{sat}\left(a\right)}{2\pi }, \ \ {\omega }_{sat}(a)=\sqrt{\frac{GM}{{a}^{3}},}$$

(2)

where ${\omega }_{sat}$ is the satellite’s angular velocity, $GM$ the Earth’s gravitational constant, and $a$ is the semi-major axis of the orbit, which directly correlates to the chosen altitude from the previous paragraph (a mean value of the selected range should be sufficient). Finally, the maximum number of needed satellites for a specific max. d/o can be approximated through the already defined design variables ($t, a, {l}_{max}$) by:

$${n}_{sat}\left(t\right)\le \frac{2\cdot {l}_{max}\left(t\right)}{{n}_{rev}\left(t,a\right)}\approx \left[{k}_{s}\cdot \right]\frac{4\pi }{\sqrt{GM}}\frac{{l}_{max}\left(t\right)\cdot \sqrt{{a}^{3}}}{t},$$

(3)

with some scale factor ${k}_{s}$ (see the following discussion). Note that this approximation reflects an upper limit of required satellites/pairs since the worst-case spacing in the longitudinal direction is assumed, omitting the impact of descending arcs completely. Weigelt et al. (2013) provide an analytical approach, which considers descending arcs for polar orbits. This approach is, however, not easily transferable to inclined orbits, where the characteristic diamond-shaped spatial gaps emerge when regarding the descending arcs. In addition to this simplification, it can be noted that the sampling in the along-track direction is typically much higher (only limited by the instrument sampling rate), which is why the final (normal) equation system that needs to be solved is usually strongly oversampled. Both these circumstances lead to a very unsharp requirement regarding the number of satellites resp. max. resolvable d/o. This means that there is not a concrete number where the retrieval fails and where it still succeeds. With a decreasing number of satellites (resp. increasing max. d/o), one can only observe a steady decrease of the condition number of the normal equation system (i.e., the system gets more and more unstable, c.f. Section 2.4). For a practical application of this approximation, it is hence justified to introduce a factor ${k}_{s}\in \left[1/2, 1\right]$. For the constellations investigated in the scope of this contribution, it has been shown (see Sect. 2.4) that a factor ${k}_{s}\approx 3/4$ poses a good compromise between system stability and constellation size (i.e., number of satellites). Inserting all known values in Eq. 3, applying ${k}_{s}$ as defined and approximating the altitude of a typical low earth orbit (around $500 km$), the following rules of thumb can be derived (with the Earth’s gravitational constant $GM\approx 3.986\cdot {10}^{14} {m}^{3}{s}^{-2}$):

$${n}_{sat}\approx \frac{{l}_{max}}{\left(10\pm 3\right)\cdot {n}_{days}} \leftrightarrow {l}_{max}\approx \left(10\pm 3\right)\cdot {n}_{days}\cdot {n}_{sat},$$

(4)

with ${n}_{days}$ as the TTGC $t$ in days. Obviously, as the formulas suggest, instead of the desired maximum degree, one can also define the desired number of satellites as the third design variable. The given uncertainty range has been estimated through the stability analysis discussed in Sect. 2.3. It reflects effects such as a possibly partially inhomogeneous ground track pattern (cf. Sect. 2.2) or an advantageous interplay with descending arcs for polar constellations (see Weigelt et al. 2013).

Inclinations. Having already defined the temporal and spatial resolutions, the desired altitude, and the number of satellites/pairs, one still has some degrees of freedom in the constellation design. Foremost, the choice of the inclination/s is still open. There are no general recommendations that are valid for all gravity mission concepts: as already briefly noted in Sect. 1, for SST, it is highly favorable to introduce at least one additional inclination due to the discussed reasons. However, the same can generally not be concluded for SGG, where no significant benefits from additional inclinations can be observed (at least in combination with quantum sensors, cf. Section 3.2). Hence, finding one single design pattern for the inclinations is not possible. Nevertheless, one can identify three general design variants/classes for the determination of the inclinations:

• (a) Polar-only (PO) constellations: the most straightforward variant is achieved when all satellites/pairs are located at a single (near-)polar orbit. Such constellations are robust against failures of single satellites/pairs since global coverage can still be retained. Also, since a single inclination is chosen, all satellites can be located at the same altitude for repeating PO constellations. However, from the perspective of a global homogeneous distribution of observations, polar-only constellations are not preferable since they show a strong accumulation of observations near the poles. Additionally, the ground tracks of polar-only constellations do not intersect that often (only at a very acute angle), which is unfavorable for an efficient equilibration of instrument errors (see Fig. 2a for a rationale). From the perspective of gravity field retrieval, the exact choice of the near-polar inclination is not that important as long as the introduced polar gap is sufficiently small regarding the targeted spatial resolution. PO constellations are generally more interesting for the SGG than the SST concept due to the availability of collocated multi-directional observations (see simulation results in Sect. 3).

• (b) One-satellite/pair-per-inclination (OSPI) constellations: an alternative approach is to maximize the number of inclinations given a certain number of satellites/pairs. This is obviously achieved when, on all chosen inclinations, only one satellite/pair is placed. Such OSPI constellations still have many options how to set individual inclinations. However, for gravity field missions, a favorable strategy can be identified, namely, to homogenize the observation density globally. Since the density in the longitudinal direction is anyway homogeneous, the homogenization problem can be reduced to the latitudinal coverage. For the following study, the chosen inclination can be identified with the maximum latitude covered by one satellite. For the sake of simplicity, it is further assumed that every additional satellite linearly increases the observation number per latitude in the covered latitude range. A globally approximate equal density can then be achieved by simply compensating the meridional convergence. Having ${n}_{SAT}$ satellites, this can practically be implemented by dividing the unit radius into ${n}_{SAT}$ equally spaced pieces and by mapping each generated radial distance by the arccosine to the appropriate latitude/inclination $inc\left(i, {n}_{SAT}\right)$ of satellite $i$ (cf. Figure 2b):

  $$inc\left(i, {n}_{SAT}\right)={\text{cos}}^{-1}\left(\frac{i-1}{{n}_{SAT}}\right) .$$

  (5)

Fig. 2

a Illustration of the concept of instrument error equilibration through ground track intersections for inclined OSPI and MSPI constellations. Increased long-wavelength instrument errors can be reduced through short-wavelength ties (the intra-arc network, dashed connections). In contrast, increased short-wavelength instrument errors can be reduced through long-wavelength ties (the inter-arc network, dotted connections). If the instrument noise is modeled correctly, this process happens intrinsically in a least-squares adjustment approach. Obviously, this process is impaired if the underlying functional is time-variable. b Visualization of Eq. 5 for selecting appropriate inclinations to approximate a globally homogeneous observation coverage: each time the circle of latitude increases its radius relatively by $1/{n}_{SAT}$, a new satellite is introduced to compensate the decreasing observation density in this region

When applying this formula, the first inclination is intentionally always set to 90° to retain global coverage. Note that the provided formula is just one of many ways to approximate an equal-density distribution. Independently of the actual choice of inclinations, the achieved approximation is always rather crude because the observation density of one satellite always increases towards the latitude corresponding to its inclination (which cannot be mitigated). Hence, and because there is no concrete breakdown point regarding spatial gaps (see previous discussion), the precise choice of the inclinations does not influence the global gravity field retrieval significantly (as long as the distribution is somehow equilibrated). The freedom of slightly altering single inclinations for some degrees can practically be used to further optimize the constellation (e.g., for finding better repeat/sub-cycles or for having a higher observation density over areas of higher interest).

• (iii) Multiple-satellites/pairs-per-inclination (MSPI) constellations: as the last option to distribute satellites on different inclinations remains a mixture of the previously presented variants, where one may have several satellites on several inclinations. From the perspective of gravity field retrieval, there is no clear preference for MSPI constellations over OSPI constellations. Since it is supposed to have at least one inclined satellite in such a constellation, MSPI also shares the same advantages of OSPI: multi-directional observations (in case of SST) and an abundant number of clear intersections to equilibrate instrument errors (cf. Fig. 2a). However, in MSPI one has obviously a smaller number of directions than in OSPI and also the observation density cannot be equilibrated as well with fewer inclinations. This is why it can be assumed that MSPI constellations might in general produce worse results than OSPI (empirically shown in Sect. 3). Even though OSPI provides a somewhat better homogeneity, MSPI constellations might still be necessary when very short TTGCs (e.g., below one day) are required because, for this, multiple satellites/pairs are usually needed on a single inclination (cf. Sect. 2.2). There might also be other reasons (beyond the scientific mission goal) in favor of MSPI constellations: among others, the deployment of satellites on fewer inclinations might be cheaper and, similar to OP constellations, one introduces a certain level of robustness since single satellites/pairs might fail without losing all observations of one inclination. The actual choice of the number of inclinations and the number of satellites/pairs per inclination might hence be subject to such mission parameters, which will not be treated in the scope of this contribution. Regarding the selection of the inclinations, one can apply a similar approach as presented for the OSPI approach (Eq. 5): e.g., having the satellites/pairs sorted according to their inclination in descending order and having satellites/pairs $i$ through $k$ on the same inclination, a homogeneous global observation coverage for MSPI could be approximated by simply defining this inclination as $inc\left(i, {n}_{SAT}\right)$.

2.2 Repeat and sub-cycle design

When having defined the targeted TTGCs, the altitude range, the inclinations, and the number of satellites/pairs per inclination (see Sect. 2.1), the optimal altitudes for each inclination can be determined. For this, suitable repeat and sub-cycles need to be found that implement the demanded TTGCs.

Repeat cycle. The repeat cycle of a satellite $i$ can be defined as the minimum time ${T}_{i}$ needed to solve the integer equation:

$${n}_{rev}\left({T}_{i},{a}_{i}\right)=k\cdot {n}_{E}\left({T}_{i},{a}_{i},in{c}_{i}\right),$$

(6)

where ${n}_{rev}$ is the integer number of revolutions of the satellite (cf. Eq. 2), ${n}_{E}$ the integer number of revolutions of the Earth (or any other oblate body) and k an arbitrary integer number. To ensure that $T$ is the minimum time, it is demanded that ${n}_{rev}$ and $k\cdot {n}_{E}$ are coprime (i.e., they have no common divisor other than 1). In this formula, ${n}_{E}\left({T}_{i},{a}_{i},in{c}_{i}\right)$ reflects the Earth’s rotation relative to the satellite’s nodal precession (accounting for the secular perturbation induced by the Earth’s oblateness):

$${n}_{E}\left({T}_{i},{a}_{i},in{c}_{i}\right)=\frac{{T}_{i}}{2\pi }\left({\omega }_{E}-{\omega }_{P}\left({a}_{i},in{c}_{i}\right)\right),$$

(7)

$${\omega }_{P}\left({a}_{i},in{c}_{i}\right)=\frac{3\sqrt{5}}{2}{R}^{2}{C}_{20}\sqrt{\frac{GM}{{a}_{i}^{7}}}\text{cos}\left(in{c}_{i}\right),$$

(8)

with ${\omega }_{E}$ the Earth’s angular velocity, ${\omega }_{P}$ the satellites nodal precession rate (see, e.g., Brown 2002), ${C}_{20}$ the appropriate normalized zonal SH coefficient of the Earth’s gravity field and R the reference radius to which the normalized coefficient refers to.

These formulas allow now to calculate the repeat cycle ${T}_{i}$ in several ways, depending on what is fixed/sought (for circular orbits). Since ${n}_{E}$ needs to be an integer, for solving Eq. 6, it is usually helpful to rewrite it in order that ${n}_{E}$ becomes an independent variable:

$${n}_{rev}\left({T}_{i}=T\left({n}_{E},{a}_{i},in{c}_{i}\right),{a}_{i}\right)=k\cdot {n}_{E},$$

(9)

$$T\left({n}_{E},{a}_{i},in{c}_{i}\right)=\frac{2\pi {n}_{E}}{{\omega }_{E}-{\omega }_{P}\left({a}_{i},in{c}_{i}\right)}.$$

(10)

Equation 10 implies that the repeat cycle ${T}_{i}$ cannot be freely chosen since it is just available in near-daily steps, and the precise value also depends on the chosen altitude and inclination (even if ${\omega }_{P}$ is relatively small in comparison to ${\omega }_{E}$). When having multiple inclinations, this means that ${T}_{i}$ cannot be exactly the same for all satellites and, consequently, such constellations will not exactly repeat since they will drift relatively in the longitudinal directions (due to different nodal precessions). However, these differences in ${T}_{i}$ are relatively small and do usually not significantly impact the constellation’s overall homogeneity. In the practical application, it is thus helpful to simply approximate/describe the common repeat cycle through ${n}_{E}$ and to define the effective repeat cycle time as the largest value for ${T}_{i}$ over the whole constellation (which, consequently, guarantees complete coverage).

To evaluate Eq. 9, one can insert Eqs. 2 and 8:

$$\begin{array}{cc}k\cdot {n}_{E}=& \sqrt{\frac{GM}{{a}^{3}}}\frac{{n}_{E}}{{\omega }_{E}-{\omega }_{P}\left({a}_{i},in{c}_{i}\right)},\\ \\{n}_{rev}\;\;\;=& \frac{{n}_{E}}{\frac{{\omega }_{E}}{{\omega }_{sat}\left({a}_{i}\right)}-\frac{3\sqrt{5}}{2}{\left(\frac{R}{{a}_{i}}\right)}^{2}{C}_{20}\text{cos}\left(in{c}_{i}\right)} .\end{array}$$

(11)

Since the altitude (and, hence, $a$) has been defined in an interval (see Sect. 2.1), also for ${n}_{rev}$ an allowed interval can be found when applying Eq. 11. Since the interval for $a$ is assumed to be relatively small in comparison to its amplitude, it should be sufficient to simply insert the limits for $a$ to obtain the limits for ${n}_{rev}$ (since linearity is assumed in this range). These limits for ${n}_{rev}$ lead now to a concrete set of integer samples, which can be tested if they solve Eq. 6. If no sample is found, the repeat cycle of ${n}_{E}$ days does not exist for the chosen interval of $a$. In such a case, one needs to either extend the interval or change the targeted repeat cycle. Finally, if a suitable ${n}_{rev}$ is found, Eq. 11 can be used to find (numerically) the corresponding concrete value for ${a}_{i}$ as well as ${T}_{i}$.

Sub-cycles. In real-life applications, a precise repeat cycle can only be achieved approximately since an orbit can only be kept with a certain tolerance around its nominal trajectory. This gives rise to the idea of introducing a quality measure that quantifies how “good” an achieved repeat cycle is (e.g., Massotti et al. 2021 already discussed this idea). Here, it is proposed to judge the quality according to the nodal displacement $\Delta lon$ of the last ascending node in longitudinal direction on the equator with respect to the first node and relative to the node spacing $\Delta node$. The ascending node spacing of a repeat cycle $\Delta node$ is simply calculated by:

$${\Delta }node = \frac{2\pi }{{\left\lfloor {n_{rev} } \right\rceil }},$$

(12)

where ${n}_{rev}$ can now be a positive real number according to Eq. 11 and $\left\lfloor \cdot \right\rceil$ denotes the rounding to the nearest integer number. The nodal displacement $\Delta lon$ is calculated by the angle the Earth rotates in the displacement time $\Delta t$, which the satellite still needs to reach the (nearest) ascending node (cf. Fig. 3a):

$$\begin{aligned}\hfill {{\text{ }}\Delta t =} & \hfill {\left|{n_{{rev}} - \left\lfloor {n_{rev} } \right\rceil } \right| \cdot \frac{{2\pi }}{{\omega _{{sat}} }} = } \\ \hfill {{\text{ }} = } & \hfill {\left| {n_{{rev}} - \left\lfloor {n_{rev} } \right\rceil } \right| \cdot \frac{{n_{E} }}{{n_{{rev}} }} \cdot \frac{{2\pi }}{{\omega _{E} }}} \\ \end{aligned}$$

(13)

$$\begin{aligned} \hfill {\Delta {lon} = } & \hfill {\Delta {t} \cdot \omega _{E} = } \hfill = \hfill {2 \pi \cdot \left| n_{rev} - \left\lfloor {n_{rev}} \right\rceil \right| \cdot \frac{n_{E}}{n_{rev}} } \\ \end{aligned}$$

(14)

Fig. 3

a Visualization of the nodal displacement $\Delta lon$ as a quality measure for a sub-cycle. b Illustration of an optimized combined sub-cycle tuple by a space–time diagram on the example of the combined sub-cycle pair {4,1} using 3 satellites: as seen, the period of both initial sub-cycles {12,3} can effectively be divided by 3. Each satellite simultaneously covers 1/3 (parts P1–P3) of the trajectory of the 12-day and 3-day sub-cycles (see colored boxes). For an initial 12-day repeat cycles and 3 satellites, {4,1} is, in fact, the only integer pair existing that shows this (optimal) behavior

Finally, the relative displacement $\Delta x$ is obtained by the ratio between $\Delta lon$ and the node spacing $\Delta node$:

$$\begin{aligned}\hfill {{\Delta }x\left( {n_{E} } \right): = } & \hfill {{ }\frac{{{\Delta }lon}}{{{\Delta }node}} = } \\ \hfill = & \hfill {\left| {n_{rev} - \left\lfloor {n_{rev} } \right\rceil } \right| \cdot \frac{{\left\lfloor {n_{rev} } \right\rceil }}{{n_{rev} }} \cdot n_{E} } \\ \hfill \approx & \hfill {\left| {n_{rev} - \left\lfloor {n_{rev} } \right\rceil } \right| \cdot n_{E} {, }} \\ \end{aligned}$$

(15)

with $\Delta x$, a very simple but powerful tool is provided to assess the quality of the repeat cycle: if $\Delta x=0$, a perfect repeat cycle is obtained, and the larger $\Delta x$, the worse the repeat cycle. While there is no concrete threshold, $\Delta x<1/2$ has shown to be a reasonable limit for a repeat cycle to be recognized as such when looking at an appropriate ground-track pattern. The concrete limit has to be set in agreement with the mission's requirements. With the chosen definition, $\Delta x$ directly impacts Eqs. 3 and 4 since the maximum spacing ${d}_{lon}$ (see Eq. 1) increases by a factor $1+\Delta x$:

$${n}_{sat}^{*}={n}_{sat}\cdot \left(1+\Delta x\right) ,\ \ {l}_{max}^{*}=\frac{{l}_{max}}{1+\Delta x},$$

(16)

where ${n}_{sat}^{*}$ is the modified number of satellites/pairs needed and ${l}_{max}^{*}$ is the modified maximum achievable resolution when considering an inaccurate repeat cycle.

Eventually, Eq. 16 implies that even a not precise repeat cycle can still be useful for gravity field retrieval. Equation 15 shows that approximate repeat cycles theoretically exist for all number of days. Hence, one might find for an orbit with a certain precise repeat-cycle ${n}_{R}$ several so-called sub-cycles ${n}_{k}<{n}_{R}$, where $\Delta x\left({n}_{k}\right)<{\Delta x}_{max}$ (${n}_{k}$ and $\left\lfloor {n_{rev} \left( {n_{k} } \right)} \right\rceil$ must still be coprime). If found, such an orbit produces nearly regular global patterns in ${n}_{k}$-day periods, which can then be used to implement the required TTGCs of the constellation. To effectively find desired combinations of ${n}_{k}$ sub-cycles, it is recommended not to fix the actual repeat-cycle ${n}_{R}$, but to allow a large range of possible values for it (e.g., up to several years). If the original ${n}_{R}$ is needed to implement a TTGC, it can simply be introduced as an additional sub-cycle. When establishing the repeat-cycle as a degree of freedom, one basically has a discrete 2D search space (together with the orbital altitude) which drastically increases the chance of finding the required combination. Nevertheless, even when having a 2D search space, it is not always possible to find an appropriate solution. In such cases, it might be necessary to iteratively adjust the primary orbit/constellation setup (see Sect. 2.1, e.g., TTGCs, number of satellites, inclinations) until a solution is found.

Combined repeat-/sub-cycles. For PO and MSPI constellations, more than one satellite/pair must be distributed on one inclination. Obviously, it is not really reasonable to place the satellites on the same position, as this would just increase redundancy but not the global observation density. Hence, satellites on the same inclination must operate in tandem to maximize the achievable density (so that Eqs. 3 and 4 hold). One effective way to achieve this is to distribute all ${n}_{sat}$ satellites (which have the same inclination) on the same orbit equally over its repeat cycle so that each satellite covers exactly $1/{n}_{sat}$ parts of the orbit’s trajectory. In this way, a new combined repeat cycle having a period of

$${n}_{R}^{c}=\frac{{n}_{R}}{{n}_{sat}}=\Delta n.$$

(17)

Days is created. Practically, this can be achieved by shifting the $k$th satellite on the initial orbit by $\left(k-1\right)\Delta n$ days into the future (e.g., through integration). Hence, when planning MSPI and PO constellations, the combined repeat-cycle ${n}_{R}^{c}$ (instead of the orbit’s repeat-cycle ${n}_{R}$) has to be considered when implementing the constellations TTGCs. It is noteworthy that combining satellites in this way may be the only (simple) possibility to achieve TTGCs below one day. This might be relevant if one requires a very high temporal resolution. While it is straightforward to distribute the satellites to optimize one TTGC (see Eq. 17), it gets more complicated when it is required to consider more than one TTGC. It is obviously necessary to optimize more than one (sub-)cycle in the shown way. However, generally, one can always only distribute the satellites/pairs regarding one specific (sub-)cycle in the described way (see Eq. 17). This means that the length of the other existing (sub-)cycles is generally not divided by ${n}_{sat}$ (and are, thus, not optimized). Nevertheless, even if this cannot be achieved in general, it can be implemented for a limited number of particular combinations of (sub-)cycles if the applied shift $\Delta n$ is appropriate for all chosen (sub-)cycles ${n}_{k}$ so that

$$\Delta n\text{ mod }{n}_{k}=\frac{{n}_{k}}{{n}_{sat}}\left[= {n}_{k}^{c}\right]$$

(18)

is fulfilled for all these ${n}_{k}$. This means that, for shorter sub-cycles, the observations of the different satellites/pairs are split among different longer cycles (see Fig. 3b). In this case, $\Delta n$ effectively optimizes all (sub-)cycles simultaneously. Since there exist, especially for shorter repeat cycles, usually not too many solutions, Eq. 18 can be rearranged to directly calculate all possible ${n}_{k}$ given the longest required (sub-)cycle ${n}_{0}$ (which must not necessarily coincide with the actual repeat-cycle):

$${n}_{k}=\frac{{n}_{0}}{{n}_{sat}\cdot k+1}.$$

(19)

Since ${n}_{k}$ needs to be integer, ${n}_{0}$ must practically be a product of all selected $\left({n}_{sat}\cdot k+1\right)$. In this way, one can find very effectively suitable combinations. E.g., for two satellites/pairs, setting ${n}_{0}=30$ ($\Delta n=15$) results in a possible combination of the (combined) sub-cycles {15,5,3,1}. For three satellites, ${n}_{0}=84$ ($\Delta n=28$) enables the combination {28,7,4,1}. Because parts among different cycles need to be combined for this strategy, it might occur that the observed $\Delta x\left({n}_{k}\right)$ increases since additional shifts of $\Delta x\left({n}_{k}\right)$ are introduced with every cycle skipped (cf. Figure 3a). To minimize this effect, it might be helpful to introduce ${n}_{k}\cdot k$ (or even better: ${n}_{sat}+{n}_{k}^{c}$) as an additional sub-cycle when creating the orbit. Hence, it can be concluded that finding optimal combinations of sub-cycles for multiple satellites is not trivial and it usually just succeeds for a very limited number of combinations. However, often it is just important to optimize one sub-cycle ${n}_{T}$ in this way (e.g., the shortest since it defines the temporal resolution) and for the others it is not that critical if the perfect minimum is missed. This usually succeeds since one can simply multiply ${n}_{0}$ (resp. $\Delta n$) with an arbitrary number, so that ${n}_{T}$ becomes part of the sub-cycle set. Then, by evaluating Eq. 18, one can inspect how far the optimum is missed for the other sub-cycles and, possibly, further adjust $\Delta n$.

2.3 Nominal orbit design

Keplerian elements. At this point, nearly all Keplerian elements have been determined for all orbits in the constellation (see Fig. 1): (1) the inclinations $in{c}_{i}$ from the primary orbit design; (2) the semi-major axes ${a}_{i}$ (resp. the revolution time ${T}_{rev}$) from the repeat-/sub-cycle design; (3) the eccentricity $ecc$ as (near) zero; and (4) the argument of perigee $\omega$ as zero (since it has no meaning for $ecc=0$). What is still missing is the right ascension of the ascending node $\Omega$ and the time reference (time since perigee ${t}_{per}$ or true anomaly $\nu$). Since the ascending node is drifting (see Eq. 8) for all non-polar orbits (due to the Earth’s oblateness) and, since orbits on different inclinations are also drifting relatively, setting a specific ${\Omega }_{i}$ will have no significant impact on gravity field retrieval (in the long run, if the different ${\omega }_{P,i}$ show no resonances). Hence, setting all ${\Omega }_{i}=0$ is justified and represents a worst-case moment of the constellation where the gaps on the equator will be maximum. But, also, all other choices for ${\Omega }_{i}$ are legit due to the given reasons. Eventually, even the choice of the concrete time reference ${t}_{per,i}$ will have no significant impact since the constellation’s TTGCs are solely defined by the individual (sub-)cycles. If required, ${\Omega }_{i}$ and ${t}_{per,i}$ can be chosen in such a way that the satellites always fly exactly over specific locations (every repeat cycle but at different daytimes).

Repeat ground track (RGT) design. After all orbital elements are determined, the actual constellation design is finished. However, the formulas provided in Sects. 2.1 and 2.2 for the oblate Earth are just approximate and do not reflect the real osculating behavior of the actual orbits. Thus, if one uses the initial state vector (ISV) calculated from the Keplerian elements, the desired orbit features, especially the repeat-cycle ${n}_{R}$, will probably be missed. In fact, to even have a repeat cycle, the orbit itself must be repetitive so that:

$${{\varvec{x}}}^{E}\left({{\varvec{x}}}_{0i}^{E},t\right)={{\varvec{x}}}^{E}\left({{\varvec{x}}}_{0i}^{E},t+{T}_{i}\right),$$

(20)

with ${{\varvec{x}}}^{E}$ the state vector (i.e., position and velocity) in the Earth-fixed frame at an arbitrary time $t$, ${{\varvec{x}}}_{0i}^{E}$ the ISV and ${T}_{i}$ the precise repeat cycle of satellite $i$. An orbit that satisfies this equation is called a repeat ground track (RGT) orbit. Evidently, such an orbit can just be implemented in a static environment where one has no non-conservative or time-variable forces (e.g., drag or tidal forces). Hence, in an Earth-fixed frame, only the Earth’s static gravity field can be considered for calculating RGT orbits. Since, for low Earth orbiting satellites, the Earth’s static gravity field is far more dominant than any tidal and time-variable contributions, RGT orbits are particularly suitable as nominal satellite orbits. To maintain such an orbit, just non-conservative and the (small) tidal forces need to be compensated actively (which is anyway necessary for non-decaying orbits). Thus, nominal RGT orbits should be optimal regarding fuel/energy consumption. Assuming an approximative solution (i.e., ISV) is already given (e.g., through a Kepler orbit), an RGT orbit might be found, e.g., by Newton’s method (in the sense of variational equations, see, e.g., Lara 1999):

$${\Delta }{\varvec{x}}_{i}^{E} \left( {{\varvec{x}}_{0i}^{E} } \right)\,{: = }\,{\varvec{x}}_{i}^{E} \left( {{\varvec{x}}_{0i}^{E} ,T_{i} } \right) - {\varvec{x}}_{0i}^{E} ,$$

(21)

$$\Delta {{\varvec{x}}}_{i}^{E}\left({{\varvec{x}}}_{0i}^{E}+\Delta {{\varvec{x}}}_{0i}^{E}\right)\approx\Delta {{\varvec{x}}}_{i}^{E}\left({{\varvec{x}}}_{0i}^{E}\right)+\left[\frac{\partial\Delta {{\varvec{x}}}_{i}^{E}}{\partial {{\varvec{x}}}_{0i}^{E}}\left({{\varvec{x}}}_{0i}^{E}\right)\right]\Delta {{\varvec{x}}}_{0i}^{E}=0,$$

(22)

$$\Delta {{\varvec{x}}}_{0i}^{E}=-{\left[\frac{\partial\Delta {{\varvec{x}}}_{i}^{E}}{\partial {{\varvec{x}}}_{0i}^{E}}\left({{\varvec{x}}}_{0i}^{E}\right)\right]}^{-1}\Delta {{\varvec{x}}}_{i}^{E}\left({{\varvec{x}}}_{0i}^{E}\right).$$

(23)

Equation 21 describes the remaining gap $\Delta {{\varvec{x}}}_{i}^{E}$ after one repeat cycle ${T}_{i}$ when using the approximate solution ${{\varvec{x}}}_{0i}^{E}$ (e.g., obtained through Keplerian elements). In Eq. 22, a first-order Taylor-expansion is introduced to describe the propagation of a small change $\Delta {{\varvec{x}}}_{0i}^{E}$ of the ISV to the resulting gap $\Delta {{\varvec{x}}}_{i}^{E}$. Setting Eq. 22 to zero yields Newton’s method (Eq. 23). By iterating Eq. 23 with updated ${{\varvec{x}}}_{0i}^{E}={{\varvec{x}}}_{0i}^{E,old}+\Delta {{\varvec{x}}}_{0i}^{E}$, a solution can usually be obtained in the near vicinity of the original orbit (for near-circular low Earth orbiting satellites if the approximation has been good enough). If needed, the Jacobian can also be tweaked in several ways in order to preserve certain elements (e.g., position) and, as an alternative, the period ${T}_{i}$ can also be added to an extended ISV and, thus, be varied. For longer periods ${T}_{i}$, it is usually very hard to find good approximations and it might occur that the targeted ${n}_{R,i}$ is missed (and the solution converges instead to another integer value). In such cases, it might be helpful to first solve a reduced problem assuming an equatorial symmetric gravity field (i.e., only consisting of zonal SH coefficients). In such a case, a rotated RGT condition can be established on a very short time scale, with each revolution of the satellite and Eq. 21 can be altered to:

$${\Delta }{\varvec{x}}_{i}^{{E{*}}} \left( {{\varvec{x}}_{0i}^{E} } \right)\,: = \,{\varvec{x}}_{i}^{E} \left( {{\varvec{x}}_{0i}^{E} ,\frac{{T_{i} }}{{n_{R,i} }}} \right) - {\text{R}}_{Z} \left( {\omega_{E} \frac{{T_{i} }}{{n_{R,i} }}} \right){\varvec{x}}_{0i}^{E} ,$$

(24)

with ${\text{R}}_{Z}\left(\cdot \right)$ the rotation matrix around the z-axis. Since the revolution time of low Earth orbiting satellites is short (< 2h), usually even a coarse approximation is sufficient to obtain a solution. In a second step, this approximate solution (which is already very close to the true one) can be used to solve the initial problem (Eq. 21).

2.4 Selected constellations

Overview. Now that the theoretical backgrounds have been discussed, some concrete constellations will be presented, which will be used for the simulations presented in the following sections. A self-imposed limit of 6 satellites/pairs is introduced for these exemplary constellations to confine the search space and simulation effort. Among the set of selected constellations, an attempt is made to maximize the heterogeneity regarding number of satellites and constellation type (i.e., PO, OSPI, MSPI). Concretely, constellations having 1, 2, 3, and 6 satellites resp. satellite pairs are hence proposed. For each number of satellites/pairs, one example of each constellation type is selected. This leads to a total of 9 constellations since for 1 satellite/pair, all types yield the same polar orbit, and for 2 satellites/pairs, OSPI and MSPI are also identical. The orbital altitude range for the sub-cycle search is set between 370 and 440 km. TTGCs are tweaked for weekly and daily retrieval periods. The daily period has been chosen because it is the shortest period for which global coverage can still be achieved for all investigated constellations (especially the one- and two-pair constellations). The weekly period has been chosen because it is the shortest period for which all constellations (even single-pair) reach the target resolution, which is currently deemed relevant for time-variable gravity field recovery (about 2° spacing on the equator for recovering up to ${l}_{max}\approx 90$, cf. results in Sect. 3.3). For the same reason, investigating even longer periods (e.g., months) is considered as not that crucial for future larger constellations, as their main objective is to increase the TTGCs. However, if necessary, finding/implementing longer TTGCs is usually not that problematic from the perspective of constellation design. Since it has not always been possible to find a solution that optimizes both periods (one and seven days), a compromise has been made for the weekly period so that the actual TTGC might also be somewhat shorter in those cases (e.g., 5 days). This is not considered critical since, especially for larger constellations, the observation density is already high enough to achieve a sufficient spatial resolution, even in these shorter periods. An overview of all constellations is provided in Table 1. Figure 4 (left side) exemplarily shows the ground track coverage of the 6-pair constellations after one day of retrieval time.

Table 1 Constellations selected for further investigations

Fig. 4

In the left column: global ground track coverage after one day of accumulation time for 6-satellite/pair constellations for PO6 (a), MSPI6 (c), and OSPI6 (e). In the right column: condition numbers (i.e., stability) of the solution of simulated hypothetical SST missions for different retrieval periods (see legends) and maximum retrieved SH d/o using the appropriate constellations PO6 (b), MSPI6 (d) and OSPI6 (f). The SST simulation assumes simplified white-noise instrument behavior. One curve is depicted for each TTGC implemented in the appropriate constellation

The inclinations of the constellation having two inclined orbits (MSPI2/3, OSPI2) are aligned with the inclinations chosen for the ESA MAGIC science support study in Phase A (to be comparable, see Heller-Kaikov et al. 2023). For the constellations with three inclined orbits (MSPI6, OSPI3), the lowest inclination is set intentionally to 40° which is somewhat lower than the “optimal” third inclination according to Eq. 5 (which would correspond to 48° in both cases). This is done to highlight/check that the precise choice of the inclinations does not significantly impact the achievable gravity field retrieval performance, as stated in Sect. 2.1.

Stability analysis. Having calculated the selected constellations, it is deemed important to find a measure to quantify the constellations’ performances and to verify that the previously introduced design strategies work as expected. For this, it is proposed to introduce one of the most direct stability measures possible: the condition number, induced by the ${L}^{2}$, norm of the normal equation (NEQ) system which solves for the SH coefficients of the gravity field which is observed by a given satellite gravity mission. As satellite gravity mission, the classical SST concept (with an inter-satellite distance of about 220km) is chosen with simplified white-noise assumption regarding instrument performance and also a simplified processing approach (acceleration approach, see, e.g., Mayer-Guerr 2006). By setting up the NEQ systems up to different maximum SH degree and orders, one can now investigate how the system (i.e., the constellation) behaves regarding the chosen resolution in terms of stability for different retrieval periods (i.e., TTGCs).

The results for the 6-pair missions are shown in Fig. 4 (on the right side) and they are in agreement with the rationales provided in Sect. 2.1: MSPI6 and OSPI6 constellations perform rather similarly with a slight advantage for the OSPI6 constellation. As expected for SST, the stability of PO constellations is much worse than for the inclined constellations. The effect of the missing additional observation directions (and intersections) reflects in a steady increase of the condition number with increasing maximum d/o even for longer retrieval periods. This effect can also be observed for the inclined constellations but starting only at a much higher maximum d/o (probably related to the size of the polar region where only one pair is available). For daily retrieval periods a steep change in gradient at a certain d/o (around 60) is observable which is in a very good agreement with the rule-of-thumb formula (Eq. 4) given in Sect. 2.1. Also, one can see that a solution is still obtainable with higher maximum d/o but at the cost of the system’s stability. Higher condition numbers implicate stronger correlations between coefficients and, thus, also stronger individual weights on certain observations. In presence of an under-sampled signal in the time and space domain, these strong individual weights increase the induced temporal aliasing error since the inherent de-aliasing capability of the constellation (enabled through the targeted homogeneous sampling pattern) gets corrupted. Eventually, this means that one can expect a deteriorating interaction with temporal aliasing beyond this change in gradient which will negatively affect the overall solution (which might not be worth the increase in spatial resolution). Another interesting observation is that, as soon as sufficient ground track density is achieved, a further increase has practically no impact on the system's stability. This can be observed very well, for instance, in the example of the OSPI6 constellation where more than two TTGCs could be implemented (Fig. 4f): the condition numbers for all TTGCs spanning from about 3 to 12 days are practically identical. This implies that, for larger constellations, shorter accumulation periods are usually preferred since, after a certain minimum period, one basically just adds redundancy instead of stability to the system.

Figure 5 depicts the condition numbers for the rest of the selected constellations (1–3 pairs). Basically, all statements made for the 6-pair constellations are also valid for these smaller constellations: it is seen that the change in gradient occurs now at lower degrees in agreement with Eq. 4 and OSPI3 is still somewhat more stable than MSPI3. As for PO6, the smaller polar constellations show a similar steady increase of the condition number. It shall be considered that the shown condition numbers are just valid for inline-SST observations with the measurements performed in flight direction. Especially, the stability of the polar constellations might differ (i.e., increase) significantly for other concepts (such as SGG or non-inline SST, see Sect. 4).

Fig. 5

Condition numbers (i.e. stability) of the solution of simulated hypothetical SST missions for different retrieval periods (see legends) and maximum retrieved SH d/o using the appropriate constellations PO1 (a), PO2 (b), OSPI2 (c), PO3 (d), MSPI3 (e) and OSPI3 (f). The SST simulation assumes simplified white-noise instrument behavior. One line for each TTGC implemented in the appropriate constellation

3 Satellite gravity mission simulations

With the presented constellation examples (Sect. 2.4), a broad set of samples is available now, covering all targeted constellation types and sizes. Hence, this set will further be used to examine the concrete impact of constellation type and size in conjunction with future quantum instruments on the global gravity field retrieval by simulating the (established) satellite gravity mission concepts SST and SGG for these constellations: after a brief introduction of the simulation setup/environment (Sect. 3.1), the obtained simulation results will be discussed/investigated, firstly, for a simplified static true-world model (Sect. 3.2) and, conclusively, also for a realistic time-variable model (Sect. 3.3). Larger polar (PO) SST constellations (with more than one pair) are not investigated in this contribution since it is known from earlier studies (e.g., Wiese et al. 2011) that multiple polar SST pairs will not fundamentally improve the observation geometry and, basically, just add redundancy (see discussion in 2.4).

3.1 Simulation setup

An updated version of the TUM full-scale satellite gravity field mission simulator is used to perform the SST and SGG simulations (Daras et al. 2015; Daras 2016). This full-scale simulator aims to yield realistic results that are compatible with current SH products of actual gravity data processing centers (for GRACE/-FO and GOCE). For the results shown in this paper, the simulator has been improved compared with the original version to avoid numerical problems when dealing with very low instrument noise scenarios In addition, the simulator has been extended by a new module that allows SGG observation simulation/processing (originating from the original TUM GOCE gravity field processor; see Pail et al. 2011). In the following, the simulation setup will be briefly explained: firstly, the different forward model setups will be discussed (i.e., how observations are generated from “true-world” models). Subsequently, the backward modeling will be explained (i.e., how the observations are parameterized), including the applied instrument noise model.

Forward modeling. The SST and SGG gravity observations are simulated based on existing gravity field models, which shall represent the “true world” in the simulation environment. Here, static and time-variable models can be distinguished. As static gravity field model, the GOCO05s model (see, e.g., Kvas et al. 2021) is used. As time-variable models, the ESA Earth system model (ESM, Dobslaw et al. 2015) is incorporated for the non-tidal signal components and the EOT11a ocean tide model (Savcenko and Bosch 2012) for the tidal part. The simulation period covers the first day resp. first week of January 2002. Using the appropriate functional models (for SST and SGG), error-free observations can be derived. After adding the corresponding observation noise (see Fig. 6) to it, the “true” (simulated) observations are obtained, which can then be used for the gravity field retrieval (in the scope of the backward modeling). For the simulations, two forward modeling scenarios are distinguished:

• 1. A simplified static forward model, where the Earth’s gravity is assumed constant over time (i.e., only the static gravity field model is used). Since this simplified model directly scales with the instrument performance and the system stability, it will be denoted as the product-only model.

• 2. A realistic time-variable forward model where the Earth’s gravity field is authentically changing over time according to background model data (ESM and ocean tides). Since only a static gravity field parametrization is applied in the backward model (see below), the time-variable scenario will inevitably introduce temporal aliasing (due to the insufficient parametrization) into the obtained solution (which is completely avoided for product-only). Hence, higher noise levels for these scenarios are expected because an additional error source is introduced. Therefore, this scenario is denoted as the full-noise model.

Fig. 6

ASDs of the assumed observation noise induced by the instruments for SST (blue, in terms of accelerations in line-of-sight direction) and SGG (orange, in terms of gravity gradient component). ASDs correspond to the most optimistic future instrument scenario in Encarnação et al. (2024). Sampling is assumed to be limited to 0.1Hz (10s) due to the use of CAI instruments

Note that, within this study, uncertainties related to an imprecise knowledge of the orbits are neglected (i.e., it is assumed that the satellites' positions/velocities are known sufficiently well).

Backward modeling. The TUM full-scale simulator estimates SH gravity field solutions using a short-arc least-squares adjustment (LSA) approach. This method is described in detail, e.g., by Mayer-Gürr (2006) for the SST concept but can also be applied to SGG (for the noise modeling part): in this approach, the observations are split into short arcs (e.g., with the length of several hours) and are modeled consistently within these arcs. This allows to describe the noise within one arc rigorously through covariance matrices. For SST, observations are parameterized in terms of range-rate measurements in line-of-sight direction using the integral equation approach (see Daras et al. 2015), which is a non-linear model and requires to co-estimate additional orbital parameters (per arc level). SGG, on the other hand, is parameterized by gravity gradient observations and is, in this perspective, simpler than SST since it only requires a linear model, and the orbits do not have to be co-estimated.

In addition to the primary SST or SGG observations, also GNSS observations are used for gravity field recovery and assumed to be known with a simplified (white noise) accuracy of 1 cm in each dimension. However, due to the comparable low accuracy of GNSS, the impact of these observations on the final solution is basically neglectable (especially when using quantum instruments which are long-term stable). Using this setup, global gravity fields are estimated for a daily as well as a weekly period for all investigated constellations. The unknown gravity field itself is parameterized through static SH-coefficients up to a certain maximum d/o. The maximum d/o is set according to the stability assessments in Sect. 2.4: for weekly solutions, gravity fields are always estimated up to d/o 90. For daily solutions, the maximum d/o is adjusted to the constellation size: d/o 15 for one pair, d/o 25 for two pairs, d/o 40 for three pairs, and d/o 60 for six pairs (cf. Figures 4 and 5). In the case of the full-noise forward model (see above), the observations are reduced by de-aliasing models for non-tidal atmosphere and ocean signals (from the ESA ESM data, components AO and AOerr) and tidal signals (through the ocean tide model GOT4.7, Ray 2008).

Instrument/noise modeling. The instruments are simulated by assuming noise models for the observations. To be realistic, it is supposed that these noise models already contain all significant individual contributors (e.g., accelerometers, ranging instrument, angular-rate reconstruction, temperature instabilities, misalignments, etc.). Since this study focuses on future quantum satellite gravity missions, possible future (quantum) instrument developments are considered. Especially for accelerometers and gradiometers, the current developments in the field of cold atom interferometry (CAI) may lead to significant improvements for future satellite gravity missions. Encarnação et al. (2024) provide a broad overview of such future quantum instrument scenarios. To investigate the impact of constellations, it is hence decided to pick the most optimistic (future) noise assumptions from this study for our simulations (to be minimally impacted by the limited instrument performance). The resulting observation noise models are depicted in terms of their amplitude spectral densities (ASDs) in Fig. 6 for SST (as accelerations in line-of-sight direction) and for SGG (as gradient components). Compared to the noise models of conventional electrostatic instruments, quantum instruments benefit particularly in the long wavelengths since they are not impaired by the same drift effects as their electrostatic counterparts. By applying a cosine transform, these ASDs can be converted into covariance matrices, which are then used as stochastic information for the gravity observations in the simulations. For SGG, it is assumed that one can measure all three main diagonal elements of the gravity gradient tensor with the same accuracy (which is actually needed to allow an angular rate reconstruction with sufficient performance to fully exploit the gradient signal; see Encarnação et al. 2024). Eventually, this means that, for SGG scenarios, simultaneous observations in all three directions are given in contrast to (in-line) SST, where only observations in flight directions are available. With this, SGG also accumulates three times more observations in the same time span as SST. For simulating SST, an inter-satellite distance of about 220 km (similar to GRACE/-FO) is chosen for each pair. For SGG, for each satellite, a gradiometer arm length of 1 m is assumed (the SST and SGG error curves in Fig. 6 are hence directly comparable). The SST quantum noise model consists internally mainly of two future CAI accelerometers (one for each satellite), projected on the line-of-sight, and one future laser ranging interferometer (LRI). Since it is assumed that the future LRI limits the overall performance, the projected (combined) SST noise is larger than the SGG noise in Fig. 6.

3.2 Product-only simulation results

General discussion. The product-only simulation results will be discussed first. A complete summary of all simulation results is provided in Fig. 7 in terms of empirical degree errors (i.e., closed-loop errors of the simulations) of equivalent water heights (EWH, see, e.g., Heller-Kaikov et al. 2023). The results shown lead to the following main conclusions:

• Applying the given quantum instrument-error margins, SST performs significantly better, resulting in gravity field retrieval errors about three orders of magnitude smaller than that of SGG (even though very optimistic noise assumptions for the gradiometer have been made and three times as many observations are available, see Encarnação et al. 2024). This underlines once more the sensitivity advantage of SST over SGG, which can easily be understood when interpreting SST as a kind of long-arm gradiometry: the stability of numerically derived gradients of a (sufficiently smooth) function increases linearly with the distance of the underlying sample points (accelerometer positions in the concrete case). When comparing the 220 km arm length of SST with the 1 m of SGG, it is evident that the accuracy of accelerometer measurements of SST satellites may be about five orders of magnitude lower than that of an SSG satellite to reach a comparable gradient accuracy. In the assumed instrument case, SST (line-of-sight) acceleration errors are about two orders of magnitude larger (i.e., worse) than the comparable gradient errors of SGG (see Fig. 6) due to the limiting accuracy of the inter-satellite ranging instrument (Encarnação et al. 2024). Eventually, this leads to the observable difference in the shown product-only solution of about three orders of magnitude.

• Extrapolating the achieved product-only accuracies of the SST scenarios to higher d/o suggests that retrieving time-variable gravity (EWH) becomes theoretically possible up to about d/o 200 (intersection between signal and noise curve, see Fig. 7) when applying the given instrument noise. Concerning the product-only results for SST and SGG, it can generally be stated that the noise levels in the solutions (Fig. 7) scale about linearly with the assumed noise levels of the instrument ASDs (Fig. 6) since also the underlying functional relations are relatively linear. Since the noise floor of the assumed quantum instrumentation is nearly four orders of magnitude lower than that of GRACE-FO (Darbeheshti et al. 2017), also the resulting product-only errors are about four orders of magnitude smaller (compare to Flechtner et al. 2016).

• Although the sensitivity of SST is much higher, with the assumed quantum instrument performances, even SGG becomes sensitive to time-variable gravity (up to about d/o 100). Compared to the conventional electrostatic state-of-the-art gradiometer employed in the GOCE mission (Siemes et al. 2019, Christophe et al. 2018), the noise floor of the assumed quantum gradiometer is roughly four orders of magnitude lower (about 4 µE). When comparing to the product-only retrieval errors (Fig. 7), it is evident that this low noise level is required to be sensitive to time-variable gravity (at least about 40 µE). However, these error levels can just be reached when assuming that the angular rates can be reconstructed directly through the CAI gradiometer, which requires a more sophisticated setup that is probably not realizable any time soon (Encarnação et al. 2024).

• With an increasing number of satellites, the product-only retrieval error decreases for all scenarios. This can mainly be attributed to the increased redundancy when having more observations (according to the $\sqrt{n}$-law of error propagation) since it is supposed that the system stability is reasonably good in all cases (because the resolutions have been chosen in agreement with the analysis in Sect. 2.4). This implies that the achievable error reduction with larger constellations is rather conservative within the performed simulations.

• The weekly SST single-pair scenario is an exception that displays a more significant degradation of performance, which cannot be attributed to a decreased redundancy alone. What comes into play here is (as already mentioned) the sub-optimal system stability caused by having only observations in one direction (north–south) and nearly no stabilizing intersections between ground tracks. Single satellite SGG is basically not impacted by this since even a single gradiometer provides observations in all three directions, and the white-noise instrument behavior does not significantly benefit from intersecting ground tracks.

• Interestingly, the disproportionate large performance leap between the single- and double-pair SST retrieval performance becomes less prominent in the case of a daily retrieval. When comparing the daily and weekly single-pair performance with each other, it is seen that the error level remains nearly constant. In contrast, the error levels of all other solutions decrease to some extent with the increasing retrieval period. While it is not completely clear why this happens, it is assumed that the instrument error equilibration through the ground track intersections (in the case of OSPI/MSPI, see Fig. 2a) does not work as well if the distance between the intersections becomes too large (as it might be the case for daily ground tracks).

• In the case of SST, it can be observed that the OSPI constellations perform marginally better than MSPI. This matches the prediction from the constellation design in Sect. 2.1.

• Also, for SGG, the inclined (OSPI) constellations perform, on average, slightly better than the polar constellations. However, there are also some exceptions, and some weekly scenarios show, especially in the high d/o, different behaviors between the corresponding PO and OSPI variants. This might be because different orbital altitudes had to be chosen for different constellations to implement the necessary TTGCs. Hence, the attenuation of the gravity field signal, especially in higher d/o, also slightly varies, which consequently impacts the retrieval performance. Since the differences are anyway relatively small, for SGG, no clear preference for inclined constellations over polar constellations can be expressed.

• For the daily retrieval period, it is seen that larger constellations allow to stably parameterize the gravity field to higher d/o according to the target resolutions defined in the constellation design phase. After the stability analysis in Sect. 2.4, this is a second evidence that the constellation design process works as intended and that the derived concrete constellations meet their initial expectations.

Fig. 7

Empirical degree errors of different solutions with respect to the forward-modeled gravity field in terms of EWH for product-only simulations a for a weekly (7-day) retrieval period and b for a daily retrieval period. Light colors depict SGG and intense colors SST solutions. Dotted lines describe PO, dashed lines MSPI, and solid lines OSPI constellations. Different colors are chosen for different constellation sizes: 1 satellite/pair blue, 2 green, 3 red, and 6 violet. As reference, the weekly resp. daily HIS signal is shown as a solid black line

Error structure analysis. For the six-pair solutions of the different constellations (MSPI6-SST, OSPI6-SST, and PO6-SGG), a more in-depth analysis is performed to investigate the differences in their error distributions in the SH and spatial domain. For this, the formal errors of the coefficients are plotted in triangle form along with the empirical spatial errors in Fig. 8. In the case of product-only, the formal coefficient errors are perfectly representative of the empirical errors (which are shown in Fig. 7 in terms of degree errors) since the instrument noise is modeled accurately by the simulator. Hence, the formal errors shown (Fig. 8, left column) also directly relate to the empirical error distribution in the spatial plots (Fig. 8, right column). Starting from the spatial plots, the influence of the different constellations can be clearly observed:

• For the MSPI6 constellation, the three chosen inclinations of the satellite orbits can be recognized well in the spatial plot (Fig. 8b) as the latitudes where the error amplitudes are changing (on the northern hemisphere north of Iceland and over southern Italy). In the coefficient triangle (Fig. 8a), the inclinations are even better discernible as off-zonal lobes, one lobe for each (non-polar) inclination for sine and cosine coefficients. Although these inhomogeneities are visible and impair the solution to some extent, they may not be considered significant for the overall retrieval sensitivity and achievable resolution (see Fig. 7b).

• In contrast to MSPI6, the OSPI6 error patterns are more homogeneous. This is true in the spatial and spectral domains: in the spatial domain (Fig. 8d), the individual inclinations of the orbits cannot be identified with the naked eye. Only a slightly increasing amplitude towards the equator is vaguely visible. This integral homogeneity is also observed in the spectral domain (Fig. 8c), where the individual lobes of the inclinations nearly vanish, and only a faint increase of the errors towards the sectorial coefficients remains (which roughly translates to equatorial regions in the spatial domain). From the perspective of the constellation design, this increased homogeneity of OSPI compared to MSPI has already been expected (see 2.1) due to the higher number of observation directions and better observation homogeneity.

• As previously discussed, in contrast to the six-pair SST scenarios, the SGG scenario PO6 exposes an error level about three orders of magnitudes larger. Ignoring this fact, the error patterns themselves are otherwise comparable to OSPI6: the spatial error distribution (Fig. 8f) is also relatively homogeneous with a weak increase towards the equator (slightly more visible than for OSPI6). This behavior can also be tracked well in the SH coefficients (Fig. 8e), where a small sectorial lobe with increased errors is especially visible (starting around d/o 50 and indicating a limitation of the constellation). Neglecting these sectorial lobes, the PO6 scenario shows the best performance in the zonal region (relating to polar areas), slightly degrading towards the sectorial areas (relating to equatorial regions). This is also well explained by the constellation design (see 2.1), which states that PO constellations highlight a maximally unilateral accumulation of observations around the poles at the expense of the equatorial zones.

• Additionally noteworthy, in contrast to SST, SGG enables a very stable retrieval of the lowest d/o. This indicates that the low-d/o instabilities in the case of SST are primarily induced by the measurement concept (e.g., through the single measurement direction) and not by the instrument itself (since quantum sensors are assumed that do not feature increased long-wavelength errors).

Fig. 8

Coefficient triangles of the formal errors (left column) and spatial distribution of the empirical errors (right column) of the daily solutions of the product-only six-pair scenarios MSPI6 (SST) (a–b), OSPI6 (SST) (c–d) and PO6 (SGG) (e–f) in terms of equivalent water heights (EWH). In the coefficient triangles, negative orders represent SH sine and positive orders cosine coefficients. Note that the chosen error scales of the colormaps are exactly three orders of magnitude apart between SST (a–d) and SGG (e–f)

3.3 Full-noise simulation results

General discussion. After the product-only results have been examined, the more realistic evaluation of the full-noise results will be addressed. The only difference to the product-only results of the previous section is that the observations (i.e., the forward model, see Sect. 3.1) now include realistic time variations of the gravity field signal, which will cause temporal aliasing. Similarly to the product-only results in Fig. 7, Fig. 9 summarizes the corresponding full-noise degree errors, again for a daily and weekly retrieval period. From this figure, the following insights can be gained:

• All full-noise results are limited in their accuracy (in the low d/o) at around 1 mm/degree in terms of EWH. Compared to the product-only solutions (Fig. 7), this is a deterioration of nearly five orders of magnitude for SST and still about two orders of magnitude for SGG. This leads to the conclusion that temporal aliasing will pose the largest error source by far when applying the given future instrumentation, including quantum sensor. This has already been expected from the beginning (see Sect. 1), but is now clearly proven by the simulations and highlights once more the urgent need to significantly reduce the impact of temporal aliasing for future missions.

• Larger constellations have a considerable influence on the reduction of temporal aliasing. E.g., the maximum recoverable d/o increases for the weekly SST solutions from about 15 for a single-pair, to about 40 for a double-pair, to about 50 for a three-pair, and to about 70 for a six-pair mission. For a daily retrieval period, the relative differences in the maximum recoverable d/o for the different constellation sizes are even more pronounced: it increases from about d/o 5 for a single pair to 20 for two pairs, to about 35 for three pairs and about 45 for six pairs.

• Daily SGG solutions perform slightly better but are generally very similar to daily SST solutions. This emphasizes that also the sensitivity advantage of SST over SGG (see Fig. 7b) is consequently meaningless if superimposed by temporal aliasing. The slight advantage of SGG can be explained by the collocated multi-directional measurements (except for PO6), which, eventually, help to homogenize the normal equation system and, thus, increase the mission’s intrinsic de-aliasing capability.

• Interestingly, weekly SGG solutions do not scale as well with the constellation size as SST and daily SGG. While some improvements can still be distinguished (especially in the longer wavelengths), they are relatively small, and, performance-wise, all solutions are similar to the weekly three-pair OSPI SST solution. An obvious explanation for this is a different interaction with the time-variable signal on a weekly scale, possibly caused by the different instrument noise ASDs and its dynamic interplay with denser ground track patterns (compare discussion in 3.2).

• Similar to the product-only SST solutions, also for full-noise SST, OSPI constellations perform better than their MSPI counterparts. However, for full-noise SST, the advantage of OSPI over MSPI seems to be more prominent in a way that a six-pair MSPI solution is only slightly better than a three-pair OSPI solution and, likewise, the three-pair MSPI is only marginally better than the two-pair OSPI. This suggests that, for full-noise, having more inclinations is favorable for optimizing the intrinsic de-aliasing capability of the scenario.

• In the case of SGG, for the full-noise scenarios, PO constellations seem to perform constantly slightly better than their inclined relatives. This is, to some extent, in contradiction to the product-only results where the inclined constellations slightly outperform, on average, the polar ones. This again indicates that, for SGG, no clear benefit can be obtained by applying inclined constellations (in contrast to SST).

• According to the previous results, with some minor exceptions, one can establish the following rule of thumb: if an SST (SGG) scenario performs better in the product-only case as another SST (SGG) scenario, then the same is probably also true for the full-noise case. The reason for this might again be found in the constellation’s intrinsic de-aliasing capability, which usually increases with the stability resp. homogeneity of the underlying normal equation system. Eventually, the system’s homogeneity is indicated by the product-only errors (since they follow the formal errors).

• Even though the constellation size helps to mitigate temporal aliasing to some extent, the improvements are rather conservative (within one order of magnitude) when compared to the overall temporal aliasing error contribution (which might reach up to five orders of magnitude compared to product-only scenarios of future SST mission, compare Figs. 7 and 9). Eventually, this means that the temporal aliasing problem is not fundamentally solved through the investigated constellations. As an explanation, basically, two remaining error sources can be identified (see Sect. 5.2 for a more elaborated discussion): firstly, the daily temporal sampling allows theoretically to recover just two-daily frequencies according to the Nyquist–Shannon sampling theorem. However, it is known that strong signals with daily and sub-daily frequencies (e.g., from tides, atmosphere, and ocean) exist, which, consequently, cause strong residual temporal aliasing. Secondly, in the shown simulations, a time-static parametrization (i.e., step function) is applied, which cannot even account for a linear changing signal and, hence, can never truly describe the forward modeled signal.

Fig. 9

Empirical degree errors of different solutions with respect to the analytical time-mean of the forward modeled gravity field in terms of EWH for full-noise simulations a for a weekly (7-day) retrieval period and b for a daily retrieval period. Line styles are chosen identically to Fig. 7

In addition to Fig. 9, Table 2 summarizes the performance of all conducted full-noise simulations by comparing their global cumulative mean errors at different resolutions (max. d/o). While the conclusions are generally similar to Fig. 9, the global mean errors allow an even better comparison in terms of absolute numbers. E.g., at a resolution of 4° (d/o 45) and for a weekly retrieval, an inclined two-pair SST mission improves the single-pair mission by a factor of roughly 1.7 from 171 mm to 100 mm EWH. Adding a third inclined pair further halves this error margin to about 52 mm. The six-pair OSPI6 SST constellation reduces the error once more to about 32 mm. This is a considerable improvement by a factor of roughly six over the single-pair constellation. These relative scales are more or less representative of what is achievable with larger constellations regarding the intrinsic mitigation of temporal aliasing. In comparison, without temporal aliasing, with the assumed quantum sensors, an error of less than 1 µm EWH would be expected at this resolution (cf. Fig. 7a). This highlights once again the enormous difference in scale between temporal aliasing and possible future instrument error levels. It shall be noted that all presented results are obtained without any sophisticated post-processing resp. filtering (only spectral limitation). When applying dedicated temporal-aliasing filters resp. post-processing strategies, it can be assumed that all global errors will further decrease. For GRACE, sophisticated post-processing filters (Kusche et al. 2009; Horvath et al. 2018) allow improvements by a factor of up to two compared to simple filter methods (such as Gaussian filtering or spectral limitation). Currently developed temporal aliasing filters (see, e.g., Hauk et al. 2023) may lead to further slight improvements (less than a factor of two). Since there is no specific reason why the mentioned filters will perform significantly differently on other (possibly larger) constellations and noise models, similar error reduction rates are expected when applied to the scenarios of this study. Hence, it is also not expected that the achieved improvement through filters will be will sufficiently large (i.e., more than one order of magnitude) to impact any of the assessments made within this study.

Table 2 Comparison of all conducted full-noise simulations by their global root-mean-square (RMS) errors at different resolutions in terms of mm EWH (cf. Figs. 9 and 13)

Error structure analysis. Similar to product-only, also for the full-noise scenarios, an in-depth analysis of the resulting error patterns of the different daily six-pair solutions (MSPI6-SST, OSPI6-SST, and PO6-SGG) will be performed in the spatial and spectral domain (see Fig. 10). In contrast to the product-only analysis, for investigating the coefficients, the empirical error is chosen instead of the formal. This is done because, in the presence of a temporal gravity signal, the formal errors do not realistically represent the empirical ones (since the time-variability is not modeled in the least squares adjustment approach). In fact, the estimated formal errors of the full-noise scenarios would be identical to the product-only scenarios (driven by the instrument noise model, cf. Figure 8) since the backward model is not altered between these scenarios. As previously discussed, the full-noise errors are strongly dominated by temporal aliasing, meaning that all observed patterns (in Fig. 10) are basically governed by the high-frequency time-variable signal and not by the instrument noise (as in the case of product-only). Even though the error source and magnitude have completely changed, constellation-characteristic patterns can still be observed in the case of full-noise (Fig. 10):

• For MSPI6, the chosen inclinations of the individual satellites in the constellation can well be observed in the spatial error distribution (Fig. 10b), similar to product-only but more strongly concentrated in the polar regions. The two lobes of the inclined orbits are also clearly discernible in the coefficient triangles (Fig. 10b). In comparison to the product-only formal error (Fig. 10a), the zonal lobe is more pronounced, causing larger polar spatial errors.

• In the coefficient triangle of the OSPI6 constellation (Fig. 10c), the individual lobes of the different inclinations cannot be observed anymore. Instead, a relatively wide zonal lobe is visible, and an increased sectorial error in the higher d/o. In the spatial domain, this translates to a somewhat increased error magnitude in the polar and equatorial regions. However, as already observed in the degree errors (Fig. 9b), the overall error magnitude is again somewhat lower for MSPI6 (except for the equatorial region).

• While for the two six-pair SST scenarios, the full-noise empirical errors stay at least somewhat similar to the corresponding formal errors, the same cannot be concluded for the PO6 SGG scenario: the spatial error now shows an anisotropic striping pattern in the north–south direction which increases its magnitude towards the equator (Fig. 10f). Interestingly, the zonal and near-zonal coefficients of PO6 (Fig. 10e) highlight a significantly reduced noise compared to the inclined SST scenarios, which cannot be solely explained by the increased observation density in the polar regions (since it would then more follow the behavior of the formal error). The reason for this may be found in the individual orbits of the PO6 constellations, which have, among others, also a three-day sub-cycle. This means that the combined sub-cycle of the six satellites unintentionally realizes a half-daily period, which enables a sufficient sampling of at least a part of the tidal signal (with a coarser resolution; see width of the zonal area). Eventually, this highlights the importance and the possible benefit of introducing sub-daily retrieval periods (see discussion in Sect. 5).

• Comparing the lowest d/o between SGG and SST, it is again visible that SGG allows a very stable reconstruction of the lowest wavelengths of the gravity field while SST struggles to do so.

Fig. 10

Coefficient triangles (left column) and corresponding spatial distribution (right column) of the empirical errors of the daily solutions of the product-only six-pair scenarios MSPI6 (SST) (a-b), OSPI6 (SST) (c–d) and PO6 (SGG) (e–f) in terms of equivalent water heights (EWH). Absolute coefficient values are shown in the coefficient triangles (a, c, e). Note that the chosen error scales of all colormaps are identical (in contrast to Fig. 8). To create the spatial plots (b, d, f), the maximum d/o has been limited to 50 in the SH synthesis (to not impair the signal-to-noise ratio, see Fig. 9b)

4 Across-track SST (A-SST)

The previous Sect. (3) focused solely on the already established satellite gravity mission concepts SGG and (in-line) SST. However, for future gravity missions, alternative concepts might also become feasible where the presented constellation design strategies might still be applicable. To highlight this, this section is dedicated to the evaluation of the so-called across-track SST concept, which poses one (theoretically) viable option for such an alternative gravity mission concept: in Sect. 4.1, the across-track concept is explained, and a motivation is given why and when this concept might be useful. Subsequently, in Sect. 4.2, simulation results of constellations applying the across-track concept and quantum instruments will be presented and compared to the results from the classical concepts (from Sect. 3).

4.1 The across-track SST concept

Motivation and idea. The investigations in the previous Sect. (3) indicate that gradiometry, applied on polar (PO) constellations, yields competitive solutions in presence of temporal aliasing (cf., e.g., Fig. 9). However, for gradiometry it is (at the time of writing) unrealistic to obtain the necessary measurement sensitivity to observe the Earth’s time-variable gravity field, even when employing quantum sensors (see Encarnação et al. 2024). Hence, it might be useful if an SGG-like retrieval stability on a PO constellation could also be achieved through an SST mission since SST has a fundamentally higher sensitivity (see discussion in 3.2). Additionally, using PO constellations could have some further advantages (e.g., regarding reliability and the realization of sub-daily sub-cycles, see Sect. 2). From classical inline-SST (I-SST or simply SST), it is known that the SGG full-noise retrieval performance cannot be reached on PO constellation, since only observations in in-flight direction are available, which introduces increased instabilities in the solution (see, e.g., Fig. 4b). This is in contrast to SGG, where measurements are obtained in all three directions simultaneously. Since the measurement principles of SST and SGG are otherwise strongly linked (cf. Sect. 3.2), the number of observation directions is obviously the only significant conceptual difference, which may cause the inferior performance of SST. This gives rise to the idea of measuring SST in another direction, which is maximally different (i.e., orthogonal) to the classical in-flight measurement direction to avoid the aforementioned instabilities. In general, there might be several ways to realize a second direction (e.g., through high-low SST, see Pail et al. 2019), but a straightforward idea, which implements this in a low-low configuration, is the so-called across-track SST (A-SST) concept. As the name suggests, in the A-SST concept, SST measurements are obtained in the across-track direction, roughly perpendicular to the orbit trajectory and radial position vector. This observation direction can be achieved by simply adjusting the right ascension of the ascending node $\Omega$ of one satellite so that the two satellites have the desired distance (e.g., at the equator, see Fig. 11). A-SST can be interpreted as a degenerated form of the pendulum concept, with a maximum tilt of 90° (see, Panet et al. 2013). An advantage of A-SST is that both satellite orbits can still be designed (e.g., through the method presented in 2.4) in a way that they do not drift over time relative to each other, which might be required to enable an SST mission with a sufficient lifespan. The major disadvantage of A-SST is that the orbits converge on their way from the equator to the pole, meaning that the inter-satellite distance is strongly varying. On each pole, the two satellites meet and switch their position (left–right). In an idealized Keplerian case, the satellites would, in fact, collide on the poles. However, this is not considered a fundamental problem in the real application since orbits can always be slightly adjusted if necessary. For an actual implementation, the most significant difficulties are assumed to be related to the inter-satellite ranging near the poles, which must be able to handle very small inter-satellite distances and large rotation rates to still track the other satellite. Eventually, it could be necessary to stop the measurements beyond a certain latitude, which would, introduce a polar gap. While this kind of difficulties might be relevant when actually realizing this concept, these problems will not be further considered in the scope of this more theoretical study. For the sake of simplicity, it is thus assumed that observations can be obtained on every position with equal accuracy.

Fig. 11

Illustration of the A-SST concept on a polar orbit. The inter-satellite distance ${\Delta }_{SAT}$ is maximal at the equator and converges towards the poles. On the pole, the inter-satellite distance becomes nearly zero, and the relative orientation of the satellites is changing rapidly. Beyond the pole, on the descending track, the satellite’s positions are switched relative to each other (left–right position), and the relative distance diverges again until the equator, where the cycle restarts

Combining A-SST and I-SST. Even though A-SST allows to measure in a second direction, it is not assumed that across-track measurements are inherently better suited for gravity field recovery than measurements in the in-flight direction obtainable through classical I-SST. Hence, it is also not expected that a polar A-SST-only constellation has a fundamental advantage over a comparable polar I-SST-only constellation. However, following the previous comparison with SGG, it is assumed that combining both directions within one polar (PO) constellation is the key to reaching the targeted gradiometry performance since the two observation directions should perfectly complement each other: in fact, when translating the zero-trace-condition of the (harmonic) gravity gradient to SST, it is evident that two observation directions should render the third direction redundant. Hence, two SST measurements in different directions should theoretically have the same information content as SGG when the main diagonal of the gravity gradient is measured.

IA-SST constellations. There are basically two different types of larger combined I-SST and A-SST (PO) constellations imaginable (so-called IA-SST constellations):

• The first type simply incorporates dedicated I-SST and A-SST satellite pairs into one constellation. Each pair will then cover its own ground track as defined by the constellation design (cf. Sect. 2). When using this constellation type, there are many possible ways to mix I-SST with A-SST. One straightforward way is to use both half-half and interleave I-SST and A-SST pairs on the ground track of the targeted retrieval period.

• As an alternative IA-SST constellation type, one could also create satellite triplets instead of pairs with one central satellite, one satellite orbiting ahead (for I-SST), and one aside (for A-SST). This requires one satellite less than the first type because the central satellite is targeted twice, and I-SST and A-SST observations will be collocated on (roughly) the same position. On the downside, this might require designing three different satellite types (in comparison to two when assuming a symmetric design for the former constellation type). Also, with collocated observations, the achievable spatio-temporal resolution is more limited since there are basically as many satellite triplets needed as pairs required for the former type to achieve a similar ground track coverage.

Due to these disadvantages of the latter constellation type, only the former will be investigated in this study. Additionally, when using the simpler former type, the comparison of the resulting IA-SST constellations to the classical I-SST constellations (of Sect. 3) should be fairer regarding size, cost, and performance (since pairs are compared to pairs and not to triplets).

4.2 A-SST simulation result

Simulation setup. For simulating the A-SST concept for quantum satellite gravity missions, the simulation setup is kept identical to the setup defined in Sect. 3.1 for the classical concepts. Hence, also for the A-SST investigations, daily and weekly solutions are evaluated for the product-only and full-noise case. As discussed in 4.1, to limit the complexity, the noise behavior of the line-of-sight observations for A-SST is assumed to be identical to I-SST. For implementing the IA-SST constellations, the PO constellations (see Sect. 3.4) are reused again. Concretely, the following interleaved IA-SST constellations are investigated (in brackets the SST type of each pair): PO2 (A, I), PO3 (A, I, A), PO6 (A, I, A, I, A, I). For comparison, also A-SST-only scenarios are simulated in addition on the aforementioned PO constellations.

Pre-analysis of the formal errors. In Sect. 3, it has been shown that the homogeneity of the formal errors, obtained from least squares adjustment, is a good indicator of the overall solution’s stability (cf. Sect. 2.4) and, eventually, also for the retrieval performance. This is evidently true for product-only but also for full-noise since the intrinsic de-aliasing seems to work best if the solution’s normal equation system homogeneously weights the coefficients. The formal errors of weekly solutions of the different concepts on polar orbits are shown in Fig. 12 (applying the same quantum noise models from Fig. 6). As expected, the GRACE-like I-SST (Fig. 12a) and the alternative A-SST concept (Fig. 12b) expose a highly heterogeneous error distribution on polar orbits. Eventually, this is considered the main reason why GRACE/-FO and GRACE-like scenarios perform comparatively weakly when influenced by temporal aliasing ("striping patterns”). Even though I-SST and A-SST error patterns are strongly heterogeneous, it is also evident that they are complementary: I-SST performs well in the zonal region, and A-SST performs well in the sectorial areas. Remarkably, in contrast to I-SST, A-SST also shows in the lowest d/o a good performance. This already indicates that a combination of both concepts might be promising. Indeed, the heterogeneity in the formal errors vanishes when combining I-SST and A-SST into a polar two-pair constellation (PO2, see Fig. 12c). The remaining degree dependency of the formal errors is inevitable due to the gravity signal attenuation at the satellite altitude. In 4.1, it has been further stated that SGG and IA-SST should yield roughly the same result resp. pattern due to their close physical relationship. The validity of this statement is demonstrated when comparing the IA-SST error pattern to an analogous two-pair SGG error pattern (Fig. 12d): it is evident that the shape is very similar (even if the instrument noise is not identical for both concepts). This basically proves the utility of A-SST for polar constellations, considering that the sensitivity of SGG is three orders of magnitude worse. Based on these formal error patterns (Fig. 12c), it can already be expected that the weekly two-pair IA-SST solution will perform well in the following comparisons.

Fig. 12

Coefficient triangles of the formal errors of weekly solutions of the different mission concepts on polar (PO) orbits in terms of EWH. a Formal errors of the I-SST concept (GRACE-like) on PO1. b Formal errors of the A-SST concept on PO1. c Formal errors of the IA-SST concept on PO2. d Formal errors of the SGG concept on PO2. Note that the error magnitude of SGG (d) is three orders of magnitude larger than that of SST (a–c)

General insights. An overview of all IA-SST and A-SST simulation (product-only as well as full-noise) results is given in terms of degree errors in Fig. 13 (compare also to Table 2). To have a better comparison to the results of the classical concepts (of Sect. 3), the PO SGG and OSPI SST solutions are printed again (cf. Figs. 7 and 9). When evaluating Fig. 13, the following general statements can be made:

• In the case of the 7-day solutions (product-only and full-noise), IA-SST performs well and is mostly competitive with the OSPI SST solutions and PO SGG solutions (see Fig. 13a and c). This was expected from the previous investigations of the formal errors (Fig. 12c).

• In all scenarios, IA-SST shows nearly no improvements when increasing the constellation size. This means that, despite a higher redundancy and better spatio-temporal coverage, additional polar pairs do not improve the observation geometry any further. While this may sound negative at first, it may also imply that the observation geometry is already very good with two pairs (see Fig. 12c). This is evident in the case of the 7-day product-only scenarios where the IA-SST PO2 solution is already nearly on par with the best-performing six-pair OSPI SST solution.

• Unfortunately, the IA-SST performance deteriorates somewhat when considering the shorter daily solutions. It is supposed that this is caused by the spatial separation of both measurement direction in the chosen interleaved IA-SST constellation design (see Sect. 4.1): in case of daily solutions, the targeted spatial resolution of the estimated gravity fields is close to the maximum achievable resolution of the accumulated ground track (see Sect. 2.4). It is assumed that in such cases the least squares adjustment cannot connect the interleaved I-SST and A-SST observations anymore which basically eliminates the advantage of combining both. Eventually, this means that the formulas for determining the maximum achievable resolution provided in Sect. 2 do not hold for interleaved IA-SST constellations when an optimal exploitation of the advantages of IA-SST is intended (as seen in Fig. 13b and d, the formulas still hold if one accepts a decreased performance). Without proof, a factor of roughly two (lower resolution or more satellites) is expected to adapt the formulas for IA-SST.

• As anticipated from the formal error analysis (Fig. 12), A-SST performs consistently worse than IA-SST (when disregarding the partially degenerated daily solutions). The A-SST single-pair solution performs similarly to the I-SST single-pair solution in the case of product-only. In the case of the full-noise single-pair scenarios, I-SST beats A-SST.

• In the case of product-only and similar to IA-SST, the A-SST performance does also not improve further with an increasing constellation size. So, also, for A-SST, the observation geometry cannot be further improved when more pairs are added. This is also expected since it is assumed that polar A-SST has similar deficiencies than I-SST from which this fact is already known.

• Interestingly, multi-pair A-SST full-noise scenarios perform somewhat better than what the product-only results predict (cf. Fig. 13a and c). Especially the 7-day full-noise two-pair A-SST scenario is competitive to the corresponding OSPI2 and IA-SST PO2 scenarios. This seems strange since the single-pair A-SST scenario does not share the same behavior.

Fig. 13

Empirical degree errors of IA-SST and A-SST solutions in terms of EWH for a weekly product-only solutions, b daily product-only solutions, c weekly full-noise solutions, and d daily full-noise solutions. Line color indicates constellation size. Line type indicates mission concept. Line styles are chosen identically in all subplots. The colors match Figs. 7 and 9

Error structure analysis. To further investigate the behavior of the IA-SST and A-SST constellations in the presence of temporal aliasing, the empirical error structures of the weekly six-pair (PO6) full-noise solutions are shown in Fig. 14 in the spectral and spatial domain (similar to Fig. 10). Similar to what has been found in Sect. 3.3, also the IA-SST and A-SST full-noise error patterns are closely related to their formal errors:

• For the A-SST-only six-pair (PO6) solution, the same zonal lobe is visible in the empirical coefficient errors (Fig. 14a) as it is present in the formal errors (see Fig. 12b). In the spatial domain (Fig. 14b), the zonal lobe causes a longitudinal striping, which is complementary to the latitudinal striping that would be visible for I-SST-only PO constellations (see previous discussion on the formal errors).

• Also, the empirical coefficient error of the combined IA-SST PO6 solution (Fig. 14c) follows the behavior of the IA-SST formal error (Fig. 12c). Since the error patterns are relatively homogeneous, no pronounced striping is visible in the spatial domain (Fig. 14d).

• The empirical errors of the weekly SGG PO6 solution (Fig. 14e) are again similar to IA-SST PO6 and also to the corresponding formal errors of SSG (Fig. 12d). Eventually, the six-pair SGG solution performs slightly better than IA-SST in the zonal region, which is contributed the higher redundancy and the tight collocation of the different measurement direction. The better performance in the zonal area causes a slight inhomogeneity in the overall error distribution, which is expressed in the spatial error as a somewhat pronounced latitudinal striping (Fig. 14e).

• Noteworthy, also in the empirical errors, IA-SST (but also A-SST) shows a good performance in the retrieval of the lowest d/o (Fig. 14c, e). This indicates that the inline measurement direction causes the deterioration in the long wavelengths in the case of conventional I-SST.

Fig. 14

Coefficient triangles (left column) and corresponding spatial distribution (right column) of the empirical errors of the weekly solutions of the full-noise polar six-pair (PO6) scenarios for the A-SST (a–b), the IA-SST (c–d) and the SGG concept (e–f) in terms of equivalent water heights (EWH). Absolute coefficient values are shown in the coefficient triangles (a, c, e). To create the spatial plots (b, d, f), the maximum d/o has been limited to 50 in the SH synthesis (to not impair the signal-to-noise ratio, see Fig. 13c)

5 Conclusions and outlook

At the end of this work, a summary over all study subjects is provided in Sect. 5.1, highlighting the main achievements and conclusions. Finally, to close this study, an outlook on future research topics is given in Sect. 5.2 by discussing the main (remaining) causes of temporal aliasing.

5.1 Summary and conclusions

In this contribution, a constellation design procedure for future satellite gravity missions is presented and discussed (Sect. 2). Based on exemplary larger constellations, the functionality and impact of the constellation design on the gravity field retrieval performance for the classical SST and SGG gravity mission concepts is investigated by conducting various simulations (Sect. 3). Additionally, also the alternative A-SST concept is evaluated (Sect. 4) to emphasize that the presented constellation design procedure is not limited to the classical gravity mission concepts. In the following, the most important insights and achievements of each of these three main sections will be briefly summarized and the impact of future quantum sensors is discussed.

Constellation design. The presented method allows to design constellations of arbitrary size in three different configurations: polar-only (PO), one-satellite-per-inclination (OSPI) and multiple-satellites-per-inclination (MSPI). The procedure encourages the modeling of the constellations based on central mission parameters such as the required spatial and temporal resolution. Sub-cycles even allow to optimize for multiple spatial and temporal resolutions. By using the concept of combined sub-cycles, the achievable temporal resolution is indefinitely extendible, given that enough satellites are provided. Through the repeat ground track design, the derived analytical orbits can be further adjusted to realize the desired features also in Earth’s actual (static) gravity field. Finally, the correctness of the modeling approach is empirically proven by a representative set of exemplary constellations up to six satellites/pairs and by introducing a generic stability/quality measure for the SST gravity field retrieval performance.

SST and SGG simulations. Full-scale gravity mission simulations proved that larger constellations can achieve their primary purpose and enable a stable gravity field retrieval with higher spatial resp. temporal resolution. Additionally, in most cases, also the solution’s stability can be further increased when introducing additional satellites/pairs, which, eventually, also increases the retrieval performance in the presence of temporal aliasing. With future instrument specifications, even SGG may become sensitive to time-variable gravity and could pose then a possible alternative to SST. For SGG, no significant benefit could be identified when applied on non-PO constellations. In contrast, for SST, it could be shown that maximizing the number of inclinations in a constellation yields, in most cases, the best results. However, even though larger constellations usually reduce temporal aliasing to some extent, the remaining temporal aliasing error still dominates the overall error budget by up to five(!) orders of magnitude (when compared to the product-only case). Hence, it can be concluded that temporal aliasing cannot be reduced to a satisfactory level when just trusting in the intrinsic de-aliasing capability of the constellation.

A-SST concept. Across-track SST (A-SST) combined with conventional Inline SST (I-SST, resulting in an IA-SST mission) can leverage homogeneous SGG-like error patterns on polar-only constellations. This basically allows to combine the advantage of SGG (homogeneous error structure on polar-only constellations) with the benefits of SST (significantly higher sensitivity). This is proven through simulations and the investigations of the different error patterns. Full-noise IA-SST results are mostly comparable with SGG and also competitive with the inclined I-SST constellations. The downside of A-SST is the supposed higher complexity due to strongly varying inter-satellite distances and the lower achievable spatio-temporal resolution when interleaving I-SST and A-SST pairs in a constellation.

Impact of future quantum sensing instruments. When assuming an optimistic sensor development, future instruments that employ cold atom interferometry may be able to significantly increase the sensitivity for gravity field observables by about four orders of magnitude for SST and SGG (in comparison to GRACE-FO resp. GOCE, see Encarnação et al. 2024). However, this study has also shown that SST cannot gain significant benefit from it since even constellations with up to 6 pairs are not able to reduce the temporal aliasing error to a level where this superior quantum instrument sensitivity is required. In fact, the MAGIC noise specification (Heller-Kaikov et al. 2023) would currently be more than sufficient for all investigated scenarios as long as no major leap in mitigating temporal aliasing is achieved. In contrast to SST, for SGG, the baseline is different: since the state-of-the-art GOCE performance not sufficiently sensitive to time-variable gravity (about one order of magnitude), a future quantum gradiometer can still substantially increase the gravity field retrieval performance when compared to a GOCE-like instrument by about two orders of magnitude (until reaching the temporal aliasing limit). Hence, without solving the temporal aliasing problem, SGG may currently benefit much more than SST from quantum instruments. According to Encarnação et al. (2024), for reaching the assumed quantum gradiometer noise, an elaborated 3D CAI setup would be required to enable a sufficiently accurate reconstruction of the angular rates, which is needed to determine the gravity gradient. Eventually, the availability of such an instrument is not expected any time soon. Yet, even with this complex setup, regarding the pure sensitivity on the long-wavelength gravity field signal, quantum SGG still remains about three orders of magnitude less accurate than quantum SST. However, this circumstance is currently completely shadowed by temporal aliasing when retrieving global gravity fields, which is why quantum SST and SGG show similar performance (when considering constellations with at least two pairs).

5.2 Outlook

The simulations in this study have shown that for future (quantum) satellite gravity missions, temporal aliasing will be the most critical error component by a wide margin, even when introducing larger satellite constellations. As a cause for this, two reasons can be identified, which will be briefly addressed in the following paragraphs.

Temporal and spatial signal energy distribution. Within the conducted simulations and in the constellation design, only daily retrieval periods are considered as the maximum temporal sampling rate. According to the Nyquist–Shannon sampling theorem, a daily sampling rate allows to correctly reconstruct only wavelengths longer than two days. However, in the temporal gravity signal, which is introduced in the forward model of the simulation, more than half of the total monthly signal energy is generated on daily and sub-daily wavelengths (see Fig. 15, sum of blue lines). This can be mainly attributed (1) to ocean tides (OT, Fig. 15 dotted lines) since tidal excitation frequencies are primarily located around daily and half-daily frequencies and (2) to non-tidal atmosphere and ocean signal (AO, Fig. 15 solid lines) where various processes are related to the day–night cycle. These significant signal components cannot be correctly recovered with daily sampling rates. Instead, these non-reconstructible components are then causing temporal aliasing. According to the applied ocean tide models and the non-tidal ESM model, the gravity signal energy is strongly decreasing just below half-daily wavelengths (cf., Fig. 15). This means that temporal sampling rates (retrieval periods) of less than six hours are required to correctly reconstruct these frequencies. While not impossible to achieve, in agreement with the rule of thumb established in Sect. 2.1 (Eq. 4), it would require at least about 20 satellites to realize a quarter-daily global coverage with a resolution of 3° (corresponding to a maximum d/o of 60). This underlines that rather large constellations are essential to meet future gravity mission requirements and that technological advancements that enable these may become crucial.

Fig. 15

Non-recoverable signal energy on satellite altitude of the most important time-variable gravity field components (ESM HIS, residual ESM AO, and residual ocean tides) in dependencies of the retrieval period (i.e., sampling rate) and spatial resolution (i.e., maximum recovered d/o). Signal energy of non-tidal atmosphere and ocean (AO) and ocean tides (OT) refers to residuals after applying de-aliasing products. Hence, the shown energies correspond to the actual signals within the simulation setup (cf. Sect. 3.1), effectively causing temporal aliasing. Colors correspond to different spatial resolutions (i.e., maximum d/o) and line types to the different signal components. Spectral energies are empirically derived from the individual datasets (see Sect. 3.1)

Usually, the gravity signal attenuation due to upward continuation is not considered an advantage of satellite gravity field recovery. However, in combination with temporal aliasing, it well might become one. To understand this, one can look at the decrease of the omitted gravity signal energy on the sensing instruments at satellite altitude with the increase of the resolution (i.e., maximum SH d/o): due to the outward continuation of the gravity field, the omitted signal energy strongly decreases with an increasing maximum d/o (see different colors in Fig. 15). This means that most of the energy which causes temporal aliasing can already be reconstructed when recovering the gravity field only to a relatively low maximum d/o with the highest temporal sampling. E.g., even when retrieving quarter-daily fields just up to d/o 20, the omitted signal energy can already be reduced by about a factor of four. Hence, and also due to outward continuation, spatial aliasing is considered unproblematic, which, consequently, allows to estimate lower-resolution gravity field solutions (e.g., quarter-daily solution) independently without introducing significant errors. For the stated reasons, it is deemed necessary to further investigate constellations with sub-daily retrieval periods and its impact on temporal aliasing reduction. This, by either introducing simply more satellites or by trying to find sub-daily sub-cycles with lower spatial resolution. In any case, sub-daily retrieval periods will probably require the concept of combined sub-cycles since it is not likely to find simple sub-daily sub-cycles within a close altitude range. Hence, sub-daily periods are not easily achievable with OSPI constellations.

Parametrization. Next to the insufficient temporal sampling, the second reason for the observed temporal aliasing errors is found in the static gravity field parametrization, which is inappropriate for describing time-variable gravity: in the forward model of the simulator, the time-variable gravity is described in the time-domain realistically as a continuous function (e.g., through linear or cubic splines). However, in the conventional modeling (e.g., of the standard monthly GRACE/-FO solutions) and within this study, the estimated gravity field is only introduced statically in the backward model. When deriving multiple static gravity field solutions of subsequent retrieval periods (e.g., daily or weekly solution), the resulting time-variable gravity field then only resembles a step function in the time domain. It is evident that a step function is inadequate to model a changing behavior, not even if it is just linear. Consequently, even if sufficient sampling would be available, modeling the gravity field as a step function in the time domain would still introduce a significant error. Investigating time-variable parametrization strategies is, hence, considered the second main objective for future studies. Generally, two types of such time-aware parametrization schemes can be distinguished for gravity field modeling, depending on the properties of the different signal components: for signals that consist of distinct known excitation frequencies (such as tidal signals), tailored co-parametrization strategies can be applied (e.g., see Hauk and Pail 2018). This parameterization type has the advantage that long accumulation times (e.g., years) can be used to estimate the additional parameters stably, eliminating the need for short retrieval periods and, thus, larger constellations. However, the latter approach is non-applicable for randomly occurring signals (such as non-tidal signals). The only known way these signal components can be recovered is by using a direct parameterization (e.g., through splines), which again requires short retrieval periods. Since non-tidal signal components (such as AO) significantly contribute to the overall signal energy, it is not assumed that temporal aliasing can be dramatically improved without considering these non-tidal components as well.

Eventually, a significant leap in reducing temporal aliasing can only be expected when considering both a sufficient sampling provided by an extended constellation and an adequate parametrization of signals in space and time.