Introduction

The atmosphere is constantly exposed to periodic disturbances. The disturbances range broadly in time and space, at least temporally from microseconds to Milankovitch orbital scales, and spatially from centimeters to the planetary scale. At the planetary scale, most disturbances are driven by planetary waves (i.e., Rossby waves), tides, and their nonlinear interaction waves. These waves’ amplitudes are often weak in the low atmosphere, increase with altitude, and maximize in the mesosphere–lower-thermosphere (MLT) region (e.g., Hirooka and Sciences 2000). The wave intensity and variety make the MLT an ideal nature lab for studying atmospheric waves. However, MLT observations are relatively sparse compared to other atmospheric regions since both balloons and spacecraft cannot permanently operate in the MLT. Continuous observations could only be collected remotely through either optical instruments onboard satellites or radio approaches on the ground. Both observational techniques have been used to investigate MLT waves, figuring out the salient wave behaviors in both case and statistical studies (e.g., Oberheide et al. 2011). However, most observational studies used single-station or -satellite methods and were, therefore, potentially affected by inherent spatiotemporal aliasing.

Single-station analyses cannot diagnose the horizontal wavelength of planetary-scale waves (e.g., Azeem et al. (2000)), although they enable identifying waves at expected frequencies with a high-frequency resolution. On the other hand, although space-based sensors collect data across all longitudes and allow us to determine the horizontal scale of waves, single-satellite analyses suffer from intrinsic aliasing (e.g., Tunbridge et al. 2011; Salby 1982). The aliasing can be explained in terms of the Doppler shift of waves traveling in the earth-fixed coordinate system recorded by a sun-synchronous observer because most relevant satellites obit quasi-sun-synchronously. For convenience, the current work uses [f, s] to denote a wave at the frequency f with the zonal wavenumber s in the earth-fixed coordinate system. (In some literature, s is also denoted as m. \(s>0\) and \(s<0\) denote westward and eastward traveling waves, respectively. Since [f,s] and [\(-f\),\(-s\)] denote the identical wave, the current work defines the frequency as non-negative \(f\ge 0\).) A wave [f, s] is Doppler-shifted to frequency \(f'=f-s\text {*1cpd}\) for a sun-synchronous observer, where cpd abbreviates cycles per day. Then, all waves [\(f+C\text {*1cpd}\), \(s+C\)] with an arbitrary C will be Doppler-shifted to the same \(f'\) in the sun-synchronous coordinate system and, therefore, are not distinctive from each other in single-satellite analyses. (Specially, when \(C \in {\mathbb {Z}}\) is an integer, [\(f+C\text {*1cpd}\), \(s+C\)] includes all potential secondary waves of wave-wave nonlinear interactions between [f, s] and all migrating tides.) An example is that all migrating tides [\(n\text {*1cpd}\), n] (where \(n \in {\mathbb {N}}\) is a positive integer) are Doppler-shifted to \(f'=0\) and are not distinctive from each other. Another example is the well-known zonal wave-4 structure (e.g., Immel et al. 2006). In single-satellite analyses, this structure is characterized by \(f'=\text {4cpd}\), which might be Doppler-shifted signatures of at least three potential waves [1cpd, –3], [2cpd, –2], and [0, ±4]. Although [1cpd, –3] is believed to be the main contributor (Forbes et al. 2003; Forbes et al. 2006; Hagan and Forbes 2002; Pedatella et al. 2008), [2cpd, –2] (He et al. 2011; Chen et al. 2019) and [0, ±4] (He et al. 2010; Pedatella et al. 2012a) were also reported to be the primary contributor under some conditions. Note that our Doppler-shift interpretation is equivalent to the interpretation of “space-based zonal wavenumber”\(s'\) in, e.g., Forbes and Moudden (2012) and Nguyen et al. (2016), because \(s' \equiv \vert \tfrac{f'}{1\text {cpd}}\vert\).

Many researchers tried to overcome the above aliasing by combining observations from multi-longitudinal sectors (e.g., Baumgaertner et al. 2006; Murphy et al. 2006; Manson et al. 2009; Pancheva et al. 2002, 2004; Jiang et al. 2008). In a series of works, the author developed various multi-station methods and implemented the methods to diagnose diverse planetary-scale waves. The current paper reviews these methods and results comparatively.

Methods

Experimental wave identifications typically refer to wave properties of, e.g., frequency, wavenumber, and polarization. The current section summarizes some methods identifying waves referring to zonal wavenumber s and frequency f based on observations recorded on regular time t grids from two or more irregularly separated longitudes \(\lambda\) at the same latitude. The f-s identification can be realized through a least-squares (LS) fitting to a predefined model as a function of f and s. Such a two-dimensional (2D) fitting in a sliding window can yield a temporal resolution. However, the predefined model entails much prior knowledge, and the 2D sliding fitting is typically computationally expensive. Therefore, the author performs f-s identification through two spectral analyses: linear transformations (wavelet or Fourier transformation) from the t domain to the f domain (denoted hereafter as the \(t\mapsto f\) analysis) and spectral analysis from the \(\lambda\) domain to the s domain (denoted as the \(\lambda \mapsto s\) analysis).

The phase difference technique (PDT) for diagnosing zonal wavenumber

The PDT is a dual-station method, which firstly realizes the \(t\mapsto f\) analysis through a wavelet or Fourier transformation and then deals with the \(\lambda \mapsto s\) analysis through cross-spectral analysis (e.g., He et al. (2018)).

A plane wave triggers coherent oscillations everywhere on the wave’s path. The coherence means that the phase difference between any two locations is time-independent. The phase difference equals the spatial separation multiplied by the aligned wavenumber. Therefore, the aligned wavenumber can be calculated according to the experimental estimations of the phase difference and the spatial separation. Using observations from two zonally separated stations at the same latitude, one can estimate the phase difference through cross-wavelet analyses or LS cross-spectral analyses. Two assumptions used in the wavenumber estimation are the single- and long-wave assumptions. The first requires that one wave be dominantly stronger than the rest at any frequency and instant. To satisfy this assumption, we trade off between the frequency and time resolutions differently in different circumstances. The long-wave assumption is required due to the Nyquist theorem in space that the shortest identifiable wavelength is twice longer than the station spacing. In the atmosphere, most planetary-scale waves are associated with integer zonal wavenumbers. Therefore, we often use a third assumption that the zonal wavelengths of the underlying waves are low-order harmonics of 360\(^\circ\) longitude. This integer zonal wavenumber assumption can relax the long-wave assumption slightly.

Fig. 1
figure 1

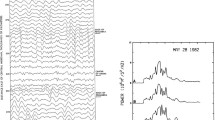
PDT implemented on synthetic data. a Temporal variations of two synthetic wave amplitudes in wind u. These waves are the diurnal and semidiurnal tides with frequency and zonal wavenumbers [f, s] = [1cpd, 1] and [2cpd, and 2], respectively. b Superposition of the waves with a unit of Gaussian noise. c The cross-wavelet spectrum of the time series was sampled along the two horizontal dashed lines, a and b in (b). Through the cross-wavelet spectrum, s can be identified through the PDT, as summarized in “The phase difference technique (PDT) for diagnosing zonal wavenumber” section

Full size image

In Fig. 1a, b, synthetic data are constructed for implementing the PDT, comprising two synthetic waves plus a unit of Gaussian noise. The synthetic waves are the diurnal and semidiurnal migrating tides, [1cpd, 1] and [2cpd, 2], which are among the most extensively studied atmospheric waves with near-zero integer zonal wavenumbers. Near-zero wavenumbers are chosen here to facilitate the long-wave assumption, while the integer wavenumbers were used since non-integer wavenumber waves can be decomposed as linear combinations of integer-wavenumber waves. Readers may overlook the frequency selection of the synthesized waves, since the methods introduced in the current work were developed to not favor any frequency.

The synthetic data are sampled at two random longitudes, labeled as a and b in Fig. 1b. The cross-wavelet spectrum between the longitudes is displayed in Fig. 1c. The red and green peaks at \(T=\)1 and 2 day indicate zonal wavenumbers of s= 1 and 2, respectively. In addition, the power of the cross-wavelet reflects the wave amplitudes. The isolation between the red and green peaks reflects that the single-wave assumption is valid. Otherwise, if the peaks overlap, the single-wave assumption fails and the dual-station PDT would not work. However, observations from more stations can help distinguish overlapping waves, as demonstrated in the subsequent two subsections.

Wavelet transformation plus least-squares (WT & LS) approaches

The PDT described in the previous subsection relies on the single- and long-wave assumptions and the integer-wavenumber assumption. These assumptions also enable the \(\lambda \mapsto s\) analysis through LS approaches using the outcomes from the \(t\mapsto f\) analysis that can be accomplished through, e.g., wavelet transformation, as introduced in the previous subsection (e.g., He et al. (2021a)). These LS approaches coupled with the \(t\mapsto f\) analysis are referred to as WT & LS throughout this study.

At each instant and frequency, the wavelet amplitudes (or Fourier or Lomb-Scargle amplitudes, e.g., He et al. 2021a; He et al. 2020) can be fitted to a predefined wavenumber model through LS approaches. The wavenumbers of underlying waves are supposed to be defined according to prior knowledge or to be determined through, e.g., the PDT or an LS optimization minimizing the error between the wavelet complex amplitudes and a single-wavenumber model (e.g., He et al. 2021a). According to the predefined wavenumbers, multi-wavenumber models can further be implemented to estimate the amplitudes of underlying waves through LS fitting (e.g., He et al. 2018).

Fig. 2
figure 2

Implementation of the WT &LS method on synthetic data. a Temporal variations of three synthetic wave amplitudes in wind u. The frequency and zonal wavenubmers are [f, s] = [1cpd, 1], [1cpd, − 1] and [2cpd, and 2], respectively. b Superposition of the waves with a unit of Gaussian noise. c The zonal wavenumber s estimation results, using the data sampled along the dashed lines in b through the WT & LS method as summarized in “Wavelet transformation plus least-squares (WT & LS) approaches” section. d–f the wave amplitudes estimated according to the s estimation in c through the WT & LS method. In b, the dashed lines indicate three randomly selected longitudes. In c, s is estimated only when the signal is above the significance level \(\alpha\) = 0.05

Full size image

As an example, Fig. 2 presents an implementation of the WT & LS approach to the synthetic data displayed in Fig. 2a, b that are composed by superposing a third wave [1cpd, − 1] on Fig. 1a, b. The third wave is superposed to illustrate the capability of the WT & LS method in resolving waves overlapping at the same frequency. In Fig. 1, the waves are separated in the frequency domain, whereas in Fig. 2, two waves with comparable amplitudes overlap at frequency f = 1cpd around \(t=\) 5 day.

The synthetic data are sampled along three randomly selected longitudes, as indicated by the dashed lines in Fig. 2b, to estimate the zonal wavenumber s of the underlying waves through an LS procedure (see, e.g., Fig. S3 in He et al. 2021a). In principle, the s estimation requires samples from a minimum of two longitudes, since the fitting uses a single-wave model. However, the fewer longitudes used, the more sensitive the fitting is to noise and longitude configuration. Here, three longitudes are selected in the s estimation. The estimated s is displayed in Fig. 2c, which reveals the three synthetic waves [f, s] = [1cpd, − 1], [1cpd, 1], and [2cpd, 2] properly. Estimating the amplitudes of three waves through the WT &LS approach requires observations from at least three longitudes (see, e.g., Equation 1 in He and Chau 2019). Accordingly, the samples collected along the three longitudes are implemented further to estimate the wave amplitudes following the procedures used, e.g., in Fig. 3a, b in He et al. (2021a). The results are displayed in Fig. 2d–f, maximizing at 7, 5, and 8 ms\(^-\), respectively, which is consistent with the corresponding amplitudes in Fig. 2a.

Compared with the dual-station PDT, the WT & LS approach can utilize as many stations as possible, but it lacks straightforward control over the Nyquist spatial aliasing due to the preassigned wavenumbers based on prior knowledge or by the LS method. An imprecise preassignment may lead to biased amplitude estimations. When observations are available at more longitudes, the preassignment can be avoided or relaxed through the approach introduced in the following subsection.

Harmonic regression plus wavelet transformation (HR & WT) approaches

Both PDT and WT &LS methods summarized in the previous two subsections realize the s-f identification by carrying out first the \(t\mapsto f\) analysis and then the \(\lambda \mapsto s\) analysis. In principle, it is also possible to perform the \(\lambda \mapsto s\) analysis before the \(t\mapsto f\) analysis (e.g., Section 4.1 in Forbes et al. 2020).

Observations from an arbitrary number of stations at any instant can be decomposed into a linear combination of zonal subharmonics \(\vert s\vert =0, 1, 2,...\), through an LS harmonic regression. Each subharmonic coefficient is a complex number that denotes the subharmonic’s amplitude and zonal phase. The wavelet transformation of the time series of each complex coefficient represents the subharmonic t-f spectrum. The t-f spectra, using the Gabor function (Torrence and Compo 1998) and its conjugate as the mother wavelet, denote the eastward and westward traveling structures, respectively. The current paper refers this method as HR & WT.

The computation cost of the HR & WT methods is proportional to the number of selected zonal harmonics, whereas the cost of the WT & LS method is proportional to the number of stations. Therefore, analyzing observations from a large number of stations, the HR & WT methods would be computationally cheaper than the WT & LS methods.

Fig. 3
figure 3

Implementation of the HR &WT method on synthetic data. a Same plot as Fig. 2b but with four more dashed lines representing more randomly selected longitudes. b–h) the wave amplitudes estimated through the HR &WT method using the data sampled on the seven dashed lines in b, as detailed in “Harmonic regression plus wavelet transformation (HR & WT) approaches” section

Full size image

Figure 3 presents an implementation of the HR &WT approach using the synthetic data displayed in Fig. 2b. The implementation aims at the wave amplitudes for seven wavenumbers \(s=\)1, 2, 3, 0, − 1, − 2, and − 3, for which the synthetic data are sampled at seven longitudes, comprising the three longitudes displayed in Fig. 2b and four more randomly selected longitudes as indicated by the dashed lines in Fig. 3a. The amplitudes for the seven wavenumbers are estimated following the procedures detailed in section 4 in Forbes et al. (2020), which are presented in Fig. 3b–h, respectively. The estimation captures the three waves properly. However, in addition to the three waves, some spectral signals appear in Fig. 3b–h which do not exist in the synthetic data, such as the peak of s = 0 at T = 1, t = 8 in Fig. 3e and the peak of s = − 1 at T = 0.5, t = 10 in Fig. 3f. These power leakages are associated with the finite number and uneven distribution of longitudinal samplings (see section 4 in Forbes et al. (2020) for discussions). This leakage will reduce with data sampled from more longitudes or evenly distributed longitudes. Therefore, the HR & WT approaches are more applicable to datasets evenly covering plenty of longitudes, such as observations from slow-processing polar-orbiting satellites and outputs from models. When longitudinal coverage is sparse or uneven, the WT & LS method will be more practical.

Evaluations of the above methods

The methods introduced in previous subsections have been evaluated crossly.

Fig. 4
figure 4

Comparison of wave amplitude of zonal wave number s=3 estimated using the ground-based WT & LS method with those estimated using the space-based MIGHTI observations. a the WT & LS estimations as a function of the day of year and period, b the MIGHTI estimation, and c and the scatter plot of the values sampled from a and b. This figure is adjusted from Fig. 3 in He et al. (2021a)

Full size image

Wave amplitudes estimated through the WT & LS methods were compared in a statistical study with a climatological tidal model of the thermosphere (CTMT, Oberheide et al. 2011) and in a case study with results derived from observations of the Michelson Interferometer for Global High-resolution Thermospheric Imaging (MIGHTI Immel et al. 2017) instrument on the ICON satellite. The comparisons, displayed in Figs. 7 and 8 in He and Chau (2019) and Fig. 3 in He et al. (2021a), respectively, exhibit reasonable consistency. The comparison with MIGHTI results is adjusted and displayed here in Fig. 4. The method was also evaluated using virtual data generated with the Whole Atmosphere Community Climate Model with thermosphere–ionosphere eXtension (SD-WACCMX) by Macotela et al. (2022). The author estimated amplitudes of selected waves through WT &LS approaches using virtual data from only three selected longitudinal sectors and compared the results with amplitudes estimated using data from all longitude sectors. The comparison exhibits reasonable consistency. Observational error propagation in the WT & LS method was analyzed through a Monte Carlo simulation (see Fig. 4 in He et al. 2018a; He et al. 2018, respectively). In addition, He and Chau (2019) quantified the susceptibility of the WT & LS amplitude estimations to neglected waves through analytical analysis and implemented the analytical solution with the empirical model CTMT. The results, displayed in Fig. 9 in He and Chau (2019), demonstrated the method’s feasibility when the neglected waves are weaker than the estimated waves.

To evaluate the PDT approach, He et al. (2020) and He et al. (2021a) collected meteor radars from multiple longitudinal sectors and used them to estimate s through the PDT using different combinations of radar pairs. The dual-station configurations result in consistent estimations (see Fig. 3 in He et al. 2020a), which are compared excellently with the WT &LS estimations (see Figures S2 and S3 in the supporting information in He et al. (2021a)).

In implementing the HR &WT approach with four longitudinally separated stations, Forbes et al. (2020) evaluated the approach using output from Thermosphere–Ionosphere–Mesosphere–Electrodynamics General Circulation Model (TIME-GCM). In Fig. 9, the author compared the four-station estimation with all-longitude estimation, and investigated the susceptibility of the four-station estimation on the longitudinal polarization of the four-station configuration. The author also quantified the error propagation and its dependence on the stations’ longitudinal separation through a Monte Carlo simulation in their Figure A1 in Forbes et al. (2020).

Spectral periodic table (SPT)

Secondary wave–wave nonlinear interactions between two waves [\(f_1\),\(s_1\)] and [\(f_2\),\(s_2\)] might generate two secondary waves (SWs), denoted hereafter as [\(f_1\),\(s_1\)]–[\(f_2\),\(s_2\)]=[\(f_1-f_2\),\(s_1-s_2\)] and [\(f_1\),\(s_1\)]+[\(f_2\),\(s_2\)]=[\(f_1+f_2\),\(s_1+s_2\)] and termed lower and upper sidebands (LSB and USB), respectively. These relations of s and f are ensured by the phase-matching among involved waves (He and Forbes 2022), and are, therefore, referred to as phase-matching relations in the current work. The phase-matching relation of f is equivalent to energy conservation according to the Manley–Rowe relation (He et al. 2017) which specifies that the energy of each wave involved in an interaction is proportional to the wave’s absolute frequency. If one planetary wave [\(f_{PW}\),\(s_{PW}\)] interacts with multiple migrating tides [n cpd,n] (\(n\in {\mathbb {N}}\)), the resultant secondary waves (SWs) [\(n\pm \frac{f_{PW}}{1\text {cpd}}\) cpd,\(n\pm s_{PW}\)] will populate the spectrum periodically. Using this periodicity, He et al. (2021b) developed the spectral periodic table (SPT) to extract the SW signatures in batches.

Fig. 5
figure 5

Spectral periodic table (SPT) as an analogy of the periodic table of elements. The left panel was wrapped from a frequency cross spectrum, so that spectral peaks in the same column share the same origin, one wave and its interactions with different migrating tides (see He et al. 2021b). For example, spectral peaks indicated by the red vertical lines, termed the red family, can be explained as either a Q2DW [\(\frac{1}{\text {50h}}\),3] or its secondary waves (SWs) through interactions with different migrating tides, while the spectral peaks indicated by the blue vertical lines can be explained as another Q2DW [\(\frac{1}{\text {41h}}\),4] and its SWs. Noted that the SPT might not be completed and can be extended to include more rows, in analogy to the potential extension of the periodic table of elements. The magenta arrow denotes increasing frequency 0\(<f<\)3.5 cpd, indicating how the cross spectrum is wrapped into the table. In each row of the table and from left to right, \(\delta f:=|\frac{f}{\text {1cpd}}-\lfloor \frac{f}{\text {1cpd}}\rceil |\), namely, the absolute spectral frequency difference to the nearest tidal frequency \(\lfloor \frac{f}{\text {1cpd}}\rceil\), increases from 0 to 0.5 cpd. The current figure is adjusted from Figure 1 in He et al. (2021b)

Full size image

To construct the SPT, the authors first calculated a frequency cross-spectrum between the two stations, \({\tilde{c}}(f)\), through the Lomb-Scargle analysis. Then, the authors chopped the \(\tilde{c}(f)\) spectrum into 0.5-cpd-width pieces, in analogy to the concept of a period in the periodic table of elements. Each piece is characterized by \(\delta f: = \left|\frac{f_{PW}}{1\text {cpd}} - \left \lfloor {\frac{f_{PW}}{1\text {cpd}}} \right\rceil \right|\) either increasing monotonically from 0 to 0.5 or decreasing from 0.5 to 0. The pieces were wrapped following the magenta arrow in Fig. 5. In the resultant spectral table, each row from left to right is associated with increasing \(\delta f\) from 0 to 0.5. In principle, all the potential SWs associated with the same PW at \(f_{PW}\) are located in the same column, which are characterized by \(\delta f \equiv \min |n\pm \frac{f_{PW}}{1\text {cpd}}|\) and termed a family, in analogy to the concept of a group in the periodic table of elements. Their product \(P(\delta f):=\prod \limits |{\tilde{c}}(\delta f)|\) is expected to be significantly beyond the noise level. Therefore, maxima of \(P(\delta f)\) were used to identify family candidates. For each candidate, the phase-matching relation of the zonal wavenumber \(n\pm s_{PW}\) can be used as a constraint of \({\tilde{c}}(\delta f)\) for estimating the zonal wavenumbers through an LS regression. Finally, the LS estimations were compared with their PDT estimations for evaluations.

Similar to the periodic table of elements which can potentially be extended with more elements and periods, the SPT in Fig. 5 can potentially be extended to include interactions of higher-order tidal harmonics.

Adjusted Feynman diagram (AFD): a representation of wave–wave interactions

Fig. 6
figure 6

Adjusted Feynman diagrams of (a) LSB and (b) USB generations of interactions between the 10-day wave [\(\frac{1}{10d}\),1] and the semidiurnal migrating tide [2cpd,2]. (c,d) Same plots as (a,b) but for the 16-day wave [\(\frac{1}{16d}\),1]. Each panel comprises three arrows, two of which go into a vertex denoting the parent waves and one comes out the vertex representing the secondary wave (SW). Since [f,s] and [\(-f\),\(-s\)] represent the same wave, we use \(f\ge 0\) in the current work to denote all waves. The red solid and blue dashed arrows represent waves exporting and accepting energy in the interaction, respectively, according to the Manley–Rowe relation (e.g. He et al. (2017)). In each panel, the blue arrows’ vector sum equals the sum of the red, entailed by the phase-matching relations

Full size image

Inspired by Hasselmann (1966), the author adjusts the Feynman diagram to represent MLT wave–wave nonlinear interactions. As an example, Fig. 6a displays an adjusted Feynman diagram (AFD) of the LSB generation between a planetary wave [\(\frac{1}{10\text {d}}\), 1] and a migrating tide [2cpd, 2]. The AFD comprises three arrows in the f-s plane, intersecting at a vertex. Each arrow denotes one wave. The arrows pointing to the vertex denote the parent waves which existed before the interaction, whereas the arrow pointing away from the vertex denotes the secondary wave (SW), which is generated in the interaction. The projections of each arrow onto the x- and y-axes denote the wave’s frequency and zonal wavenumber, respectively. Since the author defines \(f\ge 0\), the parent waves locate either at the left side of the y-axis (\(f>0\)) or on the y-axis (\(f=0\)), and the SW locates either at the right side (\(f>0\)) or on the y-axis (\(f=0\)). The red and blue colored arrows denote energy sources and sinks, respectively, according to the Manley–Rowe relation (He et al. 2017). In the interaction represented in Fig. 6a, the planetary wave is an energy sink, indicating that the wave is amplified in the interaction, although it is a parent wave. Such an amplified parent wave was called an anti-wave (e.g., Hasselmann 1966). This amplification was termed planetary wave amplification by stimulated tidal decay (PASTIDE, He et al. 2017). The Manley–Rowe relation is known as the Planck relation in Quantum mechanics. One quantum mechanic counterpart of PASTIDE is the LASER (light amplification by stimulated emission of radiation). The AFD for the USB generation between the planetary wave and tide is displayed in Fig. 6b, comprising two energy sources and one sink. In each of the AFDs, either LSB or USB, the blue arrows’ vector sum equals the red arrows’ sum, required by the phase-matching relations.

Detected planetary-scale waves

Fig. 7
figure 7

Configurations used for multi-station analyses. Dots (#1–5) in the same color denote meteor radars that were paired for implementing the PDT; crosses (#6–8) in the same color denote meteor radars that were combined for implementing the WT &LS method; and pentagrams (#9) denote surface magnetometers used in implementing the HR &WT method. Configuration #1 is also used for implementing SPT

Full size image
Fig. 8
figure 8

Planetary-scale waves diagnosed through multi-station methods in the frequency-zonal wavenumber depiction. Filled and open circles denote PWs or UFKWs and solar or lunar tides, respectively, and upward and downward triangles denote USBs and LSBs arising from wave-wave nonlinear interactions. Symbols in magenta denote waves exhibiting activities in response to SSWs. In a, the regions in the dashed boxes are zoomed in (b) and (c)

Full size image
Table 1 Waves diagnosed through multi-station methods
Full size table

The above methods were implemented on networks of meteor radars at high-, mid-, and low-latitude and surface magnetometers at the geomagnetic equator, as summarized in Fig. 7. The implementations revealed diverse planetary-scale waves as specified in Table 1 and Fig. 8. The current Section summarizes these results in three categories as follows.

Multi-day oscillations

In a series of case or statistical studies at different latitudes, various waves were diagnosed at periods longer than 1 day, as summarized in the f-s depiction in Fig. 8b. These waves can be categorized into Rossby wave normal modes (RWNMs, e.g., Sassi et al. 2012), quasi-2-day waves (Q2DWs, e.g., Salby 1981; Rojas and Norton 2007), ultra-fast Kelvin waves (UFKWs, e.g., Forbes 2000), and secondary waves (SWs, e.g., Forbes and Moudden 2012) of the previous waves’ nonlinear interactions.

Fig. 9
figure 9

Adjusted Feynman diagram of USB generation of the interaction between a stationary planetary wave [0,1] and the 16-day normal mode [\(\frac{1}{16d}\),1]

Full size image

Diagnosed RWNMs include the 16-, 10-, and 6-day normal modes, namely, [\(\frac{1}{16\text {d}}\), 1], [\(\frac{1}{10\text {d}}\), 1], and [\(\frac{1}{5-6\text {d}}\), 1] at mid- and high-latitude in the northern hemisphere, through the PDT using meteor wind observations, mostly during arctic SSWs (e.g., He et al. (2020c)). Quasi-6- and -10-day RWNMs were also diagnosed in the antarctic SSW 2019 in both the northern (He et al. 2020a) and southern hemispheres (Wang et al. 2021), through the PDT. In addition, a wave [\(\frac{1}{16\text {d}}\), 2] was detected around an SSW and was explained as the USB of the interaction between the 16-day RWNM [\(\frac{1}{16\text {d}}\), 1] and stationary planetary wave [0, 1] (He et al. 2020c), as denoted in the AFD in Fig. 9.

Through the PDT and multi-year composite analyses, He et al. (2021b) diagnosed mid-latitude Q2DWs [\(\frac{1}{41\text {h}}\), 4] and [\(\frac{1}{50\text {h}}\), 3] that maximize annually in July.

Through both the PDT and WT &LS methods, enhancements of low-latitude Q2DWs [\(\frac{1}{50\text {h}}\), 3] and [\(\frac{1}{46\text {h}}\), 2] are observed in early 2020 (He et al. 2021a). Their amplitudes compare consistently with those derived from Michelson Interferometer for Global High-resolution Thermospheric Imaging (MIGHTI) at 95–100 km altitude where the two data sets overlap (He et al. 2021a). The authors attributed these Q2DW enhancements to their seasonality.

In a case study, Forbes et al. (2020) implemented the HR &WT and detected UFKWs [\(\frac{1}{2-4\text {d}}\), –1] from surface magnetic field perturbations collected by four equatorial magnetometers. The results revealed the capabilities of the surface observations being used to infer the MLT dynamics.

Near-12-h waves

The enhancement of the semidiurnal lunar tide M2 [\(\frac{1}{12.4\text {h}}\), 2] during SSWs was broadly reported in the atmosphere and ionosphere (e.g., Yamazaki 2013; Forbes and Zhang 2012; Forbes et al. 2013; Pedatella et al. 2012b; Zhang and Forbes 2013; Liu et al. 2021). However, the M2 estimation in single-station analyses might be contaminated by another 12.4-h wave, namely, the LSB of the interaction between the semidiurnal solar migrating tide (SW2) and the 16-day RWNM: [\(\frac{1}{12.4\text {h}}\), 1]=[2cpd, 2]–[\(\frac{1}{16\text {d}}\), 1] (e.g., Kamalabadi et al. 1997) as represented in Fig. 6c. The PDT was developed originally for distinguishing these two 12.4-h waves: He et al. (2018) confirmed the M2 at boreal mid-latitude during SSW 2013 whereas He et al. (2018a) reported the LSB at boreal high-latitude during SSW 2009 which confirmed the potential contamination.

In addition to the LSB and M2, there are at least four other near-12-h waves that are reported to be active during SSW (see Fig. 8c), including the USB [\(\frac{1}{11.6\text {h}}\), 3]=[2cpd, 2]+[\(\frac{1}{16\text {d}}\), 1] (Fig. 6d), the SW2 [2cpd, 2], and non-migrating tides [2cpd, 1] and [2cpd, 3] (e.g., Pedatella and Forbes 2010; Pedatella and Liu 2013). Implementing the WT &LS method on multi-year observations of five boreal mid-latitude meteor radars, He and Chau (2019) revealed that the three tides do not enhance around the SSW center day, but the LSB, USB, and M2 do. The results suggested that the reported enhancements of the non-migrating tides are misinterpreted from the LSB and USB due to the non-orthogonality of spectral basis functions used for extracting the waves. Due to similar non-orthogonality, the experimental M2 and SW2 estimations might contaminate each other. Equation 20 in He et al. (2018) quantified the non-orthogonality between the 12.0- and 12.4-h sinusoid functions in a rectangle window as a function of the window width, which is displayed here in Fig. 11. The equation specifies that the non-orthogonality minimizes at zero when \(\ {e}^{i2\pi \Delta f\Delta T}=1\) or \(\Delta f\Delta T \in {\mathbb {N}}\), where \(\Delta f\approx \frac{1}{12.0\text {h}}-\frac{1}{12.4\text {h}}\) denotes the frequency difference between the two waves and \(\Delta T\) denotes the window width. Therefore, the non-orthogonality minimizes at \(\Delta T=\frac{1}{\Delta f}, \frac{2}{\Delta f},...\), namely, \(\Delta T\approx 14.8\text {d}, 29.5\text {d},...\). These windows should be prioritized in relevant studies to minimize the contamination between the 12.0- and 12.4-h tides. Otherwise, as a counterexample and as revealed by Fig. 11, using a 21-day window would result in approximately 20% of the SW2 amplitude being estimated as an M2 amplitude (Chau et al. 2015). It is advisable to avoid using a 21-day rectangular window for estimating M2, as it maximizes the contamination from SW2 and leads to an overestimation of M2 amplitude. When there are potentially multiple or unknown contaminating waves, the author recommends using a broad window and enveloping the data with, e.g., a Gaussian function (see the green dashed line in Fig. 11.).

Similar to the 16-day RWNM, the 10-day RWNM can also interact with SW2 (He et al. 2021a), generating near-12-h LSB ([\(\frac{1}{12.6\text {h}}\), 1]=[2cpd, 2]–[\(\frac{1}{1\text {d}}\), 1], Fig. 6a) and USB ([\(\frac{1}{11.4\text {h}}\), 1]=[2cpd, 2]+[\(\frac{1}{10\text {d}}\), 1], Fig. 6b). These LSB and USB might also be interpreted as non-migrating tides due to the non-orthogonality.

Other tides and SWs

The PDT was also used to diagnose s of other solar tidal subharmonics in two case studies using two boreal mid-latitude meteor radars. He et al. (2020) identified six subharmonics during the 2017–2018 winter and found that all subharmonics are migrating components. The 12-, 6- and 4-h components weaken around the central day of SSW 2018. Among the six migrating subharmonics, the lowest frequency four were broadly studied but the 4.8- and 4-h subharmonics have been overlooked. He et al. (2022) attributed the overlook to inappropriate noise models used in the existing literature.

Fig. 10
figure 10

Adjusted Feynman diagrams of interactions between Rossby-gravity waves ([\(\frac{1}{50h}\),3],[\(\frac{1}{41h}\),4]) and four migrating components: a [1cpd,1]–[\(\frac{1}{50h}\),3], b [1cpd,1]+[\(\frac{1}{50h}\),3], c [2cpd,2]–[\(\frac{1}{50h}\),3], d [2cpd,2]+[\(\frac{1}{50h}\),3], e [3cpd,3]–[\(\frac{1}{50h}\),3], f [1cpd,1]–[\(\frac{1}{41h}\),4], g [2cpd,2]+[\(\frac{1}{41h}\),4], h [3cpd,3]–[\(\frac{1}{41h}\),4], i [4cpd,4]–[\(\frac{1}{41h}\),4]

Full size image
Fig. 11
figure 11

Lunar semidiurnal tidal amplitude fitted from a unit solar semidiurnal tide as a function of the window width (see Equation 20 in He et al. 2018)

Full size image

The lowest frequency four migrating components were also identified in the summer 2019 (He et al. 2021b). The SPT analysis revealed that all four migrating components interacted with two Q2DWs, [\(\frac{1}{40\text {h}}\), 4] and [\(\frac{1}{50\text {h}}\), 3], generating a variety of SWs as sketched in the AFDs in Fig. 10. Among these interactions, those sketched in Fig. 10e, h, and i involving the 8- and 6-h migrating tides were observed interacting with PWs for the first time.

Summary

Observations of mesosphere and lower thermosphere (MLT) region are sparse compared to those below and above MLT. Therefore, most experimental studies on planetary-scale waves in the MLT region have been carried out using single-satellite or -station methods, which are subject to intrinsic temporal–spatial aliasing. To overcome this issue, several multi-station methods have been developed recently that use ground-based observations recorded on a regular time grid in multiple longitudinal sectors. These methods transform the observations from the time and longitude domain to the frequency and zonal wavenumber domain using various techniques such as Fourier and wavelet transforms, Lomb–Scargle spectral analyses, and least-squares regression. By implementing these methods to meteor winds and surface magnetic field observations from low-, mid- and high-latitudes, researchers have identified various waves, including Rossby wave normal modes (RWNMs), quasi-2-day waves (Q2DWs), ultra-fast Kelvin waves (UFKWs), and tides and their upper and lower sidebands (USB and LSB) arising from nonlinear interactions with RWNMs or Q2DWs. The activities of these waves during sudden stratospheric warming events (SSWs) have also been investigated in detail, such as the amplification of 16-, 10-, and 6-day RWNMs, semidiurnal lunar (M2) tide, and the 11.4- and 11.6-h USBs (zonal wavenumber 3) and 12.4- and 12.6-h LSBs (zonal wavenumber 1) of tide-RWNM interactions, and the weakening of 6- and 4-h migrating tides. These works revealed that the estimation of M2 might be contaminated by the 12.4-h LSB in single-station analyses in existing literature due to zonal wavenumber ambiguity. The M2 estimation might also be contaminated by the 12-h solar migrating tide (SW2) due to non-orthogonal spectral basis functions used for extracting the waves. On the other way around, the existence of M2 can also contaminate the SW2 estimation due to the non-orthogonality. Similarly, the contamination associated with the non-orthogonality also occurs potentially between the USBs and the 12-h non-migrating tide with zonal wavenumber 3 (SW3), and between the LSBs and the 12-h zonal-wavenumber-1 tide (SW1). A multi-year composite analysis revealed that the LSB and USB amplifications might have been misinterpreted as SW1 and SW3 amplifications, respectively, in some existing literature. In addition, LSBs and USBs generated by interactions between four solar migrating tides and two quasi-2-day waves were observed 3 months before the Antarctic SSW 2019.

The results summarized above were obtained by applying the methods at specific latitudes, primarily at mid-latitudes in the Northern Hemisphere. To broaden the scope of these findings and overcome aliasing issues, future studies should expand to different latitudes and the Southern Hemisphere. To further improve the methodology and remove the assumptions made in multi-station approaches, future research should incorporate data from both satellite and ground-based observations across various latitudes, as demonstrated in pioneering work by Zhou et al. (2018).